第3章C++的函数
C语言第3章 数据描述与基本操作

C语言使用的基本表达式有: 语言使用的基本表达式有: 语言使用的基本表达式有 ⑴赋值表达式,如:a=3 赋值表达式, ⑵算数表达式,如:3+4*2 算数表达式, ⑶关系表达式,如:3>2 关系表达式, ⑷逻辑表达式,如:3>5&&a>=b 逻辑表达式, ⑸条件表达式,如:a>b?a:b 条件表达式, ⑹逗号表达式,如:a=3,b=4,c=5 逗号表达式,
● 赋值运算符的结合性是自右向左
(3) 赋值运算符的使用 设变量定义如下: char c1=‘a’,c2; int n1=65,n2,n3,n4,n5,n6; float f1=3.0,f2; 则: ① c2=n1运算后,c2的值是65,n1的值不变。 n2 !c1 n2 0 c1 ② n2=!c1运算后,n2的值是0,c1的值不变。 ③ f2=f1+0.001运算后,f2的值是3.001,f1的值不变。 ④ n3=c1==n1||c1!=n1运算后,n3的值是1,c1和n1 的值不变。 注:运算顺序相当于 n3=((c1==n1)||(c1!=n1)) ⑤ n4=n5=n6=-(――n1)运算后,n4,n5,n6的值 均是-64,n1的值是64。 注意:上述表达式的值就等于赋值表达式中的最左边的变量值。 注意
三.赋值运算符 赋值运算符
1.赋值运算符
赋值运算符是双目运算符,赋值运算符的左边必须是变量, 右边是表达式。 (1) 赋值运算符的运算对象及有关规则如下表:
对象数 名称 运算符 运算规则 运算结果 结合性 表达式的 自右向左 将表达式的 双目 赋值 =
值赋予变量 类型
(2) 赋值运算符的优先级 ● 算术运算符 优先于 关系运算符 优先于 双目逻为2,
则:① b=a+3,c=b+4 运算结果:a不变,b为5,c为9,表达式的值为9 ② d=a――,e=d――,f=――e 运算结果:a为1,d为1,e为1,f为1,表达式的值为1
C语言课件第三章

三、 自增、自减运算符 ++ --
++、- -运算符的作用是使变量的值加1或减1
1)该运算符为单目运算符,其运算对象只能是 变量,不能为常量或者表达式。 例如: i++ 、x- - 都是正确的 5++ 、(x+y)++ 都是错误的
2)该运算符作前缀、后缀都可以 例如 i++、++i、i- - 、- -i 都是正确的
3)对变量而言 i++ 或者++i都相当于i=i+1 i- -或者- -i都相当于i=i-1
例如: main( ) { int i=3 , j=3; +i+++i; j---j;; printf (“%d, %d\n”, i, j ); }
运行结果:4,2
4)但如果作为表达式,前缀和后缀则不同: 后缀:先取值再运算(i++,先取i值,i再自加) 前缀:先运算再取值(++i,i先自加,再取i值)
2)强制类型转换运算符优先级高于算术运算符
float x=3.6; int y; y=(int)x%3+2;
x = ?3.6 y=?2
计算下列表达式的值 设 x=2.5, a=7,y=4.7
x+a%3 * (int)(7x7+.2y ) % 2 / 4
设 a=2,b=3,x=3.5,y=2.5
(float5).(0a+b )/2+(int3)(x)%(int2)(y)
例如: main() { int i=3; printf(“%d\n”+, +i+i+ ); printf(“%d”, i ); }
(精选试题附答案)高中数学第三章函数的概念与性质知识点题库

(名师选题)(精选试题附答案)高中数学第三章函数的概念与性质知识点题库单选题1、下列图形能表示函数图象的是()A.B.C.D.答案:D分析:根据函数的定义,判断任意垂直于x轴的直线与函数的图象的交点个数,即可得答案.由函数的定义:任意垂直于x轴的直线与函数的图象至多有一个交点,所以A、B显然不符合,C在x=0与函数图象有两个交点,不符合,只有D符合要求.故选:D2、“幂函数f(x)=(m2+m−1)x m在(0,+∞)上为增函数”是“函数g(x)=2x−m2⋅2−x为奇函数”的()条件A.充分不必要B.必要不充分C.充分必要D.既不充分也不必要答案:A分析:要使函数f(x)=(m2+m−1)x m是幂函数,且在(0,+∞)上为增函数,求出m=1,可得函数g(x)为奇函数,即充分性成立;函数g (x )=2x −m 2⋅2−x 为奇函数,求出m =±1,故必要性不成立,可得答案.要使函数f (x )=(m 2+m −1)x m 是幂函数,且在(0,+∞)上为增函数,则{m 2+m −1=1m >0,解得:m =1,当m =1时,g (x )=2x −2−x ,x ∈R , 则g (−x )=2−x −2x =−(2x −2−x )=−g (x ),所以函数g (x )为奇函数,即充分性成立;“函数g (x )=2x −m 2⋅2−x 为奇函数”,则g (x )=−g (−x ),即2x −m 2⋅2−x =−(2−x −m 2⋅2x )=m 2⋅2x −2−x ,解得:m =±1,故必要性不成立,故选:A .3、已知定义在R 上的奇函数f (x )在(0,+∞)上单调递增,且f(1)=0,若实数x 满足xf (x −12)≤0,则x 的取值范围是( )A .[−12,0]∪[12,32]B .[−12,12]∪[32,+∞)C .[−12,0]∪[12,+∞)D .[−32,−12]∪[0,12] 答案:A分析:首先根据函数的奇偶性和单调性得到函数f (x )在R 上单调递增,且f (1)=f (−1)=0,从而得到x ∈(−∞,−1),f (x )<0,x ∈(−1,0),f (x )>0,x ∈(0,1),f (x )<0,x ∈(1,+∞),f (x )>0,再分类讨论解不等式xf (x −12)≤0即可.因为奇函数f (x )在(0,+∞)上单调递增,定义域为R ,f(1)=0,所以函数f (x )在R 上单调递增,且f (1)=f (−1)=0.所以x ∈(−∞,−1),f (x )<0,x ∈(−1,0),f (x )>0,x ∈(0,1),f (x )<0,x ∈(1,+∞),f (x )>0.因为xf (x −12)≤0,当x <0时,f (x −12)≥0,即−1≤x −12≤0或x −12≥1,解得−12≤x <0.当x =0时,符合题意.当x >0时,f (x −12)≤0,x −12≤−1或0≤x −12≤1, 解得12≤x ≤32.综上:−12≤x ≤0或12≤x ≤32. 故选:A4、下列四个函数在(−∞,0)是增函数的为( )A .f (x )=x 2+4B .f (x )=1−2xC .f (x )=−x 2−x +1D .f (x )=2−3x答案:D分析:根据各个函数的性质逐个判断即可对A ,f (x )=x 2+4二次函数开口向上,对称轴为y 轴,在(−∞,0)是减函数,故A 不对.对B ,f (x )=1−2x 为一次函数,k <0,在(−∞,0)是减函数,故B 不对.对C ,f (x )=−x 2−x +1,二次函数,开口向下,对称轴为x =−12,在(−∞,−12)是增函数,故C 不对. 对D ,f (x )=2−3x 为反比例类型,k <0,在(−∞,0)是增函数,故D 对.故选:D5、已知函数f(x)={−3x +3,x <0−x 2+3,x ≥0,则不等式f (a )>f (3a −4)的解集为( ) A .(−12,+∞)B .(2,+∞)C .(−∞,2)D .(−∞,−12)答案:B分析:由分段函数表达式,判断其单调性,利用单调性,求解不等式.根据题目所给的函数解析式,可知函数f (x )在(−∞,+∞)上是减函数,所以a <3a −4,解得a >2.故选:B6、设函数f(x)=x2+2(4−a)x+2在区间(−∞,3]上是减函数,则实数a的取值范围是()A.a≥−7B.a≥7C.a≥3D.a≤−7答案:B分析:根据二次函数的图象和性质即可求解.函数f(x)的对称轴为x=a−4,又∵函数在(−∞,3]上为减函数,∴a−4⩾3,即a⩾7.故选:B.小提示:本题考查由函数的单调区间求参数的取值范围,涉及二次函数的性质,属基础题.7、若函数y=f(x)在R上单调递增,且f(2m−3)>f(−m),则实数m的取值范围是()A.(−∞,−1)B.(−1,+∞)C.(1,+∞)D.(−∞,1)答案:C分析:由单调性可直接得到2m−3>−m,解不等式即可求得结果.∵f(x)在R上单调递增,f(2m−3)>f(−m),∴2m−3>−m,解得:m>1,∴实数m的取值范围为(1,+∞).故选:C.8、已知f(x)是定义在(−2,2)上的单调递减函数,且f(2a−3)<f(a−2),则实数a的取值范围是()A.(0,4)B.(1,+∞)C.(12,52)D.(1,52)答案:D分析:根据函数自变量的定义域以及函数单调递减列式,求出a的取值范围. ∵f(x)是定义在(−2,2)上的单调递减函数,且f(2a−3)<f(a−2),则{2a−3>a−2−2<a−2<2−2<2a−3<2,解得1<a<52故选:D..9、函数f (x )在(−∞,+∞)上是减函数,且a 为实数,则有( )A .f (a )<f (2a )B .f (a 2)<f (a )C .f (a 2+1)<f (a )D .f (a 2−a )<f (a )答案:C分析:利用a =0可排除ABD ;根据函数单调性和a 2+1>a 恒成立可知C 正确.当a =0时,ABD 中不等式左右两侧均为f (0),不等式不成立,ABD 错误;∵a 2+1−a >0对于a ∈R 恒成立,即a 2+1>a 恒成立,又f (x )为R 上的减函数,∴f (a 2+1)<f (a ),C 正确.故选:C.10、已知幂函数y =f(x)的图象过点P(2,4),则f(3)=( )A .2B .3C .8D .9答案:D分析:先利用待定系数法求出幂函数的解析式,再求f(3)的值解:设f(x)=x α,则2α=4,得α=2,所以f(x)=x 2,所以f(3)=32=9,故选:D填空题11、已知f (x )={(3a −1)x +4a,x <1−x +1,x ⩾1是定义在R 上的减函数,那么a 的取值范围是___. 答案:[17,13) 分析:利用函数在R 上是减函数,可列出不等式组{3a −1<0(3a −1)+4a ⩾−1+1 ,由此求得a 的取值范围.由于f (x )={(3a −1)x +4a,x <1−x +1,x ⩾1是定义在R 上的减函数,∴{3a −1<0(3a −1)+4a ⩾−1+1 , 求得17⩽a <13,所以答案是:[17,13). 12、函数y =√7+6x −x 2的定义域是_____.答案:[−1,7].分析:由题意得到关于x 的不等式,解不等式可得函数的定义域.由已知得7+6x −x 2≥0,即x 2−6x −7≤0解得−1≤x ≤7,故函数的定义域为[−1,7].小提示:求函数的定义域,其实质就是以函数解析式有意义为准则,列出不等式或不等式组,然后求出它们的解集即可.13、函数y =√x 2−1的单调递减区间为___________.答案:(−∞,−1](或(−∞,−1)都对)解析:利用复合函数的单调性,同增异减,即可得到答案;令t =x 2−1,则y =√t ,∵ t =x 2−1在(−∞,−1)单调递减,y =√t 在(0,+∞)单调递增,根据复合函数的单调性可得:y =√x 2−1在(−∞,−1)单调递减,所以答案是:(−∞,−1).14、已知函数f (x )=mx 2+nx +2(m,n ∈R )是定义在[2m,m +3]上的偶函数,则函数g (x )=f (x )+2x 在[−2,2]上的最小值为______.答案:-6分析:先利用题意能得到f(−x)=f(x)和2m+m+3=0,解得n=0和m=−1,代入f(x)中,再代入g(x),再结合二次函数的性质求最小值因为函数f(x)=mx2+nx+2(m,n∈R)是定义在[2m,m+3]上的偶函数,故{f(−x)=f(x)2m+m+3=0,即{mx2−nx+2=mx2+nx+2m=−1,则{2nx=0m=−1解得{n=0m=−1,所以g(x)=f(x)+2x=−x2+2x+2=3−(x−1)2,x∈[−2,2],所以g(−2)=−(−2)2+2×(−2)+2=−6,g(2)=−22+2×2+2=2,则g(x)min=−6,所以答案是:-615、已知函数y=f(2x+1)的定义域为[−1,2],则函数y=f(x−1)的定义域为_________.答案:[0,6]分析:根据抽象函数的定义域求解规则求解即可.函数y=f(2x+1)的定义域为[−1,2],即−1≤x≤2,所以−1≤2x+1≤5,所以−1≤x−1≤5,即0≤x≤6,所以函数的定义域为[0,6].所以答案是:[0,6].解答题16、上海市某地铁项目正在紧张建设中,通车后将给更多市民出行带来便利,已知该线路通车后,地铁的发车时间间隔t(单位:分钟)满足2≤t≤20,t∈N∗,经测算,在某一时段,地铁载客量与发车时间间隔t相关,当10≤t≤20时地铁可达到满载状态,载客量为1200人,当2≤t<10时,载客量会减少,减少的人数与(10−t)的平方成正比,且发车时间间隔为2分钟时载客量为560人,记地铁载客量为p(t).(1)求p(t)的解析式;(2)若该时段这条线路每分钟的净收益为Q=6p(t)−3360t−360(元),问当发车时间间隔为多少时,该时段这条线路每分钟的净收益最大?答案:(1)p(t)={−10t 2+200t +200,2≤t <101200,10≤t ≤20(t ∈N ∗);(2)6分钟. 分析:(1)2≤t <10时,求出正比例系数k ,写出函数式即可得解;(2)求出每一段上的最大值,再比较大小即可得解.(1)由题意知p(t)={1200−k(10−t)2,2≤t <101200,10≤t ≤20(t ∈N ∗ ),(k 为常数), 因p(2)=1200−k(10−2)2=1200−64k =560,则k =10,所以p(t)={−10t 2+200t +200,2≤t <101200,10≤t ≤20(t ∈N ∗); (2)由Q =6p(t)−3360t −360得Q ={6(−10t 2+200t+200)−3360t −360,2≤t <103840t −360,10≤t ≤20 ,即Q ={840−60(t +36t ),2≤t <103840t−360,10≤t ≤20 (t ∈N ∗), ①当2≤t <10时,Q =840−60(t +36t )≤840−60×12=120,当且仅当t =6等号成立; ②当10≤t ≤20时,Q =3840t −360在[10,20]上递减,当t =10时Q 取最大值24,由①②可知,当发车时间间隔为t =6分钟时,该时段这条线路每分钟的净收益最大,最大为120元.17、已知集合A ={x |2<x <4},集合B ={x |m −1<x <m 2}.(1)若A ∩B =∅;求实数m 的取值范围;(2)命题p:x ∈A ,命题q:x ∈B ,若p 是q 的充分条件,求实数m 的取值集合.答案:(1)−√2≤m ≤√2或m ≥5(2){m |m ≤−2 或2≤m ≤3}分析:(1)讨论B =∅或B ≠∅,根据A ∩B =∅列不等式组即可求解.(2)由题意得出A ⊆B ,再由集合的包含关系列不等式组即可求解.(1)∵A ∩B =∅,∴当B =∅时,m -1≥m 2,解得:m ∈∅.当B ≠∅时,m -1≥4或m 2≤2,∴−√2≤m ≤√2或m ≥5.(2)∵x∈A是x∈B的充分条件,∴A⊆B,∴{m−1≤2m2≥4,解得:m≤-2或2≤m≤3.所以实数m的取值集合为{m|m≤−2或2≤m≤3}18、已知幂函数f(x)=x m2−m−2(m∈Z)是偶函数,且在(0,+∞)上是减函数,求函数f(x)的解析式.答案:f(x)=x−2分析:根据幂函数的单调性,可知m2−m−2<0,又m∈Z,则m=0,1,再根据函数f(x)是偶函数,将m= 0,1分别代入验证可得答案.因为幂函数f(x)在区间(0,+∞)上单调递减,则m2−m−2<0,得m∈(−1,2),又∵m∈Z,∴m=0或1.因为函数f(x)是偶函数,将m=0,1分别代入,当m=0时,m2−m−2=−2,函数为f(x)=x−2是偶函数,满足条件.当m=1时,m2−m−2=−2,函数为f(x)=x−2是偶函数,满足条件.∴f(x)的解析式为f(x)=x−2.19、判断下列函数的奇偶性:(1)f(x)=√4−x2|x+3|−3;(2)f(x)=(x−1)√1+x1−x;(3)f(x)=√1−x2+√x2−1;(4)f(x)={x2−2x+3,x>00,x=0−x2−2x−3,x<0. 答案:(1)奇函数(2)既不是奇函数也不是偶函数(3)既是奇函数又是偶函数(4)奇函数分析:根据函数奇偶性的概念,逐问判断即可.(1)由{4−x 2≥0|x +3|−3≠0,得−2≤x ≤2,且x ≠0, 所以f (x )的定义域为[−2,0)∪(0,2],关于原点对称,所以f (x )=√4−x 2|x+3|−3=√4−x 2x+3−3=√4−x 2x . 又f (−x )=√4−(−x )2−x =−√4−x 2x =−f (x ),所以f (x )是奇函数.(2)因为f (x )的定义域为[−1,1),不关于原点对称,所以f (x )既不是奇函数也不是偶函数.(3)对于函数f (x )=√1−x 2+√x 2−1,{1−x 2≥0x 2−1≥0,∴x =±1,其定义域为{−1,1},关于原点对称. 因为对定义域内的每一个x ,都有f (x )=0,所以f (−x )=f (x ),f (−x )=−f (x ), 所以f (x )=√1−x 2+√x 2−1既是奇函数又是偶函数.(4)函数f (x )的定义域为R ,定义域关于原点对称.①当x =0时,−x =0,所以f (−x )=f (0)=0,f (x )=f (0)=0,所以f (−x )=−f (x );②当x >0时,−x <0,所以f (−x )=−(−x )2−2(−x )−3=−(x 2−2x +3)=−f (x ); ③当x <0时,−x >0,所以f (−x )=(−x )2−2(−x )+3=−(−x 2−2x −3)=−f (x ). 综上,可知函数f (x )为奇函数.。
C语言_第3章
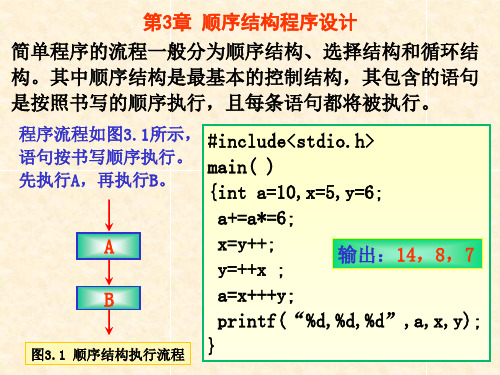
简单程序的流程一般分为顺序结构、选择结构和循环结 构。其中顺序结构是最基本的控制结构,其包含的语句 是按照书写的顺序执行,且每条语句都将被执行。
程序流程如图3.1所示, #include<stdio.h> 语句按书写顺序执行。 main( ) 先执行A,再执行B。 {int a=10,x=5,y=6;
三、复合语句
用一对花括号,把若干条语句括起来,
就形成了一条复合语句。形式如下:
{[内部数据描述语句]
其中定义的变量是
语句1; …… 语句n;}
复合语句结束的 “}”之后,不需
局部变量,仅在复 合语句中有效。
要再加分号。
花括号中的语句,可以是简单语句、空语句、复合 语句、流程控制语句,所有这些语句括在一起,在 语法上看成是一条语句,执行时顺序执行花括号中 的每条语句。复合语句多用于流程控制语句中。
printf(“\n%d,%d”,a+i,i++);}
四、格式输入函数 格式输入函数一般形式 scanf(“格式控制字符串”,地址列表); 功能:按指定的格式从键盘上把数据输入到指定的 变量之中 。 在scanf语句的格式控制字符串中,有两类字符: 普通字符:必须按原样输入,不能省略; 格式说明部分:由%引导的格式字符串组成。
scanf语句格式说明部分的一般格式为: %[*][width][F|N][h|L]type type是必须的,表示输入后转换的数据类型。
d(D) o(O) x(X) i(I) u(U)
c s f,e,g F,E,G n
%
十进制整数 八进制整数 十六进制整数 自动根据数头分辨十、八、十六进制 无符号十进制整数 单个字符 字符串 实数
第3章 C语言的运算符

普通高等教育“十一五 ” 国家级规划教材
3.2. 算术运算符与算术表达式
3、C语言的运算符和表达式
3.1.2 运算符的优先级和结合性
例如:
普通高等教育“十一五 ” 国家级规划教材
3*5/3 :表达式中出现了二个运算符即*和/。按 照优先级的次序,5的两侧“*”和“/”优先级相同, 则按结合性处理。“*”和“/”运算符的结合性为从 左到右,则先乘后除,表达式的值为5。
d=a+b-c :表达式中出现了三个运算符即=(赋 值)、+、-。按照优先级的次序,加和减的运算优先 级相同,而赋值运算符优先级较低。根据加和减的结 合性是从左到右,因此先计算加,再计算减,最后进 行赋值。
3 C语言的运算符和表达式
普通高等教育“十一五 ” 国家级规划教材
3.1.1运算符的优先级和结合性
注意所有的单目运算符、赋值运算符
和条件运算符都是从右向左结合的,要 予以特别关注,其余均为从左向右结合 的,与习惯一致。
普通高等教育“十一五 ” 国家级规划教材
学习 C语言的运算符,不仅要掌握各种 运算符的功能,以及它们各自可连接的运算 对象个数,而且还要了解各种运算符彼此之
普通高等教育“十一五 ” 国家级规划教材
第3章 运算符与表达式
作为一种程序设计语言,C 语言规定了一套严密的字符 集和语法规则,程序设计就是根据这些基本字符和语法规则
C语言第3章简单程序

这种如同乱麻一样的算法称为BS型算 法,意为一碗面条(A Bowl of Spaghetti),乱无头绪。
• 三种基本结构
Bohra和Jacopini提出了以下三种基本 结构: 顺序结构、选择结构、循环结构
用这三种基本结构作为表示一个良好算 法的基本单元。
三种基本结构的图示:
顺序结构
选择结构
循环结构的图示:
主要内容
3.1 算法概述 3.2 程序的三种基本结构 3.3 C语句综述 3.4 赋值表达式和赋值语句 3.5 数据输入输出的概念 3.6 字符数据的输入输出 3.7 简单的格式输入与输出 3.8 顺序结构程序设计举例
3.1 算法概述
一个程序应包括两个方面的内容: • 对数据的描述:数据结构(data structure) • 对操作的描述:算法(algorithm) 著名计算机科学家沃思提出一个公式: 数据结构 + 算法 = 程序
includestdiohincludestdiohvoidmainvoidmain定义字符变量定义字符变量abc从键盘输入一个字符送给字符变量从键盘输入一个字符送给字符变量a从键盘输入一个字符送给字符变量从键盘输入一个字符送给字符变量b从键盘输入一个字符送给字符变量从键盘输入一个字符送给字符变量c将变量将变量aa的值输出的值输出将变量将变量aa的值输出的值输出将变量将变量aa的值输出的值输出pu• 传统流程图的弊端 传统流程图用流程线指出各框的执行 顺序,对流程线的使用没有严格限制。因 此,使用者可以毫不受限制地使流程随意 地转向,使流程图变得毫无规律,阅读者 要花很大精力去追踪流程,使人难以理解 算法的逻辑。如图:
缺点:难以阅读、修改,使算法的 传统流程图的流程可以是: 可靠性和可维护性难以保证。 解决办法:必须限制箭头的滥用, 即不允许无规律地使流程随意转向, 只能顺序地进行下去。
C语言第3章(A-6(函数调用语句))

标准输入输出函数
printf scanf 例题: 注意: main() 必须为地址,“&”是地运算符, &a指a在内的地址。 { int a ,b ,c; scanf(“%d%d%d”, &a,&b,&c ); printf(“%d,%d,%d”,a,b,c); }
C语言程序设计
标准输入输出函数
C语言程序设计
标准输入输出函数
printf
用法:
1) %f :不指定输出的宽 度,由系统自动指定, 使整数部分全部输出, 并输出6位小数。
scanf
main() { float x,y; x=1111.2222; y=2222.4444; printf(“%f”,x+y); } 结果:3333.666608
实例:
printf(“ i= %d , c= %c ” , i , c);
格式控制:是用双引号括起来的字符串,也称为 “转换控制字符串”,它包括两部分信息: 1) 格式说明:由“%”和格式字符组成,如%d,%f等。 它的作用是将输出的数据转换为指定的格式输出。 2) 普通字符:需要原样输出的字符。如双引号中的 逗号、空格和换行符。
标准输入输出函数
printf scanf
2) %ms,输出的字符串占m列,如字符串本身长度大 于m,则按实际长度输出;如串长度小于m,则左补 空格。
printf(“%3s”,”china”);
输出结果:
printf(“%6s”,”china”);
china
china
C语言程序设计
标准输入输出函数
printf(“%ld”,e);
如果用%d输出,就会发生错误,因为整型数 据的范围为-32768-32767。
四川大学《c语言程序设计》课件-第3章 键盘输入与屏幕输出

Please input a and b: 123456↙ a=12, b=56, a+b = 68
30/44
输入数据的格式控制——例3.9
#include <stdio.h> main() {
int a, b;
12 34↙
scanf("%d %d", &a, &b); printf("a = %d, b = %d\n", a, b); }
%d decimal 以带符号十进制整数输出
%f float 以小数形式输出浮点数(6位小数)
%e exponent 以标准指数形式输出(6位小数)
%g
选用%f,%e中输出宽度较小的一种格式
%o octal 以八进制无符号整数输出(无前导0)
%x hex
以十六进制无符号整数输出(无前导0x)
%u unsigned 以十进制无符号整数输出
例:
printf("Value is:%10f", 32.6784728);
6 digits (default) Value is: 32.678473
10 个字符长度
19/44
printf 函数 – 浮点数输出
例:
printf("Value is:%10.5f", 32.6784);
5 digits Value is: 32.67840
break
do~while() return
变量定义语句
int a, b, c; 表达式语句
c = a + b; 函数调用语句
printf("Hello World!"); 复合语句 空语句
高中数学第三章函数的概念与性质3-1函数3-1-1对函数概念的再认识学生用书湘教版必修第一册

3.1 函数3.1.1 对函数概念的再认识教材要点要点一函数的概念(1)非空性:函数定义中的集合A,B必须是两个非空实数集.(2)任意性:即定义域中的每一个元素都有函数值.(3)单值性:每一个自变量有唯一的函数值与之对应.(4)方向性:函数是一个从定义域到值域的对应关系,如果改变这个对应方向,那么新的对应所确定的关系就不一定是函数关系.要点二两个函数相等两个函数f(x)和g(x),当且仅当有相同的定义域U且对每个x∈U都有f(x)=g(x)时,叫作相等.状元随笔由于值域是由定义域和对应关系决定的,所以确定一个函数只需要两个要素:定义域和对应关系.即要检验给定的两个变量(变量均取数值)之间是否具有函数关系,只要检验:(1)定义域和对应关系是否给出;(2)根据给出的对应关系,自变量x在定义域中的每一个值是否都有唯一的函数值y和它对应.要点三常见函数的定义域和值域1.一次函数f(x)=ax+b(a≠0)的定义域为________,值域是________.2.二次函数f(x)=ax2+bx+c(a≠0)的定义域是__________,当a>0时,值域为__________________,当a<0时,值域为__________________.基础自测1.思考辨析(正确的画“√”,错误的画“×”)(1)函数的定义域和值域一定是无限集合.( )(2)任何两个集合之间都可以建立函数关系.( )(3)函数的定义域必须是数集,值域可以为其他集合.( )(4)两个函数的定义域和值域相同就表示同一函数.( )2.下列可作为函数y=f(x)的图象的是( )的定义域是( )3.函数y=√x−1A.{x|x≥1}B.{x|x≤1}C.{x|x>1}D.{x|x<1}4.若f(x)=x-√x+1,则f(3)=________.题型1 函数关系的判断例1 (1)下列从集合A到集合B的对应关系f是函数的是( )A.A={-1,0,1},B={0,1},f:A中的数平方B.A={0,1},B={-1,0,1},f:A中的数开方C.A=Z,B=Q,f:A中的数取倒数D.A={平行四边形},B=R,f:求A中平行四边形的面积(2)设A={x|0≤x≤2},B={x|1≤x≤2},能表示从集合A到集合B的函数关系的是( )方法归纳(1)判断所给对应是否为函数的方法 ①首先观察两个数集A ,B 是否非空;②其次验证对应关系下,集合A 中x 的任意性,集合B 中y 的唯一性,既不能没有数y 对应数x ,也不能有多于一个的数y 对应x .(2)根据图形判断对应是否为函数的方法步骤 ①任取一条垂直于x 轴的直线l ; ②在定义域内平行移动直线l ;③若l 与图形有且只有一个交点,则是函数;若在定义域内没有交点或有两个或两个以上的交点,则不是函数.跟踪训练1 (1)(多选)已知集合M ={-1,1,2,4},N ={1,2,4},给出下列四个对应关系:①y =x 2,②y =x +1,③y =x -1,④y =|x |.其中不能构成从M 到N 的函数的是( )A .①B .②C .③D .④(2)图中所给图象是函数图象的个数为( )A .1B .2C .3D .4题型2 求函数的定义域 例2 (1)函数f (x )=√1−x +1x+3的定义域为( )A .{x |-3<x ≤0}B .{x |-3<x ≤1}C .{x |x <-3或-3<x ≤0}D .{x |x <-3或-3<x ≤1}(2)函数f (x )=(x −12)0+√x +2的定义域为( )}A.{x|x≥−2且x≠12B.{x|x≥-2}}C.{x|x>−2且x≠12D.{x|x>-2}方法归纳求给出解析式的函数的定义域的基本步骤常见函数的定义域(1)f(x)为整式型函数时,定义域为R;(2)由于分式的分母不为0,所以当f(x)为分式型函数时,定义域为使分母不为零的实数的集合;(3)由于偶次根式的被开方数非负,所以当f(x)为偶次根式型函数时,定义域为使被开方数为非负的实数的集合;(4)函数y=x0中的x不为0;(5)如果函数是由一些简单函数通过四则运算构成的,那么它的定义域是各个简单函数定义域的交集.跟踪训练2 (1)函数f(x)=√−x的定义域为( )2x2−3x−2A.{x|x≤0}}B.{x|x≤−12}C.{x|x≤0且x≠−12<x≤0}D.{x|−12的定义域为________.(2)函数y=√x+3x−2题型3 两个函数是相等函数的判断例3 (多选)下列各组函数是相等函数的是( )A.f(x)=√−2x3与g(x)=x·√−2xB .f (x )=x 与g (x )=√x 2C .f (x )=x 0与g (x )=1xD .f (x )=x 2-x +1与g (t )=t 2-t +1方法归纳判断相等函数的三个步骤和两个注意点(1)判断相等函数的三个步骤(2)两个注意点:①在化简解析式时,必须是等价变形; ②与用哪个字母表示无关.跟踪训练3 下列函数中与函数y =x 2是相等函数的是( ) A .u =v 2B .y =x ·|x |C .y =x 3x D .y =(√x )4题型4 函数值与函数的值域例4 (1)设f (x )=2x 2+2,g (x )=1x+2,求: ①f (2),f (a +3),g (a )+g (0)(a ≠-2); ②g (f (2)),f (g (2)). (2)求下列函数的值域. ①y =3-4x ,x ∈(-1,3]; ②y =2xx+1; ③y =x -√1−2x .方法归纳1.函数求值的方法(1)已知f(x)的表达式时,只需用a替换表达式中的x即得f(a)的值.(2)求f(g(a))的值应遵循由里往外的原则.2.求函数值域的常用方法(1)观察法:对于一些比较简单的函数,其值域可通过观察法得到.(2)配方法:是求“二次函数”类值域的基本方法.(3)换元法:运用新元代换,将所给函数化成值域易确定的函数,从而求得原函数的值域.对于f(x)=ax+b±√cx+d(其中a,b,c,d为常数,且ac≠0)型的函数常用换元法.(4)分离常数法:此方法主要是针对有理分式,即将有理分式转化为“反比例函数类”的形式,便于求值域.跟踪训练4 (1)下列函数中,值域为(0,+∞)的是( )A.y=√x B.y=√xC.y=1xD.y=x2+1(2)已知函数f(x)=x+1x+2.求f(2);f(f(1)).易错辨析忽略参数取值范围致误例5 若函数f(x)=√mx2−mx+2的定义域为R,则实数m的取值范围是________.解析:函数f(x)=√mx2−mx+2的定义域为R,即mx2-mx+2>0恒成立.当m=0时,易知成立,当m≠0时,需满足{m>0,Δ=m2−8m<0,∴0<m<8,综上所述,0≤m<8.答案:0≤m<8易错警示课堂十分钟1.下列各图中,一定不是函数图象的是( )2.函数f (x )=√1−3xx的定义域为( )A .{x|x ≤13}B .{x|x <13}C .{x|0<x ≤13}D .{x|x ≤13且x ≠0}3.下列各组函数中,表示相等函数的是( ) A .f (x )=√x 2,g (x )=(√x )2B .f (x )=√x 2,g (x )=|x |C .f (x )=1,g (x )=x 0D .f (x )=x+1x 2−1,g (x )=1x−14.已知函数f (x )=11+x ,又知f (t )=6,则t =________. 5.已知函数f (x )=1x+1+√x +2.(1)求f (x )的定义域; (2)若a >0,求f (a -1)的值.第三章 函数的概念与性质3.1 函数3.1.1 对函数概念的再认识新知初探·课前预习要点一实数集 唯一确定 x 要点三 1.R R 2.R [4ac−b 24a,+∞) (−∞,4ac−b 24a][基础自测]1.答案:(1)× (2)× (3)× (4)× 2.解析:由函数的定义可知D 正确. 答案:D3.解析:要使函数y =√x−1有意义,则必须{x −1≥0,√x −1≠0.∴x >1,故选C. 答案:C4.解析:f (3)=3-√3+1=3-2=1. 答案:1题型探究·课堂解透例1 解析:(1)对B ,集合A 中的元素1对应集合B 中的元素±1,不符合函数的定义;对C ,集合A 中的元素0取倒数没有意义,在集合B 中没有元素与之对应,不符合函数的定义;对D ,A 集合不是数集,故不符合函数的定义.综上,选A.(2)A 中,函数的值域为{y |0≤y ≤2},不满足条件;B 中,函数的值域为{y |0≤y ≤2},不满足条件;C 中,在0≤x <2内,一个x 有两个y 与之对应,不满足条件;D 中,每个x 都有唯一确定的y 与之对应,是函数关系.故选D.答案:(1)A (2)D跟踪训练1 解析:(1)①中,当x =4时,y =42=16∉N ,故不能构成函数.②中,当x =-1时,y =-1+1=0∉N ,故不能构成函数;③中,当x =-1时,y =-1-1=-2∉N ,故不能构成函数;④中,当x =±1时,y =|x |=1∈N ,当x =2时,y =|x |=2∈N ,当x =4时,y =|x |=4∈N ,故构成函数.故选ABC.(2)根据函数的概念可知③④是函数的图象.故选B. 答案:(1)ABC (2)B例2 解析:(1)要使函数f (x )有意义, 则{1−x ≥0,x +3≠0,解得x ≤1且x ≠-3, 所以函数f (x )的定义域为{x |x ≤1且x ≠-3},即{x |x <-3或-3<x ≤1}.故选D. (2)要使函数f (x )有意义,则{x ≠12,x +2≥0,解得x ≥-2且x ≠12,故选A. 答案:(1)D (2)A跟踪训练2 解析:(1)要使函数f (x )有意义, 则{−x ≥0,2x 2−3x −2≠0,解得x ≤0且x ≠-12,故选C. (2)∵函数解析式为y =√x+3x−2, ∴x +3≥0且x ≠2, ∴x ≥-3且x ≠2.答案:(1)C (2){x |x ≥-3且x ≠2}例3 解析:A 中,定义域都是(-∞,0],但解析式不相同;B 中,g (x )=√x 2=|x |与f (x )=x 解析式不同;C 、D 是相等函数.答案:CD跟踪训练3 解析:函数y =x 2的定义域为R ,对于A 项,u =v 2的定义域为R ,对应法则与y =x 2一致,则A 正确;对于B 项,y =x ·|x |的对应法则与y =x 2不一致,则B 错误;对于C 项,y =x 3x 的定义域为{x |x ≠0},则C 错误;对于D 项,y =(√x )4的定义域为{x |x ≥0},则D 错误;故选A.答案:A例4 解析:(1)①f (2)=2×22+2=10;f (a +3)=2(a +3)2+2=2a 2+12a +20;g (a )+g (0)=1a+2+12;②g (f (2))=g (10)=110+2=112;f (g (2))=f (14)=2×(14)2+2=178.(2)①因为x ∈(-1,3],所以-12≤-4x <4,所以-9≤3-4x <7, 所以函数y =3-4x ,x ∈(-1,3]的值域是[-9,7). ②因为y =2xx+1=2(x+1)−2x+1=2-2x+1≠2,所以函数y =2x x+1的值域为{y |y ≠2}. ③设√1−2x =t ,则t ≥0,x =1−t 22,所以y =1−t 22-t =12(-t 2-2t +1)=-12(t +1)2+1,因为t ≥0,所以y ≤12,所以函数y =x -√1−2x 的值域为(−∞,12].跟踪训练4 解析:(1)A 中,由x ≥0得y =√x ≥0,∴y =√x (x ≥0)的值域为[0,+∞),A 不符合;B 中,设√x =t ,由x >0得t =√x >0,由y =1t (t >0)的图象知其值域为(0,+∞),B 符合;C 中,由y =1x (x ≠0)的图象知,y =1x 的值域为(-∞,0)∪(0,+∞),C 不符合;D 中,y =x 2+1≥1,值域为[1,+∞),不符合.(2)①f (2)=2+12+2=34; ②∵f (1)=1+11+2=23;∴f (f (1))=f (23)=23+123+2=58.答案:(1)B (2)见解析[课堂十分钟]1.解析:对于A 选项,由图象可知,存在x 同时对应两个函数值y ,A 选项中的图象不是函数图象;对于B 选项,由图象可知,每个x 有唯一的函数值y 与之对应,B 选项中的图象是函数图象;对于C 选项,由图象可知,每个x 有唯一的函数值y 与之对应,C 选项中的图象是函数图象;对于D 选项,由图象可知,每个x 有唯一的函数值y 与之对应,D 选项中的图象是函数图象.故选A.答案:A2.解析:要使f (x )有意义,只需满足{1−3x ≥0,x ≠0,即x ≤13且x ≠0.故选D.11 答案:D3.解析:对于选项A :f (x )=√x 2的定义域为R ,g (x )=(√x )2的定义域为[0,+∞),定义域不同不是相等函数,故A 不正确;对于选项B :f (x )=√x 2=|x |,g (x )=|x |是相等函数,故B 正确;对于选项C :f (x )=1定义域为R ,g (x )=x 0=1,定义域为{x |x ≠0},定义域不同不是相等函数,故C 不正确;对于选项D :f (x )=x+1x 2−1的定义域为{x |x ≠±1},g (x )=1x−1的定义域为{x |x ≠1},定义域不同不是相等函数,故D 不正确;故选B.答案:B4.解析:由f (t )=6,得11+t =6,即t =-56.答案:-565.解析:(1)由{x +1≠0x +2≥0,解得x ≥-2且x ≠-1,故f (x )的定义域为{x |x ≥−2且x ≠−1};(2)若a >0,f (a -1)=1a−1+1+√a −1+2=1a +√a +1.。
C语言电子教案第3章 输入输出及顺序结构

o
o
o
在%与格式符之间插入一个整数表示指定输出的宽度.若 指定的输出宽度大于实际数据的宽度,那么数据向右靠齐, 左边补空格;若指定的宽度小于实际数据的宽度,那么按 实际数据的宽度输出. 可以采用"m.n"的格式修饰格式符来输出一个实数,这里m 和n是两个整数. 对于字符串,采用"m.n"的附加格式符来修饰格式符表示 指定字符串的总宽度为m,不足m则向右靠齐,左补空格.n 表示指定截取实际字符串的前n个字符输出.也可以省略m, 不指定总宽度. 可以在宽度之前加一个""来指定输出的数据向左靠齐.
输出表列 o 输出表列是需要输出的数据,可以是变量,常量或表达 式.输出表列可以是零项,一项或多项,若多于一项则 各项之间用逗号分隔. o 输出表列和格式说明符在个数与类型上应相匹配. 例如,printf("\n x = %d , y = %f ", x , y+1);
3.2 常用输出与输入函数 printf的格式说明符
3.2 常用输出与输入函数
程序的运行结果是: 57 5 7 67.856400,-789.124023 67.856400,-789.124023 67.86,-789.12,67.856400,789.124023,67.856400,-789.124023 6.785640e+01,-7.9e+02 A,65,101,41 1234567,4553207,d687 65535,177777,ffff,-1 COMPUTER,COM
3.2 常用输出与输入函数
printf函数在使用时的注意事项
printf函数可以输出常量,变量和表达式的值.但 格式控制中的格式符必须按从左到右的顺序,与 输出项表中每个数据在类型上一一匹配,否则将 导致数据输出错误. 类型转换字符x,e,g可以用小写字母,也可以用大 写字母.使用大写字母时,输出数据中包含的字 母也要大写.除x,e,g外,其他类型转换字符必须 用小写字母,例如%f不能写成%F. 在输入long整型数据时,一定要使用格式%ld.如 果只用了%d,将输出错误数据. 若需要输出百分号"%",则应在格式串中用连续 的两个百分号"%%"表示. 类型转换字符紧跟在"%"后面时作为类型转换字 符,否则将作为普通字符处理. printf函数的返回值通常是本次调用中输出字符的 个数.
C语言程序设计第3章 顺序结构编程2018版

类型 变量长度(单位:字节) 数值范围
short int
2
-215 ~ 215-1
4
-23311 ~ 23311-1
long
unsigned short
unsigned int
unsigned long
4
-231 ~ 231-1
2
0 ~ 216-1
4
0 ~ 232-1
4
0 ~ 232-1
➢ 整型常量三种形式
例:total = money*num; int money=10, num=10;
注:int money=num=10;
3.2.3 赋值语句
➢ 复合赋值运算符 a += b 等价于 a = a + b a -= b 等价于 a = a – b a *= b 等价于 a = a * b a /= b 等价于 a = a / b a %= b 等价于 a = a % b
案例二:共享单车费用程序运行结果
案例三:孩子身高预测
问题描述:孩子的身高可以利用遗传因素 即利用父母的身高进行预测。女儿身高计 算公式为:女儿成人时的身高=(父高× 0.96 + 母高)÷2 (注:此方法未考虑环 境因素的影响)。
解析C程序设计-第3章自定义函数设计精品文档

2019/10/18
《解析C程序设计》第3章 自定义函数设计
3
• 事实上,C程序可以
– 只包含一个主函数 – 也可以包含一个主函数和若干个其它函数(库
函数和自定义函数)
• C语言是一个函数式语言。
2019/10/18
《解析C程序设计》第3章 自定义函数设计
求最大值和最小值可以使用条件运算符完成,当然还有其 他办法(你知道吗?)。
另外还涉及到函数的定义、函数的调用、函数值的返回、 参数的传递、函数的声明等基本知识。下面逐步介绍。
2019/10/18
《解析C程序设计》第3章 自定义函数设计
8
条件表达式运算符
一般形式: expr1 ? expr2 : expr3
max=(x>y) ? x : y; return(max); } int minmum(int x,int y) { int min; min=(x<y) ? x : y; return min; } void main() { int a,b; scanf("%4d,%4d",&a,&b); printf("max=%d\n", maxmum(a,b)); printf("min=%d\n", minmum(a,b)); }
22
例3-2:求两个整数的最大值和最小值
【分析】 首先定义两个函数:求最大值和最小值,然后在主函数中调用。
#include <stdio.h>
/* 定义求最大值的函数 */
void maxmum(int x,int y)
C语言第3章_数据的输入输出

如: scanf(“%c%c%c”,&c1,&c2,&c3); 若输入a• b• c 则ac1, • c2, b c3
17/22
例:有以下程序 #include<stdio.h> main() { int a1,a2; char c1,c2; float x,y,z; char a,b,c; scanf("%d%c%d%c",&a1,&c1,&a2,&c2); printf("%d,%c,%d,%c",a1,c1,a2,c2); } 若想通过键盘输入,使得al的值为12,a2的值为34 ,cl的值为字符a,c2的值为字符b,程序输出结果是 :12,a,34,b则正确的输入格式是(以下□代表空格, <CR>代表回车)( A )。 A)12a34b<CR> B)12□a□34□b<CR> C)12,a,34,b<CR> D)12□a34□b<CR>
4/22
d(int) o x(X)
以带符号的10进制形式输出整数 以8进制无符号形式输出整数 以16进制无符号形式输出整数
u(unsighed) 以无符号10进制形式输出整数
c(char) s f(float) e(E) 以字符形式输出一个字符 输出字符串
注意: long(%ld) double(%lf)
23/22
16/22
实数不许规定小数精度,像%10.4f不合法 输入格式中不能含有\n,如: scanf(“%d%d\n”,&a,&b); long型数据一定要用%ld格式输入,double型数 据一定要用%lf格式输入,否则运行结果错误。 用‚%c”格式符时,空格和转义字符作为有 效字符输入
第三章 C语言数据的输入与输出复习

l L
从上表可知:双精度实型数据的输出不要用%lf, 只要用%f即可。但长双精度实型数据的输出必须加 长度修饰符L, 例如%Lf、%Le等。
格式化输出函数printf()
printf函数的输出格式说明
每个格式说明都必须用%开头,以一个格式字
符作为结束,在此之间根据需要可以插入"宽度说
明"、长度修饰符'l'和'L"等。
(1)格式字符:格式字符用于规定输出不同的数据 类型,格式字符和它们的作用如下表,可详见附录 D。
格式化输出函数printf()
scanf函数的功能是从标准输入流中按指定格式 接收输入的数据; scanf函数的调用格式为: scanf(格式控制字符串, 地址列表);
格式控制字符串同printf
地址列表是由若干个地址组成的表列,可以是变 量的地址,或字符串的首地址
格式化输入函数scanf()
例:用scanf函数输入数据 #include "stdio.h" a在内存中的地 main() 址 &是地址运算符 {int a,b,c; scanf("%d%d%d",&a,&b,&c); printf("%d,%d,%d\nf",a,b,c); } 运行情况: 3 4 5<回车> (输入a,b,c的值) 3 ,4 ,5 (输出a,b,c的值)
计算机二级C语言_第3章输入输出函数

横向跳格(跳向下一输出区)(8列)
竖向跳格
后退一格
回车(回本行第一列)
走纸换页
输出反斜杠字符
输出单引号字符
1到3位8进制数所代表的字符
1到2位16进制数所代表的字符
printf函数举例
#include <stdio.h>
main() {int a=29; long b=123456; double x=123.456; char c=':';
首地址。
&:取地址符 格式: &变量名
➢ 一般格式
scanf (“格式控制字符串”,变量1的地址,变量2的地址,…,变量n的地 址);
➢ 格式控制符与后续参数中的变量地址的对应关系
已 知: int a , b; 函数调用: scanf ("%d%d", &a , &b); 假设输入: 10□20↙ 变量的值: a的值是10,b的值是20
格式
1、%s 按字符串的实际长度输出。 printf("%s","china");
china 2、%ms 输出的字符串占m列。
printf("%3s,%7s","china","china"); china,△△china 1.当字符串实际长度>m,则按实际长度输出。 2.当字符串实际长度≤m 。则左端补空格。 3、%-ms 输出的字符串占m列。 printf("%3s,%-7s","china","china"); china,china △△ 1.当字符串实际长度>m,则按实际长度输出。 2.当字符串实际长度≤m 。则右端补空格。
C语言第3章_

o,x
f
e g c
计算机基础教学部
17
二、printf格式符说明
■ 另外,还有其他格式符如:
■m
■l ■ 将在需要的时候用实例讲解。
计算机基础教学部
18
二、printf一般格式
■
%[标志][输出最小宽度][.精度][长度]格式字符
#include <stdio.h> #include <stdio.h> main() main() { { 输出结果:10,3.4 int a=10; 10 3.4 int a=10; 输出结果:103.4 float b=3.4; float b=3.4; printf(“%d%f\n”,a,b);/*a是int类型,用%d格 printf(“%d ,%f\n”,a,b); 式, b是float类型,用 %f格式*/ } printf(“%d%6.2f\n”,a,b) }
}
计算机基础教学部
23
四、格式输入函数scanf
输入数据赋给变量:
#include <stdio.h> #include <stdio.h> #include <stdio.h> #include <stdio.h> main() main() main() #include <stdio.h> main() { { { main() { int a,b; float h,w; int a;{ float b; scanf(“%d%d”,&a,&b); printf(“请输入身高(米):”); scanf(“%d”,&a); double c; scanf(“%f”,&b); scanf(“%f”,&h); } scanf(“%lf”,&c); } } printf(“请输入体重(千克):”); } scanf(“%f”,&w); printf(“肥胖指数为:%.2f\n”,w/h/h);
高考数学一轮复习第3章三角函数解三角形3.5两角和与差的正弦余弦与正切公式学案理

高考数学一轮复习第3章三角函数解三角形3.5两角和与差的正弦余弦与正切公式学案理052121743.5 两角和与差的正弦、余弦与正切公式[知识梳理]1.两角和与差的正弦、余弦、正切公式(1)C (α∓β):cos(α∓β)=cos αcos β±sin αsin β. (2)S (α±β):sin(α±β)=sin αcos β±cos αsin β.(3)T (α±β):tan(α±β)=tan α±tan β1∓tan αtan β⎝ ⎛⎭⎪⎫α,β,α±β≠π2+k π,k ∈Z .2.二倍角的正弦、余弦、正切公式 (1)S 2α:sin2α=2sin αcos α.(2)C 2α:cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α. (3)T 2α:tan2α=2tan α1-tan 2α⎝ ⎛⎭⎪⎫α≠±π4+k π,且α≠k π+π2,k ∈Z . 3.公式的常用变形(1)tan α±tan β=tan(α±β)(1∓tan αtan β). (2)cos 2α=1+cos2α2,sin 2α=1-cos2α2.(3)1±sin2α=(sin α±cos α)2, sin α±cos α=2sin ⎝⎛⎭⎪⎫α±π4.(4)a sin α+b cos α=a 2+b 2sin(α+φ),其中cos φ=a a 2+b2,sin φ=b a 2+b 2,tan φ=ba(a ≠0).特别提醒:(1)角:转化三角函数式中往往出现较多的差异角,注意观察角与角之间的和、差、倍、互补、互余等关系,运用角的变换,化多角为单角或减少未知角的数目,连接条件角与待求角,使问题顺利获解.对角变换时:①可以通过诱导公式、两角和与差的三角公式等;②注意倍角的相对性;③注意拆角、拼角技巧,例如,2α=(α+β)+(α-β),α=(α+β)-β=(α-β)+β,β=α+β2-α-β2=(α+2β)-(α+β),α-β=(α-γ)+(γ-β),15°=45°-30°,π4+α=π2-⎝ ⎛⎭⎪⎫π4-α等.(2)将三角变换与代数变换密切结合:三角变换主要是灵活应用相应的三角公式,对于代数变换主要有因式分解、通分、提取公因式、利用相应的代数公式等,例如,sin 4x +cos 4x =(sin 2x +cos 2x )2-2sin 2x cos 2x =1-12sin 22x .[诊断自测] 1.概念思辨(1)两角和与差的正弦、余弦公式中的角α,β是任意的.( ) (2)存在实数α,β,使等式sin(α+β)=sin α+sin β成立.( ) (3)在锐角△ABC 中,sin A sin B 和cos A cos B 大小关系不确定.( ) (4)公式tan(α+β)=tan α+tan β1-tan αtan β可以变形为tan α+tan β=tan(α+β)(1-tan αtan β),且对任意角α,β都成立.( )答案 (1)√ (2)√ (3)× (4)× 2.教材衍化(1)(必修A4P 131T 5)sin20°cos10°-cos160°sin10°=( ) A .-32 B.32 C .-12 D.12答案 D解析 原式=sin20°cos10°+cos20°sin10°=sin(20°+10°)=sin30°=12,故选D.(2)(必修A4P 146A 组T 3)已知tan ⎝ ⎛⎭⎪⎫α+π6=12,tan ⎝⎛⎭⎪⎫β-π6=13,则tan(α+β)=________.答案 1解析 ∵α+β=⎝⎛⎭⎪⎫α+π6+⎝ ⎛⎭⎪⎫β-π6, ∴tan(α+β)=tan ⎝ ⎛⎭⎪⎫α+π6+tan ⎝⎛⎭⎪⎫β-π61-tan ⎝ ⎛⎭⎪⎫α+π6tan ⎝ ⎛⎭⎪⎫β-π6=12+131-16=1.3.小题热身(1)sin7°+cos15°sin8°cos7-sin15°sin8°的值为( )A .2+ 3B .2- 3C .2 D.12答案 B解析 原式=sin (15°-8°)+cos15°sin8°cos (15°-8°)-sin15°sin8°=sin15°cos8°cos15°cos8°=tan15°=tan(45°-30°)=tan45°-tan30°1+tan45°tan30°=1-331+33=3-13+1=2- 3.故选B.(2)若sin(α-β)sin β-cos(α-β)cos β=45,且α是第二象限角,则tan ⎝ ⎛⎭⎪⎫π4+α等于( )A .7B .-7 C.17 D .-17答案 C解析 ∵sin(α-β)sin β-cos(α-β)cos β=45,∴cos α=-45.又α是第二象限角,∴sin α=35,则tan α=-34.∴tan ⎝ ⎛⎭⎪⎫π4+α=tan π4+tan α1-tan π4tan α=1-341+34=17.故选C.题型1 求值问题典例 已知cos ⎝ ⎛⎭⎪⎫π4+x =35,若17π12<x <7π4,求sin2x +2sin 2x 1-tan x 的值. 本题采用“函数转化法”.解 由17π12<x <7π4,得5π3<x +π4<2π.又cos ⎝⎛⎭⎪⎫π4+x =35,所以sin ⎝ ⎛⎭⎪⎫π4+x =-45,所以cos x =cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫π4+x -π4=cos ⎝ ⎛⎭⎪⎫π4+x cos π4+sin ⎝ ⎛⎭⎪⎫π4+x sin π4=35×22-45×22=-210,从而sin x =-7210,tan x =7.则sin2x +2sin 2x 1-tan x =2sin x cos x +2sin 2x 1-tan x=2⎝ ⎛⎭⎪⎫-7210·⎝ ⎛⎭⎪⎫-210+2⎝ ⎛⎭⎪⎫-721021-7=-2875.方法技巧三角恒等变换的变“角”与变“名”问题的解题思路1.角的变换:明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角),熟悉角的拆分与组合的技巧,半角与倍角的相互转化.2.名的变换:明确各个三角函数名称之间的联系,常常用到同角关系、诱导公式,把正弦、余弦化为正切,或者把正切化为正弦、余弦.冲关针对训练已知锐角α,β满足sin α=55,cos β=31010,则α+β等于( ) A.3π4 B.π4或3π4C.π4D .2k π+π4(k ∈Z )答案 C 解析 由sin α=55,cos β=31010,且α,β为锐角,可知cos α=255,sin β=1010, 故cos(α+β)=cos αcos β-sin αsin β=255×31010-55×1010=22,又0<α+β<π,故α+β=π4.故选C.题型2 三角恒等变换的综合应用角度1 研究三角函数的性质典例 (2017·临沂一模)已知函数f (x )=4sin ⎝ ⎛⎭⎪⎫x -π3cos x + 3.(1)求函数f (x )的最小正周期和单调递增区间;(2)若函数g (x )=f (x )-m 在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的零点x 1,x 2,求实数m 的取值范围,并计算tan(x 1+x 2)的值.本题采用转化法、数形结合思想.解 函数f (x )=4sin ⎝⎛⎭⎪⎫x -π3cos x +3,化简可得f (x )=2sin x cos x -23cos 2x + 3=sin2x -23⎝ ⎛⎭⎪⎫12+12cos2x + 3=sin2x -3cos2x =2sin ⎝⎛⎭⎪⎫2x -π3. (1)函数的最小正周期T =2π2=π,由2k π-π2≤2x -π3≤2k π+π2时单调递增,解得k π-π12≤x ≤k π+5π12(k ∈Z ),∴函数的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z .(2)函数g (x )=f (x )-m 在⎣⎢⎡⎦⎥⎤0,π2上有两个不同的零点x 1,x 2,转化为函数f (x )与函数y =m 有两个交点.令u =2x -π3,∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴u ∈⎣⎢⎡⎦⎥⎤-π3,2π3可得f (x )=2sin u 的图象(如图).由图可知:m 在[3,2),函数f (x )与函数y =m 有两个交点,其横坐标分别为x 1,x 2. 故得实数m 的取值范围是m ∈[3,2), 由题意可知x 1,x 2是关于对称轴是对称的: 那么函数在⎣⎢⎡⎦⎥⎤0,π2的对称轴为x =5π12, ∴x 1+x 2=5π12×2=5π6.那么tan(x 1+x 2)=tan 5π6=-33.方法技巧三角函数综合性试题涉及三角函数的性质研究.首先将三角函数化为f (x )=A sin(ωx +φ)的形式,在转化过程中需要三角恒等变换.如典例.这是高考的重点题型.冲关针对训练(2017·河北区二模)已知函数f (x )=sin ⎝⎛⎭⎪⎫x -π6+cos x .(1)求函数f (x )的最小正周期;(2)若α是第一象限角,且f ⎝ ⎛⎭⎪⎫α+π3=45,求tan ⎝⎛⎭⎪⎫α-π4的值.解 (1)f (x )=sin ⎝⎛⎭⎪⎫x -π6+cos x=32sin x -12cos x +cos x =32sin x +12cos x =sin ⎝⎛⎭⎪⎫x +π6,所以函数f (x )的最小正周期为T =2π1=2π.(2)由于f (x )=sin ⎝⎛⎭⎪⎫x +π6,则f ⎝ ⎛⎭⎪⎫α+π3=sin ⎝ ⎛⎭⎪⎫α+π2=cos α=45,由于α是第一象限角, 所以sin α=35,则tan α=34,则tan ⎝ ⎛⎭⎪⎫α-π4=tan α-11+tan α=-17. 角度2 三角恒等变换与向量的综合典例(2017·南京三模)已知向量a =(2cos α,sin 2α),b =(2sin α,t ),α∈⎝ ⎛⎭⎪⎫0,π2,t 为实数.(1)若a -b =⎝ ⎛⎭⎪⎫25,0,求t 的值;(2)若t =1,且a ·b =1,求tan ⎝⎛⎭⎪⎫2α+π4的值. 本题采用向量法、平方法.解 (1)向量a =(2cos α,sin 2α),b =(2sin α,t ),α∈⎝ ⎛⎭⎪⎫0,π2,t 为实数.若a -b =⎝ ⎛⎭⎪⎫25,0,则(2cos α-2sin α,sin 2α-t )=⎝ ⎛⎭⎪⎫25,0,可得cos α-sin α=15,平方可得sin 2α+cos 2α-2cos αsin α=125,即为2cos αsin α=1-125=2425(cos α>0,sin α>0),由sin 2α+cos 2α=1,解得cos α+sin α=(cos α-sin α)2+4sin αcos α =125+4825=75, 即有sin α=35,cos α=45,则t =sin 2α=925.(2)若t =1,且a ·b =1,即有4cos αsin α+sin 2α=1, 即有4cos αsin α=1-sin 2α=cos 2α,由α为锐角,可得cos α∈(0,1),即有tan α=sin αcos α=14,则tan2α=2tan α1-tan 2α=121-116=815, tan ⎝ ⎛⎭⎪⎫2α+π4=tan2α+11-tan2α=1+8151-815=237.方法技巧三角恒等变换与向量的综合问题是高考中经常出现的问题,一般以向量的坐标形式给出与三角函数有关的条件,并结合简单的向量运算进行化简.冲关针对训练(2017·南通模拟)已知向量m =⎝ ⎛⎭⎪⎫sin x 2,1,n =⎝⎛⎭⎪⎫1,3cos x2,函数f (x )=m ·n .(1)求函数f (x )的最小正周期;(2)若f ⎝ ⎛⎭⎪⎫α-2π3=23,求f ⎝⎛⎭⎪⎫2α+π3的值.解 (1)f (x )=sin x 2+3cos x 2=2sin ⎝ ⎛⎭⎪⎫x 2+π3,∴f (x )的最小正周期T =2π12=4π.(2)∵f ⎝ ⎛⎭⎪⎫α-2π3=2sin α2=23,∴sin α2=13, ∴cos α=1-2sin2α2=79,∴f ⎝ ⎛⎭⎪⎫2α+π3=2sin ⎝⎛⎭⎪⎫α+π2=2cos α=149.1.(2016·全国卷Ⅱ)若cos ⎝ ⎛⎭⎪⎫π4-α=35,则sin2α=( )A.725 B.15 C .-15 D .-725答案 D解析 cos ⎝ ⎛⎭⎪⎫π4-α=22(cos α+sin α)=35⇒cos α+sin α=325⇒1+sin2α=1825,∴sin2α=-725.故选D.2.(2014·全国卷Ⅰ)设α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫0,π2,且tan α=1+sin βcos β,则( )A .3α-β=π2B .3α+β=π2C .2α-β=π2D .2α+β=π2答案 C解析 由tan α=1+sin βcos β得sin αcos α=1+sin βcos β,即sin αcos β=cos α+sin βcos α,所以sin(α-β)=cos α,又cos α=sin ⎝ ⎛⎭⎪⎫π2-α,所以sin(α-β)=sin ⎝ ⎛⎭⎪⎫π2-α,又因为α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝⎛⎭⎪⎫0,π2,所以-π2<α-β<π2,0<π2-α<π2,因此α-β=π2-α,所以2α-β=π2,故选C.3.(2014·全国卷Ⅱ)函数f (x )=sin(x +2φ)-2sin φcos(x +φ)的最大值为________.答案 1解析 f (x )=sin[(x +φ)+φ]-2sin φcos(x +φ) =sin(x +φ)cos φ+cos(x +φ)sin φ-2sin φcos(x +φ) =sin(x +φ)cos φ-sin φcos(x +φ) =sin(x +φ-φ) =sin x ,∴f (x )的最大值为1.4.(2017·全国卷Ⅱ)函数f (x )=sin 2x +3cos x -34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0,π2的最大值是________.答案 1解析 f (x )=1-cos 2x +3cos x -34=-⎝ ⎛⎭⎪⎫cos x -322+1.∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴cos x ∈[0,1],∴当cos x =32时,f (x )取得最大值,最大值为1.[重点保分 两级优选练]A 级一、选择题1.计算sin43°cos13°+sin47°cos103°的结果等于( ) A.12 B.33 C.22 D.32 答案 A解析 原式=sin43°cos13°-cos43°sin13°=sin(43°-13°)=sin30°=12.故选A.2.sin47°-sin17°cos30°cos17°=( )A .-32 B .-12 C.12 D.32答案 C解析 sin47°=sin(30°+17°)=sin30°cos17°+cos30°·sin17°, ∴原式=sin30°cos17°cos17°=sin30°=12.故选C.3.已知过点(0,1)的直线l :x tan α-y -3tan β=0的斜率为2,则tan(α+β)=( ) A .-73 B.73 C.57 D .1答案 D解析 由题意知tan α=2,tan β=-13.∴tan(α+β)=tan α+tan β1-tan αtan β=2-131-2×⎝ ⎛⎭⎪⎫-13=1.故选D.4.(2017·云南一检)cos π9·cos 2π9·cos ⎝ ⎛⎭⎪⎫-23π9=( )A .-18B .-116 C.116 D.18答案 A解析 cos π9·cos 2π9·cos ⎝ ⎛⎭⎪⎫-23π9 =cos20°·cos40°·cos100°=-cos20°·cos40°·cos80° =-sin20°·cos20°·cos40°·cos80°sin20°=-12sin40°·cos40°·cos80°sin20°=-14sin80°·cos80°sin20°=-18sin160°sin20°=-18sin20°sin20°=-18.故选A.5.(2017·衡水中学二调)3cos10°-1sin170°=( )A .4B .2C .-2D .-4 答案 D 解析 3cos10°-1sin170°=3cos10°-1sin10°=3sin10°-cos10°sin10°cos10°=2sin (10°-30°)12sin20°=-2sin20°12sin20°=-4.故选D.6.若0<α<π2,-π2<β<0,cos ⎝ ⎛⎭⎪⎫π4+α=13,cos ⎝ ⎛ π4-⎭⎪⎫β2=33,则cos ⎝⎛⎭⎪⎫α+β2=( )A.33 B .-33 C.539 D .-69答案 C解析 cos ⎝ ⎛⎭⎪⎫α+β2=cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫π4+α-⎝ ⎛⎭⎪⎫π4-β2 =cos ⎝ ⎛⎭⎪⎫π4+αcos ⎝ ⎛⎭⎪⎫π4-β2+sin ⎝ ⎛⎭⎪⎫π4+αsin ⎝ ⎛⎭⎪⎫π4-β2,由0<α<π2,得π4<α+π4<3π4,则sin ⎝ ⎛⎭⎪⎫π4+α=223. 由-π2<β<0,得π4<π4-β2<π2,则sin ⎝ ⎛⎭⎪⎫π4-β2=63,代入上式,得cos ⎝⎛⎭⎪⎫α+β2=539,故选C.7.(2018·长春模拟)已知tan(α+β)=-1,tan(α-β)=12,则sin2αsin2β的值为( )A.13 B .-13 C .3 D .-3 答案 A 解析 sin2αsin2β=sin[(α+β)+(α-β)]sin[(α+β)-(α-β)]=sin (α+β)cos (α-β)+cos (α+β)sin (α-β)sin (α+β)cos (α-β)-cos (α+β)sin (α-β)=tan (α+β)+tan (α-β)tan (α+β)-tan (α-β)=13.故选A.8.(2017·山西八校联考)若将函数f (x )=sin(2x +φ)+3cos(2x +φ)(0<φ<π)的图象向左平移π4个单位长度,平移后的图象关于点⎝ ⎛⎭⎪⎫π2,0对称,则函数g (x )=cos(x +φ)在⎣⎢⎡⎦⎥⎤-π2,π6上的最小值是( )A .-12B .-32 C.22 D.12答案 D解析 ∵f (x )=sin(2x +φ)+3cos(2x +φ)=2sin ( 2x +φ+π3 ),∴将函数f (x )的图象向左平移π4个单位长度后,得到函数解析式为y =2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +π4+φ+π3=2cos ⎝ ⎛⎭⎪⎫2x +φ+π3的图象.∵该图象关于点⎝ ⎛⎭⎪⎫π2,0对称,对称中心在函数图象上,∴2cos ⎝ ⎛⎭⎪⎫2×π2+φ+π3=2cos ⎝⎛⎭⎪⎫π+φ+π3=0,解得π+φ+π3=k π+π2,k ∈Z ,即φ=k π-5π6,k ∈Z . ∵0<φ<π,∴φ=π6,∴g (x )=cos ⎝⎛⎭⎪⎫x +π6,∵x ∈⎣⎢⎡⎦⎥⎤-π2,π6,∴x +π6∈⎣⎢⎡⎦⎥⎤-π3,π3, ∴cos ⎝⎛⎭⎪⎫x +π6∈⎣⎢⎡⎦⎥⎤12,1,则函数g (x )=cos(x +φ)在⎣⎢⎡⎦⎥⎤-π2,π6上的最小值是12.故选D.9.(2018·兰州检测)在斜三角形ABC 中,sin A =-2cos B ·cos C ,且tan B tan C =1-2,则角A 的值为( )A.π4 B.π3 C.π2 D.3π4答案 A解析 由题意知,-2cos B cos C =sin A =sin(B +C )=sin B cos C +cos B sin C ,等式-2cos B cos C =sin B cos C +cos B sin C 两边同除以cos B cos C ,得tan B +tan C =-2,又tan(B +C )=tan B +tan C 1-tan B tan C =-1=-tan A ,即tan A =1,所以A =π4.故选A.10.(2018·河北模拟)已知θ∈⎝ ⎛⎭⎪⎫0,π4,且sin θ-cos θ=-144,则2cos 2θ-1cos ⎝ ⎛⎭⎪⎫π4+θ等于( )A.23B.43C.34D.32 答案 D解析 由sin θ-cos θ=-144,得sin ⎝ ⎛⎭⎪⎫π4-θ=74,∵θ∈⎝ ⎛⎭⎪⎫0,π4,∴π4-θ∈⎝⎛⎭⎪⎫0,π4,∴cos ⎝ ⎛⎭⎪⎫π4-θ=34,∴2cos 2θ-1cos ⎝ ⎛⎭⎪⎫π4+θ=cos2θsin ⎝ ⎛⎭⎪⎫π4-θ=sin ⎝ ⎛⎭⎪⎫π2-2θsin ⎝ ⎛⎭⎪⎫π4-θ=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4-θsin ⎝ ⎛⎭⎪⎫π4-θ=2cos ⎝ ⎛⎭⎪⎫π4-θ=32.故选D.二、填空题11.已知cos(α+β)cos(α-β)=13,则cos 2α-sin 2β=________.答案 13解析 ∵(cos αcos β-sin αsin β)(cos αcos β+sin αsin β)=13,∴cos 2αcos 2β-sin 2αsin 2β=13.∴cos 2α(1-sin 2β)-(1-cos 2α)sin 2β=13.∴cos 2α-sin 2β=13.12.已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,则2α-β的值为________.答案 -3π4解析 ∵tan α=tan[(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β=12-171+12×17=13>0,又α∈(0,π),∴0<α<π2.又∵tan2α=2tan α1-tan 2α=2×131-⎝ ⎛⎭⎪⎫132=34>0, ∴0<2α<π2,∴tan(2α-β)=tan2α-tan β1+tan2αtan β=34+171-34×17=1.∵tan β=-17<0,∴π2<β<π,-π<2α-β<0,∴2α-β=-3π4.13.(2017·江苏模拟)已知α、β为三角形的两个内角,cos α=17,sin(α+β)=5314,则β=________.答案π3解析 因为0<α<π,cos α=17,所以sin α=1-cos 2α=437,故π3<α<π2,又因为0<α+β<π,sin(α+β)=5314<32,所以0<α+β<π3或2π3<α+β<π.由π3<α<π2,知2π3<α+β<π, 所以cos(α+β)=-1-sin 2(α+β)=-1114,所以cos β=cos[(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α=12,又0<β<π,所以β=π3.14.已知sin α=12+cos α,且α∈⎝⎛⎭⎪⎫0,π2,则cos2αsin ⎝⎛⎭⎪⎫α-π4的值为________. 答案 -142解析 ∵sin α=12+cos α,∴sin α-cos α=12,∴(sin α-cos α)2=1-2sin αcos α=14,∴2sin αcos α=34,∵α∈⎝⎛⎭⎪⎫0,π2,∴sin α+cos α=sin 2α+cos 2α+2sin αcos α = 1+34=72,∴cos2αsin ⎝ ⎛⎭⎪⎫α-π4=(cos α+sin α)(cos α-sin α)22(sin α-cos α) =-2(sin α+cos α)=-142. B 级三、解答题15.(2017·合肥质检)已知a =(sin x ,3cos x ),b =(cos x ,-cos x ),函数f (x )=a ·b +32. (1)求函数y =f (x )图象的对称轴方程;(2)若方程f (x )=13在(0,π)上的解为x 1,x 2,求cos(x 1-x 2)的值.解 (1)f (x )=a ·b +32=(sin x ,3cos x )·(cos x ,-cos x )+32=sin x ·cos x -3cos 2x +32=12sin2x -32cos2x =sin ⎝⎛⎭⎪⎫2x -π3. 令2x -π3=k π+π2(k ∈Z ),得x =5π12+k π2(k ∈Z ),即函数y =f (x )图象的对称轴方程为x =5π12+k π2(k ∈Z ).(2)由条件知sin ⎝ ⎛⎭⎪⎫2x 1-π3=sin ⎝ ⎛⎭⎪⎫2x 2-π3=13>0,设x 1<x 2,则0<x 1<5π12<x 2<2π3,易知(x 1,f (x 1))与(x 2,f (x 2))关于直线x =5π12对称,则x 1+x 2=5π6,∴cos(x 1-x 2)=cos ⎣⎢⎡⎦⎥⎤x 1-⎝ ⎛⎭⎪⎫5π6-x 1=cos ⎝ ⎛⎭⎪⎫2x 1-5π6=cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2x 1-π3-π2=sin ⎝⎛⎭⎪⎫2x 1-π3=13.16.(2017·黄冈质检)已知函数f (x )=2cos 2x -sin ⎝ ⎛⎭⎪⎫2x -7π6.(1)求函数f (x )的最大值,并写出f (x )取最大值时x 的取值集合;(2)已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若f (A )=32,b +c =2.求实数a的取值范围.解 (1)f (x )=2cos 2x -sin ⎝ ⎛⎭⎪⎫2x -7π6=(1+cos2x )-⎝ ⎛⎭⎪⎫sin2x cos 7π6-cos2x sin 7π6 =1+32sin2x +12cos2x =1+sin ⎝⎛⎭⎪⎫2x +π6.∴函数f (x )的最大值为2.当且仅当sin ⎝⎛⎭⎪⎫2x +π6=1,即2x +π6=2k π+π2(k ∈Z ),即x =k π+π6,k ∈Z 时取到.∴函数f (x )的最大值为2时x 的取值集合为x ⎪⎪⎪⎭⎬⎫x =k π+π6,k ∈Z .(2)由题意,f (A )=sin ⎝ ⎛⎭⎪⎫2A +π6+1=32,化简得sin ⎝⎛⎭⎪⎫2A +π6=12.∵A ∈(0,π),∴2A +π6∈⎝ ⎛⎭⎪⎫π6,13π6,∴2A +π6=5π6,∴A =π3.在△ABC 中,根据余弦定理,得a 2=b 2+c 2-2bc cos π3=(b +c )2-3bc .由b +c =2,知bc ≤⎝⎛⎭⎪⎫b +c 22=1,即a 2≥1.∴当且仅当b =c =1时,取等号.又由b +c >a 得a <2.所以a 的取值范围是[1,2).17.(2017·青岛诊断)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且a sin B +3a cos B =3c .(1)求角A 的大小;(2)已知函数f (x )=λcos 2⎝ ⎛⎭⎪⎫ωx +A 2-3(λ>0,ω>0)的最大值为2,将y =f (x )的图象的纵坐标不变,横坐标伸长到原来的32倍后便得到函数y =g (x )的图象,若函数y =g (x )的最小正周期为π.当x ∈⎣⎢⎡⎦⎥⎤0,π2时,求函数f (x )的值域.解 (1)∵a sin B +3a cos B =3c , ∴sin A sin B +3sin A cos B =3sin C . ∵C =π-(A +B ),∴sin A sin B +3sin A cos B =3sin(A +B ) =3(sin A cos B +cos A sin B ). 即sin A sin B =3cos A sin B .∵sin B ≠0,∴tan A =3,∵0<A <π,∴A =π3.(2)由A =π3,得f (x )=λcos 2⎝ ⎛⎭⎪⎫ωx +π6-3=λ·1+cos ⎝ ⎛⎭⎪⎫2ωx +π32-3=λ2cos ⎝⎛⎭⎪⎫2ωx +π3+λ2-3,∴λ-3=2,λ=5.∴f (x )=5cos 2⎝ ⎛⎭⎪⎫ωx +π6-3=52cos ⎝ ⎛⎭⎪⎫2ωx +π3-12,从而g (x )=52cos ⎝ ⎛⎭⎪⎫43ωx +π3-12,∴2π43ω=π,得ω=32, ∴f (x )=52cos ⎝⎛⎭⎪⎫3x +π3-12.当x ∈⎣⎢⎡⎦⎥⎤0,π2时,π3≤3x +π3≤11π6,∴-1≤cos ⎝⎛⎭⎪⎫3x +π3≤32,从而-3≤f (x )≤53-24,∴f (x )的值域为⎣⎢⎡⎦⎥⎤-3,53-24.18.(2017·江西南昌三校模拟)已知函数f (x )=sin ⎝⎛⎭⎪⎫5π6-2x -2sin ⎝ ⎛⎭⎪⎫x -π4cos ⎝⎛⎭⎪⎫x +3π4.(1)求函数f (x )的最小正周期和单调递增区间; (2)若x ∈⎣⎢⎡⎦⎥⎤π12,π3,且F (x )=-4λf (x )-cos ⎝⎛⎭⎪⎫4x -π3的最小值是-32,求实数λ的值.解 (1)∵f (x )=sin ⎝ ⎛⎭⎪⎫5π6-2x -2sin ⎝ ⎛⎭⎪⎫x -π4cos ⎝⎛⎭⎪⎫x +3π4=12cos2x +32sin2x +(sin x-cos x )(sin x +cos x )=12cos2x +32sin2x +sin 2x -cos 2x =12cos2x +32sin2x -cos2x =sin ⎝⎛⎭⎪⎫2x -π6.∴函数f (x )的最小正周期T =2π2=π.由2k π-π2≤2x -π6≤2k π+π2得k π-π6≤x ≤k π+π3(k ∈Z ),∴函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈Z ).(2)F (x )=-4λf (x )-cos ⎝ ⎛⎭⎪⎫4x -π3 =-4λsin ⎝ ⎛⎭⎪⎫2x -π6-⎣⎢⎡⎦⎥⎤1-2sin 2⎝ ⎛⎭⎪⎫2x -π6=2sin 2⎝ ⎛⎭⎪⎫2x -π6-4λsin ⎝ ⎛⎭⎪⎫2x -π6-1 =2⎣⎢⎡⎦⎥⎤sin ⎝ ⎛⎭⎪⎫2x -π6-λ2-1-2λ2.∵x ∈⎣⎢⎡⎦⎥⎤π12,π3,∴0≤2x -π6≤π2,∴0≤sin ⎝⎛⎭⎪⎫2x -π6≤1. ①当λ<0时,当且仅当sin ⎝ ⎛⎭⎪⎫2x -π6=0时,F (x )取得最小值,最小值为-1,这与已知不相符;②当0≤λ≤1时,当且仅当sin ⎝ ⎛⎭⎪⎫2x -π6=λ时,F (x )取得最小值,最小值为-1-2λ2,由已知得-1-2λ2=-32,解得λ=-12(舍)或λ=12;③当λ>1时,当且仅当sin ⎝ ⎛⎭⎪⎫2x -π6=1时,F (x )取得最小值,最小值为1-4λ,由已知得1-4λ=-32,解得λ=58,这与λ>1矛盾.综上所述,λ=12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22
• 使用引用类型以减少编译器的大量 拷贝数据时间,并希望不改变其值, 声明为:const type& arg • 局部变量不可当成引用类型返回值。
23
2. inline (内联)函数
24
2.1 为什么使用inline 函数
• 利用inline函数可以增加程序执行的 速度。一般用于程序码相当小的函 数(1~5行代码)。 • 原理:一个小函数若设定为一般函 数,则程序在进出函数之间所用去 的时间可能就多于函数本身执行所 用去的时间。
• 但有时希望函数能改变所传递的参数值,这 时可以用传址(passing by address)来达到目的。 • 传址法是要借助于所传递过来的地址,(这 些地址被存放在栈中),更改该地址所指向 的值,而不是要更改地址的值。 • 如果更改地址的值,而这些值存放在堆栈中, 即使更改它,当函数结束时,这些存放地址 值的存储空间便被释放回系统。对于原来调 用该函数的程序并无影响,所以会有同传值 法的结果。
5
• 其中stime 便是所谓的形式参数,在 函数定义中,用来接收当调用函数 时所传过来的数据的变量便称为形 式参数。 • 所有在函数中定义的变量,连同形 式参数,都是属于局部变量,当程 序离开该函数的有效范围则这些变 量所占的存储空间也会被释放回系 统而不能再使用。
6
1.2 传值(passing by value)
25
2.2 什么是inline函数 • 使用内联函数,编译器在编 译时并不生成真正的函数, 而是将程序中出现的每一个 内联函数调用表达式直接用 该内联函数的函数体替换。
26
2.3 设定inline函数
见inliner.cpp 将一函数设定为inline,必须完成: • 在函数定义前加上关键字inline; • 该函数的定义必须在第一次被 调用前出现。
4
பைடு நூலகம்
1.1 实在参数(actual arguemnt)与形式 参数(formal argument)
所谓实在参数便是当调用函数时,所给与函数的参数。 void main( ) { … int times; //第一次调用show函数 int count = show(times); … } 则times称为函数show的实在参数。而在函数show的定 义中: int show(int stime ) { … }
21
1.4.4 引用类型(Reference type) 总结
• 引用类型: & 定义时需赋初值。 • 类似指针,但如变量使用,主要用 于参数或函数返回值的类型。 • 使用引用类型作为函数参数,实质 上是形参可如实参使用。 –函数原形中声明为Reference, & , 这是唯一区别是否为Reference 的 方法。 –函数调用中直接引用实参。
9
• 也就是无论我们在函数showchar中 如何更改c, count的值,都不会影响 到main中ch, times的值。 当我们调用函数时,希望所传递的参 数不被更改时,就用传值法。 更多例子见:PassValue.cpp, PassValueStruct.cpp
10
1.3 传址(passing by address)
3. 函数名称的重载 (overloaded functions)
30
• 函数名称可以被重复使用,也就是 程序中一个有效范围中可以有两个 或两个以上的函数名称与返回值类 型是完全一样的。 • 具有相同名称的函数只要其参数表 (参数个数或参数数据类型)不一 样,则可视为不同的函数。
31
• 例如: void showchar(int times, const char c); void showchar(const char c, int times); void showchar(int times); 都是属于重载的函数。 见:overload.cpp及overengl.cpp
20
• 局部变量不可当成引用类型返回值。如 下定义不允许。
Grade& specadd(Grade& stu) { Grade temp = stu; temp.Chin+ = 10; temp.Eng1+ =10; temp.Math+ = 10; temp.Chem+ = 10; return temp; }
35
4. 函数默认(缺省)参数 Default Argument
36
• C++允许函数对于参数可以有默认值, 当用户忽略对函数指定参数时,函数便 会自动使用参数的默认值。 • 只需在提供函数原形的同时,对于参数 指定初值即可: double square(double x=2); 则当以下形式调用函数square时: square(); 如同:square(2); 见:missarg.cpp
14
–可见调用函数swap_by_ref后的 确将两变量的值交换了,与传址 一样的效果。
–注意:&出现在函数原型时,表 示以引用为参数,而若出现在调 用函数时,则表示以传址法来传 递参数。
15
1.4.2 使用引用传递结构
• 引用类型另一个好处便是可以 减少编译器拷贝实在参数的值 到堆栈中的时间。(注意:指 针也能达到同样的效果。)
34
• 如函数参数的数据类型中有引用类型, 则应格外小心,因为引用类型变量的使 用与一般的普通变量一样。如: void count(int x); void count(int& x); 则我们以下列语句调用是:int times =10; count(times); 编译器无法辨别应使用哪一个函数。
8
1.2 传值(passing by value)
参数传递的方法中,传值法是最简单的。 原理: • 编译器会将传递来的实在参数值(ch, times)拷贝到栈中,并产生形式参数 (c,count)来接收这个值。 • 而等到函数showchar(char c,int count) 执行完成后,便将c, count所占用的存储 空间释放回系统,所以,c和ch有相同的 值,但却是完全独立。
19
1.4.3 以引用类型数据为函数的返 回值(return by reference)
• 引用类型作为函数结束时的返回值。 例如:int& coun(int *num); • 函数返回引用,把返回值当作一般函数 对待,return 后面一般跟着引用类型。 还可以是:数组元素,static变量,指针 所指的值…… • 见RefReturn.cpp
• 引用类型使用户可以在局部的函数范围 中使用非函数范围的实在参数,但有时 我们担心传递过来的实在参数的值被改 变,又不想用传值法浪费时间来拷贝实 在参数的值到栈中。(注:指向const的 指针也可达到同样的效果) • 解决的方法:在定义函数时,特别在引 用类型结构数据参数的前方加上关键字 const. • 见 PassRefStruct.cpp
16
• 如果用户以结构为函数的参 数,采用传值法,结构中所 含有多项的数据在传递过程 中必会造成编译器在拷贝结 构中数据到堆栈时的过度负 载。
17
• 以引用类型的结构为函数的参 数,如同只传进一个指向此结 构的指针,则可以省去编译器 的大量拷贝整个结构数据,使 用时也如同一般参数的用法。
18
以引用类型为参数可能产生的问题
27
• inline 函数体内不允许有循环和 switch 语句;对于一些程序码 太大的函数,即使设定成inline, 编译器仍就视为一般函数。 • 不宜过长,1~5 行为宜。
28
/*This file is an example that the program contains a short function which is a inline function*/ #include <iostream.h> #include<conio.h> inline double add(double x, double y) { return(x+y); } void main() { cout<<“2+2:” <<add(2.0,2.0);<<endl; cout<<“2.2+3.134is: ”<<add(13.134,3.134) 29 <<endl; }
/*This file is an example of how to pass argument by value.*/
#include <iostream.h> #include <conio.h> void showcar(char c, int count); void main( ) { char ch; //what character to be shown out int times; //how many times to be shown out cout<<“Please input what character to show: ”; cin>>ch; //get a character cout<<“How many times to show: ” ; cin>>time; showchar(ch,times);
12
• 而在调用函数时,若其参数为引用 类型参数,则只要给与变量的名称 即可,如同传值的方法一般,但效果 如同传址。 • 可以把引用看作是使语法更加便利 的工具。 • 见例:chpt3, PassReference.cpp
13
• 从例chpt3, PassReference.cpp中可看出:
–以引用类型为参数的函数原型为: void swap_by_ref(int &arg1, int &arg2); –其参数与swap_by_val唯一不同的便是所有 参数前都加上了&,而其定义部分除了说明 符外其余都同于swap_by_val void swap_by_ref(int &arg1,int &arg2) { int temp = arg1; arg1 = arg2; arg2 = temp; }
