北京第五十四中学数学轴对称填空选择中考真题汇编[解析版]
北京第五十四中学数学整式的乘法与因式分解中考真题汇编[解析版]
![北京第五十四中学数学整式的乘法与因式分解中考真题汇编[解析版]](https://img.taocdn.com/s3/m/fb82d5b6cc17552706220835.png)
北京第五十四中学数学整式的乘法与因式分解中考真题汇编[解析版]一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为()A.6 B.7 C.8 D.9【答案】C【解析】【分析】设2为a,3为b,则根据5张边长为2的正方形纸片的面积是5a2,4张边长分别为2、3的矩形纸片的面积是4ab,6张边长为3的正方形纸片的面积是6a2,得出a2+4ab+4b2=(a+2b)2,再根据正方形的面积公式将a、b代入,即可得出答案.【详解】解:设2为a,3为b,则根据5张边长为2的正方形纸片的面积是5a2,4张边长分别为2、3的矩形纸片的面积是4ab,6张边长为3的正方形纸片的面积是6b2,∵a2+4ab+4b2=(a+2b)2,(b>a)∴拼成的正方形的边长最长可以为a+2b=2+6=8,故选C.【点睛】此题考查了完全平方公式的几何背景,关键是根据题意得出a2+4ab+4b2=(a+2b)2,用到的知识点是完全平方公式.2.已知n16++是一个有理数的平方,则n不能取以下各数中的哪一个() 221-D.9A.30 B.32 C.18【答案】B【解析】【分析】分多项式的三项分别是乘积二倍项时,利用完全平方公式分别求出n的值,然后选择答案即可.【详解】2n是乘积二倍项时,2n+216+1=216+2×28+1=(28+1)2,此时n=8+1=9,216是乘积二倍项时,2n +216+1=2n +2×215+1=(215+1)2,此时n=2×15=30,1是乘积二倍项时,2n +216+1=(28)2+2×28×2-9+(2-9)2=(28+2-9)2,此时n=-18,综上所述,n 可以取到的数是9、30、-18,不能取到的数是32.故选B .【点睛】本题考查了完全平方式,难点在于要分情况讨论,熟记完全平方公式结构是解题的关键.3.()()()()242212121......21n ++++=( )A .421n -B .421n +C .441n -D .441n + 【答案】A【解析】【分析】 先乘以(2-1)值不变,再利用平方差公式进行化简即可.【详解】()()()()242n 212121......21++++=(2-1)()()()()242n 212121......21++++ =24n -1.故选A.【点睛】本题考查乘法公式的应用,熟练掌握并灵活运用平方差公式是解题关键.4.已知三角形三边长为a 、b 、c ,且满足247a b -=, 246b c -=-, 2618c a -=-,则此三角形的形状是( )A .等腰三角形B .等边三角形C .直角三角形D .无法确定【答案】A【解析】解:∵a 2﹣4b =7,b 2﹣4c =﹣6,c 2﹣6a =﹣18,∴a 2﹣4b +b 2﹣4c +c 2﹣6a =7﹣6﹣18,整理得:a 2﹣6a +9+b 2﹣4b +4+c 2﹣4c +4=0,即(a ﹣3)2+(b ﹣2)2+(c ﹣2)2=0,∴a =3,b =2,c =2,∴此三角形为等腰三角形.故选A .点睛:本题考查了因式分解的应用,解题的关键是正确的进行因式分解.5.计算,得( ) A . B .C .D .【答案】C【解析】【分析】直接提取公因式(-3)m-1,进而分解因式即可.【详解】(-3)m +2×(-3)m-1=(-3)m-1(-3+2)=-(-3)m-1.故选C .【点睛】此题主要考查了提取公因式法分解因式,正确分解因式是解题关键.6.如图将4个长、宽分别均为a ,b 的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )A .a 2+2ab+b 2=(a+b )2B .a 2﹣2ab+b 2=(a ﹣b )2C .4ab=(a+b )2﹣(a ﹣b )2D .(a+b )(a ﹣b )=a 2﹣b 2【答案】C【解析】【分析】根据图形的组成以及正方形和长方形的面积公式,知:大正方形的面积﹣小正方形的面积=4个矩形的面积.【详解】∵大正方形的面积﹣小正方形的面积=4个矩形的面积,∴(a+b )2﹣(a ﹣b )2=4ab ,即4ab=(a+b )2﹣(a ﹣b )2.故选C .7.通过计算几何图形的面积可表示代数恒等式,图中可表示的代数恒等式是( )A .22()()a b a b a b +-=-B .222()2a b a ab b +=++C .22()22a a b a ab +=+D .222()2a b a ab b -=-+【答案】A【解析】【分析】 根据阴影部分面积的两种表示方法,即可解答.【详解】图1中阴影部分的面积为:22a b -,图2中的面积为:()()a b a b +-,则22()()a b a b a b +-=-故选:A.【点睛】本题考查了平方差公式的几何背景,解决本题的关键是表示阴影部分的面积.8.如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是 ( )A .30B .20C .60D .40【答案】A【解析】【分析】 设大正方形的边长为x ,小正方形的边长为y ,表示出阴影部分的面积,结合大正方形与小正方形的面积之差是60即可求解.【详解】设大正方形的边长为x ,小正方形的边长为y ,则2260x y -=,∵S 阴影=S △AEC +S △AED =11()()22x y x x y y -+- =1()()2x y x y -+ =221()2x y - =1602⨯ =30.故选A.【点睛】此题主要考查了平方差公式的应用,读懂图形和熟练掌握平方差公式是解此题的关键.9.下列等式由左边向右边的变形中,属于因式分解的是 ( )A .x 2+5x -1=x(x+5)-1B .x 2-4+3x=(x+2)(x -2)+3xC .(x+2)(x -2)=x 2-4D .x 2-9=(x+3)(x -3)【答案】D【解析】【分析】根据因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,判断求解.【详解】解:A 、右边不是积的形式,故A 错误;B 、右边不是积的形式,故B 错误;C 、是整式的乘法,故C 错误;D 、x 2-9=(x+3)(x -3),属于因式分解.故选D .【点睛】此题主要考查因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.10.若2149x kx ++是完全平方式,则实数k 的值为( ) A .43 B .13 C .43± D .13± 【答案】C【解析】【分析】本题是已知平方项求乘积项,根据完全平方式的形式可得出k 的值.【详解】由完全平方式的形式(a±b )2=a 2±2ab+b 2可得: kx=±2•2x•13, 解得k=±43. 故选:C【点睛】本题关键是有平方项求乘积项,掌握完全平方式的形式(a±b )2=a 2±2ab+b 2是关键.二、八年级数学整式的乘法与因式分解填空题压轴题(难)11.如图,有一张边长为x 的正方形ABCD 纸板,在它的一个角上切去一个边长为y 的正方形AEFG ,剩下图形的面积是32,过点F 作FH ⊥DC ,垂足为H.将长方形GFHD 切下,与长方形EBCH 重新拼成一个长方形,若拼成的长方形的较长的一边长为8,则正方形ABCD 的面积是____.【答案】36.【解析】【分析】根据题意列出2232,8x y x y -=+=,求出x-y=4,解方程组得到x 的值即可得到答案.【详解】由题意得: 2232,8x y x y -=+= ∵22()()x y x y x y -=+-,∴x -y=4, 解方程组48x y x y -=⎧⎨+=⎩,得62x y =⎧⎨=⎩, ∴正方形ABCD 面积为236x =,故填:36.【点睛】此题考查平方差公式的运用,根据题意求得x-y=4是解题的关键,由此解方程组即可.12.已知a-b=4,ab=6,则22a b += _________.【答案】28【解析】【分析】对完全平方公式进行变形即可解答.【详解】解:∵222()216a b a ab b -=-+=∴22a b +=2()a b -+2ab=16+2×6=28故答案为28.【点睛】本题考查了完全平方公式的应用,掌握完全平方公式并能够进行灵活变形是解答本题的关键.13.如果关于x 的二次三项式24x x m -+在实数范围内不能因式分解,那么m 的值可以是_________.(填出符合条件的一个值)【答案】5【解析】【分析】根据前两项,此多项式如用十字相乘方法分解,m 应是3或-5;若用完全平方公式分解,m 应是4,若用提公因式法分解,m 的值应是0,排除3、-5、4、0的数即可.【详解】当m=5时,原式为245x x -+,不能因式分解,故答案为:5.【点睛】此题考查多项式的因式分解方法,熟记每种分解的因式的特点及所用因式分解的方法,掌握技巧才能熟练运用解题.14.将4个数a ,b ,c ,d 排列成2行、2列,两边各加一条竖直线记成a b c d ,定义a bad bc c d =-,上述记号就叫做2阶行列式.若11611x x x x --=-+,则x=_________.【答案】4【解析】【分析】根据题目中所给的新定义运算方法可得方程 (x-1)(x+1)- (x-1)2=6,解方程求得x 即可.【详解】由题意可得,(x-1)(x+1)- (x-1)2=6,解得x=4.故答案为:4.【点睛】本题考查了新定义运算,根据新定义运算的运算方法列出方程是解本题的关键.15.多项式18x n+1-24x n 的公因式是_______.【答案】6x n【解析】运用公因式的概念,找出系数的最大公约数是6,相同字母的最低指数次幂是x n ,可得公因式为6x n .故答案为:6x n .16.因式分解:3222x x y xy +=﹣__________. 【答案】()2x x y -【解析】【分析】先提取公因式x ,再对余下的多项式利用完全平方公式继续分解.【详解】解:原式()()2222x x xy y x x y =-+=-, 故答案为:()2x x y -【点睛】本题考查提公因式,熟练掌握运算法则是解题关键.17.计算:))201820192的结果是_____.2【解析】【分析】逆用积的乘方运算法则以及平方差公式即可求得答案.【详解】))201820192=)))2018201822⨯⨯=)))201822⎡⎤⎣⎦⨯⨯=(5-4)2018×)2=,【点睛】本题考查了积的乘方的逆用,平方差公式,熟练掌握相关的运算法则是解题的关键.18.因式分解:3x 3﹣12x=_____.【答案】3x (x+2)(x ﹣2)【解析】【分析】先提公因式3x ,然后利用平方差公式进行分解即可.【详解】3x 3﹣12x=3x (x 2﹣4)=3x (x+2)(x ﹣2),故答案为3x (x+2)(x ﹣2).【点睛】本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.19.若(2x ﹣3)x+5=1,则x 的值为________.【答案】2或1或-5【解析】(1)当2x −3=1时,x=2,此时()2+543-=1,等式成立;(2)当2x −3=−1时,x=1,此时()1523+-=1,等式成立; (3)当x+5=0时,x=−5,此时()0103--=1,等式成立.综上所述,x 的值为:2,1或−5.故答案为2,1或−5.20.若m+n=3,则2m 2+4mn+2n 2-6的值为________.【答案】12【解析】原式=2(m 2+2mn +n 2)-6,=2(m +n )2-6,=2×9-6,=12.。
中考数学复习《轴对称》专题训练-带含有参考答案

中考数学复习《轴对称》专题训练-带含有参考答案一、选择题1.下列交通标志中,是轴对称图形的是()A.B.C.D.2.点P关于x轴对称点M的坐标为(4,﹣5),那么点P关于y轴对称点N的坐标为()A.(﹣4,5)B.(4,5)C.(﹣4,﹣5)D.(﹣5,4)3.如图,方格纸中每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,线段AB 的顶点均在格点上.在图中画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N均为格点,这样的线段能画()条.A.2 B.3 C.5 D.64.如图,在△ABC中,DE是AC的垂直平分线AB=5cm,BC=8cm,则△ABD的周长为()A.10cm B.13cm C.15cm D.16cm5.等腰三角形的周长为11,其中一边长为3,则该等腰三角形的底边长为()A.3B.5C.4或5D.3或56.如图,在Rt△ABC中∠ACB=90°,∠B=15°,AB的垂直平分线交AB于点E,交BC于点D,且BD=12cm,则AC的长是()A.12cm B.6cm C.4cm D.6√3cm7.如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G,F,若FG=3,ED=6,则EB+DC的值为()A.7 B.8 C.9 D.108.如图,已知ΔABC是正三角形,D是BC边上任意一点,过点D作DF⊥AC于点F,ED⊥BC交AB于点E,则∠EDF等于()A.50°B.65°C.60°D.75°二、填空题9.某车标是一个轴对称图形,有条对称轴.10.在平面直角坐标系中,点M(a,3)与点N(5,b)关于y轴对称,则a﹣b=.11.如图,在△ABC中,边AB的垂直平分线分别交BC于点D,交AB于点E.若AE=3,△ADC的周长为8,则△ABC的周长为.12.如图,在△ABC中,AB=AC,AD=BD,∠A=36°,则图中等腰三角形的个数是.13.如图,在△ABC中AB=AC,∠C=30°,AB⊥AD,AD=6,BC的长是.三、解答题14.图①、图②均是由边长为1的小正方形组成的网格,每个小正方形的顶点称为格点,点A、B、C均在格点上.请用无刻度的直尺按下列要求在网格中作图.(1)在图①中,连接AC,以线段AC为腰作一个等腰直角三角形ACD;(2)在图②中确定一个格点D,并画出以A、B、C、D为顶点的四边形.使其为轴对称图形.15.如图,在中,的垂直平分线分别交线段,于点M,P,的垂直平分线分别交线段,于点N,Q.(1)如图,当时,求的度数;(2)当时,求的度数.16.如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).(1)求出△ABC的面积.(2)在图中作出△ABC关于y轴的对称图形△A1B1C1.(3)写出点△A1B1C1的坐标.17.如图,在△ABC中,AB=AC,点D、E、F分别在△ABC的三条边上,且BF=CD,BD=CE.(1)求证:△DFE是等腰三角形;(2)若∠A=56°,求∠EDF的度数.18.如图,在△ABC中AB=AC,点D在△ABC内BD=BC,∠DBC=60°点E在△ABC外∠BCE=150°,∠ABE=60° .(1)求∠ADB的度数;(2)判断△ABE的形状并加以证明;(3)连接DE,若DE⊥BD,DE=8求AD的长.参考答案1.B2.A3.C4.B5.D6.B7.C8.C9.310.﹣811.1412.313.1814.(1)解:如图①所示(2)解:如图②所示15.(1)解:∵、分别是的垂直平分线∴∵∴∵∴∴(2)解:∵分别是的垂直平分线∴∴∴当P点在Q点右侧时,如图:∵∴∵∴.当P点在Q点左侧时∵∴∵∴.综上或.16.(1)解:S△ABC= 12×5×3=152(或7.5)(平方单位)(2)解:如图.(3)解:A1(1,5),B1(1,0),C1(4,3). 17.(1)证明:∵AB=AC∴∠B=∠C在△FBD与△DCE中{BF=CD∠B=∠CBD=CE∴△FBD≌△DCE.∴DF=ED,即△DEF是等腰三角形(2)解:∵AB=AC,∠A=56°∴∠B=∠C= 12(180°−56°)=62°.∴∠EDF=∠B=62°.18.(1)解:∵BD=BC,∠DBC=60°∴△DBC是等边三角形,∴DB=DC,∠BDC=∠DBC=∠DCB=60°在△ADB和△ADC中{AB=ACAD=ADDB=DC∴△ADB≌△ADC,∴∠ADB=∠ADC,∴∠ADB= 12(360°﹣60°)=150°.(2)解:结论:△ABE是等边三角形.理由:∵∠ABE=∠DBC=60°,∴∠ABD=∠CBE在△ABD和△EBC中{AB=EB∠ADB=∠BCE=150°∠ABD=∠CBE∴△ABD≌△EBC ∴AB=BE,∵∠ABE=60°,∴△ABE是等边三角形.(3)解:连接DE.∵∠BCE=150°,∠DCB=60°,∴∠DCE=90°,∵∠EDB=90°,∠BDC=60°∴∠EDC=30°,∴EC= 12DE=4,∵△ABD≌△EBC,∴AD=EC=4.。
北京市第五十四中学2024-2025学年九年级上学期期中考试数学试卷

北京市第五十四中学2024-2025学年九年级上学期期中考试数学试卷一、单选题1.下列图形中是轴对称图形但不是中心对称图形的是()A .B .C .D .2.若3x =是关于x 的方程220x x m --=的一个根,则m 的值是()A .15-B .3-C .3D .153.关于二次函数22(1)2y x =-+,下列说法正确的是()A .当1x =时,有最小值为2B .当1x =时,有最大值为2C .当=1x -时,有最小值为2D .当=1x -时,有最大值为24.如图,四边形ABCD 内接于O ,若80ADC ︒∠=,则ABC ∠的度数是()A .40°B .80°C .100°D .120°5.圆心角是90︒,半径为20的扇形的弧长为()A .5πB .10πC .15πD .20π6.已知点()13,A y -,()21,B y -,()32,C y 在函数22y x x b =--+的图象上,则1y 、2y 、3y 的大小关系为()A .132y y y <<B .312y y y <<C .321y y y <<D .213y y y <<7.如图,在小正方形网格中,将ABC V 绕某一点旋转变换得到DEF ,则旋转中心为()A .点MB .点OC .点ND .点P8.如图,P 是抛物线y =x 2﹣x ﹣4在第四象限的一点,过点P 分别向x 轴和y 轴作垂线,垂足分别为A 、B ,则四边形OAPB 周长的最大值为()A .10B .8C .7.5D .9.如图,点A ,B ,C 均在O 上,若70ACB ∠=︒,则OAB ∠的度数是()A .10︒B .20︒C .25︒D .30︒10.二次函数2(0)y ax bx c a =++≠的图象如图所示,下列结论:①0abc <;②20a b +=;③m 为任意实数,则()a b m am b +≤+;④0a b c -+>;⑤若221122ax bx ax bx +=+,且12x x ≠,则122x x +=.其中正确的个数是()A .2个B .3个C .4个D .5个二、填空题11.在平面直角坐标系中,点()1,2P -关于原点对称的点的坐标是.12.用配方法将一元二次方程2820x x --=变形为()2x m n +=的形式是.13.关于x 的一元二次方程2440kx x -+=有实数根,k 的取值范围是.14.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P 表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O 为圆心,5m 为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB 长为8m ,则筒车工作时,盛水桶在水面以下的最大深度为m .15.已知二次函数()20y ax bx c a =++≠的图象如图所示,则不等式20ax bx c ++>的解集是.16.如图,在ABC V 中,70CAB ∠=︒,将ABC V 在平面内绕点A 旋转到A B C ''' 的位置,使CC AB '∥,则旋转角的度数为.17.如图,AD 是⊙O 的直径,A 、B 、C 、D 是O 上的点,过点C 作为O 切线交AD 延长线于点P ,若1PD =,OB AB BC ==,则O 半径是.18.如图,等边三角形ABC 中,5,AB P =为AB 边上一动点,,PD BC PE AC ⊥⊥,垂足分别为,D E 则DE 的最小值为.三、解答题19.用适当的方法解下列方程:(1)210x -+=;(2)()2121x x -=+.20.在平面直角坐标系xOy 中,ABC V 的三个顶点的坐标分别为()2,5A -,()3,0B -,()1,2C .将ABC V 绕原点O 顺时针旋转90°得到A B C ''' ,点A ,B ,C 的对应点分别为A ',B ',C '.(1)画出旋转后的A B C ''' ;(2)直接写出点C '的坐标;(3)记线段B C ''与线段BC 的交点为G ,直接写出BGC '∠的大小.21.已知二次函数2=23y x x --.(1)将2=23y x x --化成()2y a x h k =-+的形式,并写出它的顶点坐标;(2)在所给的平面直角坐标系中画出此函数的图象;(3)当12x -<<时,结合图象,直接写出函数值y 的取值范围.22.如图,O 是ABC V 的外接圆,AD 是O 的直径,AD BC ⊥于点E .(1)求证:BAD CAD ∠=∠;(2)连接BO 并延长,交O 于点G ,连接GC .若O 的半径为5,3OE =,求GC 和BC 的长.23.关于x 的一元二次方程2(2)420k x x --+=有两个不相等的实数根.(1)求k 的取值范围;(2)如果符合条件的最大整数k 是一元二次方程210k mk ++=的根,求m 的值.24.如图,AB 是⊙O 的直径,AC 与⊙O 交于点F ,弦AD 平分BAC ∠,DE AC ⊥,垂足为E(1)试判断直线DE与⊙O的位置关系,并说明理由;(2)若⊙O的半径为2,60∠=,求线段EF的长.BAC︒25.某公园在人工湖里建造一道喷泉拱门,工人在垂直于湖面的立柱上安装喷头,从喷头喷出的水柱的形状可以看作是抛物线的一部分.安装后,通过测量获得如下数据,喷头高出湖面3米,在距立柱水平距离为d米的地点,水柱距离湖面高度为h米.d(米)0.50 1.00 1.50 2.00 2.50 3.00h(米) 3.75 4.00 3.75 3.00 1.750请解决以下问题:(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;(2)结合表中所给数据或所画图象,直接写出水柱最高点距离湖面的高度;(3)求h关于d的函数表达式;(4)公园希望游船能从喷泉拱门下穿过,已知游船的宽度约为2米,游船的平顶棚到湖面的高度约为1米,从安全的角度考虑,要求游船到立柱的水平距离不小于1米,顶棚到水柱的竖直距离也不小于1米.工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求,调整高度至少______米.26.在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2)在抛物线y=﹣x2+(2a﹣2)x﹣a 2+2a 上,其中x 1<x 2.(1)求抛物线的对称轴(用含a 的式子表示);(2)①当x =a 时,求y 的值;②若y 1=y 2=0,求x 1的值(用含a 的式子表示).(3)若对于x 1+x 2<﹣4,都有y 1<y 2,求a 的取值范围.27.已知正方形ABCD 和一动点E ,连接CE ,将线段CE 绕点C 顺时针旋转90︒得到线段CF ,连接BE ,DF .(1)如图1,当点E 在正方形ABCD 内部时,①依题意补全图1;②求证:BE DF =;(2)如图2,当点E 在正方形ABCD 外部时,连接AF ,取AF 中点M ,连接AE ,DM ,用等式表示线段AE 与DM 的数量关系,并证明.28.在平面直角坐标系xOy 中,旋转角α满足0180α︒≤≤︒,对图形M 与图形N 给出如下定义:将图形M 绕原点逆时针旋转α得到图形M '.P 为图形M '上任意一点,Q 为图形N上的任意一点,称PQ 长度的最小值为图形M 与图形N 的“转后距”.已知点(A ,点()4,0B ,点()2,0C .(1)当90α=︒时,记线段OA 为图形M .①画出图形M ';②若点C 为图形N ,则“转后距”为______;③若线段AC 为图形N ,求“转后距”;(2)已知点(),0P t ,点1,2Q t ⎛- ⎝⎭,记线段AB 为图形M ,线段PQ 为图形N ,对任意旋转角α,“转后距”大于1,直接写出t 的取值范围.。
北京第五十四中学数学几何图形初步中考真题汇编[解析版]
![北京第五十四中学数学几何图形初步中考真题汇编[解析版]](https://img.taocdn.com/s3/m/8437cb3483d049649b6658d2.png)
一、初一数学几何模型部分解答题压轴题精选(难)1.如图(1),在△ABC和△EDC中,D为△ABC边AC上一点,CA平分∠BCE,BC=CD,AC=CE.(1)求证:△ABC≌△EDC;(2)如图(2),若∠ACB=60°,连接BE交AC于F,G为边CE上一点,满足CG=CF,连接DG交BE于H.①求∠DHF的度数;②若EB平分∠DEC,试说明:BE平分∠ABC.【答案】(1)证明:∵CA平分∠BCE,∴∠ACB=∠ACE.在△ABC和△EDC中.∵BC=CD,∠ACB=∠ACE,AC=CE.∴△ABC≌△EDC(SAS).(2)解:①在△BCF和△DCG中∵BC=DC, ∠BCD=∠DCE,CF=CG,∴△BCF≌△DCG(SAS),∴∠CBF=∠CDG.∵∠CBF+∠BCF=∠CDG+∠DHF∴∠BCF=∠DHF=60°.②∵EB平分∠DEC,∴∠DEH=∠BEC.∵∠DHF=60°,∴∠HDE=60°-∠DEH.∵∠BCE=60°+60°=120°,∴∠CBE=180°-120°-∠BEC=60°-∠BEC.∴∠HDE=∠CBE. ∠A=∠DEG.∵△ABC≌△EDC, △BCF≌△DCG(已证)∴∠BFC=∠DGC,∵∠ABF=∠BFC-∠A, ∠HDE=∠DGC-∠DEG,∴∠ABF=∠HDE,∴∠ABF=∠CBE,∴BE平分∠ABC.【解析】【分析】(1)由角平分线定义得出∠ACB=∠ACE,由ASA证明△ABC≌△EDC即可.(2)①由ASA证明△BCF≌△DCG,得出∠CBF=∠CDG;在△BCF,△DHF中,由三角形内角和定理得出∠BCF=∠DHF=60°.②由全等三角形的性质得出∠A=∠DEG,∠ABF=∠BFC-∠A, ∠HDE=∠DGC-∠DEG,从而得出∠ABF=∠HDE,∠ABF=∠CBE,即BE平分∠ABC.2.探究题学习完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题。
北京第五十四中学数学三角形填空选择中考真题汇编[解析版]
![北京第五十四中学数学三角形填空选择中考真题汇编[解析版]](https://img.taocdn.com/s3/m/e2d9dc08fd0a79563c1e72c8.png)
北京第五十四中学数学三角形填空选择中考真题汇编[解析版]一、八年级数学三角形填空题(难)1.如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,则∠E=_____度.【答案】80【解析】【详解】如图,根据角平分线的性质和平行线的性质,可知∠FMA=12∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE=2∠FMA,即∠E=2∠F=2×40°=80°.故答案为80.2.将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=40°,∠2=50°,那么∠ 3的度数等于______________.【答案】12°【解析】等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是108°,则∠3=360°-60°-90°-108°-∠1-∠2=12°.点睛:本题考查的是多边形的内角,熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键.3.△ABC的两边长为4和3,则第三边上的中线长m的取值范围是_______.【答案】17 22m<<【解析】【分析】作出草图,延长AD到E,使DE=AD,连接CE,利用“边角边”证明△ABD和△ECD全等,然后根据全等三角形对应边相等可得CE=AB,再根据三角形的任意两边之和大于第三边,两边之和小于第三边求出AE的取值范围,便不难得出m的取值范围.【详解】解:如图,延长AD到E,使DE=AD,连接CE,∵AD是△ABC的中线,∴BD=CD,在△ABD和△ECD中,AD DEADB EDCBD CD=⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△ECD(SAS),∴CE=AB,∵AB=3,AC=4,∴4-3<AE<4+3,即1<AE<7,∴1722m<<.故答案为:1722m<<.【点睛】本题主要考查倍长中线法构造全等三角形和三边关系,解决本题的关键是要熟练掌握倍长中线法构造全等三角形.4.如图,有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ改变位置,但始终满足经过B、C两点.如果△ABC中,∠A=52°,则∠ABX+∠ACX=_________________.【答案】38°【解析】∠A=52°,∴∠ABC+∠ACB=128°,∠XBC+∠XCB=90°,∴∠ABX+∠ACX=128°-90°=38°.5.一个正多边形的每个外角为60°,那么这个正多边形的内角和是_____.【答案】720°.【解析】【分析】先利用多边形的外角和为360°计算出这个正多边形的边数,然后再根据内角和公式进行求解即可.【详解】这个正多边形的边数为36060︒︒=6,所以这个正多边形的内角和=(6﹣2)×180°=720°,故答案为720°.【点睛】本题考查了多边形内角与外角:内角和定理:(n﹣2)•180 (n≥3)且n为整数);多边形的外角和等于360度.6.一个多边形的内角和是外角和的72倍,那么这个多边形的边数为_______.【答案】9【解析】【分析】根据多边形的内角和公式(n-2)•180°与外角和定理列出方程,然后求解即可.【详解】解:设这个多边形是n边形,根据题意得,(n-2)•180°=72×360°,解得:n=9.故答案为:9.【点睛】本题考查了多边形的内角和公式与外角和定理,多边形的外角和与边数无关,任何多边形的外角和都是360°.7.一个等腰三角形的两边长分别为4cm和9cm,则它的周长为__cm.【答案】22【解析】【分析】底边可能是4,也可能是9,分类讨论,去掉不合条件的,然后可求周长.【详解】试题解析:①当腰是4cm,底边是9cm时:不满足三角形的三边关系,因此舍去.②当底边是4cm,腰长是9cm时,能构成三角形,则其周长=4+9+9=22cm.故填22.【点睛】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答.8.如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2,则S△ABC=_____cm2.【答案】12cm2.【解析】【分析】根据三角形的面积公式,得△ACE的面积是△ACD的面积的一半,△ACD的面积是△ABC 的面积的一半.【详解】解:∵CE是△ACD的中线,∴S△ACD=2S△ACE=6cm2.∵AD是△ABC的中线,∴S△ABC=2S△ACD=12cm2.故答案为12cm2.【点睛】此题主要是根据三角形的面积公式,得三角形的中线把三角形的面积分成了相等的两部分.9.如果一个n边形的内角和是1440°,那么n=__.【答案】10【解析】∵n边形的内角和是1440°,∴(n−2)×180°=1440°,解得:n=10.故答案为:10.10.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC=_____度.【答案】45【解析】【分析】根据三角形全等的判定和性质,先证△ADC≌△BDF,可得BD=AD,可求∠ABC=∠BAD=45°.【详解】∵AD⊥BC于D,BE⊥AC于E∴∠EAF+∠AFE=90°,∠DBF+∠BFD=90°,又∵∠BFD=∠AFE(对顶角相等)∴∠EAF=∠DBF,在Rt△ADC和Rt△BDF中,CAD FBDBDF ADCBF AC∠∠⎧⎪∠∠⎨⎪⎩===,∴△ADC≌△BDF(AAS),∴BD=AD,即∠ABC=∠BAD=45°.故答案为45.【点睛】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.二、八年级数学三角形选择题(难)11.在多边形内角和公式的探究过程中,主要运用的数学思想是()A.化归思想B.分类讨论C.方程思想D.数形结合思想【答案】A【解析】【分析】根据多边形内角和定理:(n-2)·180(n≥3)且n为整数)的推导过程即可解答.【详解】解:多边形内角和定理:(n-2)·180(n≥3)且n为整数),该公式推导的基本方法是从n 边形的一个顶点出发引出(n-3)条对角线,将n边形分割为(n-2)个三角形,这(n-2)个三角形的所有内角之和正好是n边形的内角和,体现了化归思想.故答案为A.【点睛】本题主要考查了在数学的学习过程应用的数学思想,弄清推导过程是解答此题的关键. 12.如图,在△ABC中,点D、E分别是边AC,AB的中点,BD,CE相交于点O,连接O在AO上取一点F,使得OF=12AF若S△ABC =12,则四边形OCDF的面积为()A.2 B.83C.3 D.103【答案】B【解析】【分析】重心定理:三角形的三条边的中线交于一点,该点叫做三角形的重心.重心和三角形任意两个顶点组成的3个三角形面积相等.【详解】解:∵点D、E分别是边AC,AB的中点,∴O为△ABC的重心,∴13AOCS=ABCS=4,∴12DOC DOAS S==AOCS=2,∵OF=12 AF,∴13DOFS=AODS=23,∴S 阴=DOC S +DOF S =83. 故选:B.【点睛】本题考查了重心及重心定理,熟练掌握相关定理是解题关键.13.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )A .B .C .D .不能确定【答案】B【解析】如图,∵等边三角形的边长为3,∴高线AH=3×333= S △ABC =1111••••2222BC AH AB PD BC PE AC PF ==+ ∴11113?3?3?3?2222AH PD PE PF ⨯=⨯+⨯+⨯ ∴PD+PE+PF=AH=33 即点P 到三角形三边距离之和为33. 故选B.14.已知△ABC 的两条高的长分别为5和20,若第三条高的长也是整数,则第三条高的长的最大值为( )A .5B .6C .7D .8【答案】B【解析】设△ABC 的面积为S ,所求的第三条高线的长为h ,则三边长分别为,,,根据三角形的三边关系为,解得,所以h的最大整数值为6,即第三条高线的长的最大值为6.故选B.点睛:本题主要考查了三角形的面积公式,三角形三边关系定理及不等式组的解法,有一定难度.利用三角形的面积公式,表示出△ABC三边的长度,从而运用三角形三边关系定理,列出不等式组是解题的关键,难点是解不等式组.15.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是()A.2 B.4 C.3 D.5【答案】B【解析】如图,满足条件的点C共有4个.故选B.16.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为1:3,则这个多边形为()A.三角形B.四边形C.六边形D.八边形【答案】D【解析】【分析】一个外角与一个内角的比为1 : 3,则内角和是外角和的3倍,根据多边形的外角和是360°,即可求得多边形的内角的度数,依据多边形的内角和公式即可求解.【详解】解:多边形的内角和是:360°×3=1080°.设多边形的边数是n,则(n-2)•180=1080,解得:n=8.即这个多边形是正八边形.故选D.【点睛】本题考查了多边形的内角和定理以及多边形的外角和定理,注意多边形的外角和不随边数的变化而变化.17.如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为()A.35°B.40°C.45°D.55°【答案】C【解析】【分析】根据三角形的一个外角等于与它不相邻的两个内角的和,得到∠4的度数,再根据平行线的性质,即可得出∠2的度数.【详解】解:如图,根据三角形外角性质,可得∠3=∠1+∠4,∴∠4=∠3-∠1=95°-50°=45°,∵a∥b,∴∠2=∠4=45°.故选C.【点睛】本题考查了平行线的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.18.如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数()A.24°B.25°C.30°D.35°【答案】D【解析】【分析】首先根据三角形内角和定理可得∠AEF+∠AFE=120°,再根据邻补角的性质可得∠FEB+∠EFC=360°-120°=240°,再根据由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=240°,然后计算出∠1+∠2的度数,进而得到答案.【详解】解:∵∠A=60°,∴∠AEF+∠AFE=180°-60°=120°,∴∠FEB+∠EFC=360°-120°=240°,∵由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=240°,∴∠1+∠2=240°-120°=120°,∵∠1=85°,∴∠2=120°-85°=35°.故选:D.【点睛】此题主要考查了翻折变换,关键是根据题意得到翻折以后,哪些角是对应相等的.19.如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于()A.110︒B.115︒C.120︒D.125︒【答案】A【解析】【分析】根据三角形外角的性质三角形的一个外角等于和它不相邻的两个内角的和可得∠AEB=∠A+∠C=65°,∠DFE=∠B+∠AEC,进而可得答案.【详解】解:∵∠A=27°,∠C=38°,∴∠AEB=∠A+∠C=65°,∵∠B=45°,∴∠DFE=65°+45°=110°,故选:A.【点睛】此题主要考查了三角形外角的性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.20.一个多边形的每个内角均为108º,则这个多边形是()A.七边形 B.六边形 C.五边形 D.四边形【答案】C【解析】试题分析:因为这个多边形的每个内角都为108°,所以它的每一个外角都为72°,所以它的边数=360÷72=5(边).考点:⒈多边形的内角和;⒉多边形的外角和.。
北京第五十四中学八年级数学上册第三单元《轴对称》测试卷(答案解析)
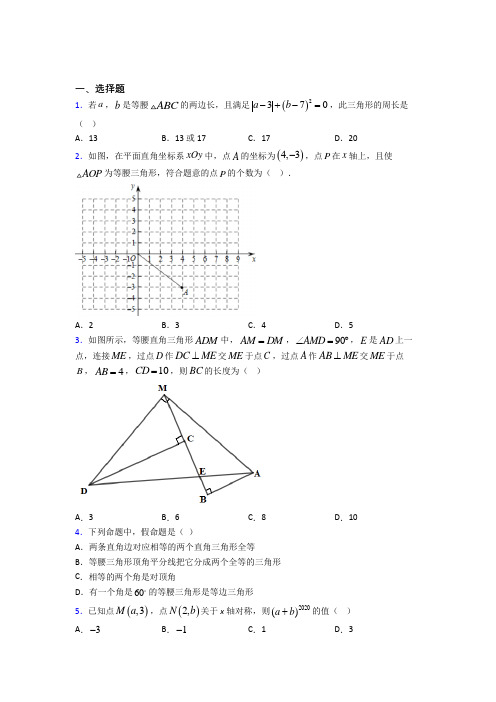
一、选择题1.若a ,b 是等腰ABC 的两边长,且满足()2370a b -+-=,此三角形的周长是( ) A .13B .13或17C .17D .202.如图,在平面直角坐标系xOy 中,点A 的坐标为()4,3-,点P 在x 轴上,且使AOP 为等腰三角形,符合题意的点P 的个数为( ).A .2B .3C .4D .53.如图所示,等腰直角三角形ADM 中,AM DM =,90AMD ∠=︒,E 是AD 上一点,连接ME ,过点D 作DC ME ⊥交ME 于点C ,过点A 作AB ME ⊥交ME 于点B ,4AB =,10CD =,则BC 的长度为( )A .3B .6C .8D .104.下列命题中,假命题是( )A .两条直角边对应相等的两个直角三角形全等B .等腰三角形顶角平分线把它分成两个全等的三角形C .相等的两个角是对顶角D .有一个角是60的等腰三角形是等边三角形5.已知点(),3M a ,点()2,N b 关于x 轴对称,则2020()a b +的值( )A .3-B .1-C .1D .36.如图,在△ABC 中,∠C =84°,分别以点A ,B 为圆心,以大于12AB 的长为半径画弧,两弧分别交于点M ,N ,作直线MN 交AC 于点D ;以点B 为圆心,适当长为半径画弧,分别交BA ,BC 于点E ,F ,再分别以点E ,F 为圆心,大于12EF 的长为半径画弧,两弧交于点P .若此时射线BP 恰好经过点D ,则∠A 的大小是( )A .30°B .32°C .36°D .42°7.如图,C 是线段AB 上的一点,ACD △和BCE 都是等边三角形,AE 交CD 于M ,BD 交CE 于N ,交AE 于O ,则①DB AE =;②AMC DNC ∠=∠;③60AOB ∠=︒;④DN AM =;⑤CMN △是等边三角形.其中,正确的有( )A .2个B .3个C .4个D .5个8.已知一个等腰三角形ABC 的两边长为5,7,另一个等腰三角形ABC 的两边为23x -,35x -,若两个三角形全等,则x 的值为( )A .5B .4C .4或5D .1039.如图,在ABC 中,DE 是AC 的垂直平分线,交AC 边于E ,交BC 边于D ,连接AD ,若3AE =,ABD △的周长为13,则ABC 的周长( )A .16B .19C .20D .2410.如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,DH ⊥BC 于H ,交BE 于G ,下列结论:①BD =CD ;②AD +CF =BD ;③CE =12BF ;④AE =BG .其中正确的是( )A .①②B .①③C .①②③D .①②③④11.如图,在Rt ABC 中,∠BAC =90°,以点A 为圆心,以AB 长为半径作弧交BC 于点D ,再分别以点B ,D 为圆心,以大于12BD 的长为半径作弧,两弧交于点P ,作射线AP 交BC 于点E ,如果AB =3,AC =4,那么线段AE 的长度是( )A .125B .95C .85D .7512.已知等腰三角形的一个内角为50°,则它的顶角为( ) A .50°B .80°C .65°或80°D .50°或80°二、填空题13.平面直角坐标系中,已知A (8,0),△AOP 为等腰三角形,且△AOP 的面积为16,则满足条件的P 点个数是______.14.如图,在ABC 中,90ACB ︒∠=,30B,6AC =,P 为BC 边的垂直平分线DE 上一个动点,则ACP △周长的最小值为________.15.如图,点C 在DE 上,,,45B E AB AE CAD BAE ∠=∠=∠=∠=︒,则ACB =∠_____________.16.如图,在△ABC 中,点D 是BC 上一点,∠BAD =80°,AB =AD =DC ,则∠C =________17.如图,25AOB ∠=︒,点M ,N 分别是边OA ,OB 上的定点,点P ,Q 分别是边OB ,OA 上的动点,记MPQ α∠=,PQN β∠=,当MP PQ QN ++的值最小时,βα-的大小=__________(度).18.如图,在等边△ABC 中,AC =9,点O 在AC 上,且AO =3,点P 是AB 上一动点,连接OP ,以O 为圆心,OP 长为半径画弧交BC 于点D ,连接PD ,如果PO =PD ,那么AP 的长是________.19.△ABC 中,∠A =50°,当∠B =____________时,△ABC 是等腰三角形.20.如图,△ABC 中,AB =AC ,点D 、E 、F 分别在AB 、BC 、CA 边上,且BE =CF ,BD =CE ,如果∠A =44°,则∠EDF 的度数为__.三、解答题21.如图,ABC 是边长为10的等边三角形,现有两点P 、Q 沿如图所示的方向分别从点A 、点B 同时出发,沿ABC 的边运动,已知点P 的速度为每秒1个单位长度,点Q 的运度为每秒2个单位长度,当点P 第一次到达B 点时,P 、Q 同时停止运动. (1)点P 、Q 运动几秒后,可得到等边三角形APQ ? (2)点P 、Q 运动几秒后,P 、Q 两点重合?(3)当点P 、Q 在BC 边上运动时,能否得到以PQ 为底边的等腰APQ ?如存在,请求出此时P 、Q 运动的时间.22.已知AOB ∠及一点P ,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法)(1)过点P 作OA 、OB 的垂线,垂足分别为点M 、N ; (2)猜想MPN ∠与AOB ∠之间的数量关系,并说明理由.23.如图,在Rt ABC △中,90ACB ∠=︒,CAP 和CBQ △都是等边三角形,BQ 和CP 交于点H ,求证:BQ CP ⊥.24.如图,,ABC AEF ∆∆均为等边三角形,连接BE ,连接并延长CF 交BE 于点D . (1)求证:CAF BAE ∆≅∆; (2)连接AD ,求证DA 平分CDE ∠.25.在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,ABC 的顶点均在格点上,点A 的坐标是(3,1)--.(1)将ABC 关于x 轴对称得到111A B C △,画出111A B C △,并写出点1B 的坐标; (2)把111A B C △平移,使点B 平移到2(3,4)B ,请作出111A B C △平移后的222A B C △,并写出2A 的坐标;(3)已知ABC 中有一点(,)D a b ,求222A B C △中的对应点2D 的坐标.26.如图,在12×10的正方形网格中,△ABC 是格点三角形,点B 的坐标为(﹣5,1),点C 的坐标为(﹣4,5).(1)请在方格纸中画出x 轴、y 轴,并标出原点O ;(2)画出△ABC 关于直线l 对称的△A 1B 1C 1;C 1的坐标为(3)若点P (a ,b )在△ABC 内,其关于直线l 的对称点是P 1,则P 1的坐标是 .【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据绝对值非负性的性质以及平方的非负性可知a和b的值,然后根据等腰三角形的性质分情况计算即可;【详解】∵()2-+-=,a b370∴ a=3,b=7,若腰为3时,3+3<7,三角形不成立;若腰为7时,则周长为7+7+3=17,故选:C.【点睛】本题考查了非负性的性质以及等腰三角形的性质,熟练掌握知识点是解题的关键;.2.C解析:C【分析】以O为圆心,AO长为半径画圆可得与x轴有2个交点,再以A为圆心,AO长为半径画圆可得与x轴有1个交点,然后再作AO的垂直平分线可得与x轴有1个交点.【详解】解:如图所示:点P在x轴上,且使△AOP为等腰三角形,符合题意的点P的个数共4个,故选:C.【点睛】此题主要考查了等腰三角形的判定,关键是考虑全面,作图不重不漏.3.B解析:B 【分析】通过先证明AMB MDC △≌△,得到=4AB MC =,=10MB CD =,即可求得=BC MB MC -,即可得到答案. 【详解】解:∵DC ME ⊥,AB ME ⊥,90AMD ∠=︒∴DCM B ∠=∠,+90AMB DMC ∠∠=︒,+90MDC DMC ∠∠=︒ ∴AMB ∠=MDC ∠ ∵AM DM =∴AMB MDC △≌△∴AB MC =,MB CD = ∵4AB =,10CD =∴4MC =,10MB = ∴=1046BC MB MC -=-= 故选B . 【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的定义,熟练掌握全等三角形判定和性质,并能进行推理计算是解决问题的关键.4.C解析:C 【分析】利用全等三角形的判定和等腰三角形的性质判断A 、B ,根据对顶角的定义判断C ,根据等边三角形的判定判断D . 【详解】解:A .两条直角边对应相等的两个直角三角形,符合两三角形的判定定理“SAS”;故本选项是真命题;B .已知等腰三角形的两腰相等,且顶角的平分线即为底边上的高,则可根据为HL 可以得出两个三角形全等,故本选项是真命题;C 、相等的角不一定是对顶角,故错误,是假命题;D 、有一个角为60°的等腰三角形是等边三角形,正确,是真命题; 故选C . 【点睛】本题考查了命题和定理,解题的关键是明确题意,可以判断题目中的命题的真假,对于假命题能举出反例或者说明理由.5.C解析:C 【分析】根据关于坐标轴对称的规律,关于谁对称谁不变,另一个坐标变为相反数即可获得a 和b 的值,然后即可得解. 【详解】∵点(),3M a ,点()2,N b 关于x 轴对称 ∴2a =,3b =- ∴()()20182018231a b +=-=故选:C .【点睛】本题考查了在坐标平面直角坐标系中关于x 轴对称的点的坐标的变化规律,点(),x y 关于x 轴对称的点的坐标为()x y -,,熟记规律即可得到正确答案.6.B解析:B 【分析】根据题中作图知:DM 垂直平分AB ,BD 平分∠ABC ,利用三角形内角和定理计算即可. 【详解】由题意得:DM 垂直平分AB ,BD 平分∠ABC , ∵DM 垂直平分AB , ∴AD=BD , ∴∠A=∠ABD , ∵BD 平分∠ABC , ∴∠ABD=∠CBD ,∵∠A+∠ABD+∠CBD+∠C=180︒,∠C =84°, ∴∠A=32︒, 故选:B . 【点睛】此题考查线段垂直平分线作图及性质,角平分线作图及性质,三角形的内角和定理,根据题意得到DM 垂直平分AB ,BD 平分∠ABC 是解题的关键.7.C解析:C 【分析】易证△ACE ≌△DCB ,可得①正确;即可求得∠AOB =120°,可得③错误;再证明△ACM ≌△DCN ,可得②④正确和CM =CN ,即可证明⑤正确;即可解题. 【详解】解:∵ACD △和BCE 都是等边三角形 ∵∠ACD =∠BCE =60°, ∴∠DCE =60°, 在△ACE 和△DCB 中,AC DC ACE DCB CB CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACE ≌△DCB (SAS ),∴∠BDC =∠EAC ,DB =AE ,①正确; ∠CBD =∠AEC ,∵∠AOB =180°−∠OAB−∠DBC ,∴∠AOB =180°−∠AEC−∠OAB =120°,③错误; 在△ACM 和△DCN 中,60BDC EAC DC ACACD DCN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴△ACM ≌△DCN (ASA ), ∴AM =DN ,④正确; ∠AMC =∠DNC ,②正确; CM =CN ,∵∠ACD =∠BCE =60°,∴∠MCN =180°-∠ACD-∠BCE =60°, ∴△CMN 是等边三角形,⑤正确; 故有①②④⑤正确. 故选:C . 【点睛】本题考查了全等三角形的判定和全等三角形对应边、对应角相等的性质,本题中求证△ACE ≌△DCB 和△ACM ≌△DCN 是解题的关键.8.B解析:B 【分析】根据等腰ABC 的两边长为5,7,得到ABC 的三边长为5,7,7;或5,5,7;之后根据全等分2x-3=5,2x-3=7,3x-5=5,3x-5=7四种情况分类讨论,舍去不合题意的即可求解.【详解】解:∵等腰ABC 的两边长为5,7,∴ABC 的三边长为5,7,7;或5,5,7;由题意得另一个等腰三角形的两边为23x -,35x -,且与等腰ABC 全等(1)当2x-3=5时,解得x=4,则3x-5=7,符合题意;(2)当2x-3=7时,解得x=5,则3x-5=10,不合题意;(3)当3x-5=5时,解得103x =,则2x-3=113,不合题意; (4)当3x-5=7时,解得x=4,则2x-3=5,符合题意;综上所述:x 的值为4.故答案为:B【点睛】 本题考查了等腰三角形的定义,全等三角形的性质,根据题意分类讨论是解题关键. 9.B解析:B【分析】根据线段垂直平分线性质得出 AD = DC ,求出和 AB + BC 的长,即可求出答案.【详解】DE 是 AC 的垂直平分线,AE=3cm,.∴ AC=2AE=6cm ,AD = DC ,△ ABD 的周长为13cm ,∴ AB + BD +AD=13cm ,∴AB + BD + DC = AB +BC=13cm∴ △ ABC 的周长为 AB + BC +AC=13cm+6cm=19cm ,故选 B .【点睛】本题考查了线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.10.C解析:C【分析】根据∠ABC=45°,CD ⊥AB 可得出BD=CD ,利用ASA 判定Rt △DFB ≌Rt △DAC ,从而得出DF=AD ,BF=AC .则CD=CF+AD ,即AD+CF=BD ;再利用ASA 判定Rt △BEA ≌Rt △BEC ,得出CE=AE=12AC ,又因为BF=AC 所以CE=12AC=12BF ,连接CG .因为△BCD 是等腰直角三角形,即BD=CD .又因为DH ⊥BC ,那么DH 垂直平分BC .即BG=CG .在Rt △CEG 中,CG 是斜边,CE 是直角边,所以CE <CG .即AE <BG .【详解】解:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD.故①正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC.∴BF=AC;DF=AD.∵CD=CF+DF,∴AD+CF=BD;故②正确;在Rt△BEA和Rt△BEC中∵BE平分∠ABC,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt△BEA≌Rt△BEC.∴CE=AE=12AC.又由(2),知BF=AC,∴CE=12AC=12BF;故③正确;连接CG.∵△BCD是等腰直角三角形,∴BD=CD又DH⊥BC,∴DH垂直平分BC.∴BG=CG 在Rt△CEG中,∵CG是斜边,CE是直角边,∴CE<CG.∵CE=AE,∴AE<BG.故④错误.∴正确的选项有①②③;故选:C.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.在复杂的图形中有45°的角,有垂直,往往要用到等腰直角三角形,要注意掌握并应用此点.11.A解析:A【分析】根据作图过程可得AP是BD的垂直平分线,根据勾股定理可得BC的长,再根据等面积法求出AE的长即可.【详解】解:∵∠BAC=90°,AB=3,AC=4,∴BC5=,根据作图过程可知:AP是BD的垂直平分线,∴BE=DE,AE⊥BD,∴△ABC的面积:12AB•AC=12BC•AE,∴5AE=12,∴AE=125.故选:A.【点睛】本题考查垂直平分线和勾股定理,需要有一定的数形结合能力,熟练掌握垂直平分线的定义,结合题意进行解题是解决本题的关键.12.D解析:D【分析】由50︒的角是顶角或底角,依据三角形内角和计算得出顶角的度数.【详解】当50︒的角为顶角时,它的顶角为50︒,当50︒的角为底角时,它的顶角为18050280︒-︒⨯=︒,∴它的顶角为50︒或80︒,故选:D.【点睛】此题考查等腰三角形等边对等角的性质,三角形内角和定理,熟记等边对等角的性质是解题的关键.二、填空题13.10【分析】使△AOP为等腰三角形只需分两种情况考虑:OA当底边或OA 当腰当OA是底边时有2个点;当OA是腰时有8个点即可得出答案【详解】∵A(80)∴OA=8设△AOP的边OA上的高是h则×8×h解析:10【分析】使△AOP为等腰三角形,只需分两种情况考虑:OA当底边或OA当腰.当OA是底边时,有2个点;当OA是腰时,有8个点,即可得出答案.【详解】∵A(8,0),∴OA=8,设△AOP的边OA上的高是h,则12×8×h=16,解得:h=4,在x轴的两侧作直线a和直线b都和x轴平行,且到x轴的距离都等于4,如图:①以A为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,②以O为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,③作AO的垂直平分线分别交直线a、b于一点,即共2个点符合,其中,没有重复的点,∴4+4+1+1=10.故选:B.【点睛】本题主要考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.14.18【分析】因为BC的垂直平分线为DE所以点C和点B关于直线DE对称所以当点动点P和E重合时则△ACP的周长最小值再结合题目的已知条件求出AB的长即可【详解】解:如图∵P为BC边的垂直平分线DE上一解析:18【分析】因为BC的垂直平分线为DE,所以点C和点B关于直线DE对称,所以当点动点P和E重合时则△ACP的周长最小值,再结合题目的已知条件求出AB的长即可.【详解】解:如图,∵P为BC边的垂直平分线DE上一个动点,∴点C和点B关于直线DE对称,∴当点动点P和E重合时则△ACP的周长最小值,∵∠ACB=90°,∠B=30°,AC=6,∴AB=2AC=12,∵AP+CP=AP+BP=AB=12,∴△ACP的周长最小值=AC+AB=18,故答案为:18.【点睛】本题考查了轴对称-最短路线的问题以及垂直平分线的性质,正确确定P点的位置是解题的关键,确定点P的位置这类题在课本中有原题,因此加强课本题目的训练至关重要.15.【分析】由条件可证得△ABC≌△AED则可求得∠ACB=∠ADEAD=AC再利用等腰三角形的性质可求得答案【详解】解:∵∠CAD=∠BAE∴∠CAD+∠CAE=∠BAE+∠CAE即∠BAC=∠DAE解析:67.5【分析】由条件可证得△ABC≌△AED,则可求得∠ACB=∠ADE,AD=AC,再利用等腰三角形的性质可求得答案.【详解】解:∵∠CAD=∠BAE,∴∠CAD+∠CAE=∠BAE+∠CAE,即∠BAC=∠DAE,在△ABC和△AED中,B E AB AEBAC EAD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ABC ≌△AED (ASA ),∴AD=AC ,∠ACB=∠ADE ,∴∠ACD=∠ADC ,∵∠CAD=45°,∴∠ADC=67.5°,∴∠ACB=67.5°,故答案为:67.5.【点睛】本题主要考查全等三角形的判定和性质及等腰三角形的性质,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(全等三角形的对应边相等、对应角相等)是解题的关键.16.25°【分析】先根据AB=AD 利用三角形内角和定理求出∠B 和∠ADB 的度数再根据三角形外角的性质即可求出∠C 的大小【详解】解:∵AB=AD ∴∠B=∠ADB ∵∠BAD=80°∴∠B=∠ADB==50°解析:25°【分析】先根据AB=AD ,利用三角形内角和定理求出∠B 和∠ADB 的度数,再根据三角形外角的性质即可求出∠C 的大小.【详解】解:∵AB=AD ,∴∠B=∠ADB ,∵∠BAD=80°,∴∠B=∠ADB =180802︒︒-=50°, ∵AD=DC ,∴∠C=∠ACD ,∴∠C=12∠ADB=25°, 故答案为:25°.【点睛】此题主要考查学生对等腰三角形的性质和三角形内角和定理的理解和掌握,解答此题的关键是利用三角形一个外角等于与它不相邻的两个内角的和.17.50【分析】作M 关于OB 的对称点N 关于OA 的对称点连接交OB 于点P 交OA 于点Q 连接MPQN 可知此时最小此时再根据三角形外角的性质和平角的定义即可得出结论【详解】作M 关于OB 的对称点N 关于OA 的对称点【分析】作M 关于OB 的对称点M ',N 关于OA 的对称点N ',连接M N '',交OB 于点P ,交OA 于点Q ,连接MP ,QN ,可知此时MP PQ QN ++最小,此时OPM OPM NPQ OQP AQN AQN ''∠=∠=∠∠=∠=∠,,再根据三角形外角的性质和平角的定义即可得出结论.【详解】作M 关于OB 的对称点M ',N 关于OA 的对称点N ',连接M N '',交OB 于点P ,交OA 于点Q ,连接MP ,QN ,如图所示.根据两点之间,线段最短,可知此时MP PQ QN++最小,即MP PQ QN M N ''++=, ∴OPM OPM NPQ OQP AQN AQN ''∠=∠=∠∠=∠=∠,,∵MPQ PQN αβ∠=∠=,, ∴11(180)(180)22QPN OQP αβ∠=︒-∠=︒-,, ∵QPN AOB OQP ∠=∠+∠,25AOB ∠=︒, ∴11(180)25(180)22αβ︒-=︒+︒- , ∴50βα-=︒ . 故答案为:50.【点睛】本题考查轴对称-最短问题、三角形内角和,三角形外角的性质等知识,灵活运用所学知识解决问题是解题的关键,综合性较强.18.6【分析】连接OD 由题意可知OP =DP =OD 即△PDO 为等边三角形所以∠OPA =∠PDB =∠DPA=60°推出△OPA ≌△PDB 根据全等三角形的对应边相等知OA =BP =3则AP =AB−BP =6【详解解析:6连接OD .由题意可知OP =DP =OD ,即△PDO 为等边三角形,所以∠OPA =∠PDB =∠DPA=60°,推出△OPA ≌△PDB ,根据全等三角形的对应边相等知OA =BP =3,则AP =AB−BP =6.【详解】解:如图,连接OD ,∵PO =PD ,∴OP =DP =OD ,∴△PDO 为等边三角形,即∠DPO =60°,∵等边△ABC ,∴∠A =∠B =60°,AC =AB =9,∴∠OPA =180°−60°−∠DPA=120°−∠DPA∠PDB =180°−∠DPA−60°=120°−∠DPA∴∠OPA=∠PDB ,∴ 在△OPA 和△PDB 中,A B OPA PDB PO PD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△OPA ≌△PDB (AAS ),∵AO =3,∴AO =PB =3,∴AP =6.故答案是:6.【点睛】本题主要考查全等三角形的判定和性质、等边三角形的性质,关键在于求证△OPA ≌△PDB .19.50°或80°或65°【分析】由已知条件根据题意分三种情况讨论:①∠A 是顶角;②∠A 是底角∠B =∠A 时③∠A 是底角∠B =∠A 时利用三角形的内角和进行求解【详解】①∠A 是顶角∠B =(180°−∠A )÷解析:50°或80°或65°【分析】由已知条件,根据题意,分三种情况讨论:①∠A 是顶角;②∠A 是底角,∠B =∠A时,③∠A 是底角,∠B =∠A 时,利用三角形的内角和进行求解.【详解】①∠A 是顶角,∠B =(180°−∠A )÷2=65°;②∠A 是底角,∠B =∠A =50°.③∠A 是底角,∠A =∠C =50°,则∠B =180°−50°×2=80°,∴当∠B 的度数为50°或65°或80°时,△ABC 是等腰三角形.故答案为:50°或65°或80°.【点睛】本题考查了等腰三角形的判定及三角形的内角和定理;分情况讨论是正确解答本题的关键.20.56°【分析】根据可求出根据△DBE ≌△ECF 利用三角形内角和定理即可求出的度数【详解】解:∵AB =AC ∴∠ABC =∠ACB 在△DBE 和△CEF 中∴△DBE ≌△ECF (SAS )∴DE =EF ∴△DEF解析:56°【分析】根据44A ∠=︒可求出68ABC ACB ∠=∠=︒,根据△DBE ≌△ECF ,利用三角形内角和定理即可求出 EDF ∠的度数.【详解】解:∵AB =AC ,∴∠ABC =∠ACB ,在△DBE 和△CEF 中BE CF ABC ACB BD CE =⎧⎪∠=∠⎨⎪=⎩,∴△DBE ≌△ECF (SAS ),∴DE =EF ,∴△DEF 是等腰三角形,∵△DBE ≌△ECF ,∴∠1=∠3,∠2=∠4,∵∠A +∠B +∠C =180°,∴()118044682B ∠=︒-︒=︒, ∴1218068∠+∠=︒-︒,∴3218068∠+∠=︒-︒,∴∠DEF =68°, ∴18068562EDF ︒-︒∠==︒. 故答案为:56°.【点睛】 此题主要考查全等三角形的判定与性质的理解和掌握,主要应用了三角形内角和定理和平角是180︒,根据等腰三角形的性质得出B C ∠=∠是解题的关键.三、解答题21.(1)点P 、Q 运动103秒后,可得到等边三角形APQ ;(2)点P 、Q 运动10秒后,P 、Q 两点重合;(3)当点P 、Q 在BC 边上运动时,能得到以PQ 为底边的等腰三角形,此时P 、Q 运动的时间为403秒. 【分析】(1)设点P 、Q 运动t 秒后,可得到等边三角形APQ ,利用,AP AQ = 列方程,解方程可得答案;(2)设点P 、Q 运动x 秒后,P 、Q 两点重合,由追及问题中的相等关系:Q 的运动路程等于P 的运动路程加上相距的路程,列方程,解方程即可得到答案;(3)当点P 、Q 在BC 边上运动时,可以得到以PQ 为底边的等腰三角形.先证明:ACP △≌ABQ △,可得CP BQ =,再列方程,解方程并检验即可得到答案.【详解】解:(1)设点P 、Q 运动t 秒后,可得到等边三角形APQ ,如图①,AP t =,102AQ AB BQ t =-=-,∵三角形APQ 是等边三角形,,AP AQ ∴=∴102t t =-,解得103t =, ∴点P 、Q 运动103秒后,可得到等边三角形APQ .(2)设点P 、Q 运动x 秒后,P 、Q 两点重合,102x x +=,解得:10x =.∴点P 、Q 运动10秒后,P 、Q 两点重合.(3)当点P 、Q 在BC 边上运动时,可以得到以PQ 为底边的等腰三角形.理由如下: 由(2)知10秒时P 、Q 两点重合,恰好在C 处,如图②,假设APQ 是等腰三角形,∴AP AQ =,∴APQ AQP ∠=∠,∴APC AQB ∠=∠,∵ACB △是等边三角形,∴C B ∠=∠,在ACP △和ABQ △中,,,,AC AB C B APC AQB =⎧⎪∠=∠⎨⎪∠=∠⎩, ∴ACP △≌ABQ △,∴CP BQ =,设当点P 、Q 在BC 边上运动时,P 、Q 运动的时间y 秒时,APQ 是等腰三角形, 由题意得:10CP y =-,302QB y =-,∴ 10302y y -=-, 解得:403y =, P 的最长运动时间为2020,1s = Q 从B A C B →→→的最长时间为30=152s ,由403<15, ∴ 403y =符合题意, ∴当点P 、Q 在BC 边上运动时,能得到以PQ 为底边的等腰三角形,此时P 、Q 运动的时间为403秒. 【点睛】 本题考查的是三角形全等的判定与性质,等腰三角形的判定与性质,等边三角形的判定与性质,动点问题,掌握以上知识是解题的关键.22.(1)见解析;(2)∠MPN+∠AOB=180°或∠MPN=∠AOB ,理由见解析【分析】(1)根据垂线的定义画出图形即可解决问题;(2)根据四边形内角和为360°或“8字型”的性质即可解决问题;【详解】(1)过点P 作OA 、OB 的垂线PM 、PN 如图所示;(2)猜想:∠MPN+∠AOB=180°或∠MPN=∠AOB .理由:左图中,在四边形PMON 中,∵∠PMO=∠PNO=90°,∴∠MPN+∠AOB=180°.右图中,∵∠PJM=∠OJN ,∠PMJ=∠JNO=90°,∴∠MPN=∠AOB .【点睛】本题考查了作图-基本作图,解题的关键是熟练掌握基本知识,属于中考常考题型. 23.见解析【分析】由已知条件证得∠BHC=90°即可得到解答.【详解】∵CAP 和CBQ △都是等边三角形;∴60ACP CBQ ∠=∠=︒,∵90ACB ∠=︒,∴30BCP ACB ACP ∠=∠-∠=︒在BCH 中,18090BHC BCH CBH ∠=︒-∠-∠=︒∴BQ CP ⊥【点睛】本题考查等边三角形和直角三角形的综合运用,熟练掌握等边三角形、直角三角形的性质并灵活运用是解题关键.24.(1)见解析;(2)详见解析.【分析】(1)利用SAS 证明即可;(2)逆用角的平分线性质定理证明.【详解】(1)∵△ABC,△AEF 是等边三角形,∴AC=AB,AF=AE,∠CAB=∠EAF,∴∠CAB-∠FAB =∠EAF-∠FAB,∴∠CAF=∠BAE,∴△CAF ≌△BAE;(2)过点A 分别作AH ⊥CD 于点H,AG ⊥BE,交BE 的延长线于点G,由(1)知,△CAF ≌△BAE ,∴CF=BE ,CAF BAE SS =, ∴1122CE AH BE AG ⨯⨯=⨯⨯, ∴AH=AG ,∴DA 平分∠CDE.【点睛】本题考查了三角形的全等,等边三角形的性质,角平分线性质定理的逆定理,准确选择全等判定方法,活用角的平分线的逆定理是解题的关键.25.(1)图见解析,点B 1的坐标为(-2,4);(2)图见解析,A 2的坐标为(2,1);(3)D 2的坐标为(a+5,-b ).【分析】(1)分别作出点A 、B 、C 关于x 轴对称得到的对应点,再顺次连接可得;(2)根据B 1(-2,4)和2(3,4)B ,可得平移方式为向右平移5个单位,分别作出△A 1B 1C 1向右平移5个单位所得对应点,再顺次连接可得;D的坐标.(3)根据图形的变换方式即可得出D点的变换方式,从而可得点2【详解】解:(1)如图所示,△A1B1C1即为所求,点B1的坐标为(-2,4);(2)如图所示,△A2B2C2即为所求,A2的坐标为(2,1);(3)△A2B2C2中的对应点D2的坐标为(a+5,-b).【点睛】本题考查坐标与图形变换—轴对称和平移.理解点的变换和对应图形变换的关系是解题关键.26.(1)见解析;(2)见解析;(0,5);(3)(﹣a﹣4,b)【分析】(1)利用A、C点的坐标画出直角坐标系;(2)利用网格点和对称的性质画出A、B、C关于直线l的对称点A1、B1、C1即可;(3)先把P点向右平移2个单位(a+2,b)(相当于把直线l右平移2个单位),点(a+2,b)关于y轴的对称点为(-a-2,b),然后把(-a-2,b)向左平移2个单位,相当于把直线l向左平移2个单位回到原来位置,于是得到P1的坐标为(-a-2-2,b).【详解】解:(1)如图,就是所求作的坐标轴与原点;(2)如图,△A1B1C1为所作的三角形;C1的坐标为:(0,5);(3)先把P点向右平移2个单位(a+2,b)(相当于把直线l右平移2个单位),点(a+2,b)关于y轴的对称点为(-a-2,b),然后把(-a-2,b)向左平移2个单位,相当于把直线l向左平移2个单位回到原来位置,于是得到P1的坐标为(-a-2-2,b).∴P1的坐标是(﹣a﹣4,b).【点睛】本题考查了作图——轴对称变换:几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的,。
北京第五十四中学七年级数学下册期末试卷选择题汇编精选模拟考试试题

一、选择题1.如图,在数轴上表示1,3的对应点分别为A B、,点B关于点A的对称点为C,则点C表示的数为()A31B.13C.23D32答案:C解析:C【分析】首先根据表示13A、点B可以求出线段AB的长度,然后根据点B 和点C关于点A对称,求出AC的长度,最后可以计算出点C的坐标.【详解】解:∵表示13A、点B,∴AB31,∵点B关于点A的对称点为点C,∴CA=AB,∴点C的坐标为:1−31)=3故选:C.【点睛】本题考查的知识点为实数与数轴,解决本题的关键是求数轴上两点间的距离就让右边的数减去左边的数.知道两点间的距离,求较小的数,就用较大的数减去两点间的距离.2.若整数a使关于x的不等式组125262x xx a++⎧≤⎪⎨⎪->⎩至少有4个整数解,且使关于x,y的方程组206ax yx y+=⎧⎨+=⎩的解为正整数,那么所有满足条件的整数a的值的和是( ).A.-3 B.-4 C.-10 D.-14答案:D解析:D【分析】根据不等式组求出a的范围,然后再根据关于x,y的方程组206ax yx y+=⎧⎨+=⎩的解为正整数得到26a-=-或12-,从而确定所有满足条件的整数a的值的和.【详解】解:125262x x x a++⎧⎪⎨⎪->⎩, 不等式组整理得:22x x a ⎧⎨>+⎩, 由不等式组至少有4个整数解,得到21a +<-,解得:3a <-,解方程组206ax y x y +=⎧⎨+=⎩,得12262x a a y a ⎧=-⎪⎪-⎨⎪=⎪-⎩, 又关于x ,y 的方程组206ax y x y +=⎧⎨+=⎩的解为正整数, 26a ∴-=-或12-,解得4a =-或10a =-,∴所有满足条件的整数a 的值的和是14-.故选:D .【点睛】本题考查解一元一次不等式组,学生的计算能力以及推理能力,解题的关键是根据不等式组以及二元一次方程组求出a 的范围,本题属于中等题型.3.如图,一个粒子在第一象限内及x 轴、y 轴上运动,在第一分钟,它从原点运动到点(1,0),第二分钟,它从点(1,0)运动到点(1,1),而后它接着按图中箭头所示在与x 轴,y 轴平行的方向上来回运动,且每分钟移动1个单位长度,那么在第2019分钟时,这个粒子所在位置的坐标是( )A .(44,5)B .(5,44)C .(44,6)D .(6,44)答案:A解析:A【解析】【分析】要弄清粒子的运动规律,先观察横坐标和纵坐标的相同点:(0,0),粒子运动了0分钟.(1,1)就是运动了2=1×2分钟,将向左运动!(2,2)粒子运动了6=2×3分钟,将向下运动!(3,3),粒子运动了12=3×4分钟.将向左运动…(44,44)点处粒子运动了44×45=1980分钟!此时粒子会将向下移动,进而得出答案.【详解】粒子所在位置与运动时间的情况如下:位置:(1,1),运动了2=1×2(分钟),方向向左;位置:(2,2),运动了6=2×3(分钟),方向向下;位置:(3,3),运动了12=3×4(分钟),方向向左;位置:(4,4),运动了20=4×5(分钟),方向向下,由上式规律,到(44,44)处时,粒子运动了44×45=1980(分钟),方向向下,故到2019分钟,须由(44,44)再向下运动2019-1980=39(分钟),所以在第2019分钟时,这个粒子的纵坐标为44-39=5,所以其坐标为(44,5), 故选A.【点睛】本题考查了点的坐标的确定.本题也是一个阅读理解并猜想规律的题目,解答此题的关键是总结规律首先确定点所在的大致位置,然后就可以进一步推得点的坐标.4.为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间,小聪把它抽象成图2的数学问题:已知AB ∥CD ,∠EAB =80°,110ECD ∠=︒,则∠E 的度数是( )A .30°B .40°C .60°D .70°答案:A解析:A【分析】过点E 作//EF AB ,先根据平行线的性质可得100AEF ∠=︒,再根据平行公理推论、平行线的性质可得70CEF ∠=︒,然后根据角的和差即可得.【详解】解:如图,过点E 作//EF AB ,80EAB ∠=︒,180100A E B E A F ∠=︒-=∴∠︒,//AB CD ,∴,CD EF//∴∠+∠=︒,CEF ECD180∠=︒,ECD110∴∠=︒-∠=︒,CEF ECD18070∴∠=∠-∠=︒-︒=︒,1007030AEC AEF CEF故选:A.【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的性质是解题关键.,运动到5.如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(00)(0)1,,然后接着按图中箭头所示方向运动,即(00)(01)(11)(10),,,,…,且每秒移→→→→动一个单位,那么第80秒时质点所在位置的坐标是()A.(0,9)B.(9,0)C.(0,8)D.(8,0)答案:C解析:C【解析】【分析】由题目可以知道,质点每秒运动一次,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒钟,2秒钟,3秒钟,到(1,1)用2秒,到(2,2)用6秒,到(3,3)用12秒,到(4,4)用20秒,依此类推:到点(n,n),用n2+n秒,这样可以先确定,第80秒钟时所在的点所在正方形,然后就可以进一步推得点的坐标.【详解】质点每秒运动一次,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒钟,2秒钟,3秒钟,到(1,1)用2秒,到(2,2)用6秒,到(3,3)用12秒,到(4,4)用20秒,依此类推:到点(n,n),用n2+n秒,∵当n=8时,n2+n=82+8=72,∴当质点运动到第72秒时到达(8,8),∴质点接下来向左运动,运动时间为80-72=8秒,∴此时质点的横坐标为8-8=0,∴此时质点的坐标为(0,8),∴第80秒后质点所在位置的坐标是(0,8),故选C.【点睛】本题考查了规律题——点的坐标,解决本题的关键是读懂题意,并总结出一定的规律,难度较大.6.如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳运1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P 第100次跳动至点P 100的坐标是( )A .(-24,49)B .(-25,50)C .(26,50)D .(26,51) 答案:C解析:C【详解】经过观察可得:1P 和2P 的纵坐标均为1,3P 和4P 的纵坐标均为2,5P 和6P 的纵坐标均为3,因此可以推知99P 和100P 的纵坐标均为100÷2=50;其中4的倍数的跳动都在y 轴的右侧,那么第100次跳动得到的横坐标也在y 轴右侧.1P 横坐标为1,4P 横坐标为2,8P 横坐标为3,依此类推可得到:n P 的横坐标为n÷4+1(n 是4的倍数). 故点100P 的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P 第100次跳动至点100P 的坐标是(26,50).故答案为(26,50).7.如图,将整数按规律排列,若有序数对(a ,b )表示第a 排从左往右第b 个数,则(9,4)表示的数是( )A .49B .﹣40C .﹣32D .25答案:B解析:B【分析】根据有序数对(m ,n )表示第m 行从左到右第n 个数,对如图中给出的有序数对和(3,2)表示整数5可得规律,进而可求出(9,4)表示的数.【详解】解:根据有序数对(m ,n )表示第m 行从左到右第n 个数,对如图中给出的有序数对和(3,2)表示整数5可知:(3,2):3(31)2⨯-25+=; (3,1):()331142⎡⎤⨯--+=-⎢⎥⎣⎦;(4,4):()4414102⎡⎤⨯--+=-⎢⎥⎣⎦; …由此可以发现,对所有数对(m ,n )(n ≤m )有,()12m m n ⨯-+.表示的数是偶数时结果为负数,奇数时结果为正数,所以(9,4)表示的数是:()9914402⎡⎤⨯--+=-⎢⎥⎣⎦. 故选:B .【点睛】本题考查了规律型-图形的变化类,解决本题的关键是观察数字的变化寻找规律,总结规律.8.已知: []x 表示不超过x 的最大整数,例: ][3.93, 1.82⎡⎤=-=-⎣⎦,令关于k 的函数()][1k 44k k f +⎡⎤=-⎢⎥⎣⎦ (k 是正整数),例:()][313344f +⎡⎤=-⎢⎥⎣⎦=1,则下列结论错误..的是( ) A .()10f =B .()()4f k f k +=C .()()1f k f k +≥D .()0f k =或1答案:C解析:C【分析】根据新定义的运算逐项进行计算即可做出判断.【详解】A. ()f 1=][11144+⎡⎤-⎢⎥⎣⎦=0-0=0,故A 选项正确,不符合题意; B. ()f k 4+=][k 41k 444+++⎡⎤-⎢⎥⎣⎦=][k 1k 1144+⎡⎤+-+⎢⎥⎣⎦=][k 1k 44+⎡⎤-⎢⎥⎣⎦,()f k =][k 1k 44+⎡⎤-⎢⎥⎣⎦, 所以()()f k 4f k +=,故B 选项正确,不符合题意;C. ()f k 1+=k 11k 1k 2k 14444+++++⎡⎤⎡⎤⎡⎤⎡⎤-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦,()f k = ][k 1k 44+⎡⎤-⎢⎥⎣⎦, 当k=3时,()f 31+=323144++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=0,()f 3= ][31344+⎡⎤-⎢⎥⎣⎦=1, 此时()()f k 1f k +<,故C 选项错误,符合题意;D.设n 为正整数,当k=4n 时,()f k =4n 14n 44+⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0, 当k=4n+1时,()f k =4n 24n 144++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0,当k=4n+2时,()f k =4n 34n 244++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n-n=0, 当k=4n+3时,()f k =4n 44n 344++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦=n+1-n=1, 所以()f k 0=或1,故D 选项正确,不符合题意,故选C.【点睛】本题考查了新定义运算,明确运算的法则,运用分类讨论思想是解题的关键.9.数轴上表示1,2的对应点分別为A ,B ,点B 关于点A 的对称点为C ,则点C 所表示的数是( )A .21-B .12-C .22-D .22- 答案:C解析:C【分析】根据数轴上两点之间的距离计算、对称的性质即可解决.【详解】根据对称的性质得:AC =AB设点C 表示的数为a ,则121a -=-解得:22a =-故选:C .【点睛】本题考查了数轴上两点之间的距离,图形对称的性质,关键是由对称的性质得到AC =AB . 10.已知A ,B ,C 是数轴上三点,点B 是线段AC 的中点,点A ,B 对应的实数分别为1-和2,则点C 对应的实数是( )A .21+B .22+C .221-D .221+ 答案:D解析:D【分析】由B 为AC 中点,得到AB BC =,求出AB 的长,即为BC 的长,从而确定出C 对应的实数即可.【详解】解:如图:根据题意得:21AB BC ==+,则点C 对应的实数是2(12)221++=+,故选:D .【点睛】此题考查了实数与数轴,弄清数轴上两点间的距离表示方法是解本题的关键. 11.若实数p ,q ,m ,n 在数轴上的对应点的位置如图所示,且满足0p q m n +++=,则绝对值最小的数是( )A .pB .qC .mD .n答案:C解析:C【分析】根据0p q m n +++=,并结合数轴可知原点在q 和m 之间,且离m 点最近,即可求解.【详解】解:∵0p q m n +++=结合数轴可得:()-=p q m n ++, 即原点在q 和m 之间,且离m 点最近,∴绝对值最小的数是m ,故选:C .【点睛】本题考查实数与数轴,解题的关键是明确数轴的特点,利用数形结合的思想解答. 12.已知T 122119311242++,T 22211497123366++,T 32211134++21313()1212,⋯,T 22111(1)n n +++n 为正整数.设S n =T 1+T 2+T 3+⋯+T n ,则S 2021值是( ) A .202120212022 B .202120222022 C .120212021 D .120222021 答案:A解析:A【分析】根据数字间的规律探索列式计算【详解】解:由题意可得:T 122119312+11=124212⨯++⨯, T 2221149723+11=2336623⨯++⨯,T 31334+1=1234⨯⨯∴T ()()1+11n n n n ++ ∴T 2021=20212022+120212022⨯⨯ ∴S 2021=T 1+T 2+T 3+⋯+T 2021 =371320212022+1+++ (261220212022)⨯+⨯ =11111++1++1++...1+261220212022+⨯ =11112021++++...+261220212022⨯ =11112021++++...+12233420212022⨯⨯⨯⨯ =11111112021+1++...+2233420212022⎛⎫-+--- ⎪⎝⎭ =12021+12022⎛⎫- ⎪⎝⎭=202120212022故选:A .【点睛】本题考查实数数字类的规律探索,探索规律,准确计算是解题关键.13.在平面直角坐标系xOy 中,对于点P (x ,y ),我们把P 1(y -1,-x -1)叫做点P 的友好点,已知点A 1的友好点为A 2,点A 2的友好点为A 3,点A 3的友好点为A 4,,这样依次得到各点.若A 2020的坐标为(-3,2),设A 1(x ,y ),则x +y 的值是( )A .-5B .-1C .3D .5答案:C解析:C【分析】列出部分An 点的坐标,根据坐标的变化寻找规律,规律和A 2020的坐标结合起来,即可得出答案.【详解】解:∵设A 1(x ,y ),∴A2(y-1,-x-1),∴A3(-x-1-1,-y+1-1),即A3(-x-2,-y ),∴A4(-y-1,x+2-1),即A4(-y-1,x+1),∴A5(x+1-1,y+1-1),即A5(x ,y )与A1相同,可以观察到友好点是4个一组循环的,∵2020÷4=505,∴A 2020(-3,2)与A4是相同的,1312y x --=-⎧∴⎨+=⎩, 解得12x y =⎧⎨=⎩, ∴x+y=1+2=3;故答案为:C .【点睛】本题考查了规律型中点的坐标变化,解题的关键是找出变化的规律,规律找到之后即可解答本题.14.估算193+的值应在( )A .5和6之间B .6和7之间C .7和8之间D .8和9之间 答案:C解析:C【分析】先根据19位于两个相邻平方数16和25之间,估算19的取值范围进而得出结论.【详解】解:由于16<19<25,所以4195<<,因此71938<+<,故选:C .【点睛】本题主要考查了估算无理数的大小的能力,现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法.15.如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…,则第100个点的横坐标为( )A .12B .13C .14D .15答案:C解析:C【分析】设横坐标为n的点的个数为a n,横坐标≤n的点的个数为S n(n为正整数),结合图形找出部分a n的值,根据数值的变化找出变化规律“a n=n”,再罗列出部分S n的值,根据数值的变化找出变化规律()12nn nS+=,依次变化规律解不等式()11002n n+≥即可得出结论.【详解】设横坐标为n的点的个数为a n,横坐标≤n的点的个数为S n(n为正整数),观察,发现规律:a1=1,a2=2,a3=3,…,∴a n=n.S1=a1=1,S2=a1+a2=3,S3=a1+a2+a3=6,…,∴S n=1+2+…+n=()12n n+.当100≤S n,即100≤()12n n+,解得:n≤(舍去),或n≥∵1413,故选:C.【点睛】本题考查了规律型中得点的坐标的变化,解题的关键是根据点的坐标的找出变化规律“()12nn nS+=”.16.若1a>,则a,a-,1a的大小关系正确的是()A.1a aa>->B.1a aa>->C.1a aa>>-D.1a aa->>答案:C 解析:C 【分析】可以用取特殊值的方法,因为a>1,所以可设a=2,然后分别计算|a|,-a,1a,再比较即可求得它们的关系.【详解】解:设a=2,则|a|=2,-a=-2,112a=,∵2>12>-2,∴|a|>1a>-a ; 故选:C .【点睛】此类问题运用取特殊值的方法做比较简单.17.有下列说法:①在1和2②实数与数轴上的点一一对应;③两个无理数的积一定是无理数;④2π是分数.其中正确的为( ) A .①②③④ B .①②④ C .②④D .② 答案:D解析:D【分析】根据无理数的定义与运算、实数与数轴逐个判断即可得.【详解】①在1和2之间的无理数有无限个,此说法错误;②实数与数轴上的点一一对应,此说法正确;③两个无理数的积不一定是无理数,如2=-,此说法错误; ④2π是无理数,不是分数,此说法错误; 综上,说法正确的为②,故选:D .【点睛】本题考查了无理数的定义与运算、实数与数轴,熟练掌握运算法则和定义是解题关键. 18.对于任意不相等的两个实数a ,b ,定义运算:a ※b =a 2﹣b 2+1,例如3※2=32﹣22+1=6,那么(﹣5)※4的值为( )A .﹣40B .﹣32C .18D .10答案:D解析:D【分析】直接利用题中的新定义给出的运算公式计算得出答案.【详解】解:(-5)※4=(﹣5)2﹣42+1=10.故选:D .【点睛】本题主要考查了实数运算,以及定义新运算,正确运用新定义给出的运算公式是解题关键.19.如图,已知//AB CD ,M 为平行线之间一点连接AM ,CM ,N 为AB 上方一点,连接AN ,CN ,E 为NA 延长线上一点.若AM ,CM 分别平分BAE ∠,DCN ∠,则M ∠与N ∠的数量关系为( ).A .90M N ∠-∠=︒B .2180M N ∠-∠=︒C .180M N ∠+∠=︒D .2180M N ∠+∠=︒答案:B解析:B【分析】过点M 作//MO AB ,过点N 作//NP AB ,则//////MO AB CD NP ,根据平行线的性质可得12AMC ∠=∠+∠,223CNE ∠=∠-∠,318021∠=︒-∠,即可得出结论.【详解】解:过点M 作//MO AB ,过点N 作//NP AB ,//AB CD ,//////MO AB CD NP ∴,1AMO ∴∠=∠,OMC MCD ∠=∠, AM ,CM 分别平分BAE ∠,DCN ∠,21BAE ∴∠=∠,22NCD ∠=∠,2MCD ∠=∠,12AMC ∴∠=∠+∠,//CD NP ,22PNC NCD ∴∠=∠=∠,223CNE ∴∠=∠-∠,//NP AB ,318021NAB ∴∠=∠=︒-∠,22(18021)2(12)1802180CNE AMC ∴∠=∠-︒-∠=∠+∠-︒=∠-︒,2180AMC CNE ∴∠-∠=︒,故选:B .【点睛】本题考查了平行线的性质,邻补角的定义,解题的关键是熟练掌握平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等. 20.如图所示,若AB ∥EF ,用含α、β、γ的式子表示x ,应为( )A .αβγ++B .βγα+-C .180αγβ︒--+D .180αβγ︒++- 答案:C解析:C【分析】过C 作CD ∥AB ,过M 作MN ∥EF ,推出AB ∥CD ∥MN ∥EF ,根据平行线的性质得出α+∠BCD=180°,∠DCM=∠CMN ,∠NMF=γ,求出∠BCD=180°-α,∠DCM=∠CMN=β-γ,即可得出答案.【详解】过C 作CD ∥AB ,过M 作MN ∥EF ,∵AB ∥EF ,∴AB ∥CD ∥MN ∥EF ,∴α+∠BCD=180°,∠DCM=∠CMN ,∠NMF=γ,∴∠BCD=180°-α,∠DCM=∠CMN=β-γ,∴x =∠BCD+∠DCM=180αγβ︒--+,故选:C .【点睛】本题考查了平行线的性质的应用,主要考查了学生的推理能力.21.如图所示,若∠1=∠2=45°,∠3=70°,则∠4等于( )A.70°B.45°C.110°D.135°答案:C解析:C【分析】根据对顶角的性质可得∠1=∠5,再由等量代换得∠2=∠5,即可得到到a∥b,利用两直线平行同旁内角互补可得∠3+∠4=180°,最后根据∠3的度数即可求出∠4的度数.【详解】解:∵∠1与∠5是对顶角,∴∠1=∠2=∠5=45°,∴a∥b,∴∠3+∠6=180°,∵∠3=70°,∴∠4=∠6=110°.故答案为C.【点睛】本题考查了对顶角的性质、平行线的性质及判定,其中掌握平行线的性质和判定是解答本题的关键.22.如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=100°,则∠D等于()A.70°B.80°C.90°D.100°答案:B解析:B【详解】因为AB∥DF,所以∠D+∠DEB=180°,因为∠DEB与∠AEC是对顶角,所以∠DEB=100°,所以∠D=180°﹣∠DEB=80°.故选B.23.给出下列说法:(1)两条直线被第三条直线所截,同位角相等;(2)不相等的两个角不是同位角;(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(4)从直线外一点到这条直线的垂线段,叫做该点到直线的距离;(5)过一点作已知直线的平行线,有且只有一条.其中真命题的有( )A .0个B .1个C .2个D .3个答案:B解析:B【详解】试题分析:根据两平行线被第三条直线所截,同位角相等,故(1)不正确;同位角不一定相等,只有在两直线平行时,同位角相等,故(2)不正确;平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交,故(3)正确; 从直线外一点到这条直线的垂线段的长度,叫做该点到直线的距离,故(4)不正确; 过直线外一点作已知直线的平行线,有且只有一条,故(5)不正确.故选B.24.如图,直线AB ,CD 相交于点O ,EO ⊥AB ,垂直为点O ,∠BOD =50°,则∠COE =( )A .30°B .140°C .50°D .60°答案:B解析:B【详解】试题解析:EO ⊥AB ,90,AOE ∴∠=50,AOC BOD ∠=∠=5090140.COE AOC AOE ∴∠=∠+∠=+=故选B.25.如图,已知//BC DE ,BF 平分ABC ∠,DC 平分ADE ∠,则下列判断:①ACB E ∠=∠;②DF 平分ADC ∠;③BFD BDF ∠=∠;④ABF BCD ∠=∠中,正确的有( )A .1个B .2个C .3个D .4个答案:B解析:B【分析】根据平行线的性质求出ACB E ∠=∠,根据角平分线定义和平行线的性质求出ABF CBF ADC EDC ∠=∠=∠=∠,推出//BF DC ,再根据平行线的性质判断即可.【详解】∵//BC DE ,∴ACB E ∠=∠,∴①正确;∵//BC DE ,∴ABC ADE ∠=∠,∵BF 平分ABC ∠,DC 平分ADE ∠, ∴12ABF CBF ABC ∠=∠=∠,12ADC EDC ADE ∠=∠=∠, ∴ABF CBF ADC EDC ∠=∠=∠=∠,∴//BF DC ,∴BFD FDC ∠=∠,∴根据已知不能推出ADF CDF ∠=∠,∴②错误;③错误;∵ABF ADC ∠=∠,ADC EDC ∠=∠,∴ABF EDC ∠=∠,∵//DE BC ,∴BCD EDC ∠=∠,∴ABF BCD ∠=∠,∴④正确;即正确的有2个,故选:B .【点睛】本题考查了平行线的性质和判定,角平分线定义的应用,能灵活运用平行线的性质和判定进行推理是解此题的关键.26.如图,C 为AOB ∠的边OA 上一点,过点C 作//CD OB 交AOB ∠的平分线OE 于点F ,作CH OB ⊥交BO 的延长线于点H ,若EFD α∠=,现有以下结论:①COF α∠=;②1802AOH α∠=︒-;③CH CD ⊥;④290OCH α∠=-︒.结论正确的个数是( )A .1个B .2个C .3个D .4个答案:D解析:D【分析】根据平行线的性质可得EOB EFD α∠=∠=,结合角平分线的定义可判断①;再由平角的定义可判断②;由平行线的性质可判断③;由余角及补角的定义可判断④.【详解】解://CD OB ,EFD α∠=,EOB EFD α∴∠=∠=, OE 平分AOB ∠,COF EOB α∴∠=∠=,故①正确;2AOB α∠=,180AOB AOH ∠+∠=︒,1802AOH α∴∠=︒-,故②正确;//CD OB ,CH OB ⊥,CH CD ∴⊥,故③正确;90HCO HOC ∴∠+∠=︒,180AOB HOC ∠+∠=︒,290OCH α∴∠=-︒,故④正确.正确为①②③④,故选:D .【点睛】本题主要考查平行线的性质,角平分线的定义,垂直的定义,灵活运用平行线的性质是解题的关键.27.如图,//AB CD ,AC 平分BAD ∠,B CDA ∠=∠,点E 在AD 的延长线上,连接EC ,2B CED ∠=∠,下列结论:①//BC AD ;②CA 平分BCD ∠;③AC EC ⊥;④ECD CED ∠=∠.其中正确的个数为( )A .1个B .2个C .3个D .4个答案:D解析:D【分析】结合平行线性质和平分线判断出①②正确,再结合平行线和平分线根据等量代换判断出③④正确即可.【详解】解:∵AB//CD,∴∠1=∠2,∵AC平分∠BAD,∴∠2=∠3,∴∠1=∠3,∵∠B=∠CDA,∴∠1=∠4,∴∠3=∠4,∴BC//AD,∴①正确;∴CA平分∠BCD,∴②正确;∵∠B=2∠CED,∴∠CDA=2∠CED,∵∠CDA=∠DCE+∠CED,∴∠ECD=∠CED,∴④正确;∵BC//AD,∴∠BCE+∠AEC= 180°,∴∠1+∠4+∠DCE+∠CED= 180°,∴∠1+∠DCE = 90°,∴∠ACE= 90°,∴AC⊥EC,∴③正确故其中正确的有①②③④,4个,故选:D.【点睛】此题考查平行线的性质和角平分线的性质,难度一般,利用性质定理判断是关键.28.以下11个命题:①负数没有平方根;②内错角相等;③同旁内角互补,两直线平行;④一个正数有两个立方根,它们互为相反数;⑤无限不循环小数是无理数;⑥数轴上的点与实数有一一对应关系;⑦过一点有且只有一条直线和已知直线垂直;⑧不相交的两条直线叫做平行线;⑨从直线外一点到这条直线的垂线段,叫做这点到直线的距离.⑩开方开不尽的数是无理数;⑪相等的两个角是对顶角;其中真命题的个数为()A .5B .6C .7D .8答案:A解析:A【分析】根据相关知识逐项判断即可求解.【详解】解:①“负数没有平方根”,是真命题②“内错角相等”,缺少两直线平行这一条件,是假命题;③“同旁内角互补,两直线平行”,是真命题;④“一个正数有两个立方根,它们互为相反数”,一个正数有一个立方根,是假命题;⑤“无限不循环小数是无理数”,是真命题;⑥“数轴上的点与实数有一一对应关系”,是真命题;⑦“过一点有且只有一条直线和已知直线垂直”,缺少在同一平面内条件,是假命题;⑧“不相交的两条直线叫做平行线”,缺少在同一平面内条件,是假命题;⑨“从直线外一点到这条直线的垂线段,叫做这点到直线的距离”,应为“从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离”,是假命题.⑩“开方开不尽的数是无理数”,是真命题;⑪“相等的两个角是对顶角”,相等的角有可能是对顶角,但不一定是对顶角,是假命题.所以真命题有5个.故选:A【点睛】本题考查判断真假命题、平方根、立方根、平行线的判定、无理数、实数与数轴关系、直线外一点到直线的距离、对顶角等知识,综合性较强,熟知相关知识点是解题关键. 29.小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了 5 支笔和 10 本笔记本共花了 42 元钱,第二次买了 10 文笔和 5 本笔记本共花了 30 元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔 记本的价格分别是( )A .0.8 元/支,2.6 元/本B .0.8 元/支,3.6 元/本C .1.2 元/支,2.6 元/本D .1.2 元/支,3.6 元/本答案:D解析:D【分析】首先设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,根据关键语句“第一次买了5支笔和10本笔记本共花了42元钱,”可得方程5x+10y=42,“第二次买了10支笔和5本笔记本共花了30元钱”可得方程10x+5y=30,联立两个方程,再解方程组即可.【详解】解:设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,由题意得:5104210530x y x y +=⎧⎨+=⎩ 解得: 1.23.6x y =⎧⎨=⎩ 故答案为D.【点睛】本题主要考查了二元一次方程组的应用,关键是弄懂题意,找出题目中的等量关系,再列出方程组即可.30.若关于x 的不等式组式020x a x b -≥⎧⎨-<⎩的整数解为x=1和x=2,则满足这个不等式组的整数a ,b 组成的有序数对(a ,b )共有( )对A .0B .1C .3D .2答案:D解析:D【分析】首先解不等式组的解集即可利用a 、b 表示,根据不等式组的整数解仅为1,2即可确定a 、b 的范围,即可确定a 、b 的整数解,即可求解.【详解】020x a x b -≥⎧⎨-<⎩①② 由①得:x a ≥由②得:2b x < 不等式组的解集为:2b a x ≤<∵整数解为为x=1和x=2∴01a <≤,232b <≤ 解得:01a <≤,46b <≤∴a =1,b=6,5∴整数a 、b 组成的有序数对(a ,b )共有2个故选D【点睛】本题考查一元一次不等式组的整数解,难度较大,熟练掌握一元一次不等式组相关知识点是解题关键.31.关于x 的不等式组0321x a x -≤⎧⎨+>-⎩的整数解共有4个,则a 的取值范围( ) A .3a = B .23a << C .23a ≤< D .23a <≤ 答案:C解析:C【分析】分别求出每一个不等式的解集,根据不等式组的整数解的个数可得答案.【详解】解不等式x-a≤0得x≤a ,解不等式3+2x >-1得x >-2,∵不等式组的整数解共有4个,∴这4个整数解为-1、0、1、2,则2≤a <3,故选:C .【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.32.小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了 5 支笔和 10 本笔记本共花了 42 元钱,第二次买了 10 文笔和 5 本笔记本共花了 30 元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔 记本的价格分别是( )A .0.8 元/支,2.6 元/本B .0.8 元/支,3.6 元/本C .1.2 元/支,2.6 元/本D .1.2 元/支,3.6 元/本答案:D解析:D【分析】首先设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,根据关键语句“第一次买了5支笔和10本笔记本共花了42元钱,”可得方程5x+10y=42,“第二次买了10支笔和5本笔记本共花了30元钱”可得方程10x+5y=30,联立两个方程,再解方程组即可.【详解】解:设小红所买的笔的价格是x 元/支,笔记本的价格是y 元/本,由题意得:5104210530x y x y +=⎧⎨+=⎩ 解得: 1.23.6x y =⎧⎨=⎩ 故答案为D.【点睛】本题主要考查了二元一次方程组的应用,关键是弄懂题意,找出题目中的等量关系,再列出方程组即可.33.若实数x 和y 满足x >y ,则下列式子中错误的是( )A .x +1>y +1B .2x -6>2y -6C .-3x >-3yD .-3x <-3y 答案:C解析:C【分析】直接利用不等式的基本性质:①不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;②不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;③不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;分别分析得出答案.【详解】解:A .∵x >y ,∴x +1>y +1,故此选项不合题意;B .∵x >y ,∴2x >2y ,∴2x −6>2y −6,故此选项不合题意;C .∵x >y ,∴−3x <−3y ,故此选项符合题意;D .∵x >y ,∴-3x <-3y ,故此选项不合题意; 故选:C .【点睛】本题主要考查了不等式的性质,掌握不等式的基本性质是解题关键.34.已知关于x 的一元一次不等式组10,20.x x a ->⎧⎨-<⎩有2个整数解,若a 为整数,则a 的值为( )A .5B .6C .6或7D .7或8答案:D解析:D【分析】先解出每个不等式的解集,即可得到该不等式组的解集,然后根据该不等式组有2个整数解确定a 的取值范围,从而求出a 的整数值.【详解】10,20.x x a ->⎧⎨-<⎩解不等式①,得:x > 1,解不等式②,得:2a x <, ∴不等式组的解集为12a x <<, 又该不等式组有2个整数解,∴2个整数解为2和3,342a ∴<≤, 解得:68a <≤,∴整数a 的值为7或8,故选:D .【点睛】本题考查的是解一元一次不等式组,不等式组的整数解,属于基础题,难度一般,熟知“同大取大;同小取小;大小小大中间找,大大小小找不到”的原则是解题的关键. 35.下列说法错误..的是( )A .由20x +>,可得2x >-B .由102x <,可得0x <C .由24x >-,可得2x <-D .由312x ->-,可得23x < 答案:C解析:C【分析】根据不等式的性质求解判断即可.【详解】解:A .由20x +>,可得2x >-,故A 说法正确,不符合题意;B .由102x <,可得0x <,故B 说法正确,不符合题意;C .由24x >-,可得2x <-,故C 说法错误,符合题意;D .由312x ->-,可得,23x <,故D 说法正确,不符合题意; 故选:C .【点睛】本题考查了不等式的性质,熟记不等式的性质是解题的关键.36.若关于x 的不等式0ax b ->的解集是12x <,则关于x 的不等式bx a <的解集是( ) A .2x <- B .2x < C .2x >- D .2x >答案:D解析:D【分析】由题意可知,a 、b 均为负数,且可得a =2b ,把a =2b 代入bx <a 中,则可求得bx <a 的解集.【详解】由0ax b ->得:ax b >∵不等式0ax b ->的解集为12x <∴a <0 ∴12b x a <= ∴a =2b∴b <0由bx a <,得2bx b <∵b <0∴x >2故选:D .【点睛】本题考查了解一元一次不等式,关键是由条件确定字母a 的符号,从而确定a 与b 的关系,易出现错误的地方是求bx <a 的解集时,忽略b 的符号,从而导致结果错误. 37.设[x )表示大于x 的最小整数,如[3)=4,[-1.2)=-1,下列结论:①[0)=0;②[x )-x 的最小值是0;③[x )-x 的最大值是1;④存在实数x ,使[x )-x =0.5成立,其中正确的是( )A .①②B .③④C .①②③D .②③④ 答案:B解析:B【分析】利用题中的新定义计算即可求出值.【详解】解:由题意可知:∵[x )表示大于x 的最小整数,∴设[x )=n ,则n -1≤x <n ,∴[x )-1≤x <[x ),∴0<[x )-x ≤1,∴①[0)1=,故①错误;②[)x x -可无限接近0,但取不到0,无最小值,故②错误;③[)x x -的最大值是1,当x 为整数时,故③正确;④存在实数x ,使[)0.5x x -=成立,比如x =1.5,故④正确,故选:B .【点睛】此题考查了解一元一次不等式,读懂新定义,并熟练掌握运算法则是解本题的关键.38.关于x 、y 的方程组731x y a x y a +=+⎧⎨-=+⎩的解恰好是第二象限内一个点的坐标(,)x y ,则a 的取值范围是( )A .3a <B .2a <-C .23a -<<D .32a -≤≤ 答案:B解析:B【分析】先解不等式组求出x 、y ,然后根据第二象限内点坐标的特点列式求解即可.【详解】解:解不等式组731x y a x y a +=+⎧⎨-=+⎩,得243x a y a =+⎧⎨=-+⎩ ∵点(,)x y 在第二象限∴24030a a +⎧⎨-+⎩<>,解得:2a <-. 故选B .【点睛】本题主要考查了解二元一次方程组和解不等式组,根据点的特点列出不等式是解答本题的关键.39.七(1)班全体同学进行了一次转盘得分活动.如图,将转盘等分成8格,每人转动一次,指针指向的数字就是获得的得分,指针落在边界则重新转动一次.根据小红、小明两位同学的对话,可得七(1)班共有学生()人.A.38 B.40 C.42 D.45答案:A解析:A【分析】根据题意,分别假设未知数,再根据对话内容列出方程组,即可求解答案.【详解】解:设得3分,4分,5分和6分的共有x人,它们平均得分为y分,分两种情况:(1)得分不足7分的平均得分为3分,xy+3×2+5×1=3(x+5+3),xy﹣3x=13①,(2)得3分及以上的人平均得分为4.5分,xy+3×7+4×8=4.5(x+3+4),4.5x﹣xy=21.5②,①+②得1.5x=34.5,解得x=2.3,故七(1)班共有学生23+5+3+3+4=38(人).故选:A.【点睛】考查了二元一次方程组的应用,解题的关键是了解题意,根据数量关系列出方程组,即可求出结果.40.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…第n次移动到A n.则△OA6A2020的面积是()。
北京第五十四中学七年级下册数学期末压轴难题试卷

北京第五十四中学七年级下册数学期末压轴难题试卷一、选择题1.“9的平方根”这句话用数学符号表示为()A .9B .±9C .3D .±32.下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( ) A . B . C . D . 3.如图,小手盖住的点的坐标可能为( )A .()2,3B .()2,3-C .()2,3--D .()2,3-4.下列六个命题 ①有理数与数轴上的点一一对应②两条直线被第三条直线所截,内错角相等③平行于同一条直线的两条直线互相平行; ④同一平面内,垂直于同一条直线的两条直线互相平行;⑤直线外一点到这条直线的垂线段叫做点到直线的距离⑥如果一个角的两边分别平行于另一个角的两边,那么这两个角相等,其中假命题的个数是( )A .2个B .3个C .4个D .5个 5.若A ∠的两边与B 的两边分别平行,且20B A ∠=∠+︒,那么A ∠的度数为( ) A .80︒ B .60︒ C .80︒或100︒ D .60︒或100︒ 6.下列说法:①两个无理数的和可能是有理数:②任意一个有理数都可以用数轴上的点表示;③33mn π-+是三次二项式;④立方根是本身的数有0和1;其中正确的是( ) A .①② B .①③ C .①②③ D .①②④ 7.如图,将一张长方形纸片折叠,若250∠=︒,则1∠的度数是( )A .80°B .70°C .60°D .50°8.如图,已知在平面直角坐标系中,点A 坐标是(1,1).若记点A 坐标为(a 1,a 2),则一个点从点A 出发沿图中路线依次经过B (a 3,a 4),C (a 5,a 6),D (a 7,a 8),…,每个点的横纵坐标都是整数,按此规律一直运动下去,则a 2016+a 2017+a 2018的值为( )A .1009B .1010C .1513D .2521二、填空题9.425⨯=______.10.将点()14P -,先关于x 轴对称,再关于y 轴对称的点的坐标为_______. 11.若(,)A a b 在第一、三象限的角平分线上,a 与b 的关系是_________.12.如图,已知直线EF ⊥MN 垂足为F ,且∠1=138°,则当∠2等于__时,AB ∥CD .13.如图,将一张长方形纸条折成如图的形状,若170∠=︒,则2∠的度数为____.14.观察下列等式:1﹣12=12,2﹣25=85,3﹣310=2710,4﹣417=6417,…,根据你发现的规律,则第20个等式为_____.15.平面直角坐标系中,已知点A (2,0),B (0,3),点P (m ,n )为第三象限内一点,若△PAB 的面积为18,则m ,n 满足的数量关系式为________.16.在平面直角坐标系中,111,4P ⎛⎫ ⎪⎝⎭,()22,1P ,393,4P ⎛⎫ ⎪⎝⎭,()44,4P ,5255,4P ⎛⎫ ⎪⎝⎭,…,按照此规律排列下去,点10P 的坐标为________.三、解答题17.计算:(13981-(223427(3)--(32(23)(4)353325-++18.求下列各式中的x 的值.(1)21(1)24x -=; (2)32(2)160x --=. 19.完成下列证明过程,并在括号内填上依据.如图,点E 在AB 上,点F 在CD 上,∠1=∠2,∠B =∠C ,求证AB ∥CD .证明:∵∠1=∠2(已知),∠1=∠4∴∠2= (等量代换),∴ ∥BF ( ), ∴∠3=∠ ( ).又∵∠B =∠C (已知),∴∠3=∠B∴AB ∥CD ( ).20.如图,在平面直角坐标系中,已知P (a ,b )是△ABC 的边AC 上一点,△ABC 经平移后点P 的对应点为P 1(a +6,b +2).(1)请画出上述平移后的△A 1B 1C 1,并写出点A 1,C 1的坐标;(2)写出平移的过程;(3)求出以A ,C ,A 1,C 1为顶点的四边形的面积.21.在学习《实数》内容时,我们通过“逐步逼近”2的近似值,得出1.42 1.5.利用“逐步逼近“法,请回答下列问题:(117介于连续的两个整数a 和b 之间,且a <b ,那么a = ,b = . (2)x 17的小数部分,y 171的整数部分,求x = ,y = . (317x )y 的平方根.二十二、解答题22.如图,用两个面积为28cm 的小正方形纸片剪拼成一个大的正方形.(1)大正方形的边长是________cm ;(2)请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为214cm 的长方形纸片,使它的长宽之比为2:1,若能,求出这个长方形纸片的长和宽,若不能,请说明理由.二十三、解答题23.如图,已知直线//AB 射线CD ,110CEB ∠=︒.P 是射线EB 上一动点,过点P 作//PQ EC 交射线CD 于点Q ,连接CP .作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠.(1)若点P ,F ,G 都在点E 的右侧.①求PCG ∠的度数;②若30EGC ECG ∠-∠=︒,求CPQ ∠的度数.(不能使用“三角形的内角和是180︒”直接解题)(2)在点P 的运动过程中,是否存在这样的偕形,使:3:2EGC EFC ∠∠=?若存在,直接写出CPQ ∠的度数;若不存在.请说明理由.24.如图,直线//PQ MN ,一副三角板(90ABC CDE ∠=∠=︒,30ACB ∠=︒,60,45EAC DCE DEC ∠=︒∠=∠=︒)按如图①放置,其中点E 在直线PQ 上,点,B C 均在直线MN 上,且CE 平分ACN ∠.(1)求DEQ ∠的度数.(2)如图②,若将三角形ABC 绕B 点以每秒5︒的速度按逆时针方向旋转(,A C 的对应点分别为,F G ).设旋转时间为t 秒(036)t ≤≤.①在旋转过程中,若边//BG CD ,求t 的值;②若在三角形ABC 绕B 点旋转的同时,三角形CDE 绕E 点以每秒4︒的速度按顺时针方向旋转(,C D 的对应点分别为,H K ).请直接写出当边//BG HK 时t 的值.25.(生活常识)射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图 1,MN 是平面镜,若入射光线 AO 与水平镜面夹角为∠1,反射光线 OB 与水平镜面夹角为∠2,则∠1=∠2 .(现象解释)如图 2,有两块平面镜 OM ,ON ,且 OM ⊥ON ,入射光线 AB 经过两次反射,得到反射光线 CD .求证 AB ∥CD .(尝试探究)如图 3,有两块平面镜 OM ,ON ,且∠MON =55︒ ,入射光线 AB 经过两次反射,得到反射光线 CD ,光线 AB 与 CD 相交于点 E ,求∠BEC 的大小.(深入思考)如图 4,有两块平面镜 OM ,ON ,且∠MON = α ,入射光线 AB 经过两次反射,得到反射光线 CD ,光线 AB 与 CD 所在的直线相交于点 E ,∠BED =β , α 与 β 之间满足的等量关系是 .(直接写出结果)26.如图,△ABC 和△ADE 有公共顶点A ,∠ACB =∠AED =90°,∠BAC =45°,∠DAE =30°. (1)若DE //AB ,则∠EAC = ;(2)如图1,过AC 上一点O 作OG ⊥AC ,分别交A B 、A D 、AE 于点G 、H 、F . ①若AO =2,S △AGH =4,S △AHF =1,求线段OF 的长;②如图2,∠AFO 的平分线和∠AOF 的平分线交于点M ,∠FHD 的平分线和∠OGB 的平分线交于点N ,∠N +∠M 的度数是否发生变化?若不变,求出其度数;若改变,请说明理由.【参考答案】一、选择题1.B解析:B【分析】b≥),那么a就叫做b的平方根,解答即可.根据平方根的定义:如果2a b=(0【详解】解:∵(299=∴“9的平方根”这句话用数学符号表示为:9,故选B.【点睛】本题考查了平方根的定义,是基础概念题,熟记概念是解题的关键.2.B【分析】根据图形的平移只改变图形的位置,而不改变图形的形状和大小对各个选项进行逐一判断即可.【详解】A,C,D选项中的图案不能通过平移得到,B选项中的图案通过平移后可以得到.故选B.解析:B【分析】根据图形的平移只改变图形的位置,而不改变图形的形状和大小对各个选项进行逐一判断即可.【详解】A,C,D选项中的图案不能通过平移得到,B选项中的图案通过平移后可以得到.故选B.【点睛】本题考查了平移的性质和平移的应用等有关知识,熟练掌握平移的性质是解答本题的关键.3.C【分析】根据平面直角坐标系的象限内点的特点判断即可;【详解】∵盖住的点在第三象限,∴()2,3--符合条件;故答案选C .【点睛】本题主要考查了平面直角坐标系象限内点的特征,准确分析判断是解题的关键. 4.C【分析】利用实数的性质、平行线的性质及判定、点到直线的距离等知识分别判断后即可确定答案.【详解】解:①实数与数轴上的点一一对应,故原命题错误,是假命题,符合题意;②两条平行直线被第三条直线所截,内错角相等,故原命题错误,是假命题,符合题意; ③平行于同一条直线的两条直线互相平行,正确,是真命题,不符合题意;④同一平面内,垂直于同一条直线的两条直线互相平行,正确,是真命题,不符合题意; ⑤直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故原命题错误,是假命题,符合题意;⑥如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补,故原命题错误,是假命题,符合题意,假命题有4个,故选:C .【点睛】本题主要考查了命题与定理的知识,解题的关键是了解实数的性质、平行线的性质及判定、点到直线的距离的定义等知识,难度不大.5.A【分析】根据当两角的两边分别平行时,两角的关系可能相等也可能互补,即可得出答案.【详解】解:当∠B 的两边与∠A 的两边如图一所示时,则∠B =∠A ,又∵∠B =∠A +20°,∴∠A +20°=∠A ,∵此方程无解,∴此种情况不符合题意,舍去;当∠B 的两边与∠A 的两边如图二所示时,则∠A +∠B =180°;又∵∠B =∠A +20°,∴∠A +20°+∠A =180°,解得:∠A =80°;综上所述,A ∠的度数为80°,故选:A .【点睛】本题考查了平行线的性质,本题的解题关键是明确题意,画出相应图形,然后分类讨论角度关系即可得出答案.6.A【分析】根据无理数的运算、数轴的定义、多项式的定义、立方根的运算逐个判断即可.【详解】①两个无理数的和可能是有理数,说法正确 如:2和2-是无理数,2(2)0+-=,0是有理数②有理数属于实数,实数与数轴上的点是一一对应关系,则任意一个有理数都可以用数轴上的点表示,说法正确③3327mn mn ππ=-+-+是二次二项式,说法错误④立方根是本身的数有0和±1,说法错误综上,说法正确的是①②故选:A .【点睛】本题考查了无理数的运算、数轴的定义、多项式的定义、立方根的运算,熟记各运算法则和定义是解题关键.7.A【分析】先由折叠的性质得出∠4=∠2=50°,再根据矩形对边平行可以得出答案.【详解】解:如图,由折叠性质知∠4=∠2=50°,∴∠3=180°-∠4-∠2=80°,∵AB∥CD,∴∠1=∠3=80°,故选:A.【点睛】本题主要考查平行线的性质,解题的关键是掌握两直线平行同位角相等的性质和折叠的性质.8.B【分析】观察已知点的坐标可得,所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2017=1009,偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数解析:B【分析】观察已知点的坐标可得,所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2017=1009,偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数,不能整除的,等于结果的整数部分加1,且符号为正,进而可得结果.【详解】解:由直角坐标系可知A(1,1),B(2,﹣1),C(3,2),D(4,﹣2),……,即a1=1,a2=1,a3=2,a4=﹣1,a5=3,a6=2,a7=4,a8=﹣2,……,所有数列奇数个都是从1开始逐渐递增的,且都等于所在的个数加上1再除以2,则a2017=1009,偶数列等于所在的个数除以4,能够整除的,结果的相反数就是所求出的数,不能整除的,等于结果的整数部分加1,且符号为正,∴a2016=﹣504,2018÷4=504……2,∴a2018=505,故a2016+a2017+a2018=1010,故选:B.【点睛】本题主要考查了规律型:点的坐标,探索数字与字母规律是解题关键.二、填空题9.10【分析】先计算乘法,然后计算算术平方根,即可得到答案.【详解】解:;故答案为:10.【点睛】本题考查了算术平方根,解题的关键是掌握算术平方根的计算方法. 解析:10【分析】先计算乘法,然后计算算术平方根,即可得到答案.【详解】10=;故答案为:10.【点睛】本题考查了算术平方根,解题的关键是掌握算术平方根的计算方法.10.(1,-4)【分析】直角坐标系中,关于x 轴对称的两点,横坐标相同,纵坐标互为相反数.关于y 轴对称的两点,纵坐标相同,横坐标互为相反数,由此即可求解.【详解】设关于x 轴对称的点为则点的坐标为解析:(1,-4)【分析】直角坐标系中,关于x 轴对称的两点,横坐标相同,纵坐标互为相反数.关于y 轴对称的两点,纵坐标相同,横坐标互为相反数,由此即可求解.【详解】设()14P -,关于x 轴对称的点为P' 则P'点的坐标为(-1,-4)设点P'和点''P 关于y 轴对称则''P 的坐标为(1,-4)故答案为:(1,-4)【点睛】本题考查了关于坐标轴对称的点的坐标特征,关于x 轴对称的两点,横坐标相同,纵坐标互为相反数,关于y 轴对称的两点,纵坐标相同,横坐标互为相反数.11.a=b .【详解】根据第一、三象限的角平分线上的点的坐标特征,易得a=b.解析:a=b .【详解】根据第一、三象限的角平分线上的点的坐标特征,易得a=b.12.48°【分析】先假设,求得∠3=∠4,由∠1=138°,根据邻补角求出∠3,再利用即可求出∠2的度数.【详解】解:若AB//CD ,则∠3=∠4,又∵∠1+∠3=180°,∠1=138°,解析:48°【分析】先假设//AB CD ,求得∠3=∠4,由∠1=138°,根据邻补角求出∠3,再利用EF MN 即可求出∠2的度数.【详解】解:若AB //CD ,则∠3=∠4,又∵∠1+∠3=180°,∠1=138°,∴∠3=∠4=42°;∵EF ⊥MN ,∴∠2+∠4=90°,∴∠2=48°;故答案为:48°.【点睛】本题主要考查平行线的性质,两直线垂直,平角定义,解题思维熟知邻补角、垂直的角度关系.13.55°【分析】依据平行线的性质以及折叠的性质,即可得到∠2的度数.【详解】解:如图所示,∵∠1=70°,∴∠3+∠4=180°-∠1=110°,又∵折叠,∴∠3=∠4=55°,解析:55°【分析】依据平行线的性质以及折叠的性质,即可得到∠2的度数.【详解】解:如图所示,∵∠1=70°,∴∠3+∠4=180°-∠1=110°,又∵折叠,∴∠3=∠4=55°,∵AB//DE,∴∠2=∠3=55°,故答案为:55°.【点睛】本题主要考查了平行线的性质,解题时注意:两条平行线被第三条直线所截,内错角相等.14.20﹣.【分析】观察已知等式,找出等式左边和右边的规律,再归纳总结出一般规律,由此即可得出答案.【详解】观察已知等式,等式左边的第一个数的规律为,第二个数的规律为:分子为,分母为等式右边的解析:20﹣208000= 401401.【分析】观察已知等式,找出等式左边和右边的规律,再归纳总结出一般规律,由此即可得出答案.【详解】观察已知等式,等式左边的第一个数的规律为1,2,3,,第二个数的规律为:分子为1,2,3,,分母为222112,215,3110,+=+=+=等式右边的规律为:分子为3331,2,3,,分母为222112,215,3110,+=+=+= 归纳类推得:第n 个等式为32211n n n n n -=++(n 为正整数) 当20n =时,这个等式为322202020201201-=++,即20800020401401-= 故答案为:20800020401401-=. 【点睛】 本题考查了实数运算的规律型问题,从已知等式中归纳类推出一般规律是解题关键. 15.【分析】 连接OP ,将PAB 的面积分割成三个小三角形,根据三个小三角形的面积的和为18进行整理即可解答.【详解】解:连接OP ,如图:∵A (2,0),B (0,3),∴OA=2,OB=3,解析:3230m n +=-【分析】连接OP ,将∆PAB 的面积分割成三个小三角形,根据三个小三角形的面积的和为18进行整理即可解答.【详解】解:连接OP ,如图:∵A (2,0),B (0,3),∴OA=2,OB=3,∵∠AOB=90°,∴11=23322OAB S OA OB ⋅=⨯⨯=,∵点P (m ,n )为第三象限内一点,m <0,n <0∴,11y 222OAP P S OA n n ∴=⋅=⨯⋅=-, 1133222OBP P S OB x m m =⋅=⨯⋅=-, 33182PAB OAB OAP OBP S S S S n m ∴=++=--+=, 整理可得:3230m n +=-;故答案为:3230m n +=-.【点睛】本题考查的是平面直角坐标系中面积的求解,要注意在计算面积的时候,可根据题意适当添加辅助线,帮助自己分割图形.16.【分析】观察前面几个点的坐标得到的横坐标为,纵坐标为,即可求解.【详解】解:观察前面几个点的坐标得到的横坐标为,纵坐标为,将代入得∴故答案为:【点睛】此题考查了平面直角坐标系中点坐解析:()10,25【分析】观察前面几个点的坐标得到n P 的横坐标为n ,纵坐标为24n ,即可求解. 【详解】解:观察前面几个点的坐标得到n P 的横坐标为n ,纵坐标为24n , 将10n =代入得2254n = ∴10(10,25)P故答案为:()10,25【点睛】此题考查了平面直角坐标系中点坐标规律的探索,根据已知点找到规律是解题的关键.三、解答题17.(1)6;(2)-4;(3);(4).【分析】(1)利用算术平方根和立方根、绝对值化简,再进一步计算即可;(2)利用算术平方根和立方根化简,再进一步计算即可;(3)类比单项式乘多项式展开计算解析:(1)6;(2)-4;(3)2+;(4)【分析】(1)利用算术平方根和立方根、绝对值化简,再进一步计算即可;(2)利用算术平方根和立方根化简,再进一步计算即可;(3)类比单项式乘多项式展开计算;(4)利用绝对值的性质化简,再进一步合并同类二次根式.【详解】解:(11-=3+2+1=6;(2=2-3-3=-4;(33)=2+;(4+=故答案为(1)6;(2)-4;(3)2+4)【点睛】本题考查立方根和算术平方根,实数的混合运算,先化简,再进一步计算,注意选择合适的方法简算.18.(1)或;(2).【分析】(1)两边开平方即可得出两个一元一次方程,求出方程的解即可;(2)先整理变形为(x﹣2)3=8,开立方根得出x﹣2=2,求出即可.【详解】解:(1),,,或解析:(1)52x=或12x=-;(2)4x=.【分析】(1)两边开平方即可得出两个一元一次方程,求出方程的解即可;(2)先整理变形为(x ﹣2)3=8,开立方根得出x ﹣2=2,求出即可.【详解】解:(1)29(1)4x -=, 312x -=±, 312x =±, 52x =或12x =-; (2)32(2)160x --=,32(2)16x -=,3(2)8x -=,22x -=,4x =.【点睛】本题是根据平方根和立方根的定义解方程,将方程系数化为1变形为:x 2=a (a ≥0)或x 3=b 的形式,再根据定义开平方或开立方,注意开平方时,有两个解.19.∠4;CE ;同位角相等,两直线平行;C ;两直线平行,同位角相等;内错角相等,两直线平行【分析】根据平行线的判定和性质解答.【详解】解∵∠1=∠2(已知),∠1=∠4(对顶角相等),∴∠2=解析:∠4;CE ;同位角相等,两直线平行;C ;两直线平行,同位角相等;内错角相等,两直线平行【分析】根据平行线的判定和性质解答.【详解】解∵∠1=∠2(已知),∠1=∠4(对顶角相等),∴∠2=∠4(等量代换),∴CE ∥BF (同位角相等,两直线平行),∴∠3=∠C (两直线平行,同位角相等).又∵∠B =∠C (已知),∴∠3=∠B (等量代换),∴AB ∥CD (内错角相等,两直线平行).故答案为:对顶角相等;CE ∥BF ;同位角相等,两直线平行;两直线平行,同位角相等;内错角相等,两直线平行.【点睛】此题考查平行线的判定和性质,关键是根据平行线的判定和性质解答.20.(1)图见详解;;(2)平移过程为先向右平移6个单位长度,再向上平移2个单位长度;(3)以A ,C ,A1,C1为顶点的四边形的面积为14.【分析】(1)根据点P 的对应点P1(a+6,b+2)可分别解析:(1)图见详解;()()113,4,4,2A C ;(2)平移过程为先向右平移6个单位长度,再向上平移2个单位长度;(3)以A ,C ,A 1,C 1为顶点的四边形的面积为14.【分析】(1)根据点P 的对应点P 1(a +6,b +2)可分别得出A 、B 、C 的对应点A 1,B 1,C 1的坐标,然后连接即可得出图象;(2)由(1)可直接进行求解;(3)由(1)的图象可直接利用割补法进行求解面积.【详解】解:(1)由点P 的对应点P 1(a +6,b +2)可得如图所示图象:∴由图象可得()()113,4,4,2A C ;(2)由图象可得:平移过程为先向右平移6个单位长度,再向上平移2个单位长度; (3)连接11,,AA CC ,如图所示:∵点()()13,2,4,2A C -,∴点1,A C 在同一条直线上,且与x 轴平行, ∴1111272142AC C ACC A S S =⨯=⨯=四边形.【点睛】本题主要考查平移的性质及坐标与图形,熟练掌握坐标的平移是解题的关键. 21.(1)4;5;(2);3;(3)±8.【分析】(1)首先估算出的取值范围,即可得出结论;(2)根据 (1)的结论,得到,即可求得答案;(3)根据(2)的结论代入计算即可求得答案.【详解】解析:(1)4;5;(24;3;(3)±8.【分析】(1的取值范围,即可得出结论;(2)根据 (1)的结论45<<,得到627<<,即可求得答案;(3)根据(2)的结论代入计算即可求得答案.【详解】解:(1)∵16<17<25, ∴45<,∴a =4,b =5.故答案为:4;5(2)∵45<<, ∴627<<,2的整数部分为64, ∴4x =,3y =.4;3(3)当4x ,3y =时,代入,)33)4464y x ⎤===⎦. ∴64的平方根为:8±.【点睛】本题考查了平方和平方根估算无理数大小应用,正确计算是解题的关键,注意平方根是一对互为相反数的两个数.二十二、解答题22.(1)4;(2)不能,理由见解析.【分析】(1)根据已知正方形的面积求出大正方形的边长即可;(2)先设未知数根据面积=14(cm2)列方程,求出长方形的边长,将长方形的长与正方形边长比较大小再解析:(1)4;(2)不能,理由见解析.【分析】(1)根据已知正方形的面积求出大正方形的边长即可;(2)先设未知数根据面积=14(cm2)列方程,求出长方形的边长,将长方形的长与正方形边长比较大小再判断即可.【详解】解:(1)两个正方形面积之和为:2×8=16(cm2),∴拼成的大正方形的面积=16(cm2),∴大正方形的边长是4cm;故答案为:4;(2)设长方形纸片的长为2xcm,宽为xcm,则2x•x=14,解得:x=2x,∴不存在长宽之比为2:1且面积为214cm的长方形纸片.【点睛】本题考查了算术平方根,能够根据题意列出算式是解此题的关键.二十三、解答题23.(1)①35°;(2)55°;(2)存在,或【分析】(1)①依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;②依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=20°解析:(1)①35°;(2)55°;(2)存在,52.5︒或7.5︒【分析】(1)①依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;②依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=20°,再根据PQ∥CE,即可得出∠CPQ=∠ECP=60°;(2)设∠EGC=3x,∠EFC=2x,则∠GCF=3x-2x=x,分两种情况讨论:①当点G、F在点E 的右侧时,②当点G、F在点E的左侧时,依据等量关系列方程求解即可.【详解】解:(1)①∵AB∥CD,∴∠CEB+∠ECQ=180°,∵∠CEB=110°,∴∠ECQ=70°,∵∠PCF=∠PCQ,CG平分∠ECF,∴∠PCG=∠PCF+∠FCG=12∠QCF+12∠FCE=12∠ECQ=35°;②∵AB∥CD,∴∠QCG=∠EGC,∵∠QCG+∠ECG=∠ECQ=70°,∴∠EGC+∠ECG=70°,又∵∠EGC-∠ECG=30°,∴∠EGC=50°,∠ECG=20°,∴∠ECG=∠GCF=20°,∠PCF=∠PCQ=12(70°−40°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=∠ECQ-∠PCQ=70°-15°=55°.(2)52.5°或7.5°,设∠EGC=3x°,∠EFC=2x°,①当点G、F在点E的右侧时,∵AB∥CD,∴∠QCG=∠EGC=3x°,∠QCF=∠EFC=2x°,则∠GCF=∠QCG-∠QCF=3x°-2x°=x°,∴∠PCF=∠PCQ=12∠FCQ=12∠EFC=x°,则∠ECG=∠GCF=∠PCF=∠PCD=x°,∵∠ECD=70°,∴4x=70°,解得x=17.5°,∴∠CPQ=3x=52.5°;②当点G、F在点E的左侧时,反向延长CD到H,∵∠EGC=3x°,∠EFC=2x°,∴∠GCH=∠EGC=3x°,∠FCH=∠EFC=2x°,∴∠ECG=∠GCF=∠GCH-∠FCH=x°,∵∠CGF=180°-3x°,∠GCQ=70°+x°,∴180-3x=70+x,解得x=27.5,∴∠FCQ=∠ECF+∠ECQ=27.5°×2+70°=125°,∴∠PCQ=12∠FCQ=62.5°,∴∠CPQ=∠ECP=62.5°-55°=7.5°,【点睛】本题主要考查了平行线的性质,掌握两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.24.(1)60°;(2)①6s;②s或s【分析】(1)利用平行线的性质角平分线的定义即可解决问题.(2)①首先证明∠GBC=∠DCN=30°,由此构建方程即可解决问题.②分两种情形:如图③中,当解析:(1)60°;(2)①6s;②103s或703s【分析】(1)利用平行线的性质角平分线的定义即可解决问题.(2)①首先证明∠GBC=∠DCN=30°,由此构建方程即可解决问题.②分两种情形:如图③中,当BG∥HK时,延长KH交MN于R.根据∠GBN=∠KRN构建方程即可解决问题.如图③-1中,当BG∥HK时,延长HK交MN于R.根据∠GBN+∠KRM=180°构建方程即可解决问题.【详解】解:(1)如图①中,∵∠ACB=30°,∴∠ACN=180°-∠ACB=150°,∵CE平分∠ACN,∴∠ECN=12∠ACN=75°,∵PQ∥MN,∴∠QEC+∠ECN=180°,∴∠QEC=180°-75°=105°,∴∠DEQ=∠QEC-∠CED=105°-45°=60°.(2)①如图②中,∵BG∥CD,∴∠GBC=∠DCN,∵∠DCN=∠ECN-∠ECD=75°-45°=30°,∴∠GBC=30°,∴5t=30,∴t=6s.∴在旋转过程中,若边BG∥CD,t的值为6s.②如图③中,当BG∥HK时,延长KH交MN于R.∵BG∥KR,∴∠GBN=∠KRN,∵∠QEK=60°+4t,∠K=∠QEK+∠KRN,∴∠KRN=90°-(60°+4t)=30°-4t,∴5t=30°-4t,∴t=10s.3如图③-1中,当BG∥HK时,延长HK交MN于R.∵BG∥KR,∴∠GBN+∠KRM=180°,∵∠QEK=60°+4t,∠EKR=∠PEK+∠KRM,∴∠KRM=90°-(180°-60°-4t)=4t-30°,∴5t+4t-30°=180°,∴t=703s.综上所述,满足条件的t的值为103s或703s.【点睛】本题考查几何变换综合题,考查了平行线的性质,旋转变换,角平分线的定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.25.【现象解释】见解析;【尝试探究】BEC 70;【深入思考】2.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用∠2+∠3=90°得出∠1+∠2+∠解析:【现象解释】见解析;【尝试探究】∠BEC = 70︒;【深入思考】β= 2α.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用∠2+∠3=90°得出∠1+∠2+∠3+∠4=180°,即可得出∠DCB+∠ABC=180°,即可证得AB∥CD;[尝试探究]根据三角形内角和定理求得∠2+∠3=125°,根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用平角的定义得出∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,即可得出∠EBC+BCE=360°-250°=110°,根据三角形内角和定理即可得出∠BEC=180°-110°=70°;[深入思考]利用平角的定义得出∠ABC=180°-2∠2,∠BCD=180°-2∠3,利用外角的性质∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,而∠BOC=∠3-∠2=α,即可证得β=2α.【详解】[现象解释]如图2,∵OM⊥ON,∴∠CON=90°,∴∠2+∠3=90°∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=180°,∴∠DCB+∠ABC=180°,∴AB∥CD;【尝试探究】如图3,在△OBC中,∵∠COB=55°,∴∠2+∠3=125°,∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=250°,∵∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,∴∠EBC+BCE=360°-250°=110°,∴∠BEC=180°-110°=70°;【深入思考】如图4,β=2α,理由如下:∵∠1=∠2,∠3=∠4,∴∠ABC=180°-2∠2,∠BCD=180°-2∠3,∴∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,∵∠BOC=∠3-∠2=α,∴β=2α.【点睛】本题考查了平行线的判定,三角形外角的性质以及三角形内角和定理,熟练掌握三角形的性质是解题的关键.26.(1)45°;(2)①1;②是定值,∠M+∠N=142.5°【分析】(1)利用平行线的性质求解即可.(2)①利用三角形的面积求出GH,HF,再证明AO=OG=2,可得结论.②利用角平分线的定解析:(1)45°;(2)①1;②是定值,∠M+∠N=142.5°【分析】(1)利用平行线的性质求解即可.(2)①利用三角形的面积求出GH,HF,再证明AO=OG=2,可得结论.②利用角平分线的定义求出∠M,∠N(用∠FAO表示),可得结论.【详解】解:(1)如图,∵AB∥ED∴∠E=∠EAB=90°(两直线平行,内错角相等),∵∠BAC=45°,∴∠CAE=90°-45°=45°.故答案为:45°.(2)①如图1中,∵OG⊥AC,∴∠AOG=90°,∵∠OAG=45°,∴∠OAG=∠OGA=45°,∴AO=OG=2,∵S△AHG=12•GH•AO=4,S△AHF=12•FH•AO=1,∴GH=4,FH=1,∴OF=GH-HF-OG=4-1-2=1.②结论:∠N+∠M=142.5°,度数不变.理由:如图2中,∵MF,MO分别平分∠AFO,∠AOF,∴∠M=180°-12(∠AFO+∠AOF)=180°-12(180°-∠FAO)=90°+12∠FAO,∵NH,NG分别平分∠DHG,∠BGH,∴∠N=180°-12(∠DHG+∠BGH)=180°-12(∠HAG+∠AGH+∠HAG+∠AHG)=180°-12(180°+∠HAG)=90°-12∠HAG=90°-12(30°+∠FAO+45°)=52.5°-12∠FAO,∴∠M+∠N=142.5°.【点睛】本题考查平行线的性质,角平分线的定义,三角形内角和定理,三角形外角的性质等知识,最后一个问题的解题关键是用∠FAO表示出∠M,∠N.。
北京第五十四中学八年级上册期末数学模拟试卷及答案

北京第五十四中学八年级上册期末数学模拟试卷及答案一、选择题1.下列说法:①三角形的一个外角等于它的任意两个内角和;②内角和等于外角和的多边形只有四边形;③角是轴对称图形,角的对称轴是角平分线.其中正确的有( )个. A .0 B .1 C .2 D .32.下列因式分解正确的是( )A .221(21)1x x x x --=--B .2244(2)x x x -+=-C .256(6)(1)x x x x -+=-+D .()321x x x x -=- 3.如图,AB//CD ,F 为,BAC ACD ∠∠的平分线的交点,EF AC ⊥于点E ,且EF=6,则AB 与CD 之间的距离是( )A .6B .8C .10D .124.如图,ABD ∆与AEC ∆都是等边三角形,AB AC ≠,下列结论中,正确的个数是( )①BE CD =;②60BOD ︒∠=;③BDO CEO ∠=∠;④若90BAC ︒∠=,且DA BC ,则BC CE ⊥.A .1B .2C .3D .4 5.已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )A .2B .3C .2或3D .不能确定 6.在四边形ABCD 中,若∠A 与∠C 之和等于四边形外角和的一半,∠B 比∠D 大15°,则∠B 的度数等于( )A .150°B .97.5°C .82.5°D .67.5° 7.有下列长度的三条线段,能组成三角形的是( )A .2cm ,3cm ,4cmB .1cm ,4cm ,2cmC .1cm ,2cm ,3cmD .6cm ,2cm ,3cm 8.如图,△ABC 的三边长分别是6,9,12,其三条角平分线将其分为三个三角形,则::ABO BCO CAO S S S ∆∆∆等于( )A .1:1:1B .1:2:3C .2:3:4D .3:4:59.如图,点A,B,C 在一条直线上,△ABD,△BCE 均为等边三角形,连接AE 和CD,AE 分别交CD,BD 于点M,P ,CD 交BE 于点Q,连接PQ,BM,下面的结论:①△ABE ≌△DBC;②∠DMA=60°;③△BPQ 为等边三角形;④MB 平分∠AMC,其中结论正确的有( )A .1个B .2个C .3个D .4个10.已知△ABC ,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB ,AC 上,且这组对应边所对的顶点重合于点M ,点M 一定在( ).A .∠A 的平分线上B .AC 边的高上 C .BC 边的垂直平分线上D .AB 边的中线上二、填空题11.如图,在△ABC 中,DE 是AB 的垂直平分线,且分别交AB 、AC 于点D 和E ,∠A =50°,∠C =60°,则∠EBC 等于_____度.12.计算:()322177a a a -÷=__________. 13.如图,在△ABC 中,已知点D 、E 、F 分别为BC 、AD 、CE 的中点,且S △ABC =1cm 2,则S △BEF =_____cm 2.14.计算:()32ab b b +÷=______.15.等腰三角形一腰上的高与另一腰的夹角为60°,那么这个等腰三角形的底角为__________.16.若103a =,102b =,则210a b -=______.17.等腰三角形中,两条边长分别为4cm 和5cm ,则此三角形的周长为 ____cm .18.因式分解:2a 4-=________19.已知等腰△ABC 中∠A=50°,则∠B=_______.20.当 x_____ 时,分2x x+式有意义. 三、解答题21.如图,在ABC 中,110ABC ∠=,40A ∠=.(1)作ABC 的角平分线BE (点E 在AC 上;用尺规作图,不写作法,保留作图痕迹);(2)在(1)的条件下,求BEC ∠的度数.22.已知如图,点A 、点B 在直线l 异侧,以点A 为圆心,AB 长为半径作弧交直线l 于C 、D 两点.分别以C 、D 为圆心,AB 长为半径作弧,两弧在l 下方交于点E,连结AE. (1)根据题意,利用直尺和圆规补全图形;(2)证明:l 垂直平分AE.23.如图,在四边形ABCD 中,//AD BC ,ABC ∠的平分线交CD 于点E ,交AD 的延长线于点F ,DEF F ∠=∠.(1)写出3对由条件//AD BC 直接推出的相等或互补的角;___________、_____________、_______________.(2)3∠与F ∠相等吗?为什么?(3)证明://DC AB .请在下面括号内,填上推理的根据,完成下面的证明://AD BC ,2F ∴∠=∠.(①_________);3F∠=∠(已证), 23∴∠=∠,(②__________); 又12∠=∠(③___________),13∠∠∴=,//DC AB ∴(④_____________).24.已知:230m mn +=,210mn n -=-,求下列代数式的值:(1)222m mn n +-;(2)227m n +-.25.如图,在ABC 中,4654,B C AD ∠=︒∠=︒,平分BAC ∠交BC 于点D ,点E 是边AC 上一点,连接DE ,若40ADE ∠=︒,求证://DE AB .26.(1)解方程组:202321x y x y -=⎧⎨+=⎩. (2)解不等式组:202(21)15x x x -<⎧⎨-≤+⎩. (3)分解因式:3x x -.(4)分解因式:221x x -++.27.如图,AB =AD =BC =DC ,∠C =∠D =∠ABE =∠BAD =90°,点E 、F 分别在边BC 、CD 上,∠EAF =45°,过点A 作∠GAB =∠FAD ,且点G 在CB 的延长线上.(1)△GAB 与△FAD 全等吗?为什么?(2)若DF =2,BE =3,求EF 的长.28.如图,如果AD ∥BC ,∠B =∠C ,那么AD 是∠EAC 的平分线吗?请说明你判别的理由.29.已知x =3+1,y =3﹣1,求:(1)代数式xy 的值;(2)代数式x 3+x 2y +xy 2+y 3的值.30.如图,已知ABC ∠、ACB ∠的平分线相交于点O ,EF 过点O 且//EF BC .(1)若50ABC ∠=︒,60ACB ∠=︒,求BOC ∠的度数;(2)若130BOC ∠=︒,1:23:2∠∠=,求ABC ∠、ACB ∠的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据三角形的外角和定理、三角形的内角和定理、角的性质、对称轴的定义知识点逐个判断即可.【详解】解: ①应为三角形的一个外角等于与它不相邻的两个内角的和,故本选项错误; ②内角和等于外角和的多边形只有四边形,故正确;③角是轴对称图形,角的对称轴是角的平分线所在的直线,③错误;综上所述, ②正确,故选B .【点睛】本题考查了三角形的外角和定理、三角形的内角和定理、角的性质、对称轴的定义相关知识点,能熟记知识点的内容是解此题的关键.2.B解析:B【解析】【分析】根据因式分解的定义进行选择即可.【详解】A. 221(21)1x x x x --=--,不是因式分解,故本选项不符合题意;B. 2244(2)x x x -+=-,故本选项符合题意,C. 256(2)(-3)-+=-x x x x ,故本选项不符合题意;D. ()321=x x+1x-1()()-=-x x x x ,故本选项不符合题意; 故选B【点睛】此题考查提公因式法与公式法的综合运用,因式分解-十字相乘法,掌握运算法则是解题关键3.D解析:D【解析】【分析】过点F 作MN AB ⊥于点M ,交CD 于点N ,根据角平分线上的点到角的两边距离相等可得MF EF FN ==,再根据平行线间的距离的定义解答.【详解】解:如图,过点F 作MN AB ⊥于点M ,交CD 于点N ,//AB CD ,M N CD ∴⊥. F 为BAC ∠、ACD ∠的平分线的交点,6EF =,6MF EF FN ∴===,AB ∴与CD 之间的距离12MF FN =+=.故选:D .【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,平行线间的距离的求解,熟记性质并作出辅助线是解题的关键.4.C解析:C【解析】【分析】利用全等三角形的判定和性质一一判断即可.【详解】解:∵ABD ∆与AEC ∆都是等边三角形∴AD=AB,AC=AE,∠DAB=∠EAC=60°∴∠DAB+∠BAC=∠EAC +∠BAC即∠DAC=∠EAB∴DAC BAE ≅∴BE CD =,①正确;∵DAC BAE ≅∴∠ADO=∠ABO∴∠BOD=∠DAB=60°,②正确∵∠BDA=∠CEA=60°,∠ADC≠∠AEB∴∠BDA -∠ADC≠∠CEA -∠AEB∴BDO CEO ∠≠∠,③错误∵DA BC∴∠DAC+∠BCA=180°∵∠DAB=60°,90BAC ︒∠=∴∠BCA=180°-∠DAB -∠BAC=30°∵∠ACE=60°∴∠BCE=∠ACE+∠BCA=60°+30°=90°∴BC CE ⊥④正确故由①②④三个正确,故选C【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、角平分线的判定定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.5.B解析:B【解析】【分析】根据等腰三角形性质和已知条件,进行分类讨论,即可得到答案,要注意的是一定要符合构成三角形的三边关系.【详解】已知三角形一边长为2,(1)当这一边是等腰三角形的腰时,它的腰长就为2,则底边是4根据三角形三边关系,这种情况不符合条件;(2)当这一边是等腰三角形的底边时∵ 周长为8,底边为2∴ 腰长为:822=3 (等腰三角形两腰相等) 根据三角形三边关系,这种情况符合条件;综上所述,这个等腰三角形的腰长为3.故答案选B.【点睛】本题考查了三角形的三边关系与等腰三角形的性质,解题的关键是熟练的掌握三角形的三边关系与等腰三角形的性质.6.B解析:B【解析】【分析】根据∠A 与∠C 之和等于四边形外角和的一半,四边形的外角和为360°,得到∠A+∠C=180°,根据四边形的内角和为360°∠B+∠D=360°-(∠A+∠C )=180°①,根据∠B 比∠D 大15°,得到∠B-∠D=15°②,所以①+②得:2∠B=195°,所以∠B=97.5°.【详解】解:∵∠A 与∠C 之和等于四边形外角和的一半,四边形的外角和为360°,∴∠A+∠C =180°,∴∠B+∠D =360°﹣(∠A+∠C )=180°①,∵∠B 比∠D 大15°,∴∠B ﹣∠D =15°②,①+②得:2∠B =195°,∴∠B =97.5°.故选:B .【点睛】本题考查了多边形的内角与外角,解决本题的关键是熟记四边形的内角和与外角和.7.A解析:A【解析】【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的之差一定小于第三边;进行解答即可.【详解】A、2+3>4,能围成三角形;B、1+2<4,所以不能围成三角形;C、1+2=3,不能围成三角形;D、2+3<6,所以不能围成三角形;故选:A.【点睛】本题主要考查了三角形的三边关系的应用,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.8.C解析:C【解析】过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,∵O是三角形三条角平分线的交点,∴OD=OE=OF,∵AB=6,BC=9,AC=12,∴S△ABO:S△BCO:S△CAO=2:3:4,故选C.【点睛】本题主要考查了角平分线的性质和三角形面积的求法,难度不大,作辅助线很关键.9.D解析:D【解析】试题分析:∵△ABD、△BCE为等边三角形,∴AB=DB,∠ABD=∠CBE=60°,BE=BC,∴∠ABE=∠DBC,∠PBQ=60°,在△ABE和△DBC中,,∴△ABE≌△DBC(SAS),∴①正确;∵△ABE≌△DBC,∴∠BAE=∠BDC,∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,∴②正确;在△ABP和△DBQ中,,∴△ABP≌△DBQ(ASA),∴BP=BQ,∴△BPQ为等边三角形,∴③正确;∵∠DMA=60°,∴∠AMC=120°,∴∠AMC+∠PBQ=180°,∴P、B、Q、M四点共圆,∵BP=BQ,∴BP BQ,∴∠BMP=∠BMQ,即MB平分∠AMC;∴④正确;综上所述:正确的结论有4个;故选D.考点:等边三角形的性质与判定、全等三角形的判定与性质、四点共圆、圆周角定理.10.A解析:A【解析】【分析】根据角平分线的判定推出M在∠BAC的角平分线上,即可得到答案.【详解】如图,∵ME⊥AB,MF⊥AC,ME=MF,∴M在∠BAC的角平分线上,故选:C.【点睛】本题主要考查对角平分线的判定定理的理解和掌握,能熟练地利用角平分线的判定定理进行推理是解此题的关键.二、填空题11.20【解析】【分析】根据三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到EA=EB,得到∠EBA=∠A=50°,结合图形计算,得到答案.【详解】解:∵A=50°,∠C=60°,解析:20【解析】【分析】根据三角形内角和定理求出∠ABC,根据线段垂直平分线的性质得到EA=EB,得到∠EBA=∠A=50°,结合图形计算,得到答案.【详解】解:∵A=50°,∠C=60°,∴∠ABC=180°-50°-60°=70°,∵DE是AB的垂直平分线,∴EA=EB,∴∠EBA=∠A=50°,∴∠EBC=∠ABC-∠EBA=70°-50°=20°,故答案为:20.【点睛】本题考查的是线段的垂直平分线的性质、三角形内角和定理,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.12.【解析】【分析】根据整式的除法法即可求解.【详解】故填:【点睛】此题主要考查整式的除法,解题的关键是熟知多项式除单项式的运算法则.解析:23a a【解析】【分析】根据整式的除法法即可求解.【详解】()322177a a a -÷=23a a -故填:23a a -【点睛】此题主要考查整式的除法,解题的关键是熟知多项式除单项式的运算法则.13.【解析】【分析】由于D 、E 、F 分别为BC 、AD 、CE 的中点,可判断出AD 、BE 、CE 、BF 为△ABC 、△ABD 、△ACD 、△BEC 的中线,根据中线的性质可知将相应三角形分成面积相等的两部分,从 解析:14【解析】【分析】由于D 、E 、F 分别为BC 、AD 、CE 的中点,可判断出AD 、BE 、CE 、BF 为△ABC 、△ABD 、△ACD 、△BEC 的中线,根据中线的性质可知将相应三角形分成面积相等的两部分,从而完成解答.【详解】∵由于D 、E 、F 分别为BC 、AD 、CE 的中点∴△ABE 、△DBE 、△DCE 、△AEC 的面积相等S △BEC =12S △ABC =12 S △BEF =12S △BEC =12×12=14故答案为:14. 【点睛】本题考察了三角形中线的知识;求解的关键是熟练掌握三角形中线的性质,从而完成求解.14.3a+2【解析】【分析】直接根据多项式除以单项式的运算法则进行计算即可.【详解】解:.故答案为:3a+2.【点睛】此题主要考查了多项式除以单项式,熟练掌握运算法则是解答此题的关键. 解析:3a+2【解析】【分析】直接根据多项式除以单项式的运算法则进行计算即可.【详解】解:()323232ab b b ab b b b a +÷=÷+÷=+.故答案为:3a+2.【点睛】此题主要考查了多项式除以单项式,熟练掌握运算法则是解答此题的关键.15.或【解析】【分析】首先根据题意画出图形,然后分别从锐角三角形与钝角三角形分析求解即可求得答案.【详解】解:根据题意得:AB=AC ,BD⊥AC,如图(1),∠ABD=60°,则∠A=3解析:75︒或15︒【解析】【分析】首先根据题意画出图形,然后分别从锐角三角形与钝角三角形分析求解即可求得答案.【详解】解:根据题意得:AB=AC ,BD ⊥AC ,如图(1),∠ABD=60°,则∠A=30°,∴∠ABC=∠C=75°;如图(2),∠ABD=60°,∴∠BAD=30°,∴∠ABC=∠C=12∠BAD=15°. 故这个等腰三角形的底角是:75°或15°.故答案为:75︒或15︒.【点睛】此题考查了等腰三角形的性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.16.【解析】【分析】根据同底数幂的除法和幂的乘方得出,代入求出即可.【详解】∵10a=3,10b=2,∴=102a ÷10 b==32÷2=.故答案为.【点睛】本题考查同底数幂 解析:92【解析】【分析】根据同底数幂的除法和幂的乘方得出()21010a b ÷,代入求出即可. 【详解】∵10a =3,10b =2,∴210a b -=102a ÷10 b=()21010a b ÷ =32÷2 =92. 故答案为92.本题考查同底数幂的除法和幂的乘方的应用,关键是得出关于10a 和10b 的式子,用了整体代入思想.17.13或14【解析】【分析】分是腰长和是腰长两种情况,再根据等腰三角形的定义可得出此三角形的三边长,然后根据三角形的周长公式即可得.【详解】由题意,分以下两种情况:(1)当是腰长时,此三角解析:13或14【解析】【分析】分4cm 是腰长和5cm 是腰长两种情况,再根据等腰三角形的定义可得出此三角形的三边长,然后根据三角形的周长公式即可得.【详解】由题意,分以下两种情况:(1)当4cm 是腰长时,此三角形的三边长分别为4,4,5cm cm cm ,满足三角形的三边关系定理,能组成三角形,则此三角形的周长为44513()cm ++=;(2)当5cm 是腰长时,此三角形的三边长分别为4,5,5cm cm cm ,满足三角形的三边关系定理,能组成三角形,则此三角形的周长为45514()cm ++=;综上,此三角形的周长为13cm 或14cm ,故答案为:13或14.【点睛】本题考查了等腰三角形的定义,难点在于分情况讨论并利用三角形的三边关系判断是否能组成三角形.18.=(a+2)(a-2)【解析】【分析】直接利用平方差公式分解因式得出即可.【详解】a2﹣4=(a+2)(a ﹣2).故答案为:(a+2)(a ﹣2).此题主要考查了公式法分解因式解析:2a4=(a+2)(a-2)【解析】【分析】直接利用平方差公式分解因式得出即可.【详解】a2﹣4=(a+2)(a﹣2).故答案为:(a+2)(a﹣2).【点睛】此题主要考查了公式法分解因式,熟练应用平方差公式是解题关键.19.50°或65°或80°【解析】【分析】分∠A、∠B、∠C为顶点三种情况,根据等腰三角形的性质,利用三角形内角和求出∠B的度数即可.【详解】①∠A为顶角时,∵∠A=50°,∴∠B=∠C=解析:50°或65°或80°【解析】【分析】分∠A、∠B、∠C为顶点三种情况,根据等腰三角形的性质,利用三角形内角和求出∠B 的度数即可.【详解】①∠A为顶角时,∵∠A=50°,∴∠B=∠C=12(180°-∠A)=65°,②当∠B为顶角时,∵∠A=50°,∴∠C=∠A=50°,∴∠B=180°-∠A-∠C=80°,③当∠C为顶角时,∠B=∠A=50°,综上所述:∠B的度数为50°或65°或80°,故答案为:50°或65°或80°本题考查等腰三角形的性质及三角形内角和定理,等腰三角形的两个底角相等;三角形的内角和是180°;运用分类讨论的思想是解题关键.20.【解析】【分析】直接利用分式有意义的条件分析得出即可.【详解】解:根据分式有意义得:2+x≠0,解得:x≠-2.故答案为:≠-2.【点睛】本题考查了分式有意义的条件,关键是熟练掌握解析:2≠-【解析】【分析】直接利用分式有意义的条件分析得出即可.【详解】解:根据分式有意义得:2+x≠0,解得:x≠-2.故答案为:≠-2.【点睛】本题考查了分式有意义的条件,关键是熟练掌握知识点:分式有意义,分母不为0.三、解答题21.(1)见解析;(2)95°【解析】【分析】(1)依据角平分线的作法,即可得到△ABC的角平分线BE;(2)依据三角形内角和定理,即可得到∠AEB的度数,再根据邻补角的定义,即可得到∠BEC的度数.【详解】(1)如图(满足“三弧一线”可得)线段BE 即为所求(2)由(1)得,BE 平分ABC ∠∵110ABC ∠=︒ ∴1552ABE ABC ∠=∠=︒ ∵40A ∠=︒∴180554085AEB ∠=︒-︒-︒=︒∵180AEB BEC ∠+∠=︒∴1808595BEC ∠=︒-︒=︒【点睛】本题主要考查了三角形内角和定理以及基本作图,解决问题的关键是掌握角平分线的作法.22.(1)见解析;(2)证明见解析.【解析】【分析】(1)根据题意进行作图即可;(2)根据题意可证明△ACD ≌△ECD ,再利用全等的性质及等腰三角形“三线合一”的性质即可证明结论.【详解】解:(1)如图所示;(2)证明:由题意可知,AC=AD=AB ,CE=ED=AB ,∴AC=CE ,AD=DE ,又∵CD=CD ,∴△ACD ≌△ECD ,∴∠ACD=∠ECD ,又∵AC=CE ,∴CO 垂直平分AE ,∴l 垂直平分AE.【点睛】本题考查了作图及线段的垂直平分线,需熟练掌握全等三角形的判定及性质,等腰三角形的性质,学会应用“三线合一”证明线段的垂直平分线.23.(1)2F ∠=∠,C CDF ∠=∠,180A ABC ∠+∠=︒或180C ADC ∠+∠=︒ (2)相等,理由见解析(3)见解析【解析】【分析】(1)根据平行线的性质解答;(2)根据对顶角的性质解答;(3)根据平行线的性质及等量代换,平行线的判定定理解答.【详解】(1)∵//AD BC ,∴2F ∠=∠,C CDF ∠=∠,180A ABC ∠+∠=︒或180C ADC ∠+∠=︒;故答案为:2F ∠=∠,C CDF ∠=∠,180A ABC ∠+∠=︒或180C ADC ∠+∠=︒; (2)3∠与F ∠相等.理由如下:DEF F ∠=∠,3DEF ∠=∠,3F ∴∠=∠.(3)//AD BC ,2F ∴∠=∠.(①两直线平行,内错角相等);3F∠=∠(已证), 23∴∠=∠,(②等量代换); 又12∠=∠(③角平分线的定义),13∠∠∴=,//DC AB ∴(④内错角相等,两直线平行).故答案为:①两直线平行,内错角相等;②等量代换;③角平分线的定义;④内错角相等,两直线平行.【点睛】此题考查平行线的性质定理及判定定理,角平分线的性质定理,等量代换的推理依据,熟练掌握平行线的判定及性质定理是解题的关键.24.(1)20;(2)33.【解析】【分析】(1)将已知两等式左右两边相加,即可求出所求代数式的值;(2)将已知两等式左右两边相减,即可求出所求代数式的值.【详解】(1)∵230m mn +=,210mn n -=-,∴222m mn n +-=(2m mn +)+(2mn n -)=30-10=20;(2)∵230m mn +=,210mn n -=-,∴227m n +-=(2m mn +)-(2mn n -)-7=30-(-10)-7=30+10-7=33.【点睛】此题考查了代数式求值,利用了整体代入的思想,是一道基本题型.25.证明见解析【解析】【分析】先求出∠BAC 的度数,进而得出∠BAD ,因为∠BAD=40°=∠ADE ,由“内错角相等,两直线平行”即可判断.【详解】证明:在ABC ∆中,46,54,B C ︒︒∠=∠=180465480BAC ︒︒︒︒∴∠=--=, AD 平分,BAC ∠ 1402BAD BAC ︒∴∠=∠=, 40,ADE ︒∠=.ADE BAD ∴∠=∠//.DE AB ∴【点睛】本题考查角的运算,角平分线的性质定理以及平行线的判定,掌握角平分线的性质是解题的关键.26.(1)63x y =⎧⎨=⎩;(2)32x -≤<;(3)()()11x x x +-;(4)()21x - 【解析】【分析】(1)加减消元法解方程组;(2)先分别解不等式,再找解集的公共部分;(3)先提公因式,再用平方差公式;(4)应用完全平方公式.【详解】(1)解:202321x y x y -=⎧⎨+=⎩①②, ②-①×2,得:721y =,解得:3y =,把3y =代入①得:6x =,∴原方程组的解为:63x y =⎧⎨=⎩; (2)解:202(21)15x x x -<⎧⎨-≤+⎩①②, 由①得:2x <,由②得:4-215x x ≤+,解得:3x ≥-,∴原不等式组的解为:32x -≤<;(3)原式=()()()211-1x x x x x -=+; (4)原式=221x x -++=()21x -.【点睛】本题考查二元一次方程组的解法,一元一次不等式组的解法,因式分解的方法,熟练掌握基础知识是关键.27.(1)全等,理由详见解析;(2)5【解析】【分析】(1)由题意易得∠ABG =90°=∠D ,然后问题可求证;(2)由(1)及题意易得△GAE ≌△FAE ,GB =DF ,进而问题可求解.【详解】解:(1)全等.理由如下∵∠D =∠ABE =90°,∴∠ABG =90°=∠D ,在△ABG 和△ADF 中, GAB FAD AB AD ABG D ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△GAB ≌△FAD (ASA );(2)∵∠BAD =90°,∠EAF =45°,∴∠DAF +∠BAE =45°,∵△GAB ≌△FAD ,∴∠GAB =∠FAD ,AG =AF ,∴∠GAB +∠BAE =45°,∴∠GAE =45°,∴∠GAE =∠EAF ,在△GAE 和△FAE 中,AG AF GAE EAF AE AE =⎧⎪∠=∠⎨⎪=⎩, ∴△GAE ≌△FAE (SAS )∴EF =GE∵△GAB ≌△FAD ,∴GB =DF ,∴EF =GE =GB +BE =FD +BE =2+3=5.【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.28.AD 是∠EAC 的平分线,理由见解析【解析】【分析】根据平行线和等腰三角形的性质可证得∠EAD=∠DAC ,可得出结论.【详解】AD 是∠EAC 的平分线,∵AD ∥BC ,∴∠EAD =∠B ,∠DAC =∠C ,又∵∠B =∠C ,∴∠EAD =∠DAC ,∴AD 是∠EAC 的平分线.【点睛】本题主要考查了等腰三角形的性质和平行线的性质,掌握等边对等角和平行线的性质是解题的关键.29.(1)2;(2)【解析】【分析】(1)直接代入平方差公式计算即可;(2)先计算出x+y 和x 2+y 2,原式整理成(x 2+y 2)(x+y )代入计算即可;【详解】(1)xy=)=2-1=2;(2)∵x,y1,xy=2,∴∴x 2+y 2=(x+y )2-2xy=8,则x3+x2y+xy2+y3= x2(x+y)+y2(x+y)=(x2+y2)(x+y)=8×23=163.【点睛】此题考查整式的化简求值,平方差公式,完全平方公式,解题关键在于掌握运算法则. 30.(1)∠BOC=125°;(2)∠ABC=60°,∠ACB=40°.【解析】【分析】(1)由角平分线的性质可求出∠OBC、∠OCB的度数,再根据三角形内角和即可得出答案;(2)由邻补角的定义可求出∠1+∠2=50°,再根据1:23:2∠∠=即可分别求出∠1和∠2的度数,最后根据两直线平行内错角相等及角平分线的性质即可得出答案.【详解】解:(1)因为∠ABC和∠ACB的平分线BO与CO相交于点O,所以∠EBO=∠OBC12ABC=∠,∠FCO=∠OCB12ACB=∠又∠ABC=50°,∠ACB=60°,所以∠OBC=25°,∠OCB=30°所以∠BOC=180°-∠OBC -∠OCB=125°(2)因为∠BOC=130°,所以∠1+∠2=50°因为∠1: ∠2=3:2所以3150305∠=⨯︒=︒,2250205∠=⨯︒=︒因为 EF∥BC所以∠OBC=∠1=30°,∠OCB=∠2=20°因为∠ABC和∠ACB的平分线BO与CO相交于点O,所以∠ABC=60°,∠ACB=40°.【点睛】本题考查了角平分线的性质、平行线的性质、三角形内角和性质,熟练掌握性质定理是解题的关键.。
【精选试卷】北京第五十四中学中考数学解答题专项练习习题(含答案)

一、解答题1.某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: (1)这次调查的学生共有多少名;(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数; (3)如果要在这个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A 、B 、C 、D 、E ).2.材料:解形如(x+a )4+(x+b )4=c 的一元四次方程时,可以先求常数a 和b 的均值a+b 2,然后设y =x+a+b 2.再把原方程换元求解,用种方法可以成功地消去含未知数的奇次项,使方程转化成易于求解的双二次方程,这种方法叫做“均值换元法. 例:解方程:(x ﹣2)4+(x ﹣3)4=1解:因为﹣2和﹣3的均值为−52,所以,设y =x ﹣52,原方程可化为(y+12)4+(y ﹣12)4=1,去括号,得:(y 2+y+14)2+(y 2﹣y+14)2=1y 4+y 2+116+2y 3+12y 2+12y+y 4+y 2+116﹣2y 3+12y 2﹣12y =1整理,得:2y 4+3y 2﹣78=0(成功地消去了未知数的奇次项) 解得:y 2=14或y 2=−74(舍去)所以y =±12,即x ﹣52=±12.所以x =3或x =2.(1)用阅读材料中这种方法解关于x 的方程(x+3)4+(x+5)4=1130时,先求两个常数的均值为______.设y =x+____.原方程转化为:(y ﹣_____)4+(y+_____)4=1130. (2)用这种方法解方程(x+1)4+(x+3)4=7063.计算:()()()21a b a 2b (2a b)-+--;()221m 4m 421m 1m m -+⎛⎫-÷ ⎪--⎝⎭.4.将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D'处,折痕为EF.(1)求证:ABE AD F'≌;(2)连结CF,判断四边形AECF是什么特殊四边形?证明你的结论.5.小华想复习分式方程,由于印刷问题,有一个数“?”看不清楚:?1322x x+=--.(1)她把这个数“?”猜成5,请你帮小华解这个分式方程;(2)小华的妈妈说:“我看到标准答案是:方程的增根是2x=,原分式方程无解”,请你求出原分式方程中“?”代表的数是多少?6.某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x (元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:销售单价x(元)8595105115日销售量y(个)17512575m日销售利润w(元)87518751875875(注:日销售利润=日销售量×(销售单价﹣成本单价))(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;(2)根据以上信息,填空:该产品的成本单价是元,当销售单价x=元时,日销售利润w最大,最大值是元;(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?7.为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.整理情况频数频率非常好0.21 较好 70 0.35一般 m 不好36请根据图表中提供的信息,解答下列问题: (1)本次抽样共调查了 名学生; (2)m= ;(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A 1、A 2),1本“较好”(记为B ),1本“一般”(记为C ),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.8.4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A ,小江抓着风筝线的一端站在D 处,他从牵引端E 测得风筝A 的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC =30米)的居民楼顶B 处测得风筝A 的仰角是45°,已知小江与居民楼的距离CD =40米,牵引端距地面高度DE =1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈1213,cos67°≈513,tan67°≈125,2≈1.414).9.已知关于x 的方程220x ax a ++-=.(1)当该方程的一个根为1时,求a 的值及该方程的另一根; (2)求证:不论a 取何实数,该方程都有两个不相等的实数根. 10.如图,在四边形ABCD 中,ABDC ,AB AD =,对角线AC ,BD 交于点O ,AC 平分BAD ∠,过点C 作CE AB ⊥交AB 的延长线于点E ,连接OE .(1)求证:四边形ABCD 是菱形;(2)若5AB =2BD =,求OE 的长.11.荆门市是著名的“鱼米之乡”.某水产经销商在荆门市长湖养殖场批发购进草鱼和乌鱼(俗称黑鱼)共75千克,且乌鱼的进货量大于40千克.已知草鱼的批发单价为8元/千克,乌鱼的批发单价与进货量的函数关系如图所示.(1)请直接写出批发购进乌鱼所需总金额y (元)与进货量x (千克)之间的函数关系式;(2)若经销商将购进的这批鱼当日零售,草鱼和乌鱼分别可卖出89%、95%,要使总零售量不低于进货量的93%,问该经销商应怎样安排进货,才能使进货费用最低?最低费用是多少?12.如图,BD 是△ABC 的角平分线,过点D 作DE∥BC 交AB 于点E ,DF∥AB 交BC 于点F . (1)求证:四边形BEDF 为菱形;(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF 的面积.13.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y (千克)与每千克降价x (元)(020)x <<之间满足一次函数关系,其图象如图所示:(1)求y 与x 之间的函数关系式;(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?14.某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y 1(元/件),销量y 2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).(1)求y1与y2的函数解析式.(2)求每天的销售利润W与x的函数解析式.(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?15.在一个不透明的盒子中装有三张卡片,分别标有数字1,2,3,这些卡片除数字不同外其余均相同.小吉从盒子中随机抽取一张卡片记下数字后放回,洗匀后再随机抽取一张卡片.用画树状图或列表的方法,求两次抽取的卡片上数字之和为奇数的概率.16.2x=600答:甲公司有600人,乙公司有500人.点睛:本题考查了分式方程的应用,关键是分析题意找出等量关系,通过设未知数并根据等量关系列出方程.17.垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对本校甲、乙两班各60名学生进行了垃极分类相关知识的测试,并分别随机抽取了15份成绩,整理分析过程如下,请补充完整(收集数据)甲班15名学生测试成绩统计如下:(满分100分)68,72,89,85,82,85,74,92,80,85,78,85,69,76,80乙班15名学生测试成绩统计如下:(满分100分)86,89,83,76,73,78,67,80,80,79,80,84,82,80,83(整理数据)按如下分数段整理、描述这两组样本数据组别班级65.6~70.570.5~75.575.5~80.580.5~85.585.5~90.590.5~95.5甲班224511乙班11a b20在表中,a=,b=.(分析数据)(1)两组样本数据的平均数、众数、中位数、方差如下表所示:班级平均数众数中位数方差甲班80x8047.6乙班8080y26.2在表中:x=,y=.(2)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃圾分类相关知识合格的学生有人(3)你认为哪个班的学生掌握垃圾分类相关知识的情况较好,说明理由.18.在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:(Ⅰ)图1中a的值为;(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.19.数学活动课上,张老师引导同学进行如下探究:如图1,将长为12cm的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上,一端A固定在桌面上,图2是示意图.活动一如图3,将铅笔AB绕端点A顺时针旋转,AB与OF交于点D,当旋转至水平位置时,铅笔AB的中点C与点O重合.数学思考(1)设CD=x cm,点B到OF的距离GB=y cm.①用含x的代数式表示:AD的长是_________cm,BD的长是________cm;②y与x的函数关系式是_____________,自变量x的取值范围是____________.活动二(2)①列表:根据(1)中所求函数关系式计算并补全..表格. x(cm ) 6 5 4 3.5 3 2.5 2 1 0.5 0y(cm )0.551.21.581.02.4734.295.08②描点:根据表中数值,描出①中剩余的两个点(x,y).③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象. 数学思考(3)请你结合函数的图象,写出该函数的两条性质或结论.20.国家自2016年1月1日起实行全面放开二胎政策,某计生组织为了解该市家庭对待这项政策的态度,准备采用以下调查方式中的一种进行调查: A .从一个社区随机选取1 000户家庭调查;B .从一个城镇的不同住宅楼中随机选取1 000户家庭调查;C .从该市公安局户籍管理处随机抽取1 000户城乡家庭调查.(1)在上述调查方式中,你认为比较合理的一个是 .(填“A”、“B”或“C”) (2)将一种比较合理的调查方式调查得到的结果分为四类:(A )已有两个孩子;(B )决定生二胎;(C )考虑之中;(D )决定不生二胎.将调查结果绘制成如下两幅不完整的统计图.请根据以上不完整的统计图提供的信息,解答下列问题: ①补全条形统计图.②估计该市100万户家庭中决定不生二胎的家庭数. 21.先化简,再求值:(2)(2)(4)a a a a +-+-,其中14a =.22.如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.(1)求线段AD的长度;(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.23.某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?24.“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;C.仅家长自己参与; D.家长和学生都未参与.请根据图中提供的信息,解答下列问题:(1)在这次抽样调查中,共调查了________名学生;(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数. 25.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.26.解方程:x21 x1x-= -.27.已知222111 x x x Ax x++=---.(1)化简A;(2)当x满足不等式组1030xx-≥⎧⎨-<⎩,且x为整数时,求A的值.28.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.29.修建隧道可以方便出行.如图:A,B两地被大山阻隔,由A地到B地需要爬坡到山顶C地,再下坡到B地.若打通穿山隧道,建成直达A,B两地的公路,可以缩短从A地到B地的路程.已知:从A到C坡面的坡度1:3i=,从B到C坡面的坡角45CBA∠=︒,42BC=公里.(1)求隧道打通后从A到B的总路程是多少公里?(结果保留根号)(2)求隧道打通后与打通前相比,从A地到B地的路程约缩短多少公里?(结果精确到0.01 1.4141.732)30.对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)甲组抽到A小区的概率是多少;(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、解答题1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.无17.18.19.20.21.22.23.24.25.26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、解答题1.(1)280名;(2)补图见解析;108°;(3)0.1.【解析】【分析】(1)根据“平等”的人数除以占的百分比得到调查的学生总数即可;(2)求出“互助”与“进取”的学生数,补全条形统计图,求出“进取”占的圆心角度数即可;(3)列表或画树状图得出所有等可能的情况数,找出恰好选到“C”与“E”的情况数,即可求出所求的概率.【详解】解:(1)56÷20%=280(名),答:这次调查的学生共有280名;(2)280×15%=42(名),280﹣42﹣56﹣28﹣70=84(名),补全条形统计图,如图所示,根据题意得:84÷280=30%,360°×30%=108°,答:“进取”所对应的圆心角是108°;(3)由(2)中调查结果知:学生关注最多的两个主题为“进取”和“感恩”用列表法为:A B C D EA(A,B)(A,C)(A,D)(A,E)B(B,A)(B,C)(B,D)(B,E)C(C,A)(C,B)(C,D)(C,E)D(D,A)(D,B)(D,C)(D,E)E(E,A)(E,B)(E,C)(E,D)用树状图为:共20种情况,恰好选到“C”和“E”有2种,∴恰好选到“进取”和“感恩”两个主题的概率是0.1.2.(1)4,4,1,1;(2)x =2或x =﹣6. 【解析】 【分析】(1)可以先求常数3和5的均值4,然后设y =x+4,原方程可化为(y ﹣1)4+(y+1)4=1130;(2)可以先求常数1和3的均值2,然后设y =x+2,原方程可化为(y ﹣1)4+(y+1)4=706,再整理化简求出y 的值,最后求出x 的值. 【详解】(1)因为3和5的均值为4,所以,设y =x+4,原方程可化为(y ﹣1)4+(y+1)4=1130,故答案为4,4,1,1;(2)因为1和3的均值为2,所以,设y =x+2,原方程可化为(y ﹣1)4+(y+1)4=706,去括号,得:(y 2﹣2y+1)2+(y 2+2y+1)2=706, y 4+4y 2+1﹣4y 3+2y 2﹣4y+y 4+4y 2+1+4y 3+2y 2+4y =706,整理,得:2y 4+12y 2﹣704=0(成功地消去了未知数的奇次项), 解得:y 2=16或y 2=﹣22(舍去)所以y =±4,即x+2=±4.所以x =2或x =﹣6. 【点睛】本题考查了解高次方程,求出均值把原方程换元求解是解题的关键.3.(1)223a 5ab 3b -+-;(2)mm 2-. 【解析】 【分析】()1根据多项式乘多项式、完全平方公式展开,然后再合并同类项即可; ()2括号内先通分进行分式的减法运算,然后再进行分式的除法运算即可.【详解】()()()21a b a 2b (2a b)-+--=2222a 2ab ab 2b 4a 4ab b +---+-223a 5ab 3b =-+-;(2)221m 4m 41m 1m m -+⎛⎫-÷ ⎪--⎝⎭ =()2m m 1m 2m 1(m 2)--⋅--mm 2=-. 【点睛】 本题考查了整式的混合运算、分式的混合运算,熟练掌握它们的运算法则是解题的关键.4.(1)证明见解析;(2)四边形AECF 是菱形.证明见解析. 【解析】 【分析】(1)根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′,AB=AD′,∠1=∠3,从而利用ASA 判定△ABE ≌△AD′F ;(2)四边形AECF 是菱形,我们可以运用菱形的判定,有一组邻边相等的平行四边形是菱形来进行验证. 【详解】解:(1)由折叠可知:∠D=∠D′,CD=AD′, ∠C=∠D′AE .∵四边形ABCD 是平行四边形, ∴∠B=∠D ,AB=CD ,∠C=∠BAD . ∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD , 即∠1+∠2=∠2+∠3. ∴∠1=∠3. 在△ABE 和△AD′F 中∵{13D B AB AD ∠'=∠='∠=∠ ∴△ABE ≌△AD′F (ASA ).(2)四边形AECF 是菱形.证明:由折叠可知:AE=EC ,∠4=∠5. ∵四边形ABCD 是平行四边形, ∴AD ∥BC . ∴∠5=∠6. ∴∠4=∠6. ∴AF=AE .∵AE=EC,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.又∵AF=AE,∴平行四边形AECF是菱形.考点:1.全等三角形的判定;2.菱形的判定.5.x=;(2)原分式方程中“?”代表的数是-1.(1)0【解析】【分析】(1)“?”当成5,解分式方程即可,(2)方程有增根是去分母时产生的,故先去分母,再将x=2代入即可解答.【详解】x-得(1)方程两边同时乘以()2()x+-=-5321x=解得0x=是原分式方程的解.经检验,0(2)设?为m,x-得方程两边同时乘以()2()+-=-321m xx=是原分式方程的增根,由于2x=代入上面的等式得所以把2()m+-=-3221m=-1所以,原分式方程中“?”代表的数是-1.【点睛】本题考查了分式方程解法和增根的定义及应用.增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.增根确定后可按如下步骤进行:①化分式方程为整式方程;②把增根代入整式方程即可求得相关字母的值.6.(1)25;(2)80,100,2000;(3)该产品的成本单价应不超过65元.【解析】分析:(1)根据题意和表格中的数据可以求得y关于x的函数解析式;(2)根据题意可以列出相应的方程,从而可以求得生产成本和w的最大值;(3)根据题意可以列出相应的不等式,从而可以取得科技创新后的成本.详解;(1)设y关于x的函数解析式为y=kx+b,8517595125k b k b +⎧⎨+⎩==,得5600k b ==-⎧⎨⎩, 即y 关于x 的函数解析式是y=-5x+600, 当x=115时,y=-5×115+600=25, 即m 的值是25; (2)设成本为a 元/个,当x=85时,875=175×(85-a ),得a=80,w=(-5x+600)(x-80)=-5x 2+1000x-48000=-5(x-100)2+2000, ∴当x=100时,w 取得最大值,此时w=2000, (3)设科技创新后成本为b 元, 当x=90时,(-5×90+600)(90-b )≥3750, 解得,b≤65,答:该产品的成本单价应不超过65元.点睛:本题考查二次函数的应用、一元二次方程的应用、不等式的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数和数形结合的思想解答.7.(1)200;(2)52;(3)840人;(4)16【解析】分析:(1)用较好的频数除以较好的频率.即可求出本次抽样调查的总人数; (2)用总人数乘以非常好的频率,求出非常好的频数,再用总人数减去其它频数即可求出m 的值;(3)利用总人数乘以对应的频率即可; (4)利用树状图方法,利用概率公式即可求解.详解:(1)本次抽样共调查的人数是:70÷0.35=200(人); (2)非常好的频数是:200×0.21=42(人), 一般的频数是:m=200﹣42﹣70﹣36=52(人),(3)该校学生整理错题集情况“非常好”和“较好”的学生一共约有:1500×(0.21+0.35)=840(人);(4)根据题意画图如下:∵所有可能出现的结果共12种情况,并且每种情况出现的可能性相等, 其中两次抽到的错题集都是“非常好”的情况有2种, ∴两次抽到的错题集都是“非常好”的概率是21=126. 点睛:此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.8.风筝距地面的高度49.9m.【解析】【分析】作AM⊥CD于M,作BF⊥AM于F,EH⊥AM于H.设AF=BF=x,则CM=BF=x,DM=HE=40-x,AH=x+30-1.5=x+28.5,在Rt△AHE中,利用∠AEH的正切列方程求解即可.【详解】如图,作AM⊥CD于M,作BF⊥AM于F,EH⊥AM于H.∵∠ABF=45°,∠AFB=90°,∴AF=BF,设AF=BF=x,则CM=BF=x,DM=HE=40-x,AH=x+30-1.5=x+28.5,在Rt△AHE中,tan67°=AH HE,∴1228.5 540xx+=-,解得x≈19.9 m.∴AM=19.9+30=49.9 m.∴风筝距地面的高度49.9 m.【点睛】本题考查了解直角三角形的应用,解决此问题的关键在于正确理解题意得基础上建立数学模型,把实际问题转化为数学问题.9.(1)12,32-;(2)证明见解析.【解析】试题分析:(1)根据一元二次方程根与系数的关系列方程组求解即可.(2)要证方程都有两个不相等的实数根,只要证明根的判别式大于0即可.试题解析:(1)设方程的另一根为x1,∵该方程的一个根为1,∴1111{211a x a x +=--⋅=.解得132{12x a =-=. ∴a 的值为12,该方程的另一根为32-.(2)∵()()222241248444240a a a a a a a ∆=-⋅⋅-=-+=-++=-+>, ∴不论a 取何实数,该方程都有两个不相等的实数根.考点:1.一元二次方程根与系数的关系;2. 一元二次方程根根的判别式;3.配方法的应用.10.(1)证明见解析;(2)2. 【解析】分析:(1)根据一组对边相等的平行四边形是菱形进行判定即可. (2)根据菱形的性质和勾股定理求出2OA ==.根据直角三角形斜边的中线等于斜边的一半即可求解. 详解:(1)证明:∵AB ∥CD , ∴CAB ACD ∠=∠ ∵AC 平分BAD ∠ ∴CAB CAD ∠=∠, ∴CAD ACD ∠=∠ ∴AD CD = 又∵AD AB = ∴AB CD = 又∵AB ∥CD ,∴四边形ABCD 是平行四边形 又∵AB AD = ∴ABCD 是菱形(2)解:∵四边形ABCD 是菱形,对角线AC 、BD 交于点O . ∴AC BD ⊥.12OA OC AC ==,12OB OD BD ==, ∴112OB BD ==. 在Rt AOB 中,90AOB ∠=︒.∴2OA =.∵CE AB ⊥, ∴90AEC ∠=︒.在Rt AEC 中,90AEC ∠=︒.O 为AC 中点.∴122OE AC OA===.点睛:本题考查了平行四边形的性质和判定,菱形的判定与性质,直角三角形的性质,勾股定理等,熟练掌握菱形的判定方法以及直角三角形斜边的中线等于斜边的一半是解题的关键.11.(1)y=26(2040)24(40)x xx x⎧⎨>⎩;(2)该经销商应购进草鱼25千克,乌鱼50千克,才能使进货费用最低,最低费用为1400元.【解析】【分析】【详解】(1)批发购进乌鱼所需总金额y(元)与进货量x(千克)之间的函数关系式y=26(2040) 24(40)x xx x⎧⎨>⎩;(2)设该经销商购进乌鱼x千克,则购进草鱼(75﹣x)千克,所需进货费用为w元.由题意得:4089%(75)95%93%75 xx x>⎧⎨⨯-+⨯⎩解得x≥50.由题意得w=8(75﹣x)+24x=16x+600.∵16>0,∴w的值随x的增大而增大.∴当x=50时,75﹣x=25,W最小=1400(元).答:该经销商应购进草鱼25千克,乌鱼50千克,才能使进货费用最低,最低费用为1400元.12.(1)见解析.【解析】【分析】(1)根据平行四边形的和菱形的判定证明即可;(2)根据含30°的直角三角形的性质和勾股定理以及菱形的面积解答即可.【详解】证明:(1)∵DE∥BC,DF∥AB,∴四边形BFDE是平行四边形,∵BD是△ABC的角平分线,∴∠EBD=∠DBF,∵DE∥BC,∴∠EDB=∠DBF,∴∠EBD=∠EDB,∴BE=ED ,∴平行四边形BFDE 是菱形; (2)连接EF ,交BD 于O ,∵∠BAC=90°,∠C=30°, ∴∠ABC=60°, ∵BD 平分∠ABC , ∴∠DBC=30°, ∴BD=DC=12, ∵DF ∥AB , ∴∠FDC=∠A=90°, ∴4333== 在Rt △DOF 中,()222243623DF OD -=-=∴菱形BFDE 的面积=12×EF •BD =12×12×33 【点评】此题考查了菱形的判定和性质,熟练掌握菱形的判定和性质是解题的关键.13.(1)10100y x =+;(2)商贸公司要想获利2090元,则这种干果每千克应降价9元. 【解析】 【分析】(1)根据图象可得:当2x =,120y =,当4x =,140y =;再用待定系数法求解即可;(2)根据这种干果每千克的利润×销售量=2090列出方程,解方程即可. 【详解】解:(1)设一次函数解析式为:y kx b =+,根据图象可知:当2x =,120y =;当4x =,140y =;∴21204140k b k b +=⎧⎨+=⎩,解得:10100k b =⎧⎨=⎩,∴y 与x 之间的函数关系式为10100y x =+; (2)由题意得:(6040)(10100)2090x x --+=,整理得:21090x x -+=,解得:11x =.29x =,∵让顾客得到更大的实惠,∴9x =.答:商贸公司要想获利2090元,这种干果每千克应降价9元.【点睛】本题考查了一元二次方程的应用和一次函数的应用,读懂图象信息、熟练掌握待定系数法、正确列出一元二次方程是解题的关键.14.(1)y 2与x 的函数关系式为y 2=-2x+200(1≤x<90);(2)W=22x 180x 2?000(1x 50),120?x 12?000(50x 90).⎧-++≤<⎨-+≤<⎩ (3)销售这种文化衫的第45天,销售利润最大,最大利润是6050元.【解析】【分析】(1)待定系数法分别求解可得;(2)根据:销售利润=(售价-成本)×销量,分1≤x <50、50≤x <90两种情况分别列函数关系式可得;(3)当1≤x <50时,将二次函数关系式配方后依据二次函数性质可得此时最值情况,当50≤x <90时,依据一次函数性质可得最值情况,比较后可得答案.【详解】(1)当1≤x<50时,设y 1=kx+b ,将(1,41),(50,90)代入,得k b 41,50k b 90,+=⎧⎨+=⎩解得k 1,b 40,=⎧⎨=⎩∴y 1=x+40,当50≤x<90时,y 1=90,故y 1与x 的函数解析式为y 1=x 40(1x 50),90(50x 90);+≤<⎧⎨≤<⎩ 设y 2与x 的函数解析式为y 2=mx+n(1≤x<90),将(50,100),(90,20)代入,得50m n 100,90m n 20,+=⎧⎨+=⎩解得:m 2,n 200,=-⎧⎨=⎩故y 2与x 的函数关系式为y 2=-2x+200(1≤x<90).(2)由(1)知,当1≤x<50时,W=(x+40-30)(-2x+200)=-2x 2+180x+2000;当50≤x<90时,W=(90-30)(-2x+200)=-120x+12000;综上,W=22x180x2?000(1x50), 120?x12?000(50x90).⎧-++≤<⎨-+≤<⎩(3)当1≤x<50时,∵W=-2x2+180x+2000=-2(x-45)2+6050,∴当x=45时,W取得最大值,最大值为6050元;当50≤x<90时,W=-120x+12000,∵-120<0,W随x的增大而减小,∴当x=50时,W取得最大值,最大值为6000元;综上,当x=45时,W取得最大值6050元.答:销售这种文化衫的第45天,销售利润最大,最大利润是6050元.15.49.【解析】【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次抽取的卡片上数字之和是奇数的情况,再利用概率公式即可求得答案即可.【详解】解:画树状图得:∵共有9种等可能的结果,两次抽取的卡片上数字之和是奇数的有4种情况,∴两次两次抽取的卡片上数字之和是奇数的概率为49.【点睛】本题考查列表法与树状图法.16.17.【整理数据】:7,4;【分析数据】(1)85,80;(2)40;(3)乙班的学生掌握垃圾分类相关知识的整体水平较好,见解析.【解析】【分析】由收集的数据即可得;(1)根据众数和中位数的定义求解可得;(2)用总人数乘以乙班样本中合格人数所占比例可得;(3)甲、乙两班的方差判定即可.【详解】解:乙班75.5~80.5分数段的学生数为7,80.5~85.5分数段的学生数为4,故a=7,b=4,故答案为:7,4;(1)68,72,89,85,82,85,74,92,80,85,78,85,69,76,80,众数是x=85,67,73,76,78,79,80,80,80,80,82,83,83,84,86,89,中位数是y=80,故答案为:85,80;(2)60×1015=40(人),即合格的学生有40人,故答案为:40;(3)乙班的学生掌握垃圾分类相关知识的整体水平较好,∵甲班的方差>乙班的方差,∴乙班的学生掌握垃圾分类相关知识的整体水平较好.【点睛】本题考查了频数分布直方图,众数,中位数,正确的理解题意是解题的关键.18.(1) 25 ; (2) 这组初赛成绩数据的平均数是1.61.;众数是1.65;中位数是1.60;(3)初赛成绩为1.65 m的运动员能进入复赛.【解析】【分析】【详解】试题分析:(1)、用整体1减去其它所占的百分比,即可求出a的值;(2)、根据平均数、众数和中位数的定义分别进行解答即可;(3)、根据中位数的意义可直接判断出能否进入复赛.试题解析:(1)、根据题意得:1﹣20%﹣10%﹣15%﹣30%=25%;则a的值是25;(2)、观察条形统计图得:1.502 1.554 1.605 1.656 1.70324563x⨯+⨯+⨯+⨯+⨯=++++=1.61;∵在这组数据中,1.65出现了6次,出现的次数最多,∴这组数据的众数是1.65;将这组数据从小到大排列为,其中处于中间的两个数都是1.60,则这组数据的中位数是1.60.(3)、能;∵共有20个人,中位数是第10、11个数的平均数,∴根据中位数可以判断出能否进入前9名;∵1.65m>1.60m,∴能进入复赛考点:(1)、众数;(2)、扇形统计图;(3)、条形统计图;(4)、加权平均数;(5)、中位数19.(1) )(6+x),(6−x),y=6(6−x)6+x,0⩽x⩽6;(2)见解析;(3)①y随着x的增大而减小;②图象关于直线y=x对称;③函数y的取值范围是0⩽y⩽6.【解析】【分析】(1)①利用线段的和差定义计算即可.②利用平行线分线段成比例定理解决问题即可.(2)①利用函数关系式计算即可.②描出点(0,6),(3,2)即可.③由平滑的曲线画出该函数的图象即可.(3)根据函数图象写出两个性质即可(答案不唯一).【详解】解:(1)①如图3中,由题意AC=OA=12AB=6(cm),∵CD=xcm,∴AD=(6+x)(cm),BD=12−(6+x)=(6−x)(cm),故答案为:(6+x),(6−x).②作BG⊥OF于G.∵OA⊥OF,BG⊥OF,∴BG//OA,∴BGOA =BDAD,∴y6=6−x6+x,∴y=36−6x6+x(0⩽x⩽6),故答案为:y=36−6x6+x,0⩽x⩽6.(2)①当x=3时,y=2,当x=0时,y=6,故答案为2,6.②点(0,6),点(3,2)如图所示.③函数图象如图所示.。
七年级上册北京第五十四中学数学期末试卷中考真题汇编[解析版]
![七年级上册北京第五十四中学数学期末试卷中考真题汇编[解析版]](https://img.taocdn.com/s3/m/305bf7d3caaedd3382c4d38a.png)
七年级上册北京第五十四中学数学期末试卷中考真题汇编[解析版]一、初一数学上学期期末试卷解答题压轴题精选(难)1.将一副三角板放在同一平面内,使直角顶点重合于点O(1)如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.(2)如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.(3)如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.【答案】(1)解:∵而同理:∴∴(2)解:∠AOD与∠BOC的大小关系为:∠AOB与∠DOC存在的数量关系为:(3)解:仍然成立.理由如下:∵又∵∴【解析】【分析】(1)先计算出再根据(2)根据(1)中得出的度数直接写出结论即可.(3)根据即可得到利用周角定义得∠AOB+∠COD+∠AOC+∠BOD=360°,而∠AOC=∠BOD=90°,即可得到∠AOB+∠DOC=180°.2.已知 (本题中的角均大于且小于 )(1)如图1,在内部作,若,求的度数;(2)如图2,在内部作,在内,在内,且,,,求的度数;(3)射线从的位置出发绕点顺时针以每秒的速度旋转,时间为秒( 且 ).射线平分,射线平分,射线平分 .若,则 ________秒.【答案】(1)解:∵∠AOD+∠BOC=∠AOC+∠COD+∠BOD+∠COD=∠AOB+∠COD又∵∠AOD+∠BOC=160°且∠AOB=120°∴(2)解:,设,则,则,(3) s或15s或30s或45s【解析】【解答】(2)解:当OI在直线OA的上方时,有∠MON=∠MOI+∠NOI= (∠AOI+∠BOI))= ∠AOB= ×120°=60°,∠PON= ×60°=30°,∵∠MOI=3∠POI,∴3t=3(30-3t)或3t=3(3t-30),解得t= 或15;当OI在直线AO的下方时,∠MON═(360°-∠AOB)═ ×240°=120°,∵∠MOI=3∠POI,∴180°-3t=3(60°- )或180°-3t=3( -60°),解得t=30或45,综上所述,满足条件的t的值为 s或15s或30s或45s【分析】(1)利用角的和差进行计算便可;(2)设,则,,通过角的和差列出方程解答便可;(3)分情况讨论,确定∠MON在不同情况下的定值,再根据角的和差确定t的不同方程进行解答便可.3.探究题:如图①,已知线段AB=14cm,点C为AB上的一个动点,点D、E分别是AC 和BC的中点.(1)若点C恰好是AB中点,则DE=________cm;(2)若AC=4cm,求DE的长;(3)试利用“字母代替数”的方法,设AC=a cm请说明不论a取何值(a不超过14cm),DE的长不变;(4)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE 分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.【答案】(1)7(2)解:∵AC=4cm ∴BC=AB-AC=10cm 又∵D为AC中点,E为BC中点∴CD=2cm,CE=5cm ∴DE=CD+CE=7cm.(3)解:∵AC=acm ∴BC=AB-AC=(14-a)cm 又∵D为AC中点,E为BC中点∴CD=cm,CE= cm ∴DE=CD+CE= +∴无论a取何值(不超过14)DE的长不变。
北京第五十四中学七年级下册数学期末试卷真题汇编[解析版]
![北京第五十四中学七年级下册数学期末试卷真题汇编[解析版]](https://img.taocdn.com/s3/m/e9b4b1cb0d22590102020740be1e650e52eacfed.png)
北京第五十四中学七年级下册数学期末试卷真题汇编[解析版]一、解答题1.已知//AB CD ,点E 在AB 与CD 之间.(1)图1中,试说明:BED ABE CDE ∠=∠+∠;(2)图2中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请利用(1)的结论说明:2BED BFD ∠=∠.(3)图3中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请直接写出BED ∠与BFD ∠之间的数量关系.2.已知:直线AB ∥CD ,M ,N 分别在直线AB ,CD 上,H 为平面内一点,连HM ,HN . (1)如图1,延长HN 至G ,∠BMH 和∠GND 的角平分线相交于点E .求证:2∠MEN ﹣∠MHN =180°;(2)如图2,∠BMH 和∠HND 的角平分线相交于点E . ①请直接写出∠MEN 与∠MHN 的数量关系: ;②作MP 平分∠AMH ,NQ ∥MP 交ME 的延长线于点Q ,若∠H =140°,求∠ENQ 的度数.(可直接运用①中的结论)3.阅读下面材料: 小亮同学遇到这样一个问题:已知:如图甲,AB //CD ,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED . 求证:∠BED =∠B +∠D .(1)小亮写出了该问题的证明,请你帮他把证明过程补充完整. 证明:过点E 作EF //AB , 则有∠BEF = . ∵AB //CD , ∴ // , ∴∠FED = .∴∠BED =∠BEF +∠FED =∠B +∠D .(2)请你参考小亮思考问题的方法,解决问题:如图乙,已知:直线a //b ,点A ,B 在直线a 上,点C ,D 在直线b 上,连接AD ,BC ,BE 平分∠ABC ,DE 平分∠ADC ,且BE ,DE 所在的直线交于点E .①如图1,当点B 在点A 的左侧时,若∠ABC =60°,∠ADC =70°,求∠BED 的度数; ②如图2,当点B 在点A 的右侧时,设∠ABC =α,∠ADC =β,请你求出∠BED 的度数(用含有α,β的式子表示).4.如图,已知直线//AB 射线CD ,110CEB ∠=︒.P 是射线EB 上一动点,过点P 作//PQ EC 交射线CD 于点Q ,连接CP .作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠.(1)若点P ,F ,G 都在点E 的右侧. ①求PCG ∠的度数;②若30EGC ECG ∠-∠=︒,求CPQ ∠的度数.(不能使用“三角形的内角和是180︒”直接解题)(2)在点P 的运动过程中,是否存在这样的偕形,使:3:2EGC EFC ∠∠=?若存在,直接写出CPQ ∠的度数;若不存在.请说明理由.5.如图,已知直线//AB 射线CD ,100CEB ∠=︒.P 是射线EB 上一动点,过点P 作PQ //EC 交射线CD 于点Q ,连接CP .作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠.(1)若点P ,F ,G 都在点E 的右侧,求PCG ∠的度数;(2)若点P ,F ,G 都在点E 的右侧,30EGC ECG ∠-∠=︒,求CPQ ∠的度数; (3)在点P 的运动过程中,是否存在这样的情形,使:4:3EGC EFC ∠∠=?若存在,求出CPQ ∠的度数;若不存在,请说明理由.二、解答题6.如图1,E 点在BC 上,A D ∠=∠.180ACB BED ∠+∠=︒.(1)求证://AB CD(2)如图2,//,AB CD BG 平分ABE ∠,与EDF ∠的平分线交于H 点,若DEB ∠比DHB ∠大60︒,求DEB ∠的度数.(3)保持(2)中所求的DEB ∠的度数不变,如图3,BM 平分,EBK DN ∠平分CDE ∠,作//BP DN ,则PBM ∠的度数是否改变?若不变,请直接写出答案;若改变,请说明理由.7.如图1所示:点E 为BC 上一点,∠A =∠D ,AB ∥CD (1)直接写出∠ACB 与∠BED 的数量关系;(2)如图2,AB ∥CD ,BG 平分∠ABE ,BG 的反向延长线与∠EDF 的平分线交于H 点,若∠DEB 比∠GHD 大60°,求∠DEB 的度数;(3)保持(2)中所求的∠DEB 的度数不变,如图3,BM 平分∠EBK ,DN 平分∠CDE ,作BP ∥DN ,则∠PBM 的度数是否改变?若不发生变化,请求它的度数,若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角).8.如图,已知//AB CD P ,是直线AB CD ,间的一点,PF CD ⊥于点F PE ,交AB 于点120E FPE ∠=︒,.(1)求AEP ∠的度数;(2)如图2,射线PN 从PF 出发,以每秒40︒的速度绕P 点按逆时针方向旋转,当PN 垂直AB 时,立刻按原速返回至PF 后停止运动:射线EM 从EA 出发,以每秒15︒的速度绕E 点按逆时针方向旋转至EB 后停止运动,若射线PN ,射线EM 同时开始运动,设运动间为t 秒.①当20MEP ∠=︒时,求EPN ∠的度数; ②当 //EM PN 时,求t 的值. 9.综合与探究综合与实践课上,同学们以“一个含30角的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线a ,b ,且//a b ,三角形ABC 是直角三角形,90BCA ∠=︒,30BAC ∠=︒,60ABC ∠=︒操作发现:(1)如图1.148∠=︒,求2∠的度数;(2)如图2.创新小组的同学把直线a 向上平移,并把2∠的位置改变,发现21120∠-∠=︒,请说明理由. 实践探究:(3)填密小组在创新小组发现的结论的基础上,将图2中的图形继续变化得到图3,AC 平分BAM ∠,此时发现1∠与2∠又存在新的数量关系,请写出1∠与2∠的数量关系并说明理由.10.如图,已知AM ∥BN ,∠A =64°.点P 是射线AM 上一动点(与点A 不重合),BC 、BD 分别平分∠ABP 和∠PBN ,分别交射线AM 于点C ,D .(1)①∠ABN 的度数是 ;②∵AM ∥BN ,∴∠ACB =∠ ; (2)求∠CBD 的度数;(3)当点P 运动时,∠APB 与∠ADB 之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律; (4)当点P 运动到使∠ACB =∠ABD 时,∠ABC 的度数是 .三、解答题11.如图,直线//AB CD ,E 、F 是AB 、CD 上的两点,直线l 与AB 、CD 分别交于点G 、H ,点P 是直线l 上的一个动点(不与点G 、H 重合),连接PE 、PF .(1)当点P 与点E 、F 在一直线上时,GEP EGP ∠=∠,60FHP ∠=︒,则PFD ∠=_____.(2)若点P 与点E 、F 不在一直线上,试探索AEP ∠、EPF ∠、CFP ∠之间的关系,并证明你的结论.12.Rt △ABC 中,∠C=90°,点D 、E 分别是△ABC 边AC 、BC 上的点,点P 是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P 在线段AB 上,如图(1)所示,且∠α=50°,则∠1+∠2= °;(2)若点P 在边AB 上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;(3)若点P 运动到边AB 的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P 运动到△ABC 形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: . 13.【问题探究】如图1,DF ∥CE ,∠PCE=∠α,∠PDF=∠β,猜想∠DPC 与α、β之间有何数量关系?并说明理由; 【问题迁移】如图2,DF ∥CE ,点P 在三角板AB 边上滑动,∠PCE=∠α,∠PDF=∠β. (1)当点P 在E 、F 两点之间运动时,如果α=30°,β=40°,则∠DPC= °.(2)如果点P 在E 、F 两点外侧运动时(点P 与点A 、B 、E 、F 四点不重合),写出∠DPC 与α、β之间的数量关系,并说明理由.(图1) (图2)14.在ABC 中,100BAC ∠=︒,A ABC CB =∠∠,点D 在直线BC 上运动(不与点B 、C 重合),点E 在射线AC 上运动,且ADE AED ∠=∠,设DAC n ∠=︒.(1)如图①,当点D 在边BC 上,且40n =︒时,则BAD ∠=__________︒,CDE ∠=__________︒;(2)如图②,当点D 运动到点B 的左侧时,其他条件不变,请猜想BAD ∠和CDE ∠的数量关系,并说明理由;(3)当点D 运动到点C 的右侧时,其他条件不变,BAD ∠和CDE ∠还满足(2)中的数量关系吗?请在图③中画出图形,并给予证明.(画图痕迹用黑色签字笔加粗加黑) 15.如果三角形的两个内角α与β满足290αβ+=︒,那么我们称这样的三角形是“准互余三角形”.(1)如图1,在Rt ABC 中,90ACB ∠=︒,BD 是ABC 的角平分线,求证:ABD △是“准互余三角形”;(2)关于“准互余三角形”,有下列说法:①在ABC 中,若100A ∠=︒,70B ∠=︒,10C ∠=︒,则ABC 是“准互余三角形”; ②若ABC 是“准互余三角形”,90C ∠>︒,60A ∠=︒,则20B ∠=︒; ③“准互余三角形”一定是钝角三角形.其中正确的结论是___________(填写所有正确说法的序号);(3)如图2,B ,C 为直线l 上两点,点A 在直线l 外,且50ABC ∠=︒.若P 是直线l 上一点,且ABP △是“准互余三角形”,请直接写出APB ∠的度数.【参考答案】一、解答题1.(1)说明过程请看解答;(2)说明过程请看解答;(3)∠BED=360°-2∠BFD . 【分析】(1)图1中,过点E 作EG ∥AB ,则∠BEG=∠ABE ,根据AB ∥CD ,EG ∥AB ,所以CD ∥EG ,解析:(1)说明过程请看解答;(2)说明过程请看解答;(3)∠BED =360°-2∠BFD . 【分析】(1)图1中,过点E 作EG ∥AB ,则∠BEG =∠ABE ,根据AB ∥CD ,EG ∥AB ,所以CD ∥EG ,所以∠DEG =∠CDE ,进而可得∠BED =∠ABE +∠CDE ;(2)图2中,根据∠ABE 的平分线与∠CDE 的平分线相交于点F ,结合(1)的结论即可说明:∠BED =2∠BFD ;(3)图3中,根据∠ABE 的平分线与∠CDE 的平分线相交于点F ,过点E 作EG ∥AB ,则∠BEG +∠ABE =180°,因为AB ∥CD ,EG ∥AB ,所以CD ∥EG ,所以∠DEG +∠CDE =180°,再结合(1)的结论即可说明∠BED 与∠BFD 之间的数量关系. 【详解】解:(1)如图1中,过点E 作EG ∥AB , 则∠BEG =∠ABE ,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG=∠CDE,所以∠BEG+∠DEG=∠ABE+∠CDE,即∠BED=∠ABE+∠CDE;(2)图2中,因为BF平分∠ABE,所以∠ABE=2∠ABF,因为DF平分∠CDE,所以∠CDE=2∠CDF,所以∠ABE+∠CDE=2∠ABF+2∠CDF=2(∠ABF+∠CDF),由(1)得:因为AB∥CD,所以∠BED=∠ABE+∠CDE,∠BFD=∠ABF+∠CDF,所以∠BED=2∠BFD.(3)∠BED=360°-2∠BFD.图3中,过点E作EG∥AB,则∠BEG+∠ABE=180°,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG+∠CDE=180°,所以∠BEG+∠DEG=360°-(∠ABE+∠CDE),即∠BED=360°-(∠ABE+∠CDE),因为BF平分∠ABE,所以∠ABE=2∠ABF,因为DF平分∠CDE,所以∠CDE=2∠CDF,∠BED=360°-2(∠ABF+∠CDF),由(1)得:因为AB∥CD,所以∠BFD=∠ABF+∠CDF,所以∠BED=360°-2∠BFD.【点睛】本题考查了平行线的性质,解决本题的关键是掌握平行线的性质.2.(1)见解析;(2)①2∠MEN+∠MHN=360°;②20°【分析】(1)过点E作EP∥AB交MH于点Q,利用平行线的性质、角平分线性质、邻补角和为180°,角与角之间的基本运算、等量代换等即解析:(1)见解析;(2)①2∠MEN+∠MHN=360°;②20°【分析】(1)过点E作EP∥AB交MH于点Q,利用平行线的性质、角平分线性质、邻补角和为180°,角与角之间的基本运算、等量代换等即可得证.(2)①过点H作GI∥AB,利用(1)中结论2∠MEN﹣∠MHN=180°,利用平行线的性质、角平分线性质、邻补角和为180°,角与角之间的基本运算、等量代换等得出∠AMH+∠HNC=360°﹣(∠BMH+∠HND),进而用等量代换得出2∠MEN+∠MHN=360°.②过点H作HT∥MP,由①的结论得2∠MEN+∠MHN=360°,∠H=140°,∠MEN=110°.利用平行线性质得∠ENQ+∠ENH+∠NHT=180°,由角平分线性质及邻补角可得∠ENQ+∠ENH+140°﹣12(180°﹣∠BMH)=180°.继续使用等量代换可得∠ENQ度数.【详解】解:(1)证明:过点E作EP∥AB交MH于点Q.如答图1∵EP∥AB且ME平分∠BMH,∴∠MEQ=∠BME=12∠BMH.∵EP∥AB,AB∥CD,∴EP∥CD,又NE平分∠GND,∴∠QEN=∠DNE=12∠GND.(两直线平行,内错角相等)∴∠MEN=∠MEQ+∠QEN=12∠BMH+12∠GND=12(∠BMH+∠GND).∴2∠MEN=∠BMH+∠GND.∵∠GND+∠DNH=180°,∠DNH+∠MHN=∠MON=∠BMH.∴∠DHN=∠BMH﹣∠MHN.∴∠GND+∠BMH﹣∠MHN=180°,即2∠MEN﹣∠MHN=180°.(2)①:过点H作GI∥AB.如答图2由(1)可得∠MEN=12(∠BMH+∠HND),由图可知∠MHN=∠MHI+∠NHI,∵GI∥AB,∴∠AMH=∠MHI=180°﹣∠BMH,∵GI∥AB,AB∥CD,∴GI∥CD.∴∠HNC=∠NHI=180°﹣∠HND.∴∠AMH+∠HNC=180°﹣∠BMH+180°﹣∠HND=360°﹣(∠BMH+∠HND).又∵∠AMH+∠HNC=∠MHI+∠NHI=∠MHN,∴∠BMH+∠HND=360°﹣∠MHN.即2∠MEN+∠MHN=360°.故答案为:2∠MEN+∠MHN=360°.②:由①的结论得2∠MEN+∠MHN=360°,∵∠H=∠MHN=140°,∴2∠MEN=360°﹣140°=220°.∴∠MEN=110°.过点H作HT∥MP.如答图2∵MP∥NQ,∴HT∥NQ.∴∠ENQ+∠ENH+∠NHT=180°(两直线平行,同旁内角互补).∵MP平分∠AMH,∴∠PMH=12∠AMH=12(180°﹣∠BMH).∵∠NHT=∠MHN﹣∠MHT=140°﹣∠PMH.∴∠ENQ+∠ENH+140°﹣12(180°﹣∠BMH)=180°.∵∠ENH=12∠HND.∴∠ENQ+12∠HND+140°﹣90°+12∠BMH=180°.∴∠ENQ+12(HND+∠BMH)=130°.∴∠ENQ+12∠MEN=130°.∴∠ENQ=130°﹣110°=20°.【点睛】本题考查了平行线的性质,角平分线的性质,邻补角,等量代换,角之间的数量关系运算,辅助线的作法,正确作出辅助线是解题的关键,本题综合性较强.3.(1)∠B,EF,CD,∠D;(2)①65°;②180°﹣【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图1,过点E作EF∥AB,当点B在点A的左侧时,根据∠ABC=60°,解析:(1)∠B,EF,CD,∠D;(2)①65°;②180°﹣11 22 aβ+【分析】(1)根据平行线的判定定理与性质定理解答即可;(2)①如图1,过点E作EF∥AB,当点B在点A的左侧时,根据∠ABC=60°,∠ADC=70°,参考小亮思考问题的方法即可求∠BED的度数;②如图2,过点E作EF∥AB,当点B在点A的右侧时,∠ABC=α,∠ADC=β,参考小亮思考问题的方法即可求出∠BED的度数.【详解】解:(1)过点E作EF∥AB,则有∠BEF=∠B,∵AB∥CD,∴EF∥CD,∴∠FED=∠D,∴∠BED=∠BEF+∠FED=∠B+∠D;故答案为:∠B;EF;CD;∠D;(2)①如图1,过点E作EF∥AB,有∠BEF=∠EBA.∵AB∥CD,∴EF∥CD.∴∠FED=∠EDC.∴∠BEF+∠FED=∠EBA+∠EDC.即∠BED=∠EBA+∠EDC,∵BE平分∠ABC,DE平分∠ADC,∴∠EBA=12∠ABC=30°,∠EDC=12∠ADC=35°,∴∠BED=∠EBA+∠EDC=65°.答:∠BED 的度数为65°;②如图2,过点E 作EF ∥AB ,有∠BEF +∠EBA =180°.∴∠BEF =180°﹣∠EBA ,∵AB ∥CD ,∴EF ∥CD .∴∠FED =∠EDC .∴∠BEF +∠FED =180°﹣∠EBA +∠EDC .即∠BED =180°﹣∠EBA +∠EDC ,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =12α,∠EDC =12∠ADC =12β, ∴∠BED =180°﹣∠EBA +∠EDC =180°﹣1122a β+. 答:∠BED 的度数为180°﹣1122a β+. 【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质. 4.(1)①35°;(2)55°;(2)存在,或【分析】(1)①依据平行线的性质以及角平分线的定义,即可得到∠PCG 的度数; ②依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=20° 解析:(1)①35°;(2)55°;(2)存在,52.5︒或7.5︒【分析】(1)①依据平行线的性质以及角平分线的定义,即可得到∠PCG 的度数;②依据平行线的性质以及角平分线的定义,即可得到∠ECG =∠GCF =20°,再根据PQ ∥CE ,即可得出∠CPQ =∠ECP =60°;(2)设∠EGC =3x ,∠EFC =2x ,则∠GCF =3x -2x =x ,分两种情况讨论:①当点G 、F 在点E 的右侧时,②当点G 、F 在点E 的左侧时,依据等量关系列方程求解即可.【详解】解:(1)①∵AB ∥CD ,∴∠CEB +∠ECQ =180°,∵∠CEB =110°,∴∠ECQ =70°,∵∠PCF =∠PCQ ,CG 平分∠ECF ,∴∠PCG=∠PCF+∠FCG=12∠QCF+12∠FCE=12∠ECQ=35°;②∵AB∥CD,∴∠QCG=∠EGC,∵∠QCG+∠ECG=∠ECQ=70°,∴∠EGC+∠ECG=70°,又∵∠EGC-∠ECG=30°,∴∠EGC=50°,∠ECG=20°,∴∠ECG=∠GCF=20°,∠PCF=∠PCQ=12(70°−40°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=∠ECQ-∠PCQ=70°-15°=55°.(2)52.5°或7.5°,设∠EGC=3x°,∠EFC=2x°,①当点G、F在点E的右侧时,∵AB∥CD,∴∠QCG=∠EGC=3x°,∠QCF=∠EFC=2x°,则∠GCF=∠QCG-∠QCF=3x°-2x°=x°,∴∠PCF=∠PCQ=12∠FCQ=12∠EFC=x°,则∠ECG=∠GCF=∠PCF=∠PCD=x°,∵∠ECD=70°,∴4x=70°,解得x=17.5°,∴∠CPQ=3x=52.5°;②当点G、F在点E的左侧时,反向延长CD到H,∵∠EGC=3x°,∠EFC=2x°,∴∠GCH=∠EGC=3x°,∠FCH=∠EFC=2x°,∴∠ECG=∠GCF=∠GCH-∠FCH=x°,∵∠CGF=180°-3x°,∠GCQ=70°+x°,∴180-3x=70+x,解得x=27.5,∴∠FCQ=∠ECF+∠ECQ=27.5°×2+70°=125°,∴∠PCQ=12∠FCQ=62.5°,∴∠CPQ=∠ECP=62.5°-55°=7.5°,【点睛】本题主要考查了平行线的性质,掌握两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.5.(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠G解析:(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=25°,再根据PQ∥CE,即可得出∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=4x-3x=x,分两种情况讨论:①当点G、F在点E 的右侧时,②当点G、F在点E的左侧时,依据等量关系列方程求解即可.【详解】解:(1)∵∠CEB=100°,AB∥CD,∴∠ECQ=80°,∵∠PCF=∠PCQ,CG平分∠ECF,∴∠PCG=∠PCF+∠FCG=12∠QCF+12∠FCE=12∠ECQ=40°;(2)∵AB∥CD∴∠QCG=∠EGC,∠QCG+∠ECG=∠ECQ=80°,∴∠EGC+∠ECG=80°,又∵∠EGC-∠ECG=30°,∴∠EGC=55°,∠ECG=25°,∴∠ECG=∠GCF=25°,∠PCF=∠PCQ=12(80°-50°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=∠FCD=4x-3x=x,①当点G、F在点E的右侧时,则∠ECG=x,∠PCF=∠PCD=32 x,∵∠ECD=80°,∴x +x +32x +32x =80°, 解得x =16°,∴∠CPQ=∠ECP =x +x +32x =56°; ②当点G 、F 在点E 的左侧时,则∠ECG =∠GCF =x ,∵∠CGF =180°-4x ,∠GCQ =80°+x ,∴180°-4x =80°+x ,解得x =20°,∴∠FCQ =∠ECF +∠ECQ =40°+80°=120°,∴∠PCQ =12∠FCQ =60°,∴∠CPQ =∠ECP =80°-60°=20°.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等. 二、解答题6.(1)见解析;(2)100°;(3)不变,40°【分析】(1)如图1,延长交于点,根据,,可得,所以,可得,又,进而可得结论; (2)如图2,作,,根据,可得,根据平行线的性质得角之间的关系,再 解析:(1)见解析;(2)100°;(3)不变,40°【分析】(1)如图1,延长DE 交AB 于点F ,根据180ACB BED ∠+∠=︒,180CED BED ∠+∠=︒,可得ACB CED ∠=∠,所以//AC DF ,可得A DFB ∠=∠,又A D ∠=∠,进而可得结论; (2)如图2,作//EM CD ,//HN CD ,根据//AB CD ,可得//////AB EM HN CD ,根据平行线的性质得角之间的关系,再根据DEB ∠比DHB ∠大60︒,列出等式即可求DEB ∠的度数;(3)如图3,过点E 作//ES CD ,设直线DF 和直线BP 相交于点G ,根据平行线的性质和角平分线定义可求PBM ∠的度数.【详解】解:(1)证明:如图1,延长DE 交AB 于点F ,180ACB BED ∠+∠=︒,180CED BED ∠+∠=︒,ACB CED ∴∠=∠,//AC DF ∴,A DFB ∴∠=∠,A D ∠=∠,DFB D ∴∠=∠,//AB CD ∴;(2)如图2,作//EM CD ,//HN CD ,//AB CD ,//////AB EM HN CD ∴,1180EDF ∴∠+∠=︒,MEB ABE ∠=∠, BG 平分ABE ∠,12ABG ABE ∴∠=∠, //AB HN ,2ABG ∴∠=∠,//CF HN ,23β∴∠+∠=∠, ∴132ABE β∠+∠=∠, DH 平分EDF ∠,132EDF ∴∠=∠, ∴1122ABE EDF β∠+∠=∠,1()2EDF ABE β∴∠=∠-∠, 2EDF ABE β∴∠-∠=∠,设DEB α∠=∠,1180180()1802MEB EDF ABE EDF ABE αβ∠=∠+∠=︒-∠+∠=︒-∠-∠=︒-∠,DEB ∠比DHB ∠大60︒,60αβ∴∠-︒=∠,1802(60)αα∴∠=︒-∠-︒解得100α∠=︒DEB ∴∠的度数为100︒;(3)PBM ∠的度数不变,理由如下:如图3,过点E 作//ES CD ,设直线DF 和直线BP 相交于点G ,BM 平分EBK ∠,DN 平分CDE ∠,12EBM MBK EBK ∴∠=∠=∠, 12CDN EDN CDE ∠=∠=∠, //ES CD ,//AB CD ,////ES AB CD ∴,DES CDE ∴∠=∠,180BES ABE EBK ∠=∠=︒-∠,G PBK ∠=∠,由(2)可知:100DEB ∠=︒,180100CDE EBK ∴∠+︒-∠=︒,80EBK CDE ∴∠-∠=︒,//BP DN ,CDN G ∴∠=∠,12PBK G CDN CDE ∴∠=∠=∠=∠, PBM MBK PBK ∴∠=∠-∠1122EBK CDE =∠-∠ 1()2EBK CDE =∠-∠ 1802=⨯︒ 40=︒.【点睛】本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质. 7.(1) ;(2) ;(3)不发生变化,理由见解析【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出;(2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥E 解析:(1) +180ACB BED ∠∠=︒;(2) 100︒;(3)不发生变化,理由见解析【分析】(1)如图1,延长DE 交AB 于点F ,根据平行线的性质推出+180ACB BED ∠∠=︒;(2)如图2,过点E 作ES ∥AB ,过点H 作HT ∥AB ,根据AB ∥CD ,AB ∥ES 推出BED ABE CDE ∠=∠+∠,再根据AB ∥TH ,AB ∥CD 推出GHD THD THB ∠=∠-∠,最后根据BED ∠比BHD ∠大60︒得出BED ∠的度数;(3)如图3,过点E 作EQ ∥DN ,根据DEB CDE ABE ∠=∠+∠得出βα-的度数,根据条件再逐步求出PBM ∠的度数.【详解】(1)如答图1所示,延长DE 交AB 于点F .AB ∥CD ,所以D EFB ∠=∠,又因为A D ∠=∠,所以A EFB ∠=∠,所以AC ∥DF ,所以ACB CED ∠=∠.因为+180CED BED ∠∠=︒,所以+180ACB BED ∠∠=︒.(2)如答图2所示,过点E 作ES ∥AB ,过点H 作HT ∥AB .设ABG EBG α∠=∠=,FDH EDH β∠=∠=,因为AB ∥CD ,AB ∥ES ,所以ABE BES ∠=∠,SED CED ∠=∠,所以21802BED BES SED ABE CDE αβ∠=∠+∠=∠+∠=+︒-,因为AB ∥TH ,AB ∥CD ,所以ABG THB ∠=∠,FDH DHT ∠=∠,所以GHD THD THB βα∠=∠-∠=-,因为BED ∠比BHD ∠大60︒,所以2+1802()60αββα︒---=︒,所以40βα-=︒,所以40BHD ∠=︒,所以100BED ∠=︒(3)不发生变化如答图3所示,过点E 作EQ ∥DN .设CDN EDN α∠=∠=,EBM KBM β∠=∠=,由(2)易知DEB CDE ABE ∠=∠+∠,所以2+1802100αβ︒-=︒,所以40βα-=︒, 所以180()180DEB CDE EDN EBM PBM PBM αβ∠=∠+∠+︒-∠+∠=+︒--∠, 所以80()40PBM βα∠=︒--=︒.【点睛】本题考查了平行线的性质,求角的度数,正确作出相关的辅助线,根据条件逐步求出角度的度数是解题的关键.8.(1);(2)①或;②秒或或秒【分析】(1)通过延长作辅助线,根据平行线的性质,得到,再根据外角的性质可计算得到结果;(2)①当时,分两种情况,Ⅰ当在和之间,Ⅱ当在和之间,由,计算出的运动时间解析:(1)30;(2)①2803︒或403︒;②185秒或5411或9011秒 【分析】(1)通过延长PG 作辅助线,根据平行线的性质,得到90∠=︒PGE ,再根据外角的性质可计算得到结果;(2)①当20MEP ∠=︒时,分两种情况,Ⅰ当ME 在AE 和EP 之间,Ⅱ当ME 在EP 和EB 之间,由20MEP ∠=︒,计算出EM 的运动时间t ,根据运动时间可计算出FPN ∠,由已知120FPE ∠=︒可计算出EPN ∠的度数; ②根据题意可知,当//EM PN 时,分三种情况,Ⅰ射线PN 由PF 逆时针转动,//EM PN ,根据题意可知15AEM t ∠=︒,40FPN t ∠=︒,再平行线的性质可得AEM AHP ∠=∠,再根据三角形外角和定理可列等量关系,求解即可得出结论;Ⅱ射线PN 垂直AB 时,再顺时针向PF 运动时,//EM PN ,根据题意可知,15AEM t ∠=︒,//ME PN ,15GHP t ∠=︒,可计算射线PN 的转动度数1809015t ︒+︒-︒,再根据PN 转动可列等量关系,即可求出答案;Ⅲ射线PN 垂直AB 时,再顺时针向PF 运动时,//EM PN ,根据题意可知,15AEM t ∠=︒,940()2GPN t ∠=-︒,根据(1)中结论,30PEG ∠=︒,60PGE ∠=,可计算出PEM ∠与EPN ∠代数式,再根据平行线的性质,可列等量关系,求解可得出结论.【详解】解:(1)延长FP 与AB 相交于点G ,如图1,PF CD ⊥,90PFD PGE ∴∠=∠=︒,EPF PGE AEP ∠=∠+∠,1209030AEP EPF PGE ∴∠=∠-∠=︒-︒=︒;(2)①Ⅰ如图2,30AEP ∠=︒,20MEP ∠=︒,10AEM ∴∠=︒,∴射线ME 运动的时间102153t ==(秒), ∴射线PN 旋转的角度2804033FPN ︒∠=⨯︒=, 又120EPF ∠=︒,8028012033EPN EPF EPN ︒︒∴∠=∠-∠=︒-=;Ⅱ如图3所示,30AEP ∠=︒,20MEP ∠=︒, 50AEM ∴∠=︒,∴射线ME 运动的时间5010153t ==(秒), ∴射线PN 旋转的角度104004033FPN ︒∠=⨯︒=, 又120EPF ∠=︒,4004012033EPN FPN EPF ︒︒∴∠=∠-∠=-︒=; EPN ∴∠的度数为2803︒或403︒;②Ⅰ当PN 由PF 运动如图4时//EM PN , PN 与AB 相交于点H ,根据题意可知,经过t 秒, 15AEM t ∠=︒,40FPN t ∠=︒, //EM PN ,15AEM AHP t ∴∠=∠=︒,又=FPN PGH PHA ∠∠+∠, 409015t t ∴︒=︒+︒,解得185t =(秒);Ⅱ当PN 运动到PG ,再由PG 运动到如图5时//EM PN ,PN 与AB 相交于点H ,根据题意可知,经过t 秒,15AEM t ∠=︒,//EM PN ,15GHP t ∴∠=︒,9015GPH t ∠=︒-︒,PN ∴运动的度数可得,18040GPH t ︒+∠=︒,解得5411t =;Ⅲ当PN 由PG 运动如图6时,//EM PN ,根据题意可知,经过t 秒,15AEM t ∠=︒,40180GPN t ∠=-︒,30AEP ∠=︒,60EPG ∠=︒,1530PEM t ∴∠=︒-︒,24040EPN t ∠=︒-,又//EM PN ,180PEM EPN ∴∠+∠=︒,153040240180t t ∴︒-︒+-︒=︒,解得9011t =(秒), 当t 的值为185秒或5411或9011秒时,//EM PN .【点睛】本题主要考查平行线性质,合理添加辅助线和根据题意画出相应的图形时解决本题的关键.9.(1);(2)理由见解析;(3),理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠ 解析:(1)242∠=︒;(2)理由见解析;(3)12∠=∠,理由见解析.【分析】(1)由平角定义求出∠3=42°,再由平行线的性质即可得出答案;(2)过点B 作BD ∥a .由平行线的性质得∠2+∠ABD =180°,∠1=∠DBC ,则∠ABD =∠ABC−∠DBC =60°−∠1,进而得出结论;(3)过点C 作CP ∥a ,由角平分线定义得∠CAM =∠BAC =30°,∠BAM =2∠BAC =60°,由平行线的性质得∠1=∠BAM =60°,∠PCA =∠CAM =30°,∠2=∠BCP =60°,即可得出结论.【详解】解:(1)如图1 148∠=︒,90BCA ∠=︒,3180142BCA ∴∠=︒-∠-∠=︒,//a b ,2342∴∠=∠=︒;图1(2)理由如下:如图2. 过点B 作//BD a ,图22180ABD ∴∠+∠=︒,//a b ,//b BD ∴,1∴∠=∠DBC ,601ABD ABC DBC ∴∠=∠-∠=︒-∠,2601180∴∠+︒-∠=︒,21120∴∠-∠=︒;(3)12∠=∠,图3理由如下:如图3,过点C 作//CP a , AC 平分BAM ∠,30CAM BAC ∴∠=∠=︒,260BAM BAC ∠=∠=︒,又//a b ,//CP b ∴,160BAM ∠=∠=︒,30PCA CAM ∴∠=∠=︒,903060BCP BCA PCA ∴∠=∠-∠=︒-︒=︒,又//CP a ,260BCP ∴∠=∠=︒,12∠∠∴=.【点睛】本题是三角形综合题目,考查了平移的性质、直角三角形的性质、平行线的判定与性质、角平分线定义、平角的定义等知识;本题综合性强,熟练掌握平移的性质和平行线的性质是解题的关键.10.(1)① ②;(2);(3)不变,,理由见解析;(4)【分析】(1)①由平行线的性质,两直线平行,同旁内角互补可直接求出;②由平行线的性质,两直线平行,内错角相等可直接写出;(2)由角平分线的解析:(1)①116,︒②CBN;(2)58︒;(3)不变,:2:1∠∠=,理由见解析;APB ADB(4)29.︒【分析】(1)①由平行线的性质,两直线平行,同旁内角互补可直接求出;②由平行线的性质,两直线平行,内错角相等可直接写出;∠ABN,即可求出结果;(2)由角平分线的定义可以证明∠CBD=12(3)不变,∠APB:∠ADB=2:1,证∠APB=∠PBN,∠PBN=2∠DBN,即可推出结论;(4)可先证明∠ABC=∠DBN,由(1)∠ABN=116°,可推出∠CBD=58°,所以∠ABC+∠DBN=58°,则可求出∠ABC的度数.【详解】解:(1)①∵AM//BN,∠A=64°,∴∠ABN=180°﹣∠A=116°,故答案为:116°;②∵AM//BN,∴∠ACB=∠CBN,故答案为:CBN;(2)∵AM//BN,∴∠ABN+∠A=180°,∴∠ABN=180°﹣64°=116°,∴∠ABP+∠PBN=116°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=116°,∴∠CBD=∠CBP+∠DBP=58°;(3)不变,∠APB:∠ADB=2:1,∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM//BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN∴∠ABC=∠DBN,由(1)∠ABN=116°,∴∠CBD=58°,∴∠ABC+∠DBN=58°,∴∠ABC=29°,故答案为:29°.【点睛】本题考查了角平分线的定义,平行线的性质等,解题关键是能熟练运用平行线的性质并能灵活运用角平分线的定义等.三、解答题11.(1)120°;(2)∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP,证明见详解.【分析】(1)根据题意,当点与点、在一直线上时,作出图形,由AB∥CD,∠FHP=60°,可以推出解析:(1)120°;(2)∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP,证明见详解.【分析】(1)根据题意,当点P与点E、F在一直线上时,作出图形,由AB∥CD,∠FHP=60°,可∠=∠=60°,计算∠PFD即可;以推出GEP EGP(2)根据点P是动点,分三种情况讨论:①当点P在AB与CD之间时;②当点P在AB 上方时;③当点P在CD下方时,分别求出∠AEP、∠EPF、∠CFP之间的关系即可.【详解】(1)当点P与点E、F在一直线上时,作图如下,∠=∠,∵AB∥CD,∠FHP=60°,GEP EGP∠=∠=∠FHP=60°,∴GEP EGP∴∠EFD=180°-∠GEP=180°-60°=120°,∴∠PFD=120°,故答案为:120°;(2)满足关系式为∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP.证明:根据点P是动点,分三种情况讨论:①当点P在AB与CD之间时,过点P作PQ∥AB,如下图,∵AB∥CD,∴PQ∥AB∥CD,∴∠AEP=∠EPQ,∠CFP=∠FPQ,∴∠EPF=∠EPQ+∠FPQ=∠AEP+∠CFP,即∠EPF =∠AEP+∠CFP;②当点P在AB上方时,如下图所示,∵∠AEP=∠EPF+∠EQP,∵AB∥CD,∴∠CFP=∠EQP,∴∠AEP=∠EPF+∠CFP;③当点P在CD下方时,∵AB∥CD,∴∠AEP=∠EQF,∴∠EQF=∠EPF+∠CFP,∴∠AEP=∠EPF+∠CFP,综上所述,∠AEP、∠EPF、∠CFP之间满足的关系式为:∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP,故答案为:∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP.【点睛】本题考查了平行线的性质,外角的性质,掌握平行线的性质是解题的关键,注意分情况讨论问题.12.(1)140°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α.【详解】试题分析:(1)根据四边形内角和定理以及邻补角的定义,得出∠1+∠2解析:(1)140°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α.【详解】试题分析:(1)根据四边形内角和定理以及邻补角的定义,得出∠1+∠2=∠C+∠α,进而得出即可;(2)利用(1)中所求的结论得出∠α、∠1、∠2之间的关系即可;(3)利用三角外角的性质,得出∠1=∠C+∠2+α=90°+∠2+α;(4)利用三角形内角和定理以及邻补角的性质可得出∠α、∠1、∠2之间的关系.试题分析:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°,故答案为140;(2)由(1)得∠α+∠C=∠1+∠2,∴∠1+∠2=90°+∠α.故答案为∠1+∠2=90°+∠α.(3)∠1=90°+∠2+∠α.理由如下:如图③,设DP与BE的交点为M,∵∠2+∠α=∠DME,∠DME+∠C=∠1,∴∠1=∠C+∠2+∠α=90°+∠2+∠α.(4)如图④,设PE与AC的交点为F,∵∠PFD=∠EFC,∴180°-∠PFD=180°-∠EFC,∴∠α+180°-∠1=∠C+180°-∠2,∴∠2=90°+∠1-∠α.故答案为∠2=90°+∠1-∠α点睛:本题考查了三角形内角和定理和外角的性质、对顶角相等的性质,熟练掌握三角形外角的性质是解决问题的关键.13.∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析.【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠C解析:∠DPC=α+β,理由见解析;(1)70 ;(2) ∠DPC=α –β,理由见解析.【解析】(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(2)化成图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【问题探究】解:∠DPC=α+β如图,过P作PH∥DF∵DF∥CE,∴∠PCE=∠1=α,∠PDF=∠2∵∠DPC=∠2+∠1=α+β【问题迁移】(1)70(图1)(图2)(2) 如图1,∠DPC=β -α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1-∠FDP=∠1-α.∴∠DPC=β -α如图2,∠DPC= α -β∵DF∥CE,∴∠PDF=∠1=α∵∠DPC=∠1-∠ACE=∠1-β.∴∠DPC=α - β14.(1)60,30;(2)∠BAD=2∠CDE,证明见解析;(3)成立,∠BAD=2∠CDE,证明见解析【分析】(1)如图①,将∠BAC=100°,∠DAC=40°代入∠BAD=∠BAC-∠DAC解析:(1)60,30;(2)∠BAD=2∠CDE,证明见解析;(3)成立,∠BAD=2∠CDE,证明见解析【分析】(1)如图①,将∠BAC=100°,∠DAC=40°代入∠BAD=∠BAC-∠DAC,求出∠BAD.在△ABC 中利用三角形内角和定理求出∠ABC=∠ACB=40°,根据三角形外角的性质得出∠ADC=∠ABC+∠BAD=100°,在△ADE中利用三角形内角和定理求出∠ADE=∠AED=70°,那么∠CDE=∠ADC-∠ADE=30°;(2)如图②,在△ABC和△ADE中利用三角形内角和定理求出∠ABC=∠ACB=40°,∠ADE=∠AED=1802n︒-.根据三角形外角的性质得出∠CDE=∠ACB-∠AED=1002n-︒,再由∠BAD=∠DAC-∠BAC得到∠BAD=n-100°,从而得出结论∠BAD=2∠CDE;(3)如图③,在△ABC和△ADE中利用三角形内角和定理求出∠ABC=∠ACB=40°,∠ADE=∠AED=1802n︒-.根据三角形外角的性质得出∠CDE=∠ACD-∠AED=1002n︒+,再由∠BAD=∠BAC+∠DAC得到∠BAD=100°+n,从而得出结论∠BAD=2∠CDE.【详解】解:(1)∠BAD=∠BAC-∠DAC=100°-40°=60°.∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,∴∠ABC=∠ACB=40°,∴∠ADC=∠ABC+∠BAD=40°+60°=100°.∵∠DAC=40°,∠ADE=∠AED,∴∠ADE=∠AED=70°,∴∠CDE=∠ADC-∠ADE=100°-70°=30°.故答案为60,30.(2)∠BAD=2∠CDE,理由如下:如图②,在△ABC中,∠BAC=100°,∴∠ABC=∠ACB=40°.在△ADE中,∠DAC=n,∴∠ADE=∠AED=1802n︒-,∵∠ACB=∠CDE+∠AED,∴∠CDE=∠ACB-∠AED=40°-1802n︒-=1002n-︒,∵∠BAC=100°,∠DAC=n,∴∠BAD=n-100°,∴∠BAD=2∠CDE.(3)成立,∠BAD=2∠CDE,理由如下:如图③,在△ABC中,∠BAC=100°,∴∠ABC=∠ACB=40°,∴∠ACD=140°.在△ADE中,∠DAC=n,∴∠ADE=∠AED=1802n︒-,∵∠ACD=∠CDE+∠AED,∴∠CDE =∠ACD -∠AED =140°-1802n ︒-=1002n ︒+, ∵∠BAC =100°,∠DAC =n ,∴∠BAD =100°+n ,∴∠BAD =2∠CDE .【点睛】 本题考查了三角形内角和定理,三角形外角的性质,从图形中得出相关角度之间的关系是解题的关键.15.(1)见解析;(2)①③;(3)∠APB 的度数是10°或20°或40°或110°【分析】(1)由和是的角平分线,证明即可;(2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角解析:(1)见解析;(2)①③;(3)∠APB 的度数是10°或20°或40°或110°【分析】(1)由90ABC A ∠+∠=︒和BD 是ABC 的角平分线,证明290ABD A ∠+∠=︒即可; (2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角形”的定义,分类讨论:①2∠A +∠ABC =90°;②∠A +2∠APB =90°;③2∠APB +∠ABC =90°;④2∠A +∠APB =90°,由三角形内角和定理和外角的性质结合“准互余三角形”的定义,即可求出答案.【详解】(1)证明:∵在Rt ABC 中,90ACB ∠=︒,∴90ABC A ∠+∠=︒,∵BD 是ABC ∠的角平分线,∴2ABC ABD ∠=∠,∴290ABD A ∠+∠=︒,∴ABD △是“准互余三角形”;(2)①∵70,10B C ∠=︒∠=︒,∴290B C ∠+∠=︒,∴ABC 是“准互余三角形”,故①正确;②∵60A ∠=︒, 20B ∠=︒,∴210090A B ∠+∠=︒≠︒,∴ABC 不是“准互余三角形”,故②错误;③设三角形的三个内角分别为,,αβγ,且αβγ<<,∵三角形是“准互余三角形”,∴290αβ+=︒或290αβ+=︒,∴90αβ+<︒,∴180()90γαβ=︒-+>︒,∴“准互余三角形”一定是钝角三角形,故③正确;综上所述,①③正确,故答案为:①③;(3)∠APB 的度数是10°或20°或40°或110°;如图①,当2∠A +∠ABC =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A =20°,∴∠APB =110°;如图②,当∠A +2∠APB =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A +∠APB =50°,∴∠APB =40°;如图③,当2∠APB +∠ABC =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠APB =20°;如图④,当2∠A +∠APB =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A+∠APB=50°,所以∠A=40°,所以∠APB=10°;综上,∠APB的度数是10°或20°或40°或110°时,ABP△是“准互余三角形”.【点睛】本题是三角形综合题,考查了三角形内角和定理,三角形的外角的性质,解题关键是理解题意,根据三角形内角和定理和三角形的外角的性质,结合新定义进行求解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、八年级数学全等三角形填空题(难)1.如图,在ABC ∆和ADE ∆中,90BAC DAE ∠=∠=︒,AB AC =,AD AE =,C ,D ,E 三点在同一条直线上,连接BD ,则下列结论正确的是___________.①ABD ACE ∆≅∆②45ACE DBC ∠+∠=︒③BD CE ⊥④180EAB DBC ∠+∠=︒【答案】①②③④【解析】【分析】根据全等三角形的判定和性质,以及等腰三角形的性质解答即可.【详解】解:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC ,即:∠BAD=∠CAE ,∵AB=AC ,AE=AD ,∴△BAD ≌△CAE (SAS ),故①正确;∵△BAD ≌△CAE ,∴∠ABD=∠ACE ,∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,故②正确;∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD ⊥CE ,故③正确;∵90BAC DAE ∠=∠=︒,∴∠BAE+∠DAC=180°,∵∠ADB=∠E=45°,∴DAC DBC ∠=∠,∴180EAB DBC ∠+∠=︒,故④正确;故答案为:①②③④.【点睛】此题主要考查了全等三角形的判定及性质,以及等腰三角形的性质,注意细心分析,熟练应用全等三角形的判定以及等腰三角形的性质是解决问题的关键.2.如图,在△ABC 中,∠C=090,点D 在AB 上,BC=BD,DE ⊥AB 交AC 于点E ,△ABC 的周长为12,△ADE 的周长为6,则BC 的长为_______【答案】3【解析】【分析】连接BE ,由斜边直角边判定Rt BDE ∆≅ Rt BCE ∆,从而DE CE =,再由△ABC 的周长 △ADE 的周长即可求得BC 的长.【详解】如图:连接BE ,DE ⊥AB ,090BDE ∴∠=, 在Rt BDE ∆和Rt BCE ∆中,BE BE BD BC =⎧⎨=⎩, ∴Rt BDE ∆≅ Rt BCE ∆,DE CE ∴=,∴△ABC 的周长=AB+BC+AC=2BC+AD+AE+DE=12,△ADE 的周长= AD+AE+DE =6,∴BC=3,故答案为3.【点睛】本题考查三角形全等的判定和性质以及和三角形有关的线段,连接BE 构造全等三角形是解答此题的关键.3.如图,在等腰三角形ABC 中,90ABC ∠=,D 为AD 边上中点,多D 点作DE DF ⊥,交AB 于E ,交BC 于F ,若3AE =,2CF =,则ABC ∆的面积为______.【答案】252【解析】【分析】 利用等腰直角三角形斜边中点D 证明AD=BD ,∠DBC=∠A=45︒,再利用DE DF ⊥证得∠ADE=∠BDF ,由此证明△ADE ≌△BDF ,得到BC 的长度,即可求出三角形的面积.【详解】∵90ABC ∠=︒,AB=BC,∴∠A=45︒,∵D 为AC 边上中点,∴AD=CD=BD ,∠DBC=∠A=45︒,∠ADB=90︒,∵DE DF ⊥,∴∠EDB+∠BDF=∠EDB+∠ADE=90︒,∴∠ADE=∠BDF,∴△ADE ≌△BDF,∴BF==AE=3,∵CF=2,∴AB=BC=BF+CF=5,∴ABC ∆的面积为212BC ⋅=252, 故答案为:252. 【点睛】此题考查等腰直角三角形的性质,三角形全等的判定及性质.4.如图,10AB =,45A B ∠=∠=︒,32AC BD ==E ,F 为线段AB 上两点.现存在以下条件:①4CE DF ==;②AF BE =;③CEB DFA ∠=∠;④5CE DF ==.请在以上条件中选择一个条件,使得ACE △一定..和BDF 全等,则这个条件可以为________.(请写出所有正确的答案)【答案】②③④【解析】【分析】根据三角形全等的判定定理逐个判断即可.【详解】①如图1,过点C作CM AB⊥,过点D作DN AB⊥32,45A BAC BD∠=∠===︒3CM AM DN BN∴====4CE DF==由勾股定理得:22227,7ME CE CM NF DF DN=-==-=37,37AE AM ME BF BN NF∴=-=-=+=+,即AE BF≠此时,ACE∆和BDF∆不全等②AF BE=AF EF BE EF∴+=+,即AE BF=又452,3AC DA B B∠=∠=︒==则由SAS定理可得,ACE BDF∆≅∆③CEB DFACEB C ADFA D B∠=∠⎧⎪∠=∠+∠⎨⎪∠=∠+∠⎩C AD B∴∠+∠=∠+∠又A B∠=∠C D∴∠=∠32AC BD==则由ASA定理可得,ACE BDF∆≅∆④由(1)知,当5CE DF==时,22224,4ME CE CM NF DF DN-=-=此时,,,CE CA DF BDME AM NF BN>>⎧⎨>>⎩则点E在点M的右侧,点F在点N的左侧又10AM BN ME AM BN NF AB++=++==则点E与点N重合,点F与点M重合,如图2所示因此必有347AE BF==+=由SSS定理可得,ACE BDF∆≅∆故答案为:②③④.【点睛】本题考查了三角形全等的判定定理,熟记各判定定理是解题关键.5.在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,∠C<90°,若∠B满足条件:______________,则△ABC≌△DEF.【答案】∠B≥∠A.【解析】【分析】虽然题目中∠B为锐角,但是需要对∠B进行分类探究会理解更深入:可按“∠B是直角、钝角、锐角”三种情况进行,最后得出∠B、∠E都是锐角时两三角形全等的条件.【详解】解:需分三种情况讨论:第一种情况:当∠B是直角时:如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,可知:△ABC与△DEF一定全等,依据的判定方法是HL;第二种情况:当∠B是钝角时:如图②,过点C作CG⊥AB交AB的延长线于G,过点F作DH⊥DE交DE的延长线于H.∵∠B=∠E,且∠B、∠E都是钝角.∴180°-∠B=180°-∠E,即∠CBG=∠FEH.在△CBG和△FEH中,CBG FEHG HBC EF∠∠⎧⎪∠∠⎨⎪⎩===∴△CBG≌△FEH(AAS),∴CG=FH,在Rt△ACG和Rt△DFH中,AC DF CG FH⎧⎨⎩=,= ∴Rt △ACG ≌Rt △DFH (HL ),∴∠A=∠D , 在△ABC 和△DEF 中,A DB EAC DF ∠∠⎧⎪∠∠⎨⎪⎩==,=∴△ABC ≌△DEF (AAS );第三种情况:当∠B 是锐角时:在△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B=∠E ,且∠B 、∠E 都是锐角,小明在△ABC 中(如图③)以点C 为圆心,以AC 长为半径画弧交AB 于点D ,假设E 与B 重合,F 与C 重合,得到△DEF 与△ABC 符号已知条件,但是△AEF 与△ABC 一定不全等,所以有两边和其中一边的对角对应相等的两个三角形不一定全等;由图③可知,∠A=∠CDA=∠B+∠BCD ,∴∠A >∠B ,∴当∠B≥∠A 时,△ABC 就唯一确定了,则△ABC ≌△DEF .故答案为:∠B≥∠A .【点睛】本题是三角形综合题,考查全等三角形的判定与性质,应用与设计作图,熟练掌握三角形全等的判定方法是解题的关键.6.AD ,BE 是△ABC 的高,这两条高所在的直线相交于点O ,若BO=AC ,BC=a ,CD=b ,则AD 的长为______.【答案】AD 的长为a-b 或b-a 或a+b 或12a 或b. 【解析】【分析】分别讨论△ABC 为锐角三角形时、∠A 、∠B 、∠C 分别为钝角时和∠A 为直角时五种情况,利用AAS 证明△BOD ≌△ACD ,可得BD=AD ,根据线段的和差关系即可得答案.【详解】①如图,当△ABC 为锐角三角形时,∵AD、BE为△ABC的两条高,∴∠CAD+∠AOE=90°,∠CBE+∠BOD=90°,∵∠BOD=∠AOE,∴∠CAD=∠OBD,又∵∠ODB=∠ADC=90°,OB=AC,∴△BOD≌△ACD,∴AD=BD,∵BC=a,CD=b,∴AD=BD=BC-CD=a-b.②如图,当∠B为钝角时,∵∠C+∠CAD=90°,∠O+∠CAD=90°,∴∠C=∠O,又∵∠ADC=∠ODB=90°,OB=AC,∴△BOD≌△ACD,∴BD=AD,∴AD=CD-BC=b-a.③如图,当∠A为钝角时,同理可证:△BOD≌△ACD,∴AD=BC-CD=a-b.④如图,当∠C为钝角时,同理可证:△BOD≌△ACD,∴AD=BD=BC+CD=a+b.⑤当∠B为直角时,点O、D、B重合,OB=0,不符合题意,当∠C为直角时,点O、C、D、E重合,CD=0,不符合题意,如图,当∠A为直角时,点A、E、O重合,∵OB=AC,∠CAB=90°,∴△ABC是等腰直角三角形,∵AD⊥BC,∴AD是Rt△ABC斜边中线,∴AD=AD=12BC=12a=b.综上所述:AD的长为a-b或b-a或a+b或12a或b.故答案为:a-b或b-a或a+b或12a或b【点睛】本题主要考查全等三角形的判定与性质,全等三角形的判定方法有:SSS、AAS、ASA、SAS、HL等,注意:SAS时,角必须是两边的夹角,SSA和AAA不能判定两个三角形全等.灵活运用分类讨论的思想是解题关键.7.如图,三角形△ABO中,∠OAB=∠AOB=15°,点B在x轴的正半轴,坐标为B(6,0).OC平分∠AOB,点M在OC的延长线上,点N为边OA上的点,则MA+MN的最小值是______.【答案】3【解析】【分析】在x轴正半轴上取点N’,使ON’=ON,作AD⊥x轴于D点.易证△N’OM≌△NOM,可得MN’=MN,则MA+MN的最小值即为MA+MN’的最小值,由于A点固定,故当N’点与D点重合时,MA+MN’的值最小,即MA+MN的值最小.【详解】解:在x轴正半轴上取点N’,使ON’=ON,作AD⊥x轴于D点.∵ON’=ON,∠N’OM=∠NOM,OM=OM,∴△N’OM≌△NOM,∴MN’=MN,∴MA+MN=MA+MN’,∵A点固定,∴MA+MN’的最小值为当N’与D点重合时的MA+MN’值,∴MA+MN’的最小值为AD,∵∠OAB=∠AOB=15°,OB=6,∴∠ABD=30°,AB=6,∴AD=0.5×6=3,∴MA+MN的最小值为3,故答案为3.【点睛】理解A点是固定点,而M和N均为动点,然后运用三点共线及点到直线的最短距离概念进行解答是本题的关键.8.如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE 上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=22,则DF=________.【答案】3.【解析】【分析】由题意可证的△ABF≌△ACE,可得△AEF 为等腰直角三角形,取AF的中点O,连接CO交BE与点G,连接AG,可得△AGF, △AGE,△CEG均为等腰直角三角形,可得AG 平行等于CE,可得四边形AGCE为平行四边形,可得FD的长.【详解】解:如图Rt△ABC中,AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,又∠BAC=90°,BE⊥CE,∠DAE为∠BAC与EAF的公共角∴∠BAF=∠CAE,∠ABC=∠ACB=45°, BE⊥CE∴∠ABF+∠CBE=45°,∠CBE+∠ACB+∠ACE=90°,即: ∠CBE+∠ACE=45°,∴∠ABF=∠ACE,在△ABF与△ACE中,有AB ACBAF CAEABF ACE=⎧⎪∠=∠⎨⎪∠=∠⎩,∴△ABF≌△ACE,∴AE=AF, △AEF为等腰直角三角形, 取AF的中点O,连接CO交BE与点G,连接AG,C是线段AF的垂直平分线上的点,易得△AGF, △AGE,△CEG均为等腰直角三角形,AF=22∴AG=GE=CE=FG=2,又AG⊥BE,CE⊥BE,可得AG∥CE,∴四边形AGCE为平行四边形,∴GD=DE=1,∴DF=FG+GD=2+1=3.【点睛】本题主要考查三角形全等及性质,综合性强,需综合运用所学知识求解.9.如图,已知AC平分∠DAB,CE⊥AB于点E,AB=AD+2BE,则下列结论:①AB+AD= 2AE;②∠DAB+∠DCB=180°;③CD=CB;④S ACE﹣S BCE=S ACD.其中正确的是______.【答案】①②③④.【解析】【分析】【详解】①在AE取点F,使EF=BE,连接CF.∵AB=AD+2BE=AF+EF+BE,EF=BE,∴AB=AD+2BE=AF+2BE,∴AD=AF,∴AB+AD=AF+EF+BE+AD=2AF+2EF=2(AF+EF)=2AE,∴AB+AD= 2AE,故①正确;②在AB上取点F,使EF=BE,连接CF.在△ACD与△ACF中,∵AD=AF,∠DAC=∠FAC,AC=AC,∴△ACD≌△ACF,∴∠ADC=∠AFC.∵CE垂直平分BF,∴CF=CB,∴∠CFB=∠B.又∵∠AFC+∠CFB=180°,∴∠ADC+∠B=180°,∴∠DAB+∠DCB=180°故②正确;③由②知,△ACD≌△ACF,∴CD=CF,又∵CF=CB,∴CD=CB,故③正确;④易证△CEF≌△CEB,∴S△ACE﹣S△BCE=S△ACE﹣S△FCE=S△ACF,又∵△ACD≌△ACF,∴S△ACF=S△ADC,∴S△ACE﹣2S△BCE=S△ADC,故④正确.综上所述,正确的结论是①②③④,故答案为①②③④.10.如图,AD=AB,∠C=∠E,AB=2,AE=8,则DE=_________.【答案】6【解析】根据三角形全等的判定“AAS”可得△ADC≌△ABE,可得AD=AB=2,由AE=8可得DE=AE-AD=6.故答案为:6.点睛:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.二、八年级数学全等三角形选择题(难)=,D、E是斜边BC上两点,且∠DAE=45°,将11.如图,在Rt△ABC中,AB AC△ADC绕点A顺时针旋转90︒后,得到△AFB,连接EF.列结论:+=①△ADC≌△AFB;②△ABE≌△ACD;③△AED≌△AEF;④BE DC DE其中正确的是( )A.②④B.①④C.②③D.①③【答案】D【解析】解:∵将△ADC绕点A顺时针旋转90︒后,得到△AFB,∴△ADC≌△AFB,故①正确;②无法证明,故②错误;③∵△ADC≌△AFB,∴AF=AD,∠FAB=∠DAC.∵∠DAE=45°,∴∠BAE+∠DAC=45°,∠FA E=∠DAE=45°.在△FAE和△DAE中,∵AF=AD,∠FAE=∠DAE,AE=AE,∴△FAE≌△DAE,故③正确;④∵△ADC≌△AFB,∴DC=BF,∵△FAE≌△DAE,∴EF=ED,∵BF+BE>EF,∴DC+BE>ED .故④错误.故选D.12.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD平分∠BAC;②作图依据是S.A.S;③∠ADC=60°;④点D在AB的垂直平分线上A.1个B.2个C.3个D.4个【答案】C【解析】①根据作图的过程可以判定AD是∠BAC的∠平分线;②根据作图的过程可以判定出AD的依据;③利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质求∠ADC的度数;④利用等角对等边可以证得△ADB的等腰三角形,由等腰三角形的“三合一”的性质可以证明点在AB的中垂线上.解:如图所示,①根据作图的过程可知,AD是∠BAC的∠平分线;故①正确;②根据作图的过程可知,作出AD的依据是SSS;故②错误;③∵在△ABC中,∠C=90°,∠B=30°,∴∠CBA=60°.又∵AD是∠BAC的平分线,∴∠1=∠2=12∠CAB=30°, ∴∠3=90°-∠2=60°,即∠ADC=60°.故③正确;④∵∠1=∠B=30°,∴AD=BD,∴点D 在AB 的中垂线上.故④正确;故选C.“点睛”此题主要考查的是作图-基本作图,涉及到角平分线的作法以及垂直平分线的性质,熟练根据角平分线的性质得出∠ADC 的度数是解题的关键.13.如图,Rt ABC ∆中,90C =∠,3,4,5,AC BC AB ===AD 平分BAC ∠.则:ACD ABD S S ∆∆=( )A .3:4B .3:5C .4:5D .2:3【答案】B【解析】 如图,过点D 作DE ⊥AB 于点E ,由角平分线的性质可得出DE=CD ,由全等三角形的判定定理HL 得出△ADC ≌△ADE ,故可得出AE=AC=3,由AB=5求出BE=2,设CD=x ,则DE=x ,BD=4﹣x ,再根据勾股定理知DE 2+BE 2=BD 2,即x 2+22=(4﹣x )2,求出x=32,进而根据等高三角形的面积,可得出:S △ACD :S △ABD =CD :BD=12×32×3:12×32×5=3:5.故选:B .点睛:本题考查的是角平分线的性质,熟知角平分线上的点到角两边的距离相等是解答此题的关键.14.如图,点P、Q分别是边长为6cm的等边ABC△边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论:①BQ AM=②ABQ△≌CAP△③CMQ∠的度数不变,始终等于60︒④当第2秒或第4秒时,PBQ△为直角三角形,正确的有()个.A.1B.2C.3D.4【答案】C【解析】∵点P、Q速度相同,∴AP BQ=.在ACP△和ABQ△中,60AP BQCAP ABQAC BA=⎧⎪∠==︒⎨⎪=⎩,∴ACP△≌BAQ△,故②正确.则AQC CPB∠=∠.即B BAQ BAQ AMP∠+∠=∠+∠.∴60AMP B∠=∠=︒.则60CMQ AMP∠=∠=︒,故③正确.∵APM∠不一定等于60︒.∴AP AM≠.∴BQ AM≠.故①错误.设时间为t,则AP=BQ=t,PB=4-t①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得6-t=2t,t=2 ;②当∠BPQ=90°时,∵∠B=60°,∴BQ =2BP ,得t =2(6-t ),t =4;∴当第2秒或第4秒时,△PBQ 为直角三角形.∴④正确.故选C.点睛:本题考查了等边三角形的性质、全等三角形的判定与性质、直角三角形的性质等知识点,综合性强,难度较大.15.如图在ABC △中,P ,Q 分别是BC 、AC 上的点,作PR AB ⊥,PS AC ⊥,垂足分别是R ,S ,AQ PQ =,PR PS =,下面三个结论:①AS AR =;②PQ AB ∥;③BRP △≌CSP △.其中正确的是().A .①②B .②③C .①③D .①②③ 【答案】A【解析】连接AP ,由题意得,90ARP ASP ∠=∠=︒,在Rt APR 和Rt APS 中,AP APPR PS =⎧⎨=⎩,∴△APR ≌()APS HL ,∴AS AR =,故①正确.BAP SAP ∠=∠,∴2SAB BAP SAP SAP ∠=∠+∠=∠,在AQP △中,∴AQ PQ =,∴QAP APQ ∠=∠,∴22CQP QAP APQ QAP SAP ∠=∠+∠=∠=∠,∴PQ AB∥,故②正确;在Rt BRP和Rt CSP中,只有PR PS=,不满足三角形全等的条件,故③错误.故选A.点睛:本题主要考查三角形全等的判定方法以及角平分线的判定和平行线的判定,准确作出辅助线是解决本题的关键.16.如图,AD是△ABC的外角平分线,下列一定结论正确的是()A.AD+BC=AB+CD,B.AB+AC=DB+DC,C.AD+BC<AB+CD,D.AB+AC<DB+DC【答案】D【解析】【分析】在BA的延长线上取点E,使AE=AC,连接ED,证△ACD≌△AED,推出DE=DC,根据三角形中任意两边之和大于第三边即可得到AB+AC<DB+DC.【详解】解: 在BA的延长线上取点E, 使AE=AC,连接ED,∵AD是△ABC的外角平分线,∴∠EAD=∠CAD,在△ACD和△AED中,AD ADEAD CADAC AE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△AED(SAS)∴DE=DC,在△EBD中,BE<BD+DE,∴AB+AC<DB+DC故选:D.【点睛】本题主要考查三角形全等的证明,全等三角形的性质,三角形的三边关系,作辅助线构造以AB、AC、DB、DC的长度为边的三角形是解题的关键,也是解本题的难点.17.如图,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为()A.2 B.3 C.4 D.5【答案】C【解析】【分析】可延长DE至F,使EF=BC,利用SAS可证明△ABC≌△AEF,连AC,AD,AF,再利用SSS证明△ACD≌△AFD,可将五边形ABCDE的面积转化为两个△ADF的面积,进而求解即可.【详解】延长DE至F,使EF=BC,连AC,AD,AF,在△ABC与△AEF中,=90AB AEABC AEFBC EF⎧⎪∠∠⎨⎪⎩===,∴△ABC≌△AEF(SAS),∴AC=AF,∵AB=CD=AE=BC+DE,∠ABC=∠AED=90°,∴CD=EF+DE=DF,在△ACD与△AFD中,AC AFCD DFAD AD⎧⎪⎨⎪⎩===,∴△ACD≌△AFD(SSS),∴五边形ABCDE的面积是:S=2S△ADF=2×12•DF•AE=2×12×2×2=4.故选C.【点睛】本题主要考查了全等三角形的判定及性质以及三角形面积的计算,正确作出辅助线,利用全等三角形把五边形ABCDE的面积转化为两个△ADF的面积是解决问题的关键.18.如图,等腰直角△ABC中,∠BAC=90︒,AD⊥BC于D,∠ABC的平分线分别交AC、AD 于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有()A.1个B.2个C.3个D.4个【答案】C【解析】试题解析:∵∠BAC=90°,AC=AB,AD⊥BC,∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,∴∠BAD=45°=∠CAD,∵BE平分∠ABC,∴∠ABE=∠CBE=12∠ABC=22.5°,∴∠BFD=∠AEB=90°-22.5°=67.5°,∴∠AFE=∠BFD=∠AEB=67.5°,∴AF=AE,故①正确;∵M为EF的中点,∴AM⊥EF,故②正确;过点F作FH⊥AB于点H,∵BE 平分∠ABC ,且AD ⊥BC ,∴FD=FH <FA ,故③错误;∵AM ⊥EF ,∴∠AMF=∠AME=90°,∴∠DAN=90°-67.5°=22.5°=∠MBN ,在△FBD 和△NAD 中{FBD DANBD ADBDF ADN∠∠∠∠=== ∴△FBD ≌△NAD ,∴DF=DN ,故④正确;故选C .19.在ABC 中,2,72A B ACB ∠=∠∠≠︒,CD 平分ACB ∠,P 为AB 的中点,则下列各式中正确的是()A .AD BC CD =-B .AD BC AC =- C .AD BC AP =-D .AD BC BD =-【答案】B【解析】【分析】 可在BC 上截取CE=CA ,连接DE ,可得△ACD ≌△ECD ,得DE=AD ,进而再通过线段之间的转化得出线段之间的关系.【详解】解:∵∠A=2∠B,∴∠A﹥∠B∴BC﹥AC∴可在BC上截取CE=CA,连接DE(如图),,∴∠ACD=∠BCD∵CD平分ACB又∵CD=CD,CE=CA∴△ACD≌△ECD,∴AD=ED,∠CED=∠A=2∠B又∠CED=∠B+∠BDE∴∠B=∠BDE∴AD=DE=BE,∴BC=BE+EC=AD+AC所以AD=BC-AC故选:B若A选项成立,则CD=AC,∴∠A=∠CDA=∠CDE=∠CED=2∠B=2∠EDB∴∠CDA+∠CDE+∠EDB=180°即5∠EDB=180°∴∠EDB=36°∴∠A=72°,∠B=36°∴∠ACB=72°与已知∠ACB≠72°矛盾,故选项A不正确;假设C选项成立,则有AP=AC,作∠BAC的平分线,连接FP,∴△CAF≌△PAF≌△PBF,∴∠CFA=∠AFP=∠PFB=60°∠B=30°,∠ACB=90°当∠ACB=90°时,选项C才成立,∴当∠ACB≠72°时,选项C不一定成立;假设D选项成立,则AD=BC-BD由图可知AD=BA-BD∴AB=BC∴∠A=∠ACB=2∠B∴∠A+∠ACB+∠B=180°∴∠B=36°,∠ACB=72这与已知∠ACB≠72°矛盾,故选项D不成立.故选:B【点睛】本题考查的是考查的是利用角的平分线的性质说明线段之间的关系.,,20.如图,点 D 是等腰直角△ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C;正确的个数是()A.1 B.2 C.3 D.4【答案】B【解析】【分析】依据点D是等腰直角△ABC腰BC上的中点,可得tan∠BAD=12,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.【详解】∵点D是等腰直角△ABC腰BC上的中点,∴BD=12BC=12AB,∴tan∠BAD=12,∴∠BAD≠30°,故①错误;如图,连接B'D,∵B、B′关于AD对称,∴AD垂直平分BB',∴∠AFB=90°,BD=B'D=CD,∴∠DBB'=∠BB'D,∠DCB'=∠DB'C,∴∠BB'C=∠BB'D+∠DB'C=90°,∴∠AFB=∠BB'C,又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF,∴∠BAF=∠CBB',∴△ABF≌△BCB',∴BF=CB'=B'F,∴△FCB'是等腰直角三角形,∴∠CFB'=45°,即∠BFC=135°,故②正确;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C,故③正确;∵AF>BF=B'C,∴△AEF与△CEB'不全等,∴AE≠CE,∴S△AFE≠S△FCE,故④错误;故选B.【点睛】本题主要考查了轴对称的性质以及全等三角形的判定与性质的运用,如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.21.如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是()A.AB﹣AD>CB﹣CD B.AB﹣AD=CB﹣CDC.AB﹣AD<CB﹣CD D.AB﹣AD与CB﹣CD的大小关系不确定【答案】A【解析】如图,在AB上截取AE=AD,连接CE.∵AC平分∠BAD,∴∠BAC=∠DAC,又AC是公共边,∴△AEC≌△ADC(SAS),∴AE=AD,CE=CD,∴AB-AD=AB-AE=BE,BC-CD=BC-CE,∵在△BCE中,BE>BC-CE,∴AB-AD>CB-CD.故选A.22.如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,连结AO,则图中共有全等三角形的对数为()A.2对B.3对C.4对D.5对【答案】C【解析】【分析】先根据条件,利用AAS可知△ADB≌△AEC,然后再利用HL、ASA即可判断△AOE≌△AOD,△BOE≌△COD,△AOC≌△AOB.【详解】∵AB=AC,BD⊥AC于D,CE⊥AB于E,∴∠ADB=∠AEC=90°,∵∠A为公共角,∴△ADB≌△AEC,(AAS)∴AE=AD,∠B=∠C∴BE=CD,∵AE=AD,OA=OA,∠ADB=∠AEC=90°,∴△AOE≌△AOD(HL),∴∠OAC=∠OAB,∵∠B=∠C ,AB=AC ,∠OAC=∠OAB ,∴△AOC ≌△AOB.(ASA )∵∠B=∠C ,BE=CD ,∠ODC=∠OEB=90°,∴△BOE ≌△COD (ASA ).综上:共有4对全等三角形,故选C.【点睛】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要从已知条件开始结合全等的判定方法逐一验证,由易到难,不重不漏.23.如图,四边形ABCD 中,∠A 、∠B 、∠C 、∠D 的角平分线恰相交于一点P ,记△APD 、△APB 、△BPC 、△DPC 的面积分别为S 1、S 2、S 3、S 4,则有( )A .1324S S S S +=+B .1234S S S S +=+C .1423S S S S +=+D .13S S =【答案】A【解析】【分析】作辅助线,利用角平分线性质定理,明确8个三角形中面积两两相等即可解题.【详解】四边形ABCD,四个内角平分线交于一点P,即点p 到四边形各边距离相等,(角平分线性质定理),如下图,可将四边形分成8个三角形,面积分别是a 、a 、b 、b 、c 、c 、d 、d,则S 1=a+d, S 2=a+b, S 3=b+c, S 4=c+d,∴S 1+S 3=a+b+c+d= S 2+S 4故选A【点睛】本题考查了角平分线性质定理,作高线和理解角平分线性质定理是解题关键.24.如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是().A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】如图,连接AP,根据HL判定△APR和△APS全等,即可说明①正确;由△APR和△APS 全等可得∠RAP=∠PAC,再根据等腰三角形性质推出∠QAP=∠QPA,得到∠QPA=∠BAP,根据平行线判定推出OP//AB,即②正确;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等;连接RS,与AP交于点D,先证△ARD≌△ASD,即RD=SD;运用等腰三角形的性质即可判定.【详解】解:如图,连接AP∵PR⊥AB,PS⊥AC,PR=PS∴△APR≌△APS∴AS=AR,∠RAP=∠PAC即①正确;又∵AQ=PQ∴∠QAP=∠QPA∴∠QPA=∠BAP∴OP//AB,即②正确.在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等,故③错误.如图,连接PS∵△APR≌△APS∴AR=AS,∠RAP=∠PAC∴AP垂直平分RS,即④正确;故答案为C.【点睛】本题主要考查了全等三角形的性质和判定,角平分线性质的应用,熟练掌握全等三角形的判定和性质是解答本题的关键25.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有()A.1个B.2个C.3个D.4个【答案】C【解析】【分析】利用“角边角”证明△APE和△CPF全等,根据全等三角形的可得AE=CF,再根据等腰直角三角形的定义得到△EFP是等腰直角三角形,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半.【详解】∵AB=AC,∠BAC=90°,点P是BC的中点,∴AP⊥BC,AP=PC,∠EAP=∠C=45°,∴∠APF+∠CPF=90°,∵∠EPF是直角,∴∠APF+∠APE=90°,∴∠APE=∠CPF,在△APE和△CPF中,45APE CPFAP PCEAP C∠∠⎧⎪⎨⎪∠∠︒⎩====,∴△APE≌△CPF(ASA),∴AE=CF,故①②正确;∵△AEP≌△CFP,同理可证△APF≌△BPE,∴△EFP是等腰直角三角形,故③错误;∵△APE≌△CPF,∴S△APE=S△CPF,∴四边形AEPF =S △AEP +S △APF =S △CPF +S △BPE =12S △ABC .故④正确, 故选C .【点睛】 本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,根据同角的余角相等求出∠APE=∠CPF ,从而得到△APE 和△CPF 全等是解题的关键,也是本题的突破点.26.如图,已知∠DCE=90°,∠DAC=90°,BE ⊥AC 于B ,且DC=EC .若BE=7,AB=3,则AD 的长为( )A .3B .5C .4D .不确定【答案】C【解析】 根据同角的余角相等求出∠ACD=∠E ,再利用“角角边”证明△ACD ≌△BCE ,根据全等三角形对应边相等可得AD=BC ,AC=BE=7,然后求解BC=AC-AB=7-3=4.故选:C .点睛:本题考查了全等三角形的判定与性质,等角的余角相等的性质,熟练掌握三角形全等的判定方法是解题的关键.27.如图,AOB ∆的外角,CAB DBA ∠∠的平分线,AP BP 相交于点P ,PE OC ⊥于E ,PF OD ⊥于F ,下列结论:(1)PE PF =;(2)点P 在COD ∠的平分线上;(3)90APB O ∠=︒-∠,其中正确的有 ( )A .0个B .1个C .2个D .3个【答案】C【解析】【分析】 过点P 作PG ⊥AB ,由角平分线的性质定理,得到PE PG PF ==,可判断(1)(2)正确;由12APB EPF ∠=∠,180EPF O ∠+∠=︒,得到1902APB O ∠=︒-∠,可判断(3)错误;即可得到答案.解:过点P 作PG ⊥AB ,如图:∵AP 平分∠CAB ,BP 平分∠DBA ,PE OC ⊥,PF OD ⊥,PG ⊥AB ,∴PE PG PF ==;故(1)正确;∴点P 在COD ∠的平分线上;故(2)正确;∵12APB APG BPG EPF ∠=∠+∠=∠, 又180EPF O ∠+∠=︒, ∴11(180)9022APB O O ∠=⨯︒-∠=︒-∠;故(3)错误; ∴正确的选项有2个;故选:C .【点睛】 本题考查了角平分线的判定定理和性质定理,解题的关键是熟练掌握角平分线的判定和性质进行解题.28.已知:如图,在长方形ABCD 中,AB=4,AD=6.延长BC 到点E ,使CE=2,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC-CD-DA 向终点A 运动,设点P 的运动时间为t 秒,当t 的值为_____秒时,△ABP 和△DCE 全等.A .1B .1或3C .1或7D .3或7 【答案】C【解析】【分析】 分两种情况进行讨论,根据题意得出BP=2t=2和AP=16-2t=2即可求得.【详解】解:因为AB=CD ,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS 证得△ABP ≌△DCE , 由题意得:BP=2t=2,所以t=1,因为AB=CD ,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS 证得△BAP ≌△DCE ,由题意得:AP=16-2t=2,所以,当t的值为1或7秒时.△ABP和△DCE全等.故选C.【点睛】本题考查全等三角形的判定,判定方法有:ASA,SAS,AAS,SSS,HL.29.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论,其中正确的是()①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.A.①②③B.①②④C.①②D.①②③④【答案】A【解析】【分析】根据题意结合图形证明△AFB≌△AEC;利用四点共圆及全等三角形的性质问题即可解决.【详解】如图,∵∠EAF=∠BAC,∴∠BAF=∠CAE;在△AFB与△AEC中,AF AEBAF CAEAB AC⎧⎪∠∠⎨⎪⎩===,∴△AFB≌△AEC(SAS),∴BF=CE;∠ABF=∠ACE,∴A、F、B、C四点共圆,∴∠BFC=∠BAC=∠EAF;故①、②、③正确,④错误.故选A..【点睛】本题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是准确找出图形中隐含的全等三角形,灵活运用四点共圆等几何知识来分析、判断、推理或证明.30.已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为()A.6 B.5C.4.5 D.与AP的长度有关【答案】A【解析】【分析】作DQ⊥AB,交直线AB的延长线于点Q,连接DE,PQ,根据全等三角形的判定定理得出△APE≌△BDQ,再由AE=BQ,PE=QD且PE∥QD,可知四边形PEDQ是平行四边形,进而可得出EF=12AB,由等边△ABC的边长为12可得出DE=6.【详解】解;如图,作DQ⊥AB,交AB的延长线于点F,连接DE,PQ,又∵PE⊥AB于E,∴∠BQD=∠AEP=90°,∵△ABC是等边三角形,∴∠A=∠ABC=∠DBQ=60°,在△APE和△BDQ中,A DBQ AEP BQD AP BD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△APE ≌△BDQ (AAS ),∴AE=BQ ,PE=QD 且PE ∥QD ,∴四边形PEDQ 是平行四边形,∴EF=12EQ , ∵EB+AE=BE+BQ=AB , ∴EF=12AB , 又∵等边△ABC 的边长为12,∴EF=6.故选:A.【点睛】本题主要考查全等三角形的判定与性质,平行四边形的判定与性质,解此题的关键在于根据题中PE ⊥AB 作辅助线构成全等的三角形.。
