课后习题一(第一章、第二章)
信息安全技术使用教程第二版课后习题

信息安全技术使用教程(第版)课后习题第一章(信息安全概述)习题一、1、填空题(1)信息安全是指秘密信息在产生、传输、使用、和存储的过程中不被泄露或破坏(2)信息安全的4个方面是;保密性、完整性、可用性、和不可否认性。
(3)信息安全主要包括系统安全和数据安全俩个方面。
(4)一个完整的信息安全技术体系结构由物理安全技术、基础安全技术、系统安全技术、网络完全技术及应用安全技术组成。
(5)一个常见的网络安全模型是PDRR模型。
(6)木桶原则是指对信息均衡、全面的进行保护。
木桶的最大容积取决于最短的一块木板。
2、思考与解答题:(1)简述信息安全技术面临的威胁。
(2)简述PDRR网络安全模型的工作过程。
第二章(物理安全技术)习题二1、填空题(1)物理安全又称为实体安全、是保护计算机设备、设施(网络及通信线路)免遭地震、火灾、水灾、有害气体和其他环境事故(如电磁污染等)破坏的措施和过程。
(2)物理安全包括环境安全、设备安全电源系统安全和通信线路安全、(3)计算机的电子元器件、芯片都密封在机箱中,有的芯片工作时表面温非常高,一般电子元器件的工作温度在0---45摄氏度。
(4)在放置计算机的房间内,湿度最好保持在40%--60% 之间,湿度过高或过低对计算机的可靠性与安全性都有影响。
2、思考与解答:(1)为计算机系统提供合适的安全环境的目的是什么。
(2)简述计算机机房的外部环境要求、内部环境要求。
第三章(基础安全技术)习题三、1、填空题(1)一般来说,信息安全主要包括系统安全和数据安全俩个方面。
(2)面膜技术是保障信息安全的核心技术、它以很小的代价,对信息提供一种强有力的安全保护。
(3)加密使用某种方法将文字转换成不能直接阅读的形式的过程。
(4)加密一般分为3类,是对称加密、非对称加密和单向散列函数。
(5)从密码学的发展历程来看,共经历了古典密码、对称密钥密码和公开密钥密码。
(6)对称加密算法又称为传统密码算法或单密钥算法,它采用了对称密码编码技术,其特点是文件加密和加密使用相同的密钥。
生物学选择性必修一第一二章课后习题

选择性必修一第一章人体内环境与稳态第一节细胞生活的环境一、概念检测1.人在进行一定强度的体力劳动后,手掌或脚掌上可能会磨出水疱。
水疱中的液体主要是组织液,一段时间后水疱可自行消失。
请判断以下有关说法是否正确。
(1)水疱的成分中蛋白质的含量最高。
( )(2)水疱主要是由血浆中的水大量渗出到组织液形成的。
( )(3)水疱自行消失是因为其中的液体可以渗入毛细血管和毛细淋巴管。
( )(4)水疱的形成和消失说明内环境中物质是不断更新的。
( )2. 人体内环境是体内细胞直接生活的环境。
下列属于人体内环境的是( )A. 膀胱内的尿液B. 大脑细胞间隙的液体C. 肺泡腔内的气体D.小肠腔内的消化液3.右上图表示人体内细胞与外界环境之间进行物质交换的过程,A、B、C表示直接与内环境进行物质交换的几种器官,①②是有关的生理过程。
请回答下列问题。
(1)A、B、C分别是。
(2)B内的营养物质通过①过程进入内环境,则①表示。
(3)②表示。
二、拓展应用剧烈运动会使肌肉产生大量乳酸等酸性物质,这会影响血浆的pH吗?在这种情况下,机体是如何维持细胞外液的酸碱度的?第二节内环境的稳态一、概念检测1.稳态是生命统的特征,也是机体存活的条件。
判断下列与人体稳态有关的表述是否正确。
(1)人吃进酸性或碱性的食物会使血浆pH发生紊乱。
( )(2)有的人常吃咸鱼、咸菜,但他细胞外液的渗透压仍能保持相对稳定。
( )(3)在正常情况下,一个人的体温是恒定不变的。
( )(4)CO2是人体细呼吸产生的废物,不参与维持内环境的稳态。
( )2. 在长跑比赛时,运动员的体内会发生复杂的生理变化,如机体大量产热、出汗等。
下列相关叙述正确的是( )A.大量产热会使体温急剧升高B.大量出汗会使血浆的pH下降C. 大量出汗可使血浆渗透压降低个D. 大量出汗有利于机体体温的稳定二、拓展应用2017年,科学家研制了一个充满的大塑料袋,并用它来抚育早产的羊羔。
羊羔在此“人造子宫”中待了4周。
微生物学课后习题(第一部分)

微生物学课后习题(第一部分)第一章原核生物的形态、构造和功能复习思考题1.试设计一张表格,比较一下6个大类原核生物的主要特性。
2.典型细菌的大小和重量是多少?试设想几种形象化的比喻并加以说明。
3.试图示G+和G-细菌细胞壁的主要构造,并简要说明其异同。
4.试图示肽聚糖的模式构造,并指出G+和G-细菌肽聚糖结构的差别。
5.什么是缺壁细菌?试列表比较4类缺壁细菌的形成、特点和实际应用。
6.试述革兰氏染色法的机制并说明此法的重要性。
7.何谓“拴菌试验”?它何以能证明鞭毛的运气机制?8.渗透调节皮层膨胀学说是如何解释芽孢耐热机制的?9.什么是菌落?试讨论细菌的细胞形态与菌落形态间的相关性。
10.名词解释:磷壁酸,LPS,假肽聚糖,PHB,伴胞晶体,基内菌丝,孢囊链霉菌,横割分裂,异形胞,原体与始体,类支原体,羧酶体,孢囊,磁小体。
第二章真核微生物的形态、构造和功能复习思考题1.试解释菌物、真菌、酵母菌、霉菌和蕈菌。
2.试图示并说明真核微生物“9+2”型鞭毛的构造和生理功能。
3.试简介真菌所特有的几种细胞器――膜边体、几丁质酶体和氢化酶体。
4.什么是单细胞蛋白(SCP)?为什么酵母菌是一种优良的单细胞蛋白?5.试图示Saccharomyces cerevisiae 的生活史,并说明其各阶段的特点。
6.试简介菌丝、菌丝体、菌丝球、真酵母、假酵母、芽痕、蒂痕、真菌丝、假菌丝等名词。
7.霉菌的营养菌丝和气生菌丝各有何特点?它们分别可分化出哪些特化结构8.试以Neurospora crassa 为例,说明菌丝尖端细胞的分化过程及其成分变化。
9.试列表比较各种真菌孢子的特点。
10.细菌、放线菌、酵母菌和霉菌四大类微生物的菌落有何不同?为什么? 11.为什么说蕈菌也是真核微生物?12.什么叫锁状联合?其生理意义如何?试图示其过程。
13.试比较细菌、放线菌、酵母菌和霉菌细胞壁成分的异同,并讨论它们的原生质体制备方法。
第三章病毒和亚病毒复习思考题1.什么是真病毒?什么是亚病毒?2.病毒的一般大小如何?试图示病毒的典型构造。
线性代数课后习题1-4作业答案(高等教育出版社)

第一章 行列式1. 利用对角线法则计算下列三阶行列式: (1)381141102---;解 381141102---=2⨯(-4)⨯3+0⨯(-1)⨯(-1)+1⨯1⨯8 -0⨯1⨯3-2⨯(-1)⨯8-1⨯(-4)⨯(-1) =-24+8+16-4=-4. (3)222111c b a c b a ; 解 222111c b a c b a=bc 2+ca 2+ab 2-ac 2-ba 2-cb 2 =(a -b )(b -c )(c -a ).4. 计算下列各行列式:(1)71100251020214214; 解 7110251020214214010014231020211021473234-----======c c c c 34)1(143102211014+-⨯---= 143102211014--=01417172001099323211=-++======c c c c .(2)2605232112131412-;解 2605232112131412-260503212213041224--=====c c 041203212213041224--=====r r 000003212213041214=--=====r r . (3)efcf bf de cd bd aeac ab ---;解 ef cf bf de cd bd ae ac ab ---e c b e c b ec b adf ---=abcdef adfbce 4111111111=---=.(4)dc b a 100110011001---. 解d c b a 100110011001---dc b aab ar r 10011001101021---++===== dc a ab 101101)1)(1(12--+--=+01011123-+-++=====cd c ada ab dc ccdad ab +-+--=+111)1)(1(23=abcd +ab +cd +ad +1. 6. 证明:(1)1112222b b a a b ab a +=(a -b )3;证明1112222b b a a b ab a +00122222221213a b a b a a b a ab a c c c c ------=====ab a b a b a ab 22)1(22213-----=+21))((a b a a b a b +--==(a -b )3 . (2)y x z x z y zy x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++;证明bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++bz ay by ax x by ax bx az z bxaz bz ay y b bz ay by ax z by ax bx az y bx az bz ay x a +++++++++++++=bz ay y x by ax x z bxaz z y b y by ax z x bx az y z bz ay x a +++++++=22z y x y x z xz y b y x z x z y z y x a 33+=y x z x z y zy x b y x z x z y z y x a 33+=yx z x z y zy x b a )(33+=.8. 计算下列各行列式(D k 为k 阶行列式): (1)aa D n 1 1⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa a a x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得 ax x a ax x a a x x a a a a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(=[x +(n -1)a ](x -a )n 第二章 矩阵及其运算 1. 计算下列乘积:(5)⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x ;解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x=(a 11x 1+a 12x 2+a 13x 3 a 12x 1+a 22x 2+a 23x 3 a 13x 1+a 23x 2+a 33x 3)⎪⎪⎭⎫⎝⎛321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=.2. 设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B , 求3AB -2A 及A TB .解 ⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=-1111111112150421321111111111323A AB⎪⎪⎭⎫⎝⎛----=⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-=2294201722213211111111120926508503, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=092650850150421321111111111B A T . 3.已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4.设⎪⎭⎫ ⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B , 问: (1)AB =BA 吗? 解 AB ≠BA .因为⎪⎭⎫ ⎝⎛=6443AB , ⎪⎭⎫ ⎝⎛=8321BA , 所以AB ≠BA .(3)(A +B )(A -B )=A 2-B 2吗? 解 (A +B )(A -B )≠A 2-B 2.因为⎪⎭⎫ ⎝⎛=+5222B A , ⎪⎭⎫ ⎝⎛=-1020B A ,⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=-+906010205222))((B A B A ,而 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-718243011148322B A ,故(A +B )(A -B )≠A 2-B 2.5. 举反列说明下列命题是错误的: (1)若A 2=0, 则A =0;解 取⎪⎭⎫ ⎝⎛=0010A , 则A 2=0, 但A ≠0. (2)若A 2=A , 则A =0或A =E ;解 取⎪⎭⎫ ⎝⎛=0011A , 则A 2=A , 但A ≠0且A ≠E . (3)若AX =AY , 且A ≠0, 则X =Y .解 取⎪⎭⎫ ⎝⎛=0001A , ⎪⎭⎫ ⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y ,则AX =AY , 且A ≠0, 但X ≠Y .7. 设⎪⎪⎭⎫⎝⎛=λλλ001001A , 求A k .解 首先观察⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎭⎫⎝⎛=222002012λλλλλ,⎪⎪⎭⎫⎝⎛=⋅=3232323003033λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=43423434004064λλλλλλA A A ,⎪⎪⎭⎫⎝⎛=⋅=545345450050105λλλλλλA A A ,⋅ ⋅ ⋅ ⋅ ⋅ ⋅,⎝⎛=kA kk kk k k k k k k λλλλλλ0002)1(121----⎪⎪⎪⎭⎫. 用数学归纳法证明: 当k =2时, 显然成立. 假设k 时成立,则k +1时,⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ,由数学归纳法原理知:⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121.8. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵.证明 因为A T =A , 所以(B T AB )T =B T (B T A )T =B T A T B =B T AB , 从而B T AB 是对称矩阵. 11. 求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221; 解 ⎪⎭⎫ ⎝⎛=5221A . |A |=1, 故A -1存在. 因为 ⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛=1225*22122111A A A A A ,故 *||11A A A =-⎪⎭⎫ ⎝⎛--=1225. (3)⎪⎪⎭⎫⎝⎛---145243121; 解 ⎪⎪⎭⎫⎝⎛---=145243121A . |A |=2≠0, 故A -1存在. 因为⎪⎪⎭⎫⎝⎛-----=⎪⎪⎭⎫ ⎝⎛=214321613024*332313322212312111A A A A A A A A A A ,所以 *||11A A A =-⎪⎪⎪⎭⎫ ⎝⎛-----=1716213213012.(4)⎪⎪⎪⎭⎫ ⎝⎛n a a a 0021(a 1a 2⋅ ⋅ ⋅a n ≠0) .解 ⎪⎪⎪⎭⎫ ⎝⎛=n a a a A 0021, 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 10011211 . 12. 利用逆矩阵解下列线性方程组: (1)⎪⎩⎪⎨⎧=++=++=++3532522132321321321x x x x x x x x x ;解 方程组可表示为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛321153522321321x x x ,故 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x ,从而有 ⎪⎩⎪⎨⎧===001321x x x .19.设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 解 由P -1AP =Λ, 得A =P ΛP -1, 所以A 11= A =P Λ11P -1.|P |=3, ⎪⎭⎫ ⎝⎛-=1141*P , ⎪⎭⎫ ⎝⎛--=-1141311P ,而 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=Λ11111120 012001,故 ⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=31313431200111411111A ⎪⎭⎫ ⎝⎛--=68468327322731. 20. 设AP =P Λ, 其中⎪⎪⎭⎫⎝⎛--=111201111P , ⎪⎪⎭⎫ ⎝⎛-=Λ511, 求ϕ(A )=A 8(5E -6A +A 2). 解 ϕ(Λ)=Λ8(5E -6Λ+Λ2)=diag(1,1,58)[diag(5,5,5)-diag(-6,6,30)+diag(1,1,25)] =diag(1,1,58)diag(12,0,0)=12diag(1,0,0). ϕ(A )=P ϕ(Λ)P -1*)(||1P P P Λ=ϕ⎪⎪⎭⎫ ⎝⎛------⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---=1213032220000000011112011112⎪⎪⎭⎫⎝⎛=1111111114.21. 设A k =O (k 为正整数), 证明(E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1. 证明 因为A k =O , 所以E -A k =E . 又因为 E -A k =(E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1), 所以 (E -A )(E +A +A 2+⋅ ⋅ ⋅+A k -1)=E , 由定理2推论知(E -A )可逆, 且 (E -A )-1=E +A +A 2+⋅ ⋅ ⋅+A k -1.证明 一方面, 有E =(E -A )-1(E -A ).另一方面, 由A k =O , 有E =(E -A )+(A -A 2)+A 2-⋅ ⋅ ⋅-A k -1+(A k -1-A k ) =(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 故 (E -A )-1(E -A )=(E +A +A 2+⋅ ⋅ ⋅+A k -1)(E -A ), 两端同时右乘(E -A )-1, 就有(E -A )-1(E -A )=E +A +A 2+⋅ ⋅ ⋅+A k -1.22. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.证明 由A 2-A -2E =O 得 A 2-A =2E , 即A (A -E )=2E , 或 E E A A =-⋅)(21,由定理2推论知A 可逆, 且)(211E A A -=-.由A 2-A -2E =O 得A 2-A -6E =-4E , 即(A +2E )(A -3E )=-4E , 或 E A E E A =-⋅+)3(41)2(由定理2推论知(A +2E )可逆, 且)3(41)2(1A E E A -=+-.证明 由A 2-A -2E =O 得A 2-A =2E , 两端同时取行列式得 |A 2-A |=2, 即 |A ||A -E |=2, 故 |A |≠0,所以A 可逆, 而A +2E =A 2, |A +2E |=|A 2|=|A |2≠0, 故A +2E 也可逆. 由 A 2-A -2E =O ⇒A (A -E )=2E⇒A -1A (A -E )=2A -1E ⇒)(211E A A -=-,又由 A 2-A -2E =O ⇒(A +2E )A -3(A +2E )=-4E ⇒ (A +2E )(A -3E )=-4 E ,所以 (A +2E )-1(A +2E )(A -3E )=-4(A +2 E )-1, )3(41)2(1A E E A -=+-.第三章 矩阵的初等变换与线性方程组 1. 把下列矩阵化为行最简形矩阵:(1)⎪⎪⎭⎫⎝⎛--340313021201;解 ⎪⎪⎭⎫⎝⎛--340313021201(下一步: r 2+(-2)r 1, r 3+(-3)r 1. )~⎪⎪⎭⎫⎝⎛---020*********(下一步: r 2÷(-1), r 3÷(-2). )~⎪⎪⎭⎫⎝⎛--010*********(下一步: r 3-r 2. )~⎪⎪⎭⎫⎝⎛--300031001201(下一步: r 3÷3. )~⎪⎪⎭⎫⎝⎛--100031001201(下一步: r 2+3r 3. )~⎪⎪⎭⎫⎝⎛-100001001201(下一步: r 1+(-2)r 2, r 1+r 3. )~⎪⎪⎭⎫⎝⎛100001000001.(3)⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311; 解 ⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311(下一步: r 2-3r 1, r 3-2r 1, r 4-3r 1. )~⎪⎪⎪⎭⎫⎝⎛--------1010500663008840034311(下一步: r 2÷(-4), r 3÷(-3) , r 4÷(-5). )~⎪⎪⎪⎭⎫⎝⎛-----22100221002210034311(下一步: r 1-3r 2, r 3-r 2, r 4-r 2. )~⎪⎪⎪⎭⎫⎝⎛---00000000002210032011. 3. 已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=32133212311542322y y y x y y y x y y x ,⎪⎩⎪⎨⎧+-=+=+-=323312211323z z y z z y z z y , 求从z 1, z 2, z 3到x 1, x 2, x 3的线性变换.解 由已知⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z ,所以有⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236z z z x z z z x z z z x .4. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:(1)⎪⎪⎭⎫⎝⎛323513123;解 ⎪⎪⎭⎫ ⎝⎛100010001323513123~⎪⎪⎭⎫⎝⎛---101011001200410123~⎪⎪⎭⎫ ⎝⎛----1012002110102/102/3023~⎪⎪⎭⎫⎝⎛----2/102/11002110102/922/7003~⎪⎪⎭⎫⎝⎛----2/102/11002110102/33/26/7001故逆矩阵为⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267.(2)⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023.解 ⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023~⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321 ~⎪⎪⎪⎭⎫⎝⎛----------10612631110`1022111000010000100021 ~⎪⎪⎪⎭⎫⎝⎛-------106126311101042111000010000100001 故逆矩阵为⎪⎪⎪⎭⎫⎝⎛-------10612631110104211. 5. (2)设⎪⎪⎭⎫ ⎝⎛---=433312120A , ⎪⎭⎫ ⎝⎛-=132321B , 求X 使XA =B . 解 考虑A T X T =B T . 因为⎪⎪⎭⎫ ⎝⎛----=134313*********) ,(T T B A ⎪⎪⎭⎫⎝⎛---411007101042001 ~r ,所以 ⎪⎪⎭⎫⎝⎛---==-417142)(1T T T B A X ,从而 ⎪⎭⎫ ⎝⎛---==-4741121BA X . 9. 求作一个秩是4的方阵, 它的两个行向量是(1, 0, 1, 0, 0), (1, -1, 0, 0, 0).解 用已知向量容易构成一个有4个非零行的5阶下三角矩阵:⎪⎪⎪⎪⎭⎫ ⎝⎛-0000001000001010001100001, 此矩阵的秩为4, 其第2行和第3行是已知向量.12. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3. P106/ 1.已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示.证明 由 ⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r ⎪⎪⎪⎭⎫⎝⎛------531400251552000751610421301 ~r ⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r 知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示.由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示. 4. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.5. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解 以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.9.设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关.证明 由已知条件得a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1,于是 a 1 =b 1-b 2+a 3 =b 1-b 2+b 3-a 4 =b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.11.(1) 求下列向量组的秩, 并求一个最大无关组:(1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解 由⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a , 知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.12.利用初等行变换求下列矩阵的列向量组的一个最大无关组:(1)⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125;解 因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513121433~r r r r r r ---⎪⎪⎪⎭⎫ ⎝⎛531053103210431731253423~rr r r --⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2)⎪⎪⎪⎭⎫⎝⎛---140113*********12211. 解 因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221113142~rr r r --⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122112343~rr r r +↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组. 13. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解 设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=52001110311161101110311131********) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5. 20.求下列齐次线性方程组的基础解系: (1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解 对系数矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T . 因此方程组的基础解系为ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x .解 对系数矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x .取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ; 取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .26. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . 当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x . 解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B . 与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x . 当x 3=x 4=0时, 得所给方程组的一个解η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .。
生物化学课后习题1-3

生物化学(上册)课后习题第一章糖类1、环状己醛糖有多少个可能的旋光异构体?为什么?25=32因为环状己醛糖含有5个不对称碳原子。
单糖由直链变成环状结构后,羰基碳原子成为新的手性中心,导致C1差向异构化,产生两个非对映异构体。
羰基碳上形成的差向异构体称异头物。
2、含D-吡喃半乳糖和D-吡喃葡萄糖的双糖可能含有多少个异构体(不包括异头物)?含同样残基的糖蛋白上的二糖将有多少个异构体?每个单糖单位都能作为羰基供体,与另一个单糖单位的5个羟基形成糖苷键(C1,C2,C3,C4,C6),于是α-D-吡喃半乳糖-D-吡喃葡萄糖苷、β-D-吡喃半乳糖-D-吡喃葡萄糖苷、α-D-吡喃葡萄糖-D-吡喃半乳糖苷和β-D-吡喃葡萄糖-D-吡喃半乳糖苷各有五种,共5*4=20种。
糖蛋白上的二糖链其中一个单糖的C1用于连接多肽,C2,C3,C4,C6用于和另一单糖的C1形成糖苷键,算法同上,共有4*4=16个,考虑到二糖与多肽相连时的异头构象,异构体数目为16*2=32个。
5、D-葡萄糖的α、β异头物的比旋(【α】20D)分别为+112.2º和+18.7º.当α-D-吡喃葡萄糖晶体溶于水时,比旋将由+112.2º降至平衡值+52.7º.计算平衡混合液中α和β异头物的比率。
假设开链形式和呋喃形式可忽略。
忽略开链形式和呋喃形式。
设:α-D-吡喃葡萄糖所占比例x%,则β-D-吡喃葡萄糖所占比例为(100-x)%。
已知25℃,1ml溶液和1dm旋光管中,α-D-吡喃葡萄糖旋光度+112.2º,β-D-吡喃葡萄糖+18.7º,平衡时葡萄糖溶液的旋光度+52.7º。
根据平衡时旋光度是组成各成分旋光度的加和,列出关系式如下:112.2x%+18.7(100-x)%=52.7,解方程得x=36.5α-D-吡喃葡萄糖比例为36.5%,β-D-吡喃葡萄糖比例为63.5%。
课后习题

课后习题第一章绪论(一) 选择题1.国际经济学在研究资源配置时,是以()作为基本的经济单位来划分的。
A. 企业B.个人C.政府D.国家2.国际经济学研究的对象是()A国际商品流动B世界范围内的稀缺资源的最优配置C国际收支平衡D各国之间的经济活动和经济关系3.从国际间经济资源流动的难易度看,()流动最容易A商品B资本C人员D技术(二)问答题1.试述国际经济学和国内经济学的关系。
第二章古典的国际贸易理论(一)选择题本国生产A、B、C、D四种产品的单位劳动投入分别为1、2、4、15,外国生产这四种产品的单位劳动投入分别为12、18、24、30,根据李嘉图模型,本国在哪种产品上拥有最大比较优势?在哪种产品上拥有最大比较劣势?()(a)D、A(b)C、B(c)A、D(d)B、C(二)问答题1.亚当·斯密对国际贸易理论的主要贡献有哪些?2.绝对优势理论和比较优势理论的区别是什么?(三)计算题1.根据下面两个表中的数据,确定(1)贸易前的相对价格;(2)比较优势型态。
表1 X、Y的单位产出所需的劳动投入A国 B国X Y621512表2 X、Y的单位产出所需的劳动投入 A国 B国X Y 104552.假设A、B两国的生产技术条件如下所示,那么两国还有进行贸易的动机吗?解释原因。
表3 X、Y的单位产出所需的劳动投入A BX Y 42843.证明即使一国在某一商品上具有绝对优势,也未必具有比较优势。
4.试对下列说法加以评价:(1)由于发达国家工资水平高于发展中国家,所以发达国家与发展中国家进行贸易会无利可图;(2)因为美国的工资水平很高,所以美国产品在世界市场缺乏竞争力;(3)发展中国家的工资水平比较低是因为国际贸易的缘故。
5. 计算说明题英、美两国生产情况表(1) 什么是绝对优势?分别指出美国、英国在各种情况下具有绝对优势和绝对劣势的产品?(2) 什么是比较优势?分别指出美国、英国在各种情况下比较优势与比较劣势的商品?并说明在各种情况下贸易的可能性及贸易基础?(3) 假设在B种情况下,美国用4单位小麦与英国4单位布交换:1)美国获利多少?2)英国获利多少?3)互惠贸易的范围由多大?4)如果改用4单位小麦于6单位布交换,两国分别获利多少?与第(3)对比说明了什么问题?(4) 假设B种情况下,劳动是唯一生产要素而且是同质的。
大学基础化学课后习题解答(1)

大学基础化学课后习题解答第一章 溶液和胶体溶液 第二章 化学热力学基础2-1 什么是状态函数?它有什么重要特点?2-2 什么叫热力学能、焓、熵和自由能?符号H 、S 、G 、∆H 、∆S 、∆G 、θf m H ∆、θc m H ∆、θf m G ∆、θr mH ∆、θm S 、θr m S ∆、θr m G ∆各代表什么意义? 2-3 什么是自由能判据?其应用条件是什么? 2-4 判断以下说法是否正确,并说明理由。
〔1〕指定单质的θf m G ∆、θf m H ∆、θm S 皆为零。
〔2〕,反应 O 2(g) +S(g) = SO 2(g) 的θr m G ∆、θr m H ∆、θr m S ∆分别等于SO 2(g)的θf m G ∆、θf m H ∆、θm S 。
〔3〕θr m G ∆<0的反应必能自发进行。
2-5 298.15K 和标准状态下,HgO 在开口容器中加热分解,假设吸热22.7kJ 可形成Hg 〔l 〕50.10g ,求该反应的θr m H ∆。
假设在密闭的容器中反应,生成同样量的Hg 〔l 〕需吸热多少?解:HgO= Hg(l)+1/2O 2(g)θr mH ∆=22.7× kJ·mol -1 kJ·mol -1 2-6 随温度升高,反应〔1〕:2M(s)+O 2(g) =2MO(s)和反应〔2〕:2C(s) +O 2(g) =2CO(g)的摩尔吉布斯自由能升高的为 (1) ,降低的为 (2) ,因此,金属氧化物MO 被硫复原反应2MO(s)+ C(s) =M(s)+ CO(g)在高温条件下 正 向自发。
2-7 热力学第一定律说明热力学能变化与热和功的关系。
此关系只适用于:A.理想气体;2-8 纯液体在其正常沸点时气化,该过程中增大的量是:A.蒸气压;B.汽化热;2-9 在298K 时,反应N 2(g)+3H 2(g) = 2NH 3(g),θr m H ∆<0则标准状态下该反应A.任何温度下均自发进行;B.任何温度下均不能自发进行;C.高温自发;2-10 298K ,标准状态下,1.00g 金属镁在定压条件下完全燃烧生成MgO(s),放热24.7kJ 。
人教版高中化学必修一课后习题答案

44高一化学必修1课后习题参考答案第一章第一节1.C2.C3.CD4.略5.乳化原理或萃取原理6.利用和稀盐酸反应产生气体7.不可靠,因为碳酸钡也是白色沉淀,碳酸根干扰了硫酸根的检验。
由于硫酸钡是难溶的强酸盐,不溶于强酸,而碳酸钡是难溶弱酸盐,可溶于强酸,因此可先取样,再滴入氯化钡溶液和几滴稀硝酸或稀盐酸,如果出现白色沉淀,说明有硫酸根。
第一章第二节1.D2.B3.B4.B5.65mg/dL~110mg/dL(1mmol=10-3m ol)6.这种操作会使得结果偏低,因为倒出去的溶液中含有溶质,相当于容量瓶内的溶质有损失。
7.14mL8.n(Ca):n(Mg):n(Cu):n(Fe)=224:140:35:29.1)0.2mol2)Cu2+:0.2mol Cl-:0.4mol10.40(M=40g/mo l,该气体的相对分子质量为40。
)第一章复习题1.C2.B3.A4.BC5.C6.(1)不正确。
(标况下)(2)不正确。
(溶液体积不为1L)(3)不正确。
(水标况下不是气体)(4)正确。
(同温同压下气体的体积比即为物质的量之比,也就是分子个数比)7.(1)5%(2)0.28mol/L8.稀硫酸铁粉过滤Fe、CuFeSO溶液过滤FeSO溶液蒸发9.1.42g,操作步骤略。
结晶第二章第一节1.②⑧①④⑤⑥⑦⑩⑨2.树状分类法略5.分散系分散质粒子大小主要特征举例(3) 强 酸 +CaCO 9 . (1) SO 4 2-+Ba 2 + =BaSO 4(2) 2Al+3Hg 2+ =3Hg+2Al 2(2) 强 酸 + 强 碱 = 可 溶 盐= 可 溶 钙 盐 +H 2 O+CO 2(4) 强 酸 + 可 溶 盐 = 可 溶 >100 nm <1 nm浊液 不稳定,不均一 泥浆水溶液 稳定,均一 饱 和 NaCl 溶 液 胶体 1 ~ 100 nm 较稳定,均一 豆浆 6 . BD7 .胶 体 区 别 于 其 他 分 散 系 得 本 质 特 征 是 胶 体 粒 子 的 大 小 在 1~100n m范 围。
《发动机原理》课后习题答案

《发动机原理》课后习题答案第⼀章1简述发动机的实际⼯作循环过程。
发动机的实际循环是由进⽓、压缩、燃烧、膨胀和排⽓五个过程组成的,较理论循环复杂很多。
1) 进⽓过程。
为了使发动机连续运转,必须不断吸⼊新鲜⼯质,此时进⽓门开启,排⽓门关闭,活塞由上⽌点向下⽌点移动。
、2) 压缩过程。
此时进排⽓门均关闭,活塞由下⽌点向上⽌点移动,缸内⼯质受到压缩,温度、压⼒不断上升,增⼤作功过程的温差,获得最⼤限度的膨胀⽐,提⾼热功转化效率,为燃烧过程创造有利条件。
3) 燃烧过程。
此时进排⽓门均关闭,活塞处在上⽌点前后,作⽤是将燃料的化学能转变为热能,使⼯质的压⼒、温度升⾼。
4) 膨胀过程。
也称作功过程,此时进排⽓门均关闭,⾼温、⾼压的⼯质推动活塞,由上⽌点向下⽌点移动⽽膨胀作功,⽓体的压⼒和温度也随即迅速降低。
5) 排⽓过程。
当膨胀过程接近终了时,排⽓门打开,废⽓开始靠⾃⾝压⼒⾃由排⽓,膨胀过程结束后,活塞由下⽌点返回上⽌点,将⽓缸内的废⽓排除。
2画出四冲程发动机实际循环的⽰功图,它与理论⽰功图有什么不同?说明指⽰功的概念和意义。
图a、b分别为柴油机和汽油机实际循环和理论循环的⽰功图⽐较,理论循环中假设⼯质⽐热容是定值,⽽实际⽓体随温度等因素影响会变⼤,⽽且实际循环中还存在泄露损失。
换⽓损失燃烧损失等,这些损失的存在,会导致实际循环放热率低于理论循环。
指⽰功时指⽓缸内完成⼀个⼯作循环所得到的有⽤功Wi,指⽰功Wi反映了发动机⽓缸在⼀个⼯作循环中所获得的有⽤功的数量。
3 提⾼发动机实际⼯作循环热效率的基本途径是什么?可采取哪些基本措施?提⾼实际循环热效率的基本途径为:减⼩⼯质传热损失,燃烧损失,换⽓损失,不完全燃烧损失,⼯质流动损失,⼯质泄漏损失,提⾼⼯质的绝热指数。
可采取的基本措施是:1)减⼩燃烧室⾯积,缩短后燃⽓能减⼩传热损失。
2)采⽤最佳点⽕提前⾓和供油提前⾓能减少提前燃烧损失或后燃损失。
3)采⽤多⽓门,最佳配⽓相位和最优进排⽓系统能减少换⽓损失。
高等有机化学课后习题

⾼等有机化学课后习题第⼀章习题1. ⽤共振式说明苯甲醚分⼦中甲氧基的邻/对位效应。
2. ⽐较下列各组化合物的酸性⼤⼩并予以解释。
(1) HOCH2CH2COOH 和CH3CH(OH)COOH (2)⼄酸、丙⼆酸、⼄⼆酸和甲酸(3) COOHNO 2和COOHHO(4)H 2C CH 2H 3C CH 3HC CH 、和3. ⽐较碱性。
H 2N(1) CH 3CH 2NH 2 和(2)NH 2HO NH 2O 2N和(3)N HN和⽐较C-Br 键断裂的难易次序和CH 3CH 2CHCH 2CH 3CH 3OCHCH 2CH 3CH 3CH 2CHCF 2CF 3在极性条件下,、4.5. 下列共振式哪⼀个贡献⼤,为什么?C C C C OAB6. 在亲核加成反应中ArCH 2COR 和ArCOR 哪⼀个活性⾼,为什么?7. 解释酸性⼤⼩。
COOH<COOH(1)COOH COOH(2)>8. 为什么ArCOR 被HI 断裂时,得到的产物是RI 和ArOH ,⽽不是ROH 和ArI 。
9. 下列反应中⼏乎不会⽣成PhCH 2CBr(CH 3)2,为什么?PhCH 2CH(CH 3)2 + Br 2 PhCHBrCH(CH 3)2 + HBr10. ⽐较拗CH 3COCH 2COCH 3和CH 3COCH 2COOC 2H 5的酸性,并简要说明原因。
11. 为什么胺的碱性⼤于酰胺?12. 羧酸及其衍⽣物的亲核取代反应活性为什么是RCOCl>(RCO)2O>RC OOR’~RCOOH>RCONH 2。
13.为什么顺丁烯⼆酸的p K a1⽐反丁烯⼆酸⼩,p K a2却正相反?14. 排列下列化合物与HCN反应的活性顺序。
NO2CHO(H3C)2N CHOCHO CHOCl(1)(2)(3)(4)15. 五元杂环⽐苯更易进⾏亲电取代,为什么?第⼆章习题1. 2-丁烯的顺反异构体,分别经稀、冷、碱性KMnO4⽔溶液氧化后,为什么⽣成的2,3-丁⼆醇都不能测出旋光度?2. (R)-CH3CH2CH2CHDI在丙酮NaI溶液中共热,试解释下属现象,①化合物外消旋化;②有过量NaI128存在下,外消旋化速度是同位素交换的两倍;3. 请根据下述现象,为反应H2C CH OC2H5 + H2O C2H5OH + CH3CHO提出反应机理:(1)该反应符合普通的酸催化反应.(2)⽔解反应速度在⽔中⽐在重⽔中快1.9倍.(3)如果⽤同位素标记的⽔进⾏⽔解,所得⼄醇不含18O.(4)若在D2O中进⾏⽔解,只在⼄醛中出现⼀个D.第4章习题1.完成下列反应。
基础会计学课后练习题答案

基础会计学课后练习题答案第一章会计概要二、练习题单选1——5:AADCA多选1.BCD.AC .ABC . ABCD . ABD . ABD第二章会计信息二、练习题单选1——:CAABC ——9: CDAA多选1.ABCD .ABCD .BCD . ABC第三章会计要素二、练习题单项选择题1——5: CBADD——10: CCBDB多项选择题1.ABC.ACD. AB.BCD.ABC.AD.ABC业务题1.该项业务会使资产“银行存款”增加万元,同时负债“预收账款”增加万元。
“应付账款”增加万元。
该项业务会使一项资产“原材料”增加1万元,同时另外一项资产“银行存款”减少 1万元。
该项业务会使一项资产“固定资产”增加20 万元,同时所有者权益“实收资本”增加0 万元。
该项业务会使资产“银行存款”增加1万元,同时负债“短期借款”增加1万。
该项业务会使一项资产“银行存款”增加万元,同时另一项资产“应收账款”减少万元。
该项业务会使一项资产“其他应收款”增加1000 元,另外一项资产“银行存款”减少 1000 元。
该项业务会使资产“银行存款”减少10 万元,同时负债“短期借款”减少10 万元。
该项业务会使资产“固定资产”增加1万元,同时所有者权益“资本公积”增加1万元。
该项业务会使一项资产“库存现金”增加12000 元,同时另一项资产“银行存款” 减少12000 元。
该项业务会使一项所有者权益“盈余公积”减少万元,同时另外一项所有者权益“实收资本”增加万元。
该项业务会使资产“银行存款”减少万元,同时负债“应付账款”减少万元。
“应交税费”减少万元。
该项业务会使一项负债“短期借款”增加86000 元,同时另一项负债“应付账款”减少86000 元。
该项业务会使一项资产“银行存款”增加4000 元,另一项资产“库存现金”减少4000 元。
2.月末资产总额=1842000+30000+80000+120000-120000+200000+160000+80 000-80000+1000-1000-100000+120000+12000-12000-60000-20000+4000-4000=2252000 负债总额=+30000+80000+160000-100000-60000-20000+86000-86000= 932000所有者权益总额=+200000+120000+40000-40000=1320000第四章会计科目和账户二、练习题单选1——7: BCABAAC多选1.ABD .ABCD . ABC . AC .B .ABC 第五章借贷记账法二、练习题单选1——7: ACBCBCC多选1.ABCD.ACD.ABCD.ACD. ABCD.ABCD 1.1)借:银行存款00000贷:实收资本000002)借:固定资产8000贷:实收资本80003)借:银行存款0000贷:短期借款00002.借:原材料——甲9200应交税费——应交增值税6460贷:银行存款5660借:预付账款——琼山钢厂8000贷:银行存款8000借:原材料5050应交税费——应交增值税4080贷:预付帐款8000银行存款 1130借:在建工程 164000应交税费——应交增值税27200贷:银行存款 191200借:在建工程 12000贷:原材料000应付职工薪酬000安装完毕,交付使用时借:固定资产 176000贷:在建工程 1760003.借:生产成本8400制造费用000贷:原材料4400借:管理费用20贷:库存现金20借:生产成本6000制造费用 10000贷:应付职工薪酬6000借:库存现金6000贷:银行存款6000借:应付职工薪酬6000贷:库存现金6000借:制造费用600贷:累计折旧600借:制造费用000贷:预提费用000借:制造费用400贷:待摊费用400借:生产成本6000贷:制造费用6000借:库存商品7200贷:生产成本72004.1)借:生产成本——A产品1000 ——B产品9000制造费用 1100贷:原材料 1011002)借:制造费用00贷:待摊费用003)借:生产成本——A产品 18000 ——B产品 10000制造费用000贷:应付职工薪酬10004)借:制造费用00贷:银行存款005)借:制造费用100贷:累计折旧1006)借:制造费用 1200贷:预提费用 12007)借:制造费用600贷:银行存款600制造费用生产成本1100 100000 00010018000000 1000000本期发生额:128000100 期末余额: 1280001200600本期发生额:218005.编制会计分录:借:银行存款6000贷:预收账款6000借:应收票据1528贷:主营业务收入 18400应交税费——应交增值税128借:预收账款6000银行存款 1674贷:主营业务收入2200应交税费——应交增值税借:银行存款2200贷:应收账款2200借:营业税金及附加 1800贷:应交税费 1800借:主营业务成本4100贷:库存商品4100借:财务费用200贷:预提费用200借:银行存款9200贷:营业外收入9200借:本年利润6500贷:营业税金及附加 1800主营业务成本4100财务费用200管理费用400借:主营业务收入0600营业外收入9200贷:本年利润980074利润总额=79800-46500=33300所得税=33300×25%=8325借:所得税费用325贷:应交税费——应交所得税325借:本年利润——未分配利润325贷:所得税费用325净利润:33300-8325=24975借:利润分配497.5贷:盈余公积497.5第六章会计凭证二、练习题1——7: BBDAADA三、业务题付款凭证贷方科目:银行存款00年月1 日银付字第 1 号金额摘要借方总账科目明细科目千百十万千百十元角分提取备用金库存现金 0 0 0 0 0 合计¥ 0 0 0 0 0 财务主管记账黎明出纳国山审核海军制单王彦转账凭证200年月日转字第 1 号借方金额贷方金额摘要总账科目明细科目千百十万千百十元角分千百十万千百十元角分李明报销差旅费管理费用差旅费 0 0 0 0其他应收款李明 0 0 0 0合计¥0 0 0 0¥0 0 0 0 财务主管记账黎明出纳国山审核海军制单王彦收款凭证借方科目:库存现金 00年月日现收字第 1 号金额摘要借方总账科目明细科目千百十万千百十元角分预借差旅费其他应收款李明 0 0 0 0 余款退回合计¥ 0 0 0 0 财务主管记账黎明出纳国山审核海军制单王彦收款凭证借方科目:库存现金 00年月日现收字第号金额摘要借方总账科目明细科目千百十万千百十元角分第一章总论复习思考题一、单项选择题1.会计所使用的主要计量尺度是。
《现代工业发酵调控学》课后习题

《现代工业发酵调控学》课后习题《第一章》1,不同学科对微生物生长的定义的着重点有何不同?什么是分化?答:细胞生物学家关注单细胞的形态变化,特别是细胞的分裂方式;而生化学者对成千个与生长有关的酶反应,动力学及代谢途径感兴趣,认为生长是所有化学成分有秩序的相互作用的结果。
生物物理学者则认为细胞是热力学不平衡的开放系统,与其周围环境进行物质与能量的交流,特别是在熵的溢流上。
生化工程师把生长看做是生物催化剂数量的增长,通常以质量和细胞数目的增长来表达细胞的生长。
分化是生物的细胞形态和功能向不同的方向发展,由一般变为特殊的现象。
2,有些霉菌,如产黄青霉在培养液中生长过程,其菌丝会形成菌团,有哪些因素影响菌球的松紧?答:生长过程中添加易利用的碳源,如葡萄糖,加快搅拌,供氧改善能使菌团变得密实;反之,用乳糖、搅拌缓慢或供氧跟不上,则菌团变得疏松。
3,微生物生长可以分为几期?停滞期的长短由哪些因素决定?答:微生物生长可分为三个时期,延滞期、对数生长期、静止期。
停滞期的长短影响因素有接种量、接种种子生长期、种子培养基与发酵培养基的相似度、培养基的营养富集度等。
4,生物量的测定为什么对次级代谢产物的生产尤为重要?对谷氨酸,青霉素发酵菌浓的测定,您倾向于用什么方法,说出你的理由答:因为生通过长量的测定可以判断菌体代谢情况,从而控制菌体的发酵得到所需发酵产物。
对谷氨酸、青霉素发酵菌浓的测定,可用比浊法。
操作简便、快速有效、精密度高。
8,有哪些因素会影响微生物的生长答:物理环境,如温度搅拌、空气流量、渗透压、水活度;化学环境,如pH值、溶氧度二氧化碳、碳源、氮源、有机酸等。
9,温度对微生物的生长影响表现在哪些方面答:温度会影响没得活性,从而影响微生物的生长。
温度过高会使酶失活,低温,酶活性弱,不同的温度,可能改变酶的合成种类,从而改变微生物的代谢形式。
10,水的活度用什么表示?它对微生物比生长速率有何影响?答:水活度用同一温度下溶液蒸汽压与纯水蒸汽压的比值表示。
电路分析基础第四版课后习题第一章第二章第三章第四章答案
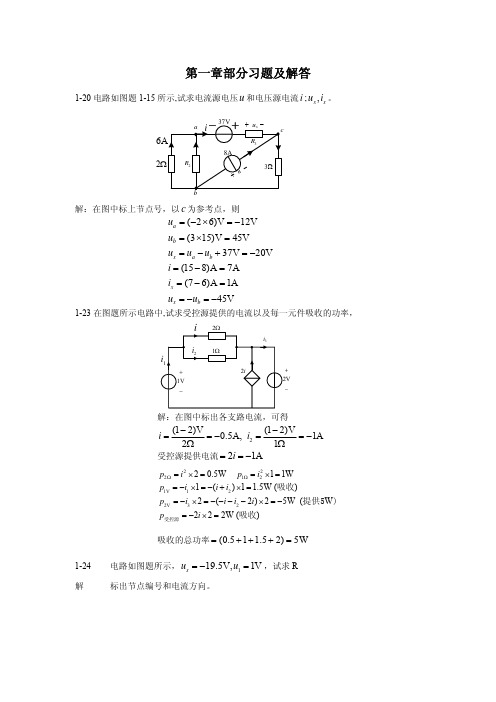
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ,列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向,
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
(完整版)电路原理课后习题答案

第五版《电路原理》课后作业 第一章“电路模型和电路定律”练习题1- 1 说明题 1-1 图(a )、(b )中:(1)u 、i 的参考方向是否关联? ( 2)ui 乘积表示什么功率? ( 3)如果在图( a )中 u>0、 i<0;图( b )中 u>0、i>0,元件实际发出还是吸收功率?元件( a )( b )题 1-1 图解( 1 ) u 、 i 的参考方向是否关联?答: (a ) 关联——同一元件上的电压、电流的参考方向一致,称为关联参考方向;(b ) 非关联——同一元件上的电压、电流的参考方向相反,称为非关联参考方向。
( 2 ) ui 乘积表示什么功率?答: (a ) 吸收功率——关联方向下,乘积 p = ui > 0 表示吸收功率;(b ) 发出功率——非关联方向, 调换电流 i 的参考方向之后, 乘积 p= ui < 0,表示 元件发出功率。
( 3)如果在图 (a ) 中 u>0, i<0,元件实际发出还是吸收功率? 答:(a ) 发出功率——关联方向下, u > 0,i < 0,功率 p 为负值下,元件实际发出功率;(b ) 吸收功率——非关联方向下,调换电流 i 的参考方向之后, u > 0,i > 0,功率 p 为正值 下,元件实际吸收功率;解 (a )电阻元件, u 、i 为关联参考方向。
由欧姆定律 u = R i = 104i(b )电阻元件, u 、i 为非关联参考方向 由欧姆定律 u = - R i = -10i(c )理想电压源与外部电路无关,故 u = 10V (d )理想电压源与外部电路无关,故 u = -5V元件1-4 在指定的电压 u 和电流 i 的参考方向下,写出题 1-4 图所示各元件的 u 和 i 的约束方程 (即 VCR )。
10V +i+u u(c )i 10mA + i u10mA(f )10ka )5V+ud )i10+b )10mA u(e ) 题 1-4 图(e ) 理想电流源与外部电路无关,故i=10 ×10-3A=10-2Af )理想电流源与外部电路无关,故 i=-10 ×10-3A=-10-2A故 电阻功率 PR 吸ui 10 2 20W (吸收 20W )电流源功率PI 吸ui 52 10W ( 吸收 10W )电压源功率 PU 发 ui 15 2 30W (发出30W )b )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解 1-5 图(b )故 电阻功率 P R 吸 12 3 45W (吸收45W ) 电流源功率PI 发 15 2 30W (发出30W ) 电压源功率PU 发15 1 15W(发出15W )c )由基尔霍夫电压定律和电流定律可得各元件的电压电流如解 1-5 图(c )电阻功率 PR 吸15 3 45W (吸收45W ) 电流源功率P I 吸15 2 30W (吸收 30W )电流源及电阻的功率(须说明是吸收还是发出)15V+15V2A电流如解 1-5 图a (b ) 题 1-52A5(发出电压源功率P U发15 5 75W75W)1- 16 电路如题 1-16 图所示,试求每个元件发出或吸收的功率。
人工智能 (马少平 朱小燕 著) 清华大学出版社 课后答案 - 完整版(习题部分+答案部分)

人工智能(马少平朱小燕著) 清华大学出版社课后答案习题部分第一章课后习题1、对N=5、k≤3时,求解传教士和野人问题的产生式系统各组成部分进行描述(给出综合数据库、规则集合的形式化描述,给出初始状态和目标条件的描述),并画出状态空间图。
2、对量水问题给出产生式系统描述,并画出状态空间图。
有两个无刻度标志的水壶,分别可装5升和2升的水。
设另有一水缸,可用来向水壶灌水或倒出水,两个水壶之间,水也可以相互倾灌。
已知5升壶为满壶,2升壶为空壶,问如何通过倒水或灌水操作,使能在2升的壶中量出一升的水来。
3、对梵塔问题给出产生式系统描述,并讨论N为任意时状态空间的规模。
相传古代某处一庙宇中,有三根立柱,柱子上可套放直径不等的N个圆盘,开始时所有圆盘都放在第一根柱子上,且小盘处在大盘之上,即从下向上直径是递减的。
和尚们的任务是把所有圆盘一次一个地搬到另一个柱子上去(不许暂搁地上等),且小盘只许在大盘之上。
问和尚们如何搬法最后能完成将所有的盘子都移到第三根柱子上(其余两根柱子,有一根可作过渡盘子使用)。
求N=2时,求解该问题的产生式系统描述,给出其状态空间图。
讨论N为任意时,状态空间的规模。
4、对猴子摘香蕉问题,给出产生式系统描述。
一个房间里,天花板上挂有一串香蕉,有一只猴子可在房间里任意活动(到处走动,推移箱子,攀登箱子等)。
设房间里还有一只可被猴子移动的箱子,且猴子登上箱子时才能摘到香蕉,问猴子在某一状态下(设猴子位置为a,箱子位置为b,香蕉位置为c),如何行动可摘取到香蕉。
5、对三枚钱币问题给出产生式系统描述及状态空间图。
设有三枚钱币,其排列处在"正、正、反"状态,现允许每次可翻动其中任意一个钱币,问只许操作三次的情况下,如何翻动钱币使其变成"正、正、正"或"反、反、反"状态。
6、说明怎样才能用一个产生式系统把十进制数转换为二进制数,并通过转换141.125这个数为二进制数,阐明其运行过程。
第一章和第二章习题生态

第一章绪论单选择题1.下列表述正确的是[]。
A.生态学是研究生物形态的一门科学B.生态学是研究人与环境相互关系的一门科学C.生态学是研究生物与其周围环境之间相互关系的一门科学D.生态学是研究自然环境因素相互关系的一门科学。
2.生态学作为一个科学名词,最早是由谁提出并定义的[]。
A.E.Haeckel B.E.P.Odum C.A.G.Tansley D.Darwin3.当代环境问题和资源问题,使生态学的研究日益从以生物为研究主体发展到[]。
A.以动物为研究主体 B.以人类为研究主体C.以植物为研究主体 D.以种群为研究主体4.种群生态学研究的对象是[]。
A.种群 B.群落 C.生态系统 D.有机个体5.景观生态学的研究对象是[]。
A.生物圈 B.群落 C.种群 D.景观单元6.全球生态学的研究对象是[]。
A.全球陆地 B.全球海洋 C.整个生物圈 D.整个宇宙7.臭氧层破坏属于[]。
A.地区性环境问题 B.全球性环境问题C.某个国家的环境问题 D. 以某个大陆的环境问题8.生态学发展大致经历了生态学的萌芽时期,建立时期,巩固时期和[]。
A.生物学时期 B.环境科学时期 C.现代生态学时期 D.现代生物学时期9.生态学是研究[]相互关系的一门科学。
A.动物与植物 B.人类与环境 C.有机环境与无机环境 D.生物与环境第二章生物与环境1.具体的生物个体和群体生活地段上的生态环境称为[]。
A.环境 B.生境 C.内环境 D.地球环境2.生物生存不可缺少的因子是[]。
A.生存因子 B.生态因子 C.环境因子 D.生物因子3.根据生态因子的性质,可将生态因子分为土壤因子、地形因子、生物因子、人为因子和[]。
A.气候因子 B.地球因子 C.非生物因子 D.外来因子4.根据生态因子的稳定性程度可把生态因子分为稳定因子和[]。
A.气候因子 B.地形因子 C.外来因子 D.变动因子5.下列生态因子中,属于间接因子的是[]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课后习题一(第一章、第二章)1、ENIAC所用的主要元件是( C )A. 集成电路B. 晶体管C. 电子管D. 以上均不对2、电子计算机问世至今,新型机器不断推陈出新,不管怎么更新,依然保有“存储程序”的概念,最早提出这种概念的是( B )A. 巴贝奇B. 冯.诺依曼C. 帕斯卡D. 贝尔3、个人计算机(PC)是属于( C )类计算机A. 大型计算机B. 小型机C. 微型计算机D. 超级计算机4、电子计算机的算术/逻辑运算单元、控制单元合并为( A )A. CPUB. ALUC. 主机D. I/O5、1字节(BYTE)对应( B )位二进制数A. 1B. 8C. 16D. 不确定6、计算机中关于ALU的描述,正确的是( D )A. 只做算术运算,不做逻辑运算B. 只做加法C. 能存放运算结果D. 以上均不对7、完整的计算机系统应包括( D )A. 运算器、存储器、控制器B. 外部设备和主机C. 主机和实用程序D. 配套的硬件设备和软件系统8、至今为止,计算机中的所有信息仍以二进制方式表示的理由主要是(C )A. 节约元件B. 运算速度快C. 物理器件性能所致D. 信息处理方便9、冯.诺依曼计算机工作方式的基本特点是( B )A. 多指令流单数据流B. 按地址访问并顺序执行指令C. 堆栈操作D. 存储器按内容选择地址10、某寄存器中的值可能是操作数,也可能是地址,只有计算机的( C )才能识别它A. 译码器B. 判断程序C. 指令D. 时序信号11、比特(bit)也称作字位,1比特对应( A )位二进制数A. 1B. 8C. 16D. 不确定12、下列( A )是软件A. 操作系统B. 键盘C. CPUD. 液晶显示器13、下列( D )不是输入设备A. 磁盘驱动器B. 键盘C. 鼠标器D. 打印机14、下列各装置中,( A )具有输入及输出功能A. 磁盘驱动器B. 键盘C. 传统显示器(无触控功能)D. 打印机15、基本上计算机能直接处理的语言是由0与1组成的语言,此种语言称为( C )A. 人工语言B. 汇编语言C. 机器语言D. 高级语言16、某微机系统以16位来表示地址,则该计算机系统有( C )个地址空间21665536A. 256B. 65535C. 65536D. 13107217、一片1MB的磁盘能存储( B )的数据A. 210字节B. 220字节C. 230字节D. 240字节18、计算机中( B )负责指令译码A. ALUB. 控制单元C. 存储器译码电路D. 输入输出译码电路19、下列数中最小的数是( A )A. 101001B=41B. 52Q(八进制=42)C. 2BH=43D. 4420、设寄存器为8位,机器数采用补码形式(含1位符号位),对应于十进制数—27,则寄存器中内容为( C )A. 27HB. 9BHC. 0E5HD. 1BH21、对真值0表示形式唯一的机器数是( B )A. 原码B. 补码和移码C. 补码D. 反码22、在小数定点机中,下述第( B )种说法是正确的A. 只有原码能表示—1B. 只有补码能表示—1C. 只有反码能表示—1D. 原码、补码和反码均能表示—123、某机字长8位,采用补码形式(含1位符号位),则机器数所能表示的范围是(C )A. —127~127B. —128~128C. —128~127D. —127~12824、在小型和微型计算机里,最普遍采用的字母与字符编码是( C )A. BCD码B. 16进制C. ASCII码D. 海明码25、32位字长的浮点数,其中阶符1位,阶码7位,数符1位,尾数23位,则其对应的最大正数为( A ),最小负数为( B ),最小的绝对值为( F ),若机器数采用补码表示,且尾数为规格化形式,则对应的最大正数为( A ),最小正数为( C ),最小负数为( D )A. 2127(1—2-23)B. —2127(1—2-23)C. 2-129D. —2127E. 2-128×2-23F. 2-127×2-2326、[X]补=1.0000000,它代表的真值是( B )A. —0B. —1C. +1D. 无具体意义27、设X为整数,[X]补=1,X1X2X3X4X5,若要X﹤—16,X1~X5应满足( D )条件A. X1~X5至少有一个为1B. X1必须为0,X2~X5至少有一个为1C. X1~X5至少有一个为0D. X1必须为0,X2~X5任意28、设寄存器内容为10000000,若它等于—128,则为( B )A. 原码B. 补码C. 移码D. 反码29、大部分计算机内的减法是用( C )实现A. 将被减数加到减数中B. 从被减数中减去减数C. 补数的相加D. 从减数中减去被减数30、在定点机中执行算术运算时会产生溢出,其原因是( D )A. 主存容量不够B. 操作数过大C. 操作数地址过大D. 运算结果无法表示31、两补码相加,采用1位符号位,则当( D )时,表示结果溢出A. 最高位有进位B. 最高位进位和次高位进位异或结果为0C. 最高位为1D. 最高位进位和次高位进位异或结果为132、在浮点机中,下列( C )是正确的A. 尾数的第一数位为1时,即为规格化形式B. 尾数的第一数位与数符不同时,即为规格化形式C. 不同的机器数有不同的规格化形式D. 尾数的第一数位为0时,即为规格化形式33、在浮点机中,判断补码规格化形式的原则是( C )A. 尾数的第一数位为1时,数符任意B. 尾数的符号位与第一数位相同C. 尾数的符号位与第一数位不同D. 阶符与数符不同34、补码的加减法是指( C )A. 操作数用补码表示,两尾数相加减,符号位单独处理,减法用加法替代B. 操作数用补码表示,符号位和尾数一起参加运算,结果的符号与加减相同C. 操作数用补码表示,连同符号位直接相加减,减某数用加负某数的补码替代,结果的符号在运算中形成D. 操作数用补码表示,由数符决定两尾数的操作,符号位单独处理35、在原码乘法中,符号单独处理,参加操作的数是( D )A. 原码B. 补码C. 绝对值D. 绝对值的补码36、设机器数字长8位(含2位符号位),若机器数DAH为补码,分别对其进行算术左移一位和算术右移一位,其结果分别为( A )A. B4H,EDHB. F4H,6DHC. B5H,EDHD. B4H,6DH注:两位符号位左移后可根据符号关系判断溢出,上例左移后负溢37、运算器的主要功能是进行( C )A. 算术运算B. 逻辑运算C. 算逻运算D. 初等函数运算38、运算器由许多部件组成,其核心部件是( B )A. 数据总线B. 算术逻辑运算单元C. 累加寄存器D. 多路开关以下为书上相关例题39、下列存储器中,汇编语言程序员可见的是( B )A. 存储器地址寄存器(MAR)B. 程序计数器(PC)C. 存储器数据寄存器(MDR)D. 指令寄存器(IR)40、假定基准程序A在某计算机上的运行时间为100秒,其中90秒为CPU时间,其余为I/O时间。
若CPU速度提高50%,I/O速度不变,则运行程序A所耗费的时间是(D )A. 55秒B. 60秒C. 65秒D. 70秒41、假定编译器规定int和short类型长度分别为32位和16位,执行下列C语言语句:unsigned short x=65530;unsigned int y=x;则得到y的机器数为( B )A. 00007FFAHB. 0000FFFAHC. FFFF7FFAHD. FFFFFFFAH42、一个C语言程序在一台32位机器上运行,程序中定义了三个变量x、y和z,其中x 和z为int型,y 为short型,当x=127,y=—9时,执行赋值语句z=x+y后,x、y和z的值分别是( D )A. x=0000007FH,y=FFF9H,z=00000076HB. x=0000007FH,y=FFF9H,z=FFFF0076HC. x=0000007FH,y=FFF7H,z=FFFF0076HD. x=0000007FH,y=FFF7H,z=00000076H43、设浮点数的阶码和尾数均用补码表示,且位数分别为5位和7位(内含2位符号位),若有两个数X=27×29/32,Y=25×5/8,则浮点加法运算X+Y的最终结果为( D )A. 00111 1100010B. 00111 0100010C. 01000 0010001D. 发生溢出问答题44、冯.诺依曼计算机的特点是什么?45、画出以存储器为中心的计算机硬件组成框图,并说明各部件的作用。
46、若x=0.11011,y=—0.11101,分别用原码一位乘和补码一位乘(Booth比较法)计算x ×y。
47、若x=3.3125,y=6.125,假设不包括符号位阶码取3位,尾数取6位,阶符和尾符均取2位,计算x+y。
*答案略。
