湖南省五市十校204-2015学年高二下学期期末联考试题(2015年7月) 化学 Word版含答案

合集下载

2015年高二联考试卷参考答案

2015年高二联考试卷参考答案水平检测二、填空题（每空2分，共16分）17. 2.235-2.238 、10.235 18. 负、2×10-7 19. 减少、200 20. 1.5、2三、计算题（每小题10分，共20分）()()()212222122122221.(10)(1)= 264= 16=12cm 306cm 2 6>12cm3QE k r Q Q kk x x Q x Q x x x Q Q kk x x x ---=-=----<<--->----分分分(2)分分22.(10)(1)= 30.090.01=10080V 20.1= 380==0.1A 279010E ntE EI R r I ∆Φ---∆-⨯=------+---+分分分(2)分分能力检测四、选择题（每小题5分，共20分）五、填空题（每空3分，共15分）28. 3200 29. E 2 、R 1 、短路、变大六、计算题（第30题6分，第31题9分，共,15分）3000200001112291030.(6)(1)===18A 1500==6A 11==13(2)=1500V 1-=1440V 11440200P I U P I Rt I n I n I U nU U nU U IR n U n U ⨯---⇒------=⇒---=---==损分升压原线圈：分输电线路上：分升压变压器原副线圈之比：分升压变压器原副线圈电压之比：分降压变压器原线圈电压：分降压变压器原副线圈电压之比：72111=---分231.(9)(1)2(2)22==2 0.51(3)442AP N 212M M M M M M N MM M N M N M M N N N M v vqv B m R m R qB mT qBT m T m T t nT n T Tt t nT nT n R qBR v mv π=⇒=---=---=+==+=+---==-==---分带负电、分分（取正整数）（取正整数）故线段为粒子轨迹圆的直径分由图知分分。

湖南省五市十校204-2015学年高二下学期期末联考试题(2015年7月) 数学(理)

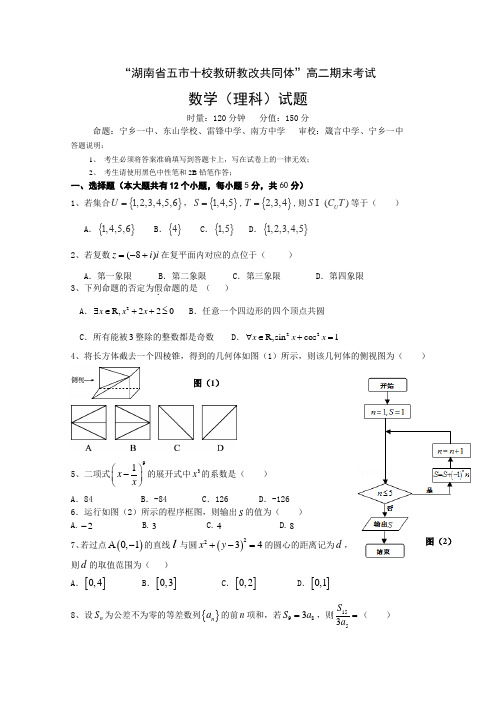
“湖南省五市十校教研教改共同体”高二期末考试数学（理科）试题时量：120分钟分值：150分命题：宁乡一中、东山学校、雷锋中学、南方中学审校：箴言中学、宁乡一中答题说明：1、考生必须将答案准确填写到答题卡上，写在试卷上的一律无效；2、考生请使用黑色中性笔和2B 铅笔作答；一、选择题（本大题共有12个小题，每小题5分，共60分）1、若集合}{,,,,,U =123456，}{,,S =145,}{,,T =234,则)(T C S U 等于（） A ．}{,,,1456 B ．}{4 C ．}{,15D ．}{,,,,12345 2、若复数i i z )8(+-=在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3、下列命题的否定为假．命题的是（） A ．2R,220x x x ∃∈++≤ B ．任意一个四边形的四个顶点共圆 C ．所有能被3整除的整数都是奇数 D ．22R,sin cos 1x x x ∀∈+=4、将长方体截去一个四棱锥，得到的几何体如图（1）所示，则该几何体的侧视图为（）5、二项式91x x ⎛⎫- ⎪⎝⎭的展开式中3x 的系数是（）A ．84B ．-84C ．126D ．-1266．运行如图（2）所示的程序框图，则输出S 的值为（） A.2- B.3 C.4 D.87、若过点()0,1A -的直线l 与圆()2234x y +-=的圆心的距离记为d ，则d 的取值范围为（）A ．[]0,4B ．[]0,3C ．[]0,2D ．[]0,1 8、设n S 为公差不为零的等差数列{}n a 的前n 项和，若983S a =，则1553S a =（）图（1）图（2）A ．15B ．17C ．19D ．219、四边形ABCD 为长方形，O BC AB ,1,2==为AB 的中点。

在长方形ABCD 内随机取一点，取到的点到O 的距离大于1的概率为（）A 、81π-B 、8πC 、41π- D 、4π10、设函数3()f x x x =+，x R ∈．若当02πθ<<时，不等式0)1()sin (>-+m f m f θ恒成立，则实数m 的取值范围是（）A ．(,1]-∞B ．[1,)+∞C ．1(,1)2D ．1(,1]211、已知P 是抛物线x y 42=上的一个动点,Q 是圆()()22311x y -+-=上的一个动点,)0,1(N 是一个定点,则PQ PN +的最小值为（）A ．3B ．4C ．5D 112、已知函数x x f +=1)(—22x +33x —44x +…+20152015x ，g （x ）=1—x +22x —33x +44x —…—20152015x ,设函数()(3)(F x f x g x =+⋅-，且函数()F x 的零点均在区间),,](,[Z ∈<b a b a b a 内，则-b a 的最小值为（）A 、11B 、10C 、9D 、8 二、非选择题（共90分）（一）填空题（本大题共有4个小题，每题5分，将正确答案填入答题卡上） 13、dx x⎰211= 。

(全优试卷)湖南省五市十校教研教改共同体高二下学期期末考试数学(理)试题 Word版含答案

“五市十校教研教改共同体”2015-2016高二第二学期期末考试数学（理科）时量：120分钟总分150分考试学校：沅江一中、箴言中学、桃江一中、宁乡一中、雷锋学校、东山学校、南方中学、岳阳市第十四中学、岳阳市第十五中学、南县一中等第Ⅰ卷一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求） 1．复数12ii-+ (i 是虚数单位)的虚部是( ) A ．13 B ．13i C ．－15 D ．－15iA ．(0，1)B ．[0，1)C ．(1，2)D ．[1，2)3．设数列{}n a 是单调递减的等差数列，前三项的和为12，前三项的积为28，则1a =（） A ．1 B ． 4 C ．7 D ．1或74．将函数()2cos2f x x x =-的图象向左平移6π个单位，所得图象其中一条对称轴方程为( )A ．0x =B ．6x π=C ．4x π=D ．2x π=5．某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆)，则该几何体的体积为( )A ．8010π+B ．8020π+C ．9214π+D ．12010π+6．已知函数2()sin 2cos f x x x x x =+，(2,2)x ππ∈-，则其导函数'()f x 的图象大致是（）A B C D7．给出下列三个命题：①“若2230x x +-≠，则3x ≠-”为假命题； ② 若p q ∨为真命题，则p ,q 均为真命题；③ 命题:,30xp x R ∀∈>，则00:,30x p x R ⌝∃∈≤．其中正确的个数是( )A ．0B ．1C ．2D ．38．定义在R 上的奇函数()f x 满足()(4)f x f x =-，且在[)0,2上单调递增，则下列结论中正确的是（）A ．0(1)(5)f f <->在第一象限的某点，1F 、2F 为双曲线的焦点．若P 在以12F F 为直径的圆上且满足213PF PF =，则双曲线的离心率为（）A ．5B ．25 C．4D ．210 11．如图，设区域{}()|0101D x y x y =≤≤≤≤，，，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y =2y x =所围成阴影区域内的概率是（）A ．16 B ． 13 C ．12 D ． 2312．在平面直角坐标系中，(2,0)A -，(2,0)B ，(8,0)M ，(0,8)N ，若5AP BP =，12()()()33OQ t OM t ON t =-++为实数，则||PQ 的最小值是（）A．3 B．3 C．1 D ． 5第II 卷本卷包括必考题和选考题两部分. 第13～21题为必考题，每个试题考生都必须作答. 第22～24题为选考题，考生根据要求作答. 二、填空题（本题共4小题，每小题5分）13．数列{}n a 的前n 项和记为()11,3,21n n n S a a S n +==≥，则n S =__________． 14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有种不同参加方案（用数字作答）．15．若实数x ，y 满足约束条件4210440y xx y x y ≤-⎧⎪-+≥⎨⎪--≤⎩，则46y z x +=-的最大值是．16．将三项式()21nx x ++展开，当0,1,2,3,n =⋅⋅⋅时，得到以下等式：()0211xx ++=()12211x x x x ++=++()2243212321xx x x x x ++=++++()32654321367631x x x x x x x x ++=++++++……观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数(不足3数的，缺少的数计为0)之和，第k 行共有2k+1个数．若在()()5211ax x x +++的展开式中，8x 项的系数为75，则实数a 的值为．三、解答题（解答应写出文字说明、证明过程或演算步骤）17．(本小题满分12分) 如图，设△ABC 的三个内角A 、B 、C 对应的三条边分别为a b c 、、，且角A 、B 、C 成等差数列，2a =，线段AC 的垂直平分线分别交线段AB 、AC 于D 、E 两点．（Ⅰ）若△BCD ，求线段CD 的长；（Ⅱ）若CD =，求角A 的值．18．（本小题满分12分）如图，已知长方形ABCD 中，AB =，AD =M 为DC 的中点．将ADM ∆沿AM 折起，使得平面ADM ⊥平面ABCM ．（Ⅰ）求证：AD BM ⊥；（Ⅱ）若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为．19．（本小题满分12分）近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X：①求对商品和服务全好评的次数X的分布列；②求X的数学期望和方差．附临界值表：2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828 P K kk≥2K的观测值：2()()()()()n ad bcka b c d a c b d-=++++（其中n a b c d=+++）关于商品和服务评价的2×2列联表：20．（本小题满分12分）已知椭圆222:1(0)3x y M a a +=>的一个焦点为(1,0)F -，左右顶点分别为,A B ，经过点F 的直线l 与椭圆M 交于,C D 两点.（Ⅰ）求椭圆方程；（Ⅱ）记ABD ∆与ABC ∆的面积分别为1S 和2S ，求12||S S -的最大值.21．（本小题满分12分）已知函数()ln 1f x x x =-+，(0,)x ∈+∞；3()g x x ax =-．（Ⅰ）求()f x 的最大值；（Ⅱ）若对1(0,)x ∀∈+∞，总存在2[1,2]x ∈使得12()()f x g x ≤成立，求a 的取值范围；（Ⅲ）证明不等式12()()()1nnn n e nnn e +++<-．请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分．答时用2B 铅笔在答题卡上把所选题目的题号涂黑． 22．（本小题满分10分）选修41-：几何证明选讲如图直线AB 经过圆O 上的点C ，OA=OB ，CA=CB ，圆O 交直线OB 于点E 、D ，其中D 在线段OB 上，连接EC 、CD ．（Ⅰ）证明：直线AB 是圆O 的切线；（Ⅱ）若1tan 2CED ∠=，圆O 的半径为3，求线段OA 的长．23．（本小题满分10分）选修44-：坐标系与参数方程在极坐标系中，圆C 的方程为2sin (0)a a ρθ=>．以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，设直线l 的参数方程为⎩⎨⎧+=+=34,13t y t x （t 为参数）．（Ⅰ）求圆C 的标准方程和直线l 的普通方程；（Ⅱ）若直线l 与圆C 交于,A B 两点，且AB ≥，求实数a 的取值范围．24．（本小题满分10分）选修4—5：不等式选讲已知函数()2f x x x a =-+-．（Ⅰ）当1a =时，解不等式()2f x ≤；（Ⅱ）若()2f x ≥，求实数a 的取值范围．参考答案第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．复数12ii-+ (i 是虚数单位)的虚部是( ) A ．13 B ．13i C ．－15 D ．－15i【答案】CA ．(0，1)B ．[0，1)C ．(1，2)D ．[1，2) 【答案】D3．设数列{}n a 是单调递减的等差数列，前三项的和为12，前三项的积为28，则1a =（） A ．1 B ． 4 C ．7 D ．1或7 【答案】C4．将函数()2cos2f x x x =-的图象向左平移6π个单位，所得图象其中一条对称轴方程为( )A ．0x =B ．6x π= C ．4x π=D ．2x π=【答案】B5．某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆)，则该几何体的体积为( )A ．8010π+B ．8020π+C ．9214π+D ．12010π+ 【答案】A6．已知函数2()sin 2cos f x x x x x =+，(2,2)x ππ∈-，则其导函数'()f x 的图象大致是（）A B C D【答案】C7．给出下列三个命题：①“若2230x x +-≠，则3x ≠-”为假命题； ② 若p q ∨为真命题，则p ,q 均为真命题；③ 命题:,30x p x R ∀∈>，则00:,30xp x R ⌝∃∈≤．其中正确的个数是( )A ．0B ．1C ．2D ．3【答案】B8．定义在R 上的奇函数()f x 满足()(4)f x f x =-，且在[)0,2上单调递增，则下列结论中正确的是（）A ．0(1)(5)f f <->在第一象限的某点，1F 、2F 为双曲线的焦点．若P 在以12F F 为直径的圆上且满足213PF PF =，则双曲线的离心率为（）A ．5B ．25 C ．4D ．210 【答案】D11．如图，设区域{}()|0101D x y x y =≤≤≤≤，，，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y =2y x =所围成阴影区域内的概率是（）A ．16 B ． 13 C ．12 D ． 23【答案】B12．在平面直角坐标系中，(2,0)A -，(2,0)B ，(8,0)M ，(0,8)N ，若5AP BP =，12()()()33OQ t OM t ON t =-++为实数，则||PQ 的最小值是（）A．3 B．3 C．1 D ． 5 【答案】A第II 卷本卷包括必考题和选考题两部分. 第13 ~ 21题为必考题，每个试题考生都必须作答. 第22 ~ 24题为选考题，考生根据要求作答. 二、填空题：本题共4小题，每小题5分.13．数列{}n a 的前n 项和记为()11,3,21n n n S a a S n +==≥，则n S =__________．【答案】3n14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有种不同参加方案（用数字作答）．【答案】4215．若实数x ，y 满足约束条件4210440y xx y x y ≤-⎧⎪-+≥⎨⎪--≤⎩，则46y z x +=-的最大值是．【答案】-216．将三项式()21nx x ++展开，当0,1,2,3,n =⋅⋅⋅时，得到以下等式：()0211x x ++=()12211x x x x ++=++()2243212321xx x x x x ++=++++()32654321367631x x x x x x x x ++=++++++……观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数(不足3数的，缺少的数计为0)之和，第k 行共有2k+1个数．若在()()5211ax x x +++的展开式中，8x 项的系数为75，则实数a 的值为．【答案】2三、解答题：解答应写出文字说明、证明过程或演算步骤．17．(本小题满分12分) 如图，设△ABC 的三个内角A 、B 、C 对应的三条边分别为a b c 、、，且角A 、B 、C 成等差数列，2a =，线段AC 的垂直平分线分别交线段AB 、AC 于D 、E 两点．（Ⅰ）若△BCD 的面积为3，求线段CD 的长；（Ⅱ）若CD =A 的值．解：（Ⅰ）∵角A,B,C成等差数列，A B C π++=，∴3B π=…………1分又∵△BCD 2a =，∴11sin 222BCDS BD BC B BD ==⨯= ∴23BD =…………3分在△BCD 中，由余弦定理可得3CD ==………6分（Ⅱ）由题意，在△BCD 中，sin sin CD BCB BDC=∠2sin BDC =∠，………8分 ∴sin 1BDC ∠=，则90oBDC ∠=，即C D A B ⊥ …………10分又DE 为AC 的垂直平分线，故4A B π∠=∠=…………12分18．（本小题满分12分）如图，已知长方形ABCD 中，AB =，AD =M 为DC 的中点．将ADM ∆沿AM 折起，使得平面ADM ⊥平面ABCM ．（Ⅰ）求证：AD BM ⊥；（Ⅱ）若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为．解：（Ⅰ）证明：∵长方形ABCD 中，AB=22，AD=2，M 为DC 的中点，∴AM=BM=2，∴BM ⊥AM. ……2分 ∵平面ADM ⊥平面ABCM ，平面ADM∩平面ABCM=AM ，BM ⊂平面ABCM∴BM ⊥平面ADM ……4分 ∵AD ⊂平面ADM ∴AD ⊥BM. ……5分（Ⅱ）建立如图所示的直角坐标系，设DE DB λ=，则平面AMD 的一个法向量(0,1,0)n =，(1,2,1),ME MD DB λλλλ=+=--(2,0,0)AM =-， ……8分设平面AME 的一个法向量(,,),m x y z = 则202(1)0x y z λλ=⎧⎨+-=⎩ 取y =1，得20,1,,1x y z λλ===- 所以2(0,1,)1m λλ=-， ……10分因为5cos ,||||m n m n m n ⋅<>==⋅，求得12λ=，所以E为BD的中点．……12分19．（本小题满分12分）近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X：①求对商品和服务全好评的次数X的分布列；②求X的数学期望和方差．附临界值表：2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828 P K kk≥2K的观测值：2()()()()()n ad bcka b c d a c b d-=++++（其中n a b c d=+++）关于商品和服务评价的2×2列联表：解：（1）由题意可得关于商品和服务评价的2×2列联表如下：2分22200(80104070)11.11110.828,1505012080K ⨯⨯-⨯=≈>⨯⨯⨯ ………4分故能在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关. …5分(2)①每次购物时,对商品和服务都好评的概率为25,且X 的取值可以是0,1,2,3. 其中3327(0)()5125P X ===; 1232354(1)()()55125P X C ===;………7分22132336(2)()()55125P X C ===; 3303238(3)()()55125P X C ===. ………9分X 的分布列为：10分②由于2~(3,)5X B ,则26()3,55E X =⨯=2218()3(1).5525D X =⨯⨯-=……12分20．（本小题满分12分）已知椭圆222:1(0)3x y M a a +=>的一个焦点为(1,0)F -，左右顶点分别为,A B ，经过点F 的直线l 与椭圆M 交于,C D 两点.（Ⅰ）求椭圆方程；（Ⅱ）记ABD ∆与ABC ∆的面积分别为1S 和2S ，求12||S S -的最大值. （Ⅰ）因为)0,1(-F 为椭圆的焦点，所以1=c ，又32=b ，所以42=a ，所以椭圆方程为13422=+y x . ……………………………………4分（Ⅱ）当直线l 无斜率时,直线方程为1-=x ,此时3(1,)2D -,3(1,)2C --,021=-S S . ……………………………………5分当直线l 斜率存在时，设直线方程为)0)(1(≠+=k x k y ，设),(),,(2211y x D y x C ，联立得⎪⎩⎪⎨⎧+==+)1(13422x k y y x ，消掉y 得01248)43(2222=-+++k x k x k ，显然0>∆，方程有根，且2221222143124,438k k x x k k x x +-=+-=+.………………8分此时)1()1(22212121221+++=+=-=-x k x k y y y y S S212122(+)234kk x x k k =+=+. ………………………………10分因为0≠k ，上式312212432124312==⋅≤+=k kk k，（23±=k 时等号成立），所以21S S -的最大值为3. …………………………12分21．（本小题满分12分）已知函数()ln 1f x x x =-+，(0,)x ∈+∞；3()g x x ax =-．（Ⅰ）求()f x 的最大值；（Ⅱ）若对1(0,)x ∀∈+∞，总存在2[1,2]x ∈使得12()()f x g x ≤成立，求a 的取值范围；（Ⅲ）证明不等式12()()()1nnn n e nnn e +++<-．，， ……………………1分时，，时，， ……………………3分，∴的最大值为. ……………………4分，使得成立，等价于……………………5分，当时，在时恒为正，满足题意. ……………………6分时，2()3g x x a '=-，令()0g x '=，解得，上单调递增，……………………7分，∴，∴.时，在递减，递增，而，在为正，在为负，∴，，而时，，不合题意，的取值范围为. …………9分即， …………10分，∴，即，…………11分. …………12分请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分．答时用2B 铅笔在答题卡上把所选题目的题号涂黑． 22．（本小题满分10分）选修41-：几何证明选讲如图直线AB 经过圆O 上的点C ，OA=OB ，CA=CB ，圆O 交直线OB 于点E 、D ，其中D 在线段OB 上，连接EC 、CD ．（Ⅰ）证明：直线AB 是圆O 的切线；（Ⅱ）若1t a n 2C ED ∠=，圆O 的半径为3，求线段OA 的长．解：（1）连结,,,OC OA OB CA CB OC AB ==∴⊥.又OC 是圆O 的半径，AB ∴是圆O 的切线. …………5分（2）直线AB 是圆O 的切线，BCD E ∴∠=∠.又CBD EBC ∠=∠，BCD BEC ∴∆∆，则有BC BD CD BE BC EC ==，又1t a n 2CD CED EC ∠==，故12B DC DB C E C==. 设BD x =，则2BC x =，又2BC BD BE =，故()()226x x x =+，即2360x x -=.解得2x =，即2BD =.325OA OB OD DB ∴==+=+=. …………10分23．（本小题满分10分）选修44-：坐标系与参数方程在极坐标系中，圆C 的方程为2sin (0)a a ρθ=>．以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，设直线l 的参数方程为⎩⎨⎧+=+=34,13t y t x （t 为参数）．（Ⅰ）求圆C 的标准方程和直线l 的普通方程；（Ⅱ）若直线l 与圆C 交于,A B 两点，且AB ≥，求实数a 的取值范围．23.解：（Ⅰ）C 的直角坐标方程为222()x y a a +-=，在直线l 的参数方程中消t 得：4350x y -+= ………5分（Ⅱ）要满足弦AB ≥及圆的半径为a 可知只需圆心(0,)a 到直线l 的距离12d a ≤即12a ≤, 整理得：2111201000a a -+≤即(1110)(10)0a a --≤解得：101011a ≤≤，故实数a 的取值范围为：101011a ≤≤ ………10分24．（本小题满分10分）选修4—5：不等式选讲已知函数()2f x x x a =-+-．（Ⅰ）当1a =时，解不等式()2f x ≤；（Ⅱ）若()2f x ≥，求实数a 的取值范围．解：（Ⅰ）当1a =时，231()112232x x f x x x x -+<⎧⎪=≤≤⎨⎪->⎩， ……………1分当1x <时，232x -+≤，所以12x >。

湖南省五市十校204-2015高二数学下学期期末联考试题理

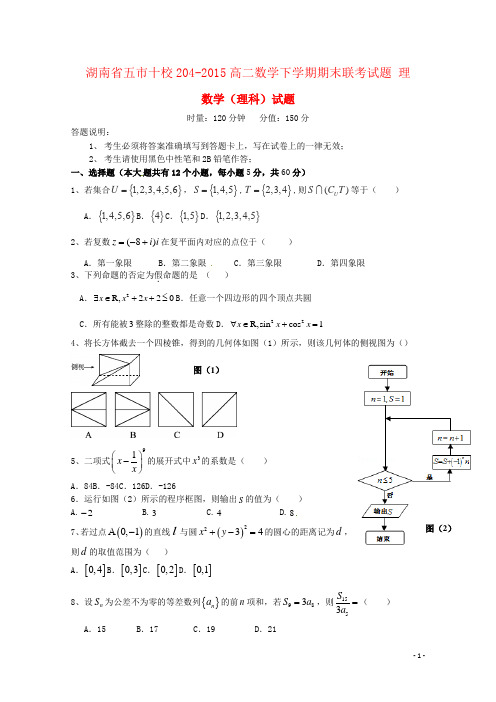
湖南省五市十校204-2015高二数学下学期期末联考试题理数学（理科）试题时量：120分钟分值：150分答题说明：1、考生必须将答案准确填写到答题卡上，写在试卷上的一律无效；2、考生请使用黑色中性笔和2B 铅笔作答；一、选择题（本大题共有12个小题，每小题5分，共60分）1、若集合}{,,,,,U =123456，}{,,S =145,}{,,T =234,则)(T C S U 等于（） A ．}{,,,1456B ．}{4C ．}{,15D ．}{,,,,12345 2、若复数i i z )8(+-=在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3、下列命题的否定为假．命题的是（） A ．2R,220x x x ∃∈++≤B ．任意一个四边形的四个顶点共圆 C ．所有能被3整除的整数都是奇数D ．22R,sin cos 1x x x ∀∈+=4、将长方体截去一个四棱锥，得到的几何体如图（1）所示，则该几何体的侧视图为（）5、二项式91x x ⎛⎫- ⎪⎝⎭的展开式中3x 的系数是（）A ．84B ．-84C ．126D ．-1266．运行如图（2）所示的程序框图，则输出S 的值为（） A.2- B.3 C.4 D.87、若过点()0,1A -的直线l 与圆()2234x y +-=的圆心的距离记为d ，则d 的取值范围为（）A ．[]0,4B ．[]0,3C ．[]0,2D ．[]0,18、设n S 为公差不为零的等差数列{}n a 的前n 项和，若983S a =，则1553S a =（） A ．15 B ．17 C ．19 D ．21图（1）图（2）9、四边形ABCD 为长方形，O BC AB ,1,2==为AB 的中点。

在长方形ABCD 内随机取一点，取到的点到O 的距离大于1的概率为（）A 、81π-B 、8πC 、41π- D 、4π10、设函数3()f x x x =+，x R ∈．若当02πθ<<时，不等式0)1()sin (>-+m f m f θ恒成立，则实数m 的取值范围是（）A ．(,1]-∞B ．[1,)+∞C ．1(,1)2D ．1(,1]211、已知P 是抛物线x y 42=上的一个动点,Q 是圆()()22311x y -+-=上的一个动点,)0,1(N 是一个定点,则PQ PN +的最小值为（） A ．3 B ．4 C ．5 D ．21+12、已知函数x x f +=1)(—22x +33x —44x +…+20152015x ，g （x ）=1—x +22x —33x +44x —…—20152015x ,设函数()(3)(4)F x f x g x =+⋅-，且函数()F x 的零点均在区间),,](,[Z ∈<b a b a b a 内，则-b a 的最小值为（）A 、11B 、10C 、9D 、8 二、非选择题（共90分）（一）填空题（本大题共有4个小题，每题5分，将正确答案填入答题卡上） 13、dx x⎰211=。

湖南省五市十校204-2015学年高二下学期期末联考试题(2015年7月) 语文 Word版含答案

“湖南省五市十校教研教改共同体”高二期末考试语文试题时量：150分钟总分 150分命题：箴言中学、桃江一中、南县一中审校：箴言中学、宁乡一中答题说明:1.本试卷分第I卷(阅读题)和第II卷(表达题)两部分，共150分。

考试时间150分钟。

2.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

作答时请认真阅读答题卡上的注意事项，将答案写在答题卡上，在本试卷上答题无效。

3.考生请使用黑色中性笔和2B铅笔作答。

第I卷阅读题(70分)甲必做题一、现代文阅读(9分，每小题3分)阅读下面文字，完成1-3题（9分）小说敢不敢拒绝影视改编？王彦自1987年出版《商州》，到2014年9月《老生》问世，27年间贾平凹共创作15部长篇小说。

但其中被改编为影视剧的仅有3部，改编后成为口碑之作的更近乎为零。

作为一代名家，贾平凹似乎与时下小说改编影视剧成风的潮流格格不入。

对此，有学者提出，当今文学界紧缺的恰是敢于逆流而行，让影视剧改编无从入手的纯文学性小说。

文学评论家徐兆寿举例为证：2012年中国作家海外影响力排行榜上，莫言、余华、苏童分列前三。

“作家本身功底之外，不可忽视的因素是，每人背后都有一部由小说改编的经典电影。

”在他看来，莫言背后有《红高粱》，余华有《活着》，苏童则有《大红灯笼高高挂》。

它们既成就了张艺谋，也成全了作家在海外声名鹊起。

“国内书市同样如此，书店的畅销小说半数以上都有‘触电’背景”。

徐兆寿说，影视与文学联姻，常常能让一些作家为更多读者认识，具有更大的阅读市场，像莫言、王朔、余华、刘恒、刘震云、麦家、严歌苓等，他们的作品随着影视剧的热播在小说热销榜上扶摇直上。

影视对文学作品的推广作用不仅中国有，国外同样早有先河，美国当代电影理论家乔治·布鲁斯东就在著作《从小说到电影》中写道：“《大卫・科波菲尔》在克利夫兰的影院公映时，借阅小说的人数陡增，当地图书馆不得不在一周内添购132册；《呼啸山庄》被拍成电影后，小说在2年内的销售数量超出过去92年的总和。

湖南省五市十校近年-近年学年高二数学下学期期末联考试题文(扫描版)(最新整理)

高二文科数学参考答案一、选择题：（本大题共12小题，每小题5分，在每小题给出的四个选项中,只有一项是符合题目要求的．）123456789101112题号答B AC C B C A B BD C D案二、填空题：（本大题共4小题，每小题5分,共20分）13． 14． 15 . 16.三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤（一)必考题17。

解：（1） 2×2列联表如下:通过人数未通过人总计数甲校204060乙校302050总计5060110由上表数据算得:所以有99％的把握认为学生的自主招生通过情况与所在学校有关……………6分(2) 按照分层抽样的方法，应从甲校中抽2 人,乙校中抽3人,甲校2 人记为A，B，乙校3人记为，从5 人中任取2人共有10种情况，其中2 人全部来自乙校的情况有共3种，所以所求事件的概率为……………………12分。

18.解: ( 1 ）由成等差数列，可求得，由已知及正弦定理可求得 (5)( 2 ）解法一：三角形的周长为所以周长的取值范围是………………12分解法二：，,19。

解: （I）取中点,连结；平面，平面,平面。

………………5分 (II）………………6分又平面平面平面平面……8分过作的线,垂足为，则为四棱锥的高。

底面四边形为直角梯形，其面积…………10分…………12分20.解: （1）由已知点代入椭圆方程得由得可转化为由以上两式解得所以椭圆C的方程为：………………….4分(2）存在这样的直线。

当l的斜率不存在时，显然不满足，所以设所求直线方程代入椭圆方程化简得：设所求直线与椭圆相交两点由已知条件可得综合上述式子可解得符合题意所以所求直线方程为：……………12分21。

解（1)由已知可知函数f（x）的定义域为，由当时,所以在为增函数当时,所以f(x）的单调递增区间为,单调递减区间为…………………5分( 2）当时，由（1)可知知在为增函数,在为减函数。

湖南省五市十校204-2015学年高二数学下学期期末联考试题文

“湖南省五市十校教研教改共同体”高二期末考试数学（文科）试题时量：120分钟分值：150分答题说明：1、考生必须将答案准确填写到答题卡上，写在试卷上的一律无效；2、考生请使用黑色中性笔和2B 铅笔作答；一、选择题（每小题5分，共60分） 1. 设集合{x x U =}3<， {}1<=x x A ，则A C U = （）A ．{}31<≤x xB ．{}31≤<x xC ．}{31<<x x D ．{}1x x ≥2.复数11i+的虚部是（） A ．12- B ．12 C ．12i D ．i 21-3.已知命题:,sin p x x x ∀∈>R ，则p 的否定形式为（） A ．000,sin x x x ∃∈<R B ．000,sin x x x ∃∈≤R C ．,sin x x x ∀∈≤RD ．,sin x x x ∀∈<R4.设函数2()23,[5,5]f x x x x =-++∈-.若从区间[5,5]-内随机选取一个实数0x ,则所选取的实数0x 满足0()0f x ≤的概率为（） A ．0.3 B ．0.4 C ．0.5 D ．0.65.已知P 是圆122=+y x 上的动点，则 P 点到直线 022:=-+y x l 的距离的最小值为（）A ． 1B ．2C ． 2D．6.极坐标方程2sin()2ρπθ=+和参数方程2cos (3sin x y θθθ=⎧⎨=⎩为参数）所表示的图形分别是（）A ．圆与直线 B.圆与椭圆 C.直线与圆 D.直线与椭圆7. 某产品的广告费用错误！未找到引用源。

与销售额错误！未找到引用源。

的统计数据如下表：为错误！未找到引用源。

，据此模型预报广告费用为6万元时销售额为( )A ．63.6万元 B.65.5万元 C.67.7万元 D.72.0万元8.函数错误！未找到引用源。

的图象向右平移错误！未找到引用源。

【英语】湖南省五市十校204-2015学年高二下学期期末联考试题

“湖南省五市十校教研教改共同体”高二期末考试第Ⅰ卷（选择题）第二部分阅读理解(共两节，满分40分)第一节(共15小题；每小题2分，满分30分)阅读下列短文，从每题所给的四个选项(A、B、C、和D)中，选出最佳选项，并在答题卡上将该项涂黑。

AGlastonbury Festival:Time and place: 22nd～26th June, Pilton, Somerse. Recognized as the best summer festival season, Glasto nbury is one of the biggest and oldest festivals in the UK. Last year‟s 40th anniversary was their best ever, even though the supergroup U2 canceled last minute because of Bono injuring his back.Latitude Festival:Time and place:14th～17th July, Henham Park, Suffolk. Now in its sixth year, this festival is the choice for more families. It is providing visitors with a range of entertainment to accompany the music, including comedy, show, theatre and literature.Shrewsbury Folk Festival:Time and place: 26th～29th August, West Mids Show Ground, Shrewsbury. Announced as one of the best folk festivals in the UK, this festival is only in its sixth year. It takes place over the 4 days of the August bank holiday weekend, and moved to Shrewsbury in 2006.Download Festival:Time and place: 10th and 12th, June, Donington Park Derby. It is a three-day rock music festival held every year. The name Download was chosen for the festival for two reasons. Downloading was a dirty work in the music industry at the time because of file sharing and rock is seen as a rebellious (反叛) type of music.21. Which festival is one of the oldest festivals in the UK?A. Download FestivalB. Latitude FestivalC. Shrewsbury Folk FestivalD. Glastonbury Festival22. When and where is the rock music festival held?A. 22nd～26th June, Pilton, SomerseB. 26th～29th August, West Mids Show GroundC. 10th and 12th, June, Donington Park DerbyD. 14th～17th July, Henham Park, Suffolk23. What is special about Latitude Festival?A. It is one of the best folk festivals in the UK.B. It has a long history and is held every year.C. It is the best summer festival in the UK.D. It is attractive and joyful for many families.BBelieve it or not but it is true. There are people who lose the ability to understand or use words due to brain damage. But they become extremely good at something else. They become experts at spotting liars. The condition in which people lose their power to understand or use words due to brain damage are called aphasia(失语症). A study conducted in Massachusetts, U.S., has clearly proved that aphasics make good lie detectors(测谎仪).In the last 100 years, many doctors studying the brain have mentioned examples of this amazing power of patients suffering from aphasia. Recently, scientists conducted tests to see if all that was said about aphasics was true. They studied the powers of a mixed group of people. Some were normal; others were aphasic. And it was proved clearly that the normal volunteers still got fooled by words. The aphasics were far ahead of them in recognizing false speech. The results of the study were reported in the magazine Nature.`Fourteen years ago, famous American doctor, Dr. Oliver Sacks, wrote about his experiences with aphasic patients in a book. He remembered a particular incident in a hospital. Patients from the aphasia room were watching TV. Their president, Ronald Reagan, was giving a speech. He was trying to put feelings into each and every word of his speech. But his speech had an opposite effect on the patients. They were not impressed. On the contrary, the whole room shook with their laughter. The aphasics knew that he did not mean a word of what he was saying.Dr. Sacks saw aphasics as more gifted than normal people. Normal people “get carried away”by words. An aphasic cannot understand words. But he or she can still understand what is being said. He said most of the aphasics had this superior understanding. So, while normal people think of aphasic patients as brain damaged, they actually seem to understand human expressions better.24. We can know from the first paragraph ___.A. how aphasics get their special abilityB. that aphasics can tell if you are lyingC. that aphasics are good at telling liesD. why aphasics are experts at spotting liars25. The phrase “get carried away” in the last paragraph means ___.A. get fooledB. get excitedC. get misunderstoodD. get discouraged26. Dr. Oliver Sacks thinks that aphasics ___.A. can be cured totallyB. can not understand what is being saidC. are specially gifted in a wayD. should be treated equally and nicely27. Which would be the best title of the passage?A. A great discoveryB. The great lie detectorsC. Why aphasics can‟t ta lkD. A special way of understandingCJames Cleveland Owens was the son of a farmer and the grandson of black slaves. His family moved to Cleveland when he was 9. There, a school teacher asked the youth his name.“J.C., ”he replied.She t hought he had said “Jesse”, and he had a new name.Owens ran his first race at age 13. After high school, he went to Ohio State University. He had to work part time so as to pay for his education. As a second year student, in the Big Ten games in 1935, he set even more records than he would in the Olympic Games a year later.A week before the Big Ten Meet, Owens accidentally fell down a flight of stairs. His back hurt so much that he could not exercise all week, and he had to be helped in and out of the car that drove him to the meet. He refused to listen to the suggestions that he give up and said he would try, event by event. He did try, and the results are in the record book.The stage was set for Owens victory at the Olympic Games in Berlin the next year, and his success would come to be regarded as not only athletic but also political. Hitler did notcongratulate any of the African American winners.“It was all right with me,” he said years later. “I didn‟t go to Berlin to shake hands with him, anyway. ”Having returned from Berlin, he received no telephone calls from the president of his own country, either. In fact, he was not honored by the United States until 1976, four years before his death.Owens Olympic victories made little difference to him. He earned his living by looking after a school playground, and accepted money to race against cars, trucks, motorcycles and dogs.“Sure, it bothered me, ”he said later. “But at least it was an honest living. I had to eat.”In time, however, his gold medals ch anged his life. “They have kept me alive over the years,” he once said. “Time has stood still for me. That golden moment dies hard.”28. In the Big Ten Meet, Owens ___.A. hurt himself in the backB. succeeded in setting many recordsC. tried every sports event but failedD. had to give up some events29. We can infer from the text that Owens was treated unfairly in the US at that time because ___.A. he did not talk to the US president on the phoneB. he was the son of a poor farmerC. he did not shake hands with HitlerD. he was not of the right race30. When Owens says “They have kept me alive over the years”, he means that the medals ___.A. have been changed for money to help him live onB. have made him famous in the USC. have encouraged him to overcome difficulties in lifeD. have kept him busy with all kinds of jobs31. What would be the best title for the text?A. Jesse Owens, a great American athleteB. Golden Moment — a life time struggleC. Making a living as a sportsmanD. How to be a successful athleteDParents and kids today dress alike, listen to the same music, and are friends. Is it a goodthing? Sometimes when Mr. Ballmer and his 16-year-old daughter, Elizabeth, listen to rock music together and talk about interests both enjoy, such as pop culture, he remembers his more distant relationship with his parents when he was a teenager.“I would never have said to my mom, …Hey, the new Weezer album is really great. How do you like it‟?” says Ballmer. “There was just a complete gap in taste.”Music was not the only gulf. From clothing and hairstyles to activities and expectations, earlier generations of parents and children often appeared to move in separate orbits.Today, the generation gap has not disappeared, but it is getting narrow in many families. Conversations on subjects such as sex and drugs would not have taken place a generation ago. Now they are comfortable and common. And parent-child activities, from shopping to sports, involve a feeling of trust and friendship that can continue into adulthood.No wonder greeting cards today carry the message, “To my mother, my best friend.”But family experts warn that the new equality can also result in less respect for parents.“There‟s still a lot of strictness a nd authority on the part of parents out there, but there is a change happening,” says Kerrie, a psychology professor at Lebanon Valley College. “In the middle of that change, there is a lot of confusion among parents.”Family researchers offer a variety of reasons for these evolving roles and attitudes. They see the 1960s as a turning point. Great cultural changes led to more open communication and a more democratic process that encourages everyone to have a say.“My parents were on the …before‟ side of tha t change, but today‟s parents, the 40-year-olds, were on the …after‟ side,” explains Mr. Ballmer. “It‟s not something easily accomplished by parents these days, because life is more difficult to understand or deal with, but sharing interests does make it more fun to be a parent now.”32. The underlined word “gulf” in Paragraph 3 most probably means ___.A. interestB. differenceC. distanceD. separation33. Which of the following shows that the generation gap is disappearing?A. Parents help their children develop interests in more activities.B. Parents put more trust in their children‟s abilities.C. Parents and children talk more about sex and drugs.D. Parents share more interests with their children.34. The change in today‟s parent child relationship is ___.A. more confusion among parentsB. more equality between parents and childrenC. less respect for parents from childrenD. more strictness and authority on the part of parents35. By saying “today‟s parents, the 40-year-olds, were on the …after‟ side,” the author means thattoday‟s parents ___.A. follow the trend of the changeB. can set a limit to the changeC. fail to take the change seriouslyD. have little difficulty adjusting to the change第二节(共5小题，每小题2分，满分10分)根据短文内容，从短文后的选项中选出能填入空白处的最佳选项。

【精选高中试题】湖南省五市十校教研教改共同体高二下学期期末考试数学(理)试题 Word版含答案

“五市十校教研教改共同体”2015-2016高二第二学期期末考试数学（理科）时量：120分钟总分150分考试学校：沅江一中、箴言中学、桃江一中、宁乡一中、雷锋学校、东山学校、南方中学、岳阳市第十四中学、岳阳市第十五中学、南县一中等第Ⅰ卷一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求） 1．复数12ii-+ (i 是虚数单位)的虚部是( ) A ．13 B ．13i C ．－15 D ．－15iA ．(0，1)B ．[0，1)C ．(1，2)D ．[1，2)3．设数列{}n a 是单调递减的等差数列，前三项的和为12，前三项的积为28，则1a =（） A ．1 B ． 4 C ．7 D ．1或74．将函数()cos2f x x x =-的图象向左平移6π个单位，所得图象其中一条对称轴方程为( )A ．0x =B ．6x π=C ．4x π=D ．2x π=5．某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆)，则该几何体的体积为( )A ．8010π+B ．8020π+C ．9214π+D ．12010π+6．已知函数2()sin 2cos f x x x x x =+，(2,2)x ππ∈-，则其导函数'()f x 的图象大致是（）A B C D7．给出下列三个命题：①“若2230x x +-≠，则3x ≠-”为假命题； ② 若p q ∨为真命题，则p ,q 均为真命题；③ 命题:,30x p x R ∀∈>，则00:,30x p x R ⌝∃∈≤．其中正确的个数是( ) A ．0B ．1C ．2D ．38．定义在R 上的奇函数()f x 满足()(4)f x f x =-，且在[)0,2上单调递增，则下列结论中正确的是（）A ．0(1)(5)f f <->在第一象限的某点，1F 、2F 为双曲线的焦点．若P 在以12F F 为直径的圆上且满足213PF PF =，则双曲线的离心率为（）A ．5B ．25 C D ．21011．如图，设区域{}()|0101D x y x y =≤≤≤≤，，，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y =2y x =所围成阴影区域内的概率是（）A ．16 B ． 13 C ．12 D ． 2312．在平面直角坐标系中，(2,0)A -，(2,0)B ，(8,0)M ，(0,8)N ，若5AP BP =，12()()()33OQ t OM t ON t =-++为实数，则||PQ 的最小值是（）A．3 B．3 C．1 D ． 5第II 卷本卷包括必考题和选考题两部分. 第13～21题为必考题，每个试题考生都必须作答. 第22～24题为选考题，考生根据要求作答. 二、填空题（本题共4小题，每小题5分）13．数列{}n a 的前n 项和记为()11,3,21n n n S a a S n +==≥，则n S =__________． 14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有种不同参加方案（用数字作答）．15．若实数x ，y 满足约束条件4210440y xx y x y ≤-⎧⎪-+≥⎨⎪--≤⎩，则46y z x +=-的最大值是．16．将三项式()21nx x ++展开，当0,1,2,3,n =⋅⋅⋅时，得到以下等式：()0211x x ++=()12211xx x x ++=++()2243212321x x x x x x ++=++++()32654321367631x x x x x x x x ++=++++++……观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数(不足3数的，缺少的数计为0)之和，第k 行共有2k+1个数．若在()()5211ax x x +++的展开式中，8x 项的系数为75，则实数a 的值为．三、解答题（解答应写出文字说明、证明过程或演算步骤）17．(本小题满分12分) 如图，设△ABC 的三个内角A 、B 、C 对应的三条边分别为a b c 、、，且角A 、B 、C 成等差数列，2a =，线段AC 的垂直平分线分别交线段AB 、AC 于D 、E 两点．（Ⅰ）若△BCD CD 的长；（Ⅱ）若CD ，求角A 的值．18．（本小题满分12分）如图，已知长方形ABCD 中，AB =，AD =M 为DC 的中点．将ADM ∆沿AM 折起，使得平面ADM ⊥平面ABCM ．（Ⅰ）求证：AD BM ⊥；（Ⅱ）若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为．19．（本小题满分12分）近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X：①求对商品和服务全好评的次数X的分布列；②求X的数学期望和方差．附临界值表：2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828 P K kk≥2K的观测值：2()()()()()n ad bcka b c d a c b d-=++++（其中n a b c d=+++）关于商品和服务评价的2×2列联表：20．（本小题满分12分）已知椭圆222:1(0)3x yM aa+=>的一个焦点为(1,0)F-，左右顶点分别为,A B，经过点F的直线l与椭圆M交于,C D两点. （Ⅰ）求椭圆方程；（Ⅱ）记ABD ∆与ABC ∆的面积分别为1S 和2S ，求12||S S -的最大值.21．（本小题满分12分）已知函数()ln 1f x x x =-+，(0,)x ∈+∞；3()g x x ax =-．（Ⅰ）求()f x 的最大值；（Ⅱ）若对1(0,)x ∀∈+∞，总存在2[1,2]x ∈使得12()()f x g x ≤成立，求a 的取值范围；（Ⅲ）证明不等式12()()()1n n n n e n n n e +++<-．请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分．答时用2B 铅笔在答题卡上把所选题目的题号涂黑． 22．（本小题满分10分）选修41-：几何证明选讲如图直线AB 经过圆O 上的点C ，OA=OB ，CA=CB ，圆O 交直线OB 于点E 、D ，其中D 在线段OB 上，连接EC 、CD ．（Ⅰ）证明：直线AB 是圆O 的切线；（Ⅱ）若1tan 2CED ∠=，圆O 的半径为3，求线段OA 的长．23．（本小题满分10分）选修44-：坐标系与参数方程在极坐标系中，圆C 的方程为2sin (0)a a ρθ=>．以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，设直线l 的参数方程为⎩⎨⎧+=+=34,13t y t x （t 为参数）．（Ⅰ）求圆C 的标准方程和直线l 的普通方程；（Ⅱ）若直线l 与圆C 交于,A B 两点，且AB ≥，求实数a 的取值范围．24．（本小题满分10分）选修4—5：不等式选讲已知函数()2f x x x a =-+-．（Ⅰ）当1a =时，解不等式()2f x ≤；（Ⅱ）若()2f x ≥，求实数a 的取值范围．参考答案第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．复数12ii-+ (i 是虚数单位)的虚部是( ) A ．13 B ．13i C ．－15 D ．－15iA ．(0，1)B ．[0，1)C ．(1，2)D ．[1，2) 【答案】D3．设数列{}n a 是单调递减的等差数列，前三项的和为12，前三项的积为28，则1a =（） A ．1 B ． 4 C ．7 D ．1或7 【答案】C4．将函数()cos2f x x x =-的图象向左平移6π个单位，所得图象其中一条对称轴方程为( )A ．0x =B ．6x π= C ．4x π=D ．2x π=【答案】B5．某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆)，则该几何体的体积为( )A ．8010π+B ．8020π+C ．9214π+D ．12010π+ 【答案】A6．已知函数2()sin 2cos f x x x x x =+，(2,2)x ππ∈-，则其导函数'()f x 的图象大致是（）A B C D【答案】C7．给出下列三个命题：①“若2230x x +-≠，则3x ≠-”为假命题； ② 若p q ∨为真命题，则p ,q 均为真命题；③ 命题:,30x p x R ∀∈>，则00:,30x p x R ⌝∃∈≤．其中正确的个数是( ) A ．0 B ．1C ．2D ．3【答案】B8．定义在R 上的奇函数()f x 满足()(4)f x f x =-，且在[)0,2上单调递增，则下列结论中正确的是（）A ．0(1)(5)f f <->在第一象限的某点，1F 、2F 为双曲线的焦点．若P 在以12F F 为直径的圆上且满足213PF PF =，则双曲线的离心率为（）A ．5B ．25CD ．210 【答案】D11．如图，设区域{}()|0101D x y x y =≤≤≤≤，，，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y =与2y x =所围成阴影区域内的概率是（）A ．16 B ． 13 C ．12 D ． 23【答案】B12．在平面直角坐标系中，(2,0)A -，(2,0)B ，(8,0)M ，(0,8)N ，若5AP BP =，12()()()33OQ t OM t ON t =-++为实数，则||PQ 的最小值是（）A．3 B．3 C．1 D ． 5 【答案】A第II 卷本卷包括必考题和选考题两部分. 第13 ~ 21题为必考题，每个试题考生都必须作答. 第22 ~ 24题为选考题，考生根据要求作答. 二、填空题：本题共4小题，每小题5分.13．数列{}n a 的前n 项和记为()11,3,21n n n S a a S n +==≥，则n S =__________．【答案】3n14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有种不同参加方案（用数字作答）．【答案】4215．若实数x ，y 满足约束条件4210440y xx y x y ≤-⎧⎪-+≥⎨⎪--≤⎩，则46y z x +=-的最大值是．【答案】-216．将三项式()21nx x ++展开，当0,1,2,3,n =⋅⋅⋅时，得到以下等式：()0211x x ++=()12211xx x x ++=++()2243212321x x x x x x ++=++++()32654321367631x x x x x x x x ++=++++++……观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数(不足3数的，缺少的数计为0)之和，第k 行共有2k+1个数．若在()()5211ax x x +++的展开式中，8x 项的系数为75，则实数a 的值为．【答案】2三、解答题：解答应写出文字说明、证明过程或演算步骤．17．(本小题满分12分) 如图，设△ABC 的三个内角A 、B 、C 对应的三条边分别为a b c 、、，且角A 、B 、C 成等差数列，2a =，线段AC 的垂直平分线分别交线段AB 、AC 于D 、E 两点．（Ⅰ）若△BCD CD 的长；（Ⅱ）若CD =，求角A 的值．解：（Ⅰ）∵角A,B,C 成等差数列，A B C π++=，∴3B π=…………1分又∵△BCD 的面积为3，2a =，∴11sin 22223BCDS BD BC B BD ==⨯⨯=∴23BD =…………3分在△BCD 中，由余弦定理可得CD ==………6分（Ⅱ）由题意，在△BCD 中，sin sin CD BC B BDC =∠2sin BDC=∠，………8分 ∴sin 1BDC ∠=，则90oBDC ∠=，即CD A B ⊥ …………10分又DE 为AC 的垂直平分线，故4A B π∠=∠=…………12分18．（本小题满分12分）如图，已知长方形ABCD 中，AB =，AD =M 为DC 的中点．将ADM ∆沿AM 折起，使得平面ADM ⊥平面ABCM ．（Ⅰ）求证：AD BM ⊥；（Ⅱ）若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为．解：（Ⅰ）证明：∵长方形ABCD 中，AB=22，AD=2，M 为DC 的中点，∴AM=BM=2，∴BM ⊥AM. ……2分 ∵平面ADM ⊥平面ABCM ，平面ADM∩平面ABCM=AM ，BM ⊂平面ABCM∴BM ⊥平面ADM ……4分 ∵AD ⊂平面ADM ∴AD ⊥BM. ……5分（Ⅱ）建立如图所示的直角坐标系，设DE DB λ=，则平面AMD 的一个法向量(0,1,0)n =，(1,2,1),ME MD DB λλλλ=+=--(2,0,0)AM =-， ……8分设平面AME 的一个法向量(,,),m x y z = 则202(1)0x y z λλ=⎧⎨+-=⎩取y =1，得20,1,,1x y z λλ===- 所以2(0,1,)1m λλ=-， (10)分因为5cos ,||||m n m n m n ⋅<>==⋅，求得12λ=，所以E 为BD 的中点． ……12分19．（本小题满分12分）近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X ：① 求对商品和服务全好评的次数X 的分布列； ② 求X 的数学期望和方差．附临界值表：2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828P K k k ≥2K 的观测值：2()()()()()n ad bc k a b c d a c b d -=++++（其中n a b c d =+++）关于商品和服务评价的2×2列联表：解：（12分22200(80104070)11.11110.828,1505012080K ⨯⨯-⨯=≈>⨯⨯⨯ ………4分故能在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关. …5分(2)①每次购物时,对商品和服务都好评的概率为25,且X 的取值可以是0,1,2,3. 其中3327(0)()5125P X ===; 1232354(1)()()55125P X C ===;………7分22132336(2)()()55125P X C ===; 3303238(3)()()55125P X C ===. ………9分X 的分布列为：10分②由于2~(3,)5X B ,则26()3,55E X =⨯=2218()3(1).5525D X =⨯⨯-=……12分20．（本小题满分12分）已知椭圆222:1(0)3x y M a a +=>的一个焦点为(1,0)F -，左右顶点分别为,A B ，经过点F 的直线l 与椭圆M 交于,C D 两点. （Ⅰ）求椭圆方程；（Ⅱ）记ABD ∆与ABC ∆的面积分别为1S 和2S ，求12||S S -的最大值. （Ⅰ）因为)0,1(-F 为椭圆的焦点，所以1=c ，又32=b ，所以42=a ，所以椭圆方程为13422=+y x . ……………………………………4分（Ⅱ）当直线l 无斜率时,直线方程为1-=x ,此时3(1,)2D -,3(1,)2C --,021=-S S . ……………………………………5分当直线l 斜率存在时，设直线方程为)0)(1(≠+=k x k y ，设),(),,(2211y x D y x C ，联立得⎪⎩⎪⎨⎧+==+)1(13422x k y y x ，消掉y 得01248)43(2222=-+++k x k x k ，显然0>∆，方程有根，且2221222143124,438k k x x k k x x +-=+-=+.………………8分此时)1()1(22212121221+++=+=-=-x k x k y y y y S S212122(+)234kk x x k k=+=+. ………………………………10分因为0≠k ，上式312212432124312==⋅≤+=k kk k，（23±=k 时等号成立），所以21S S -的最大值为3. …………………………12分21．（本小题满分12分）已知函数()ln 1f x x x =-+，(0,)x ∈+∞；3()g x x ax =-．（Ⅰ）求()f x 的最大值；（Ⅱ）若对1(0,)x ∀∈+∞，总存在2[1,2]x ∈使得12()()f x g x ≤成立，求a 的取值范围；（Ⅲ）证明不等式12()()()1n n n n e n n n e +++<-．，， ……………………1分，时，， ……………………3分，∴的最大值为. ……………………4分，使得成立，等价于……………………5分，当时，在时恒为正，满足题意. ……………………6分时，2()3g x x a '=-，令()0g x '=，解得，上单调递增，……………………7分，∴，∴.时，在递减，递增，而，在为正，在为负，∴，，而时，，不合题意，的取值范围为. …………9分即，…………10分，∴，即，…………11分. …………12分请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分．答时用2B 铅笔在答题卡上把所选题目的题号涂黑． 22．（本小题满分10分）选修41-：几何证明选讲如图直线AB 经过圆O 上的点C ，OA=OB ，CA=CB ，圆O 交直线OB 于点E 、D ，其中D 在线段OB 上，连接EC 、CD ．（Ⅰ）证明：直线AB 是圆O 的切线；（Ⅱ）若1tan 2CED ∠=，圆O 的半径为3，求线段OA 的长．解：（1）连结,,,OC OA OB CA CB OC AB ==∴⊥.又OC 是圆O 的半径，AB ∴是圆O 的切线. …………5分（2）直线AB 是圆O 的切线，BCD E ∴∠=∠.又CBD EBC ∠=∠，BCD BEC ∴∆∆，则有BC BD CD BE BC EC ==，又1t a n 2CD CED EC ∠==，故12B DC DB C E C==. 设BD x =，则2BC x =，又2BC BD BE =，故()()226x x x =+，即2360x x -=.解得2x =，即2BD =.325OA OB OD DB ∴==+=+=. …………10分23．（本小题满分10分）选修44-：坐标系与参数方程在极坐标系中，圆C 的方程为2sin (0)a a ρθ=>．以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，设直线l 的参数方程为⎩⎨⎧+=+=34,13t y t x （t 为参数）．（Ⅰ）求圆C 的标准方程和直线l 的普通方程；（Ⅱ）若直线l 与圆C 交于,A B两点，且AB ≥，求实数a 的取值范围． 23.解：（Ⅰ）C 的直角坐标方程为222()x y a a +-=，在直线l 的参数方程中消t 得：4350x y -+= ………5分（Ⅱ）要满足弦AB ≥及圆的半径为a 可知只需圆心(0,)a 到直线l 的距离12d a ≤即12a ≤, 整理得：2111201000a a -+≤即(1110)(10)0a a --≤解得：101011a ≤≤，故实数a 的取值范围为：101011a ≤≤ ………10分24．（本小题满分10分）选修4—5：不等式选讲已知函数()2f x x x a =-+-．（Ⅰ）当1a =时，解不等式()2f x ≤；（Ⅱ）若()2f x ≥，求实数a 的取值范围．解：（Ⅰ）当1a =时，231()112232x x f x x x x -+<⎧⎪=≤≤⎨⎪->⎩， ……………1分当1x <时，232x -+≤，所以12x >。

湖南省五市十校教研教改共同体高二下学期期末考试数学(理)试题 Word版含答案

“五市十校教研教改共同体”2015-2016高二第二学期期末考试数学（理科）时量：120分钟总分150分考试学校：沅江一中、箴言中学、桃江一中、宁乡一中、雷锋学校、东山学校、南方中学、岳阳市第十四中学、岳阳市第十五中学、南县一中等第Ⅰ卷一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求） 1．复数12ii-+ (i 是虚数单位)的虚部是( ) A ．13 B ．13i C ．－15 D ．－15iA ．(0，1)B ．[0，1)C ．(1，2)D ．[1，2)3．设数列{}n a 是单调递减的等差数列，前三项的和为12，前三项的积为28，则1a =（） A ．1 B ． 4 C ．7 D ．1或74．将函数()cos2f x x x =-的图象向左平移6π个单位，所得图象其中一条对称轴方程为( )A ．0x =B ．6x π=C ．4x π=D ．2x π=5．某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆)，则该几何体的体积为( )A ．8010π+B ．8020π+C ．9214π+D ．12010π+6．已知函数2()sin 2cos f x x x x x =+，(2,2)x ππ∈-，则其导函数'()f x 的图象大致是（）A B C D7．给出下列三个命题：①“若2230x x +-≠，则3x ≠-”为假命题； ② 若p q ∨为真命题，则p ,q 均为真命题；③ 命题:,30x p x R ∀∈>，则00:,30x p x R ⌝∃∈≤．其中正确的个数是( ) A ．0B ．1C ．2D ．38．定义在R 上的奇函数()f x 满足()(4)f x f x =-，且在[)0,2上单调递增，则下列结论中正确的是（）A ．0(1)(5)f f <->在第一象限的某点，1F 、2F 为双曲线的焦点．若P 在以12F F 为直径的圆上且满足213PF PF =，则双曲线的离心率为（）A ．5B ．25 C D ．21011．如图，设区域{}()|0101D x y x y =≤≤≤≤，，，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y =2y x =所围成阴影区域内的概率是（）A ．16 B ． 13 C ．12 D ． 2312．在平面直角坐标系中，(2,0)A -，(2,0)B ，(8,0)M ，(0,8)N ，若5AP BP =，12()()()33OQ t OM t ON t =-++为实数，则||PQ 的最小值是（）A．3 B．3 C．1 D ． 5第II 卷本卷包括必考题和选考题两部分. 第13～21题为必考题，每个试题考生都必须作答. 第22～24题为选考题，考生根据要求作答. 二、填空题（本题共4小题，每小题5分）13．数列{}n a 的前n 项和记为()11,3,21n n n S a a S n +==≥，则n S =__________． 14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有种不同参加方案（用数字作答）．15．若实数x ，y 满足约束条件4210440y xx y x y ≤-⎧⎪-+≥⎨⎪--≤⎩，则46y z x +=-的最大值是．16．将三项式()21nx x ++展开，当0,1,2,3,n =⋅⋅⋅时，得到以下等式：()0211x x ++=()12211xx x x ++=++()2243212321x x x x x x ++=++++()32654321367631x x x x x x x x ++=++++++……观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数(不足3数的，缺少的数计为0)之和，第k 行共有2k+1个数．若在()()5211ax x x +++的展开式中，8x 项的系数为75，则实数a 的值为．三、解答题（解答应写出文字说明、证明过程或演算步骤）17．(本小题满分12分) 如图，设△ABC 的三个内角A 、B 、C 对应的三条边分别为a b c 、、，且角A 、B 、C 成等差数列，2a =，线段AC 的垂直平分线分别交线段AB 、AC 于D 、E 两点．（Ⅰ）若△BCD CD 的长；（Ⅱ）若CD ，求角A 的值．18．（本小题满分12分）如图，已知长方形ABCD 中，AB =，AD =M 为DC 的中点．将ADM ∆沿AM 折起，使得平面ADM ⊥平面ABCM ．（Ⅰ）求证：AD BM ⊥；（Ⅱ）若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为．19．（本小题满分12分）近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X：①求对商品和服务全好评的次数X的分布列；②求X的数学期望和方差．附临界值表：2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828 P K kk≥2K的观测值：2()()()()()n ad bcka b c d a c b d-=++++（其中n a b c d=+++）关于商品和服务评价的2×2列联表：20．（本小题满分12分）已知椭圆222:1(0)3x yM aa+=>的一个焦点为(1,0)F-，左右顶点分别为,A B，经过点F的直线l与椭圆M交于,C D两点. （Ⅰ）求椭圆方程；（Ⅱ）记ABD ∆与ABC ∆的面积分别为1S 和2S ，求12||S S -的最大值.21．（本小题满分12分）已知函数()ln 1f x x x =-+，(0,)x ∈+∞；3()g x x ax =-．（Ⅰ）求()f x 的最大值；（Ⅱ）若对1(0,)x ∀∈+∞，总存在2[1,2]x ∈使得12()()f x g x ≤成立，求a 的取值范围；（Ⅲ）证明不等式12()()()1n n n n e n n n e +++<-．请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分．答时用2B 铅笔在答题卡上把所选题目的题号涂黑． 22．（本小题满分10分）选修41-：几何证明选讲如图直线AB 经过圆O 上的点C ，OA=OB ，CA=CB ，圆O 交直线OB 于点E 、D ，其中D 在线段OB 上，连接EC 、CD ．（Ⅰ）证明：直线AB 是圆O 的切线；（Ⅱ）若1tan 2CED ∠=，圆O 的半径为3，求线段OA 的长．23．（本小题满分10分）选修44-：坐标系与参数方程在极坐标系中，圆C 的方程为2sin (0)a a ρθ=>．以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，设直线l 的参数方程为⎩⎨⎧+=+=34,13t y t x （t 为参数）．（Ⅰ）求圆C 的标准方程和直线l 的普通方程；（Ⅱ）若直线l 与圆C 交于,A B 两点，且AB ≥，求实数a 的取值范围．24．（本小题满分10分）选修4—5：不等式选讲已知函数()2f x x x a =-+-．（Ⅰ）当1a =时，解不等式()2f x ≤；（Ⅱ）若()2f x ≥，求实数a 的取值范围．参考答案第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．复数12ii-+ (i 是虚数单位)的虚部是( ) A ．13 B ．13i C ．－15 D ．－15iA ．(0，1)B ．[0，1)C ．(1，2)D ．[1，2) 【答案】D3．设数列{}n a 是单调递减的等差数列，前三项的和为12，前三项的积为28，则1a =（） A ．1 B ． 4 C ．7 D ．1或7 【答案】C4．将函数()cos2f x x x =-的图象向左平移6π个单位，所得图象其中一条对称轴方程为( )A ．0x =B ．6x π= C ．4x π=D ．2x π=【答案】B5．某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆)，则该几何体的体积为( )A ．8010π+B ．8020π+C ．9214π+D ．12010π+ 【答案】A6．已知函数2()sin 2cos f x x x x x =+，(2,2)x ππ∈-，则其导函数'()f x 的图象大致是（）A B C D【答案】C7．给出下列三个命题：①“若2230x x +-≠，则3x ≠-”为假命题； ② 若p q ∨为真命题，则p ,q 均为真命题；③ 命题:,30x p x R ∀∈>，则00:,30x p x R ⌝∃∈≤．其中正确的个数是( ) A ．0 B ．1C ．2D ．3【答案】B8．定义在R 上的奇函数()f x 满足()(4)f x f x =-，且在[)0,2上单调递增，则下列结论中正确的是（）A ．0(1)(5)f f <->在第一象限的某点，1F 、2F 为双曲线的焦点．若P 在以12F F 为直径的圆上且满足213PF PF =，则双曲线的离心率为（）A ．5B ．25CD ．210 【答案】D11．如图，设区域{}()|0101D x y x y =≤≤≤≤，，，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y =与2y x =所围成阴影区域内的概率是（）A ．16 B ． 13 C ．12 D ． 23【答案】B12．在平面直角坐标系中，(2,0)A -，(2,0)B ，(8,0)M ，(0,8)N ，若5AP BP =，12()()()33OQ t OM t ON t =-++为实数，则||PQ 的最小值是（）A．3 B．3 C．1 D ． 5 【答案】A第II 卷本卷包括必考题和选考题两部分. 第13 ~ 21题为必考题，每个试题考生都必须作答. 第22 ~ 24题为选考题，考生根据要求作答. 二、填空题：本题共4小题，每小题5分.13．数列{}n a 的前n 项和记为()11,3,21n n n S a a S n +==≥，则n S =__________．【答案】3n14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有种不同参加方案（用数字作答）．【答案】4215．若实数x ，y 满足约束条件4210440y xx y x y ≤-⎧⎪-+≥⎨⎪--≤⎩，则46y z x +=-的最大值是．【答案】-216．将三项式()21nx x ++展开，当0,1,2,3,n =⋅⋅⋅时，得到以下等式：()0211x x ++=()12211xx x x ++=++()2243212321x x x x x x ++=++++()32654321367631x x x x x x x x ++=++++++……观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数(不足3数的，缺少的数计为0)之和，第k 行共有2k+1个数．若在()()5211ax x x +++的展开式中，8x 项的系数为75，则实数a 的值为．【答案】2三、解答题：解答应写出文字说明、证明过程或演算步骤．17．(本小题满分12分) 如图，设△ABC 的三个内角A 、B 、C 对应的三条边分别为a b c 、、，且角A 、B 、C 成等差数列，2a =，线段AC 的垂直平分线分别交线段AB 、AC 于D 、E 两点．（Ⅰ）若△BCD CD 的长；（Ⅱ）若CD =，求角A 的值．解：（Ⅰ）∵角A,B,C 成等差数列，A B C π++=，∴3B π=…………1分又∵△BCD 的面积为3，2a =，∴11sin 22223BCDS BD BC B BD ==⨯⨯=∴23BD =…………3分在△BCD 中，由余弦定理可得CD ==………6分（Ⅱ）由题意，在△BCD 中，sin sin CD BC B BDC =∠2sin BDC=∠，………8分 ∴sin 1BDC ∠=，则90oBDC ∠=，即CD A B ⊥ …………10分又DE 为AC 的垂直平分线，故4A B π∠=∠=…………12分18．（本小题满分12分）如图，已知长方形ABCD 中，AB =，AD =M 为DC 的中点．将ADM ∆沿AM 折起，使得平面ADM ⊥平面ABCM ．（Ⅰ）求证：AD BM ⊥；（Ⅱ）若点E 是线段DB 上的一动点，问点E 在何位置时，二面角E AM D --的余弦值为．解：（Ⅰ）证明：∵长方形ABCD 中，AB=22，AD=2，M 为DC 的中点，∴AM=BM=2，∴BM ⊥AM. ……2分 ∵平面ADM ⊥平面ABCM ，平面ADM∩平面ABCM=AM ，BM ⊂平面ABCM∴BM ⊥平面ADM ……4分 ∵AD ⊂平面ADM ∴AD ⊥BM. ……5分（Ⅱ）建立如图所示的直角坐标系，设DE DB λ=，则平面AMD 的一个法向量(0,1,0)n =，(1,2,1),ME MD DB λλλλ=+=--(2,0,0)AM =-， ……8分设平面AME 的一个法向量(,,),m x y z = 则202(1)0x y z λλ=⎧⎨+-=⎩取y =1，得20,1,,1x y z λλ===- 所以2(0,1,)1m λλ=-， (10)分因为5cos ,||||m n m n m n ⋅<>==⋅，求得12λ=，所以E 为BD 的中点． ……12分19．（本小题满分12分）近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量X ：① 求对商品和服务全好评的次数X 的分布列； ② 求X 的数学期望和方差．附临界值表：2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828P K k k ≥2K 的观测值：2()()()()()n ad bc k a b c d a c b d -=++++（其中n a b c d =+++）关于商品和服务评价的2×2列联表：解：（12分22200(80104070)11.11110.828,1505012080K ⨯⨯-⨯=≈>⨯⨯⨯ ………4分故能在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关. …5分(2)①每次购物时,对商品和服务都好评的概率为25,且X 的取值可以是0,1,2,3. 其中3327(0)()5125P X ===; 1232354(1)()()55125P X C ===;………7分22132336(2)()()55125P X C ===; 3303238(3)()()55125P X C ===. ………9分X 的分布列为：10分②由于2~(3,)5X B ,则26()3,55E X =⨯=2218()3(1).5525D X =⨯⨯-=……12分20．（本小题满分12分）已知椭圆222:1(0)3x y M a a +=>的一个焦点为(1,0)F -，左右顶点分别为,A B ，经过点F 的直线l 与椭圆M 交于,C D 两点. （Ⅰ）求椭圆方程；（Ⅱ）记ABD ∆与ABC ∆的面积分别为1S 和2S ，求12||S S -的最大值. （Ⅰ）因为)0,1(-F 为椭圆的焦点，所以1=c ，又32=b ，所以42=a ，所以椭圆方程为13422=+y x . ……………………………………4分（Ⅱ）当直线l 无斜率时,直线方程为1-=x ,此时3(1,)2D -,3(1,)2C --,021=-S S . ……………………………………5分当直线l 斜率存在时，设直线方程为)0)(1(≠+=k x k y ，设),(),,(2211y x D y x C ，联立得⎪⎩⎪⎨⎧+==+)1(13422x k y y x ，消掉y 得01248)43(2222=-+++k x k x k ，显然0>∆，方程有根，且2221222143124,438k k x x k k x x +-=+-=+.………………8分此时)1()1(22212121221+++=+=-=-x k x k y y y y S S212122(+)234kk x x k k=+=+. ………………………………10分因为0≠k ，上式312212432124312==⋅≤+=k kk k，（23±=k 时等号成立），所以21S S -的最大值为3. …………………………12分21．（本小题满分12分）已知函数()ln 1f x x x =-+，(0,)x ∈+∞；3()g x x ax =-．（Ⅰ）求()f x 的最大值；（Ⅱ）若对1(0,)x ∀∈+∞，总存在2[1,2]x ∈使得12()()f x g x ≤成立，求a 的取值范围；（Ⅲ）证明不等式12()()()1n n n n e n n n e +++<-．，， ……………………1分，时，， ……………………3分，∴的最大值为. ……………………4分，使得成立，等价于……………………5分，当时，在时恒为正，满足题意. ……………………6分时，2()3g x x a '=-，令()0g x '=，解得，上单调递增，……………………7分，∴，∴.时，在递减，递增，而，在为正，在为负，∴，，而时，，不合题意，的取值范围为. …………9分即，…………10分，∴，即，…………11分. …………12分请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分．答时用2B 铅笔在答题卡上把所选题目的题号涂黑． 22．（本小题满分10分）选修41-：几何证明选讲如图直线AB 经过圆O 上的点C ，OA=OB ，CA=CB ，圆O 交直线OB 于点E 、D ，其中D 在线段OB 上，连接EC 、CD ．（Ⅰ）证明：直线AB 是圆O 的切线；（Ⅱ）若1tan 2CED ∠=，圆O 的半径为3，求线段OA 的长．解：（1）连结,,,OC OA OB CA CB OC AB ==∴⊥.又OC 是圆O 的半径，AB ∴是圆O 的切线. …………5分（2）直线AB 是圆O 的切线，BCD E ∴∠=∠.又CBD EBC ∠=∠，BCD BEC ∴∆∆，则有BC BD CD BE BC EC ==，又1t a n 2CD CED EC ∠==，故12B DC DB C E C==. 设BD x =，则2BC x =，又2BC BD BE =，故()()226x x x =+，即2360x x -=. 解得2x =，即2BD =.325OA OB OD DB ∴==+=+=. …………10分23．（本小题满分10分）选修44-：坐标系与参数方程在极坐标系中，圆C 的方程为2sin (0)a a ρθ=>．以极点为坐标原点，极轴为x 轴的正半轴建立平面直角坐标系，设直线l 的参数方程为⎩⎨⎧+=+=34,13t y t x （t 为参数）．（Ⅰ）求圆C 的标准方程和直线l 的普通方程；（Ⅱ）若直线l 与圆C 交于,A B两点，且AB ≥，求实数a 的取值范围． 23.解：（Ⅰ）C 的直角坐标方程为222()x y a a +-=，在直线l 的参数方程中消t 得：4350x y -+= ………5分（Ⅱ）要满足弦AB ≥及圆的半径为a 可知只需圆心(0,)a 到直线l 的距离12d a ≤即12a ≤, 整理得：2111201000a a -+≤即(1110)(10)0a a --≤解得：101011a ≤≤，故实数a 的取值范围为：101011a ≤≤ ………10分24．（本小题满分10分）选修4—5：不等式选讲已知函数()2f x x x a =-+-．（Ⅰ）当1a =时，解不等式()2f x ≤；（Ⅱ）若()2f x ≥，求实数a 的取值范围．解：（Ⅰ）当1a =时，231()112232x x f x x x x -+<⎧⎪=≤≤⎨⎪->⎩， ……………1分当1x <时，232x -+≤，所以12x >。

湖南省五市十校204-2015学年高二物理下学期期末联考试题

“湖南省五市十校教研教改共同体”高二期末考试物理试题时量：80分钟分值：110分答题说明：1、考生必须将答案准确填写到答题卡上写在试卷上的一律无效；2、考生请使用黑色中性笔和2B 铅笔作答；物理选择题（本题共9小题每小题6分1-6为单项选择；7-9题为多项选择全部选对得6分选对但选不全的得3分有选错的得0分)1．关于物理科学家和他们的贡献下列说法中正确的是A.奥斯特发现了电流的磁效应并发现了电磁感应现象B.库仑提出了库仑定律并最早用实验测得元电荷e 的数值C.牛顿发现了万有引力定律并通过实验测出了引力常量D.法拉第发现了电磁感应现象。

2．一物体在三个共点恒力作用下做匀速直线运动若突然撤去其中一个力其余两力不变此物体不可能做A.匀加速直线运动B.匀减速直线运动C.类似于平抛运动D.匀速圆周运动3．如图所示一同学分别在同一直线上的A 、B 、C 三个位置投掷篮球结果都垂直击中篮筐速度分别为1v 、2v 、3v 。

若篮球出手时高度相同出手速度与水平夹角分别为1θ、2θ、3θ下列说法正确的是A. 1v ＜2v ＜3vB. 1v ＞2v ＞3vC. 1θ＞ 2θ＞3θD.错误!未找到引用源。

4．示波管原理如图所示电子在电压为U PK 的加速电场中由静止开始运动然后进入电压为U AB 的偏转电场最后打在荧光屏上的O ′点要使电子打在荧光屏上的位置O ′到荧光屏中心O 的距离增大下列措施可行的是A.只增大U PKB.只增大U ABC.增大U PK 同时减小U ABD.将电子换成比荷(q/m )较大的带电粒子5．在如图所示的电路中,闭合开关S,在滑动变阻器滑片P 缓慢向右移动的过程中,A.灯泡L变暗B.电源内部消耗的功率先变大后变小C.电容器C上的电荷量增加D.流过R1的电流方向由左向右6．人造地球卫星绕地球运转它的轨道半径、周期和环绕速度的关系是：（）A．半径越小速度越小周期越小 B．半径越小速度越大周期越小C．半径越大速度越大周期越小 D．半径越大速度越小周期越小7．质量为1.0kg的物体以某一初速度在水平面上滑行由于滑动摩擦力的作用其动能随位移变化的情况如图所示若g取10m/s2则下列判断正确的是A.物体与水平面间的动摩擦因数为0.30B.物体与水平面间的动摩擦因数为0.25C.物体滑行的总时间为4.0sD.物体滑行的总时间为3.0s8．如图甲所示在匀强磁场中一矩形金属线框绕与磁场方向垂直的轴匀速转动产生交流电电动势e随时间t的变化关系如图乙所示则A.该交流电的频率为100HzB.该交流电电动势的有效值为220VC.t=0.01s时穿过线框的磁通量为零D.t=0.01s时穿过线框的磁通量的变化率为零9．如图甲所示,abcd 为导体做成的框架,其所在平面与水平面成θ角,导体棒PQ 与ad 、bc 接触良好,整个装置放在垂直于框架平面的变化磁场中,磁场的磁感应强度B 随时间t 的变化情况如图乙所示(设图甲中B 的方向为正方向),在0~t 1时间内导体棒PQ 始终静止,下面判断正确的是A.导体棒PQ 中电流方向由Q 至PB.导体棒PQ 所受安培力的方向沿框架向下C.导体棒PQ 所受安培力的大小在增大D.导体棒PQ 所受安培力的大小在减小10.（6分）在研究匀变速直线运动的实验中如图所示为一条记录小车运动情况的纸带图中A 、B 、C 、D 、E 为相邻的计数点相邻计数点间的时间间隔T=0.1s 。

湖南省五市十校教研共同体高二数学下学期期末试卷理(含解析)

2015-2016学年湖南省五市十校教研共同体高二（下）期末数学试卷（理科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．复数（i是虚数单位）的虚部是（）A．B． i C．﹣ D．﹣i2．若集合A={x|x2﹣2x＜0}，函数f（x）=的定义域为集合B，则A∩B等于（）A．（0，1）B．[0，1）C．（1，2）D．[1，2）3．设数列{a n}是单调递减的等差数列，前三项的和为12，前三项的积为28，则a1=（）A．1 B．4 C．7 D．1或74．将函数f（x）=sin2x﹣cos2x的图象向左平移个单位，所得图象其中一条对称轴方程为（）A．x=0 B．x=C．x=D．x=5．某个几何体的三视图如图所示（其中正视图中的圆弧是半径为2的半圆），则该几何体的体积为（）A．80+10πB．80+20πC．92+14πD．120+10π6．已知函数f（x）=x2sinx+2xcosx，x∈（﹣2π，2π），则其导函数f′（x）的图象大致是（）A．B．C．D．7．给出下列三个命题：①“若x2+2x﹣3≠0，则x≠﹣3”为假命题；②若p∨q为真命题，则p，q均为真命题；③命题p：∀x∈R，3x＞0，则￢p：∃x0∈R，3≤0．其中正确的个数是（）A．0 B．1 C．2 D．38．定义在R上的奇函数f（x）满足f（x）=f（x﹣4），且在[0，2）上单调递增，则下列结论中正确的是（）A．0＜f（﹣1）＜f（5）B．f（﹣1）＜f（5）＜0 C．f（5）＜f（﹣1）＜0 D．f（﹣1）＜0＜f（5）9．阅读如图所示的程序框图，若输入n=2017，则输出的S值是（）A．B．C．D．10．点P是双曲线﹣=1（a＞0，b＞0）在第一象限的某点，F1、F2为双曲线的焦点．若P在以F1F2为直径的圆上且满足|PF1|=3|PF2|，则双曲线的离心率为（）A．B．C．D．11．如图，设区域D={（x，y）|0≤x≤1，0≤y≤1，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y=与y=x2所围成阴影区域内的概率是（）A．B．C．D．12．在平面直角坐标系中，A（﹣2，0），B（2，0），M（8，0），N（0，8），若•=5，=（﹣t）+（+t）（t为实数），则||的最小值是（）A．4﹣3 B．4+3 C．4﹣1 D．5二、填空题：本题共4小题，每小题5分.13．数列{a n}的前n项和记为S n，a1=3，a n+1=2S n（n≥1），则S n= ．14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有种不同参加方案（用数字作答）15．若实数x，y满足约束条件，则z=的最小值是16．将三项式（x2+x+1）n展开，当n=0，1，2，3，…时，得到以下等式：（x2+x+1）0=1（x2+x+1）1=x2+x+1（x2+x+1）2=x4+2x3+3x2+2x+1（x2+x+1）3=x6+3x5+6x4+7x3+6x2+3x+1…观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数（不足3数的，缺少的数计为0）之和，第k行共有2k+1个数．若在（1+ax）（x2+x+1）5的展开式中，x7项的系数为75，则实数a的值为．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．如图，设△ABC的个内角A、B、C对应的三条边分别为a、b、c，且角A、B、C成等差数列，a=2，线段AC的垂直平分线分别交线段AB、AC于D、E两点．（1）若△BCD的面积为，求线段CD的长；（2）若DE=，求角A的值．18．如图，已知长方形ABCD中，AB=2，AD=，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM（Ⅰ）求证：AD⊥BM（Ⅱ）若点E是线段DB上的一动点，问点E在何位置时，二面角E﹣AM﹣D的余弦值为．19．近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率，某人在该购物平台上进行的3次购物中，设对商品和服务全好评的次数为随机变量X：①求对商品和服务全好评的次数X的分布列；②求X的数学期望和方差．附临界值表：P（K2≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 k）k 2.072 2.706 3.841 5.024 6.635 7.897 10.828 K2的观测值：k=（其中n=a+b+c+d）关于商品和服务评价的2×2列联表：对服务好评对服务不满意合计对商品好评a=80 b=对商品不满意c= d=10合计n=20020．已知椭圆M： +=1（a＞0）的一个焦点为F（﹣1，0），左右顶点分别为A，B，经过点F的直线l与椭圆M交于C，D两点．（Ⅰ）求椭圆方程；（Ⅱ）记△ABD与△ABC的面积分别为S1和S2，求|S1﹣S2|的最大值．21．已知函数f（x）=lnx﹣x+1，x∈（0，+∞），g（x）=x3﹣ax．（1）求f（x）的最大值；（2）若对∀x1∈（0，+∞），总存在x2∈[1，2]使得f（x1）≤g（x2）成立，求a的取值范围；（3）证明不等式：（）n+（）n+…+（）n＜．[选修4-1：几何证明选讲]22．如图，直线AB经过圆O上的点C，并且OA=OB，CA=CB，圆O交直线OB于点E、D，其中D在线段OB上．连结EC，CD．（Ⅰ）证明：直线AB是圆O的切线；（Ⅱ）若tan∠CED=，圆O的半径为3，求OA的长．[选修4-4：坐标系与参数方程]23．在极坐标系中，圆C的方程为ρ=2asinθ （a＞0）．以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，设直线l的参数方程为（t为参数）．（Ⅰ）求圆C的标准方程和直线l的普通方程；（Ⅱ）若直线l与圆C交于A，B两点，且．求实数a的取值范围？[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣2|+|x﹣a|．（Ⅰ）当a=1时，解不等式f（x）≤2（Ⅱ）若f（x）≥2，求实数a的取值范围．2015-2016学年湖南省五市十校教研共同体高二（下）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．复数（i是虚数单位）的虚部是（）A．B． i C．﹣ D．﹣i【考点】复数代数形式的乘除运算．【分析】直接由复数代数形式的乘除运算化简复数得答案．【解答】解： =，则复数（i是虚数单位）的虚部是：．故选：C．2．若集合A={x|x2﹣2x＜0}，函数f（x）=的定义域为集合B，则A∩B等于（）A．（0，1）B．[0，1）C．（1，2）D．[1，2）【考点】交集及其运算．【分析】求出A中不等式的解集确定出A，求出f（x）的定义域确定出B，找出两集合的交集即可．【解答】解：由A中不等式变形得：x（x﹣2）＜0，解得：0＜x＜2，即A=（0，2），由f（x）=，得到x﹣1≥0，解得：x≥1，即B=[1，+∞），则A∩B=[1，2），故选：D．3．设数列{a n}是单调递减的等差数列，前三项的和为12，前三项的积为28，则a1=（）A．1 B．4 C．7 D．1或7【考点】等差数列的通项公式．【分析】利用等差数列的通项公式列出方程组，由此能求出等差数列的公差．【解答】解：∵数列{a n}是单调递减的等差数列，前三项的和为12，前三项的积为28，∴，且d＜0，解得a1=7，d=﹣3．∴a1=7．故选：C．4．将函数f（x）=sin2x﹣cos2x的图象向左平移个单位，所得图象其中一条对称轴方程为（）A．x=0 B．x=C．x=D．x=【考点】函数y=Asin（ωx+φ）的图象变换；三角函数中的恒等变换应用．【分析】利用两角和差的正弦公式化简函数的解析式，利用函数y=Asin（ωx+φ）的图象变换规律求得所得图象对应的函数解析式，再利用正弦函数的图象的对称性，得出结论．【解答】解：将函数f（x）=sin2x﹣cos2x=2sin（2x﹣）的图象向左平移个单位，所得图象对应的函数解析式为y=2sin[2（x+）﹣）]=2sin（2x+），令2x+=kπ+，x=+，可得函数的图象的对称轴方程为 x=+，k∈Z，令k=0，可得其中一条对称轴方程为x=，故选：B．5．某个几何体的三视图如图所示（其中正视图中的圆弧是半径为2的半圆），则该几何体的体积为（）A．80+10πB．80+20πC．92+14πD．120+10π【考点】由三视图求面积、体积．【分析】几何体是半圆柱与长方体的组合体，根据三视图判断长方体的长、宽、高及半圆柱的半径和高，把数据代入，即可计算体积．【解答】解：由三视图知：几何体是半圆柱与长方体的组合体，下面长方体的长、宽、高分别为4、5、4，体积为4×5×4=80上面半圆柱的半径为2，高为5，体积为=10π∴几何体的体积V=V半圆柱+V长方体=80+10π．故选：A．6．已知函数f（x）=x2sinx+2xcosx，x∈（﹣2π，2π），则其导函数f′（x）的图象大致是（）A．B．C．D．【考点】函数的图象．【分析】求出f′（x）的解析式，判断其奇偶性，单调性，特殊点，结合选项得出答案．【解答】解：f′（x）=2xsinx+x2cosx+2cosx﹣2xsinx=x2cosx+2cosx．∴f′（﹣x）=（﹣x）2cos（﹣x）+2cos（﹣x）=x2cosx+2cosx=f′（x），∴f′（x）是偶函数，图象关于y轴对称，排除A，B；又f′（0）=2≠0，排除D．故选C．7．给出下列三个命题：①“若x2+2x﹣3≠0，则x≠﹣3”为假命题；②若p∨q为真命题，则p，q均为真命题；③命题p：∀x∈R，3x＞0，则￢p：∃x0∈R，3≤0．其中正确的个数是（）A．0 B．1 C．2 D．3【考点】命题的真假判断与应用．【分析】①根据不等式的解法进行判断，②根据复合命题的真假关系进行判断③根据全称命题的否定是特称命题进行判断．【解答】解：①“若x2+2x﹣3≠0，则x≠﹣3且x≠1，故①为真命题，则①错误；②若p∨q为真命题，则p，q至少有一个为真命题；故②错误③命题p：∀x∈R，3x＞0，则￢p：∃x0∈R，3≤0．故③正确，故选：B8．定义在R上的奇函数f（x）满足f（x）=f（x﹣4），且在[0，2）上单调递增，则下列结论中正确的是（）A．0＜f（﹣1）＜f（5）B．f（﹣1）＜f（5）＜0 C．f（5）＜f（﹣1）＜0 D．f（﹣1）＜0＜f（5）【考点】奇偶性与单调性的综合．【分析】由题意可得f（x）是周期为4的周期函数，故有f（5）=f（1），f（x）在一个周期（﹣2，2）上单调递增，且f（0）=0，从而得出结论．【解答】解：定义在R上的奇函数f（x）满足f（x）=f（x﹣4），则f（x）是周期为4的周期函数，故有f（5）=f（1）．由于f（x）在[0，2）上单调递增，故它在（﹣2，0]上单调递增，故有f（x）在一个周期（﹣2，2）上单调递增，且f（0）=0，故有f（﹣1）＜0＜f（5）=f（1），故选：D．9．阅读如图所示的程序框图，若输入n=2017，则输出的S值是（）A．B．C．D．【考点】程序框图．【分析】根据程序框图的流程，依次写出每次循环得到的S，k的值，当k=2017时，不满足条件k＜2017，退出循环，输出S的值，用裂项相消法求和即可得解．【解答】解：模拟程序的运行，可得：n=2017，k=1，S=0执行循环体，S=0+，k=2；满足条件k＜2017，执行循环体，S=0++，k=3；…满足条件k＜2017，执行循环体，S=0+++…+，k=2017；此时，不满足条件k＜2017，退出循环，输出S的值．由于：S=0+++…+=×[（1﹣）+（）+…+（﹣）]=（1﹣）=．故选：A．10．点P是双曲线﹣=1（a＞0，b＞0）在第一象限的某点，F1、F2为双曲线的焦点．若P在以F1F2为直径的圆上且满足|PF1|=3|PF2|，则双曲线的离心率为（）A．B．C．D．【考点】双曲线的简单性质．【分析】根据双曲线的定义结合圆的性质可知PF1⊥PF2，由已知结合双曲线的定义求得|PF1|，|PF2|，再由勾股定理得答案．【解答】解：如图，∵P在以F1F2为直径的圆上，∴F1F2为圆的直径，则PF1⊥PF2，∵|PF1|=3|PF2|，∴由，解得|PF1|=3a，|PF2|=a，∴，即，得e=．故选：D．11．如图，设区域D={（x，y）|0≤x≤1，0≤y≤1，向区域内随机投一点，且投入到区域内任一点都是等可能的，则点落到由曲线y=与y=x2所围成阴影区域内的概率是（）A．B．C．D．【考点】几何概型；定积分在求面积中的应用．【分析】根据积分的几何意义求出阴影区域的面积，然后根据几何概型的概率公式即可得到结论．【解答】解：根据积分的几何意义可知区域M的面积为=（）=，区域D的面积为1×1=1，则由几何概型的概率公式可得点落到由曲线y=与y=x2所围成阴影区域内的概率等于，故选：B．12．在平面直角坐标系中，A（﹣2，0），B（2，0），M（8，0），N（0，8），若•=5，=（﹣t）+（+t）（t为实数），则||的最小值是（）A．4﹣3 B．4+3 C．4﹣1 D．5【考点】平面向量数量积的运算；平面向量的基本定理及其意义．【分析】利用向量知识，确定P、Q的轨迹方程，进而利用点到直线的距离公式，即可求||的最小值．【解答】解：，A（﹣2，0），B（2，0），若•=5，设P（a，b），可得（a+2）（a﹣2）+b2=5，即a2+b2=9，可得：M（8，0），N（0，8），∵=（﹣t）+（+t），∴P的轨迹是以半径为3、圆心在原点的圆，∴Q，M，N三点共线，∴Q的轨迹方程为直线MN：x+y﹣8=0，∴||的最小值是圆心到直线的距离减去半径，即﹣3=4﹣3．故选：A．二、填空题：本题共4小题，每小题5分.13．数列{a n}的前n项和记为S n，a1=3，a n+1=2S n（n≥1），则S n= 3n．【考点】数列递推式．【分析】由a n+1=2S n（n≥1），可得S n+1﹣S n=2S n，即S n+1=3S n利用等比数列的通项公式即可得出．【解答】解：∵a n+1=2S n（n≥1），∴S n+1﹣S n=2S n，即S n+1=3S n，∴数列{S n}是等比数列，首项为S1=3，公比为q=3，∴S n=3•3n﹣1=3n．故答案为：3n．14．某校高二成立3个社团，有4名同学，每人只选一个社团，恰有1个社团没有同学选，共有42 种不同参加方案（用数字作答）【考点】计数原理的应用．【分析】第一步：从3个社团中选2个，第二步：把4名同学分为（3，1）或（2，2）两组，把这两组同学分配到两个社团中，根据分步计数原理可得．【解答】解：第一步：从3个社团中选2个，共有C32=3种，第二步：把4名同学分为（3，1）或（2，2）两组，把这两组同学分配到两个社团中有A22C43+C42=14，根据分步计数原理可得，共有3×14=42种，故答案为：42．15．若实数x，y满足约束条件，则z=的最小值是﹣2【考点】简单线性规划．【分析】作出不等式组对应的平面区域，利用直线斜率公式，利用数形结合进行判断即可．【解答】解：z=的几何意义是区域内的点到定点D（6，﹣4）的斜率，作出不等式组对应的平面区域，由图象知AD的斜率最大，BD的斜率最小，由得，即B（4，0），此时z==﹣2，故答案为：﹣2．16．将三项式（x2+x+1）n展开，当n=0，1，2，3，…时，得到以下等式：（x2+x+1）0=1（x2+x+1）1=x2+x+1（x2+x+1）2=x4+2x3+3x2+2x+1（x2+x+1）3=x6+3x5+6x4+7x3+6x2+3x+1…观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它头上与左右两肩上3数（不足3数的，缺少的数计为0）之和，第k行共有2k+1个数．若在（1+ax）（x2+x+1）5的展开式中，x7项的系数为75，则实数a的值为 1 ．【考点】归纳推理．【分析】由题意可得广义杨辉三角形第5行为1，5，15，30，45，51，45，30，15，5，1，所以（1+ax）（x2+x+1）5的展开式中，x7项的系数为30+45a=75，即可求出实数a的值．【解答】解：由题意可得广义杨辉三角形第5行为1，5，15，30，45，51，45，30，15，5，1，所以（1+ax）（x2+x+1）5的展开式中，x7项的系数为30+45a=75，所以a=1．故答案为：1．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．如图，设△ABC的个内角A、B、C对应的三条边分别为a、b、c，且角A、B、C成等差数列，a=2，线段AC的垂直平分线分别交线段AB、AC于D、E两点．（1）若△BCD的面积为，求线段CD的长；（2）若DE=，求角A的值．【考点】正弦定理；余弦定理．【分析】（1）先根据三角形的内角A，B，C成等差数列，求出B的度数，再根据三角的面积公式求出BD，再根据余弦定理即可求出，（2）根据垂直平分线的性质得到AC=2AE=，再根据正弦定理，即可求出答案．【解答】解：（1）三角形的内角A，B，C成等差数列，则有2B=A+C．又A+B+C=180°，∴B=60°，∵△BCD的面积为，a=2∴BD•BC•sin60°=，∴BD=，由余弦定理，CD2=BD2+BC2+2BD•BC•cos60°=+4+2××2×=，∴CD=，（2）∵线段AC的垂直平分线分别交线段AB、AC于D、E两点，DE=，∴AE=，∴AC=2AE=2×=，由正弦定理可得=，即=，∴cosA=，∵0＜A＜180°，∴A=45°18．如图，已知长方形ABCD中，AB=2，AD=，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM（Ⅰ）求证：AD⊥BM（Ⅱ）若点E是线段DB上的一动点，问点E在何位置时，二面角E﹣AM﹣D的余弦值为．【考点】二面角的平面角及求法；空间中直线与直线之间的位置关系．【分析】（Ⅰ）根据线面垂直的性质证明BM⊥平面ADM即可证明AD⊥BM（Ⅱ）建立空间坐标系，求出平面的法向量，利用向量法建立二面角的夹角关系，解方程即可．【解答】（1）证明：∵长方形ABCD中，AB=2，AD=，M为DC的中点，∴AM=BM=2，∴BM⊥AM．∵平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，BM⊂平面ABCM∴BM⊥平面ADM∵AD⊂平面ADM∴AD⊥BM；（2）建立如图所示的直角坐标系，设，则平面AMD的一个法向量=（0，1，0），=+=（1﹣λ，2λ，1﹣λ），=（﹣2，0，0），设平面AME的一个法向量为=（x，y，z），则，取y=1，得x=0，z=，则=（0，1，），∵cos＜，＞==，∴求得，故E为BD的中点．19．近年来我国电子商务行业迎来发展的新机遇．2016年618期间，某购物平台的销售业绩高达516亿人民币．与此同时，相关管理部门推出了针对电商的商品和服务的评价体系．现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．（Ⅰ）先完成关于商品和服务评价的2×2列联表，再判断能否在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关？（Ⅱ）若将频率视为概率，某人在该购物平台上进行的3次购物中，设对商品和服务全好评的次数为随机变量X：①求对商品和服务全好评的次数X的分布列；②求X的数学期望和方差．附临界值表：P（K2≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 k）k 2.072 2.706 3.841 5.024 6.635 7.897 10.828 K2的观测值：k=（其中n=a+b+c+d）关于商品和服务评价的2×2列联表：对服务好评对服务不满意合计对商品好评a=80 b= 40 120对商品不满意c= 70 d=10 80合计150 50 n=200【考点】独立性检验的应用．【分析】（Ⅰ）由已知列出关于商品和服务评价的2×2列联表，代入公式求得k2的值，对应数表得答案；（Ⅱ）①每次购物时，对商品和服务全好评的概率为0.4，且X的取值可以是0，1，2，3，X～B（3，0.4）．求出相应的概率，可得对商品和服务全好评的次数X的分布列（概率用组合数算式表示）；②利用二项分布的数学期望和方差求X的数学期望和方差．【解答】解：（1）由题意可得关于商品和服务评价的2×2列联表如下：对服务好评对服务不满意合计对商品好评80 40 120对商品不满意70 10 80合计150 50 200…2分K2=≈11.111＞10.828 …4分故能在犯错误的概率不超过0.001的前提下，认为商品好评与服务好评有关．…5分（2）①每次购物时，对商品和服务都好评的概率为0.4，且X的取值可以是0，1，2，3．其中P（X=0）=0.63=； P（X=1）=C31•0.4•0.62=；…7分P（X=2）=C32•0.42•0.6=； P（X=3）=C33•0.43=．…9分X的分布列为：X 0 1 2 3P…10分②由于X～B（3，0.4），则E（X）=3×0.4=1.2，D（X）=3×0.4×0.6=0.72…12分．20．已知椭圆M： +=1（a＞0）的一个焦点为F（﹣1，0），左右顶点分别为A，B，经过点F的直线l与椭圆M交于C，D两点．（Ⅰ）求椭圆方程；（Ⅱ）记△ABD与△ABC的面积分别为S1和S2，求|S1﹣S2|的最大值．【考点】椭圆的简单性质．【分析】（Ⅰ）由焦点F坐标可求c值，根据a，b，c的平方关系可求得a值；（Ⅱ）当直线l不存在斜率时可得，|S1﹣S2|=0；当直线l斜率存在（显然k≠0）时，设直线方程为y=k（x+1）（k≠0），与椭圆方程联立消y可得x的方程，根据韦达定理可用k表示x1+x2，x1x2，|S1﹣S2|可转化为关于x1，x2的式子，进而变为关于k的表达式，再用基本不等式即可求得其最大值．【解答】解：（Ⅰ）因为F（﹣1，0）为椭圆的焦点，所以c=1，又b=，所以a=2，所以椭圆方程为=1；（Ⅱ）直线l无斜率时，直线方程为x=﹣1，此时D（﹣1，），C（﹣1，﹣），△ABD，△ABC面积相等，|S1﹣S2|=0，当直线l斜率存在（显然k≠0）时，设直线方程为y=k（x+1）（k≠0），设C（x1，y1），D（x2，y2），和椭圆方程联立，消掉y得（3+4k2）x2+8k2x+4k2﹣12=0，显然△＞0，方程有根，且x1+x2=﹣，x1x2=，此时|S1﹣S2|=2||y1|﹣|y2||=2|y1+y2|=2|k（x2+1）+k（x1+1）|=2|k（x2+x1）+2k|==≤=，（k=±时等号成立）所以|S1﹣S2|的最大值为．21．已知函数f（x）=lnx﹣x+1，x∈（0，+∞），g（x）=x3﹣ax．（1）求f（x）的最大值；（2）若对∀x1∈（0，+∞），总存在x2∈[1，2]使得f（x1）≤g（x2）成立，求a的取值范围；（3）证明不等式：（）n+（）n+…+（）n＜．【考点】导数在最大值、最小值问题中的应用；不等式的证明．【分析】（1）求导函数，确定函数的单调性，可得f（x）≤f（1）=0，从而可求f（x）的最大值；（2）若对∀x1∈（0，+∞），总存在x2∈[1，2]使得f（x1）≤g（x2）成立，等价于f（x）≤g（x）max，max由（1）知f（x）max=0，分类讨论，求出g（x）max，即可求a的取值范围；（3）由（1）知f（x）≤0即lnx≤x﹣1（x＞0），取x=，可得ln≤﹣1=，从而可得（）n≤e k﹣n，即可证明结论．【解答】（1）解：∵f（x）=lnx﹣x+1 （x＞0）∴f′（x）=，∴当0＜x＜1时，f′（x）＞0，x＞1时，f′（x）＜0，∴f（x）≤f（1）=0，∴f（x）的最大值为0；（2）解：∀x1∈（0，+∞），总存在x2∈[1，2]使得f（x1）≤g（x2）成立，等价于f（x）max≤g（x）max，由（1）知f（x）max=0，当a≤0时，g（x）=x3﹣ax在x∈[1，2]时恒为正，满足题意．当a＞0时，g′（x）=3x2﹣a，令g′（x）=0，解得x=±，∴g（x）在（﹣∞，﹣），（，+∞）上单调增若≤1即0＜a≤3时，g（x）max=g（2）=8﹣2a，∴8﹣2a≥0，∴a≤4，∴0＜a≤3若1＜≤2即3＜a≤12时，g（x）在[1，]，[，2]而g（1）=1﹣a＜0，g（2）=8﹣2a在（3，4]为正，在（4，12）为负∴3＜a≤4当＞2而a＞12时g（1）＜0，g（2）＜0不合题意综上a的取值范围为 a≤4．（3）证明：由（1）知f（x）≤0即lnx≤x﹣1（x＞0）取x=，∴ln≤﹣1=，∴nln≤k﹣n，即（）n≤e k﹣n，∴（）n+（）n+…+（）n≤e1﹣n+e2﹣n+…+e n﹣n==＜．[选修4-1：几何证明选讲]22．如图，直线AB经过圆O上的点C，并且OA=OB，CA=CB，圆O交直线OB于点E、D，其中D在线段OB上．连结EC，CD．（Ⅰ）证明：直线AB是圆O的切线；（Ⅱ）若tan∠CED=，圆O的半径为3，求OA的长．【考点】相似三角形的性质．【分析】（Ⅰ）连结OC，推导出OC⊥AB，由此能证明AB是圆O的切线．（Ⅱ）由题意先推导出△BCD∽△BEC，从而得到，由此能求出OA．【解答】证明：（Ⅰ）连结OC，∵OA=OB，CA=CB，∴OC⊥AB，又OC是圆O的半径，∴AB是圆O的切线．解：（Ⅱ）∵直线AB是圆O的切线，∴∠BCD=∠E，又∠CBD=∠EBC，∴△BCD∽△BEC，∴，又tan∠CED==，设BD=x，则BC=2x，又BC2=BD•BE，∴（2x）2=x（x+6），即3x2﹣6x=0，解得x=2，即BD=2，∴OA=OB=OD+DB=3+2=5．[选修4-4：坐标系与参数方程]23．在极坐标系中，圆C的方程为ρ=2asinθ （a＞0）．以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，设直线l的参数方程为（t为参数）．（Ⅰ）求圆C的标准方程和直线l的普通方程；（Ⅱ）若直线l与圆C交于A，B两点，且．求实数a的取值范围？【考点】简单曲线的极坐标方程；参数方程化成普通方程．【分析】（Ⅰ）利用极坐标方程进行转化即可求圆C的标准方程，消去参数即可求直线l的普通方程；（Ⅱ）利用直线和圆相交的弦长公式进行转化求解即可．【解答】解：（Ⅰ）∵ρ=2asinθ （a＞0）．∴ρ2=2aρsinθ，即x2+y2=2ay，即x2+（y﹣a）2=a2，（a＞0）．则圆C的标准方程为x2+（y﹣a）2=a2，（a＞0）．由，消去参数t得4x﹣3y+5=0，即直线l的普通方程为4x﹣3y+5=0；（Ⅱ）由圆的方程得圆心C（0，a），半径R=a，则圆心到直线的距离d=，∵．∴2≥a，即a2﹣d2≥a2，则d2≤，即d≤，则﹣≤≤，由得得≤a≤10．即实数a的取值范围是≤a≤10．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣2|+|x﹣a|．（Ⅰ）当a=1时，解不等式f（x）≤2（Ⅱ）若f（x）≥2，求实数a的取值范围．【考点】绝对值不等式的解法；绝对值三角不等式．【分析】（Ⅰ）将a=1代入f（x），通过讨论x的范围，求出不等式的解集即可；（Ⅱ）根据绝对值的意义得到|a﹣2|≥2，解出即可．【解答】解：（Ⅰ）当a=1时，f（x）=，当x＜1时，﹣2x+3≤2，所以x＞．故＜x＜1，当1≤x≤2时，1≤2恒成立，当x＞2时，2x﹣3＜2，所以x＜，故2＜x＜，综上可知x∈（，）；（Ⅱ）∵|x﹣2|+|x﹣a|≥|x﹣2+a﹣x|=|a﹣2|，由题意有|a﹣2|≥2，∴a﹣2≥2或a﹣2≤﹣2，解得：a≥4或a≤0．。

湖南省五市十校教研教改共同体高二物理下学期期末考试试题

“五市十校教研教改共同体”2015-2016高二第二学期期末考试物理时量：80分钟总分：110分考试学校：沅江一中、箴言中学、桃江一中、宁乡一中、雷锋学校、东山学校、南方中学、岳阳市第十四中学、岳阳市第十五中学、南县一中等一、选择题（本题共12小题，每小题4分，共48分。

在每小题给出的四个选项中，第1——8题只有一项符合题目要求，第9-12题有多项符合题目要求。

） 1．如图所示为锥形齿轮的传动示意图，大齿轮带动小齿轮转动，已知A 、B 分别为大、小齿轮边缘处的两点，A 、B 线速度大小分别为v 1、v 2，向心加速度大小分别为a 1、a 2，则 ( )A. v 1=v 2，a 1<a 2B. v 1=v 2，a 1>a 2C. v 1>v 2，a 1=a 2D. v 1<v 2，a 1=a 22．A 、B 两物体在同一直线上运动的v -t 图象如图所示。

已知在第3s 末两物体相遇，则下列说法正确的是 ( )A.两物体从同一地点出发B.出发时A 在B 前方3m 处C.两物体运动过程中，A 的加速度大于B 的加速度D.第3s 末两物体相遇之后，两物体可能再相遇3．理想变压器连接电路如图甲所示，已知原、副线圈匝数比为5∶1，当输入电压波形如图乙时，电流表读数为2A ，则 ( )A.电压表读数为200VB.电压表读数为56.4VC.输入功率为80WD.输入功率为112.8W 4．如图，放在光滑斜面上的物块，受到平行斜面向下的力F 作用，沿斜面向下运动，斜面体在粗糙水平地面上保持静止。

下列说法正确的是（） A ．地面对斜面体的支持力大于斜面体和物块的重力之和 B ．地面对斜面体的摩擦力的方向水平向左 C ．若F 反向，地面对斜面体的支持力不变 D ．若F 增大，地面对斜面体的摩擦力也增大5．位于赤道上随地球自转的物体P 和地球的同步通信卫星Q 均在赤道平面上绕地心做匀速圆周运动。

湖南省五市十校204-2015学年高二生物下学期期末联考试题

“湖南省五市十校教研教改共同体”高二期末考试生物试题时量：70分钟分值：90分答题说明：1、考生必须将答案准确填写在答题卡上，写在试卷上的一律无效；2、考生请使用黑色中性笔和2B铅笔作答；3、试题卷请留存备讲。

一、选择题（每题有且只有一项正确答案，每题4分，共36分）1．下图是高等动物细胞亚显微结构示意图，下列叙述错误的是 ( ) A．若⑦是糖蛋白(如干扰素)，则该蛋白中的糖基与蛋白质分子的连接场所可以是图中的②B．若⑦是抗体，则⑦由高尔基体通过囊泡分泌到细胞外不需要载体，不消耗能量C．在图中的结构①和⑧中都能发生碱基A--U互补配对D．若⑦是性激素，则该激素合成的场所可能是②2. 下列有关酶的叙述正确的是（）A．酶的合成场所都在核糖体B．酶通过为反应物供能和降低活化能来提高化学反应速率C．DNA聚合酶和RNA聚合酶催化形成的化学键不同D．细胞内发生的化学反应所需要的酶都由细胞合成3．基因位于染色体上的实验证据是摩尔根的果蝇杂交试验，所用科学方法是假说—演绎法，摩尔根在实验中所发现的新问题是：（）A．F1果蝇全是红色 B．F2果蝇出现性状分离C．F2果蝇红眼和白眼之间的数量比是3:1 D．白眼性状的表现总是与性别相联系4．下列现象属于基因重组的是：（）A．精子与卵细胞随机结合 B．植物组织培养中出现新品种C．非同源染色体之间片段互换 D．减数分裂中的交叉互换5．现有一个数目庞大的哺乳动物种群，个体基因型情况为AA占25%，Aa占50%，aa占25%；若让该种群分别进行自由交配和自交（特指基因型相同雌雄个体间交配），两种交配方式的F1中AA的基因型频率、a基因频率变化情况分别是： ( )A．上升、不变和上升、下降 B．不变、不变和上升、不变C．不变、不变和不变、不变 D．上升、不变和上升、上升6．现有一份自然的辣椒种子，将它们分成两份，分别标记为甲组和乙组。

甲组自然种植；乙组随宇宙飞船到太空遨游一番后返回地面，同样也和甲组一样的条件自然种植，试分析并预测两组辣椒的性状表现情况： ( ) A．乙组都好于甲组 B．乙组都不如甲组C．乙组大部分好于甲组 D．乙组大部分不如甲组7．右图表示高等动物细胞(2N)在分裂过程中某一时期的染色体(a)、染色单体(b)、DNA(c)三者之间的数量关系。

五市十校204-2015学年高二下学期期末考试联考化学试题及答案

“湖南省五市十校教研教改共同体”高二期末考试化学试题时量：70分钟分值：100分命题：宁乡一中、东山学校、雷锋中学、南方中学审校：箴言中学、宁乡一中答题说明：1. 考生必须将答案准确填写到答题卡上，写在试卷上的一律无效；2. 考生请使用黑色中性笔和2B铅笔作答；3. 可能用到的相对原子质量：H—1 O—16 C—12 Cu—64 Mg—24 N—14 K—39 Mn—55一、选择题（每小题4分，共40分）1．化学与人类生活、社会可持续发展密切相关，下列措施有利于节能减排、保护环境的是（）①加快化石燃料的开采与使用；②研发易降解的生物农药；③应用高效洁净的能源转换技术；④田间焚烧秸秆；⑤推广使用节能环保材料。

A.①③⑤B.②③⑤C.①②④D.②④⑤2．下列离子方程式中正确的是（）A.向碳酸钠溶液中加入足量的盐酸CO32-+ 2H+ = CO2↑+H2OB.单质铁和三氯化铁溶液反应生成氯化亚铁Fe + Fe3+＝2Fe2+C.金属钠与水反应生成氢氧化钠和氢气Na + H2O＝Na++OH -+H2↑D.氯化铵晶体和石灰粉共热产生氨气NH4+ +OH -＝NH3↑+H2O3．下列有关物质性质的说法错误．．的是（）A.热稳定性：HCl＞HIB.原子半径：Na＞MgC.酸性：H2SO3＞H2SO4D.结合质子能力：S2—＞Cl—4．N A表示阿伏加德罗常数的值，下列说法正确的是()A．标准状况下，22.4 L二氯甲烷的分子数约为N A个B．盛有SO2的密闭容器中含有N A个氧原子，则SO2的物质的量为0.5 molC．17.6 g丙烷中所含的极性共价键为4N A个D．电解精炼铜时，若阴极得到电子数为2N A个，则阳极质量一定减少64 g5．分子式为C5H10O且能发生银镜反应的有机物种数是（）A.3种B.4种C.5种D.6种6．下列说法不正确．．．的是（）A．化学反应达到化学平衡状态的正逆反应速率相等，是指同一物质的消耗速率和生成速率相等，若用不同物质表示时，反应速率不一定相等。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B．标准状况下，1 L辛烷完全燃烧生成CO2 8 LC．2.4 g Mg无论与O2还是与N2完全反应，转移电子数都是0.2N AD．1 L 1 mol·L－1 CH3COOH溶液中，所含CH3COO－、CH3COOH的总数为N A7．一种新型燃料电池，以镍板为电极插入KOH溶液中，分别向两极通入乙烷(C2H6)和氧气，其中某一电极反应式为C2H6＋18OH－－14e－===2CO2－3＋12H2O。

有关此电池的描述不正确．．．的是()A．通入氧气的电极为正极B．参加反应的O2与C2H6的物质的量之比为7∶2C．放电一段时间后，KOH的物质的量浓度将下降D．放电一段时间后，正极区附近溶液的pH减小8．已知某有机物X的结构简式为，下列有关叙述正确的是()① 1 mol X分别与足量的Na、NaOH溶液、NaHCO3溶液反应，消耗这三种物质的物质的量分别为3 mol、4 mol、1 mol②X在一定条件下能与FeCl3溶液发生显色反应③X在一定条件下能发生消去反应和酯化反应④X的化学式为C10H8O6A．①②B．①③C．②④D．③④9．下列描述正确的个数是()①聚乳酸的结构为，聚乳酸是由单体之间通过加聚而合成②完全燃烧等物质的量的乙醛和乙醇，消耗氧气的质量相等③蔗糖.麦芽糖的分子式都是C12H22O11，二者互为同分异构体④用甘氨酸()和丙氨酸()缩合最多可形成4种二肽⑤的系统命名法的名称为2,2,3-三甲基戊烷A. 1B.2C.3D.410．某密闭容器中充入等物质的量的A和B，一定温度下发生反应A(g)＋x B(g) 2C(g)，达到平衡后，在不同的时间段，分别改变影响反应的一个条件，测得容器中物质的物质的量浓度.反应速率分别随时间的变化如下图所示：下列说法中正确的是()A．30～40 min间该反应使用了催化剂B．反应方程式中的x＝1，正反应为吸热反应t/minC ．30 min 时降低温度，40 min 时升高温度D ．8 min 前A 的反应速率为0.08 mol·L －1·min －1二、非选择题（共60分） 11．（I 题三分，II 题毎空3分，15分） “低碳循环”、如何降低大气中CO 2的含量、有效地开发利用CO 2，引起了全世界的普遍重视。

I ．用电弧法合成的储氢纳米碳管，可用如下氧化法提纯，请完成下述反应：___ C+ ___ KMnO 4 + 6 H 2SO 4→____CO 2↑+ ____MnSO 4 + ____K 2SO 4 + 6 H 2O II ．某研究小组现将三组CO(g)与H 2O(g)的混合气体分别通入体积为2 L 的恒容密闭容器中，一定条件下发生反应：CO(g)+H 2O(g)2(g)+H 2(g) △H ＜0，得到如下数据：（1）实验I 中，前5min 的反应速率υ(CO 2)＝ mol•L -1•min -1。

（2）下列能判断在800℃实验条件下CO(g)与H 2O(g)反应一定达到平衡状态的是。

A ．容器内压强不再变化B ．C ．混合气体密度不变D ．υ正(CO) ＝υ逆（CO 2）（3）实验III 中：y= 。

（4）若实验Ⅲ的容器改为在绝热的密闭容器中进行，实验测得H 2O(g)的转化率a(H 2O)随时间变化的示意图，如右图所示，b 点：υ正 υ逆（填“＜”.“＝”或“＞”）。

12. （毎空3分，15分）为了保护环境，充分利用资源，某研究小组通过如下简化流程，将工业制硫酸的硫铁矿烧渣（含Fe 2O 3.SiO 2.Al 2O 3等）转变成重要的工业原料FeSO 4（反应条件略）活化硫铁矿还原Fe 3+的主要反应为：FeS 2+7Fe 2(SO 4)3+8H 2O=15FeSO 4+8H 2SO 4，不考虑其它反应，请回答下列问题：（1）第1步H2SO4与Fe2O3反应的离子方程式是。

（2）检验第II步中Fe3+是否完全还原，应选择（填字母编号）。

A．KMnO4溶液B．K3[Fe(CN)6]溶液C．KSCN溶液（3）第III步加FeCO3调溶液pH=6时，利用相关数据计算，判断Al3+是否沉淀完全？（填“是”或“否”）（已知Ksp【Al(OH)3】=1.9×10-33，当离子浓度小于1×10-5mol·L-1时，可认为沉淀完全）（4）FeCO3在空气中加热反应可制得铁系氧化物材料。

∆= —1648kJ/mol 已知25℃，101kPa时：4Fe(s)+3O2(g)=2Fe2O3(s) H∆= —393kJ/molC(s)+O2(g)=CO2(g) H∆= —1480kJ/mol2Fe(s)+2C(s)+3O2(g)=2FeCO3(s) HFeCO3在空气中加热反应生成Fe2O3的热化学方程式是。

（5）FeSO4在一定条件下可制得FeS2(二硫化亚铁)纳米材料，该材料可用于制造高容量锂电池，电池放电时的总反应为4Li + FeS2= Fe + 2Li2S，正极反应式是。

13.（16分）由烃A合成有机化合物G（二乙酸乙二酯），采用如图所示的合成路线：Array回答下列问题：⑴已知有机物CH3OOC-COOCH3的名称为乙二酸二甲酯，请写出G的结构简式：。

⑵在上述反应中属于取代反应的有 (填序号)。

⑶E中官能团的名称：。

与A互为同系物的C3H6 分子中最多共面原子有个。

⑷写出反应④的化学方程式(3分): 。

⑸满足下列条件：①能发生水解反应，②能发生银镜反应，③能与碳酸氢钠反应的G的同分异构体共有（3分）。

其中， G的一种同分异体其核磁共振氢谱只有6个峰，面积之比为1:1:1:1:3:3，写出其结构简式。

14．（毎空2分，14分）苯甲酸广泛用于医药、食品、染料、化工等领域。

以下是实验室制备苯甲酸的一种方法。

反应原理如下：实验步骤：下图组装反应装置（冷凝水.夹持及加热装置未画出），并在三颈烧瓶中依次加入120mL水、9.4g高锰酸钾和3.0mL甲苯。

②将三颈烧瓶中的混合液体搅拌，加热至沸腾，直到甲苯完全反应。

③趁热过滤反应混合物。

若滤液呈紫色，则需加入适量的亚硫酸氢钠溶液至紫色褪去后再过滤，用热水洗涤滤渣，洗涤液合并至滤液中。

④用冰水冷却滤液，然后用浓盐酸酸化，过滤，用少量冷水洗涤滤渣，得到苯甲酸粗产品，经重结晶得到精制的苯甲酸。

回答下列问题：（1）本实验应选择的三颈烧瓶规格为（填字母序号）。

A．100 mL B．250 mL C．500 mL D．1000 mL（2）判断甲苯已完全反应的现象是、回流液不再出现油珠。

（3）实验步骤④中，用少量冷水而不用热水洗涤滤渣的目的是；苯甲酸粗产品除了可用重结晶法精制外，还可用法。

A．蒸发 B．升华 C．过滤 D．分液（4）精制的苯甲酸纯度测定：称取1.220g样品，用稀乙醇溶解并配成100 mL溶液，分别取25.00mL溶液，用0.1000 mo1·L－1NaOH标准溶液滴定，三次滴定消耗NaOH溶液的体积分别为V1=24.70mL、V2=24.80 mL、V3= 25.80mL。

①配制溶液时用稀乙醇而不用蒸馏水作溶剂的原因是。

②若用酚酞作指示剂，确定滴定终点的现象是。

③产品的纯度为。

化学参考答案1-10：BACBB BDABD【11答案】（每空3分，共15分）I ．_5_ C+ _4_ KMnO 4+ 6 H 2SO 4→_5_CO 2↑+ _4_MnSO 4 + _2_K 2SO 4+ 6 H 2O （3分） II ．（1）0.1（3分）（2）D （ 3分）（3）1（3分）＞（3分）【12答案】（每空3分，共15分）（1）Fe 2O 3+6H +＝2Fe 3++3H 2O （2）C （3）是（4）4FeCO 3(s)+O 2(g) =2Fe 2O 3(s)+ 4CO 2(g) H =－260kJ ·mol -1。

（5）FeS 2+4e －= Fe +2S 2－或FeS 2+4Li ++4e －= Fe +2Li 2S【13答案】（1）CH 3COOCH 2CH 2OOCCH 3 （ 2分）(2) ②⑥ （ 2分） (3)醛基（ 2分） 7（ 2分）（4）2CH 3CH 2OH + O 2 → 2CH 3CHO + 2H 2O （ 3分）(5) 12 （ 3分）（ 2分）【14答案】（每空2分，共14分）（1）B （2）三颈烧瓶中混合液不再分层（或甲苯层消失）（3）减少苯甲酸因溶解造成损失， B（4）①常温下苯甲酸微溶于水而易溶于乙醇②滴加最后一滴氢氧化钠标准溶液后，溶液由无色变为浅红色，且30秒不褪色 ③99.00%。