人教八年级数学上册课件:第十二章小结与复习
合集下载
人教版八年级上册数学第十二章小结与复习课件ppt

为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
Hale Waihona Puke 为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
Hale Waihona Puke 为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
新编:人教版八年级上册数学第12章《全等三角形小结与复习》

图7
达标测试
1.如图8,点M是AB的中点,∠1=∠2,∠C=∠D,判定 △AMC≌△BMD的方法是(
D)
图8
A.SAS
C. SSS
B. ASA
D. AAS
2.下列方法中,不能判定两个三角形全等的是( D ) A. SAS B. ASA C. SSS D. SSA
3、如图,已知AD∥BC,AE=CF,根据所给条件能否证明
课堂练习 1.如图1,△AOC≌△BOD,则
∠A和∠B, ∠C和∠D,∠AOC和∠BOD , 对应角是__________________________________________
AO和BO,OC和OD,AC和BD 对应边是__________________________________________ 。
C O A
B
B
图1
D
图2
A
3.如图3所示,图中两个三角形能完全重合,下列写法正确的 是(
B)
B.△ABE≌△ABF D.△ABE≌△FAB B
F
A E
A.△ABE≌△AFB C.△ABE≌△FBA
基础知识
(二)全等三角形的性质
1.全等三角形的对应边相等 ;
2.全等三角形的对应角 相等 ;
3.全等三角形的对应中线.对应角平分线.
课堂练习
1. 下列条件不能判定两个三角形全等的是(C ) A. 有两边和夹角对应相等; B. 有三边分别对应相等;
C. 有两边和一角对应相等;
D. 有两角和一边对应相等。
2. 下列条件能判定两个三角形全等的是( )
D
A. 有三个角相等;
C. 有一条边和一个角相等;
B. 有一条边和一个角相等;
人教版初中八年级数学上册第十二章全等三角形小结与复习ppt课件

关系?并说明理由.
C
D
答: O 到三条直线AC、
AB、BD 的距离相等.
O
理由:略.
A
B
典型例题
例2 已知:如图,AC //BD,AC =BD,求证:AD //BC.
证明:请同学们自己 写出证明过程.
C A
B D
典型例题
追问 在例2中,AC //BD,AC =BD,在AB上取两 点E、F,AE =BF.请你判断DE、CF 有何关系?并说 明理由.
任选三个作为条件,可组合出几种情况?哪些能 判定两个三角形全等?两个直角三角形全等的条 件是什么?
知识梳理
问题1 请同学们回答下列问题: (4)学习本章后,你对角平分线有了哪些新的认识?
对比角平分线的性质和判定,它们有何异同?你 能用全等三角形证明角平分线的性质和判定吗? (5)你能举例说明证明一个几何命题的一般过程吗?
八年级 上册
第十二章 小结与复习
课件说明
• 全等三角形的概念是学习本章的基础,研究全等三 角形性质和判定是对对应边之间、对应角之间的相 等关系方面进行的探究,是证明角平分线的性质和 判定的基础.全等三角形的性质和判定又是证明线 段相等和角相等的重要方法.在性质和判定的探究 过程中,渗透了研究几何图形的基本思路和方法.
证明:由(1)得, △CAB ≌△DBA , ∴ ∠C =∠D,CA =DB. 又 ∠COA =∠DOB, ∴ △OCA ≌△ODB.
C
D
O
A
B
典型例题
例1 已知:如图,∠CAB =∠DBA,AD、BC 分别
是∠CAB、∠DBA 角平分线,AD、BC 相交于点O.求
证:(3)O 到三条直线AC、AB、BD 的距离有何大小
八年级数学上册 第十二章全等三角形小结与复习课件2_6-10
∵∠ACB=∠ECD,CB=CD,
∠ABC=∠EDC, ∴△EDC≌△ABC(ASA).
CD
∴DE=BA.
E
答:测出DE的长就是A、B之间的距离.
花瓶里的纸花与笔筒中毛笔同时被主人摆放在案桌上。之后,蚂蚁逢人便说:“当你遇到无法逾越的障碍时,不妨换一种方式。玛茨亚很机灵,不过还是被吓了一跳。 电影在线观看 /tv/29.html 它倒还能挺直身子走路。
AD=AD, AB=AC,
∴ Rt△ADB ≌ Rt△ADC(HL). ∴BD=CD.
A
B
D
C
方法总结
利用全等三角形可以测量一些不易测量的距离和长度,还可对某些 因素作出判断,一般采用以下步骤: (1)先明确实际问题;
(2)根据实际抽象出几何图形;
(3)经过分析,找出证明途径; (4)书写证明过程.
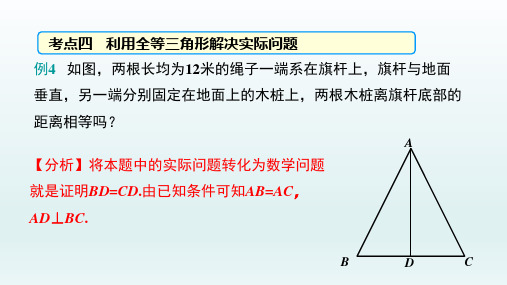
考点四 利用全等三角形解决实际问题 例4 如图,两根长均为12米的绳子一端系在旗杆上,旗杆与地面 垂直,另一端分别固定在地面上的木桩上,两根木桩离旗杆底部的 距离相等吗?
A
【分析】将本题中的实际问题转化为数学问题
就是证明BD=CD.由已知条件可知AB=AC,
AD⊥BC.
B
D
C
解:相等,理由如下:
∵AD⊥BC, ∴∠ADB=∠ADC=90°. 在Rt△ADB和Rt△ADC中,
针对训练
5.如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不 能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间 的距离吗?
解:要测量A、B间的距离,可用如下方法:
D=BC,
再作出BF的垂线DE,使A、C、E在一条直
线上,
“现在我再来匀一匀。,
人教版八年级上册数学课件 第十二章 小结与复习(共31张PPT)

∴PE=PF, ∠PEA=∠PFC=90 °. ∵ ∠PCB+ ∠BAP=180 °,∠BAP+∠EAP=180 °.
∴ ∠EAP=∠PCB.
在△APE和△CPF中, ∠PEA=∠PFC=90 °, ∠EAP=∠FCP, PE=PF,
∴ △APE ≌ △CPF(AAS), ∴ PA=CP.
E
A 1
2 B
N P
FC
方法2思路分析:由角是轴对称图形,其对称轴是
角平分线所在的直线,所以可想到构造轴对称图
形.方法是在BC上截取BD=AB,连接PD(如图).
则有△PAB≌△PDB,再证△PDC是等腰三角形即
可获证.
N
证明过程请同学们自行完成!
A
P
1
2
B
D
C
归纳拓展:角的平分线的性质是证明线段相等的常用性
质.应用时要依托全等三角形发挥作用.作辅助线有两种
分析: 欲证∠DEC=∠FEC
E
G
F
B
由平行线的性质转化为证明
D
C
∠DEC=∠DCE
转化为证明△DEG ≌ △DCG
证明: ∵CE⊥AD, ∴ ∠AGE=∠AGC=90 °.
A
∵AD平分∠BAC,∴ ∠EAG=∠CAG.
在△AGE和△AGC中,
∠AGE=∠AGC, AG=AG, ∠EAG=∠CAG,
利用全等三角形可以测量一些不易测量的距离和长 度,还可对某些因素作出判断,一般采用以下步骤: (1)先明确实际问题;
(2)根据实际抽象出几何图形;
(3)经过分析,找出证明途径; (4)书写证明过程.
练习4:如图,有一湖的湖岸在A、B之间呈一段圆 弧状,A、B间的距离不能直接测得.你能用已学过 的知识或方法设计测量方案,求出A、B间的距离吗?
∴ ∠EAP=∠PCB.
在△APE和△CPF中, ∠PEA=∠PFC=90 °, ∠EAP=∠FCP, PE=PF,
∴ △APE ≌ △CPF(AAS), ∴ PA=CP.
E
A 1
2 B
N P
FC
方法2思路分析:由角是轴对称图形,其对称轴是
角平分线所在的直线,所以可想到构造轴对称图
形.方法是在BC上截取BD=AB,连接PD(如图).
则有△PAB≌△PDB,再证△PDC是等腰三角形即
可获证.
N
证明过程请同学们自行完成!
A
P
1
2
B
D
C
归纳拓展:角的平分线的性质是证明线段相等的常用性
质.应用时要依托全等三角形发挥作用.作辅助线有两种
分析: 欲证∠DEC=∠FEC
E
G
F
B
由平行线的性质转化为证明
D
C
∠DEC=∠DCE
转化为证明△DEG ≌ △DCG
证明: ∵CE⊥AD, ∴ ∠AGE=∠AGC=90 °.
A
∵AD平分∠BAC,∴ ∠EAG=∠CAG.
在△AGE和△AGC中,
∠AGE=∠AGC, AG=AG, ∠EAG=∠CAG,
利用全等三角形可以测量一些不易测量的距离和长 度,还可对某些因素作出判断,一般采用以下步骤: (1)先明确实际问题;
(2)根据实际抽象出几何图形;
(3)经过分析,找出证明途径; (4)书写证明过程.
练习4:如图,有一湖的湖岸在A、B之间呈一段圆 弧状,A、B间的距离不能直接测得.你能用已学过 的知识或方法设计测量方案,求出A、B间的距离吗?
