【金识源】高中数学 1.1.3 集合的基本运算导学案 新人教A版必修1
高中数学 1.1.3(集合的基本运算)教案 新人教A版必修1 教案

§ 集合的基本运算一. 教学目标:1. 知识与技能(1)理解两个集合的并集与交集的含义,会求两个简单集合的交集与并集.(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.(3)能使用Venn 图表达集合的运算,体会直观图示对理解抽象概念的作用.2. 过程与方法学生通过观察和类比,借助Venn 图理解集合的基本运算.3.情感.态度与价值观(1)进一步树立数形结合的思想.(2)进一步体会类比的作用.(3)感受集合作为一种语言,在表示数学内容时的简洁和准确.重点:交集与并集,全集与补集的概念.难点:理解交集与并集的概念.符号之间的区别与联系.1.学法:学生借助Venn 图,通过观察.类比.思考.交流和讨论等,理解集合的基本运算.2.教学用具:投影仪.四. 教学思路(一)创设情景,揭示课题问题1:我们知道,实数有加法运算。
类比实数的加法运算,集合是否也可以“相加”呢? 请同学们考察下列各个集合,你能说出集合C 与集合A .B 之间的关系吗?(1){1,3,5},{2,4,6},{1,2,3,4,5,6};A B C ===(2){|},{|},{|}A x x B x x C x x ===是理数是无理数是实数引导学生通过观察,类比.思考和交流,得出结论。
教师强调集合也有运算,这就是我们本节课所要学习的内容。
(二)研探新知—般地,由所有属于集合A 或属于集合B 的元素所组成的集合,称为集合A 与B 的并集. 记作:A ∪B.读作:A 并B.其含义用符号表示为:{|,}A B x x A x B =∈∈或用Venn 图表示如下:请同学们用并集运算符号表示问题1中A ,B ,C 三者之间的关系.练习.检查和反馈(1)设A={4,5,6,8),B={3,5,7,8),求A ∪B.(2)设集合A {|12},{|13},.A x x B x x AB =-<<=<<集合求让学生独立完成后,教师通过检查,进行反馈,并强调:(1)在求两个集合的并集时,它们的公共元素在并集中只能出现一次.(2)对于表示不等式解集的集合的运算,可借助数轴解题.(1)思考:求集合的并集是集合间的一种运算,那么,集合间还有其他运算吗?请同学们考察下面的问题,集合A .B 与集合C 之间有什么关系?①{2,4,6,8,10},{3,5,8,12},{8};A B C ===②{|20049}.A x x =是国兴中学年月入学的高一年级女同学B={x |x 是国兴中学2004年9月入学的高一年级同学},C={x |x 是国兴中学2004年9月入学的高一年级女同学}.教师组织学生思考.讨论和交流,得出结论,从而得出交集的定义;一般地,由属于集合A 且属于集合B 的所有元素组成的集合,称为A 与B 的交集. 记作:A ∩B.读作:A 交B其含义用符号表示为:{|,}.A B x x A x B =∈∈且接着教师要求学生用Venn 图表示交集运算.(2)练习.检查和反馈①设平面内直线1l 上点的集合为1L ,直线1l 上点的集合为2L ,试用集合的运算表示1l 的位置关系.②学校里开运动会,设A={x |x 是参加一百米跑的同学},B={x |x 是参加二百米跑的同学},C={x |x 是参加四百米跑的同学},学校规定,在上述比赛中,每个同学最多只能参加两项比赛,请你用集合的运算说明这项规定,并解释集合运算A ∩B 与A ∩C 的含义.学生独立练习,教师检查,作个别指导.并对学生中存在的问题进行反馈和纠正.(三)学生自主学习,阅读理解1.教师引导学生阅读教材第11~12页中有关补集的内容,并思考回答下例问题:(1)什么叫全集?(2)补集的含义是什么?用符号如何表示它的含义?用Venn 图又表示?(3)已知集合{|38},R A x x A =≤<求.(4)设S={x |x 是至少有一组对边平行的四边形},A={x |x 是平行四边形},B={x |x 是菱形},C={x |x 是矩形},求,,A S B C B A .在学生阅读.思考的过程中,教师作个别指导,待学生经过阅读和思考完后,请学生回答上述问题,并及时给予评价.(四)归纳整理,整体认识1.通过对集合的学习,同学对集合这种语言有什么感受?2.并集.交集和补集这三种集合运算有什么区别?(五)作业1.课外思考:对于集合的基本运算,你能得出哪些运算规律?2.请你举出现实生活中的一个实例,并说明其并集.交集和补集的现实含义.3.书面作业:教材第14页习题组第7题和B组第4题.。
高中数学 1.1.3 集合的基本运算 第一课时教案精讲 新人教A版必修1
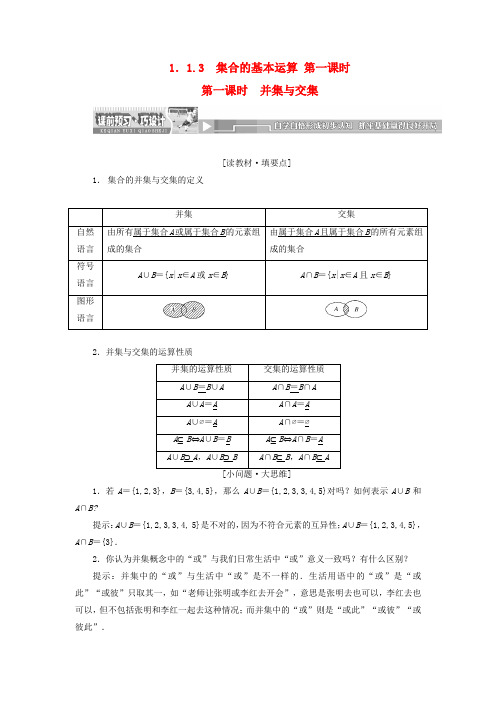
1.1.3 集合的基本运算第一课时第一课时并集与交集[读教材·填要点]1.集合的并集与交集的定义2.并集与交集的运算性质1.若A={1,2,3},B={3,4,5},那么A∪B={1,2,3,3,4,5}对吗?如何表示A∪B和A∩B?提示:A∪B={1,2,3,3,4, 5}是不对的,因为不符合元素的互异性;A∪B={1,2,3,4,5},A∩B={3}.2.你认为并集概念中的“或”与我们日常生活中“或”意义一致吗?有什么区别?提示:并集中的“或”与生活中“或”是不一样的.生活用语中的“或”是“或此”“或彼”只取其一,如“老师让张明或李红去开会”,意思是张明去也可以,李红去也可以,但不包括张明和李红一起去这种情况;而并集中的“或”则是“或此”“或彼”“或彼此”.3.若集合A 与集合B 没有公共元素,能否说集合A 与集合B 没有关系?提示:当两集合A 与B 没有公共元素时,不能说集合A 与B 没有关系,而是A ∩B =∅.[例1] 已知集合A ={x |(x -1)(x +2)=0},B ={x |(x +2)(x -3)=0},则集合A ∪B 是( )A .{-1,2,3}B .{-1,-2,3}C .{1,-2,3}D .{1,-2,-3}[自主解答] A ={x |(x -1)(x +2)=0}={1,-2};B ={x |(x +2)(x -3)=0}={-2,3},∴A ∪B ={1,-2}∪{-2,3}={-2,1,3}. [答案] C ——————————————————解决此类问题首先应看清集合中元素的范围,简化集合,若是用列举法表示的数集,可以根据交集、并集的定义直接观察或用Venn 图表示出集合运算的结果;若是用描述法表示的数集,可借助数轴分析写出结果,此时要注意当端点不在集合中时,应用“空心点”表示. ————————————————————————————————————————1.已知集合A ={x |-1<x ≤3},B ={x |x ≤0,或x ≥52},求A ∩B ,A ∪B .解:∵A ={x |-1<x ≤3},B ={x |x ≤0,或x ≥52},把集合A 与B 表示在数轴上,如图.∴A ∩B ={x |-1<x ≤3}∩{x |x ≤0或x ≥52}={x |-1<x ≤0或52≤x ≤3};A ∪B ={x |-1<x ≤3}∪{x |x ≤0或x ≥52}=R .[例2] 已知集合A ={1,3,x },B ={1,x 2},A ∪B ={1,3,x },求满足条件的实数x 的值.[自主解答] ∵A ∪B ={1,3,x },A ={1,3,x },B ={1,x 2}, ∴A ∪B =A ,即B ⊆A , ∴x 2=3或x 2=x .①当x 2=3时,得x =± 3.若x =3,则A ={1,3,3},B ={1,3},符合题意; 若x =-3,则A ={1,3,-3},B ={1,3},符合题意. ②当x 2=x 时,则x =0或x =1.若x =0,则A ={1,3,0},B ={1,0},符合题意; 若x =1,则A ={1,3,1},B ={1,1},不成立,舍去; 综上可知,x =±3或x =0. ——————————————————在利用集合的交集、并集性质解题时,常常会遇到A ∩B =A ,A ∪B =B 等这类问题,解答时常借助于交、并集的定义及上节学习的集合间的关系去分析,如A ∩B =A ⇔A⊆B ,A ∪B =B ⇔A ⊆B 等,解答时应灵活处理.对于含有参数的问题要分类讨论,同时要检验,利用好集合中元素的互异性.————————————————————————————————————————2.已知集合A ={4,6},B ={2,m },A ∪B ={2,4,6},则m 的值为________. 解析:∵A ={4,6},B ={2,m }, 而A ∪B ={2,4,6}, ∴m =4或m =6. 答案:4或6 高手妙解题 同样的结果,不一样的过程,节省解题时间,也是得分!集合A ={x |x 2-ax +a 2-19=0},B ={x |x 2-5x +6=0},C ={x |x 2+2x -8=0}.(1) 若A ∩B =A ∪B ,求a 的值; (2)若∅A ∩B ,A ∩C =∅,求a 的值.[巧思] (1)A ∩B =A ∪B ⇔A =B ;(2)∅A ∩B ⇔A ∩B ≠∅. [妙解] 由已知,得B ={2,3},C ={2,-4}.(1)∵A ∩B =A ∪B ,∴A =B .于是2,3是一元二次方程x 2-ax +a 2-19=0的两个根,由根与系数之间的关系知:⎩⎪⎨⎪⎧2+3=a ,2×3=a 2-19解之得a =5.(2)由A ∩B ∅⇒A ∩B ≠∅,又A ∩C =∅,得3∈A,2∉A ,-4∉A . 由3∈A 得32-3a +a 2-19=0, 解得a =5或a =-2.当a =5时,A ={x |x 2-5x +6=0}={2,3},与2∉A 矛盾; 当a =-2时, A ={x |x 2+2x -15=0}={3,-5},符合题意. ∴a =-2.1.已知集合M ={1,2,3,4},N ={-2,2},下列结论成立的是( ) A .N ⊆M B .M ∪N =M C .M ∩N =ND .M ∩N ={2}解析:因为-2∉M ,可排除A ;M ∪N ={-2,1,2,3,4},可排除B ;M ∩N ={2}. 答案:D2.设A ={x ∈N |1≤x ≤10},B ={x ∈R |x 2+x -6=0},则如图中阴影部分表示的集合为( )A .{2}B .{3}C .{-3,2}D .{-2,3}解析:注意到集合A 中的元素为自然数,因此易知A ={1,2,3,4,5,6,7,8,9,10},而直接解集合B 中的方程可知B ={-3,2},因此阴影部分显然表示的是A ∩B ={2}.答案:A3.设集合M ={x |-3≤x <7},N ={x |2x +k ≤0},若M ∩N ≠∅,则k 的取值范围是( ) A .k ≤3B .k ≥-3C .k >6D .k ≤6解析:因为N ={x |2x +k ≤0}={x |x ≤-k2},且M ∩N ≠∅,所以-k2≥-3⇒k ≤6.答案:D4.已知集合A ={x |x 是平行四边形},B ={x |x 是菱形},C ={x |x 是矩形},则A ∩B ∩C =________.解析:∵A ∩B ={x |x 是菱形} ∴A ∩B ∩C ={x |x 是正方形}. 答案:{x |x 是正方形}5.已知集合M ={0,1,2},N ={x |x =2a ,a ∈M },则集合M ∩N =________. 解析:由M ={0,1,2},知N ={0,2,4},M ∩N ={0,2}.答案:{0,2}6.设集合A ={a 2,a +1,-3},B ={a -3,2a -1,a 2+1},A ∩B ={-3},求实数a . 解:∵A ∩B ={-3},∴-3∈B . ∵a 2+1≠-3,∴①若a -3=-3,则a =0,此时A ={0,1,-3},B ={-3,-1,1}, 但由于A ∩B ={1,-3}与已知A ∩B ={-3}矛盾, ∴a ≠0.②若2a -1=-3,则a =-1,此时A ={1,0,-3},B ={-4,-3,2},A ∩B ={-3},综上可知a =-1.一、选择题1.已知集合A ={x |x ≥0},B ={x |-1≤x ≤2},则A ∪B =( ) A .{x |x ≥-1} B .{x |x ≤2} C .{x |0<x ≤2}D .{x |1≤x ≤2}解析:结合数轴得A ∪B ={x |x ≥-1}.答案:A2.设集合M ={x |-3<x <2},N ={x |1≤x ≤3},则M ∩N =( ) A .{x |1≤x <2}B .{x |1≤x ≤2}C .{x |2<x ≤3}D .{x |2≤x ≤3}解析:∵M ={x |-3<x <2}且N ={x |1≤x ≤3},∴M ∩N ={x |1≤x <2}. 答案:A3.设A ={x |-3≤x ≤3},B ={y |y =-x 2+t }.若A ∩B =∅,则实数t 的取值范围是( ) A .t <-3 B .t ≤-3 C .t >3D .t ≥3解析:B ={y |y ≤t },结合数轴可知t <-3.答案:A4.已知集合A ={x |-2≤x ≤7},B ={x |m +1<x <2m -1},且B ≠∅,若A ∪B =A ,则( ) A .-3≤m ≤4 B .-3<m <4 C .2<m <4D .2<m ≤4解析:∵A ∪B =A ,∴B ⊆A .又B ≠∅,∴⎩⎨⎧m +1≥-2,2m -1≤7m +1<2m -1即2<m ≤4.答案:D 二、填空题5.已知集合A ={1,2,4},B ={2,4,6},则A ∪B =________. 解析:集合A ,B 都是以列举法的形式给出,易得A ∪B ={1,2,4,6}. 答案:{1,2,4,6}6.已知集合A ={x |x ≥5},集合B ={x |x ≤m },且A ∩B ={x |5≤x ≤6},则实数m =________.解析:用数轴表示集合A 、B 如图所示,由于A ∩B ={x |5≤x ≤6}, 则m =6. 答案:67.已知集合A ={x |x ≤1},B ={x |x ≥a },且A ∪B =R ,则实数a 的取值范围是________.解析:如图所示,若A ∪B =R ,则a ≤1.答案:a ≤18.已知集合A ={(x ,y )|y =ax +3},B ={(x ,y )|y =3x +b },A ∩B ={(2,5)},则a =________,b =________.解析:∵A ∩B ={(2,5)}. ∴5=2a +3.∴a =1. ∴5=6+b .∴b =-1. 答案:1 -1 三、解答题9.已知集合A ={x |-1≤x <3},B ={x |2x -4≥x -2}. (1)求A ∩B ;(2)若集合C ={x |2x +a >0},满足B ∪C =C ,求实数a 的取值范围. 解:(1)∵B ={x |x ≥2},A ={x |-1≤x <3}, ∴A ∩B ={x |2≤x <3}.(2)∵C ={x |x >-a2},B ∪C =C ⇔B ⊆C ,∴a >-4.10.已知集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎩⎪⎨⎪⎧ 3-x >0,3x +6>0,集合B ={m |3>2m -1},求A ∩B ,A ∪B . 解:解不等式组⎩⎪⎨⎪⎧3-x >0,3x +6>0,得-2<x <3,则A ={x |-2<x <3},解不等式3>2m -1,得m <2,则B ={m |m <2}. 用数轴表示集合A 和B ,如图所示,则A ∩B ={x |-2<x <2},A ∪B ={x |x <3}.。
高中数学:1.1.3《集合的基本运算》全集与补集 教学案(新人教A版必修1)

1.1.3集合的基本运算(全集、补集)【教学目标】1、了解全集的意义,理解补集的概念.2、能用韦恩图表达集合的关系及运算,体会直观图示对理解抽象概念的作用3、进一步体会数学语言的简洁性与明确性,发展运用数学语言交流问题的能力。
【教学重难点】教学重点:会求给定子集的补集。
教学难点:会求给定子集的补集。
【教学过程】(一)复习集合的概念、子集的概念、集合相等的概念;两集合的交集,并集.(二)教学过程一、情景导入观察下面两个图的阴影部分,它们同集合A 、集合B 有什么关系?二、检查预习1、在给定的问题中,若研究的所有集合都是某一给定集合的子集,那么称这个给定的集合为 .2、若A 是全集U 的子集,由U 中不属于A 的元素构成的集合,叫做 ,记作 。
三、合作交流Φ=⋂A C A U ,U A C A U =⋃,A A C C U U =)(B C A C B A C U U U ⋂=⋃)(,B C A C B A C U U U ⋃=⋂)(注:是否给出证明应根据学生的基础而定.四、精讲精练例⒈设U={2,4,3-a 2},P={2,a 2+2-a },CU P={-1},求a . 解:∵-1∈CU P∴-1∈U∴3-a 2=-1得a =±2.当a =2时,P={2,4}满足题意.当a =-2时,P={2,8},8∉U舍去.因此a =2.[点评]由集合、补集、全集三者关系进行分析,特别注意集合元素的互异性,所以解题时不要忘记检验,防止产生增解。
变式训练一:已知A={0,2,4,6},CS A={-1,-3,1,3},CS B={-1,0,2},用列举法写出集合B.解:∵A={0,2,4,6},CS A={-1,-3,1,3}∴S={-3,-1,0,1,2,3,4,6}又CS B={-1,0,2} ∴B={-3,1,3,4,6}.例⒉设全集U=R,A={x|3m-1<x<2m},B={x|-1<x<3},B⊂≠CU A,求m的取值范围.解:由条件知,若A=Φ,则3m-1≥2m即m≥1,适合题意;若A≠Φ,即m<1时,CU A={x|x≥2m或x≤3m-1},则应有-1≥2m即m≤-21; 或3m-1≥3即m≥43与m<1矛盾,舍去. 综上可知:m的取值范围是m≥1或m≤-21. 变式训练二:设全集U={1,2,3,4},且A={x|x2-mx+n=0,x∈U},若CU A={2,3},求m,n的值.解:∵U={1,2,3,4},CU A={2,3}∴A={1,4}.∴1,4是方程x2-mx+n=0的两根.∴m=1+4=5,n=1×4=4.【板书设计】一、 基础知识1. 全集与补集2. 全集与补集的性质二、 典型例题例1: 例2:小结:【作业布置】本节课学案预习下一节。
高中数学人教A版必修1《1.1.3集合的基本运算》教案5

必修一集合的基本运算教案教学内容:人教版普通高中课程标准实验教科书数学必修一第一章 1.1.3,教材9~12页。
教学目标:1、让学生清楚把握并集、交集、补集的概念。
2、让学生把握如何求出并集、交集、补集。
3、让学生能清楚区分并集、交集、补集,并把握它们之间的关系。
4、培养学生的类比迁移的数学方法,提高学生学习的兴趣。
教学重点:让学生把握如何求出并集、交集、补集。
教学难点:能用图示法表示出集合的关系,能从图示中看出集合的关系。
教学用具:多媒体教学过程:一、导入:同学们,我们之前学习过了数的运算,那么我们的集合是否也具备一些运算呢?好,那我们今天就来研究一下集合的基本运算。
二、新授:1、并集我们知道,实数有加法运算,类比实数的加法运算,集合是否也可以“相加”呢?考察下面的集合,你能说出集合C与集合A、B之前的关系吗?(1)A=﹛x|x是有理数﹜B=﹛x|x是无理数﹜C=﹛x|x是实数﹜(2)A=﹛1、3、5﹜B=﹛2、4、6﹜C=﹛1、2、3、4、5、6﹜让学生根据这个问题各抒己见,教师根据学生的回答,适时引入并集的概念。
同学们,刚才你们发现A和B相加就是C,我们还可以得到这样一种关系:集合C是有所有属于集合A或属于集合B的元素组成,那么像这样由所有属于集合A或集合B的元素组成的集合,我们称为A与B的并集,记做:A∪B,读作:A并B即A∪B=﹛x|x∈A或x∈B﹜韦恩图表示为那么像刚才我们引入的题目我们就可以有C=A∪B又C=A∪B同学们能不能得出它们的另一个关系呢?A⊆C、B⊆C教师讲解例4、例5例4教师向学生提问A∪B=﹛4、5、6、8、3、5、7、8﹜对不对?为什么不对?(让学生对前面学习集合元素的互异性进行巩固,让学生明白并集并不是两个集合的简单相加)例5让学生清楚用数轴表示出集合,并能从数轴上看出集合的并集A∪A=A A∪空集=A ?2、交集考察下面问题,集合A、B与集合C之间有什么关系?(1)A=﹛2、4、6、8、10﹜ B=﹛3、5、8、12﹜C=﹛8﹜(2)A=﹛x|x是新华中学2004年9月在校的女同学﹜B=﹛x|x是新华中学2004年9月在校的高一年级同学﹜C=﹛x|x是新华中学2004年9月在校的高一年级女同学﹜让学生根据这个问题各抒己见,教师根据学生的回答,适时引入交集的概念。
人教A版《必修1》“1.1.3集合的基本运算(一):交集、并集“导学案

高一数学?必修1? 1.1.3集合的根本运算〔一〕---------- 并集与交集【学习目标】1.理解两个集合并集与交集的含义;2、会求两个集合的并集与交集;3、能用韦恩图(Venn)表达集合的关系与运算。
【课前导学】先阅读课本P8—9内容,然后开始做学案;(注意:集合的交集、并集结果还是集合.)1、一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的,记作(读作)符号语言:AjB={x∣xw礴x∈8}图形语言:(请用阴影表示A B)(读作).符号语言:Ai8={xk∈4,且x∈B}图形语言:(请你仿照上题画出韦恩图,并用阴影表示4'B)【预习自测】1、设A={锐角三角形},B={钝角三角形},那么ADB=。
2、A={x∣x>3},8={x∣xv6},那么AkJB=:AC3=。
3、A={5,6},4=0,那么ADB= ___________________ ;ACB= __________ ;An0= ____________ ;Au0=__________ 。
4、设集合A={x∈Z卜2≤x≤2},8={x∈Z∣0<xv3},求AkJaAC8。
5、试根据Venn图分析后,用适当的符号填空(1)A<J A=,AuO=,A<J BB<J A,AuB=A=>;(2)ACA=,Λn0=,AnB Br∖A,AcB=An;(3)假设AUB,那么AuB=,AcB=;【课中导学】首先独立思考探究,然后合作交流展示探究一:设集合A={R-2≤x≤2},B={x卜3v2x—3v3},求AkJB,AcB0探究二:设A={x∣χ2—4x—5=0},8={1产=1},求AUaACBo变式:设A={0,y)∣4R+y=6},3={(x,y)∣3x+2y=7},求AC探究三:平面内直线上上的点的集合为1.,直线入上的点的集合为1.2,用集合表示▲和A的位置关系。
【总结提升】学完本节课,你在知识、方法等方面有什么收获与感受?请写下来【课后作业】(注:①解答题的解答过程请写在作业本;②笫7题普通班选做,1、4、12班必做)1.设A={1,2,4},B={2,6},那么AUB= _____________________ ,A∩B= ______________2.设人=,一9<%<1},8={乂-3<%<2},。
高中数学 第一章 1.1.3 集合的基本运算导学案(2) 新人教版必修1

§1.1.3 集合的基本运算(2) 学习目标 2. 能使用Venn 图表达集合的运算,体会直观图示对理解抽象概念的作用. 学习过程一、课前准备1011复习1:集合相关概念及运算.① 如果集合A 的任意一个元素都是集合B 的元素,则称集合A 是集合B 的 ,记作 .若集合A B ⊆,存在元素x B x A ∈∉且,则称集合A 是集合B 的 ,记作 . 若A B B A ⊆⊆且,则 .② 两个集合的 部分、 部分,分别是它们交集、并集,用符号语言表示为:A B =I ;A B =U .复习2:已知A ={x |x +3>0},B ={x |x ≤-3},则A 、B 、R 有何关系?二、新课导学※ 学习探究探究:设U ={全班同学}、A ={全班参加足球队的同学}、B ={全班没有参加足球队的同学},则U 、A 、B 有何关系?新知:全集、补集.① 全集:如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集(Universe ),通常记作U .② 补集:已知集合U , 集合A ⊆U ,由U 中所有不属于A 的元素组成的集合,叫作A 相对于U 的补集(complementary set ),记作:U C A ,读作:“A 在U 中补集”,即{|,}U C A x x U x A =∈∉且.补集的Venn 图表示如右:说明:全集是相对于所研究问题而言的一个相对概念,补集的概念必须要有全集的限制. 试试:(1)U ={2,3,4},A ={4,3},B =∅,则U C A = ,U C B = ;(2)设U ={x |x <8,且x ∈N },A ={x |(x -2)(x -4)(x -5)=0},则U C A = ;(3)设集合{|38}A x x =≤<,则R A ð= ;(4)设U ={三角形},A ={锐角三角形},则U C A = .反思:(1)在解不等式时,一般把什么作为全集?在研究图形集合时,一般把什么作为全集?(2)Q 的补集如何表示?意为什么?※ 典型例题例1 设U ={x |x <13,且x ∈N }, A ={8的正约数},B ={12的正约数},求U C A 、U C B .例2 设U =R ,A ={x |-1<x <2},B ={x |1<x <3},求A ∩B 、A ∪B 、U C A 、U C B .变式:分别求()U C A B U 、()()U U C A C B I .※ 动手试试练 1. 已知全集I ={小于10的正整数},其子集A 、B 满足()(){1,9}I I C A C B =I ,(){4,6,8}I C A B =I ,{2}A B =I . 求集合A 、B .练2. 分别用集合A 、B 、C 表示下图的阴影部分.(1) ; (2) ;(3) ; (4) .反思:结合Venn 图分析,如何得到性质:(1)()U A C A =I ,()U A C A =U ; (2)()U U C C A = .三、总结提升※ 学习小结1. 补集、全集的概念;补集、全集的符号.2. 集合运算的两种方法:数轴、Venn 图.※ 知识拓展试结合Venn 图分析,探索如下等式是否成立?(1)()()()U U U C A B C A C B =U I ;(2)()()()U U U C A B C A C B =I U .学习评价).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. 设全集U =R ,集合2{|1}A x x =≠,则U C A =( )A. 1B. -1,1C. {1}D. {1,1}-2. 已知集合U ={|0}x x >,{|02}U C A x x =<<,那么集合A =( ).A. {|02}x x x ≤≥或B. {|02}x x x <>或C. {|2}x x ≥D. {|2}x x >3. 设全集{}0,1,2,3,4I =----,集合{}0,1,2M =--, {}0,3,4N =--,则()I M N =I ð( ).A .{0}B .{}3,4--C .{}1,2--D .∅4. 已知U ={x ∈N |x ≤10},A ={小于11的质数},则U C A = .5. 定义A —B ={x |x ∈A ,且x ∉B },若M ={1,2,3,4,5},N ={2,4,8},则N —M = .1. 已知全集I =2{2,3,23}a a +-,若{,2}A b =,{5}I C A =,求实数,a b .2. 已知全集U =R ,集合A ={}220x x px ++=,{}250,B x x x q =-+= 若{}()2U C A B =I ,试用列举法表示集合A。
精品推荐高中数学 1.1.3 集合的基本运算导学案 新人教A版必修1

1.1.3 集合的基本运算班级:__________姓名:__________设计人__________日期__________课前预习· 预习案【温馨寄语】昨天,已经是历史;明天,还是个未知数;把昨天和明天连接在一起的是今天。
愿你紧紧地把今天攥在手心里!【学习目标】1.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.2.能使用Venn图表示集合的并集和交集,体会直观图对理解抽象概念的作用.3.掌握有关的术语和符号,并会用它们正确进行集合的并集与交集运算.4.了解全集的含义及符号表示.5.理解在给定集合中一个子集的补集的含义,会求一个给定集合在全集中的补集.6.能正确运用补集的符号和表示形式,会用Venn图表示一个集合及其子集的补集.【学习重点】1.求两个简单集合的并集2.求两个简单集合的交集3.补集的含义,会求给定子集的补集4.集合的交、并、补的概念及运算【学习难点】1.并集的含义2.交集概念中“且”字的含义的理解3.补集的运算【自主学习】1.并集与交集的性质=_________________ =_________________2.交集的概念(1)自然语言:由属于集合______________属于集合的所有元素组成的集合,记作(读作_____________).(2)符号语言:=___________________.(3)图形语言:3.并集的概念(1)自然语言:由所有属于集合______________属于集合的元素组成的集合,记作(读作___________).(2)符号语言:=______________.(3)图形语言:4.补集对于一个集合,由全集中合称为集合相对于全集的补集,记作=__________5.全集(1)元素的组成:含有我们所研究问题中涉及的________.(2)符号表示:通常记作_______________.【预习评价】1.全集,,则=A. B.C. D.2.全集,集合,则=A. B.C. D.3.已知全集,,,则=_____________.4.设集合,,且,则实数=_____________.5.集合,,则=_______,=_______.6.设集合.,则_________.高效课堂· 探究案【合作探究】1.交集的概念根据集合考虑:若集合与集合没有公共元素,则集合与集合有没有交集?2.并集的概念观察集合,,,探究下面的问题:(1)集合,中的元素与集合的关系是什么?(2)集合与集合,集合与集合的关系是什么?(3)集合与集合有什么关系?3.全集、补集的概念及性质观察集合,,,探究下列问题:(1)集合与集合,集合与集合,集合与集合之间分别有何关系?(2)如何用图示法表示集合,,的关系?(3)若把看作全集,则=___________________.4.全集、补集的概念及性质根据方程在不同范围内的解集,探究下面的问题:(1)该方程在有理数集内的解集为_______________;在实数集内的解集为_______________.(2)有理数集、实数集相对于方程的解集来说称为什么?【教师点拨】1.对交集概念的两点说明(1)对于,不能仅认为中的任一元素都是与的公共元素,同时还有与的公共元素都属于的含义.(2)并不是任何两个集合总有公共元素,当两个集合没有公共元素时.2.对并集概念的两点说明(1)并集概念中的“或”字与生活中的“或”字含义不同,生活中的“或”字是非此即彼,必居其一,而并集中的“或”字可以兼有,它是由所有至少属于,两者之一的元素组成的.(2)中含有和的所有元素.3.对全集、补集的三点说明(1)补集是相对于全集而存在的,研究一个集合的补集之前一定要明确对应的全集.(2)补集既是集合之间的一种关系,同时也是集合之间的一种运算.(3)若,则和二者必居其一.【交流展示】1.集合,,则=A.B.C.D.2.若集合,,则集合=A. B.C. D.3.集合,,则下列关系正确的是A. B. C. D.4.设集合,若,则合集=A. B. C. D.5.已知集合,且,求实数的取值范围.6.已知集合,,(1)若,求实数的取值范围.(2)若,求实数的取值范围.【学习小结】1.利用集合交集、并集的性质解题的方法及关注点(1)方法:当题目中含有条件,.解答时常借助于交集、并集的定义及集合间的关系去分析,将关系进行等价转化如:,等.(2)关注点:当题目条件中出现时,若集合不确定,解答时要注意讨论的情况.2.求集合交集的方法3.求集合并集的两种情况和方法提醒:求集合的并集时,要注意集合元素的互异性的检验4.求解交、并、补集综合运算的三种方法(1)定义法:若所给集合是有限集,则先把集合中的元素一一列举出来,然后结合补集的定义来求解.(2)Venn图法:当集合中的元素能一一列举出来是时,也可借助于Venn图求解,这样处理起来,直观、形象且解答时不易出错.(3)数轴法:若所给集合有无限集,如不等式的解集,则常借助于数轴,把已知集合及全集分别表示在数轴上,然后在根据补集的定义求解.提醒:利用数轴求解集合补集运算时,要注意集合端点的虚实.5.求解补集的两个步骤和注意事项(1)两个步骤:①明确全集:根据题中所研究的对象,确定全集.②借助数轴和补集的定义:利用,求集合的补集.(2)注意事项:①实点变虚点、虚点变实点.②通过改变原不等式的不等号方向取补集时,要防止漏解.【当堂检测】1.已知集合,,则=A. B.C. D.2.已知集合且,则实数的取值范围是A. B. C. D.3.满足条件的集合的个数是______________.4.已知集合,,,则实数的取值范围是___________. 5.已知,,,若. (l)求的值.(2)若,求的值.6.已知全集,集合,,求.1.1.3 集合的基本运算详细答案课前预习· 预习案【自主学习】1.A A2.(1)且“A交B”(2){x|x∈A,且x∈B}3.(1)或“A并B”(2){x|x∈A,或x∈B}4.不属于集合A{x|x∈U,且x∉A}5.(1)所有元素(2)U【预习评价】1.B2.B3.24.-15.{0} {0,1,2,3,4}6.{x|x>-2}高效课堂· 探究案【合作探究】1.有.若集合A与集合B没有公共元素,则A∩B为空集.2.(1)通过观察可发现集合A中的所有元素都属于集合C;集合B中的所有元素都属于集合C.(2)因为集合A中的元素都是集合C中的元素,所以;同理.(3)因为集合C中的元素是由集合A或集合B中的元素组成,所以C=A∪B.3.(1)A中的所有元素都是U中的元素,所以,同理,集合A是集合U中除去集合B中元素之后剩余的元素组成的集合.(2)用图示法表示.如图所示:(3)由(2)图可知,ðU A=B.答案 B4.(1){3}(2)有理数集、实数集是所研究问题的所有元素组成的集合,即全集.【交流展示】1.C2.C3.A4.D5.6.(1)-6≤m≤-2(2)m≤-11或m≥3【当堂检测】1.A2.C3.4小初高K12学习教材4.m≥55.(1)(2)0或.6.因为全集U=R,A={x|x>1},B={x|0≤x≤2},所以ðU A={x|x≤1},ðU B={x|x<0或x>2}. 小初高K12学习教材。
高中数学 (1.3 集合的基本运算第1课时)示范教案 新人教A版必修1

1.1.3 集合的基本运算整体设计教学分析课本从学生熟悉的集合出发,结合实例,通过类比实数加法运算引入集合间的运算,同时,结合相关内容介绍子集和全集等概念.在安排这部分内容时,课本继续注重体现逻辑思考的方法,如类比等.值得注意的问题:在全集和补集的教学中,应注意利用图形的直观作用,帮助学生理解补集的概念,并能够用直观图进行求补集的运算.三维目标1.理解两个集合的并集与交集、全集的含义,掌握求两个简单集合的交集与并集的方法,会求给定子集的补集,感受集合作为一种语言,在表示数学内容时的简洁和准确,进一步提高类比的能力.2.通过观察和类比,借助Venn图理解集合的基本运算.体会直观图示对理解抽象概念的作用,培养数形结合的思想.重点难点教学重点:交集与并集,全集与补集的概念.教学难点:理解交集与并集的概念,以及符号之间的区别与联系.课时安排2课时教学过程第1课时导入新课思路1.我们知道,实数有加法运算,两个实数可以相加,例如5+3=8.类比实数的加法运算,集合是否也可以“相加”呢?教师直接点出课题.思路2.请同学们考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?(1)A={1,3,5},B={2,4,6},C={1,2,3,4,5,6};(2)A={x|x是有理数},B={x|x是无理数},C={x|x是实数}.引导学生通过观察、类比、思考和交流,得出结论.教师强调集合也有运算,这就是我们本节课所要学习的内容.思路3.(1)①如图1131甲和乙所示,观察两个图的阴影部分,它们分别同集合A、集合B有什么关系?图1-1-3-1②观察集合A与B与集合C={1,2,3,4}之间的关系.学生思考交流并回答,教师直接指出这就是本节课学习的课题:集合的运算.(2)①已知集合A={1,2,3},B={2,3,4},写出由集合A,B中的所有元素组成的集合C.②已知集合A={x|x>1},B={x|x<0},在数轴上表示出集合A与B,并写出由集合A与B中的所有元素组成的集合C.推进新课新知探究提出问题①通过上述问题中集合A与B与集合C之间的关系,类比实数的加法运算,你发现了什么?②用文字语言来叙述上述问题中,集合A与B与集合C之间的关系.③用数学符号来叙述上述问题中,集合A与B与集合C之间的关系.④试用Venn图表示A∪B=C.⑤请给出集合的并集定义.⑥求集合的并集是集合间的一种运算,那么,集合间还有其他运算吗?请同学们考察下面的问题,集合A与B与集合C之间有什么关系?(ⅰ)A={2,4,6,8,10},B={3,5,8,12},C={8};(ⅱ)A={x|x是国兴中学2007年9月入学的高一年级女同学},B={x|x是国兴中学2007年9月入学的高一年级男同学},C={x|x是国兴中学2007年9月入学的高一年级同学}.⑦类比集合的并集,请给出集合的交集定义?并分别用三种不同的语言形式来表达.活动:先让学生思考或讨论问题,然后再回答,经教师提示、点拨,并对回答正确的学生及时表扬,对回答不准确的学生提示引导考虑问题的思路,主要引导学生发现集合的并集和交集运算并能用数学符号来刻画,用Venn图来显示.讨论结果:①集合之间也可以相加,也可以进行运算,但是为了不和实数的运算相混淆,规定这种运算不叫集合的加法,而是叫做求集合的并集.集合C叫集合A与B的并集.记为A∪B=C,读作A并B.②所有属于集合A或属于集合B的元素所组成了集合C.③C={x|x∈A,或x∈B}.④如图1131所示.⑤一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集.其含义用符号表示为A∪B={x|x∈A,或x∈B},用Venn图表示,如图1131所示.⑥集合之间还可以求它们的公共元素组成集合的运算,这种运算叫求集合的交集,记作A∩B,读作A交B.(ⅰ)A∩B=C,(ⅱ)A∪B=C.⑦一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集.其含义用符号表示为:A∩B={x|x∈A,且x∈B}.用Venn图表示,如图1132所示.图1-1-3-2应用示例思路11.设A={4,5,6,8},B={3,5,7,8},求A∪B,A∩B.图1-1-3-3活动:让学生回顾集合的表示法和交集、并集的含义,由于本例题难度较小,让学生自己解决,重点是总结集合运算的方法.根据集合并集、交集的含义,借助于Venn图写出.观察这两个集合中的元素,或用Venn图来表示,如图1133所示.解:A∪B={4,5,6,8}∪{3,5,7,8}={3,4,5,6,7,8}.A∩B={4,5,6,8}∩{3,5,7,8}={5,8}.点评:本题主要考查集合的并集和交集.用列举法表示的集合,运算时常利用Venn图或直接观察得到结果.本题易错解为A∪B={3,4,5,5,6,7,8,8}.其原因是忽视了集合元素的互异性.解决集合问题要遵守集合元素的三条性质.变式训练1.集合M={1,2,3},N={-1,5,6,7},则M∪N=________.M∩N=________.答案:{-1,1,2,3,5,6,7} ∅2.集合P={1,2,3,m},M={m2,3},P∪M={1,2,3,m},则m=_________.-,0.因m=1不合题意,故舍去.分析:由题意得m2=1或2或m,解得m=-1,1,2,2-,0答案:-1,2,23.2007河南实验中学月考,理1满足A∪B={0,2}的集合A与B的组数为 ( )A.2B.5C.7D.9分析:∵A∪B={0,2},∴A⊆{0,2}.则A=∅或A={0}或A={2}或A={0,2}.当A=∅时,B={0,2};当A={0}时,则集合B={2}或{0,2};当A={2}时,则集合B={0}或{0,2};当A={0,2}时,则集合B=∅或{0}或{2}或{0,2},则满足条件的集合A与B的组数为1+2+2+4=9.答案:D4.2006辽宁高考,理2设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是 ( )A.1B.3C.4D.8分析:转化为求集合A子集的个数.很明显3∉A,又A∪B={1,2,3},必有3∈B,即集合B中至少有一个元素3,其他元素来自集合A中,则集合B的个数等于A={1,2}的子集个数,又集合A 中含有22=4个元素,则集合A有22=4个子集,所以满足条件的集合B共有4个.答案:C2.设A={x|-1<x<2},B={x|1<x<3},求A∪B,A∩B.活动:学生回顾集合的表示法和并集、交集的含义.利用数轴,将A、B分别表示出来,则阴影部分即为所求.用数轴表示描述法表示的数集.解:将A={x|-1<x<2}及B={x|1<x<3}在数轴上表示出来.如图1134所示的阴影部分即为所求.图1-1-3-4由图得A∪B={x|-1<x<2}∪{x|1<x<3}={x|-1<x<3},A∩B={x|-1<x<2}∩{x|1<x<3}={x|1<x<2}.点评:本类题主要考查集合的并集和交集.用描述法表示的集合,运算时常利用数轴来计算结果.变式训练1.设A={x|2x-4<2},B={x|2x-4>0},求A∪B,A∩B.答案:A∪B=R,A∩B={x|2<x<3}.2.设A={x|2x-4=2},B={x|2x-4=0},求A∪B,A∩B.答案:A∪B={3,2},A∩B=∅.3.2007惠州高三第一次调研考试,文1设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于( )A.[0,2]B.[1,2]C.[0,4]D.[1,4]分析:在同一条数轴上表示出集合A、B,如图1135所示.由图得A∩B=[0,2].图1-1-3-5答案:A课本P11例6、例7.思路21.A={x|x<5},B={x|x>0},C={x|x≥10},则A∩B,B∪C,A∩B∩C分别是什么?活动:学生先思考集合中元素特征,明确集合中的元素.将集合中元素利用数形结合在数轴上找到,那么运算结果寻求就易进行.这三个集合都是用描述法表示的数集,求集合的并集和交集的关键是找出它们的公共元素和所有元素.解:因A={x|x<5},B={x|x>0},C={x|x≥10},在数轴上表示,如图1136所示,所以A∩B={x|0<x<5},B∪C={x|x>0},A∩B∩C=∅.图1-1-3-6点评:本题主要考查集合的交集和并集.求集合的并集和交集时,①明确集合中的元素;②依据并集和交集的含义,借助于直观(数轴或Venn图)写出结果.变式训练1.设A={x|x=2n,n∈N*},B={x|x=2n,n∈N},求A∩B,A∪B.解:对任意m∈A,则有m=2n=2·2n-1,n∈N*,因n∈N*,故n-1∈N,有2n-1∈N,那么m∈B,即对任意m∈A有m∈B,所以A⊆B.而10∈B但10∉A,即A B,那么A∩B=A,A∪B=B.2.求满足{1,2}∪B={1,2,3}的集合B的个数.解:满足{1,2}∪B={1,2,3}的集合B一定含有元素3,B={3};还可含1或2其中一个,有{1,3},{2,3};还可含1和2,即{1,2,3},那么共有4个满足条件的集合B.3.设A={-4,2,a-1,a2},B={9,a-5,1-a},已知A∩B={9},求a.解:因A∩B={9},则9∈A,a-1=9或a2=9,a=10或a=±3,当a=10时,a-5=5,1-a=-9;当a=3时,a-1=2不合题意.当a=-3时,a-1=-4不合题意.故a=10,此时A={-4,2,9,100},B={9,5,-9},满足A∩B={9}.4.2006北京高考,文1设集合A={x|2x+1<3},B={x|-3<x<2},则A∩B等于 ( )A.{x|-3<x<1}B.{x|1<x<2}C.{x|x>-3}D.{x|x<1}分析:集合A={x|2x+1<3}={x|x<1},观察或由数轴得A∩B={x|-3<x<1}.答案:A2.设集合A={x|x 2+4x=0},B={x|x 2+2(a+1)x+a 2-1=0,a∈R},若A∩B=B,求a 的值.活动:明确集合A 、B 中的元素,教师和学生共同探讨满足A∩B=B 的集合A 、B 的关系.集合A 是方程x 2+4x=0的解组成的集合,可以发现,B ⊆A,通过分类讨论集合B 是否为空集来求a 的值.利用集合的表示法来认识集合A 、B 均是方程的解集,通过画Venn 图发现集合A 、B 的关系,从数轴上分析求得a 的值.解:由题意得A={-4,0}.∵A∩B=B,∴B ⊆A.∴B=∅或B≠∅.当B=∅时,即关于x 的方程x 2+2(a+1)x+a 2-1=0无实数解,则Δ=4(a+1)2-4(a 2-1)<0,解得a<-1.当B≠∅时,若集合B 仅含有一个元素,则Δ=4(a+1)2-4(a 2-1)=0,解得a=-1,此时,B={x|x 2=0}={0}⊆A,即a=-1符合题意.若集合B 含有两个元素,则这两个元素是-4,0,即关于x 的方程x 2+2(a+1)x+a 2-1=0的解是-4,0.则有⎩⎨⎧=⨯+=+ 1.-a 04-1),-2(a 04-2解得a=1,则a=1符合题意.综上所得,a=1或a≤-1.变式训练1.已知非空集合A={x|2a+1≤x≤3a -5},B={x|3≤x≤22},则能使A ⊆(A∩B)成立的所有a 值的集合是什么?解:由题意知A ⊆(A∩B),即A ⊆B,A 非空,利用数轴得⎪⎩⎪⎨⎧≤-≥+-≤+.2253,312,5312a a a a 解得6≤a≤9,即所有a 值的集合是{a|6≤a≤9}.2.已知集合A={x|-2≤x≤5},集合B={x|m+1≤x≤2m -1},且A∪B=A,试求实数m 的取值范围. 分析:由A∪B=A 得B ⊆A,则有B=∅或B≠∅,因此对集合B 分类讨论.解:∵A∪B=A,∴B ⊆A.又∵A={x|-2≤x≤5}≠∅,∴B=∅,或B≠∅.当B=∅时,有m+1>2m-1,∴m<2.当B≠∅时,观察图1-1-3-7:图1-1-3-7由数轴可得⎪⎩⎪⎨⎧≤-+≤--≤+.512,12,121m m m m 解得-2≤m≤3.综上所述,实数m 的取值范围是m<2或-2≤m≤3,即m≤3.点评:本题主要考查集合的运算、分类讨论的思想,以及集合间关系的应用.已知两个集合的运算结果,求集合中参数的值时,由集合的运算结果确定它们的关系,通过深刻理解集合表示法的转换,把相关问题化归为其他常见的方程、不等式等数学问题.这称为数学的化归思想,是数学中的常用方法,学会应用化归和分类讨论的数学思想方法解决有关问题.知能训练课本P11练习1、2、3.【补充练习】1.设a={3,5,6,8},B={4,5,7,8},(1)求A∩B,A∪B.(2)用适当的符号(⊇、⊆)填空:A∩B________A,B________A∩B,A∪B________A,A∪B________B,A∩B________A∪B.解:(1)因A、B的公共元素为5、8,故两集合的公共部分为5、8,则A∩B={3,5,6,8}∩{4,5,7,8}={5,8}.又A、B两集合的元素3、4、5、6、7、8,故A∪B={3,4,5,6,7,8}.(2)由文氏图可知A∩B⊆A,B⊇A∩B,A∪B⊇A,A∪B⊇B,A∩B⊆A∪B.2.设A={x|x<5},B={x|x≥0},求A∩B.解:因x<5及x≥0的公共部分为0≤x<5,故A∩B={x|x<5}∩{x|x≥0}={x|0≤x<5}.3.设A={x|x是锐角三角形},B={x|x是钝角三角形},求A∩B.解:因三角形按角分类时,锐角三角形和钝角三角形彼此孤立.故A、B两集合没有公共部分. 所以A∩B={x|x是锐角三角形}∩{x|x是钝角三角形}=∅.4.设A={x|x>-2},B={x|x≥3},求A∪B.解:在数轴上将A、B分别表示出来,得A∪B={x|x>-2}.5.设A={x|x是平行四边形},B={x|x是矩形},求A∪B.解:因矩形是平行四边形,故由A及B的元素组成的集合为A∪B,A∪B={x|x是平行四边形}.6.已知M={1},N={1,2},设A={(x,y)|x∈M,y∈N},B={(x,y)|x∈N,y∈M},求A∩B,A∪B.分析:M、N中元素是数.A、B中元素是平面内点集,关键是找其元素.解:∵M={1},N={1,2},则A={(1,1),(1,2)},B={(1,1),(2,1)},故A∩B={(1,1)},A∪B={(1,1),(1,2),(2,1)}.7.2006江苏高考,7若A、B、C为三个集合,A∪B=B∩C,则一定有( )A.A⊆CB.C⊆AC.A≠CD.A=∅分析:思路一:∵(B∩C)⊆B,(B∩C)⊆C,A∪B=B∩C,∴A∪B⊆B,A∪B⊆C.∴A⊆B⊆C.∴A⊆C.思路二:取满足条件的A={1},B={1,2},C={1,2,3},排除B、D,令A={1,2},B={1,2},C={1,2},则此时也满足条件A∪B=B∩C,而此时A=C,排除C.答案:A拓展提升观察:(1)集合A={1,2},B={1,2,3,4}时,A∩B,A∪B这两个运算结果与集合A,B的关系;(2)当A=∅时,A∩B,A∪B这两个运算结果与集合A,B的关系;(3)当A=B={1,2}时,A∩B,A∪B这两个运算结果与集合A,B的关系.由(1)(2)(3)你发现了什么结论?活动:依据集合的交集和并集的含义写出运算结果,并观察与集合A,B的关系.用Venn图来发现运算结果与集合A,B的关系.(1)(2)(3)中的集合A,B均满足A⊆B,用Venn图表示,如图1138所示,就可以发现A∩B,A∪B与集合A,B的关系.图1-1-3-8解:A∩B=A⇔A⊆B⇔A∪B=B.可用类似方法,可以得到集合的运算性质,归纳如下:A∪B=B∪A,A⊆(A∪B),B⊆(A∪B);A∪A=A,A∪∅=A,A⊆B⇔A∪B=B;A∩B=B∩A;(A∩B)⊆A,(A∩B)⊆B;A∩A=A;A∩∅=∅;A⊆B⇔A∩B=A.课堂小结本节主要学习了:1.集合的交集和并集.2.通常借助于数轴或Venn图来求交集和并集.作业1.课外思考:对于集合的基本运算,你能得出哪些运算规律?2.请你举出现实生活中的一个实例,并说明其并集、交集和补集的现实含义.3.书面作业:课本P12习题1.1A组6、7、8.设计感想由于本节课内容比较容易接受,也是历年高考的必考内容之一,所以在教学设计上注重加强练习和拓展课本内容.设计中通过借助于数轴或Venn图写出集合运算的结果,这是突破本节教学难点的有效方法.。
高中数学 1.1.3集合的基本运算教案 新人教A版必修1

1.1.3 集合的基本运算学习目标:(1)理解交集与并集的概念;(2)掌握两个较简单集合的交集、并集的求法;(3)通过对交集、并集概念的讲解,培养学生观察、比较、分析、概括、等能力,使学生认识由具体到抽象的思维过程;(4)通过对集合符号语言的学习,培养学生符号表达能力,培养严谨的学习作风,养成良好的学习习惯。
教学重点:交集和并集的概念教学难点:交集和并集的概念、符号之间的区别与联系合作探究展示:一、问题衔接我们知道两个实数除了可以比较大小外,还可以进行加法运算,类比实数的加法运算,两个集合是否也可以“相加”呢?思考(P8思考题),引入并集概念。
二、新课教学1.并集一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union)记作:A∪B 读作:“A并B”即: A∪B={x|x∈A,或x∈B}Venn图表示:说明:B的所有元素组成的集合(重复元素只看成一个元素)。
例题(P8-9例4、例5)说明:连续的(用不等式表示的)实数集合可以用数轴上的一段封闭曲线来表示。
问题:在上图中我们除了研究集合A与B的并集外,它们的公共部分(即问号部分)还应是我们所关心的,我们称其为集合A与B的交集。
2.交集一般地,由属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集(intersection)。
记作:A∩B 读作:“A交B”即: A∩B={x|∈A,且x∈B}交集的Venn图表示说明:两个集合求交集,结果还是一个集合,是由集合A 与B 的公共元素组成的集合。
例题(P 9-10例6、例7)拓展:求下列各图中集合A 与B 的并集与交集当两个集合没有公共元素时,两个集合的交集是空集,集3. 探索研究A ∩B ⊆A ,A ∩B ⊆B ,A ∩A=A ,A ∩∅=∅,A ∩B=B ∩AA ⊆A ∪B ,B ⊆A ∪B ,A ∪A=A ,A ∪∅=A,A ∪B=B ∪A三、归纳小结(略)四、作业布置书面作业:P 12习题1.1,第6-8题拓展提高:题型一 已知集合的交集、并集求参数问题例1 已知集合{}{}22,1,3,3,21,1A a a B a a a =+-=--+,若{}3A B =-,求实数a 的值解:∵{}3A B =-,∴3B -∈,而213a +≠-,∴当{}{}33,0,0,1,3,3,1,1a a A B -=-==-=--,这样{}3,1A B =-与{}3A B =-矛盾;当213,1,a a -=-=-符合{}3AB =- ∴1a =-练习1已知集合{}{},9,1,5,,1a 2,42a a B a A --=--=若{},9=⋂B A 求a 的值 答案 a=-3例 2.已知{}{},51,32>-<=+≤≤=x x x B a x a x A 或若,φ=⋂B A 求a 的取值范围.解(1)若,,φφ=⋂=B A A 由此时332>∴+>a a a A(2)若221325312,,≤≤-⎪⎩⎪⎨⎧+≤≤+-≥∴=⋂≠a a a a a B A A 解得由φφ 综上所述,a 的取值范围是.3221⎭⎬⎫⎩⎨⎧>≤≤-a a a 或 练习2上题中若的取值范围求a R B A ,=⋃。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.3 集合的基本运算
班级:__________姓名:__________设计人__________日期__________
课前预习· 预习案
【温馨寄语】
昨天,已经是历史;明天,还是个未知数;把昨天和明天连接在一起的是今天。
愿你紧紧地把今天攥在手心里!
【学习目标】
1.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
2.能使用Venn图表示集合的并集和交集,体会直观图对理解抽象概念的作用. 3.掌握有关的术语和符号,并会用它们正确进行集合的并集与交集运算.
4.了解全集的含义及符号表示.
5.理解在给定集合中一个子集的补集的含义,会求一个给定集合在全集中的补集. 6.能正确运用补集的符号和表示形式,会用Venn图表示一个集合及其子集的补集. 【学习重点】
1.求两个简单集合的并集
2.求两个简单集合的交集
3.补集的含义,会求给定子集的补集
4.集合的交、并、补的概念及运算
【学习难点】
1.并集的含义
2.交集概念中“且”字的含义的理解
3.补集的运算
【自主学习】
1.并集与交集的性质
=_________________ =_________________
2.交集的概念
(1)自然语言:由属于集合______________属于集合的所有元素组成的集合,记作
(读作_____________).
(2)符号语言:=___________________.
(3)图形语言:
3.并集的概念
(1)自然语言:由所有属于集合______________属于集合的元素组成的集合,记作
(读作___________).
(2)符号语言:=______________.
(3)图形语言:
4.补集
,由全集
合称为集合相对于全集的补集,记作
=__________
5.全集
(1)元素的组成:含有我们所研究问题中涉及的________.
(2)符号表示:通常记作_______________.
【预习评价】
1.全集,,则= A. B.
C. D.
2.全集,集合,则=
A. B.
C. D.
3.已知全集,,
,则=_____________.
4.设集合,,且,则实数=_____________.
5.集合,,则=_______,
=_______.
6.设集合.,则_________.
高效课堂· 探究案
【合作探究】
1.交集的概念
根据集合考虑:若集合与集合没有公共元素,则集合与集合有没有交集?
2.并集的概念
观察集合,,,探究下面的问题:
(1)集合,中的元素与集合的关系是什么?
(2)集合与集合,集合与集合的关系是什么?
(3)集合与集合有什么关系?
3.全集、补集的概念及性质
观察集合,
,
,
探究下列问题:
(1)集合与集合,集合与集合,集合与集合之间分别有何关系?
(2)如何用图示法表示集合,,的关系?
(3)若把看作全集,则=___________________.
4.全集、补集的概念及性质
根据方程在不同范围内的解集,探究下面的问题:
(1)该方程在有理数集内的解集为_______________;在实数集内的解集为
_______________.
(2)有理数集、实数集相对于方程的解集来说称为什么?
【教师点拨】
1.对交集概念的两点说明
(1)对于,不能仅认为中的任一元素都是与的公共元素,同时还有与的公共元素都属于的含义.
(2)并不是任何两个集合总有公共元素,当两个集合没有公共元素时. 2.对并集概念的两点说明
(1)并集概念中的“或”字与生活中的“或”字含义不同,生活中的“或”字是非此即彼,必居其一,而并集中的“或”字可以兼有,它是由所有至少属于,两者之一的元素组成的.
(2)中含有和的所有元素.
3.对全集、补集的三点说明
(1)补集是相对于全集而存在的,研究一个集合的补集之前一定要明确对应的全集.
(2)补集既是集合之间的一种关系,同时也是集合之间的一种运算.
(3)若,则和二者必居其一.
【交流展示】
1.集合,,则=
A.
B.
C.
D.
2.若集合,,则集合=
A. B.
C. D.
3.集合,,则下列关系正确的是
A. B. C. D.
4.设集合,若
,则合集=
A. B. C. D.
5.已知集合,且,求实数的取值范围.
6.已知集合,,
(1)若,求实数的取值范围.
(2)若,求实数的取值范围.
【学习小结】
1.利用集合交集、并集的性质解题的方法及关注点
(1)方法:当题目中含有条件,.解答时常借助于交集、并集的定义及集合间的关系去分析,将关系进行等价转化如:,
等.
(2)关注点:当题目条件中出现时,若集合不确定,解答时要注意讨论
的情况.
2.求集合交集的方法
3.求集合并集的两种情况和方法
提醒:求集合的并集时,要注意集合元素的互异性的检验
4.求解交、并、补集综合运算的三种方法
(1)定义法:若所给集合是有限集,则先把集合中的元素一一列举出来,然后结合补集的定义来求解.
(2)Venn图法:当集合中的元素能一一列举出来是时,也可借助于Venn图求解,这样处理起来,直观、形象且解答时不易出错.
(3)数轴法:若所给集合有无限集,如不等式的解集,则常借助于数轴,把已知集合及全集分别表示在数轴上,然后在根据补集的定义求解.
提醒:利用数轴求解集合补集运算时,要注意集合端点的虚实.
5.求解补集的两个步骤和注意事项
(1)两个步骤:
①明确全集:根据题中所研究的对象,确定全集.
②借助数轴和补集的定义:利用,求集合的补集.
(2)注意事项:
①实点变虚点、虚点变实点.
②通过改变原不等式的不等号方向取补集时,要防止漏解.
【当堂检测】
1.已知集合,,则=
A. B.
C. D.
2.已知集合且,则实数的取值范围是A. B. C. D.
3.满足条件的集合的个数是______________.
4.已知集合,,,则实数的取值范围是
___________.
5.已知,,,若
.
(l)求的值.
(2)若,求的值.
6.已知全集,集合,,求.
答案
课前预习· 预习案
【自主学习】
1.A A
2.(1)且“A交B”
(2){x|x∈A,且x∈B}
3.(1)或“A并B”
(2){x|x∈A,或x∈B}
4.不属于集合A{x|x∈U,且x∉A}
5.(1)所有元素(2)U
【预习评价】
1.B
2.B
3.2
4.-1
5.{0} {0,1,2,3,4}
6.{x|x>-2}
高效课堂· 探究案
【合作探究】
1.有.若集合A与集合B没有公共元素,则A∩B为空集.
2.(1)通过观察可发现集合A中的所有元素都属于集合C;集合B中的所有元素都属于集合C.
(2)因为集合A中的元素都是集合C中的元素,所以;同理.
(3)因为集合C中的元素是由集合A或集合B中的元素组成,所以C=A∪B.
3.(1)A中的所有元素都是U中的元素,所以,同理,集合A是集合U中除去集合B中元素之后剩余的元素组成的集合.
(2)用图示法表示.如图所示:
(3)由(2)图可知,ðU A=B.
答案 B
4.(1){3}
(2)有理数集、实数集是所研究问题的所有元素组成的集合,即全集.
【交流展示】
1.C
2.C
3.A
4.D
5.
6.(1)-6≤m≤-2
(2)m≤-11或m≥3
【当堂检测】
1.A
2.C
3.4
4.m≥5
5.(1)(2)0或.
6.因为全集U=R,A={x|x>1},B={x|0≤x≤2},所以ðU A={x|x≤1},ðU B={x|x<0或x>2}.。
