【IT专家】实现全排列的两种算法：字典序列法以及递归算法(java)

合集下载

java 全组合算法思路

java 全组合算法思路
在Java中，实现全组合算法的思路有很多种，下面列举两种常见的思路：
解法一：递归实现全排列算法。

输入一串字符，然后对字符进行全排列，如“abc”，全排列结果为:"abc","acb","bac","bca","cab","cba"。

具体步骤如下：
1. 从字符串中选择一个作为第一个字符，然后对剩下的字符串进行全排列，如此递归下去，直到打印出全部排列。

2. 如:"abc":
- 选a作为第一个字符:”abc“，”acb“；
- 选b作为第一个字符:”bac“，”bca“；
- 选c作为第一个字符:”cab“，”cba“。

解法二：从大到小排序算法。

将字符串从小到大倒排序，以此得到整体的最小顺序，然后找到次小顺序，直到得到最大顺序，也就是从大到小的顺序。

找下一个顺序的算法如下：
1. 假设到了”21543“，从后往前找到i-1位置小于i位置的下标，1<5，所以要找的下标pos=1。

2. 将下标为1的数字1，和它后面最小的且大于它的数替换，”21543”---> "23541"。

3. 然后再将下标1后面的字符串翻转得到:"23145"，这就得到了“21543”下一个顺序值“23145”。

需要注意的是，全组合算法的时间复杂度至少为$n!$级别，因此在处理大规模数据时可能会比较耗时。

在实际应用中，你需要根据具体需求选择合适的算法和实现方式。

java全排列递归算法

java全排列递归算法全排列是指将一组元素按照一定的顺序进行排列，使得每个元素都能够出现在每个位置上，且每个元素只能出现一次。

在Java中，可以使用递归算法来实现全排列。

递归算法是一种通过调用自身来解决问题的方法。

在全排列问题中，可以通过递归的方式来生成所有可能的排列。

首先，我们需要定义一个递归函数，该函数接受一个数组和两个整数作为参数。

其中，数组表示待排列的元素，第一个整数表示当前排列的起始位置，第二个整数表示当前排列的结束位置。

在递归函数中，我们首先判断当前排列是否已经完成。

如果起始位置等于结束位置，说明已经完成了一次排列，我们可以将当前排列输出。

否则，我们需要对当前排列进行递归调用。

在递归调用中，我们需要将当前排列的起始位置与结束位置进行交换，然后对剩余的元素进行递归调用。

递归调用完成后，我们需要将当前排列的起始位置与结束位置进行交换，以便进行下一次排列。

下面是一个使用递归算法实现全排列的Java代码示例：```javapublic class Permutation {public static void permute(int[] nums, int start, int end) {if (start == end) {for (int num : nums) {System.out.print(num + " ");}System.out.println();} else {for (int i = start; i <= end; i++) {swap(nums, start, i);permute(nums, start + 1, end);swap(nums, start, i);}}}public static void swap(int[] nums, int i, int j) { int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}public static void main(String[] args) {int[] nums = {1, 2, 3};permute(nums, 0, nums.length - 1);}}```在上述代码中，我们定义了一个`permute`函数来实现全排列。

解决不重复序列的全排列问题的两个方法：递归和字典序法

解决不重复序列的全排列问题的两个方法：递归和字典序法简介
给定{1, 2, 3, , , n}，其全排列为n! 个，这是最基础的高中组合数学知识。

我们以n=4 为例，其全部排列如下图（以字典序树形式来呈现）：
我们很容易想到用递归来求出它的所有全排列。

仔细观察上图，
以1 开头，下面跟着{2, 3, 4} 的全排列；
以2 开头，下面跟着{1, 3, 4} 的全排列；
以3 开头，下面跟着{1, 2, 4} 的全排列；
以4 开头，下面跟着{1, 2, 3} 的全排列。

代码如下：
/**
*
* author : 刘毅（Limer）
* date : 2017-05-31
* mode : C++++
*/
#include
#include
using namespacestd;
voidFullPermutation(intarray[],intleft,intright)
{
if(left == right)
{
for(inti = 0;i
咦~ 递归写出的全排列有点不完美，它并不严格遵循字典序。

但是熟悉C++ 的朋友肯定知道另一种更简单，更完美的全排列方法。

全排列字典序全排列

全排列字典序全排列全排列递归的⽅法参考 leetcode 47字典序算法：升序实现：判断了是否相等计算全排列的数量⽅法为 n!/ (m!*p!*...) m，p为重复的数字的重复量#include<iostream>#include<algorithm>#include<vector>using namespace std;vector<int>nums;void Permutation(int len,vector<int>nums){int j, k;int flag=1; //start 0swhile (true){for(int i=0;i<len;i++){if(nums[i]==0&&flag)continue;else{flag=0;printf("%d",nums[i]);}}printf("");flag=1;for (j = len - 2; j >= 0 && nums[j] >= nums[j + 1]; j--);//注意此处 j >= 0 判断条件在前,加个等号即可if (j < 0) return;//结束for (k = len - 1; k > j&&nums[k] <= nums[j]; k--);//加个等号即可swap(nums[k], nums[j]);for (int l = j + 1, r = len - 1; l < r; l++, r--)swap(nums[l], nums[r]);}}int calc(int len){int summ=1;for(int i=1;i<=len;i++)summ*=i;return summ;}int main(){int n;while(cin>>n)nums.push_back(n);sort(nums.begin(),nums.end());int len=nums.size();//all 0int flag=0;for(int i=0;i<len;i++)if(nums[i]!=0){flag==1;break;}if(flag){cout<<"1 0"<<endl;return0;}vector<int>dup;int cnt=1;int bef=nums[0];for(int i=1;i<len;i++)if(bef==nums[i]){cnt++;continue;}else{dup.push_back(cnt);cnt=1;bef=nums[i];}//dup.push_back(cnt);vector<int>::iterator iter=dup.begin();int divide=1;for(iter;iter!=dup.end();iter++)divide*=calc(*iter);int summ=calc(len)/divide;printf("%d ",summ);Permutation(len,nums);system("pause");return0;}。

全排列递归算法_概述及举例说明

全排列递归算法概述及举例说明1. 引言1.1 概述在计算机科学中，全排列递归算法是一种常见且重要的算法。

它能够通过递归的方式生成给定元素集合的所有可能排列组合。

全排列递归算法的实现原理相对简单，但其应用领域十分广泛，并在许多其他算法中扮演着关键角色。

1.2 文章结构本文将首先介绍全排列递归算法的概述，包括其定义、特点和应用场景等。

随后，我们将深入探讨该算法的实现原理，并对其优缺点进行详尽分析。

接下来，我们会通过三个具体的举例说明来展示全排列递归算法的具体运用情况。

在最后部分，我们将探究该算法在其他领域中的应用以及进一步扩展与改进思路。

1.3 目的本文旨在提供一个清晰而全面的介绍全排列递归算法及其应用示例。

通过阅读本文，读者将能够了解该算法的基本原理、实现方法和优缺点，并对其在不同场景下的具体应用有更深入、更具体的认识。

此外，本文还将探讨该算法的拓展和改进思路，为读者提供继续研究和应用的思路。

2. 全排列递归算法概述2.1 什么是全排列递归算法全排列递归算法是一种用于确定给定元素集合所有可能排列方式的算法。

它通过递归的方式将原始集合分解成更小的子问题，并且在每个步骤中交换不同位置上的元素来生成新的排列。

这个过程会一直持续到达到基本情况，也就是无法再进一步交换元素位置为止。

2.2 实现原理全排列递归算法可以通过以下方法实现：1) 确定基本情况：当待排序集合只包含一个元素时，即达到了基本情况。

此时，我们可以认为该集合已经被排列好了。

2) 对于超过一个元素的集合，选择其中一个元素作为固定元素，并将其与其他每个位置上的元素进行交换。

这样，我们就得到了以不同元素开头的一系列子问题。

3) 对于每个子问题，重复步骤2中的操作，对其余部分进行递归地全排列。

4) 在重复进行步骤2和3后，我们可以得到最终的全排列结果。

2.3 优缺点分析全排列递归算法具有以下优点：- 算法逻辑简单易懂，易于实现和理解。

- 能够生成给定元素集合的所有可能排列方式。

java 常用算法总结 -回复

java 常用算法总结-回复Java常用算法总结在Java程序开发中，算法是非常重要的一部分，它们能够解决各种问题，并为程序提供高效的解决方案。

本文将总结Java中常用的算法，并为每种算法的主题进行详细解释。

以下是本文的主要内容：1. 基础算法：涵盖了常见的算法思想和数据结构，例如递归、排序、查找等。

1.1 递归：递归是一种调用自身的算法。

它常用于解决可以被分解为规模较小的子问题的问题。

1.2 排序算法：排序算法用于对一组数据进行排序，常见的算法包括冒泡排序、插入排序、选择排序、快速排序、归并排序等。

1.3 查找算法：查找算法用于在一组数据中查找指定的元素，常见的算法包括线性查找、二分查找、哈希查找等。

2. 图算法：图算法用于解决与图相关的问题，例如找到两个节点之间的最短路径、判断图是否连通等。

2.1 广度优先搜索（BFS）：BFS算法用于在图中寻找最短路径。

它从给定的起始节点开始，逐层遍历图中的节点，直到找到目标节点或遍历完所有节点。

2.2 深度优先搜索（DFS）：DFS算法用于在图中寻找路径。

它从给定的起始节点开始，沿着一条路径一直遍历直到不能继续才回溯，继续遍历其他路径。

2.3 最小生成树（MST）：最小生成树算法用于在给定的图中找到一棵包含所有节点的树，并使得树的所有边的权重之和最小。

2.4 拓扑排序：拓扑排序算法用于对有向无环图进行排序。

它将图中的节点按照依赖关系进行排序，使得每个依赖关系的节点都排在其依赖的节点之后。

3. 动态规划：动态规划是一种通过将问题分解为子问题并解决子问题来解决复杂问题的算法。

它通常用于解决最优化问题。

3.1 斐波那契数列：斐波那契数列是一个经典的动态规划问题，它的定义为f(n) = f(n-1) + f(n-2)，其中f(0) = 0，f(1) = 1。

3.2 背包问题：背包问题是一个经典的动态规划问题，它的目标是在给定的背包容量下，将价值最大化。

常见的背包问题包括01背包问题、完全背包问题和多重背包问题。

全排列的几种实现（含字典序排列算法分析）

全排列的⼏种实现（含字典序排列算法分析）始于⼀个很简单的问题：⽣成｛0，1，2，3，...，n-1｝的n！种排列，即全排列问题。

下⾯介绍⼏种全排列的实现，以及探讨⼀下其解题思路。

基于枚举/递归的⽅法思路：基于枚举的⽅法，也可以说是基于递归的⽅法，此⽅法的思路是先将全排列问题的约束进⾏放松，形成⼀个较容易解决的新问题，解新问题，再对新问题进⾏约束，解出当前问题。

以上全排列问题是⽣成｛0，1，2，...，n-1｝的n！个排列，隐含的⼀个约束是这个n个位置上的数必须是给出的集合中的数，不能重复使⽤。

当我们将此约束放松的时候，问题就变成了n个位置每个位置上有0~n-1种可能出现的数字，列出所有n n种数列，即在每⼀位上枚举所有的可能。

新问题的算法⾮常简单：private Integer[] perm;private void permut(int pos, int n) {if (pos == n) {for (int i = 0; i < perm.length; i++) {System.out.print(perm[i]);}System.out.println();return;}for (int i = 0; i < n; i++) {perm[pos] = i;permut(pos+1, n);}} ⽽我们实际的问题只要保证每⼀位上的数字在其他位置上没有使⽤过就⾏了。

private boolean[] used;private Integer[] perm;private void permut(int pos, int n) {if (pos == n) {for (int i = 0; i < perm.length; i++) {System.out.print(perm[i]);}System.out.println();return;} //针对perm的第pos个位置，究竟使⽤0~n-1中的哪⼀个进⾏循环for (int i = 0; i < n; i++) {if (used[i] == false) {perm[pos] = i;used[i] = true; //i已经被使⽤了，所以把标志位设置为Truepermut(pos+1, n);used[i] = false; //使⽤完之后要把标志复位}}} 或者完全按递归是思想，对｛0，1，2，...，n-1｝进⾏排列，分别将每个位置交换到最前⾯位，之后全排列剩下的位：private static void PermutationList(int fromIndex, int endIndex){if (fromIndex == endIndex)Output();else{for (int index = fromIndex; index <= endIndex; ++index){// 此处排序主要是为了⽣成字典序全排列，否则递归会打乱字典序Sort(fromIndex, endIndex);Swap(fromIndex, index);PermutationList(fromIndex + 1, endIndex);Swap(fromIndex, index);}}}基于字典序的⽅法基于字典序的⽅法，⽣成给定全排列的下⼀个排列，所谓⼀个的下⼀个就是这⼀个与下⼀个之间没有其他的。

两种常用的全排列算法（java）

两种常⽤的全排列算法（java）问题：给出⼀个字符串，输出所有可能的排列。

全排列有多种算法，此处仅介绍常⽤的两种：字典序法和递归法。

1、字典序法：如何计算字符串的下⼀个排列了？来考虑"926520"这个字符串，我们从后向前找第⼀双相邻的递增数字，"20"、"52"都是⾮递增的，"26 "即满⾜要求，称前⼀个数字2为替换数，替换数的下标称为替换点，再从后⾯找⼀个⽐替换数⼤的最⼩数（这个数必然存在），0、2都不⾏，5可以，将5和2交换得到"956220"，然后再将替换点后的字符串"6220"颠倒即得到"950226"。

算法概括：从后向前遍历，找出第⼀个交换点，再按照规则找出第⼆个交换点，将两者进⾏交换，对第⼀个交换点之后的字符进⾏颠倒操作package algorithm;import java.util.Arrays;public class DictionaryPermutation {private char[] data;private int length;public void permutate(String input) {// change the data type to we neededchangeToData(input);// sort the data from small to bigArrays.sort(data);// output all the orderSystem.out.println(data);while (nextPermutate()) {System.out.println(data);}}private void changeToData(String input) {if (input == null)return;data = input.toCharArray();length = data.length;}private boolean nextPermutate() {int end = length - 1;int swapPoint1 = end, swapPoint2 = end;// the actual swap-point is swapPoint1 - 1while (swapPoint1 > 0 && data[swapPoint1] <= data[swapPoint1 - 1])swapPoint1--;if (swapPoint1 == 0)return false;else {while (swapPoint2 > 0 && data[swapPoint2] <= data[swapPoint1 - 1])swapPoint2--;swap(data, swapPoint1 - 1, swapPoint2);reverse(data, swapPoint1, end);return true;}}private void swap(char[] data, int left, int right) {char temp = data[left];data[left] = data[right];data[right] = temp;}private void reverse(char[] data, int left, int right) {for (int i = left, j = right; i < j; i++, j--)swap(data, i, j);}public static void main(String... args) {DictionaryPermutation p = new DictionaryPermutation();p.permutate("aab");}}2、递归法为⽅便起见，⽤123来⽰例下。

字典排序算法实现全排列

字典排序算法实现全排列相关资料免积分下载：字典排序算法实现全排列的步骤：总结：1.从右向左找，找到第⼀个⽐下⼀个元素还⼩的地⽅，记下位置，标注为左元素。

2.从右向左找，找到第⼀个⽐左元素⼤的元素，记下位置，标注为右元素。

3.交换左元素和右元素。

4.不管现在左元素位置上放的是谁，将左元素右边的序列逆序。

5.这样就得到了⼀个新数了。

6.可以继续重复1-5，来继续得到下⼀个排列。

7.如果再也找不到⼀个⽐下⼀个元素还⼩的地⽅，那么意味着这个序列已经降序了，排列完成了，那就结束吧。

代码如下：<?php/*** 打印数组** @param int $num 数组内的元素个数*/function printArr($num){global$array;//全局数组for($i=0;$i<$num;$i++)echo$array[$i];echo "<br>";}/*** 交换值** @param string $a* @param string $b*/function swap(&$a,&$b){$temp= $a;$a = $b;$b = $temp;}/*** 将第$m个和$n个之间的数据倒置排序** @param int $m 数组中的位序$m* @param int $n 数组中的位序$n*/function convert($m,$n){global$array;//全局数组for ($i=$m,$j=$n;$j>$i;$i++,$j--)swap($array[$i],$array[$j]);}/*** 对1~n进⾏全排列** @param int $num 元素的总个数* @return 1*/function dictionary_sort($num){global$array;//全局数组if ($num==1){echo "1<br>";return 1;}while (1){printArr($num); //打印数组for ($i=$num-2;$i>=0;$i--){ //步骤1:从后向前找,找到第⼀个⽐下⼀个元素还⼩的地⽅,记下位置,标注$iif ($array[$i]<$array[$i+1])break;//得到$iif ($i==0)return 1; //函数出⼝}for ($j=$num-1;$j>$i;$j--){ //步骤2:从后向前找，找到第⼀个⽐$i元素⼤的元素，记下位置，标注为$jif ($array[$j]>$array[$i])break;}swap($array[$i],$array[$j]);//步骤3:交换$array[$i]和$array[$j]的数据convert($i+1,$num-1); //步骤4: 将$i个元素右边的序列逆序}}$array=array();$num=5;for ($i=0;$i<$num;$i++){$array[$i]=$i+1;}dictionary_sort($num);原创⽂章：转载请注明出处：。

全排列问题的递归算法

全排列问题是一种经典的算法问题，它要求对一组元素进行排列，得到所有可能的排列方式。

全排列问题可以使用递归算法进行求解。

递归算法的基本思路是将原问题分解为若干个子问题，然后求解这些子问题，最后将子问题的解组合起来得到原问题的解。

对于全排列问题，可以将其分解为两个子问题：
1.考虑第一个元素在排列中的位置，将其与后面的元素进行全排列。

2.不考虑第一个元素在排列中的位置，对后面的元素进行全排列。

3.通过递归地求解这两个子问题，可以得到所有可能的排列方式。

具体实现过程如下：
1.定义一个递归函数permute，它接受一个整数n和一个整数数组arr作为参
数。

n表示要排列的元素个数，arr表示要排列的元素。

2.如果n等于0，说明已经排列完了所有的元素，此时直接返回空数组。

3.如果n等于1`，说明只有一个元素需要排列，此时直接返回包含这个元素的
数组。

4.否则，将arr数组分成两部分：第一个元素和后面的元素。

递归地求解以下
两个子问题：
a. 考虑第一个元素在排列中的位置，将其与后面的元素进行全排列。

b. 不考虑第一个元素在排列中的位置，对后面的元素进行全排列。

5.将两个子问题的解组合起来，得到原问题的解。

6.返回原问题的解。

这个算法的时间复杂度是指数级的，因为对于每一个排列方式，它需要递归地求解两个子问题。

因此，当元素个数较大时，这个算法可能会非常耗时。

java全排列从普通循环到递归

java全排列从普通循环到递归⾸先是给出⼀步步交换的过程，例如abc三个字母的全排列，思路就是先a在前得到abc，交换后边两个字母得到acb再交换回来abc，然后b在前，最后c在前，依次交换后边的字母输出，然后交换回abc。

代码如下：public class TestDemo3 {public static void trans( String str ) {char[] arr = str.toCharArray();permute(arr,3);}public static void permute( char[] arr, int a ) { //a在⾸字母swap(arr,arr.length-3,arr.length-3);for(int i=0;i<arr.length;i++) {System.out.print(arr[i]);}System.out.print(" ");swap(arr,arr.length-2,arr.length-1);for(int i=0;i<arr.length;i++) {System.out.print(arr[i]);}swap(arr,arr.length-2,arr.length-1);swap(arr,arr.length-3,arr.length-3);System.out.println();//b在⾸字母swap(arr,arr.length-3,arr.length-2);for(int i=0;i<arr.length;i++) {System.out.print(arr[i]);}System.out.print(" ");swap(arr,arr.length-2,arr.length-1);for(int i=0;i<arr.length;i++) {System.out.print(arr[i]);}swap(arr,arr.length-2,arr.length-1);swap(arr,arr.length-3,arr.length-2);System.out.println();//c在⾸字母swap(arr,arr.length-3,arr.length-1);for(int i=0;i<arr.length;i++) {System.out.print(arr[i]);}System.out.print(" ");swap(arr,arr.length-2,arr.length-1);for(int i=0;i<arr.length;i++) {System.out.print(arr[i]);}swap(arr,arr.length-2,arr.length-1);swap(arr,arr.length-3,arr.length-1);public static void swap( char[] arr, int a, int b ) {char temp;temp = arr[a];arr[a] = arr[b];arr[b] = temp;}public static void main( String[] args ) {trans("abcd");}} 接下来对重复的代码进⾏重构，重复的部分可以⽤循环替代，代码如下：public class TestDemo3 {public static void trans( String str ) {char[] arr = str.toCharArray();permute(arr,0);}public static void permute( char[] arr, int a ) {for(int j=a;j<arr.length;j++) {swap(arr,a,j);for(int k=0;k<arr.length;k++) {System.out.print(arr[k]);}System.out.print(" ");swap(arr,arr.length-2,arr.length-1);for(int k=0;k<arr.length;k++) {System.out.print(arr[k]);}System.out.println();swap(arr,arr.length-2,arr.length-1);swap(arr,a,j);}}public static void swap( char[] arr, int a, int b ) {char temp;temp = arr[a];arr[a] = arr[b];arr[b] = temp;}public static void main( String[] args ) {trans("abc");}} 对于4个字符的字符串，显然以上⽅法不⾏，利⽤循环嵌套可以解决，思路就是，先a在前，按照交换3个字符的字符串的⽅式交换bcd，再将a与bcd依次交换进⾏排列。

算法——快速排序迭代式和递归式的Java实现

算法——快速排序迭代式和递归式的Java实现快速排序迭代式和递归式的Java实现快速排序基于分治法的思想，在待排序表中任选⼀值作为中枢值 pivot，⼀趟快排将所有⼤于该值的元素置于⼀边，⼩于该值的元素置于另⼀边，这样⼀个元素在排序中的最终位置就已确定。

接下来将中枢值左右两边的区域分别进⾏下⼀趟快排，直到所有的元素都有序排列。

空间效率：最好情况为 O(log2(n+1))，最坏情况为 O(n)，平均空间复杂度 O(log2(n))。

时间效率：最好情况为 O(n*log2(n))，最坏情况 O(n^2)，平均时间复杂度 O(n*log2(n))。

快速排序是所有内部排序中平均性能最优的算法，同时也是⼀个不稳定的排序算法。

递归式1public class Test {23public static void main(String[] args) {45int[] nums = {2, 12, 32, 32, 43, 5, 74, 13, 87, 12, 44, 2, 41, 5, 33};67 recursiveQuicksort(nums,0,nums.length-1);89 System.out.println("Sorted array : " + Arrays.toString(nums));1011 }1213//recursiveQuicksort(int[] 被排序数组, int 数组下界, int 数组上界)14private static void recursiveQuicksort(int[] nums, int low, int high) {1516if(low < high){1718int pivotpos = partition(nums, low, high);1920 recursiveQuicksort(nums, low, pivotpos -1);21 recursiveQuicksort(nums, pivotpos + 1, high);2223 }24 }2526private static int partition(int[] nums, int low, int high) {2728//将当前列表中第⼀个元素设为中枢值29int pivot = nums[low];3031while(low < high){3233//找到第⼀个⼩于中枢值的数，置于low的位置34while(low < high && nums[high] >= pivot){35 --high;36 }37 nums[low] = nums[high];3839//找到第⼀个⼤于中枢值的数，置于high的位置40while(low < high && nums[low] <= pivot){41 ++low;42 }43 nums[high] = nums[low];44 }4546//这样⼀趟下来nums[low]左端都是⼩于中枢值的数，右端都是⼤于中枢值的数，⼀个元素的最终排序位置确定47 nums[low] = pivot;4849return low;50 }51 }迭代式递归的操作更加便于理解，但是递归频繁的调⽤函数会不断让参数和其它额外的变量⼊栈，从⽽造成栈空间的极⼤浪费，如果调⽤层次很深，还有可能造成栈溢出，⽽⼊栈也会有性能损失。

java算法实现排列组合的方法介绍

java算法实现排列组合的方法介绍java算法实现排列组合的方法介绍一.利用二进制状态法求排列组合，此种方法比较容易懂，但是运行效率不高，小数据排列组合可以使用代码如下:import java.util.Arrays;//利用二进制算法进行全排列//count1:170187//count2:291656public class test {public static void main(String[] args) {long start=System.currentTimeMillis();count2();long end=System.currentTimeMillis();System.out.println(end-start);}private static void count2(){int[] num=new int []{1,2,3,4,5,6,7,8,9};for(int i=1;i<Math.pow(9, 9);i++){String str=Integer.toString(i,9);int sz=str.length();for(int j=0;j<9-sz;j++){str="0"+str;}char[] temp=str.toCharArray();Arrays.sort(temp);String gl=new String(temp);if(!gl.equals("012345678")){continue;}String result="";for(int m=0;m<str.length();m++){result+=num[Integer.parseInt(str.charAt(m)+"")]; }System.out.println(result);}}public static void count1(){int[] num=new int []{1,2,3,4,5,6,7,8,9};int[] ss=new int []{0,1,2,3,4,5,6,7,8};int[] temp=new int[9];while(temp[0]<9){temp[temp.length-1]++;for(int i=temp.length-1;i>0;i--){if(temp[i]==9){temp[i]=0;temp[i-1]++;}}int []tt=temp.clone();Arrays.sort(tt);if(!Arrays.equals(tt,ss)){continue;}String result="";for(int i=0;i<num.length;i++){result+=num[temp[i]];}System.out.println(result);}}二.用递归的思想来求排列跟组合，代码量比较大代码如下: package practice;import java.util.ArrayList;import java.util.List;public class Test1 {/*** @param args*/public static void main(String[] args) {// TODO Auto-generated method stubObject[] tmp={1,2,3,4,5,6};// ArrayListrs=RandomC(tmp);ArrayListrs=cmn(tmp,3);for(int i=0;i<rs.size();i++){// System.out.print(i+"=");for(int j=0;j<rs.get(i).length;j++){System.out.print(rs.get(i)[j]+",");}System.out.println();}}// 求一个数组的任意组合static ArrayListRandomC(Object[] source)ArrayListresult=new ArrayList();if(source.length==1){result.add(source);}else{Object[] psource=new Object[source.length-1];for(int i=0;i<psource.length;i++){psource[i]=source[i];}result=RandomC(psource);int len=result.size();//fn组合的长度result.add((new Object[]{source[source.length-1]})); for(int i=0;i<len;i++){Object[] tmp=new Object[result.get(i).length+1]; for(int j=0;j<tmp.length-1;j++){tmp[j]=result.get(i)[j];}tmp[tmp.length-1]=source[source.length-1]; result.add(tmp);}}return result;static ArrayListcmn(Object[] source,int n){ArrayListresult=new ArrayList();if(n==1){for(int i=0;i<source.length;i++){result.add(new Object[]{source[i]});}}else if(source.length==n){result.add(source);}else{Object[] psource=new Object[source.length-1]; for(int i=0;i<psource.length;i++){psource[i]=source[i];}result=cmn(psource,n);ArrayListtmp=cmn(psource,n-1);for(int i=0;i<tmp.size();i++){Object[] rs=new Object[n];for(int j=0;j<n-1;j++){rs[j]=tmp.get(i)[j];}rs[n-1]=source[source.length-1];result.add(rs);}}return result;}}三.利用动态规划的思想求排列和组合代码如下: package Acm;//强大的.求组合数public class MainApp {public static void main(String[] args) {int[] num=new int[]{1,2,3,4,5};String str="";//求3个数的组合个数// count(0,str,num,3);// 求1-n个数的组合个数count1(0,str,num);}private static void count1(int i, String str, int[] num) { if(i==num.length){System.out.println(str);return;}count1(i+1,str,num);count1(i+1,str+num[i]+",",num);}private static void count(int i, String str, int[] num,int n) { if(n==0){System.out.println(str);return;}if(i==num.length){return;}count(i+1,str+num[i]+",",num,n-1);count(i+1,str,num,n);}}下面是求排列代码如下:package Acm;//求排列，求各种排列或组合后排列import java.util.Arrays;import java.util.Scanner;public class Demo19 {private static boolean f[];public static void main(String[] args) {Scanner sc=new Scanner(System.in);int sz=sc.nextInt();for(int i=0;i<sz;i++){int sum=sc.nextInt();f=new boolean[sum];Arrays.fill(f, true);int[] num=new int[sum];for(int j=0;j<sum;j++){num[j]=j+1;}int nn=sc.nextInt();String str="";count(num,str,nn);}}/**** @param num 表示要排列的数组* @param str 以排列好的字符串* @param nn 剩下需要排列的个数，如果需要全排列，则nn为数组长度*/private static void count(int[] num, String str, int nn) {if(nn==0){System.out.println(str);return;}for(int i=0;i<num.length;i++){if(!f[i]){continue;}f[i]=false;count(num,str+num[i],nn-1);f[i]=true;}}}【java算法实现排列组合的方法介绍】。

java中全排列是如何生成算法

java中全排列是如何生成算法全排列的生成算法就是对于给定的字符集，用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。

任何n个字符集的排列都可以与1～n的n个数字的排列一一对应，因此在此就以n个数字的排列为例说明排列的生成法。

n个字符的全体排列之间存在一个确定的线*顺序关系。

所有的排列中除最后一个排列外，都有一个后继；除第一个排列外，都有一个前驱。

每个排列的后继都可以从它的前驱经过最少的变化而得到，全排列的生成算法就是从第一个排列开始逐个生成所有的排列的方法。

全排列的生成法通常有以下几种：字典序法递增进位数制法递减进位数制法邻位交换法递归类算法1.字典序法效率高且顺序自然字典序法中，对于数字1、2、3......n的排列，不同排列的先后关系是从左到右逐个比较对应的数字的先后来决定的。

例如对于5个数字的排列12354和12345，排列12345在前，排列12354在后。

按照这样的规定，5个数字的所有的排列中最前面的是12345，最后面的是54321。

字典序算法如下：设P是1～n的一个全排列:p=p1p2......pn=p1p2......pj-1pjpj+1......pk-1pkpk+1......pn1）从排列的右端开始，找出第一个比右边数字小的数字的序号j （j从左端开始计算），即j=max{i|pi<pi+1}2）在pj的右边的数字中，找出所有比pj大的数中最小的数字pk，即k=max{i|pi>pj}（右边的数从右至左是递增的，因此k是所有大于pj的数字中序号最大者）3）对换pi，pk4）再将pj+1......pk-1pkpk+1pn倒转得到排列p'=p1p2.....pj-1pjpn.....pk+1pkpk-1.....pj+1，这就是排列p的下一个下一个排列。

例如839647521是数字1～9的一个排列。

从它生成下一个排列的步骤如下：自右至左找出排列中第一个比右边数字小的数字4839647521在该数字后的数字中找出比4大的数中最小的一个5839647521将5与4交换839657421将7421倒转839651247所以839647521的下一个排列是839651247。

全排列算法（java实现）组合算法实现

全排列算法（java实现）组合算法实现100题⽬之53题⽬和70题⽬在做100题⽬的时候，全排列的困扰了很久，虽然⽹上了搜了⼀些资料，可是并没有搞懂。

今天花了⼀个下午的时间，从新梳理了⼀遍，终于弄明⽩了。

全排列的算法，递归分析⽹上都有：设⼀组数p = {r1, r2, r3, ... ,rn}, 全排列为perm(p)，pn = p - {rn}。

因此perm(p) = r1perm(p1), r2perm(p2), r3perm(p3), ... , rnperm(pn)。

当n = 1时perm(p} = r1。

实现代码如下：[c-sharp]1. public class permutate {2. public static int total = 0;3. public static void swap(String[] str, int i, int j)4. {5. String temp = new String();6. temp = str[i];7. str[i] = str[j];8. str[j] = temp;9. }10. public static void arrange (String[] str, int st, int len)11. {12. if (st == len - 1)13. {14. for (int i = 0; i < len; i ++)15. {16. System.out.print(str[i]+ " ");17. }18. System.out.println();19. total++;20. }21. else22. {23. for (int i = st; i < len; i ++)24. {25. swap(str, st, i);26. arrange(str, st + 1, len);27. swap(str, st, i);28. }29. }30.31. }32. /**33. * @param args34. */35. public static void main(String[] args) {36. // TODO Auto-generated method stub37. String str[] = {"a","b","c"};38. arrange(str, 0, str.length);39. System.out.println(total);40. }41. }关键的就是arrange⽅法的else⾥⾯的内容，我的理解是（以求str[] = {"a","b","c"}的排列为例⼦）：⽤i从str[st]做⼀遍循环：每⼀次循环中，都要将str[i]与str[i]互相调换位置：第⼀次开始，"a"与⾃⼰换，这时候，递归调⽤arrange[str,st + 1, len]这是在求取str[str...len - 1]的排列即"b","c"的排列；第⼆次，"a"与"b"互相调换，递归调⽤arrange[str,str + 1, len]就是在求取{"a","c"}的排列。

全排列递归算法详解

全排列递归算法详解
哎呀，啥是全排列递归算法呀？我一个小学生刚开始听到这个词的时候，简直是一头雾水，就好像走进了一个黑漆漆的迷宫，找不到出口。

咱们先来说说啥叫排列吧。

比如说，有三个数字1、2、3，把它们排排队，123 是一种排法，213 是一种排法，321 又是一种排法，这就是排列。

那全排列呢，就是把所有可能的排法都找出来。

那递归算法又是啥呢？这就像我们玩的搭积木。

我们先搭一层，然后在这一层的基础上再搭一层，一层一层地往上加。

递归算法也是这样，它自己调用自己，就像搭积木一样，一层一层地解决问题。

比如说，我们要对三个数字1、2、3 进行全排列。

那我们可以先固定第一个数字1，然后对剩下的2 和3 进行全排列。

怎么排呢？再固定2，剩下3 自己就是一种排法；然后固定3，剩下2 又是一种排法。

这是不是有点像我们做数学题的时候，一步一步来，每一步都为下一步打下基础？这不就和我们一层一层搭积木一样嘛！
再想想，如果数字更多了，比如1、2、3、4 这四个数字，那我们还是用同样的方法。

先固定一个数字，然后对剩下的数字进行全排列。

这是不是有点像我们解决难题的时候，把大问题分成一个个小问题，然后一个个解决？
哎呀，说了这么多，我感觉全排列递归算法就像是一个神奇的魔法，能把一堆乱七八糟的数字变得整整齐齐，让我们能找到所有的可能性。

反正我觉得全排列递归算法虽然有点难，但是只要我们认真去想，去琢磨，就一定能搞明白！。

用Java实现排列、组合算法

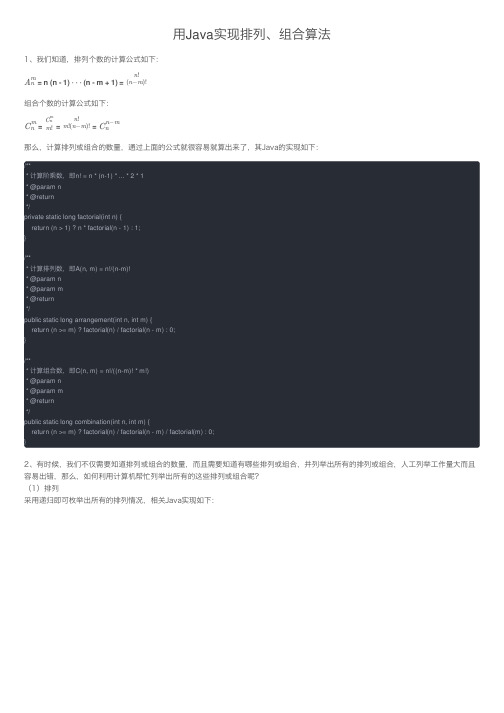
⽤Java 实现排列、组合算法1、我们知道，排列个数的计算公式如下：= n (n - 1) (n - m + 1) = 组合个数的计算公式如下：= = = 那么，计算排列或组合的数量，通过上⾯的公式就很容易就算出来了，其Java的实现如下：/*** 计算阶乘数，即n! = n * (n-1) * ... * 2 * 1* @param n* @return*/private static long factorial(int n) {return (n > 1) ? n * factorial(n - 1) : 1;}/*** 计算排列数，即A(n, m) = n!/(n-m)!* @param n* @param m* @return*/public static long arrangement(int n, int m) {return (n >= m) ? factorial(n) / factorial(n - m) : 0;}/*** 计算组合数，即C(n, m) = n!/((n-m)! * m!)* @param n* @param m* @return*/public static long combination(int n, int m) {return (n >= m) ? factorial(n) / factorial(n - m) / factorial(m) : 0;}2、有时候，我们不仅需要知道排列或组合的数量，⽽且需要知道有哪些排列或组合，并列举出所有的排列或组合，⼈⼯列举⼯作量⼤⽽且容易出错，那么，如何利⽤计算机帮忙列举出所有的这些排列或组合呢？（1）排列采⽤递归即可枚举出所有的排列情况，相关Java实现如下：A n m⋯(n −m )!n !C n m m !C n m m !(n −m )!n !C n n −m*/public static void arrangementSelect(String[] dataList, int n) {System.out.println(String.format("A(%d, %d) = %d", dataList.length, n, arrangement(dataList.length, n))); arrangementSelect(dataList, new String[n], 0);}/*** 排列选择* @param dataList 待选列表* @param resultList 前⾯（resultIndex-1）个的排列结果* @param resultIndex 选择索引，从0开始*/private static void arrangementSelect(String[] dataList, String[] resultList, int resultIndex) {int resultLen = resultList.length;if (resultIndex >= resultLen) { // 全部选择完时，输出排列结果System.out.println(Arrays.asList(resultList));return;}// 递归选择下⼀个for (int i = 0; i < dataList.length; i++) {// 判断待选项是否存在于排列结果中boolean exists = false;for (int j = 0; j < resultIndex; j++) {if (dataList[i].equals(resultList[j])) {exists = true;break;}}if (!exists) { // 排列结果不存在该项，才可选择resultList[resultIndex] = dataList[i];arrangementSelect(dataList, resultList, resultIndex + 1);}}}（2）组合采⽤递归即可枚举出所有的排列情况，相关Java实现如下：*/public static void combinationSelect(String[] dataList, int n) {System.out.println(String.format("C(%d, %d) = %d", dataList.length, n, combination(dataList.length, n)));combinationSelect(dataList, 0, new String[n], 0);}/*** 组合选择* @param dataList 待选列表* @param dataIndex 待选开始索引* @param resultList 前⾯（resultIndex-1）个的组合结果* @param resultIndex 选择索引，从0开始*/private static void combinationSelect(String[] dataList, int dataIndex, String[] resultList, int resultIndex) {int resultLen = resultList.length;int resultCount = resultIndex + 1;if (resultCount > resultLen) { // 全部选择完时，输出组合结果System.out.println(Arrays.asList(resultList));return;}// 递归选择下⼀个for (int i = dataIndex; i < dataList.length + resultCount - resultLen; i++) {resultList[resultIndex] = dataList[i];combinationSelect(dataList, i + 1, resultList, resultIndex + 1);}}3、测试（1）完整的测试代码如下/*** 从n个数⾥取出m个数的排列或组合算法实现* @author chengesheng* @date 2016年9⽉28⽇下午3:18:34*/import java.util.Arrays;public class MathTest {public static void main(String[] args) {arrangementSelect(new String[] {"1", "2", "3", "4"}, 2);combinationSelect(new String[] {"1", "2", "3", "4", "5"}, 3);}/*** 排列选择（从列表中选择n个排列）* @param dataList 待选列表* @param n 选择个数*/public static void arrangementSelect(String[] dataList, int n) {System.out.println(String.format("A(%d, %d) = %d", dataList.length, n, arrangement(dataList.length, n))); arrangementSelect(dataList, new String[n], 0);}/*** 排列选择* @param dataList 待选列表* @param dataList 待选列表* @param resultList 前⾯（resultIndex-1）个的排列结果* @param resultIndex 选择索引，从0开始*/private static void arrangementSelect(String[] dataList, String[] resultList, int resultIndex) {int resultLen = resultList.length;if (resultIndex >= resultLen) { // 全部选择完时，输出排列结果System.out.println(Arrays.asList(resultList));return;}// 递归选择下⼀个for (int i = 0; i < dataList.length; i++) {// 判断待选项是否存在于排列结果中boolean exists = false;for (int j = 0; j < resultIndex; j++) {if (dataList[i].equals(resultList[j])) {exists = true;break;}}if (!exists) { // 排列结果不存在该项，才可选择resultList[resultIndex] = dataList[i];arrangementSelect(dataList, resultList, resultIndex + 1);}}}/*** 组合选择（从列表中选择n个组合）* @param dataList 待选列表* @param n 选择个数*/public static void combinationSelect(String[] dataList, int n) {System.out.println(String.format("C(%d, %d) = %d", dataList.length, n, combination(dataList.length, n))); combinationSelect(dataList, 0, new String[n], 0);}/*** 组合选择* @param dataList 待选列表* @param dataIndex 待选开始索引* @param resultList 前⾯（resultIndex-1）个的组合结果* @param resultIndex 选择索引，从0开始*/private static void combinationSelect(String[] dataList, int dataIndex, String[] resultList, int resultIndex) {int resultLen = resultList.length;int resultCount = resultIndex + 1;if (resultCount > resultLen) { // 全部选择完时，输出组合结果System.out.println(Arrays.asList(resultList));return;}// 递归选择下⼀个for (int i = dataIndex; i < dataList.length + resultCount - resultLen; i++) {resultList[resultIndex] = dataList[i];combinationSelect(dataList, i + 1, resultList, resultIndex + 1);}}/*** 计算阶乘数，即n! = n * (n-1) * ... * 2 * 1* @param n* @return*/public static long factorial(int n) {return (n > 1) ? n * factorial(n - 1) : 1;}/*** 计算排列数，即A(n, m) = n!/(n-m)!* @param n* @param m* @return*/public static long arrangement(int n, int m) {return (n >= m) ? factorial(n) / factorial(n - m) : 0;}/*** 计算组合数，即C(n, m) = n!/((n-m)! * m!)* @param n* @param m* @return*/public static long combination(int n, int m) {return (n >= m) ? factorial(n) / factorial(n - m) / factorial(m) : 0; }}（2）测试结果A(4, 2) = 12[1, 2][1, 3][1, 4][2, 1][2, 3][2, 4][3, 1][3, 2][3, 4][4, 1][4, 2][4, 3]C(5, 3) = 10[1, 2, 3][1, 2, 4][1, 2, 5][1, 3, 4][1, 3, 5][1, 4, 5][2, 3, 4][2, 3, 5][2, 4, 5][3, 4, 5]转⾃该⼤佬的博客：。

递归排序算法java

递归排序算法java递归排序是一种基于分治思想的排序算法，其主要思想是将待排序的数组按照一定的规则划分成两个子数组，然后对这两个子数组分别进行递归排序，最后将这两个有序的子数组合并成一个有序的数组。

递归排序的核心思想是将大的问题拆分成小的问题来解决，这是递归的本质。

因此，递归排序可以通过递归调用来实现。

递归排序的基本流程如下：1. 判断数组是否为空或者只有一个元素，如果是，则表示已经有序，直接返回。

2. 如果数组有多个元素，则将数组划分成两个子数组，分别对这两个子数组进行递归排序。

3. 对于每个子数组，递归排序时重复以上步骤，直到子数组中只有一个元素或为空。

4. 合并两个有序的子数组，得到一个有序的数组。

因此，递归排序算法可以分为两个部分：分治和合并。

分治的实现：定义一个函数，其输入为待排序的数组arr，以及数组的起始位置low和终止位置high，函数的输出为一个有序的数组。

在函数内部先判断数组是否为空或者只有一个元素，如果是，则直接返回；否则，将数组中间位置mid作为分界点，将数组分成左右两个子数组，然后对左右两个子数组分别进行递归排序，最后将两个有序的子数组合并成一个有序的数组。

定义一个函数，其输入为两个已排序的数组leftArr和rightArr，以及数组的长度leftLen和rightLen，函数的输出为合并后的有序数组。

在函数内部，定义一个新的数组result，长度为leftLen+rightLen，然后使用两根指针i和j分别指向leftArr和rightArr的第一个元素，对比i和j指向的元素大小，将较小的元素存入result中，直到其中一个指针到达数组尾部，最后将剩余的元素添加到result中即可。

最终整个递归排序算法的代码实现如下：public static void mergeSort(int[] arr, int low, int high) {if (low >= high) return; // 数组为空或者只有一个元素，已经有序，直接返回int mid = (low + high) / 2; // 将数组以中间元素为分界点，分成两个子数组mergeSort(arr, low, mid); // 对左子数组进行递归排序mergeSort(arr, mid + 1, high); // 对右子数组进行递归排序int i = low, j = mid + 1, k = 0;int[] temp = new int[high - low + 1];while (i <= mid && j <= high) {if (arr[i] < arr[j]) temp[k++] = arr[i++];else temp[k++] = arr[j++];}while (i <= mid) temp[k++] = arr[i++];while (j <= high) temp[k++] = arr[j++];System.arraycopy(temp, 0, arr, low, temp.length);}总结：递归排序算法是一种时间复杂度较为稳定的排序算法，其时间复杂度为O(nlogn)，空间复杂度为O(n)，具有稳定性和扩展性。

数组全排列递归算法

数组全排列递归算法
哎呀呀，我是一名小学生，数组全排列递归算法？这对我来说简直像个超级大怪兽！
我先试着给您讲讲我理解的“数组”吧。

就好像我们班同学排队，一排同学站成一列，这一列同学就像是一个数组。

那全排列是啥呢？假如这一排同学可以随便换位置，有好多好多不同的站法，每一种站法就是一种全排列。

递归算法呢？这可难倒我啦！就好像我们做数学题，一道难题不会做，我们去想一个简单一点的类似的题目，从那个简单的题目里找到方法，再用这个方法来解决难题。

递归算法好像就是这样，自己调用自己，一层一层地解决问题。

我想想啊，比如说有三个数字1、2、3 组成的数组，那全排列不就是123、132、213、231、312、321 这六种嘛。

那怎么用递归算法来实现呢？这就像是搭积木，先确定第一个数字，然后剩下的数字再进行全排列。

比如说先确定1 ，那剩下2 和3 ，它们又可以有两种排列23 和32 ，这样就得到123 和132 啦。

哎呀，我说清楚了吗？我感觉自己都有点晕乎乎的呢！反正我觉得这数组全排列递归算法就像个神秘的魔法，我还在努力探索怎么能完全搞懂它！
我的观点就是，这东西太难啦，但是我不会放弃，我要继续努力，总有一天我能把它拿下！。