八年级上学期全等三角形期中复习经典题
2024年八年级数学上册《全等三角形》及答案解析

第十二章全等三角形(单元重点综合测试)班级_________姓名________学号__________分数__________考试范围:全章的内容;考试时间:120分钟;总分:120分一、选择题(本大题共10小题,每小题3分,共30分)1.下列说法中,正确的有()①形状相同的两个图形是全等形;②面积相等的两个图形是全等形;③全等三角形的周长相等,面积相等;④若△ABC≌△DEF,则∠A=∠D.A.1个B.2个C.3个D.4个2.下列各组图形中,是全等形的是()A. B.C. D.3.如图,点B在线段AD上,△ABC≌△EBD,AB=2cm,BD=5cm,则CE的长度为()A.2cmB.2.5cmC.3cmD.5cm4.小红用如图所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,CD⊥BC,BO=OC,点A、O、D在同一直线上,就能保证△ABO≌△DCO,可作为证明△ABO≌△DCO的依据的是()A.SSSB.ASAC.SASD.HL5.如图,在△ABC和△DEF中,点A,E,B,AC∥DF,AC=DF,能判定△ABC≌△DEF的是()A.BC=DEB.AE=DBC.∠A=∠DEFD.∠ABC=∠D6.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中全等三角形有()A.1对B.2对C.3对D.4对7.现要在一块三角形形状的草坪上安装一个洒水龙头,要使洒水龙头到草坪三条边的距离相等,洒水龙头的位置应选在( )处A.三角形三边的垂直平分线的交点B.三角形的三条角平分线的交点C.三角形的三条高所在直线的交点D.三角形的三条中线的交点8.如图,在△ABC中,CD平分∠ACB,DE⊥BC于点E,S△ABC=30,DE=4,BC=10,则AC的长是()A.5B.6C.7D.89.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列五个结论:①DE=DF;②BC=2DB;③AD⊥BC;④AB=3BF;⑤S△ADB=2S△BDF;其中正确的结论共有()A.4个B.3个C.2个D.1个10.新定义:已知三条平行直线,相邻两条平行线间的距离相等,我们把三个顶点分别在这样的三条平行线上的三角形称为“格线三角形”.如图,a∥b∥c,相邻两条平行线间的距离为m,等腰Rt△ABC为“格线三角形”,且∠BAC=90°,则△ABC的面积为()A.5m2 B.2m2 C.5m2 D.4m22二、填空题(本大题共6小题,每小题3分,共18分)11.如图,AD=AB,∠C=∠E,∠CDE=50°,则∠ABE=.12.如图,四边形ABCD≌四边形A B C D .若∠B=90°,∠C=60°,∠D =105°,则∠A的大小为度.13.如图,D,E是边BC上的两点,BD=CE,∠ADB=∠AEC,现要直接用“AAS”定理来证明△ABD≌△ACE,请你再添加一个条件:.14.已知△ABC面积为24,将△ABC沿BC的方向平移到△A B C 的位置,使B 和C重合,连接AC 交A C于D,则△C DC的面积为.15.如图,△ABC中∠A=66°,点M、N是∠ABC与∠ACB三等分线的交点,则∠BMN的度数是.16.如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=15cm,AC=6cm.动点E从A点出发以3cm/s的速度沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.若点E的运动时间为t秒t>0,则当t=秒时,△DEB与△BCA全等.三、(本大题共4小题,每小题6分,共24分)17.已知:如图,AB=AE,∠1=∠2,∠C=∠D.求证:BC=ED.18.如图,已知AB∥CD,AB=CD.(1)求证:△ABC≌△CDA;(2)判断BC与AD的位置关系,并说明理由.19.如图,已知AB=CD,AD=BC,O为AC的中点,过O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形?请把它们都写出来;(2)求证:∠MAE=∠NCF.20.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B(1)求证:△ABC≌△CDE(2)若∠A=55°,求∠BCD的度数.四、(本大题共3小题,每小题8分,共24分)21.如图,△ABC中,点D在边BC延长线上,∠ACB=106°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=53°.(1)求∠ACE的度数;(2)求证:AE平分∠CAF;(3)若AC+CD=16,AB=10,且S△ACD=24,则△ABE的面积.22.问题提出:如图1,在四边形ABCD中,∠BAD与∠BCD互补,∠B与∠D互补,AB=AD,∠BAD=x°0<x<180,∠ACB=y°,数学兴趣小组在探究y与x的数量关系时,经历了如下过程:实验操作:(1)数学兴趣小组通过电脑软件“几何画板”进行探究,测量出部分结果如下表所示:x⋯304050607080β130y757065α555040θ这里α=,β=,θ=.猜想证明:(2)根据表格,猜想:y与x之间的关系式为;数学兴趣小组发现证明此猜想的一种方法:如图2,延长CB到E,使BE=DC,连接AE,⋯,请你根据其思路将证明过程补充完整,并验证(1)中结论的正确性.应用拓广:(3)如图3,若x+y=135,AC=10,求四边形ABCD的面积.23.(1)【问题解决】如图①,∠AOB=∠DFE=90°,OC平分∠AOB,点F在OC上,∠DFE的两边分别与OA,OB交于点D,E.当FE⊥OB,FD⊥OA时,则FD与FE的数量关系为;(2)【问题探究】如图②,在(1)的条件下,过点F作两条相互垂直的射线FM,FN,分别交OA,OB于点M,N,判断FM与FN的数量关系,说明理由;(3)【迁移应用】某学校有一块四边形的空地ABCD,如图③所示,∠DAB=∠DCB=90°,AC是∠DAB的平分线,AB= 50m,AD=30m,直接写出该空地的面积.五、(本大题共2小题,每小题12分,共24分)24.综合探究:如题图1是一种用刻度尺画角平分线的方法,在OA、OB上分别取点C、E、D、F,使得OC=OD,OE=OF,连接CF、DE,交点为P,则射线OP为∠AOB的角平分线.【验证】(1)试说明OP平分∠AOB,且PE=PF;【应用】(2)如题图2,若C、E、D、F分别为OA、OB上的点,且OC=OD,CF⊥OA,DE⊥OB,试用(1)中的原理说明OP平分∠AOB;【猜想】(3)如题图3,P是∠AOB角平分线上一点,C、D分别为OA、OB上的点,且PC=PD,请补全图形,并直接写出∠PCO与∠PDO的数量关系.25.【模型呈现】(1)如图1,∠BAD=90°,AB=AD,BC⊥CA于点C,DE⊥AE于点E.求证:BC=AE.【模型应用】(2)如图2,EA⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形ABCDE的面积.【深入探究】(3)如图3,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC、DE,且BC⊥AF于点F,DE与直线AF交于点G.①求证DG=GE;②若BC=21,AF=12,求△ADG的面积.第十二章全等三角形(单元重点综合测试)班级_________姓名________学号__________分数__________考试范围:全章的内容;考试时间:120分钟;总分:120分一、选择题(本大题共10小题,每小题3分,共30分)1.下列说法中,正确的有()①形状相同的两个图形是全等形;②面积相等的两个图形是全等形;③全等三角形的周长相等,面积相等;④若△ABC≌△DEF,则∠A=∠D.A.1个B.2个C.3个D.4个【答案】B【分析】根据全等形的定义,全等三角形的判定与性质,即可判断.【详解】解:能够完全重合的两个图形叫做全等形,即形状和大小相同的两个图形是全等形,故①②说法错误;全等三角形能够完全重合,所以全等三角形的周长相等,面积相等,故③说法正确;若△ABC≌△DEF,∠A的对应角为∠D,所以∠A=∠D,故④说法正确;说法正确的有③④,共2个.故选:B.【点睛】本题考查全等形,理解能够完全重合的两个图形叫做全等形是解题关键.2.下列各组图形中,是全等形的是()A. B.C. D.【答案】B【分析】本题考查全等形,掌握能完全重合的两个图形是全等形是解题的关键.【详解】观察发现:A,C,D选项中两个图形不能完全重合,不是全等形;B选项中两个图形能完全重合,是全等形,故选B.3.如图,点B在线段AD上,△ABC≌△EBD,AB=2cm,BD=5cm,则CE的长度为()A.2cmB.2.5cmC.3cmD.5cm【答案】C【分析】此题考查了全等三角形的性质,解题的关键熟练掌握性质的应用.根据全等三角形的对应边相等,再利用线段和差即可求解.【详解】∵△ABC≌△EBD,∴BE=AB=2cm,BC=BD=5cm,∴CE=BC-BE=3cm,故选:C.4.小红用如图所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,CD⊥BC,BO=OC,点A、O、D在同一直线上,就能保证△ABO≌△DCO,可作为证明△ABO≌△DCO的依据的是()A.SSSB.ASAC.SASD.HL【答案】B【分析】本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.直接利用全等三角形的判定方法即可得出答案.【详解】解:∵AB⊥BC,CD⊥BC,∴∠ABO=∠DCO=90°,在△ABO和△DCO中,∠ABO=∠DCOBO=OC=CO∠BOA=∠COD,∴△ABO≌△DCO ASA∴证明△ABO≌△DCO的依据的是ASA,故选:B.5.如图,在△ABC和△DEF中,点A,E,B,AC∥DF,AC=DF,能判定△ABC≌△DEF的是()A.BC=DEB.AE=DBC.∠A=∠DEFD.∠ABC=∠D【答案】B【分析】本题考查三角形全等的判定,先根据平行线的性质得到∠A=∠D,加上AC=DF,则可根据全等三角形的判定方法对各选项进行判断即可,掌握全等三角形的判定方法:SSS、SAS、ASA、AAS,HL是解题的关键.【详解】解:∵AC∥DF,∴∠A=∠D,∵AC=DF,A、添加BC=DE,不能判定△ABC≌△DEF;B、添加AE=DB,能判定△ABC≌△DEF;C、添加∠A=∠DEF,不能判定△ABC≌△DEF;D、添加∠ABC=∠D,不能判定△ABC≌△DEF;故选:B.6.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中全等三角形有()A.1对B.2对C.3对D.4对【答案】C【分析】本题主要考查三角形全等的判定定理,角平分线的性质,熟练掌握三角形全等的判定方程是解题的关键.根据全等三角形的判定分别证明△AOP≌△BOP(SAS),Rt△P AE≌Rt△PBF HL,△OEP≌△OFP (AAS),即可得到答案.【详解】解:∵OP平分∠MON,∴∠AOP=∠BOP,∵OA=OB,OP=OP,∴△AOP≌△BOP(SAS);∴AP=BP,∵OP平分∠MON,PE⊥OM,PF⊥ON∴PE=PF,∵PE⊥OM于点E,PF⊥ON于点F,∴Rt△P AE≌Rt△PBF HL;∵OP平分∠MON,∴∠AOP=∠BOP,又∵∠OEP=∠OFP=90°,OP=OP,∴△OEP≌△OFP(AAS).∴图中全等三角形有3对故选C.7.现要在一块三角形形状的草坪上安装一个洒水龙头,要使洒水龙头到草坪三条边的距离相等,洒水龙头的位置应选在( )处A.三角形三边的垂直平分线的交点B.三角形的三条角平分线的交点C.三角形的三条高所在直线的交点D.三角形的三条中线的交点【答案】B【分析】本题考查的是三角形的角平分线的性质,掌握角平分线上的点到角的两边的距离相等是解题的关键.根据角平分线上的点到角的两边的距离相等解答即可.【详解】解:要使洒水龙头到草坪三条边的距离相等,则洒水龙头的位置应选在三角形三条角平分线的交点,故选:B8.如图,在△ABC 中,CD 平分∠ACB ,DE ⊥BC 于点E ,S △ABC =30,DE =4,BC =10,则AC 的长是()A.5B.6C.7D.8【答案】A 【分析】本题主要考查了角平分线的性质定理.过点D 作DF ⊥AC 于点F ,根据角平分线的性质可得DE =DF =4,再由S △ABC =S △DBC +S △DAC ,即可求解.【详解】解:如图,过点D 作DF ⊥AC 于点F ,∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,DE =4,∴DE =DF =4,∵S △ABC =S △DBC +S △DAC ,S △ABC =30,BC =10,∴30=12DE ×BC +12DF ×AC ,∴30=12×4×10+12×4×AC ,∴AC =5,故选:A .9.如图,AD 是△ABC 的角平分线,DE ⊥AC ,垂足为E ,BF ∥AC 交ED 的延长线于点F ,若BC 恰好平分∠ABF ,AE =2BF ,给出下列五个结论:①DE =DF ;②BC =2DB ;③AD ⊥BC ;④AB =3BF ;⑤S △ADB =2S △BDF ;其中正确的结论共有()A.4个B.3个C.2个D.1个【答案】A 【分析】本题考查了全等三角形判定和性质,角平分线的性质,等腰三角形的判定和性质,由角平分线的性质和平行线的性质可证∠ACB=∠ABC,可得AC=AB,由等腰三角形的性质可得AD⊥BC,CD= BD,由“ASA”可证△CDE≌△BDF,可得S△CDE=S△BDF,CE=BF,DE=DF,即可求解.【详解】解:∵BC恰好平分∠ABF,∴∠ABC=∠CBF,∵BF∥AC,∴∠ACB=∠CBF,∴∠ACB=∠ABC,∴AC=AB,且AD是△ABC的角平分线,∴AD⊥BC,BC=2DB,故②,③正确,符合题意;在△CDE和△BDF中,∠ACB=∠CBF CD=BD∠CDE=∠BDF,∴△CDE≌△BDF ASA,∴S△CDE=S△BDF,CE=BF,DE=DF,故①正确,符合题意;∵AE=2BF,∴AC=3BF=AB,故④正确,符合题意;∵BD=CD,∴S△ADB=S△ACD,∵AE=2BF,∴S△ADB=S△ACD=3S△CDE=3S△BDF,故⑤错误,不符合题意;故选:A.10.新定义:已知三条平行直线,相邻两条平行线间的距离相等,我们把三个顶点分别在这样的三条平行线上的三角形称为“格线三角形”.如图,a∥b∥c,相邻两条平行线间的距离为m,等腰Rt△ABC为“格线三角形”,且∠BAC=90°,则△ABC的面积为()A.52m2 B.2m2 C.5m2 D.4m2【答案】A【分析】本题主要考查平行线间的距离,全等三角形的判定与性质,过点B作BE⊥直线a于点E,延长EB交直线c于点F,过点C作CD⊥直线a于点D,证明△CDA≌△AEB(AAS),得出AE=CD=2m,AD=BE=m,CF=DE=AD+AE=m+2m=3m,再根据=S四边形DEFE-S△ACD×2-S△BCF求解即可【详解】解:过点B作BE⊥直线a于点E,延长EB交直线c于点F,过点C作CD⊥直线a于点D,则∠CDA=∠AEB=90°,如图,∵a∥b∥c,相邻两条平行线间的距离为m,∴BF⊥直线c,CD=2m,BE=BF=m,∵∠CAB=90°,∠CDA=90°∴∠DCA+∠DAC=90°,∴∠DCA=∠EAB,在△CDA和△AEB中,∠DCA=∠EAB∠CDA=∠AEBAC=AB,∴△CDA≌△AEB(AAS),∴AE=CD=2m,AD=BE=m,∴CF=DE=AD+AE=m+2m=3m∴△ABC的面积=S四边形DEFE -S△ACD×2-S△BCF=3m×2m-12×2m×m×2-12×3m×m=52m2故选:A二、填空题(本大题共6小题,每小题3分,共18分)11.如图,AD=AB,∠C=∠E,∠CDE=50°,则∠ABE=.【答案】130°/130度【分析】本题考查了全等三角形的性质与判定,邻补角的定义,掌握全等三角形的性质与判定是解题的关键.证明△ADC≌△ABE AAS得出∠ADC=∠ABE,根据邻补角即可求解.【详解】解:∵在△ADC和△ABE中,∠C=∠E∠A=∠AAD=AB,∴△ADC≌△ABE AAS,∴∠ADC=∠ABE,∵∠CDE=50°,∴∠ADC=180°-50°=130°,∴∠ABE=130°.故答案为:130°.12.如图,四边形ABCD≌四边形A B C D .若∠B=90°,∠C=60°,∠D =105°,则∠A的大小为度.【答案】105【分析】本题考查了全等图形的性质和四边形内角和公式,解题的关键在于熟练掌握全等图形的性质.根据全等的性质求出∠D=∠D ,利用四边形的内角和公式求出∠A的度数即可.【详解】解:∵四边形ABCD≌四边形A B C D .∴∠D=∠D ,∵∠D =105°,∴∠D=105°,∵∠B=90°,∠C=60°,∴∠A=360°-90°-60°-105°=105°,故答案为:105.13.如图,D,E是边BC上的两点,BD=CE,∠ADB=∠AEC,现要直接用“AAS”定理来证明△ABD≌△ACE,请你再添加一个条件:.【答案】∠BAD=∠CAE【分析】在△ABE与△ACD中,已知AE=AD,∠AED=∠ADE,即已知一角及角的一边对应相等,根据“AAS”的判定方法,可以添加已知边的对角对应相等即可.本题考查了全等三角形的判定定理:AAS:两角及其中一个角的对边对应相等的两个三角形全等.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.根据已知结合图形及判定方法选择条件是正确解答本题的关键.【详解】解:可添加一个条件:∠BAD=∠CAE,使△ABD≌△ACE.理由:在△ABD与△ACE中,∠BAD=∠CAE∠AED=∠ADEBD=CE,∴△ABD≌△ACE(AAS).故答案为∠BAD=∠CAE14.已知△ABC面积为24,将△ABC沿BC的方向平移到△A B C 的位置,使B 和C重合,连接AC 交A C于D,则△C DC的面积为.【答案】12【分析】根据平移的性质可得AC=A C ,BC=B C ,AC∥A C ,证明△ADC≌△C DA ,得到AD=C D,则S△C DC =12S△ACC,再推出S△ABC=S△ACC=24,则S△C DC=12S△ACC=12.【详解】解:由平移的性质可得AC=A C ,BC=B C ,AC∥A C ,∴∠DCA=∠DA C ,∠DAC=∠DC A ,∴△ADC≌△C DA ASA,∴AD=C D,∴S△C DC =12S△ACC,∵BC=CC ,△ABC的面积为24,∴S△ABC=S△ACC=24,∴S△C DC =12S△ACC=12.故答案为:12.【点睛】本题主要考查了平移的基本性质,全等三角形的性质与判定,三角形中线的性质,熟知平移的性质是解题的关键:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.15.如图,△ABC中∠A=66°,点M、N是∠ABC与∠ACB三等分线的交点,则∠BMN的度数是.【答案】52°/52度【分析】本题考查与角平分线有关的三角形的内角和定理.过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,根据角平分线上的点到角的两边的距离相等可得NE=NG=NF,再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC,然后根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角的三等分求出∠MBC+∠MCB的度数,然后利用三角形内角和定理求出∠BMC的度数,从而得解.【详解】解:如图,过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,∵点M、N是∠ABC与∠ACB三等分线的交点,∴BN平分∠MBC,CN平分∠MCB,∴NE=NG,NF=NG,∴NE=NF,∴MN平分∠BMC,∴∠BMN=12∠BMC,∵∠A=66°,∴∠ABC+∠ACB=180°-∠A=180°-66°=114°,∴∠MBC+∠MCB=23∠ABC+∠ACB=76°,在△BMC中,∠BMC=180°-∠MBC+∠MCB=180°-76°=104°∴∠BMN=12∠BMC=52°.故答案为:52°.16.如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=15cm,AC=6cm.动点E从A点出发以3cm/s的速度沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.若点E的运动时间为t秒t>0,则当t=秒时,△DEB与△BCA全等.【答案】3或7或10【分析】本题考查全等三角形的性质,关键是要分情况讨论.分情况,当E在线段AB上,或当E在线段AB延长线上,由HL即可求解.【详解】解:∵CA⊥AB,BM⊥AB,∠CAB=∠DBE=90°,∵ED=CB,当E在线段AB上时,若BE=AC,∴Rt△DEB≌Rt△BCA(HL),∵AE=3tcm,∴BE=AB-AE=15-3tcm,∴15-3t=6,∴t=3;若BE=AB,∴Rt△DEB≌Rt△CBA(HL),∴AE=0,∴t=0(舍去),当E在线段AB延长线上时,若BE=AC,∴Rt△DEB≌Rt△BCA(HL),∵AE=3t=AB+BE=15+6=21(cm),∴t=7,若BE=AB,∴Rt△DEB≌Rt△CBA(HL),∵AE=3t=AB+BE=15+15=30(cm),∴t=10,∴当t=3或7或10秒时,△DEB与△BCA全等.故答案为:3或7或10.三、(本大题共4小题,每小题6分,共24分)17.已知:如图,AB=AE,∠1=∠2,∠C=∠D.求证:BC=ED.【答案】见解析【分析】本题考查了全等三角形的判定与性质,由∠1=∠2可得∠EAD=∠BAC,再根据条件AB=AE,∠C=∠D,可利用AAS证明△ABC≌△AED AAS,再根据全等三角形对应边相等即可得出结论.【详解】证明:∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即∠EAD=∠BAC,在△EAD和△BAC中,∠C=∠D∠BAC=∠EADAB=AE,∴△ABC≌△AED AAS,∴BC=ED.18.如图,已知AB∥CD,AB=CD.(1)求证:△ABC≌△CDA;(2)判断BC与AD的位置关系,并说明理由.【答案】(1)见解析(2)BC∥AD,理由见解析【分析】本题考查了全等三角形的判定与性质,解决本题的关键是得到△ABC≌△CDA.(1)利用SAS证明△ABC≌△CDA即可;(2)由△ABC≌△CDA,得∠BCA=∠CAD,进而可以判断BC与AD的位置关系.【详解】(1)证明:∵AB∥CD,∴∠BAC=∠ACD,在△ABC与△CDA中,AB=CD∠BAC=∠ACDAC=CA,∴△ABC≌△CDA SAS;(2)解:BC∥AD,理由如下:∵△ABC≌△CDA,∴∠BCA=∠CAD,∴BC∥AD.19.如图,已知AB=CD,AD=BC,O为AC的中点,过O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形?请把它们都写出来;(2)求证:∠MAE=∠NCF.【答案】(1)4;△ABC≌△CDA,△AMO≌△CNO,△OAE≌△OCF,△AME≌△CNF(2)证明见解析【分析】本题主要考查了全等三角形的性质与判定,找出判定三角形全等的条件是解题的关键.(1)结合已知条件,再根据全等三角形的四个判定方法,即可找出所有的全等三角形;(2)先证明△AME≌△CNF SSS,即可证明∠MAE=∠NCF.【详解】(1)解:有4对全等三角形,分别为:△ABC≌△CDA,△AMO≌△CNO,△OAE≌△OCF,△AME≌△CNF,理由如下:∵AB=CD,BC=AD=DA,AC=CA,∴△ABC≌△CDA SSS,∴∠BAC=∠DCA,即∠MAO=∠NCO,∵O为AC的中点,∴OA=OC,又∵∠AOM=∠CON,∴△AMO≌△CNO ASA,∴AM=CN,OM=ON,∵OA=OC,∠AOE=∠COF,OE=OF,∴△OAE≌△OCF SAS,∴AE=CF,∵OE=OF,OM=ON,∴OE-OM=OF-ON,即ME=NF,又∵AM=CN,∴△AME≌△CNF SSS;(2)证明:∵AB=CD,BC=AD=DA,AC=CA,∴△ABC≌△CDA SSS,∴∠BAC=∠DCA,即∠MAO=∠NCO,∵O为AC的中点,∴OA=OC,又∵∠AOM=∠CON,∴△AMO≌△CNO ASA,∴AM=CN,OM=ON,∵OA=OC,∠AOE=∠COF,OE=OF,∴△OAE≌△OCF SAS,∴AE=CF,∵OE=OF,OM=ON,∴OE-OM=OF-ON,即ME=NF,又∵AM=CN,∴△AME≌△CNF SSS,∴∠MAE=∠NCF.20.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B(1)求证:△ABC≌△CDE(2)若∠A=55°,求∠BCD的度数.【答案】(1)详见解析(2)125°【分析】本题考查了平行线性质和全等三角形的性质和判定的应用,证得△ABC≌△CDE是解题的关键.(1)根据平行线求出∠ACD=∠CDE,∠ACB=∠CED,再说明∠B=∠CDE,最后结合AC=CE运用AAS即可证明结论;(2)根据全等三角形性质得出∠A=∠E=55°,进而根据平角定义即可解答.【详解】(1)证明∶∵AC∥DE,∴∠ACD=∠CDE,∠ACB=∠CED,∵∠ACD=∠B,∴∠B=∠CDE,∵AC=CE,∴△ABC≌△CDE AAS.(2)解:∵∠A=55°,∵△ABC≌△CDE,∴∠A=∠ECD=55°,∴∠BCD=180°-∠ECD=180°-55°=125°.四、(本大题共3小题,每小题8分,共24分)21.如图,△ABC中,点D在边BC延长线上,∠ACB=106°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=53°.(1)求∠ACE的度数;(2)求证:AE平分∠CAF;(3)若AC+CD=16,AB=10,且S△ACD=24,则△ABE的面积.【答案】(1)∠ACE=37°(2)证明见解析(3)15【分析】本题主要考查了邻补角的性质、角平分线的性质与判定定理、三角形的面积等知识点,灵活运用相关知识点成为解答本题的关键.(1)根据邻补角的定义和垂直的定义可得∠ACD=74°、∠CHE=90°,进而得到∠ECH=37°,然后根据∠ACE=∠ACD-∠ECH即可解答;(2)如图:过E点分别作EM⊥BF于M,EN⊥AC与N,根据角平分线的性质定理以及角平分线的定义可得EM=EH、CE平分∠ACD、EN=EH,最后根据角平分线的判定定理即可解答;(3)根据S△ACD=S△ACE+S△CED结合已知条件可得EM=3,最后运用三角形的面积公式即可解答.【详解】(1)解:∵∠ACB=106°,∴∠ACD=180°-106°=74°,∵EH⊥BD,∴∠CHE=90°,∵∠CEH=53°,∴∠ECH=90°-53°=37°,∴∠ACE=∠ACD-∠ECH=74°-37°=37°.(2)证明:如图:过E点分别作EM⊥BF于M,EN⊥AC与N,∵BE平分∠ABC,∴EM=EH,∵∠ACE =∠ECH =37°,∴CE 平分∠ACD ,∴EN =EH ,∴EM =EN ,∴AE 平分∠CAF .(3)解:∵AC +CD =16,S △ACD =24,EM =EN =EH ,∴S △ACD =S △ACE +S △CED =12AC ⋅EN +12CD ⋅EH =12(AC +CD )⋅EM =24,即12×16⋅EM =24,解得EM =3,∵AB =10,∴S △ABE =12AB ⋅EM =15.22.问题提出:如图1,在四边形ABCD 中,∠BAD 与∠BCD 互补,∠B 与∠D 互补,AB =AD ,∠BAD =x °0<x <180 ,∠ACB =y °,数学兴趣小组在探究y 与x 的数量关系时,经历了如下过程:实验操作:(1)数学兴趣小组通过电脑软件“几何画板”进行探究,测量出部分结果如下表所示:x⋯304050607080β130y 757065α555040θ这里α=,β=,θ=.猜想证明:(2)根据表格,猜想:y 与x 之间的关系式为;数学兴趣小组发现证明此猜想的一种方法:如图2,延长CB 到E ,使BE =DC ,连接AE ,⋯,请你根据其思路将证明过程补充完整,并验证(1)中结论的正确性.应用拓广:(3)如图3,若x +y =135,AC =10,求四边形ABCD 的面积.【答案】(1)60,100,15;(2)y =90-12x ,理由见详解;(3)S 四边形ABCD =50【分析】(1)观察表格发现:x 每增加10,y 减小5,由此即可得出α、β、θ的值.(2)根据表格猜想:y =90-12x .延长CB 到E ,使BE =DC ,连接AE ,则可得△ABE ≌△ADE ,进而可得AE =AC ,∠EAB =∠CAD ,则可得∠EAC =x °.在△AEC 中,根据三角形内角和定理即可得出y 于x 之间的关系式.(3)延长CB 到E ,使BE =DC ,连接AE .由(2)得△ABE ≌△ADE ,则S △ABE =S △ADE ,进而可得S 四边形ABCD =S △AEC .由x +y =135,y =90-12x 可得x =90,y =45.则可得∠EAC =90°,∠AEC =∠ACE =45°,进而可得AE =AC =10,可得S △AEC 的值,即可得S 四边形ABCD 的值.【详解】(1)观察表格发现:x每增加10,y减小5,∴α=65-5=60,β=80+2×10=100,θ=40-3×5=15.故答案为:60,100,15,x.(2)根据表格猜想:y=90-12证明:如图2,延长CB到E,使BE=DC,连接AE,则∠ABC+∠ABE=180°,又∵∠ABC+∠D=180°,∴∠ABE=∠D,又∵AB=AD,∴△ABE≌△ADE(SAS),∴AE=AC,∠EAB=∠CAD,∴∠E=∠ACB=y°,∠EAC=∠EAB+∠BAC=∠CAD+∠BAC=∠BAD=x°.在△AEC中,∠EAC+∠E+∠ACE=180°,∴x°+2y°=180°,y=90-1x.2(3)如图,延长CB到E,使BE=DC,连接AE.由(2)得△ABE≌△ADE,∴S△ABE=S△ADE,=S△ACD+S△ABC=S△ABE+S△ABC=S△AEC,∴S四边形ABCD∵x+y=135,y=90-1x,2x=135,∴x+90-12解得x=90,y=45,∴∠EAC=90°,∠AEC=∠ACE=45°,∴AE=AC=10,×10×10=50,∴S△AEC=12∴S=50.四边形ABCD【点睛】本题考查了数字类探索规律问题,以及全等三角形的判定和性质,三角形内角和定理.熟练掌握以上知识,证明出y与x之间的关系式是解题的关键.23.(1)【问题解决】如图①,∠AOB =∠DFE =90°,OC 平分∠AOB ,点F 在OC 上,∠DFE 的两边分别与OA ,OB 交于点D ,E .当FE ⊥OB ,FD ⊥OA 时,则FD 与FE 的数量关系为;(2)【问题探究】如图②,在(1)的条件下,过点F 作两条相互垂直的射线FM ,FN ,分别交OA ,OB 于点M ,N ,判断FM 与FN 的数量关系,说明理由;(3)【迁移应用】某学校有一块四边形的空地ABCD ,如图③所示,∠DAB =∠DCB =90°,AC 是∠DAB 的平分线,AB =50m ,AD =30m ,直接写出该空地的面积.【答案】(1)FD =FE ;(2)FM =FN ,理由见详解;(3)1600m 2【分析】(1)根据“角平分线上的点到角两边的距离相等”可得FD =FE ;(2)先根据四边形内角和等于360°可得∠DFE =90°,由∠DFE =∠FMN =90°可得∠DFM =∠EFN ,再根据ASA 证明△DFM ≌△EFN ,则可得FM =FN ;(3)过C 点作CE ⊥AB 于E 点,CF ⊥AD 的延长线于F 点.由(2)得△CFD ≌△CEB ,则可得FD =EB ,S △CFD =S △CEB ,进而可得S 四边形ABCD =S 四边形AECF .证明△ACF ≌△ACE (,则可得AF =AE ,由AE =AB -BE 、AF =AD +DF 可求得BE 的长,进而可得AF 、AE 的长,由此可得S 四边形AECF 的值,即可得S 四边形ABCD 的值.【详解】(1)解:∵OC 平分∠AOB ,点F 在OC 上,且FE ⊥OB ,FD ⊥OA ,∴FD =FE .(2)解:FD =FE ,理由如下:∵FD ⊥OA ,FE ⊥OB ,∴∠FDO =∠FEO =∠FEN =90°,∵四边形DOEF 中,∠FDO =∠FEO =∠AOB =90°,∴∠DFE =360°-∠FDO -∠FEO -∠AOB =90°,∴∠DMF +∠MFE =90°,又∵FM ⊥FN ,∴∠FMN =90°,∴∠DFM =∠EFN ,在△DFM 和△EFN 中,∠FDM =∠FENFD =FE ∠DFM =∠EFN,∴△DFM ≌△EFN (ASA ),∴FM =FN .(3)解:如图,过C 点作CE ⊥AB 于E 点,CF ⊥AD 的延长线于F 点,由(2)得△CFD≌△CEB,∴FD=EB,S△CFD=S△CEB,∴S四边形ABCD =S四边形AECF,∵AC是∠DAB的平分线,∴∠DAC=∠CAB,又∵∠CFB=∠CEA=90°,AC=AC,∴△ACF≌△ACE(AAS),∴AF=AE,又∵AE=AB-BE,AF=AD+DF,∴AB-BE=AD+DF,∴50-BE=30+BE,解得BE=10,∴AF=AE=40,∴S四边形AECF=40×40=1600m2,∴S四边形ABCD=1600m2,答:该空地的面积为1600m2.【点睛】本题主要考查了角平分线的性质、全等三角形的判定和性质,熟练掌握以上知识,正确的作出辅助线是解题的关键.五、(本大题共2小题,每小题12分,共24分)24.综合探究:如题图1是一种用刻度尺画角平分线的方法,在OA、OB上分别取点C、E、D、F,使得OC=OD,OE=OF,连接CF、DE,交点为P,则射线OP为∠AOB的角平分线.【验证】(1)试说明OP平分∠AOB,且PE=PF;【应用】(2)如题图2,若C、E、D、F分别为OA、OB上的点,且OC=OD,CF⊥OA,DE⊥OB,试用(1)中的原理说明OP平分∠AOB;【猜想】(3)如题图3,P是∠AOB角平分线上一点,C、D分别为OA、OB上的点,且PC=PD,请补全图形,并直接写出∠PCO与∠PDO的数量关系.【答案】(1)见解析;(2)见解析;(3)补全图形见解析,∠PCO=∠PDO或∠PCO+∠PDO=180°【分析】本题是三角形综合题目,考查了全等三角形的判定与性质、角平分线的性质等知识,本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键,属于中考常考题型.(1)先证明△DOE≌△COF(SAS),得∠PEC=∠PFD,再证△CPE≌△DPF(AAS),得PE=PF,然后证△OPE≌△OPF(SSS),得∠POE=∠POF,即可得出结论;(2)先证明△OCF≌△ODE(ASA),可得OF=OE,由(1)可得OP平分∠AOB;(3)过点P分别作PM⊥OA于M,PN⊥OB于N,分两种情况进行求解即可.【详解】解:(1)∵OC=OD,∠DOE=∠COF,OE=OF,∴CE=DF,△DOE≌△COF(SAS),∴∠PEC=∠PFD,∵∠CPE=∠DPF,CE=DF,∴△CPE≌△DPF(AAS),∴PE=PF,∵OE=OF,PE=PF,OP=OP,∴△OPE≌△OPF(SSS),∴∠POE=∠POF,即∠POA=∠POB,∴射线OP平分∠AOB;(2)∵CF⊥OA,DE⊥OB,∴∠OCF=∠ODE=90°,∴∠COF=∠DOE,OC=OD,∴△OCF≌△ODE(ASA),∴OF=OE,由(1)可得OP平分∠AOB;(3)补全图形如下,过点P分别作PM⊥OA于M,PN⊥OB于N,∵OP是∠AOB的平分线,∴PM=PN,∠PMC=∠PND=90°,当PC=PD1时,在Rt△PMC和Rt△PND1中,PC=PD1,PM=PN∴Rt△PMC≌Rt△PND1(HL),∴∠PCO=∠PD1O;当PC=PD2时,同理得Rt△PMC≌Rt△PND2HL,∴∠PCM=∠PD2N;∵∠PD2N+∠PD2O=180°,∴∠PCO+∠PD2O=180°,综上所述,∠PCO与∠PDO的数量关系为∠PCO=∠PDO或∠PCO+∠PDO=180°;25.【模型呈现】(1)如图1,∠BAD=90°,AB=AD,BC⊥CA于点C,DE⊥AE于点E.求证:BC=AE.【模型应用】(2)如图2,EA⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形ABCDE的面积.【深入探究】(3)如图3,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC、DE,且BC⊥AF于点F,DE与直线AF交于点G.①求证DG=GE;②若BC=21,AF=12,求△ADG的面积.【答案】(1)见解析;(2)50;(3)①见解析;63【分析】(1)证明△ABC≌△DAE AAS,即可得证;(2)同(1)法得到△AEP≌△BAG,△CBG≌△DCH,分割法求出图形面积即可;(3)①过点D作DP⊥AG于P,过点E作EQ⊥AG交AG的延长线于Q,易证△AFB≌△DP A,△AFC ≌△EQA,得到DP=AF,EQ=AF,再证明△DPG≌△EQG AAS,即可得出结论;②根据全等三角形的性质,求出AG的长,进而利用面积公式进行求解即可.【详解】解:(1)证明:∵∠BAD=90°,∴∠BAC+∠DAE=90°,∵BC⊥CA,DE⊥AE,∴∠ACB=∠DEA=90°,∴∠BAC+∠ABC=90°,∴∠ABC=∠DAE,在△ABC和△DAE中,∠ACB=∠DEA∠ABC=∠DAEBA=AD∴△ABC≌△DAE AAS,∴BC=AE.(2)由模型呈现可知,△AEP≌△BAG,△CBG≌△DCH,∴AP=BG=3,AG=EP=6,CG=DH=4,CH=BG=3,则S实线围成的图形=12×4+6×3+6+4+3-12×3×6-12×3×6-12×3×4-12×3×4=50.(3)①过点D作DP⊥AG于P,过点E作EQ⊥AG交AG的延长线于Q.图3由【模型呈现】可知,△AFB≌△DP A,△AFC≌△EQA,∴DP=AF,EQ=AF∴DP=EQ,∵DP⊥AG,EQ⊥AG∴∠DPG=∠EQG=90°,在△DPG和△EQG中,∠DPG=∠EQG∠DGP=∠EGQDP=EQ∴△DPG≌△EQG AAS,∴DG=GE.②由①可知,BF=AP,FC=AQ,∴BC=BF+FC=AP+AQ,∵BC=21,∴AP+AQ=21,∴AP+AP+PG+GQ=21,由①△DPG≌△EQG得∴PG=GQ,∴AP+AP+PG+PG=21,∴AP+PG=10.5,∴AG=10.5,∴S△ADG=1×10.5×12=63.2。
初二全等三角形经典练习题及答案

初二全等三角形经典练习题及答案一、选择题1. 设ABC和DEF是两个全等三角形,已知∠A=∠D=63°,∠B=∠E=75°,则∠C=_____。
A. 63°B. 75°C. 105°D. 123°2. 若△ABC≌△PQR,已知AB=7.5cm,BC=9cm,PR=6cm,令P是B的重点,则AP的长度是_____。
A. 6.75cmB. 5.25cmC. 3.75cmD. 3cm3. 在△ABC和△PQR中,已知∠A=80°,∠C=60°,∠Q=80°。
如果BC=PQ=4cm,则BQ的长度是_____。
A. 4cmB. 5cmC. 6cmD. 8cm4. 设ABC和DEF是两个全等三角形,已知AB=DE=12cm,BC=EF=16cm,AC=DF=20cm,则△ABC和△DEF的周长之比是_____。
A. 3:4B. 4:3C. 5:6D. 6:5二、填空题1. 在△ABC中,已知AB=AC,∠B=30°,BD为边AB的中线,DE⊥AC交BC于点E,则∠DEB=_____。
2. 在△ABC与△DEF中,AB=DE,AC=DF,∠A=∠D,若AD平行于BF,则BC平行于_____。
3. 在△ABC和△DEF中,BC=EF,AB=2DE,∠B=∠E=90°,∠C=∠F=60°,则BC的长度是_____。
4. 在△ABC中,AB=AC,∠A=40°,点D是边BC的中点,则∠ACD的度数是_____。
三、综合题1. 在△ABC中,AB=AC,∠B=40°。
点D和点E分别在线段AB和AC上,且AD=CE。
若∠CDE=80°,求∠DBE的度数。
解答:已知∠B=40°,AB=AC,AD=CE,且∠CDE=80°。
利用全等三角形的性质,我们可以得到以下等式:∠BAC = ∠CAB (等腰三角形的性质)∠ADE = 180° - ∠D = 180° - 80° = 100°∠AED = 180° - ∠A - ∠ADE = 180° - 40° - 100° = 40°由∠ADE = ∠AED,得到△ADE是一个等腰三角形。
人教版八年级数学上册 第12章 全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
专题 全等三角形压轴题(30题)(原卷版)

八年级上册数学《第十二章全等三角形》专题全等三角形压轴题训练(30题)1.(2022秋•忠县期末)在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.2.如图,△ABC中,AB=AC,D为AC边上一点,E为AB延长线上一点,且CD=BE,DE与BC相交于点F.(1)求证:DF=EF.=5,求EG的长.(2)过点F作FG⊥DE,交线段CE于点G,若CE⊥AC,CD=4,S△EFG3.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点P为BC边上的一个动点,连接AP,以AP为直角边,A为直角顶点,在AP右侧作等腰直角三角形PAD,连接CD.(1)当点P在线段BC上时(不与点B重合),求证:△BAP≌△CAD;(2)当点P在线段BC的延长线上时(如图2),试猜想线段BP和CD的数量关系与位置关系分别是什么?请给予证明.4.在△ABC中,∠ABC=90°.点G在直线BC上,点E在直线AB上,且AG与CE相交于点F,过点A 作边AB的垂线AD,且CD∥AG,EB=AD,AE=BC.(1)如图①,当点E在△ABC的边AB上时,求∠DCE的度数;(2)如图②,当点E在线段BA的延长线上时,求证:AB=BG.5.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.(1)求证:AB=BD;(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.6.(2023春•市南区期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.7.(2022秋•新市区校级期中)已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.求证:(1)AD=AE=EC.(2)BA+BC=2BF.8.(2023春•余江区期末)如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.(1)找出图中的全等三角形,并说明理由;(2)当AD=AB=4cm,则AE的长度为 cm.(3)猜想AE与BD的位置关系,并说明理由.9.已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE(1)如图1,当AE平分∠BAC时,EH⊥AB于H,△EHB的周长为10m,求AB的长;(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.10.在△ABC中,∠ABC=45°,AM⊥MB,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,点D在线段AM上,且DM=CM.求证:△BDM≌△ACM;(2)如图②,在(1)的条件下,点E是△ABC外一点,且满足EC=AC,连接ED并延长交BC于点F,且F为线段BC的中点,求证:∠BDF=∠CEF.11.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.12.(2022秋•渝北区校级期末)已在等腰Rt△ABC中,∠ABC=90°,AB=CB,D为直线AB上一点,连接CD,过点C作CE⊥CD,且CE=CD,连接DE,交AC于点F.(1)如图1,当点D在线段AB上,且∠DCB=30°时,请探究DF,EF,CF之间的数量关系,并说明理由;(2)如图2,在(1)的条件下,在FC上任取一点G,连接DG,作射线GP使∠DGP=60°,交∠DFG 的平分线于点Q,求证:FD+FG=FQ.13.(2022春•运城期末)综合与探究如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.(1)求证:△ACE≌△ABD.(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.14.(2022春•沙坪坝区校级期中)如图,在△ABC中,∠ABC、∠ACB的平分线交于点D,延长BD交AC 于E,G、F分别在BD、BC上,连接DF、GF,其中∠A=2∠BDF,GD=DE.(1)当∠A=80°时,求∠EDC的度数;(2)求证:CF=FG+CE.15.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线交BC于点D,过D作DE⊥BA于点E,点F在AC上,且BD=DF.(1)求证:AC=AE;(2)求证:∠BAC+∠FDB=180°;(3)若AB=9.5,AF=1.5,求线段BE的长.16.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接DE,CE.(1)如图,当点D在BC延长线上移动时,求证:BD=CE.(2)设∠BAC=α,∠DCE=β.①当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由.②当点D分别在线段BC上、线段BC的反向延长线上移动时,α与β之间有什么数量关系?请说明理由.17.(2022春•南海区校级月考)如图,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD.以AD为直角边且在AD的上方作等腰直角三角形ADF.(1)若AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),试探讨CF与BD的数量关系和位置关系;②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应的图形并说明理由;(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BD 的位置关系.18.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)△ABC≌△ADE吗?为什么?(2)求∠FAE的度数;(3)延长BF到G,使得FG=FB,试说明CD=2BF+DE.19.Rt△ABC中,∠C=90°,点D在直线AC上,点E在直线AB上,∠ADE=∠ABC.(1)如图1,当点D、E分别在边AC、AB上时,求证:DE⊥AB;(2)如图2,当点D在CA延长线上,点E在BA延长线上时,DE、BC延长线交于点F,作∠EAC的角平分线AG交DF于点G,求证:∠D+2∠DGA=90°;(3)如图3,在(2)的条件下,连接BG交CD于点H,若∠DGH=∠DHG,∠AGB=3∠CBH,求∠DGA的度数.20.(2023春•新市区期末)在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明;(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.21.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F 不重合),并说明理由.22.(1)如图1,∠B=∠D=90°,E是BD的中点,AE平分∠BAC,求证:CE平分∠ACD.(2)如图2,AM∥CN,∠BAC和∠ACD的平分线并于点E,过点E作BD⊥AM,分别交AM、CN于B、D,请猜想AB、CD、AC三者之间的数量关系,请直接写出结论,不要求证明.(3)如图3,AM∥CN,∠BAC和∠ACD的平分线交于点E,过点E作不垂直于AM的线段BD,分别交AM、CN于B、D点,且B、D两点都在AC的同侧,(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.23.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.24.(2023春•沙坪坝区校级期中)如图,在△ABC和△DCE中,∠ACB=90°,CA=CB,∠DCE=90°,CD=CE.= 32 ;(1)如图1,当点D在BC上时,CB=10,AE=4,则S四边形ABDE(2)如图2,当B、C、E三点共线时,D在AC上,连接BD、AE,F是AD的中点,过点A作AG∥BD,交BF的延长线于点G,求证:AG=AE且AG⊥AE;(3)如图3,B、C、E三点共线,且∠DBE=15°,将线段AE绕点A以每秒10°的速度逆时针旋转,同时线段BE绕点E以每秒20°的速度顺时针旋转180°后立即以相同速度回转,设转动时间为t秒,当BE回到出发时的位置时同时停止旋转,则在转动过程中.当BE和AE互相平行或者垂直时,请直接写出此时t的值.25.如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(1)延长MP交CN于点E(如图2),①求证:△BPM≌△CPE;②求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由.26.已知∠BAM+∠MDC=180°,AB=AM,DC=DM,连接BC,N为BC的中点.(1)①定理“等边对等角”即:对于任意△ABC若满足AB=AC,则∠ABC=∠ ;②如图1若A、M、D共线,若∠BAM=70°,求∠NDC的大小;(2)如图2,A、M、D不共线时,求∠ANB+∠DNC的值.27.(2023春•将乐县校级期中)如图,等腰三角形ABC和等腰三角形ADE,其中AB=AC,AD=AE.(1)如图1,若∠BAC=90°,当C、D、E共线时,AD的延长线AF⊥BC交BC于点F,则∠ACE= ;(2)如图2,连接CD、BE,延长ED交BC于点F,若点F是BC的中点,∠BAC=∠DAE,证明:AD ⊥CD;(3)如图3,延长DC到点M,连接BM,使得∠ABM+∠ACM=180°,延长ED、BM交于点N,连接AN,若∠BAC=2∠NAD,请写出∠ADM、∠DAE之间的数量关系,并写出证明过程.28.在平面直角坐标系中,点A的坐标为(3,3),AB=BC,AB⊥BC,点B在x轴上.(1)如图1,AC交x轴于点D,若∠DBC=10°,则∠ADB= ;(2)如图1,若点B在x轴正半轴上,点C(1,﹣1),求点B坐标;(3)如图2,若点B在x轴负半轴上,AE⊥x轴于点E,AF⊥y轴于点F,∠BFM=45°,MF交直线AE于点M,若点B(﹣1,0),BM=5,求EM的长.29.(2023春•贵港期末)如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,4),A (4,4),过C点作∠ECF分别交线段AB、OB于E、F两点(1)若OF+BE=AB,求证:CF=CE.(2)如图(2),且∠ECF =45°,S △ECF =6,求S △BEF 的值.30.(1)阅读理解:如图①,在△ABC 中,若AB =10,AC =6,求BC 边上的中线AD 的取值范围.解决此问题可以用如下方法:延长AD 到点E 使DE =AD ,再连接BE (或将△ACD 绕着点D 逆时针旋转180°得到△EBD ),把AB 、AC ,2AD 集中在△ABE 中,利用三角形三边的关系即可判断.中线AD 的取值范围是 ;(2)问题解决:如图②,在△ABC 中,D 是BC 边上的中点,DE ⊥DF 于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,求证:BE +CF >EF ;(3)问题拓展:如图③,在四边形ABCD 中,∠B +∠D =180°,CB =CD ,∠BCD =140°,以C 为顶点作一个70°角,角的两边分别交AB ,AD 于E 、F 两点,连接EF ,探索线段BE ,DF ,EF 之间的数量关系,并加以证明.。
专题05全等三角形压轴题训练 期中专题复习(含解析)2023年秋人教版数学八年级上册

A .2B .4.如图, 中,分别为 、 上的动点,那么2m ABC V AC =BD BCA .B 7.如图,点P 为定角在绕点P 旋转的过程中,其两边分别与论:①恒成立;A .3B .28.如图,在中,于点.下列结论187∠MPN ∠PM PN =ABC V A ∠OF AB ⊥F9.已知:中,,线右侧作,且的值为 .10.如图,在直角三角形,过点作①;②11.如图,已知四边形,连接,则的面积等于ABC V 90ACB ∠=︒AC AE AD ⊥AE AD =ADB AEMS S △△O O OF AD ⊥45BOD ∠=︒::ACD ABD S S CD BD =△△ABCD 5AD =ABD △12.如图,在中,,延长线于点,若,则13.如图,在中,上一点,连接、,且满足为 .14.已知中,与交于点(1)如图,求证:(2)如图,连接,求证:(3)如图,若,ABC V 10.5BAC ∠=︒AD BC M BM BA AC =+ABC V AB AE CE ABC V BE CD 12OA 360BAC ∠=︒15.如图,在中,(1)如图1,若.①求的度数;②试探究线段与、(2)如图2,点,分别在.求证:.16.我们现给出如下结论:“直角三角形斜边上的中线等于斜边的一半如图1所示,在中,请结合上述结论解决如下问题:已知:P 是边上的一动点垂线,垂是分别为点E 点F ,ABC V 60A ∠=︒BDF ∠BC BF N M DN DE =CM MN CE =+Rt ABC △ABC V AB(1)如图2所示,当点P 与点Q 重合时,与的位置关系是____________,与的数量关系是____________.(2)如图3所示,当点P 在线段上不与点Q 重合时,试判断与的数量关系,并给与证明.(3)如图4所示,当点P 在线段的延长线上时,此时(2)中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由.17.某校八年级(1)班数学兴趣小组在一次活动中进行了试验探究活动,请你和他们一起活动吧.【探究与发现】(1)如图1,是的中线,延长至点E ,使,连接,写出图中全等的两个三角形:__________;【理解与运用】(2)如图2,是的中线,若,,设,求的取值范围;(3)如图3,是的中线,,点Q 在的延长线上,,求证:.18.如图,在中,,是的角平分线交于点,过作于点,点在上,且.(1)求证:;(2)求证:;AE BF QE QF AB QE QF BA AD ABC V AD ED AD =BE EP DEF V 5EF =3DE =EP x =x AD ABC V BAC ACB ∠=∠BC QC AB =2AQ AD =ABC ∆90C ∠=︒AD BAC ∠BC D D DE BA ⊥E F AC BD DF =AC AE =180BAC FDB ∠+∠=︒(3)若,,求线段的长.19.如图,在中,、的平分线交于点D ,延长交于E ,G 、F 分别在上,连接,其中,.(1)当时,求的度数;(2)求证:.20.(1)【初步探索】如图①,在四边形中,,.E 、F 分别是、上的点.且.探究图中、、之间的数量关系.小王同学探究此问题的方法:延长到点G ,使.连接.先证明,再证,可得出结论.他的结论应是_____.(2)【灵活运用】如图②,在四边形中,,,E 、F 分别是、上的点,且,上述结论是否仍然成立?请说明理由.(3)【延伸拓展】如图③,在四边形中,,.若点E 在的延长线上,点F 在的延长线上,仍然满足,请写出与的数量关系,并给出证明过程.21.问题引入:课外兴趣小组活动时,老师提出这样的问题:如图1,在中,,,求边上的中线的取值范围.小华在组内经过合作交流,得到了如下的解决方法:延长到,使得,再连接,把集中在中,利用三角形的三边关系可得,则.从中他总结出:解题时,条件中若出现“中线”“中点”等条件,可以考虑将中线加倍延长,构造全等三角形,把分散的条件和需求证的结论集中到同一个三角形中.9.5AB = 1.5AF =BE ABC V ABC ∠ACB ∠BD AC BD BC 、DF GF 、2A BDF ∠=∠GD DE =80A ∠=︒FDC ∠CF FG CE =+ABCD BA BC =90A C ∠=∠=︒AD CD EF AE CF =+CBF ∠EBF ∠ABE ∠EA AG CF =BG BCF BAG V V ≌BEF BEG ≌△△ABCD BA BC =180A C ∠+∠=︒AD CD EF AE CF =+ABCD 180BAD BCD ∠+∠=︒BA BC =DA DC EF AE CF =+EBF ∠ABC ∠ABC V 5AB =3AC =BC AD E DE AD =BE ,,2AB AC AD ABE V 28AE <<14AD <<参考答案:【分析】过点作于,如图,根据角平分线的性质得到,则可根据“”判断,所以,然后利用得到.【详解】解:过点作于,如图,是的角平分线,,,,在和中,,,,,.故选:A .【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了直角三角形全等的判定与性质.利用角平分线性质构造全等三角形是解题关键.3.C【分析】根据题意和图形,作出合适的辅助线,然后根据直角三角形的面积和梯形的面积,可以计算出凸五边形ABCDE 的面积.【详解】解:作EG ⊥AC 于点G ,作BF ⊥AC 于点F ,作DH ⊥AC 于点H ,D DH AC ⊥H DF DH =HL Rt DFE Rt DHG ≅V V DEF DGH ∠=∠180AED DEF ∠+∠=︒180AED AGD ∠+∠=︒D DH AC ⊥H AD Q ABC V DF AB ⊥DH AC ⊥DF DH ∴=Rt DFE △Rt DHG V DE DG DF DH=⎧⎨=⎩(HL)Rt DFE Rt DHG ∴≅V V DEF DGH ∴∠=∠180AED DEF ∠+∠=︒Q 180AED AGD ∴∠+∠=︒则∠EGA=∠AFB=∠BFC ∴∠EAG+∠AEG=90°,∵AB⊥AE,BC⊥CD,∴∠EAB=∠BCD=90°,∴∠EAG+∠FAB=90°,【点睛】此题考查了角平分线的性质定理最短路线问题,解题的关键是找到使5.A∴,∵,∴,∴,∴,在和中,,∴,∴,∴.故选:A .【点睛】本题考查了全等三角形的性质和判定,坐标与图形性质,关键是推出AM =BN 和推出.6.B【分析】证明得出,证明得出,进而即可求解.【详解】解:如图,在上截取,连接平分,平分,4OM ON CN CM ====90ACB ∠=︒ACB MON ∠∠=9090MCA ACN BCN ACN ∠∠∠∠=︒-=︒-,ACM BCN ∠∠=ACM V BCN V ACM BCN CM CNCMA CNB ∠=∠⎧⎪=⎨⎪∠=∠⎩ACM BCN ASA V V ≌()AM BN =OA OB+OA ON BN=++OA ON AM=++ON OM=+44=+8=OA OB OM ON +=+BOE BOH V V ≌60EOH BOH ∠=∠=︒COD COH V V ≌CD CH =BC BH BE =OHBD Q ABC ∠CE ACB ∠【分析】作于E ,于F ,根据平分可知,结合即可证明.根据图中各角的数量关系可得,进而还可证明;利用全等三角形的性质可以得到多组相等的边,由此判断①的正误.根据全等三角形的性质得到,据此可得定值,还可判断③的正误;【详解】解:如图,作于E ,于F .∵,∴,∵,∴,∴,∵平分,于E ,于F ,∴.在和中,∴,∴.在和中,∴,∴,故①正确.∴定值,故③正确.∴定值,故②正确.PE OA ⊥PF OB ⊥OP AOB ∠PE PF =OP OP =POE POF V V ≌MPE NPF PEM PFN ∠∠∠∠==、PEM PFN V V ≌PEM PNF S S =V V PMON PEOF S S ==四边形四边形PE OA ⊥PF OB ⊥90PEO PFO ∠∠==︒180EPF AOB ∠∠+=︒180MPN AOB ∠∠+=︒EPF MPN ∠∠=EPM FPN ∠∠=OP AOB ∠PE OA ⊥PF OB ⊥PE PF =POE V POF V PE PF OP OP ==,()Rt Rt HL POE POF V V ≌OE OF =PEM V PFN V MPE NPF PE PF PEM PFN ∠∠∠∠===,,()ASA PEM PFN V V ≌PEM PNF EM NF PM PN S S ===V V ,,PMON PEOF S S ==四边形四边形2OM ON OE ME OF NF OE +=++-==∵平分,,∴,∴故结论①正确;∵,BD ABC ∠OF AB ⊥OG OF OG =11:2:2BOC BOE S S BC OG BE OF =⨯⨯V V 60A ∠=︒∴,∴,又∵,∴,故结论②错误;在上截取,连接,在和中,,∴,∴,,∵,,∴,∴在和中,,∴,∴,∴,故结论③正确;∵,,∴,,9050BOF OBA ∠=︒-∠=︒605010EOF BOE BOF ∠=∠-∠=︒-︒=︒806020ABC A ∠-∠=︒-︒=︒EOF ABC A ∠∠∠≠-BC BM BE =OM BOE △BOM V BE BM OBE OBM OB OB =⎧⎪∠=∠⎨⎪=⎩(SAS)BOE BOM V V ≌OE OM =60BOM BOE ∠=∠=︒60OD B E C O ︒==∠∠18060COM BOE BOM ∠=︒-∠-∠=︒COD COM ∠=∠COD △COM V OCD OCM OC OCCOD COM ∠=∠⎧⎪=⎨⎪∠=∠⎩(ASA)COD COM V V ≌CD CM =BE CD BM CM BC +=+=BOE BOM V V ≌COD COM V V ≌BOE BOM S S =V V COD COM S S =V V∴,∴,∵,∴,即:∴,90ACB AGE CGE ∠=∠=∠=︒90DAC ADC ∠+∠=°AE AD ⊥90DAE ∠=︒90DAC GAE ∠+∠=ADC GAE ∠=∠∴,∴,∵,∴,即:,∴,在和中,90ACB AHE ∠=∠=︒90DAC ADC ∠+∠=°AD AE ⊥90DAE ∠=︒90DAC HAE ∠+∠=︒ADC HAE ∠=∠ADC △EAH V∴,又∵,,∴,∴,,∴,∴,∴,∴,,∴,∵,,∴,故③正确;∵,,∴,∴,∴,∵,,∴,∴,又∵,,∴,∴,∴,故②错误;90AOG AOH ∠=∠=︒HAO GAO ∠=∠AO AO =(ASA)AOH AOG ≌V V AG AH =OG OH =18045BOH BOD DOF ∠=︒-∠-∠=︒45BOH BOD ∠=∠=︒(ASA)BOD BOH ≌V V BD BH =OH OD =AB AH BH AG BD =+=+3BD =8AG =11AB =135BOA BOH AOH ∠=∠+∠=︒135BOF BOD DOF ∠=∠+∠=︒BOA BOF ∠=∠(ASA)BOA BOF ≌V V AO OF =OH OD =OG OH =OD OG =AD AO OD OF OG =+=+90OGE F ∠=︒-∠90BEC EBC ∠=︒-∠OGE BEC ∠≠∠OE OG ≠AD OF OG OF OE =+≠+∴,,∴,∴,即∵,,,∴,∴,5AE AD ==EAD ADC ∠=∠CD AE ∥BAC CAD CAD EAD ∠+∠=∠+∠BAD ∠AB AC =BAD CAE ∠=∠AD AE =()SAS ABD ACE △≌△112555222ABD ACE S S AE AD ==⨯=⨯⨯=V V∵,∴.∴.∵,是∴BE BA AE =+BM BA =BE BM =AEM BME ∠=∠10.5BAC ∠=︒AD BAC ∠12DAC BAD BAC ∠=∠=∠=∵,∴∵,∴∴90ADB ∠=︒180ADO ∠=︒-AD AD =OD ≌ADO ADE V V OAD EAD ∠=∠平分,平分,,,点在的平分线上,,平分,BE Q ABC ∠CD ∠OM ON ∴=ON OK =OM OK ∴=∴O BAC ∠60BAC ∠=︒Q 1902BOC BAC ︒∴∠=+∠180BOD COE ︒∴∠=∠=-OF Q BOC ∠,∵,∴∴∵FBD GBD ∠=∠BD BD=()FBD GBD SAS ≌△△BDF BDG∠=∠60BDF ∠=︒120BDC ∠=︒∵平分,∴,在和中,∴,CD ACB ∠ACD BCD ∠=∠ECD V HCD V CH CE =()ECD HCD SAS ≌△△∵,∴,∴,∴.【点睛】本题考查了全等三角形的判定与性质,角平分线的定义,三角形内角和与外角的性质等,添加适当的辅助线是解题的关键.16.(1);(2),证明见解析(3)成立,证明见解析【分析】(1)根据得到,得到、,根据内错角相等两直线平行,得到;(2)延长交于,求出,根据全等三角形的性质得出,根据直角三角形斜边上中点性质得出即可;(3)延长交于,求出,根据全等三角形的性质得出,根据直角三角形斜边上中点性质得出即可【详解】(1)如图1,当点与点重合时,与的位置关系是,与的数量关系是,理由:为的中点,,,,DM DM =()NDM HDM SAS ≌△△MN MH =CM MN CE =+AE BF ∥QE QF=QE QF =AAS AEQ BFQ ≌△△AEQ BFQ ∠=∠QE QF =AE BF ∥EQ BF D AEQ BDQ ≌V V EQ QD =EQ FB D AEQ BDQ ≌V V EQ QD =P Q AE BF AE BF ∥QE QF AE BF =Q Q AB AQ BQ ∴=AE CQ ⊥Q BF CQ ⊥,,在和中,,,故答案为:;;(2)证明:延长交于,,(3)当点在线段延长线上时,此时()中结论成立证明:延长交的延长于∵,∴∴AE BF ∥90AEQ BFQ ∠=∠=︒AEQ △V BFQ AQE BQF AEQ BFQ AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS AEQ BFQ ∴V V ≌QE QF ∴=AE BF ∥QE QF =QE QF=EQ BF D ,AE CP BF CP⊥⊥Q AE ∴BF∥AEQ BDQ∴∠=∠AQE BQD AEQ BDQ AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩AEQ BDQ∴V V ≌EQ DQ∴=90BFE ∠=︒Q QE QF∴=P BA 2EQ FB DAE BF ∥AEQ BDQ∠=∠【点睛】本题考查了三角形全等的判定方法:,平行线的性质,根据点位置不同,画出正确的图形,找到的条件是解决本题的关键.17.(1)≌(2)(3)证明见解析【分析】(1)≌,根据全等三角形的判定即可得到.(2)根据(1)中的辅助线作法,延长至点Q ,使,再证明≌,得到,再在中,利用三边关系进行计算即可.(3)根据(1)中辅助线作法,延长至点M ,使,证明≌,得到,,再证明≌,根据全等三角形的性质即可得证.【详解】(1)是的中线,,在和中,,≌.AQE BQD AEQ BDQAQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩Q AEQ BDQ∴V V ≌EQ QF∴=90BFE ∠=︒Q QE QF∴=AAS P AAS ADC △EDB△14x <<ADC △EDB △SAS EP PQ PE =PDE △PFQ △DE FQ =FQE △AD MD AD =BMD V CAD V BM CA =DBM DCA ∠=∠ACQ V MBA △AD Q ABC V BD DC ∴=ADC △EDB △DC BD ADC EDB AD ED =⎧⎪∠=∠⎨⎪=⎩∴ADC △EDB △()SAS(2)如图2,延长至点Q ,使,连接,是的中线,在和中,,≌,,,在中,即,∴.(3)如图3,延长至点M ,使,连接,∴,∵是的中线,∴,在和中,,EP PQ PE =FQ EP Q DEF V PD PF∴=PDE △PFQ △PD PF DPE FPQ PE PQ =⎧⎪∠=∠⎨⎪=⎩PDE ∴V PFQ △()SAS 3DE FQ ∴==PE PQ x ==FQE △EF FQ QE EF FQ-<<+53253x -<<+14x <<AD MD AD =BM 2AM AD =AD ABC V BD CD =BMD V CAD V MD AD BDM CDA BD CD =⎧⎪∠=∠⎨⎪=⎩∴≌,∴,,∵,,,∴,在和中,,∴≌,∴.【点睛】本题考查三角形全等的证明,三角形全等的证明方法以及倍长中线的辅助线作法是本题关键,准确的作出辅助线是本题难点.18.(1)见解析(2)见解析(3)4【分析】(1)证,即可得出结论;(2)设,在上截取,连接,证,得,,再证,得,然后证,即可得出结论;(3)求出,由全等三角形的性质得,即可求解.【详解】(1)证明:平分,,,,,,在和中,BMD V CAD V ()SAS BM CA =DBM DCA ∠=∠BAC ACB ∠=∠ACQ BAC ABC ∠=∠+∠MBA DBM ABC ∠=∠+∠ACQ MBA ∠=∠ACQ V MBA △CA BM ACQ MBA QC AB =⎧⎪∠=∠⎨⎪=⎩ACQ V MBA △()SAS 2AQ AM AD ==(AAS)ACD AED V V ≌DAC DAE α∠=∠=AB AM AF =MD (SAS)FAD MAD V V ≌FD MD =ADF ADM ∠=∠Rt Rt (HL)MDE BDE V V ≌DME B ∠=∠909021802FDB αα∠=︒+︒-=︒-8MB AB AM =-=ME BE =AD Q BAC ∠DAC DAE ∴∠=∠DE BA ⊥Q 90DEA DEB ∴∠=∠=︒90C ∠=︒Q 90C DEA ∴∠=∠=︒ACD V AED V,,;(2)证明:设,,,,则,在上截取,连接,如图所示:在和中,,,,,,,在和中,,,,C DEA DAC DAE AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)ACD AED ∴△≌△AC AE ∴=DAC DAE α∠=∠=90C DEA ∠=∠=︒Q 90ADC α∴∠=︒-90ADE α∠=︒-90FDB FCD DFC DFC ∠=∠+∠=︒+∠AB AM AF =MD FAD V MAD V AF AM DAF DAM AD AD =⎧⎪∠=∠⎨⎪=⎩(SAS)FAD MAD ∴V V ≌FD MD ∴=ADF ADM ∠=∠BD DF =Q BD MD ∴=Rt MDE △Rt BDE △MD BD DE DE=⎧⎨=⎩Rt Rt (HL)MDE BDE ∴V V ≌DME B ∴∠=∠DAC DAE α∠=∠=Q平分,,在和中,CD Q ACB ∠DCE DCH ∴∠=∠DCE △DCH V CE CH =⎧在和中,BCF △BAG △,∴,∴,又∵,在和中,,∴,∴,故答案为:;(2)仍成立,理由如下:延长到点G ,使,连接,∵,,∴,在和中,,∴,∴,又∵,90BC BA C BAG CF AG =⎧⎪∠=∠=︒⎨⎪=⎩()SAS BCF BAG V V ≌BF BG =GE GA AE AE CF EF =+=+=BEF △BEG V BF BG BE BE EF GE =⎧⎪=⎨⎪=⎩()SSS BEF BEG V V ≌EBF EBG ABE ABG ABE CBF ∠=∠=∠+∠=∠+∠EBF CBF ABE ∠=∠+∠EA AG CF =BG 180BAE C ∠+∠=︒180BAE BAG ∠+∠=︒C BAG ∠=∠BCF △BAG △BC BA C BAG CF AG =⎧⎪∠=∠⎨⎪=⎩()SAS BCF BAG V V ≌BF BG =GE GA AE AE CF EF =+=+=∵∴,在和中,,180BAD BCD ∠+∠=BAD BCF ∠=∠BCF △BAG △BC AB BAD BCF CF AG =⎧⎪∠=∠⎨⎪=⎩D BC∵是中点,∴,在和中,,∴,∴,在中,∴;即:,(2)如图,延长至点,使得,连接,则,∵是中点,∴,在和中,,∴,∴,,,∵,,,∴,在和中,BD DC =ACD V EBD △BD CD ADC EDB AD ED =⎧⎪∠=∠⎨⎪=⎩()SAS ACD EBD V V ≌AC EB =ABE V 2AB EB AE AD +>=2AB AC AD +>AE F EF AE =DF 2AF EF AE AE =+=E BD DE BE =EDF V EBA △DE BE DEF BEA EF EA =⎧⎪∠=∠⎨⎪=⎩()SAS EDF EBA V V ≌DF AB CD ==B EDF ∠=∠F EAB ∠=∠CDA B BAD ∠=∠+∠ADF BDA EDF ∠=∠+∠BDA BAD ∠=∠ADC ADF ∠=∠AFD △ACD V同(2)理可证:∴,,∵,∴∵,∴(SAS AMO DMH ≌V V OA DH OB ==H AOM ∠=∠∠90AOB COD ∠=∠=︒BOC AOB COD AOD ∠=∠+∠-∠=180HDO H HDO ∠=︒-∠-∠180180HDO AOM HDO ∠=︒-∠-∠=等三角形是解题的关键.。
人教版八年级上册数学课堂作业同步期中复习:全等三角形训练(一)

人教版八年级上册数学课堂作业同步期中复习:全等三角形训练(一)1.已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.2.如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从C出发以每秒2个单位的速度在线段CA上向点A运动,连接AD、DE,设D、E两点运动时间为t秒(0<t<4)(1)运动秒时,AE=DC;(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;(3)若△ABD≌△DCE,∠BAC=α,则∠ADE=(用含α的式子表示).3.如图,在△ABC中,∠ACB=45°,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.(1)求证:△ABD≌△CED;(2)若CE为∠ACD的角平分线,求∠BAC的度数.4.如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为E、F,且AB=CD.(1)△ABF与△CDE全等吗?为什么?(2)求证:EG=FG.5.如图1,CA=CB,CD=CE,∠ACB=∠DCE=α(1)求证:BE=AD;(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.6.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.【问题解决】如图1,若点D在边BC上,求证:CE+CF=CD;【类比探究】如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.7.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.8.已知,在△ABC中,AC=BC.分别过A,B点作互相平行的直线AM和BN.过点C 的直线分别交直线AM,BN于点D,E.(1)如图1.若CD=CE.求∠ABE的大小;(2)如图2.∠ABC=∠DEB=60°.求证:AD+DC=BE.9.如图,在△ABC中,AB=AC=2,∠B=36°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=36°,DE交线段AC于点E.(1)当∠BDA=128°时,∠EDC=,∠AED=;(2)线段DC的长度为何值时,△ABD≌△DCE?请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.10.如图,在△ABC中,∠BAC=90°,E为边BC上的任意点,D为线段BE的中点,AB=AE,EF⊥AE,AF∥BC.(1)求证:∠DAE=∠C;(2)求证:AF=BC.11.如图,△ABC中,AB=AC,点D在AB边上,点E在AC的延长线上,且CE=BD,连接DE交BC于点F.(1)求证:EF=DF;(2)过点D作DG⊥BC,垂足为G,求证:BC=2FG.12.在∠MAN内有一点D,过点D分别作DB⊥AM,DC⊥AN,垂足分别为B,C.且BD=CD,点E,F分别在边AM和AN上.(1)如图1,若∠BED=∠CFD,请说明DE=DF;(2)如图2,若∠BDC=120°,∠EDF=60°,猜想EF,BE,CF具有的数量关系,并说明你的结论成立的理由.13.在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连结BD,E、F分别是AB、BC上的点,且DE⊥DF.(1)如图1,若D为AC边上的中点.①填空:∠C=,∠DBC=;②求证:△BDE≌△CDF.(2)如图2,D从点C出发,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤t≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.14.已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,(1)求证:△ABC≌△EDF;(2)当∠CHD=120°,求∠HBD的度数.15.以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.(1)说明BD=CE;(2)延长BD,交CE于点F,求∠BFC的度数;(3)若如图2放置,上面的结论还成立吗?请简单说明理由.参考答案1.解:(1)∵BD⊥AC,CF⊥AB,∴∠DCE+∠DEC=∠DCE+∠FAC=90°,∴∠DEC=∠BAC,∠DEC+∠BEC=180°,∴∠BAC+∠BEC=180°;(2)∵BD平分∠ABC,CF平分∠ACB,∴∠EBC=ABC,∠ECB=ACB,∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠BAC)=90°∠BAC;(3)作∠BEC的平分线EM交BC于M,∵∠BAC=60°,∴∠BEC=90°+BAC=120°,∴∠FEB=∠DEC=60°,∵EM平分∠BEC,∴∠BEM=60°,在△FBE与△EBM中,,∴△FBE≌△EBM(ASA),∴EF=EM,同理DE=EM,∴EF=DE.2.解:(1)由题可得,BD=CE=2t,∴CD=12﹣2t,AE=8﹣2t,∴当AE=DC,时,8﹣2t=(12﹣2t),解得t=3,故答案为:3;(2)当△ABD≌△DCE成立时,AB=CD=8,∴12﹣2t=8,解得t=2,∴运动2秒时,△ABD≌△DCE能成立;(3)当△ABD≌△DCE时,∠CDE=∠BAD,又∵∠ADE=180°﹣∠CDE﹣∠ADB,∠B=∠180°﹣∠BAD﹣∠ADB,∴∠ADE=∠B,又∵∠BAC=α,AB=AC,∴∠ADE=∠B=(180°﹣α)=90°﹣α.故答案为:90°﹣α.3.(1)证明:∵AD⊥BC,∠ACB=45°,∴∠ADB=∠CDE=90°,△ADC是等腰直角三角形,∴AD=CD,∠CAD=∠ACD=45°,在△ABD与△CED中,,∴△ABD≌△CED(SAS);(2)解:∵CE为∠ACD的角平分线,∴∠ECD=∠ACD=22.5°,由(1)得:△ABD≌△CED,∴∠BAD=∠ECD=22.5°,∴∠BAC=∠BAD+∠CAD=22.5°+45°=67.5°.4.(1)解:△ABF与△CDE全等,理由如下:∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°,∵AE=CF,∴AE+EF=CF+EF,即AF=CE,在Rt△ABF和Rt△CDE中,,∴Rt△ABF≌Rt△CDE(HL);(2)证明:∵Rt△ABF≌Rt△CDE,∴BF=DE,在△DEG和△BFG中,,∴△DEG≌△BFG(AAS),∴EG=FG.5.解:(1)如图1,∵∠ACB=∠DCE=α,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴BE=AD;(2)△CPQ为等腰直角三角形.证明:如图2,由(1)可得,BE=AD,∵AD,BE的中点分别为点P、Q,∴AP=BQ,∵△ACD≌△BCE,∴∠CAP=∠CBQ,在△ACP和△BCQ中,,∴△ACP≌△BCQ(SAS),∴CP=CQ,且∠ACP=∠BCQ,又∵∠ACP+∠PCB=90°,∴∠BCQ+∠PCB=90°,∴∠PCQ=90°,∴△CPQ为等腰直角三角形6.【问题解决】证明:在CD上截取CH=CE,如图1所示:∵△ABC是等边三角形,∴∠ECH=60°,∴△CEH是等边三角形,∴EH=EC=CH,∠CEH=60°,∵△DEF是等边三角形,∴DE=FE,∠DEF=60°,∴∠DEH+∠HEF=∠FEC+∠HEF=60°,∴∠DEH=∠FEC,在△DEH和△FEC中,,∴△DEH≌△FEC(SAS),∴DH=CF,∴CD=CH+DH=CE+CF,∴CE+CF=CD;【类比探究】解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:∵△ABC是等边三角形,∴∠A=∠B=60°,过D作DG∥AB,交AC的延长线于点G,如图2所示:∵GD∥AB,∴∠GDC=∠B=60°,∠DGC=∠A=60°,∴∠GDC=∠DGC=60°,∴△GCD为等边三角形,∴DG=CD=CG,∠GDC=60°,∵△EDF为等边三角形,∴ED=DF,∠EDF=∠GDC=60°,∴∠EDG=∠FDC,在△EGD和△FCD中,,∴△EGD≌△FCD(SAS),∴EG=FC,∴FC=EG=CG+CE=CD+CE.7.证明:(1)∵AD∥BC(已知),∴∠ADC=∠ECF(两直线平行,内错角相等),∵E是CD的中点(已知),∴DE=EC(中点的定义).∵在△ADE与△FCE中,,∴△ADE≌△FCE(ASA),∴FC=AD(全等三角形的性质).(2)∵△ADE≌△FCE,∴AE=EF,AD=CF(全等三角形的对应边相等),∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF,∵AD=CF(已证),∴AB=BC+AD(等量代换).8.(1)解:如图1,延长AC交BN于点F,∵AM∥BN,∴∠DAF=∠AFB,在△ADC和△FEC中,,∴△ADC≌△FEC(AAS),∴AC=FC,∵AC=BC,∴BC=AC=FC=AF,∴△ABF是直角三角形,∴∠ABE=90°;(2)证明:如图2,在EB上截取EH=EC,连CH,∵AC=BC,∠ABC=60°,∴△ABC为等边三角形,∵∠DEB=60°,∴△CHE是等边三角形,∴∠CHE=60°,∠HCE=60°,∴∠BHC=120°,∵AM∥BN,∴∠ADC+∠BEC=180°,∴∠ADC=120°,∴∠DAC+∠DCA=60°,又∵∠DCA+∠ACB+∠BCH+∠HCE=180°,∴∠DCA+∠BCH=60°,∴∠DAC=∠BCH,在△DAC与△HCB中,,∴△DAC≌△HCB(AAS),∴AD=CH,DC=BH,又∵CH=CE=HE,∴BE=BH+HE=DC+AD,即AD+DC=BE.9.解:(1)∵AB=AC,∴∠C=∠B=36°,∵∠ADE=36°,∠BDA=128°,∵∠EDC=180°﹣∠ADB﹣∠ADE=16°,∴∠AED=∠EDC+∠C=16°+36°=52°,故答案为:16°;52°;(2)当DC=2时,△ABD≌△DCE,理由:∵AB=2,DC=2,∴AB=DC,∵∠C=36°,∴∠DEC+∠EDC=144°,∵∠ADE=36°,∴∠ADB+∠EDC=144°,∴∠ADB=∠DEC,在△ABD和△DCE中,,∴△ABD≌△DCE(AAS);(3)当∠BDA的度数为108°或72°时,△ADE的形状是等腰三角形,①当DA=DE时,∠DAE=∠DEA=72°,∴∠BDA=∠DAE+∠C=72°+36°=108°;②当AD=AE时,∠AED=∠ADE=36°,∴∠DAE=108°,此时,点D与点B重合,不合题意;③当EA=ED时,∠EAD=∠ADE=36°,∴∠BDA=∠EAD+∠C=36°+36°=72°;综上所述,当∠BDA的度数为108°或72°时,△ADE的形状是等腰三角形.10.证明:(1)∵AB=AE,D为线段BE的中点,∴AD⊥BC,(三线合一没有学习到,可以用全等证明)∴∠C+∠DAC=90°,∵∠BAC=90°∴∠BAD+∠DAC=90°∴∠C=∠BAD,∵AB=AE,AD⊥BE,∴∠BAD=∠DAE,∴∠DAE=∠C(2)∵AF∥BC∴∠FAE=∠AEB∵AB=AE∴∠B=∠AEB∴∠B=∠FAE,且∠AEF=∠BAC=90°,AB=AE∴△ABC≌△EAF(ASA)∴AC=EF11.证明:(1)过点D作DH∥AC,DH交BC于H,如图1所示:则∠DHB=∠ACB,∠DHF=∠ECF,∵AB=AC,∴∠B=∠ACB,∴∠B=∠DHB,∴BD=HD,∵CE=BD,∴HD=CE,在△DHF和△ECF中,,∴△DHF≌△ECF(AAS),∴EF=DF;(2)如图2,由(1)知:BD=HD,∵DG⊥BC,∴BG=GH,由(1)得:△DHF≌△ECF,∴HF=CF,∴GH+HF=BH+CH=BC,∴BC=2FG.12.解:(1)∵DB⊥AM,DC⊥AN,∴∠DBE=∠DCF=90°,在△BDE和△CDF中,∵∴△BDE≌△CDF(AAS).∴DE=DF;(2)EF=FC+BE,理由:过点D作∠CDG=∠BDE,交AN于点G,在△BDE和△CDG中,,∴△BDE≌△CDG(ASA),∴DE=DG,BE=CG.∵∠BDC=120°,∠EDF=60°,∴∠BDE+∠CDF=60°.∴∠FDG=∠CDG+∠CDF=60°,∴∠EDF=∠GDF.在△EDF和△GDF中,,∴△EDF≌△GDF(SAS).∴EF=GF,∴EF=FC+CG=FC+BE.13.(1)①解:∵在等腰三角形ABC中,∠ABC=90度,D为AC边上的中点,∴∠C=45°,∠DBC=45°;故答案为:45°;45°;②证明:在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,故BD⊥AC,∵ED⊥DF,∴∠BDE=∠FDC,∴∠C=∠DBC=45°,∴BD=DC,在△BDE和△CDF中,,∴△BDE≌△CDF(ASA);(2)解:如图①所示:当t=0时,△PBE≌△CAE一对;如图②所示:当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共3对;如图③所示:当t=4时,△PBA≌△CAB一对.14.(1)证明:∵AD=BE,∴AB=ED,在△ABC和△EDF中,,∴△ABC≌△EDF(SAS);(2)∵△ABC≌△EDF,∴∠HDB=∠HBD,∵∠CHD=∠HDB+∠HBD=120°,∴∠HBD=60°.15.解:(1)∵△ABC、△ADE是等腰直角三角形,∴AB=AC,∠BAD=∠EAC=90°,AD=AE,∵在△ADB和△AEC中,,∴△ADB≌△AEC(SAS),∴BD=CE;(2)∵△ADB≌△AEC,∴∠ACE=∠ABD,而在△CDF中,∠BFC=180°﹣∠ACE﹣∠CDF又∵∠CDF=∠BDA∴∠BFC=180°﹣∠DBA﹣∠BDA=∠DAB=90°;(3)BD=CE成立,且两线段所在直线互相垂直,即∠BFC=90°.理由如下:∵△ABC、△ADE是等腰直角三角形∴AB=AC,AD=AE,∠BAC=∠EAD=90°,∵∠BAC+∠CAD=∠EAD+∠CAD∴∠BAD=∠CAE,∵在△ADB和△AEC中,,∴△ADB≌△AEC(SAS)∴BD=CE,∠ACE=∠DBA,∴∠BFC=∠CAB=90°.。
专题三 全等三角形的判定-浙教版八年级数学上册期中复习专题训练

浙教版数学(八上)期中复习专题三全等三角形一、选择题1. 下列命题中:①形状相同的两个三角形是全等形;①在两个全等三角形中,相等的角是对应角相等的边是对应边;①全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命的个数为( )。
A.3个B.2个C.1个D.0个【答案】C2. 在下列的条件中,不能说明①ABC①①AB'C'的是( )。
A.①A=①A',①C=①C',AC=A'CB.①A=①A',AB=A'B',BC=B′C′C.①B=①B',①C=①C',AB=A'B′D. AB=A′B′,BC=B′C′,AC=A′C′【答案】B3. 有下列说法:①有一个外角是钝角的三角形是锐角三角形;①有两条边和一个角对应相等的两个三角形全等;①若三条线段ab,满足a≥b≥c,且a<b+C,则这三条线段必能组成一个三角形;①有两个角和一条边彼此相等的两个三角形全等。
其中正确的个数是( )。
A.4个B.3个C.2个D.1个【答案】D4.用尺规作一个角的平分线的示意图如图所示,则能说明①AOC=①BOC的依据是( )。
A. SSSB. ASAC. AASD.角平分线上的点到角两边距离相等【答案】A5.如图所示,点B、C、E在同一条直线上,①ABC与①CDE都是等边三角形则下列结论不一定成立的是( )。
A.①ACE①①BCDB.①BGC①①AFCC.①DCG①①ECFD.①ADB①①CEA【答案】D6.如图,已知①1=①2,则不一定能使①ABD①①ACD的条件是( )。
A. AB=ACB. BD=CDC.①B=①CD.①BDA=①CDA7. 要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明①EDC①①ABC,得ED=AB,因此测得ED的长就是AB的长,判定①EDC①①ABC最恰当的理由是( )。
8年级数学全等三角形经典例题

8年级数学全等三角形经典例题一、全等三角形经典例题1。
例1:如图,在△ABC中,AB = AC,AD是BC边上的中线,求证:△ABD≌△ACD。
解析:1. 在△ABD和△ACD中:- 已知AB = AC(题目中给出的等腰三角形的两腰相等)。
- 因为AD是BC边上的中线,所以BD = CD(中线的定义)。
- AD = AD(公共边)。
2. 根据SSS(边边边)全等判定定理,可得△ABD≌△ACD。
二、全等三角形经典例题2。
例2:已知:如图,AB = AD,∠B = ∠D,∠1=∠2,求证:△ABC≌△ADE。
解析:1. 因为∠1 = ∠2,所以∠1+∠DAC = ∠2+∠DAC,即∠BAC = ∠DAE。
2. 在△ABC和△ADE中:- 已知AB = AD。
- ∠B = ∠D。
- 且∠BAC = ∠DAE(已证)。
3. 根据ASA(角边角)全等判定定理,可得△ABC≌△ADE。
三、全等三角形经典例题3。
例3:如图,在△ABC中,∠C = 90°,AC = BC,AD平分∠CAB交BC于D,DE⊥AB于E,AB = 6cm,求△DEB的周长。
解析:1. 因为AD平分∠CAB,∠C = 90°,DE⊥AB,根据角平分线的性质,可知CD = DE。
2. 在Rt△ACD和Rt△AED中:- AD = AD(公共边)。
- CD = DE(已证角平分线性质)。
- 根据HL(斜边直角边)定理,可得Rt△ACD≌Rt△AED。
- 所以AC = AE。
3. 因为AC = BC,AB = 6cm,设AC = BC=x,根据勾股定理AC^2+BC^2=AB^2,即x^2+x^2=6^2,2x^2=36,x^2=18,x = 3√(2)。
4. 又因为AE = AC = 3\sqrt{2}\),所以BE=AB - AE = 6 - 3\sqrt{2}\)。
5. 而△DEB的周长为DE+DB+BE,因为CD = DE,BC = BD + CD,所以△DEB的周长为BC+BE = 3\sqrt{2}+6 - 3\sqrt{2}=6cm。
八年级上册典型题

八年级上册典型题一、三角形全等证明类(5题)1. 如图,在△ABC和△DEF中,AB = DE,BC = EF,∠A = ∠D。
求证:△ABC≌△DEF。
- 解析:- 在△ABC和△DEF中,已知AB = DE,BC = EF,∠A = ∠D。
- 但是“SSA”(边 - 边 - 角)不能判定三角形全等,所以这两个三角形不全等。
这是一个易错点,让学生明确全等三角形的判定定理中没有“SSA”。
2. 已知:如图,AC = BD,∠CAB=∠DBA。
求证:△CAB≌△DBA。
- 解析:- 在△CAB和△DBA中,AC = BD,∠CAB = ∠DBA,AB是公共边。
- 根据三角形全等判定定理中的“SAS”(边角边),因为AC = BD,∠CAB = ∠DBA,AB = BA,所以△CAB≌△DBA。
3. 如图,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE = AC,延长BE交AC于F。
求证:△AEF≌△DEB。
- 解析:- 因为AD是BC边上的中线,所以BD = CD。
- 在△AEF和△DEB中,- 对顶角∠AEF = ∠DEB。
- 因为BD = CD,AD是中线,∠BDE = ∠CDA(对顶角相等),可证△BDE≌△CDA (SAS),所以∠BED = ∠CAD,又因为BE = AC。
- 根据“AAS”(角角边),所以△AEF≌△DEB。
4. 如图,AB = AC,AD = AE,∠1 = ∠2。
求证:△ABD≌△ACE。
- 解析:- 因为∠1 = ∠2,所以∠1+∠CAD = ∠2 + ∠CAD,即∠BAD = ∠CAE。
- 在△ABD和△ACE中,AB = AC,AD = AE,∠BAD = ∠CAE。
- 根据“SAS”(边角边),所以△ABD≌△ACE。
5. 如图,点B、F、C、E在一条直线上,FB = CE,AB∥ED,AC∥FD。
求证:△ABC≌△DEF。
- 解析:- 因为FB = CE,所以FB+FC = CE + FC,即BC = EF。
八年级上册数学全等三角形必考题

八年级上册数学全等三角形必考题全文共5篇示例,供读者参考八年级上册数学全等三角形必考题1《全等三角形的判定》这一课,要求学生会通过观察几何图形识别两个三角形全等,并能通过正确的分类动手探索出两个三角形全等的条件。
具体说:(1)正确识别两个三角形全等——会将两个三角形相等的边和角对应重叠在一起,看是否重合;(2)相信判定两个三角形全等不一定要3条边和3个角都相等,可能一边或一角相等就足够(这个判断不一定要正确,但要有这种想法,探索命题的真假才有可能);(3)能正确地将三角形的6个元素按条件的个数分成:①一个元素:一个边或一条角对应相等。
②两个元素:两边或一边一角或两角对应相等。
③三个元素:三边或两边和一角或一边和两角或三角对应相等。
或者按:①边(一条边或两条边或三条边分别对应相等)。
②角(一个角或两个角或三个角分别对应相等)。
③边和角[一条边和一个角或一条边和两个角(又分为角边角和角角边两种)或两条边和一个角(又分为边角边和边边角两种)分别对应相等];(4)能将分好的三大类(12小类)条件用画图的方法进行验证,找出能判定两个三角形全等的三条公理和一条定理;(5)能用这四个判定,直接判定两个三角形是否全等或能补充一个条件使两个三角形全等。
基于知识的完整性和分类的数学思想的渗透,我认为这个教学设计体现了知识与技能目标。
增强学生的观察、猜想和动手操作能力。
八年级上册数学全等三角形必考题2一、制订好复习课的复习目标复习要对以前多节新课中的知识点或数学思想方法进行压缩整理,所以要制订好复习课的复习目标。
首先,选择合适的知识范围非常重要。
其次,应确定对所选知识点中重点的复习深度,过易会让学生索然无味,过难会让学生畏惧前行,失去信心。
我对这节课的难度把握是保全突尖,教学流程本身有梯度,例题与配套变式也有梯度。
不过对于例3“求证两线段相等”这个问题既需要添加辅助线,又要连续两次证全等。
问题的梯度设置过大,许多学生还观察不出。
专题02全等三角形-八年级数学上学期期中真题分类汇编(人教版,吉林专用)【含答案】

专题02 全等三角形(8种经典基础练+4种优选提升练)全等图形(2023秋•永年区期中)1.下列各组中的两个图形属于全等图形的是()A.B.C.D.(2024春•龙岗区期中)2.下列说法正确的是()A.形状相同的两个图形一定全等B.两个长方形是全等图形C.两个全等图形面积一定相等D.两个正方形一定是全等图形(2023秋•二道区校级期中)3.如图,已知方格纸中是9个相同的小正方形,则12Ð+Ð的度数为°.全等三角形的性质(2023秋•铁西区期中)4.已知图中的两个三角形全等,则1Ð等于( )A .50°B .58°C .60°D .72°(2023秋•南关区校级期中)5.如图,ABC DEC ≌△△,若85DCB Ð=°,40BCE Ð=°,则ACE Ð的度数为( )A .5°B .10°C .15°D .20°(2023秋•双阳区校级期中)6.如图,ABC FDE ≌△△,AB FD =,20cm =AE ,10cm FC =,则AF 的长是 cm .(2023秋•船营区校级期中)7.两个全等的直角三角形重叠在一起. 将其中的一个三角形沿着点B 到C 的方向平移到DEF V 的位置,4AB =,1DO =,平移距离为2.则阴影部分面积为 .全等三角形的判定(2023秋•通榆县期中)8.工人师傅常用角尺平分一个任意角,做法是:如图在AOB Ð的边OA OB 、上分别取OM ON =,移动角尺,使角尺的两边相同的刻度分别与M 、N 重合,得到AOB Ð的平分线OP ,做法中用到三角形全等的判定方法是( )A .SSSB .SASC .ASAD .HL(2023秋•二道区校级期中)9.如图,已知AE AC =,C E Ð=Ð,下列条件中,无法判定ABC ADE △≌△的是( )A .B D Ð=ÐB .BC DE =C .12Ð=ÐD .AB AD =(2023秋•乾安县期中)10.如图,已知AD 与BC 交于O 点,OA OB =,要使AOC BOD ≌V V ,添加一个你认为合适的条件为 .(2023秋•德惠市期中)11.如图,已知AB AD =,AC AE =,BAD CAE Ð=Ð,求证:ABC ADE V V ≌.(2023秋•德惠市期中)12.如图,在ABC V 中,90ACB Ð=°,6AC =,8BC =.点D 从点A 出发,沿折线AC CB -以每秒1个单位长度的速度向终点B 运动,点E 从点B 出发,沿折线BC CA -以每秒3个单位长度的速度向终点A 运动,D 、E 两点同时出发.分别过D 、E 两点作垂直于过点C 的直线,垂足分别为点F 、G .设点D 的运动时间为t (秒):(1)当D 、E 两点相遇时,求t 的值;(2)在整个运动过程中,求CD 的长(用含t 的代数式表示)(3)当DFC △与EGC V 全等时,请直接写出t 的值.直角三角形全等的判定(2023秋•乾安县期中)13.如图,Rt ABC D 和Rt EDF D 中,//BC DF ,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt ABC D 和Rt EDF D 全等.(2023秋•前郭县期中)14.如图,在ABC V 中,CB AB ^,45BAC Ð=°,F 是AB 延长线上一点,点E 在BC 上,且AE CF =.求证:ABE CBF △≌△.(2023秋•前郭县期中)15.如图,已知90A D Ð=Ð=°,E 、F 在线段BC 上,DE 与AF 交于点O ,且AB CD =,BE CF =.求证:Rt Rt ABF DCE ≌△△.全等三角形的判定与性质(2023秋•船营区校级期中)16.如图,在ACB △中,90ACB Ð=°,AC BC =,点C 的坐标为()2,0-,点A 的坐标为()6,3-,求点B 的坐标.(2023秋•龙潭区校级期中)17.如图,()4,0A ,()0,6B ,若AB BC =,90ABC Ð=°,则C 点的坐标为 .(2023秋•船营区校级期中)18.如图,点F 、C 在BE 上,BF CE =,AB DE =,DF AC =.求证:A D Ð=Ð.(2023秋•前郭县期中)19.如图,在ABC V 和DBC △中,90ACB DBC Ð=Ð=°,点E 是BC 的中点,DE AB ^于点F ,且AB DE =.(1)求证:V V ≌ACB EBD ;(2)若12DB =,求AC 的长.全等三角形的应用(2023秋•乾安县期中)20.如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )A .SASB .ASAC .AASD .SSS(2023秋•前郭县期中)21.生活中的数学:(1)如图①,一扇窗户打开后,用窗钩AB 可将其固定利用了_____;(2)如图②,要测量池塘沿岸上两点A 、E 之间的距离,可以在池塘周围取两条互相平行的线段AB 和CD ,且使AB CD =,连接BC 、AD 交于点E ,要想知道A 、E 之间的距离,只需要测量线段DE 的长度,这样做合适吗?请说明理由.(2023秋•通榆县期中)22.如图,有两个长度相等的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角B Ð和F Ð的大小有什么关系?(2023秋•双辽市期中)23.王强同学用10块高度都是2cm 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC BC =,90ACB Ð=°),点A 和B 分别与木墙的顶端重合.(1)求证:ADC CEB △≌△;(2)求两堵木墙之间的距离.(2023秋•宁江区期中)24.如图,A ,B 两点位于高墙外,不能直接到达.为在该高楼的楼顶上搭建一个支架,需要在地面测量出A ,B 间的距离.学习了三角形全等知识后,小明给出了如下的方案:先在地面上取一点可以直接到达A 点和B 点的点O ,连接AO 并延长到C ,使OC OA =;连接BO 并延长到D ,使OD OB =,连接CD 并测量出CD 的长度,CD 的长度就是A ,B 间的距离.请根据以上的信息,说明AB CD =.角平分线的性质(2023秋•吉林期中)25.如图,在Rt ABC △中,90ACB Ð=°,BD 平分ABC Ð,DE AB ^于点E ,9AC =,5AD =,则DE 的长 .(2023秋•朝阳区校级期中)26.如图,ABC V 中,90C Ð=°,AD 平分BAC Ð,10AB =,3CD =,则ABD △的面积为 .(2023秋•通榆县期中)27.在ABC V 中,90,A BD Ð=°平分,3,10ABC AD BC Ð==,ABC V 的面积为27,求AB 的长.(2023秋•铁西区期中)28.如图,180CB CD D ABC CE AD =Ð+Ð=°^,,于E ,CF AB ^交AB 的延长线于点F .(1)求证:AC 平分DAB Ð;(2)若82AE DE ==,,求AB 的长.(2023秋•船营区校级期中)29.如图,AD 是ABC D 的角平分线,且DE AB ^,50B Ð=°,60C Ð=°.(1)求ADC Ð的度数;(2)若8DE =,点F 是AC 上的动点,求DF 的最小值.作图—尺规作图的定义(2023秋•双阳区校级期中)30.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )A .SSSB .ASAC .AASD .SAS(2023秋•信丰县期中)31.如图,在Rt ABC △中,90C Ð=°,以点A 为圆心,适当长为半径作弧,分别交AB ,AC于点D ,E ,再分别以点D ,E ,为圆心,以大于12DE 的长度为半径作弧,两弧交于点F ,作射线AF 交BC 于点G ,若12AB =,3CG =,则ABG V 的面积是( )A .12B .18C .24D .36(2023秋•泗水县期中)32.如图,Rt ABC △中,90ACB Ð=°,30B Ð=°,要求用圆规和直尺作图,把它分成两个三角形,其中至少有一个三角形是等腰三角形,其作法错误的是( )A .B .C .D .全等三角形模型之“旋转模型”(22-23八年级上·湖北孝感·期中)33.已知:ABC DEC ≌△△,90ACB Ð=o ,32B Ð=o .(1)如图1当点D 在AB 上,ACD Ð______.(2)如图2猜想BDC V 与ACE △的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)(21-22八年级上·江苏宿迁·期中)34.(1)如图①,在正方形ABCD 中,E 、F 分别是BC 、DC 上的点,且45EAF Ð=°,连接EF ,探究BE 、DF 、EF 之间的数量关系,并说明理由;(2)如图②,在四边形ABCD 中,AB AD =,180B D Ð+Ð=°,E 、F 分别是BC 、DC 上的点,且12EAF BAD Ð=Ð,此时(1)中的结论是否仍然成立?请说明理由.全等三角形模型之“倍长中线模型”(23-24八年级上·山西长治·期中)35.如图,AD ,AF 分别是ABC V 的中线和高,BE 是ABD △的角平分线(1)若60,40BED BAD Ð=°Ð=°,求BAF Ð的度数.(2)若8,6AB AC ==,求中线AD 长的取值范围.(22-23八年级上·河南安阳·期中)36.如图,在ABC V 中,CM 是AB 边上的中线,8AC =,12BC =,求CM 的取值范围.全等三角形模型之“一线三等角模型”(21-22八年级上·天津和平·期中)37.在BAC V 中,90BAC Ð=°,AB AC =,AE 是过A 的一条直线,BD AE ^于点D ,CE AE ^于E ,(1)如图(1)所示,若B ,C 在AE 的异侧,易得BD 与DE ,CE 的关系是DE =____________;(2)若直线AE 绕点A 旋转到图(2)位置时,(BD CE <),其余条件不变,问BD 与DE ,CE 的关系如何?请予以证明;(3)若直AE 绕点A 旋转到图(3)的位置,(BD CE >),问BD 与DE ,CE 的关系如何?请直接写出结果,不需证明.(20-21八年级上·广东韶关·期中)38.如图,已知ABC V 中,10cm AB AC ==,8cm BC =,点D 为AB 的中点.如果点P 在线段BC 上以3cm/s 的速度由点B 向C 点运动,同时,点Q 在线段CA 上由点C 向A 点运动.(1)用含t 的式子表示PC 的长为______________;(2)若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP V 是否全等,请说明理由.(3)若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP V 全等?全等三角形模型之“截长补短模型”(22-23八年级上·福建莆田·期中)39.如图,锐角三角形ABC 与等腰直角三角形DBC 是共边三角形,90BDC Ð=°,BD DC =,过点D 作EF AB ^于F ,E 为AC 的中点.(1)求证:EDC ABD Ð=Ð;(2)求证:;AF FD =(3)若,AB a DE b ==,求BF 的长(23-24八年级上·广东珠海·期中)40.如图,Rt ACB △中,90,ACB ABC °Ð=V 的角平分线AD BE 、相交于点P ,过P 作PF AD^交BC 的延长线于点F ,交AC 于点H .(1)求APB Ð度数;(2)求证:AP FP =;(3)猜想线段,,AH AB BD 的数量关系,并证明.1.B【分析】此题主要考查了全等图形,关键是掌握能够完全重合的两个图形叫做全等形.利用全等图形的定义进行判断即可.【详解】解:A 、两个图形不属于全等图形, 故此选项不符合题意;B 、两个图形属于全等图形, 故此选项符合题意;C 、两个图形不属于全等图形, 故此选项不符合题意;D 、两个图形不属于全等图形, 故此选项不符合题意.故选:B .2.C【分析】直接利用全等图形以及全等图形的性质判断得出答案.【详解】解:选项A 中,形状相同、大小相等的两个图形一定全等,故选项A 错误;选项B 中,长方形不一定是全等图形,故选项B 错误;选项C 中,两个全等图形面积一定相等,故选项C 正确;选项D 中,两个正方形不一定是全等图形,故选项D 错误;故选C.【点睛】本题主要考查了全等图形和全等图形的性质,掌握全等图形和全等图形的性质是解题关键.3.45【分析】本题考查了利用全等的性质求网格中的角度,三角形外角的性质,等腰直角三角形的性质,得出13Ð=Ð是解题的关键.观察图形可知3Ð与1Ð所在的直角三角形全等,则13Ð=Ð,根据外角的性质卡得423Ð=Ð+Ð,即可求解.【详解】解:观察图形可知3Ð与1Ð所在的直角三角形全等(两直角边分别为1和2),∴13Ð=Ð,∵445Ð=°,∴1232445Ð+Ð=Ð+Ð=Ð=°,故答案为:45.4.B【分析】本题考查了全等三角形的性质,三角形内角和定理;根据全等三角形的性质得出1B Ð=Ð,50A D Ð=Ð=°,72F C Ð=Ð=°,进而根据三角形内角和定理即可求解.【详解】解:如图所示,ABC QV 和DEF V 全等,AC DF b ==,DE AB a ==,1B \Ð=Ð,50A D Ð=Ð=°,72F C Ð=Ð=°,118058D F \Ð=°-Ð-Ð=°,故选:B .5.A【分析】本题考查的是全等三角形的性质,掌握全等三角形的对应角相等是解题的关键.根据角的和差得到45DCE Ð=°,再根据全等三角形的性质得到45ACB DCE Ð=Ð=°,再根据角的和差即可求出ACE Ð的度数.【详解】解:85DCB Ð=°Q ,40BCE Ð=°,45DCE DCB BCE \Ð=Ð-Ð=°,ABC DEC Q △≌△,45ACB DCE \Ð=Ð=°,45405ACE ACB BCE \Ð=Ð-Ð=°-°=°.故选:A .6.5【分析】根据全等三角形的对应边相等得到AC EF =,结合等式的性质推出AF CE =,结合已知相关线段的长度解答.【详解】解:∵20cm =AE ,10cm FC =,∴10cm AF CE AE FC +=-=.∵ABC FDE ≌△△,∴AC EF =.∴AC FC EF FC -=-,∴AF CE =.∴()15cm 2AF AF CE =+=.故答案为:5.【点睛】此题主要考查了全等三角形的性质,正确得出AF CE =是解题关键.7.7【分析】先根据全等三角形的性质可得ABC DEF S S =V V ,再根据平移的性质可得4DE AB ==,2BE =,从而可得3OE =,然后根据阴影部分的面积等于直角梯形ABEO 的面积即可得.【详解】解:由题意得:90B DEF Ð=Ð=°,ABC DEF ≌△△,ABC DEF S S \=△△,AB OE ∥,\四边形ABEO 是直角梯形,由平移的性质得:4DE AB ==,2BE =,1DO =Q ,3OE DE DO \=-=,则阴影部分面积为DEF COES S -V V ABC COES S =-V V ABEOS =直角梯形()2OE AB BE+×=()3422+´=7=,故答案为:7.【点睛】本题考查了全等三角形的性质、平移的性质,熟练掌握平移的性质是解题关键.8.A【分析】此题考查了全等三角形的判定和性质、角平分线的定义等知识.用SSS 证明ONP OMP V V ≌,则NOP MOP Ð=Ð,即可得到解答.【详解】解:做法中用到的三角形全等的判定方法是SSS ,证明如下:由题意得,PN PM =,在ONP △和OMP V 中,ON OM PN PM OP OP =ìï=íï=î,∴()SSS ONP OMP V V ≌,∴NOP MOP Ð=Ð,即OP 为AOB Ð的平分线.故选:A .9.D【分析】由全等三角形的判定依次判断可求解.【详解】A 、添加B D Ð=Ð,由“AAS ”可证ABC ADE △≌△,故选项A 不符合题意;B 、添加BC DE =,由“SAS ”可证ABC ADE △≌△,故选项B 不符合题意;C 、添加12ÐÐ=,由“ASA ”可证ABC ADE △≌△,故选项C 不符合题意;D 、添加AB AD =,不能证明ABC ADE △≌△,故选项D 符合题意;故选:D .【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定是本题的关键.10.OC OD =(答案不唯一)【分析】可以是OC OD =,根据SAS 可证明AOC BOD ≌V V ,从而得到答案.【详解】解:OC OD =,理由是:在AOC △和BOD V 中,OA OB AOC BOD OC OD =ìïÐ=Ðíï=î,()SAS AOC BOD \V V ≌,故答案为:OC OD =(答案不唯一).【点睛】本题考查了全等三角形的判定定理,熟练掌握证明三角形全等的方法有:SAS 、SSS 、AAS 、ASA 、HL 是解题的关键.11.证明见解析【分析】本题主要考查了全等三角形的判定,解题的关键是通过BAD CAE Ð=Ð得出BAC DAE Ð=Ð.根据BAD CAE Ð=Ð可得BAC DAE Ð=Ð,再根据SAS 即可证明.【详解】证明:∵BAD CAE Ð=Ð,∴BAD DAC CAE DAC Ð+Ð=Ð+Ð,即BAC DAE Ð=Ð,在ABC V 和ADE V 中,AB AD BAC DAE AC AE =ìïÐ=Ðíï=î,∴()SAS ABC ADE V V ≌.12.(1)72秒(2)6(06)6(614)t t t t -££ìí-<£î(3)1t =, 3.5t =,12t =【分析】本题考查了三角形全等的判定和性质,线段的动点问题,根据题意得出关于t 的方程是解题的关键.(1)由题意得368t t +=+,即可求得t 的值;(2)根据题意即可得出CD 的长为6(06)6(614)t t t t -££ìí-<£î;(3)分情况讨论得出关于t 的方程,解方程求得t 的值.【详解】(1)解:由题意得368t t +=+,解得:72t =(秒),当D 、E 两点相遇时,t 的值为72秒;(2)解:由题意可知AD t =, 6AC =,8BC =,则CD 的长为6(06)6(614)t t t t -££ìí-<£î;(3)解:当D 在AC 上,E 在BC 上时,∵90ACB Ð=°,∴90DCF ECG Ð+Ð=°,∵PF l ^于E ,EG l ^于F .∴9090DCF FDC DFC CGE Ð+Ð=°Ð=Ð=°,,∴CDF ECG Ð=Ð,∴DCF CEG V V ≌,∴CD CE =,∴683t t -=-,解得1t =,当D 在AC 上,E 在AC 上时,即D 、E 重合时,则CD CE =,由题意得,638t t -=-,解得: 3.5t =,当D 在BC 上,E 在AC 上时,即A 、E 重合时,则6CE AC CD ===,解得12t =综上,当DFC △与EGC V 全等时,满足条件的t 等于1或3.5或12.13.AB ED =,答案不唯一【分析】本题是一道开放型的题目,答案不唯一,可以是AB =ED 或BC =DF 或AC =EF 或AE =CF 等,只要符合全等三角形的判定定理即可.【详解】∵Rt ABC D 和Rt EDF D 中,∴90BAC DEF Ð=Ð=°,∵//BC DF ,∴DFE BCA Ð=Ð,∴添加AB ED =,在Rt ABC D 和Rt EDF D 中DFE BCA DEF BAC AB ED Ð=ÐìïÐ=Ðíï=î,∴()Rt Rt AAS ABC EDF D D ≌,故答案为:AB ED =答案不唯一.【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理的内容是解此题的关键,注意:两直角三角形全等的判定定理有SAS ,ASA ,AAS ,SSS ,HL 等.14.见解析【分析】本题考查了全等三角形的判定与性质,结合等角对等边,得出AB CB =,再通过“HL ”证明Rt Rt ABE CBF △≌△,即可作答.【详解】证明:CB AB ^Q ,90ABC FBC Ðа\==45BAC Ð=°Q ,45BCA BAC \Ð=°=Ð,ABC \V 为等腰直角三角形,AB CB\=在Rt ABE △和Rt CBF △中,AE CF AB CB=ìí=î()Rt Rt HL ABE CBF \V V ≌15.见解析.【分析】此题考查了直角三角形全等的判定,解题关键是由BE CF =推出BF CE =,利用HL 进行判定.【详解】证明:BE CF =Q ,BE EF CF EF \+=+,即BF CE =,90A D Ð=Ð=°Q ,ABF \V 与DCE △都为直角三角形,在Rt ABF V 和Rt DCE V 中,BF CE AB CD=ìí=î\Rt Rt (HL)ABF DCE ≌△△.16.B 点的坐标是()1,4【分析】本题主要查了坐标与图形,全等三角形的判定和性质.过点A 和点B 分别作AD x ^轴于点D ,BE x ⊥轴于点E ,证明ADC CEB △≌△,可得DC BE =,=AD CE ,从而得到4BE =,即可求解.【详解】解:过点A 和点B 分别作AD x ^轴于点D ,BE x ⊥轴于点E ,90ACB Ð=°Q ,90ACD CAD \Ð+Ð=°,90ACD BCE Ð+Ð=°,CAD BCE \Ð=Ð,在ADC △和CEB V 中,90ADC CEB CAD BCEAC BC Ð=Ð=°ìïÐ=Ðíï=î,()AAS ADC CEB \V V ≌,DC BE \=,=AD CE ,∵点C 的坐标为()2,0-,点A 的坐标为()6,3-,2OC \=,3AD CE ==,6OD =,4CD OD OC \=-=,321OE CE OC =-=-=,4BE \=,∴B 点的坐标是(1,4).17.()6,10【分析】过点C 作CD y ^轴于点D ,通过角的计算即可得出ABO BCD ÐÐ=,再结合90CDB BOA Ðа==即可利用AAS 证出ABO BCD V V ≌,由此即可得出BD CD 、的长度,进而可得出点C 的坐标.【详解】解:过点C 作CD y ^轴于点D ,如图所示.∵CD BD BO AO ^^,,∴90CDB BOA Ð=Ð=°.∵90ABC Ð=°,∵9090CBD ABO CBD BCD Ð+Ð=°Ð+Ð=°,,∴ABO BCD Ð=Ð.又∵AB BC =,∴()AAS ABO BCD ≌△△,∴BD AO CD BO ==,,∵()()4006A B ,,,,∴46BD AO CD BO ====,,∴10OD OB BD =+=∴点C 的坐标为()6,10,故答案为:()6,10.【点睛】本题结合等腰直角三角形和坐标点综合考查,关键在于辅助线的作法,过C 点作垂直于x 轴的垂线还是垂直于y 轴的垂线是解题关键.18.见解析【分析】本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证()SSS ABC DEF ≌△△是解题的关键 .先证明BC EF =,即可证明()SSS ABC DEF ≌△△,可得结论.【详解】证明:BF CE =Q ,BF FC CE FC \+=+,BC EF \=,在ABC V 和DEF V 中,∵,,,BC EF AC DF AB ED =ìï=íï=î∴()SSS ABC DEF ≌△△,∴A D Ð=Ð.19.(1)见解析(2)6【分析】本题考查全等三角形的判定与性质、三角形的内角和定理、余角性质,熟练掌握全等三角形的判定与性质是解答的关键.(1)先证明DEB A Ð=Ð,再根据全等三角形的判定定理可得结论;(2)根据全等三角形的性质得得BC DB =,AC EB =,结合线段中点定义可求解.【详解】(1)证明:∵90ACB DBC Ð=Ð=°,DE AB ^,∴90Ð+Ð=°DEB ABC ,90A ABC Ð+Ð=°,∴DEB A Ð=Ð,在ACB △和EBD △中,90ACB EBD A DEBAB DE Ð=Ð=°ìïÐ=Ðíï=î,∴()AAS ACB EBD V V ≌;(2)解:由(1)得:V V ≌ACB EBD ,∴BC DB =,AC EB =,∵E 是BC 的中点,∴12EB BC =,∵12DB =,BC DB =,∴12BC =,∴162AC EB BC ===.20.B【分析】本题考查了全等三角形的性质与判定;根据图形可知两角及夹边是已知条件即可判断.【详解】解:由图可知,左上角和左下角可测量,为已知条件,两角的夹边也可测量,为已知条件,故可根据ASA 即可得到与原图形全等的三角形,即小亮画图的依据是ASA ,故选:B .21.(1)三角形的稳定性(2)这样做合适,理由见解析【分析】(1)根据三角形的稳定性解答即可;(2)首先证明AEB DEC △△≌,根据全等三角形的性质可得AE DE =.【详解】(1)解:一扇窗户打开后,用窗钩AB 可将其固定利用了三角形具有稳定性,故答案为:三角形的稳定性.(2)解:这样做合适,理由:∵AB CD ∥,∴A D Ð=Ð,B C Ð=Ð,在AEB V 与DEC V 中,A D AB CD BC Ð=Ðìï=íïÐ=Ðî,∴()ASA AEB DEC ≌V V ,∴AE DE =.【点睛】此题主要考查了三角形的稳定性,全等三角形的应用,解题的关键是掌握全等三角形,对应边相等.22.90B F Ð+Ð=°【分析】根据HL 证明Rt BAC Rt EDF V V ≌即可.【详解】解:根据题意,可知90BAC EDF Ð=Ð=°,,BC EF AC DF ==,∴()HL Rt BAC Rt EDF V V ≌.∴B DEF Ð=Ð(全等三角形的对应角相等).∵90DEF F Ð+Ð=°(直角三角形的两锐角互余),∴90B F Ð+Ð=°.【点睛】本题考查了直角三角形的全等,熟练掌握直角三角形全等的判定方法是解题的关键.23.(1)见解析(2)20cm【分析】(1)根据题意可得AC BC =,90ACB Ð=°,AD DE ^,BE DE ^,进而得到90ADC CEB Ð=Ð=°,再根据等角的余角相等可得BCE DAC Ð=Ð,再利用“AAS ”证明ADC CEB △≌△即可;(2)利用全等三角形的性质进行解答即可;熟练掌握全等三角形的判定和性质是解题关键.【详解】(1)证明:由题意可得AC BC =,90ACB Ð=°,BE DE ^,AD DE ^,∴90ADC CEB Ð=Ð=°,∴90ACD BCE Ð+Ð=°,90ACD DAC Ð+Ð=°,∴BCE DAC Ð=Ð,在ADC △和CEB V 中,ADC CEB DAC BCE AC BC Ð=ÐìïÐ=Ðíï=î,∴(AAS)ADC CEB ≌V V ;(2)解:由题意可得236AD =´=(cm ),7214BE =´=(cm ),∵ADC CEB △△≌,∴6EC AD ==cm ,14DC BE ==cm ,∴20DE DC CE =+=(cm ),答:两堵木墙之间的距离为20cm .24.见解析【分析】利用SAS 证得△AOB ≌△COD ,则其对应边相等.【详解】解:在△AOB 与△COD 中,OA OC AOB COD OB OD =ìïÐ=Ðíï=î,则△AOB ≌△COD (SAS ).所以AB =CD .【点睛】本题考查全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.25.4【分析】由线段的和差关系可得CD 的长,再根据角平分线的性质可得答案.【详解】解:∵9AC =,5AD =,∴4CD =,∵90ACB Ð=°,∴DC BC ^,∵BD 平分ABC Ð,DE AB ^于点E ,∴4DE CD ==,故答案为:4.【点睛】此题考查了角平分线的性质,理解角的平分线上的点到角的两边的距离相等是解题的关键.26.15【分析】本题考查角平分线的性质,三角形的面积,先作辅助线DE AB ^,然后根据角平分线的性质即可得到DE DC =,再根据三角形的面积公式即可计算出ABD △的面积.解答本题的关键是作出合适的辅助线,求出DE 的长.【详解】解:作DE AB ^于点E ,如图所示,∵AD 平分BAC Ð,90C Ð=°,∴DE DC =,∴3DE =,∵10AB =,∴1031522ABD AB DE S ×´===V ,故答案为:15.27.8【分析】过点D 作DE BC ^于E ,根据角平分线上的点到角的两边距离相等可得DE AD =,然后利用三角形的面积公式列式计算即可得解,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【详解】解:过点D 作DE BC ^于E ,∵BD 平分,90ABC A ÐÐ=°,∴3DE AD ==,∵ABC DBC DBA S S S D D +=V ,ABC V 的面积为27,∴112722BC DE AB AD ×+×=,∴1110332722AB ´´+´=,解得:8AB =.28.(1)见解析(2)6【分析】此题考查了全等三角形的判定和性质、角平分线的判定定理,证明()AAS CDE CBF V V ≌是解题的关键.(1)()AAS CDE CBF V V ≌,则CE CF =,根据角平分线的判定即可得到结论;(2)由(1)可得2BF DE ==,证明()Rt HL ACE Rt ACF V V ≌,则8AE AF ==,即可得到【详解】(1)证明:∵CE AD ^,CF AB ^,∴90DEC CFB Ð=Ð=°,∵180180D ABC CBF ABC Ð+Ð=°Ð+Ð=°,,∴D CBF Ð=Ð,在CDE V 与CBF V 中,D CBF DEC CFB CD CB Ð=ÐìïÐ=Ðíï=î,∴()AAS CDE CBF V V ≌,∴CE CF =,又,CE AD CF AB ^^,∴AC 平分DAB Ð;(2)解:由(1)可得2BF DE ==,在Rt ACE V 和Rt ACF △中,CE CF AC AC =ìí=î,∴()Rt HL ACE Rt ACF V V ≌,∴8AE AF ==,∴6AB AF BF =-=.29.(1)85°(2)8【分析】本题主要考查了三角形内角和定理,角平分线定义和性质,垂线段最短,(1)先根据三角形内角和计算出70BAC Ð=°,再利用角平分线的定义得到35BAD Ð=°,然后根据三角形外角性质可计算出ADC Ð的度数;(2)过D 点作DH AC ^于H 点,如图,先根据角平分线的性质得到8DH DE ==,然后垂线段最短求解.【详解】(1)解:50B Ð=°Q ,60C Ð=°,18070BAC B C \Ð=°-Ð-Ð=°.AD Q 是ABC V 的角平分线,1352CAD BAC \Ð=Ð=°,180180603585ADC C CAD \Ð=°-Ð+Ð=°-°-°=°;(2)过D 点作DH AC ^于H 点,如图,AD Q 是ABC V 的角平分线,DE AB ^,DH AC ^,8DH DE \==.Q 点F 是AC 上的动点,根据垂线段最短,可知DF 的最小值为DH 的长,即DF 的最小值为8.30.A【分析】本题考查了尺规作图—做一个角等于已知角,全等三角形的判定和性质,熟练掌握尺规作图的方法和步骤,以及全等三角形的判定方法SSS,SAS,AAS,ASA,HL ,以及全等三角形对应角相等,即可解答.【详解】解:由作图可知,AC AB DE DF BC EF ====,在ABC V 和DEF V 中,AC DF AB DE BC EF =ìï=íï=î,∴()SSS ABC DEF ≌△△,∴BAC EDF Ð=Ð,故选:A .31.B【分析】本题考查角分线的尺规作图和性质,过点G 作GH AB ^于点H ,根据题意得,AF 是CAB Ð的角平分线,得CG GH =,根据三角形面积公式,即可求出ABG V 的面积.解题的关键是掌握角平分线的性质.【详解】解:过点G 作GH AB ^于点H ,根据题意得,AF 是CAB Ð的角平分线,∵90C Ð=°,∴AC CG ^,∵GH AB ^,∴CG GH =,∵3CG =,∴111231822ABG S AB GH =´´=´´=V ,故选:B .32.C【分析】本题主要考查了作图-复杂作图以及等腰三角形的性质,熟练掌握尺规作图的五个基本图形是解决问题的关键.由作法知AD AC =,可判断A ;由作法知,AD 是BAC Ð的平分线,BAD B =∠∠,可判断B ;由作法知所作图形是线段BC 的垂直平分线,可判断C ; 由作法知,所作图形是线段AB 的垂直平分线,根据线段垂直平分线的性质得到DA DB =,可判断D .【详解】解:A 、由作法知AD AC =,∴ACD V 是等腰三角形,故选项A 不符合题意;B 、由作法知,AD 是BAC Ð的平分线,∴BAD B =∠∠,∴ABD △是等腰三角形,故选项B 不符合题意;C 、90,30,60C B BAC Ð=°Ð=°Ð=°,由作法知所作直线是BC 的垂直平分线,∴BD CD =,∴不能判定ABD △是等腰三角形,故选项C 符合题意;D 、由作法知所作图形是线段AB 的垂直平分线,∴AD BD =,∴ABD △是等腰三角形,故选项D 不符合题意;故选:C .33.(1)64°(2)BDC ACE S S =V V ,理由见解析【分析】(1)由全等可知CA CD =,所以当点D 在AB 上时,CAD V 为等腰三角形,依据已知计算即可.(2)因为两个三角形中有一边相等,只要找到这两个底对应高之间的关系即可.【详解】(1)解:Q ABC DEC ≌△△,\CA CD =,又Q 90ACB Ð=o ,32B Ð=o ,\903258A ADC Ð=Ð=°-°=°,\在ACD V 中,180********ACD A ADC Ð=°-Ð-Ð=°-´°=°,故答案为:64°.(2)解:如下图所示:过点B 作BDC V 的边CD 上的高BG ,过点E 作ACE △的边AC 上的高,由作图及ABC DEC ≌△△知:90BCG DCF Ð+Ð=°,90ECF DCF Ð+Ð=°,CD AC =,\BCG ECF Ð=Ð(同角的余角相等),\在Rt BCG V 与Rt ECF △中有:90BCG ECF BGC EFC BC EC Ð=ÐìïÐ=Ð=°íï=î\Rt BCG Rt ECF V V ≌(AAS ),\BG EF =,Q 12BDC S CD BG =×V ,12ACE S AC EF =×V ,Q CD AC =,BG EF =,\BDC ACE S S =V V ,故答案为:BDC ACE S S =V V .【点睛】本题考查了全等三角形性质和判定,关键是使用分析法找到:两个三角形面积相等时,底相等则高相等,从而构造全等证明对应高相等.34.(1)EF BE DF =+,理由见解析;(2)成立,理由见解析【分析】(1)典型的“夹半角模型”,延长CB 到M 使得BM DF =,先证ADF ABM V V ≌,再证EAM EAF V V ≌,最后根据边的关系即可证明;(2)图形变式题可以参考第一问的思路,延长CB 到M 使得BM DF =,先证ADF ABM V V ≌,再证EAM EAF V V ≌,最后根据边的关系即可证明;【详解】解:(1)EF BE DF =+证明:延长CB 到M ,使得BM DF= 连接AM∵四边形ABCD 是正方形∴AB AD =,D ABM Ð=Ð又∵BM DF =∴()ADF ABM SAS V V ≌ ∴AF AM =,12Ð=Ð ∵45EAF Ð=°∴1345Ð+Ð=°∴2345MAE EAFÐ+Ð=Ð=°=Ð 又∵AE AE= ∴()EAM EAF SAS V V ≌ ∴EF EM BE BM==+ 又∵BM DF= ∴EF EB DF=+(2)EF BE DF=+证明:延长CB 到M ,使得BM DF= 连接AM∵180ABC D Ð+Ð=°,4180ABC Ð+Ð=°∴4D Ð=Ð 又∵AB AD =,BM DF =∴()ADF ABM SAS V V ≌ ∴AF AM =,12Ð=Ð ∵12EAF BADÐ=Ð ∴13EAFÐ+Ð=Ð ∴23MAE EAFÐ=Ð+Ð=Ð 又∵AE AE= ∴()EAM EAF SAS V V ≌ ∴EF EM BE BM ==+又∵BM DF= ∴EF EB DF=+【点睛】本题考查了全等三角形的判定和性质,正确的根据“夹半角模型”作出辅助线是解题的关键.35.(1)50°(2)17AD <<【分析】(1)利用三角形的外角先求解20ABE Ð=°,可得40ABC Ð=°,再结合高与三角形的内角和定理可得答案;(2)延长AD 至K ,使AD DK =,再证明ADB KDC V V ≌,可得8AB CK ==,而6AC =,则214AK <<,再结合中线的含义可得答案.【详解】(1)解:BED ABE BAE Ð=Ð+ÐQ ,60,40BED BAD Ð=°Ð=°,604020ABE \Ð=°-°=°,BE Q 平分ABC Ð,240ABC ABE \Ð=Ð=°,AF Q 为高,90AFB \Ð=°,90904050BAF ABF \Ð=°-Ð=°-°=°;(2)延长AD 至K ,使AD DK =,∵AD 是ABC V 的中线,∴BD CD =,∵ADB CDK Ð=Ð,∴ADB KDC V V ≌,∴8AB CK ==,而6AC =,∴214AK <<,∴17AD <<.【点睛】本题考查的是三角形的中线,高,角平分线的含义,三角形的外角的性质,内角和定理的应用,全等三角形的判定与性质,三角形三边关系的应用,熟记基础概念是解本题的关键.36.210CM <<【分析】倍长中线CM 至点N ,构造BNM V ,易得ACM BNM @△△,再利用三角形的三边关系找到CN 的取值范围,进而得到CM 的取值范围.【详解】解:如图,延长CM 到点N ,使CM MN =,连接BN ,在ACM △和BNM V 中,CM NM AMC BMN AM BM =ìïÐ=Ðíï=î,\ACM BNM @△△(SAS ),\8AC BN ==,在BCN △中,BC BN CN BC BN -<<+,\128128CN -<<+,即420CN <<,\4220CM <<,即210CM <<.【点睛】本题考查了全等三角形的性质与判定以及三角形的三边关系,解决本题的关键是倍长中线构造全等三角形.37.(1)DE BD CE =-;(2)DE BD CE =+,证明过程见解析;(3)DE BD CE=+【分析】(1)根据已知条件证明ABD CAE @V V 即可得解;(2)根据已知条件证明ABD CAE @V V 即可得解;(3)根据已知条件证明ABD CAE @V V 即可得解;【详解】(1)在ABD △和CAE V中,∵90CAD BAD Ð+Ð=°,90BAD ABD Ð+Ð=°,∴CAD ABD Ð=Ð,又∵90ADB AEC Ð=Ð=°,AB AC =,∴ABD CAE @V V ,∴BD AE =,=AD CE ,又AE AD DE =+,∴AE DE CE =+,即DE BD CE =-;故答案是:BD CE -;(2)答:DE BD CE =+;证明:∵BD AE ^于D ,CE AE ^于E ,∴90ADB CEA Ð=Ð=°.∴90ABD BAD Ð+Ð=°,∵18090CAE BAD BAC Ð+Ð=°-Ð=°,∴ABD CAE Ð=Ð.在ABD △和CAE V 中,ADB CEA ABD CAE AB AC Ð=ÐìïÐ=Ðíï=î,∴ABD CAE ≌V V (AAS ),∴BD AE =,=AD CE ,∴DE AE AD BD CE =+=+;(3)∵BD AE ^于D ,CE AE ^于E ,∴90ADB CEA Ð=Ð=°.∴90ABD BAD Ð+Ð=°,∵18090CAE BAD BAC Ð+Ð=°-Ð=°,∴ABD CAE Ð=Ð.在ABD △和CAE V 中,ADB CEA ABD CAE AB CA Ð=ÐìïÐ=Ðíï=î,∴ABD CAE ≌V V (AAS ),∴BD AE =,=AD CE ,∴DE BD CE =+;【点睛】本题主要考查了全等三角形的综合应用,准确分析证明是解题的关键.38.(1)(83)cmt -(2)全等,理由见详解(3)15cm/s 4【分析】(1)根据题意可得出答案;(2)由“SAS ”可证BPD CQP V V ≌;(3)根据全等三角形的性质得出4cm BP PC ==,5cm CQ BD ==,则可得出答案.本题考查了等腰三角形的性质,全等三角形的性质和判定的应用等知识,熟练运用这些性质解决问题是解此题的关键.【详解】(1)解:∵8cm BC =,点D 为AB 的中点.如果点P 在线段BC 上以3cm/s 的速度由点B 向C 点运动,∴(83)cm PC BC BP t =-=-,故答案为:(83)cm t -.(2)解:全等,理由:1t s =Q ,点Q 的运动速度与点P 的运动速度相等,313(cm)BP CQ \==´=,10cm AB =Q ,点D 为AB 的中点,5(cm)BD \=.又PC BC BP =-Q ,8cm BC =,835(cm)PC \=-=,PC BD \=,又AB AC =Q ,B C \Ð=Ð,在BPD △和CQP V 中,。
人教版版八年级上册数学期中常考题《全等三角形的性质》专项复习

人教版八年级上册数学期中常考题《全等三角形的性质》专项复习一.选择题(共5小题)1.如图,△ABC≌△DEF.若BC=5cm,BF=7cm,则EC=()A.1cm B.2cm C.3cm D.4cm2.(2020秋•巩义市期末)已知图中的两个三角形全等,则∠1等于()A.72°B.60°C.50°D.58°3.(2021•浦东新区模拟)在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是()A.(6,0)B.(4,0)C.(4,﹣2)D.(4,﹣3)4.(2021•新华区模拟)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是()A.90°B.120°C.135°D.180°5.(2021春•衡阳期末)如图,已知Rt△ABC≌Rt△CDE,下列结论中不正确的是()A.AC=CE B.∠BAC=∠ECD C.∠ACB=∠ECD D.∠B=∠D二.填空题(共5小题)6.(2020秋•河东区期末)如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为.7.(2020秋•吉林期末)如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是.8.(2020秋•射阳县期末)如图,△ABC≌△ADE,∠EAC=35°,则∠BAD=°.9.(2021春•泰兴市期末)如图,两个三角形全等,根据图中所给条件,可得∠α=°.10.(2021春•雁塔区校级期末)一个三角形的三条边的长分别是5,7,10,另一个三角形的三条边的长分别是5,3x﹣2,2y+1,若这两个三角形全等,则x+y的值是或.三.解答题(共5小题)11.(2020秋•章贡区期末)如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.12.(2021春•市中区期末)如图,△ABD≌△EBC,AB=3cm,BC=6cm,(1)求DE的长.(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?13.(2021春•碑林区校级期中)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=10,BC=4,∠D=30°,∠C=70°.(1)求线段AE的长.(2)求∠DBC的度数.14.(2021春•铁西区期中)如图,点B、C、E、F在同一直线上,AB⊥BC于点B,△DEF ≌△ABC,且BC=6,CE=3.(1)求CF的长;(2)判断DE与EF的位置关系,并说明理由.15.(2021春•宝安区期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.(1)求证:CE⊥AB;(2)已知BC=7,AD=5,求AF的长.参考答案一.选择题(共5小题)1.【解答】解:∵BC=5cm,BF=7cm,∴CF=BF﹣BC=2cm,∵△ABC≌△DEF,∴FE=BC=5cm,∴EC=EF﹣CF=5cm﹣2cm=3cm,故选:C.2.【解答】解:如图,由三角形内角和定理得到:∠2=180°﹣50°﹣72°=58°.∵图中的两个三角形全等,∴∠1=∠2=58°.故选:D.3.【解答】解:如图所示:△ABC与△EFB全等,点F的坐标可以是:(4,﹣3).故选:D.4.【解答】解:如图所示:由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,∵三个全等三角形,∴∠4+∠9+∠6=180°,又∵∠5+∠7+∠8=180°,∴∠1+∠2+∠3+180°+180°=540°,∴∠1+∠2+∠3的度数是180°.故选:D.5.【解答】解:∵Rt△ABC≌Rt△CDE,∴AC=CE,故A正确;∴∠BAC=∠ECD,故B正确;∴∠B=∠D,故D正确;但不能得出∠ACB=∠ECD,故C错误;故选:C.二.填空题(共5小题)6.【解答】解:∵△ABE≌△ACF∴AC=AB=5∴EC=AC﹣AE=5﹣2=3,故答案为:3.7.【解答】解:∵△AOB≌△COD,∴OD=OB,∴点D的坐标是(﹣2,0).故答案为:(﹣2,0).8.【解答】解:∵△ABC≌△ADE,∴∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠BAD=∠EAC,∵∠EAC=35°,∴∠BAD=35°,故答案为:35.9.【解答】解:左边的三角形中,b所对的角为180°﹣65°﹣55°=60°,两个全等三角形中,相等的边是对应边,两三角形中,长度为b的边是对应边,它们对的角是对应角,∴∠α=60°故答案为:60.10.【解答】解:由题意得,①,解得,,∴x+y=3+=;②,解得,,∴x+y=4+3=7;故答案为:或7.三.解答题(共5小题)11.【解答】证明:∵△ABC≌△DEC,∴∠B=∠DEC,BC=EC,∴∠B=∠BEC,∴∠BEC=∠DEC,∴CE平分∠BED.12.【解答】解:(1)∵△ABD≌△EBC,∴BD=BC=6cm,BE=AB=3cm,∴DE=BD﹣BE=3cm;(2)DB⊥AC.理由如下:∵△ABD≌△EBC,∴∠ABD=∠EBC,又∵∠ABD+∠EBC=180°,∴∠ABD=∠EBC=90°,∴DB⊥AC.13.【解答】解:(1)∵△ABC≌△DEB,DE=10,BC=4,∴AB=DE=10,BE=BC=4,∴AE=AB﹣BE=6;(2)∵△ABC≌△DEB,∠D=30°,∠C=70°,∴∠BAC=∠D=30°,∠DBE=∠C=70°,∴∠ABC=180°﹣30°﹣70°=80°,∴∠DBC=∠ABC﹣∠DBE=10°.14.【解答】解:(1)∵△DEF≌△ABC,∴BC=EF,∵BC=6,CE=3,∴EF=6,∴CF=EF+EC=6+3=9;(2)DE⊥EF,理由:∵AB⊥BC,∴∠ABC=90°,∴∠ABC=∠DEF=90°,∴DE⊥EF.15.(【解答】(1)证明:∵△ABD≌△CFD,∴∠BAD=∠DCF,又∵∠AFE=∠CFD,∴∠AEF=∠CDF=90°,∴CE⊥AB;(2)解:∵△ABD≌△CFD,∴BD=DF,∵BC=7,AD=DC=5,∴BD=BC﹣CD=2,∴AF=AD﹣DF=5﹣2=3.。
苏科版八年级数学上册 第1章全等三角形 期中复习综合练习题 (含答案和解析)-doc
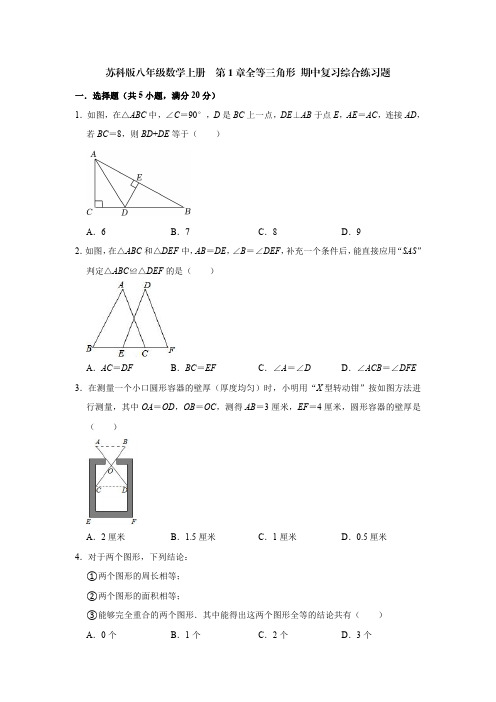
苏科版八年级数学上册第1章全等三角形期中复习综合练习题一.选择题(共5小题,满分20分)1.如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于点E,AE=AC,连接AD,若BC=8,则BD+DE等于()A.6B.7C.8D.92.如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充一个条件后,能直接应用“SAS”判定△ABC≌△DEF的是()A.AC=DF B.BC=EF C.∠A=∠D D.∠ACB=∠DFE 3.在测量一个小口圆形容器的壁厚(厚度均匀)时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=3厘米,EF=4厘米,圆形容器的壁厚是()A.2厘米B.1.5厘米C.1厘米D.0.5厘米4.对于两个图形,下列结论:①两个图形的周长相等;②两个图形的面积相等;③能够完全重合的两个图形.其中能得出这两个图形全等的结论共有()A.0个B.1个C.2个D.3个5.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=7,CF=4,则BD的长是()A.5B.4C.3D.2二.填空题(共5小题,满分20分)6.如图.两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位,AB=8,DP=3,平移距离为6,则阴影部分的面积为.7.如图,在等腰△ABC中,∠ACB=90°,点D是AC的中点,过点A作直线BD的垂线交BC的延长线于点E,若BC=4,则CE的长为.8.如图,在网格中(每个小正方形的边长为1)有一个格点△ABC(三角形的顶点都在格点上),则∠1﹣∠2=°.9.如图,△ABC的面积为10cm2,AP垂直∠B的平分线BP于P,则△BCP的面积为cm2.10.如图,在△ABC中,点E是中线AD上的一点且AE=ED,连接CE,且CE=6,若∠AEC=4∠BAD=120°,则AC的长为.三.解答题(共12小题,满分80分)11.如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.若∠A=55°,求∠EDF的度数.12.已知:如图,在四边形ABCD中,连接AC,DE⊥AC,垂足为点E,BF⊥AC,垂足为点F,AD=BC,DE=BF.请说明AB与CD的数量关系和位置关系,并说明理由.13.如图所示,∠A=∠D=90°,AB=DC,点E,F在AD上且BE=CF.(1)求证:∠BEA=∠CFD;(2)若PO平分∠EPF,则PO与线段EF有什么关系?请证明你的结论.14.如图,点E、C在线段BF上,点A、D在BF同侧,AC、DE相交于点O.若OE=OC,BE=CF,∠B=∠F,则∠A与∠D相等吗?说明理由.15.如图,已知点C、点D都在线段AF上,AC=DF,BC∥EF,∠B=∠E.(1)求证:△ABC≌△DEF;(2)求证:AB∥DE.16.如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥EF于E,CF⊥EF 于F,AE=CF,连接BD,求证:Rt△ADE≌Rt△CDF.17.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.18.如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC 上,且AE=CF.求证:Rt△ABE≌Rt△CBF.19.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.(1)Rt△ADE与Rt△BEC全等吗?并说明理由;(2)△CDE是不是直角三角形?并说明理由.20.如图,在△ABC中,点D为AB边上一点,DE∥BC交AC于点E,点F为BC延长线上一点,BF=AD,∠ACF=∠ADF.(1)求证:AE=FD;(2)若∠FDB=80°,∠B=70°,求∠1的度数.21.校园内有一块四边形的草坪造型,课外活动小组实地测量,并记录数据,根据造型画如图的四边形ABCD,其中AB=CD=2米,AD=BC=3米,∠B=30°.(1)求证:△ABC≌△CDA;(2)求草坪造型的面积.22.为了测量一池塘的两端A,B之间的距离,同学们想出了如下的两种方案:方案①如图1,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,BC至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长;方案②如图2,过点B作AB的垂线BF,在BF上取C,D两点,使BC=CD,接着过D作BD的垂线DE,在垂线上选一点E,使A、C、E三点在一条直线上,则测出DE的长即是AB的距离.问:(1)方案①是否可行?请说明理由;(2)方案②是否可行?请说明理由;(3)小明说在方案②中,并不一定需要BF⊥AB,DE⊥BF,只需要就可以了,请把小明所说的条件补上.参考答案一.选择题(共5小题,满分20分)1.解:∵DE⊥AB,∴∠DEB=90°,在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴CD=DE,∴BD+DE=BD+CD=BC,∵BC=8,∴BD+DE=BC=8.故选:C.2.解:A.AB=DE,AC=DF,∠B=∠DEF,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;B.AB=DE,∠B=∠DEF,BC=EF,符合全等三角形的判定定理SAS,能推出△ABC ≌△DEF,故本选项符合题意;C.∠A=∠D,AB=DE,∠B=∠DEF,符合全等三角形的判定定理ASA(不是SAS),能推出△ABC≌△DCB,故本选项不符合题意;D.∠ACB=∠F,∠ABC=∠DEF,AB=DE,符合全等三角形的判定定理AAS(不是SAS),能推出△ABC≌△DCB,故本选项不符合题意;故选:B.3.解:在△AOB和△DOC中,,∴△AOB≌△DOC(SAS),∴AB=CD=3厘米,∵EF=4厘米,∴圆柱形容器的壁厚是×(4﹣3)=0.5(厘米),故选:D.4.解:①周长相等的两个图形不一定重合,所以这两个图形不一定全等;②面积相同而形状不同的两个图形不全等;③两个图形能够完全重合,则这两个图形全等.所以只有1个结论正确.故选B.5.解:∵CF∥AB,∴∠A=∠FCE,∠ADE=∠F,在△ADE和△FCE中,,∴△ADE≌△CFE(AAS),∴AD=CF=4,∵AB=7,∴DB=AB﹣AD=7﹣4=3.故选:C.二.填空题(共5小题,满分20分)6.解:由平移的性质知,BE=6,DE=AB=8,∴PE=DE﹣DP=8﹣3=5,∵△ABC≌△DEF,=S△DEF,∴S△ABC=S梯形ABEO=(AB+PE)•BE=(8+5)×6=39,∴S四边形ODFC故答案为:39.7.解:在等腰△ABC中,∠ACB=90°,点D是AC的中点,∴AC=BC=4,AD=CD=2,∵∠E+∠CAE=90°=∠E+∠EBD,∴∠EBD=∠CAE,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴CE=CD=2,故答案为:2.8.解:∵AB2=AC2=22+32=13,BC2=12+52=26,∴AB2+AC2=BC2,∴∠BAC=90°,∴∠ABC=45°,∴90°﹣∠2+45°+∠1=180°,∴∠1﹣∠2=45°,故答案为:45.9.解:延长AP交BC于E,∵AP垂直∠B的平分线BP于P,∴∠ABP=∠EBP,又∵BP=BP,∠APB=∠BPE=90°,∴△ABP≌△BEP(ASA),=S△BEP,AP=PE,∴S△ABP∴△APC和△CPE等底同高,=S△PCE,∴S△APC=S△PBE+S△PCE=S△ABC=5cm2,∴S△PBC故答案为:5.10.解:延长CE交AB于点F,过点D作DG∥CF,交AB于点G,如图所示:∵∠AEC=4∠BAD=120°,∴∠AEF=60°,∠BAD=30°,∴∠AFE=90°,设EF=x,则AE=2x,AF=x,∵AE=ED,∴DE=3x,∵DG∥CF,∴∠AEF=∠ADG,∠AFE=∠AGD,∴△AEF∽△ADG,∴FE:DG=AE:AD=2:5,∴DG=EF=x,∵D是BC的中点,∴DG=,∵CE=6,∴x=(x+6),解得x=,∴AF=,CF=,根据勾股定理,得AC=.故答案为:.三.解答题(共12小题,满分80分)11.解:∵AD=CF,∴AD+DC=DC+CF,即AC=DF,在△ABC和△DEF中,,∴△ABC≌△DEF(SSS),∴∠EDF=∠A,∵∠A=55°,∴∠EDF=55°.12.解:AB=CD,AB∥CD,理由如下:∵DE⊥AC,BF⊥AC,∴∠DEA=∠BFC=90°,在Rt△ADE和Rt△CBF中,,∴Rt△ADE≌Rt△CBF(HL),∴∠DAE=∠BCF,∴AD∥BC,∵AD=BC,∴四边形ABCD是平行四边形,∴AB=CD,AB∥CD.13.(1)证明:在Rt△ABE和Rt△DCF中,,∴Rt△ABE≌Rt△DCF(HL),∴∠BEA=∠CFD;(2)解:PO垂直平分EF,理由如下:∵∠BEA=∠CFD,∴PE=PF,∵PO平分∠EPF,∴PO⊥EF,FO=EO,∴PO垂直平分EF.14.解:∠A=∠D,理由如下:∵OE=OC,∴∠ACB=∠DEF,∵BE=CF,∴BC=EF,在△ABC和△DFE中,,∴△ABC≌△DFE(ASA),∴∠A=∠D.15.(1)证明:如图,∵AD=CF,∴AD+CD=CF+CD,∴AC=DF,∵BC∥EF,∴∠ACB=∠F,在△ABC和△DEF中,,∴△ABC≌△DEF(AAS);(2)证明:∵△ABC≌△DEF,∴∠A=∠EDF,∴AB∥DE.16.证明:∵∠BAD=∠BCD=90°,在Rt△ABD和Rt△CBD中,,∴Rt△ABD≌Rt△CBD(HL),∴AD=CD,∵AE⊥EF于E,CF⊥EF于F,∴∠E=∠F=90°,在Rt△ADE和Rt△CDF中,,∴Rt△ADE≌Rt△CDF(HL).17.证明:∵∠A=∠D=90°,AC=BD,BC=BC,∴Rt△BAC≌Rt△CDB(HL)∴∠ACB=∠DBC.∴∠OCB=∠OBC.∴OB=OC(等角对等边).18.证明:在Rt△ABE和Rt△CBF中,∵,∴Rt△ABE≌Rt△CBF(HL).19.解:(1)全等,理由是:∵∠1=∠2,∴DE=CE,在Rt△ADE和Rt△BEC中,,∴Rt△ADE≌Rt△BEC(HL);(2)是直角三角形,理由是:∵Rt△ADE≌Rt△BEC,∴∠3=∠4,∵∠3+∠5=90°,∴∠4+∠5=90°,∴∠DEC=90°,∴△CDE是直角三角形.20.(1)证明:∵∠ACF=∠ADF,∴∠B+∠A=∠B+∠F,∴∠A=∠F,∵DE∥BC,∴∠ADE=∠B,在△ADE和△FBD中,,∴△ADE≌△FBD(ASA),∴AE=FD;(2)解:∵∠FDB=80°,∠B=70°,∴∠F=30°,∴∠ACF=∠ADF=∠B+∠F=100°,∴∠1=∠F+∠ACF=130°.21.(1)证明:在△ABC和△CDA中,∵,∴△ABC≌△CDA(SSS);(2)解:过点A作AE⊥BC于点E,∵AB=2米,∠B=30°,∴AE=1米,=×3×1=(平方米),∴S△ABC=(平方米),则S△CDA∴草坪造型的面积为:2×=3(平方米).22.解:(1)方案①可行,理由如下:在△DCE和△ACB中,,∴△DCE≌△ACB(SAS),∴DE=AB,∴方案①可行;(2)方案②可行,理由如下:∵AB⊥BF,DE⊥BF,∴∠ABC=∠EDC=90°,在△ABC和△EDC中,,∴△ABC≌△EDC(ASA),∴DE=AB,故方案②可行;(3)只需要AB∥DE,此时∠ABC=∠EDC,证明步骤同(2),故答案为:AB∥DE。
2020-2021学年八年级数学人教版上册 全等三角形 期中专项练习

2020-2021年八年级数学人教版(上)全等三角形期中专项练习2一、解答题(本大题共16道小题)1. 已知:如图,在梯形ABCD中,AD∥BC,E是AB的中点,CE的延长线与DA的延长线相交于点F.(1)求证:△BCE≌△AFE;(2)连接AC、FB,则AC与FB的数量关系是,位置关系是.FEBC A D2. 如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是.(只填一个即可)3. (1)已知:如图,△ABE≌△A CD,∠1=∠2,∠B=∠C,指出其他的对应边和对应角.(2)由对应边找对应角,由对应角找对应边有什么规律?4. 已知:如图,AB∥CD,AB=CD.求证:AD∥BC.分析:要证AD ∥BC ,只要证∠______=∠______,又需证______≌______.证明:∵ AB ∥CD ( ),∴ ∠______=∠______ ( ),在△______和△______中,⎪⎩⎪⎨⎧===),______(______),______(______),______(______ ∴ Δ______≌Δ______ ( ).∴ ∠______=∠______ ( ).∴ ______∥______( ).5. 如图,A 、C 、D 、B 四点共线,且AC =BD ,∠A =∠B ,∠ADE =∠BCF.求证:DE =CF.6. (12分)如图在△AFD 和△CEB 中,点A 、E 、F 、C 在同一条直线上.有下面四个论断:(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD ∥BC.请用其中三个作为条件,余下一个作为结论,进行证明.条件是:结论是:证明:7. 如图,木工师傅常用角尺来作任意一个角的平分线,请你设计一个方案,只用角尺来作∠AOB 的平分线,并说明理由.8. 如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;(2)求出∠FHG的度数.9. 在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.(1)求∠DFG的度数;(2)设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.10. 已知:如图,OD平分∠POQ,在OP、OQ边上取OA=OB,点C在OD上,CM⊥AD于M,CN⊥BD于N.求证:CM=CN.11. 四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠ADC+∠B=180°求证:2AE=AB+AD.12. 如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,•若AB=CD,试证明BD平分EF.13. (8分)如图所示,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.14. 已知△ABC为等边三角形,D为AB边所在的直线上的动点,连接DC,以DC为边在DC 两侧作等边△DCE和等边△DCF(点E在DC的右侧或上侧,点F在DC左侧或下侧),连接AE、BF(1)如图1,若点D在AB边上,请你通过观察,测量,猜想线段AE、BF和AB有怎样的数量关系?并证明你的结论;(2)如图2,若点D在AB的延长线上,其他条件不变,线段AE、BF和AB有怎样的数量关系?请直接写出结论(不需要证明);(3)若点D在AB的反向延长线上,其他条件不变,请在图3中画出图形,探究线段AE、BF和AB有怎样的数量关系,并直接写出结论(不需要证明)15. 如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为,线段CF、BD的数量关系为;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.16. 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.(1)如果点P在线段BC上以4cm/秒的速度由B点向C点运动,同时,点Q在线段CD上以acm/秒的速度由C点向D点运动,设运动的时间为t秒,①CP的长为cm(用含t的代数式表示);②若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,求a的值.(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动.则点P与点Q会不会相遇?若不相遇,请说明理由.若相遇,求出经过多长时间点P与点Q第一次在正方形ABCD的何处相遇?。
2021年北京重点校初二(上)期中数学试卷汇编:全等三角形1
2021北京重点校初二(上)期中数学汇编全等三角形1一、单选题1.(2021·北京四中八年级期中)某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最少要带第()块去玻璃店就可以买到完全一样的玻璃.A.①B.②C.③D.①②③2.(2021·北京四中八年级期中)正方形网格中,AOB∠的位置如图所示,到AOB∠两边距离相等的点是()A.点M B.点N C.点P D.点Q△≌△,3.(2021·北京四中八年级期中)如图,点B,D,E,C在同一条直线上,若ABD ACEAEC∠=︒,则DAE110∠的度数为()A.30B.40︒C.50︒D.60︒4.(2021·北京·101中学八年级期中)如图,A、B是两个居民小区,快递公司准备在公路l上选取点P处建一个服务中心,使P A=PB.下面四种选址方案,符合要求的是()A .B .C .D .5.(2021·北京市第一六一中学八年级期中)下列各组条件中,能判定△ABC ≌△DEF 的是( )A . AB =DE ,BC =EF ,AC =DFB .AB =DE ,BC =EF ,∠A =∠D C .∠A =∠D ,∠C =∠F ,AC =EF D .∠A =∠D ,∠B =∠E ,∠C =∠F6.(2021·北京·101中学八年级期中)如图,在ABC 中,BC 的垂直平分线分别交AC ,BC 于点D ,E .若ABD △的周长为13,BE =5,则ABC 的周长为( )A .14B .28C .18D .237.(2021·北京市第一六一中学八年级期中)如图,在四边形ABCD 中,对角线AC 平分BAD ∠,AB AC >,下列结论正确的是( )A .AB AD CB CD −>−B .AB AD CB CD −=−C .AB AD CB CD −<− D .AB AD −与CB CD −的大小关系不确定8.(2021·北京·首都师范大学附属中学八年级期中)已知图中的两个三角形全等,则∠α等于( )A.50°B.60°C.70°D.80°9.(2021·北京市第十二中学八年级期中)如图,若△ABC≌△DEF,四个点B、E、C、F在同一直线上,BC=7,EC=5,则CF的长是()A.2B.3C.5D.7二、填空题10.(2021·北京·清华附中八年级期中)如图,在ABC中,BC的垂直平分线MN交AB于点D,若BD=,3+的最小值是______.5AD=,P是直线MN上的任意一点,则PA PC=,点D,E在边BC上,11.(2021·北京·清华附中八年级期中)如图,在ABC中,AB AC∠=∠,若16BAD CAEBC=,6DE=,则CE的长为______.12.(2021·北京师大附中八年级期中)如图,A、B、C、D四点共线,且AB=CD,CE⊥AB于C,DF⊥AB于D,请添加一个条件使△ACE≌△BDF,并证明.添加条件____________________.证明:13.(2021·北京师大附中八年级期中)如图,在△ABC 中,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,若△ABC 的周长是20,且OD =3,则△ABC 的面积为________.14.(2021·北京四中八年级期中)如图,DE 是ABC 中AC 边的垂直平分线,若4BC =,5AB =,则EBC 的周长是_________.15.(2021·北京四中八年级期中)如图,在ABC 中,BD 是边AC 上的高,CE 平分ACB ∠,交BD 于点E ,4DE =,10BC =,则BCE 的面积为___________.16.(2021·北京四中八年级期中)如图,已知12∠=∠,添加一个条件______________,使得ABC ADC △≌△.17.(2021·北京市第十二中学八年级期中)在△ABC 中,若AB =5,AC =7,AD 是BC 边上的中线,则AD 的取值范围是___.18.(2021·北京·101中学八年级期中)如图,BE 与CD 交于点A ,且B E ∠=∠.请添加一个条件使得ABC AED ≌△△,这个条件是:_________(写出一个即可)19.(2021·北京八中八年级期中)如图,OP 平分∠MON ,P A ⊥ON 于点A ,点Q 是射线OM 上一个动点,若P A=2,则PQ 的最小值为__________.20.(2021·北京市第一六一中学八年级期中)如图,在ABC ∆中,边AB 的垂直平分线交BC 于点D ,交AB 于点E ,若3AE =,ADC ∆的周长为9,则ABC ∆的周长=__________.21.(2021·北京市第十二中学八年级期中)如图,△ABC ≌△DEC ,∠ACD =28°,则∠BCE =_____°.22.(2021·北京师大附中八年级期中)如图,要测量池塘两岸相对的两点A ,B 的距离,可以在池塘外取AB 的垂线BF 上的两点C ,D ,使BC =CD ,再画出BF 的垂线DE ,使E 与A ,C 在一条直线上.若想知道两点A ,B 的距离,只需要测量出线段______________即可.三、解答题23.(2021·北京四中八年级期中)我们类比学习“三角形全等的判定”获得的经验与方法,对“四边形全等的判定”进行探究.根据全等形的定义,如果四边形满足四条边分别相等,四个角分别相等,就能判定这两个四边形全等.【初步思考】一定要满足四条边分别相等,四个角也分别相等,才能保证两个四边形全等吗?能否在上述八个条件中选择部分条件,简捷地判定两个四边形全等呢?通过画图可以发现,满足上述八个条件中的四个条件的两个四边形不一定全等,举反例如图1或图2:【深入探究】满足上述八个条件中的五个,能保证两个四边形全等吗?小萍所在学习小组进行了研究,她们认为五个条件可分为以下四种类型:Ⅰ.一条边和四个角分别相等;Ⅱ.二条边和三个角分别相等;Ⅲ.三条边和二个角分别相等;Ⅳ.四条边和一个角分别相等.(1)小齐认为“Ⅰ.一条边和四个角分别相等”的两个四边形不一定全等,请你画图举反例说明,并写出分别相等的一条边和四个角.(2)小栗认为“Ⅳ.四条边和一个角分别相等”的两个四边形全等,请你结合下图进行证明.已知:如图,四边形ABCD 和四边形1111D C B A 中,11AB A B =,11BC B C =,11CD C D =,11=DA D A ,1B B ∠=∠.求证:四边形ABCD ≌四边形1111D C B A .(3)小熊认为还可以对“Ⅱ.二条边和三个角分别相等”进一步分类,他以四边形ABCD 和四边形1111D C B A 为例,分为以下几类:①1111111,,,,==∠=∠∠=∠∠=∠AB A B AD A D A A B B C C ;②1111111,,,,==∠=∠∠=∠∠=∠AB A B AD A D A A B B D D ;③1111111,,,,==∠=∠∠=∠∠=∠AB A B AD A D B B C C D D ;④1111111,,,,==∠=∠∠=∠∠=∠AB A B CD C D A A B B C C .其中能判定四边形ABCD 和四边形1111D C B A 全等的是__________(填序号),概括可得一个“全等四边形的判定方法”,这个判定方法是_________________.24.(2021·北京四中八年级期中)已知:如图1,在ABC 中,AD 是BAC ∠的平分线.E 是线段AD 上一点(点E 不与点A ,点D 重合),满足2∠=∠ABE ACE .(1)如图2,若18∠=︒ACE ,且EA EC =,则DEC ∠=________︒,AEB ∠=_______︒.(2)求证:AB BE AC +=.(3)如图3,若BD BE =,请直接写出ABE ∠和BAC ∠的数量关系.25.(2021·北京四中八年级期中)如图,已知AOB ∠.按照以下步骤作图:①以点O 为圆心,以适当的长为半径作弧,分别交OA 、OB 于M 、N 两点;②分别以点M ,N 为圆心,以大于12线段MN 的长为半径作弧,两弧在AOB ∠内部交于点C . 则射线OC 是AOB ∠的角平分线.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出射线OC (请保留作图痕迹);(2)完成下面证明过程.(注:括号里填写推理的依据).连接MC ,NC .在OCM 和OCN 中,∵,,,OM ON OC OC MC NC =⎧⎪=⎨⎪=⎩∴≌OCM OCN ( ),∴AOC ∠=________( ),即OC 平分AOB ∠.26.(2021·北京师大附中八年级期中)如图,AB =AC ,BD =CD ,DE ⊥AB 于E ,DF ⊥AC 于F .求证:DE =DF证明:在△ABD 和△ACD 中,AB AC =, ,∴△ABD≌△ACD()∴∠=∠()∴AD是∠BAC的角平分线又∵DE⊥AB于E,DF⊥AC于F,∴DE=DF()27.(2021·北京·101中学八年级期中)如图,在△ABC中,AB=AC,过点B作BD⊥AC于点D,点E在△ABC内部,连结AE,BE,CE,其中AE,BE分别平分∠BAD,∠ABD.(1)求∠AEB的度数:(2)试判断△BEC的形状,并说明理由.28.(2021·北京·首都师范大学附属中学八年级期中)已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,试问:DE和DF相等吗?说明理由.29.(2021·北京市第一六一中学八年级期中)已知:如图,∠B=∠C=90°,M是BC的中点,且DM平分∠ADC.(1)求证:AM平分∠DAB.(2)试说明线段DM与AM有怎样的位置关系?并证明你的结论.30.(2021·北京四中八年级期中)如图,已知AB=AC,E为AB上一点,ED∥AC,ED=AE.求证:BD=CD.参考答案1.C【分析】根据全等三角形的判定定理解答.【详解】解:第③保留有原三角形的两个角和一条边,可以利用ASA 证明两个三角形全等, 故选:C .【点睛】此题考查全等三角形的判定定理:SSS 、ASA 、AAS 、SAS 、HL ,熟记各判定定理并熟练应用解决问题是解题的关键.2.A【分析】角平分线上的点到角两边的距离相等,根据角平分线的性质解答.【详解】解:如图,作AOB ∠的平分线,点M 在该角平分线上,∴点M 到AOB ∠两边距离相等,故选:A .【点睛】此题考查角平分线的性质,熟记性质定理并正确作出角平分线是解题的关键.3.B【分析】由全等三角形的性质,得到110ADB AEC ∠=∠=︒,然后得到70ADE AED ∠=∠=︒,利用三角形的内角和定理,即可求出答案.【详解】解:根据题意,∵ABD ACE △≌△,∴110ADB AEC ∠=∠=︒,∴18011070ADE AED ∠=∠=︒−︒=︒,∴180707040DAE ∠=︒−︒−︒=︒;故选:B .【点睛】本题考查了全等三角形的性质,三角形的内角和定理,解题的关键是掌握所学的知识,正确的进行解题.4.C【分析】根据题意,使P A=PB ,即P 点在AB 的垂直平分线上,进而观察选项即可求得答案 【详解】P A=PB ,∴P 点在AB 的垂直平分线上,只有C 选项的P 点的位置满足题意,故选C【点睛】本题考查了垂直平分线的应用,掌握垂直平分线的性质是解题的关键.5.A【分析】根据三角形全等的判定方法逐个判断即可.判定三角形全等的方法有:SSS ,SAS ,AAS ,ASA ,HL (直角三角形).【详解】解:A 、AB =DE ,BC =EF ,AC =DF ,可以根据SSS 判断两个三角形全等,符合题意;B 、AB =DE ,BC =EF ,∠A =∠D ,两边及其一边的对角相等的两个三角形不一定全等,不符合题意;C 、∠A =∠D ,∠C =∠F ,AC =EF ,不能判定两个三角形全等,,不符合题意;D 、∠A =∠D ,∠B =∠E ,∠C =∠F ,三组角对应相等的两个三角形不一定全等,不符合题意. 故选:A .【点睛】此题考查了三角形全等的判定方法,解题的关键是熟练掌握三角形全等的判定方法.判定三角形全等的方法有:SSS ,SAS ,AAS ,ASA ,HL (直角三角形).6.D【分析】利用线段的垂直平分线的性质证明△ABD 的周长=AB +AC ,再求出BC =2BC 解答即可.【详解】解:∵BC 的垂直平分线分别交AC ,BC 于点D ,E ,∴DB =DC ,BE =EC ,∵BE =5,∴BC =10,∵△ABD 的周长=AB +AD +BD =AB +AD +DC =AB +AC =13,∴△ABC 的周长为AB +AC +BC =13+10=23,故选:D .【点睛】本题考查线段垂直平分线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.7.A【分析】先通过在AB 上截取AE =AD ,得到一对全等三角形,利用全等三角形的性质得到对应边相等,再利用三角形的三边关系和等量代换即可得到A 选项正确.【详解】解:如图,在AB 上取AE AD =,对角线AC 平分BAD ∠,BAC DAC ∴∠=∠,在ACD ∆和ACE ∆中,AD AE BAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩,()ACD ACE SAS ∴∆≅∆,CD CE ∴=,BE CB CE >−,AB AD CB CD ∴−>−.故选:A .【点睛】本题考查了全等三角形的判定与性质、角平分线的定义和三角形的三边关系,要求学生能根据已知条件做出辅助线构造全等三角形,并能根据全等三角形的性质得到不同线段之间的关系,利用三角形三边关系判断大小,解决本题的关键是牢记概念和公式,正确作辅助线构造全等三角形等.8.C【分析】利用全等三角形的性质及三角形内角和可求得答案.【详解】解:如图,∵两三角形全等,∴∠2=60°,∠1=52°,∴∠α=180°-50°-60°=70°,故选:C.【点睛】本题主要考查全等三角形的性质,掌握全等三角形的对应角相等是解题的关键.9.A【分析】根据全等三角形的性质证得EF=BC=7,从而求得答案.【详解】∵△ABC≌△DEF,∴BC=EF= 7∴ CF=EF-EC=7-5=2故选:A.【点睛】本题考查了全等三角形的性质.题目简单,熟记全等三角形的性质是解题的关键.10.8【分析】如图,连接PB.利用线段的垂直平分线的性质,可知PC=PB,推出P A+PC=P A+PB≥AB,即可解决问题.【详解】解:如图,连接PB.∵MN 垂直平分线段BC ,∴PC =PB ,∴P A +PC =P A +PB ,∵P A +PB ≥AB =BD +DA =5+3=8,∴P A +PC ≥8,∴P A +PC 的最小值为8.故答案为:8.【点睛】本题考查轴对称﹣最短问题,线段的垂直平分线的性质等知识,解题的关键是学会利用两点之间线段最短解决最短问题,属于中考常考题型.11.5【分析】由题意易得B C ∠=∠,然后可证ABD ACE △≌△,则有BD CE =,进而问题可求解.【详解】解:∵AB AC =,∴B C ∠=∠,∵BAD CAE ∠=∠,∴ABD ACE △≌△(ASA ),∴BD CE =,∵16BC =,6DE =,∴10BD CE BC DE +=−=,∴5BD CE ==;故答案为5.【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.12.∠E =∠F (不唯一)【分析】添加条件∠E =∠F ,利用AAS 证明两个三角形全等即可.【详解】解:添加条件:∠E =∠F ,∵AB =CD ,∴AB +BC =CD +BC ,即AC =BD ,∵CE ⊥AB ,DF ⊥AB ,∴∠ACE =∠BDF =90°,在△ACE 和△BDF 中,=ACE BDF E FAC BD ∠=∠⎧⎪∠∠⎨⎪=⎩, ∴△ACE ≌△BDF (AAS ),故答案为:∠E =∠F (不唯一).【点睛】本题主要考查了添加条件证明三角形全等,解题的关键在于能够熟练掌握全等三角形的判定条件.13.30【分析】过点O 作OE ⊥AB 于E ,作OF ⊥AC 于F ,连接AO 根据角平分线上的点到角的两边的距离相等可得OE =OD =OF ,然后根据三角形的面积列式计算即可得解.【详解】解:如图,过点O 作OE ⊥AB 于E ,作OF ⊥AC 于F ,连接AO∵OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC ,∴OE =OD =OF =3,∴=ABC ABO ACO BCO S S S S ++△△△△111222AB OE AC OF BC OD =++ ()32AB AC BC =++, ∵△ABC 的周长为20,∴AB +AC +BC =20,∴=30ABC S △,故答案为:30.【点睛】本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键. 14.9 【分析】由垂直平分线的性质,得到AE =CE ,然后得到BE +CE =5,即可求出答案.【详解】解:∵DE 是ABC 中AC 边的垂直平分线,∴AE CE =,∴5BE CE BE AE AB +=+==,∴EBC 的周长是:549BE CE BC ++=+=;故答案为:9.【点睛】本题考查了垂直平分线的性质,解题的关键是掌握垂直平分线的性质,正确得到5BE CE +=.15.20【分析】作EF ⊥BC 于F ,根据角平分线的性质求得EF =DE =4,然后根据三角形面积公式求得即可.【详解】解:作EF ⊥BC 于F ,∵CE 平分∠ACB ,BD ⊥AC ,EF ⊥BC ,∴EF =DE =4,∴S △BCE =12BC •EF =12×10×4=20.故答案为:20.【点睛】本题考查了角平分线的性质以及三角形的面积,作出辅助线求得三角形的高是解题的关键. 16.AB AD =或34∠=∠或B D ∠=∠【分析】根据全等三角形全等的方法判断即可.【详解】解:根据SAS 判定ABC ADC △≌△,可以添加AB AD =;根据ASA 判定ABC ADC △≌△,可以添加34∠=∠;根据AAS 判定ABC ADC △≌△,可以添加B D ∠=∠;故答案为:AB AD =或34∠=∠或B D ∠=∠.【点睛】本题考查全等三角形的判定,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.17.1 6.AD【分析】如图,过B 作,BE AC ∥ 交AD 的延长线于,E 证明,ADC EDB ≌可得,,ADED AC BE 再利用三角形的三边关系可得答案.【详解】解:如图,过B 作,BE AC ∥ 交AD 的延长线于,E,C EBDAD 是BC 边上的中线,,ADC EDB,CD BD ∴= ,ADC EDB ≌,7,AD ED AC BE5,AB =,BE AB AE BE AB75275,AD1 6.AD故答案为:1 6.AD【点睛】本题考查的是三角形中线的定义,平行线的性质,全等三角形的判定与性质,三角形三边之间的关系,作出适当的辅助线构建三角形全等是解题的关键.18.AB AE =(答案不唯一)【分析】根据题意可知已有两组对应角相等,再确定一组对应边相等即可判定ABC AED ≌△△. 【详解】B E ∠=∠,BAC EAD ∠=∠∴当AB AE =时,依据ASA 可得,ABC AED ≌△△,故答案为:AB AE =(答案不唯一)【点睛】本题考查了全等三角形的判定,两角及其夹边对应相等的两个三角形全等,掌握三角形全等的判定定理是解题的关键.19.2【分析】根据题意点Q 是射线OM 上的一个动点,要求PQ 的最小值,需要找出满足题意的点Q ,根据直线外一点与直线上各点连接的所有线段中,垂线段最短,所以我们过点P 作PQ 垂直OM ,此时的PQ 最短,然后根据角平分线上的点到角两边的距离相等可得PA=PQ ,利用已知的PA 的值即可求出PQ 的最小值.【详解】解:过点P 作PQ ⊥OM ,垂足为Q ,则PQ 为最短距离,∵OP 平分∠MON ,PA ⊥ON ,PQ ⊥OM ,∴PA=PQ=2,故答案为:2.【点睛】本题考查角平分线的性质和点到直线的距离.理解角平分线上的点到角的两边的距离相等是解题关键.20.15【分析】根据垂直平分线的性质及定义可得AD=BD ,AB=2AE=6,然后根据三角形的周长公式和等量代换可得BC +AC=9,从而求出△ABC 的周长.【详解】解:∵DE 垂直平分AB ,3AE =∴AD=BD ,AB=2AE=6∆的周长为9,∵ADC∴AD+DC+AC=9∴BD+DC+AC=9即BC+AC=9∆的周长=BC+AC+AB=9+6=15∴ABC故答案为:15.【点睛】此题考查的是垂直平分线的性质的应用,掌握直平分线的性质及定义是解决此题的关键.21.28【分析】根据全等三角形对应角相等可得∠ACB=∠DCE,再根据等式的性质两边同时减去∠ACE可得结论.【详解】证明:∵△ABC≌△DEC,∴∠ACB=∠DCE,∴∠ACB﹣∠ACE=∠DCE﹣∠ACE,即∠ACD=∠BCE=28°.故答案是:28.【点睛】本题考查了全等三角形的性质,三角形的内角和定理的应用,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等.22.DE【分析】由对顶角相等,两个直角相等及BD=CD,可以判断两个三角形全等;所以AB=DE.【详解】根据题意可知∠B=∠D=90°,BC=CD,∠ACB=∠ECD∴△ABC≌△EDC∴AB=DE即只需要测量出线段DE即可.故答案为:DE【点睛】解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系,做题时要认真观察图形,根据已知选择方法.23.(1)见解析;(2)见解析;(3)①②③,有一组邻边和三个角对应相等的两个四边形全等【分析】(1)可以利用正方形与矩形进行说明;(2)根据四条边对应相等,和一个角对应相等,结合图形即可写出已知与求证.证明时可以连接AC、A1C1,转化为证明△ABC≌△A1B1C1,和△ACD≌△A1C1D1.即可证得;(3)根据条件能证明①②③中△ABD≌△A1B1D1(SAS),和△BCD≌△B1C1D1(AAS或ASA),从而利用全等三角形的性质与等式的性质得出两个四边形四条边对应相等,四个角对应相等,因而这两个四边形全等.【详解】解:(1)如正方形与矩形有一条边对应相等,但显然不一定全等.如图,已知AB=A1B1,∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,正方形ABCD和矩形A1B1C1D1不一定全等;(2)已知:如图,四边形ABCD和四边形A1B1C1D1中,AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1,∠B=∠B1.求证:四边形ABCD≌四边形A1B1C1D1.证明:连接AC、A1C1.∵AB=A1B1,∠B=∠B1,BC=B1C1,∴△ABC≌△A1B1C1,∴AC=A1C1,∠BAC=∠B1A1C1,∠BCA=∠B1C1A1.又∵CD=C1D1,DA=D1A1,∴△ACD≌△A1C1D1.∴∠D=∠D1,∠DAC=∠D1A1C1,∠DCA=∠D1C1A1,∴∠BAD=∠B1A1D1,∠BCD=∠B1C1D1,∴四边形ABCD≌四边形A1B1C1D1;(3)①②③;①已知:如图,四边形ABCD和四边形A1B1C1D1中,AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.求证:四边形ABCD≌四边形A1B1C1D1.证明:连接BD、B1D1.∵AB=A1B1,A=∠A1,AD=A1D1,∴△ABD≌△A1B1D1,∴BD =B 1D 1,∠ABD =∠A 1B 1D 1,∠ADB =∠A 1D 1B 1,又∵∠ABC =∠A 1B 1C 1,∠C =∠C 1,∴∠DBC =∠D 1B 1C 1,∴△BCD ≌△B 1C 1D 1.∴BC =B 1C 1,CD =C 1D 1,∠BDC =∠B 1D 1C 1,∴∠ADC =∠A 1D 1C 1,∴四边形ABCD ≌四边形A 1B 1C 1D 1;同理可证明②③成立;④如图,四边形ABCD 和四边形A 1B 1C 1D 1中,已知AB =A 1B 1,CD =C 1D 1,∠A =∠A 1,∠B =∠B 1,∠C =∠C 1.显然四边形ABCD 和四边形A 1B 1C 1D 1不一定全等.概括可得一个“全等四边形的判定方法”,这个判定方法是:有一组邻边和三个角对应相等的两个四边形全等.故答案为:①②③;有一组邻边和三个角对应相等的两个四边形全等.【点睛】本题考查了四边形综合题,涉及的知识点有:四边形的全等,三角形全等的判定与性质,解题的关键是注意:多边形的全等可以通过作辅助线转化为证明三角形全等的问题.24.(1)36,126;(2)见解析;(3)3180∠+∠=︒ABE BAC【分析】(1)18∠=︒ACE ,且EA EC =,再结合三角形的外角定理即可求DEC ∠,18∠=︒ACE ,且EA EC =,AD 是BAC ∠的平分线,2∠=∠ABE ACE 再结合三角形内角和定理即可求解AEB ∠; (2)在AC 上截取AF AB =,连接FE ,可证()≌AEF AEB SAS ,故EF EB =,AFE ABE ,从而可得FEC FCE ∠=∠,所以EF FC =进而可证得:=+=+AC AF FC AB BE(3)由BD BE =,可得BED BDE ∠=∠,BED ABE BAE ∠=∠+∠,∠=∠+∠BDE DAC ACD ,又AD 是BAC ∠的平分线,可得ABE ACD ∠=∠,故CE 是ACD ∠的平分线,所以BE 是ABD ∠的平分线,故∠=∠=∠ABE ACD DBE ,又180ACB ABC BAC ∠+∠+∠=︒,所以ABE ∠和BAC ∠的数量关系即可求解.【详解】(1)∵18∠=︒ACE ,且EA EC =,∴∠EAC =∠ACE =18°,∴∠DEC =∠EAC +∠ACE =36°,又∵AD 是BAC ∠的平分线,∴∠BAD =∠CAD =18°,∵2∠=∠ABE ACE ,∴∠ABE =36°,∴1801836126∠=︒−︒−︒=︒AEB ; 故答案为:36,126(2)在AC 上截取AF AB =,连接FE , 又∵AE =AE ,EAF EAB ∠=∠,∴()≌AEF AEB SAS ,∴EF EB =,AFE ABE∵∠AFE =∠ACE +∠FEC ,∠ABE =2∠ACE , ∴FEC FCE ∠=∠,∴EF FC =∴=+=+AC AF FC AB BE ;(3)∵BD BE =,∴BED BDE ∠=∠,∵BED ABE BAE ∠=∠+∠,∠=∠+∠BDE DAC ACD ,∠CAD =∠BAE , ∴∠ACD =∠ABE ,∵∠ABE =2∠ACE ,∴∠ACD =2∠ACE ,∴CE 平分∠ACB ,∴点E 到CA 、CB 的距离相等,又∵AD 是BAC ∠的平分线,∴点E 到AC 、AB 的距离相等,∴点E 到BA 、BC 的距离相等,∴BE 是ABD ∠的平分线,∴∠ABE =∠CBE ,∴∠=∠=∠ABE ACD DBE ,又∵180ACB ABC BAC ∠+∠+∠=︒,∴2180∠+∠+∠=︒ABE ABE BAC ,即3180∠+∠=︒ABE BAC .【点睛】本题考查了三角形外角的性质、三角形的内角和定理、角平分线的性质、三角形全等的判定和性质,解题的关键是熟练掌握各知识点,准确作出辅助线,熟练运用数形结合的思想.25.(1)见解析;(2)SSS ,BOC ∠,全等三角形的对应角相等【分析】(1)根据题目中的作图步骤画图即可;(2)根据全等三角形的判定定理和性质,补充完整即可.【详解】(1)如图所示,射线OC 即为所求;(2)连接MC ,NC .在OCM 和OCN 中,∵,,,OM ON OC OC MC NC =⎧⎪=⎨⎪=⎩∴≌OCM OCN ( SSS ),∴AOC ∠=∠BOC ( ,即OC 平分AOB ∠.【点睛】本题考查了角平分线的画法和全等三角形的判定与性质,解题关键是明确角平分线画法,熟练运用全等三角形的判定与性质进行证明.26.BD CD =,AD AD =,SSS ,BAD ,CAD ,全等三角形的对应角相等,角平分线上的点到角两边的距离相等【分析】根据全等三角形的判定与性质,结合上下文以及条件,求解即可.【详解】在△ABD 和△ACD 中,AB AC =,BD CD =,AD AD =∴△ABD ≌△ACD (SSS )∴BAD CAD ∠=∠(全等三角形的对应角相等)∴AD 是∠BAC 的角平分线又∵DE ⊥AB 于E ,DF ⊥AC 于F ,∴DE =DF (角平分线上的点到角两边的距离相等)故答案为:BD CD =,AD AD =,SSS ,BAD ,CAD,全等三角形的对应角相等,角平分线上的点到角两边的距离相等【点睛】此题考查了全等三角形的判定与性质,角平分线的性质,熟练掌握相关基本性质是解题的关键.27.(1)∠AEB =135°;(2)△BEC 是等腰直角三角形.理由见解析【分析】(1)根据角平分线的定义得到∠1=∠2,∠3=∠4,再根据三角形内角和定理求得∠1+∠4=45°,然后根据三角形内角和定理即可求解;(2)利用SAS 证明△BEA ≅△CEA ,易证明△BEC 是等腰直角三角形.【详解】解:(1)∵AE ,BE 分别平分∠BAD ,∠ABD ,∴∠1=∠2,∠3=∠4,∵BD ⊥AC ,∴∠BDA =90°,∴∠1+∠2+∠3+∠4=90°,即2∠1+2∠4=90°,∴∠1+∠4=45°,在△BEA 中,∠AEB =180°-(∠1+∠4)=135°;(2)△BEC 是等腰直角三角形.理由如下:在△BEA 和△CEA 中,12AB AC AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△BEA ≅△CEA (SAS ),∴BE =CE ,∠AEC =∠AEB =135°,∴∠BEC =180°-∠AEC -∠AEB =180°-135°-135°=90°,∴△BEC 是等腰直角三角形..【点睛】本题考查了角平分线的定义,三角形内角和定理,全等三角形的判定和性质,熟记各图形的性质并准确识图是解题的关键.28.相等,理由见解析【分析】连接AD ,证明ACD ≌△ABD ,可得DAE DAF ∠=∠,进而根据角平分线的性质即可证明DE 和DF 相等.【详解】连接AD ,如图,在△ACD 和△ABD 中,AB AC AD AD BD CD =⎧⎪=⎨⎪=⎩,∴ACD ≌△ABD (SSS ),DAB DAC ∴∠=∠即DAE DAF ∠=∠∵DE ⊥AE ,DF ⊥AF ,∴DE =DF .【点睛】本题考查了角平分线的性质,三角形全等的性质与判定,掌握角平分线的性质是解题的关键.29.(1)见解析;(2)AM ⊥DM ,证明见解析.【分析】(1)过M 作ME ⊥AD 于E ,根据角平分线性质求出ME=MC=MB ,再根据角平分线的判定即可;(2)根据平行线性质求出∠BAD+∠ADC=180°,结合已知求出∠MAD+∠MDA=90°,即可求出答案.【详解】(1)证明:过M 作ME ⊥AD 于E ,∵DM 平分∠ADC ,∠C=90°,ME ⊥AD ,∴MC=ME ,∵M 为BC 的中点,∴BM=MC=ME ,∵∠B=90°,ME ⊥AD ,∴AM 平分∠DAB ;(2)AM ⊥DM ,证明如下:∵∠B=∠C=90°,∴∠B+∠C=180°,∴AB//DC ,∴∠BAD+∠ADC=180°,∵AM 平分∠DAB ,DM 平分∠ADC ,∴∠MAD=12∠BAD ,∠MDA=12∠ADC ,∴∠MAD+∠MDA=90°,∴∠AMD=90°,∴AM ⊥DM .【点睛】本题考查了平行线的性质,角平分线性质和判定的应用,主要考查学生综合运用性质进行推理的能力,难度适中.30.见解析.【分析】根据平行线性质得∠EDA =∠DAC ,由ED=AE ,得∠EAD =∠EDA .证△ADB ≌△ADC (SAS )可得.【详解】证明:∵ED ∥AC ,∴∠EDA =∠DAC ,∵ED=AE ,∴∠EAD =∠EDA .∴∠EAD =∠DAC .在△ADB 和△ADC 中, ,,,AB AC DAB DAC AD AD =⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△ADC (SAS ).∴BD=CD .【点睛】考核知识点:全等三角形判定,等腰三角形性质.判定三角形全等是关键.。
人教版2020年八年级数学上册期中复习卷《全等三角形》(含答案)

人教版2020年八年级数学上册期中复习卷《全等三角形》一、选择题1.边长都为整数的△ABC≌△DEF ,AB与DE是对应边, AB=2 ,BC=4,若△DEF的周长为偶数,则 DF的取值为()(A)3 (B)4 (C)5 (D)3或4或52.已知图中的两个三角形全等,则∠1等于()A.50°B.58°C.60°D.72°3.下列说法正确的是()A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等4.如图,已知△ABC≌△ADE,∠D=55°,∠AED=76°,则∠C的大小是()A.50°B.6O°C.76°D.55°5.如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为()A.15°B.20°C.25°D.30°6.如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不成立的是( )A.BD=CEB.∠ABD=∠ACEC.∠BAD=∠CAED.∠BAC=∠DAE7.如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,则图中全等的直角三角形有( )A.3对B.4对C.5对D.6对8.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC大小是()A.40°B.45°C.50°D.60°9.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC长是()A.3B.4C.5D. 610.在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是()。
