期末作业3(含答案)
(最新)部编版五年级语文上册 期末考试卷3【含答案】

2022年部编版五年级语文上册期末测试卷(时间:90分满分:100分)一、看拼音,写词语。
(8分)xián yídǎn qièyúchuán zhēbì()()()()qǐdíjiàn zhùsīchóu róng shù()()()()二、多音字组词。
(3分)guān()guī()sì()冠龟似guàn()jūn()shì()三、读句子,写出带有读音“lì”的字。
(3分)1.圆明园不但建筑宏伟,还收藏着最珍贵的()史文物。
2.母亲还是一如既往地鼓()我。
3.我有个慈祥的母亲,我还有个严()的父亲。
4.上课铃声响了,教室里的嘈杂声()刻停止下来。
5.春种一()粟,秋收万颗子。
6.美()的三峡风光,像一幅幅绚丽的图画。
四、比一比,再组词。
(8分)悔()律()拨()煌()诲()津()拔()蝗()捧()衰()畔()噪()棒()蓑()伴()躁()五、根据语境,用“理”字组成不同的词语填入括号里。
(3分)1.我们是少先队员,()要戴红领巾上学。
2.这位律师在法庭上()地为被告辩护。
3.一些人在广场上(),被巡警带走了。
六、按要求改写句子。
(8分)(1)小鸟在树上叫个不停。
(改写成拟人句)(2)教室里非常安静。
(改写成夸张句)___(3)父亲说:“对,这是我对你们的希望。
”(改为转述句)(4)漂亮的校园里洋溢着孩子们欢乐的笑声。
(缩写句子)___七、根据积累和课文内容填空。
(12分)1.(1)有关惜时的名言:(1分)(2)有关勤俭的名言:(1分)(3)古人谈读书的名言:(1分)(4)有关思乡的名句:(1分)(5)我喜欢本册所学的一篇民间故事。
(1分)2.这学期我们学习了第九册《语文》,这本书中我最喜欢的课文是,因为。
(2分)3.《长相思》作者是代词人。
人教版数学五年级上册期末测试卷3(含答案)(高分必备)

人教新课标数学五年级上学期期末测试卷一、我会填.(每空1分,共27分)1.在下面横线里填上适当的最简分数.800cm3=dm335分=小时吨=80千克75cm2=dm2L=500mL625dm3=m3.2.五(1)班有学生60人,其中男生33人,男生占全班人数的,女生占全班人数的,女生人数是男生人数的.3.的分数单位是,它有个这样的分数单位,再加个这样的单位就是最小的质数.4.要使75□含有因数3,□里最小应填;要使它同时是2和3的倍数,□里最大应填.5.把4个棱长是1厘米的正方体拼成一个长方体,这个长方体的棱长总和是厘米.6.一根铁丝长3米,平均分成6段,每段占全长的,每段长米.7.9÷36==(填小数)==.8.时钟从下午1时到4时,时针是方向旋转了度.9.向一个长40厘米、宽30厘米、高30厘米的长方体鱼缸里倒入20厘米深的水,鱼缸里水的体积是升.10.在一个长方体中,相交于同一顶点的三条棱长之和是30厘米,则这个长方体的棱长总和是厘米.11.一个合唱队有28人,老师要用打电话的方式尽快通知每一个队员演出的消息.每分钟通知1人,最少花分钟就能通知到每个人.12.一个多位数,它既是5的倍数,又是2的倍数,这个数个位上的数应是.二、我能判断.(对的在括号里画“√”,错的画“×”)(每题1分,共5分)13.一个数的倍数一定大于它的因数..(判断对错)14.把一个正方体切成两个相同的长方体后,体积不变,表面积也不变.(判断对错)15.分数都比整数小.(判断对错)16.2的倍数一定是合数..(判断对错)17.7和13的公因数只有1..(判断对错)三、我会选.(将正确答案的序号填在括号里)(共5分)18.把的分子加上15,要使分数的大小不变,分母应加上()A.15 B.27 C.3619.下列分数中不能化成有限小数的是()A.B.C.220.一个分数,分母比分子大20,且它与相等,那么这个分数是()A.B.C.D.21.要使是一个假分数,是一个真分数,则a等于()A.14 B.15 C.1622.下面展开图可以围成一个正方体的是()A.B.C.四、我会算.+0.2= += ﹣= ++== += =++﹣1﹣﹣+﹣﹣.25.解方程.x﹣=+x=3(x﹣15)=2.7.五、我会画.26.画一画:看图1,在方格图2中分别画出从上面、正面和左面所看到的图形.27.在图中画出三角形AOB绕O点逆时针旋转90°后的图形.28.请你用图中的图形,运用平移和旋转的方法,设计一副美丽的图案.六、解决问题我能行.(1小题共3分,5小题7分,其余每小题3分,共25分)29.有8瓶钙片,其中一瓶少了5片,用天平称,至少称几次能确保找出少了5片的那一瓶?请你设计一个方案.30.在一个长30米,宽15米,深2米的游泳池里面贴瓷砖,瓷砖是边长为3分米的正方形,贴完这个游泳池共需瓷砖多少块?31.把一个棱长为20cm的正方体铁块锻造成长40cm,宽25cm的长方体,长方体铁块的高是多少cm?32.一个工厂去年上半年完成了全年计划产值的,下半年完成了全年计划产值的,去年这个工厂的产值超过了全年计划产值的几分之几?33.如图是某市两个商场2009﹣2014年营业额情况统计图.(1)哪个商场的营业额增长得快?(2)2014年,甲、乙两个商场的营业额相差多少?(3)如果你是甲商场的负责人,你有什么想法?参考答案与试题解析一、我会填.(每空1分,共27分)1.在下面横线里填上适当的最简分数.800cm3=dm335分=小时吨=80千克75cm2=dm2L=500mL625dm3=m3.【考点】体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算;面积单位间的进率及单位换算.【专题】综合填空题;长度、面积、体积单位;质量、时间、人民币单位.【分析】把800立方厘米换算为立方分米数,用800除以进率1000;把35分换算为小时数,用35除以进率60;把80千克换算为吨,用80除以进率1000;把75平方厘米换算为平方分米数,用75除以进率100;把500毫升化成升数,用500除以进率1000;把625立方分米换算为立方米数,用625除以进率1000.【解答】解:在下面横线里填上适当的最简分数.800cm3=dm335分=小时吨=80千克75cm2=dm2L=500mL625dm3=m3故答案为:,,,,,,.【点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率.2.五(1)班有学生60人,其中男生33人,男生占全班人数的,女生占全班人数的,女生人数是男生人数的.【考点】分数的意义、读写及分类.【专题】综合填空题;分数和百分数.【分析】根据求一个数是另一个数的几分之几,用除法计算.【解答】解:33÷60=(60﹣33)÷60=(60﹣33)÷33=27÷33=答:男生占全班人数的,女生占全班人数的,女生人数是男生人数的.故答案为:;;.【点评】解答本题的关键是找到题目中的单位“1”,再根据求一个数是另一个数的几分之几,用除法计算.3.的分数单位是,它有7个这样的分数单位,再加9个这样的单位就是最小的质数.【考点】分数的意义、读写及分类;合数与质数.【分析】将单位“1”平均分成若干份,表示其中这样一份的数为分数单位.据此可知,的分数单位是,它有7个这样的分数单位;最小的质数为2,2﹣=,里有8个,所以再加上9个这样的分数单位就是最小的质数.【解答】解:根据分数单位的意义可知,的分数单位是,它有7个这样的分数单位;2﹣=,所以再加上9个这样的分数单位就是最小的质数.故答案为:,7,9.【点评】根据分数单位的意义可知,一个分数的分母是几,其分数单位就是几分之一,分子是几其就含有几个这样的分数单位(带分数除外).4.要使75□含有因数3,□里最小应填0;要使它同时是2和3的倍数,□里最大应填6.【考点】2、3、5的倍数特征.【专题】综合填空题;数的整除.【分析】要使75□含有因数3,百位、十位上数的和是:7+5=12,12再加0、3、6、9的和是3的倍数,最小的数是0,个位数是0和6,满足2的倍数特征,其中6是最大的,据此解答.【解答】解:要使75□含有因数3,□里最小应填0;要使它同时是2和3的倍数,□里最大应填6.故答案为:0;6.【点评】本题主要考查2和3的倍数特征,注意掌握2和3的倍数特征:2的倍数的特征是;个位上是0、2、4、6、8的数;3的倍数的特征是:各个数位上的数字和是3的倍数.5.把4个棱长是1厘米的正方体拼成一个长方体,这个长方体的棱长总和是32或24厘米.【考点】长方体的特征.【专题】立体图形的认识与计算.【分析】4个正方体拼成一个长方体,有两个拼法,当4个正方体排成一排拼成长方体时,则减少4×6=24条正方体的棱长;当4个正方体两个在下两个在上拼成长方体时,则减少的4×4=16条正方体的棱长,据此根据正方体的棱长总和公式计算即可解答.【解答】解:当4个正方体排成一排拼成长方体时,棱长总和为:1×12×4﹣1×4×6=48﹣24=24(厘米),当4个正方体两个在下,两个在上拼成长方体时,棱长总和为:1×12×4﹣1×4×4=48﹣16=32(厘米),答:这个长方体的棱长总和是24厘米或者32厘米.故答案为:24或32.【点评】本题是考查图形的切拼问题、长方体和正方体的棱长总和.解答此题的关键是理解4个正方体拼成一个长方体后,减少了几条棱长.6.一根铁丝长3米,平均分成6段,每段占全长的 ,每段长 米.【考点】分数的意义、读写及分类;分数除法.【分析】一根铁丝长3米,平均分成6段,根据分数的意义可知,即将这根铁丝当做单位“1”平均分成6份,则每段占全长的1÷6=,每段的长为3×=米.【解答】解:每段占全长的:1÷6=,每段的长为:3×=(米).故答案为:,. 【点评】完成本题要注意前后两个空的不同,前一个空是求每段占全长的分率,后一个空是求每段的具体长度.7.9÷36== 0.25 (填小数)==.【考点】小数与分数的互化;分数的基本性质.【专题】计算题;综合填空题;运算顺序及法则.【分析】首先求出9÷36的结果用分数表示是;然后判断出分子由1变成5,扩大了5倍,根据分数的基本性质,分母也要扩大5倍,由4变成20;最后判断出分母由4变成100,扩大了25倍,根据分数的基本性质,分子也要扩大25倍,由1变成25;再用1除以4,求出分数的大小用小数表示是多少即可.【解答】解:根据分析,可得9÷36==0.25(填小数)==.故答案为:、0.25、20、25.【点评】此题主要考查了小数与分数的互化,以及分数的基本性质的应用,要熟练掌握.8.时钟从下午1时到4时,时针是 顺时针 方向旋转了 90 度.【考点】旋转;时、分、秒及其关系、单位换算与计算.【专题】图形与变换.【分析】时钟从下午1时到4时,时针沿顺时针方向旋转了3个大格,是30×3=90度;由此解答即可.【解答】解:时钟从下午1时到4时,时针是顺时针方向旋转了 90度. 故答案为:顺时针,90.【点评】解答此题的关键是弄清从下午1时到4时时针在钟面上运动的轨迹.9.向一个长40厘米、宽30厘米、高30厘米的长方体鱼缸里倒入20厘米深的水,鱼缸里水的体积是24升.【考点】长方体和正方体的体积.【专题】综合填空题;立体图形的认识与计算.【分析】首先根据长方体的容积公式:v=abh把数据代入公式求出鱼缸中水的体积,然后换算成容积单位即可.【解答】解:50×30×20=1200×20=24000(立方厘米)24000立方厘米24升答鱼缸里水的体积是24升.故答案为:24.【点评】此题主要考查长方体的容积公式的灵活运用,注意:体积单位与容积单位的换算.10.在一个长方体中,相交于同一顶点的三条棱长之和是30厘米,则这个长方体的棱长总和是120厘米.【考点】长方体的特征.【专题】综合填空题;立体图形的认识与计算.【分析】根据长方体的特征,12条棱分为互相平行的3组(长、宽、高),每组4条棱的长度相等,已知相交于一个顶点的三条棱长总和是30厘米,也就是长、宽、高的和是30厘米,长方体的棱长总和=(长+宽+高)×4,由此列式解答.【解答】解:30×4=120(厘米),答:这个长方体的棱长总和是120厘米.故答案为:120.【点评】此题主要考查长方体的特征和棱长总和的计算方法,要明确一个长方体相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高.11.一个合唱队有28人,老师要用打电话的方式尽快通知每一个队员演出的消息.每分钟通知1人,最少花5分钟就能通知到每个人.【考点】最佳方法问题.【专题】综合填空题;优化问题.【分析】老师首先用1分钟通知第一个学生,第二分钟由老师和1个学生两人分别通知1个学生,现在通知的一共1+2=3个学生,第三分钟可以推出通知的一共3+4=7个学生,以此类推,第四分钟通知的一共7+8=15个学生,第五分钟还剩下13个学生通知,由此问题解决.【解答】解:第一分钟通知到1个学生;第二分钟最多可通知到1+2=3个学生;第三分钟最多可通知到3+4=7个学生;第四分钟最多可通知到7+8=15个学生;第五分钟最多可通知到15+16=31个学生;31>20.故答案为:5.【点评】解决此题的关键是利用已通知的学生的人数加上老师是下一次要通知的学生人数.12.一个多位数,它既是5的倍数,又是2的倍数,这个数个位上的数应是0.【考点】2、3、5的倍数特征.【专题】综合填空题;数的整除.【分析】根据能被2和5整除的数的特点解答即可.【解答】解:2的倍数,即能被2整除的数,个位上是0,2,4,6,8;5的倍数,即能被5整除的数,个位上是0,5;所以既是2的倍数又是5的倍数,则它的个位数字一定是0.故答案为:0.【点评】本题也可以这样想:2和5互质,它们的倍数一定是2×5=10的倍数,10的倍数末尾一定是0.二、我能判断.(对的在括号里画“√”,错的画“×”)(每题1分,共5分)13.一个数的倍数一定大于它的因数.×.(判断对错)【考点】找一个数的倍数的方法;找一个数的因数的方法.【专题】数的整除.【分析】根据因数、倍数的意义,一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数.据此判断即可.【解答】解:因为一个数的最大因数是它本身,一个数的最小倍数也是它本身,如:6的最大因数是6,6的最小倍数是6.所以,一个数的倍数一定大于它的因数.此说法错误.故答案为:×.【点评】此题考查的目的是理解因数、倍数的意义,明确:一个数的最大因数是它本身,一个数的最小倍数也是它本身.14.把一个正方体切成两个相同的长方体后,体积不变,表面积也不变.×(判断对错)【考点】简单的立方体切拼问题.【专题】立体图形的认识与计算.【分析】一个正方体切成两个大小相等的长方体后,增加了两个面,所以表面积就增加了;而分成的两个长方体所占据空间的大小和就等于原来正方体的体积,所以体积不变,据此解答.【解答】解:把一个正方体切成两个相同的长方体后,体积不变,表面积增加.故答案为:×.【点评】此题主要考查长方体与正方体的表面积和体积的定义.15.分数都比整数小×.(判断对错)【考点】分数的意义、读写及分类;分数大小的比较.【分析】最小的正整数为1,根据假分数的意义可知,假分数≥1,所以分数都比整数小的说法是错误的.【解答】解:由于假分数≥1,所以分数都比整数小的说法是错误的.故答案为:×.【点评】在分数中,真分数<1,假分数≥1.16.2的倍数一定是合数.×.(判断对错)【考点】合数与质数.【专题】数的整除.【分析】在自然数中,除了1和它本身外,没有别的因数的数为质数,由此可知,最小的质数是2,而2是2的最小的倍数,所以2的倍数一定是合数说法错误.【解答】解:由于最小的质数是2,而2是2的最小的倍数,所以2的倍数一定是合数说法错误.故答案为:×.【点评】明确2是最小的质数同是也是2的倍数,是完成本题的关键.17.7和13的公因数只有1.√.(判断对错)【考点】因数、公因数和最大公因数.【专题】综合填空题;数的整除.【分析】7是质数、13也是质数,所以7和13是互质数,那么它们的公因数只有1.据此判断即可.【解答】解:因为7是质数、13也是质数,所以7和13是互质数,那么它们的公因数只有1.因此,7和13的公因数只有1.这种说法是正确的.故答案为:√.【点评】此题考查的目的是理解掌握公因数的意义以及求两个数的公因数的方法及应用.三、我会选.(将正确答案的序号填在括号里)(共5分)18.把的分子加上15,要使分数的大小不变,分母应加上()A.15 B.27 C.36【考点】分数的基本性质.【专题】综合判断题;分数和百分数.【分析】根据分数的基本性质:分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变,从而进行解答.【解答】解:的分子增加15,变成5+15=20,扩大了20÷5=4倍,要使分数的大小不变,分母也应扩大4倍,变成9×4=36,所以应增加36﹣9=27;故选:B.【点评】此题主要利用分数的基本性质解决问题.19.下列分数中不能化成有限小数的是()A.B.C.2【考点】小数与分数的互化.【专题】综合填空题;综合判断题;运算顺序及法则.【分析】首先把每个分数化成最简分数,如果分母中除了2与5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数,据此解答即可.【解答】解:,因为分母中含有质因数3,所以分数不能化成有限小数;因为的分母中只含有质因数2,所以分数能化成有限小数;2,因为2的分母中只含有质因数5,所以分数2能化成有限小数.故选:A.【点评】此题主要考查了小数与分数的互化,解答此题的关键是要明确:一个最简分数,如果分母中除了2与5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数.20.一个分数,分母比分子大20,且它与相等,那么这个分数是()A.B.C.D.【考点】分数的基本性质.【专题】综合判断题;分数和百分数.【分析】根据“一个分数的分母比分子大20,约分后是,逐项分析是否符合以上条件,再做出选择.【解答】解:A、的分母比分子大20,且约分后是,此数不符合题意;B、的分母比分子大15,不符合题意;C、的分母比分子大15,不符合题意;D、的分母比分子大20,且约分后是,符合题意.故选:D.【点评】考查了分数的基本性质,解决此题关键是逐项分析,找出符合条件的分数:必须是分母比分子大20,约分后是.21.要使是一个假分数,是一个真分数,则a等于()A.14 B.15 C.16【考点】用字母表示数;分数的意义、读写及分类.【专题】综合填空题;分数和百分数;用字母表示数.【分析】假分数是指分子等于或大于分母的分数,据此分母是15的假分数分子得大于或等于15;真分数是指分子小于分母的分数,据此分母是16的真分数的分子得小于16;据此即可求得a一定是15.【解答】解:是真分数,可得a<16,是假分数,可得a≥15,所以a应该是15.故选:B.【点评】解决此题关键是明确真分数和假分数的意义.22.下面展开图可以围成一个正方体的是()A.B.C.【考点】正方体的展开图.【专题】立体图形的认识与计算.【分析】根据正方体展开图的11种特征,选项A和选项B都不属于正方体展开图,不能围成正方体;选项C属于正方体展开图的“1﹣4﹣1”型,能围成正方体.【解答】解:根据正方体展开图的11种特征,选项A和选项B都不能围成正方体;选项C能围成正方体.故选:C.【点评】正方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.四、我会算. +0.2+﹣++= +=【专题】计算题;运算顺序及法则.【分析】根据分数加减法运算的计算法则进行计算即可,++运用加法交换律简算. +0.2=0.+=﹣++=1=1+==0用.24.计算下面各题,能简算的要简算.++﹣1﹣﹣ +﹣﹣. 【考点】分数的简便计算.【专题】计算题;运算顺序及法则;运算定律及简算.【分析】(1)先把同分母分数相加减,再计算即可;(2)先把同分母分数相加减,再计算即可;(3)根据减法的性质,先把同分母分数相加减,再计算即可.【解答】解:(1)++﹣=()+() =1+=;(2)1﹣﹣ =(1﹣)﹣=1﹣=;(3)+﹣﹣=()﹣()=﹣1=.【点评】此题主要考查分数运算,注意运算顺序和应用运算定律进行简便计算.25.解方程.x﹣=+x=3(x﹣15)=2.7.【考点】方程的解和解方程.【专题】计算题;消去法;简易方程.【分析】(1)根据等式的性质,方程两边同时加上求解;(2)根据等式的性质,方程两边同时减去求解;(3)根据等式的性质,方程两边同时除以3,再两边同时加上15求解.【解答】解:(1)x﹣=x﹣+=+x=;(2)+x=+x﹣=﹣x=;(3)3(x﹣15)=2.73(x﹣15)÷3=2.7÷3x﹣15=2.7x﹣15+15=2.7+15x=17.7.【点评】此题考查利用等式的性质解方程的能力,解方程式同时注意“=”上下要对齐.五、我会画.26.画一画:看图1,在方格图2中分别画出从上面、正面和左面所看到的图形.【考点】从不同方向观察物体和几何体.【专题】立体图形的认识与计算.【分析】观察图形可知,从上面看到的图形是两行:上面一行3个正方形,下面一行1个正方形靠中间,从正面看到的图形是2层:下层3个正方形,上层1个靠中间;从左面看到的图形是2层:下层2个正方形,上层1个靠左边;据此即可画图.【解答】解:根据题干分析可得:【点评】此题考查了从不同方向观察问题和几何体,锻炼了学生的空间想象力和抽象思维能力.27.在图中画出三角形AOB绕O点逆时针旋转90°后的图形.【考点】作旋转一定角度后的图形.【专题】作图题;图形与变换.【分析】根据旋转的特征,三角形AOB绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形.【解答】解:在图中画出三角形AOB绕O点逆时针旋转90°后的图形(下图):【点评】旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.28.请你用图中的图形,运用平移和旋转的方法,设计一副美丽的图案.【考点】运用平移、对称和旋转设计图案.【专题】作图题;图形与变换.【分析】图中是一个小菱形,通过平移、旋转可设计出一幅美丽的花边.【解答】解:【点评】本题主要是考查利用一个简单图形通过平移、旋转等手段设计图案.六、解决问题我能行.(1小题共3分,5小题7分,其余每小题3分,共25分)29.有8瓶钙片,其中一瓶少了5片,用天平称,至少称几次能确保找出少了5片的那一瓶?请你设计一个方案.【考点】找次品.【专题】创新题型;优化问题.【分析】将8瓶钙片分成2瓶、3瓶、3瓶,共三组,先称各3瓶的两组,若天平平衡,则少5片的那瓶在2瓶的那组里,再称一次,即可找出少5片的那瓶;若天平不平衡,从向上翘的那3瓶中取出一瓶,再称另外的两瓶,若平衡,则拿出的那瓶是次品,若不平衡,则轻松就能判断哪瓶是次品,从而问题得解.【解答】解:将8瓶钙片分成2瓶、3瓶、3瓶,共三组,先称各3瓶的两组,若天平平衡,则次品在2瓶的那组里,再称一次,即可找出少5片的那瓶;若天平不平衡,从向上翘的那3瓶中取出一瓶,再称另外的两瓶;若平衡,则拿出的那瓶是次品,若不平衡,则向上翘的哪瓶是次品;所以,用天平称至少称2次能把这瓶药找出来.【点评】解答此题的关键是,将8钙片药进行合理的分组,从而只用2次就可以将次品药找出来.30.在一个长30米,宽15米,深2米的游泳池里面贴瓷砖,瓷砖是边长为3分米的正方形,贴完这个游泳池共需瓷砖多少块?【考点】长方体和正方体的表面积.【专题】应用题;立体图形的认识与计算.【分析】求出要贴瓷砖的面积,即四周面加上底面积,四周面积是(长×高+宽×高)×2,底面是长×宽;用这面积除以每块瓷砖的面积;代入数据计算即可求解.【解答】解:30×15+(30×2+15×2)×2=450+(60+30)×2=450+90×2=450+180=630(平方米),630平方米=63000平方分米63000÷(3×3)=63000÷9=7000(块)答:贴完这个游泳池共需7000块瓷砖.【点评】此题主要是考查长方体的表面积、整数除法的应用,解题时值得注意的是游泳池需要贴瓷砖的是底面和侧面五个面的面积.31.把一个棱长为20cm的正方体铁块锻造成长40cm,宽25cm的长方体,长方体铁块的高是多少cm?【考点】长方体和正方体的体积.【专题】应用题;立体图形的认识与计算.【分析】把正方体钢材锻造成长方体只是形状变了,但体积不变.首先根据正方体的体积公式:v=a3,求出钢材的体积,再根据长方体的体积公式:v=sh,用钢材体积除以长方体的底面积即可.【解答】解:20×20×20÷(40×25)=8000÷1000=8(cm)答:长方形的高是8cm.【点评】此题主要考查正方体、长方体的体积公式的灵活运用.32.一个工厂去年上半年完成了全年计划产值的,下半年完成了全年计划产值的,去年这个工厂的产值超过了全年计划产值的几分之几?【考点】分数加减法应用题.【专题】分数百分数应用题.【分析】把去年计划的总产值看成单位“1”,用上半年完成的分率加上下半年完成的分率,求出一共完成计划产值的几分之几,然后再减去1,就是超产了几分之几.【解答】解:+﹣1=﹣1=,答:去年这个工厂的产值超过了全年计划产值的.【点评】本题中的单位“1”都是计划的产值,直接用加减法求解即可.33.如图是某市两个商场2009﹣2014年营业额情况统计图.(1)哪个商场的营业额增长得快?(2)2014年,甲、乙两个商场的营业额相差多少?(3)如果你是甲商场的负责人,你有什么想法?【考点】复式折线统计图.【专题】综合题;图示法;统计数据的计算与应用.【分析】(1)根据折线统计图知道:乙商场的营业额增长得快;(2)2014年,甲商场的营业额是800万元,乙商场的营业额是1200万元,用乙商场的营业额减去甲商场的营业额,列式解答即可;(3)如果我是甲商场的负责人,我会认真观察分析营业额上不去的原因,改进进货渠道,搞一些促销活动等.【解答】解:(1)根据某市两个商场2009﹣2014年营业额情况统计图可知:乙商场的营业额增长得快;(2)1200﹣800=400(万元)答:甲、乙两个商场的营业额相差400万元.(3)如果我是甲商场的负责人,我会认真观察分析营业额上不去的原因,改进进货渠道,搞一些促销活动等.【点评】本题主要考查了从折线统计图中获取知识的能力及根据基本的数量关系解决问题的能力.。
五年级下册英语试题—期末复习训练3(含答案)人教pep

期末复习训练一、选出画线部分发音不同的一项。
()1.A.clever B. plant C. play()2.A.mother B. third C. thin()3.A.look B. good C. bamboo()4.A.when B. where C. who()5.A.meat B. bread C. season二、根据图片及句意,填写单词补全句子。
1. 2. 3. 4. 5.1. —Which________ do you like best?—________. Farmers are very busy.2. —Your T-shirt is so dirty. Please keep it ________.—Sorry. I'll ________ it.3. My birthday is on ____________. (写完全形式)4. I often ____________ on Sundays.5. Jack is ____________ in his bedroom.三、单项选择。
()1.—Are these books ________?—Yes, ________ are.A. we; theseB. ours; thereC. ours; they()2.I often go for a walk and ________ sports with my friends.A. to playB. to doC. play()3.I often watch TV in the evening, but ________ I go for a walk with my mum.A. usuallyB. alwaysC. sometimes()4.I get up very early ________ Saturday morning.A. onB. inC. at()5.________ is Dragon Boat Festival?A. WhereB. WhenC. Who()6.Children's Day is ________ June.A. inB. atC. on()7.I like spring best because I can ________.A. pick applesB. make a snowmanC. plant trees()8.There are________ tigers in the zoo.A. thirdB. threeC. thirteenth()9.Look! The pandas are ________ now.A. will drinkB. to drinkC. drinking()10.What ________ the monkeys doing?A. areB. isC. am四、用所给词的正确形式填空。
罗阳小学三年级语文期末复习练习作业3

三年级语文题姓名:评分:
习作:介绍自己的外貌、性格或爱好。
例:她鞠了一躬。她向大家深深地鞠了一躬。王华看小说。
根据意思写出相应的词语:弯曲的小路把恩引向优雅的境地。()
中国加入世贸,奥运会举办成功,足球走向世界,全国人民心情十分愉快,你想到的词语有:___________ ____________ _______________
用自己的话说说下面词语的意思,并用它说一句话:引人注目:
泉眼无声惜细流,树阴照水爱晴柔。(),()。
填量词:一()楼房一()老马一()报纸一()蝴蝶一()小说一()诗歌
组词:校( )期( )安( )罢( )
造句:纷纷……
选词填空:<震惊震动>一声ቤተ መጻሕፍቲ ባይዱ雷()着整个山谷。
不爬崎岖的高山,不知大地的平坦。
中国加入世贸,奥运会举办成功,足球走向世界,全国人民心情十分愉快,你想到的词语有:___________ ____________ _______________
写出下列词语的近义词:发现()奋力()雄伟()闻名()
把词语补充完整:()日当空意味()长()光溢彩孜孜()求
选字填空:<愿望希望失望>老师( )同学们好好学习,将来为祖国多做贡献。大姐想当一名人民教师的( )终于实现了。遇到困难时,大家不能( ),应当增强信心去战胜它。
2023年三年级语文第二学期 期末检测卷3(含答案)

2023年三年级语文(下)期末检测卷题次一二三四五六合计得分一、书写展示。
抄写下面的句子,做到规范、端正、整洁。
(整张卷面2分)(3分)迟日江山丽,春风花草香。
二、词句检阅。
(25分)(一)拼拼写写,我能行。
(8分)pǔtōng fǎng fúmógu mìfēngzhān jiāo qiān xūmóxíng zhìhuì(二)给加点字选择正确的读音,打“√”。
(4分)1.妈妈加班没回家,他只好到隔壁一个作.(zuōzuò)坊里写作.(zuōzuò)业。
2.这种鲜.(xiān xiǎn)花来自美洲,我们这边鲜.(xiān xiǎn)少有人见过。
3.跟老板折.(zhēzhé)腾了半天,总算让他同意打折.(zhēzhé)了。
4.透过门缝.(féngfèng),他看见妻子正在灯下缝.(féngfèng)补衣服。
(三)选择正确的字打“√”。
(2分)1.请不要打(继断)他的话,让他(继断)续把话说完吧。
2.由于(旋旅)途劳累,她刚下车就感到天(旋旅)地转。
(四)一字多义。
(5分)信:①信用;②相信;③信奉(宗教);④听凭,随意,放任;⑤凭据;⑥书信。
1.我们的庆龄是个守信.用的孩子。
()2.我才不信.咧,你别小人说大话啦!()3.爸爸很久没回家了,我决定写一封信.给他。
()4.他们一家都只信科学,不信.宗教。
()5.不要信.口开河,说话一定要负责任。
()(五)按要求改写句子。
(6分)1.到那时我就把头发烫起来。
(改为“被”字句)2.小蘑菇长出来了。
(改为拟人句)3.婷婷做完了老师所有布置的作业。
(修改病句)三、课文盘点。
(20分)1.根据课文内容连一连。
(4分)《肥皂泡》萧红万寿菊凌晨四点《蜜蜂》谢婉莹牵牛花下午三点《荷花》叶圣陶夜来香傍晚六点《火烧云》法布尔烟草花晚上八点2.《我不能失信》中,宋庆龄教会我做人要;《剃头大师》让我认识了小沙,他怕鬼,怕喝中药、怕做噩梦、还怕剃头,是一个;《小真的长头发》带我走进想象的世界,除此之外,我们还学了另一篇关于想象的课文《》。
浙教版七年级数学下册期末刷题3(含答案)

2021学年浙教版七下数学期末刷题31.下列调查中,适合采用全面调查方式的是()A.了解一批灯管的使用寿命B.了解居民对废电池的处理情况C.了解一个班级的数学考试成绩D.了解全国七年级学生的视力情况2.下列计算中,结果是a6的是()A.a2+a4B.a2•a3C.a12÷a2D.(a2)3 3.如图,下列说法错误的是()A.∠A与∠B是同旁内角B.∠3与∠1是同旁内角C.∠2与∠3是内错角D.∠1与∠2是同位角4.下列分式中,与相等的是()A.B.C.﹣D.5.二元一次方程组的解为()A.B.C.D.6.如图,说法正确的是()A.∠A和∠1是同位角B.∠A和∠2是内错角C.∠A和∠3是同旁内角D.∠A和∠B是同旁内角7.在义卖活动中,小华负责卖一种圆珠笔,第一天小华卖得60元,第二天多卖了10支,卖得75元,设小华第一天卖了x支这种圆珠笔,则下列方程正确的是()A.B.C.D.8.如图,用四个长和宽分别为a,b(a>b)的长方形拼成面积是64的大正方形,中间围成的小正方形的面积是S,()A.若S=4,则ab=8B.若S=16,则ab=10C.若ab=12,则S=16D.若ab=14,则S=49.多项式(2a+1)x2+bx,其中a,b为整数,()A.若公因式为3x,则a=1B.若公因式为5x,则a=2C.若公因式为3x,则a=3k+1(k为整数)D.若公因式为5x,则a=5k+1(k为整数)10.如图,a∥b,设∠1=(3m+10)°,∠4=(7m﹣30)°,正确的选项是()A.若∠2=∠3,则∠2=(3m﹣10)°B.若∠1=∠4,则∠3=(m+30)°C.若∠1=2∠2=2∠3,则∠2=(3m)°D.若∠1=∠2=∠3,则∠2=(5m﹣10)°11.计算:﹣a×(﹣a)2×(﹣a)3=.12.将一个有50个数据的一组数分成四组,绘制频数直方图,已知各小长方形的高的比为1:2:3:4,则第一个小组的频率为,第二个小组的频数为.13.已知代数式x2+bx+c,当x=1时,它的值是﹣4;当x=2时,它的值是﹣3,则b=,c=.14.现定义运算a⊗b=2ab﹣a﹣b,则计算(1⊗12)﹣(2⊗3)的结果为.15.若•|m+3|=,则m=.16.如图,一个啤酒瓶的高度为30cm,瓶中装有高度12cm的水,将瓶盖盖好后倒置,这时瓶中水面高度20cm,则瓶中水的体积和瓶子的容积之比为.(瓶底的厚度不计)17.解方程:(1)﹣=﹣2(2)﹣=3.18.化简求值:已知|a﹣4|+(b+1)2=0,求5ab2﹣[a2b﹣2(2ab2﹣a2b)]+4a2b的值.19.定义:若a+b=ab,则称a、b是“相伴数”例如:3+1.5=3×1.5,因此3和1.5是一组“相伴数”(1)﹣1与是一组“相伴数”;(2)若m、n是一组“相伴数”,2mn﹣[3m+2(n﹣m)+3mn﹣6]的值.20.在图中,利用网格点和三角板画图或计算:(1)在给定方格纸中画出平移后的△A′B′C′;(2)画出AB边上的中线CD;(3)画出BC边上的高线AE;(4)记网格的边长为1,则在平移的过程中线段BC扫过区域的面积为.21.中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:频数频率分布表成绩x(分)频数(人)频率50≤x<60100.0560≤x<70300.1570≤x<8040n80≤x<90m0.3590≤x≤100500.25根据所给信息,解答下列问题:(1)m=,n=;(2)补全频数分布直方图;(3)这200名学生成绩的中位数会落在分数段;(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?22.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系?为什么?23.某汽车专卖店销售A,B两种型号的新能源汽车第一周售出1辆A型车和3辆B型车,销售额为96万元;第二周售出2辆A型车和1辆B型车,销售额为62万元.(1)求每辆A型车和B型车的售价各为多少万元;(2)甲公司拟向该店购买A、B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?(3)为了提高营业额,除了A、B两种型号,第三周、第四周专卖店新增了售价为12万元的C种型号的汽车.据统计,第三周第四周总营业额达到380万元,且A、B两种型号共卖出10辆,C不少于12辆,则A型车至少卖出了几辆?24.平面直角坐标系中,已知A(﹣1,5),B(﹣3,1),C(1,0).(1)求△ABC的面积;(提示:三角形ABC的面积可以看作一个长方形的面积减去一些小三角形的面积)(2)在x轴上找一点P,使△P AC的面积等于△ABC面积的2倍;(3)将线段AB沿水平方向以每秒1个单位的速度平移至MN(A对应M、B对应N),几秒后,△MNO的面积与△ABC面积相等?参考答案1.解:A、了解一批灯管的使用寿命调查具有破坏性适合抽样调查,故A不符合题意;B、了解居民对废电池的处理情况调查范围广适合抽样调查,故B不符合题意;C、了解一个班级的数学考试成绩适合普查,故C符合题意;D、了解全国七年级学生的视力情况调查范围广适合抽样调查,故D不符合题意;故选:C.2.解:∵a2+a4≠a6,∴选项A的结果不是a6;∵a2•a3=a5,∴选项B的结果不是a6;∵a12÷a2=a10,∴选项C的结果不是a6;∵(a2)3=a6,∴选项D的结果是a6.故选:D.3.解:A、∠A与∠B是同旁内角,说法正确;B、∠3与∠1是同旁内角,说法正确;C、∠2与∠3是内错角,说法正确;D、∠1与∠2是邻补角,原题说法错误,故选:D.4.解:A、≠,此选项不符合题意;B、=,符合题意;C、﹣=﹣≠,不符合题意;D、=≠,不符合题意;故选:B.5.解:①+②,得3x=9,解得x=3,把x=3代入①,得3+y=5,y=2,所以原方程组的解为.故选:C.6.解:∵∠A和∠1是内错角,∠A和∠2不是同位角、内错角和同旁内角,∠A和∠3是同位角,∠A和∠B是同旁内角,∴D选项正确,故选:D.7.解:设小华第一天卖了x支这种圆珠笔,则第二天卖了(x+10)支这种圆珠笔,依题意,得:=.故选:B.8.解:根据大正方形的面积求得该正方形的边长是8,则a+b=8,若S=4,则根据小正方形的面积可以求得该正方形的边长是2,则a﹣b=2,解得a=5,b=3,ab=15,故选项A、D错误;若S=16,则根据小正方形的面积可以求得该正方形的边长是4,则a﹣b=4,解得a=6,b=2,ab=12,故选项B错误;故选项C正确.故选:C.9.解:若公因式为3x,则a=3k+1(k为整数);若公因式为5x,则a=5k+2(k为整数).观察选项,只有选项C符合题意.故选:C.10.解:如图,∵a∥b,∴∠1=∠5,∵∠2+∠4=∠3+∠5,当∠2=∠3时,可以推出∠1=∠4,∠2与∠3是变化的,选项A,B中∠2∠3 不确定表示不了,C选项成立时m=10°,此时∠1=∠4=40°按照题目给的代数式∠C=30°不存在前面条件的二倍关系.故A,B,C错误.如图,当∠1=∠2=∠3时,∵∠1=∠2,∴a∥c,∵a∥b,∴c∥b,∴∠3=∠4,∵∠1=∠2=∠3,∴∠1=∠2=∠3=∠4,∴∠2=(∠1+∠4)=[(3m+10)°+(7m﹣30)°]=(5m﹣10)°,故选项D正确,故选:D.11.解:原式=(﹣a)1+2+3=(﹣a)6=a6,故答案为:a6.12.解:∵一个有50个数据的一组数分成四组,各小长方形的高的比为1:2:3:4,∴第一个小组的频率为:=0.1,第二个小组的频数为:50×=10,故答案为:0.1,10.13.解:根据题意得:,整理得:,②﹣①得:b=﹣2,把b=﹣2代入①得:c=﹣3,则b=﹣2,c=﹣3.故答案为:﹣2,﹣3.14.解:根据题中的新定义得:(1⊗12)﹣(2⊗3)=212﹣1﹣12﹣26﹣2﹣3=2﹣1﹣21=﹣2=﹣1.故答案为:﹣1.15.解:|m+3|=÷=1,∴m+3=±1,∴m=﹣4或m=﹣2,∵m≠﹣2,∴m=﹣4,当m=2时,此时=0,也符合题意,故答案为:﹣4或0.16.解:设瓶的底面积为Scm2,则左图V水=12Scm3,右图V空=10Scm3,∵V瓶=V水+V空=22Scm3,∴V水:V瓶=6:11.故答案为.17.解:(1)3(x﹣1)﹣2(1+2x)=2x﹣1﹣12,3x﹣3﹣2﹣4x=12x﹣13,3x﹣4x﹣2x=﹣13+3+2,﹣3x=﹣8,x=;(2)﹣=3,5x﹣10﹣2x﹣2=3,5x﹣2x=3+10+2,3x=15,x=5.18.解∵|a﹣4|+(b+1)2=0,∴a﹣4=0,b+1=0,∴a=4,b=﹣1,原式=5ab2﹣(a2b﹣4ab2+2a2b)+4a2b=5ab2﹣3a2b+4ab2+4a2b=9ab2+a2b当a=4,b=﹣1时原式=9×4×(﹣1)2+42×(﹣1)=36﹣16=20.19.解:(1)设﹣1与m是一组“相伴数”,由题意得,﹣1+m=﹣m,解得,m=,故答案为:;(2)∵m、n是一组“相伴数”,∴m+n=mn,则2mn﹣[3m+2(n﹣m)+3mn﹣6]=2mn﹣m﹣(n﹣m)﹣mn+3=2mn﹣m﹣n+m﹣mn+3=mn﹣(m+n)+3=3.20.解:(1)如图所示:△A′B′C′,即为所求;(2)如图所示:线段CD即为所求;(3)如图所示:高线AE即为所求;(4)在平移的过程中线段BC扫过区域的面积为:4×7=28.故答案为:28.21.解:(1)本次调查的总人数为10÷0.05=200,则m=200×0.35=70,n=40÷200=0.2,故答案为:70,0.2;(2)频数分布直方图如图所示,(3)200名学生成绩的中位数是第100、101个成绩的平均数,而第100、101个数均落在80≤x<90,∴这200名学生成绩的中位数会落在80≤x<90分数段,故答案为:80≤x<90;(4)该校参加本次比赛的3000名学生中成绩“优”等的约有:3000×0.25=750(人).22.平行.证明:∵CD∥AB,∴∠ABC=∠DCB=70°;又∵∠CBF=20°,∴∠ABF=∠ABC﹣∠CBF=70°﹣20°=50°;∴∠ABF+∠EFB=50°+130°=180°;∴EF∥AB(同旁内角互补,两直线平行).23.解:(1)设每辆A型车的售价为x万元,每辆B型车的售价为y万元,依题意,得:,解得:.答:每辆A型车的售价为18万元,每辆B型车的售价为26万元.(2)设购买A型车m辆,则购买B型车(6﹣m)辆,依题意,得:,解得:2≤m≤3.∵m为正整数,∴m的值可以为2,3,∴共有2种购车方案,方案1:购买A型车2辆,B型车4辆;方案2:购买A型车3辆,B型车3辆.(3)设A型车卖出了a辆,则B型车卖出了(10﹣a)辆,依题意,得:≥12,解得:a≥3.答:A型车至少卖出了3辆.24.解:(1)S△ABC=4×5﹣×2×5﹣×2×4﹣×4×1=9;(2)如图,设AC与y轴交于点E,∵A(﹣1,5),C(1,0),∴直线AC解析式为:y=﹣x+,当x=0时,y=,∴点E(0,),∵△P AC的面积等于△ABC面积的2倍,∴×PE×2=2×9,∴PE=18,∴点P(0,)或(0,﹣);(3)设x秒后,△MNO的面积与△ABC面积相等,由题意可得:﹣﹣=9,∴t=,答:秒后,△MNO的面积与△ABC面积相等。
三年级语文上册期末模拟试卷三(部编版)(含答案)

⑤目瞪口呆:眼睛直盯着不动,嘴张着说不出话来。形容因吃惊或害怕而发愣。
⑥自言自语:自己跟自己说话。
(1)“百发百中”结构是ABAC式,类似的词语有:百战百胜、自由自在。
(2)形容人或动物很多,聚集在一起的词语是“成群结队”。
(3)根据词义,为了能在期末考试中取得好成绩,同学们都在抓紧时间复习,应选“争分夺秒”。
4.根据所学知识填空。
(1)《山行》一诗是唐代诗人杜牧写的。诗中描述的“__________,__________”的美景让诗人忍不住停下来。
(2)苏轼的《赠刘景文》中诗人认为秋天是最好的诗句是“__________,___________”。
(3)当我们在长江上顺流而下,看到天门山,便会吟诵起李白的《望天门山》中写的“___________,____________”。
①百( )百( )②提( )瞪口( )⑥自( )自( )
(1)写出两个与第①个结构相同的词语:_______________。
(2)_____________的意思是形容人或动物很多,聚集在一起。
(3)为了能在期末考试中取得好成绩,同学们都在_____________地复习。
小羊羔不再打嗝儿了,她依偎着老狼毛草茸的脸颊,在他的怀里睡着了。
“唉!”老狼叹了口气,“如果我一口把她吃掉,应该可以吧?”于是,他张开大嘴,要把小羊羔吞掉。可这时,小羊羔睡醒了,她看到老狼张着大嘴,以为是要亲她,于是她先使劲地亲了老狼一口!
……
16.联系上下文,我知道“狼吞虎咽”的意思是______。
15.如果你是英子的同学,在英子不敢站到讲台上时,你会对英子说些什么?
课外阅读。
阅读文段
【数学】苏教版数学三年级下册试题期末试卷3(含答案)

苏教版数学三年级下册试题期末试卷3(含答案)时间:90分钟 分值:100分一、填空(2、4、5每题2分其余每空1分,共19分)1.两位数乘两位数,所得的积最可以是( )位数,可以是( )位数。
三位数除以一位数,求得的商最少是( )位数。
2.东东3分钟跳绳180下,小雨1分钟跳绳140下。
这两位小朋友,( )跳得慢一些。
3. 在○中填上“<”、“>”、“=”。
4000克○3吨 米107○70厘米 10平方米○20平方分米 300÷2÷3○300÷5 25×14○24×15 1千米○1000分米4.2016年第一季度共有( )天。
5.小红买了12个桃,吃了43,剩下的...全送给了爷爷,共送了( )个。
6.① ② ③( )号图和( )号图的面积相等,( )号图和( )号图的周长相等。
二、选择,将正确答案的序号填入括号内(每小2分,计10分 )1.三年级三(2)有48名队员,他们的体重都在38~42千克之间。
这些队员的体重合起来大约重 ( )吨?A. 1吨B. 2吨C. 3吨2.兰兰每天步行到学校要用10分钟,他家到学校的路程大约是( )?A.1000米B.2千米C. 20千米3.到2019年10月1日,中华人民共和国正好建国( )周年。
A.68周年B. 69周年C. 70周年4.把2×3=6、360÷6=60合并成综合算式应是下面哪一道算式( )?A. 360÷2×3B. (360÷2)×3C. 360÷(2×3)5.甲长方形包含16个小正方形,乙长方形包含12个小正方形。
甲长方形与乙长方形的面积相比,结果是什么? ( )A. 甲的面积大B. 乙的面积大C. 无法确定三、判断(每小题2分,计10分 )1.两个数相乘的积一定大于这两个数相加的和。
( )2.边长是4厘米的正方形,它的周长和面积相等。
2022年宁夏吴忠市七年级(上)语文期末测试卷含答案(三)

2022年宁夏吴忠市七年级(上)语文期末测试卷(三)一、积累运用1.(12分)默写。
(1),铁马冰河入梦来。
(陆游《十月四日风雨大作》)(2),崔九堂前几度闻。
(杜甫《江南逢李龟年》)(3)晴空一鹤排云上,。
(刘禹锡《秋词》)(4),山入潼关不解平。
(谭嗣同《潼关》)(5)《观沧海》中描写秋风萧瑟,惊涛拍岸的句子是:,。
(6)李白《闻王昌龄左迁龙标遥有此寄》采用寄情于景的手法,既点明时令,又表明了漂泊之感和落寞之情的句子是:,。
(7)《论语》中强调复习的重要性的句子是:,。
(8)《诫子书》中阐述过度享乐和急躁对修身养性的不利影响的句子是:,。
2.(4分)根据提示完成下面的题目。
初中语文课本为我们打开一扇文学之门,开启一段学习之旅。
在旅途中,欣赏《春》,我们闻到了酝酿. _____在空气里的泥土气息;阅读《纪念白求恩》,我们知道了对工作不能niān_____轻怕重;徜徉《动物笑谈》,我们见识了研究动物行为科学家们的怪诞不jīng_____;吟诵《十一月四日风雨大作》,我们读到了诗人的爱国热忱._____……语文学习让我们流连忘返。
(1)给文段中加点的字注音。
①酝酿.②热忱.(2)根据拼音写出相应的汉字。
①niān 轻怕重②怪诞不jīng3.(4分)阅读下面一段文字,完成后面的题目。
行者丢下扇子道:“不停当!不停当!被那厮哄了!”三藏只道:“怎生是好!”……八戒道:“只拣无火处走便罢。
”三藏道:“哪方无火?”八戒道:“东方南方北方俱无火。
”(1)这段对话选自《西游记》中这一故事情节,八戒说“东方南方北方俱无火”的潜台词是。
(2)《西游记》中孙悟空踏上取经之路后,曾几度返回花果山,请选择其中一次简要叙述经过。
4.(4分)阅读下面文字,完成题目。
在抗击新冠肺炎疫情斗争中作出杰出贡献的功勋模范人物之一﹣﹣84岁的钟南山院士被授予“共和国勋章”。
“千羊之皮,不如一狐之腋;千人之诺诺,不如一士之谔谔”。
钟南山院士是一名共产党员,他在特殊时期的“敢言”正与共产党的“讲真话”要求丝丝入扣,他“擅言”的能力与“敢言”的勇气,为新时代的奋斗者树立了标尺。
七年级(上)期末数学试卷(含答案) (3)
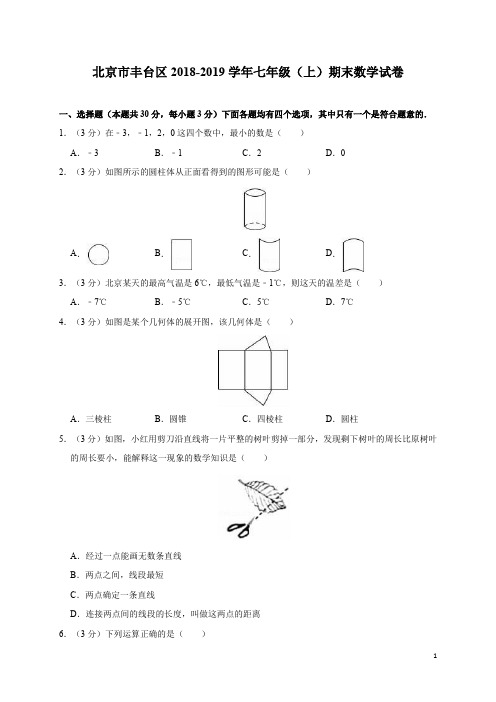
北京市丰台区2018-2019学年七年级(上)期末数学试卷一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.(3分)在﹣3,﹣1,2,0这四个数中,最小的数是()A.﹣3 B.﹣1 C.2 D.02.(3分)如图所示的圆柱体从正面看得到的图形可能是()A.B.C.D.3.(3分)北京某天的最高气温是6℃,最低气温是﹣1℃,则这天的温差是()A.﹣7℃B.﹣5℃C.5℃D.7℃4.(3分)如图是某个几何体的展开图,该几何体是()A.三棱柱B.圆锥C.四棱柱D.圆柱5.(3分)如图,小红用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能解释这一现象的数学知识是()A.经过一点能画无数条直线B.两点之间,线段最短C.两点确定一条直线D.连接两点间的线段的长度,叫做这两点的距离6.(3分)下列运算正确的是()A.4m﹣m=3 B.a3﹣a2=a C.2xy﹣yx=xy D.a2b﹣ab2=07.(3分)2018年10月24日珠港澳大桥正式通车,它是中国境内一座连接珠海、香港和澳门的桥隧工程.其中海底隧道由33节巨型沉管等部件组成,已知每节沉管重约74000吨,那么珠港澳大桥海底隧道所有巨型沉管的总重量约为()A.7.4×104吨B.7.4×105吨C.2.4×105吨D.2.4×106吨8.(3分)有理数a,b在数轴上的对应点的位置如图所示,则下列各式成立的是()A.a>b B.﹣ab<0 C.|a|<|b| D.a<﹣b9.(3分)如图,一副三角尺按不同的位置摆放,摆放位置中∠α与∠β不相等的图形是()A.B.C.D.10.(3分)如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()A.63 B.70 C.96 D.105二、填空题(本题共16分,每小题2分)11.(2分)绝对值等于3的数是.12.(2分)单项式﹣x2y3的系数是,次数是.13.(2分)若a,b互为相反数,则5a+5b的值为.14.(2分)若∠α=47°30′,则∠α的补角的度数为.15.(2分)若x=4是关于x的一元一次方程ax=x﹣1的解,则a=.16.(2分)学习直线、射线、线段时,老师请同学们交流这样一个问题:直线上有三点A,B,C,若AB=6,BC=2,点D是线段AB的中点,请你求出线段CD的长.小华同学通过计算得到CD的长是5.你认为小华的答案是否正确(填“是”或“否”).你的理由是.17.(2分)中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了6天才到达目的地.若设此人第一天走的路程为x里,依题意可列方程为.18.(2分)一般地,我们把研究对象统称为元素,把一些元素组成的总体称为集合.集合中的元素是互不相同的,如一组数1,2,2,3,4就可以构成一个集合,记为A={1,2,3,4}.类比有理数可以进行加法运算,集合也可以“相加”.我们规定:集合A与集合B中的所有元素组成的集合称为集合A与集合B的和,记为A+B.若已知A={﹣2,0,1,4,6},B={﹣1,0,4},则A+B.三、解答题(本题共54分,第19题3分,第20-21题,每小题3分,第22-26题,每小题3分,第27-29题,每小题3分)19.(3分)计算:﹣7﹣(﹣13)+(﹣9).20.(4分)计算:﹣8×(+﹣)21.(4分)计算:(﹣1)2019+|﹣|÷(﹣4)×822.(5分)解方程:2x+3(5﹣x)=4.23.(5分)=1﹣.24.(5分)如图,平面上有三个点A,O,B.(1)画直线OA,射线OB;(2)连接AB,用圆规在射线OB上截取OC=AB(保留作图痕迹);(3)用量角器测量∠AOB的大小(精确到度).25.(5分)先化简,再求值:3(a2b+ab2)﹣(3a2b﹣1)﹣ab2﹣1,其中a=1,b=﹣3.26.(5分)如图,∠CAB+∠ABC=90°,AD平分∠CAB,与BC边交于点D,BE平分∠ABC与AC 边交于点E.(1)依题意补全图形,并猜想∠DAB+∠EBA的度数等于;(2)证明以上结论.证明:∵AD平分∠CAB,BE平分∠ABC,∴∠DAB=∠CAB,∠EBA=.(理由:)∵∠CAB+∠ABC=90°,∴∠DAB+∠EBA=×(∠+∠)=.27.(6分)某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动,两班学生共104人,其中初一(1)班有40多人,不足50人,教育基地门票价格如下:原计划两班都以班为单位购票,则一共应付1136元,请回答下列问题:(1)初一(1)班有多少人?(2)你作为组织者如何购票最省钱?比原计划省多少钱?28.(6分)如图,数轴上点A对应的有理数为10,点P以每秒1个单位长度的速度从点A出发,点Q以每秒3个单位长度的速度从原点O出发,且P、Q两点同时向数轴正方向运动,设运动时间为t秒.(1)当t=2时,P,Q两点对应的有理数分別是,,PQ=;(2)当PQ=8时,求t的值.29.(6分)阅读下面一段文字:问题:0.能化为分数形式吗?探求:步骤①设x=0.,步骤②10x=10×,步骤③10x=7.,则10x=7×,步骤④10x=7+x,解得:x=.根据你对这段文字的理解,回答下列问题:(1)步骤①到步骤②的依据是;(2)仿照上述探求过程,请你尝试把0.化为分数形式:步骤①设x=0.,步骤②100x=100×,步骤③;步骤④,解得x=;(3)请你将0.3化为分数形式,并说明理由.参考答案一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.解:如图所示,,由图可知,四个数中﹣3最小.故选:A.2.解:一个直立在水平面上的圆柱体,从正面看是一个矩形,故选:B.3.解:这天的温差为6﹣(﹣1)=6+1=7(℃),故选:D.4.解:观察图形可知,这个几何体是三棱柱.故选:A.5.解:小红用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能解释这一现象的数学知识是两点之间,线段最短,故选:B.6.解:(A)原式=3m,故A错误;(B)原式=a3﹣a2,故B错误;(D)原式=a2b﹣ab2,故D错误;故选:C.7.解:74000×33=2442000(吨),2442000吨≈2.4×106吨.故选:D.8.解:∵由图可知a<0<b,且|a|>|b|,∴a<﹣b.故选:D.9.解:A、∠α=∠β=90°﹣45°=90°,能判断∠α和∠β相等,故本选项错误;B、∠α和∠β都等于90°减去重合的角,故本选项错误;C、不能判断∠α和∠β相等,故本选项正确;D、∠α=∠β=180°﹣45°=135°,能判断∠α和∠β相等,故本选项错误.故选:C.10.解:设“H”型框中的正中间的数为x,则其他6个数分别为x﹣8,x﹣6,x﹣1,x+1,x+6,x+8,这7个数之和为:x﹣8+x﹣6+x﹣1+x+1+x+x+6+x+8=7x.由题意得A、7x=63,解得:x=9,能求得这7个数;B、7x=70,解得:x=10,能求得这7个数;C、7x=96,解得:x=,不能求得这7个数;D、7x=105,解得:x=15,能求得这7个数.故选:C.二、填空题(本题共16分,每小题2分)11.解:绝对值等于3的数是±3.12.解:单项式﹣x2y3的系数为﹣,次数为5.故答案为:﹣,5.13.解:∵a,b互为相反数,∴5a+5b=5(a+b)=0.故答案为:0.14.解:180°﹣47°30′=132°30′,故答案为:132°30′.15.解:把x=4代入方程ax=x﹣1得:4a=4﹣1,解得:a=,故答案为:.16.解:如图1,∵AB=6,点D是线段AB的中点,∴DB=3,又BC=2,∴DC=5;如图2,∵AB=6,点D是线段AB的中点,∴DB=3,又BC=2,∴DC=1,∴小华的答案不正确,因为线段DC的长为1或5,故答案为:否;当点C在线段AB上时,CD=1或5.17.解:设此人第一天走的路程为x里,根据题意得:x+++++=378.故答案为:x+++++=378.18.解:∵A={﹣2,0,1,4,6},B={﹣1,0,4},∴由集合的定义,可得A+B={﹣2,﹣1,0,1,4,6}.故答案为:={﹣2,﹣1,0,1,4,6}.三、解答题(本题共54分,第19题3分,第20-21题,每小题3分,第22-26题,每小题3分,第27-29题,每小题3分)19.解:原式=﹣7+13﹣9=﹣3.20.解:原式=﹣1﹣2+12=9.21.解:原式=﹣1﹣××8=﹣1﹣1=﹣2.22.解:去括号得:2x+15﹣3x=4,移项合并得:﹣x=﹣11,解得:x=11.23.解:去分母得:4x﹣1=6﹣6x+2,移项合并得:10x=9,解得:x=0.9.24.解:(1)如图所示,直线OA和射线OB即为所求;(2)如图所示,线段OC即为所求;(3)∠AOB约为40°.25.解:原式=3a2b+3ab2﹣3a2b+1﹣ab2﹣1=2ab2,当a=1,b=﹣3时,原式=2×1×(﹣3)2=2×9=18.26.解:(1)补全图形,并猜想∠DAB+∠EBA的度数等于45°;(2)证明:∵AD平分∠CAB,BE平分∠ABC,∴∠DAB=∠CAB,∠EBA=∠CBA.(理由:角平分线的定义)∵∠CAB+∠ABC=90°,∴∠DAB+∠EBA=×(∠CAB+∠ABC)=45°.故答案为:45°,∠CAB,角平分线的定义,,∠CAB,∠ABC,45°.27.解:(1)设初一(1)班有x人,则初一(2)班有(104﹣x)人,12x+10(104﹣x)=1136,解得,x =48,答:初一(1)有48人; (2)两个班一起购票最省钱,1136﹣8×104=1136﹣832=304(元), 即可以节省304元.28.解:(1)∵10+2×1=12,3×2=6,∴当t =2时,P ,Q 两点对应的有理数分别是12,6, ∴PQ =12﹣6=6. 故答案为:12;6;6;(2)运动t 秒时,P ,Q 两点对应的有理数分别是10+t ,3t . ①当点P 在点Q 右侧时, ∵PQ =8,∴(10+t )﹣3t =8, 解得:t =1;②当点P 在点Q 左侧时, ∵PQ =8,∴3t ﹣(10+t )=8, 解得:t =9.综上所述,t 的值为1秒或9秒.29.解:(1)步骤①到步骤②的依据是等式的基本性质2. 故答案为等式的基本性质2;(2)把0.化为分数形式:步骤①设x =0.,步骤②100x =100×,步骤③100x =37.,则100x =37+0.;步骤④100x =37+x ,解得x =.故答案为100x =37.,则100x =37+0.;100x =37+x ,;11(3)设x =0.,10x =10×0.,10x =8.,10x =8+0.,10x =8+x ,解得:x =.设m =0.3,10m =3.=3+=,m =. 即0.3=.。
高中数学必修二期末考试试卷(三)(含答案解析)

高中数学必修二期末考试试卷(三)(含答案解析)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分) 1.直线l 经过原点和(1,-1),则l 的倾斜角是( ) A.45° B.-45° C.135° D.45°和135° 答案 C解析 ∵直线l 经过坐标原点和点(1,-1),∴直线l 的斜率k =-11=-1,∴直线l 的倾斜角α=135°,故选C.2.已知过点M (-2,a ),N (a,4)的直线的斜率为-12,则|MN |等于( )A.10B.180C.6 3D.6 5考点 两点间的距离公式 题点 求两点间的距离 答案 D 解析 k MN =a -4-2-a=-12,解得a =10,即M (-2,10),N (10,4),所以|MN |=(-2-10)2+(10-4)2=65,故选D.3.设点A (2,-3),B (-3,-2),直线过P (1,1)且与线段AB 相交,则l 的斜率k 的取值范围是( )A.k ≥34或k ≤-4B.-4≤k ≤34C.-34≤k ≤4D.以上都不对考点 直线的图象特征与倾斜角、斜率的关系 题点 倾斜角和斜率关系的其他应用 答案 A解析 建立如图所示的直角坐标系.由图可得k ≥k PB 或k ≤k P A .∵k PB =34,k P A =-4,∴k ≥34或k ≤-4.4.若光线从点P (-3,3)射到y 轴上,经y 轴反射后经过点Q (-1,-5),则光线从点P 到点Q 走过的路程为( ) A.10 B.5+17 C.4 5D.217考点 对称问题的求法 题点 光路可逆问题 答案 C解析 Q (-1,-5)关于y 轴的对称点为Q 1(1,-5),易知光线从点P 到点Q 走过的路程为|PQ 1|=42+(-8)2=4 5.5.到直线3x -4y -1=0的距离为2的直线方程是( ) A.3x -4y -11=0B.3x -4y -11=0或3x -4y +9=0C.3x -4y +9=0D.3x -4y +11=0或3x -4y -9=0 答案 B解析 直线3x -4y -11=0与3x -4y +9=0到直线3x -4y -1=0的距离均为2, 又因为直线3x -4y +11=0到直线3x -4y -1=0的距离为125,故不能选择A ,C ,D ,所以答案为B.6.过两点(-1,1)和(3,9)的直线在x 轴上的截距为( ) A.-32 B.-23 C.25 D.2考点 直线的两点式方程 题点 利用两点式求直线方程 答案 A解析 由两点式y -19-1=x +13+1,得y =2x +3,令y =0,得x =-32,即为在x 轴上的截距.7.若直线mx +ny +2=0平行于直线x -2y +5=0,且在y 轴上的截距为1,则m ,n 的值分别为( ) A.1和2 B.-1和2 C.1和-2D.-1和-2 考点 直线的一般式方程与直线的平行关系 题点 根据平行求参数的值答案 C解析 由已知得直线mx +ny +2=0过点(0,1),则n =-2,又因为两直线平行,所以-m n =12,解得m =1.8.若直线(2m -3)x -(m -2)y +m +1=0恒过某个点P ,则点P 的坐标为( ) A.(3,5) B.(-3,5) C.(-3,-5) D.(3,-5)答案 C解析 方程(2m -3)x -(m -2)y +m +1=0可整理得m (2x -y +1)-(3x -2y -1)=0,联立⎩⎪⎨⎪⎧ 2x -y +1=0,3x -2y -1=0,得⎩⎪⎨⎪⎧x =-3,y =-5.故P (-3,-5).9.若直线l 1:y =k (x -4)与直线l 2关于点(2,1)对称,则直线l 2过定点( ) A.(0,4) B.(0,2) C.(-2,4)D.(4,-2)考点 对称问题的求法 题点 直线关于点的对称问题 答案 B解析 ∵l 1:y =k (x -4)过定点M (4,0), 而点M 关于点(2,1)的对称点为N (0,2), 故直线l 2过定点(0,2).10.直线y =ax +1a的图象可能是( )考点 直线的斜截式方程 题点 直线斜截式方程的应用 答案 B解析 根据斜截式方程知,斜率与直线在y 轴上的纵截距同正负.11.若直线x -2y +5=0与直线2x +my -6=0互相垂直,则实数m 等于( ) A.-1 B.1 C.12 D.-12考点 直线的一般式方程与直线的垂直关系 题点 根据垂直求参数的值 答案 B解析 由两直线垂直,得12×⎝⎛⎭⎫-2m =-1,解得m =1. 12.已知直线x -2y +m =0(m >0)与直线x +ny -3=0互相平行,且两者之间的距离是5,则m +n 等于( ) A.-1 B.0 C.1 D.2考点 两条平行直线间的距离公式及应用 题点 利用两条平行直线间的距离求参数的值 答案 B解析 由题意知,所给两条直线平行,∴n =-2. 由两条平行直线间的距离公式,得d =|m +3|12+(-2)2=|m +3|5=5,解得m =2或m =-8(舍去),∴m +n =0.二、填空题(本大题共4小题,每小题5分,共20分)13.过点(-2,-3)且在x 轴,y 轴上的截距相等的直线方程为____________. 考点 直线的截距式方程 题点 利用截距式求直线方程 答案 x +y +5=0或3x -2y =0解析 当直线过原点时,所求直线的方程为3x -2y =0;当直线不过原点时,所求直线的方程为x +y +5=0.14.过两直线x -3y +1=0和3x +y -3=0的交点,并且与原点的最短距离为12的直线的方程为________.答案 x =12或x -3y +1=0解析 易求得两直线交点的坐标为⎝⎛⎭⎫12,32,当斜率不存在时,显然直线x =12满足条件.当斜率存在时,设过该点的直线方程为y -32=k ⎝⎛⎭⎫x -12, 化为一般式得2kx -2y +3-k =0, 因为直线与原点的最短距离为12,所以|3-k |4+4k 2=12,解得k =33,所以所求直线的方程为x -3y +1=0.15.已知直线x -2y -2k =0与两坐标轴围成的三角形的面积不大于1,则实数k 的取值范围是________________. 答案 [-1,0)∪(0,1]解析 令x =0,得y =-k ,令y =0,得x =2k , ∴三角形的面积S =12|xy |=k 2.又S ≤1,即k 2≤1.∴-1≤k ≤1.又当k =0时,直线过原点,与两坐标轴构不成三角形,故应舍去. ∴实数k 的取值范围是[-1,0)∪(0,1].16.已知直线l 与直线y =1,x -y -7=0分别相交于P ,Q 两点,线段PQ 的中点坐标为(1,-1),那么直线l 的斜率为________. 考点 中点坐标公式 题点 求过中点的直线方程 答案 -23解析 设P (x,1),则Q (2-x ,-3),将点Q 的坐标代入x -y -7=0,得2-x +3-7=0. ∴x =-2,∴P (-2,1),∴k l =-23.三、解答题(本大题共6小题,共70分)17.(10分)已知点M 是直线l :3x -y +3=0与x 轴的交点,将直线l 绕点M 旋转30°,求所得直线l ′的方程. 考点 直线的一般式方程题点 求直线的一般式方程及各种方程的互化 解 在3x -y +3=0中,令y =0,得x =-3, 即M (-3,0).∵直线l 的斜率k =3,∴其倾斜角θ=60°. 若直线l 绕点M 逆时针方向旋转30°, 则直线l ′的倾斜角为60°+30°=90°, 此时斜率不存在,故其方程为x =- 3.若直线l 绕点M 顺时针方向旋转30°,则直线l ′的倾斜角为60°-30°=30°,此时斜率为tan 30°=33, 故其方程为y =33(x +3),即x -3y +3=0. 综上所述,所求直线方程为x +3=0或x -3y +3=0.18.(12分)已知直线l 经过点(0,-2),其倾斜角的大小是60°. (1)求直线l 的方程;(2)求直线l 与两坐标轴围成的三角形的面积.解 (1)由直线的点斜式方程得直线l 的方程为y +2=tan 60°·x ,即3x -y -2=0. (2)设直线l 与x 轴、y 轴的交点分别为A ,B , 令y =0得x =233;令x =0得y =-2.所以S △AOB =12|OA |·|OB |=12×233×2=233,故所求三角形的面积为233.19.(12分)已知直线l 1的方程为x +2y -4=0,若l 2在x 轴上的截距为32,且l 1⊥l 2.(1)求直线l 1与l 2的交点坐标;(2)已知直线l 3经过l 1与l 2的交点,且在y 轴上的截距是在x 轴上的截距的2倍,求l 3的方程. 解 (1)设l 2的方程为2x -y +m =0, 因为l 2在x 轴上的截距为32,所以3-0+m =0,m =-3, 即l 2:2x -y -3=0.联立⎩⎪⎨⎪⎧ x +2y -4=0,2x -y -3=0得⎩⎪⎨⎪⎧x =2,y =1.直线l 1与l 2的交点坐标为(2,1). (2)当l 3过原点时,l 3的方程为y =12x .当l 3不过原点时,设l 3的方程为x a +y2a =1(a ≠0),又直线l 3经过l 1与l 2的交点, 所以2a +12a =1,得a =52,l 3的方程为2x +y -5=0.综上,l 3的方程为x -2y =0或2x +y -5=0.20.(12分)已知点A (5,1)关于x 轴的对称点为B (x 1,y 1),关于原点的对称点为C (x 2,y 2). (1)求△ABC 中过AB ,BC 边上中点的直线方程; (2)求△ABC 的面积. 考点 中点坐标公式 题点 与中位线有关的问题解 (1)∵点A (5,1)关于x 轴的对称点为B (x 1,y 1),∴B (5,-1), 又∵点A (5,1)关于原点的对称点为C (x 2,y 2), ∴C (-5,-1),∴AB 的中点坐标是(5,0),BC 的中点坐标是(0,-1).过(5,0),(0,-1)的直线方程是y -0-1-0=x -50-5, 整理得x -5y -5=0.(2)易知|AB |=|-1-1|=2,|BC |=|-5-5|=10,AB ⊥BC , ∴△ABC 的面积S =12|AB |·|BC |=12×2×10=10.21.(12分)已知直线l 1:y =-k (x -a )和直线l 2在x 轴上的截距相等,且它们的倾斜角互补,又知直线l 1过点P (-3,3).如果点Q (2,2)到直线l 2的距离为1,求l 2的方程. 考点 直线的一般式方程题点 求直线的一般式方程及各种方程的互化 解 由题意,可设直线l 2的方程为y =k (x -a ), 即kx -y -ak =0,∵点Q (2,2)到直线l 2的距离为1,∴|2k -2-ak |k 2+1=1,①又∵直线l 1的方程为y =-k (x -a ), 且直线l 1过点P (-3,3),∴ak =3-3k .② 由①②得|5k -5|k 2+1=1,两边平方整理得12k 2-25k +12=0,解得k =43或k =34.∴当k =43时,代入②得a =-34,此时直线l 2的方程为4x -3y +3=0;当k =34时,代入②得a =1,此时直线l 2的方程为3x -4y -3=0.综上所述,直线l 2的方程为4x -3y +3=0或3x -4y -3=0.22.(12分)已知直线l :y =4x 和点P (6,4),点A 为第一象限内的点且在直线l 上,直线P A 交x 轴的正半轴于点B ,(1)当OP ⊥AB 时,求AB 所在直线的方程;(2)求△OAB 面积的最小值,并求当△OAB 面积取最小值时点B 的坐标. 考点 点到直线的距离题点 与点到直线的距离有关的最值问题解 (1)∵点P (6,4),∴k OP =23.又∵OP ⊥AB ,∴k AB =-32.∵AB 过点P (6,4),∴直线AB 的方程为y -4=-32(x -6),化为一般式可得3x +2y -26=0.(2)设点A (a,4a ),a >0,点B 的坐标为(b,0),b >0,当直线AB 的斜率不存在时,a =b =6,此时△OAB 的面积S =12×6×24=72.当直线AB 的斜率存在时,有4a -4a -6=0-4b -6,解得b =5aa -1, 故点B 的坐标为⎝⎛⎭⎫5a a -1,0,故△OAB 的面积S =12·5a a -1·4a =10a 2a -1,即10a 2-Sa +S =0.①由题意可得方程10a 2-Sa +S =0有解, 故判别式Δ=S 2-40S ≥0,∴S ≥40,故S 的最小值为40,此时①为a 2-4a +4=0,解得a =2. 综上可得,△OAB 面积的最小值为40, 当△OAB 面积取最小值时,点B 的坐标为(10,0).。
人教版七年级数学上册期末测试题含答案 (3)

七年级(上)期末目标检测数学试卷(三)一、选择题(每小题3分,共30分)1.a 、b ,在数轴上表示如图1,下列判断正确的是( )A .0>+b aB .01>+bC .01<--bD .01>+a 2.如图2,在下列说法中错误的是( )A .射线OA 的方向是正西方向B .射线OB 的方向是东北方向C .射线OC 的方向是南偏东60°D .射线OD 的方向是南偏西55°3.下列运算正确的是( )A.235=-x xB.ab b a 532=+C.ab ba ab =-2D.a b b a +=--)(4.如果有理数b a ,满足0>ab ,0<+b a ,则下列说法正确的是( )A.0,0>>b aB.0,0><b aC.0,0<<b aD.0,0<>b a 5.若0|2|)1(2=++-n m ,如n m +的值为( )A.1-B.3-C.3D.不确定 6.若0||>a ,那么( )A.0>aB.0<aC.0≠aD.a 为任意有理数 7.平面内有三个点,过任意两点画一条直线,则可以画直线的条数是( ) A.2条 B.3条 C.4条 D.1条或3条 8.将长方形的纸ABCD 沿AE 折叠,得到如图3 所示的图形,已知∠CED′=60º.则∠AED 的是( ) A.60º B.50º C.75º D.55º9.在正方体的表面上画有如图4 a 所示的粗线,图4 b 是其展开图的示意图,但只在A 面上有粗线,那么将图4 a 中剩余两个面中的粗线画入图4 b 中,画法正确的是( )10.一家三口人(父亲、母亲、女儿)准备参加旅游团外出旅游,甲旅行社告知“父母全票,女儿半价优惠”,乙旅行社告知家庭可按团体票计价,即每人均按全价54收费。
浙教版2020-2021学年八年级上册数学期末复习试题3(含答案)

2020-2021学年浙教新版八年级上册数学期末复习试题一.选择题1.在平面直角坐标系中,将点(﹣2,﹣4)向下平移3个单位长度后得到的点的坐标是()A.(﹣2,﹣1)B.(﹣5,﹣4)C.(1,﹣4)D.(﹣2,﹣7)2.直线y=﹣2x+6与两坐标轴围成的三角形的面积是()A.8B.6C.9D.23.如图,在△ABC中,画出AC边上的高,正确的图形是()A.B.C.D.4.某校网课学习的要求是每周听课时长至少达到480分钟算合格.张飞前3天平均每天听课时长为90分钟,问张飞后2天平均每天听课时长不得少于多少分钟才能合格?设张飞后2天平均听课时长为x分钟,以下所列不等式正确的是()A.90×3+2x≥480B.90×3+2x≤480C.90×3+2x<480D.90×3+2x>4805.在等腰△ABC中,∠A=70°,则∠C的度数不可能是()A.40°B.55°C.65°D.70°6.点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于()A.5B.3C.﹣3D.﹣17.若不等式组的解集为x<﹣a,则下列各式中正确的是()A.a+b≤0B.a+b≥0C.a﹣b<0D.a﹣b>08.如图,把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换,你认为在滑动对称变换过程中,对应点不在变换直线上的两个对应三角形的对应点所具有的性质是()A.对应点连线与对称轴垂直B.对应点连线被对称轴平分C.对应点连线被对称轴垂直平分D.对应点连线互相平行9.如图,OA和BA分别表示甲乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定跑260米时,快者比慢者少用多少秒()A.6秒B.6.5秒C.7秒D.7.5秒10.下列命题中是真命题的有()①面积相等的两个三角形全等;②平方根是它本身的数有1和0;③10的平方根是;④在数轴上可以找到表示的点;⑤已知直角三角形中两边长为3和4,则第三边长为5;⑥若(x﹣y)2+A=(x+y)2成立,则A=4xy.A.1个B.2个C.3个D.4个二.填空题11.请写出适合不等式x<﹣1的一个整数解.12.将点A(2,1)变换到点B(2,﹣1),写出一种轴对称或平移方法:.13.如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠C=40°,则∠CDO+∠CFO的度数为.14.已知一次函数y=kx﹣3的图象与x轴的交点坐标为(x0,0),且2≤x0≤3,则k的取值范围是.15.如图,在△ABC中,AB=AC,∠A=50°,EF垂直平分AB,则∠FBC的度数为.16.A,B两地相距240km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止.在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止.两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD﹣DE﹣EF所示.其中点C的坐标是(0,240),点D的坐标是(2.4,0),则点E的坐标是.三.解答题17.已知不等式组的解集为﹣1<x<1,求(a+1)(b﹣1)的值.18.已知∠O及其两边上点A和B(如图),用直尺和圆规作一点P,使点P到∠O的两边距离相等,且到点A,B的距离也相等,并保证其距离最短.(不写作法,保留作图痕迹)19.如图,每个小正方形的边长为1,△ABC经过平移得到△A′B′C′.根据下列条件,利用网格点和直尺画图:(1)补全△A′B′C′;(2)作出中线CD;(3)画出BC边上的高线AE;(4)△ABC的面积为.20.若直线y1=k1x+b1(k1≠0),y2=k2x+b2(k2≠0),则称直线y=(k1+k2)x+b1b2为这两条直线的友好直线.(1)直线y=3x+2与y=﹣4x+3的友好直线为.(2)已知直线l是直线y=﹣2x+m与y=3mx﹣6(m≠0)的友好直线,且直线l经过第一、三、四象限.①求m的取值范围;②若直线l经过点(3,12),求m的值.21.定义:若a,b,c是△ABC的三边,且a2+b2=2c2,则称△ABC为“方倍三角形”.(1)对于①等边三角形②直角三角形,下列说法一定正确的是.A.①一定是“方倍三角形”B.②一定是“方倍三角形”C.①②都一定是“方倍三角形”D.①②都一定不是“方倍三角形”(2)若Rt△ABC是“方倍三角形”,且斜边AB=,则该三角形的面积为;(3)如图,△ABC中,∠ABC=120°,∠ACB=45°,P为AC边上一点,将△ABP沿直线BP进行折叠,点A落在点D处,连结CD,AD.若△ABD为“方倍三角形”,且AP=,求△PDC的面积.22.已知一次函数y1=2x+m(m为常数)和y2=﹣x+1.(1)当m=2时,若y1>y2,求x的取值范围;(2)当x1>1时,y1>y2;当x1<1时,y1<y2,则m的值是.(3)判断函数y=y1•y2的图象与x轴的交点个数情况,并说明理由.23.在△ABC和△DBE中,CA=CB,EB=ED,点D在AC上.(1)如图1,若∠ABC=∠DBE=60°,求证:∠ECB=∠A;(2)如图2,设BC与DE交于点F.当∠ABC=∠DBE=45°时,求证:CE∥AB;(3)在(2)的条件下,若tan∠DEC=时,求的值.参考答案与试题解析一.选择题1.解:将点(﹣2,﹣4)向下平移3个单位长度,所得到的点的坐标是(﹣2,﹣7),故选:D.2.解:在直线y=﹣2x+6中,当x=0时,y=6;当y=0时,x=3;∴直线y=﹣2x+6与坐标轴交于(0,6),(3,0)两点,∴直线y=﹣2x+6与两坐标轴围成的三角形面积=×6×3=9.故选:C.3.解:根据三角形高线的定义,AC边上的高是过点B向AC作垂线垂足为D,纵观各图形,A、B、C都不符合高线的定义,D符合高线的定义.故选:D.4.解:设张飞后2天平均听课时长为x分钟,根据题意,得:3×90+2x≥480,故选:A.5.解:当∠A=∠C时,∠C=70°;当∠A=∠B=70°时,∠C=180°﹣∠A﹣∠B=40°;当∠B=∠C时,∠C=∠B=(180°﹣∠A)=55°;即∠C的度数可以是70°或40°或55°,故选:C.6.解:∵点P(a,b)在函数y=3x+2的图象上,∴b=3a+2,则3a﹣b=﹣2.∴6a﹣2b+1=2(3a﹣b)+1=﹣4+1=﹣3故选:C.7.解:∵不等式组的解集为x<﹣a,∴﹣a≤b,∴a+b≥0.故选:B.8.解:两个对应三角形的对应点所具有的性质是对应点连线被对称轴平分.故选:B.9.解:如图所示:快者的速度为:64÷8=8(m/s),慢者的速度为:(64﹣12)÷8=6.5(m/s),快者跑260米所用的时间为(m/s),慢者跑260米所用的时间为(m/s),∴快者比慢者少用的时间为(秒).故选:D.10.解:①面积相等的两个三角形全等,是假命题;②平方根是它本身的数有1和0,是假命题;③10的平方根是,是真命题;④在数轴上可以找到表示的点,是真命题;⑤已知直角三角形中两边长为3和4,则第三边长为5,是假命题;⑥若(x﹣y)2+A=(x+y)2成立,则A=4xy,是真命题.真命题共3个,故选:C.二.填空题11.解:适合不等式x<﹣1的一个整数解为﹣2(答案不唯一),故答案为:﹣2.12.解:将点A(2,1)向下平移2个单位得到点B(2,﹣1),点A关于x轴的对称点为B(2,﹣1),故答案为向下平移2个单位或关于x轴对称13.解:∵将△ABC沿DE,EF翻折,顶点A,B均落在点O处,∴∠A=∠DOE,∠B=∠EOF,∴∠DOF=∠A+∠B,∵∠A+∠B+∠C=180°,∴∠A+B=180°﹣∠C,∵∠DOF=∠C+∠CDO+∠CFO=180°﹣∠C,∴∠CDO+∠CFO+40°=180°﹣40°,∴∠CDO+∠CFO=100°,故答案为:100°.14.解:将(2,0)代入y=kx﹣3得:0=2k﹣3,∴k=.将(3,0)代入y=kx﹣3得:0=3k﹣3∴k=1.∵一次函数y=kx﹣3过定点(0,﹣3),函数图象与x轴的交点坐标为(x0,0),且2≤x0≤3,∴1≤k≤.故答案为:1≤k≤.15.解:∵AB=AC,∠A=50°,∴∠ABC=∠C=65°.∵EF垂直平分AB,∴AF=BF,∴∠ABF=∠A=50°.∴∠FBC=∠ABC﹣∠ABF=65°﹣50°=15°.故答案为:15°.16.解:根据题意可得,乙货车的速度为:240÷2.4﹣40=60(km/h),∴乙货车从B地到A地所用时间为:240÷60=4(小时),当乙货车到达A地时,甲货车行驶的路程为:40×4=160(千米),∴点E的坐标是(4,160).故答案为:(4,160).三.解答题17.解:由2x﹣a<1得:x<由x﹣2b>3得:x>3+2b∴不等式组的解集为:3+2b<x<又∵﹣1<x<1∴∴,∴(a+1)(b﹣1)=(1+1)(﹣2﹣1)=﹣6.18.解:如图,点P即为所求.19.解:(1)如图,△A′B′C′即为所求.(2)如图线段CD即为所求.(3)如图,线段AE即为所求.=×4×4=8.(4)S△ABC故答案为8.20.解:(1)直线y=3x+2与y=﹣4x+3的友好直线为:y=(3﹣4)x+2×3=﹣x+6,故答案为:y=﹣x+6;(2)①∵直线l是直线y=﹣2x+m与y=3mx﹣6(m≠0)的友好直线,∴直线l的解析式为:y=(﹣2+3m)x﹣6m,∵直线l经过第一、三、四象限,∴,解得;②∵直线l经过点(3,12),∴3(﹣2+3m)﹣6m=12,∴m=6.21.解:(1)对于①等边三角形,三边相等,设边长为a,则a2+a2=2a2,根据“方倍三角形”定义可知:等边三角形一定是“方倍三角形”;对于②直角三角形,三边满足关系式:a2+b2=c2,根据“方倍三角形”定义可知:直角三角形不一定是“方倍三角形”;故选A.故答案为:A;(2)设Rt△ABC其余两条边为a,b,则满足a2+b2=3,根据“方倍三角形”定义,还满足:a2+3=2b2,联立解得,则Rt△ABC的面积为:;故答案为:;(3)由题意可知:△ABP≌△DBP,∴BA=BD,∠ABP=∠DBP,根据“方倍三角形”定义可知:BA2+BD2=2AD2=2BA2,∴AD=AB=BD,∴△ABD为等边三角形,∠BAD=60°,∴∠ABP=∠DBP=30°,∴∠PBC=90°,∵∠CPB=45°,∴∠APB=180°﹣45°=135°,∴∠DPC=90°,∵∠ABC=120°,∠ACB=45°,∴∠BAC=15°,∴∠CAD=45°,∴△APD为等腰直角三角形,∴AP=DP=,∴AD=2,延长BP交AD于点E,如图,∵∠ABP=∠PBD,∴BE⊥AD,PE=AD=AE=1,∴BE===,∴PB=BE﹣PE=﹣1,∵∠CPB=∠PCB=45°,∴△PBC为等腰直角三角形,∴PC=PB=﹣,=PC•PD=(﹣)×=﹣1.∴S△PDC22.解:(1)当m=2时,y1=2x+2,∵y1>y2,y2=﹣x+1,∴2x+2>﹣x+1,解得x>﹣;(2)如果y1>y2,那么2x+m>﹣x+1,解得x>,如果y1<y2,那么2x+m<﹣x+1,解得x<,∵当x1>1时,y1>y2;当x1<1时,y1<y2,∴=1,解得m=﹣2.故答案为:﹣2;(3)y=y1•y2=(2x+m)(﹣x+1),令y=0,则(2x+m)(﹣x+1)=0,解得x1=﹣,x2=1,当﹣=1,即m=﹣2时,该方程有两个相等的实数根,则函数图象与x轴只有一个交点;当﹣≠1,即m≠﹣2时,该方程有两个不相等的实数根,则函数图象与x轴有两个交点.23.(1)证明:∵CA=CB,EB=ED,∠ABC=∠DBE=60°,∴△ABC和△DBE都是等边三角形,∴AB=BC,DB=BE,∠A=60°.∵∠ABC=∠DBE=60°,∴∠ABD=∠CBE,∴△ABD≌△CBE(SAS).∴∠A=∠ECB;(2)证明:∵∠ABC=∠DBE=45°,CA=CB,EB=ED,∴△ABC和△DBE都是等腰直角三角形,∴∠CAB=45°,∴,∴,∵∠ABC=∠DBE,∴∠ABD=∠CBE,∴△ABD∽△CBE,∴∠BAD=∠BCE=45°,∵∠ABC=45°,∴∠ABC=∠BCE,∴CE∥AB;(3)解:过点D作DM⊥CE于点M,过点D作DN∥AB交CB于点N,∵∠ACB=90°,∠BCE=45°,∴∠DCM=45°,∴∠MDC=∠DCM=45°,∴DM=MC,设DM=MC=a,∴a,∵DN∥AB,∴△DCN为等腰直角三角形,∴DN=DC=2a,∵tan∠DEC=,∴ME=2DM,∴CE=a,∴,∵CE∥DN,∴△CEF∽△NDF,∴.。
人教版数学七年级上学期期末测试题 (3)含答案

人教版数学七年级上学期期末测试题一、选择题(本大题共8小题,共24.0分)1.如图,数轴上点()表示的数是-2的相反数.A. 点AB. 点BC. 点CD. 点D2.如图是一个正方体的展开图,则“文”字的对面的字是()A. 青B. 岛C. 城D. 市3.下列调查中,适宜采用全面调查(普查)方式的是()A. 调查江北市民对“江北区创建国家食品安全示范城市”的了解情况B. 调查央视节目《国家宝藏》的收视率C. 调查我校某班学生喜欢上数学课的情况D. 调查学校一批白板笔的使用寿命4.莫拉、沃姆两位博士及其同事在《PloSBio log y》期刊发表了一篇关于地球物种数量预测的文章,根据他们采用的最新分析方法,这个星球总共拥有8700000个物种,8700000用科学记数法可以表示为()A. 8.7×105B. 8.7×106C. 8.7×107D. 0.87×1075.用一副三角板不能画出下列那组角()A. 45∘,30∘,90∘B. 75∘,15∘,135∘C. 60∘,105∘,150∘D. 45∘,80∘,120∘6.方程2x-1=3与方程1-3a−x3=0的解相同,则a的值为()A. 3B. 2C. 1D. 537.在如图所示的2018年1月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是()A. 23B. 51C. 65D. 758.把夏禹时代的“洛书”用数学符号翻译出来就是一个三阶幻方,它的每行、每列、每条对角线上三个数之和均相等,则幻方中a的值是()A. 6B. 12C. 18D. 24二、填空题(本大题共6小题,共18.0分)9.单项式-13πa2b3c的系数为______,次数为______.10.若a=-2×32,b=(-2×3)2,c=-(2×3)2,将a、b、c三个数用“<”连接起来应为______.11.半径为2的圆中,扇形AOB的圆心角为90°,则这个扇形的面积是______.12.某种商品的进价为300元,售价为550元.后来由于该商品积压,商店准备打折销售,但要保证利润率为10%,则该商品可打______折.13.如图,把一张边长为15cm的正方形硬纸板的四个角各剪去一个同样大小的正方形,再折成一个无盖的长方体盒子(纸板的厚度忽略不计),当剪去的正方形边长从4cm变为6cm后,长方体的纸盒容积变______(填大或小)了______cm3.14.一个由13个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,则这个几何体的搭法共有______种.三、计算题(本大题共2小题,共18.0分)15.计算:(1)7+(-15)-2×(-9)(2)(-3)2÷(-134)×0.75×|-213|.16.(1)化简:-14(2k3+4k2-28)+12(k3-2k2+4k).(2)已知A-B=7a2-7ab,且B=-4a2+6ab+7.①求A+B;②若a=-1,b=2,求A+B的值.四、解答题(本大题共8小题,共60.0分)17.如图,已知线段a、b(1)画一条射线AB;(2)在射线AB上作一条线段AC,使AC等于a-b.18.解方程(1)2(100-15x)=60+5x(2)2x−13−10x+16=1.19.某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选,同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)通过计算补全条形统计图;(3)在扇形统计图中,“私家车”部分所对应的圆心角是多少度?(4)若全校共有1800名学生,估计该校乘坐私家车上学的学生约有多少名?20.某水泥仓库一周7天内进出水泥的吨数如下(“+”表示进库,“-”表示出库):+30、-25、-30、+28、-29、-16、-15、(1)经过这7天,仓库里的水泥是增多还是减少了?增多或减少了多少吨?(2)经过这7天,仓库管理员结算发现库里还存200吨水泥,那么7天前,仓库里存有水泥多少吨?(3)如果进仓库的水泥装卸费是每吨a元、出仓库的水泥装卸费是每吨b元,求这7天要付多少元装卸费?21.在市南区某住房小区建设中,为了提高业主的宜居环境,某小区因地制宜规划修建一个广场(图中阴影部分).(1)用含m、n的代数式表示该广场的周长C;(2)用含m、n的代数式表示该广场的面积S;(3)若m、n满足(m-6)2+|n-8|=0,求出该广场的周长和面积.22.如图①,已知线段AB=20cm,CD=2cm,线段CD在线段AB上运动,E、F分别是AC、BD的中点.(1)若AC=4cm,则EF=______cm.(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变,请求出EF的长度;如果变化,请说明理由.(3)我们发现角的很多规律和线段一样,如图②,已知∠COD在∠AOB内部转动,OE、OF分别平分∠AOC和∠BOD,若∠AOB=142°,∠COD=38°,则∠EOF=______.由此,你猜想∠EOF、∠AOB和∠COD会有怎样的数量关系.(直接写出猜想即可)23.我区有着丰富的莲藕资.某企业已收购莲藕52.5吨.根据市场信息,将莲藕直接销售,每吨可获利100元;如果对莲藕进行粗加工,每天可加工8吨,每吨可获利1000元;如果进行精加工,每天可加0.5吨,每吨可获利5000元.由于受条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批莲藕全部销售.为此研究了二种方案:方案一:将莲藕全部粗加工后销售,则可获利______ 元.方案二:30天时间都进行精加工,未来得及加工的莲藕,在市场上直接销售,则可获利______ 元.问:是否存在第三种方案,将部分莲藕精加工,其余莲藕粗加工,并且恰好在30天内完成?若存在,求销售后所获利润;若不存在,请说明理由.24.阅读以下材料并填空问题:在一条直线上有n个点(n≥2),每两个点确定一条线段,一共有多少条线段?【探究】:当仅有2个点时,有1×22=1条线段;当有3个点时,有2×32=3条线段;当有4个点时,有3×42=6条线段;当有5个点时,有______条线段;……当有n个点时,从这些点中任意取一点,如1,以这个点为端点和其余各点能组成(n-1)条线段,这样总共有n×(n-1)条线段.在这些线段中每条线段都重复了两次,如:线段A1A2和A2A1是同一条线段,所以,一条直线上有n个点,一共有______条线段.【应用】(1)在一条直线上有10个点,直线外一点分别与这10个点连接成线段,一共可以组成______个三角形.(2)平面上有50个点,且任意三个点不在同一直线上,过这些点作直线,一共能作出______条不同的直线.【拓展】平面上有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形,一共能作出多少个不同的三角形?当有3个点时,可作1个三角形;当有4个点时,可作______个三角形;当有5个点时,可作______个三角形;……当有n个点时,可连成______个三角形.答案和解析1.【答案】D【解析】解:∵-2的相反数是2,而数轴上点D表示的数是2,∴数轴上点D表示的数是-2的相反数,故选:D.由-2的相反数是2且点D表示数2可得.本题主要考查数轴,解题的关键是掌握数轴上的点所表示的数及相反数的定义.2.【答案】B【解析】解:这是一个正方体的平面展开图,共有六个面,其中“文”字的对面的字是岛.故选:B.利用正方体及其表面展开图的特点求解即可.本题考查了正方体相对两个面上文字的知识,解答本题的关键是从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念.3.【答案】C【解析】解:A、调查江北市民对“江北区创建国家食品安全示范城市”的了解情况,故应当采用抽样调查,故本选项错误;B、调查央视节目《国家宝藏》的收视率,故应当采用抽样调查,故本选项错误;C、调查我校某班学生喜欢上数学课的情况,适宜采用全面调查,故本选项正确;D、调查学校一批白板笔的使用寿命,故应当采用抽样调查,故本选项错误;故选:C.普查和抽样调查的选择.调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.此题考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.4.【答案】B【解析】解:8700000=8.7×106.故选:B.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.此题主要考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.【答案】D【解析】解:A、45°,30°,90°,可以,B、75°,15°,135,可以,C、60°,105°,150,可以,D、45°,80°,120°,其中80°、120°不能.故选:D.A、45° 30°90°,可以,B、75°15°135,可以,C、60° 105° 150,可以,D、45° 80° 120°,其中80°、120°不能.本题考查的是角的计算,根据题意提供的角度,画出图形即可解答.6.【答案】D【解析】解:解方程2x-1=3,得x=2,把x=2代入方程1-=0,得1-=0,解得,a=.故选:D.先解方程2x-1=3,求得x的值,因为这个解也是方程1-=0的解,根据方程的解的定义,把x代入求出a的值.此题考查同解方程,本题的关键是正确解一元一次方程.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.7.【答案】B【解析】解:设第一个数为x,则第二个数为x+7,第三个数为x+14故三个数的和为x+x+7+x+14=3x+213x+21=23,解得x=(舍去);3x+21=51,解得x=10;3x+21=65,解得x=14(舍去);3x+21=75,解得x=18(舍去).故这三个数的和可能是51.故选:B.设第一个数为x,则第二个数为x+7,第三个数为x+14.列出三个数的和的方程,再根据选项解出x,看是否存在.此题主要考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.8.【答案】C【解析】解:设中心数为x,根据题意得,6+x+16=4+x+a,∴a=18,故选:C.根据三阶幻方的特点,可得三阶幻方的和,根据三阶幻方的和,可得a、b的值,根据有理数的加法,可得答案.本题主要考查了有理数的加法,解决此题的关键利用中心数求幻和,再由幻和与已知数求得a、b,最后是有理数的加法.9.【答案】-13π 6【解析】解:单项式-πa2b3c的系数为-π,次数为6,故答案为:-π,6.单项式的系数是数字部分,单项式的次数是字母指数的和,可得答案.本题考查了单项式,单项式的系数是数字因数,单项式的次数是字母指数和.10.【答案】c<a<b【解析】解:a=-2×32=-2×9=-18,b=(-2×3)2=(-6)2=36,c=-(2×3)2=-62=-36,∵-36<-18<36,∴c<a<b.故答案为:c<a<b.先求出各数的值,再比较大小即可.本题考查的是有理数的大小比较,熟知负数与负数比较大小的法则是解答此题的关键.11.【答案】π【解析】解:由题意扇形的面积==π,故答案为π.利用扇形的面积公式计算即可.本题考查扇形的面积公式,解题的关键是熟练掌握基本知识,属于中考常考题型.12.【答案】6【解析】解:设商店可打x折则550×0.1x-300=300×10%,解得x=6.即商店可打6折.故答案为:6.可设商店可打x折,则售价是550×0.1x=55x元.根据等量关系:利润率为10%就可以列出方程,解方程即可求解.本题考查一元一次方程的应用,正确理解利润率的含义,理解利润=进价×利润率,是解题的关键.13.【答案】小142【解析】解:当剪去的正方形边长从4cm变为6cm后,长方体的纸盒容积从(15-4×2)2×4=196cm3变为(15-6×2)2×6=54cm3.故长方体的纸盒容积变小了196-54=142cm3.故答案为:小,142.分别求得剪去的正方形边长从4cm变为6cm后,长方体的纸盒容积即可得到结论.本题考查了展开图折叠成几何体,长方体的体积,熟记长方体的体积公式是解题的关键.14.【答案】3【解析】解:由题意俯视图:除了A,B,C不能确定,其余位置上的小立方体是确定的数字如图所示.∵由13个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,∴A为1,B为2,C为2或A为2,B为2,C为1或A为2,B为1,C为2,共三种情形,故答案为3.由题意俯视图:除了A,B,C不能确定,其余位置上的小立方体是确定的数字如图所示.根据俯视图即可解决问题.本题考查三视图判定几何体,解题的关键是理解题意,灵活运用所学知识解决问题.15.【答案】解:(1)7+(-15)-2×(-9)=7+(-15)+18=10;(2)(-3)2÷(-134)×0.75×|-213|=9×(-47)×34×73=-9.【解析】(1)根据有理数的乘法和加减法可以解答本题;(2)根据有理数的乘除法和绝对值可以解答本题.本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.16.【答案】解:(1)原式=-12k3-k2+7+12k3-k2+2k=-2k2+2k+7;(2)①A+B=A-B+2B=7a2-7ab+2(-4a2+6ab+7)=7a2-7ab-8a2+12ab+14=-a2+5ab+14,②当a=-1,b=2时,原式=-(-1)2+5×(-1)×2+14=-1-10+14=3.【解析】(1)先去括号,再合并同类项即可得;(2)①由A+B=A-B+2B,再将A、B所表示的多项式代入,去括号、合并同类项即可得;②将a和b的值代入所得代数式计算可得.本题主要考查整式的加减,解题的关键是掌握去括号和合并同类项法则.17.【答案】解:线段AC即为所求.【解析】作射线AB,在射线AB上截取AD=a,在线段DA上截取DC=b,线段AC即为所求.本题考查作图-复杂作图,解题的关键是熟练掌握五种基本作图,属于中考常考题型.18.【答案】解:(1)去括号得:200-30x=60+5x移项、合并同类项得:-35x=-140系数化为1得:x=4(2)去分母得:2(2x-1)-(10x+1)=6去括号得:4x-2-10x-1=6移项、合并同类项得:-6x=9系数化为1得:x=-32【解析】(1)方程去括号,移项合并,把x系数化为1,即可求出解.(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.本题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.19.【答案】解:(1)24÷30%=80(名),答:在这次调查中,一共抽取了80名学生.(2)乘坐公交车的人数=80×20%=16(名),条形图如图所示:(3)“私家车”部分所对应的圆心角=360°×3280=144°.(4)全校共有1800名学生,估计该校乘坐私家车上学的学生约有1800×3280=720(名)【解析】(1)根据步行的人数以及百分比求出总人数即可.(2)求出乘坐公交车的人数,画出条形图即可.(3)根据圆心角=360°×百分比计算即可.(4)利用样本估计总体的思想解决问题即可.本题考查条形统计图,扇形统计图,样本估计总体等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.20.【答案】解:(1)∵+30-25-30+28-29-16-15=-57;∴经过这7天,仓库里的水泥减少了57吨;(2)∵200+57=257,∴那么7天前,仓库里存有水泥257吨.(3)依题意:进库的装卸费为:[(+30)+(+28)]a=58a;出库的装卸费为:[|-25|+|-30|+|-29|+|-16|+|-15|]b=115b,∴这7天要付多少元装卸费58a+115b.【解析】(1)根据有理数的加法运算,可得答案;(2)根据有理数的减法运算,可得答案;(3)根据装卸都付费,可得总费用.本题考查了正数和负数及列代数式的知识,(1)有理数的加法是解题关键;(2)剩下的减去多运出的就是原来的,(3)装卸都付费.21.【答案】解:(1)C=6m+4n;(2)S=2m×2n-m(2n-n-0.5n)=4mn-0.5mn=3.5mn;(3)由题意得m-6=0,n-8=0,∴m=6,n=8,代入,可得原式=3.5×6×8=168.【解析】(1)根据周长公式解答即可;(2)由广场的面积等于大矩形面积减去小矩形面积表示出S即可;(3)利用非负数的性质求出m与n的值,代入S中计算即可得到结果.此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.22.【答案】11 90°【解析】解:(1)∵AB=20cm,CD=2cm,AC=4cm,∴DB=14cm,∵E、F分别是AC、BD的中点,∴CE=AC=2cm,DF=DB=7cm,∴EF=2+2+7=11cm,故答案为:11;(2)EF的长度不变.∵E、F分别是AC、BD的中点,∴EC=AC,DF=DB,∴EF=EC+CD+DF=AC+CD+DB=(AC+BD)+CD=(AB-CD)+CD=(AB+CD),∵AB=20cm,CD=2cm,∴EF=×(20+2)=11cm;(3)∠EOF=(∠AOB+∠COD).理由:∵OE、OF分别平分∠AOC和∠BOD,∴∠COE=∠AOC,∠DOF=∠BOD,∴∠EOF=∠COE+∠COD+∠DOF=∠AOC+∠COD+∠BOD=(∠AOC+∠BOD)+∠COD=(∠AOB-∠COD)+∠COD=(∠AOB+∠COD)..故答案为:90(1)依据AB=20cm,CD=2cm,AC=4cm可得DB=14cm,再根据E、F分别是AC、BD的中点,即可得到CE=AC=2cm,DF=DB=7cm,进而得出EF=2+2+7=11cm;(2)依据E、F分别是AC、BD的中点,可得EC=AC,DF=DB,再根据EF=EC+CD+DF进行计算,即可得到EF=×(20+2)=11cm;(3)依据OE、OF分别平分∠AOC在∠BOD,可得∠COE=∠AOC,∠DOF=∠BOD,再依据∠EOF=∠COE+∠COD+∠DOF进行计算,即可得到结果.本题主要考查角平分线、线段的中点的定义及线段的和差关系的运用,关键在于认真的进行计算,熟练运用相关的性质定理.23.【答案】52500 78750【解析】解:方案一:由已知得:将莲藕全部粗加工后销售,则可获利为:1000×52.5=52500(元).故答案为:52500.方案二:30天时间都进行精加工,未来得及加工的莲藕,在市场上直接销售,则可获利为:0.5×30×5000+(52.5-0.5×30)×100=78750(元).故答案分为:78750.由已知分析存在第三种方案.设粗加工x天,则精加工(30-x)天,依题意得:8x+0.5×(30-x)=52.5,解得:x=5,30-x=25.销售后所获利润为:1000×5×8+5000×25×0.5=102500(元).答:存在第三种方案,将部分莲藕精加工,其余莲藕粗加工,并且恰好在30天内完成,销售后所获利润为102500元.方案一:根据总利润=每吨利润×总质量即可求出结论;方案二:根据总利润=精加工部分的利润+未加工部分的利润即可求出结论;分析方案一、二可知存在方案三,设粗加工x天,则精加工(30-x)天,根据总质量为52.5吨即可得出关于x的一元一次方程,解之即可得出x的值,再根据总利润=精加工部分的利润+粗加工部分的利润即可算出结论.本题考查了一元一次方程的应用,根据数量关系列出关于x的一元一次方程是解题的关键.24.【答案】10 S n=n(n−1)245 1225 4 10 n(n−1)(n−2)6【解析】解:【探究】:当仅有2个点时,有=1条线段;当有3个点时,有=3条线段;当有4个点时,有=6条线段;当有5个点时,有=10条线段;…一条直线上有n个点,一共有S n=条线段.故答案为10,S n=;【应用】(1)∵n=10时,S10==45,∴在一条直线上有10个点,直线外一点分别与这10个点连接成线段,一共可以组成45个三角形.(2)∵n=50时,S50==1225,∴平面上有50个点,且任意三个点不在同一直线上,过这些点作直线,一共能作出1225条不同的直线.故答案为45,1225;【拓展】当有3个点时,可作1个三角形,1=;当有4个点时,可作4个三角形,4=;当有5个点时,可作10个三角形,10=;…当有n个点时,可连成个三角形.故答案为1,4,10,.【探究】结合右面的图形,正确地数出有5个点时线段的数量即可;根据一条直线上有2、3、4、5个点时对应的线段条数以及阅读材料,总结出规律,即可得出一条直线上有n个点时的线段条数;【应用】结合总结出点数与直线的规律S n=,将n=10或50代入前面的式子,求得所作出的直线数量即可;【拓展】画出图形,得出当有4个点时,可作4个三角形;当有5个点时,可作10个三角形;依此类推得出当有n个点时,可作个三角形.此题考查了规律型:图形的变化类,关键是通过归纳与总结,得到其中的规律,并用得到的规律解题.体现了由特殊到一般,并由一般到特殊的方法.。
2020年PEP人教版小学英语三年级下学期期末测试卷3(含答案)

小学三年级英语期末综合题(考试时间:30分钟,满分100分)亲爱的同学们,学习英语是不是一件快乐的事情呀!现在为大家提供一个展示的机会,让大家开始我们的知识之旅吧!要仔细认真哦!听力部分(70分)一、Listen and choose:听录音,选出相符的一项,圈住其字母代号。
每小题读两遍。
(10分,每小题1分)4. 5. 6.7. 8. 9. 10.内容一二三四五六七八九十合计得分A BA BA BA BA BA BA BA BA BA B123二、Listen and choose :下面的单词开头缺了一个字母,听录音,选出正确的答案,并将其字母编号填在横线上,每小题读两遍。
(10分,每小题1分)例如:_B wo ( A. c B. t C. g )1、___ce-cream ( A. i B. b C. g )2、___ each ( A. t B. p C. f )3、___alkman ( A. w B. s C. c )4、___all ( A. b B. w C. f )5、___eep ( A. p B. d C. j )6、___ike ( A. l B. f C. b )7、___ine ( A. n B. m C. f ) 8、___oodbye ( A. d B. g C. m ) 9、___other ( A. m B. n C. s ) 10、___gg ( A. o B. u C. e )三、Listen and judge: 根据录音内容,判断下面的图片是否与录音内容相符合。
相符的在图片上方的括号里打“√”,不相符打“×”,每小题读两遍。
(10分,每小题2分)1. ()2.()3. ()4.()5.()四、Listen and number:听一听,排一排,根据听到的内容给下面图片用阿拉伯数字排序,每小题读两遍(10分,每小题2分)( ) ( ) ( ) ( ) ( )五、Listen and tick: 听听小朋友们喜欢什么水果,请在相应的空格中用“√”表示,每小题读两遍。
七年级英语期末综合测试卷(三)含答案

七年级英语期末综合测试卷(三)(时间:90分钟满分:100分)班级_______ _______ 得分_______听力部分(20分)一、根据你所听到的容,选择正确答案(5分)( )1.A.five boxes B.fifteen books C.fifty bags( )2.A.tall and slim B.short and slim C.short and strong( )3.A.1ater B.1atter C.1etter( )4.88010667 B.88010676 C.88010677( )5.go to school B.go home C.go to the zoo二、根据你所听到的对话及问题选择正确答案(5分)( )6.A.One. B.Four. C.Three.( )7.A.4:15. B.4:50. C.5:50.( )8.A.At schoo1. B.At home. C.In a book shop.( )9.A.On Thursday. B.On Friday. C.On Saturday.( )10.A.White. B.Yellow. C.Red.三、根据你所听到的对话及问题选择正确答案(5分)(听第一段对话回答第11、12小题,第二段对话回答13、14、15)( )11.A.3:25. B.4:25. C.5:25.( )12.A.12 yuan. B.12.5 yuan. C.13 yuan.( )13.A.A pair of trousers. B.A pair of football boots. C.A sweater.( )14.A.Size 6. B.Size 7. C.Size 8.( )15.A.$68 B.$58 C.$45四、根据你所听到的短文填入正确的单词(5分)Millie is 16 clothes for me now.Look at the 17 .It is 18 and the colour is young 19 favourite.I think it looks 20 on anyone.Oh,how nice the 21 boots are 11 think it is 22 to wear boots.Let me 23 them on.I don’t want them to be 24 tight.I think 1 will be 25 in the clothes.16._______17._______18._______19._______20._______21._______ 22._______ 23._______ 24._______ 25._______笔试部分(80分)一、选择填空(15分)( )1.-Could you buy _______milk for me.please?一Sorry,I don’t have_______ money.A.some;some B.any,anyC.any,some D.some,any( )2.Would you like _______ at home or go for a walk?A.to stay B.stayingC.stay D.stays( )3.I don’t mind _______the window.It is not in the room.A.to open B.openedC.opening D.is coming( )4.My words made him _______very sad.A.feels B.feelC.to feel D.D felt( )5.China is a country _______a 1ong history.A.has B.haveC.in D.with( )6.The library is a good place _______books.A.to look B.to seeC.to watch D.to read( )7. 一I called you yesterday,_______nobody answered it.Where _______you?-Our family went to Hang Zhou.A.and;are B.but;wereC.so;were D.but;did( )8.Mr. White has two children._______is a doctor,and _______is a nurse. A.One;another B.One;othersC.One;other D.One;the other( )9. The actor _______of medium build and _______straight.black hair,.A.is;has B.is:isC.has;has D.has;is( )10.We have a job _______you _______a teacher.A. for; forB. to;forC. for;as D.for;to( )11.We’re so tired。
七年级数学下册期末考试真题卷含答案解析(3)

七年级数学下册期末考试真题卷一.选择题(共10小题,满分30分)1.下面有4个汽车标致图案,其中不是轴对称图形的是()A.B.C.D.2.永定河,“北京的母亲河”.近年来,我区政府在永定河治理过程中,有时会将弯曲的河道改直,图中A、B两地间的河道改直后大大缩短了河道的长度.这一做法的主要依据是()A.两点确定一条直线B.垂线段最短C.过一点有且只有一条直线与已知直线垂直D.两点之间,线段最短3.下列计算正确的是()A.x3÷x3=0B.(﹣3x)2=6x2C.2x﹣2=D.(x3)2=x6 4.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为()A.16B.14C.12D.105.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有()﹣+从袋子中随机摸出一个球,摸到红球的概率是,那么=,=∠=×21.如图,已知△ABC.(1)尺规作图,画出线段AB的垂直平分线(不写作法,保留作图痕迹);(2)设AB的垂直平分线与BA交于点D,与BC交于点E,连接AE.若∠B=40°,求∠BEA的度数.22.某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买200元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券,(转盘被等分成20个扇形),已知甲顾客购物220元.(1)他获得购物券的概率是多少?(2)他得到100元、50元、20元购物券的概率分别是多少?(3)若要让获得20元购物券的概率变为,则转盘的颜色部分怎样修改?(直接写出修改方案即可).23.如图,在△ABC中,AB=AC,D是边BC延长线上一点,连接AD,过A作AE=AD,且∠DAE=∠BAC,连接CE交AD于点F.(1)求证:△ABD≌△ACE;(2)若∠FCD=34°,求∠B的度数.参考答案一.选择题1.D.2.D.3.D.4.B.5.C.6.C.7.C.8.C.9.C.10.B.二.填空题11.108°.12.2.13.4.14.8.15.﹣1.16.70°.17.y=x.三.解答题18.解:(1)原式=﹣a3•a2﹣9a6÷a=﹣a5﹣9a5=﹣10a5;(2)原式=20212﹣(2021+1)×(2021﹣1)=20212﹣20212+1=1.19.解:原式=x2﹣2xy﹣y2﹣(x2﹣y2)=x2﹣2xy﹣y2﹣x2+y2=﹣2xy,当x=,y=1时,原式=﹣2××1=﹣1.20.解:∵AD∥BC,(已知)∴∠1=∠B=60°.(两直线平行,同位角相等)∵∠1=∠C,(已知)∴∠C=∠B=60°.(等量代换)∵AD∥BC,(已知)∴∠C+∠ADC=180°.(两直线平行,同旁内角互补)∴∠ADC=180°﹣∠C=180°﹣60°=120°.(等式的性质)∵DE平分∠ADC,(已知)∴∠ADE=∠ADC=×120°=60°.(角平分线定义)∴∠1=∠ADE.(等量代换)∴AB∥DE.(内错角相等,两直线平行.)故答案为:B,两直线平行,同位角相等,ADC,两直线平行,同旁内角互补,ADC,角平分线定义,内错角相等,两直线平行.四.解答题21.解:(1)线段AB的垂直平分线如图所示;(2)∵DE是AB的垂直平分线,∴AE=BE∴∠BAE=∠B=40°∴∠BEA=180°﹣∠B﹣∠BAE=180°﹣40°﹣40°=100°答:∠BEA的度数为100°22.解:(1)∵共有20种等可能事件,其中满足条件的有11种,∴P(中奖)=;(2)由题意得:共有20种等可能结果,其中获100元购物券的有2种,获得50元购物券的有4种,获得20元购物券的有5种,∴P(获得100元)==;P(获得50元)==;P(获得20元)==;(3)直接将3个无色扇形涂为黄色.23.(1)证明:∵∠DAE=∠BAC,∴∠DAE+∠DAC=∠BAC+∠DAC,即∠EAC=∠DAB,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS).(2)由(1)可知∠B=∠ACB=ACE,∵∠ACB+∠ACE+∠FCE=180°,即2∠B+34°=180°,∴∠B=73°.24.解:(1)由图象可知,小钱开始营业前微信零钱有50元;(2)由图象可知,销售草莓20kg后,小钱的微信零钱为650元,∴销售草莓20kg,销售收入为650﹣50=600元,∴降价前草莓每千克售价为:600÷20=30(元);(3)降价后草莓每千克售价为:30﹣10=20元,∴小钱卖完所有草莓微信零钱为:650+5×20=750(元),答:小钱卖完所有草莓微信零钱应该有750元.25.解:(1)如图①,∵△ACB和△DCE均为等边三角形,∴AC=BC,DC=CE,∠ACB=∠DCE=60°,∵点A、D、E在同一条直线上,∴∠ADC=120°,∵∠ACB﹣∠DCB=∠DCE﹣∠DCB,∴∠ACD=∠BCE,且AC=BC,DC=CE,∴△CAD≌△CBE(SAS)(2)如图①∵△DCE为等边三角形,∴∠CDE=∠CED=60°,∵点A、D、E在同一条直线上,∴∠ADC=120°,∵△CAD≌△CBE,∴AD=BE,∠BEC=∠ADC=120°,∴∠AEB=120°﹣60°=60°,故答案为:60°,AD=BE;(3)结论:∠AEB=90°,AE=BE+2CM,理由:如图②,∵△ACB和△DCE均为等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°,∵点A,D,E在同一直线上,∴∠ADC=135°,∴∠BEC=135°,∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,∵CD=CE,CM⊥DE,∴DM=ME,∵∠DCE=90°,∴DM=ME=CM,∴AE=AD+DE=BE+2CM.故答案为:90°,AE=BE+2CM.。
四年级上册英语试题-期末测试英语试卷(三)人教PEP版含答案

一、选择题(题型注释)) 1.A.bed B.me C.let 2.A.excuse e C.duck 3.A.not B.nose C.home 4.A.five B.pig C.like 5.A.date B.makeC.hat6.—What’s your uncle’s ? ( )—He is a cook. A.phone B.jobC.family7.—Would you like some vegetables? ( )— . A.No, pleaseB.No, thanksC.Yes, I am8.My friend short and thin. He glasses. ( ) A.is; have B.is; hasC.are; has9.—What is on the desk? ( )—A.An orange and a book.B.The desk is yellow.C.I like orange.10.—Let’s clean the blackboard. ( ) — A.Good job. B.OK.C.You’re welcome.二、阅读理解(题型注释)判断正 “T” 误 “F”。
)My name is Sarah. I’m a student. There are four people in my family. My father is aworker. He is tall and strong. My mother is a teacher. She is pretty. My sister is a nurse. She is thin. We are having dinner. I like rice and eggs. I have a friend. He’s Tom. He is short and thin.11.Sarah is a student. (____)12.There are five people in Sarah’s family. (____) 13.Tom is Sarah’s friend. (____) 14.Sarah likes rice and beef. (____) 15.Sarah’s mother is a worker. (____) 三、匹配题,选择正确的答语。
三年级下册数学试题-期末检测卷 扬州市 苏教版(含答案)(3)

3237274扬州市小学数学三年级下册期末检测卷 2020.7一、计算题1.直接写出得数。
3.4-0.3 = 42×30 = 540÷9 = 8×600 = + = 50×20 = 82-28= 7.1+0.1= 612÷3 = 1- = 2.用竖式计算。
(带“★”的需写出验算过程。
)9.3-3.9= 60×52= ★ 49×25=验算3.用递等式计算。
85-15×2 80×20÷4 24×(64-59)二、填空题1. 43×38的积大约是( ),59×48的积接近( )千, 40的60倍是( )个十, 125×8的积的末尾有( )个0。
2. 在1002、26.7、200.1、8、0、0.9、1这7个数中,整数有( )个,小数有( )个。
3.按规律填数:1.6 , 2.1 , 2.6 ,( ),( )。
4.在○里填上>、<或=。
50××(4+6)240÷2÷÷(2×4) 13××23 195平方分米平方米 5.在括号里填上合适的单位。
桐桐家一个月大约用水8( )。
港珠澳大桥全长约55( )。
一根跳绳长2.5( )。
数学书封面的面积大约是5( )。
6.用“3、6、7”这三个数算24点,写成综合算式是( )。
7.6只蜻蜓2天吃害虫1200只,6只蜻蜓平均每天吃害虫( )只。
8.分针从数字12走到数字6,走了一圈的( )(填分数)2020年5月9.仔细观察右图,这个月共有( )个星期日。
这个月学生在校( )天(5月1日--3日为法定休息日)。
今年的儿童节是星期( ),在第( )季度。
10.用一张长19厘米、宽5厘米的长方形纸可以剪出( )个尽可能大的正方形,剩下图形的面积是( )平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ECDB初三数学期末作业3一、单项选择题:(本大题共6题,每题4分,满分24分)1.在锐角三角形ABC 中,如果各边长都扩大2倍,那么∠B 的余弦值( ) . (A )扩大2倍; (B )缩小2倍; (C )大小不变; (D )不能确定. 2.下列各组图形中,一定相似的是( ) .(A )两个矩形; (B )两个菱形; (C )两个正方形; (D )两个等腰梯形. 3.如果k <0(k 为常数),那么二次函数y =kx 2-2x +k 2的图像大致是( ).4.下列说法中正确的是( ). (A )三个点确定一个圆;(B )当半径大于点到圆心的距离时,点在圆外; (C )圆心角相等,它们所对的弧相等;(D )边长为R 的正六边形的边心距等于23R .5.如图1,在△ABC 中,点D 、E 、F 分别在边AB 、AC 、BC 上,如果DE ∥BC ,DF ∥AC ,那么下列比例式一定成立的是( ). (A )BCDEEC AE =; (B )BCCF AC AE=; (C )BCBFAB AD = ; (D )ACDFBC DE =.6.如图2,由5个同样大小的正方形合成一个矩形,那么∠ABD +∠ADB 的度数是( ). (A )90°; (B )60°; (C )45°; (D )不能确定.二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:tan30°×cos60°= . 8.已知抛物线的表达式是y=-254x ,那么它的顶点坐标是 .9.把抛物线y =2(x -2)2+5向右平移310.已知线段a =4,c =9,那么a 和c 的比例中项b = .11.如果两个相似三角形的相似比为1:4,那么它们的周长比为 . 12.小王在楼下点A 处看到楼上点B 处的小明的仰角是35度,那么点B 处的小明 看点A 处的小王的俯角等于 度.13.如图3,平行四边形ABCD 中,点E 在边BC 上,AE 交BD 于点F , 如果32=FD BF ,那么=BCBE.14.如图4,DE //BC ,31=BA DA ,请用向量ED 表示向量BC ,那么BC = .15.G 为△ABC 的重心,如果EF 过点G 且EF ∥BC ,分别交AB 、AC于点E 、F ,那么BCEF 的值为__ ____.FE D CBA图1DBCB A图4ABCDE16.已知两圆相切,半径分别为2厘米和5厘米,那么两圆的圆心距等于 厘米. 17.如图5是一张直角三角形的纸片,直角边AC =6cm , sin B =53,现将△ABC 折叠,使点B 与点A 重合,折痕为DE ,那么DE 的长等于 .18.在平面直角坐标系中,△ABC 的顶点分别是A (-1,0),B (3,0),C (0,2),已知动直线y =m (0<m <2)与线段AC 、BC 分别交于D 、E 两点,而在x 轴上存在点P ,使得△DEP 为等腰直角三角形,那么m 的值等于 . 三、解答题:(本大题共7题,满分78分)19.如图6,已知两个不平行的向量→a 、→b .先化简,再求作:2(→a -21→b )-21 (2→a +4→b ).(不要求写作法,但要指出图中表示结论的向量)20.如图7,点A ,B 是⊙O 上两点,AB =10,点P 是⊙O 上的动点(P 与A ,B 不重合),联结AP ,PB ,过点O 分别作OE ⊥AP ,OF ⊥PB ,点E 、F 分别是垂足.(1)求线段EF 的长;(2)点O 到AB 的距离为2,求⊙O 的半径.212与自变量x 的部分对应值如下表:(1)(2)设m ≥2,且A (m ,y 1),B (m +1,y 2)两点都在该函数的图像上,试比较y 1与y 2的大小:y 1 y 2(填“大于”“等于”或“小于”).图6→a →b图722.如图8所示,A 、B 两地隔河相望,原来从A 地到B 地需要经过桥DC ,沿折线A →D →C →B 到达B 地,现在直线AB (与桥DC 平行)上建了新桥EF ,可沿直线AB 从A 地直达B 地.已知BC =1000m ,∠A =45°,∠B =37°.问:现在从A 地到达B 地可比原来少走多少路程?(结果精确到1m .参考数据:2≈1.41,sin37°≈0.60,cos37°≈0.80)23.如图9,在△ABC 中,D 是AB 上一点,E 是AC 上一点,∠ACD =∠B ,AD 2=AE·AC . 求证:(1)DE //BC ;(2)2⎪⎪⎭⎫ ⎝⎛=BCDDECABCADE SS S S △△△△.24. 如图10,梯形OABC ,BC//OA ,边OA 在x 轴正半轴上,边OC 在y 轴正半轴上,点B (3,4),AB =5. (1)求∠BAO 的正切值; (2)如果二次函数y =94x 2+bx+c 的图像经过O 、A 两点,求这个二次函数的解析式并求图像顶点M 的坐标;(3)点Q 在x 轴上,以点Q 、点O 及(2)中的点M 为顶点的三角形与△ABO 相似,求点Q 的坐标.EDCBA图925、把两块边长为4的等边三角板ABC 和DEF 先如图11-1放置,使三角板DEF 的顶点D 与三角板ABC 的AC 边的中点重合,DF 经过点B ,射线DE 与射线AB 相交于点M ,接着把三角形板ABC 固定不动,将三角形板DEF 由图11-1所示的位置绕点D 按逆时针方向旋转,设旋转角为α.其中0°<α<90°,射线DF 与线段BC 相交于点N (如图11-2所示). (1)当0°<α<60°时,求AM ·CN 的值. (2)当0°<α<60°时,设AM =x ,两块三角形板重叠部分的面积为y ,求y 与x 的函数解析式并求定义域. (3)当B M = 2时,求两块三角形板重叠部分的面积.MFEDCBA图11-1NBCDM EFA图11-2AB备用图参考答案1.(C); 2.(C); 3.(D); 4.(D); 5.(B); 6.(C). 7.6; 8. ()0,0; 9. ()2255y x =-+ ;10. 6; 11.1:4; 12. 35;13.23; 14.3E D -; 15.23;16.3或7; 17. 154; 18.1或43.19.解:原式=22a b a b ---………………………………………………………………………2′=3a b -. …………………………………………………………………………………2′图形正确………………………………………………………………………………………5′ ∴结论. ………………………………………………………………………………………1′ 20.解:(1)在⊙O 中,O E A P ⊥, ∴P E A E =. ……………………………………2′同理PF B F =∴EF 为△A P B 的中位线. ………………………1′ ∵10A B =, ∴EF =152AB =.……………………………2′(2)过点O 作O H A B ⊥,点H 为垂足,联结OA ,…………………1′ 2O H =,152AH AB ==…………………………………………2′在R t A O H △中,由勾股定理得:A O =……………………………………2′即⊙O21.解:(1)根据题意,当2x =时,1y =;当1x =-时,10y =. 所以142510 5.a b a b =++⎧⎨=-+⎩, ……………………………………………………………………2′解得14.a b =⎧⎨=-⎩, ……………………………………………………………………2′所以,该二次函数关系式为245y x x =-+.………………………………………………… 1′ 对称轴为:直线2x =.………………………………………………………………………… 2′ (2)小于 ……………………………………………………………………………………………3′ 22、解:过点D 作AB DM ⊥,垂足为M .过点C 作AB CE ⊥,垂足为N .………………………………… 2′ 在CBN Rt ∆中,︒=∠37B , BCCNB BC BNB ==sin ,cos ,B BC CN B BC BN sin ,cos ⋅=⋅=.NM︒=∠=37,1000B m BC ,∴800,600BN m CN m == .…………………………………………………………… 2′AB DC //∴CN DM ==600m ,MN DC = …………………………………………………… 1′ 在ADM Rt ∆中,︒=∠45DAM , ∴m DM AM 600== .∴2600=AD .………………………………………………………………………… 1′ ∴846≈AD . ………………………………………………………………………… 1′ BN AM BC AD BN MN AM BC DC AD --+=++-++)(m 4468006001000846=--+= . ……………………………………………………… 2′答:现在从A 地到B 地可以比原来少走446米.…………………………………………1′ 23.(1)证明: 2AD AE AC = ,∴A DA EA C A D=.A ∠为公共角,∴A D E △∽A C D △.……………………………………………………3’ ∴A D E A C D ∠=∠.……………………………………………………1’ A C D B ∠=∠,∴A D E B ∠=∠.………………………………………………………………1’ ∴DE ∥BC .………………………………………………………………………1’ (2)证明:∵DE ∥BC ,∴A D E △∽A B C △.∴22A D E AB CS D E S B C=△△.…………………………………………………………3’∵DE ∥BC ,∴D E C △与C D B △同高, ∴D E C B C D S D ES B C=△△.…………………………………………………………2’∴2A D ED E C A B C B C D S S S S ⎛⎫= ⎪⎝⎭△△△△.…………………………………………………………1’24.解:(1)过点B 作BH ⊥OA ,垂足为H . ∵B (3,4),∴CB =OH =3,BH =4.…………………………………………………………………1′ 在R t B H A △中,由勾股定理得:3A H =,………………………………………………………1′∴4tan 3BAO ∠=.……………………………………………………………1′(2)∵OH =3,3A H =;∴点A 的坐标为()6,0.……………………………………………………………1′ 因为图像经过O 、A 两点,∴求得83b =-,0c =.∴二次函数的解析式为24893y x x =-.………………………………………2′所以()24349y x =--,顶点M 的坐标为(3,-4).……………………1′ (3)设点(),0Q x ,∵M (3,-4),∴4tan 3M OQ ∠=.所以MOQ BAO ∠=∠.……………………………………………………………1′ ∴△QOM 与△A B O 相似有两种可能性, ①O A A B O MO Q=655x =,解得:256x =,∴25,06Q ⎛⎫ ⎪⎝⎭.……………………………………………………………2′②O A A B O QO M=655x=,解得:x =6,∴()6,0Q .……………………………………………………………2′ 综上所述:符合要求的点Q 有两个,分别是25,06⎛⎫⎪⎝⎭和()6,0 . 25.解:(1)∵△ABC 和△DEF 是等边三角形,∴3=60C A ∠=∠=∠.∵132C ∠+∠=∠+∠,, ∴12∠=∠.∴A M D △∽C D N △.…………………………………2′ ∴A MA DC D C N=.∴A M C N A D C D ∙=∙ ∵A D C D ==2,∴4A M C N ∙=.…………………………………2′(2)过点D 作DP ⊥AB ,DQ ⊥BC ,垂足分别是点P 、Q ,在R t A P D △中,得PD =同理:D Q =.…………………………………1′321NBCD M EFA PDM EA∵AM = x ,4C N x=.…………………………………………………………1′ M BNC ABC AM D CDN S S S S =--△△△y 2x x=-()14x <<.…………………………………2′+1′(3)①如图11-2,当BM = 1时,AM = 2,即2x =所以y =,即:两块三角形板重叠部分的面积为…………………………2′ ②如图11-3,过点D 作DG ∥BC ,交AB 于点G , DG =2设DE 与BC 的交点为R ,由DG ∥BC ,得BR BMDG M G =,1B R = ∵AM =6,∴CN=23∴73R N =,6D R N S =△.……………………………………………………………3′综上所述,两块三角形板重叠部分的面积为6.R G A FEM D CBN 图11-3。
