必修三第二章测试题
必修三第2章综合检测以及答案

第2章综合检测A.激素X是促性腺激素,激素Y为雌性激素一、选择题 B.激素Y到达靶细胞后,其跨膜运输方式是主动运输1.如图为反射弧结构示意图,下列有关说法不正确的是( ) C.该生理过程中存在反馈调节D.长期注射激素Y会导致性腺衰退5.下图为人体甲状腺激素分泌的调节示意图,图中①②③为激素。
下列叙述不正确的是( ) A.由abcde组成了一个完整的反射弧B.若从③处剪断神经纤维,刺激①处,效应器仍能产生反应A.含量很少的①经过分级调节作用,可明显增加③的分泌C.图中②的结构决定了神经元之间的兴奋传递只能是单向的B.激素②是调节甲状腺细胞分泌功能的主要激素D.若从①处剪断神经纤维,刺激③处,效应器仍能产生反应C.血中③的浓度过低时,对下丘脑和垂体的促进作用减弱2.下图为某一传出神经元与肌细胞形成的突触。
下列说法错误的是( ) D.③几乎作用于全身的靶细胞,促进其细胞代谢6.如图表示人体和人体细胞内某些信息传递机制的模式图,图示中箭头表示信息的传递方向。
下列有关叙述中,正确的是( ) A.①的形成与高尔基体有关 A.如果该图表示反射弧,则其中的信息是以局部电流的形式传导的B.参与突触形成的肌细胞膜面积增大有利于神经递质的作用B.如果该图中的a为下丘脑、b为垂体、c为甲状腺,则c分泌的甲状腺激素增加到一定程度后,C.④兴奋时,其两侧的电位表现为内正外负对a分泌d,b分泌e具有抑制作用D.②释放的神经递质一定会使肌细胞兴奋C.如果该图表示细胞中遗传信息的传递过程,则过程d只发生于细胞核中 3.如图表示突触的亚显微结构,下列说法正确的是( ) D.如果该图表示细胞免疫过程,则a为效应T细胞,b为靶细胞,c为抗体7.如图所示,①②分别代表不同的细胞,a代表物质,下列各项不符合该示意图的是( ) +A.①中内容物使b兴奋时,兴奋部位的膜对Na通透性减小A.①为前一神经元、②为后一神经元、a为神经递质B.②处的液体为组织液,③一定是一个神经元的树突膜B.①为垂体细胞、②为甲状腺细胞、a 为促甲状腺激素释放激素C.在a中发生电信号→化学信号的转变,信息传递需要能量C.①为下丘脑细胞、②为肾小管细胞、a为抗利尿激素D.当兴奋沿b神经元传导时,其膜内电流方向与兴奋传导方向相D.①为甲状腺细胞、②为下丘脑细胞、a为甲状腺激素反 8.细胞间和细胞内的信息传递过程中,需要受体对信号的识别。
人教版高中英语必修第三册课后习题 Unit 2 Morals and Virtues 第二单元测评卷

第二单元测评(时间:120分钟满分:150分)第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.How does the man come here?A.By taxi.B.By bus.C.By car.2.Why is Helen absent?A.She forgot to come.B.She wasn’t invited.C.She changed her decision.3.What’s the probable relationship between the two speakers?A.Husband and wife.B.Mother and son.C.Doctor and patient.4.How much will the woman pay?A.20 dollars.B.12 dollars.C.2 dollars.5.What does the man mean?A.He can’t go to the cinema.B.He can go to the cinema on Saturday evening.C.He can go to the cinema on Saturday morning.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6.When will the man go on holiday?A.In winter.B.In summer.C.In spring.7.Where is the man going?A.Italy.B.Switzerland.C.Austria.听第7段材料,回答第8至10题。
必修三第二章综合测试题
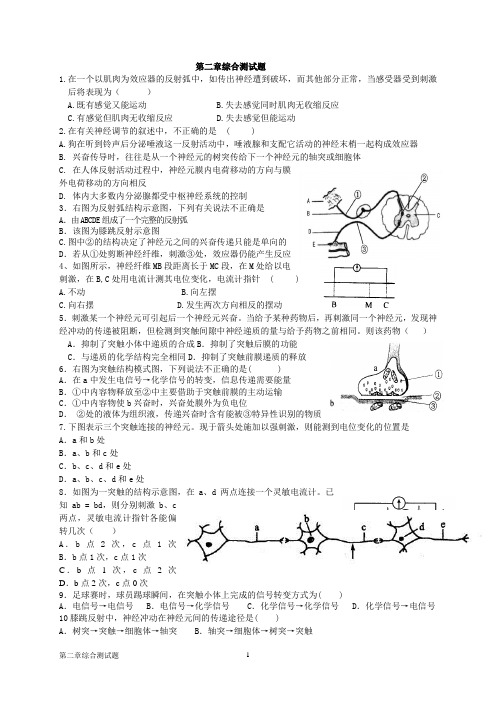
第二章综合测试题1.在一个以肌肉为效应器的反射弧中,如传出神经遭到破坏,而其他部分正常,当感受器受到刺激后将表现为()A.既有感觉又能运动B.失去感觉同时肌肉无收缩反应C.有感觉但肌肉无收缩反应D.失去感觉但能运动2.在有关神经调节的叙述中,不正确的是 ( )A.狗在听到铃声后分泌唾液这一反射活动中,唾液腺和支配它活动的神经末梢一起构成效应器B. 兴奋传导时,往往是从一个神经元的树突传给下一个神经元的轴突或细胞体C. 在人体反射活动过程中,神经元膜内电荷移动的方向与膜外电荷移动的方向相反D. 体内大多数内分泌腺都受中枢神经系统的控制3.右图为反射弧结构示意图,下列有关说法不正确是A.由ABCDE组成了一个完整的反射弧B.该图为膝跳反射示意图C.图中②的结构决定了神经元之间的兴奋传递只能是单向的D.若从①处剪断神经纤维,刺激③处,效应器仍能产生反应4、如图所示,神经纤维MB段距离长于MC段,在M处给以电刺激,在B,C处用电流计测其电位变化,电流计指针 ( )A.不动B.向左摆C.向右摆D.发生两次方向相反的摆动5.刺激某一个神经元可引起后一个神经元兴奋。
当给予某种药物后,再刺激同一个神经元,发现神经冲动的传递被阻断,但检测到突触间隙中神经递质的量与给予药物之前相同。
则该药物()A.抑制了突触小体中递质的合成B.抑制了突触后膜的功能C.与递质的化学结构完全相同D.抑制了突触前膜递质的释放6.右图为突触结构模式图,下列说法不正确的是( )A.在a中发生电信号→化学信号的转变,信息传递需要能量B.①中内容物释放至②中主要借助于突触前膜的主动运输C.①中内容物使b兴奋时,兴奋处膜外为负电位D.②处的液体为组织液,传递兴奋时含有能被③特异性识别的物质7.下图表示三个突触连接的神经元。
现于箭头处施加以强刺激,则能测到电位变化的位置是A.a和b处B.a、b和c处C.b、c、d和e处D.a、b、c、d和e处8.如图为一突触的结构示意图,在a、d两点连接一个灵敏电流计。
高中地理必修三第二章测试题

第二章区域可持续发展综合检测一、选择题(2分×25=50分)2010年6月17日是第15个“世界防治荒漠化和干旱日”(World Day to Combat Desertification and Drought)。
2009年“世界防治荒漠化和干旱日”的主题是“荒漠化与气候变化——一个全球性的挑战”。
思考并完成1~3题。
1.为迎接今年的“世界防治荒漠化和干旱日”,某校地理兴趣小组制作了四幅景观图片,其中属于土地荒漠化的是( )A.①②④B.①②③C.②③④ D.①③④2.导致①中现象的主要外力作用是( )A.风蚀B.水蚀C.冰川侵蚀D.海蚀3.导致②中现象出现的自然原因是( )A.气候干旱,大风频繁B.降水少,但有时强度大C.人口增长迅速D.不合理的生产活动读“我国部分区域简图”,完成4~5题。
4.图例所示的某环境问题主要是( )A.水土流失 B.土地荒漠化C.环境污染 D.湿地破坏5.治理该环境问题的根本措施是( )A.退耕还林还草B.修建水电站C.增加灌溉面积武汉已总体规划了6大放射状楔形绿色生态走廊:①大东湖水系;②武湖水系;③府河水系;④后官湖水系;⑤青菱湖水系;⑥汤逊湖水系。
结合“武汉城市规划图”,完成6~8题。
6.打通这些湿地风道可以( )A.缓解城区的热岛效应B.发展城区水上观光旅游C.改善城市交通拥堵状况D.缓解城市用水紧张的局面7.武汉市有众多的湖泊,这些湖泊的主要功能是( )①改善城市环境②调节径流,减少洪灾③提供供水和航运之便④土地后备资源A.①② B.①③C.②④ D.③④8.武汉市夹“二江三岸”,有丰富的河滩地资源,对这些河滩地的科学开发应( )A.兴建高档观景(观江)建筑B.修建道路、桥梁C.发展城市观光农业D.兴建防洪设施田纳西河源出阿巴拉契亚高地西坡……大部分流经阿巴拉契亚高原区……水力资源丰富,仅能通行小汽轮。
下游河谷较开阔,从帕迪尤卡至弗洛伦斯之间450千米河道,通航便利。
人教A版高中数学必修三试卷第二章测试.doc

高中数学学习材料鼎尚图文*整理制作第二章测试(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的) 1.某商场想通过检查发票及销售记录的2%来快速估计每月的销售总额.采取如下方法:从某本50张的发票存根中随机抽一张,如15号,然后按顺序往后将65号,115号,165号,…抽出,发票上的销售额组成一个调查样本.这种抽取样本的方法是() A.简单随机抽样B.系统抽样C.分层抽样D.其他方式的抽样答案 B2.①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②一次数学月考中,某班有10人在100分以上,32人在90~100分,12人低于90分,现从中抽取9人了解有关情况;③运动会工作人员为参加4×100 m接力赛的6支队伍安排跑道.就这三件事,恰当的抽样方法分别为() A.分层抽样、分层抽样、简单随机抽样B.系统抽样、系统抽样、简单随机抽样C .分层抽样、简单随机抽样、简单随机抽样D .系统抽样、分层抽样、简单随机抽样解析 ①中总体容量较多,抽取的样本容量较大,用系统抽样比较恰当;②中考试成绩各分数段之间的同学有明显的差异,应按分层抽样比较恰当;③中个体较少,按简单随机抽样比较恰当.答案 D3.某中学有高一学生400人,高二学生300人,高三学生500人,现用分层抽样的方法在这三个年级中抽取120人进行体能测试,则从高三抽取的人数应为( )A .40B .48C .50D .80解析 ∵一、二、三年级的人数比为,∴从高三应抽取的人数为120×512=50.答案 C4.将一个样本容量为100的数据分组,各组的频数如下: (17,19],1;[19,21),1;(21,23],3;(23,25],3;(25,27],18;(27,29],16;(29,31],28;(31,33],30.根据样本频率分布,估计小于或等于29的数据大约占总体的( )A .58%B .42%C .40%D .16%解析 依题意可得1+1+3+3+18+16100=42%. 答案 B5.工人的月工资y (元)依劳动生产率x (千元)变化的回归方程为y^=50+80x,下列判断正确的是()A.劳动生产率为1000元时,工资为130元B.劳动生产率提高1000元,则工资提高80元C.劳动生产率提高1000元,则工资提高130元D.当月工资为210元时,劳动生产率为2000元解析由回归系数b^的意义知,当b^>0时,自变量和因变量正相关,当b^<0时,自变量和因变量负相关,回归直线的斜率b^=80,所以x每增加1个单位(千元),工人工资y平均增加80个单位(元),即劳动生产率提高1000元时,工资提高80元,故选B.答案 B6.甲、乙两名同学在五次数学测试中的成绩统计用茎叶图表示如下,若甲、乙两人的平均成绩分别用X甲,X乙表示,则下列结论正确的是()A.X甲>X乙,甲比乙成绩稳定B.X甲>X乙,乙比甲成绩稳定C.X甲<X乙,甲比乙成绩稳定D.X甲<X乙,乙比甲成绩稳定解析由茎叶图知,X甲=15×(68+69+70+71+72)=70,X乙=15×(63+68+69+69+71)=68,∴X甲>X乙,且甲比乙成绩稳定.答案 A7.已知数据x1,x2,x3的中位数为k,众数为m,平均数为n,方差为p,则下列说法中,错误的是()A.数据2x1,2x2,2x3的中位数为2kB.数据2x1,2x2,2x3的众数为2mC.数据2x1,2x2,2x3的平均数为2nD.数据2x1,2x2,2x3的方差为2p解析2x1,2x2,2x3的方差应为4p,∴选项D错.答案 D8.随机调查某校50个学生在“六一\”儿童节的午餐费,结果如下表:餐费(元)34 5人数102020 这50个学生“六一\”儿童节午餐费的平均数和方差分别为()A.4.2,0.56 B.4,0.6C.4,0.6 D.4.2,0.56解析平均数x=3×10+4×20+5×2050=4.2.方差s2=150×[(4.2-3)2×10+(4.2-4)2×20+(4.2-5)2×20]=150×(14.4+0.8+12.8)=150×28=0.56.答案 A9.甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数是1.8,全年进球数的标准差为0.3.下列说法中,正确的个数为()①甲队的技术比乙队好;②乙队发挥比甲队稳定;③乙队几乎每场都进球;④甲队的表现时好时坏.A.1 B.2C.3 D.4解析由平均数及方差的意义知,①,②,③,④都正确.答案 D10.10名工人某天生产同一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有()A.a>b>c B.b>c>aC.c>a>b D.c>b>a解析把10个数据从小到大排列为10,12,14,14,15,15,16,17,17,17.∴中位数b=15,众数c=17,平均数a=110×(10+12+14×2+15×2+16+17×3)=14.7.∴a <b <c . 答案 D11.观察新生婴儿的体重,其频率分布直方图如图,则新生婴儿体重在(2700,3000)的频率为( )A .0.001B .0.1C .0.2D .0.3解析 由直方图可知,所求频率为0.001×300=0.3. 答案 D12.设矩形的长为a ,宽为b ,其比满足b :a =5-12≈0.618,这种矩形给人以美感,称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:甲批次:0.598 0.625 0.628 0.595 0.639 乙批次:0.618 0.613 0.592 0.622 0.620根据上述两个样本来估计两个批次的总体平均数与标准值0.618比较,正确结论是( )A .甲批次的总体平均数与标准值更接近B.乙批次的总体平均数与标准值更接近C.两个批次总体平均数与标准值接近程度相同D.两个批次总体平均数与标准值接近程度不能确定解析甲批次的样本平均数为15×(0.598+0.625+0.628+0.595+0.639)=0.617;乙批次的样本平均数为15×(0.618+0.613+0.592+0.622+0.620)=0.613.所以可估计:甲批次的总体平均数与标准值更接近.答案 A二、填空题(本大题共4小题,每小题5分,满分20分.把答案填在题中横线上)13.若x1,x2,…,x2010,x2011的方差为3,则3(x1-2),3(x2-2),…,3(x2010-2),3(x2011-2)的方差为________.解析由方差的计算公式知,方差为原来方差的9倍,因此,所求的方差为27.答案2714.如图是CBA篮球联赛中,甲、乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的运动员是________.解析由茎叶图知平均得分高的运动员是甲,或计算得x甲=20.4,x2=19.3,x甲>x乙.答案甲15.防疫站对学生进行身体健康调查,采用分层抽样法抽取.某中学共有学生1600名,抽取一个容量为200的样本,已知女生比男生少抽了10人,则该校的女生人数应为________人.解析由题意知,样本中有女生95人,男生105人,则全校共有女生为95÷2001600=760人.答案76016.某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为________.解析 由频率分布图知,设90~100分数段的人数为x ,则0.40x =0.0590,∴x =720.答案 720三、解答题(本大题共6小题,满分70分.解答应写出必要的文字说明、证明过程或演算步骤)17.(10分)某中学初中部有三个年级,其中初二、初三共有学生1500人,采用分层抽样从初中部抽取一个容量为75的样本,初二年级抽取30人,初三年级抽取20人.问初中部共有多少学生?解 设初中部共有x 名学生,依题意可得75x =30+201500,解得x =2250.即初中部共有2250人.18.(12分)为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组频率分别为0.1,0.3,0.4,第一小组的频数为5.(1)求第四小组的频率;(2)参加这次测试的学生有多少人;(3)若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率是多少.解(1)由累积频率为1知,第四小组的频率为1-0.1-0.3-0.4=0.2.(2)设参加这次测试的学生有x人,则0.1x=5,∴x=50.即参加这次测试的学生有50人.(3)达标率为0.3+0.4+0.2=90%,所以估计该年级学生跳绳测试的达标率为90%.19.(12分)对某400件元件进行寿命追踪调查情况频率分布如下:寿命(h)频率[500,600)0.10[600,700)0.15[700,800)0.40[800,900)0.20[900,1000]0.15合计 1(1)列出寿命与频数对应表;(2)估计元件寿命在[500,800)内的频率;(3)估计元件寿命在700 h以上的频率.解(1)寿命与频数对应表:寿命(h)[500,600)[600,700)[700,800)[800,900)[900,1000] 频数40601608060(2)估计该元件寿命在[500,800)内的频率为0.10+0.15+0.40=0.65.(3)估计该元件寿命在700 h以上的频率为0.40+0.20+0.15=0.75.20.(12分)两台机床同时生产一种零件,在10天中,两台机床每天的次品数如下:甲1,0,2,0,2,3,0,4,1,2乙1,3,2,1,0,2,1,1,0,1(1)哪台机床次品数的平均数较小?(2)哪台机床的生产状况比较稳定?解(1)x甲=(1+0+2+0+2+3+0+4+1+2)×110=1.5,x乙=(1+3+2+1+0+2+1+1+0+1)×110=1.2. ∵x甲>x乙,∴乙车床次品数的平均数较小.(2)s2甲=110[(1-1.5)2+(0-1.5)2+(2-1.5)2+(0-1.5)2+(2-1.5)2+(3-1.5)2+(0-1.5)2+(4-1.5)2+(1-1.5)2+(2-1.5)2]=1.65,同理s2乙=0.76,∵s2甲>s2乙,∴乙车床的生产状况比较稳定.21.(12分)某良种培育基地正在培育一种小麦新品种A.将其与原有的一个优良品种B进行对照试验.两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:品种A:357,359,367,368,375,388,392,399,400,405,412,414,415,421,423,423,427 ,430,430,434,443,445,445,451,454品种B:363,371,374,383,385,386,391,392,394,394,395,397,397,400,401,401,403 ,406,407,410,412,415,416,422,430(1)完成数据的茎叶图;(2)用茎叶图处理现有的数据,有什么优点?(3)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论.解(1)(2)由于每个品种的数据都只有25个,样本不大,画茎叶图很方便;此时茎叶图不仅清晰明了地展示了数据的分布情况,便于比较,没有任何信息损失,而且还可以随时记录新的数据.(3)通过观察茎叶图可以看出:①品种A 的亩产平均数(或均值)比品种B 高;②品种A 的亩产标准差(或方差)比品种B 大,故品种A 的亩产量稳定性较差.22.(12分)某个体服装店经营各种服装,在某周内获纯利润y (元)与该周每天销售这种服装件数x 之间的一组数据关系如下表:x3456789y66 69 73 81 89 90 91已知:∑i =17x 2i =280,∑i =17x i y i =3487.(1)求x ,y ; (2)画出散点图;(3)观察散点图,若y 与x 线性相关,请求纯利润y 与每天销售件数x 之间的回归直线方程.解 (1)x =3+4+5+6+7+8+97=6, y =66+69+73+81+89+90+917=5597≈79.86. (2)散点图如图所示.(3)观察散点图知,y 与x 线性相关.设回归直线方程为y ^=b^x +a ^. ∵∑i =17x 2i =280,∑i =17x i y i =3487, x =6,y =5597,∴b ^=3487-7×6×5597280-7×36=13328=4.75.a ^=5597-6×4.75≈51.36.∴回归直线方程为y ^=4.75x +51.36.。
高中数学必修3第二章:统计测试题及其答案

高中数学必修3第二章(统计)检测题班级姓名得分一、选择题:(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.某单位有老年人28人,中年人54人,青年人81人.为了调查他们的身体状况,需从他们中抽取一个容量为36的样本,最适合抽取样本的方法是( D ).A.简单随机抽样B.系统抽样C.分层抽样D.先从老年人中剔除一人,然后分层抽样2.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12.设其平均数为a,中位数为b,众数为c,则有( D ).A.a>b>c B.b>c>a C.c>a>b D.c>b>a3.下列说法错误的是( B ).A.在统计里,把所需考察对象的全体叫作总体B.一组数据的平均数一定大于这组数据中的每个数据C.平均数、众数与中位数从不同的角度描述了一组数据的集中趋势D.一组数据的方差越大,说明这组数据的波动越大4.下列说法中,正确的是( C ).A.数据5,4,4,3,5,2的众数是4B.一组数据的标准差是这组数据的方差的平方C.数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半D.频率分布直方图中各小长方形的面积等于相应各组的频数5.从甲、乙两班分别任意抽出10名学生进行英语口语测验,其测验成绩的方差分别为S12= 13.2,S22=26.26,则( A ).A.甲班10名学生的成绩比乙班10名学生的成绩整齐B.乙班10名学生的成绩比甲班10名学生的成绩整齐C.甲、乙两班10名学生的成绩一样整齐D.不能比较甲、乙两班10名学生成绩的整齐程度6.下列说法正确的是( C ).A.根据样本估计总体,其误差与所选择的样本容量无关B.方差和标准差具有相同的单位C.从总体中可以抽取不同的几个样本D.如果容量相同的两个样本的方差满足S12<S22,那么推得总体也满足S12<S22是错的7.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输人为15,那么由此求出的平均数与实际平均数的差是( B ).A.3.5 B.-3 C.3 D.-0.58.在一次数学测验中,某小组14名学生分别与全班的平均分85分的差是:2,3,-3,-5,12,12,8,2,-1,4,-10,-2,5,5,那么这个小组的平均分是(B )分.A.97.2 B.87.29 C.92.32 D.82.869A.37.0%10.如果一组数中每个数减去同一个非零常数,则这一组数的( 10 ).A.平均数不变,方差不变B.平均数改变,方差改变C.平均数不变,方差改变D.平均数改变,方差不变11. 为调查参加运动会的1 000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下列说法正确的是(A)A.1 000名运动员是总体B.每个运动员是个体C.抽取的100名运动员是样本D.样本容量是10012.为了调查某产品的销售情况,销售部门从下属的92家销售连锁店中抽取30家了解情况.若用系统抽样法,则抽样间隔和随机剔除的个体数分别为(A)A.3,2 B.2,3 C.2,30 D.30,213.某城区有农民、工人、知识分子家庭共计2 000家,其中农民家庭1 800户,工人家庭100户.现要从中抽取容量为40的样本,调查家庭收入情况,则在整个抽样过程中,可以用到下列抽样方法(D)①简单随机抽样;②系统抽样;③分层抽样.A.②③B.①③C.③D.①②③14.下列说法不正确的是(A)A.频率分布直方图中每个小矩形的高就是该组的频率B.频率分布直方图中各个小矩形的面积之和等于1C.频率分布直方图中各个小矩形的宽一样大D.频率分布直方图能直观地表明样本数据的分布情况15A.0.35 B.0.45 C.0.55 D.0.6516.已知10名工人生产同一零件,生产的件数分别是16,18,15,11,16,18,18,17,15,13,设其平均数为a,中位数为b,众数为c,则有(D)A.a>b>c B.a>c>b C.c>a>b D.c>b>a17. 已知一个样本中的数据为1,2,3,4,5,则该样本的标准差为(B)A.1 B. 2 C. 3 D.218. 如图是2012年某校举行的元旦诗歌朗诵比赛中,七位评委为某位选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和方差分别为(C)A.84,4.84 B.84,1.6 C.85,1.6 D.85,0.419.某中学有高中生3500人,初中生1500人.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为(A)A.100 B.150 C.200 D.25020.样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是(A)A.32,0.4 B.8,0.1C.32,0.1 D.8,0.4二、填空题:(本题共4小题,每小题3分,共12分)21.一个公司共有240名员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为20的样本.已知某部门有60名员工,那么从这一部门抽取的员工人数是 5 。
(压轴题)高中数学必修三第二章《算法初步》测试卷(答案解析)
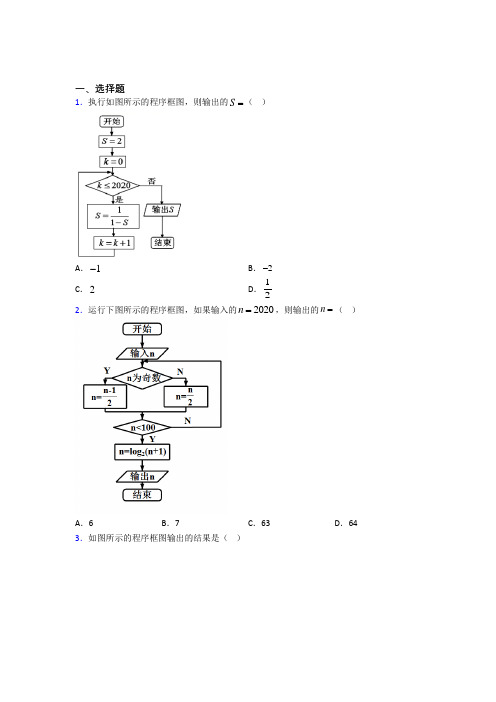
一、选择题1.执行如图所示的程序框图,则输出的S=()A.1-B.2-C.2D.1 22.运行下图所示的程序框图,如果输入的2020n=,则输出的n=()A.6 B.7 C.63 D.64 3.如图所示的程序框图输出的结果是()A.34 B.55 C.78 D.894.执行如图所示的程序框图,若输入x=9,则循环体执行的次数为()A.1次B.2次C.3次D.4次5.明代数学家程大位(1533~1606年),有感于当时筹算方法的不便,用其毕生心血写出《算法统宗》,可谓集成计算的鼻祖.如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题.执行该程序框图,若输出的y的值为2,则输入的x的值为()A .74B .5627C .2D .164816.某程序框图如图所示,其中21()g n n n =+,若输出的20192020S =,则判断框内可以填入的条件为( )A .2020?n <B .2020?nC .2020?n >D .2020?n 7.鸡兔同笼,是中国古代著名的趣味题之一.《孙子算经》中就有这样的记载:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各有几何?设计如右图的算法来解决这个问题,则判断框中应填入的是( )A .94m >B .94m =C .35m = D .35m ≤8.如图,执行程序框图后,输出的结果是( )A .140B .204C .245D .300 9.如图给出的是计算1111246102+++⋅⋅⋅+的值的一个程序框图,其中判断框中应填入的是( )A .102i >B .102i ≤C .100i >D .100i ≤ 10.执行如图所示的程序框图,若输入的6n =,则输出S =A .514B .13C .2756D .31011.《数书九章》是我国宋代数学家秦九韶的著作,其中给出了求多项式的值的秦九韶算法,如图所示的程序框图给出了一个利用秦九韶算法求某多项式值的实例,若输入的13x =,输出的12181=y 则判断框“”中应填入的是( )A .2?k ≤B .3?k ≤C .4?k ≤D .5?≤k 12.执行如下图的程序框图,那么输出S 的值是( )A .2B .1C .12D .-1二、填空题13.执行下面的程序框图,若输入的a ,b ,k 分别为1,2,3,则输出的M =_____14.执行如图所示的程序框图若输人x 的值为3,则输出y 的值为______.15.执行如图所示的伪代码,若输出的y的值为10,则输入的x的值是________.16.我国元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没有壶中酒,借问此壶中,当原多少酒?”用程序x=,问一开始输入的x=______斗.遇店添一倍,逢框图表达如图所示,即最终输出的0友饮一斗,意思是碰到酒店就把壶里的酒加1倍,碰到朋友就把壶里的酒喝一斗,店友经三处,意思是每次都是遇到店后又遇到朋友,一共是3次.17.如图是一个算法流程图,则输出的S的值为______.18.如图所示的程序框图,输出S的结果是__________.19.运行如图所示的程序,输出结果为___________.20.一个算法的程序框图如图所示,则该程序运行后输出的结果是.三、解答题21.如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为22cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.22.用程序框图描述算法:已知梯形的两底边长分别为a,b,高为h,求梯形面积.23.下面程序的功能是输出1~100之间的所有偶数.程序:i=1DOm=iMOD2IF①THENPRINTiENDIF②LOOPUNTILi>100END(1)试将上面的程序补充完整;(2)改写为WHILE型循环结构程序.24.已知函数f(x)=221(0)25(0)x xx x⎧-≥⎨-<⎩每输入一个x值,都得到相应的函数值,画出程序框图并写出程序.25.分别标有1,2,3,4,5,6六个号码的小球,有一个最重,写出挑出最重球的算法,并画出程序框图.26.写出计算102+202+…+1 0002的算法程序,并画出相应的程序框图.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】列举出前四次循环,可知,该算法循环是以3为周期的周期循环,利用周期性可得出输出的S 的值.【详解】第一次循环,02020k =≤成立,1112S ==--,011k =+=; 第二次循环,12020k =≤成立,()11112S ==--,112k =+=; 第三次循环,22020k =≤成立,12112S ==-,213k =+=;第四次循环,32020k =≤成立,1112S ==--,314k =+=; 由上可知,该算法循环是周期循环,且周期为3,依次类推,执行最后一次循环,20202020k =≤成立,且202036731=⨯+,此时12S =, 202012021k =+=,20212020k =≤不成立,跳出循环体,输出S 的值为12. 故选:D.【点睛】本题考查利用程序框图计算输出结果,推导出循环的周期性是解题的关键,考查计算能力,属于中等题.2.A解析:A【分析】根据题中所给的框图,模拟执行程序框图,求得结果.【详解】输入2020100n =>,且不是奇数,赋值1010100n =>,且不是奇数,赋值505100n =>,且是奇数,赋值252100n =>,且不是奇数,赋值126100n =>,且不是奇数,赋值63100n =<,赋值()2log 6316n =+=,输出6.故选:A【点睛】该题考查的是有关程序框图的问题,涉及到的知识点有计算程序框图的输出结果,属于简单题目.3.B解析:B【分析】通过不断的循环赋值,得到临界值,即可得解.【详解】1,1,21,2,32,3,53,5,85,8,138,13,2113,21,3421,34,55x y z x y z x y z x y z x y z x y z x y z x y z ======================== 不满足50z ≤,输出即可,故选:B.【点睛】本题考查了程序框图循环结构求输出结果,考查了计算能力,属于中当题.4.C解析:C【分析】根据程序框图依次计算得到答案.【详解】9,5x y ==,41y x -=>;115,3x y ==,413y x -=>; 1129,39x y ==,419y x -=<;结束. 故选:C .【点睛】本题考查了程序框图的循环次数,意在考查学生的理解能力和计算能力.5.C解析:C【分析】根据程序框图依次计算得到答案.【详解】34y x =-,1i =;34916y y x =-=-,2i =;342752y y x =-=-,3i =; 3481160y y x =-=-,4i =;34243484y y x =-=-,此时不满足3i ≤,跳出循环,输出结果为243484x -,由题意2434842y x =-=,得2x =.故选:C【点睛】本题考查了程序框图的计算,意在考查学生的理解能力和计算能力.6.A解析:A【分析】因为()()2111111g n n n n n n n ===-+++,此程序框图是对函数()g n 求和,利用裂项相消法求和,可知201912020n S n ==+,可知2019满足条件进入循环,2020不满足条件没有进入循环,根据选项得到正确结果.【详解】 由2221111111112019(1111222231112020n S n n n n n n ⎫⎛⎫⎛⎫=++⋯+=-+-+⋯+-=-==⎪ ⎪ ⎪++++++⎭⎝⎭⎝⎭,解得2019n =,可得n 的值为2019时.满足判断框内的条件,当n 的值为2020时,不满足判断框内的条件,退出循环,输出S 的值,故判断框内可以填人的条件为“2020n <?”.故选A.【点睛】本题考查根据循环框图的输出结果填写判断框的内容,关键是分析出满足输出结果时的n 值,再根据选项判断结果.7.B解析:B【分析】由题意知i 为鸡的数量,j 为兔的数量,m 为足的数量,根据题意可得出判断条件.【详解】由题意可知i 为鸡的数量,j 为兔的数量,m 为足的数量,根据题意知,在程序框图中,当计算足的数量为94时,算法结束,因此,判断条件应填入“94m =”.故选B.【点睛】本题考查算法程序框图中判断条件的填写,考查分析问题和解决问题的能力,属于中等题. 8.B【分析】根据程序框图列举出算法的每一步,可得出输出结果.【详解】18n =>不成立,执行第一次循环,211b ==,011s =+=,112n =+=;28n =>不成立,执行第二次循环,224b ==,145s =+=,213n =+=; 38n =>不成立,执行第三次循环,239b ==,5914s =+=,314n =+=; 48n =>不成立,执行第四次循环,2416b ==,141630s =+=,415n =+=; 58n =>不成立,执行第五次循环,2525b ==,302555s =+=,516n =+=; 68n =>不成立,执行第六次循环,2636b ==,553691s =+=,617n =+=; 78n =>不成立,执行第七次循环,2749b ==,9149140s =+=,718=+=n ; 88n =>不成立,执行第八次循环,2864b ==,14064204s =+=,819n =+=; 98n =>成立,跳出循环体,输出s 的值为204,故选B.【点睛】本题考查程序框图运行结果的计算,一般利用算法程序框图将算法的每一步列举出来,考查计算能力,属于中等题.9.B解析:B【解析】【分析】 根据题目所求表达式1111246102+++⋅⋅⋅+中最后一个数字1102,确定填写的语句. 【详解】 由于题目所求是1111246102+++⋅⋅⋅+,最后一个数字为1102,即当102i =时,判断是,继续循环,2104i i =+=,判断否,退出程序输出S 的值,由此可知应填102i ≤.故选B.【点睛】本小题主要考查填写程序框图循环条件,属于基础题. 10.B解析:B【解析】【分析】首先确定流程图所实现的功能,然后利用裂项求和的方法即可确定输出的数值.【详解】 由流程图可知,程序输出的值为:1111023344556S =++++⨯⨯⨯⨯, 即1111111123344556S ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭111263=-=.【点睛】本题主要考查流程图功能的识别,裂项求和的方法等知识,意在考查学生的转化能力和计算求解能力.11.C解析:C【解析】【分析】模拟程序的运行过程,即可得出输出y 的值时判断框中应填入的是什么.【详解】模拟程序的运行过程如下, 输入114,1,11333x k y ===⨯+=, 41132,1339k y ==⨯+=, 131403,19327k y ==⨯+=, 4011214,127381k y ==⨯+=, 此时不满足循环条件,输出12181=y ; 则判断框中应填入的是4?k ≤. 故选:C .【点睛】本题考查了算法与程序框图的应用问题,理解框图的功能是解题的关键,是基础题. 12.A解析:A【解析】【分析】模拟程序的运行,依次写出每次循环得到的k 和S 值,根据题意即可得到结果.【详解】程序运行如下,k=0, S =112-=﹣1, k =1,S =()111--=12; k =2,S =12112=-;k =3,S =11-2=-1… 变量S 的值以3为周期循环变化,当k=2018时,s=2,K=2019时,结束循环,输出s 的值为2.故选:A .【点睛】本题考查程序框图,是当型结构,即先判断后执行,满足条件执行循环,不满足条件,跳出循环,算法结束,解答的关键是算准周期,是基础题.二、填空题13.12【分析】由题意可知从开始判断框条件成立执行第一次循环得到一组新的的值再从开始判断框条件成立执行第一次循环得到一组新的的值当时判断条件框不成立输出此时的值即可得出答案【详解】当时执行程序框图得;当 解析:12【分析】由题意可知,从1n =开始,判断框条件成立,执行第一次循环,得到一组新的,,M a b 的值,再从2n =开始,判断框条件成立,执行第一次循环,得到一组新的,,M a b 的值,当3n =时,判断条件框不成立,输出此时M 的值,即可得出答案.【详解】当1n =时,执行程序框图得,1225,2,5M a b =+⨯===;当2n =时,执行程序框图得,22512,5,12M a b =+⨯===;当3n =时,不满足判断条件框,直接输出 12M =.故答案为12.【点睛】本题主要考查了根据程序框图写出执行结果的问题,对于这类题目,首先要弄清框图的结构和执行过程,本题为循环结构的程序框图.14.63【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量y 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】解:模拟程序的运行可得x=3y=7不满足条件|x-y|解析:63【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量y 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【详解】解:模拟程序的运行,可得x=3y=7不满足条件|x-y|>31,执行循环体,x=7,y=15不满足条件|x-y|>31,执行循环体,x=15,y=31不满足条件|x-y|>31,执行循环体,x=31,y=63此时,满足条件|x-y|>31,退出循环,输出y 的值为63.故答案为63.【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.15.3【解析】【分析】分析出算法的功能是求分段函数的值根据输出的值为10分别求出当时和当时的值即可【详解】由程序语句知:算法的功能是求的值当时解得(或不合題意舍去);当时解得舍去综上的值为3故答案为3【 解析:3【解析】【分析】分析出算法的功能是求分段函数22,31,3x x y x x <⎧=⎨+≥⎩的值,根据输出的值为10 ,分别求出当3x <时和当3x ≥时的x 值即可.【详解】由程序语句知:算法的功能是求22,31,3x x y x x <⎧=⎨+≥⎩的值, 当3x ≥时,2110y x =+=,解得3x =(或3- ,不合題意舍去);当3x <时,210y x ==,解得5x = ,舍去,综上,x 的值为3,故答案为3 .【点睛】本题主要考查条件语句以及算法的应用,属于中档题 .算法是新课标高考的一大热点,其中算法的交汇性问题已成为高考的一大亮,这类问题常常与函数、数列、不等式等交汇自然,很好地考查考生的信息处理能力及综合运用知识解决问題的能力,解决算法的交汇性问题的方:(1)读懂程序框图、明确交汇知识,(2)根据给出问题与程序框图处理问题即可. 16.【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件输出令即可得结果【详解】第一次输入执行循环体执行循环体执行循环体输出的值为0解得:故答案为【点睛】本题主要考查程序框图的 解析:78【分析】模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件输出87x -,令870x -=即可得结果.【详解】第一次输入x x =,1i =执行循环体,21x x =-,2i =,执行循环体,()221143x x x =--=-,3i =,执行循环体,()243187x x x =--=-,43i =>,输出87x -的值为0,解得:78x =, 故答案为78. 【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可. 17.【解析】【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】模拟程序的运行可得满足条件执行循环体满足条件执行循 解析:7【解析】【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【详解】模拟程序的运行,可得1S =,1i =满足条件4i <,执行循环体,2S =,2i =满足条件4i <,执行循环体,4S =,3i =满足条件4i <,执行循环体,7S =,4i =此时,不满足条件4i <,退出循环,输出S 的值为7.故答案为7.【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.18.【解析】阅读流程图可得该流程图计算的数值为:解析:【解析】阅读流程图可得,该流程图计算的数值为:sin 0sin 1sin 5262626S ππππππ⎛⎫⎛⎫⎛⎫=⨯++⨯+++⨯+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 19.【详解】试题分析:第一次运行条件成立;第二次运行条件成立;第三次运行条件成立;第四次运行条件不成立;输出故答案应填:1考点:算法及程序语言解析:1【详解】试题分析:第一次运行,5,4s n ==条件14s <成立;第二次运行,9,3s n ==条件14s <成立;第三次运行,12,2s n ==条件14s <成立;第四次运行,14,1s n ==条件14s <不成立;输出1n =,故答案应填:1.考点:算法及程序语言.20.4【分析】执行程序当时循环结束即可得出【详解】因为第一次进入循环后;第二次进入循环后;第三次进入循环后;第四次进入循环后循环结束所以输出的结果为4【点睛】本题主要考查了程序框图求输出的值做题时要仔细 解析:4【分析】执行程序,当4K =时循环结束,即可得出【详解】因为第一次进入循环后1,1S K ==;第二次进入循环后3,2S K ==;第三次进入循环后11,3S K ==;第四次进入循环后2059,4S K ==,循环结束,所以输出的结果为4【点睛】本题主要考查了程序框图求输出的值,做题时要仔细点,属于基础题.三、解答题21.221,02222,251(7)10,572x x y x x x x ⎧≤≤⎪⎪=-<≤⎨⎪⎪-+<<⎩,程序框图和程序见解析. 【分析】根据直线l 将梯形分割的左边部分的形状进行分类讨论,求出函数关系式,即可根据条件结构画出程序框图,并写出程序.【详解】过点A ,D 分别作AG ⊥BC ,DH ⊥BC ,垂足分别是G ,H .∵四边形ABCD 是等腰梯形,底角是45°,AB =2cm ,∴BG =AG =DH =HC =2 cm .又BC =7cm ,∴AD =GH =3cm ,当02x ≤≤时,212yx =; 当25x <≤时,22y x =-; 当57x <<时,21(7)102y x =-+, 所以221,02222,251(7)10,572x x y x x x x ⎧≤≤⎪⎪=-<≤⎨⎪⎪-+<<⎩ . 程序框图如下:程序:INPUT “x =”;xIF x >=0 AND x <=2 THENy =0.5 *x ^2ELSEIF x <=5 THENy =2*x -2ELSEy =-0.5*(x -7) ^2+10END IFEND IFPRINT yEND【点睛】本题主要考查分段函数解析式的求法、程序框图的画法以及程序语句的书写,意在考查学生分类讨论思想和算法语句的理解和书写.22.答案详见解析.【分析】分三步完成,先输入上下底和高,再计算面积S ,最后输出计算结果S.【详解】梯形面积S =12(上底+下底)×高, ∵梯形的两底边长分别为a ,b ,高为h ,∴程序算法如下:第一步:输入a ,b ,h 的值,第二步:计算S =()2a b h +, 第三步:输出S ,程序框图如下:【点睛】本题主要考查了算法及程序框图,属于中档题.23.(1)①m=0②i=i+1;(2)见解析【分析】(1)如果除以2的余数为零,则为偶数,故填0m =.i 每次增加1,故填1i i =+.(2)根据WHILE 型循环的结构,对原有程序进行改写.【详解】(1)①m=0②i=i+1(2)改写为WHILE 型循环程序如下:i=1WHILE i<=100m=I MOD 2IF m=0 THENPRINT iEND IFi=i+1WENDEND【点睛】本小题主要考查循环结构的两种编写程序的方法,属于基础题.24.见解析【分析】由条件可得函数为分段函数,这样就要进行判断,然后进行求解【详解】用变量x y ,分别表示自变量和函数值,步骤如下:第一步,输入x 的值第二步,判断x 的范围,若0x ≥,则用解析式21y x =-求函数值;否则,用225y x =-求函数值第三步,输出y 的值程序框图和程序如下.【点睛】本题考查的知识点是设计程序解决问题,由已知条件不难发现函数为分段函数,故需要进行对输入值的判定,然后再代入求解.25.见解析【解析】分析:挑最重的球需要把最重的一个球与其它都想比较,运用循环结构即可得出结果.详解:设六个小球的重量分别为ω1,ω2,…,ω6.算法如下:S1将1号球放在天平左边,2号球放在天平右边.S2比较两球的重量后,若两球一样重,则淘汰天平右边的球;若两球不一样重,则淘汰较轻的球,将较重的球放在天平左边.S3将下一号球放在天平右边比较重量,重复执行S2.S4最后留在天平左边的球是最重的球.程序框图如下图所示:点睛:本题的重点是掌握算法流程图书写的基本步骤,书写规范和方法,当需要解决的问题需要多次重复的相同的步骤时,实现算法需要通过循环结构来实现,在写算法和流程图时注意语言的表达要清晰,步骤要简洁完整.26.见解析【解析】试题分析:确定循环体为:S=S+i^2,i=i+10,再确定初始值和结束的条件即可试题程序如下:S=0;i=10;while i<=1000S=S+i^2;i=i+10;endprint(%io(2),S);程序框图如图所示:。
必修三第二章测试题

统计三一、选择题(题型注释)1.一名小学生的年龄和身高(单位:cm )的数据如下表:由散点图可知,身高y 与年龄x 之间的线性回归方程为8.8y x a =+,则a 的值为( )A .65B .74C .56D .472.设某中学的女生体重y (kg )与身高x (cm )具有线性相关关系,根据一组样本数(),i i x y ()1,2,3,,i n =,用最小二乘法建立的线性回归直线方程为ˆ0.8585.71yx =-,给出下列结论,则错误的是( ) A .y 与x 具有正的线性相关关系B .若该中学某女生身高增加1cm ,则其体重约增加0.85kgC .回归直线至少经过样本数据(),i i x y ()1,2,3,,i n =中的一个D .回归直线一定过样本点的中心点(,)x y3.为了解某商品销售量y (单位:件)与销售价格x (单位:元/件)的关系,统计了(,x y )的10组值,并画成散点图如图,则其回归方程可能是A .ˆ10198yx =-- B .ˆ10198yx =-+ C .ˆ10198yx =+ D .ˆ10198yx =- 4.下列判断中不正确的是( )A .r 为变量间的相关系数,r 值越大,线性相关程度越高B .在平面直角坐标系中,可以用散点图发现变量之间的变化规律C .线性回归方程代表了观测值x 、y 之间的关系D .任何一组观测值都能得到具有代表意义的回归直线方程5.已知呈线性相关关系的变量x ,y 之间的关系如下表所示,则回归直线一定过点( )A .()0.1,2.11B .()0.2,2.85C .()0.3,4.08D .()0.275,4.79756.(2015•烟台二模)某产品的广告费用x 与销售额y 的统计数据如下表:根据上表可得回归方程=x+a 中的b=10.6,据此模型预报广告费用为10万广告费用x (万元)4 2 35 销售额y (万元) 49 26 39 58 万元7.对于下列表格所示的五个散点,已知求得的线性回归直线方程为y =0.8x x 196 197 200 203 204 y 1 3 6 7 m 则实数m 的值为( )A .8.4B .8.2C .8D .8.5 8.对变量x ,y 观测数据11(,)(1,2,,10)x y i =,得散点图1;对变量u ,v 有观测数据11(,)(1,2,,10)u v i =⋅⋅⋅,得散点图2.由这两个散点图可以判断( )A .变量x 与y 正相关,u 与v 正相关B .变量x 与y 正相关,u 与v 负相关C .变量x 与y 负相关,u 与v 正相关D .变量x 与y 负相关,u 与v 负相关9.已知某种产品的支出广告额x 与利润额y (单位:万元)之间有如下对应数据:则回归直线方程必过( )A .()5,36B .()5,35C .()5,30D .()4,3010.下列反映两个变量的相关关系中,不同于其它三个的是A .名师出高徒B .水涨船高C .月明星稀D .登高望远 11.下面是两个变量的一组数据: X 1 2 3 4 5 6 7 8 y 1 4 9 16 25 36 49 64则这两个变量之间的线性回归方程是( )A .y=-16+9xB .y=31-xC .y=30-xD .y=-15+9x12.在下列各图中,两个变量具有线性相关关系的图是( )A .(1)(2)B .(1)(3)C .(2)(4)D .(2)(3) 13.下面哪些变量是相关关系( )A .出租车费与行驶的里程B .房屋面积与房屋价格C .身高与体重D .铁的大小与质量 14.已知,x y 的取值如下表所示:x 2 3 4 y6 4 5如果y 与x 呈线性相关,且线性回归方程为ˆ2ybx =+,则b = . 15.根据如图样本数据得到的回归方程为=bx+a ,若样本点的中心为(5,0.9).则当x 每增加1个单位时,y 就( )A .增加1.4个单位B .减少1.4个单位C .增加7.9个单位D .减少7.9个单位16.如图所示,图中有5组数据,去掉 组数据后(填字母代号),剩下的4组数据的线性相关性最大( )A.E B.C C.D D.A17.为了考察两个变量x 和y 之间的线性相关性,甲、乙两同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为1t 和2t ,已知两个人在试验中发现对变量x 的观测值的平均值都是s ,对变量y 的观测值的平均值都是t ,那么下列说法正确的是() A .1t 和2t 有交点(),s tB .1t 和2t 相交,但交点不是(),s tC .1t 和2t 必定重合D .1t 和2t 必定不重合18.四名同学根据各自的样本数据研究变量,x y 之间的相关关系,并求得回归直线方程,分别得到以下四个结论: ①y 与x 负相关且 2.347 6.423y x ∧=-; ②y 与x 负相关且 3.476 5.648y x ∧=-+; ③y 与x 正相关且 5.4378.493y x ∧=+; ④y 与x 正相关且 4.326 4.578y x ∧=--.其中一定不正确的结论的序号是()A .①②B .②③C .③④D .①④二、填空题(题型注释)^20.下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是 .(将所有正确的序号填上) 21.下列说法:①从匀速传递的产品生产流水线上,质检员第10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样②某地气象局预报:5月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 ④在回归直线方程0.110y x =+中,当解释变量x 每增加一个单位时,预报变量平均增加0.1个单位其中正确的是 (填上你认为正确的序号)22.某商场在销售过程中投入的销售成本x 与销售额y 的统计数据如下表:根据上表可得,该数据符合线性回归方程:9y bx =-.由此预测销售额为100万元时,投入的销售成本大约为 ;23.下表为某公司员工连续加班时间与制造产品的几组数据,根据表中提供的数据,求出y 关于x 的线性回归方程为ˆ0.70.35yx =+,则表中t 的值25.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是________________.26.小华的妈妈经营一家饮品店,经常为进货数量而烦恼,于是小华代妈妈进行统计,其中某种饮料的日销售量y (瓶)与当天的气温x (℃)的几组对照数据根据上表得回归方程y bx a =+中的48a =,据此模型估计当气温为35℃时,该饮料的日销售量为 瓶.27.高三某学生高考成绩y (分)与高三期间有效复习时间x (天)正相关,且回归方程是503ˆ+=x y,若期望他高考达到560分,那么他的有效复习时间应不低于______天.三、解答题(题型注释)28.某种产品的广告费用支出x (百万)与销售额y (百万)之间有如下的对应数(2)求回归直线方程;(3)据此估计广告费用为10(百万)时,销售收入y 的值.29.下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量y(吨标准煤)的几组对应数据. (1)求线性回归方程a x b y+=ˆ所表示的直线必经过的点; (2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程a xb y+=ˆ; 并预测生产1000吨甲产品的生产能耗多少吨标准煤?(参考:1221,ni ii nii x y nx yb a y bx xnx==-==--∑∑)30.某城市理论预测2000年到2004年人口总数与年份的关系如下表所示(1)请画出上表数据的散点图;(2)请根据上表提供的数据,求最小二乘法求出y 关于x 的线性回归方程y=bx+a ;(3) 据此估计2012年.该 城市人口总数.(参考数值:0×5+1×7+2×8+3×11+4×19=132,222220123430++++=,公式见卷首)参考答案1.A 【解析】 试题分析:67897.54x +++==,1181261361441314y +++==,所以样本中心点为()7.5,131,将样本中心点()7.5,131代入回归方程8.8y x a =+可得1318.87.5a =⨯+,解得65a =.故A 正确.考点:线性回归方程. 2.C 【解析】试题分析:085.0>=k ,所以y 与x 具有正的线性相关关系,该中学某女生身高增加1cm ,则其体重约增加0.85kg ,回归直线一定过样本点的中心点(,)x y ,回归直线有可能不经过样本数据,故选C . 考点:回归直线方程 3.B 【解析】试题分析:由散点图可知负相关,回归方程x 的系数为负,方程在y 轴上的截距为正,因此B 正确 考点:散点图 4.D 【解析】试题分析:A 项正确,r 为变量间的相关系数,r 值越大,线性相关程度越高,相反则线性相关程度越低;B 项正确,因为变量都是围绕着某一中心变化,所以可以用散点图发现变量之间的变化规律;C 项中,因为变量始终在线性回归方程附近,所以线性回归方程表示的就是观测值x 、y 之间的关系;D 项中,回归直线方程指在一组具有相关关系的变量的数据(),x y 间,一条最好地反映x 与y 之间的关系直线,所以并不是任何一组观测值都能得到又代表意义的回归直线方程.考点:变量的相关性以及回归直线方程. 5.D 【解析】试题分析:回归直线恒过样本的中心点),(y x ,由样本可求得0.275, 4.7975x y ==,所以回归直线恒过点()0.275,4.7975.考点:回归直线. 6.C 【解析】试题分析:求出所给数据的平均数,得到样本中心点,根据线性回归直线过样本中心点,求出方程中的一个系数,得到线性回归方程,把自变量为10代入,预报出结果. 解:∵==3.5,==43,∵数据的样本中心点在线性回归直线上,=x+a 中的b=10.6,∴43=10.6×3.5+a, ∴a=5.9,∴线性回归方程是y=10.6x+5.9,∴广告费用为10万元时销售额为10.6×10+5.9=111.9万元, 故选:C .考点:线性回归方程. 7.C 【解析】 试题分析:由题意可知196197200203204136717200,555m m x y +++++++++====,所以中心点为17200,5m +⎛⎫ ⎪⎝⎭,代入回归方程成立,8m ∴=考点:回归方程8.C 【解析】试题分析:由题图1可知,y 随x 的增大而减小,各点整体呈下降趋势,x 与y 负相关,由题图2可知,u 随v 的增大而增大,各点整体呈上升趋势,u 与v 正相关 考点:散点图 9.A 【解析】试题分析:因为3456755x ++++==,2030304060365y ++++==,所以回归直线方程必过(5,36),故选A .考点:回归直线方程.10.C 【解析】试题分析:对于A ,名师出高徒是正相关;对于B ,水涨船高是正相关;对于C ,月明星稀是负相关;对于D ,登高望远是正相关,故答案为C . 考点:变量间的相关关系. 11.D【解析】试题分析:由表格数据可知线性正相关,因此x 系数为正,128149644.5,25.588x y +++++++====,代入回归方程可知y=-15+9x 成立考点:回归方程 12.D 【解析】 试题分析:(2)中两变量线性正相关,(3)中两变量线性负相关 考点:变量线性相关问题 13.C 【解析】试题分析:答案ABD 中两个变量之间是一个确定的函数关系,只有答案C 中的关系是 相关关系。
(经典)高中数学必修三单元测试题附答案解析

(数学3必修)第二章:统计 [基础训练A 组] 一、选择题1.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ,则有( )A . c b a >>B .a c b >>C .b a c >>D .a b c >>2.下列说法错误的是 ( )A .在统计里,把所需考察对象的全体叫作总体B .一组数据的平均数一定大于这组数据中的每个数据C .平均数、众数与中位数从不同的角度描述了一组数据的集中趋势D .一组数据的方差越大,说明这组数据的波动越大3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( ) A .3.5 B .3- C .3 D .5.0- 4. 要了解全市高一学生身高在某一范围的学生所占比例的大小,需知道相应样本的( )A . 平均数B . 方差C . 众数D . 频率分布5.要从已编号(160)的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是( )A .5,10,15,20,25,30B .3,13,23,33,43,53C .1,2,3,4,5,6D .2,4,8,16,32,48 6.容量为100的样本数据,按从小到大的顺序分为8组,如下表:组号 1 2 3 4 5 6 7 8 频数 10 13 x 14 15 13 12 9第三组的频数和频率分别是 ( )A .14和0.14B .0.14和14C .141和0.14 D . 31和141二、填空题1.为了了解参加运动会的2000名运动员的年龄情况,从中抽取100名运动员;就这个问题,下列说法中正确的有 ;① 2000名运动员是总体;②每个运动员是个体;③所抽取的100名运动员是一个样本;④样本容量为100;⑤这个抽样方法可采用按年龄进行分层抽样;⑥每个运动员被抽到的概率相等。
必修3第2章试题及答案

必修3第2章试题及答案一、选择题1. 下列关于必修3第2章内容的描述,哪一项是不正确的?A. 该章节主要介绍了基础概念B. 该章节详细阐述了理论应用C. 该章节包含了大量的实践案例D. 该章节内容与必修1的知识点完全无关2. 根据必修3第2章的理论,以下哪个选项是正确的实践方法?A. 忽略理论直接进行实践B. 先理解理论再进行实践C. 只依赖经验进行实践D. 理论与实践无关,可以独立进行3. 在必修3第2章中,哪个概念是整个章节的核心?A. 基础概念B. 理论应用C. 实践案例D. 知识点关联4. 必修3第2章中提到的“X理论”主要用于解决什么问题?A. 实践操作问题B. 理论理解问题C. 知识点记忆问题D. 综合应用问题二、填空题5. 必修3第2章中提到的“Y理论”强调了________的重要性。
6. 在解决实际问题时,我们需要将________与________相结合。
7. 必修3第2章中,通过________案例,展示了理论的实际应用。
8. “Z理论”是必修3第2章中的一个关键概念,它与________紧密相关。
三、简答题9. 简述必修3第2章中提到的“基础概念”的作用。
10. 描述必修3第2章中“理论应用”的具体步骤。
四、论述题11. 根据必修3第2章的内容,论述如何将理论与实践相结合以提高解决问题的效率。
五、答案1. 答案:D2. 答案:B3. 答案:A4. 答案:D5. 答案:理论联系实际6. 答案:理论与实践7. 答案:具体案例分析8. 答案:实际操作技巧9. 答案:基础概念在必修3第2章中的作用是为理解和应用更复杂的理论打下坚实的基础,帮助学生建立起对学科的基本认识。
10. 答案:必修3第2章中“理论应用”的步骤包括:首先理解理论的基本原理,然后通过案例分析将理论应用到实际问题中,最后通过实践检验理论的有效性并进行调整。
11. 答案:要将理论与实践相结合提高解决问题的效率,首先需要深入理解理论的内涵和应用范围。
必修三第二单元练习题

必修三第二单元练习题一、选择题A. 力是改变物体运动状态的原因B. 物体在没有外力作用下保持静止或匀速直线运动C. 作用力和反作用力大小相等,方向相反D. 物体间的相互作用力与其距离的平方成反比A. 在只有重力做功的情况下,物体的机械能守恒B. 在只有弹力做功的情况下,物体的机械能守恒C. 在所有外力做功的情况下,物体的机械能守恒D. 在没有外力做功的情况下,物体的机械能守恒A. 镜子中的倒影B. 水中的鱼看起来比实际位置浅C. 太阳光通过三棱镜形成彩虹D. 月亮在水中形成的倒影二、填空题1. 动能的大小与物体的质量和______有关。
2. 重力势能的大小与物体的质量和______有关。
3. 在自由落体运动中,物体的加速度为______。
三、简答题1. 请简要说明摩擦力的分类及其产生原因。
2. 简述影响压强的因素。
3. 如何区分扩散现象和布朗运动?四、计算题1. 一辆质量为2吨的汽车以20m/s的速度行驶,求其动能。
2. 一物体从10m高空自由落体,不考虑空气阻力,求落地时的速度。
3. 一物体在水平面上受到10N的力作用,沿力的方向移动了5m,求该力所做的功。
五、实验题1. 设计一个实验,验证牛顿第二定律。
2. 如何利用实验方法测量物体的密度?3. 请描述一个实验,观察光的反射现象。
六、作图题1. 请画出力的合成与分解的示意图,并标明力的方向和大小。
2. 画出物体在斜面上受到的各个力的分解图,包括重力、支持力和摩擦力。
3. 绘制一个完整的反射光路图,包括入射光线、反射光线和法线。
七、应用题1. 一名学生用20N的力将一个物体沿水平桌面推动,已知物体与桌面间的摩擦力为5N,求物体的加速度。
2. 一质量为m的物体从高度h自由下落,求物体落地前0.1s内的位移。
3. 一辆汽车以恒定功率P行驶,行驶过程中速度从v1增加到v2,求汽车行驶的距离。
八、综合题1. 结合实际生活,举例说明杠杆原理在日常生活中的应用。
教科版高中物理必修第三册课后习题 第二章 电路及其应用 第二章测评

第二章测评(时间:75分钟满分:100分)一、单项选择题(本题共7小题,每小题4分,共28分。
在每小题给出的四个选项中,只有一个选项符合题目要求)1.(陕西汉中期中)一段粗细均匀的金属导体两端加一定电压后产生了恒定电流。
已知该导体单位体积内的自由电子数为n,电子的电荷量为e,自由电子定向移动的速率为v,要想得出通过导体的电流,除以上给出的条件外,还需要以下哪个条件( )A.导体的长度LB.导体的电阻RC.导体的横截面积SD.导体两端的电压U2.(江苏宿迁期末)如图所示,将灯泡的灯丝与小灯泡串联接入电路,闭合开关使小灯泡发光。
用酒精灯给灯丝加热,下列说法正确的是( )A.小灯泡变暗,灯丝电阻率变大B.小灯泡变暗,灯丝电阻率变小C.小灯泡变亮,灯丝电阻率变大D.小灯泡变亮,灯丝电阻率变小3.(浙江绍兴柯桥模拟)高压线是非常危险的远距离输电线,但是我们也经常会看到许多鸟儿双脚站上面却相安无事。
小蒋为了弄清其中的道理特别查阅了当地的一组数据:高压线输送电功率P=6.4×104kW,输送电压为22万伏,导线所用的是LGJ型钢芯铝绞线,其横截面积是95 mm2,其电阻率ρ=3.0×10-8Ω·m,则一只小鸟双脚停留在高压线上时承受的电压大小为( )A.2.0 VB.2.0×10-1 VC.2.0×10-3 VD.2.0×10-5 V4.(湖南岳阳平江月考)一电动机如图所示,其线圈电阻是r,当它两端所加的电压为U时,通过的电流是I,则这台电动机( )A.发热功率为I2rB.消耗的电功率为UI-I 2rC.所做机械功的功率为UID.t 时间内所做的机械功为U 2r t 5.(四川内江开学)电源的效率定义为外电路电阻消耗的功率与电源的总功率之比。
直线A 、B 和C 分别是电源a 、电源b 和电阻R 的伏安特性图线。
将这个电阻R 分别接到a 、b 两电源上,那么( )A.电源a 、b 电动势一样大,b 内阻较大B.R 接到电源a 上,电路中的电流较小C.R 接到电源b 上,电源的输出功率较大D.R 接到电源b 上,电源效率较高6.在温控电路中,通过热敏电阻阻值随温度的变化可实现对电路相关物理量的控制。
教科版高中物理必修第三册课后习题 第二章 第二章测评

第二章测评(时间:60分钟满分:100分)一、选择题(本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,第1~5题只有一项符合题目要求,第6~8题有多项符合题目要求。
全部选对的得5分,选对但不全的得3分,有选错的得0分)1.两个小灯泡,分别标有“1 A 4 W”和“2 A 1 W”的字样,则它们均正常发光时的电阻阻值之比为( )A.2∶1B.16∶1C.4∶1D.1∶16P=I2R知R=PI2,所以R1∶R2=41∶14=16∶1。
2.在正常照射下,太阳能电池的光电转换效率可达23%。
单片单晶硅太阳能电池可产生0.6 V的电动势,可获得0.1 A的电流,则每秒照射到这种太阳能电池上的太阳光的能量是( )A.0.24 JB.0.25 JC.0.26 JD.0.28 JW=UIt可得每秒太阳能电池产生的能量为W=0.6×0.1×1J=0.06J,设太阳能每秒照射的能量为Q,则由能量守恒定律得Q×23%=W,所以Q=0.26J。
3.如图所示,电池电动势为E,内阻为r。
当可变电阻的滑片P向b点移动时,电压表V1的读数U1与电压表V2的读数U2的变化情况是( )A.U1变大,U2变小B.U1变大,U2变大C.U1变小,U2变小D.U1变小,U2变大变小。
由于路端电压P向b移动时,总电阻变大,干路中I=ER+rU=E-Ir,U增大,即V1表示数U1变大。
由于V2表示数U2=IR,U2减小,所以A 正确。
4.导体中电流I的表达式I=nqSv,其中S为导体的横截面积,n为导体每单位体积内的自由电荷数,q为每个自由电荷所带的电荷量,v是( )A.导体运动的速率B.导体传导的速率C.电子热运动的速率D.自由电荷定向移动的速率,电流决定于导体中单位体积内的自由电荷数、每个自由电荷的电荷量、定向移动速率,还与导体的横截面积有关,公式I=nqSv中的v就是自由电荷定向移动的速率。
教科版高中物理必修第三册课后习题 第二章 第二章测评(B)

第二章测评(B)(时间:60分钟满分:100分)一、选择题(本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,第1~5题只有一项符合题目要求,第6~8题有多项符合题目要求。
全部选对的得5分,选对但不全的得3分,有选错的得0分)1.下列关于电源电动势的说法,正确的是( )A.在某电池的电路中,每通过2 C的电荷量,电池提供的电能是4 J,那么这个电池的电动势是0.5 VB.电源的路端电压增大时,其电源的电动势一定也增大C.无论内电压和外电压如何变化,其电源的电动势一定不变D.电源的电动势越大,电源所能提供的电能就越多得E=2V,选项A错误;电源的电动势与外电,由E=Wq路无关,只由电源自身的性质决定,选项B错误,选项C正确;电源的电动势大,所提供的能量不一定大,电源提供的电能等于通过电源的电荷量与电动势之积,选项D错误。
2.两个用同种材料制成的均匀导体A、B,其质量相同,当它们接入电压相同的电路时,其电流之比I A∶I B=1∶4,则横截面积之比S A∶S B为( )A.1∶2B.2∶1C.1∶4D.4∶1R=UI可知,在U一定时,I与R成反比,即R A∶R B=4∶1。
又根据电阻定律R=ρlS =ρVSS=ρVS2可知,当ρ、V一定时,R∝1S2,即有S A2S B2=R B R A =14,所以S AS B=√14=12。
3.如图所示,电源A的电压为6 V,电源B的电压为8 V,电容器的电容为200 pF,当开关S合向A,稳定后再合向B,再次达到稳定,则在这个过程中通过电流计的电荷量为( )A.4×10-9 CB.1.2×10-9 CC.1.6×10-9 CD.2.8×10-9 CS打在A时,电容器的电压为U1=6V,电荷量为Q1=CU1=2×10-10×6C=1.2×10-9C。
开关S打在B时,稳定时,电容器的电压为U2=8V,电荷量为Q2=CU2=2×10-10×8C=1.6×10-9C。
北师大版高中数学必修三第二章过关测试卷(.docx

第二章过关测试卷(100分,45分钟)一、选择题(每题5分,共30分)1.〈北京期末考〉如果输入2,那么执行下面算法的结果是()第一步:输入n第二步:n=n+1第三步:n=n+1第四步:输出nA.输出2 B.输出3C.输出4 D.程序出错,输不出任何结果2.〈福州模拟〉执行如图1所示的程序框图后,若输出结果为-1,则输入x的值不可能是()A.2 B.1 C.-1 D.-2图1 图23.〈茂名二模〉某银行开发出一套网银验证程序,验证规则如下:(1)有两组数,这两组数存在一种对应关系:第一组数a,b,c对应第二组数2a+b,c+2b,a+3c;(2)进行验证时程序在电脑屏幕上依次显示出第二组数,由用户计算出第一组数后依次输入电脑,只有准确输入方能进入,其流程图如图2,试问用户应输入()A.3,4,5 B.4,2,6 C.2,6,4 D.3,5,7 4.〈密云一模〉如图3是关于闰年的流程图,则以下年份是闰年的为()图3A.2012年B.2010年C.2100年D.1998年5.阅读下面两个算法:算法一:算法二:i=0 S=0S=0 For i=1 To 20Do S=S+1iS=S+1Next1ii=i+1 输出SLoop While i<20输出S以上两个算法()A.程序相同,结果相同B.程序不同,结果相同C.程序相同,结果不同D.程序不同,结果不同6.已知某程序框图如图4,则该程序运行后,输出的结果为()A.35B.45C.12D. 15图4 图5二、填空题(每题5分,共20分)7.〈浙江期末考〉为了在运行下面的程序之后输出25,键盘输入的x 的值应该是.If x<0 Theny=(x+1)*(x+1)Elsey=(x-1)*(x-1)End If输出y8.〈广东模拟〉利用如图5所示的算法在平面直角坐标系上打印一系列点,则打印的点既满足y-x-4>0,又在直线y=4.5的下方的有个.9.〈福建,有改动〉阅读如图6所示的程序框图,运行相应的程序.如果输入某个正整数n后,输出的S∈(10,20),那么n的值为.图6 图710.〈广东文〉某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:队员i 1 2 3 4 5 6三分球个数a1a2a3a4a5a6如图7所示的是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图7中判断框中应填,输出的s= .三、解答题(13题18分,其余每题16分,共50分)11. 甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图8和如图9.图8 图9(1)根据图8和图9,试判断甲、乙两位同学编写的程序框图输出的结果是否一致,当n=20时分别求它们输出的结果;(2)若希望通过对图9虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的程序框图.12.〈海南中学期末考〉数学的美是令人惊异的!如三位数153,它满足153=13+53+33,即这个整数等于它各位上的数字的立方的和,我们称这样的数为“水仙花数”.请您设计一个算法,找出大于100,小于1 000的所有“水仙花数”.(1)用自然语言写出算法;(2)画出流程图.13.某汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当每辆销售价为图10的输出结果p万元时,平均每周能售出8辆,而当每辆销售价每降低1万元时,平均每周能多售出8辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)图10 (1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x 的取值范围;(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?参考答案及点拨一、1. C 点拨:第一步:输入n=2;第二步:n=2+1=3;第三步:n=3+1=4;第四步:输出4.故答案为C.2. D 点拨:利用代入法求解.输入2,执行y=-1,输出-1;输入1,执行y=-1,输出-1;输入-1,执行y=(-1)3,输出-1;输入-2,执行y=(-2)3,输出-8.故选D.3. A 学科思想:利用方程思想求解,通过输入值与输出值的关系,建立方程组求解.解方程组:210,213,318,a bc ba c+=+=+=⎧⎪⎨⎪⎩得3,4,5abc===⎧⎪⎨⎪⎩. 用户应输入:3,4,5,故选A.4.A 点拨:由流程图可知:要判断输入的代表年份的y是否为闰年,则要判断y能否被4整除但不能被100整除,或者能否被400整除.5. B6. D 点拨:该程序在运行过程中各变量的值如下:A=0.2;n=1,第一次循环:A=0.4,n=2; 第二次循环:A=0.8,n=3; 第三次循环:A=0.6,n=4; 第四次循环:A=0.2,n=5;第五次循环:A=0.4,n=6,因此输出结果的周期为4.又2 013=4×503+1,因此输出结果为0.2.二、7. 6或-6 学科思想:利用化归转化思想,将条件语句转化为分段函数问题,再利用分类讨论思想、方程思想求解.因为输出y=25,由25=(x+1)2,x<0,可得x=-6;由25=(x-1)2,x≥0,可得x=6,故x=6或-6.8.1 学科思想:根据算法框图的功能,写出各点坐标,然后在平面直角坐标系上,描绘出直线与各点的位置,根据数形结合思想求解.根据算法框图所示的顺序,该程序的作用是打印如下点:(-3,6),(-2,5),(-1,4),(0,3),(1,2),其中点(-3,6),(-2,5),(-1,4)满足y-x-4>0,点(-1,4),(0,3),(1,2)在直线y=4.5的下方,即只有点(-1,4)既满足y-x-4>0,又在直线y=4.5的下方.故答案为:1.9. 4 点拨: S=0,k=1, 第一次循环:S=1,k=2,第二次循环:S =3,k=3,第三次循环:S=7,k=4,第四次循环:S=15,k=5>4,故n的值为4.10.i≤6;a1+a2+…+a6.三、11. 解:(1)甲、乙两位同学编写的程序框图输出的结果是一致的.题图8中程序框图的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.题图9中程序框图的功能是求2+4+6+…+2n的和,当n=20时,S=2+4+6+…+40=420.(2)修改后虚框部分的程序框图如答图1.答图112. 解:(1)算法如下:第一步:i=101;第二步:若i不大于999,则执行第三步,否则算法结束;第三步:若这个数i等于它各位上的数字的立方的和,则输出这个数; 第四步:i=i+1,返回第二步.(2)如答图2.答图213. 解:(1)由程序框图知,p=29,故当每辆销售价为程序框图的输出结果p万元时,平均每周能售出8辆,则y=29-x-25=-x+4(0≤x≤4).(2)由于当每辆销售价每降低1万元时,平均每周能多售出8辆,故每辆汽车降价x万元时,平均第周销售量为(8+8x)辆,故z=y(8+8x)=8(-x+4)(1+x)=-8x2+24x+32.(3)∵z=-8x2+24x+32=-8(x-1.5)2+50(0≤x≤4),∴当x=1.5时,平均每周的销售利润最大,此时29-x=27.5,即当每辆汽车的定价为27.5万元时.平均每周的销售利润最大,最大利润为50万元.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计三一、选择题(题型注释)1.一名小学生的年龄和身高(单位:cm)的数据如下表:由散点图可知,身高y与年龄x之间的线性回归方程为8.8=+,则a的y x a值为()A.65 B.74 C.56 D.472.设某中学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数(),i i=,用最小二乘法建立的线性回归直线方程i nx y()1,2,3,,为ˆ0.8585.71=-,给出下列结论,则错误的是()y xA.y与x具有正的线性相关关系B.若该中学某女生身高增加1cm,则其体重约增加0.85kgC.回归直线至少经过样本数据(),i i=中的一个i nx y()1,2,3,,D.回归直线一定过样本点的中心点(,)x y3.为了解某商品销售量y(单位:件)与销售价格x(单位:元/件)的关系,统计了(,x y)的10组值,并画成散点图如图,则其回归方程可能是A.ˆ10198=--y xB.ˆ10198=-+y xC.ˆ10198y x=+D.ˆ10198y x=-4.下列判断中不正确的是()A.r为变量间的相关系数,r值越大,线性相关程度越高B.在平面直角坐标系中,可以用散点图发现变量之间的变化规律C.线性回归方程代表了观测值x、y之间的关系D.任何一组观测值都能得到具有代表意义的回归直线方程5.已知呈线性相关关系的变量x,y之间的关系如下表所示,则回归直线一定过点()A .()0.1,2.11B.()0.2,2.85C.()0.3,4.08D.()0.275,4.79756.(2015•烟台二模)某产品的广告费用x与销售额y的统计数据如下表:根据上表可得回归方程=x+a中的b=10.6,据此模型预报广告费用为10万元时销售额为()广告费用x(万元)4235销售额y(万元)49263958A.112.1万元B.113.1万元C.111.9万元D.113.9万元7.对于下列表格所示的五个散点,已知求得的线性回归直线方程为y=0.8x -155.x 196 197 200 203 204 y 1367m则实数m 的值为( )A .8.4B .8.2C .8D .8.5 8.对变量x ,y 观测数据11(,)(1,2,,10)x y i =,得散点图1;对变量u ,v 有观测数据11(,)(1,2,,10)u v i =⋅⋅⋅,得散点图2.由这两个散点图可以判断( )A .变量x 与y 正相关,u 与v 正相关B .变量x 与y 正相关,u 与v 负相关C .变量x 与y 负相关,u 与v 正相关D .变量x 与y 负相关,u 与v 负相关9.已知某种产品的支出广告额x 与利润额y (单位:万元)之间有如下对应数据:则回归直线方程必过( )A .()5,36B .()5,35C .()5,30D .()4,30 10.下列反映两个变量的相关关系中,不同于其它三个的是A .名师出高徒B .水涨船高C .月明星稀D .登高望远 11.下面是两个变量的一组数据:y 1 4 9 16 25 36 49 64则这两个变量之间的线性回归方程是( )A .y=-16+9xB .y=31-xC .y=30-xD .y=-15+9x12.在下列各图中,两个变量具有线性相关关系的图是( )A .(1)(2)B .(1)(3)C .(2)(4)D .(2)(3) 13.下面哪些变量是相关关系( )A .出租车费与行驶的里程B .房屋面积与房屋价格C .身高与体重D .铁的大小与质量 14.已知,x y 的取值如下表所示:x2 3 4 y645如果y 与x 呈线性相关,且线性回归方程为ˆ2ybx =+,则b = . 15.根据如图样本数据得到的回归方程为=bx+a ,若样本点的中心为(5,0.9).则当x 每增加1个单位时,y 就( )A .增加1.4个单位B .减少1.4个单位C .增加7.9个单位D .减少7.9个单位16.如图所示,图中有5组数据,去掉 组数据后(填字母代号),剩下的4组数据的线性相关性最大( )A.E B.C C.D D.A17.为了考察两个变量x 和y 之间的线性相关性,甲、乙两同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为1t 和2t ,已知两个人在试验中发现对变量x 的观测值的平均值都是s ,对变量y 的观测值的平均值都是t ,那么下列说法正确的是() A .1t 和2t 有交点(),s tB .1t 和2t 相交,但交点不是(),s tC .1t 和2t 必定重合D .1t 和2t 必定不重合18.四名同学根据各自的样本数据研究变量,x y 之间的相关关系,并求得回归直线方程,分别得到以下四个结论: ①y 与x 负相关且 2.347 6.423y x ∧=-; ②y 与x 负相关且 3.476 5.648y x ∧=-+; ③y 与x 正相关且 5.4378.493y x ∧=+; ④y 与x 正相关且 4.326 4.578y x ∧=--. 其中一定不正确的结论的序号是()A .①②B .②③C .③④D .①④二、填空题(题型注释)19.已知回归方程为^y =0.4x-0.8,则当x= 20时,y 的估计值为 20.下列结论:①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.其中正确的是 .(将所有正确的序号填上) 21.下列说法:①从匀速传递的产品生产流水线上,质检员第10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样②某地气象局预报:5月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 ④在回归直线方程0.110y x =+中,当解释变量x 每增加一个单位时,预报变量平均增加0.1个单位其中正确的是 (填上你认为正确的序号)22.某商场在销售过程中投入的销售成本x 与销售额y 的统计数据如下表:根据上表可得,该数据符合线性回归方程:9y bx =-.由此预测销售额为100万元时,投入的销售成本大约为 ;23.下表为某公司员工连续加班时间与制造产品的几组数据,根据表中提供的数据,求出y 关于x 的线性回归方程为ˆ0.70.35yx =+,则表中t 的值为 .24.已知x 与y 之间的一组数据:则y 与x 的线性回归方程为y=bx+a 必过点__________________________. 25.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是________________.26.小华的妈妈经营一家饮品店,经常为进货数量而烦恼,于是小华 代妈妈进行统计,其中某种饮料的日销售量y (瓶)与当天的气温x (℃)的几组对照数据 如下:根据上表得回归方程y bx a =+中的48a =,据此模型估计当气温为35℃时,该饮料的日销售量为 瓶.27.高三某学生高考成绩y (分)与高三期间有效复习时间x (天)正相关,且回归方程是503ˆ+=x y ,若期望他高考达到560分,那么他的有效复习时间应不低于______天.三、解答题(题型注释)28.某种产品的广告费用支出x (百万)与销售额y (百万)之间有如下的对应数据:(1)画出散点图; (2)求回归直线方程;(3)据此估计广告费用为10(百万)时,销售收入y 的值.29.下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量x (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.(1)求线性回归方程a x b y+=ˆ所表示的直线必经过的点; (2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程a xb y+=ˆ; 并预测生产1000吨甲产品的生产能耗多少吨标准煤?(参考:1221,ni ii nii x y nx yb a y bx xnx==-==--∑∑)30.某城市理论预测2000年到2004年人口总数与年份的关系如下表所示 (1)请画出上表数据的散点图;(2)请根据上表提供的数据,求最小二乘法求出y 关于x 的线性回归方程y=bx+a ;(3) 据此估计2012年.该 城市人口总数.(参考数值:0×5+1×7+2×8+3×11+4×19=132,222220123430++++=,公式见卷首)参考答案1.A 【解析】试题分析:67897.54x +++==,1181261361441314y +++==,所以样本中心点为()7.5,131,将样本中心点()7.5,131代入回归方程8.8y x a =+可得1318.87.5a =⨯+,解得65a =.故A 正确. 考点:线性回归方程. 2.C 【解析】试题分析:085.0>=k ,所以y 与x 具有正的线性相关关系,该中学某女生身高增加1cm ,则其体重约增加0.85kg ,回归直线一定过样本点的中心点(,)x y ,回归直线有可能不经过样本数据,故选C . 考点:回归直线方程 3.B 【解析】试题分析:由散点图可知负相关,回归方程x 的系数为负,方程在y 轴上的截距为正,因此B 正确 考点:散点图 4.D 【解析】试题分析:A 项正确,r 为变量间的相关系数,r 值越大,线性相关程度越高,相反则线性相关程度越低;B项正确,因为变量都是围绕着某一中心变化,所以可以用散点图发现变量之间的变化规律;C项中,因为变量始终在线性回归方程附近,所以线性回归方程表示的就是观测值x、y之间的关系;D项中,回归直线方程指在一组具有相关关系的变量的数据(),x y间,一条最好地反映x与y之间的关系直线,所以并不是任何一组观测值都能得到又代表意义的回归直线方程.考点:变量的相关性以及回归直线方程.5.D【解析】试题分析:回归直线恒过样本的中心点)x,由样本可求得,(y0.275,4.7975.==,所以回归直线恒过点()x y0.275, 4.7975考点:回归直线.6.C【解析】试题分析:求出所给数据的平均数,得到样本中心点,根据线性回归直线过样本中心点,求出方程中的一个系数,得到线性回归方程,把自变量为10代入,预报出结果.解:∵==3.5,==43,∵数据的样本中心点在线性回归直线上,=x+a中的b=10.6,∴43=10.6×3.5+a,∴a=5.9,∴线性回归方程是y=10.6x+5.9,∴广告费用为10万元时销售额为10.6×10+5.9=111.9万元,故选:C .考点:线性回归方程.7.C【解析】试题分析:由题意可知196197200203204136717200,555m m x y +++++++++====,所以中心点为17200,5m +⎛⎫ ⎪⎝⎭,代入回归方程成立,8m ∴= 考点:回归方程8.C【解析】试题分析:由题图1可知,y 随x 的增大而减小,各点整体呈下降趋势,x 与y 负相关,由题图2可知,u 随v 的增大而增大,各点整体呈上升趋势,u 与v 正相关 考点:散点图9.A【解析】 试题分析:因为3456755x ++++==,2030304060365y ++++==,所以回归直线方程必过(5,36),故选A .考点:回归直线方程.10.C【解析】试题分析:对于A ,名师出高徒是正相关;对于B ,水涨船高是正相关;对于C ,月明星稀是负相关;对于D ,登高望远是正相关,故答案为C .考点:变量间的相关关系.11.D【解析】试题分析:由表格数据可知线性正相关,因此x 系数为正,128149644.5,25.588x y +++++++====,代入回归方程可知y=-15+9x 成立考点:回归方程12.D【解析】试题分析:(2)中两变量线性正相关,(3)中两变量线性负相关考点:变量线性相关问题 13.C【解析】试题分析:答案ABD 中两个变量之间是一个确定的函数关系,只有答案C 中的关系是 相关关系。
