高等传热学非稳态导热理论2
传热学第四章非稳态导热1125

2 sin( n ) ( x, ) x a 2 cos( n ) exp( 2 n ) 0 n 1 n sin n cos n
Fo a 2
傅里叶准则
2 2 单位时间通过 面积厚为的导热量 2 Fo a 3 c 单位时间体积为 3的内能变化
(b) (c)
边界条件(3)代入(b) 得
将 右端整理成:
y h
tg ( )
h
h 1
Bi
注意,这里Bi数的尺度为 平板厚度的一半。 显然,β是两曲线交点 对应的所有值。式(c) 称为特征方程。 β称 为特征值。分别为β1、 β2…… βn。
至此,我们获得了无穷个特解:
( x, ) 2 sin 1 x cos( 1 ) e 0 1 sin 1 cos 1
2 1 F0
(0, ) m ( ) 2 sin 1 e 0 0 1 sin 1 cos 1
2 1 F0
( x, ) 2 sin 1 x F cos( 1 ) e 0 1 sin 1 cos 1
以上两式的通解为:
C1e
于是
a 2
X C2 cos( x) C3 sin( x)
( x, ) e
a 2
[ A cos( x) B sin( x)]
( x, ) e
a 2
[ A cos( x) B sin( x)]
( a)
此处Bn为离散面(特征值)
2 n a
n n 若令 则上式可改写为:
2 sin n ( x , ) x cos( n ) e 0 n 1 n sin n cos n
热传导-非稳态热传导

体积为 V 表面积为 A 物性 r, l, c 初始温度 t0 >t∞
2. 数学描写
1)控制方程
t a 2t Φ
rc
空间导数为零
dt Φ
d rc
初始条件 0, t t0 (不需要边界条件)
2)如何确定广义热源项 Φ
与分析肋片导热问题类似-发生热量交换的边界不是计算边界,无法通过边界条件 来反应边界上的热交换,需将界面上交换的热量折算成整个物体的体积热源。
均为齐次条件!可以采用分离变量法求解
x , - x h x
(2)分离变量法求解
取
X (x) ( )
则原方程
2
a x2
化为
1 d 1 d 2 X a d X dx2
只为 的函数
只为 x 的函数
左右端只能为常数: 1 d 1 d 2 X const a d X dx2
初始条件(IC): t f ( x, y, z, 0) f ( x, y, z )
边界条件(BC)可能有三种: 第1,2,3 类边界条件。
第三类边界条件较常见:
(
t n
)
w
h(tw
tf
)
h, t f 已知
n
未知的 换热表 已知的表 未知的 已知的
表面法 面外法 面对流传 表面温 流体温
正规 状况 阶段
渐消失,不同时刻温度分布主要取决于 边界条件及物性(分布 P-D, P-E, P-G
非正 规阶
等)。
段
N
4. 非稳态导热问题数学描写
用矢量表示的三个坐标系下控制方程的统一形式:
传热学第三章 非稳态导热

时、物体中最大与最小的过余温度之差小于5%,对于一 般工程计算,此时已经足然特确地可以认为整个物体温度 均匀。按照这样要求,由于l=V/A对圆柱有球分别是半轻 的1/2与1/3、因而如果以l作为Bi数的特征长度,则该Bi数 对平板、国柱与球应该分别小于0.1、0.05和0. 033。
方程中指数的量纲:
hA
W m2K
m2
w1
Vc
kg m3
Jkg K
[
m3
]
J
s
第三章 非稳态导热
9
即与 1 的量纲相同,当 Vc 时,则
hA
hA
1 Vc
此时,
e1 36.8%
0
称
Vc
hA
为时间常数,用 c 表示。
第三章 非稳态导热
10
如果导热体的热容量( Vc )小、换热条件好(h大),
有一直径为 5cm 的钢球,初始温度为 450 ℃,将其突然置 于温度为 30 ℃空气中。设钢球表面与周围环境间的总换热 系数为 24w/(m2 . K),试计算钢球冷却到 300 ℃所需的 时间。已知钢球的 c=0.48kJ/(kg·K ) , ρ =7753kg/m3 , λ =33w/(m. K ).
Fo
l2
a
换热时间 边界热扰动扩散到l 2面积上所需的时间
无量纲 热阻
Fo越大,热扰动就能越深入地传播到物体 内部,因而,物体各点地温度就越接近周
围介质的温度。
无量纲 时间
第三章 非稳态导热
12
对于平板、圆柱、球的一维非稳态第三类边界条件条件下 的导热问题,当按特征长度
l= 、厚度为2 的平板,
l=R、圆柱 l=R.球 定义的Bi数满足
传热学第3章非稳态导热

•第3章 非稳态导热——§3-4半无限大的物体
§3-4 半无限大的物体
半无限大物体的概念
• 第一类边界条件: • 第二类边界条件: • 第三类边界条件:
•* - 31 -
•第3章 非稳态导热——§3-4半无限大的物体
问题的解:
•
误差函数 无量纲变量
• 第一类边界:
• 第二类边界:
• ● 非周期性(瞬态导热):物体的温度随时间的推移逐渐趋于恒定。
• 3、工程上几种典型非稳态导热过程温度变化率的数量级
•* - 2 -
•第3章 非稳态导热——§3-1 非稳态导热的基本概念
着重讨论瞬态非稳态导热
• 4、温度分布:
•t
• 开始的一段时间,物体内部温度变化一层
层逐渐深入到内部,温度变化速度不一样,反映 到吸热量上,吸热量不一样。
• 此时x处的温度可认为完全不变,因而可以把
视为惰性时间。
•
当
时x处的温度可以认为等于t0。
•对于有限大的实际物体,半无限大物体的概念只适用于物体的非稳态导热的 初始阶段,那在惰性时间以内。
•* - 35 -
•第3章 非稳态导热——§3-4半无限大的物体
即任一点的热流通量: 令 即得边界面上的热流通量
• 第三类边界:
•* - 32 -
•第3章 非稳态导热——§3-4半无限大的物体
• 误差函数:
• 无量纲 坐标
• 说明:(1) 无量纲温度仅与无量纲坐标 有关
•
(2) 一旦物体表面发生了一个热扰动,无论经历多么短的时间无论 x 有多么
大,
•
该处总能感受到温度的化。?
•
(3) 但解释Fo, a 时,仍说热量是以一定速度传播的,这是因为,
第三章非稳态导热_传热学

tm m tf 9 8= 17c C
m 2 0.9064 exp 1.1347 2 0.22 0.9 0 1.1347 0.9064 0.4224
平壁表面处 x 的过余温度为:
w 2sin 1 cos 1 exp 12 Fo 0 1 sin 1 cos 1
(2)在垂直于热量传递的方向上,每个截面上热流量不相等; (3)温度随时间变化,热流也随时间变化。
3.讨论非稳态导热问题的目的:
(1)在加热和冷却时,物体内部某一点温度达到预定温度 时所需要的时间,以及该时间内物体吸收和放出的热量;
(2)对物体加热或冷却之后,物体内部温度分布以及物体 温度随时间的变化率
1 0
1 d a d
c1 exp a
c1 exp a
2
1 d2 X 2 2 X dx
X c2 cos x c3 sin x
x, X x
第三章 非稳态导热
§3-1 §3-2 §3-3 §3-4 §3-5 非稳态导热的基本概念 无限大平壁的瞬态导热 半无限大物体的瞬态导热 其他形状物体的瞬态导热 周期性非稳态导热(自学)
• • • •
1.加热冷却过程 2.动力机械中的开关车
应用背景
3.地球的气候变化
4.医疗中激光技术(控制温度范围)
x, 2sin 1 x cos 1 exp 12 Fo 0 1 sin 1 cos 1
查表3-1,当Bi=2.5时, 1 1.1347
180 sin 1 sin 1.1347 0.9064
x A sin 0 B cos 0 exp a 2 0
3-非稳态热传导2

0
exp(u 2 )du
称为余误差函数或误差函数的补函数。 几个有关的函数的值列于表中。
23
半无限大物体的非稳态导热
24
半无限大物体的非稳态导热
25
令
yx
4a
若 即
y 2 erf (2) 0.9953 可认为该处温度没有变化 w 1 0.9953
erf ( y )
17
半无限大物体的非稳态导热
建立相似性变量的方法在开始时采用“自 由参数法” 。它没有一个常规的程序,而 是依赖于对问题本质的深入领悟。以后发 展了数群理论法,可以按照一定的规则导 得相似性变量。有关该方法的细节可参阅 相关文献。
18
半无限大物体的非稳态导热
0 x , 0 x 0, 0 w t w t0 , x 0, 0 对由上式所描述的定解问题,引入相似性变量 2 a 2 , x 0,
2 2 2 a 2 , y y 0, 0, y H , 0,
0, 0 y H ,
0 y H , 0 2 0 y 2 h2 2 0 y 2 f2 ( y)
13
半无限大物体的非稳态导热
有限厚平壁的温度响应一般需要用无穷级数的形 式表示,而半无限大物体中的温度响应则常常可 表示为某种积分函数的形式,因此较为简明。 求解半无限大物体中的导热问题也可采用分离变 量法(涉及傅里叶积分),或采用格林函数法和拉 普拉斯变换法。 本节将结合几个常见的问题讨论相似性解和积分 近似解的概念。这些方法对于解决其他的复杂问 题,例如流体流动和对流换热,也是有帮助的。
非稳态导热

rVc
华北电力大学
梁秀俊
高等传热学
从0到任意时刻 积分
1 d hA
d
0
rVc 0
t t
hA
e rVc
0 t0 t
上式中右端的指数可作如下变化
hA rVc
h(V /
A)
a
(V / A)2
BiV FoV
式中BiV是特征尺度l用V/A表示的毕渥数。
华北电力大学
梁秀俊
高等传热学
梁秀俊
高等传热学
(x, ) (x, ) m ( ) ;
0
m ( ) 0
m ( ) f (Bi, Fo) 0
无限大平板中心无量纲过余温度曲线
华北电力大学
梁秀俊
高等传热学
(x, ) (x, ) m ( ) ; (x, ) f (Bi, x )
0
m ( ) 0
m ( )
四、无限长圆柱 过程类似 图线类似
无限大平板无量纲过 华北电力大学 余温度曲线
梁秀俊
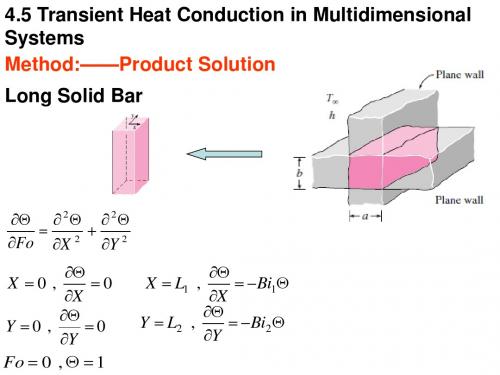
四、乘积解
高等传热学
在二维和三维非稳态导热问题中,几种典型几何 形状物体的非稳态导热问题可以利用一维非稳态导 热分析解的组合求得。无限长方柱体、短圆柱体及 短方柱体就是这类典型几何形状的例子。
华北电力大学
梁秀俊
高等传热学
矩形截面的无限长方柱体是由两个无限大平壁垂 直相交而成;短圆柱是由一个无限长圆柱和一个无 限大平壁垂直相交而成 ;短方柱体(或称垂直六面 体)是由三个无限大平壁垂直相交而成;
z
d d
C1 exp( 2 )
再 积 分 得 :
C1
exp( 2 )d
0
C2
代 入 定 解 C1 2w / 条 件 可 得 :C2 w
传热学-第三章 非稳态导热

[J ]
当物体被加热时(t<t∞),将上两式中的θ0=t0-t∞ 改为θ0=t∞-t0,其余计算式相同(为什么?)
4. BiV·FoV的物理意义
Bi
=
hl
λ
=
l
λ=
物体内部导热热阻
1 物体表面对流换热热阻
h
无量纲 热阻
BiV数越小,计算结果越接近实际情况。比如热电
偶测温,其BiV数只有0.001。
=
h ⋅ 4(l + d
cp dl
/ 2)
=
140× 4× (0.3 + 0.05 / 2)
0.48×103 × 7753× 0.05× 0.3
=
0.326
×10−2
s -1
θ θ0
=
t − t∞ t0 − t∞
= exp⎜⎜⎝⎛ −
hA
ρcV
⋅τ ⎟⎟⎠⎞
⇓
( ) 800 −1200 = exp − 0.326×10−2 ×τ
解:① 建立非稳态导热数学模型
方法一:椐非稳态有内热源的导热微分方程:
∂t
∂τ
=
λ ⎜⎛ ∂2t ρc ⎜⎝ ∂x 2
+
∂2t ∂y 2
+
∂2t ∂z 2
⎟⎟⎠⎞ +
Φ&
ρc
∵ 物体内部导热热阻很小,忽略不计。
∴ 物体温度在同一瞬间各点温度基本相等,即t仅是τ
的一元函数,而与坐标x、y、z无关,即:
例 一 直 径 为 5cm , 长 为 30cm 的 钢 圆 柱 体 , 初 始 温 度 为 30℃ , 将 其 放 入 炉 温 为 1200℃ 的 加 热 炉 中 加 热 , 升 温 到 800℃时方可取出。已知钢圆柱体与烟气间的表面传热系数 为 140w/(m2K) , 钢 球 的 比 热 c=0.48kJ/(kgK) , 密 度 ρ=7753kg/m3,导热系数λ=33w/(mK)。问需要多少时间才 能达到加热要求? 解:首先检验是否可以采用集总参数法。为此计算Biv数:
《传热学》第 章 非稳态热传导

(2) 毕渥数的定义:
Bir h rh 1h
两个热阻比值的量纲一的量
tf h
t
tf
h
0
x
2020/3/2
0
x
第3章 非稳态热传导
3.1.3 第三边界条件下Bi数对温度分布的影响
Bir rh
1h h
当 B i 时,rrh,可以忽略对流换热热阻 当 B i 0时,rrh,可以忽略导热热阻
第3章 非稳态热传导
3-1 非稳态导热基本概念 3-2 零维问题的分析法——集中参数法 3-3 典型一维非稳态导热的分析解 3-4 半无限大物体的非稳态导热 3-5 简单几何形状物体多维非稳态导热的分析解
2020/3/2
第3章 非稳态热传导
3.1 非稳态导热的基本概念
定义:物体的温度随时间而变化的导热过程称为非稳态导热 分类:物体温度随时间推移逐渐趋近于恒定的值(金属热处理)
未知)
w
2020/3/2
第3章 非稳态热传导
唯一解定律:如果某一函数满足导热微分方程以及一定的初始条件与 边界条件,那么此函数就是这一特定导热问题的唯一解。
3.1.3 第三边界条件下Bi数对温度分布的影响
(1) 问题的分析
如图所示,存在两个换热环节:
tf
a 流体与物体表面的对流换热环节 rh 1h h
导热微分方程变为 d hA d Vc
2020/3/2
导热微分方程推导:
t cP
体积热源折算
VA(th t )
VcddthA (tt)
零维问题的数学描述:
零维问题的导热微分方程
引入过余温度tt, 则有
传热学课件-第三章非稳态热传导共66页文档

0
物体中的温度 呈指数分布
方程中指数的量纲:
hA
mW2Km2
w1
cV
kg m3
JKkg[m3]
J
s
即与 1 的量纲相同,当
时hVAc,则
hA 1
Vc
此时, e1 36.8% 0
上式表明:当传热时间等于 Vc时,物体的过余温度已经达
到了初始过余温度的36.8%。hA称 为Vc 时间常数,用 表示 。c
非周期性非稳态导热:物体的温度随时间的推移逐渐趋 近于恒定的值
非周期性非稳态导热实例(汽轮机外壳)
冷态启动前:tf1=tw1=tw2=tf2
进汽后 tf1
内壁 q1=h1(tf1-tw1) 到某一时刻 h1A1(tf1-tw1)=h2A2(tw2-tf2) 以后为稳态导热
3 温度分布:
问题描述:
3 、了解内容:
①无限大物体非稳态导热的基本特点。 ②二维非稳态导热问题。
§3-1 非稳态导热的基本概念
一、非稳态导热的特点及类型
1 非稳态导热的定义
物体的温度随时间而变化的导热过程称非稳态导热。
2 非稳态导热的分类
周期性非稳态导热:物体的温度随时间而作周期性的变化
例如太阳辐射的周期性变化引起的房屋的墙壁温度随时间的变化。
这 时 , 由 于 导 热 热 阻 δ/λ几乎可以 忽略,因而任一时刻平板中各点的 温度接近均匀,并随着时间的推移, 整体地下降,逐渐趋近于t∞ 。
(3) δ/λ与 1/h 的数值比较接近
这时,平板中不同时刻的温度分布介于上述两种极 端情况之间。
由此可见,上述两个热阻 的相对大小对于物体中非稳态 导热的温度场的变化具有重要 影响。为此,我们引入表征这 两个热阻比值的无量纲数毕渥 数: Bi h
高等传热学_第一章_导热理论和导热微分方程

导热系数的单位是W/(m·K)。导热系数与材料的种类及其所处的
状态有关。固体、液体与气体,金属与介电质的内部结构不同,
导热的机理也有很大的差异。
• 对于绝大多数材料,现在还不能根据其结构和导热机理来计算其 导热系数。各种实际应用材料的导热系数主要是通过实验的方法 得到的。目前已有一系列不同的实验方法可用来测定各种材料在 不同温度范围内的导热系数,特别是20世纪60年代以来发展起来 的多种非稳态的方法,由于其测试时间短(几秒至几十秒)、适 应性强等优点,已被广泛采用。
傅里叶定律的局限性
• 热扰动应该以一定的速度传播。
修正的傅里叶定律
• a 热扩散率 • c 热传播速度 • 松弛时间
在深冷时或在热负荷急剧变化的场合,左边第一项不 能略去。
俄罗斯流变学家Alxander Malkin的流变学教材 Rheology: Concepts, Methods and Applications在第2 章介绍粘弹性的时候,专门用一块小字号的阅读材 料来解释什么叫松弛时间——而且是作为物理学的 一般性概念来介绍,简短明快,值得借鉴。
where k is a kinetic rate constant with the dimension of reciprocal time.
• The parameter X in the initial state equals to X0. Then, the solution of
this equation is
• 连续温度场内的每—点都对应一个温度梯度向量,所以温度梯度
构成一个向量场。
1-1 导热基本定律
• 1-1-3 热流向量
• 单位时间内通过单位面积传递的热量称为热流密度,记作q,单 位为W/m2。对确定的空间点、在不同方向上热流密度是不同的。 与定义温度梯度的方法一样,可以定义一点处的热流向量。热流 向量的方向是热流密度最大的方向,其大小等于该方向的热流密 度。热流向量记作q。任一方向的热流密度等于热流向量在该方 向的投影。在连续温度场内的每一点都对应一个热流向量,所以 热流向量也构成一个热流向量场,或称热流场。在直角坐标系中
高等传热学-热传导理论幻灯片

描述导热过程中的温度场 。 各向同性、热传递速度无限大、温度场光滑时(满足傅立叶 定律成立的条件),由能量守衡得(常物性)
12:03
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
有了方程以后还要有单值性条件以确定某个问题的定解。导 热微分方程只反应了导热问题的共性,每个确定的导热问题 还有其个性。 单值条件 1)几何条件:物体形状、大小; 2)物理条件:材料的热物性; 3)时间条件:说明过程进行在时间上的特点; 4)边界条件:说明在物体边界上,热过程进行的特点,反应
12:03
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
傅里叶定律例题1,任意方向的热流密度
12:03
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
傅里叶定律例题2,沿边界面总换热
12:03
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
规则的周期性变化:温度是时间的简谐函数。
由于周期性问题与工程问题相差较远重点为瞬态导热问题。
12:03
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
2.瞬态导热的物理过程 以第三类边界条件为例,以BI数区分几种情况讨论。
1) 内热阻远远小于外热阻 特点:内热阻小,物体内部温差小,内部温度趋于一致。
12:03
Copyright by HIT
时间条件的一般表达式
哈尔滨工业大学航空航天热物理研究所
三类边界条件的一般表达式
12:03
Copyright by HIT
哈尔滨工业大学航空航天热物理研究所
传热学-第2、3章 稳态热传导、非稳态热传导

(√ )
问题:通过平直肋片的导热
Heat Transfer
t∞
空气
h
绝热条件 t : n0
t0
λ
t(x)=? x
问题:通过平直肋片的导热
假定肋片温度仅在x方向发生变化。
k
d2t dx2
q
0
Heat Transfer ct kx2t2y2t2 z2t2q
(4)会计算通过平壁、圆筒壁、球壳、肋壁的稳态 导热和传热过程;
(5)掌握肋片效率的影响因素及提高肋片效率的方 法。
问题1:通过平壁的导热总结
Heat Transfer
首先,根据物理问题写出控制方程与边界条件/初始条件
2t x 2
0
t
ttw1f oxr0
ttw 2foxr
tw1
tw2
Heat Transfer
总结
本章主要讲述导热的基本概念、基本定律 、导热 现象的数学描述方法及通过平壁、圆筒壁、球壳和肋 壁稳态导热的分析计算方法,重点掌握以下内容:
(1)温度场、温度梯度、导热系数、热阻、肋片效 率等基本概念;
(2)付里叶定律的内容、表达式及其适用条件;
(3)掌握导热问题的数学描述方法,能够正确建立 导热问题的物理模型和数学模型;
什么?
答:
霜会容易结在树叶的上表面,因为树叶上表面朝向 太空,而太空表面的温度会低于摄氏零度;下表面 朝向地面,而地球表面的温度一般在零度以上。相 对于下表面来说,树叶上表面向外辐射热量较多, 温度下降的快,一旦低于零度时便会结霜。
练习题6:对流换热过程微分方程式与导热过程的第 三类边界条件表达式有什么不同之处?
传热学-非稳态导热2

二、无限长直角柱体、有限长圆柱体和六面体
1、无限长直角柱体中的瞬态导热
2x 2y
可以证明:无限长直角柱体
的温度场是这两块无限大平
壁温度场的乘积
可以看成是厚度为2δx 和厚度
为2δy 的两块无限大平壁垂直
相交形成的
在室外综合温度t e 的周期波
波动振幅:温度波动的最
大值与平均值之差
m
max t t A −=由上图:综合温度振幅:37.1度;屋顶外表面温度振幅:28.6度屋顶内表面温度的振幅:4.9度
——温度波的衰减
不同地点温度最大值出现的时
间不同:
综合温度最大值—中午12点
12点半
16点
大值约在22点左右出现——时间延迟
迟的现象——时间延迟
夏天晚上人们喜欢在室外乘凉,原因何在?故宫的墙壁厚度很厚,为什么?——温度波的衰减
实测综合温度简谐波
随着x 的增大,振幅是衰减的——物体材料对温度波的阻尼作用
深度越深,振幅衰减越甚——当深度足够大时,温认为终年保持不变——等温层
360087602.3×T x
⎛−
x
ππ
2
λ
0w ==A A ϕD 45=ψ时 022
=λaT
h ⇒↑ 2aT h。
传热学第10讲非稳态导热2
3)源项积分
t t n e
Sdxdydt
t s w
( S c S PTP ) x y t
4)结果整理
,
a P T P a E T E a W TW a N T N a S T S b
[ke A( x)e
TE TP ( x ) e
0
0
kw A( x)w
T P TW ( x ) w
0
0
] t
0 0
( c ) P A ( x ) P (T P T P ) x [ k e A ( x ) e
0
TE TP ( x ) e
0
kw A( x)w
0 0
1 ( X , Fo 1 ) 2 ( Y , Fo 2 )
Fo
2ຫໍສະໝຸດ 1 2 ' 1 ' 2
1
2
X
2
2
X
2
2 1"
2
Y
2
1
2
2
Y
2
1 2 "
Fo
X
2
2
Y
2
问题:如何建立恰当的模型?有没有理论分析解? 数值解与理论解会有什么相同点和不同点?解的结 果如何表示,表示内容有哪些为好?
多维导热问题处理
直角坐标系
圆柱轴对称坐标系
极坐标系
二维非稳态导热全隐格式的通用离散方程
直角坐标系下的为例,根据二维非稳态导热方程:
c
T t
x
(k
T x
)
d T dx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等传热学导热理论
第四讲 非稳态导热
描述非稳态导热问题的微分方程:
p
C t a t ρτΦ+
∇=∂∂ 2
共有四维,不好解。
最简单的情况,如果系统内部无温度差(即无导热),
它的温度变化规律如何?这就是所谓的薄壁问题,此时无需考虑系统的空间坐标,所以又是0维问题。
1.薄壁问题(P 40-45)即集总参数系统适用条件 薄壁理论:
如果系统内部无温度差,由热力学第一定律可得:
MCdt d A d q =∙Ω
τ
1-4-1
当热流密度与边界相互垂直时,有:
VCdt qAd ρτ= 1-4-2
如边界上的热流密度为)(t t h q f -=
VCdt d t t hA f ρτ=-)( 1-4-3
00
t t ==τ
实际情况 t 不可能相同。
什么条件下可用薄壁公式呢? 工程界用得最多的判据是:
1.0≤Bi 1-4-4
对平壁,圆柱和球,此时内部温差小于()()(,)(0,)/(0,)5%t r t t t τττ∞--≤,即实际判据为:
()()(,)(0,)/(0,)t r t t t τττε∞--≤,即某时刻平壁内最大温差与该时刻平壁和
环境间的最大温差之比小于给定小量。
有人对此判据提出异议:在加热初期极短时间内,任何有限薄壁可看作半无限大体,温度只影响边界附近薄层中,与薄壁概念不符。
判据1-4-4的缺点是没有F o 的影响。
R o s e n o w 提出另一个判据,()()(,)(0,)/(,)(,0)t r t t t ττδτδε--≤,物理意义是在某时刻平壁内最大温差与该时间段内平壁最大温度变化之比小于给定小量。
该判据含F o ,但存在B i 越小,薄壁区越小的缺点,与判据1-4-4不相容。
俞佐平提出了含F o 的新判据,
()()()()
(,)(,0)(,)/1//(,0)t t t t t t Bi h t t δτδδτεδλδ∞∞∞∞---=≤-
该判据规律与1-4-4相似。
本人从理论上证明了判据1-4-4的合理性,发现异议者的误区在于但B i 很小时,无论时间如何短,与该薄壁相应的半无限大体中的最大温差也不会超过我们限定的温差。
这就是问题的实质。
证明:00,()w t t h c t t t t t n ρλττλ
∞∂∂=∇∇==-=-∂∂ V
V t
c
dV tdV ρλτ∂=∇∇∂⎰
⎰ ,()()(,)(0,)/(0,)t r t t t τττε∞--≤ (0,)(0,)V
V
t dt dt c
dV c dV c V d d ττρρρτττ∂≈=∂⎰
⎰ ()((0,))((0,))w
V
S
S
w
S
S
t
tdV t dS dS
n
h t t dS h t t dS h t t S
λλλ
ττ∞∞∞∂∇∇=∇=-∂=--≈-=-⎰
⎰⎰⎰⎰
(0,)(0,)((0,))((0,))dt dt hS
c
V h t t S t t d d cV ττρττττρ∞∞
=-→=- 此即集总参数法公式。
证毕。
2.薄壁加热理论:
由式1-4-2,得:()H C VC qA d dt ==ρτ//叫升温速度。
由此式可以清楚地看到形
状和密度对升温速度的影响。
()V A C q C H ρ//⨯=
其中: ()球圆柱=平壁32/13/2//===⎪⎩
⎪
⎨⎧=k k k R k R R R
A V ρρρρρ
()R k C q C H ρ//⨯=
在R 相同时,球的升温速度最快,是厚为2R 平壁的3倍,平壁最慢。
因为物体体积都是有限的,令2/1A L A =和3/1V L v =,V A L L E /=叫形状参数
3/22V E A =, 2//E L A V V =,得:
()V H L E C q C ρ//2⨯=
球:E =2.20, 高径相等的圆柱:E =2.33, 立方体E =2.45 无限长圆柱(L 趋向无穷大): (
)1/6
/E L R π=a ×a ×n a 的正方形柱 E =
a ×m a ×n a 的长方形柱 E =当m =n 趋向无穷大,为无限大平壁:E =在体积相同时,平壁具有最大的形状参数,升温速度最快,球有最小的形状参数,升温速度最慢,与上面的结论完全相反,但两个结论都是对的。
3.加热方式的影响:
A . 等热流加热,q =c o n s t
()0/t CV qA t +∆=ρτ
B . 等温加热:
对流加热 式1-4-3f t 为常量时的解:
()()()CV hA t t t t f ρτ/exp 0∆--=- 辐射加热:)(440T T q f -=εσ,解为
⎪⎪⎭
⎫ ⎝⎛-=∆)()(030f f f T T T T AT CV ψψεσρτ θθθθψarctan 2
1
11ln
4
1)(+-+= 适用条件,02.0≤Mo
C .动态温度加热,测温理论 等速升温:
τ∆+=v t t f f 0,0.,0f t t ==τ
解为:()())(/exp 0t t f v CV hA v t t ττρττ-+∆-=- 温度出现滞后现象,滞后时间()t τ,滞后温差:t v τ
正弦温度加热:
ωτsin 0B t t f f += 0.,0f t t ==τ
解为:()
()()()
()φωτωτρτωτφ-++
∆-+=
-sin 1/exp 1sin 2
2
0t t f B CV hA B t t
温度频率不变,但出现滞后现象,滞后相位差φ,温度振幅减小,减小到
()
2
11ωτt +,()ωτφt arctan =
以上分析告诉我们,若用热电偶一类的温度计测量动态温度,即时显示温度
总是跟不上实际温度变化,必须采取措施,尽量减小误差。
其中测温系统的时间常数是影响精度的主要指标。
4. 动态温度测试仪分析。
用热电偶等测量燃气温度温度,可以看成是薄壁系统。
在低马赫数条件下,可用下面方程进行描述:
))16.273()16.273(()(440+-++-=t t A t t hA d dt VC w f εστ
ρ
在壁面温度比燃气温度低得多时,上式中壁面辐射热量可以忽略不计。
我们整理
成: ))16.273()16.273((440
+-+++
=w f t t h d dt hA VC t t εστρ R M f t t t t ∆+∆+=
动态误差 辐射误差
减小动态误差的方法:
减小密度,体积和比热容,增加燃气和测温元件间的换热系数和感温元件的换热面积。
即减小系统时间常数。
减小辐射误差的方法:减小系统黑度(测温元件表面涂黑度小的材料,元件和低温壁面之间加遮热罩,增加辐射热阻,调整位置减小角系数),增加换热系数,提高壁面温度。
设计新形式,修正误差,如测出时间常数和温度变化曲线,即可算出动态误差。
5 厚壁的非稳态导热:
1D 时无内热源,常物性,有通用方程:
Sphere
n Cylinder n Plate
n dr dt r n dr t d a t
2
1022===⎪⎪⎭⎫ ⎝⎛+=∂∂τ 解有海撕勒图。
现介绍半无限大体的解。
有限
t or x
t
x t t x
t
or q q or t t x t t dx t d a t
f w w 0)(0
0022=∂∂∞
=-=∂∂-=====⎪⎪⎭
⎫ ⎝⎛=∂∂λ
ττ
1s t B C 的解:(相似法):令 τ
ηa x
2=
代入上式:得 02
2,
,
02t t q q or
t t d t d d dt w
w
=∞=====
-ηηηηη
当t w =t a 常数时:
)2(0τ
a x
erf t t t t w w =--
当2cos(
)a t t B T πτ=+时 )2cos()exp(aT
x T aT x B t t a π
τππ--+= 振幅得衰减系数:)exp(aT
x
π
-
相位延迟量:aT
x
π
温度波传播速度:T
a
x u πτ2
=∆= 温度波周期不变。
