苏教版高中数学(必修2)测试试卷及答案[1]
最新苏教版高中数学必修2全册单元练习题(共4份)及解析.docx

(新课标)2018-2019学年苏教版高中数学必修二必修2练习题(一)(时间:60分钟,满分:100分)班别 座号 姓名 成绩 一、选择题(本大题共10小题,每小题5分,共50分)1.下列命题中,正确的是( )A .一个平面把空间分成两部分落千丈 B. 两个平面把空间分成三部分 C. 三个平面把空间分成四部分 D. 四个平面把空间分成五部分 2.下列函数中,奇函数是( )A. y = ( 1- x )( 1 + x )B. 31x y =C.x1x x y 2--= D.)1lg(2x x x y ++=3.||2)(2x x x f -=的单调递增区间为( )A. (-1,0)B.(0,1)C.(1,+∞)D.(-1,0)和(1,+∞) 4.函数xx x f 2ln )(-=的零点所在的大致区间是( ) A.(1,2) B.(2,3) C.和,⎪⎭⎫⎝⎛e 11(3,4) D.)(∞+,e 5.一个正方体的顶点都在球面上,此球与正方体的表面积之比是( ) A. π:3 B.π:4 C. π:2 D. π:16. 4、设f (x)是奇函数,且当x > 0时,f (x) = x -1. 则当x < 0时,有 (A) f (x) < 0 (B) f (x) > 0 (C) f (x)f (-x) < 0 (D) f (x)f (-x) < 07.两个球的表面积之差为48π,它们的大圆周长之和为12 π,这两个球的半径之差为A 4B 3C 2D 18.如图所示的直观图,其平面图形的面积为A 3B 6 C23D2239.圆锥和圆柱的底面半径和高都是R ,则圆锥的全面积与圆柱的全面积之比为( ) (A )2:2 (B )4:)21(+(C )1:2 (D )2:)21(+10.正六棱台的两底面的边长分别为a 和2a ,高为a ,则它的体积为A32321a B 3233a C 337a D 3237a 选择题答题表 题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题(本大题共4小题,每小题5分,共20分)11.一个平面的斜二测图形是边长为2的正方形,则原图形的高是 . 12. 棱长都是1的三棱锥的表面积为 . 13. 函数 定义域是3lg x y = .14.已知y a =<log 341,那么a 的取值范围是: .三、解答题(本大题共3小题,每小题10分,共30分)15.有一个几何体的三视图及其尺寸如下 16.一个三棱柱的底面是3的正三角形,侧棱45032(单位cm ),求该几何体的表面积及体积: 垂直于底面,它的三视图如图所示。
2020-2021学年苏教版高中数学必修二全册综合练习及答案解析

(新课标)2018-2019学年苏教版高中数学必修二全册综合练习一、填空题1. 圆C:x2+y2+2x-4y-4=0的圆心到原点的距离是________.2. 已知直线l过直线l1:3x-5y-10=0和l2:x+y+1=0的交点,且平行于l3:x+2y -5=0,则直线l的方程是________________.3. 已知圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则线段AB的垂直平分线的方程是________________.4. 不论m为何实数,直线(m-1)x+(2m-1)y=m-5都过定点________.5. 半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为__________________.6. 给出下列说法:①正方形的直观图是一个平行四边形,其相邻两边长的比为1∶2,有一内角为45°;②水平放置的正三角形的直观图是一个底边长不变,高为原三角形高的一半的三角形;③不等边三角形水平放置的直观图是不等边三角形;④水平放置的平面图形的直观图是平面图形.其中,正确的说法是________.(填序号)7. 如图,正方体的棱长为1,C,D分别是两条棱的中点,A,B,M是顶点,那么点M 到截面ABCD的距离是________.(第7题)(第8题)8. 如图,正四棱锥SABCD 的底面边长和各侧棱长都为2,点S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为________.9. 已知一圆的方程为x 2+y 2-6x -8y =0,设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为________.10. 如图,在直三棱柱ABCA 1B 1C 1中,AB =1,BC =2,BB 1=3,∠ABC =90°,点D 为侧棱BB 1上的动点.当AD +DC 1最小时,三棱锥DABC 1的体积为__________.二、 解答题11. 已知直线l 1:(a +1)x +y -a +1a 2+1=0,l 2:x -y -a 2-3a 2+1=0.(1) 当a 为何值时,l 1∥l 2? 当a 为何值时,l 1⊥l 2?(2) 若l 1与l 2相交,且交点在第一象限,求a 的取值范围.12. 如图,在长方体ABCD A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E 是棱AA1上任意一点.(1) 求证:BD⊥EC1;(2) 如果AB=2,AE=2,OE⊥EC1,求AA1的长.13. 如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.求证:(1) 直线OG∥平面EFCD;(2) 直线AC⊥平面ODE.14. 已知直线x -2y +2=0与圆C :x 2+y 2-4y +m =0相交,截得的弦长为255.(1) 求圆C 的方程;(2) 过原点O 作圆C 的两条切线,与抛物线y =x 2相交于M ,N 两点(异于原点).求证:直线MN 与圆C 相切.1. 5 解析:圆心C(-1,2)到原点距离d =(-1)2+22= 5.2. 8x +16y +21=0 解析:由直线l 过l 1与l 2的交点,故可设直线l 的方程为3x -5y -10+λ(x +y +1)=0,即(3+λ)x +(λ-5)y +λ-10=0.∵ l ∥l 3,∴ 3+λ1=λ-52≠λ-10-5,∴ λ=-11. ∴ 直线l 的方程为-8x -16y -21=0,即8x +16y +21=0.3. 3x -y -9=0 解析:AB 的垂直平分线经过两圆的圆心(2,-3),(3,0),所以AB 的垂直平分线的方程是y =3(x -3),即3x -y -9=0.4. (9,-4) 解析:在(x +2y -1)m -(x +y -5)=0中,令⎩⎨⎧x +2y -1=0,x +y -5=0,解得⎩⎨⎧x =9,y =-4.5. (x +4)2+(y -6)2=36或(x -4)2+(y -6)2=36解析:设圆心坐标为(a ,b),由所求圆与x 轴相切且与圆x 2+(y -3)2=1相内切可知,所求圆的圆心必在x 轴的上方,且b =6,即圆心为(a ,6).由两圆内切可得a 2+(6-3)2=6-1=5,所以a =±4.所以所求圆的方程为(x +4)2+(y -6)2=36或(x -4)2+(y -6)2=36.6. ④ 解析:对于①,若以该正方形的一组邻边所在的直线为x 轴、y 轴,则结论正确;但若以该正方形的两条对角线所在的直线为x 轴、y 轴,由于此时该正方形的各边均不在坐标轴上,则其直观图中相邻两边长不一定符合“横不变,纵减半”的规则.对于②,水平放置的正三角形的直观图是一个底边长不变,高比原三角形高的一半还要短的三角形.对于③,只要坐标系选取恰当,不等边三角形水平放置的直观图可以是等边三角形.7. 23 解析:设点M 到截面ABCD 的距离为h ,由V C ABM =V M ABC 知13·S △ABM ·1=13·S △ABC ·h ,又S △ABM =12,S △ABC =12·2·1+⎝ ⎛⎭⎪⎫242=34,∴ h =23.8. 43π 解析:如图,过S 作SO 1⊥平面ABCD ,由已知O 1C =12AC =1.在Rt △SO 1C 中, ∵ SC =2,∴ SO 1=SC 2-O 1C 2=1,∴ O 1S =O 1A =O 1B =O 1C =O 1D ,故O 1是过S ,A ,B ,C ,D 点的球的球心,∴ 球的半径为r =1,∴ 球的体积为43π·r 3=43π.9. 20 6 解析:圆的方程可化为(x -3)2+(y -4)2=52,∴ 圆心为P(3,4).∴ 过点(3,5)的最长弦为直径AC =10, 过点(3,5)的最短弦长BD =4 6.故四边形ABCD 的面积=12·AC ·BD =12×10×46=20 6. 10. 1311. 解:(1) 当(a +1)·(-1)-1=0且-a 2-3a 2+1-a +1a 2+1≠0时,l 1∥l 2,上式无解,即不存在a ∈R ,使l 1∥l 2.当(a +1)·1-1=0,即a =0时,l 1⊥l 2.(2) 方程联立得交点为(a -1a 2+1,-a 2+a +2a 2+1),所以⎩⎪⎨⎪⎧a -1a 2+1>0,-a 2+a +2a 2+1>0,解得1<a <2.12. (1) 证明:由题设条件,容易证明BD ⊥平面AA 1C 1C.又EC ⊂平面AA 1C 1C ,所以BD ⊥EC 1.(2) 解:设A 1E =x ,在Rt △AEB 中,AE =2,AB =2,则BE =6; 在Rt △BCC 1中,BC =2,CC 1=x +2,则BC 21=BC 2+CC 21=22+(x +2)2;在Rt △EA 1C 1中,EC 21=A 1E 2+A 1C 21=x 2+(22)2.又由(1)知BD ⊥EC 1且OE ⊥EC 1,BD ∩OE =O , ∴ EC 1⊥平面BDE.又BE ⊂平面BDE ,∴ EC 1⊥BE.∴ △BEC 1为直角三角形.∴ BC 21=BE 2+EC 21,即22+(x +2)2=6+x 2+(22)2,解得x =2 2.又AE =2,∴ AA 1=3 2.13. 证明:(1) ∵ 四边形ABCD 是菱形,AC ∩BD =O , ∴ 点O 是BD 的中点.∵ 点G 为BC 的中点,∴ OG ∥CD. ∵ OG ⊄平面EFCD ,CD ⊂平面EFCD ,∴ 直线OG ∥平面EFCD.(2) ∵ BF =CF ,点G 为BC 的中点, ∴ FG ⊥BC.∵ 平面BCF ⊥平面ABCD ,平面BCF ∩平面ABCD =BC ,FG ⊂平面BCF ,FG ⊥BC , ∴ FG ⊥平面ABCD.∵ AC ⊂平面ABCD ,∴ FG ⊥AC.∵ OG ∥AB ,OG =12AB ,EF ∥AB ,EF =12AB ,∴ OG ∥EF ,OG =EF ,∴ 四边形EFGO 为平行四边形, ∴ FG ∥EO. ∴ AC ⊥EO.∵ 四边形ABCD 是菱形,∴ AC ⊥DO. ∵ EO ∩DO =O ,EO ,DO 在平面ODE 内, ∴ AC ⊥平面ODE.14. (1) 解:∵ C(0,2),∴ 圆心C 到直线x -2y +2=0的距离为d =|0-4+2|5=25.∵ 截得的弦长为255,∴ r 2=⎝ ⎛⎭⎪⎫252+⎝ ⎛⎭⎪⎫552=1,∴ 圆C 的方程为x 2+(y -2)2=1.(2) 证明:设过原点的切线方程为y =kx ,即kx -y =0,∴ |0-2|k 2+1=1,解得k =±3, ∴ 过原点的切线方程为y =±3x. 不妨设y =3x 与抛物线的交点为M ,则⎩⎨⎧y =3x ,y =x 2,解得M(3,3),同理可求得N(-3,3), ∴ 直线MN :y =3.∵ 圆心C(0,2)到直线MN 的距离为1且r =1,。
苏教版高中数学(必修2)单元测试-月考.docx

江苏省运河中学高二年级数学学科阶段性检测试卷考试时间为120分钟,试卷满分160分.一、填空题:(本大题共14小题,每小题5分,共70分)1. ______________________________________________________________________ 已知直线px + qy-l = Q(p,q e 7?)经过第二、三、四象限,则满足的条件是_________________ .2.已知直线/:(l + 4Qx —(2 —3Qy + (2 —3Q = 0 ( k w R),则直线/一定通过定点3.已知直线x + ay = 2a + 2与直线ax + y = a + 1平彳亍,则实数a的值为 ________ .4.某商品的市场需求量儿(万件)、市场供应量力(万件)与市场价格x (元/件)分别近似地满足下列关系:=-x + 70,y2 =2x-20.当儿=力时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.现对每件商品征税3元时新的平衡价格为—元.5.已知两条直线a l x + b l y +1 = 0和a2x + b2y + 1 = 0都过点4(2,3),则过两点片⑷,勺),厶(如#2)的直线方程为______________________ .6.已知直线I过点M (3,-4),且在两坐标轴上的截距相等,则I的方程为______________ .7. ______________________________________________________________________ 用长、宽分别是3龙与兀的矩形硬纸卷成的圆柱的侧面,则该圆柱底面的半径为___________ . &已知平面a外的一条直线/上有两点到a距离相等,贝强与a的位置关系是____________ .9.如图,在正方体ABCD-A{B{C X D X中,二面角C;—BD-C的正切值为________________ .10.若直线y + xsin 0 + 3 = 0的倾斜角为a,则a的取值范围为______________________ ,11.直线ax + (l-a)y-l = 0与直线(a — l)x + (2a + 3)y - 2 = 0互相垂直,则实数a的值为____________ •12.设、n是异面直线,则⑴一定存在平面a ,使m c a且”〃a ;⑵一定存在平面a ,使m c a且”丄a; (3) —定存在平面了,使m , n到y的距离相等;(4) 一定存在无数对平面a 与0,使"U0,且a // (3上述4个命题中正确命题的序号为 ________________________________ .13.一个几何体的三视图如图所示,该几何体的内接圆柱侧面积的最大值为_______ .俯视图第13题图14. 设a 和0为不重合的两个平面,给出下列命题:① 若a u a,b u a,a Cl b = 4, / u 0,"?. u 0,a 〃/,/?//m,则 a 〃0;② 若/ <Z a,m u a,/〃m,贝!]///a;③ 若 a Cl 0 = Z, m u a,丄/,则 a 丄 0;④ 若m u u a ,则/丄a o l 丄 加,/丄".上面命题中,真命題的序号 _______________ (写出所有真命题的序号)二.解答题(本大题共有6小题,要求写出必要的过程)15. (本小题满分14分)已知直线(2m 2 + m - 3)x + (m~ -m )y = 4m -1.(1)当加为何值时,直线倾斜角为45° ? (2)当〃?为何值时,直线与x 轴平行? (3) 当加为何值时,直线与直线2x —3y = 5垂直?16. (木小题满分14分)如图,在四面体ABCD 中,CB = CD, 4D 丄BD,点E, F 分别是AB, BD 的中点.求证:(1) 直线 EF//面 ACD-,(2) 平面EFC 丄面BCD. 17. (本小满分14分)、(4)当加为何值时, 直线与直线2x —3y = 5平行?R在长方体ABCD - A.B.C.D,中,底面ABCD是边长为41的正方体,侧棱长为V3, E,F分别是AB l,CB l的中点,求证:平面QEF丄平面A5.C.18.(本小题满分16分)在路边安装路灯,路宽23m,灯杆长2.5m ,且与灯柱成120。
苏教版高中数学必修二期末综合测试题含答案

苏教版高中数学必修二期末综合测试题含答案一、单选题1.已知复数是虚数单位),则在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.已知一组数据1,2,3,4,5,那么这组数据的方差为()A .B.2C.D.33.调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是()A.互联网行业从业人员中90后占一半以上B.互联网行业中从事技术岗位的人数超过总人数的C.互联网行业中从事运营岗位的人数90后比80前多D.互联网行业中从事运营岗位的人数90后比80后多4.高一2班有45名学生,学号为01-45,为弘扬中国古诗词文化,现采用随机数表法从该班抽取7名同学参加校园诗词朗诵大赛,从随机数表第5行第15个数开始向右数,随机数表的第5行和第6行,则抽取的第7个同学的学号是( ) 162277943949544354821737932378873520964384263491 64844217533157245506887704744767217633502583921206 76A.26B.35C.20D.435.若,则()A.3B.4C.5D.66.已知复数,则复数z的共轭复数在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限7.已知非零向量,,若,且,则与的夹角为()A.B.C.D.8.若,则( )A.B.C.2D.9.若是平行四边形的中心,,则等于()A .B.C.D.10.中,分别是角的对边,向量,,∥且,则=()A.30°B.60°C.120°D.150°11.古希腊数学家阿基米德的墓碑上,刻着一个“圆柱容球”的几何图形,就是圆柱容器里放了一个球,这个球顶天立地,四周碰边(如图).若记这个球的表面积和体积分别为和,圆柱的表面积和体积分别为和,则()A.B.C.D.与的大小关系不确定12.A,B,C是的内角,其中,则的取值范围A.B.C.D.二、多选题13.在四棱锥中,侧面平面,,四边形是正方形,点是棱的中点,则()A.平面B.平面C.D.14.下列关于说法中正确的是()A.过平面外一点有且仅有一个平面与已知平面平行B.过平面外一点有且仅有一个平面与已知平面垂直C.两条异面直线不能垂直于同一个平面D.空间中与两条异面直线同时平行的平面有无数个15.已知复数(其中为虚数单位),则()A.复数在复平面上对应的点可能落在第二象限B.可能为实数C.D.的实部为16.下列命题中不正确的是()A.是共线的充要条件B.若共线,则C.三点不共线,对空间任意一点,若,则四点共面D.若为空间四点,且有不共线,则是三点共线的充分不必要条件。
苏教版高中数学必修二9月份高二阶段高二试卷参考答案.docx

高中数学学习材料马鸣风萧萧*整理制作高二数学阶段测试参考答案一、填空题1.1或无数个 2. 1∶4 3.相交或异面 4.垂直 5. 16.无数条7.38.直角梯形9.9∶49 10. 4或1211. 180 12.3 13. ②14. 24或408二、解答题15.(本题14分)证法1:(反证法)假定a、b异面,任取B∈b,则a与B确定平面γ,且γ∩α=ι1,γ∩β=ι2,由已知a∥α,a∥β知a∥ι1,且a∥ι2,由公理4知ι1∥ι2,与ι1∩ι2=B矛盾,故假设不成立,∴a∥b。
证法2:(同一法)任取B∈b,则a与B确定平面γ,且γ∩α=ι1,γ∩β=ι2,且B∈ι1,B∈ι2。
∵a∥α,a∥β,∴a∥ι1,a ∥ι2,由平行公理知ι1与ι2重合,即为α与β的交线b,∴a∥b。
证法3:(直接证法)过a作平面γ1,γ2,γ1∩α=c,γ2∩β=d,∵a∥α,a∥β∴a∥c,a∥d∴c∥d∴c∥β(d⊂β)∴c∥b∴a∥b16. (本题14分)证明:取BD中点E,连结AE,CE∵AB=AD,CB=CD且E是BD中点∴AE⊥BD,CE⊥BD又∵AE∩CE=E∴BD⊥平面ACE∵AC⊂平面ACE∴AC⊥BD17. (本题14分)证明:(1)连结PG,由题知△PAD为正三角形,G 是AD的中点,∴PG⊥AD.又平面PAD⊥平面ABCD,∴PG⊥平面ABCD,∴PG⊥BG.又∵四边形ABCD是菱形且∠DAB=60°,∴BG⊥AD.又AD∩PG=G,∴BG⊥平面PAD.(2)由(1)可知BG⊥AD,PG⊥AD.所以AD⊥平面PBG,所以AD⊥PB.18. (本题16分)证明:(1)∵AP AB =,AF PB ⊥∴F 分别是PB 的中点 ∵E .F 分别是PA .PB 的中点 ∴EF ∥AB 又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF ∥平面ABC 同理:FG ∥平面ABC又∵EF FG=F, EF .FG ⊆平面ABC ∴平面//EFG 平面ABC (2)∵平面PAB ⊥平面PBC 平面PAB 平面PBC =BC AF ⊆平面PAB AF ⊥PB∴AF ⊥平面PBC 又∵BC ⊆平面PBC ∴AF ⊥BC又∵BC AB ⊥, AB AF=A, AB .AF ⊆平面PAB ∴BC ⊥平面PAB 又∵PA ⊆平面PAB ∴BC ⊥PA19. (本题16分)(1)证明:连接A 1C 1,DC 1,则Q 为A 1C 1的中点 ∴ PQ ∥DC 1且PQ =21 DC 1 ∴ PQ ∥平面DD 1C 1C (2)解:PQ =21DC 1=22 (3)解:∵ PQ ∥DC 1 ∴ PQ 、DC 1与平面AA 1D 1D 所成的角相等∵DC1与平面AA1D1D所成的角为45°∴PQ与平面AA1D1D所成的角为45°20. (本题16分)证明(1)∵E,F分别是AB,BD的中点,∴EF是△ABD的中位线,∴EF∥AD,∵EF⊄面ACD,AD⊂面ACD,∴EF∥面ACD.(2)∵AD⊥BD,EF∥AD,∴EF⊥BD.∵CB=CD,F是BD的中点,∴CF⊥BD.又EF∩CF=F,∴BD⊥面EFC.∵BD⊂面BCD,∴面EFC⊥面BCD.。
全册苏教版高中数学必修2全册同步练习及单元检测含答案

苏教版高中数学必修2 全册同步练习及检测第1章立体几何§1.1空间几何体1.1.1 棱柱、棱锥和棱台1.1.2 圆柱、圆锥、圆台和球【课时目标】认识柱、锥、台、球的结构特征,并能运用这些特征描述现实生活中简单物体的结构.1.一般地,由一个________________沿某一方向平移形成的空间几何体叫做棱柱.平移起止位置的两个面叫做棱柱的________,多边形的边平移所形成的面叫做棱柱的________,两侧面的公共边叫________.2.当棱柱的一个底面__________________时,得到的几何体叫做棱锥(如图所示).3.棱台是棱锥被平行于底面的一个平面所截后,______和________之间的部分.4.将________、________________、______________分别绕着它的________、______________、____________________所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥、圆台,这条直线叫做______,垂直于轴的边旋转而成的圆面叫做________,不垂直于轴的边旋转而成的曲面叫做________,无论旋转到什么位置,这条边都叫做________.5.________绕着它的______所在的直线旋转一周所形成的曲面叫做球面,球面围成的几何体叫做______,简称______.一、填空题1.将梯形沿某一方向平移形成的几何体是________.2.有下列命题:①棱柱的底面一定是多边形;②棱台的底面一定是梯形;③棱柱被平面截成的两部分可以都是棱柱;④棱锥被平面截成的两部分不可能都是棱锥.其中正确命题的序号是________.3.棱台具备的性质是________(填序号).①两底面相似;②侧面都是梯形;③侧棱都相等;④侧棱延长后都交于一点.4.下列命题中正确的是________(填序号).①有两个面平行,其余各面都是四边形的几何体叫棱柱;②有两个面平行,其余各面都是平行四边形的几何体叫棱柱;③有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱;④用一个平面去截棱锥,底面和截面之间的部分组成的几何体叫棱台.5.以任意方式截一个几何体,各个截面都是圆,则这个几何体一定是________.6.右图所示的几何体是由下列哪个平面图形通过旋转得到的________(填序号).7.下列叙述中错误的是________.(填序号)①以直角三角形的一边为轴旋转所得的旋转体是圆锥;②以直角梯形的一腰为轴旋转所得的旋转体是圆台;③圆柱、圆锥、圆台的底面都是圆;④用一个平面去截圆锥,得到一个圆锥和一个圆台.8.如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是______(填序号).9.在下面的四个平面图形中,哪几个是侧棱都相等的四面体的展开图?其序号是______.二、解答题10.如图所示为长方体ABCD—A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由;如果是,指出底面及侧棱.11.如图所示,已知△ABC,以AB为轴,将△ABC旋转360°.试指出这个旋转体是由怎样的简单几何体构成的?画出这个旋转体的直观图.能力提升12.一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面是下列______图形.(填序号)13.如图,在底面半径为1,高为2的圆柱上A点处有一只蚂蚁,它要围绕圆柱由A 点爬到B点,问蚂蚁爬行的最短距离是多少?1.学习本节知识,要注意结合集合的观点来认识各种几何体的性质,还要注意结合动态直观图从运动变化的观点认识棱柱、棱锥和棱台的关系.2.在讨论旋转体的性质时轴截面具有极其重要的作用,它决定着旋转体的大小、形状,旋转体的有关元素之间的关系可以在轴截面上体现出来.轴截面是将旋转体问题转化为平面问题的关键.3.几何体表面距离最短问题需要把表面展开在同一平面上,然后利用两点间距离的最小值是连结两点的线段长求解.第1章立体几何初步§1.1空间几何体1.1.1棱柱、棱锥和棱台1.1.2圆柱、圆锥、圆台和球答案知识梳理1.平面多边形底面侧面侧棱2.收缩为一个点3.截面底面4.矩形直角三角形直角梯形一边一直角边垂直于底边的腰轴底面侧面母线5.半圆直径球体球作业设计1.四棱柱 2.①③3.①②④解析用棱台的定义去判断.4.③解析①、②的反例图形如图所示,④显然不正确.5.球体 6.①7.①②③④8.(1)(5)解析一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是矩形除去一条边,圆锥的轮廓是三角形除去一条边或抛物线的一部分.9.①②10.解截面BCFE右侧部分是棱柱,因为它满足棱柱的定义.它是三棱柱BEB′—CFC′,其中△BEB′和△CFC′是底面.EF,B′C′,BC是侧棱,截面BCFE左侧部分也是棱柱.它是四棱柱ABEA′—DCFD′.其中四边形ABEA′和四边形DCFD′是底面.A′D′,EF,BC,AD为侧棱.11.解这个旋转体可由一个大圆锥挖去一个同底面的小圆锥而得到,直观图如图所示.12.②13.解把圆柱的侧面沿AB剪开,然后展开成为平面图形——矩形,如图所示,连结AB′,则AB′即为蚂蚁爬行的最短距离.∵AB=A′B′=2,AA′为底面圆的周长,且AA′=2π×1=2π,∴AB′=A′B′2+AA′2=4+(2π)2=21+π2,即蚂蚁爬行的最短距离为21+π2.1.1.3中心投影和平行投影【课时目标】1.了解中心投影和平行投影.2.能画出简单空间图形(柱、锥、台、球及其组合体)的三视图.3.能识别三视图所表示的立体模型.1.平行投影与中心投影的不同之处在于:平行投影的投影线是________,而中心投影的投影线________.2.三视图包括__________、__________和__________,其中几何体的____________和__________高度一样,__________与____________长度一样,__________与__________宽度一样.一、选择题1.人在灯光下走动,当人逐渐远离灯光时,其影子的长度将________.2.两条相交直线的平行投影是________.3.如图所示,下列几何体各自的三视图中,有且仅有两个视图相同的是(填序号)________.4.一个长方体去掉一角的直观图如图所示,关于它的三视图,下列画法正确的是________(填序号).5.某几何体的三视图如图所示,那么这个几何体是________________________________.6.若一个三棱柱的三视图如图所示,则这个三棱柱的高(两底面之间的距离)和底面边长分别是________和________.7.用小正方体搭成一个几何体,如图是它的主视图和左视图,搭成这个几何体的小正方体的个数最多为________个.8.根据如图所示俯视图,找出对应的物体.(1)对应________;(2)对应________;(3)对应________;(4)对应________;(5)对应________.9.如图1所示,E,F分别为正方体的面AD1,BC1的中心,则四边形BFD1E在该正方体的面上的正投影可能是图2中的________.(填上可能的序号)二、解答题10.在下面图形中,图(b)是图(a)中实物画出的主视图和俯视图,你认为正确吗?如果不正确,请找出错误并改正,然后画出左视图(尺寸不作严格要求).11.如图是截去一角的长方体,画出它的三视图.能力提升12.如图,螺栓是棱柱和圆柱的组合体,画出它的三视图.13.用小立方体搭成一个几何体,使它的主视图和俯视图如图所示,搭建这样的几何体,最多要几个小立方体?最少要几个小立方体?在绘制三视图时,要注意以下三点:1.若两相邻物体的表面相交,表面的交线是它们的原分界线,在三视图中,分界线和可见轮廓都用实线画出,不可见轮廓用虚线画出.2.一个物体的三视图的排列规则是:俯视图放在主视图的下面,长度和主视图一样.左视图放在主视图的右面,高度和主视图一样,宽度和俯视图一样,简记为“长对正,高平齐,宽相等”.3.在画物体的三视图时应注意观察角度,角度不同,往往画出的三视图不同.1.1.3中心投影和平行投影答案知识梳理1.平行的交于一点2.主视图左视图俯视图左视图主视图俯视图主视图左视图俯视图作业设计1.变长解析中心投影的性质.2.两条相交直线或一条直线3.②④解析在各自的三视图中①正方体的三个视图都相同;②圆锥有两个视图相同;③三棱台的三个视图都不同;④正四棱锥有两个视图相同.4.① 5.四棱锥6.2 4解析三棱柱的高同左视图的高,左视图的宽度恰为底面正三角形的高,故底边长为4.7.78.(1)D(2)A(3)E(4)C(5)B9.②③解析图②为四边形BFD1E在正方体前后及上下面上的正投影,③为其在左右侧面上的正投影.10.解图(a)是由两个长方体组合而成的,主视图正确,俯视图错误,俯视图应该画出不可见轮廓线(用虚线表示),左视图轮廓是一个矩形,有一条可视的交线(用实线表示),正确画法如图所示.11.解该图形的三视图如图所示.12.解该物体是由一个正六棱柱和一个圆柱组合而成的,主视图反映正六棱柱的三个侧面和圆柱侧面,左视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体投影后是一个正六边形和一个圆(中心重合).它的三视图如图所示.13.解由于主视图中每列的层数即是俯视图中该列的最大数字,因此,用的立方块数最多的情况是每个方框都用该列的最大数字,即如图①所示,此种情况共用小立方块17块.而搭建这样的几何体用方块数最少的情况是每列只要有一个最大的数字,其他方框内的数字可减少到最少的1,即如图②所示,这样的摆法只需小立方块11块.1.1.4直观图画法【课时目标】1.了解斜二测画法的概念.2.会用斜二测画法画出一些简单的平面图形和立体图形的直观图.用斜二测画法画水平放置的平面图形直观图的步骤:(1)在空间图形中取互相________的x轴和y轴,两轴交于O点,再取z轴,使∠xOz =________,且∠yOz=________.(2)画直观图时把它们画成对应的x′轴、y′轴和z′轴,它们相交于O′,并使∠x′O′y′=______(或______),∠x′O′z′=________,x′轴和y′轴所确定的平面表示水平面.(3)已知图形中平行于x轴、y轴或z轴的线段,在直观图中分别画成平行于x′轴、y′轴或z′轴的线段.(4)已知图形中平行于x轴或z轴的线段,在直观图中保持原长度________;平行于y 轴的线段,长度为原来的________.一、填空题1.下列结论:①角的水平放置的直观图一定是角;②相等的角在直观图中仍然相等;③相等的线段在直观图中仍然相等;④两条平行线段在直观图中对应的两条线段仍然平行.其中正确的有__________(填序号).2.具有如图所示直观图的平面图形ABCD的形状是____________.3.如图,正方形O′A′B′C′的边长为1 cm,它是水平放置的一个平面图形的直观图,则原图的周长是________ cm.4.下面每个选项的2个边长为1的正△ABC的直观图不是全等三角形的一组是______(填序号).5.△ABC面积为10,以它的一边为x轴画出直观图,其直观图的面积为________.6.一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于__________.7.利用斜二测画法得到:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形.以上结论,正确的是______________.8.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为____________.9.如图所示,为一个水平放置的正方形ABCO,它在直角坐标系xOy中,点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为______.二、解答题10.如图所示,已知几何体的三视图,用斜二测画法画出它的直观图.11.如图所示,梯形ABCD中,AB∥CD,AB=4 cm,CD=2 cm,∠DAB=30°,AD =3 cm,试画出它的直观图.能力提升12.已知△ABC的平面直观图△A′B′C′是边长为a的正三角形,那么原△ABC的面积为________.13.在水平放置的平面α内有一个边长为1的正方形A′B′C′D′,如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.直观图与原图形的关系1.斜二测画法是联系直观图和原图形的桥梁,可根据它们之间的可逆关系寻找它们的联系;在求直观图的面积时,可根据斜二测画法,画出直观图,从而确定其高和底边等;而求原图形的面积可把直观图还原为原图形;此类题易混淆原图形与直观图中的垂直关系而出错,在原图形中互相垂直的直线在直观图中不一定垂直,反之也是.所以在求面积时应按照斜二测画法的规则把原图形与直观图都画出来,找出改变量与不变量.用斜二测画法画出的水平放置的平面图形的直观图的面积是原图形面积的24倍.2.在用斜二测画法画直观图时,平行线段仍然平行,所画平行线段之比仍然等于它的真实长度之比,但所画夹角大小不一定是其真实夹角大小.1.1.4直观图画法答案知识梳理(1)垂直90°90°(2)45°135°90°(4)不变一半作业设计1.①②⑤解析由斜二测画法的规则判断.2.直角梯形3.8解析根据直观图的画法,原几何图形如图所示,四边形OABC 为平行四边形,OB =22,OA =1,AB =3,从而原图周长为8 cm .4.③ 5.522 解析 设△ABC 面积为S , 则直观图面积S ′=24S =522. 6.2+ 2解析 如图1所示,等腰梯形A ′B ′C ′D ′为水平放置的原平面图形的直观图,作D ′E ′∥A ′B ′交B ′C ′于E ′,由斜二测直观图画法规则,直观图是等腰梯形A ′B ′C ′D ′的原平面图形为如图2所示的直角梯形ABCD ,且AB =2,BC =1+2,AD =1,所以S ABCD =2+2.图1 图27.①②解析 斜二测画法得到的图形与原图形中的线线相交、相对线线平行关系不会改变,因此三角形的直观图是三角形,平行四边形的直观图是平行四边形. 8.2.5解析 由直观图知,原平面图形为直角三角形,且AC =A ′C ′=3,BC =2B ′C ′=4,计算得AB =5,所求中线长为2.5.9.22 解析画出直观图,则B ′到x ′轴的距离为22·12OA =24OA =22.10.解 (1)作出长方体的直观图ABCD -A 1B 1C 1D 1,如图a 所示;(2)再以上底面A 1B 1C 1D 1的对角线交点为原点建立x ′,y ′,z ′轴,如图b 所示,在z ′上取点V ′,使得V ′O ′的长度为棱锥的高,连结V ′A 1,V ′B 1,V ′C 1,V ′D 1,得到四棱锥的直观图,如图b ;(3)擦去辅助线和坐标轴,遮住部分用虚线表示,得到几何体的直观图,如图c .11.解 (1)如图a 所示,在梯形ABCD 中,以边AB 所在的直线为x 轴,点A 为原点,建立平面直角坐标系xOy .如图b 所示,画出对应的x ′轴,y ′轴,使∠x ′O ′y ′=45°. (2)在图a 中,过D 点作DE ⊥x 轴,垂足为E .在x ′轴上取A ′B ′=AB =4 cm ,A ′E ′=AE =323≈2.598 cm ;过点E ′作E ′D ′∥y ′轴,使E ′D ′=12ED ,再过点D ′作D ′C ′∥x ′轴,且使D ′C ′=DC =2 cm .(3)连结A ′D ′、B ′C ′,并擦去x ′轴与y ′轴及其他一些辅助线,如图c 所示,则四边形A ′B ′C ′D ′就是所求作的直观图.12.62a 2解析 画△ABC 直观图如图(1)所示:则A ′D ′=32a ,又∠x ′O ′y ′=45°,∴A ′O ′=62a . 画△ABC 的实际图形,如图(2)所示,AO =2A ′O ′=6a ,BC =B ′C ′=a , ∴S △ABC =12BC·AO =62a 2.13.解四边形ABCD的真实图形如图所示,∵A′C′在水平位置,A′B′C′D′为正方形,∴∠D′A′C′=∠A′C′B′=45°,∴在原四边形ABCD中,DA⊥AC,AC⊥BC,∵DA=2D′A′=2,AC=A′C′=2,∴S四边形ABCD=AC·AD=22.§1.2 点、线、面之间的位置关系1.2.1 平面的基本性质【课时目标】 1.了解平面的概念及表示法.2.了解公理1、2、3及推论1、2、3,并能用文字语言、图形语言和符号语言分别表述.1.公理1:如果一条直线上的________在一个平面内,那么这条直线上所有的点都在这个平面内.用符号表示为:________________.2.公理2:如果________________________________,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的______________.用符号表示为:⎭⎪⎬⎪⎫P ∈αP ∈β⇒α∩β=l 且P ∈l . 3.公理3:经过不在同一条直线上的三点,________________________.公理3也可简单地说成,不共线的三点确定一个平面.(1)推论1 经过________________________________________,有且只有一个平面. (2)推论2 经过____________,有且只有一个平面. (3)推论3 经过____________,有且只有一个平面.一、填空题 1.下列命题: ①书桌面是平面;②8个平面重叠起来,要比6个平面重叠起来厚; ③有一个平面的长是50 m ,宽是20 m ;④平面是绝对的平、无厚度,可以无限延展的抽象数学概念. 其中正确命题的个数为________. 2.若点M 在直线b 上,b 在平面β内,则M 、b 、β之间的关系用符号可记作____________. 3.已知平面α与平面β、γ都相交,则这三个平面可能的交线有________条.4.已知α、β为平面,A 、B 、M 、N 为点,a 为直线,下列推理错误的是__________(填序号).①A ∈a ,A ∈β,B ∈a ,B ∈β⇒a ⊂β;②M ∈α,M ∈β,N ∈α,N ∈β⇒α∩β=MN ; ③A ∈α,A ∈β⇒α∩β=A ;④A 、B 、M ∈α,A 、B 、M ∈β,且A 、B 、M 不共线⇒α、β重合. 5.空间中可以确定一个平面的条件是________.(填序号) ①两条直线; ②一点和一直线; ③一个三角形; ④三个点. 6.空间有四个点,如果其中任意三个点不共线,则经过其中三个点的平面有__________个.7.把下列符号叙述所对应的图形(如图)的序号填在题后横线上.(1)AD/∈α,a ⊂α________.(2)α∩β=a,PD/∈α且PD/∈β________.(3)a⊄α,a∩α=A________.(4)α∩β=a,α∩γ=c,β∩γ=b,a∩b∩c=O________.8.已知α∩β=m,a⊂α,b⊂β,a∩b=A,则直线m与A的位置关系用集合符号表示为________.9.下列四个命题:①两个相交平面有不在同一直线上的三个公共点;②经过空间任意三点有且只有一个平面;③过两平行直线有且只有一个平面;④在空间两两相交的三条直线必共面.其中正确命题的序号是________.二、解答题10.如图,直角梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线,并说明理由.11.如图所示,四边形ABCD中,已知AB∥CD,AB,BC,DC,AD(或延长线)分别与平面α相交于E,F,G,H,求证:E,F,G,H必在同一直线上.能力提升12.空间中三个平面两两相交于三条直线,这三条直线两两不平行,证明三条直线必相交于一点.13.如图,在正方体ABCD -A 1B 1C 1D 1中,对角线A 1C 与平面BDC 1交于点O ,AC 、BD 交于点M ,E 为AB 的中点,F 为AA 1的中点.求证:(1)C 1、O 、M 三点共线; (2)E 、C 、D 1、F 四点共面; (3)CE 、D 1F 、DA 三线共点.1.证明几点共线的方法:先考虑两个平面的交线,再证有关的点都是这两个平面的公共点,或先由某两点作一直线,再证明其他点也在这条直线上.2.证明点线共面的方法:先由有关元素确定一个基本平面,再证其他的点(或线)在这个平面内;或先由部分点线确定平面,再由其他点线确定平面,然后证明这些平面重合.注意对诸如“两平行直线确定一个平面”等依据的证明、记忆与运用.3.证明几线共点的方法:先证两线共点,再证这个点在其他直线上,而“其他”直线往往归结为平面与平面的交线.§1.2 点、线、面之间的位置关系1.2.1 平面的基本性质答案知识梳理1.两点⎭⎪⎬⎪⎫A ∈αB ∈α⇒AB ⊂α 2.两个平面有一个公共点 一条直线 3.有且只有一个平面 (1)一条直线和这条直线外的一点 (2)两条相交直线 (3)两条平行直线作业设计 1.1解析 由平面的概念,它是平滑、无厚度、可无限延展的,可以判断命题④正确,其余的命题都不符合平面的概念,所以命题①、②、③都不正确.2.M∈b⊂β3.1,2或34.③解析∵A∈α,A∈β,∴A∈α∩β.由公理可知α∩β为经过A的一条直线而不是A.故α∩β=A的写法错误.5.③6.1或4解析四点共面时有1个平面,四点不共面时有4个平面.7.(1)C(2)D(3)A(4)B8.A∈m解析因为α∩β=m,A∈a⊂α,所以A∈α,同理A∈β,故A在α与β的交线m上.9.③10.解很明显,点S是平面SBD和平面SAC的一个公共点,即点S在交线上,由于AB>CD,则分别延长AC和BD交于点E,如图所示.∵E∈AC,AC⊂平面SAC,∴E∈平面SAC.同理,可证E∈平面SBD.∴点E在平面SBD和平面SAC的交线上,连结SE,直线SE是平面SBD和平面SAC的交线.11.证明因为AB∥CD,所以AB,CD确定平面AC,AD∩α=H,因为H∈平面AC,H∈α,由公理3可知,H必在平面AC与平面α的交线上.同理F、G、E都在平面AC与平面α的交线上,因此E,F,G,H必在同一直线上.12.证明∵l1⊂β,l2⊂β,l1l2,∴l1∩l2交于一点,记交点为P.∵P∈l1⊂β,P∈l2⊂γ,∴P∈β∩γ=l3,∴l1,l2,l3交于一点.13.证明(1)∵C1、O、M∈平面BDC1,又C1、O、M∈平面A1ACC1,由公理3知,点C1、O、M在平面BDC1与平面A1ACC1的交线上,∴C1、O、M三点共线.(2)∵E,F分别是AB,A1A的中点,∴EF∥A1B.∵A1B∥CD1,∴EF∥CD1.∴E、C、D1、F四点共面.(3)由(2)可知:四点E、C、D1、F共面.又∵EF=12A1B.∴D1F,CE为相交直线,记交点为P.则P∈D1F⊂平面ADD1A1,P∈CE⊂平面ADCB.∴P∈平面ADD1A1∩平面ADCB=AD.∴CE、D1F、DA三线共点.1.2.2空间两条直线的位置关系【课时目标】1.会判断空间两直线的位置关系.2.理解两异面直线的定义及判定定理,会求两异面直线所成的角.3.能用公理4及等角定理解决一些简单的相关证明.1.空间两条直线的位置关系有且只有三种:________、____________、____________.2.公理4:平行于同一条直线的两条直线____________.3.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角________.4.异面直线(1)定义:________________________的两条直线叫做异面直线.(2)判定定理:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是______________.5.异面直线所成的角:直线a,b是异面直线,经过空间任一点O,作直线a′,b′,使__________,__________,我们把a′与b′所成的________________叫做异面直线a与b所成的角.如果两条直线所成的角是________,那么我们就说这两条异面直线互相垂直,两条异面直线所成的角α的取值范围是____________.一、填空题1.若空间两条直线a,b没有公共点,则其位置关系是____________.2.若a和b是异面直线,b和c是异面直线,则a和c的位置关系是______________.3.在正方体ABCD—A1B1C1D1中,与对角线AC1异面的棱共有________条.4.空间四边形的两条对角线相互垂直,顺次连结四边中点的四边形的形状是________.5.给出下列四个命题:①垂直于同一直线的两条直线互相平行;②平行于同一直线的两直线平行;③若直线a,b,c满足a∥b,b⊥c,则a⊥c;④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.其中假命题的个数是________.6.有下列命题:①两条直线和第三条直线成等角,则这两条直线平行;②四条边相等且四个角也相等的四边形是正方形;③经过直线外一点有无数条直线和已知直线垂直;④若∠AOB=∠A1O1B1,且OA∥O1A1,则OB∥O1B1.其中正确命题的序号为________.7.空间两个角α、β,且α与β的两边对应平行且α=60°,则β为________.8.已知正方体ABCD—A′B′C′D′中:(1)BC′与CD′所成的角为________;(2)AD与BC′所成的角为________.9.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论:①AB⊥EF;②AB与CM所成的角为60°;③EF与MN是异面直线;④MN∥CD.以上结论中正确结论的序号为________.二、解答题10.已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD、AD的中点.求证:(1)四边形MNA1C1是梯形;(2)∠DNM=∠D1A1C1.11.如图所示,在空间四边形ABCD中,AB=CD且AB与CD所成的角为30°,E、F 分别是BC、AD的中点,求EF与AB所成角的大小.能力提升12.如图所示,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有________(填序号).13.如图所示,在正方体AC1中,E、F分别是面A1B1C1D1和AA1D1D的中心,则EF 和CD所成的角是______.1.判定两直线的位置关系的依据就在于两直线平行、相交、异面的定义.很多情况下,定义就是一种常用的判定方法.另外,我们解决空间有关线线问题时,不要忘了我们生活中的模型,比如说教室就是一个长方体模型,里面的线线关系非常丰富,我们要好好地利用它,它是我们培养空间想象能力的好工具.2.在研究异面直线所成角的大小时,通常把两条异面直线所成的角转化为两条相交直线所成的角.将空间问题向平面问题转化,这是我们学习立体几何的一条重要的思维途径.需要强调的是,两条异面直线所成角α的范围为0°<α≤90°,解题时经常结合这一点去求异面直线所成的角的大小.作异面直线所成的角,可通过多种方法平移产生,主要有三种方法:①直接平移法(可利用图中已有的平行线);②中位线平移法;③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).1.2.2空间两条直线的位置关系答案知识梳理1.相交直线平行直线异面直线2.互相平行3.相等4.(1)不同在任何一个平面内(2)异面直线5.a′∥a b′∥b锐角(或直角)直角0°<α≤90°作业设计1.平行或异面2.相交、平行或异面解析异面直线不具有传递性,可以以长方体为载体加以说明a、b异面,直线c的位置可如图所示.3.64.矩形解析易证四边形EFGH为平行四边形.又∵E,F分别为AB,BC的中点,∴EF∥AC,又FG∥BD,∴∠EFG或其补角为AC与BD所成的角.而AC与BD所成的角为90°,∴∠EFG=90°,故四边形EFGH为矩形.5.2解析①④均为假命题.①可举反例,如a、b、c三线两两垂直.④如图甲时,c、d与异面直线l1、l2交于四个点,此时c、d异面,一定不会平行;当点A在直线a上运动(其余三点不动),会出现点A与B重合的情形,如图乙所示,此时c、d共面相交.6.③7.60°或120°8.(1)60°(2)45°解析连结BA′,则BA′∥CD′,连结A′C′,则∠A′BC′就是BC′与CD′所成的角.由△A′BC′为正三角形,知∠A′BC′=60°,由AD∥BC,知AD与BC′所成的角就是∠C′BC.易知∠C′BC=45°.9.①③解析把正方体平面展开图还原到原来的正方体,如图所示,AB⊥EF,EF与MN是异面直线,AB∥CM,MN⊥CD,只有①③正确.10.。
苏教版高中数学必修二测试题全套及答案.docx

正确的是( 若若若若帕)a, a, a, a, “〃0, nlB, 刀〃 0, "丄B, a 丄0,则皿丄" a 丄0,则加丄“ a 〃 0,则 m// n a 丄 0,则 m// n 对于A, m 与n 还可能平行或相交或异面;对于C,皿与力还可能相 交或异面;对于D,皿与门还可能相交或异面.答案:B5. (2015 •浙江卷)某几何体的三视图如图所示(单位:cm ),则该几何体的 体积是() /M 2 A. 8 cm 3 B. 12 cm 3 最新苏教版高中数学必修二测试题全套及答案章末过关检测卷(一)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四 个选项中,只有一项是符合题目要求的)1. 已知平面a 和直线Z,则a 内至少有一条宜线与Z ( )A. 平行B.相交C.垂直D.异面解析:无论/在a 内,还是与a 平行或相交,都可在a 内找到一条直线 与Z 垂直.答案:C2. 对两条异面直线a 与〃,必存在平面a ,使得( )C. a± a,方丄 a解析:已知两条异面直线a 和方,可以在直线a 上任取一点力,则朋方.过点 力作直线c//b,则过a, c 确定平面a ,且使得aU a , b// a.答案:B3. 已知直线〃,"和平面a , 0满足m 丄n, ml a , a 丄0 ,贝!]( )A. 77丄 0B. nil B 或 z?u 0C. Z7丄 aD. n// a 或 a解析:在平面B 内作直线/垂直于a, B 的交线,则由a 丄〃得直线/丄a. 又因为皿丄a,所以l//m.若mUB,要满足题中限制条件,显然只能n 〃 a 或 nU a ;同理nflB,仍有n// a 或“Ua.综上所述,D 正确.答案:D4. 已知空间两条不同的直线"和两个不同的平面a , B,则下列命题 A. aU a, bu a B. aU a, b// a侧视图正视图 俯视图解析:该几何体是由一个正方体和一个正四棱锥构成的组合体.下面是棱 长为2 cm 的正方体,体积K=2X2X2=8(cm 3);上面是底面边长为2 cm,高1 O为2 cm 的正四棱锥,体积^=-X2X2X2=-(cm 3),所以该几何体的体积V= %+ %=m (cm 3).答案:C6. (2015 •北京卷)某三棱锥的三视图如图所示,则该三棱锥的表面积是B. 4+^5 D. 5解析:该三棱锥的直观图如图所示,且过点"作加丄EG交%于点仗连 S 表= *Sk 跑 + S^ACD~y S'ABD + 5'A ^=|X 2X2+|X A /5X1+|X A /5X1+|X 2X躬=2+2甫.答案:C7. (2015 •课标全国I 卷)圆柱被一个平面截去一部分后与半球(半径为r) 组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体 的表面积为16+20 or ,则r=( )正视图A. 1B. 2C. 4D. 8 A. 2+萌C. 2 + 2萌 接应则 BC=2, EC=\, AD=\,正视图 侧视图俯视图 俯视图解析:由题意知,2r •2_r+* *2 n r *2r+^ n r+| JT r*4 n r =4r + 5 n r = 16+20",解得 r=2.答案:B8. (2015 •广东卷)若空间中门个不同的点两两距离都相等,则正整数“的 取值()A. 大于5B.等于5C. 至多等于4D.至多等于3解析:当72=3时显然成立,故排除A 、B ;由正四面体的四个顶点,两两距 离相等,得77=4时成立.答案:C9. 如左下图所示,有一个水平放置的透明无盖的正方体容器,容器高8 cm, 将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm, 如果不计容器的厚度,则球的体积为()500 兀 < A. —-—cm'1 372 n , C. cm' 解析:作出该球轴截面的图象,如图所示,依题意BE=2, AE=CE=4, 设DE=x,故AD=2+x,因为肋=力芒+血,解得x=3,故该球的半径血4 , 500 n *=5,所以心§兀用=―-—(cm ).答案:A10. 如图所示,等边三角形力氏的边长为4, M,"分别为ME 的中点, 沿侧将△皿W 折起,使得平面测与平面沟脳所成的二面角为30° ,则四棱 锥力-妣?的体积为( )866 兀, B. ---cm'解析:如图所示,作出二面角力-她的平面角ZAED, A0気厶AED 嵐迪.ED 上的髙,也是四棱锥才廠方的高.由题意,得AO^.答案:A11. 轴截面为正方形的圆柱的侧面积与全面积的比是()A. 1 : 2B. 2 : 3D. 1 : 4 答案:B12. 已知平面a 丄平面J3, a C B = l,在/上取线段仙=4, AC. BD 分 别在平面a 和平面B 内,且ACLAB, DBLAB, AC^3,劭=12,则如的长度为()A. 13B. V151C. 12^3D. 15 答案:D二、填空题(本大题共4小题,每小题5分,共20分.将正确答案填在题 中的横线上) _13. 已知正四棱锥沪必⑦的体积为誓,底面边长为乂§,则以0为球心, OA 为半径的球的表面积为 ______ .解析:设正四棱锥的高为h,则卜(羽)纺=誓,解得高力=享.底面正表面积为4 JI (、荷尸=24 JI. 答案:24 JI14. (2014 •北京卷)某三棱锥的三视图如图所示,则该三棱锥最长棱的棱 长为 • 解析:根据三视图还原几何体,得如图所示的三棱锥严由三视图的形C. 1 : 3方形的对角线长为型X 遍卡,所以创= —\[Q ,所以球的 1正视图 侧视图■^亠俯视图状特征及数据,可推知场丄平面且PA=2.底面为等腰三角形,AB=BC, 设〃为川7中点,AC^2,则AD^DC^X,且勿=1,易得AB=B片电,所以最长的棱为PC,P*g+AC=2返答案:2^215.(2015 •江苏卷)现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为____________ .解析:底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱的总体积为討・52X4+n •22X8=^|JL.设新的圆锥和圆柱的底面半径为r,则扌2, 2 28 兀2 196 皿/-Ji • r • 4+ n • r X8=_~r=_-,解得r=y]l.答案:^716.设甲、乙两个圆柱的底面积分别为S, 体积分别为K, V2,若它们的侧面积相等,且鲁諾,则辛的值是_______ .解析:设甲、乙两个圆柱的底面半径和高分别为益,乙和仏,h2,则 2 n riAi=2 a r2h2,所以^r=~,S x JI H 9 乂犷石TY 所以霁所以匕=王鱼=呂.鱼=宜.空=3V2 n 处力2 d A -d -Ti 2'答案:|三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程及演算步骤)17.(本小题满分10分)(2014 •课标全国II卷)如图所示,四棱锥严力磁中,底面力磁为矩形,刊丄平面力磁,E为刃的中点.B1(1)证明:PB//平両AEC;(2) 设力41, AX 远,三棱锥严砂的体积卩=计,求力到平面磁的距⑴证明:如图所示,设劭与M 的交点为0,连接00.因为四边形仙(刃为 矩形,所以0为勿的中点.又0为刃的中点, 所以 EO//PB.因为EOu 平面AEC,刃□平面AEC, 所以刃〃平面AEC.丹于点圧由题设知方C 丄平面宓,所以牝丄也 故的丄平面PBC.在Rt △加中,由勾股定理可得刃=华,18. (本小题满分12分)如图所示,四棱锥严力磁的底面曲⑦是边长为2 的菱形,Z 磁=60° .已知PB=PX2,场=托.(1) 证明:PCLBD-,(2) 若£为刊的中点,求三棱锥斤磁的体积.(1) 证明:如图所示,连接勿,/C 交于点0. 因为PB=PD,.所以 POLBD.又因为磁"是菱形,所以BDLAC.而牝「化2=0, 所以勿丄面PAC.乐以BDIPC.(2) 解:由(1)知別丄面刊Q(2)解:由 V=~PA • AB* AD= A (3 3 又 片讣,可得AB=2-作初丄刃交所以力到平面磁的距离为蛰3E2由已知得BD=2, AC=2y[3, PO^y^.] ] ] 3所以5^彩=空5\加=空X — X 2寸^ X寸^ —~.19.(本小题满分12分)将圆心角为120°,面积为3兀的扇形,作为圆锥的侧面,求圆锥的表面积和体积.解:设扇形的半径和圆锥的母线都为厶圆锥的底面半径为r,小120 …, 2n则—n 7 =3 Ji , 7=3;—X3 = 2 nr, r=l;S表页积=S侧両+S底页=n r_Z+ n * = 4 n ,心寺協=寺>< n • 1欣2边=冷^“.20.(本小题满分12分)一个几何体按比例绘制出的三视图如图所示(单位:(1)试画出其直观图;(2)求它的体积.解:(1)几何体的直观图如图所示.(2)由直观图知,该几何体可看成底面立起来的四棱柱,其体积为K=|x (1+2) XlXl=-(m3).21.(本小题满分12分)如图所示,四棱锥严力磁中,底面磁?是矩形,以丄底面曲⑦,PA=AB=\,血=萌,点尸是刃的中点,点g在边EC上移动.(1)求三棱锥罗门40的体积; (2)点0为血的中点时,试判断防与平面丹Q 的位置关系,并说明理由; (3)求证:无论点0在牝边的何处,都有丹'丄 (1) 解:因为刃丄底面宓9,所以PALAD,所以三棱锥孚切的体积为V=^S^PAD - ^=|x|x 1 X^/3X 1 =^.(2) 解:当点g 为比的中点时,刃'与平面刃C 平行. 因为在△磁中,E, F 分鈕为BC,丹的中点, 所以肿〃比又历□平面刃C,而PCu 平面场C, 所以防〃平面PAC.(3) 证明:因为以丄平面宓9, BEu 平両ABCD, 所以EBLPA.因为 EBLAB, ABC\AP=A, AB, APu 平面 PAB, 所以场丄平面PAB.又因为AFu 平面PAB,所以〃'丄庞:因为刃=AB=\,点尸是刃的中点,所以AFLPB.因为 PBCBE=B, PB, BEu 平両 PBE, 所以磨丄平面磁因为丹u 平面PBE,所以AFLPE.22. (本小题满分12分)(2014 -广东卷)如图①所示,四边形曲⑦为矩形, PDL 平固ABCD, AB=\, BXP 片2,按图②方式折叠,折痕励//必其中点仗 尸分别在线段刃,PC 匕 沿费折叠后点P 叠在线段血上的点记为必 并且肪 LCF.(1) 证明:CF 丄平面磁';(2) 求三棱锥/宓的体积.(1)证明:如图所示,因为刃丄平面 個⑦,血?U 平面 曲仞,所以PDLAD.又因为曲⑦是矩形,CDIAD,刃与切交于点D, 所以血丄平面PQZ A B 图① A B图②A B又CFu 平面PCD,所以〃丄刖即MDLCF.灭 MFICF, MDCMF=M,所以CF 丄平面DMF.(2)解:固为 PDIDC, BC=2, CD=\, ZPCD=60° , 所以刃=、启,由(1)知月9丄刖 在直角三角形册中,CF=^CD=^.过点尸作略丄如,得 FG=FGsix\ 60° =£><¥=乎, 所以故曲=円=住-¥=誓.所以 MD=^Me-De=1 1 A /3 S ^CDE =~^DE • Dc=~y< 4X1=8,LL 1 1 A /6 A /3 A /2故 V M ~ CDE —~^MD • <Sk«®=§X 2 X & =]6,章末过关检测卷(二)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四 个选项中,只有一项是符合题目要求的)1. 若直线过点(1, 2), (4, 2+书),则此直线的倾斜角是()A. 30°B. 45°C. 60°D. 90° 解析:直线斜率为£+比2=尊故倾斜角为30。
苏教版高中数学必修二试卷.docx

高中数学学习材料鼎尚图文*整理制作江苏省宿迁中学2010-2011学年度第一学期 高一第二次调研测试试题 数 学(满分160分,时间120分钟 命题:贺恒月 审校:彭清峰)一、填空题:(共14题,每题5分共70分。
请把答案填写在答题卡相应的位置上..........) 1.已知集合{}3,1,0,1,3U =--,{}3,0,1A =-,{1,0,1}B =-,则(U C A )B = ▲ 。
2. 函数lg(6)1x y x -=-的定义域是 ▲ 。
3.已知幂函数221(55)m y m m x +=--在(0)+∞,上为减函数,则实数m = ▲ 。
4.设 1.20.320.6,2,log 0.2a b c ===,则c b a 、、的大小关系为 ▲ 。
5. 如图,在正方体ABCD-A 1B 1C 1D 1中,M 、N 分别为棱BC 和棱CC 1的中点,则直线AC 和MN 所成的角的度数是 ▲ 。
6. 如图,在边长为a 的正方体ABCD-A 1B 1C 1D 1中,E 是棱AB 上一点,M 是棱D 1C 1上一点,则三棱锥M-DEC 的体积是 ▲ 。
7. 定义在实数集R 上的奇函数()f x ,当0x <时,2()f x x x =-,则当0x >时,()f x ACD1A 1B 1C 1D MNB(第5题图)D C1A 1B 1C 1D .BAM.(第6题图)的解析式为 ▲ 。
8. 设x 0是方程lg x+x -8=0的解,且0(,1)()x k k k ∈+∈Z ,则k = ▲ 。
9. 函数2121log ()2y x x =++的值域为 ▲ 。
10.已知集合}023|{2=+-=x ax x A ,.若集合A 中至多有一个元素,则实数a 的取值范围是 ▲ 。
11.已知l n m ,,是直线,βα、是平面,下列命题中,正确的命题是 ▲ 。
(填序号) ①若l 垂直于α内两条直线,则α⊥l ; ②若l 平行于α,则α内可有无数条直线与l 平行; ③若m l l m ⊥⊂⊂且,,βα,则βα⊥; ④若m ⊥n ,n ⊥l 则m ∥l ; ⑤若βαβα//,,且⊂⊂l m ,则l m //;12.已知函数8log (3)9a y x =+-(0,1a a >≠)的图像恒过定点A ,若点A 也在函数()3x f x b =+的图像上,则3(log 2)f = ▲ 。
苏教版高中数学必修二单元测试题(共4份).docx
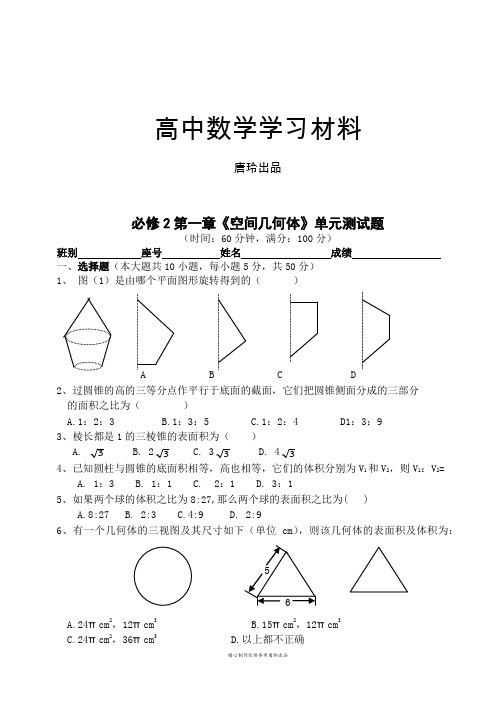
精心制作仅供参考唐玲出品高中数学学习材料唐玲出品必修2第一章《空间几何体》单元测试题(时间:60分钟,满分:100分)班别 座号 姓名 成绩 一、选择题(本大题共10小题,每小题5分,共50分) 1、 图(1)是由哪个平面图形旋转得到的( )A B C D2、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分 的面积之比为( )A.1:2:3B.1:3:5C.1:2:4 D1:3:9 3、棱长都是1的三棱锥的表面积为( )A. 3B. 23C. 33D. 434、已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2=A. 1:3B. 1:1C. 2:1D. 3:15、如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:96、有一个几何体的三视图及其尺寸如下(单位cm ),则该几何体的表面积及体积为:A.24πcm 2,12πcm 3B.15πcm 2,12πcm3C.24πcm 2,36πcm 3D.以上都不正确65精心制作仅供参考唐玲出品7、一个球的外切正方体的全面积等于6 cm 2,则此球的体积为 ( ) A.334cm π B.386cm π C. 361cm π D. 366cm π 8、一个体积为38cm 的正方体的顶点都在球面上,则球的表面积是A .28cm πB .212cm πC .216cm πD .220cm π9、一个正方体的顶点都在球面上,此球与正方体的表面积之比是( ) A. 3π B. 4π C. 2π D. π10、如右图为一个几何体的三视图,其中府视图为 正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为(A)6+3 (B)24+3(C)24+23 (D)32选择题答题表 题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题(本大题共4小题,每小题5分,共20分)11. 长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为_______________. 12.一个半球的全面积为Q ,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 ______.13、球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.14、一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.三、解答题(本大题共3小题,每小题10分,共30分)15.将圆心角为1200,面积为3π的扇形, 16. (如图)在底半径为2母线长为4的 作为圆锥的侧面,求圆锥的表面积和体积. 圆锥中内接一个高为3的圆柱,求圆柱的表面积A B A 1B 1CC 1正视图侧视图 府视图精心制作仅供参考唐玲出品*16、如图,在四边形ABCD 中,,,,,AD=2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.参考答案:1.A ;2.B ;3.A ;4.D ;5.C ;6.A ;7.C ;8.B ;9.C ;10.C.11.15;12.910Q;13.8;14.2:1 15.解:l=3,R=1;S=4π;V=322π.16.R=1,h=3,S=2π+2π3.17.S=60π+4π2;V=52π-38π=3148π.必修2第二章《点、直线、平面之间的位置关系》单元测试题(时间:60分钟,满分:100分)班别座号姓名成绩一、选择题(本大题共10小题,每小题5分,共50分)1.若直线a不平行于平面α,则下列结论成立的是()A. α内所有的直线都与a异面;B. α内不存在与a平行的直线;C. α内所有的直线都与a相交;D.直线a与平面α有公共点.2.已知两个平面垂直,下列命题①一个平面内的已知直线必垂直于另一个平面的任意一条直线;②一个平面内的已知直线必垂直于另一个平面的无数条直线;③一个平面内的任一条直线必垂直于另一个平面;④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面.其中正确的个数是() A.3 B.2 C.1 D.03.空间四边形ABCD中,若AB AD AC CB CD BD=====,则AC与BD所成角为A、09060 D、030 B、045 C、04. 给出下列命题:(1)直线a与平面α不平行,则a与平面α内的所有直线都不平行;(2)直线a与平面α不垂直,则a与平面α内的所有直线都不垂直;(3)异面直线a、b不垂直,则过a的任何平面与b都不垂直;(4)若直线a和b共面,直线b和c共面,则a和c共面其中错误命题的个数为()(A)0 (B) 1 (C)2 (D)35.正方体ABCD-A1B1C1D1中,与对角线AC1异面的棱有()条 A 3 B 4 C 6 D 8精心制作仅供参考唐玲出品精心制作仅供参考唐玲出品6. 点P 为ΔABC 所在平面外一点,PO ⊥平面ABC ,垂足为O ,若PA=PB=PC ,则点O 是ΔABC 的( ) (A )内心 (B )外心 (C )重心 (D )垂心7.如图长方体中,AB=AD=23,CC 1=2,则二面角C 1—BD —C 的大小为( )(A )300 (B )450 (C )600 (D )900 8.直线a,b,c 及平面α,β,γ,下列命题正确的是( )A 、若a ⊂α,b ⊂α,c ⊥a, c ⊥b 则c ⊥αB 、若b ⊂α, a//b 则 a//αC 、若a//α,α∩β=b 则a//bD 、若a ⊥α, b ⊥α 则a//b 9.平面α与平面β平行的条件可以是( )A.α内有无穷多条直线与β平行;B.直线a//α,a//βC.直线a α⊂,直线b β⊂,且a//β,b//αD.α内的任何直线都与β平行 10、 a, b 是异面直线,下面四个命题:①过a 至少有一个平面平行于b ; ②过a 至少有一个平面垂直于b ; ③至多有一条直线与a ,b 都垂直;④至少有一个平面与a ,b 都平行。
(完整word版)苏教版高中数学必修二练习及答案

苏教版高中数学必修二练习及答案一、选择题(每题3分,共54分)1、在直角坐标系中,直线033=-+y x 的倾斜角是( )A .6πB .3π C .65π D .32π 2、若圆C 与圆1)1()2(22=-++y x 关于原点对称,则圆C 的方程是()A .1)1()2(22=++-y x B .1)1()2(22=-+-y x C .1)2()1(22=++-y xD .1)2()1(22=-++y x3、直线0=++c by ax 同时要经过第一、第二、第四象限,则c b a 、、应满足( )A .0,0<>bc abB .0,0<>bc abC .0,0>>bc abD .0,0<<bc ab4、已知直线221:1+=x y l ,直线2l 过点)1,2(-P ,且1l 到2l 的夹角为ο45,则直线2l 的方程是( ) A .1-=x y B .5331+=x y C .73+-=x y D .73+=x y5、不等式062>--y x 表示的平面区域在直线062=--y x 的() A .左上方B .右上方C .左下方D .左下方6、直线0943=--y x 与圆422=+y x 的位置关系是() A .相交且过圆心B .相切C .相离D .相交但不过圆心7、已知直线)0(0≠=++abc c by ax 与圆122=+y x 相切,则三条边长分别为c b a 、、的三角形( )A .是锐角三角形B .是直角三角形C .是钝角三角形D .不存在8、过两点)9,3()1,1(和-的直线在x 轴上的截距是()A .23-B .32-C .52 D .29、点)5,0(到直线x y 2=的距离为()A .25B .5C .23 D .25 10、下列命题中,正确的是()A .点)0,0(在区域0≥+y x 内B .点)0,0(在区域01<++y x 内C .点)0,1(在区域x y 2>内D .点)1,0(在区域01<+-y x 内11、由点)3,1(P 引圆922=+y x 的切线的长是 ()A .2B .19C .1D .412、三直线102,1034,082=-=+=++y x y x y ax 相交于一点,则a 的值是( )A .2-B .1-C .0D .113、已知直线01:,03:21=+-=+y kx l y x l ,若1l 到2l 的夹角为ο60,则k 的值是 ( )A .03或B .03或-C .3D .3-14、如果直线02012=-+=++y x y ax 与直线互相垂直,那么a 的值等于()A .1B .31-C .32-D .2-15、若直线023022=--=++y x y ax 与直线 平行,那么系数a 等于()A .3-B .6-C .23-D .32 16、由422=+=y x x y 和圆所围成的较小图形的面积是() A .4πB .πC .43πD .23π 17、动点在圆122=+y x 上移动时,它与定点)0,3(B 连线的中点的轨迹方程是()A .4)3(22=++y x B .1)3(22=+-y x C .14)32(22=+-y xD .21)23(22=++y x 18、参数方程⎩⎨⎧+-=+=θθsin 33cos 33y x 表示的图形是( ) A .圆心为)3,3(-,半径为9的圆 B .圆心为)3,3(-,半径为3的圆 C .圆心为)3,3(-,半径为9的圆D .圆心为)3,3(-,半径为3的圆二、填空题(每题3分,共15分)19、以点)1,5()3,1(-和为端点的线段的中垂线的方程是 20、过点023)4,3(=+-y x 且与直线平行的直线的方程是 21、直线y x y x 、在0623=+-轴上的截距分别为22、三点)2,5()3,4(32k及),,(-在同一条直线上,则k 的值等于23、若方程014222=+++-+a y x y x 表示的曲线是一个圆,则a 的取值范围是 三、解答题(第24、25两题每题7分,第26题8分,第27题9分,共31分) 24、若圆经过点)2,0(),0,4(),0,2(C B A ,求这个圆的方程。
苏教版高中数学必修二练习及答案

苏教版高中数学必修二练习及答案TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-苏教版高中数学必修二练习及答案一、 选择题(每题3分,共54分)1、在直角坐标系中,直线033=-+y x 的倾斜角是( )A .6πB .3π C .65πD .32π2、若圆C 与圆1)1()2(22=-++y x 关于原点对称,则圆C 的方程是()A .1)1()2(22=++-y xB .1)1()2(22=-+-y xC .1)2()1(22=++-y xD .1)2()1(22=-++y x3、直线0=++c by ax 同时要经过第一、第二、第四象限,则c b a 、、应满足( )A .0,0<>bc abB .0,0<>bc abC .0,0>>bc abD .0,0<<bc ab4、已知直线221:1+=x y l ,直线2l 过点)1,2(-P ,且1l 到2l 的夹角为 45,则直线2l 的方程是() A .1-=x yB .5331+=x yC .73+-=x yD .73+=x y5、不等式062>--y x 表示的平面区域在直线062=--y x 的( ) A .左上方B .右上方C .左下方D .左下方6、直线0943=--y x 与圆422=+y x 的位置关系是( ) A .相交且过圆心 B .相切C .相离D .相交但不过圆心7、已知直线)0(0≠=++abc c by ax 与圆122=+y x 相切,则三条边长分别为c b a 、、的三角形( )A .是锐角三角形B .是直角三角形C .是钝角三角形D .不存在8、过两点)9,3()1,1(和-的直线在x 轴上的截距是()A .23-B .32-C .52D .29、点)5,0(到直线x y 2=的距离为() A .25B .5C .23D .25 10、下列命题中,正确的是( )A .点)0,0(在区域0≥+y x 内B .点)0,0(在区域01<++y x 内C .点)0,1(在区域x y 2>内D .点)1,0(在区域01<+-y x 内 11、由点)3,1(P 引圆922=+y x 的切线的长是 () A .2B .19C .1D .412、三直线102,1034,082=-=+=++y x y x y ax 相交于一点,则a 的值是( ) A .2-B .1-C .0D .113、已知直线01:,03:21=+-=+y kx l y x l ,若1l 到2l 的夹角为 60,则k 的值是 ()A .03或B .03或-C .3D .3-14、如果直线02012=-+=++y x y ax 与直线互相垂直,那么a 的值等于( )A .1B .31-C .32-D .2-15、若直线023022=--=++y x y ax 与直线 平行,那么系数a 等于()A .3-B .6-C .23-D .32 16、由422=+=y x x y 和圆所围成的较小图形的面积是()A .4πB .πC .43πD .23π17、动点在圆122=+y x 上移动时,它与定点)0,3(B 连线的中点的轨迹方程是( )A .4)3(22=++y xB .1)3(22=+-y xC .14)32(22=+-y xD .21)23(22=++y x18、参数方程⎩⎨⎧+-=+=θθsin 33cos 33y x 表示的图形是( )A .圆心为)3,3(-,半径为9的圆B .圆心为)3,3(-,半径为3的圆C .圆心为)3,3(-,半径为9的圆D .圆心为)3,3(-,半径为3的圆二、填空题(每题3分,共15分)19、以点)1,5()3,1(-和为端点的线段的中垂线的方程是 20、过点023)4,3(=+-y x 且与直线平行的直线的方程是 21、直线y x y x 、在0623=+-轴上的截距分别为22、三点)2,5()3,4(32k及),,(-在同一条直线上,则k 的值等于23、若方程014222=+++-+a y x y x 表示的曲线是一个圆,则a 的取值范围是 三、解答题(第24、25两题每题7分,第26题8分,第27题9分,共31分) 24、若圆经过点)2,0(),0,4(),0,2(C B A ,求这个圆的方程。
最新苏教版高中数学必修二模块综合测评及答案解析.docx

(新课标)2018-2019学年苏教版高中数学必修二模块综合测评(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分.请把答案填写在题中横线上)1.下列叙述中不正确的序号是________.①若直线的斜率存在,则必有倾斜角与之对应;②每一条直线都有唯一对应的倾斜角;③与坐标轴垂直的直线的倾斜角为0°或90°;④若直线的倾斜角为α,则直线的斜率为tan α.【解析】当α=90°时,tan α不存在,所以④错误,由直线斜率和倾斜角的知识知①②③正确.【答案】④2.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是________.【解析】如图所示,由V=Sh得,S=4,即正四棱柱底面边长为2.∴A1O1=2,A1O=R= 6.∴S 球=4πR 2=24π. 【答案】 24π3.已知直线l 1:ax +4y -2=0与直线l 2:2x -5y +b =0互相垂直,垂足为(1,c ),则a +b +c 的值为________.【解析】 垂足(1,c )是两直线的交点,且l 1⊥l 2,故-a 4·25=-1,∴a =10.l 1:10x +4y -2=0.将(1,c )代入l 1,得c =-2;将(1,-2)代入l 2,得b =-12.则a +b +c =10+(-12)+(-2)=-4. 【答案】 -44.圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角的度数为________.【解析】 S 底+S 侧=3S 底,2S 底=S 侧,即2πr 2=πrl ,得2r =1. 设侧面展开图的圆心角为θ,则θπl180°=2πr ,∴θ=180°.【答案】 180°5.过点(3,-4)且在两坐标轴上的截距相等的直线的方程是________. 【导学号:60420098】【解析】 当截距均为0时,设方程为y =kx ,将点(3,-4),代入得k =-43,即直线方程为4x +3y =0;当截距不为0时,设方程为x a +ya =1,将点(3,-4)代入得a =-1,即直线方程为x +y +1=0.【答案】 4x +3y =0或x +y +1=06.若x ,y 满足x 2+y 2-2x +4y -20=0,则x 2+y 2的最小值为________.【解析】配方得(x-1)2+(y+2)2=25,圆心坐标为(1,-2),半径r=5,所以x2+y2的最小值为半径减去原点到圆心的距离,即5-5,故可求x2+y2的最小值为30-10 5.【答案】30-10 57.设α,β是两个不同的平面,l是一条直线,以下命题正确的是________.(填序号)①若l⊥α,α⊥β,则l⊂β;②若l∥α,α∥β,则l⊂β;③若l⊥α,α∥β,则l⊥β;④若l∥α,α⊥β,则l⊥β.【解析】当l⊥α,α⊥β时不一定有l⊂β,还有可能l∥β,故①不对;当l∥α,α∥β时,l⊂β或l∥β,故②不对;若α∥β,α内必有两条相交直线m,n与平面β内的两条相交直线m′,n′平行,又l⊥α,则l⊥m,l⊥n,即l⊥m′,l⊥n′,故l⊥β,因此③正确;若l∥α,α⊥β,则l与β相交或l∥β或l⊂β,故④不对.【答案】③8.在正方体ABCDA1B1C1D1中,直线BD1与平面A1B1CD所成角的正切值是________.【解析】连结B1C交BC1于O,则B1C⊥BC1,又A1B1⊥BC1,所以BC1⊥平面A1B1CD,取D1B的中点O1,连结O1O,则∠BO1O就是直线BD1与平面A1B1CD所成的角.不妨设正方体棱长为1,则BD1=3,BO=22,O1O=12,在Rt△BOO1中,tan∠BO1O=BOO1O= 2.【答案】 29.已知直线l:y=x+m(m∈R),若以点M(2,0)为圆心的圆与直线l相切于点P,且点P在y轴上,则该圆的方程为__________.【解析】由题意知P(0,m),又直线l与圆相切于点P,则MP⊥l,且直线l的倾斜角为45°,所以点P的坐标为(0,2),|MP|=22,于是所求圆的方程为(x-2)2+y2=8.【答案】(x-2)2+y2=810.从直线3x+4y+8=0上一点P向圆C:x2+y2-2x-2y+1=0引切线PA,PB,A,B为切点,则四边形PACB的周长的最小值为__________.【解析】圆心到直线的距离为d=|3+4+8|5=3,圆的半径为1,所以四边形PACB的周长的最小值为232-12+2=42+2.【答案】42+211.图1如图1,在正方体ABCDA1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于________.【解析】如图,取A1B1的中点M,连结GM,HM.由题意易知EF∥GM,且△GMH为正三角形.∴异面直线EF与GH所成的角即为GM与GH的夹角∠HGM.而在正三角形GMH中,∠HGM=60°.【答案】60°12.侧棱长为a的正三棱锥PABC的侧面都是直角三角形,且四个顶点都在一个球面上,则该球的表面积为__________.【解析】侧棱长为a的正三棱锥PABC其实就是棱长为a的正方体的一角,所以球的直径就是正方体的对角线,所以球的半径为3a2,该球的表面积为3πa2.【答案】3πa213.若圆x2+y2=4与圆x2+y2+2ay-6=0(a>0)的公共弦的长为23,则a=________.【解析】两圆的方程相减,得公共弦所在的直线方程为(x2+y2+2ay-6)-(x2+y2)=0-4⇒y=1a,又a>0,结合图象(略),再利用半径、弦长的一半及弦心距所构成的直角三角形,可知1a=22-(3)2=1⇒a=1.【答案】 114.(2014·全国卷Ⅱ改编)设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是________.【解析】如图,过点M 作⊙O 的切线,切点为N ,连接ON .M 点的纵坐标为1,MN 与⊙O 相切于点N .设∠OMN =θ,则θ≥45°,即sin θ≥22,即ONOM ≥22.而ON =1,∴OM ≤2.∵M 为(x 0,1),∴x 20+1≤2,∴x 20≤1,∴-1≤x 0≤1,∴x 0的取值范围为[-1,1]. 【答案】 [-1,1]二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)已知两直线l 1:mx +8y +n =0和l 2:2x +my -1=0.试确定m ,n 的值,使(1)l 1∥l 2;(2)l 1⊥l 2,且l 1在y 轴上的截距为-1.【解】 (1)∵l 1∥l 2,∴A 1B 2-A 2B 1=0,且B 1C 2-B 2C 1≠0, 即⎩⎪⎨⎪⎧m ·m -2×8=0,8×(-1)-m ×n ≠0,∴⎩⎪⎨⎪⎧m =4,n ≠-2,或⎩⎪⎨⎪⎧m =-4,n ≠2.(2)由l 1在y 轴上的截距为-1,得m ·0+8×(-1)+n =0,∴n =8. 又l 1⊥l 2,∴A 1A 2+B 1B 2=0, 即m ×2+8m =0,∴m =0. ∴⎩⎪⎨⎪⎧m =0,n =8.16.(本小题满分14分)在三棱柱ABC A 1B 1C 1中,已知平面BB 1C 1C ⊥平面ABC ,AB =AC ,D 是BC 的中点,且B 1D ⊥BC 1.(1)求证:A 1C ∥平面B 1AD ; (2)求证:BC 1⊥平面B 1AD .图2【证明】 (1)如图,连结BA 1交AB 1于点O ,连结OD .由棱柱知侧面AA 1B 1B 为平行四边形,所以O 为BA 1的中点.又D 是BC 的中点,所以OD ∥A 1C .因为A 1C ⊄平面B 1AD ,OD ⊂平面B 1AD ,所以A 1C ∥平面B 1AD . (2)因为D 是BC 的中点,AB =AC ,所以AD ⊥BC .因为平面BB 1C 1C ⊥平面ABC ,平面BB 1C 1C ∩平面ABC =BC ,AD ⊂平面ABC ,所以AD ⊥平面BB 1C 1C .因为BC 1⊂平面BB 1C 1C ,所以AD ⊥BC 1.又BC 1⊥B 1D ,且AD ∩B 1D =D ,所以BC 1⊥平面B 1AD .图317.(本小题满分14分)如图3所示,圆x 2+y 2=8内有一点P (-1,2),AB 为过点P 且倾斜角为α的弦.(1)当α=135°时,求|AB |;(2)当弦AB 被点P 平分时,求直线AB 的方程.【解】 (1)过点O 作OG ⊥AB 于G ,连接OA ,当α=135°时,直线AB 的斜率为-1,故直线AB 的方程为x +y -1=0,∴|OG |=|0+0-1|2=22,∴|GA |=8-12=152=302, ∴|AB |=2|GA |=30.(2)连结OP .当弦AB 被P 平分时,OP ⊥AB ,此时k OP =-2,∴k AB =12,∴直线AB 的方程为y -2=12(x +1),即x -2y +5=0.图418.(本小题满分16分)(2015·安徽高考)如图4,三棱锥P ABC 中,PA ⊥平面ABC ,PA =1,AB =1,AC =2,∠BAC =60°.(1)求三棱锥P ABC 的体积;(2)证明:在线段PC 上存在点M ,使得AC ⊥BM ,并求PM MC的值.【解】 (1)由题设AB =1,AC =2,∠BAC =60°, 可得S △ABC =12·AB ·AC ·sin 60°=32.由PA ⊥平面ABC ,可知PA 是三棱锥P ABC 的高.又PA =1, 所以三棱锥P ABC 的体积V =13·S △ABC ·PA =36.(2)证明:在平面ABC 内,过点B 作BN ⊥AC ,垂足为N .在平面PAC 内,过点N 作MN ∥PA 交PC 于点M ,连接BM .由PA ⊥平面ABC 知PA ⊥AC ,所以MN ⊥AC . 由于BN ∩MN =N ,故AC ⊥平面MBN . 又BM ⊂平面MBN ,所以AC ⊥BM .在直角△BAN 中,AN =AB ·cos ∠BAC =12,从而NC=AC-AN=32.由MN∥PA,得PMMC=ANNC=13.19.(本小题满分16分)(2014·全国卷Ⅰ)已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.(1)求M的轨迹方程;(2)当|OP|=|OM|时,求l的方程及△POM的面积.【解】(1)圆C的方程可化为x2+(y-4)2=16,所以圆心为C(0,4),半径为4.设M(x,y),则CM→=(x,y-4),MP→=(2-x,2-y).由题设知CM→·MP→=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.(2)由(1)可知M的轨迹是以点N(1,3)为圆心,2为半径的圆.由于|OP|=|OM|,故O在线段PM的垂直平分线上.又P在圆N上,从而ON⊥PM.因为ON的斜率为3,所以l的斜率为-1 3,故l的方程为y=-13x+83.又|OM|=|OP|=22,O到l的距离为4105,|PM|=4105,所以△POM的面积为165. 20.(本小题满分16分)如图5(1),在边长为1的等边三角形ABC 中,D ,E 分别是AB ,AC 上的点,AD =AE ,F 是BC 的中点,AF 与DE 交于点G .将△ABF 沿AF 折起,得到如图5(2)所示的三棱锥A BCF ,其中BC =22.(1) (2)图5(1)证明:DE ∥平面BCF ;(2)证明:CF ⊥平面ABF ;(3)当AD =23时,求三棱锥F DEG 的体积V F DEG . 【解】 (1)证法一:在折叠后的图形中,因为AB =AC ,AD =AE ,所以ADAB =AEAC ,所以DE ∥BC .因为DE ⊄平面BCF ,BC ⊂平面BCF ,所以DE ∥平面BCF .证法二:在折叠前的图形中,因为AB =AC ,AD =AE , 所以AD AB =AE AC ,所以DE ∥BC ,即DG ∥BF ,EG ∥CF .在折叠后的图形中,仍有DG ∥BF ,EG ∥CF .又因为DG ⊄平面BCF ,BF ⊂平面BCF ,所以DG ∥平面BCF ,同理可证EG ∥平面BCF .又DG ∩EG =G ,DG ⊂平面DEG ,EG ⊂平面DEG ,故平面DEG ∥平面BCF .又DE ⊂平面DEG ,所以DE ∥平面BCF .(2)证明:在折叠前的图形中,因为△ABC 为等边三角形,BF =CF , 所以AF ⊥BC ,则在折叠后的图形中,AF ⊥BF ,AF ⊥CF .又BF =CF =12,BC =22, 所以BC 2=BF 2+CF 2,所以BF ⊥CF .又BF ∩AF =F ,BF ⊂平面ABF ,AF ⊂平面ABF ,所以CF ⊥平面ABF .(3)由(1)知,平面DEG ∥平面BCF ,由(2)知AF ⊥BF ,AF ⊥CF ,又BF ∩CF =F ,所以AF ⊥平面BCF ,所以AF ⊥平面DEG ,即GF ⊥平面DEG .在折叠前的图形中,AB =1,BF =CF =12,AF =32. 由AD =23知AD AB =23,又DG ∥BF , 所以DG BF =AG AF =AD AB =23,所以DG=EG=23×12=13,AG=23×32=33,所以FG=AF-AG=3 6.故三棱锥FDEG的体积为V三棱锥F-DEG=13S△DEG·FG=13×12×⎝⎛⎭⎪⎪⎫132×36=3 324.。
苏教版高中数学(必修2)期末测试题(一).docx

苏州市2009-2010学年度第一学期期末调研试题高二数学一、填空题:本大题共14小题,每小题5分,共70分。
1. 抛物线y = 2x 2的焦点坐标是 _________________ein Y2. 已知函数 /■(*) =「-,则 /'(%)= _________________x3. 命题"存在X 。
wR ,2*。
V0”的否定是 ____________________2 24. 双曲线冷—刍= l (a>0, b 〉0)离心率为血,则此双曲线的渐近线方程为 _______________a~ b~5. 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得到这个几何体的P 是Gd 上的任意一点,则直线BM 与OP 所成的角大小为 _________________7.如图所示的等腰直角三角形,表示一个水平放置的平面图形的平面直观图,则这个平面 图形的 面积是 ____________&a,0,y 为不重合的平面,l,m,n 表示直线,下列叙述正确的序号是 _________________ ①若 P & a,Qea ,则 PQua ;②若 AB u a , AB u 0,则 A e (tz n 0)且 B w (a c 0);③若a 〃0且0 〃了,则a // y •,④若/丄,"且也丄”,贝0 /丄“。
9. 若关于“的方程乱+七=1表示的曲线为焦点在x 轴上的椭圆,肌的取值范围 为10. 以椭圆/ +L = 1的焦点为顶点、两顶点为焦点的双曲线标准方程是 ________________211. 将圆x 2 + y 2 =4上所有点的纵坐标保持不变,横坐标变为原来的一半,则所得曲线的 离心率为 ____________ 的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 _______________ (结果用兀表 示)。
12.有一根高为3兀,底面半径为1的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝 您积是 _____________ (结果用71表示)6.如右上图,正方体ABCD- A X B X C X D X ,点M 是人%的中点,点O 是底面ABCD 的中心,13•若kwZ ,则椭圆丄 +丿一= 1的离心率是1 + k 3-k-14.有一只(底面圆半径是2 )装有半杯水的圆柱形透明水杯竖直放在水平桌面上,现将水杯轻轻向一侧倾斜,使得圆柱母线与桌面成60°角,这时杯中水平水面截杯壁所得的椭圆的焦距大小(不考虑杯壁厚度)是 ________________ 解答题:本大题共6小题,共90分.15.(本题满分14分)已知曲线y = |x3+| (1)求曲线在点P (2,4)处的切线方程;(2)求曲线过点P (2,4)的切线方程(3)求斜率为4的曲线的切线方程16.(本题满分14分)如图,已知双曲线二-与=1 (a>0,b>0)其右准线交x轴于点A ,a b双曲线虚轴的下端点为B ,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P ,若点D 满足:2OD^OF + OP(O为原点)且AB =0)(1)求双曲线的离心率;(2)若a = 2,过点B的直线/交双曲线于M、N两点,问在y轴上是否存在定点C ,使CM・CN为常数,若存在,求出C点的坐标,若不存在,请说明理由.17.(本题满分15分)如图,在三棱柱ABC-A^Q中,AB丄BC,BC丄= , E,F分别为线段4G ,£C]的中点。
【金版学案】苏教版高中数学必修2测试模块综合检测卷二含解析

所以 |5k - 1 + 2-2k| k 2+(-1) 2 =10,解得 k= 3. 模块综合检测卷(二)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题 给出的四个选项中,只有一项是符合题目要求的 )1.若PQ 是圆x 2 + y 2= 9的弦,PQ 的中点是M (1, 2),则直线PQ 的方程是()A . x + 2y - 3= 0 C . 2x -y + 4= 0 B . x + 2y -5= 0 D . 2x -y = 02-0 解析:由题意知k oM = = 2, 1 — 0 1 所以k pQ =- 2 所以直线PQ 的方程为: y - 2=- ;(x -1), 即:x + 2y - 5= 0. 答案:B 2.直线I 通过两直线7x + 5y -24= 0和x -y = 0的交点,且点(5, 1)到l 的距离为10,则l 的方程是( ) A . 3x +y + 4= 0 B . 3x -y + 4= 0 C . 3x -y -4= 0 D . x - 3y - 4 = 0 7x + 5y - 24= 0, 解析:由 得交点(2 , 2). lx —y = 0, 设l 的方程为y - 2 = k(x - 2), 即 kx - y + 2- 2k = 0,所以I 的方程为3x —y — 4= 0.答案:C3.在坐标平面xOy 上,到点A(3, 2, 5), B(3, 5, 1)距离相等的点有(B . 2个解析:在坐标平面xOy 内,设点P(x , y , 0),依题意得(x — 3) 1 2 3 4 5+( y — 2) 2 + 25= (x — 3) 2+ (y -5) 2+ 1,1整理得y = — 2 x € R ,所以符合条件的点有无数个.答案:D4 已知直线 I : x + ay — 1 = 0(a € R)是圆 C : x 2 + y 2 — 4x — 2y +1 = 0的对称轴.过点A( — 4, a)作圆C 的一条切线,切点为B,则|AB|=() A . 2 B . 4 2 C . 6 D . 2 10解析:圆C 的标准方程为(x — 2)2 + (y — 1)2= 4,圆心为C(2, 1),半径为r = 2,因此 2 + a 1— 1 = 0, a = — 1,即卩 A( — 4,— 1),|AB|= |AC|2— r 2 =(— 4— 2) 2 +(— 1 — 1) 2— 4 = 6. 答案:C5 已知两点A( — 2, 0), B(0, 2).点C 是圆x 2+ y 2— 2x = 0上任意 一点,则△ ABC 面积的最小值是() A . 3— 2 B . 3+ 2C .不存在D .无数个解析:I AB: x —y+ 2 = 0,圆心(i ,o )到I 的距离d = |32 =3所以AB 边上的高的最小值为迈一1・1 L 1 3 、 L所以 S min = 2X 2 2X 2 —1 = 3— 2. 答案:A 6.若点P( — 4,— 2, 3)关于坐标平面xOy 及y 轴的对称点的坐标 分别是(a , b , c), (e , f , d),则c 与e 的和为() A . 7 B .— 7 C . — 1 D . 1答案:D7. 一个多面体的三视图如左下图所示, 则该多面体的体积为()解析:该几何体是正方体去掉两个角所形成的多面体,如图所示,1 123其体积为 V = 2X 2X 2— 2X 3X 2X 1X 1X 1= 3. A. 23答案:A8.如图所示,在正方体ABCD-A1B1C1D1中,E, F , G, H分别为AA1, AB, BB1, BC的中点,则异面直线EF与GH所成的角等于()j] k a A . 45° B . 60° C . 90° D . 120 解析:如图所示,取A 1B 1的中点M ,连接GM , HM •由题意易知 EF // GM ,且△ GMH 为正三角形.所以异面直线 EF 与GH 所成的角 即为GM 与GH 的夹角/ HGM.而在正三角形 GMH 中/ HGM = 60° ,答案:B9.若曲线 C 1: x 2+ y 2-2x = 0 与曲线 C 2: y(y - mx — m)= 0 有四个 不同的交点,则实数m 的取值范围是(A -」」I 3, 3 丿B (-富J b ,割解析:C i : (x — 1)2 + y 2= 1,C 2: y = 0 或 y = mx +m = m(x +1).如图所示,当m = 0时,C 2: y = 0,此时C i 与C 2显然只有两个交 DL D.——oo Sf3 <3,占;J \\、‘当m z 0时,要满足题意,需圆(x — 1)2 + y 2= 1与直线y = m(x + 1)有两交点,当圆与直线相切时,m =±33 即直线处于两切线之间时满足题意, 贝jvmvO 或 0<m<3.答案:B10.已知实数 x , y 满足 x 2+ y 2 = 4,贝S S = x 2+ y 2 — 6x — 8y + 25 的 最大值和最小值分别为()A . 49, 9B . 7, 3 C. 7, 3 D . 7, 3解析:函数 S = x 2 + y 2 — 6x — 8y + 25 化为(x — 3)2 + (y — 4)2= S ,它是以点C(3, 4)为圆心,半径为 S 的圆,当此圆和已知圆x 2 + y 2= 4外切 和内切时,对应的S 的值即为要求的最小值和最大值.当圆 C 与已知 圆x 2 + y 2 = 4相外切时,对应的S 为最小值,此时两圆圆心距等于两圆 半径之和,即5= S min + 2,求得S min = 9;当圆C 与已知圆X 2+亍=4 相内切时,对应的S 为最大值,此时两圆圆心距等于两圆半径之差,即5= S m ax — 2,求得 S max = 49・答案:A 11.圆 x 2 +『+ 2x — 4y + 1 = 0 关于直线 2ax — by + 2 = 0(a , b € R)C.:-i ,0)解析:圆 x 2+ y 2 + 2x — 4y + 1 = 0 关于直线 2ax — by + 2= 0(a , b € R)对称,则圆心在直线上,求得 a + b = 1, ab = a(1 — a)= — a 2+a =— a —4<4, ab 的取值范围是;—x, 〔故选A.答案:A对称,则ab 的取值范围是(A.) B.12. 已知半径为1的动圆与圆(x—5)2+ (y+ 7)2= 16相切,则动圆圆心的轨迹方程是()A. (x—5)2+ (y+ 7)2= 25B. (x—5)2+ (y+ 7)2= 17或(x —5)2+ (y+ 7)2= 15C. (x—5)2+ (y+ 7)2= 9D. (x—5)2+ (y+ 7)2= 25 或(x—5)2+ (y+ 7)2= 9解析:设动圆圆心为P,已知圆的圆心为A(5,—7),则外切时|PA| =5,内切时|PA|= 3,所以P的轨迹为以A为圆心,3或5为半径的圆,选D.答案:D二、填空题(本大题共4小题,每小题5分,共20分.将正确答案填在题中的横线上)113. 若函数y= ax+ 8与y=—qx+ b的图象关于直线y=x对称,贝H a + b= ______ .解析:直线y= ax+ 8关于y= x对称的直线方程为x= ay+ 8,1所以x=ay+ 8与y= —?x+ b为同一直线,[a= —2,故得所以a+ b= 2.b= 4,答案:214. 圆x2+(y+ 1)2= 3绕直线kx—y— 1 = 0旋转一周所得的几何体的表面积为________ .解析:由题意,圆心为(0,—1),又直线kx—y—1 = 0恒过点(0, —1),所以旋转一周所得的几何体为球,球心即为圆心,球的半径即是圆的半径,所以S= 4n(3)2= 12 n答案:12n15.过点(3, 1)作圆(x—2)2+ (y—2)2= 4的弦,其中最短弦的长为解析:借助圆的几何性质,确定圆的最短弦的位置,利用半径、弦心距及半弦长的关系求弦长.设A(3, 1),易知圆心C(2, 2),半径r= 2,当弦过点A(3, 1)且与|CA|= (2—3) 2+( 2—1) 2= 2.所以半弦长= r2—|CA|2= 4—2= 2.所以最短弦长为2 2.答案:2 216.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于 ___________ cm5.---- —t3172\正视图側视图俯视图解析:由三视图可知该几何体为一个直三棱柱被截去了一个小三棱锥,如图所示.三棱柱的底面为直角三角形,且直角边长分别为3和4,1三棱柱的高为5,故其体积V1 =十3X 4X 5= 30(cm3),小三棱锥的底1 1面与三棱柱的上底面相同,高为3,故其体积V2= 3x2x 3X4X3=6(cm3),所以所求几何体的体积为30— 6 = 24(cm3).答案:24三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程及演算步骤)17.(本小题满分10分)已知两条直线l i: mx+8y+ n= 0和b: 2x+ my— 1 = 0,试确定m, n的值,使:(1)l i与12相交于点(m,—1);(2) h// I2;(3) 11 ± I2,且I1在y轴上的截距为一1.解:⑴因为I1与I2相交于点(m,—1),所以点(m,—1)在h, I2上.将点(m,—1)代入I2,得2m —m— 1 = 0,解得m= 1.又因为m = 1,把(1,—1)代入h,所以n = 7.故m = 1, n= 7.m2—16= 0,(2)要使I1 // I2,则有/八小C、m x (—1)—2n z 0,m= 4, m= —4,解得或ln^ —2 ln^ 2.⑶要使I1丄I2,则有m 2 + 8X m = 0,得m = 0.则h为y= —$,由于h在y轴上的截距为一1,所以一8= —1,即卩n= &故m= 0, n = 8.18.(本小题满分12分)有一块扇形铁皮OAB,/AOB= 60° OA =72 cm,要剪下来一个扇环形ABCD,作圆台容器的侧面,并且在余下的扇形OCD 内能剪下一块与其相切的圆形使它恰好作圆台容器的下底面(大底面).(1) AD应取多长?(2) 容器的容积为多大?解:(1)如图①和图②所示,设圆台上、下底面半径分别为r, R, AD = x,贝卩OD = 72 —x.60 Xn “ 2K R = 180 了2, 由题意得」 60X n 、 2n = 180 (72 —x ), 72- x = 3R. 所以 R = 12, r = 6, x = 36, 所以 AD = 36 cm. (2)圆台所在圆锥的高H = 722 — R 2 = 12 35, H 圆台的高h = H = 6\巧5,小圆锥的高h = 6侮,19.(本小题满分12分)如图所示,在三棱锥S-ABC 中,平面SAB 丄平面SBC ,AB 丄BC , AS = AB •过A 作AF 丄SB ,垂足为F ,点E , G 分别是棱SA , SC 的中点.求证:(1) 平面EFG //平面 ABC ;(2) BC 丄 SA.证明:(1)因为AS = AB , AF 丄SB , 所以V 容=V 大锥—V 小锥 =3n R 2H — 3 n r 2h ' =504 35 n垂足为F,所以F是SB的中点.又因为E是SA的中点,所以EF // AB.因为EF ?平面ABC, AB?平面ABC,所以EF //平面ABC. 同理EG //平面ABC•又EF A EG = E,所以平面EFG //平面ABC.(2)因为平面SAB丄平面SBC,且交线为SB,又AF?平面SAB,AF丄SB,所以AF丄平面SBC.因为BC?平面SBC,所以AF丄BC.又因为AB丄BC, AF A AB= A, AF?平面SAB, AB?平面SAB. 所以BC丄平面SAB.因为SA?平面SAB,所以BC丄SA.20. (本小题满分12分)已知圆x2+ y2= 4上一定点A(2, 0), B(1, 1)为圆内一点, P, Q 为圆上的动点.(1) 求线段AP 中点的轨迹方程;(2) 若/ PBQ= 90°,求线段PQ中点的轨迹方程.解:(1)设AP中点为M(x, y),由中点坐标公式可知,P点坐标为(2x—2, 2y).因为P点在圆x2+ y2= 4上,所以(2x—2)2+ (2y)2= 4.故线段AP中点的轨迹方程为(x—1)2+ y2= 1.(2)设PQ 的中点为N(x, y).在Rt△ PBQ 中,|PN|= |BN|,设O 为坐标原点,连接ON,贝卩ON丄PQ,所以|OP|2=|ON|2+ |PN|2=|ON|2+ |BN|2.所以x2+ y2+ (x—1)2+ (y—1)2= 4.故线段PQ中点的轨迹方程为x2+ y2—x —y—1 = 0.21. (本小题满分12分)如图所示,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB丄BC, AA1= AC = 2, BC= 1, E, F 分别是A1C1, BC 的中点.fl(1)求证:平面ABE丄平面B i BCC i;⑵求证:GF //平面ABE;(3)求三棱锥E-ABC的体积.(1) 证明:在三棱柱ABC-A i B i C i中,BB i丄底面ABC,所以BB i丄AB.又因为AB丄BC,所以AB丄平面B i BCC i.又AB?平面ABE ,所以平面ABE丄平面B i BCC i・(2) 证明:如图所示,取AB的中点G,连接EG, FG.因为E, F分别是A i C i, BC的中点,i所以FG // AC, 且FG = 2AC・因为AC / A i C i,且AC= A i C i,所以FG // EC i,且FG = EC i,所以四边形FGEC i为平行四边形.所以C i F // EG.又因为EG?平面ABE, C i F?平面ABE,所以C i F //平面ABE.(3)解:因为AA i = AC = 2, BC= i, AB丄BC, 所以AB= AC2- BC2= 3・所以三棱锥E-ABC的体积1 11 3 V = 3SS BC • AA i = 3X 2^ 3X 1 X 2= 3 . 22.(本小题满分12分)已知过原点的动直线I 与圆C 1: x2 + y 2- 6x + 5 = 0相交于不同的两点 A , B. (1) 求圆C 1的圆心坐标; (2) 求线段AB 的中点M 的轨迹C 的方程; (3) 是否存在实数k ,使得直线L : y = k(x — 4)与曲线C 只有一个交 点?若存在,求出k 的取值范围;若不存在,说明理由. 解:⑴圆C 1的标准方程为(x — 3)2 + y 2 = 4. 所以圆C 1的圆心坐标为(3, 0). (2)设动直线I 的方程为y = kx. 〔(x —3)2+y =4, 2 2 联立 ?(k 2 + 1)x 2 — 6x + 5= 0, ly = kx 贝卩△= 36— 4(k 2 + 1)X 5>0? k 2v ;・ 设A , B 两点坐标为(%, y)(X 2, y 2), 6 则X 1 + X 2= k 2+1? AB 中点M 的轨迹C 的参数方程为⑶联立 ?(1 + k 2)x 2— (3+ 8k)x + 16k 2=0.y = k (x — 4)令△= (3+ 8k)2— 4(1 + k 2)16k 2 = 0? k = ±又因为轨迹c (即圆弧)的端点3,士 235与点(4,0)决定的直线斜率即轨迹C 的方程为 '3f 2 9 5 L2丿+ y = 4,严3・ x 2— 3x + y 2= 0, 3为¥75所以当直线y= k(x—4)与曲线C只有一个交点时,k的取值范围为L 7,7 丿U、— 4, 4丿。
苏教版高中数学必修二综合测试(一).docx

综合测试(一)一 填空题1.在直角坐标系中,直线01=+y 的倾斜角α的大小是__________弧度. 2.直线0534=+-y x 与直线0568=+-y x 的距离为__________.3.若直线1:(1)3l ax a y +-=与2:(1)(23)2l a x a y -++=互相垂直,则实数a 的值为__________.4.设直线0132=++y x 和圆03222=--+x y x 相交于点,A B ,则弦AB 的垂直平分线 的方程是_________.5.点(4,5)A 关于直线l 的对称点为(2,7)B - 则直线l 的方程为_________. 6.以)9,4(A ,(6,3)B -为直径的圆的方程是________________________ . 7.已知直线5120x y a -+=与圆2220x x y -+=相切,则a 的值为_________. 8.已知直线1)0(022=+≠=++y x abc c by ax 与圆相切,则三条边长分别为||,||,||a b c 的 三角形的形状是____________.9.已知圆C :4)2()(22=-+-y a x (0>a )及直线l :03=+-y x ,当直线l 被C 截得的弦长为32时,则a 的值为_________.10已知线段AB ,(1,9)A ,B 在圆22:(3)(1)16C x y -++=,则AB 中点M 的轨迹方__________.11 . 已知直线L 经过点P(-4,-3),且被圆22(1)(2)25x y +++=截得的弦长为8,则直线L 的方程 是 ;12 .过点(1,2)P 的直线L 把圆22450x y x +--=分成两个弓形,当其中较小弓形面积最小时,直线L 的方程是_________.13 .若方程2222110x y kx y k ++++-=表示的曲线是圆,则实数k 的取值范围是_______. 14.如果过点(1,2)总可以作两条直线和圆2222110x y kx y k ++++-=相切,则实数k 的取值范围是_______________. 二 解答题15.在ABC ∆中,点(1,2),(5,5),(6,2)A B C --y求(1)ABC ∆的面积(2)ABC ∆的外接圆的方程16.已知正方形ABCD 一边CD 所在直线的方程为3130x y +-=,对角线,AC BD 的交点为(1,5)P求(1)正方形ABCD 其它三边所在直线的方程: (2)正方形ABCD 的外接圆方程。
苏教版高中数学必修二练习及答案

苏教版高中数学必修二练习及答案一、选择题(每题3分,共54分)1、在直角坐标系中,直线033=-+y x 的倾斜角是( )A .6πB .3π C .65π D .32π 2、若圆C 与圆1)1()2(22=-++y x 关于原点对称,则圆C 的方程是()A .1)1()2(22=++-y x B .1)1()2(22=-+-y x C .1)2()1(22=++-y xD .1)2()1(22=-++y x3、直线0=++c by ax 同时要经过第一、第二、第四象限,则c b a 、、应满足( )A .0,0<>bc abB .0,0<>bc abC .0,0>>bc abD .0,0<<bc ab4、已知直线221:1+=x y l ,直线2l 过点)1,2(-P ,且1l 到2l 的夹角为ο45,则直线2l 的方程是( ) A .1-=x y B .5331+=x y C .73+-=x y D .73+=x y5、不等式062>--y x 表示的平面区域在直线062=--y x 的() A .左上方B .右上方C .左下方D .左下方6、直线0943=--y x 与圆422=+y x 的位置关系是() A .相交且过圆心B .相切C .相离D .相交但不过圆心7、已知直线)0(0≠=++abc c by ax 与圆122=+y x 相切,则三条边长分别为c b a 、、的三角形( )A .是锐角三角形B .是直角三角形C .是钝角三角形D .不存在8、过两点)9,3()1,1(和-的直线在x 轴上的截距是()A .23-B .32-C .52 D .29、点)5,0(到直线x y 2=的距离为()A .25B .5C .23 D .25 10、下列命题中,正确的是()A .点)0,0(在区域0≥+y x 内B .点)0,0(在区域01<++y x 内C .点)0,1(在区域x y 2>内D .点)1,0(在区域01<+-y x 内11、由点)3,1(P 引圆922=+y x 的切线的长是 ()A .2B .19C .1D .412、三直线102,1034,082=-=+=++y x y x y ax 相交于一点,则a 的值是( )A .2-B .1-C .0D .113、已知直线01:,03:21=+-=+y kx l y x l ,若1l 到2l 的夹角为ο60,则k 的值是 ( )A .03或B .03或-C .3D .3-14、如果直线02012=-+=++y x y ax 与直线互相垂直,那么a 的值等于()A .1B .31-C .32-D .2-15、若直线023022=--=++y x y ax 与直线 平行,那么系数a 等于()A .3-B .6-C .23-D .32 16、由422=+=y x x y 和圆所围成的较小图形的面积是() A .4πB .πC .43πD .23π 17、动点在圆122=+y x 上移动时,它与定点)0,3(B 连线的中点的轨迹方程是()A .4)3(22=++y x B .1)3(22=+-y x C .14)32(22=+-y xD .21)23(22=++y x 18、参数方程⎩⎨⎧+-=+=θθsin 33cos 33y x 表示的图形是( ) A .圆心为)3,3(-,半径为9的圆 B .圆心为)3,3(-,半径为3的圆 C .圆心为)3,3(-,半径为9的圆D .圆心为)3,3(-,半径为3的圆二、填空题(每题3分,共15分)19、以点)1,5()3,1(-和为端点的线段的中垂线的方程是 20、过点023)4,3(=+-y x 且与直线平行的直线的方程是 21、直线y x y x 、在0623=+-轴上的截距分别为22、三点)2,5()3,4(32k 及),,(-在同一条直线上,则k 的值等于23、若方程014222=+++-+a y x y x 表示的曲线是一个圆,则a 的取值范围是 三、解答题(第24、25两题每题7分,第26题8分,第27题9分,共31分) 24、若圆经过点)2,0(),0,4(),0,2(C B A ,求这个圆的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏教版高中数学(必修2)测试试卷及答案一、选择题(每小题5分,共50分,每小题只有一个正确答案) 1、正方体1AC 中,与面ABCD 的对角线AC 异面的棱有(B )A .4条 B.6条 C.8条 D.10条 2、有下列四个命题:1)过三点确定一个平面 2)矩形是平面图形 3)三条直线两两相交则确定一个平面4)两个相交平面把空间分成四个区域,其中错误命题的序号是(B ). (A )1)和2) (B )1)和3) (C )2)和4) (D )2)和3) 3、如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( D ) A .平行 B .相交且垂直C . 异面D .相交成60°4.给出下列关于互不相同的直线l n m ,,和平面βα,的四个命题: ①,,,m A A l m ∉=⊂点αα 则l 与m 不共面;②l 、m 是异面直线,ααα⊥⊥⊥n m n l n m l 则且,,,//,//; ③若m l m l //,//,//,//则βαβα;④若ββαα//,//,,,m l A m l m l 点=⊂⊂ ,则βα// 其中真命题个数是(C )A .1B .2C .3D .45、在直角坐标系中,已知两点(4,2),(1,3)M N -,沿x 轴把直角坐标平面折成直二面角后,,M N 两点的距离为 ( C ) A B C D 6、直线053=+-y x 的倾斜角是(A )(A )30° (B )120° (C )60° (D )150°7.已知直线3430x y +-=与直线6140x my ++=平行,则它们之间的距离是(D )A .1710 B . 175C .8D .2 8.点24P(,)在直线0ax y b ++=上的射影是43Q(,),则a,b 的值依次为( A )DCABA .25,-B .211,-C .152,- D .112,-- 9.过点P(2,1)且被圆C :x 2+y 2-2x +4y =0 截得弦长最长的直线l 的方程是(A ) A .3x -y -5=0B .3x +y -7=0C .x +3y -5=0D .x -3y +5=010.若直线ax+by=1与圆122=+y x 相交,则点P(a,b)与圆的位置关系是( B ) A .在圆上 B .在圆外 C .在圆内 D .不能确定 二、填空题(每小题5分,共6小题30分)11.设点M 是点(2,3,5)N -关于坐标平面xoy 的对称点,则线段MN 的长度等于 ▲ 。
12.设,m 表示两条不同的直线,α表示一个平面,从“//、⊥”中选择适当的符号填入下列空格,使其成立真命题:αα____▲_________m l m l ⇒⎭⎬⎫13.已知圆22:(3)(4)4C x y -+-=,过点A(1,0)与圆C 相切的直线方程为 ▲ . 14.用一张圆弧长等于12π分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于 ▲ 立方分米。
15.已知球内接正方体的表面积为S ,那么球的体积等于 ▲ 16. 正三棱锥P -ABC 侧棱长为a,∠APB=30o,D 、E 分别在PB 、PC 上, 则△ADE 的周长的最小值为 ▲ . 三、解答题(共5大题,共70分)17、(12 分 )写出过两点A(5,0)、B(0,-3) 的直线方程的两点式、点斜式、斜截式、截距式和一般式方程.18、(12 分 )如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗? 请用你的计算数据说明理由.19、本题满分14分如图,圆1O 与圆2O 的半径都是1,1O 2O =4,过动点P 分别作圆1O 、圆2O 的切线PM 、PN (M 、N 分别为切点),使得PN 2PM =,试建立适当的坐标系,并求动点P 的轨迹方程。
1C B1A ACD 1B 20、本题满分12分在长方体ABCD-A 1B 1C 1D 1中,, B 1B=BC=1,(1)求D D 1与平面ABD 1所成角的大小; (2)求面B D 1C 与面A D 1D(3)求AD 的中点M 到平面D 1B C 的距离.21、本题满分12分已知圆C :x 2+y 2-2x+4y -4=0,是否存在斜率为1的直线m ,使以m 被圆C 截得的弦 AB 为直径的圆过原点?若存在,求出直线m 的方程;若不存在,说明理由。
22.(本小题满分14分)如图,正三棱柱111ABC A B C -的底面边长为a ,侧,点D 在棱11A C 上. (1) 若11A D DC =,求证:直线1//BC 平面1AB D ;(2)是否存点D , 使平面1AB D ⊥平面11ABB A ,若存在,请确定点D 的位置,若不存在,请说明理由;(3)请指出点D 的位置,使二面角11A AB D --平面角的正切值的大小为2,并证明你的结论。
参考答案一、选择题1.B .解析:棱AB 、BC 、CD 、AD 、AA 1、CC 1与AC 共面,其余6条棱与AC 异面,故选B 。
2.B .解析:三点共线时不能确定一个平面,故1)不正确;三条直线两两相交,所确定的平面个数为1个或3个,故3)不正确;故选B 。
3. D .解析:将平面展开图还原成立体图形,如下图所示,其中无上底面,连接AC ,易知,△ABC 为等边三角形,∴AB 与CD 相交成600,故选D 4. C .解析:由异面直线判定定理,知①正确; ∵α//l ,过l 作平面a =⋂αγ,∴a l // ∵α//m ,过m 作平面b =⋂αθ,∴b m //m l , 是异面直线,a ∴与b 相交,又α⊥∴⊥⊥∴⊥⊥n b n a n m n l n ,,,, ,故②正确; 由两个平面平行的判定定理知④正确,而两个平行平面中的任意两条直线的位置关系为平行或异面,故③错误。
综上知选C 。
5. C .解析: 沿x 轴把直角坐标平面折成直二面角后,线段MN 可看成长方体的对角线,此长方体的过同一顶点的三条棱长分别为2、3、3,由长方体的对角线公式,得22332222=++=MN ,故选C 。
6. A .解析:直线053=+-y x 的斜率33=k ,设直线的倾斜角为,α则由)180,0[,33tan 00∈=αα,得030=α,故选A 。
7. D .解析: ∵直线3430x y +-=与直线6140x my ++=平行,∴8,463==m m, ∴直线6140x my ++=即为0743=++y x ,∴此两平行直线间的距离243)3(722=+--=d ,故选D 。
8.A .解析:∵431242PQ k -==--,且与直线PQ 垂直的直线为0ax y b ++=,∴直线0ax y b ++=的斜率为12PQk a k =-==-,∴2a =-,而点(4,3)Q 在直线0ax y b ++=上,∴2430b -⨯++=,即5b =.故选A .9.A .解析:过点P(2,1)且被圆C :x 2+y 2-2x +4y =0 截得弦长最长的直线l 必过圆C 的圆心,而圆心C 的坐标为C (1,-2),易求得过P 、C 两点的直线方程为3x -y -5=0,故选A 。
10.B .解析:∵直线ax+by=1与圆122=+y x 相交,∴圆心到直线的距离小于圆的半径,即1,112222>+∴<+b a b a ,即点P 到圆心(0,0)的距离大于圆的半径,∴点P 在圆外,故选B 。
二、填空题11.10 解析:易知,M 点的坐标为(2,-3,-5),所以MN =1012.m m αα//⎫⇒⊥⎬⊥⎭13.1x =或3430x y --=。
解析:过点A (1,0)且直线的斜率存在时,圆22:(3)(4)4C x y -+-=,则过点A(1,0)与圆C 相切的直线方程可设为)1(-=x k y ,即0=--k y kx 。
由圆心到切线的距离等于圆的半径,得43,21432==+--k k k k 得,故此时过点A(1,0)与圆C 相切的直线方程为0343=--y x ,又易知,过点A(1,0)且直线的斜率不存在时,其方程为1=x 也是圆C 的切线。
14.立方分米π96.解析:设此圆锥体模型的底面半径为r ,则6,122==r r ππ,又易知此圆锥体模型的母线长为10,所以此圆锥体模型的高861022=-=h ,因此其体积为ππ96312==h r V 立方分米. 解析: 设球内接正方体的棱长为a ,则6,62Sa S a =∴=。
又球内接正方体的对角线是球的直径,设球的半径为R ,则,42,232S R Sa R =∴==所以球的体积242343ππS S R V ==. 16.a 2解析: 将正三棱锥P -ABC 的侧面展开,得三个相邻的全等的等腰三角形,其顶角为030,腰长为a,要使△ADE 的周长的取得最小值,则A-D-E-A 共线,其长度为a 2 三、解答题17.解析:两点式方程:5)3(00)3(---=---x y ; 点斜式方程:)0(05)3(0)3(----=--x y ,即)0(53)3(-=--x y ; 斜截式方程:305)3(0-⋅---=x y ,即353-⋅=x y ; 截距式方程:135=-+y x ; 一般式方程:01553=--y x . 18.解析:因为)(134434213421333cm R V ≈⨯⨯=⨯=ππ半球 )(2011243131322cm h r V ≈⨯⨯==ππ圆锥因为圆锥半球V V <所以,冰淇淋融化了,不会溢出杯子.19.解析:以1O 2O 的中点O 为原点,1O 2O 所在的直线为x 轴,建立平面直角坐标系,则1O (-2,0),2O (2,0),由已知PN 2PM =,得222PN PM =。
因为两圆的半径均为1,所以)1(212221-=-PO PO 。
设),(y x P ,则]1)2[(21)2(2222-+-=-++y x y x ,即33)6(22=+-y x ,所以所求轨迹方程为33)6(22=+-y x 。
(或031222=+-+x y x )20. 解析:(1)连接A 1D 交AD 1于O ,∵ABCD-A 1B 1C 1D 1为长方体,而B 1B=BC ,则四边形A 1ADD 1为正方形,∴A 1D AD 1,又∵AB 面A 1ADD 1,A 1D ⊂面A 1ADD 1,∴ABA 1D ,∴A 1D面ABD 1,∴DD 1O 是D D 1与平面ABD 1所成角, 2分∵四边形A 1ADD 1为正方形,∴DD 1O=450,则D D 1与平面ABD 1所成角为450.4分(2)连接A 1B ,∵A 1A 面D 1DCC 1,D 1D 、DC ⊂面D 1DCC 1,∴A 1AD 1D 、A 1A DC ,∴DD 1C 是面B D 1C 与面A D 1D 所成二面角的平面角, 6分在直角三角形D 1DC 中,∵DC=,D 1D=B 1B =1,∴DD 1C=600,即DD 1C 是面B D 1C 与面A D 1D 所成的二面角为600. 8分(3)∵AD//BC ,∴AD//面BCD 1,则AD 的中点M 到平面D 1B C 的距离即为A 点到平面D 1B C 的距离,∵BC 面A 1ABB 1,∴面BCD 1A 1面A 1ABB 1,过A 作AH A 1B ,垂足为H ,由AH 面BCD 1A 1可得,AH 即为所求. 10分在直角三角形A 1AB 中,∵,A 1A=B 1B =1,∴A 1B =2,112A A AB AH A B ⋅==, ∴AD 的中点M 到平面D 1B C的距离为2. 12分 (评分说明:第(3)问也可以用等体积法求M 到平面D 1B C 的距离,一样给分) 21. 解析:设这样的直线存在,其方程为y x b =+,它与圆C 的交点设为A 11(,)x y 、B 22(,)x y ,则由222440x y x y y x b ⎧+-+-=⎨=+⎩得2222(1)440x b x b b ++++-=(*),∴12212(1)442x x b b b x x +=-+⎧⎪⎨+-⋅=⎪⎩.∴1212()()y y x b x b =++=21212()x x b x x b +++. 由O A ⊥OB 得12120x x y y +=,∴212122()0x x b x x b +++=,即2244(1)0b b b b b +--++=,2340b b +-=,∴1b =或4b =-.容易验证1b =或4b =-时方程(*)有实根.故存在这样的直线,有两条,其方程是1y x =+或4-=x y 22.(1)证明:连接1A B 交1AB 于E 点,在平行四边形11ABB A 中,有1A E BE =,又11A D DC = ……(2分)1CB1AACD1BENMF∴DE 为11A BC ∆的中位线,从而1//DE BC ,又DE ⊂平面1AB D ,D AB BC 11平面⊄,∴直线1//BC 平面1AB D ; ……(4分) (2)解:假设存在点D ,使平面1AB D ⊥平面11ABB A , 过点D 作1DN AB ⊥于N ,则DN ⊥平面11ABB A ,又过D 作11DM A B ⊥于M ,则DM ⊥平面11ABB A , ……(6分) 而过平面外一点有且仅有一条直线与已知平面垂直,故M 、N 应重合于1B 点,此时应有111DB A B ⊥,故01190A B D ∠=, ……(7分)又点D 在棱11A C 上,故01111160A B D A B C ∠≤∠=,显然矛盾,故不存在这样的点D ,使平面1AB D ⊥平面11ABB A . ……(9分) (3)解:连接MN ,过1A 作11A F AB ⊥于F .由(2)中的作法可知:MND ∠为二面角11A AB D --平面角, ……(10分) 设111A DA C λ=,则1112A M AB λ=,则可得2DM λ=,13A F a =,11)22MN MN A F λλ=-⇒=-, ……(12分)∴6tan 32DM MN θλ===-+-.∴643225λλ-+=⇒=-即点D 在棱11A C 上,且11145A D A C =时, 二面角11A AB D --平面角的正切值的大小为2。
