对向量求导
matlab中diff函数求导的的用法

Matlab中的diff函数是用来求解导数的一个方便而强大的工具。
它可以对向量或矩阵进行导数运算,以便在数学建模和数据分析中进行快速准确的计算。
本文将对Matlab中diff函数的用法进行详细介绍,帮助读者更好地理解和应用这一功能。
一、基本用法1. 对向量求导在Matlab中使用diff函数对向量进行求导,可以直接调用该函数并输入要求导的向量作为参数即可。
例如:```matlabx = linspace(0, 2*pi, 100); 生成一个0到2π的100个点的向量y = sin(x); 计算sin(x)的值dydx = diff(y) ./ diff(x); 对y进行求导```上述代码中,我们首先使用linspace函数生成了一个包含100个点的等间距向量x,然后根据x计算了对应的sin(x)值作为向量y。
我们使用diff函数对向量y进行求导,得到了dydx。
2. 对矩阵求导除了对向量进行求导,diff函数也能够处理矩阵。
在对矩阵进行求导时,需要指定求导的维度,即对行进行求导还是对列进行求导。
例如:```matlabA = [1 2 3; 4 5 6; 7 8 9]; 定义一个3x3的矩阵dAdx = diff(A, 1, 2); 对A的行进行求导dAdy = diff(A, 1, 1); 对A的列进行求导```在上述代码中,我们定义了一个3x3的矩阵A,并分别对其行和列进行了求导运算。
二、高阶导数的计算除了一阶导数外,diff函数还可以用来计算高阶导数。
通过多次调用diff函数,可以得到任意阶的导数。
例如:```matlabx = linspace(0, 2*pi, 100); 生成一个0到2π的100个点的向量y = sin(x); 计算sin(x)的值d2ydx2 = diff(y, 2) ./ diff(x, 2); 对y进行二阶导数运算```在上述代码中,我们通过两次调用diff函数,分别对向量y和x进行了二阶导数的计算,得到了d2ydx2。
简单的求导公式大全

简单的求导公式大全当涉及到求导公式时,需要考虑一元函数和多元函数的情况。
下面是一些常见的求导公式:一元函数的求导公式:1. 常数函数的导数为0,(c)' = 0,其中c为常数。
2. 幂函数的导数,(x^n)' = nx^(n-1),其中n为常数。
3. 指数函数的导数,(e^x)' = e^x。
4. 对数函数的导数,(ln(x))' = 1/x。
5. 三角函数的导数:正弦函数的导数,(sin(x))' = cos(x)。
余弦函数的导数,(cos(x))' = -sin(x)。
正切函数的导数,(tan(x))' = sec^2(x)。
6. 反三角函数的导数:反正弦函数的导数,(arcsin(x))' = 1/√(1-x^2)。
反余弦函数的导数,(arccos(x))' = -1/√(1-x^2)。
反正切函数的导数,(arctan(x))' = 1/(1+x^2)。
多元函数的求导公式:1. 偏导数,对于多元函数f(x1, x2, ..., xn),其关于变量xi的偏导数表示为∂f/∂xi。
2. 多元函数的链式法则,若z=f(g(x)),则dz/dx = (df/dg) (dg/dx)。
3. 多元函数的梯度,对于向量值函数f(x1, x2, ..., xn),其梯度表示为∇f = (∂f/∂x1, ∂f/∂x2, ..., ∂f/∂xn)。
以上只是一些常见的求导公式,实际上还有更复杂的函数和求导规则,如乘积法则、商规则、复合函数求导等。
在具体问题中,可以根据需要使用不同的求导公式来求解。
向量微积分理解向量微积分的概念与计算方法

向量微积分理解向量微积分的概念与计算方法向量微积分是微积分学中的重要分支,是研究向量函数导数、积分、微分方程和曲线、曲面的基础工具。
本文将从向量微积分的概念入手,逐步介绍向量微积分的计算方法。
一、向量微积分的概念向量是具有大小和方向的量,常用箭头表示。
向量微积分则是对向量进行微积分运算的过程,包括求导、求积分等。
在向量微积分中,我们经常用到矢量的点乘和叉乘。
矢量的点乘表示为“·”,计算方法为将两个矢量对应分量相乘后求和。
矢量的叉乘表示为“×”,计算方法为用行列式的形式计算。
利用矢量的点乘,我们可以计算出向量的模长,两个向量的夹角以及向量的投影。
利用矢量的叉乘,我们可以计算出两个向量的乘积向量及其模长。
二、向量的导数在向量微积分中,我们常常需要对向量函数进行求导。
向量函数的导数表示为关于自变量的导数矢量,即函数值在各个自变量分量上的导数。
向量函数的导数计算方法与标量函数的导数类似,只需要对每个分量分别求导即可。
求导的规则包括基本的四则运算法则以及链式法则等。
通过求导,我们可以获得向量函数的切向量,从而研究曲线的切线方向以及曲面的法线方向。
三、向量的积分向量函数的积分表示为函数的定积分对应的矢量。
向量函数的积分可以用于计算曲线以及曲面的面积、体积等物理量。
与求导相反,求积分需要对向量函数的每个分量进行积分。
求积分的规则包括基本的定积分法则以及换元法等。
通过积分,我们可以得到曲线的弧长、曲面的面积以及体积等重要信息。
四、向量微分方程向量微分方程是包含矢量未知函数及其导数的微分方程。
求解向量微分方程的方法主要包括变量分离法、常数变易法、矢量积分因子法等。
通过求解向量微分方程,我们可以得到矢量未知函数的解析表达式,从而研究物理现象以及工程问题。
综上所述,向量微积分是研究向量函数导数、积分、微分方程以及曲线、曲面的基础工具。
通过了解向量微积分的概念和计算方法,我们可以更好地理解和应用微积分学中的向量运算。
矩阵对向量求导

矩阵、向量求导法则(1)行向量对元素求导设 []n Ty y 1=y 是 n 维行向量,x 是元素,则⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂x y xy x n T1y 。
(2)列向量对元素求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m y y 1y 是 m 维列向量,x 是元素,则 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂=∂∂x y x y x m 1y 。
(3)矩阵对元素求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=mn m n y y y y Y1111 是 n m ⨯ 矩阵,x 是元素,则 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂x y xyx y xy x Y mn m n1111。
(4)元素对行向量求导 设 y 是元素,][1q Tx x =x 是 q 维行向量,则⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂=∂∂q T x y x yy 1x 。
(5)元素对列向量求导设 y 是元素,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=p x x 1x 是 p 维列向量,则 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂=∂∂p x y x y y 1x。
(6)元素对矩阵求导设 y 是元素,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=pq p q y x x x X 1111 是 q p ⨯ 矩阵,则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂pq p q x y x yx y x yX y1111。
(7)行向量对列向量求导设 []n Ty y 1=y 是 n 维行向量,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=p x x 1x 是 p 维列向量,则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂p n pn Tx y x yx y x y1111x y。
(8)列向量对行向量求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m y y 1y 是 m 维列向量,][1q Tx x =x 是 q 维行向量,则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂q m mq Tx y x y x y x y1111x y 。
(9)行向量对行向量求导设 []n Ty y 1=y 是 n 维行向量,][1q T x x =x 是 q 维行向量,则⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂=∂∂qTTTT x x y y x y1 。
二次型对列向量求导

二次型对列向量求导
英文回答:
The derivative of a quadratic form with respect to a column vector is a linear transformation. It is given by the following formula:
∇[x^T A x] = 2Ax.
where:
x is a column vector.
A is a symmetric matrix.
The gradient of a quadratic form is a vector that points in the direction of the steepest ascent of the form. It can be used to find the maximum or minimum of a quadratic form.
中文回答:
二次型的对列向量求导。
二次型对列向量的导数是一个线性变换。
其公式如下:
∇[x^T A x] = 2Ax.
其中:
x 是列向量。
A 是对称矩阵。
二次型的梯度是一个指向该形式最陡上升方向的向量。
它可以用来求二次型的最大值或最小值。
求导过程:
设二次型为:
Q(x) = x^T A x.
则其对列向量 x 的偏导数为:
∂Q/∂x_i = 2A_ix.
其中:
A_i 是矩阵 A 的第 i 列。
将所有偏导数按列组成雅可比矩阵,得到:
∇Q(x) = [∂Q/∂x_1, ∂Q/∂x_2, ..., ∂Q/∂x_n] = 2Ax.
因此,二次型对列向量的导数为 2Ax。
导数与函数的向量值函数求导

导数与函数的向量值函数求导导数是微积分中的重要概念,用于描述函数在某一点上的变化率。
而函数的向量值函数则是指函数的输出为向量的情况。
在本文中,我们将探讨导数与函数的向量值函数求导的相关内容。
一、导数的定义导数表示函数在某一点处的变化率,通常记为 f'(x),可以通过极限的方法来定义。
对于实数域上的函数 f(x),其在 x 点处的导数定义如下:f'(x) = lim┬(h→0)〖(f(x+h)-f(x))/h〗二、向量值函数的概念向量值函数是指函数的输出是一个向量。
一般形式为 F(t) = (f₁(t),f₂(t), ..., fₙ(t)),其中 f₁(t)、f₂(t)、...、fₙ(t) 分别是关于 t 的实值函数。
向量值函数可以表示多维空间中的曲线、曲面等几何对象。
三、向量值函数的导数对于向量值函数 F(t) = (f₁(t), f₂(t), ..., fₙ(t)),其导数 F'(t) = (f'₁(t),f'₂(t), ..., f'ₙ(t)) 是一个向量,其中 f'₁(t)、f'₂(t)、...、f'ₙ(t) 分别是f₁(t)、f₂(t)、...、fₙ(t) 的导数。
四、向量值函数的求导方法向量值函数的求导方法与一般函数的求导方法类似,对每个分量分别求导。
例如,对于二维向量值函数 F(t) = (x(t), y(t)),其导数 F'(t) =(x'(t), y'(t)),其中 x'(t)、y'(t) 分别是 x(t)、y(t) 的导数。
五、基本导数规则以下是常用的向量值函数导数规则:1. 常数规则:若 c 是一个常数,则 (cF(t))' = cF'(t)2. 和差规则:若 F(t) 和 G(t) 是两个向量值函数,则 (F(t) ± G(t))' = F'(t) ± G'(t)3. 数乘规则:若 F(t) 是一个向量值函数,c 是一个常数,则 (cF(t))' = cF'(t)4. 函数乘法规则:若 F(t) 和 G(t) 是两个向量值函数,则 (F(t)·G(t))' = F'(t)·G(t) + F(t)·G'(t)5. 向量点积规则:若 F(t) 和 G(t) 是两个向量值函数,则 (F(t)·G(t))' = F'(t)·G(t) + F(t)·G'(t)六、实例分析考虑一个二维向量值函数 F(t) = (t², sin(t)),我们将通过求导来计算其导数。
向量点乘 求导

向量点乘求导
向量点乘求导是指对两个向量进行点乘运算后,对其中一个向量进行求导的过程。
点乘运算的结果是一个标量,因此对其中一个向量求导可以转化为对结果的求导。
根据向量点乘的定义,点乘的结果等于两个向量对应分量相乘后的和,因此可以利用链式法则和求导的基本规则对点乘进行求导。
具体来说,如果有向量
$mathbf{a}=(a_1,a_2,cdots,a_n)$和向量
$mathbf{b}=(b_1,b_2,cdots,b_n)$,则它们的点乘结果可以表示为$mathbf{a}cdot mathbf{b}=a_1 b_1+a_2 b_2+cdots+a_n b_n$。
如果要对向量$mathbf{a}$进行求导,则需要先将点乘转化为函数形式,即$f(mathbf{a})=mathbf{a}cdot mathbf{b}$,然后利用链式法则和求导的基本规则进行求导。
最终的结果是$frac{df}{da_i}=b_i$,即向量$mathbf{b}$中第$i$个分量的值。
- 1 -。
向量范数求导

向量范数求导向量范数是向量的大小或长度的度量方式。
在机器学习和优化领域中,向量范数是一个非常常见的概念。
要想求导向量范数,我们需要了解一些基础知识。
首先,向量的范数有不同的定义方式,其中最常见的是欧几里得范数(也称为L2范数)和曼哈顿范数(也称为L1范数)。
欧几里得范数定义为向量各元素平方和的平方根,即||x||_2 =sqrt(sum(x_i^2)),而曼哈顿范数定义为向量各元素绝对值之和,即||x||_1 = sum(|x_i|)。
对于向量的范数求导,我们需要使用链式法则。
设f(x)是一个标量函数,y=g(x)是一个向量,那么f(g(x))的导数可以表示为:df/dx = (df/dg) * (dg/dx)其中,df/dg是f对向量g的导数,dg/dx是向量g对向量x的导数。
对于欧几里得范数的求导,我们可以先将其展开成平方根形式,即:||x||_2 = sqrt(x^Tx)其中x^T表示x的转置,x^Tx表示x的内积。
我们定义y=x^Tx,则有:||x||_2 = sqrt(y)对y求导,得到:dy/dx = 2x然后再代入链式法则的公式,得到欧几里得范数对向量x的导数: d||x||_2/dx = (1/2) * (1/sqrt(y)) * (dy/dx) = (1/2) *x/||x||_2对于曼哈顿范数的求导,我们可以先将其转化为:||x||_1 = sum(sqrt(x_i^2))然后对每个元素x_i求导,得到:d||x||_1/dx_i = (x_i/|x_i|) * (1/sqrt(x_i^2)) = (x_i/|x_i|) * (1/|x_i|)因为|x_i|取值可能是x_i本身或者-x_i,所以我们可以写成:d||x||_1/dx_i = sign(x_i)其中sign函数表示取x_i的符号。
将每个元素的导数组合起来,得到曼哈顿范数对向量x的导数:d||x||_1/dx = [sign(x_1), sign(x_2), ..., sign(x_n)] 这些是求解向量范数的导数的基本方法。
基本矢量求导

基本矢量求导在向量微积分中,我们经常需要对向量函数进行求导。
基本矢量的求导主要涉及标量函数对矢量的求导以及矢量函数对矢量的求导。
1.标量函数对矢量的求导:假设我们有一个标量函数f(x, y, z) 和一个矢量(\vec{r} = x\hat{i} + y\hat{j} + z\hat{k})。
标量函数对矢量的求导通常指的是梯度。
梯度定义为:(\nabla f = \frac{\partial f}{\partial x}\hat{i} + \frac{\partial f}{\partial y}\hat{j} + \frac{\partial f}{\partial z}\hat{k})这表示函数 f 在点(x, y, z) 处的变化率或斜率。
2.矢量函数对矢量的求导:假设我们有一个矢量函数(\vec{A} = A_x(x, y, z)\hat{i} + A_y(x, y, z)\hat{j} + A_z(x, y, z)\hat{k}) 和另一个矢量(\vec{r} = x\hat{i} + y\hat{j} + z\hat{k})。
矢量函数对矢量的求导通常涉及到雅可比矩阵或全导数矩阵。
雅可比矩阵是一个m×n 矩阵,其中m 和n 是矢量函数和自变量的维数。
对于上述的(\vec{A}) 和(\vec{r}),雅可比矩阵为:(\begin{bmatrix}\frac{\partial A_x}{\partial x} & \frac{\partial A_x}{\partial y} & \frac{\partial A_x}{\partial z} \\frac{\partial A_y}{\partial x} & \frac{\partial A_y}{\partial y} & \frac{\partial A_y}{\partial z} \\frac{\partial A_z}{\partial x} & \frac{\partial A_z}{\partial y} & \frac{\partial A_z}{\partial z} \\end{bmatrix})每一行代表(\vec{A}) 的一个分量对(\vec{r}) 的各个分量的偏导数。
向量值函数及其极值和导数

向量值函数及其极值和导数在高等数学中,向量值函数是函数的一种,它将自变量映射到向量空间中的向量。
向量值函数在物理、工程和计算机图形学等领域中经常被使用,因为它们可以用来描述物体的位置、速度和加速度。
向量值函数的定义向量值函数是一个从实数集合到向量空间的映射,通常可以表示为:$f(t) = \begin{pmatrix} f_1(t) \\ f_2(t) \\ \vdots \\ f_n(t)\end{pmatrix}$其中 $t$ 是自变量, $f_i(t)$ 是 $i$ 维向量的第 $i$ 个分量,$n$ 表示向量的维数。
例如,可以将二维平面上的一条曲线表示为向量值函数:$r(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix}$其中 $x(t)$ 和 $y(t)$ 分别是 $t$ 的函数,表示曲线上每个点的横坐标和纵坐标。
向量值函数的极值类似于标量函数,向量值函数也可以有极值。
但是,向量值函数的极值不是在某个点上取得的,而是在某个时间或区间内取得的。
在一维情况下,一个函数在局部极值的必要条件是它的导数为零或不存在。
同样地,在向量值函数中,它的导数也是一个向量值函数。
只有当这个导数在某个时间或区间内为零或不存在时,原始函数才能取得极值。
一个向量值函数 $f(t) = \begin{pmatrix} f_1(t) \\ f_2(t) \\ \vdots \\ f_n(t) \end{pmatrix}$ 在 $[a, b]$ 区间内取得极大值或极小值的必要条件是 $f'(t) = \begin{pmatrix} f_1'(t) \\ f_2'(t) \\ \vdots \\ f_n'(t)\end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix}$ 或$f'(t)$ 不存在。
导数常用方法

导数常用方法
常用的计算导数的方法有:
1. 使用定义法计算导数:根据导数的定义,对函数求极限得到导数。
2. 使用求导法则计算导数:对于一些常见的函数,可以使用求导法则进行导数计算,如常数乘法法则、幂函数法则、指数函数法则、对数函数法则、三角函数法则等等。
3. 使用积分法计算导数:如果已知一个函数的原函数,可以通过对原函数求导得到导数。
4. 使用链式法则计算导数:对于复合函数,可以使用链式法则对函数求导。
5. 使用隐函数法计算导数:对于隐函数,可以使用隐函数法进行导数计算。
6. 使用参数方程法计算导数:对于参数方程表示的曲线,可以通过对参数方程求导得到曲线的切线斜率。
7. 使用向量法计算导数:对于向量函数,可以对向量函数的每一个分量求导得到导数。
8. 使用导数表求导:可以利用一些常见函数的导数表进行导数计算。
关于向量求导的一些公式

1 单因子幂对向量的导数
定理 1 设 x′ = ( x1 , …, x n ) 是 1 ×n 的变数向量 , a′ = ( a1 , …, a n ) 是 1 ×n 的常数向量 ,则对于任一 自然数 m ∈N ,有 9 ( a′ x) 9x 证明 用归纳法证 ( 1) 当 m = 1 时 9 ( a′ x) 9 ( n = 6 a x ) = ai 9xi 9x i j = i j j 9 ( a′ x) 9 = ( x′ a) = a 9x 9x 上式说明当 m = 1 时 , ( 111) 式成立
证毕 。
2 多因子幂对向量的导数
定理 3 设 x′ = ( x1 , …, x n ) 为 1 ×n 变数向量 , a′ = ( a1 , …, a n ) , b′ = ( b1 , …, bn ) , …, c′ = ( c1 , …,
cn ) 为有限个 1 ×n 常数变量 ,对任一自然数 m ,则有
=
( 212)
9 ( x′ Ax ) 9 ( x′ Bx) m m m ( x′ B x ) …( x′ Cx ) + ( x′ Ax ) ・ 9xi 9xi 9 ( x′ Cx ) 9xi
m
m
…
m m m ( x′ Cx ) + …+ ( x′ Ax ) ( x′ B x) …
= m ( x′ Ax )
k- 2 k- 1 k- 1 k- 1 k- 1 = ( k - 1) ( a′ x) ai ( a′ x ) + ( a′ x) ai = ( k - 1) ( a′ x) ai + ( a′ x) ai = k ( a′ x) ai
9 ( a′ x) k- 1 = k ( a′ x) a ,即当 m = k 时 , ( 111) 式成立 。 9x 综上可知对任一自然数 m ∈N , ( 111) 式成立 于是
向量求导——精选推荐

向量求导1. 矩阵Y对标量x求导:相当于每个元素求导数后转置⼀下,注意M×N矩阵求导后变成N×M了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导:注意与上⾯不同,这次括号内是求偏导,不转置,对N×1向量求导后还是N×1向量 y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'3. ⾏向量Y'对列向量X求导:注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每⼀列对X求偏导,将各列构成⼀个矩阵。
重要结论:dX'/dX = Id(AX)'/dX = A'4. 列向量Y对⾏向量X’求导:转化为⾏向量Y’对列向量X的导数,然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则:注意与标量求导有点不同。
d(UV')/dX = (dU/dX)V' + U(dV'/dX)d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'重要结论:d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = Ad(AX)/dX' = (d(X'A')/dX)' = (A')' = Ad(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X6. 矩阵Y对列向量X求导:将Y对X的每⼀个分量求偏导,构成⼀个超向量。
注意该向量的每⼀个元素都是⼀个矩阵。
矩阵对向量求导
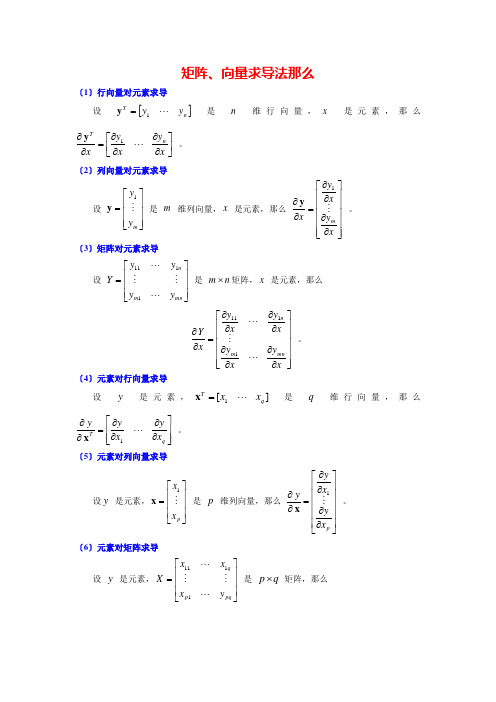
矩阵、向量求导法那么〔1〕行向量对元素求导设 []n Ty y1=y 是 n 维行向量,x 是元素,那么⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂x y x y x n T 1y 。
〔2〕列向量对元素求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m y y 1y 是 m 维列向量,x 是元素,那么 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂=∂∂x y x y x m 1y 。
〔3〕矩阵对元素求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=mn m n y y y y Y 1111 是 n m ⨯矩阵,x 是元素,那么⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂x y x yx y x y x Y mn m n1111。
〔4〕元素对行向量求导 设y 是元素,][1q T x x =x 是 q 维行向量,那么⎥⎥⎦⎤⎢⎢⎣⎡∂∂∂∂=∂∂q Tx y x yy1x 。
〔5〕元素对列向量求导设y 是元素,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=p x x 1x 是 p 维列向量,那么 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂=∂∂p x y x y y 1x 。
〔6〕元素对矩阵求导设 y 是元素,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=pq p q y x x x X1111 是 q p ⨯ 矩阵,那么⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂pq p q x y x yx y x y X y1111。
〔7〕行向量对列向量求导设 []n Ty y1=y 是 n 维行向量,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=p x x 1x 是 p 维列向量,那么⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂p n pn Tx y x yx y x y1111x y。
〔8〕列向量对行向量求导设 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=m y y 1y 是 m 维列向量,][1q Tx x =x 是 q 维行向量,那么⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∂∂q m m q T x y x yx y x y1111x y 。
向量点积求导

向量点积求导
向量点积是矢量分析中的一个重要工具。
在求导的过程中,有一些技巧和注意事项需要掌握。
首先,我们需要知道向量点积的定义:若两个向量a和b的夹角为θ,则它们的点积为a·b=|a||b|cosθ。
其中,|a|和|b|分别表示向量a和b的模长。
接下来,我们来推导一下向量点积的导数。
假设a=a1i+a2j+a3k,b=b1i+b2j+b3k,则a·b=a1b1+a2b2+a3b3。
根据导数的定义,我们有:
(d/dx)(a·b) = (d/dx)(a1b1+a2b2+a3b3)
= a1(d/dx)b1 + b1(d/dx)a1 + a2(d/dx)b2 + b2(d/dx)a2 + a3(d/dx)b3 + b3(d/dx)a3
根据向量的乘法规则,我们可以将上式写成:
(d/dx)(a·b) = (da/dx)·b + a·(db/dx)
其中,·表示向量的点积运算。
这个式子就是求向量点积的导数的公式。
最后,我们需要注意一些求导的技巧。
首先,我们可以利用向量的坐标表达式,将求导的问题转化为常规的求导问题。
其次,我们需要注意向量的模长在求导时也需要考虑。
此外,对于向量函数中的向量点积,我们也可以利用链式法则进行求导。
总之,向量点积的导数是一个比较基础的知识点,但在实际应用中仍然需要注意一些技巧和注意事项。
范数求导公式(一)

范数求导公式(一)范数求导公式1. L1范数求导公式L1范数是向量的绝对值之和,其求导公式如下:∂∂x ||x||1={1, if x>0−1, if x<0undefined, if x=0举例说明:假设有向量x=[−2,3,1],则其L1范数为||x||1= |−2|+|3|+|1|=6。
对于该向量的元素进行求导,得到∂∂x||x||1= [1,1,1]。
2. L2范数求导公式L2范数是向量的平方和的平方根,其求导公式如下:∂∂x ||x||2=x||x||2举例说明:假设有向量x=[3,4],则其L2范数为||x||2=√32+42=5。
对于该向量的元素进行求导,得到∂∂x ||x||2=[3,4]5=[,]。
3. Lp范数求导公式Lp范数是向量元素的绝对值的p次方和的1/p次方,其求导公式如下:∂∂x ||x||p=|x|p−1⋅sign(x)||x||p p−1举例说明:假设有向量x=[−1,2,−3],要求其L3范数的导数。
首先计算L3范数为||x||3=√|−1|3+|2|3+|−3|33=√1+8+273=3。
然后根据Lp范数求导公式,对向量元素进行求导,得到∂∂x ||x||3=[|−1|3−1⋅sign(−1),|2|3−1⋅sign(2),|−3|3−1⋅sign(−3)]32=[−1,4,−9]9。
4. Frobenius范数求导公式Frobenius范数是矩阵元素的绝对值的平方和的平方根,其求导公式如下:∂∂X ||X||F=X||X||F举例说明:假设有矩阵X=[21−34],则其Frobenius范数为||X||F=√22+12+(−3)2+42=√30。
对于该矩阵的元素进行求导,得到∂∂X ||X||F=[21−34]√305. 其他范数求导公式除了常见的L1范数、L2范数、Lp范数和Frobenius范数外,还有其他范数求导公式,如最大值范数、最小值范数等。
向量函数导数

向量函数导数向量函数是一种将实数域映射到向量空间的函数,即对于每个实数t,向量函数f(t)都会返回一个向量。
向量函数是向量微积分、向量微分方程和向量场理论的基础。
在计算机图形学、机器学习和控制理论等领域中经常使用向量函数来描述物理系统。
向量函数的导数也被称为向量值函数的导数,它是描述向量函数在每个点的切线方向和强度的向量。
向量函数的导数在物理学、工程学和自然科学中都有广泛的应用。
一般来说,向量函数f(t)=<f1(t), f2(t), f3(t)>的导数f'(t)被定义为:f'(t) = df1/dt i + df2/dt j + df3/dt k其中,i、j和k是三个互相垂直的单位向量,den/dt代表f关于t的导数。
向量函数的导数具有一些与标量函数的导数类似的性质,如乘法法则、链式法则等。
此外,它还有一些特殊的性质。
例如,向量函数f(t)的定积分可以用来计算其导数:f(t) = ∫f'(t)dt此时,向量函数的导数可以被看作是向量函数的原函数。
这个性质在计算机图形学和数值分析中经常使用。
对于向量函数f(t)的导数,还有一个重要的概念是方向导数。
方向导数是指向量函数在给定方向上的导数。
对于给定的向量v,函数f在点p上沿着v方向的导数可以使用以下公式计算:Dvf(p) = lim(h→0) [f(p + hv)−f(p)]/h其中,Dvf(p)是函数f在点p上沿着v方向的方向导数。
最后,需要注意的是,向量函数的导数不一定是一定存在的。
在某些情况下,向量函数的导数可能不存在或是无限大。
例如,考虑向量函数f(t)=<sin t, cos t>在t=π/2的导数,会发现该导数不存在,因为左导数和右导数的值不同。
总的来说,向量函数的导数是向量微积分中的重要概念。
它不仅有着广泛的应用,还与向量场、物理学、工程学和计算机图形学等领域有着密切的联系。
理解向量函数导数的定义和性质,是学习向量微积分和相关学科的关键。
范数的导数法则

范数的导数法则主要有以下三种:
L1范数(向量的绝对值之和):它的求导公式如下:。
举例说明:假设有向量,则其L1范数为。
对于该向量的元素进行求导,得到。
L2范数(向量的平方和的平方根):其求导公式如下:。
举例说明:假设有向量,则其L2范数为。
对于该向量的元素进行求导,得到。
Lp范数(向量元素的绝对值的p次方和的1/p次方):其求导公式如下:。
举例说明:假设有向量,要求其L3范数的导数。
首先计算L3范数为。
然后根据Lp范数求导公式,对向量元素进行求导,得到。
另外,矩阵范数还可以由向量范数诱导出来,一般称为这种范数为算子范数。
