流体力学 第二章习题解答fx
化工流体力学第二章习题解答精选全文

可编辑修改精选全文完整版习题2-2 一元流动用拉格朗日变数表示x =x (a,t ),p =p(a,t ),试证明:拉格朗日变数表示压力p 的当地变化率为:(,)(,)(,)(,)/p a t p a t x a t x a t t t a t ∂∂∂∂⎡⎤-⎢⎥∂∂∂∂⎣⎦证明:压力的导数为Dp p u p Dt t∂=+•∇∂ p 的当地变化率为p Dp u p t Dt ∂=-•∇∂ 式中:Dp Dt 用拉氏变数表示为(,)p a t t ∂∂ u 用拉氏变数表示为(,)x a t t∂∂ p ∇用拉氏变数表示为(,)p a t a a t ∂∂•∂∂ 所以有:(,)(,)(,)(,)/p p a t p a t x a t x a t t t t a t ∂∂∂∂∂⎡⎤=-⎢⎥∂∂∂∂∂⎣⎦习题2-3已知速度分布,t t x y u y u x e e -==++,求迹线方程。
解:x dx u y dt== 又t t y dy u x e e t -==++∂ 22t t d x dy x e e dt dt-∴==++ 积分可得:()()12121212t t t t t t t t x C e C e te te y C e C e te te ----=++-=+++如果t=0时,质点位置(,)a b ,则可得:12,22a b a bC C +-==2-4解:流线x ydxdyu u dx dy A Bt C∴==+可得:'Cy x C A Bt ∴=++上式为一直线轨线:()223'331(1)2(2)dxA Btdt x At Bt C dyCdt y Ct C y C y t C C C ∴=+=++==+-==+ 式2代入式(1)可得:()()2''3321(3)2y y x A C B C C C C =++++可见轨线为抛物线。
2-5解:Q AU =(1)等截面A=const , Q=const 所以:0x duuua u dt t x ∂∂==+=∂∂(2)变截面 A=A(x), ()x Qu A x ='22'3()()()()()x x u du u a u dt t xQ Q A x A x A x Q A x A x ∂∂==+∂∂⎛⎫=- ⎪⎝⎭=- 2-6解:22222211220.03750.0375d x d y d z a i j k dt dt dtt i t k=++=+ x=8时,t=12.9则加速度为0.1350.135a i k =+2-7解: 双曲正切函数()21tanh tanh 'cosh x xx x e e x x e e x ---==+2=tanh 1cosh UtlU t l θθθ∂=∂令 x x u u a u t x ∂∂=+∂∂其中:222222211cosh 2cosh 11cosh 2cosh u U x U U U t l l l U x U l l θθθθ∂=-∂=- tanh tanh tanh 22x x u U U u U x x l l θθθ∂⎡⎤==•-⎢⎥∂⎣⎦可得加速度计算:2222222211tanh tanh tanh cosh 2cosh 22111(1)22cosh tanh x x u u U x U U U a u U x t x l l l l U x Ut Ut l l l l θθθθθ∂∂⎡⎤=+==--•-⎢⎥∂∂⎣⎦⎡⎤⎢⎥⎢⎥=--⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦(2)当x=L 时,其加速度为 222112cosh 2tanh U a Ut Ut l l l ⎡⎤⎢⎥⎢⎥=-⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦当a=0时,222222222110cosh 2tanh cosh 2tanh cosh cosh 2tanh 2sinh sinh 2Ut Ut l l Ut Ut l l θθθθθ-=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭===或 其中:22sinh 2e e θθθ-⎛⎫-= ⎪⎝⎭(222100=52Ut ln 5e e e l θθθ-+-=±=±解得:所对应时间:(ln 52l t U =± 2-9流体质点的速度与质点到OX 轴的距离成正比,并且与OX 轴平行。
流体力学 第二章 例题与习题答案

R cos
1 2
gR2b sin 2
22366kN
7
8
图示水箱,左端为一半球形端 盖,右端为一平板端盖。水箱 上部有一加水管,已知:
h 600mm, R 150mm。
求两端盖上所受到的总压力大 小及其方向。
右端是平板:
Ar R2
其上总压力
FPr g(h R) Ar 520N
方向垂直于端盖。水平向右。
21
14
习题2-21
15
习题2-24
T ???
hc F2 F1
A b
B
l
hc 2m,l 2m, b 1m, 45
mA(F) 0
F1
l 2
F2
2 3
l
Tl
cos
0
16
习题2-25 h 3m,宽b 2m, h1 6m,h2 4.5m
求:(1)作用在闸门上的总压力; (2)压力中心位置。
yc2
h2 2
,
A
bh
Fp2 gyc2 A2 78480N
作用点:
yD2
yc2
Ic2 yc2 A2
1.33m
将闸门两侧的总压力及绳索拉力对转动轴O取矩:
m0 (F ) 0
可以求出绳索拉力: F 348895.92N
(2)闸门关闭时,绳索上拉力为零,闸板下端支承于A点,有力 Fp作用:将闸板上的力对O点取矩,即可以得到Fp。
左端盖:
FPx g(h R) Ar 520N
由于半球面对称于y轴,故有
FPy 0
Z方向总压力由压力体来求。
V VABCDEA VBCDEB VABEA V 1 4 R3
23
半个球的体积
流体力学三版第2章课后答案

第一章 流体的基本概念1-1 单位换算:1.海水的密度ρ=1028公斤/米3,以达因/厘米3,牛/米3为单位,表示此海水的重度γ值。
解:2.酒精在0℃时的比重为0.807,其密度ρ为若干公斤/米3 ? 若干克/厘米3 ? 其重度γ为若干达因/厘米3 ? 若干牛/米3 ? 解:l-2 粘度的换算:1.石油在50℃时的重度γ=900达因/厘米3,动力粘度μ=58.86×10-4牛.秒/米2。
求此石油的运动粘性系数ν。
解:2.某种液体的比重为1.046,动力粘性系数μ=1.85厘泊,其运动粘性系数为若干斯? 解:3.求在1大气压下,35℃时空气的动力粘性系数μ及运动粘性系3323333w /8.790/7908/8.9/807 0.807g/cm 807kg/m 1000kg/m cm dy m N s m m kg ==⨯===⨯γ酒精√sm s cm cmdy s cm cm s dy g /104.6/1064 /900/)/980101086.58( 26233224--⨯=⨯=⨯⋅⨯==∴γμν)(/017686.0 /1046.1/1085.1 232w 斯比重s cm cmg cm s g =⨯⋅⨯=⨯=∴-ρμν33235/44.1007/4.10074/8.9/1028 101 ; cm dy m N s m m kg dyN g ==⨯=∴==γργ数ν之值。
解:1-3 相距10毫米的两块相互平行的板子,水平放置,板间充满20℃的蓖麻油(动力粘度μ=9.72泊)。
下板固定不动,上板以1.5米/秒的速度移动,问在油中的切应力τ是多少牛/米2? 解:1-4 直径为150毫米的圆柱,固定不动。
内径为151.24毫米的圆筒,同心地套在圆柱之外。
二者的长度均为250毫米。
柱面与筒内壁之间的空隙充以甘油。
转动外筒,每分钟100转,测得转矩为9.091牛米。
假设空隙中甘油的速度按线性分布,也不考虑末端效应。
流体力学课后习题答案第二章

第二章 流体静力学2-1 密闭容器测压管液面高于容器内液面h=1.8m,液体密度为850kg/m3, 求液面压强。
解:08509.8 1.814994Pa p gh ρ==⨯⨯=2-2 密闭水箱,压力表测得压强为4900Pa,压力表中心比A 点高0.4米,A 点在液面下1.5m ,液面压强。
解:0()490010009.8(0.4 1.5) 49009800 1.15880PaM B A p p g h h ρ=+-=+⨯⨯-=-⨯=-2-3 水箱形状如图,底部有4个支座。
试求底面上的总压力和四个支座的支座反力,并讨论总压力和支座反力不相等的原因。
解:底面上总压力(内力,与容器内的反作用力平衡)()10009.81333352.8KN P ghA ρ==⨯⨯+⨯⨯=支座反力支座反力(合外力)3312()10009.8(31)274.4KN G g V V ρ=+=⨯⨯+=2-4盛满水的容器顶口装有活塞A ,直径d=0.4m ,容器底直径D=1.0m ,高h=1.8m 。
如活塞上加力为2520N(包括活塞自重)。
求容器底的压强和总压力。
解:压强2252010009.8 1.837.7kPa (0.4)/4G p gh A ρπ=+=+⨯⨯= 总压力 237.71/429.6KN P p A π=⋅=⨯⋅=2-5多管水银测压计用来测水箱中的表面压强。
图中高程单位为m ,试求水面的绝对压强。
解:对1-1等压面02(3.0 1.4)(2.5 1.4)p g p g ρρ+-=+-汞对3-3等压面 2(2.5 1.2)(2.3 1.2)a p g p g ρρ+-=+-汞将两式相加后整理0(2.3 1.2)(2.5 1.4)(2.5 1.2)(3.0 1.4)264.8kPap g g g g ρρρρ=-+-----=汞汞绝对压强 0.0264.8+98=362.8kPa abs a p p p =+=2-6水管A 、B 两点高差h 1=0.2m ,U 形管压差计中水银液面高差h 2=0.2m 。
流体力学三版第2章课后答案

第一章 流体的基本概念1-1 单位换算:1.海水的密度ρ=1028公斤/米3,以达因/厘米3,牛/米3为单位,表示此海水的重度γ值。
解:2.酒精在0℃时的比重为0.807,其密度ρ为若干公斤/米3 ? 若干克/厘米3 ? 其重度γ为若干达因/厘米3 ? 若干牛/米3 ? 解:l-2 粘度的换算:1.石油在50℃时的重度γ=900达因/厘米3,动力粘度μ=58.86×10-4牛.秒/米2。
求此石油的运动粘性系数ν。
解:2.某种液体的比重为1.046,动力粘性系数μ=1.85厘泊,其运动粘性系数为若干斯? 解:3.求在1大气压下,35℃时空气的动力粘性系数μ及运动粘性系3323333w /8.790/7908/8.9/807 0.807g/cm 807kg/m 1000kg/m cm dy m N s m m kg ==⨯===⨯γ酒精√sm s cm cmdy s cm cm s dy g /104.6/1064 /900/)/980101086.58( 26233224--⨯=⨯=⨯⋅⨯==∴γμν)(/017686.0 /1046.1/1085.1 232w 斯比重s cm cmg cm s g =⨯⋅⨯=⨯=∴-ρμν33235/44.1007/4.10074/8.9/1028 101 ; cm dy m N s m m kg dyN g ==⨯=∴==γργ数ν之值。
解:1-3 相距10毫米的两块相互平行的板子,水平放置,板间充满20℃的蓖麻油(动力粘度μ=9.72泊)。
下板固定不动,上板以1.5米/秒的速度移动,问在油中的切应力τ是多少牛/米2? 解:1-4 直径为150毫米的圆柱,固定不动。
内径为151.24毫米的圆筒,同心地套在圆柱之外。
二者的长度均为250毫米。
柱面与筒内壁之间的空隙充以甘油。
转动外筒,每分钟100转,测得转矩为9.091牛米。
假设空隙中甘油的速度按线性分布,也不考虑末端效应。
流体力学与流体机械第二章重要概念及其重要课后习题及其答案

流体力学第二章作业(流体力学与流体机械)思考题1流体力学的平衡有哪些?共同特点是什么?答:流体的平衡状态有两种,一种是绝对平衡,即重力场的平衡,流体对地球没有相对运动,另一种平衡是相对平衡,即流体相对与运动容器或流体质点相互之间没有相对运动。
这分为匀加速运动,以及流体处于等角速度旋转状态。
处于平衡状态的流体的共性是流体质点之间没有相对运动,流体的黏性作用表现不出来,切向应力等于 0.。
2什么是流体的静压强,试述其特性。
答:流体处于平衡时的压强称为流体的静压强。
他有两个特性:第一是流体的静压强的方向与作用面相互垂直,并指向作用面的内法线方向;第二平衡流体中任意一点处各个方向上作用的静压强大小相等,与作用面的方位无关,只是坐标的函数3什么是等压面,等压面有何性质?答:流体中压强相等的各点组成的平面或曲面称为等压面。
第一等压面也是等势面,第二等压面与质量力垂直,第三两种互不相混的液体平衡时,交界面必是等压面。
4写出流体静力学基本方程,并阐述其物理几何意义?答:物理意义:z+P/pg=单位重量流体的位置势能+单位重量流体的压强势能=常数,该方程式表示静止流体中各点单位重量流体的重势能保持不变。
几何意义:方程式中的 z 表示某一点在基准面以上的高度,P/pg 代表一定的液柱高度,即两者都可以用线段高度表示。
计算题流体力学第二次作业思考题:1什么是面积矩与惯性矩?能否为零?等于零的条件是什么?答:假定某块面积具有均匀的面密度,于是具有均匀的质量分布;对某固定点求该面积的重力的力矩,最后把这个力矩值除以面密度,就得到了面积对该点的面积矩。
惯性矩是物体相对与一个点而言的(围绕旋转的点)惯性矩是物体相对与一个点而言的(围绕旋转的点) 质量M*质心到该点的距离 L,角动惯量=惯性矩*角速度。
惯性矩的数值恒大于零,面积矩可以等于零。
面积矩为零的条件:若截面图形有对称轴,则对于对称轴的面积矩必为零。
2简述压力体的概念及其特性。
吴望一《流体力学》第二章部份习题参考答案

吴望一《流体力学》第二章部份习题参考答案一、基本概念1.连续介质假设适用条件:在研究流体的宏观运动时,如果所研究问题的空间尺度远远大于分子平均间距,例如研究河流、空气流动等;或者在研究流体与其他物体(固体)的相互作用时,物体的尺度要远远大于分子平均间距,例如水绕流桥墩、飞机在空中的飞行(空气绕流飞机)。
若不满足上述要求,连续介质假设不再适用。
如在分析空间飞行器和高层稀薄大气的相互作用时,飞行器尺度与空气分子平均自由程尺度相当。
此时单个分子运动的微观行为对宏观运动有直接的影响,分子运动论才是解决问题的正确方法。
2.(1)不可;(2)可以,因为地球直径远大于稀薄空气分子平均间距,同时与地球发生相互作用的是大量空气分子。
3.流体密度在压强和温度变化时会发生改变,这个性质被称作流体的可压缩性。
流体力学中谈到流体可压缩还是不可压缩一般要结合具体流动。
如果流动过程中,压力和温度变化较小,流体密度的变化可以忽略,就可以认为流体不可压缩。
随高度的增加而减少只能说明密度的空间分布非均匀。
判断流体是否不可压缩要看速度场的散度V ∇⋅ 。
空气上升运动属可压缩流动,小区域内的水平运动一般是不可压缩运动。
4.没有, 没有, 不是。
5 三个式子的物理意义分别是:流体加速度为零;流动是定常的;流动是均匀的。
6 欧拉观点:(),0d r t dt ρ= ,拉格朗日观点:(),,,0a b c t tρ∂=∂ 7 1)0=∇ρ,2)const =ρ,3) 0=∂∂tρ 8 不能。
要想由()t r a , 唯一确定()t r v ,还需要速度场的边界条件和初始条件。
9 物理意义分别为:初始坐标为(,)a b 的质点在任意时刻的速度;任意时刻场内任意点(,)x y 处的速度。
10 1)V s ∂∂ ,3)V V V⋅∇ 11 见讲义。
12 分别是迹线和脉线。
13 两者皆不是。
该曲线可视为从某点流出的质点在某一时刻的位置连线,即脉线。
流体力学习题及答案-第二章

第二章 流体静力学2-1如果地面上空气压力为0.MPa ,求距地面100m 和1000m 高空处的压力。
答:取空气密度为()3/226.1m kg =ρ,并注意到()()Pa a 610MP 1=。
(1)100米高空处:()()()()()()()Pa Pa Pa m s m m kg Pa gh p p 523501000122.11203101325100/81.9/226.11001325.1⨯=-=⨯⨯-⨯=-=ρ(2)1000米高空处:()()()()()()()Pa Pa Pa m s m m kg Pa gh p p 523501089298.0120271013251000/81.9/226.11001325.1⨯=-=⨯⨯-⨯=-=ρ2-2 如果海面压力为一个工程大气压,求潜艇下潜深度为50m 、500m 和5000m 时所承受海水的压力分别为多少?答:取海水密度为()33/10025.1m kg ⨯=ρ,并注意到所求压力为相对压力。
(1)当水深为50米时:()()()()Pa m s m m kg gh p 523310028.550/81.9/10025.1⨯=⨯⨯⨯==ρ。
(2)当水深为500米时:()()()()Pa m s m m kg gh p 623310028.5500/81.9/10025.1⨯=⨯⨯⨯==ρ。
(3)当水深为5000米时:()()()()Pa m s m m kg gh p 723310028.55000/81.9/10025.1⨯=⨯⨯⨯==ρ。
2-3试决定图示装置中A ,B 两点间的压力差。
已知:mm 500h 1=,mm 200h 2=,mm 150h 3=,mm 250h 4=,mm 400h 5=;酒精重度31/7848m N =γ,水银重度32/133400m N =γ,水的重度33/9810m N =γ。
答:设A ,B 两点的压力分别为A p 和B p ,1,2,3,4各个点处的压力分别为1p ,2p ,3p 和4p 。
《流体力学》徐正坦主编课后答案第二章..

第二章习题简答2-1 题2-1图示中的A 、B 点的相对压强各为多少?(单位分别用N/m 2和mH 2O 表示)题2-1图解:()OmH Pa gh P O mH Pa gh p B B A A 2232940038.910005.0490035.38.91000==⨯⨯==-=-=-⨯⨯==ρρ2-2 已知题2-2图中z = 1m , h = 2m ,试求A 点的相对压强。
解:取等压面1-1,则Pagh gz P ghgz P A A 3108.9)21(8.91000⨯-=-⨯⨯=-=-=-ρρρρ2-3 已知水箱真空表M 的读数为0.98kPa ,水箱与油箱的液面差H =1.5m ,水银柱差m 2.02=h ,3m /kg 800=油ρ,求1h 为多少米?解:取等压面1-1,则()()()()()mgh H g P gh h gh gh P h h H g P P Hg Hg a a 6.58.980010002.05.198009802.01332802212121=⨯-+⨯-+⨯=-+-+=++=+++-油油ρρρρρρρ2-4 为了精确测定密度为ρ的液体中A 、B 两点的微小压差,特设计图示微压计。
测定时的各液面差如图示。
试求ρ与ρ'的关系及同一高程上A 、B 两点的压差。
解:如图取等压面1-1,以3-3为基准面,则()a b g gb -=ρρ' (对于a 段空气产生的压力忽略不计)得()⎪⎭⎫ ⎝⎛-=-=b a ba b 1'ρρρ取等压面2-2,则gHbagH gH p p p gHp gH p B A B A ρρρρρ=-=-=∆-=-''2-5 图示密闭容器,压力表的示值为4900N/m 2,压力表中心比A 点高0.4m ,A 点在水面下1.5m,求水面压强。
解:PagH gh P P ghP gH P 5880)5.14.0(9800490000-=-⨯+=-+=+=+ρρρρ2-6 图为倾斜水管上测定压差的装置,已知cm 20=z ,压差计液面之差cm 12=h ,求当(1)31kg/m 920=ρ的油时;(2)1ρ为空气时;A 、B 两点的压差分别为多少?解:(1)取等压面1-1OmH Pa ghgZ gh P P gh gZ P gh P A B B A 21119.092.1865)12.02.0(980012.08.9920==-⨯+⨯⨯=-+=---=-ρρρρρρ(2)同题(1)可得OmH Pa ghgZ P P gZ P gh P A B B A 208.0784)12.02.0(9800==-⨯=-=--=-ρρρρ2-7 已知倾斜微压计的倾角︒=30α,测得0.5m =l ,容器中液面至测压管口高度m 1.0=h ,求压力p 。
【流体力学】流体第二章作业答案

2.2解:欧拉平衡方程是平衡流体中普遍适用的一个基本公式,因为在推导过程中,质量力是空间任意方向,故它既适应于绝对静止,也适于相对静止。
同时推导过程中也不涉及流体的密度是否发生变化,故它不仅适应于不可压缩流体,也适于可压缩流体。
2.5解:(1)表达式:C g p z =+ρ。
(2)物理意义:静止的不可压缩均质重力流体中,任何一点的压强势能和位置势能之和是常数,即总势能保持不变(平衡流体中任意点的总势能(包括位置势能和压强势能)保持不变。
)。
(3)几何意义:在重力作用下的连续均质不可压缩静止流体中,静水头线和计示静水头线均为水平线。
2.9解:(1)绝对压强是以绝对真空为起点,其值恒大于0;相对压强是以当地大气压为起点,其值可正可负,也可为0.相对压强又称计示压强;相对压强小于0时,其数值的绝对值又称真空度。
(2)单位:帕(Pa )、巴(bar )、米水柱(mH 2O)、毫米汞柱(mmHg)2.16解:实压力体:液体与压力体位于曲面的同一侧,方向铅直向下,通常用正体积表示;虚压力体:液体与压力体位于曲面的两侧,方向铅直向上,通常用负体积表示。
2.22解:如图所示1-1、2-2、3-3均为等压面,应用流体静力学法可得:B A p h h g gh gh gh gh p =---+-+)(45143322311ρρρρρ即 32114514323)(gh gh h h g gh gh p p B A ρρρρρ---++=-将各已知数带入,得=-B A p p 67864Pa2.36题2-36 图解:半球盖所受的水平总压力为: )(N 2048.76sin 2==θπρR gh F X半球盖所受的垂向总压力为:(压力体为斜椭圆锥台(虚压力体,方向向上)—半球(实压力体,方向向下)),即:()(N)74.109832cos 32B=⎪⎭⎫ ⎝⎛-=-=R h R g V V g F ABDC CF EA Z πθπρρ则半球所受的中静水压力为:(N)79.232422=+=Z X F F F 合力与水平方向的夹角为:。
《流体力学》课后习题详细解答

1-8解:
或,由 积分得
1-9解:法一:5atm
10atm
=0.537 x 10-9x (10-5) x98.07 x 103= 0.026%
法二: ,积分得
1-10解:水在玻璃管中上升高度
h =
水银在玻璃管中下降的高度
H= mm
第二章流体静力学
2-1解:已知液体所受质量力的x向分量为–a ,z向分量为-g。液体平衡方程为
重心C位于浮心之上,偏心距
沉箱绕长度方向的对称轴y轴倾斜时稳定性最差。浮面面积A=15m2。浮面关于y
轴的惯性矩和体积排量为
定倾半径
可见, >e,定倾中心高于重心,沉箱是稳定的。
第三章流体运动学
3-1解:质点的运动速度
质点的轨迹方程
3-Байду номын сангаас解:
由 和 ,得
故
3-3解:当t=1s时,点A(1,2)处的流速
线速度u = 0r,速度环量
(2)半径r+dr的圆周封闭流线的速度环量为
得
忽略高阶项2 0dr2,得d
(3)设涡量为 ,它在半径r和r+dr两条圆周封闭流线之间的圆环域上的积分为d 。因为 在圆环域上可看作均匀分布,得
将圆环域的面积dA=2 rdr代入该式,得
可解出 =2 + dr/r。忽略无穷小量 dr/r,最后的涡量
沉箱绕长度方向的对称轴y倾斜时稳定性最差。浮面面积A=15m2.浮面关于y轴的惯性矩和体积排量为
定倾半径
可见, ,定倾中心低于重心,沉箱是不稳定的。
(2)沉箱的混凝土体积
沉箱的重量
沉箱水平截面面积
设吃水深度为h,取水的密度 =1000kg/m3.浮力F等于重量G。有
化工流体力学第二章习题解答

习题2-2一元流动用拉格朗日变数表示x =x a ,t ,p =p (a ,t ),试证明:拉格朗日变数表示压力p 的当地变化率为:(,)(,)(,)(,)/p a t p a t x a t x a t t ta t ∂∂∂∂⎡⎤-⎢⎥∂∂∂∂⎣⎦ 证明:压力的导数为Dp p u p Dt t∂=+∙∇∂ p 的当地变化率为p Dp u p t Dt ∂=-∙∇∂ 式中:Dp Dt 用拉氏变数表示为(,)p a t t ∂∂ u 用拉氏变数表示为(,)x a t t∂∂ p ∇用拉氏变数表示为(,)p a t a a t ∂∂∙∂∂ 所以有:(,)(,)(,)(,)/p p a t p a t x a t x a t t t ta t ∂∂∂∂∂⎡⎤=-⎢⎥∂∂∂∂∂⎣⎦ 习题2-3已知速度分布,t t x y u y u x e e -==++,求迹线方程。
解:x dx u y dt== 又t t y dy u x e e t -==++∂ 22t t d x dy x e e dt dt-∴==++ 积分可得:()()12121212t t t t t t t t x C e C e te te y C e C e te te ----=++-=+++如果t=0时,质点位置(,)a b ,则可得:12,22a b a b C C +-==2-4解:流线x ydx dyu u dx dy A Bt C∴==+可得:'Cy x C A Bt ∴=++上式为一直线轨线:()223'331(1)2(2)dxA Btdt x At Bt C dyCdt y Ct C y C y t C C C ∴=+=++==+-==+ 式2代入式(1)可得:()()2''3321(3)2y y x A C B C C C C =++++可见轨线为抛物线。
2-5解:Q AU =(1)等截面A=const , Q=const 所以:0x du uua u dt t x ∂∂==+=∂∂(2)变截面 A=A(x),()x Qu A x ='22'3()()()()()xx u duua u dt t xQ Q A x A x A x Q A x A x ∂∂==+∂∂⎛⎫=- ⎪⎝⎭=-22222211220.03750.0375d x d y d z a i j k dt dt dtt i t k=++=+ x=8时,t=12.9则加速度为0.1350.135a i k =+2-7解: 双曲正切函数()21tanh tanh 'cosh x xx x e e x x e e x ---==+2=tanh 1cosh UtlU t l θθθ∂=∂令 x x u u a u t x ∂∂=+∂∂ 其中:222222211cosh 2cosh 11cosh 2cosh u U x U U U t l l l U x U l l θθθθ∂=-∂=- tanh tanh tanh 22x x u U U u U x x l l θθθ∂⎡⎤==∙-⎢⎥∂⎣⎦可得加速度计算:2222222211tanh tanh tanh cosh 2cosh 22111(1)22cosh tanh x x u u U x U U U a u U x t x l l l l U x Ut Ut l l l l θθθθθ∂∂⎡⎤=+==--∙-⎢⎥∂∂⎣⎦⎡⎤⎢⎥⎢⎥=--⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦(2)当x=L 时,其加速度为 222112cosh 2tanh U a Ut Ut l l l ⎡⎤⎢⎥⎢⎥=-⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦222222222110cosh 2tanh cosh 2tanh cosh cosh 2tanh 2sinh sinh 2Ut Ut l l Ut Ut l l θθθθθ-=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭===或 其中:22sinh 2e e θθθ-⎛⎫-= ⎪⎝⎭(222100=52Ut ln 5e e e l θθθ-+-=±=±解得:所对应时间:(ln 52l t U =± 2-9流体质点的速度与质点到OX 轴的距离成正比,并且与OX 轴平行。
流体力学三版第2章课后答案

第一章 流体的基本概念1-1 单位换算:1.海水的密度ρ=1028公斤/米3,以达因/厘米3,牛/米3为单位,表示此海水的重度γ值。
解:2.酒精在0℃时的比重为0.807,其密度ρ为若干公斤/米3 ? 若干克/厘米3 ? 其重度γ为若干达因/厘米3 ? 若干牛/米3 ? 解:l-2 粘度的换算:1.石油在50℃时的重度γ=900达因/厘米3,动力粘度μ=58.86×10-4牛.秒/米2。
求此石油的运动粘性系数ν。
解:2.某种液体的比重为1.046,动力粘性系数μ=1.85厘泊,其运动粘性系数为若干斯? 解:3.求在1大气压下,35℃时空气的动力粘性系数μ及运动粘性系3323333w /8.790/7908/8.9/807 0.807g/cm 807kg/m 1000kg/m cm dy m N s m m kg ==⨯===⨯γ酒精√sm s cm cmdy s cm cm s dy g /104.6/1064 /900/)/980101086.58( 26233224--⨯=⨯=⨯⋅⨯==∴γμν)(/017686.0 /1046.1/1085.1 232w 斯比重s cm cmg cm s g =⨯⋅⨯=⨯=∴-ρμν33235/44.1007/4.10074/8.9/1028 101 ; cm dy m N s m m kg dyN g ==⨯=∴==γργ数ν之值。
解:1-3 相距10毫米的两块相互平行的板子,水平放置,板间充满20℃的蓖麻油(动力粘度μ=9.72泊)。
下板固定不动,上板以1.5米/秒的速度移动,问在油中的切应力τ是多少牛/米2? 解:1-4 直径为150毫米的圆柱,固定不动。
内径为151.24毫米的圆筒,同心地套在圆柱之外。
二者的长度均为250毫米。
柱面与筒内壁之间的空隙充以甘油。
转动外筒,每分钟100转,测得转矩为9.091牛米。
假设空隙中甘油的速度按线性分布,也不考虑末端效应。
《流体力学》徐正坦主编课后答案第二章..

第二章习题简答2-1 题2-1图示中的A 、B 点的相对压强各为多少?(单位分别用N/m 2和mH 2O 表示)题2-1图解:()OmH Pa gh P O mH Pa gh p B B A A 2232940038.910005.0490035.38.91000==⨯⨯==-=-=-⨯⨯==ρρ2-2 已知题2-2图中z = 1m , h = 2m ,试求A 点的相对压强。
解:取等压面1-1,则Pagh gz P ghgz P A A 3108.9)21(8.91000⨯-=-⨯⨯=-=-=-ρρρρ2-3 已知水箱真空表M 的读数为0.98kPa ,水箱与油箱的液面差H =1.5m ,水银柱差m 2.02=h ,3m /kg 800=油ρ,求1h 为多少米?解:取等压面1-1,则()()()()()mgh H g P gh h gh gh P h h H g P P Hg Hg a a 6.58.980010002.05.198009802.01332802212121=⨯-+⨯-+⨯=-+-+=++=+++-油油ρρρρρρρ2-4 为了精确测定密度为ρ的液体中A 、B 两点的微小压差,特设计图示微压计。
测定时的各液面差如图示。
试求ρ与ρ'的关系及同一高程上A 、B 两点的压差。
解:如图取等压面1-1,以3-3为基准面,则()a b g gb -=ρρ' (对于a 段空气产生的压力忽略不计)得()⎪⎭⎫ ⎝⎛-=-=b a ba b 1'ρρρ取等压面2-2,则gHbagH gH p p p gHp gH p B A B A ρρρρρ=-=-=∆-=-''2-5 图示密闭容器,压力表的示值为4900N/m 2,压力表中心比A 点高0.4m ,A 点在水面下1.5m,求水面压强。
解:PagH gh P P ghP gH P 5880)5.14.0(9800490000-=-⨯+=-+=+=+ρρρρ2-6 图为倾斜水管上测定压差的装置,已知cm 20=z ,压差计液面之差cm 12=h ,求当(1)31kg/m 920=ρ的油时;(2)1ρ为空气时;A 、B 两点的压差分别为多少?解:(1)取等压面1-1OmH Pa ghgZ gh P P gh gZ P gh P A B B A 21119.092.1865)12.02.0(980012.08.9920==-⨯+⨯⨯=-+=---=-ρρρρρρ(2)同题(1)可得OmH Pa ghgZ P P gZ P gh P A B B A 208.0784)12.02.0(9800==-⨯=-=--=-ρρρρ2-7 已知倾斜微压计的倾角︒=30α,测得0.5m =l ,容器中液面至测压管口高度m 1.0=h ,求压力p 。
工程流体力学第二版答案
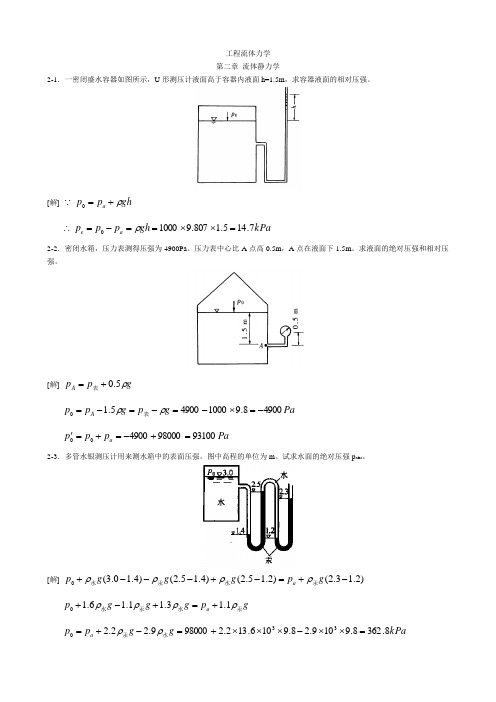
工程流体力学 第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
[解] gh p p a ρ+=0kPa gh p p p a e 7.145.1807.910000=⨯⨯==-=∴ρ2-2.密闭水箱,压力表测得压强为4900Pa 。
压力表中心比A 点高0.5m ,A 点在液面下1.5m 。
求液面的绝对压强和相对压强。
[解]g p p A ρ5.0+=表Pa g p g p p A 49008.9100049005.10-=⨯-=-=-=ρρ表 Pa p p p a 9310098000490000=+-=+=' 2-3.多管水银测压计用来测水箱中的表面压强。
图中高程的单位为m 。
试求水面的绝对压强p abs 。
[解])2.13.2()2.15.2()4.15.2()4.10.3(0-+=-+---+g p g g g p a 汞水汞水ρρρρ g p g g g p a 汞水汞水ρρρρ1.13.11.16.10+=+-+kPa g g p p a 8.3628.9109.28.9106.132.2980009.22.2330=⨯⨯-⨯⨯⨯+=-+=水汞ρρ2-4. 水管A 、B 两点高差h 1=0.2m ,U 形压差计中水银液面高差h 2=0.2m 。
试求A 、B 两点的压强差。
(22.736N /m 2)[解] 221)(gh p h h g p B A 水银水ρρ+=++Pa h h g gh p p B A 22736)2.02.0(8.9102.08.9106.13)(33212=+⨯⨯-⨯⨯⨯=+-=-∴水水银ρρ2-5.水车的水箱长3m,高1.8m ,盛水深1.2m ,以等加速度向前平驶,为使水不溢出,加速度a 的允许值是多少?[解] 坐标原点取在液面中心,则自由液面方程为:x gaz -=0 当m lx5.12-=-=时,m z 6.02.18.10=-=,此时水不溢出 20/92.35.16.08.9s m x gz a =-⨯-=-=∴2-6.矩形平板闸门AB 一侧挡水。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
更多精品文档请关注本人主页(下载后删除页眉即可)欢迎阅览第2 章流体静力学 2.1 大气压计的读数为100.66kPa(755mmHg),水面以下7.6m 深处的绝对压力为多少?知: a a KP P 66 . 100 3 / 1 0 0 0 m kg 水 m h 6 . 7 求:水下h 处绝对压力P 解:a a KP gh P P 175 6 . 7 1000 807 . 9 6 . 100 2.2 烟囱高H=20m,烟气温度ts=300℃,压力为ps,确定引起火炉中烟气自动流通的压力差。
烟气的密度可按下式计算:p= (1.25-0.0027ts)kg/m 3 ,空气ρ =1.29kg/m 3 。
解:把t 300 s C 代入 3 s (1.25 0.0027 ) / s t kg m 得3 s (1.25 0.0027 ) / s t kg m 3 3 ( 1 . 2 5 0 .0 0 2 7 3 0 0 ) / 0 . 4 4 / k g m k g m 压力差s = - p a ()gH ,把3 1 . 2 9 / a k g m ,3 0.44 / s kg m ,9.8 / g N kg ,20 H m 分别代入上式可得s = - 20 p Pa a ()gH =(1.29-0.44) 9.8 166.6 Pa 2.3 已知大气压力为98.1kN/m 2 。
求以水柱高度表示时:(1)绝对压力为117.2kN/m 2 时的相对压力;(2)绝对压力为68.5kN/m 2 时的真空值各为多少?解:(1)相对压力:pa =p-p 大气=117.72-98.1=19.62KN/ 2 m 以水柱高度来表示:h= pa/ g =19.62* 3 10 /(9.807* 3 10 )=2.0m (2)真空值:2 v a p =p p=98.1 68.5=29.6 / m KN 以水柱高度来表示:h= pa/ g =29.6* 3 10 /(9.807* 3 10 )=3.0m 更多精品文档请关注本人主页(下载后删除页眉即可)欢迎阅览 2.4 如图所示的密封容器中盛有水和水银,若 A 点的绝对压力为300kPa,表面的空气压力为180kPa,则水高度为多少?压力表B 的读数是多少?解:水的密度1000kg/m 3 ,水银密度13600 kg/m 3 A 点的绝对压力为:) 8 .0 ( 2 0 g gh p p Hg o h A 300 3 10 =180 3 10 +1000 9.8 h+13600 9.8 0.8 求得:h=1.36m 压力表B 的读数p (300 101) 199 g a p p KPa KPa 2.5 如图所示,在盛有油和水的圆柱形容器的盖上加载F=5788N 已知h1=50cm,h2=30cm,d=0.4cm,油密度ρ 油=800kg/m 3 水银密度ρ Hg=13600kg/m 3 ,求U 型管中水银柱的高度差H。
解:盖上压强 1 2 5788 46082.8 0.2 F p Pa S 2 2 1 1 1 2 1 1 1 2 46082.8 1000 9.807 0.5 800 9.807 0.3 13600 9.807 0.4 Hg H O H O Hg gH p gh gh p gh gh H g m 2.6 如右图所示为一密闭水箱,当U 形管测压计的读数为12cm 时,试确定压力表的读数。
解:容器内真空压强:0 13600 9.8 0.12 16005.24 Hg p gh 压力表的读数2 0 0 9.807 3 1000 16005.24 13415.8 g H O p p p gh p Pa 更多精品文档请关注本人主页(下载后删除页眉即可)欢迎阅览 2.7 如图所示,一密闭容器内盛有油和水,并装有水银测压管,已知油层h1=30cm,h2=50cm,h=40cm,油的密度ρ 油=800kg/m 3 ,水银密度ρHg=13600kg/m 3 求油面上的相对压力。
解:设油面的绝对压力为p 在水和汞接触面上有如下压力平衡关系: a 1 2 1 2 ( ) Hg P g h h h p gh gh 油水则油面的相对压力 a 1 2 1 2 ( ) Hg p P g h h h gh gh 油水a 13600 9.807 0.4 800 9.807 0.3 1000 9.807 0.5 46093 a p P p 2.8 如图所示,容器A 中液体的密度ρ A=856.6kg/m3,容器B 中液体的密度ρ B=1254.3kg/m 3 ,U 形差压机中的液体为水银。
如果B 中的压力为200KPa,求A 中的压力。
解:设水银U 形管两边的水银面分别为1、2,则有KPa KPa m m kg KPa gh P P b b 5 . 138 10 5 807 .9 / 3 . 1254 200 3 3 1 1 KPa KPa m KP P P 2 . 133 10 04 . 0 807 . 9 / kg 13600 - a 5 . 138 gh 3 3 1 2 贡 KPa KPa m m kg KPa gh P P A A 3 . 150 10 2 807 . 9 / 6 . 856 2 . 133 3 3 2 更多精品文档请关注本人主页(下载后删除页眉即可)欢迎阅览 2.9 U 形管测压计与气体容器K 相连,如图所示已知h=500mm,H=2m。
求U 形管中水银面的高度差△H 为多少?解:设K 中真空压强为P,大气压为Pa,依题意得2 a H O a Hg p p gH P p g H 得2 2 1000 2 0.147 13600 H O hg H O Hg gH g H gH H m g 2.10 试按复式测压计的读数算出锅炉中水面上蒸汽的绝对压力p。
已知:H=3m,h1=1.4m,h2=2.5m,h3=1.2m,h4=2.3m,水银密度ρ =13600kg/m 3 。
解:如图所示标出分界面1、2 和3,根据等压面条件,分界面为等压面。
3 点的绝对压力为:P 3 =P a + Hg g(h 4 - h 3 ) 2 点的绝对压力为:P 2 =P 3 - H2O g(h 2 - h 3 ) 1 点的绝对压力为:P 1 =P 2 + Hg g(h 2 - h 1 ) 蒸汽的绝对压力为:P=P 1 - H2O g(H- h 1 ) 整理上式得:P= P a + Hg g(h 4 - h 3 +h 2 - h 1 ) - O H 2 g(H -h 1 ) 将数据代入上式得:P=10132.5+13600×9.8×(2.3-1.2+2.5-1.4)-1000×9.8×(3-1.4)=361004.44 P a 2.11 如图所示,试确定 A 与 B 两点的压力差;已知:h1=500mm,h2=200mm,h3=150mm,h4=400mm。
酒精的密度ρ 1=800kg/m,水银的密度ρ Hg=13600kg/m 3 水的密度ρ =1000kg/m 3. 解:如图,可写处各个液面分界面的压强表达式:1 gh p p p c a 水 更多精品文档请关注本人主页(下载后删除页眉即可)欢迎阅览 2 gh p p p c d 汞 3 gh p p p d e 酒 ) ( 4 5 4 h h g p gh p p p e b 水汞联立方程,代入数据解得h h h h h h P p g g g B A 3 5 4 14 2 ) ( ) ( 酒水汞 15 . 0 8 .9 800 ) 4 . 0 25 . 0 5 . 0 ( 8 . 9 1000 ) 25 . 0 2 . 0 ( 8 . 9 13600 =55370 p a 2.12 用倾斜微压计来测量通风管道中的A,B 两点的压力差△p,如图所示。
(1)若微压计中的工作液体是水,倾斜角α =45°,L=20cm,求压力差△p 为多少?(2)若倾斜微压计内为酒精(ρ =800kg/m 3 ),α =30°,风管A,B 的压力差同(1)时,L 值应为多少?解:(1)a 1387 45 sin 2 . 0 807 .9 1000 45 sin P gL P (2)a gL P sin 酒 cm m a g P L 35 . 35 3535 . 0 5 . 0 807 .9 800 1387 sin 酒 2.13 有运水车以30km/h 的速度行驶,车上装有长L=3.0m,高h=1.0m,宽b=2.0m 的水箱。
该车因遇到特殊情况开始减速,经100m 后完全停下,此时,箱内一端的水面恰到水箱的上缘。
若考虑均匀制动,求水箱的盛水量。
解:设水车做匀减速运动的加速度为a,初速度Vo=(30*103 )/3600=8.3m/s 由运动学公式2 2 1 at t v s at v v 。
式中,; 3 . 8 s m v 。
更多精品文档请关注本人主页(下载后删除页眉即可)欢迎阅览当 2 347 . 0 100 s m a m s 时,解得则a=-0.347m/s�0�5,其中负号表示加速度的方向与车的行驶方向相反。
设运动容器中流体静止时液面距离边缘为x m,则根据静力学公式有:x/1.5=a/g 求出:x=0.053m 则h=1-0.053=0.947m 水体积:V=2*3*h=6x0.947=5.682m�0�6 则水箱内的盛水量为:m=ρ V=1000x5.682 ㎏=5682 ㎏ 2.14 如图所示,一正方形容器,底面积为b×b=(200×200)mm 2 ,m1 =4Kg。
当它装水的高度h=150mm 时,在m2 =25Kg 的载荷作用下沿平面滑动。
若容器的底与平面间的摩擦系数C f =0.3,试求不使水溢出时容器的最小高度H 是多少?解:由题意有,水的质量kg V m 6 10 150 200 200 10 0 . 1 9 3 0 由牛顿定律a m m m gC m m g m f ) ( ) ( 0 2 1 0 1 2 a 35 3 . 0 8 . 9 10 8 . 9 25 解得2 16 . 6 s m a 倾斜角 152 . 32 8 . 9 16 . 6 arctan arctan g a 超高mm b g a z s 5 . 67 100 8 . 9 16 . 6 ) 2 ( 所以最小高度m mm z h H s 217 . 0 217 5 . 67 150 2.15 如图所示,为矩形敞口盛水车,长L=6mm,宽b=2.5mm,高h=2mm,静止时水深h1=1m,当车以加速度a=2 s m 2 前进时,试求(1)作用在前、后壁的压力;(2)如果车内充满水,以a=1.5 s m 2 ,的等加速前进,有多少水溢出?解:(1)前壁处的超高m x g a zs 612 . 0 2 6 * 8 .9 2 则前壁水的高度m z h s 388 . 0 h1 前更多精品文档请关注本人主页(下载后删除页眉即可)欢迎阅览形心高度m 1 9 4 . 0 2 h hc 前前壁受到的压力N ghcA F 1847 5 . 2 * 388 . 0 * 194 . 0 * 8 . 9 * 1000 ρ 前后壁压力N A ghc F 31832 5 . 2 * ) 612 . 0 1 ( * 2 / ) 612 . 0 1 * 8 . 9 * 1000 2 (ρ 后(2)当s m a 2 5 . 1 时。
