C++标准库的数值极限
数值修约规则与极限数值的表示和判定

3.2.2拟舍弃数字的最左一位数字大于5,则 进一,即保留数字的末位数字加1。 例:将1268修约到“百”数位,得13×102 (特定场合可写为1300) “特定场合”系指修约间隔明确时。 例:将下列数字修约到个数位 10.68 15.74 200.89 199.63
修约后:11 16 201 200
3.2.4拟舍弃数字的最左一位数字为5,且其 后无数字或皆为0时,若所保留的末位数字为 奇数(1,3,5,7,9)则进一,即保留数 字的末位数字加1;若所保留的末位数字为偶 数(0,2,4,6,8),则舍去。 例1:修约间隔为0.1(或10-1) 拟修约数值 修约值 1.050 1.0 0.35 0.4 1.250 1.2 1.75 1.8
例:将下列数字修约到“个”数位的0.5单位修约 拟修约数值X 2X 2X修约值 X修约值 60.25 120.50 120 60.0 60.38 120.76 121 60.5 60.28 120.56 121 60.5 -60.75 -121.50 -122 -61.0
3.4.2 0.2单位修约 0.2单位修约是指按指定修约间隔对拟修约的 数值0.2单位进行的修约。 0.2单位修约方法如下:将拟修约数值X乘以5, 按指定修约间隔对5X依3.2的规则修约,所得 数值(5X修约值)再除以5。
3.2进舍规则
3.2.1拟舍弃数字的最左一位数字小于5,则 舍去,保留其余各位数字不变。 例:将12.1498修约到个位数,得12;将 12.1498修约到一位小数,得12.1。 例:将下列数字按0.1单位修约 10.5025 19.428 0.0395 0.04959 修约后: 10.5 19.4 0.0 0.0
数值修约规则与极限数值的表示和判定

数值修约规则与极限数值的表示和判定1范围本标准规定了对数值进行修约的规则、数值极限数值的表示和判定方法,有关用语及其符号,以及将测定值或其计算值与标准规定的极限数值作比较的方法。
本标准适用于科学技术与生产活动中试验测定和计算得出的各种数值。
当所得数值需要修约时,应按本标准给出的规则进行。
本标准适用于各种标准或其他技术规范的编写和对测试结果的判定。
2 术语和定义下列术语和定义适用于本标准。
2.1数值修约 rounding off for numerical values通过省略原数值的最后若干数字,调整所保留的末位数字,使最后所得到的值最接近原数值的过程。
注:经数值修约后的数值称为(原数值的)修约值。
2.2修约间隔 rounding interval修约值的最小数值单位。
注:修约间隔的数值一经确定,修约值即应为该数值的整数倍。
例l:如指定修约间隔为0.l,修约值应在0.1的整数倍中选取,相当于将数值修约到一位小数。
例2:如指定修约间隔为100,修约值应在100的整数倍中选取,相当于将数值修约到“百”数位。
2.3极限数值 limiting values标准(或技术规范)中规定考核的以数量形式给出且符合该标准(或技术规范)要求的指标数值范围的界限值。
3数值修约规则3.1确定修约间隔a)指定修约间隔为10-n(n为正整数),或指明将数值修约到n位小数;b)指定修约间隔为1,或指明将数值修约到“1”数位;c)指定修约间隔为10n(n为正整数),或指明将数值修约到10n数位,或指明将数值修约到“十”、“百”、“千”……数位。
3.2 进舍规则3.2.1 拟舍弃数字的最左一位数字小于5,则舍去,保留其余各位数字不变。
例:将12.1498修约到个数位,得12;将12.1 498修约到一位小数,得12。
1。
3.2.2 拟舍弃数字的最左一位数字大于5;则进一,即保留数字的末位数字加1。
例:将1268修约到“百”数位,得13×102(特定时可写为1300)。
有效数字和数值的修约及极限数值的表

4 0.2单位修约
• 指修约间隔为指定数位的0.2单位,即修约 到指定数位的0.2单位。
• 例如,将832修约到“百"数位的0.2单位, 得840(修约方法见本规则5.2)。
6
二 数值修约规则
• 1 指定修约间隔 • a.指定修约间隔为10-n(n为正整数),或指明
将数值修约到n位小数; • b.指定修约间隔为1,或指明将数值修约到
个数位; • c.指定修约间隔为10n,或指明将数值修约
到10n数位(n为正整数),或指明将数值修约 到“十","百","千"……数位。
7
2 进舍规则
四舍六入五考虑,五后非零 则进一,五后是零看前位, 前位为奇则进一,前位为偶 应舍去。
8
• a)拟舍弃数字的最左一位数字小于 5时,则舍去,即保留的各位数字不 变。(四舍)
• 例1:将12.1498修约到一位小数, 得12.1。
• 例2:将12.1498修约成两位有效位 数,得12。
9
• b) 拟舍弃数字的最左一位数字大于5, 或者是5,而其后跟有并非全部为0的数 字时,则进一,即保留的末位数字加l。 (六入;五后非零则进一)
• 例l:将1268修约到百数位,得13×102 (特定时可写为1300)。
• 例2:3.2,0.32,0.032,0.0032均为两位有效位数, 0.0320为三位有效位数。
• 例3:12.490为五位有效位数,10.00为四位有效位数。
4
3 0.5单位修约(半个单位修约)
• 指修约间隔为指定数位的0.5单位,即修约 到指定数位的0.5单位。
• 例如,将60.28修约到个位数的0.5单位,得 60.5。
标准公差表
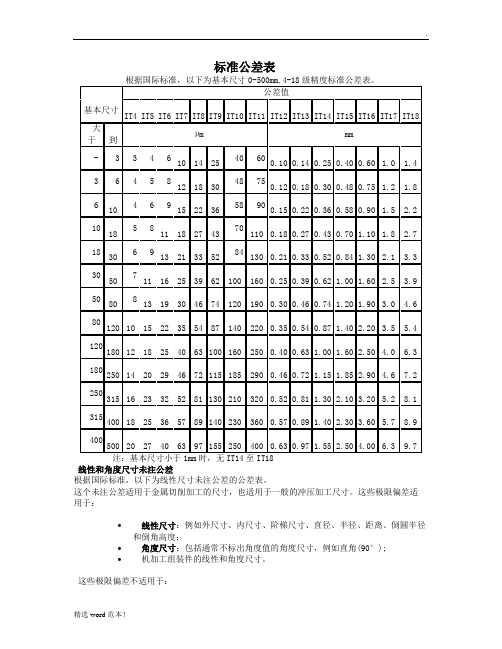
标准公差表线性和角度尺寸未注公差根据国际标准,以下为线性尺寸未注公差的公差表。
这个未注公差适用于金属切削加工的尺寸,也适用于一般的冲压加工尺寸。
这些极限偏差适用于:•线性尺寸:例如外尺寸、内尺寸、阶梯尺寸、直径、半径、距离、倒圆半径和倒角高度;•角度尺寸:包括通常不标出角度值的角度尺寸,例如直角(90°);•机加工组装件的线性和角度尺寸。
这些极限偏差不适用于:•已有其他一般公差标准规定的线性和角度尺寸;•括号内的参考尺寸;•矩形框格内的理论正确尺寸。
形状位置公差零件在加工过程中,由于机床-夹具-刀具系统存在几何误差,以及加工中出现受力变形、热变形、振动和磨损等影响,使被加工零件的几何要素不可避免地产生误差。
这些误差包括尺寸偏差、形状误差(包括宏观几何误差、波度和表面粗糙度)及位置误差。
形状公差形状公差是指单一实际要素的形状所允许的变动全量。
形状公差用形状公差带表达。
形状公差带包括公差带形状、方向、位置和大小等四要素。
形状公差项目有:直线度、平面度、圆度、圆柱度、线轮廓度、面轮廓度等6项。
位置公差位置公差是指关联实际要素的位置对基准所允许的变动全量。
定向公差定向公差是指关联实际要素对基准在方向上允许的变动全量。
这类公差包括平行度、垂直度、倾斜度3项。
定位公差定位公差是关联实际要素对基准在位置上允许的变动全量。
这类公差包括同轴度、对称度、位置度3项。
跳动公差跳动公差是以特定的检测方式为依据而给定的公差项目。
跳动公差可分为圆跳动与全跳动。
零件的形位公差共14项,其中形状公差6个,位置公差8个,列于下表。
分类项目符号简要描述形状公差直线度直线度是表示零件上的直线要素实际形状保持理想直线的状况。
也就是通常所说的平直程度。
直线度公差是实际线对理想直线所允许的最大变动量。
也就是在图样上所给定的,用以限制实际线加工误差所允许的变动范围。
平面度平面度是表示零件的平面要素实际形状,保持理想平面的状况。
也就是通常所说的平整程度。
数值修约与极限数值的判定

数值修约与极限数值的判定(GB/T8170-2008数值修约规则与极限数值的表示和判定代替GB/T1250-1989、GB/T8170-1987)1.数值修约方法1.1数值修约例:圆周率:3.1415926……数值修约的目的:简化计算、准确表达测量结果。
数学定义:对某一拟修约数,根据保留位数的要求,将多余位数的数字进行取舍,按一定规则,选取一个其值为修约间隔整数倍的数(即修约数)来代替拟修约数的过程。
又称数的化整。
标准定义(GB8170):例:圆周率原数值:3.1415926……要求调整到小数点后2位数字3.1415926=3.14此过程称为数值修约1.2有效位数(有效数字)对没有小数位且以若干个零结尾的数值,从非零数字最左一位向右数得到的位数减去无效零即(仅为定位用的零)的个数,就是有效位数;对其他十进位数,从非零数字最左一位向右数而得到的位数,就是有效位数例1: 35000没有小数位且以3个0结尾的数值,非0数字为35,最左一位为3,向右数得到的位数为5位,如最后2个0为无效0,则有效位数为3位;如最后3个0为无效0,则有效位数为2位。
有效数字表示:若有两个无效零则为三位有效位数,应写为350×102若有三个无效零则为两位有效位数,应写为35×103实例1项目技术要求实测值(报出值) 绝缘电阻接插件与接插件间 600000 MΩ 6×105 MΩ6.0×105 MΩ接插件与保护套间 2500000 MΩ 2.5×106 MΩ例2: 3.20.320.0320.03200.00320.0302其他十进位数,从非零数字最左一位向右数而得到的位数,就是有效位数3.2,0.32,0.032,0.0032均为两位有效位数0.0320,0.0302为三位有效位数例3: 12.490,10.0012.490为五位有效位数10.00为四位有效位数1.3修约间隔(化整间隔)是确定修约保留位数的一种方式。
数值修约规则与极限数值的表示和判定GBT8170-2008代替GBT1250

数值修约规则与极限数值的表示和判定GB/T 8170-2008代替GB/T 1250-1989,GB/T8170-19872008-07-16发布2009-01-01实施1 范围本标准规定了对数值进行修约的规则、数值极限数值的表示和判定方法,有关用语及其符号,以及将测定值或其计算值与标准规定的极限数值作比较的方法。
本标准适用于科学技术与生产活动中测试和计算得出的各种数值。
当所有数值需要修约时,应按本标准给出的规则进行。
本标准适用于各种标准或其他技术规范的编写和对测试结果的判定。
2术语和定义下列术语和定义使用于本标准2.1 数值修约(rounding off for numerical values)通过省略原数值的最后若干位数字,调整所保留的末尾数字,使最后所得到的数值最接近原数值的过程。
注:经数值修约后数值称为(原数值的)修约值。
2.2修约间隔(rounding interval)修约值的最小数值单位。
注:修约间隔的数值一经确定,修约值即为该数值的整数倍。
例1:如指定修约间隔为0.1,修约值应在0.1的整数倍中选取,相当于将数值修约到一位小数。
例2:如指定修约间隔为100,修约值应在100的整数倍中选取,相当于将数值修约到“百”数位。
2.3极限数值(limiting values)标准(或技术规范)中规定考核的以数量形式给出且符合该标准(或技术规范)要求的指标数值范围的界限值。
3数值修约间隔3.1 确定修约间隔a)指定修约间隔为10-n (n为正整数),或指明将数值修约到n位小数。
b)指定修约间隔为1,或指明将数值修约到“个”数位。
c)指定修约间隔为10n (n为正整数),或指明将数值修约到10n数位,或指明将数值修约到“十”、“百”、“千”……数位。
3.2 进舍规则3.2.1 拟舍弃数字的最左一位数字小于5,则舍去,保留其余各位数字不变。
例:将12.1498修约到个数位,得12;将12.1498修约到一位小数,得12.1.3.2.2 拟舍弃数字的最左一位数字大于5,则进一,即保留数字的末位数字加1.例:将1268修约到“百”数位,得13×102(特定场合可写为1300).注:本标准示例中,“特定场合”系指修约间隔明确时。
产品标准和工程技术标准中测量结果的极限值判定研究

I研究与探讨I Research and Discussion产品标准和工程技术标准中测量结果的极限值判定研究丁百湛▽景盛名V1淮安市建筑科学研究院有限公司2淮安市建筑工程质量检测中心有限公司摘要:在现行产品标准和工程技术标准中,极限值的判定大多未注明采用GB/T8170中的全数值比较法或修约值比较法,同时产品标准的指标和试验方法的检测值数值修约的修约间隔也不一致,给检测结果的判定带来困难,本文对产品标准和工程技术标准中测量结果的极限值判定进行研究,关键词:极限值结果判定修约间隔一致性1引言在我们日常使用的检测标准中,有的产品标准或工程技术标准中有关于极限值判定方法的规定,许多情况下则没有。
如钢材类、涂料类、化工类标准可能会有,而墙体材料类、管材管件类则没有,有时给检测结果的符合性判定造成困难。
下面对比问题进行分析,不妥之处,敬请指正。
2标准起草的规则中关于极限值和判定的规定产品标准起草需要依据两个标准:一是GB/T1.1-2020《标准化工作导则第1部分:标准化文件的结构和起草规则》;二是GB/T20001.10-2014《标准编写规则第10部分:产品标准》。
根据GB/T1.1-2020中第5.4条规定:标准的表述原则遵循“一致性原则、协调性原则和易用性原则”。
其中一致性原则是指"每个文件内或分为部分的文件各部分之间,其结构以及要素的表述需保持一致”[1]o在GB/T20001.10-2014的第5章规定:规范性要素包含"技术要求、试验方法和检验规则”,产品标准中可根据产品特性的用途可规定极限值同、可选值及由供方确定的数值。
通常极限值体现在产品标准的技术要求中,如在GB/ T1596-2017《用于水泥混凝土中的粉煤灰》第6章技术要求中规定粉煤灰密度极限值为2.6g/cm3o而判定规则通常在“检验规则”中体现。
3产品标准或工程技术标准采用数值修约规则或规定极限值判定方法示例在涂料产品、钢产品、有害物质限量等产品标准或工程技术标准有极限值判定方法的规定,见表1O66工程建设标准化-2020年第10M研究与探讨Research and Discussion表1产品标准或工程技术标准中有关极限值判定的描述示例序号标准名称及代号极限值判定相关条款1GB/T3077-2015合金结构钢8.4.复验与判定规则8.4.3钢棒的检测和检测结果应采用修约值比较法修约到与规定值末位数字所标识的数位相一致,其修约规则应符合GB/T8170-2008第3章的规定2JMT206-2018外墙外保温用丙烯酸涂料7.试验方法7.3数值修约按GB/T8170-2008中修约值比较法进行3JGJ144-2019外墙外保温工程技术标准3.基本规定3.0.9检测数据的判定应采用现行国家标准《数值修约规则与极限数值的表示和判定》GB/T8170中规定的修约值比较法4GB18582-2020建筑用墙面涂料中有害物质限量7检验规则7.2检验结果的判定7.2.1检验结果的判定,按GB/F8170-2008中修约值比较法进行5GB50325-2020民用建筑工程室内环境污染控制规范6.0.4民用建筑工程竣工验收时,必须进行室内环境污染物浓度检测。
浅谈检验数据的处理

不
规 的
,
则依据 ( 数字 0 修 约 规则 )进 行数据处 理 否 则应 侠
用 GB 12 5 0 标准 过 早 一 步到位
, 。
G B8 l 7
定使用 也应将
G B8 1 7 O《 数字修约规则 )
过早地 反 报 出数 一 步修约到标
准 要 求 的 精度往 往 不 能体 现 试验精
报出数修约 不 宜
这 样才 能 较 好 地 解 决 原 始记 录 中 的
报出数 和 检 验报 告 中的 报告数 的表
达 问题
。
二 报告数的形成 报 出 数 出来 后
,
:
位非
5
数字 不 进 行取舍 处 理 (
十
,
出现
就 需 要 配合标 准
。
GB 1 2 5O 对
报
5 这 个数字 需 用
)(
一
)符 号 表 示
数值修约规则中指出 : 本标 准
一 位 报 出数就精确
, 。 ,
将报 出数 整理 成报告数时应 视 标 准 规定 是 否 使 用 修约 规 则
规 定 了 使 用 修 约 规则的
, 。
(l )
何表 达
,
目前大体有 三 种 意 见
,
:
(l )
就 可 以把
有 的 人认为原始 记 录 中计算 后 所得 数据 即 报 出 数 度
,
前 面 约定 的 报 出数 用修约规则处理
, 。
丰 王 苑 丽 晓
标 准 中没有规定对数据采取修约规 则对报 出 数 报 告 数 均 应 采 用 CB1 2 5 0 ( 极 限 数值 的 表 示 方 法 和 判
定 方 法 》 书 写 方式 也应 按 G B 1 2 5 O 表
数值修约规则与极限数值的表示和判定201007

综合运算 例:2.0×104+15000×2.5 解:[分析]先乘除后加减
2.0×104+15000×2.5 =2.0×104+150×102×2.5 =2.0×104+375×102 =2.0×104+3.75×104 =5.75×104 ≈5.8×104
–将2:将12.1498修约到小数点后一位, 得12.1;
2.2.拟舍去数字的最左一位数字大于5时, 或是5,而其后跟有并非全部为0的数 字时,则进1,即保留的末位数字加1;
例1:将1268修约到“百”位数,得 13×102(特定时可写成1300);
特定时—指修约间隔或有数位数明 确时
例2:将1268修约成3位有效位数,得 127×10 ;
例3:将下列数字修约到十数位
拟修约值
修约值
-355 可写为-360)
-36 ×10(特定时
3.不得连续修约:拟修约的数字在确定 修约位数后一次修约获得结果,不得 多次连续修约。
例1: 修约15.4546,修约间隔1,结果为 15。
–错误:15.4546 → 15.455 15.46 → 15.5 → 16
例2:60.38
60.38×2=120.76 →121 → 120/2=60.5
• 例:将下列数字修约到“百”数位的 0.5单位(或修约间隔为50)
• 例:930
• 930×2=1860,按100间隔修约为 1900/2=950
三、近似数运算
又称数字运算,如对测量结果进行 加、减、乘、除、开方、乘方、三角 函数运算等。 运算时必须注意有效数字。
c语言中无穷的符号

c语言中无穷的符号
在C语言中,无穷的符号是用来表示无穷大和无穷小的特殊值。
C语言中没有直接定义无穷的符号,但可以通过一些技巧来表示无
穷大和无穷小。
1. 无穷大的表示:
在C语言中,可以使用宏定义来表示无穷大,例如:
c.
#define INFINITY_POSITIVE 1e1000 // 正无穷大。
#define INFINITY_NEGATIVE -1e1000 // 负无穷大。
这里使用了一个非常大的数来表示无穷大,超过了浮点数的表
示范围。
2. 无穷小的表示:
同样地,在C语言中,可以使用宏定义来表示无穷小,例如:
c.
#define INFINITY_SMALL 1e-1000 // 无穷小。
这里使用了一个非常接近于零的数来表示无穷小,超过了浮点
数的精度范围。
需要注意的是,这种表示方式只是近似地表示无穷大和无穷小,并不是真正的无穷。
在实际计算中,这些宏定义可以用于比较大小
或判断边界条件。
此外,在C标准库中也提供了一些函数来处理无穷大和无穷小,例如`isinf()`函数用于判断一个浮点数是否为无穷大,`isnan()`
函数用于判断一个浮点数是否为非数值(NaN)。
总结起来,虽然C语言中没有直接定义无穷的符号,但可以通
过宏定义或使用标准库函数来近似表示无穷大和无穷小。
这样可以
方便地处理与无穷相关的数值计算和判断。
国家标准极限与配合

2.4 公差带 和配合的表示法
公差带的表示: 基本偏差字母+公差等级数字
孔的孔公的差公差带带代代号号
φ6φ5H675H7
公差公等差级等级数数字字 孔的孔基的本基本偏偏差差代代号号((大大写写)) 孔的孔基的本基本尺尺寸寸
φφ65k6
轴轴的的公公差差带带代代号号
公公差差等等级级数数字字 轴轴的的基基本本偏偏差差代代号号((大小写)写) 轴轴的的基基本本尺尺寸寸
❖ 场合:
主要用于较低精度的非配合尺寸
❖ 作用:
简化制图 节省图样设计时间 一般不用检验
㈡.国家标准 GB/T1804-2000
《一般公差 未注公差的线性和角度尺寸的公差》
等级: 精密级 f
中等级 m
粗糙级 c
最粗级 v
这4个公差等级相当于ITl2、ITl4、IT16和IT17。
在基本尺寸0.5~4000mm范围内分为8个尺 寸段。极限偏差均对称分布。同时也对倒圆半径 与倒角高度尺寸的极限偏差的数值作了规定。
❖ 尺寸偏差可为正值负值或零,而公差只能是正 值或零。( )
选择:
❖ 最大极限尺寸( )基本尺寸。
A大于
B 小于
C 等于
D 大于、 小于或等于
❖ 利同一加工方法,加工φ45H7孔和 φ50H6孔,应理解为: ( )
㈢.标注方法
❖ 图样上 只标注基本尺寸,不标注基本偏差
❖ 技术要求中的有关技术文件或标准中: 用本标准和公差等级代号表示 例: GB/T 1804-m
应用
主要用于不重要的,较低精度的非配合 尺寸及以工艺方法可保证的尺寸(铸、 模锻)。(简化制图,节约设计、检验
时间,突出重要尺寸)
练习
判断: ❖ 任意尺寸的上偏差一定大于其下偏差。( )
混凝土设计强度标准值规定

混凝土设计强度标准值规定混凝土设计强度标准值是指在混凝土设计时所规定的混凝土强度等级的标准值,通常以标号形式表示,如C20、C25、C30等。
混凝土设计强度标准值是混凝土设计的基础,也是混凝土工程质量的重要指标,因此必须严格按照规范要求进行确定和控制。
一、混凝土设计强度标准值的确定(一)混凝土设计强度等级的选择混凝土设计强度等级的选择应根据工程用途、荷载类型、结构形式、施工要求等因素综合考虑。
一般情况下,混凝土设计强度等级应根据规范要求选择。
(二)混凝土设计强度标准值的确定混凝土设计强度标准值的确定应按照规范中相应的计算公式进行计算,包括混凝土强度等级的标准值、设计强度、极限状态设计值、可靠度系数等。
1.混凝土强度等级的标准值混凝土强度等级的标准值是指规范规定的混凝土强度等级的标准数值,具体数值可参考国家标准《建筑结构用混凝土设计规范》(GB 50010)中相应的表格。
2.设计强度设计强度是指根据结构要求和施工条件确定的混凝土强度值,其数值应不低于规范规定的混凝土强度等级的标准值。
3.极限状态设计值极限状态设计值是指混凝土在荷载作用下达到极限状态时的强度值,其计算公式为:fcd=fck/γc+αcc,其中fck为混凝土标准强度值,γc 为混凝土的安全系数,αcc为混凝土的荷载系数。
4.可靠度系数可靠度系数是指在考虑各种不确定因素的情况下,为保证结构安全可采用的安全系数,其数值应根据规范要求确定。
二、混凝土设计强度标准值的控制混凝土设计强度标准值的控制是指在混凝土施工过程中,对混凝土强度标准值进行控制,确保混凝土工程质量达到规范要求。
具体控制措施如下:(一)材料控制混凝土施工中应根据规范要求对材料进行严格的控制,包括水泥、骨料、砂子、水等。
(二)配合比控制混凝土配合比应按照设计要求进行控制,其中水灰比、骨料粒径、配合比中各材料的比例等应符合规范要求。
(三)搅拌控制混凝土搅拌应按照规范要求进行,包括搅拌时间、搅拌速度、搅拌次数等。
numeric_limits方法

numeric_limits方法`numeric_limits` 是 C++ 标准库 `<limits>` 头文件中定义的一个模板类。
这个类用于查询数值类型的各种属性,例如最小值、最大值、精度等。
以下是一些常见的使用示例:```cppinclude <iostream>include <limits>int main() {std::cout << "The minimum value for int is: " <<std::numeric_limits<int>::min() << std::endl;std::cout << "The maximum value for int is: " <<std::numeric_limits<int>::max() << std::endl;std::cout << "The precision for double is: " <<std::numeric_limits<double>::digits << std::endl;return 0;}```在这个例子中,我们查询了 `int` 和 `double` 类型的最小值、最大值和精度。
注意,`std::numeric_limits` 的`min()` 和`max()` 方法返回的是类型本身,所以我们需要使用 `std::numeric_limits<T>::min()` 的形式来调用它们。
`digits` 是用于表示精度的一个属性,但它的值并不是以小数点后的位数来表示的,而是一个表示可以表示的最大非零位数的概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C++标准库的数值极限numeric_limits
一般来说,数值类型的极值是一个与平台相关的特性。
c++标准程序库通过template numeric_limits提供这些极值,取代传统C语言所采用的预处理常数。
你仍然可以使用后者,其中整数常数定义于<climits>和<limits.h>,浮点常数定义于<cfloat>和<float.h>,新的极值概念有两个优点,一是提供了更好的类型安全性,二是程序员可借此写出一些template以核定
#include<iostream>
#include<string>
#include<limits> //头文件
using namespace std;
int main(){
cout<<"numeric_limits<int>::min()= "<<numeric_limits<int>::min()<<endl; //最小值
cout<<"numeric_limits<int>::max()= "<<numeric_limits<int>::max()<<endl; /最大值
cout<<"numeric_limits<short>::min()= "<<numeric_limits<short>::min()<<endl;
cout<<"numeric_limits<short>::max()= "<<numeric_limits<short>::max()<<endl;
cout<<"numeric_limits<double>::min()= "<<numeric_limits<double>::min()<<endl;
cout<<"numeric_limits<double>::max()= "<<numeric_limits<double>::max()<<endl;
cout<<"numeric_limits<int>::is_signed()= "<<numeric_limits<int>::is_signed<<endl;//正负号
cout<<"numeric_limits<string>::is_specialized()= "<<numeric_limits<string>::is_specialized<<end l;//是否定义了数值极限
system("pause");
return 0;
}。
