第3章部分习题参考解答
(仅供参考)第3章扭转作业参考解答
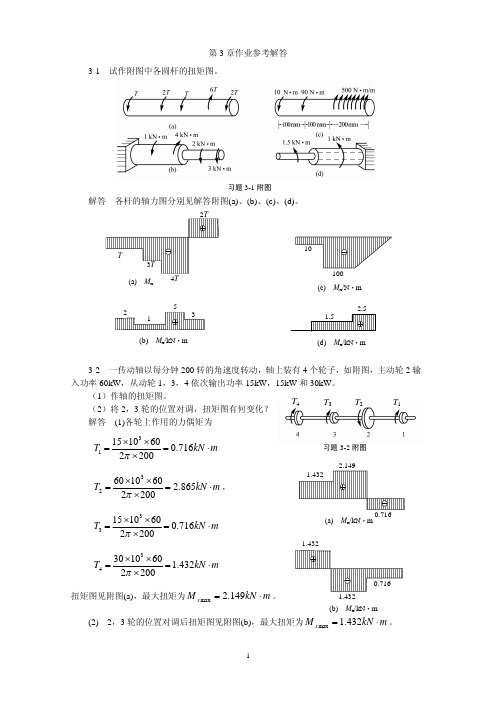
第3章作业参考解答3-1 试作附图中各圆杆的扭矩图。
习题3-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
3-2 一传动轴以每分钟200转的角速度转动,轴上装有4个轮子,如附图,主动轮2输入功率60kW ,从动轮1,3,4依次输出功率15kW ,15kW 和30kW 。
(1)作轴的扭矩图。
(2)将2,3轮的位置对调,扭矩图有何变化? 解答 (1)各轮上作用的力偶矩为m kN T ×=´´´=716.0200260101531pm kN T ×=´´´=865.2200260106032p ,m kN T ×=´´´=716.0200260101533pm kN T ×=´´´=432.1200260103034p扭矩图见附图(a),最大扭矩为m kN M x ×=149.2max 。
(2) 2,3轮的位置对调后扭矩图见附图(b),最大扭矩为m kN M x ×=432.1max 。
(a) M x(c) M x /N ·m(b)M x /kN ·m(d) M x /kN ·m习题3-2附图T 1T 2 T 3 T 4 (a)M x /kN ·m1.432(b) M x /kN ·m3-3 一直径d =60mm 的圆杆,其两端受T =2kN·m 的外力偶矩作用而发生扭转,如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
解答 1,2,3点处的切应力分别为MPaMPa W T p 4.313/22.4716/06.014.320000.031332===´===t t t t 切应力方向见附图(1)。
计量经济学第三章练习题及参考全部解答

第三章练习题及参考解答3.1为研究中国各地区入境旅游状况,建立了各省市旅游外汇收入(Y,百万美元)、旅行社职工人数(X1,人)、国际旅游人数(X2,万人次)的模型,用某年31个省市的截面数据估计结果如下:Y = -151.0263 0.1179X1i1.5452X2it=(-3.066806)(6.652983)(3.378064)2 2R2=0.934331 R 0.92964 F=191.1894 n=311)从经济意义上考察估计模型的合理性。
2)在5%显著性水平上,分别检验参数M, :2的显著性。
3)在5%显著性水平上,检验模型的整体显著性。
练习题3.1参考解答:(1)由模型估计结果可看出:从经济意义上说明,旅行社职工人数和国际旅游人数均与旅游外汇收入正相关。
平均说来,旅行社职工人数增加1人,旅游外汇收入将增加0.1179百万美元;国际旅游人数增加1万人次,旅游外汇收入增加 1.5452百万美元。
这与经济理论及经验符合,是合理的。
矚慫润厲钐瘗睞枥庑赖。
(2)取。
=0.05,查表得t0.025(31 — 3) = 2.048因为3个参数t统计量的绝对值均大于t0.025(31 — 3) =2.048,说明经t检验3个参数均显著不为0,即旅行社职工人数和国际旅游人数分别对旅游外汇收入都有显著影响。
聞創沟燴鐺險爱氇谴净。
(3)取G =0.05,查表得F0.O5(2,28) =3.34,由于F =199.1894 a F0.05(2,28^ 3.34,说明旅行社职工人数和国际旅游人数联合起来对旅游外汇收入有显著影响,线性回归方程显著成立。
残骛楼諍锩瀨濟溆塹籟。
3.2表3.6给出了有两个解释变量X2和.X3的回归模型方差分析的部分结果:n=14+1=15因为TSS=RSS+ESS 残差平方和RSS=TSS-ESS=66042-65965=77回归平方和的自由度为:k-仁3-仁2残差平方和RSS的自由度为:n-k=15-3=12(2)可决系数为:R2=65965 =0£98834TSS 660422 n -1 ' e215 -1 77修正的可决系数:R 1 "2=1 0.9986n —k送y, 15—3 66042(3)这说明两个解释变量X2和.X3联合起来对被解释变量有很显著的影响,但是还不能确定两个解释变量X2和.X3各自对Y 都有显著影响。
电工技术第3章课后习题及详细解答

第3章单相正弦电路分析已知正弦电压(V)、(V),则u1与u2的相位差为,是否正确?为什么?分析讨论相位差问题时应当注意,只有同频率正弦量才能对相位进行比较。
这是因为只有同频率正弦量在任意时刻的相位差是恒定的,能够确定超前、滞后的关系,而不同频率正弦量的相位差是随时间变化的,无法确定超前、滞后的关系,因此不能进行相位的比较。
解不正确。
因为u1的角频率为ω,而u2的角频率为2ω,两者的频率不同,相位差随时间变化,无法确定超前、滞后的关系,因此不能进行相位的比较。
已知某正弦电流的有效值为10 A,频率为50 Hz,初相为45°。
(1)写出该电流的正弦函数表达式,并画出波形图;(2)求该正弦电流在s时的相位和瞬时值。
解(1)由题设已知正弦电流的有效值A,频率Hz,初相。
由频率f可得角频率ω为:(rad/s)所以,该电流的正弦函数表达式为:(A)波形图如图所示。
(2)s时的相位为:(rad)瞬时值为:(A)已知正弦电流(A)、(A),试求i1与i2的振幅、频率、初相、有效值和相位差,并画出其波形图。
解i1与i2的振幅分别为:(A)(A)频率分别为:(Hz)初相分别为:有效值分别为:(A)(A)i1与i2的相位差为:说明i1超前i2。
波形图如图所示。
图习题解答用图图习题解答用图设,,试计算、、AB、。
分析复数可用复平面上的有向线段、代数型、三角函数型和指数型(极坐标型)等形式表示。
复数的加减运算就是将实部和虚部分别进行加减,因而采用代数型比较方便。
复数的乘法运算就是将模相乘而辐角相加,复数的除法运算就是将模相除而辐角相减,因而采用指数型(极坐标型)比较方便。
解写出下列各正弦量所对应的相量,并画出其相量图。
(1)(mA)(2)(A)(3)(V)(4)(V)分析用相量来表示正弦量,就是用一个复数来反映正弦量的振幅(或有效值)和初相,即用相量的模来代表正弦量的振幅(或有效值),用相量的辐角来代表正弦量的初相。
第3章CPU构成习题参考解答

6.按照图 3.3 所示的双总线数据通路,写出 SUB R2,R3 指令取指阶段和执行阶段的 微操作序列。 答:SUB R2,R3。这是一条减法指令,属于寄存器寻址方式,操作数和结果都存在寄 存器中。其功能是用寄存器 R2 的内容减去 R3 的内容,结果存入寄存器 R2 中。其指令流程 如表 3.26: 表 3.26 SUB R2,R3 指令双总线流程分析表 步骤 ( 1) ( 2) ( 3) ( 4) ( 5) 微 操 作 (PC)→MAR; (PC)+1→C (C ) →PC; M[MAR] →MDR (MDR)→IR (R2)-(R3)→C (C)→R2 控 制 信 号 解 释 PCOUT1、 CPMAR、 EMAR、 指令地址送到 MAR , PC RD、+1、CPC 内容和 1 相加后送 C。 COUT、CP2PC、SMDR MDROUT1、CP1IR 完成 PC 的修改, 将读出的 指令送 MDR。 将读出的指令送 IR,取指 阶段完成。
表 3.27 SUB R2,R3 指令三总线流程分析表 步骤 ( 1) ( 2) ( 3) ( 4) 微 操 作 (PC)→MAR; (PC)+1→PC M[MAR] →MDR (MDR)→IR (R2)-(R3)→R2 控 制 信 号 解 释 PCOUT3、 CPMAR、 EMAR、 指令地址送到 MAR , PC RD、+1、CP1PC 内容和 1 相加后送 PC。 SMDR MDROUT3、CP1IR R2OUT2 、 R3OUT3 、 ADD、PC1R1 将读出的指令送 MDR。 将读出的指令送 IR,取指 阶段完成。 R2 减去 R3 的内容后送 R2。
8.根据表 3.7 分析,参考表 3.8,说明此模型机有几种指令格式。 答:模型机有如下 9 种指令格式: ⑴ 31 27 26 22 21 17 16 0 OP ra rb C2 指令:LOAD、STORE、LOADA、ADDI、ANDI 和 ORI 使用此格式。 ⑵ 31 27 26 22 21 0 OP ra C1 指令:LOADR、STORER 和 LOADR 使用此格式。 ⑶ 31 27 26 22 21 17 16 12 11 0 OP ra rc 未用 指令:NEG、NOT 使用此格式。 ⑷ 31 27 26 22 21 17 16 12 11 OP 未用 rb rc 未用 指令:BRxx 使用此格式。 ⑸ 31 27 26 22 21 17 16 12 11 OP ra rb rc 未用 指令:BRLxx 使用此格式。 ⑹ 31 27 26 22 21 17 16 12 11 OP ra rb rc 未用 0 指令:ADD、SUB、AND 和 OR 使用此格式。 ⑺ 31 27 26 22 21 17 16 5 4 未用 3 2 C4 3 2 C4 0 0 0
数据与计算机通信答案(第3章)

而对于数字彩色电视机,相当不错了。如果不提高数据率,还可以通过降低分辨率或刷新速 率,来换取色彩数的提高,但这也不实用的方法。
已知视频带宽 B=5MHz,所以有 5=P/105,则每行的像素数 P=5x105=525。 然而,通常 CCIR-M/NTSC 制式每行只约有 450 像素,带宽 B=P/105=450/105=4.3MHz (实 际技术指标 4.2Hz) 。 带宽由 4.2MHz 增加到 5MHz 时,水平分辨率约增加 75 像素,增幅 16.7%。 (2)计算垂直分辨率的增幅 由于信号最高频率 fH=5MHz,即最短的信号周期 1/fH=0.2υs。 又因为每个最短周期包含 2 个像素,则有 225 周期/行。那么,每行扫描时间为 0.2υs×225=45υs。加上水平回扫 11υs,每行往返扫描时间为 56υs ,即 56x10-6 s, 假定每屏 V 行,每秒扫描 30 场(帧、屏),则每秒扫描行数为 30V。 因此对于画面刷新,有 30V×56x10-6 = 1s,V = 595 行/屏。目前 NSTL 制式每行只有 525 行。垂直分辨率增加了 70 行,增幅 13.3%。
cos 2 t = cos t cos t = 1 (cos 2t + cos 0) = 1 (cos 2t + 1)
2
2
所以, f (t) = (10 cos t)2 = 100 cos 2 t = 50 + 50 cos 2t
编译原理 第3章习题解答
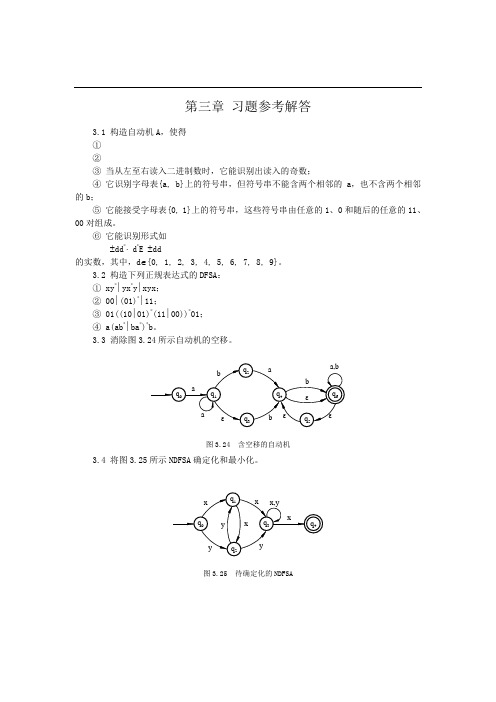
第三章习题参考解答3.1 构造自动机A,使得①②③当从左至右读入二进制数时,它能识别出读入的奇数;④它识别字母表{a, b}上的符号串,但符号串不能含两个相邻的a,也不含两个相邻的b;⑤它能接受字母表{0, 1}上的符号串,这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数,其中,d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA:① xy*∣yx*y∣xyx;② 00∣(01)*∣11;③ 01((10∣01)*(11∣00))*01;④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
bεq1q2q3aba,bqaq6q4q5abεεε图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
xyqq1q2q4q3xyxyx,yx图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式,试证明① e∣e=e;② {{e}}={e};③ {e}=ε∣e{e};④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机,指明该自动机是不是确定的,并写出它相应的语言: G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中,f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA确定化。
3.8 设文法G[〈单词〉]:〈单词〉→〈标识符〉∣〈无符号整数〉〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉〈字母〉→a∣b〈数字〉→1∣2试写出相应的有限自动机和状态图。
结构力学第三章习题参考解答

FAy 6 FAx 2 0
1 ql 2A
1 ql 4
取整体:M A 0
Fy 0
取AC: MC 0
取整体: Fx 0
l
l
0.45ql
FBy
1 2l
ql 3l 2
3 ql 4
FAy
ql
3 4
ql
1 4
ql
FAx
2 ql 2 l4
1 ql 2
FBx
1 ql 2
l 2
1 ql B2 3 ql 4
取左段
FNK
ql cos
3l 4
1 q 3 l 2 2 4
9 ql 2 32
D
C
q
3 ql
4
A
1 ql
l
4
1 ql
4
1 ql 4
3 ql
4
FQ KN
1 ql 2
E
4
1 ql 2 4
9 ql2 32
1 ql
B
4
ql 2 8
M KNm
l
1 ql
4
1 ql
4
1 ql
4
FN KN
1 ql2 4
1 ql 4
3-12解:
q C
q
3 ql
4
A
l
1 ql
B
4
Fy 0
FAy
1 ql 4
1 ql 4
l
l
1 ql
4
取BC:
MC 0
FBx
1 4
ql
取整体:
Fx 0
FAx
ql
1 ql 4
3 ql 4
AD段的最大弯矩 M x 3 qlx 1 qx2 dM 3 ql qx 0
机械设计基础课后习题答案
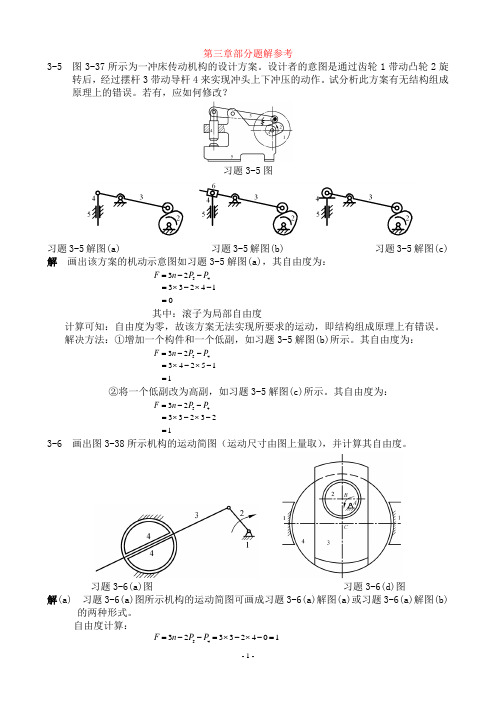
第三章部分题解参考3-5 图3-37所示为一冲床传动机构的设计方案。
设计者的意图是通过齿轮1带动凸轮2旋转后,经过摆杆3带动导杆4来实现冲头上下冲压的动作。
试分析此方案有无结构组成原理上的错误。
若有,应如何修改?习题3-5图习题3-5解图(a) 习题3-5解图(b) 习题3-5解图(c) 解 画出该方案的机动示意图如习题3-5解图(a),其自由度为:14233 2345=-⨯-⨯=--=P P n F 其中:滚子为局部自由度计算可知:自由度为零,故该方案无法实现所要求的运动,即结构组成原理上有错误。
解决方法:①增加一个构件和一个低副,如习题3-5解图(b)所示。
其自由度为:115243 2345=-⨯-⨯=--=P P n F ②将一个低副改为高副,如习题3-5解图(c)所示。
其自由度为:123233 2345=-⨯-⨯=--=P P n F 3-6 画出图3-38所示机构的运动简图(运动尺寸由图上量取),并计算其自由度。
习题3-6(a)图 习题3-6(d)图解(a) 习题3-6(a)图所示机构的运动简图可画成习题3-6(a)解图(a)或习题3-6(a)解图(b)的两种形式。
自由度计算:1042332345=-⨯-⨯=--=P P n F习题3-6(a)解图(a)习题3-6(a)解图(b)解(d) 习题3-6(d)图所示机构的运动简图可画成习题3-6(d)解图(a)或习题3-6(d)解图(b)的两种形式。
自由度计算:1042332345=-⨯-⨯=--=P P n F习题3-6(d)解图(a) 习题3-6(d)解图(b)3-7 计算图3-39所示机构的自由度,并说明各机构应有的原动件数目。
解(a) 10102732345=-⨯-⨯=--=P P n FA 、B 、C 、D 为复合铰链原动件数目应为1说明:该机构为精确直线机构。
当满足BE =BC =CD =DE ,AB =AD ,AF =CF 条件时,E 点轨迹是精确直线,其轨迹垂直于机架连心线AF解(b) 1072532345=-⨯-⨯=--=P P n FB 为复合铰链,移动副E 、F 中有一个是虚约束 原动件数目应为1说明:该机构为飞剪机构,即在物体的运动过程中将其剪切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ρ
,即
D2
=
ρ R03 3r 2
,
E2
=
D1 ε0
=
ρ R03 3ε 0 r 2
故介质球中心点的电位为
∫ ∫ ∫ ∫ ϕ(0) =
R0 0
E1dr
+
∞
R0 E2dr
=
R0 0
ρr 3ε rε 0
dr +
∞ R0
ρ R03 3ε0r 2
dr
= ρ R02 6ε rε 0
+
ρ R02 3ε 0
=
2εr + 2ε r
3.1 数ϕ
长度为 L 的线电荷,电荷密度为常数 ρl ;(2) 利用直接积分法计算平分面上的
0EG。,(1并) 用计E算G =线−电∇ϕ荷由平(分1)验面证上(的2)电所位得函结
果。
图题 3.1 解:(1) 建立如图题 3.1 所示坐标系。根据电位的积分表达式,线电荷平分面上 任意点 P 的电位为
两板间加电压U0 ,试证明液面升高
h
=
1 2ρ g
(ε
−
ε
0
)
⎛ ⎜⎝
U0 d
⎞2 ⎟⎠
式中的 ρ 为液体的质量密度, g 为重力加速度。
U0
L h
ε
d
图题 3.10
解:设金属板的宽度为 a 、高度为 L 。当金属板间的液面升高为 h 时,其电容为
C = ε ah + ε0a(L − h)
d
d
金属板间的静电能量为
(1)
∂2 ∂x2
(e− y
cosh
x)
+
∂2 ∂y2
(e− y
cosh
x)
+
∂2 ∂z2
(e− y
cosh
x)
=
2e− y
cosh
x
≠
0
所以函数 e− y cosh x 不是 y > 0 空间中的电位解;
(2)
∂2 ∂x2
(e− y
cos
x)
+
∂2 ∂y2
(e− y
cos
x)
+
∂2 ∂z2
(e− y
(a < ρ < c) (a < ρ < b) (b < ρ < c)
由于
∫ ∫ U0 =
b a
G E1
⋅
dρG
+
c b
G E2
⋅ dρG
=
I 2πσ1
ln
⎛ ⎜⎝
b a
⎞ ⎟⎠
+
I 2πσ 2
ln
⎛ ⎜⎝
c b
⎞ ⎟⎠
于是得到
I=
2πσ1σ 2U0
σ 2 ln(b / a) + σ1 ln(c / b)
cosφ
,
⎠
ρ≥a
(1) 求圆柱内、外的电场强度;(2) 这个圆柱是什么材料制成的?其表面上有电
荷分布吗?试G 求之。
解:(1) ρ
由 E = −∇Gϕ ,可得 ≤ a 时, E = −∇ϕ =
0
ρ
≥
G a 时, E
=
−∇ϕ
=
G −eρ
∂ ∂ρ
⎡ ⎢
A(ρ
⎣
−
a2 ρ
)
cos
φ
⎤ ⎥ ⎦
−
G eφ
∂ ρ∂φ
cos
x)
=
−e− y
cos
x
+
e− y
cos
x
=
0
所以函数 e− y cos x 是 y > 0 空间中可能的电位解;
(3)
∂ (e− 2 sin x cos x) + ∂ (e− 2 sin x cos x) + ∂ (e− 2 sin x cos x)
∂x2
∂y2
∂z 2
= −4e− 2 sin x cos x + 2e− 2 sin x cos x ≠ 0 所以函数 e− 2 sin x cos x 不是 y > 0 空间中的电位解;
q
−
2q
⎤ ⎥
4πε0 ⎢⎣ (x + a)2 + y2 + z2 (x − a)2 + y2 + z2 ⎥⎦
令ϕ(x, y, z) = 0 ,则有
1
−
2
=0
(x + a)2 + y2 + z2 (x − a)2 + y2 + z2
即
4[(x + a)2 + y2 + z2 ] = (x − a)2 + y2 + z2
G eρ
ρl 0 4πε 0 ρ
z' ρ 2 + (L / 2)2
3.2 点电荷 q1 = q 位于 P1(−a, 0, 0) ,另一点电荷 q2 = −2q 位于 P2 (a, 0, 0) ,求空间的 零电位面。 解:两个点电荷 +q 和 −2q 在空间产生的电位
ϕ(x, y, z) =
1
⎡ ⎢
+
(L /
2)2
+
L
/
2
⎤ ⎥
2πε0 ⎢⎣
ρ
⎥⎦
=
G −eρ
ρl0 2πε 0
d dρ
[ln(
ρ 2 + (L / 2)2 + L / 2) − ln ρ]
=
G −eρ
ρl0 2πε 0
⎧⎪ ⎨ ⎪⎩[L / 2 +
ρ ρ 2 + (L / 2)2 ]
ρ2
+ (L / 2)2
−
1 ⎫⎪
ρ
⎬ ⎪⎭
=
We
=
1 2
CU
2
0
=
aU
2
0
2d
[hε
+
(L
−
h)ε0 ]
液体受到竖直向上的静电力为
Fe
=
∂We ∂h
=
aU
2
0
2d
(ε
−ε0)
而液体所受重力 Fg = mg = ahd ρ g
Fe 与 Fg 相平衡,即
aU
2 0
2d
(ε
−ε0)
=
ahdg ρ
故得到液面上升的高度
h
=
(ε
−
ε0
)U
2 0
2d 2ρ g
−ε0)
∂ϕ2 ∂r
r=a
=
3ε0 (ε − ε0 ) ε + 2ε0
E0
cosθ
3.7 两块无限大导体平板分别置于 x = 0 和 x = d 处,板间充满电荷,其体电荷密
度为
ρ
=
ρ0 x d
,极板的电位分别设为
0
和U0
,如图题
3.7
所示,求两导体板之间
的电位和电场强度。
ϕ = 0 ρ(x) ϕ = U0
所以
E
=
q 2πr2 (ε1
+
ε2)
∫ ∫ 导体球的电位
ϕ(a) =
∞
Edr =
q
∞ 1 dr =
q
a
2π(ε1 + ε2 ) a r 2
2π(ε1 + ε2 )a
故导体球的电容
C
=
q ϕ(a)
=
2π(ε1
+
ε2
)a
(2) 总的静电能量为
We
=
1 2
qϕ (a)
=
q2 4π(ε1 +
ε 2 )a
3.10 两平行的金属板,板间距离为 d ,竖直地插入介电常数为 ε 的液态介质中,
自由电荷,试证明该介质球中心点的电位为 G
2εr +1 2ε r
ρ 3ε 0
R02
。
解:由高斯定理 v∫S D ⋅ dS = q ,得
r
< R0 时, 4πr 2D1
=
4πr 3 3
ρ
,即 D1
=
ρr 3
, E1
=
D1 ε rε 0
=
ρr 3ε rε 0
r
>
R0 时, 4πr 2D2
=
4πR03 3
故两种介质中的电流密度和电场强度分别为
G J
=
G eρ
ρ[σ 2
同轴线单位长度的静电储能为
∫ ∫ We
=
1 2
ε E2dV = 1
V
2
bε
a
⎛ ⎜⎝
ql 2περ
⎞2 ⎟⎠
2πρdρ
=
1 2
q2 l
2πε
ln
⎛ ⎜⎝
b a
⎞ ⎟⎠
=
1 2
q2 l
C
3.9 有一半径为 a 、带电量 q 的导体球,其球心位于介电常数分别为 ε1 和 ε2 的两
种介质分界面上,设该分界面为无限大平面。试求:(1)导体球的电容;(2) 总的 静电能量。
ql2 2C
。式中
ql
为单位长度上的电荷
量, C 为单位长度上的电容。 证:由高斯定理可求得同轴线内、外导体间的电场强度为
E(ρ) = ql 2περ
内外导体间的电压为
∫ ∫ U =
b Edρ =
a
b a
ql dρ 2περ
=
ql 2πε
ln
⎛ ⎜⎝
