最新高考文科数学全国卷1试题及详细解析(Word精美版)
高考全国1卷文科数学带答案

绝密★启用前普通高等学校招生全国统一考试文科数学注意事项:1.答卷前, 考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时, 选出每小题答案后, 用铅笔把答题卡对应题目的答案标号涂黑。
如需改动, 用橡皮擦干净后, 再选涂其它答案标号。
回答非选择题时, 将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后, 将本试卷和答题卡一并交回。
一、选择题:本题共12小题, 每小题5分, 共60分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
1.已知集合{}02A =,, {}21012B =--,,,,, 则A B =I A .{}02, B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++, 则z = A .0B .12C .1D .23.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况, 统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A .新农村建设后, 种植收入减少B .新农村建设后, 其他收入增加了一倍以上C .新农村建设后, 养殖收入增加了一倍D .新农村建设后, 养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为(20),, 则C 的离心率为 A .13B .12C 2D .2235.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形, 则该圆柱的表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数, 则曲线()y f x =在点()00,处的切线方程为 A .2y x =-B .y x =-C .2y x = D.y x =7.在△ABC 中, AD 为BC 边上的中线, E 为AD 的中点, 则EB =u u u rA .3144AB AC -u u ur u u u rB .1344AB AC -u u ur u u u rC .3144AB AC +u u ur u u u rD .1344AB AC +u u ur u u u r8.已知函数()222cos sin 2f x x x =-+, 则 A .()f x 的最小正周期为π, 最大值为3 B .()f x 的最小正周期为π, 最大值为4 C .()f x 的最小正周期为2π, 最大值为3 D .()f x 的最小正周期为2π, 最大值为4 9.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B , 则在此圆柱侧面上, 从M 到N 的路径中, 最短路径的长度为 A .217B .25C .3D .210.在长方体1111ABCD A B C D -中, 2AB BC ==, 1AC 与平面11BB C C 所成的角为30︒, 则该长方体的体积为 A .8B .62C .82D .8311.已知角α的顶点为坐标原点, 始边与x 轴的非负半轴重合, 终边上有两点()1A a ,, ()2B b ,, 且2cos 23α=, 则a b -=A .15B .5 C .25D .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,, 则满足()()12f x f x +<的x 的取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题(本题共4小题, 每小题5分, 共20分)13.已知函数()()22log f x x a =+, 若()31f =, 则a =________.14.若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤, 则32z x y =+的最大值为________.15.直线1y x =+与圆22230x y y ++-=交于A B ,两点, 则AB =________.16.△ABC 的内角A B C ,,的对边分别为a b c ,,, 已知sin sin 4sin sin b C c B a B C +=, 2228b c a +-=, 则△ABC 的面积为________.三、解答题:共70分。
最新高考文科数学全国新课标卷1试题与答案word解析版

2013年普通高等学校招生全国统一考试(新课标全国卷I)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(2013课标全国Ⅰ,文1)已知集合A ={1,2,3,4},B ={x |x =n 2,n ∈A },则A ∩B =( ).A .{1,4}B .{2,3}C .{9,16}D .{1,2} 【答案】A【考点】本题主要考查集合的基本知识。
【解析】∵B ={x |x =n 2,n ∈A }={1,4,9,16}, ∴A ∩B ={1,4}.2.(2013课标全国Ⅰ,文2)212i1i +(-)=( ).A. −1−12i B .11+i 2- C .1+12i D .1−12i 【答案】B【考点】本题主要考查复数的基本运算。
【解析】212i 12i 12i i 2i 1i 2i 22++(+)-+===(-)-=11+i 2-.3.(2013课标全国Ⅰ,文3)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( ).A .12B .13C .14D .16【答案】B【考点】本题主要考查列举法解古典概型问题的基本能力。
【解析】由题意知总事件数为6,且分别为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),满足条件的事件数是2,所以所求的概率为13. 4.(2013课标全国Ⅰ,文4)已知双曲线C :2222=1x y a b-(a >0,b >0)C 的渐近线方程为( ).A . y =±14x B .y =±13x C .12y x =± D .y =±x【答案】C【考点】本题主要考查双曲线的离心率、渐近线方程。
【解析】∵2e =2c a =,即2254c a =.∵c 2=a 2+b 2,∴2214b a =.∴12b a =.∵双曲线的渐近线方程为by x a=±,∴渐近线方程为12y x =±.故选C.5.(2013课标全国Ⅰ,文5)已知命题p :∀x ∈R,2x <3x ;命题q :∃x ∈R ,x 3=1-x 2,则下列命题中为真命题的是( ).A .p ∧qB .⌝p ∧qC .p ∧⌝qD .⌝p ∧⌝q 【答案】B【考点】本题主要考查常用逻辑用语等基本知识。
最新整理高考全国卷ⅰ数文科试题含答案全word.doc

普通高等学校招生全国统一考试文科数学(必修+选修Ⅰ)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页,第II 卷3至9页.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷考生注意: 1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ,并贴好条形码.请认真核准条形码上的准考证号、姓名和科目. 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效..........3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 参考公式: 如果事件A B ,互斥,那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是P ,那么34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(01,2)k kn k n n P k C P P k n -=-=,,,一、选择题 1.函数y = )A .{|1}x x ≤B .{|0}x x ≥C .{|10}x x x ≥或≤D .{|01}x x ≤≤2.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图像可能是( )A .B .C .D .3.512x ⎛⎫+ ⎪⎝⎭的展开式中2x 的系数为( )A .10B .5C .52D .14.曲线324y x x =-+在点(13),处的切线的倾斜角为( ) A .30°B .45°C .60°D .120°5.在ABC △中,AB c =,AC b =.若点D 满足2BD DC =,则AD =( ) A .2133b c + B .5233c b -C .2133b c - D .1233b c +6.2(sin cos )1y x x =--是( ) A .最小正周期为2π的偶函数 B .最小正周期为2π的奇函数 C .最小正周期为π的偶函数D .最小正周期为π的奇函数7.已知等比数列{}n a 满足122336a a a a +=+=,,则7a =( ) A .64B .81C .128D .2438.若函数()y f x =的图象与函数1y =的图象关于直线y x =对称,则()f x =( ) A .22ex -B .2e xC .21ex +D .2+2ex9.为得到函数πcos 3y x ⎛⎫=+ ⎪⎝⎭的图象,只需将函数sin y x =的图像( ) A .向左平移π6个长度单位 B .向右平移π6个长度单位 C .向左平移5π6个长度单位 D .向右平移5π6个长度单位10.若直线1x y a b+=与圆221x y +=有公共点,则( )A .221a b +≤B .221a b +≥ C .22111a b+≤D .2211a b +≥1 11.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( )A .13B .3C .3D .2312.将1,2,3填入33⨯的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( )A .6种B .12种C .24种D .48种普通高等学校招生全国统一考试文科数学(必修+选修Ⅰ)第Ⅱ卷注意事项:1.答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,然后贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.第Ⅱ卷共7页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.......... 3.本卷共10小题,共90分.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.(注意:在试题卷上作答无效.........) 13.若x y ,满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩,,,≥≥≤≤则2z x y =-的最大值为 .14.已知抛物线21y ax =-的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 . 15.在ABC △中,90A ∠=,3tan 4B =.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .16.已知菱形ABCD 中,2AB =,120A ∠=,沿对角线BD 将ABD △折起,使二面角A BD C --为120,则点A 到BCD △所在平面的距离等于 .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)(注意:在试题卷上作答无效.........) 设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且cos 3a B =,sin 4b A =. (Ⅰ)求边长a ;(Ⅱ)若ABC △的面积10S =,求ABC △的周长l .18.(本小题满分12分)(注意:在试题卷上作答无效.........) 四棱锥A BCDE -中,底面BCDE 为矩形,侧面ABC ⊥底面BCDE ,2BC =,CD =AB AC =.(Ⅰ)证明:AD CE ⊥;(Ⅱ)设侧面ABC 为等边三角形,求二面角C AD E --的大小.19.(本小题满分12分)(注意:在试题卷上作答无效.........) 在数列{}n a 中,11a =,122nn n a a +=+.(Ⅰ)设12nn n a b -=.证明:数列{}n b 是等差数列; (Ⅱ)求数列{}n a 的前n 项和n S . 20.(本小题满分12分)(注意:在试题卷上作答无效.........) 已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方案: 方案甲:逐个化验,直到能确定患病动物为止.方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.求依方案甲所需化验次数不少于依方案乙所需化验次数的概率.CDE AB21.(本小题满分12分)(注意:在试题卷上作答无效.........) 已知函数32()1f x x ax x =+++,a ∈R . (Ⅰ)讨论函数()f x 的单调区间;(Ⅱ)设函数()f x 在区间2133⎛⎫-- ⎪⎝⎭,内是减函数,求a 的取值范围. 22.(本小题满分12分)(注意:在试题卷上作答无效.........) 双曲线的中心为原点O ,焦点在x 轴上,两条渐近线分别为12l l ,,经过右焦点F 垂直于1l 的直线分别交12l l ,于A B ,两点.已知OA AB OB 、、成等差数列,且BF 与FA 同向. (Ⅰ)求双曲线的离心率;(Ⅱ)设AB 被双曲线所截得的线段的长为4,求双曲线的方程.普通高等学校招生全国统一考试 文科数学(必修+选修Ⅰ)参考答案一、1.D 2.A 3.C 4.B 5.A 6.D 7.A 8.A 9.C 10.D 11.B 12.B二、13.9 14.12 15.1216.2三、17.解:(1)由cos 3a B =与sin 4b A =两式相除,有:3cos cos cos cot 4sin sin sin a B a B b BB b A A b B b ==== 又通过cos 3a B =知:cos 0B >,则3cos 5B =,4sin 5B =,则5a =.(2)由1sin 2S ac B =,得到5c =.由222cos 2a c b B ac+-=,解得:b =最后10l =+.18.解:(1)取BC 中点F ,连接DF 交CE 于点O , AB AC =,∴AF BC ⊥,又面ABC ⊥面BCDE , ∴AF ⊥面BCDE , ∴AF CE ⊥.tan tan 2CED FDC ∠=∠=, ∴90OED ODE ∠+∠=,90DOE ∴∠=,即CE DF ⊥,CE ∴⊥面ADF , CE AD ∴⊥.(2)在面ACD 内过C 点做AD 的垂线,垂足为G . CG AD ⊥,CE AD ⊥,AD ∴⊥面CEG , EG AD ∴⊥,则CGE ∠即为所求二面角.233AC CD CG AD ==,3DG =,3EG ==,CE =则222cos 210CG GE CE CGE CG GE +-∠==-,πarccos CGE ∴∠=-⎝⎭.19.解:(1)122nn n a a +=+,11122n nn n a a +-=+, 11n n b b +=+,则n b 为等差数列,11b =,n b n =,12n n a n -=.(2)01211222(1)22n n n S n n --=+++-+12121222(1)22n n n S n n -=+++-+两式相减,得01121222221n n n n n S n n -=---=-+.20.解:对于甲:次数 1 2 3 4 5 概率 0.20.2 0.2 0.20.2 对于乙:次数 2 3 4 概率0.40.40.20.20.40.20.80.210.210.64****+++=.21.解:(1)32()1f x x ax x =+++ 求导:2()321f x x ax '=++ 当23a≤时,0∆≤,()0f x '≥()f x 在R 上递增当23a >,()0f x '=求得两根为3a x -±=即()f x在⎛-∞ ⎝⎭递增,⎝⎭递减,3a ⎛⎫-++∞⎪ ⎪⎝⎭递增 (2)2313--,且23a >解得:74a ≥22.解:(1)设OA m d =-,AB m =,OB m d =+由勾股定理可得:222()()m d m m d -+=+得:14d m =,tan b AOF a ∠=,4tan tan 23AB AOB AOF OA ∠=∠==由倍角公式∴22431ba b a =⎛⎫- ⎪⎝⎭,解得12b a =则离心率2e =.(2)过F 直线方程为()ay x c b =-- 与双曲线方程22221x y a b -=联立将2a b =,c =代入,化简有22152104x x b -+=124x =-=将数值代入,有4=解得3b=最后求得双曲线方程为:221 369x y-=.点评:本次高考题目难度适中,第12道选择题是北京市海淀区第二次模拟考试题,新东方在寒假强化班教材的220页33题选用此题进行过详细讲解,在春季冲刺班教材30页33题也选用此题,新东方的老师曾在多种场合下对此题做过多次讲解.第19道计算题也是一个非常典型的题型,在12月31日,新东方在石家庄的讲座上曾经讲过这类问题的解法,在的讲课中也多次提过此题型是重点.其他的题型也都很固定,没有出现偏题怪题,应该说,本次高考题的难度,区分度都非常恰当.。
高考真题——数学文(全国Ⅰ卷) Word版含答解析

绝密★启用前2020年普通高等学校招生全国统一考试文科数学本试卷共5页,满分150分。
考生注意:1.答卷前,考生务必将自己的准考证号、姓名填写在答题卡上。
考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,监考员将试题卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={}|2x x <,B ={}|320x x ->,则 A .A I B =3|2x x ⎧⎫<⎨⎬⎩⎭B .A I B =∅C .A U B 3|2x x ⎧⎫=<⎨⎬⎩⎭D .A U B=R【答案】A【解析】由320x ->得32x <,所以33{|2}{|}{|}22A B x x x x x x ⋂=<⋂<=<,选A. 2.为评估一种农作物的种植效果,选了n 块地作试验田.这n 块地的亩产量(单位:kg )分别为x 1,x 2,…,x n ,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 A .x 1,x 2,…,x n 的平均数 B .x 1,x 2,…,x n 的标准差 C .x 1,x 2,…,x n 的最大值D .x 1,x 2,…,x n 的中位数【答案】B【解析】刻画评估这种农作物亩产量稳定程度的指标是标准差,故选B 3.下列各式的运算结果为纯虚数的是 A .i(1+i)2B .i 2(1-i)C .(1+i)2D .i(1+i)【答案】C【解析】由2(1)2i i +=为纯虚数知选C.4.如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,学 科&网则此点取自黑色部分的概率是A .14B .π8C .12D .π 4【答案】B5.已知F 是双曲线C :x 2-23y =1的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3).则△APF 的面积为 A .13B .1 2C .2 3D .3 2【答案】D【解析】由2224c a b =+=得2c =,所以(2,0)F ,将2x =代入2213y x -=,得3y =±,所以3PF =,又A 的坐标是(1,3),故APF 的面积为133(21)22⨯⨯-=,选D. 6.如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是【答案】A【解析】由B ,AB ∥MQ ,则直线AB ∥平面MNQ ;由C ,AB ∥MQ ,则直线AB ∥平面MNQ ;由D ,AB ∥NQ ,则直线AB ∥平面MNQ.故A 不满足,选A. 7.设x ,y 满足约束条件33,1,0,x y x y y +≤⎧⎪-≥⎨⎪≥⎩则z =x +y 的最大值为A .0B .1C .2D .3【答案】D【解析】如图,目标函数z x y =+经过(3,0)A 时最大,故max 303z =+=,故选D.8..函数sin21cos xy x=-的部分图像大致为【答案】C【解析】由题意知,函数sin 21cos xy x=-为奇函数,故排除B ;当x π=时,0y =,排除D ;当1x =时,sin 201cos 2y =>-,排除A.故选C.9.已知函数()ln ln(2)f x x x =+-,则 A .()f x 在(0,2)单调递增B .()f x 在(0,2)单调递减C .y =()f x 的图像关于直线x =1对称D .y =()f x 的图像关于点(1,0)对称【答案】C10.如图是为了求出满足321000n n ->的最小偶数n ,学|科网那么在和两个空白框中,可以分别填入A .A >1000和n =n +1B .A >1000和n =n +2C .A ≤1000和n =n +1D .A ≤1000和n =n +2【答案】D【解析】由题意选择321000n n->,则判定框内填1000A ≤,由因为选择偶数,所以矩形框内填2n n =+,故选D.11.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c 。
(版)高考文科数学全国1卷(附答案)

(版)高考文科数学全国1卷(附答案)_ -__ -___ -__:-号-学-__ -___-___-____线__封__密___-_-名姓---班-___-___-_年-____线__封_密__-___-___-___-___-___-___ -:校-学-12B-SX-0000022绝密★启用前2021年普通高等学校招生全国统一考试文科数学全国I卷本试卷共23小题,总分值 150分,考试用时120分钟(适用地区:河北、河南、山西、山东、江西、安徽、湖北、湖南、广东、福建)考前须知:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.答复选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答复非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:此题共12小题,每题5分,共60分。
在每个小题给出的四个选项中,只有一项为哪一项符合题目要求的。
1.设z3i,那么z=12iA.2B.3C.2D.12.集合U1,2,3,4,5,6,7,A2,3,4,5,B2,3,6,7,那么BIeAUA.1,6B.1,7C.6,7D.1,6,7.a,那么log20.2,b2,c3A.a b c B.a c bC.c a b D.b c a4.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之(版)高考文科数学全国1卷(附答案)比是5 1〔51≈,称为黄金分割比例),著名22 的“断臂维纳斯〞便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是5 1.假设某人满足2上述两个黄金分割比例,且腿长为105cm ,头顶至脖子下端的长度为26cm ,那么其身高可能是 A.165cm B.175cm C.185cmD.190cm函数f(x)=sinxx2在[—π,π]的图像大致为cosxxA.B.C.D.6.某学校为了解 1000名新生的身体素质,将这些学生编号为 1,2, ,1000,从这些新生中用系统抽样方法等距抽取 100名学生进行体质测验 .假设46号学生被抽到,那么下面 4名学生中被抽到的是A .8号学生B .200号学生C .616号学生D .815号学生7.tan255=° A .-2-3B .-2+3C .2-3D .2+3-1--2-(版)高考文科数学全国1卷(附答案)12B-SX-00000228.非零向量a ,b 满足a =2b ,且〔a –b 〕b ,那么a 与b 的夹角为A .ππ2π5π6B .C .D .3 3 619.如图是求21 的程序框图,图中空白框中应填入2 12A.A=12 AB.A= 21AC.A=11 2AD.A= 112Ax 2 y 2 1(a0,b0)的一条渐近线的倾斜角为130°,那么C 的10.双曲线C :b 2 a 2离心率为A .2sin40°B .2cos40°C .1 1D .cos50sin5011.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,asinA -bsinB=4csinC ,cosA=-1 ,那么b=4cA .6B .5C .4D .312.椭圆C 的焦点为F 1(1,0),F 2(1,0),过F 2的直线与C 交于A ,B 两点.假设|AF| 2|FB|,|AB||BF|,那么C 的方程为221A .x 2y21B .x 2y 2 1232x 2 y 2 1x 2y 2 1C .3D .445二、填空题:此题共4小题,每题 5分,共20分。
(word版)全国高考文科数学试题及参考答案全国卷1

绝密★启用前2021年普通高等学校招生全国统一考试文科数学本试卷共5页,总分值150分。
考生注意:1.答卷前,考生务必将自己的准考证号、姓名填写在答题卡上。
考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目〞与考生本人准考证号、姓名是否一致。
2.答复选择题时,选出每题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答复非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,监考员将试题卷和答题卡一并交回。
一、选择题:本大题共12小题,每题5分,共60分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
1.集合A=x|x2,B=x|32x0,那么3B.AIBA.AIB=x|x2C.AUB3D.AUB=R x|x22.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量〔单位:kg〕分别为x1,x2,,x n,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是A.x1,x2,,x n的平均数B.x1,x2,,x n的标准差C.x1,x2,,x n的最大值D.x1,x2,,x n的中位数3.以下各式的运算结果为纯虚数的是A.i(1+i)2B.i2(1-i)C.(1+i)2D.i(1+i)4.如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色局部和白色局部关于正方形的中心成中心对称.在正方形内随机取一点,那么此点取自黑色局部的概率是A.1B.π48精心整理C .1πD .245.F 是双曲线 2y 2 C :x-=1的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3).3那么△APF 的面积为A .1B .1C .2D .332 3 26.如图,在以下四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,那么在这四个正方体中,直接AB 与平面MNQ 不平行的是x 3y 3,7.设x ,y 满足约束条件xy1,y 0,那么z=x+y 的最大值为A .0B .1C .2D .38..函数ysin2x 的局部图像大致为1cosx9.函数f(x)lnxln(2x),那么A .f(x)在〔0,2〕单调递增B .f(x)在〔0,2〕单调递减C .y=f(x)的图像关于直线x=1对称D .y=f(x)的图像关于点〔1,0〕对称10.如图是为了求出满足3n2n 1000的最小偶数n ,那么在和 两个空白框中,可以分别填入A .A>1000和n=n+1B .A>1000和n=n+2C .A ≤1000和n=n+1D .A ≤1000和n=n+211.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c 。
2020年高考文科数学全国卷1附答案解析版

1| 2
PF1 ||
PF2 | 中计算即可.
由已知,不妨设 F1 2,0,F2 2,0,
则a
1,c
2 ,因为| OP | 1
1| 2
F
1F2
|,
所以点 P 在以 F1F2为直径的圆上, 即 △F1F2P 是以 P 为直角顶点的直角三角形,
【解析】根据已知条件求得q 的值,再由a 6 a 7 a 8 q a5 1a 2 a3 可求得结果. 设等比数列an的公比为q ,则 a 1 a2 a3 a1 1 q q 2 1 , a2 a3 a4 a1q a1q 2 a1q3 a1q 1 q q 2 q 2 , 因此, a6 a7 a8 a1 q5 a1 q6 a1 q7 a1 q5 1 q q 2 q5 32 .
数学试卷 第 6 页(共 6 页)
2020年普通高等学校招生全国统一考试·全国I卷
文科数学答案解析
一、选择题 1.【答案】D 【解析】首先解一元二次不等式求得集合 A,之后利用交集中元素的特征求得 A 由 x2 3x 4<0 解得1<x<4,
所以 A x | 1<x<4, 又因为 B 4,1,3,5,所以 A B 1,3,
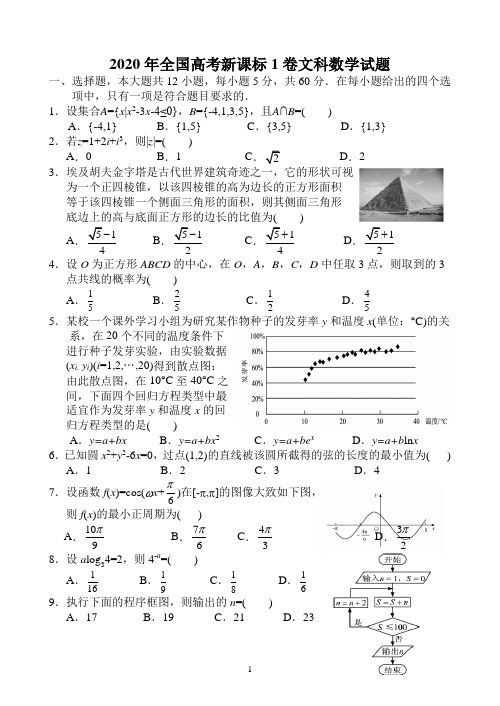
xi,yi i 1,2,,20得到下面的散点图:
由此散点图,在10℃ 至 40℃之间,下面四个回归方程类型中最适宜作为发芽率 y 和
温度 x 的回归方程类型的是
()
A. y a bx
B. y a bx2
C. y a bex
D. y a b ln x
6.已知圆 x2 y2 6x 0 ,过点1,2的直线被该圆所截得的弦的长度的最小值为
数学试卷 第 4 页(共 6 页)
毕业学校
姓名
考生号
2020年全国卷一文科数学高考试题(word版+详细解析版)

2020年普通高等学校招生全国统一考试全国卷一文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合2{|340}A x x x =--<,{4,1,3,5}B =-,则A B =A .{4,1}-B .{1,5}C .{3,5}D .{1,3}答案:D解析:2{|340}{|14}A x x x x x =--<=-<<,则交集的定义可得,{13},A B =,故选D 2.若312i i z =++,则||z =A .0B .1C .2D .2答案:C解析:因为312i i 12i (i)1i z =++=++-=+,所以22||=112z +=,故选C3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A.14 B.12C.14 D.12 答案:C解析:如图,P ABCD -是正四棱锥,过P 作PO ABCD ⊥平面,O 为垂足,则O 是正方形ABCD 的中心,取BC 的中点E ,则OE BC ⊥,因为PO ABCD ⊥平面,所以BC PO ⊥,又PO OE O =,所以BC POE ⊥平面,因为PE POE ⊂平面,所以PE BC ⊥,设BC a =,PO h =,由勾股定理得PE =1122PBCS BC PE =⋅=212h =,所以221142PE a aPE -=,解得PE =或PE =(舍去),故选CE OPA B C D4.设O 为正方形ABCD 的中心,在O ,A ,B ,C ,D 中任取3点,则取到的3点共线的概率为A .15B .25C .12D .45答案:A解析:O ,A ,B ,C ,D 中任取3点的取法用集合表示有{,,}O A B ,{,,}O A C ,{,,}O A D ,{,,}O B C ,{,,}O B D ,{,,}O C D ,{,,}A B C ,{,,}A B D ,{,,}A C D ,{,,}B C D ,共有10种取法,其中3点共线的取法有{,,}O A C ,{,,}O B D ,共2种,故取到的3点共线的概率为21105=,故选AODCBA5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(,)(1,2,,20)i ix y i=得到下面的散点图:由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是A.y a bx=+B.2y a bx=+C.e xy a b=+D.lny a b x=+答案:D解析:本题考查回归方程及一次函数、二次函数、指数函数、对数函数的图象,观察散点图可知,散点图用光滑曲线连接起来比较接近对数函数的图象,故选D。
(完整word版)高考数学试卷全国卷1文科真题附答案解析

2019 年全国一致高考数学试卷(文科)(新课标Ⅰ)一、选择题:此题共12 小题,每题 5 分,共60 分。
在每题给出的四个选项中,只有一项为哪一项切合题目要求的。
1.( 5 分)设 z 3 i,则 | z | ( )1 2iA .2B . 3 C. 2 D. 12.( 5 分)已知会合U { 1 ,2,3,4, 5,6, 7} , A {2 ,3,4, 5} , B {2 ,3,6, 7} ,则 B I e U A ( )A . {1 , 6}B . {1 , 7} C. {6 , 7} D. {1 , 6, 7} 3.( 5 分)已知 a log2 0.2 , b 2 , c ,则 ( )A . a b cB . a c b C. c a b D. b c a4.( 5 分)古希腊期间,人们以为最佳人体的头顶至肚脐的长度与肚脐至足底的长度之比是5 1 5 12 (20.618 ,称为黄金切割比率),有名的“断臂维纳斯”即是这样.别的,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是5 1 .若某人知足上述两个黄金分2割比率,且腿长为 105cm ,头顶至脖子下端的长度为26cm ,则其身高可能是 ()A . 165cmB . 175cm C. 185cm D. 190cm 5.( 5 分)函数 f ( x) sin x x 的图象在 [ ,] 的大概为 ( )cos x x2A.B.C.D .6.( 5 分)某学校为认识1000 名重生的身体素质,将这些学生编号1, 2,,1000,从这些重生顶用系统抽样方法等距抽取100 名学生进行体质测试.若46 号学生被抽到,则下边4 名学生中被抽到的是( )A .8 号学生B .200 号学生C. 616 号学生D. 815 号学生7.( 5 分) tan 255 ( )A . 2 3B . 23 C. 23 D. 2 38.( 5 分)已知非零向量r r r r r r r r ra ,b 知足 | a | 2| b | ,且 (a b) b ,则 a 与 b 的夹角为 ()A .B .3 C.2D.56 3 69.( 5 分)如图是求1的程序框图,图中空白框中应填入( ) 121221 1 1 1A . AB . A 2 C. A D. A 12 A A 1 2 A 2 Ax 2y2130 C 10.( 5 分)双曲线C :a2 b2 1(a 0,b 0) 的一条渐近线的倾斜角为,则的离心率为 ( )A . 2sin40B . 2cos401D.1C.cos50sin50bbsin B 4c sin C ,11.( 5 分) ABC 的内角A,B,C 的对边分别为a,,c,已知 a sin Acos A 1 ,则 b ( )4 cA .6B .5 C. 4 D. 312.( 5 分)已知椭圆 C 的焦点为 F1( 1,0) , F2 (1,0) ,过 F2的直线与 C 交于A,B两点.若| AF2 | 2 | F2 B | , | AB | | BF1 | ,则 C 的方程为 ( )A. x2 y2 1 B. x2 y2 1 C. x2 y2 1 D. x2 y2 12 3 2 4 3 5 4二、填空题:此题共 4 小题,每题 5 分,共20 分。
高考文科数学全国新课标卷1试题与答案word解析版

答案: C
解析: ∵ e
5, ∴c
2
a
5, 2
即
c2 a2
5. 4
∵c2=a2+b2,
∴
b2
2
1 .∴ b
1.
a 4 a2
∵双曲线的渐近线方程为 y
b x, a
6
∴渐近线方程为 y
1 x .故选 C. 2
5.
答案: B
解析: 由 20=30 知, p 为假命题.令 h(x)=x3- 1+ x2,
答案: A 解析: ∵B={ x| x=n2, n∈ A} = {1,4,9,16},
∴A ∩B={1,4} .
3.
答案: B
解析: 由题意知总事件数为 6, 且分别为 (1,2), (1,3), (1,4), (2,3), (2,4), (3,4), 满足
条件的事件数是 2, 所以所求的概率为 1 . 3
3
19.(本小题满分 12 分 )如图, 三棱柱 ABC-A1B1C1 中, CA=CB, AB= AA1, ∠BAA 1= 60°. (1)证明: AB ⊥A1C; (2)若 AB= CB= 2, A1C= 6 , 求三棱柱 ABC-A 1B1C1 的体积.
20. (本小题满分 12 分 )已知函数 f ( x) ex (ax b) x2 4x ,曲线 y f ( x) 在点 (0, f (0)) 处的切 线方程为 y 4x 4 . (1)求 a, b的值; (2)讨论 f (x) 的单调性, 并求 f (x) 的极大值. 21.(本小题满分 12 分)已知圆 M : ( x 1)2 y 2 1 , 圆 N : ( x 1) 2 y2 9 , 动圆 P 与圆 M 外 切并且与圆 N 内切, 圆心 P 的轨迹为曲线 C . (1)求 C 的方程; (2)l 是与圆 P , 圆 M 都相切的一条直线, l 与曲线 C 交于 A, B 两点, 当圆 P 的半径最长时, 求 | AB |.
2020年高考文科数学全国卷1试题解析(word版)

2020年普通高等学校招生全国统一考试(新课标卷I)文科数学试题解析一、选择题,本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={x|x2-3x-4≤0},B={-4,1,3,5},且A∩B=( )A.{-4,1} B.{1,5} C.{3,5} D.{1,3}解析:A={x|-1≤x≤4},∴A∩B={1,3},故选D2.若z=1+2i+i3,则|z|=( )A.0 B.1 C2D.2解析:z=1+i,∴|z2 C3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.514B.512C.514D.512解析:设四棱锥的高为h,底面边长为2a,侧面三角形的高为m,依题h2=am,且h2+a2=m2,联立消去h得m2-am -a2=0,152 hm±∴=,舍去负号,故选C. 4.设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )A.15B.25C.12D.45解析:任取三点有:O-A-B,C,D,O-B-C,D,O-C-D,A-B-C,D,A-C-D,B-C-D,共有10种。
其中3点共线的有2种,故选A.5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(x i. y i)(i=1,2,···,20)得到散点图:由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是( )A .y=a+bxB .y=a+bx 2C .y=a+be xD .y=a+b ln x解析:根据散点图可排除A .B .C .故选D.6.已知圆x 2+y 2-6x =0,过点(1,2)的直线被该圆所截得的弦的长度的最小值为( ) A .1 B .2 C .3D .4解析:依题圆心为C (3,0),半径r =3,过点A (1,2)的最短弦是垂直AC 的弦. 又AC 2,由勾股关系可得最短弦长=2,故选B. 7.设函数f (x )=cos(ωx +6π)在[-π,π]的图像大致如下图, 则f (x )的最小正周期为( ) A .109πB .76π C .43π D .32π 解析:依图49π-是(-π,0)的一个零点。
word完整版高考教学文科数学全国1卷附答案

word 完整版高考教学文科数学全国1卷附答案_-__-__ _ -_ _:-号-学-_ _-_ _ _-___- _ _ _ _ 线_ _ 封_ _ 密_ __-_-名姓-- -班-___-_ __-_年-__ _ _ 线 _ _ 封_密__-_ __-___-_ __-__ _ -___-___ - :校-学-12B-SX-0000022绝密★启用前2019年一般高等学校招生全国一致考试 文科数学全国I 卷 本试卷共23小题,满分 150分,考试用时 120分钟 (合用地域:河北、河南、山西、山东、江西、安徽、湖北、湖南、广东、福建) 注意事项: 1.答卷前,考生务势必自己的姓名、考生号等填写在答题卡和试卷指定地点上。
2.回答选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需变动,用橡皮擦洁净后,再选涂其余答案标号。
回答非选择题时,将答案写在 答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:此题共 12小题,每题 5分,共60分。
在每个小题给出的四个选 项中, 只有一项为哪一项切合题目要求的。
1.设z 3 i ,则z=1 2iA .2B .3C . 2D .12.已知会合U 1,2,3,4,5,6,7 ,A2,3,4,5 ,B2,3,6,7,则BIeAUA .1,6B .1,7C .6,7D .1,6,7.已知a,则log 20.2,b2,c3A .a b cB .a c bC .c a bD .b c a4.古希腊期间,人们以为最佳人体的头顶至肚脐的长度与肚脐至足底的长度之word 完整版高考教学文科数学全国1卷附答案比是5 1(51≈,称为黄金切割比率),有名 22 的“断臂维纳斯”即是这样.别的,最佳人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是5 1.若某人知足2上述两个黄金切割比率,且腿长为105cm ,头顶至脖子下端的长度为26cm ,则其身高可能是 A.165cm B.175cm C.185cmD.190cm函数f(x)=sinxx2在[—π,π]的图像大概为cosxxA.B.C.D.6.某学校为认识 1000名重生的身体素质,将这些学生编号为 1,2, ,1000,从这些重生顶用系统抽样方法等距抽取 100名学生进行体质测试 .若46号学生被抽到,则下边 4名学生中被抽到的是A .8号学生B .200号学生C .616号学生D .815号学生7.tan255=° A .-2-3B .-2+3C .2-3D .2+3-1- -2-word 完整版高考教学文科数学全国1卷附答案12B-SX-00000228.已知非零向量 a ,b 知足a =2b ,且(a –b )b ,则a 与b 的夹角为A .ππ2π5π6B .C .D .3 3 619.如图是求21 的程序框图,图中空白框中应填入2 12A.A=12 AB.A= 21AC.A=11 2AD.A= 112Ax 2 y 2 1(a0,b0)的一条渐近线的倾斜角为130°,则C 的10.双曲线C :b 2 a 2离心率为A .2sin40°B .2cos40°C .1 1D .cos50sin5011.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知asinA -bsinB=4csinC ,cosA=- 1 ,则b=4 cA .6B .5C .4D .312.已知椭圆C 的焦点为F 1(1,0),F 2(1,0),过F 2 的直线与C 交于A ,B 两点.若|AF|2|FB|,|AB||BF|,则C 的方程为221A .x 2y21B .x 2y 2 123 2x 2 y 2 1x 2y 2 1C .3D .445二、填空题:此题共4小题,每题5分,共20分。
高考文科数学全国卷1试题及详细解析

2021年普通高等学校招生全国统一测试文科数学考前须知:1 .答卷前,考生务必将自己的姓名和准考证号填写在做题卡上.2 .答复选择题时,选出每题答案后,用铅笔把做题卡对应题目的答案标号涂黑.如需改动,用橡皮 擦干净后,再选涂其它答案标号.答复非选择题时,将答案写在做题卡上.写在本试卷上无效.3 .测试结束后,将本试卷和做题卡一并交回.一、选择题:此题共 12小题,每题5分,共60分.在每题给出的四个选项中,只有一项为哪一项符合题目 要求的. 1,集合 A 0,2, B 2, 1, 0,1, 2,那么 AI BA. 0, 2B, 1,2C. 0D. 2 , 1 , 0 , 1 , 22 .设 z 1-- 2i ,那么 z1 iA. 0B. 1C. 1D. 223.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:那么下面结论中不正确的选项是 A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半y- 1的一个焦点为〔2,0〕,那么C 的离心率为 42/2D. jO 1 , 02,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,那么该圆柱的外表积为绝密★启用前2X 4.椭圆C:七 aC 2 C.5.圆柱的上、下底面的中央分别为6.7.8.9. A. 12 .. 2兀设函数f xA. y 2x在^ ABC中,3uurA. -AB3 uurC. 4 AB函数A.B.C.D.B. 12兀 D. 10711 x2 ax .假设f x为奇函数,那么曲线B. y xC. y 2xAD为BC边上的中线,E为AD的中点,那么1 uur-AC41 uur-AC 42 ・ 2 cl,f x 2cos x sin x 2,那么在点0,0处的切线方程为D. y x的最小正周期为的最小正周期为的最小正周期为的最小正周期为2 Tt,最大值为2 Tt,最大值为uurEB1 uuu 3 uuirB. -AB -AC4 41 uuu 3 uuirD. AB -AC4 4某圆柱的高为2,底面周长为16,其三视图如右图. 圆柱外表上的点M在正视图上的对应点为A,圆柱外表上的点N在左视图上的对应点为B,那么在此圆柱侧面上,从到N的路径中,最短路径的长度为A. 2 17B. 2,5C. 3D. 210.在长方体ABCD A1B1c l D1中,AB BC 2, AC1与平面BB1c l e所成的角为30 ,那么该长方体的体积为A. 8 D. 8、311.角的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点cos 2 2 i一,那么a3 B. r 2 5C. ------5D.12.设函数xW0x 1 f 2x的x的取值范围是A. B.,C. 1,0 D.、填空题〔此题共4小题,每题5分,共20分〕13 .函数f x log2x2a ,假设f 3 1 ,贝U a .x 2y 2w 014 .假设x, y满足约束条件x y 1 > 0 ,那么z 3x 2y的最大值为 .y w 015 .直线y x 1与圆x2y22y 3 0交于A, B两点,那么|AB .16 . △ ABC 的内角A, B , C 的对边分别为a, b, c,bsinC csin B 4asinBsinC , b2c2a28 , 那么^ ABC的面积为.三、解做题:共70分.解容许写出文字说明、证实过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.〔一〕必考题:共60分.17 . 〔 12 分〕a.数列a n满足& 1 , na n 1 2 n 1 a n,设b n — . n〔1〕求 D , b2 , A ;〔2〕判断数列bn是否为等比数列,并说明理由;〔3〕求a n的通项公式.学,科网18 . 〔12 分〕如图,在平行四边形ABCM中,AB AC 3, /ACM 90 ,以AC为折痕将^ ACM折起,使点M 到达点D的位置,且AB ± DA .〔1〕证实:平面ACD,平面ABC ;22〕 Q为线段AD上一点,P为线段BC上一点,且BP DQ - DA ,求三棱锥Q ABP的体积.319 . 〔12 分〕某家庭记录了未使用节水龙头50天的日用水量数据〔单位:m3〕和使用了节水龙头50天的日用水量数据,得到频数分布表如下:日用0, 0.1 0.1 , 0.2 0.2, 0.3 0.3, 0.4 0.4, 0.5 0.5, 0.6 0.6, 0.7 水量频数 1 3 2 4 9 26 5日用0 , 0.1 0.1, 0.2 0.2 , 0.3 0.3, 0.4 0.4 , 0.5 0.5, 0.6水量频数 1 5 13 10 16 5 (1)(2)估计该家庭使用节水龙头后,日用水量小于m3的概率;(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)20 . (12 分)设抛物线C:y22x,点A 2, 0 , B 2 , 0 ,过点A的直线l与C交于M , N两点.(1)当l与x轴垂直时,求直线BM的方程;(2)证实:/ ABM / ABN .21 . ( 12 分)函数f x ae x ln x 1 .(1)设x 2是f x的极值点.求a,并求f x的单调区间;1(2)证实:当a>—时,fx>0. e(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,那么按所做的第一题计分.22 .[选彳4-4:坐标系与参数方程](10分)在直角坐标系xOy中,曲线C1的方程为y k x 2.以坐标原点为极点, x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为22 cos 3 0.(1)求C2的直角坐标方程;(2)假设C1与C2有且仅有三个公共点,求G的方程.23 .[选彳4-5:不等式选讲](10分)f x x 1 ax 1 .1)当a 1 时,求不等式 f x 1 的解集;(2)假设xC 0, 1时不等式f x x成立,求a的取值范围.绝密★启用前2021年普通高等学校招生全国统一测试文科数学试题参考答案一、选择题1 . A 2. C 3. A 4. C 5. B 6. D7. A 8. B 9. B 10. C 11 . B 12. D二、填空题13. -7 14. 6 15. 2 2 16.生3三、解做题17 .解:(1)由条件可得a n+i=2(n 1)a n将n=1代入得,a2=4a,而a1=1,所以,a2=4.将n=2代入得,a3=3a2,所以,a3=12.从而b1=1, b2=2, b3=4.(2) {b n}是首项为1,公比为2的等比数列.由条件可得-al±空L,即b n+1=2b n,又b1 = 1,所以{b n}是首项为1,公比为2的等比数歹U. n 1 n(3)由(2)可得包2n 1,所以a n=n- 2n-1. n18 .解:(1)由可得, BAC=90 , BA± AC .又BAL AD 所以AB1平面ACD又AB平面ABC所以平面ACD_平面ABC(2)由可得, DGCMAB=3, DA=3班.又BP DQ 2DA ,所以BP 272 .3作Qa AC,垂足为E,那么QE P 1 DC .3由及(1)可得DCL平面ABC所以QEL平面ABC QE=1.因此,三棱锥Q ABP的体积为V Q ABP - QE S A ABP -1-3 242sin45 1 . 3 3 2解:(1) (2)根据以上数据,该家庭使用节水龙头后 50天日用水量小于的频率为X +1 x + x +2X=,因此该家庭使用节水龙头后日用水量小于的概率的估计值为. (3)该家庭未使用节水龙头 50天日用水量的平均数为 - 1 __ _ / c/ CCC CCC _ cc cccc 、ccXI —(0.05 1 0.15 3 0.252 0.354 0.459 0.5526 0.655) 0.48 .50该家庭使用了节水龙头后 50天日用水量的平均数为 - 1,cc / C/ CC "CC "C "C 、ccX 2 —(0.05 1 0.15 5 0.25 13 0.35 10 0.45 16 0.55 5) 0.35 .50 估计使用节水龙头后,一年可节省水(0.48 0.35) 365 47.45(m 3).20 .解:(1)当l 与x 轴垂直时,l 的方程为x=2,可得M 的坐标为(2, 2)或(2, -2).所以直线BM 勺方程为y =lx 1或y 2x 1. 22(2)当l 与x 轴垂直时,AB 为MN 勺垂直平分线,所以/ ABIMZ ABN当 l 与 x 轴不垂直时,设 l 的方程为 y k(x 2)(k 0), M(x1,y1),N (x 2, y 2),那么 x 1>0, x 2>0.r y k(x 2) 一口 2一' 2由得 ky - 2y - 4k =0,可知 y 1+y 2=- , y 1y 2= - 4.y 3 2xk直线BM BN 的斜率之和为 y 2x 2y 1 x 1y 2 2( y 1 ① x 2 2(x 1 2)(x 2 2)比 2及y“y 2, y/2的表达式代入①式分子,可得 k2y 1y 2 4k(y 〔 y 2) 8 8 y 2) 0 • k k所以k BM +k BN =0,可知BM BN 的倾斜角互补,所以/ ABM/ABN 综上,/ ABM/ABN121 .解:(1) f (x)的定义域为(0,), f ' (x) =a e x --.x1由题设知,f(2) =0,所以a =—2 .2e当 0<x<2 时,f ' (x) <0;当 x>2 时,f ' (x) >0.2 V.1 V 1从而 f (x) =2e ln x 1, f(x) =-2e - .2e2e x19.k BMk BNx 1 2 将 X " 2 , x 2 k x 2y 1 x 1y 2 2( y 1所以f (x)在(0, 2)单调递减,在(2, +8)单调递增. x(2)当a>1 时,f (x) > 旦lnx 1 . e ex x .e e 1设g (x) =— In x 1 ,那么g (x) — e e x当0<x<1时,g' (x) <0;当x>1时,g' (x) >0.所以x=1是g (x)的最小值点.故当x>0 时,g (x) >g (1) =0.1因此,当a工时,f(x) 0. e22 .[选彳4-4 :坐标系与参数方程](10分)解:(1)由x cos , y sin得C2的直角坐标方程为2 2(x 1) y 4.(2)由(1)知C2是圆心为A( 1,0),半径为2的圆.由题设知,C I是过点B(0,2)且关于y轴对称的两条射线.记y轴右边的射线为1I, y轴左边的射线为l2 .由于B在圆C2的外面,故C I与C2有且仅有三个公共点等价于1I与C2只有一个公共点且l2与C2有两个公共点,或l2与C2只有一个公共点且1I与C2有两个公共点.| k 2| 4当1I与C2只有一个公共点时, A到l1所在直线的距离为2 ,所以2 2 4 5 ,故k —或k 0 ..k 1 34 一一经检验,当k 0时,1I与C2没有公共点;当k —时,1I与C2只有一个公共点,l2与C2有两个公共3点.|k 2| 4当l2与C2只有一个公共点时, A到l2所在直线的距离为 2 ,所以T=2= 2 ,故k 0或k -.k 1 34 一经检验,当k 0时,1I与C2没有公共点;当k7时,l2与C2没有公共点.34 综上,所求G的万程为y -|x| 2 .323.[选彳4-5 :不等式选讲](10分)2,x 1,解:(1)当a 1 时,f(x) | x 1| | x 1| ,即 f (x) 2x, 1 x 1,2,x 1.(2)当x (0,1)时|x 1| |ax 1| x成立等彳^于当x (0,1)时|ax 1| 1成立.假设 a 0 ,那么当x (0,1)时| ax 1| 1 ;2 2假设a 0, |ax 1| 1的解集为0 x —,所以—1,故0 a 2 .a a4故不等式f(x) 1的解集为{x|x 1}.5综上,a的取值范围为(0,2].。
2020年全国高考新课标1卷文科数学试题(word文档完整版小题也有详解)
2020年全国高考新课标1卷文科数学试题一、选择题,本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A ={x |x 2-3x -4≤0},B ={-4,1,3,5},且A ∩B =( )A .{-4,1}B .{1,5}C .{3,5}D .{1,3} 2.若z =1+2i +i 3,则|z |=( )A .0B .1C 2D .2 3.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积 等于该四棱锥一个侧面三角形的面积,则其侧面三角形 底边上的高与底面正方形的边长的比值为( )A .514B .512C .514D .5124.设O 为正方形ABCD 的中心,在O ,A ,B ,C ,D 中任取3点,则取到的3点共线的概率为( )A .15B .25C .12D .455.某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:°C)的关系,在20个不同的温度条件下 进行种子发芽实验,由实验数据 (x i . y i )(i =1,2,···,20)得到散点图:由此散点图,在10°C 至40°C 之 间,下面四个回归方程类型中最 适宜作为发芽率y 和温度x 的回 归方程类型的是( ) A .y=a+bx B .y=a+bx 2 C .y=a+be xD .y=a+b ln x6.已知圆x 2+y 2-6x =0,过点(1,2)的直线被该圆所截得的弦的长度的最小值为( )A .1B .2C .3D .47.设函数f (x )=cos(ωx +6π)在[-π,π]的图像大致如下图,则f (x )的最小正周期为( )A .109πB .76πC .43πD .32π8.设a log 34=2,则4-a =( )A .116B .19C .18D .169.执行下面的程序框图,则输出的n =( )A .17B .19C .21D .2310.设{a n}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=( ) A.12 B.24 C.30 D.3211.设F1, F2是双曲线C:2213yx-=的两个焦点,O为坐标原点,点P在C上且|OP|=2,则∆PF1F2的面积为( )A.72B.3 C.52D.212.已知A,B,C为球O的球面上的三个点,⊙O1为∆ABC的外接圆,若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( )AA.64πB.48πC.36πD.32π二、填空题:本大题共4小题,每小题5分,共20分.把答案填在横线上.13.若x,y满足约束条件220,10,10,x yx yy+-≤⎧⎪--≥⎨⎪+≥⎩则z=x+7y的最大值为.14.设为(1,1)(1,24),a b m m a b-=+-⊥=,若,则m= .15.曲线y=ln x+x+1的一条切线的斜率为2,则该切线的方程为.16.数列{a n}满足a n+2+(-1)n a n=3n-1,前16项和为540,则a1= .三、解答题:解答应写出文字说明,证明过程或演算步骤。
普通高等学校招生全国统一考试数学文科试题(全国I卷)全解析(部分解析)

2020 年一般高等学校招生全国一致考试文科数学 ( 必修 +选修 )分析版本试卷分第I 卷 ( 选择题 ) 和第Ⅱ卷 ( 非选择题 ) 两部分。
第I 卷 1 至 2 页。
第Ⅱ卷3至 4 页。
考试结束后,将本试卷和答题卡一并交回。
第 I 卷注意事项:1.答题前,考生在答题卡上务必用直径0.5 毫米黑色墨水署名笔将自己的姓名、准考据号填写清楚,并贴好条形码。
请仔细批准条形码上的准考据号、姓名和科目。
2.每题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需变动,用橡皮擦洁净后,再选涂其余答案标号,在试题卷上作答无效。
.........3.第 I 卷共 12 小题,每题 5 分,共 60 分。
在每题给出的四个选项中,只有一项为哪一项切合题目要求的。
参照公式:假如事件 A、 B互斥,那么球的表面积公式P( A B) P( A) P(B)假如事件 A、 B互相独立,那么P( AgB) P(A)gP(B)假如事件 A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件 A 恰巧发生 k 次的概率P n (k) C n k p k (1 p) n k (k 0,1,2,⋯ n)一、选择题(1)cos300S 4R2此中 R 表示球的半径球的体积公式V 3 R34此中 R 表示球的半径31(C)1(D)3(A)(B)-22221.C 【命题企图】本小题主要考察引诱公式、特别三角函数值等三角函数知识【分析】 cos300 cos 360601 cos602(2) 设全集U1,2,3,4,5,会合 M1,4, N 1,3,5,则 N e MUA. 1,3B.1,5C.3,5D.4,52.C 【命题企图】本小题主要考察会合的观点、会合运算等会合相关知识【分析】 e M2,3,5 , N1,3,5 ,则 N e M1,3,52,3,5= 3,5 U Uy1,(3) 若变量x, y知足拘束条件x y0,则 z x 2 y 的最大值为x y20,(A)4(B)3(C)2(D)1( 4)已知各项均为正数的等比数列{ a n } ,a1a2a3 =5,a7a8a9 =10,则a4a5a6 =(A) 5 2 (B) 7 (C) 6 (D) 4 24.A 【命题企图】本小题主要考察等比数列的性质、指数幂的运算、根式与指数式的互化等知识,侧重考察了转变与化归的数学思想.【解析】由等比数列的性质知 a1a2a3(a1a3 )ga2 a23 5 ,a7a8a9 (a7 a9 )ga8 a831 10, 因此a2a8503,1因此 a4 a5a6 ( a4a6 )ga5a53( a2a8 )3(506 )3 5 2(5) (1x) 4 (1x ) 3的睁开式x2的系数是(A)-6 (B)-3 (C)0(D)35.A.【命题企图】本小题主要考察了考生对二项式定理的掌握状况,特别是睁开式的通项公式的灵巧应用,以及可否划分睁开式中项的系数与其二项式系数,同时也考察了考生的一些基本运算能力 .【分析】 (1 x)4 (1 x )3 1 4x 6x24x3x413 1 3x23x x 2x2的系数是-12+6=-6(6) 直三棱柱ABC A1B1C1中,若BAC90, AB AC AA1,则异面直线BA1与AC1所成的角等于(A)30°(B)45° (C)60°(D)90°( 8)已知F1、F2为双曲线C: x2y21的左、右焦点,点P 在 C上,∠F1P F2 = 600,则| PF1 |g| PF2 |(A)2(B)4(C) 6(D) 88.B 【命题企图】本小题主要考察双曲线定义、几何性质、余弦定理,考察转变的数学思想,.经过此题能够有效地考察考生的综合运用能力及运算能力【分析 1】 . 由余弦定理得cos ∠F1 P F2 =| PF1 |2| PF2 |2| F1F2 |22| PF1 ||PF2 |PF1PF22 2 PF1 PF2F1 F22222PF1 PF2 2 221cos6002 PF1 PF2 2 PF1PF22| PF1|g| PF2|4【解析2】由焦点三角形面积公式得:S FPF b2260031PF2sin 6001PF1PF232cot1 cot PF1122222 | PF1|g| PF2|4( 9)正方体ABCD -A1 B1C1D1中, BB1与平面 ACD1所成角的余弦值为( A)2( B)3(C)2( D)63333【分析 2】设上下底面的中心分别为O 1 , O ;O 1 O 与平面AC D1所成角就是B B1与平面AC D1所成角, cos O1OD1O1O361/23 OD1( 10)设 a log 3 2,b ln 2,c 15 2则( A ) a bc (B ) b c a(C)c a b (D) c b a11.D 【命题企图】本小题主要考察向量的数目积运算与圆的切线长定理,侧重考察最值的求法——鉴别 式法 , 同时也考察了考生综合运用数学知识解题的能力及运算能力 .【分析 1】如下图: 设 PA=PB=x (x0) , ∠ APO= , 则∠ AAPB=,PO=1 2, sin1,O2x 1 x 2Puuuv uuuv uuuv uuuvx 2 (1 2sin 2)PA? PB | PA | | PB | cos 2= =B224 2 uuuv uuuv42y ,则 y xx ,x ( x 1) = x x,令 PA ? PBx 2 1 x 21x 2 1即 x 4 (1 y) x 2 y 0 ,由 x 2 是实数,因此[ (1 y)] 2 4 1 ( y)0 , y 2 6 y 10 ,解得 y32 2 或 y322.故uuuv uuuv(PA ? PB)min3 2 2 . 此时 x21.uuuvuuuv2【分析 2】设 APB,0, PA?PBPA PB cos1/ tancos2cos21sin212sin 2 212sin222 222sinsin22uuuv uuuv 1x 1 2x2x 12 2 3PA? PBx3 x(12)已知在半径为 2 的球面上有 A、 B、C、 D四点,若大值为23432 3(D)(A)(B)(C)332换元:x sin,0 x 1,AB=CD=2,则四周体ABCD的体积的最8 3312.B 【命题企图】本小题主要考察几何体的体积的计算、球的性质、异面直线的距离, 经过球这个载体考察考生的空间想象能力及推理运算能力.【分析】过CD 作平面 PCD,使 AB⊥平面 PCD,交 AB 与 P, 设点 P 到 CD 的距离为h , 则有V四周体ABCD1 212 h2h ,当直径经过AB与CD的中点时,h max 2 2212 2 3,故32343Vmax.3第Ⅱ卷注意事项:1.答题前,考生先在答题卡上用直径毫米黑色墨水署名笔将自己的姓名、准考据号填写清楚,而后贴好条形码。
2020年全国统一高考数学试卷(文科)(全国卷一)(含详细解析)

c 保密★启用前2020年全国统一高考数学试卷(文科)(全国卷一)您题号—总分得分注意事项:1.答题前垃写好自己的姓名、班级、考号等信息2.请将答案正确填写在答超卡上o:n o评卷人得分1.己知集合/!={x\xA.{—4,1}一、单选题3—4<0},8={-4,1,3,5},则』口=()B.(1,5}C.{3,5}D.{1,3}2.若z= l+2i+i3,则回=()A.0B.1C.41D.23.埃及胡夫金字塔是古代世界建筑志迹之一,它的形状可视为-个正四棱锥,以该四校锥的高为边长的正方形面积等于该四梭推一个侧面三角形的面积,鲫其侧面三角形底边上的高与底面正方形的边长的比值为()oO A旦R岂 C.旦 D.旦4242的概率为()5.某校一个课外学习小组为研充某作物种了•的发芽率.p 和温度工(单位:°C )的关系. 在20个不同的温度条件下进行种子发芽实验,由实验数据(.t r.Z )(/ = 1.2.-.2O )得到下 面的散点图;由此散点图•在10。
至40也之间・卜.面四个回归方程类型中最适宜作为发芽率*和温度X 的问归方程类型的是()A. ,= 〃 +版B. y = a + hx 2C. y-a + be l D・ y = a + b\nx6.已知圆xf 尸-6“0,过点(1, 2)的直线被该圆所截得的弦的忙度的最小值为A. 1C. 3B. 2D. 47 .设函数f (x ) = COS (5 +兰)在[-兀,71]的图像大致如卜图,则用)的最小止周期为()610n A. B.Inc. 8. A. 9.4丸设g4=2,则4"= <)1 B.1. 169执行下面的程序框图,则输出的〃=()D.C.A.3兀D.417 B.19 C.21 D.2310.设{虬}是等比数列,旦0+七+%=】•%+江/久=2.则%+"%=(A.12B.24C.30D.32y11.设%足是双仙线C:x2-^-=l的两个焦点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B =A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z = A .0B .12C .1D .23.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为(20),,则C 的离心率为 A .13B .12C .22D .2235.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC +D .1344AB AC + 8.已知函数()222cos sin 2f x x x =-+,则 A .()f x 的最小正周期为π,最大值为3 B .()f x 的最小正周期为π,最大值为4 C .()f x 的最小正周期为2π,最大值为3 D .()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为 A .217 B .25 C .3D .210.在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为 A .8B .62C .82D .8311.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且2cos 23α=,则a b -= A .15B .55C .255D .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题(本题共4小题,每小题5分,共20分)13.已知函数()()22log f x x a =+,若()31f =,则a =________.14.若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+的最大值为________.15.直线1y x =+与圆22230x y y ++-=交于A B ,两点,则AB =________.16.△ABC 的内角A B C ,,的对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则△ABC 的面积为________.三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)已知数列{}n a 满足11a =,()121n n na n a +=+,设nn a b n=. (1)求123b b b ,,; (2)判断数列{}n b 是否为等比数列,并说明理由; (3)求{}n a 的通项公式.学,科网 18.(12分)如图,在平行四边形ABCM 中,3AB AC ==,90ACM =︒∠,以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB DA ⊥. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.19.(12分)某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:未使用节水龙头50天的日用水量频数分布表日用水量[)00.1,[)0.10.2,[)0.20.3,[)0.30.4,[)0.40.5,[)0.50.6,[)0.60.7,频数 1 3 2 4 9 26 5使用了节水龙头50天的日用水量频数分布表日用水量[)00.1,[)0.10.2,[)0.20.3,[)0.30.4,[)0.40.5,[)0.50.6,频数 1 5 13 10 16 5 (1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:(2)估计该家庭使用节水龙头后,日用水量小于0.35 m 3的概率;(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.) 20.(12分)设抛物线22C y x =:,点()20A ,,()20B -,,过点A 的直线l 与C 交于M ,N 两点. (1)当l 与x 轴垂直时,求直线BM 的方程; (2)证明:ABM ABN =∠∠. 21.(12分)已知函数()e ln 1xf x a x =--.(1)设2x =是()f x 的极值点.求a ,并求()f x 的单调区间; (2)证明:当1ea ≥时,()0f x ≥.(二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,则按所做的第一题计分。
22.[选修4—4:坐标系与参数方程](10分)在直角坐标系xOy 中,曲线1C 的方程为2y k x =+.以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为22cos 30ρρθ+-=. (1)求2C 的直角坐标方程;(2)若1C 与2C 有且仅有三个公共点,求1C 的方程. 23.[选修4—5:不等式选讲](10分)已知()11f x x ax =+--.(1)当1a =时,求不等式()1f x >的解集;(2)若()01x ∈,时不等式()f x x >成立,求a 的取值范围.绝密★启用前2018年普通高等学校招生全国统一考试文科数学试题参考答案一、选择题 1.A 2.C 3.A 4.C 5.B 6.D 7.A8.B9.B10.C11.B12.D二、填空题 13.-7 14.6 15.22 16.233三、解答题17.解:(1)由条件可得a n +1=2(1)n n a n+. 将n =1代入得,a 2=4a 1,而a 1=1,所以,a 2=4. 将n =2代入得,a 3=3a 2,所以,a 3=12. 从而b 1=1,b 2=2,b 3=4.(2){b n }是首项为1,公比为2的等比数列. 由条件可得121n na a n n+=+,即b n +1=2b n ,又b 1=1,所以{b n }是首项为1,公比为2的等比数列. (3)由(2)可得12n n a n-=,所以a n =n ·2n -1. 18.解:(1)由已知可得,BAC ∠=90°,BA AC ⊥.又BA ⊥AD ,所以AB ⊥平面ACD . 又AB ⊂平面ABC , 所以平面ACD ⊥平面ABC .(2)由已知可得,DC =CM =AB =3,DA =32.又23BP DQ DA ==,所以22BP =. 作QE ⊥AC ,垂足为E ,则QE =13DC .由已知及(1)可得DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE =1. 因此,三棱锥Q ABP -的体积为1111322sin 451332Q ABP ABP V QE S -=⨯⨯=⨯⨯⨯⨯︒=△.19.解:(1)(2)根据以上数据,该家庭使用节水龙头后50天日用水量小于0.35m 3的频率为0.2×0.1+1×0.1+2.6×0.1+2×0.05=0.48,因此该家庭使用节水龙头后日用水量小于0.35m 3的概率的估计值为0.48.(3)该家庭未使用节水龙头50天日用水量的平均数为11(0.0510.1530.2520.3540.4590.55260.655)0.4850x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=.该家庭使用了节水龙头后50天日用水量的平均数为21(0.0510.1550.25130.35100.45160.555)0.3550x =⨯+⨯+⨯+⨯+⨯+⨯=. 估计使用节水龙头后,一年可节省水3(0.480.35)36547.45(m )-⨯=.20.解:(1)当l 与x 轴垂直时,l 的方程为x =2,可得M 的坐标为(2,2)或(2,–2).所以直线BM 的方程为y =112x +或112y x =--.(2)当l 与x 轴垂直时,AB 为MN 的垂直平分线,所以∠ABM =∠ABN .当l 与x 轴不垂直时,设l 的方程为(2)(0)y k x k =-≠,M (x 1,y 1),N (x 2,y 2),则x 1>0,x 2>0. 由2(2)2y k x y x=-⎧⎨=⎩,得ky 2–2y –4k =0,可知y 1+y 2=2k ,y 1y 2=–4.直线BM ,BN 的斜率之和为 1221121212122()22(2)(2)BM BN y y x y x y y y k k x x x x ++++=+=++++.① 将112y x k =+,222yx k=+及y 1+y 2,y 1y 2的表达式代入①式分子,可得 121221121224()882()0y y k y y x y x y y y k k++-++++===.所以k BM +k BN =0,可知BM ,BN 的倾斜角互补,所以∠ABM +∠ABN . 综上,∠ABM =∠ABN .21.解:(1)f (x )的定义域为(0)+∞,,f ′(x )=a e x –1x. 由题设知,f ′(2)=0,所以a =212e . 从而f (x )=21e ln 12e x x --,f ′(x )=211e 2e x x-. 当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.所以f (x )在(0,2)单调递减,在(2,+∞)单调递增.(2)当a ≥1e 时,f (x )≥e ln 1exx --.设g (x )=e ln 1e x x --,则e 1()e x g x x'=-.当0<x <1时,g ′(x )<0;当x >1时,g ′(x )>0.所以x =1是g (x )的最小值点. 故当x >0时,g (x )≥g (1)=0.因此,当1ea ≥时,()0f x ≥.22.[选修4-4:坐标系与参数方程](10分)解:(1)由cos x ρθ=,sin y ρθ=得2C 的直角坐标方程为 22(1)4x y ++=.(2)由(1)知2C 是圆心为(1,0)A -,半径为2的圆.由题设知,1C 是过点(0,2)B 且关于y 轴对称的两条射线.记y 轴右边的射线为1l ,y 轴左边的射线为2l .由于B 在圆2C 的外面,故1C 与2C 有且仅有三个公共点等价于1l 与2C 只有一个公共点且2l 与2C 有两个公共点,或2l 与2C 只有一个公共点且1l 与2C 有两个公共点. 当1l 与2C 只有一个公共点时,A 到1l 所在直线的距离为2,所以2|2|21k k -+=+,故43k =-或0k =.经检验,当0k =时,1l 与2C 没有公共点;当43k =-时,1l 与2C 只有一个公共点,2l 与2C 有两个公共点.当2l 与2C 只有一个公共点时,A 到2l 所在直线的距离为2,所以2|2|21k k +=+,故0k =或43k =.经检验,当0k =时,1l 与2C 没有公共点;当43k =时,2l 与2C 没有公共点. 综上,所求1C 的方程为4||23y x =-+.23.[选修4-5:不等式选讲](10分)解:(1)当1a =时,()|1||1|f x x x =+--,即2,1,()2,11,2, 1.x f x x x x -≤-⎧⎪=-<<⎨⎪≥⎩故不等式()1f x >的解集为1{|}2x x >.(2)当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立. 若0a ≤,则当(0,1)x ∈时|1|1ax -≥; 若0a >,|1|1ax -<的解集为20x a <<,所以21a≥,故02a <≤.综上,a的取值范围为(0,2].。
