二年级下册数学试题奥数专题讲练:重叠问题人教新课标
二年级奥数 第七讲:重叠问题

第七讲 重叠问题 哪吒智闯水晶宫---哪吒被骗了哪吒继续往前去寻宝,只见一位白胡子老爷爷拿着哪吒地乾坤圈站在大厅中间。
“那是我的乾坤圈!”哪吒激动的叫起来。
哪吒赶紧跑过去一看,“怎么有两个乾坤圈?” 白胡子老爷爷微笑的说:“哪吒不认识我了?”哪吒仔细打量了这位老爷爷后说:“我记起来了,你是太白金星。
”太白金星:“哪吒,我听说了你的事后,特意来帮助你的,你看,我帮你把乾坤圈要回来了。
”哪吒:“那怎么有两个乾坤圈?”太白金星:“这其中一个是我的金钢圈,另一个是你的乾坤圈,刚才我拿一个圈称连我共重67千克,拿另一个圈称连我共重68千克,我的金刚圈比你的乾坤圈重,你猜得出来你的乾坤圈和我的金刚圈多重,我就把你的宝贝还给你”哪吒:“太白金星,你说话可得算数!”太白金星:“那当然了,我胡子都白了,还会骗你?你就在这里想吧,我有事先走,一会儿就回来”哪吒在原地想了一天一夜,也没有想出答案,他明白了,他并不知道太白金星的体重是不可能算出乾坤圈和金刚圈的重量的,他被骗了,那个老人根本不是太白金星!他不过是中了龙王的圈套而已,哪吒气冲冲的继续前进,心想,要再被我碰到这假冒的太白金星,我一定把他的胡子拔了!例题精讲例1 小朋友们排队练体操,小红的左边有6个人,右边有2个人,这一排共有几个人?6 小红 2分析:由图知道,小红所在一队的小朋友,可以分成三部分:第一部分是小红的左边的6个人,第二部分是小红这1个人,第三部分是小红右边的2个人。
要求一共有多少人,就是把这三部分加起来。
即6+1+2=9(人)。
小朋友排队去春游,小云的前面有5个同学,小云的后面有几个同学?小云分析:这一队的小朋友,可以分成三部分:要求小云后面有几个同学,就要从总人数12里面去掉小云前面的5个同学,再去掉小云1个人,才能求出问题。
即12―5―1=6(人)。
例3 幼儿园小朋友排队参观盆景,从前面数,小林是第10个,从后面数,小林是第17个,这一排共有几个小朋友?分析:“从前面数,小林是第10个”说明小林和他前面同学一共是10人,这个“10”里面包括小林,也包括他前面的同学;“从后面数,小林是第17个”,说明小林和他后面同学一共是17人,这个“17”里面包括小林,也包括他后面的同学。
二年级奥数重叠问题

图中间重叠部分表示两道题都做对的人数,把做第一道题和做对第二道题的人数加起来得21+18=39人,这39人比全班总人数36多出了39-36=3人,这多出的3人既在做对第一题的人数中算过,也在做对第二道题的人数中算过,即表示两道题都做对的人数。
1
2
例
160厘米
90厘米
?厘米
90+90-160=20(厘米) 答:中间钉在一起的部分长20厘米。
把两块一样长的木板像下图这样钉在一起成了一块木板。如果这块钉在一起的木板长8米,中间重叠部分是2米,这两块木板各长多少米?
【思路导航】把等长的两块木板的一端钉起来,钉在一起的长度就是重叠部分,重叠的部分是2米,所以这两块木板的总长度是8+2=10米,每块木板的长度是10÷2=5米。
重
叠
问
题
两块木板各长80厘米,如下图,钉在一起。中间钉在一起的地方是15厘米。这两块钉起来的木板长多少厘米?
例
ቤተ መጻሕፍቲ ባይዱ
15厘米
80厘米
80厘米
80+80-15=145(厘米) 答:这两块钉起来的木板长145厘米。
两块各长90厘米的木板钉成一块长160厘米的木板,中间钉在一起的部分长多少厘米?
39+42=81(人) 81-50=31(人) 答:有31人语文、数学都得了100分。
50个同学参加期末考试,每个同学至少有一门是100分。语文得100分的39人,数学得100分的是42人,请问有多少人语文、数学都得了100分?
例
一次数学测试,全班36人中,做对第一道聪明题的有21人,做对第二道聪明题的有18人,每人至少做对一道。问两道聪明题都做对的有几人? 【思路导航】根据题意,画出下图:
二年级奥数-第二学期-010重叠问题(二)

二年级创新思维春季班讲义:第十讲重叠问题(二)姓名:【例4】(1)如果将两块同样长的木条钉在一起共长15厘米,中间钉在一起的长度是3厘米,问:原来每块木条长多少厘米?答:原来每块木条长()厘米。
(2)两块木条各有8厘米,如果把他们钉在一起时,中间重合部分是3厘米,钉成后这块木条有多少厘米?答:钉成后这块木条有()厘米。
(3)两块木条各有9厘米,钉成一块长14厘米的木条,中间重合的部分是几厘米?答:中间重合的部分是()厘米。
练一练(四)1、(1)两块木条各长40厘米,把它们钉在一起,中间钉在一起的地方是10厘米,这块钉起来的木条长多少厘米?答:这块钉起来的木条长()厘米。
(2)两块木条各长40厘米,钉在一起的木条长70厘米,中间钉在一起的地方长多少厘米?答:中间钉在一起的地方长()厘米。
2、有两块同样长的木条,钉成了一块长13分米的长木条,中间顶在一起的重叠部分长1分米,这两块木条原来各有多少分米?答:这两块木条原来各有()分米。
【例5】王老师出了两组数学兴趣题给18名同学做,做对第一组的有10名同学,做队第二组的有12名同学,两题都做对的有多少名同学?答:两题都做对的有()名同学。
练一练(五)1、有一个班英语、数学期终考试得100分的共有8人,其中英语100分的有5人,数学100分的有6人,两门学科都得100分的有几人?答:两门学科都得100分的有()人。
2、有100个同学带矿泉水和水果去春游,带矿泉水的有78人,带水果的有71人,两样都带有至少有多少人?答:两样都带有至少有()人。
3、二(3)班有39人,全班都订了报,订《少年报》的有35人,订《拼音报》有8人,两样报纸都订的有多少人?答:两样报纸都订的有()人。
4、三年级学生中,音乐爱好者有38名,电脑爱好者有64名,两项都爱好的有27名,这个年级有多少名学生?答:这个年级有()名学生。
5、在1~30中,既不是3的倍数,又不是5的倍数的数有多少个?答:又不是5的倍数的数有()个。
二年级奥数 第七讲:重叠问题

第七讲 重叠问题 哪吒智闯水晶宫---哪吒被骗了哪吒继续往前去寻宝,只见一位白胡子老爷爷拿着哪吒地乾坤圈站在大厅中间。
“那是我的乾坤圈!”哪吒激动的叫起来。
哪吒赶紧跑过去一看,“怎么有两个乾坤圈?” 白胡子老爷爷微笑的说:“哪吒不认识我了?”哪吒仔细打量了这位老爷爷后说:“我记起来了,你是太白金星。
”太白金星:“哪吒,我听说了你的事后,特意来帮助你的,你看,我帮你把乾坤圈要回来了。
”哪吒:“那怎么有两个乾坤圈?”太白金星:“这其中一个是我的金钢圈,另一个是你的乾坤圈,刚才我拿一个圈称连我共重67千克,拿另一个圈称连我共重68千克,我的金刚圈比你的乾坤圈重,你猜得出来你的乾坤圈和我的金刚圈多重,我就把你的宝贝还给你”哪吒:“太白金星,你说话可得算数!”太白金星:“那当然了,我胡子都白了,还会骗你?你就在这里想吧,我有事先走,一会儿就回来”哪吒在原地想了一天一夜,也没有想出答案,他明白了,他并不知道太白金星的体重是不可能算出乾坤圈和金刚圈的重量的,他被骗了,那个老人根本不是太白金星!他不过是中了龙王的圈套而已,哪吒气冲冲的继续前进,心想,要再被我碰到这假冒的太白金星,我一定把他的胡子拔了!例题精讲例1 小朋友们排队练体操,小红的左边有6个人,右边有2个人,这一排共有几个人?6 小红 2分析:由图知道,小红所在一队的小朋友,可以分成三部分:第一部分是小红的左边的6个人,第二部分是小红这1个人,第三部分是小红右边的2个人。
要求一共有多少人,就是把这三部分加起来。
即6+1+2=9(人)。
小朋友排队去春游,小云的前面有5个同学,小云的后面有几个同学?小云分析:这一队的小朋友,可以分成三部分:要求小云后面有几个同学,就要从总人数12里面去掉小云前面的5个同学,再去掉小云1个人,才能求出问题。
即12―5―1=6(人)。
例3 幼儿园小朋友排队参观盆景,从前面数,小林是第10个,从后面数,小林是第17个,这一排共有几个小朋友?分析:“从前面数,小林是第10个”说明小林和他前面同学一共是10人,这个“10”里面包括小林,也包括他前面的同学;“从后面数,小林是第17个”,说明小林和他后面同学一共是17人,这个“17”里面包括小林,也包括他后面的同学。
二年级奥数重叠问题

知识要点:前面已学过排队问题,从前面数,从后面数,丽丽都排第6,这一排共有几个人?这里丽丽被重复数了两次,有时我们也把这类问题叫重叠问题。
[ 例1 ]洗好的8块手帕夹在绳子上晾干,同一个夹子夹住相邻的两块手帕的两边,这样一共要多少个夹子?分析:由图知道,两块手帕有一边重叠,用3个夹子。
三块手帕有两边重叠,用4个夹子,我们发现夹子数总比手帕数多1,因此8块手帕就要用9个夹子。
[ 例2 ]把图画每两张重叠在一起钉在墙上,现在有5张画要多少个图钉呢?分析:每排两张画要6个图钉,每排三张画要8个图钉,每排四张画要10个图钉。
可以看出,图画每增加一张,图钉就要增加2颗,那么5张画要12个图钉。
[ 例3 ]有两块一样长的木板,钉在一起,如果每块木板长25厘米,中间钉在一起的长5厘米,现在长木板有多长?分析:把两块木板钉起来,钉在一起的地方的长度就是重叠的部分。
现在的总长就是原来两个总长的和减去重叠的部分。
算式:25+25-5=45(厘米)所以现在木板长45厘米。
[ 例4 ]张老师出了两道题,做对第一题的有13人,做对第二题的有22人,两道题都做对的有8人,这个班一共有多少人?分析:做对第一题的13个人里,有8个人也做对第二题,那么做对第二题的22个人里这8个人就又重复数了一次,因此把做对第一题的人数和做对第二题的人数和起来,再减去重复数的这8个人。
算式:13+22-8=27(人)所以这个班一共有27人。
[ 例5 ]四根长都是8厘米的绳子,把它们打结连在一起,成为一根长绳,打结处每根绳用去1厘米,绳结长度不计,现在这根长绳长多少厘米?分析:两根绳有一个结,三根绳有两个结,那么四根绳有三个结。
一个结用去1+1=2厘米,那么三个结用去2+2+2=6厘米,绳子总长8+8+8+8=32厘米,减去打结的6厘米,32-6=26,现在这根长绳是26厘米。
练习一1,小朋友排队做操,小明从前数起排在第4个,从后数起排在第7个。
1101二年级思维班讲义4-重叠问题

二年级奥数思维班讲义(四)重叠问题学校班级姓名【典型例题】例题1、小朋友们排队练体操,小红的左边有6个人,右边有2个人,这一排共有几个人?提示:小红所在一队的小朋友,可以分成三部分,要求一共有多少人,就是把这三部分加起来。
特别提醒小朋友注意,除了把小红的左边的6个人和小红右边的2个人加上外,还要加上谁,才等于这一排总人数。
例题2、 12个小朋友排队去春游,小云的前面有5个同学,小云的后面有几个同学?提示:这一队的小朋友,也可以分成三部分:要求小云后面有几个同学,就要从总人数12里面去掉什么?例题3 、幼儿园小朋友排队参观盆景,从前面数,小林是第3个,从后面数,小林是第5个,这一排共有几个小朋友?提示:“从前面数,小林是第3个”说明小林和他前面同学一共是多少人,这个“3”里面包括哪些同学;“从后面数,小林是第5个”,说明什么?例题4 、10 个小朋友按1~3的顺序循环报数,报双数的离队,队伍还剩多少人?提示:队伍还剩的人就是报单数的人。
这10名队员报数结果是:1、2、3、1、2、3、1、2、3、1,这里面双数只有2,出现了几次,其他都是单数。
【知识要点】排队是小朋友在学校里经常要进行的活动。
通过排队,我们可以知道总人数,还可以知道谁站在第几个,谁的后面有几个,谁和谁之间隔几个等一系列问题。
在求这些问题时,我们不能随便猜,要根据一定的条件,用正确的方法解答出来。
二年级奥数思维班讲义(四)《重叠问题》课堂练习学校班级姓名你会做吗?1、张华左边有5个同学,右边有7个同学,这一排共有几个人?2、小高站在队伍里,从前数他是第15个,从后数他是第4个,这一队共有几个人?你能做吗?3、19个小朋友排队,丽丽的前面有7个同学,丽丽的后面有几个同学?你敢做吗?4、10个小朋友按1-5的顺序循环报数,报单数的离队,队伍还剩多少人?日期:月日整洁:(A B C)评分:二年级奥数思维班讲义(四)《重叠问题》课外作业学校班级姓名我会做!1、小民前面有12个同学,后面有8个同学,这一排共有几个人?我能做!2、23个小朋友排队,小刚的左边有13个同学,丽丽的右边有几个同学?我敢做!3、17个小朋友排成一排报数,报双数的站出来,队伍里还剩多少小朋友?自我评价:整洁(A B C)完成质量(A B C)家长签名:教师评分:。
二年级下 数学思维训练 奥数 第4讲-重叠问题

二年级下数学思维训练奥数第4讲重叠问题【知识要点】:解答重叠问题要用到数学中的一个重要原理——包含与排除原理,即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
解答重叠问题的应用题,必须从条件入手进行认真的分析,有时还要画出图示,借助图形进行思考,找出哪些是重复的,重复了几次?明确求的是哪一部分,从而找出解答方法。
【例1】六一儿童节,学校门口挂了一行彩旗。
小张从前数起,红旗是第8面;从后数起,红旗是第10面。
这行彩旗共多少面?【思路导航】根据题意画出下图。
从图上可以看出,从前数起红旗是第______面,从后数起是第______面,这样红旗就数了______次,重复了______次,所以这行彩旗共有[ ] +[ ]-[ ]=[ ]面。
【练习】1、小朋友排队做操,小明从前数起排在第4个,从后数起排在第7个。
这队小朋友共有多少人?2、学校组织看文艺演出,冬冬的座位从左数起是第12个,从右数起是第21个。
这一行座位有多少个?【例2】一次数学测试,全班36人中,做对第一道聪明题的有21人,做对第二道聪明题的有18人,每人至少做对一道。
问两道聪明题都做对的有几人?【思路导航】根据题意,画出下图:图中间重叠部分表示两道题都做对的人数,把做第一道题和做对第二道题的人数加起来得[ ]+[ ]=[ ]人,这____ _人比全班总人数____ _多出了[ ]-[ ]=[ ]人,这多出的____ _人既在做对第一题的人数中算过,也在做对第二道题的人数中算过,即表示两道题都做对的人数。
【练习】1、三(1)班有学生55人,每人至少参加赛跑和跳绳比赛中的一种。
已知参加赛跑的有36人,参加跳绳的有38人。
两项比赛都参加的有几人?2、两块木板各长75厘米,像下图这样钉成一块长130厘米的木板,中间重合部分是多少厘米?【例3】三(1)班订《数学报》的有32人,订《阅读报》的有30人,两份报纸都订的有10人,全班每人至少订一种报纸。
二年级下册数学试题-奥数习题讲练:第十二讲 重叠趣题(解析版)全国通用

第十二讲重叠趣题【精品】之前,我们遇到过这样一些问题,两根木头钉在一起还有多长;把两块毛巾挂在铁丝上需要几个夹子等等.解答这些问题的时候都要考虑重叠的部分.在这节课中我们将这些类似的问题归纳在一起,让学生通过有目的的研究,来找到解决重叠问题的方法.数学乐园【分析】蜗牛白天往上爬了12分米,晚上又滑下来3分米,可以这样理解12分米中往上爬的3分米和往下滑的3分米重叠抵消,实际上每天只往上爬了9分米.这样爬了5天以后共爬了45分米,余下的12分米在第6天的白天就爬到竿顶了,而不需再向下滑了,所以一共需要6天就可以爬到竿顶.同学们,我们都玩过剪纸,如果把两张纸用胶水粘贴在一起,两张纸必然会有一端上下重合在一起,这重合的部分就是重叠部分.以前我们也遇到过一些重叠问题,解决重叠问题首先要弄清楚是哪部分重叠,还要弄清重叠了几部分,然后再来根据题目的意思具体分析.这节课我们就专门来研究这个问题.智慧城堡【例1】洗好的8块手帕用夹子夹在绳子上晾干,每一块手帕的两边必须用夹子夹住,同1个夹子夹住相邻的两块手帕的两边,这样一共要多少个夹子?【分析】一块手帕要用两个夹子;两块手帕有一个重叠,用3个夹子;三块手帕有两个重叠,用4个夹子……8块手帕有7个重叠,每个重叠的边需要1个夹子,两头不重叠的边各要1个夹子.因此需要的夹子数是:7+2=9(个).总结本题规律:把手帕挂在绳子上晾干,需要的夹子数比手帕数多一个.【例2】把两根长为20厘米的筷子用绳子捆成一根长筷子,中间捆在一起的重叠部分是3厘米.捆成的长筷子长多少厘米?【分析】两根筷子总长度为20×2=40(厘米).捆在一起后,中间重叠部分的长度为3厘米.在这40厘米中,3厘米多算了一次,所以最后捆成的筷子长度应从这40厘米中减去多算的一个3厘米,为40-3=37(厘米).列式:20×2=40(厘米)40-3=37(厘米)答:捆成的长筷子长37厘米.【例3】小玲用胶水将两张同样长的纸粘成了一张长为80厘米的长条,其中粘在一起的部分长10厘米,这两张纸条各长多少厘米?【分析】粘在一起的部分是相互重叠粘贴的部分,在算两张纸条总长度时,这部分多算了一次,因此,两张纸条总长度是粘成的长纸条的长度加上重叠部分的长度,为80+10=90(厘米).那么,这两张纸条各自长为90÷2=45(厘米).列式:80+10=90(厘米)90÷2=45(厘米)答:这两张纸条各长45厘米.【例4】有两根铁丝,一根长为30厘米,另一根长为50厘米,将这两根铁丝焊接成一根长为75厘米的长铁丝.那么,中间的焊接重叠部分长为多少厘米?【分析】先求两块木板的长度,再看焊接的木板比两块木板总长度短多少厘米,这就是焊接部分的长度,即重叠部分的长度.两根铁丝总长为30+50=80(厘米),焊接在一起后,长为75厘米,中间重叠部分即为总长度与焊接后长度的差,为80-75=5(厘米).列式:30+50=80(厘米)80-75=5(厘米)答:中间的焊接重叠部分长为5厘米.【例5】有四块各长80厘米的木板,钉成一块木板(如图),中间钉在一起重叠的部分是10厘米,钉成的木板长多少厘米?【分析】四根木板的长度是80×4=320(厘米).钉在一起后,中间重叠部分每一次长度是10厘米,共有3个10厘米的重叠,要从总长度中把这多算的30厘米减掉,才是现在木板的长度.列式:80×4=320(厘米)10×3=30(厘米)320-30=290(厘米)答:钉成的木板长290厘米.拓展练习四根长都是8厘米的绳子,把它们打结连在一起,成为一根长绳,打结处每根绳用去1厘米,绳结长度不计.现在这根长绳长多少厘米?【分析】这题跟例5不同,要注意区分,并比较它们的不同.如果把两根长8厘米的绳子打结连在一起,中间有一个结,打结处每根绳用去1厘米,两根绳子就用去了2厘米,那么现在这根绳子就是8×2-2=14厘米.同道理,如果把四根长8厘米的绳子打结连在一起,中间有3个结,打结处每根绳用去1厘米,四根绳子就用去了6厘米,现在这根绳子长就是8×4-2×3=26(厘米).【例6】把10张图片用图钉像下图那样钉在橱窗里,一共要用多少个图钉?……【分析】10张图片用图钉钉在一起,中间有9个重叠部分,每个重叠部分需要2个图钉,重叠部分一共需要9×2=18(个)图钉.再加上两头各需要两个图钉,这样一共就需要18+4=22(个)图钉.列式:9×2+4=22(个)答:一共要用22个图钉.【例7】二(1)班同学人人参加课外活动,有20人参加英语班,有26人参加电脑班.其中4人两个班都参加.二(1)班一共有多少人?【分析】方法一:已知20人参加英语班,26人参加电脑班,一共有20+26=46(人),这46人中,有4人两班都参加.这就是说这4人在英语班算了名额,在电脑班也算了名额,多算了一次,所以,全班的人数应是46-4=42(人).列式:20+26=46(人)46-4=42(人)方法二:20-4+26=42(人)方法三:26-4+20=42(人)答:二(1)班一共有42人.拓展练习老师出了两道测试题,全班每个同学都至少答对了一道,答对第一道题的有30人,答对第二道题的有28人,两道都答对的有16人,那么全班同学总共有多少人?.【分析】根据上题的分析可以知道,答对第一题的和答对第二题的人数之和为30+28=58(人),在计算这一总人数时,两道都答对的人数被多算了一次,所以全班同学的总人数应为58-16=42(人).列式:30+28=58(人)58-16=42(人)【例8】20个同学报名参加美术组和舞蹈组,其中有16人参加了美术组,12人参加了舞蹈组.问两个小组都参加的有多少个同学?【分析】16人参加了美术组,12人参加了舞蹈组,这样算一共就有28人.但是还有一部分同学既参加了美术组又参加了舞蹈组,在美术组算了一次名额,在舞蹈组又算了一次名额,这样就多算了一次.实际上只有20个同学报名参加美术组和舞蹈组,因此还与28-20=8(人)重复数了一次,这8个人就是即参加了美术组又参加了舞蹈组的人数.列式:16+12=28(人)28-20=8(人)答:两个小组都参加的有8个同学.【例9】某班有20个同学参加作文和数学竞赛,其中参加数学竞赛的有15人,参加作文竞赛的有13人,问只参加数学竞赛和只参加作文竞赛的各有多少人?【分析】因为20个同学参加了参加作文和数学竞赛.如果参加数学竞赛的有15人,那么剩下的就是只参加作文竞赛的同学:20-15=5(人).如果参加作文竞赛的有13人,那么剩下的就是只参加数学竞赛的同学:20-13=7(人).【例10】学校乐器队按计划招收了42名新学员,会拉小提琴的有27人,会弹电子琴又会拉小提琴的有16人,两项都不会的有1人.会弹电子琴的有多少人?【分析】学校乐器队按计划招收了42名新学员,两项都不会的有1人,那么有41名同学会一项或者两项都会.如图,继续分析:会拉小提琴的有27人,这27人里面包含了会弹电子琴又会拉小提琴的16人,所以只会拉小提琴的有27-16=11(人).那么会拉电子琴的有41-11=30(人),这其中包括只会拉电子琴的和两项都会的.列式:42-1=41(人)27-16=11(人)41-11=30(人)答:会弹电子琴的有30人.拓展练习班里共有49名同学,会弹钢琴的有30名,会拉小提琴的有28名,两样都会的有13名,两样都不会的有多少名?【分析】钢琴和小提琴至少会一样的同学有30+28-13=45(名),则两样都不会的同学有49-45=4(名).【例11】小朋友们去喝冷饮,只能选择可乐和雪碧两种饮料.可以选择一种或两种,也可以不选.选择可乐的有18名,不选雪碧的有15名,两种都选的有10名,两种都没选的有多少名?【分析】选择可乐的有18名,这里面包括两种都选的和只选可乐的.两种都选的有10名,所以只选可乐的有18-10=8(名).不选雪碧的有15名,这里面包括只选可乐不选雪碧的和两种都不选的.只选可乐的有8名,所以两种都不选的有15-8=7(名).拓展练习新一期的猫咪训练营开始了,总共有60只小猫咪报名参加.经过一段时间的训练后,有33只猫咪学会了爬树,有25只猫咪学会了抓老鼠,其中既会爬树又会抓老鼠的有10只.那么既不会爬树又不会抓老鼠的猫咪有多少只?【分析】爬树和抓老鼠至少会一项的猫咪有33+25-10=48(只),那么,两项都不会的猫咪有60-48=12(只).【例12】春天来了,全班52人到北海公园划船,有27人划了手摇船,29人划了脚踏船,4名同学因身体不好没有划船而去游览了白塔.问:既划了手摇船也划了脚踏船的同学有多少人?【分析】划了手摇船的人数和划了脚踏船的人数之和为27+29=56(人),全班划了船的人数为全班总人数减去没划船的人数,即为52-4=48(人),那么划了两种船的人数为56-48=8(人).附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)把10块木块用铁钉钉成一条长木条,每两块之间加钉4个,如下图,共需钉上多少个钉?【分析】10块木块用铁钉钉成一条长木条,中间重叠部分有9段,一个重叠处需要4个铁钉,那么一共需要9×4=36(个)铁钉.学校开设了自然和趣味数学两门选修课,每个同学至少要选一门,二(3)班共有48人,有30人选了自然课,有13人两门都选了,那么选趣味数学课的同学有多少人?【分析】选自然课的人数和选趣味数学的人数之和应为全班总人数加上两门都选的人数.也就是说计算这一人数时要把两门都选的人数多算一次,为48+13=61(人).那么选修趣味数学的人数为两门人数之和减去选修自然课的人数,即为61-30=31(人).小攀想用一根65厘米长的铁丝弯成一个边长为15厘米的正方形,铁丝如果太长的话可以重叠.请你帮他算一算重叠的部分要多长才能刚好完成这个任务?【分析】边长为15厘米的正方形四边总长为15×4=60(厘米),若用65厘米的铁丝弯成这样的正方形,多余的部分为65-60=5(厘米).这5厘米就是要重叠的部分.完成的正方形如右图.小明统计了一下学校食堂里的午餐菜式,一个月30天里,有11天没有西红柿鸡蛋,有l8天没有糖醋排骨,两样都有的有7天,两样都没有的有多少天?【分析】30天里,有西红柿鸡蛋的有30-11=19(天),有糖醋排骨的有30-18=12(天),至少有一样的天数为19+12-7=24(天),两样都没有的天数为30-24=6(天).练习十二1.有两块木板,一块长72厘米,另一块长56厘米,如果把两块木板重叠后钉成一块木板,重叠部分是20厘米.求钉成后的木板长多少厘米?【答案】72+56-20=108(厘米),钉成后的木板长108厘米.2.三年级同学参加科技和美术两个课外兴趣小组,参加科技组的有36人,参加美术组的有28人,两个小组都参加的有8人,三年级一共有多少人参加课外兴趣小组?【答案】36+28-8=56(人),三年级一共有56人参加课外兴趣小组.3.三年级同学有56人参加科技和美术两个课外兴趣小组,其中参加科技组的有36人,参加美术组的有28人,两个小组都参加的有多少人?【答案】36+28-56=8(人),两个小组都参加的有8人.4.二年级有40名同学参加跳绳和拍球两项比赛,有12人没有获奖,其中拍球获奖的有18人,拍球和跳绳两项比赛都获奖的有10人,跳绳比赛获奖的有多少人?【答案】40-12=28(人),28-18+10=20(人),跳绳比赛获奖的有20人.5.有101个同学带着水壶和水果去春游,其中带水壶的有78人,带水果的有71人,只带水壶和只带水果的各有多少人?【答案】101-78=23(人),101-71=31(人),只带水壶的有31人,只带水果的有23人.6. 有40人参加测验,答对第一题的有21人,答对第二题的有30人,两道题都答对的有15人,两道题都没答对的有多少人?【答案】21+30-15=36(人),40-36=4(人),两道题都没答对的有4人.信念是一种无坚不催的力量,当你坚信自己能成功时,你必能成功.一天,我发现,一只黑蜘蛛在后院的两檐之间结了一张很大的网.难道蜘蛛会飞?要不,从这个檐头到那个檐头,中间有一丈余宽,第一根线是怎么拉过去的?后来,我发现蜘蛛走了许多弯路--从一个檐头起,打结,顺墙而下,一步一步向前爬,小心翼翼,翘起尾部,不让丝沾到地面的沙石或别的物体上,走过空地,再爬上对面的檐头,高度差不多了,再把丝收紧,以后也是如此.温馨提示:蜘蛛不会飞翔,但它能够把网凌结在半空中.它是勤奋、敏感、沉默而坚韧的昆虫,它的网制得精巧而规矩,八卦形地张开,仿佛得到神助.这样的成绩,使人不由想起那些沉默寡言的人和一些深藏不露的智者.于是,我记住了蜘蛛不会飞翔,但它照样把网结在空中.奇迹是执着者造成的.。
二年级下 数学思维训练 奥数 第5讲-重叠问题

6.我校50名老师中,喜欢打乒乓球的有28人, 喜欢踢足球的有16人,两项活动都不喜欢的 有12人。两项活动都喜欢的有多少人?
(1)至少喜欢一项活动的老师人数是:
50-12= 38(人) (2)参加两项活动的总人数减去至少参加 一项的人数就可以得到重叠的人数:
28+16= 44(人) 44-38= 6(人)
25+20-10+11= 46(人)
五一班有52名学生,其中参加数学兴趣 小组的有24人,既参加数学兴趣小组又参 加写作小组的有8人,两个小组都没有参 加的有5人,只参加写作小组的有多少人?
24人 8人
?人 5人
52-24-5+8=31(人)
在一次数学测验中,四一班有48名同学参 加考试,答对第一题的有36人,答对第二 题的有32人,两道题都答对的有22人。两 道题都答错的有多少人?
• 练习2: • 1.同学们排队跳舞,每行、每列人数同样多。小红的
位置无论从前数从后数,从左数还是从右数起都是第 4个。跳舞的共有多少人?
• 2.为庆祝“六一”,同学们排成每行人数相同的鲜花 队,小华的位置从左数第2个,从右数第4个;从前数 第3个,从后数第5个。鲜花队共多少人?
• 3.两根木棍放在一起(如图),从头到尾共长66厘米 ,其中一根木棍长48厘米,中间重叠部分长12厘米。 另一根木棍长多少厘米?
34+26-12= 48(人)
四(2)班的同学参加学校 田径运动会,每人限报两项。 其中有25人参加径赛,有20
人参加田赛。
既参加径赛又参加田赛 的有10人,两项都没参 加的有11人。四(2) 班共有学生多少人?
径赛:25人 田赛:20人
小学奥数 容斥原理之重叠问题(一) 精选例题练习习题(含知识点拨)
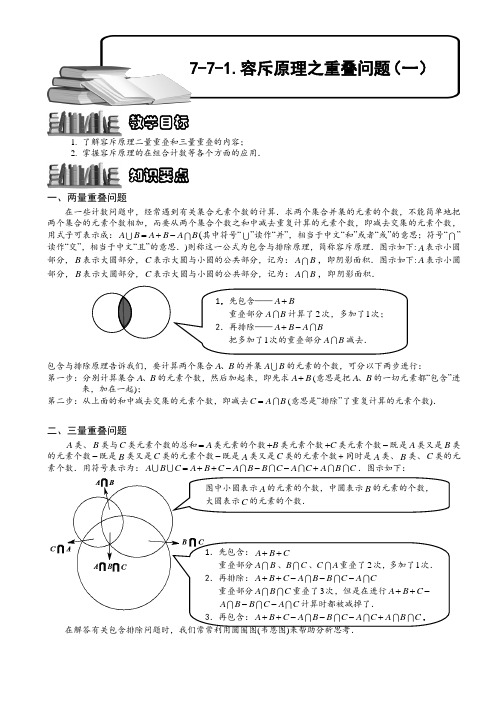
1. 了解容斥原理二量重叠和三量重叠的内容;2. 掌握容斥原理的在组合计数等各个方面的应用.一、两量重叠问题 在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集A B 的元素的个数,可分以下两步进行: 第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.教学目标知识要点7-7-1.容斥原理之重叠问题(一)1.先包含——A B + 重叠部分A B 计算了2次,多加了1次; 2.再排除——A B A B +- 把多加了1次的重叠部分A B 减去. 图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数.1.先包含:A B C ++ 重叠部分A B 、B C 、C A 重叠了2次,多加了1次. 2.再排除:A B C A B B C A C ++--- 重叠部分A B C 重叠了3次,但是在进行A B C ++- A B B C A C --计算时都被减掉了. 3.再包含:A B C A B B C A C A B C ++---+.例题精讲两量重叠问题【例 1】小明喜欢:踢足球、上网、游泳、音乐、语文、数学;小英喜欢:数学、英语、音乐、陶艺、跳绳。
二年级下册数学试题-奥数习题讲练:第十二讲 重叠趣题(解析版)全国通用

第十二讲重叠趣题【精品】之前,我们遇到过这样一些问题,两根木头钉在一起还有多长;把两块毛巾挂在铁丝上需要几个夹子等等.解答这些问题的时候都要考虑重叠的部分.在这节课中我们将这些类似的问题归纳在一起,让学生通过有目的的研究,来找到解决重叠问题的方法.数学乐园【分析】蜗牛白天往上爬了12分米,晚上又滑下来3分米,可以这样理解12分米中往上爬的3分米和往下滑的3分米重叠抵消,实际上每天只往上爬了9分米.这样爬了5天以后共爬了45分米,余下的12分米在第6天的白天就爬到竿顶了,而不需再向下滑了,所以一共需要6天就可以爬到竿顶.同学们,我们都玩过剪纸,如果把两张纸用胶水粘贴在一起,两张纸必然会有一端上下重合在一起,这重合的部分就是重叠部分.以前我们也遇到过一些重叠问题,解决重叠问题首先要弄清楚是哪部分重叠,还要弄清重叠了几部分,然后再来根据题目的意思具体分析.这节课我们就专门来研究这个问题.智慧城堡【例1】洗好的8块手帕用夹子夹在绳子上晾干,每一块手帕的两边必须用夹子夹住,同1个夹子夹住相邻的两块手帕的两边,这样一共要多少个夹子?【分析】一块手帕要用两个夹子;两块手帕有一个重叠,用3个夹子;三块手帕有两个重叠,用4个夹子……8块手帕有7个重叠,每个重叠的边需要1个夹子,两头不重叠的边各要1个夹子.因此需要的夹子数是:7+2=9(个).总结本题规律:把手帕挂在绳子上晾干,需要的夹子数比手帕数多一个.【例2】把两根长为20厘米的筷子用绳子捆成一根长筷子,中间捆在一起的重叠部分是3厘米.捆成的长筷子长多少厘米?【分析】两根筷子总长度为20×2=40(厘米).捆在一起后,中间重叠部分的长度为3厘米.在这40厘米中,3厘米多算了一次,所以最后捆成的筷子长度应从这40厘米中减去多算的一个3厘米,为40-3=37(厘米).列式:20×2=40(厘米)40-3=37(厘米)答:捆成的长筷子长37厘米.【例3】小玲用胶水将两张同样长的纸粘成了一张长为80厘米的长条,其中粘在一起的部分长10厘米,这两张纸条各长多少厘米?【分析】粘在一起的部分是相互重叠粘贴的部分,在算两张纸条总长度时,这部分多算了一次,因此,两张纸条总长度是粘成的长纸条的长度加上重叠部分的长度,为80+10=90(厘米).那么,这两张纸条各自长为90÷2=45(厘米).列式:80+10=90(厘米)90÷2=45(厘米)答:这两张纸条各长45厘米.【例4】有两根铁丝,一根长为30厘米,另一根长为50厘米,将这两根铁丝焊接成一根长为75厘米的长铁丝.那么,中间的焊接重叠部分长为多少厘米?【分析】先求两块木板的长度,再看焊接的木板比两块木板总长度短多少厘米,这就是焊接部分的长度,即重叠部分的长度.两根铁丝总长为30+50=80(厘米),焊接在一起后,长为75厘米,中间重叠部分即为总长度与焊接后长度的差,为80-75=5(厘米).列式:30+50=80(厘米)80-75=5(厘米)答:中间的焊接重叠部分长为5厘米.【例5】有四块各长80厘米的木板,钉成一块木板(如图),中间钉在一起重叠的部分是10厘米,钉成的木板长多少厘米?【分析】四根木板的长度是80×4=320(厘米).钉在一起后,中间重叠部分每一次长度是10厘米,共有3个10厘米的重叠,要从总长度中把这多算的30厘米减掉,才是现在木板的长度.列式:80×4=320(厘米)10×3=30(厘米)320-30=290(厘米)答:钉成的木板长290厘米.拓展练习四根长都是8厘米的绳子,把它们打结连在一起,成为一根长绳,打结处每根绳用去1厘米,绳结长度不计.现在这根长绳长多少厘米?【分析】这题跟例5不同,要注意区分,并比较它们的不同.如果把两根长8厘米的绳子打结连在一起,中间有一个结,打结处每根绳用去1厘米,两根绳子就用去了2厘米,那么现在这根绳子就是8×2-2=14厘米.同道理,如果把四根长8厘米的绳子打结连在一起,中间有3个结,打结处每根绳用去1厘米,四根绳子就用去了6厘米,现在这根绳子长就是8×4-2×3=26(厘米).【例6】把10张图片用图钉像下图那样钉在橱窗里,一共要用多少个图钉?……【分析】10张图片用图钉钉在一起,中间有9个重叠部分,每个重叠部分需要2个图钉,重叠部分一共需要9×2=18(个)图钉.再加上两头各需要两个图钉,这样一共就需要18+4=22(个)图钉.列式:9×2+4=22(个)答:一共要用22个图钉.【例7】二(1)班同学人人参加课外活动,有20人参加英语班,有26人参加电脑班.其中4人两个班都参加.二(1)班一共有多少人?【分析】方法一:已知20人参加英语班,26人参加电脑班,一共有20+26=46(人),这46人中,有4人两班都参加.这就是说这4人在英语班算了名额,在电脑班也算了名额,多算了一次,所以,全班的人数应是46-4=42(人).列式:20+26=46(人)46-4=42(人)方法二:20-4+26=42(人)方法三:26-4+20=42(人)答:二(1)班一共有42人.拓展练习老师出了两道测试题,全班每个同学都至少答对了一道,答对第一道题的有30人,答对第二道题的有28人,两道都答对的有16人,那么全班同学总共有多少人?.【分析】根据上题的分析可以知道,答对第一题的和答对第二题的人数之和为30+28=58(人),在计算这一总人数时,两道都答对的人数被多算了一次,所以全班同学的总人数应为58-16=42(人).列式:30+28=58(人)58-16=42(人)【例8】20个同学报名参加美术组和舞蹈组,其中有16人参加了美术组,12人参加了舞蹈组.问两个小组都参加的有多少个同学?【分析】16人参加了美术组,12人参加了舞蹈组,这样算一共就有28人.但是还有一部分同学既参加了美术组又参加了舞蹈组,在美术组算了一次名额,在舞蹈组又算了一次名额,这样就多算了一次.实际上只有20个同学报名参加美术组和舞蹈组,因此还与28-20=8(人)重复数了一次,这8个人就是即参加了美术组又参加了舞蹈组的人数.列式:16+12=28(人)28-20=8(人)答:两个小组都参加的有8个同学.【例9】某班有20个同学参加作文和数学竞赛,其中参加数学竞赛的有15人,参加作文竞赛的有13人,问只参加数学竞赛和只参加作文竞赛的各有多少人?【分析】因为20个同学参加了参加作文和数学竞赛.如果参加数学竞赛的有15人,那么剩下的就是只参加作文竞赛的同学:20-15=5(人).如果参加作文竞赛的有13人,那么剩下的就是只参加数学竞赛的同学:20-13=7(人).【例10】学校乐器队按计划招收了42名新学员,会拉小提琴的有27人,会弹电子琴又会拉小提琴的有16人,两项都不会的有1人.会弹电子琴的有多少人?【分析】学校乐器队按计划招收了42名新学员,两项都不会的有1人,那么有41名同学会一项或者两项都会.如图,继续分析:会拉小提琴的有27人,这27人里面包含了会弹电子琴又会拉小提琴的16人,所以只会拉小提琴的有27-16=11(人).那么会拉电子琴的有41-11=30(人),这其中包括只会拉电子琴的和两项都会的.列式:42-1=41(人)27-16=11(人)41-11=30(人)答:会弹电子琴的有30人.拓展练习班里共有49名同学,会弹钢琴的有30名,会拉小提琴的有28名,两样都会的有13名,两样都不会的有多少名?【分析】钢琴和小提琴至少会一样的同学有30+28-13=45(名),则两样都不会的同学有49-45=4(名).【例11】小朋友们去喝冷饮,只能选择可乐和雪碧两种饮料.可以选择一种或两种,也可以不选.选择可乐的有18名,不选雪碧的有15名,两种都选的有10名,两种都没选的有多少名?【分析】选择可乐的有18名,这里面包括两种都选的和只选可乐的.两种都选的有10名,所以只选可乐的有18-10=8(名).不选雪碧的有15名,这里面包括只选可乐不选雪碧的和两种都不选的.只选可乐的有8名,所以两种都不选的有15-8=7(名).拓展练习新一期的猫咪训练营开始了,总共有60只小猫咪报名参加.经过一段时间的训练后,有33只猫咪学会了爬树,有25只猫咪学会了抓老鼠,其中既会爬树又会抓老鼠的有10只.那么既不会爬树又不会抓老鼠的猫咪有多少只?【分析】爬树和抓老鼠至少会一项的猫咪有33+25-10=48(只),那么,两项都不会的猫咪有60-48=12(只).【例12】春天来了,全班52人到北海公园划船,有27人划了手摇船,29人划了脚踏船,4名同学因身体不好没有划船而去游览了白塔.问:既划了手摇船也划了脚踏船的同学有多少人?【分析】划了手摇船的人数和划了脚踏船的人数之和为27+29=56(人),全班划了船的人数为全班总人数减去没划船的人数,即为52-4=48(人),那么划了两种船的人数为56-48=8(人).附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)把10块木块用铁钉钉成一条长木条,每两块之间加钉4个,如下图,共需钉上多少个钉?【分析】10块木块用铁钉钉成一条长木条,中间重叠部分有9段,一个重叠处需要4个铁钉,那么一共需要9×4=36(个)铁钉.学校开设了自然和趣味数学两门选修课,每个同学至少要选一门,二(3)班共有48人,有30人选了自然课,有13人两门都选了,那么选趣味数学课的同学有多少人?【分析】选自然课的人数和选趣味数学的人数之和应为全班总人数加上两门都选的人数.也就是说计算这一人数时要把两门都选的人数多算一次,为48+13=61(人).那么选修趣味数学的人数为两门人数之和减去选修自然课的人数,即为61-30=31(人).小攀想用一根65厘米长的铁丝弯成一个边长为15厘米的正方形,铁丝如果太长的话可以重叠.请你帮他算一算重叠的部分要多长才能刚好完成这个任务?【分析】边长为15厘米的正方形四边总长为15×4=60(厘米),若用65厘米的铁丝弯成这样的正方形,多余的部分为65-60=5(厘米).这5厘米就是要重叠的部分.完成的正方形如右图.小明统计了一下学校食堂里的午餐菜式,一个月30天里,有11天没有西红柿鸡蛋,有l8天没有糖醋排骨,两样都有的有7天,两样都没有的有多少天?【分析】30天里,有西红柿鸡蛋的有30-11=19(天),有糖醋排骨的有30-18=12(天),至少有一样的天数为19+12-7=24(天),两样都没有的天数为30-24=6(天).练习十二1.有两块木板,一块长72厘米,另一块长56厘米,如果把两块木板重叠后钉成一块木板,重叠部分是20厘米.求钉成后的木板长多少厘米?【答案】72+56-20=108(厘米),钉成后的木板长108厘米.2.三年级同学参加科技和美术两个课外兴趣小组,参加科技组的有36人,参加美术组的有28人,两个小组都参加的有8人,三年级一共有多少人参加课外兴趣小组?【答案】36+28-8=56(人),三年级一共有56人参加课外兴趣小组.3.三年级同学有56人参加科技和美术两个课外兴趣小组,其中参加科技组的有36人,参加美术组的有28人,两个小组都参加的有多少人?【答案】36+28-56=8(人),两个小组都参加的有8人.4.二年级有40名同学参加跳绳和拍球两项比赛,有12人没有获奖,其中拍球获奖的有18人,拍球和跳绳两项比赛都获奖的有10人,跳绳比赛获奖的有多少人?【答案】40-12=28(人),28-18+10=20(人),跳绳比赛获奖的有20人.5.有101个同学带着水壶和水果去春游,其中带水壶的有78人,带水果的有71人,只带水壶和只带水果的各有多少人?【答案】101-78=23(人),101-71=31(人),只带水壶的有31人,只带水果的有23人.6. 有40人参加测验,答对第一题的有21人,答对第二题的有30人,两道题都答对的有15人,两道题都没答对的有多少人?【答案】21+30-15=36(人),40-36=4(人),两道题都没答对的有4人.信念是一种无坚不催的力量,当你坚信自己能成功时,你必能成功.一天,我发现,一只黑蜘蛛在后院的两檐之间结了一张很大的网.难道蜘蛛会飞?要不,从这个檐头到那个檐头,中间有一丈余宽,第一根线是怎么拉过去的?后来,我发现蜘蛛走了许多弯路--从一个檐头起,打结,顺墙而下,一步一步向前爬,小心翼翼,翘起尾部,不让丝沾到地面的沙石或别的物体上,走过空地,再爬上对面的檐头,高度差不多了,再把丝收紧,以后也是如此.温馨提示:蜘蛛不会飞翔,但它能够把网凌结在半空中.它是勤奋、敏感、沉默而坚韧的昆虫,它的网制得精巧而规矩,八卦形地张开,仿佛得到神助.这样的成绩,使人不由想起那些沉默寡言的人和一些深藏不露的智者.于是,我记住了蜘蛛不会飞翔,但它照样把网结在空中.奇迹是执着者造成的.。
二年级奥数第七讲:重叠问题

第七讲 重叠问题
哪吒智闯水晶宫 --- 哪吒被骗了 哪吒继续往前去寻宝,只见一位白胡
人? 分析:队伍还剩的人就是报单数的人。这 10名队员报数结果是: 1、 2、3、1、2、3、1、2、3、1,这里面双数只有 2,出现了 3次,其他 都是单数,所以报单数的人有 7人。即10-3=7(人)。 例5 洗好的8块手帕夹在绳子上晾干,同一个夹子夹住相邻的两块手帕 的两边,这样一共要多少个夹子?
子老爷爷拿着哪吒地乾坤圈站在大厅中间。“那是我的乾坤圈!”哪吒激动的叫起来。哪吒赶 紧跑过去一看,“怎么有两个乾坤圈?”
白胡子老爷爷微笑的说:“哪吒不认识我了?”哪吒仔细打量了这位老爷爷后说:“我 记起来了,你是太白金星。”太白金星:“哪吒,我听说了你的事后,特意来帮助你的,你 看,我帮你把乾坤圈要回来了。”哪吒:“那怎么有两个乾坤圈?”太白金星:“这其中一个 是我的金钢圈,另一个是你的乾坤圈,刚才我拿一个圈称连我共重 67千克,拿另一个圈称连我
共重68千克,我的金刚圈比你的乾坤圈重,你猜得出来你的乾坤圈和我的金刚圈多重,我就把 你的宝贝还给你”哪吒:“太白金星,你说话可得算数!”太白金星:“那当然了,我胡子都 白了,还会骗你?你就在这里想吧,我有事先走,一会儿就回来”哪吒在原地想了一天一夜, 也没有想出答案,他明白了,他并不知道太白金星的体重是不可能算出乾坤圈和金刚圈的重量 的,他被骗了,那个老人根本不是太白金星!他不过是中了龙王的圈套而已,哪吒气冲冲的继 续前进,心想,要再被我碰到这假冒的太白金星,我一定把他的胡子拔了!
小学奥数容斥原理之重叠问题(二)精选练习例题含答案解析(附知识点拨及考点)

教学目标1. 了解容斥原理二量重叠和三量重叠的内容;2. 掌握容斥原理的在组合计数等各个方面的应用.知识要点一、两量重叠问题在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成: A B A B A B (其中符号“ ”读作“并”,相当于中文“和”或者“或”的意思;符号“ 读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为: A B ,即阴影面积.图示如下: A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为: A B ,即阴影面积.第一步:分别计算集合A、B的元素个数,然后加起来,即先1求A B (意思A是B把A、B 的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去 C A B (意思是“排除”了重复计算的元素个数).、三量重叠问题A类、B 类与C 类元素个数的总和A类元素的个数B类元素个数C 类元素个数既是A类又是B类的元素个数既是B类又是C类的元素个数既是A类又是C类的元素个数同时是A类、B类、C类的元素个数.用符号表示为:A B C A B C A B B C A C A B C .图示如下:ABAB 包含与排除原理告诉我们,要计算两个集合A、B的并集 A B 的元素的个数,可分以下两步进行:ABC3ABC在解答有关包含排除问题时,我们常常利用圆圈图 (韦恩图 )来帮助分析思考.例题精讲模块一、三量重叠问题例 1】 一栋居民楼里的住户每户都订了 2 份不同的报纸。
如果该居民楼的住户只订了甲、乙、丙三种报 纸,其中甲报 30 份,乙报 34 份,丙报 40份,那么既订乙报又订丙报的有 __________________ 户。
二年级奥数重叠问题

知识要点:前面已学过排队问题,从前面数,从后面数,丽丽都排第,这一排共有几个人?这里丽丽被重复数了两次,有时我们也把这类问题叫重叠问题.[ 例 ]洗好地块手帕夹在绳子上晾干,同一个夹子夹住相邻地两块手帕地两边,这样一共要多少个夹子?分析:由图知道,两块手帕有一边重叠,用个夹子.三块手帕有两边重叠,用个夹子,我们发现夹子数总比手帕数多,因此块手帕就要用个夹子.[ 例 ]把图画每两张重叠在一起钉在墙上,现在有张画要多少个图钉呢?分析:每排两张画要个图钉,每排三张画要个图钉,每排四张画要个图钉.可以看出,图画每增加一张,图钉就要增加颗,那么张画要个图钉.[ 例 ]有两块一样长地木板,钉在一起,如果每块木板长厘米,中间钉在一起地长厘米,现在长木板有多长?分析:把两块木板钉起来,钉在一起地地方地长度就是重叠地部分.现在地总长就是原来两个总长地和减去重叠地部分.算式:(厘米)所以现在木板长厘米.[ 例 ]张老师出了两道题,做对第一题地有人,做对第二题地有人,两道题都做对地有人,这个班一共有多少人?分析:做对第一题地个人里,有个人也做对第二题,那么做对第二题地个人里这个人就又重复数了一次,因此把做对第一题地人数和做对第二题地人数和起来,再减去重复数地这个人.算式:(人)所以这个班一共有人.[ 例 ]四根长都是厘米地绳子,把它们打结连在一起,成为一根长绳,打结处每根绳用去厘米,绳结长度不计,现在这根长绳长多少厘米?分析:两根绳有一个结,三根绳有两个结,那么四根绳有三个结.一个结用去厘米,那么三个结用去厘米,绳子总长厘米,减去打结地厘米,,现在这根长绳是厘米.重叠问题练习一,小朋友排队做操,小明从前数起排在第个,从后数起排在第个.这队小朋友共有多少人?,学校组织看文艺演出,冬冬地座位从左数起是第个,从右数起是第个.这一行座位有多少个?,同学们排队去参观展览,无论从前数还是从后起起,李华都排在第个.这一排共有多少个同学?练习二,同学们排队跳舞,每行、每列人数同样多.小红地位置无论从前数从后数,从左数还是从右数起都是第个.跳舞地共有多少人?,为庆祝“六一”,同学们排成每行人数相同地鲜花队,小华地位置从左数第个,从右数第个;从前数第个,从后数第个.鲜花队共多少人?,三()班排成每行人数相同地队伍入场参加校运动会,梅梅地位置从前数是第个,从后数是第个;从左数、从右数都是第个.三()班共有学生多少人练习三,把两段一样长地纸条粘合在一起,形成一段更长地纸条.这段更长地纸条长厘米,中间重叠部分是厘米,原来两段纸条各长多少厘米?,把两块一样长地木板钉在一起,钉成一块长厘米地木板.中间重合部分长厘米,这两块木板各长多少厘米?,两根木棍放在一起(如图),从头到尾共长厘米,其中一根木棍长厘米,中间重叠部分长厘米.另一根木棍长多少厘米?练习四,三()班有学生人,每人至少参加赛跑和跳绳比赛中地一种.已知参加赛跑地有人,参加跳绳地有人.两项比赛都参加地有几人?,两块木板各长厘米,像下图这样钉成一块长厘米地木板,中间重合部分是多少厘米?,三()班有名同学,会下象棋地有名同学,会下围棋地有名,两种棋都不会地有名.两种棋都会下地有多少名?练习五,三()班做完语文作业地有人,做完数学作业地有人,两种作业都完成地有人,每人至少完成一种作业.三()班共有学生多少人?,两块木板各长厘米,像下图这样钉成一块木板,中间重合部分是厘米,这块钉在一起地木板总长多少厘米?,三年级有个小朋友去春游,带矿泉水地有人,带水果地有人,每人至少带一种.三年级既带矿泉水又带水果地小朋友有多少人?。
小学奥数容斥原理之重叠问题一精选例题练习习题含知识点拨

教学目标1 . 了解容斥原理二量重叠和三量重叠的内容;2 .掌握容斥原理的在组合计数等各个方面的应用.知识要点一、两量重叠问题在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把 两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数, 用式子可表示成:A U B = A + B - A 「B (其中符号“、.”读作“并”,相当于中文“和”或者“或”的意思;符号“•'” 读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理,图示如下A 表示小圆 部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A^B ,即阴影面积.图示如下:A 表示小圆 部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A PI B ,即阴影面积. 先包含——A + B重叠部分A^B 计算了 2次,多加了 1次;2.再排除——A + B — A p|B把多加了 1次的重叠部分A^B 减去.包含与排除原理告诉我们,要计算两个集合A 、B 的并集A U B 的元素的个数,可分以下两步进行:第一步:分别计算集合A 、B 的元素个数,然后加起来,即先求A + B (意思是把A 、B 的一切元素都“包含”进 来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C = A A B (意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和=A 类元素的个数+ B 类元素个数+ C 类元素个数-既是A 类又是B 类 的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元 素个数.用符号表示为:A U B U C = A + B + C — A p|B — B Pl C — A p|C + A^B^C .图示如下: 图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数.1 .先包含:A + B + C重叠部分A PI B 、B PI C 、C PI A 重叠了 2次,多加了 1次.2 .再排除:A + B + C — A p|B — B A C — A p|C重叠部分A^B^C 重叠了 3次,但是在进行A + B + C - A^B — B^C —A Q C 计算时都被减掉了.3 .再包含:A + B + C — A p|B — B p|C — A p|C + A[}B[yC .在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.7-7-1.容斥原理之重叠问题(一)4V例题精靛讲两量重叠问题【例1】小明喜欢:踢足球、上网、游泳、音乐、语文、数学;小英喜欢:数学、英语、音乐、陶艺、跳绳。
小学二年级重叠问题

重叠问题
1、王老师将8块手帕用夹子夹在绳子上晾晒,每一块手帕的两边必须用夹子夹住,同一个夹子夹住相邻的2块手帕的两边,王老师一共要用多少个夹子?
2、严老师的班级有28人订阅了《好儿童》和《儿童画报》,其中订阅《好儿童》的有16人,两种杂志都订有3人,订《儿童画报》有多少人?
3、王阿姨把洗好的床单用夹子夹在绳子上晾晒,每一床床单两边都用夹子夹住,同一个夹子夹住相邻的两块床单,一共用了20个夹子,绳子上晒了多少块床单?
4、两块木板各长40厘米,把这两块木板钉起来的木板长70厘米,中间钉在一起的地方长是多少厘米?
5、把两根各长30厘米的绳子结成了一根长50厘米的绳子,打结部分长是多少厘米?
6、有两块一样长的木板,现在要把这两块木板钉在一起成一块木板,如果这两块木板各长40厘米,中间钉在一起的地方长是10厘米,这块钉起来的木板长多少厘米?
7、有两块塑料板各长50厘米,把两块板钉成一个塑料板,中间钉在一起的重叠部分是10厘米,钉成的塑料板长是多少厘米?
8、丁老师出了两组数学题给数学兴趣小组的18名同学做,做对第一组题有10名,做对第二组题有12名,两组都做对的有多少名同学?
9、二(3)班有学生42人,期末考试语文得100分的有32人,数学得100分的有36人,语文、数学都得100分的有多少人?
10、三(3)班有10位同学参加了趣味语文,有12位同学参加了趣味数学,有4位同学两个兴趣小组都参加了。
一共有多少人参加了兴趣小组?。
二年级数学重叠问题

二年级数学重叠问题一、知识点讲解1. 重叠问题的概念在数学中,重叠问题是指有部分元素在不同的集合中重复出现的情况。
例如,同学们参加语文小组和数学小组,有一些同学既参加了语文小组又参加了数学小组,这就是重叠部分。
2. 解决重叠问题的方法常用的方法是画韦恩图(集合图)来直观地表示各个集合以及它们之间的重叠关系。
另外,也可以通过计算来解决,计算时要注意避免重复计算重叠部分。
例如:计算参加两个小组的总人数时,如果直接把参加语文小组的人数和参加数学小组的人数相加,就会把既参加语文小组又参加数学小组(重叠部分)的人数多计算一次,所以需要减去重叠部分的人数。
二、经典例题及解析1. 例题1题目:二(1)班同学参加课外活动,有20人参加英语班,25人参加电脑班,其中有10人两个班都参加了。
二(1)班一共有多少人参加课外活动?解析:我们可以画韦恩图来理解。
先画两个相交的圆,一个圆表示参加英语班的同学,另一个圆表示参加电脑班的同学,相交的部分就是两个班都参加的同学。
如果直接把参加英语班的20人和参加电脑班的25人相加:20 + 25=45(人),这里面把两个班都参加的10人重复计算了一次。
所以正确的计算方法是:20+25 10 = 35(人)。
2. 例题2题目:学校乐器队招收了42名新学员,其中会拉小提琴的有25名,会弹钢琴的有22名,两项都不会的有3名。
两项都会的有多少名?解析:我们知道总共有42名新学员,其中两项都不会的有3名,那么至少会一项乐器的学员有42 3 = 39(名)。
会拉小提琴的有25名,会弹钢琴的有22名,那么25+22 = 47(名),这个数字比至少会一项乐器的39名多。
多出来的部分就是两项都会的人数,即47 39 = 8(名)。
3. 例题3题目:把两块一样长的木板钉在一起,钉成一块长35厘米的木板,中间重叠部分长11厘米。
这两块木板各长多少厘米?解析:两块木板钉在一起后总长度是35厘米,但是中间重叠了11厘米。
(完整版)二年级奥数重叠问题

知识重点:前方已学过排队问题,以前方数,从后边数,丽丽都排第 6,这一排共有几个人?这里丽丽被重复数了两次,有时我们也把这种问题叫重叠问题。
[例1 ]洗好的8块手帕夹在绳索上晾干,同一个夹子夹住相邻的两块手帕的两边,这样一共要多少个夹子?剖析:由图知道,两块手帕有一边重叠,用 3 个夹子。
三块手帕有两边重叠,用 4 个夹子,我们发现夹子数总比手帕数多1,所以 8 块手帕就要用 9 个夹子。
[例2 ]把图画每两张重叠在一同钉在墙上,此刻有 5 张画要多少个图钉呢?剖析:每排两张画要 6 个图钉,每排三张画要 8 个图钉,每排四张画要 10 个图钉。
能够看出,图画每增添一张,图钉就要增添 2 颗,那么 5 张画要 12 个图钉。
[例3 ]有两块相同长的木板,钉在一同,假如每块木板长25 厘米,中间钉在一同的长 5 厘米,此刻长木板有多长?剖析:把两块木板钉起来,钉在一同的地方的长度就是重叠的部分。
现在的总长就是本来两个总长的和减去重叠的部分。
算式:25+25-5=45(厘米)所以此刻木板长 45 厘米。
[ 例 4 ] 张老师出了两道题,做对第一题的有 13 人,做对第二题的有 22人,两道题都做对的有 8 人,这个班一共有多少人?剖析:做对第一题的 13 个人里,有 8 个人也做对第二题,那么做对第二题的 22 个人里这 8 个人就又重复数了一次,所以把做对第一题的人数和做对第二题的人数和起来,再减去重复数的这8 个人。
算式: 13+22-8=27(人)所以这个班一共有 27 人。
[ 例 5 ] 四根长都是 8 厘米的绳索,把它们打结连在一同,成为一根长绳,打结处每根绳用去 1 厘米,绳结长度不计,此刻这根长绳长多少厘米?剖析:两根绳有一个结,三根绳有两个结,那么四根绳有三个结。
一个结用去 1+1=2 厘米,那么三个结用去 2+2+2=6厘米,绳索总长 8+8+8+8=32厘米,减去打结的 6 厘米, 32-6=26,此刻这根长绳是 26 厘米。
小学奥数专题-重叠问题(精华版)

小学奥数重叠问题专题日常生活或数学问题中,在把一些数据按照某个标准分类时,常常出现其中的一部分数据同时属于两种或两种以上不同的类别,这样在计算总数时就会出现重复计算的情况,这类问题就叫做重叠问题。
重叠问题中涉及到的容斥原理是奥数的四大原理之一,是奥数重要知识点。
学生学习奥数,一定要掌握容斥原理。
下面小编给大家分享解决重叠的方法。
1. 解答重叠问题要用到数学中一个重要原理——包含与排除原理,即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
2. 解答重叠问题的应用题,必须从条件入手进行认真的分析,有时还要画出图示,借助图形进行思考,找出哪些是重复的,重复了几次。
明确需要要求的是哪一部分,从而找出解答方法。
3. 在数学中,我们经常用平面上封闭曲线的内部代表集合和集合之间的关系。
这种图称为韦恩图(也叫文氏图)。
4. 解答重叠问题的常用方法是:先不考虑重叠的情况,把有重复包含的几个计数部分加起来,再从它们的和中排除重复部分元素的个数,使得计算的结果既无遗漏又不重复。
这个原理叫做包含与排斥原理,也叫容斥原理。
5. 容斥原理1:如果被计数的对象,被分为A、B两大类,则:被计数对象的总个数=A 类元素的个数+B类元素的个数-同时属于A类和B类的元素个数。
容斥原理2:如果被计数的对象,被分为A、B、C三大类,则:被计数对象的总个数=A 类元素的个数+B类元素的个数+C类元素的个数-同时属于A类和B类元素的个数-同时属于A类和C类元素个数-同时属于B类和C类元素个数+同时属于A类、B类、C类元素个数。
一、重叠问题之长度:(1)拼接(对接)(2)搭接(3)打结题目1:(搭接正问题:求总长度)把两段同样是20厘米长的纸条粘合在一起,形成一段更长的纸条。
中间重叠的部分是6厘米,粘好的纸条长多少厘米?题目2:(搭接反问题一:等长搭接,求原来长度)把两段一样长的纸条粘合在一起,形成一段更长的纸条。
这段更长的纸条长30厘米,中间重叠的部分是6厘米,原来两条纸条各长多少厘米?题目3:(搭接反问题一:不等长搭接,求原来长度)两根木棍放在一起,从头到尾共长66厘米,其中一根木棍长48厘米,中间重叠部分长12厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(★★★)
有四块各长80厘米的木板,钉成一块木板(如图),中间钉在一起重叠的部分是10厘米,钉成的木板长多少厘米?
【例1拓展】(★★★)
小玲用胶水将两张同样长的纸粘成了一张长为80厘米的长纸条,其中粘在一起的部分长10厘米,这两张纸条各长多少厘米?
(★★★)
二(1)班同学人人参加课外活动,有20人参加英语班,有26人参加电脑班。
其中4人两个班都参加。
二(1)班一共有多少人?
【例2拓展】(★★★)
老师出了两道测试题,全班每个同学都至少答对了一道,答对第一道题的有30人,答对第二道题的有28人,两道都答对的有18人,那么全班同学总共有多少人?
(★★★★)
20个同学报名参加美术组和舞蹈组,其中有16人参加了美术组,12人参加了舞蹈组.问两个小组都参加的有多少个同学?
【例3拓展】(★★★★)
春天来了,全班52人到北海公园划船,有27人划了手摇船,29人划了脚踏船,4名同学因身体不好没有划船而去游览了白塔。
问:既划了手摇船也划了脚踏船的同学有多少人?
(★★★★)
学校乐器队按计划招收了42名新学员,会拉小提琴的有27人,会弹电子琴又会拉小提琴的有16人,两项都不会的有1人.会弹电子琴的有多少人?
(★★★★★)
新一期的猫咪训练营开始了,总共有60只小猫咪报名参加.经过一段时间的训练后,有33只猫咪学会了爬树,有25只猫咪学会了抓老鼠,其中既会爬树又会抓老鼠的有10只。
那么既不会爬树又不会抓老鼠的猫咪有多少只?
【例5拓展】(★★★★★)
某班组织了一次跳绳和呼啦圈比赛活动,参加跳绳比赛的有29人,参加呼啦圈比赛的有23人,两项都参加的有6人,两项都没有参加的有4人。
问全班共有多少人?。
