2019-2020年高考数学二轮复习难点2.7 立体几何中的空间角与距离教学案理

合集下载

2020版高考数学二轮复习第2部分专题4立体几何第2讲空间向量与立体几何教案理

第2讲空间向量与立体几何[做小题——激活思维]1．在正方体A 1B 1C 1D 1ABCD 中，AC 与B 1D 所成角的大小为( ) A.π6 B.π4 C.π3D.π2D [如图，连接BD ，易证AC ⊥平面BB 1D ， ∴AC ⊥B 1D ，∴AC 与B 1D 所成角的大小为π2.] 2．已知两平面的法向量分别为m ＝(0,1,0)，n ＝(0,1,1)，则两平面所成的二面角为( ) A ．45° B ．135° C ．45°或135°D ．90°C [∵m ＝(0,1,0)，n ＝(0,1,1)， ∴|m |＝1，|n |＝2，m ·n ＝1，∴cos〈m ，n 〉＝m ·n |m ||n |＝12＝22，设两平面所成的二面角为α，则 |cos α|＝22，∴α＝45°或135°，故选C.] 3．用a ，b ，c 表示空间中三条不同的直线，γ表示平面，给出下列命题： ①若a ⊥b ，b ⊥c ，则a ∥c ；②若a ∥b ，a ∥c ，则b ∥c ； ③若a ∥γ，b ∥γ，则a ∥b ；④若a ⊥γ，b ⊥γ，则a ∥b . 其中真命题的序号是( ) A ．①② B ．②③ C ．①④D ．②④D [对于①，正方体从同一顶点引出的三条直线a ，b ，c ，满足a ⊥b ，b ⊥c ，但是a ⊥c ，所以①错误；对于②，若a ∥b ，a ∥c ，则b ∥c ，满足平行线公理，所以②正确；对于③，平行于同一平面的两条直线的位置关系可能是平行、相交或者异面，所以③错误；对于④，由垂直于同一平面的两条直线平行，知④正确．故选D.]4．已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则l 与α所成的角为________．π6[设l 与α所成的角为θ，则 sin θ＝|cos 〈m ，n 〉|＝12，又θ∈⎣⎢⎡⎦⎥⎤0，π2，∴θ＝π6.][扣要点——查缺补漏]1．证明线线平行和线线垂直的常用方法(1)证明线线平行：①利用平行公理；②利用平行四边形进行平行转换；③利用三角形的中位线定理；④利用线面平行、面面平行的性质定理进行平行转换．如T 3.(2)证明线线垂直：①利用等腰三角形底边上的中线即高线的性质；②勾股定理；③线面垂直的性质．2．证明线面平行和线面垂直的常用方法(1)证明线面平行：①利用线面平行的判定定理；②利用面面平行的性质定理． (2)证明线面垂直：①利用线面垂直的判定定理；②利用面面垂直的性质定理． 3．异面直线所成的角求法 (1)平移法：解三角形．(2)向量法：注意角的范围．如T 1. 4．二面角的求法cos θ＝cos 〈m ，n 〉＝m ·n|m ||n |，如T 2.5．线面角的求法sin θ＝|cos 〈m ，n 〉|，如T 4.利用空间向量求空间角(5年15考)[高考解读] 主要考查通过建立空间直角坐标系，解决空间图形中的线线角、线面角和面面角的求解，考查学生的空间想象能力、运算能力、三种角的定义及求法等.(2018·全国卷Ⅱ)如图，在三棱锥P ABC 中，AB ＝BC ＝22，PA ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角M PA C 为30°，求PC 与平面PAM 所成角的正弦值．切入点：(1)借助勾股定理，证明PO ⊥OB ；(2)建立空间直角坐标系，利用二面角M PA C 为30°求出点M 的坐标，进而求出PC 与平面PAM 所成角的正弦值．[解](1)证明：因为AP ＝CP ＝AC ＝4，O 为AC 的中点，所以OP ⊥AC ，且OP ＝2 3. 连接OB .因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2.由OP 2＋OB 2＝PB 2知PO ⊥OB .由OP ⊥OB ，OP ⊥AC ，OB ∩AC ＝O ，知PO ⊥平面ABC . (2)如图，以O 为坐标原点，OB →的方向为x 轴正方向，建立空间直角坐标系O xyz .由已知得O (0,0,0)，B (2,0,0)，A (0，－2,0)，C (0,2,0)，P (0,0,23)，AP →＝(0,2,23)．取平面PAC 的一个法向量OB →＝(2,0,0)．设M (a,2－a,0)(0≤a ≤2)，则AM →＝(a,4－a,0)．设平面PAM 的法向量为n ＝(x ，y ，z )．由AP →·n ＝0，AM →·n ＝0得⎩⎨⎧2y ＋23z ＝0，ax ＋－a y ＝0，可取n ＝(3(a －4)，3a ，－a )，所以cos 〈OB →，n 〉＝23a －2a －2＋3a 2＋a2.由已知可得|cos 〈OB →，n 〉|＝32，所以23|a －4|2a －2＋3a 2＋a2＝32，解得a ＝－4(舍去)，a ＝43，所以n ＝⎝ ⎛⎭⎪⎫－833，433，－43.又PC →＝(0,2，－23)，所以cos 〈PC →，n 〉＝34.所以PC 与平面PAM 所成角的正弦值为34. [教师备选题]1.(2015·全国卷Ⅰ)如图，四边形ABCD 为菱形，∠ABC ＝120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE ＝2DF ，AE ⊥EC .(1)证明：平面AEC ⊥平面AFC ；(2)求直线AE 与直线CF 所成角的余弦值．[解](1)证明：如图，连接BD ，设BD ∩AC ＝G ，连接EG ，FG ，EF . 在菱形ABCD 中，不妨设GB ＝1.由∠ABC ＝120°，可得AG ＝GC ＝ 3.由BE ⊥平面ABCD ，AB ＝BC ，可知AE ＝EC . 又AE ⊥EC ，所以EG ＝3，且EG ⊥AC . 在Rt△EBG 中，可得BE ＝2，故DF ＝22. 在Rt△FDG 中，可得FG ＝62. 在直角梯形BDFE 中，由BD ＝2，BE ＝2，DF ＝22，可得EF ＝322. 从而EG 2＋FG 2＝EF 2，所以EG ⊥FG . 又AC ∩FG ＝G ，所以EG ⊥平面AFC . 因为EG平面AEC ，所以平面AEC ⊥平面AFC .(2)如图，以G 为坐标原点，分别以GB →，GC →的方向为x 轴，y 轴正方向，|GB →|为单位长度，建立空间直角坐标系G xyz .由(1)可得A (0，－3，0)，E (1,0，2)，F －1,0，22，C (0，3，0)，所以A E →＝(1，3，2)，CF →＝⎝ ⎛⎭⎪⎫－1，－3，22.故cos 〈A E →，CF →〉＝A E →·CF →|A E →||CF →|＝－33.所以直线AE 与直线CF 所成角的余弦值为33. 2．(2019·全国卷Ⅰ)如图，直四棱柱ABCD A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．(1)证明：MN ∥平面C 1DE ； (2)求二面角A MA 1N 的正弦值．[解](1)连接B 1C ，ME .因为M ，E 分别为BB 1，BC 的中点，所以ME ∥B 1C ，且ME ＝12B 1C .又因为N 为A 1D 的中点，所以ND ＝12A 1D .由题设知A 1B 1DC ，可得B 1C A 1D ，故ME ND ，因此四边形MNDE 为平行四边形，MN ∥ED .又MN平面EDC 1，所以MN ∥平面C 1DE .(2)由已知可得DE ⊥D A.以D 为坐标原点，DA →的方向为x 轴正方向，建立如图所示的空间直角坐标系D xyz ，则A (2,0,0)，A 1(2,0,4)，M (1，3，2)，N (1,0,2)，A 1A →＝(0,0，－4)，A 1M →＝(－1，3，－2)，A 1N →＝(－1,0，－2)，MN →＝(0，－3，0)．设m ＝(x ，y ，z )为平面A 1MA 的法向量，则 ⎩⎪⎨⎪⎧m ·A 1M →＝0，m ·A 1A →＝0.所以⎩⎨⎧－x ＋3y －2z ＝0，－4z ＝0.可取m ＝(3，1,0)．设n ＝(p ，q ，r )为平面A 1MN 的法向量，则 ⎩⎪⎨⎪⎧n ·MN →＝0，n ·A 1N →＝0.所以⎩⎨⎧－3q ＝0，－p －2r ＝0.可取n ＝(2,0，－1)．于是cos 〈m ，n 〉＝m·n |m||n|＝232×5＝155，所以二面角A MA 1N 的正弦值为105.1．利用向量法求线面角的两种方法(1)法一：分别求出斜线和它在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)；(2)法二：通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角．2．利用向量计算二面角大小的常用方法(1)找法向量法：分别求出二面角的两个半平面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐(钝)二面角．(2)找与棱垂直的方向向量法：分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，则这两个向量的夹角的大小就是二面角的大小．提醒：判断二面角的平面角是锐角还是钝角，可结合图形进行．1．[一题多解](以圆柱为载体)如图，圆柱的轴截面ABCD 为正方形，E 为弧BC 的中点，则异面直线AE 与BC 所成角的余弦值为 ( )A.33 B.55 C.306D.66D [法一：(平移法)取BC 的中点H ，连接EH ，AH ，∠EHA ＝90°，设AB ＝2，则BH ＝HE ＝1，AH ＝5，所以AE ＝6，连接ED ，ED ＝6，因为BC ∥AD ，所以异面直线AE 与BC 所成角即为∠EAD ，在△EAD 中cos∠EAD ＝6＋4－62×2×6＝66，故选D.法二：(向量法)取圆柱底面的圆心O 为原点，建立空间直角坐标系O xyz ，设AB ＝2，则A (1,0,0)，B (1,0,2)，C (－1,0,2)，E (0,1,2)，∴A E →＝(－1,1,2)，BC →＝(－2,0,0)∴cos〈A E →，BC →〉＝26×2＝66，故选D.] 2．(以棱柱为载体)在三棱柱ABC A1B 1C 1中， AB ⊥平面BCC 1B 1，∠BCC 1＝π3， AB ＝BC ＝2, BB 1＝4，点D 在棱CC 1上，且CD ＝λCC 1(0<λ≤1)．建立如图所示的空间直角坐标系．(1)当λ＝12时，求异面直线AB 1与A 1D 的夹角的余弦值；(2)若二面角A B 1D A 1的平面角为π3，求λ的值．[解](1)易知A ()0，0，2， B 1()0，4，0， A 1()0，4，2. 当λ＝12时，因为BC ＝CD ＝2, ∠BCC 1＝π3，所以C ()3，－1，0，D ()3，1，0.所以AB 1→＝()0，4，－2， A 1D →＝()3，－3，－2. 所以cos 〈AB 1→，A 1D →〉＝AB 1→·A 1D→||AB 1→||A 1D →＝0×3＋4×()－3＋()－2×()－242＋()－22·()32＋()－32＋()－22＝－55. 故异面直线AB 1与A 1D 的夹角的余弦值为55. (2)由CD ＝λCC 1可知， D ()3，4λ－1，0，所以DB 1→＝()－3，5－4λ，0，由(1)知， AB 1→＝()0，4，－2.设平面AB 1D 的法向量为m ＝()x ，y ，z ，则⎩⎪⎨⎪⎧AB 1→·m ＝0，DB 1→·m ＝0，即⎩⎨⎧4y －2z ＝0，()5－4λy －3x ＝0，令y ＝1，解得x ＝5－4λ3， z ＝2，所以平面AB 1D 的一个法向量为m ＝⎝ ⎛⎭⎪⎫5－4λ3，1，2.设平面A 1B 1D 的法向量为n ＝()x ，y ，z ，则⎩⎪⎨⎪⎧B 1A 1→·n ＝0，DB 1→·n ＝0，即⎩⎨⎧2z ＝0，()5－4λy －3x ＝0，令y ＝1，解得x ＝5－4λ3， z ＝0，所以平面A 1B 1D 的一个法向量为n ＝⎝ ⎛⎭⎪⎫5－4λ3，1，0.因为二面角A B 1D A 1的平面角为π3，所以||cos 〈m ，n 〉＝|m·n |||m ||n＝⎪⎪⎪⎪⎪⎪5－4λ3×5－4λ3＋1×1＋2×0⎝ ⎛⎭⎪⎫5－4λ32＋12＋22·⎝ ⎛⎭⎪⎫5－4λ32＋12＝12，即()5－4λ2＝1，解得λ＝32(舍)或λ＝1，故λ的值为1.3.(以棱台为载体)如图，在三棱台DEF ABC 中，AB ＝2DE ，G ，H 分别为AC ，BC 的中点． (1)求证：BD ∥平面FGH ；(2)若CF ⊥平面ABC ，AB ⊥BC ，CF ＝DE ，∠BAC ＝45°，求平面FGH 与平面ACFD 所成的角(锐角)的大小．[解](1)证明：在三棱台DEF ABC 中，由BC ＝2EF ，H 为BC 的中点，可得BH ∥EF ，BH ＝EF ，所以四边形BHFE 为平行四边形，可得BE ∥HF .在△ABC 中，G 为AC 的中点，H 为BC 的中点，所以GH ∥AB .又GH ∩HF ＝H ，所以平面FGH ∥平面ABED . 因为BD平面ABED ，所以BD ∥平面FGH .(2)设AB ＝2，则CF ＝1.在三棱台DEF ABC 中，G 为AC 的中点，由DF ＝12AC ＝GC ，可得四边形DGCF 为平行四边形，因此DG ∥FC . 又FC ⊥平面ABC ，所以DG ⊥平面ABC .连接GB ，在△ABC 中，由AB ⊥BC ，∠BAC ＝45°，G 是AC 的中点，所以AB ＝BC ，GB ⊥GC ，因此GB ，GC ，GD 两两垂直．以G 为坐标原点，建立如图所示的空间直角坐标系G xyz .所以G (0,0,0)，B (2，0,0)，C (0，2，0)，D (0,0,1)．可得H ⎝⎛⎭⎪⎫22，22，0，F (0，2，1)．故GH →＝⎝ ⎛⎭⎪⎫22，22，0，GF →＝(0，2，1)．设n ＝(x ，y ，z )是平面FGH 的法向量，则由⎩⎪⎨⎪⎧n ·GH →＝0，n ·GF →＝0，可得⎩⎨⎧x ＋y ＝0，2y ＋z ＝0.可得平面FGH 的一个法向量n ＝(1，－1，2)．因为GB →是平面ACFD 的一个法向量，GB →＝(2，0,0)，所以cos 〈GB →，n 〉＝GB →·n |GB →|·|n |＝222＝12.所以平面FGH 与平面ACFD 所成角(锐角)的大小为60°. 4.(以五面体为载体)如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，平面ABEF 为正方形，AF ＝2FD ，∠AFD ＝90°，且二面角D AF E 与二面角C BE F 都是60°.(1)证明：平面ABEF ⊥平面EFDC ； (2)求二面角E BC A 的余弦值．[解](1)证明：由已知可得AF ⊥DF ，AF ⊥FE ，DF ∩EF ＝F ，所以AF ⊥平面EFDC .又AF 平面ABEF ，故平面ABEF ⊥平面EFDC .(2)过D 作DG ⊥EF ，垂足为G ，由(1)知DG ⊥平面ABEF . 以G 为坐标原点，GF →的方向为x 轴正方向，|GF →|为单位长，建立如图所示的空间直角坐标系G xyz .由(1)知∠DEF 为二面角D AF E 的平面角，故∠DFE ＝60°，则|DF |＝2，|DG |＝3，可得A (1,4,0)，B (－3,4,0)，E (－3,0,0)，D (0,0，3)．由已知得，AB ∥EF ，所以AB ∥平面EFDC . 又平面ABCD ∩平面EFDC ＝CD ，故AB ∥CD ，CD ∥EF .由BE ∥AF ，可得BE ⊥平面EFDC ，所以∠CEF 为二面角C BE F 的平面角，∠CEF ＝60°.从而可得C (－2,0，3)．连接AC ，所以E C →＝(1,0，3)，E B →＝(0,4,0)，AC →＝(－3，－4，3)，AB →＝(－4,0,0)．设n ＝(x ，y ，z )是平面BCE 的法向量，则 ⎩⎪⎨⎪⎧n ·E C →＝0，n ·E B →＝0，即⎩⎨⎧x ＋3z ＝0，4y ＝0.所以可取n ＝(3,0，－3)．设m 是平面ABCD 的法向量，则⎩⎪⎨⎪⎧m ·AC →＝0，m ·AB →＝0.同理可取m ＝(0，3，4)．则cos 〈n ，m 〉＝n ·m |n ||m |＝－21919. 故二面角E BC A 的余弦值为－21919.利用空间向量解决折叠性问题(5年3考)[高考解读] 以平面图形的翻折为载体，考查空间想象能力，在线面位置关系的证明中考查逻辑推理能力，在空间角的求解中，考查转化化归及数学运算的核心素养.1．(2018·全国卷Ⅰ)如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P的位置，且PF ⊥BF .(1)证明：平面PEF ⊥平面ABFD ； (2)求DP 与平面ABFD 所成角的正弦值．切入点：(1)对照折叠前后的线面关系给予证明； (2)建立空间直角坐标系通过向量法求解． [解](1)由已知可得，BF ⊥PF ，BF ⊥EF ，又PF 平面PEF ，EF平面PEF ，且PF ∩EF ＝F ，所以BF ⊥平面PEF .又BF平面ABFD ，所以平面PEF ⊥平面ABFD .(2)作PH ⊥EF ，垂足为H .由(1)得，PH ⊥平面ABFD . 以H 为坐标原点，HF →的方向为y 轴正方向，|BF →|为单位长，建立如图所示的空间直角坐标系H xyz .由(1)可得，DE ⊥PE .又DP ＝2，DE ＝1，所以PE ＝ 3.又PF ＝1，EF ＝2，PF 2＋PE 2＝EF 2，故PE ⊥PF .可得PH ＝32，EH ＝32. 则H (0,0,0)，P ⎝ ⎛⎭⎪⎫0，0，32，D ⎝ ⎛⎭⎪⎫－1，－32，0，DP →＝⎝ ⎛⎭⎪⎫1，32，32，HP →＝⎝⎛⎭⎪⎫0，0，32为平面ABFD 的法向量．设DP 与平面ABFD 所成角为θ，则sin θ＝⎪⎪⎪⎪⎪⎪⎪⎪HP →·DP →|HP →||DP →|＝343＝34. 所以DP 与平面ABFD 所成角的正弦值为34. [教师备选题](2016·全国卷Ⅱ)如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB ＝5，AC ＝6，点E ，F 分别在AD ，CD 上，AE ＝CF ＝54，EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置，OD ′＝10.(1)证明：D ′H ⊥平面ABCD ； (2)求二面角B D ′A C 的正弦值． [解](1)证明：由已知得AC ⊥BD ，AD ＝CD .又由AE ＝CF 得A EAD ＝CFCD，故AC ∥EF .因此EF ⊥HD ，从而EF ⊥D ′H .由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4.由EF ∥AC ，得OH DO ＝A E AD ＝14.所以OH ＝1，D ′H ＝DH ＝3.于是D ′H 2＋OH 2＝32＋12＝10＝D ′O 2，故D ′H ⊥OH . 又D ′H ⊥EF ，而OH ∩EF ＝H ，所以D ′H ⊥平面ABCD . (2)如图，以H 为坐标原点，HF →的方向为x 轴正方向，建立空间直角坐标系H xyz ，则H (0,0,0)，A (－3，－1,0)，B (0，－5,0)，C (3，－1,0)，D ′(0,0,3)，AB →＝(3，－4,0)，AC →＝(6,0,0)，AD ′→＝(3,1,3)．设m ＝(x 1，y 1，z 1)是平面ABD ′的法向量，则 ⎩⎪⎨⎪⎧ m ·AB →＝0，m ·AD ′→＝0，即⎩⎪⎨⎪⎧ 3x 1－4y 1＝0，3x 1＋y 1＋3z 1＝0，所以可取m ＝(4,3，－5)．设n ＝(x 2，y 2，z 2)是平面ACD ′的法向量，则 ⎩⎪⎨⎪⎧n ·AC →＝0，n ·AD ′→＝0，即⎩⎪⎨⎪⎧6x 2＝0，3x 2＋y 2＋3z 2＝0，所以可取n ＝(0，－3,1)．于是cos 〈m ，n 〉＝m·n |m||n |＝－1450×10＝－7525.sin 〈m ，n 〉＝29525.因此二面角B D ′A C 的正弦值是29525.平面图形翻折问题的求解方法(1)解决与折叠有关的问题的关键是搞清折叠前后的变和不变，一般情况下，线段的长度是不变量，而位置关系往往会发生变化，抓住不变量是解决问题的突破口．(2)在解决问题时，要综合考虑折叠前后的图形，既要分析折叠后的图形，也要分析折叠前的图形．(以梯形为载体)如图，等腰梯形ABCD 中，AB ∥CD ，AD ＝AB ＝BC ＝1，CD ＝2，E 为CD 中点，以AE 为折痕把△ADE 折起，使点D 到达点P 的位置(P 平面ABCE )．(1)证明：AE ⊥PB ；(2)若直线PB 与平面ABCE 所成的角为π4，求二面角A PE C 的余弦值．[解](1)证明：连接BD ，设AE 的中点为O ， ∵AB ∥CE ，AB ＝CE ＝12CD ，∴四边形ABCE 为平行四边形，∴AE ＝BC ＝AD ＝DE ， ∴△ADE ，△ABE 为等边三角形， ∴OD ⊥AE ，OB ⊥AE ，又OP ∩OB ＝O ， ∴AE ⊥平面POB ，又PB 平面POB ，∴AE ⊥PB .(2)在平面POB 内作PQ ⊥平面ABCE ，垂足为Q ，则Q 在直线OB 上， ∴直线PB 与平面ABCE 夹角为∠PBO ＝π4，又OP ＝OB ，∴OP ⊥OB ，∴O 、Q 两点重合，即PO ⊥平面ABCE ，以O 为原点，OE 为x 轴，OB 为y 轴，OP 为z 轴，建立空间直角坐标系，则P ⎝ ⎛⎭⎪⎫0，0，32，E ⎝ ⎛⎭⎪⎫12，0，0，C ⎝ ⎛⎭⎪⎫1，32，0，∴P E →＝⎝ ⎛⎭⎪⎫12，0，－32，E C →＝⎝ ⎛⎭⎪⎫12，32，0，设平面PCE 的一个法向量为n 1＝(x ，y ，z )，则⎩⎪⎨⎪⎧n 1·P E →＝0，n 1·E C →＝0，即⎩⎪⎨⎪⎧12x －32z ＝0，12x ＋32y ＝0，令x ＝3得n 1＝(3，－1,1)，又OB ⊥平面PAE ，∴n 2＝(0,1,0)为平面PAE 的一个法向量，设二面角A EP C 为α，则|cos α|＝cos 〈n 1，n 2〉＝|n 1·n 2||n 1||n 2|＝15＝55，易知二面角A EP C 为钝角，所以cos α＝－55.立体几何的综合问题(5年3考)[高考解读] 将圆的几何性质、空间线面的位置关系、空间几何体的体积等知识融于一体，综合考查学生的逻辑推理能力.(2018·全国卷Ⅲ)如图，边长为2的正方形ABCD 所在的平面与半圆弧CD ︵所在平面垂直，M 是CD ︵上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)当三棱锥M ABC 体积最大时，求平面MAB 与平面MCD 所成二面角的正弦值．切入点：(1)借助圆的几何性质得出DM ⊥CM ，进而借助面面垂直的判定求解． (2)借助体积公式先探寻M 点的位置，建系借助坐标法求解． [解](1)由题设知，平面CMD ⊥平面ABCD ，交线为CD .因为BC ⊥CD ，BC 平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM .因为M 为CD ︵上异于C ，D 的点，且DC 为直径，所以DM ⊥CM . 又BC ∩CM ＝C ，所以DM ⊥平面BMC . 而DM平面AMD ，故平面AMD ⊥平面BMC .(2)以D 为坐标原点，DA →的方向为x 轴正方向，建立如图所示的空间直角坐标系D xyz . 当三棱锥M ABC 体积最大时，M 为CD ︵的中点．由题设得D (0,0,0)，A (2,0,0)，B (2,2,0)，C (0,2,0)，M (0,1,1)，AM →＝(－2,1,1)，AB →＝(0,2,0)，DA →＝(2,0,0)．设n ＝(x ，y ，z )是平面MAB 的法向量，则⎩⎪⎨⎪⎧n ·AM →＝0，n ·AB →＝0，即⎩⎪⎨⎪⎧－2x ＋y ＋z ＝0，2y ＝0.可取n ＝(1,0,2)．DA →是平面MCD 的法向量，因为cos 〈n ，DA →〉＝n ·DA →|n ||DA →|＝55，sin 〈n ，DA →〉＝255.所以平面MAB 与平面MCD 所成二面角的正弦值是255.存在性问题的求解策略(1)对于存在判断型问题的求解，应先假设存在，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“是否有解”“是否有规定范围内的解”等．(2)对于位置探究型问题，通常是借助向量，引入参数，综合条件和结论列方程，解出参数，从而确定位置．(3)在棱上是否存在一点时，要充分利用共线向量定理．(探索位置型)如图所示，四棱锥P ABCD 中，PA ⊥底面ABCD .四边形ABCD 中，AB ⊥AD ，AB ＋AD ＝4，CD ＝2，∠CDA ＝45°，且AB ＝AP .(1)若直线PB 与平面PCD 所成的角为30°，求线段AB 的长；(2)在线段AD 上是否存在一点G ，使得点G 到点P ，B ，C ，D 的距离都相等？说明理由． [解] (1)以A 为坐标原点，建立空间直角坐标系A xyz ，如图1所示．图1在平面ABCD 内，作CE ∥AB ，交AD 于点E ，则CE ⊥AD . 在Rt△CDE 中，DE ＝CD ·cos 45°＝1，CE ＝CD ·sin 45°＝1. 设AB ＝AP ＝t (t ＞0)，则B (t,0,0)，P (0,0，t )．由AB ＋AD ＝4得AD ＝4－t ，∴E (0,3－t,0)，C (1,3－t,0)，D (0,4－t,0)， ∴CD →＝(－1,1,0)，PD →＝(0,4－t ，－t )．设平面PCD 的法向量为n ＝(x ，y ，z )，由n ⊥CD →，n ⊥PD →得⎩⎪⎨⎪⎧－x ＋y ＝0，－t y －tz ＝0.取x ＝t ，得平面PCD 的一个法向量n ＝(t ，t,4－t )． cos 60°＝|n ·PB →||n |·|PB →|，即|2t 2－4t |t 2＋t 2＋－t 2·2t 2＝12，解得t ＝45或t ＝4(舍去，因为AD ＝4－t ＞0)，∴AB ＝45.(2)法一：(向量法)假设在线段AD 上存在一点G (如图2所示)，使得点G 到点P ，B ，C ，D 的距离都相等．设G (0，m,0)(其中0≤m ≤4－t )，则GC →＝(1,3－t －m,0)，GD →＝(0,4－t －m,0)，GP →(0，－m ，t )．图2由|GC →|＝|GD →|得12＋(3－t －m )2＝(4－t －m )2，即t ＝3－m . ①由|GD →|＝|GP →|，得(4－m －t )2＝m 2＋t 2. ② 由①，②消去t ，化简得m 2－3m ＋4＝0. ③由于方程③没有实数根，所以在线段AD 上不存在点G 到点P ，B ，C ，D 的距离都相等．法二：(几何法)假设在线段AD 上存在一点G ，使得点G 到点P ，B ，C ，D 的距离都相等．图3由GC ＝GD 得∠GCD ＝∠GDC ＝45°， ∴∠CGD ＝90°，即CG ⊥AD ， ∴GD ＝CD ·cos 45°＝1.设AB ＝λ，则AD ＝4－λ，AG ＝AD －GD ＝3－λ. 如图3所示，在Rt△ABG 中，GB ＝AB 2＋AG 2＝λ2＋－λ2＝2⎝⎛⎭⎪⎫λ－322＋92＞1，这与GB ＝GD 矛盾．∴在线段AD 上不存在点G 到点P ，B ，C ，D 的距离都相等．。

数学必修2空间几何体中的夹角和距离知识点

数学必修2空间几何体中的夹角和距离知识点高中数学课本中，空间几何体角与距离这部分内容是教学的难点，下面是店铺给大家带来的数学必修2空间几何体中的夹角和距离知识点，希望对你有帮助。

空间几何体中的夹角和距离知识点一、距离空间中的距离是立体几何的重要内容，其内容主要包括：点点距，点线距，点面距，线线距，线面距，面面距。

其中重点是点点距、点线距、点面距以及两异面直线间的距离.因此，掌握点、线、面之间距离的概念，理解距离的垂直性和最近性，理解距离都指相应线段的长度，懂得几种距离之间的转化关系，所有这些都是十分重要的。

求距离的重点在点到平面的距离，直线到平面的距离和两个平面的距离可以转化成点到平面的距离，一个点到平面的距离也可以转化成另外一个点到这个平面的距离。

1、两条异面直线的距离两条异面直线的公垂线在这两条异面直线间的线段的长度，叫做两条异面直线的距离;求法：如果知道两条异面直线的公垂线，那么就转化成求公垂线段的长度。

2、点到平面的距离平面外一点P，在该平面上的射影为P'，则线段PP'的长度就是点到平面的距离;求法：(1)”一找二证三求”，三步都必须要清楚地写出来。

(2)、等体积法。

3、直线与平面的距离一条直线和一个平面平行，这条直线上任意一点到平面的距离，叫做这条直线和平面的距离;4、平行平面间的距离两个平行平面的公垂线段的长度，叫做两个平行平面的距离。

二、线面垂直空间中的各种角包括异面直线所成的角，直线与平面所成的角和二面角，要理解各种角的概念定义和取值范围，其范围依次为(0°，90°]、[0°，90°]和[0°，180°]。

1、两条异面直线所成的角求法：①、先通过其中一条直线或者两条直线的平移，找出这两条异面直线所成的角，然后通过解三角形去求得;②、通过两条异面直线的方向量所成的角来求得，但是注意到异面直线所成角得范围是(0,90°]，向量所成的角范围是(0,180°]，如果求出的是钝角，要注意转化成相应的锐角。

高中数学知识要点重温(19)空间中的角和距离知识点分析

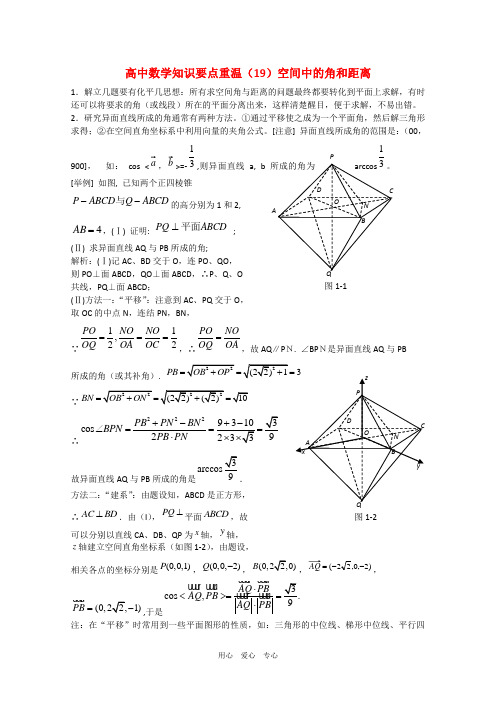
QBCPADON 图1-1图1-2高中数学知识要点重温（19）空间中的角和距离1．解立几题要有化平几思想：所有求空间角与距离的问题最终都要转化到平面上求解，有时还可以将要求的角（或线段）所在的平面分离出来，这样清楚醒目，便于求解，不易出错。

2．研究异面直线所成的角通常有两种方法。

①通过平移使之成为一个平面角，然后解三角形求得；②在空间直角坐标系中利用向量的夹角公式。

[注意] 异面直线所成角的范围是：（00，900]，如： cos <，>=-31,则异面直线 a, b 所成的角为arccos 31。

[举例] 如图, 已知两个正四棱锥ABCD Q ABCD P --与的高分别为1和2,4=AB ，(Ⅰ) 证明: ABCD PQ 平面⊥ ;(Ⅱ) 求异面直线AQ 与PB 所成的角;解析：(Ⅰ)记AC 、BD 交于O ，连PO 、QO ，则PO ⊥面ABCD ，QO ⊥面ABCD ，∴P 、Q 、O 共线，PQ ⊥面ABCD ； (Ⅱ)方法一：“平移”：注意到AC 、PQ 交于O ，取OC 的中点N ，连结PN ，BN ，∵11,22PO NO NO OQ OA OC ===，∴PONOOQ OA =，故AQ ∥P Ｎ. ∠BP Ｎ是异面直线AQ 与PB 所成的角（或其补角）. PB ==∵BN ===∴222cos 29PB PN BN BPN PB PN+-∠===⋅ 故异面直线AQ 与PB 所成的角是．方法二：“建系”：由题设知，ABCD 是正方形， ∴AC BD ⊥．由（I ），PQ ⊥平面ABCD ，故可以分别以直线CA 、DB 、QP 为x 轴，y 轴， z 轴建立空间直角坐标系（如图1-2），由题设，相关各点的坐标分别是(0,0,1)P ，(0,0,2)Q -，B，)2,0,22(--=AQ ，(0,1)PB =-,于是3cos ,AQ PB AQ PB AQ PB⋅<>==⋅注：在“平移”时常用到一些平面图形的性质，如：三角形的中位线、梯形中位线、平行四边形、平行线分线段成比例定理的逆定理甚至三角形相似等。

2019年高考数学二轮复习试题：专题三第3讲空间中的角和距离(附答案解析)

2019年高考数学二轮复习试题第3讲空间中的角和距离选题明细表巩固提高A一、选择题1. 在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC 与BD所成角的余弦值为( A )(A)(B)-(C) (D)-解析: 由题意,可补形成正方体如图.所以异面直线AC与BD所成角就是ED与BD所成角,而△BDE为等边三角形,所以所成角为,cos=.故选A.2.在正四面体ABCD中,E为AB的中点,则CE与BD所成角的余弦值为( A )(A) (B)(C) (D)解析:如图,取AD中点F,连接EF,CF,因为E为AB的中点,所以EF∥BD,则∠CEF为异面直线BD与CE所成的角,因为ABCD为正四面体,E,F分别为AB,AD的中点,所以CE=CF.设正四面体的棱长为2a,则EF=a,CE=CF== a.在△CEF中,由余弦定理得cos∠CEF===.故选A.3.(2018·杭州二模)已知三棱锥S ABC的底面ABC为正三角形,SA<SB<SC,平面SBC,SCA,SAB与平面ABC所成的锐二面角分别为α1,α2,α3则( A )(A)α1<α2(B)α1>α2(C)α2<α3(D)α2>α3解析:由题意,设三角形SBC,SCA的高分别为h 1,h2,三棱锥S-ABC的高为h,易知h1>h2,根据正弦函数的定义得,sin α1=,sin α2=,所以sin α1<sin α2,又α1,α2均为锐角,所以α1<α2,故选A.4. 如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1中心,则O到平面ABC1D1的距离是( A )(A)(B)(C)(D)解析:法一过O作A1B1的平行线,交B1C1于E,则O到平面ABC1D1的距离为E到平面ABC1D1的距离.作EF⊥BC1于F,易证明EF⊥平面ABC1D1,连接B1C,可求得EF=B1C=.故选A.法二因为O是A1C1的中点且C1∈平面ABC1D1,所以点O到平面ABC1D1距离为点A1到平面ABC1D1距离的一半,过A1作A1G⊥AD1于G,(图略),由正方体性质得A1G⊥平面ABC1D1,在等腰Rt△A1AD中,A1G=A1D=,所以A1到平面ABC1D1距离为,所以O到平面ABC1D1距离为.故选A.5. 如图,三棱锥P ABC中,△ABC为边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,PA=,PB=,则PA与平面CDE所成角的正切值为( A )(A) (B) (C) (D)解析:由勾股定理PA2+PB2=AB2⇒PA⊥PB,过P作PM⊥AB于M,由⇒AB⊥平面DCE,所以∠APM为PA与平面CDE所成的角,在直角三角形APB中,∠APM=∠PBA,tan∠APM=tan∠PBA==.故选A.6. 如图,在正方体ABCD-A1B1C1D1中,点P在正方体表面运动,如果=,那么这样的点P共有( C )(A)2个(B)4个(C)6个(D)无数个解析:设点A到直线BD1的距离为d,则满足题意的点位于以BD1为轴,以d为半径的圆柱上,即满足题意的点为圆柱与正方体的交点,设正方体棱长为1,则由=,得××1=××d得d=,在正方体内易证BD1⊥平面A1C1D,BD1⊥平面ACB1,记两个垂足分别为M,N,如图(1),则M,N分别为等边△A1C1D与等边△ACB1的中心,这两个三角形的六个顶点到对角线BD1的距离都相等,在对角面BB1D1D 中,如图(2).BD1=,D1M=,所以DM==,所以正方体的六个顶点D,A,C,A1,B1,C1到对角线BD1距离都为,这又是正方体上到对角线BD1距离最远的点.由此得满足条件的点P有6个.故选C. 7.(2018·新高考研究联盟第三次联考)在平面α内,已知AB⊥BC,过直线AB,BC分别作平面β,γ,使锐二面角α-AB-β为,锐二面角α-BC-γ为,则平面β与平面γ所成的锐二面角的余弦值为( A )(A)(B) (C)(D)解析:cos θ=cos 60°cos 60°=,也可以构造一个三棱锥来解决,故选A.二、填空题8.在正方体ABCD-A1B1C1D1中,异面直线AD1与BD所成角的大小是.解析:如图所示,连接BC1,DC1,由正方体的性质可得,∠DBC1即为所求,且△DBC1为等边三角形,则直线AD1与BD所成角的大小是60°.答案:60°9. 长方体ABCD-A1B1C1D1中,底面ABCD是边长为4的正方形,高为2,则顶点A1到截面AB1D1的距离为.解析:由题意可得:AD1=AB1==2,B1D1==4,据此可得=×4×=4,设顶点A1到截面AB1D1的距离为h,对三棱锥A1-AB1D1由等体积法得=,即×4×h=×(×4×4)×2,解得h=.答案:10. 正三棱锥P-ABC中,CM=2PM,CN=2NB,对于以下结论:①二面角B-PA-C的取值范围是(,π);②若MN⊥AM,则PC与平面PAB所成角的大小为;③过点M与异面直线PA和BC都成的直线有3条;④若二面角B PA C为,则过点N与平面PAC和平面PAB都成的直线有3条.正确的序号是.解析:根据题意,由于正三棱锥P ABC中,CM=2PM,CN=2NB,那么对于①当PA→+∞时二面角趋近于,当P无限接近于△ABC外心时,趋近于π,二面角B-PA-C 的取值范围是(,π);成立.②若MN⊥AM,则PC与平面PAB所成角的大小为;成立.③过点M与异面直线PA和BC都成的直线有3条;不成立.④若二面角B PA C为,则过点N与平面PAC和平面PAB都成的直线有3条;成立.答案:①②④11.如图,已知正方体ABCD A1B1C1D1,则二面角C1-BD-C的正切值为.解析:设正方体棱长为a,取BD中点O,连接CO,C1O,因为CD=CB=a,C1B=C1D=a,所以CO⊥BD,C1O⊥BD,所以∠COC1是二面角C1-BD-C的平面角,因为CC1=a,CO=a,所以tan∠COC1===.所以二面角C1-BD-C的正切值为.答案:12.平面α,β,γ两两垂直且交于一点O,若空间有一点P到这三个平面的距离分别是3,4,12,则点P到点O的距离为.解析:由题意,构造长方体图形,这个长方体过一个顶点的三条棱长分别为3,4,12,所求PO的长度即为体对角线长,所以PO==13.答案:1313. 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则= .解析:连接AC交BD于点O,连接OE,OC′(图略),在△OAE中,由正弦定理得:=,所以AE=sin 30°=,在△C′OE中,由正弦定理得:=,所以EC′=sin 45°=,因为sin ∠C′EO=sin ∠OEA,所以=.答案:14.正三棱锥V-ABC中,VB=,BC=2,则二面角V-AC-B的大小为.解析:取AC中点为O,连接VO,BO,在正三棱锥V ABC中,VB=,BC=2,因为VA=VC=VB=,AB=AC=BC=2,AO=CO=,所以VO⊥AC,BO⊥AC,VO==2,BO==3,所以cos∠VOB==,所以∠VOB=60°.答案:60°15.已知△ABC与平面α,且∠ACB=,CD⊥AB于D,若边AB⊂平面α,边BC,AC 与平面α所成的角分别为和,则CD与平面α所成角的大小为.解析:如图,过点C作CE⊥α于E,连DE,则∠CDE即为CD与平面α所成角.连AE,BE,则∠CAE,∠CBE分别为AC,BC与平面α所成的角,即∠CAE=,∠CBE=.设CE=1,则AC=2,BC=,于是AB==.由等面积法得CD===,所以sin∠CDE==,所以∠CDE=.答案:三、解答题16.(2018·北京卷) 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D, E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC=AA1=2.(1)求证:AC⊥平面BEF;(2)求二面角B-CD-C1的余弦值;(3)证明:直线FG与平面BCD相交.(1)证明:在三棱柱ABC A1B1C1中,因为CC1⊥平面ABC,所以四边形A1ACC1为矩形.又E,F分别为AC,A1C1的中点,所以AC⊥EF.因为AB=BC,所以AC⊥BE,因为BE∩EF=E,所以AC⊥平面BEF.(2)解: 由(1)知AC⊥EF,AC⊥BE,EF∥CC1.又CC1⊥平面ABC,所以EF⊥平面ABC.因为BE⊂平面ABC,所以EF⊥BE.如图,建立空间直角坐标系Exyz.由题意得B(0,2,0),C(-1,0,0),D(1,0,1),E(0,0,0), F(0,0,2),G(0,2,1),所以=(-1,-2,0),=(1,-2,1).设平面BCD的法向量为n=(x0,y0,z0),则即令y0=-1,则x0=2,z0=-4,于是n=(2,-1,-4).又因为平面CC1D的法向量为=(0,2,0),所以cos<n,>==-.由题知二面角B CD C1为钝角,所以其余弦值为-.(3)证明:由(2)知平面BCD的法向量为n=(2,-1,-4),=(0,2,-1).因为n·=2×0+(-1)×2+(-4)×(-1)=2≠0,所以直线FG与平面BCD相交.巩固提高B一、选择题1. 如图,在正方体ABCD A1B1C1D1中,点E为正方形ABCD的两条对角线的交点,点F是棱AB的中点,则异面直线AC1与EF所成角的正切值为( D )(A)-(B)- (C)(D)解析:因为点E为正方形ABCD的两条对角线的交点,点F是棱AB的中点,所以EF∥AD,所以∠DAC1就是异面直线AC1与EF所成的角,正切值等于=.故选D.2. 将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦值为( C )(A)(B)(C)(D)解析:过点E作EF⊥BD,垂足为F,则∠EAF为直线AE与平面ABD所成的角,不妨设正方形的边长为2,则BF=EF=,AB=2,在△ABF中,由余弦定理:AF2=AB2+BF2-2×AB×BF×cos∠ABF=,所以AF=,在Rt△AEF 中,AE2=AF2+EF2=3,所以AE=,故cos∠EAF==.故选C.3. 如图,二面角α-l-β的大小是45°,线段AB⊂α,B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是( D )(A) (B) (C) (D)解析:如图,过点A作AC⊥β于C,在β内过C作CD⊥l于D,连接AD,BC,由三垂线定理可知AD⊥l,故∠ADC为二面角α-l-β的平面角,为45°,又由已知,∠ABD=30°,则∠ABC为AB与平面β所成的角,设AD=2,则AC=,AB=4,所以sin∠ABC==.故选D.4.在正方体ABCD-A1B1C1D1中,过它的任意两条棱作平面,则能作得与A1B成30°角的平面的个数为( B )(A)2个(B)4个(C)6个(D)8个解析:画出图形如图所示,由图可知,正方体表面6个面与A1B所成的角不是30°.符合题意的面为平面AA1C1C,平面A1B1CD,平面ABC1D1和平面BDD1B1,共4个.故选B.5.平面α过正方体ABCD A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( A )(A) (B) (C) (D)解析:由题意直线m∥BD,直线n∥A1B,易知△A1DB为等边三角形,∠DBA1=60°,sin 60°=,所以m,n所成角的正弦值为,故选A.6.(2018·嵊州市适应性考试)如图,已知矩形ABCD,E是边AB上的点(不包括端点),且AE=AD,将△ADE沿DE翻折至△A′DE,记二面角A′-BC-D为α,二面角A′-CD-E为β,二面角A′-DE-B为γ,则( B )(A)α≥β(B)α≤β(C)β≥γ(D)β≤γ解析: 要比较α,β,γ之间的大小关系,只需比较A′在底面BCD上的射影O 到三边BC,CD,DE的距离d1,d2,d3,之间的大小关系,当O从A点运动到F时,必有d1>d2,即有α≤β;而d2,d3关系不确定,故选B.7.(2018·全国Ⅰ卷)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为( A )(A)(B)(C)(D)解析: 如图所示,在正方体ABCD A1B1C1D1中,平面AB1D1与棱A1A,A1B1,A1D1所成的角都相等,又正方体的其余棱都分别与A1A,A1B1,A1D1平行,故正方体ABCD A1B1C1D1的每条棱所在直线与平面AB1D1所成的角都相等.如图所示,取棱AB,BB1,B1C1,C1D1,DD1,AD的中点E,F,G,H,M,N,则正六边形EFGHMN所在平面与平面AB1D1平行且面积最大,此截面面积为S正六边形×××sin 60°=.故选A.EFGHMN=68. 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BC的中点,点E为A1C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为时,实数m的值为( A )(A)1 (B)2 (C)(D)3解析: 由题意知m>0,过点A在平面ABC内作Ox⊥AC,则以A为原点O,分别以Ox,OC,OA1为x,y,z轴,建立空间直角坐标系Oxyz,如图所示,则E(0,,),=(,,0),=(0,,),设平面ADE的法向量为n=(x,y,z),则⇒n=(,-1,),取平面ADC法向量为m=(0,0,1),由二面角E-AD-C余弦值为,则|cos<n,m>|=,所以==⇒m2=1⇒m=1.故选A.二、填空题9. 在边长为a的等边三角形ABC中,AD⊥BC于D,沿AD折成二面角B AD C 后,BC=,这时二面角B-AD-C的大小为.解析:根据已知中AD⊥BC于D,易得沿AD折成二面角B-AD-C后,∠BDC即为二面角B-AD-C的平面角,解三角形BDC即可求出二面角B-AD-C的大小.因为AD⊥BC,所以沿AD折成二面角B-AD-C后,AD⊥BD,AD⊥CD,故∠BDC即为二面角B-AD-C的平面角,又因为BD=CD=BC=,所以△BDC为等边三角形,所以∠BDC=60°.答案:60°10. 如图,60°的二面角棱上有A′,B′两点,直线AA′,BB′分别在这个二面角的半平面内,且都垂直于A′B′,已知A′B′=3AA′=3,BB′=5,则AB的长度为.解析:运用基向量表示空间的向量,结合模长的计算得到AB的长度为2. 答案:211.矩形ABCD满足AB=2,AD=1,点A,B分别在射线ON,OM上运动,∠MON为直角,当C到点O的距离最大时,∠ABO的大小为.解析:如图,设∠ABO=θ,因AB=2,BC=AD=1,则OB=2cos θ,在△CBO中,由余弦定理得OC===,当OC最大时,sin(2θ+)=1,即2θ+=,也即θ=,所以∠ABO=.答案:12. 如图,三棱锥S-ABC中,若AC=2,SA=SB=SC=AB=BC=4,E为棱SC的中点,则直线AC与BE所成角的余弦值为,直线AC与平面SAB所成的角为.解析:(1)如图(1),取SA中点M,连ME,BM,则ME∥AC,所以直线AC与BE所成角等于直线ME与BE所成角,则ME=,BM=BE=2,cos∠MEB==,所以直线AC与BE所成角的余弦值为.(2)如图(2),取SB中点N,连接AN,CN,则AN⊥SB,CN⊥SB⇒SB⊥平面ACN⇒平面SAB⊥平面ACN,因此直线AC与平面SAB所成的角为∠CAN,因为AN=CN=AC=2,所以∠CAN=60°,因此直线AC与平面SAB所成的角为60°. 答案:60°13. 如图所示,等边△ABC的边长为4,D为BC中点,沿AD把△ADC折叠到△ADC′处,使二面角B-AD-C′为60°,则折叠后二面角A-BC′-D的正切值为.解析:由题意知∠BDC′即为二面角B-AD-C′的平面角,即∠BDC′=60°,所以BC′=2,作DM⊥BC′于点M,连接AM,则AM⊥BC′,则∠AMD为二面角A-BC′-D的平面角,因为△ABC为等边三角形且BC=4.所以AD=2.DM=.所以tan ∠AMD===2.答案:214.在长方体ABCD A1B1C1D1中,底面ABCD是边长为的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则CF与平面ABCD所成角的正切值为.解析: 连接AC与BD交于点O,因为四边形ABCD是正方形,AA1⊥底面ABCD,所以BD⊥平面ACC1A1,则当C1F与EO垂直时,C1F⊥平面BDE,所以∠ACF是CF与平面ABCD所成角,在矩形ACC1A1中,△C1A1F∽△EAO,则=,因为A1C1=2AO=AB=2,AE=,所以A1F=,所以AF=,所以tan∠ACF===.所以CF与平面ABCD所成角的正切值为.答案:15.已知三棱锥A BCD中,AB⊥CD,且AB与平面BCD成60°角.当的值取到最大值时,二面角A-CD-B的大小为.解析: 如图所示,作AE⊥CD于点E,连接BE,因为AB⊥CD,CD⊥AE,AB∩AE=A,所以CD⊥平面ABE,且CD⊂平面BCD,所以平面BCD⊥平面ABE,又因为平面BCD∩平面ABE=BE,所以点A在平面BCD的射影在BE上,所以∠ABE=60°,在△ABE中由余弦定理得AE2=AB2+BE2-2AB×BE×,所以=()2-+1=(-)2+,当=,即BE=2AB时,最小,此时=最大,所以AE=AB,由二面角的定义可知∠AEB为二面角A CD B的平面角,cos∠AEB==,所以∠AEB=.答案:16.高为的四棱锥S-ABCD的底面是边长为1的正方形,点S,A,B,C,D均在同一球面上,底面ABCD的中心为O1,球心O到底面ABCD的距离为,则异面直线SO1与AB所成角的余弦值的范围为.解析:建立如图所示的空间直角坐标系,设S(x,y,),O(,,),O1(,,0),BC中点M(1,,0),由题设外接球的半径R==1,则(x-)2+(y-)2+=1,即(x-)2+（y-）2=.由于=（x-,y-,）,=（,0,0）,因此·=（x-）,又因为（x-）2=-（y-）2≤,即︱x-︱≤,所以cos<,>==≤.即异面直线SO1与AB所求角的余弦值的范围为［0,］.答案:［0,］三、解答题17.(2018·天津卷) 如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(2)求二面角E-BC-F的正弦值;(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP 的长.解:依题意,可以建立以D为原点,分别以,,的方向为x轴、y轴、z轴的正方向的空间直角坐标系(如图),可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M（0,,1）,N(1,0,2).(1)依题意得=(0,2,0),=(2,0,2).设n0=(x,y,z)为平面CDE的法向量,则即不妨令z=-1,可得n0=(1,0,-1).又=（1,-,1）,可得·n0=0,又因为直线MN⊄平面CDE,所以MN∥平面CDE.(2)依题意,可得=(-1,0,0),=(1,-2,2),=(0,-1,2).设n=(x,y,z)为平面BCE的法向量,则即不妨令z=1,可得n=(0,1,1). 设m=(x,y,z)为平面BCF的法向量,则即不妨令z=1,可得m=(0,2,1).因此有cos<m,n>==,于是sin<m,n>=.所以二面角E-BC-F的正弦值为.(3)设线段DP的长为h(h∈[0,2]),则点P的坐标为(0,0,h), 可得=(-1,-2,h).易知,=(0,2,0)为平面ADGE的一个法向量,故︱cos<,>︱==,由题意,可得=sin 60°=,解得h=∈[0,2].所以线段DP的长为.。

高考数学复习考点题型专题讲解15 空间角、距离的计算(几何法、向量法)

高考数学复习考点题型专题讲解专题15 空间角、距离的计算(几何法、向量法) 高考定位 1.以空间几何体为载体考查空间角(以线面角为主)是高考命题的重点，常与空间线面位置关系的证明相结合，热点为空间角的求解，常以解答题的形式进行考查.高考注重利用向量方法解决空间角问题，但也可利用几何法来求解；2.空间距离(特别是点到面的距离)也是高考题中的常见题型，多以解答题的形式出现，难度中等.1.(多选)(2022·新高考Ⅰ卷)已知正方体ABCD－A1B1C1D1，则( )A.直线BC1与DA1所成的角为90°B.直线BC1与CA1所成的角为90°C.直线BC1与平面BB1D1D所成的角为45°D.直线BC1与平面ABCD所成的角为45°答案ABD解析如图，连接AD1，在正方形A1ADD1中，AD1⊥DA1，因为AD1∥BC1，所以BC1⊥DA1，所以直线BC1与DA1所成的角为90°，故A正确；在正方体ABCD－A1B1C1D1中，CD⊥平面BCC1B1，又BC1⊂平面BCC1B1，所以CD⊥BC1.连接B1C，则B1C⊥BC1.因为CD∩B1C＝C，CD，B1C⊂平面DCB1A1，所以BC1⊥平面DCB1A1，又CA1⊂平面DCB1A1，所以BC1⊥CA1，所以直线BC1与CA1所成的角为90°，故B正确；连接A1C1，交B1D1于点O，则易得OC1⊥平面BB1D1D，连接OB. 因为OB⊂平面BB1D1D，所以OC1⊥OB，∠OBC1为直线BC1与平面BB1D1D所成的角.设正方体的棱长为a，则易得BC1＝2a，OC1＝2a 2，所以在Rt△BOC1中，OC1＝12BC1，所以∠OBC1＝30°，故C错误；因为C1C⊥平面ABCD，所以∠CBC1为直线BC1与平面ABCD所成的角，易得∠CBC1＝45°，故D正确.故选ABD.2.(2019·全国Ⅰ卷)已知∠ACB＝90°，P为平面ABC外一点，PC＝2，点P到∠ACB两边AC，BC的距离均为3，那么P到平面ABC的距离为________.答案 2解析如图，过点P作PO⊥平面ABC于O，则PO为P到平面ABC的距离.再过O作OE⊥AC于E，OF⊥BC于F，连接OC，PE，PF，则PE⊥AC，PF⊥BC.所以PE＝PF＝3，所以OE＝OF，所以CO为∠ACB的平分线，即∠ACO＝45°.在Rt△PEC中，PC＝2，PE＝3，所以CE＝1，所以OE＝1，所以PO＝PE2－OE2＝（3）2－12＝ 2.3.(2022·新高考Ⅱ卷)如图，PO是三棱锥P－ABC的高，PA＝PB，AB⊥AC，E为PB的中点.(1)证明：OE∥平面PAC；(2)若∠ABO＝∠CBO＝30°，PO＝3，PA＝5，求二面角C－AE－B的正弦值.(1)证明如图，取AB的中点D，连接DP，DO，DE.因为AP＝PB，所以PD⊥AB.因为PO为三棱锥P－ABC的高，所以PO⊥平面ABC.因为AB⊂平面ABC，所以PO⊥AB.又PO，PD⊂平面POD，且PO∩PD＝P，所以AB⊥平面POD.因为OD⊂平面POD，所以AB⊥OD，又AB⊥AC，AB，OD，AC⊂平面ABC，所以OD∥AC.因为OD⊄平面PAC，AC⊂平面PAC，所以OD∥平面PAC.因为D，E分别为BA，BP的中点，所以DE∥PA.因为DE⊄平面PAC，PA⊂平面PAC，所以DE∥平面PAC.又OD，DE⊂平面ODE，OD∩DE＝D，所以平面ODE∥平面PAC.又OE⊂平面ODE，所以OE∥平面PAC.(2)解连接OA，因为PO⊥平面ABC，OA，OB⊂平面ABC，所以PO⊥OA，PO⊥OB，所以OA＝OB＝PA2－PO2＝52－32＝4.易得在△AOB中，∠OAB＝∠ABO＝30°，所以OD＝OA sin 30°＝4×12＝2，AB＝2AD＝2OA cos 30°＝2×4×32＝4 3.又∠ABC＝∠ABO＋∠CBO＝60°，所以在Rt△ABC 中，AC ＝AB tan 60°＝43×3＝12.以A 为坐标原点，AB ，AC 所在直线分别为x ，y 轴，以过A 且垂直于平面ABC 的直线为z 轴建立空间直角坐标系，如图所示，则A (0，0，0)，B (43，0，0)，C (0，12，0)， P (23，2，3)，E ⎝⎛⎭⎪⎫33，1，32，所以AE →＝⎝ ⎛⎭⎪⎫33，1，32，AB →＝(43，0，0)，AC →＝(0，12，0).设平面AEC 的一个法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·AE →＝0，n ·AC →＝0，即⎩⎨⎧33x ＋y ＋32z ＝0，12y ＝0，令z ＝23，则n ＝(－1，0，23).设平面AEB 的一个法向量为m ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧m ·AE →＝0，m ·AB →＝0，即⎩⎨⎧33x 1＋y 1＋32z 1＝0，43x 1＝0，令z 1＝2，则m ＝(0，－3，2)，所以|cos 〈n ，m 〉|＝⎪⎪⎪⎪⎪⎪n ·m |n |·|m |＝4313.设二面角C －AE －B 的大小为θ，则sin θ＝1－⎝⎛⎭⎪⎫43132＝1113.4.(2021·浙江卷)如图，在四棱锥P－ABCD中，底面ABCD是平行四边形，∠ABC＝120°，AB＝1，BC＝4，PA＝15，M，N分别为BC，PC的中点，PD⊥DC，PM⊥MD.(1)证明：AB⊥PM；(2)求直线AN与平面PDM所成角的正弦值.(1)证明因为底面ABCD是平行四边形，∠ABC＝120°，BC＝4，AB＝1，且M为BC的中点，所以CM＝2，CD＝1，∠DCM＝60°，易得CD⊥DM.又PD⊥DC，且PD∩DM＝D，PD，DM⊂平面PDM，所以CD⊥平面PDM.因为AB∥CD，所以AB⊥平面PDM.又PM⊂平面PDM，所以AB⊥PM.(2)解法一由(1)知AB⊥平面PDM，所以∠NAB为直线AN与平面PDM所成角的余角.连接AM，因为PM⊥MD，由(1)知PM⊥DC，又MD，DC⊂平面ABCD，MD∩DC＝D，所以PM⊥平面ABCD，又AM⊂平面ABCD，所以PM⊥AM.因为∠ABC＝120°，AB＝1，BM＝2，所以由余弦定理得AM＝7，又PA＝15，所以PM＝22，所以PB＝PC＝2 3.连接BN，结合余弦定理得BN＝11.连接AC，则由余弦定理得AC＝21，在△PAC中，结合余弦定理得PA2＋AC2＝2AN2＋2PN2，所以AN＝15.所以在△ABN中，cos∠BAN＝AB2＋AN2－BN22AB·AN＝1＋15－11215＝156.设直线AN与平面PDM所成的角为θ，则sin θ＝cos ∠BAN＝15 6.故直线AN与平面PDM所成角的正弦值为15 6.法二因为PM⊥MD，由(1)知PM⊥DC，又MD，DC⊂平面ABCD，MD∩DC＝D，所以PM ⊥平面ABCD . 连接AM ，则PM ⊥AM .因为∠ABC ＝120°，AB ＝1，BM ＝2，所以AM ＝7，又PA ＝15，所以PM ＝2 2. 由(1)知CD ⊥DM ，过点M 作ME ∥CD 交AD 于点E ，则ME ⊥MD.故可以以M 为坐标原点，MD ，ME ，MP 所在直线分别为x ，y ，z 轴建立如图所示的空间直角坐标系，则A (－3，2，0)，P (0，0，22)，C (3，－1，0)，所以N ⎝ ⎛⎭⎪⎫32，－12，2，所以AN →＝⎝ ⎛⎭⎪⎫332，－52，2.易知平面PDM 的一个法向量为n ＝(0，1，0). 设直线AN 与平面PDM 所成的角为θ，则sin θ＝|cos 〈AN →，n 〉|＝|AN →·n ||AN →|·|n |＝5215＝156.故直线AN 与平面PDM 所成角的正弦值为156.热点一异面直线所成的角求异面直线所成角的方法方法一：综合法.步骤为：①利用定义构造角，可固定一条直线，平移另一条直线，或将两条直线同时平移到某个特殊的位置；②证明找到(或作出)的角即为所求角；③通过解三角形来求角.方法二：空间向量法.步骤为：①求出直线a ，b 的方向向量，分别记为m ，n ；②计算cos 〈m ，n 〉＝m ·n |m ||n |；③利用cos θ＝|cos 〈m ，n 〉|，以及θ∈⎝⎛⎦⎥⎤0，π2，求出角θ.例1 在正方体ABCD －A 1B 1C 1D 1中，P 为B 1D 1的中点，则直线PB 与AD 1所成的角为( ) A.π2B.π3C.π4D.π6 答案 D解析法一如图，连接C 1P ，因为ABCD －A 1B 1C 1D 1是正方体，且P 为B 1D 1的中点，所以C 1P ⊥B 1D 1，又C 1P ⊥BB 1，B 1D 1∩BB 1＝B 1，B 1D 1，BB 1⊂平面B 1BP ，所以C 1P ⊥平面B 1BP . 又BP ⊂平面B 1BP ，所以有C 1P ⊥BP .连接BC 1，则AD 1∥BC 1，所以∠PBC 1为直线PB 与AD 1所成的角. 设正方体ABCD －A 1B 1C 1D 1的棱长为2，则在Rt△C 1PB 中，C 1P ＝12B 1D 1＝2，BC 1＝22，sin ∠PBC 1＝PC 1BC 1＝12，所以∠PBC 1＝π6，故选D. 法二如图，以A 为坐标原点，AB ，AD ，AA 1所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，设正方体ABCD －A 1B 1C 1D 1的棱长为2，则A (0，0，0)，B (2，0，0)，P (1，1，2)，D 1(0，2，2)，PB →＝(1，－1，－2)，AD →1＝(0，2，2). 设直线PB 与AD 1所成的角为θ，则cos θ＝⎪⎪⎪⎪⎪⎪⎪⎪PB →·AD →1|PB →||AD →1|＝|－6|6×8＝32. 因为θ∈⎝⎛⎦⎥⎤0，π2，所以θ＝π6，故选D.法三如图，连接BC1，A1B，A1P，PC1，则易知AD1∥BC1，所以直线PB与AD1所成的角等于直线PB与BC1所成的角.由P为正方形A1B1C1D1的对角线B1D1的中点，知A1，P，C1三点共线，且P为A1C1的中点.易知A1B＝BC1＝A1C1，所以△A1BC1为等边三角形，所以∠A1BC1＝π3，又P为A1C1的中点，所以可得∠PBC1＝12∠A1BC1＝π6，故直线PB与AD1所成的角为π6，故选D.易错提醒 1.利用几何法求异面直线所成的角时，通过平移直线所得的角不一定就是两异面直线所成的角，也可能是其补角.2.用向量法时，要注意向量夹角与异面直线所成角的范围不同.训练1 (1)(2022·湖州质检)在长方体ABCD－A1B1C1D1中，BB1＝2AB＝2BC，P，Q分别为B 1C1，BC的中点，则异面直线AQ与BP所成角的余弦值是( )A.55B.21717C.8585D.28585 答案 C解析法一不妨设AB ＝2，则BC ＝2，BB 1＝4，连接A 1P ，A 1B (图略)，则A 1P ∥AQ ， ∴∠A 1PB (或其补角)为异面直线AQ 与BP 所成的角.由勾股定理得BP ＝17，A 1P ＝5，A 1B ＝25，在△A 1BP 中，由余弦定理的推论得，cos∠A 1PB ＝（17）2＋（5）2－（25）22×17×5＝8585.故选C.法二如图建立空间直角坐标系，设直线AQ 与BP 所成的角为θ，不妨设AB ＝2，则BC ＝2，BB 1＝4.故B (2，0，0)，P (2，1，4)，Q (2，1，0)，所以BP →＝(0，1，4)，AQ →＝(2，1，0)，所以cos θ＝|cos 〈BP →，AQ →〉|＝⎪⎪⎪⎪⎪⎪117×5＝8585. (2)(2022·河南顶尖名校联考)如图，圆锥的底面直径AB ＝2，其侧面展开图为半圆，底面圆的弦AD ＝3，则异面直线AD 与BC 所成的角的余弦值为( )A.0B.3 3C.34D.22答案 C解析法一如图，延长DO交圆于E，连接BE，CE，易知AD＝BE＝3，AD∥BE，∴∠EBC(或其补角)为异面直线AD与BC所成的角.由圆锥侧面展开图为半圆，易得BC＝2，在△BEC中，BC＝CE＝2，BE＝3，∴cos∠EBC＝22＋（3）2－222×2×3＝34.法二由圆锥侧面展开图为半圆，易得BC＝2，又BO＝1，所以CO＝3，在△AOD中，AO＝DO＝1，AD＝3，由余弦定理得cos∠AOD＝12＋12－（3）22×1×1＝－12，则∠AOD＝2π3，以O 为坐标原点，OB 所在直线为y 轴，OC 所在直线为z 轴，建立空间直角坐标系如图，则A (0，－1，0)，D ⎝ ⎛⎭⎪⎫32，12，0，B (0，1，0)，C (0，0，3)，所以AD →＝⎝ ⎛⎭⎪⎫32，32，0，BC →＝(0，－1，3)，故cos 〈AD →，BC →〉＝－323×2＝－34，又异面直线所成角的范围是⎝ ⎛⎦⎥⎤0，π2，故直线AD 与BC 所成角的余弦值为34. 热点二直线与平面所成的角求直线与平面所成角的方法方法一：几何法.步骤为：①找出直线l 在平面α上的射影；②证明所找的角就是所求的角；③把这个角置于一个三角形中，通过解三角形来求角.方法二：空间向量法.步骤为：①求出平面α的法向量n 与直线AB 的方向向量AB →；②计算cos 〈AB →，n 〉＝AB →·n |AB →||n |；③利用sin θ＝|cos 〈AB →，n 〉|，以及θ∈⎣⎢⎡⎦⎥⎤0，π2，求出角θ.例2(2022·南京模拟)如图，在三棱柱ABC－A1B1C1中，AA1＝13，AB＝8，BC＝6，AB⊥BC，AB＝B1C，D为AC的中点，平面AB1C⊥平面ABC.1(1)求证：B1D⊥平面ABC；(2)求直线C1D与平面AB1C所成角的正弦值.(1)证明因为AB1＝B1C，D为AC的中点，所以B1D⊥AC.又平面AB1C⊥平面ABC，平面AB1C∩平面ABC＝AC，B1D⊂平面AB1C，所以B1D⊥平面ABC.(2)解法一在平面ABC内，过点D作BC的平行线，交AB于点E，过点D作AB的平行线，交BC于点F，连接DE，DF，BD.由(1)知B 1D ⊥平面ABC ，所以B 1D ⊥AC ，B 1D ⊥BD . 因为AB ⊥BC ，所以DE ⊥DF ，故以{DE →，DF →，DB 1→}为基底建立如图所示的空间直角坐标系D －xyz .因为AB ＝8，BC ＝6，AB ⊥BC ，所以AC ＝AB 2＋BC 2＝10，BD ＝12AC ＝5.又AA 1＝BB 1＝13，AB ⊥BC ，所以B 1D ＝BB 21－BD 2＝12.易得D (0，0，0)，A (3，－4，0)，B (3，4，0)，C (－3，4，0)，B 1(0，0，12)，则AC →＝(－6，8，0)，BC →＝(－6，0，0)，B 1C →＝(－3，4，－12). 设点C 1(x ，y ，z )，则B 1C 1→＝(x ，y ，z －12)，由BC →＝B 1C 1→，得(－6，0，0)＝(x ，y ，z －12)，所以⎩⎨⎧x ＝－6，y ＝0，z ＝12，即C 1(－6，0，12)，所以C 1D →＝(6，0，－12).设平面AB 1C 的法向量为n ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧n ·AC →＝－6x 1＋8y 1＝0，n ·B 1C →＝－3x 1＋4y 1－12z 1＝0，得3x 1＝4y 1，z 1＝0.不妨取x 1＝4，则y 1＝3，得平面AB 1C 的一个法向量为n ＝(4，3，0). 设直线C 1D 与平面AB 1C 所成的角为θ，则sin θ＝|cos 〈n ，C 1D →〉|＝|n ·C 1D →||n |·|C 1D →|＝|4×6＋3×0＋0×（－12）|42＋32＋02×62＋02＋（－12）2＝4525. 所以直线C 1D 与平面AB 1C 所成角的正弦值为4525. 法二连接BC 1，交B 1C 于点M ，易知BM ＝MC 1，所以点C 1到平面AB 1C 的距离d 和点B 到平面AB 1C 的距离相等.过点B 作BH ⊥AC ，垂足为H .又平面AB 1C ⊥平面ABC ，平面AB 1C ∩平面ABC ＝AC ，BH ⊂平面ABC ，所以BH ⊥平面AB 1C ，则BH 为点B 到平面AB 1C 的距离. 在Rt△ABC 中，因为AB ＝8，BC ＝6，AB ⊥BC ，所以AC ＝10，则BH ＝6×810＝245，所以d ＝BH ＝245.由(1)知B 1D ⊥平面ABC ，又BC ⊂平面ABC ，所以B 1D ⊥BC . 又B 1C 1∥BC ，所以B 1D ⊥B 1C 1，则△DB 1C 1为直角三角形. 连接BD ，则B 1D ⊥BD .因为D 为AC 的中点，所以BD ＝12AC ＝5.又AA 1＝BB 1＝13，所以B 1D ＝12. 又B 1C 1＝BC ＝6，所以C 1D ＝6 5. 设直线C 1D 与平面AB 1C 所成的角为θ，则sin θ＝d C 1D ＝24565＝4525. 所以直线C 1D 与平面AB 1C 所成角的正弦值为4525. 规律方法 1.几何法求线面角的关键是找出线面角(重点是找垂线与射影)，然后在三角形中应用余弦定理(勾股定理)求解；2.向量法求线面角时要注意：线面角θ与直线的方向向量a 和平面的法向量n 所成的角〈a ，n 〉的关系是〈a ，n 〉＋θ＝π2或〈a ，n 〉－θ＝π2，所以应用向量法求的是线面角的正弦值，而不是余弦值.训练2(2022·湖北十校联考)如图，在四棱锥A－BCDE中，CD∥BE，CD＝12EB＝1，CB⊥BE，AE＝AB＝BC＝2，AD＝3，O是AE的中点.(1)求证：DO∥平面ABC；(2)求DA与平面ABC所成角的正弦值. (1)证明取AB的中点为F，连接CF，OF，因为O，F分别为AE，AB的中点，所以OF∥BE，且OF＝12 BE.又CD∥BE，CD＝12 EB，所以OF∥CD，且OF＝CD，所以四边形OFCD为平行四边形，所以DO∥CF，又CF⊂平面ABC，DO⊄平面ABC，所以DO∥平面ABC.(2)解法一取EB的中点为G，连接AG，DG，易得DG綊BC.因为AE＝AB＝2，BE＝2，所以AE2＋AB2＝BE2，所以AB⊥AE，△ABE为等腰直角三角形，所以AG⊥BE，AG＝1，又AD＝3，DG＝BC＝2，所以AG2＋DG2＝AD2，所以DG⊥AG.又BE⊥AG，BE∩DG＝G，BE，DG⊂平面BCDE，所以AG⊥平面BCDE. 记h为点D到平面ABC的距离，连接BD，则V D－ABC＝V A－BCD，即13S△ABC·h＝13S△BCD·AG，因为BC⊂平面BCDE，所以BC⊥AG，又CB⊥BE，BE∩AG＝G，BE，AG⊂平面ABE，所以BC⊥平面ABE，又AB⊂平面ABE，所以BC⊥AB，所以S△ABC＝12×AB×BC＝12×2×2＝1，又S△BCD＝12×BC×CD＝12×2×1＝22，所以h＝2 2，设DA与平面ABC所成的角为θ，则sin θ＝h AD ＝223＝66.所以DA 与平面ABC 所成角的正弦值为66. 法二如图，取EB 的中点为G ，连接AG ，OG ，DG ，由(2)法一可知AG ⊥BE ，AB ⊥AE ，BC ⊥平面ABE ，BC ∥DG ，所以DG ⊥平面ABE .以G 为坐标原点，以GA →，GB →，GD →的方向分别为x 轴，y 轴，z 轴正方向建立空间直角坐标系，则G (0，0，0)，A (1，0，0)，D (0，0，2)，E (0，－1，0)，AD →＝(－1，0，2). 因为AE ⊂平面ABE ，所以BC ⊥AE ，又AB ⊥AE ，BC ∩AB ＝B ，BC ，AB ⊂平面ABC ，所以AE ⊥平面ABC ，故平面ABC 的一个法向量为AE →＝(－1，－1，0). 设DA 与平面ABC 所成角为θ，则sin θ＝|cos 〈AD →，AE →〉|＝|AD →·AE →||AD →|·|AE →|＝16＝66.所以DA 与平面ABC 所成角的正弦值为66.热点三平面与平面的夹角求平面与平面的夹角方法方法一：几何法.步骤为：①找出二面角的平面角(以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角就是二面角的平面角)；②证明所找的角就是要求的角；③把这个平面角置于一个三角形中，通过解三角形来求角.求二面角的平面角的口诀：点在棱上，边在面内，垂直于棱，大小确定.方法二：空间向量法.步骤为：①求两个平面α，β的法向量m，n；②计算cos〈m，n〉＝m·n|m|·|n|；③设两个平面的夹角为θ，则cos θ＝|cos〈m，n〉|.例3(2022·济南质测)如图，在三棱锥D－ABC中，DA⊥底面ABC，AC＝BC＝DA＝1，AB ＝2，E是CD的中点，点F在DB上，且EF⊥DB.(1)证明：DB⊥平面AEF；(2)求平面ADB与平面DBC夹角的大小.法一(1)证明∵DA⊥平面ABC，且BC⊂平面ABC，∴DA⊥BC.∵AC＝BC＝1，AB＝2，∴AC2＋BC2＝AB2，∴AC⊥BC.∵DA∩AC＝A，DA，AC⊂平面DAC，∴BC ⊥平面DAC ，又AE ⊂平面DAC ， ∴BC ⊥AE .∵DA ＝AC ，E 是CD 的中点， ∴DC ⊥AE ，又BC ∩DC ＝C ，BC ，DC ⊂平面DBC ， ∴AE ⊥平面DBC ，又DB ⊂平面DBC ，∴DB ⊥AE ，又EF ⊥DB ，EF ∩AE ＝E ，EF ，AE ⊂平面AEF ， ∴DB ⊥平面AEF .(2)解∵EF ⊥DB ，由(1)得DB ⊥AF ， ∴∠AFE 为平面ADB 与平面DBC 的夹角. ∵DA ⊥平面ABC ， ∴DA ⊥AC ，DA ⊥AB ，又AC ＝DA ＝1，E 为CD 的中点， ∴AE ＝12DC ＝22.∵AB ＝2，∴S △DAB ＝12×DA ×AB ＝12×DB ×AF ，∴AF ＝DA ×AB DB ＝1×212＋（2）2＝63. 由(1)知，AE ⊥平面DBC ，∵EF ⊂平面DBC ，∴AE ⊥EF ，∴sin∠AFE ＝AE AF ＝2263＝32. ∵∠AFE 为锐角，∴∠AFE ＝π3， ∴平面ADB 与平面DBC 夹角的大小为π3.法二 (1)证明∵DA ⊥平面ABC ，且BC ⊂平面ABC ，∴DA ⊥BC . ∵AC ＝BC ＝1，AB ＝2， ∴AC 2＋BC 2＝AB 2， ∴AC ⊥BC .∴DA ∩AC ＝A ，DA ，AC ⊂平面DAC ， ∴BC ⊥平面DAC ，如图，过点A 作AG ∥BC ，则AG ⊥平面DAC .以A 为坐标原点，分别以向量AC →，AG →，AD →的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系A －xyz ，则A (0，0，0)，B (1，1，0)，D (0，0，1)，E ⎝ ⎛⎭⎪⎫12，0，12，∴DB →＝(1，1，－1)，AE →＝⎝ ⎛⎭⎪⎫12，0，12.∵DB →·AE →＝1×12＋1×0＋(－1)×12＝0，∴DB →⊥AE →，∴DB ⊥AE .又DB ⊥EF ，且AE ∩EF ＝E ，AE ，EF ⊂平面AEF ， ∴DB ⊥平面AEF .(2)解由(1)知AD →＝(0，0，1)，BD →＝(－1，－1，1)，CD →＝(－1，0，1). 设平面ADB 的法向量为m ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧m ·AD →＝0，m ·BD →＝0，∴⎩⎨⎧z 1＝0，－x 1－y 1＋z 1＝0，令y 1＝1，则m ＝(－1，1，0).设平面DBC 的法向量为n ＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧n ·CD →＝0，n ·BD →＝0，∴⎩⎨⎧－x 2＋z 2＝0，－x 2－y 2＋z 2＝0，令x 2＝1，则n ＝(1，0，1). 设平面ADB 与平面DBC 的夹角为θ，则cos θ＝|cos 〈m ，n 〉|＝|－1|2×2＝12.所以θ＝π3，即平面ADB 与平面DBC 夹角的大小为π3.规律方法 (1)用几何法求解二面角的关键是：先找(或作)出二面角的平面角，再在三角形中求解此角.(2)利用法向量的依据是两个半平面的法向量所成的角和二面角的平面角相等或互补，在求二面角的大小时，一定要判断出二面角的平面角是锐角还是钝角，否则解法是不严谨的.训练3(2022·沈阳质检)如图，在四棱锥P －ABCD 中，PA ⊥平面ABCD ，四边形ABCD 是直角梯形，BC ∥AD ，AB ⊥AD ，PA ＝AB ＝2，AD ＝2BC ＝2 2.(1)求证：BD ⊥平面PAC ；(2)求平面BPC 与平面PCD 夹角的余弦值.(1)证明法一由题意得，四边形ABCD 是直角梯形，BC ∥AD ，AB ⊥AD ，PA ＝AB ＝2，AD ＝2BC ＝22，所以tan ∠ACB ＝tan∠DBA ＝2，可知∠ACB ＝∠DBA ，所以∠DBC ＋∠ACB ＝90°，则AC ⊥BD . 又PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA ⊥BD ，又AC∩PA＝A，PA，AC⊂平面PAC，故BD⊥平面PAC.法二由题意PA⊥平面ABCD，AB⊥AD，分别以AB→，AD→，AP→的方向为x轴，y轴，z轴正方向建立空间直角坐标系A－xyz，如图所示，则A(0，0，0)，B(2，0，0)，C(2，2，0)，D(0，22，0)，P(0，0，2)，BD→＝(－2，22，0)，AP→＝(0，0，2)，BD→·AP→＝0，即BD⊥AP，AC→＝(2，2，0)，BD→·AC→＝－4＋4＝0，即BD⊥AC，又AC∩AP＝A，AC，AP⊂平面PAC，故BD⊥平面PAC.(2)解由题意PA⊥平面ABCD，AB⊥AD，分别以AB→，AD→，AP→的方向为x轴，y轴，z轴正方向建立空间直角坐标系A－xyz，如图所示，则A(0，0，0)，B(2，0，0)，C(2，2，0)，D(0，22，0)，P(0，0，2)，在平面PBC中，BC→＝(0，2，0)，BP→＝(－2，0，2)，设平面PBC的法向量为n＝(x1，y1，z1)，则⎩⎪⎨⎪⎧n ·BC →＝2y 1＝0，n ·BP →＝－2x 1＋2z 1＝0，所以y 1＝0，令x 1＝1，则z 1＝1，所以n ＝(1，0，1).在平面PCD 中，CD →＝(－2，2，0)， CP →＝(－2，－2，2)，设平面PCD 的法向量为m ＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧m ·CD →＝－2x 2＋2y 2＝0，m ·CP →＝－2x 2－2y 2＋2z 2＝0，令x 2＝1，则y 2＝2，z 2＝2，所以m ＝(1，2，2).设平面BPC 与平面PCD 夹角的大小为θ，则cos θ＝|cos 〈m ，n 〉|＝|1＋0＋2|2×7＝31414，所以平面BPC 与平面PCD 夹角的余弦值为31414. 热点四距离问题1.空间中点、线、面距离的相互转化关系2.空间距离的求解方法有：(1)作垂线段；(2)等体积法；(3)等价转化；(4)空间向量法.例4 在直三棱柱ABC－A1B1C1中，AB＝AC＝AA1＝2，∠BAC＝90°，M为BB1的中点，N为BC的中点.(1)求点M到直线AC1的距离；(2)求点N到平面MA1C1的距离.解法一(1)如图，连接AM，MC1，AC1，易知MC1＝MB21＋A1B21＋A1C21＝22＋22＋12＝3，AC1＝22，MA＝5，在△MAC1中，由余弦定理得cos ∠MAC1＝5＋8－92×5×22＝1010，则sin ∠MAC1＝310 10，所以M到直线AC1的距离为MA·sin ∠MAC1＝5×31010＝322.(2)如图，S△MNC1＝S矩形B1BCC1－S△B1MC1－S△BMN－S△NCC1＝42－2－22－2＝322，设点N到平面MA1C1的距离为h，由V N－MA1C1＝V A1－MNC1，得1 3×12×2×5×h＝13×322×2，得h ＝355，即N 到平面MA 1C 1的距离为355. 法二 (1)建立如图所示的空间直角坐标系，则A (0，0，0)，A 1(0，0，2)，M (2，0，1)，C 1(0，2，2)，直线AC 1的一个单位方向向量为s 0＝⎝⎛⎭⎪⎫0，22，22，AM →＝(2，0，1)，故点M 到直线AC 1的距离d ＝|AM →|2－|AM →·s 0|2＝5－12＝322. (2)设平面MA 1C 1的法向量为n ＝(x ，y ，z )，因为A 1C 1→＝(0，2，0)，A 1M →＝(2，0，－1)，则⎩⎪⎨⎪⎧n ·A 1C 1→＝0，n ·A 1M →＝0，即⎩⎨⎧2y ＝0，2x －z ＝0，取x ＝1，得z ＝2，故n ＝(1，0，2)为平面MA 1C 1的一个法向量，因为N (1，1，0)，所以MN →＝(－1，1，－1)，故N 到平面MA 1C 1的距离d ＝|MN →·n ||n |＝35＝355.规律方法 1.在解题过程中要对“点线距离”、“点面距离”、“线面距离”与“面面距离”进行适当转化，从而把所求距离转化为点与点的距离进而解决问题. 2.解决点线距问题注意应用等面积法，解决点面距问题注意应用等体积法.训练4 在四棱柱ABCD－A1B1C1D1中，A1A⊥平面ABCD，AA1＝3，底面是边长为4的菱形，且∠DAB＝60°，AC∩BD＝O，A1C1∩B1D1＝O1，E是O1A的中点，则点E到平面O1BC的距离为( )A.2B.1C.32D.3答案 C解析法一如图，连接OO1，则OO1⊥平面ABCD，OO1＝AA1＝3，∵四边形ABCD是边长为4的菱形，且∠DAB＝60°，∴OB＝2，OC＝23，AC＝2OC＝43，OB⊥AC.∴O1B＝13，O1C＝21，又BC＝4，∴cos∠BO1C＝913×21，sin∠BO1C＝8313×21，故S△BO1C＝12×13×21×8313×21＝4 3.设A到平面O1BC的距离为h，则由V A－BO1C＝V O1－ABC得13×43×h＝13×12×43×2×3，解得h ＝3，又∵E 是O 1A 的中点， ∴E 到平面O 1BC 的距离为32.法二易得OO 1⊥平面ABCD ，所以OO 1⊥OA ，OO 1⊥OB . 又OA ⊥OB ，所以建立如图所示的空间直角坐标系Oxyz . 因为底面ABCD 是边长为4的菱形，∠DAB ＝60°，所以OA ＝23，OB ＝2，则A (23，0，0)，B (0，2，0)，C (－23，0，0)，O 1(0，0，3)，所以O 1B →＝(0，2，－3)，O 1C →＝(－23，0，－3). 设平面O 1BC 的法向量为n ＝(x ，y ，z ). 则⎩⎪⎨⎪⎧n ·O 1B →＝0，n ·O 1C →＝0，所以⎩⎨⎧2y －3z ＝0，－23x －3z ＝0，取z ＝2，则x ＝－3，y ＝3，则n ＝(－3，3，2)是平面O 1BC 的一个法向量. 设点E 到平面O 1BC 的距离为d .因为E 是O 1A 的中点，所以E ⎝⎛⎭⎪⎫3，0，32，EO 1→＝⎝⎛⎭⎪⎫－3，0，32，则d ＝|EO 1→·n ||n |＝⎪⎪⎪⎪⎪⎪⎝ ⎛⎭⎪⎫－3，0，32·（－3，3，2）（－3）2＋32＋22＝32，所以点E 到平面O 1BC 的距离为32.一、基本技能练1.如图，四棱锥P －ABCD 中，∠ABC ＝∠BAD ＝90°，BC ＝2AD ，△PAB 和△PAD 都是边长为2的等边三角形.(1)证明：PB ⊥CD ；(2)求点A 到平面PCD 的距离.(1)证明取BC 的中点E ，连接DE ，则ABED 为正方形.过P 作PO ⊥平面ABCD ，垂足为O . 连接OA ，OB ，OD ，OE .由△PAB 和△PAD 都是等边三角形知PA ＝PB ＝PD ，所以OA ＝OB ＝OD ，即点O 为正方形ABED 对角线的交点，故OE ⊥BD ，从而PB ⊥OE .因为O 是BD 的中点，E 是BC 的中点，所以OE ∥CD .因此PB ⊥CD . (2)解取PD 的中点F ，连接OF ，则OF ∥PB .由(1)知，PB ⊥CD ，故OF ⊥CD .又OD ＝12BD ＝2，OP ＝PD 2－OD 2＝2，故△POD 为等腰三角形，因此OF ⊥PD . 又PD ∩CD ＝D ，PD ，CD ⊂平面PCD ，所以OF ⊥平面PCD .因为AE ∥CD ，CD ⊂平面PCD ，AE ⊄平面PCD ，所以AE ∥平面PCD .因此O 到平面PCD 的距离OF 就是A 到平面PCD 的距离，而 OF ＝12PB ＝1，所以A 到平面PCD 的距离为1.2.(2022·广州调研)如图，在三棱锥P －ABC 中，BC ⊥平面PAC ，AD ⊥BP ，AB ＝2，BC ＝1，PD ＝3BD ＝3.(1)求证：PA ⊥AC ；(2)求平面PAC与平面ACD夹角的余弦值.(1)证明法一由AB＝2，BD＝1，AD⊥BP，得AD＝ 3. 由PD＝3，AD＝3，AD⊥BP，得PA＝2 3.由BC⊥平面PAC，AC，PC⊂平面PAC，得BC⊥AC，BC⊥PC.所以AC＝AB2－BC2＝3，PC＝PB2－BC2＝15.因为AC2＋PA2＝15＝PC2，所以PA⊥AC.法二由AB＝2，BD＝1，AD⊥BP，得AD＝ 3.由PD＝3，AD＝3，AD⊥BP，得PA＝2 3.因为PB＝4，所以PB2＝AB2＋PA2，所以PA⊥AB.由BC⊥平面PAC，PA⊂平面PAC，得BC⊥PA.又BC，AB⊂平面ABC，BC∩AB＝B，故PA⊥平面ABC.因为AC⊂平面ABC，所以PA⊥AC.(2)解法一如图，过点D作DE∥BC交PC于点E，因为BC⊥平面PAC，所以DE⊥平面PAC.因为AC⊂平面PAC，所以DE⊥AC.过点E作EF⊥AC交AC于点F，连接DF，又DE∩EF＝E，DE，EF⊂平面DEF，所以AC⊥平面DEF.因为DF⊂平面DEF，所以AC⊥DF.则∠DFE为平面PAC与平面ACD的夹角.由PD＝3BD＝3，DE∥BC，得DE＝3 4，由EF⊥AC，PA⊥AC，且EF，PA⊂平面PAC，得EF∥PA，且EFPA＝CECP＝BDBP＝14，得EF＝3 2.易知DE⊥EF，则DF＝DE2＋EF2＝21 4.所以cos∠DFE ＝EF DF ＝277.所以平面PAC 与平面ACD 夹角的余弦值为277. 法二如图，作AQ ∥CB ，以AQ ，AC ，AP 所在直线分别为x ，y ，z 轴，建立空间直角坐标系.因为AB ＝2，BC ＝1，BD ＝1，BP ＝4，所以AC ＝3，AP ＝2 3.故A (0，0，0)，B (1，3，0)，C (0，3，0)，P (0，0，23). 由BD →＝14BP →，得D ⎝ ⎛⎭⎪⎫34，334，32，则AD →＝⎝ ⎛⎭⎪⎫34，334，32，AC →＝(0，3，0).设平面ACD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·AC →＝0，n ·AD →＝0，即⎩⎨⎧3y ＝0，34x ＋334y ＋32z ＝0，令x ＝2，则z ＝－3，y ＝0，所以n ＝(2，0，－3)为平面ACD 的一个法向量. 由于BC ⊥平面PAC ，因此CB →＝(1，0，0)为平面PAC 的一个法向量. 设平面PAC 与平面ACD 夹角的大小为θ，则cos θ＝|cos 〈CB →，n 〉|＝|CB →·n ||CB →||n |＝27＝277.所以平面PAC 与平面ACD 夹角的余弦值为277. 3.(2022·泉州质检)在三棱锥A －BCD 中，已知CB ＝CD ＝5，BD ＝2，O 为BD 的中点，AO ⊥平面BCD ，AO ＝2，E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值；(2)若点F 在BC 上，满足BF ＝14BC ，设平面FDE 与平面DEC 夹角的大小为θ，求sin θ的值.解 (1)如图，连接OC ，因为CB ＝CD ，O 为BD 的中点，所以CO ⊥BD .又AO ⊥平面BCD ，OB ，OC ⊂平面BCD ，所以AO ⊥OB ，AO ⊥OC .以{OB →，OC →，OA →}为基底，建立空间直角坐标系O －xyz .因为BD ＝2，CB ＝CD ＝5，AO ＝2，所以B (1，0，0)，D (－1，0，0)，C (0，2，0)，A (0，0，2). 因为E 为AC 的中点，所以E (0，1，1)，所以AB →＝(1，0，－2)，DE →＝(1，1，1)，所以|cos 〈AB →，DE →〉|＝|AB →·DE →||AB →|·|DE →|＝|1＋0－2|5×3＝1515.因此，直线AB 与DE 所成角的余弦值为1515. (2)因为点F 在BC 上，BF ＝14BC ，BC →＝(－1，2，0)，所以BF →＝14BC →＝⎝ ⎛⎭⎪⎫－14，12，0.又DB →＝(2，0，0)，故DF →＝DB →＋BF →＝⎝ ⎛⎭⎪⎫74，12，0.设平面DEF 的法向量为n 1＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧DE →·n 1＝0，DF →·n 1＝0，即⎩⎨⎧x 1＋y 1＋z 1＝0，74x 1＋12y 1＝0，取x 1＝2，得y 1＝－7，z 1＝5，所以n 1＝(2，－7，5)为平面DEF 的一个法向量.设平面DEC 的法向量为n 2＝(x 2，y 2，z 2)，又DC →＝(1，2，0)，则⎩⎪⎨⎪⎧DE →·n 2＝0，DC →·n 2＝0，即⎩⎨⎧x 2＋y 2＋z 2＝0，x 2＋2y 2＝0，取x 2＝2，得y 2＝－1，z 2＝－1，所以n 2＝(2，－1，－1)为平面DEC 的一个法向量. 故|cos θ|＝|n 1·n 2||n 1|·|n 2|＝|4＋7－5|78×6＝1313.所以sin θ＝1－cos 2θ＝23913.二、创新拓展练4.如图，三棱柱ABC －A 1B 1C 1中，侧面BCC 1B 1为矩形，若平面BCC 1B 1⊥平面ABB 1A 1，平面BCC 1B 1⊥平面ABC 1.(1)求证：AB ⊥BB 1；(2)记平面ABC 1与平面A 1B 1C 1的夹角为α，直线AC 1与平面BCC 1B 1所成的角为β，异面直线AC 1与BC 所成的角为φ，当α，β满足：cos α·cos β＝m (0<m <1，m 为常数)时，求sin φ的值.(1)证明∵四边形BCC 1B 1是矩形，∴BC ⊥BB 1，图1 又平面ABB1A1⊥平面BCC1B1，平面ABB1A1∩平面BCC1B1＝BB1，BC⊂平面BCC1B1，∴BC⊥平面ABB1A1，又AB⊂平面ABB1A1，∴AB⊥BC.如图1，过C作CO⊥BC1，∵平面BCC1B1⊥平面ABC1，平面BCC1B1∩平面ABC1＝BC1，CO⊂平面BCC1B1，∴CO⊥平面ABC1，又AB⊂平面ABC1，∴AB⊥CO，又AB⊥BC，CO∩BC＝C，CO，BC⊂平面BCC1B1，∴AB⊥平面BCC1B1，又BB1⊂平面BCC1B1，∴AB⊥BB1.(2)解由题意知AB∥A1B1，又AB⊥平面BCC1B1，∴A1B1⊥平面BCC1B1.以B 1为原点，B 1A 1，B 1B ，B 1C 1所在直线分别为x ，y ，z 轴建立空间直角坐标系，如图2，图2不妨设B 1A 1＝a ，B 1B ＝b ，B 1C 1＝c ，则B 1(0，0，0)，A 1(a ，0，0)，B (0，b ，0)，C 1(0，0，c )，A (a ，b ，0)， BA →＝B 1A 1→＝(a ，0，0)，BC →＝B 1C 1→＝(0，0，c )，BC1→＝(0，－b ，c ). 设n 1＝(x 1，y 1，z 1)为平面ABC 1的法向量，则⎩⎪⎨⎪⎧n 1·BA →＝ax 1＝0，n 1·BC 1→＝－by 1＋cz 1＝0，∴x 1＝0，令y 1＝c ，则z 1＝b ， ∴n 1＝(0，c ，b ).取平面A 1B 1C 1的一个法向量n ＝(0，1，0)，由图知，α为锐角，则cos α＝|cos 〈n 1，n 〉|＝c b 2＋c 2.取平面BCC 1B 1的一个法向量n 2＝(1，0，0)，由C 1A →＝(a ，b ，－c )，得sin β＝|cos 〈C 1A →，n 2〉|＝aa 2＋b 2＋c2. 又β∈⎣⎢⎡⎦⎥⎤0，π2，∴cos β＝b 2＋c 2a 2＋b 2＋c 2，则cos αcos β＝ca 2＋b 2＋c2. |cos 〈C 1A →，BC →〉|＝cos φ＝|（a ，b ，－c ）·（0，0，c ）|c a 2＋b 2＋（－c ）2＝c a 2＋b 2＋c 2，∴cos φ＝cos αcos β.∵cos αcos β＝m 且m ∈(0，1)，φ∈⎝ ⎛⎦⎥⎤0，π2，∴sin φ＝1－cos 2φ＝1－m 2.。

高考数学二轮复习考点知识与题型专题讲解45 求空间角和距离

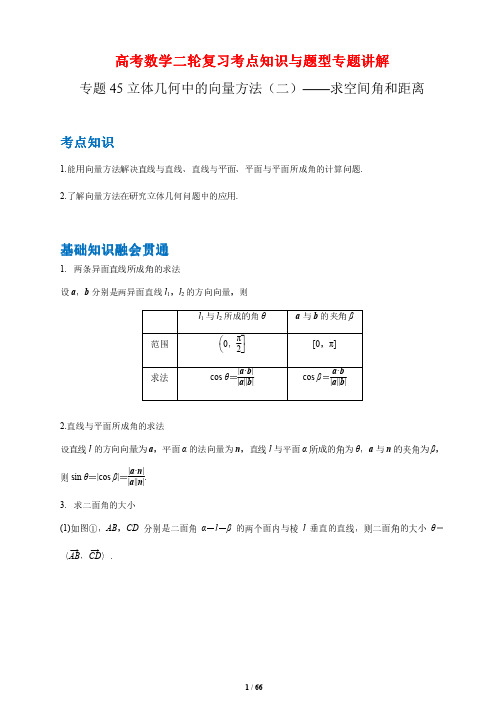
由
⇒CG⊥面
，∴∠ VAD
CVG
是
CV
与平面
VAD
所成的角………………
VC
2m；CG＝m，∴∠CVG＝30°
∴CV 与平面 VAD 所成角为 30°………………
法 2：以 A 为原点，射线，， AB AD AV 所在直线为 x，y，z 轴正半轴，建立空间直角坐标系，则平
面 VAD 法向量（m，0，0），又
又| | ，| | ，
∴cos ，
6分
证明：（2）A1（1，0，2），C1（0，0，2），B1（0，1，2），N（1，0，1），
∴M（，，2），∴ （，，2），（1，0，﹣1），（1，﹣1，1），
∴•
1 （﹣1）+1×0＝0，同理可求 • 0，
∴ ⊥ ， ⊥ ，＝， C1M∩C1N C1 ∴BN⊥平面 C1MN…12 分．
rt△PHC PH
4，
在中，＝，＝ Rt△PHD PH 4 DH 2 ，所以 PD
2．
由 DH＝2HK，得点 H 到直线 PD 的距离为，即所以点 E 到平面 PCD 的距离为．
，得 h ．
【再练一题】如图，PA⊥平面 ABCD，四边形 ABCD 是正方形，PA＝AD＝2，M、N 分别是 A ．B PC 的中点．（1）求证：平面 MND⊥平面； PCD （2）求点 P 到平面 MND 的距离．
【题型二】求直线与平面所成的角
【典型例题】
如图所示，在直角梯形 ABCD 中，已知 ∥ ， ⊥ ，＝ BC AD AB AD BC BA （1）求证：CD⊥平面； VAC
（2）若 VA m，求 CV 与平面 VAD 所成角的大小．

上海高三数学高考二轮复习教案立体几何专题之空间的角与距离(1)含答案

沪教版（上海）高中数学度高三数学二轮复习立体几何专题之空间的角与距离①教学目标1、理解点到平面、直线和直线、直线和平面、平面和平面距离的概念；会用求距离的常用方法（如：直接法、转化法、向量法）2、理解线线角、线面角、面面角的概念定义和取值范围；会用求角的方法“一作二证三计算”。

知识梳理1、空间角：（1）空间角的计算步骤一作、二证、三算。

（2）异面直线所成角：1>范围：___________ (0°，90°]；2>计算方法:<1>平移法：一般情况下应用平行四边形的对边、梯形的平行对边、三角形的中位线进行平移;<2>补体法；（3）直线与平面所成的角：1>定义：平面的一条斜线和它在这个平面内的射影所成的锐角，叫做这条直线和这个平面所成的角；一条直线垂直于平面，我们说它们所成的角是直角；2>范围：_____________ [0°，90°]；3>斜线与平面所成角的计算：<1>直接法：关键是作垂线，找射影可利用面面垂直的性质；<2>平移法：通过三角形的中位线或平行四边形的对边平移，计算其平行线与平面所成的角（也可平移平面）。

<3>通过等体积法求出斜线任一点到平面的距离d，计算这点与斜足之间的线段长l，则sindl θ=.(6)二面角：1>定义：平面内的一条直线把平面分为两部分，其中的每一部分叫做半平面.从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，每个半平面叫做二面角的面。

二面角的平面角：以二面角的棱上任一点为端点，在两个半平面内分别作垂直于棱的两条射线，这两条射线所成的角，叫做这个二面角的平面角.规定：二面角的两个半平面重合时，二面角为0，当两个半平面合成一个平面时，二面角为π，因此，二面角的大小范围为_______ [0°，180°]；2>确定二面角的方法：<1>定义法；<2>垂面法；注：空间角的计算步骤：一作、二证、三算2、空间距离（1）七种距离：点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离，其中点与点、点与直线、点到平面的距离是基础，求其它几种距离一般化归为求这三种距离；（2）点与点的距离： 1>解三角形及多边形；2>空间任意两点A 、B 间的距离即线段AB 的长度：设()111,,A x y z 、()222,,B x y z ，则()()()222121212AB x x y y z z =-+-+-（3）两条异面两条异面直线的距离：直线的公垂线段的长度；说明：两条异面直线的距离等于其中一条直线到过另一条直线且与这条直线平行的平面的距离。

高考数学复习第十一讲立体几何之空间距离

第^一讲立体几何之空间距离一、空间距离包括:点与点、点与线、点与面、线与线（异面直线）、线与面（线面平行）、面与面（面面平行）的距离。

要理解各个距离的概念。

二、空间距离的求法重点掌握：线线距离、点面距离、尤其点面距离（1）线线距离：找公垂线段（2）点面距离①直接法（过点向面作作垂线段，即求公垂线段长度）②等体积法（三棱锥）③向量法：设平面的法向量为n , P为平面外一点，Q是平面内任一点,一n PQ 则点P到平面的距离为d等于PQ在法向量n上的投影绝对值。

d --------------------n三、例题讲解1、下列命题中：①PA 矩形ABCD所在的平面，则P、B间的距离等于P到BC的距离；②若a//b,a ,b ,则a与b的距离等于a与的距离；③直线a、b是异面直线，a ,b// ,则a、b之间的距离等于b与的距离④直线a 、b 是异面直线，a ,b ,且// ,则a 、b 之间的距离等于、间的距离其中正确的命题个数有（ C ）A. 1个B. 2个C. 3个D. 4个1，C 、D 为两条棱的中点，A 、B 、M 是顶点，那么点 M 到截面ABCD 的距离是 ________________解析：取AB 、CD 中点P 、Q ,易证 MPQ 中，PQ 边长的高 MH 为所求，PM丄PQ 口MH2243A-BCDE 中，AE 底面 BCDE 且 AE=CD=a, G 、H 是 BE 、ED 的中点，贝U GH 到面ABD 的距离是解析：连结EC ,交BD 于0,且交GH 于0，则有平面 AEO 面ABD 。

2、如图所示，正方形的棱长为3、在底面是正方形的四棱锥1 i AE EO :"3过E作EK AO于K，则所求距离等于—EK a2 2 AO 64、如图，在棱长为a的正方体ABCD A1B1C1D1中，E、F分别为棱AB和BC的中点, G为上底面A1B1C1D1的中心，则点D到平面B1EF的距离_______________ _解：方法1 :建立如图直角坐标系，a a a a则Aa,0,0,B a,a,0,C 0,a,0,E a,2,0 , F2,a,0 ,B1a,a,a ,G 2,2,a设平面B1FE的法向量为n1 x,y,zEFa a —2,2,0 ,EB10,|,an1EF 0, n1 EB, 0a—x2ayaz 0取y 2,则x 2,z可取n12,2, 1DB1ri| 又DB1 a, a, a D到平面B1 EF的距离d —厂l n12a 2a aa3方法2 :等体积法3h a即D到平面B1EF的距离为a 。

高考数学二轮专题复习第14课时空间角与空间距离课件文

14
在RtPOD中，PD2 PO2 OD2，
在RtPDB中，PB2 PD2 BD2，
所以PB2 PO2 OD2 BD2 36，得PB 6.在RtPOA中，
PA2 AO2 OP2 25，得PA 5.
又cosBPA PA2 PB2 AB2 1，从而sinBPA 2 2 .
16
(1)证明：因为AB、BC、CD两两垂直，所以CD⊥BC，CD⊥AB. 又因为AB、BC为平面ABC内的两条相交直线，所以CD⊥平面ABC，而CD⊂平面ACD，所以平面ACD⊥平面ABC. (2)因为AB⊥CD，AB⊥BC，而BC、CD是平面BCD 内的两条相交直线，所以AB⊥平面BCD. 而BD⊂平面BCD，所以AB⊥BD，所以∠CBD为二面角C-AB-D的平面角．又因为BC=CD=1，BC⊥CD，所以∠CBD=45°，即二面角C-AB-D的平面角为45°.
在RtDCA中，CG CD2 22 4 5 .
AC
22 12
5
45
在RtPCG中，tanCPG CG 5 2 5 ， PC 2 5
即直线PC与平面PDE所成的角的正弦值为 2 . 3
22
3由于BF 1 CF，所以可知点B到平面PDE的距离等于
4 点C到平面PDE的距离 1 ，即 1 CH.
24
【变式训练】如图，在四棱锥P-ABCD中，底面 ABCD 是矩形， PA⊥ 平面 ABCD ， PA=AD=4 ， AB=2，BM⊥PD，垂足为M，O为BD的中点． (1)求证：PD⊥平面ABM； (2)求点O到平面ABM的距离； (3)求直线OA与平面ABM所成角的正弦值．
25
(1)证明：因为PA⊥平面ABCD，而AB⊂平面ABCD，所以PA⊥AB，又因为AB⊥AD，PA、AD为平面PAD内的两条相交直线，所以AB⊥平面PAD，所以AB⊥PD，又因为BM⊥PD，AB、BM为平面ABM内的两条相交直线，所以PD⊥平面ABM.

高三数学二轮专题复习27 空间角与空间距离

立体几何—空间角与空间距离专题综述空间角度与空间距离的推理、比较与计算，是高考考查的重点.求解方法既可以选择几何法，又可以选择向量法，在解决空间背景下及建系困难的几何体中的角与距离时，几何法更具优势，在解决简单几何体中的角与距离及探究性问题时，向量法更具优势.因此,选择合适的方法，确保快速解决问题.另外，两种方法都要求熟练准确的运算，且具有较高的直观想象、逻辑推理及数学运算的核心素养.专题探究探究1：综合法解决立体图形中角度和距离问题的思路：立体几何平面化→平面几何三角化→三角问题定理化.即把空间立体几何的问题转化为平面几何的问题，再把平面几何的问题转化为解三角形问题.答题思路一：综合法求解空间角（1）求异面直线成角的方法①平移：平移已有的平行线，或选择适当的点（线段的中点或端点），做平线性平移，或补形平移；② 证明：证明所作的角是异面直线所成的角或是其补角；③ 寻找：在立体图形中，寻找或作出含有此角的三角形，解三角形； ④ 取舍：因为异面直线所成角θ的取值范围是0,2π⎛⎤⎥⎝⎦，所以所作的角为钝角时，应取它的补角作为异面直线所成的角．（2）求线面角的方法：（I ）定义法：① 先确定斜线与平面，找到线面的交点A 为斜足；找线在面外的一点B ，过点B 向平面α做垂线，确定垂足O ；② 连结斜足A 与垂足O ,OA 为斜线AB 在面α内的投影；投影OA 与斜线AB 之间的夹角为线面角；③ 把投影OA 与斜线AB 归到三角形中进行求解. （2）间接法：设斜线PA 与平面α所成角为θ，则sin Ph PAθ=（P h 为点P 到平面α的距离），转化为求点P 到平面α的距离，可利用等积转化或借助其他点求距离. （3）求二面角的方法：l αβ--① 点A 为平面α内一点，过点A 作AO l ⊥于点O ； ② 证明过点A 的直线AB ⊥平面β于点B ,连接OB ，AB l l ⇒⊥⇒⊥平面AOB ,OB l ⇒⊥，⇒AOB ∠即为二面角l αβ--的平面角；③ 解Rt AOB ∆.答题思路二：综合法求解空间距离空间中的距离：平行平面间的距离、平行平面的直线到平面的距离、点到平面的距离⇒转化为点到平面的距离求点A 到平面α距离的方法：（1）直接法：① 求证过点A 的直线AB ⊥平面α于点B ，则线段AB 的长即为点A 到平面α的距离； ② 利用求三棱锥体积的等积转化思想进行求解；（2）间接法：转化为其他点到平面的距离① 直线AB 平面α，转化为求点B 到平面的距离；② ,A B ∈平面β，平面β平面α，转化为求点B 到平面的距离.（2021.福建省福州市月考试卷）如图，在棱长为2的正方体1111ABCD A B C D -中，下列结论正确的有（） A.二面角11A CD D --的大小为045 B.异面直线11D B 与CD 所成的角为060 C. 直线11D B 与平面11A DCB 所成的角为030 D. 1D 到平面11A DCB 的距离为2【审题视点】以简单几何体或者空间位置背景下的多选题，选项中涉及求空间角、距离、体积的问题，若建系，运算量较大，可以优先选择综合法解题.【思维引导】将综合法求空间角和距离的方法，以“流程化”的形式，将需要寻找的点，或需要作出的辅助线呈现出来，即可锁定所求的角或线段长.综合法的关键是，“按步骤进行”.【规范解析】解：在棱长为2的正方体1111ABCD A B C D -中，连接1AD 交1A D 于点O ，则11A D AD ⊥CD ⊥平面11ADD A1CD AD ∴⊥11,,A D CD D A D CD =⊂平面11A DCB 1AD ∴⊥平面11A DCB确定过点1D 垂直于平面11A DCB 的垂线1DD CD⊥11A DD ∴∠是二面角11ACD D --的平面角，又1145A DD ∠=,∴二面角11A CD D --的大小为045故A 正确11CD C D111B D C ∴∠是异面直线11D B 与CD 所成角或其补角又011145B D C ∠=∴异面直线11D B 与CD 所成角为045故B 错误01130OB D ∴∠=∴直线11D B 与平面11A DCB 所成的角为030故C 正确方法一：1OD ⊥平面11A DCB∴1OD 的长即为点1D 到平面11A DCB 的距离 ∴点1D 到平面11A DCB方法二：三棱锥111D A B D -中111111D A B D B A D D V V --=1111111133D A B D B A D D h S h S ∆∆∴⋅⋅=⋅⋅11111112222122B A D DDA B Dh ShS∆∆⋅⋅⋅⋅∴===⋅∴点1D到平面11A DCB方法三：111111,C D A B A B ⊂平面11A DCB，11C D⊄平面11A DCB三棱锥111C A B C-中111111C A B C A C B CV V--=11111112222122A CB CCA B Ch ShS∆∆⋅⋅⋅⋅∴===⋅∴点1C到平面11A DCB，即点1D到平面11A DCB故D正确.【探究总结】求空间角和距离，不能单一的只利用空间向量法求解，对于一些简单的几何体，或者建系定坐标需花费较多时间的题目，选择用综合法求解会缩短解题时间.空间三大角中，二面角的求解较为困难，记住一点出发，作两垂线，连接两垂足，解三角形即可.1111111133C A B C A C B Ch S h S∆∆∴⋅⋅=⋅⋅（2021年全国新高考Ⅰ卷）如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点. （1）证明：OA CD ⊥；（2）若OCD ∆是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.探究2：向量法利用空间向量求空间角与距离的思路：寻找从同一点出发的三条两两相互垂直的直线（条件不足需证明垂直）⇒建立空间直角坐标系⇒确定点的坐标⇒求出向量（方向向量或法向量）坐标 ⇒带入空间向量求角或距离的公式，求解. 答题思路三：向量法求解空间角与空间距离（1）求空间角① 设异面直线,m n 的方向向量分别为,m n ，则异面直线,m n 所成角的余弦值为cos ,m n m n m n⋅=； ② 设直线m平面A α=，直线m 的方向向量为m ，平面α的法向量为a ，则直线m 与平面α所成角的正弦值为cos ,m a m a m a⋅=； ③ 设平面α平面l β=，平面α，平面β的法向量分别为,a b ，则法向量,a b 夹角的余弦值为cos ,a b a b a b⋅=.（2）求点到平面的距离点P ∉平面α，点A ∉平面α，平面α的法向量为n ，则点P 到平面α的距离为PA n n⋅.强调：方向向量所成角的余弦值的绝对值分清所求角是二面角还是平面与平面所成角，对结果进行转化注意是角的正弦值（1）利用空间向量求解空间角或者空间距离①通过建立空间直角坐标系，利用向量的坐标运算进行；②利用空间向量基本定理表示向量，结合空间向量数量积，求角或距离.（2）求解空间角或者距离范围、最值的问题依然利用上述的求解思路，只是点的坐标含有参数，导致最终的结果是一个含参表达式.结合题干条件明确参数范围，转化为函数求范围、最值问题.AB=，（2021广东省佛山市期中考试）如图，已知矩形ABCD中，21∆沿AM折起，使得平面ADM⊥平面ABCM，AD=，M为DC的中点，将ADM连接BM.（1）求证：BM⊥平面ADM；--的余弦值；（2）求二面角A DM C-的体积为（3）若点E是线段DB上的一动点，问点E在何位置时，三棱锥M ADE212【审题视点】题干条件中边长关系较多，联想到利用勾股定理或等腰三角形的三线合一的结论得出垂直结论，平面ADM⊥平面ABCM转化为线面垂直，故图形中垂直结论较多，第一问不难证明，同样容易建系求解后续两问.【思维引导】这是一道立体几何部分的常规题型，图形中垂直条件较多，不难证明BM⊥平面ADM，第一问的结论又为建系提供条件.题中需要求二面角的余弦值，及探究点E位置，用空间向量解决问题的思路更清晰一些.【规范解析】（1）证明：∵矩形ABCD 中，2AB =，1AD =，M 为DC 的中点2AM BM ∴==，222AM BM AB ∴+=AM BM ∴⊥平面ADM ⊥平面ABCM ,平面ADM平面ABCM AM =BM ⊂平面ABCM BM ∴⊥平面ADM（2）解：分别取,AM AB 的中点O 和N ，则ONBM ，ON ∴⊥平面ADM ,ON AM ON OD ∴⊥⊥ AD AM = OD AM ∴⊥建立如图所示空间直角坐标系则2220,0,,,0,0,2,,0222D M C ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 2222,0,,,,02222DM MC ⎛⎫⎛⎫∴=--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭设(),,m x y z =为平面CDM 的一个法向量，则2202222022DM m x z MC m x y ⎧⋅=--=⎪⎪⎨⎪⋅=-+=⎪⎩令1x =，则1,1y z ==-，即()1,1,1m =- 又()0,1,0n =是平面ADM 的一个法向量，3cos ,3m n m n m n⋅==∴二面角A DM C --的余弦值为33建系：凑齐建系条件找点坐标，表示向量坐标，若直接表求向量的坐标难度大，可利用向量间的关系，间接表示求法向量，与坐标平面重合或者平行的平面可直接给出法向量结合图形，分析二面角的范围，对结果进行转化（3）由（2）得22,0,0,,2,022A B ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ 22,2,22DB ⎛⎫∴=-- ⎪ ⎪⎝⎭设[],0,1DE DB λλ=∈22,2,22DE λλλ⎛⎫∴=-- ⎪ ⎪⎝⎭ 则222,2,222E λλλ⎛⎫=-- ⎪ ⎪⎝⎭2222,2,2222AE λλλ⎛⎫∴=--- ⎪ ⎪⎝⎭∴点E 到平面ADM 的距离2AE n d nλ⋅==则1223612M ADB ADM V S d λ-∆=⋅==解得12λ=，则E 为BD 的中点．【探究总结】向量法解决问题的前提是合理建系（条件不足时，有必要的证明）,写出点的坐标，求解二面角、点面距的前提是准确求出法向量.向量法本质是几何问题代数化，准确计算是保障.（2021浙江省期中考试）如图,在四棱柱1111ABCD A B C D -中,底面ABCD是等腰梯形, AB CD ,14,2AB BC CD D C ====, 1D C ⊥底面ABCD ,则（） A.BC ⊥平面1ACDB.直线1DD 与底面ABCD 所成的角为4πC.平面11ABC D 与平面ABCD 所成锐二面角的余弦值为217过点E 的斜线的方向向量+平面的法向量，求点面距离专题升华对于空间角与空间距离的计算问题，综合法与向量法都需要掌握.综合法要求一作（作辅助线）、二证（证明作图的合理性，即平行垂直的依据）、三计算（利用平面几何的知识计算角或边长），注重考查空间想象能力（判别平行与垂直的位置关系），推理论证能力（平行与垂直关系的辅助线作图与论证），运算求解能力（利用余弦定理,计算三角形的内角与边长）.空间向量法要求建立坐标系、写出点坐标、计算角的三角函数值与距离或选择空间向量基底表示其他向量, 利用空间向量数量积运算计算各种角的三角函数值与距离.两种方法针对不同的题型，各具优势，做题时选择合适的方法，快速准确的解题.【答案详解】变式训练1 【解析】解：（1）AB AD =，O 为BD 中点OA BD ∴⊥平面ABD 平面BCD =BD ,平面ABD ⊥平面BCD ，AO ⊂平面ABD OA ∴⊥平面BCDOA CD ∴⊥（2）作EF BD ⊥于F , 作EM BC ⊥于M ,连FM ,则EF OA OA ⊥平面BCD ,EF OAEF ∴⊥平面BCDEF BC ∴⊥平面BCD,EM BC EM EF E ⊥=BC ∴⊥平面EFMBC FM ∴⊥EMF ∴∠为二面角E BC D --的平面角, 即4EMF π∠=BO OD =,OCD ∆为正三角形BCD ∴∆为直角三角形2DE EA =1223FM BF ∴== 33122OA EF FM ∴===11131133326A BCD BCD V OA S -∆∴=⋅=⨯⨯⨯⨯= 变式训练2【解析】解：如图，易知1D C ⊥平面.ABCD BC ⊂平面ABCD1.BC D C ∴⊥在等腰梯形ABCD 中，过点C 作CG AB ⊥于点.G 则3AG =，1BG =，22213CG =-=，所以22223(3)2 3.AC AG CG =+=+= 因此满足22216AC BC AB +==，所以.BC AC ⊥ 又1D C ，AC ⊂平面1AD C ，1D C AC C =， BC ∴⊥平面1AD C1D C ⊥平面ABCD14D DC π∴∠=，即直线1DD 与底面ABCD 所成的角为.4π 建立如图所示空间直角坐标系则(0,0,0)C ，(23,0,0)A ，(0,2,0)B ，1(0,0,2)D ， (23,2,0)AB ∴=-，1(23,0,2).AD =-设平面11ABC D 的法向量(,,)n x y z =，由10,0,AB n AD n ⎧⋅=⎪⎨⋅=⎪⎩得2320,2320,x y x z ⎧-+=⎪⎨-+=⎪⎩ 取1x =，可得平面11ABC D 的一个法向量(1,3,3).n = 又1(0,0,2)CD =为平面ABCD 的一个法向量设平面11ABC D 与平面ABCD 所成锐二面角为θ，则11||2321cos ||||727CD n CD n θ⋅===，因此平面11ABC D 与平面ABCD 所成锐二面角的余弦值为7 故点C 到平面11ABC D 的距离为1||221||7CD n n ⋅= 故选.ABC。

2021年高考数学二轮复习难点.7 立体几何中的空间角与距离教学案理

2021年高考数学二轮复习难点2.7 立体几何中的空间角与距离教学案理立体几何中的“角”与“距离”是定量分析空间几何元素（点、线、面）间位置关系的两个重要的几何量,在研究这些“角”和“距离”时,常将空间问题转化为平面问题来处理,这是化归思想在立体几何中的具体应用. 空间角是考查学生对立体几何中的视图、空间想象能力、逻辑推理能力以及运算能力的一个综合知识点;空间距离既能考查学生的空间想象能力和逻辑推理能力,又能考查学生的转化思想及运算能力,空间距离的计算也是学生感觉较难的部分.在求解空间的角与距离的问题时,一般应包括三个部分:求作、论证和计算,这三部分是一个统一的整体.求空间中的角或距离的常用方法注意根据定义找出或作出所求的角或距离，给出证明，一般情况下，力求明确所求角或距离的位置.求角与距离的关键是将空间的角与距离灵活地转化为平面上的角与距离，然后将所求量置于一个三角形中，通过解三角形最终求得所需的角与距离. 空间向量是高中数学立体几何中新增加的内容 .借助于空间向量工具，可以对一些传统解法中较为繁琐的问题加以定量化 ,从而降低了思维难度 ,增强了可操作性 ,使学生对立体几何更容易产生兴趣 .空间向量在角和距离的处理上有着独特的优势 ,它最大限度地避开了思维的高强度转换 ,避开了各种辅助线添加的难处 ,代之以空间向量的计算 ,有利于我们较好地解决问题 .1 异面直线所成的角异面直线所成角的大小，是由空间一点分别引它们的平行线所成的锐角（或直角）来定义的.因此，通常我们要求异面直线所成的角会要求学生通过平移直线，形成角，然后在某个三角形中求出角的方法来得到异面直线所成角的大小.在这一方法中，平移直线是求异面直线所成角的关键，而如何平移直线要求学生有良好的空间观和作图能力.新教材对立体几何的处理有了一些新的变化，淡化了对学生作图能力的要求，引进了空间向量的方法（实际上是把空间问题代数化），避开了一些繁杂的作图，其中在求异面直线所成的角中运用空间向量的方法有很大的优点.另外，对异面直线所成的角的求法我们还可以借用一些固定的模型，引用一些已知的公式来求出角的大小.例１在直三棱柱中，底面是直角三角形，，为侧棱的中点.（1）求异面直线、所成角的余弦值；（2）求二面角的平面角的余弦值.思路分析：建立空间直角坐标系，由题意写出相关点的坐标；（1）求出异面直线所在的方向向量，直接计算即可；（2）求出平面与平面的法向量，计算即可.（2）因为，，，所以，，所以为平面的一个法向量.因为，，设平面的一个法向量为， .由得令，则，.所以42cos(,).323||||n CBn CBn CB⋅===⨯所以二面角的余弦值为点评：本题考查空间向量的应用，属中档题；在空间求线线角、线面角、二面角，是通过建立恰当的空间直角坐标系,正确写出各点的坐标，则通直线所在的方向向量、平面的法向量，通过向量的夹角间接求解，准确运算是解决这类问题的关键.2 直线与平面所成的角直线与平面所成角是空间三大角之一,它既是教与学的难点,又是高考的热点,求直线与平面所成角的常用方法.一、直接法直接法就是根据斜线与平面所成角的定义,直接作出斜线在平面内的射影,则斜线与射影所成角就是斜线与平面所成角,这是解题时首先要考虑的方法,直接法的关键是确定斜线在平面内的射影,下列结论常作为找斜线在平面内射影的依据.(1)(两平面垂直的性质定理)如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.(2)如果一个角所在平面外一点到角的两边的距离相等,那么这个点在平面内的射影在这个角的平分线上.(3)经过一个角的顶点引这个角所在平面的斜线,设它和已知角的两边的夹角为锐角且相等,则这条斜线在平面的射影是这个角的平分线.(4)若三棱锥的三条侧棱相等,则其顶点在底面上的射影是底面三角形的外心. 二、借助于空间向量工具，利用直线的方向向量与平面的法向量的夹角来转化，当直线的方向向量与平面的法向量夹角为锐角时，通过直角三角形可以知道，直线与平面所成的角与直线的方向向量与平面的法向量夹角互余，因此直线与平面所成的角的正弦就等于直线的方向向量与平面的法向量夹角的余弦，当直线的方向向量与平面的法向量夹角为钝角时，其补角跟直线与平面所成的角互余，因此因此直线与平面所成的角的正弦就等于直线的方向向量与平面的法向量夹角的余弦的相反数.例2【西南名校联盟高三xx年元月】如图，在等腰梯形中，，上底，下底，点为下底的中点，现将该梯形中的三角形沿线段折起，形成四棱锥.（1）在四棱锥中，求证：；（2）若平面与平面所成二面角的平面角为，求直线与平面所成角的正弦值.思路分析：（1）由，，，点为的中点，得三角形沿线段折起后可得四边形为菱形，边长为，，取的中点，连接，，，可证，，即可证平面，从而平面，即可得证；（2）以为坐标原点，建立空间直角坐标系，由（1）可证为平面与平面所成二面角的平面角，从而求出，，，，再求出平面的一个法向量，即可求出直线与平面所成角的正弦值.∴，而，∴且，得点的横坐标为，点的竖坐标为，则，，，，故，，，设平面的一个法向量为， ∴()()()333·0?022{ ·020?0BD n x y z AD n x y z ⎛⎫=-= ⎪ ⎪⎝⎭=-=，，，，，，，，，，得3330 220x z y -=-=，，点评：直线与平面所成的角解题的一般思路为：首先建立适当的空间直角坐标系并正确写出各点的空间坐标，并求出平面的法向量，最后运用公式即可得出结果. 利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.3 二面角二面角及其平面角的概念是立体几何最重要的概念之一，在历年高考中几乎都要涉及.尤其是在数学新课改的大环境下，要求对二面角求法的掌握变得更加灵活，二面角的概念发展、完善了空间角的概念；而二面角的平面角不但定量描述了两相交平面的相对位置，同时它也是空间中线线、线面、面面位置关系的一个汇集点.研究二面角的求法，可以进一步培养学生的空间想象能力和逻辑思维能力，为培养学生的创新意识和创新能力提供了一个良好的契机. 在求解二面角的问题中，通常首先要定位出二面角的平面角，而这也是学生在解题中感到最为陌生和棘手的问题.特别是若二面角的棱隐而不露其解题的难度又会增大.求解二面角是立体几何中最基本、最重要的题型，也是各地高考中的“热点”问题，虽然对此可说是“千锤百炼”，但我们必须面对新的情境、新的变化，如何以基本方法的“不变”去应对题目中的“万变”就是我们研究的中心话题. 总的来说，求解二面角的大体步骤为：“作、证、求”.其中“作、证”是关键也是难点，“求”依靠的计算，也决不能忽视，否则因小失大，功亏一篑，也是十分遗憾之事.例3【北京市朝阳区xx届期末】如图，在三棱柱中，，是线段的中点，且平面．（Ⅰ）求证：平面平面；（Ⅱ）求证：平面；（Ⅲ）若，，求二面角的余弦值.思路分析：（Ⅰ）由，可得，由平面可得．根据线面垂直的判定定理可得平面，再利用面面垂直的判定定理可得结论；（Ⅱ）连接，设，根据三角形中位线定理可得，从而根据线面平行的判定定理可得平面；（Ⅲ）取的中点，则，因为，所以，又因为平面，所以两两垂直．以为原点，分别以为轴建立空间坐标系，利用向量垂直数量积为零列方程组，分别求出平面的一个法向量与平面的一个法向量，根据空间向量夹角余弦公式，可得结果.，所以，即设，则．故317cos,772m nm nm n⋅-+〈〉===⋅⨯．由图知，二面角的平面角为锐角，所以二面角的余弦值为．点评：本题考查了线面平行性质定理及判定定理、二面角的求解、空间向量的运算等知识点的应用，其中对于垂直、平行关系证明中应用转化与化归思想的常见类型.（1）证明线面、面面平行，需转化为证明线线平行.（2）证明线面垂直，需转化为证明线线垂直.（3）证明线线垂直，需转化为证明线面垂直. 利用空间向量求二面角，首先利用垂直关系建立恰当的空间直角坐标系，设立各点坐标，利用方程组解两个平面的法向量，利用向量数量积求夹角，最后根据向量夹角与二面角之间关系得结果.其解题过程中最容易出现以下错误：其一是对于第一问不能熟练运用线线平行、线面平行和面面平行的判定定理和性质定理，进而不能正确处理线面平行的问题；其二是对于第二问不能正确运用空间向量求二面角的大小，其关键是正确地求出各面的法向量.4 空间距离空间中距离的求法是历年高考考查的重点，其中以点与点、点到线、点到面的距离为基础，求其他几种距离一般化归为这三种距离. 空间中的距离主要指以下七种： (1)两点之间的距离. (2)点到直线的距离. (3)点到平面的距离. (4)两条平行线间的距离. (5)两条异面直线间的距离. (6)平面的平行直线与平面之间的距离. (7)两个平行平面之间的距离. 七种距离都是指它们所在的两个点集之间所含两点的距离中最小的距离.七种距离之间有密切联系，有些可以相互转化，如两条平行线的距离可转化为求点到直线的距离，平行线面间的距离或平行平面间的距离都可转化成点到平面的距离. 在七种距离中，求点到平面的距离是重点，求两条异面直线间的距离是难点. 求点到平面的距离：(1)直接法：即直接由点作垂线，求垂线段的长.(2) 转移法：转化成求另一点到该平面的距离.(3)体积法. 求异面直线的距离：(1)定义法：即求公垂线段的长.(2)转化成求直线与平面的距离.(3)函数极值法：依据是两条异面直线的距离是分别在两条异面直线上两点间距离中最小的.例4.是的直径，点是上的动点，过动点的直线垂直于所在的平面，分别是的中点．（1）试判断直线与平面的位置关系，并说明理由；（2）若已知当三棱锥体积最大时，求点到面的距离．思路分析：（1）要判断直线与平面的位置关系，注意到分别是的中点，可知，只需判断直线与平面的位置关系，由已知是的直径，点是上的动点，得，又直线垂直于所在的平面，可得面，从而可得面．（2）求点到面的距离，首先确定点的位置，有已知当三棱锥体积最大，需写出三棱锥的体积表达式，故设，则，从而可得，由基本不等式可得点为的中点，最后利用公式即可得出点到面的距离．点评：本题考查是空间的直线与平面的垂直问题和点与平面的距离的计算问题.解答时第一问充分借助已知条件与判定定理,探寻直线与平行,再推证与平面垂直即可.关于第二问中的最值问题,解答时巧妙运用基本不等式,探求出三棱锥的体积取得最大值时成立的条件,然后运用等积法求出点到平面的距离.综合以上四类问题，立体几何中的空间角与距离问题都是高考中的热点问题，在高考试题的新颖性越来越明显，能力要求也越来越高，并且也越来越广泛．异面直线所成的角，通过作平行线，转化为相交直线所成的角.具体地，有以下两种方法：一是在其中一条上的适当位置选一点，过该点作另一条的平行线；二是在空间适当位置选一点，过该点作两条异面直线的平行线.求异面直线所成的角，点的选取很重要.运用空间向量坐标运算求异面直线所成的角的一般步骤：①建立恰当的空间直角坐标系；②求出相关点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤转化为几何结论．注意：两异面直线所成的角不一定是直线的方向向量的夹角. 直线与平面所成的角就是直线与其在该平面内的射影所成的角.求线面角的关键是找出斜线在平面内的射影，一般在斜线上的某个特殊的位置找一点，过该点平面的垂线，从而作出射影；运用空间向量坐标运算求直线与平面所成的角的一般步骤：①建立恰当的空间直角坐标系；②求出相关点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤转化为几何结论．注意：直线与平面所成的角的正弦等于直线与平面的法向量的夹角的余弦的绝对值. 求二面角的方法:①直接法.直接法求二面角大小的步骤是：一作（找）、二证、三计算.即先作(找)出表示二面角大小的平面角,并证明这个角就是所求二面角的平面角,然后再计算这个角的大小. 用直接法求二面角的大小,其关键是确定表示二面角大小的平面角.而确定其平面角,可从以下几个方面着手:①利用三垂线定理(或三垂线定理的逆定理)确定平面角,自二面角的一个面上一点向另一面引垂线，再由垂足向棱作垂线得到棱上的点（即垂足），斜足与面上一点连线和斜足与垂足连线所夹的角，即为二面角的平面角；；②利用与二面角的棱垂直的平面确定平面角, 自空间一点作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角；③利用定义确定平面角, 在棱上任取一点，过这点在两个平面内分别引棱的垂线，这两条射线所成的角，就是二面角的平面角；②射影面积法.利用射影面积公式＝；此方法常用于无棱二面角大小的计算；对于无棱二面角问题还有一条途径是设法作出它的棱，作法有“平移法”“延伸平面法”等.③空间向量法:法一: 是二面角的两个面内与棱l垂直的直线，则二面角的大小．法二：设,是二面角的两个半平面的法向量，其方向一个指向内侧，另一个指向外侧（同等异补），则二面角的平面角或.求距离的关键是化归.即空间距离向平面距离化归，具体方法如下：（1）求空间中两点间的距离，一般转化为解直角三角形或斜三角形.（2）求点到直线的距离和点到平面的距离，一般转化为求直角三角形斜边上的高；或利用三棱锥的底面与顶点的轮换性转化为三棱锥的高，即用体积法.（3）求距离的一般方法和步骤：应用各种距离之间的转化关系和“平行移动”的思想方法，把所求的距离转化为点点距、点线距或点面距求之，其一般步骤是：①找出或作出表示有关距离的线段；②证明它符合定义；③归到解某个三角形．若表示距离的线段不容易找出或作出，可用体积等积法计算求之.2.用法向量球距离：（1）用法向量求异面直线间的距离：如右图所示，a、b是两异面直线，是a和b 的法向量，点E∈a，F∈b，则异面直线 a与b之间的距离是d=；（2）用法向量求点到平面的距离：已知AB是平面α的一条斜线，为平面α的法向量，则 A到平面α的距离为d=；（3）用法向量求直线到平面间的距离：首先必须确定直线与平面平行，然后将直线到平面的距离问题转化成直线上一点到平面的距离问题；（4）用法向量求两平行平面间的距离：首先必须确定两个平面是否平行，这时可以在一个平面上任取一点，将两平面间的距离问题转化成点到平面的距离问题.解答这些问题，需要主观的意志力，不要见到此类问题先发怵，进行消极的自我暗示，要通过一些必要的练习，加强解题信心的培养，确定解题的一般规律，积极的深入分析问题的特征，进而实现顺利解答．。

2020年高考数学(文科)二轮复习第二章《空间角与距离》讲义案及拔高题型归纳附答案解析

2020年高考数学（文科）二轮复习第二章《空间角与距离》讲义案及题型归纳一、考纲解读1.掌握各种角的定义，弄清异面直线所成的角与两直线所成的角，二面角与二面角的平面角，直线与平面所成的角和斜线与平面所成的角，二面角与两平面所成的角的联系与区别，弄清他们各自的取值范围。

2.细心体会求空间角的转化和数形结合思想，熟练掌握平移，射影等方法。

二、命题趋势探究异面直线所成角，线面角，二面角时高考中考查的热点，解答与空间角有关的问题时既可用传统法，又可用向量法。

在新课程标准下，对立体几何的基本理论知识要求有所降低，因此应用向量这一工具解题更为重要，特别是要熟练掌握利用空间图形的特殊性，构造适当的空间直角坐标系解决问题的方法，并能灵活应用。

空间角是立体几何中的一个重要概念，它是空间图形的一个突出量化指标，是空间图形位置关系的具体体现，故以高频的考点出现在历届高考试题中，在选择题，填空题及解答题中均有出现。

三、知识点精讲(一).空间角的定义和范围（1）两条异面直线所成角θ的范围是(0]2π，，当θ=2π时，这两条异面直线互相垂直。

（2）斜线AO 与它在平面α内的射影AB 所成角θ叫做直线与平面所成的角。

平面的斜线和平面所成的角，是这条斜线和这个平面内的任一直线所成角中最小的角，如果直线和平面垂直，那么直线与平面所成的角为2π；如果直线和平面平行或直线在平面内，那么就是直线和平面所成的角为0.直线和平面所成的角的范围为[0]2π，；斜线和平面所成的角的范围为(0,).2π（3）从一条直线出发的两个半平面所组成的角叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面，棱为l ，两个平面分别为α，β的二面角记做α-l -β，二面角的范围是[0,]π（4）一个平面垂直于二面角的公共棱l ，且与两个半平面的交线分别是射线OA ，OB ，则∠AOB 叫做二面角的平面角，平面角是直角的二面角叫做直二面角，相交成直二面角的两个平面垂直.(二).点到平面距离的定义与常用术语点到平面的距离即点到它在平面内的正射影的距离.常用术语有以下4点.1．点在直线上的射影．自点A 向直线l 引垂线，垂足1A 叫做点A 在直线l 上的射影．点A 到垂足的距离叫点到直线的距离．2．点在平面内的射影．自点A 向平面α引垂线，垂足1A 叫做点A 在平面α内的射影，这点和垂足间的线段叫做这点到平面的垂线段．垂线段的长度叫做这点到这个平面的距离．3．斜线在平面内的射影．一条直线和一个平面相交，但不和这个平面垂直，这条直线叫做这个平面的斜线，斜线和平面的交点叫做斜足，斜线上一点和斜足间的线段，叫做这点到平面的斜线段．过斜线上斜足以外的一点向平面引垂线，过垂足和斜足的直线叫做斜线在这个平面内的射影，垂足与斜足间的线段叫做这点到平面的斜线段在这个平面内的射影．4．求点面距离的方法：①直接法：直接作面的垂线，确定垂足的位置；②等体积法：对同一个三棱锥，从不同的角度选择底和高计算体积并加以比较即可．③转化法：转化成求另一点到该平面的距离，常见的是转化为求与面平行的直线上的点到面的距离．五、解答题题型总结核心考点一：点到面的距离与等体积法【例1】⑴如图，正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E ，F ，且12EF =，则下列结论中错误的是（）A ．AC BE⊥B ．EF ∥平面ABCDC ．三棱锥A BEF -的体积为定值D ．AEF △的面积与BEF △的面积相等⑵在正四面体A BCD -中，棱长为4，M 是BC 的中点，P 在线段AM 上运动（P 不与A 、M 重合），过点P 作直线l ⊥平面ABC ，l 与平面BCD 交于点Q ，给出下列命题：①BC ⊥面AMD ；②Q 点一定在直线DM 上；③42C AMD V -=．其中正确的是（）A ．①②B ．①③C ．②③D ．①②③⑶如图，正方体1111ABCD A B C D -的棱长为2，动点E ，F 在棱11A B 上，动点P ，Q 分别在棱AD ，CD 上，若1EF =，1A E x =，DQ y =，DP z =（x y z ,,大于零），则四面体PEFQ的体积（）A ．与x y z ，，都有关B ．与x 有关，与y z ，无关C ．与y 有关，与x z ，无关D ．与z 有关，与x y ，无关QP FEB 1C 1D 1A 1D C BA⑴⑵⑶【解析】⑴D,⑵A,⑶D【例2】已知直四棱柱1111ABCD A B C D -的各棱长均为3，60BAD ∠=︒．长为2的线段MN 的一个端点M 在1DD 上运动，另一个端点N 在底面ABCD 上运动，则MN 的中点的轨迹（曲面）与共一顶点的三个面围成的几何体的体积为_______．【解析】2π9；【例3】ABC △中，90C ∠=︒，30B ∠=︒，2AC =，M 是AB 的中点，将ACM △沿CM 翻折，使得A B ，两点间的距离为22，则三棱锥A BCM -的体积等于（）A ．23B ．23C ．63D ．223原图：【解析】D ；由已知有2AM AC CM BM ====，又22AB =，∴90AMB ∠=︒．由2AC =，22AB =，23BC =，∴90BAC ∠=︒．过B 作面ACM 的垂线，设垂足为H ，则BH AM ⊥．又AM BM ⊥，∴AM ⊥面BHM ，∴AM MH ⊥．同理，CA AH ⊥．∴2433AH AM =⋅=，22273CH AH AC =+=，于是()222227262333BH BC CH ⎛⎫=-=-= ⎪ ⎪⎝⎭，∴21132622233433A BCMB ACM ACM V V S BH --==⋅=⋅⋅⋅=△．。

新教材高考数学二轮专题复习第一部分专题攻略专题四立体几何第二讲空间位置关系空间角与空间距离课件

AC
10
2．[2022·广东茂名二模]正三棱锥S - ABC的底面边长为4，侧棱长为
2 3 ， D 为棱 AC 的中点，则异面直线 SD 与 AB 所成角的余弦值为
2
________.
4
解析：取BC的中点E，连接SE，DE，则∠SDE(或其补
角)为异面直线SD与AB所成的角，
解决问题；
2．必要时可以借助空间几何模型，如从长方体、四面体等模型中观
察线面位置关系，并结合有关定理来进行判断．
巩固训练1
1.[2022·湖南衡阳二模]设m、n是空间中两条不同的直线，α、β是两
个不同的平面，则下列说法正确的是(
)
A．若m⊥α，n⊥β，m⊥n，则α⊥β
B．若m⊂α，n⊂β，α∥β，则m∥n
面ABCD，且PA＝AB，AD＝3AB，则PC与底面ABCD所成角的正切值为
(
)
1
A．
B．3
3
C．
10
10
D． 10
答案：C
解析：因为PA⊥底面ABCD，AC⊂底面ABCD，
所以PA⊥AC，则PC与底面ABCD所成角为∠PCA.
设AB＝1，则PA＝1，AD＝3，AC＝ 10.
所以tan
PA
10
∠PCA＝＝ .
1 ·2
为θ.则sin θ＝|cos 〈n1，n2〉|＝
.
1 2
3．平面与平面的夹角
若n1，n2分别为平面α，β的法向量，θ为平面α，β的夹角，则cos θ＝
1 ·2
|cos 〈n1，n2〉|＝
.
1 2
4．点到直线的距离：已知A，B是直线l上任意两点， P是l外一点，