人教A版高中数学空间立体几何知识点归纳

合集下载

新人教A版高中数学选修2-1第三章《空间向量与立体几何》知识点汇总及解题方法总计

第三章空间向量与立体几何单元小结[核心速填]1．空间向量的有关定理和推论(1)共线向量定理：对空间任意两个向量a ，b (b ≠0)，a ∥b 的充要条件是存在实数λ，使得a ＝λb .(2)共线向量定理的推论：若OA →，OB →不共线，则P ，A ，B 三点共线的充要条件是OP →＝λOA →＋μOB →，且λ＋μ＝1.(3)共面向量定理：如果两个向量a ，b 不共线，那么向量p 与向量a ，b 共面的充要条件是存在惟一的有序实数对(x ，y )，使得p ＝x a ＋y b .(4)共面向量定理的推论：已知空间任意一点O 和不共线的三点A ，B ，C ，则P ，A ，B ，C 四点共面的充要条件是OP →＝xOA →＋yOB →＋zOC →(其中x ＋y ＋z ＝1)．(5)空间向量基本定理：如果三个向量a ，b ，c 不共面，那么对空间任一向量p ，存在有序实数组{x ，y ，z }，使得p ＝x a ＋y b ＋z c ，其中{a ，b ，c }叫做空间的一个基底．2．空间向量运算的坐标表示设a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3)． (1)a ＋b ＝(a 1＋b 1，a 2＋b 2，a 3＋b 3)，a －b ＝(a 1－b 1，a 2－b 2，a 3－b 3)，λa ＝(λa 1，λa 2，λa 3)，a ·b ＝a 1b 1＋a 2b 2＋a 3b 3.(2)重要结论：a ∥b ⇔a ＝λb ⇔a 1＝λb 1，a 2＝λb 2，a 3＝λb 3(λ∈R )； a ⊥b ⇔a ·b ＝0⇔a 1b 1＋a 2b 2＋a 3b 3＝0.3．模、夹角和距离公式(1)设a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3)，则①|a |＝a ·a②cos 〈a ，b 〉＝a ·b |a ||b |＝(2)设A (a 1，b 1，c 1)，B (a 2，b 2，c 2)，则d AB ＝|AB →|4．空间向量的结论与线面位置关系的对应关系(1)设直线l 的方向向量是u ＝(a 1，b 1，c 1)，平面α的法向量v ＝(a 2，b 2，c 2)，则l ∥α⇔u ⊥v ⇔u ·v ＝0⇔a 1a 2＋b 1b 2＋c 1c 2＝0，l ⊥α⇔u ∥v ⇔u ＝k v ⇔(a 1，b 1，c 1)＝k (a 2，b 2，c 2)⇔a 1＝ka 2，b 1＝kb 2，c 1＝kc 2(k ∈R )．(2)设直线l ，m 的方向向量分别为a ，b ，平面α，β的法向量分别为u ，v ，则l ∥m ⇔a ∥b ⇔a ＝k b ，k ∈R ； l ⊥m ⇔a ⊥b ⇔a ·b ＝0； l ∥α⇔a ⊥u ⇔a ·u ＝0； l ⊥α⇔a ∥u ⇔a ＝k u ，k ∈R ；α∥β⇔u ∥v ⇔u ＝k v ，k ∈R ； α⊥β⇔u ⊥v ⇔u ·v ＝0. 5．空间向量与空间角的关系(1)设异面直线l 1，l 2的方向向量分别为m 1，m 2，则l 1与l 2的夹角θ满足cos θ＝|cos 〈m 1，m 2〉|.(2)设直线l 的方向向量和平面α的法向量分别为m ，n ，则直线l 与平面α的夹角θ满足sin θ＝|cos 〈m ，n 〉|.(3)求二面角的大小：(ⅰ)如图31①，AB ，CD 是二面角αl β的两个半平面α，β内与棱l 垂直的直线，则二面角的大小θ＝〈AB →，CD →〉．图31(ⅱ)如图31②③，n 1，n 2分别是二面角αl β的两个半平面α，β的法向量，则二面角的大小θ满足cos θ＝cos 〈n 1，n 2〉或－cos 〈n 1，n 2〉．[体系构建][题型探究]类型一、空间向量的基本概念及运算例1、如图32，在四棱锥S ABCD 中，底面ABCD 是边长为1的正方形，S 到A 、B 、C 、D 的距离都等于2.给出以下结论：图32①SA →＋SB →＋SC →＋SD →＝0； ②SA →＋SB →－SC →－SD →＝0； ③SA →－SB →＋SC →－SD →＝0； ④SA →·SB →＝SC →·SD →； ⑤SA →·SC →＝0.其中正确结论的序号是________．【答案】 ③④【解析】容易推出SA →－SB →＋SC →－SD →＝BA →＋DC →＝0，所以③正确；又因为底面ABCD 是边长为1的正方形，SA ＝SB ＝SC ＝SD ＝2，所以SA →·SB →＝2·2·cos∠ASB ，SC →·SD →＝2·2·cos ∠CSD ，而∠ASB ＝∠CSD ，于是SA →·SB →＝SC →·SD →，因此④正确，其余三个都不正确，故正确结论的序号是③④.[规律方法] 1.空间向量的线性运算包括加、减及数乘运算，选定空间不共面的三个向量作为基向量，并用它们表示出目标向量，这是用向量法解决立体几何问题的基本要求，解题时可结合已知和所求，根据图形，利用向量运算法则表示所需向量．2．空间向量的数量积(1)空间向量的数量积的定义表达式a ·b ＝|a |·|b |·cos 〈a ，b 〉及其变式cos 〈a ，b 〉＝a ·b|a | ·|b |是两个重要公式． (2)空间向量的数量积的其他变式是解决立体几何问题的重要公式，如a 2＝|a |2，a 在b 上的投影a ·b|b |＝|a |·cos θ等．[跟踪训练]1.如图33，已知ABCD A ′B ′C ′D ′是平行六面体．设M 是底面ABCD 的中心，N 是侧面BCC ′B ′对角线BC ′上的34分点，设MN →＝αAB →＋βAD→＋γAA ′→，则α＋β＋γ＝________.图33【答案】32[连接BD ，则M 为BD 的中点，MN →＝MB →＋BN →＝12DB →＋34BC ′→＝12(DA →＋AB →)＋34(BC →＋CC ′→)＝12(－AD →＋AB →)＋34(AD →＋AA ′→)＝12AB →＋14AD →＋34AA ′→.∴α＝12，β＝14，γ＝34.∴α＋β＋γ＝32.]类型二、空间向量的坐标运算例2、(1)已知a ＝(2,3，－4)，b ＝(－4，－3，－2)，b ＝12x －2a ，则x ＝( )A ．(0,3，－6)B ．(0,6，－20)C ．(0,6，－6)D ．(6,6，－6)(2)已知向量a ＝(x,1,2)，b ＝(1，y ，－2)，c ＝(3,1，z )，a ∥b ，b ⊥C ． ①求向量a ，b ，c ；②求a ＋c 与b ＋c 所成角的余弦值.【答案】(1)B [由b ＝12x －2a 得x ＝4a ＋2b ，又4a ＋2b ＝4(2,3，－4)＋2(－4，－3，－2)＝(0,6，－20)，所以x ＝(0,6，－20)．](2)①∵向量a ＝(x,1,2)，b ＝(1，y ，－2)，c ＝(3,1，z )，且a ∥b ，b ⊥c ，∴⎩⎪⎨⎪⎧x 1＝1y ＝2－23＋y －2z ＝0，解得⎩⎪⎨⎪⎧x ＝－1，y ＝－1，z ＝1，∴向量a ＝(－1,1,2)，b ＝(1，－1，－2)，c ＝(3,1,1)． ②∵a ＋c ＝(2,2,3)，b ＋c ＝(4,0，－1)， ∴(a ＋c )·(b ＋c )＝2×4＋2×0＋3×(－1)＝5，|a ＋c |＝22＋22＋32＝17，|b ＋c |＝42＋02＋(－1)2＝17， ∴a ＋c 与b ＋c 所成角的余弦值为(a ＋c )·(b ＋c )|a ＋c ||b ＋c |＝517.[规律方法] 熟记空间向量的坐标运算公式设a ＝(x 1，y 1，z 1)，b ＝(x 2，y 2，z 2)， (1)加减运算：a ±b ＝(x 1±x 2，y 1±y 2，z 1±z 2). (2)数量积运算：a ·b ＝x 1x 2＋y 1y 2＋z 1z 2. (3)向量夹角：cos 〈a ，b 〉＝x 1x 2＋y 1y 2＋z 1z 2x 21＋y 21＋z 21x 22＋y 22＋z 22. (4)向量长度：设M 1(x 1，y 1，z 1)，M 2(x 2，y 2，z 2)，则|M 1M 2→|＝(x 1－x 2)2＋(y 1－y 2)2＋(z 1－z 2)2. 提醒：在利用坐标运算公式时注意先对向量式子进行化简再运算. [跟踪训练]2．在空间直角坐标系中，已知点A (1，－2,11)，B (4,2,3)，C (6，－1,4)，则△ABC 一定是( )A ．等腰三角形B ．等边三角形C ．直角三角形D ．等腰直角三角形【答案】C [∵AB →＝(3,4，－8)，AC →＝(5,1，－7)，BC →＝(2，－3,1)，∴|AB →|＝32＋42＋(－8)2＝89，|AC →|＝52＋12＋(－7)2＝75，|BC →|＝22＋(－3)2＋1＝14，∴|AC →|2＋|BC →|2＝|AB →|2，∴△ABC 一定为直角三角形．]类型三、利用空间向量证明平行、垂直问题例3、在四棱锥P ABCD 中，AB ⊥AD ，CD ⊥AD ，PA ⊥底面ABCD ，PA ＝AD ＝CD ＝2AB ＝2，M 为PC 的中点．(1)求证：BM ∥平面PAD ；(2)平面PAD 内是否存在一点N ，使MN ⊥平面PBD ？若存在，确定N 的位置；若不存在，说明理由．[思路探究] (1)证明向量BM →垂直于平面PAD 的一个法向量即可；(2)假设存在点N ，设出其坐标，利用MN →⊥BD →，MN →⊥PB →，列方程求其坐标即可．【答案】以A 为原点，以AB ，AD ，AP 分别为x 轴、y 轴、z 轴建立空间直角坐标系如图所示，则B (1,0,0)，D (0,2,0)，P (0,0,2)，C (2,2,0)，M (1，1,1)，(1)证明：∵BM →＝(0,1,1)，平面PAD 的一个法向量为n ＝(1,0,0)， ∴BM →·n ＝0，即BM →⊥n ，又BM ⊄平面PAD ，∴BM ∥平面PAD ． (2)BD →＝(－1,2,0)，PB →＝(1,0，－2)，假设平面PAD 内存在一点N ，使MN ⊥平面PBD ．设N (0，y ，z )，则MN →＝(－1，y －1，z －1)，从而MN ⊥BD ，MN ⊥PB ， ∴⎩⎪⎨⎪⎧MN →·BD →＝0，MN →·PB →＝0，即⎩⎪⎨⎪⎧1＋2(y －1)＝0，－1－2(z －1)＝0，∴⎩⎪⎨⎪⎧y ＝12，z ＝12，∴N ⎝ ⎛⎭⎪⎫0，12，12，∴在平面PAD 内存在一点N ⎝ ⎛⎭⎪⎫0，12，12，使MN ⊥平面PBD ．[规律方法]利用空间向量证明空间中的位置关系(1)线线平行：证明两条直线平行，只需证明两条直线的方向向量是共线向量． (2)线线垂直：证明两条直线垂直，只需证明两直线的方向向量垂直． (3)线面平行：①证明直线的方向向量与平面的法向量垂直；②证明可在平面内找到一个向量与直线的方向向量是共线向量；③利用共面向量定理，即证明直线的方向向量可用平面内两不共线向量线性表示．(4)线面垂直：①证明直线的方向向量与平面的法向量平行；②利用线面垂直的判定定理转化为线线垂直问题．(5)面面平行：①证明两个平面的法向量平行(即是共线向量)；②转化为线面平行、线线平行问题．(6)面面垂直：①证明两个平面的法向量互相垂直；②转化为线面垂直、线线垂直问题．[跟踪训练]3．如图34，长方体ABCDA1B1C1D1中，点M，N分别在BB1，DD1上，且AM⊥A1B，AN⊥A1D．图34(1)求证：A1C⊥平面AMN.(2)当AB＝2，AD＝2，A1A＝3时，问在线段AA1上是否存在一点P使得C1P∥平面AMN，若存在，试确定P的位置.【答案】(1)证明：因为CB⊥平面AA1B1B，AM⊂平面AA1B1B，所以CB⊥AM，又因为AM⊥A1B，A1B∩CB＝B，所以AM⊥平面A1BC，所以A1C⊥AM，同理可证A1C⊥AN，又AM∩AN＝A，所以A1C⊥平面AMN.(2)以C 为原点，CD 所在直线为x 轴，CB 所在直线为y 轴，CC 1所在直线为z 轴，建立空间直角坐标系，因为AB ＝2，AD ＝2，A 1A ＝3，所以C (0,0,0)，A 1(2,2,3)，C 1(0,0,3)，CA 1→＝(2,2,3)，由(1)知CA 1⊥平面AMN ，故平面AMN 的一个法向量为CA 1→＝(2,2,3)．设线段AA 1上存在一点P (2,2，t )，使得C 1P ∥平面AMN ，则C 1P →＝(2,2，t －3)，因为C 1P ∥平面AMN ，所以C 1P →·CA 1→＝4＋4＋3t －9＝0，解得t ＝13.所以P ⎝⎛⎭⎪⎫2，2，13，所以线段AA 1上存在一点P ⎝ ⎛⎭⎪⎫2，2，13，使得C 1P ∥平面AMN .类型四、利用空间向量求空间角例4、如图35，在等腰直角三角形ABC 中，∠A ＝90°，BC ＝6，D ，E 分别是AC ，AB 上的点，CD ＝BE ＝2，O 为BC 的中点．将△ADE 沿DE 折起，得到如图(2)所示的四棱锥A ′BCDE ，其中A ′O ＝ 3.(1) (2)图35(1)证明：A ′O ⊥平面BCDE ；(2)求二面角A ′CD B 的平面角的余弦值．[思路探究] (1)利用勾股定理可证A ′O ⊥OD ，A ′O ⊥OE ，从而证得A ′O ⊥平面BCDE ；(2)用“三垂线”法作二面角的平面角后求解或用向量法求两个平面的法向量的夹角．【答案】(1)证明：由题意，得OC ＝3，AC ＝32，AD ＝2 2. 如图，连接OD ，OE ，在△OCD 中，由余弦定理，得OD ＝OC 2＋CD 2－2OC ·CD cos 45°＝ 5.由翻折不变性，知A ′D ＝22，所以A ′O 2＋OD 2＝A ′D 2，所以A ′O ⊥OD ．同理可证A ′O ⊥OE .又因为OD ∩OE ＝O ，所以A ′O ⊥平面BCDE .(2)如图，过点O 作OH ⊥CD 交CD 的延长线于点H ，连接A ′H .因为A ′O ⊥平面BCDE ，OH ⊥CD ，所以A ′H ⊥CD ．所以∠A ′HO 为二面角A ′CD B 的平面角．结合图(1)可知，H 为AC 的中点，故OH ＝322，从而A ′H ＝OH 2＋A ′O 2＝302. 所以cos ∠A ′HO ＝OH A ′H ＝155. 所以二面角A ′CD B 的平面角的余弦值为155. [规律方法] 用向量法求空间角的注意点(1)异面直线所成角：两异面直线所成角的范围为0°<θ≤90°，需找到两异面直线的方向向量，借助方向向量所成角求解．(2)直线与平面所成的角：要求直线a 与平面α所成的角θ，先求这个平面α的法向量n 与直线a 的方向向量a 夹角的余弦cos 〈n ，a 〉，易知θ＝〈n ，a 〉－π2或者π2－〈n ，a 〉．(3)二面角：如图36，有两个平面α与β，分别作这两个平面的法向量n 1与n 2，则平面α与β所成的角跟法向量n 1与n 2所成的角相等或互补，所以首先应判断二面角是锐角还是钝角．图36[跟踪训练]4．在如图37所示的圆台中，AC 是下底面圆O 的直径，EF 是上底面圆O ′的直径，FB是圆台的一条母线．图37(1)已知G ，H 分别为EC ，FB 的中点，求证：GH ∥平面ABC ． (2)已知EF ＝FB ＝12AC ＝23，AB ＝BC ，求二面角F BC A 的余弦值.【答案】 (1)证明：设CF 的中点为I ，连接GI ，HI .在△CEF 中，因为点G ，I 分别是CE ，CF 的中点，所以GI ∥EF .又EF ∥OB ，所以GI ∥OB ．在△CFB 中，因为H ，I 分别是FB ，CF 的中点，所以HI ∥BC ．又HI ∩GI ＝I ，BC ∩OB ＝B ，所以平面GHI ∥平面ABC ．因为GH ⊂平面GHI ，所以GH ∥平面ABC ．(2)连接OO ′，则OO ′⊥平面ABC ．又AB ＝BC ，且AC 是圆O 的直径，所以BO ⊥AC ．以O 为坐标原点，建立如图所示的空间直角坐标系．由题意得B (0,23，0)，C (－23，0,0)．过点F 作FM ⊥OB 于点M ，所以FM ＝FB 2－BM 2＝3，可得F (0，3，3)．11 故BC →＝(－23，－23，0)，BF →＝(0，－3，3)．设m ＝(x ，y ，z )是平面BCF 的法向量．由⎩⎪⎨⎪⎧m ·BC →＝0，m ·BF →＝0可得⎩⎨⎧ －23x －23y ＝0，－3y ＋3z ＝0.可得平面BCF 的一个法向量m ＝⎝ ⎛⎭⎪⎫－1，1，33.因为平面ABC 的一个法向量n ＝(0,0,1)，所以cos 〈m ，n 〉＝m ·n|m |·|n |＝77，所以二面角F BC A 的余弦值为77.。

(完整版)高中数学空间几何体知识点总结

空间几何体知识点总结一、空间几何体的结构特征1．柱、锥、台、球的结构特征由若干个平面多边形围成的几何体称之为多面体。

围成多面体的各个多边形叫叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做顶点。

把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体称之为旋转体，其中定直线称为旋转体的轴。

（1）柱棱柱：一般的，有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱；棱柱中两个互相平行的面叫做棱柱的底面，简称为底；其余各面叫做棱柱的侧面；相邻侧面的公共边叫做棱柱的侧棱；侧面与底面的公共顶点叫做棱柱的顶点。

底面是三角形、四边形、五边形……的棱柱分别叫做三棱柱、四棱柱、五棱柱……注：相关棱柱几何体系列（棱柱、斜棱柱、直棱柱、正棱柱）的关系：棱柱的性质：①侧棱都相等，侧面是平行四边形；②两个底面与平行于底面的截面是全等的多边形；③过不相邻的两条侧棱的截面是平行四边形；④直棱柱的侧棱长与高相等，侧面与对角面是矩形。

圆柱：以矩形的一边所在的直线为旋转轴，其余边旋转形成的曲面所围成的几何体叫做圆柱；旋转轴叫做圆柱的轴；垂直于轴的边旋转而成的曲面叫做圆柱的侧面；无论旋转到什么位置，不垂直于轴的边都叫做圆柱侧面的母线。

圆柱的性质：上、下底及平行于底面的截面都是等圆；过轴的截面（轴截面）是全等的矩形。

棱柱与圆柱统称为柱体；（2）锥棱锥：一般的有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥；这个多边形面叫做棱锥的底面或底；有公共顶点的各个三角形面叫做棱锥的侧面；各侧面的公共顶点叫做棱锥的顶点；相邻侧面的公共边叫做棱锥的侧棱。

底面是三角锥、四边锥、五边锥……的棱柱分别叫做三棱锥、四棱锥、五棱锥……正棱锥：如果有一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥。

注：棱锥的性质：①平行于底面的截面是与底面相似的正多边形，相似比等于顶点到截面的距离与顶点到底面的距离之比；②正棱锥各侧棱相等，各侧面是全等的等腰三角形；③正棱锥中六个元素，即侧棱、高、斜高、侧棱在底面内的射影、斜高在底面的射影、底面边长一半，构成四个直角三角形。

新课标人教A版高一数学必修二定理知识要点

第一章空间几何体1．2 空间几何体的三视图和直观图我们把一束平行光线照射下形成的投影，叫做平行投影.平行投影的投影线是平行的.在平行投影中，投影线正对着投影面时，叫做正投影，否则叫做斜投影.（a ）中心投影（b ）斜投影（c ）正投影正视图、侧视图、俯视图统称为三视图1.一个几何体的正视图和侧视图的高度一样；2.正视图与俯视图的长度一样；3.侧视图与俯视图宽度一样；定义：上述画水平放置的平面图形的直观图的方法叫做斜二测画法，有如下步骤和规则(1)在原图形中建立平面直角坐标系xoy ，同时建立直观图坐标系y o x '''，确定水平面，045='''∠y o x ； (2)与坐标轴平行的线段保持平行；（3）水平线段等长，竖直线段减半. 1．3 空间几何体的表面积与体积表中S 表示面积，C ’、C 分别表示上、下底面周长，h 表示高，h ’表示斜高，l 表示侧棱长。

表示l 、h 分别表示母线、高，r 表示圆柱、圆锥与球冠的底半径，r1、r2分别表示圆台上、下底面半径，R 表示半径。

第二章点、直线、平面之间的位置关. 2．1 空间点、直线、平面之间的位.平面特征：平面没有大小、厚薄和宽窄，几何里的平面是无限延展的.平面内有无数个点，平面可以看成点的集合. 点A 在平面α内，记作A ∈α；点B 在平面α外，记作B ∉α.直线 l 在平面α内表示为α⊂l ;直线l 不在平面α内表示为α⊄m . 公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内. 公理2：过不在一条直线上的三点，有且只有一个平面.公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.公理2 推论1：经过一条直线和这条直线外一点，有且只有一个平面。

公理2 推论2：经过两条相交直线，有且只有一个平面。

公理2 推论3：经过两条平行直线，有且只有一个平面。

新课标人教A版高中数学必修二空间几何体知识点总结

高中数学必修2空间几何体知识点总结1.1柱、锥、台、球的结构特征（1）棱柱：定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体。

分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。

表示：用各顶点字母，如五棱柱 ABCDE —AB 'CDE '或用对角线的端点字母，女口五棱柱AD '几何特征：两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形。

（2）棱锥定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示：用各顶点字母，如五棱锥P -A 'B 'C 'D 'E '几何特征：侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。

（3）棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示：用各顶点字母，如五棱台P -A 'B 'C 'D 'E '几何特征：①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点（4）圆柱：定义：以矩形的一边所在的直线为轴旋转，其余三边旋转所成的曲面所围成的几何体几何特征：①底面是全等的圆；②母线与轴平行；③轴与底面圆的半径垂直； ④侧面展开图是一个矩形。

（5）圆锥：定义：以直角三角形的一条直角边为旋转轴，旋转一周所成的曲面所围成的几何体几何特征：①底面是一个圆；②母线交于圆锥的顶点；③侧面展开图是一个扇形。

（6）圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的下底面部分几何特征：①上下底面是两个圆；②侧面母线交于原圆锥的顶点；③侧面展开图是一个弓形。

人教高中数学必修二A版《基本立体图形》立体几何初步说课复习(棱柱、棱锥、棱台的结构特征)

课件
课件课件
课件课件
课件课件
课件课件
栏目导引
第八章立体几何初步
在三棱锥
课件
课件
课件
课件
课件
课件
课件
个人简历：课件/j ia nli/
课件
课件
手抄报：课件/shouchaobao/
课件
课件课件
课件课件
课件课件
课件课件
课件
课件
A-BCD
中，可以当作棱锥底面的三角形的个数为
()
A．1
B．2
C．3
D．4
解析：选 D.每个面都可作为底面，有 4 个．
展开成平面图形
第八章立体几何初步
课件
课件
课件
课件
课件
课件
课件
个人简历：课件/j ia nli/
课件
课件
手抄报：课件/shouchaobao/
课件
课件课件
课件课件
课件课件
课件课件
课件
课件
问题导学
预习教材 P97－P100 的内容，思考以下问题： 1．空间几何体的定义是什么？ 2．空间几何体分为哪几类？ 3．常见的多面体有哪些？ 4．棱柱、棱锥、棱台有哪些结构特征？
课件课件
课件
课件
③棱台的侧棱所在直线均相交于同一点．
解析：棱锥是由棱柱的一个底面收缩为一个点而得到的几何体，因
而其侧面均是三角形，且所有侧面都有一个公共点，故①对．棱台
是棱锥被平行于底面的平面所截后，截面与底面之间的部分，因而
其侧面均是梯形，且所有的侧棱延长后均相交于一点(即原棱锥的顶
点)，故②错，③对．因而正确的有①③. 答案：①③

人教A版高中数学选择性必修第一册精品课件复习课第1课时空间向量与立体几何

(
)
(12)若向量n与直线l的方向向量垂直,A∈l,P∉l,则点P到直线l的距离可以
看成是在n上的投影向量的长度.(
)
(13)设直线l与平面α所成的角为θ,直线l的方向向量为u,平面α的法向量为
n,则cos θ=|cos<u,n>|. ( × )
专题归纳核心突破
专题一
空间向量的线性运算
提示:空间向量共线的充要条件:对任意两个空间向量a,b(b≠0),a∥b的充
要条件是存在实数λ,使a=λb.
空间向量共面的充要条件:如果两个向量a,b不共线,那么向量p与向量a,b
共面的充要条件是存在唯一的有序实数对(x,y),使p=xa+yb.
2.空间向量基本定理与空间向量的坐标表示的内容是什么?
模就越大.(
)
(3)不论λ取什么实数,λa与a一定共线.(
)
(4)若a·b=0,则a,b中至少有一个为0.( × )
(5)若 a·b=k,则

a= 或

b= .

( × )
(6)对于三个不共面向量a1,a2,a3,不存在实数组(λ1,λ2,λ3),使
λ1a1+λ2a2+λ3a3=0.( × )
(7)已知 A,B,M,N 是空间四点,若{, , }是空间的一个基底,则
(2)平面PAD内是否存在一点N,使MN⊥平面PBD?若存
在,确定N的位置;若不存在,说明理由.
分析:(1)证明向量垂直于平面 PAD 的一个法向量即可;
(2)假设存在点 N,设出其坐标,利用 ⊥ , ⊥ ,
列方程求其坐标即可.
解:以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角

人教高中数学必修二A版《空间直线、平面的平行》立体几何初步说课复习(直线与平面平行)

如果_平__面__外___一条直线与___此__平__面__内_______的一条直线__平__行____，那么该直线与此平面平行
符号语言 _a_⊄_α_，__b_⊂__α_，__且__a_∥__b__ ⇒a∥α
图形语言
栏目导引
第八章立体几何初步
■名师点拨课件
课件
课件
课件
课件
课件
课件
个人简历：课件/j ia nli/
课件
课件
手抄报：课件/shouchaobao/
课件
课件课件
课件课件
课件课件
课件课件
课件
课件
用该定理判断直线 a 和平面 α 平行时，必须同时具备三个条件：
(1)直线 a 在平面 α 外，即 a⊄α.
(2)直线 b 在平面 α 内，即 b⊂α.
(3)两直线 a，b 平行，即 a∥b.
栏目导引
栏目导引
第八章立体几何初步
解：过点 E 作 EG∥FD 交 AP 于点 G，连接 CG，连接 AC 交
BD 于点 O，
课件
课件
课件
课件
课件
课件
课件
个人简历：课件/j ia nli/
课件
课件
手抄报：课件/shouchaobao/
课件
课件课件
课件课件
课件课件
课件课件
课件
课件
连接
FO.
因为 EG∥FD，EG⊄平面 BDF，
课件
个人简历：课件/j ia nli/
课件
课件
手抄报：课件/shouchaobao/
课件
课件课件
课件课件
课件课件

高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

描述：例题：描述：高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征，能运用这些结构特征描述现实生活中简单物体的结构．二、知识清单典型空间几何体空间几何体的结构特征组合体展开图截面分析三、知识讲解1.典型空间几何体空间几何体的概念只考虑物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体．2.空间几何体的结构特征多面体由若干个平面多边形围成的几何体叫做多面体．围成多面体的各个多边形叫做多面体的面；相邻两个面的公共边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点；连接不在同一个面上的两个顶点的线段叫做多面体的对角线．按多面体的面数可把多面体分为四面体、五面体、六面体．其中，四个面均为全等的正三角形的四面体叫做正四面体．旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体．这条定直线叫做旋转体的轴．棱柱的结构特征一般地，有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱（prism）．棱柱中，两个互相平行的面叫做底面，简称底；其余各面叫做棱柱的侧面；相邻侧面的公共边叫做棱柱的侧棱；侧棱与底面的公共顶点叫做棱柱的用一个平行于棱锥底面的平面去截棱锥，得到两个几何体，一个是______，另一个是______．解：棱锥；棱台．⋯⋯余各面叫做棱柱的侧面；相邻侧面的公共边叫做棱柱的侧棱；侧棱与底面的公共顶点叫做棱柱的顶点．底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱，可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱，如下图的六棱柱可以表示为棱柱或棱柱．侧棱与底面不垂直的棱柱叫做斜棱柱；侧棱与底面垂直的棱柱叫做直棱柱；底面是正多边形的直棱柱叫做正棱柱；底面是平行四边形的棱柱叫做平行六面体；侧棱与底面垂直的平行六面体叫做直平行六面体．棱锥的结构特征一般地，有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥（pyramid）．这个多边形面叫做棱锥的底面或底；有公共顶点的各个三角形面叫做棱锥的侧面；各侧面的公共顶点叫做棱锥的顶点；相邻侧面的公共边叫做棱锥的侧棱．底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体．棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示，如下图的四棱锥表示为棱锥或者棱锥．棱锥的底面是正多边形，且它的顶点在过底面中心且与底面垂直的直线上，这个棱锥叫做正棱锥．正棱锥各侧面都是全等的等腰三角形，这些等腰三角形底边上的高都相等，叫做棱锥的斜高．⋯⋯⋯⋯ABCDEF−A′B′C′D′E′F′DA′⋯⋯⋯⋯S−ABCD S−AC棱台的结构特征用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分，这样的多面体叫做棱台（frustum of a pyramid）．原棱锥的底面和截面分别叫做棱台的下底面和上底面；其他各面叫做棱台的侧面；相邻两侧面的公共边叫做棱台的侧棱；两底面的距离叫做棱台的高．由正棱锥截得的棱台叫做正棱台，正棱台的各个侧面都是全等的等腰梯形，这些等腰梯形的高叫做棱台的斜高．圆柱的结构特征以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱（circular cylinder）．旋转轴叫做圆柱的轴；垂直于轴的边旋转而成的圆面叫做圆柱的底面；平行于轴的边旋转而成的曲面叫做圆柱的侧面；无论旋转到什么位置，不垂直于轴的边都叫做圆柱侧面的母线．圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥（circular cone）．圆台的结构特征例题：用平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做圆台（frustum of a cone）．棱台与圆台统称为台体．球的结构特征以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫做球体，简称球（solid sphere）．半圆的圆心叫做球的球心，半圆的半径叫做球的半径，半圆的直径叫做球的直径．球常用表示球心的字母表示．O下列命题中，正确的是（）A．有两个面互相平行，其余各面都是四边形的几何体叫棱柱B．棱柱中互相平行的两个面叫做棱柱的底面C．棱柱的侧面是平行四边形，而底面不是平行四边形D．棱柱的侧棱长相等，侧面是平行四边形解：D如图(1)，满足 A 选项条件，但不是棱柱；对于 B 选项，如图(2)，构造四棱柱，令四边形是梯形，可知，但这两个面不能作为棱柱的底面；C选项中，若棱柱是平行六面体，则它的底面是平行四边形．ABCD−A1B1C1D1ABCD面AB∥面DCB1A1C1D1若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是（）A．三棱锥 B．四棱锥 C．五棱锥 D．六棱锥解：D如下图，正六边形中，，那么正六棱锥中，，即侧棱长大于底面边长．ABCDEF OA=OB=⋯=AB S−ABCDEF SA>OA=AB描述：3.组合体简单组合体的构成有两种基本形式：一种是由简单几何体拼接而成，一种是由简单几何体截去或挖去一部分而成．如图所示的几何体中，是台体的是（）A．①② B．①③ C．③ D．②③解：C利用棱台的定义求解．①中各侧棱的延长线不能交于一点；②中的截面不平行于底面；③中各侧棱的延长线能交于一点且截面与底面平行．有下列四种说法：①圆柱是将矩形旋转一周所得的几何体；②以直角三角形的一直角边为旋转轴，旋转所得几何体是圆锥；③圆台的任意两条母线的延长线，可能相交也可能不相交；④半圆绕其直径所在直线旋转一周形成球．其中错误的有（）A．个 B．个 C．个 D．个解：D圆柱是矩形绕其一条边所在直线旋转形成的几何体，故①错；以直角三角形的一条直角边所在直线为轴，旋转一周，才能构成圆锥，②错；圆台是由圆锥截得，故其任意两条母线延长后一定交于一点，③错；半圆绕其直径所在直线旋转一周形成的是球面，故④错误．1234例题：描述：4.展开图空间形体的表面在平面上摊平后得到的图形，是画法几何研究的一项内容．描述图中几何体的结构特征．解：图（1）所示的几何体是由两个圆台拼接而成的组合体；图（2）所示的几何体是由一个圆台挖去一个圆锥得到的组合体；图（3）所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体．下图中的几何体是由哪个平面图形旋转得到的（）解：D）不在同一平面内的有______对．3内．解：C描述：例题：5.截面分析截面用平面截立体图形所得的封闭平面几何图形称为截面．平行截面、中截面与立体图形底面平行的截面称为平行截面，等分立体图形的高的平行截面称为中截面．轴截面包含立体图形的轴线的截面称为轴截面．球截面球的截面称为球截面．球的任意截面都是圆，其中通过球心的截面称为球的大圆，不过球心的截面称为球的小圆．球心与球的截面的圆心连线垂直于截面，并且有，其中为球的半径，为截面圆的半径，为球心到截面的距离．+=r 2d 2R 2R r d 下面几何体的截面一定是圆面的是（）A．圆台 B．球 C．圆柱 D．棱柱解：B如图所示，是一个三棱台，试用两个平面把这个三棱台分成三部分，使每一部分都是一个三棱锥．解：如图，过，，三点作一个平面，再过，，作一个平面，就把三棱台分成三部分，形成的三个三棱锥分别是，，．ABC −A ′B ′C ′A ′B C A ′B C ′ABC −A ′B ′C ′−ABC A ′−B B ′A ′C ′−BC A ′C ′如图，正方体中，，，分别是，，的中点，那么正方体中过点，，的截面形状是（）A．三角形 B．四边形 C．五边形 D．六边形ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P QR作截面图如图所示，可知是六边形．ii）若两平行截面在球心的两侧，如图(2)所示，则解：四、课后作业（查看更多本章节同步练习题，请到快乐学）答案：1.如图，能推断这个几何体可能是三棱台的是．A ．B ．C ．D ．C ()=2,AB =3,=3,BC =4A 1B 1B 1C 1=1,AB =2,=1.5,BC =3,=2,AC =3A 1B 1B 1C 1A 1C 1=1,AB =2,=1.5,BC =3,=2,AC =4A 1B 1B 1C 1A 1C 1AB =,BC =,CA =A 1B 1B 1C 1C 1A 1答案：2. 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北．现在沿该正方体的一些棱将正方体剪开、外面朝上展平，得到如图所示的平面图形，则标" "的面的方位是．A ．南B ．北C ．西D ．下B △()3. 向高为的水瓶中注水，注满为止，如果注水量与水深的函数关系的图象如图所示，那么水瓶的形状是．A ．H V h ()高考不提分，赔付1万元，关注快乐学了解详情。

2019新人教A版高中数学选择性必修一全册重点知识点归纳总结(复习必背)【可编辑全文】

2019新人教版高中数学选择性必修一全册重点知识点归纳总结（复习必背）第一章空间向量与立体几何一、知识要点1、空间向量的概念：在空间，我们把具有大小和方向的量叫做向量。

注：（1）向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量。

（2）向量具有平移不变性2、空间向量的运算定义：与平面向量运算一样，空间向量的加法、减法与数乘运算如下（如图）。

OB OA AB a b =+=+ ;BA OA OB a b =-=- ;()OP a R λλ=∈运算律：（1）加法交换律：a b b a +=+（2）加法结合律：)()(c b a c b a ++=++（3）数乘分配律：ba b aλλλ+=+)(运算法则：三角形法则、平行四边形法则、平行六面体法则3、共线向量（1）如果表示空间向量的有向线段所在的直线平行或重合，那么这些向量也叫做共线向量或平行向量，a 平行于b ，记作b a//。

（2）共线向量定理：空间任意两个向量a 、b （b ≠0 ），a //b 存在实数λ，使a＝λb 。

（3）三点共线：A 、B 、C 三点共线<=>ACAB λ=<=>OB y OA x OC +=（其中x +y =1）（4）与a 共线的单位向量为4、共面向量（1）定义：一般地，能平移到同一平面内的向量叫做共面向量。

说明：空间任意的两向量都是共面的。

（2）共面向量定理：如果两个向量,a b 不共线，p与向量,a b 共面的条件是存在实数x ，y 使p xa yb =+。

（3）四点共面：若A 、B 、C 、P 四点共面<=>ACy AB x AP +=<=>)1(=++++=z y x OC z OB y OA x OP 其中5、空间向量基本定理：如果三个向量,,a b c不共面，那么对空间任一向量p ，存在一个唯一的有序实数组,,x y z ，使p xa yb zc =++。

第8章立体几何初步章末知识梳理(教学课件)-高中数学人教A版(2019)必修第二册

又 MA∥PB 且 MA＝12PB， ∴PF∥MA 且 PF＝MA， ∴四边形 AFPM 是平行四边形， ∴AF∥PM. 又 AF⊄平面 PMD，PM⊂平面 PMD， ∴AF∥平面 PMD. 又 AF∩OF＝F，AF⊂平面 AFC，OF⊂平面 AFC， ∴平面 AFC∥平面 PMD.
【对点练习】❷ 如图，△ABC为正三角形，EC⊥平面 ABC，DB⊥平面ABC，CE＝CA＝2BD，M是EA的中点，N是EC 的中点，求证：平面DMN∥平面ABC.
第八章
立体几何初步
章末知识梳理
一、空间几何体的结构特征 1．多面体及其结构特征 (1)棱柱：①有两个平面(底面)互相平行；②其余各面都是平行四边形；③每相邻两个平行四边形的公共边互相平行. (2)棱锥：①有一个面(底面)是多边形； ②其余各面(侧面)是有一个公共顶点的三角形. (3)棱台：①上、下底面互相平行，且是相似图形；②各侧棱延长线相交于一点.
(3)判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直.
(4)性质定理：垂直于同一个平面的两条直线平行.
2．平面与平面垂直
(1)平面和平面垂直的定义：
两个平面相交，若所成的二面角是直二面角，则这两个平面垂直.
(2)判定定理：一个平面过另一个平面的垂线，则这两个平面互相垂直.
(2)性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒ 线线平行”).
2．平面与平面平行
(1)判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为“线面平行⇒面面平行”).
(2)性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行.

高中数学人教A版第八章立体几何初步知识梳理

第八章立体几何初步一、凸多面体的概念1、棱柱：两个面互相平面，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱．1）分类：斜棱柱：侧棱不垂直于底面的棱柱；直棱柱：侧棱垂直于底面的棱柱；正棱柱：底面是正多边形的直棱柱；2）常见几何体平行六面体：底面是平行四边形的棱柱；直平行六面体：侧棱垂直于底面的平行六面体；长方体：底面是矩形的直平行六面体；2、棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥．2）常见几何体正棱锥：底面是正多边形，且顶点在底面的射影是底面的中心；正四面体：所有棱长都相等的三棱锥．3、棱台：用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫做棱台，由正棱锥截得的棱台叫做正棱台．二、简单旋转体概念（圆柱、圆锥、圆台、球）1、圆柱：以矩形的一边所在的直线为旋转轴，其余三边旋转形成的面所围成的几何体叫做圆柱．2、圆柱：以直角三角形的一条直角边所在的直线为旋转轴，将其旋转一周形成的面所围成的几何体叫做圆锥．3、圆台：用平行于圆锥底面的平面去截圆锥，底面和截面之间的部分叫做圆台．4、球：以半圆的直径所在的直线为旋转轴，半圆面旋转一周形成的旋转体叫做球体，简称为球（球面距离：经过两点的大圆在这两点间的劣弧长度）．三、常见几何体的表面积与体积计算公式表面积公式表面积柱体2直棱柱底=+S ch S2(斜棱柱底''=+S c l S c为直截面周长)2222()圆锥=+=+S r rl r r lπππ一、知识点明晰体积公式四、空间几何体的直观图1、斜二测画法（主要步骤如下）1）建立直角坐标系．在已知水平放置的平面图形中取互相垂直的Ox ，Oy ，建立直角坐标系． 2）画出斜坐标系．在画直观图的纸上（平面上）画出对应图形．在已知图形平行于x 轴的线段，在直观图中画成平行于''O x ，''O y ，使45'''∠=x O y （或135），它们确定的平面表示水平平面．3）画出对应图形．在已知图形平行于x 轴的线段，在直观图中画成平行于'x 轴的线段，且长度保持不变；在已知图形平行于y轴的线段，在直观图中画成平行于'y轴，且长度变为原来的一般．可简化为“横不变，纵减半”．4）擦去辅助线．图画好后，要擦去'x轴、'y轴及为画图添加的辅助线（虚线）．被挡住的棱画虚线．2、常用结论：1）直观图和平面图形的面积比为S=原直。

新教材人教A版高中数学必修第二册第八章立体几何初步知识点汇总及解题规律方法提炼

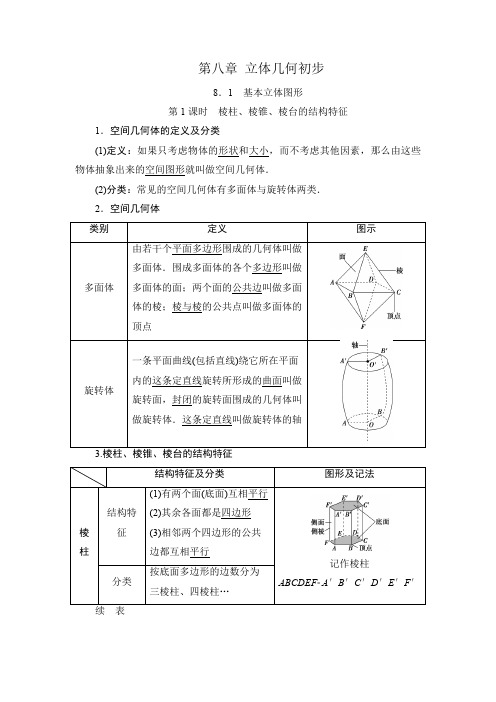
第八章立体几何初步8．1基本立体图形第1课时棱柱、棱锥、棱台的结构特征1．空间几何体的定义及分类(1)定义：如果只考虑物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体．(2)分类：常见的空间几何体有多面体与旋转体两类．2．空间几何体记作棱柱ABCDEFA′B′C′D′E′F′记作棱锥SABCD按底面多边形的边数分为三棱锥、记作棱台ABCDA′B′C′D′得的棱台分别为三棱台、四棱台、(1)棱柱、棱锥、棱台的关系在运动变化的观点下，棱柱、棱锥、棱台之间的关系可以用下图表示出来(以三棱柱、三棱锥、三棱台为例)．(2)各种棱柱之间的关系①棱柱的分类棱柱⎩⎨⎧直棱柱⎩⎨⎧正棱柱（底面为正多边形）一般的直棱柱斜棱柱②常见的几种四棱柱之间的转化关系典型应用1棱柱的结构特征下列关于棱柱的说法：①所有的面都是平行四边形；②每一个面都不会是三角形；③两底面平行，并且各侧棱也平行；④被平面截成的两部分可以都是棱柱．其中正确说法的序号是__________．【解析】①错误，棱柱的底面不一定是平行四边形；②错误，棱柱的底面可以是三角形；③正确，由棱柱的定义易知；④正确，棱柱可以被平行于底面的平面截成两个棱柱，所以正确说法的序号是③④.【答案】③④棱柱结构特征的辨析技巧(1)扣定义：判定一个几何体是否是棱柱的关键是棱柱的定义．①看“面”，即观察这个多面体是否有两个互相平行的面，其余各面都是四边形；②看“线”，即观察每相邻两个四边形的公共边是否平行．(2)举反例：通过举反例，如与常见几何体或实物模型、图片等不吻合，给予排除．典型应用2棱锥、棱台的结构特征下列关于棱锥、棱台的说法：①用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；②棱台的侧面一定不会是平行四边形；③棱锥的侧面只能是三角形；④由四个面围成的封闭图形只能是三棱锥；⑤棱锥被平面截成的两部分不可能都是棱锥．其中正确说法的序号是________．【解析】①错误，若平面不与棱锥底面平行，用这个平面去截棱锥，棱锥底面和截面之间的部分不是棱台．②正确，棱台的侧面一定是梯形，而不是平行四边形．③正确，由棱锥的定义知棱锥的侧面只能是三角形．④正确，由四个面围成的封闭图形只能是三棱锥．⑤错误，如图所示四棱锥被平面截成的两部分都是棱锥．所以正确说法的序号为②③④.【答案】②③④判断棱锥、棱台形状的两种方法(1)举反例法结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确．(2)直接法棱锥棱台定底面只有一个面是多边形，此面即为底面两个互相平行的面，即为底面看侧棱相交于一点延长后相交于一点空间几何体的平面展开图(1)水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的平面展开图(图中数字写在正方体的外表面上)，若图中的“2”在正方体的上面，则这个正方体的下面是()A．1 B．9C．快D．乐(2)如图是三个几何体的侧面展开图，请问各是什么几何体？【解】(1)选B.由题意，将正方体的展开图还原成正方体，“1”与“乐”相对，“2”与“9”相对，“0”与“快”相对，所以下面是“9”．(2)题图①中，有5个平行四边形，而且还有两个全等的五边形，符合棱柱的特点；题图②中，有5个三角形，且具有共同的顶点，还有一个五边形，符合棱锥的特点；题图③中，有3个梯形，且其腰的延长线交于一点，还有两个相似的三角形，符合棱台的特点，把侧面展开图还原为原几何体，如图所示：所以①为五棱柱，②为五棱锥，③为三棱台．多面体展开图问题的解题策略(1)绘制展开图：绘制多面体的平面展开图要结合多面体的几何特征，发挥空间想象能力或者是亲手制作多面体模型．在解题过程中，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面，便可得到其平面展开图．(2)由展开图复原几何体：若是给出多面体的平面展开图，来判断是由哪一个多面体展开的，则可把上述过程逆推，同一个几何体的平面展开图可能是不一样的，也就是说，一个多面体可有多个平面展开图．圆柱、圆锥、圆台、球、简单组合体的结构特征1．圆柱、圆锥、圆台和球的结构特征(1)圆柱的结构特征(1)圆柱有无数条母线，它们平行且相等．(2)平行于底面的截面是与底面大小相同的圆，如图1所示．(3)过轴的截面(轴截面)都是全等的矩形，如图2所示．(4)过任意两条母线的截面是矩形，如图3所示．(2)圆锥的结构特征(1)圆锥有无数条母线，它们有公共点即圆锥的顶点，且长度相等．(2)平行于底面的截面都是圆，如图1所示．(3)过轴的截面是全等的等腰三角形，如图2所示．(4)过任意两条母线的截面是等腰三角形，如图3所示．(3)圆台的结构特征(1)圆台有无数条母线，且长度相等，延长后相交于一点．(2)平行于底面的截面是圆，如图1所示．(3)过轴的截面是全等的等腰梯形，如图2所示．(4)过任意两条母线的截面是等腰梯形，如图3所示．(4)球的结构特征(1)球心和截面圆心的连线垂直于截面．(2)球心到截面的距离d与球的半径R及截面圆的半径r有如下关系：r＝R2－d2.2．简单组合体(1)概念由简单几何体组合而成的几何体叫做简单组合体．(2)两种构成形式①由简单几何体拼接而成；②由简单几何体截去或挖去一部分而成．典型应用1圆柱、圆锥、圆台、球的概念(1)给出下列说法：①圆柱的底面是圆面；②经过圆柱任意两条母线的截面是一个矩形面；③圆台的任意两条母线的延长线可能相交，也可能不相交；④夹在圆柱的两个截面间的几何体还是一个旋转体．其中说法正确的是________．(2)给出以下说法：①球的半径是球面上任意一点与球心所连线段的长；②球的直径是球面上任意两点间所连线段的长；③用一个平面截一个球，得到的截面可以是一个正方形；④过圆柱轴的平面截圆柱所得截面形状是矩形．其中正确说法的序号是________．【解析】(1)①正确，圆柱的底面是圆面；②正确，如图所示，经过圆柱任意两条母线的截面是一个矩形面；③不正确，圆台的母线延长相交于一点；④不正确，圆柱夹在两个平行于底面的截面间的几何体才是旋转体．(2)根据球的定义知，①正确；②不正确，因为球的直径必过球心；③不正确，因为球的任何截面都是圆面；④正确．【答案】(1)①②(2)①④(1)判断简单旋转体结构特征的方法①明确由哪个平面图形旋转而成；②明确旋转轴是哪条直线．(2)简单旋转体的轴截面及其应用①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量；②在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想．典型应用2简单组合体的结构特征如图所示的几何体是由下面哪一个平面图形旋转而形成的()【解析】该几何体自上而下由圆锥、圆台、圆台、圆柱组合而成，故应选A.【答案】A[变条件、变问法]若将本例选项B中的平面图形旋转一周，试说出它形成的几何体的结构特征．解：①是直角三角形，旋转后形成圆锥；②是直角梯形，旋转后形成圆台；③是矩形，旋转后形成圆柱，所以旋转后形成的几何体如图所示．通过观察可知，该几何体是由一个圆锥、一个圆台和一个圆柱自上而下拼接而成的．不规则平面图形旋转形成几何体的结构特征的分析策略(1)分割：首先要对原平面图形适当分割，一般分割成矩形、梯形、三角形或圆(半圆或四分之一圆)等基本图形．(2)定形：然后结合圆柱、圆锥、圆台、球的形成过程进行分析．典型应用3旋转体中的计算问题如图所示，用一个平行于圆锥SO底面的平面截这个圆锥，截得圆台上、下底面的面积之比为1∶16，截去的圆锥的母线长是3 cm，求圆台O′O的母线长．【解】设圆台的母线长为l cm，由截得的圆台上、下底面面积之比为1∶16，可设截得的圆台的上、下底面的半径分别为r cm，4r cm.过轴SO作截面，如图所示，则△SO′A′∽△SOA，SA′＝3 cm.所以SA′SA＝O′A′OA，所以33＋l＝r4r＝14.解得l＝9，即圆台O′O的母线长为9 cm.解决旋转体中计算问题的方法用平行于底面的平面去截柱、锥、台等几何体，注意抓住截面的性质(与底面全等或相似)，同时结合旋转体中的轴截面(经过旋转轴的截面)的几何性质，利用相似三角形中的相似比，列出相关几何变量的方程(组)而解得．[注意]在研究与截面有关的问题时，要注意截面与物体的相对位置的变化．由于相对位置的改变，截面的形状也会随之发生变化．8．2立体图形的直观图1．用斜二测画法画水平放置的平面图形的直观图的步骤(1)建系：在已知图形中取互相垂直的x轴和y轴，两轴相交于点O.画直观图时，把它们画成对应的x′轴与y′轴，两轴交于点O′，且使∠x′O′y′＝45°(或135°)，它们确定的平面表示水平面．(2)平行不变：已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴或y′轴的线段．(3)长度规则：已知图形中平行于x轴的线段，在直观图中保持原长度不变，平行于y轴的线段，长度为原来的一半．2．空间几何体直观图的画法(1)与平面图形的直观图画法相比多了一个z轴，直观图中与之对应的是z′轴．(2)直观图中平面x′O′y′表示水平平面，平面y′O′z′和x′O′z′表示竖直平面．(3)已知图形中平行于z轴(或在z轴上)的线段，在其直观图中平行性和长度都不变．(4)成图后，去掉辅助线，将被遮挡的部分改为虚线.■名师点拨(1)画水平放置的平面图形的直观图，关键是确定多边形顶点的位置，借助于平面直角坐标系确定顶点后，只需把这些顶点顺次连接即可．(2)用斜二测画法画直观图要掌握水平长不变，垂线长减半，直角画45°(或135°)．典型应用1画水平放置的平面图形的直观图画水平放置的直角梯形的直观图，如图所示．【解】(1)在已知的直角梯形OBCD中，以底边OB所在直线为x轴，垂直于OB的腰OD所在直线为y轴建立平面直角坐标系．如图①所示．(2)画相应的x′轴和y′轴，使∠x′O′y′＝45°，在x′轴上截取O′B′＝OB，在y′轴上截取O′D′＝12OD，过点D′作x′轴的平行线l，在l上沿x′轴正方向取点C′使得D′C′＝DC.连接B′C′，如图②.(3)所得四边形O′B′C′D′就是直角梯形OBCD的直观图．如图③.画水平放置的平面图形的直观图的关键及注意事项(1)在画水平放置的平面图形的直观图时，选取适当的直角坐标系是关键，一般要使平面多边形尽可能多的顶点在坐标轴上或边与坐标轴平行，以便于画图．(2)画图时要注意原图和直观图中线段的长度的关系是否发生变化．典型应用2画简单几何体的直观图已知一个正四棱台的上底面边长为2，下底面边长为6，高为4，用斜二测画法画出此正四棱台的直观图．【解】(1)画轴．如图①，画x轴、y轴、z轴，三轴相交于点O，使∠xOy ＝45°，∠xOz＝90°.(2)画下底面．以O为中点，在x轴上取线段EF，使得EF＝6，在y轴上取线段GH，使得GH＝3，再过G，H分别作AB綊EF，CD綊EF，且使得AB的中点为G，CD的中点为H，连接AD，BC，这样就得到了正四棱台的下底面ABCD 的直观图．(3)画上底面．在z轴上截取线段OO1＝4，过O1作O1x′∥Ox，O1y′∥Oy，使∠x′O1y′＝45°，建立坐标系x′O1y′，在x′O1y′中仿照(2)的步骤画出上底面A1B1C1D1的直观图．(4)连接AA1、BB1、CC1、DD1，擦去辅助线，得到的图形就是所求的正四棱台的直观图(如图②)．画空间图形的直观图的原则(1)用斜二测画法画空间图形的直观图时，图形中平行于x 轴、y 轴、z 轴的线段在直观图中应分别画成平行于x ′轴、y ′轴、z ′轴的线段．(2)平行于x 轴、z 轴的线段在直观图中长度保持不变，平行于y 轴的线段长度变为原来的12.典型应用3直观图的还原与计算如图所示，梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图．若A 1D 1∥O ′y ′，A 1B 1∥C 1D 1，A 1B 1＝23C 1D 1＝2，A 1D 1＝O ′D 1＝1.试画出原四边形，并求原图形的面积．【解】如图，建立直角坐标系xOy ，在x 轴上截取OD ＝O ′D 1＝1，OC ＝O ′C 1＝2.在过点D 与y 轴平行的直线上截取DA ＝2D 1A 1＝2.在过点A 与x 轴平行的直线上截取AB ＝A 1B 1＝2.连接BC ，便得到了原图形(如图)．由作法可知，原四边形ABCD 是直角梯形，上、下底长度分别为AB ＝2，CD ＝3，直角腰长度为AD ＝2.所以面积为S ＝2＋32×2＝5.(1)直观图的还原技巧由直观图还原为平面图的关键是找与x ′轴、y ′轴平行的直线或线段，且平行于x ′轴的线段还原时长度不变，平行于y ′轴的线段还原时放大为直观图中相应线段长的2倍，由此确定图形的各个顶点，顺次连接即可．(2)直观图与原图面积之间的关系若一个平面多边形的面积为S ，其直观图的面积为S ′，则有S ′＝24S 或S ＝22S ′.利用这一公式可由原图形面积求其直观图面积或由直观图面积求原图形面积．柱、锥、台的表面积和体积1．棱柱、棱锥、棱台的表面积多面体的表面积就是围成多面体各个面的面积的和．棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和．2．棱柱、棱锥、棱台的体积(1)V棱柱＝Sh；(2)V棱锥＝13Sh；V棱台3S′，S分别是棱台的上、下底面面积，h为棱台的高．3．圆柱、圆锥、圆台的表面积和体积1．柱体、锥体、台体的体积(1)柱体：柱体的底面面积为S ，高为h ，则V ＝Sh . (2)锥体：锥体的底面面积为S ，高为h ，则V ＝13Sh .(3)台体：台体的上、下底面面积分别为S ′、S ，高为h ，则V ＝13()S ′＋SS ′＋S h .2．圆柱、圆锥、圆台的侧面积公式之间的关系 S 圆柱侧＝2πrl ――→r ′＝r S 圆台侧＝π(r ′＋r )l ――→r ′＝0S 圆锥侧＝πrl . 3．柱体、锥体、台体的体积公式之间的关系V 柱体＝Sh ――→S ′＝S V 台体＝13(S ′＋S ′S ＋S )h ――→S ′＝0V 锥体＝13Sh . 典型应用1柱、锥、台的表面积(1)若圆锥的正视图是正三角形，则它的侧面积是底面积的( ) A.2倍 B ．3 倍 C ．2 倍D ．5 倍(2)已知正方体的 8 个顶点中，有 4 个为侧面是等边三角形的三棱锥的顶点，则这个三棱锥与正方体的表面积之比为( )A ．1∶ 2B ．1∶3C ．2∶ 2D ．3∶6(3)已知某圆台的一个底面周长是另一个底面周长的 3 倍，母线长为 3 ，圆台的侧面积为 84π，则该圆台较小底面的半径为( )A ．7B ．6C ．5D ．3【解析】 (1)设圆锥的底面半径为 r ，母线长为 l ，则由题意可知，l ＝2r ，于是 S 侧＝πr ·2r ＝2πr 2，S 底＝πr 2，可知选 C.(2)棱锥 B ′ACD ′为适合条件的棱锥，四个面为全等的等边三角形，设正方体的棱长为 1，则 B ′C ＝2，S △B ′AC ＝32.三棱锥的表面积 S 锥＝4×32＝23，又正方体的表面积S正＝6.因此S锥∶S正＝23∶6＝1∶ 3.(3)设圆台较小底面的半径为r，则另一底面的半径为3r.由S侧＝3π(r＋3r)＝84π，解得r＝7.【答案】(1)C (2)B (3)A空间几何体表面积的求法技巧(1)多面体的表面积是各个面的面积之和．(2)组合体的表面积应注意重合部分的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展开为平面图形计算，而表面积是侧面积与底面圆的面积之和．典型应用2柱、锥、台的体积如图所示，正方体ABCDA1B1C1D1的棱长为a，过顶点B，D，A1截下一个三棱锥．(1)求剩余部分的体积；(2)求三棱锥AA1BD的体积及高．【解】(1)V三棱锥A1ABD＝13S△ABD·A1A＝13×12·AB·AD·A1A＝16a3.故剩余部分的体积V＝V正方体－V三棱锥A1ABD＝a3－16a3＝56a3.(2)V三棱锥AA1BD＝V三棱锥A1ABD＝1 6a 3.设三棱锥AA1BD的高为h，则V三棱锥AA1BD＝13·S△A1BD·h＝13×12×32(2a)2h＝36a2h，故36a2h＝16a3，解得h＝3 3a.求几何体体积的常用方法(1)公式法：直接代入公式求解．(2)等积法：例如四面体的任何一个面都可以作为底面，只需选用底面积和高都易求的形式即可．(3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，棱台补成棱锥等．(4)分割法：将几何体分割成易求解的几部分，分别求体积．[提醒]求几何体的体积时，要注意利用好几何体的轴截面(尤其为圆柱、圆锥时)，准确求出几何体的高和底面积．典型应用3组合体的表面积和体积如图在底面半径为2，母线长为 4 的圆锥中内接一个高为3的圆柱，求圆柱的表面积．【解】设圆锥的底面半径为R，圆柱的底面半径为r，表面积为S.则R＝OC＝2，AC＝4，AO＝42－22＝2 3.如图所示，易知△AEB∽△AOC，所以AEAO＝EBOC，即323＝r2，所以r＝1，S 底＝2πr 2＝2π，S 侧＝2πr ·h ＝23π. 所以 S ＝S 底＋S 侧＝2π＋23π ＝(2＋23)π.1．[变问法]本例中的条件不变，求圆柱的体积与圆锥的体积之比．解：由例题解析可知：圆柱的底面半径为 r ＝1，高 h ＝3，所以圆柱的体积 V 1＝πr 2h ＝π×12×3＝3π.圆锥的体积 V 2＝13π×22×23＝833π. 所以圆柱与圆锥的体积比为 3∶8.2．[变问法]本例中的条件不变，求图中圆台的表面积与体积．解：由例题解析可知：圆台的上底面半径 r ＝1，下底面半径 R ＝2，高 h ＝3，母线 l ＝2，所以圆台的表面积 S ＝π(r 2＋R 2＋r ·l ＋Rl )＝π(12＋22＋1×2＋2×2)＝11π.圆台的体积 V ＝13π(r 2＋rR ＋R 2)h ＝13π(12＋2＋22)×3＝733π.3．[变条件、变问法]本例中的“高为3”改为“高为 h ”，试求圆柱侧面积的最大值．解：设圆锥的底面半径为 R ，圆柱的底面半径为 r ，则 R ＝OC ＝2，AC ＝4， AO ＝42－22＝2 3.如图所示易知△AEB ∽△AOC ，所以AE AO ＝EB OC ，即23－h 23＝r2，所以 h ＝23－3r ，S 圆柱侧＝2πrh ＝2πr (23－3r ) ＝－23πr 2＋43πr ，所以当 r ＝1，h ＝3时，圆柱的侧面积最大，其最大值为 23π.求组合体的表面积与体积的步骤(1)分析结构特征：弄清组合体的组成形式，找准有关简单几何体的关键量．(2)设计计算方法：根据组成形式，设计计算方法，特别要注意“拼接面”面积的处理，利用“切割”“补形”的方法求体积．(3)计算求值：根据设计的计算方法求值．球的体积和表面积1．球的表面积设球的半径为R，则球的表面积S＝4πR2．2．球的体积设球的半径为R，则球的体积V＝43πR3．■名师点拨对球的体积和表面积的几点认识(1)从公式看，球的表面积和体积的大小，只与球的半径相关，给定R都有唯一确定的S和V与之对应，故表面积和体积是关于R的函数．(2)由于球的表面不能展开成平面，所以，球的表面积公式的推导与前面所学的多面体与旋转体的表面积公式的推导方法是不一样的．(3)球的表面积恰好是球的大圆(过球心的平面截球面所得的圆)面积的4倍．典型应用1球的表面积与体积(1)已知球的体积是32π3，则此球的表面积是()A．12πB．16πC.16π3 D.64π3(2)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径，若该几何体的体积是28π3，则它的表面积是()A．17πB．18πC．20πD．28π【解析】(1)设球的半径为R，则由已知得V＝43πR3＝32π3，解得R＝2.所以球的表面积S＝4πR2＝16π.(2)由三视图可得此几何体为一个球切割掉18后剩下的几何体，设球的半径为r，故78×43πr3＝283π，所以r＝2，表面积S＝78×4πr2＋34πr2＝17π，选A.【答案】(1)B(2)A球的体积与表面积的求法及注意事项(1)要求球的体积或表面积，必须知道半径R或者通过条件能求出半径R，然后代入体积或表面积公式求解．(2)半径和球心是球的最关键要素，把握住了这两点，计算球的表面积或体积的相关题目也就易如反掌了．典型应用2球的截面问题如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器厚度，则球的体积为()A.500π3cm3 B.866π3cm3C.1 372π3cm 3D.2 048π3cm 3【解析】如图，作出球的一个截面，则MC ＝8－6＝2(cm)， BM ＝12AB ＝12×8＝4(cm)．设球的半径为R cm ，则 R 2＝OM 2＋MB 2 ＝(R －2)2＋42，所以R ＝5，所以V 球＝43π×53＝5003π (cm 3)．【答案】 A球的截面问题的解题技巧(1)有关球的截面问题，常画出过球心的截面圆，将问题转化为平面中圆的问题．(2)解题时要注意借助球半径R ，截面圆半径r ，球心到截面的距离d 构成的直角三角形，即R 2＝d 2＋r 2.典型应用3与球有关的切、接问题角度一球的外切正方体问题将棱长为 2 的正方体木块削成一个体积最大的球，则该球的体积为( )A.4π3B.2π3C.3π2D.π6【解析】由题意知，此球是正方体的内切球，根据其几何特征知，此球的直径与正方体的棱长是相等的，故可得球的直径为 2，故半径为 1，其体积是43×π×13＝4π3.【答案】 A角度二球的内接长方体问题一个长方体的各个顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1，2，3，则此球的表面积为________．【解析】长方体外接球直径长等于长方体体对角线长，即2R＝12＋22＋32＝14，所以球的表面积S＝4πR2＝14π.【答案】14π角度三球的内接正四面体问题若棱长为a的正四面体的各个顶点都在半径为R的球面上，求球的表面积．【解】把正四面体放在正方体中，设正方体棱长为x，则a＝2x，由题意2R＝3x＝3×2a2＝62a，所以S球＝4πR2＝32πa2.角度四球的内接圆锥问题球的一个内接圆锥满足：球心到该圆锥底面的距离是球半径的一半，则该圆锥的体积和此球体积的比值为________．【解析】①当圆锥顶点与底面在球心两侧时，如图所示，设球半径为r，则球心到该圆锥底面的距离是r2，于是圆锥的底面半径为r2－⎝⎛⎭⎪⎫r22＝3r2，高为3r 2.该圆锥的体积为13×π×⎝⎛⎭⎪⎫3r22×3r2＝38πr3，球体积为43πr3，所以该圆锥的体积和此球体积的比值为38πr343πr3＝932.②同理，当圆锥顶点与底面在球心同侧时，该圆锥的体积和此球体积的比值为332.【答案】 932或332角度五球的内接直棱柱问题设三棱柱的侧棱垂直于底面，所有棱的长都为 a ，顶点都在一个球面上，则该球的表面积为( )A ．πa 2 B.73πa 2 C.113πa 2D ．5πa 2【解析】由题意知，该三棱柱为正三棱柱，且侧棱与底面边长相等，均为 a ．如图，P 为三棱柱上底面的中心，O 为球心，易知 AP ＝23×32a ＝33a ，OP ＝12a ，所以球的半径 R ＝ OA 满足R 2＝⎝ ⎛⎭⎪⎫33a 2＋⎝ ⎛⎭⎪⎫12a 2＝712a 2，故 S 球＝4πR 2＝73πa 2.【答案】 B(1)正方体的内切球球与正方体的六个面都相切，称球为正方体的内切球，此时球的半径为 r 1＝a2，过在一个平面上的四个切点作截面如图(1)．(2)长方体的外接球长方体的八个顶点都在球面上，称球为长方体的外接球，根据球的定义可知，长方体的体对角线是球的直径，若长方体过同一顶点的三条棱长为 a ，b ，c ，过球心作长方体的对角线，则球的半径为 r 2＝12a 2＋b 2＋c 2，如图(2)．(3)正四面体的外接球正四面体的棱长a与外接球半径R的关系为：2R＝6 2a.8．4.1平面1．平面(1)平面的概念几何里所说的“平面”，是从课桌面、黑板面、海面这样的一些物体中抽象出来的．平面是向四周无限延展的．(2)平面的画法我们常用矩形的直观图，即平行四边形表示平面．当水平放置时，常把平行四边形的一边画成横向；当平面竖直放置时，常把平行四边形的一边画成竖向．(3)平面的表示方法我们常用希腊字母α，β，γ等表示平面，如平面α、平面β、平面γ等，并将它写在代表平面的平行四边形的一个角内；也可以用代表平面的平行四边形的四个顶点，或者相对的两个顶点的大写英文字母作为这个平面的名称．如图中的平面α，也可以表示为平面ABCD、平面AC或者平面BD．■名师点拨(1)平面和点、直线一样，是只描述而不加定义的原始概念，不能进行度量．(2)平面无厚薄、无大小，是无限延展的．2．点、线、面之间的关系及符号表示A是点，l，m是直线，α，β是平面．从集合的角度理解点、线、面之间的关系(1)直线可以看成无数个点组成的集合，故点与直线的关系是元素与集合的关系，用“∈”或“∉”表示．(2)平面也可以看成点集，故点与平面的关系也是元素与集合的关系，用“∈”或“∉”表示．(3)直线与平面都是点集，它们之间的关系可看成集合与集合的关系，故用“⊂”或“⊄”表示．3．平面的性质在画两个相交平面时，如果其中一个平面的一部分被另一个平面挡住，通常把被挡住的部分画成虚线或不画，这样可使画出的图形立体感更强一些．如下图①，图②所示：4．平面性质的三个推论推论1经过一条直线和这条直线外一点，有且只有一个平面．如图(1)．推论2经过两条相交直线，有且只有一个平面．如图(2)．推论3经过两条平行直线，有且只有一个平面．如图(3)．典型应用1图形、文字、符号语言的相互转化(1)用符号语言表示下面的语句，并画出图形．平面ABD与平面BDC交于BD，平面ABC与平面ADC交于AC.(2)将下面用符号语言表示的关系用文字语言予以叙述，并用图形语言予以表示．α∩β＝l，A∈l，AB⊂α，AC⊂β.【解】(1)符号语言表示：平面ABD∩平面BDC＝BD，平面ABC∩平面ADC＝AC.用图形表示如图①所示．(2)文字语言叙述为：点A在平面α与平面β的交线l上，直线AB，AC分别在平面α，β内，图形语言表示如图②所示．。

高中数学立体几何知识点总结新人教A版选修2

第三章空间向量与立体几何一、空间向量1.在空间既有，又有的量叫空间向量.空间向量用表示. 平行四边形法则和三角形法则例如：1.若a 与b 共线，b 与共c 线，则a 与c 共线 ( )2.已知A(1,2，-3)，B （3，-4,5），向量AB 按照 =（-1,2,4）平移后得到向量AB 为 .3.化简=+-MN PN PM . =+++ .4.在长方体AC 1中，化简=-+-+-B A B A B B C B DB DA 11111 .在空间四边形ABCD 中，M ，G 分别是BC ，CD 的中点，则)(21BC BD AB ++= .二、两个向量共线,共面1.非零向量21,e e 不共线，若21e e k +与21e k e +共线，则k ＝______．2.若O 为直线MN 外一点，且 ON OM OP μλ+=，若P,M,N 共线，则μλ+= 。

3.已知A 、B 、C 三点不共线，对平面ABC 外任一点O ，有OM 414321-+=，则A 、B 、C 、M ______(共面、不共面)4.已知A 、B 、C 、D 四点满足任三点不共线，但四点共面，且O 是平面ABCD 外一点，.432,432=++⋅+⋅+⋅=z y x DO z CO y BO x OA .三、空间基底及应用平面内，不共线的两个非0向量可以作为一组基底；空间中，不共面的三个非0向量可以作为一组基底。

设x=a+b,y=b+c,z=c+a,且a,b,c 是空间的一个基底，给出下列向量：（1）a,b,x (2)x,y,z (3)b,c,z (4)x,y,a+b+c 其中可以作为空间基底的为 . ⒈已知平行六面体ABCD －A 1B 1C 1D 1，若,3211C z y x AC ++=则x ＋y ＋z ＝( )A ．1B ．67 C ．65 D ．322.平行六面体OABC －O ′A ′B ′C ′中，设,,,O ='==G 为BC ′的中点，用a ，b ，c 表示向量OG ，则OG ＝ .3.设A 、B 、C 、D 是空间不共面的四点，且满足0,0,0===⋅⋅⋅AD AB AD AC AC AB ，则△BCD 是( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定4.已知平行六面体ABCD －A 1B 1C 1D 1中，以顶点A 为端点的三条棱长都等于1，且两两夹角是60°，则对角线AC 1的长是______，=⋅11BD AC .5.已知空间四边形ABCD 中，AB ⊥CD,AC ⊥BD,则<⋅>= . 四、向量的直角坐标运算：设a ＝123(,,)a a a ，b ＝123(,,)b b b ，则⑴a ＋b ＝； ⑵a －b ＝； ⑶λa ＝ ()R λ∈； ⑷a ·b ＝ . 两个向量共线或垂直的判定：设a ＝123(,,)a a a ，b ＝123(,,)b b b ，则 ⑴ a //b ⇔a ＝λb ⇔ ； ⑵ a ⊥b ⇔a ·b =0⇔ ．向量的模：设a ＝123(,,)a a a ，｜a ｜＝.（5）向量在空间直角坐标系中的坐标的求法：设A 111(,,)x y z ，B 222(,,)x y z ，则AB ＝OA OB -＝222(,,)x y z －111(,,)x y z ＝这个公式的几何意义是表示长方体的对角线的长度．在空间直角坐标系中，已知点111(,,)A x y z ，222(,,)B x y z ，则A B d =、A B d 、表示A 与B 两点间的距离．已知△ABC 的三个顶点为A （3，3，2），B （4，－3，7），C （0，5，1），则BC 边上的中线长为（）A ．2B ．3C ．4D ．5五、向量的数量积a ·b ＝ = .由此可以得出：cos ＜a ,b ＞＝ = ,><,cos = .＜a ,b ＞的范围是，＜a ,-b ＞与＜a ,b ＞的关系是。

新课标人教A版高中数学知识点总结专题立体几何

专题六立体几何【知识概要】一、多面体●1. 多面体——由若干个平面多边形围成的几何体叫做多面体。

多面体有几个面就称为几面体。

棱柱棱锥棱台定义由一个平面多边形沿某一方向平移形成的空间几何体。

当棱柱的一个底面收缩为一点时，得到的几何体。

棱锥被一个平行于底面的平面所截后，截面和底面之间的部分。

性质(1) 两个底面与平行于底面的截面是对应边互相平行的全等多边形； (2) 侧面都是平行四边形，侧棱都相等；(3) 过棱柱不相邻的两条侧棱的截面都是平行四边形。

(1) 底面是多边形；(2) 平行于底面的截面与底面相似；(3) 侧面是有一个公共顶点的三角形。

(1) 两个底面是相似多边形； (2) 两个底面以及平行于底面的截面是对应边互相平行的相似多边形；(3) 侧面都是梯形。

●2.二、中心投影和平行投影●1. 投影——是光线（投射线）通过物体，向选定的面（投影面）投射，并在该面上得到图形的方法。

投射线交于一点的投影称为中心投影。

投射线相互平行的投影称为平行投影。

平行投影按投射方向是否正对着投影面，可分为斜投底面是平行四边形侧棱与底面垂直底面是矩形棱长相等四棱柱平行六面体直平行六面体长方体正方体影和正投影。

●2. 视图——物体按正投影向投影面投射所得的图形。

光线从物体的前面向后投射所得的投影称为主视图或正视图，自上向下的称为俯视图，自左向右的称为左视图。

正视图、俯视图、左视图称为三视图；作图关键：按“长对正、高平齐、宽相等”。

●3. 空间几何体画在纸上，要体现立体感，底面常用斜二侧画法，画出它的直观图。

三角形ABC 的面积为S ，用斜二测画法画得它的直观图三角形A B C '''的面积为S '，则24S S '=。

作图关键：倾斜45︒，横“等”纵“半”。

三、平面基本性质：（三公理三推论）名称内容公理1如果一条直线的两点在一个平面内，那么这条直线上的所有点都在这个平面内。

人教A版高中数学空间立体几何知识点归纳

第一章空间几何体知识点归纳1、空间几何体的结构：空间几何体分为多面体和旋转体和简单组合体⑴常见的多面体有：棱柱、棱锥、棱台；常见的旋转体有：圆柱、圆锥、圆台、球。

简单组合体的构成形式：一种是由简单几何体拼接而成，一种是由简单几何体截去或挖去一部分而成。

⑵棱柱：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱。

⑶棱台：用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分，这样的多面体叫做棱台。

1、空间几何体的三视图和直观图投影：中心投影平行投影（1）定义：几何体的正视图、侧视图和俯视图统称为几何体的三视图。

（2）三视图中反应的长、宽、高的特点：“长对正”，“高平齐”，“宽相等”2、空间几何体的直观图（表示空间图形的平面图）. 观察者站在某一点观察几何体，画出的图形.3、斜二测画法的基本步骤：①建立适当直角坐标系xOy （尽可能使更多的点在坐标轴上）②建立斜坐标系'''x O y ∠，使'''x O y ∠=450（或1350），注意它们确定的平面表示水平平面；③画对应图形，在已知图形平行于X 轴的线段，在直观图中画成平行于X ‘轴，且长度保持不变；在已知图形平行于Y 轴的线段，在直观图中画成平行于Y ‘轴，且长度变为原来的一半；一般地，原图的面积是其直观图面积的22倍，即22S S 原图直观＝4、空间几何体的表面积与体积⑴圆柱侧面积；l r S ⋅⋅=π2侧面⑵圆锥侧面积：l r S ⋅⋅=π侧面 ⑶圆台侧面积：()S r R l π=+侧面⑷体积公式：h S V ⋅=柱体；h S V ⋅=31锥体； ()13V h S S S S =+⋅+下下台体上上⑸球的表面积和体积：32344R V R S ππ==球球，.一般地，面积比等于相似比的平方，体积比等于相似比的立方。

O 2O 1h lr R第二章点、直线、平面之间的位置关系及其论证1 、公理1：如果一条直线上两点在一个平面内，那么这条直线在此平面内公理1的作用：判断直线是否在平面内2、公理2：过不在一条直线上的三点，有且只有一个平面。

人教A版高中数学空间立体几何知识点归纳

新人教A版高中数学选修2-1第三章《空间向量与立体几何》知识点汇总及解题方法总计

(完整版)高中数学空间几何体知识点总结

新课标人教A版 高一数学必修二定理知识要点

新课标人教A版高中数学必修二空间几何体知识点总结

人教高中数学必修二A版《基本立体图形》立体几何初步说课复习(棱柱、棱锥、棱台的结构特征)

人教A版高中数学选择性必修第一册精品课件 复习课 第1课时 空间向量与立体几何

人教高中数学必修二A版《空间直线、平面的平行》立体几何初步说课复习(直线与平面平行)

高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

2019新人教A版高中数学选择性必修一全册重点知识点归纳总结(复习必背)【可编辑全文】

第8章 立体几何初步 章末知识梳理(教学课件)-高中数学人教A版(2019)必修第二册

高中数学人教A版第八章立体几何初步知识梳理

新教材 人教A版高中数学必修第二册 第八章 立体几何初步 知识点汇总及解题规律方法提炼

高中数学 立体几何知识点总结 新人教A版选修2

新课标人教A版高中数学知识点总结专题立体几何

人教A版高中数学空间立体几何知识点归纳

新课标人教A版高一数学必修二定理知识要点

人教A版高中数学选择性必修第一册精品课件复习课第1课时空间向量与立体几何

第8章立体几何初步章末知识梳理(教学课件)-高中数学人教A版(2019)必修第二册

新教材人教A版高中数学必修第二册第八章立体几何初步知识点汇总及解题规律方法提炼

高中数学立体几何知识点总结新人教A版选修2