机械学基础(轮系-习题课)
机械原理-轮系集合例题

第5章轮系典型例题例1在图示轮系中,已知各轮齿数为:z1 =z1' = 40,z2=z4=30,z3=z5=100,试求传动比i1H。
解:齿轮1',4,5和系杆H组成了一个差动轮系。
齿轮1,2,3和齿轮5(充当系杆)组成了一个行星轮系。
在由齿轮1,2,3和齿轮5(系杆)组成的行星轮系中由于n 3=0,故有在由齿轮1',4,5和系杆H组成的差动轮系中即分析两个基本轮系的联系,可知n1= n1'(c)将(a),(c)两式代入(b),可得计算结果为正,表明从动系杆H和主动齿轮1的转向相同。
例2 在图示轮系中,已知各轮齿数为:z 1 = 90,z 2 = 60,z 2' = 30,z 3 =30,z 3' = 24,z 4 = 18,z 5 = 60,z 5' = 36,z 6 = 32。
运动从A,B两轴输入,由构件H输出。
已知n A=100r/min,n B=900r/min,转向如图所示。
试求输出轴H的转速n H的大小和方向。
解:齿轮3',4,5和系杆H组成了一个差动轮系齿轮1,2,2',3组成了一个定轴轮系,齿轮5',6组成了另一个定轴轮系。
对于齿轮3',4,5和系杆H组成的差动轮系,有即对于齿轮1,2,2',3组成的定轴轮系,有即对于齿轮5,6组成的定轴轮系,有即分析三个轮系之间的基本联系,有将该结果带入(a)式,可得化简整理后得计算结果为负,说明n H转向与n 5 相同,即n A,n B转向相反。
例3 在图示轮系中,已知齿轮1的转速为n 1 =1650 r/min,齿轮4的转速n4=1000r/min,所有齿轮都是标准齿轮,且z 2=z 5=z 6=20。
求各个齿轮中未知的齿轮齿数。
解:由齿轮1与齿轮3和齿轮6与齿轮4的同轴条件得齿轮1,2,3及系杆H1组成差动轮系;齿轮4,5,6及系杆H2组成行星轮系。
机械基础习题课

18、在曲柄滑块机构中,若以曲柄为主动件,则可把曲柄的旋 转运动转换成滑块的往复直线移动。
19、改变曲柄滑块机构中的机架,可演化出转动导杆机构、曲 柄摇块机构和移动导杆机构。
20、曲柄滑块机构中,当极位夹角q > 00时,机构具有急回特性; 当极位夹角q=00时,机构无急回特性。
杆的刚度
。
A降低 B提高
C不变
5、与齿轮传动相比,蜗杆传动轮齿间的相对滑动速度 。
ቤተ መጻሕፍቲ ባይዱ
A较大 B较小
C相同
6、蜗杆传动中,以下参数中标准化的有
。
A蜗杆头数 B蜗杆分度圆直径 C蜗杆导程角
7、 当两轴相距较远且要求传动比准确时,应采用 。
A带传动 B轮系传动 D蜗杆传动
8、定轴轮系传动比的大小与轮系中惰轮的齿数 。
21、曲柄摇杆机构中,当出现急回运动时,曲柄为主动件,摇 杆为从动件。
22、凸轮机构的基本特点在于能使从动件获得预期的运动规律。
23、按凸轮的形状分类,凸轮机构可分为盘形凸轮机构、移动 凸轮机构和圆柱凸轮机构。
24、按从动件端部形状分类,齿轮机构可分为尖顶从动件凸轮 机构、滚子从动件凸轮机构和平底从动件凸轮机构。
9、蜗杆传动,蜗杆头数确定后,直径系数越小,导程角越大。
10、轮系中的惰轮只改变从动轮的转向,不改变轮系传动比的 大小。
11、定轴轮系末端为螺旋传动,已知输入运动的主动轮转速 n1=1450r/min,轮系传动比i=50,双线螺杆的螺距P=1mm,则 螺母的移动速度为 58 mm/min。
12、周转轮系中,轴线固定的齿轮称为中心轮,兼有自转和公 转的齿轮称为行星轮。
机械基础轮系习题

1定轴轮系的传动比等于各对齿轮传动比的连乘积。
〔〕周转轮系的传动比等于各对齿轮传动比的连乘积。
〔〕那么反之不论什么状况,以中心轮为原行星轮系中假定系杆为原动件可驱动中心轮,动件时也必定可驱动系杆。
〔〕平面定轴轮系传动比的大小等于〔1〕;从动轮的展转方向可用〔1〕方法来确立。
所谓定轴轮系是指①〔1〕,而周转轮系是指②〔1〕在图示轮系中,:蜗杆为单头且右旋,转速n11440r/min,转动方向如图示,其他各轮齿数为:z2?40,z2'20,z330,z3'18,z4?54,试:〔1〕说明轮系属于何种种类;〔2〕计算齿轮4的转速n4;〔3〕在图中标出齿轮4的转动方向。
在图示轮系中,依据齿轮1的转动方向,在图上标出蜗轮4的转动方向。
1、在图示的轮系中,各轮齿数为z1,齿轮1、4、z2z3z5z6205、7为同轴线,试求该轮系的传动比i17。
2、在图示的轮系中,z124,z218,z315,z3'30,4105,当轴转z速n I19r/min时,试求轴和轮2的转速n II,n2。
3、计算图示轮系的传动比i1H,并确立输出杆H的转向。
各轮齿数z11,z240,z2'24,z372,z3'18,z4114,蜗杆左旋,n1转向如图示。
4、在图示增速器轮系中,设各轮齿数为z1,z2,z3,z4,z5,z6。
试求传动比i16。
5、在图示轮系中,各轮齿数分别为z11(右旋),z240,z2'20,z318, z420,z'30,z520,z655,n11000r/min,试求n B的大小和方向(方向可4用箭头表示)。
6、轮系如图示,由电动机带动齿轮1,其转速为n11296r/min,转向如图示,z120,z224,z320,z428,z528,z617,z762,z82,z980。
求:1〕蜗轮9的每分钟转数;32〕蜗轮9的转向〔以箭头表示在题图上〕;45〕蜗轮齿的倾斜方向。
机械设计基础第5章 轮系习题解答2
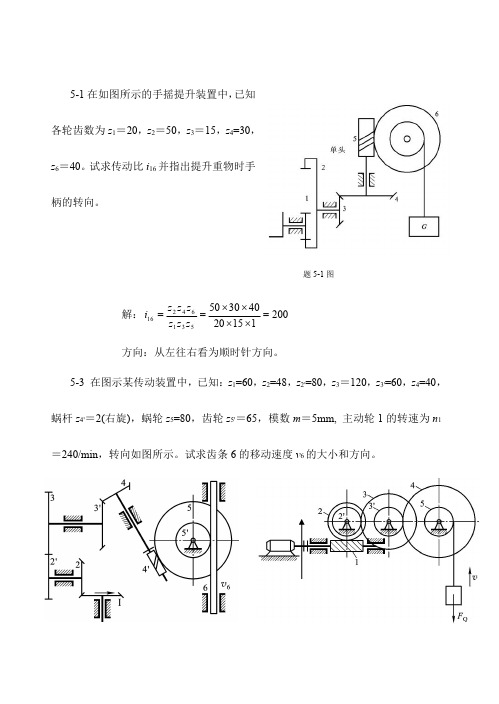
5-1在如图所示的手摇提升装置中,已知各轮齿数为z 1=20,z 2=50,z 3=15,z 4=30,z 6=40。
试求传动比i 16并指出提升重物时手柄的转向。
题5-1图解:2001152040305053164216=⨯⨯⨯⨯==z z z z z z i 方向:从左往右看为顺时针方向。
5-3在图示某传动装置中,已知:z 1=60,z 2=48,z 2'=80,z 3=120,z 3'=60,z 4=40,蜗杆z 4'=2(右旋),蜗轮z 5=80,齿轮z 5'=65,模数m =5mm,主动轮1的转速为n 1=240/min ,转向如图所示。
试求齿条6的移动速度v 6的大小和方向。
题5-3图题5-4图解:齿条的移动方向如图所示,其轮系传动比为:322608060804012048'4'3'2154325115=⨯⨯⨯⨯⨯⨯===z z z z z z z z n n i 则齿轮5’的转速为:min /5.7322401515r i n n ===又齿轮5’分度圆直径为:mm m z d 325565'5'5=⨯==所以齿条的移动速度为:s m n d v /128.0600005.73251000605'56=⨯⨯=⨯=ππ5-4如图所示为一电动卷扬机的传动简图。
已知蜗杆1为单头右旋蜗杆,蜗轮2的齿数z 2=42,其余各轮齿数为z 2'=18,z 3=78,z 3'=18,z 4=55;卷筒5与齿轮4固联,其直径D 5=400mm ,电动机转速。
n 1=1500r/min ,试求:(1)转筒5的转速n 5的人小和重物的移动速度v 。
(2)提升重物时,电动机应该以什么方向旋转?解:1.其轮系传动比为:11.5569500518181557842'3'214324114==⨯⨯⨯⨯===z z z z z z n n i 则齿轮4的转速(即转筒5的转速)为:min /70.211.556150014145r i n n n ====所以重物的移动速度为:s m n D v /057.0600007.2400100060556=⨯⨯=⨯=ππ5-5在如图所示周转轮系中,已知各轮齿数为z 1=60,z 2=20,z 2'=20,z 3=20,z 4=20,z 5=100,试求传动比i 41。
机械设计课后习题--轮系
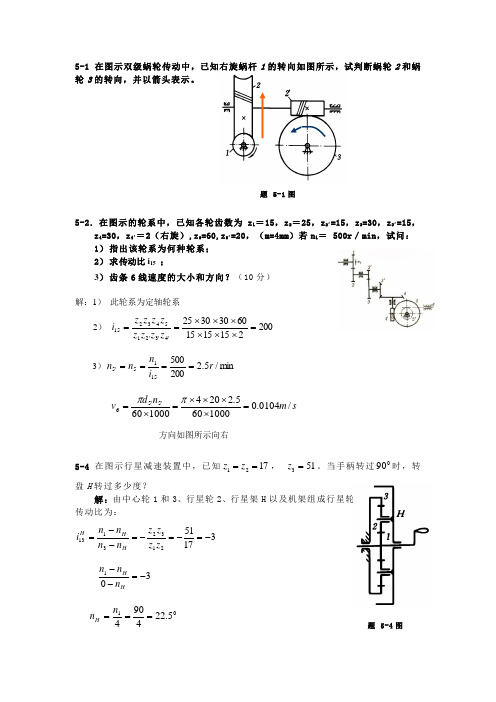
5-1 在图示双级蜗轮传动中,已知右旋蜗杆1的转向如图所示,试判断蜗轮2和蜗轮3的转向,并以箭头表示。
5-2.在图示的轮系中,已知各轮齿数为z l =15,z 2=25,z 2´=15,z 3=30,z 3´=15,z 4=30,z 4´=2(右旋),z 5=60,z 5´=20,(m=4mm )若n l = 500r /min ,试问:1) 指出该轮系为何种轮系;2) 求传动比i 15 ; 3) 齿条6线速度的大小和方向?(10分)解:1) 此轮系为定轴轮系2) 200215151560303025'4'3'21543215=⨯⨯⨯⨯⨯⨯==z z z z z z z z i 3)min /5.22005001515'5r i n n n ==== s m n d v /0104.01000605.2204100060'5'56=⨯⨯⨯⨯=⨯=ππ方向如图所示向右5-4 在图示行星减速装置中,已知1721==z z , 513=z 。
当手柄转过090时,转盘H 转过多少度?解:由中心轮1和3、行星轮2、行星架H 以及机架组成行星轮系,转化轮系的传动比为:3175121323113-=-=-=--=z z z z n n n n i H H H 301-=--HH n n n 015.224904===n n H 题 5-4图题 5-1图方向相同5-5 在图示的手动葫芦中,S 为手动链轮,H 为起重链轮。
已知121=z ,282=z ,142='z ,543=z ,求传动比SH i 。
解:由中心轮1和3、行星轮2-2’、行星架H 行星轮系,故()914125428''1213221321313113-=⨯⨯-=-=-=--==z z z z z z z z n n n n n n i H H H H H 03=n ,1n n s =101===∴HH s sH n n n n i 5-8 在图示圆锥齿轮组成的行星轮系中,已知各轮的齿数为201=z ,302=z ,502='z ,803=z ,m in /501r n =,求H n 的大小和方向。
大连理工大学 机械设计基础 作业解答:第5章-轮系

齿轮1、2组成定轴轮系,齿轮3、4、 4’、5和行星架组成周转轮系
定轴轮系
i12
n1 n2
Z2 Z1
Z2 17
周转轮系
i3H5
n3H n5H
n3 nH n5 nH
Z5Z4 Z4'Z3
2419 114 20 23 115
nH
n2 , n3
0,所以 n2 n5 n2
114 115
n1 n3
Z3 Z1
85 17
5,所以n3
n1 5
周转轮系中,i4H7
n4H n7H
n4 nH n7 nH
Z7Z5 Z6Z4
63 24 4 2118
nH
n3, n7
nP
,
所以
n4 nP
n1 / 5 n1 / 5
4, nP
n1
n4 4
(1)当n1
10001r
/ min 、n4
5-2 Z1=15, Z2=25 ,Z2'=15 ,Z3=30,Z3'=15, Z4=30, Z4'=2(右旋),Z5=60,Z5'=20(m=4mm), 若
n1=500(r/min),求齿条6的线速度。
传动4 .Z 3 .Z 2 Z 4' .Z 3' .Z 2' .Z1
的传动比 iSM 和分针与时针的传动比 iMH 。
秒针S到分针M的传动路线为齿轮 6—5—4—3,所以
i SM
Z3.Z5 Z 4 .Z 6
64 60 88
60
分针M到时针H的传动路线为 齿轮9—10—11—12,所以
iMH
Z12 .Z10 Z11.Z9
24 24 68
12
5-4 Z1 = Z2 =17, Z3 =51。当手柄转过90°时,转盘 H 转过 多少角度?
机械原理题目轮系

机械原理题目轮系第六章轮系及其设计计算及分析题1、已知:Z1=30,Z2=20,Z2’=30,Z3 = 25,Z4 = 100,求i1H。
2、图示轮系,已知各轮齿数Z1=18,Z2= Z4=30,Z3=78,Z5=76,试计算传动比i15。
12345H3、在图示轮系中,已知各轮齿数为Z1=Z3=30,Z2=90,Z2’=40,Z3’=40,Z4=30,试求传动比i1H,并说明I、H轴的转向是否相同4、在图示轮系中,已知各轮齿数为Z1 =15,Z2=20,Z2’ = Z3’= Z4=30,Z3=40,Z5= 90,试求传动比i1 H,并说明H的转向是否和齿轮1相同1I22’33’4H5、在图示轮系中,已知各轮的齿数为Z1= 20,Z2=30,Z3=80,Z4=25,Z5=50,试求传动比i15。
6、在图示轮系中,已知各轮齿数为Z1=19,Z2=76,Z2’= 40,Z3=20,Z4= 80,试求传动比i1H。
7、在图示轮系中,已知各轮齿数为Z1= 20,Z2’= 25,Z2= Z3=30,Z3’= 20,Z4=75,试求:(1)轮系的传动比i1H。
(2)若n1=1000r/min,转臂H的转速n H=8、已知图示轮系中各轮的齿数Z1=20,Z2=40,Z3=15,Z4=60,轮1的转速为n1=120r/min,转向如图。
试求轮3的转速n3的大小和转向。
1232’3’4H45123H122’3453’H9、在图示轮系中,已知各轮齿数为Z 1= Z 3= Z 4=20,Z 2=40,Z 5= 60, n 1 = 800r/min ,方向如图所示,试求n H 的大小及转10、在图示轮系中,已知各轮齿数为Z 1=16 ,Z 2=24, Z 2’= 20,Z 3=40,Z 3’= 30, Z 4= 20,Z 5=70试求轮系的传动比i 1H 。
11、在图示轮系中,已知各轮齿数为Z 1= 15,Z 2=25,Z 2’= 20,Z 3=60,Z 4=10,Z 5=30,n 1=200r/min ,n 3=50r/min ,试求n 1、n 3转向相反时,n 5=。
机械学基础(轮系-习题课)

M H 6'
因 n H n M = 1 12 ? 故由式( ),( ),(c) 故由式(b),( )得
nH n1 nM = nM n1 nH = z2′′ z6′ 1 = z6 z7 12 z2 z = 1 z 2 z6 z7 zz z 1 2′′ 6′
3 100 n H 20 × 25 H nH=-100r/min i 13 = = 200 n H 30 × 25 2) n1与n3 反向,即用 n1=100r/min,n3= ห้องสมุดไป่ตู้200r/min代入, 反向, 代入, ) , 代入 100 n H 20 × 25 H i 13 = = 可得 nH=700r/min 30 × 25 200 n H 所求转速的方向,须由计算结果得正负号来决定, 所求转速的方向,须由计算结果得正负号来决定,决不 能在图形中直观判断! 能在图形中直观判断!
右图轮系中, 例1 右图轮系中,已知各轮的齿数 为:z1=48,z2=48,z2'=18,z3=24, , , , , 又n1=250r/min, n3=100r/min,转向 , , 如图所示.试求系杆的转速n 如图所示.试求系杆的转速 H的大 小和方向. 小和方向. 解:这是一个由锥齿轮所组成的周转轮 先计算其转化机构的传动比. 系.先计算其转化机构的传动比.
�
因
=1, n1=1,n3=-1
nH=-1/2
i1H =
n1 1 = = 2 1 nH 行星架与中心轮1转向相反. 行星架与中心轮1转向相反. 2
H n1 n1 n H z2 H i 12 = H = = n2 nH z1 n2
求n2.
注:转速有方 向.
n1=1,nH=-1/2 ,
机械基础轮系试题及答案

机械基础轮系试题及答案一、选择题(每题2分,共10分)1. 轮系中,若主动轮转速为n1,从动轮转速为n2,传动比i为:A. n1/n2B. n2/n1C. n1*n2D. n1-n2答案:B2. 轮系中,若主动轮齿数为Z1,从动轮齿数为Z2,传动比i为:A. Z1/Z2B. Z2/Z1C. Z1*Z2D. Z1-Z2答案:B3. 轮系中,若主动轮直径为D1,从动轮直径为D2,传动比i为:A. D1/D2B. D2/D1C. D1*D2D. D1-D2答案:B4. 轮系中,若主动轮扭矩为T1,从动轮扭矩为T2,传动比i为:A. T1/T2B. T2/T1C. T1*T2D. T1-T2答案:B5. 轮系中,若主动轮功率为P1,从动轮功率为P2,传动比i为:A. P1/P2B. P2/P1C. P1*P2D. P1-P2答案:B二、填空题(每题2分,共10分)1. 轮系中,传动比i的计算公式为_________。
答案:主动轮转速/从动轮转速或主动轮齿数/从动轮齿数或主动轮直径/从动轮直径2. 轮系中,若主动轮转速为n1,从动轮转速为n2,则传动比i=_________。
答案:n1/n23. 轮系中,若主动轮齿数为Z1,从动轮齿数为Z2,则传动比i=_________。
答案:Z1/Z24. 轮系中,若主动轮直径为D1,从动轮直径为D2,则传动比i=_________。
答案:D1/D25. 轮系中,若主动轮扭矩为T1,从动轮扭矩为T2,则传动比i=_________。
答案:T2/T1三、简答题(每题5分,共20分)1. 描述轮系中传动比的物理意义。
答案:传动比表示轮系中主动轮与从动轮转速或齿数或直径的比值,反映了轮系的减速或增速效果。
2. 轮系中,为什么主动轮与从动轮的转速比等于它们的齿数比?答案:因为轮系中齿轮的啮合关系使得主动轮与从动轮的齿数比决定了它们的转速比,即齿数多的轮转速慢,齿数少的轮转速快。
轮系练习
将n4=0代入上式得
则,nH=n1/7=350/7 (r/min) =50 r/min,与n1转向相同。
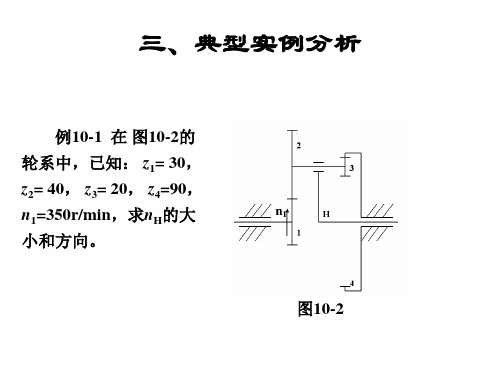
三、典型实例分析
例10-2 在图10-3所示的轮系中,已知 z1=z3=50,z2=30 , nH=60r/min (方向从左轴端观察为顺时针)。求 ⑴ 当 n1=0时,n3是多少? ; ⑵ 当 n1=200 r/min(方向为顺时针)时, n3是多少?
四、复习题
⒊ 计算题
⑴ 在图10-4所示的轮系中,已知 z1=15,z2=25,z3=15, z4=30,z5=15,z6=15,求i16的大小和各轮的转动方向。 2、3的齿数分别为z1、z2、z3,求模数相同时的z4及i14。
⑵ 图10-5轮系的各齿轮为标准齿轮、标准安装,已知齿轮1、
图10-4
6
n1 3 5
2 定轴轮系传动比 4 2 4 n1 z2 H i12 n2 z1 n1 1 n2 n2 r/ min i12 99 差动轮系 蜗轮2转动方向向下 n1 z5 z4 n1 101 i14 n4 n4 r/ min n4 z1 z5 i14 10000
z2 z3 ) H z1 z2 1 代入各轮齿数 101 99 9999 1 iH1 10000 i1H 1 1 100 100 10000 10000 z3=100 系杆H与齿轮1转向相同 101 100 10100 1 i1H 1 1 iH1 100 100 100 10000 100 系杆H与齿轮1转向相反 i1 H 1 (
2 2 3
H 1
200 5 50 nH 75 r/ min 系杆H与齿轮1、3转向相同 6 n1、n3转向相反时 200 5 50 25 nH r/ min 系杆H与齿轮3转向相同 6 3
机械原理补充习题(轮系)

第11章轮系重点内容:轮系传动比的计算11-1 已知:z1=24,z1’=30,z2=95,, z3 =89,z3’=102,z4 = 80,z4’=40,z5=17.求i15。
11-2 已知:z1=22,z2=60,, z3 =z3’=142,z4 =22,z5=60.求i AB。
11-3已知:z1=30,z2=20,z2’=30,z3 =25,z4 =100 n1=100r/min,求i1H。
11-4 在图示的电动三爪卡盘传动轮系中,已知各齿轮的齿数分别为:z1=6,z2=z2’=25,z3 =57,z4 =56,求传动比i1411-5 图示轮系,已经各齿轮齿数为:z1=24,z1’=34,z2=40,z2’=40,z3 =18,z3’=38,z4 =36,z4’=22,求该轮系传动比i AH,11-6 图示轮系,已经各齿轮齿数为:z1=22,z3 =z5,求该轮系传动比i1511-7 .图示轮系中,已知z z z z134420====',z280=,z560=。
若nA=1000r/min,求nB的大小及方向。
11-8 .图示轮系中,已知各轮齿数,试求轮系的传动比i AB。
(写成齿数比的形式〕11-9 .在 图 示 轮 系 中, 已 知 各 轮 的 齿 数z z 1380==',z z 3520==, 及 齿 轮1 的 转 速n 170= r/min, 方 向 如 图 示。
试 求 齿 轮5 的 转 速n 5 的 大 小 及 方 向。
11-10 .在 图 示 轮 系 中, 已 知 各 轮 的 齿 数z 117=,z 223=,z 220'=,z 360=,z 320'=,z 440=, 构 件B 的 转 速n B=200r/min, 转 向 如 图 示。
试 求 轴A 转 速n A 的 大 小 和 方 向。
11-11图 示 轮 系 中, 已 知z 124=,z 226=,z 220'=,z 330=,z 326'=,z 428=。
轮系-习题及答案

轮系一、复习思考题1.为什么要应用轮系?试举出几个应用轮系的实例?2.何谓定轴轮系?何谓周转轮系?行星轮系与差动轮系有何区别? 3.什么叫惰轮?它在轮系中有什么作用?4.定轴轮系的传动比如何计算?式中(-1)m有什么意义? 5.定轴轮系末端的转向怎样判别?6.如果轮系的末端轴是螺旋传动,应如何计算螺母的移动量?二、填空题1.由若干对齿轮组成的齿轮机构称为 。
2.根据轮系中齿轮的几何轴线是否固定,可将轮系分 轮系、 轮系和 轮系三种。
3.对平面定轴轮系,始末两齿轮转向关系可用传动比计算公式中 的符号来判定。
4.行星轮系由 、 和 三种基本构件组成。
5.在定轴轮系中,每一个齿轮的回转轴线都是 的。
6.惰轮对 并无映响,但却能改变从动轮的 方向。
7.如果在齿轮传动中,其中有一个齿轮和它的 绕另一个 旋转,则这轮系就叫周转轮系。
8.旋转齿轮的几何轴线位置均 的轮系,称为定轴轮系。
9.轮系中 两轮 之比,称为轮系的传动比。
10.加惰轮的轮系只能改变 的旋转方向,不能改变轮系的 。
11.一对齿轮的传动比,若考虑两轮旋转方向的同异,可写成±==21n n i ——。
12.定轴轮系的传动比,等于组成该轮系的所有 轮齿数连乘积与所有 轮齿数连乘积之比。
13.在周转转系中,凡具有 几何轴线的齿轮,称中心轮,凡具有 几何轴线的齿轮,称为行星轮,支持行星轮并和它一起绕固定几何轴线旋转的构件,称为 。
14.周转轮系中,只有一个 时的轮系称为行星轮系。
15.转系可获得 的传动比,并可作 距离的传动。
16.转系可以实现 要求和 要求。
17.转系可以 运动,也可以 运动。
18.采用周转轮系可将两个独立运动 为一个运动,或将一个独立的运动 成两个独立的运动。
19.差动轮系的主要结构特点,是有两个。
20.周转轮系结构尺寸,重量较。
21.周转轮系可获得的传动比和的功率传递。
三、判断题1.转系可分为定轴轮系和周转轮系两种。
轮系习题课

图示轮系,已知各轮齿数:z2=32,z3=34,z4=36,z5=64,z7=32,z8=17, z9=24。轴A按图示方向以1250r/min的转速回转,轴B按图示方向以600r/min的转 速回转,求轴C的转速nC的大小和方向。
在图示的轮系中,已知各轮齿数为z2=z4=25,z2′=20,各轮的模数相同, n4=1000r/min。试求行星架的转速nH的大小和方向。
在图示轮系中,设已知双头右旋蜗杆的转速n1=900r/min,z2=60,z2′=25,z3=20, z3′=25,z4=20,z4′=30,z5=35,z5′=28,z6=135,求n6的大小和方向。
图示轮系中,各轮模数和压力角均相同,都是标准齿轮,各轮齿数为z1=23,z2=51, z3=92,z3′=40,z4=40,z4′=17,z5=33,n1=1500r/min,转向如图示。试求齿轮2'的 齿数z2′及nA的大小和方向。
在图示轮系中,各轮模数相同,均为标准齿轮,各轮齿数为z1=30,z3=70,z5=80, z6=40,z8=20,z9=30,z10=90。试求传动比iⅠⅡ。
在图示轮系中,已知各轮齿数为z1=20,z2=36,z2′=18,z3=60,z3′=70,z4=28, z5=14,nA=60r/min,nB=300r/min,方向如图示。试求轮5的转速n5的大小和方向。
在图所示轮系中,设转速n1为19r/min,已知各轮齿数为z1=90,z2=60,z2´=z3=30, z3´=24,z4=18,z5=15,z5´=30,z6=105,z8=35,z7=32,试求转速n7。
轴a按图示方向以1250rmin的转速回转轴b按图示方向以600rmin的转速回转求轴c的转速nc的大小和方向
(完整版)机械基础轮系练习题

XXXXX 学校《机械根底》练习题一、 填空题1.由一系列相互啮合齿轮所构成的传动系统称为_________.2.按照轮系传动时各齿轮的轴线位置是否固定,轮系分为________和________两大类. 3.当轮系运转时,所有齿轮几何轴线的位置相对于机架固定不变的轮系称为_______. 4.轮系中,既有定轴轮系又有行星轮系的称为________.5.采用行星轮系,可以将两个独立的运动_______为一个运动,或将一个运动_______为两个独立的运动. 6.轮系中含有圆锥齿轮、蜗轮蜗杆、齿轮齿条,其各轮转向只能用_________的方法表示.7.定轴轮系中的传动比等于_________的转速之比,也等于该轮系中________与_______之比.8.在各齿轮轴线相互平行的轮系中,假设齿轮的外啮合对数是偶数,那么首轮与末轮的转向_______;假设为奇数,那么首轮与末轮的转向__________.9.在轮系中,惰轮常用于传动距离稍__________和需要改变________的场合.10.在轮系中,末端件假设是齿轮齿条,它可以把主动件的________运动变为齿条的______运动. 11.轮系的特点:(1)可获得_________的传动比;(2)可实现__________距离传动;(3)可实现________、________要求;(4)可_________或__________运动.12.平面定轴轮系中传动比计算公式为_________,其中(-1)的n 次方,n 表示 ________.假设(-1) 的n 次方为正,那么首、末两轮转向____.13.定釉轮系中任一从动件的转速计算公式为______________________.14.定轴轮系末端通常有以下三种传动形式,那么末端件的移动速度v(或移动距离L)的计算公式分别为: (1)末端为螺旋传动时:________________ (2)末端为滚动轮传动时:______________ (3)末端为齿轮齿条传动时:_____________ 二、单项选择题 1.假设齿轮与轴之间( ),那么齿轮与轴各自转动,互不影响. A.空套 B .固定 c .滑移 D .空间配合 2.如下图的轮系中,设Z1= Z2=Z3′=Z4= 20,Z3=Z5= 60,又齿轮1、3、3′ 与5同轴线,试求传动比i15。
轮系习题课

i4H 5 5 4 H H
z5 z4
1005 20
精选完整ppt课件
10
4 15 4 H
由(1)和(2)式得
1 4
4
3 8
1
• 传动比为:
i41
4 1
3 2
精选完整ppt课件
11
11.图示轮系。已知齿数z1=30,z2=20,z2/= z3 = 25, n1=100r/min,n3=200r/min且轮1与轮3转向相反。求nH。 解:
7、图示轮系,已知各轮的齿数分别为Z1=40, Z2=30,Z3=100,Z3/=48,
。 Z4=24,Z5=96。试求:i1H
解:轮系分析 该轮系是由定轴轮系3/、4、5和周转轮系1、2、3、H组成。
i3 /5
( 1)1
z4 z3/
z5 z4
2
i3 /5
n3/ n5
Hale Waihona Puke 2而n5nH
n3/
2nH
n 13 H
z6 z5
24 35
n6
0
n4 nH 2
11 35
而
n4
nH1
3n1 nH 2
11 35
i1 H 2
0 . 105
1和
H
转向相同。
2
精选完整ppt课件
6
5、图示轮系,均采用标准齿轮传动。已知各轮的齿数分别为Z1=80, Z1/=40,Z2=20,Z2/=30,Z3=40,Z4=30。 试求:Z3/及i1H。 解:
• 解:(1)该轮系为定轴轮系;
• (2)
i14 n n1 4 zz1 2
z3 z2/
z4 z3/
403054 120 18180
5.5 轮系 (答案)

轮系一、填空题1.传动时,各轴线位置固定不变的轮系称为定轴轮系。
2.轮系中惰轮只能改变齿轮的传动方向,不改变传动比。
3.行星轮系由行星轮、中心轮和系杆三种基本构件组成。
4.周转轮系按其自由度数目不同,可分行星轮系和差动轮系。
5.在周转轮系中,几何轴线固定的齿轮称为太阳轮,几何轴线运动的齿轮称为行星轮,支承行星轮并和它一起绕固定轴线旋转的构件称为系杆。
6. 定轴轮系的传动比,等于组成该轮系的所有从动轮齿数连乘积与所有主动轮齿数连乘积之比。
7.下图所示,属于定轴轮系轮系。
9.下图所示,属于周转轮系轮系。
二、判断题1.轮系可分为定轴轮系和周转轮系两种。
(×)2.旋转齿轮的几何轴线位置均不能固定的轮系,称之为周转轮系。
(×)3.至少有一个齿轮和它的几何轴线绕另一个齿轮旋转的轮系,称为定轴轮系。
(×)4.定轴轮系首末两轮转速之比,等于组成该轮系的所有从动齿轮齿数连乘积与所有主动齿轮齿数连乘积之比。
(√)5.在周转轮系中,凡具有旋转几何轴线的齿轮,就称为中心轮。
(×)6.在周转轮系中,凡具有固定几何轴线的齿轮,就称为行星轮。
(×)三、选择题1、轮系( B )A.不能获得很大的传动比B.可以实现变向和变速要求C 不适宜作较远距离传动 D. 可以实现运动的合成但不能分解运动2、定轴轮系的传动比大小与惰轮的齿数( B )A.有关B.无关C.成正比D.成反比3、一对外啮合圆柱齿轮传动,传动比公式计算正确的是( D )A. i12=Z1/Z2B. i12= -Z1/Z2C.i12=Z2/ Z1D.i12= -Z2/ Z14、定轴轮系中各齿轮的几何轴线位置都是( A )。
A.固定的B.活动的C.相交的D. 交错的5、轮系不可实现( D )。
A.大的传动比B.较远距离的传动C.改变从动轴回转方向D.过载保护6、惰轮在轮系中,不影响传动比大小,只影响从动轮( A )。
A.旋转方向B.转速C. 传动比D.齿数四、思考题1.如图下所示,已知各齿轮齿数:Z1=20;;Z2=28;Z3=20; Z3′=60;Z4=40; Z4′=30; Z5=50;转向如图所示,求传动比i15,并判定齿轮5的转向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
能在图形中直观判断!
例1.图示轮系中,已知各轮的齿数 为: z1 z2 30, z3 90
试求当n1=1,n3=-1时nH及i1H的值。
解:这是一个差动轮系。
i1H3
1 H 3 H
n1 nH n3 nH
z2z3 z1z2
90 30
3
因 n1=1,n3=-1
解:H,4组成定轴轮系;齿轮1、2-2’、3和H 组成周转轮系
由于n3 0
n1 nH nH
16 25
解得n1
9 25
nH
所以
i14
n1 n4
9 25
nH
5nH
9 125
,
n1与n4 方向相反
3K型
(3个中心轮 和一个系杆)
系杆既不是输入 件也不是输出件, 只起支承行星轮 的作用。
例:已知齿数z1=30, z2=20, z2’= z3 = 25, n1=100r/min, n3=200r/min。 求nH。
2 2’ 2
解: 2’
i1H3
n1 nH n3 nH
z2z3 z1z 2'
H 13
1
3
1) n1与n3 同向, n1=100r/min n3=200r/min代入,可得
4'
成定轴轮系,得
3'
E
3
4 N
2 2"
2' 6
1
7S
M H 6'
i1H
n1 nH
n1 n7
(1)3 z2z6z7 z1 z2 z6
(c)
因 nM ns 1 60
3'
5
E
3
故由式(a)、(b)得
nM ns
n1 ns n1 nM
z2 z3 z4 z1 z2 z3
nH=-1/2
i1H
n1 nH
1 1
2
2
行星架与中心轮1转向相反。
求n2。
i1H2
n1H nH2
n1 nH n2 nH
z2 z1
n1=1,nH=-1/2
n2=-2,方向与n1相反。
注:转速有方 向。
例1 右图轮系中,已知各轮的齿数 为:z1=48,z2=48,z2’=18,z3=24, 又n1=250r/min, n3=100r/min,转向 如图所示。试求系杆的转速nH的大 小和方向。
i1H3
100 nH 200 nH
20 25 30 25
nH=-100r/min
2) n1与n3 反向,即用 n1=100r/min,n3= -200r/min代入,
i1H3
100 nH 200 nH
20 25 30 25
可得 nH=700r/min
所求转速的方向,须由计算结果得正负号来决定,决不
nH=50r/min 系杆H的转向与齿轮1相同,与齿轮3相反。
例 图示轮系,各轮齿数 z3=z2’=60 , z2=20 , z1=30,
n3=60rpm, nH=180rpm, n3、nH转向相同,求n1 ?
解: 此轮系需用箭头法确定式中正负号
i1H3
n1H n3H
n1 nH n3 nH
轮系习题课
例: 钟表传动示意图如下。E为擒纵轮,N为
发条盘,S、M及H各为秒针、分针及时针。设
Z1=72, Z2=12, Z2'=64 , Z3=8, Z3’=60 ,
Z4'=60, Z5 =6, Z2"=8, Z6=24, Z6’=6,问
Z4、Z7各为多少? 解:(1) 走秒传动,由 5
3'
E
3
z2 z1
4'
N
4
2 2"
2' 6
1
z3z4 1 z2z3 60
故
z4
z2 z3 60 z3
64 60 60 8
8
7S
M H 6'
因 nH nM 1 12 ? 故由式(b)、(c)得
nH
n1
nM
z2 z1
nM n1 nH
z2z3 z1z2'
设n3转向为正,则
n1 180 2060 2 60 180 3060 3
3
H
得 n1=260 r/min 正值说明轮1、3转向相同
2'
2
1
例2:在图示的轮系中,已知各轮齿轮为Z1=Z2’=25,Z2=Z3=20, ZH=100,Z4=20。求传动比i14。
轮1,2(2'),3(3'),4组成
2 2"
7S
定轴轮系,得
4
i1S
n1 ns
n1 n4
(1)3
z2 z3z4 z1 z2 z3
4' (a) N
2' 6
1
M H 6'
(2) 走分传动,由轮1, 2组成定轴轮系,得 5
i1M
n1 nM
n1 n2
z2 z1
(b)
(3) 走时传动,由轮1, 2(2"),6(6'),7组
z2 z6 z7 z1 z2 z6
z2z6 1 z6z7 12
3'
5
E
3
2 2"
4 4'
N
2' 6
1
故
z7
12 z2z6 z6
12 8 6 24
24
7S M
H 6'
本题为分路传动的定轴轮系。各路的首末两 轮的转向关系用传动比正、负号表示,并可 直接用外啮合的数目m来确定,即(-1)m。
解:这是一个由锥齿轮所组成的周转轮 系。先计算其转化机构的传动比。
i1H3
n1 nH n3 nH
(1) z2z3 z1z2
48 24 48 18
4 3
n1=250r/min n3=-100r/min ?
规定n1为正
n1 nH 250 nH 4 n3 nH 100 nH 3
