四川省攀枝花七中2011-2012学年高二上学期第一次月考数学试卷

合集下载

2011-2012年高二数学上学期第一次月考试卷及答案

2011-2012学年度高二上学期第一次月考数学试卷（考试时间120分钟，满分：150分）卷Ⅰ 选择题一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项是符合题目要求的.）1．直线2x ＋ay ＋3＝0的倾斜角为120°，则a 的值是A.233 B ．－233C ．2 3D ．－2 32．直线l 过点(－1,2)且与直线2x －3y ＋4＝0垂直，则l 的方程是A ．3x ＋2y －1＝0B ．3x ＋2y ＋7＝0C ．2x －3y ＋5＝0D ．2x －3y ＋8＝03．经过圆C ：(x ＋1)2＋(y －2)2＝4的圆心且斜率为1的直线方程为 A ．x －y ＋3＝0 B ．x －y －3＝0 C ．x ＋y －1＝0 D ．x ＋y ＋3＝04．圆x 2＋y 2－4x －4y ＋5＝0上的点到直线x ＋y －9＝0的最大距离与最小距离的差为A. 3 B ．2 3 C ．3 3 D ．65．方程2x 2＋ky 2＝1表示的曲线是长轴在y 轴上的椭圆，则实数k 的取值范围是 A ．(0，＋∞) B ．(2，＋∞) C ．(0,2) D ．(0，2) 6．圆221:20O x y x +-=和圆222:40O x y y +-=的位置关系是.A 相离.B 相交 .C 外切 .D 内切7．若椭圆x 25＋y 2m ＝1的离心率e ＝105，则m 的值为A ．1 B.15或5315 C.15D ．3或2538．已知两点M （－2，0），N （2，0），点P 满足⋅=12，则点P 的轨迹方程为A ．11622=+y xB ．822=-x yC ． 1622=+y xD ．822=+y x9．如果直线12,l l 的斜率分别为二次方程2410x x -+=的两个根，那么1l 与2l 的夹角为A ．3π B ．4π C ．6π D ．8π10．椭圆x 24＋y 23＝1的左、右焦点是F 1、F 2，P 是椭圆上一点，若|PF 1|＝3|PF 2|，则P 点到左准线的距离是A ．8B ．6C ．4D ．211．F 1，F 2是椭圆C ：x 28＋y24＝1的两个焦点，在C 上满足PF 1⊥PF 2的点P 的个数为A ．4B ．2C ．1D ．0 12．若直线220(,0)ax by a b +-=>始终平分圆224280x y x y +---=的周长，则12a b+ 的最小值为A ．1B ．5C． D．3+卷Ⅱ 非选择题二、填空题：（本大题共4小题，每小题5分，共20分）13．已知直线0125=++a y x 与圆0222=+-y x x 相切，则a 的值为________.14．若椭圆长轴长与短轴长之比为2，它的一个焦点是(215，0)，则椭圆的标准方程是15．将参数方程⎩⎨⎧=+=θθsin 2cos 21y x （θ为参数）化为普通方程，所得方程是_____.16．设1,m >在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下，目标函数5z x y =+的最大值为4，则m 的值为．三、解答题：（本大题共6小题，共70分. 解答应写出文字说明，证明过程或演算步骤.）17. (本小题满分10分）已知直线l 1的方程为3x ＋4y －12＝0.(1)若直线l 2与l 1平行，且过点(－1,3)，求直线l 2的方程；(2)若直线l 2与l 1垂直，且l 2与两坐标轴围成的三角形面积为4，求直线l 2的方程．18. (本小题满分12分)椭圆的中心在原点，焦点在x 轴上，焦距为2，且经过点A )23,1(-；（1）求满足条件的椭圆方程；（2）求该椭圆的顶点坐标，长轴长，短轴长，离心率．19. (本小题满分12分）设圆满足：①截y 轴所得弦长为2；②被x 轴分成两段圆弧，其弧长之比为3：1；③圆心到直线:20l x y -=，求该圆的方程．20. (本小题满分12分）营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素C.另外，该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？21.（本小题满分12分）设M 是圆22680x y x y +--=上的动点，O 是原点，N 是射线OM 上的点，若150||||=⋅ON OM ，求点N 的轨迹方程。

四川攀枝花七中2011高三上期末模拟考试(12月)--数学(文)

攀枝花市七中高2011届上期期末模拟考试数学试题（文科）第I 卷一、选择题：（本大题共12小题，每小题5分，共60分）1．已知等差数列{}n a 中，247,15a a ==，则前10项的和10S =A ．100B ．210C ．380D ．4002．已知已知2{|4}M x x =≤，2{|1}1N x x =≥-，则M N = A ．{|12}x x <≤ B ．{|21}x x -≤≤C ．{|12}x x ≤≤D ．{|2}x x <3．“a =1”是“函数()||f x x a =-在区间[1,)+∞上为增函数”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件4．若直线()1:4l y k x =-与直线2l 关于点)1,2(对称，则直线2l 恒过定点（）A . ()0,4B . ()0,2C . ()2,4-D . ()4,2- 5．已知3sin()45x π-=，则sin 2x 的值为A ．1925B ．1625C ．1425D ．7256．函数cos()sin()23y x x ππ=++-具有性质A ．最大值为6x π=对称B ．最大值为1，图像关于直线6x π=对称C ，图像关于（,06π）对称D ．最大值为1，图像关与(,0)6π对称7．若等比数列{}n a 的前n 项和为13n n S a +=+，则常数a 的值等于A ．13-B ．1-C ．13D ．3-8．已知函数()f x 在R 上可导，且2()2'(2)f x x x f =+ ，则(1)f -与(1)f 的大小关系为 A ．(1)(1)f f -= B ．(1)(1)f f -> C ．(1)(1)f f -< D ．不确定 9．圆cos :1sin x C y θθ=⎧⎨=-+⎩（θ为参数）与直线0x y a ++=有公共点，那么实数a 的取值范围是A ．（1，2）B ．[0，C ．[1-+D ．1,1]10．若双曲线22221(0)x y a b ab-=>>的左右焦点分别为1F 、2F ，线段1F 2F 被抛物线22y bx =的焦点分成7：5的两段，则此双曲线的离心率为A ．98B．37 C．4 D．1011．已知正数,x y 满足等式042=+-+xy y x ，则A ．xy 的最大值是4，且y x +的最小值是4B ．xy 的最小值是4，且y x +的最大值是4C ．xy 的最大值是4，且y x +的最大值是4D ．xy 的最小值是4，且y x +的最小值是412．定义域为R 的函数()f x =1,1|1|1,1x x x ⎧≠⎪-⎨⎪=⎩，若关于x 的函数21()()()2h x f x bf x =++有5个不同的零点12345,,,,x x x x x ，则2222212345x x x x x ++++等于A ．2222b b+ B ．16 C ．5 D ．15第II 卷二、填空题：（本大题共4小题，每小题4分，共16分，把答案填在题中横线上） 13．若110,a b a ba<<-则与的大小关系为．14．若曲线4()2f x x x =-+在点发P 处的切线与直线310x y +-=垂直，则点P 的坐标是． 15．某单位邀请10位教师中的6人参加一个研讨会，其中甲、乙两位教师不能同时参加，则邀请的不同方法有．16. 锐角三角形ABC 中，若2A B =，①sin 3sin 2B C =；②3tan tan 122B C =； ③64B ππ<<④ab∈则叙述正确的是．三、解答题：（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）17（12分）已知向量(1,1)m = ,向量n 与向量m 夹角为34π，且1m n =- ．（1）求向量;n（2）若向量n 与向量q =(1,0)的夹角为2π，向量2(cos ,2cos )2Cp A = ，其中A 、B 、C 为∆ABC 的内角，且A 、B 、C 依次成等差数列。

四川省攀枝花市高二数学上学期期中检测试题文新人教A版

D ．3
C
4
4
4
4
第Ⅱ卷（非选择题共 90 分）
B 二、填空题（本大题 4 个小题，每小题 4 分，共 16 分，只填结果，不要过程） 13．如图，已知四面体 P－ ABC中， PA＝ PB＝ PC，且 AB＝ AC，∠ BAC＝90°，则异
A 面直线 PA与 BC所成的角为 ________．
14．三棱锥 A BCD 中 DA , DB, DC 两两垂直且长度都为 1，则三棱锥的体积为 _____．
C．所有能被 2 整除的整数都不是偶数
D ．存在一个能被 2 整除的整数不是偶数
4 ．设 P 是椭圆 x2 25
y2 16
1 上的点．若
F1，F2 是椭圆的两个焦点，则
PF1 PF2 等于 (
)
A． 4
B ．5
C． 8
D ．10
5．正方体的全面积为 6，它的顶点都在球面上，则这个球的表面积是
（）
A． 3
∴
EF＝
AE· DE 3×６
AD
＝ 3
＝ 5
6
5
5 ，在
Rt△ EFG中， FG＝ AB＝3
EF 2 5，∴ tan ∠ EGF＝ FG＝ 5，
3
5
综上可知， a 的取值范围是 2，2 或 2，4 .
21．（ I ）证明：在矩形 ADEF 中， ED AD ∵ 平面 ADEF 平面 ABCD ，且平面 ADEF 平面 ABCD AD
∴ ED 平面 ABCD ∴ ED AC --------------6
分
（Ⅱ）由（ I ）知： ED 平面 ABCD
（ 1）求证：平面 ABCD⊥平面 ADE；（ 2）求二面角 D－ BC－ E的平面角的正切值．

攀枝花市七中2010—2011学年度第二学期高三第一次周考(答案)

数学试题（文）参考解答BACDB CACBD AB 13、135 14、22－1 15、45° 16、④ 17．（1）解：∵)cos 2sin 2,sin 2cos 2(βαβα++=+n m 2分∴)sin(222)cos (sin )sin (cos 2||22βαβαβα++=+++=+∴.558)sin(222=++βα ∴53)sin(=+βα 6分（2）解：∵,02,20<<-<<βππα∴22πβαπ<+<- 又∵.135sin ,53)sin(-=∴=+ββα8分∵ββαα-+=)( ∴ββαββααsin )sin(cos )cos(cos +++==.6533135********=⨯-⨯ 12分18、（1）第3号小球恰好放入第3号小盒记为时间A ，则P(A)=445515A A =（2）1号小球不落入1号小盒且5号小球不落入5号小盒的事件记为B ，则P(B)=5435435521320A A A A -+= 19．解析：（I ）ABCD 是矩形，AD CD ⊥∴ --------------1分又CD AB AB SD //,⊥，则SD CD ⊥ -------------2分 SD AD ⊥ -------------3分 ∴⊥CD 平面ADS -------------4分（II ）由AD SD ⊥，及（I ）结论可知DA 、DC 、DS, 两两互相垂直，建立如图所示的空间直角坐标系)0,0,3(S ∴ ,)0,0,0(),2,0,0(),2,1,0(),0,1,0(D C B A)2,1,3(),0,1,0(-=-=∴SB AD --------------6分 42,cos -=>=<∴ --------------7分 AD 与SB 所成的角的余弦为42--------------8分（III ）)2,1,0(),0,0,3(==DB DS 设面SBD 的一个法向量为),,(z y x n =⎪⎩⎪⎨⎧=∙=∙∴0DB n ⎩⎨⎧=-=⇔0203z y x )1,2,0(-=⇒ --------------9分又)0,1,3(),2,0,0(== ∴设面SAB 的一个法向量为),,(z y x =⎪⎩⎪⎨⎧=∙=∙∴00SA m ⎩⎨⎧=+-=⇔0302y x z )0,3,1(=⇒m --------------10分515,cos =>=<∴ ------11分所以所求的二面角的余弦为515------12分解法二：（I ）同解法一（II ）矩形ABCD ，BC AD //∴，即a BC =∴要求AD 与SB 所成的角，即求BC 与SB 所成的角，………………5分在SBC ∆中，由（I ）知⊥SD 平面ABCD ∴a a a ，SC SBC Rt 7)2()3(22=+=∆中CD 是CS 在面ABCD 内的射影，且CD BC ⊥BC SC ⊥∴ --------------6分77tan ===∠a a CB SC SBC ，42cos =∠SBC --------------8分从而SB 与AD 的成的角的余弦为42（III ）AB SD AD SD SAD ⊥⊥∆且中,, ，⊥∴SD 面ABCD ． ∴ 面SDB ⊥面ABCDBD 为面SDB 与面ABCD 的交线．∴过A 作AE ⊥DB 于E ，∴AE ⊥面SDB ，又过A 作AF ⊥SB 于F ，连接EF ，从而得：EF ⊥SB∴AFE ∠为二面角A —SB —D 的平面角 -------10分在矩形ABCD 中，对角线a a a BD 5)2(22=+= ∴在ABD ∆中， a aa a BD CD AB AE 55252=⋅=⋅= 由（II ）知在而222,2,2,AB SA SB a AB a SA SAD Rt +=∴==∆且中SAB ∆∴为等腰直角三角形，且SAB ∠为直角，a AB AF 222==∴ 5102552sin ===∠∴aaAF AE AFE 所以所求的二面角的余弦为515----12分20．解：（Ⅰ）12n n a S +=，12n n n S S S +∴-=，13n nS S +∴=．………2分又111S a ==，∴数列{}n S 是首项为1，公比为3的等比数列，1*3()n n S n -=∈N ．当2n ≥时，21223(2)n n n a S n --==≥，………………4分21132n n n a n -=⎧∴=⎨2⎩，，，≥．………………6分（Ⅱ）12323n n T a a a na =++++，当1n =时，11T =； ………………7分当2n ≥时，0121436323n n T n -=++++，…………①12133436323n n T n -=++++，………………………②-①②得：12212242(333)23n n n T n ---=-+++++-213(13)222313n n n ---=+--11(12)3n n -=-+-．1113(2)22n n T n n -⎛⎫∴=+- ⎪⎝⎭≥．………………10分又111T a ==也满足上式， 1*113()22n n T n n -⎛⎫∴=+-∈ ⎪⎝⎭N ．………………12分 21．解：（I ）由题易得椭圆方程为13422=+y x ………………4分（II ）如图，设),(11y x M ，),(22y x N ，直线MN 的方程为1+=my x ，则),4(11y M ，),4(21y N ，111+=my x ，122+=my x ，联立方程组⎩⎨⎧=++=1243122y x my x 消去x 得096)34(22=-++my y m ，由韦达定理得⎪⎪⎩⎪⎪⎨⎧+-=+-=+439436221221m y y m m y y ………………6分221131)4(21)4(21y x y x S S -∙-=因为 2222121)43()1(81)3)(3(41++=--=m m y y my my ………………8分 []2222122122122)43()1(3244)(49321++=-+=⎪⎭⎫ ⎝⎛∙-=m m y y y y y y S ……10分所以有43122=S S S ，即存在这样的4=λ ………………12分22．解析：(Ⅰ)当m ＝3时，f (x )＝ 13x 3－3x 2＋5x ，f ′ (x )＝x 2－6x ＋5．（1分）因为f (2)＝ 23，f ′ (2)＝－3，所以切点坐标为（2，23），切线的斜率为－3，则所求的切线方程为y －23＝－3(x －2)，即9x ＋3y －20＝0。

四川省攀枝花市中学初中部高二数学理月考试题含解析

四川省攀枝花市中学初中部高二数学理月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 在等比数列中，，公比.若，则m =（）A.9B.10C.11D.12参考答案：选C。

方法一：由得。

又因为，所以。

因此。

方法二：因为，所以。

又因为，，所以。

所以，即。

2. 下列函数中，定义域是且为增函数的是（）A. B. C. D.参考答案：A3. 若直线x+（1+m）y+m﹣2=0与直线2mx+4y+16=0没有公共点，则m的值是（）A．﹣2 B．1 C．1或﹣2 D．2或﹣1参考答案：B【考点】直线的一般式方程与直线的平行关系．【专题】方程思想；转化思想；直线与圆．【分析】利用两条直线平行的充要条件即可得出．【解答】解：∵直线x+（1+m）y+m﹣2=0与直线2mx+4y+16=0没有公共点，∴两条直线平行．两条直线方程分别化为：y=﹣x+，y=﹣mx﹣4，（1+m≠0），∴﹣=﹣，≠﹣4，解得m=1．故选：B．【点评】本题考查了两条直线平行的充要条件，考查了推理能力与计算能力，属于中档题．4. 已知点是球表面上的点，平面，四边形的边长为的正方形. 若，则球的表面积为（）A. B. C. D.参考答案：A5. 如图，△PAB所在的平面和四边形ABCD所在的平面垂直，且，，AD=4，BC=8，AB=6，，则点P在平面内的轨迹是A．圆的一部分B．一条直线C．一条线段D．两条直线参考答案：A6. 已知点A（3，2），F为抛物线的焦点，点P在抛物线上移动，当取得最小值时，点P的坐标是（）（A）（0，0）；（B）（2，2）；（C）（－2，－2）（D）（2，0）参考答案：B略7. 已知点M（0，﹣1），点N在直线x﹣y+1=0上，若直线MN垂直于直线x+2y﹣3=0，则点N的坐标是（）B略8. 在空间直角坐标系中，点P（1，2，﹣3）关于坐标平面xOy的对称点为（）A．（﹣1，﹣2，3）B．（﹣1，﹣2，﹣3）C．（﹣1，2，﹣3）D．（1，2，3）参考答案：D【考点】空间中的点的坐标．【分析】点（a，b，c）关于坐标平面xOy的对称点为（a，b，﹣c）．【解答】解：在空间直角坐标系中，点P（1，2，﹣3）关于坐标平面xOy的对称点为（1，2，3）．故选：D．【点评】本题考查点的坐标的求法，是基础题，解题时要认真审题，注意空间直角坐标系的性质的合理运用．9. 计算机执行下面的程序段后，输出的结果是（）A． B． C． D．参考答案：B10. 设函数f（x），g（x）在[a，b]上均可导，且f′（x）＜g′（x），则当a＜x＜b时，有（）A．f（x）＞g（x）B．f（x）＜g（x）C．f（x）+g（a）＜g（x）+f（a）D．f（x）+g（b）＜g（x）+f（b）参考答案：C【考点】6B：利用导数研究函数的单调性．【分析】比较大小常用方法就是作差，构造函数F（x）=f（x）﹣g（x），研究F（x）在给定的区间[a，b]上的单调性，F（x）在给定的区间[a，b]上是增函数从而F（x）＞F（a），整理后得到答案．【解答】解：设F（x）=f（x）﹣g（x），∵在[a，b]上f'（x）＜g'（x），F′（x）=f′（x）﹣g′（x）＜0，∴F（x）在给定的区间[a，b]上是减函数．∴当x＞a时，F（x）＜F（a），即f（x）﹣g（x）＜f（a）﹣g（a）即f（x）+g（a）＜g（x）+f（a）故选C．二、填空题:本大题共7小题,每小题4分,共28分11. 已知＝2，＝3，＝4…，若＝6，(a，t为互质的正整数)，由以上等式，可推测a，t的值，则a＋t＝________.参考答案：41根据题中所列的前几项的规律可知其通项应为，所以当n＝6时，，.12. 由下列各式：……请你归纳出一个最贴切的一般性结论:参考答案：13. 设等比数列的前项和为，若=，则实数=参考答案：-114.已知两点A( –2, 0 ) , B( 0 , 2 ), 点P 是椭圆=1上任意一点，则点P 到直线 AB 距离的最大值是 ______________.参考答案：略15. 侧棱与底面垂直的三棱柱A 1B 1C 1﹣ABC 的所有棱长均为2，则三棱锥B ﹣AB 1C 1的体积为．参考答案：【考点】棱柱、棱锥、棱台的体积．【分析】先求出，AA 1=2，由此能求出三棱锥B ﹣AB 1C 1的体积．【解答】解：∵侧棱与底面垂直的三棱柱A 1B 1C 1﹣ABC 的所有棱长均为2， ∴==，AA 1=2，∴三棱锥B ﹣AB 1C 1的体积为： V==．故答案为：．【点评】本题考查三棱锥的体积的求不地，是基础题，解题时要认真审题，注意空间思维能力的培养． 16. 已知函数的零点，则整数a 的值为______.参考答案：3根据函数单调性可知若存在零点则零点唯一，由零点存在定理可判断出零点所在区间，从而求得结果. 【详解】由题意知：在上单调递增若存在零点，则存在唯一一个零点又，由零点存在定理可知：，则本题正确结果：【点睛】本题考查零点存在定理的应用，属于基础题. 17. 二次函数的图像与轴的交点为和，则函数的最大值为 ▲ ．参考答案：略三、解答题：本大题共5小题，共72分。

四川省攀枝花市民族中学校高二数学理月考试卷含解析

四川省攀枝花市民族中学校高二数学理月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 函数、均为偶函数，且当x∈[0，2]时，是减函数，设，,则a、b、c的大小是（）A．B．C． D．参考答案：A略2. 2x2＋5x－3<0的解集为________________.参考答案：{x|－3<x<}3. 已知数列，那么9是数列的（）A．第12项 B．第13项 C．第14项 D．第15项参考答案：C4. 已知数列的通项公式为，那么是这个数列的 ( )A．第3项B．第4项 C．第5项D．第6项参考答案：A5. 下列说法中正确的是（请将你认为正确的序号填在横线上）①平均数不受少数几个极端值的影响，中位数受样本中的每一个数据影响；②抛掷两枚硬币，出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大；③用样本的频率分布估计总体分布的过程中，样本容量越大，估计越准确；④向一个圆面内随机地投一个点，如果该点落在圆内任意一点都是等可能的，则该随机试验的数学模型是古典概型．参考答案：③6. 若点O和点F分别为椭圆的中心和左焦点，点P为椭圆上的任意一点，则的最大值为()A．2B．3C．6D．8参考答案：C略7. 函数的定义域是（）A． B． C．D．参考答案：A8. 已知双曲线的一个焦点与抛物线的焦点重合,且其渐近线的方程为,则该双曲线的标准方程为（）A. B. C. D.参考答案：C略9. 设函数f(x)＝ax3－3x＋1(x∈R)，若对于任意x∈[－1,1]，都有f(x)≥0成立，则实数a的值为（）．A .0 B.2 C.4 D .1参考答案：A10. 已知复数z满足，则z的虚部为（）A．4 B．4i C．－2 D．－2i参考答案：A二、填空题:本大题共7小题,每小题4分,共28分11. 已知甲箱子里装有3个白球、2个黑球，乙箱子里装有2个白球、2个黑球，从这两个箱子里分别随机摸出1个球，则恰有一个白球的概率为__________.参考答案：【分析】通过分析恰有一个白球分为两类：“甲中一白球乙中一黑球”，“甲中一黑球乙中一白球”，于是分别计算概率相加即得答案.【详解】恰有一个白球分为两类：甲中一白球乙中一黑球，甲中一黑球乙中一白球。

高二数学上学期第一次月考试题文含解析 (2)

智才艺州攀枝花市创界学校一中二零二零—二零二壹上学期第一次月考高二年级文科数学试题第一卷〔一共60分〕一、选择题：本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的.1.一个圆锥的外表积为，它的侧面展开图是圆心角为的扇形，那么该圆锥的高为〔〕A.1B.C.2D.【答案】B...............考点：圆锥的面积2.程度放置的的直观图〔斜二测画法〕是边长为的正三角形，那么原的面积为〔〕A. B. C. D.【答案】D【解析】正三角形A′B′C′复原回原三角形如图，过C′作C′D垂直于x′轴于D，因为ΔA′B′C′是边长为√2a的正三角形，，过C′作C′E平行于x′轴交y′轴于E，那么A′E=√2C′D=√3a，所以C′D=√6a2所以，C′对应的原图形中的点C在平面直角坐标系xoy下的纵坐标为2√3a，即原三角形ABC底边AB上的高为2√3a，所以，原三角形ABC面积S=12×√2a×2√3a=√6a，应选D.点睛:平面图形与其直观图的关系(1)在斜二测画法中，要确定关键点及关键线段．“平行于x轴的线段平行性不变，长度不变；平行于y轴的线段平行性不变，长度减半．〞S原图形．(2)按照斜二测画法得到的平面图形的直观图，其面积与原图形的面积的关系：S直观图=√243.在正方体ABCD−A1B1C1D1中，与对角线BD1异面的棱有〔〕条A.3B.4C.6D.8【答案】C【解析】与对角线BD1异面的棱有AD,AA1,A1B1,CC1,C1B1,C1D1六条，选C.4.如图，在以下四个正方体中，A,B为正方体的两个顶点，M,N,Q为所在棱的中点，那么在这四个正方体中，直接AB与平面MNQ不平行的是〔〕A. B.C. D.【答案】A【解析】对于B，易知AB∥MQ，那么直线AB∥平面MNQ；对于C，易知AB∥MQ，那么直线AB∥平面MNQ；对于D，易知AB∥NQ，那么直线AB∥平面MNQ．故排除B，C，D，选A．点睛:此题主要考察线面平行的断定定理以及空间想象才能，属容易题．证明线面平行的常用方法：①利用线面平行的断定定理，使用这个定理的关键是设法在平面内找到一条与直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者者构造平行四边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面．5.圆心(2,−3)，一条直径的两个端点恰好在两坐标轴上，那么这个圆的方程是〔〕A.x2+y2−4x+6y+8=0B.x2+y2−4x+6y=0C.x2+y2−4x−6y=0D.x2+y2−4x+6y−8=0【答案】B【解析】由题意可设圆的直径两端点坐标为A(a,0),B(0,b)，由圆心坐标可得a=4,b=−6，可求得2R=|AB|=2√13∴R=√13，可得圆的方程为(x−2)2−(y+3)2=13即x2+y2−4x+6y=0.应选B.6.m,n是不同的直线，α,β,γ1〕假设m//α，n//α，那么m//n；〔2〕假设m//α，m//β，那么α//β；〔3〕假设m⊥α，n⊥α，那么m//n；〔4〕假设m⊥α，m⊥β，那么α//β；〔5〕假设α⊥β，α⊥γ，那么β//γ〕A.1B.2C.3D.4【答案】C【解析】(1)平行于同一平面的两直线并不一定平行，可能相交，可能异面，所以错〔2〕平行于同一直线的两平面可能相交，可能平行，所以错〔3〕垂直同一平面的两直线平行，对〔4〕垂直同一直线两平面平行，对〔5〕垂直于同一平面的两平面，可能平行，可能相交，错。

四川省攀枝花市第七高级中学校高二数学理月考试题含解析

四川省攀枝花市第七高级中学校高二数学理月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知函数在处取极值10，则a= ( )A. 4或－3B. 4或－11C. 4D. －3参考答案：C2. 函数在[0，3]上的最大值和最小值分别是（）A．5，15 B．5，C．5，D．5，参考答案：C略3. 曲线在点处的切线与坐标轴所围成的三角形的面积为（）A． B． C．3 D．参考答案：B略4. 函数的图象是（）的.A．关于直线对称Ｂ．关于x轴对称Ｃ．关于y轴对称Ｄ．关于原点对称参考答案：C略5. 某几何体的三视图如右图所示，则其侧面积为A．B．C． D．参考答案：A略6. 设函数在区间D上可导，则“时> 0”是“ 函数在区间D上是增函数”的（）Ａ、充分不必要条件Ｂ、必要不充分条件Ｃ、充要条件Ｄ、既不充分也不必要条件参考答案：A7. 一个长方体去掉一个小长方体，所得几何体的正(主)视图与侧(左)视图分别如下图所示，则该几何体的俯视图为()参考答案：C略8. 已知各顶点都在一个球面上的正四棱柱（其底面是正方形，且侧棱垂直于底面）高为4，体积为16，则这个球的表面积是（）A. 16πB. 20πC. 24πD. 32π参考答案：C【分析】根据正四棱柱的底面是正方形,高为4,体积为16,求得底面正方形的边长,再求出其对角线长,然后根据正四棱柱的体对角线是外接球的直径可得球的半径,再根据球的表面积公式可求得.【详解】依题意正四棱柱的体对角线是其外接球的直径,的中点是球心,如图:依题意设,则正四棱柱的体积为:,解得,所以外接球的直径,所以外接球的半径,则这个球的表面积是.故选C.【点睛】本题考查了球与正四棱柱的组合体,球的表面积公式,正四棱柱的体积公式,属中档题.9. 设为等差数列的前项和，若，公差，，则A．5 B．6 C．7D．8参考答案：B10. 在正三棱柱ABC﹣A1B1C1中，若AB=2，AA1=1，则点A到平面A1BC的距离为( )A．B．C．D．参考答案：B【考点】棱柱、棱锥、棱台的体积；棱柱的结构特征．【专题】计算题．【分析】要求点A到平面A1BC的距离，可以求三棱锥底面A1BC上的高，由三棱锥的体积相等，容易求得高，即是点到平面的距离．【解答】解：设点A到平面A1BC的距离为h，则三棱锥的体积为即∴∴．故选：B．【点评】本题求点到平面的距离，可以转化为三棱锥底面上的高，用体积相等法，容易求得．“等积法”是常用的求点到平面的距离的方法．二、填空题:本大题共7小题,每小题4分,共28分11. 一组数据中的每一个数据都乘以2，再减去3 ，得到一组新的数据，如果求得新数据的平均数为7，方差为4，则原来数据的平均数为为，方差为。

高二数学上学期第一次月考试题 60(共10页)

第七中学2021-2021学年高二数学(sh ùxu é)上学期第一次月考试题一、选择题(本大题一一共13小题，每一小题4分，一共52分．前10题为单项选择，11-13三题为多项选择)〔一〕单项选择题(本大题一一共10小题，每一小题4分，一共40分．在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的) 1．数列，，，，……的一个通项公式为〔〕A ．B ．C ．D ．2．数列满足，，那么〔〕A ．B ．12C ．D ．3．设等差数列{}n a 的前项和为，假设，，那么〔〕A ．B ．C ．D ．4．中国古代数学著作?算法统宗?中有这样一个问题：有一人走了378里路，第一天健步行走，从第二天起，由于脚痛，每天走的路程是前一天的一半，走了6天后到达目的地，那么此人第二天走的路程为〔〕 A ．96里B ．189里C ．192里D ．288里 {}n a 是各项均为正数的等比数列，其前n 项和为n S ，假设，，那么〔〕 A ．B ．C ．D ．6．设等差数列{}n a 的前n 项和为n S ，假设，，那么当n S 最大时，〔〕 A ．B ．C ．D ．{}n a 满足，，，那么数列的前10项和为〔〕 A ．B ．C ．D ．8. 函数(hánshù)f〔x〕=，M=f〔1n〕+f〔〕+…+f〔〕+f〔〕〔n∈N*，且n为奇数〕，那么M为〔〕A．2n﹣1 B．n﹣12C．2n+2 D．2n+129.设等差数列{}n a的前n项和为n S，，．记，其中表示不超过的最大整数，如，，那么数列{}n b的前项和为〔〕A． B． C．D．10．数列{}n a满足且，那么2019a 〔〕A．B． C．D．〔二〕多项选择题(本大题一一共3小题，每一小题4分，一共12分．在每一小题给出的四个选项里面，有至少两项符合要求，全部选对得4分，局部选对得2分，错选得0分)11．不等式x2﹣2ax﹣8a2＜0的解集为〔x1，x2〕，且x2﹣x1=15，那么a=〔〕．A． B． C． D．12.假如函数满足：对于任意的等比数列{}n a，仍是等比数列，那么称函数()f x为“保等比数列函数〞．在以下函数中，是“保等比数列函数〞的有〔〕A．B． C． D．13．a＞b＞0，c＜0，那么以下结论中正确的选项是〔〕A. B. C. D.二、填空题(本大题一一共4小题，每一小题4分，一共16分． 17题每空2分)14．{}n a是等比数列，且，与的等差中项为18，那么___________．15．数列{a n}满足：a1＋3a2＋5a3＋…＋(2n－1)·a n＝(n－1)·3n＋1＋3(n∈N*)，那么数列{a n}的通项公式a n=____________.16．数列(shùliè){}n a的通项公式为，假设{}n a是递减数列，那么的取值范围为________.17.正数a，b满足ab=a+2b．①那么ab的最小值为_________，②那么2a+b的最小值为________．三、解答题(本大题一一共6小题，一共82分．解容许写出文字说明，证明过程或者演算步骤) 18．(本小题满分是12分)数列{}n a满足，．（1）求证数列是等差数列；〔2〕求数列{}n a的通项公式；〔3〕试判断是否为数列{}n a中的项，并说明理由．19．(本小题满分是14分)建筑公司用万元购得一块空地，方案在该地块上建造一栋至少层、每层平方米的楼房.初步估计得知，假如将楼房建为层，那么每平方米的平均建筑费用为(单位:元).〔1〕求楼房每平方米的平均综合费用的解析式；〔2〕为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？每平方米的平均综合费用最小值是多少？20．(本小题满分是14分)数列{a n}的前n项和为S n，且a1=1，S n=2a n+1．〔1〕求数列(shùliè){a n}的通项公式a n及S n；〔2〕求数列{na n+12n}的前n项和．21．(本小题满分是14分)等差数列{a n}满足a2+a3=7，其前9项和为54．设数列{b n}的前n项和为S n，满足b1=1，〔n∈N*〕．〔1〕求数列{a n}，{b n}的通项公式；〔2〕令，数列{c n}的前n项和为T n，假设对任意n∈N*，都有T n≥a恒成立，务实数a的取值范围．22.(本小题满分是14分)数列{a n}的前n项和为S n，满足2S n-na n=n,n∈N*,且a2=3〔1〕求数列{a n}的通项公式；〔2〕设，数列{b n}的前n项和为T n,求使成立的最小正整数n的值。

四川省攀枝花市第七中学高二数学文联考试卷含解析

四川省攀枝花市第七中学高二数学文联考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 假设关于某设备的使用年限（年）和所支出的费用（万元），有如下表所示的统计资料：42.23.8 6.5 7.0根据上表提供的数据，求出了关于的线性回归方程为，那么统计表中的值为( )A. 5.5B. 5.0C. 4.5D. 4.8参考答案：A2. 一次函数与二次函数在同一坐标系中的图象大致是（）参考答案：C3. 函数的图象大致是（）A. B. C. D.参考答案：A【分析】先判断函数的奇偶性排除B,D，再根据f(1)排除C得解.【详解】由题得，所以函数是奇函数，排除选项B,D.由题得，所以排除选项C.故选：A【点睛】本题主要考查函数图像的识别，考查函数的奇偶性的判断，意在考查学生对这些知识的理解掌握水平，属于基础题.4. 设f（x）是（﹣∞，+∞）上的减函数，则不等式f（2）＜f（）的解集是（）A．（0，）B．（﹣∞，）C．（，+∞）D．（﹣∞，0）∪（，+∞）参考答案：D【考点】函数单调性的性质．【分析】根据函数单调性的性质进行转化求解即可得到结论．【解答】解：∵f（x）是（﹣∞，+∞）上的减函数，则由不等式f（2）＜f（）可得 2＞，∴x＜0，或x＞，故选：D．5. 若，则“”是“方程表示双曲线”的( )A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件参考答案：A略6. 已知数列{a n}为等比数列，S n是它的前n项和，若a2?a3=2a1，且a4与2a7的等差中项为，则S5=( )A．35 B．33 C．31 D．29参考答案：C考点：等比数列的性质；等比数列的前n项和．专题：等差数列与等比数列．分析：用a1和q表示出a2和a3代入a2?a3=2a1求得a4，再根据a4+2a7=a4+2a4q3，求得q，进而求得a1，代入S5即可．解答：解：a2?a3=a1q?a1q2=2a1∴a4=2a4+2a7=a4+2a4q3=2×∴q=，a1==16故S5==31故选C．点评：本题主要考查了等比数列的性质．属基础题．7. 函数f（x）=log2（x+3）（x﹣5）的定义域是A，函数g（x）=x3+m在x∈[1，2]上的值域为B，又已知B?A，则实数m的取值范围是（）A．（﹣∞，﹣11）∪（4，+∞）B．（﹣11，4）C．（﹣4，﹣3）D．（﹣∞，﹣4]∪[﹣3，+∞）参考答案：A【考点】函数的值域；函数的定义域及其求法．【分析】求出函数f（x）的定义域A和函数g（x）在x∈[1，2]上的值域B，再根据B?A列不等式求出实数m的取值范围．【解答】解：函数f（x）=log2（x+3）（x﹣5），∴（x+3）（x﹣5）＞0，解得x＜﹣3或x＞5，∴f（x）的定义域是A=（﹣∞，﹣3）∪（5，+∞）；又函数g（x）=x3+m在x∈[1，2]上是增函数，∴g（x）的值域为B=[1+m，8+m]；又B?A，∴1+m＞5或8+m＜﹣3，解得m＞4或m＜﹣11；∴实数m的取值范围是（﹣∞，﹣11）∪（4，+∞）．故选：A．8. 若满足, 则直线过定点( )A. B. C. D.参考答案：B略9. 用反证法证明命题：“若a,b∈N，ab能被3整除，那么a,b中至少有一个能被3整除”时，假设应为（）A．a、b都能被3整除 B．a、b都不能被3整除C．a、b不都能被3整除 D．a不能被3整除参考答案：B略10. x=5y=6PRINT xy=11ENDA.xy=11B.11C.xy=11D.出错信息参考答案：D二、填空题:本大题共7小题,每小题4分,共28分11. 已知圆O的方程为x2+y2=2，圆M的方程为（x﹣1）2+（y﹣3）2=1，过圆M上任一点P作圆O的切线PA，若直线PA与圆M的另一个交点为Q，则当弦PQ的长度最大时，直线PA的斜率是．参考答案：1或﹣7【考点】直线与圆的位置关系．【专题】计算题．【分析】由题意得，弦PQ的长度最大为圆M的直径，用点斜式设出直线PA的方程，根据直线PA和圆O相切，圆心O到直线PA的距离等于圆O的半径，求出PA的斜率k，即得直线PA的方程．【解答】解：当直线PA过圆M的圆心M（1，3）时，弦PQ的长度最大为圆M的直径．设直线PA的斜率为k，由点斜式求得直线PA的方程为 y﹣3=k（x﹣1），即 kx﹣y+3﹣k=0．由直线PA和圆O相切得=，∴k=1或 k=﹣7，故答案为：1或﹣7．【点评】本题考查直线和圆的位置关系，点到直线的距离公式的应用，判断弦PQ的长度最大为圆M 的直径是解题的关键．12. 展开式中二项式系数最大的项为 .(求出具体的项)参考答案：略13.给出以下四个问题：①输入一个数x，输出它的绝对值；②求面积为6的正方形的周长；③求三个数a，b，c中的最大数；④求函数f(x)＝的函数值．其中需要用选择结构来描述算法的有________个．参考答案：314. 甲、乙、丙三名同学中只有一人考了满分，当他们被问到谁考了满分时，甲说：丙没有考满分；乙说：是我考的；丙说：甲说真话．事实证明：在这三名同学中，只有一人说的是假话，那么得满分的同学是_____．参考答案：甲试题分析：采用反证法，如果甲说的是假话，那丙就是满分，那么乙也说的是假话，就不成立了，如果乙说的是假话，那乙没有考满分，丙也没有考满分，那只有甲考满分．考点：1．合情推理；2．反证法．15. 在等差数列3，7，11…中，第5项为_______.参考答案：19略16. 若x、y∈R+, x+4y=20,则xy的最大值为．参考答案：2517. 设变量满足约束条件，且目标函数的最小值是－10，在a的值是．参考答案：2三、解答题：本大题共5小题，共72分。

攀枝花市三中2011数学月考

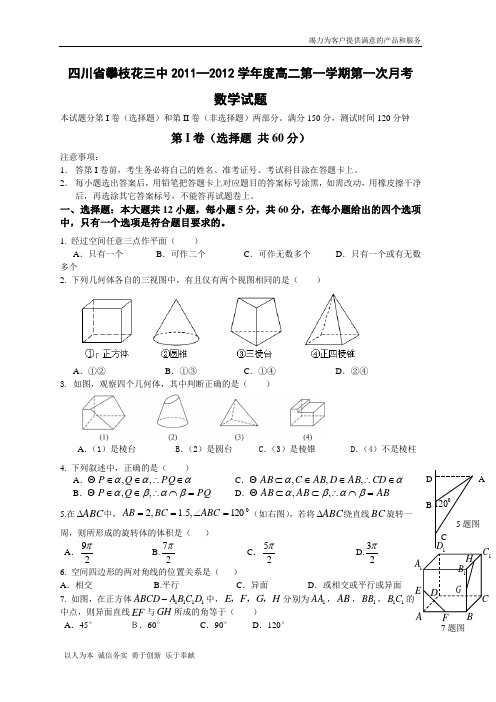
A FD BCG E 1BH1C1D1A7题图四川省攀枝花三中2011—2012学年度高二第一学期第一次月考数学试题本试题分第I 卷（选择题）和第II 卷（非选择题）两部分。

满分150分，测试时间120分钟第I 卷（选择题共60分）注意事项：1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目涂在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，不能答再试题卷上。

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个选项是符合题目要求的。

1. 经过空间任意三点作平面（）A ．只有一个B ．可作二个C ．可作无数多个D ．只有一个或有无数多个2. 下列几何体各自的三视图中，有且仅有两个视图相同的是（）A ．①②B ．①③C ．①④D ．②④3. 如图，观察四个几何体，其中判断正确的是（）A ．（1）是棱台B ．（2）是圆台C ．（3）是棱锥D ．（4）不是棱柱 4. 下列叙述中，正确的是（） A ．ααα∈∴∈∈PQ Q P ,,C ．αα∈∴∈∈⊂CD AB D AB C AB ,,, B ．PQ Q P =⋂∴∈∈βαβα,,D ．AB AB AB =⋂∴⊂⊂βαβα,,5.在ABC ∆中，0120,5.1,2=∠==ABC BC AB （如右图），若将ABC ∆绕直线BC 旋转一周，则所形成的旋转体的体积是（） A ．29π B.27π C ．25π D.23π6. 空间四边形的两对角线的位置关系是（）A ．相交 B.平行 C ．异面 D ．或相交或平行或异面 7. 如图，在正方体1111ABCD ABCD -中，EFGH ，，，分别为1AA ，AB ，1BB ，11B C 的中点，则异面直线EF 与GH 所成的角等于（） A ．45° Ｂ．60° C ．90° D ．120°ACB D 01205题图8. 设n m ,是不同的直线，α、β、γ是不同的平面，有以下四个命题，其中正确的命题是（）①γβγαβα//////⇒⎭⎬⎫；②βαβα⊥⇒⎭⎬⎫⊥m m //；③βαβα⊥⇒⎭⎬⎫⊥//m m ；④αα////m n n m ⇒⎭⎬⎫⊂；Ａ．①④；B ．②③；C ．①③；D ．②④；9.菱形ABCD 在平面α内，BD PA PC 与对角线则,α⊥的位置关系是（） A ．平行 B ．相交但不垂直 C ．垂直相交 D ．异面垂直 10.已知正ABC △的边长为a ，那么ABC △的平面直观图AB C △'''的面积为（） A22 C2D2 11．已知球面上过,,A B C 三点的截面和球心的距离是球半径的一半，且2AB BC CA ===，则球的表面积为.A.169πB.83πC.4πD.649π12. 如图，正方体1111ABCD A B C D -，则下列四个命题：其中正确命题的是（）①P 在直线1BC 上运动时，三棱锥1A D PC -的体积不变；②P 在直线1BC 上运动时，直线AP 与平面ACD 1所成角的大小不变； ③P 在直线1BC 上运动时，二面角1P AD C --的大小不变；④M 是平面1111A B C D 上到点D 和1C 距离相等的点，则M 点的轨迹是过1D 点的直线A ．①③B ．①②③C ． ②④D ．①③④第II 卷（非选择题共90分）注意事项：1．用钢笔或圆珠笔直接答在答题卷中规定的方框内，答错位置直接按零分计算； 2．答题前将密封线内的项目填写清楚二．填空题：本大题共4个小题，每小题4分，共16分，将答案填在题中横线上。

四川省攀枝花七中-度高二数学上学期期中检测题(理)

四川省攀枝花七中2008-2009学年度高二数学上学期期中检测题（理）注意事项：本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟。

第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．点(1,1)在圆22()()4x a y a -++=的内部，则a 的取值范围是 A ．01a << B ．11a -<< C ．1a <-或1a > D ．1a =±2．双曲线22134y x -=的两条准线的距离等于A B C ．65 D ．353．椭圆221916x y +=的焦点坐标是 A ．1(5,0)F -、2(5,0)F B ．1(0,5)F -、2(0,5)FC ．1(F 、2FD ．1(0,F 、2F4．两个圆1C ：222220x y x y +---=与2C ：226440x y x y ++++=的公切线有且仅有A ．1条B ．2条C ．3条D ．4条5．与直线l ：23y x =+平行且与圆222440x y x y +--+=相切的直线方程是 A ．05=±-y x B ．052=±-y xC ．052=±+y xD ．052=±-y x6．方程222-=-y x xy 所表示的曲线的对称性是 A ．关于原点对称 B ．关于两坐标轴对称 C ．关于直线y =x 对称 D ．关于直线y =－x 对称7．斜率为2的直线l 过双曲线)0,0(12222>>=-b a by a x 的右焦点，且与双曲线的左、右两支分别相交，则双曲线的离心率e 的取值范围A ．2>e B ．5>e C ．51<<e D ．31<<e8．已知点（x ，y ）在如图所示平面区域内运动（包含边界），目标函数.y kx z -=当且仅当54,32==y x 时，目标函数z 取最小值，则实数k 的取值范围是 A ．)103,512(--B ．]103,512[--C ．)310,125(--D ．]310,125[--9．如图，ABCDEF 为正六边形，则以F 、C 为焦点，且经过A 、E 、D 、B 四点的双曲线的离心率为A1B1 C1D110．已知(2,1)M ，(1,2)N -，在下列方程的曲线上，存在点P 满足||||MP NP =的曲线方程是A ．310x y -+=B ．22430x y x +-+=C ．1222=+y x D ．1222=-y x 11．已知椭圆的焦点是F 1、F 2，P 是椭圆上的一个动点，过点F 2向∠F 1PF 2的外角平分线作垂线，垂足为M ，则点M 的轨迹是A ．圆B ．椭圆C ．直线D ．双曲线的一支12．已知直线.127))(3(22=-∈-=y m x R k x k y 与双曲线某学生作了如下变形：由 ⎪⎩⎪⎨⎧=--=127)3(22y m x x k y 消去y 后得到形如02=++C Bx Ax 的方程，当A=0时，该方程有一解；当A ≠0时，240B AC ∆=-≥恒成立.假设学生的演算过程是正确的，则实数m 的取值范围为A ．),9[+∞B ．]9,0(C ．]3,0(D ．),3[+∞四川省攀枝花七中08-09学年高二上学期期中检测（数学理）总分表第Ⅱ卷（非选择题共90分）二、填空题（本大题4个小题，每小题4分，共16分，只填结果，不要过程） 13．点(,)P x y 在椭圆2244x y +=上，则x y +的最大值为。

攀枝花七中—学年月考统一检测试卷。12.doc

攀枝花七中—20XX 学年月考统一检测试卷。

12高一数学（满分150分，120分钟完成）注意事项：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷答案填涂到答题卡上；第Ⅰ卷（60分）一、选择题（本题共12个小题，每小题5分，共60分，在每小题列出的四个选项中，只有一项是符合题目要求的。

）1．条件甲：A B A = ；条件乙：A 是B 的真子集，则甲是乙的 ( )A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要 2．已知},1|{},1|{22-==-==x y y N x y x M 那么M N= （）A ．∅B ．MC ．ND ．R3、下列各组函数中，表示同一函数的是（）2)x y x y A ==和 111)2+=--=x y x x y B 和 x y x y C lg 2lg )2==和 100lg2lg )x y x y D =-=和 4．有下列命题：①“若1=xy ，则x 、y 互为倒数”的逆命题；②“面积相等的两个三角形全等”的否命题；③“若1≤m ，则022=+-m x x 有实数根”的逆否命题；④“若M N N N M ⊆=则, ”的逆否命题。

其中正确的是（）A ①②B ②③C ①②③D ③④5．)(x f 的定义域为]4,2[-, 则)43(-x f 的定义域为）A ]38,32[ B ]10,8[- C ]2,0[ D ]4,2[-6．函数)(x g 的图象与函数9)1(log )(3+-=x x f 的图象关于直线x y =对称，则)10(g的值为 ( )A 2B 4C 11D 127．如果函数2)1(2)(2+-+=x a x x f 在区间（－∞，4]上是减函数，那么实数a 的取值范围是（）A a ≥ 3B a ≤－3C a ≤5D a ≥ －38．=≠-=-)21(),0(1)21(22f x xx x f 那么（） A 1 B 3 C 15D 309．设0<a <1，实数,x y 满足log 0a x y +=，则y 关于x 轴的函数图像大致形状是（）A B C D10．2210ax x ++=至少．．有一个负．的实根．．的充要条件．．．．是（）A ．0<a ≤1B ．a <1C ．a ≤1D ．0<a ≤1或a <011．拟定从甲地到乙地通话m 分钟的电话费由f(m)＝1.06(0.50×[m]＋1)给出，其中m ＞0，[m]是大于或等于m 的最小整数（如[3]＝3，[3.7]＝4， [3.1]＝4），则从甲地到乙地通话时间为5.5分钟的话费为（）A ．3.71B ．3.97C ．4.24D ．4.7712．已知定义在实数R 上的函数)(x f y =不恒为零，同时满足),()()(y f x f y x f =+且当x >0时，f (x )>1，那么当x <0时，一定有（）A ．1)(-<x fB ．0)(1<<-x fC ．1)(>x fD ．1)(0<<x f攀枝花七中—20XX 学年月考统一检测试卷高一数学总分表第Ⅱ卷（非选择题，共90分）二、填空题（本小题4个小题，每小题4分，共16分） 13．含有三个实数的集合既可表示为}1,,{aba 也可表示为}0,,{2b a a +，则 20042003b a+= 。

攀枝花市高2012级高三

6.方茴说："我觉得之所以说相见不如怀念，是因为相见只能让人在现实面前无奈地哀悼伤痛，而怀念却可以把已经注定的谎言变成童话。

"7.在村头有一截巨大的雷击木，直径十几米，此时主干上唯一的柳条已经在朝霞中掩去了莹光，变得普普通通了。

1."噢，居然有土龙肉，给我一块！"2.老人们都笑了，自巨石上起身。

而那些身材健壮如虎的成年人则是一阵笑骂，数落着自己的孩子，拎着骨棒与阔剑也快步向自家中走去。

攀枝花市高2012级高三第一次统考 2011.11数学（理工类）试题卷本试题卷分第一部分（选择题）和第二部分（非选择题）两部分，共4页．考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效．满分150分，考试时间120分钟．考试结束后，将答题卡交回．注意事项：1. 答题前，务必将自己的姓名、考号填写在答题卡规定的位置上．并用2B 铅笔将答题卡考号对应数字标号涂黑．2. 答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．第一部分（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．） 1、设全集U R =，集合{|14}A x x x =<->或，2{|0}3x B x x -=≤+，则()U A B =ð（）A ．{|12}x x -≤≤B ．{|31}x x -<<-C ．{|24}x x ≤≤D ．{|34}x x x ≤->或 2、已知等差数列{}n a 中，23412a a a ++=，则{}n a 的前5项的和5S 的值为（）A ．5B ．10C ．20D ．40 3、已知角α的终边经过点(4,3)P -，则tan()4πα+的值等于（）A ．17-B ．17C ．37D ．474、如图是某条公共汽车线路收支差额y 与乘客量x 的图像，由于目前线路亏损，公司领导决定：支出不变，适当提高票价。

四川省攀枝花市第七中学高二数学文模拟试卷含解析

四川省攀枝花市第七中学高二数学文模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 在等差数列{a n}中，a4+a6=6，且a2=1，则公差d等于（）A．B．C．D．参考答案：A【考点】等差数列的通项公式．【分析】由已知结合等差数列的通项公式化为关于d的方程求解．【解答】解：在等差数列{a n}中，由a4+a6=6，且a2=1，得a2+2d+a2+4d=6，即2+6d=6，∴d=．故选：A．2. 若，且，则下列不等式一定成立的是（）A.． B． C． D．参考答案：D略3. 已知x1，x2是函数f（x）=e﹣x﹣|ln x|的两个零点，则（）A．B．1＜x1x2＜e C．1＜x1x2＜10 D．e＜x1x2＜10参考答案：A【考点】函数的零点．【分析】若的两个零点，则x1，x2是函数y=e﹣x和y=|lnx|的图象交点的横坐标，在同一个坐标系中，画函数y=e﹣x和y=|lnx|的图象，利用对数函数的性质，可判断出x1x2的范围．【解答】解：若的两个零点，则x1，x2是函数y=e﹣x和y=|lnx|的图象交点的横坐标在同一个坐标系中，画函数y=e﹣x和y=|lnx|的图象如下图所示：由图可得即﹣1＜ln（x1?x2）＜1即又∵﹣lnx1＞lnx2∴ln（x1?x2）＜0∴x1?x2＜1综上故选A4. 如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE，若M为线段A1C 的中点，则在△ADE翻折过程中，下面四个命题中不正确的是( )A．|BM|是定值B．点M在某个球面上运动C．存在某个位置，使DE⊥A1CD．存在某个位置，使MB∥平面A1DE参考答案：C考点：平面与平面之间的位置关系．专题：综合题；空间位置关系与距离．分析：取CD中点F，连接MF，BF，则平面MBF∥平面A1DE，可得D正确；由余弦定理可得MB2=MF2+FB2﹣2MF?FB?cos∠MFB，所以MB是定值，M是在以B为圆心，MB为半径的圆上，可得A，B正确．A1C在平面ABCD中的射影为AC，AC与DE不垂直，可得C不正确．解答：解：取CD中点F，连接MF，BF，则MF∥DA1，BF∥DE，∴平面MBF∥平面A1DE，∴MB∥平面A1DE，故D正确由∠A1DE=∠MFB，MF=A1D=定值，FB=DE=定值，由余弦定理可得MB2=MF2+FB2﹣2MF?FB?cos∠MFB，所以MB是定值，故A正确．∵B是定点，∴M是在以B为圆心，MB为半径的圆上，故B正确，∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，∴存在某个位置，使DE⊥A1C不正确．故选：C．点评：掌握线面、面面平行与垂直的判定和性质定理及线面角、二面角的定义及求法是解题的关键．5. 已知a=，b=log2，c=log，则（）A．a＞b＞c B．a＞c＞b C．c＞b＞a D．c＞a＞b参考答案：D【考点】4H：对数的运算性质．【分析】利用指数式的运算性质得到0＜a＜1，由对数的运算性质得到b＜0，c＞1，则答案可求．【解答】解：∵0＜a=＜20=1，b=log2＜log21=0，c=log=log23＞log22=1，∴c＞a＞b．故选：D．6. 函数在处切线斜率为（）A．0 B．－1 C. 1 D．参考答案：C则，即函数在处切线斜率为.本题选择C选项.7. 下列求导运算正确的是：（）A． B．C．D．参考答案：D8. 已知定义在R上的奇函数满足，当时，，且，则（）A. 2B. 1C. －2D. －1参考答案：C【分析】根据题意，结合函数的奇偶性与对称性可得函数f（x）是周期为8的周期函数，由函数的奇偶性可得f（﹣2）＝8，结合函数的解析式求出a的值，进而求出f（﹣1）的值，进而结合函数的奇偶性与对称性分析可得答案．【详解】根据题意，函数f（x）是定义在R上的奇函数，则f（﹣x）＝﹣f（x），若函数f（x）满足f（x+2）＝f（2﹣x），则有f（﹣x）＝f（x+4），则有f（x+4）＝﹣f（x），变形可得f（x+8）＝﹣f（x+4）＝f（x），则函数f（x）是周期为8的周期函数，又由函数f（x）是定义在R上的奇函数，且f（2）＝﹣8，则f（﹣2）＝8，若当﹣2≤x ＜0时，f （x ）＝a x ﹣1（a ＞0），且f （﹣2）＝a ﹣2﹣1＝8，解可得a，则f （﹣1）＝（）﹣1﹣1＝2，则f （1）＝﹣2，又由函数f （x ）是周期为8的周期函数，则f （2019）＝f （3+2016）＝f （3）＝f （1）＝﹣2；故选：C ．【点睛】本题考查函数的奇偶性与周期性的应用，关键是分析函数的周期性，属于中档题． 9. 下图为两幂函数y ＝x α和y ＝x β的图像，其中α，β∈{－，，2,3}，则不可能的是( )参考答案：B12. 中，=A ．B ．C ．D ．或参考答案： B 略二、填空题:本大题共7小题,每小题4分,共28分11. 若命题“?x∈R，使x 2+（a ﹣1）x+1＜0”是假命题，则实数a 的取值范围为．参考答案：﹣1≤a≤3【分析】先求出命题的否定，再用恒成立来求解【解答】解：命题“?x∈R，使x 2+（a ﹣1）x+1＜0”的否定是：““?x∈R，使x 2+（a ﹣1）x+1≥0”即：△=（a ﹣1）2﹣4≤0，∴﹣1≤a≤3 故答案是﹣1≤a≤312. 抛物线y 2=4x 与直线y=2x ﹣4所围成图形的面积为．参考答案：9【考点】定积分．【分析】先联立方程，组成方程组，求得交点坐标，可得被积区间，再用定积分表示出曲线yy 2=4x 与直线y=2x ﹣4所围成的封闭图形的面积，即可求得结论【解答】解：联立方程组，解得或，∴曲线y=x 2与直线y=x 围成的封闭图形的面积为S=（y+2﹣y 2）dy=（y 2+2y ﹣）|=9，故答案为：913. 正三棱锥P -ABC 的底面边长为，E 、F 、G 、H 分别是PA 、AC 、BC 、PB 的中点，四边形EFGH 面积记为，则的取值范围是 ▲.参考答案：14. 古希腊著名的毕达哥拉斯学派把1、3、6、10……这样的数称为“三角形数”，而把1、4、9、16……这样的数称为“正方形数”.如图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式中，符合这一规律的表达式是①13=3+10； ②25=9+16 ③36=15+21； ④49=18+31； ⑤64=28+36 参考答案： ③⑤ 略15. 若三角形的内切圆半径为r ，三边的长分别为a ，b ，c ，则三角形的面积S=r （a+b+c ），根据类比思想，若四面体的内切球半径为R ，四个面的面积分别为S 1、S 2、S 3、S 4，则此四面体的体积V= ．参考答案：R （S 1+S2+S 3+S 4）【考点】类比推理；棱柱、棱锥、棱台的体积．【分析】根据平面与空间之间的类比推理，由点类比点或直线，由直线类比直线或平面，由内切圆类比内切球，由平面图形面积类比立体图形的体积，结合求三角形的面积的方法类比求四面体的体积即可．【解答】解：设四面体的内切球的球心为O ，则球心O 到四个面的距离都是R ，所以四面体的体积等于以O 为顶点，分别以四个面为底面的4个三棱锥体积的和．故答案为： R （S 1+S 2+S 3+S 4）．16. 在等比数列中，若＞0且则．参考答案： 8 略17. 已知实数x, y 满足方程x2+y2=4, 则y-x 的最小值为_____参考答案：略三、解答题：本大题共5小题，共72分。