实验5 积分与微分电路实验
积分电路和微分电路实验报告

竭诚为您提供优质文档/双击可除积分电路和微分电路实验报告篇一:实验6积分与微分电路实验6积分与微分电路1.实验目的学习使用运放组成积分和微分电路。
2.实验仪器双踪示波器、信号发生器、交流毫伏表、数字万用表。
3.预习内容1)阅读op07的“数据手册”,了解op07的性能。
2)复习关于积分和微分电路的理论知识。
3)阅读本次实验的教材。
4.实验内容1)积分电路如图5.1。
在理想条件下,为零时,则dV(t)Vi(t)??co,当c两端的初始电压RdtVo(t)??1tVi(t)dtRc?o因此而得名为积分电路。
(1)取运放直流偏置为?12V,输入幅值Vi=-1V的阶跃电压,测量输出饱和电压和有效积分时间。
若输入为幅值Vi=-1V阶跃电压时,输出为Vo(t)??Vi1tVdt??t,(1)iRc?oRc这时输出电压将随时间增长而线性上升。
通常运放存在输入直流失调电压,图6.1所示电路运放直流开路,运放以开环放大倍数放大输入直流失调电压,往往使运放输出限幅,即输出电压接近直流电源电压,输出饱和,运放不能正常工作。
在op07的“数据手册”中,其输入直流失调电压的典型值为30μV;开环增益约为112db,即4×105。
据此可以估算,当Vi=0V时,Vo=30μV×4×105=12V。
电路实际输出接近直流偏置电压,已无法正常工作。
建议用以下方法。
按图6.1接好电路后,将直流信号源输出端与此同时Vi相接,调整直流信号源,使其输出为-1V,将输出Vo接示波器输入,用示波器可观察到积分电路输出饱和。
保持电路状态,关闭直流偏置电源,示波器x轴扫描速度置0.2sec/div,Y轴输入电压灵敏度置2V/div,将扫描线移至示波器屏的下方。
等待至电容上的电荷放尽。
当扫描光点在示波器屏的左下方时,即时打开直流偏置电源,示波器屏上积分电路的输出为线性上升的直线,大约1秒后,积分电路输出由线性上升的直线变为水平直线,即积分电路已饱和,立即按下示波器的“stop”键。
积分电路和微分电路 实验报告书

积分电路和微分电路实验报告书学号:姓名:学习中心:(1)按如图连接电路(2)设置信号发生器的输出频率为1HZ,幅值为5V的方波,如图(3)激活仿真电路双击示波器图标弹出示波器面板,观察并分析示波器波形(4)按表1给出的电路参数依次设置R和C的取值,分别激活仿真运行,双击示波器图标,弹出示波器面板,给出输入/输出信号的波形图,并说明R和C的取值对输出信号的影响表1 实验电路参数序号输入为方波信号电路参数频率/HZ幅值/V R/KO C/uF1 1 5 100 12 1 5 100 23 1 5 100 4.72.微分电路实验(1)按图连接电路(2)设置R和C(3)激活电路仿真运行,(4)双击示波器的面板,给出输入/输出信号的波形图(5)说明R和C的取值对输出信号的影响表2 实验电路参数序号输入为方波信号电路参数频率/HZ幅值/V R/KO C/uF1 1 5 100 12 1 5 100 23 1 5 100 4.7三、实验过程原始数据(数据、图表、计算等)1.积分电路实验R=100KO,C=1uFR=100 KO C=2UFR=100KO C=4.7uF2.微分电路实验R=100KO,C=1uFR=100 KO C=2UFR=100KO C=4.7uF四、实验结果及分析积分电路实验由积分电路的特点:时间常数t远大于输入信号的周期T,在此条件下Uc(t)<<UR(t)因此i(t)=UR(t)/R=Ui(t)/RU0(t)=Uc(t)=1/C(i(t)dt=1/RC(ui(t)dt即输出电压与输入电压的积分成正比,若输出电压为周期方波,则输出电压为周期三角波由实验数据知道,随着C的增大,积分方波越明显微分电路实验由微分电路的特点:Uo(t)=UR(t)=RC*duc(t)/dt=RC*dui(t)/dt即输出电压与输入电压的微分成正比;若输入为周期方波,则输出电压为周期窄脉冲;从实验数据知道:随着C的增大,微分脉冲越明显如有侵权请联系告知删除,感谢你们的配合!。
积分电路和微分电路的设计实验报告

积分电路和微分电路的设计实验报告一、实验目的本实验旨在通过设计积分电路和微分电路,掌握基本的积分和微分电路的原理、设计方法和实验技能,加深对模拟电子技术的理解。
二、实验器材1.双踪示波器2.函数信号发生器3.直流稳压电源4.万用表5.集成运放(LM741)三、积分电路设计实验1.原理简介:积分电路是一种能够将输入信号进行积分运算的电路,通常由一个运放、一个电容和一个反馈电阻组成。
在输入信号为正弦波时,输出信号为余弦波,并且幅度随时间增加而增大。
2.设计步骤:(1)选择合适的运放:本次实验选用LM741运放。
(2)确定反馈电阻Rf:根据公式Rf=1/(2πfC),其中f为输入信号频率,C为选定的电容值。
本次实验选用C=0.01μF,当输入频率为1kHz时,计算得到Rf=15.92kΩ。
(3)确定输入阻抗Rin:为了保证输入信号不被积分电路影响,需要满足Rin>>Rf。
本次实验选用Rin=1MΩ。
(4)确定电源电压:根据运放数据手册,LM741的最大工作电压为±18V。
本次实验选用±15V的直流稳压电源。
3.实验步骤:(1)按照上述设计步骤连接电路图,并接通电源。
(2)调节函数信号发生器输出正弦波信号,频率为1kHz,幅度为2V。
(3)使用双踪示波器观察输入和输出信号波形,并记录数据。
(4)更改输入信号频率和幅度,重复步骤(2)和(3),记录数据。
4.实验结果分析:根据实验记录的数据,可以得到输入和输出信号的波形图。
当输入为正弦波时,输出为余弦波,并且幅度随时间增加而增大。
当输入频率增加时,输出幅度也相应增加;当输入幅度增加时,输出幅度也相应增加。
五、微分电路设计实验1.原理简介:微分电路是一种能够将输入信号进行微分运算的电路,通常由一个运放、一个电阻和一个反馈电容组成。
在输入信号为正弦波时,输出信号为余弦波,并且幅度随时间减小而减小。
2.设计步骤:(1)选择合适的运放:本次实验选用LM741运放。
积分与微分电路实验报告

积分与微分电路实验报告这次的实验其实说起来也不复杂,就是做一个积分电路和微分电路,听起来很高大上对吧?不过,做起来其实没那么神秘,反而有点像做菜,材料准备好,步骤走一遍,最后成果就出来了。
先说说积分电路吧,这玩意儿简单得很,就是通过运算放大器来实现输入信号的积分。
其实就是把电压信号“积”在电容上,输出一个跟输入信号积分相关的结果。
你可以想象成,输入信号就像下雨,电容就像一个大水桶,输入信号越大,积累的水越多,输出的电压就越高。
真有点像这小雨变大雨的感觉!做这个电路的时候,最重要的就是把电容和电阻选对了,不然信号一来,电路就“崩了”,啥也没有。
然后说微分电路,哎,这个就有点儿像是小汽车的刹车系统了,输入信号一来,它立马做出反应,把信号的变化量放大输出。
微分电路的关键就是把输入信号变化的速度抓住,简而言之就是“快、狠、准”!只要一有信号的突变,输出信号就会像火箭一样飞出去,这就有点像看到路口红灯时,车子猛地刹车的感觉。
如果把积分电路比作“慢慢积累”,那微分电路就是“迅速反应”。
不过,微分电路也有点难搞,稍微电路设计得不对,输出信号就容易出现“尖刺”——噼里啪啦乱响的那种,简直是让人抓狂。
实验做的时候,我一开始有点儿紧张,毕竟这些电路在书本上看着简单,可一旦自己动手弄,事情就复杂了。
记得第一次接好电路后,开机的时候,心里那是忐忑不安的,简直像是在做某个高难度的挑战。
输入信号一开始就不对,整个人都傻眼了。
那个波形一看,心想:哎呀妈呀,咋回事啊?完全不像书上的样子嘛!不过,再一看,发现是电容接错了,真是晕了。
于是,我又赶紧换了下接线,结果,哇塞,居然成功了!看到输出信号渐渐符合预期,心里那个小激动,简直快要跳起来。
做电路嘛,最终的目的就是“问题解决”!当你看到那个波形对上了,真是像突然得到了人生的答案,所有的辛苦和焦虑都值了。
说到这里,你可能会想,积分电路和微分电路做起来有啥不一样?其实不瞒你说,差别还真不小。
微分与积分电路分析
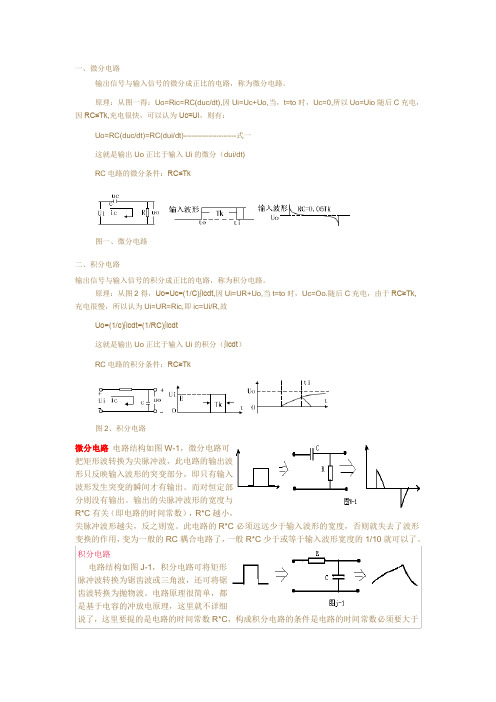
一、微分电路输出信号与输入信号的微分成正比的电路,称为微分电路。
原理:从图一得:Uo=Ric=RC(duc/dt),因Ui=Uc+Uo,当,t=to时,Uc=0,所以Uo=Uio随后C充电,因RC≤Tk,充电很快,可以认为Uc≈Ui,则有:Uo=RC(duc/dt)=RC(dui/dt)---------------------式一这就是输出Uo正比于输入Ui的微分(dui/dt)RC电路的微分条件:RC≤Tk图一、微分电路二、积分电路输出信号与输入信号的积分成正比的电路,称为积分电路。
原理:从图2得,Uo=Uc=(1/C)∫icdt,因Ui=UR+Uo,当t=to时,Uc=Oo.随后C充电,由于RC≥Tk,充电很慢,所以认为Ui=UR=Ric,即ic=Ui/R,故Uo=(1/c)∫icdt=(1/RC)∫icdt这就是输出Uo正比于输入Ui的积分(∫icdt)RC电路的积分条件:RC≥Tk图2、积分电路微分电路电路结构如图W-1,微分电路可把矩形波转换为尖脉冲波,此电路的输出波形只反映输入波形的突变部分,即只有输入波形发生突变的瞬间才有输出。
而对恒定部分则没有输出。
输出的尖脉冲波形的宽度与R*C有关(即电路的时间常数),R*C越小,尖脉冲波形越尖,反之则宽。
此电路的R*C必须远远少于输入波形的宽度,否则就失去了波形变换的作用,变为一般的RC耦合电路了,一般R*C少于或等于输入波形宽度的1/10就可以了。
积分电路电路结构如图J-1,积分电路可将矩形脉冲波转换为锯齿波或三角波,还可将锯齿波转换为抛物波。
电路原理很简单,都是基于电容的冲放电原理,这里就不详细说了,这里要提的是电路的时间常数R*C,构成积分电路的条件是电路的时间常数必须要大于或等于10倍于输入波形的宽度。
名盛汽车电子发表于2005-11-10 21:37:00限幅电路图X是一个限幅电路,在输入端没信号输入时由于二极管D反向连接,所以输出电压为零。
积分与微分电路

实验七 积分与微分电路一、 实验目的1. 进一步了解集成运算放大器的性质和特点2. 用集成运算放大器组成积分、微分电路二、 实验原理本实验采用通用型集成运算放大器。
1. 积分运算电路用集成运算放大器组成的积分运算电路如图7-1所示。
该电路输出与输入之间的关系为: ⎰-=dt t u RCu i o )(1 。
当输入电压信号为阶跃信号时该电路的输出电压为: 图7-1 积分电路如图7-2所示。
输出为一个线性变化的电压,其幅度受集成运放饱和输出电压的限制。
方波信号可以看成是多个阶跃信号的组合,因此,当输入信号为方波信号时,积分运算电路输出三角波。
如图7-3所示。
当然,实际积分电路的特性不可能与理想的完全一致,其误差来源很多。
图7-2 输入阶跃信号 7-3 输入方波信号2. 微分运算电路微分运算是积分运算的逆运算,基本微分电路如图7-4所示。
电路输出为:dtt du RC u i o )(-= 但是,图7-4所示电路在频率较高时不稳定,容易产生自激。
因此,实验中一般采用图7-5所示电路,该电路可以消除自激并抑制电路的高频噪声。
当微分运算电路输入方波信号时,输出尖脉冲波,如图7-6所示。
输入三角波时,输出为方波。
t V RC dt t u RC u I i o 1)(1-=-=⎰图7-4 基本微分电路 图7-5实验用微分电路三、 实验仪器模拟电路实验箱,示波器,晶体管毫伏表等。
四、 实验内容与步骤1. 积分运算电路(1)按图7-1接电路,检查无误后通电。
(2)令u i =0,调节调零电位器使输出为零。
调节完毕,将输入与地断开。
(3)输入f=1kHz ,幅度为1V 的方波信号,用示波器观察输出信号波形并记录。
(效果不好时,接电容) 图7-6 微分波形2. 微分运算电路(1)按图7-5接电路,检查无误后通电。
(2)令u i =0,调节调零电位器使输出为零。
调节完毕,将输入与地断开。
(3)分别输入f=1kHz ,幅度为1V 的方波信号和三角波信号,用示波器观察输出信号波形并记录。
积分电路和微分电路的设计实验报告

积分电路和微分电路的设计实验报告实验报告:在本次实验中,我们将对积分电路和微分电路进行设计和测试。
积分电路和微分电路是电子电路中常见的两种基本电路,分别具有将输入信号进行积分和微分运算的功能。
首先我们设计了一个积分电路。
积分电路的基本原理是将输入信号进行积分运算,输出信号为输入信号的积分。
我们选择了一个运算放大器和一个电容器来构建积分电路。
通过适当选择电阻和电容的数值,我们成功设计出一个稳定的积分电路。
在实验中,我们输入了一个方波信号,观察到输出信号为方波信号的积分波形,验证了积分电路的功能。
接着,我们设计了一个微分电路。
微分电路的基本原理是将输入信号进行微分运算,输出信号为输入信号的微分。
我们同样选择了一个运算放大器和一组电阻来构建微分电路。
通过适当选择电阻的数值,我们成功设计出一个稳定的微分电路。
在实验中,我们输入了一个正弦信号,观察到输出信号为正弦信号的微分波形,验证了微分电路的功能。
在实验过程中,我们遇到了一些问题和挑战。
首先是在选择电阻和电容数值时,需要考虑电路的稳定性和频率响应。
另外,在电路的搭建和测试过程中,需要保证电路连接正确,避免引入干扰和误差。
通过仔细分析和调试,我们最终成功设计并测试出了积分电路和微分电路,实现了实验的预期目标。
总的来说,本次实验对积分电路和微分电路的设计和测试提供了宝贵的经验和实践机会。
通过动手实验,我们更深入地理解了电子电路的基本原理和工作原理,提升了我们的实验技能和电路设计能力。
希望在未来的学习和研究中,我们能够更加熟练地应用电子电路知识,为解决实际问题和创新设计电路做出贡献。
感谢老师和同学们的帮助和支持,让我们共同完成了这次有意义的实验。
模拟电子技术实验 运放组成积分、微分实验

实验五 集成运放积分、微分运算电路一、实验目的1、进一步理解运算放大器的基本性质和特点。
2、熟悉集成运放构成的几种运算电路的结构及特点,测定其运算关系。
3、学习区别运算放大器的非线性电路和线性电路,掌握非线性电路的应用。
二、实验原理在自动控制系统中广泛使用比例—积分—微分电路,本实验所涉及的积分运算电路、微分运算电路即是这种电路的基础。
⒈ 积分运算电路基本积分运算电路是以电阻作为输入回路,反馈回路以电容作为积分元件,电路如图5-1所示。
当运算放大器的开环电压增益足够大时,可认为:i C R i =1R v i IR =()td t v d Ci o C −=其中 图5-1 积分运算电路()()()∫+⋅−=01Oio V t d t v RCt v 输入与输出间的关系为:在初始时电容上的电压为零,则 ;当输入信号 是幅度为V 的阶跃电压,则有:()0()t V V i 0=O即:输出电压 是随时间线性减小,见图5-2积分电路的应用时,应注意运算放大器的输入电压和输出电流不允许超过它的额定工作电压U SCM 和工作电流I SCM 。
为了减小输出的直流漂移,若将电容C上并联 一个反馈 图5-2 积分状态图()()t V CR t d V C R t d t V C R t v tti o ⋅−=−=⋅−=∫∫10101111()V t o电阻R F ,电路如图5-4所示。
输入与输出间的关系为:()()∫⋅−≈td t v RCt v io 1由于R F 的加入将对电容产生分流作用,从而导致积分误差。
在考虑克服误差时,一般满足 。
C太小,会加剧积分漂移,C太大,电容漏电也随着增大。
通常取 , 。
CR C R f 11R R f ≥F C 〉〉μ1≥⒉ 微分运算电路微分运算放大电路是对输入信号实现微分运算,它是积分运算的逆运算。
如图5-3所示为基本微分运算电路;其输出电压为:()图5-3 基本微分运算电路()t d t v d t F o ≈CR v i −从上式可以看出:当输入信号 是三角波时,其输出 既是矩形波。
积分微分电路实验报告

积分微分电路实验报告积分微分电路实验报告引言:积分微分电路是电子工程中常见的一种电路,它具有对输入信号进行积分或微分运算的功能。
在本次实验中,我们将通过搭建积分和微分电路,探索它们的工作原理和应用。
实验目的:1. 了解积分和微分电路的基本原理;2. 掌握积分和微分电路的搭建方法;3. 分析积分和微分电路对不同输入信号的响应特性。
实验材料:1. 电源供应器;2. 电阻、电容元件;3. 示波器;4. 函数发生器。
实验步骤:1. 搭建积分电路a. 将一个电阻和一个电容连接成串联电路;b. 将该串联电路与一个函数发生器相连;c. 将函数发生器的正负极分别与示波器的输入端相连;d. 调节函数发生器的频率和幅度,观察示波器上电压波形的变化。
2. 搭建微分电路a. 将一个电阻和一个电容连接成并联电路;b. 将该并联电路与一个函数发生器相连;c. 将函数发生器的正负极分别与示波器的输入端相连;d. 调节函数发生器的频率和幅度,观察示波器上电压波形的变化。
实验结果与分析:1. 积分电路实验结果在积分电路中,当输入信号为正弦波时,输出信号将呈现出相位滞后的特性。
随着输入信号频率的增加,输出信号的幅度逐渐减小,且相位滞后的程度增加。
这是因为电容器对输入信号的积分作用,导致输出信号的幅度和相位发生变化。
2. 微分电路实验结果在微分电路中,当输入信号为正弦波时,输出信号将呈现出相位超前的特性。
随着输入信号频率的增加,输出信号的幅度逐渐增大,且相位超前的程度增加。
这是因为电容器对输入信号的微分作用,导致输出信号的幅度和相位发生变化。
实验总结:通过本次实验,我们深入了解了积分和微分电路的工作原理和特性。
积分电路在信号处理中常用于对输入信号进行积分运算,以实现对信号的累加效果;而微分电路则常用于对输入信号进行微分运算,以实现对信号的变化率检测。
这两种电路在电子工程中有着广泛的应用,如滤波器、控制系统等。
然而,需要注意的是,在实际应用中,我们需要根据具体的信号特性和要求来选择合适的电路。
积分电路和微分电路的设计实验报告

积分电路和微分电路的设计实验报告摘要:本文是一份关于积分电路和微分电路设计实验的报告。
首先介绍了积分电路和微分电路的定义和原理。
接着分别描述了积分电路和微分电路的设计步骤,并给出了具体的设计实例。
最后进行了实验结果的分析和讨论。
一、引言积分电路和微分电路是电子电路中非常重要的两种基本电路。
积分电路可以将输入信号进行积分运算,微分电路可以将输入信号进行微分运算。
它们在信号处理、滤波器设计、控制系统中起着重要作用。
本实验旨在研究和实现积分电路和微分电路的设计与应用。
二、积分电路的设计1. 原理介绍积分电路是将输入信号进行积分运算的电路,它由电容器和电阻器组成。
当输入信号为正弦波时,经过积分电路后输出为余弦波。
积分电路的输入电压与输出电压之间存在一个相位差90度。
2. 设计步骤(1)选择合适的电容和电阻值,根据输入信号频率和幅值来确定。
(2)计算电容器的充电时间常数τ,可以通过以下公式计算:τ = RC。
(3)根据所要求的积分运算时间,计算所需的电容器充放电时间,根据时间和电导率来确定电容值。
(4)根据计算结果,选取合适的电容和电阻器。
3. 设计实例以RC积分电路为例,假设输入信号为5V峰峰值的正弦波,频率为1kHz,要求积分时间为2s。
根据电容器的充电时间常数τ = RC,可以计算出为τ = 2s/RC。
根据所需积分时间为2s,电阻值选取为10kΩ,可以求得电容器的充放电时间为RC = 0.2s,电容值为1μF。
三、微分电路的设计1. 原理介绍微分电路是将输入信号进行微分运算的电路,它由电阻器和电容器组成。
当输入信号为正弦波时,经过微分电路后输出为正弦波的导数波形。
2. 设计步骤(1)选择合适的电容和电阻值,根据输入信号频率和幅值来确定。
(2)计算电容器的放电时间常数τ,可以通过以下公式计算:τ = RC。
(3)根据所要求的微分运算时间,计算所需的电容器放电时间,根据时间和电导率来确定电容值。
(4)根据计算结果,选取合适的电容和电阻器。
积分与微分电路实验

积分与微分电路实验1.实验目的(1)掌握用运算放大器组成的积分、微分电路。
(2)理解积分、微分电路的特点及性能。
2.实验仪器(1)数字万用表。
(2)信号发生器。
(3)双踪示波器。
(4)集成运算放大电路模块。
3.预习要求(1)分析图5.7.1所示电路,若输入正弦波,V o 与V i 相位差是多少? 当输入信号为l00Hz ,有效值为2V 时,输出电压V o =?(2)分析图5.7.2所示电路,若输入方波,V o 与V i 相位差多少? 当输入信号为l60Hz ,幅值为lV 时,输出电压V o =?(3)拟定实验步骤,做好记录表格。
4.实验原理(1)积分电路是模拟计算机中的基本单元。
利用它可以实现对微分方程的模拟,同时它也是控制和测量系统中的重要单元。
利用它的充、放电过程,可实现延时、定时以及产生各种波形。
在图5.7.1的积分电路中(与反相比例放大器相比,它的不同之处是用C 代替反馈电阻R f ),利用虚地的概念可知i i =V i /Rdt 1dt 1⎰⎰-=-==i C C o V RC i C V V 即输出电压与输入电压成积分关系。
(2)微分电路是积分运算的逆运算。
图5.7.2为微分电路图,与图5.7.1相比,其区别仅在于电容C 变换了位置。
利用虚地的概念则有:tV RC t V RCR i R i V d d d d i C C R o -=-=⋅-=⋅-= 因此,输出电压是输入电压的微分。
5.实验内容(1)积分电路。
实验电路如图5.7.1所示。
图5.7.1积分电路①取i V=-1V,断开开关K(开关K用一连线代替,拔出连线一端作为断开),用示波器观察V o变化。
做此步骤时,建议示波器X轴扫描速度置0.2sec/div,Y 轴输入电压灵敏度置2V/div,将扫描线移至示波器屏的下方,并把示波器的“AC、GND、DC”的开关档放置到DC档。
若实验箱没有470μF的电容C,可以选择一个几十μF的电容进行替代。
比例、求和、 积分、微分电路

深圳大学实验报告课程名称:电路与电子学实验项目名称:比例、求和、积分、微分电路学院:专业:指导教师:报告人:学号:班级:实验时间:实验报告提交时间:教务处制一、实验目的1、掌握用集成运算放大电路组成比例、求和电路的特点及性能;2、掌握用运算放大器组成积分微分电路;3、学会上述电路的测试和分析方法二、实验环境1、数字万用表2、双踪示波器3、信号发生器三、实验内容与步骤:1.电压跟随电路实验电路图如下,按表1内容实验并测量记录。
V i(V) -2 -0.5 0 +0.5 1R L=∞V0(V)R L=5.1KΩ2.反相比例放大器实验电路如图,U0=-R F*U i/R1,按表2内容实验并测量记录。
表23.同相比例放大电路实验电路如下所示,U 0=(1+R F /R 1)U i ,按表3实验测量并记录。
直流输入电压V i (mV)30 100 300 1000 3000 输出电压V 0理论估算(V)实际值(V) 误差(mV )4.反相求和放大电路直流输入电压V i (mV)30 100 300 1000 3000 输出电压V 0理论估算(V)实际值(V )误差(mV)实验电路如图,U0=-RF(Ui1/R1+Ui2/R2),按表4内容进行实验测量。
Vi1(V) 0.3 -0.3Vi2(V) 0.2 0.2V0(V)V0估(V)表4四、实验结果与数据分析:五、实验体会及自我评价:六、诚信承诺:本人郑重承诺在完成该项目的过程中不发生任何不诚信现象,一切不诚信所导致的后果均由本人承担。
签名:2、教师批改学生实验报告时间应在学生提交实验报告时间后10日内。
积分与微分电路

积分与微分电路一、 实验目的1、 熟悉Multisim 软件的使用方法。
2、 掌握积分运算与微分运算关系及基本测量方法。
二、 实验原理1. 积分运算电路反相积分电路如图 332-1所示。
在理想化条件下,输出电压 uO(t)等于式中 UC(o)是t = 0时刻电容C 两端的电压值,即初始值。
如果ui(t)是幅值为E 的阶跃电压,并设 Uc(o) = 0,贝U1 t E u 0 (t) Edtt 片C 0 R 1C即输出电压 uo(t)随时间增长而线性下降。
显然RC 的数值越大,达到给定的 uo 值所需的时间就越 长。
积分输出电压所能达到的最大值受集成运放最大输出范围的限值。
实用积分实验电路如图 332-2所示。
U o (t)-- t0U i dt U c(0)在进行积分运算之前,首先应对运放调零。
为了便于调节,将图中 K1闭合,即通过电阻 R2(R2)的负反馈作用帮助实现调零。
但在完成调零后,应将 K1打开,以免因R2的接入造成积分误差。
K2的 设置一方面为积分电容放电提供通路,同时可实现积分电容初始电压 UC(o) = 0,另一方面,可控制积 分起始点,即在加入信号 ui 后,只要K2 一打开,电容就将被恒流充电,电路也就开始进行积分运算。
2. 微分电路微分是积分的逆运算。
将积分电路中R 和c 的位置互换,可组成基本微分电路。
在理想化条件下,输出电压u o 等于:u 0 = -眈叫 dt可见输出电压正比于输入电压对时间的微分。
微分电路可以实现波形变换,例如将矩形波变换为尖脉冲,此外,微分电路也可以移相作用。
基本微分电路的主要缺点是,当输入信号频率升高时,电容的容抗减小,则放大倍数增大,造成电 路对输入信号中的高频噪声非常敏感,因而输出信号中的噪声成分严重增加,信噪比大大下降。
另一个 缺点是微分电路中的 RC 元件形成一个滞后的移相环节,它和集成运放中原有的滞后环节共同作用,很 容易产生自激振荡,使电路的稳定性变差。
微分电路与积分电路的实验研究

*6.3
二阶电路动态响应的实验研究 (设计性实训)
6.3.1 实训目的
1)加深对二阶电路动态响应的理解。 2)了解二阶电路动态响应的实验研究方法。 3)初步掌握设计性实训的思路和方法。
6.3.2 实训原理
1 ) RLC 串联电路,无论是零输入响应,或是零状态响 应,二阶电路动态过程的性质, 完全由特征方程
3)示波器的探头与电路连接时,接地点不能接错,否 则信号将被短路。
4)信号发生器、示波器和实验电路的地端应连在一起, 即共地,以防止干扰。
6.3.7
设计报告要求
主要内容:
1)实训目的、基本原理和实训设计方案。 2)电路图、所需仪表、元器件和电路参数。 3)实验内容和操作步骤。 4)数据测量与分析。
积分实验电路
图6-6
积分实验电路
6.1.6
注意事项
1)用示波器观察信号发生器产生的方波,防止失真。 2)示波器的探头与电路连接时,接地点不能接错,否则 信号将被短路。 3)信号发生器、示波器和电路的地端应连接在一起,即 共地,以防止干扰。 4)用示波器观察UC和IC波形时,由于信号幅值相差较大, 要缓慢调节Y轴的灵敏度,使波形清晰可测。
L为电感线圈, C为可变电容, R 为可变电阻。改变电 容或电阻的参数可获得各种响应状态。信号发生器接地端 与示波器的接地端并联接地。 振荡电路中电流I,在电阻R上产生电压作为取样信号 电压加到示波器的 Y 输入端,即能观察到测量值的波形与 数值。
实验电路
图6-11
RLC串联的二阶电路
操作步骤
调节信号发生器的方波输出频率为50~100HZ,输出电 压2V固定不变,L为电感线圈,C选用0.2μf电容,R为可变 电阻4.7KΩ ,在0~500Ω ~2KΩ 范围可调。用示波器观察分 析R<2 、R=2 L/C L/C 以及 R>2
积分电路和微分电路实验报告

积分电路和微分电路实验报告篇一:积分电路与微分电路实验报告四、积分电路与微分电路目的及要求:(1)进一步掌握微分电路和积分电路的相关知识。
(2)学会用运算放大器组成积分微分电路。
(3)设计一个RC微分电路,将方波变换成尖脉冲波。
(4)设计一个RC积分电路,将方波变换成三角波。
(5)进一步学习和熟悉Multisim软件的使用。
(6)得出结论进行分析并写出仿真体会。
一.积分电路与微分电路1. 积分电路及其产生波形1.1运算放大器组成的积分电路及其波形设计电路图如图所示:图 1.1积分电路其工作原理为:积分电路主要用于产生三角波,输出电压对时间的变化率与输入阶跃电压的负值成正比,与积分时间常数成反比,即?U0?t??UinR1C式中,R1C积分时间常数,Uin为输入阶跃电压。
反馈电阻Rf的主要作用是防止运算放大器LM741饱和。
C为加速电容,当输入电压为方波时,输入端U01的高电平等于正电源?Vcc,低电平等于负电源电压?Vdd,比较器的U??U??0时,比较器翻转,输入U01从高电平跳到低电平?Vdd。
输出的是一个上升速度与下降速度相等的三角波形。
图1.2积分电路产生的波形1.2微分电路及其产生波形2. 运算放大器组成的微分电路及其波形设计的微分电路图:图2.1微分电路其工作原理为:将积分电路中的电阻与电容对换位子,并选用比较小的时间常数RC,便得到了微分电路。
微分电路中,输出电压与输入电压对时间的变化率的负值成正比,与微分时间常数成反比,所以RinU0??RfC?U?tin的主要作用是防止运放LM741产生自激振荡。
v0??RCdV/dt,输出电压正比与输入电压对时间的微商,符号表示相位相反,当输入电压为方波时,当t?o时输出电压为一个有限制。
随着C的充电,输出电压v0将逐渐衰减,最后趋于零,就回形成尖顶脉冲波。
微分电路中用信号发生器输入方波信号,经过微分电路就会产生输出脉冲波信号。
结论与体会:通过此设计学会了用运算放大器组成的积分电路和微分电路,还学会了Multisim 软件的应用和使用方法。
积分与微分电路

积分与微分电路一、实验目的1、熟悉Multisim 软件的使用方法。
2、掌握积分运算与微分运算关系及基本测量方法。
二、实验原理1. 积分运算电路反相积分电路如图3.3.2-1所示。
图3.3.2-1 反相积分电路在理想化条件下,输出电压u0(t)等于)0(1)(010c ti u dt u CR t u +-=⎰式中 UC(o)是t =0时刻电容C 两端的电压值,即初始值。
如果ui(t)是幅值为E 的阶跃电压,并设Uc(o)=0,则⎰-=-=t t CR EEdt C R t u 01101)( 即输出电压 uo(t)随时间增长而线性下降。
显然RC 的数值越大,达到给定的uo 值所需的时间就越长。
积分输出电压所能达到的最大值受集成运放最大输出范围的限值。
实用积分实验电路如图3.3.2-2所示。
图3.3.2-2 实用积分实验电路在进行积分运算之前,首先应对运放调零。
为了便于调节,将图中K1闭合,即通过电阻R2(R2)的负反馈作用帮助实现调零。
但在完成调零后,应将K1打开,以免因R2的接入造成积分误差。
K2的设置一方面为积分电容放电提供通路,同时可实现积分电容初始电压UC(o)=0,另一方面,可控制积分起始点,即在加入信号ui 后,只要K2一打开,电容就将被恒流充电,电路也就开始进行积分运算。
2. 微分电路微分是积分的逆运算。
将积分电路中R 和c 的位置互换,可组成基本微分电路。
在理想化条件下,输出电压u O 等于:dtdu RCu i-=0 可见输出电压正比于输入电压对时间的微分。
微分电路可以实现波形变换,例如将矩形波变换为尖脉冲,此外,微分电路也可以移相作用。
基本微分电路的主要缺点是,当输入信号频率升高时,电容的容抗减小,则放大倍数增大,造成电路对输入信号中的高频噪声非常敏感,因而输出信号中的噪声成分严重增加,信噪比大大下降。
另一个缺点是微分电路中的RC 元件形成一个滞后的移相环节,它和集成运放中原有的滞后环节共同作用,很容易产生自激振荡,使电路的稳定性变差。
积分电路与微分电路

积分电路与微分电路1 实验目的及要求:(1)进一步掌握微分电路和积分电路的相关知识。
(2)学会用运算放大器组成积分微分电路。
(3)设计一个RC微分电路,将方波变换成尖脉冲波。
(4)设计一个RC积分电路,将方波变换成三角波。
(5)进一步学习和熟悉Multisim软件的使用。
(6)得出结论进行分析并写出仿真体会。
工作原理:积分电路:积分是一种常见的数学运算,同时,积分电路是一种常见的波形变换电路,它是将矩形脉冲(或方波)变换成三角波的一种电路。
最简单的积分电路(一阶RC电路)。
本实验中,加入运算放大器,其原理图如图所示:利用虚地和虚断的概念:,0=n ,21i i i ==电容器C 以电流R v i /11=进行充电。
假设电容器C 初始电压,0)(=o c v 则 输出电压:V 0=dt v RC⎰-11上式表明,输出电压V 0为输入电压Vi 对时间的积分,负号表示它们在相位上是相反的。
当输入信号Vi 为阶跃电压(方波)时,在它的作用下,电容器将以近似恒流方式进行充电,输出电压V 0与时间T 近似成线性关系,因此t v t RC v v ii o τ-=-=式中τ=RC 为时间常数。
由此推知运放输出电压的最大值Vom 受到直流稳压电源的限制,致使运放进入到饱和状态,Vo 保持不变,而停止积分。
微分电路:将积分电路中的电阻和电容元件对换位置,并选取较小的时间常数RC ,便得到如图4所示的微分电路。
这个电路同样存在虚地和虚断。
图4 含运放的微分电路设t=0时,电容器的初始电压Vc(0)=0,当信号牌电压Vi接入后,便有dtdvCi i-=1dtdvRCv io-=上式表明,输出电压Vo正比于输入电压Vi对时间的微分,负号表示它们的相位相反。
当输入信号为方波时,该电路可将方波变换为尖顶脉冲波。
实验内容我们先画出微分和积分电路图就进行了实验和观察输出波形微分电路图:微分波形图:积分电路图:积分波形图:分析:输出信号与输入信号的积分成正比的电路,称为积分电路,即。
积分与微分电路

实验微积分电路2010级电子信息工程胡俊2010117114 实验目的1.掌握集成运算放大器的特点、性能及使用方法。
2.掌握比例求和电路、微积分电路的测试和分析方法。
3.掌握各电路的工作原理和理论计算方法。
实验仪器1.数字万用表2.直流稳压电源3.双踪示波器4.信号发生器5.交流毫伏表。
实验原理与测量原理集成运算放大器是高电压放大倍数、高输入阻抗、低输出阻抗的多级直接耦合放大器,具有两个输入端和一个输出端,可对直流及交流信号进行放大,外接负反馈电路后,输出电压UO 与输出电压Ui的运算关系仅取决于外接反馈网络和输入端的外接阻抗,而与运算放大器本身无关。
运算放大器型号、品种繁多,应用十分广泛。
本次实验采用通用型集成运放μA741。
1、集成运放积分电路①ui= -1V,用示波器观察波形uo,并测量运放输出电压的正向饱和电压值。
积分电路的运算关系:②ui= 1V,测量运放的负向饱和电压值。
③电路中的积分电容改为0.1μF,ui分别输入1kHz幅值为2V的方波和正弦信号,观察ui和uo的大小及相位关系,并记录波形,计算电路的有效积分时间。
④变电路的输入信号的频率,观察ui和uo的相位,幅值关系。
随着频率的增加,Vi与Vo的幅值减小,相位增大。
2、集成运放微分电路微分电路的运算关系:①输入正弦波信号,f =500Hz,有效值为1V,用示波器观察ui 和uo的波形并测量输出电压值。
当输入Ui=时,Uo=2.6Ui由图可知:Ui=1V,Uo=2.765V②变正弦波频率(20Hz -- 40Hz),观察ui和uo的相位、幅值变化情况并记录。
随着频率的增加,Vi与Vo的幅值增大,相位减小。
输入方波,f = 200Hz,U = +5V,用示波器观察uo波形。
在电容前加一个电阻后③输入三角波,f = 200Hz,U = ±2V,用示波器观察uo波形。
重复上述实验。
3、积分—微分电路1.输入f = 200Hz,U = +5V的方波信号,用示波器观察ui和uo的波形并记录。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验5 积分与微分电路实验一、实验目的学习使用运放组成积分和微分电路。
二、实验仪器示波器、信号发生器、交流毫伏表、数字多用表。
三、预习内容(1)阅读 OP07的“数据手册”,了解 OP07的性能。
(2)复习关于积分和微分电路的理论知识。
(3)阅读本次实验的教材。
四、实验内容(1)积分电路如图1。
在理想条件下,()()1d d I O v t v t C R t =-当C 两端的初始电压为0时,则()()011d tO I v t v t tR C =-⎰因此而得名为积分电路。
1)取运放直流偏置为±12V ,输入辐值v I =-1V 的阶跃电压,测量输出饱和电压和有效积分时间。
若输入为幅值v I =-1V 阶跃电压时,输出为()()011d tO I v t v t t R C =-⎰在输出饱和前,输出电压将随时间增长而线性上升。
通常运放存在输入直流失调电压,图1所示电路运放直流开路,运放以开环放大倍数放大输入直流失调电压,往往使运放输出限幅,即输出电压接近直流电图1 积分电路源电压,输出饱和,运放不能正常工作。
在OP07的 “数据手册”中,其输入直流失调电压的典型值为 30μV ;开环增益约为112dB ,即4×105。
据此可以估 算,当v I =0时,v O =30μV×4×105=12V 。
电路实际输出约等于直流偏置电压,已无法正常工作。
建议用以下方法。
按图1接好电路后,将直流信号源输出端与v I 相接,调整 直流信号源,使其输出为-1V ,将输出v O 接示波器输入,用示波器可观察到积分电路输出饱和。
保持电路状态,关闭直流偏置电源,示波X 轴扫描速度置 0.2sec/div ,Y 轴输入电压灵敏度置2V/div ,扫描线移至示波器屏的下方。
等待至电容上的电荷放尽。
当扫描光点在示波器屏的左下方时,即时打开直流偏置电源, 示波器屏上积分电路的输出为线性上升的直线,大约1秒后,积分电路输出由线性上升的直线变为水平直线,即积分电路已饱和,立即按下示波器的“stop ”键。
再用示波器的光标测量示波器屏上电压曲线线性上升段的电压变化量和所用的时间,即积分电路的输出饱和电压和有效积分时间。
由于打开直流偏置电源后电路有过渡过程,所以用上述方法测量得到的曲线,在打开直流偏置电源后的很短的时间内不是线性上升的直线,这一时间及其对应的电压,实验者可用曲线拟合的方法估计。
有的实验者测量到的还可能是弯曲的上升曲线,这是因为本实验电路 使用的积分电容是电解电容,这是电解电容漏电所致。
这使得电路的传递函数背离积分关系。
若上升曲线弯曲得较严重,在实用电路中应更换电容。
2)改取C = 0.1μF ,v I =0.5sin2πf i t V ,f i ∈(10Hz ,20kHz),测量积分电路的幅频特性曲线。
观察输入输出波形的相位差。
通常,输出会有直流飘移,甚至输出被限幅。
解决的办法之一是在电容两端并接一个100k Ω的电阻。
建议先按表1要求测量,再绘制幅频特性曲线。
图1所示电路的传递函数为()11H s R Cs I =-图 2 直流闭环的积分电路一阶低通滤波器若运放为理想运放,上式在无限宽的频带上满足积分关系。
但是,由于运放的输入直流失调电压和很大的开环增益,运放输出饱和,电路无法正常工作。
在电容两端并接100k Ω电阻后,电路如图2所示,其传递函数为()()()211211o i V s R H s V s R R Cs I ==-+该电路对输入直流失调电压仅仅放大了10倍,由 OP07“数据手册”给出的输入直流失调电压的数据,输出失调电压可估计为约300μV ,这对电路的影响往往是可以忽略的。
但是,上式满足积分规律的下限频率大大提高了,约为15.9Hz 。
由 OP07“数据手册”可见,其设有输出调零电路。
对于图 1所示电路,调零灵敏度很高,即调零电位器的很小变化,可使输出失调电压急剧变化,电路的稳定性不好。
对于图2所示电路,可通过调整调零电位器,使输出失调电压几乎为零。
本实验电路未安装调零电位器,有兴趣者可用面包板做OP07的输出直流漂移调零实验。
根据OP07“数据手册”给出的Fig.1 Simplified Schematic ,将20k Ω多圈电位器的两个固定短点分别接运放的1,8脚,中间的动触点接正电源V CC ,调整多圈电位器,可使OP07输出直流为零。
3)取V I 的高电平V H 为0.5V 、低电平V L 为-0.5V 、占空比V H /V L 为1的方波,方波基频为f i ∈(10Hz ,2kHz),观察输入输出波形。
通常,输出会有直流漂移,甚至输出被限幅。
解决的办法之一是在电容两端并接一个100k Ω的电阻R 2。
若无 100k Ω电阻,假设运放没有输入直流漂移,在稳态,取t ∈(0,τ)做积分,τ为输入方波的半周期,则输出幅值为om 0111d H H V V V t C R R ττ-=-=-⎰的三角波,如图3所示。
其中,V H 为输入方波的幅值0.5V ;T 1=R 1C 为电路的积常数。
因为在半周期内,来自R 1支路的电流是恒定的。
若接了电阻R 2后,R 2支路对来自R 1支路的电流进行分流,分流电流随输出电压的变化而不断变化,从而使电容的充电(或放电)电流也不断变化,电容上的电压不再是线性上升的,输出电压v O 不再是三角波。
图3 图1所示电路的方波响应设在稳态,取t ∈(0,τ),电路的响应可可看作阶跃输入的零状态响应和初始条件为V om 的零输入响应。
阶跃输入的零状态响应的Laplace 变换为()2im os 1211R V V s R R Cs s =-⋅⋅+V im 为输入阶跃的幅值。
做Laplace 逆变换可得()212im 11T os R v t eV R -⎛⎫=-- ⎪ ⎪⎝⎭其中,T 2=R 2C 为电路的时间常数。
由前式可得电路零输入时的微分方程()()()oh 2oh oh omd 0,0d v t T v t v V t +==容易得到电路的零输入响应为()2oh om tT v t V e-=电路的输出为零状态响应v os (t )与零输入响应v oh (t )之和()()()222o os oh im om 11t tT T R v t v t v t eV V e R --⎛⎫=+=--+ ⎪ ⎪⎝⎭其波形如图4所示。
再求V om ,在输入半周期结束时刻,输出电压为-V om ,所以222omim om 11T T R V eV V e R ττ--⎛⎫-=--+ ⎪ ⎪⎝⎭输出电压峰值为222om im111T T R e V V R e ττ---=⋅+(2)微分电路 电路如图5所示。
1)v i =0.5sin2πf i t V ,f i ∈(10Hz ,10kHz),测量微分电路的幅频特性曲线。
观察输入输出波形的相位差。
在图5中,若假设运放为理想运放,其传递函数为H 1(s )=-R 1Cs =-0.0022s 图4 图2所示电路的方波响应由上式绘制的幅频响应如图6所示。
由实验测量得到的幅频响应曲线亦绘制于图6。
微分电路处6.6kHz 处有一尖峰,而满足微分关系的上限频率小于1kHz ,在大于6.6kHz 后,电路的放大倍数急剧下降。
这与图6所示的、由理想运放得出的传递函数所绘制幅频响应相差甚远。
这是由于理想运放与实际运放的差别造成的,其中主要是实际运放的频率特性造成的。
在图5中,若计及运放幅频特性,求微分电路的传递函数。
对图5中运放反相输入端v n 点处的电流方程和运放的电压传输方程分别为101i n o nv v v v R sC --+=()o o nv A s v =-其中A o (s )为运放的频率特性函数,如实验4中的图3,经代数运算可得其传递函数为()()()()()()011121101111111111o o o sR Cs T s H s s R Cs T s A s A s A s ωω=-=-=-⎛⎫++++++ ⎪⎝⎭其中T 1= R 1C =0.0022s ,ω01=1/ T 1,其频率特性函数为()()01201111o jH j j A s ωωωωω=-⎛⎫++ ⎪⎝⎭由实验5图3可知,对于本例,可以认为运放是一个一阶单元,即图5 微分电路 图6 微分电路的幅频特性曲线()021o k A s T s =+其中k 0=4×105,T 2=1/(2π×1.5Hz)≈0.1061s 。
代入前式,得()()()()()0112201212210020020222202200202121211111111k T sT s H s k T T s TT sT s T s k k H s sQ T k s s s s Q T T TT ωωω=-=-+++++++=-=-⎛⎫++++++⎪⎝⎭其中,ω02=41396rad/s ;f 02≈6.59kHz ;Q 02≈89;H 02=8125,约为78.2dB 。
若用上式绘制幅频特性曲线,其与图6中由实验测得的幅频曲线几乎重合,故不再另绘图了。
图7是用Protel 仿真得到的电路幅频特性曲线。
将图7的曲线与图6的曲线相比较,可见两者十分相似。
由此可见,对图5所示的微分电路,用计及运放频率特性的分析方法分析所得结果,Protel 仿真的结果,对实际电路测量的结果,三者几乎相同。
用线性系统的知识分析图5所示电路可知,该电路是一个开环增益很大的、闭环的、二阶带通电路,所以其幅频特性出现尖峰是必然的。
在高频端,其幅频特性可近似为运放的幅频特性,所以其幅频特性在高频端随频率增大而减小也是必然的。
图7 幅频特性仿真图计及频率特性的有源微分电路的优化设计方法:由图7可知,该电路满足微分关系的上限频率小于1kHz ,由前式可知,要消除图6中的尖峰就要降低Q 值,若要使电路具有最平坦幅频响应,应取Q图8是一种改进的电路。
v n 点处的电流方程和运放电压传输方程分别为1201i n o n v v v vR R sC --+=+()o o nv A s v =-由该式经代数运算可得()()()()1312211o o o R CsH s R Cs R Cs R Cs A s A s A s =-++++记R 2C =T 3,则()()()()1312311o o o T sH s T s R Cs T s A s A s A s =-++++将A o (s )代入,得()()()()0132122312303003003032220320300303213122312231111k T s H s TT T T s T T T k T s k k H s sQ T k T k s s s s Q T T T TT T T TT T T ωωω=-++++++=-=-⎛⎫+++++++ ⎪+++⎝⎭其中()010********k T Q H T T T k ω===+++令Q 03,则可得()()()2123001223121T T T k k TT T T +++=++⎡⎤⎣⎦从中可解得()()2122112332000220111T T T TT T T k k k +++-=+++图8 幅微分电路优化设计由上式可解出30T =由于k 0>>1,k 0 >>T 1,k 0 >>T 2,又由T 3=R 2C ,可得R 2的表达式为20R ≈=其中,f 0为运放幅频特性的转折频率,对于本例f 0≈1.5Hz 。
