数值分析上机实验课件
数值分析学习课件

对任意 u ≠ 0 ∈ R n +1 ,必有 Φ u ≠ 0 。 则 u T B u = u T Φ T Φ u =|| Φ u || 2 > 0 2 若不然, 若不然,则 存在唯一解 ⇒ B为正定阵,则非奇异,所以法方程组存在唯一解。 为正定阵,则非奇异,所以法方程组存在唯一 n +1 存在一个 u ≠ 0 ∈ R 使得 Φ u = 0 … 即
则 (ϕ i , ϕ j ) =
∫
1 0
x i x j dx =
1 i + j+1
Hilbert阵! 阵
若能取函数族Φ={ ϕ0(x), ϕ1(x), … , ϕn(x), … }, , 两两( 使得任意一对ϕi(x)和ϕj(x)两两(带权)正交, 和 两两 带权)正交, 改进: 改进: 对角阵! 就化为对角阵 则 B 就化为对角阵! (ϕ k , y ) 这时直接可算出a 这时直接可算出 k = (ϕ k , ϕ k ) 正交多项式的构造: 正交多项式的构造: 多项式的构造 取为k 多项式,为简单起见, 将正交函数族中的ϕk 取为 阶多项式,为简单起见,可取 ϕk 的首项系数为 1 。
①
总体上尽可能小 尽可能小。 这时没必要取 P(xi) = yi , 而要使 P(xi) − yi 总体上尽可能小。 常见做法: 常见做法:
m
不可导, 不可导,求解困难
太复杂
使 max | P ( x i ) − y i | 最小 /* minimax problem */ 1≤ i ≤ m 使 ∑ | P ( x i ) − y i | 最小 使 ∑ | P ( x ) − y | 最小 /* Least-Squares method */ 定义 最佳平方逼近:即连续型 逼近,在 || f ||2 = 最佳平方逼近:即连续型L-S逼近 平方逼近 逼近,
数值分析-第一章ppt课件

数及其图形作出判断. 整理版课件
6
由分部积分法可得:
Ine101xndex
n=1,2,4,6, 8,10,15
e 1 x n ex|1 0 e 1 0 1 nn 1 x ex dx
1 nn 1 I (n 1 ,2 , ).
如果取 I0 = 1–e–1 = 0.63212056 (八位有效数字).
x1,2b
b24ac 2a
直接进行计算则得: x1=109, x2=0. 其中的x2=0明பைடு நூலகம்失真, 这也是由于舍入误差造成的.
整理版课件
8
§1 误差的来源
实际 问题
建立数 学模型
确定计 算方法
编程 上机
由抽象简 化产生的 模型误差 及参数的 观测误差
由计算方 法本身产 生的截断 误差或称 方法误差
er(x* )e(x x* )x xx*
同样, 由于精确值 x 经常是未知的, 所以, 需要另
外的近似表达形式. 我们注意如下公式的推导,
当
|
e ( x*) x*
|
较小时,
有
e(x* )e(x* )e(x*x )* (x)
x x*
xx*
[x*[ee((xx**))2]x] *1[e(exx(**x*)]2)
整理版课件
18
乘法相关的误差公式: 设 f (x1, x2)= x1 x2 . e ( x 1 x 2 ) x 2 e ( x 1 ) x 1 e ( x 2 ) e r ( x 1 x 2 ) e r ( x 1 ) e r ( x 2 ) |e ( x 1 x 2 ) | |e ( x 1 ) | |e ( x 2 ) | |e r ( x 1 x 2 ) | |e r ( x 1 ) | |e r ( x 2 ) |
数值分析上机实验

目录1 绪论 (1)2 实验题目(一) (2)2.1 题目要求 (2)2.2 NEWTON插值多项式 (3)2.3 数据分析 (4)2.3.1 NEWTON插值多项式数据分析 (4)2.3.2 NEWTON插值多项式数据分析 (6)2.4 问答题 (6)2.5 总结 (7)3 实验题目(二) (8)3.1 题目要求 (8)3.2 高斯-塞德尔迭代法 (8)3.3 高斯-塞德尔改进法—松弛法 (9)3.4 松弛法的程序设计与分析 (9)3.4.1 算法实现 (9)3.4.2 运算结果 (9)3.4.3 数据分析 (11)4 实验题目(三) (13)4.1 题目要求 (13)4.2 RUNGE-KUTTA 4阶算法 (13)4.3 RUNGE-KUTTA 4阶算法运算结果及数值分析 (14)总结 (16)附录A (17)1绪论数值分析是计算数学的一个主要部分,它主要研究各类数学问题的数值解法,以及分析所用数值解法在理论上的合理性。
实际工程中的数学问题非常复杂,所以往往需要借助计算机进行计算。
运用数值分析解决问题的过程:分析实际问题,构建数学模型,运用数值计算方法,进行程序设计,最后上机计算求出结果。
数值分析这门学科具有面向计算机、可靠的理论分析、好的计算复杂性、数值实验、对算法进行误差分析等特点。
本学期开设了数值分析课程,该课程讲授了数值分析绪论、非线性方程的求解、线性方程组的直接接法、线性方程组的迭代法、插值法、函数逼近与曲线拟合、数值积分和数值微分、常微分方程初值问题的数值解法等内容。
其为我们解决实际数学问题提供了理论基础,同时我们也发现课程中很多问题的求解必须借助计算机运算,人工计算量太大甚至无法操作。
所以学好数值分析的关键是要加强上机操作,即利用计算机程序语言实现数值分析的算法。
本报告就是基于此目的完成的。
本上机实验是通过用计算机来解答数值分析问题的过程,所用的计算工具是比较成熟的数学软件MATLAB。
数值分析上机实验指导书

“数值计算方法”上机实验指导书实验一 误差分析实验1.1(病态问题)实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。
对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。
通过本实验可获得一个初步体会。
数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。
病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。
问题提出:考虑一个高次的代数多项式)1.1()()20()2)(1()(201∏=−=−−−=k k x x x x x p显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。
现考虑该多项式的一个扰动)2.1(0)(19=+x x p ε其中ε是一个非常小的数。
这相当于是对(1.1)中19x 的系数作一个小的扰动。
我们希望比较(1.1)和(1.2)根的差别,从而分析方程(1.1)的解对扰动的敏感性。
实验内容:为了实现方便,我们先介绍两个MATLAB 函数:“roots ”和“poly ”。
roots(a)u =其中若变量a 存储n+1维的向量,则该函数的输出u 为一个n 维的向量。
设a 的元素依次为121,,,+n a a a ,则输出u 的各分量是多项式方程01121=+++++−n n n n a x a x a x a的全部根;而函数 poly(v)b =的输出b 是一个n+1维向量,它是以n 维向量v 的各分量为根的多项式的系数(从高到低排列)。
可见“roots ”和“poly ”是两个互逆的运算函数。
))20:1((;)2();21,1(;000000001.0ve poly roots ess ve zeros ve ess +===上述简单的MATLAB 程序便得到(1.2)的全部根,程序中的“ess ”即是(1.2)中的ε。
《数值分析教程》课件

一种适用于大规模计算的数值方法
详细描述
谱方法适用于大规模计算,通过将问题分解为较小的子问 题并利用多线程或分布式计算等技术进行并行计算,可以 有效地处理大规模的计算任务。
感谢您的观看
THANKS
具有简单、稳定和可靠的优点。
05
数值积分与微分
牛顿-莱布尼兹公式
要点一
总结词
牛顿-莱布尼兹公式是数值积分中的基本公式,用于计算定 积分。
要点二
详细描述
牛顿-莱布尼兹公式基于定积分的定义,通过选取一系列小 区间上的近似值,将定积分转化为一系列小矩形面积之和 ,从而实现了数值积分。
复化求积公式
总结词
算机实现各种算法,为各个领域的科学研究和技术开发提供了强有力的支持。
数值分析的应用领域
总结词
数值分析的应用领域非常广泛,包括科学计算、工程 、经济、金融、生物医学等。
详细描述
数值分析的应用领域非常广泛,几乎涵盖了所有的科学 和工程领域。在科学计算方面,数值分析用于模拟和预 测各种自然现象,如气候变化、生态系统和地球科学等 。在工程领域,数值分析用于解决各种复杂的工程问题 ,如航空航天、机械、土木和电子工程等。在经济和金 融领域,数值分析用于进行统计分析、预测和优化等。 在生物医学领域,数值分析用于图像处理、疾病诊断和 治疗等。总之,数值分析已经成为各个领域中不可或缺 的重要工具。
03
线性方程组的数值解法
高斯消去法
总结词
高斯消去法是一种直接求解线性方程组的方法,通过一系列 行变换将系数矩阵变为上三角矩阵,然后求解上三角方程组 得到解。
详细描述
高斯消去法的基本思想是将系数矩阵通过行变换化为上三角 矩阵,然后通过回带求解得到方程组的解。该方法具有较高 的稳定性和精度,适用于中小规模线性方程组的求解。
课件-数值分析(第五版)1-3章

x x
f ( x) f ( x* ) f ( x)
x x
xf ( x) f ( x)
C p 10 即认为是病态
f ( x) x n
9 第1章 数值分析与科学计算引论
研究对象 作用特点
数值计算 误差
误差分析 避免危害
数值计算 算法设计
数学软件
2. 算法的数值稳定性 定义3 一个算法如果输入数据有误差,而在计算过程中舍入误 差不增长,则称此算法是数值稳定的,否则称此算法为不稳定 的。 例1.1:P.9 I n e
x 0.003
y 1
2017/3/12
1000
1.00314 , y * 1.003
6 第1章 数值分析与科学计算引论
研究对象 作用特点
数值计算 误差
误差分析 避免危害
数值计算 算法设计
数学软件
注: 有效位数与小数点后有多少位无关; m相同情况下,有效位数越多,误差限越小; 相对误差及相对误差限是无量纲的,绝对误差及误差限是有量纲的。
数值计算 算法设计
数学软件
1.1 数值分析的对象、作用与特点
1 研究对象
用计算机求解数学问题的数值计算方法、理论及软件实现
实际问题 数学模型 数值计算方法 程序设计(数学软件) 上机计算求出结果
应用数学
计算数学即数值分析
数值分析(计算方法) 插值与函数逼近(2、3)数值微分与数值积分(4) 的研究对象
第一章习题
1, 5,7,12,14
谢
谢 !
2017/3/12
14 第1章 数值分析与科学计算引论
第2章 插值法
引言
拉格朗日(Lagrange)插值 均差与牛顿(Newton)插值 埃尔米特(Hermite)插值 分段低次插值 三次样条插值
《数值分析》上机实验报告

数值分析上机实验报告《数值分析》上机实验报告1.用Newton 法求方程 X 7-X 4+14=0在(0.1,1.9)中的近似根(初始近似值取为区间端点,迭代6次或误差小于0.00001)。
1.1 理论依据:设函数在有限区间[a ,b]上二阶导数存在,且满足条件{}αϕ上的惟一解在区间平方收敛于方程所生的迭代序列迭代过程由则对任意初始近似值达到的一个中使是其中上不变号在区间],[0)(3,2,1,0,)(')()(],,[x |))(),((|,|,)(||)(|.4;0)(.3],[)(.20)()(.110......b a x f x k x f x f x x x Newton b a b f a f mir b a c x f ab c f x f b a x f b f x f k k k k k k ==-==∈≤-≠>+令)9.1()9.1(0)8(4233642)(0)16(71127)(0)9.1(,0)1.0(,1428)(3225333647>⋅''<-=-=''<-=-='<>+-=f f x x x x x f x x x x x f f f x x x f故以1.9为起点⎪⎩⎪⎨⎧='-=+9.1)()(01x x f x f x x k k k k 如此一次一次的迭代,逼近x 的真实根。
当前后两个的差<=ε时,就认为求出了近似的根。
本程序用Newton 法求代数方程(最高次数不大于10)在(a,b )区间的根。
1.2 C语言程序原代码:#include<stdio.h>#include<math.h>main(){double x2,f,f1;double x1=1.9; //取初值为1.9do{x2=x1;f=pow(x2,7)-28*pow(x2,4)+14;f1=7*pow(x2,6)-4*28*pow(x2,3);x1=x2-f/f1;}while(fabs(x1-x2)>=0.00001||x1<0.1); //限制循环次数printf("计算结果:x=%f\n",x1);}1.3 运行结果:1.4 MATLAB上机程序function y=Newton(f,df,x0,eps,M)d=0;for k=1:Mif feval(df,x0)==0d=2;breakelsex1=x0-feval(f,x0)/feval(df,x0);ende=abs(x1-x0);x0=x1;if e<=eps&&abs(feval(f,x1))<=epsd=1;breakendendif d==1y=x1;elseif d==0y='迭代M次失败';elsey= '奇异'endfunction y=df(x)y=7*x^6-28*4*x^3;Endfunction y=f(x)y=x^7-28*x^4+14;End>> x0=1.9;>> eps=0.00001;>> M=100;>> x=Newton('f','df',x0,eps,M);>> vpa(x,7)1.5 问题讨论:1.使用此方法求方解,用误差来控制循环迭代次数,可以在误差允许的范围内得到比较理想的计算结果。
数值分析课件(第1章)

使用教材:数值分析 华南理工大学出版社 韩国强 林伟健等编著
数值分析
林伟健
制作
华南理工大学计算机学院
本课程介绍的内容:使用计算机来 解决某些数学问题的近似方法。
《数 值 分 析》目录
第 1 章 误差 第 2 章 代数插值与数值微分 第 3 章 数据拟合 第 4 章 数值积分 第 5 章 解线性代数方程组的直接法 第 6 章 解线性代数方程组的迭代法 第 7 章 非线性方程和非线性方程组的数值解 第 8 章 矩阵特征值和特征向量的数值解法 第 9 章 常微分方程初值问题的数值解法
2
从而得到
p n 3
而
3.1415 0.31415101 p 1
近似值 3.1415 的误差限为该值小数点后
第三位的半个单位,由有效数字的定义得知,
具有4位有效数字。 顺便指出,准确值我们通常称它具有无穷多位有效
数字。
4. 有效数字与误差限的关系
设准确值 x 的近似值为 x* ,且将 x* 表示为
x 0.1 2 m 10 p(p为整数,1,2,,m
3.1416 1 104
2 3.14159
1 105
2
2
这个数经过四舍五入之后所得到的近似值,它的误差
限是它末位的半个单位。
可以证明:对任何数经过四舍五入之后所得到的 近似值,它的误差限都是它末位的半个单位。
定义1-3 若近似值x*的误差限为该值的某一位的半个单位,
例如, 0.045678 0.0457 3 位 具有3 位有效数字 又如, 8.0005 8.00 3 位 具有3位有效数字
例1-2 若 的近似值为 3.141,5 则 有多少位有效数字?
《数值分析》ppt课件
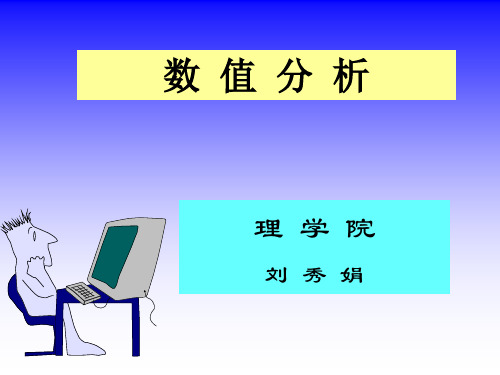
e r(b) e (b) 0.5 2.08%,
b 24
311.5mm x 312.5mm, 23.5mm y 24.5mm
例2 设 a=-2.18 , b=2.1200 是分别由准确值x和y
经过四舍五入而得到的近似值,
问: e(a),e(b),e r(a),er(b) 各是多少?
e(u)
n i 1
f
(a1
,ห้องสมุดไป่ตู้
a2 , xi
,a
n
) e(ai
)
e (u)
n i 1
f
(a1, a2 xi
,
,
an
)
e
(ai
)
( 5) ( 6)
问题三:四则运算结果的误差估计
设a,b 分别是准确值x,y 的近似值,则
1. e (a b) e (a) e (b)
解: e (a) 0.005 , e (b) 0.000 05 e r(a) e (a) 0.005 0.23%,
a 2.18
e r(b) e (b) 0.00005 0.0024%
b 2.1200
有效数字 ( significant digits)
四舍五入带来的绝对误差限
凡是由准确值 x 经四舍五入而得到近似值 x*,其绝对误差 限等于该近似值末位的半个单位。
定义 有效数字
设 x* 是数 x 的近似值,如果 x* 的绝对误差限是它的 某一位的半个单位,并且从该位到它的第一位非零数字共 有 n 位,则称用 x* 近似 x 时,具有 n 位有效数字。
有效数字的确定方法
提问:数值分析是做什么用的?
《数值分析》上机实验报告

数值分析上机实验报告x k x k - f(X k) f (X k)《数值分析》上机实验报告1. 用Newt on法求方程X7-X4+14=0在(0.1,1.9)中的近似根(初始近似值取为区间端点,迭代6次或误差小于0.00001 )。
1.1理论依据:设函数在有限区间[a,b]上二阶导数存在,且满足条件1. f(x)f(b) 02. f(x)在区间[a, b]上不变号3f(x) = 0;4」f (c)〔f .(x) |,其中c是a,b中使mir(| f .(a), f .(b) |)达到的一个b -a则对任意初始近似值x0• [a,b],由Newton迭代过程込f(x k )X“ M(Xk) = Xk — T^,k = 0,1,2,3…f'(X k)所生的迭代序列 % [平方收敛于方程f(x)=0在区间[a,b]上的惟一解: 令7 4f(x)=x -28x 14, f (0.1) 0, f(1.9) ::0f (x) =7x6-112x3=7x3(x3-16) ::: 0f (x) =42x5-336x2=42x2(x3-8) :: 0f (1.9) f (1.9) 0故以1.9为起点x0 =1.9如此一次一次的迭代,逼近X的真实根。
当前后两个的差<=出寸,就认为求出了近似的根。
本程序用Newton法求代数方程(最高次数不大于10)在(a,b )区间的根//限制循环次数1.2 C 语言程序原代码:#i nclude<stdio.h> #in clude<math.h> mai n() {double x2,f,f1; double x1=1.9; // 取初值为 1.9do {x2=x1;f=pow(x2,7)-28*pow(x2,4)+14; f1=7*pow(x2,6)-4*28*pow(x2,3); x 仁 x2-f/f1;}while(fabs(x1-x2)>=0.00001||x1<0.1); printf("计算结果:x=%f\n",x1);}1.3运行结果:* D:\VC + +\EXERCIS E\Debu g\l1.4 MATLAB上机程序fun cti on y=Newt on( f,df,x0,eps,M)d=0;for k=1:Mif feval(df,x0)==0d=2; breakelsex1=x0-feval(f,x0)/feval(df,x0);ende=abs(x1-x0);x0=x1;if e<=eps&&abs(feval(f,x1))v=epsd=1; breakendendif d==1y=x1;elseif d==0y='迭代M次失败';elsey=奇异’endfun cti on y=df(x)y=7*x A6-28*4*x A3;Endfunction y=f(x) y=x A7-28*x A4+14;End>> x0=1.9;>> eps=0.00001;>> M=100;>> x=Newto n('f,'df,x0,eps,M);>> vpa(x,7)1.5问题讨论:1•使用此方法求方解,用误差来控制循环迭代次数,可以在误差允许的范围内得到比较理想的计算结果。
数值分析第一章PPT课件

= f ’( )(x* x)
x* 与 x 非常接近时,可认为 f ’( ) f ’(x*) ,则有:
|e*(y)| | f ’(x*)|·|e*(x)|
即:x*产生的误差经过 f 作用后被放大/缩小了| f ’(x*)| 倍。故称| f ’(x*)|为放大因子 /* amplification factor */ 或 绝对条件数 /* absolute condition number */.
r* (x ) ln x * r* (y )
11 0n1lnx*0.1% 2a1
n4
.
10
1.3 避免误差危害的若干原则
算法的数值稳定性
用一个算法进行计算,如果初始数据误差在计算中 传播使计算结果的误差增长很快,这个算法就是数值不 稳定的.
.
11
1.3 避免误差危害的若干原则
病态问题与条件数
Cp
x f (x) f (x)
x nxn1 xn
n,
它表示相对误差可能放大 n倍.
如 n10,有 f(1 ) 1 ,f(1 .0)2 1 .2,4 若取 x 1, x*1.02, 自变量相对误差为 2% ,函数值相对误差为 24%, 这时问题可以认为是病态的.
一般情况下,条件数
Cp
10就认为是病态,
εr*21 a11 0n10.0 0% 1
已知 a1 = 3,则从以上不等式可解得 n > 6 log6,即
n 6,应取 * = 3.14159。
.
8
1.2 数值计算的误差
问题:对于y = f (x),若用x* 取代x,将对y 产生什么影响?
分析:e*(y) = f (x*) f (x)
e*(x) = x* x
《数值分析》ppt课件
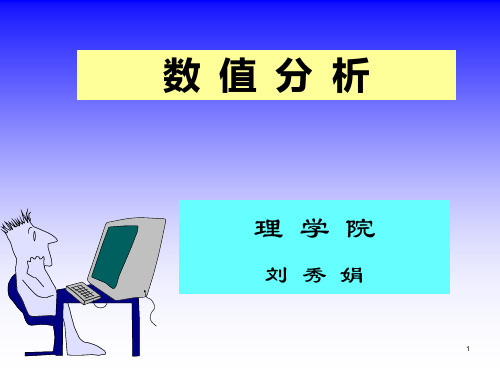
7.
er
a b
er
(a)
er
(b)
30
例4
ε(p)
设有三个近似数
p ≈ 6.6332
≈0.02585
a=2.31,b=1.93,c=2.24
它们都有三位有效数字,试计算p=a+bc,e ( p)和e r ( p) 并问:p的计算结果能有几位有效数字?
2位
例5
设f (x, y) cos y , x 1.30 0.005, y 0.871 0.0005. x
er
e x
x x x
.
由于精确值 x 未知, 实际上总把
e x
作为x*的
相对误差,并且仍记为er , 即
er
e x
.
❖定义 近似值 x* 的相对误差上限(界) (relative accuracy)
εr
|
ε x
|.
注:相对误差一般用百分比表示.
17
例1 用最小刻度为毫米的卡尺测量直杆甲和直杆
注:理论上讲,e 是唯一确定的, 可能取正, 也可能取负.
e > 0 不唯一,当然 e 越小越具有参考价值。
15
提问:绝对误差限的大小能否完全地 表示近似值的好坏? 例如:有两个量
x 10 1 , y 1000 5
思考
问:谁的近似程度要好一些?
16
❖定义 近似值 x* 的相对误差 (relative error)
a 2.18
e r(b) e (b) 0.00005 0.0024%
b 2.1200
19
➢有效数字 ( significant digits)
数值分析课件第5章

cn1xn1
fn1
an bn xn fn
其中|i-j|>1时,aij=0,且满足如下的对角占优条件:
(1)|b1|>|c1|>0,|bn|>|an|>0
(2)|bi|≥|ai|+|ci|, aici≠0, i=2,3,…,n-1.
工科研究生公共课程数学系列
机动 上页 下页 首页 结束
b1 c1
为单位下三角矩阵
这就是说,高斯消去法实质上产生了一个将A分解为 两个三角形矩阵相乘的因式分解,于是我们得到如下重要 定理。
工科研究生公共课程数学系列
机动 上页 下页 首页 结束
定理 7矩 ( 阵L的 U 分解 )设A为n阶矩阵, A的如 顺果 序主 Di 0(i1,2,,n1),则 A可分解为一个 角单 矩L和 位 阵下 一个上三U的 角乘 矩积 阵,且这 唯种 一分 的解 。是
a(2) m2
a1(1n) a2(2n)
b1(1) b2(2)
mi2aa22((2221))
(a2(22) 0)
(i3,,m)
am(2n)
bn(2)
a1(11) 0
a(1) 12
a(2) 22
a1(1n)
a2(2n)
b1(1) b2(2)
A(3)
: b(3)
0
0
am(3n)
a(k) kk
工科研究生公共课程数学系列
()
机动 上页 下页 首页 结束
高斯消去法的条件
定理5 设Axb,其中ARnn
(1) 如果ak(kk) 0(k 1,2,,n),则可通过高斯将 消去法 Axb约化为等价的三组 角(方 ),程且计算公 (式 )。
数值计算方法上机实验

用追赶法解三角方程组Ax=d,A= , d=
实验过程:
1.利用C语言编程求解,程序如下:
#include<stdio.h>
#include<math.h>
void main()
{int i;
double a[5]={0,-1,-1,-1,-1},b[5]={2,1,1,1,1},c[4]={2,2,2,2},f[5]={6,7,9,11,1};
{double x=-0.99,y;
int n=0;
printf("%d ,%lf\n",n,x);
do
{y=x;
x=x-(x*x*x/3-x)/(x*x-1);
n++;
printf("n= %d ,x= %lf\n",n,x);
}while(fabs(y-x)>1e-5);
}
1.2.命令窗口结果截屏如下:
}
2.2.命令窗口结果截屏如下:
实验结果分析:
从运算截图中我们可以知道,一方面运用牛顿迭代法和牛顿下山迭代法的程序运算的结果是一致的,若出现小小的差异的话,可能是由于设置的变量类型不同导致,另一方面运用牛顿下山迭代法比运用一般牛顿迭代法计算的步骤要少一些,这证明对于同一个题,牛顿下山迭代法的优越性比一般的牛顿迭代要高。
实验内容:
用列主元法解线性方程组
=
实验过程:
1.利用C语言编程求解,程序如下:
#include<stdio.h>
#include<math.h>
void main()
{double t,m1,m2,m3,x1,x2,x3,x4,a[4][5]={1.1348,3.8326,1.1651,3.4017,9.5342,0.5301,1.7875,2.5330,1.5435,6.3941,3.4129,4.9317,8.7643,1.3142,18.4231,1.2371,4.9998,10.6721,0.0147,16.9237};
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录1 绪论 (1)2 实验题目(一) (2)2.1 题目要求 (2)2.2 NEWTON插值多项式 (3)2.3 数据分析 (4)2.3.1 NEWTON插值多项式数据分析 (4)2.3.2 NEWTON插值多项式数据分析 (6)2.4 问答题 (6)2.5 总结 (7)3 实验题目(二) (8)3.1 题目要求 (8)3.2 高斯-塞德尔迭代法 (8)3.3 高斯-塞德尔改进法—松弛法 (9)3.4 松弛法的程序设计与分析 (9)3.4.1 算法实现 (9)3.4.2 运算结果 (9)3.4.3 数据分析 (11)4 实验题目(三) (13)4.1 题目要求 (13)4.2 RUNGE-KUTTA 4阶算法 (13)4.3 RUNGE-KUTTA 4阶算法运算结果及数值分析 (14)总结 (16)附录A (17)1绪论数值分析是计算数学的一个主要部分,它主要研究各类数学问题的数值解法,以及分析所用数值解法在理论上的合理性。
实际工程中的数学问题非常复杂,所以往往需要借助计算机进行计算。
运用数值分析解决问题的过程:分析实际问题,构建数学模型,运用数值计算方法,进行程序设计,最后上机计算求出结果。
数值分析这门学科具有面向计算机、可靠的理论分析、好的计算复杂性、数值实验、对算法进行误差分析等特点。
本学期开设了数值分析课程,该课程讲授了数值分析绪论、非线性方程的求解、线性方程组的直接接法、线性方程组的迭代法、插值法、函数逼近与曲线拟合、数值积分和数值微分、常微分方程初值问题的数值解法等内容。
其为我们解决实际数学问题提供了理论基础,同时我们也发现课程中很多问题的求解必须借助计算机运算,人工计算量太大甚至无法操作。
所以学好数值分析的关键是要加强上机操作,即利用计算机程序语言实现数值分析的算法。
本报告就是基于此目的完成的。
本上机实验是通过用计算机来解答数值分析问题的过程,所用的计算工具是比较成熟的数学软件MATLAB。
MATLAB是Matrix Laboratory的缩写,是以矩阵为基础的交互式程序计算语言。
MATLAB是一款具有强大的矩阵运算、数据处理和图形显示功能的软件,其输出结果可视化,编程效率极高,用极少的代码即可实现复杂的运行,因此它使工程技术人员摆脱了繁琐的程序代码,以便快速地验证自己的模型和算法。
其主要特点包括:强大的数值运算功能;先进的资料视觉化功能高阶但简单的程序环境;开方及可延展的构架;丰富的程式工具箱。
在科学研究和工程计算领域经常会遇到一些非常复杂的计算问题,利用计算器或手工计算是相当困难或无法实现的,只能借助计算机编程来实现。
MATLAB将高性能的数值计算和可视化的图形工具集成在一起,提供了大量的内置函数,使其在科学计算领域具有独特的优势。
最后感谢数值分析课程任课教师赵海良老师的悉心指导!2实验题目(一)2.1题目要求已知:a=-5,b=5, 以下是某函数f(x)的一些点(x k,y k), 其中x k=a+0.1(k-1) ,k=1,..,101 请用插值类方法给出函数f(x)的一个解决方案和具体结果。
并通过实验考虑下列问题(1)Ln(x)的次数n越高,逼近f(x)的程度越好?(2)高次插值收敛性如何?(3)如何选择等距插值多项式次数?(4)若要精度增高,你有什么想法?比如一定用插值吗?(5)逼近某个函数不用插值方式,有何变通之举?(6)函数之间的误差如何度量,逼近的标准又是什么?(7)如何比较好的使用插值多项式呢?x k =-5.0000:0.1:5.0000;y(x k)=y k=Columns 1 through 725.0000 24.0100 23.0400 22.0900 21.1600 20.2500 19.3600 Columns 8 through 1418.4900 17.6400 16.8100 16.0000 15.2100 14.4400 13.6900Columns 15 through 2112.9600 12.2500 11.5600 10.8899 10.2397 9.6093 8.9991 Columns 22 through 288.4092 7.8405 7.2941 6.7705 6.2693 5.7866 5.3144 Columns 29 through 354.8403 4.3522 3.8463 3.3402 2.8832 2.5554 2.4475 Columns 36 through 422.61543.0219 3.4920 3.7149 3.3232 2.0435 -0.1277 Columns 43 through 49-2.8066 -5.2470 -6.5469 -5.9893 -3.3862 0.7365 5.2312Columns 50 through 568.6985 10.0000 8.6985 5.2312 0.7365 -3.3862 -5.9893 Columns 57 through 63-6.5469 -5.2470 -2.8066 -0.1277 2.0435 3.3232 3.7149 Columns 64 through 703.4920 3.0219 2.6154 2.4475 2.5554 2.8832 3.3402 Columns 71 through 773.84634.3522 4.84035.3144 5.78666.2693 6.7705 Columns 78 through 847.2941 7.8405 8.4092 8.9991 9.6093 10.2397 10.8899 Columns 85 through 9111.5600 12.2500 12.9600 13.6900 14.4400 15.2100 16.0000 Columns 92 through 9816.8100 17.6400 18.4900 19.3600 20.2500 21.1600 22.0900Columns 99 through 10123.0400 24.0100 25.00002.2 Newton 插值多项式n 阶差商的定义:[][]0110211010,,,,,)(],,,[],,,[x x x x x f x x x f x f x x x x x x f n n n n n --==-牛顿插值公式 )()()(x R x P x f n n +=牛顿插值多项式)())(](,,,[)](,[)()(110100100----++-+=n n n x x x x x x x x x f x x x x f x f x P牛顿插值余项)(],,,,[)(010i n i n n x x x x x x f x R -∏==其差商表如下所示:表1差商标计算规律:任一个k(≥1) 阶均差的数值等于一个分式的值,其分子为所求均差左侧的数减去左上侧的数,分母为所求均差同一行最左边的基点值减去由它往上数第k 个基点值。
2.3数据分析2.3.1Newton插值多项式数据分析图1各阶牛顿插值的结果取x1=[-5 0 5],y1=[25 10 25]时,进行牛顿二阶插值:图2二阶牛顿插值的结果取x2=[-5:2.5:5];,y2=[25 6.2693 10 6.2693 25]时,进行牛顿四阶插值:图3四阶牛顿插值的结果取x3=[-5:2:5],y3=[25 8.9991 2.0435 2.0435 8.9991 25]时,进行牛顿五阶插值:图4五阶牛顿插值的结果取x4=[-5:1:5],y4=[25 16 8.9991 3.8463 2.0435 10 2.0435 3.8463 8.9991 16 25]时,进行牛顿十阶插值:图5十阶牛顿插值的结果2.3.2 Newton 插值多项式数据分析从上面的计算结果绘图可以看出以下几点:(1)当等距选取的插值节点过少时,会产生较大的插值误差,相应增加等距选取的插值节点能减小插值的误差,这从二阶插值倒三、四阶插值插值计算结果越来越接近原函数可以看出。
(2)过大的选取等距插值节点的个数会造成龙格现象,插值的效果反而不好,这可以从十阶插值的结果绘图看出。
总的来说,适当的选取等距插值节点的个数对于提高插值误差和避免龙格现象很重要。
2.4 问答题(1)Ln(x)的次数n 越高,逼近f(x)的程度越好?答:这说法不正确,并非次数越高逼近程序越好,事实上对于高次的拉格朗日插值,在插值的次数过大时会发生龙格现象,导致在节点两端的波动很大,从而Ln(x)不能一致逼近于f(x)。
(2)高次插值收敛性如何?答:对于高次的拉格朗日插值,误差满足下式:1max |()()|()0()(1)!n n a x b M f x L x b a n n +≤≤-≤-→→∞+式中,[a,b]为插值区间,(1)1max |()|n n a x bM f x M ++≤≤=≤。
由此看出,当插值节点的个数越多(即n+1越大),误差越小,但不能简单地认为对所有插值问题当插值节点的个数越多,误差就越小,这是因为误差估计式是有条件的,在[a,b]上函数f(x)要有高阶导数,而高阶导数要一致有界,如果M n+1无限增大,就不能保证Ln(x)收敛于f(x)。
故高次插值的收敛性是有条件的,其取决于其高阶导数是否有界,如果其高阶导数有界则,其高次插值收敛,否则不收敛。
(3)如何选取等距插值多项式次数?答:在本题当中,f(x)的高阶导数有界,故高次插值收敛,在进行插值时我在101个点当中选择了部分点进行牛顿插值,通过画图比较插值函数和原函数,得出图像是收敛的,另外对于高阶导数无界的函数,在用多项式插值时不宜选取高次多项式插值(七八次以上),这样就能有效的避免龙格现象。
(4)若要精度增高,你有什么想法?比如一定用插值么?答:采用曲线拟合,通过拟合出的曲线带入插值点的值计算插值点的函数值;插值函数曲线是通过所给全部插值节点的,这将使插值函数保留数据的全部测量误差,并且当插值函数的阶数较高时,曲线摆动很大,而求得的插值函数与实验规律较远,而数值拟合构造的数学函数则能从整体上较好地逼近函数,从而保持比较好的精度。
(5) 逼近某个函数不用插值方式,有何变通之举?答:曲线拟合。
(6) 函数之间的误差如何度量,逼近的标准又是什么?答:函数之间的误差可以通过求其余项来进行比较得到度量,而逼近的标准在于n 趋近于无穷时,余项趋近于0,这样插值函数就无限接近于f(x)即实现逼近了。
(7)如何比较好的使用插值多项式呢?答:根据插值数据的特点选取适当的插值方式,要注意避免龙格现象,总之,具体情况具体分析,使用插值多项式应当从插值对象出发选取适合的插值多项式。
