第五章单元测验

合集下载

浙教版数学七年级上册第五章一元一次方程单元测试 (含答案)

浙教版数学七年级上册第五章一元一次方程一、选择题1．下列方程是一元一次方程的是（）A ．y =2x−1B ．x−1=0C ．x 2=9D ．3x−52．下列利用等式的基本性质变形错误的是（）A ．若x−2=7，则x =7+2B ．若−5x =15，则x =−3C ．若13x =9，则x =3D ．若2x +1=6，则2x =53．若x =2是关于x 的方程x−a =0的解，则a 的值是（）A ．2B ．1C ．−1D ．−24．由x 2−y3=1可以得到用x 表示y 的式子是（）A ．y =3x−22B ．y =32x−12C ．y =3−32xD ．y =32x−35．解方程x−13=1−3x +16，去分母后正确的是（）A ．2x−1=1−(3x +1)B ．2(x−1)=1−(3x +1)C ．2(x−1)=6−(3x +1)D ．(x−1)=6−3x +16．我国明代珠算家程大位的名著《直指算法统宗》里有一道算题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，试问大、小和尚各多少人？设小和尚有x 人，依题意列方程得（）A ．x3+3(100−x )=100B ．3x +100−x3=100C ．x3−3(100−x )=100D ．3x−100−x3=1007．下列方程的变形中，正确的是（）A ．方程3x−2=2x +1，移项，得3x−2x =−1+2；B ．方程3−x =2−5(x−1)，去括号，得3−x =2−5x−1；C ．方程23x =32，未知数系数化为1，得x =1；D ．方程x−12−x5=1化成5(x−1)−2x =10．8．将 6 块形状、大小完全相同的小长方形，放入长为 m ，宽为 n 的长方形中，当两块阴影部分A,B 的面积相等时，小长方形其较短一边长的值为（）A ．m 6B ．m 4C ．n 6D ．n 49．已知|a−1|+(ab−2)2=0，则关于x 的方程xab+x (a +1)(b +1)+x (a +2)(b +2)+⋅⋅⋅+x(a +2021)(b +2021)=2022的解是（）A ．2021B ．2022C ．2023D ．202410．我国古代的“九宫图”是由3×3的方格构成的，每个方格均有不同的数，每一行、每一列以及每一条对角线上的三个数之和相等．如图给出了“九宫图”的一部分，请推算x 的值是（）2025x 23A ．2020B ．−2020C ．2019D ．−2019二、填空题11．已知4x +2y =3，用含x 的式子表示y =　　．12．如图，在数轴上，点A,B 表示的数分别为a,b ，且a +b =0，若AB =2，则点A 表示的数为．13．一张试卷有25道必答题，答对一题得4分，答错一题扣1分，某学生解答了全部试题共得70分，他答对了道题．14．甲对乙说：“当我岁数是你现在的岁数时，你才4岁．”乙对甲说：“当我的岁数是你现在岁数时，你61岁．”则乙现在为岁．15．如图，数轴上A ，B 点对应的实数分别是1和3．若点A 关于点B 的对称点为点C （即2AB =BC ），则点C 所对应的实数为．16．一个四位正整数M ，如果千位数字与十位数字之和的两倍等于百位数字与个位数字之和，则称M 为“共进退数”，并规定F (M )等于M 的前两位数所组成的数字与后两位数所组成的数字之和，G (M )等于M 的前两位数所组成的数字与后两位数所组成的数字之差，如果F (M )=60，那么M 各数位上的数字之和为　　；有一个四位正整数N =1101+1000x +10y +z （0≤x ≤4,0≤y ≤9,0≤z ≤8，且为整数）是一个“共进退数”，且F (N )是一个平方数，G (N )13是一个整数，则满足条件的数N 是．三、解答题17．解方程：2x +13−6x−16=1．18．当m 为何值时，关于x 的方程x−m 2−1=2x +m3的解是非负数．19．一艘轮船从A 地顺水航行到B 地用了4小时，从B 地逆水航行返回A 地比顺水航行多用了2小时，已知轮船在静水中的速度是25千米/时．（1）求水流的速度和A ，B 两地之间的距离；（2）若在A ，B 两地之间的C 地建立新的码头，使该轮船从A 地顺水航行到C 码头的时间是它从B 地逆水航行到C 码头所用时间的一半，问A ，C 两地相距多少千米？20．关于x 的两个一元一次方程x−1=a ①，3x +1=2a ②，已知方程①的解比方程②的解大1，求a的值．21．我们规定，若关于x 的一元一次方程ax =b 的解为x =b−a ，则称该方程为“差解方程”．例如：2x =4的解为x =2，且2=4−2，则该方程2x =4是差解方程．（1）判断：方程3x =4.5差解方程（填“是”或“不是”）（2）若关于x 的一元一次方程4x =m +3是差解方程，求m 的值．22．甲、乙两人加工机器零件，已知甲、乙两人一天共加工零件35个，甲每天加工零件的个数比乙每天加工零件的个数多5个．（1）问甲、乙两人每天各加工多少个零件？（2）现在工厂需要加工零件600个，先由两人合作一段时间，剩下的全部由乙单独完成，恰好20天完成任务，求两人合作的天数．23．某条城际铁路线共有A ，B ，C 三个车站，每日上午均有两班次列车从A 站驶往C 站，其中D1001次列车从A 站始发，经停B 站后到达C 站，G1002次列车从A 站始发，直达C 站，两个车次的列车在行驶过程中保持各自的行驶速度不变．某校数学学习小组对列车运行情况进行研究，收集到列车运行信息如下表所示．列车运行时刻表A 站B 站C 站车次发车时刻到站时刻发车时刻到站时刻D10018：009：309：5010：50G10028：25途经B站，不停车10：30请根据表格中的信息，解答下列问题：（1）D1001次列车从A站到B站行驶了分钟，从B站到C站行驶了分钟；（2）记D1001次列车的行驶速度为v1，离A站的路程为d1；G1002次列车的行驶速度为v2，离A站的路程为d2．①v1v=▲；2②从上午8：00开始计时，时长记为t分钟（如：上午9：15，则t=75），已知v1=240千米/小时（可换算为4千米/分钟），在G1002次列车的行驶过程中(25≤t≤150)，若|d1−d2|=60，求t的值．答案解析部分1．【答案】B2．【答案】C3．【答案】A4．【答案】D5．【答案】C6．【答案】A7．【答案】D8．【答案】A9．【答案】C10．【答案】D11．【答案】32−2x12．【答案】−113．【答案】1914．【答案】2315．【答案】33−216．【答案】15；310517．【答案】x=−3218．【答案】m≤−6519．【答案】（1）解：设水流的速度为x千米/时，A，B两地之间的距离为y千米，则轮船在顺水中的速度为(25+x)千米/时，在逆水中的速度为(25−x)千米/时．由题意，得{4(25+x)=y6(25−x)=y，解得{x=5 y=120．答：水流的速度为5千米/时，A，B两地之间的距离为120千米．（2）解：设A，C两地相距m千米．由题意，得m25+5=12×120−m25−5，解得m=3607．答：A，C两地相距3607千米．20．【答案】a=−121．【答案】（1）是（2）7322．【答案】（1）甲每天加工零件个数为20个，乙每天加工15个（2）两人合作的天数15天23．【答案】（1）90；60（2）解：①5 6；②解法示例：∵v1=4（千米/分钟），v1v2=56，∴v2=4.8（千米/分钟）．∵4×90=360，∴A与B站之间的路程为360．∵360÷4.8=75，∴当t=100时，G1002次列车经过B站．由题意可如，当90≤t≤110时，D1001次列车在B站停车．∴G1002次列车经过B站时，D1001次列车正在B站停车．ⅰ．当25≤t<90时，d1>d2，∴|d1−d2|=d1−d2，∴4t−4.8(t−25)=60，t=75（分钟）；ⅱ．当90≤t≤100时，d1≥d2，∴|d1−d2|=d1−d2，∴360−4.8(t−25)=60，t=87.5（分钟），不合题意，舍去；ⅲ．当100<t≤110时，d1<d2，∴|d1−d2|=d2−d1，∴4.8(t−25)−360=60，t=112.5（分钟），不合题意，舍去；ⅳ．当110<t≤150时，d1<d2，∴|d1−d2|=d2−d1，∴4.8(t−25)−[360+4(t−110)]=60，t=125（分钟）．综上所述，当t=75或125时，|d1−d2|=60．。

人教版七年级下册数学第五章《相交线与平行线》单元练习题(含答案)

人教版七年级下册数学第五章《相交线与平行线》单元练习题（含答案）一、单选题1．如图，AB CD ∥ ，点E 在CA 的延长线上若50BAE ∠=︒，则ACD ∠的大小为( )A ．100°B ．120°C ．130°D ．110°2．如图，要修建一条公路，从A 村沿北偏东75°方向到B 村，从B 村沿北偏西25°方向到C 村.若要保持公路CE 与从A 村到B 村的方向一致，则应顺时针转动的度数为（）A ．50°B ．75°C ．100°D ．105°3．如图，直线AB ∥CD ，如果∠1=70°，那么∠BOF 的度数是（）A ．70°B ．100°C ．110°D ．120°4．具有下列关系的两角：①互为补角；②同位角；③对顶角；④内错角；⑤邻补角；⑥同旁内角．其中一定有公共顶点的两角的对数为( )A ．1对B ．2对C ．3对D ．4对5．如图，将三角板与直尺贴在一起，使三角板的直角顶点C （∠ACB ＝90°）在直尺的一边上，若∠2＝65°，则∠1的度数是（）A ．15°B ．25°C ．35°D ．65°6．下列命题中，真命题是（）A ．一条直线截另外两条直线所得到的同位角相等B ．两个无理数的和仍是无理数C ．有公共顶点且相等的两个角是对顶角D ．等角的余角相等7．如图，AB ∥CD ，AE 平分∠CAB 交CD 于点E ，若∠C=70°，则∠AED=（）A ．55°B ．125°C ．135°D ．140°8．如图，12l l //，点O 在直线1l 上，若90AOB ︒∠=，135︒∠=，则2∠的度数为（）A ．65°B ．55°C ．45°D ．35°9．下列命题是真命题的是（）A ．如果一个数的相反数等于这个数本身，那么这个数一定是0B ．如果一个数的倒数等于这个数本身，那么这个数一定是1C ．如果一个数的平方等于这个数本身，那么这个数一定是0D ．如果一个数的算术平方根等于这个数本身，那么这个数一定是010．如图，直线AB ∥ CD ，∠ B=50°，∠ C=40°，则∠E 等于（）A ．70°B ．80°C ．90°D ．100°二、填空题 11．如图，AD ∥BC ，EF ∥BC ，BD 平分∠ABC ，图中与∠ADO 相等的角有_______ 个，分别是___________．因为AB ∥CD ，EF ∥AB ，根据_____________________________，所以_____________．12．如图，在正方形网格中，三角形DEF 是由三角形ABC 平移得到的，则点C 移动了________格．13．如图，在ABC ∆中，4AB =，6BC =，60B ∠=︒，将ABC ∆沿射线BC 的方向平移2个单位后，得到A B C '''∆，连结A C '，则A B C ∆''的周长为______.14．下面三个命题： ①若是方程组的解，则或； ②函数通过配方可化为； ③最小角等于的三角形是锐角三角形．其中正确命题的序号为．15．设圆上有n 个不同的点，连接任两点所得线段，将圆分成若干个互不重合的区域，记()f n 为区域数的最大值，则(5)_________f =，(6)________f =．16．如图，已知AB ∥ED,∠ABC=300,∠EDC=400，则∠BCD 的度数是．17．点M ，N 在线段AB 上，且MB ＝6cm ，NB ＝9cm ，且N 是AM 的中点，则AB ＝___cm ，AN ＝____cm .18．把命题“三个角都相等的三角形是等边三角形”改写成“如果……，那么……”的形式是_____；该命题的条件是_____，结论是_____．三、解答题19．如图，已知点A 是射线OP 上一点．（1）过点A 画OQ 的垂线，垂足为B ；过点B 画OP 的平行线BC ；（2）若50POQ ∠=，求ABC ∠的度数．20．（1）问题背景：已知：如图①-1，//AB CD ，点P 的位置如图所示，连结,PA PC ，试探究APC ∠与PAB ∠、PCD ∠之间有什么数量关系，并说明理由．(将下面的解答过程补充完整，括号内写上相应理由或数学式)解：（1）APC ∠与PAB ∠、PCD ∠之间的数量关系是：360APC PAB PCD ∠+∠+∠=︒(或360()APC PAB PCD ∠=︒∠+∠只要关系式形式正确即可)理由：如图①-2，过点P 作//PE AB ．∵//PE AB (作图)，∴180PAB APE ∠+∠=︒( )，∴//AB CD (已知)//PE AB (作图)，∴//PE _______( )，∴CPE PCD ∠+∠=_______( )，∴180180360PAB APE CPE PCD ∠+∠+∠+∠=+︒=︒(等量代换)又∵APE CPE APC ∠+∠=∠(角的和差)，∴360APC PAB PCD ∠+∠+∠=︒(等量代换)总结反思：本题通过添加适当的辅助线，从而利用平行线的性质，使问题得以解决．（2）类比探究：如图②，//AB CD ，点P 的位置如图所示，连结PA 、PC ，请同学们类比（1）的解答过程，试探究APC ∠与PAB ∠、PCD ∠之间有什么数量关系，并说明理由．（3）拓展延伸：如图③，//AB CD ，ABP ∠与CDP ∠的平分线相交于点1P ，若128P ∠=︒，求P ∠的度数，请直接写出结果，不说明理由．21．如图，抛物线y ＝ax 2+bx ﹣3与x 轴交于A （﹣1，0），B （3，0），与y 轴交于点C ，顶点为D ．（1）求抛物线的解析式及点D的坐标．（2）在线段BC下方的抛物线上，是否存在异于点D的点E，使S△BCE＝S△BCD？若存在，求出点E的坐标；若不存在，请说明理由．（3）点M3,2m⎛⎫- ⎪⎝⎭在抛物线上，点P为y轴上一动点，求2MP+2PC的最小值．22．如图，在96⨯网格中，已知△ABC，请按下列要求画格点三角形A' B' C'(三角形的三个顶点都是小正方形的顶点)．(1)在图①中，将△ABC平移，使点O落在△ABC的边AB(不包括点A和点B)上；(2)在图②中，将△ABC平移，使点O落在△ABC的内部．23．如图．一次函数y＝12x+1的图象L1交y轴于点A，一次函数y＝﹣x+3的图象L2交x轴于点B，L1与L2交于点C．（1）求点A与点B的坐标；（2）求△ABC的面积．24．在如图所示的方格纸中，每个小正方形的边长为1，每个小正方形的顶点都叫做格点．△ABC的顶点A、B、C都在格点上．(1)过B作AC的平行线BD．(2)作出表示B到AC的距离的线段BE．(3)线段BE与BC的大小关系是：BE BC(填“＞”、“＜”、“=”)．(4)△ABC的面积为．25．如图，点E在直线DF上，点B在直线AC上，若∠1=∠2，∠3=∠4，则∠A=∠F，请说明理由．解：∵∠1=∠2(已知)∠2=∠DGF∴∠1=∠DGF(____________)∴BD∥CE∴∠3+∠C=180°( )又∵∠3=∠4(已知)∴∠4+∠C=180°∴∥(同旁内角互补，两直线平行)∴∠A=∠F( )．26．如图，所有小正方形的边长都为1，A、B、C都在格点上．（1）过点C画直线AB的平行线（不写画法，下同）；（2）过点A画直线BC的垂线，并注明垂足为G；过点A画直线AB的垂线，交BC于点H．（3）线段_____的长度是点A到直线BC的距离；（4）线段AG、AH的大小关系为AG_____AH．（填“＞”或“＜”或“＝”），理由________．27．如图，AB∥CD，∠1＝∠2，求证：AM∥CN参考答案1．C2．C3．C4．B5．B6．D7．B8．B9．A10．C11．4 ∠DOF、∠EOB、∠ABD、∠DBC平行于同一直线的两条直线平行CD∥EF 12．513．1214．②③15．16；3116．70°17． 12 318．如果一个三角形的三个角都相等，那么这个三角形是等边三角形一个三角形的三个角都相等这个三角形是等边三角形19．（2）40°20．（1）∠APC+∠PAB+∠PCD=360°，理由见解析；两直线平行，同旁内角互补；CD，如果两条直线都和第三条直线平行，那么这两条直线也互相平行；180°，两直线平行，同旁内角互补；（2）∠APC=∠PAB+∠PCD，（3）∠P=56°．21．（1）y＝x2﹣2x﹣3，D的坐标为（1，﹣4）；（2）存在异于点D的点E，使S△BCE＝S△BCD，点E的坐标为（2，﹣3）；（3）最小值为23．（1）A（0，1），B（3，0）；（2）5 324． (3) ＜；(4) 9 26．（3）AG；（4）<.。

第五章《抛体运动》单元测试含答案(人教版2019)

试卷第1页，共5页第五章抛体运动单元测试姓名：___________班级：___________考号：___________一、选择题（本大题共11 小题，1～7题是单选，8～11题是多选，每小题4分，共44 分。

多选题全部选对得4分，选对但不全得2分，有选错的得0分）1．如图所示，一物块仅在三个共点恒力F 1、F 2、F 3的作用下以速度v 0水平向右做匀速直线运动，其中F 1斜向右上方，F 2竖直向下，F 3水平向左．某时刻撤去其中的一个力，其他力的大小和方向不变，一段时间后恢复该力，则下列说法不正确的是（）A ．如果撤去的是F 1，则物块先做匀变速曲线运动，恢复该力之后将做匀速直线运动B ．如果撤去的是F 1，恢复F 1时物块的速度大小可能为v 0C ．如果撤去的是F 3，物块将向右做匀加速直线运动，恢复该力之后做匀速直线运动D ．如果撤去的是F 2，在恢复该力之前的时间内，因物块做曲线运动，故在相等时间间隔内其速度的变化量Δv 的方向时刻在改变2．以6m/s 的初速度竖直向上抛出一个小球，不计空气阻力，取g =10m/s 2。

则小球回到抛出点的速度大小和上升的最大高度分别为（）A ．0，1.8mB ．0，3.6mC ．6m/s ，1.8mD ．6m/s ，3.6m3．如图所示，某救援队利用如下装置转运救灾物资，物资穿在竖直固定光滑杆上，若汽车速度为1v ，物资运动速度为2v ，定滑轮左右两侧轻绳与竖直方向夹角分别为α、β。

不计滑轮质量以及绳与滑轮间的摩擦，下列关系正确的是（）A ．12v v =B ．21cos sin v v αβ= C ．122sin cos v v αα= D ．21cos sin v v βα=4．从航母起飞的战斗机在空中水平方向匀速直线飞行，在模拟训练中，先后投放多枚炸弹轰炸正前方静止的“敌方”舰船，投放每枚炸弹的时间间隔相同，且轰炸机投放炸弹后速度不变（炸弹离开飞机后，空气阻力忽略不计），则（）A ．空中飞行的炸弹在相等时间内速度变化都相同B ．战斗机上的飞行员看到投放在空中的炸弹位于一条抛物线上C ．战斗机的速度越大，炸弹在空中飞行时间越短D ．炸弹击中“敌方”舰船时，轰炸机位于“敌方”舰船的前上方试卷第2页，共5页5．在空中，一枚石子以某一水平速度被抛出。

第五章单元检测题

第五章单元检测题一、选择题1、下列关于透镜的说法中，正确的是（）A 凸透镜只对平行光有会聚作用 B.凸透镜两个焦点之间的距离叫做焦距 C.平行光经过凸透镜折射后一定会聚于一点 D 凸透镜任何光束都有会聚作用 2．一束光在空气中经凸透镜折射后，下列说法中正确的是（）A ．一定是平行光束B ．一定是会聚光束C ．折射光束比原光束会聚一些D ．一定是发散光束3．光学器件在我们的生活、学习中有着广泛的应用。

下面的介绍有一项不切实际，它是（）A ．近视眼镜利用了凹透镜对光线的发散作用B ．照相时，被照者与相机的距离是在镜头的二倍焦距之外C ．借助放大镜看地图时，地图到放大镜的距离应略大于一倍焦距D ．阳光通过凸透镜可以点燃纸屑，这利用了凸透镜对光的会聚作用4．下图是“探究凸透镜成像的规律”实验装置示意图，凸透镜的焦距是20cm ，如图的情景，眼睛可能观察到烛焰经凸透镜折射所成的虚像.5．如右图所示是利用航空摄影拍摄到的铜仁市碧江区一角，如果拍摄时所用照像机的镜头焦距是50mm,则胶片到镜头的距离应（）A ．大于100mmB ．大于50mm 小于100mmC ．小于50mmD ．等于50mm6．小明同学在“探究凸透镜成像的规律”实验时，烛焰在光屏上成了一个清晰的像，如图所示。

下面给出的生活中常用物品工作时原理与此现象相同的是（）A.投影仪B.照相机C.放大镜D.近视镜7．在探究凸透镜成像规律的实验中，当烛焰、凸透镜、光屏位于如图所示的位置时，烛焰在光屏上呈现一个清晰放大的像。

要使烛焰在光屏上呈现一个清晰缩小的像，调节的方法是A.透镜不动，蜡烛远离透镜移动，光屏靠近透镜移动B.透镜不动，蜡烛远离透镜移动，光屏远离透镜移动C.透镜不动，蜡烛靠近透镜移动，光屏远离透镜移动D.透镜不动，蜡烛靠近透镜移动，光屏靠近透镜移动 8．（2012浙江绍兴）图中人手持的是一枚（）A ．凹透镜，可以矫正近视B ．凹透镜，可以矫正远视C ．凸透镜，可以矫正近视D ．凸透镜，可以矫正远视9.如图所示，画出了光通过透镜前后的方向，在图中Ｏ处应填的适当类型的透镜是（）A. 凸透镜B.凹透镜C.凸、凹透镜都有可能D.凸、凹透镜都不行10．如果在屏幕上想看到一个正常的“F ”投影片放置的情况应是（）11．(2012河北)透镜在我们的生活、学习中应用广泛。

人教版七年级数学下册第五章相交线与平行线单元检测卷(共6套)

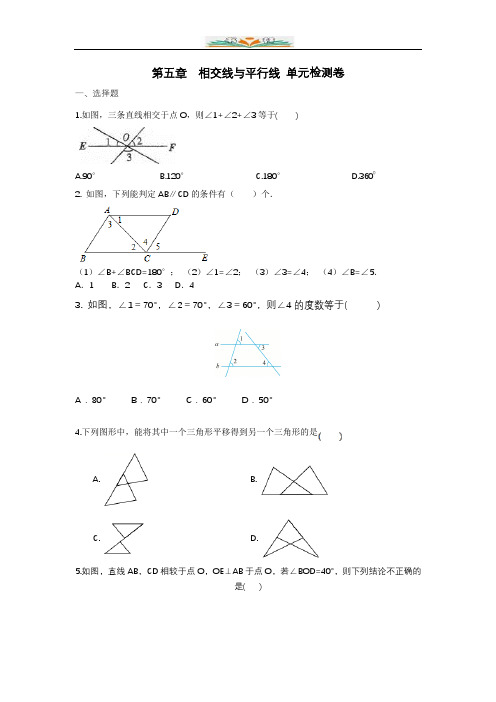
第五章相交线与平行线单元检测卷一、选择题1.如图，三条直线相交于点O，则∠1+∠2+∠3等于( )A.90°B.120°C.180°D.36002. 如图，下列能判定AB∥CD的条件有（）个．（1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5．A．1 B．2 C．3 D．43. 如图，∠1＝70°，∠2＝70°，∠3＝60°，则∠4的度数等于( )A．80°B．70°C．60°D．50°4.下列图形中，能将其中一个三角形平移得到另一个三角形的是A. B.C. D.5.如图，直线AB，CD相较于点O，OE⊥AB于点O，若∠BOD=40°，则下列结论不正确的是( )A.∠AOC=40°B.∠COE=130°C.∠EOD=40°D.∠BOE=90°6.如图，直线a,b被c,d所截，且a∥b，则下列结论中正确的是( )A.∠1=∠2 C.∠3+∠4=180°B.∠3=∠4 D.∠1+∠4=180°7.如图，点A在直线BG上,AD∥BC，AE平分∠GAD，若∠CBA=80°,则( )A.60°B.50°C.40°D.30°8.下列各图中，∠1与∠2互为邻补角的是( )9.对于图中标记的各角，下列条件能推理得到a∥b的是（）A．∠1=∠2 B．∠2=∠4 C．∠3=∠4 D．∠1+∠4=18010．下列说法正确的是( )A.一个角的补角一定比这个角大B.一个角的余角一定比这个角小C.一对对顶角的两条角平分线必在同一条直线上D.有公共顶点并且相等的两个角是对顶角二、填空题11.如图，直线AB，CD相交于点O, EO⊥AB于点O，∠EOD=50°，则∠BOC的度数为______.12. 如图是由五个形状、大小完全相同的三角形组成的图案，三角形的三个角分别为36°，72°，72°，则图中共有_____对平行线．13.如图，，则的度数等于14．如图，点0是直线AB上一点平分，图中与互余的角有______ ．图中与互补的角有______ ．15. 说明命题“x>－4，则x2>16”是假命题的一个反例可以是x＝____________．16.如图，现要从村庄A修建一条连接公路PQ的最短小路，过点A作AH⊥PQ于点H，沿AH修建公路，则这样做的理由是三、解答题17.如图，直线AB，CD 相交于点O，∠AOD=3∠BOD+20°.(1)求∠BOD的度数；(2)以O为端点引射线OE,OF ,射线OE平分∠BOD，且∠EOF= 90°，求∠BOF的度数.18．已知：如图，AB∥CD，∠1=∠2，∠3=∠4．（1）求证：AD∥BE；（2）若∠B=∠3=2∠2，求∠D的度数．19.如图，D，E，F是线段AB的四等分点.(1)过点D画DH∥BC交于点H,过点E画EG∥BC交AC于点G，过点F画FM∥BC交AC 于点M;(2)量出线段AH,HG,GM,MC的长度，你有什么发现？(3)量出线段HD,EG,FM,BC的长度，你又有什么发现？20.请写出命题“两直线平行，同位角相等”的题设和结论：题设：，结论：．21.观察下图，寻找对顶角：(1)如图1，图中共有对对顶角(2)如图2，图中共有对对顶角(3)如图3，图中共有对对顶角(4)若有n条直线相交于一点，则可形成多少对对顶角？22.如图，已知直线AB∥DF,∠D+∠B=180°.(1)试说明DE∥BC；(2)若∠AMD=75°，求∠AGC的度数.【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

第五章发展与合作同单元测试卷(原题卷)

第五章发展与合作同单元测试卷一、选择题（每题2分，共40分）1．领土是指一个国家国界线以内的（）A．陆地、领海B．陆地、领水C．陆地、领空D．陆地、领海、内水和领空2．朝鲜和韩国的分界线是（）A．河流B．经线C．山脉D．纬线3．和平与发展是当今世界两大主题，加强国际合作显得尤为重要，这是因为（）A．发达国家要从发展中国家购买全部原料，并售出全部产品B．发展中国家要从发达国家引进全部资金、设备、技术及管理经验C．如果离开了某一大国，其他国家就无法生存D．任何国家都不是孤立存在的，总与其他国家发生不同程度的联系4．下列图例表示国界线的是（）A．B．C．D．5．2021年3月27日，中国与伊朗签署全面合作计划，两国之间的合作被称为（）A．南北对话B．南南合作C．南北互助D．南南互助6．下列国家之间的政治、经济商谈属于“南北对话”的是（）A．中国和巴西B．美国和英国C．澳大利亚和印度D．日本和法国7．当今世界矛盾冲突的主要原因是（）A．发展中国家与发达国家之间日益扩大的贫富差距B．发展中国家无法忍受发达国家长期的经济封锁C．发达国家介入发展中国家之间的一些争端D．石油输出国组织通过提高石油价格维护自身的利益8．英文缩写“WTO”的国际组织是（）A．联合国B．国际红十字会C．世界贸易组织D．欧洲联盟9．下列国家中符合“北半球，发达国家”两个条件的有（）A．美国、印度B．澳大利亚、法国C．中国、巴西D．美国、日本10．下列国家中全部属于发达国家的是（）A．美国、加拿大、中国B．英国、澳大利亚、日本C．法国、美国、马来西亚D．新加坡、印度尼西亚、巴西11．如图示意2017年世界部分国家的人口状况，读图，图示国家中人口最稠密的是（）A．日本B．中国C．巴基斯坦D．巴西12．下列有关国际贸易的叙述，正确的是（）A．在国际贸易中，发达国家和发展中国家的经济合作是平等的B．发达国家出口初级产品，进口高科技工业产品C．发展中国家出口初级产品，进口高科技工业产品D．在国际贸易中，发达国家赚钱少，发展中国家赚钱多13．与发展中国家相比，发达国家具有的特征是（）①农业机械化水平高②人均教育经费低③出口工业半成品为主④高新技术产业领先A．①③B．②④C．②③D．①④14．2020年11月15日，东盟十国（东南亚国家联盟）及中国、日本、韩国、澳大利亚、新西兰共15个国家正式签署区域全面经济伙伴关系协定（RCEP），以下对伙伴国描述正确的是（）①RCEP成员中国土面积最大的是中国②澳大利亚以白色人种为主③日本和韩国地处东亚④RCEP成员国全都为发达国家A．①②③B．①③④C．①②④D．②③④15．关于领土的说法，正确的是（）A．领土一般指陆地面积B．领土是一个国家行使主权的空间C．领土一般不包括岛屿D．领土指国界范围以内的领陆、领水和领海16．下列关于国界的说法正确的是（）①国界是一国与邻国或公海之间的界线②国界是国家主权范围的边界③国界是人为划分的④国界是依据宗教来划分的．A．①②B．②③④C．①②③D．③④17．联合国安理会常任理事国是（）A．中国、意大利、美国、英国、法国B．中国、德国、法国、英国、美国C．中国、日本、美国、德国、法国D．中国、俄罗斯、法国、英国、美国18．划分发达国家和发展中国家的依据是（）A．国家面积大小B．国家人口多少C．国家历史长短D．国家经济发展水平19．人类共同生活在地球家园，人类社会永恒的主题是（）A．冲突B．联系C．发展D．合作20．下列生产、生活现象中不能体现国际经济合作的是（）A．中国的棉花、淡水产品大量出口到日本B．在中国可以买到产自美国的电子产品C．在北京的超市可以买到来自吐鲁番的葡萄干D．上海宝钢的铁矿石主要来自澳大利亚二、填空题（每空1分，共41分）21．根据经济发展水平，世界上的国家划分为两类即、．22．和平共处的五项基本原则是、、、、。

第五章相交线与平行线单元试卷测试卷(解析版)

第五章相交线与平行线单元试卷测试卷（解析版）一、选择题1．如图，AB∥EF，设∠C＝90°，那么x、y和z的关系是（）A．y＝x+z B．x+y﹣z＝90°C．x+y+z＝180°D．y+z﹣x＝90°2．如图，AB∥CD，∠1=120°，则∠2＝（）A．50°B．70°C．120°D．130°3．如图，已知直线AB、CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB、CD、AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC的度数可能是（）A．①②③B．①②④C．①③④D．①②③④4．两条平行线被第三条直线所截，则下列说法错误的是（）A．一对邻补角的平分线互相垂直 B．一对同位角的平分线互相平行C．一对内错角的平分线互相平行 D．一对同旁内角的平分线互相平行5．下列说法不正确的是（）A．过任意一点可作已知直线的一条平行线 B．在同一平面内两条不相交的直线是平行线C．在同一平面内，过直线外一点只能画一条直线与已知直线垂直D．直线外一点与直线上各点连接的所有线段中，垂线段最短6．如图，直线AB，CD相交于点O，EO⊥AB，垂直为点O，∠BOD＝50°，则∠COE＝（）A．30°B．140°C．50°D．60°7．如图，在△ABC中，AB=AC，CD∥AB，点E在BC的延长线上.若∠A=30°，则∠DCE的大小为（）A．30° B．52.5° C．75° D．85°8．命题“垂直于同一条直线的两条直线互相平行”的条件是（）A．垂直B．两条直线互相平行C．同一条直线D．两条直线垂直于同一条直线9．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为（）A．10°B．20°C．25°D．30°10．下列选项中，不是运用“垂线段最短”这一性质的是（）A．立定跳远时测量落点后端到起跳线的距离 B．从一个村庄向一条河引一条最短的水渠C．把弯曲的公路改成直道可以缩短路程D．直角三角形中任意一条直角边的长度都比斜边短11．下列说法中不正确的个数为（）．①在同一平面内，两条直线的位置关系只有两种：相交和垂直．②有且只有一条直线垂直于已知直线．③如果两条直线都与第三条直线平行，那么这两条直线也互相平行．④从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离．⑤过一点，有且只有一条直线与已知直线平行．A．2个B．3个C．4个D．5个12．如图，△ABC经平移得到△EFB，则下列说法正确的有（）①线段AC 的对应线段是线段EB ；②点C 的对应点是点B ；③AC ∥EB ；④平移的距离等于线段BF 的长度．A ．1B ．2C ．3D ．4二、填空题13．如图，已知AB ∥CD ，点E ，F 分别在直线AB ，CD 上点P 在AB ，CD 之间且在EF 的左侧．若将射线EA 沿EP 折叠，射线FC 沿FP 折叠，折叠后的两条射线互相垂直，则∠EPF 的度数为 _____．14．如果∠α与∠β的两边分别平行，∠α比∠β的3倍少40°，则∠α的度数为_______．15．小明将一副三角板中的两块直角三角尺的直角顶点C 按如图所示的方式叠放在一起，当∠ACE ＜180°且点E 在直线AC 的上方时，他发现若∠ACE ＝_____，则三角板BCE 有一条边与斜边AD 平行．16．如图，AB //CD BED 110BF ，，∠=平分ABE DF ∠，平分CDE ∠，则BFD ∠= ______ ．17．规律探究：同一平面内有直线1a 、2a 、3a ，⋯，100a ，若12//a a ，23a a ⊥，34//a a ，45a a ⊥，⋯，按此规律，1a 与100a 的位置关系是______．18．如图，1∠与2∠是对顶角，110α∠=+︒，250∠=︒，则α=______．19．如图，AD ∥BC ，∠D=100°，CA 平分∠BCD ，则∠DAC=________度．20．如图，直线////a b c ，直角三角板的直角顶点落在直线b 上，若135∠=︒，则2∠等于_______．三、解答题21．（1）如图a 所示，//AB CD ，且点E 在射线AB 与CD 之间，请说明AEC A C ∠=∠+∠的理由．（2）现在如图b 所示，仍有//AB CD ，但点E 在AB 与CD 的上方，①请尝试探索1∠，2∠，E ∠三者的数量关系．②请说明理由．22．问题情境（1）如图1，已知//AB CD ，125PBA ︒∠=，155PCD ︒∠=，求BPC ∠的度数．佩佩同学的思路：过点P 作PG//AB ，进而//PG CD ，由平行线的性质来求BPC ∠，求得BPC ∠=________．问题迁移（2）图2．图3均是由一块三角板和一把直尺拼成的图形，三角板的两直角边与直尺的两边重合，90ACB ︒∠=，//DF CG ，AB 与FD 相交于点E ，有一动点P 在边BC 上运动，连接PE ，PA ，记PED α∠=∠，PAC β∠=∠．①如图2，当点P 在C ，D 两点之间运动时，请直接写出AOE ∠与α∠，β∠之间的数量关系；②如图3，当点P 在B ，D 两点之间运动时，APE ∠与α∠，β∠之间有何数量关系？请判断并说明理由；拓展延伸（3）当点P 在C ，D 两点之间运动时，若PED ∠，PAC ∠的角平分线EN ，AN 相交于点N ，请直接写出ANE ∠与α∠，β∠之间的数量关系．23．如图，//AB CD ，EG 平分DEF ∠，FG 平分BFE ∠．（1）求证：90EFG GEF ∠+∠=︒；（2）在（1）问的条件下，过点G 作GH AB ⊥，垂足为H ，FGH ∠的平分线GI 交AB 于点I ，EGH ∠的平分线GJ 交AB 于点J ，求IGJ ∠的度数．24．已知AB ∥CD ，点C 在点D 的右侧，连接AD ，BC ，BE 平分∠ABC ，DE 平分∠ADC ，BE ，DE 相交于点E ．（1）如图1，当点B 在点A 的左侧时，①若∠ABC =50º，∠ADC =70º，求∠BED 的度数；②请直接写出∠BED 与∠ABC ，∠ADC 的数量关系；（2）如图2，当点B 在点A 的右侧时，试猜想∠BED 与∠ABC ，∠ADC 的数量关系，并说明理由．25．（1）方法感悟如图①所示，求证：BCF B F ∠=∠+∠．证明：过点C 作//CD EF//AB EF (已知)//CD AB ∴(平行于同一条直线的两条直线互相平行)1,2B F ∴∠=∠∠=∠(两直线平行，内错角相等 )12B F ∴∠+∠=∠+∠即BCF B F ∠=∠+∠（2）类比应用如图②所示，//,AB EF 求证：360B BCF F ∠+∠+∠=︒．证明：（3）拓展探究如图③所示，//,AB EF BCF ∠与B F ∠∠、的关系是 (直接写出结论即可)．如图④所示，//,AB EF BCF ∠与B F ∠∠、的关系是 (直接写出结论即可)．26．如图1，直线AB 与直线OC 交于点O ，()090BOC αα∠=︒<<．小明将一个含30的直角三角板PQD 如图1所示放置，使顶点P 落在直线AB 上，过点Q 作直线MN AB 交直线OC 于点H (点H 在Q 左侧)．（1）若PD OC ∥，45NQD ∠=︒，则α=__________︒．（2）若PQH ∠的角平分线交直线AB 于点E ，如图2．①当QE OC ∥，60α=︒时，求证：OCPD ． ②小明将三角板保持PD OC ∥并向左平移，运动过程中，PEQ ∠=__________．(用α表示)． 27．如图`，已知：直线AD BC ∥，且直线AB 、CD 与AD 、BC 分别交于A 、D 和B 、C 两点，点P 在直线AB 上．∠、(1)如图1,当点P在A、B两点之间时(点P不与点A、B重合)，探究ADP、DPC ∠之间的关系，并说明理由.BCP∠、(2)若点P不在A、B两点之间，在备用图中画出图形，直接写出ADP、DPC∠之间的关系，不需说理．BCP28．如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC＝50°，∠ADC＝30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于E．（1）求∠AEC的度数；（2）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1，CE平分∠ACD1，A1E与CE相交于E，∠PAC＝50°，∠A1D1C＝30°，求∠A1EC 的度数．（3）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（2）相同，求此时∠A1EC的度数．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】过C作CM∥AB，延长CD交EF于N，根据三角形外角性质求出∠CNE＝y﹣z，根据平行线性质得出∠1＝x，∠2＝∠CNE，代入求出即可．【详解】解：过C作CM∥AB，延长CD交EF于N，则∠CDE＝∠E+∠CNE，即∠CNE＝y﹣z∵CM∥AB，AB∥EF，∴CM∥AB∥EF，∴∠ABC＝x＝∠1，∠2＝∠CNE，∵∠BCD＝90°，∴∠1+∠2＝90°，∴x+y﹣z＝90°．故选：B．【点睛】本题考查了平行线的性质和三角形外角性质的应用，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补．2．C解析：C【分析】由平行线性质和对顶角相等可以得到解答．【详解】解：如图，由对顶角相等可以得到∠3＝∠1=120°又AB∥CD，∴∠2＝∠3=120°．故选C．【点睛】本题考查平行线和对顶角的综合应用，由题意发现角的相等关系是解题关键．3．D解析：D【分析】根据E点有4中情况，分四种情况讨论分别画出图形，根据平行线的性质与三角形外角定理求解.【详解】E点有4中情况，分四种情况讨论如下：由AB∥CD，可得∠AOC=∠DCE1=β∵∠AOC=∠BAE1+∠AE1C，∴∠AE1C=β-α过点E2作AB的平行线，由AB∥CD，可得∠1=∠BAE2=α,∠2=∠DCE2=β∴∠AE2C=α+β由AB∥CD，可得∠BOE3=∠DCE3=β∵∠BAE3=∠BOE3+∠AE3C，∴∠AE3C=α-β由AB∥CD，可得∠BAE4+∠AE4C+∠DCE4=360°，∴∠AE4C=360°-α-β∴∠AEC的度数可能是①α+β，②α﹣β，③β-α，④360°﹣α﹣β，故选D.【点睛】此题主要考查平行线的性质与外角定理，解题的关键是根据题意分情况讨论.4．D解析：D【解析】试题分析：A、两条平行线被第三条直线所截，一对邻补角的平分线互相垂直，故本选项正确；B、两条平行线被第三条直线所截，同位角的平分线互相平行，故本选项正确；C、两条平行线被第三条直线所截，内错角的平分线互相平行，故本选项正确；D、两条平行线被第三条直线所截，同旁内角的平分线互相垂直，故本选项错误；故选：D．5．A解析：A【解析】试题分析：平面内，过直线外一点有且只有一条直线与已知直线平行，故A不正确；在同一平面内两条不相交的直线是平行线，这是平行线的概念，故B正确；在同一平面内，过直线外一点只能画一条直线与已知直线垂直，故C正确；直线外一点与直线上各点连接的所有线段中，垂线段最短，故D正确；故选：A.6．B解析：B【解析】试题解析：EO⊥AB，∴∠=AOE90,∠=∠=AOC BOD50,∴∠=∠+∠=+=COE AOC AOE5090140.故选B.7．C解析：C【解析】试题分析：根据等腰三角形的性质：等边对等角，可得∠B=∠ACB，然后根据三角形的内角和可求得∠B=75°，然后根据平行线的性质可得∠B=∠DCE=75°.故选：C.点睛：此题主要考查了等腰三角形的性质，解题关键是利用等腰三角形的性质求得两底角的值，然后根据平行线的性质可求解问题.8．D解析：D【分析】命题有条件和结论两部分组成，条件是已知的部分，结论是由条件得出的推论．【详解】“垂直于同一条直线的两条直线互相平行”的条件是“两条直线垂直于同一条直线”，结论是“两条直线互相平行”．故选：D．【点睛】本题考查了对命题的题设和结论的理解，解题的关键在于利用直线垂直的定义进行判断．9．C解析：C【解析】分析：如图，延长AB交CF于E，∵∠ACB=90°，∠A=30°，∴∠ABC=60°．∵∠1=35°，∴∠AEC=∠ABC﹣∠1=25°．∵GH∥EF，∴∠2=∠AEC=25°．故选C．10．C解析：C【分析】垂线段最短，指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．据此逐个分析即可.【详解】解：A．立定跳远时测量落点后端到起跳线的距离，运用“垂线段最短”这一性质；B．从一个村庄向一条河引一条最短的水渠，运用“垂线段最短”这一性质；C．把弯曲的公路改成直道可以缩短路程，运用“两点之间，线段最短”这一性质；D．直角三角形中任意一条直角边的长度都比斜边短，运用“垂线段最短”这一性质；故选：C．【点睛】本题主要考查了垂线段最短，实际问题中涉及线路最短问题时，其理论依据应从“两点之间，线段最短”和“垂线段最短”这两个中去选择．11．C解析：C【分析】根据在同一平面内，根据两条直线的位置关系、垂直的性质、平行线平行公理及推论、点到直线的距离等逐一进行判断即可．【详解】∵在同一平面内，两条直线的位置关系只有两种：相交和平行，故①不正确；∵过直线外一点有且只有一条直线垂直于已知直线．故②不正确；如果两条直线都与第三条直线平行，那么这两条直线也互相平行．故③正确；从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离．故④不正确；过直线外一点，有且只有一条直线与已知直线平行．故⑤不正确；∴不正确的有①②④⑤四个．故选：C．【点睛】本题考查了直线的知识；解题的关键是熟练掌握直线相交、直线垂直、直线平行以及垂线的性质，从而完成求解．12．D解析：D【分析】根据平移的特点分别判断各选项即可．【详解】∵△ABC经平移得到△EFB∴点A、B、C的对应点分别为E、F、B，②正确∴BE是AC的对应线段，①正确∴AC∥EB，③正确平移距离为对应点连线的长度，即BF的长度，④正确故选：D【点睛】本题考查平移的特点，注意，在平移过程中，一定要把握住对应点，仅对应点的连线之间才有平行、相等的一些关系．二、填空题13．45°或135°【分析】根据题意画出图形，然后利用平行线的性质得出∠EMF与∠AEM和∠CFM的关系，然后可得答案．【详解】解：如图1，过作，，，，，，，同理可得，由折叠可解析：45°或135°【分析】根据题意画出图形，然后利用平行线的性质得出∠EMF与∠AEM和∠CFM的关系，然后可得答案．【详解】解：如图1，过M 作//MN AB ，//AB CD ，////AB CD NM ∴，AEM EMN ∴∠=∠，NMF MFC ∠=∠，90EMF ∠=︒，90AEM CFM ∴∠+∠=︒，同理可得P AEP CFP ∠=∠+∠，由折叠可得：12AEP PEM AEM ∠=∠=∠，12PFC PFM CFM ∠=∠=∠， 1()452P AEM CFM ∴∠=∠+∠=︒，如图2，过M 作//MN AB ，//AB CD ， ////AB CD NM ∴，180AEM EMN ∴∠+∠=︒，180NMF MFC ∠+∠=︒，360AEM EMF CFM ∴∠+∠+∠=︒，90EMF ∠=︒，36090270AEM CFM ∴∠+∠=︒-︒=︒，由折叠可得：12AEP PEM AEM ∠=∠=∠，12PFC PFM CFM ∠=∠=∠， 12701352P ∴∠=︒⨯=︒，综上所述：EPF ∠的度数为45︒或135︒，故答案为：45°或135°．【点睛】本题主要考查了平行线的性质，关键是正确画出图形，分两种情况分别计算出∠EPF 的度数．14．或【分析】由两角的两边互相平行可得出两角相等或互补，再由题意，其中一个角比另一个角的3倍少，可得出答案．【详解】解：设为x ，则为，若两角互补，则，解得，；若两角相等，则，解得，．故答案解析：125︒或20︒【分析】由两角的两边互相平行可得出两角相等或互补，再由题意，其中一个角比另一个角的3倍少40︒，可得出答案．【详解】解：设β∠为x ，则α∠为340x -︒，若两角互补，则340180x x +-︒=︒，解得55x =︒，125α∠=︒；若两角相等，则340x x =-︒，解得20x =︒，20α∠=︒．故答案为：125︒或20︒．【点睛】本题考查了平行线的性质，解题的关键是注意若∠α与∠β的两边分别平行，即可得∠α与∠β相等或互补，注意方程思想与分类讨论思想的应用．15．或或【分析】分三种情形画出图形分别建立好几何模型求解，即可解决问题．【详解】解：有三种情形： ①如图1中，当AD∥BC 时．∵AD∥BC， ∴∠D＝∠BCD＝30°，∵∠ACE+∠E解析：30或120︒或165︒【分析】分三种情形画出图形分别建立好几何模型求解，即可解决问题．【详解】解：有三种情形： ①如图1中，当AD ∥BC 时．∵AD ∥BC ， ∴∠D ＝∠BCD ＝30°，∵∠ACE+∠ECD ＝∠ECD+∠DCB ＝90°，∴∠ACE＝∠DCB＝30°．②如图2中，当AD∥CE时，∠DCE＝∠D＝30°，可得∠ACE＝90°+30°＝120°．③如图2中，当AD∥BE时，延长BC交AD于M．∵AD∥BE，∴∠AMC=∠B=45°，∴∠ACM＝180°-60°-45°＝75°，∴∠ACE＝75°+90＝165°，综上所述，满足条件的∠ACE的度数为30°或120°或165°．故答案为30°或120°或165°．【点睛】本题考查旋转变换、平行线的判定和性质、三角形内角和定理等知识，解题的关键是学会用分类讨论的首先思考问题，属于中考常考题型．16．【解析】【分析】首先过点E作EM∥AB，过点F作FN∥AB，由AB∥CD，即可得EM∥AB∥CD∥FN，然后根据两直线平行，同旁内角互补，由∠BED=110°，即可求得∠ABE+∠CDE=25解析：125【解析】【分析】首先过点E作EM∥AB，过点F作FN∥AB，由AB∥CD，即可得EM∥AB∥CD∥FN，然后根据两直线平行，同旁内角互补，由∠BED=110°，即可求得∠ABE+∠CDE=250°，又由BF平分∠ABE，DF平分∠CDE，根据角平分线的性质，即可求得∠ABF+∠CDF的度数，又由两只线平行，内错角相等，即可求得∠BFD的度数．【详解】过点E作EM∥AB，过点F作FN∥AB，∵AB∥CD，∴EM∥AB∥CD∥FN，∴∠ABE+∠BEM=180°，∠CDE+∠DEM=180°，∴∠ABE+∠BED+∠CDE=360°，∵∠BED=110°，∴∠ABE+∠CDE=250°，∵BF平分∠ABE，DF平分∠CDE，∴∠ABF=12∠ABE，∠CDF=12∠CDE，∴∠ABF+∠CDF=12（∠ABE+∠CDE）=125°，∵∠DFN=∠CDF，∠BFN=∠ABF，∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°．故答案为125°【点睛】此题考查了平行线的性质与角平分线的定义．此题难度适中，解题的关键是注意数形结合思想的应用，注意辅助线的作法．17．互相垂直．【解析】【分析】依据，，，，，可得，即可得到与的位置关系是互相垂直．【详解】解：，，，，按此规律，，又，，，以此类推，，，故答案为：互相垂直．【点睛】本题主要解析：互相垂直．【解析】【分析】依据12a //a ，23a a ⊥，34a //a ，45a a ⊥，⋯，可得14n a a ⊥，即可得到1a 与100a 的位置关系是互相垂直．【详解】解：12a //a ，23a a ⊥，34a //a ，14a a ∴⊥，按此规律，58a a ⊥，又45a a ⊥，⋯，18a a ∴⊥，以此类推，14n a a ⊥100425=⨯，1100a a ∴⊥，故答案为：互相垂直．【点睛】本题主要考查了平行线的性质，解决问题的关键是根据已知条件得出规律：14n a a ⊥． 18．40°【分析】先根据对顶角相等的性质得出∠1=∠2，即可求出α的度数．【详解】解：∵∠1与∠2是对顶角，，∠2=50°，∴∠1=∠2，∵，∠2=50°，∴α+10°=50°，∴α=4解析：40°【分析】先根据对顶角相等的性质得出∠1=∠2，即可求出α的度数．【详解】解：∵∠1与∠2是对顶角，110α∠=+︒，∠2=50°，∴∠1=∠2，∵110α∠=+︒，∠2=50°，∴α+10°=50°，∴α=40°．故答案为：40°．【点睛】本题考查了对顶角相等的性质以及角度的计算．19．40°【分析】本题主要利用两直线平行，同旁内角互补、两直线平行，内错角相等以及角平分线的定义进行做题．【详解】∵AD∥BC，∴∠BCD=180°-∠D=80°，又∵CA 平分∠BCD，∴解析：40°【分析】本题主要利用两直线平行，同旁内角互补、两直线平行，内错角相等以及角平分线的定义进行做题．【详解】∵AD ∥BC ，∴∠BCD=180°-∠D=80°，又∵CA 平分∠BCD ，∴∠ACB=12∠BCD=40°， ∴∠DAC=∠ACB=40°．【点睛】本题重点考查了平行线的性质及角平分线的定义，是一道较为简单的题目．20．【分析】如图，利用平行线的性质得出∠3=35°，然后进一步得出∠4的度数，从而再次利用平行线性质得出答案即可.【详解】如图所示，∵，，∴，∴∠4=90°−∠3=55°，∵，∴∠2解析：55︒【分析】如图，利用平行线的性质得出∠3=35°，然后进一步得出∠4的度数，从而再次利用平行线性质得出答案即可.【详解】如图所示，∵//a b ，135∠=︒，∴335∠=︒，∴∠4=90°−∠3=55°，∵////a b c ，∴∠2=∠4=55°.故答案为：55°.【点睛】本题主要考查了平行线的性质，熟练掌握相关概念是解题关键.三、解答题21．（1）；（2）①∠1+∠2-∠E=180°；②见解析【分析】（1）过点E 作EF ∥AB ，根据平行线的性质得到∠A=∠AEF 和∠FEC=∠C ，再相加即可；（2）①、②过点E 作EF ∥AB ，根据平行线的性质可得∠AEF+∠1=180°和∠FEC=∠2，从而可得三者之间的关系．【详解】解：（1）过点E 作EF ∥AB ，∴∠A=∠AEF ，∵AB ∥CD ，∴EF ∥CD ，∴∠FEC=∠C ，∵∠AEC=∠AEF+∠FEC ，∴∠AEC=∠A+∠C ；（2）①∠1+∠2-∠E=180°，②过点E 作EF ∥AB ，∴∠AEF+∠1=180°，∵AB ∥CD ，∴EF ∥CD ，∴∠FEC=∠2，即∠CEA+∠AEF=∠2，∴∠AEF=∠2-∠CEA ，∴∠2-∠CEA+∠1=180°，即∠1+∠2-∠AEC=180°．【点睛】本题考查了平行线的性质，作辅助线并熟记性质是解题的关键．22．（1）80︒；（2）①APE αβ∠=∠+∠，②APE βα∠=∠-∠，理由见解析；（3）1()2ANE αβ∠=∠+∠ 【分析】（1）过点P 作//PG AB ，则//PG CD ，由平行线的性质可得BPC ∠的度数；（2）①过点P 作FD 的平行线，依据平行线的性质可得APE ∠与α∠，β∠之间的数量关系；②过P 作//PQ DF ，依据平行线的性质可得QPA β∠=∠，QPE α∠=∠，即可得到APE APQ EPQ βα∠=∠-∠=∠-∠；（3）过P 和N 分别作FD 的平行线，依据平行线的性质以及角平分线的定义，即可得到ANE ∠与α∠，β∠之间的数量关系为1()2ANE αβ∠=∠+∠．【详解】解：（1）如图1，过点P 作//PG AB ，则//PG CD ，由平行线的性质可得180B BPG ︒∠+∠=，180C CPG ︒∠+∠=，又∵125PBA ︒∠=，155PCD ︒∠=，∴36012515580BPC ︒︒︒︒∠=--=，故答案为：80︒；（2）①如图2，APE ∠与α∠，β∠之间的数量关系为APE αβ∠=∠+∠；过点P 作PM∥FD，则PM∥FD∥CG，∵PM∥FD，∴∠1=∠α，∵PM∥CG，∴∠2=∠β，∴∠1+∠2=∠α+∠β，即：APE αβ∠=∠+∠，②如图，APE ∠与α∠，β∠之间的数量关系为APE βα∠=∠-∠；理由：过P 作//PQ DF ，∵//DF CG ，∴//PQ CG ，∴QPA β∠=∠，QPE α∠=∠，∴APE APQ EPQ βα∠=∠-∠=∠-∠；（3）如图，由①可知，∠N=∠3+∠4，∵EN 平分∠DEP，AN 平分∠PAC， ∴∠3=12∠α，∠4=12∠β， ∴1()2ANE αβ∠=∠+∠，∴ANE ∠与α∠，β∠之间的数量关系为1()2ANE αβ∠=∠+∠．【点睛】本题主要考查了平行线的性质，解决问题的关键是过拐点作平行线，利用平行线的性质得出结论．23．（1）证明见解析；（2）45IGJ ∠=︒．【分析】（1）根据平行线的性质可得180DEF BFE ∠+∠=︒，再利用角平分线的定义即可得证；（2）过点G 作//GK AB ，则////AB GK CD ，根据平行线的性质可得DEG EGK ∠=∠，KGF GFB ∠=∠，再结合（1）的结论易得90EGK KGF ∠+∠=︒，利用角平分线的定义及垂线的定义即可求解．【详解】（1）证明：∵//AB CD ，∴180DEF BFE ∠+∠=︒．∵EG 平分DEF ∠，FG 平分BFE ∠，∴22DEF GEF DEG ∠=∠=∠，22BFE EFG GFB ∠=∠=∠，∴22180GEF EFG ∠+∠=︒，∴90EFG GEF ∠+∠=︒．（2）解：过点G 作//GK AB ．∵//AB CD ，∴////AB GK CD ，∴DEG EGK ∠=∠，KGF GFB ∠=∠．由（1）得90DEG GFB ∠+∠=︒，∴90EGK KGF ∠+∠=︒．∵GH AB ⊥，∴GH KG ⊥，即90KGH KGF HGF ∠=∠+∠=︒，∴EGK HGF ∠=∠．∵GJ 平分EGH ∠，∴EGJ HGJ ∠=∠．又KGJ EGJ EGK ∠=∠-∠，FGJ HGJ HGF ∠=∠-∠，∴KGJ FGJ ∠=∠，∴2KGF FGJ ∠=∠．∵GI 平分HGF ∠，∴2HGF FGI ∠=∠，∴2290FGJ FGI ∠+∠=︒，即45FGJ FGI ∠+∠=︒，∴45IGJ FGJ FGI ∠=∠+∠=︒．【点睛】本题考查平行线的性质、角平分线的定义等内容，掌握平行线的性质是解题的关键．24．（1）①∠BED =60º；②∠BED =12∠ABC +12∠ADC ；（2）∠BED =180º-12∠ABC +12∠ADC ，理由见解析．【分析】（1）①过点E 作EF ∥AB ，然后说明AB ∥CD ∥EF ，再运用平行线的性质、角平分线的性质和角的和差即可解答；②利用平行线的性质和角平分线的性质即可确定它们的关系．（2）过点E 作EF ∥AB ，再运用平行线的性质、角平分线的定义和角的和差即可确定它们的关系．【详解】（1）①如图1，过点E作EF∥AB．∵AB∥CD∴AB∥CD∥EF∴∠ABE=∠BEF，∠EDC=∠DEF．∵BE平分∠ABC，DE平分∠ADC，∴∠ABC=50º，∠ADC=70º∴∠ABE=12∠ABC=150252⨯=°°，∠EDC=12∠ADC=170352⨯︒=︒，∴∠BEF=25º，∠DEF=35º，∴∠BED=∠BEF+∠DEF=25º+35º=60º；②∵AB∥CD∴AB∥CD∥EF∴∠ABE=∠BEF=12∠ABC，∠EDC=∠DEF=12∠ADC；．∴∠BED=∠BEF +∠DEF =12∠ABC+12∠ADC∴∠BED=12∠ABC+12∠ADC（2）如图2，过点E作EF∥AB．∵AB∥CD∴AB∥CD∥EF∴∠EDC=∠DEF，∵∠ABE+∠BEF=180º，∴∠BEF=180º-∠ABE．∵BE平分∠ABC，DE平分∠ADC，∴∠ABE=12∠ABC，∠DEF=12∠ADC，∴∠BED=∠BEF+∠DEF=180º-12∠ABC+12∠ADC．【点睛】本题考查了平行线的判定与性质，添加辅助线构造平行线并灵活利用平行线的性质是解答本题的关键．25．（2）见解析；（2）BCF F B ∠=∠-∠，BCF B F ∠=∠-∠．【分析】（2）过点C 作CD ∥AB ，由平行线的性质，得到180B BCD ∠+∠=︒，180DCF F ∠+∠=︒，即可得到结论成立；（3）①过点C 作CD ∥AB ，由平行线的性质和（2）的证明方法，即可得到答案； ②过点C 作CD ∥AB ，由平行线的性质和（2）的证明方法，即可得到答案；【详解】()2证明:过点C 作//CD AB//AB EF (已知)//CD EF ∴(平行于同一条直线的两条直线互相平行)180,180B BCD DCF F ∴∠+∠=︒∠+∠=︒(两相线平行，同旁内角补)，∵BCF BCD DCF ∠=∠+∠，∴360B BCF F ∠+∠+∠=︒；（3）①过点C 作//CD AB ，如图：∵AB ∥CD ∥EF ，∴180,180B BCD DCF F ∠+∠=︒∠+∠=︒，∵BCD BCF DCF ∠=∠+∠，∴BCF F B ∠=∠-∠；故答案为：BCF F B ∠=∠-∠；②过点C 作//CD AB ，如图：∵AB ∥CD ∥EF ，∴180,180B BCD DCF F ∠+∠=︒∠+∠=︒，∵BCD BCF DCF ∠+∠=∠，∴BCF B F ∠=∠-∠．故答案为：BCF B F ∠=∠-∠．【点睛】本题考查了平行线的判定和性质，解题的关键是熟练掌握题意，以及掌握平行线的判定和性质进行证明．26．（1）45；（2）①详见解析；②302α︒+或602α︒-；【分析】（1）根据平行线性质可得180********BPD ∠=︒-︒-︒-︒=︒，再根据平行线性质得BOC BPD ∠=∠；（2）①根据平行线性质得160BOC ∠=∠=︒，2160∠=∠=︒，结合角平分线定义可证180DQE PDQ ∠+∠=︒，得PD QE ∥，根据平行线传递性可再证PD OC ∥； ②分两种情况分析：当Q 在H 的右侧时，根据平行线性质可得∠BPD=∠BOC=α，∠MQP=∠QPB=60°+α，根据角平分线性质∠MQE=12（60°+α），故∠PEQ=∠MQE ；当Q 在H 的右侧时，与上面同理，∠NQE=12（180°-60°-α），∠PEQ=∠NQE ．【详解】（1）由45NQD ∠=︒，MNAB ,可得180********BPD ∠=︒-︒-︒-︒=︒，而PD OC ∥，则有BOC BPD ∠=∠．故45BPD α=∠=︒ （2）∵QE OC ∥，60BOC α∠==︒，∴160BOC ∠=∠=︒，又∵MN AB ，∴2160∠=∠=︒，又∵QE 平分PQH ∠，∴3260∠=∠=︒，又∵430∠=︒，∴4390DQE ∠=∠+∠=︒，且90PDQ ∠=︒，∴180DQE PDQ ∠+∠=︒，∴PD QE ∥，∵QE OC ∥，∴PD OC ∥．②当Q 在H 的右侧时，∵PD ∥OC∴∠BPD=∠BOC=α∵MN ∥AB∴∠MQP=∠QPB=60°+α又∵QE 平分∠MQP∴∠MQE=12（60°+α）=30°+12α ∴∠PEQ=∠MQE=30°+12α 当Q 在H 的左侧时∵PD ∥OC∴∠BPD=∠BOC=α∵MN ∥AB∴∠NQP=180°-60°-α又∵QE 平分∠NQP∠NQE=12（180°-60°-α）=60°-12α ∴∠PEQ=∠NQE=60°-12α∴302PEQ α∠=︒+或602α︒-．【点睛】考核知识点：平移、平行线判定和性质综合运用．熟练运用平行线性质和判定，分类讨论问题是关键．27．（1）∠ADP+∠BCP=∠DPC，理由见解析；（2）∠ADP=∠DPC+∠BCP，理由见解析【分析】（1）过P作直线PQ∥AD，交CD于点Q，根据平行线的性质进行推理；（2）过P作直线PQ∥AD，交CD于点Q，根据平行线的性质进行推理；【详解】解：（1）过P作直线PQ∥AD，交CD于点Q，∵AD∥BC，∴PQ∥AD∥BC，∴∠ADP=∠DPQ，∠BCP=∠CPQ，∴∠ADP+∠BCP=∠DPC；（2）∠ADP=∠DPC+∠BCP.过P作直线PQ∥AD，交CD于点Q，∵AD∥BC，∴PQ∥AD∥BC，∴∠ADP=∠DPQ=∠DPC+∠CPQ，∠BCP=∠CPQ，∴∠ADP=∠DPC+∠BCP.【点睛】本题考查了平行线的性质，利用平行线的性质得出角的和差关系是解题的关键. 28．（1）∠AEC＝130°；（2）∠A1EC＝130°；（3）∠A1EC＝40°．【解析】【分析】(1)由直线PQ∥MN，∠ADC=∠QAD=30°，可得∠PAD=150°，再求∠PAE=75°，可得∠CAE=25°；由∠PAC=∠ACN，求得∠ECA=25°，故∠AEC=180°﹣25°﹣25°；(2)先求出∠QA1D1=30°，∠PA1D1=150°，再求出∠PA1E=∠EA1D1=75°，再求出∠CAQ=130°，∠ACN=50°，根据平分线定义得∠ACE=25°，再利用四边形内角和性质可求∠CEA1；(3)根据平行线性质和角平分线定义可求得∠QA1E=∠2=15°，∠ACE=∠ECN=∠1=25°，再由∠CEA1=∠1+∠2即可求得答案.【详解】(1)如图1所示：∵直线PQ∥MN，∠ADC＝30°，∴∠ADC＝∠QAD＝30°，∴∠PAD＝150°，∵∠PAC＝50°，AE平分∠PAD，∴∠PAE＝75°，∴∠CAE＝25°，可得∠PAC＝∠ACN＝50°，∵CE平分∠ACD，∴∠ECA＝25°，∴∠AEC＝180°﹣25°﹣25°＝130°；(2)如图2所示：∵∠A1D1C＝30°，线段AD沿MN向右平移到A1D1，PQ∥MN，∴∠QA1D1＝30°，∴∠PA1D1＝150°，∵A1E平分∠AA1D1，∴∠PA1E＝∠EA1D1＝75°，∵∠PAC＝50°，PQ∥MN，∴∠CAQ＝130°，∠ACN＝50°，∵CE平分∠ACD1，∴∠ACE＝25°，∴∠CEA1＝360°﹣25°﹣130°﹣75°＝130°；(3)如图3所示：过点E作FE∥PQ，∵∠A1D1C＝30°，线段AD沿MN向左平移到A1D1，PQ∥MN，∴∠QA1D1＝30°，∵A1E平分∠AA1D1，∴∠QA1E＝∠2＝15°，∵∠PAC＝50°，PQ∥MN，∴∠ACN＝50°，∵CE平分∠ACD1，∴∠ACE＝∠ECN＝∠1＝25°，∴∠CEA1＝∠1+∠2＝15°+25°＝40°．【点睛】本题考查了平行线性质，角平分线定义，熟练运用平行线性质和角平分线定义推出角的度数是解题的关键.。

七年级数学下册第五章《相交线与平行线》单元测试题-人教版(含答案)

七年级数学下册第五章《相交线与平行线》单元测试题-人教版（含答案）一、单选题1．在下图中，1∠和2∠是同位角的是（）A ．（1）、（2）B ．（1）、（3）C ．（2）、（3）D ．（2）、（4） 2．如图，直线AB 与CD 相交于点O ，75AOC ∠=︒，125∠=︒，则2∠的度数是（）A ．25°B ．30°C ．40°D ．50° 3．如图，直线1l 与2l 相交于点O ，1OM l ⊥，若4418α=︒'，则β的度数是（）A ．5542'︒B ．4542'︒C ．'4552︒D ．4642'︒ 4．如图，两条直线交于点O ，若1280∠+∠=︒，则3∠的度数为（）A ．40︒B ．80︒C ．100D ．140︒ 5．如图，,AB CD BC EF ∥∥．若158∠=︒，则2∠的大小为（）A ．120︒B ．122︒C ．132︒D ．148︒ 6．如图，直线a ∥b ，将三角尺直角顶点放在直线b 上，若∠1＝50°，则∠2的度数是（）A ．20°B ．30°C ．40°D ．50° 7．如图，将一副三角板按如图放置，则下列结论：∠13∠=∠；∠2180CAD ∠+∠=︒；∠如果235∠=︒，则有BC AD ∥；∠4275∠+∠=︒．其中正确的序号是（）A ．∠∠∠∠B ．∠∠∠C ．∠∠∠D ．∠∠∠ 8．如图，点E 在BC 的延长线上，下列条件中不能判定//AB CD 的是（）A ．3=4∠∠B ．12∠=∠C ．B DCE ∠=∠D ．13180D ∠+∠+∠=︒9．下列语句是命题的是（）A ．画出两个相等的角B ．所有的直角都相等吗C ．延长线段AB 到C ，使得BC BA =D ．两直线平行，内错角相等10．如图，下列条件中能判定AB CE ∥的是（）A ．∠B ＝∠ACE B ．∠B ＝∠ACBC ．∠A ＝∠ECD D ．∠A ＝∠ACE＝180°；∠∠7＝∠5．其中能够说明a ∥b 的条件为（）A ．∠∠B ．∠∠C ．∠∠D ．∠∠ 12．如图，直线AB ，CD 相交于点E ，EF AB ⊥于点E ，若20FEC AEC ∠-∠=︒，那么AED ∠的度数为（）A ．125°B ．135°C ．140°D ．145°二、填空题 13．已知如图，三条直线1l 、2l 、3l 交于一点，则∠1+∠2+∠3=_________．14．如图，要把池水引到C 处，可作CD AB ⊥于点D ，然后沿CD 开渠，可使所开渠道最短，依据是______．15．如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工，若干天后，公路准确接通，则乙地所修公路的走向是南偏西16．如图，AB CD ∥，若40A ∠=︒，26C ∠=︒，则∠E =______．17．如图，将∠ABE 向右平移2cm 得到∠DCF ，如果∠ABE 的周长是16cm ，那么四边形ABFD 的周长是_____．18．如图，在四边形ABCD 中．点E 为AB 延长线上一点，点F 为CD 延长线上一点，连接EF ，交BC 于点G ，交AD 于点H ，若12∠=∠，A C ∠=∠，求证：E F ∠=∠．证明：13∠=∠（），12∠=∠（已知）． ∠ = （等量代换）．∴AD BC ∥（）4180A ∴∠+∠=（）， A C ∠=∠（已知），4180C ∴∠+∠=（等量代换）． ∠ ∥ （同旁内角互补，两直线平行）．19．如图直线AD 与直线BC 相交于点O ，OE 平分AOB ∠，130∠=︒，则EOD ∠的度数为___________°．三、解答题20．如图，直线AB 、CD 相交于点O ，OE 平分∠BOD ，OF 平分∠COE ．(1)若∠AOC =76°，求∠BOF 的度数；(2)若∠BOF =36°，求∠AOC 的度数；21．如图，已知AD BC ⊥，EF BC ⊥，12∠=∠．(1)求证：EF AD ∥；(2)求证：180BAC AGD ∠+∠=︒．22．如图，直线AB 和CD 相交于O 点，OE CD ⊥，142EOF ∠=︒，13BOD BOF ∠∠=：：，求AOF ∠的度数.23．如图，两直线AB ，CD 相交于点O ，OE 平分∠BOD ，∠AOC ：∠AOD =7：11.(1)求∠COE 的度数；(2)若OF ∠OE ，求∠COF 的度数．24．如图，直线CD 、EF 交于点O ，OA ，OB 分别平分COE ∠和DOE ∠，已知1290∠+∠=︒，且2:32:5∠∠=．(1)求BOF ∠的度数；(2)试说明AB CD 的理由．参考答案1．B2．D解：由题可知75BOD AOC ∠=∠=︒，125∠=︒，217525BOD ∴∠=∠-∠=︒-︒=50︒．3．B解：由题意得90180αβ++︒=︒，∠180904542βα'=︒-︒-=︒，4．D解：12∠=∠，1280∠+∠=︒，140∴∠=︒，13180∠+∠=︒，31801140∴∠=︒-∠=︒．5．B解：设CD 与EF 交于G ，∠AB ∠CD∠∠1=∠C =58°∠BC ∠FE ，∠∠C +∠CGE =180°，∠∠CGE =180°-58°=122°，∠∠2=∠CGE =122°，6．C解：如图，由题意得：∠3=180°-90°-∠1=40°，∠a ∥b ，∠∠2=∠3＝40°，7．B解：∠1290CAB ∠=∠+∠=︒，3290EAD ∠=∠+∠=︒，∠13∠=∠，故∠正确；∠212329090180CAD ∠+∠=∠+∠+∠+∠=︒+︒=︒故∠正确；∠235∠=︒，∠3902903565∠=︒-∠=︒-︒=︒，1(18090)452B ∠=︒-︒=︒， ∠BC 与AD 不平行，故∠错误；∠43CBA EDA ∠+∠=∠+∠，即445330∠+︒=∠+︒，又∠2+3=90∠∠︒，∠44590230∠+︒=︒∠+︒-42=75∠+∠︒,故∠正确；综上，∠∠∠正确，8．A解：A 、∠3=4∠∠，∠//AD BC ，故选项A 不能判定//AB CD ，符合题意；B 、∠12∠=∠，∠//AB CD ，故选项B 能判定//AB CD ，不符合题意；C 、∠B DCE ∠=∠，∠//AB CD ，故选项C 能判定//AB CD ，不符合题意；D 、∠13180D ∠+∠+∠=︒，即180D DAB ∠+∠︒＝，∠//AB CD ，故选项D 能判定//AB CD ，不符合题意；9．D解：A 、画出两个相等的角，没有做错判断，不是命题；B 、所有的直角都相等吗，没有做错判断，不是命题；C 、延长线段AB 到C ，使得BC BA =，没有做错判断，不是命题；D 、两直线平行，内错角相等，是命题；10．DA ． ∠B ＝∠ACE ，不是同位角，内错角，不能判定AB CE ∥，不符合题意；B ． ∠B ＝∠ACB ，不是同位角，内错角，不能判定AB CE ∥，不符合题意；C ． ∠A ＝∠ECD ，不是同位角，内错角，不能判定AB CE ∥，不符合题意； D ． ∠A ＝∠ACE ，内错角相等，两直线平行，能判定AB CE ∥，符合题意；11．A∠∠∠1＝∠5，∠a ∥b ，故正确；∠∠∠5＝∠7，∠1＝∠7，∠∠1＝∠5，∠a ∥b ，故正确；∠∠2+∠3＝180°，∠2和∠3是邻补角，不能说明任何一组直线平行，故错误； ∠∠7＝∠5，∠7和∠5是对顶角，不能说明任何一组直线平行，故错误．12．D设AEC ∠为x ，则+20FEC x ∠=︒，∠EF AB ⊥，∠90AEF ∠=︒，∠90AEC FEC ∠+∠=︒，∠2090x x ++︒=︒，解得35x =︒，即35AEC ∠=︒，∠18035145AED ∠=︒-︒=︒．13．180°解：如图，14∠=∠，123423180∴∠+∠+∠=∠+∠+∠=︒．故答案为：180︒．14．垂线段最短15．48°先根据题意画出图形，利用平行线的性质解答即可．解：如图，∠AC∠BD ，∠1=48°，∠∠2=∠1=48°，根据方向角的概念可知，乙地所修公路的走向是南偏西48°．16．66︒解：如图所示，过点E 作EF AB ∥，∠EF AB AB CD ∥，∥，∠AB CD EF ∥∥，∠4026AEF A CEF C ==︒==︒∠∠，∠∠，∠66AEC AEF CEF =+=︒∠∠∠，故答案为：66︒．17．20cm解：∠∠ABE 向右平移2cm 得到∠DCF ，∠DF ＝AE ，∠四边形ABFD 的周长＝AB +BE +DF +AD +EF ，＝AB +BE +AE +AD +EF ，＝∠ABE 的周长+AD +EF ，∠平移距离为2cm ，∠AD ＝EF ＝2cm ，∠∠ABE 的周长是16cm ，∠四边形ABFD 的周长＝16+2+2＝20cm ．故答案为：20cm ．18．对顶角相等；23∠∠，；同位角相等，两直线平行；两直线平行，同旁内角互补；CF ，EA ；两直线平行，内错角相等．证明：13∠=∠（对顶角相等），12∠=∠（已知）， 23∴∠=∠（等量代换），∴AD BC ∥（同位角相等，两直线平行），4180A ∴∠+∠=（两直线平行，同旁内角互补）， A C ∠=∠（已知），4180C ∴∠+∠=（等量代换）， ∴CF EA ∥（同旁内角互补，两直线平行），E F ∴∠=∠（两直线平行，内错角相等）；故答案为：对顶角相等；23∠∠，；同位角相等，两直线平行；两直线平行，同旁内角互补；CF ，EA ；两直线平行，内错角相等．19．105解：∠130∠=︒，∠180118030150AOB ∠=︒-∠=︒-︒=︒，∠OE 平分AOB ∠， ∠111507522BOE AOB ∠=∠=⨯︒=︒， ∠2130∠=∠=︒，∠27530105EOD BOE ∠=∠+∠=︒+︒=︒故答案为：10520．(1)∠BOF =33°(2)∠AOC =72°（1）∠∠AOC 、∠BOD 是对顶角，∠∠BOD=∠AOC=76°，∠OE 平分∠BOD ， ∠∠DOE=∠BOE=12∠BOD=38°∠∠COE=142°，∠OF 平分∠COE ． ∠∠EOF=12∠COE=71°，又∠BOE+∠BOF=∠EOF ，∠∠BOF=∠EOF−∠BOE=71°−38°=33°，（2）∠OE 平分∠BOD ，OF 平分∠COE ，∠BOE EOD COF FOE ∠=∠∠=∠，，∠设BOE x ∠=，则EOD x ∠=，故2COA x ∠=，36EOF COF x ∠=∠=+︒，则23636180AOC COF BOF x x ∠+∠+∠=++︒+︒=︒，解得36x =︒，故∠AOC =72°．21．(1)见解析(2)见解析（1）证明：∠AD BC ⊥，EF BC ⊥， ∠90EFB ∠=︒，90ADB ∠=︒（垂直的定义）， ∠∠=∠EFB ADB （等量代换），∠EF AD ∥（同位角相等，两直线平行）；（2）证明：∠EF AD ∥，∠1BAD ∠=∠（两直线平行，同位角相等），又12∠=∠（已知），∠2BAD ∠=∠（等量代换），∠DG BA ∥（内错角相等，两直线平行）， ∠180BAC AGD ∠+∠=︒（两直线平行，同旁内角互补）． 22．102AOF ∠=︒解：∠OE CD ⊥，∠90EOD ∠=︒，∠142EOF ∠=︒，∠1429052DOF ∠=︒-︒=︒，∠13BOD BOF ∠∠=：：， ∠1262BOD DOF ∠=∠=︒， ∠78BOF BOD DOF ∠=∠+∠=︒，∠180AOF BOF ∠+∠=︒，∠180********AOF BOF ∠=︒-∠=︒-︒=︒． ∠102AOF ∠=︒．23．(1)145︒(2)125︒1）解：∠711180AOC AOD AOC AOD ∠∠=∠+∠=︒：：，， ∠∠AOC =71818070⨯︒=︒， ∠∠DOB =∠AOC =70°，又∠OE 平分∠BOD ，∠DOE ∠=12DOB ∠=127035⨯︒=︒，∠180********COE DOE ∠=︒-∠=︒-︒=︒，（2）∠OF OE ⊥，∠90EOF ∠=︒，∠90903555FOD DOE ∠=︒-∠=︒-︒=︒， ∠180********COF FOD ∠=︒-∠=︒-︒=︒． 24．(1)BOF ∠的度数为140︒(2)见解析（1）解：∠OA ，OB 分别平分COE ∠和DOE ∠， ∠12AOE AOC COE ∠=∠=∠，122BOE DOE ∠=∠=∠， ∠180COE DOE ∠+∠=°，∠290AOC ∠+∠=︒，∠3COE ∠=∠， ∠132AOC ∠=∠， ∠123902∠+∠=︒，∠2:32:5∠∠=， ∠5322∠=∠， ∠15229022∠+⨯∠=︒，∠240∠=︒，∠3100∠=︒，∠23140BOF ∠=∠+∠=︒；（2）解：1290∠+∠=︒，290AOC ∠+∠=︒， ∠1AOC ∠=∠，∠AB CD ．。

精编北师大版七年级数学下册第五章《生活中的轴对称》单元测试卷(5套试题)含答案

第五章《生活中的轴对称》单元测试卷1一、选择题1．下列说法中，不正确的是 ( )A．等腰三角形底边上的中线就是它的顶角平分线B．等腰三角形底边上的高就是底边的垂直平分线的一部分C．一条线段可看作以它的垂直平分线为对称轴的轴对称图形D．两个三角形能够重合，它们一定是轴对称的2．下列推理中，错误的是 ( )A．∵∠A＝∠B＝∠C，∴△ABC是等边三角形B．∵AB＝AC，且∠B＝∠C，∴△ABC是等边三角形C．∵∠A＝60°，∠B＝60°，∴△ABC是等边三角形D．∵AB＝AC，∠B＝60°，∴△ABC是等边三角形3．在等边三角形ABC中，CD是∠ACB的平分线，过D作DE∥BC交AC于E，若△ABC的边长为a，则△ADE的周长为 ( )4A．2a B．a3C．1．5a D．a4．等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是( )A．9cm B．12cmC．9cm和12cm D．在9cm与12cm之间5．观察图7—108中的汽车商标，其中是轴对称图形的个数为 ( )A.2B.3C.4D.56．对于下列命题：(1)关于某一直线成轴对称的两个三角形全等；(2)等腰三角形的对称轴是顶角的平分线；(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点；(4)如果两个三角形全等，那么它们关于某直线成轴对称．其中真命题的个数为 ( )A ．0B ．1C ．2D ．37．△ABC 中，AB ＝AC ，点D 与顶点A 在直线BC 同侧，且BD ＝AD ．则BD 与CD 的大小关系为 ( )A ．BD ＞CDB ．BD ＝CDC ．BD ＜CDD ．BD 与CD 大小关系无法确定8．下列图形中，不是轴对称图形的是 ( ) A ．互相垂直的两条直线构成的图形 B ．一条直线和直线外一点构成的图形C ．有一个内角为30°，另一个内角为120°的三角形D ．有一个内角为60°的三角形9．在等腰△ABC 中，AB ＝AC ，O 为不同于A 的一点，且OB ＝OC ，则直线AO 与底边BC 的关系为 ( )A ．平行B ．垂直且平分C ．斜交D ．垂直不平分10．三角形的三个顶点的外角平分线所在的直线两两相交，所围成的三角形一定是 ( )A ．锐角三角形B ．钝角三角形C ．等腰三角形D ．直角三角形二、填空题1．正五角星形共有_______条对称轴． 2．黑板上写着在正对着黑板的镜子里的像是__________.3．已知等腰三角形的腰长是底边长的34，一边长为11cm ，则它的周长为________. 4．(1)等腰三角形，(2)正方形，(3)正七边形，(4)平行四边形，(5)梯形，(6)菱形中，一定是轴对称图形的是_____________.5．如果一个图形沿某一条直线折叠后，直线两旁的部分能够_______，那么这个图形叫做轴对称图形，这条直线叫做___________.6．如图7—109，在△ACD中，AD＝BD＝BC，若∠C＝25°，则∠ADB＝________.7．已知：如图7—110，△ABC中，AB＝AC，BE∥AC，∠BDE＝100°，∠BAD＝70°，则∠E ＝_____________.8．如图7—111，在Rt△ABC中，B为直角，DE是AC的垂直平分线，E在BC上，∠BAE：∠BAC＝1：5，则∠C＝_________.9．如图7—112，∠BAC＝30°，AM是∠BAC的平分线，过M作ME∥BA交AC于E，作MD⊥BA，垂足为D，ME＝10cm，则MD＝_________.10．如图7—113，OE是∠AOB的平分线，BD⊥OA于D，AC⊥BO于C，则关于直线OE对称的三角形有________对．三、解答题1．如图7—114，∠XOY内有一点P，在射线OX上找出一点M，在射线OY上找出一点N，使PM＋MN＋NP最短．2．如图7—115，图中的图形是轴对称图形吗?如果是轴对称图形，请作出它们的对称轴．3．已知∠AOB＝30°，点P在OA上，且OP＝2，点P关于直线OB的对称点是Q，求PQ之长．4．如图7—116，在△ABC中，C为直角，∠A＝30°，CD⊥AB于D，若BD＝1，求AB之长．5．如图7—117，在△ABC中，C为直角，AB上的高CD及中线CE恰好把∠ACB三等分，若AB＝20，求△ABC的两锐角及AD、DE、EB各为多少?6．如图7—118，AD、BE分别是等边△ABC中BC、AC上的高．M、N分别在AD、BE的延长线上，∠CBM＝∠ACN．求证：AM＝BN．7．如图7—119，点G在CA的延长线上，AF＝AG，∠ADC＝∠GEC．求证：AD平分∠BAC．8．已知：如图7—120，等腰直角三角形ABC中，∠A＝90°，D为BC中点，E、F分别为AB、AC上的点，且满足EA＝CF．求证：DE＝DF．参考答案一、1．D 2．B 3．C 4．B 5．C 6．C 7．D 8．D 9．B 10．A 二、1．5 2．3．cm 3121或cm 41214．等腰三角形，正方形，正七边形，菱形5．互相重合，对称轴 6．80° 7．50° 8．40° 9．5cm 10．4 三、1．分别以直线Ox ，Oy 为对称轴，作P 点的对应点P '和P ''，连结P P '''交Ox 于M ，交Oy 于N 则PM ＋MN ＋NP 最短.如图所示.2．略 3．2 4．45．∠A＝60°，∠B＝30°，AD ＝5cm ，DE ＝5cm ，EB ＝10cm 6．先证△ENC≌△DMB（ASA ）， ∴ DM＝EN. 再加上AD ＝BE 即可.7．∵ AF＝AG ，∴ ∠G＝∠AFG.又∵ ∠ADC＝∠GEC，∴ AD∥GE.∴ ∠G＝∠CAD. ∴ ∠AFG＝∠BAD.∴ ∠CAD＝∠BAD. ∴ AD 平分∠BAC.8．连结AD.在△ADF 和△BDE 中，可证得： BD ＝AD ，BE ＝AF ，∠B＝∠D AF. ∴ △ADF≌△BDE.∴ DE＝DF.第五章《生活中的轴对称》单元测试卷2选择题（每题5分，共30分）1、下列图形中，不是轴对称图形的是（）A．等腰三角形 B.线段 C.钝角 D.直角三角形2、下列图案中，有且只有三条对称轴的是（）3、等腰三角形一腰上的高与底边所成的角等于（）A.顶角B.顶角的一半C.顶角的两倍D.底角的一半4、等腰三角形两边的长分别是2cm和5cm，则这个三角形的周长是( )A.9cmB.12cmC.9cm或12cmD.在9cm和12cm之间5、下列图案中，不能用折叠剪纸方法得到的是（）6、将写有字母F的纸条正对镜面，则镜中出现的会是（）二、填空题（每题5分，共25分）1、把一张纸对折，任意剪成一个形状，把它打开后所得到的图形关于这条折痕成______图形.2、我国传统木结构房屋，窗子常用各种图案装饰，如右图所示是一种常见的图案，这个图案有______条对称轴.3、前后两辆车，从前一辆的反光镜里看到后一辆车的车牌号是则后面这辆车的实际车牌号是___________.4、等腰三角形的三个内角与顶角相邻的一个外角之和是310°，则底角度数为________.5、如图，在△ABC 中，∠BAC=110°，PM 和QN 分别垂直平分AB 和AC ，则∠PAQ=_________. 三、画图题（每题5分，共10分）把下列各图补成以直线l 为对称轴的轴对称图形. 1、 2、四、解答题（第1题5分，第2、3、4题10分，共35分） 1、如图是由一个等腰三角形（AB=AC ）和一个圆（O 为圆心）所成的轴对称图形，则AO 与BC 有怎样的位置关系？试说明理由。

七年级数学下册《第五章分式》单元测试卷-附答案(浙教版)

七年级数学下册《第五章分式》单元测试卷-附答案(浙教版)一、单选题1．当x=-2时，下列各式哪个无意义（）A ．-1x x B ．224x - C ．2224x x -+ D ．24x x ++ 2．如果把分式32a bab+中的a 和b 都扩大两倍，则分式的值（） A ．变为原来的4倍 B ．变为原来的12C ．不变D ．变为原来的2倍3．计算 2310635x y y x -⋅ ，结果是（） A ．24x y -B ．24y x-C ．4yx- D ．215yx-4．计算12a a +的值是（） A ．3a B ．32aC ．22a D ．23a 5．下列方程中，是分式方程的个数是（）①113x += ，②341x =+ ，③2111x x -=+ ，④1223x x -+= ，⑤12x x π++= ． A ．1个B ．2个C ．3个D ．4个6．不论x 取何值，下列代数式的值不可能为0的是()A ．21x -B ．11x - C ．()21x -D ．11x x -+ 7．把分式2xyx y- 中x ，y 的值都扩大为原来的3倍，则分式的值（） A ．为原来的6倍B ．为原来的3倍C ．不变D ．为原来的9倍8．计算-a 2÷（ 2a b ）•（ 2b a）的结果是（）A ．1B ．3b a-C ．-3a b D ．-149．如果 4x y -= ，那么代数式222222x yx y x y +-- 的值是（）A ．-2B ．2C ．12D ．12-10．甲、乙两人做某种机械零件，已知甲做350个零件的时间是乙做240个零件所用时间的54倍，两人每天共做130个零件．七（1）班同学根据条件提出了不同的问题，设出相应的未知数x ，并列出如下方程，数学老师批阅后，发现一个不正确，这个不正确的方程一定是（）A ．35052404130x x =⨯- B ．35024054130x x⨯=⨯-C ．35024013054x x+= D ．35024013054x x+= 二、填空题11．化简： 22224ab a b ＝．12．23(2)x y y ⎛⎫-⋅- ⎪⎝⎭= 。

第五章一元函数的导数及其应用单元综合测试卷(原卷版)

第五章一元函数的导数及其应用单元综合测试卷第Ⅰ卷一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若函数()f x 在1x =处的导数为2，则()()011lim2x f x f x ∆→+∆-=∆ ( ) A ．2 B ．1 C ．12 D ．62．已知函数()()22cos f x t g x x ==，，则（）A ．()()0,2sin f x g x x ''==-B ．()()2,2sin f x t g x x =-''=C ．()()02sin f x g x x ''==，D ．()()2,2sin f x t g x x =''=3．2022年2月，第24届冬季奥林匹克运动会在北京隆重举行，中国代表团获得了9金4银2铜的优异成绩，彰显了我国体育强国的底蕴和综合国力.设某高山滑雪运动员在一次滑雪训练中滑行的路程l （单位：m ）与时间t （单位：s ）之间的关系为()2322l t t t =+，则当3s t =时，该运动员的滑雪速度为（） A ．7.5m /s B ．13.5m /s C ．16.5m /s D ．22.5m /s4．函数()f x 的定义域为开区间(),a b ，导函数()f x '在(),a b 内的图象如图所示，则函数()f x 在开区间(),a b 内有极小值点（）A ．1个B ．2个C ．3个D ．4个5．函数(=cos2ln y x x ⋅的图像可能是（） A ． B ．C ．D ．6．设定义在[)0,∞+上的函数()0f x ≠恒成立，其导函数为()f x '，若()()()()1ln 10f x x f x x '-++<，则（） A ．()()2130f f >>B ．()()2130f f <<C ．()()2310f f >>D ．()()2310f f <<7．给定函数()()1e x f x x =-，则下列结论不正确的是（）A ．函数()f x 有两个零点B ．函数()f x 在()1,+∞上单调递增C ．函数()f x 的最小值是1-D ．当1a =-或0a ≥时，方程()f x a =有1个解8．若120x x a <<≤都有211212ln ln x x x x x x -<-成立，则a 的最大值为（）A ．12 B ．1 C ．e D ．2e二、选择题：本题共4小题，每小题5分，共20分。

(完整版)第五章透镜及其应用单元测试题(含答案)

第五章透镜及其应用一、单选题1.学习了透镜知识后，小勇回家认真研究爷爷的老花镜，并得出以下结论，你认为他的这些结论中不妥当的是（）A．老花镜是一种凹透镜B．老花镜可以用来做放大镜C．老花镜能在阳光下点燃白纸D．爷爷是个远视眼2.如图所示，将凸透镜看作是眼睛的晶状体，光屏看作是眼睛的视网膜，烛焰看作是被眼睛观察的物体．拿一个远视眼镜给“眼睛”戴上，光屏上出现烛焰清晰的像，而拿走远视眼镜则烛焰的像变得模糊．在拿走远视眼镜后，为了能在光屏上重新得到清晰的像，下列操作可行的是（）A．将蜡烛靠近凸透镜B．将光屏靠近凸透镜C．将光屏远离凸透镜D．将光屏和蜡烛同时靠近凸透镜3.一支蜡烛位于焦距为10cm的凸透镜前，调节好透镜和光屏的位置后，光屏上呈现倒立、缩小的像，这支蜡烛可能距离透镜（）A． 10cmB． 15cmC． 20cmD． 25cm4.如图所示有四幅图，能说明远视眼的成因及矫正的是（）A．甲、丁B．乙、丙C．乙、丁D．甲、丙5.使用下列光学器材，使物体成正立、放大的虚像的是（）A．放大镜B．照相机C．幻灯机D．平面镜6.下列光学设备中，应用的原理与如图5所示的凸透镜成像规律相同的是（）A．幻灯机B．老花镜C．照相机D．放大镜7.下列透镜中，属于凹透镜的是（）A．B．C．D．二、填空题8.某些手表上有一个圆滑的透明凸起，通过它看日期会觉得很清楚，这是因为这个圆滑的凸起相当于一个________，我们看到的实际上是一个________（选填“放大”或“缩小”）的________（选填“实像”或“虚像）9.在“探究凸透镜成像规律”的实验中，当蜡烛、凸透镜和光屏位置如图所示时，恰能在光屏上成一个清晰的像，该像的性质为______ （包括倒立或正立、放大或缩小、虚像或实像），利用此原理可以制成 ______ ．10.如图是微型手电筒所用的小灯泡，小灯泡前端的A部分相当于 ______ ，对光有 ______ 作用．11.一般放大镜的放大倍数有限，要想看清楚动植物的细胞等非常小的物体，就要使用____________．这种仪器镜筒的两端各有一组透镜，每组透镜的作用都相当于一个____________透镜．12.小莉看不清黑板上的字，她向黑板靠近几步就看清了，说明她是______ 眼（选填“近视”或“远视”）．如果小莉仍坐在原位，为了使物体的像刚好落在小莉的视网膜上，她应该配戴适当度数的______ 透镜制作的眼镜来矫正视力，使远处物体在视网膜上成倒立、 ______ 的实像．13.有一种望远镜也是由两组______ 组成的，靠近眼睛的叫做______ ，靠近被观测物体的叫做______ ．物镜的作用是使远处的物体在焦点附近成 ______ （填“放大”或“缩小”）的 ______ （填“实像”或“虚像”），目镜的作用当于一个 ______ ，用来把这个像放大．由于像被拉近，靠近人眼，______ 较大，所以使我们看到远处物体的像大而清晰．14.有一种交通标志牌，由基板和背面涂有反射胶的玻璃微珠组成，结构如图．黑夜中，当汽车灯光射来时，光线经过玻璃微珠____________(填“反射”“折射”)后，在玻璃微珠背面发生____________(填“反射”或“折射”)，然后沿原路返回，这样司机就可以看清黑夜中的标志牌．这里的玻璃微珠对光线起____________作用(填“会聚”或“发散”)．三、实验题15.用如图所示装置模拟人眼成像情况，此时烛焰在光屏上成清晰的像.（1）实验时，应使烛焰和 ______ 的中心位于凸透镜的主光轴上．（2）图中物距u应满足 ______ ．（3）当蜡烛远离凸透镜时，烛焰的像将落在光屏的 ______ 方．（4）在第（3）小题的情况下，若用此实验模拟人眼的调节功能，重新在光屏上得到清晰的像，应该进行的操作是 ______ ．A．将光屏靠近凸透镜B．将光屏远离凸透镜C．换焦距更大的凸透镜D．换焦距更小的凸透镜．（5）在第（3）小题的情况下，若拿来一只眼镜放在蜡烛和凸透镜之间，且较靠近凸透镜，结果重新在光屏上得到清晰的像，这只眼镜是 ______ 透镜．16.小组同学在做“验证凸透镜成像规律”实验的过程中发现：当发光物体与光屏之间的距离L确定时，将凸透镜从发光物体处缓慢向光屏移动的过程中，有时能在光屏上成两次清晰的像，有时只能成一次清晰的像，有时不能在光屏上成像．为了研究产生这些现象的条件，该小组同学进行实验，并将每次实验中的相关数据及现象记录在表中．（1）分析比较实验序号1、2、3（或5、6、7）的第一次成像数据中像距v和物距u的变化关系及相关条件，可得出的结论： ______ ；（2）分析比较实验序号1（或2、或5、或6）的第一次和第二次成像数据中物距与像距的关系及相关条件，可得出的结论：同一凸透镜，当______ 一定，移动凸透镜能在光屏上成两次像时，______ ；（3）继续分析比较表格物屏距离L与凸透镜焦距f的数据及观察到的现象，可得出的结论：只要适当移动凸透镜，可以在光屏上得到一次放大的像和一次缩小的像．请你对他所得出的结论做出点评．17.小华在做探究凸透镜成像规律的实验时，将焦距为10cm的薄凸透镜固定在光具座上50cm刻度线处，将点燃的蜡烛放置在光具座上20cm刻度线处，移动光屏至65cm刻度线处，使烛焰在光屏上成清晰的像．如图所示．请结合此实验完成下列问题：（1）如图所示的实验现象能够说明 ______ 的成像特点．A．照相机 B．幻灯机 C．放大镜（2）保持透镜在50cm刻度线处不动，如果想在光屏上得到更大的清晰的像，应该进行的操作是______ ．A．将蜡烛左移，光屏左移 B．将蜡烛左移，光屏右移C．将蜡烛右移．光屏左移 D．将蜡烛右移．光屏右移（3）保持透镜在50cm刻度线处不动，若将点燃的蜡烛放在光具座上80cm刻度线处，将光屏放在光具座上透镜的左侧，通过移动光屏，在光屏上可呈现烛焰清晰 ______ 的像．A．倒立放大 B．倒立缩小 C．正立放大．四、计算题18.如图所示，物体AB经凸透镜折射后所成像为A′B′，已知AB的高为h1，物距u，像距v，试用h1、u、v表示像高h2．五、作图题19.在下图所示的光路图中，分别填入合适的透镜．20.如图，根据近视眼成因及矫正方法，在如图所示方框内画出矫正所需的透镜并完成光路图．21.我国古代的“千里眼”是富有想象力的神话，随着科学技术的飞速发展，天文望远镜已将神话变成现实．图中天文望远镜是由两个透镜组成的，请完成两条入射光线经过两个透镜的光路（其中F1是透镜L1的焦点，F2是透镜L2的焦点）．六、阅读理解题22.你了解实像和虚像吗？自从学习光现象以来，我们分别学习了实像和虚像，对于这两种像的区别与联系掌握起来却有点麻烦．实像是由实际光线会聚的，而且是倒立的，并且能用光屏承接；虚像是由实际光线的反向延长线会聚的，因此不能用光屏承接，并且都是正立的；无论是实像还是虚像都能用眼睛看到．请根据上述信息回答一下问题：（1）下列现象中，只能成虚像的是（）A．照相机照相 B．平面镜成像 C．凸透镜成像 D．小孔成像（2）透过放大镜可以看到物体被放大的虚像，关于放大镜的说法中正确的是（）A．透过放大镜总能看到物体被放大的虚像B．透过放大镜看到放大物体的虚像与物体在放大镜的两侧C．物体距离放大镜越近成的虚像就越小D．放大镜其实就是凹透镜（3）对实像和虚像的认识正确的是（）A．只有通过光的反射才可以成虚像B．只有通过光的折射才可以成虚像C．通过光的反射可以成实像和虚像D．通过光的折射可以成实像和虚像．23.请仔细阅读下文，按要求回答问题人类的眼睛人类的眼睛很像一架照相机，眼睛与照相机的不同之处是：人的眼睛是通过调节晶状体的弯曲程度，改变晶状体的焦距来获得清晰的像，如图所示；普通照相机是在物距确定的情况下通过改变像距使像变得清晰.由眼睛的调节作用所能看清楚的最远点，叫远点，正常眼的远点在极远处；眼睛所能看清楚的最近点，叫近点，正常眼的近点约距眼睛10cm.眼睛是人体的重要器官，长时间的用眼，如看书、看电视、计算机，都可以引起眼睛的疲劳，眼睛疲劳的常见症状是头疼脑胀、眼睛发干，看物体时间较长也不易感到疲劳的距离叫明视距离，正常眼的明视距离为25cm.如果眼睛长期使用不当就会造成眼睛缺陷，常见的有近视和远视，它们都需要配戴眼镜（透镜）来矫正视力.人们通常所说的眼镜度数φ和焦距f之间的关系可用下列公式表示：眼镜的度数（其中f用m作单位）（1）人的眼睛是通过改变晶状体的来获得清晰的像；普通照相机是在物距确定的情况下通过改变使像变得清晰.（2）小明是近视眼，则应配戴_______透镜。

大学计算机第五章单元测验

1单选(2分)关于计算机程序，下列叙述正确的是（）。

A.只有可执行程序（.exe）才能在计算机中运行。

B.计算机程序是用自然语言书写的关于问题求解的方法和步骤的描述。

C.计算机程序编程人员利用某种计算机程设计语言，根据用户业务需求来编写完成，从概念上讲，计算机程序有数据和代码两部分。

D.用高级程序设计语言书写的程序都可以直接在计算机中运行。

E.从本质上讲，计算机程序是在计算机中运行的指令序列。

正确答案： C、E2单选(2分)世界上第一个计算机高级程序设计语言是（）。

正确答案： D 你选对了3单选(2分)与计算机硬件系统紧密相关的程序设计语言是（）。

A.符号语言B.脚本语言C.汇编语言D.机器语言E.高级语言正确答案： D 你选对了4单选(2分)关于计算机软件开发，下列叙述正确的是（）。

A.软件开发就是编写程序。

B.软件开发中的生命周期和原型法不能混合使用。

C.软件开发包括几个典型的阶段，包括：需求分析，系统设计，系统实施，系统测试，运行和维护等。

D.软件开发完成后就可以一劳永逸的运行。

E.软件开发需遵循相应的方法，例如生命周期法和原型法等。

正确答案： C、E 你选对了5单选(2分)下面是一个将十进制正整数转换为2进制数的函数定义：void tobinary(int x){while (x>0) {printf("%1d",x%2);}}要实现函数的功能，则在空白处应该填写的程序语句是（）。

=x/2;=x/10;=x%2;=x%10;正确答案： A 你选对了6单选(2分)关于数据库管理系统（Data Base Management System，DBMS），下列说法正确的是（）。

A.用户程序对数据文件直接操作和数据库管理系统对文件进行管理效果一样。

B.在数据库应用系统中，用户程序可以直接对数据库进行添加、查询、修改和删除操作。

C.用户通过DBMS创建数据库，创建完成后，程序对数据的操作与DBMS无关。

人教版八年级物理第五章《透镜及其应用》单元测试题及答案

人教版八年级物理第五章《透镜及其应用》单元测试题及答案题号得分（满分：100分时间：60分钟）一、选择题（每小题3 分，共36 分）1.如图是用来他那就凸透镜成像规律的实验装置示意图（屏未画出），当蜡烛和透镜放在图示位置时，通过移动光屏，可以在光屏上得到与物体等大的像；若透镜位置不变，将蜡烛移到刻度为40cm 处，则（）A.移动光屏，可以在屏上得到倒立放大的像B.移动光屏，可以在屏上得到倒立缩小的像C.移动光屏，可以在屏上得到正立放大的像D.不论光屏移到什么位置，都不能在屏上得到蜡烛的像2.将一个凸透镜正对着太阳光，在凸透镜另一侧15cm 处的纸上出现一个最小、最亮的光斑，将一个物体放在该凸透镜主光轴上距光心20cm 处，则在凸透镜的另一侧光屏上会出现一个（）A.正立、放大的虚像B.正立、缩小的虚像C.倒立、放大的实像D.倒立、缩小的实像3.透镜在我们的生活、学习中应用广泛.下列说法正确的是（）A.阳光通过凸透镜可以点燃纸屑，这利用了凸透镜对光的会聚作用B.近视眼镜可利用凸透镜矫正C.照相时，被照者应站在镜头两倍焦距以内D.投影仪能使物体在屏幕上成正立、缩小的虚像4.如图所示，为小明用透镜观察字的情况，下列说法正确的是( )A.字到透镜的距离大于此透镜的焦距B.该透镜只能成放大的像C.该透镜可以用作近视眼镜D.该透镜可以用作照相机镜头5.凸透镜成像实验中，移动物体到某位置时，能在光屏上成清晰缩小的像，则下列能成立的是（）①如果将物体靠近凸透镜，仍要在光屏上得到清晰的像，光屏必须远离凸透镜，且光屏移动距离先大于后小于物体移动距离；②同时移动物体与光屏，且移动距离相同，有可能在光屏上成清晰缩小的像；③换用焦距较小的凸透镜后，仍要在光屏上得到清晰的像，如果只移动光屏，光屏必须靠近凸透镜；④保持物体和光屏位置不变，一定可以在光屏上的到另一个清晰的像.A.①③B.②④C.②③D.③④6.智能手机的出现和普及，极大的方便了人们的生活.下列有关智能手机的说法正确的是（）A.智能手机的摄像头相当于一个凹透镜B.给智能手机电池充电是将化学能转化为电能C.使用智能手机打电话是利用超声波来传递信息的D.使用智能手机上网是利用电磁波来传递信息的7.在做凸透镜成像实验时，将点燃的蜡烛沿着光具座，从凸透镜二倍焦距以外的某位置向焦点移动，在此过程中，像的大小及像距的变化情况是（）A.像和像距都逐渐变大B.像和像距都逐渐变小C.像逐渐变大，像距逐渐变小D.像逐渐变小，像距逐渐变大8.某凸透镜的焦距为10 厘米，若物理在光屏上所成的像离该透镜的距离大于30厘米，则物体离该透镜的距离可能为（）A.3 厘米B.13 厘米C.23 厘米D.33 厘米9.在“探究凸透镜成像规律”的实验中，所用凸透镜的焦距为15cm，当物体距离凸透镜40cm 时，在光屏上得到清晰的像是（）A.倒立、缩小的实像B.倒立、等大的实像C.倒立、放大的实像D.正立、放大的虚像10.如图所示，是王爷爷小孙女的照片，王爷爷用放大镜贴近照片所看到的像是（）C.11.小露同学在做探究凸透镜成像规律时，出现了如下图的情形，则凸透镜的焦距可能是（）A.3cmB.6cmC.9cmD.20cm12. 小明同学在做凸透镜成像规律的实验中，光屏上得到烛焰清晰的像，同组的小华不小心将手指尖触摸到凸透镜，这时光屏上（）A.出现手指的实像B.出现手指的影子C.烛焰的像变得不完整D.烛焰的像完整，但变暗二、填空题（每空2 分，共30 分）13.人的球好像照相机，晶状体和角膜共同作用相当于一个_______；小丽的眼睛成像情况如图所示，为矫正视力应当佩戴眼镜片为_________的眼镜（均选填“凸透镜”或“凹透镜”）14.如图所示，F和F'为凸透镜的焦点，P和P'到凸透镜的距离为二倍焦距。

人教版地理八年级下册第五章中国的地理差异单元测试(有答案)

第五章单元测试题.选择题（共25小题）2.下列山脉中属于我国地势第一级和第二级阶梯分界线的是（）A.昆仑山B.大兴安岭C.太行山脉D.长白山脉3.下列山脉位于我国地势第一、二级阶梯分界线上的是（）A.阿尔泰山脉B.祁连山脉C.太行山脉D.长白山脉4.下列山脉中，既位于我国第二、三级阶梯分界线，又是省级行政区大致界线的是（A.昆仑山B.太行山C.大兴安岭D.南岭5.构成我国地势第二和第三阶梯分界线的山脉由北向南依次是（）A.大兴安岭-雪峰山-太行山B.昆仑山-祁连山-横断山C.祁连山-六盘山-雪峰山D.大兴安岭-太行山-巫山-雪峰山6.我国地势第一、二级阶梯的分界线是下列哪一组山脉构成的（）A.大兴安岭-阴山-贺兰山-祁连山B.大兴安岭-阴山-贺兰山-巴颜喀拉山C.大兴安岭-太行山-巫山-云贵高原东南部D ,昆仑山----- 祁连山----- 横断山7.下列山脉中既是我国地势第二、三级阶梯的分界线，又是山西省和河北省分界线的是（A.大兴安岭B.太行山C.巫山D.雪峰山8.下列为我国地势第二、三级阶梯分界线的是（A.四川盆地B.横断山脉C.巫山D.长江中下游平原9.贵州省位于我国地势（）A.第一级阶梯B.第二级阶梯C.第三级阶梯D.第二、三级阶梯10.我国地势第二、三级阶梯的分界线是（）A.长白山-武夷山B.昆仑山-祁连山-横断山脉C.天山-阴山D.大兴安岭-太行山-巫山-雪峰山11.下列属于我国地势第一二级阶梯分界线的是（）B.横断山脉C.巫山12.下列各组出脉是我国第一级阶梯和第二级阶梯分界线的是（）A .大兴安岭太行山、巫山、雪峰山B.昆仑山、祁连山、横断山脉C.长白山、武夷山、台湾山脉D.天山、阿尔泰山、喜马拉雅山13.我国地势第二级阶梯和第三级阶梯的分界线上的山脉是（）A.阿尔泰山、祁连山、横断山B.昆仑山、祁连山、横断山C.大兴安岭、祁连山、横断山D .大兴安岭、太行山、巫山、雪峰山14.我国四大地理区域中具有得天独厚水运条件的是（）A .北方地区 B.南方地区 C.青藏地区 D.西北地区15.我国四大地理区域的地形对应不正确的是（）A.北方地区平原、高原B.南方地区平原、高原、丘陵、盆地C.西北地区山地、丘陵D .青藏地区高原、盆地16.关于我国四大地理区域叙述正确的是（）A .种植业区与非种植业区的界线大致与800毫米年等降水量线一致B.从干湿状况看，我国种植业区主要分布在湿润地区和半湿润地区C.我国的林业、畜牧业主要分布在西北地区D.南方地区主要种植水稻、棉花、苹果等17.北方地区和西北地区在自然地理方面具有共同的特征是（）A.都以干旱为主的自然环境特征B.都有丰富的能源矿产C.都以高原和盆地为主的地形类型D.都主要位于地势的第二级阶梯18.我国南方地区和北方地区的分界线是（）A.黑河一腾冲一线B.昆仑山一祁连山一横断山一线C.秦岭一淮河一线D .大兴安岭一太行山一巫山一雪峰山一线19.秦岭，是以下哪两条河流的分水岭（）A .珠江、黑龙江 B.长江、黄河C.辽河、渭河D.渭河、汉江20.读秦岭南北两侧①②两地图，判断下列说法正确的是（）A . 1月份②地比①地气温高的主要原因是②地纬度高B.②地受寒潮影响较小的原因是秦岭等山脉的阻挡作用C.②地农作物以小麦为主，①地农作物以水稻为主D.②地比①地降水多的原因是②地海拔较低21 .下列地理界线接近秦岭淮河一线的是（)A . 800 mm年降水量线B.中温带与暖温带的分界线C.干旱区与半干旱区的分界线D. 7月份0c等温线22.北方地区与南方地区划分的自然依据（）A.地形因素B.气候因素C.交通条件D.受夏季风影响23.南方地区和北方地区分界线的确定，主导因素是（）A.地形因素B.气候因素C.经济因素D.文化因素24.下列地理界线中，不属于我国四大地理区域分界线的是（）A .秦岭--淮河一线B. 400mm等降水量线C.我国地势一、二级阶梯的分界线D. 200mm等降水量线25.南方地区与北方地区的界限大体在（）A .大兴安岭、太行山、巫山、雪峰山一线B.秦岭-淮河一线C.昆仑山、祁连山、横断山一线D.大兴安岭、阴山、贺兰山、巴颜喀拉山、冈底斯山一线二.填空题（共10小题）26.《中国国家地理》杂志社特别策划了“三纵一横”四条寻访中国路线，即东线（A线）、中线（B线）、西线（C线）和北纬35。

六年级数学北师大版上册第5章《单元测试》01(含答案)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！北师大版六年级上单元测试第5单元班级________姓名________一、选择题1．要清楚地表示出亮亮1－13岁的身高变化情况，应选择（）。

A．条形统计图B．折线统计图C．扇形统计图D．以上三种都可以2．下面的信息资料中，适合用条形统计图表示的是（）。

A．工厂各车间的人数B．亮亮家7月份各项支出占总支出的百分比C．病人一天的体温变化情况D．明明这学期成绩的变化情况3．要表示某个学生一至六年级身高变化情况，采用（）比较适合。

A．条形统计图B．折线统计图C．扇形统计图D．以上三种统计图4．下面是红星果园各种果树栽种情况统计图。

根据图中提供的信息，下列说法中错误的是（）。

A．果园里苹果树最多B．果园里橘子树最少C．从统计图无法看出哪种果树最少D．桃树和梨树一样多5．如果要反映“新冠肺炎”全球确诊人数的变化情况，选用（）。

第五章单元测验 (§5.4-§5.5)

第五章单元测验（§5.4-§5.5）上海市文来中学秦婵一、填空题1. 同号两数相加，取________的符号，并把________相加。

异号两数相加，取________的加数的符号，并把较大的绝对值________较小的绝对值.2. 互为相反数的两数相加，和为________.3. 数轴上点A 、点B 分别表示数3.4与4.3-，那么点A 与点B 之间的距离为________.4. 如果一个加数是9，另一个加数比9的相反数大4，那么它们的和是________.5. 3175比8.5-大________. 6. 9.75-比________小1114. 7. 9-，7，13-三个数的和比这三个数的绝对值的和________（填“大”或“小”）________.8. 下面各式的空格中填入适当的数，使等式成立.（1）18_____8--=-；（2）34(5)_____277-+-+=. 9. 如果某一时间上海气温为15+℃，哈尔滨气温为5-℃，那么哈尔滨气温比上海气温低________℃，哈尔滨气温升高________℃才能和上海气温相同.10.如果4a =，6b =，则a b +=________.二、选择题11．两个有理数的和是正数，那么这两个数（）.()A 都是正数 ()B 都是负数()C 至少有一个正数 ()D 至少有一个负数12．如果0b <，那么在下列各数中，最大的是（）.()A a - ()B a b -- ()C a b -+ ()D a b --三、简答题13．计算：（1）21112(1)(2).3246---+-（2）1311(2)5.4444--+---14．根据条件列式计算：（1）758-减去什么数所得的差是5.875。

（2）什么数加上113-与2-的差所得的和是9.四、解答题15．一辆旅行巴士载着游客在某南北方向的观光隧道里行驶，从隧道口出发向北行驶了880米，然后向南行驶1300米，再向北行驶5300米，最后又向南行驶了2500米。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

选修五《进入合成有机高分子化合物的时代》单元测验本试卷分选择题和非选择题两部分，共4页，满分100分，考试用时60分钟。

常用相对原子质量：H:1 C:12 N:14 O:16 Na:23 Cl:35.5
出题人：广东实验中学程俊
第一卷（48分）
一、选择题（每题4分，共48分。

1~8每题只有一个选项，9~12每题有1~2个选项，）
1.下列物质中属于合成纤维的是( )
A.人造丝
B.蚕丝
C.腈纶
D.羊毛绒
2.下列高分子在空气中燃烧只生成CO2和H2O的是( )
A.白明胶(动物胶)
B.粘胶纤维
C.氯丁橡胶
D.毛发
3.新科技革命三大支柱通常是指( )
①能源②交通③通讯④材料⑤信息
A.①②③
B.①③⑤
C.②③⑤
D.①④⑤
4.下列高分子材料属于功能高分子材料的是( )
①玻璃钢②高分子分离膜③丁苯橡胶④硅聚合物⑤聚氨脂⑥酚醛树脂⑦聚甲基丙烯酸甲酯
A.①②⑤
B.②③⑦
C.②④⑥
D.②④⑤
5.“不粘锅”饮具是在金属锅的内壁上涂一薄层聚四氟乙烯制成，下列各项对聚四氟乙烯的叙述中正确的是( )
A.在聚四氟乙烯的单体中不含有碳碳双键
B.聚四氟乙烯在高温时容易燃烧
C.聚四氟乙烯的化学性质很稳定，正常使用时不会发生化学变化
D.聚四氟乙烯的分子内支链很多，且彼此缠绕，不会污染食物
6.下述对乙烯和聚乙烯的描述不正确的是( )
A.乙烯性质比聚乙烯活泼
B.乙烯是纯净物，常温下为气态，聚乙烯为固态，是混合物
C.取等物质的量的乙烯和聚乙烯，完全燃烧一生成的CO2和H2O的物质的量分别相等
D.取等质量乙烯和聚乙烯，完全燃烧后，生成的CO2和H2O的质量分别相等
7.下列叙述正确的是( )
A.单体的质量之和等于所生成高聚物的质量
B.单体为一种物质时，则单体发生加聚反应
C.缩聚反应的单体至少有两种物质
D.淀粉和纤维素的链节都是C6H10O5，但聚合度不同，彼此不是同分异构体
8.某种具有较好耐热性、耐水性和高频电绝缘性的高分子化合物的结构片断为：
则生成该树脂的单体的种数和化学反应所属类型正确的是( )
A.1种，加聚反应
B.2种，缩聚反应
C.3种，加聚反应
D.3种，缩聚反应
9.硅橡胶是由二甲基二氯硅烷()经两种反应而制得的，这两种反应依次是( )
A.消去、加聚
B.水解、缩聚
C.氧化、缩聚
D.取代、缩聚
10.做为单体，能在一定条件下发生加聚反应生成的是( )
A.氯乙烯
B.氯乙烯和乙烯
11.下列高聚物必须是由两种单体缩聚而成的是( )
12.现已为婴儿特制成了一种新型的尿布——“尿不湿”。

这种尿布表面涂有一种既能吸水又能保留水的物质。

依你的推测，这种特殊物质的结构可能是( )
第二卷（52分）
二、填空题（7分）
13．(7分)为了保护人类的生存环境，人们开始着手利用废弃塑料，使它成为有用的资源：
(1)_____________ (2) _____________ (3) _____________
科学家展望，21世纪的高分子化学，要制造出对环境友好的高分子，包括在环境中可降解的塑料。

例如，以_____________和_____________为原料制成聚乙烯光降解塑料；以_____________和_____________为原料制成微生物降解塑料等。

三、实验题（10分）
14．（10分）如下图是实验室制取酚醛树脂的装置图。

(1)装置中的一处错误是_______________________________。

(2)试管上方长玻璃管的作用是_______________________________。

(3)浓盐酸在该反应中的作用是_______________________________。

(4)此反应需水浴加热，不用温度计控制水浴温度的原因是______________________。

(5)生成的酚醛树脂为_______色_______态。

(6)实验完毕后，若试管用水不易洗涤，可以加入少量_______浸泡几分钟，然后洗净。

(7)（3分）写出实验室制取酚醛树脂的化学方程式______________________________
____________________________________，此有机反应类型是_____________________。

四、推断题
15．（7分）聚苯乙烯的结构为，试回答下列问题：
（1）（4分）聚苯乙烯的联结是_________________，单体是___________________；
（2）（1分）实验测得聚苯乙烯的相对分子质量（平均值）为52000，则该高聚物的聚合度n为________________。

（3）（2分）已知聚苯乙烯为线性结构的高分子化合物，试推测：_________（“能”与“不能”）溶于CHCl3，具有__________（填“热塑”或“热固”）性。

16.（6分）写出下列化合物作为单体聚合生成的高分子化合物的结构简式：
(1)聚合得___________________________(此聚合物用作合成橡胶)。

(2)已知在虚线处开环聚合得CH2CH2O n(此聚合物用作表面活性剂，)则
开环聚合得_______________________________(此聚合物用作合成纤维)。

17.(12分)已知涤纶树脂的结构简式为：
(1)（4分）写出合成涤纶树脂所需要单体的结构简式：
________________________________和__________________________________
(2)（8分）写出以对二甲苯、乙烯、食盐、氧化剂和水为原料，制备这两种单体的各步反应的化学方程式。

18．.(10分)已知-NH2连在苯环上显碱性，连在苯环上显中性，化学式为C7H7NO2的有机物中其分子结构中有一个苯环，两个侧链(间位)，符合下列条件的结构简式为：
(A)既有酸性又有碱性__________________________；
(B)只有酸性_____________________________；
(C)只有碱性_____________________________；
(D)显中性______________________________。

由于-COOH能跟-NH2形成，所以可用乙二醇、对苯二甲酸跟上述既显酸性
又显碱性的物质发生反应，生成高分子化合物［(C17H13NO5)n］。

该化合物为高强度纤维材料，其结构简式为
___________________________________。

参考答案：
13.(1)直接用作材料(2)热解成单体(3)制成燃油和燃气乙烯CO 纤维素淀粉14．(1)试管底部不应与烧杯底部接触；(2)冷凝回流作用；(3)催化剂；(4)因反应条件为沸水浴；(5)粉红；粘稠；(6)乙醇
15．（1）；。

（2）500。

（3）能；热塑。

16．
17．
18．。