华东师大初中数学九年级上册《23.3.3 相似三角形的性质(第1课时)课件
合集下载
华师大九年级数学上23.3.1《相似三角形》课件(共12张PPT)

巩固练习
1 3
答案:1.△OAB∽△OBC∽△OCD∽△ODA∽ △BAC∽△ABD∽△CBD. 2.90 1 .
3ቤተ መጻሕፍቲ ባይዱ
归纳小结
1.书写相似三角形时,通常把对应顶点写在对应位置上, 以便比较容易找到相似三角形中的对应角、对应边。 2.相似比有顺序性。 3.相似三角形中,对应角所对的边是对应边,对应边 所对的角是对应角。 4.最大(小)的边(角)与最大(小)的边(角)是 对应边(角)。
谢谢观赏
You made my day!
我们,还在路上……
第23章 图形的相似
23.3.1 相似三角形
驶向胜利 的彼岸
复习导入
什么是相似图形?识别两个多边形 是否相似的标准是什么?
探索新知
相似三角形与全等三角形的关系
全等三角形是相似三角形的特例;但 相似三角形不一定是全等三角形,只有 当相似比k=1时,两个相似三角形才是 全等三角形。
例1 如图,在△ABC中,D为AB 上的任一点,作DE∥BC,交边 AC于点E,试判断:△ADE与 △ABC是否相似。
发现每一个新的群体在形式上都 是数学的,因为我们不可能有其 他的指导。
——C·G·达尔文。
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月28日星期一2022/2/282022/2/282022/2/28 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/282022/2/282022/2/282/28/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/282022/2/28February 28, 2022 •4、享受阅读快乐,提高生活质量。2022/2/282022/2/282022/2/282022/2/28
九年级数学上册23.3.3相似三角形的性质教学课件新版华东师大版
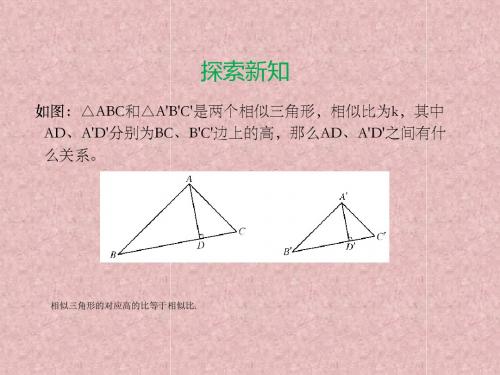
探索新知
如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中 AD、A'D',那么AD、A'D'之间有什 么关系。
相似三角形的对应高的比等于相似比.
证明:∵AD⊥BC,A'D'⊥B'C' ∴∠ABD=∠A'B'D',且∠B=∠B' ∴△ABD∽△A'B'D' AD AB k ∴ A D AB
课后作业
2.若将上图中的高改为中线、角分线,那么 它们对应中线的比,对应角平分线的比等于 多少?
结论:相似三角形对应中线的比等于相似比. 结论:相似三角形对应角的角平分线的比等于相似比.
3.相似三角形的周长比等于相似比.
4.相似三角形的面积比等于相似比的平方.
归纳小结
利用相似三角形的性质解题时,应特别注意 “对应”,切忌混淆对应边的比与相似比中的 前后项的位置。
如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中 AD、A'D',那么AD、A'D'之间有什 么关系。
相似三角形的对应高的比等于相似比.
证明:∵AD⊥BC,A'D'⊥B'C' ∴∠ABD=∠A'B'D',且∠B=∠B' ∴△ABD∽△A'B'D' AD AB k ∴ A D AB
课后作业
2.若将上图中的高改为中线、角分线,那么 它们对应中线的比,对应角平分线的比等于 多少?
结论:相似三角形对应中线的比等于相似比. 结论:相似三角形对应角的角平分线的比等于相似比.
3.相似三角形的周长比等于相似比.
4.相似三角形的面积比等于相似比的平方.
归纳小结
利用相似三角形的性质解题时,应特别注意 “对应”,切忌混淆对应边的比与相似比中的 前后项的位置。
九年级数学上3.3.3相似三角形的性质教学课件(新版)华东师大

•最新精品中小学课件
九年级数学上册· 华师
第23章 图形的相似
23.3.3 相似三角形的性质
•最新精品中小学课件
ห้องสมุดไป่ตู้
•1
23.3.3 相似三角形的性质
复习导入
1.相似三角形的判定方法有 哪些? 2.相似三角形有哪些性质? 3.三角形中的主要线段有哪 些?
•最新精品中小学课件
•2
探索新知
如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中 AD、A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什 么关系。
课后作业
•最新精品中小学课件
•8
谢谢!
墨子,( 约前468~前376) 名翟,鲁人 ,一说 宋人, 战国初 期思想 家,政 治家, 教育家 ,先秦 堵子散 文代表 作家。 曾为宋 国大夫 。早年 接受儒 家教育 ,后聚 徒讲学 ,创立 与儒家 相对立 的墨家 学派。 主张•兼 爱”“ 非攻“ 尚贤” “节用 ”,反 映了小 生产者 反对兼 并战争 ,要求 改善经 济地位 和社会 地位的 愿望, 他的认 识观点 是唯物 的。但 他一方 面批判 唯心的 宿命论 ,一方 面又提 出同样 是唯心 的“天 志”说 ,认为 天有意 志,并 且相信 鬼神。 墨于的 学说在 当时影 响很大 ,与儒 家并称 为 •显 学”。 《墨子》是先秦墨家著作,现存五 十三篇 ,其中 有墨子 自作的 ,有弟 子所记 的墨子 讲学辞 和语录 ,其中 也有后 期墨家 的作品 。《墨 子》是 我国论 辩性散 文的源 头,运 用譬喻 ,类比 、举例 ,推论 的论辩 方法进 行论政 ,逻辑 严密, 说理清 楚。语 言质朴 无华, 多用口 语,在 先秦堵 子散文 中占有 重要的 地位。 公输,名盘,也作•“般”或•“班 ”又称 鲁班, 山东人 ,是我 国古代 传说中 的能工 巧匠。 现在, 鲁班被 人们尊 称为建 筑业的 鼻祖, 其实这 远远不 够.鲁 班不光 在建筑 业,而 且在其 他领域 也颇有 建树。 他发明 了飞鸢 ,是人 类征服 太空的 第一人 ,他发 明了云 梯 ( 重武 器) ,钩 钜( 现 在还用) 以及其 他攻城 武器, 是一位 伟大的 军事科 学家, 在机械 方面, 很早被 人称为 “机械 圣人” ,此外 还有许 多民用 、工艺 等方面 的成就 。鲁班 对人类 的贡献 可以说 是前无 古人, 后无来 者,是 我国当 之无愧 的科技 发明之 父。
(新)华东师大版九年级数学上册 23.3《相似三角形》课件(极品)

1、已知:如图,分别写出各组相似三角形的对应边比例式
AD AE DE (1)如图1,DE//BC.则_______________________________ AB AC BC
AD AE DE (2)如图2,DE//BC.则_______________________________ AB AC BC AB AC BC AE AD ED (3)如图3,∠ABC=∠AED.则_____________________________
(4) 、相似的两个三角形一定大小不等。
√
×
试一试身手
3、填 一填 : ① 、如果两个三角形的相似比为1,那么这两个三角 全等 形_____ ② 、若△ABC ∽△A′B′C′,一组对应边的长AB=3 cm,A′B′=4 cm,那么△A′B′C′与△ABC的相似比 4 是____ 3 ③ 、若△ABC的三条边长为3cm、5cm、6cm,与其相似 的另一个△A′B′C′的最小边长为12 cm,那么△ 24cm A′B′C′的最大边长是___ ④ 、已知△ABC的三条3cm,4cm,5cm,△ABC∽△A1B1C1, 那么△A1B1C1的形状是直角三角形 ______,又知△A1B1C1的最大边 长为25cm,那么△A1B1C1的面积为 150cm ____ 2
华东师大版《数学 ·九年级(上)》
第23章
图形的相似
§23.3 相似三角形
第一课时 相似三角形的概念
学习目标 1.了解两个三角形相似的概念,能熟练地找出相似三角 形的对应角和对应边。 2.掌握相似的符号和“相似比”的意义。 3.探究并证明:平行于三角形一边的直线,和其他两边 (或两边的延长线)相交所构成的三角形与原三角形相 似。能灵活应用此结论解题。 学习重点 “相似比”的意义,对应边、对应角的确定 学习难点 平行于三角形一边的直线,和其他两边(或两边的延 长线)相交所构成的三角形与原三角形相似的理解及 灵活运用。
AD AE DE (1)如图1,DE//BC.则_______________________________ AB AC BC
AD AE DE (2)如图2,DE//BC.则_______________________________ AB AC BC AB AC BC AE AD ED (3)如图3,∠ABC=∠AED.则_____________________________
(4) 、相似的两个三角形一定大小不等。
√
×
试一试身手
3、填 一填 : ① 、如果两个三角形的相似比为1,那么这两个三角 全等 形_____ ② 、若△ABC ∽△A′B′C′,一组对应边的长AB=3 cm,A′B′=4 cm,那么△A′B′C′与△ABC的相似比 4 是____ 3 ③ 、若△ABC的三条边长为3cm、5cm、6cm,与其相似 的另一个△A′B′C′的最小边长为12 cm,那么△ 24cm A′B′C′的最大边长是___ ④ 、已知△ABC的三条3cm,4cm,5cm,△ABC∽△A1B1C1, 那么△A1B1C1的形状是直角三角形 ______,又知△A1B1C1的最大边 长为25cm,那么△A1B1C1的面积为 150cm ____ 2
华东师大版《数学 ·九年级(上)》
第23章
图形的相似
§23.3 相似三角形
第一课时 相似三角形的概念
学习目标 1.了解两个三角形相似的概念,能熟练地找出相似三角 形的对应角和对应边。 2.掌握相似的符号和“相似比”的意义。 3.探究并证明:平行于三角形一边的直线,和其他两边 (或两边的延长线)相交所构成的三角形与原三角形相 似。能灵活应用此结论解题。 学习重点 “相似比”的意义,对应边、对应角的确定 学习难点 平行于三角形一边的直线,和其他两边(或两边的延 长线)相交所构成的三角形与原三角形相似的理解及 灵活运用。
23.相似三角形的判定第1课时PPT课件(华师大版)

(1) 证明:∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC.
(2) 解:∵△ACD∽△ABC, ∴AC=AD,即 4 =3, AB AC AB 4 ∴A B =16. 3
第23章 图形的类似
4.如图,在△ABC中,∠C=90°,DE⊥AB于点E,DF⊥BC于点F. 求证:△DEH∽△BCA.
第23章 图形的类似
两角判定两个三角形类似
| 23.3.2 类似三角形的判定 第1课时 |
华师版(2012)九年级上册数学
回顾知识
类似多边形
第23章 图形的类似
性质
对应边成比例,对应角相等,类似比等于对应 边的比)
当类似比等于 1 时,类似图形即是全等图形, 全等是一种特殊的类似
定义
平行于三角形一边的直线与其他两边(或两边的 延长线)相交,所构成的三角形与原三角形类似
第23章 图形的类似
2.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角 分别为60° ,80 ,则这两个三角形( C )
A.一定不类似
B.不一定类似
C.一定类似
D.全等
第23章 图形的类似
3.如图,在△ABC中,若D是AB上的一点,且∠ACD=∠B. 求证:△ACD∽△ABC; 若AD=3,AC=4,求AB的长.
.
新知探究
活动一 1.视察学生与老师的直角三角板(30° 与 60°),会类似吗?测量 测量,得出你的猜想.
第23章 图形的类似
活动一 2.两个人画出两个三角形 ,使三个角分别为60°,45°,75° . ①分别量出两个三角形三边的长度; ②这两个三角形类似吗?
第23章 图形的类似
活动二 2.与同伴合作,一人画 △ABC,另一人画 △A′B′C′,使∠A =∠A′,
∴△ACD∽△ABC.
(2) 解:∵△ACD∽△ABC, ∴AC=AD,即 4 =3, AB AC AB 4 ∴A B =16. 3
第23章 图形的类似
4.如图,在△ABC中,∠C=90°,DE⊥AB于点E,DF⊥BC于点F. 求证:△DEH∽△BCA.
第23章 图形的类似
两角判定两个三角形类似
| 23.3.2 类似三角形的判定 第1课时 |
华师版(2012)九年级上册数学
回顾知识
类似多边形
第23章 图形的类似
性质
对应边成比例,对应角相等,类似比等于对应 边的比)
当类似比等于 1 时,类似图形即是全等图形, 全等是一种特殊的类似
定义
平行于三角形一边的直线与其他两边(或两边的 延长线)相交,所构成的三角形与原三角形类似
第23章 图形的类似
2.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角 分别为60° ,80 ,则这两个三角形( C )
A.一定不类似
B.不一定类似
C.一定类似
D.全等
第23章 图形的类似
3.如图,在△ABC中,若D是AB上的一点,且∠ACD=∠B. 求证:△ACD∽△ABC; 若AD=3,AC=4,求AB的长.
.
新知探究
活动一 1.视察学生与老师的直角三角板(30° 与 60°),会类似吗?测量 测量,得出你的猜想.
第23章 图形的类似
活动一 2.两个人画出两个三角形 ,使三个角分别为60°,45°,75° . ①分别量出两个三角形三边的长度; ②这两个三角形类似吗?
第23章 图形的类似
活动二 2.与同伴合作,一人画 △ABC,另一人画 △A′B′C′,使∠A =∠A′,
华东师大版九年级数学上册23.3 《相似三角形的应用》(共20张PPT)

You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
给你,一把皮尺,一 面平面镜.你能利 用所学知识来测
出塔高吗?
B
皮尺
平面镜
D
┐
┐
C
A
E
给你一条1米高 的木杆,一把皮尺. 你能利用所学知 识来测出塔高吗?
1 2
D
D
E
A
C
(1)
B
E
C
(2)
小小旅行家
胡夫金字塔是埃及现存规模最大的金字塔,被喻为 “世界古代七大奇观之一”.塔的4个斜面正对东南西北 四个方向,塔基呈正方形,每边长约230多米.据考证, 为建成大金字塔,共动用了10万人花了20年时间.原高 146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀. 所以高度有所降低 .
O
A A′
O′
B′C
B
如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木 棒O′B′,比较棒子的影长A′B′与金字塔影长AB,即可近似算出金 字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔 的高度OB.
解: ∵太阳光是平行光线, ∴ ∠OAB=∠O′A′B′.
又∵ ∠ABO=∠A′B′O′=90°.
(1)当t=3秒时,求S的值. (2)当t=5秒时,求S的值.
A
D
P
B l
G
C
Q
E
R
∴ △OAB∽△O′A′B′,
OB∶O′B′=AB∶A′B′,
OB= AB OB27411(3米7)
AB
2
答:该金字塔高为137米.
给你,一把皮尺,一 面平面镜.你能利 用所学知识来测
出塔高吗?
B
皮尺
平面镜
D
┐
┐
C
A
E
给你一条1米高 的木杆,一把皮尺. 你能利用所学知 识来测出塔高吗?
1 2
D
D
E
A
C
(1)
B
E
C
(2)
小小旅行家
胡夫金字塔是埃及现存规模最大的金字塔,被喻为 “世界古代七大奇观之一”.塔的4个斜面正对东南西北 四个方向,塔基呈正方形,每边长约230多米.据考证, 为建成大金字塔,共动用了10万人花了20年时间.原高 146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀. 所以高度有所降低 .
O
A A′
O′
B′C
B
如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木 棒O′B′,比较棒子的影长A′B′与金字塔影长AB,即可近似算出金 字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔 的高度OB.
解: ∵太阳光是平行光线, ∴ ∠OAB=∠O′A′B′.
又∵ ∠ABO=∠A′B′O′=90°.
(1)当t=3秒时,求S的值. (2)当t=5秒时,求S的值.
A
D
P
B l
G
C
Q
E
R
∴ △OAB∽△O′A′B′,
OB∶O′B′=AB∶A′B′,
OB= AB OB27411(3米7)
AB
2
答:该金字塔高为137米.
九级数学上册 23.3.3 相似三角形的性质课件 华东师大版精品

别是△ABC、△ A´B´C´ 对应边BC、B´C´上的高,求证:
S ABC k 2
S ABC
A
证明:∵△ABC∽△ A´B´C´
B
∴ ADk, BCk
AD BC
A' DC源自∴ SABC 1 AD•BC 2
B' k2
SABC 1 AD•BC
D'
C'
2
结论:相似三角形面积的比等于相似比的平方.
•最新中小学课件
第23章 图形的相似
3.相似三角形的性质
•最新中小学课件
•1
复习回顾
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形, 叫做相似三角形.
(2)如何判定两个三角形相似?
①平行得相似; ②两个角对应相等; ③两边对应成比例, 夹角相等; ④三边对应成比例.
•最新中小学课件
•2
(3)相似三角形有何性质? A´
∴
AB △BCCAk
AB BC CA
∴ ABBC CAk
ABBCCA
即△ABC、△AB的C周长比等于相似比
结论:相似三角形对应角的周长
的比等于相似比.
•最新中小学课件
•10
问题5:两个相似三角形的面积与 相似比之间有什么关系呢?
•最新中小学课件
•11
已知△ABC∽△A´B´C´,且相似比为k,AD、A´D´分
•5
问题 1:如图 ,ABC∽ ABC,相似比k为 ,
其中AD、AD分别为 BC、BC边上的, 高
由ABD∽ABD能否得A到D等于什?么
AD
因为ABD∽ ABD,
图18.3.9
所以 AD AB (相似三角形的对应边成比例)
华师大版数学九上23.3.3《相似三角形的性质》ppt课件

∴ SADE 9 ∴ SADE 36cm2 100 25
∴ S四边形BCDE SABC SADE 100 36 64cm2
2020/10/1
练习: 1、 已知:△ ABC∽△ A' B'C',它们的周长分别
为144cm和120cm ,且BC=48cm,
A' B' 30cm。
求:AB、AC、B 'C'、A'C'的长
3.7 相似三角形的性质
2020/10/1
复习 定理 例题 小结
2020/10/1
填空:
两个相似三角形的_对__应__角__相等,_对__应__边__成比例。
__相__似___三__角__形___对__应__高__的___比__、 ___相__似__三__角___形__对__应___中__线__的__比___、 _相___似__三__角___形__对__应__角___平__分__线___的__比___都等于相似比。
AC AB 5
D
求四边形BCDE的面积。
解:∵ AE AD 3 ,∠A=∠A
B
C
AC AB 5
∴ △ ADE∽△ ABC(两边对应成比例,且夹角相等,两三角形相似)
∴
SADE SABC
AE2 (相似三角形面积的比等于相似比的平方)
AC2
∴
SADE SABC
32 52
9 25
∵ SABC 100 cm2
∴
2020/10/1
SABC SA'B 'C '
AB A' B'
AB A' B'
AB2 A' B'2
华师大版九年级数学上册课件:23.3 相似三角形 23.3.3 相似三角形的性质

【解答】∵点D、E分别在AB、AC边上,且DE∥BC,∴△ADE∽△ABC
, ∵AD∶AB=1∶4,∴其周长比为1∶4, ∵BC=8cm,三角形ABC为等边三角形,
跟踪训练
1.(2017青海)如图,在平行四边形ABCD中,点E在边DC上,
DE∶EC=3∶1,连接AE交DB于点F,则△DEF的面积与△BAF的面
名师讲解
【例2】如图, ABCD中,E是CD的延长线上一点,BE与AD交 于点F,DE= CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
【解答】(1)∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD, ∴∠ABF=∠CEB,∴△ABF∽△CEB; (2)∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD且AB=CD , ∴△DEF∽△CEB,△DEF∽△ABF,∵DE= CD,
第二十三章 图形的相似源自23.3 相似三角形
23.3.3 相似三角形的性质
轻松预习
相似三角形的性质
(1)相似三角形对应边上的高、对应边上的中线和对 应角的平分线的比都等于 相似比 ;
(2)相似三角形的周长之比等于 相似比 ;
【思考】相似多边形的周长之比等于相似比吗?
(3)相似三角形面积的比等于 相似比的平方 .
跟踪训练
5.如图,在四边形ABCD中,E是AB上一点,EC∥AD,DE∥BC ,若S△BEC=1,S△ADE=3,求△CDE的面积. 解:∵AD∥CE,DE∥BC, ∴∠A=∠BEC,∠AED=∠EBC, ∴△ADE∽△ECB, 又△ADE与△ECB的面积比为3∶1, ∴相似比为DE∶BC= ∶1,又∵DE∥BC, ∴△CDE与△BEC的面积之比为DE∶BC,即 ∶1, ∴S△CDE= .
, ∵AD∶AB=1∶4,∴其周长比为1∶4, ∵BC=8cm,三角形ABC为等边三角形,
跟踪训练
1.(2017青海)如图,在平行四边形ABCD中,点E在边DC上,
DE∶EC=3∶1,连接AE交DB于点F,则△DEF的面积与△BAF的面
名师讲解
【例2】如图, ABCD中,E是CD的延长线上一点,BE与AD交 于点F,DE= CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
【解答】(1)∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD, ∴∠ABF=∠CEB,∴△ABF∽△CEB; (2)∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD且AB=CD , ∴△DEF∽△CEB,△DEF∽△ABF,∵DE= CD,
第二十三章 图形的相似源自23.3 相似三角形
23.3.3 相似三角形的性质
轻松预习
相似三角形的性质
(1)相似三角形对应边上的高、对应边上的中线和对 应角的平分线的比都等于 相似比 ;
(2)相似三角形的周长之比等于 相似比 ;
【思考】相似多边形的周长之比等于相似比吗?
(3)相似三角形面积的比等于 相似比的平方 .
跟踪训练
5.如图,在四边形ABCD中,E是AB上一点,EC∥AD,DE∥BC ,若S△BEC=1,S△ADE=3,求△CDE的面积. 解:∵AD∥CE,DE∥BC, ∴∠A=∠BEC,∠AED=∠EBC, ∴△ADE∽△ECB, 又△ADE与△ECB的面积比为3∶1, ∴相似比为DE∶BC= ∶1,又∵DE∥BC, ∴△CDE与△BEC的面积之比为DE∶BC,即 ∶1, ∴S△CDE= .
九年级数学上册(华师大版 教学课件):23.3.3相似三角

,
∴
AD k AD
BC k BC
SABC
1 AD BC 2
k2
SABC 1 AD BC
2
如图,在正方形网格上有 A1B1C1 和 A2 B2C2 ,这两
个三角形相似吗?如果相似,请给出证明,并求出 A1B1C1 和 A2 B2C2 的面积比.
相似三角形的面积比等于相似比的平方 图 24.3.10
已知:△ABC∽△A′B′C′,且相似比为k,AD、 A′D′分 别是△ABC、 △A′B′C′对应边
BC、 B′C′上的高,求证:
S ABC k 2 S ABC
A
证明 ∵ △ABC∽△A′B′C′,
.
B
B’
D
C
A’
D’ C’
,
∴
(第 3 题)
两个相相似似三角三形角的形的周长比等于相似比
周图长24比.是3.什1么1中?,△ABC和△A′B′C′相似, AD、A′D′分别为对应边上的中线,BE、 B′E′分别为对应角的角平分线,那么它们之 间有什么关系呢?
你可以从中探索 对应边上图的24中.3.1线1 的到比什等么于呢相?似比; 对应角上的角平分线的比等于相似比。
相似比 4
1
10
k
3
周长比 4
1
10
k
3
面积比 16
1
100
k2
9
2. 如果两个相似三角形的面积之比为1:9,则它 们对应边的比为_1_:_3___,对应高的比为_1__:_3__ ,周长 的比为_1_:_3___ 。
3. 如果两个相似三角形的面积之比为2:7,较大 三角形一边上的高为7,则较小三角形对应边上的高为
∴
AD k AD
BC k BC
SABC
1 AD BC 2
k2
SABC 1 AD BC
2
如图,在正方形网格上有 A1B1C1 和 A2 B2C2 ,这两
个三角形相似吗?如果相似,请给出证明,并求出 A1B1C1 和 A2 B2C2 的面积比.
相似三角形的面积比等于相似比的平方 图 24.3.10
已知:△ABC∽△A′B′C′,且相似比为k,AD、 A′D′分 别是△ABC、 △A′B′C′对应边
BC、 B′C′上的高,求证:
S ABC k 2 S ABC
A
证明 ∵ △ABC∽△A′B′C′,
.
B
B’
D
C
A’
D’ C’
,
∴
(第 3 题)
两个相相似似三角三形角的形的周长比等于相似比
周图长24比.是3.什1么1中?,△ABC和△A′B′C′相似, AD、A′D′分别为对应边上的中线,BE、 B′E′分别为对应角的角平分线,那么它们之 间有什么关系呢?
你可以从中探索 对应边上图的24中.3.1线1 的到比什等么于呢相?似比; 对应角上的角平分线的比等于相似比。
相似比 4
1
10
k
3
周长比 4
1
10
k
3
面积比 16
1
100
k2
9
2. 如果两个相似三角形的面积之比为1:9,则它 们对应边的比为_1_:_3___,对应高的比为_1__:_3__ ,周长 的比为_1_:_3___ 。
3. 如果两个相似三角形的面积之比为2:7,较大 三角形一边上的高为7,则较小三角形对应边上的高为
华师大九年级上23.3.3相似三角形的性质课件(共10张PPT)

答案:1.3∶5. 2.0.4 0.4 0.4 0.16. 3.100cm 4.32 16
归纳小结
利用相似三角形的性质解题时,应特别注意 “对应”,切忌混淆对应边的比与相似比中的 前后项的位置。
课后作业
观察可能导致发现,观察将揭示某 种规则、模式或定律。
——波利亚
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月28日星期一2022/2/282022/2/282022/2/28 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/282022/2/282022/2/282/28/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/282022/2/28February 28, 2022 •4、享受阅读快乐,提高生活质量。2022/2/282022/2/282022/2/282022/2/28
第24章 图形的相似
23.3.3 相似三角形的性质
驶向胜利 的彼岸
23.3.3 相似三角形的性质
复习导入
1.相似三角形的判定方法有 哪些? 2.相似三角形有哪些性质? 3.三角形中的主要线段有哪 些?
探索新知
如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中 AD、A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么 关系。
相似三角形的对应高的比等于相似比.
证明:∵AD⊥BC,A'D'⊥B'C'
归纳小结
利用相似三角形的性质解题时,应特别注意 “对应”,切忌混淆对应边的比与相似比中的 前后项的位置。
课后作业
观察可能导致发现,观察将揭示某 种规则、模式或定律。
——波利亚
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月28日星期一2022/2/282022/2/282022/2/28 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/282022/2/282022/2/282/28/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/282022/2/28February 28, 2022 •4、享受阅读快乐,提高生活质量。2022/2/282022/2/282022/2/282022/2/28
第24章 图形的相似
23.3.3 相似三角形的性质
驶向胜利 的彼岸
23.3.3 相似三角形的性质
复习导入
1.相似三角形的判定方法有 哪些? 2.相似三角形有哪些性质? 3.三角形中的主要线段有哪 些?
探索新知
如图:△ABC和△A'B'C'是两个相似三角形,相似比为k,其中 AD、A'D'分别为BC、B'C'边上的高,那么AD、A'D'之间有什么 关系。
相似三角形的对应高的比等于相似比.
证明:∵AD⊥BC,A'D'⊥B'C'
华东师大版九年级数学上册《23章 图形的相似 23.3 相似三角形 相似三角形的性质》精品课件_9

三角形的性质:
对应角 。对应边 。对
应高的比等
。
对应中线的比等于 。
对应角平分线的比等于 。
周长比等于 。
面积比等于
。
巩固练习
提升练习
观察可能导致发现,观察将揭示某 种规则、模式或定律。
——波利亚
第24章 图形的相似
23.3.3 相似三角形的性质
驶向胜利 的彼岸
23.3.3 相似三角形的性质 复习导入
1.相似三角形的判定方法有哪些? 2.相似三角形有哪些性质?
3.三角形中的主要线段有哪些? 4.什么是相似三角形的相似比?
探索新知
两个三角形相似,除了对应边成比例、对应角相等之外,还可以 得到许多有用的结论,如图:△ABC和△A'B'C'是两个相似三角形, 相似比为k,其中AD、A'D'分别为BC、B'C'边上的高,那么AD、 A'D'之间有什么关系。
△ABC和△A'B'C'是两个相 似三角形,相似比为k,其中AD、 A'D'分别为角BAC、角B'A'C'边 上中线, ,那么AD、A'D'之间有 什么关系?
△ABC和△A‘B’C‘是两个相似 三角形,相似比为k,那么它们 的周长比与相似比之间有什么 关系?
△ABC和△A‘B’C‘是两个相似 三角形,相似比为k,那么它们 的面积比与相似比之间有什么 关系?
相似三角形的对应高的比等于相似比.
三、小组合作探究 1、两相似三角形对应边上的 角平分线之比、中线之比和 相似比有什么关系? 2、两相似三角形的周长比、 面积比和相似比有什么关系?
△ABC和△A'B'C'是两个相 似三角形,相似比为k,其中AD、 A'D'分别为角BAC、角B'A'C'边 上的角平分线,那么AD、A'D' 之间有什么关系?
对应角 。对应边 。对
应高的比等
。
对应中线的比等于 。
对应角平分线的比等于 。
周长比等于 。
面积比等于
。
巩固练习
提升练习
观察可能导致发现,观察将揭示某 种规则、模式或定律。
——波利亚
第24章 图形的相似
23.3.3 相似三角形的性质
驶向胜利 的彼岸
23.3.3 相似三角形的性质 复习导入
1.相似三角形的判定方法有哪些? 2.相似三角形有哪些性质?
3.三角形中的主要线段有哪些? 4.什么是相似三角形的相似比?
探索新知
两个三角形相似,除了对应边成比例、对应角相等之外,还可以 得到许多有用的结论,如图:△ABC和△A'B'C'是两个相似三角形, 相似比为k,其中AD、A'D'分别为BC、B'C'边上的高,那么AD、 A'D'之间有什么关系。
△ABC和△A'B'C'是两个相 似三角形,相似比为k,其中AD、 A'D'分别为角BAC、角B'A'C'边 上中线, ,那么AD、A'D'之间有 什么关系?
△ABC和△A‘B’C‘是两个相似 三角形,相似比为k,那么它们 的周长比与相似比之间有什么 关系?
△ABC和△A‘B’C‘是两个相似 三角形,相似比为k,那么它们 的面积比与相似比之间有什么 关系?
相似三角形的对应高的比等于相似比.
三、小组合作探究 1、两相似三角形对应边上的 角平分线之比、中线之比和 相似比有什么关系? 2、两相似三角形的周长比、 面积比和相似比有什么关系?
△ABC和△A'B'C'是两个相 似三角形,相似比为k,其中AD、 A'D'分别为角BAC、角B'A'C'边 上的角平分线,那么AD、A'D' 之间有什么关系?
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC于D,
求DSE的A长DE度。S梯形BCDE
A
E
D
B
C
变式练习:
下图是一个照相机成像的示意图。如 果底片AB宽35mm,焦距是70mm, 拍摄5m外的景物70Amm′B ′有5多m 宽?如B′ 果 焦距是50mm呢A?
BO A′
• 今天我们学习相似三角形哪些性质?
1、相似三角形对应高的比等于相似比, 相似三角形对应中线的比等于相似比, 相似三角形对应角平分线的比等于相似比。
∵ AD、A′D′分别是△ABC与 △A′B′C′的高 ∴∠ADB=∠A′D′B′=90O ∴ △ABD∽△A ′ B ′ D ′
AD A' D '
AB A' B'
k
A
B
D
C
A’
ቤተ መጻሕፍቲ ባይዱ
B’
D’ C’
信不信不由你
•我也做一做:
A组,求证:相似三角形对应中线 的比等于相似比。
B组,求证:相似三角形对应角平分 线的比等于相似比
周长为
cm.
3、如果把一个三角形每条边的长都扩大为原来
的5倍,那么它的周长扩大为原来的
倍,
而面积扩大为原来的 倍。
A
4、如图,已知△ABC∽△ADE,
且BC=2DE,则△ADE与四
E
D
边形BCDE的面积比为(B) B
C
(A)1:2 (B)1:3 (C)1;4 (D)1:5
思考题:
在△ABC中,BC=m,DE∥BC,交AB于E,交
往事新忆
1.回忆全等三角形的性质: 两个全等三角形具有哪些性质? 全等三角形的 ①对应角相等 ②对应边相等 ③对应高相等 ④对应中线相等 ⑤对应角平分线相等
新知猜想
• 展开想象的翅膀: • 相似三角形的对应角、对应边、 • 对应高、对应中线及对应角平分线 • 有何关系?
根据相似三角形的定义我们可以知道哪 些性质?
B
C D
B′
C′
D′
上述结论是否适用于一般
的相似三角形?
证明:分别过A、A′,作A' D' B'C'于D'
∴
作AD⊥BC于D,
SABC
1 AD BC 2
AD BC
∴
SABC S A'B 'C '
AB A' B'
AB A' B'
AB2 A' B'2
SA’B’C’ 1 A' D'B'C' A' D' B'C' 2
相似三角形周长的比等于相似比。
已知: △ABC∽△ A' B'C'
A
A′
求证: AB BC CA AB A' B'B'C'C' A' A' B'
B 证明:∵ △ABC∽△ A' B'C'
C B′
C′
∴ AB BC CA (相似三角形对应边成比例) A' B' B'C' C' A'
∴ AB BC CA AB (等比性质) A' B'B'C'C' A' A' B'
如下图⑴、⑵、⑶分别是边长为 1、2、3的等边三角形,它们都相似。
⑵
⑴
做一做
⑶
⑵与⑴的相似比=( 2:1 ) ⑵与⑴的面积比=( 4:1 ) ⑶与⑴的相似比=( 3:1 ) ⑶与⑴的面积比=( 9:1 )
由此我们可以得到什么结论? 对等边三角形而言,面积比=相似比的平方。
A
A′
动动你聪明的 脑子,想一想
结论3 相似三
∵ △ ABC∽ △A' B'C'
角形的面积比为相似
∴
BC B'C'
AB A' B'
AD AB A' D' A' B'
比的平方。
感悟与反思
通过前面的思考、探索、推理,我们得到 相似三角形有如下性质;
相似三角形对应高的比、对应中线的 比、对应角平分线的比、周长的比等于相 似比。
相似三角形面积的比等于相似比的平 方。
两个相相似似三三角角形形的的周长比等于相似比
图 周2长4比.是3.什1么1中?,△ABC和△A′B′C′相似,AD、 A′D′分别为对应边上的中线,BE、B′E′分别为 对应角的角平分线,那么它们之间有什么关系 呢?
对应边图上24的.3.1中1 线的比等你于可相以似从比中;探对索 应角上的角平分线的比等到于什相么似呢比?。
40 60
AE SR .(相似三角形对应高
解得,x=24. 所以正方形PQRS
AD BC 的比等于相似比) 的面积为576cm2.
实战演习
A
D
1.已知:四边形ABCD
中,AC平分∠DAB,
∠ACD= ∠ABC.
求证:AC2=AB·ADB
C
2.已知:梯形ABCD 中,AD∥BC,AD=36,BC=60cm,延长两 腰BA,CD交于点O,OF⊥BC,交AD于 E,EF=32cm,则OF=_______.
对应角相等,对应边成比例。 我们来研究其它性质
J我们把相似三角形对应边的比值 称为相似比 猜想EQ相似三角形对应高的比是 否等于相似比
• 已知:如图, △ABC∽
△A′B′C′, △ABC
与 △A′B′C′的相
似比是k,AD、A′D′ AA'是DD' 对k 应高。 • 求∴证证∠明B:=∵:∠△BA′BC∽△A ′ B ′ C ′
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
学习目标
1.在理解相似三角形基本性质的基础上,掌 握 相似三角形对应中线、对应高线、对应角平 分线的比等于相似比,周长的比等于相似比, 面积的比等于相似比的平方。
2.通过实践体会相似三角形的性质,会用性质解 决相关的问题。
之比为_4__:_3_,对应中线之比为_4__:__3
已知两个三角形相似,请完成下列表格:
相似比 2
k
……
周长比
1
……
3
面积比
10000
……
自我测试
1、两个矩形相似,它们的对角线之比是1:3,那么
它们的相似比是 ,周长比是 ,面积比是 .
2、若两个相似三角形的相似比是3:5,其中第一
个三角形的周长为21cm,则第二个三角形的
挑战自我
小王有一块三角形余料ABC,它的边 BC=60cm,高线AD=40cm,要把它加 工成正方形零件,使正方形的一边在BC上, 其余两个顶点分别在AB,AC上。
(1) △ ASR与△ ABC相似吗?为什么A?
(2)求正方形SPQR的面积。S E R
B
P DQ C
例题解析
A
(1)△ASR与△ABC相似吗?为什么?
S ER
(2)求正方形PQRS的面积.
40
分析:(1) △ASR∽△ABC.理由是:
B P60 D Q
四边形PQRS是正方形
RS∥B C
∠ASR= ∠B ∠ARS= ∠C
△ASR∽△ABC.
设正方形PQRS的边长 为x cm, 则AE=(40-
x)cm4, 0 x x .
(2)由(1)可知, △ASR∽△ABC.
2、相似三角形周长的比等于相似比, 相似三角形面积的比等于相似比的平方。
你今天努力了吗?
知识象一艘船 让它载着我们
驶向理想的……
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
O A ED
B
FC
1.如果两个三角形相似,相似比为3∶5,那么对
应角的角平分线的比等于多少? 3∶5
2.相似三角形对应边的比为2:5,那么相似比为
_2_:_5___,对应角的角平分线的比为_2__:5___,周长 的比为__2_:_5__,面积的比为_4__:2__5_.
3、若两个三角形面积之比为16:9,则它们的对高
