2015年四川省高考数学(理)试卷真题word工整排版
2015年高考理数真题试卷(四川卷)
第1页,总16页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………姓名:____________班级:____________学号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………2015年高考理数真题试卷(四川卷)考试时间:**分钟 满分:**分姓名:____________班级:____________学号:___________题号 一 二 三 总分 核分人 得分注意事项:1、填写答题卡的内容用2B铅笔填写2、提前 15 分钟收取答题卡第Ⅰ卷 客观题第Ⅰ卷的注释评卷人 得分一、单选题(共9题)(x+1)(x -2)<0},集合B={x|1<x<3},则AB=( )A . {x|-1<x<3}B . {x|-1<x<1}C . {x|1<x<2}D . {x|2<x<3} 2.1. (2015·四川)执行如图所示的程序框图,输出S 的值是( )A . -B .C . -D .3.1. (2015·四川)下列函数中,最小正周期为且图象关于原点对称的函数是( )答案第2页,总16页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………A . y=cos(2x+)B . y=sin(2x+)C . y=sin2x+cos2xD . y=sinx+cosx4. (2015·四川)设a , b 都是不等于1的正数,则“3a >3b >3”是“log a 3<log b 3”的 ( ) A . 充要条件 B . 充分不必要条件C . 必要不充分条件D . 既不充分也不必要条件5. (2015·四川)过双曲线 x 2-=1的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则|AB|=( )A .B . 2C . 6D . 46.1. (2015·四川)设i 是虚数单位,则复数i 3-( ) A . -i B . -3i C . i D . 3i 7.1. (2015·四川)设直线l 与抛物线y 2=4x 相交于A ,B 两点,与圆(x -5)2+y 2=r 2(r>0)相切于点M ,且M为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是( )A . (1,3)B . (1, 4)C . (2,3)D . (2,4) 8.1. (2015·四川)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( ) A . 144个 B . 120个 C . 96个 D . 72个 9.1. (2015·四川)如果函数f(x)=(m -2)x 2+(n -8)x+1(m≥0, n≥0)在区间[, 2]上单调递减,则mn 的最大值为( )A . 16B . 18C . 25D .。
高考理科数学(精校解析版、公式可编辑)四川2015
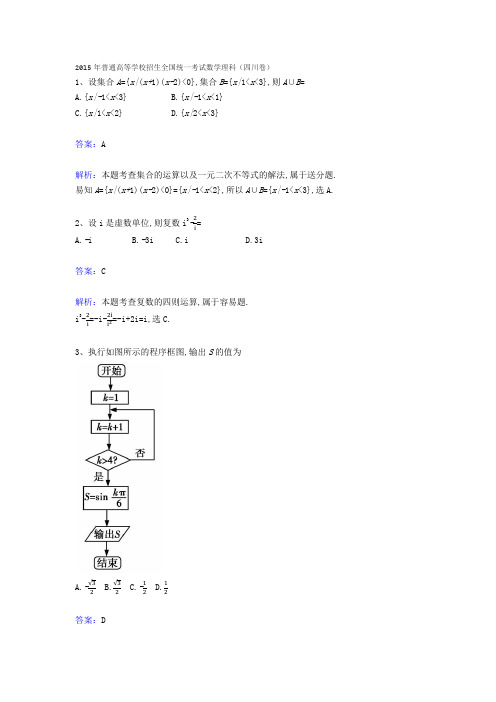
2015年普通高等学校招生全国统一考试数学理科(四川卷)1、设集合A={x|(x+1)(x-2)<0},集合B={x|1<x<3},则A∪B=A.{x|-1<x<3}B.{x|-1<x<1}C.{x|1<x<2}D.{x|2<x<3}答案:A解析:本题考查集合的运算以及一元二次不等式的解法,属于送分题. 易知A={x|(x+1)(x-2)<0}={x|-1<x<2},所以A∪B={x|-1<x<3},选A.2、设i是虚数单位,则复数i3-=A.-iB.-3iC.iD.3i答案:C解析:本题考查复数的四则运算,属于容易题.i3-=-i-=-i+2i=i,选C.3、执行如图所示的程序框图,输出S的值为A.-B.C.-D.答案:D解析:本题考查程序框图与特殊角的三角函数值的计算,求解的关键是读懂循环结束的条件“k>4 ?”.由程序框图与循环结束的条件“k>4 ?”可知,最后输出的S=sinπ=sinπ,选D.4、下列函数中,最小正周期为π且图象关于原点对称的函数是A.y=cos(2x+π)B.y=sin(2x+π)C.y=sin 2x+cos 2xD.y=sin x+cos x答案:A解析:本题考查三角函数的周期性和奇偶性,只需将已知函数化为正弦型函数f(x)=A sin(ωx+φ),即可判断.采用验证法.由y=cos(2x+π)=-sin 2x,可知该函数的最小正周期为π且为奇函数,故选A.5、过双曲线x2-=1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A,B两点,则|AB|=A. B.2 C.6 D.4答案:D解析:本题考查双曲线的标准方程、简单几何性质以及两点间的距离公式,属于基础题.由双曲线的标准方程x2-=1得,右焦点F(2,0),两条渐近线方程为y=±x,直线AB:x=2,所以不妨取A(2,2),B(2,-2),则|AB|=4,选D.6、用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有A.144个B.120个C.96个D.72个答案:B解析:本题考查两个计数原理的灵活运用、排列组合的概念及运算,求解的关键是按最高位分两类处理:①万位为4,②万位为5.当五位数的万位为4时,个位可以是0,2,此时满足条件的偶数共有=48(个);当五位数的万位为5时,个位可以是0,2,4,此时满足条件的偶数共有=72(个),所以比40 000大的偶数共有48+72=120(个),选B.7、设四边形ABCD为平行四边形,||=6,||=4.若点M,N满足=3,=2,则·=A.20B.15C.9D.6答案:C解析:本题考查平面向量的线性运算、平面向量基本定理等.选择,为基向量.∵=3,∴+++,又=2,∴+-,于是·=(+)·(-)=(4+3)·(4-3)=(16||2-9||2)=9,故选C.8、设a,b都是不等于1的正数,则“3a>3b>3”是“log a3<log b3”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件答案:B解析:本题考查指数函数、对数函数的图象和性质,考查充要关系的判定,属于中档题.由指数函数的性质知,若3a>3b>3,则a>b>1,由对数函数的性质,得log a 3<log b 3;反之,取a=,b=,显然有log a 3<log b 3,此时0<b<a<1,于是3>3a>3b,所以“3a>3b>3”是“log a 3<log b 3”的充分不必要条件,选B.9、如果函数f(x)=(m-2)x2+(n-8)x+1(m≥0,n≥0)在区间[,2]上单调递减,那么mn的最大值为A.16B.18C.25D.答案:B解析:本题考查二次函数的图象、单调区间、最值的求法以及线性规划的综合运用.由已知得f'(x)=(m-2)x+n-8,又对任意的x∈[,2],f'(x)≤0,所以′′,即.画出该不等式组表示的平面区域如图中阴影部分所示,令mn=t,则当n=0时,t=0,当n≠0时,m=.由线性规划的相关知识知,只有当直线2m+n=12与曲线m=相切时,t 取得最大值.由,解得n=6,t=18,所以(mn)max=18,选B.10、设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是A.(1,3)B.(1,4)C.(2,3)D.(2,4) 答案:D解析:本题考查直线与抛物线、圆的位置关系的判定,考查化归与转化思想、数形结合思想. 当直线l的斜率不存在时,这样的直线l恰有2条,即x=5±r,所以0<r<5;所以当直线l的斜率存在时,这样的直线l有2条即可.设A(x1,y1),B(x2,y2),M(x0,y0),则.又,两式相减得(y1+y2)(y1-y2)=4(x1-x2),k AB=.设圆心为C(5,0),则k CM=.因为直线l与圆相切,所以·=-1,解得x0=3,于是=r2-4,r>2,又<4x0,即r2-4<12,所以0<r<4,又0<r<5,r>2,所以2<r<4,选D.11、在(2x-1)5的展开式中,含x2的项的系数是(用数字填写答案).答案:-40解析:本题主要考查二项展开式指定项的系数的求解,属于基础题.由二项展开式的通项T r+1=(2x)5-r(-1)r(r=0,1,…,5)知,当r=3 时,T4=(2x)5-3(-1)3=-40x2,所以含x2的项的系数是-40.12、sin 15°+sin 75°的值是.答案:解析:本题主要考查两角和与差的正弦公式的运用,考查考生的运算求解能力.sin15°+sin75°=sin(45°-30°)+sin(45°+30°)=2sin45°·cos30°=.13、某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是小时.答案:24解析:本题是指数函数的简单应用题,考查幂的运算法则及函数与方程思想.由题意得,即,所以该食品在33 ℃的保鲜时间是y=e33k+b=·e b=()3×192=24(小时).14、如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F 分别为AB,BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.答案:解析:本题考查异面直线的概念及异面直线所成角的余弦值的求法,考查考生的空间想象能力.取BF的中点N,连接MN,EN,则EN∥AF,所以直线EN与EM所成的角就是异面直线EM与AF所成的角.在△EMN中,当点M与点P重合时,EM⊥AF,所以当点M逐渐趋近于点Q时,直线EN与EM的夹角越来越小,此时cos θ越来越大.故当点M与点Q重合时,cos θ取最大值.设正方形的边长为4,连接EQ,NQ,在△EQN中,由余弦定理,得cos∠QEN==-,所以cos θ的最大值为.15、已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=,n=.现有如下命题:①对于任意不相等的实数x1,x2,都有m>0;②对于任意的a及任意不相等的实数x1,x2,都有n>0;③对于任意的a,存在不相等的实数x1,x2,使得m=n;④对于任意的a,存在不相等的实数x1,x2,使得m=-n.其中的真命题有(写出所有真命题的序号).答案:①④解析:本题主要考查函数的图象、性质、导数及其应用,考查考生利用所学知识解决问题的能力.因为f(x)=2x在R上是单调递增的,所以对于不相等的实数x1,x2,m=>0恒成立,①正确;因为g(x)=x2+ax,所以n==x1+x2+a,正负不定,②错误;由m=n,整理得f(x1)-g(x1)=f(x2)-g(x2).令函数p(x)=f(x)-g(x)=2x-x2-ax,则p'(x)=2x ln 2-2x-a,令t(x)=p'(x),则t'(x)=2x(ln 2)2-2,又t'(1)=2(ln 2)2-2<0,t'(3)=8(ln 2)2-2>0,从而存在x0∈(1,3),使得t'(x0)=(ln 2)2-2=0,于是p'(x)有极小值p'(x0)=ln2-2x0-a=-2log2-a,所以存在a=-2log2,使得p'(x0)=>0,此时p(x)在R上单调递增,故不存在不相等的实数x1,x2,使得f(x1)-g(x1)=f(x2)-g(x2),不满足题意,③错误;由m=-n,得f'(x)=-g'(x),即-a=2x ln 2+2x.设h(x)=2x ln 2+2x,则h'(x)=2x(ln 2)2+2>0,所以h(x)在R上是单调递增的,且当x→+∞时,h(x)→+∞,当x→-∞时,h(x)→-∞,所以对于任意的a,y=-a与y=h(x)的图象一定有交点,④正确.16、设数列{a n}(n=1,2,3,…)的前n项和S n满足S n=2a n-a1,且a1,a2+1,a3成等差数列. (Ⅰ)求数列{a n}的通项公式;(Ⅱ)记数列{}的前n项和为T n,求使得|T n-1|<成立的n的最小值.答案:(Ⅰ)由已知S n=2a n-a1,有a n=S n-S n-1=2a n-2a n-1(n≥2),即a n=2a n-1(n≥2).从而a2=2a1,a3=2a2=4a1.又因为a1,a2+1,a3成等差数列,即a1+a3=2(a2+1).所以a1+4a1=2(2a1+1),解得a1=2.所以,数列{a n}是首项为2,公比为2的等比数列.故a n=2n.(Ⅱ)由(Ⅰ)得.所以T n=++…+=1-.由|T n-1|<,得|1--1|<,即2n>1 000.因为29=512<1 000<1 024=210,所以n≥10.于是,使|T n-1|<成立的n的最小值为10.解析:本题考查等差数列与等比数列的概念、等比数列的通项公式与前n项和等基础知识,考查运算求解能力.由S n=2a n-a1,得a2=2a1,a3=4a1,再通过a1,a2+1,a3成等差数列确定首项a1=2是解决(Ⅰ)的切入点;由(Ⅰ)知{}是首项为,公比为的等比数列,所以T n=1-,然后解不等式即可.17、某市A,B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.(Ⅰ)求A中学至少有1名学生入选代表队的概率;(Ⅱ)某场比赛前,从代表队的6名队员中随机抽取4人参赛.设X表示参赛的男生人数,求X 的分布列和数学期望.答案:(Ⅰ)由题意,参加集训的男、女生各有6名.代表队中的学生全从B中学抽取(等价于A中学没有学生入选代表队)的概率为. 因此,A中学至少有1名学生入选代表队的概率为1-.(Ⅱ)根据题意,X的可能取值为1,2,3.P(X=1)==,P(X=2)==,P(X=3)==.所以X的分布列为X 1 2 3P因此,X的数学期望为E(X)=1×P(X=1)+2×P(X=2)+3×P(X=3)=1×+2×+3×=2.概率、分布列、数学期望等相关概念不熟,从题干中提取数据时被无关信息干扰,或计算出错.解析:本题主要考查随机事件的概率、古典概型、随机变量的分布列、数学期望等基础知识,考查运算求解能力、应用意识,考查运用概率与统计的知识与方法分析和解决实际问题的能力.(Ⅰ)先求对立事件“A中学没有学生入选代表队”的概率,然后利用对立事件的概率计算公式即可得解;(Ⅱ)参赛的男生人数X的可能取值为1,2,3,分别求出X=1,2,3的概率,由此求出X的分布列和数学期望.18、一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M,GH的中点为N.(Ⅰ)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(Ⅱ)证明:直线MN∥平面BDH;(Ⅲ)求二面角A-EG-M的余弦值.答案:(Ⅰ)点F,G,H的位置如图所示.(Ⅱ)连接BD,设O为BD的中点,连接OM,OH.因为M,N分别是BC,GH的中点,所以OM∥CD,且OM=CD,HN∥CD,且HN=C D.所以OM∥HN,OM=HN.所以MNHO是平行四边形,从而MN∥OH.又MN⊄平面BDH,OH⊂平面BDH,所以MN∥平面BDH.(Ⅲ)方法一连接AC,过M作MP⊥AC于P.在正方体ABCD-EFGH中,AC∥EG,所以MP⊥E G.过P作PK⊥EG于K,连接KM.所以EG⊥平面PKM,从而KM⊥E G.所以∠PKM是二面角A-EG-M的平面角.设AD=2,则CM=1,PK=2.在Rt△CMP中,PM=CM sin 45°=.在Rt△PKM中,KM=.所以cos∠PKM=.即二面角A-EG-M的余弦值为.方法二如图,以D为坐标原点,分别以,,的方向为x,y,z轴的正方向,建立空间直角坐标系D-xyz.设AD=2,则M(1,2,0),G(0,2,2),E(2,0,2),O(1,1,0),所以=(2,-2,0),=(-1,0,2).设平面EGM的一个法向量为n1=(x,y,z),由得取x=2,得n1=(2,2,1).在正方体ABCD-EFGH中,DO⊥平面AEGC,则可取平面AEG的一个法向量为n2==(1,1,0),所以cos<n1,n2>=,故二面角A-EG-M的余弦值为.解析:本题主要考查简单空间图形的直观图、空间线面平行的判定与性质、空间面面夹角的计算等基础知识,考查空间想象能力、推理论证能力、运算求解能力.(Ⅰ)利用平面展开图的有关知识求解;(Ⅱ)考虑用三角形的中位线寻找平行于平面BDH的直线即可证明;(Ⅲ)作出二面角的平面角,在三角形中求解,也可以建立空间直角坐标系,求出平面ACGE的法向量、平面MEG的法向量,即可求得结论.19、如图,A,B,C,D为平面四边形ABCD的四个内角.(Ⅰ)证明:tan;(Ⅱ)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan+tan+tan+tan的值.答案:(Ⅰ)tan .(Ⅱ)由A+C=180°,得C=180°-A,D=180°-B.由(Ⅰ),有tan +tan +tan +tan=++°°+°°=+.连接B D.在△ABD中,有BD2=AB2+AD2-2AB·AD cos A,在△BCD中,有BD2=BC2+CD2-2BC·CD cos C,所以AB2+AD2-2AB·AD cos A=BC2+CD2+2BC·CD cos A. 则cos A=.于是sin A=.连接A C.同理可得cos B=,于是sin B =. 所以tan +tan +tan +tan= + =+ = .解析:本题主要考查二倍角公式、诱导公式、余弦定理、简单的三角恒等变换等基础知识,考查运算求解能力、推理论证能力,考查函数与方程、化归与转化等数学思想.第(Ⅰ)问三角恒等式的证明,利用二倍角公式化简即得;第(Ⅱ)问,首先由A 与C 、B 与D 互补及(Ⅰ)的结果,得tan +tan ,tan +tan ,然后由余弦定理,得cos A = ,cos B = ,即可获解.20、如图,椭圆E : + =1(a >b >0)的离心率是,过点P (0,1)的动直线l 与椭圆相交于A ,B 两点.当直线l 平行于x 轴时,直线l 被椭圆E 截得的线段长为2 .(Ⅰ)求椭圆E 的方程;(Ⅱ)在平面直角坐标系xOy 中,是否存在与点P 不同的定点Q ,使得 恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.答案:(Ⅰ)由已知,点( ,1)在椭圆E 上.因此,解得a =2,b = . 所以椭圆E 的方程为 + =1.(Ⅱ)当直线l 与x 轴平行时,设直线l 与椭圆相交于C ,D 两点.如果存在定点Q 满足条件,则有 =1,即|QC|=|QD|.所以Q 点在y 轴上,可设Q 点的坐标为(0,y 0).当直线l与x轴垂直时,设直线l与椭圆相交于M,N两点,则M,N的坐标分别为(0,),(0,-).由,有,解得y0=1,或y0=2.所以,若存在不同于点P的定点Q满足条件,则Q点坐标只可能为(0,2).下面证明:对任意直线l,均有.当直线l的斜率不存在时,由上可知,结论成立.当直线l的斜率存在时,可设直线l的方程为y=kx+1,A,B的坐标分别为(x1,y1),(x2,y2). 联立得(2k2+1)x2+4kx-2=0.其判别式Δ=(4k)2+8(2k2+1)>0,所以x1+x2=-,x1x2=-.因此+=2k.易知,点B关于y轴对称的点B'的坐标为(-x2,y2).又k QA==k-,K QB'==-k+=k-,所以k QA=k QB',即Q,A,B'三点共线..所以′故存在与P不同的定点Q(0,2),使得恒成立.解析:本题主要考查椭圆的标准方程与几何性质、直线方程、直线与椭圆的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合、化归与转化、特殊与一般、分类与整合等数学思想.(Ⅰ)由题意得点(,1)在椭圆E上,然后进行求解;(Ⅱ)分动直线l的斜率存在与不存在两种情况讨论,其中对运算的变形是求解的难点所在.21、已知函数f(x)=-2(x+a)ln x+x2-2ax-2a2+a,其中a>0.(Ⅰ)设g(x)是f(x)的导函数,讨论g(x)的单调性;(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.答案:本题主要考查导数的运算、导数在研究函数中的应用、函数的零点等基础知识,考查推理论证能力、运算求解能力、创新意识,考查函数与方程、数形结合、分类与整合、化归与转化等数学思想.(Ⅰ)由已知得g(x)=2(x-a)-2ln x-2(1+),g'(x)=,通过判断函数y=x2-x+a(x>0,a>0)的正负确定g(x)的单调性;(Ⅱ)通过构造新函数,结合函数的零点存在性定理进行证明.解析:(Ⅰ)由已知,函数f(x)的定义域为(0,+∞),g(x)=f'(x)=2(x-a)-2ln x-2(1+),所以g'(x)=2-+.当0<a<时,g(x)在区间(0,),(,+∞)上单调递增,在区间(,)上单调递减;当a≥时,g(x)在区间(0,+∞)上单调递增.(Ⅱ)由f'(x)=2(x-a)-2ln x-2(1+)=0,解得a=.令φ(x)=-2(x+)ln x+x2-2()x-2()2+.则φ(1)=1>0,φ(e)=--2()2<0.故存在x0∈(1,e),使得φ(x0)=0.令a0=,u(x)=x-1-ln x(x≥1).由u'(x)=1-≥0知,函数u(x)在区间(1,+∞)上单调递增.所以0==a0<<1.即a0∈(0,1).当a=a0时,有f'(x0)=0,f(x0)=φ(x0)=0.由(Ⅰ)知,f'(x)在区间(1,+∞)上单调递增,故当x∈(1,x0)时,f'(x)<0,从而f(x)>f(x0)=0;当x∈(x0,+∞)时,f'(x)>0,从而f(x)>f(x0)=0.所以,当x∈(1,+∞)时,f(x)≥0.综上所述,存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.。
2015年四川省高考数学试卷(理科)

2015年四川省高考数学试卷(理科)一、选择题:本大题共10小题.每小题5分.共50分。
在每小题给出的四个选项中.只有一个是符合题目要求的。
1.(5分)(2015•四川)设集合A={x|(x+1)(x﹣2)<0}.集合B={x|1<x<3}.则A∪B=()A.{x|﹣1<x<3} B.{x|﹣1<x<1} C.{x|1<x<2} D.{x|2<x<3}2.(5分)(2015•四川)设i是虚数单位.则复数i3﹣=()A.﹣i B.﹣3i C.i D.3i3.(5分)(2015•四川)执行如图所示的程序框图.输出s的值为()A.﹣B.C.﹣ D.4.(5分)(2015•四川)下列函数中.最小正周期为π且图象关于原点对称的函数是()A.y=cos(2x+)B.y=sin(2x+)C.y=sin2x+cos2x D.y=sinx+cosx5.(5分)(2015•四川)过双曲线x2﹣=1的右焦点且与x轴垂直的直线.交该双曲线的两条渐近线于A、B两点.则|AB|=()A.B.2 C.6 D.46.(5分)(2015•四川)用数字0.1.2.3.4.5组成没有重复数字的五位数.其中比40000大的偶数共有()A.144个B.120个C.96个D.72个7.(5分)(2015•四川)设四边形ABCD为平行四边形.||=6.||=4.若点M、N满足..则=()A.20 B.15 C.9 D.68.(5分)(2015•四川)设a、b都是不等于1的正数.则“3a>3b>3”是“log a3<log b3”的()A.充要条件 B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件9.(5分)(2015•四川)如果函数f(x)=(m﹣2)x2+(n﹣8)x+1(m≥0.n≥0)在区间[]上单调递减.那么mn的最大值为()A.16 B.18 C.25 D.10.(5分)(2015•四川)设直线l与抛物线y2=4x相交于A、B两点.与圆(x﹣5)2+y2=r2(r>0)相切于点M.且M为线段AB的中点.若这样的直线l恰有4条.则r的取值范围是()A.(1.3)B.(1.4)C.(2.3)D.(2.4)二、填空题:本大题共5小题.每小题5分.共25分。
2015年高考理科数学四川卷及答案

数学试卷 第1页(共24页)数学试卷 第2页(共24页)数学试卷 第3页(共24页)绝密★启用前2015年普通高等学校招生全国统一考试(四川卷)数学(理科)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).第Ⅰ卷1至2页,第Ⅱ卷3至6页,共6页.满分150分.考试时间120分钟.考生作答时,须将答案答在答题卡上.在本试题卷、草稿纸上答题无效.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将选答案对应的标号涂黑. 第Ⅰ卷共10小题.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|(1)(2)0}A x x x =+-<,集合{|13}B x x =<<,则AB = ( )A .{|13}x x -<<B .{|11}x x -<<C .{|12}x x <<D .{|23}x x <<2.设i 是虚数单位,则复数32i i-=( )A .-iB .-3iC .iD .3i3.执行如图所示的程序框图,输出S 的值为( )A .32- B .32 C .12-D .124.下列函数中,最小正周期为π且图象关于原点对称的函数是( )A .πcos(2)2y x =+ B .πsin(2)2y x =+ C .sin 2cos2y x x =+D .sin cos y x x =+5.过双曲线的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则||AB =( )A .433B .23C .6D .436.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( )A .144个B .120个C .96个D .72个7.设四边形ABCD 为平行四边形,||=6AB ,||=4AD .若点M ,N 满足=3BM MC ,DN=2NC ,则AM NM = ( )A .20B .15C .9D .68.设a ,b 都是不等于1的正数,则“3>3>3a b ”是“log 3log 3a b <”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件9.如果函数1()(2)(8)10022f x =m x +n x+m n --(≥,≥)在区间1[,2]2上单调递减,那么mn 的最大值为( )A .16B .18C .25D .81210.设直线l 与抛物线24y x =相交于A ,B 两点,与圆222(5)(0)x y r r -+=>相切于点M ,且M 为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是( )A .(1,3)B .(1,4)C .(2,3)D .(2,4) 第Ⅱ卷(非选择题 共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷、草稿纸上无效.第Ⅱ卷共11小题.二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上. 11.在5(21)x -的展开式中,含2x 的项的系数是_________(用数字填写答案). 12.sin15+sin75的值是_________.13.某食品的保鲜时间y (单位:小时)与储存温度x (单位:℃)满足函数关系y =e kx b +(e 2.718=…为自然对数的底数,k ,b 为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是_________小时.14.如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,E ,F 分别为AB 、BC 的中点.设异面直线EM 与AF 所成的角为θ,则cos θ 的最大值为_________.15.已知函数()2x f x =,2()g x x ax =+(其中a ∈R ).对于不相等的实数1x ,2x ,设1212()()f x f x m x x -=-,1212()()g x g x n x x -=-.现有如下命题:(1)对于任意不相等的实数1x ,2x ,都有0m >;(2)对于任意的a 及任意不相等的实数1x ,2x ,都有0n >; (3)对于任意的a ,存在不相等的实数1x ,2x ,使得m n =;(4)对于任意的a ,存在不相等的实数1x ,2x ,使得m n =-. 其中的真命题有_________(写出所有真命题的序号). 2213y x -=---------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________数学试卷 第4页(共24页)数学试卷 第5页(共24页) 数学试卷 第6页(共24页)三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤. 16.(本小题满分12分)设数列{}n a (1,2,3,)n =⋅⋅⋅的前n 项和n S 满足12n n S a a =-,且1a ,21a +,3a 成等差数列.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)记数列1{}n a 的前n 项和为n T ,求使得1|1| 1 000n T -<成立的n 的最小值.17.(本小题满分12分)某市A ,B 两所中学的学生组队参加辩论赛,A 中学推荐了3名男生、2名女生,B 中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队. (Ⅰ)求A 中学至少有一名学生入选代表队的概率;(Ⅱ)某场比赛前,从代表队的6名队员中随机抽取4人参赛.记X 表示参赛的男生人数,求X 的分布列和数学期望.18.(本小题满分12分)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC 的中点为M ,GH 的中点为N .(Ⅰ)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由); (Ⅱ)证明:直线MN ∥平面BDH ; (Ⅲ)求二面角A EG M --的余弦值.19.(本小题满分12分)如图A ,B ,C ,D 为平面四边形ABCD 的四个内角. (Ⅰ)证明:1cos tan2sin A AA-=; (Ⅱ)若180A C +=,6AB =,3BC =,4CD =,5AD =,求tantan 22A B++tantan 22C D+的值. 20.(本小题满分13分)2015年普通高等学校招生全国统一考试(四川卷)理科数学答案解析【解析】解:∵四边形ABCD为平行四边形,点M、N满足3BM MC=,2DN NC=,∴根据图形可得:3344AM AB BC AB AD=+=+,2233AN AD DC AD AB=+=+,∴NM AM AN=-,∵2()AM NM AM AM AN AM AM AN=-=-,22239216AM AB AB AD AD=++,22233342AM AN AB AD AB AD=++,||6AB=,||4AD=,∴22131239316AM NM AB AD=-=-=故选;C【提示】根据图形得出3344AM AB BC AB AD=+=+,2233AN AD DC AD AB=+=+,2()AM NM AM AM AN AM AM AN=-=-,结合向量结合向量的数量积求解即可.数学试卷第7页(共24页)数学试卷第8页(共24页)数学试卷第9页(共24页)。
四川省高考数学理科试题附解析

2015年四川省高考数学理科试题(附解析)2015年四川省高考数学理科试题(附解析)第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合集合,则A.{x|-1x3}B.{x|-1x1}C.{x|1x2}D.{x|2x3}【答案】A【解析】试题分析:,选A.2.设i是虚数单位,则复数A.-iB.-3iC.i.D.3i【答案】C【解析】试题分析:3.执行如图所示的程序框图,输出S的值是A.B.C.-D.【答案】D【解析】试题分析:4.下列函数中,最小正周期为且图象关于原点对称的函数是【答案】A【解析】试题分析:5.过双曲线的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A,B两点,则(A)(B)(C)6(D)【答案】D【解析】试题分析:6.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有(A)144个(B)120个(C)96个(D)72个【答案】B【解析】试题分析:7.设四边形ABCD为平行四边形,,.若点M,N满足,,则(A)20(B)15(C)9(D)6【答案】【解析】试题分析:8.设a,b都是不等于1的正数,则“”是“”的(A)充要条件(B)充分不必要条件(C)必要不充分条件(D)既不充分也不必要条件【答案】B【解析】试题分析:9.如果函数在区间单调递减,则mn的最大值为(A)16(B)18(C)25(D)【答案】B【解析】试题分析:10.设直线l与抛物线相交于A,B两点,与圆相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是(A)(B)(C)(D)【答案】D【解析】试题分析:第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.在的展开式中,含的项的系数是(用数字作答). 【答案】.【解析】试题分析:12【答案】.【解析】试题分析:考点:13.某食品的保鲜时间y(单位:小时)与储存温度x(单位:)满足函数关系(为自然对数的底数,k、b为常数)。
2015四川高考理科数学试题(word精编版)

2015年普通高等学校招生全国统一考试(四川)
数学(理工农医类)
本试题卷分第 卷(选择题)和第 卷(非选择题)。第 卷1至2页,第 卷2至4页,共4页。满分150分。考试时间120分钟。考生作答时,必须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。考试结束后,将本试题卷和答题卡一并交回。
第 卷共11小题。
二、填空题:本大题共5小题,每小题5分,共25分。
11.在(2x 1)8的展开式中,含的项的系数是(用数字作答)。
12. sin15 +sin75 =。
13.某食品的保鲜时间y(单位:小时)与储存温度x(单位: C)满足函数关系y=ekx+b(e=2.718 为自然对数的底数,k、b为常数)。若该食品在0 C的保鲜时间设计192小时,在22 C的保鲜时间是45小时,则该食品在33 C的保鲜时间是小时。
2.设i是虚数单位,则复数i3 =
A.-iB. -3iC. i.D. 3i
3.执行如图1所示的程序框图,输出S的值是
A. B. C. D.
4 .下列函数中,最小正周期为且图象关于原点对称的函数是
A.y=cos(2x+ )
B.y=cos(2x+ )
C.y=sin2x +cos2x
D.y=sinx +cosx
(1)对于任意不相等的实数x1,x2,都有m> 0;
(2)对于任意的a及任意不相等的实数x1,x2,都有n> 0;
(3)对于任意的a,存在不相等的实数x1,x2,使得m=n;
(4)对于任意的a,存在不相等的实数x1,x2,使得m= -n。
其中的真命题有(写出所有真命题的序号)。
三、解答题:本大题共6小题,共75分。解答时应写出文字说明、证明过程或演算步骤。
2015年四川省高考数学试卷(理科)解析

2015年四川省高考数学试卷(理科)解析2015年四川省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.(5分)(2015•四川)设集合A={x|(x+1)(x ﹣2)<0},集合B={x|1<x <3},则A ∪B=( )A . {x|﹣1<x <3}B . {x|﹣1<x <1}C . {x|1<x <2}D . {x|2<x<3}2.(5分)(2015•四川)设i 是虚数单位,则复数i 3﹣=( )A . ﹣iB . ﹣3iC . iD . 3i3.(5分)(2015•四川)执行如图所示的程序框图,输出s 的值为( )6.(5分)(2015•四川)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有()A.144个B.120个C.96个D.72个7.(5分)(2015•四川)设四边形ABCD为平行四边形,||=6,||=4,若点M、N满足,,则=()A.20 B.15 C.9D.68.(5分)(2015•四川)设a、b都是不等于1的正数,则“3a>3b>3”是“log a3<log b3”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件9.(5分)(2015•四川)如果函数f(x)=(m ﹣2)x 2+(n﹣8)x+1(m≥0,n≥0)在区间[]上单调递减,那么mn的最大值为()A.16 B.18 C.25 D.10.(5分)(2015•四川)设直线l与抛物线y2=4x 相交于A、B两点,与圆(x﹣5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是()A.(1,3)B.(1,4)C.(2,3)D.(2,4)二、填空题:本大题共5小题,每小题5分,共25分。
11.(5分)(2015•四川)在(2x﹣1)5的展开式中,含x2的项的系数是(用数字填写答案).12.(5分)(2015•四川)sin15°+sin75°的值是.13.(5分)(2015•四川)某食品的保鲜时间y (单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k、b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是小时.14.(5分)(2015•四川)如图,四边形ABCD 和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为.15.(5分)(2015•四川)已知函数f(x)=2x,g (x)=x2+ax(其中a∈R).对于不相等的实数x1、x2,设m=,n=.现有如下命题:①对于任意不相等的实数x1、x2,都有m>0;②对于任意的a及任意不相等的实数x1、x2,都有n>0;③对于任意的a,存在不相等的实数x1、x2,使得m=n;④对于任意的a,存在不相等的实数x1、x2,使得m=﹣n.其中的真命题有(写出所有真命题的序号).三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
2015年四川省高考数学试卷(理科)

2015年四川省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.(5分)设集合A={x |(x +1)(x ﹣2)<0},集合B={x |1<x <3},则A ∪B=( )A .{x |﹣1<x <3}B .{x |﹣1<x <1}C .{x |1<x <2}D .{x |2<x <3} 2.(5分)设i 是虚数单位,则复数i 3﹣2i=( ) A .﹣i B .﹣3i C .iD .3i3.(5分)执行如图所示的程序框图,输出s 的值为( )A .﹣√32B .√32 C .﹣12 D .124.(5分)下列函数中,最小正周期为π且图象关于原点对称的函数是( )A .y=cos (2x +π2)B .y=sin (2x +π2)C .y=sin2x +cos2xD .y=sinx +cosx5.(5分)过双曲线x 2﹣y 23=1的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A 、B 两点,则|AB |=( )A .4√33B .2√3C .6D .4√36.(5分)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )A .144个B .120个C .96个D .72个7.(5分)设四边形ABCD 为平行四边形,|AB →|=6,|AD →|=4,若点M 、N 满足BM →=3MC →,DN →=2NC →,则AM →⋅NM →=( ) A .20 B .15 C .9D .68.(5分)设a 、b 都是不等于1的正数,则“3a >3b >3”是“log a 3<log b 3”的( ) A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件9.(5分)如果函数f (x )=12(m ﹣2)x 2+(n ﹣8)x +1(m ≥0,n ≥0)在区间[12,2]上单调递减,那么mn 的最大值为( ) A .16 B .18 C .25 D .81210.(5分)设直线l 与抛物线y 2=4x 相交于A 、B 两点,与圆(x ﹣5)2+y 2=r 2(r >0)相切于点M ,且M 为线段AB 的中点,若这样的直线l 恰有4条,则r 的取值范围是( )A .(1,3)B .(1,4)C .(2,3)D .(2,4)二、填空题:本大题共5小题,每小题5分,共25分。
2015年全国高考理科数学试题及答案-四川卷

2015年普通高等学校招生全国统一考试(四川)数学(理科)第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|(1)(2)0}A x x x =+-<,集合{|13}B x x =<<,则AB( )A.{x|-1<x<3}B.{x|-1<x<1}C.{x|1<x<2}D.{x|2<x<3} 2.设i 是虚数单位,则复数32i i- =( ) A.-i B.-3i C.i. D.3i3.执行如图所示的程序框图,输出S 的值是( ) A.32 B.32C.-12D.124.下列函数中,最小正周期为π且图象关于原点对称的函数是( ) A. cos(2)2y x π=+B. sin(2)2y x π=+ C. sin 2cos 2y x x =+ D sin cos y x x =+5.过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则AB =( )(A) (B ) (C )6 (D )6.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( ) (A )144个 (B )120个 (C )96个 (D )72个7.设四边形ABCD 为平行四边形,6AB =,4AD =.若点M ,N 满足3BM MC =,2DN NC =,则.AM NM =( )(A )20 (B )15 (C )9 (D )6 8.设a ,b 都是不等于1的正数,则“333a b >>”是“log 3log 3a b <”的 (A )充要条件 (B )充分不必要条件 (C )必要不充分条件 (D )既不充分也不必要条件 9.如果函数()()()()21281002f x m x n x m n =-+-+≥≥,在区间122⎡⎤⎢⎥⎣⎦,单调递减,则mn 的最大值为( )(A )16 (B )18 (C )25 (D )81210.设直线l 与抛物线24y x =相交于A ,B 两点,与圆()()22250x y r r -+=>相切于点M ,且M 为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是( ) (A )()13, (B )()14, (C )()23, (D )()24,第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.在5(21)x -的展开式中,含2x 的项的系数是 (用数字作答). 12. sin15sin 75+的值是 .13.某食品的保鲜时间y (单位:小时)与储存温度x (单位:C)满足函数关系bkx ey +=(718.2=e为自然对数的底数,k 、b 为常数)。
2015年四川省高考数学试卷真题及答案(理科)

2015年四川省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.(5分)设集合A={x|(x+1)(x﹣2)<0},集合B={x|1<x<3},则A∪B=()A.{x|﹣1<x<3}B.{x|﹣1<x<1}C.{x|1<x<2}D.{x|2<x<3} 2.(5分)设i是虚数单位,则复数i3﹣=()A.﹣i B.﹣3i C.i D.3i3.(5分)执行如图所示的程序框图,输出s的值为()A.﹣B.C.﹣ D.4.(5分)下列函数中,最小正周期为π且图象关于原点对称的函数是()A.y=cos(2x+) B.y=sin(2x+)C.y=sin2x+cos2x D.y=sinx+cosx5.(5分)过双曲线x2﹣=1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A、B两点,则|AB|=()A.B.2 C.6 D.46.(5分)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有()A.144个B.120个C.96个D.72个7.(5分)设四边形ABCD为平行四边形,||=6,||=4,若点M、N满足,,则=()A.20 B.15 C.9 D.68.(5分)设a、b都是不等于1的正数,则“3a>3b>3”是“log a3<log b3”的()A.充要条件B.充分不必要条件C.必要不充分条件 D.既不充分也不必要条件9.(5分)如果函数f(x)=(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[]上单调递减,那么mn的最大值为()A.16 B.18 C.25 D.10.(5分)设直线l与抛物线y2=4x相交于A、B两点,与圆(x﹣5)2+y2=r2(r >0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是()A.(1,3) B.(1,4) C.(2,3) D.(2,4)二、填空题:本大题共5小题,每小题5分,共25分。
2015高考数学四川(理工科类)试卷真题与答案解析

2015 年四川省高考数学(理)试卷真题答案及解析一、选择题1. 设集合A { x |(x1)( x2) 0} ,集合B { x |1 x 3} ,则A BA.{ x | 1 x 3}B. { x | 1 x 1}C. {x|1 x 2}D. { x | 2 x 3} 【答案】A【解析】 A { x | 1 x 2} ,且B { x |1 x 3}A B x x ,故选A{ | 1 3}2. 设i 是虚数单位,则复数i 3 2iA. iB. 3iC. iD. 3i 【答案】C2 2i【解析】3i i i2i i,故选C3. 执行如图所示的程序框图,输出S 的值是A.32B.32B. C. 12D.12【答案】D【解析】进入循环,当k 5时才能输出k 的值,则5 1S sin ,故选D6 24. 下列函数中,最小正周期为且图象关于原点对称的函数是A. y cos(2 x)B. y sin(2 x )2 2C. y sin 2x cos 2xD. y sin x cos x【答案】A【解析】1/ 20A. y cos(2 x ) sin 2x 可知其满足题意2kB. y sin(2 x ) cos 2x 可知其图像的对称中心为( ,0)( k Z),最小正2 4 2周期为C. sin 2 cos 2 2 sin(2 )y x x x 可知其图像的对称中心为4k( ,0)( k Z),最小正周期为2 8D. sin cos 2 sin( )y x x x 可知其图像的对称中心为(k,0)( k Z)小4 4正周期为25.过双曲线2y2 1x 的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线3于A 、B 两点,则| AB |A. 4 33B. 2 3C. 6D. 4 3【答案】D【解析】由题可知渐近线方程为y 3x ,右焦点(2,0) ,则直线x 2 与两条渐近线的交点分别为 A (2,2 3) ,B (2, 2 3) ,所以| AB | 4 36.用数字0,1,2,3,4,5 组成没有重复数字的五位数,其中比40000 大的偶数共有(A)144 个(B)120 个(C)96 个(D)72 个【答案】 B【解析】分类讨论2/ 20①当5 在万位时,个位可以排0、2、4 三个数,其余位置没有限制,故有 1 3C A3 4 72种。
2015年四川省高考数学试题及标准答案(理科)【解析版】

2015年四川省高考数学试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.(5分)(2015•四川)设集合A={x|(x+1)(x﹣2)<0},集合B={x|1<x<3},则A∪B=()A. {x|﹣1<x<3} B.{x|﹣1<x<1}C.{x|1<x<2} D. {x|2<x<3}考点: 并集及其运算.专题:函数的性质及应用.分析:求解不等式得出集合A={x|﹣1<x<2},根据集合的并集可求解答案.解答:解:∵集合A={x|(x+1)(x﹣2)<0},集合B={x|1<x<3},∴集合A={x|﹣1<x<2},∵A∪B={x|﹣1<x<3},故选:A点评:本题考查了二次不等式的求解,集合的运算,属于容易题.2.(5分)(2015•四川)设i是虚数单位,则复数i3﹣=()A. ﹣i B.﹣3i C. i D.3i考点: 复数代数形式的乘除运算.专题: 计算题.分析:通分得出,利用i的性质运算即可.解答:解:∵i是虚数单位,则复数i3﹣,∴===i,故选;C点评:本题考查了复数的运算,掌握好运算法则即可,属于计算题.3.(5分)(2015•四川)执行如图所示的程序框图,输出s的值为()A.﹣B. C.﹣D.考点:程序框图.专题:图表型;算法和程序框图.分析:模拟执行程序框图,依次写出每次循环得到的k的值,当k=5时满足条件k>4,计算并输出S的值为.解答:解:模拟执行程序框图,可得k=1k=2不满足条件k>4,k=3不满足条件k>4,k=4不满足条件k>4,k=5满足条件k>4,S=sin=,输出S的值为.故选:D.点评:本题主要考查了循环结构的程序框图,属于基础题.4.(5分)(2015•四川)下列函数中,最小正周期为π且图象关于原点对称的函数是()A.y=cos(2x+) B.y=sin(2x+)C.y=sin2x+cos2x D.y=sinx+cosx考点: 两角和与差的正弦函数;三角函数的周期性及其求法.专题: 三角函数的图像与性质.分析:求出函数的周期,函数的奇偶性,判断求解即可.。
2015年全国高考理科数学试题及答案-四川卷

2015年普通高等学校招生全国统一考试(四川)数学(理科)第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|(1)(2)0}A x x x =+-<,集合{|13}B x x =<<,则A B =U ( )A.{x|-1<x<3}B.{x|-1<x<1}C.{x|1<x<2}D.{x|2<x<3} 2.设i 是虚数单位,则复数32i i-=( ) A.-i B.-3i C.i.D.3i3.执行如图所示的程序框图,输出S 的值是( )A.32-B.32 C.-12D.124.下列函数中,最小正周期为π且图象关于原点对称的函数是( )A. cos(2)2y x π=+B. sin(2)2y x π=+C. sin 2cos 2y x x =+D. sin cos y x x =+5. 过双曲线2213y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则AB =( )(A)43(B )23 (C )6 (D )43 6.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )(A )144个 (B )120个 (C )96个 (D )72个7. 设四边形ABCD 为平行四边形,6AB =u u u r ,4AD =u u u r.若点M ,N 满足3BM MC =u u u u r u u u u r ,2DN NC =u u u r u u u r ,则.AM NM =u u u u r u u u u r( )(A )20 (B )15 (C )9 (D )68.设a ,b 都是不等于1的正数,则“333a b >>”是“log 3log 3a b <”的(A )充要条件 (B )充分不必要条件 (C )必要不充分条件 (D )既不充分也不必要条件 9. 如果函数()()()()21281002f x m x n x m n =-+-+≥≥,在区间122⎡⎤⎢⎥⎣⎦,单调递减,则mn 的最大值为( ) (A )16(B )18 (C )25(D )81210. 设直线l 与抛物线24y x =相交于A ,B 两点,与圆()()22250x y r r -+=>相切于点M ,且M为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是( ) (A )()13, (B )()14, (C )()23, (D )()24,第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11. 在5(21)x -的展开式中,含2x 的项的系数是 (用数字作答). 12. sin15sin 75+o o 的值是 .13. 某食品的保鲜时间y (单位:小时)与储存温度x (单位:C ο)满足函数关系bkx e y +=(Λ718.2=e 为自然对数的底数,k 、b 为常数)。
四川卷(理)

四川卷(理)第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.(2015高考四川卷,理1)设集合A={x|(x+1)(x-2)<0},集合B={x|1<x<3},则A∪B等于( A )(A){x|-1<x<3} (B){x|-1<x<1}(C){x|1<x<2} (D){x|2<x<3}解析:A={x|-1<x<2},B={x|1<x<3},利用数轴可知A∪B={x|-1<x<3}.故选A.2.(2015高考四川卷,理2)设i是虚数单位,则复数i3-等于( C )(A)-i (B)-3i (C)i (D)3i解析:i3-=-i+2i=i.故选C.3.(2015高考四川卷,理3)执行如图所示的程序框图,输出S的值为( D )(A)-(B)(C)-(D)解析:由程序框图可知,当k=5时,S=sin =.故选D.4.(2015高考四川卷,理4)下列函数中,最小正周期为π且图象关于原点对称的函数是( A )(A)y=cos(2x+) (B)y=sin(2x+)(C)y=sin 2x+cos 2x (D)y=sin x+cos x解析:选项A,y=cos(2x+)=-sin 2x,符合题意,故选A.5.(2015高考四川卷,理5)过双曲线x2-=1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A,B两点,则|AB|等于( D ) (A)(B)2 (C)6 (D)4解析:双曲线x2-=1的右焦点为F(2,0),其渐近线方程为x±y=0.不妨设A(2,2),B(2,-2),所以|AB|=4,故选D.6.(2015高考四川卷,理6)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( B )(A)144个(B)120个(C)96个(D)72个解析:当五位数的万位为4时,个位可以是0,2,此时满足条件的偶数共有=48(个);当五位数的万位为5时,个位可以是0,2,4,此时满足条件的偶数共有=72(个),所以比40000大的偶数共有48+72=120(个).故选B.7.(2015高考四川卷,理7)设四边形ABCD为平行四边形,||=6,||=4,若点M,N满足=3,=2,则·等于( C )(A)20 (B)15 (C)9 (D)6解析:依题意有=+=+,=+=-=-,所以·=(+)·(-)=-=9.故选C.8.(2015高考四川卷,理8)设a,b都是不等于1的正数,则“3a>3b>3”是“log a3<log b3”的( B )(A)充要条件(B)充分不必要条件(C)必要不充分条件 (D)既不充分也不必要条件解析:“3a>3b>3”等价于“a>b>1”,“log a3<log b3”等价于“a>b>1或0<a<1<b或0<b<a<1”,从而“3a>3b>3”是“log a3<log b3”的充分不必要条件.故选B.9.(2015高考四川卷,理9)如果函数f(x)=(m-2)x2+(n-8)x+1(m≥0,n ≥0)在区间[,2]上单调递减,那么mn的最大值为( B )(A)16 (B)18 (C)25 (D)解析:当m=2时,f(x)=(n-8)x+1在区间[,2]上单调递减,则n-8<0⇒n<8,于是mn<16,则mn无最大值.当m∈[0,2)时,f(x)的图象开口向下且过点(0,1),要使f(x)在区间[,2]上单调递减,需-≤,即2n+m≤18,又n≥0,则mn≤m(9-)=-m2+9m.而g(m)=-m2+9m在[0,2)上为增函数,所以m∈[0,2)时,g(m)<g(2)=16,故不合题意,故m∈[0,2)时,mn无最大值.当m>2时,f(x)的图象开口向上且过点(0,1),要使f(x)在区间[,2]上单调递减,需-≥2,即2m+n≤12,而2m+n≥2,所以mn≤18,当且仅当即时,取“=”,此时满足m>2.故(mn)max=18.故选B.10.(2015高考四川卷,理10)设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( D )(A)(1,3) (B)(1,4) (C)(2,3) (D)(2,4)解析:当直线l的斜率不存在时,这样的直线l恰有2条,即x=5±r,所以0<r<5;所以当直线l的斜率存在时,这样的直线l有2条即可.设A(x1,y1),B(x2,y2),M(x0,y0),则又两式相减得(y1+y2)(y1-y2)=4(x1-x2),k AB===.设圆心为C(5,0),则k CM=.因为直线l与圆相切,所以·=-1,解得x0=3,于是=r2-4,r>2,又<4x 0,即r2-4<12,所以0<r<4,又0<r<5,r>2,所以2<r<4.故选D.第Ⅱ卷(非选择题共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.(2015高考四川卷,理11)在(2x-1)5的展开式中,含x2的项的系数是(用数字填写答案).解析:T r+1=·(2x)5-r·(-1)r=(-1)r·25-r··x5-r,令5-r=2,则r=3,所以含x2的项的系数是-40.答案:-4012.(2015高考四川卷,理12)sin 15°+sin 75°的值是. 解析:sin 15°+sin 75°=sin 15°+cos 15°=sin(15°+45°)=sin 60°=.答案:13.(2015高考四川卷,理13)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是小时.解析:依题意有192=e b,48=e22k+b=e22k·e b,所以e22k===,所以e11k=或-(舍去),于是该食品在33 ℃的保鲜时间是e33k+b=(e11k)3·e b=()3×192=24(小时).答案:2414.(2015高考四川卷,理14)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.解析:如图,建立空间直角坐标系A-xyz,设AB=2,QM=m(0≤m≤2),则F(2,1,0),E(1,0,0),M(0,m,2),=(2,1,0),=(1,-m,-2),cos θ=|cos<,>|=||=||=.设y=(0≤m≤2),则y′===.当0≤m≤2时,y′≤0,所以y=在[0,2]上单调递减. 所以当m=0时,y取最大值,此时cos θ取最大值,(cos θ)max==.答案:15.(2015高考四川卷,理15)已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=,n=现有如下命题:①对于任意不相等的实数x1,x2,都有m>0;②对于任意的a及任意不相等的实数x1,x2,都有n>0;③对于任意的a,存在不相等的实数x1,x2,使得m=n;④对于任意的a,存在不相等的实数x1,x2,使得m=-n.其中的真命题有(写出所有真命题的序号).解析:m=,n=的几何意义分别是函数f(x),g(x)图象上两点连线的斜率,由f′(x)=2x·ln 2>0,g′(x)=2x+a可知m>0,n∈R.从而①是真命题,②是假命题.当a<0时,y1=f′(x)与y2=g′(x)的图象显然无交点,即不存在x1,x2,使m=n,故③是假命题;因为对任意的a,y3=-f′(x)=-2x·ln 2与y2=g′(x)=2x+a的图象恒有交点,即说明对任意的a,恒存在x1,x2,使m=-n.故④是真命题.答案:①④三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)(2015高考四川卷,理16)设数列{a n}(n=1,2,3,…)的前n项和S n满足S n=2a n-a1,且a1,a2+1,a3成等差数列.(1)求数列{a n}的通项公式;(2)记数列{}的前n项和为T n,求使得|T n-1|<成立的n的最小值. 解:(1)由已知S n=2a n-a1,有a n=S n-S n-1=2a n-2a n-1(n≥2),即a n=2a n-1(n≥2).从而a2=2a1,a3=2a2=4a1.又因为a1,a2+1,a3成等差数列,即a1+a3=2(a2+1).所以a1+4a1=2(2a1+1),解得a1=2.所以数列{a n}是首项为2,公比为2的等比数列.故a n=2n.(2)由(1)得=,所以T n=++…+==1-.由|T n-1|<,得|1--1|<,即2n>1000.因为29=512<1000<1024=210,所以n≥10.于是,使|T n-1|<成立的n的最小值为10.17.(本小题满分12分)(2015高考四川卷,理17)某市A,B两所中学的学生组队参加辩论赛,A 中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.(1)求A中学至少有1名学生入选代表队的概率;(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛.设X表示参赛的男生人数,求X的分布列和数学期望.解:(1)由题意,参加集训的男、女生各有6名.参赛学生全从B中学抽取(等价于A中学没有学生入选代表队)的概率为=.因此,A中学至少有1名学生入选代表队的概率为1-=.(2)根据题意,X的可能取值为1,2,3.P(X=1)==,P(X=2)==,P(X=3)==.所以X的分布列为因此,X的数学期望为E(X)=1×P(X=1)+2×P(X=2)+3×P(X=3)=1×+2×+3×=2.18.(本小题满分12分)(2015高考四川卷,理18)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M,GH的中点为N.(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(2)证明:直线MN∥平面BDH;(3)求二面角A-EG-M的余弦值.解:(1)点F,G,H的位置如图所示.(2)连接BD,设O为BD的中点.因为M,N分别是BC,GH的中点,所以OM∥CD,且OM=CD,HN∥CD,且HN=CD.所以OM∥HN,OM=HN.所以MNHO是平行四边形,从而MN∥OH.又MN⊄平面BDH,OH⊂平面BDH,所以MN∥平面BDH.(3)法一连接AC,过M作MP⊥AC于P.在正方体ABCD-EFGH中,AC∥EG,所以MP⊥EG.过P作PK⊥EG于K,连接KM,所以EG⊥平面PKM,从而KM⊥EG.所以∠PKM是二面角A-EG-M的平面角.设AD=2,则CM=1,PK=2.在Rt△CMP中,PM=CMsin 45°=.在Rt△PKM中,KM==.所以cos∠PKM==.即二面角A-EG-M的余弦值为.法二如图,以D为坐标原点,分别以,,的方向为x,y,z轴的正方向,建立空间直角坐标系D xyz.设AD=2,则M(1,2,0),G(0,2,2),E(2,0,2),O(1,1,0),所以=(2,-2,0),=(-1,0,2).设平面EGM的法向量为n1=(x,y,z),由得取x=2,得n1=(2,2,1)在正方体ABCD EFGH中,DO⊥平面AEGC,则可取平面AEG的一个法向量为n2==(1,1,0),所以cos<n1,n2>===,故二面角A-EG-M的余弦值为.19.(本小题满分12分)(2015高考四川卷,理19)如图,A,B,C,D为平面四边形ABCD的四个内角.(1)证明:tan =;(2)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan +tan +tan + tan 的值.(1)证明:tan ===.(2)解:由A+C=180°,得C=180°-A,D=180°-B.由(1),有tan +tan +tan +tan=+++=+.连接BD(图略),在△ABD中,有BD2=AB2+AD2-2AB·ADcos A,在△BCD中,有BD2=BC2+CD2-2BC·CDcos C,所以AB2+AD2-2AB·ADcos A=BC2+CD2+2BC·CDcos A.则cos A===.于是sin A===. 连接AC,同理可得cos B===,于是sin B===. 所以tan +tan +tan +tan=+=+=.20.(本小题满分13分)(2015高考四川卷,理20)如图,椭圆E:+=1(a>b>0)的离心率是,过点P(0,1)的动直线l与椭圆相交于A,B两点.当直线l平行于x轴时,直线l被椭圆E截得的线段长为2.(1)求椭圆E的方程;(2)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得=恒成立?若存在,求出点Q的坐标;若不存在,请说明理由. 解:(1)由已知,点(,1)在椭圆E上.因此,解得a=2,b=.所以椭圆E的方程为+=1.(2)当直线l与x轴平行时,设直线l与椭圆相交于C,D两点.如果存在定点Q满足条件,则有==1,即|QC|=|QD|.所以Q点在y轴上,可设Q点的坐标为(0,y0).当直线l与x轴垂直时,设直线l与椭圆相交于M,N两点,则M,N的坐标分别为(0,),(0,-).由=,有=,解得y0=1或y0=2.所以,若存在不同于点P的定点Q满足条件,则Q点坐标只可能为(0,2).下面证明:对任意直线l,均有=.当直线l的斜率不存在时,由上可知,结论成立.当直线l的斜率存在时,可设直线l的方程为y=kx+1,A,B的坐标分别为(x1,y1),(x2,y2).联立得(2k2+1)x2+4kx-2=0.其判别式Δ=(4k)2+8(2k2+1)>0,所以x1+x2=-,x1x2=-.因此+==2k.易知,点B关于y轴对称的点B′的坐标为(-x2,y2).又k QA===k-,k QB′===-k+=k-,所以k QA=k QB′,即Q,A,B′三点共线.所以===.故存在与P不同的定点Q(0,2),使得=恒成立.21.(本小题满分14分)(2015高考四川卷,理21)已知函数f(x)=-2(x+a)ln x+x2-2ax-2a2+a,其中a>0.(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;(2)证明:存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.(1)解:由已知,函数f(x)的定义域为(0,+∞),g(x)=f′(x)=2(x-a)-2ln x-2(1+),所以g′(x)=2-+=.当0<a<时,g(x)在区间(0,),(,+∞)上单调递增,在区间(,)上单调递减;当a≥时,g(x)在区间(0,+∞)上单调递增.(2)证明:由f′(x)=2(x-a)-2ln x-2(1+)=0,解得a=.令φ(x)=-2(x+)ln x+x2-2··x-2()2+.则φ(1)=1>0,φ(e)=--2()2<0.故存在x0∈(1,e),使得φ(x0)=0.令a0=,u(x)=x-1-ln x(x≥1).由u′(x)=1-≥0知,函数u(x)在区间(1,+∞)上单调递增. 所以0=<=a0<=<1.即a0∈(0,1).当a=a0时,有f′(x0)=0,f(x0)=φ(x0)=0.由(1)知,f′(x)在区间(1,+∞)上单调递增,故当x∈(1,x0)时,f′(x)<0,从而f(x)>f(x0)=0;当x∈(x0,+∞)时,f′(x)>0,从而f(x)>f(x0)=0.所以,当x∈(1,+∞)时,f(x)≥0.综上所述,存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立, 且f(x)=0在区间(1,+∞)内有唯一解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年四川省高考数学(理)试卷真题
一、选择题
1. 设集合{|(1)(2)0}A x x x =+-<,集合{|13}B x x =<<,则A B ⋃= A.{|13}x x -<< B. {|11}x x -<< C. {|12}x x << D. {|23}x x <<
2. 设i 是虚数单位,则复数32
i i
-
=
A.i -
B. 3i -
C. i
D. 3i 3. 执行如图所示的程序框图,输出S 的值是
A. -
B.
C. 12-
D. 12
4. 下列函数中,最小正周期为且图象关于原点对称的函数是 A. c o s (2)2y x π=+ B. s in (2)2y x π
=+
C. s i n 2c o s 2y x x =+
D. s i n c o s y x x
=+ 5. 过双曲线2
2
13
y x -=的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A 、B 两点,则||AB =
A.
B. C. 6 D. 6. 用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有
(A )144个 (B )120个 (C )96个 (D )72个 7. 设四边形ABCD 为平行四边形,
6,4A B A D ==.若点M,N 满足
3B M M C =,2D N N C =,则A MN M ⋅=
( ) (A )20 (B )15 (C )9 (D )6
8. 设,a b 都是不等于1的正数,则“333a b
>>”是“l o g3l o g3a b <”的
(A )充要条件 (B )充分不必要条件 (C )必要不充分条件 (D )既不充分也不必要条件
9. 如果函数()()()()
2
1281002fx m x n x mn =-+-+≥≥,在区间122⎡⎤⎢⎥⎣⎦
,单调递减,则mn 的最大值为
(A )16 (B )18 (C )25 (D )
81
2
10. 设直线l 与抛物线24y x =相交于,A B 两点,与圆()()
2
22
50x y r r -+=>相切于点M ,且M 为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是
(A )()13,
(B )()14, (C )()23, (D )()24, 二、填空题
11.在()8
21x -的展开式中,含2x 的项的系数是________(用数字填写答案)
12. °°
s i n 15s i n 75
+的值是________ 13.某食品的保鲜时间y (单位:小时)与储藏温度x (单位:°C )满足函数关系k x b y e +=( e =2.718⋅⋅⋅为自然对数的底数,k ,b 为常数)。
若该食品在°0C 的保鲜时间是192小时,在23°C 的保鲜时间是48小时,则该食品在33°C 的保鲜时间是________小时。
14.如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面相互垂直,动点M 在线段PQ 上,E ,F 分别为AB ,BC 中点,设异面直线EM 与AF 所成的角为θ,则cos θ的最大值为________
A
15.已知函数)
()(,2)(f 2
R a ax x x g x x ∈+==其中。
对于不相等的实数1x ,2x ,设2121)()(x x x f x f m --=
,2
121)()(n x x x g x g --=。
现有如下命题:
(1) 对于任意不相等的实数1x ,2x ,都有0m >;
(2) 对于任意a 的及任意不相等的实数1x ,2x ,都有0n >; (3) 对于任意的a ,存在不相等的实数1x ,2x ,使得n =m ; (4) 对于任意的a ,存在不相等的实数1x ,2x ,使得n m -=. 其中的真命题有_________________(写出所有真命题的序号)。
三、简答题
16.(本小题12分)设数列{}n a 的前n 项和12n n S a a =-,且123,1,a a a +成等差数列。
(1)求数列{}n a 的通项公式; (2)记数列1
{}n
a 的前n 项和n T ,求得使1|1|1000n T -<成立的n 的最小值。
17.(本小题12分)某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
(1)求A中学至少有1名学生入选代表队的概率.
(2)某场比赛前。
从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X得分布列和数学期望.
18.(本小题满分12分)
一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设B C的中点为M,GH的中点为N。
(I)请将字母标记在正方体相应的顶点处(不需说明理由)
M N平面B D H
(II)证明:直线//
--余弦值
(III)求二面角AE GM
G
F
H
E
C D
A B
19.(本题满分12分)
如图,,,,ABCD 为平面四边形A
B C D 的四个内角. (1)证明:1c o s t a n 2s i n A A A
-=
; (2)若180o
AC +=,6A B =,3B C =,4C D =,5A D =,求
ta n ta n ta n 222A B C ++t a n 2
D +.
20.(本小题13分)如图,椭圆2
2
22:
1+
=x y E a
b
,过点(0,1)P 的动
直线l 与椭圆相交于,A B 两点。
当直线l 平行于x 轴时,直线l 被椭圆E 截得的线
段长为。
(1) 球椭圆E 的方程;
(2) 在平面直角坐标系xoy 中,是否存在与点P 不同的定点Q ,使得
=
QA PA QB
PB
恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由。
D
C
B
A
21.(本小题14分)已知函数()()
22
2l n 22=-++--+f x x a x x a x a a ,其中0>a 。
(1)设()g x 是()f x 的导函数,讨论()g x 的单调性;
(2)证明:存在()0,1∈a ,使得()0≥f x 在区间()1,+∞内恒成立,且()0=f x 在区间()1,+∞内有唯一解。
