2012年数值分析第一次作业和参考答案与解析

合集下载

数值分析参考答案

数值分析参考答案数值分析参考答案数值分析是一门研究使用数值方法解决数学问题的学科。

它涉及到数值计算、数值逼近、数值解法等方面的内容。

在实际应用中，数值分析可以帮助我们解决各种各样的问题，如线性方程组的求解、非线性方程的根的求解、插值、数值积分等等。

本文将给出一些数值分析常见问题的参考答案。

1. 线性方程组的求解线性方程组的求解是数值分析中的一个重要问题。

常见的求解方法有直接法和迭代法。

直接法包括高斯消元法、LU分解法等，迭代法包括雅可比迭代法、高斯-赛德尔迭代法等。

2. 非线性方程的根的求解非线性方程的根的求解是数值分析中的另一个重要问题。

常见的求解方法有二分法、牛顿法、割线法等。

其中，牛顿法是一种迭代法，通过不断迭代逼近方程的根。

3. 插值插值是数值分析中的一个常见问题，它可以用于构造函数的近似值。

常见的插值方法有拉格朗日插值法、牛顿插值法等。

这些方法通过已知的数据点来构造一个多项式函数，从而近似原函数。

4. 数值积分数值积分是数值分析中的另一个重要问题，它可以用于计算函数的定积分。

常见的数值积分方法有梯形法则、辛普森法则等。

这些方法通过将定积分转化为求和的形式，从而进行数值计算。

5. 常微分方程的数值解法常微分方程的数值解法是数值分析中的一个重要问题。

常见的数值解法有欧拉法、改进的欧拉法、龙格-库塔法等。

这些方法通过将微分方程转化为递推关系，从而逐步逼近解。

6. 线性规划问题的求解线性规划问题是数值分析中的一个重要问题，它可以用于求解最优化问题。

常见的线性规划求解方法有单纯形法、内点法等。

这些方法通过不断迭代来逼近最优解。

7. 矩阵特征值和特征向量的计算矩阵特征值和特征向量的计算是数值分析中的一个重要问题。

常见的计算方法有幂法、反幂法、QR方法等。

这些方法通过迭代来逼近矩阵的特征值和特征向量。

总结起来，数值分析是一门研究使用数值方法解决数学问题的学科。

它涉及到线性方程组的求解、非线性方程的根的求解、插值、数值积分、常微分方程的数值解法、线性规划问题的求解以及矩阵特征值和特征向量的计算等方面的内容。

2012数值分析试题及答案

aii
(bi

n
aij
x
(k j
)
)
,
j 1
i 1,2,, n
(1) 求此迭代法的迭代矩阵 M ；
(2) 证明：当 A 是严格对角占优矩阵， 0.5 时，此迭代格式收敛.
解：迭代法的矩阵形式为：
x(k1) x(k) D 1 (b Ax (k) ) D 1 (D A)x(k) D 1b
x2 3/5
）.
线 …
8．对离散数据 xi yi
1 0 1 2 的拟合曲线 y 5 x 2 的均方差为( 2.5 1.58 ).
2 1 1 3
6
…
…
…
9．设求积公式
2
f (x)dx
1
A0 f (1) A1 f (0) A2 f (1) 是插值型求积公式，则积分系
… 数 A0 3/ 4 , A1 0 , A2 9 / 4 .
2
2
2
2
2
2
R[ f ] 0 f (x)dx 0 p1 (x)dx 0 f (x)dx 0 H 3 (x)dx 0 H 3 (x)dx 0 p1(x)dx
2 f (4) ( x ) (x 1 )2 (x 1 )2 dx f (4) () 2 (x2 1)2 dx
…
四、(10 分)利用复化 Simpson 公式 S2 计算定积分 I
2
cos
xdx
的近似值，并估
0
… 计误差。
… …
解：
I

S2

1 [cos0 6
cos2

数值分析课第一次作业答案answer1

2 2 答案：利用重节点均差（差商）表。P (x) = 1 4 x (x − 3) 。
计算机习题： 1. 作多项式 p，以 −1，0，1 为零点，首项系数为 2，并计算 p(3)。 4
答案：p = poly ([−1, 0, 1])，s = polyval(p, 3)。 2. 已知函数在下列各点的值为 xi 0.2 0.4 0.6 0.8 1.0
2
a 6 6e+154 0 1 1
b 10 10e+154 1 -1e+5 -4
c -4 -4e+154 1 1 3.999999
-1e+155 -7e+155 1e+155 答案：第二种方法更准确，因为第一种方法是一个累加的过程。 matlab 的 x = a : h : b 和 x = a + (0 : n) ∗ h 是第二种方法实现的。代码： format long e a = 0; b = 8; n = 9; h = (b-a)/n; x(1) = a; y(1) = a; for j = 1:n, x(j+1) = x(j) + h; y(j+1) = y(1) + j*h; end [x',y',(a:h:b)',a+(0:n)’*h] 第二章插值法 1. 当 x = 1, −1, 2 时，f (x) = 0, −3, 4，求 f (x) 的二次插值多项式。（计算两遍，分别用拉格朗日插值和牛顿插值）
5
f (xi ) 0.98 0.92 0.81 0.64 0.38 求 4 次牛顿插值多项式 P4 (x) 并画图。答案：代码： x=0.2:0.2:1.0; y=[0.98,0.92,0.81,0.64,0.38]; n = length(y); if length(x)~=n, error('x and y are not compatible'); end D = zeros(n,n); D(:,1)=y(:); for j=2:n for i=j:n D(i,j) = (D(i,j-1)-D(i-1,j-1))/(x(i)-x(i-j+1)); end end p=D(1,1)*[zeros(1,n-1),1]; for k=2:n p=p+D(k,k)*[zeros(1,n-k),poly(x(1:k-1))]; end x=0.2:0.01:1.0; z=polyval(p,x); plot(x,z) 比较：p = polyf it(x, y, 4)。

《数值分析》参考答案

参考答案第1章一、选择题1. D2. C3. A4. B5. B二、填空题1. 函数题头 H1行帮助信息函数体注释部分函数题头2. nargin varargin3. A=rand(4)4. 单引号三、解答题1. for 语句和while 语句均可以实现循环执行的功能。

二者的区别在于，for 循环语句一般适用于已知道循环次数，而不知道循环运算的目标的问题，而while 循环语句则相反，一般适用于已知循环目标，而循环次数未知的问题。

2. 程序如下：function [highavg,weightavg]=avg_high_weight(varargin) n=length(varargin); highsum=0; weightsum=0; for i=1:n highsum=highsum+varargin{i}(1);weightsum=weightsum+varargin{i}(2);endhighavg=highsum/n; weightavg=weightsum/n;第2章一、选择题1. A2. B3. A4. C5. D二、填空题1. 1.7 1.73 1.7322. 3 13. 5％4. 3三、解答题1. 解：1*()()nn x nxx x ε-≈-1***()()n nr nxx x x x x nnxxε---≈=()0.02r ne x n ==2数值分析2. 解：*1 1.1021x =有五位有效数字；*20.031x =有两位有效数字；*3385.6x =有四位有效数字；*47 1.0x =⨯有一位有效数字。

3. 解：（1）*******124124()()()()x x x x x x εεεε++≤++433111101010222---=⨯+⨯+⨯3*1.0510ε-=⨯=（2）*********123231113()()x x x x x x x x x ε⋅⋅≈⋅-+⋅****221233()()x x x x x x -+⋅-*0.197ε≈=（3）******2242244**2441(/) |()()|()x x x x x x x xx ε≤---****2224**44|()()|r r x x x x xxεε=-***224*4||[|()||()|]r r x e x e x x≤+331110100.0312256.4800.03156.480--⎡⎤⨯⨯⎢⎥=+⎢⎥⎢⎥⎣⎦5*10ε-≤=4. 解：33**34433()43r R RV Rππεπ-=*2**2R R R R R RRR R-++=⋅*223R R R RR-≈⋅*3R R R-=⋅1%=故*1300R R R-=5. 解：设Y =*27.983Y =，*31102Y Y δ-=-≤⨯，028Y =，*028Y =，*0000Y Y δ=-=*111282827.983100Y Y ⎛⎛⎫-=---⨯ ⎪⎝⎝⎭1100δ≤，**22111127.983100100Y Y Y Y ⎛⎛⎫-=-⨯--⨯ ⎪⎝⎝⎭**111()()100Y Y Y Y =---112100100100δδδ≤+=仿此可得：*100n n n Y Y δ-≤则*31001001001101002Y Y δδ--≤==⨯即计算100Y 的误差界不超过31102-⨯参考答案 36. 解：解方程25610x x -+=得：28282x =±±由第5题知27.983具有五位有效数字，故可取：1282827.98355.983x =++=21280.0178655.983x =-≈=7. 解：设正方形的边长为x ，则其面积为2y x =。

2012年春季学期(本科生)数值分析课程考试试卷(A卷)答案及评分标准

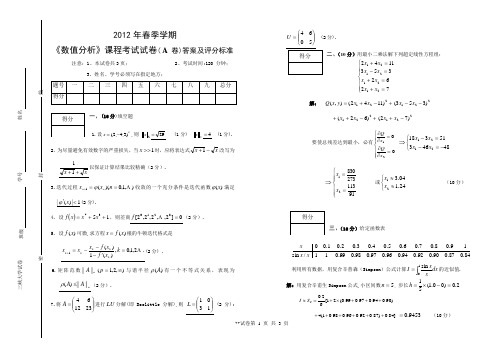
线封密三峡大学试卷班级姓名学号2012年春季学期《数值分析》课程考试试卷( A 卷)答案及评分标准注意：1、本试卷共3页；2、考试时间:120 分钟；3、姓名、学号必须写在指定地方；一、(16分)填空题1.设T x )3,4,2(-=,则 2x 29= (1分) ∞x4= (1分).2. 为尽量避免有效数字的严重损失，当1>>x 时，应将表达式x x -+1改写为xx ++11以保证计算结果比较精确（2分）.3.迭代过程),1,0)((1 ==+n x x n n ϕ收敛的一个充分条件是迭代函数)(x ϕ满足1|)(|<'x ϕ(2分).4. 设()1537++=x x x f ，则差商0]2,,2,2,2[821= f （2分）.5. 设)(x f 可微,求方程)(x f x =根的牛顿迭代格式是.2,1,0,)(1)(1='---=+k x f x f x x x k k k k k (2分) .6.矩阵范数),2,1(||||∞=p A p 与谱半径)(A ρ有一个不等式关系，表现为p A A ||||)(≤ρ（2分）.7.将⎪⎪⎭⎫ ⎝⎛=231264A 进行LU 分解(即Doolittle 分解),则 ⎪⎪⎭⎫⎝⎛=1301L (2分);⎪⎪⎭⎫ ⎝⎛=5064U (2分).二、（10分）用最小二乘法解下列超定线性方程组：⎪⎪⎩⎪⎪⎨⎧=+=+=-=+7262353114221212121x x x x x x x x 解： +-+=221)1142(),(x x y x Q 221)353(--x x+-++221)62(x x 221)72(-+x x要使总残差达到最小，必有⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂0021x Q x Q⇒⎩⎨⎧-=-=-48463513182121x x x x⇒⎪⎪⎩⎪⎪⎨⎧==9111327383021x x 或⎩⎨⎧≈≈24.104.321x x （10分）三、（10分）给定函数表84.087.090.092.094.096.097.098.099.011/sin 19.08.07.06.05.04.03.02.01.00x x x 利用所有数据，用复合辛普森（Simpson ）公式计算dxx xI ⎰=10sin 的近似值. 解: 用复合辛甫生Simpson 公式,小区间数5=n , 步长2.0)00.1(51=-⨯=h)90.094.097.099.0(21[62.05+++⨯+=≈S I]84.0)87.092.096.098.01(4++++++ 9453.0= （10分）线封密三峡大学试卷班级姓名学号四、（12分）设nn ij Ra A ⨯∈=)(对称,顺序主子式),,2,1(0n i i =≠∆则T LDL A =分解存在,其中L 为单位下三角形矩阵,D 为对角阵, 试写出求方程组b Ax =解的计算步骤(用矩阵表示), 此法称为改进平方根法. 试用它求解方程组：⎩⎨⎧=+=+635310121022121x x x x 解: 由T LDL A =可得b Ax =的方程为b x LDL T=,令y x DL T =,则b Ly =.计算步骤： (1) 将A 直接分解TLDL A =，求出 D L , (2) 求解方程b Ly =(3) 求解方程y D x L T 1-= （4分）⎢⎣⎡102 ⎥⎦⎤5310⎥⎦⎤⎢⎣⎡=10121l ⎥⎦⎤⎢⎣⎡2100d d ⎥⎦⎤⎢⎣⎡10121l 比较矩阵两边的元素,可得: ,521=l ,21=d .32=d由b Ly =可得 ⎥⎦⎤⎢⎣⎡1501⎥⎦⎤⎢⎣⎡21y y ⎥⎦⎤⎢⎣⎡=6312 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒31221y y 由y D x L T1-=得 ⎥⎦⎤⎢⎣⎡1051⎥⎦⎤⎢⎣⎡21x x ⎥⎦⎤⎢⎣⎡=16 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒1112x x （12分）五、(12分) 取节点1,010==x x ,写出x e x y -=)(的一次插值多项式),(1x L 并估计插值误差.解: 建立Lagrange 公式为 ()x L 110100101y x x x x y x x x x --+--=1101101-⨯--+⨯--=e x x x e x 11-+-=. （8分） ())1)(0(!2)()()(11--''=-=x x y x L x y x R ξ )10(<<ξ ()1)0(max 2110--≤≤≤x x x 令 ),1()(-=x x x h 由0)(='x h ，求得一个驻点得211=x于是 =≤≤|)(|max 10x h x 41)}1(),(),0({max 110=≤≤h x h h x 所以有())()(11x L x y x R -=)(max 2110x h x ≤≤≤81= （12分）六、(10分) 在区间[0,2]上利用压缩映像原理验证迭代格式1012.k x k +==，，，的敛散性. 解：(1) 记x x +=2)(ϕ，则xx +='221)(ϕ.当]2,0[∈x 时,];2,0[]2,2[)]2(),0([)(⊂=∈ϕϕϕx (5分) (2) .1221)0(|)(|<='≤'ϕϕx 因此,对]2,0[0∈∀x ,迭代格式1012.k x k +==，，，产生的序列∞=0}{k k x 收敛. (10分)线封密三峡大学试卷班级姓名学号七、（12分）已知方程组⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛121212212321x x x a a a （1）写出解此方程组的雅可比(Jacobi)迭代法公式；（2）证明当4>a 时，雅可比(Jacobi)迭代法收敛；（3）取5=a ,T x)101,51,101()0(=，求出)2(x . 解：（1）对.,3,2,1 =i 从第i 个方程解出i x ，得雅可比法迭代公式为：⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=--=--=+++ ,1,0,)21(1)222(1)21(1)(2)(1)1(3)(3)(1)1(2)(3)(2)1(1n x x a x x x a x x x a x n n n n n n n n n （5分）（2）当4>a 时，A 为严格对角占优矩阵，所以雅可比迭代法收敛. （10分）（3）取5=a ，Tx )101,51,101()0(= 由迭代公式计算得 101)1(1=x ， 258)1(2=x ， 101)1(3=x . 25013)2(1=x ， 258)2(2=x ， 25013)2(3=x . （12分）八、（10分）设初值问题:⎩⎨⎧=≤≤++='0)0(10,122y x y x y , (1) 写出用Euler 方法、取步长1.0=h 解上述初值问题数值解的公式； (2) 写出用改进Euler 方法、取步长1.0=h 解上述初值问题数值解的公式. 解: （1）取步长1.0=h 解上述初值问题数值解的Euler 公式为；9,,1,0),1(1.0),(0221==++⨯+=+=+y n y x y y x hf y y n n n n n n n （5分）（2）取步长1.0=h 解上述初值问题数值解的改进Euler 公式为：)2(21.0)1(1.002121221221=⎪⎩⎪⎨⎧+++++=++⨯+=++++y y x y x y y y x y y n n n n n n n n n n （10分）九、（8分）学完《数值分析》这门课程后，请你简述一下“插值、逼近、拟合”三者的区别和联系.解: 答案略.。

数值分析练习题及答案

数值分析练习题及答案数值分析练习题及答案数值分析是应用数学的一个分支，它研究如何使用数值方法解决实际问题。

在数值分析的学习过程中，练习题是非常重要的一部分，通过练习题的完成，我们可以更好地理解和掌握数值分析的原理和方法。

本文将给出一些数值分析的练习题及其答案，希望对读者有所帮助。

一、插值与拟合1. 插值是指根据已知数据点的函数值，通过某种方法推导出在这些数据点之间的函数值。

请问插值的目的是什么？答案：插值的目的是通过已知数据点的函数值，推导出在这些数据点之间的函数值，以便于我们在这些数据点之间进行计算和分析。

2. 拟合是指根据已知数据点的函数值，通过某种方法找到一个函数，使得该函数与这些数据点尽可能接近。

请问拟合的目的是什么？答案：拟合的目的是通过已知数据点的函数值，找到一个函数，使得该函数与这些数据点尽可能接近，以便于我们对数据的趋势和规律进行分析和预测。

二、数值积分1. 数值积分是指通过数值方法计算一个函数在某个区间上的积分值。

请问数值积分的应用领域有哪些？答案：数值积分在科学计算、工程设计、金融分析等领域都有广泛的应用。

例如，在物理学中，数值积分可以用来计算物体的质心、重心等重要物理量；在金融分析中，数值积分可以用来计算期权的价格和风险价值等。

2. 辛普森法则是一种常用的数值积分方法，它通过将积分区间划分为若干个小区间，并在每个小区间上使用一个二次多项式来逼近被积函数。

请问辛普森法则的原理是什么？答案：辛普森法则的原理是通过将积分区间划分为若干个小区间，并在每个小区间上使用一个二次多项式来逼近被积函数。

然后，通过对这些小区间上的二次多项式进行积分，最后将这些积分值加起来，就可以得到整个积分区间上的积分值。

三、数值微分1. 数值微分是指通过数值方法计算一个函数在某个点处的导数值。

请问数值微分的作用是什么？答案：数值微分的作用是通过数值方法计算一个函数在某个点处的导数值，以便于我们对函数的变化趋势和规律进行分析和预测。

数值分析练习题附答案

1
2-3 对矩阵 A 进行 LDLT 分解和 GGT 分解，求解方程组 Ax=b,其中
16 4 8
1
A=( 4 5 −4) ， b＝(2)
8 −4 22
3
解：（注：课本 P26 P27 根平方法）
设 L=(l i j )，D=diag(di)，对 k=1,2,…,n,
其中��=��－∑��=−11 ��2��
��31=(��31 − ∑0��=1 ��3��1�� )/ ��1=186=12
��32=(��32
−
∑1��=1
��3��2��
�� )/
6.6667
，得 ��3 ＝ 1.78570
−1 209
��4
0
��4
0.47847
(
56
−1
780 (��5) 209)
(200)
(��5) ( 53.718 )
1 −1
4
1 −4
15
��1
25
��2
6.6667再由1源自− 15561
− 56
209

x (k1) 1

1 5
(12

2 x2( k )

x (k) 3
)

2 5
x (k) 2

数值分析习题集及答案[1](精)

数值分析习题集（适合课程《数值方法A 》和《数值方法B 》）长沙理工大学第一章绪论1. 设x >0,x 的相对误差为δ,求ln x 的误差.2. 设x 的相对误差为2％,求nx 的相对误差.3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====⨯4. 利用公式(3.3)求下列各近似值的误差限:********12412324(),(),()/,i x x x ii x x x iii x x ++其中****1234,,,x x x x 均为第3题所给的数.5. 计算球体积要使相对误差限为1％,问度量半径R 时允许的相对误差限是多少?6. 设028,Y =按递推公式1n n Y Y -= ( n=1,2,…)计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差?7. 求方程25610x x -+=的两个根,使它至少具有四位有效数字≈27.982).8. 当N 充分大时,怎样求211Ndx x +∞+⎰?9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2?10. 设212S gt =假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加,而相对误差却减小.11. 序列{}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字),计算到10y 时误差有多大?这个计算过程稳定吗?12. 计算61)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好?3--13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式ln(ln(x x =-计算,求对数时误差有多大?14. 试用消元法解方程组{101012121010;2.x x x x +=+=假定只用三位数计算,问结果是否可靠?15. 已知三角形面积1sin ,2s ab c =其中c 为弧度,02c π<<,且测量a ,b ,c 的误差分别为,,.a b c ∆∆∆证明面积的误差s ∆满足.s a b c s a b c ∆∆∆∆≤++第二章插值法1. 根据(2.2)定义的范德蒙行列式,令2000011211121()(,,,,)11n n n n nn n n n x x x V x V x x x x x x x xx x ----==证明()n V x 是n 次多项式,它的根是01,,n x x -,且 101101()(,,,)()()n n n n V x V x x x x x x x ---=--.2. 当x = 1 , -1 , 2 时, f (x)= 0 , -3 , 4 ,求f (x )的二次插值多项式.3.4. 给出cos x ,0°≤x ≤90°的函数表,步长h =1′=(1/60)°,若函数表具有5位有效数字,研究用线性插值求cos x 近似值时的总误差界.5. 设0k x x kh =+,k =0,1,2,3,求032max ()x x x l x ≤≤.6. 设jx 为互异节点(j =0,1,…,n ),求证:i) 0()(0,1,,);nk kj jj x l x x k n =≡=∑ii) 0()()1,2,,).nk jj j xx l x k n =-≡0(=∑7. 设[]2(),f x C a b ∈且()()0f a f b ==,求证21()()().8max max a x ba xb f x b a f x ≤≤≤≤≤-"8. 在44x -≤≤上给出()xf x e =的等距节点函数表,若用二次插值求xe 的近似值,要使截断误差不超过610-,问使用函数表的步长h 应取多少? 9. 若2nn y =,求4n y ∆及4n y δ. 10. 如果()f x 是m 次多项式,记()()()f x f x h f x ∆=+-,证明()f x 的k 阶差分()(0)k f x k m ∆≤≤是m k -次多项式,并且()0(m l f x l +∆=为正整数).11. 证明1()k k k k k k f g f g g f +∆=∆+∆. 12. 证明110010.n n kkn n k k k k f gf g f g g f --+==∆=--∆∑∑13. 证明1200.n j n j y y y -=∆=∆-∆∑14. 若1011()n n n n f x a a x a x a x --=++++有n 个不同实根12,,,n x x x ,证明{10,02;, 1.1()n k njk n a k n j jx f x -≤≤-=-=='∑15. 证明n 阶均差有下列性质: i)若()()F x cf x =,则[][]0101,,,,,,n n F x x x cf x x x =;ii) 若()()()F x f x g x =+,则[][][]010101,,,,,,,,,n n n F x x x f x x x g x x x =+.16. 74()31f x x x x =+++,求0172,2,,2f ⎡⎤⎣⎦及0182,2,,2f ⎡⎤⎣⎦.17. 证明两点三次埃尔米特插值余项是(4)22311()()()()/4!,(,)k k k k R x f x x x x x x ++=ξ--ξ∈并由此求出分段三次埃尔米特插值的误差限.18. 求一个次数不高于4次的多项式()P x ,使它满足(0)(1)P P k =-+并由此求出分段三次埃尔米特插值的误差限. 19. 试求出一个最高次数不高于4次的函数多项式()P x ,以便使它能够满足以下边界条件(0)(0)0P P ='=,(1)(1)1P P ='=,(2)1P =.20. 设[](),f x C a b ∈,把[],a b 分为n 等分,试构造一个台阶形的零次分段插值函数()n x ϕ并证明当n →∞时,()n x ϕ在[],a b 上一致收敛到()f x .21. 设2()1/(1)f x x =+,在55x -≤≤上取10n =,按等距节点求分段线性插值函数()h I x ,计算各节点间中点处的()h I x 与()f x 的值,并估计误差.22. 求2()f x x =在[],a b 上的分段线性插值函数()h I x ,并估计误差.23. 求4()f x x =在[],a b 上的分段埃尔米特插值,并估计误差.试求三次样条插值并满足条件i) (0.25) 1.0000,(0.53)0.6868;S S '='= ii)(0.25)(0.53)0.S S "="=25. 若[]2(),f x C a b ∈,()S x 是三次样条函数,证明i)[][][][]222()()()()2()()()bbbbaaaaf x dx S x dx f x S x dx S x f x S x dx"-"="-"+""-"⎰⎰⎰⎰;ii) 若()()(0,1,,)i i f x S x i n ==,式中i x 为插值节点,且01n a x x x b =<<<=,则[][][]()()()()()()()()()b aS x f x S x dx S b f b S b S a f a S a ""-"="'-'-"'-'⎰.26. 编出计算三次样条函数()S x 系数及其在插值节点中点的值的程序框图(()S x 可用(8.7)式的表达式).第三章函数逼近与计算1. (a)利用区间变换推出区间为[],a b 的伯恩斯坦多项式.(b)对()sin f x x =在[]0,/2π上求1次和三次伯恩斯坦多项式并画出图形,并与相应的马克劳林级数部分和误差做比较. 2. 求证:(a)当()m f x M ≤≤时,(,)n m B f x M ≤≤. (b)当()f x x =时,(,)n B f x x =. 3. 在次数不超过6的多项式中,求()sin 4f x x =在[]0,2π的最佳一致逼近多项式. 4. 假设()f x 在[],a b 上连续,求()f x 的零次最佳一致逼近多项式. 5. 选取常数a ,使301max x x ax≤≤-达到极小,又问这个解是否唯一?6. 求()sin f x x =在[]0,/2π上的最佳一次逼近多项式,并估计误差.7. 求()xf x e =在[]0,1上的最佳一次逼近多项式.8. 如何选取r ,使2()p x x r =+在[]1,1-上与零偏差最小?r 是否唯一?9. 设43()31f x x x =+-,在[]0,1上求三次最佳逼近多项式.10. 令[]()(21),0,1n n T x T x x =-∈,求***0123(),(),(),()T x T x T x T x .11. 试证{}*()nTx 是在[]0,1上带权ρ=的正交多项式.12. 在[]1,1-上利用插值极小化求11()f x tg x -=的三次近似最佳逼近多项式.13. 设()xf x e =在[]1,1-上的插值极小化近似最佳逼近多项式为()n L x ,若nf L ∞-有界,证明对任何1n ≥,存在常数n α、n β,使11()()()()(11).n n n n n T x f x L x T x x ++α≤-≤β-≤≤14. 设在[]1,1-上234511315165()128243843840x x x x x x ϕ=-----,试将()x ϕ降低到3次多项式并估计误差.15. 在[]1,1-上利用幂级数项数求()sin f x x =的3次逼近多项式,使误差不超过0.005.16. ()f x 是[],a a -上的连续奇(偶)函数,证明不管n 是奇数或偶数,()f x 的最佳逼近多项式*()n n F x H ∈也是奇(偶)函数.17. 求a 、b 使[]220sin ax b x dx π+-⎰为最小.并与1题及6题的一次逼近多项式误差作比较.18. ()f x 、[]1(),g x C a b ∈,定义 ()(,)()();()(,)()()()();b baaa f g f x g x dxb f g f x g x dx f a g a =''=''+⎰⎰问它们是否构成内积?19. 用许瓦兹不等式(4.5)估计6101x dx x +⎰的上界,并用积分中值定理估计同一积分的上下界,并比较其结果.20. 选择a ,使下列积分取得最小值:1122211(),x ax dx x ax dx----⎰⎰.21. 设空间{}{}10010121,,,span x span x x 1ϕ=ϕ=,分别在1ϕ、2ϕ上求出一个元素,使得其为[]20,1x C ∈的最佳平方逼近,并比较其结果.22. ()f x x =在[]1,1-上,求在{}2411,,span x x ϕ=上的最佳平方逼近.23.sin (1)arccos ()n n x u x +=是第二类切比雪夫多项式,证明它有递推关系()()()112n n n u x xu x u x +-=-.24. 将1()sin2f x x=在[]1,1-上按勒让德多项式及切比雪夫多项式展开,求三次最佳平方逼近多项式并画出误差图形,再计算均方误差.25. 把()arccos f x x =在[]1,1-上展成切比雪夫级数.26.2y a bx =+.27.用最小二乘拟合求.29. 编出用正交多项式做最小二乘拟合的程序框图. 30. 编出改进FFT 算法的程序框图. 31. 现给出一张记录{}{}4,3,2,1,0,1,2,3k x =,试用改进FFT 算法求出序列{}k x 的离散频谱{}k C (0,1,,7).k =第四章数值积分与数值微分1. 确定下列求积公式中的待定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度:(1)101()()(0)()hhf x dx A f h A f A f h --≈-++⎰; (2)21012()()(0)()hh f x dx A f h A f A f h --≈-++⎰;(3)[]1121()(1)2()3()/3f x dx f f x f x -≈-++⎰;(4)[][]20()(0)()/1(0)()hf x dx h f f h ah f f h ≈++'-'⎰.2. 分别用梯形公式和辛普森公式计算下列积分:(1)120,84xdx n x =+⎰; (2)1210(1),10x e dx n x --=⎰;(3)1,4n =⎰;(4),6n =.3. 直接验证柯特斯公式(2.4)具有5次代数精度.4. 用辛普森公式求积分10x e dx-⎰并计算误差. 5. 推导下列三种矩形求积公式:(1)2()()()()()2ba f f x dxb a f a b a 'η=-+-⎰; (2)2()()()()()2baf f x dx b a f b b a 'η=---⎰; (3)3()()()()()224baa b f f x dx b a f b a +"η=-+-⎰. 6. 证明梯形公式(2.9)和辛普森公式(2.11)当n →∞时收敛到积分()baf x dx⎰.7. 用复化梯形公式求积分()baf x dx⎰,问要将积分区间[],a b 分成多少等分,才能保证误差不超过ε(设不计舍入误差)?8.1x e dx-,要求误差不超过510-.9. 卫星轨道是一个椭圆,椭圆周长的计算公式是S a =θ,这里a 是椭圆的半长轴,c 是地球中心与轨道中心(椭圆中心)的距离,记h 为近地点距离,H 为远地点距离,6371R =公里为地球半径,则(2)/2,()/2a R H h c H h =++=-.我国第一颗人造卫星近地点距离439h =公里,远地点距离2384H =公里,试求卫星轨道的周长.10. 证明等式3524sin3!5!n n nnππππ=-+-试依据sin(/)(3,6,12)n n n π=的值,用外推算法求π的近似值.11. 用下列方法计算积分31dyy ⎰并比较结果.(1) 龙贝格方法;(2) 三点及五点高斯公式;(3) 将积分区间分为四等分,用复化两点高斯公式.12. 用三点公式和五点公式分别求21()(1)f x x =+在x =1.0,1.1和1.2处的导数值,并估计误()f x第五章常微分方程数值解法1. 就初值问题0)0(,=+='y b ax y 分别导出尤拉方法和改进的尤拉方法的近似解的表达式，并与准确解bx ax y +=221相比较。

数值分析习题参考答案1

部分习题参考答案习题一1. 分别有3位、5位与4位有效数字2. 分别有５位、3位、4位与３位有效数字3. 有３位有效数字; 绝对误差为－０、0012;相对误差-０、0005570514. (1) (2）(3)６、提示:注意字长为８位得计算机上得机器数系得特点与计算机对数得接收与运算处理。

7、提示:通过证明进行说明,这里 8、,不稳定 9、最好10、采用j 从10000到２得顺序相加,或通过进行化简计算。

11、本题有递推公式得出得就就就是。

算法１、2、For k=n-1,n-2,…,1,0 做12、提示：仿照例１、9做之。

习题二 2、提示:3、取迭代函数讨论之。

4、由确定k,迭代次数59、5、迭代公式及区间为,数列得极限值。

6、x 3=０、567１43 ７、，用New ｔo ｎ迭代公式及定理６做，根1、03０ 8、两个根: ;9、取,当时，取区间,用定理6做，当时,由做转换讨论。

极限为１1提示:由可得,或由用定理2、4 １2、()()()()()()()()()()()()()()()()()222******1*22*****1*2***2*3(),()2'()2!()'()'()2'()'()'()2()'()2k k kk k k k k k k k k k k k kk k k k k k f f y x x x f y f x f x y x y x f x f x f f y x x y x y x y x y x f x f x f x y x f f x f x y x f x y x f x x f f x ξξξξξξ+'''''-=-=+-+-'''∴-=--=------''⎛⎫'=--- ⎪⎝⎭-''''=-+()()()()()2*13*121*32()2'()()()()4'()2'()k k kk k k f x x f x x xf f f f x x f x f x ξξξξξ⎛⎫''⨯- ⎪⎝⎭''-''''⎛⎫''=+- ⎪⎝⎭１3、提示:借助代入中约化。

《数值分析》练习题及答案解析

《数值分析》练习题及答案解析第一章绪论主要考查点：有效数字，相对误差、绝对误差定义及关系；误差分类；误差控制的基本原则；。

1. 3.142和3.141分别作为π的近似数具有（）和（）位有效数字.A ．4和3B ．3和2C ．3和4D ．4和4 答案：A2. 设 2.3149541...x *=，取5位有效数字，则所得的近似值x=___________ .答案：2.31503.若近似数2*103400.0-⨯=x 的绝对误差限为5105.0-⨯,那么近似数有几位有效数字解：2*103400.0-⨯=x ，325*10211021---⨯=⨯≤-x x 故具有3位有效数字。

4 . 14159.3=π具有4位有效数字的近似值是多少？解：10314159.0⨯= π，欲使其近似值*π具有4位有效数字，必需！41*1021-⨯≤-ππ，3*310211021--⨯+≤≤⨯-πππ，即14209.314109.3*≤≤π即取（ , ）之间的任意数，都具有4位有效数字。

第二章非线性方程求根主要考查点：二分法N 步后根所在的区间，及给定精度下二分的次数计算；非线性方程一般迭代格式的构造，（局部）收敛性的判断，迭代次数计算；牛顿迭代格式构造；求收敛阶；1.用二分法求方程012=--x x 的正根，要求误差小于0.05。

（二分法）解：1)(2--=x x x f ，01)0(<-=f ，01)2(>=f ，)(x f 在[0，2]连续，故[0，2]为函数的有根区间。

"（1）计算01)1(<-=f ，故有根区间为[1，2]。

（2）计算041123)23()23(2<-=--=f ，故有根区间为]2,23[。

（3）计算0165147)47()47(2>=--=f ，故有根区间为]47,23[。

（4）计算06411813)813()813(2>=--=f ，故有根区间为]813,23[。

数值分析第一次作业答案

作业1.用如下数值表构造不超过3次的插值多项式2. P55 11题.给出概率积分⎰-=xxdxey 022π的数据表用2次插值计算，试问：(1) 当x = 0.472时，积分值等于多少? (2) 当x 为何值时，积分值等于0.5？解：(1) 取x 0 = 0.47， x 1 = 0.48, x 2 = 0.4980.4955530040.04093346-80.1809899240.355496540.51166830.50274980.4937452=+=----⨯+----⨯+----⨯==----+----+----≈)48.049.0)(47.049.0()48.0472.0)(47.0472.0()49.048.0)(47.048.0()49.0472.0)(47.0472.0()49.0472.0)(48.047.0()49.0472.0)(48.0472.0()472.0())(())(())(())(())(())(()472.0(2120210221120121210y Lxx xx xxy x x x x x x y x x x x x x x x x x x x y(2)90.4769359350.05272367-80.4362204360.093439170.50274980.51166830.49374520.51166830.50274980.49374520.49 0.51166830.50274980.49374520.50274980.51166830.49374520.48 0.51166830.49374520.50274980.49374520.51166830.50274980.47=+=----⨯+----⨯+----⨯==----+----+----≈))(()5.0)(5.0())(()5.0)(5.0())(()5.0)(5.0()5.0())(())(())(())(())(())(()5.0(212210221120121210Lyyy y yy xy y yy y y xyyyy yy xy y y y y y x3. 证明方程e x +10x －2＝0在区间[0，1]内有一个根，如果使用二分法求该区间内的根，且误差不超过10－6，试问需要二分区间[0，1]多少次？4. 设x t ＝451.01为准确值，x a ＝451.023为x t 的近似值，试求出x a 有效数字的位数及相对误差作业答案1.解：N 2(x ) = f (0)+f [0，1](x -0)+ f [0，1，2](x -0) (x -1) 1＋1×(x -0) ＋3×(x -0) (x -1)＝3x 2-2x +1 为求得P 3(x )，根据插值条件知，P 3(x )应具有下面的形式 P 3(x )＝N 2(x )＋k (x -0) (x -1) (x -2)，这样的P 3(x )自然满足：P 3(x i )= f (x i )由P 3’(1 )=3P 3’(1 )= N 2’(1 )+k (1-0) (1-2) =N 2’(1 )－k = 4－k=3∴ k =1∴ P 3(x )＝N 2(x )＋ (x -0) (x -1) (x -2)=x 3+1 3. 证明令f (x )＝e x +10x －2，∵ f (0)=-1<0，f (1)=e+8> 0∴ f (x )= e x +10x －2 =0在[0，1]有根。

数值分析课后习题答案

数值分析课后习题答案数值分析课后习题答案数值分析是一门应用数学的学科，主要研究用数值方法解决数学问题的理论和方法。

在学习数值分析课程时，习题是非常重要的一部分，通过解答习题可以加深对数值方法的理解和掌握。

下面将为大家提供一些数值分析课后习题的答案，希望能对大家的学习有所帮助。

1. 插值法是数值分析中常用的一种数值逼近方法。

给定一组已知数据点，我们希望通过插值方法找到一个函数，使得该函数在已知数据点上的取值与给定数据点的值尽可能接近。

常见的插值方法有拉格朗日插值法和牛顿插值法。

下面是一个使用拉格朗日插值法求解的习题：已知函数f(x)=sin(x)，求在区间[0, π/2]上的插值多项式P(x)，使得P(0)=0，P(π/2)=1。

解答：根据拉格朗日插值法的原理，我们需要构造一个满足条件的插值多项式。

首先，我们需要确定插值节点。

根据题目要求，我们取两个插值节点：x0=0，x1=π/2。

然后，我们需要确定插值多项式的系数。

设插值多项式为P(x)=a0+a1x，代入已知条件可得到两个方程：P(0)=a0=0P(π/2)=a0+a1(π/2)=1解方程组可得，a0=0，a1=2/π。

因此，插值多项式为P(x)=2x/π。

2. 数值积分是数值分析中的另一个重要内容。

它主要研究如何用数值方法计算函数的定积分。

常见的数值积分方法有梯形法则、辛普森法则等。

下面是一个使用梯形法则求解的习题：计算定积分∫[0, 1] e^(-x^2) dx。

解答：根据梯形法则的原理，我们可以将定积分转化为离散的求和问题。

首先，我们将积分区间[0, 1]等分为n个小区间，每个小区间的宽度为h=1/n。

然后，我们在每个小区间的两个端点上计算函数值，并将其加权求和。

根据梯形法则的公式，我们可以得到近似解为：∫[0, 1] e^(-x^2) dx ≈ h/2 * (f(0) + 2f(x1) + 2f(x2) + ... + 2f(x(n-1)) + f(1))其中，f(x)表示函数e^(-x^2)在点x处的取值。

数值分析2012考试卷

研究生考试命题纸沈阳工业大学 2012 / 2013 学年第一学期课程名称：数值分析课程编号：000304 任课教师：陈欣曲绍波考试形式：闭卷一、填空（每题3分，共15分）1. 二分法是求解方程f (x )=0的根一种方法，其前提是f (x )在有根区间[a ,b ]内单调且。

2. 设矩阵⎪⎪⎭⎫ ⎝⎛-=0112A ，则1A = 、=2A 、)(A ρ= 。

3. 对于正数a ，使用牛顿法于方程02=-a x 所得到的迭代格式为，其收敛阶为、求110（取x 0=10）的第一个近似值为。

4. 幂法用来计算实矩阵A 的特征值及对应的，在计算过程中进行“归一化”处理的原因是为了。

5. 高斯求积公式)33()33()(11f f dx x f +-≈⎰-的代数精度为，当区间不是[-1,1]，而是一般区间[a , b ]时，需要做变换，使用该公式计算≈⎰311dx x。

二、解答下列各题（每题5分，共10分）1. 请写出经过点A (0,1)，B (2,3)，C (4,5)的拉格朗日插值多项式形式。

说明插值基函数的性质以及拉格朗日插值法的优缺点。

2. 设n 阶可逆矩阵A 已经分解成A =LU ，其中L 下三角矩阵，U 单位上三角矩阵，推导出解线性方程组AX =b 的计算公式。

三、（10分）用不选主元的直接三角分解法解下面线性方程组⎪⎪⎩⎪⎪⎨⎧=+-=-+-=-+-=-342424344343232121x x x x x x x x x x 四、（20分，每题10分）对于线性方程组⎪⎩⎪⎨⎧=++=++=-+9223122321321321x x x x x x x x x 1. 分别写出使用GS 迭代法，SOR 迭代法（ω=1.3）求解的迭代格式，并对初始向量（1，0，0）T ，分别计算第一步近似解向量；2. 分别讨论求解此方程的J —方法和GS —方法的收敛性。

五、（10分）给出函数表如下，用牛顿向前插值公式求f (2.03)的近似值。

数值分析习题及答案解析

数值分析习题及答案解析第⼀章绪论习题⼀1.设x>0,x*的相对误差为δ，求f(x)=ln x的误差限。

解：求lnx的误差极限就是求f(x)=lnx的误差限，由公式(1.2.4)有已知x*的相对误差满⾜，⽽，故即2.下列各数都是经过四舍五⼊得到的近似值，试指出它们有⼏位有效数字，并给出其误差限与相对误差限。

解：直接根据定义和式(1.2.2)(1.2.3)则得有5位有效数字，其误差限，相对误差限有2位有效数字，有5位有效数字，3.下列公式如何才⽐较准确？（1）（2）解：要使计算较准确，主要是避免两相近数相减，故应变换所给公式。

（1）（2）4.近似数x*=0.0310,是 3 位有数数字。

5.计算取，利⽤：式计算误差最⼩。

四个选项：第⼆、三章插值与函数逼近习题⼆、三1. 给定的数值表⽤线性插值与⼆次插值计算ln0.54的近似值并估计误差限. 解：仍可使⽤n=1及n=2的Lagrange插值或Newton插值,并应⽤误差估计（5.8）。

线性插值时，⽤0.5及0.6两点，⽤Newton插值误差限，因，故⼆次插值时，⽤0.5，0.6，0.7三点，作⼆次Newton插值误差限，故2. 在-4≤x≤4上给出的等距节点函数表，若⽤⼆次插值法求的近似值，要使误差不超过，函数表的步长h 应取多少?解：⽤误差估计式（5.8），令因得3. 若，求和.解：由均差与导数关系于是4. 若互异，求的值，这⾥p≤n+1.解：，由均差对称性可知当有⽽当P＝n＋1时于是得5. 求证.解：解：只要按差分定义直接展开得6. 已知的函数表求出三次Newton均差插值多项式，计算f(0.23)的近似值并⽤均差的余项表达式估计误差.解：根据给定函数表构造均差表由式(5.14)当n=3时得Newton均差插值多项式N3(x)=1.0067x+0.08367x(x-0.2)+0.17400x(x-0.2)(x-0.3) 由此可得f(0.23) N3(0.23)=0.23203由余项表达式(5.15)可得由于7. 给定f(x)=cosx的函数表⽤Newton等距插值公式计算cos 0.048及cos 0.566的近似值并估计误差解：先构造差分表计算，⽤n=4得Newton前插公式误差估计由公式（5.17）得其中计算时⽤Newton后插公式（5.18)误差估计由公式（5.19）得这⾥仍为0.5658．求⼀个次数不⾼于四次的多项式p(x),使它满⾜解：这种题⽬可以有很多⽅法去做，但应以简单为宜。

2012数值分析试卷Microsoft Word 文档

一．填空题（每小题3分，共27分）：1．计算40的近似值时，要使其相对误差限001.0*<r ε，只需取位有效数字； 2．设近似数1,2*2*1-==x x 的误差限分别为01.0和02.0，则≈)(*2*1x x ε ；3．设求积公式)()(0k ban k k x f A dx x f ⎰∑=≈是插值型求积公式，则0nk k A ==∑.4．若)(x P 是],[)(b a C x f ∈的最佳4次逼近多项式，则)(x P 在],[b a 上至少有个偏差点； 5．在求积公式中，辛甫生公式至少具有次代数精度；6．将⎪⎪⎭⎫ ⎝⎛-=1111A 分解为下三角阵L 与上三角阵U 之积, 即LU A =,则L =, U =；7.用牛顿迭代法解方程10x xe -=的迭代公式为8. 将],[b a 区间n 等分，步长n ab h -=，分点),,1,0(n k kh a x k =+=，则],[b a 等分为n 个子区间，即∑-==1],[n k k I b a ，子区间],[1+=k k k x x I .则计算定积分()baI f x dx =⎰的复化辛普森公式为n S =.9. 计算定积分()b aI f x dx =⎰的复化梯形公式的误差表达式为n I T -= 二．单选题（每小题3分，共24分）：1. 根据数值运算误差分析的方法与原则, 无需避免的是 ( );A. 绝对值很大的数除以绝对值很小的数B. 两个非常相近的数相乘C. 绝对值很大的数加上绝对值很小的数D. 两个非常相近的数相减2. 设 )(,),(),(10x l x l x l n 分别为节点 n x x x ,,,10 上的 n 次拉格朗日插值基函数，则 ∑=≡-ni iix l x 0)()2(（）；A ．2-x B.2-i xC.0D. 13. 设 n ()[,],()f x C a b P x ∈是)(x f 的最佳一致逼近多项式, 则其逼近标准是依据( )； A. 2min[()()]kbn aa f x P x dx -⎰C. n minmax ()()ia a x bf x P x ≤≤- D. n maxmin()()ka x ba f x P x ≤≤-4. 设 )(],,[)(x P b a C x f ∈是)(x f 的最佳平方逼近多项式, 则其逼近标准是依据( )； A. 2min[()()]kbn aa f x P x dx -⎰B.C. n minmax ()()ia a x bf x P x ≤≤- D. n maxmin()()ka x ba f x P x ≤≤-5. 若牛顿-柯特斯公式只有一个求积节点, 则柯特斯系数 =)0(0C ( A )；A.1B.0C.2/1D.a b - 6．插值型求积公式 ∑==nk k kn x f AI 0)( 的代数精度最高可达到 ( ) 次；A.nB.1+nC.n 2D.12+n7. 用迭代法解方程 )5.1(01023==--x x x , 则该方程最好改写为 ( ) ； A.2/11x x += B.321x x += C.13-=x x D. 1/1-=x x8. 迭代法)()()1(k k k x Ax b x+-=+解线性方程组b Ax =收敛的充要条件是（）；A ．1)(<A ρB. 1)(<-A b ρC. 1)(<-A I ρD. 1)(<+A I ρ三．解答题(共39分)1.(7分) 求 32()21f x x x x =++- 在区间 [-1,1] 上的２次最佳一致逼近多项式()2P x2. (15分) 己知)(x f 的函数表如下，解答下述问题:(1)填写差商表.i x)(i x f ],[1+i i x x f ],,[21++i i i x x x f ],,[3+i i x x f ],,[4+i i x x f6 1 10 3 46 4 82 6212(2)写出函数)(x f 的牛顿插值多项式. (3)写出插值余项的表达式.3．(7分)求简单迭代法),...2,1,0(,121=+=+k x x x kk k 的收敛阶。

数值分析试题(A)参考答案2012.6

湖南大学研究生课程考试命题专用纸考试科目：数值分析（A 卷）参考答案专业年级： 11级各专业考试形式：闭卷（可用计算器）考试时间：120分钟……………………………………………………………………………………………………………………… 注：答题（包括填空题、选择题）必须答在专用答卷纸上，否则无效。

一、简答题(20分)1、避免误差危害的主要原则有哪些？答：（1）两个同号相近的数相减（或异号相近的数相减），会丧失有效数字，扩大相对误差，应该尽量避免。

（2分）（2）很小的数做分母（或乘法中的大因子）会严重扩大误差，应该尽量避免。

（3分）（3）几个数相加减时，为了减少误差，应该按照绝对值由大到小的顺序进行。

（4分）（4）采用稳定的算法。

（5分）2．求解线性方程组的高斯消元法为什么要选主元？哪些特殊的线性方程组不用选主元？答：（1）若出现小主元，将会严重扩大误差，使计算失真，所以高斯消元法选主元。

（3分）（2）当系数矩阵是对称正定矩阵时，高斯消元法不用选主元。

（4分）（3）当系数矩阵是严格对角占优或不可约对角占优时，高斯消元法不用选主元。

（5分）3．求解非线性方程的Newton 迭代法的收敛性如何？答：（1） Newton 迭代法是局部收敛的，即当初值充分靠近根时，迭代是收敛的。

（2分）（2）用Newton 迭代法求方程0)(=x f 的单根时，其收敛至少是平方收敛，若求重根，则只有线性收敛。

（5分）4．Newton-Cotes 积分公式的稳定性怎么样？答：（1）Newton-Cotes 积分公式当7≤n 时，Cotes 系数都为小于1的正数，因此是稳定的。

（3分）（2）当8>n 时，出现了绝对值大于1的Cotes 系数，因此是不稳定。

（5分）二、(10分) 证明函数)(x f 关于点k x x x ,...,,10的k 阶差商],...,,[10k x x x f 可以写成对应函数值k y y y ,...,,10的线性组合，即∑==k j jjk x w y x x x f 010)('],...,,[ 其中节点))...()(()(10k x x x x x x x w ---=。

2012数值分析试卷答案

##理工大学2012级硕士研究生试卷科目：数值分析考试时间：出题教师：集体考生__专业：__予计分；可带计算器.一、填空题〔每空2分,共40分〕1．设*0.231x =是真值0.228x =的近似值,则*x 有位有效数字,*x 的相对误差限为.2．设133)(47+++=x x x x f ,则=]2,,2,2[710 f ,=]2,,2,2[810 f . 3. 过点)0,2(),0,1(-和)3,1(的二次拉格朗日插值函数为)(2x L =, 并计算=)0(2L . 4．设32()3245f x x x x =+-+在[]1,1-上的最佳二次逼近多项式为,最佳二次平方逼近多项式为. 5．高斯求积公式)()()(11010x f Ax f A dx x f x +≈⎰的系数0A =,1A =,节点0x =,1x =.6．方程组b Ax =,,U L D A --=建立迭代公式f Bx xk k +=+)()1(,写出雅可比迭代法和高斯-赛德尔迭代法的迭代矩阵,=Jacobi B ,=-Seidel Gauss B .7．00100A ⎤⎥⎥=⎢⎥⎢⎥,其条件数2()Cond A =.8．设⎥⎦⎤⎢⎣⎡=2113A ,计算矩阵A 的X 数,1||||A = , 2||||A = .9．求方程()x f x =根的牛顿迭代格式是.10．对矩阵⎪⎪⎪⎭⎫ ⎝⎛=513252321A 作LU 分解,其L=________________, U= __________________.二、计算题〔每题10分,共50分〕1. 求一个次数不高于4次的多项式P <x >,使它满足:1)1(,0)0(,0)0('===p p p ,1)1(,'=p,1)2(=p 并写出其余项表达式〔要求有推导过程〕.2. 若用复合梯形公式计算积分dx e x ⎰1,问区间[0, 1]应分成多少等分才能使截断误差不超过51021-⨯? 若改用复合辛普森公式,要达到同样的精度区间[0, 1]应该分成多少等份? 由下表数据,用复合辛普森公式计算该积分的近似值.3. 线性方程组b Ax =,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=18.04.08.014.04.04.01A ,T b ]3,2,1[=,〔1〕建立雅可比迭代法和高斯-赛德尔迭代法的分量形式.〔2〕问雅可比迭代法和高斯-赛德尔迭代法都收敛吗?4. 已知如下实验数据4,,1,0),,( =i y x i i , 用最小二乘法求形如x a a y 10+=的经验公式,并计算最小二乘法的误差.5.用改进的欧拉公式<预估-校正方法>,解初值问题0)0(,10022=+=y y x dx,取步长,1.0=h 计算到2.0=x〔保留到小数点后四位〕.三、证明题〔共10分〕1．如果 A 是对称正定矩阵,则A 可唯一地写成T LL A =,其中L 是具有正对角元的下三角阵.##理工大学2012级硕士研究生试卷答案一填空题〔每空2分,共40分〕1. 2 0.025或0.02162. 3 03. )2)(1(23-+-x x ,34. 2754x x -+2119255x x -+ 5. 0.28 0.39 0.29 0.826. U L D H U L D H S G J 11)(),(----=+=7. 18. | A ||1 = 3_,2316299||||2++=A9. 1()1'()k k k k k x f x x x f x +-=--10. ⎪⎪⎪⎭⎫ ⎝⎛-=153012001L ,⎪⎪⎪⎭⎫ ⎝⎛--=2400410321U二、计算题〔每空10分,共50分〕1．求一个次数不高于4次的多项式P <x >,使它满足:P <0> =0,P’<0> =0,P <1> =1,P’<1>=1,P <2> =1,并写出其余项表达式.解：由题意P <x > = x 2<ax 2 + b x + c >,由插值条件得方程组求解,得 a =1/4,b= – 3/2 ,c =9/4.所以插值余项为)2()1()(!51)(22)5(--=x x x f x R ξ2．若用复合梯形公式计算积分dx e x ⎰1,问区间[0, 1]应分成多少等分才能使截断误差不超过51021-⨯？若改用复合辛普森公式,要达到同样的精度区间[0, 1]应该分成多少等分？由下表数据用复合辛普森公式计算该积分.解：由于xe xf =)(,则x e x fx f ==)()()4(''在区间[0,1]上为单调增函数,b-a=1,设区间分成n 等分,则h=1/n., 故对复合梯形公式,要求≤--=|)(12|)(''2ηf h a b f R T 521021)1(121-⨯≤e n ,)1,0(∈η 即52106⨯≥en ,85.212≥n ,因此n=213,即将区间[0,1]分成213等分时,用复合梯形计算,截断误差不超过51021-⨯.若用复合辛普森公式,则要求≤⎪⎭⎫ ⎝⎛--=|)(2180|)(()42ηf h a b f R S 5441021)1(21801-⨯≤⨯e n,)1,0(∈η4410144⨯≥en ,7066.3≥n ,因此n=4,即将区间[0,1]分成8等分时,用复合梯形计算,截断误差不超过51021-⨯.3. 线性方程组b Ax =,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=18.04.08.014.04.04.01A ,Tb ]3,2,1[=,〔1〕建立Jacobi 迭代法和Gauss-Seidel 迭代法的分量形式.〔2〕问Jacobi 迭代和Gausse-Seidel 迭代法都熟收敛吗？解：（1） Jacobi 迭代法的分量形式⎪⎩⎪⎨⎧=--=--=--=+++ ,2,1,0,)8.04.03()8.04.02()4.04.01()(2)(1)1(3)(3)(1)1(2)(3)(2)1(1k x x x x x x x x x k k k k k k k k k ,)0(x 为任意初始值. Gauss-Seidel 迭代法的分量形式⎪⎩⎪⎨⎧=--=--=--=++++++ ,2,1,0,)8.04.03()8.04.02()4.04.01()1(2)1(1)1(3)(3)1(1)1(2)(3)(2)1(1k x x x x x x x x x k k k k k k k k k ,)0(x 为任意初始值. <2>Jacobi 迭代法的迭代矩阵10928203.1)(>=J B ρ,故Jacobi 迭代法不收敛.Gauss-Seidel 迭代法的迭代矩阵18.0)(<=-S G B ρ,故G-S 迭代法收敛.4. 已知实验数据5,,2,1),,( =k y x k k ,如下表,用最小二乘法求形如x a a y 10+=的经解：令x a a x S 101)(+= 故由法方程得线性方程组解得25.1,45.210==a a 于是所求拟合曲线为 2-X 数的误差5.用改进的欧拉公式〔预估-校正方法〕解初值问题0)0(,10022=+=y y x dxdy,h 为步长,〔1〕取步长,1.0=h 计算到2.0=x 〔保留到小数点后四位〕. 解：〔1〕由改进的欧拉公式因为,1.0=h 00=y ,22100),(y x y x f += 所以2.0,1.0,0210===x x x=+=),(0001y x hf y y 0,),(),([2110001y x f y x f hy y ++==0.0005=+=),(1112y x hf y y 0.0015)],(),([2|221112.02y x f y x f hy y x ++===0.0030三、证明题〔共10分〕1、证明：如果 A 是对称正定矩阵,则A 可唯一地写成T LL A =,其中L 是具有正对角元的下三角阵.法一：因为A 对称正定,A 的所有顺序主子式不为零. A 有唯一的Doolittle 分解其中D 为对角阵,0U 为单位上三角矩阵. 又因为A 是对角正定矩阵T A A DU L ==0=TTL D U 0由分解的唯一性TU L 0=,代入分解式子又A 对称正定知道2121221122112211D D u u u u u u u u u D nn nn nn =⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=所以TTLL D L D L A ==)(2121,其中21D L 为对角元为正的下三角矩阵.。