等差与等比数列专题复习
等差数列与等比数列专题辅导(小编推荐)

等差数列与等比数列专题辅导(小编推荐)第一篇:等差数列与等比数列专题辅导(小编推荐)等差数列与等比数列专题辅导(1)在等差数列{an}中, a7=9, a13=-2, 则a25=()A-22B-24C60D64(2)在等比数列{an}中, 存在正整数m, 有am=3,am+5=24, 则am+15=()A864B1176C1440D1536(3)已知等差数列{an}的公差为2,若a1,a3,a4成等比数列, 则a2=()A–4B–6C–8D–10(4)设数列{an}是等差数列,且a2=-6,a8=6,Sn是数列{an}的前n 项和,则()AS4>S3BS4=S2CS6(5)已知由正数组成的等比数列{an}中,公比q=2, a1·a2·a3·…·a30=245, 则a1·a4·a7·…·a28=5101520A 2B2C2D2(6)若{an}是等差数列,首项a1>0,a2003+a2004>0,a2003.a2004<0,则使前n项和Sn>0成立的最大自然数n是:()A.4005B.4006C.4007D.4008(7)在等比数列{an}中, a1<0, 若对正整数n都有anAq>1B0a1(3n-1)(8)设数列{an}的前n项和为Sn,Sn=(对于所有n≥1),且a4=54,则a1=__________.2(9)等差数列{an}的前m项和为30, 前2m项和为100, 则它的前3m项和为_________.(10)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列{an}是等和数列, 且a1=2, 公和为5,那么a18的值为_______,这个数列的前21项和S21的值为.(11)已知等差数列{an}共2n+1项, 其中奇数项之和为290, 偶数项之和为261,求第n+1项及项数2n+1的值.(12)设{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110且a1,a2,a4成等比数列.(Ⅰ)证明a1=d;(Ⅱ)求公差d的值和数列{an}的通项公式.(13)已知等比数列{an}的各项都是正数, Sn=80, S2n=6560, 且在前n项中, 最大的项为54, 求n的值.(14)ΔOBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2), 设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n, Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn), an=(Ⅰ)求a1,a2,a3及an;(Ⅱ)证明yn+4=1-(Ⅲ)若记bn=y4n+41yn+yn+1+yn+2.2yn,n∈N*;4-y4n,n∈N*,证明{bn}是等比数列.答案:1-7 BDBDA BB8.29.21010.3, 5211.29, 1912.(2)d=2 an=2n13.n=414.(1)an=2(2)(3)证明略第二篇:等差数列与等比数列等差数列与等比数列⎧>0,递增数列⎪一、等差数列的定义:an+1-an=d(d:公差)(常数)⎨=0,常数列,⎪<0,递减数列⎩1.证明数列{an}为等差数列:(1)定义:an+1-an=d(常数)(2)等差中项:2an+1=an+an+2注:(1)不可用a2-a1=a3-a2=a4-a3=Λ=“常数”证(2)a1=⎨例1.(1)已知数列{an}为等差数列,求证:数列{an+an+1}为等差数列;变式:①已知数列{an}为等差数列,求证:数列{an+t}(t为常数)为等差数列;②已知数列{an}为等差数列,求证:数列{tan}(t为常数)为等差数列;③已知数列{an}、{bn}均为等差数列,求证:数列{an+bn}为等差数列(2)已知数列{an}的前n项和为Sn,且Sn=n2,求证:数列{an}为等差数列;变式:①已知数列{an}的前n项和为Sn,且Sn=n2+1,求:an②已知数列{an}的前n项和为Sn,且Sn=an2+bn,求:an ③已知数列{an}的前n项和为Sn,且Sn=an2+bn+c,求:an(3)已知数列{an}满足:a1=1,an+1=数列;(4)已知数列{an},a1=1,an+1=为等差数列(5)设数列{an}的前n项和为Sn,求证:数列{an}为等差数列的充要条件是{an}为等差数列⎧S1,n=1⎩Sn-Sn-1,n≥2an1,且bn=,求证:数列{bn}为等差an+1ann1an+,且bn=nan,求证:数列{bn}n+1n+1Sn=n(a1+an)22.证明数列{an}为单调数列:an+1-an=f(n)⎨⎧>0,递增数列递减数列⎩<0,注:(1)求数列{an}中an的极值也可采用此方法(2)已知数列{an}为等差数列ⅰ.若a1<0,d>0,则Sn有最小值;解法:①令an≤0{bn}②Snⅱ.若a1>0,d<0,则Sn有最大值;解法:①令an≥0②Sn例2.已知an=(11-2n)2n,求数列{an}的最大项例3.(1)已知等差数列{an}的前n项和为Sn,且an=10-2n,求Sn的最大值;(2)已知等差数列{an}的前n项和为Sn,且an=2n-13,求Sn的最小值;3.叠加法:已知a1=a,an+1-an=f(n),求an例4.(1)已知数列{an}为等差数列,首项为a1,公差为d,求an;(2)已知数列{an},a1=1,an+1=4.通项公式:an=a1+(n-1)d(1)an=am+(n-m)d(2)an是关于n的一次函数,且n的系数为公差d.例5.已知数列{an}为等差数列,a5=-3,a9=13,求an5.等差中项:若a、b、c成等差数列,则b=(1)若数列{an}为等差数列,则2an+1n+11an+,求an nna+c称为a、c的等差中项2=an+an+2;(2)若已知三个数成等差数列,且其和为定值,则可设这三个数为a-d、a、a+d;(3)若数列{an}为等差数列,且公差d≠0,则am+an=ap+aq⇔m+n=p+q(4)在有穷等差数列{an}中,与首尾两项距离相等的两项的和等于首尾两项的和.即:a1+an=a2+an-1=a3+an-2=Λ=ak+an-k+1例6.(1)已知:等差数列中连续三项的和为21,平方和为179,求这三项(2)在3与19之间插入3个数后成等差数列,求这三个数(3)已知:a、b、c成等差数列求证:①b+c、a+c、a+b成等差数列;②a(b+c)、b(a+c)、c(a+b)成等差数列;③a-bc、b-ac、c-ab 成等差数列(4)已知:a、b、c成等差数列,求证:2222111成等差数列 b+ca+ca+blg(a-c)、lg(a+c-2b)成等差(5)已知:成等差数列,求证:lg(a+c)、数列(6)若方程a(b-c)xb(c-a)x+c(a-b)=0有相等实根,求证:成等差111abc111abc数列例7.在等差数列{an}中,(1)若a5+a10=12,求S14;(2)若a8=m,求S15;(3)若a4+a6+a15+a17=50,求S20;(4)若a2+a4=18,a3+a5=32,求S6;(5)若a2+a5+a12+a15=36,求S16;(6)若a3+a4+a5+a6+a7=450,求a2+a8(7)若等差数列{an}的各项都是负数,且a32+a82+2a3⋅a8=9,则其前10项和S10= ____________(8)在等差数列{an}中,若a3+a15=a5+an,则n=_______6.数列{an}的前n项和Sn=注:(1)倒序法求和;(2)等差数列{an}的前n项和Sn是关于自然数n的二次函数,且n的系数为n(a1+an)n(n-1)n(n-1)=na1+d=nan-d 222d,2常数项为零,即:Sn=An2+Bn(当A=0时数列{an}为常数列);(3)①S2n-1=(2n-1)an(可以将项与和之间进行相互转化)。
高考数学复习:等差数列与等比数列

Sn=an2+bn(a,b为 常数)
Sn=kqn-k(k≠0,q≠0,1)
证明数列为等差(比)数列一般使用定义法.
例3 (2019·全国Ⅱ)已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an- bn+4,4bn+1=3bn-an-4. (1)证明:{an+bn}是等比数列,{an-bn}是等差数列;
(2)已知函数 f(x)=1+2 x2(x∈R),若等比数列{an}满足 a1a2 020=1,则 f(a1)
+f(a2)+f(a3)+…+f(a2 020)等于
√A.1 D.2
解析 ∵a1a2 020=1,
∴f(a1)+f(a2 020)=1+2 a21+1+2a22 ∵{an}为等比数列,
a3+a4=2,则a6+a7+a8等于
A.12
B.24
√ C.30
D.32
解析 设等比数列{an}的公比为q, 则 q=aa21++aa32++aa43=21=2,
所以a6+a7+a8=(a1+a2+a3)·q5=1×25=32.
(2)已知正项等比数列{an}的前n项和为Sn,且S10=10,S30=130,则S40等于
∴an=2×2n-1=2n. 又∵ak+1+ak+2+…+ak+10=215-25,
∴2k+111--2210=215-25,
即2k+1(210-1)=25(210-1),
∴2k+1=25,∴k+1=5,∴k=4.
(2)(多选)(2020·威海模拟)等差数列{an}的前n项和记为Sn,若a1>0,S10=
证明 由题设得4(an+1+bn+1)=2(an+bn),
即 an+1+bn+1=12(an+bn). 因为a1+b1=1, 所以{an+bn}是首项为 1,公比为12的等比数列. 由题设得4(an+1-bn+1)=4(an-bn)+8, 即an+1-bn+1=an-bn+2. 又a1-b1=1, 所以{an-bn}是首项为1,公差为2的等差数列.
等差数列与等比数列复习

[前15项]
5.等差数列 4, 8, 12, 16 … 的前多少
项和是480? 解:
a1 4, d 8 4 4, Sn 480
n( n 1) 则由公式得到: 4n 4 480 2
n n 240 0
2
解得: n1 15, n2 16 (舍去)
2 3 4
1 1 1 1 , , , , 2 4 8 16
1 公比 q= 递减数列 2
5,5,5,5,5,5,… 1,-1,1,-1,1,…
公比 q=1 非零常数列 公 比q= -1 摆动数列
定义:如果一个数列从第2项起,每一项与它的前一项的比等 于同一个常数(指与n无关的数),这个数列就叫做等比数列, 这个常数叫做等比数列的公比,公比通常用字母q表示。
(a1 an ) (a1 an ) (a1 an )
n(a1 an )
n(a1 an ) Sn 2
(2).如果已知等差数列的首项为a1,公差为d, 项数为n,把an=a1+(n-1)d代入
Sn
n( a 1 a n ) 2
可得到等差数列前n项和的另一个公式。
等差数列 定 义 数 学 表 达 式 通项公 式证明 通 项 公 式
等比数列
等比数列用“比”代替了等差数列中的 “差”
常数
an q(q 0) an 1
an-an-1=d
(n≥2)
减—除 加—乘
迭加法
迭乘法
加-乘
an a1 (n 1)d
an a1 qn1 (a1 q 0)
3
由此可知,等比数列
a
n
a5 a4 q a1 q 4
等差数列与等比数列(题型归纳)

等差数列与等比数列【考情分析】【题型一】等差、等比数列基本运算【题组练透】1.(山东省淄博市2021届高三二模数学试题)已知{}n a 为等比数列,n S 为其前n 项和,若32342S a a a =++,则公比q =().A .12B .12-C .1D .2【答案】D 【解析】因为32342S a a a =++,所以()3412232a a a a a a ++=++,即41232a a a a ++=,因为10a ≠,所以232q q q ++=,即()()2210q q q -++=,因为210q q ++≠,所以q =2.故选:D2.我国明代数学家程大位的《算法统宗》中有这样一个问题:今有钞二百三十八贯,令五等人从上作互和减半分之,只云戊不及甲三十三贯六百文,问:各该钞若干?其意思是:现有钱238贯,采用等差数列的方法依次分给甲、乙、丙、丁、戊五个人,现在只知道戊所得钱比甲少33贯600文(1贯=1000文),问各人各得钱多少?在这个问题中,戊所得钱数为()A .30.8贯B .39.2贯C .47.6贯D .64.4贯【答案】A【继续】依次记甲、乙、丙、丁、戊五个人所得钱数为a 1,a 2,a 3,a 4,a 5,由数列{a n }为等差数列,可记公差为d ,依题意得:()123451155223833.6a a a a a a d a a ⎧++++=+=⎨-=⎩,解得a 1=64.4,d =﹣8.4,所以a 5=64.4﹣33.6=30.8,即戊所得钱数为30.8贯.故选:A.3.(2021·武汉市第一中学高三二模)等差数列{a n }的前n 项和记为S n ,若a 1>0,S 10=S 20,则()A .d <0B .a 16<0C .S n ≤S 15D .当且仅当S n <0时n ≥32【答案】ABC【解析】设等差数列{a n }的公差为d ,∵S 10=S 20,∴10a 1+45d =20a 1+190d ,∴2a 1+29d =0,∵a 1>0,∴d <0,故A 正确;∴a 1+14d +a 1+15d =0,即a 15+a 16=0,∵d <0,∴a 15>a 16,∴a 15>0,a 16<0,故B 正确;∴S n ≤S 15,故C 正确;又131311631()3102a a S a +==<,130********()15()02a a S a a +==+=,∴当且仅当S n <0时,n ≥31,故D 错误.故选:ABC .4.(2021·湖南长沙市·高三其他模拟)已知等比数列{}n a 中,22a =,514a =,则满足12231212n n a a a a a a +++⋅⋅⋅+≤成立的最大正整数n 的值为______.【答案】3【解析】已知{}n a 为等比数列,设其公比为q ,由352a a q =⋅得,3124q ⋅=,318q =,解得12q =,又22a =.∴14a =.因为21211==4n n n n a a q a a +++,所以数列{}1n n a a +也是等比数列,其首项为128a a =,公比为14.∴()1223132211432nn n a a a a a a -+++⋅⋅⋅+=-≤,从而有11464n⎛⎫≥ ⎪⎝⎭.∴3n ≤.故max 3n =.故答案为:3.【提分秘籍】1.在等差(比)数列中,a 1,d(q),n,a n ,S n 五个量中知道其中任意三个,就可以求出其他两个.解这类问题时,一般是转化为首项a 1和公差d(公比q)这两个基本量的有关运算.2.对于等比数列的前n 项和公式,应按照公比q 与1的关系分类讨论,一般地,若涉及n 较小的等比数列前n 项和问题,为防止遗忘分类讨论,可直接利用通项公式写出,而不必使用前n 项和公式.【题型二】等差、等比数列的性质【题组练透】1.(2021·陕西西安市·西北工业大学附属中学高三其他模拟(文))等比数列{}n a 的各项均为正数,且154a a =,则2122232425log log log log log a a a a a ++++=()A .10B .5C .8D .4【答案】B 【分析】应用等比数列等比中项的性质可得32a =,运用对数的运算性质可得原式为235log a ,代入3a 可计算结果.【详解】解:因为154a a =,且0n a >,则有32a =521222324252323log log log log log log 5log 5a a a a a a a ++++===.故选:B.2.(2021·山东青岛市·高三三模)行列式是近代数学中研究线性方程的有力工具,其中最简单的二阶行列式的运算定义如下:1112112221122122a a a a a a a a =-,已知n S 是等差数列{}n a 的前n 项和,若()7911001a a -=,则15S =()A .152B .45C .75D .150【答案】C 【分析】先由行列式的定义化简,再根据等差数列的前n 项和公式求和即可.【详解】由行列式的定义有9711(10)0a a ⨯-⨯-=,即1875a d a +==,所以11581515()1527522a a a S +⨯===.故选:C.3.(2021·广东潮州市·高三二模)已知数列{}n a 满足()*,01nn a n k n N k =⋅∈<<,下列命题正确的有()A .当12k =时,数列{}n a 为递减数列B .当45k =时,数列{}n a 一定有最大项C .当102k <<时,数列{}n a 为递减数列D .当1kk-为正整数时,数列{}n a 必有两项相等的最大项【答案】BCD 【分析】分别代入12k =和45k =计算判断AB 选项;再利用放缩法计算判断C 选项;设1=-k n k ,则1=+k nn ,所以化简得11n na a +=,可知数列{}n a 为常数数列,可判断D ;【详解】当12k=时,1212a a==,知A错误;当45k=时,1415nna na n++=⋅,当4n<,11nnaa+>,4n>,11nnaa+<,所以可判断{}n a一定有最大项,B正确;当12k<<时,11112nna n nka n n+++=<≤,所以数列{}n a为递减数列,C正确;当1kk-为正整数时,其值不妨取为n,则1=+k nn,所以11111+++==⋅=+nna n n nka n n n,可知数列{}n a为常数数列,D正确;故选:BCD.4.已知数列{a n}为等差数列,若a2+a8=23π,则tan(a3+a7)的值为A .33B .-33CD【解析】∵数列{a n}为等差数列,∴a3+a7=a2+a8=23π.∴tan(a3+a7)=tan 2 3π【提分秘籍】1.利用等差(等比)数列的性质求解的关键是抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.2.活用函数的性质:数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的这些性质解题.【题型三】等差、等比数列的判断与证明【典例分析】【典例】若数列{a n }的前n 项和为S n ,且满足a n +2S n S n -1=0(n ≥2),a 1=12.(1)求证:}1{nS 成等差数列;(2)求数列{a n }的通项公式.(1)证明当n ≥2时,由a n +2S n S n -1=0,得S n -S n -1=-2S n S n -1,所以1S n -1S n -1=2,又1S 1=1a 1=2,故}1{nS 是首项为2,公差为2的等差数列.(2)由(1)可得1S n =2n ,∴S n =12n .当n ≥2时,a n =S n -S n -1=12n -12(n -1)=n -1-n 2n (n -1)=-12n (n -1).当n =1时,a 1=12不适合上式.故a n n =1,-12n (n -1),n ≥2.【变式探究1】本例条件不变,判断数列{a n }是否为等差数列,并说明理由.【解析】因为a n =S n -S n -1(n ≥2),a n +2S n S n -1=0,所以S n -S n -1+2S n S n -1=0(n ≥2).所以1S n -1S n -1=2(n ≥2).又1S 1=1a 1=2,所以}1{nS 是以2为首项,2为公差的等差数列.所以1S n =2+(n -1)×2=2n ,故S n =12n.所以当n ≥2时,a n =S n -S n -1=12n -12(n -1)=-12n (n -1),所以a n +1=-12n (n +1),又a n +1-a n =-12n (n +1)--12n (n -1)=-12n }1111{--+n n =1n (n -1)(n +1).所以当n ≥2时,a n +1-a n 的值不是一个与n 无关的常数,故数列{a n }不是一个等差数列.【变式探究2】本例中,若将条件变为a 1=35,na n +1=(n +1)a n +n (n +1),试求数列{a n }的通项公式.【解析】由已知可得a n +1n +1=a n n +1,即a n +1n +1-a nn=1,又a 1=35,∴}{na n 是以a 11=35为首项,1为公差的等差数列,∴a n n =35+(n -1)·1=n -25,∴a n =n 2-25n .【提分秘籍】1.常见的判定等差数列的方法(1)定义法:对于数列{a n },若a n+1-a n =d(n ∈N *)(d 为常数),则数列{a n }是等差数列;(2)等差中项法:对于数列{a n },若2a n+1=a n +a n+2(n ∈N *),则数列{a n }是等差数列.2.常见的判定等比数列的方法(1)定义法:若n n a a 1+=q(q≠0,n ∈N *)或1-n n a a=q(q≠0,n≥2,n ∈N *),则数列{a n }是等比数列;(2)等比中项法:若数列{a n }中,a n ≠0且21-n a =a n ·a n-2(n≥3,n ∈N *),则数列{a n }是等比数列.注意:如果要证明一个数列是等差(等比)数列,则必须用定义法或等差(等比)中项法.判断时易忽视定义中从第2项起,以后每项与前一项的差(比)是同一常数,即易忽视验证a 2-a 1=d(12a a =q)这一关键条件【变式演练】1.(2021·广东省级名校联考)已知S n 是数列{a n }的前n 项和,且满足S n -2a n =n -4.(1)证明:{S n -n +2}为等比数列;(2)求数列{S n }的前n 项和T n .(1)证明因为a n =S n -S n -1(n ≥2),所以S n -2(S n -S n -1)=n -4(n ≥2),则S n =2S n -1-n +4(n ≥2),所以S n -n +2=2[S n -1-(n -1)+2](n ≥2),又由题意知a 1-2a 1=-3,所以a 1=3,则S 1-1+2=4,所以{S n -n +2}是首项为4,公比为2等比数列.(2)由(1)知S n -n +2=2n +1,所以S n =2n +1+n -2,于是T n =(22+23+…+2n +1)+(1+2+…+n )-2n=4(1-2n )1-2+n (n +1)2-2n =2n +3+n 2-3n -82.1.(2021·山西阳泉市·高三三模(文))在正项等比数列{}n a 中,34a a m +=,1314a a n +=,则2324a a +的值为()A .nmB .22n m C .2n mD .2n m 【答案】C 【分析】利用广义通项公式计算,可得10nq m=,即可得到答案;【详解】10101010131434n a a a q a q q m n q m+=+=⋅=⇒=,∴()14210232413n n a a a a q n m m+=+⋅=⋅=,故选:C.2.(2021·宁波市北仑中学高三其他模拟)设n S 是某个等差数列的前n 项和,若201920202020S S ==,则2021S =()A .220202019-B .220202019+C .120201010-D .120201010+【答案】A 【分析】由题设易得12019a d =-且20212020S S d =+,利用等差数列前n 项和公式,由20192020S =求d ,即可求2021S .【详解】由题意知:20200a =即12019a d =-,且20212020S S d =+,∴201912019201820192019(1010)20202S a d d ⨯=+=⨯-=,故22019d =-,∴2021220202019S =-.故选:A3.(2021·济南市·山东省实验中学高三二模)已知等差数列{}n a 的项数为奇数,其中所有奇数项之和为319,所有偶数项之和为290,则该数列的中间项为()A .28B .29C .30D .31【答案】B 【分析】本题可设等差数列{}n a 共有21n +项,然后通过S S -奇偶即可得出结果.【详解】设等差数列{}n a 共有21n +项,则13521n S a a a a +=++++ 奇,2462n S a a a a =++++ 偶,中间项为1n a +,故()()()13254212n nS S a a a a a a a +-=+-+-++- 奇偶111n a d d d a nd a +=++++=+= ,131929029n a S S +=-=-=奇偶,故选:B.4.(2021·安徽马鞍山市·高三三模(文))在天然气和煤气还未普及时,农民通常会用水稻秸秆作为生火做饭的材料.每年水稻收割结束之后,农民们都会把水稻秸秆收集起来,然后堆成如图的草堆,供生火做饭使用.通常他们堆草堆的时候都是先把秸秆先捆成一捆一捆的,然后堆成下面近似成一个圆柱体,上面近似成一个圆锥体的形状.假设圆柱体堆了7层,每层所用的小捆草数量相同,上面收小时,每层小捆草数量是下一层的12倍.若共用255捆,最上一层只有一捆,则草堆自上往下共有几层()A .13B .12C .11D .10【答案】B 【分析】由题可知,上面的圆锥每层的数量是以1为首项,2为公比的等比数列;设草堆自上往下共有x 层,则圆锥有()7x -层,依题意列关系式.【详解】设草堆自上往下共有x 层,则圆锥有()7x -层,由题可知,上面的圆锥每层的数量是以1为首项,2为公比的等比数列,则287122272255x x --+++++⨯= ,()771127225512x x --⨯-+⨯=-,解得:12x =∴草堆自上往下共有12层.故选:B.【点睛】知识点点睛:等比数列前n 项和()111n n a q S q-=-.5.(2021·全国高三其他模拟)已知数列{}n a 满足12a =,()11312,n n n n a a a a n n N *--+=-≥∈,若123nn Ta a a a =⋅⋅⋅,当10n T >时,n 的最小值为()A .3B .5C .6D .7【答案】C 【分析】将已知递推关系式变形可得1111112n n a a --=--,由此可知数列11n a ⎧⎫⎨⎬-⎩⎭为等差数列,由等差数列通项公式可取得11n a -,进而得到n a ;由123n n T a a a a =⋅⋅⋅可上下相消求得n T ,结合n *∈N 解不等式可求得n 的最小值.【详解】由1131n n n n a a a a --+=-得:11311n n n a a a ---=+,()11111121312211111n n n n n n n a a a a a a a ---------∴-=-==+++,()()111111121111212112n n n n n n a a a a a a -----+-+∴===+----,即1111112n n a a --=--,∴数列11n a ⎧⎫⎨⎬-⎩⎭是以1111a =-为首项,12为公差的等差数列,()11111122n n n a +∴=+-=-,则31n n a n +=+,()()123234562323416n n n n n n T a a a a n n ++++=⋅⋅⋅=⨯⨯⨯⋅⋅⋅⨯⨯=+∴,由10n T >得:()()23106n n ++>,又n *∈N ,6n ∴≥且n *∈N ,n ∴的最小值为6.故选:C.【点睛】关键点点睛:本题考查数列中的不等式的求解问题,解题关键是能够根据已知的递推关系式,构造出全新的等差数列,利用等差数列通项公式求得通项后,即可确定n a .6.(2021·四川内江市·高三一模(理))若数列{}n a 满足1120n na a +-=,则称{}n a 为“梦想数列”,已知正项数列1nb ⎧⎫⎨⎬⎩⎭为“梦想数列”,且1231b b b ++=,则678b b b ++=()A .4B .8C .16D .32【答案】D 【分析】利用等比数列的定义可推导出“梦想数列”{}n a 是公比为12的等比数列,进而结合题意可知数列{}n b 是公比为2的等比数列,由此可得()56781232b b b b b b ++=++,即可得解.【详解】由题意可知,若数列{}n a 为“梦想数列”,则1120n n a a +-=,可得112n n a a +=,所以,“梦想数列”{}n a 是公比为12的等比数列,若正项数列1n b ⎧⎫⎨⎬⎩⎭为“梦想数列”,则1112n n b b +=,所以,12n n b b +=,即正项数列{}n b 是公比为2的等比数列,因为1231b b b ++=,因此,()5678123232b b b b b b ++=++=.故选:D.【点睛】关键点点睛:本题考查数列的新定义“梦想数列”,解题的关键就是紧扣新定义,本题中,“梦想数列”就是公比为12的等比数列,解题要将这种定义应用到数列1n b ⎧⎫⎨⎬⎩⎭中,推导出数列{}n b 为等比数列,然后利用等比数列基本量法求解.7.(2021·全国高三其他模拟)已知n S 为等差数列{}n a 的前n 项和,且220a =,798S =,则()A .1534a a +=B .89a a <C .9n S S ≤D .满足0nS <的n 的最小值为17【答案】AD 【分析】先由等差数列的性质及798S =求得414a =,结合220a =及等差数列的性质即可判断选项A ;由选项A 得到数列{}n a 的公差,进而得到等差数列{}n a 的通项公式,然后求出8a ,9a 的值,结合{}n a 的增减性即可判断选项B ,C ;由等差数列的性质及8a ,9a 易得到16S ,17S 的值,结合{}n a 的增减性即可判断选项D .【详解】因为()177477982a a S a +===,所以414a =.又220a =,所以152434a a a a +=+=,A 选项正确;设等差数列{}n a 的公差为d ,由4226a a d -==-,解得3d =-,所以()()223263n a a n n =+-⨯-=-.826382a =-⨯=,926391a =-⨯=-.所以89a a >,B 选项不正确;由3d =-知数列{}n a 为递减数列,又820a =>,910a =-<.所以8S 为n S 的最大值,C 选项不正确;因为()()1161689168802a a S a a +==+=>,()11717917171702a a S a +==⨯=-<.所以满足0n S <的n 的最小值为17,D 选项正确.故选AD .【点睛】结论点睛:在处理等差数列及其前n 项和问题时,通常会用到如下的一些性质结论;1.通项性质:若m +n =p +q =2k (m ,n ,p ,q ,k ∈N *),则有a m +a n =a p +a q =2a k .2.前n 项和的性质:(1)S m ,S 2m -S m ,S 3m -S 2m ,…成等差数列(2)S 2n -1=(2n -1)a n .8.(2021·全国(文))《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).关于这个问题,下列说法正确的是()A .甲得钱是戊得钱的2倍B .乙得钱比丁得钱多12钱C .甲、丙得钱的和是乙得钱的2倍D .丁、戊得钱的和比甲得钱多13钱【答案】AC 【分析】由等差数列的性质,可设甲、乙、丙、丁、戊所得钱分别为2a d -,a d -,a ,a d +,2a d +,结合已知求a ,d ,即可得甲、乙、丙、丁、戊所得钱,进而判断选项的正误.【详解】依题意,设甲、乙、丙、丁、戊所得钱分别为2a d -,a d -,a ,a d +,2a d +,且22a d a d a a d a d -+-=++++,即6a d =-,又2255a d a d a a d a d a -+-+++++==,∴1a =,16d =-,即1421263a d ⎛⎫-=-⨯-= ⎪⎝⎭,17166a d ⎛⎫-=--= ⎪⎝⎭,15166a d ⎛⎫+=+-= ⎪⎝⎭,1221263a d ⎛⎫+=+⨯-= ⎪⎝⎭,∴甲得43钱,乙得76钱,丙得1钱,丁得56钱,戊得23钱,则有如下结论:甲得钱是戊得钱的2倍,故A 正确;乙得钱比丁得钱多751663-=钱,故B 错误;甲、丙得钱的和是乙得钱的413276+=倍,故C 正确;丁、戊得钱的和比甲得钱多52416336+-=钱,故D 错误.故选:AC .9.(2021·全国高二专题练习)数列{}n a 为等比数列,公比q >1,其前n 项和为S n ,若a 5﹣a 1=15,2416a a ⋅=,则下列说法正确的是()A .S n +1=2S n +1B .a n =2nC .数列{log 3(S n +1)}是等比数列D .对任意的正整数k (k 为常数),数列{log 2(S n +k ﹣S n )}是公差为1的等差数列【答案】AD 【分析】根据条件可求出12n n a -=,21nn S =-,然后逐一判断即可.【详解】因为公比为q >1,由512415,16,a a a a -=⎧⎨⋅=⎩可得41131115,16,a q a a q a q ⎧-=⎨⋅=⎩,即421154q q -=,所以4q 4﹣15q 2﹣4=0,解得q 2=4,所以112a q =⎧⎨=⎩,所以12n n a -=,()1122112n n nS ⋅-==--,所以112121n n n S S ++=-=+,S n +1=2n ,所以log 3(S n +1)=n log 32,所以数列{log 3(S n +1)}是等差数列,对任意的正整数n ,k ,S n +k ﹣S n =2n +k ﹣2n =(2k ﹣1)2n ,所以log 2(S n +k ﹣S n )=n +log 2(2k ﹣1),所以数列{log 2(S n +k ﹣S n )}是公差为1的等差数列,故选:AD10.(2021·济南市历城第二中学高二开学考试)设等差数列{}n a 的前n 项和为n S ,若20212020220212020S S -=,则数列{}n a 公差为___________.【答案】4【分析】由等差数列性质可知,112n S n a d n -=+,从而得到结果.【详解】由等差数列性质可知,112n S n a d n -=+又20212020220212020S S -=,∴2019101022d d -=,解得,4d =故答案为:411.(2021·河南高三月考(理))已知数列{}n b ,()1*12N n n b b b n +-==∈,等比数列{}n a 中,11a b =,48a b =,若数列{}n b 中去掉与数列{}n a 相同的项后余下的项按原顺序组成数列{}n c ,则{}n c 前200项的和为___________.【答案】42962【分析】根据等差数列的定义,结合等比数列的通项公式、等差数列和等比数列的前n 项和公式进行求解即可.【详解】∵12n n b b +-=,∴{}n b 为等差数列,又12b =,∴2n b n =,∴12a =,416a =,则等比数列{}n a 的公比为2=,∴2n n a =.∵208416b =,12a =,24a =,38a =,416a =,532a =,664a =,7128a =,8256a =,9512a =.∴()()1220012208128c c c b b b a a a ++⋅⋅⋅+=++⋅⋅⋅+-++⋅⋅⋅+()()82122082416212⨯-⨯+=--()920920822=⨯--42962=.故答案为:4296212.(2021·广东汕头市·高三三模)已知数列{}n a 满足()12335213nn a a a n a ++++-= ,则3a =__________,若对任意的N n *∈,()1nn a λ≥-恒成立,则λ的取值范围为_____________.【答案】185[]3,2-【分析】由1n =可求得1a 的值,令2n ≥由()12335213nn a a a n a ++++-= 可得出()1123135233n n a a a n a --++++-= ,两式作差可得出数列{}n a 的通项公式,可得出3a 的值,然后分n 为奇数和偶数两种情况讨论,分析数列{}n a 的单调性,由此可求得实数λ的取值范围.【详解】当1n =时,13a =;当2n ≥时,()()12313523213nn n a a a n a n a -++++-+-= ,可得()1123135233n n a a a n a --++++-= ,上述两式作差可得()11213323nn n n n a ---=-=⋅,即12321n n a n -⋅=-,13a =不满足12321n n a n -⋅=-,所以,13,123,221n n n a n n -=⎧⎪=⎨⋅≥⎪-⎩,则23231855a ⨯==.当2n ≥时,()()()118312323021212121n n n n n n a a n n n n -+⋅⋅-⋅⋅-=-=>+--+,即1n n a a +>,所以,数列{}n a 从第二项开始为递增数列,对任意的N n *∈,()1nn a λ≥-恒成立.①若n 为正奇数,则n a λ≥-,1351835a a a =<=<< ,则3λ-≤,可得3λ≥-;②若n 为正偶数,则n a λ≥,可得22a λ≤=.综上所述,32λ-≤≤.故答案为:185;[]3,2-.【点睛】思路点睛:已知数列{}n a 的前n 项和n S ,求通项公式n a 的步骤:(1)当1n =时,11a S =;(2)当2n ≥时,根据n S 可得出1n S -,化简得出1n n n a S S -=-;(3)如果1a 满足当2n ≥时1nn n a S S -=-的通项公式,那么数列{}n a 的通项公式为1n n n a S S -=-;如果1a 不满足当2n ≥时1n n n a S S -=-的通项公式,那么数列{}n a 的通项公式要分段表示为11,1,2n nn S n a S S n -=⎧=⎨-≥⎩.13.(2021·山东临沂市·高三二模)已知正项数列{}n a 的前n 项和为n S ,数列{}n b 为等比数列,满足21444n n S a n +=--,且1112a b =+=,44a b =.(1)求证:数列{}n a 为等差数列;(2)若从数列{}n a 中去掉数列{}n b 的项后余下的项按原来的顺序组成数列{}n c ,求123100c c c c +++⋅⋅⋅+.【答案】(1)证明见解析;(2)11302.【分析】(1)由递推公式,将n 换成1n -,与原式作差,化简,求出1a ,结合等差数列的定义可证明.(2)先求出,n n a b 的通项公式,求出数列{}n a 的前100项中,与{}n b 重合的项,然后再求和即可.【详解】(1)证明:∵21444n n S a n +=--,∴当2n ≥时,2144n n S a n -=-,所以22n n 1n4a a a 4+=--,∴()2212n n a a +=+,又0na >,所以12n n a a +=+.当1n =时,21248S a =-,即21248a a =-,又12a =,∴24a =,212a a -=适合上式,所以数列{}n a 是首项为2,公差为2的等差数列.(2)由(1)可知2n a n =,设{}n b 的公比为q ,又448b a ==,1111b a =-=,∴38q =,∴2q =,∴12n n b -=.∴11b =,212b a ==,324b a ==,448b a ==,5816b a ==,61632b a ==,73264b a ==,864128b a ==,9128256b a ==.∴()()123100123107238c c c c a a a a b b b +++⋅⋅⋅+=+++⋅⋅⋅+-++⋅⋅⋅+()()7212107221411302212-+=-=-.【点睛】关键点睛:本题考查利用递推关系证明数列为等差数列,数列求和问题,解答本题的关键是应用1111n nn S n a S S n -=⎧=⎨->⎩时,注意n 的范围,以及求和时根据条件123100c c c c +++⋅⋅⋅+()()123107238a a a a b b b =+++⋅⋅⋅+-++⋅⋅⋅+,属于中档题.14.(2021·山东枣庄市·高三二模)已知数列{}n a 中,121a a ==,且212n n n a a a ++=+.记1n n n b a a +=+,求证:(1){}n b 是等比数列;(2){}n b 的前n 项和n T 满足:3121223112n n n b b b T T T T T T ++++⋅⋅⋅+<⋅⋅⋅.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)将212n n n a a a ++=+变形为()2112n n n n a a a a ++++=+,并计算1b 的值,由此根据定义可证明{}n b 是等比数列;(2)先根据等比数列的前n 项和公式求解出n T ,然后根据1111n n n n n n n b T T T T T T ++++-=⋅⋅并采用裂项相消的方法求解出11n n n b T T ++⎧⎫⎨⋅⎩⎭的前n 项和,最后分析11n n n b T T ++⎧⎫⎨⎬⋅⎩⎭的前n 项和并完成证明.【详解】(1)证明:由212n n n a a a ++=+,得()121122n n n n n n b a a a a b ++++=+=+=,又11220b a a =+=≠,所以{}n b 是以2为首项,2为公比的等比数列.(2)由(1)知,()22222112n n n T -⨯==--.于是1111111111122121n n n n n n n n n n n b T T T T T T T T ++++++-⎛⎫==-=- ⎪⋅⋅--⎝⎭.31212231n n n b b b T T T T T T ++++⋅⋅⋅+⋅⋅⋅1223111111112212121212121n n +⎡⎤⎛⎫⎛⎫⎛⎫=-+-+⋅⋅⋅+ ⎪ ⎪ ⎪⎢⎥------⎝⎭⎝⎭⎝⎭⎣⎦1111221n +⎛⎫=- ⎪-⎝⎭.因为11021n +>-,所以3121223112n n n b b b T T T T T T ++++⋅⋅⋅+<⋅⋅⋅.。
等差数列与等比数列的知识点总结

等差数列与等比数列的知识点总结
等差数列和等比数列是数学中的两个重要概念,它们在日常生活和科学研究中有着广泛的应用。
以下是关于等差数列和等比数列的主要知识点总结:
等差数列:
1. 定义:一个数列,其中任意两个相邻项的差是一个常数,这个数列被称为等差数列。
2. 通项公式:$a_n = a_1 + (n - 1)d$,其中 $a_1$ 是首项,$d$ 是公差,$n$ 是项数。
3. 求和公式:$S_n = \frac{n}{2} [2a_1 + (n - 1)d]$,其中 $S_n$ 是前$n$ 项的和。
4. 等差中项:任意两项的算术平均值等于第三项。
5. 等差数列的性质:如果两个数列都是等差数列,那么它们的和也是一个等差数列。
等比数列:
1. 定义:一个数列,其中任意两个相邻项的比是一个常数,这个数列被称为等比数列。
2. 通项公式:$a_n = a_1 \times q^{n-1}$,其中 $a_1$ 是首项,$q$ 是公比,$n$ 是项数。
3. 求和公式:对于 $q \neq 1$,有 $S_n = \frac{a_1(1 - q^n)}{1 - q}$;对于 $q = 1$,有 $S_n = na_1$。
4. 等比中项:任意两项的几何平均值等于第三项。
5. 等比数列的性质:如果两个数列都是等比数列,那么它们的乘积是一个等比数列。
以上是关于等差数列和等比数列的主要知识点总结。
在学习这些内容时,可以通过做练习题来加深理解和巩固知识。
数列的等差数列与等比数列知识点总结

数列的等差数列与等比数列知识点总结数列是数学中经常出现的概念,它是按照一定规律排列的一组数的集合。
其中,等差数列和等比数列是两种常见的数列类型。
本文将对等差数列和等比数列的基本概念、性质、求和公式以及应用进行总结。
一、等差数列等差数列是指数列中相邻两项之差均相等的数列。
用通项公式表示为:an = a1 + (n-1)d,其中an表示第n项,a1为首项,d为公差。
1. 等差数列的基本概念等差数列中,每一项与它的前一项的差值都相等,这个差值称为公差。
等差数列可以是正差、零差或负差的数列。
2. 等差数列的性质(1)首项和末项之和等于中间项之和的两倍:a1 + an = 2Sn,其中Sn表示前n项和。
(2)任意一项与首项之和等于任意一项与末项之和:ai + aj = a1 + an。
(3)等差数列的前n项和Sn等于首项与末项之和乘以项数的一半:Sn = (a1 + an) × n / 2。
3. 求等差数列的和求解等差数列的和可以利用求和公式Sn = (a1 + an) × n / 2,其中n 为项数。
4. 等差数列的应用等差数列在实际问题中有广泛的应用,如金融投资、房贷分期还款等均可以利用等差数列的性质进行计算。
二、等比数列等比数列是指数列中相邻两项之比均相等的数列。
用通项公式表示为:an = a1 × r^(n-1),其中an表示第n项,a1为首项,r为公比。
1. 等比数列的基本概念等比数列中,每一项与它的前一项的比值都相等,这个比值称为公比。
等比数列可以是正比、零比或负比的数列。
2. 等比数列的性质(1)相邻两项之商等于任意一项与首项之商等于任意一项与末项之商:ai/aj = a1/ai = ai/an。
(2)等比数列的前n项和Sn等于首项与末项之差除以公比减1:Sn = (a1 - an × r^n) / (1 - r)。
3. 求等比数列的和求解等比数列的和可以利用求和公式Sn = (a1 - an × r^n) / (1 - r),其中r不等于1。
高考数学《等差数列、等比数列》复习

(1)等差数列通项公式:an=a1+(n-1)d.
(2)等差数列前 n 项和公式:Sn=n
a1+an 2
=na1+n
n- 2
d.
(3)等差中项公式:2an=an-1+an+1(n∈N*,n≥2).
2.等比数列
(1)等比数列通项公式:an=a1qn-1.
na1 q=
(2)等比数列前n项和公式:Sn= a1 -qn 1-q
高考数学《等差数列、等比数列》复习
高考考点
1. 等差(比)数列的基本运算 2. 等差(比)数列的判断与证明 3. 等差(比)数列的性质
考点解读
1. 在等差(比)数列中, a1,an, Sn,n,d(q) 这五个量中已知其中的三个量, 求另外两个量 2. 考查等差(比)数列的通项公式,前n项和公式, 考查方程的思想以及运算能力
(2)等差数列中连续 k 项的和成等差数列,即 Sk,S2k-Sk,S3k-S2k,…成等差数列, 公差为 k2d.
5.若 A2n-1,B2n-1 分别为等差数列{an},{bn}的前 2n-1 项的和, 则an=A2n-1.
bn B2n-1
解题技巧
判断或证明数列是否为等差或等比数列, 一般是依据等差数列、等比数列的定义, 或利用等差中项、等比中项进行判断.
A.15
B.30
C.45
√D.60
S100 a1 a2 a100 90 ,设 S a1 a3 a99 ,则 2S a2 a4 a100 ,S 2S S100 90,S 30 , 故 a2 a4 a100 2S 60 .故选 D.
1.不能忽视等比数列的条件:判断一个数列是等比数列时, 注意各项都不为零的条件. 2.不能漏掉等比中项:正数a,b的等比中项是±,不能漏掉-. 3.对等比数列的公比的讨论: 应用等比数列前n项和公式时应首先讨论公式q是否等于1
等差数列与等比数列+课件-2024届高三数学二轮复习专题

5
为 ak+1+ak+2+…+ak+10=2 -2 ,所以
5
10
k+1
5
+ (- )
-
15
5
k+1
10
=2 -2 ,即 2 (2 -
1)=2 (2 -1),所以 2 =2 ,所以 k+1=5,所以 k=4.故选 C.
4.[等差数列基本量](2023·全国甲卷)记Sn为等差数列
列{an}中,a1=2,am+n=aman.若ak+1+ak+2+…+ak+10=215-25,则
k等于(
A.2
)
B.3
C.4
√
D.5
解析:因为 a1=2,am+n=aman,令 m=1,则 an+1=a1an=2an,所以{an}是
n-1
n
以 a1=2 为首项,2 为公比的等比数列,所以 an=2×2 =2 .又因
可得
即
- = ,
(- ) = ,
= ,
5
解得
所以 a6=a1q =3.故选 D.
= ,
法二
设等比数列{an}的首项为 a1,公比为 q,由题意可得
+ + = ,
- = ,
(- )
即
-
= ,
(- ) = ,
所以{an}是以 a1 为首项,2a1 为公差的等差数列.
考法聚焦 讲练突破
热点一
等差、等比数列的基本运算
典例 1
(2023·新课标Ⅰ卷)设等差数列{an}的公差为 d,且
数列中的等比数列与等差数列——数列知识要点

数列中的等比数列与等差数列——数列知识要点数列是数学中的一个重要概念,广泛应用于各个领域。
其中,等差数列和等比数列是数列中的两种常见类型。
本文将重点介绍数列中的等差数列和等比数列的基本概念、性质以及应用。
一、等差数列等差数列是指数列中相邻两项之差保持恒定的数列。
设数列为{an},其中a1为首项,d为公差,则有以下关系式:an = a1 + (n-1)d等差数列的性质如下:1. 公差d:等差数列中相邻两项之差保持恒定,这个差值称为公差。
2. 通项公式:等差数列的通项公式为an = a1 + (n-1)d,可以通过该公式计算数列中任意一项的值。
3. 首项和末项:等差数列的首项为a1,末项为an。
4. 数列元素之和:等差数列的前n项和Sn可以通过以下公式计算:Sn = (n/2)(a1 + an)等差数列在实际问题中的应用非常广泛,例如计算机算法中的循环结构、金融领域中的利息计算等都可以归纳为等差数列的应用。
二、等比数列等比数列是指数列中相邻两项之比保持恒定的数列。
设数列为{an},其中a1为首项,r为公比,则有以下关系式:an = a1 * r^(n-1)等比数列的性质如下:1. 公比r:等比数列中相邻两项之比保持恒定,这个比值称为公比。
2. 通项公式:等比数列的通项公式为an = a1 * r^(n-1),可以通过该公式计算数列中任意一项的值。
3. 首项和末项:等比数列的首项为a1,末项为an。
4. 数列元素之和:等比数列的前n项和Sn可以通过以下公式计算(当r≠1时):Sn = a1 * (1 - r^n) / (1 - r)等比数列也有广泛的应用,例如在科学领域中的指数增长问题、经济领域中的复利计算等都可以归纳为等比数列的应用。
三、等差数列与等比数列的联系与区别等差数列和等比数列都是数列中常见的类型,它们之间有一些联系和区别。
联系:1. 通项公式:等差数列和等比数列都有通项公式,可以通过该公式计算数列中任意一项的值。
高考数学二轮复习 专题3 数列 第一讲 等差数列与等比数列 理

高考数学二轮复习 专题3 数列 第一讲 等差数列与等比数列 理第一讲 等差数列与等比数列1.等差数列的定义.数列{a n }满足a n +1-a n =d (其中n∈N *,d 为与n 值无关的常数)⇔{a n }是等差数列. 2.等差数列的通项公式.若等差数列的首项为a 1,公差为d ,则a n =a 1+(n -1)d =a m +(n -m )d (n ,m ∈N *). 3.等差中项.若x ,A ,y 成等差数列,则A =x +y2,其中A 为x ,y 的等差中项.4.等差数列的前n 项和公式.若等差数列首项为a 1,公差为d ,则其前n 项和S n =n (a 1+a n )2=na 1+n (n -1)d2.1.等比数列的定义. 数列{a n }满足a n +1a n=q (其中a n ≠0,q 是与n 值无关且不为零的常数,n ∈N *)⇔{a n }为等比数列.2.等比数列的通项公式.若等比数列的首项为a 1,公比为q ,则a n =a 1·q n -1=a m ·qn -m(n ,m ∈N *).3.等比中项.若x ,G ,y 成等比数列,则G 2=xy ,其中G 为x ,y 的等比中项,G 值有两个. 4.等比数列的前n 项和公式.设等比数列的首项为a 1,公比为q ,则S n =⎩⎪⎨⎪⎧na 1,q =1,a 1(1-q n )1-q=a 1-a n q 1-q ,q ≠1.判断下面结论是否正确(请在括号中打“√”或“×”).(1)若一个数列从第二项起每一项与它的前一项的差都是常数,则这个数列是等差数列.(×)(2)数列{a n }为等差数列的充要条件是对任意n ∈N *,都有2a n +1=a n +a n +2.(√) (3)数列{a n }为等差数列的充要条件是其通项公式为n 的一次函数.(×) (4)满足a n +1=qa n (n ∈N *,q 为常数)的数列{a n }为等比数列.(×) (5)G 为a ,b 的等比中项⇔G 2=ab .(×) (6)1+b +b 2+b 3+b 4+b 5=1-b51-b.(×)1.在等差数列{a n }中,a 2=1,a 4=5,则数列{a n }的前5项和S 5=(B ) A .7 B .15 C .20 D .25解析:2d =a 4-a 2=5-1=4⇒d =2,a 1=a 2-d =1-2=-1,a 5=a 2+3d =1+6=7,故S 5=(a 1+a 5)×52=6×52=15.2. (2015·北京卷)设{a n }是等差数列,下列结论中正确的是(C ) A .若a 1+a 2>0,则a 2+a 3>0 B .若a 1+a 3<0,则a 1+a 2<0 C .若0<a 1<a 2,则a 2>a 1a 3 D .若a 1<0,则(a 2-a 1)(a 2-a 3)>0解析:设等差数列{a n}的公差为d,若a1+a2>0,a2+a3=a1+d+a2+d=(a1+a2)+2d,由于d正负不确定,因而a2+a3符号不确定,故选项A错;若a1+a3<0,a1+a2=a1+a3-d=(a1+a3)-d,由于d正负不确定,因而a1+a2符号不确定,故选项B错;若0<a1<a2,可知a1>0,d>0,a2>0,a3>0,∴a22-a1a3=(a1+d)2-a1(a1+2d)=d2>0,∴a2>a1a3,故选项C正确;若a1<0,则(a2-a1)(a2-a3)=d·(-d)=-d2≤0,故选项D错.3.(2015·新课标Ⅱ卷)已知等比数列{a n}满足a1=3,a1+a3+a5=21,则a3+a5+a7=(B)A.21 B.42C.63 D.84解析:∵ a1=3,a1+a3+a5=21,∴ 3+3q2+3q4=21.∴ 1+q2+q4=7.解得q2=2或q2=-3(舍去).∴a3+a5+a7=q2(a1+a3+a5)=2×21=42.故选B.4.等差数列{a n}的公差不为零,首项a1=1,a2是a1和a5的等比中项,则数列的前10项之和是(B)A.90 B.100C.145 D.190解析:设公差为d,则(1+d)2=1·(1+4d).∵d≠0,解得d=2,∴S10=100.一、选择题1.已知等差数列{a n}中,前n项和为S n,若a3+a9=6,则S11=(B)A.12 B.33 C.66 D.99解析:∵{a n}为等差数列且a3+a9=6,∴a 6+a 6=a 3+a 9=6. ∴a 6=3. ∴S 11=a 1+a 112×11=a 6+a 62×11=11a 6=11×3=33.2.在等比数列{a n }中,若a 1+a 2=20,a 3+a 4=40,则数列{a n }的前6项和S 6=(B ) A .120 B .140 C .160 D .180 解析:∵{a n }为等比数列,∴a 1+a 2,a 3+a 4,a 5+a 6为等比数列. ∴(a 3+a 4)2=(a 1+a 2)(a 5+a 6). 即a 5+a 6=(a 3+a 4)2a 1+a 2=40220=80.∴S 6=a 1+a 2+a 3+a 4+a 5+a 6=20+40+80=140.3.已知数列{a n }的前n 项和S n =n 2-2n -1,则a 3+a 17=(C ) A .15 B .17 C .34 D .398 解析:∵S n =n 2-2n -1, ∴a 1=S 1=12-2-1=-2. 当n ≥2时,a n =S n -S n -1=n 2-2n -1-[(n -1)2-2(n -1)-1] =n 2-(n -1)2+2(n -1)-2n -1+1 =n 2-n 2+2n -1+2n -2-2n =2n -3.∴a n =⎩⎪⎨⎪⎧-2,n =1,2n -3,n ≥2.∴a 3+a 17=(2×3-3)+(2×17-3)=3+31=34. 4.(2014·陕西卷)原命题为“若a n +a n +12<a n ,n ∈N *,则{a n }为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是(A )A .真,真,真B .假,假,真C .真,真,假D .假,假,假 解析:由a n +a n +12<a n ⇒a n +1<a n ⇒{a n }为递减数列,所以原命题为真命题;逆命题:若{a n }为递减数列,则a n +a n +12<a n ,n ∈N +;若{a n }为递减数列,则a n +1<a n ,即a n +a n +12<a n ,所以逆命题为真;否命题:若a n +a n +12≥a n ,n ∈N +,则{a n }不为递减数列;由a n +a n +12≥a n ⇒a n ≤a n +1⇒{a n }不为递减数列,所以否命题为真;因为逆否命题的真假为原命题的真假相同,所以逆否命题也为真命题. 故选A.5.某棵果树前n 年的总产量S n 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为(C )A .5B .7C .9D .11解析:由图可知6,7,8,9这几年增长最快,超过平均值,所以应该加入m =9,因此选C.二、填空题6.(2015·安徽卷)已知数列{a n }中,a 1=1,a n =a n -1+12(n ≥2),则数列{a n }的前9项和等于27.解析:由a 1=1,a n =a n -1+12(n ≥2),可知数列{a n }是首项为1,公差为12的等差数列,故S 9=9a 1+9×(9-1)2×12=9+18=27.7.设公比为q (q >0)的等比数列{a n }的前n 项和为S n .若S 2=3a 2+2,S 4=3a 4+2,则q =32. 解析:将S 2=3a 2+2,S 4=3a 4+2两个式子全部转化成用a 1,q 表示的式子,即⎩⎪⎨⎪⎧a 1+a 1q =3a 1q +2,a 1+a 1q +a 1q 2+a 1q 3=3a 1q 3+2,两式作差得:a 1q 2+a 1q 3=3a 1q (q 2-1),即:2q 2-q -3=0,解得q =32或q =-1(舍去).8.(2014·广东卷)等比数列{a n }的各项均为正数,且a 1a 5=4,则log 2a 1+log 2a 2+log 2a 3+log 2a 4+log 2a 5=5.解析:由题意知a 1a 5=a 23=4,且数列{a n }的各项均为正数,所以a 3=2, ∴a 1a 2a 3a 4a 5=(a 1a 5)·(a 2a 4)·a 3=(a 23)2·a 3=a 53=25,∴log 2a 1+log 2a 2+log 2a 3+log 2a 4+log 2a 5=log 2(a 1a 2a 3a 4a 5)=log 225=5. 三、解答题9.已知数列{a n }满足,a 1=1,a 2=2,a n +2 =a n +a n +12,n ∈N *.(1)令b n =a n +1-a n ,证明:{b n }是等比数列; (2)求{a n }的通项公式. 解析:(1)b 1=a 2-a 1=1, 当n ≥2时,b n =a n +1-a n =a n -1+a n2-a n =-12(a n -a n -1)=-12b n -1,所以{b n }是以1为首项,-12为公比的等比数列.(2)由(1)知b n =a n +1-a n =⎝ ⎛⎭⎪⎫-12n -1,当n ≥2时,a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=1+1+⎝ ⎛⎭⎪⎫-12+…+⎝ ⎛⎭⎪⎫-12n -2=1+1-⎝ ⎛⎭⎪⎫-12n -11-⎝ ⎛⎭⎪⎫-12=1+23⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-12n -1=53-23⎝ ⎛⎭⎪⎫-12n -1, 当n =1时,53-23⎝ ⎛⎭⎪⎫-121-1=1=a 1.所以a n =53-23⎝ ⎛⎭⎪⎫-12n -1(n ∈N *).10.(2015·安徽卷)已知数列{a n }是递增的等比数列,且a 1+a 4=9,a 2a 3=8. (1)求数列{a n }的通项公式; (2)设S n 为数列{a n }的前n 项和,b n =a n +1S n S n +1,求数列{b n }的前n 项和T n . 解析:(1)由题设知a 1·a 4=a 2·a 3=8,又a 1+a 4=9,可解得⎩⎪⎨⎪⎧a 1=1,a 4=8或⎩⎪⎨⎪⎧a 1=8,a 4=1(舍去). 由a 4=a 1q 3得公比q =2,故a n =a 1qn -1=2n -1.(2)S n =a 1(1-q n )1-q=2n-1.又b n =a n +1S n S n +1=S n +1-S n S n S n +1=1S n -1S n +1, 所以T n =b 1+b 2+…+b n =⎝ ⎛⎭⎪⎫1S 1-1S 2+⎝ ⎛⎭⎪⎫1S 2-1S 3+…+⎝ ⎛⎭⎪⎫1S n -1S n +1=1S 1-1S n +1=1-12n +1-1.。
等差等比数列基础知识复习

数列专题复习(一)等差数列1.定义:2.通项公式:3.前n 项和公式:4.性质:基础训练:1.已知为等差数列,且-2=-1, =0,则公差d =2.在等差数列中,,则.3.数列{}n a 满足112n n a a -=+(*2,n n N ≥∈), 21a =,n S 是{}n a 的前n 项和, 则21S = .4.设等差数列的前项和为,若则 .5.等差数列的前项和为,且则6. 已知首项为23,公差为整数的等差数列{}n a ,且670,0a a ><(1)求数列的公差;(2)求前n 项和n S 的最大值;(3)当n S >0时,求n 的最大值。
{}n a 7a 4a 3a }{n a 6,7253+==a a a ____________6=a {}n a n n S 535a a =95S S ={}n a n n S 53655,S S -=4a =7.数列{n a }的前n 项和为210n S n n =-,求数列{}n a 的通项公式。
8. 等差数列的判定和证明(1)已知数列{}n a ,*12112,2232)n n a a a a n n N +===+≥∈,(,判断{}n a 是等差数列吗?(2)已知各项均为正数的数列{}n a 满足1n n a a -=2*2)n n N ≥∈(,,判断数列{lg n a }是否是等差数列。
(3)已知数列{}n a 中,135a =,112n n a a -=-*2)n n N ≥∈(,,数列{}n b 满足11n n b a =- (*n N ∈)①求证数列{}n b 是等差数列;②求数列{}n a 中的最大项与最小项,并说明理由。
(一)等比数列1.定义:2.通项公式:3.前n 项和公式:4.性质:基础训练:1.在各项都为正数等比数列{}n a 中,首项13a =,前三项和为21,则345a a a ++等于A 33B 72C 84D 1892.等比数列{}n a 中,29a =,5243a =,则{}n a 前4项和为3.等比数列{}n a 中,若331,3a S ==,则q =4.等比数列{}n a 中,7116a a ⋅=,4145a a +=,则2010a a 等于5. 在数列{}n a 中,()10,1n n S ka k k =+≠≠,(1)求证:{}n a 是等比数列; (2)求通项公式n a 。
等差数列与等比数列知识点复习总结

等差数列与等比数列知识点复习总结的公比计算方法:①后一项除以前一项:q = an+1an②前两项之比:q = a2a1③前一项与后一项的平方根之比:q = √(an+1an3、等比数列an的通项式:①ana1q^(n-1)②anamq^(n-m)③anb*q^n (b为常数)4、等比数列an的性质:①两项性质:若m+n=p+q,则 a manapaq②等比中项性质:若x,A,y成等比数列,则 2A = x+y③下标成等比数列的项仍成等比数列。
若数列an是等比数列,公比为q,则数列akak+mak+2mak+3m仍构成等比数列,公比为q^m。
5、等比数列an的前n项和:Sna1q^n-1)/(q-1)等比数列前n项和性质:①首项为a1,公比为q的等比数列的前n项和为Sn=a1(1-q^n)/(1-q)②首项为a1,公比为q的等比数列的前n项和为Sn=a1(q^n-1)/(q-1)③特别地,首项为1,公比为q的等比数列的前n项和为Sn=(1-q^n)/(1-q)6、等比数列前n项和性质:①首项为a1,公比为q的等比数列的前n项和为Sn=a1(1-q^n)/(1-q)②首项为a1,公比为q的等比数列的前n项和为Sn=a1(q^n-1)/(q-1)③特别地,首项为1,公比为q的等比数列的前n项和为Sn=(1-q^n)/(1-q)等差数列前n项和性质:①片段和性质:等差数列{an}的前n项和为Sn,公差为d,则Sn,S2n-Sn,S3n-S2n。
即a1+a2+。
+am,am+1+am+2+。
+a2m,a2m+1+a2m+2+。
+a3m也成等差数列,公差为md。
②若两个等差数列{an},{bn}的前n项和分别是An,Bn,则a1+b1,a2+b2.an+bn也成等差数列,公差为d1+d2.其它性质:(任何数列都适用)①Sn与Sn-1之间的关系:an=Sn-Sn-1(n=1),a1=S1②S2n-1与S2n之间的关系:an=1/2(S2n-S2n-1)(n≥2)③通项公式:an=S(n)-S(n-1)④题型:已知Sn与n的关系,求数列的通项公式an;已知Sn与an的关系,求数列的通项公式an。
等差数列与等比数列知识点及题型归纳总结

等差数列与等比数列知识点及题型归纳总结知识点精讲一、基本概念 1.数列(1)定义:按照一定顺序排列的一列数就叫做数列. (2)数列与函数的关系.从函数的角度来看,数列是特殊的函数.在()y f x =中,当自变量x N *∈时,所对应的函数值(1),(2),(3),f f f 就构成一数列,通常记为{}n a ,所以数列有些问题可用函数方法来解决.2.等差数列 (1)定义:一般地,如果一个数列从第2项起,每一项与它前一项的差等于同一常数,则该数列叫做等差数列,这个常数叫做公差,常用字母d 表示,即1()n n a a d n N *+-=∈.(2)等差数列的通项公式.若等差数列{}n a 的首项是1a ,公差是d ,则其通项公式为11(1)()n a a n d nd a d =+-=+-,是关于n 的一次型函数.或()n m a a n m d =+-,公差n m a a d n m-=-(直线的斜率)(,,m n m n N *≠∈).(3)等差中项.若,,x A y 成等差数列,那么A 叫做x 与y 的等差中项,即2x yA +=或2A x y =+,.在一个等差数列中,从第2项起(有穷等差数列的末项除外),每一项都是它的前一项与后一项的等差中项;事实上,等差数列中每一项都是与其等距离的前后两项的等差中项.(4)等差数列的前n 项和2111()2(1)2222n n a a n a dn n d d S na n n +--==+=+(类似于2n S An Bn =+),是关于n 的二次型函数(二次项系数为2d且常数项为0).n S 的图像在过原点的直线(0)d =上或在过原点的抛物线(0)d ≠上.3.等比数列(1)定义.:一般地,如果一个数列从第2项起,每一项与它前一项的比等于同一个非零常数,则该数列叫做等比数列,这个常数叫做公比,常用字母q 表示,即1(q 0,)n na q n N a *+=≠∈. (2)等比数列的通项公式. 等比数列的通项1111()(,0)n n n a a a qc q c a q q-==⋅=≠,是不含常数项的指数型函数. (3)m n mna q a -=. (4)等比中项如果,,x G y 成等比数列,那么G 叫做x 与y 的等比中项,即2G xy =或G =两个同号实数的等比中项有两个).(5)等比数列的前n 项和111(1)(1)(1)11n n n na q S a a qa q q q q =⎧⎪=--⎨=≠⎪--⎩注①等比数列的前n 项和公式有两种形式,在求等比数列的前n 项和时,首先要判断公比q 是否为1,再由q 的情况选择相应的求和公式,当不能判断公比q 是否为1时,要分1q =与1q ≠两种情况讨论求解.②已知1,(1),a q q n ≠(项数),则利用1(1)1n n a q S q -=-求解;已知1,,(1)n a a q q ≠,则利用11n n a a qS q-=-求解.③111(1)(0,1)111n n n n a q a aS q kq k k q q q q--==⋅+=-≠≠---,n S 为关于n q 的指数型函数,且系数与常数互为相反数.例如等比数列{}n a ,前n 项和为212n n S t +=+,则t =.解:等比数列前n 项和21224n n n S t t +=+=⋅+,则2t =-.二、基本性质1.等差数列的性质 (1)等差中项的推广.当(,,,)m n p q m n p q N *+=+∈时,则有m n p q a a a a +=+,特别地,当2m n p +=时,则有2m n p a a a +=.(2)等差数列线性组合.①设{}n a 是等差数列,则{}(,)n a b b R λλ+∈也是等差数列.②设{},{b }n n a 是等差数列,则1212{}(,)n n a b R λλλλ+∈也是等差数列. (3)有限数列.①对于项数为2n 的等差数列,有: (Ⅰ)21()n n n S n a a +=+.(Ⅱ)11,,,n n n nS a S na S na S S nd S a ++==-==偶奇奇偶偶奇. ②对于项数为21n -的等差数列,有; (Ⅰ)21(21)n n S n a -=-.(Ⅱ),(1),,1n n n S nS na S n a S S a S n ==--==-奇奇奇偶偶偶.(4)等差数列的单调性及前n 项和n S 的最值. 公差0{}n d a >⇔为递增等差数列,n S 有最小值; 公差0{}n d a <⇔为递减等差数列,n S 有最大值; 公差0{}n d a =⇔为常数列. 特别地 若10a d >⎧⎨<⎩,则n S 有最大值(所有正项或非负项之和);若100a d <⎧⎨>⎩,则n S 有最小值(所有负项或非正项之和).(5)其他衍生等差数列.若已知等差数列{}n a ,公差为d ,前n 项和为n S ,则: ①等间距抽取2(1),,,,p p t p t p n t a a a a +++-为等差数列,公差为td . ②等长度截取232,,,m m m m m S S S S S --为等差数列,公差为2m d .③算术平均值312,,,123S S S 为等差数列,公差为2d . 2.等差数列的几个重要结论(1)等差数列{}n a 中,若,(,,)n m a m a n m n m n N *==≠∈,则0m n a +=. (2)等差数列{}n a 中,若,(,,)n m S m S n m n m n N *==≠∈,则()m n S m n +=-+. (3)等差数列{}n a 中,若(,,)n m S S m n m n N *=≠∈,则0m n S +=.(4)若{}n a 与{b }n 为等差数列,且前n 项和为n S 与n T ,则2121m m m m a S b T --=. 3.等比数列的性质 (1)等比中项的推广.若m n p q +=+时,则m n p q a a a a =,特别地,当2m n p +=时,2m n p a a a =.(2)①设{}n a 为等比数列,则{}n a λ(λ为非零常数),{}n a ,{}mn a 仍为等比数列.②设{}n a 与{b }n 为等比数列,则{b }n n a 也为等比数列.(3)等比数列{}n a 的单调性(等比数列的单调性由首项1a 与公比q 决定).当101a q >⎧⎨>⎩或1001a q <⎧⎨<<⎩时,{}n a 为递增数列;当1001a q >⎧⎨<<⎩或101a q <⎧⎨>⎩时,{}n a 为递减数列.(4)其他衍生等比数列.若已知等比数列{}n a ,公比为q ,前n 项和为n S ,则: ①等间距抽取2(1),,,,p p t p t p n t a a a a +++-为等比数列,公比为tq .②等长度截取232,,,m m m m m S S S S S --为等比数列,公比为mq (当1q =-时,m 不为偶数).4.等差数列与等比数列的转化(1)若{}n a 为正项等比数列,则{log }(c 0,c 1)c n a >≠为等差数列. (2)若{}n a 为等差数列,则{c }(c 0,c 1)n a>≠为等比数列. (3)若{}n a 既是等差数列又是等比数列{)n a ⇔是非零常数列. 题型归纳及思路提示题型1 等差、等比数列的通项及基本量的求解 思路提示利用等差(比)数列的通项公式或前n 项和公式,列出关于1,()a d q 基本量的方程或不等式从而求出所求的量.一、求等差数列的公差及公差的取值范围例6.1 记等差数列{}n a 的前n 项和为n S ,若244,20S S ==,则该数列的公差d =( ). A.7 B.6 C.3 D.2解析 212124S a a a d =+=+= ①414620S a d =+= ②由式①②可解得3d =,故选C.评注 求解基本量用的是方程思想.变式1 (2012福建理2)等差数列{}n a 中,15410,7a a a +==则数列{}n a 的公差为( ). A.1 B.2 C.3 D.4变式2 已知等差数列首项为31,从第16项起小于1,则此数列公差d 的取值范围是( ). A.(,2)-∞- B.15,27⎡⎫--⎪⎢⎣⎭ C.(2,)-+∞ D.15,27⎛⎫-- ⎪⎝⎭二、求等比数列的公比例6.2 在等比数列{}n a 中,201320108a a =,则公比q 的值为( ). A.2 B.3 C.4 D.8 解析 因为201320108a a =,所以3201320108,a q a ==则2q =,故选A. 变式1 等比数列{}n a 的前n 项和为n S ,且1234,2,a a a 成等差数列,若11a =,则4S =( ). A.7 B.8 C.15 D.16变式2 (2012浙江理13)设公比为(0)q q >的等比数列{}n a 的前n 项和为n S ,若224432,32S a S a =+=+,则q =.变式3 等比数列{}n a 的前n 项和为n S ,若123,2,3S S S 成等差数列,则{}n a 的公比为.三、求数列的通项n a例6.3 (1)(2012广东理11)已知递增等差数列{}n a 满足21321,4a a a ==-,则n a =.(2)(2012辽宁理14)已知等比数列{}n a 为递增数列,且251021,2()5n n n a a a a a ++=+=,则数列{}n a 的通项公式n a =.解析 (1)利用等差数列的通项公式求解.设等差数列公差为d ,则由2324a a =-得,212(1)4d d +=+-,所以24d =,得2d =±,又该数列为递增的等差数列,所以2d =.故1(1)21()n a a n d n n N *=+-=-∈.(2)由数列{}n a 为等比数列,设公比为q ,由212()5n n n a a a +++=,得22()5n n n a a q a q +=,即22(1)5q q +=,解得12q =或2.又25100a a =>,且数列{}n a 为递增数列,则2q =. 因此5532q a ==,所以2()n n a n N *=∈.变式1 n S 为等差数列{}n a 的前n 项和,264,1S S a ==,则n a =.变式2 已知两个等比数列{},{b }n n a ,满足11122331,1,2,4a b a b a b a =-=-=-=,求数列{}n a 的通项公式.例6.4 在等差数列{}n a 中,138a a +=,且4a 为2a 和9a 的等比中项,求数列{}n a 的前n 项和为n S .解析 设该数列的公差为d ,前n 项和为n S .由已知,得211228,(3)a d a d +=+=11()(8)a d a d ++,所以114,(3)0a d d d a +=-=,解得14,0a d ==或11,3a d ==,即数列{}n a 的首项为4,公差为0,或首项为1,公差为3.所以数列的前n 项和为4n S n =或232n n nS -=.变式1 已知数列{}n a 的前n 项和29n S n n =-,则其通项n a =;若它的第k 项满足58k a <<,则k =.变式2 已知数列{}n a 的前n 项和1(nn S a a =-为非零实数),那么{}n a ( ).A.一定是等差数列B.一定是等比数列C.或者是等差数列,或者是等比数列D.既不可能是等差数列,也不可能是等比数列题型2 等差、等比数列的求和 思路提示求解等差或等比数列的前n 项和n S ,要准确地记住求和公式,并合理选取公式,尤其是要注意其项数n 的值;对于奇偶项通项不统一和含绝对值的数列的求和问题要注意分类讨论.主要是从n 为奇数、偶数,项n a 的正、负进行分类.一、公式法(准确记忆公式,合理选取公式)例6.5 在等比数列{}()n a n N *∈中,若1411,8a a ==,则该数列的前10项和为( ). 8910111111.2.2 C.2 D.22222A B ----解析 由334111,82a a q q q ====得,所以1010911()1221212S -==--,故选B. 变式1 {}n a 是由正数组成的等比数列,n S 为前n 项和,已知2431,7a a S ==,则n S =.变式2 设4710310()22222()n f n n N +=+++++∈,则()()f n =.1342222.(81).(81).(81).(81)7777n n n n A B C D +++----二、关于等比数列求和公式中q 的讨论例6.6 设等比数列{}n a 的前n 项和为n S ,若396,,S S S 成等差数列,求数列的公比q .解析 若1q =,则3161913,6,9S a S a S a ===,因为10a ≠,所以3692S S S +≠,与396,,S S S 成等差数列矛盾,故1q ≠.由题意可得3692S S S +=,即有369111(1)(1)2(1)111a q a q a q q q q---+=---,整理得363(21)0q q q --=,又0q ≠,故63210q q --=,即33(21)(1)0q q +-=.因为31q ≠,所以312q =-,所以q ==变式1 设数列{}n a 是等比数列,其前n 项和为n S ,且333S a =,则其公比q =.变式2 求和2311357(21)(2,,)n n S x x x n x n n N x R -*=+++++-≥∈∈.三、关于奇偶项求和问题的讨论例6.7 已知数列{}n a 的通项公式为12(1)n n a n -=-,求其前n 项和为n S . 解析 (1)当n 为偶数时,222221234(1)n S n n =-+-++--22222(12)(34)[(1)]n n =-+-++--[37(21)]n =-+++-(321)(1)222nn n n +-+=-=-. (2)当n 为奇数时,则1n +为偶数,所以211(1)(2)(1)(1)22n n n n n n n S S a n +++++=-=-++=. 综上,(1)()2(1)()2n n n n S n n n +⎧-⎪⎪=⎨+⎪⎪⎩为正偶数为正奇数.评注:本题中,将n 为奇数的情形转化为n 为偶数的情形,可以避免不必要的计算,此技巧值得同学们借鉴和应用。
等差数列与等比数列知识点复习总结知识讲解

等差数列
等比数列
1、数列 为等差数列的判定方法
定义法: (后一项减前一项等于常数)
等差中项法: (两倍的中项等于前后项之和)
通项式法: ( 是关于 的一次函数)
前 项和公式法(公差不为零时): (求和公式是关于 的二次函数且常数项为零,且公差 首项 )
1、数列 为等比数列的判定方法
题型: 已知 与 的关系,求数列的通项公式 ; 已知 与 的关系,求数列的通项公式 。
数列的求和方法
1、分组求和法
例1、若数列 的通项式为 ,求数列 的前 项
练习1、(1)已知数列 的通项式为
,求数列 的前 项
(2)有穷数列1,1+2,1+2+4,…, 所有项的和为____________
2、错位相减法
6、等差数列前 项和性质
片段和性质:
等差数列 的前 项和为 ,公差为 ,则
即 , ,
也成等差数列,公差为 。
若两个等差数列 的前 项和分别是 ,则 。
6、等比数列前 项和性质
7、其它性质:(任何数列都适用)
与 之间的关系: ,步骤: ________________ ________________ _____________________ _____________
两项性质:若 ,则________________
等比中项性质:若 成等比数列 ______________
5、等差数列 的前 项和
5、等比数列 的前 项和
__________________ _________________ ________________
特别地,__________________________
等差数列与等比数列的知识点总结

等差数列与等比数列的知识点总结等差数列与等比数列是数学中常见的两种数列,它们在数学和实际生活中都有着重要的应用。
下面将从定义、性质、求和公式和应用等几个方面对等差数列和等比数列进行全面总结。
**一、等差数列的基本概念**等差数列是指一个数列中,从第二项起,每一项与它的前一项的差等于同一个常数的数列。
一般来说,等差数列的通项公式为:a_n=a_1+(n-1)d,其中a_n表示数列的第n项,a_1表示数列的首项,n表示项数,d表示公差。
**二、等差数列的性质**1. 等差数列的通项公式:a_n=a_1+(n-1)d2. 等差数列的前n项和公式:S_n=\frac{n}{2}(2a_1+(n-1)d)3. 等差数列的性质:任意三项成等差数列,等差中项相等。
4. 等差数列的性质:首项与末项的关系。
**三、等差数列的应用**等差数列在实际生活中有着广泛的应用,比如在金融领域中的等额还款、在物理学中的匀速运动等等。
**四、等比数列的基本概念**等比数列是指一个数列中,从第二项起,每一项与它的前一项的比等于同一个常数的数列。
一般来说,等比数列的通项公式为:a_n=a_1 \cdot q^{n-1},其中a_n表示数列的第n项,a_1表示数列的首项,n表示项数,q表示公比。
**五、等比数列的性质**1. 等比数列的通项公式:a_n=a_1 \cdot q^{n-1}2. 等比数列的前n项和公式:S_n=\frac{a_1(1-q^n)}{1-q},当|q|<1时成立3. 等比数列的性质:首项、末项、项数的关系。
4. 等比数列的性质:任意三项成等比数列,等比中项与等比积。
**六、等比数列的应用**等比数列同样在实际中有着广泛的应用,比如在利息计算中的等比增长、在生物学中的细胞分裂等等。
**结语**等差数列与等比数列是数学中基础而重要的概念,它们不仅在数学理论中有着重要的意义,而且在实际生活中也有着广泛的应用。
专题06 等差数列与等比数列(解析版)
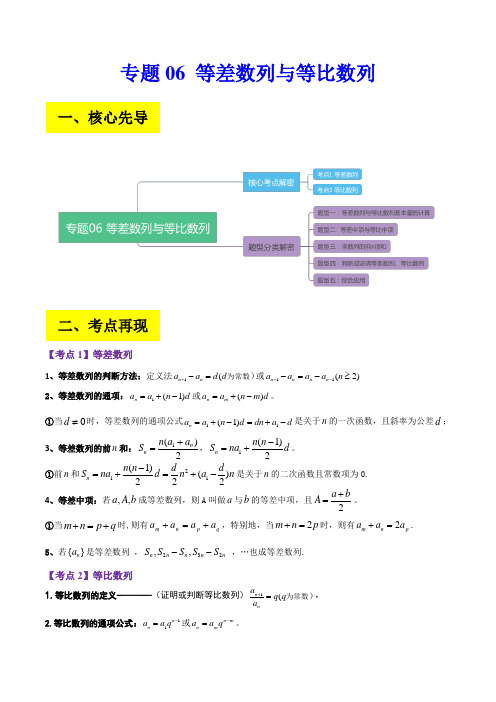
专题06 等差数列与等比数列【考点1】等差数列1、等差数列的判断方法:定义法1(n n a a d d +-=为常数)或11(2)n n n n a a a a n +--=-≥2、等差数列的通项:1(1)n a a n d =+-或()n m a a n m d =+-。
①当0d ≠时,等差数列的通项公式11(1)n a a n d dn a d =+-=+-是关于n 的一次函数,且斜率为公差d ;3、等差数列的前n 和:1()2n n n a a S +=,1(1)2n n n S na d -=+。
①前n 和211(1)()222n n n d dS na d n a n -=+=+-是关于n 的二次函数且常数项为0.4、等差中项:若,,a A b 成等差数列,则A 叫做a 与b 的等差中项,且2a bA +=。
①当m n p q +=+时,则有q p n m a a a a +=+,特别地,当2m n p +=时,则有2m n p a a a +=. 5、若{}n a 是等差数列 ,232,,n n n n n S S S S S -- ,…也成等差数列.【考点2】等比数列1.等比数列的定义--------(证明或判断等比数列)1(n na q q a +=为常数),2.等比数列的通项公式:11n n a a q -=或n m n m a a q -=。
二、考点再现一、核心先导3.等比数列的前n 和:①当1q =时,1n S na =;②当1q ≠时,1(1)1n n a q S q -=-11n a a qq-=-。
4、等比中项:⑴、若,,a A b 成等比数列,那么A 叫做a 与b 的等比中项,⑵、当m n p q +=+时,则有。
5、若{}n a 是等比数列 ,232,,n n n n n S S S S S -- ,…也成等比数列.等差数列与等比数列作为两种基本的数列,是高考中数列考查的重中之重,值得关注 . 考查的形式主要有等差数列、等比数列的实际应用以及等差数列、等比数列与其他知识的综合 . 在复习中,要紧抓以下几个方面 :方法1. 关注两种基本方法:研究等差数列、等比数列的基本方法就是“基本量法”及活用好它们的“对称性”;方法2. 领悟等差数列、等比数列的两类本质:等差数列、等比数列是两类特殊数列,又是两类特殊的函数,这种双重身份,注定它们必然是高考中的重点、难点,故而,学习中,要从“函数”及“数列”这两个方面来认识它们;方法3. 两类数学思想:分类讨论思想以及函数与方程的思想是解决数列问题所经常使用的两类数学思想题型一:等差数列与等比数列基本量的计算例1.(1)、(2022·四川省遂宁市教育局模拟预测(文))若{}n a 为等差数列,n S 是数列{}n a 的前n 项和,4614a a +=,735S =,则31a a -等于( )A .7B .6C .5D .4【答案】D【分析】根据题意,设等差数列{}n a 的公差为d ,进而建立方程组求解得2d =,再计算31a a -即可. 【详解】解:根据题意,设等差数列{}n a 的公差为d ,四、考点解密三、解法解密因为4614a a +=,735S =所以46171281472135a a a d S a d +=+=⎧⎨=+=⎩,解得121d a =⎧⎨=-⎩,所以3124a a d -==. 故选:D(2)、(2022·福建福州·高二期末)(多选题)已知等差数列{}n a 的公差为d ,前n 项和为n S ,5316,12a a ==.则( ) A .2d =- B .120a =C .2628a a +=D .n S 取得最大值时,11n =【答案】ABC 【解析】 【分析】利用基本量代换,求出通项公式,即可验证A 、B 、C ;由通项公式判断出10n ≤时,0n a >,110a =,12n ≥时,0n a <可以得到1011S S =最大,即可判断选项D. 【详解】因为5316,12a a ==,所以3151216412a a d a a d =+=⎧⎨=+=⎩,解得:1202a d =⎧⎨=-⎩,故选项A 、B 正确; 所以()11222n a n n d a +==--.对于C :因为222n a n =-,所以26181028a a +=+=,故C 正确; 对于D :因为222n a n =-,所以11222110a =-⨯=.因为10n ≤时,0n a >;12n ≥时,0n a <;所以1011S S =最大.故D 错误. 故选:ABC【变式训练1-1】、(2022·四川·宜宾市叙州区第二中学校模拟预测(文))已知等比数列{}n a 中,34a =,119a =,则7a =______.【答案】6【分析】由等比数列的性质求解即可【详解】由等比数列的性质可得:2731136a a a ==,由等比数列中奇数项的符号相同, 所以76a =, 故答案为:6【变式训练1-2】、(2021·云南·模拟预测(文))已知{}n a 为等差数列,n S 为其前n 项和.若137,15a S =-=-,则8a =______. 【答案】7 【解析】 【分析】根据题意得等差数列{}n a 的公差为2d =,再根据通项公式求解即可. 【详解】解:设等差数列{}n a 的公差为d ,因为137,15a S =-=-所以13173315a S a d =-⎧⎨=+=-⎩,解得2d =,所以29n a n =-,所以82897a =⨯-=. 故答案为:7题型二:等差中项与等比中项的应用例2.(1)、(2022·山东泰安·模拟预测)若等差数列{}n a 满足8926a a -=,则它的前13项和为( ) A .110 B .78 C .55 D .45(2).(2022·河南焦作·一模(文))设{}n a 和{}n b 都是等差数列,前n 项和分别为n S 和n T ,若17136a a a ++=,1391112b b b b +++=,则1311S T =( ) A .2633B .23C .1322D .1311【答案】A 【解析】 【分析】利用等差数列的性质分别求得72a =,63b =,再利用等差数列前n 项和公式求解. 【详解】由等差数列的性质可得1713736a a a a ++==, 所以72a =;因为139********b b b b b b +++=+=, 所以63b =.由等差数列的前n 项和公式可得()113137131322262a a a S ⨯==+=,()111611*********b b b T +⨯===, 所以13112633S T =. 故选:A【变式训练2-1】、(2022·安徽黄山·一模(文))在等比数列{}n a 中,1a ,13a 是方程21390x x -+=的两根,则2127a a a 的值为( )AB .3 C.D .3±故选:B.【变式训练2-2】、(2022·湖北·荆门市龙泉中学二模)正项等比数列{}n a 中,312,,a a a -成等差数列,且存在两项*,(,N )m n a a m n ∈14a ,则15m n+ 的最小值是( ) A .2 B .74C.1 D .不存在2q ,进而有0>,则q 2q,14n a a ⋅=,则,可得m n +=51(6m n m +=号不成立,1455(3,4)-∈题型三:求数列的前n 项和例3.(1)、(2022·山西运城·模拟预测(文))已知数列{}n a 中,14a =,()11333n n n a a a +=-+,数列1n a 的前n 项和为n S ,则( ) A .202201S << B .2022312S <<C .2022322S <<D .202223S <<20,又1a }是递增数列3-,所以122311111111333333n n n a a a a a a a +⎛⎫⎛⎫⎛⎫++=-+-++-=⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭11133n a +=--,所以20222023113S a =--,又20234a >,所以202331a ->,所以1. (2).(2022·安徽·合肥市第七中学高二期末)已知数列{}n a 的前n 项和221n S n n =-+,则其通项公式n a =______.【答案】*2,143,2,n n n n N =⎧⎨-≥∈⎩【解析】 【分析】利用当2n ≥时,1n n n a S S -=-,可求出此时的通项公式,验证n =1时是否适合,可得答案. 【详解】当2n ≥时,()()22121211143n n n a S S n n n n n -⎡⎤=-=-+----+=-⎣⎦, 当1n =时,12112a =-+=不适合上式,∴*2,143,2,n n a n n n N =⎧=⎨-≥∈⎩,故答案为:*2,143,2,n n n n N =⎧⎨-≥∈⎩. 【变式训练3-1】、(2022·四川绵阳·一模(理))已知等比数列{}n a 的各项均为正数,设n S 是数列{}n a 的前n 项和,且22a =,48a =,则5S =______. 【答案】31【分析】利用等比数列通项公式,结合0q >,可求得公比2q ,进而得到1a ,利用等比数列求和公式可求得结果.【详解】设等比数列{}n a 的公比为q ,0n a >,51S ⨯∴=故答案为:【变式训练3-2】、(2022·河南·开封市东信学校模拟预测(理))已知数列{}n a 满足()112,22N n n a a a n n *+=-=+∈,则数列1na 的前2022项的和为___________. 18,,n n a a --)()3124682n n a a a n --++-=+++++.∴(1)n a n n =+,则1111(1)1n a n n n n ==-++. 数列1na 的前n 项和为31111111122311n a n n n n 1++=-+-++-=-=+++20222023=. 故答案为:20222023.题型四:判断或证明等差、等比数列例4、(2022·吉林长春·模拟预测)已知数列{}n a 满足:12a =,()()()31121n n na n n a n +++=+++.(1)证明:数列()1n a n n ⎧⎫⎪⎪⎨⎬+⎪⎪⎩⎭是等差数列;(2)设()122n n nn n b a ++=,求数列{}n b 的前n 项和n S .【变式训练4-1】、(2022·河南·模拟预测(理))若数列{}n a 满足12a =,1123n n n a a -+-=.(1)证明:{}13n n a a +-是等比数列;(2)设{}n a 的前n 项和为n S ,求满足2023n S <的n 的最大值. n a ++)()10112333n n --++++++()3331222n n n-=+-,为递增数列,12202023<,835352023S =>,题型五:综合应用例5.(1)、(2022·河南省叶县高级中学模拟预测(文))中国公民身份号码编排规定,女性公民的顺序码为偶数,男性为奇数,反映了性别与数字之间的联系;数字简谱以1,2,3,4,5,6,7代表音阶中的7个基本音阶,反映了音乐与数字之间的联系,同样我们可以对几何图形赋予新的含义,使几何图形与数字之间建立联系.如图1,我们规定1个正方形对应1个三角形和1个正方形,1个三角形对应1个正方形,在图2中,第1行有1个正方形和1个三角形,第2行有2个正方形和1个三角形,则在第9行中的正方形的个数为( )A .53B .55C .57D .59【答案】B【分析】根据题意将题中所给的信息转化为数列递推公式关系1n n n a a b +=+,1n n b a +=,通过递推从而得出结果.【详解】设n a 为第n 行中正方形的个数,n b 为第n 行中三角形的个数,由于每个正方形产生下一行的1个三角形和1个正方形,每个三角形产生下一行的1个正方形,则有1n n n a a b +=+,1n n b a +=, 整理得()112n n n a a a n +-=+≥,且11a =,22a =,则3213a a a =+=,4325a a a =+=,5438a a a =+=,65413a a a =+=, 76521a a a =+=,87634a a a =+=,98755a a a =+=.故选:B.(2)、(2021·全国·模拟预测)在流行病学中,基本传染数0R 是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数.0R 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定.假设某种传染病的基本传染数03R =(注:对于01R >的传染病,要隔离感染者,以控制传染源,切断传播途径),那么由1个初始感染者经过六轮传染被感染(不含初始感染者)的总人数为______(注:初始感染者传染0R 个人为第一轮传染,这0R 个人每人再传染0R 个人为第二轮传染……) 【答案】1092【解析】由题意分析,传染模型为一个101,3a q R ===等比数列,可解. 【详解】由题意:101,3a q R ===所以1113n n n a a q --==第六轮的传染人数为7a所以前六轮被传染的人数为771131109213S a --=-=-.故答案为:1092【点睛】数学建模是高中数学六大核心素养之一,在高中数学中,应用题是常见考查形式:求解应用性问题时,首先要弄清题意,分清条件和结论,抓住关键词和量,理顺数量关系,然后将文字语言转化成数学语言,建立相应的数学模型;【变式训练5-1】、(2022·浙江宁波·一模)南宋的数学家杨辉“善于把已知形状、大小的几何图形的求面积、体积的连续量问题转化为离散量的垛积问题”,在他的专著《详解九章算法•商功》中,杨辉将堆垜与相应立体图形作类比,推导出了三角垛、方垛、刍童垛等的公式,例如三角垛指的是如图顶层放1个,第二层放3个,第三层放6个,第四层放10个第n 层放n a 个物体堆成的堆垛,则1210111a a a +++=__________.【答案】2011【分析】由累加法即可求得n a ,再利用裂项相消法即可求解. 【详解】由题可知:1231,3,6a a a ===,即有()12n n a a n n --=≥, 所以121321()()()n n n a a a a a a a a -=+---+++(1)12342n n n +=+++++=,当n=1成立所以1222(1)1n a n n n n ==-++, 所以121011122222222223341011a a a +++=-+-+-++- 22021111=-=. 故答案为:2011【变式训练5-2】、(2021·河南郑州·三模(文))1967年,法国数学家蒙德尔布罗的文章《英国的海岸线有多长?》标志着几何概念从整数维到分数维的飞跃.1977年他正式将具有分数维的图形成为“分形”,并建立了以这类图形为对象的数学分支——分形几何.分形几何不只是扮演着计算机艺术家的角色,事实表明它们是描述和探索自然界大量存在的不规则现象的工具.下面我们用分形的方法来得到一系列图形,如图1,线段AB 的长度为1,在线段AB 上取两个点C ,D ,使得13AC DB AB ==,以CD 为一边在线段AB 的上方做一个正三角形,然后去掉线段CD ,得到图2中的图形;对图2中的线段EC 、ED 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:记第n 个图形(图1为第一个图形)中的所有线段长的和为n S ,对任意的正整数n ,都有n S a <,则a 的最小值为__________. 【答案】2.【分析】根据图形之间的关系可得n S 的递推关系,从而可求{}n S 的通项公式,故可求a 的最小值.【详解】设第n 个图形中新出现的等边三角形的边长为n a ,则当2n ≥时,21111333n n n a --⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭,设第n 个图形中新增加的等边三角形的个数为n b ,则当2n ≥时,22n n b -=,故121123n n n n S S ---⎛⎫-=⨯ ⎪⎝⎭,其中2n ≥,由累加法可得121121222123111223332313n n n S --⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=++++=+⨯⨯-⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦- 1223n -⎛⎫=- ⎪⎝⎭,A 组 基础巩固1.(2022·全国·安阳市第二中学模拟预测(理))我国《洛书》中记载着世界上最古老的一个幻方,如图所示,将1,2,3,…,9填入33⨯的方格内,使得三行、三列、对角线的三个数之和都等于15,便得到一个3阶幻方;一般地,将连续的正整数1,2,3,…,2n 填入n n ⨯个方格中,使得每行、每列、每条对角线上的数的和都相等,这个正方形叫作n 阶幻方.记n 阶幻方的数的和(即方格内的所有数的和)为n S ,如345S =,那么10阶幻方每行、每列、每条对角线上的数的和均为( )A .555B .101C .505D .1010【答案】C【分析】利用等差数列求和公式得到105050S =,进而求出10阶幻方每行、每列、每条对角线上的数的和. 【详解】由题意得:()10100110012310050502S ⨯+=++++==,故10阶幻方每行、每列、每条对角线上的数的和均为505010505÷=. 故选:C2.(2022·四川省遂宁市教育局模拟预测(理))设数列{}n a 是等差数列,n S 是数列{}n a 的前n 项和,4614a a +=,735S =,则5S 等于( )A .10B .15C .20D .25【答案】B【分析】根据给定条件求出等差数列{}n a 的首项及公差即可得解. 【详解】因数列{}n a 是等差数列,由等差数列的性质知:46572a a a +==, 而177477352a a S a +=⨯==,则45a =, 五、分层训练3.(2022·四川绵阳·一模(理))已知n S 是等差数列{}n a 的前n 项和,若1957S =,则5143a a a --=( ) A .2 B .3 C .4 D .64.(2022·黑龙江·哈九中模拟预测(理))在等差数列{}n a 中n S 为前n 项和,7624a a =- ,则9S =( ) A .28 B .30C .32D .365.(2022·云南云南·模拟预测)设等差数列{}n a 的前n 项和为n S ,383235a a +=,则9S =( ) A .56 B .63 C .67 D .726.(2022·北京·北师大实验中学模拟预测)设等差数列{}n a 的前n 项和为n S ,若19a =,642a a +=,则当n S 取最大值n 等于( ) A .4 B .5 C .6 D .77.(2022·山东淄博·三模)已知正项等比数列{}n a 的前n 项和为n S ,且123,,a S S -成等差数列.若存在两项*,(,N )m n a a m n ∈18a =,则19m n+的最小值是( ) A .16 B .2 C .103 D .832q ,结合的代换求目标式的最小值,注意等号成立条件.23(a q a +=2q,n a >18n a a ⋅=,则8m n +=,911(8n m =⨯8.(2022·全国·模拟预测(文))在数列{}n a 中,()()()111,11N n n a n n a a n *+=+-=∈,则2022a =( )A .40432022B .20212022C .40402021D .20202021()21111111111212a a a n n n n ⎛⎫⎛⎫⎛⎫++-+=-+-++-+ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭9.(2022·四川省内江市第六中学模拟预测(理))已知数列{}n a 的前n 项和n S 满足()()*41N n S n n n =+∈,若数列{}n b 满足34n n a b +=,则122320212022111b b b b b b ++⋅⋅⋅+=( ) A .5052021B .20202021C .20212022D .2021808810.(2022·辽宁·模拟预测)如图是美丽的“勾股树”,将一个直角三角形分别以它的每一条边向外作正方形而得到如图①的第1代“勾股树”,重复图①的作法,得到如图②的第2代“勾股树”,…,以此类推,记第n 代“勾股树”中所有正方形的个数为n a ,数列{}n a 的前n 项和为n S ,若不等式2022n S >恒成立,则n 的最小值为( )A .7B .8C .9D .10【答案】C【分析】根据第1代“勾股树”,第2代“勾股树”中,正方形的个数,以此类推,得到第n 代“勾股树”中所有正方形的个数,即n a ,从而得到n S 求解.【详解】解:第1代“勾股树”中,正方形的个数为11321+=-,第2代“勾股树”中,正方形的个数为21721+=-,…,以此类推,第n 代“勾股树”中所有正方形的个数为121n +-,即121n n a +=-,所以()24122412n n n S n n +-=-=---,因为0n a >,所以数列{}n S 为递增数列, 又810122022S =<,920352022S =>, 所以n 的最小值为9. 故选:C .11.(2022·河南·模拟预测(文))已知数列{an }的前n 项和Sn 满足2n S n =,记数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为Tn ,n ∈N *.则使得T 20的值为( ) A .1939B .3839C .2041D .4041【答案】C113941++-12.(2022·山东济南·模拟预测)设{}n a 是首项为1的等比数列,n S 是其前n 项和,若34520a a a -=,则5S =______.2q,所以故答案为:31.13.(2022·四川省南充高级中学模拟预测(文))记n S 为正项等比数列{}n a 的前n 项和,若314S =,12a =,则2514a a a a ++的值为__________. 【答案】22q (q =-,所以21a a ++14.(2022·山东泰安·二模)已知数列{}n a 是公差大于0的等差数列,12a =,且32a +,4a ,64a -成等比数列,则10a =______. 【答案】20【分析】先利用()()243624a a a =+-解出公差d ,再通过等差数列计算10a 即可.【详解】设公差为d ,则()()243624a a a =+-,即()()()223222254d d d +=+++-,化简得24120d d +-=,解得2d =或6d =-,又0d >,故2d =,则101920a a d =+=. 故答案为:20.15.(2022·新疆石河子一中模拟预测(理))等差数列{}n a 的公差为2,前n 项和为n S,若2a ,4a ,8a 构成等比数列,则n S =___________.16.(2022·广东·模拟预测)已知数列{}n a 是首项为1的等差数列,其前n 项和为n S ,且962354S S -=,记()()1111n n n b a a +=++,则数列{}n b的前n 项和n T =______.【详解】设等差数列{}n a 的公差为d ,则由11a =,962354S S -=, 得()()91186115235422d d ++++⨯-⨯=, 解得2d =,所以()12121n a n n =+-=-, 所以()()()111111114141n n n b a a n n n n +⎛⎫===- ⎪++++⎝⎭,所以数列{}n b 的前n 项和11111114223144n nT n n n ⎛⎫=-+-+⋅⋅⋅+-= ⎪++⎝⎭. 故答案为:44nn +. 17.(2022·陕西·西安中学模拟预测(文))在等差数列{}n a 中,72615,18a a a =+=,若数列{}(1)nn a -的前n 项之和为n S ,则100S =__________. 【答案】100【分析】根据给定条件,利用等差数列性质计算首项、公差,再借助并项求和法求解作答. 【详解】设等差数列{}n a 公差为d ,由426218a a a =+=得:49a =,则741592743a a d --===-, ()4421n a a n d n =+-=+,当n 为偶数时,()()111112n nn n n n a a a a d ----+-=-==,所以100214310099()()()502100a a a a a a S =-+-++-=⨯=.故答案为:10018.(2022·内蒙古·赤峰二中模拟预测(理))如图所示,是毕达哥拉斯(Pythagoras )的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形,…,如此继续,若一共能得到1023个正方形.设初始正方形的边长为2,则最小正方形的边长为_____.【答案】116【分析】记初始正方形的边长为1a ,经过n 1-次生长后的正方形的边长为n a ,经过n 1-次生长后正方形的12n -++,由此次生长后正方形的112n -++=10n =,10121216-==19.(2022·河南·模拟预测(理))已知数列{}n a 为等比数列,公比0q >,首项11a =,前三项和为7,121024n a a a =,则n =______.2q,所以21222=⋅⋅⋅200-=,解得:故答案为:520.(2022·湖南益阳·模拟预测)在单调递增数列{}n a 中,已知11a =,22a =,且21n a -,2n a ,21n a +成等比数列,2n a ,21n a +,22n a + 成等差数列()*n N∈,那么100a=__________.21.(2022·上海交大附中模拟预测)已知各项均为正数的等比数列{}n a ,若4562a a a -=,则23a 的值为___________. 22.(2022·黑龙江·哈九中三模(文))设函数()12ln x f x x-=+,11a =,()*21N 1,23n n a f f n f f n n n n n -⎛⎫=+++⋅ ⎪⋅⋅+∈≥ ⎪⎝⎛⎫⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭⎝⎭⎭.则数列{}n a 的前n 项和n S =______.23.(2022·四川·宜宾市叙州区第二中学校模拟预测(文))已知数列{}n a 的前n 项和n S 满足2392222n n S a n n =-+-.(1)求1a ,并证明数列{}3n a n +为等比数列; (2)若(3)n n b n a n =+,求数列{}n b 的前n 项和n T . 11,S a =∴当2n ≥时,131a +⨯∴{}3n a n +(2)n a +13122n n T n =⨯+⨯①4122n n +++⨯23222n n ++-⨯11)22n n +-⋅-,24.(2022·贵州·模拟预测(理))已知数列{}n a ,满足12a =,2142n n n a a a +=++.(1)证明:数列(){}2log 2n a +是等比数列,并求数列{}n a 的通项公式; (2)求数列{}2n a +的前n 项积n T . 2q ,首项.(2)解:由(1)可得222nn a +=, ∴123112312222222222222222n n n nn T --+++++=⨯⨯⨯⨯⨯=,∵123112222222n n n -++++++=-,∴1222n n T +-=,*n ∈N .B 组 能力提升25.(2022·山东青岛·一模)我国古代数学著作《九章算术》中有如下问题:“今有人持金出五关,前关二税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.问本持金几何?”其意思为“今有人持金出五关,第1关收税金为持金的12,第2关收税金为剩余金的13,第3关收税金为剩余金的14,第4关收税金为剩余金的15,第5关收税金为剩余金的16,5关所收税金之和恰好重1斤.问原来持金多少?”.记这个人原来持金为a 斤,设()101,115,01x x f x x x +>⎧=⎨-<≤⎩,则()f a =( )A .5-B .7C .13D .2626.(2020·安徽·寿县第一中学模拟预测(文))右面的数表为“森德拉姆筛”,其特点是表中的每行每列上的数都成等差数列,则第n 行第n 个数字是( )A .21n -B .2(1)1n ++C .21n +D .2n【答案】C【分析】设第n 行第n 个数字是n n a ,由题意知第n 行是首项为1n +,公差为n 的等差数列,从而得出答案. 【详解】设第n 行第n 个数字是n n a ,由题意知第n 行是首项为1n +,公差为n 的等差数列,所以()()2111nn a n n n n =++-⨯=+故选:C【点睛】本题考查行列模型的等差数列求法,观察得出规律是关键,属于基础题. 27.(2022·全国·安阳市第二中学模拟预测(文))已知数列{}n a 的前n 项和为n S ,且2n n S na +=,若1n na S n nλ-≤-恒成立,则实数λ的最大值为( )A .12 B .1 C .23D .34,)()g n < 28.(2022·黑龙江·哈尔滨市第一二二中学校三模(文))公比为q 的等比数列{}n a ,其前n 项和为n S ,前n 项积为n T ,满足2021120212022202211,1,01a a a a a ->⋅><-.则下列结论正确的是( )A .201120331a a ⋅>B .n T 的最大值为2021TC .n S 的最大值为2023SD .1q >29.(2022·全国·武功县普集高级中学模拟预测(理))记n S 为各项均为正数的等比数列{}n a 的前n 项和,378S =,312a =,则5a =( )A .14B .18C .1D .230.(2022·安徽·芜湖一中模拟预测)已知正项等比数列{}n a 的前n 项和为n S ,前n 项积为n T ,满足12311,238a a S a ==-,则n T 的最小值是( )A .116B .132C .164D .11282q 或1-(舍去),211,,84a a =111264⨯⨯=31.(2022·吉林·长春吉大附中实验学校模拟预测)(多选题)意大利数学家列昂纳多•斐波那契提出的“兔子数列”:1,1,2,3,5,8,13,21,34,55,89,144,233,⋯,在现代生物及化学等领域有着广泛的应用,它可以表述为数列{}n a 满足()12211,n n n a a a a a n +++===+∈N .若此数列各项被3除后的余数构成一个新数列{}n b ,记{}n b 的前n 项和为n S ,则以下结论正确的是( )A .910n n b b ++-=B .1029n n S S ++=+C .20222b =D .20222696S =【答案】ABC【分析】根据数列{}n a 可得出数列{}n b 是以8为周期的周期数列,依次分析即可判断. 【详解】数列{}n a 为1,1,2,3,5,8,13,21,34,55,89,144,233,…, 被3除后的余数构成一个新数列{}n b ,∴数列{}n b 为1,1,2,0,2,2,1,0,1,1,2,0,2,2,1,0,…,观察可得数列{}n b 是以8为周期的周期数列,故910n n b b ++-=,A 正确; 且1289b b b +++=,故10234102...9n n n n n n S S b b b S ++++++=++++=+,B 正确;82502262262=b b b ⨯+==,C 正确;则{}n b 的前2022项和为202225291120222276S ⨯++++++==,D 错误. 故选:ABC32.(2022·广东·肇庆市外国语学校模拟预测)(多选题)将数列{}n a 中的所有项排成如下数阵: 234567891...a a a a a a a a a已知从第二行开始每一行比上一行多两项,第一列数1a 、2a 、5a 、成等差数列,且24a =,1010a =.从第二行起,每一行中的数按从左到右的顺序均构成以12为公比的等比数列,则( ) A .11a = B .2021a 位于第84列C .221n na a +<D .2021841332a =193644=则2021a 为第21n n b a ++=a b =C 组 真题实战练33.(2021·全国·高考真题(文))记n S 为等比数列{}n a 的前n 项和.若24S =,46S =,则6S =( ) A .7 B .8C .9D .10【答案】A【分析】根据题目条件可得2S ,42S S -,64S S -成等比数列,从而求出641S S -=,进一步求出答案. 【详解】∵n S 为等比数列{}n a 的前n 项和, ∴2S ,42S S -,64S S -成等比数列 ∴24S =,42642S S -=-= ∴641S S -=, ∴641167S S =+=+=. 故选:A.34.(2021·北京·高考真题)已知{}n a 是各项均为整数的递增数列,且13a ≥,若12100n a a a ++⋅⋅⋅+=,则n 的最大值为( ) A .9 B .10C .11D .12【答案】C【分析】使数列首项、递增幅度均最小,结合等差数列的通项及求和公式求得n 可能的最大值,然后构造数列满足条件,即得到n 的最大值. 【详解】若要使n 尽可能的大,则,递增幅度要尽可能小,不妨设数列是首项为3,公差为1的等差数列,其前n 项和为,则,,所以11n ≤. 对于,,取数列各项为(1,2,10)n =⋯,1125a =,则1211100a a a ++⋅⋅⋅+=, 所以n 的最大值为11.故选:C .35.(2021·北京·高考真题)《中国共产党党旗党徽制作和使用的若干规定》指出,中国共产党党旗为旗面缀有金黄色党徽图案的红旗,通用规格有五种.这五种规格党旗的长12345,,,,a a a a a (单位:cm)成等差数列,对应的宽为12345,,,,b b b b b (单位: cm),且长与宽之比都相等,已知1288a =,596=a ,1192b =,则3b = A .64 B .96 C .128 D .160【答案】C【分析】设等差数列{}n a 公差为d ,求得48d =-,得到3192a =,结合党旗长与宽之比都相等和1192b =,列出方程,即可求解.【详解】由题意,五种规格党旗的长12345,,,,a a a a a (单位:cm)成等差数列,设公差为d , 因为1288a =,596=a ,可得519628848513a a d --===--, 可得3288(31)(48)192a =+-⨯-=, 又由长与宽之比都相等,且1192b =,可得3113a ab b =,所以3131192192=128288a b b a ⋅⨯==. 故选:C.36.(2020·全国·高考真题(理))北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )A .3699块B .3474块C .3402块D .3339块【答案】C【分析】第n 环天石心块数为n a ,第一层共有n 环,则{}n a 是以9为首项,9为公差的等差数列,37.(2020·全国·高考真题(文))设{}n a 是等比数列,且1231a a a ++=,234+2a a a +=,则678a a a ++=( ) A .12 B .24 C .30 D .32【答案】D【分析】根据已知条件求得q 的值,再由()5678123a a a q a a a ++=++可求得结果.【详解】设等比数列{}n a 的公比为q ,则()2123111a a a a q q ++=++=,()232234111112a a a a q a q a q a q q q q ++=++=++==,因此,()5675256781111132a a a a q a q a q a q q q q ++=++=++==.故选:D.【点睛】本题主要考查等比数列基本量的计算,属于基础题.38.(2020·全国·高考真题(文))记Sn 为等比数列{an }的前n 项和.若a 5–a 3=12,a 6–a 4=24,则nnS a =( ) A .2n –1 B .2–21–nC .2–2n –1D .21–n –1【答案】B【分析】根据等比数列的通项公式,可以得到方程组,解方程组求出首项和公比,最后利用等比数列的通项公式和前n 项和公式进行求解即可.39.(2020·全国·高考真题(文))记n S 为等差数列{}n a 的前n 项和.若1262,2a a a =-+=,则10S =__________. 【详解】{根据等差数列前力和计算能力,属于基础题.40.(2020·全国·高考真题(文))数列{}n a 满足2(1)31nn n a a n ++-=-,前16项和为540,则1a =______________. 【答案】7【分析】对n 为奇偶数分类讨论,分别得出奇数项、偶数项的递推关系,由奇数项递推公式将奇数项用1a 表示,由偶数项递推公式得出偶数项的和,建立1a 方程,求解即可得出结论.【详解】2(1)31nn n a a n ++-=-,当n 为奇数时,231n n a a n +=+-;当n 为偶数时,231n n a a n ++=-. 设数列{}n a 的前n 项和为n S , 16123416S a a a a a =+++++13515241416()()a a a a a a a a =+++++++111111(2)(10)(24)(44)(70)a a a a a a =++++++++++ 11(102)(140)(5172941)a a ++++++++118392928484540a a =++=+=, 17a ∴=.故答案为:7.【点睛】本题考查数列的递推公式的应用,以及数列的并项求和,考查分类讨论思想和数学计算能力,属于较难题.41.(2021·全国·高考真题)记n S 是公差不为0的等差数列{}n a 的前n 项和,若35244,a S a a S ==. (1)求数列{}n a 的通项公式n a ; (2)求使n n S a >成立的n 的最小值. 【答案】(1)26n a n =-;(2)7.【分析】(1)由题意首先求得3a 的值,然后结合题意求得数列的公差即可确定数列的通项公式; (2)首先求得前n 项和的表达式,然后求解二次不等式即可确定n 的最小值.42.(2021·浙江·高考真题)已知数列{}n a 的前n 项和为n S ,194a =-,且1439n n S S +=-.(1)求数列{}n a 的通项;(2)设数列{}n b 满足*3(4)0()n n b n a n N +-=∈,记{}n b 的前n 项和为n T ,若n n T b λ≤对任意N n *∈恒成立,求实数λ的取值范围.(4)n ++-3(5)(4nn ⎛⎫++-⋅+ ⎪⎝⎭3433(44n⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭,43.(2021·全国·高考真题)已知数列{}n a 满足11a =,11,,2,.n n na n a a n ++⎧=⎨+⎩为奇数为偶数 (1)记2n n b a =,写出1b ,2b ,并求数列{}n b 的通项公式;(2)求{}n a 的前20项和.2111()121221+a a a a +-+=+++++++12(n n =+⨯的通项公式31n b n =-. 201924620++++()()a a a a a a a +=+++10101)b b ++-++300=. 满足12121,2n n a a a ==+,1924260)()a a a a a +++++++101012=⨯+方法一:由题意讨论{}n b 的性质为最一般的思路和最优的解法;方法二:利用递推关系式分类讨论奇偶两种情况,然后利用递推关系式确定数列的性质;方法三:写出数列{}n a 的通项公式,然后累加求数列{}n b 的通项公式,是一种更加灵活的思路n 44.(2021·全国·高考真题(文))设{}n a 是首项为1的等比数列,数列{}n b 满足3nn na b =.已知1a ,23a ,39a 成等差数列.(1)求{}n a 和{}n b 的通项公式;(2)记n S 和n T 分别为{}n a 和{}n b 的前n 项和.证明:2nn S T <.113n n --+++121111333-⎫+++⎪⎭n ,230121*********323333n n n -⎫⎛⎫++++-++++=⎪ ⎪⎭⎝⎭0101233--+++113---n n 2111111212233-----+++n n , ⑧ 311212233---+++nn . ⑨211133-⎫++-⎪⎭n 123--⨯n n . 03<⨯nn. 113n n --+++3213n n -+++2111133333n n n n =++++-1n b c ++=:导函数法 23+++=nx x x )()(1'1n x x ⎡⎤⎤-⎣⎦1-++=n nx1-n ,2111111233333n n b n -⎡⎤⎛⎫⎛⎫++=+⨯+⨯++⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦1133f ⎛⋅ ⎝'13311)34423nnn ⎤⎛⎫⎛⎫⎛⎫+=-+⎥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎥⎦,下同方法二. 【整体点评】本题主要考查数列的求和,涉及到等差数列的性质,错位相减法求数列的和,考查学生的数。
等比数列等差数列知识点归纳总结

等比数列等差数列知识点归纳总结等比数列和等差数列是数学中常见且重要的概念之一。
在解决各种数学问题和应用中,它们都有着广泛的应用。
本文将对等比数列和等差数列的知识点进行归纳总结,以帮助读者更好地理解和掌握这两个数列的特点和应用。
一、等差数列等差数列是一种特殊的数列,其中每一项与前一项之差保持恒定。
具体来说,对于一个等差数列a₁, a₂, a₃, ..., an,它的通项公式可以表示为:an = a₁ + (n-1)d其中,a₁表示首项,d表示公差,n表示项数。
等差数列的常用术语包括首项、公差、通项公式和项数等。
1. 首项(a₁):等差数列的第一项称为首项。
2. 公差(d):等差数列中相邻两项的差称为公差。
公差可以是正数、负数或零。
3. 通项公式:等差数列的第n项通项公式可以用来求出数列中任意一项的值。
在通项公式中,n表示项数。
4. 项数:等差数列包含的项的个数称为项数。
等差数列的主要特点是任意两项之差相等,这使得我们可以根据已知的条件,快速求解未知项的值。
一些常见的应用包括求和公式、平均数问题、等差数列的图像和几何问题等。
二、等比数列等比数列是一种特殊的数列,其中每一项与前一项之比保持恒定。
具体来说,对于一个等比数列a₁, a₂, a₃, ..., an,它的通项公式可以表示为:an = a₁ * r^(n-1)其中,a₁表示首项,r表示公比,n表示项数。
等比数列的常用术语包括首项、公比、通项公式和项数等。
1. 首项(a₁):等比数列的第一项称为首项。
2. 公比(r):等比数列中相邻两项的比称为公比。
公比可以是正数、负数或零,但不能为1。
3. 通项公式:等比数列的第n项通项公式可以用来求出数列中任意一项的值。
在通项公式中,n表示项数。
4. 项数:等比数列包含的项的个数称为项数。
等比数列的主要特点是任意两项之比相等,这使得我们可以根据已知的条件,快速求解未知项的值。
一些常见的应用包括求和公式、计算几何问题和金融领域的应用等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等差与等比数列专题复习等差与等比数列是最重要且应用广泛的有通项公式的数列,在高考中占有重要地位,成为每年必考的重点内容,这部分内容的基础知识有:等差、等比数列的定义及通项公式,前几项和公式以及等差、等比数列的性质,在解决有关等差,等比数列问题时,要注意运用方程的思想和函数思想以及整体的观点,培养分析问题与解决问题的能力。
一、知识结构与要点:等差、等比数列的性质推广2等比数列- L 定义:且a n基本概念-通项_ q a n 2an 11an 1 a nq n m S n前n 项和 1等比中项:a b c 成等比数列b 2 acaw(q 1)印(1 q n )a iL 与首末两端等距离的两项之积相等a 1ana 2an 1a i an i 1—基本性质一二、典型例题 am a n a p a q{a n }成等比,若 n 「n 2,…n k 成等差 贝V a 1,a n2,...a nk 当a 1或q成等比a 1 q 1a 1时{ a n }为递增数列 0 q 10或a 1 0时{a n }为递减数列 0 q 1q<0时 q=1时 { a n }为摆动数列 { a n }为常数数列例1 •在等差数列中a 6 a 9a 12 a 15 20求S 20解法 a n a1(n l)da 6 a 9 a12 2(2a 1 19d) a1520(a 1 5d) (a 1 8d) (a 1 11d) (a 1 14d)2a 1 19d 10那么S 2010(2a 1 19d)100解法二:由m nq am a n a p a qa 6 a 9 a i2 a i5 2(a 6 a i5)2(a i a 2o ) 20点评:在等差数列中,由条件不能具体求出a 1和d ,但可以求出 a 1与d 的组合式,而所求的量往往可以用这个组合式表示,那么用“整体代值”的方法将值求出(2)利用:m n p q a m a n a p a q 将所求量化为已知量也是“整体代值”的思 想,它比用a 1和d 表示更简捷。
例2 .等差数列前 m 项和为30,前2m 项和为100,则它的前3m 项和为 _____________________ 解法一 用方程的思想,由条件知...(a 1 a m )m 30\ 2 (a i a m )m 60 ①⑻ a 2m )2m 100(a i a 2m )m 100 ②2am a 2m a 3m 也成等数列解:在等差数列中由性质知 s ms 2m s m S 3m s 2m 成等差数列S3m S 2m 2( S 2m S m ) S m S3m 3(S 2m S m ) 210解法三等差数列{a n }中 S na 〔n 丄n(n 1)d 爼 a (n 1) —2 n2即{§斗为以a 1为首项公差为—的等差数列 依题意条件知n12S3m 3(S 2m S m ) 210点评:三种解法从不同角度反映等差数列所具有的特性,运用方程的方法、性质或构造新的等 差数列都是数列中解决问题的常用方法且有价值,对解决某些问题极为方便。
例3在等比数列中 S 5 93 a 2 a 3 a 4 a 5 a 6 186求a 8S3m3m .y (a 1a3m )3尹⑻2a 2m a m )由②x2-①得m(a 1 a 2m a m )140 代入-140 2102m 2m 3m2 Em S 2m S m 2m 3m m分析:在等比数列中对于 a 〔q n a n S n 五个量一般“知三求二”其中首项 5元比是关键,第4页共17页因此 解法一a 2 a 3 a 4a 5 a6 186S5a 6a 1 186a6a 1 93a 1 q 5a 1 93又S 5 a 1 a 1q 5 93a 〔 a 〔 9393 q 2a 1 31 q 1 q则a 8 a 1 q 7384解法二S593而a 2 a3a 4 a5a6(a 1 a 2 a 3 a 4 a 5)q 186q 2代入a1(11 q 5) q93 中得a 〔 3故 a 8 a 1 q 7 384点评:根据等比数列定义运用方程的方法解决数列问题常用解法二更为简捷。
例4•在等差数列{a n }中S 936 Sn 104等比数列{b n }中例5•设等差数列{a n }前n 项和为S n 已知a 3 12 S 12 0S 13 0(1)求公差d 的范围 (2)指出S 1S 2……S 12中哪一个值最大,并说明理由解: S 9a 1 a 9 x (12 9)9 a 5 936a 54S13a1a13213 a 713 104a 7 8b 5 b 7 a 5 a 732b)2 324.3b5a5b7a7 贝廿 b 6----------------------------点评:此题也可以把a i 和d 看成两个未知数,通过 S 936 S 13104列方程,联立解之 d= 2 a 14。
再求出a 5a 7但计算较繁,运用a i2a n 计算较为方便。
S1212a 1 0 032解:(1 )由题义有S1313a1由a312a 1 12 2d (2 S n a〔n d<0所以[n 1(5 24 12 (12 1)d 0 2 13 (13 1)d 0则代入上式有1n(12 2d)2n(n24)]2最小时S n 最大d24 1)d7d 01 -. 6 2(5 T )6.5 所以当n=6时[n 1 2(5 点评:本题解法体现了函数思想在处理数列问题中的运用, 法与判断函数增减性的方法相同。
例6已知a>0 a 1数列{a n }是首项5元比都为2a 1 11d a 1 6d 1 2(524 2d 1 24 22[2(5 尹24 )]2最小d 判断数列随 a 的等比数列, 数列{b n }中每一项总小于它后面的项,求 a 的取值范围。
解:由已知有 a n a a n 1所以 b na n lga nn . na lgab n因此由题意 对任意nbnb n 1成立即na n alg(n 即 a n lg a [(n 1)a n]对任N 总成立,那么 由a>0 即(i ) 由i 知a>1故a 的取值范围为1)a n 1)nS 6最大N 增大而变化规律的方a n lg a n (n N)如果n .na lg a1)a n1 alg知a n—为递增的函数n 1所以「)min1a 或 a>12点评:这是道数列与不等式综合的题目,既含有字母分类讨论又要运用极限的思想和函数最值的最大值.第6页共17页数列求和的基本方法和技巧数列是高中代数的重要内容,又是学习高等数学的基础•在高考和各种数学竞赛中都占有重要的地位.数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部 分数列的求和都需要一定的技巧 •下面,就几个历届高考数学和数学竞赛试题来谈谈数列求和的基本方法和技巧.一、利用常用求和公式求和 利用下列常用求和公式求和是数列求和的最基本最重要的方法3、 Sn nk k 1 ^n(n 2 1)4、 S nnk 2 h(n 1)(2n1)k 1 6n31 25S nk[二 1)]k 12123[例1]已知log 3 x,求XX xlog 2 3[例 2]设 S= 1+2+3+…+ n , n € N,求 f(n)的观点来解决问题,同时还要判断函数的单调性,具有一定的综合性。
解:由log 3 x1 log2 3log 3 xlog 3 2由等比数列求和公式得S n x x 2 x 3x n (利用常用公式)x(1 x n ) 1 x1 11(1戶 1 1 21=1 — 2n1、等差数列求和公式:S nn(n 1)dna (q 1) 2、等比数列求和公式:S nd(1 q n )(q 1)x n 的前n 项和.&(n 32)S n 1解:由等差数列求和公式得S 1 1丄n(n 1) , S n丄5 1)(n 2)(利用常用公式) 2 2S n …f(门)(n 32)S n 1n~2~n 34 n 64n1 _64 二34 ( ., nn___ 丄250 50 n= 8 时, f ( n)max150二、错位相减法求和这种方法是在推导等比数列的前项和公式时所用的方法,这种方法主要用于求数列{a n • b n}的前n项和, 其中}分别是等差数列和等比数列[例3]求和: S n 1 3x 5x27x3(2n 1)x n 1解:由题可知, {(2n 1)x n1}的通项是等差数列{2n —1}的通项与等比数列{x n 1}的通项之积设xS n 1x 3x2 5x3 7x4(2n 1)x n.②(设制错位)①一②得(1x)S n 1 2x 2x22x32x42x n 1(2n 1)x n(错位相减)再利用等比数列的求和公式得: (1 X)Snn 11 x2x -1 x(2n 1)x nS nn 1(2n 1)x 1)x n(1 x)2(2n (1x)[例4]求数列-2 4 622,23,尹前n项的和.解:由题可知,{军}的通项是等差数列{2n}的通项与等比数列2n}的通项之积设S n2n2n(设制错位)①一②得(1;)S n 22 22 222 23_2_24_22n(错位相减)2【i I1 2n2n 1 n 1n 2 4、反序相加法求和这是推导等差数列的前 n 项和公式时所用的方法,就是将一个数列倒过来排列(反序) ,再把它与原数列相加,就可以得到 n 个(印 a n ). [例5]求证:C 3C : 5C ; (2n 1)C : (n 1)2n证明:设S nc : 3C : 5C n 2(2n 1)C ;••…•…①把①式右边倒转过来得S n (2n 1)C ; (2n 1)C n n 13C : Co (反序)又由c m C 1 m可得S n (2n 1)C° (2n 1)C ;n 1n 3Cncn……..②①+②得2S n (2n 2)(C : c :c : 1 C :)2(n 1) 2n (反序相加)S n (n 1)2n[例6]求sin 21 sin 22sin 2 3sin 2 88 sin 89 的值解:设 S sin 21 sin 22 sin 23sin 2 88 sin 2 89 …①将①式右边反序得non、、,sin 3 sin 2 sin 1 …②(反序)2 2 22 S (sin 1 cos 1 ) (sin 2四、分组法求和有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等 差、等比或常见的数列,然后分别求和,再将其合并即可11 1 [例7]求数列的前n 项和:11, 4,— 7,,十 3n 2,a aa1 1解:设 S n (11) (— 4)(飞 7)a a1(F 3n 2) 将其每一项拆开再重新组合a2n2 2S sin 89 sin 88又因为 sin x cos(902 2x),sin x cos x 1①+②得(反序相加)2小、cos 2 )2 2(sin 89 cos 89 ) = 89 /• S = 44.511 1 S n(1 - -2―) (1 4 7 3n 2)(分组) a aa当 a = 1 时,S nn (3n 1)n = (3n 1)n (分组求和)22当a1 !1时,S n即1 - a(3n 1)n1 naa (3n 1)n2—a 12[例 8] 求数列{n(n+1)(2n+1)} 的前n 项和.解:设 a k k(k 1)(2k 1) 2k 3 3k 2k nS nk(k 1)(2k 1)=k 1n(2 k 3 3k 2 k )k 1将其每一项拆开再重新组合得s=nn n2 k3 3 k 2k( 分 组)——k 1k 1k 1332(1 2n 3) 3(1222n 2) (1 2n)=n 2(n 1)2n(n 1)(2n1) n(n 1)(分组求和) n(n 1)2(n 2)22 22五、裂项法求和这是分解与组合思想在数列求和中的具体应用 •裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的si n1(2)cos n cos(n 1)1 1] n(n 1)(n 2) 2 n(n 1) (n 1)(n 2)(3) a n1 - 1n(n 1) n n 1(2n)21丄(丄丄 (2n 1)(2n 1)2 2n 1 2n 1通项分解(裂项)如:tan(n 1) tan n(1)a nf(n 1) f(n)(5) a na nn 2n(n 1)2(n 1) n 1nn(n 1) 21 ,则S" 1儿(n 1)2n[例9]1求数列1, ,1 2 2 3的前n项和.解:S na n(2 .J)■/n(裂项)(裂项求和)(.3 ,2) C.n• n)=、n 110] 在数列{a n}中,a n,又b n,求数列{b n}的前n项的和.解:T a n•••b n数列{b n}的前n项和anan 1(裂项)S n 8[(1 11112)1)(1(丄n[例11] 求证:解:设S cosO cos1 cos1 cos2cosO cos1 cos1 cos 2 sin1由cos n cos(n 1)tan(n 1)• Scos0 cos1 cos1 cos21{(tan 1 tan 0 ) (tan 2 sin 11)](裂项求和)18(1冷8nn 1 cos88 cos89cos1sin21cos88 cos89tan n (裂项)cos88 cos89(裂项求和)tan 1 ) (tan 3 tan 2 ) [tan 89 tan 88 ]}第11页共17六、合并法求和针对一些特殊的数列,将某些项合并在一起就具有某种特殊的性质,因此,在求数列的和 时,可将这些项放在一起先求和,然后再求S.[例 12] 求 cos1 ° + cos2 ° + cos3 ° + •…+ cos178 ° + cos179 ° 的值. 解:设 S n = cos1 ° + cos2 ° + cos3 ° + •…+ cos178 ° + cos179 °••• cosn cos(180 n)(找特殊性质项)• S= (cos1 ° +cos179 °)+(cos2 ° +cos178 °)+(cos3 ° +cos177 °) + • • • + (cos89 ° +cos91 °)+cos90 ° (合并求和)=0= a 1999a 2000 a 2001 a 2002由等比数列的性质 m n p q a m a n a p a q (找特殊性质项)sin1(tan 89 tanO )= ------- sin 1 coslcotl = 2—sin 1原等式成立解:设 S 2002 = a 1a 2 a 3a :2002由a 1 1, a 23,a32, a n2an 1an 可得a 41, a 53, a 62, a 7 1, a 83, a 92, aw 1, an3, a 122a6k 11,a6k 23, a 6k 32,a6k 41, a 6k 53,a6k 62'a6k 1a6k2a6k 3 a6k 4a(5k 5a6k 6(找特殊性质项)•-S E 002 = =a 1 a 2 a 3a2002(合并求和)=(a-ia 2 a 3 a 6)(a 7a8a12)(a6k 1a6k 2a6k 6)[例 13]数列{a n }: a 1 1, a 2 3, a 3 2, a . 2 a . 1 a * ,求 S 2002.(a 1 993 a 1994a 1998 ) a 1999 a 2000 a 2001 a 2002a6k 1a6k 2a6k 3 a6k 4[例14]在各项均为正数的等比数列中,若 a §a 69,求 log 3 a 1 log 3 a 2log 3 a 10 的值.解:设 S n log 3 a 1log 3a 2log3 a 10和对数的运算性质log a M log a N log a M N 得 S n (log 3 a 1log 3 a 10 )(log 3 a 2 log 3 a 9)(log 3 a 5 log 3 a 6)(合并求和)=(log 3 a 1 a 10)(log3 a 2 a 9)(log3 a 5 a 6)=log 3 9 log 3 9 log 3 9 =10七、利用数列的通项求和先根据数列的结构及特征进行分析,找出数列的通项及其特征,然后再利用数列的通项揭=4(池示的规律来求数列的前 [例 15]求 1 11n 项和,是一个重要的方法111 111 1之和.n 个1解:由于111k 个1999k 个 199(10k1)(找通项及特征)1 11 111111n 个=1(101 1)9丄(1021)91)1丄(10" 1)(分组求和)9(101102 103n 、10 )1(11)1 10(10n 1) n 9 10 199n)[例16]已知数列{a n } : a(n1)( n 3),求(n n 11)(a na n 1 )的值.解:••• (n 1)(a na n 1) 8(n1)[( n 1)(n 3)(n 2)( n 4)](找通项及特征)—8[(n 2)(n4) (n](设制分组)3)( n 4)(裂项)(n1)(a n a n 1 1 1 1) 4 ( 1')8(' ')(分组、裂项求和) n 1n1n2n4 n1n3n4,,11、 c 113=4 (-—)83443等差与等比数列1(北京)已知数列{a n}中,a i 1 12,Sn为数列的前n项和,且Sn与二的一个等比中项为n(n N'),则lim S n的值为( )n/八3 3 2(A) ( B) (C) ( D) 14 2 32(黄冈)在等差数列{a n}中,a1 + a2 + + a50 = 200,a51 + a52 + …+ a1oo = 2700 ,贝V a1 等于((A)—1221 (B)—21.5 (C)—20.5 (D)—20第13页共1712a n (0 a n —)6i2若 3i -,贝U a 8 ( )1 7— a n 1( a n 1)—1 (D)-7—a 1 1, a n 1 a n 1,则此数列前4项之和为( )(C) — (D)-—5 (天津)在等差数列{a n }中,n —,公差d<0,前n 项和是S n ,则有( )(A ) na n S nna j (B )na j S n na n ( C ) S n na j ( D )S nna n16(北京)等差数列{a n }中,已知a 1 ,a —+ a 5=4, a n =33,贝U n 为( ) 3A 、 48B 49C 、 50D 、517、如果数列 满足是首项为1,公比为—的等比数列,则。
