数电第一章
合集下载
数电 第1章 数字逻辑电路基础
第1章 数字逻辑电路基础
两类信号: 模拟信号;数字信号. 在时间上和幅值上均连续 的信号称为模拟信号; 在时间上和幅值上均离散 的信号称为数字信号.
处理数字信号的电路称为数字电路.
数字电路特点:
1) 工作信号是二进制表示的二值信号(具有“0”和“1”
两种取值);
2) 电路中器件工作于“开”和“关”两种状态,电路的输
与逻辑电路
若将开关断开和灯的熄灭状态用逻辑量“0”表示;将开关 合上和灯亮的状态用逻辑量“1”表示,则上述状态表可表 示为:
A 0 0 1 1 与逻辑真值表 B F=A ·B 0 1 0 1 0 0 0 1
A B
&
F=AB
与门逻辑符号
与门的逻辑功能概括： 1）有“0”出“0”； 2）全“1”出“1”。
非逻辑电路
•
与门和或门均可以有多个输入端.
1.3.2
复合逻辑运算
1. 与非逻辑 (将与逻辑和非逻辑组合而成)
与非逻辑真值表 B F=A ·B 0 1 0 1 1 1 1 0
A 0 0 1 1
A
&
B
F=AB
与非门逻辑符号
2. 或非逻辑 (将或逻辑和非逻辑组合而成)
A 0 0 1 1 或非逻辑真值表 B F=A +B
表示二进制数的方法有三种，即原码、反码和补码
符号位(+)
真实二进制数
B6 B 5 B4 B3 B2 B1 B0 1 0 1 0 0 1 1 =－4510
符号位(－)
补码
用补码系统表示有符号数
1.3.3
+9 +4
补码系统中的加法
0 1001 (被加数) 0 0100 (加数) 0 1101 (和=+13)
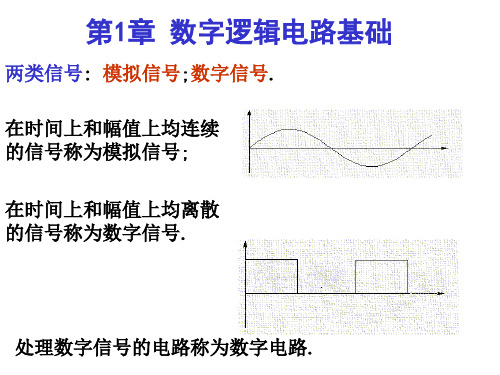
两类信号: 模拟信号;数字信号. 在时间上和幅值上均连续 的信号称为模拟信号; 在时间上和幅值上均离散 的信号称为数字信号.
处理数字信号的电路称为数字电路.
数字电路特点:
1) 工作信号是二进制表示的二值信号(具有“0”和“1”
两种取值);
2) 电路中器件工作于“开”和“关”两种状态,电路的输
与逻辑电路
若将开关断开和灯的熄灭状态用逻辑量“0”表示;将开关 合上和灯亮的状态用逻辑量“1”表示,则上述状态表可表 示为:
A 0 0 1 1 与逻辑真值表 B F=A ·B 0 1 0 1 0 0 0 1
A B
&
F=AB
与门逻辑符号
与门的逻辑功能概括： 1）有“0”出“0”； 2）全“1”出“1”。
非逻辑电路
•
与门和或门均可以有多个输入端.
1.3.2
复合逻辑运算
1. 与非逻辑 (将与逻辑和非逻辑组合而成)
与非逻辑真值表 B F=A ·B 0 1 0 1 1 1 1 0
A 0 0 1 1
A
&
B
F=AB
与非门逻辑符号
2. 或非逻辑 (将或逻辑和非逻辑组合而成)
A 0 0 1 1 或非逻辑真值表 B F=A +B
表示二进制数的方法有三种，即原码、反码和补码
符号位(+)
真实二进制数
B6 B 5 B4 B3 B2 B1 B0 1 0 1 0 0 1 1 =－4510
符号位(－)
补码
用补码系统表示有符号数
1.3.3
+9 +4
补码系统中的加法
0 1001 (被加数) 0 0100 (加数) 0 1101 (和=+13)
精品课件-数字电子技术-第1章
(3) 重复做第（2）步，直到商为0 (4) 将各个余数按照和运算过程相反的顺序排列起来， 即为所求的R
第1章 数字逻辑基础
【例1.3】 (47)10=(?)2
即
(47)10=(101111)2
第1章 数字逻辑基础
【例1.4】 (435)10=(?)16 解
即
(435)10=(1B3)16
第1章 数字逻辑基础
Y=F（A，B，C，…）
第1章 数字逻辑基础
在逻辑函数中，不管是变量还是函数，它们都只有两个 取值，即逻辑0和逻辑1。0和1称为逻辑常量，并不表示数值 的大小，而是表示某一种事物两种对立的逻辑状态。这一点 从事件发生的因果关系去想很容易理解。因为决定事件是否 发生的条件相当于变量，尽管条件可能很多，但对于一个条 件来说，都只有具备和不具备两种可能，而事件相当于函数，
由于在实际工作中人们大都习惯于使用正逻辑体系，因此 在本教材及以后的实际工作中，如无特殊说明，所遇到的逻辑
第1章 数字逻辑基础
1.2.3 基本逻辑运算有与、或、非三种。为了便于理解，我们
用开关控制电路为例来说明这三种运算。将开关作为条件，
在图1.1（a）所示电路中，只有当两个开关同时闭合时， 指示灯才会亮，即决定事物结果的全部条件同时具备时，结 果才会发生。这种因果关系叫做逻辑与， 用符号“·”表示 与运算，
第1章 数字逻辑基础
图1.2 (a) 与门；(b) 或门；(c)
第1章 数字逻辑基础
1.2.4 实际的逻辑问题往往比与、或、非逻辑要复杂得多，不
过它们都可以用与、或、非的逻辑组合来实现。最常见的组 合逻辑运算有与非、或非、与或非、异或、同或等。实现组
第1章 数字逻辑基础
3) 十六进制数的每一位有十六个不同的数码，分别用0~9、 A(10)、B(11)、C(12)、D(13)、E(14)、F(15) 表示。计 数基数为16。其计数规则是“逢16进1”，各位的权值是16i。
第1章 数字逻辑基础
【例1.3】 (47)10=(?)2
即
(47)10=(101111)2
第1章 数字逻辑基础
【例1.4】 (435)10=(?)16 解
即
(435)10=(1B3)16
第1章 数字逻辑基础
Y=F（A，B，C，…）
第1章 数字逻辑基础
在逻辑函数中，不管是变量还是函数，它们都只有两个 取值，即逻辑0和逻辑1。0和1称为逻辑常量，并不表示数值 的大小，而是表示某一种事物两种对立的逻辑状态。这一点 从事件发生的因果关系去想很容易理解。因为决定事件是否 发生的条件相当于变量，尽管条件可能很多，但对于一个条 件来说，都只有具备和不具备两种可能，而事件相当于函数，
由于在实际工作中人们大都习惯于使用正逻辑体系，因此 在本教材及以后的实际工作中，如无特殊说明，所遇到的逻辑
第1章 数字逻辑基础
1.2.3 基本逻辑运算有与、或、非三种。为了便于理解，我们
用开关控制电路为例来说明这三种运算。将开关作为条件，
在图1.1（a）所示电路中，只有当两个开关同时闭合时， 指示灯才会亮，即决定事物结果的全部条件同时具备时，结 果才会发生。这种因果关系叫做逻辑与， 用符号“·”表示 与运算，
第1章 数字逻辑基础
图1.2 (a) 与门；(b) 或门；(c)
第1章 数字逻辑基础
1.2.4 实际的逻辑问题往往比与、或、非逻辑要复杂得多，不
过它们都可以用与、或、非的逻辑组合来实现。最常见的组 合逻辑运算有与非、或非、与或非、异或、同或等。实现组
第1章 数字逻辑基础
3) 十六进制数的每一位有十六个不同的数码，分别用0~9、 A(10)、B(11)、C(12)、D(13)、E(14)、F(15) 表示。计 数基数为16。其计数规则是“逢16进1”，各位的权值是16i。
数字电路 第 1 章 绪论
二-十进制代码（BCD码）
二-十进制码(BCD码)
BCD码：将十进制数的0～9十个数字，用二进制数表示的代码，称为
二-十进制码，简称BCD码 。 每四位二进制码为一组，代表一个十进制数。既具有二进制码的形 式，又有十进制数的特点。四位二进制数表示十进制数的方案数：
A
16! 10 2.91010 = 16 (16-10)!
赋予）
二-十进制代码（BCD:Binary Coded Decimal）：采用二进制码表
示一个十进制数的代码。
数字系统中常用的编码有两类：二进制码、二-十进制码。
二进制码 二进制码：自然码、循环二进制码
1、自然码：有权码(结构形式同二进制数：各位的权值为2i) 2、循环二进制码（格雷码）：无权码(相邻的代码只相差一位)
(N) R= (kn-1kn-2…k1k0.k-1k-2…k-m)R n-表示整数位数，-m表示小数位数 Ki为R进制中的一个数码，0≤Ki ≤R－1
ⅱ) 多项式记数法：（按权展开）
(N) R=kn-1Rn-1+…+k0R0 +k-1R-1+…+k-mR–m
常用的进位制
十进制(Decimal)
(1) R=10(0,1,2,3,4,5,6,7,8,9；逢十进一：9+1=(10)10)
解 (10101.11)B=1×24+0×23+1×22+0×21 +1×20+1×2-1+1×2-2 =16+0+4+0+1+0.5+0.25=(21.75)D
十进制数转换成其它进制数
需将十进制数的整数部分和小数部分分别进行转换，然后将 它们合并起来 。 1. 整数转换——采用逐次除以基数R取余数的方法
数电第一章
4、十六进制（ Hexadecimal ）
基数R=16，它有16个符号，即0~9和 A(10),B(11),C(12)， D(13),E(14),F(15)；计数时，逢十六进一
不同数位上的数具有不同的权值16i。
第一章 逻辑代数基础
常用数制对照表
十 0 1 2 3 4 5 6 7 二 0 0 0 0 0 0 0 0 000 001 010 011 100 101 110 111 八 0 1 2 3 4 5 6 7 十 六 0 1 2 3 4 5 6 7 十 8 9 1 1 1 1 1 1 二 1 1 1 1 1 1 1 1 000 001 010 011 100 101 110 111 八 1 1 1 1 1 1 1 1 0 1 2 3 4 5 6 7 十 六 8 9 A B C D E F
小数点为分界
3
2
7
2
3
4
第一章 逻辑代数基础
非十进制间的转换
二进制与十六进制间的转换
以小数点为分界，整数部分向左、小数部分 分向右，每四位分为一组，不足四位的分别在整 数的最高位前和小数的最低位后加“0‖补足，然 后每组用等值的十六进制码替代，即得目的数。 例： 111011.10101 BB= ?(3B.A8)H (111011.10101) = H
权 权 权 权 权
第一章 逻辑代数基础
2、二进制（ Binary ）
(N)2= ( Kn-1 K1 K0 . K-1 K-m )2
= Kn-1 2n-1++K121+K020+K-1 2-1++K-m 2-m
n1 i K 2 i i m
特点：⑴ i可为-m到n-1之间的任意整数 ⑵ 基数2，逢2进一，即1+1=10 ⑶ K i表示第i位的数符，数码K i从0-1。 ⑷ 不同数位上的数具有不同的权值2i。
数电第1章
利用运算规则可以对逻辑式进行化简。 例如：
AB CD AB D( E F ) AB CD
被吸收
大连交通大学电气信息学院 30
②反变量的吸收：A AB 证明： A
A B
长中含反，去掉反。
AB A AB AB
A B( A A) A B
例如： A ABC DC A BC DC 被吸收
=AB +AC 推论：AB+AC+BCDE… =AB+AC
大连交通大学电气信息学院 37
例1.3 试利用与非门来组成非门、与门和或门
非门： A 与门：
A B
& &
F
F A AA
&
F
F A B A B
或门： A
& &
F A B A B
F
AB
B
&
大连交通大学电气信息学院 38
A 0 A , A 1 1, A A A, A A 1
乘运算规则:
0•0=0
0•1=0
1•0=0
1•1=1
A 0 0 , A 1 A, A A A, A A 0
非运算规则:
1 0
0 1
AA
27
大连交通大学电气信息学院
2. 逻辑代数的运算规律
(25.375 )10 (?)2
整数部分 除二倒取余
+
小数部分
大连交通大学电气信息学院
乘二正取整
8
2
2
25 12
余 1 余 0 余 0 余 1 余 1
数电-第一章
D = Σ(ki ×16i )
¾十六进制数ABCD.EF可表示成： ¾(ABCD.EF)16=(10×163+11×162+12×161+1
3×160+14×16-1+15×16-2)10
2011-3-2
26
1.1.3八进制数和十六进制数
¾对R(R为正整数)进位计数制的特点总结如下： ¾1、R进位计数制的基数是R，各数位能选用的数
模拟信号
数字信号
时间上和幅度上都 连续变化的信号
时间上和幅度上都 断续高变电化平的信号
2011-3-2
低电平 9
二、数字电路的分类
¾根据电路结构不同分 分立元件电路
集成电路
将晶体管、电阻、电 容等元器件用导线在线路 板上连接起来的电路。
将上述元器件和导线通过半 导体制造工艺做在一块硅片上而 成为一个不可分割的整体电路。
-1+2×8-2)10
2011-3-2
24
4
2011-3-2
1.1.3八进制数和十六进制数
¾十六进制数 ¾组成：0、1、2、3、4、5、6、7、8、
9、A、B、C、D、E、F ¾进位规则：逢十六进一 ¾权值：16i ¾基数：16
2011-3-2
25
1.1.3八进制数和十六进制数
¾对任意一个十六进制数D，也可以用一个多 项式形式表示，并可计算出它所表示的十 进制数的大小 。
¾根据半导体的导电类型不同分
双极型数字集成电路 单极型数字集成电路
以双极型晶体管 作为基本器件2011-3-2例如 TTL
以单极型晶体管 作为基本器件
例如 CMOS 10
¾根据集成密度不同分
集成电路的分类 集成度
¾十六进制数ABCD.EF可表示成： ¾(ABCD.EF)16=(10×163+11×162+12×161+1
3×160+14×16-1+15×16-2)10
2011-3-2
26
1.1.3八进制数和十六进制数
¾对R(R为正整数)进位计数制的特点总结如下： ¾1、R进位计数制的基数是R，各数位能选用的数
模拟信号
数字信号
时间上和幅度上都 连续变化的信号
时间上和幅度上都 断续高变电化平的信号
2011-3-2
低电平 9
二、数字电路的分类
¾根据电路结构不同分 分立元件电路
集成电路
将晶体管、电阻、电 容等元器件用导线在线路 板上连接起来的电路。
将上述元器件和导线通过半 导体制造工艺做在一块硅片上而 成为一个不可分割的整体电路。
-1+2×8-2)10
2011-3-2
24
4
2011-3-2
1.1.3八进制数和十六进制数
¾十六进制数 ¾组成：0、1、2、3、4、5、6、7、8、
9、A、B、C、D、E、F ¾进位规则：逢十六进一 ¾权值：16i ¾基数：16
2011-3-2
25
1.1.3八进制数和十六进制数
¾对任意一个十六进制数D，也可以用一个多 项式形式表示，并可计算出它所表示的十 进制数的大小 。
¾根据半导体的导电类型不同分
双极型数字集成电路 单极型数字集成电路
以双极型晶体管 作为基本器件2011-3-2例如 TTL
以单极型晶体管 作为基本器件
例如 CMOS 10
¾根据集成密度不同分
集成电路的分类 集成度
数电第一章逻辑代数基础
计数的基数是16，进位规则是“逢十六进一” 任意一个十六进制数D可按“权”展开为：D=ΣkiX16i 如：(2F.8)16=2×161+15×160+8×16-1=(47.5)10 下标16代表十六进制数，有时也用H（Hexadecimal）代
替下标16。
如：2F.8H=47.5D 二进制、十六进制数广泛应用于数字电路
低位
所以：(44.375)10＝(101100.011)2
3.二进制—十六进制转换 十六进制实际上也应属于二进制的范畴 将4位二进制数（恰好有16个状态）看作一个整体时，它的 进位关系正好是“逢十六进一” 所以只要以小数点为界，每4位二进制数为一组（高位不足4 位时，前面补0，低位不足4位时，后面补0），并代之以等值
注意： 不要漏掉 将十进制数展成Σki×2i的形式 0 得到二进制数:knkn-1……k1k0（有小数时还会有k-1……） =1×64+1×32+1×16+1×8+0×4+1×2+1×1 =(1111011)2
例：(123)10=64+32+16+8+0+2+1
或者：采用的方法 — 除2取余、乘2取整 原理：将整数部分和小数部分分别进行转换。 整数部分采用除 2取余法，小数部分采用乘2取整法。转换后再合并。 整数部分采用除2取余法， 先得到的余数为低位，后 得到的余数为高位。
数 字 电 路
车晓镭
第一章 逻辑代数基础
1.1 概述 1.2 逻辑代数的基本运算 1.3 逻辑代数的基本公式和常用公式 1.4 逻辑代数的基本定理 1.5 逻辑函数及其表示方法 1.6 逻辑函数的公式化简 1.7 逻辑函数的卡诺图化简法
替下标16。
如：2F.8H=47.5D 二进制、十六进制数广泛应用于数字电路
低位
所以：(44.375)10＝(101100.011)2
3.二进制—十六进制转换 十六进制实际上也应属于二进制的范畴 将4位二进制数（恰好有16个状态）看作一个整体时，它的 进位关系正好是“逢十六进一” 所以只要以小数点为界，每4位二进制数为一组（高位不足4 位时，前面补0，低位不足4位时，后面补0），并代之以等值
注意： 不要漏掉 将十进制数展成Σki×2i的形式 0 得到二进制数:knkn-1……k1k0（有小数时还会有k-1……） =1×64+1×32+1×16+1×8+0×4+1×2+1×1 =(1111011)2
例：(123)10=64+32+16+8+0+2+1
或者：采用的方法 — 除2取余、乘2取整 原理：将整数部分和小数部分分别进行转换。 整数部分采用除 2取余法，小数部分采用乘2取整法。转换后再合并。 整数部分采用除2取余法， 先得到的余数为低位，后 得到的余数为高位。
数 字 电 路
车晓镭
第一章 逻辑代数基础
1.1 概述 1.2 逻辑代数的基本运算 1.3 逻辑代数的基本公式和常用公式 1.4 逻辑代数的基本定理 1.5 逻辑函数及其表示方法 1.6 逻辑函数的公式化简 1.7 逻辑函数的卡诺图化简法
精品课件-数字电子技术-第1章
在八进制中，各相邻位之间，低位逢八向高位进一。它的 基数为8，各位的权为8i，各位的系数Ki可以是0～7八个数字 中的任意一个，因而任意一个n位八进制数(M)8可以表示为
(M )2 Kn1 16n1 Kn2 16n2
n1
Ki 16i i0
K1 161 K0 160
第1 如:
[9FE]=9×162+14×161+15×160
(2)系数：N进制中，第i位的数字符号Ki称为第i位的系数。
(3)权：N进制中，Ni称为第i位的权。
第1
1．十进制 十进制是我们最熟悉的数制，它用0～9这10个数字符号 以一定的规律排列起来，表示数值的大小。其计数规则是，相 邻位之间，低位逢十向高位进一,即“逢十进一”。它的基数 为10，各位的系数Ki可以是0～9这10个数字中的任意一个，各 位的权为10i,因而任意一个n位十进制数(M)10可以表示为
类型 小规模集成 电路 中规模集成 电路 大规模集成 电路 超大规模集成 电路
英文缩写 SSI MSI LSI VL SI
属性 1-10 门/片或 10-100 门/片 10-100 门/片或 100-1000 门/片 100-1000 门/片或 1000-100000 门/片 1000 门以上或 100000 门以上
第1 第1
1.1 数字信号与数字电路 1.2 数制和码制
第1 1.1
1.1.1 数字信号 在模拟电子技术中，电子线路主要处理的是模拟信号，而
在模拟电子技术学习中，我们知道模拟信号是在时间和数 值上均作连续变化的电信号，如收音机、电视机通过天线接收 到的音频信号和视频信号都是随时间作连续变化的物理量，信 号电压在正常情况下是不会发生突变的。
第1 在数字电子技术中，我们遇到的大量电信号是在数值和时
(M )2 Kn1 16n1 Kn2 16n2
n1
Ki 16i i0
K1 161 K0 160
第1 如:
[9FE]=9×162+14×161+15×160
(2)系数：N进制中，第i位的数字符号Ki称为第i位的系数。
(3)权：N进制中，Ni称为第i位的权。
第1
1．十进制 十进制是我们最熟悉的数制，它用0～9这10个数字符号 以一定的规律排列起来，表示数值的大小。其计数规则是，相 邻位之间，低位逢十向高位进一,即“逢十进一”。它的基数 为10，各位的系数Ki可以是0～9这10个数字中的任意一个，各 位的权为10i,因而任意一个n位十进制数(M)10可以表示为
类型 小规模集成 电路 中规模集成 电路 大规模集成 电路 超大规模集成 电路
英文缩写 SSI MSI LSI VL SI
属性 1-10 门/片或 10-100 门/片 10-100 门/片或 100-1000 门/片 100-1000 门/片或 1000-100000 门/片 1000 门以上或 100000 门以上
第1 第1
1.1 数字信号与数字电路 1.2 数制和码制
第1 1.1
1.1.1 数字信号 在模拟电子技术中，电子线路主要处理的是模拟信号，而
在模拟电子技术学习中，我们知道模拟信号是在时间和数 值上均作连续变化的电信号，如收音机、电视机通过天线接收 到的音频信号和视频信号都是随时间作连续变化的物理量，信 号电压在正常情况下是不会发生突变的。
第1 在数字电子技术中，我们遇到的大量电信号是在数值和时
数电第一章讲解
模拟电子电路（Analog electronic circuit）
Temperature (℉)
100 95 90 85 80 75 70
1 2 3 4 5 6 7 8 9 101112 1 2 3 4 5 6 7 8 9 101112
A.M.
P.M.
Time of day
数字电子电路（Digital electronic circuit）
A compact disk (CD) player
CD driver
sound waves
Digital data
Digital-to-analog converter
Linear amplifier Analog reproduction of music audio signal
Speaker
５×１００＝ ＋
５ 可以表示为各位上的
５ ５即：５(55５55)10＝5×103 ＋＝5５×1５0５2＋５5×1数乘01码 积＋与之5其和×1对，00应称位按权权的展
同样的数码在不同的数
位开号式不。同，位权不同。
位上代表的数值不同。
概述
电 子
模拟信号 时间和数值连续变化
电
的信号，如压力，温度，
路
正弦波电压等。
中
的
信
号
数字信号 时间和数值都是离散的，
如人数，产品的个数，开关
的通与断，电平的高与低，0
和1等。
模拟信号 正弦波信号 u
t
锯齿波信号
u
t
模拟电路：处理模拟信号的电路。
研究模拟信号时，我们注重电路 输入、输出信号间的大小、相位关系 。相应的电子电路就是模拟电路，包 括交直流放大器、滤波器、信号发生 器等。
数字电子技术基础-第一章PPT课件
•15
第一章：数字逻辑基础
【例1-3】将十六进制数8A.3按权展开。 解：(8A.3)16=8×161+10×160+3×16-1
•16
第一章：数字逻辑基础
1.2.2 不同进制数的转换 1. 十进制数转换为二进制、八进制和十六进制数 转换方法： (1) 十进制数除以基数(直到商为0为止)。 (2) 取余数倒读。
•17
第一章：数字逻辑基础
【例1-4】将十进制数47转换为二进制、八进制和十六进制数。 解：
(47)10=(101111)2=(57)8=(2F)16。
•18
第一章：数字逻辑基础
【例1-5】将十进制数0.734375转换为二进制和八进制数。
解：
(1)转换为二进制数。
首先用0.734375×2=1.46875 (积的整数部分为1，积的小数部分为
•25
第一章：数字逻辑基础
按选取方式的不同，可以得到如表1.1所示常用的几种BCD编码。 表1.1 常用的几种BCD编码
•26
第一章：数字逻辑基础
2. 数的原码、反码和补码 在实际中，数有正有负，在计算机中人们主要采用两种
方法来表示数的正负。第一种方法是舍去符号，所有的数字 均采用无符号数来表示。
•7
第一章：数字逻辑基础
2. 数字电路的分类
1) 按集成度划分 按集成度来划分，数字集成电路可分为小规模、中规模、大规模和超大
规模等各种集成电路。 2) 按制作工艺划分
按制作工艺来划分，数字电路可分为双极型(TTL型)电路和单极型(MOS 型)电路。双极型电路开关速度快，频率高，工作可靠，应用广泛。单极型 电路功耗小，工艺简单，集成度高，易于大规模集成生产。 3) 按逻辑功能划分
第一章：数字逻辑基础
【例1-3】将十六进制数8A.3按权展开。 解：(8A.3)16=8×161+10×160+3×16-1
•16
第一章：数字逻辑基础
1.2.2 不同进制数的转换 1. 十进制数转换为二进制、八进制和十六进制数 转换方法： (1) 十进制数除以基数(直到商为0为止)。 (2) 取余数倒读。
•17
第一章：数字逻辑基础
【例1-4】将十进制数47转换为二进制、八进制和十六进制数。 解：
(47)10=(101111)2=(57)8=(2F)16。
•18
第一章：数字逻辑基础
【例1-5】将十进制数0.734375转换为二进制和八进制数。
解：
(1)转换为二进制数。
首先用0.734375×2=1.46875 (积的整数部分为1，积的小数部分为
•25
第一章：数字逻辑基础
按选取方式的不同，可以得到如表1.1所示常用的几种BCD编码。 表1.1 常用的几种BCD编码
•26
第一章：数字逻辑基础
2. 数的原码、反码和补码 在实际中，数有正有负，在计算机中人们主要采用两种
方法来表示数的正负。第一种方法是舍去符号，所有的数字 均采用无符号数来表示。
•7
第一章：数字逻辑基础
2. 数字电路的分类
1) 按集成度划分 按集成度来划分，数字集成电路可分为小规模、中规模、大规模和超大
规模等各种集成电路。 2) 按制作工艺划分
按制作工艺来划分，数字电路可分为双极型(TTL型)电路和单极型(MOS 型)电路。双极型电路开关速度快，频率高，工作可靠，应用广泛。单极型 电路功耗小，工艺简单，集成度高，易于大规模集成生产。 3) 按逻辑功能划分
数字电子技术第一章.ppt
1 0001 1
1
2 0010 2
2
3 0011 3
3
4 0100 4
4
5 0101 5
5
6 0110 6
6
7 0111 7
7
8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F
20
+
3
23
第一节 数制与编码
十进制（Decimal）
按权展开式
(652.5)D = 6 102 + 5 101 + 2 100 + 5 10-1
位置计数法 下标D表权示十进制权
权
权
任意一个十进制数，都可按其权位展成多项式的形式。
(N)D=(Kn-1 K1 K0. K-1 K-m)D
=Kn-1 10n-1 + +K1101 + K0100 + K-1 10-1 + + K-m 10-m
二进制原码、补码及反码
各种数制都有原码和补码之分。
二进制数N 的基数的补码又称为2的补码， 常简称上为一节补介码绍，的其十定进义制和为二进制数都属于原码。
补码分为两种N：补基数2 n的补N码和降基数的补码。
n是二进制数N整数部分的位数。
例：[1010]补=24-1010=10000-1010=0110 [1010.101]补=24-1010.101=10000.000- 1010.101 =0101.011
例：（11010111.0100111）B = （?3）27Q.234 ）Q
数电~第一章总结
第一章逻辑代数基础本章介绍了数字电路逻辑功能的数字方法。
首先介绍数字波形、数制、码制，逻辑代数的基本公式、常用公式和重要规则，然后又介绍了逻辑函数及表示方法，最后介绍利用公式、卡诺图化简逻辑函数。
一、数制和码制数电中常用到的数制有十进制、二进制和十六进制。
十进制转换成其他进制时整数部分采用基数除法，小数部分采用基数乘法。
二进制转换成十六进制时从小数点开始向右和向左划分成4位二进制一组，整数部分不足的左边用0补充，小数部分不足的右边用0补充。
二进制转化成八进制时类似，3位二进制一组；反过来转化与上述过程相反。
二进制可以进行加减乘除等运算。
运算时用补码进行。
二进制数的补码：最高位为符号位（0位正，1为负）;正数的补码和原码相同；负数的补码为对原码求反加一。
二、基本逻辑函数及运算定律逻辑代数的基本运算有与、或、非三种。
三种逻辑运算的真值表及标准符号大家可以要熟悉。
还有其他的一些复合逻辑运算：与非、或非、与或非、异或、同或等大家了解一下。
逻辑运算的运算定律定律公式公式0-1定律1*A=A 1+A=1 0+A=A交换律A*B=B*A A+B=B+A结合律A*(B*C)=(A*B)*C A+（B+C）=(A+B)+C 分配律A*(B+C)=A*B+A*C A+B*C=（A+B ）*(A+C) 吸收律A*(A+B)=A A+A*B=A重复律A*A=A A+A=A互补律A*A+还原律反演律=A*B逻辑代数的常用公式A+B=A+BAB+A=AAB+C+BC=AB+C (添加项公式)A*=A*; *=A B=A+A逻辑代数的基本规则有：带入规则；对偶规则；反演规则。
三、 逻辑函数的表示方法要掌握函数表述方法：逻辑函数表达式，真值表，逻辑图和卡诺图。
真值表和卡诺图是逻辑函数的最小项表示法，具有唯一性。
最大项表示法仅需要了解即可。
最小项的性质：◆ 在输入变量任意取值下，有且仅有一个最小项的值为1； ◆ 全体最小项的之和为1； ◆ 任意两个最小项之积为0；◆ 两个相邻的最小项之和可以合并，消去一对因子，只留下公共因子。
大学 数字电子技术基础-第一章--数字逻辑基础
（175.0625)D
•
23
例1-6 将(154.375)D 转化为十六进制数。 解：（1）整数部分 ：“除16取余”
连续“除16取余”的 过程直到商为0为止
24
（2）小数部分：“乘16取整”
0.375×16=6.0 ……… 整数部分为6
(154.375)D=(9A.6)H
直到小数部分为0 为止
25
四、八进制----二进制
二进制数和八进制数之间 有很简单的对应关系，三 位二进制数对应一位八进 制数。对应关系如表所示。
三位二进制数 000 001 010 011 100 101 110 111
一位八进制数 0 1 2 3 4 5 6 7
(374.26)O = (011111100 . 010110)B
1
1
0
0
1
1
0
0
0
33
三、ASCII码
ASCII码是国际上最通用的一种字符码，用7位二进制码来表示128个十进制 数、英文大小写字母、控制符、运算符以及特殊符号
34
第五节 逻辑问题的描述ห้องสมุดไป่ตู้
• 一、自然界中三种基本逻辑关系：
❖1、与逻辑关系：决定某一事物结果的所有条件
同时具备，结果才会发生。这一因果关系称与逻 辑关系
32
二、格雷码
二进制数
b3
b2
b1
b0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
•
23
例1-6 将(154.375)D 转化为十六进制数。 解：（1）整数部分 ：“除16取余”
连续“除16取余”的 过程直到商为0为止
24
（2）小数部分：“乘16取整”
0.375×16=6.0 ……… 整数部分为6
(154.375)D=(9A.6)H
直到小数部分为0 为止
25
四、八进制----二进制
二进制数和八进制数之间 有很简单的对应关系，三 位二进制数对应一位八进 制数。对应关系如表所示。
三位二进制数 000 001 010 011 100 101 110 111
一位八进制数 0 1 2 3 4 5 6 7
(374.26)O = (011111100 . 010110)B
1
1
0
0
1
1
0
0
0
33
三、ASCII码
ASCII码是国际上最通用的一种字符码，用7位二进制码来表示128个十进制 数、英文大小写字母、控制符、运算符以及特殊符号
34
第五节 逻辑问题的描述ห้องสมุดไป่ตู้
• 一、自然界中三种基本逻辑关系：
❖1、与逻辑关系：决定某一事物结果的所有条件
同时具备，结果才会发生。这一因果关系称与逻 辑关系
32
二、格雷码
二进制数
b3
b2
b1
b0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
《数电第一章》课件
设计工具：状态机、卡诺 图、逻辑门等。
06 数电第一章复习 题
选择题
选择题1
二进制数10101010转换为十进制 数是____。
答案
A. 106
选择题2
逻辑或运算的运算规则是____。
答案
B. 0 OR 0 = 0, 0 OR 1 = 1, 1 OR 0 = 1, 1 OR 1 = 1
选择题3
在数字电路中，通常使用____来表示 逻辑关系。
数字电路的基本概念
数字信号、数字电路等。
逻辑门电路
与门、或门、非门等。
逻辑代数
基本逻辑运算、逻辑函数等。
组合逻辑电路
加法器、比较器、多路选择器 等。
学习方法
理论学习
通过阅读教材和课件， 掌握数字电路的基本概
念和原理。
实验操作
通过实验，加深对数字 电路的理解，提高实际
操作能力。
习题练习
通过练习习题，巩固所 学知识，提高解题能力
02
或门
当至少一个输入端为高电平时，输出 端就为高电平；否则输出端为低电平 。
01
或非门
当至少一个输入端为高电平时，输出 端为低电平；否则输出端为高电平。
05
03
非门
输入端与输出端的电平状态相反，即 输入高电平时输出低电平，输入低电 平时输出高电平。
04
与非门
当所有输入端都为高电平时，输出端 为低电平；否则输出端为高电平。
。
小组讨论
通过小组讨论，互相交 流学习心得，提高学习
效果。
02 数字电路基础
数字电路概述
01
02
03
数字电路的定义
数字电路是处理离散信号 的电路，其输入和输出信 号通常为二进制形式（0 和1）。
数电第1章
第一章 数 制 与 代 码
小结：
进位计数制： 1、进位基数 R 2、数位的权数 Ri
权值表示法： (N )R
i a R i n 1
i m
二、八、十六进制数转换十进制数 (D)
多项式法
十进制数 (D) 转换二、八、十六进制数 整数连除法 （小数连乘法）
第一章 数 制 与 代 码
作业：
0………… 1
即 (11)D=(1011)B
最高位
第一章 数 制 与 代 码
2. 纯小数转换——基数连乘法
把十进制的纯小数 M 转换成 R 进制数的步骤如下： (1) 将M乘以R，记下整数部分。 (2) 将上一步乘积中的小数部分再乘以 R ，记下 整数部分。 (3) 重复做第 (2) 步，直到小数部分为 0 或者满足 精度要求为止。 (4) 将各步求得的整数转换成 R 进制的数码，并 按照和 运算过程相同的顺序 排列起来，即为所求 的R进制数。
在计算机应用系统中： 二进制主要用于机器内部的数据处理， 八进制和十六进制主要用于书写程序， 十制主要用于运算最终结果的输出。
第一章 数 制 与 代 码
1.2 数制转换
1.2.1 非十进制数 转换 成十进制数 不同数制之间的转换方法有若干种。把非十进制 数转换成十进制数采用按权展开相加法。 具体步骤是，首先把非十进制数写成按权展开的 多项式，然后按十进制数的计数规则求其和。
例9
解
(11.375)D=( ? )B
2 11 2 5………… 2 2………… 2 1………… 0………… 1 1 0 1
即 (11)D=(1011)B
0.375×2=0.75………0 0.75×2=1.5 0.5×2=1.0
………1 ………1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0 1 1 0 0 1 1 1 1 1 0 1
19
无符号数算术运算
2．二进制减法
无符号二进制数的减法规则：
0-0=0， 1-1=0，1-0=1 0-1=11 (前面的1是借位)
例1.3.2 计算两个二进制数1010和0101的差。 解：
1 0 1 0 0 1 0 1 0 1 0 1
20
无符号数算术运算
1.数字逻辑基础
模拟信号与数字信号 数制 二进制的算术运算 二进制码
二值逻辑变量与基本逻辑运算 逻辑函数与逻辑问题的描述
1
1.1 模拟信号与数字信号
模拟信号 数字信号
- 数字信号表示 - 数字波形及主要参数 - 模拟与数字信号的相互转换
2
模拟信号
模拟信号: 时间和数值上都是连续变化的物理量
无权码 5421 码
0000 0001 0010 0011 0100 1000 1001 1010 1011 1100
余 3码
0011 0100 0101 0110 0111 1000 1001 1010 1011 1100
余 3循
环码 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010
14
二进制数与十进制数间的转换
(N)B→ (N)D ：将(N)B写成按权展开的多项式， 按十进制规则求各乘积项的积并相加。
(N)D→ (N)B ：需将整数部分和小数部分分别转换， 然后合成。 整数部分：除2取余或分解为2的乘幂项之和 小数部分：乘2取整
15
十进制数→二进制数举例
例：(58.625)D → (N)B 整数部分 2 58 2 29 —— 余0 2 14 —— 余1 2 7 —— 余0 2 3 —— 余1 2 1 —— 余1 0 —— 余1 小数部分 0 . 625 × 2 1 . 250 × 2 0 . 500 × 2 1 . 000
设：n位二进制数表示为Bn-1Bn-2 … B0 n位Gray码表示为Gn-1Gn-2 … G0 二进制数 Gray码 Gray码 Gn-1= Bn-1 Gi = Bi +1 Bi (0 i n-2) Bn-1 = Gn-1 Bi = Bi +1 Gi (0 i n-2) （上式中“”是异或运算）
3、乘法和除法 例1.3.3 计算两个二进制数1010和0101的积。 解：
+
0
1 0
1
1 × 0 1 0 0 0 1 0 0
0
0 1 1 0 0 1 0 0 0
0 1
0 1 0
1
0
21
无符号数算术运算
例1.3.4 计算两个二进制数1010和111之商。 解： 1. 0 1 1 111 1 0 1 0
R进制的多项式表示：
( N ) R an 1R n 1 an 2 R n 2 a1R1 a0 R 0 a1R 1 am R m
常用数制 十进制 二进制 八进制 十六进制 (N)R (N)D (N)B (N)O (N)H R 10 2 8 16 a 0,1,2,3,4,5,6,7,8,9 0,1 0,1,2,3,4,5,6,7 0,1,2,3,4,5,6,7,8, 9,A,B,C,D,E,F 进制规则 逢十进一 逢二进一 逢八进一 逢十六进一
( AB 6) H 10 16 2 11 161 6 16 0 ( 2742) D
13
几种进制数之间的对应关系
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 二进制 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 八进制 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F
8
时序图
表明多个数字信号在时间上的对应关系的波形图 例： T
Q3 Q2 Q1 Q0
CP
加 计 数 器
CP Q0
Q1 Q2 Q3
9
模拟与数字信号的相互转换
数-模转换
模-数转换
n位二进制数
模拟电压
模拟电压
n位二进制数
10
1.2 数 制
进位计数制的一般表示 常用进制之间的相互转换
11
进位计数制的一般表示
(257.0254)O=(10101111.0001011011)B=(AF.16C)H
18
1.3
二进制数的算术运算
1.3.1 无符号数算术运算 1、二进制加法 无符号二进制的加法规则：
0+0=0，0+1=1+0=1，1+1=10 (前面的1是进位) 例1.3.1 计算两个二进制数0110和0111的和。 解：
二-十进制码(BCD码) 可靠性编码 - 格雷码 - 奇偶校验码 ASCII码
27
1. 二-十进制码(BCD码)
BCD — Binary Coded Decimal 用 4 位二进制代码b3b2b1b0表示十进制数的十个数码(0~9) 4位二进制数码最多可产生16种取值组合，故有多种编码 方案，分为两大类：有权码和无权码。 有权码 令N为0~9中的一个十进制数, b3b2b1b0为其对应的BCD 码， 则：N b W b W b W b W 3 3 2 2 1 1 0 0
25
带符号二进制的减法运算
5. 溢出的判别 如何判断是否产生溢出？
4 ) 3 7
2 ) 6 8
0 1 0 0 0 0 1 1
5 ) 3 8
1 0 1 1 1 1 0
1
1 0 0 0
3 ) 6 9
23
带符号二进制的减法运算
3. 二进制补码的减法运算 减法运算的原理 : 减去一个正数相当于加上一个负数 AB=A+(B)，对(B)求补码，然后进行加法运算。 例1.3.7 试用4位二进制补码计算52。 解：因为(52)补 =(5)补 +(2) 补 =0101+1110 =0011 所以 52=3
LSB
1
0 1
MSB
或 (58)D=25+ 24 + 23 + 21 = (111010)B
∴ (58.625)D=(111010.101)B
16
常用的2n数值
20 21 22 23 24 25 26 27 1 2 4 8 16 32 64 128
28 29
210
256 512
1024
17
八、十六进制与二进制的转换
其中W3 W2 W1 W0为b3 b2 b1 b0各位对应的权值 常用的有权码：8421BCD、 2421BCD、5421BCD
28
BCD码
8421BCD、2421BCD、5421BCD的权值分配
权值权 码 8421 2421 5421 D3 W3 8 2 5 D3 W2 4 4 4 D1 W 1 2 2 2 D0 W0 1 1 1
1 1 1 1 1 0 0 1 1 1 1 0 1 0 1 1 1 1 1 余数
22
1.3.2 带符号二进制数的减法运算
有符号的二进制数可用原码、反码和补码来表示。
1. 原码 二进制数的原码最高位表示符号位，且用0表示正数， 用1表示负数，其余部分为数值位。 例：(+13)D =(0 1101) B , (13)D =(1 1101) B 2. 反码与补码 反码或补码的最高位为符号位，正数为0，负数为1。 • 当二进制数为正数时，其反码、补码与原码相同。 • 当二进制数为负数时，将原码的数值位逐位求反(即为反码)， 然后在最低位加1得到补码。 例： (13)D =(1 1101) B原 =(1 0010) B反 =(1 0011) B补
在实际数字电路中，通常用逻辑电平的高低表示0和1。 正逻辑体系规定： 高电平(H) - 1 ， 低电平(L) - 0。 不同类型或系列的数字IC对应高低电平的电压范围不相同。
4
数字波形
数字波形：是信号逻辑电平-时间的图形表示. 例:
5
数字波形的两种类型
*非归零型(电平型 )和归零型( 脉冲型) 高电平 低电平
(Gray)
（注意：每种编码方式中都有六个无效码字）
30
数制/码制转换例
例：将十进制数157分别转换为二进制数、十六 进制数、8421BCD码和余3码。 解： (157)D = (10011101)B = (9D)H
= (0001 0101 0111) 8421BCD = (0100 1000 1010) 余3码
有脉冲
无脉冲
(本书中采用的都是电平型表示)
6
数字波形的周期性和非周期性
A B tw C T 数字周期信号主要参数：周期T、频率f、占空比q等 周 期
非周期
tw 占空比q（%） 100% T
7
实际数字信号波形
非理想脉冲波形
脉冲宽度 (tw ) ：脉冲幅值的50%的两个时间所跨越的时间
上升时间tr 和下降时间tf ：从脉冲幅值的10%到90% 上升 下降所经历的时间( 典型值ns )
例：
正弦波信号
三角波信号
3
数字信号
数字信号: 时间和数值上都是离散的信号, 可以用二值数字
逻辑和数字波形表示。 由 0 和 1 组成的n位数字信号可以表示2n 个数值或编码 - 数值，例：数值8 用4位二进制数表示为1000； - 编码，例：字母A 用ASCII码表示为1000001；