力矩作功 刚体绕定轴转动的动能定理
合集下载
力矩的功刚体动能定理
3.一根长l质量为m 的匀质细杆，其一端固定在光滑的 水平轴O，可以在竖直平面内转动。最初杆静止在水 平位置。求:杆由初始位置下摆 时的角速度?
θβ
解: 方法一用转动定律求解(略)
方法二用转动动能定理求解
杆处在β时,力矩 M mg l cos
杆转过d时, dA Md mg l cosd
2
2
A EK
k = 2.74×10-4 N·m·rad-2·s2. 求（2）吊扇由静止匀加
速的达到第二档转速经历的时间为 5s . 在此时间内阻力
矩做了多少功 ?
解: 吊扇由静止作匀角加速度运动
2
t5
t
阻力矩做功 W Mf 2d k3dt
W t k 3t3dt 1 k 3t 4
0
4
在 t ＝ 5s 时间内 W 84.8 J
EkA EpA EkB EpB
EkA EpA EkB EpB
o
m, l A
EkA EPA 0
m
EkB
1 2
J 2
J J1 J2
J 1 ml2 ml2 4 ml2
mg
B
mg
3
3
EpB
(mg
l 2
sin
mgl sin )
3 mgl sin
2
0 3 ml22 3 mgl sin 3 ( g sin )1 2
合外力矩对绕定轴转动的刚体所作的功等于刚 体转动动能的增量。
与质点运动类似，若刚体转动过程中，只有 保守力做功，同样刚体的机械能守恒。
3. 刚体的重力势能
y
N
N
mi yi
E p
mi gyi
i 1
Mg
i 1
刚体转动的动能定理
一、力矩的功 1 力矩的定义若作用的质点上的力为F ,则将r ×F 定义为力F 对O 点的力矩，记为M 。
M r F =⨯M 、F 、r 三者的方向构成右手螺旋关系。
M大小：方向：右手法则2 力矩的功设：；转盘上的微小质量元Δm 在力F 作用下以R 为半径绕O 轴转动，在dt 时间内转过角度d ，对应位移d r,路程ds,此时F 所做的元功为则总功为二、转动惯量设初速为零，质量元Δm 的动能为转盘的总动能1 定义：为物体的转动惯量。
意义：由质量和质量对于转轴的分布情况决定。
描述转动的惯性。
o z FtF nF tF ord rd θt t d d d d A F r F s F r θ=⋅==d d A M θ=21d A M θθθ=⎰αrsin t M Fr F rα==d θFtF ord r12ki i iE m v =212k ki i i i i E E m ==∆∑∑v 221()2i i i m r ω=∆∑2i i iI m r =∆∑单位：SI 制 kg m 22 定轴转动物体转动惯量的计算质量不连续分布的质点系：转动惯量定义为各个质点对该定轴的转动惯量之和2i i iI m r =∑质量连续分布的刚体：转动惯量定义为各个质点对该定轴的转动惯量的积分。
2mI r dm =⎰转动惯量的大小不仅取决于物体的质量，还与质量的分布和轴线的位置有关。
例1 求小球m 的转动惯量。
解：m 看作质点 I = m R 2例2 质量为m 的细圆环，求I 。
解：把环分成无限多个质量为dm 的小段，对每个d m 有d J = R 2对整个环有I = R 2d m = mR 2例3质量m ，半径 R 的薄圆盘，求I 。
解：把盘分成无限多个环。
取其中的一个环(半径r ，宽d r ，质量 d m )， 其转动惯量 d I = r 2d m22mdm rdr Rππ=整个盘的转动惯量d rd md SrRd mRRm22322200002122R R R Rm m I dI r dm r rdr r dr mR R R ππ=====⎰⎰⎰⎰例4 长为L 、质量为m 的细长直杆，转轴垂直于细杆且通过杆中心 解：杆长为L,质量为m, 则密度为＝m / L 。
刚体绕定轴转动的动能定理
刚体绕定轴转动的动能定理1. 引言刚体是指其内部各点之间的相对位置关系在运动过程中不会发生改变的物体。
刚体绕定轴转动是指刚体在固定轴线上做圆周运动的情况。
动能定理是物理学中的一条重要定理，描述了物体运动过程中动能的变化与外力做功之间的关系。
本文将对刚体绕定轴转动的动能定理进行全面详细、完整且深入的阐述。
2. 刚体绕定轴转动在刚体绕定轴转动的情况下，我们需要考虑刚体的转动惯量和角速度等因素。
转动惯量是描述刚体对转动运动抵抗程度的物理量，通常用符号I表示。
角速度是描述刚体旋转快慢程度的物理量，通常用符号ω表示。
根据牛顿第二定律和角动量守恒定律，我们可以得到刚体绕定轴转动时的基本方程：τ=Iα其中，τ表示作用于刚体上产生转矩（力矩）大小，α表示角加速度。
刚体绕定轴转动的运动规律与作用在刚体上的转矩和转动惯量有关。
3. 动能定理的推导根据刚体绕定轴转动的基本方程，我们可以推导出刚体绕定轴转动的动能定理。
我们来考虑刚体上某一质点的动能T。
由于刚体上各质点都在绕着同一个轴旋转，因此它们具有相同的角速度ω。
设某一质点到轴心的距离为r，则该质点具有的线速度v为v=rω。
该质点的动能T′可以表示为：T′=12mv2=12m(rω)2=12mr2ω2其中，m表示质点的质量。
由于刚体是由众多质点组成的，因此整个刚体的动能T 可以表示为所有质点动能之和：T=∑Tni=1′i其中，n表示刚体上质点的总数。
根据牛顿第二定律和角动量守恒定律，我们知道刚体绕定轴转动时转动惯量I和角加速度α之间存在关系τ=Iα。
将该关系代入动能的表达式中，得到：T=12Iω2其中，ω表示整个刚体的角速度。
刚体绕定轴转动的动能可以表示为12Iω2。
这就是刚体绕定轴转动的动能定理。
4. 动能定理的物理意义刚体绕定轴转动的动能定理描述了刚体在转动过程中动能的变化与外力做功之间的关系。
根据动能定理，我们可以得出以下物理结论：1.外力对刚体做功会改变刚体的动能。
3.3刚体定轴转动中的功与能
−1 1
解：以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
二、刚体的转动动能和重力势能
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳，绳的一端悬挂质量为m的物体 的物体。 动，滑轮上绕有轻绳，绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少？ 当物体从静止下降距离 时，物体速度是多少？ 以滑轮、 解：以滑轮、物体和地球组成系统为研究对 由于只有保守力做功，故机械能守恒。 象。由于只有保守力做功，故机械能守恒。 设终态时重力势能为零 初态：动能为零，重力势能为mgh 初态：动能为零，重力势能为 末态： 末态：动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
解：以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
二、刚体的转动动能和重力势能
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳，绳的一端悬挂质量为m的物体 的物体。 动，滑轮上绕有轻绳，绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少？ 当物体从静止下降距离 时，物体速度是多少？ 以滑轮、 解：以滑轮、物体和地球组成系统为研究对 由于只有保守力做功，故机械能守恒。 象。由于只有保守力做功，故机械能守恒。 设终态时重力势能为零 初态：动能为零，重力势能为mgh 初态：动能为零，重力势能为 末态： 末态：动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
力矩作功与刚体绕定轴转动的动能定理
Ek0 0
1 mgl 1 J 2 0
2
2
m,l
o
J 1 ml 2
3
3g
mg
l
练习2、一质量 M、半径 R 圆盘绕一无摩檫 轴转动，盘上绕有轻绳，下端挂物体 m。 求：当 m 由静止下落h时速度 v ？
解：
刚体 M
N T
o
对m：
G
TP
m
v 2 mgh h
M 2m
注意和前面的方法比较！
练习3、一匀质细棒长l ，质量m，可绕通过 其端点O水平轴转动。当棒从水平位置自由释
放后，它在竖直位置上与放在地面上的物体
相撞。该物体的质量也为m ，地面的摩擦系 数为 。撞后物体沿地面滑行s后而停止。求 相撞后棒的质心C 离地面的最大高度h，并说
明棒在碰撞后将向重力外，其余内力与外力都 O
（3）
由匀减速直线运动的公式得
亦即
（4）
由（1）（2）与（4）联合求解，即得
（5）
当 >0 则棒向左摆条件： 亦即L>6s；
当0，则棒向右摆条件：
亦即L <6s
由机械能守恒定律，棒上升的最大高度：
(6)
把（5）代入上式，求得：
练习4：工程上，两飞轮常用摩擦啮合器使它们
以相同的转速一起转动。如图所示，A和B两飞
动量守恒；
动量不守恒；
角动量守恒；
角动量守恒；
机械能不守恒 .
机械能不守恒 .
圆锥摆系统 动量不守恒； 角动量守恒； 机械能守恒 .
直线运动与定轴转动规律对照
质点的直线运动
刚体的定轴转动
P126书例2 一长为 l , 质
量为m 的竿可绕支点O自由转 动．一质量为m’、速率为v
刚体定轴转动的动能定理
2
3 2
g.
又因棒在竖直位置时的角加速度 0（因此时合力矩为（4）可以由质心运动定理求出棒在竖直位置时，O 轴对棒的 反力 Fx 和 Fy：
Fy
Fx mact 0
Fx O
Fy mg macn
对于刚体，因其内部质点间无相对位移， 任何一对内力作功为零（对刚体的任何运动形式都 是成立的）。
若A外 A内非 0 E Ek EP 常量
则刚体系统的机械能守恒。
直线运动与定轴转动规律对照
质点的直线运动
v dx dt
a dv d2 x dt dt2
P mv F
EK
1 2
mv2
m
dA Fdx Fdt
A
Ek 2
Ek1
1 2
I22
1 2
I12
合外力矩对绕定轴转动的刚体做的功 = 刚体转动动能的增量
—— 刚体绕定轴转动的动能定理
刚体的重力势能：
刚体受保守力作用也有势能概念.
对于一个不太大的质量为 m 的物体，它的重
力势能应是组成刚体的各个质点的重力势能之和。
C • mi
hc
EP 0
h Epi mi ghi i
力的空间累积效应 力的功,动能,动能定理.
力矩的空间累积效应 力矩的功,转动动能,动能定理.
§7.4 定轴转动中的功能关系
F 一、力矩的功：
α
（设力F 在转动平面内）
dr P
d r
Z
rd
x dA F dr F dr sin rF sin d
力矩的元功：dA Ftrd Md
力矩作功：当刚体在外力矩作用下绕定轴转
B、对于定轴转动刚体，所有内力的功总和在任何过程 中均为零。（内力成对，大小相等方向相反，一对内力矩 的的功代数dA和为F零2 ；dr∴ 内相力对矩位的移功为总零和.）为零。另一角度，内力
3 2
g.
又因棒在竖直位置时的角加速度 0（因此时合力矩为（4）可以由质心运动定理求出棒在竖直位置时，O 轴对棒的 反力 Fx 和 Fy：
Fy
Fx mact 0
Fx O
Fy mg macn
对于刚体，因其内部质点间无相对位移， 任何一对内力作功为零（对刚体的任何运动形式都 是成立的）。
若A外 A内非 0 E Ek EP 常量
则刚体系统的机械能守恒。
直线运动与定轴转动规律对照
质点的直线运动
v dx dt
a dv d2 x dt dt2
P mv F
EK
1 2
mv2
m
dA Fdx Fdt
A
Ek 2
Ek1
1 2
I22
1 2
I12
合外力矩对绕定轴转动的刚体做的功 = 刚体转动动能的增量
—— 刚体绕定轴转动的动能定理
刚体的重力势能：
刚体受保守力作用也有势能概念.
对于一个不太大的质量为 m 的物体，它的重
力势能应是组成刚体的各个质点的重力势能之和。
C • mi
hc
EP 0
h Epi mi ghi i
力的空间累积效应 力的功,动能,动能定理.
力矩的空间累积效应 力矩的功,转动动能,动能定理.
§7.4 定轴转动中的功能关系
F 一、力矩的功：
α
（设力F 在转动平面内）
dr P
d r
Z
rd
x dA F dr F dr sin rF sin d
力矩的元功：dA Ftrd Md
力矩作功：当刚体在外力矩作用下绕定轴转
B、对于定轴转动刚体，所有内力的功总和在任何过程 中均为零。（内力成对，大小相等方向相反，一对内力矩 的的功代数dA和为F零2 ；dr∴ 内相力对矩位的移功为总零和.）为零。另一角度，内力
定轴转动的动能定理
例题2 一根质量为m、长为 l 的均匀细棒OA （如图），可绕通过其一
端的光滑轴O在竖直平面内转动，今使棒从水平位置开始自由下摆，求细棒
摆到竖直位置时其中点C和端点A的速度。
C
解 先对细棒OA 所受的力作一分析；重力G O
作用在棒的中心点C，方向竖直下；轴和棒之间没
A
有摩擦力，轴对棒作用的支承力 N 垂直于棒和 轴
的接触 面且通过O点，在棒的下摆过程中，此力
的方向和大小是随时改变的。
A
在棒的下摆过程中，对转轴O而言，支撑力N通
G
过O点，所以支撑力N的力矩等于零，重力G的力矩则
是变力矩，大小等于mg(l /2) cos ，棒转过一极小的角位移d 时，重力
矩所作的元功是
dW mg l cosd
2
在使棒从水平位置下摆到竖直位置过程中，重力矩所作的功是
度ω0=0,转动动能为0，重力势能为 mg（2l 选下摆到竖直位置hc=0），下摆到竖
直位置时角速度ω=ω,转动动能为
1 2
J重2 力势能为0。
mg l 1 J 2
22
由此得
3g l
mgl
J
所以细棒在竖直位置时，端点A和中心点C的速度分别为
vA l 3gl
vC
l
2
1 2
3gl
J2
2
1 2
J12
刚体定轴转动的动能定理：总外力矩对刚体所做的功等于刚体转动动能
的增量。
注：
1. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点的动能之和。
设刚体中第i个质点的质量为 mi ，速度为 vi
刚体做定轴转动时，各质点的角速度相同。
,则该质点的动能为
力矩做功
dw 为合外力矩对刚体作的元功 当刚体在合外力矩的作 为合外力矩对刚体作的元功.当刚体在合外力矩的作
∫
∫
2
2
2
1
W合内力矩=?
刚体的重力势能
E p = ∑ mi ghi = g ∑ mi hi mi hi = mg ∑ m = mghc
一个不太大的刚体它的重力势能与它的质量都集中在质心 所具有的势能一样
J
故
1 2 E k = Jω 2
四 刚体绕定轴转动的动能定理 由转动定律 或
dW = Mdθ = Jωdω
dω dω dθ dω M=J =J = Jω dt dθ dt dθ
用下,角速度由 用下 角速度由 ω 1变为ω 2 ,合外力矩对刚体所作的功为 合外力矩对刚体所作的功为 ω2 合外力矩对作定轴转动的刚 W = Mdθ = Jωdω 体所作的功等于刚体转动动 ω1 能的增量---刚体绕定轴转动 能的增量 刚体绕定轴转动 1 1 2 2 的动能定理 即W = Jω Jω
r r r r r , r , ∴ mv r = mv , r , LL(1) Q r // v 2 , r ⊥v1 , r ⊥v 1
卫星进入椭圆轨道后,卫星, 卫星进入椭圆轨道后,卫星,地球系统只有万有引力 保守内力)作用,机械能守恒: (保守内力)作用,机械能守恒:
r r r r, r, r × m ( v1 + v 2 ) = r × m v
1 1 1 2 2 2 mv 0 = mv + Jω 2 2 2
的球体, 例14, 地球可看作是半径 R= 6400 km 的球体,一颗 , 的圆形轨道上, 人造地球卫星在地面上空 h=800km 的圆形轨道上,以 v1=7.5 km/s的速度绕地球运动. 的速度绕地球运动. 的速度绕地球运动 火箭, 突然点燃 一 火箭,其冲力使卫星附加一个 向外的径向分 使卫星的轨道变成椭圆形. 速度 v2=0.2 km/s使卫星的轨道变成椭圆形. 使卫星的轨道变成椭圆形 求此后卫星轨道的最低点和最高点位于地面上空多高? 求此后卫星轨道的最低点和最高点位于地面上空多高? 解:分析 r r
大学物理3_4 刚体绕定轴转动的动能定理
t 3 3 3 5 3 2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端， 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩
M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端， 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩
M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0
4.4力矩的功动能定理
v R
求解得
2mgh kh v 2 mJ /R
2
§4.力矩功、转动动能定理 / 五、机械能守恒定律
设计制作
干耀国
山东科技大学济南校区
§4.力矩功、转动动能定理
§4.力矩功、转动动能定理 / 五、机械能守恒定律
解：在物体 m 下落过程中只有 重力和弹力保守 力作功，物体系 机械能守恒。 E0 E
k
J,R
h
m
选择弹簧原长为弹性 0 势点， 物体下落 h 时为重力 0 势点。
1 1 1 2 2 2 mgh mv J kh 2 2 2
§4.力矩功、转动动能定理 / 五、机械能守恒定律
第四节 力矩的功 刚体绕定轴转 动的动能定理
在功和能一章中我们研究了力对空间 的累积效应——功，在这节中要介绍力矩 对空间的累积效应——力矩的功。
一、力矩的功
o
将F分解为 切向力和法向力。
F
d
r
Fn
ds
F
刚体转过 d, 作用点的位移为 ds, 法向力 Fn 不作功，只有切向力作功，
§4.力矩功、转动动能定理 / 一、力矩的功
§4.力矩功、转动动能定理 / 四、解题方法及举例
摩擦力矩的功：W阻 M阻d 2 2 0 mgRd mgR 3 3 由动能定理： W Ek Ek 0
2 1 2 mgR J0 3 2 1 其中 J mR 2 2 2 3J0 4mgR 2 3R 0 n 2 16g
§4.力矩功、转动动能定理 / 四、解题方法及举例
圆盘的面密度为： m 2 R 圆环的质量为： dm dS 2rdr
0
m
dr
4-4力矩的功定轴转动的动能定理
l
dt
2l
8
例（习题4-33）在题 习题 ）在题3-30的冲击摆问 的冲击摆问 题中， 题中，若以质量为 m′ 的均匀细棒代 替柔绳，子弹速率的最小值应是多少？ 替柔绳，子弹速率的最小值应是多少？
解：
(1)若为绳时（题3-30的解法） 若为绳时（ 的解法） 若为绳时 的解法 a、子弹与物块在最低点碰 、 撞，系统的动量守恒 b、物块做圆周运动的过程 、 中机械能守恒 c、物块做圆周运动能越过 、 最高点的条件： 最高点的条件：
F向心力 ≥ M 物 g
(2)当绳变为细棒时： 当绳变为细棒时： 当绳变为细棒时 分析： ①细棒和摆钟构成一个刚体，可绕O 分析： 细棒和摆钟构成一个刚体，可绕 轴作定轴转动。 轴作定轴转动。在A处，子弹与摆钟碰撞， 处 子弹与摆钟碰撞， 使刚体获得绕O轴转动的角速度 轴转动的角速度w。 使刚体获得绕 轴转动的角速度 。若取子 摆钟和细杆为系统， 弹、摆钟和细杆为系统，在碰撞过程中刚体 受到定轴O的水平方向作用力 的水平方向作用力， 受到定轴 的水平方向作用力，系统所受合 外力不等于零，系统的动量不守恒。但由于 外力不等于零，系统的动量不守恒。 转轴对刚体的作用的作用线过转轴O,不产生 转轴对刚体的作用的作用线过转轴 不产生 转动力矩，因而作用于系统的合外力矩为零， 转动力矩，因而作用于系统的合外力矩为零， 系统的角动量守恒。 系统的角动量守恒。 设摆钟对O点的转动惯量为 ， 设摆钟对 点的转动惯量为J，则J=m1l 2 点的转动惯量为 细棒对O点的转动惯量为 细棒对 点的转动惯量为 J ' ，则 J ' = 1 m ' l 2
O v0 l A R
α
作业： 作业：
一匀质细棒长为l 质量为m， 可绕通过其端点O 一匀质细棒长为 ， 质量为 ， 可绕通过其端点 的水平轴转动，如图所示。 的水平轴转动，如图所示。当棒从水平位置自由释放后 它在竖直位置上与放在地面上的物体相撞。 ，它在竖直位置上与放在地面上的物体相撞。该物体的 质量也为m ， 它与地面的摩擦系数为 µ。 相撞后物体 质量也为 沿地面滑行一距离s而停止 求相撞后棒的质心C 而停止。 沿地面滑行一距离 而停止。求相撞后棒的质心 离地 面的最大高度h， 面的最大高度 ， 并说明棒在碰撞后将向左摆或向右摆 的条件。 的条件。
dt
2l
8
例（习题4-33）在题 习题 ）在题3-30的冲击摆问 的冲击摆问 题中， 题中，若以质量为 m′ 的均匀细棒代 替柔绳，子弹速率的最小值应是多少？ 替柔绳，子弹速率的最小值应是多少？
解：
(1)若为绳时（题3-30的解法） 若为绳时（ 的解法） 若为绳时 的解法 a、子弹与物块在最低点碰 、 撞，系统的动量守恒 b、物块做圆周运动的过程 、 中机械能守恒 c、物块做圆周运动能越过 、 最高点的条件： 最高点的条件：
F向心力 ≥ M 物 g
(2)当绳变为细棒时： 当绳变为细棒时： 当绳变为细棒时 分析： ①细棒和摆钟构成一个刚体，可绕O 分析： 细棒和摆钟构成一个刚体，可绕 轴作定轴转动。 轴作定轴转动。在A处，子弹与摆钟碰撞， 处 子弹与摆钟碰撞， 使刚体获得绕O轴转动的角速度 轴转动的角速度w。 使刚体获得绕 轴转动的角速度 。若取子 摆钟和细杆为系统， 弹、摆钟和细杆为系统，在碰撞过程中刚体 受到定轴O的水平方向作用力 的水平方向作用力， 受到定轴 的水平方向作用力，系统所受合 外力不等于零，系统的动量不守恒。但由于 外力不等于零，系统的动量不守恒。 转轴对刚体的作用的作用线过转轴O,不产生 转轴对刚体的作用的作用线过转轴 不产生 转动力矩，因而作用于系统的合外力矩为零， 转动力矩，因而作用于系统的合外力矩为零， 系统的角动量守恒。 系统的角动量守恒。 设摆钟对O点的转动惯量为 ， 设摆钟对 点的转动惯量为J，则J=m1l 2 点的转动惯量为 细棒对O点的转动惯量为 细棒对 点的转动惯量为 J ' ，则 J ' = 1 m ' l 2
O v0 l A R
α
作业： 作业：
一匀质细棒长为l 质量为m， 可绕通过其端点O 一匀质细棒长为 ， 质量为 ， 可绕通过其端点 的水平轴转动，如图所示。 的水平轴转动，如图所示。当棒从水平位置自由释放后 它在竖直位置上与放在地面上的物体相撞。 ，它在竖直位置上与放在地面上的物体相撞。该物体的 质量也为m ， 它与地面的摩擦系数为 µ。 相撞后物体 质量也为 沿地面滑行一距离s而停止 求相撞后棒的质心C 而停止。 沿地面滑行一距离 而停止。求相撞后棒的质心 离地 面的最大高度h， 面的最大高度 ， 并说明棒在碰撞后将向左摆或向右摆 的条件。 的条件。
05-3刚体绕定轴转动的动能定理
2
物体下滑的速率 是物体在斜面上 位置的函数
2）物体在斜面上能滑多远 ） 物体的速率
R
m
2
2mgx sin θ − kx v= 2 m+ J /R
2
m
θ
x
k
当v= 0 时物体在斜面上停止下滑
2mgx sin θ − kx = 0
2mg sin θ x= k
1 2 2 = (∑ mi ri )ω 2
z
1 2 2 Ek = (∑ mi ri )ω 2 i =1
刚体对定轴 的转动惯量
n
ω
vi
mi
J = ∑ mi ri
i =1
n
2
v o ri
1 2 Ek = Jω 2
对比质点 的动能
——刚体的转动动能 刚体的转动动能
1 2 Ek = mv 2
v dr
v F
当力作用在质点上使它在力的方向发 生位移， 生位移，该力就对质点做功
v v dW = F ⋅ dr
z
刚体绕固定轴转动时， 刚体绕固定轴转动时，外力使刚体上 的质点都作圆周运动， 的质点都作圆周运动，外力也在做功 外力对刚体做功要用力矩和角位移 的乘积形式来表示， 的乘积形式来表示，称为力矩的功
ω
vi
4-4 刚体绕定轴转动的动能定理 -
力矩是改变刚体转动状态的原因
刚体定轴 转动定律
M = Jα
——力矩的瞬时作用效应 力矩的瞬时作用效应 还应该研究力矩的累积效应—— 还应该研究力矩的累积效应 力矩对时间累积效应 刚体的角动量定理 力矩对空间的累积 刚体定轴转动的动能定理 如何表示刚体的转动动能呢？ 如何表示刚体的转动动能呢？ 高速转动的砂轮具有 转动动能， 转动动能，它能通过 摩擦转化为热能
3-3刚体转动的动能定理
T2
( m1
1 2
M )m 2 g
1 2
m1 m 2
M
以上两种方法，都是求解这类问题的基本方法, 都 应该理解和掌握。
例4：一个转动惯量为2.5 kgm2 、直径为60cm 的飞轮，正以130 rads1 的角速度旋转。现用闸瓦 将其制动, 如果闸瓦对飞轮的正压力为 500 N,闸瓦 与飞轮之间的摩擦系数为0.50。求：
设刚体有n个质点组成，其中第i个质点的质 量 为 mi ，它到转轴的距离为 ri，速度大小为vi ，则该质 1 1 E m vБайду номын сангаас，因 vi ri w ,所以 E m r w 。因 点的动能 2 2 此，整个刚体的动能为
2 ki i i
2
2
ki
i i
1 1 n 2 2 Ek mi vi mi ri w2 2 i 1 i 1 2
m2
m1
解：物体m1、m2和滑轮的受力情况如图所示。 列方程
T1 =m1 a
（ 1）
FN
m2 g T2 = m2 a （2）
对于滑轮
T1 T1 T2 T2
α
1 2 T2 r T1r I M r 2
辅助方程
（ 3）
m1 g
a
（ 4）
m2 g
r = a
n
式中 i 1 是刚体的转动惯量I，所以绕定轴转 动的动能可以写为
mi vi
n
2
1 2 E k Iw 2
三、定轴转动的动能定理
设刚体在 合 外力矩M的作用下,绕定轴转过角位 移 d ,合外力矩对刚体作的元功为
dA Md
1-4 力矩做功 动能定理 动量守恒定理
第一章 力学基本定律
1-4 力矩做功 动能定理 动量守恒定理
解:把飞船和排出的废气 看作一个系统，废气质 量为m。可以认为废气质 量远小于飞船的质量， dm/2
u Lg u r L0
dm/2
所以原来系统对于飞船中心轴的角动量近似地等于飞船自 身的角动量，即
L＝J 0
在喷气过程中，以dm表示dt时间内喷出的气体，这些气体 对中心轴的角动量为dm r(u+v)，方向与飞船的角动量相同。 因u=50m/s远大于飞船的速率v(= r) ，所以此角动量近似地 等于dm ru。在整个喷气过程中喷出废气的总的角动量Lg应为
当M z 0时， Lz J11 J 22 恒量
c.若系统内既有平动也有转动现象发生， 若对某一定轴的合外力矩为零,则系统对该 轴的角动量守恒。 例1: 一匀质细棒长为l ，质量为m，可绕通过O的水平轴转动 ，如图。当棒从水平位置自由释放后，它在竖直位置上与放 在地面上的物体相撞。该物体的质量也为m ，它与地面的摩 擦系数为 。相撞后物体沿地面滑行s而停止。求撞后棒的 质心C 离地面的最大高度h，并说明棒在碰撞后将向左摆或 向右摆的条件。
1 2 l E0 J mg (a ) 2 2
l a E m0 ga(1 cos ) mg (a cos ) 2
m0
势能零点
第一章 力学基本定律
1-4 力矩做功 动能定理 动量守恒定理 由机械能守恒，E=E0, 代入=300，得：
1 2 l 1 l 1 J mg (a ) m0 ga(1 ) mg (a ) 2 2 2 22
1 2 J 2
2n飞 2n电 d电 60 60 d飞
2
力矩的功转动动能动能定理
第四章 刚体的转动
8
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
例2 一长为 l , 质量为m’ o 的竿可绕支点O自由转动．一 30 / m 质量为m 、速率为v 的子弹 a m 射入竿内距支点为a 处，使竿 o 的偏转角为30 . 问子弹的初 v 速率为多少? 解 子弹、竿组成一系统，应用角动量守恒
第四章 刚体的转动
4
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
解 (1) 如图取面 积元ds = drdl，该面元 所受的摩擦力为
df
df
mg
πR
2
drdl
R
o
r
dl dr
此力对点o的力矩为
rdf
mg
πR
2
rdrdl
刚体的转动
5
第四章
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
一
力矩作功 dW F dr Ft ds
v
d
Ft
F
Ft rd
dW Md
力矩的功 W
dr
o
r
x
2
1
Md
刚体的转动
1
第四章
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
二
dW d 力矩的功率 P M M dt dt 比较 W F dr P F v
——刚体绕定轴转动的动能定理
比较
1 1 2 2 W F dr mv2 mv1 2 2
8
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
例2 一长为 l , 质量为m’ o 的竿可绕支点O自由转动．一 30 / m 质量为m 、速率为v 的子弹 a m 射入竿内距支点为a 处，使竿 o 的偏转角为30 . 问子弹的初 v 速率为多少? 解 子弹、竿组成一系统，应用角动量守恒
第四章 刚体的转动
4
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
解 (1) 如图取面 积元ds = drdl，该面元 所受的摩擦力为
df
df
mg
πR
2
drdl
R
o
r
dl dr
此力对点o的力矩为
rdf
mg
πR
2
rdrdl
刚体的转动
5
第四章
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
一
力矩作功 dW F dr Ft ds
v
d
Ft
F
Ft rd
dW Md
力矩的功 W
dr
o
r
x
2
1
Md
刚体的转动
1
第四章
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
二
dW d 力矩的功率 P M M dt dt 比较 W F dr P F v
——刚体绕定轴转动的动能定理
比较
1 1 2 2 W F dr mv2 mv1 2 2
4.4刚体绕定轴转动的动能定理(7)
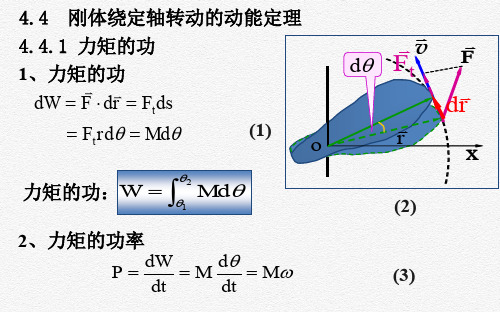
mv
3 4
l
1 3
M
l
2
m
3 4Hale Waihona Puke l2
解得棒开始运动时刚体系的角速度为：
mv
3 4
=8.88rads-1
1 3
M
9 16
m
l
（2）把木棒、子弹、地球视为刚体系统，由于子弹射
入木棒后，木棒的摆动过程只有重力作功，重力属
于保守内力，故系统的机械能守恒。选取初态木棒A
点和
l 2
处，分别为子弹、棒重力势能零势点，注意
到，初态仅有动能末态只有势能，由机械能守恒定
律得：
1
1
Ml 2
m
3
l
2
2
Mg
l
(1
cos
)
mg
3l
(1
cos
)
2 3
4
2
4
cos
1
2 3
M
9 8
m
l
2
0.074
94.3
(6)
刚体绕定轴转动动能定理：合外力矩对定轴转 动刚体所作的功，等于刚体转动动能的增量.
刚体绕定轴转动的机械能：
E
Ek
Ep
E
1 2
J2
Ep
(6)
例题4.4.1 长 l 0.4m、质量 M 1.0kg 的匀质木棒如 图所示，可绕水平轴O在铅直平面内转动，初态木棒
自然铅直悬垂，设质量为 m 8g的子弹以v 200m s1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5
4-4 力矩作功 刚体绕定轴转动的动能定理
四章作业 《大学物理习题精选I》P. 19
1. 选择题: 1,3,4,6,8； 2. 填空题: 1,2,4,5,6,8,9、 3.计算题: 2,3,7
6
第四章 刚体的转动
4-4 力矩作功 刚体绕定轴转动的动能定理
一
dW F dr F cosdr Ft ds Ft rd dW Md
力矩作功
d Ft
v
F
dr en
力矩的功 W 二 转动动能
2
1
o
r
Md
1 2 dE m v 质量元： ki i i 2
例1 一长为 l , 质量为 m 的竿可绕支点O自由 转动 . 一质量为 m、速率为 v 的子弹射入竿内距支 点为 a 处， 问角速度为多少 ? 解 把子弹和竿看作一个系统 . 子弹射入竿的过程系统角动量守恒
1 2 2 mva m l m a 3 3mva 2 2 m' l 3ma
三
定轴转动刚体的动能定理
2 1W 2 d 源自 Jd Md Jd J 1 1 1 dt 2 1 1 2 2 W Md J 2 J1 1 2 2
合外力矩对绕定轴转动的刚体所作的功等于刚体 转动动能的增量 .
3
4-4 力矩作功 刚体绕定轴转动的动能定理
o
30
a
v
m
4
4-4 力矩作功 刚体绕定轴转动的动能定理
注意
子细 弹绳 击质 入量 沙不 袋计
o
v
子 弹 击 入 杆
o
圆 锥 摆
o
T
'
m
v
p
o
v
R
以子弹和沙袋为系统 以子弹和杆为系统 圆锥摆系统 动量守恒； 动量不守恒； 动量不守恒； 角动量守恒； 角动量守恒； 角动量守恒； 机械能不守恒 . 机械能不守恒 . 机械能守恒 .
x
1 2 1 1 2 2 Ek mi vi ( mi ri ) J 2 i 2 2 i 2
刚体的转动动能 E k
1 2 J 2
4-4 力矩作功 刚体绕定轴转动的动能定理
力矩的功 W
刚体的转动动能
2
1
Md
转动定律：
1 2 Ek J 2
2
1
M J
4-4 力矩作功 刚体绕定轴转动的动能定理
四章作业 《大学物理习题精选I》P. 19
1. 选择题: 1,3,4,6,8； 2. 填空题: 1,2,4,5,6,8,9、 3.计算题: 2,3,7
6
第四章 刚体的转动
4-4 力矩作功 刚体绕定轴转动的动能定理
一
dW F dr F cosdr Ft ds Ft rd dW Md
力矩作功
d Ft
v
F
dr en
力矩的功 W 二 转动动能
2
1
o
r
Md
1 2 dE m v 质量元： ki i i 2
例1 一长为 l , 质量为 m 的竿可绕支点O自由 转动 . 一质量为 m、速率为 v 的子弹射入竿内距支 点为 a 处， 问角速度为多少 ? 解 把子弹和竿看作一个系统 . 子弹射入竿的过程系统角动量守恒
1 2 2 mva m l m a 3 3mva 2 2 m' l 3ma
三
定轴转动刚体的动能定理
2 1W 2 d 源自 Jd Md Jd J 1 1 1 dt 2 1 1 2 2 W Md J 2 J1 1 2 2
合外力矩对绕定轴转动的刚体所作的功等于刚体 转动动能的增量 .
3
4-4 力矩作功 刚体绕定轴转动的动能定理
o
30
a
v
m
4
4-4 力矩作功 刚体绕定轴转动的动能定理
注意
子细 弹绳 击质 入量 沙不 袋计
o
v
子 弹 击 入 杆
o
圆 锥 摆
o
T
'
m
v
p
o
v
R
以子弹和沙袋为系统 以子弹和杆为系统 圆锥摆系统 动量守恒； 动量不守恒； 动量不守恒； 角动量守恒； 角动量守恒； 角动量守恒； 机械能不守恒 . 机械能不守恒 . 机械能守恒 .
x
1 2 1 1 2 2 Ek mi vi ( mi ri ) J 2 i 2 2 i 2
刚体的转动动能 E k
1 2 J 2
4-4 力矩作功 刚体绕定轴转动的动能定理
力矩的功 W
刚体的转动动能
2
1
Md
转动定律：
1 2 Ek J 2
2
1
M J