【免费下载】人教版第十一章三角形测试题
人教版八年级数学上册第十一章三角形单元测试卷-(含答案)

人教版八年级数学上册第十一章三角形单元测试卷一、单选题(共30分,每小题3分)1.能用三角形的稳定性解释的生活现象是()A.B.C.D.2.如图,BE、CF都是ABC的角平分线,且115BDC∠=︒,则A∠=()A.45°B.50°C.65°D.70°3.如果一个多边形的每一个外角都是90︒,那么这个多边形的内角和是()A.180︒B.360︒C.540︒D.720︒4.若一个多边形的每个内角都等于150°,则这个多边形的边数是()A.10B.11C.12D.135.一个多边形截去一个角后,得到的多边形的内角和为1980,那么原来的多边形的边数为().A.12或13取14B.13或14C.12或13D.13或14或15 6.下列命题正确的是()A.三角形的角平分线、中线、高均在三角形内部B.三角形中至少有一个内角不小于60︒C.直角三角形仅有一条高D .直角三角形斜边上的高等于斜边的一半7.下列各组线段,能构成三角形的是( )A .1,3,5cm cm cmB .2,4,6cm cm cmC .4,4,1cm cm cmD .8,8,20cm cm cm8.在三角形的①三条中线;①三条角平分线;①三条高中,一定相交于一点的是( )A .①①①B .①C .①D .①① 9.如图,在①ABC 中,D 是BC 延长线上一点,①B =40°,①ACD =120°,则①A 等于A .60°B .70°C .80°D .90° 10.如图在△ABC 中,BO ,CO 分别平分①ABC ,①ACB ,交于O ,CE 为外角①ACD 的平分线,BO 的延长线交CE 于点E ,记①BAC =①1,①BEC =①2,则以下结论①①1=2①2,①①BOC =3①2,①①BOC =90°+①1,①①BOC =90°+①2正确的是( )A .①①①B .①①①C .①①D .①①①二、填空题(共24分,每小题3分) 11.若一个多边形的内角和是 1980°,则这个多边形的边数为________. 12.等腰三角形一边长为5,另一边长为7,则周长为__________.13.如图,①BCD =145°,则①A +①B +①D 的度数为_____.14.一个多边形的每一个外角都等于60°,则这个多边形的内角和为_____度. 15.如果一个多边形的内角和为1260°,那么从这个多边形的一个顶点可以连___________条对角线.16.小华从点A 出发向前走10m ,向右转36︒然后继续向前走10m ,再向右转36︒,他以样的方法继续走下去,当他走回到点A 时共走_________米.17.如图,在①ABC 中,①CAD =①CDA ,①CAB −①ABC =30°,则①BAD =________︒.18.如图,在ABC 中,12∠=∠,34∠=∠,80A ∠=︒,则x =______.三、解答题(共66分) 19.如图,ABCD 是四根木条钉成的四边形,为了使它不变形,小明加了根木条AE ,小明的做法正确吗?说说你的理由.(共6分)20.如图①A =20°,①B =45°,①C =40°,求①DFE 的度数.(共6分)21.已知,如图,在ABC ∆中,AD 、AE 分别是ABC ∆的高和角平分线,若30ABC ∠=,60ACB ∠=(共8分)(1)求DAE ∠的度数;(2)写出DAE ∠与C B ∠-∠的数量关系 ,并证明你的结论22.若一个多边形的内角和比外角和多540°,求这个多边形的边数.(共8分)23.如图:(共8分)(1)画出△ABC 的BC 边上的高线AD ;(2)画出△ABC 的角平分线CE .24.已知在△ABC 中,∠A :∠B :∠C =2:3:4,CD 是∠ACB 平分线,求∠A 和∠CDB 的度数.(共10分)25.如图,已知:点P 是ABC ∆内一点.(共10分)(1)求证:BPC A ∠>∠;(2)若PB 平分ABC ∠,PC 平分ACB ∠,40A ︒∠=,求P ∠的度数.26.如图,五边形ABCDE的内角都相等,且AB=BC,AC=AD,求①CAD的度数.(共10分)答案第1页,共1页 参考答案:1.C2.B3.B4.C5.A6.B7.C8.D9.C10.C 11.1312.17或1913.145°14.72015.616.10017.1518.13020.小明的做法正确,21.105°22.(1)15°;(2)()12DAE C B ∠=∠-∠, 23.724.略25.∠A =40°,∠CDB =80°.26.(1)略;(2)110°27.①CAD =36°.。
人教版八年级数学第十一章《三角形》单元测试题(含答案)

人教版八年级数学第十一章《三角形》单元测试题(含答案)时间:120分钟满分:120分一、选择题(共10小题,满分30分,每小题3分)1.(3分)如图,在四边形ABCD中,AB>AD,对角线AC平分∠BAD,下列结论正确的是()A.AB﹣AD>|CB﹣CD|B.AB﹣AD=|CB﹣CD|C.AB﹣AD<|CB﹣CD|D.AB﹣AD与|CB﹣CD|的大小关系不确定2.(3分)有两条高在三角形外部的三角形是()A.锐角三角形B.直角三角形C.钝角三角形D.不确定3.(3分)如图,为了估计池塘两岸A,B间的距离,在池塘的一侧选取点P,测得P A=15米,PB=11米那么A,B间的距离不可能是()A.5米B.8.7米C.27米D.18米4.(3分)一个三角形的两边长分别为3和4,且第三边长为整数,这样的三角形的周长最大值是()A.11B.12C.13D.145.(3分)如图,在△ABC中,AF平分∠BAC交BC于点F、BE平分∠ABC交AC于点E,AF与BE相交于点O,AD是BC边上的高,若∠C=50°,BE⊥AC,则∠DAF的度数为()A.10°B.12°C.15°D.20°6.(3分)如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,以下结论:①AD∥BC,②∠ACB=∠ADB,③∠ADC+∠ABD=90°,④∠ADB=45°﹣∠CDB,其中正确的结论有()A.1个B.2个C.3个D.4个7.(3分)如图,在三角形ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①AH⊥EF;②∠ABF=∠EFB;③AC∥BE;④∠E=∠ABE.其中正确的结论有()A.4个B.3个C.2个D.1个8.(3分)如图,四边形ABCD为一长方形纸带,AD∥BC,将四边形ABCD沿EF折叠,C、D两点分别与C′、D′对应,若∠1=2∠2,则∠3的度数为()A.50°B.54°C.58°D.62°9.(3分)若n边形的内角和与外角和相加为1800°,则n的值为()A.7B.8.C.9D.1010.(3分)如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α,再沿直线前进8米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度α为()A.30°B.40°C.45°D.60°二、填空题(共5小题,满分15分,每小题3分)11.(3分)如图,正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH的边长为6,则正六边形ABCDEF的边长为.12.(3分)如图,在△ABC中,∠B=80°,∠C=42°,AD⊥BC于点D,AE平分∠BAC,则∠DAE=.13.(3分)如图,在△ABC中,∠A=65°,则∠1+∠2=°.14.(3分)如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC是半高三角形,且斜边AB=10,则它的周长等于.15.(3分)如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=4cm,则.三、解答题(共10小题,满分75分)16.(7分)如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC =10cm,∠CAB=90°.试求:(1)AD的长;(2)△ABE的面积;(3)△ACE和△ABE的周长的差.17.(7分)如图,P为△ABC内任意一点,求证:AB+AC>PB+PC.18.(7分)已知a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.(1)求c的取值范围;(2)若△ABC的周长为12,求c的值.19.(7分)如图所示,在△ABC中,CD⊥AB于点D,EF⊥CD于点G,∠ADE=∠EFC.(1)证明AB∥EF.(2)请说明∠AED=∠ACB的理由.(3)若∠BDE=2∠B+36°,求∠DEF的度数.20.(7分)已知:在△ABC中,AE平分∠BAC,BF平分∠ABC,AE、BF交于点G.(1)如图1:若∠C=60°,求∠AGB的度数;(2)如图2:点D是AE延长线上一点,连接BD、CD,∠ADC=∠ABG+∠BAG,求证:CD∥BF;(3)如图3:在(2)的条件下,过点G作GK∥AB,交BD于点K,点M在线段DC 的延长线上,连接KM,若∠ACB=∠BDA,∠ABC+∠BAE=2∠DKM,∠M=16°,求∠BAC的度数.21.(7分)如图所示,在△ABC中,AD平分∠BAC交BC于点D,BE平分∠ABC交AD 于点E.(1)若∠C=60°,∠BAC=80°,求∠ADB的度数;(2)若∠BED=60°,求∠C的度数.22.(7分)如图,在三角形ABC中,点D是BC上一点,点F是AC上一点,连接AD、DF,点E是AD上一点,连接EF,且∠1+∠2=180°,∠B=∠3.(1)求证:AB∥DF;(2)若FD平分∠CFE,∠BAD=50°,∠3=70°,求∠CAD的度数.23.(8分)如图,四边形ABCD中,∠A=75°,∠C=105°,BE平分∠ABC,DF平分∠ADC.求:(1)∠ABC+∠ADC的值;(2)∠BED+∠BFD的值.24.(9分)已知如图1,线段AB,CD相交于O点,连接AD,CB,我们把如图1的图形称之为“8字形”.那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:(1)在图1中,请写出∠A,∠B,∠C,∠D之间的数量关系,并说明理由;(2)如图2,计算∠A+∠B+∠C+∠D+∠E+∠F的度数.25.(9分)△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数;(2)如图2(∠B<∠C),试说明∠DAE与∠B、∠C的数量关系;(3)拓展:如图3,四边形ABDC中,AE是∠BAC的角平分线,DA是∠BDC的角平分线,猜想:∠DAE与∠B、∠C的数量关系是否改变.说明理由.参考答案一、选择题(共10小题,满分30分,每小题3分)1.A;2.C;3.C;4.C;5.C;6.B;7.B;8.B;9.D;10.B;二、填空题(共5小题,满分15分,每小题3分)11.4;12.19°;13.245;14.10+10或610;15.;三、解答题(共10小题,满分75分)16.解:∵∠BAC=90°,AD是边BC上的高,∴AB•AC BC•AD,∴AD 4.8(cm),即AD的长度为4.8cm;(2)方法一:如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,∴S△ABC AB•AC6×8=24(cm2).又∵AE是边BC的中线,∴BE=EC,∴BE•AD EC•AD,即S△ABE=S△AEC,∴S△ABE S△ABC=12(cm2).∴△ABE的面积是12cm2.方法二:因为BE BC=5,由(1)知AD=4.8,所以S△ABE BE•AD5×4.8=12(cm2).∴△ABE的面积是12cm2.(3)∵AE为BC边上的中线,∴BE=CE,∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE)=AC﹣AB=8﹣6=2(cm),即△ACE和△ABE的周长的差是2cm.17.证明:延长BP交AC于点D,在△ABD中,PB+PD<AB+AD①在△PCD中,PC<PD+CD②①+②得PB+PD+PC<AB+AD+PD+CD,即PB+PC<AB+AC,即:AB+AC>PB+PC.18.解:(1)∵a,b,c分别为△ABC的三边,a+b=3c﹣2,a﹣b=2c﹣6,∴,解得:1<c<6.故c的取值范围为1<c<6;(2)∵△ABC的周长为12,a+b=3c﹣2,∴a+b+c=4c﹣2=12,解得c=3.5.故c的值是3.5.19.解:(1)证明:∵CD⊥AB于点D,EF⊥CD于点G,∴∠BDC=∠FGC,=90°,∴AB∥EF(同位角相等,两直线平行).(2)证明:由(1)得AB∥EF,∴∠B=∠EFC(两直线平行,同位角相等),又∵∠ADE=∠EFC.∴∠B=∠ADE;(3)由(2)得∠B=∠ADE,∴DE∥BC,由(1)得AB∥EF,∴四边形BDEF是平行四边形(两组对边平行的四边形是平行四边形),∴∠DEF=∠B(平行四边形对角相等),∵∠B=∠ADE,∠BDE=2∠B+36°,∴180°﹣∠B=2∠B+36°,∴∠B=48°,∴∠DEF=48°.20.(1)证明:如图1,∵AE、BF分别平分∠BAC与∠ABC,∴,,在△ABC中,∠ABC+∠ACB+∠C=180°,∠C=60°,∴∠ABC+∠BAC=180°﹣60°=120°,∴∠ABF+∠BAE∠ABC∠BAC(∠ABC+∠BAC)120°=60°,∴∠AGB=180°﹣60°=120°;(2)证明:如图2,∵∠BGD是△ABG得一个外角,∴∠BGD=∠BAG+∠ABG,∵∠ADC=∠BAG+∠ABG,∴∠BGD=∠ADC,∴CD∥BF;(3)解:如图3,∵∠BED=∠AEC,∠ACB=∠BDA,∴∠CAE=∠DBE,∵AE平分∠BAC,BF平分∠ABC,设∠ABF=∠CBF=α,∠BAD=∠CAD=∠DBC=β,∴∠AEC=2α+β,∵∠ABC+∠BAE=2∠DKM,∴,∵GK∥AB,∴∠BGK=∠ABG=α,∴∠GKD=∠GBK+∠BGK=2α+β,∴,∵GB∥DM,∠M=16°,∴∠GBK+∠MDK=180°,∵∠GBK+∠GKB+∠BGK+∠MKD+∠KDM+∠M=360°,∠BKG+∠MKD=180°﹣∠GKM,∴180°+180°﹣∠GKM+∠BGK+∠M=360°,∴∠GKM=∠BGK+∠M,∴,∴β=32°,∴∠BAC=2×32°=64°.21.解:(1)∵AD平分∠BAC,∠BAC=80°,∴∠DAC∠BAC=40°,∵∠ADB是△ADC的外角,∠C=60°,∴∠ADB=∠C+∠DAC=100°;(2)∵∠BED是△ABE的外角,∠BED=60°,∴∠BAD+∠ABE=∠BED=60°,∵AD平分∠BAC,BE平分∠ABC,∴∠BAC=2∠BAD,∠ABC=2∠ABE,∴∠BAC+∠ABC=2(∠BAD+∠ABE)=120°,∵∠BAC+∠ABC+∠C=180°,∴∠C=180°﹣(∠BAC+∠ABC)=60°.22.(1)证明:∵∠1+∠2=180°,∠1+∠DEF=180°,∴∠DEF=∠2.∴EF∥BC.∴∠3=∠FDC.∵∠B=∠3,∴∠B=∠FDC.∴AB∥DF.(2)解:∵AB∥DF,∴∠BAD=∠EDF=50°.∵FD平分∠CFE,∴∠EFC=2∠3=140°.∴∠AFE=180°﹣∠EFC=40°,∠1=∠3+∠EDF=70°+50°=120°.∴∠CAD=180°﹣∠1﹣∠AFE=20°.23.解:(1)∵四边形ABCD中,∠A=75°,∠C=105°,∴∠ABC+∠ADC=360°﹣75°﹣105°=180°;(2)如图,∵BE平分∠ABC,DF平分∠ADC,∴∠1∠ABC,∠2∠ADC,∴∠1+∠2(∠ABC+∠ADC)=90°,由三角形外角的性质可得,∠BED=∠1+∠A,∠BFD=∠2+∠A,∴∠BED+∠BFD=∠1+∠A+∠2+∠A=∠1+∠2+2∠A=90°+150°=240°.24.解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,在△BOC中,∠BOC=180°﹣∠B﹣∠C,∵∠AOD=∠BOC(对顶角相等),∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,∴∠A+∠D=∠B+∠C;(2)如图3,连接AD,则∠BAD+∠B+∠C+∠ADC=360°,根据“8字形”数量关系,∠E+∠F=∠EDA+∠F AD,所以,∠A+∠B+∠C+∠D+∠E+∠F=360°.25.解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,∴∠BAC=80°,∵AD是∠BAC的角平分线,∴∠CAD=∠BAD∠BAC=40°,∵AE是△ABC的高,∴∠AEC=90°,∵∠C=60°,∴∠CAE=90°﹣60°=30°,∴∠DAE=∠CAD﹣∠CAE=10°;(2)∵∠BAC+∠B+∠C=180°,∴∠BAC=180°﹣∠B﹣∠C,∵AD是∠BAC的角平分线,∴∠CAD=∠BAD∠BAC,∵AE是△ABC的高,∴∠AEC=90°,∴∠CAE=90°﹣∠C,∴∠DAE=∠CAD﹣∠CAE∠BAC﹣(90°﹣∠C)(180°﹣∠B﹣∠C)﹣90°+∠C∠C∠B,即∠DAE∠C∠B;(3)不变,理由:连接BC交AD于F,过点A作AM⊥BC于M,过点D作DN⊥BC于N,∵AE是∠BAC的角平分线,AM是高,∴∠EAM(∠ACB﹣∠ABC),同理,∠ADN(∠BCD﹣∠CBD),∵∠AFM=∠DFN,∠AMF=∠DNF=90°,∴∠MAD=∠ADN,∴∠DAE=∠EAM+∠MAD=∠EAM+∠ADN(∠ACB﹣∠ABC)(∠BCD﹣∠CBD)(∠ACD﹣∠ABD).。
八年级数学上册《第十一章 三角形》单元测试卷及答案(人教版)

八年级数学上册《第十一章三角形》单元测试卷及答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列长度的三条线段能组成三角形的是()A.3,3,7 B.3,4,8 C.5,6,11 D.5,6,102.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的数学原理是()A.三角形具有稳定性B.两点确定一条直线C.两点之间线段最短D.三角形的两边之和大于第三边3.一个正多边形,它的每一个内角都等于140°,则该正多边形是()A.正六边形B.正七边形C.正八边形D.正九边形4.把一块直角三角板和一把直尺如图放置,若∠1=35°,则∠2的度数等于()A.65°B.55°C.45°D.60°5.如图,AD是△ABC的边BC上的高,若BC=3,AB=6,AD=4则AB边上的高为()A.1 B.2 C.3 D.无法计算6.如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图2是八角形空窗的示意图,它的一个外角∠1=()A.45°B.60°C.110°D.135°7.如图,在△ABC中,点I到△ABC的三边距离相等,连接AI、BI,若∠ACB=70∘,则∠AIB的大小为()A.160∘B.140∘C.130∘D.125∘8.如图AB∥CD,点E在线段BC上(不与点B,C重合),连接DE,若∠D=40°,∠BED=60°则∠B=()A.10°B.20°C.40°D.60°二、填空题9.一个不等边三角形的两边分别为5cm和7cm,第三边的长度为奇数,则满足条件的三角形共有个.10.正十边形的每个内角是度.11.如图,在△ABC中,AD是BC边上的中线,若S△ABC=12,AC=3则点D到AC的距离为.12.如图,在△ABC中,点O是△ABC角平分线的交点,若∠A=70°,∠BOC=.13.如图,在△ABC中AB=AC,点D、E分别在边BC、AB上AD=DE,如果∠CAD=60°,∠BDE=15°那么∠C=°.14.如图,AB//CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=.三、解答题15.AD、BE为△ABC的高,AD、BE相交于H点∠C=50°,求∠BHD.16.如图,△ABC中∠ACB=90°,CD为AB边上的高,BE平分∠ABC,且分别交CD,AC于点F,E求证:CE=CF.17.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=100°,求∠A和∠ACE的度数.18.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.(1)求∠CBE的度数;(2)若∠F=25°,求证:BE∥DF.19.(本题满分10分)如图AC∥EF,∠1+∠3=180°.(1)求证AF∥CD;(2)若AC平分∠FAB,AC⊥EB于点C,∠4=78°求∠BCD的度数.参考答案1.D2.A3.D4.B5.B6.A7.D8.B9.510.14411.412.125°13.3514.125°15.解:∵AD是△ABC的高∴∠BHD+∠HBD=90°∵BE是△ABC的高∴∠HBD+∠C=90°∴∠BHD=∠C∵∠C=50°∴∠BHD=50°.16.证明:∵∠ACB=90°∴∠ACD+∠BCD=90°∵CD为AB边上的高∴∠ADC=90°∴∠A+∠ACD=90°∴∠A=∠BCD∵BE是∠ABC的平分线∴∠ABE=∠CBE∴∠CFE=∠BCD+∠CBE=∠A+∠ABE∵∠CEF=∠A+∠ABE∴∠CEF=∠CFE∴CE=CF.17.解:∵∠ADB=∠DBC+∠ACB∴∠DBC=∠ADB﹣∠ACB=100°﹣60°=40°.∵BD是角平分线∴∠ABC=80°∴∠A=180°﹣∠ABC﹣∠ACB=40°;∵CE是高∴∠AEC=90°∴∠ACE=90°﹣∠A=50°18.(1)解:∵∠ACB=90°,∠A=40°∴∠CBD=∠A+∠ACB=130°∵BE平分∠CBD∠CBD=65°∴∠CBE=12(2)证明:∵∠ACB=90°∴∠BCE=90°∵∠CBE=65°∴∠BEC=90°-65°=25°∵∠F=25°∴∠F=∠BEC∴BE∥DF19.(1)证明:∵AC∥EF∴∠1+∠2=180°.又∵∠1+∠3=180°∴∠2=∠3.∴AF∥CD.(2)解:∵AC平分∠FAB∴∠2=∠CAD.∵∠2=∠3∴∠CAD=∠3.∵∠4+∠ADC=180°且∠4=78°∴∠ADC=180°−78°=102°.∴∠CAD=∠3=180°−102°2=39°∵AC⊥EB ∴∠ACB=90°.∴∠BCD=90°−∠3=90°−39°=51°.。
八年级数学上册试题 第十一章 三角形章节测试卷--人教版(含详解)

第十一章《三角形》章节测试卷一.选择题(共12小题,满分48分,每小题4分)1.已知△ABC中,∠A=20°,∠B=70°,那么△ABC是( )A.直角三角形B.锐角三角形C.钝角三角形D.正三角形2.下面四个图形中,线段BD是△ABC的高的是( )A.B.C.D.3.要使如图所示的五边形木架不变形,至少要再钉上几根木条( )A.1根B.2根C.3根D.4根4.能把一个任意三角形分成面积相等的两部分是( )A.以上都可以B.高C.中线D.角平分线5.长度分别为3,8,x的三条线段能组成一个三角形,x的值可以是( )A.4B.5C.6D.116.如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )A.90°B.20°C.45°D.70°7.如图所示,∠1=∠2=150°,则∠3=( )A.30°B.150°C.120°D.60°8.如图,在△ABC中,AB=2021,AC=2018,AD为中线,则△ABD与△ACD的周长之差为( )A.1B.2C.3D.49.若一个多边形的每个内角都等于150°,则这个多边形的边数是( )A.10B.11C.12D.1310.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )A.90°B.135°C.270°D.315°11.△ABC的两边是方程组{x+2y=104x+3y=20的解,第三边长为奇数.符合条件的三角形有( )A.1个B.2个C.3个D.4个12.如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( )A.∠A+∠D﹣45°B.12(∠A+∠D)+45°C.180°-(∠A+∠D)D.12∠A+12∠D二.填空题(共4小题,满分16分,每小题4分)13.如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=20°,则∠1= °.14.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A= .15.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠AFD的度数为 .16.如图,D,E,F分别是△ABC的边AB,BC,AC上的中点,连接AE,BF,CD交于点G,AG:GE=2:1,△ABC的面积为6,设△BDG的面积为S1,△CGF的面积为S2,则S1+S2= .三.解答题(共8小题,满分86分)17.已知一个多边形的内角和是外角和的三倍,则这个多边形是几边形?18.如图,∠ABC=∠FEC=∠ADC=90°.(1)在△ABC中,BC边上的高是 ;(2)在△AEC中,AE边上的高是 ;(3)若AB=2.4cm,CD=2cm,AE=3cm,求△AEC的面积及CE的长.19.如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数;(2)∠AEF的度数.20.已知一等腰三角形的两边长x,y满足方程组{3x−y=55x+2y=23求此等腰三角形的周长.21.一个零件的形状如图,按规定∠A=90°,∠B和∠C应分别是32°和21°,检验工人量得∠BDC=149°,就判断这个零件不合格,运用三角形的有关知识说出零件不合格的理由.22.如图1所示,将一副三角板的直角顶点重合在点O处.(1)∠AOD ∠BOC;(填“>”“<”“=”)(2)若将三角尺按图2的位置摆放,∠AOC和∠BOD在数量上有何关系?说明理由;(3)在图2中,已知∠BOC与∠AOC的度数比为m:n,当a6m b11与a n+1b2n﹣11是同类项时,求∠BOD的度数.23.问题1现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.研究(1):如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系是 研究(2):如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是 研究(3):如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.问题2研究(4):将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .24.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.(1)如图1,若∠B=40°,∠C=60°,求∠DAE的度数;(2)如图2(∠B<∠C),试说明∠DAE与∠B、∠C的数量关系;(3)拓展:如图3,四边形ABDC中,AE是∠BAC的角平分线,DA是∠BDC的角平分线,猜想:∠DAE与∠B、∠C的数量关系是否改变.说明理由.答案一.选择题1.【解答】解:∵△ABC中,∠A=20°,∠B=70°,∴∠C=180°﹣20°﹣70°=90°,∴△ABC是直角三角形.故选:A.2.【解答】解:由图可得,线段BD是△ABC的高的图是D选项.故选:D.3.【解答】解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.故选:B.4.【解答】解:三角形的中线把三角形分成等底同高的两个三角形,面积相等,所以,能把一个任意三角形分成面积相等的两部分是中线.故选:C.5.【解答】解:8﹣3<x<8+3,5<x<11,只有选项C符合题意.故选:C.6.【解答】解:∵∠BAC=90°,∴∠DAC+∠BAD=90°,∵AD是△ABC的高,∴∠ADB=∠BAD+∠B=90°,∴∠DAC=∠B=20°,故选:B.7.【解答】解:∵∠1=∠2=150°,∴∠ABC=∠BAC=180°﹣150°=30°,∴∠3=∠ABC+∠BAC=60°.故选:D.8.【解答】解:∵AD为中线,∴DB=DC,∴△ABD与△ACD的周长之差为:(AB+AD+BD)﹣(AD+DC+AC)=AB+AD+BD﹣AD﹣DC﹣AC=AB﹣AC=2021﹣2018=3,故选:C.9.【解答】解:由题意可得:180°•(n﹣2)=150°•n,解得n=12.故多边形是12边形.故选:C.10.【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.故选:C.11.【解答】解:方程组{x+2y=104x+3y=20的解为:{x=2 y=4,∵△ABC的两边是方程组{x+2y=104x+3y=20的解,第三边长为奇数,∴2<第三边长<6,1∴第三边长可以为:3,5.∴这样的三角形有2个.故选:B.12.【解答】解:∵四边形的内角和=360°,∴∠ABC+∠BCD=360°﹣(∠A+∠D),∵∠ABC与∠BCD的平分线的交点E恰好在AD边上,∴2∠EBC=∠ABC,2∠ECB=∠BCD,∴∠EBC+∠ECB=12(∠ABC+∠BCD)=12×[360°−(∠A+∠D)],∴∠BEC=180°﹣(∠EBC+∠ECB)=180°−12×[360°−(∠A+∠D)]=12(∠A+∠D),故选:D.二.填空题13.【解答】解:∵∠A=60°,∠C=50°,∴∠ABC=180°﹣∠A﹣∠C=180°﹣60°﹣50°=70°,∴∠1=∠ABC﹣∠D=50°﹣20°=50°.故答案为:50.14.【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠ABC=2∠ABP,∠ACM=2∠ACP,又∵∠ABP=20°,∠ACP=50°,∴∠ABC=2×20°=40°,∠ACM=2×50°=100°,∴∠A=∠ACM﹣∠ABC=60°,故答案为60°.15.【解答】解:∵∠B=40°,∠C=30°,∴∠BAC=110°,由折叠的性质得,∠E=∠C=30°,∠EAD=∠CAD,∵DE∥AB,∴∠BAE=∠E=30°,∴∠CAD=40°,∴∠ADC=180°﹣∠CAD﹣∠C=110°,∴∠AFD=110°﹣40°=70°,故答案为:70°.16.【解答】解:∵D,E,F分别是△ABC的边AB,BC,AC上的中点,∴AD=DB,AF=CF,∴△BDG的面积=△ADG的面积,△CFG的面积=△AGF的面积,∴设△BDG的面积为S1,△CGF的面积为S2,则S1+S2=四边形ADGF的面积,∵△ABC的面积为6,AG:GE=2:1,∴四边形ADGF的面积=23×12×6=2,∴S1+S2=2,故答案为:2三.解答题17.解:设这个多边形为n边形,n边形的内角和为:(n﹣2)×180°,n边形的外角和为:360°,根据题意得:(n﹣2)×180°=3×360°,解得:n=8,答:这个多边形是八边形.18.解:(1)在△ABC中,BC边上的高是线段AB;故答案为线段AB;(2)在△AEC中,AE边上的高是线段CD;故答案为线段CD;(3)∵S△AEC=12×AE×CD=12×CE×AB,∴CE=AE⋅CDAB= 2.5(cm).19.解:(1)∵DF⊥AB,∴∠B=90°﹣∠D=48°,∵∠ACD是△ABC的一个外角,∴∠ACD=∠A+∠B=83°;(2)∵DF⊥AB,∴∠AFD=90°,∴∠AEF=90°﹣∠A=55°.20.解:解方程组组{3x−y=55x+2y=23得{x=3 y=4,所以,等腰三角形的两边长为3,4.若腰长为3,底边长为4,由3+3=6>4知,三角形的周长为10.若腰长为4,底边长为3,则三角形的周长为11.所以,这个等腰三角形的周长为10或11.21.解:延长CD交AB于点E,∵∠BEC是△ACE的一个外角,∴∠BEC=∠A+∠C=90°+21°=111°,同理,∠BDC=∠BEC+∠B=111°+32°=143°,而检验工人量得∠BDC=149°,所以零件不合格.22.解:(1)∵∠AOB=∠COD=90°,∴∠AOB+∠BOD=∠COD+∠BOD,即∠AOD=∠BOC.故答案为:=;(2)∵∠AOB=∠COD=90°,∴∠AOC+∠BOD=180°.故∠AOC和∠BOD在数量上的关系为:∠AOC+∠BOD=180°;(3)∵a6m b11与a n+1b2n﹣11是同类项,∴{6m=n+111=2n−11,解得{m=2n=11,∵∠BOC与∠AOC的度数比为m:n,11﹣2=9,∴∠BOC=90°×2=20°,11−2∴∠BOD=90°﹣20°=70°.故∠BOD的度数是70°.23.解:(1)如图1,∠1=2∠A,理由是:由折叠得:∠A=∠DA′A,∵∠1=∠A+∠DA′A,∴∠1=2∠A;故答案为:∠1=2∠A;(2)如图2,猜想:∠1+∠2=2∠A,理由是:由折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,∵∠ADB+∠AEC=360°,∴∠1+∠2=360°﹣∠ADE﹣∠A′DE﹣∠AED﹣∠A′ED=360°﹣2∠ADE﹣2∠AED,∴∠1+∠2=2(180°﹣∠ADE﹣∠AED)=2∠A;故答案为:∠1+∠2=2∠A;(3)如图3,∠2﹣∠1=2∠A,理由是:∵∠2=∠AFE+∠A,∠AFE=∠A′+∠1,∴∠2=∠A′+∠A+∠1,∵∠A=∠A′,∴∠2=2∠A+∠1,∴∠2﹣∠1=2∠A;(4)如图4,由折叠得:∠BMN=∠B′MN,∠ANM=∠A′NM,∵∠DNA+∠BMC=360°,∴∠1+∠2=360°﹣2∠BMN﹣2∠ANM,∵∠BMN+∠ANM=360°﹣∠A﹣∠B,∴∠1+∠2=360°﹣2(360°﹣∠A﹣∠B)=2(∠A+∠B)﹣360°,故答案为:∠1+∠2=2(∠A+∠B)﹣360°.24.解:(1)∵∠B=40°,∠C=60°,∠BAC+∠B+∠C=180°,∴∠BAC=80°,∵AD是∠BAC的角平分线,∠BAC=40°,∴∠CAD=∠BAD=12∵AE是△ABC的高,∴∠AEC=90°,∵∠C=60°,∴∠CAE=90°﹣60°=30°,∴∠DAE=∠CAD﹣∠CAE=10°;(2)∵∠BAC+∠B+∠C=180°,∴∠BAC =180°﹣∠B ﹣∠C ,∵AD 是∠BAC 的角平分线,∴∠CAD =∠BAD =12∠BAC ,∵AE 是△ABC 的高,∴∠AEC =90°,∴∠CAE =90°﹣∠C ,∴∠DAE =∠CAD ﹣∠CAE =12∠BAC ﹣(90°﹣∠C )=12(180°﹣∠B ﹣∠C )﹣90°+∠C =12∠C −12∠B ,即∠DAE =12∠C −12∠B ; (3)不变,理由:连接BC 交AD 于F ,过点A 作AM ⊥BC 于M ,过点D 作DN ⊥BC 于N ,∵AE 是∠BAC 的角平分线,AM 是高,∴∠EAM =12(∠ACB ﹣∠ABC ),同理,∠ADN =12(∠BCD ﹣∠CBD ),∵∠AFM =∠DFN ,∠AMF =∠DNF =90°,∴∠MAD =∠ADN ,∴∠DAE =∠EAM+∠MAD =∠EAM+∠ADN =12(∠ACB ﹣∠ABC )+12(∠BCD ﹣∠CBD )=12(∠ACD ﹣∠ABD ).。
人教版八年级数学上册第十一章《三角形》测试题(含答案)

人教版八年级数学上册第十一章《三角形》测试题(含答案)一、选择题(30分)1.下列说法错误的是()A.三角形的角平分线把三角形分成面积相等的两部分B.三角形的三条中线相交于一点C.直角三角形的三条高交于三角形的直角顶点处D.钝角三角形的三条高所在直线的交点在三角形的外部2.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是()A.①②③B.①③④C.①④D.①②④3.如果线段AB=3cm,BC=1cm,那么A,C两点的距离d的长度为()A.4cm B.2cm C.4cm或2cm D.小于或等于4cm,且大于或等于2cm4.如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=()A.40°B.50°C.60°D.70°5.如图,△ABC中,BD,BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE,∠F, ②2∠BEF,∠BAF,∠C,③∠F,∠BAC,∠C,④∠BGH,∠ABE,∠C,其中正确个数是()A.4个B.3个C.2个D.1个6.小明同学在用计算器计算某n边形的内角和时,不小心多输入一个内角,得到和为2016°,则n等于()A.11B.12C.13D.147.如图,直线AB,CD被BC所截,若AB,CD,,1,45°,,2,35°,则∠3,( )A.80°B.70°C.60°D.90°8.如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE和∠CHG的大小关系为()A.∠AHE>∠CHG B.∠AHE<∠CHG C.∠AHE=∠CHG D.不一定9.若a,b,c是△ABC的三边的长,则化简|a,b,c|,|b,c,a|,|a,b,c|的结果是()A.a,b,c B.,a,3b,c C.a,b,c D.2b,2c10.已知正多边形的一个外角等于40,那么这个正多边形的边数为()A.6B.7C.8D.9二、填空题(15分)11.如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB 平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.12.设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x,150°时,对应的和谐数对有一个,它为(10,20);当x,66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________,13.根据如图所示的已知角的度数,求出其中∠α的度数为______.14.在图中过点P任意画一条直线,最多可以得到____________个三角形.15.如图,点O是△ABC的两条角平分线的交点,若△BOC=118°,则△A的大小是。
人教版八年级上册数学三角形试卷

第十一章三角形单元测试人教版数学八年级上册时间:60分钟,满分:100分一、选择题(每题3分,共24分)1.下列长度的三条线段能组成三角形的是()A.1cm 2cm 3cm B.6cm 2cm 3cmC.4cm 6cm 8cm D.5cm 12cm 6cm2.安装空调一般会采用如图的方法固定,其根据的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短3.多边形的内角和不可能是()A.B.C.D.4.如图,在中,点D是的中点,,若的面积为10,则的面积是()A.B.1.5 C.D.25.如图,是的外角,,则的度数为()A.B.C.D.6.一副三角板,按如图所示叠放在一起,则图中的度数是()A.B.C.D.7.如图,在中,是的高,是的角平分线,,,则的度数是()A.B.C.D.8.如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=()A.90°B.180°C.120°D.270°二、填空题(每题4分,共20分)9.已知的三条边长为,则x的取值范围是.10.已知一个三角形三个内角度数的比是1:3:6,则其最小内角的度数为.11.一个多边形的内角和与外角和的差是,则它的边数为.12.如图,△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是.13.如图,BE、CF是△ABC的角平分线,BE、CF相交于点D,若,则∠CDE的度数为°.三、解答题(共56分)14.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.15.如图,在△ABC中,∠A=46°,CE是∠ACB的平分线,B,C,D在同一条直线上,DF∥EC,∠D=42°.求∠B的度数.16.如图,中,已知为的平分线,于,,,求的度数.17.如图,在△ABC中,,,CF平分交AB于点E.(1)求的度数:(2)若于点D, .判断△CFD的形状,并说明理由. 18.如图,五边形中, .(1)求的度数;(2)直接写出五边形的外角和.参考答案1.C2.A3.C4.A5.D6.D7.B8.B9.10.18°11.712.80°13.60;14.解:设这个多边形的边数是n,依题意得(n﹣2)×180°=3×360°﹣180°,n﹣2=6﹣1,n=7.∴这个多边形的边数是715.解:∵FD∥EC,∴∠BCE=∠D=42°,∵CE是∠ACB的平分线,∴∠ACB=2∠BCE=84°,∵∠A=46°,∴∠B=180°-84°-46°=50°.16.解:,,,,,,,平分,.17.(1)解:中,,,,又平分,,即;(2)解:是直角三角形,理由:于点D,,,又,,又,,是直角三角形.18.(1)解:∵AE∥CD,∴∠D+∠E=180°,∵五边形ABCDE中,∠A=100°,∠B=120°,∴.(2)解:根据多边形的外角和定理:五边形的外角和是:。
人教版八年级数学上册《第11章三角形》单元测试题含答案

第十一章三角形测试题一、选择题(每小题3分,共30分)1.三角形按边分类可分为( )A.不等边三角形、等边三角形B.等腰三角形、等边三角形C.不等边三角形、等腰三角形、等边三角形D.不等边三角形、等腰三角形2.如图1,图中三角形的个数是( )图1A.6 B.7 C.8 D.93.如图2,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )图2A.△AGC中,CF是AG边上的高B.△GBC中,CF是BG边上的高C.△ABC中,GC是BC边上的高D.△GBC中,GC是BC边上的高4.如图3,小明做了一个长方形框架,发现很容易变形,请你帮他选择一个最好的加固方案( )图3图45.如图5,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )图5A.118° B.119° C.120° D.121°6.如图6是六边形ABCDEF,则该图形的对角线的条数是( )图6A.6 B.9 C.12 D.187.如图7,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B,C处开工挖出“V”字型通道.如果∠DBA=130°,∠ECA=135°,那么∠A的度数是( )图7A.75° B.80° C.85° D.90°8.如图8,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )图8A.x=y+z B.x=y-zC.x=z-y D.x+y+z=1809.如图9,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形(含三角形).若这两个多边形的内角和分别为M和N,则M+N不可能是( )图9A.360° B.540° C.720° D.630°10.某木材市场上木棒规格与对应价格如下表:规格 1 m 2 m 3 m 4 m 5 m 6 m价格(元/根)101520253035小明的爷爷要做一个三角形的木架养鱼用,现有两根长度分别为3 m和5 m的木棒,还需要到该木材市场上购买一根木棒.则小明的爷爷至少带的钱数应为( )A.10元 B.15元 C.20元 D.25元请将选择题答案填入下表:题号12345678910总分答案第Ⅱ卷(非选择题共70分)二、填空题(每小题3分,共18分)11.已知一个等腰三角形两边的长分别为3和6,则该等腰三角形的周长是________.12.如图10,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为________cm.图1013.如图11,直角三角形的两条直角边AC,BC分别经过正九边形的两个顶点,则图中∠1+∠2的度数是________.1114.有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图12方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为________.图1215.有一程序,如果机器人在平地上按如图13所示的步骤行走,那么机器人回到A点处行走的路程是________.图1316.如图14所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,D,E分别为垂足.若∠AFD=158°,则∠EDF=________°.图14三、解答题(共52分)17.(6分)如图15,佳佳和音音住在同一小区(A点),每天一块去学校(B点)上学.一天,佳佳要先去文具店(C点)买练习本再去学校,音音要先去书店(D点)买书再去学校.这天两人从家到学校谁走的路远?为什么?图1518.(6分)已知一个多边形的内角和与外角和之比为11∶2.(1)求这个多边形的内角和;(2)求这个多边形的边数.19.(6分)如图16,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB =60°,∠ADB=97°,求∠A和∠ACE的度数.图1620.(6分)如图17,用钉子把木棒AB,BC和CD分别在端点B,C处连接起来,AB,CD 可以转动,用橡皮筋把AD连接起来,设橡皮筋AD的长是x cm.(1)若AB=5 cm,CD=3 cm,BC=11 cm,求x的最大值和最小值;(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?图1721.(6分)如图18,它是一个大型模板,设计要求BA与CD相交成20°角,DA与CB 相交成40°角,现测得∠A=145°,∠B=75°,∠C=85°,∠D=55°,就断定这块模板是合格的,这是为什么?图1822.(7分)已知△ABC的周长是20,三边分别为a,b,c.(1)若b是最大边,求b的取值范围;(2)若△ABC是三边均不相等的三角形,b是最大边,c是最小边,且b=3c,a,b,c 均为整数,求△ABC的三边长.23.(7分)如图19,在△ABC中,点E在AC上,∠AEB=∠ABC.(1)如图①,作∠BAC的平分线AD,分别交CB,BE于点D,F.求证:∠EFD=∠ADC;(2)如图②,作△ABC的外角∠BAG的平分线AD,交CB的延长线于点D,反向延长AD 交BE的延长线于点F,则(1)中的结论是否仍然成立?为什么?图1924.(8分)已知:如图20,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.图20答案1.D 2.C 3.C . 4.B . 5.C 6.B . 7.C 8.A . 9.D 10.C 11.15 12.19 13.190° 14.105° . 15.30米 16.68 .17.解:佳佳从家到学校走的路远. 理由:佳佳从家到学校走的路是AC +CD +BD ,音音从家到学校走的路是AD +BD.∵在△ACD 中,AC +CD >AD ,∴AC +CD +BD >AD +BD ,即佳佳从家到学校走的路远.18.解:(1)360°×112=1980°.即这个多边形的内角和为1980°.(2)设该多边形的边数为n,则(n-2)×180°=1980°,解得n=13.即这个多边形的边数为13.19.解:∵∠ADB=∠DBC+∠ACB,∴∠DBC=∠ADB-∠ACB=97°-60°=37°.∵BD是∠ABC的平分线,∴∠ABC=74°,∴∠A=180°-∠ABC-∠ACB=46°.∵CE是AB边上的高,∴∠AEC=90°,∴∠ACE=90°-∠A=44°.20.解:(1)x的最大值是5+3+11=19,最小值是11-3-5=3.(2)由(1)得橡皮筋长x的取值范围为3<x<19.21.解:如图,延长DA,CB相交于点F,延长BA,CD相交于点E.∵∠C+∠ADC=85°+55°=140°,∴∠F=180°-140°=40°.∵∠C+∠ABC=85°+75°=160°,∴∠E=180°-160°=20°.符合设计要求,故这块模板是合格的.22.解:(1)依题意有b≥a,b≥c.∵a +c >b ,∴a +b +c ≤3b 且a +b +c >2b ,则2b <20≤3b ,解得203≤b <10. (2)∵203≤b <10,b 为整数, ∴b =7,8,9.∵b =3c ,且c 为整数,∴b =9,c =3,∴a =20-b -c =8.故△ABC 的三边长分别为a =8,b =9,c =3.23.解:(1)证明:∵AD 平分∠BAC ,∴∠BAD =∠DAC.∵∠EFD =∠DAC +∠AEB ,∠ADC =∠ABC +∠BAD ,且∠AEB =∠ABC ,∴∠EFD =∠ADC.(2)∠EFD =∠ADC 仍然成立.理由:∵AD 平分∠BAG ,∴∠BAD =∠GAD.∵∠FAE =∠GAD ,∴∠FAE =∠BAD.∵∠EFD =∠AEB -∠FAE ,∠ADC =∠ABC -∠BAD ,且∠AEB =∠ABC ,∴∠EFD =∠ADC.24.解:(1)证明:∵∠BAE =180°-∠ABC -∠AEB ,∠EFC =180°-∠BCD -∠CEF ,且∠ABC =∠BCD ,∠AEB =∠CEF ,∴∠BAE =∠EFC.∵AE 平分∠BAD ,∴∠BAE=∠DAE,∴∠EFC=∠DAE.∵∠EFC+∠EFD=180°,∴∠DAE+∠EFD=180°,∴∠AEF+∠D=360°-(∠DAE+∠EFD)=180°.∵∠D=90°,∴∠AEF=90°,∴EF⊥AE.(2)EF⊥AE仍成立.理由如下:如图.∵∠1=∠ABC-∠AEB,∠F=∠BCD-∠CEF,且∠ABC=∠BCD,∠AEB=∠CEF,∴∠1=∠F.∵AE平分四边形ABCD的外角,∴∠1=∠2,∴∠F=∠2.∵∠2+∠EAD=180°,∴∠F+∠EAD=180°,∴∠AEF+∠D=360°-(∠F+∠EAD)=180°.∵∠D=90°,∴∠AEF=90°,∴EF⊥AE.。
初中数学人教版八年级上册 第十一章 三角形单元测试(含简单答案)
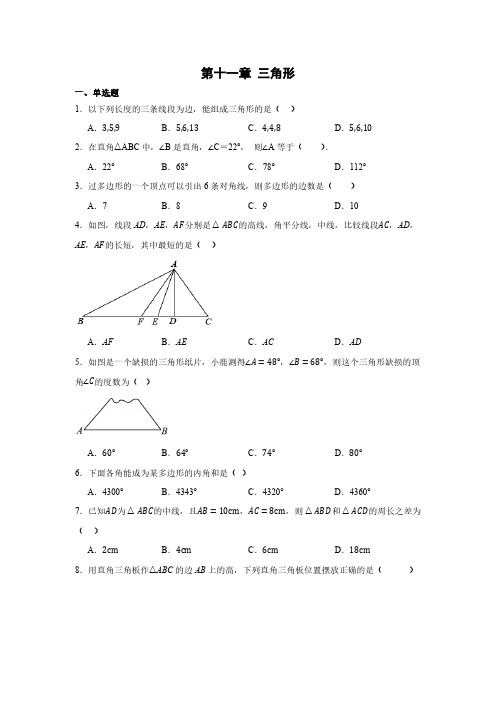
第十一章三角形一、单选题1.以下列长度的三条线段为边,能组成三角形的是()A.3,5,9B.5,6,13C.4,4,8D.5,6,102.在直角△ABC中,∠B是直角,∠C=22°,则∠A等于( ).A.22°B.68°C.78°D.112°3.过多边形的一个顶点可以引出6条对角线,则多边形的边数是( )A.7B.8C.9D.104.如图,线段AD,AE,AF分别是△ABC的高线,角平分线,中线,比较线段AC,AD,AE,AF的长短,其中最短的是()A.AF B.AE C.AC D.AD5.如图是一个缺损的三角形纸片,小鹿测得∠A=48°,∠B=68°,则这个三角形缺损的顶角∠C的度数为()A.60°B.64°C.74°D.80°6.下面各角能成为某多边形的内角和是()A.4300°B.4343°C.4320°D.4360°7.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD和△ACD的周长之差为()A.2cm B.4cm C.6cm D.18cm8.用直角三角板作△ABC的边AB上的高,下列直角三角板位置摆放正确的是( )A.B.C.D.9.如图,AD为△ABC的中线,BE为△ABD的中线.若△ABC的面积为12,BD=3,则△BDE中BD边上的高为( )A.1B.4C.3D.2二、填空题10.椅子是一种日常生活家具,现代的椅子追求美观时尚,在如图所示的椅子的设计中,将椅子脚设计成三角形,椅子非常稳固,其所利用的数学原理是.11.在△ABC中,∠A=35°,∠B=45°,则∠C为.12.如图,∠BCD是△ABC的外角,∠BCD=100°,∠A=70°,那么∠B=°.13.如图,∠A+∠B+∠C+∠D+∠E=.14.如图,AD是△ABC的中线,E为线段AD的中点,过点E作EF⊥BC于点F.若S△ABC=16,BD=3,则EF长为.15.将两块分别含有30°和45°角的直角三角板按如图所示叠放,若∠1=∠2,则∠3=°.16.已知一个包装盒的底面是内角和为720°的多边形,它是由另一个多边形纸片剪掉一个角以后得到的,则原多边形是边形.17.如图,△ABC中,E为AD与CF的交点,AE=ED,已知△ABC的面积是36,△BEF的面积是3.6,则△AEF的面积是.18.如图,在△ABC中,点D、E分别为边BC、AC上的点,连接DE,将△CDE沿DE翻折得到△C′DE,使C′D∥AB.若∠A=75°,∠B=60°,则∠C′EA的大小为.19.如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;④∠ADB=45°−1∠CDB,其中正确的结论有.2三、解答题20.已知和多边形一个内角相邻的外角与其余各内角度数总和为600°,求该多边形的边数.21.已知:a、b、c为△ABC的三边长,且a、b满足|2a−b+2|+(a+b−8)2=0.(1)求c的取值范围;(2)在(1)的条件下,若2x−c=1,求x的取值范围.22.一个零件的形状如图所示,按规定∠A=90°,∠B、∠D分别是32°和21°,要测量这个零件是否合格,检验工人测量∠BCD的度数,如果∠BCD=150°,就判定这个零件不合格,你知道这是为什么吗?请说明原因.23.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°;求:(1)求∠ACB的度数.(2)∠BCD的度数;(3)∠ECD的度数.24.综合与探究 小明在学习中遇到这样一个问题:如图1,∠MON =90°,点A ,B 分别在OM ,ON 上运动(不与点O 重合).探究与发现:若BC 是∠ABN 的平分线,BC 的反向延长线与∠BAO 的平分线交于点D .(1)①若∠BAO =70°,则∠D =________°;②猜想:∠D 的度数是否随A ,B 的运动而发生变化?并说明理由;(2)拓展延伸:如图2,若∠ABC =13∠ABN ,∠BAD =13∠BAO ,求∠D 的度数.(3)在图1的基础上,如果∠MON =α,其余条件不变,随着点A 、B 的运动(如图3),∠D =________(用含α的代数式表示)参考答案:1.D2.B3.C4.D5.B6.C7.A8.D9.D10.三角形的稳定性11.100°12.3013.180度/180°14.83/22315.67.516.五或六或七17.2.418.30°/30度19.①②③④20.边数为5或6.21.(1)4<c <8(2)52<x <9222.这个零件合格23.(1)100°(2)30°(3)20°24.(1)①45②∠D 的度数不发生变化(2)30°(3)12α。
2023-2024学年人教版八年级数学上册第11章三角形 单元同步达标测试题(含答案)

2023年秋人教版八年级数学上册《第11章三角形》同步达标测试题一、单选题(满分40分)1.下列长度的三条线段能组成三角形的是()A.4cm,5cm,9cm B.5cm,5cm,11cmC.8cm,9cm,15cm D.7cm,12cm,20cm2.正十二边形的外角和为( )A.30°B.150°C.360°D.1800°3.如图,在△ABC中,BC边上的高为()A.线段AD B.线段BF C.线段BE D.线段CG4.如图,有一个与水平地面成20°角的斜坡,现要在斜坡上竖起一根与水平地面垂直的电线杆,电线杆与斜坡所夹的角∠1的度数为()A.50°B.60°C.70°D.80°5.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠的铺成一片,就是平面图形的镶嵌.只用下面一种图形能够进行平面镶嵌的是()A.正三角形B.正五边形C.正八边形D.正十二边形6.如图,在△ABC中,D是BC中点,E是AD中点,连结BE、CE,若△ABC的面积为20,则△BCE的面积为()A.5B.10C.15D.187.将一副直角三角板如图放置,已知∠E=60°,∠C=45°,EF∥BC,则∠BND的大小为()A.100°B.105°C.110°D.115°8.如图,∠B=20°,∠C=60°,AD平分∠BAC,AE⊥BC,则∠DAE度数是()A.30°B.25°C.20°D.15°10.一个多边形的内角和是外角和的14.如图,在△ABC中,D为AC边的中点,积为4,则△BFC的面积为.15.如图,在△ABC中,∠ABC∠A的度数为____________.16.图①是一盏可折叠台灯,图为固定支撑杆,∠A是∠B的两倍,灯体旋转到CD′位置(图②中虚线所示∠BCD−∠DCD′=120°,则∠DCD三、解答题(满分40分)17.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是多少?18.如图,在ΔABC中,AD是高,∠DAC=10°,AE是ΔABC外角∠MAC的平分线,交BC 的延长线于点E,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB和∠E的度数.19.画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.(1)将△ABC向左平移5格,再向下平移1格.请在图中画出平移后的△A′B′C′;(2)利用网格在图中画出△ABC的中线CD,高线AE;(3)△A′B′C′的面积为__________;(4)在图中能使S△ABC=S△PBC的格点P的个数有__________个(点P异于A).20.如图,已知∠1=∠BDC,∠2+∠3=180°.(1)求证:AD∥EC;(2)若CE⊥AE于点E,∠F=50°,求∠ADF的度数.21.如图,已知△ABC中,点D、E分别在边AB、AC上,点F在BE上.(1)若∠ADE=∠ABC,(2)若D、E、F分别是△ABC的面积.(1)如图1,这是一个五角星,则(2)如图2,将五角星截去一个角后多出一个角,求参考答案∵电线杆与水平地面垂直,∴∠2=90°,∴∠1=∠3=180°−20°−90°故答案为:三角形具有稳定性.10.解:由题意,得:(n−2)180°=2×360°,解得:n=6;∴这个多边形的边数为6;故答案为:611.解:∵a+b>c,b−a<c,c+b>a,∴a+b−c>0,b−a−c<0,c−a+b>0,∴|a+b−c|+|b−a−c|+|c−a+b|=a+b−c+a+c−b+c−a+b=a+b+c故答案为:a+b+c.12.解:由折叠的性质得∠ADE=∠ADC=110°,∵∠ADB=180°−∠ADC=70°,∴∠BDE=110°−∠ADB=110°−70°=40°,∵DE∥AB,∴∠B=∠BDE=40°.故答案为:40.13.解:∵AB∥CD,∠B+∠D=70°,∴∠B=∠HGD,∵∠EHF是△HGD的一个外角,∴∠EHF=∠HGD+∠D,∴∠EHF=∠B+∠D=70°,∵∠1+∠2+∠EHF=180°,∴∠1+∠2=180°−∠EHF=110°.∵CD∥OE,∴OA⊥CD,∵AO⊥OE,D′G⊥AB,∴∠AGC=∠AFC=90°,在四边形AFCG中,∠AGC+∠GCF+∠AFC(4)如图,利用等高模型,在图中能使S△ABC=S△PBC的格点P在直线m,n上(除点A 外),总共有21个;故答案为21.20.(1)证明:∵∠1=∠BDC,∴AB∥CD,∴∠2=∠ADC,∵∠2+∠3=180°,∴∠ADC+∠3=180°,∴AD∥CE;(2)解:∵CE⊥AE,∴∠CEF=90°,由(1)知AD∥CE,∴∠DAF=∠CEF=90°,在△AFD中,∠F=50°∴∠ADF=180°−90°−50°=40°.21.(1)证明:∵∠ADE=∠ABC,∴DE∥BC,∴∠AED=C,∵∠EDF=∠C,∴∠EDF=∠AED,∴DF∥AC;(2)解:∵点F是BE中点,∴S△DEF=S△DBF,设S△DEF=S△DBF=x,∵D是AB中点,∴S△ADE=S△BDE=2x,∵E是AC中点,∴S△ABE=S△CBE=4x,S△CEF=2x,=3x∴S四边形DECF∵S=9,四边形DECF∴3x=9,x=3,∴S△ABC=2S△ABE=8x=24.22. 解:(1)如图,由三角形的外角性质,得∠A+∠C=∠1,∠B+∠D=∠2,∵∠2+∠1+∠E=180°∴∠A+∠B+∠C+∠D+∠E=180°,故答案为:180°;(2)如图,延长CA与DG相较于点H,∠CAG和∠AGD是△HAG的两个外角,则∠CAG=∠H+∠AGH,∠AGD=∠H+∠HAG,∴∠CAG+∠AGD=∠H+∠HGA+∠H+∠HAG=∠H+180°,∴∠GAC+∠B+∠C+∠D+∠E+∠AGD=180°+180°=360°,故∠A+∠B+∠C+∠D+∠E+∠G的度数为360°.(3)由(2)知,每截去图1中的一个角,剩余角的度数会增加180°,图1中,∠A+∠B+∠C+∠D+∠E=180°,在题图3中,去掉五个角后,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J =180°+5×180°=1080°.。
人教版八年级数学上册 第十一章 三角形 单元测试(含解析)

第十一章 《三角形》单元测试一、单选题(本大题共10小题,每小题3分,共30分)1.下列图形中,具有稳定性的是( )A .B .C .D .2.如图,在中,边上的高作法正确的是( )A .B .C .D .3.盒中有的小棒各一根,取出和的小棒后,至少再取( )的小棒才能围成一个三角形A .3B .4C .5D .64.如图,的面积为4,取的中点D ,E ,连接,则图中阴影部分面积是( )A.B .C .3D .5.如图,、是边、上的点,沿翻折后得到,沿翻ABC AB 110cm 3cm 7cm cm ABC AB AC ,DE 528372M N ABC AB AC AMN MN DMN BMD BD折后得到,且点在边上,沿翻折后得到,且点在边上,若,则( )A .B .C .D .6.小明制作简易工具来测量物体表面的倾斜程度,方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的刻度线与三角板的底边平行.将用细线和铅锤做成的重锤线顶端固定在量角器中心点O 处,现将三角板底边紧贴被测物体表面,如图所示,此时重锤线在量角器上对应的刻度为,那么被测物体表面的倾斜角为( )A .B .C .D .7.已知四边形,求证:.在证明该结论时,需要添加辅助线,则添加辅助线不正确的是( )A .B .C .D .8.如图,A ,B ,C ,D ,E 分别在的两条边上,若,,,,,则下列结论中错误的是()BED E BC CND △CD CFD △F BC 70A ∠=︒12∠+∠=65︒70︒75︒85︒90︒27︒α63︒36︒27︒18︒ABCD 360BAD ABC BCD ADC ∠+∠+∠+∠=︒MON ∠120∠=︒240∠=︒360∠=︒AB CD BC DE ∥A .B .C .D .9.如图,直线,点C 为直线MN 上一点,连接AC 、BC ,∠CAB =40°,∠ACB =90°,∠BAC 的角平分线交MN 于点D ,点E 是射线AD 上的一个动点,连接CE 、BE ,∠CED 的角平分线交MN 于点F .当∠BEF =70°时,令,用含的式子表示∠EBC 为( ).A.B .C .D .10.如图,点A 是直线l 外一点,点B 、C 是直线l 上的两动点,且,连接,点D 、E 分别为的中点,为的中线,连接,若四边形的面积为5,则的最小值为( )A .2B .3C .4D .5二、填空题(本大题共8小题,每小题4分,共32分)11如果一个多边形的每个外角都等于,那么它的内角和为 °.12如图,∠1= .13.(2023秋·全国·八年级专题练习)如图,点B ,C ,D 都在直线l 上,点A 是直线外一点,.若,,,则长的最小值为 .480∠=︒100BAO ∠=︒40CDE ∠=︒120CBD ∠=︒AB MN ∥ECM α∠=α52α10α︒-1102α︒-1102α-︒4BC =AB AC 、AC BC 、AF ABD △EF AFEC AB 72︒90BAD ∠=︒12AB =5AD =13BD =AC14.如图,点E 是长方形纸片AD 边的中点,过E 点将∠A 和∠D 分别翻折,得到折痕EM 和EN ,且折后A 、D 两点均与MN 上的点H 重合.若∠DEN =62°,则∠AEM = .15.清初数学家梅文鼎在著作《平三角举要》中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明,证明过程中创造性地设计直角三角形,得出了一个结论:如图,是锐角的高,则.当,时, .16.如图,两条交叉水管的接口在处,为了测量两条交叉水管所在直线和的夹角,工程师傅在直线上选取点,并过点作直线,量得与的夹角,由此可知:的度数为.AD ABC 2212AB AC BD BC BC ⎛⎫-=+ ⎪⎝⎭7,6AB BC ==5AC =CD =A 1l 2l β2l B B 31l l ⊥2l 3l 35α=︒β17.如图,三角形是由三角形平移得到的,点在边上,连接.若和中其中一个角是另一个角的倍,,则的度数为 .18.有一副直角三角板、,其中,,.如图,将三角板的顶点E 放在上,移动三角板,当点E 从点A 沿向点B 移动的过程中,点E 、C 、D 始终保持在一条直线上.下列结论:①当时,;②逐渐变小;③若直线与直线交于点M ,则为定值;④若的一边与的某一边平行,则符合条件的点E 的位置有3个.正确的有 .(填序号)三、解答题(本大题共6小题,共58分)19.(8分).已知一个多边形的内角和与外角和相加等于,求这个多边形的边数及对角线的条数.DEF ABC D AC CE BCE ∠CED ∠360B ∠=︒CED ∠ABC DEF 90ACB DEF ∠=∠=︒30A ∠=︒45D ∠=︒DEF AB DEF AB DE AB ⊥60ACE ∠=︒BEF ∠DF AB ACE DME ∠+∠ABC DEF 2160︒20.(8分)已知 的周长为,(1)若,求的长;(2)若,求三条边的长.21.(10分)如图,是的角平分线,,P 为线段上一点,交的延长线于点E .(1),,求的度数;(2)试猜想与、之间的数量关系,并证明你的结论.22.(10分)如图,已知,.(1)求证:;(2)求证:;(3)若、、分别是、、边上的中点,,则______.ABC 45cm 2AB AC BC ==BC ::2:3:4AB BC AC =ABC AD ABC ACB B ∠>∠AD PE AD ⊥BC 30B ∠=︒80ACB ∠=︒E ∠E ∠B ∠ACB ∠180BDC EFC ∠+∠=︒DEF B ∠=∠EF AB ∥AED ACB ∠=∠D E F AB AC CD 6ADFE S =四边形ABC S =23.(10分)如图,在中,于点,平分.(1)若,则 ;(2)与∠DAE 有何数量关系?证明你的结论;(3)点是线段上任一点(不与重合),作,交的延长线于点,点在的延长线上.若,求(用含代数式表示).ABC B C AD BC ∠>∠⊥,D AE BAC ∠6442B C ∠=︒∠=︒,DAE ∠=︒B C ∠∠、G CE C E 、GH CE ⊥AE H F BA FAC GHE αβ∠=∠=,B C ∠∠、αβ、24.(12分)(2023春·江苏·七年级专题练习)(1)问题解决:如图,中,、分别是和的平分线,为、交点,若,求的度数;(写出求解过程)(2)拓展与探究①如图1,中,、分别是和的平分线,为、交点,则与的关系是______;(请直接写出你的结论)②如图2,、分别是和的两个外角和的平分线,为、交点,则与的关系是______;(请直接写出你的结论)③如图3,、分别是的一个内角和一个外角的平分线,为、交点,则与的关系是______.(请直接写出你的结论)1ABC BO CO ABC ∠ACB ∠O BO CO 62A ∠=︒BOC ∠ABC BO CO ABC ∠ACB ∠O BO CO BOC ∠A ∠BO CO ABC ∠ACB ∠CBD ∠BCE ∠O BO CO BOC ∠A ∠BO CO ABC ABC ∠ACE ∠O BO CO BOC ∠A ∠一、单选题1.B【分析】根据三角形具有稳定性进行解答即可.【详解】解:A 、不具有稳定性,故此选项不符合题意;B 、具有稳定性,故此选项符合题意;C 、不具有稳定性,故此选项不符合题意;D 、不具有稳定性,故此选项不符合题意;故选:B .2.D【分析】中边上的高线是过C 点作的垂线,据此判断即可.【详解】解:中边上的高线是过C 点作的垂线,四个选项中只有D 选项正确,符合题意.故选:D .3.C【分析】设三角形的第三边长为,根据三角形三边关系得到,即可得到答案.【详解】解:设三角形的第三边长为,则,即,故选:CABC AB AB ABC AB AB cm x 410x <<cm x 7373x -<<+410x <<4.C【分析】连接,根据三角形中线平分三角形的面积求解即可.【详解】如图所示,连接,∵点D 是的中点,∴是的中线∴∵点E 是的中点∴是的中点∴∴.故选:C .5.D【分析】根据折叠的性质以及三角形内角和定理得出,,将已知数据代入,即可求解.【详解】解:如图所示,依题意,∴CD CD AB CD ABC 122BCD ACD ABC S S S ===V V V AC DE ACD 112CDE ADE ACD S S S ===V V V 213BCD CDE DBCE S S S =+=+=V V 四边形123125∠+∠+∠=︒360MDB CDN BDC MDN ∠+∠+∠+∠=︒1122MBD CBD ABC DCB DCN ACB ∠=∠=∠∠=∠=∠,180BDC DBC DCB ∠=︒-∠-∠即,∵∴∴∴∴故选:C .6.C【分析】如解析图所示,中,,,由此利用直角三角形两锐角互余即可求出答案.【详解】解:如图所示,在中,,,∴,∴,∴被测物体表面的倾斜角为,故选C .7.D【分析】根据三角形的内角和定理,在四边形中添加辅助线构成三角形即可求解.【详解】解:、根据图示可得,的内角和为,的内角和为,由此可得,故原选项正确,不符合题意;()11802ACB ACB =︒-∠+∠()1180180701252=︒-︒-︒=︒123125∠+∠+∠=︒1323BDM CDN ∠+∠=∠∠+∠=∠,70MDN A ∠=∠=︒360MDB CDN BDC MDN ∠+∠+∠+∠=︒1223123360MDN ∠+∠+∠+∠+∠+∠+∠=︒()()31231270360∠+∠+∠-∠+∠+︒=︒()31251270360⨯︒-∠+∠+︒=︒1285∠+∠=︒Rt △ABD 9090BAD ACD =︒=︒∠,∠27CAD ∠=︒Rt △ABD 9090BAD ACD =︒=︒∠,∠27CAD ∠=︒90CAD ADC ABD ADB +=︒=+∠∠∠∠27ABD CAD ==︒∠∠α27︒A ABD △180︒BCD △180︒360BAD ABC BCD ADC ∠+∠+∠+∠=︒、的内角和为,然后减去平角,可得,故原选项正确,不符合题意;、的内角和为,然减去以点为圆心的周角,可得,故原选项正确,不符合题意;、不能证明,故原选项不正确,符合题意;故选:.8.B【分析】根据两直线平行,同位角相等可得,根据平角180度,得出;根据三角形的内角和定理求出,然后根据两直线平行,同位角相等可得,然后根据三角形内角和定理求出,根据平角的定义列式计算求出即可.【详解】解:∵,∴,∴,故B 选项错误,符合题意;∵,∴,∵,∴,故A 选项正确,不符合题意;∵,∴,故C 选项正确,不符合题意;,故D 选项正确,不符合题意.故选:B .9.D【分析】先求出∠ABC ,再延长CE ,交AB 于点G ,结合平行线的性质表示出∠BCE ,然后根据三角形内角和定理表示∠CED ,再根据角平分线得定义表示出∠CEB ,最后根据三角形内角和定理得出答案.【详解】在△ABC 中,∠CAB=40°,∠ACB =90°,∴∠ABC=50°.延长CE ,交AB 于点G ,B ,,ADE ABE BCE 1803540⨯︒=︒180CED ∠=︒360BAD ABC BCD ADC ∠+∠+∠+∠=︒C ,,,AOB AOD COD BOC △△△△1804720︒⨯=︒O 360︒360BAD ABC BCD ADC ∠+∠+∠+∠=︒D D 360BAC ∠=∠=︒18060120BAO ∠=︒-︒=︒ACB ∠4ACB ∠=∠CDE ∠CBD ∠AB CD 360BAC ∠=∠=︒18060120BAO ∠=︒-︒=︒240∠=︒1802180406080ACB BAC ∠=︒-∠-∠=︒-︒-︒=︒BC DE ∥480ACB ∠=∠=︒360∠=︒18034180608040CDE ∠=︒-∠-∠=︒-︒-︒=︒180121802040120CBD ∠=︒-∠-∠=︒-︒-︒=︒∵,∴,∠ACM=∠BAC=40°,∴∠ACE =-40°,∴∠BCE=90°-(-40°)=130°-.∵∠CEA=180°-∠CAE -∠ACE ,∴∠CED=180°-∠CEA =∠CAE +∠ACE =20°+(-40°)=-20°.∵EF 平分∠CED ,∴∠CEF=,∴∠CEB =,∴∠EBC =.故选:D .10.C【分析】连接,如图,利用三角形中线的性质依次求出与的面积间的关系,然后根据四边形的面积为5求出的面积,进而可求出边上的高,即为的最小值.【详解】解:连接,如图,MN B A ∥E GB α∠=ααααα111022C ED α∠=-︒1110706022αα-︒+︒=+︒11180(60)(130)1022ααα︒-+︒-︒-=-︒CF ,,ADF CDF CEF ABC AFEC ABC BC AB CF∵点D 为的中点,∴,∵为的中线,∴,,∵点E 为中点,∴,∵四边形的面积为5,∴,即,解得,作于点G ,如图,∵,∴,∴,∵,∴的最小值是4;故选:C.AC 12ABD BCD ABC S S S == AF ABD △1124ABF ADF ABD ABC S S S S === 1124BCF DCF BCD ABC S S S S === BC 1128BEF CEF BCF ABC S S S S === AFEC 5ADF CDF CEF S S S ++= 1115448ABC ABC ABC S S S ++= 8ABC S =△AG BC ⊥4BC =1482AG ⨯⋅=4AG =AB AG ≥AB二、填空题11.【分析】根据多边形的外角和可求出多边形的边数,根据多边形的内角和定理即可求解.【详解】解:∵多边形的外角和为,每个外角都等于,∴多边形的边数为,∴多边形的内角和为:,故答案为:.【点拨】本题主要考查多边形的内角和定理与外角和的综合应用,掌握多边形的内角和的计算公式,外角和是360度是解题的关键.12.【分析】根据三角形的外角,可以求出另一个角的度数,进而得出结论.【详解】在三角形中:∵,∴,∴,故答案为:.13./【分析】根据垂线段最短,可知当时,最短,再根据面积相等即可得出答案.540360︒72︒360572=180(52)540︒⨯-=︒540120︒280140∠+︒=︒260∠=︒1180218060120∠=︒-∠=︒-︒=︒120︒60138413AC BD ⊥AC【详解】解:根据垂线段最短,可知当时,最短,∵,,,,∴,即,∴,故答案为:.14.28°【分析】根据折叠的性质得出∠DEN =∠HEN ,∠AEM =∠MEH ,根据题意结合图形即可得出结果.【详解】解:过E 点将∠A 和∠D 分别翻折,得到折痕EM 和EN ,∴∠DEN =∠HEN ,∠AEM =∠MEH ,又∵∠DEN =62°,∴∠HEN =62°,∴∠AEM =×(180°-62°-62°)=28°,故答案为:28°.15.【分析】根据公式求得,根据,即可求解.【详解】解:∵,,∴∴,故答案为:.AC BD ⊥AC 90BAD ∠=︒12AB =5AD =13BD =1122AB AD BD AC ⨯=⨯111251322AC ⨯⨯=⨯⨯6013AC =6013121BD CD BC BD =-7,6AB BC ==5AC =2212AB AC BD BC BC ⎛⎫-=+ ⎪⎝⎭149256526-⎛⎫=+= ⎪⎝⎭651CD BC BD =-=-=116.125°【分析】根据垂直的性质和对顶角的性质求出∠AOB 、∠ABO 的度数,即可求出β.【详解】解:如图,设l 3与l 1的交点为O ,∵l 3⊥l 1,∴∠AOB =90°,∵α=35°,∴∠ABO =35°,∴β=∠ABO +∠AOB =125°.故答案为:125°.17.【分析】根据图形的平移,可知,,是的外角,可得,分类讨论,当时;当时;根据角的和差倍分关系即可求解.【详解】解:如图所示,设与交于点,∵三角形平移得到三角形,∴,,∴,∵是的外角,∴,当时,,解得,;15︒AB DE ∥=60B ∠︒DGC ∠CGE DGC BCE CEG ∠=∠+∠3BCE CEG ∠=∠3BCE CEG ∠=∠BC DE G ABC DEF AB DE ∥=60B ∠︒60DGC B ∠=∠=︒DGC ∠CGE DGC BCE CEG ∠=∠+∠3BCE CEG ∠=∠360DGC CEG CEG ∠=∠+∠=︒15CEG ∠=︒当时,则,∴,解得,;综上所述,的度数为或,故答案为:或.18.①③④【分析】①由即可判断;②过点C 作,即可判断;③分别讨论当直线与线段相交、直线与线段的延长线相交即可判断;④根据平行线的判定定理即可进行判断.【详解】解:①∵,点E 、C 、D 始终保持在一条直线上∴∵∴故①正确;②如图1:过点C 作当点E 从点A 移动到点H 位置时,的度数在逐渐增大∴的度数在逐渐减小当点E 从点H 移动到点B 位置时,的度数在逐渐增大故②错误;③当直线与线段交于点M ,如图2:3BCE CEG ∠=∠13BCE CEG ∠=∠1603DGC CEG CEG ∠=∠+∠=︒45CEG ∠=︒CED ∠15︒45︒15︒45︒DE AB ⊥CH AB ⊥DF AB DF AB DE AB ⊥CE AB⊥30A ∠=︒60ACE ∠=︒CH AB ⊥DEB ∠BEF ∠BEF ∠DF AB∵∴∴当直线与线段的延长线交于点M ,如图3:∵∴∴故若直线与直线交于点M ,则为定值故③正确;④当点E 在线段上时,且,则;当点E 在线段上时,且,则;当时,则;∴若的一边与的某一边平行,则符合条件的点E 的位置有3个故④正确;故答案为:①③④三、解答题19.解:设这是边形,则,180DEB A ACE D DEB DME ∠=∠+∠∠+∠+∠=︒3045180ACE DME ∠+︒+︒+∠=︒105ACE DME ∠+∠=︒DF AB ,180DEB A ACE D DEB DME ∠=∠+∠∠+∠+∠=︒3045180ACE DME ∠+︒+︒+∠=︒105ACE DME ∠+∠=︒DF AB ACE DME ∠+∠AH 60BEF B ∠=∠=︒EF BC ∥BH 30BEF A ∠=∠=︒EF AC ∥45ECB D ∠=∠=︒DF BC ∥ABC DEF n,,.所以这个多边形的边数是12,它的对角线的条数是54.20.(1)由题意,得,解得.即的长是.(2)设,则,,由题意,得,解得.故,,.所以,,.21.(1)解:,,,平分,,,又∵,;(2)解:.设,,平分,,,,,()21802160360n -⨯︒=︒-︒210n -=12n =()()1212352243n n ⨯-=-=2245cm AB AC BC BC BC BC ++=++=9cm BC =BC 9cm 2cm AB x =3cm BC x =4cm AC x =23445x x x ++=5x =210x =315x =420x =10cm AB =15cm BC =20cm AC =30B ∠=︒ 80ACB ∠=︒70BAC ∴∠=︒AD BAC ∠35DAC ∴∠=︒18065ADC DAC ACB ∴∠=︒-∠-∠=︒PE AD ⊥9025E ADC ∴∠=︒-∠=︒1()2E ACB B ∠=∠-∠B n ∠=︒ACB m ∠=︒AD BAC ∠1122BAC ∴∠=∠=∠180B ACB BAC ∠+∠+∠=︒ B n ∠=︒ ACB m ∠=︒,,,,°,..22.(1)证明:∵,,∴,∴,(2)由()得:,∴,∵,∴,∴,∴,(3)∵为的中点,∴,∵为的中点,∴,又,即,∴,()180CAB n m ∴∠=--︒()11802BAD n m ∴∠=--︒()1113118090222B n n m n m ∴∠=∠+∠=︒+--︒=︒+︒-︒PE AD ⊥ 90DPE ∴∠=()()111190902222E n m m n ACB B ⎛⎫∴∠=︒-︒+︒-︒=-︒=∠-∠ ⎪⎝⎭180BDC EFC ∠+∠=︒180EFC DFE ∠+∠=︒BDC DFE ∠=∠EF AB ∥1EF AB ∥ADE DEF ∠=∠DEF B ∠=∠ADE B ∠=∠DE BC ∥AED ACB ∠=∠E AC 12ADE CDE ADC S S S == F DC 12DEF CEF CED S S S == 6ADFE S =四边形612ADE CDE S S += 4ADE S =△∴,∵为的中点,∴,故答案为:.23.(1)解:在中,,,,平分,,,,,,,故答案为:11;(2)解:,证明:在中,,,平分,,,,,;(3)解:是的一个外角,,,28ADC ADE S S == D AB 216ABC ADC S S == 16ABC 180B C BAC ∠+∠+∠=︒6442B C ∠=︒∠=︒ ,180644274BAC ∴∠=︒-︒-︒=︒AE BAC ∠11743722BAE BAC ∴∠=∠=⨯︒=︒AD BC ⊥ 90ADB ∴∠=︒64B ∠=︒ 906426BAD ∴∠=︒-︒=︒372611DAE BAE BAD ∴∠=∠-∠=︒-︒=︒1122DAE B C ∠=∠-∠ABC 180B C BAC ∠+∠+∠=︒180BAC B C ∴∠=︒-∠-∠AE BAC ∠()1111180902222BAE BAC B C B C ∴∠=∠=⨯︒-∠-∠=︒-∠-∠AD BC ⊥ 90ADB ∴∠=︒90BAD B ∴∠=︒-∠11111909022222DAE BAE BAD B C B B C ⎛⎫∴∠=∠-∠=︒-∠-∠-︒-∠=∠-∠ ⎪⎝⎭FAC ∠ ABC FAC B C ∴∠=∠+∠FAC α∠=,,,,,,由(2)知,,即②,①、②组成方程组得,解得,,.24.解(1)∵,∴,∵、分别是和的平分线,∴,∴,∴;(2)①,理由如下:∵,∴,∵、分别是和的平分线,∴,B C α∴∠+∠=①AD BC GH CE ⊥⊥ ,AD GH ∴∥DAE GHE ∴∠=∠GHE β∠= DAE β∴∠=1122DAE B C ∠=∠-∠1122B C β∴∠-∠=2B C β∠-∠=2B C B C βα∠-∠=⎧⎨∠+∠=⎩1212B C βααβ⎧∠=+⎪⎪⎨⎪∠=-⎪⎩∴12B βα∠=+12C αβ∠=-62A ∠=︒180118ABC ACB A +=︒-∠=︒∠∠BO CO ABC ∠ACB ∠1122OBC ABC OCB ACB ∠=∠∠=∠,115922OBC OCB ABC ACB +=+=︒∠∠∠∠180121BOC OBC OCB =︒--=︒∠∠∠1902BOC A ∠=+∠︒180A ABC ACB ∠+∠+∠=︒180ABC ACB A ∠+∠=︒-∠BO CO ABC ∠ACB ∠1122OBC ABC OCB ACB ∠=∠∠=∠,∴,∴,故答案为:;②,理由如下:∵,∴,∵分别是两个外角和的平分线,∴,∴,∴,故答案为:;③,理由如下:∵、分别是的一个内角和一个外角的平分线,,∴,又∵是的一外角,∴,∴,∵是的一外角,∴,故答案为:.11190222OBC OCB ABC ACB A +=+=︒-∠∠∠∠∠1180902BOC OBC OCB A =︒--=︒+∠∠∠1902BOC A ∠=+∠︒1902BOC A ∠=︒-∠DBC A ACB ECB A ABC ∠=∠+∠∠=∠+∠,180DBC ECB A ACB A ABC A ∠+∠=∠+∠+∠+∠=︒+∠BO CO 、ABC CBD ∠BCE ∠1122OBC DBC OCB ECB ∠=∠∠=∠,()111809022OBC OCB A A ∠+∠=︒+∠=︒+1180902BOC OBC OCB A ∠=︒-∠-∠=︒-∠1902BOC A ∠=︒-∠12BOC A ∠=∠BO CO ABC ABC ∠ACE ∠1122OBC ABC OCE ACE ∠=∠∠=∠,ACE ∠ABC ACE A ABC ∠=∠+∠()1122OCE A ABC A OBC ∠=∠+∠=∠+∠OCE ∠BOC 1122BOC OCE OBC A OBC OBC A ∠=∠-∠=∠+∠-∠=∠12BOC A ∠=∠。
八年级数学上册《第十一章 三角形》练习题-带答案(人教版)

八年级数学上册《第十一章 三角形》练习题-带答案(人教版)姓名 班级 学号 成绩一、选择题:1.三角形中,若一个角等于其他两个角的差,则这个三角形是( )A .钝角三角形B .直角三角形C .锐角三角形D .等腰三角形2.已知一个多边形的内角和与外角和的比是2∶1,则它的边数为( )A .9B .8C .7D .63.下列长度的三条线段能首尾相接构成三角形的是( )4.等腰但不等边的三角形的角平分线、高线、中线的总条数是( )A .3B .5C .7D .95.如图,AB ∥CD ,点P 在AB ,CD 之间,∠ACP=2∠PCD=40°,连结AP ,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )A .当∠P=60°时,α=30°B .当∠P=60°时,β=40°C .当=20°时,∠P=90°D .当β=0°时,∠P=90°6.如图,将三角板的直角顶点放在直尺的一边上 1=30∠︒ 2=50∠︒ 3=∠ ( )度A .10B .20C .30D .507.在△ABC 中,D 是BC 上的一点,且△ABD 与△ADC 的面积相等,则线段AD 为△ABC 的( )A .高B .角平分线C .中线D .不能确定8.如图,D ,E 是△ABC 中BC 边上的点,且BD =DE =EC ,那么( )A .S 1<S 2<S 3B .S 1>S 2>S 3C .S 1=S 2=S 3D .S 2<S 1<S 3二、填空题:9.已知一个三角形的三条边长为2、7、 x ,则 x 的取值范围是 .10.五边形从一个顶点出发,能引出 条对角线,一共有 条对角线.11.已知 AD 、AE 分别是△ABC 的高和中线,若 BD =2,CD =1,则DE 的长为 .12.如图AB CD ,AB 与DE 交于点F 40B ︒∠= 70D ︒∠= 则E ∠= .13.过m 边形的一个顶点有7条对角线,n 边形没有对角线,过k 边形一个顶点的对角线条数是边数的12,则m ﹣n+k= . 三、解答题:14.已知一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和对角线的条数.15.如图,已知FD ⊥BC 于D ,DE ⊥AB 于E ,∠B=∠C ,∠AFD=140°,求∠EDF 的度数.16.已知:在△ABC 中,AD ⊥BC ,BE 平分∠ABC 交AD 于F ,∠ABE=23°.求∠AFE 的度数.17.如图,在△ABC中、D、E分别是AB,BC上任意一点,连结DE,若BD=4,DE=5.(1)BE的取值范围;(2)若DE∥AC,∠A=85°,∠BED=35°,求∠B的度数.18.如图①,已知任意三角形ABC,过点C作DE//AB.(1)如图①,求证:三角形ABC的三个内角(即∠A,∠B,∠ACB)之和等于180°;(2)如图②,AB//CD,∠CDE=110°,GF交∠DEB的平分线EF于点F,且∠AGF=145°,结合(1)中的结论,求∠F的度数.参考答案:1.B 2.D 3.B 4.C 5.B 6.B 7.C 8.C9.5<x<910.2;511.0.5或1.512.3013.1314.解:设这个多边形的边数为n,则内角和为180°(n﹣2),依题意得:180(n﹣2)=360×3﹣180,解得n=7,对角线条数:(73)72-⨯=14.答:这个多边形的边数是7,对角线有14条15.解:∵FD⊥BC,DE⊥AB∴∠BED=∠FDC=90°∴∠B+∠BDE=90°,∠C+∠CFD=90°∵∠B=∠C∴∠BDE=∠CFD=180°﹣∠AFD=180°﹣140°=40°∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣40°﹣90°=50°.16.解:∵AD⊥BC∴∠ADB=90°∵BE平分∠ABC,∠ABE=23°∴∠FBD=∠ABE=23°∴∠BFD=180°﹣∠ADB﹣∠FBD=67°∴∠AFE=∠BFD=67°17.(1)1<BE<9(2)解:∵DE∥AC∴∠BED=∠C=35°又∵∠A=85°∴△ABC中,∠B=180°﹣∠A﹣∠C=180°﹣85°﹣35°=60°18.(1)证明:∵DE∥AB∴∠A=∠DCE,∠B=∠ECB∵∠DCE=180°∴∠DCA+∠ACB+∠ECB=180°∴∠A+∠ACB+∠B=180°.(2)解:∵AB∥CD∴∠CDE=∠BED=110°∵EF平分∠BED∴∠BEF=12∠BED=55°∵∠AGF=145°∴∠FGE=35°∵∠BEF=∠F+∠EGF∴∠F=55°﹣35°=20°。
第十一章-三角形》单元测试卷含答案(共5套)

第十一章三角形》单元测试卷含答案(共5套)第十一章三角形单元测试卷(一)时间: 120分钟满分: 120分一、选择题1.以下列每组长度的三条线段为边能组成三角形的是() A。
2.3.6.B。
2.4.6C。
2.2.4.D。
6、6、62.如图, 图中∠1的大小等于()A。
40°。
B。
50°。
C。
60°。
D。
70°3.一个多边形的每一个内角都等于140°, 则它的边数是() A。
7.B。
8.C。
9.D。
104.如图, △ABC中, ∠A=46°, ∠C=74°, BD平分∠XXX于点D, 那么∠XXX的度数是()A。
76°。
B。
81°。
C。
92°。
D。
104°5.用五根木棒钉成如下四个图形, 具有稳定性的有()A。
1个。
B。
2个。
C。
3个。
D。
4个6.如图, 点A, B, C, D, E, F是平面上的6个点, 则∠A+∠B +∠C+∠D+∠E+∠F的度数是()A。
180°。
B。
360°。
C。
540°。
D。
720°二、填空题7.已知三角形两条边长分别为3和6, 第三边的长为奇数, 则第三边的长为9.8.若n边形内角和为900°, 则边数n为10.9.将一副三角板按如图所示的方式叠放, 则∠α的度数为30°。
10.如图, 在△ABC中, ∠ACB=90°, ∠A=20°。
若将XXX沿CD所在直线折叠, 使点B落在AC边上的点E处, 则∠XXX的度数是70°。
11.如图, 在△ABC中, E、D.F分别是AD.BF、CE的中点。
若△DEF的面积是1cm², 则S△ABC=3cm²。
12.当三角形中一个内角β是另一个内角α的时, 我们称此三角形为“希望三角形”, 其中角α称为“希望角”。
如果一个“希望三角形”中有一个内角为54°, 那么这个“希望三角形”的“希望角”的度数为27°。
八年级数学上册《第十一章三角形》单元测试卷-附答案(人教版)

八年级数学上册《第十一章三角形》单元测试卷-附答案(人教版)一、单选题(本大题共12小题,每小题3分,共36分)1.下列说法中正确的是( ) A .直角三角形的高只有一条B .锐角三角形的三条高交于三角形内部C .直角三角形的高没有交点D .钝角三角形的三条高所在的直线没有交点 2.如图,在ABC 中,延长BC 至点D ,使CD BC =,记ABC 的面积为1S ,ACD 的面积为2S ,则1S 与2S 的大小关系是( )A .12S S >B .12S S <C .12S SD .不能确定3.现有长度分别为2cm 、4cm 、5cm 、7cm 的木棒,从中任取三根,能组成三角形的个数为( ) A .1 B .2 C .3 D .44.如图,在△ABC 中,∠ABC 与∠ACB 的平分线相交于点O,若∠A=70°,则∠BOC 的度数为( )A .100°B .120°C .125°D .130°5.如图,在ABC 中9065C B ∠=︒∠=︒,,点D 、E 分别在AB AC 、上,将ADE 沿DE 折叠,使点A 落在点F 处.则BDF CEF ∠-∠=( )∠∠A=∠B=2∠C;∠∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有()A.2个B.3个C.4个D.5个7.下列说法中错误的是().A.三角形的中线、角平分线、高线都是线段B.任意三角形的内角和都是180°C.三角形的一个外角大于任何一个内角D.三角形的三条高至少有一条高在三角形的内部8.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为()A.8B.7或8C.7或8或9D.8或9或10A.1B.2C.3D.4分别平分ABC的外角2A.∠∠∠B.∠∠∠C.∠∠∠D.∠∠∠∠11.如图,在直角三角形ABC中90∠=︒,AB=3,AC=4,BC=5,DE//BC,若点A到DE的距离是1,则DEA与BC之间的距离是()A.2B.1.4C.3D.2.412.从正多边形一个顶点出发共有7条对角线,则这个正多边形每个外角的度数为()A.36°B.40°C.45°D.60°二、填空题(本大题共8小题,每小题3分,共24分)13.已知三点M 、N 、P 不在同一条直线上,且MN=4厘米,NP=3厘米,M 、P 两点间的距离为x 厘米,那么x 的取值范围是 .14.如图1,为响应国家新能源建设,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线最大夹角为62︒,如图2,电池板AB 与最大夹角时刻的太阳光线相垂直,此时电池板CD 与水平线夹角为48︒,要使//AB CD ,而将电池板CD 逆时针旋转α度,则α为 .()090α<<15.如图,ABC 中55A ∠=︒,90ACB ∠=︒将ABC 沿过C 点的直线折叠,使A 点落在边BC 上的E 点处,折痕交边AB 于点D ,则BDE ∠= .16.如图,图中x 的值为 .17.三角形的三边长分别为2,5,32x -则x 的取值范围是 .18.如图,在∠ABC 中,AB >AC ,AE∠BC 于E ,AD 为∠BAC 的平分线,则∠DAE 与∠C -∠B 的数量关系 .19.如图中36B ∠=︒,76C ∠=︒且AD 、AF 分别是ABC 的角平分线和高,DAF ∠= .20.在△ABC 中,若A B C ∠=∠-∠,则B ∠的度数为 度.三、解答题(本大题共5小题,每小题8分,共40分)21.如图,△ABC 的面积为21平方厘米,DC =3DB ,AE =ED ,求阴影部分面积.22.如图:已知在ABC 中,AD 平分BAC ∠,AE BC ⊥垂足为E ,38B ∠︒=和70C ∠︒=求DAE ∠的度数.23.如图,在ABC 中,AD 是BAC ∠的平分线,DE AC ∥交AB 于点E 且55B ∠=︒,95ADC ∠=︒求AED ∠的度数.24.如图,AB△CD,AC△BE,△MAC=40,△D=50°,CH平分△ACD,BH平分△ABD(1)求△EBH的角度(2)求△BHC的角度25.如图,在△ABC中,点D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于点E.(1)若∠A=80°,求∠BDC的度数;(2)若∠EDC=40°,求∠A的度数;(3)请直接写出∠A与∠BDC之间的数量关系(不必说明理由).参考答案:1.B2.C3.B。
【新人教版】八年级数学上册:第十一章《三角形》检测题(含答案)

第十一章检测题(时间:120分钟满分:120分)一、选择题(每小题3分,共30分)1.三角形的内角和是( B)A.90° B.180° C.300° D.360°2.下列长度的三条线段能组成三角形的是( D)A.1,2,3 B.1,2,3 C.3,4,8 D.4,5,63.如图,图中∠1的大小等于( D)A.40° B.50° C.60° D.70°(第5题图) (第6题图) 4.已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( A)A.40° B.60° C.80° D.90°5.如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( C) A.60° B.75° C.90° D.105°6.如图,△ABC的角平分线BE,CF相交于点O,且∠FOE=121°,则∠A的度数是( B) A.52° B.62° C.64° D.72°7.如图,在△ABC中,∠A=80°,高BE与CH的交点为O,则∠BOC等于( C)A.80° B.120° C.100° D.150°(第7题图)(第8题图)(第9题图) 8.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中不正确的是( C)A.BE是△ABD的中线 B.BD是△BCE的角平分线C.∠1=∠2=∠3 D.BC是△ABE的高9.如图,把纸片△ABC沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请你试着找一找这个规律,你发现的规律是( B) A.∠A=∠1+∠2 B.2∠A=∠1+∠2C.3∠A=∠1+∠2 D.3∠A=2(∠1+∠2)10.如图,已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( A)A.720° B.540° C.360° D.180°(第10题图)(第13题图)(第14题图)二、填空题(每小题3分,共18分)11.(2016·镇江)正五边形每个外角的度数是__72°__.12.人站在晃动的公共汽车上,若你分开两腿站立,还需伸出一只手抓住栏杆才能站稳,这是利用了__三角形的稳定性__.13.如图,在△ABC 中,AD 是BC 边上的中线,BE 是△ABD 中AD 边上的中线,若△ABC 的面积是24,则△ABE 的面积是__6__.14.如图,∠1+∠2+∠3+∠4+∠5+∠6=__360°__.15.当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为__120°__.16.已知AD 是△ABC 的高,∠BAD =72°,∠CAD =21°,则∠BAC 的度数是__51°或93°__.三、解答题(共72分)17.(8分)如图:(1)在△ABC 中,BC 边上的高是__AB __;(2)在△AEC 中,AE 边上的高是__CD __;(3)若AB =CD =2 cm,AE =3 cm,求△AEC 的面积及CE 的长.解:S △AEC =12AE·CD =12CE·AB =3 cm 2,CE =3 cm18.(8分)等腰△ABC 的两边长x,y 满足|x -4|+(y -8)2=0,求这个等腰三角形的周长. 解:∵x ,y 满足|x -4|+(y -8)2=0,∴x =4,y =8,当4为腰时,4+4=8不成立,当4为底时,8为腰,4+8>8,满足三边关系,∴△ABC 的周长为8+8+4=2019.(8分)如图,AD 平分∠CAE ,∠B =35°,∠DAE =60°,试求∠D 与∠ACD 的度数.解:∠D =25°,∠ACD =95°20.(7分)若一个多边形的各边长均相等,周长为70 cm ,且内角和为900°,求它的边长. 解:边长是10 cm21.(7分)某工程队准备开挖一条隧道,为了缩短工期,必须在山的两侧同时开挖,为了确保两侧开挖的隧道在同一条直线上,测量人员在如图的同一高度定出了两个开挖点P 和Q,然后在左边定出开挖的方向线AP,为了准确定出右边开挖的方向线BQ,测量人员取一个可以同时看到点A,P,Q 的点O,测得∠A =28°,∠AOC =100°,那么∠QBO 应等于多少度才能确保BQ 与AP 在同一条直线上?解:在△AOB 中,∠QBO =180°-∠A -∠O =180°-28°-100°=52°.即∠QBO 应等于52°才能确保BQ 与AP 在同一条直线上22.(8分)如图,AB ∥CD,直线EF 与AB,CD 分别相交于点E,F,EP 平分∠AEF ,FP 平分∠EFC.(1)求证:△EPF 是直角三角形;(2)若∠PEF=30°,求∠PFC 的度数.解:(1)∵AB∥CD ,∴∠AEF +∠CFE =180°,∵EP 平分∠AEF ,FP 平分∠EFC ,∴∠AEP =∠FEP ,∠CFP =∠EFP ,∴∠PEF +∠PFE =12×180°=90°.∴∠EPF =180°-90°=90°,即△EPF 是直角三角形 (2)60°23.(8分)如图,在△ABC 中,∠B =26°,∠C =70°,AD 平分∠BAC ,AE ⊥BC 于点E,EF ⊥AD 于点F.(1)求∠DAC 的度数;(2)求∠DEF 的度数.解:(1)∵在△ABC 中,∠B =26°,∠C =70°,∴∠BAC =180°-∠B -∠C =180°-26°-70°=84°.∵AD 平分∠BAC ,∴∠DAC =12∠BAC =12×84°=42° (2)在△ACE 中,∠CAE =90°-∠C =90°-70°=20°,∴∠DAE =∠DAC -∠CAE =42°-20°=22°.∵∠DEF +∠AEF =∠AEF +∠DAE =90°,∴∠DEF =∠DAE =22°24.(8分)如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于点D.(1)求证:∠ACD=∠B;(2)若AF 平分∠CAB 且分别交CD,BC 于点E,F,求证:∠CEF=∠CFE.解:(1)∵∠ACB =90°,∴∠ACD +∠DCB =90°,又∵CD⊥AB 于点D ,∴∠DCB +∠B =90°,∴∠ACD =∠B (2)在△ACE 中,∠CEF =∠CAF +∠ACD ,在△AFB 中,∠CFE =∠B +∠FAB ,∵AF 平分∠CAB ,∴∠CAE =∠FAB ,∴∠CEF =∠CFE25.(10分)取一副三角板按图①拼接,固定三角板ADC,将三角板ABC 绕点A 按顺时针方向旋转得到△ABC′,如图②所示.设∠CAC′=α(0°<α≤45°).(1)当α=15°时,求证:AB∥CD;(2)连接BD,当0°<α≤45°时,∠DBC ′+∠CAC′+∠BDC 的度数是否变化,若变化 ,求出变化范围;若不变,求出其度数.解:(1)证明:∵∠CAC′=15°,∴∠BAC=∠BAC′-∠CAC′=45°-15°=30°,又∴∠C =30°,∴∠BAC=∠C,∴AB∥CD(2)∠DBC′+∠CAC′+∠BDC的度数不变.如图,连接CC′,∵∠DBC′+∠BDC=∠DCC′+∠BC′C,又∠CAC′+∠ACC′+∠AC′C=180°,∴∠CAC′+∠AC′B+∠BC′C+∠ACD+∠DCC′=180°,∵∠AC′B=45°,∠ACD=30°,∴∠DBC′+∠CAC′+∠BDC=180°-45°-30°=105°。
八年级数学上册《第十一章 三角形》单元测试题含答案(人教版)

八年级数学上册《第十一章 三角形》单元测试题含答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、单选题1.下列长度的三条线段能组成一个三角形的是( )A .1,2,4B .4,5,9C .6,8,10D .5,15,82.在△ABC 中,如果∠A :∠B :∠C =1:2:3,那么△ABC 的形状是( )A .直角三角形B .锐角三角形C .等腰三角形D .等腰直角三角形3.为了让州城居民有更多休闲和娱乐的地方,政府又新建了几处广场,工人师傅在铺设地面时,准备选用同一种正多边形地砖.现有下面几种形状的正多边形地砖,其中不能进行平面镶嵌的是( )A .正三角形B .正方形C .正五边形D .正六边形4.如图,直线a ∥b ,∠1=60°,∠2=40°,则∠3等于( )A .40°B .60°C .80°D .100°5.利用边长相等的正三角形和正六边形地砖能够铺满地板,若在每个顶点处有a 块正三角形和b 块正六边形(a >b >0),则a+b 的值为( )A .4B .5C .6D .76.如图AB CD ,点E F ,在AC 边上,已知70CED ∠=︒,128BFC ∠=︒则B D ∠+∠的度数为( )A .68︒B .58︒C .48︒D .38︒7.如图,ABC 中,BE 是AC 边上的中线,点D 为BC 边上一点,且3BC CD =,AD 、BE 交于点G ,且3GEC S =,4GDC S =则ABC 的面积是( )A .50B .40C .30D .208.如图,AD 交BC 于点O ,BAD ∠的平分线与OCD 的外角OCE ∠的平分线交于点P ,∠B=∠D ,则下列说法不正确的是( )A .90PAO PCE ∠∠+=︒B .12PAB BCD ∠∠=C .90PD ∠∠=︒+D .902P B ∠∠=︒- 二、填空题9.要使十边形木架不变形,至少要钉上 根木条.10.已知A (1,0),B (0,2),点P 在x 轴上,且△PAB 面积是5,则点P 的坐标是 .11.一副三角尺,按如图所示叠放在一起,则图中α∠的度数为 .12.如图,在ABC 中,AD 平分BAC ∠,点E 在射线BC 上,EFAD ⊥于F ,∠B=40°,∠ACE=72°,则E ∠的度数为 .13.如图,点E 、F 分别为BD 、CE 的中点,若ABC 的面积为32,则阴影部分AEF 的面积是三、解答题14.已知多边形的每个内角都相等,并且每个内角都等于相邻外角的9倍,求该多边形的边数.15.如图,在△ABC 中,AD 是BC 边上的高,∠B =30°,∠ACB =100°,AE 平分∠BAC ,求∠EAD 的度数.16.如图,在△ABC 中,AD 是BC 边上的中线,点E 是AD 的中点,过点E 作EF ⊥BC 于点F ,已知BC =8,△ABC 的面积为24,求EF 的长.17.如图,已知BC GE 和150AFG ∠=∠=︒.(1)求证:AF DE(2)若AQ 平分FAC ∠,交BC 于点Q ,且18Q ∠=︒,求ACQ ∠的度数.18.△ABC 中,AD 是∠BAC 的角平分线,AE 是△ABC 的高.(1)如图1,若∠B =40°,∠C =60°,请说明∠DAE 的度数;(2)如图2(∠B <∠C ),试说明∠DAE 、∠B 、∠C 的数量关系;(3)如图3,延长AC 到点F ,∠CAE 和∠BCF 的角平分线交于点G ,请直接写出∠G 的度数 .参考答案:1.B 2.A 3.C 4.C 5.B 6.B 7.C 8.D9.710.(﹣4,0)或(6,0)11.15°12.34°13.814.解:设一个外角为x ,则一个内角为9x∴x+9x=180°解得x=18°∵多边形的外角和为360°所以多边形的边数=360°÷18°=20即此多边形为20边形.15.解:∵AD ⊥BC∴∠D=90°∵∠ACB=100°∴∠ACD=180°-100°=80°∴∠CAD=90°-80°=10°∵∠B=30°∴∠BAD=90°-30°=60°∴∠BAC=50°∵AE 平分∠BAC∴∠CAE=12∠BAC=25°∴∠EAD=∠CAE+∠CAD=35°16.解:∵AD 是BC 边上的中线∴BD=CD.又∵△ABC 的面积为24∴ABD ACD S S = =12又∵E 是AD 的中点∴ABC BCD S S = =6又∵BC=8,EF ⊥BC 于点F∴ BD=CD=4 ∴ABDC 162S CD EF =⋅=1462EF ⨯=∴EF=3.17.(1)证明:∵BC GE∴150E ∠=∠=︒∵150AFG ∠=∠=︒∴50E AFG ∠=∠=︒∴AF DE ;(2)解:∵15018Q ∠=︒∠=︒,∴168AHD Q ∠=∠+∠=︒∵AF DE∴68FAQ AHD ∠=∠=︒∵AQ 平分 FAC ∠∴68CAQ FAQ ∠=∠=︒∴18094ACQ CAQ Q ∠=︒-∠-∠=︒ .18.(1)解:4060180B C BAC B C ∠∠∠∠∠=︒=︒++=︒,, 80BAC ∴∠=︒ AE 是ΔABC 的高90AEC ∴∠=︒,60C ∠=︒,906030CAE ∴∠=︒-︒=︒ AD 是BAC ∠的角平分线1402CAD BAD BAC ∴∠∠∠===︒ 10DAE CAD CAE ∴∠∠∠=-=︒.(2)解:180BAC B C ∠∠∠++=︒,180BAC B C ∴∠∠∠=︒-- AE 是ΔABC 的高90AEC ∴∠=︒,90CAE C ∴∠∠=︒- AD 是BAC ∠的角平分线12CAD BAD BAC ∴∠=∠=∠ ()1902DAE CAD CAE BAC C ∴∠∠∠∠=-=-︒- ()1180?Β902C C ∠∠∠=---︒+ 1122C B ∠∠=- 即1122DAE C B ∠∠∠=-; (3)45°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形单元测试
一、选择题(本大题共8小题,每小题4分,共32分.)
1.以下列各组线段为边,能组成三角形的是( )
A .2cm ,3cm ,5cm
B .5cm ,6cm ,10cm
C .1cm ,1cm ,3cm
D .3cm ,4cm ,9cm
2.等腰三角形的一边长等于4,一边长等于9,则它的周长是( ) A .17
B .22
C .17或22
D .13
3.适合条件∠A=∠B=∠C 的△ABC 是( )1213
A .锐角三角形
B .直角三角形
C .钝角三角形
D .等边三角形
4.一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是( )
A .5
B .6
C .7
D .8
5.三角形的一个外角是锐角,则此三角形的形状是( )
A .锐角三角形
B .钝角三角形
C .直角三角形
D .无法确定
6.下列命题正确的是( )
A .三角形的角平分线、中线、高均在三角形内部
B .三角形中至少有一个内角不小于60°
C .直角三角形仅有一条高
D .直角三角形斜边上的高等于斜边的一半
7.已知等腰△ABC 的底边BC=8cm ,│AC-BC│=2cm,则腰AC 的长为( )
A .10cm 或6cm
B .10cm
C .6cm
D .8cm 或6cm
8.如图1,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( ) A .∠A=∠1+∠2 B .2∠A=∠1+∠2 C .3∠A=2∠1+∠2 D .3∠A=2(∠1+∠2)
(1) (2) (3)
二、填空题(本大题共8小题,每小题4分,共32分.)
9.三角形的三边长分别为5,1+2x ,8,则x 的取值范围是________.
10.四条线段的长分别为5cm 、6cm 、8cm 、13cm , 以其中任意三条线段为边可以构成________个三角形.
11.如图2:∠A+∠B+∠C+∠D+∠E+∠F 等于________.
12.如果一个正多边形的内角和是900°,则这个正多边形是正______边形.
13.n边形的每个外角都等于45°,则n=________.
15.将一个正六边形纸片对折,并完全重合,那么,得到的图形是________边形, 它的内角和(按一层计算)是_______度.
16.如图3,已知∠1=20°,∠2=25°,∠A=55°,则∠BOC的度数是_____.
三、解答题(本大题共4小题,共36分,解答应写出文字说明, 证明过程或演算步骤)
17.(6分)如图,BD平分∠ABC,DA⊥AB,∠1=60°,∠BDC=80°,求∠C的度数.
18.(10分)如图:(1)画△ABC的外角∠BCD,再画∠BCD的平分线CE.
(2)若∠A=∠B,请完成下面的证明:
已知:△ABC中,∠A=∠B,CE是外角∠BCD的平分线.
求证:CE∥AB.
19.(10分)(1)如图4,有一块直角三角形XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_______,∠XBC+∠XCB=_______.
(4) (5)
(2)如图5,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ 仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
20.(10分)在平面内,分别用3根、5根、6根……火柴首尾依次相接, 能搭成什么形状的三角形呢?通过尝试,列表如下所示:问:(1)4根火柴能搭成三角形吗?
(2)8根、12根火柴能搭成几种不同形状的三角形?并写出它们各边长。
四.附加题(10分)
21.如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.(1)CO是△BCD的高吗?为什么?
(2)∠5的度数是多少?
(3)求四边形ABCD各内角的度数.。
