2015年二模试卷25题汇总
2015上海各区二模25汇总

黄埔25. (本题满分14分,第(1)小题满分3分,第(2)满分6分,(3)小题满分5分)如图8,Rt△ABC中,,,BC=2,CD是斜边AB上的高,点E为边AC上一点(点E不与点A、C重合),联结DE,作CF⊥DE,CF与边AB、线段DE分别交于点F、G.(1)求线段CD、AD的长;(2)设,,求y关于x的函数解析式,并写出它的定义域;(3)联结EF,当△EFG与△CDG相似时,求线段CE的长.奉贤区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图,线段AB=8,以A为圆心,5为半径作圆A,点C在⊙A上,过点C作CD//AB 交⊙A于点D(点D在C右侧),联结B C、A D.(1)若CD=6,求四边形AB CD的面积;(2)设CD=x,B C=y,求y与x的函数关系式及自变量x的取值范围;(3)设B C的中点为M,A D的中点为N,线段MN交⊙A于点E,联结CE,当CD取何值时,CE//AD.25.如图,在中,,AC=4,,点P是边上的动点,以PA为半径作⊙P.(1)若⊙P与A C边的另一交点为点D,设AP=x,△PCD的面积为y,求y关于x的函数解析式,并直接写出函数的定义域;(2)若⊙P被直线BC和直线A C截得的弦长相等,求AP的长;(3)若⊙C的半径等于1,且⊙P与⊙C的公共弦长为,求AP的长.静安、青浦区25.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)在⊙O中,OC⊥弦AB,垂足为C,点D在⊙O上.(1)如图1,已知OA=5,AB=6,如果OD//AB,CD与半径OB相交于点E,求DE的长;(2)已知OA=5,AB=6(如图2),如果射线OD与AB的延长线相交于点F,且△OCD 是等腰三角形,求AF的长;(3)如果OD//AB,CD⊥OB,垂足为E,求sin∠ODC的值.宝山嘉定25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分)在Rt△中,,,Rt△绕着点按顺时针方向旋转,使点落在斜边上的点,设点旋转后与点重合,联结,过点作直线与射线垂直,交点为M.(1)若点与点重合如图10,求的值;(2)若点在边上如图11,设边长,,点与点不重合,求与的函数关系式,并写出自变量的取值范围;(3)若,求斜边的长.松江区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)如图,已知在直角梯形ABCD中,AD∥BC,∠ABC=90º,A B=4,A D=3,,点P是对角线BD上一动点,过点P作PH⊥CD,垂足为H.(1)求证:∠BCD=∠BDC;(2)如图1,若以P为圆心、PB为半径的圆和以H为圆心、HD为半径的圆外切时,求DP的长;(3)如图2,点E在BC延长线上,且满足DP=CE,PE交DC于点F,若△ADH和△ECF 相似,求DP的长.长宁25.(本题满分14分)如图,已知矩形ABCD,AB =12 cm,AD =10 cm,⊙O与AD、AB、BC三边都相切,与DC 交于点E、F。
2015西城中考数学二模题及答案(完整版)

2015二模统一练习(二)一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.2015年羊年除夕夜的10点半,在央视春晚送红包的活动中,微信“摇一摇”峰值的摇动 次数达到8.1亿次/分钟,送出微信红包120 000 000个.将120 000 000用科学记数法表示 应为A. 90.1210⨯B. 71.210⨯C. 81.210⨯D. 71210⨯ 2.如图,BD ∥AC ,AD 与BC 交于点E ,如果∠BCA =50°,∠D =30°, 那么∠DEC 等于A. 75°B. 80°C. 100°D. 120° 3.64的立方根是A. 8±B. 4±C. 8D. 44.函数y =x 的取值范围是A.2x ≠B. x ≥2C. x >2D. x ≥2-5.如图,△ABC 中,D ,E 两点分别在AB ,AC 边上,且DE ∥BC , 如果23AD AB =,AC =6,那么AE 的长为 A. 3 B. 4 C. 9 D. 126.某居民小区开展节约用电活动,该小区100户家庭4月份的节电情况如下表所示.那么4月份这100户家庭的节电量(单位:千瓦时)的平均数是 A. 35 B. 26 C. 25 D. 20 7.若一个正六边形的半径为2,则它的边心距等于A. 2B. 1C.8.如图,△ABC 的边AC 与⊙O 相交于C ,D 两点,且经过圆心O , 边AB 与⊙O 相切,切点为B .如果∠A =34°,那么∠C 等于 A .28° B .33° C .34° D .56°9.如图,将正方形OABC 放在平面直角坐标系xOy 中,O 是原点,若点A 的坐标为,则点C 的坐标为A .B .(-C .(D .(1)-10.在平面直角坐标系xOy 中,点M 的坐标为(,1)m .如果以原点为圆心,半径为1的⊙O 上 存在点N ,使得45OMN ∠=︒,那么m 的取值范围是A .1-≤m ≤1 B. 1-<m <1 C. 0≤m ≤1 D. 0<m <1 二、填空题(本题共18分,每小题3分)11.若2(2)0m ++ 则m n -= .12.若一个凸n 边形的内角和为1080︒,则边数n = . 13.两千多年前,我国的学者墨子和他的学生做了小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上 开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小 华在学习了小孔成像的原理后,利用如下装置来验证小孔 成像的现象.已知一根点燃的蜡烛距小孔20cm ,光屏在距 小孔30cm 处,小华测量了蜡烛的火焰高度为2cm ,则光屏上火焰 所成像的高度为______cm .14.请写出一个图象的对称轴是直线1x =,且经过(0,1)点的二次函数的表达式: _____________.15.如图,在平面直角坐标系xOy 中,直线3y x =与双曲线y =(n ≠0)在第一象限的公共点是(1,)P m .小明说:以看出,满足3nx x>的x 的取值范围是1x >.”你同意他的 观点吗?答: .理由是 .16.如图,在平面直角坐标系xOy 中,点D 为直线2y x = 象限内的任意一点,1DA ⊥x 轴于点1A ,以1DA 为边在1DA 作正方形111A B C D ;直线1OC 与边1DA 交于点2A ,以2DA 2DA 的右侧作正方形222A B C D ;直线2OC 与边1DA 交于点3A ,以3DA 为边在3DA 的右侧作正方形333A B C D ,……,按这种方式进行下去,则直线1OC 对应的函数表达式为 ,直线3OC 对应的函数表达式为 . 三、解答题(本题共30分,每小题5分)17.如图,△ABC 是等边三角形,D ,E 两点分别在AB ,BC 的延长线上,BD =CE ,连接AE ,CD .求证:∠E =∠D .18.计算:1012cos 30()1(3)3π-++-.19.已知2540x x --=,求代数式(2)(2)(21)(2)x x x x +----的值.20.解方程:231233x x x x-=--.21.列方程(组)解应用题:某超市的部分商品账目记录显示内容如下:求第三天卖出牙膏多少盒.22.已知关于x 的函数 2(3)3y mx m x =+--.(1)求证:无论m 取何实数,此函数的图象与x 轴总有公共点;(2)当m >0时,如果此函数的图象与x 轴公共点的横坐标为整数,求正整数m 的值.四、解答题(本题共20分,每小题5分)23.如图,将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D的落点记为点D′ ,折痕为EF,连接CF.(1)求证:四边形AFCE是菱形;(2)若∠B=45°,∠FCE=60°,AB=D′F的长.24.1949年以来,北京市人口结构变迁经历了5个阶段,从2001年至今已进入第五个阶段——人口膨胀增长阶段.以下是根据北京市统计局2015年1月的相关数据制作的统计图.根据以上信息解决下列问题:(1)以下说法中,正确的是(请填写所有正确说法的序号)①从2011年至2014年,全市常住人口数在逐年下降;②2010年末全市常住人口数达到近年来的最高值;③ 2014年末全市常住人口比2013年末增加36.8万人;④从2011年到2014年全市常住人口的年增长率连续递减.(2)补全“2014年末北京市常住人口分布图”,并回答:2014年末朝阳、丰台、石景山、海淀四区的常住人口总数已经达到多少万人?(3)水资源缺乏制约着北京市的人口承载能力,为控制人口过快增长,到2015年底,北京市要将全市常住人口数控制在2180万以内(即不超过2180万).为实现这一目标,2015年的全市常住人口的年增长率应不超过.(精确到0.1%)25.如图1,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,点F 在线段ED 上.连接AF 并延长交 ⊙O 于点G ,在CD 的延长线上取一点P ,使PF=PG .(1)依题意补全图形,判断PG 与⊙O 的位置关系,并证明你的结论;(2)如图2,当E 为半径OA 的中点,DG ∥AB ,且OA PG 的长.26.(1)小明遇到下面一道题:如图1,在四边形ABCD 中,AD ∥BC ,∠ABC =90º,∠ACB =30º,BE ⊥AC 于点E ,且=C D E A C B ∠∠.如果AB =1,求CD 边的长.小明在解题过程中发现,图1中,△CDE 与△ 相似,CD 的长度等于 ,线段CD 与线段 的长度相等;他进一步思考:如果ACB α∠=(α是锐角),其他条件不变,那么CD 的长度可以表示为CD = ;(用含α的式子表示)(2)受以上解答过程的启发,小明设计了如下的画图题:在Rt△OMN 中,∠MON =90º,OM <ON ,OQ ⊥MN 于点Q ,直线l 经过点M ,且l ∥ON .请在直线l 上找出点P 的位置,使得NPQ ONM ∠=∠.请写出你的画图步骤,并在答题卡上完成相应的画图过程.(画出一个即可,保留画图痕迹,不要求证明)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)已知一次函数1y kx b =+(k ≠0)的图象经过(2,0),(4,1)两点,二次函数2224y x ax =-+(其中a >2).(1)求一次函数的表达式及二次函数图象的顶点坐标(用含a 的代数式表示); (2)利用函数图象解决下列问题:①若25=a ,求当10y >且2y ≤0时,自变量x 的取值范围;②如果满足10y 且2y≤0时的自变量x的取值范围内恰有一个整数,直接写出a的取值范围.28.正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是;(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.29.对于平面直角坐标系xOy中的点P和图形G,给出如下定义:在图形G上若存在两点M,N,使△PMN为正三角形,则称图形G为点P的τ型线,点P为图形G的τ型点,△PMN为图形G关于点P的τ型三角形.(1)如图1,已知点(0,A,(3,0)B,以原点O为圆心的⊙O的半径为1.在A,B 两点中,⊙O的τ型点是____,画出并回答⊙O关于该τ型点的τ型三角形;(画出一个即可)(2)如图2,已知点(0,2)F m(其中m>0).若线段EF为原点O的τ型线,E,点(,0)且线段EF关于原点O的τ,求m的值;(3)若(0,2)H-是抛物线2=+的τ型点,直接写出n的取值范围.y x n北京市西城区2015年初三二模数学试卷参考答案及评分标准 2015. 6一、选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分)三、解答题(本题共30分,每小题5分)17.证明:如图1.∵ △ABC 是等边三角形,∴ AC =BC ,∠ACB=∠ABC =60°.……………………………………………… 1分∵ D ,E 两点分别在AB ,BC 的延长线上,∴ ∠ACE =∠CBD =120°. …………………2分在△ACE 和△CBD 中,,,AC CB ACE CBD CE BD =⎧⎪∠∠⎩=⎪⎨,= ……………………… 3分∴ △ACE ≌△CBD .……………………… 4分∴ ∠E =∠D .…………………………………………………………………… 5分18.解: 1012cos 30()1(3)3π-++- 2311=+- ………………………………………………………………4分 1=. ………………………………………………………………………… 5分 19.解: (2)(2)(21)(2)x x x x +----=224(252)x x x ---+………………………………………………………………2分 =224252x x x --+-=256x x -+-.………………………………………………………………………3分 ∵ 2540x x --=,∴ 254x x -=.…………………………………………………………………… 4分∴ 原式=2(5)64610x x ---=--=-.……………………………………………5分 20.解:去分母,得 3(3)2x x --=.…………………………………………………… 1分 去括号,得 332x x -+=. ………………………………………………………2分 整理,得 21x =-.……………………………………………………………… 3分 解得 12x =-. …………………………………………………………………… 4分 经检验,12x =-是原方程的解. …………………………………………………5分 所以原方程的解是12x =-.21.解:设牙膏每盒x 元,牙刷每支y 元.…………………………………………………1分 由题意,得 713121,1415187.x y x y +=+=⎧⎨⎩…………………………………………………… 2分解得 85.x y ==⎧⎨⎩,……………………………………………………………………… 3分(124125)88-⨯=(盒). ………………………………………………………… 4分 答:第三天卖出牙膏8盒.………………………………………………………………5分 22.解:(1)当m =0 时,该函数为一次函数33y x =--,它的图象与x 轴有公共点.……………………………………………………………… 1分当m ≠0 时,二次函数2(3)3y mx m x =+--.2(3)4(3)m m ∆=--⨯-26912m m m =-++2269(3)m m m =++=+. ∵ 无论m 取何实数,总有2(3)m +≥0,即∆≥0, ∴ 方程2(3)30mx m x +--=有两个实数根.∴ 此时函数2(3)3y mx m x =+--的图象与x 轴有公共点.……………2分 综上所述,无论m 取何实数,该函数的图象与x 轴总有公共点.(2)∵m >0,∴ 该函数为二次函数,它的图象与x 轴的公共点的横坐标为(3)(3)2m m x m--±+=.∴ 11x =-,23x m=. ……………………………………………………… 3分∵ 此抛物线与x 轴公共点的横坐标为整数,∴正整数m =1或3.……………………………………………………………5分四、解答题(本题共20分,每小题5分) 23.(1)证明:如图2.∵点C 与点A 重合,折痕为EF ,∴12∠=∠,AE =EC .∵ 四边形ABCD 为平行四边形, ∴ AD ∥BC . ∴ 32∠=∠.∴ 13∠=∠.∴ AE =AF1分 ∴ AF =EC . 又∵ AF ∥EC ,∴ 四边形AFCE 是平行四边形.………………………………………… 2分 又AE =AF ,∴ 四边形AFCE 为菱形.………………………………………………… 3分(2)解:如图3,作AG ⊥BE 于点G ,则∠AGB=∠AGE=90°. ∵ 点D 的落点为点D ′ ,折痕为EF , ∴D F DF '=.∵ 四边形ABCD 为平行四边形, ∴ AD =BC .又∵AF =EC ,∴AD AF BC EC -=-,即DF BE =.∵在Rt△AGB 中,∠AGB=90°,∠B =45°,AB =∴ AG =GB =6.∵ 四边形AFCE 为平行四边形, ∴ AE ∥FC .∴ ∠4=∠5=60°.∵ 在Rt△AGE 中,∠AGE =90°,∠4=60°, ∴ tan60AGGE ==︒∴ 6BE BG GE =+=+.∴ 6D F '=+.…………………5分 24.解:(1)③④.………………………………… 2分(2)补全统计图见图4. ………………… 3分 1055万人. ………………………… 4分(3)1.3%. …………………………………………………………………………… 5分 25. 解:(1)补全图形如图5所示. ………………………………………………………… 1分 答:PG 与⊙O 相切.证明:如图6,连接OG .∵ PF =PG , ∴ ∠1=∠2.又∵OG =OA , ∴ ∠3=∠A .∵ CD ⊥AB 于点E ,∴ ∠A +∠AFE =90°.又∵∠2 =∠AFE ,∴ ∠3+∠1=90°. ……………………… 2分 即 OG ⊥PG .∵ OG 为⊙O 的半径,∴ PG 与⊙O 相切. …………………… 3分(2)解:如图7,连接CG . ∵ CD ⊥AB 于点E ,∴ ∠OEC =90°. ∵ DG ∥AB ,∴∠GDC =∠OEC =90°. ∵∠GDC 是⊙O 的圆周角, ∴ CG 为⊙O 的直径. ∵ E 为半径OA 的中点,∴ 22OA OCOE ==. ∴ ∠OCE =30°即∠GCP =30°.又∵∠CGP=90°,2CG OA ==∴tan 4PG CG GCP =⋅∠==. …………………………… 5分 26.解:(1)CADBC . …………………………………………………………… 3分1tan α.……………………………………………………………………………4分 (2)方法1:如图8,以点N 为圆心,ON 为半径作圆,交直线l 于点1P ,2P ,则点 1P ,2P 为符合题意的点.……………………………………………… 5分 方法2:如图9,过点N 画NO 的垂线1m ,画NQ 的垂直平分线2m ,直线1m 与2m 交于点R ,以点R 为圆心,RN 为半径作圆,交直线l 于点1P ,2P ,则点1P ,2P 为符合题意的点. ……………………………………… 5分五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) 27.解:(1)∵ 一次函数1y kx b =+(k ≠0)的图象经过(2,0),(4,1)两点, ∴ 20,4 1.k b k b +=⎧⎨+=⎩解得1,21.k b ⎧=⎪⎨⎪=-⎩……………………………………………………………… 1分∴ 1211-=x y . ………………………………………………………… 2分 ∵ 22224)(42a a x ax x y -+-=+-=,∴ 二次函数图象的顶点坐标为2(,4)a a -.………………………………… 3分(2)①当25=a 时,4522+-=x x y .………………………………… 4分 如图10,因为10y >且2y ≤0,由图象得2<x ≤4. (6)分②136≤a <52.……………………………7分 28.解:(1)CH=AB . ………………………………… 1分 (2)结论成立.………………………………… 2分证明:如图11,连接BE . 在正方形ABCD 中,AB=BC=CD=AD ,∠A=∠BCD=∠ABC=90°. ∵ DE=DF , ∴ AF=CE .在△ABF 和△CBE 中,,,,AB CB A BCE AF CE =⎧⎪∠=∠⎨⎪=⎩∴ △ABF ≌△CBE .∴ ∠1=∠2.……………………………………………………………………3分 ∵ EH ⊥BF ,∠BCE =90°,∴ H ,C 两点都在以BE 为直径的圆上. ∴ ∠3=∠2. ∴ ∠3=∠1.∵ ∠3+∠4=90°,∠1+∠HBC =90°, ∴ ∠4=∠HBC .∴ CH=CB .………………………………………………………………… 5分 ∴ CH=AB .………………………………………………………………… 6分(3)3.………………………………………………………………………7分29.解:(1)点A .………………………………………1分 画图见图12.(画出一个即可)…………2分 △AMN (或△AJK ). (3)分(2)如图13,作OL ⊥EF 于点L .∵ 线段EF 为点O 的τ型线, ∴ OL 即为线段EF 关于点O 的τ型三角形的高.∵线段EF 关于点O 的τ∴OL =. ……………………………… 4∵ 2OE =,OF m =,∴EL =. ∴ cos 1EL OE ∠==∴ cos 2cos 1OL OLOF ==∠∠∴m =………………………………………………………………………6分 (3)n ≤54-.……………………………………………………………………………8分。
【2015南昌二模】江西省南昌市2015届高三第二次模拟考试理科综合试题 扫描版含答案

2015 年 高 三 测 试 卷理科综合参考答案及评分标准一—二、选择题生物 化学 物理三、非选择题 (一)必考题22.(1)2k (2分),9.60~9.80;(2分) (2)12B h v gt t =-;(2分) 23.(共9分)(1)A (1分) (2)6.70(2分)(3)在坐标图中画出U —I 图线,算出水柱的电阻8.0k ΩA UR R I=-=(7.0kΩ~9.0kΩ均给2分)24R d Lπρ=(2分)(4)如图所示,(2分,电流表外接0分) 24.(1)对线圈受力分析有:cos sin F mg mg μθθ+=安(3分) 代入数据得:=0.02N F 安 (2分) (2)=F BId 安(1分)E BLv =(1分)22=E B I F L v R R=安解得:(2分)代入数据得:2m/s v = (1分)(3)由于线圈刚好匀速穿过磁场,则磁场宽度0.1m d =(1分),3=410J Q W F d -==⨯安安2(3分)25.(1)当轻杆开始运动时,弹簧的弹力等于轻杆与槽间的最大静摩擦力f ,k x f ∆=解得:0.4m x ∆=(3分)根据功能关系可得:21=1.6J 2W k x ∆=弹 (2分) 对小车,由动能定理可得:21sin =02mg x W mv θ∆--弹 (3分)联立可解得:v =m/s (2分)(2)轻杆滑动后,弹簧弹力不再变化,轻杆随小车一起做匀减速直线运动,到小车第一次速度为0的过程中,根据能量守恒定律得:21=sin 2fx mv mg x θ+滑滑 (2分)得=0.4x 滑m为使轻杆不被全部拽入槽内,则l 至少为0.4m (2分)轻杆开始滑动后,轻杆弹簧、和小车一起做匀减速直线运动,直到速度为0,由牛顿第二定律可知,加速度大小:sin 2f mg a mθ-==m/s 2(2分)又由运动学公式可得:5v t a ==s (2分) 26.(15分)(1)2MnO 4-+10Cl -+16H +==2Mn 2++5Cl 2↑+8H 2O (2分)(2)没有除去湿Cl 2中HCl (2分)(其他合理答案也给分);影响产品中NaClO 的含量,加一个盛有饱和NaCl 溶液洗气瓶(2分); (3)NaClO 的碱性溶液(1分) 尿素(1分)2NaClO+N 2H 4·H 2O==N 2+2NaCl+3H 2O (2分) (4)C (2分) (5)分馏(蒸馏)(1分) 温度计 冷凝管(2分) 27.(15分)(1)①CO 2(g)+H 2(g) HCOOH(g) △H=-70.0 kJ/moL (3分)②AC (2分)(2)小于(2分) 反应2 (2分)(3)①453K (2分); 温度越高,反应速率越快,时间越短;但463K 时,增幅不明显,能耗反而增多,故选择453K 。
山西省太原市2015届高三第二次模拟考试物理试题(含解析)

2015年山西省太原市高考物理二模试卷二、选择题:本大题共8小题,每小题6分.在每小题给出的四个选项中.1-5小题只有一项符合题目要求,6-8小题有多项符合题目要求.全部选对得6分,选对但不全得3分,有选错的得0分.1.(6分)直导线ab放在如图所示的水平导体框架上,构成了一个闭合回路;长直导线cd 和框架处在同一个平面内,且cd和ab平行,当cd中通有电流时,观察到ab向左滑动.关于cd中的电流,下列说法正确的是()A.电流一定增大,方向沿c向dB.电流一定增大,方向沿d向cC.电流一定减小,方向可能由d向cD.电流大小恒定,方向由d到c【考点】:楞次定律;磁感线及用磁感线描述磁场.【专题】:电磁感应与图像结合.【分析】:要使ab发生运动则右侧框架中一定会发生电磁感应现象,则由楞次定律可得出线框内磁场的变化.【解析】:解:导线左移时,线框的面积增大,由楞次定律可知原磁场一定是减小的;并且不论电流朝向哪个方向,只要电流减小,都会发生ab左移的情况;故选:C.【点评】:楞次定律有两种描述,一种是:增反减同,另一种是:来拒去留;本题可根据第二种描述快速求解;应明确电磁感应中的阻碍的各种含义.2.(6分)2015年莫斯科世锦赛上,我国男子短道速滑队时隔15年再次站到5000m接力的冠军颁奖台上.观察发现,“接棒”的运动员乙前面,并且开始向前滑行,待乙追上甲时,乙猛推甲,甲获得更大的速度向前冲出.在乙推甲的过程中,忽略运动员与冰面间在水平方向上的相互作用,则()A.甲对乙的作用力与乙对甲的作用力相同B.甲对乙的作用力一定做正功,乙的动能增大C.乙对甲的作用力一定做正功,甲的动能增大D.甲的动能增加量一定等于乙的动能减少量【考点】:牛顿第三定律.【专题】:常规题型.【分析】:运动员与冰面间的摩擦可忽略不计,在“交棒”过程中,“交棒”运动员猛推“接棒”运动员一把,两个运动员相互作用的力等大、反向、共线,作用时间相同,根据动量定理,两个运动员的动量变化等大、反向、共线,系统动量守恒.【解析】:解:A、由牛顿第三定律可知,作用力与反作用力大小相等,方向相反,所以甲对乙的作用力与乙对甲的作用力大小相等,方向相反,故A错误;B、甲对乙的作用力一定做负功,乙的动能减小,故B错误;C、乙对甲的作用力一定做正功,甲的动能增大,故C正确;D、甲、乙间的作用力大小相等,不知道甲、乙的质量关系,不能求出甲乙动能变化关系,故D错误;故选:C.【点评】:明确运动员间的相互作用力的冲量等于对方的动量变化,又有作用时间相同,相互作用力等大、反向,故两个运动员系统的总动量守恒.3.(6分)近年来,智能手机的普及使“低头族”应运而生.近日研究发现,玩手机时,就有可能让颈椎承受多达60磅(约270N)的重量,相当干给颈椎挂俩大西瓜,比一个7岁小孩还重.不当的姿势与一系列健康问题存在关联,如背痛、体重增加、胃痛、偏头痛和呼吸道疾病等.当人体直立时,颈椎所承受的压力等于头部的重量;但当低头时,颈椎受到的压力会随之变化.现将人体头颈部简化为如图的模型:重心在P点的头部,在可绕O转动的颈椎OP(轻杆)的支持力和沿PQ方向肌肉拉力的作用下处于静止.当低头时,颈椎与竖直方向的夹角为45°,PQ与竖直方向的夹角为60°,此时,颈椎受到的压力约为直立时颈椎受到压力的()A.4.2 B.3.7 C.2.8 D. 2.0【考点】:共点力平衡的条件及其应用;物体的弹性和弹力.【专题】:共点力作用下物体平衡专题.【分析】:对人的头部进行分析,明确其受力情况,由共点力的平衡条件可得出对应的平行四边形;由正弦定理可求得颈椎受到的压力.【解析】:解:由题意可明确人的头受力情况,如图所示:则由几何关系可知:人的颈椎对头的支持力F:所以F=;故选:B.【点评】:本题考查共点力的平衡在实际生活中的应用,要注意正确根据题意明确作出对应的图象,再由几何关系即可求解.4.(6分)假设火星可视为质量均匀分布的球体,已知“火卫一”(火星的卫星)绕火星做圆周运动的半径为R,周期为T,火星的半径为R0,自转周期为T0,则火星表面的重力加速度在赤道处大小与两极处大小的比值为()A.B.C.1﹣D.1﹣【考点】:万有引力定律及其应用.【专题】:万有引力定律的应用专题.【分析】:在赤道上,万有引力一个分力等于重力,另一个分力提供向心力,在两极,万有引力等于重力.结合火卫一的轨道半径和周期求出火星的质量,根据万有引力和重力的关系求出重力加速度的比值.【解析】:解:在赤道上的物体,有:,在两极,有:联立两式,根据,解得GM=,代入可得=1﹣.故选:D.【点评】:解决本题的关键知道万有引力与重力的关系,知道赤道上万有引力等于重力和向心力之和,两极万有引力等于重力.5.(6分)如图所示,水平地面上方矩形区域内存在垂直纸面向里的匀强磁场,两个用相同材料、相同粗细的导线绕制的单匝闭合正方形线圈l和2,其边长L1>L2,在距磁场上界面h高处由静止开始自由下落,再逐渐完全进入磁场,最后落到地面.运动过程中,线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界.设线圈l、2落地时的速度大小分别为v1、v2,在磁场中运动时产生的热世分别为Q1、Q1,通过线圈截面的电荷量分别为q1、q2,不计空气阻力,则()A.v1<v2,Q1>Q2,q1>q2 B.v1=v2,Q1=Q2,q1=q2C.v1<v2,Q1>Q2,q1=q2 D.v1=v2,Q1<Q2,q1<q2【考点】:导体切割磁感线时的感应电动势;闭合电路的欧姆定律;焦耳定律.【专题】:电磁感应与电路结合.【分析】:线圈进入磁场之前,均做自由落体运动,因下落高度一致,可知两线圈会以同样的速度进入磁场,由法拉第电磁感应定律可求出进入磁场边界时的感应电动势,从而表示出受到磁场的安培力.由电阻定律表示出两线圈的电阻,结合牛顿第二定律表示出加速度,可分析出加速度与线圈的粗细无关,从而判断出两线圈进入时运动是同步的,直到线圈2完全进入磁场后,线圈做匀加速运动,可得出落地速度的大小关系.由能量的转化与守恒可知,损失的机械能(转化为了内能)与线圈的质量有关,从而判断出产生的热量大.由q=分析电量的关系.【解析】:解:线圈从同一高度下落,到达磁场边界时具有相同的速度v,切割磁感线产生感应电流时,受到磁场的安培力大小为:F=由电阻定律有:R=ρ(ρ为材料的电阻率,L为线圈的边长,S为导线的横截面积),线圈的质量m=ρ0S•4L,(ρ0为材料的密度).当线圈的下边刚进入磁场时其加速度为:a==g﹣联立得,加速度为:a=g﹣由上式分析得知,线圈1和2进入磁场的过程先同步运动,由于当线圈2刚好全部进入磁场中时,线圈1由于边长较长还没有全部进入磁场,线圈2完全进入磁场后做加速度为g的匀加速运动,而线圈1仍先做加速度小于g的变加速运动,完全进入磁场后再做加速度为g的匀加速运动,匀加速运动的位移相同,所以落地速度v1<v2.由能量守恒可得:Q=mg(h+H)﹣mv2(H是磁场区域的高度),因为m1>m2,v1<v2,所以可得Q1>Q2.根据q==∝L知,q1>q2.故选:A.【点评】:本题要注意分析物体的运动状态及能量变化关系,关键点在于分析线圈进入磁场的过程,由牛顿第二定律得到加速度关系,分析物体的运动情况关系.6.(6分)图1是远距离输电线路的示意图,圈2是发电机输出电压随时间变化的图象,则()A.发电机输出交流电压的有效值约为500 VB.用户用电器上交流电的频率是100 HzC.输电线的电流只由升压变压器原副线圈的匝数比决定D.当用户用电器的总电阻减小时,输电线上损失的功率增大【考点】:远距离输电.【专题】:交流电专题.【分析】:根据图象可知交流电的最大值以及周期等物理量,然后进一步可求出其瞬时值的表达式以及有效值等.同时由变压器电压与匝数成正比,电流与匝数成反比.【解析】:解:A、由图象可知交流的最大值为U m=707V,因此其有效值为U==500V,故A正确;B、发电机的输出电压随时间变化的关系,由图可知,T=0.02s,故f=,故B错误;C、输电线的电流由输送的功率与电压决定的,与降压变压器原副线圈的匝数比无关,故C 错误;D、当用户用电器的总电阻增大时,用户的功率减小,降压变压器的输出功率减小,则输入的功率减小,输入的电流减小,输电线上损失的功率减小,故D正确;故选:AD.【点评】:本题考查了有关交流电描述的基础知识,要根据交流电图象正确求解最大值、有效值、周期、频率、角速度等物理量,同时要能正确书写交流电的表达式.7.(6分)某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示.则(不考虑空气阻力)()A.电场强度大小恒定,方向沿x轴负方向B.从O到x1的过程中,小球的速率越来越大,加速度越来越大C.从O到x1的过程中,相等的位移内,小球克服电场力做的功越来越大D.到达x1位置时,小球速度的大小为【考点】:电势差与电场强度的关系;牛顿第二定律;电场强度.【专题】:电场力与电势的性质专题.【分析】:从图象中能找出电场力的做功情况,根据电场力的做功情况判断出受力,继而判断出电场,在利用牛顿第二定律求的加速度【解析】:解:A、物体的机械能先减小,后保持不变,故电场力先做负功,后不做功,故电场强度方向向上,再根据机械能的变化关系可知,电场力做功越来越小,故电场强度不断减小,故A错误;B、根据牛顿第二定律可知,物体受重力与电场力,且电场力越来越小,故加速度越来越大,速度越来越大,故B正确;C、由于电场力越来越小,故相等的位移内,小球克服电场力做的功越来越小,故C错误;D、根据动能定理可得得,故D正确;故选:BD【点评】:本题主要考查了电场力做功与与物体机械能的变化关系,明确电场力做正功,电势能增加,电场力做负功,电场力减小即可8.(6分)如图,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小.这就是大家熟悉的惯性演示实验.若砝码和纸板的质量分别为M和m.各接触面间的动摩擦因数均为μ,砝码与纸板左端的距离及桌面右端的距离均为d.现用水平向右的恒定拉力F拉动纸板,下列说法正确的是()A.纸板相对砝码运动时,纸板所受摩擦力的大小为μ(M+m)gB.要使纸板相对砝码运动,F一定大于2μ(M+m)gC.若砝码与纸板分离时的速度小于,砝码不会从桌面上掉下D.当F=μ(2M+3m)g时,砝码恰好到达桌面边缘【考点】:牛顿第二定律;匀变速直线运动的速度与时间的关系.【专题】:牛顿运动定律综合专题.【分析】:应用摩擦力公式求出纸板与砝码受到的摩擦力,然后求出摩擦力大小.根据牛顿第二定律求出加速度,要使纸板相对于砝码运动,纸板的加速度应大于砝码的加速度,然后求出拉力的最小值.当F=μ(2M+3m)g时,根据牛顿第二定律分析求出砝码和纸板加速度,结合运动学公式求出分离时砝码的速度,结合速度位移公式求出砝码速度减为零的位置,从而判断出砝码的位置.【解析】:解:A、对纸板分析,当纸板相对砝码运动时,所受的摩擦力μ(M+m)g+μMg,故A错误.B、设砝码的加速度为a1,纸板的加速度为a2,则有:f1=Ma1,F﹣f1﹣f2=ma2发生相对运动需要a2>a1代入数据解得:F>2μ(M+m)g,故B正确.C、若砝码与纸板分离时的速度小于,根据知,因为开始砝码向右做匀加速运动已经有一段位移,所以砝码可能还会从桌面掉下,故C错误.D、当F=μ(2M+3m)g时,砝码未脱离时的加速度a1=μg,纸板的加速度=2μg,根据,解得t=,则此时砝码的速度,砝码脱离纸板后做匀减速运动,匀减速运动的加速度大小a′=μg,则匀减速运动的位移,可知砝码恰好到达桌面边缘,故D正确.故选:BD.【点评】:本题考查了求拉力大小,应用摩擦力公式求出摩擦力大小,知道拉动物体需要满足的条件,应用牛顿第二定律与运动学公式即可正确解题.三、非选择韪:包括必考题和选考题两部分.考生根据要求作答.(一)必考题9.(7分)用如图的电路可以精确测量定值电阻R0的电阻值和滑动变阻器R2的总阻值,图中R1为电阻箱,主要操作步骤如下,完成步骤中的填空:①将滑动变阻器滑片调到最左端,断开S2,接着闭合S、S1,读出电流表的示数I1;②再断开S1,闭合S2,调节电阻箱的电阻值,当电阻箱的电阻为5.6Ω时,电流表的示数也为I1,断开S;③将滑动变阻器滑片调到最右端,断开S2,闭合S、S1;读出电流表的示数I2;④再断开S1.闭合S2.调节电阻箱的电阻值为15.8Ω时,电流表的示数也为I2;⑤则定值电阻R0= 5.6Ω;滑动变阻器R2的总阻值为10.2Ω.【考点】:伏安法测电阻.【专题】:实验题.【分析】:分析电路结构,根据实验步骤分析实验采用的方法,再由欧姆定律分析可得出对应的电阻值.【解析】:解:由题意可知,本题应采用替代法进行测量,第①步中接入电路的只有R0,故断开S1,闭合S2,使电流仍为I1时,可知,电阻箱的阻值即为R0的阻值,则可知R0=5.6Ω;为了测量滑动变阻器的总阻值,应将滑动变阻器全部接入时得出电流值,再用电阻箱替代两电阻,得出相对的电流值,可得出滑动变阻器的总阻值与R0的阻值为电阻箱的电阻,故滑动变阻器的总阻值为:15.8﹣5.6=10.2Ω;故答案为:②S1;S2;电阻箱;④S1,S2;⑤5.6;10.2【点评】:本题考查等效替代法在电阻测量中的应用,要注意正确分析实验电路明确实验中采用的等效替代的方法.10.(8分)利用图1的装置可测量滑块与斜面间的动摩擦因数.在斜面底端O处固定一光电门,当带有遮光片的滑块自斜面上的P点从静止滑下,通过光电门时,与光电门相连的计时器显示遮光片通过光电门的时间为△t.测得P、O间的距离为x.已知遮光片的宽度为d.完成下列填空:(1)P、O间的距离x、滑块加速度的大小a、滑块经过光电门的时间△t、遮光片的宽度d四个物理量间满足的关系式是;(2)用游标卡尺测量遮光片的宽度如图2所示,则d=0.500cm,(3)多次改变滑块从斜面上开始下滑的位置,每次都让滑块由静止滑下,用米尺分别测出下滑点与O间的距离x,记下遮光片相应通过光电门的时间△t,利用所得数据作出()2﹣x图线如图3所示:①由图线可得滑块加速度的大小为 3.92m/s2;②测得斜面的高度h=60.00cm、斜面的长度L=100.00cm,取g=9.80m/s2,则滑块与斜面间的动摩擦因数的值μ=0.25.【考点】:探究影响摩擦力的大小的因素.【专题】:实验题.【分析】:(1)根据瞬时速度等于平均速度,及运动学公式,即可求解;(2)根据游标卡尺读数的方法,主尺读数加上游标读数,不需估读;(3)根据()2﹣x图线,结合运动学公式,通过图象斜率,即可求解加速度大小;(4)对滑块受力分析,结合牛顿第二定律,即可求解动摩擦因数.【解析】:解:(1)滑块经过光电门的速度为v=;根据运动学公式,那么P、O间的距离x、滑块加速度的大小a、滑块经过光电门的时间△t、遮光片的宽度d四个物理量间满足的关系式:;(2)游标卡尺的主尺读数为5mm,游标尺上第0个刻度和主尺上某一刻度对齐,所以游标读数为0×0.05mm=0.00mm,所以最终读数为:5mm+0.00mm=5.00mm=0.500cm;(3)①根据作出()2﹣x图线,结合,则有:k=2a;那么a==m/s2=3.92m/s2;②滑块受到重力、支持力与滑动摩擦力,根据力的分解,结合牛顿第二定律,则有:mg﹣μmg=ma;解得:μ==0.25;故答案为:(1);(2)0.500;(3)3.92,0.25.【点评】:考查光电门测速度的方法,知道游标卡尺的读数,理解牛顿第二定律的应用,掌握图象的作用,知道其图象斜率与加速度的关系.11.(13分)一质量为2m的卡车拖挂一质量为m的车厢,在水平直道上匀速行驶,其所受的阻力与各自的重量成正比,比例系数为k=0.2且与速度无关.某时刻车厢脱落,车厢停止运动时,卡车与车厢相距△x=96m.已知整个过程中卡车的牵引力保持不变,取g=10m/s2,求车厢脱落时的速度v0.【考点】:牛顿第二定律;匀变速直线运动的位移与时间的关系.【专题】:牛顿运动定律综合专题.【分析】:根据牛顿第二定律分别求出车厢脱落后卡车和车厢的加速度大小,结合运动学公式,结合位移关系求出车厢脱落时的速度大小.【解析】:解:设卡车的牵引力为F,车厢脱落前,对卡车和车厢整体分析有:F﹣3kmg=0.设车厢脱落后,卡车和车厢的加速度大小分别为a1和a2,由牛顿运动定律有:F﹣k×2mg=2ma1,kmg=ma2,设卡车和车厢的位移分别为x1和x2,由运动学方程有:,,△x=x1﹣x2,v0=a2t,代入数据解得v0=16m/s.答:车厢脱落时的速度为16m/s.【点评】:本题考查了牛顿第二定律和运动学公式的基本运用,通过牛顿第二定律求出加速度的大小是解决本题的关键,抓住位移关系,结合运动学公式灵活求解.12.(19分)在如图的xOy坐标系中.A(﹣L,0)、C是x轴上的两点,P点的坐标为(0,L).在第二象限内以D(﹣L,L)为圆心、L为半径的圆形区域内,分布着方向垂直xOy平面向外、磁感应强度大小为B的匀强磁场;在第一象限三角形OPC之外的区域,分布着沿y轴负方向的匀强电场.现有大量质量为m、电荷量为+q的相同粒子,从A点平行xOy 平面以相同速率、沿不同方向射向磁场区域,其中沿AD方向射入的粒子恰好从P点进入电场,经电场后恰好通过C点.已知a=30°,不考虑粒子间的相互作用及其重力,求:(1)电场强度的大小;(2)x正半袖上有粒子穿越的区间.【考点】:带电粒子在匀强磁场中的运动;带电粒子在匀强电场中的运动.【专题】:带电粒子在复合场中的运动专题.【分析】:(1)带电粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,沿AD方向的粒子由P点进入电场时,速度方向与y轴垂直,进而电场后做类平抛运动,根据牛顿第二定律结合平抛运动基本公式求解电场强度;(2)设粒子的速度方向与x轴正方向的夹角为θ,粒子从F点射出磁场,由于r=L,故四边形ADFO′为菱形,带电粒子离开磁场时,速度方向沿x轴正方向,根据几何关系结合平抛运动基本公式求出粒子到达x轴的坐标的表达式,从而求出x的范围.【解析】:解:(1)带电粒子在磁场中做匀速圆周运动,设半径为r,粒子初速度为v0,则,由几何关系得:r=L,沿AD方向的粒子由P点进入电场时,速度方向与y轴垂直,设在电场中运动的时间为t0,电场强度为E,则qE=ma,,L=解得:E=(2)若粒子的速度方向与x轴正方向的夹角为θ,粒子从F点射出磁场,由于r=L,故四边形ADFO′为菱形,O′F平行AD,v F⊥O′F,带电粒子离开磁场时,速度方向沿x轴正方向,则有:y F=L(1﹣cosθ),粒子从F′通过PC,则粒子在电场中运动的时间为t,从C′通过x轴离开电场,沿x轴方向的位移为x,x=v0t,,粒子到达x轴的坐标为x C′,x C′=x F′+x(0<θ≤90°)当θ=90°时,x C′的最小值,当时,x C′的最大值所以x正半袖上有粒子穿越的区间为答:(1)电场强度的大小为;(2)x正半袖上有粒子穿越的区间为.【点评】:带电粒子在组合场中的运动问题,首先要运用动力学方法分析清楚粒子的运动情况,再选择合适方法处理.对于匀变速曲线运动,常常运用运动的分解法,将其分解为两个直线的合成,由牛顿第二定律和运动学公式结合求解;对于磁场中圆周运动,要正确画出轨迹,由几何知识求解半径.(二)选考题:共45分.请考生从给出的三个选修中,选做一个,.如果多做,则按所做第一计分.【物理--选修3-3】(15分)13.(6分)关于热力学定律和分子动理论,下列说法正确的是()A.一定质量的理想气体,在等压膨胀过程中,气体分子的平均动能增大B.若两分子间距离减小,分子间斥力增大、引力减小,合力为斥力C.在围绕地球运行的“天宫一号”内,飘浮的水滴呈球形,这是表面张力作用的结果D.布朗运动是由于液体各部分的温度不同而引起的【考点】:* 液体的表面张力现象和毛细现象;布朗运动.【分析】:温度是分子平均动能的标志,温度越高,则分子的平均动能越大;若两分子间距离减小,分子间引力和斥力都增大.液体表面张力使液体表面呈收缩状态;布朗运动是由于固体小颗粒受撞击不平衡造成的.【解析】:解:A、一定质量的理想气体,在等压膨胀过程中,气体的温度一定升高,故气体分子的平均动能增大;故A正确;B、若两分子间距离减小,分子间斥力和引力都增大;但斥力变化快;从而导致合力为斥力;故B错误;C、在围绕地球运行的“天宫一号”内,飘浮的水滴呈球形,这是重力充当向心力,而表面张力起主要作用的结果;故C正确;D、布朗运动是由于固体小颗粒受到的撞击不平衡而导致的;故D错误;故选:AC.【点评】:本题考查分子平均动能、分子间的相互作用力、表面张力及布朗运动的性质,要注意正确理解相关内容,并且要会解释相关现象.14.(9分)如图,一根粗细均匀的玻璃管,由A、B、C三段直管及横管组成,A、C两端开口,B、C两管内装有水银且两管内液面相平.若把A管竖直插入水银槽中,当管口在水银面下8cm处且稳定时.B内水银面下降的高度为2cm;若先将c管上端封闭,再把A管竖直插入水银槽中,当管口在水银面下13cm处且处于稳定时,进入A管内的水银柱长度为5cm,求此时B管内水银面下降的高度.(已知大气压强p0=76cmHg,环境温度不变)【考点】:理想气体的状态方程.【专题】:理想气体状态方程专题.【分析】:对A管内气体进行分析,由压强的计算可求得变化前后的压强,再由玻意耳定律可列式,联立即可求得B管内水银面下降的高度.【解析】:解:设管的截面积为S,未插入水银槽前AB部分空气柱长为l0,不封闭C管的情况下,A管内封闭气体压强和长度分别为:P1=P0+ρgh1=80cmHg;l1=l0﹣4+2=l0﹣2由玻意耳定律可得:P0l0s=P1l1sC管封闭时,设B处水银下降的高度为x,AB管内封闭气体压强和长度分别为:P2=P0+ρgh2l2=l0﹣5+x由玻意耳定律可得:P1l1S=P2l2S解得:x=1.2m;答:此时B管内水银面下降的高度为1.2m.【点评】:本题考查玻意耳定律的应用,关键点是求出插入水银槽时玻璃管内气体的压强的计算方法.【物理--选修3-4](15分)15.从O点发出的甲、乙两列倚谐横波沿x正方向传播,某时刻两列波分别形成的波形如图所示,P点在甲波最大位移处,Q点在乙波最大位移处,下列说法中正确的是()A.两列波具有相同的波速B.两列波传播相同距离时,乙波所用的时间比甲波的短C.P点比Q点先回到平衡位置D.P质点完成20次全振动的时间内Q质点可完成30次全振动E.若甲、乙两列波在空间相遇时不会发生干涉【考点】:横波的图象;波长、频率和波速的关系.【专题】:振动图像与波动图像专题.【分析】:两列简谐横波在同一介质中波速相同,传播相同距离所用时间相同.Q点与P 点都要经过周期回到平衡位置.由图可两列波波长的大小,再分析周期的长短,再比较时间长短.根据频率关系研究相同时间内全振动次数关系.两列波只有频率相同时,才能产生稳定的干涉.【解析】:解:A、B两列简谐横波在同一介质中波速相同,传播相同距离所用时间相同.故A正确,B错误.C、由图可知,两列波波长之比λ甲:λ乙=3:2,波速相同,由波速公式v=得到周期之比为T甲:T乙=3:2.Q点与P点都要经过周期才回到平衡位置.所以Q点比P点先回到平衡位置.故C错误.D、两列波的频率之比为f甲:f乙=2:3,则在P质点完成20次全振动的时间内Q质点完成了30次全振动.故D正确.。
2015二模理综物理答案

页眉内容页脚内容物理部分参考答案及评分标准14.【试题答案】A【命题立意】考查学生对胡克定律和共点力平衡知识的理解和应用【解 析】对小球b 受力分析,受力平衡,弹簧B 的弹力g m F b B =;对小球a 受力分析,弹簧A 的拉力g m m F )(2b a A +=,a b 2m m =,又由胡克定律kx F =,故选项A 正确。
15.【试题答案】B【命题立意】考查学生对电荷电势能的理解。
【解 析】由电势能ϕq E =P ,把零电势面选在A 点的左侧,则B A ϕϕ>>0,可以满足1q 的电势能小于2q 的电势能,故选项B 正确16.【试题答案】D【命题立意】考查学生对交流电产生及描述问题的理解和掌握情况。
【解 析】1t 时刻线圈中感应电动势为0,A 项错误;2t 时刻线圈中感应电流为最大值,B 项错误;磁通量与线圈匝数无关,所以磁感应强度2a B ϕ=,C 项错误;线圈中瞬时感应电动势的表达式nt n N e ππϕ2cos 20=,D 项正确。
17.【试题答案】C【命题立意】考查学生应用万有引力定律和牛顿第二定律解决星体运动问题的能力。
【解 析】以月球为研究对象,r Tm r m GM 222E 4π=,E 32GM r T π=,地球质量3E E 34R M πρ=,所以周期不变,故C 选项正确。
18.【试题答案】D【命题立意】考查学生对平抛运动规律的理解和掌握及应用图象解决物理问题的能力。
【解 析】平抛运动速度偏向角的正切值t v gv v oy ==tan θ,所以θtan 0g v t =,即图象斜率为gv k 0=,所以g x ykg v ==0,故A 项错误;y 时刻的速度大小为22)()(g xy yg +,故B 项错误;由平抛运动规律可知,y页眉内容页脚内容故C 错;速度偏向角的正切值为位移偏向角正切值的2倍, D 项正确。
19.【试题答案】BCD【命题立意】考查学生应用牛顿运动定律知识解决有关连接体问题的能力 【解 析】接触面光滑时,整体分析:mFm m F a 2B A 1=+=;对B 分析:211F a m N B ==。
2015二模理数答案

长春市普通高中2015届高三质量监测(二)数学(理科)参考答案及评分标准一、选择题(本大题包括12小题,每小题5分,共60分)1. D2. A3. C4. C5. D6. D7. B8. B9. C 10.A 11. C 12. A 简答与提示:1. 【命题意图】本题主要考查集合交集与补集的运算,属于基础题.【试题解析】D 由题意可知{|1Q x x =-≤或2}x >,则{|12}Q x x =-<≤R ð,所以{|02}P Q x x =≤≤R ð. 故选D. 2. 【命题意图】本题考查复数的除法运算,以及复平面上的点与复数的关系,属于基础题.【试题解析】A131255i i i -=--,所以其共轭复数为3155i +. 故选A. 3. 【命题意图】本题考查正态分布的概念,属于基础题,要求学生对统计学原理有全面的认识.【试题解析】C (01)(12)0.5(2)P P P ξξξ==->=≤≤≤≤. 故选C. 4. 【命题意图】本题借助不等式来考查命题逻辑,属于基础题.【试题解析】C 由p 成立,则1a ≤,由q 成立,则1a >,所以p ⌝成立时1a >是q 的充要条件.故选C.5. 【命题意图】本题主要考查线性规划,是书中的原题改编,要求学生有一定的运算能力.【试题解析】D由题意可知,35x y +在(2,1)--处取得最小值,在35(,)22处取得最大值,即35[11,17]x y +∈-.故选D.6. 【命题意图】本题通过正方体的三视图来考查组合体体积的求法,对学生运算求解能力有一定要求.【试题解析】D 该几何体可视为正方体截去两个三棱锥,所以其体积为41138362--=. 故选D. 7. 【命题意图】本题考查向量模的运算.【试题解析】B |2|+==a b 故选B.8. 【命题意图】本题考查学生对茎叶图的认识,通过统计学知识考查程序流程图的认识,是一道综合题.【试题解析】B 由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图知:数学成绩大于等于90的人数为10,因此输出结果为10. 故选B. 9. 【命题意图】本题主要考查三角函数的图像和性质,属于基础题.【试题解析】C由题意()sin(2)6f x x π=+,将其图像向右平移ϕ(0)ϕ>个单位后解析式为()sin[2()]6f x x πϕ=-+,则26k πϕπ-=,即212k ππϕ=+()k ∈N ,所以ϕ的最小值为12π. 故选C.10. 【命题意图】本题借助基本不等式考查点到直线的距离,属于中档题.【试题解析】A 由直线与圆相切可知||m n +=1mn m n =++,由2()2m n mn +≤可知211()4m n m n ++≤+,解得(,2[222,)m n +∈-∞-++∞. 故选A. 11. 【命题意图】本题主要考查双曲线的几何性质,结合着较大的运算量,属于难题.【试题解析】C 由题可知,过I 、III 象限的渐近线的倾斜角为θ,则tan b a θ=,222tan 2aba bθ=-,因此△OAB 的面积可以表示为3222112tan 227a b a a a a b θ⋅⋅==-,解得34b a =,则54e =. 故选C.12. 【命题意图】本题是最近热点的复杂数列问题,属于难题.【试题解析】A 设(2)n n n b nS n a =++,有14b =,28b =,则4n b n =, 即(2)4n n n b nS n a n =++=当2n ≥时,1122(1)(1)01n n n n S S a a nn ---++-+=- 所以12(1)11n n n n a a n n -++=-,即121n n a a n n -⋅=-,所以{}n a n是以12为公比,1为首项的等比数列,所以11()2n n a n -=,12n n na -=. 故选A.二、填空题(本大题包括4小题,每小题5分,共20分)13. 6014.4915.83π16. 19(2,)8简答与提示:13. 【命题意图】本题主要考查二项式定理的有关知识,属于基础题.【试题解析】由题意可知常数项为2246(2)(60C x =. 14. 【命题意图】本题考查定积分的几何意义及微积分基本定理,属于基础题.【试题解析】由题意322023a a x ==⎰,所以49a =. 15. 【命题意图】球的内接几何体问题是高考热点问题,本题通过求球的截面面积,对考生的空间想象能力及运算求解能力进行考查,具有一定难度.【试题解析】由题意,面积最小的截面是以AB为直径,可求得3AB =,进而截面面积的最小值为283ππ=. 16. 【命题意图】本题主要考查数形结合以及函数的零点与交点的相关问题,需要学生对图像进行理解,对学生的能力提出很高要求,属于难题.【试题解析】由题意可知()f x 是周期为4的偶函数,对称轴为直线2x =. 若()F x 恰有4个零点,有(1)(1)(3)(3)g f g f >⎧⎨<⎩,解得19(2,)8a ∈.三、解答题(本大题必做题5小题,三选一选1小题,共70分)17. (本小题满分12分)【命题意图】本小题主要考查两角和的正切公式,以及同角三角函数的应用,并借助正弦定理考查边角关系的运算,对考生的化归与转化能力有较高要求.【试题解析】解:(1) +,tan tan()A B C C A B π+=∴=-+ (3分)tan 2,tan 3,tan 1,4A B C C π==∴=∴= (6分)(2)因为tan 3B =sin 3sin 3cos cos BB B B⇒=⇒=,而22sin cos 1B B +=,且B 为锐角,可求得sin B =.(9分)所以在△ABC中,由正弦定理得,sin sin AB AC B C =⨯=. (12分)18. (本小题满分12分)【命题意图】本小题主要考查统计与概率的相关知识、离散型随机变量的分布列以及数学期望的求法. 本题主要考查数据处理能力.【试题解析】(1)由图可知0.035a =,0.025b =. (4分)(2) 利用分层抽样从样本中抽取10人,其中属于高消费人群的为6人,属于潜在消费人群的为4人. (6分) 从中取出三人,并计算三人所获得代金券的总和X , 则X 的所有可能取值为:150,200,250,300.363101(150)6C P X C ===, 21643101(200)2C C P X C ===,126433(250)10C C P X C ===,343101(300)30C P X C ===,(10分) 且1131150200250300210621030EX =⨯+⨯+⨯+⨯=.(12分)19. (本小题满分12分)【命题意图】本小题主要考查立体几何的相关知识,具体涉及到线面以及面面的垂直关系、二面角的求法及空间向量在立体几何中的应用. 本小题对考生的空间想象能力与运算求解能力有较高要求. 【试题解析】解:(1) 取PB 中点N ,连结MN 、AN ,M 是PC 中点,1//,22MN BC MN BC ∴==, 又//BC AD ,//,MN AD MN AD ∴=,∴四边形ADMN 为平行四边形 ,AP AD AB AD ⊥⊥,AD ∴⊥平面PAB ,AD AN ∴⊥,AN MN ∴⊥ AP AB =,AN PB ∴⊥,AN ∴⊥平面PBC ,AN ⊂平面ADM ,∴平面ADM ⊥平面PBC .(6分) (2) 存在符合条件的λ.以A 为原点,AB 方向为x 轴,AD 方向为y 轴,AP 方向为z 轴,建立空间直角坐标系A xyz -,设(2,,0)E t ,(0,0,2)P ,(0,2,0)D ,(2,0,0)B从而(0,2,2)PD =-,(2,2,0)DE t =-,则平面PDE 的法向量为1(2,2,2)n t =-, 又平面DEB 即为xAy 平面,其法向量2(0,0,1)n =,则1212122cos ,3||||(2n n n n n n ⋅<>===⋅,解得3t =或1t =,进而3λ=或13λ=.(12分)20. (本小题满分12分)【命题意图】本小题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法,椭圆方程的求法、直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.【试题解析】解:(1) 已知11(||||||)||||22ABC A S AB AC BC r BC y ∆=++⋅=⋅,且||2BC =,||3A y r =,其中r 为内切圆半径,化简得:||||4AB AC +=,顶点A 的轨迹是以B C 、为焦点,长轴长为4的椭圆(去掉长轴端点),其中2,1,a c b ===进而其方程为22143x y +=(0)y ≠. (5分)(2) 1232k k k =+,以下进行证明:当直线PQ 斜率存在时,设直线:(1)PQ y k x =-且11(,)P x y ,22(,)Q x y ,(4,)H m联立22143(1)x y y k x ⎧+=⎪⎨⎪=-⎩可得2122834k x x k +=+,212241234k x x k -=+. (8分)由题意:13mk =,1214y m k x -=-,2324y m k x -=-.11212312()(4)()(4)(4)(4)y m x y m x k k x x --+--+=--21212121212882(5)()2424224()1636363m k kx x m k x x mk m mk x x x x k ++-+++====-+++当直线PQ 斜率不存在时,33(1,),(1,)22P Q -,231332222333m m m k k k -++=+== 综上可得1232k k k =+. (12分)21. (本小题满分12分) 【命题意图】本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述原函数的单调性、极值以及函数零点的情况. 本小题对考生的逻辑推理能力与运算求解有较高要求.【试题解析】解:(1) 对()f x 求导得:1()ln(1)1axf x a x b x-'=-++-+,根据条件知(0)0f '=,所以101b b -=⇒=. (3分)(2) 由(1)得()(1)ln(1)f x ax x x =-+-,01x ≤≤1()ln(1)11axf x a x x-'=-++-+ 22(1)(1)21()1(1)(1)a a x ax ax a f x x x x -+--++''=-+=-+++.① 当12a ≤-时,由于01x ≤≤,有221()()0(1)a a x a f x x ++''=-≥+,于是()f x '在[0,1]上单调递增,从而()(0)0f x f ''≥=,因此()f x 在[0,1]上单调递增,即()(0)0f x f ≥=而且仅有(0)0f =;②当0a ≥时,由于01x ≤≤,有221()0(1)ax a f x x ++''=-<+,于是()f x '在[0,1]上单调递减,从而()(0)0f x f ''≤=,因此()f x 在[0,1]上单调递减,即()(0)0f x f ≤=而且仅有(0)0f =;③当102a -<<时,令21min{1,}a m a+=-,当0x m ≤≤时,221()()0(1)a a x a f x x ++''=-≤+,于是()f x '在[0,]m 上单调递减,从而()(0)0f x f ''≤=,因此()f x 在[0,]m 上单调递减, 即()(0)0f x f ≤=而且仅有(0)0f =.综上可知,所求实数a 的取值范围是1(,]2-∞-. (8分)(3) 对要证明的不等式等价变形如下:2110000100010000.41000.55210001100111()()(1)(1)100001000100001000e e ++<<⇔+<<+ 所以可以考虑证明:对于任意的正整数n ,不等式215211(1)(1)n n e n n+++<<+恒成立. 并且继续作如下等价变形2152112111(1)(1)()ln(1)1()ln(1)52n n e n n n n n n+++<<+⇔++<<++ 211(1)ln(1)0()5111(1)ln(1)0()2p n n n q n n n ⎧++-<⎪⎪⇔⎨⎪++->⎪⎩对于()p 相当于(2)中21(,0)52a =-∈-,12m =情形,有()f x 在1[0,]2上单调递减,即()(0)0f x f ≤=而且仅有(0)0f =.取1x n =,当2n ≥时,211(1)ln(1)05n n n++-<成立;当1n =时,277(1)ln 21ln 210.710555+-=-<⨯-<.从而对于任意正整数n 都有211(1)ln(1)05n n n ++-<成立.对于()q 相当于(2)中12a =-情形,对于任意x ∈[0,1],恒有()0f x ≥而且仅有(0)0f =. 取1x n=,得:对于任意正整数n 都有111(1)ln(1)02n n n++->成立.因此对于任意正整数n ,不等式215211(1)(1)n n e n n+++<<+恒成立. 这样依据不等式215211(1)(1)n n e n n+++<<+,再令10000n =利用左边,令1000n = 利用右边,即可得到10000.41000.5100011001()()100001000e <<成立. (12分) 22. (本小题满分10分)【命题意图】本小题主要考查平面几何的证明,具体涉及到弦切角定理以及三角形 相似等内容.本小题重点考查考生对平面几何推理能力.【试题解析】解:(1) 由题意可知,EPC APC ∠=∠,PEB PAC ∠=∠,则△PED ∽△PAC ,则PE PD PA PC =,又PE ED PB BD =,则ED PB PDBD PA PC⋅=. (5分) (2) 由EPC APC ∠=∠,PEB PAC ∠=∠,可得CDE ECD ∠=∠, 在△ECD 中,30CED ∠=,可知75PCE ∠=. (10分)23. (本小题满分10分)【命题意图】本小题主要考查极坐标系与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、利用直线的参数方程的几何意义求解直线与曲线交点的距离等内容. 本小题考查考生的方程思想与数形结合思想,对运算求解能力有一定要求.【试题解析】解:(1) 对于曲线1C 有1x y +=,对于曲线2C 有2214x y +=.(5分) (2) 显然曲线1C :1x y +=为直线,则其参数方程可写为21x y ⎧=⎪⎪⎨⎪=-⎪⎩(t 为参数)与曲线2C :2214x y +=联立,可知0∆>,所以1C 与2C 存在两个交点,由125t t +=,1285t t =,得21||5d t t =-==. (10分) 24. (本小题满分10分)【命题意图】本小题主要考查不等式的相关知识,具体涉及到绝对值不等式及 不等式证明等内容. 本小题重点考查考生的化归与转化思想.【试题解析】解:(1) 当3a =时,174,213()5,22341,2x x f x x x x ⎧-≤⎪⎪⎪=<<⎨⎪⎪-≥⎪⎩,所以()7f x >的解集为{|0x x <或2}x >.(5分)(2) ()|21||2||212||1|f x x a x a x a x a a a =-+-+≥-+-+=-+, 由()3f x ≥恒成立,有|1|3a a -+≥,解得2a ≥ 所以a 的取值范围是[)2,+∞.(10分)。
2015北京各区中考数学二模25题全面总结及答案

2015北京各区中考数学25题汇编及答案25.如图,Rt △ABC 中,∠A =90°,以AB 为直径的⊙O 交BC 于点D ,点E 在⊙O 上, CE =CA , AB ,CE 的延长线交于点F . (1) 求证:CE 与⊙O 相切;(2) 若⊙O 的半径为3,EF =4,求BD 的长.25.如图1,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,点F 在线段ED 上.连接AF 并延长交 ⊙O 于点G ,在CD 的延长线上取一点P ,使PF=PG .(1)依题意补全图形,判断PG 与⊙O 的位置关系,并证明你的结论;(2)如图2,当E 为半径OA 的中点,DG ∥AB,且OA PG 的长.25.如图,已知AB 是⊙O 的直径,C 是⊙O 上一点,∠BAC 的平分线交⊙O 于 点D ,交⊙O 的切线BE 于点E ,过点D 作DF ⊥AC ,交AC 的延长线于点F . (1)求证:DF 是⊙O 的切线;F(2)若DF =3,DE =2.①求值;②求FAB ∠的度数.25.如图,点A B C D E 、、、、在⊙O 上,AB CB ⊥于点B ,tan 3D =,2BC=,H为CE 延长线上一点,且AH =CH =(1)求证:AH 是⊙O 的切线;(2)若点D 是弧CE 的中点,且AD 交CE 于点F ,求EF 的长.25.如图,⊙O 是△ABC 的外接圆,AB= AC ,BD 是⊙O的直径,P A ∥BC ,与DB 的延长线交于点P ,连接AD . (1)求证:P A 是⊙O 的切线;(2)若BC =4 ,求AD 的长.25.如图,△ABC 中,AB =AC ,点D 为BC 上一点,且AD =DC ,过A ,B ,D 三点作⊙O ,AE是⊙O 的直径,连结DE . (1)求证:AC 是⊙O 的切线;BEADCC(2)若4sin 5C =,AC =6,求⊙O 的直径.25.如图,AB 是⊙O 的直径.半径OD 垂直弦AC 于点E .F 是BA 延长线上一点,CDB BFD ∠=∠.(1)判断DF 与⊙O 的位置关系,并证明; (2)若AB =10,AC =8,求DF 的长.25.如图,AB 是⊙O 的直径,以AB 为边作△ABC ,使得AC = AB ,BC 交⊙O 于点D ,联结OD ,过点D 作⊙O 的切线,交AB 延长线于点E ,交AC 于点F .25.如图,⊙O 为△ABC 的外接圆,BC 为⊙O 的直径,AE 为⊙O 的切线,过点B 作BD ⊥AE 于D .(1)求证:∠DBA =∠ABC ;(2)如果BD =1,tan ∠BAD =12,求⊙O 的半径.25.如图,AB 是⊙O 的直径,点C 是⊙O 上一点, AD ⊥ DC 于D , 且AC 平分∠DAB ,延长DC 交AB 的延长线于点P ,弦CE 平分∠ACB ,交AB 于点F ,连接BE . (1)求证:PD 是⊙O 的切线; (2)若tan ABC =43∠,BE =PC 的长.25.如图,△ABC 内接于⊙O ,OC ⊥AB 于点E ,点D 在OC 的延长线上,且∠B =∠D =30°.(1)求证:AD 是⊙O 的切线;(2)若AB =求⊙O 的半径.25.如图,已知,⊙O 为△ABC 的外接圆,BC 为直径,点E 在AB 边上,过点E 作EF ⊥BC ,延长FE 交⊙O 的切线AG 于点G . (1)求证:GA =GE .PE(2)若AC =6,AB =8,BE =3,求线段OE 的长.答案25.(本小题满分5分) 证明:连接OE ,OC .在△OEC 与△OAC 中, ,,,OE OA OC OC CE CA =⎧⎪=⎨⎪=⎩F∴△OEC ≌△OAC . (1)分∴∠OEC =∠OAC .∵∠OAC =90°,∴∠OEC =90°. ∴OE ⊥CF 于E . ∴CF与⊙O相切.………………………………………………………………………………...2分(2)解:连接AD .∵∠OEC =90°, ∴∠OEF =90°. ∵⊙O 的半径为3, ∴OE =OA=3.在Rt △OEF 中,∠OEF =90°,OE = 3,EF = 4,∴5OF ,………………………………………………………………………3分3tan 4OE F EF ==. 在Rt △F AC 中,∠F AC =90°,8AF AO OF =+=, ∴tan 6AC AF F =⋅=.…………………………………………………………………………4分∵AB 为直径,∴AB =6=AC ,∠ADB =90°. ∴BD =2BC. 在Rt △ABC 中,∠BAC =90°,∴BC =F∴BD=.…………………………………………………………………………………….5分25. 解:(1)补全图形如图5所示. ………………………………………………………… 1分 答:PG 与⊙O 相切. 证明:如图6,连接OG .∵ PF =PG , ∴ ∠1=∠2.又∵OG =OA , ∴ ∠3=∠A .∵ CD ⊥AB 于点E , ∴ ∠A +∠AFE =90°. 又∵∠2 =∠AFE ,∴ ∠3+∠1=90°. ……………………… 2分 即 OG ⊥PG . ∵ OG 为⊙O 的半径,∴ PG 与⊙O 相切. …………………… 3分(2)解:如图7,连接CG . ∵ CD ⊥AB 于点E ,∴ ∠OEC =90°. ∵ DG ∥AB ,∴∠GDC =∠OEC =90°. ∵∠GDC 是⊙O 的圆周角, ∴ CG 为⊙O 的直径. ∵ E 为半径OA 的中点, ∴ 22OA OCOE ==. ∴ ∠OCE =30°即∠GCP =30°.又∵∠CGP =90°,2CG OA ==A∴tan 4PG CG GCP =⋅∠==. …………………………… 5分25. (1)连结OD , ∵AD 平分∠BAC ∴∠DAF =∠DAO ∵OA =OD ∴∠OAD =∠ODA ∴∠ DAF =∠ODA ∴AF ∥OD .┉┉1分 ∵DF ⊥AC ∴OD ⊥DF ∴DF 是⊙O 的切线┉┉2分 (2)①连接BD ∵直径AB , ∴∠ADB =90° ∵圆O 与BE 相切 ∴∠ABE =90°∵∠DAB +∠DBA =∠DBA +∠DBE =90° ∴∠DAB =∠DBE ∴∠DBE =∠F AD ∵∠BDE=∠AFD =90° ∴△BDE ∽△AFD ∴32==DF DE AD BE ┉┉3分 ②连接OC ,交AD 于G 由①,设BE =2x ,则AD =3x ∵△BDE ∽△ABE ∴BE DE AE BE =∴xx x 22232=+∵AB BC ⊥于点B∴AC 是⊙O 的直径…………………………………1分 ∵D ACB ∠=∠,∴tan tan 3D ACB =∠= 在Rt ABC ∆中,2BC =,∴36AB BC == 由勾股定理AC =在CAH ∆中,由勾股定理逆定理:22250AC AH CH +==∴90CAH ∠=°即CA AH ⊥∴AH 是⊙O 的切线…………………………………2分 (2)解:∵点D 是弧CE 的中点∴EAD DAC ∠=∠…………………………………3分 ∵AC 是⊙O 的直径 ∴AE CH ⊥∴90H EAH H HCA ∠+∠=∠+∠=° ∴EAH HCA ∠=∠∴EAD EAH DAC HCA ∠+∠=∠+∠ 即AFH HAF ∠=∠∴HF HA =∵CA AH ⊥AE CH ⊥∴2AH EH CH =⨯可得EH = ∴EF =5分25.(1)证明:连接OA 交BC 于点E ,由AB =AC 可得OA ⊥BC .………………………1分C B∵PA ∥BC , ∴∠PAO =∠BEO =90°. ∵OA 为⊙O 的半径,∴PA 为⊙O 的切线. …………………………… 2分 (2)解:根据(1)可得CE =21BC=2. Rt △ACE 中,122=-=CE AC AE . ………………………………3分∴tan C =21=CE AE . ∵BD 是直径,∴∠BAD =90°.…………………………………………………………4分 又∵∠D =∠C , ∴AD =52tan =DAB.………………………………………………………5分25. (1)证明:∵AB =AC ,AD =DC ,∴∠1=∠C =∠B ,..................................................1分 又∵∠E =∠B ,∴∠1=∠E , ∵AE 是⊙O 的直径,∴∠ADE =90°, ∴∠E +∠EAD =90°, ∴∠1+∠EAD =90°,∴AC 是⊙O 的切线............................................2分 (2)解:过点D 作DF ⊥AC 于点F , ∵DA =DC ,AC =6, ∴CF =12AC =3,..................................... ............3分 ∵4sin 5E =,∴4sin 5C =, ∴在Rt △DFC 中,DF =4,DC =5, ∴AD =5,∵∠ADE =∠DFC =90°,∠E =∠C ,∴△ADE ∽△DFC ,.............................................4分C∴AD DFAE DC =, ∴545AE =, ∴AE =254,∴⊙O 的直径为254.....................5分25.解:(1)DF 与⊙O 相切. ∵CAB CDB ∠=∠, 又∵CDB BFD ∠=∠,∴BFD CAB ∠=∠. ∴AC ∥DF . ………………………………… 2分∵半径OD 垂直于弦AC 于点E ,∴DF OD ⊥. ∴DF 与⊙O 相切. ………………………………… 3分 (2)∵半径OD 垂直于弦AC 于点E ,AC =8,∴482121=⨯==AC AE . ∵AB 是⊙O 的直径, ∴5102121=⨯===AB OD OA . 在AEORt ∆中,3452222=-=-=AE OA OE . ……………………………………… 4分∵AC ∥DF , ∴OAE ∆∽OFD ∆. ∴DF AEOD OE = . ∴DF453=. ∴321DF CEB A O320=DF . ………………………………………………… 5分25.(1)证明:联结AD .∵AB 是⊙O 的直径,∴∠ADB =90°,AD ⊥BC .∵AC = AB ,∴12∠=∠.…….1分 ∵OA OD =,∴13∠=∠. ∴23∠=∠,∴OD ∥AC .…….2分(2)∵AC = AB =10,∴B C ∠=∠.∴cos C=cos 5ABC ∠=. 在Rt △ABD 中,∠ADB =90°,cos 5BD ABC AB ∠==, ∴BDCD = BD….3分∵EF 为⊙O 的切线,∴OD ⊥EF ,由∵OD ∥AC ,∴∠DFC =90°. …….4分 在Rt △CDF 中,cos C=5CF CD =,∴CF =2.∴AF =8. ∵OD ∥AC ,∴ODE ∆∽AFE ∆.∴OE OD AE AF =.∴OB BE ODAB BE AF+=+. ∵152OB OA OD AB ====,∴103BE =.…….5分 25.(本小题满分5分)(1)证明:连接OA .(如图)∵ AE 为⊙O 的切线,BD ⊥AE , ∴ ∠DAO =∠EDB =90°. ∴ DB ∥AO .∴ ∠DBA =∠BAO . …………1分 又 ∵OA =OB , ∴ ∠ABC =∠BAO .∴ ∠D B A =∠A B C . ………………………………………………2分(2)在Rt △ADB 中,∠ADB =90°,C∵ BD =1,tan ∠BAD =12, ∴ AD =2,……………………………………………………………………3分由勾股定理得AB .∴ cos ∠DBA 又∵ BC 为⊙O 的直径, ∴ ∠BAC =90°. 又∵∠DBA =∠ABC .∴ cos ∠ABC = cos ∠DBA∴ 5.cos ABBC ABC===∠…………………………………………4分 ∴ ⊙O 的半径为5.2…………………………………………………………5分25.解:(1)∵ OC =OA∴ ∠CAO =∠OCA ∵ AC 平分∠DAB ∴ ∠DAC =∠CAO , ∴ ∠ACO =∠DAC . ∴ OC ∥AD .…………………………………………………………………….1分 ∵ AD ⊥PD , ∴OC ⊥PD . ∴ PD 是⊙O 的切线……………………………………………………………...2分(2)连接AE .∵CE 平分∠ACB ,∴AE BE =,∴AE BE == ∵AB 为⊙O 的直径, ∴∠AEB =90°.在Rt △ABE 中,14AB =………………………………………3分 ∵ ∠P AC =∠PCB ,∠P =∠P , ∴ △P AC ∽△PCB , ∴ PC AC PB BC =.…………………………………………………………………..4分 又∵4tan 3ABC =∠,∴43AC PCBC PB==, 设PC =4k ,PB =3k ,则在Rt △POC 中,PO =3k +7,OC =7,∵ PC 2+OC 2=OP 2, ∴()()2224737k k +=+, ∴ 126,0k k ==(舍去).∴ PC =4k =4×6=24. …………………………………………………………..5分25证明:(1)连接OA .∵∠B =∠D =30°,∴∠AOC =2∠B =60°,……………………….(1分) ∴∠OAD =180°-∠AOD -∠D =90°,…………….(2分) 即OA ⊥AD ,∴AD 是⊙O 的切线.……………….(3分)(2)∵OA =OC ,∠AOC =60°,∴△ACO 是等边三角形, ∵CO ⊥AB ∴ ……………………….(4分)在Rt △ABC 中∴⊙O 的半径为6.……………………………….(5分)1122AE AB ==⨯=sin sin60AEACE AC∠==︒6AC ===。
二模试题和答案

2015年中考第二次模拟考试英语科试题第一部分听力部分(共25分)一、听力理解(本大题分为A、B、C、D四部分,共25小题,每小题1分,共25分)A.听句子(共5小题,每小题1分,共5分)根据所听句子的内容和所提的问题,选出符合题意的图片回答问题,并将答案写在题前的括号内。
每小题听一遍。
( )1. How does Susan go to work?A B C( )2.What kind of clothes does the girl like?A B C( )3. What’s the boy’s favourite hobby?A B C( )4. What can be seen everywhere?A B C( )5. Where did the girl go last year?A B CB.听对话(共10小题,每小题1分,共10分)根据所听对话的内容和所提的问题,在各题所给的三个选项中选出一个最佳选项,并将答案写在题前的括号内。
每段对话听两遍。
听第一段对话,回答第6小题。
()6.Who is the man?A.Kevin’s teacher. B.Kevin’s father. C.Kevin’s brother.听第二段对话,回答第7小题。
()7.What size does the girl want?A.Size L. B.Size M. C.Size S.听第三段对话,回答第8小题。
()8.Why does the man like the red house?A.Because it has a big yard. B.Because it is beautiful. C.Because he likes red.听第四段对话,回答第9小题。
()9.What is the weather like now?A.Sunny.B.Cloudy. C.Rainy.听第五段对话,回答第10小题。
2015年上海各区二模数学卷88页

接填写结果,每题填对得 4 分,否则一律得零分.
1.函数 f ( x) lg( x 3) (x 2) 0 的定义域是
.
x1
2.函数 y log2 (x2 1)的单调递减区间是
.
2
3.已知集合 A x | x 16 0, x R , B x | x 3 a, x R ,若 B A ,则正实数 a 的
取值范围是
将它们充分混合后, 摸得一个白球计 2 分,摸得一个红球记 3 分,摸得一个黄球计 4 分,若
用随机变 量 表示随机摸一个 球的 得分, 则随机 变量 的数学期望 E 的值 是
分.
(文科 ) 一个不透明的袋中装有大小形状质地完全相同的黑球、红球、白球共
意摸出 1 个球,得到黑球的概率是 2 ,则从中任意摸出 2 个球得到至少 5
C.如果直线 l// 平面 且 l // 平面 ,那么 // D.若直线 a 与平面 M 没有公共点,则直线 a //平面 M
16.设实数 a1, a2 ,b1, b2 均不为 0,则“ a1 a2
b1 成立”是“关于 x 的不等式 a1x b1 0 与 b2
a2 x b2 0
的
[答] ( ) . A .充分非必要条件
.
4 . 若 二 次 函 数 y 2x 2 (m 2) x 3m2 1 是 定 义 域 为 R 的 偶 函 数 , 则 函 数
f ( x) xm mx 2( x 1, x R) 的反函数 f 1(x) =
5.已知角 的顶点与平面直角坐标系的原点重合,始边在
P 3a,4 a (a 0, a R) ,则 cos 2 的值是
是
.
二、选择题 (本大题满分 20 分 ) 本大题共有 4 题,每题有且只有一个正确答案,考生应在
2015年高三二模理综试卷及答案(北京市西城区)

北京市西城区2015年高三二模试卷理科综合能力测试2015.5本试卷分为选择题和非选择题两个部分,选择题1-5页,非选择题6-16页,共300分.考试时长150分钟.考生务必将答案填写在答题卡上和答题纸的相应区域内,在试卷上作答无效.考试结束后,将本试卷及答题卡和答题纸一并交回.可能用到的相对原子质量:Mg24 Si28 H1 N14 O16一、选择题(共20题每小题6分共120分)在每小题列出的四个选项中,选出符合题目要求的一项.1.下列有关细胞的叙述错误的是()A.大肠杆菌基因的转录仅发生在拟核区B.蓝藻没有叶绿体,但可以进行光合作用C.乳酸菌与醋酸杆菌异化作用类型不同D.酵母菌的细胞核和线粒体内可进行复制DNA2.下图为苯丙氨酸部分代谢途径示意图。
苯丙酮尿症是由于苯丙氨酸羟化酶基因突变所致。
患者的苯丙氨酸羟化酶失活,苯丙氨酸转化为酪氨酸受阻,组织细胞中苯丙氨酸和苯丙酮酸蓄积,表现为智力低下、毛发与皮肤颜色较浅等症状。
下列分析错误的是()A.一个基因可能会影响多个性状表现B.生物的一个性状只受一个基因的控制C.基因可通过控制酶的合成控制代谢过程,进而控制性状D.在婴幼儿时期限制对苯丙氨酸的摄入可缓解患者的病症3.为研究交感神经和副交感神经对心脏的支配作用,分别测定狗在正常情况、阻断副交感神经和阻断交感神经后的心率,结果如下表所示。
下列分析错误的是()A.副交感神经兴奋引起心脏搏动减慢B.对心脏支配占优势的是副交感神经C.交感神经和副交感神经的作用是相互协同的D.正常情况下,交感神经和副交感神经均可检测到膜电位变化CO(g)MgO(s)下列说法正确的是A.0~2 min内的平均速率为υ (CO)=0.6 mol/(L·min)B.4 min后,平衡移动的原因可能是向容器中加入了2.0 mol的SO2C.若升高温度,反应的平衡常数变为1.0,则正反应为放热反应D.其他条件不变,若起始时容器中MgSO4、CO均为1.0 mol,则平衡时n(SO2)=0.6 molPO HCl+HClO①灼烧Mg(OH)2 得到MgO的化学方程式是______。
2015西城二模试题及答案

北京市西城区2015年初三二模试卷语文 2015.6考生须知1.本试卷共8页,共四道大题,24道小题。
满分120分。
考试时间150分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和学号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题用2B铅笔作答,其他试题用黑色字迹签字笔作答。
一、基础·运用(共22分)(一)选择。
下面各题均有四个选项,其中只有一个..符合题意,选出答案后在答题卡上用铅笔把对应题目的选项字母涂黑涂满。
(共10分)成语是经过长期锤炼而形成的汉语言文化精髓.,它浓缩了中国古代传统文化的精华,承载着历代华夏儿女千百年来形成的处世哲学。
成语多来源于寓言故事,神话传说,古典诗文,也有些源自民间惯用语,谚语,歇后语等,是中华民族宝贵的文化遗产,堪称中华文化的“活化石”。
它言简意赅,以简驭繁,以极少的文字传达丰富的内涵,成为汉语言文化中的一道亮丽风景。
人们讲话、写文章都喜欢运用成语,是由于成语除了(甲),还(乙)。
而最能体现后者的,莫过于比喻的运用。
成语的比喻用法大致有两种情况。
一种是明显的比喻。
例如“如虎添翼”“门庭若市”“归心似箭”“味同嚼蜡”等,特点是带有“如”“若”“似”“同”这类比喻词。
因此不管放在什么语言环境里,一眼就能看出是比喻。
这类成语生动形象,表达效果值得__①__。
更多的一种情况是运用成语的比喻意义。
什么叫“成语的比喻意义”呢?那就是一个成语由于它的比喻用法而逐渐形成并固定下来的意义。
如“完(bì)归赵”出自蔺相如设法把国宝从秦国送回赵国的历史故事,后用来比喻原物完整无损地归还本人,这一比喻义用得多了,得到社会认可,就作为这个成语的固定意义确定下来了。
运用这类成语不仅能收到比喻的表达效果,还能提升语言的文化__②__。
1.文中加点字“髓”的注音和“完(bì)归赵”注音处应填入的汉字正确的一项是A.髓(sǔi)壁(声旁为“辟”,形旁为“土”)B.髓(suǐ)璧(声旁为“辟”,形旁为“玉”)C.髓(suǐ)壁(声旁为“辟”,形旁为“土”)D.髓(sǔi)璧(声旁为“辟”,形旁为“玉”)2.根据句意,依次填入①②两处的词语,最恰当的一项是A.①品位②品味 B.①品味②品味C.①品位②品位 D.①品味②品位3.对文中画线句标点修改正确的一项是A.成语多来源于寓言故事,神话传说,古典诗文;也有些源自民间惯用语、谚语、歇后语等B.成语多来源于寓言故事,神话传说,古典诗文。
北京2015年高三二模(理)试题分类汇编-集合

北京2015届高三二模试题分类汇编(理科)专题:集合一、 选择题。
(1)(2015年海淀区高三二模理科)已知全集U Z =,集合{1,2}A =,{1,2,3,4}A B =U ,那么()U C A B I =()(A )∅ (B ){3}x x Z ∈≥ (C ){3,4} (D ){1,2}(2)(2015年西城高三二模理科)设集合{|10}A x x =->,集合3{|}B x x =≤,则A B = ()(A )(1,3)-(B )(1,3] (C )[1,3) (D )[1,3]-(3)(2015年朝阳区高三二模理科)已知集合{}21A x x =>,集合{}(2)0B x x x =-<,则A B = A .{}12x x << B.{}2x x >C .{}02x x <<D .{1x x ≤,或}2x ≥(4)(2015年丰台区高三二模理科)已知{1}A x x =>,2{20}B x x x =-<,则A B = (A){0x x <或1}x ≥(B) {12}x x <<(C){0x x <或1}x >(D) {0}x x >(5)(2015年昌平区高三二模理科)已知集合{}2340A x x x =--=,{}0,1,4,5B =,则A B 中元素的个数为A .0个 B. 1个 C. 2个 D. 3个二、填空题。
(1)(2015年朝阳区高三二模理科)设集合{}{}123(,,)2,0,2,1,2,3i A m m m m i =?=,集合A 中所有元素的个数为;集合A 中满足条件“12325m m m ?+?”的元素个数为.(2)(2015年丰台区高三二模理科)已知非空集合A ,B 满足以下四个条件:①{1,2,3,4,5,6,7}A B = ;②A B =∅ ;③A 中的元素个数不是A 中的元素;④B 中的元素个数不是B 中的元素.(ⅰ)如果集合A 中只有1个元素,那么A =______;(ⅱ)有序集合对(A ,B )的个数是______.【答案与解析】一、 选择题。
上海2015二模试卷含答案(二套)
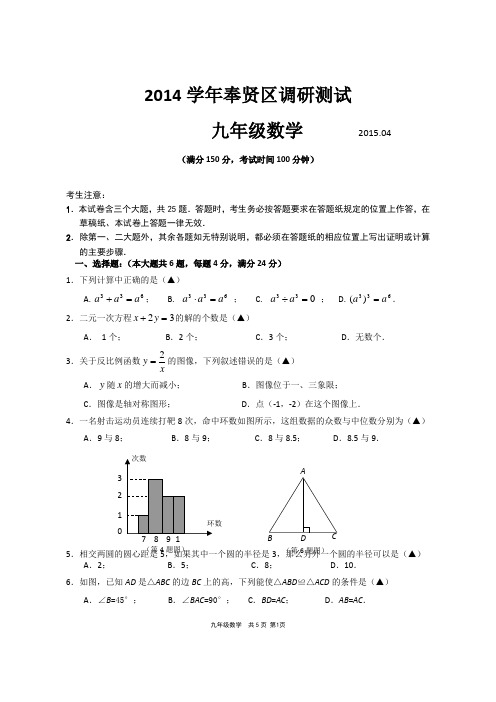
九年级数学 共5页 第1页2014学年奉贤区调研测试九年级数学 2015.04(满分150分,考试时间100分钟)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分) 1.下列计算中正确的是(▲)A .633a a a =+; B .633a a a =⋅ ; C .033=÷a a ; D .633)(a a =. 2.二元一次方程32=+y x 的解的个数是(▲)A . 1个;B .2个;C .3个;D .无数个. 3.关于反比例函数xy 2=的图像,下列叙述错误的是(▲) A .y 随x 的增大而减小; B .图像位于一、三象限;C .图像是轴对称图形;D .点(-1,-2)在这个图像上.4.一名射击运动员连续打靶8次,命中环数如图所示,这组数据的众数与中位数分别为(▲)A .9与8;B .8与9;C .8与8.5;D .8.5与9.5.相交两圆的圆心距是5,如果其中一个圆的半径是3,那么另外一个圆的半径可以是(▲)A .2;B .5;C .8;D .10. 6.如图,已知AD 是△ABC 的边BC 上的高,下列能使△ABD ≌△ACD 的条件是(▲)A .∠B =45°;B .∠BAC =90°;C .BD =AC ;D .AB =AC .(第4题图)DCB A(第6题图)九年级数学 共5页 第2页二、填空题:(本大题共12题,每题4分,满分48分) 7.用代数式表示:a 的5倍与b 的27的差: ▲ ; 8.分解因式:1522--x x = ▲ ; 9.已知函数3+=x x f )(,那么=-)(2f ▲ ;10.某红外线遥控器发出的红外线波长为0.000 000 94m ,这个数用科学记数法表示为 ▲ ; 11.若关于x 的方程022=--k x x 有两个不相等的实数根,则k 的取值范围为 ▲ ; 12.布袋中装有2个红球和5个白球,它们除颜色外其它都相同.如果从这个布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是 ▲ ;13.已知函数b x y +-=2,函数值y 随x 的增大而▲ (填“增大”或“减小”); 14.如果正n 边形的中心角是40°,那么n = ▲ ;15.已知△ABC 中,点D 在边BC 上,且BD =2DC .设AB a = ,=,那么AD →等于▲ (结果用、表示);16.小明乘滑草车沿坡比为1:2.4的斜坡下滑130米,则他下降的高度为▲米;17.我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等 腰三角形的腰长为2,“内角正度值”为45°,那么该三角形的面积等于 ▲ ;18.如图,已知钝角三角形ABC ,∠A=35°,OC 为边AB 上的中线,将△AOC 绕着点O 顺时针旋转,点C 落在BC 边上的点'C 处,点A 落在点'A 处,联结'BA ,如果点A 、C 、'A 在同一直线上,那么∠''C BA 的度数为 ▲ ;三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 计算:1o )12(45cos 22218-++--+.CBOA (第18题图)九年级数学 共5页 第3页20.(本题满分10分)解不等式组:⎪⎩⎪⎨⎧-≤-+<-x x x x 2371211513)(,将其解集在数轴上表示出来,并写出这个不等式组的最.小整数解.....21.(本题满分10分,每小题满分各5分)已知:如图,在△ABC 中,AB=AC =6,BC =4,AB 的垂直 平分线交AB 于点E ,交BC 的延长线于点D . (1)求∠D 的正弦值; (2)求点C 到直线DE 的距离.CB A(第21题图)EDS22.(本题满分10分)某学校组织为贫困地区儿童捐资助学的活动,其中七年级捐款总数为1000元,八年级捐款总数比七年级多了20%.已知八年级学生人数比七年级学生人数少25名,而八年级的人均捐款数比七年级的人均捐款数多4元.求七年级学生人均捐款数.23.(本题满分12分,每小题满分各6分)已知:如图,在四边形ABCD中,AB//CD,点E是对角线AC上一点,∠DEC=∠ABC,且CACECD⋅=2.(1)求证:四边形ABCD是平行四边形;(2)分别过点E、B作AB和AC的平行线交于点F,联结CF,若∠FCE=∠DCE,求证:四边形EFCD是菱形.D BA九年级数学共5页第4页九年级数学 共5页 第5页24.(本题满分12分,第(1)小题4分,第(2)小题8分)已知:在平面直角坐标系中,抛物线x ax y +=2的对称轴为直线x =2,顶点为A . (1)求抛物线的表达式及顶点A 的坐标; (2)点P 为抛物线对称轴上一点,联结OA 、OP .①当OA ⊥OP 时,求OP 的长;②过点P 作OP 的垂线交对称轴右侧的抛物 线于点B ,联结OB ,当∠OAP =∠OBP 时, 求点B 的坐标.九年级数学 共5页 第6页25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)已知:如图,线段AB =8,以A 为圆心,5为半径作圆A ,点C 在⊙A 上,过点C 作CD //AB 交⊙A 于点D (点D 在C 右侧),联结BC 、AD . (1)若CD=6,求四边形ABCD 的面积;(2)设CD =x ,BC =y ,求y 与x 的函数关系式及自变量x 的取值范围;(3)设BC 的中点为M ,AD 的中点为N ,线段MN 交⊙A 于点E ,联结CE ,当CD 取何值时,CE //AD .DCB (第25题图)AB(备用图)A九年级数学 共5页 第7页奉贤区初三调研考数学卷参考答案 201504一 、选择题:(本大题共8题,满分24分)1.B ; 2.D ; 3.A ; 4.C ; 5.B ; 6.D . 二、填空题:(本大题共12题,满分48分) 7.b a 725-; 8.)3)(5(+-x x ; 9.1; 10.7104.9-⨯; 11.1->k ; 12.72; 13.减小; 14.9; 15.32+; 16.50; 17.2或1; 18.20°. 三.(本大题共7题,满分78分) 19. (本题满分10分)解:原式=1222223-+--+. (2)= 122+. ………………………………………………………………………2分20.(本题满分10分)解:由①得:2x >- .………………………………………………………………………2分 由②得:4x ≤.………………………………………………………………………2分 所以,原不等式组的解集是24x -<≤.……………………………………………2分 数轴上正确表示解集.………………………………………………………………2分 所以,这个不等式组的最小整数解是-1.…………………………………………2分21. (本题满分10分)(1)过点A 作AH ⊥BC 于点H ………………………………………………………………1分 ∵ AB=AC ,BC =4 ∴BH =21BC =2 在△ABH 中,∠BHA=90°, ∴sin ∠BAH =31=AB BH …………………………………2分∵ DE 是AB 的垂直平分线 ∴∠BED=90° BE=3∴∠BED=∠BHA又∵∠B=∠B ∴∠BAH=∠D …………………………………………………1分九年级数学 共5页 第8页∴sin ∠D= sin ∠BAH=13……………………………………………………………1分 即∠D 的正弦值为13(2)解:过点C 作CM ⊥DE 于点M ………………………………………………………1分在△BED 中,∠BED=90°,sin ∠D =13,BE=3 ∴BD =9sin =∠DBE∴CD=5………………………………………………2分在△MCD 中,∠CMD=90°,sin ∠D =31=CD CM ∴CM=35.…………………2分 即点C 到DE 的距离为3522.(本题满分10分)解:设七年级人均捐款数为x 元,则八年级人均捐款数为)4(+x 元 .…………………1分根据题意,得4%)201(1000251000++=-x x .……………………………………4分 整理,得 0160122=-+x x .……………………………………………1分解得 20,821-==x x .……………………………………………………2分 经检验:20,821-==x x 是原方程的解,0202<-=x 不合题意,舍去.…………1分 答:七年级人均捐款数为8元.……………………………………………………………1分 23.(本题满分12分,每小题满分各6分) 证明:(1)CA CE CD ⋅=2 ∴CACDCD CE =∵∠ECD =∠DCA ∴△ECD ∽△DCA ……………………………………………2分 ∴∠ADC =∠DEC ∵∠DEC =∠ABC ∴∠ABC =∠ADC …………………1分∵AB ∥CD ∴∠ABC+∠BCD=1800 ∠BAD+∠ADC =1800∴∠BAD =∠BCD ………………………………………………………………………2分 ∴四边形ABCD 是平行四边形………………………………………………………1分(2)∵EF ∥AB BF ∥AE ∴四边形ABFE 是平行四边形∴ AB ∥EF AB=EF …………………………………………………………………2分 ∵四边形ABCD 是平行四边形∴AB ∥CD AB=CD九年级数学 共5页 第9页∴CD ∥EF CD=EF∴四边形EFCD 是平行四边形 ………………………………………………………2分 ∵CD ∥EF ∴∠FEC=∠ECD 又∵∠DCE=∠FCE ∴∠FEC=∠FCE ∴EF=FC∴平行四边形EFCD 是菱形 …………………………………………………………2分24.(本题满分12分,每小题4分)(1)∵ 抛物线x ax y +=2的对称轴为直线x =2.∴221=-a ∴41-=a .……………………………………………………………1分 ∴抛物线的表达式为:x x y +-=241.…………………………………………………1分 ∴顶点A 的坐标为(2,1). ……………………………………………………………2分(2)设对称轴与x 轴的交点为E .①在直角三角形AOE 和直角三角形POE 中,AE OE OAE =∠tan ,OEPEEOP =∠tan ∵OA ⊥OP ∴EOP OAE ∠=∠ ∴OEPEAE OE =……………………………2分 ∵AE =1,OE=2 ∴PE=4…………………………………………………………1分 ∴OP=524222=+……………………………………………………………1分②过点B 作AP 的垂线,垂足为F ………………………………………………………1分 设点B (a a a +-241,),则2-=a BF ,a a EF -=241 在直角三角形AOE 和直角三角形POB 中,OE AE OAE =∠cot ,OPBPOBP =∠cot ∵OBP OAE ∠=∠, ∴21==OP BP OE AE ∵PEO BFP ∠=∠,POE BPF ∠=∠∴△BPF ∽△POE ,∴OEPFPO BP PE BF == ∵OE=2, ∴PF=1,1412+-=a a PE ∴2114122=+--a a a九年级数学 共5页 第10页解得101=a ,22=a (不合题意,舍去)…………………………………………2分 ∴点B 的坐标是(10,-15).……………………………………………………………1分 25.解:(1)作AH ⊥CD ,垂足为点H ……………………………………………………1分∵ CD=6∴321===CD DH CH …………………………………………………1分 ∵AD=5∴AH=4………………………………………………………………1分∴28)(21=⋅+=AH AB CD S ABCD 梯形……………………………………………1分 (2)作CP ⊥AB ,垂足为点P ∵⊙A 中,AH ⊥CD ,CD=x∴x CH 21=∴x CH AP 21==…………… ………………………………1分 ∴x BP 218-=……………………………… ………………………………1分 222DH AD AH AHD Rt -=∆中,24125x -=∴2224125x AH CP -==…………………… ………………………………1分 在222BP CP BC BPC Rt +=∆中, 即222)218()4125(x x y -+-= 解得:()100889≤<-=x xy ………………………………………………2分(3)设AH 交MN 于点F ,联结AE∵BC 的中点为M ,AD 的中点为N ∴MN ∥CD∵CE ∥AD ∴DC=NE=x ………………………………………………………………1分 ∵MN ∥CD ∴AD AN DH NF =∵ 2xDH = ∴4x NF = ∴43x EF =……1分 在直角三角形AEF 和直角三角形AFN 中222EF AE AF -=222NF AN AF -= ∴2222)43(5)4()25(x x -=-∴265=x …………………………………………………………………2分 即当CD 长为265时,CE//AD .九年级数学 共5页 第11页崇明县2014学年第二学期教学质量调研测试卷九年级数学(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效. 3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.下列运算中,正确的是 ……………………………………………………………………( )(A)1293=±3 (C)030-=() (D)2139-=2.轨道交通给人们的出行提供了便捷的服务,据悉,上海轨道交通19号线即将开建,一期规划为自川桥路站至长兴岛,设6站,全长约为20600米.二期、远期将延伸到崇明岛、横沙岛,届时崇明县三岛将全通地铁.将20600用科学记数法表示应为 ………………………( )(A)52.0610⨯(B)320.610⨯(C)42.0610⨯(D)50.20610⨯3.从下列不等式中选择一个与12x +≥组成不等式组,如果要使该不等式组的解集为1x ≥,那么可以选择的不等式可以是 ………………………………………………………………( ) (A)1x >-(B)2x >(C)1x <-(D)2x <4.已知点11(,)A x y 和点22(,)B x y 是直线23y x =+上的两个点,如果12x x <,那么1y 与2y 的大小关系正确的是……………………………………………………………………………( )(A)12y y >(B)12y y <(C)12y y =(D)无法判断5.窗花是我国的传统艺术,下列四个窗花图案中,不是..轴对称图形的是…………………( )(A)(B) (C) (D)6.已知在四边形ABCD 中,AC 与BD 相交于点O ,那么下列条件中能判定这个四边形是正方形的是 ………………………………………………………………………………………( )九年级数学 共5页 第12页(A)AC BD =, AB CD ∥, AB CD = (B)AD BC ∥, A C ∠=∠(C)AO BO CO DO ===, AC BD ⊥(D)AO CO =, BO DO =, AB BC =九年级数学 共5页 第13页二、填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】 7.因式分解:34x x -= ▲ .8.2,那么x = ▲ .9.如果分式242x x -+的值为0,那么x 的值为 ▲ .10.已知关于x 的一元二次方程2610x x m -+-=有两个相等的实数根,那么m 的值为 ▲ .11.已知在方程222232x x x x++=+中,如果设22y x x =+,那么原方程可化为关于y 的整式方程是 ▲ . 12.布袋中有2个红球和3个黑球,它们除颜色外其他都相同,那么从布袋中取出1个球恰好是红球的概率为 ▲ .13.某学校在开展“节约每一滴水”的活动中,从初三年级的360名同学中随机选出20名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:用所学的统计知识估计这360名同学的家庭一个月节约用水的总量大约是 ▲ 吨.14.如图,在ABC ∆中,AD 是边BC 上的中线,设向量AB a = ,AD b = ,如果用向量,a b表示向量BC ,那么BC =▲ .15.如图,已知ABC ∆和ADE ∆均为等边三角形,点D 在BC 边上,DE 与AC 相交于点F ,如果9AB =,3BD =,那么CF 的长度为 ▲ .16. 如图,已知在O 中,弦CD 垂直于直径AB ,垂足为点E ,如果30BAD ∠=︒,2OE =,那么CD = ▲ .17.如果一个二次函数的二次项系数为1,那么这个函数可以表示为2y x px q =++,我们将[],p q 称为这个函数的特征数.例如二次函数242y x x =-+的特征数是[]4,2-.请根据以上的信息探究下面的问题:如果一个二次函数的特征数是[]2,3,将这个函数的图像先向左平移2个单位,再向下平移3个单位,那么此时得到的图像所对应的函数的特征数为 ▲ .(第14题图)AB C D (第15题图)AC EF D (第16题图)B九年级数学 共5页 第14页18.如图,在ABC ∆中,CA CB =,90C ∠=︒,点D 是BC的中点,将ABC ∆沿着直线EF 折叠,使点A 与点D 重合, 折痕交AB 于点E ,交AC 于点F ,那么sin BED ∠的值 为 ▲ .三、解答题(本大题共7题,满分78分)19.(本题满分10分) 先化简,再求值:2122121x x x x x x +-÷+--+,其中6tan302x =︒-. 20.(本题满分10分)解方程组:222230x y x xy y -=⎧⎨--=⎩21.(本题满分10分,第(1)小题5分、第(2)小题5分) 在Rt ABC ∆中,90BAC ∠=︒,点E 是BC 的中点,AD BC ⊥,垂足为点D .已知9AC =,3cos 5C =.(1)求线段AE 的长; (2)求sin DAE ∠的值.BACFD(第18题图)(第21题图)CABE D九年级数学 共5页 第15页22.(本题满分10分,第(1)小题4分,第(2)小题6分)周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y (km)与小明离家时间x (h)的函数图像.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.(1)小明骑电动自行车的速度为千米/小时,在甲地游玩的时间为小时;(2)小明从家出发多少小时的时候被妈妈追上?此时离家多远?23.(本题满分12分,每小题各6分)如图,ABC ∆中,2BC AB =,点D 、E 分别是BC 、AC 的中点,过点A 作AF BC ∥交线段DE 的延长线于点F ,取AF 的中点G ,联结DG ,GD 与AE 交于点H .(1)求证:四边形ABDF 是菱形; (2)求证:2DH HE HC =⋅.(第22题图))A BDHG FEC(第23题图)九年级数学 共5页 第16页24.(本题满分12分,每小题各6分)如图,已知抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C . (1)求这个抛物线的解析式,并写出顶点坐标;(2)已知点M 在y 轴上,OMB OAB ACB ∠+∠=∠,求点M 的坐标.(第24题图)(备用图)九年级数学 共5页 第17页25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分)如图,在Rt ABC ∆中,90ACB ∠=︒,8AC =,4tan 3B =,点P 是线段AB 上的一个动点,以点P 为圆心,PA 为半径的P 与射线AC 的另一个交点为点D ,射线PD 交射线BC 于点E , 点Q 是线段BE 的中点.(1)当点E 在BC 的延长线上时,设PA x =,CE y =,求y 关于x 的函数关系式,并写出定义域; (2)以点Q 为圆心,QB 为半径的Q 和P 相切时,求P 的半径;(3)射线PQ 与P 相交于点M ,联结PC 、MC ,当PMC ∆是等腰三角形时,求AP 的长.(第25题图)(备用图1)B AC (备用图2)BAC。
2015年广东省初中毕业生水平考试二模参考答案

2015年广东省初中毕业生学业考试思想品德第二次模拟试卷参考答案一、单项选择题(每小题2分,共56分)题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 答案 B A A C B C B A A B A B D A 题号1516 17 18 19 20 21 22 23 24 25 26 27 28 答案 C C B B D C C C C C A D C A二、简答题(8分)29、(1)消费者权益。
(2)我国法律保护消费者的合法权益不受侵犯。
侵权前:①练就一双慧眼,即增强判断力和选择能力。
②主动学习和掌握有关消费和法律的知识。
③自身需要具有良好的权利意识和自我保护意识,保持警惕,防止侵权行为的发生。
侵权后:当消费者合法权益受损时,要拿起法律武器,通过正当、合法途径解决:①非诉讼途径:与经营者协商和解;请求消费者协会调解;向有关行政部门申诉;根据与经营者达成的仲裁协议,提请仲裁机构仲裁。
②诉讼途径:向人民法院提起诉讼。
三、辨析题(10分)30.(1)陈中的观点是错误的。
刘华的观点是正确的。
(2)材料说明我国部分地区义务教育尚未得到保障,应加强普及义务教育的落实力度。
(3)在当今社会,教育的作用日益突出:①当今各国之间激烈的经济竞争和科技竞争,归根到底是教育的竞争,人才的竞争,教育决定一个国家和民族的未来,是一个民族最根本的事业,是民族振兴和社会进步的基石。
②接受良好的教育,已逐渐成为人们生存发展的第一需要和终身受益的财富。
③中国未来的发展,中华民族的伟大复兴,关键靠人才,基础在教育。
④发展教育有利于化人口大国为人才强国,化人口压力为人才优势,增强我国的综合办,在国际竞争中取得战略主动地位。
(4)青少年是祖国的未来,民族的希望,肩负着中华民族伟大复兴的历史重任,公民的权利和义务具有一致性一,每个人既是权利的主体,也是履行义务的主体,受教育既是公民的基本权利又是公民的基本义务。
义务教育是国家统一实施的,所有适龄儿童和少年必须接受的教育,是国家必须予以保障的公益事业,它具有强制性。
2015年中考数学二模试题附答案

2015年中考数学二模试题(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.下列运算中,正确的是 ……………………………………………………………………( )(A)1293=±3(C)030-=()(D)2139-=2.轨道交通给人们的出行提供了便捷的服务,据悉,上海轨道交通19号线即将开建,一期规划为自川桥路站至长兴岛,设6站,全长约为20600米.二期、远期将延伸到崇明岛、横沙岛,届时崇明县三岛将全通地铁.将20600用科学记数法表示应为 ………………………( )(A)52.0610⨯(B)320.610⨯(C)42.0610⨯(D)50.20610⨯3.从下列不等式中选择一个与12x +≥组成不等式组,如果要使该不等式组的解集为1x ≥,那么可以选择的不等式可以是 ………………………………………………………………( ) (A)1x >-(B)2x >(C)1x <-(D)2x <4.已知点11(,)A x y 和点22(,)B x y 是直线23y x =+上的两个点,如果12x x <,那么1y 与2y 的大小关系正确的是 …………………………………………………………………( )(A)12y y >(B)12y y <(C)12y y =(D)无法判断5.窗花是我国的传统艺术,下列四个窗花图案中,不是..轴对称图形的是…………………( )(A) (B) (C) (D) 6.已知在四边形ABCD 中,AC 与BD 相交于点O ,那么下列条件中能判定这个四边形是正方形的是 …………………………………………………………………( ) (A)AC BD =, AB CD ∥, AB CD = (B)AD BC ∥, A C ∠=∠(C)AO BO CO DO ===, AC BD ⊥(D)AO CO =, BO DO =, AB BC =二、填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】 7.因式分解:34x x -= ▲ . 8.2,那么x = ▲ .9.如果分式242x x -+的值为0,那么x 的值为 ▲ .10.已知关于x 的一元二次方程2610x x m -+-=有两个相等的实数根,那么m 的值为▲ . 11.已知在方程222232x x x x++=+中,如果设22y x x =+,那么原方程可化为关于y 的整式方程是 ▲ .12.布袋中有2个红球和3个黑球,它们除颜色外其他都相同,那么从布袋中取出1个球恰好是红球的概率为 ▲ .13.某学校在开展“节约每一滴水”的活动中,从初三年级的360名同学中随机选出20名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:用所学的统计知识估计这360名同学的家庭一个月节约用水的总量大约是 ▲ 吨.14.如图,在ABC ∆中,AD 是边BC 上的中线,设向量AB a =,AD b =,如果用向量,a b表示向量BC ,那么BC = ▲ .15.如图,已知ABC ∆和ADE∆均为等边三角形,点D 在BC 边上,DE 与AC 相交于点F ,如果9AB =,3BD =,那么CF 的长度为 ▲ .16. 如图,已知在O 中,弦CD 垂直于直径AB ,垂足为点E ,如果30BAD ∠=︒,2OE =,那么CD = ▲ .17.如果一个二次函数的二次项系数为1,那么这个函数可以表示为2y x px q =++,我们将(第14题图)ABCD(第15题图)A BCEFD(第16题图)B[],p q 称为这个函数的特征数.例如二次函数242y x x =-+的特征数是[]4,2-.请根据以上的信息探究下面的问题:如果一个二次函数的特征数是[]2,3,将这个函数的图像先向左平移2个单位,再向下平移3个单位,那么此时得到的图像所对应的函数的特征数为 ▲ .18.如图,在ABC ∆中,CA CB =,90C ∠=︒,点D 是BC的中点,将ABC ∆沿着直线EF 折叠,使点A 与点D 重合, 折痕交AB 于点E ,交AC 于点F ,那么sin BED ∠的值 为 ▲ .三、解答题(本大题共7题,满分78分) 19.(本题满分10分) 先化简,再求值:2122121x x x x x x +-÷+--+,其中6tan302x =︒-.20.(本题满分10分)解方程组:222230x y x xy y -=⎧⎨--=⎩21.(本题满分10分,第(1)小题5分、第(2)小题5分) 在Rt ABC ∆中,90BAC ∠=︒,点E 是BC 的中点, AD BC ⊥,垂足为点D .已知9AC =,3cos 5C =. (1)求线段AE 的长;(2)求sin DAE ∠的值.22.(本题满分10分,第(1)小题4分,第(2)小题6分)周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y (km)与小明离家时间x (h)的函数图像.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.(1)小明骑电动自行车的速度为 千米/小时,在甲地游玩的时间为 小时; (2)小明从家出发多少小时的时候被妈妈追上?A C FED(第18题图)(第21题图) CAB E D此时离家多远?23.(本题满分12分,每小题各6分)如图,ABC ∆中,2BC AB =,点D 、E 分别是BC 、AC 的中点,过点A 作AF BC ∥交线段DE 的延长线于点F ,取AF 的中点G ,联结DG ,GD 与AE 交于点H . (1)求证:四边形ABDF 是菱形; (2)求证:2DH HE HC =⋅.24.(本题满分12分,每小题各6分) 如图,已知抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C .(1)求这个抛物线的解析式,并写出顶点坐标;(2)已知点M 在y 轴上,OMB OAB ACB ∠+∠=∠,求点M 的坐标.(第24题图)A BDHG FEC(第23题图)25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分) 如图,在Rt ABC ∆中,90ACB ∠=︒,8AC =,4tan 3B =,点P 是线段AB 上的一个动点,以点P 为圆心,PA 为半径的P 与射线AC 的另一个交点为点D ,射线PD 交射线BC 于点E ,点Q 是线段BE 的中点.(1)当点E 在BC 的延长线上时,设PA x =,CE y =,求y 关于x 的函数关系式,并写出定义域;(2)以点Q 为圆心,QB 为半径的Q 和P 相切时,求P 的半径;(3)射线PQ 与P 相交于点M ,联结PC 、MC ,当PMC ∆是等腰三角形时,求AP 的长.(第25题图)(备用图1)BA CB九年级数学参考答案及评分说明一、选择题(本大题共6题,每题4分,满分24分) 1.D ; 2.C ;3.A ; 4.B ; 5.D ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分)7.(2)(2)x x x +- 8.1 9.2 10. 10 11. 2320y y -+= 12.2513. 540 14.22b a - 15.216. 17.[]68, 18. 35三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 先化简,再求值:2122121x x x x x x +-÷+--+,其中6302x tan =-. 解:原式=21(1)212x x x x x --+-+……………………………………………………2分 122x x x x -=-++ ………………………………………………………2分 12x =+………………………………………………………………2分∵6302x tan =-6223=⨯-=………………………………………2分 ∴原式6=………………………………………………………………2分 20. (本题满分10分) 解方程组:222230x y x xy y -=⎧⎨--=⎩...............(1) (2)解:由(2)可得:(3)()0x y x y -+=∴30x y -=,0x y += ………………………………2分∴原方程组可化为:230x y x y -=⎧⎨-=⎩,2x y x y -=⎧⎨+=⎩ …………………………4分解得原方程组的解为1131x y =⎧⎨=⎩,2211x y =⎧⎨=-⎩ ………………………………4分21.(本题满分10分,第(1)小题5分、第(2)小题5分)(1)解:909oBAC AC ∠==∵, 93cos 5AC C AB BC ===∴ …………………………………………1分 15BC =∴ ………………………………………………………………2分 90oBAC ∠=∵,点E 是BC 的中点 11522AE BC ==∴ ……………………………………………………2分 (2)解:AD BC ⊥∵ 90oADC ADB ∠=∠=∴3cos 95CD CD C AC ===∴ 275CD =∴ …………………………………………………2分∵点E 是BC 的中点,BC=15 ∴CE=152 ∴DE=2110………………………………………1分 ∵90oADB ∠= ∴sin DAE ∠=2127101525DE AE =⨯= ……………………………2分 22. (本题满分10分,第(1)小题4分,第(2)小题6分)(1) 20;0.5 ……………………………………………………………各2分 (2)解:设小明出发x 小时的时候被妈妈追上.420(1)10203()3x x -+=⨯- ……………………………………3分解得:74x =……………………………………………………1分 ∴320(1)102010254x -+=⨯+= ……………………………1分答:当小明出发74小时的时候被妈妈追上,此时他们离家25千米.…1分23.(本题满分12分,每小题各6分)(1)证明:∵点D 、E 分别是BC 、AC 的中点∴DE//AB ,BC=2BD …………………………………………………1分 ∵AF//BC∴四边形ABDF 是平行四边形 ……………………………………………2分 ∵BC=2AB∴AB=BD …………………………………………………………………1分 ∴四边形ABDF 是菱形. …………………………………………………2分(2)证明:∵四边形ABDF 是菱形 ∴AF=DF∵点G 是AF 的中点 ∴FG=12AF ∵点E 是AC 的中点 ∴AE=CE ∵AF//BC ∴1EF AEDE CE== ∴EF=12DF , ∴FG=EF ……………………………………………………………1分 在△AFE 和△DFG 中AF DF F F EF GF =⎧⎪∠=∠⎨⎪=⎩∴△AFE ≌△DFG (S.A.S )∴∠FAE=∠FDG ………………………………………………………1分 ∵AF//BC ∴∠FA E=∠C∴∠FDG=∠C ………………………………………………………1分 又∵∠EHD=∠DHC (公共角)∴△HED ∽△HDC ……………………………………………………2分 ∴HE HDHD HC= ∴2DH HE HC = ………………………………………………………1分 24.(本题满分12分,每小题各6分)(1)解:∵抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C∴44201640c a b c a b c =-⎧⎪-+=⎨⎪++=⎩……………………………………………………1分解得方程组的解为1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩………………………………………………2分∴这个抛物线的解析式为:2142y x x =-- ………………………………1分 顶点为9(1,)2- ……………………………………………………………2分(2)如图:取OA 的中点,记为点N ∵OA=OC=4,∠AOC=90° ∴∠ACB=45°∵点N 是OA 的中点 ∴ON=2 又∵OB=2 ∴OB=ON 又∵∠BON=90° ∴∠ONB=45° ∴∠ACB=∠ONB ∵∠OMB+∠OAB=∠ACB ∠NBA+∠OAB=∠ONB∴∠OMB=∠NBA ………………………………………………………………2分 1° 当点M 在点N 的上方时,记为M 1 ∵∠BAN=∠M 1AB ,∠NBA=∠OM 1B , ∴△ABN ∽△AM 1B ∴1AN ABAB AM =又∵AN=2,∴110AM = 又∵A (0,—4)∴1(0,6)M ………………………………………………………………………2分 2° 当点M 在点N 的下方时,记为M 2点M 1与点M 2关于x 轴对称,∴2(0,6)M - ……………………………………2分 综上所述,点M 的坐标为(0,6)或(0,6)-25.(本题满分14分,第(1)小题5分,第(2)小题5分,第(3)小题4分) (1)解:过点P 作PH ⊥AD ,垂足为点H∵∠ACB=90°,43tanB = ∴35sinA =∵PA x = ∴35PH x = ∵∠PHA=90° ∴222PH AH PA += ∴45AH x =……………………1分 ∵在⊙P 中,PH ⊥弦AD ∴45DH AH x ==, ∴85AD x = 又∵AC=8 ∴885CD x =- ………………………………………………1分∵∠PHA=∠BCA=90°,∴PH ∥BE ∴PH DHCE CD = ∴3455885x xy x=- ……………………………1分 ∴665y x =- (x 0<<5) (1)(2)∵PA=PD ,PH ⊥AD ∴∠1=∠2 ∵PH ∥BE∴∠1=∠B ,∠2=∠3 ∴PB=PE ∵Q 是BE 的中点∴PQ ⊥BE ………………………………………………………………………1分 ∴43PQ tanB =BQ = ∴35BQ cosB =BP = ∵PA x = ∴10PB x =- ∴365BQ x =-, 485PQ x =- 1°当⊙Q 和⊙P 外切时:PQ=AP+BQ∴438655x x x -=+- …………………………………………………………1分 53x = …………………………………………………………………1分2°当⊙Q 和⊙P 内切时,此时⊙P 的半径大于⊙Q 的半径,则PQ=A P —BQ ∴438(6)55x x x -=-- …………………………………………………………1分 321HQABP CED- 11 - 356x = ……………………………………………………………………1分 ∴当⊙Q 和⊙P 相切时,⊙P 的半径为53或356. (3)当△PMC 是等腰三角形,存在以下几种情况: 1°当MP=MC x =时 ,∵336(6)55QC x x =--= ∴45MQ x = 若M 在线段PQ 上时,PM+MQ=PQ ∴44855x x x +=- 4013x = ……………………………………………………………………1分 若M 在线段PQ 的延长线上时,PM —MQ=PQ ∴44855x x x -=- 8x = …………………………………………………………………………1分 2°当CP=CM 时∵CP=CM ,CQ ⊥PM∴PQ=QM=1122PM x = ∴41852x x -= 8013x = …………………………………………………………………………1分 3°当PM=PC x =时∵AP x = ∴PA=PC 又∵PH ⊥AC ∴AH=CH∵PH ∥BE ∴1AP AH BP CH== ∴110x x =- 5x = …………………………………………………………………………1分 综上所述:当△PMC 是等腰三角形时,AP 的长为4013或8013或5或8.。
2015年中考二模英语试题及答案

2015年高中招生文化考试全真模拟(二模)英语试题卷第I卷第一部分听力(共两节,满分25分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题:每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题。
从题中所给的A、B、C三个选项中选出最佳选项,并标在试题的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What is the weather like?A. Rainy.B. Dry.C. Hot.2. What happened to the man?A. He fell on the floor.B. He was caught in the rain.C. He fell into a river.3. How much should the man pay?A.$1.50.B.$2.C.$3.4. Where does the man want to put a new table?A. In the bedroom.B. In the livingroom.C. In the kitchen.5. Why does the boy say sorry to the girl?A. He lost the book.B. He lent the book to his grandma.C. He can’t return the book now.第二节(共10小题:每小题2分,满分20分)听下面两段对话和一段独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试题的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
每段对话或独白读两遍。
听下面一段对话,回答第6至第8三个小题。
现在,你有15秒钟时间阅读这三个小题。
2015东城二模试题及答案

北京市东城区2014-2015学年第二学期初三综合练习(二)初三语文2015.6一、基础·运用。
(共23分)(一)选择。
阅读下面文字,按要求回答问题。
(共12分。
每小题2分)青春是什么?青春是一条奔(ténɡ)①的河,是一条充满惊涛骇浪的河。
每一个少男少女都独自驾着小舟,从这条河上驶过。
然而,并非每一位水手都能乘风破.浪平安地驶到彼岸。
世界上哪一条江河没有吞没过船只?况且是这样一条吉凶难卜的河,这样一群热情大于理智的水手。
青春是什么?青春是一座高耸的山,是一座看不见路径的山。
每一个少男少女都是登山队员,怀揣着征服者的梦想。
然而,既然是高山就难免有坎坷.,难免有毒蛇猛兽出没,也难免野花的诱惑和迷路的时候。
山林之神只留下一句秘(jué)②——惟有大智大勇者脚下才有路!青春是什么?青春是一片浩(hàn)③的海,是一片不见天际的海。
每一个少男少女都是一道小溪,别无选择地汇向大海。
溪水是甜的,海水是咸的,由甜变咸根本不管你情愿还是不情愿。
道理很简单:一个人光吃甜的,并不能强身健体,只有足够地吸收盐分,骨.头才会一天天结实起来,因此,拥抱大海就是拥抱希望。
青春是什么?青春是一片蔚蓝的天,是一片辽阔无垠的天。
每一个少男少女都是一只羽翼未丰的雏燕,渴望自由翱翔。
然而,如果经不起暴风雨的考验,在天空中挥动翅膀就意味着灾难;如果没有天空一样博大的胸怀,纵然远行万里也会郁郁寡欢。
啊,让我们【甲】着河流,让我们【乙】着高山,让我们【丙】大海,让我们【丁】蓝天。
那是一个竞技场,那是一个快乐园,那也是一部青春大辞典!……(作者:孙云晓)1.对文中加点字的注音全都正确的一项是A.坎坷.(kě)骨.头(ɡū)乘风破.浪(pè)B.坎坷.(kē)骨.头(ɡū)乘风破.浪(pò)C.坎坷.(kē)骨.头(ɡǔ)乘风破.浪(pè)D.坎坷.(kě)骨.头(ɡǔ)乘风破.浪(pò)2.根据拼音书写汉字全都正确的一项是A.①腾②决③翰B.①滕②决③瀚C.①腾②诀③瀚D.①滕②诀③翰3.对文中画线词语解释有误的一项是A.渴望:迫切地希望。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页(第25题图)2015年上海中考二模25题汇总1、(2015年虹口区二模25题)如图,在Rt ABC ∆中,90ACB ∠=︒,13AB =,CD ∥AB .点E 为射线CD 上一动点(不与点C 重合),联结AE ,交边BC 于点F ,BAE ∠的平分线交BC 于点G .(1)当3CE =时,求:CEF CAF S S ∆∆的值;(2)设CE x =,AE y =,当2CG GB =时,求y 与x 之间的函数关系式; (3)当5AC =时,联结EG ,若AEG ∆为直角三角形,求BG 的长.2、(2015年静安、青浦区二模25题)在⊙O中,OC⊥弦AB,垂足为C,点D在⊙O上.(1)如图1,已知OA=5,AB=6,如果OD//AB,CD与半径OB相交于点E,求DE的长;(2)已知OA=5,AB=6(如图2),如果射线OD与AB的延长线相交于点F,且△OCD是等腰三角形,求AF的长;(3)如果OD//AB,CD⊥OB,垂足为E,求sin∠ODC的值.(第25题图1)BO A CDE(第25题图2)BOA C第2页第3页3、(2015年闵行区二模25题)如图,已知在梯形ABCD 中,AD // BC ,AB = DC = 5,AD = 4.M 、N 分别是边AD 、BC 上的任意一点,联结AN 、DN .点E 、F 分别在线段AN 、DN 上,且ME // DN ,MF // AN ,联结EF .(1)如图1,如果EF // BC ,求EF 的长;(2)如果四边形MENF 的面积是△ADN 的面积的38,求AM 的长;(3)如果BC = 10,试探索△ABN 、△AND 、△DNC 能否两两相似?如果能,求AN 的长;如果不能,请说明理由.ABCDMNEF(图1)A B CDMNEF(第25题图)第4页4、(2015年黄浦区二模25题)如图,Rt △ABC 中,90C ∠=︒,30A ∠=︒,2BC =,CD 是斜边AB 上的高,点E 为边AC 上一点(点E 不与点A 、C 重合),联结DE ,作CF ⊥DE ,CF 与边AB 、线段DE 分别交于点F 、G ;(1)求线段CD 、AD 的长;(2)设CE x =,DF y =,求y 关于x 的函数解析式,并写出它的定义域; (3)联结EF ,当△EFG 与△CDG 相似时,求线段CE 的长;第5页5、(2015年浦东新区二模25题)如图,已知在△ABC 中,射线AM ∥BC ,P 是边BC 上一动点,∠APD =∠B ,PD 交射线AM 于点D ,联结CD .AB =4,BC =6,∠B =60°. (1)求证:BP AD AP ⋅=2;(2)如果以AD 为半径的圆A 与以BP 为半径的圆B 相切,求线段BP 的长度;(3)将△ACD 绕点A 旋转,如果点D 恰好与点B 重合,点C 落在点E 的位置上,求此时∠BEP 的余切值.A B C PD (第25题图)M A B C(第25题备用图)M第6页ABC6、(2015年徐汇区二模25题)如图,在ABC Rt ∆中,90ACB ∠=︒,AC =4,14cos A =,点P 是边AB 上的动点,以PA 为半径作⊙P .(1)若⊙P 与AC 边的另一交点为点D ,设AP =x ,△PCD 的面积为y ,求y 关于x 的函数解析式,并直接写出函数的定义域;(2)若⊙P 被直线BC 和直线AC 截得的弦长相等,求AP 的长;(3)若⊙C 的半径等于1,且⊙P 与⊙C 的公共弦长为2,求AP 的长.BD C AP第7页ACBE OD 备用图7、(2015年杨浦区二模25题)在Rt △ABC 中,∠BAC =90°,BC =10,3tan 4ABC ∠=,点O 是AB 边上动点,以O 为圆心,OB 为半径的⊙O 与边BC 的另一交点为D ,过点D 作AB 的垂线,交⊙O 于点E ,联结BE 、AE 。
(1) 当AE //BC (如图(1))时,求⊙O 的半径长;(2) 设BO =x ,AE =y ,求y 关于 x 的函数关系式,并写出定义域;(3) 若以A 为圆心的⊙A 与⊙O 有公共点D 、E ,当⊙A 恰好也过点C 时,求DE 的长。
图(1)ABCD E OABC备用图第8页8、(2015年闸北区二模25题)已知:如图,△ABC 为等边三角形,43AB ,AH ⊥BC ,垂足为点H , 点D 在线段HC 上,且HD = 2,点P 为射线AH 上任意一点,以点P 为圆心,线段PD 的长为半径作⊙P ,设AP = x . (1)当x = 3时,求⊙P 的半径长;(2)如图1,如果⊙P 与线段AB 相交于E 、F 两点,且EF = y ,求y 关于x 的函数解析式,并写出它的定义域;(3)如果△PHD 与△ABH 相似,求x 的值(直接写出答案即可).ABCPDH(第25题图)(图1)A BCPDH EFABCH(备用图)第9页9、(2015年奉贤区二模25题)已知:如图,线段AB =8,以A 为圆心,5为半径作圆A ,点C 在⊙A 上,过点C 作CD //AB 交⊙A 于点D (点D 在C 右侧),联结BC 、AD .(1)若CD=6,求四边形ABCD 的面积;(2)设CD =x ,BC =y ,求y 与x 的函数关系式及自变量x 的取值范围;(3)设BC 的中点为M ,AD 的中点为N ,线段MN 交⊙A 于点E ,联结CE ,当CD 取何值时,CE //AD .DCB(第25题图)AB(备用图)A第10页10、(2015年嘉定、宝山区二模25题)在Rt △ABC 中,︒=∠90C ,2=BC ,Rt △ABC 绕着点B 按顺时针方向旋转,使点C 落在斜边AB 上的点D ,设点A 旋转后与点E 重合,联结AE ,过点E 作直线EM 与射线CB 垂直,交点为M .(1)若点M 与点B 重合如图10,求BAE ∠cot 的值;(2)若点M 在边BC 上如图11,设边长x AC =,y BM =,点M 与点B 不重合,求y 与x 的函数关系式,并写出自变量x 的取值范围; (3)若EBM BAE ∠=∠,求斜边AB 的长.A CB (M )ED图10ACBM ED图11第11页11、(2015年普陀区二模25题)如图11-1,已知梯形ABCD 中,AD ∥BC ,∠D=90°,BC=5,CD=3,cotB=1,P 是边BC 上的一个动点(不与点B 、点C 重合),过点P 作射线PE ,使射线PE 交射线BA 于点E ,∠BPE=∠CPD 。
(1)如图11-2,当点E 与点A 重合时,求∠DPC 的正切值;(2)当点E 落在线段AB 上时,设BP=x ,BE=y ,试求y 与x 之间的函数解析式,并写出x 的取值范围;(3)设以BE 长为半径的B 和以AD 长为直径的O 相切,求BP 的长。
图11-1DC BA图11-2PA(E)B CD备用图A B CD第12页12、(2015年松江区二模25题)如图,已知在直角梯形ABCD 中,AD ∥BC ,∠ABC =90º,AB =4,AD=3,552sin =∠BCD ,点P 是对角线BD 上一动点,过点P 作PH ⊥CD ,垂足为H . (1)求证:∠BCD =∠BDC ;(2)如图1,若以P 为圆心、PB 为半径的圆和以H 为圆心、HD 为半径的圆外切时,求DP 的长; (3)如图2,点E 在BC 延长线上,且满足DP =CE ,PE 交DC 于点F ,若△ADH 和△ECF 相似,求DP 的长.A BCHPD (第25题图1)ABCHPD EF(第25题图2)第13页13、(2015年长宁区二模25题)如图,已知矩形ABCD ,AB =12 cm ,AD =10 cm ,⊙O 与AD 、AB 、BC 三边都相切,与DC 交于点E 、F 。
已知点P 、Q 、R 分别从D 、A 、B 三点同时出发,沿矩形ABCD的边逆时针方向匀速运动,点P 、Q 、R 的运动速度分别是1 cm/s 、x cm/s 、1.5 cm/s ,当点Q 到达点B 时停止运动,P 、R 两点同时停止运动.设运动时间为t (单位:s ). (1)求证: DE =CF ;(2)设x = 3,当△PAQ 与△QBR 相似时,求出t 的值;(3)设△PAQ 关于直线PQ 对称的图形是△PA'Q ,当t 和x 分别为何值时,点A'与圆心O 恰好重合,求出符合条件的t 、x 的值.第25题图OFEDCBAP QR第14页14、(2015年崇明县二模25题)如图,在Rt ABC ∆中,90ACB ∠=︒,8AC =,4tan 3B =,点P 是线段AB 上的一个动点, 以点P 为圆心,PA 为半径的P 与射线AC 的另一个交点为点D ,射线PD 交射线BC 于点E ,点Q 是线段BE 的中点.(1)当点E 在BC 的延长线上时,设PA x =,CE y =,求y 关于x 的函数关系式,并写出定义域; (2)以点Q 为圆心,QB 为半径的Q 和P 相切时,求P 的半径;(3)射线PQ 与P 相交于点M ,联结PC 、MC ,当PMC ∆是等腰三角形时,求AP 的长.(第25题图)APDC EQ B(备用图1) BAC(备用图2)BAC第15页15、(2015年金山区二模25题)如图,已知在ABC ∆中,10==AC AB ,34tan =∠B (1) 求BC 的长;(2) 点D 、E 分别是边AB 、AC 的中点,不重合的两动点M 、N 在边BC 上(点M 、N 不与点B 、C 重合),且点N 始终在点M 的右边,联结DN 、EM ,交于点O ,设x MN =,四边形ADOE 的面积为y . ①求y 关于x 的函数关系式,并写出定义域;②当OMN ∆是等腰三角形且1=BM 时,求MN 的长.CB A第25题图CB A备用图。
