理论力学_第四章习题答案
理论力学(胡运康)第四章作业答案
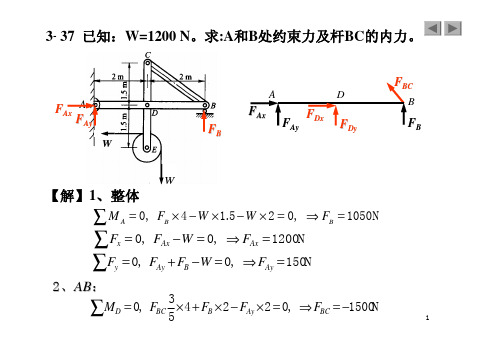
2、AB:
3 M = 0 , F N ∑ D BC × 4 + FB × 2 − FAy × 2 = 0, ⇒ F BC = −1500 5
1
3-39 已知q,M=qa2 。求铰链D受的力;铰链B受的力。
D FDx FDy
qa
C FCy FCx
FDx FDy
FB3
a 3 解: 1、整体 : ∑ M A = 0, FB 3 ⋅ a − qa ⋅ − M = 0, ⇒ FB 3 = qa 2 2 1 M = 0 , F ⋅ a + qa ⋅ a = 0 , ⇒ F = qa 2、DC: ∑ C Dy Dy 2 1 ⇒ FCy = qa ∑ Fy = 0, FDy + FCy − qa = 0, 2
∑ Fy = 0, FAy − 30 + FBC ⋅
3-73 已知M2 、M3 ,AB=d1 、BC=d2 、CD=d3 ,求M1及 A、D处约束力。
FAz FAy
【解】整体:
M3 ⇒ FAy = ∑ M z = 0, M 3 − FAy ⋅ d1 = 0, d1 M2 ⇒ FAz = ∑ M y = 0, M 2 − FAz ⋅ d1 = 0, d1
6
3-53 求桁架中杆BH、CD和GD的内力。
1
FIH 0 FBH
FE
FB 1
FBC
FE
解: FGD = 0 1、整体:
2、1-1面左边:∑ Fy = 0, FE − 60 − FBH
∑M
B
= 0, FE ×15+ 60×10 = 0, ⇒ FE = 26.67kN
1 = 0, ⇒ FBH = −47.1kN 2
∑M
G
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
经典教材——周衍柏理论力学教程及参考答案chp-4

第四章思考题4.1为什么在以角速度ω转动的参照系中,一个矢量G 的绝对变化率应当写作G ωG G ⨯+=*dt d dt d 在什么情况下0=*dtd G?在什么情况下0=⨯G ω?又在什么情况下0=dtd G? 4.2式(4.1.2)和式(4.2.3)都是求单位矢量i 、j 、k 对时间t 的微商,它们有何区别?你能否由式(4.2.3)推出式(4.1.2)?4.3在卫星式宇宙飞船中,宇航员发现自己身轻如燕,这是什么缘故? 4.4惯性离心力和离心力有哪些不同的地方?4.5圆盘以匀角速度ω绕竖直轴转动。
离盘心为r 的地方安装着一根竖直管,管中有一物体沿管下落,问此物体受到哪些惯性力的作用?4.6对于单线铁路来讲,两条铁轨磨损的程度有无不同?为什么?4.7自赤道沿水平方向朝北或朝南射出的炮弹,落地是否发生东西偏差?如以仰角 40朝北射出,或垂直向上射出,则又如何?4.8在南半球,傅科摆的振动面,沿什么方向旋转?如把它安装在赤道上某处,它旋转的周期是多大?4.9在上一章刚体运动学中,我们也常采用动坐标系,但为什么不出现科里奥利加速度?第四章思考题解答4.1.答:矢量G 的绝对变化率即为相对于静止参考系的变化率。
从静止参考系观察变矢量G 随转动系以角速度ω相对与静止系转动的同时G 本身又相对于动系运动,所以矢量G 的绝对变化率应当写作G ωG G ⨯+=*dt d dt d 。
其中dtd G *是G 相对于转动参考系的变化率即相对变化率;G ω⨯是G 随动系转动引起G 的变化率即牵连变化率。
若G 相对于参考系不变化,则有0=*dt d G ,此时牵连运动就是绝对运动,G ωG ⨯=dt d ;若0=ω即动系作动平动或瞬时平动,则有0=⨯G ω此时相对运动即为绝对运动 dtd dt d G G *=;另外,当某瞬时G ω//,则0=⨯G ω,此时瞬时转轴与G 平行,此时动系的转动不引起G 的改变。
当动系作平动或瞬时平动且G 相对动系瞬时静止时,则有0=dtd G;若G 随动系转动引起的变化G ω⨯与相对动系运动的变化dtd G *等值反向时,也有0=dt d G 。
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
理论力学---第四章空间力系习题

例4-11
已知:F、P及各尺寸
求: 杆内力
解:研究对象,长方板,列平衡方程
M
AB AE
F 0 F 0
F6 a
a 2
P 0 F6
F5 0
P 2
F D y 1 3 .0 3 K N
例 已知:各边长,载荷P、Q。 求:各杆的约束反力。 解:(1)考虑板的平衡,各杆均 为二力杆,设均受拉力。 (2)画受力图,建立坐标系,注 意各矢量的空间关系。 (3)列写平衡方程,空间一般力系有6个方程,尽量使 一个方程包含一个未知数。
M M
AB
F2 b
P F3 cos 45 b 0
F3 2 2 P
汽车后半桥传动轴,如图所示,A 处是向心推力轴承 (止推轴承),B 处是向心轴承(颈轴承)。设汽车匀 速直线行驶(平衡)。 已知:地面法向反力FD = 20 kN,锥齿轮上受的三个力 Ft = 117(kN),Fr = 36 kN,Fa =22.5 kN。齿轮节圆直 径 d = 98 mm,车轮半径R = 440 mm,尺寸如图。 求: 地面的摩擦力及两轴承的约束反力。
FOx Fx 0
F
y
0
FOy Fy 0
F
z
0
FOz Fz 0
100 FZ M x 0
30 FZ M y 0
100 Fx 30 Fy M z 0
M F 0
x
M F 0
y
M F 0
z
FOx 4.25kN, FOy 6.8kN, FOz 17kN
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学 第四章_07.8.28_
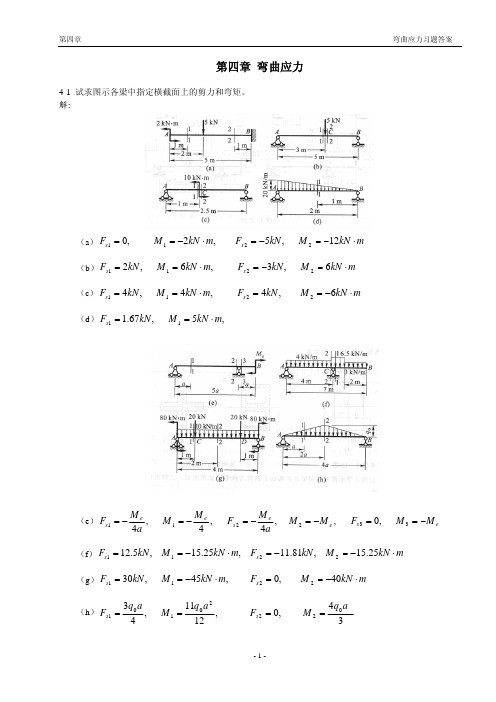
第四章 弯曲应力4-1 试求图示各梁中指定横截面上的剪力和弯矩。
解:(a )m kN M kN F m kN M F s s ⋅−=−=⋅−==12 ,5 ,2 ,02211 (b )m kN M kN F m kN M kN F s s ⋅=−=⋅==6 ,3 ,6 ,22211 (c )m kN M kN F m kN M kN F s s ⋅−==⋅==6 ,4 ,4 ,42211 (d ) ,5 ,67.111m kN M kN F s ⋅==(e )e e s e e s M M aMF M M a M F −=−=−=−=2211 ,4 ,4 ,4, e s M M F −==33 ,0 (f )m kN M kN F m kN M kN F s s ⋅−=−=⋅−==25.15 ,81.11 ,25.15 ,5.122211 (g )m kN M F m kN M kN F s s ⋅−==⋅−==40 ,0 ,45 ,302211(h )34 ,0 ,1211 ,4302220101aq M F a q M a q F s s ====4-3 试利用载荷集度、剪力和弯矩间的微分关系作下列各梁的剪力图和弯矩图。
解:(a)(b)(c)(g)(d)(e)(f)4-4 试作下列具有中间铰的梁的剪力图和弯矩图。
解:有中间铰的梁的内力图画法与普通梁无异,关键是求出约束反力。
4-6 已知简支梁的剪力图如图所示。
试作梁的弯矩图和载荷图。
已知梁上没有集中力偶作用。
解:(a )A 、B 、D 截面剪力突变,说明截面上有集中力作用,集中力的值等于该截面剪力的突变值。
CD 段剪力图为下斜直线,说明该段上有向下的均布载荷作用,载荷集度等于该段剪力图的斜率。
(b )A 、C 、D 截面剪力突变,说明截面上有集中力作用,集中力的值等于相应截面上剪力的突变值。
AC 段剪力图为下斜直线,说明该段上有向下的均布载荷作用,载荷集度等于该段剪力图的斜率。
理论力学(刘又文 彭献)答案第4章
§4.2 思考解析
思考 4-1 已知平面图形 S 的运动方程,试写出 S 上给定点 M 的运动方程, 以及该点的速度和加速度解析表达式。 答:设已知 x A = f1 (t ),
y A = f 2 (t ), ϕ = f3 (t ) 。则 M 点运动方程为
xM = x A + AM cos ϕ = f1 (t ) + AM cos f3 (t ) yM = y A + AM sin ϕ = f 2 (t ) + AM sin f3 (t ) M 点速度和加速度分量分别为
n τ aCv = aO + aC + aC vO vO n τ 其中, aC = Rω 2 , aC = Rα = a0 ,方向与 a0 相反。 vO vO
110
故
n aCv = aC , aCv = Rω 2 = vO
2 v0 R
以 Cv 为基点,M 点的加速度如图 b 所示。 故
n 2 2 aM = (aMC − aCv ) + (aτ ( Rω 2 ) 2 + (2 Rα ) 2 = 2 a0 + MCv ) = v 4 v0 4R2
所以
xM = r cos ω t + AM cos ϕ , yM = r sin ω t − AM sin ϕ
对时间 t 求一阶和二阶导数便得 M 点的速度和加速度坐标分量。
思考 4-4
试求图 a、b、c 中各平面运动刚体的速度瞬心 Cv 。
ω
B
A B
C v
A
ω
(b) (c)
(a)
ω
C
A B
B
A
ω
Cv
vC vB
理论,力学,答案,理论力学习题答案

·36·第4章 空间力系一、是非题(正确的在括号内打“√”、错误的打“×”)1.力在坐标轴上的投影是代数量,而在坐标面上的投影为矢量。
( √ )2.力对轴之矩是力使刚体绕轴转动效应的度量,它等于力在垂直于该轴的平面上的分力对轴与平面的交点之矩。
( √ )3.在平面问题中,力对点之矩为代数量;在空间问题中,力对点之矩也是代数量。
( × )4.合力对任一轴之矩,等于各分力对同一轴之矩的代数和。
( √ )5.空间任意力系平衡的必要与充分条件是力系的主矢和对任一点的主矩都等于零。
( √ ) 6.物体重力的合力所通过的点称为重心,物体几何形状的中心称为形心,重心与形心一定重合。
( × ) 7.计算一物体的重心,选择不同的坐标系,计算结果不同,因而说明物体的重心位置是变化的。
( × ) 8.物体的重心一定在物体上。
( × )二、填空题1.空间汇交力系共有三个独立的平衡方程,它们分别表示为0=∑xF、0=∑yF和0=∑zF 。
空间力偶系共有三个独立的平衡方程,它们分别表示为0=∑xM、0=∑yM和0=∑zM。
而空间任意力系共有六个独立的平衡方程,一般可表示为0=∑xF、0=∑yF、0=∑zF 、0)(=∑F xM 、 0)(=∑F yM 和0)(=∑F zM 。
2.由n 个力组成的空间平衡力系,如果其中的(n -1)个力相交于A 点,那么另一个力也必定通过点A 。
3.作用在同一刚体上的两个空间力偶彼此等效的条件是力偶矩矢相等。
4.空间力对一点的矩是一个矢量,而空间力对某轴的矩是一个代数量。
5.空间力F 对任一点O 之矩)(F M O 可用矢量积来表示,即F r F M ⨯=)(O 。
写成解析表达式为k j i F M )()()()(x y z x y z O yF xF xF zF zF yF -+-+-=。
6.当空间力与轴相交时,力对该轴的矩等于零。
F__学习_陈世民理论力学简明教程(第二版)答案_第四章 质点组动力学

又依能量守恒:
1 1 & & mυ A2 + m[(υ A − 2lθ cos θ ) 2 + (2lθ sin θ ) 2 ] = 2mgl (cos α − cos θ ) 2 2
2 & 代入 * 得: θ =
2 g (cos α − cos θ ) l (sin 2 θ + 1)
得:
2 & θ g (cos − cos α ) θ= = 2 l (2 − cos 2 )
& 劈的加速度 & x (3 )劈对物体的反作用力 F1 和水平面对劈的反作用力 p;
F2 。
解:如右图所示,建立各方向矢量,设劈与物体间的与反作用力为
F sin θ & P & = F1′ &= F1Pi = F1 sin θ i LL * F1 , F1′ ,则: & x i =− 1 i,x m′ m 1 M′ M′ m′ m′
F1 sin θ m′ g cos θ sin θ = m m′ + m sin 2 θ 代入 *1 式可得: F1 sin θ mg cos θ sin θ & & x =− M =− m′ m′+ m sin 2 θ & & x m =
水平面对劈的反作用力 F2 = m′ g (−ez ) + F1′cos θ (−ez )
< 析> 此章中许多等式的推导多用到分部积分与等量代换. 在本章的习 题解答中多用到动量定理, 角动量定理与机械能守恒定理的联立方程 组, 有时质心定理的横空出世会救你于水深火热之中.
【解题演示】
1 在一半径为 r 的圆圈上截取一段长为 s 的圆弧, 求出这段圆弧的质心 位置。 解:如右图所示建立坐标系 。则: θ0 = s 2r 设 rc = xc i + yc j 有:
理论力学静力学第四章习题答案

a tan
zC
3.在平衡位置,不破坏约束的前提下,假定杆 AB 逆时针旋转一个微小的角度 ,则质心 C 的虚位移:
a l cos tan 2
zC
4.由虚位移原理
a sin
2
l sin 2
W ( Fi ) 0 有:
a sin
2
W ( Fi ) 0 有:
(1)
FB rB cos 450 M F2 y2 cos 1500 F3 y3 0
各点的虚位移如下:
rB 6 2
代入(1)式整理可得:
y2 9
y3 3
(6 FB M
9 3 F2 3F3 ) 0 2
δθ δ rA δ rD δ rE δ rB δ rC
rA O A , rB O B , rC O1C
rD O1D , rB rC , rD rE
代入可得: rA 30rE 4.由虚位移原理
W ( Fi ) 0 有:
3.在不破坏约束的前提下给定一组虚位移 x A 0, y A 0, 0 ,如上图所示。 由虚位移原理
W ( Fi ) 0 有:
(2)
M A F 1 y1 F2 y2 F3 y3 M 0
有几何关系可得各点的虚位移如下:
R sin R l cos 杆的质心坐标可表示为: zC sin 2
坐标。由几何关系可知: z A 3.在平衡位置,不破坏约束的前提下,假定杆 AB 顺时针旋转一个微小的角度 ,则质心 C 的虚位移:
zC
4.由虚位移原理
《理论力学》第四章 力系的简化习题解
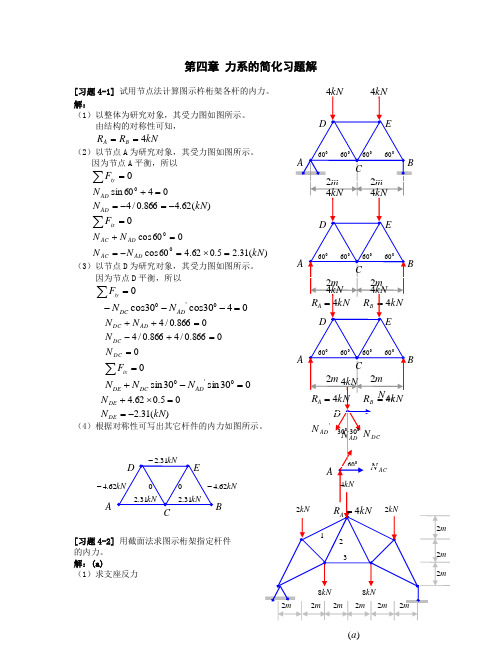
)(a 第四章 力系的简化习题解[习题4-1] 解:(1)以整体为研究对象,其受力图如图所示。
由结构的对称性可知, kN R R B A 4==(2)以节点A 为研究对象,其受力图如图所示。
因为节点A 平衡,所以0=∑iyF0460sin 0=+AD N)(62.4866.0/4kN N AD -=-=0=∑ixF060cos 0=+AD AC N N(31.25.062.460cos 0N N AD AC =⨯=-=(3)以节点D 为研究对象,其受力图如图所示。
因为节点D 平衡,所以 0=∑iyF0430cos 30cos 0'0=---AD D C N N 0866.0/4=++AD D C N N 0866.0/4866.0/4=+-D C N0=DC N0=∑ix F030sin 30sin 0'0=-+AD D C D E N N N 05.062.4=⨯+DE N )(31.2kN N DE -=(4[习题4-2] 用截面法求图示桁架指定杆件 的内力。
解:(a)(1)求支座反力kN4AB RkN 2AC 23N A以整体为研究对象,其受力图如图所示。
由对称性可知, kN R R B A 12==(2)截取左半部分为研究对象,其受力图 如图所示。
因为左半部分平衡,所以0)(=∑i CF M0612422843=⨯-⨯+⨯+⨯N 063243=⨯-++N )(123kN N =0=∑ixF0cos cos 321=++N N N αθ01252252421=+⋅+⋅N N012515221=+⋅+⋅N N0512221=++N N ……..(1) 0=∑iy F02812sin sin 21=--++αθN N025*******=+⋅+⋅N N02525121=+⋅+⋅N N052221=++N N0544221=++N N ……..(2) 05832=-N)(963.53/582kN N ==)(399.1652963.5252221kN N N -=-⨯-=--=解:(b )截取上半部分为研究对象,其受力图如图所示。
理论力学第四章习题解答
T
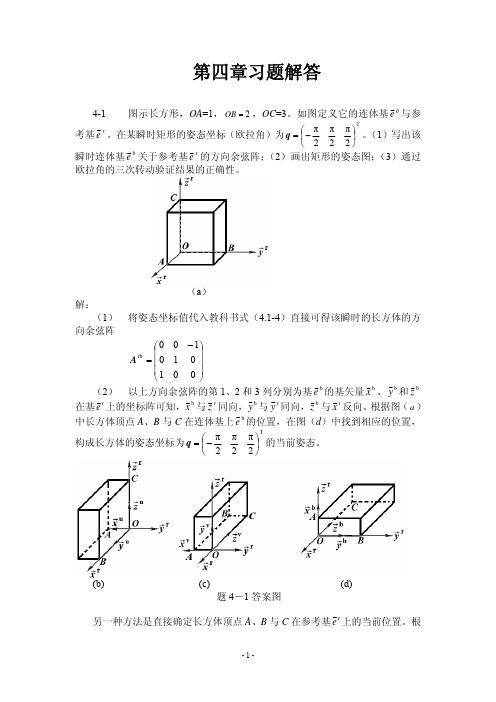
⎛ π 连体基欧拉角坐标为 q = ⎜ − ⎝ 2
-4-
顶角为 2θ 的正圆锥体,在平面上滚动而不滑动,此时顶点 A 将保持 G 、正圆 不动。设已知其高为 L,底面中心 O 点的速度为 vO , vO 为常数。求(1)
4-4
锥体的转动角速度, (2) 、底面上 C 点的速度。
-2-
4-2
试找到题 1-13 中两个基的一次转动矢量 p 在基 e 1 的坐标阵 p1 ,且验证
G
G
p 0 = p1 。 解: ⎛ 6 ⎜− ⎜ 6 ⎜ 6 根据题 1-13,已知 A 01 = ⎜ − ⎜ 3 ⎜ 6 ⎜ 6 ⎝
3 3 3 − 3 3 − 3
2⎞ ⎟ 2 ⎟ ⎟ 0 ⎟ ⎟ 2⎟ 2 ⎟ ⎠
(a) 解: (1) 向余弦阵 将姿态坐标值代入教科书式(4.1-4)直接可得该瞬时的长方体的方
⎛ 0 0 − 1⎞ ⎜ ⎟ A = ⎜0 1 0 ⎟ ⎜1 0 0 ⎟ ⎝ ⎠ G G G G (2) 以上方向余弦阵的第 1、2 和 3 列分别为基 e b 的基矢量 x b 、 y b 和 z b G G G G G G G 在基 e r 上的坐标阵可知,x b 与 z r 同向, y b 与 y r 同向,z b 与 x r 反向。 根据图 (a) Gb 中长方体顶点 A、B 与 C 在连体基上 e 的位置,在图(d)中找到相应的位置,
方向余弦阵 A 01 的本征根方程至少存在一个 λ = 1 的根,对应于本征根 λ = 1 的
G G 1 矢量为 p ,其在基 e 1 的坐标阵 p 1 = (x1
x1 2
1 x3
)
T
代入本征方程 A 01 − λI p 1 = 0 ,
哈尔滨工业大学第7版理论力学第4章课后习题答案_图文(精)

12001.013
3300⋅−=××
−××
−=x M
m N 6.361.013
220020.0100⋅−=××+×−=y M m
N 6.1033.05
22002.013
3300⋅=××
+××=z M主矢N 4262R 2R 2R R =++=x y z F F F F ,N
z B
β
A
C
θ
β
F
1
F
2
F
(a(b
图4-5
解将力F分解为F1,F2,F1垂直于AB而与CE平行,F2平行于AB,如图4-5b所示,这2个分力分别为:
α
sin
1
F
F=,α
cos
2
F
F=
(
(
(
2
1
F
M
F
M
F
M
AB
AB
AB
+
=0
sin
1
+
⋅
=θ
a
Fθ
αsin
sin
Fa
=
4-6水平圆盘的半径为r,外缘C处作用有已知力F。力F位于铅垂平面内,且与C处圆盘切线夹角为60°,其他尺寸如图4-6a所示。求力F对x,y,z轴之矩。
350×
×
+
×
×
−
×
×
−
×
×
×
=
z
M
m
N
4.
19
mm
N
400
19⋅
−
=
⋅
−
理论力学第四章

0
FBy
C 3m
M A 48kN m
1、本题是否还有其他解法? 2、本题若不要求计算1、2杆之力,试问该如何解决? 3、能否将本题进行些变化?该如何变?需要满足什么条件? 4、教材P85
求:A处的反力。 P
q
A
B
C
③
2a
②
① D
aa
aa
A 2a
P q
B ②③
① D
aa
a
C a
B
q
C
FBx
③
FBy ②
D
B FBx
4m
FBy
P2 FEx
E FEy
Y 0 , F Ay FBy FD P2 8q 0
FD
3m 2m 6m 2m
X 0 , F Ax FBx P1 0
FAy 4.75kN FBy 12.25kN
(2) 取BC部分为研究对象
q
C P2
P1
E
D
FAx A
FD 2m 2m FAy 4m
C
q
P
A E
DM 2a
θ
C a
B a
A FAx
FAy
q E FE
P B
FBC
q
例 题 5 求:A、E的约束
反力和BC杆内力。
a
a a
解:(1) 取整体为研究对象
C
X 0, FAx 0
Y 0, FAy FE qa 0
D
M E (F ) 0, FAy a qa 1.5a 0
a
解得: FAx 0 FAy 1.5qa FE 2.5qa
B FBx
4m
FBy
MC F 0 , 4FBy 8FBx 4q.2 0
理论力学课后习题及答案解析..

第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
