理论力学答案第四章
第4章 解题指导(理论力学 金尚年 第二版)

3 1 2 2 I1 I 2 m( R h ) 20 4 3 I 3 mR 2 10 Nhomakorabea
x sin ctg sin cos y 0 z cos ctg cos
I1 I 2 I3
l 2 2 2 | B | [ 1 l V (1 sin ) 2 ] 2 R 2 d dj V d k dj V 1 1 (2) a A i dt dt R dt dt R V 1V 10 j 1 k j i R R
c
解:圆锥体作定点转动,OE为转动瞬轴。所以: 3 c CE h cos 4
3 3 h sin h cos 4 4
ctg
ctg
x sin ctg sin cos y 0 z cos ctg cos
消去t,得:
2 xc yc a 3a
(抛物线)
当质心C从离A点为a处下降h距离时,有:
1 2 y a h a gt 2
t
2h g
则杆绕质心转动所转的圈数为:
t 1 n 2 2
3g 2h 1 2a g 2 3h a
例3 均匀长方形薄片的边长为a与b,质量为m,求 此长方形薄片绕其对角线以ω匀速转动时的转动惯 量和角动量。 解:如图所示,坐标轴取 在惯量主轴上,因:
角动量为:
L I e a 2b 2 m 2 2 6(a b )
例4 如图所示,均质圆锥体的高为h,质量为m, 为圆锥体与平面接触线同 ox0轴的夹角,质心C 3 3 h ,速率为 h cos 在圆锥体轴线上,且距顶点为 4 4 求该圆锥体在 ox0 y 0 平面上作无滑动滚动时的动能。 圆锥顶角为2α。
理论力学课后答案4

魏 魏 魏
后
泳 泳 泳
ww
涛 涛 涛
m
课
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
w.
kh
da
xi (2i 1)a cos , yi a sin 轨迹: xi2 yi2 a 2 2 (2i 1)
w.
co
解:以 A1 为对象研究 x a cos , y a sin 同理, Ai (i 2,3,4) 的运动方程为
kh
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.8 飞轮边缘上一点 M ,随飞轮以匀速 v 10 m s 运动。后因刹车,该点以 at 0.1t m s 2 作减速运动。设轮半径 R 0.4m ,求 M 点在减速运动过程中的运 动方程及 t 2s 时的速度、切向和法向加速度。 解:
魏
at
2 2 v vx vy 2500 4t 2
泳 泳 泳
ww
涛 涛 涛
m
加速度的直角分量 ax 0 , a y 2 切向加速度为
dv 4t dt 2500 4t 2 当 t 0s 时, at 0 ,所以
2 2 an a 2 at2 ax ay at2 2 m s 2
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
4.1 一动点按 s t 2 6t 1的规律沿直线运动,式中,时间 t 以秒( s )计,坐标 s 以 米( m )计。试求: (1)最初 5s 内的位移; (2)动点改变运动方向的时刻和所在位置; (3)最初 5s 内动点经过的路程; (4) t 5s 时动点的速度和加速度; (5)动点在哪段时间内作加速运动,哪段时间内作减速运动。
理论力学(胡运康)第四章作业答案
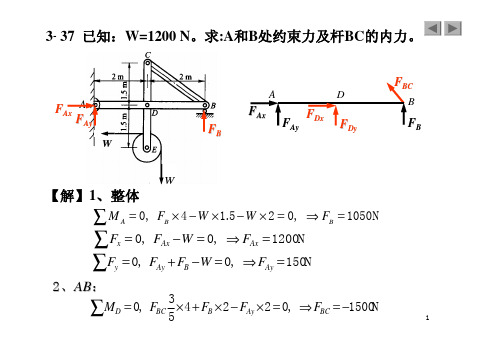
2、AB:
3 M = 0 , F N ∑ D BC × 4 + FB × 2 − FAy × 2 = 0, ⇒ F BC = −1500 5
1
3-39 已知q,M=qa2 。求铰链D受的力;铰链B受的力。
D FDx FDy
qa
C FCy FCx
FDx FDy
FB3
a 3 解: 1、整体 : ∑ M A = 0, FB 3 ⋅ a − qa ⋅ − M = 0, ⇒ FB 3 = qa 2 2 1 M = 0 , F ⋅ a + qa ⋅ a = 0 , ⇒ F = qa 2、DC: ∑ C Dy Dy 2 1 ⇒ FCy = qa ∑ Fy = 0, FDy + FCy − qa = 0, 2
∑ Fy = 0, FAy − 30 + FBC ⋅
3-73 已知M2 、M3 ,AB=d1 、BC=d2 、CD=d3 ,求M1及 A、D处约束力。
FAz FAy
【解】整体:
M3 ⇒ FAy = ∑ M z = 0, M 3 − FAy ⋅ d1 = 0, d1 M2 ⇒ FAz = ∑ M y = 0, M 2 − FAz ⋅ d1 = 0, d1
6
3-53 求桁架中杆BH、CD和GD的内力。
1
FIH 0 FBH
FE
FB 1
FBC
FE
解: FGD = 0 1、整体:
2、1-1面左边:∑ Fy = 0, FE − 60 − FBH
∑M
B
= 0, FE ×15+ 60×10 = 0, ⇒ FE = 26.67kN
1 = 0, ⇒ FBH = −47.1kN 2
∑M
G
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
《理论力学》第四章-力系平衡试题及答案
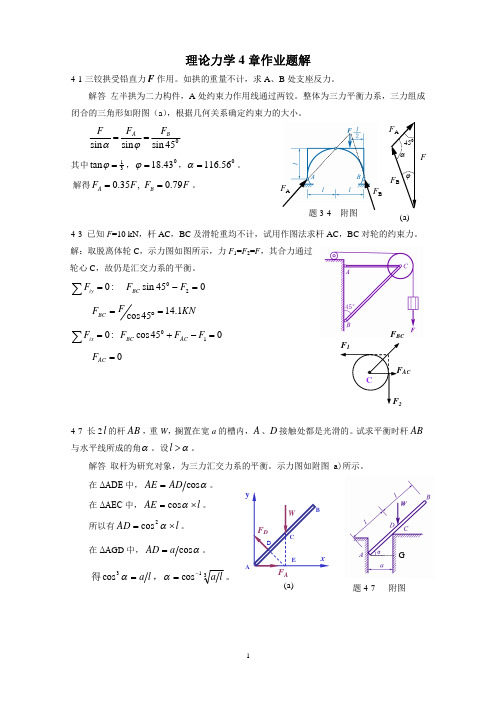
理论力学4章作业题解4-1三铰拱受铅直力F 作用。
如拱的重量不计,求A 、B 处支座反力。
解答 左半拱为二力构件,A 处约束力作用线通过两铰。
整体为三力平衡力系,三力组成闭合的三角形如附图(a ),根据几何关系确定约束力的大小。
45sin sin sin B A F F F ==j a其中31tan =j ,043.18=j ,056.116=a 。
解得F F F F B A 79.0 ,35.0==。
4-3 已知F =10 kN ,杆AC ,BC 及滑轮重均不计,试用作图法求杆AC ,BC 对轮的约束力。
解:取脱离体轮C ,示力图如图所示,力F 1=F 2=F ,其合力通过轮心C ,故仍是汇交力系的平衡。
:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ,重W ,搁置在宽a 的槽内,A 、D 接触处都是光滑的。
试求平衡时杆AB 与水平线所成的角a 。
设a >l 。
解答 取杆为研究对象,为三力汇交力系的平衡。
示力图如附图(a)所示。
在ΔADE 中,a cos AD AE =。
在ΔAEC 中,l AE ´=a cos 。
所以有l AD ´=a 2cos 。
在ΔA GD 中,a cos a AD =。
得a =a 3cos ,31cosl a -=a 。
F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ,AC ,AD 三连杆支撑一重物,如图所示。
已知W=10kN ,AB =4m ,AC =3 m ,且ABEC 在同一水平面内,试求三连杆所受的力。
解:取铰A 研究,示力图如图示,为汇交力系的平衡。
0=åix F : 05430sin =´°+AD AB F F 0=åiy F : 05330sin =´°+AD AC F F 0=åiZF: 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。
理论力学1-7章答案

习题7-1图Oυ(a)υυ(b)习题7-3图第7章 点的复合运动7-1 图示车A 沿半径R 的圆弧轨道运动,其速度为v A 。
车B 沿直线轨道行驶,其速度为v B 。
试问坐在车A 中的观察者所看到车B 的相对速度v B /A ,与坐在车B 中的观察者看到车A 的相对速度v A /B ,是否有B A A B //v v -=?(试用矢量三角形加以分析。
)答:B A A B //v v -≠1.以A 为动系,B 为动点,此时绝对运动:直线;相对运动:平面曲线;牵连运动:定轴转动。
为了定量举例,设R OB 3=,v v v B A ==,则v v 3e =∴ ⎩⎨⎧︒==6021/θv v A B2.以B 为动系,A 为动点。
牵连运动为:平移;绝对运动:圆周运动;相对运动:平面曲线。
此时⎪⎩⎪⎨⎧︒==4522/θv v B A ∴ B A A B //v v -≠7-3 图示记录装置中的鼓轮以等角速度0ω转动,鼓轮的半径为r 。
自动记录笔连接在沿铅垂方向并按)sin(1t a y ω=规律运动的构件上。
试求记录笔在纸带上所画曲线的方程。
解:t r x 0ω= (1) )sin(1t a y ω=(2)由(1)0ωr xt =代入(2),得)sin(01r xa y ωω=7-5 图示铰接四边形机构中,O 1A = O 2B = 100mm ,O 1O 2 = AB ,杆O 1A 以等角速度ω= 2rad/s 绕轴O 1转动。
AB 杆上有一套筒C ,此套筒与杆CD 相铰接,机构的各部件都在同一铅垂面内。
试求当ϕ= ︒60,CD 杆的速度和加速度。
解:1.动点:C (CD 上),动系:AB ,绝对:直线,相对:直线,牵连:平移。
2.r e a v v v +=(图a ) v e = v A01.02121.0cos e a =⨯⨯==ϕv v m/s (↑)3. r e a a a a +=(图b )4.021.022e =⨯==ωr a m/s 2 346.030cos e a =︒=a a m/s 2(↑)习题7-5图习题7-7图习题7-9图υ(a) (b)(a)7-7 图示瓦特离心调速器以角速度ω绕铅垂轴转动。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《理论力学》第四章作业参考答案
习题
4-1
解: 以棒料为研究对象,所受的力有重力P
、力偶M ,与V 型槽接触处的法向
约束力1N F 、2N F 和摩擦力1S F 、2S F
,且摩擦力的方向与棒料转动方向相反,如图所示。
建立坐标系,列平衡方程:
⎪⎪
⎩⎪
⎪⎨⎧===∑∑∑0
)(00F M F F O y x
⎪⎩
⎪⎨⎧=-+=--=-+0
125.0125.00
45sin 0
45cos 210
12021M F F P F F P F F S S S N S N 临界条件下,补充方程: 11N S S F f F = 22N S S F f F = 联立以上各式得:
223.01=s f
491.42=s f (忽略)
答:棒料与V 型槽间的静摩擦因数223.0=s f 。
习题4-6 解法一:
(1)取整体为研究对象,作用力有重力P 、提砖力F
,列平衡方程:
0=-P F
所以 )(120N F =
(2)取砖块为研究对象,其受力情况如图所示:作用力有重力P
、法向约束
力NA F 、ND F 和摩擦力SA F 、SD F
,由于其滑动趋势向下,所以其摩擦力的方向向上。
列平衡方程:
∑=0)(F M D
0250125=-SA F P
补充方程: NA S SA F f F ≤ 所以
)(60N F SA =
)(160N F NA ≥
(3)取构件AGB 为研究对象,所受的力除提砖力F
外,还有砖块对其作用的
正压力NA
F ' 、摩擦力SA F ' ,
G 点的约束力G X F 、G Y F 。
列平衡方程: ∑=0)(F M G
03095='-'+NA SA
F b F F 其中NA
F ' 与砖块所受的力NA F 、SA F ' 与砖块所受的力SA F
分别为作用力与反作用力关系,将各力的数值代入得
)(110mm b ≤
答:距离mm b 110≤时才能把砖夹起。
解法二:
取构件GCD 为研究对象,受力情况如图所示。
作用于D 点的力有正压力N F 、摩擦力S F ,作用于G 点的有约束力G X F
、G Y F。
列平衡方程:
∑=0)(F M G
0220=-S N F bF
补充方程: N S S F f F ≤
所以
)(110mm b ≤
答:距离mm b 110≤时才能把砖夹起。
解法三:
取构件GCD 为研究对象,受力情况如图所示。
作用力有D 点的全约束力D
F
和G 点的约束力G F
且二者满足二力平衡条件。
由几何关系得
ϕtan 220
=b
在平衡条件下,全约束力的作用线与法向约束力作用线的夹角不可能大于摩擦角,即
S f f =≤ϕϕtan tan
所以
)(110mm b ≤
答:距离mm b 110≤时才能把砖夹起。
习题4-23
解:(1)以均质梁AB 为研究对象,其受力情况如图所示:重力1P
作用于AB 的中点,与线圈架接触处有正压力1N F 、摩擦力1S F
,铰接处A 有约束力AX F 、
AY F。
列平衡方程:
∑=0)(F M A
02311=-P F N
我们有:)(3001N F N =
(2)以线圈架为研究对象,其受力情况如图所示:重力2P
作用于线圈架
中心,绳子的拉力F ,与梁AB 接触处的有正压力1N
F ' 、摩擦力1S F '
,与地面接触处有正压力2N F 、摩擦力2S F 。
其中1N
F ' 、1S F ' 分别与均质梁AB 所受的力1N F
、1S F
互为作用力与反作用力,即11N N
F F =',11S S F F ='。
列平衡方程:
⎪⎪
⎩⎪
⎪⎨⎧===∑∑∑0
)(00F M F F C y x
⎪⎩
⎪
⎨⎧=-'+=-'-='--0
00
2121212R F r F Fr P F F F F F S S N
N S S a.如果线圈架轴芯与梁AB 接触处先于线圈架与地面接触处滑动,则临界条件下的补充方程为:
111N S S F f F =
联立方程得:
22
240()
643()120()N S F N F N F N =⎧⎪
=⎨⎪=⎩ 所以,滑动时 240F N ≥
b.如果线圈架轴芯与梁AB 接触处晚于线圈架与地面接触处滑动,则临界条件下补充方程为:
222N S S F f F =
联立方程得:
21
257.2()643()128.6()N S F N F N F N =⎧⎪
=⎨⎪'=⎩ 所以,滑动时257.2F N ≥,而此时计算出的线圈架轴芯与梁AB 接触处的摩擦力大于它的最大摩擦力)(1203004.0111N F f F N S S =⨯==,故此种情况不可能发生。
因此,系统滑动时水平拉力的最小值应为240F N =。
答:使线圈架由静止而开始运动的水平拉力F
的最小值为240N 。
习题4-28
解:以钢管为研究对象,其受力情况如图所示。
即作用力有:钢管自身重力P 、与台架接触点C 处的正压力N F 、滑动摩擦力S F
以及滚动摩阻力偶f M 。
当钢管处于平衡状态时其平衡方程为:
⎪⎩⎪⎨
⎧==∑∑0
)(0
F M F C y ⎩⎨
⎧=-=-0
sin 0
cos f N M RP P F θθ 钢管在将要滚动时的补充方程为:
N f F M δ=
解之得:
0.5
tan 0.0225
R
δ
θ=
=
= 即 910'=θ
答:台架的最小倾角应为910'=θ。
