哈工大理论力学第七版课后习题答案(高清无水印版)
哈尔滨工业大学 第七版 理论力学 第5章 课后习题答案

第5章 摩 擦5-1 如图5-1a 所示,置于V 型槽中的棒料上作用1力偶,力偶矩m N 15⋅=M 时,刚好能转动此棒料。
已知棒料重力N 400=P ,直径m 25.0=D ,不计滚动摩阻。
求棒料与V 形槽间的静摩擦因数f s 。
(a)(b)图5-1解 圆柱体为研究对象,受力如图5-1b 所示,F s1,F s2为临界最大摩擦力。
0=∑x F ,045cos 2s 1N =°−+P F F (1) 0=∑y F ,045sin 1s 2N =°−−P F F (2) 0=∑O M ,0222s 1s =−+M DF D F(3)临界状态摩擦定律:1N s 1s F f F =(4) 2N s 2s F f F =(5)以上5式联立,化得 0145cos s2s =+°−MPDf f 代入所给数据得01714.4s 2s =+−f f 方程有2根:442.4s1=f (不合理), 223.0s2=f (是解)故棒料与V 形槽间的摩擦因数223.0s =f5-2 梯子AB 靠在墙上,其重力为N 200=P,如图5-2a 所示。
梯长为l ,并与水平面交角°=60θ。
已知接触面间的静摩擦因数均为0.25。
今有1重力为650 N 的人沿梯向上爬,问人所能达到的最高点C 到点A 的距离s 应为多少?AN F As F(a)(b)图5-2解 梯子为研究对象,受力如图5-2b 所示,刚刚要滑动时,A ,B 处都达最大静摩擦力。
人重力N 650=W ,平衡方程: 0=∑x F , 0s N =−A B F F (1) 0=∑y F , 0s N =−−+W P F F B A(2)0=∑A M ,060cos 60sin 60cos 60cos 2s N =°−°−°+°l F l F Ws lPB B (3) 临界补充方程:A s A F f F N s = (4)B s B F f F N s =(5)联立以上5式,解得 N 80012sN =++=f WP F A ,N 200s =A F N 200)(12s N =++=W P f f F sB ,N 50s =B F l PF f W l s B 456.02)3[(N s =−+=5-3 2根相同的匀质杆AB 和BC ,在端点B 用光滑铰链连接,A ,C 端放在不光滑的水平面上,如图5-3a 所示。
哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 (1)方法 1,如图 4-6b 所示,由已知得
Fxy = F cos 60° , Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学(第七版)课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示,由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象,受力及坐标如图 4-9b 所示
理论力学第七版答案、高等教育出版社出版

仅供个人学习参考哈工大理论力学(I )第7版部分习题答案1-2两个老师都有布置的题目2-3?2-6?2-14?2-?20?2-30?6-2?6-4?7-9??7-10?7-17?7-21?8-5?8-8?8-16?8-24?10-4?10-6?11-5?11-15?10-3以下题为老师布置必做题目1-1(i,j ),1-2(e,k)2-3,2-6,2-14,2-20,2-306-2,6-47-9,7-10,7-17,7-21,7-268-5,8-8(瞬心后留),8-16,8-2410-3,10-410-611-5,11-1512-10,12-15,综4,15,16,1813-11,13-15,13-166-2图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5m 在铅垂面内转动,杆AB=0.8m ,A 端为铰链,B 端有放置工件的框架。
在机构运动时,工件的速度恒为0.05m/s ,杆AB 始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B 的轨迹方程。
10-3如图所示水平面上放1均质三棱柱A ,在其斜面上又放1均质三棱柱B 。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA 三棱柱B 质量mB 的3倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A 、B 两三棱柱组成1质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统 质心位置在水平方向守恒。
设A 、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c 所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4如图所示,均质杆AB ,长l ,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A 相对图b 所示坐标系的轨迹。
哈尔滨工业大学 第七版 理论力学.13
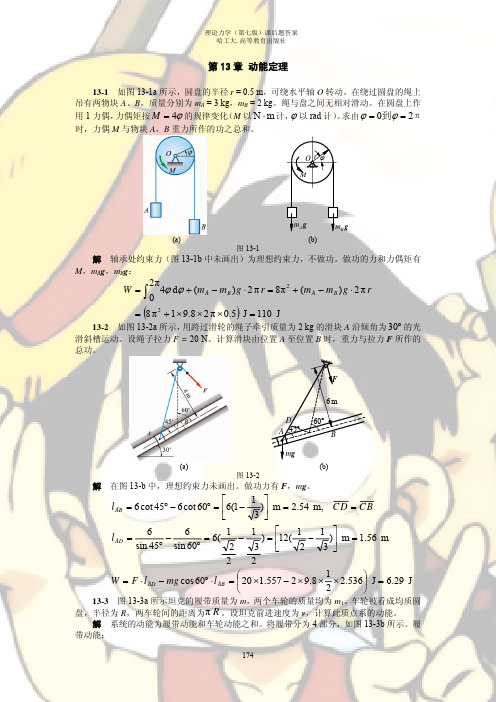
1 2 T履 = ∑ mi vi = TI + TII + TIII + TIV 2
D II A
(a) 图 13-3
IV
2v
C
ω
v
III
Iv=0
(b)
B
由于 v1 = 0, vIV = 2v ,且由于每部分履带长度均为π R ,因此
mI = mII = mIII = mIV = TI =
m 4
1 2 mI vI = 0 2 1 1 m m 2 TIV = mIV v IV = × (2v) 2 = v 2 2 2 4 2 m m 2 II、III 段可合并看作 1 滚环,其质量为 ,转动惯量为 J = R ,质心速度为 v,角速度 2 2 v 为 ω = ,则 R 1 m 1 mv 2 1 m 2 v 2 m 2 TII + TIII = ⋅ v 2 + Jω 2 = + ⋅ R ⋅ 2 = v 2 2 2 4 2 2 2 R m m T履 = 0 + v 2 + v 2 = mv 2 2 2
理论力学(第七版)课后题答案 哈工大.高等教育出版社
第 13 章 动能定理
13-1 如图 13-1a 所示,圆盘的半径 r = 0.5 m,可绕水平轴 O 转动。在绕过圆盘的绳上 吊有两物块 A、B,质量分别为 mA = 3 kg,mB = 2 kg。绳与盘之间无相对滑动。在圆盘上作 用 1 力偶, 力偶矩按 M = 4ϕ 的规律变化 (M 以 N ⋅ m 计, ϕ 以 rad 计) 。 求由 ϕ = 0到ϕ = 2π 时,力偶 M 与物块 A,B 重力所作的功之总和。
第 2 阶段 :系统通过搁板继续运动 x2 距离后静止。由动能定理
理论力学第七版答案_哈工大编_高等教育出版社出版
哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-306-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-2410-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,1813-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放 1 均质三棱柱 A ,在其斜面上又放 1 均质三棱柱 B 。
两三棱柱的横截面均为直角三角形。
三棱柱 A 的质量为 mA 三棱柱 B 质量 mB 的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱 B 沿三棱柱 A 滑下接触到水平面时,三棱柱 A 移动的距离。
11-4解取A、B 两三棱柱组成 1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)课后习题(第1~3章)【圣才出品】

圣才电子书 十万种考研考证电子书、题库视频学习平台
图 2-3 答:支座约束力不相同,如图 2-4 所示。
图 1-4
图 1-5
1-6 将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力,试画出它 们的力学简图及受力图。
(1)用两根细绳将日光灯吊挂在天花板上; (2)水面上的一块浮冰; (3)一本打开的书静止于桌面上; (4)一个人坐在一只足球上。
3 / 142
圣才电子书
答:如图 1-8 所示。
图 1-7
4 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-8 二、习题 1-1 画出图 1-1 各图中物体 A、ABC 或构件 AB、AC 的受力图。未画重力的各物体 的自重不计,所有接触处均为光滑接触。
5 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
6 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 1-1 解:各物体的受力图如图 1-2 所示。
7 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
13 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
14 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
FD
图 1-4 1-3 画出图 1-5 中每个标注字符的物体的受力图,各题的整体受力图。未画重力的物 体的自量均不计,所有接触处均为光滑接触。
15 / 142
圣才电子书 十万种考研考证电子书、题库视频学习平台
哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

tan θ =
r sin ϕ h − r cos ϕ
sin ω 0 t h − cos ω 0 t r ]
图 7-5
注意到 ϕ = ω 0 t ,得
θ = tan −1 [
(2)
自 B 作直线 BD 垂直相交 CO 于 D,则
tan θ =
r sin ω 0 t BD = DO h − r cos ω 0 t
80
理论力学(第七版)课后题答案 哈工大.高等教育出版社
7-6 如图 7-6 所示,摩擦传动机构的主动轴 I 的转速为 n = 600 r/min 。轴 I 的轮盘与轴Ⅱ的轮 盘接触,接触点按箭头 A 所示的方向移动。距离 d 的变化规律为 d = 100 − 5t ,其中 d 以 mm 计, t 以 s 计。已知 r = 50 mm , R = 150 mm 。求: (1)以距离 d 表示轴 II 的角加速度; (2)当 d = r 时,轮 B 边缘上 1 点的全加速度。 解 (1)两轮接触点的速度以及切向加速度相同
∠CBO =
π , x B = 2 R cos ϕ 2 & B = 2 R + vt (↓) x B (0) = 2 R , x
(2 R) 2 − x B
2
vt vt 1 2 − 2 2 − ( )2 R R 2R 2 v v , vC = 2 Rω = − ω =− 2 R sin ϕ sin ϕ sin ϕ = =
两边对时间 t 求导:
vt l
& sec 2 ϕ = , ϕ & = cos 2 ϕ , ϕ && = − ϕ
当ϕ =
v l
v l
2v & cos ϕ sin ϕ ⋅ ϕ l
理论力学(百度文库)-第七版答案-哈工大

哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-30 6-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-24 10-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,18 13-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放1 均质三棱柱A,在其斜面上又放1 均质三棱柱B。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA三棱柱B 质量mB的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A、B 两三棱柱组成1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A相对图b所示坐标系的轨迹。
理论力学(第七版)2

va =
得
va = 2 aω cos 30° aω 1 = 2 aω
ω=
ω1
2
= 1.5 rad/s (逆)
(b)套筒 A 为动点,动系固结于杆 O1 A ;绝对运动为绕 O2 圆周运动,相对运动为沿
va = O2 A ⋅ ω1 = 2aω cos 30° , ve = O1 Aω1 = aω 1 ve aω 1 由图 b1: v a = = cos30° cos30° aω 1 得 2aω cos 30° = cos 30° 2 ω = ω 1 = 2 rad/s (逆) 3 8-8 图 8-8a 所示曲柄滑道机构中,曲柄长 OA = r ,并以等角速度 ω 绕轴 O 转动。 装在水平杆上的滑槽 DE 与水平线成 60° 角。求当曲柄与水平线的交角分别为 ϕ = 0° , 30° , 60° 时,杆 BC 的速度。
y
如图 8-9a 所示,摇杆机构的滑杆 AB 以等速 v 向上运动,初瞬时摇杆 OC 水平。
摇杆长 OC = a ,距离 OD = l 。求当 ϕ =
va ve
C
vr
O
(a) 图 8-9
ϕ
l
(b)
A D
v
x
解 套筒 A 为动点,动系固结于杆 OC;绝对运动为上下直线,相对运动沿 OC 直线, 牵连运动为绕 O 定轴转动。速度分析如图 8-9b 所示,设杆 OC 角速度为 ω ,其转向逆时 针。由题意及几何关系可得 va = v (1)
ve1 − v r1 cos 30° = ve2 b b ω − ω ve1 − ve2 cos30° 1 cos30° 2 4b = = (ω 1 − ω 2 ) v r1 = cos30° cos30° 3 式(3)向 v r2 方向投影,得 1 2b (ω 1 − ω 2 ) = 0.4 m/s v r2 = v r1 = 2 3 0.1 ve2 = × 3 = 0.346 m/s 3 2 ⎧v = v 2 + v 2 = 0.529 m/s e2 r2 ⎪ a 所以 ⎨ ve2 0.346 = ,θ = 40.9° ⎪tan θ = 0 .4 v r2 ⎩
哈尔滨工业大学 第七版 理论力学.14
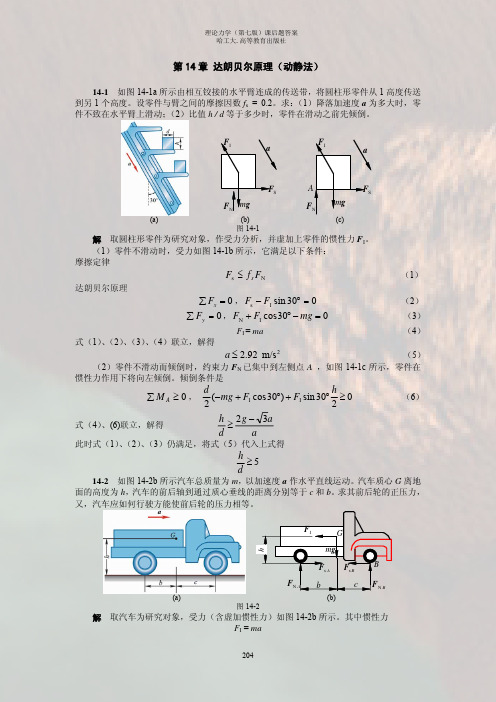
m2 g )l sin ϕ − FI l cos ϕ = 0 2
ω2 =
2m1 + m2 g tan ϕ 2m1 (a + l sin ϕ )
14-5 曲柄滑道机械如图 14-5a 所示,已知圆轮半径为 r,对转轴的转动惯量为 J,轮上 作用 1 不变的力偶 M,ABD 滑槽的质量为 m,不计摩擦。求圆轮的转动微分方程。
∑ M x = 0, M − 2 FI ⋅ l cos ϕ = 0
其中 代入前式得
FI = m ⋅ l sin ϕ ⋅ ω 2
209
理论力学(第七版)课后题答案 哈工大.高等教育出版社
k (ϕ − ϕ 0 ) − 2 ⋅ m ⋅ l sin ϕ ⋅ ω 2 ⋅ l cos ϕ = 0
ω=
k (ϕ − ϕ 0 ) ml 2 sin 2ϕ
y
m2 g 2
FAy
A FI
FAx
x
ϕ
m1 g
(a) 图 14-4
(b)
解
取调速器外壳为研究对象,由对称可知壳与圆盘接触处所受约束力为 FN = m2 g/2
取左圆盘为研究对象,受力如图 14-4b 所示,惯性力为
FI = m1 ⋅ (a + l sin ϕ )ω 2
由动静法
∑ M A = 0, (m1 g +
FI
a
FI
a
FS FN mg
(a) (b) 图 14-1
A FN mg
(c)
FS
解 取圆柱形零件为研究对象,作受力分析,并虚加上零件的惯性力 FI。 (1)零件不滑动时,受力如图 14-1b 所示,它满足以下条件: 摩擦定律
Fs ≤ f s FN
哈尔滨工业大学 第七版 理论力学.12

Lz1 = mv0 (l + r )
(1 )
在任意时刻:
Lz 2 = Jω + M z (mv M ) = Jω + M z (mv 0 ) + M z (mv e )
由图 12-5b 中,可得
Lz 2 = Jω + mv0 [l cos ϕ + r ] + m(l 2 + r 2 + 2lr cos ϕ )ω
12-4 1 半径为 R,质量为 m1 的均质圆盘,可绕通过其中心 O 的铅垂轴无摩擦地旋转, 如图 12-4a 所示。1 质量为 m2 的人在盘上由点 B 按规律 s = 开始时,圆盘和人静止。求圆盘的角速度和角加速度 α 。
1 2 at 沿半径为 r 的圆周行走。 2
R r O
(a) 图 12-4
LO = m ⋅ v A ⋅ 2 R + J Aω a 1 = m ⋅ 2 Rω O ⋅ 2 R + mR 2 ⋅ (ω O + ω r ) = 5ω O mR 2 = 20 kgm 2 /s 2
156
理论力学(第七版)课后题答案 哈工大.高等教育出版社
(3)在图 12-2c1 中,轮 A 绕 O 作圆周曲线平移
接合后,依靠摩擦使轮 2 启动。已知轮 1 和 2 的转动惯量分别为 J1 和 J2。求: (1)当离合 器接合后,两轮共同转动的角速度; (2)若经过 t 秒两轮的转速相同,求离合器应有多大的 摩擦力矩。
Mf
ω
2
(a) 图 12-6
(b)
解 (1)以轮 1 和 2 为一个系统进行研究,因为系统所受外力(包括重力和约束反力) 对转轴之矩均为零,所以系统对转轴的动量矩守恒,即
哈工大理论力学(I)第七版答案、高等教育出版社出版

哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-30 6-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-24 10-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,18 13-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放1 均质三棱柱A,在其斜面上又放1 均质三棱柱B。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA三棱柱B 质量mB的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时,三棱柱A 移动的距离。
11-4解取A、B 两三棱柱组成1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
求它从铅直位无初速地倒下时,端点A相对图b所示坐标系的轨迹。
哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

解
设轮缘上任 1 点 M 的全加速度为 a,切向加速度 a t = rα ,法向加速度 a n = ω r ,如图
2
7-11b 所示。
tan θ =
把
α=
dω , θ = 60° 代入上式,得 dt
at α = 2 an ω
dω tan 60° = dt2
ω
分离变量后,两边积分:
∫ω
得
ω
0
dω
ω
2
=∫
⎤ ⎡ ⎥ ⎢ sin ω t 0 θ = tan −1 ⎢ ⎥ ⎢ h − cos ω 0 t ⎥ ⎥ ⎢ ⎦ ⎣r
故
50 π ⋅ 600 100π r ω1 = rad/s ⋅ = 100 − 5t 30 10 − 0.5t d dω 5 000 π d ⎛ 1 000π ⎞ α2 = 2 = ⎜ ⎟= dt dt ⎝ 100 − 5t ⎠ (100 − 5π )2
故得
h1 =
h4 = 2 mm 6
图 7-7
7-8 如图 7-8 所示,纸盘由厚度为 a 的纸条卷成,令纸盘的中心不动,而以等速 v 拉纸条。求 纸盘的角加速度(以半径 r 的函数表示) 。 解 纸盘作定轴转动,当纸盘转过 2π rad 时半径减小 a。设纸盘转过 dθ 角时半径增加 dr ,则
dθ =
y
B
t aB
α j
O
vA x
ω
(a) 图 7-12
aC
(b)
i 45° A n
C
t aC
解
由图 7-12b 得出
84
理论力学(第七版)课后题答案 哈工大.高等教育出版社
v A = 0.2 j m/s , v A = ω × Ri , ω × 0.1i = 0.200 j , ω = 2k ,
理论力学(第七版)2

ω2
30°
θ ω1
(a) 图 8-11
va O
(b)
解 (1)运动分析 ① 活动销子 M 为动点,动系固结于轮 O;牵连运动为绕 O 定轴转动,相对运动为沿 轮上导槽直线,绝对运动为平面曲线。 v a = v e1 + v r1 (1) ② 活动销子 M 为动点,动系固结于杆 OA;牵连运动为绕 O 定轴转动,相对运动为 沿 OA 直线,绝对运动为平面曲线。
91
理论力学(第七版)课后题答案 哈工大.高等教育出版社
v a = v e2 + v r2
速度分析如图 8-11b 所示,由式(1) 、 (2)得 v e1 + v r1 = v e2 + v r2 方向 大小
(2) (3)
⊥ OM OM ⋅ ω 1
√ ?
⊥ OM OM ⋅ ω 2
√ ?
式(3)向 v e2 方向投影,得
ve va = sin(30° − ϕ ) sin 60°
所以
sin(30° − ϕ ) rω sin 60° 3 ϕ = 0° 时, v BC = ; rω (←) 3 ϕ = 30° 时, v BC = 0 v BC = ve =
ϕ = 60° 时, v BC = −
8-9
3 rω (→) 3 π 时点 C 的速度的大小。 4
y va vr
va v r
vr
60° 60°
杆直线运动,牵连运动为绕 O1 定轴转动。速度分析如图 8-7b1 所示。
va
A
ve
ϕ
ve
(a) (a)
60° A
(b) (b) 图 8-8 89
x
A
(c)
ω
哈尔滨工业大学 第七版 理论力学11

上式代入式(4)得
FN = 4mB g − mB
11-10 如图 11-10a 所示,质量为 m 的滑块 A,可以在水平光滑槽中运动,具有刚性系 数为 k 的弹簧 1 端与滑块相连接,另 1 端固定。杆 AB 长度为 l,质量忽略不计,A 端与滑 块 A 铰接,B 端装有质量 m1,在铅直平面内可绕点 A 旋转。设在力偶 M 作用下转动角速度 ω 为常数。求滑块 A 的运动微分方程。
质量为 m2 的小车 D,由绞车拖动,相对于平台的运动规律为 s = 不计绞车的质量,求平台的加速度。
1 2 bt ,其中 b 为已知常数。 2
m2 g
y
S D
A
vr
m1 g FN
B
ω
v
(a) 图 11-8
x
(b)
解
受力和运动分析如图 11-8b 所示
& = bt vr = & s ar = & s& = b a Da = a e + a r = a AB + a r a Da = ar − a AB m2 (a r − a AB ) − m1a AB = F F = f (m1 + m2 ) g
1
(
)
开伞后,他受重力 mg 和阻力 F 作用,如图 11-2 所示。取铅直轴 y 向下为正, 根据动量定理有
mg y
图 11-2
mv 2 − mv1 = I y = (mg − F )t
由题知:当 t=5 s 时,有 v2=4.3 m/s 即
60 × (4.3 − 44.3) = (60 × 9.8 − F ) × 5
棱柱 B 接触水平面时系统质心坐标
a b ⎤ ⎡ m A (l − ) + m B ⎢l − (a − )⎥ 3 3 ⎦ 3(m A + m B )l − a (m A + 3m B ) + m B b ⎣ ′ = xC = m A + mB 3(m A + m B )
哈尔滨工业大学第7版理论力学第4章课后习题答案_图文(精)

12001.013
3300⋅−=××
−××
−=x M
m N 6.361.013
220020.0100⋅−=××+×−=y M m
N 6.1033.05
22002.013
3300⋅=××
+××=z M主矢N 4262R 2R 2R R =++=x y z F F F F ,N
z B
β
A
C
θ
β
F
1
F
2
F
(a(b
图4-5
解将力F分解为F1,F2,F1垂直于AB而与CE平行,F2平行于AB,如图4-5b所示,这2个分力分别为:
α
sin
1
F
F=,α
cos
2
F
F=
(
(
(
2
1
F
M
F
M
F
M
AB
AB
AB
+
=0
sin
1
+
⋅
=θ
a
Fθ
αsin
sin
Fa
=
4-6水平圆盘的半径为r,外缘C处作用有已知力F。力F位于铅垂平面内,且与C处圆盘切线夹角为60°,其他尺寸如图4-6a所示。求力F对x,y,z轴之矩。
350×
×
+
×
×
−
×
×
−
×
×
×
=
z
M
m
N
4.
19
mm
N
400
19⋅
−
=
⋅
−
