第5章 能带理论 习题参考答案
材料物理基础习题
课后练习思考题:第一章晶体结构1-1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。
1-2.晶格点阵与实际晶体有何区别和了解?1-3.晶体结构可分为Bravais格子和复式格子吗?1-4.图1.34所示的点阵是布喇菲点阵(格子)吗?为什么?如果是,指明它属于那类布喇菲格子?如果不是,请说明这种复式格子的布喇菲格子属哪类?(a)(b)(c)(d)图1.341-5.以二维有心长方晶格为例,画出固体物理学原胞、结晶学原胞,并说出它们各自的特点。
1-6.倒格子的实际意义是什么?一种晶体的正格矢和相应的倒格矢是否有一一对应的关系?1-7.一个物体或体系的对称性高低如何判断?有何物理意义?一个正八面体(见图)有哪些对称操作?1-8.解理面是面指数低的晶面还是指数高的晶面?为什么?1-9. 5.晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、OB和OC分别与基矢、和重合,除O点外,OA、OB和OC上是否有格点?若ABC面的指数为(234),情况又如何?1-10.带轴为[001]的晶带各晶面,其面指数有何特点?1-11. 与晶列[l1l2l3]垂直的倒格面的面指数是什么?1-12. 在结晶学中,晶胞是按晶体的什么特性选取的?1-13. 六角密积属何种晶系?一个晶胞包含几个原子?1-14.体心立方元素晶体, [111]方向上的结晶学周期为多大?实际周期为多大?1-15. 面心立方元素晶体中最小的晶列周期为多大?该晶列在哪些晶面内?1-16. 在晶体衍射中,为什么不能用可见光?第二章固体的结合2-1.试述离子键、共价键、金属键、范德瓦尔斯键和氢键的基本特征.2-2.有人说“晶体的内能就是晶体的结合能”,对吗?2-3.当2个原子由相距很远而逐渐接近时,二原子间的力与势能是如何逐渐变化的?2-4.为什么金属比离子晶体、共价晶体易于进行机械加工并且导电、导热性良好?2-5.是否有与库仑力无关的晶体结合类型?2-6.如何理解库仑力是原子结合的动力?2-7.晶体的结合能,晶体的内能,原子间的相互作用势能有何区别?2-8.原子间的排斥作用取决于什么原因?2-9.原子间的排斥作用和吸引作用有何关系?起主导的范围是什么?2-10.共价结合为什么有“饱和性”和“方向性”?2-11.共价结合,两原子电子云交迭产生吸引,而原子靠近时,电子云交迭会产生巨大的排斥力,如何解释?2-12.试解释一个中性原子吸收一个电子一定要放出能量的现象.2-13.如何理解电负性可用电离能加亲和能来表征?2-14.何为杂化轨道?2-15.你认为固体的弹性强弱主要由排斥作用决定呢,还是吸引作用决定?第三章晶格振动与晶体的热学性质3-1.什么是简谐近似?3-2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线,并简要说明其意义。
《电磁场与电磁波》课后习题解答(第五章)

《电磁场与电磁波》课后习题解答(第五章)————————————————————————————————作者:————————————————————————————————日期:习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ,如果把它移动到无穷远处,需要作多少功?解:用镜像法计算。
导体面上的感应电荷的影响用镜像电荷来代替,镜像电荷的大小为-Q ,位于和原电荷对称的位置。
当电荷Q 离导体板的距离为x 时,电荷Q 受到的静电力为2)2(042x Q F επ-=静电力为引力,要将其移动到无穷远处,必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中,外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以,在整个过程中,外力作的总功为dq8/2επ。
也可以用静电能计算。
在移动以前,系统的静电能等于两个点电荷之间的相互作用能:d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+=移动点电荷Q 到无穷远处以后,系统的静电能为零。
因此,在这个过程中,外力作功等于系统静电能的增量,即外力作功为dq8/2επ。
5.2 一个点电荷放在直角导体内部(如图5-1),求出所有镜像电荷的位置和大小。
解:需要加三个镜像电荷代替 导体面上的感应电荷。
在(-a ,d )处,镜像电荷为-q ,在(错误!链接无效。
)处, 镜像电荷为q ,在(a ,-d )处,镜像电荷为-q 。
图5-1 5.3 证明:一个点电荷q 和一个带有电 荷Q 、半径为R 的导体球之间的作用力为]2)22(2[04R D DRq D D qR Q q F --+=επ其中D 是q 到球心的距离(D >R )。
证明:使用镜像法分析。
固体物理第五章习题及答案

.
从上式可以看出,当电子从外场力获得的能量又都输送给了晶格时, 电子的有效质量 m* 变 为 . 此时电子的加速度
a= 1 F =0
m*
,
即电子的平均速度是一常量. 或者说, 此时外场力与晶格作用力大小相等, 方向相反. 11. 万尼尔函数可用孤立原子波函数来近似的根据是什么?
[解答] 由本教科书的(5.53)式可知, 万尼尔函数可表示为
m* = 1 m 1 + 2Tn
Vn <1.
10. 电子的有效质量 m* 变为 的物理意义是什么?
[解答] 仍然从能量的角度讨论之. 电子能量的变化
(dE)外场力对电子作的功 = (dE)外场力对电子作的功 + (dE)晶格对电子作的功
m*
m
m
=
1 m
(dE ) 外场力对电子作的功
− (dE)电子对晶格作的功
i 2 nx
V (x) = Vne a
n
中, 指数函数的形式是由什么条件决定的?
[解答] 周期势函数 V(x) 付里叶级数的通式为
上式必须满足势场的周期性, 即
V (x) = Vneinx
n
显然
V (x + a) = Vnein (x+a) = Vneinx (eina ) = V (x) = Vneinx
Es (k)
=
E
at s
− Cs
−
Js
e ik Rn
n
即是例证. 其中孤立原子中电子的能量 Esat 是主项, 是一负值, − Cs和 − J s 是小量, 也是负 值. 13. 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么?
光纤通信原理参考答案

光纤通信原理参考答案第一章习题1-1 什么是光纤通信?光纤通信是利用光导纤维传输光波信号的通信方式。
1-2 光纤通信工作在什么区,其波长和频率是什么?目前使用的通信光纤大多数采用基础材料为SiO2的光纤。
它是工作在近红外区,波长为0.8~1.8μm,对应的频率为167~375THz。
1-3 BL积中B和L分别是什么含义?系统的通信容量用BL积表示,其含义是比特率—距离积表示,B为比特率,L为中继间距。
1-4 光纤通信的主要优点是什么?光纤通信之所以受到人们的极大重视,是因为和其他通信手段相比,具有无以伦比的优越性。
主要有:(1) 通信容量大(2) 中继距离远(3) 抗电磁干扰能力强,无串话(4) 光纤细,光缆轻(5) 资源丰富,节约有色金属和能源。
光纤还具有均衡容易、抗腐蚀、不怕潮湿的优点。
因而经济效益非常显著。
1-5 试画出光纤通信系统组成的方框图。
一个光纤通信系统通常由电发射机、光发射机、光接收机、电接收机和由光纤构成的光缆等组成。
1-5 试叙述光纤通信的现状和发展趋势。
略第二章习题2-1 有一频率为Hz 13103⨯的脉冲强激光束,它携带总能量W=100J ,持续 时间是τ=10ns(1ns=10-9s)。
此激光束的圆形截面半径为r=1cm 。
求:(1) 激光波长; (2) 平均能流密度; (3) 平均能量密度; (4) 辐射强度;(1)m c513810103103-=⨯⨯==νλ (2)213229/1018.3)10(1010100ms J S W S ⨯=⨯⨯⨯=∆=--πτ (3)s m J c S w 25813/1006.11031018.3⨯=⨯⨯== (4)213/1018.3ms J S I ⨯==2-2 以单色光照射到相距为0.2mm 的双缝上,双缝与屏幕的垂直距离为1m 。
(1) 从第一级明纹到同侧旁第四级明纹间的距离为7.5mm ,求单色光的波长; (2) 若入射光的波长为6×10-7m ,求相邻两明纹间的距离。
(完整word版)固体的能带理论习题.doc
第五章固体的能带理论1.布洛赫电子论作了哪些基本近似?它与金属自由电子论相比有哪些改进?解:布洛赫电子论作了 3 条基本假设,即①绝热近似,认为离子实固定在其瞬时位置上,可把电子的运动与离子实的运动分开来处理;②单电子近似,认为一个电子在离子实和其它电子所形成的势场中运动;③周期场近似,假设所有电子及离子实产生的场都具有晶格周期性。
布洛赫电子论相比于金属自由电子论,考虑了电子和离子实之间的相互作用,也考虑了电子与电子的相互作用。
2.周期场对能带形成是必要条件吗?解:周期场对能带的形成是必要条件,这是由于在周期场中运动的电子的波函数是一个周期性调幅的平面波,即是一个布洛赫波。
由此使能量本征值也称为波矢的周期函数,从而形成了一系列的能带。
3.一个能带有N 个准连续能级的物理原因是什么?解:这是由于晶体中含有的总原胞数 N 通常都是很大的,所以 k 的取值是十分密集的,相应的能级也同样十分密集,因而便形成了准连续的能级。
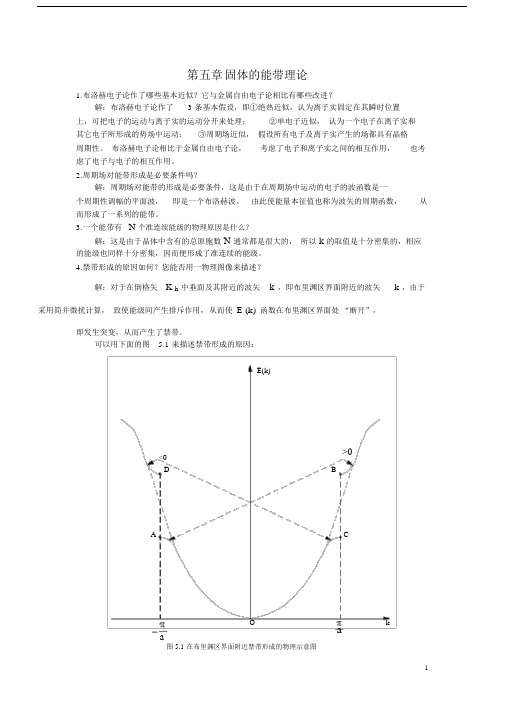
4.禁带形成的原因如何?您能否用一物理图像来描述?解:对于在倒格矢K h中垂面及其附近的波矢k ,即布里渊区界面附近的波矢k ,由于采用简并微扰计算,致使能级间产生排斥作用,从而使E (k)函数在布里渊区界面处“断开”,即发生突变,从而产生了禁带。
可以用下面的图 5.1 来描述禁带形成的原因:E(k)>0<0D BA CO kaa5.近自由电子模型与紧束缚模型各有何特点?它们有相同之处?解:所谓近自由电子模型就是认为电子接近于自由电子状态的情况,而紧束缚模型则认为电子在一个原子附近时, 将主要受到该原子场的作用, 把其它原子场的作用看成微扰作用。
这两种模型的相同之处是: 选取一个适当的具有正交性和完备性的布洛赫波形式的函数 集,然后将电子的波函数在所选取的函数集中展开, 其展开式中有一组特定的展开系数,将展开后的电子的波函数代入薛定谔方程,利用函数集中各基函数间的正交性,可以得到一组各展开系数满足的久期方程。
中山大学固体物理第五章参考答案
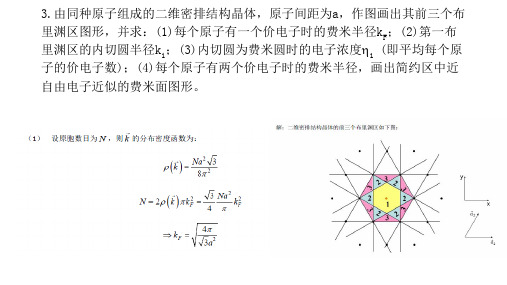
4.分别求出二维正方晶格简约区中沿M和XZM轴自由电子能量函数En(k) 能量
最低的前四条曲线的表达式,画出其示意图并给出各曲线的简并度。
二度简并
• 思考题
(1)对有限尺寸晶体(如量子点,量子线或量子井),你认为其晶体能带相 对于理想晶体会有什么变化?
周期性边界条件破坏,边界效应开始变得明显能带不再是准连续的。
反。
构造一虚拟的 空穴带,以描 述空穴动力学
k
逸失一电子 后的价带
2、能隙的由来?利用能带理论解释导体、 半导体以及绝缘体?
要点:本质是由于原子与原子的相互作用能 级分裂成能带,能带之间即是能隙。晶体中 是由于周期性势场的影响,在布里渊区边界 处bloch波的散射形成了能隙。
导体半导体绝缘体:电子的填充+能隙的大 小
(3)空穴:k(状态)空间的一种状态空缺,是存在这一空缺的整
个能带的描述,同其它电子一样,在真实空间的位置不确定,
在k空间的运动方向与其它电子相同,总带正电荷。
k 如果轨道中一个波矢为
能带是对称的,有
Ee
(ke
)
Ee
(ek的e ) 电Eh子(k逸e ) 失Eh,(k则h ),空显穴然的有波矢E为h (k-h
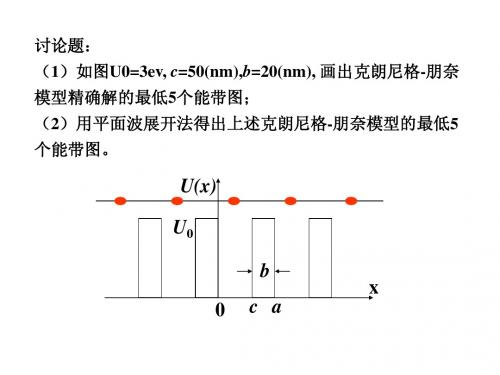
边界条件:波函数和它的一阶导数在x=c,和a处连续
U(x)
U0
1区 2区 3区
b x
0 ca Aeic Beic Cei 'c Dei 'c , ( Aeic Beic ) '(Cei 'c Dei 'c ) Cei 'a Dei 'a eika ( Aeia Beia ), '(Cei 'a Dei 'a ) eika ( Aeia Beia )
无机化学_第三版_练习及答案

第二章1.某气体在293K与9.97×104Pa时占有体积1.910-1dm3其质量为0.132g,试求这种气体的相对分子质量,它可能是何种气体?解2.一敝口烧瓶在280K时所盛的气体,需加热到什么温度时,才能使其三分之一逸出?解3.温度下,将1.013105Pa的N2 2dm3和0.5065Pa的O23 dm3放入6 dm3的真空容器中,求O2和N2的分压及混合气体的总压。
解4.容器中有4.4 g CO2,14 g N2,12.8g O2,总压为2.026105Pa,求各组分的分压。
解5.在300K,1.013105Pa时,加热一敝口细颈瓶到500K,然后封闭其细颈口,并冷却至原来的温度,求这时瓶内的压强。
解6.在273K和1.013×105Pa下,将1.0 dm3洁净干燥的空气缓慢通过H3C—O—CH3液体,在此过程中,液体损失0.0335 g,求此种液体273K时的饱和蒸汽压。
解7.有一混合气体,总压为150Pa,其中N2和H2的体积分数为0.25和0.75,求H2和N2的分压。
解8.在291K和总压为1.013×105Pa时,2.70 dm3含饱和水蒸汽的空气,通过CaCl2干燥管,完全吸水后,干燥空气为3.21 g,求291K时水的饱和蒸汽压。
解9.有一高压气瓶,容积为30 dm3,能承受2.6×107Pa,问在293K时可装入多少千克O2而不致发生危险?解10.在273K时,将同一初压的4.0 dm3 N2和1.0dm3 O2压缩到一个容积为2 dm3的真空容器中,混合气体的总压为3.26×105 Pa,试求(1)两种气体的初压;(2)混合气体中各组分气体的分压;(3)各气体的物质的量。
解P/1051.0130.675 0.507 0.338 0.253 ρ/g ·dm3-2.30741.52631.14010.757130.56660用作图外推法(p 对ρ/p )得到的数据求一氯甲烷的相对分子质量。
《固体物理学答案》第五章

第五章 晶体中电子能带理论 习题1.晶体常数为a 的一维晶体中,电子的波函数为(1)()x ai x k πψ3cos =,(2)()f la x f x k,)(-l ∑∞∞=-=ψ是某一函数,求电子在以上状态中的波矢.[解 答]由《固体物理教程》(5.14)式()()r e R r k R r i n k nψψ∙=+可知,在一维周期势场中运动的电子的波函数满足()()x e a x k ika k ψψ=+由此得(1) ()()()()x e x x ai x a i a x a i a x k ika k k ψψππππψ=-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡+=+3cos 3cos 3cos于是1-=ikae因此得 ,5,3,aa akπππ±±±= 若只取布里渊区内的值:ak aππ<-,则有ak π=(2) ()].)1([)(a l x f la a x f a x l l k ∑∑∞-∞=∞-∞=--=++=+ψ令1+='ll得 ()()()()x e x a l x f a x k ika k k ψψψ==-=+∑'.由上式知 ikae =1所以有 ,6,4,2,0aa a kπππ±±±= 因此得在布里渊区内的值为0=k2.一维周期势场为()()[]()⎪⎩⎪⎨⎧-≤≤+-+≤≤---=.1,0,21222b na x b a n b na x b na na x b mW x V 当当其中b a 4=,W 为常数,试画出此势能曲线,并求出势能的平均值.[解 答]图5.1 一维周期势场如图5.1所示,由于势能具有周期性,因此只能在一个周期内求平均即可,于是得V=a 1 ()dx x V a a ⎰-22=()dx x V b bb ⎰-2241 =dx x b mW b b b ⎰--][2141222 =b b x x b b mW --]31[8322 =2261b mW . 3.用近自由电子模型求解上题,确定晶体的第一及第二个禁带宽度. [解 答]根据教科书(5.35)式知禁带宽度的表示式为 ng V E 2=,其中n V 是周期势场()x V傅里叶级数的系数,该系数可由《固体物理教程》(5.22)式n V = a 1 ()dx e x V nx ai a a π222--⎰求得,第一禁带宽度为112V E g ==2()dxex V a a x ai ⎰--222a 1π=2⎰---b b x ai dxex b mW b π2222][241=2⎰-⎪⎭⎫ ⎝⎛-b b dx x b x b mW b 2cos ][241222π=3228πb mW .第二禁带宽度为222V E g ==2()dxex V a a x ai ⎰--224a 1π=2⎰---b b x bi dx e x b mW b π][241222 =2⎰-⎪⎭⎫ ⎝⎛-b b dx x b x b mW b πcos ][241222=222πb mW4.已知一维晶格中电子的能带可写成()⎪⎭⎫⎝⎛+-=ka ka ma k E 2cos 81cos 8722 , 式中a是晶格常数.m 是电子的质量,求(1)能带宽度,(2)电子的平均速度,(3)在带顶和带底的电子的有效质量. [解 答](1)能带宽度为 .min max E E E -=∆由极值条件 ()0=dkk dE 得上式的唯一解是0sin =ka 的解,此式在第一布里渊区内的解为 ak π,0=.当()k E k ,0时=取极小值min E ,且有 min E =()00=E当()k E ak,时π=,E(k)取极大值max E ,且有.222max ma a E E=⎪⎭⎫ ⎝⎛=π由以上可得能带宽度为.222m i nm a x ma E E E =-=∆(2)由《固体物理教程》(5.81)式,得电子的平均速度为 ().2sin 41sin 1⎪⎭⎫⎝⎛-==ka ka ma dk k dE v(3)由《固体物理教程》(5.87)式得,带顶和带底电子的有效质量分别为.322cos 21cos 1222m ka ka m k E mak ak ak -=⎪⎭⎫⎝⎛-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂=±=-±=*±=πππ.22cos 21cos 012220m ka ka m k E m k k k =⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==-==*5.对简立方结构晶体,其晶格常数为a .(1)用紧束缚方法求出对应非简并s态电子的能带;(2)分别画出第一布里渊区[110]方向的能带﹑电子的平均速度、有效质量以及沿[110]方向有恒定电场时的加速度曲线.[解 答](1)非简并s态电子的能带().e n R k ∑∙--=ns s ats s J C E k E式中n R是晶体参考格点最近邻格矢.对于简单立方晶体,任一格点有6个最近邻.取参考格点的坐标为(0,0,0),则6个最近邻点的坐标为()()().,0,0,0,,0,0,0,a a a ±±±简单立方体非简并s 态电子的能带则为()().cos cos cos 2a k a k a k J C E k E z y x s s at s s ++--=(2)在[110]方向上 ,22,0k k k k y x z === 能带变为(),22cos 40⎪⎪⎭⎫⎝⎛-=ka J E k E s s其中 ,20ss at s J C E E --=在[110]方向上,在第一布里渊区内,电子的能带如图5.2所示.图5.2[110]方向电子的能带电子的平均速度.22sin 221⎪⎪⎭⎫⎝⎛=∂∂=ka a J k E v s 平均速度曲线如图5.3所示.图5.3 平均速度曲线电子的有效质量,22cos 222222⎪⎪⎭⎫ ⎝⎛=∂∂=*ka a J k E m s 有效质量曲线如图5.4所示.图5.4 有效质量曲线 在[110]方向有恒定电场情况下,电子的受力 εe F -=电子的加速度2222cos 2⎪⎪⎭⎫⎝⎛-==*ka a J e m F a s ε.设电场方向与[110]方向相反,加速度曲线则如图5.5所示.图5.5加速度曲线6.用紧束缚方法处理面心立方体晶格的s 态电子,试导出其能带⎥⎦⎤⎢⎣⎡++--=2cos 2cos 2cos 2cos 2cos 2cos 4a k a k a k a k a k a k J C E E x z z y y x s s atss ,并求出能带底的有效质量. [解 答]用紧束缚方法处理晶格的s 态电子,当只计及最近邻格点的相互作用时,根据《固体物理教程》(5.60)式,其能带表示式为()∑∙--=ns s ats s J C E k E n R k e ,n R 是最近邻格矢.对面心立方晶格,取参考点的坐标为(0,0,0),则12个最近邻格点的坐标为 (2a ±,2a ±,0),( 2a ±,0, 2a ±),(0, 2a ±,2a±). 将上述12组坐标带入能带的表示式,得()∑∙--=ns s ats s J C E k E n R k es s ats J C E --=()()()()()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡++++⎥⎦⎤⎢⎣⎡++++⎥⎦⎤⎢⎣⎡+++---+-+---+-++---+-z y z y z y z k y k a i z k x k a i z k x k a i z k x k a i z x y x y x y x y x k k a i k k a i k k a i k k a i k k a i k k a i k k a i k k a i e e e e e e e e e e e e 222222222222()()()()()()⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧++++-+++-++--=z y z y z x z x y x y x s s ats k k a k k a k k a k k a k k a k k a J C E 2cos 2cos 2cos 2cos 2cos 2cos⎥⎦⎤⎢⎣⎡++--=2cos 2cos 2cos 2cos 2cos 2cos 4a k a k a k a k a k a k J C E x z z y y x s s ats .能带底即()k E 的最小值对应的k为(0,0,0),有《固体物理教程》(5.87)可得在能带底处电子的有效质量为2202222a J k E m s kxx xx i=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==*.同理可得222a J m s yy=*,222a J m s zz =*其它交叉项的倒数全为零.7.用紧束缚方法处理体心立方晶体,求出 (1) s 态电子的能带为()2cos 2cos 2cos 8a k a k a k J C E k E z y x s s ats s --= ; (2) 画出第一布里渊区[111]方向的能带曲线;(3) 求出带顶和带底电子的有效质量. 【解 答】(1)用紧束缚方法处理晶格的s 态电子,当只计及最近邻格点的相互作用时,其能带的表示式为().e n R k ∑∙--=ns s ats s J C E k E n R 是最近邻格矢.对体心立方晶格,取参考格点的坐标为(0,0,0),则8个最近邻格点的坐标为 (2,2,2aa a ±±±). 将上述8组坐标代入能带的表示式,的().e n R k ∑∙--=ns s ats s J C E k E()()()()()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++++++--=---+---+---++-+--+++z k y k x k a i z k y k x k a i z k y k x k a i z k y k x k ai z k y k x k a i z k y k x k a i z k y k x k a i z y x e e e e e e e e J C E k k k a i s s ats 22222222()()()()⎥⎦⎤⎢⎣⎡+++--=--+--+2cos 2cos 2cos 2cos 22222a k e a k e a k e a k e J C E z zz z k k a i s s atsy k x k ai y k x k a i y k x k a i y x ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+--=-2cos 2cos 422a k a k e e J C E z y k a i s s at s x k ai x 2cos 2cos 2cos 8ak a k a k J C E z y x s s at s --=.(2)在[111]方向上k k k k z y x 33=== , 且第一布里渊区边界在 ak k k z y x π±===,于是能带化成⎪⎪⎭⎫⎝⎛-=ka J E E s 63cos 830,其中s ats C E E -=0.图5.6为第一布里渊区[111]方向的能带曲线.图5.6 [111]方向的能带曲线(3)由能带的表示式及余弦函数的性质可知,当===z y x k k k 时,sE 取最小值,即0===z y x k k k 是能带底,电子的有效质量为2202222a J k E m s kxx xx i=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==*同理可得222a J m s yy=*,222a J m s zz =*其它交叉项的倒数全为零.而在布里渊区边界上的⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛±a a a πππ2,0,0,0,2,0,0,0,2处是能带顶,电子的有效质量为222a J m m m s zzyyxx-===***.其它交叉项的倒数也全为零.8.某晶体电子的等能面是椭球面⎪⎪⎭⎫⎝⎛++=32322212122m k m k m k E ,坐标轴1,2,3相互垂.(1) 求能态密度;(2)今加一磁场B , B与坐标轴的夹角的方向余弦分别为γβα,,,写出电子的运动方程;(3) 证明电子在磁场中的回旋频率*=m eB c ω, 其中2132********⎥⎦⎤⎢⎣⎡++=*m m m m m m m γβα.【解 答】(1) 由已知条件可将波矢空间内电子能带满足的方程化为1222232322222121=++ E m k E m k E m k .将上式与椭球公式1222222=++c z b y a x 比较可知,在波矢空间内电子的等能面是一椭球面.与椭球的体积abc π34比较可得到,能量为E 的等能面围成的椭球体积 2332132234E m m m πτ= 由上式可得dE E m m m d 21321324 πτ=.能量区间内电子的状态数目()dE E m m m V d V dz cc 1321323222πτπ== 是晶体体积.电子的能态密度()21321322E m m m VdE dz E N cπ==(2) 根据《固体物理教程》中(5.86)式得⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂∂+∂∂=331222121212211F k k EF k k E F k E a ,⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂+∂∂∂=332222221122221F k k E F k E F k k E a,⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂+∂∂∂=323222321132231F k E F k k E F k k E a .将⎪⎪⎭⎫⎝⎛++=32322212122m k m k m k E代入上述三式得运动方程为 333222111,,m F a m Fa m F a ===.即333222111,,F dtdvm F dt dv m F dt dv m ===. (1)当存在磁场B时,电子受到洛仑兹力B v e F⨯-=.其分量形式为 ()()23323223321v B v B v e B v B v e F ωνωβγ-=--=--=,()()31131331132v B v B v e B v B v e F ωνωγα-=--=--=, ()()12212112213v B v B v e B v B v e F ωνωαβ-=--=--=式中B B=,γωβωαωeB eB eB ===321,,.将上述结果代入运动方程(1)得.,,122133311322233211v v dt dvm v v dt dvm v v dt dv m ωωωωωω-=-=-= (2)(3)上述方程可用不同的方法求解.解法一:对(2)式两边作拉普拉斯变换,并采用如下初始条件 ()1010v v =,()2020v v =,().0303v v =得[]11v pL m +[]23v L ω-[]32v L ω=101v m ,-[]13v L ω+[]22v pL m +[]31v L ω=202v m ,[]12v L ω-[]21v L ω+[]33v pL m =303v m .由此解出[]∆∆=11v L . 其中()()B p Ap m m m p m m m pm p m p m +≡+++=---=∆22332222113321312123231ωωωωωωωωω.321m m m A =,321233222211m m m m m m B ωωω++=.()()322130313202121021120332302323103213130312202231011C p C p C v m v m v m pv m m v m m p v m m m pm v m p m v m v m ++≡+++-+=--=∆ωωωωωωωωωωω()203302322103211,v v m m C v m m m C ωω+==,3031320212102113v m v m v m C ωωωωω++=.因此得[]()Bp A C B p p AB C B C p AB C B p Ap C p C p C v L +++-+=+++=22231323221111.上式两边取逆拉普拉斯变换得t B BA Ct B AB C B C p AB C v sin cos 123131+-+=.同理可得t B B A C t B AB C B C p AB C v sin cos 123132'+'-'+'=.()301103312203211,v v m m C v m m m C ωω+='=', 1021130323202223v m v m v m C ωωωωω++='.及t B B A C t B AB C B C p AB C v sin cos 123133''+''-''+''=.()102201212303211,v v m m C v m m m C ωω+=''=''2032210311302333v m v m v m C ωωωωω++=''.可见电子回旋频率为B .解法二:由于电子作周期运动,将试探解t i c e v v ω101=, t i c e v v ω202=t i c e v v ω303=(这里302010,,v v v 一般为复数,电子的真实速度应为321,,v v v 的实部或虚部.) 代入(2)式得 101v m i c ω+302v ω-203v ω=0,103v ω+202v m i c ω-301v ω=0,102v ω-201v ω+303v m i c ω=0.302010,,v v v 有不全为零的解的充要条件是0312123231=----m i m i m i c c c ωωωωωωωωω. 由此得 ()02332222113321=++-c c m m m m m m ωωωωω.于是B m m m m m m c=++=3212332222112ωωωω.这样,两种方法均给出电子回旋频率为21321233222211⎪⎪⎭⎫ ⎝⎛++==m m m m m m B c ωωωω.再将γωβωαωeB eB eB ===321,,,代入上式即得*=meBc ω, 其中2132********⎪⎪⎭⎫⎝⎛++=*m m m m m m m γβα.9.求出一维、二维金属中自由的能态密度.[解 答](1)一维情况自由电子的色散关系为 mk E 222 =.由此得dk E m dk m kdE 2121222⎪⎪⎭⎫ ⎝⎛== ,即dE E m dk 212122-⎪⎭⎫⎝⎛= . 对应同一个dE ,在k ±方向各有一个dk ,因此空间中dE E E +与之间的区间为dE E m dk d 2121222-⎪⎭⎫⎝⎛== τ,在该范围内的状态数为dE E m L d LdZ 212122-⎪⎭⎫⎝⎛== πτπ,其中L 是晶格长度.于是,态密度()12122-⎪⎭⎫ ⎝⎛==E m L dE dZ E N π.(2)二维情况参照《固体物理教程》(5.102)式可知,二维情况下态密度的一般表示式为()⎰∇=Lk EdLS E N 22π.其中S 是晶格的面积,积分沿能量为E 的等能线进行.由()2222y x k k m E += 得 ()mk k k m E y x k 221222 =+=∇.于是有()21222222 mS k m k S E dL S E N Lk ππππ=⎪⎪⎭⎫ ⎝⎛=∇=-⎰.10.二维金属晶格,晶胞为简单矩形,晶格常数A a2=,A b 4=,原子为单价的.(1) 试画出第一、二布里渊区; (2) 计算自由电子费密半径;(3) 画出费密面在第一、二布里渊区的形状.【解 答】(1) 倒格子原胞基矢j bb i a b ππ2,221==.选定一倒格点为原点,原点的最近邻倒格矢有4个,它们是21,b b ±±这4个倒格矢的中垂线围成的区间即是第一布里渊区.即图5.7中Ⅰ所示区间.原点的次近邻倒格矢有4个,它们是21b b ±±这4个倒格矢的中垂线围成的区间与第一布里渊区边界围成的区间即是第二布里渊区.即图5.7中Ⅱ所示区间.图5.7 二维矩形晶格第一、二布里渊区(2)在绝对零度时,二维金属中导电电子若看成自由电子,电子的能量mk E 222 =,能量dE E E+→区间的电子占据波矢空间dk 的范围.在此范围内的波矢数目为图5.8二维波矢空间kdk S ππ2)2(2∙,其中2)2(πS是二维金属中导电电子的波矢密度,S 是金属面积。
固体物理答案第五章1

∑ f ( x la )
∞
为某一确定的函数) ( f 为某一确定的函数)
试求电子在这些状态的波矢。 试求电子在这些状态的波矢。
r r r r r ir Rn 解: 由式 ψk r + Rn = e ψk (r )
(
)
可知, 可知,在一维周期势场中运动的电子波函数满足
ψ k ( x + a ) = e ikna ψ k ( x )
v* a =
1 v i o 2A v* 1 v b = j o 4A
v* v* 以 a ,b
为基矢构成的倒格子
B3
ky
B2
A2
b
B1
A1
如图6-11所示 图中“。” 所示,图中 如图 所示 图中“
A3
o
代表倒格点。由图可见, 代表倒格点。由图可见, 矩形晶格的倒格子也是 矩形格子。 矩形格子。 第一区
(s = 0,1,2...
n = ±1,±2...)
5.2 电子在周期场中得势能
1 2 2 2 mω b ( x na ) V (x) = 2 0
[
]
当na b ≤ x ≤ na + b
当(n - 1)a + b ≤ x ≤ na b
是常数。 试画出此势能曲线,并求此势能的平均值。 且 a = 4b, ω 是常数。 试画出此势能曲线,并求此势能的平均值。 V(x) 解:
r k ya kza k xa at E k = E s A 8J cos cos cos 2 2 2
并求能带宽度。 并求能带宽度。 用紧束缚方法处理晶格的s态电子,当只计及最近邻格点 用紧束缚方法处理晶格的 态电子, 解: 态电子 的相互作用时,其能带的表示式为 的相互作用时,
大学物理第5章习题答案2(1)
(
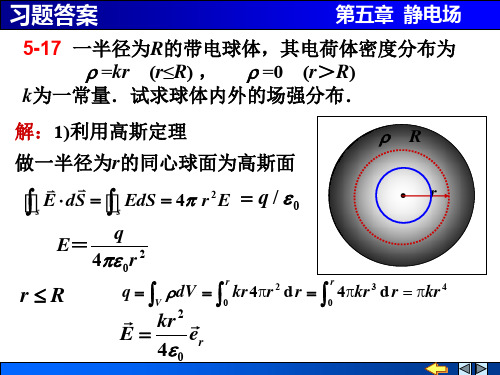
1 R1
1 R2
)
r
Q1 R1
Q2 R2
0 r R1
E
4
Q1 π 0 r
2
R1 r R2
Q1 Q2 4 π0r2
r R2
习题答案
第五章 静电场
5-30 两个很长的同轴圆柱面(R1 =3. 0010-2 m, R2 =0. 10m) , 带有等量异号的电荷,两者的电势差为450 V.
第五章 静电场
(2)
r E1 3 0 r1
r E2 3 0 r2
E E1 E2
r 3 0
r1
r2
r
a
3 0
习题答案
第五章 静电场
5-22 如图,有三个点电荷Q1 ,Q2 ,Q3沿一条直线等间 距分布,且Q1 =Q3 =Q,已知其中任一点电荷所受合力均 为零. 求在固定Q1 , Q3的情况下,将Q2从O点推到无穷 远处外力所作的功.
s
EdS 2 rhE
s
0
R1 r R2
q h
E
2 π0r
第五章 静电场
l R2
-+
r h l - + R1 - + R2 -+
习题答案
第五章 静电场
精品课件!
习题答案
第五章 静电场
精品课件!
习题答案
第五章 静电场
解(1)设两圆柱面单位长度上
分别带电
V (r) r E dr
rR2
E
dr
R2
固体物理+黄昆答案 第五章

w.
案
网
磁感应强度
kh da w. co m
v dk v v v h = qv ( k ) × B dt
课后答案网
v v hk1 hk2 hk3 v (k ) = k1 + k2 + k3 m1 m2 m3 v B = B(k1α + k2 β + k3γ )
令
k1 = k e , k 2 = k e , k 3 = k e
0 iωt 1
ww
qBγ 0 qBβ 0 dk1 0 k3 k2 dt + qB( m γ m β ) = 0 iωk1 + m k 2 m k 3 = 0 2 3 2 3 qBα 0 qBγ 0 dk 2 k3 k1 0 k1 = 0 k3 + qB( α γ ) = 0 iωk 2 + m3 m1 dt m3 m1 dk 3 qBβ 0 qBα 0 k1 k2 0 k1 k2 = 0 + qB( β α ) = 0 iωk 3 + m1 m2 m1 m2 dt
课
1 dE ( k ) v(k ) = h dk
电子的有效质量
能带底部 k = 0 能带顶部 k =
w.
π
a
ww
习题问题讨论 —— 固体物理 黄昆
kh da w. co m
后
2E m* = h 2 / 2 k
有效质量 有效质量
课后答案网
h 1 v(k ) = (sin ka sin 2ka ) ma 4
课
后
式中a为晶格常数.计算1)能带的宽度;2)电子在波矢k的状 态时的速度;3)能带底部和能带顶部电子的有效质量
答
案
能带理论(5)

空带
带隙
非导体
价带:由价电子能级分裂而形成的能带。
★通常情况下,价带为能量最高的 能带; ★价带可能被电子填满,成为满带; ★也可能未被电子填满,形成不满 带或半满带。
空带
带隙
价 带
在绝缘体中,价电子刚好填满 最低的一系列能带,最上边的 满带 —— 价带
绝缘体
再高的各能带全部都是空的 —— 空带
导体中,一部分价电子存在于不满带中,这种能 带称为导带
V 2m 1 V m 1 2 3 2 4 k E 2 CE 2 4 k 2 23
3 2
在近自由电子情况下,周期场的影响主要表现在布 里渊区边界附近,而离布里渊区边界较远处,周期场对
电子运动的影响很小。
二、费米面
1)自由电子 如果固体中有N个自由电子,按照泡利原理它们基态是由
(1)导体:能带结构有三种形式 形式1:价带中只填充了部分电子,在外加电场作用 下,这些电子很容易在该能带中从低能级跃迁到较 高能级 —— 从而形成电流
导带中电子的转移
例如:
金属Li
电子排布1s22s1
每个原子只有一个价电子,整个晶体中的价电子只 能添满半个价带 —— 实际参与导电的是不满带 中的电子 —— 电子导电型导体
导带
满带
导体
空带:若一个能带中所有的能级都没有被电子填入,
这样的能带称为空带。
空带:每一个能级上都没有 电子的能带
★与各原子的激发态能级相对应 的能带,在未被激发的正常情况 下就发的电子进入,
则空带就变成了导带。 非导体
禁带:两个相邻能带间的间隔
★禁带中不存在电子的定态; ★禁带的宽度对晶体的导电性起着 重要的作用。
带宽度比较大,不能导电。
《固体物理学答案》第五章

第五章 晶体中电子能带理论 习题1.晶体常数为a 的一维晶体中,电子的波函数为(1)()x ai x k πψ3cos =,(2)()f la x f x k,)(-l ∑∞∞=-=ψ是某一函数,求电子在以上状态中的波矢.[解 答]由《固体物理教程》(5.14)式()()r e R r k R r i n k nψψ∙=+可知,在一维周期势场中运动的电子的波函数满足()()x e a x k ika k ψψ=+由此得(1) ()()()()x e x x ai x a i a x a i a x k ika k k ψψππππψ=-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡+=+3cos 3cos 3cos于是1-=ikae因此得 ,5,3,aa akπππ±±±= 若只取布里渊区内的值:ak aππ<-,则有ak π=(2) ()].)1([)(a l x f la a x f a x l l k ∑∑∞-∞=∞-∞=--=++=+ψ令1+='ll得 ()()()()x e x a l x f a x k ika k k ψψψ==-=+∑'.由上式知 ikae =1所以有 ,6,4,2,0aa a kπππ±±±= 因此得在布里渊区内的值为0=k2.一维周期势场为()()[]()⎪⎩⎪⎨⎧-≤≤+-+≤≤---=.1,0,21222b na x b a n b na x b na na x b mW x V 当当其中b a 4=,W 为常数,试画出此势能曲线,并求出势能的平均值.[解 答]图5.1 一维周期势场如图5.1所示,由于势能具有周期性,因此只能在一个周期内求平均即可,于是得V=a 1 ()dx x V a a ⎰-22=()dx x V b bb ⎰-2241 =dx x b mW b b b ⎰--][2141222 =b b x x b b mW --]31[8322 =2261b mW . 3.用近自由电子模型求解上题,确定晶体的第一及第二个禁带宽度. [解 答]根据教科书(5.35)式知禁带宽度的表示式为 ng V E 2=,其中n V 是周期势场()x V傅里叶级数的系数,该系数可由《固体物理教程》(5.22)式n V = a 1 ()dx e x V nx ai a a π222--⎰求得,第一禁带宽度为112V E g ==2()dxex V a a x ai ⎰--222a 1π=2⎰---b b x ai dxex b mW b π2222][241=2⎰-⎪⎭⎫ ⎝⎛-b b dx x b x b mW b 2cos ][241222π=3228πb mW .第二禁带宽度为222V E g ==2()dxex V a a x ai ⎰--224a 1π=2⎰---b b x bi dx e x b mW b π][241222 =2⎰-⎪⎭⎫ ⎝⎛-b b dx x b x b mW b πcos ][241222=222πb mW4.已知一维晶格中电子的能带可写成()⎪⎭⎫⎝⎛+-=ka ka ma k E 2cos 81cos 8722 , 式中a是晶格常数.m 是电子的质量,求(1)能带宽度,(2)电子的平均速度,(3)在带顶和带底的电子的有效质量. [解 答](1)能带宽度为 .min max E E E -=∆由极值条件 ()0=dkk dE 得上式的唯一解是0sin =ka 的解,此式在第一布里渊区内的解为 ak π,0=.当()k E k ,0时=取极小值min E ,且有 min E =()00=E当()k E ak,时π=,E(k)取极大值max E ,且有.222max ma a E E=⎪⎭⎫ ⎝⎛=π由以上可得能带宽度为.222m i nm a x ma E E E =-=∆(2)由《固体物理教程》(5.81)式,得电子的平均速度为 ().2sin 41sin 1⎪⎭⎫⎝⎛-==ka ka ma dk k dE v(3)由《固体物理教程》(5.87)式得,带顶和带底电子的有效质量分别为.322cos 21cos 1222m ka ka m k E mak ak ak -=⎪⎭⎫⎝⎛-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂=±=-±=*±=πππ.22cos 21cos 012220m ka ka m k E m k k k =⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==-==*5.对简立方结构晶体,其晶格常数为a .(1)用紧束缚方法求出对应非简并s态电子的能带;(2)分别画出第一布里渊区[110]方向的能带﹑电子的平均速度、有效质量以及沿[110]方向有恒定电场时的加速度曲线.[解 答](1)非简并s态电子的能带().e n R k ∑∙--=ns s ats s J C E k E式中n R是晶体参考格点最近邻格矢.对于简单立方晶体,任一格点有6个最近邻.取参考格点的坐标为(0,0,0),则6个最近邻点的坐标为()()().,0,0,0,,0,0,0,a a a ±±±简单立方体非简并s 态电子的能带则为()().cos cos cos 2a k a k a k J C E k E z y x s s at s s ++--=(2)在[110]方向上 ,22,0k k k k y x z === 能带变为(),22cos 40⎪⎪⎭⎫⎝⎛-=ka J E k E s s其中 ,20ss at s J C E E --=在[110]方向上,在第一布里渊区内,电子的能带如图5.2所示.图5.2[110]方向电子的能带电子的平均速度.22sin 221⎪⎪⎭⎫⎝⎛=∂∂=ka a J k E v s 平均速度曲线如图5.3所示.图5.3 平均速度曲线电子的有效质量,22cos 222222⎪⎪⎭⎫ ⎝⎛=∂∂=*ka a J k E m s 有效质量曲线如图5.4所示.图5.4 有效质量曲线 在[110]方向有恒定电场情况下,电子的受力 εe F -=电子的加速度2222cos 2⎪⎪⎭⎫⎝⎛-==*ka a J e m F a s ε.设电场方向与[110]方向相反,加速度曲线则如图5.5所示.图5.5加速度曲线6.用紧束缚方法处理面心立方体晶格的s 态电子,试导出其能带⎥⎦⎤⎢⎣⎡++--=2cos 2cos 2cos 2cos 2cos 2cos 4a k a k a k a k a k a k J C E E x z z y y x s s atss ,并求出能带底的有效质量. [解 答]用紧束缚方法处理晶格的s 态电子,当只计及最近邻格点的相互作用时,根据《固体物理教程》(5.60)式,其能带表示式为()∑∙--=ns s ats s J C E k E n R k e ,n R 是最近邻格矢.对面心立方晶格,取参考点的坐标为(0,0,0),则12个最近邻格点的坐标为 (2a ±,2a ±,0),( 2a ±,0, 2a ±),(0, 2a ±,2a±). 将上述12组坐标带入能带的表示式,得()∑∙--=ns s ats s J C E k E n R k es s ats J C E --=()()()()()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡++++⎥⎦⎤⎢⎣⎡++++⎥⎦⎤⎢⎣⎡+++---+-+---+-++---+-z y z y z y z k y k a i z k x k a i z k x k a i z k x k a i z x y x y x y x y x k k a i k k a i k k a i k k a i k k a i k k a i k k a i k k a i e e e e e e e e e e e e 222222222222()()()()()()⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧++++-+++-++--=z y z y z x z x y x y x s s ats k k a k k a k k a k k a k k a k k a J C E 2cos 2cos 2cos 2cos 2cos 2cos⎥⎦⎤⎢⎣⎡++--=2cos 2cos 2cos 2cos 2cos 2cos 4a k a k a k a k a k a k J C E x z z y y x s s ats .能带底即()k E 的最小值对应的k为(0,0,0),有《固体物理教程》(5.87)可得在能带底处电子的有效质量为2202222a J k E m s kxx xx i=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==*.同理可得222a J m s yy=*,222a J m s zz =*其它交叉项的倒数全为零.7.用紧束缚方法处理体心立方晶体,求出 (1) s 态电子的能带为()2cos 2cos 2cos 8a k a k a k J C E k E z y x s s ats s --= ; (2) 画出第一布里渊区[111]方向的能带曲线;(3) 求出带顶和带底电子的有效质量. 【解 答】(1)用紧束缚方法处理晶格的s 态电子,当只计及最近邻格点的相互作用时,其能带的表示式为().e n R k ∑∙--=ns s ats s J C E k E n R 是最近邻格矢.对体心立方晶格,取参考格点的坐标为(0,0,0),则8个最近邻格点的坐标为 (2,2,2aa a ±±±). 将上述8组坐标代入能带的表示式,的().e n R k ∑∙--=ns s ats s J C E k E()()()()()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++++++--=---+---+---++-+--+++z k y k x k a i z k y k x k a i z k y k x k a i z k y k x k ai z k y k x k a i z k y k x k a i z k y k x k a i z y x e e e e e e e e J C E k k k a i s s ats 22222222()()()()⎥⎦⎤⎢⎣⎡+++--=--+--+2cos 2cos 2cos 2cos 22222a k e a k e a k e a k e J C E z zz z k k a i s s atsy k x k ai y k x k a i y k x k a i y x ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+--=-2cos 2cos 422a k a k e e J C E z y k a i s s at s x k ai x 2cos 2cos 2cos 8ak a k a k J C E z y x s s at s --=.(2)在[111]方向上k k k k z y x 33=== , 且第一布里渊区边界在 ak k k z y x π±===,于是能带化成⎪⎪⎭⎫⎝⎛-=ka J E E s 63cos 830,其中s ats C E E -=0.图5.6为第一布里渊区[111]方向的能带曲线.图5.6 [111]方向的能带曲线(3)由能带的表示式及余弦函数的性质可知,当===z y x k k k 时,sE 取最小值,即0===z y x k k k 是能带底,电子的有效质量为2202222a J k E m s kxx xx i=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂==*同理可得222a J m s yy=*,222a J m s zz =*其它交叉项的倒数全为零.而在布里渊区边界上的⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛±a a a πππ2,0,0,0,2,0,0,0,2处是能带顶,电子的有效质量为222a J m m m s zzyyxx-===***.其它交叉项的倒数也全为零.8.某晶体电子的等能面是椭球面⎪⎪⎭⎫⎝⎛++=32322212122m k m k m k E ,坐标轴1,2,3相互垂.(1) 求能态密度;(2)今加一磁场B , B与坐标轴的夹角的方向余弦分别为γβα,,,写出电子的运动方程;(3) 证明电子在磁场中的回旋频率*=m eB c ω, 其中2132********⎥⎦⎤⎢⎣⎡++=*m m m m m m m γβα.【解 答】(1) 由已知条件可将波矢空间内电子能带满足的方程化为1222232322222121=++ E m k E m k E m k .将上式与椭球公式1222222=++c z b y a x 比较可知,在波矢空间内电子的等能面是一椭球面.与椭球的体积abc π34比较可得到,能量为E 的等能面围成的椭球体积 2332132234E m m m πτ= 由上式可得dE E m m m d 21321324 πτ=.能量区间内电子的状态数目()dE E m m m V d V dz cc 1321323222πτπ== 是晶体体积.电子的能态密度()21321322E m m m VdE dz E N cπ==(2) 根据《固体物理教程》中(5.86)式得⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂∂+∂∂=331222121212211F k k EF k k E F k E a ,⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂+∂∂∂=332222221122221F k k E F k E F k k E a,⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂+∂∂∂=323222321132231F k E F k k E F k k E a .将⎪⎪⎭⎫⎝⎛++=32322212122m k m k m k E代入上述三式得运动方程为 333222111,,m F a m Fa m F a ===.即333222111,,F dtdvm F dt dv m F dt dv m ===. (1)当存在磁场B时,电子受到洛仑兹力B v e F⨯-=.其分量形式为 ()()23323223321v B v B v e B v B v e F ωνωβγ-=--=--=,()()31131331132v B v B v e B v B v e F ωνωγα-=--=--=, ()()12212112213v B v B v e B v B v e F ωνωαβ-=--=--=式中B B=,γωβωαωeB eB eB ===321,,.将上述结果代入运动方程(1)得.,,122133311322233211v v dt dvm v v dt dvm v v dt dv m ωωωωωω-=-=-= (2)(3)上述方程可用不同的方法求解.解法一:对(2)式两边作拉普拉斯变换,并采用如下初始条件 ()1010v v =,()2020v v =,().0303v v =得[]11v pL m +[]23v L ω-[]32v L ω=101v m ,-[]13v L ω+[]22v pL m +[]31v L ω=202v m ,[]12v L ω-[]21v L ω+[]33v pL m =303v m .由此解出[]∆∆=11v L . 其中()()B p Ap m m m p m m m pm p m p m +≡+++=---=∆22332222113321312123231ωωωωωωωωω.321m m m A =,321233222211m m m m m m B ωωω++=.()()322130313202121021120332302323103213130312202231011C p C p C v m v m v m pv m m v m m p v m m m pm v m p m v m v m ++≡+++-+=--=∆ωωωωωωωωωωω()203302322103211,v v m m C v m m m C ωω+==,3031320212102113v m v m v m C ωωωωω++=.因此得[]()Bp A C B p p AB C B C p AB C B p Ap C p C p C v L +++-+=+++=22231323221111.上式两边取逆拉普拉斯变换得t B BA Ct B AB C B C p AB C v sin cos 123131+-+=.同理可得t B B A C t B AB C B C p AB C v sin cos 123132'+'-'+'=.()301103312203211,v v m m C v m m m C ωω+='=', 1021130323202223v m v m v m C ωωωωω++='.及t B B A C t B AB C B C p AB C v sin cos 123133''+''-''+''=.()102201212303211,v v m m C v m m m C ωω+=''=''2032210311302333v m v m v m C ωωωωω++=''.可见电子回旋频率为B .解法二:由于电子作周期运动,将试探解t i c e v v ω101=, t i c e v v ω202=t i c e v v ω303=(这里302010,,v v v 一般为复数,电子的真实速度应为321,,v v v 的实部或虚部.) 代入(2)式得 101v m i c ω+302v ω-203v ω=0,103v ω+202v m i c ω-301v ω=0,102v ω-201v ω+303v m i c ω=0.302010,,v v v 有不全为零的解的充要条件是0312123231=----m i m i m i c c c ωωωωωωωωω. 由此得 ()02332222113321=++-c c m m m m m m ωωωωω.于是B m m m m m m c=++=3212332222112ωωωω.这样,两种方法均给出电子回旋频率为21321233222211⎪⎪⎭⎫ ⎝⎛++==m m m m m m B c ωωωω.再将γωβωαωeB eB eB ===321,,,代入上式即得*=meBc ω, 其中2132********⎪⎪⎭⎫⎝⎛++=*m m m m m m m γβα.9.求出一维、二维金属中自由的能态密度.[解 答](1)一维情况自由电子的色散关系为 mk E 222 =.由此得dk E m dk m kdE 2121222⎪⎪⎭⎫ ⎝⎛== ,即dE E m dk 212122-⎪⎭⎫⎝⎛= . 对应同一个dE ,在k ±方向各有一个dk ,因此空间中dE E E +与之间的区间为dE E m dk d 2121222-⎪⎭⎫⎝⎛== τ,在该范围内的状态数为dE E m L d LdZ 212122-⎪⎭⎫⎝⎛== πτπ,其中L 是晶格长度.于是,态密度()12122-⎪⎭⎫ ⎝⎛==E m L dE dZ E N π.(2)二维情况参照《固体物理教程》(5.102)式可知,二维情况下态密度的一般表示式为()⎰∇=Lk EdLS E N 22π.其中S 是晶格的面积,积分沿能量为E 的等能线进行.由()2222y x k k m E += 得 ()mk k k m E y x k 221222 =+=∇.于是有()21222222 mS k m k S E dL S E N Lk ππππ=⎪⎪⎭⎫ ⎝⎛=∇=-⎰.10.二维金属晶格,晶胞为简单矩形,晶格常数A a2=,A b 4=,原子为单价的.(1) 试画出第一、二布里渊区; (2) 计算自由电子费密半径;(3) 画出费密面在第一、二布里渊区的形状.【解 答】(1) 倒格子原胞基矢j bb i a b ππ2,221==.选定一倒格点为原点,原点的最近邻倒格矢有4个,它们是21,b b ±±这4个倒格矢的中垂线围成的区间即是第一布里渊区.即图5.7中Ⅰ所示区间.原点的次近邻倒格矢有4个,它们是21b b ±±这4个倒格矢的中垂线围成的区间与第一布里渊区边界围成的区间即是第二布里渊区.即图5.7中Ⅱ所示区间.图5.7 二维矩形晶格第一、二布里渊区(2)在绝对零度时,二维金属中导电电子若看成自由电子,电子的能量mk E 222 =,能量dE E E+→区间的电子占据波矢空间dk 的范围.在此范围内的波矢数目为图5.8二维波矢空间kdk S ππ2)2(2∙,其中2)2(πS是二维金属中导电电子的波矢密度,S 是金属面积。
第5章 能带理论 习题参考答案

第5章 能带理论 (习题参考答案)1. 一矩形晶格,原胞长10a 210m -=⨯,10b 410m -=⨯ (1)画出倒格子图(2)以广延图和简约图两种形式,画出第一布里渊区和第二布里渊区(3)画出自由电子的费米面(设每个原胞有2个电子)解:(1)因为a =a i=20A i b =b j=40A j倒格子基矢为12a i A*=, 014b j A*=以a * b *为基矢构成的倒格子如下图。
由图可见,矩形晶格的倒格子也是矩形格子。
(2)取任一倒格子点O作为原点,由原点以及最近邻点A i,次近邻点B i的连线的中垂线可以围成第一,第二布里渊区,上图这就是布里渊区的广延图。
如采用简约形式,将第二区移入第一区,我们得到下图。
(3) 设晶体中共有N个原胞,计及自旋后,在简约布里渊区中便有2N个状态。
简约布里渊区的面积021()8A a b A ***-=⨯=而状态密度022()16()Ng K N A A *==当每个原胞中有2个电子时,晶体电子总数为202()216Fk F N g k kdk N k ππ=⨯=⎰所以01/211111()0.2()210()8F k A m π---=≈=⨯这就是费米圆的半径。
费米圆如下图所示2. 已知一维晶体的电子能带可写成()2271cos cos 2,88E k ka ka ma ⎛⎫=-+ ⎪⎝⎭式中a 是晶格常数。
试求能带的宽度;()()()()()()()()22222min 2max 22max min 22222min 71cos cos 2,8811cos 24400,2;221sin 24sin 404k i E k ka ka ma ka ma k E k E a maE E E ma maii v E kv ka ka maiii E k k k E E m π⎛⎫=-+ ⎪⎝⎭⎡⎤=--⎢⎥⎣⎦====∆=-=∴=∇∴=--==+解:当时,当时,能带的宽度为:在能带底部,将在附近用泰勒级数展开,可得:()()()22min 22max 22max 220342203k E m m m E k k E E k m k E m m m ππδδδ****=+∴===-=+∴=- 在能带顶部,将在附近用泰勒级数展开,令k=+k 可得:aa3. 试证明:如果只计及最近邻的相互作用,用紧束缚方法导出的简单立方晶体中S 态电子的能带为()2cos 2cos 2cos 2s x y z E k E A J ak ak ak πππ⎡⎤=--++⎣⎦并求能带的宽度。
第五章晶体中电子能带理论习题解答

晶体中电子能带理论思考题1. 1. 将布洛赫函数中的调制因子)(r k u 展成付里叶级数, 对于近自由电子, 当电子波矢远离和在布里渊区边界上两种情况下, 此级数有何特点? 在紧束缚模型下, 此级数又有什么特点? [解答] 由布洛赫定理可知, 晶体中电子的波函数)()(r r k.r k i k u e =ψ,对比本教科书(5.1)和(5.39)式可得)(r k u =rKK .)(1m i mm e a N ∑Ω.对于近自由电子, 当电子波矢远离布里渊区边界时, 它的行为与自由电子近似, )(r k u 近似一常数. 因此, )(r k u 的展开式中, 除了)0(a 外, 其它项可忽略.当电子波矢落在与倒格矢K n 正交的布里渊区边界时, 与布里渊区边界平行的晶面族对布洛赫波产生了强烈的反射, )(r k u 展开式中, 除了)0(a 和)(n a K 两项外, 其它项可忽略. 在紧束缚模型下, 电子在格点R n 附近的几率)(r k ψ2大, 偏离格点R n 的几率)(r k ψ2小. 对于这样的波函数, 其付里叶级数的展式包含若干项. 也就是说, 紧束缚模型下的布洛赫波函数要由若干个平面波来构造.. 2. 2. 布洛赫函数满足)(n R r +ψ=)(r n k.R ψi e ,何以见得上式中k 具有波矢的意义? [解答]人们总可以把布洛赫函数)(r ψ展成付里叶级数rK k'h K k r ).()'()(h i he a +∑+=ψ,其中k ’是电子的波矢. 将)(r ψ代入)(n R r +ψ=)(r n k.R ψi e ,得到n k'.R i e =n k.R i e .其中利用了πp n h 2.=R K (p 是整数), 由上式可知, k =k ’, 即k 具有波矢的意义. 3. 3. 波矢空间与倒格空间有何关系? 为什么说波矢空间内的状态点是准连续的? [解答]波矢空间与倒格空间处于统一空间, 倒格空间的基矢分别为321 b b b 、、, 而波矢空间的基矢分别为32N N / / /321b b b 、、1N , N 1、N 2、N 3分别是沿正格子基矢321 a a a 、、方向晶体的原胞数目.倒格空间中一个倒格点对应的体积为*321) (Ω=⨯⋅b b b ,波矢空间中一个波矢点对应的体积为N N b N b N b *332211)(Ω=⨯⋅,即波矢空间中一个波矢点对应的体积, 是倒格空间中一个倒格点对应的体积的1/N . 由于N 是晶体的原胞数目, 数目巨大, 所以一个波矢点对应的体积与一个倒格点对应的体积相比是极其微小的. 也就是说, 波矢点在倒格空间看是极其稠密的. 因此, 在波矢空间内作求和处理时, 可把波矢空间内的状态点看成是准连续的.4. 4. 与布里渊区边界平行的晶面族对什么状态的电子具有强烈的散射作用? [解答]当电子的波矢k 满足关系式)2(=+⋅n n Kk K时, 与布里渊区边界平行且垂直于n K 的晶面族对波矢为k 的电子具有强烈的散射作用. 此时, 电子的波矢很大, 波矢的末端落在了布里渊区边界上, k 垂直于布里渊区边界的分量的模等于2/n K .5. 5. 一维周期势函数的付里叶级数nx ainn eV x V π2)(∑=中, 指数函数的形式是由什么条件决定的?[解答]周期势函数V (x ) 付里叶级数的通式为xi nn n e V x V λ∑=)(上式必须满足势场的周期性, 即xi nn a i x i nn a x i nn n n n n e V x V e e V e V a x V λλλλ∑∑∑====++)()()()(.显然1=a i n e λ.要满足上式, n λ必为倒格矢n a n πλ2=.可见周期势函数V (x )的付里叶级数中指数函数的形式是由其周期性决定的.6. 6. 对近自由电子, 当波矢k 落在三个布里渊区交界上时, 问波函数可近似由几个平面波来构成? 能量久期方程中的行列式是几阶的? [解答]设与三个布里渊区边界正交的倒格矢分别为321K ,K ,K , 则321K ,K ,K 都满足321 ,0)2(K ,K ,K K K k K ==+⋅n nn , 且波函数展式rKk K r ).()(1)(m i mm k e a N +∑=Ωψ中, 除了含有)( ,)( ,)( ,)0(321K K K a a a a 的项外, 其它项都可忽略, 波函数可近似为])( ,)( ,)( ,)0([1)().(3).(2).(1.321r K k r K k r K k r k k K K K r +++=i i i i e a e a e a e a N Ωψ.由本教科书的(5.40)式, 可得0)()()()()()()0()(233221122=-+-+-+⎥⎦⎤⎢⎣⎡-K K K K K K k a V a V a V a E m k , 0)()()()()()(2)0()(3312211221=-+-+⎥⎦⎤⎢⎣⎡-+K K K K K K K k K a V a V a E m k a V , 0)()()()(2)()()0()(3322221122=-+⎥⎦⎤⎢⎣⎡-+-+K K K K k K K K K a V a E m k a V a V , 0)()(2)()()()()0()(3222231133=⎥⎦⎤⎢⎣⎡-+-+-+K k K K K K K K K a E m k a V a V a V .由)( ,)( ,)( ,)0(321K K K a a a a 的系数行列式的值)(2)()()()()(2)()()()()(2)()()()()(222231333222122312122132122=⎥⎦⎤⎢⎣⎡----⎥⎦⎤⎢⎣⎡----⎥⎦⎤⎢⎣⎡----⎥⎦⎤⎢⎣⎡-k K K K K K K K k K K K K K K K k K K K K k E m k V V V V E m k V V V V E m k V V V V E m k .可解出电子的能量. 可见能量久期方程中的行列式是四阶的.7. 7. 在布里渊区边界上电子的能带有何特点? [解答]电子的能带依赖于波矢的方向, 在任一方向上, 在布里渊区边界上, 近自由电子的能带一般会出现禁带. 若电子所处的边界与倒格矢n K 正交, 则禁带的宽度)(2n K V E g =,)(n K V 是周期势场的付里叶级数的系数.不论何种电子, 在布里渊区边界上, 其等能面在垂直于布里渊区边界的方向上的斜率为零, 即电子的等能面与布里渊区边界正交.8. 8. 当电子的波矢落在布里渊区边界上时, 其有效质量何以与真实质量有显著差别? [解答]晶体中的电子除受外场力的作用外, 还和晶格相互作用. 设外场力为F , 晶格对电子的作用力为F l , 电子的加速度为)(1l m F F a +=.但F l 的具体形式是难以得知的. 要使上式中不显含F l , 又要保持上式左右恒等, 则只有Fa *1m =.显然, 晶格对电子的作用越弱, 有效质量m*与真实质量m 的差别就越小. 相反, 晶格对电子的作用越强, 有效质量m *与真实质量m 的差别就越大. 当电子的波矢落在布里渊区边界上时, 与布里渊区边界平行的晶面族对电子的散射作用最强烈. 在晶面族的反射方向上, 各格点的散射波相位相同, 迭加形成很强的反射波. 正因为在布里渊区边界上的电子与晶格的作用很强, 所以其有效质量与真实质量有显著差别.9. 9. 带顶和带底的电子与晶格的作用各有什么特点? [解答]由本教科书的(5.88)和(5.89)两式得m m m lF F F +=*.将上式分子变成能量的增量形式m tm t m t l d d d *ννν⋅+⋅=⋅F F F , 从能量的转换角度看, 上式可表述为mE mE m E 晶格对电子作的功外场力对电子作的功外场力对电子作的功)d ()(d )(d *+=.由于能带顶是能带的极大值,22k E∂∂<0,所以有效质量222*k E m ∂∂= <0.说明此时晶格对电子作负功, 即电子要供给晶格能量, 而且电子供给晶格的能量大于外场力对电子作的功. 而能带底是该能带的极小值,22k E∂∂>0,所以电子的有效质量222*k E m ∂∂= >0.但比m 小. 这说明晶格对电子作正功. m*<m 的例证, 不难由(5.36)式求得n nV T mm 211*+=<1.10. 电子的有效质量*m 变为∞的物理意义是什么? [解答]仍然从能量的角度讨论之. 电子能量的变化m E m E m E 晶格对电子作的功外场力对电子作的功外场力对电子作的功)d ()(d )(d *+=[]电子对晶格作的功外场力对电子作的功)d ()(d 1E E m -=.从上式可以看出,当电子从外场力获得的能量又都输送给了晶格时, 电子的有效质量*m 变为∞. 此时电子的加速度1*==F a m ,即电子的平均速度是一常量. 或者说, 此时外场力与晶格作用力大小相等, 方向相反. 11. 万尼尔函数可用孤立原子波函数来近似的根据是什么? [解答]由本教科书的(5.53)式可知, 万尼尔函数可表示为∑-=k R r k r ,R ),(1)(n n N W ααψ.紧束缚模型适用于原子间距较大的晶体. 在这类晶体中的电子有两大特点: (1) 电子被束缚在原子附近的几率大, 在原子附近它的行为同在孤立原子的行为相近, 即当r →R n 时, 电子波函数) ,(n R r k -αψ与孤立原子波函数)(n at R r -αϕ相近. (2) 它远离原子的几率很小, 即r 偏离R n 较大时, 2) ,(n R r k -αψ很小. 考虑到r 偏离R n 较大时,2)(n atR r -αϕ也很小, 所以用)(n atR r -αϕ来描述) ,(n R r k -αψ是很合适的. 取 ) ,(n R r k -αψ=)(k μ)(n atR r -αϕ. 将上式代入万尼尔函数求和中, 再利用万尼尔函数的正交性, 可得=)(r ,R n W α)(n atR r -αϕ. 也就是说, 万尼尔函数可用孤立原子波函数来近似是由紧束缚电子的性质来决定的.12. 紧束缚模型电子的能量是正值还是负值? [解答]紧束缚模型电子在原子附近的几率大, 远离原子的几率很小, 在原子附近它的行为同在孤立原子的行为相近. 因此,紧束缚模型电子的能量与在孤立原子中的能量相近. 孤立原子中电子的能量是一负值, 所以紧束缚模型电子的能量是负值. s 态电子能量(5.60)表达式∑⋅--=ni s s at s s ne J C E E R k k )(即是例证. 其中孤立原子中电子的能量ats E 是主项, 是一负值, s s J C --和是小量, 也是负值.13. 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 哪一个宽? 为什么? [解答]以s 态电子为例. 由图5.9可知, 紧束缚模型电子能带的宽度取决于积分s J 的大小, 而积分r R r R r r r d )()]()([)(*n ats n at N at s s V V J ----=⎰ϕϕΩ的大小又取决于)(r at sϕ与相邻格点的)(n at sR r -ϕ的交迭程度. 紧束缚模型下, 内层电子的)(r at s ϕ与)(n at s R r -ϕ交叠程度小, 外层电子的)(r at s ϕ与)(n at s R r -ϕ交迭程度大. 因此, 紧束缚模型下, 内层电子的能带与外层电子的能带相比较, 外层电子的能带宽. 14. 等能面在布里渊区边界上与界面垂直截交的物理意义是什么? [解答]将电子的波矢k 分成平行于布里渊区边界的分量//k 和垂直于布里渊区边界的分量k ┴. 则由电子的平均速度)(1k E k ∇=ν得到////k ∂ , ⊥⊥∂∂=k E 1ν.等能面在布里渊区边界上与界面垂直截交, 则在布里渊区边界上恒有⊥∂∂k E /=0, 即垂直于界面的速度分量⊥ν为零. 垂直于界面的速度分量为零, 是晶格对电子产生布拉格反射的结果. 在垂直于界面的方向上, 电子的入射分波与晶格的反射分波干涉形成了驻波. 15. 在磁场作用下, 电子的能态密度出现峰值, 电子系统的总能量会出现峰值吗? [解答]由(5.111)式可求出电子系统的总能量⎰∑⎰=-==FFE ln E n b E EaE E E EN U 0002/1][d d )(∑=⎭⎬⎫⎩⎨⎧-=ln n F b a b E a 0n 2/32/3)(32-][32 {}∑=-=ln n F n b a b E ab 0n 2/3)(2-2其中m eB n b m V a c c n cc =⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛=ωωπω,21 ,282/322 . 对系统的总能量求微商B U ∂∂/, 其中有一项∑=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-ln F n m eB n E m e n ab 02121 . 可见, 每当F E m eB n =⎪⎭⎫ ⎝⎛+ 21时, 总能量的斜率B U ∂∂/将趋于∞, 也即出现峰值.16. 在磁场作用下, 电子能态密度的峰值的周期是什么? 简并度Q 变小, 峰值的周期变大还是变小? [解答]由(5.111)式可知, 在磁场作用下, 电子的能态密度cln c c n E m V E N ωπω ⎪⎭⎫ ⎝⎛+-=∑=211)2(8)(02/322.从上式不难看出, 能量E 分别等于c c c c l ωωωω 212... ,25 ,23 ,21+时, 能态密度都出现峰值. 相邻峰值间的能量差, 即峰值的周期为c ω .由(5.109)式可知, 简并度yx π2.其中yx L L 和分别是晶体在x 方向和y 方向的尺寸. 因为峰值的周期正比于c ω, 所以简并度Q 变小, 峰值的周期也变小.17. 当有电场后, 满带中的电子能永远漂移下去吗? [解答]当有电场后, 满带中的电子在波矢空间内将永远循环漂移下去, 即当电子漂移到布里渊区边界时, 它会立即跳到相对的布里渊区边界, 始终保持整体能态分布不变. 具体理由可参见图5.18及其上边的说明.18. 一维简单晶格中一个能级包含几个电子? [解答]设晶格是由N 个格点组成, 则一个能带有N 个不同的波矢状态, 能容纳2N 个电子. 由于电子的能带是波矢的偶函数, 所以能级有(N /2)个. 可见一个能级上包含4个电子. 19. 本征半导体的能带与绝缘体的能带有何异同? [解答]在低温下, 本征半导体的能带与绝缘体的能带结构相同. 但本征半导体的禁带较窄, 禁带宽度通常在2个电子伏特以下. 由于禁带窄, 本征半导体禁带下满带顶的电子可以借助热激发, 跃迁到禁带上面空带的底部, 使得满带不满, 空带不空, 二者都对导电有贡献. 20. 加电场后空穴向什么方向漂移? [解答]加电场ε后空穴的加速度h m e t εν=d d ,其中h m 是空穴的质量, 是正值. 也就是说, 空穴的加速度与电场ε同方向. 因此, 加电场ε后空穴将沿电场方向漂移下去.。
能带理论——精选推荐

第五章 能带理论3.1 根据a k π±=状态简并微扰结果,求出与E+、E- 对应的本征态波函数+ψ、-ψ,说明它们都代表驻波,并比较两个电子云分布(即2ψ),说明能隙的来源。
假设( V n = V n *)。
3.2 写出一维近自由电子近似,第n 个能带(n=1,2,3)中,简约波数ak 2π=的0级波函数。
3.3 电子在周期场的势能函数⎪⎩⎪⎨⎧-≤≤+-+≤≤---=b na x b a n b na x b na ,na x b m x V )1(,0])([21)(222当当ω其中ω,4b a =为常数(1) 试画出此势能曲线,并求其平均值。
(2) 用近自由电子近似模型求出晶体的第一个及第二个带隙宽度。
3.4 设有二维正方晶格,其晶格势场)/2cos()/2cos(4),(a y a x U y x V ⋅⋅-=ππ,按弱周期场(近自由电子近似)处理,求出布里渊区角处)/,/(a a ππ的能隙。
3.5* 考虑晶格常数为a 和c 的三维简单六角晶体的第一布里渊区。
令G c 为平行于晶格c 轴的最短倒格矢。
(1) 证明对于六角密堆积结构,晶体势场V ( r ) 的傅里叶分量V ( G c )为零。
(2) V ( 2 G c ) 是否也为零?(3) 为什么二价原子构成的简单六角晶格在原则上有可能是绝缘体?(4) 为什么不可能得到由单价原子六角密堆积形成的绝缘体?3.6用紧束缚近似求出面心立方晶格和体心立方晶格s 态原子能级相对应的能带E s ( k )。
3.7 用 | n > 表示一维晶格第n 个格点的s 态,在只计入近邻作用的紧束缚近似下,写出矩阵元 < m | H | n > 的表达式。
3.8 由相同原子组成的一维原子链,每个原胞中有两个原子,原胞长度为a ,原胞内两个原子的相对距离为b :(1) 根据紧束缚近似,只计入近邻相互作用,写出原子s 态相对应的晶体波函数的形式。
L15-能带论3
L
0
( k + Gl )2 uk (Gl ) + ∑V ' (Gl − Gn )uk (Gn ) = β Gn ) + ( k + Gn )2 δ l ,n ]uk (Gn ) = β 2 uk (Gl ) ∑
n
令: A ln = V ' (Gl − Gn ) + ( k + Gn )2 δ l ,n
1 β β' cos(kzd) = cos(βc)cos(β'b) − + sin(βc)sin(β'b) 2 β' β
2m( E − U 0 ) 2mE , β'= 式中 β = h h
而
k=
2π
λ
是电子波的波矢。 是电子波的波矢。
应满足的方程,也是电子能量 上式就是电子的能量 E 应满足的方程 也是电子能量 E 之间的关系式。 与波矢 k 之间的关系式。
紧束缚近似方法的一个突出优点是它可以把晶体中 电子的能带结构与构成这种晶体的原子在孤立状态下的 电子能级联系起来。 电子能级联系起来。 一、模型与微扰计算
r-Rl V(r-Rl):Rl格点的原子势场 - : 0
ϕj(r-Rl): 原子波函数 :
的波动方程: 第l个孤立原子的波动方程: 个孤立原子的波动方程
h2 2 r r r r r r ˆ ˆ H lϕ j ( r − Rl ) = ε jϕ ( r − Rl ), H l = − ∇ + V ( r − Rl ) 2m
V(r-Rl):Rl格点的原子势场,εj:某原子能级(非简并) - : 格点的原子势场, 某原子能级(非简并)
ϕj(r-Rl): 原子波函数 :
半导体物理学(第7版)第五章习题及答案

第五章习题1. 在一个n 型半导体样品中,过剩空穴浓度为1013cm -3, 空穴的寿命为100us 。
计算空穴的复合率。
2. 用强光照射n 型样品,假定光被均匀地吸收,产生过剩载流子,产生率为,空穴寿命为τ。
(1)写出光照下过剩载流子所满足的方程; (2)求出光照下达到稳定状态时的过载流子浓度。
3. 有一块n 型硅样品,寿命是1us ,无光照时电阻率是10Ω∙cm 。
今用光照射该样品,光被半导体均匀的吸收,电子-空穴对的产生率是1022cm -3∙s-1,试计算光照下样品的电阻率,并求电导中少数在流子的贡献占多大比例?4. 一块半导体材料的寿命τ=10us ,光照在材料中会产生非平衡载流子,试求光照突然停止20us 后,其s cm pU s cm p Up 3171010010313/10U 100,/10613==∆=====∆-⨯∆-ττμτ得:解:根据?求:已知:τττττg p g p dtp d g Aet p g p dt p d L L tL=∆∴=+∆-∴=∆+=∆+∆-=∆∴-.00)2()(达到稳定状态时,方程的通解:梯度,无飘移。
解:均匀吸收,无浓度cm s pq nq q p q n pq np cm q p q n cm g n p g p pn p n p n pn L /06.396.21.0500106.1101350106.11010.0:101:1010100.1916191600'000316622=+=⨯⨯⨯+⨯⨯⨯+=∆+∆++=+=Ω=+==⨯==∆=∆=+∆-----μμμμμμσμμρττ光照后光照前光照达到稳定态后%2606.38.006.3500106.1109.,..32.01191610''==⨯⨯⨯=∆∴∆>∆Ω==-σσρp u p p p p cm 的贡献主要是所以少子对电导的贡献献少数载流子对电导的贡中非平衡载流子将衰减到原来的百分之几?5. n 型硅中,掺杂浓度N D =1016cm -3, 光注入的非平衡载流子浓度∆n=∆p=1014cm -3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 能带理论 (习题参考答案)
1. 一矩形晶格,原胞长10a 210m -=⨯,10b 410m -=⨯ (1)画出倒格子图
(2)以广延图和简约图两种形式,画出第一布里渊区和第二布里渊区
(3)画出自由电子的费米面(设每个原胞有2个电子)
解:(1)因为
a =a i=20
A i b =b j=40
A j
倒格子基矢为
12a i A
*
=
, 014b j A
*=
以a * b *为基矢构成的倒格子如下图。
由图可见,矩形晶格的倒格子也是矩形格子。
(2)取任一倒格子点O作为原点,由原点以及最近邻点
A i,次近邻点
B i的连线的中垂线可以围成第一,第二布里渊区,上图这就是布里渊区的广延图。
如采用简约形式,将第二区移入第一区,我们得到下图。
(3) 设晶体中共有N个原胞,计及自旋后,在简约布里渊区中便有2N个状态。
简约布里渊区的面积
02
1()8A a b A *
*
*
-=⨯=
而状态密度
022()16()N
g K N A A *==
当每个原胞中有2个电子时,晶体电子总数为
2
02()216F
k F N g k kdk N k ππ=⨯=⎰
所以
01/21111
1()0.2()210()8F k A m π---=≈=⨯
这就是费米圆的半径。
费米圆如下图所示
2. 已知一维晶体的电子能带可写成
()2271cos cos 2,88E k ka ka ma ⎛⎫
=-+ ⎪⎝⎭
式中a 是晶格常数。
试求能带的宽度;
()()()()()
()
()()2222
2min 2
max 2
2
max min 22
2
22
min 71
cos cos 2,
8811cos 24400,
2;221sin 24sin 404k i E k ka ka ma ka ma k E k E a ma
E E E ma ma
ii v E k
v ka ka ma
iii E k k k E E m π
⎛⎫=-+ ⎪⎝⎭⎡⎤=--⎢⎥⎣⎦====∆=-=
∴=∇∴=--==+
解:当时,当时,能带的宽度为:在能带底部,将在附近用泰勒级数展开,可得:
()()
()22
min 22
max 2
2
max 220
34220
3
k E m m m E k k E E k m k E m m m π
π
δδδ*
***
=+
∴===-=+
∴=- 在能带顶部,将在附近用泰勒级数展开,令k=
+k 可得:
a
a
3. 试证明:如果只计及最近邻的相互作用,用紧束缚方法导出的简单立方晶体中S 态电子的能带为
()
2cos 2cos 2cos 2s x y z E k E A J ak ak ak πππ⎡⎤=--++⎣⎦
并求能带的宽度。
解:若只计算最近邻的相互作用,用紧束缚近似法处理晶体中的S 态电子所得的结果
()
2()
n s n
k R R i s sn R
E k E A e
J π⋅-=--
∑
最近邻
式中s n R ,R 分别是参考原子以及最近邻的位矢。
在简单立方晶格中,有6个最紧邻,如果取s R =0,则这6个最近邻的坐标是R n
a(1,0,0); a(-1,0,0) a(0,1,0); a(0,-1,0)
a(0,0,0);a(0,0,-1)
这里a 是晶格常数。
对于S 态电子,交迭积分对各个最近邻都相等,令sn J J =-,则得
()
y y x x z z i2πak -i2πak i2πak -i2πak i2πak -i2πak s E k =E -A-J(e +e +e +e +e +e )
()
2cos 2cos 2cos 2s x y z E k E A J ak ak ak πππ⎡⎤=--++⎣⎦
在能带底处,x y z k k k 0===,对应的能量有最小值 min 0E E A 6J =--
在能带顶处,x y z k 1/2a,k 1/2a,k 1/2a =±=±=± 对应能量有最大值
max 0E E A 6J =-+ 因此能带的宽度为
max min E E E 12J ∆=-=。
