2006年高考数学模拟试题(二)

合集下载

2006年高考数学模拟试题(一)

由此可解得６．＝３
’
．
零，图象过原点，当在（，）Ｏ取值时，函数大于零．再转化为符号语言：
ｆ０。
’＞２，ｎｂａ且 ∈Ｎ，ｎ，故一１从而ｆ＝一２．
，一（＋＆＋ｃ一嬲（（）ｎｒ）一丑）一） ① ，
即ｎ＋ｆ４从而６一一ｎ．＋６一， —４ —ｆ
由①③可知ｎ，由②知ｂ，＜Ｏ再＞Ｏ
所以，～１＋，１一一ｎ一ｆ＋６２．（）（）＋６＋ｎ＋ｆ６
故选八
评析：图形语言如何正确转化为文字语言，文字
语言又如何转化为符号语言，这就是“ 读题” 如何把．
则等工。不式ｃ的，＜
Ｒ（，）０１
■ ■ ■
４５同学分别报名参加学校的足球队、．位篮球队、乒乓球队。每人限报其中的一个运动队，不同的报则名方案共有（
八１５种
崔 ■
）．
ｅ２１５种
｜｜ｌ
Ｂ８种．１
Ｃ（，ｏＯ＋ｏ）
Ｄ（。ＯＵ（，）．一。，）Ｏ１
’
３某市的邮政编码是六位数２６ ××，．４× 若后三个数字同时满足：至少有一个数字与前三个数字相 ① 同； ②与前三个数字相同的数字恰好与它所在的位号（邮编６个数字从左往右顺序依次为第１２３、、，
厶
ｆ）ｚ２（号１（一＋一）７ｘ３＋，

2006年高考理科数学摸拟试题解析样本1

2006年高考理科数学摸拟试题解析样本1一、选择题=+-2)i 3(i 31.1i 4341.A + i 4341.B -- i 2321.C + i2321.D --[分析] 本题主要考查复数的四则运算，以及简单的数值计算技能．解答本题必须正确用好复数的四则运算法则，既可用复数的代数形式进行演算，也可用三角形式进行演算．.4341)322(81 )31(813223-1 12i i i i i--=--=-=+=原式解法.i 4341 )i 31(41)i 31(i31 22--=+-=---=原式解法i.4341i)3(4i i3i i)3(i)3i(原式 32--=--=+-=++-=解法[答案]B==⎪⎭⎫⎝⎛π-∈x 2tan ,54x cos ,0,2x .2则已知247.A247.B -724.C724.D -[分析] 本题主要考查三角函数的基础知识和基本三角函数公式的简单应用，以及基本的计算技能．作为常规解法，可先由已知条件求sin x ，推得tan x 的值，再应用倍角正切公式求得答案，如解法1；作为灵活解法，可用估值快速求解，如解法2．,54x cos ,0,2x 1=⎪⎭⎫⎝⎛π-∈因为解法 ,53x cos 1x sin 2-=--=所以,43x tan -=则 . 724xtan 1x tan 2x 2tna 2-=-=由此得 (注：也可用下式得解：,724x sin x cos x cos x sin 2cos2x sin2x tan2x 22-=-==而不需求tanx ．),235422,0x 2 2<<<<π-因为解法 ,6x 454x cos π-<<π-=得则由 .,,32tan 3,22为答案得和、故排除则从而D C B A x x -<⎪⎭⎫⎝⎛--∈ππ[答案] Dx 1,)f (x 0.x ,x ,0 x .12)x (f .30021x 的取值范围是则若设涵数>⎪⎩⎪⎨⎧>≤-=-A ．（－1，1）B ．（－1，+∞）C ．（－∞，－2）∪（0，+∞）D ．（－∞，－1）∪（1，+∞）[分析] 本题主要考查分段函数的概念、指数函数与幂函数的性质、不等式组的求解等基础知识，以及简单的推理计算能力．根据函数f(x)的分段表达式，画个草图可快速判断，如解法4；也可将不等式1)x (f 0>化为等价的不等式组求解，如解法1；也可用特殊值排除法求解，如解法2；还可以利用单调性，结合解方程求解，如解法3．:1)f (x 10少有一个成立等价于下列不等式组至解法>⎪⎩⎪⎨⎧>>⎩⎨⎧≤>--.0x ,1x ② ;0x ,112①02100x 0解不等式组①得;1x 0-<解不等式组②得.1x 0>综合得0x 的取值范围为(－∞,－1)∪(1，+∞)．解法2 由,1012)0(f 0<=-=排除A 和B ；由f(0.04)=0.2<1，排除C ，得答案D ．0,x ,112 ,1)( 3x -⎩⎨⎧≤=-=由考虑方程解法x f解得x=－1；由0,x ,1x 21⎪⎩⎪⎨⎧>=解得x=1．因为f(x)在(－∞，0]上是减函数，在(0，+∞)上是增函数，所以得1)x (f 0>的取值范围为(－∞，1)∪(1，+∞)．[答案] D4．O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足),,0[,|AC |AC |AB |ABOA OP +∞∈λ⎪⎪⎪⎭⎫⎝⎛+λ+=→→→→→→则P 的轨迹一定通过△ABC 的 A ．外心B ．内心C ．重心D ．垂心[分析] 本题主要考查平面向量的线性运算等基本知识和计算技能．解法1 为书写方便与直观起见，宜作图表示(如下图)．图中，有,AP AC AB ,AC |AC |AC ,AB |AB |AB 11111→---→--→--→--→→--→--→--→--=+==则动点P 满足),0[ ,AP OA OP 1+∞∈λλ+=→---→---→---.,1AP A P 出发的射线的轨迹是由点点所以,BAC AP ,P C //AB |,AC |1|AB | 111111∠==→---→---→---→---平分所以因为因此，点P 的轨迹一定通过△ABC 的内心．得答案为B ．解法2 当λ>0时，,0|AC |AC |AB |ABOA OP AP ≠⎪⎪⎪⎭⎫⎝⎛+λ=-=→--→--→--→--→--→--→--因为,|AB ||AC |AB AC 1|AP | |AB ||AP |AB AP AB ,AP cos ⎪⎪⎪⎭⎫ ⎝⎛⋅⋅+λ=⋅⋅=〉〈→--→--→--→--→--→--→--→--→--→--→--所以.1|||||| ||||,cos ⎪⎪⎪⎭⎫⎝⎛+⋅⋅=⋅⋅=〉〈→--→--→--→---→--→--→--→--→--→--→--AC AB ACAB AP AC AP AC AP AC AP λ,,cos ,cos 〉〈=〉〈→--→--→--→--AC AP AB AP 得 ,,, 〉〈=〉〈→--→--→--→--AC AP AB AP 所以因为A ，B ，C 不共线，所以AP 平分∠BAC，得点P 的轨迹一定通过△ABC 的内心．解法3 考虑特殊情形，取△ABC 为等腰直角三角形，即：,|BC ||AB |,BC AB →--→--→--→--=⊥如图．这时，△ABC 的外心为AC 的中点D ，垂心为点B ．而由题设知点P 的轨迹是由点A 出发，方向为→--→--→--→--+|AC |AC|AB |AB 的射线l ，不经过点D ，也不经过点B ，故排除A 、D 两个选项．其次，由于|,AB ||AC |→--→--≠所以射线l 不平分BC ，即不通过△ABC 的重心，排除选项C ．从而得选项B 为答案．[答案]B的反函数为函数),1(,11ln.5+∞∈-+=x x x y),0(x ,1e 1e y .A x x +∞∈+-= ),0(x ,1e 1e y .B x x +∞∈-+= )0,(x ,1e 1e y .C x x -∞∈+-=)0,(x ,1e 1e y .D x x -∞∈-+=[分析] 本题主要考查对数函数、指数函数的性质和求反函数的方法，以及基本的计算技能．根据反函数的概念，求给定函数的反函数，可用解方程的方法，如解法1；作为选择题，还可用特殊值排除法求解，如解法2．解法1 解方程不等式组⎪⎩⎪⎨⎧>-+=,1x ,1x 1x ln y,11e 1e x y y >-+=得,01e y >+因为1e 0 y -<所以得y>O ，因此，所求的反函数为).,0(,11+∞∈-+=x e e y x x解法2 因为点(2，ln3)在原函数的图像上，所以点(1n3，2)应在反函数的图像上．因此，由In3>0，可排除选项C 、D ；由,21e 1e 3ln 3ln ≠+-可排除A ，应取B 作答． [答案] B6．棱长为a 的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为3a .A 34a .B 3 6a .C 3 12a .D 3[分析] 本题主要考查棱柱、棱锥等多面体的基本知识和体积计算，以及基本的空间想象能力．题设的八面体(记为ABCDEF)如图所示．图中将原正方体略去，以使图线清晰．该八面体的三条轴线AC 、BD 、EF 两两互相垂直，且AC=BD=EF=a ，把这个八面体看作共底(BFDE)的两个四棱锥的组合体，应用棱锥体积计算公式，得所求的八面体的体积为.6a EF BD 21AC 31V 3=⎪⎭⎫ ⎝⎛⋅⋅=对于空间想像力比较好的考生，不作图便可由心算得出答案．心算的方法比较多，例如，与上法共通地把八面体看作共底的两个四棱锥，底面积是正方体的一个面的面积之半，锥高是正方体棱长之半，即可得体积为;6a 3又如，由对称性，将正方体切成相等的八个小正方体，这时题没的八面体也被切成八个相等的三棱锥，每个三棱锥的体积等于小正方体的体积的,61所以八面体的体积是正方体体积的,61即.6a 3[答案] C7．设))x (f ,x (P )x (f y ,c bx ax )x (f ,0a 002在点曲线=++=>处切线的倾斜角的取值范围为,4,0⎥⎦⎤⎢⎣⎡π，则点P 到曲线y=f(x)对称轴距离的取值范围为⎥⎦⎤⎢⎣⎡a 1,0.A⎥⎦⎤⎢⎣⎡a 21,0.B⎥⎦⎤⎢⎣⎡a 2b ,0.C⎥⎦⎤⎢⎣⎡-a 21b ,0.D[分析] 本题主要考查导数的几何意义，多项式函数求导数的方法，点到直线的距离，二次函数的性质等基本知识，以及推理和计算技能．解答本题，宜先求出0x 的取值范围，进而根据曲线y=f(x)对称轴的方程，便可求得点P 到对称轴距离的取值范围，如解法1．此外，也可用特殊值排除法求解．解法1 依题设知点P 的横坐标0x 必须且只须满足.14tan)(00=≤'≤πx f,b ax 2)x (f +='因为.1b ax 20 0≤+≤所以因为抛物线y=f(x)的对称轴为直线l ：,a 2bx -=所以点P 到直线l 的距离为,a 2b x d 0+=0,a >因为,a 21|b ax 2|2a 1d 0≤+=所以.B .a 21，0d .0d 答案为的取值范围为即得且⎥⎦⎤⎢⎣⎡≥解法2 取特殊值a=1，b=－2，c=0．可知曲线y=f(x))x 2x y (2-=即的对称轴为直线l ：x=1．曲线在点P 处切线的斜率为,2x 2k 0-=由14tna,00tan =π=及tanx 的单调性，依题设知k 的取值范围为[0，1]，所以,12x 200≤-≤,211x 00≤-≤即得点P 到对称轴l 距离的取值范围为.21,0⎥⎦⎤⎢⎣⎡据此，可排除选项A ，C ，D ，得答案B ．[答案] B 8．已知方程0)n x 2x )(m x 2x(22=+-+-的四个根组成一个首项为41的等差数列，则|m －n|=A ．143.B21.C83.D[分析] 本题主要考查二次方程根与系数的关系，等差数列等基本知识，以及数学思维和分析处理问题的能力．注意到题设4次方程的两个2次因式中，只有常数项不同，可知等差数列的4个项中首尾两项应为其中一个因式的两根，而中间两项为另一因式的两根．所以，在此基础上，可用不同的引入方式，采取适当的计算程序，求得|m －n|的值．解法1 因为抛物线n x 2x y m x 2x y 22+-=+-=与有公共的对称轴x=1，又它们与x 轴的4个交点的横坐标(即题设方程的4个根)成等差数列，所以可设为.31 ,1 ,1 ,314321p x p x p x p x +=+=-=-=.x x ,x x ,41x 32411在另一抛物线上、在同一抛物线上、且有=413p 1 =-故 ,.41p 从而得=.218p |)p 1()9p -(1| |x x -x x ||n -m | 2223241==--==0m x 2 x 41, 22=+-=α是方程不妨设依题意解法的一个根，则方程的另一个根为,472 =α-=β .167m =αβ=所以 0n x 2x 2=+-设方程 .2 ),(111111β+α==β+αβ<αβα　则不妨设和的两个根为.,,, :，414、、、1111ββααβαβα其次序必为的等差数列个数成首项为所以,21)(31d =α-β=公差应为.1615)1(21n 11=+α⎪⎭⎫ ⎝⎛+α=βα=所以 .211615167|n m | =-=-从而解法3 依题意可设原方程的4个根为.d 341,d 241 ,d 41 ,41+++则对任意实数x ，有),n x 2x )(m x 2x (d 341x d 241x d 41x 41x 22+-+-=⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-),n x 2x ()m x 2x (d 241d 41x d 321x d 34141x d 321x 2222+-+-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-即比较系数，得.n d 241d 41,m d 34141,2d 321⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛+=+（注：m 、n 的位置也可对调，不影响结果）．,21d =解得.21|d 2||n m | 2==-所以解法4 从解原方程入手．由,0n x 2x 0m x 2x 22=+-=+-和求得原方程的根为：,n 11m 11 -±-±和由题设，这4个根组成首项为41的等差数列，所以，必有1－m>0，1－n>0，且 .41n 1141m 11=--=--或且等差数列为则若,167,4111==--m m .47 ,11 ,11 ,41 n n -+--,41473141n 11 ⎪⎭⎫⎝⎛-=---所以从而得,1615m =.211615167|n m | =-=- .21|n m |,1615m ,167n ,41n 11=-===--从而同样可得类似的推导可得则若[答案] C9．已知双曲线中心在原点且一个焦点为)0,7(F ，直线y=x －1与其相交于M 、N 两点，MN 中点的横坐标为,32-则此双曲线的方程是14y 3x .A 22=-13y 4x .B 22=- 125.22=-y x C15y 2x .D 22=-[分析] 本题主要考查双曲线的基本知识，以及推理和计算技能．本题要求确定双曲线的方程，而双曲线的已知条件比较复杂，涉及到与已知直线相交的背景．在这种情况下，宜用待定系数法求解．因为双曲线的中心在原点，点)0,7(F 又是双曲线的一个焦点．故双曲线的方程可写为① ,172222=--a y a xa>0为待定系数，可用不同方法求得．解法1 将y=x －1代人方程①，整理得,0)a 8(a x a 2x )a 27(22222=--+-由直线y=x －1与双曲线相交于M 、N 两点，故此二次方程有不等的两个实根,x ,x 21分别为点M 、N的横坐标．从而MN 中点的横坐标为,a 27a 2x x x 22210--=+=,322a 7a ,32x 220-=---=所以由题设.15y 2x ,①.2a 222=-=得所求双曲线方程为代入方程解得解法2 依题设，可记,t 35,t 32N ,t 35,t 32M ⎪⎭⎫ ⎝⎛----⎪⎭⎫⎝⎛+-+- 其中t 为某个常数，且t≠0．由M 、N 在双曲线上，得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛--=-⎪⎭⎫⎝⎛+--⎪⎭⎫ ⎝⎛+-.1a 7t 35a t 32.1a 7t 35a t 32 22222222将两式相减，整理得,a 75a 2 22-=得所求双曲线方程为代入式解得,①.2a 2= .15y 2x 22=-上述解法计算量偏大，为了快速解答，可采用定性与定量相结合的方法求解．解法3 由双曲线与直线y=x －1有两个交点M 和N ，且焦点在x 轴上，可知双曲线渐近线的斜率绝对值应大于1，由此排除B 、C ；其次，由MN 的中点的横坐标为,32-可估计双曲线的张口应比较大，D 的可能性比较大．为此，作定量检验，将直线方程代人A 所示的双曲线得,0x 6x 2=-+.D ,A ,323MN 得答案排除中点的横坐标应为可知-≠-[答案] D10．已知长方形的四个顶点A(0，0)，B(2，0)，C(2，1)和D(0，1)．一质点从AB 的中点0P 沿与AB夹角为θ的方向射到BC 上的点1P 后，依次反射到CD 、DA 和AB 上的点432P P P 和、（入射角等于反射角)．设4P 的坐标为,2x 1).0,x (44<<若则tan θ的取值范围是⎪⎭⎫⎝⎛1,31.A ⎪⎭⎫ ⎝⎛32,31.B ⎪⎭⎫ ⎝⎛21,52.C ⎪⎭⎫ ⎝⎛32,52.D[分析] 本题以运动质点碰壁反射问题为背景，主要考查直线、轴对称和函数等基础知识及其应用，以及分析解决问题的能力．依题意可知点4P 的横坐标4x 是tan θ的函数，试题要求由4x的取值范围确定tan θ的取值范围，也即由函数的值域求定义域．为此，宜从建立函数关系式入手，如解法2．不过，作为选择题，本题可以用特殊值排除法快速求解，如解法1．解法1 取特殊的θ角，当21tan =θ时，根据反射原理，得点4321P P ,P ,P 和依次是BC ，CD ，DA和AB 的中点，即有21,,1x 4因此=不属于所求的tan θ的取值范围．从而，可排除选项A 、B 和D ，应取C 作答．解法2 依题设可作图如下．记各点的坐标如下：).0,x (P ),y ,0(P ),1,x (P ),tan ,2(P ),0,1(P 44332210θ根据反射原理得：,0x y 0x 01y tan 2x tan 143232--=---=θ-=-θ-,tna 13 x 2θ-=所以,tan 32tan x 1y 23θ-=θ-= 3. tna 2tan y x 34-θ=θ=,23tna 21 214<-<<<θ等价于从而x.21tan 52tan <θ<θ的取值范围为即得[答案] C=+++++++∞→)(lim .1111413122242322n nn C C C C n C C C CA ．331.B61.CD ．6[分析] 本题主要考查组合数的性质、数列极限的计算等基本知识，以及基本的计算技能．本题要求考生计算两个和式之比的极限．由于和式的项数随n 的增加而无限增加，因而不能简单应用极限四则运算法则求极限，必须将和式化简成有限的形式．原式中，分子、分母的和式是组合数求和，应充分借助组合数性质，将其化简．例如，应用公式1m ,1n 1m n m n C C C +++=+可顺利化简原式．此外，也可采用数列求和的方法求解．3123n 2243422423332242322 C 1+=+==+++=+++=+++n n nn n C C C C C C C C C C C C C因为解法21121141323114131222114131211 1 1 C ++-=++-==+++++-=++++++-=+++n n n nn nC C C C C C C C C C C C C C C又.31)2(3)1()1(lim)1n(C C lim 221n 31n =-+-+=-=∞→++∞→n n n n n n n n 原式所以.31)2)(1(3)1)(1(limn =+--+=∞→n n n n n n 原式所以[答案] B12．一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为A ．3πB ．4ππ33.CD ．6π[分析] 本题主要考查正多面体和球的基本知识，以及空间想象能力和几何计算能力．本题给出棱长为2的正四面体，要求推断外接球的表面积．为此，必须先求该球的半径，宜作图进行推算或估算．为了图像清晰，可只作正四面体进行讨论，不画出球的图线．如附图，四面体ABCD 各棱长都为.2．解法1 如图，点O 为球心，OA 、OB 、OC 、OD 都是球的半径，因为ABCD 是正四面体，所以这四条半径的两两夹角彼此相等，设其大小为θ．由空间中的一点O ，引四条射线，两两的夹角都等于θ，则有.322π<θ<π ,3sin 2sin 4sin ,2AB ,2sin2ABOA r π<θ<π=θ==且因为球半径,232sin 22<θ<即,1r 32<<所以得,4S 38r 4S ,2<<ππ=满足球的表面积因此据此，可排除选项B 、C 和D ，应取A 作答．解法2 如图，过A 作AE⊥面BCD ，E 是垂足．连结EB ，则EB 是正△BCD 外接圆的半径．应用正弦定理，由正三角形的边长为,2得.3260sin 22EB =︒=因为 AE⊥EB.31AB EB BAE sin ==∠所以过AB 的中点F ，在平面AEB 中，作AB 的垂线交AE 于O ，则O 是四面体ABCD 外接球的球心，球的半径为,2331122 BAE cos AFAO r =-=∠==所以，所求的球之表面积为.3r 4S 2π=π=上述估计和精算的方法，计算量仍嫌偏大．若充分发挥空间想像力，可获快速判断．解法3 联想棱长为1的正方体,D C B A ABCD 1111-则四面体11D ACB 的棱长都为,2它的外接球也是正方体的外接球，其半径为正方体对角线长3的一半，即有,23r =故所求球面积为S=3π．[答案] A 二、填空题.________x x 21x .13992的系数是展开式中⎪⎭⎫ ⎝⎛-[分析] 本题主要考查二项式定理的应用，以及基本的计算技能．直接利用二项展开式的通项公式，便可求得9x 的系数，如解法1．由于二项式中的两个项都含有x ，因此将其适当变形，有利于简化计算，如解法2．试题的这种设计，体现了对计算灵活性和准确性的要求．解法1 设所求系数为a ，则由二项展开式的通项公式，知存在非负整数r ，使,ax x 21)x (C 9rr 92r9=⎪⎭⎫ ⎝⎛--.ax x 2C 9r 318rr9=⎪⎭⎫⎝⎛1⋅-即⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛⋅-==-.C 21)1(a 9,3r 18 ,r9r r 得所以解得r=3，所求系数为.221C 81a 39-=-=解法2 因为,)21x (x x 21x 93992-=⎪⎭⎫ ⎝⎛-- 的系数为该式展开式中所以9x ,.221C 81 2C a 396969-=-=⎪⎭⎫ ⎝⎛1-=-221 ][-答案14．某公司生产三种型号的轿车，产量分别为1 200辆，6 000辆和2 000辆．为检验该公司的产品质量，现用分层抽样方法抽取46辆进行检验，这三种型号的轿车依次应抽取____________，_______________，____________辆．[分析] 本题主要考查分层抽样方法在产品质量检验中的应用，以及简单的数值计算技能．设三种型号的轿车抽取数依次为x ，y ，z 辆．根据分层抽样方法的原理，知20.:60:12z :y :x 46,z y x ⎩⎨⎧==++这个方程组可用不同方法求解．解法1 由比例式知存在常数k 满足.k 20z 60y 12x ===46,20k 60k 12k =++则 10.20k z 30,60k y 6,12k x ,21k =======从而解得解法2 由此例式得60x=12y ， 20x=12z ，x 320z y =+所以46x 320x ,=+从而6, x =解得 10.x 1220z ,30x 1260y ====则[答案] 6，30，1015．某城市在中心广场建造一个花圃，花圃分为6个部分(如图)．现要栽种4种不同颜色的花，每部分栽种一种且相邻部分不能栽种同样颜色的花．不同的栽种方法有_____种．(以数字作答)[分析] 本题以花圃设计为应用背景，主要考查排列、组合的基础知识，侧重考查乘法原理和加法原理的应用，以及逻辑思维能力和计数能力．为了正确解答本题，首先必须准确理解题意：抓住花圃布局的要求，看清图形中6个部分的关系；明确每个部分只种同一种颜色的花，相邻部分应种不同颜色的花；而且4种颜色的花都要种上，缺一不可．对这些条件要求，稍有疏忽、遗漏或曲解，都会引致解答出错．其次，应设计好周全而又不出现重复计数的推算程序，关键是推算过程中分步、分类的安排要合理且严密；此外，在每一分步或分类中，计数不出错；最后，乘法原理和加法原理的运用，以及数值计算还得无误，方能得出正确的答数．采用不同的计数模式和计数程序，伴随出现不同的解法，列举解法供参考．解法1 将6个区域分4组，不同组栽种不同颜色的花，同一组栽种同一颜色的花．因为区域1与其它5个区域都有公共边，所以为了栽种方案合乎题意，分在同一组的区域至多只能有2个．因而，由图形可知,不同分组法有且只有5类，如下表(表中数字为区域号)：每一类分组法，都有44P 种不同的栽种方法．应用加法原理，得到所有符合题意的不同栽种方法的种数为.12012345P 5N 44=⨯⨯⨯⨯==解法2 按区域的顺序，依次安排各区域所栽种的花的颜色：第1区，可种4色花中的任一种，有4种不同的栽种法；接着，第2区，因与第1区相邻，两区花色必须不同，所以，第2区只能从3色花中任选一种栽种，有3种不同种法；跟着，第3区，因与第1、2区都有边界，所以，只有2种不同栽种法；随后，第4区，与2区无边界，与1、3区都有边界．因此，可分两类情形：第一类：在第4区中栽种与第2区同一色的花，有1种栽法；至此，只栽种了3种不同颜色的花，因此，第5、6区域，应有一个区域栽种第4种颜色的花，而另一区域可选的花色只有1种(这是因为与之相邻的三个区域，已种上不同颜色的3种花)．从而，在第5、6区域栽花的不同方式有2种；第二类：在第4区域中栽种与第2区域不同颜色的花，有1种栽法；不过，与第一类不同的是：至此，4种不同颜色的花都被栽种了．往后，第5区域栽花有两种选择：一种是栽与第2区域同色花，紧接着，第6区域有2种栽种方法；第五区域另一种栽花法，是栽种与第2区域不同颜色的花，只有1种选择(因为它不能与1、4区域同色)，紧接着，由于1、2、5三个区域已栽种3种不同颜色的花，故第6区域只有1种栽花的选择．综合起来，应用乘法原理和加法原理，得合乎题意的不同栽花的方法种数为 N=4×3×2×（1×2+1×2+1×1） =120解法3 因为区域1与其它5个区域都有公共边，所以当区域1栽种一种颜色的花之后，该颜色的花就不能栽于其它区域．因而可分两步走，考虑如下：第一步，在区域1中，栽上一种颜色的花，有4种栽法；第二步，在剩下的五个区域中，栽种其它三种颜色的花．为此，可将2至6号五个区域分成3组，使同一组中的不同区域没有公共边．这样的分组法有且只有5类，如下表(表中数字为区域号)：对每一类分得的3个组，将3种颜色的花分别栽于各组，共有33P 种栽法．应用乘法原理和加法原理，得合乎题意要求的不同栽种方法的种数为.120P 54N 33=⨯=解法4 由于第1、2、3区两两都有边界，所以这3个区所栽的花，彼此必须不同颜色．因而，第一步可从4种颜色的花任取3种分别栽在这3个区域上，共有3334P C 种栽法．其次将另一颜色的花栽于4、5、6三个区中的一个区或两个区，即分为两类情形：第一类：栽在4、5、6的一个区域中，有3种情形：情形1：栽于4区，则6区只有一种颜色的花可栽(因为必须不同于4、1、2区的颜色)，进而，5区周边三个区域已栽上3种不同颜色的花，故5区也只有一种颜色的花可栽；情形2：栽于6区，则与情形1同理，4、5区域分别只有1种颜色可栽；情形3：栽于5区，由于5、1、2三个区已栽上不同颜色的花，6区只有1种栽法；同理，4区也只有1种栽法．第二类：栽于4、5、6中的两个区，只有栽于4、6两个区域的一种情形，这时5区有2种栽法(因为5区的周边只有两色花)．综合起来，应用乘法原理与加法原理，得不同栽种方法的种数为.1205P C)2111111(P C N 33143334=⨯=⨯⨯+⨯+⨯=解法5 分两类情况考虑：第1类：第1、2、3、5等四个区域栽种不同颜色的4种花，共有44P 种栽法．对于每一种栽法，第4、6区分别都只有1种颜色的花可栽．第2类：第1、2、3、5等四个区域栽种不同颜色的3种花，共有3334P C 2种栽法．对于每一种栽法，要么2、5区栽同色花，要么3、5区栽同色花．对于前者，第6区有2种颜色的花可供选栽，第4区只能栽第4种颜色的花；对于后者，第4区有2种颜色的花可供选栽，第6区只能栽第4种颜色的花．即无论何种情形，第4、6区的栽法都是2种．综合上述情形，应用加法原理与乘法原理，得不同栽种方法的种数为.120P C 22P N 333444=⨯+=[答案] 12016．下列5个正方体图形中，l 是正方体的一条对角线，点M 、N 、P 分别为其所在棱的中点，能得出l ⊥面MNP 的图形的序号是_______．(写出所有符合要求的图形序号)[分析] 本题以正方体为依托，主要考查直线与平面垂直的判定，比较深刻地考查了空间想象能力．为了得到本题答案，必须对5个图形逐一进行判别．对于给定的正方体，l 位置固定，截面MNP 变动，l 与面MNP 是否垂直，可从正、反两方面进行判断．在MN 、NP 、MP 三条线中，若有一条不垂直l ，则可断定l 与面MNP 不垂直；若有两条与l 都垂直，则可断定l ⊥面MNP ；若有l 的垂面∥面MNP ，也可得l ⊥面MNP ．解法1 作正方体1111D C B A ABCD -如附图，与题设图形对比讨论．在附图中，三个截面111D CB EFGHKR D BA 和、都是对角线l )AC (1即的垂面．对比图①，由,BA //MN 1MP∥BD,D BA //MNP 1面知面，故得l ⊥面MNP ．对比图②，由MN 与面11D CB 相交，而过交点且与l 垂直的直线都应在面11D CB 内，所以MN 不垂直于l ，从而l 不垂直于面MNP ．对比图③，由MP 与面D BA 1相交，知l 不垂直于MN ，故l 不垂直于面MNP ．对比图④，由MN∥BD，,D BA //MNP ,BA //MP 11面知面故l ⊥面MNP ．对比图⑤，面MNP 与面EFGHKR 重合，故l ⊥面MNP ．综合得本题的答案为①④⑤．解法2 如果记正方体对角线l 所在的对角截面为α．各图可讨论如下：在图①中，MN ，NP 在平面α上的射影为同一直线，且与l 垂直，故l ⊥面MNP ．事实上，还可这样考虑：l 在上底面的射影是MP 的垂线，故l ⊥MP；l 在左侧面的射影是MN 的垂线，故l ⊥MN，从而l ⊥面MNP ．在图②中，由MP⊥面α，可证明MN 在平面α上的射影不是l 的垂线，故l 不垂直于MN ．从而l 不垂直于面MNP ．在图③中，点M 在α上的射影是l 的中点．点P 在α上的射影是上底面的内点，知MP 在α上的射影不是l 的垂线，得l 不垂直于面MNP ．在图④中，平面α垂直平分线段MN ，故l ⊥MN．又l 在左侧面的射影(即侧面正方形的一条对角线)与MP 垂直，从而l ⊥MP，故l ⊥面MNP ．在图⑤中，点N 在平面α上的射影是对角线l 的中点，点M 、P 在平面α上的射影分别是上、下底面对角线的4分点，三个射影同在一条直线上，且l 与这一直线垂直．从而l ⊥面MNP ．至此，得①④⑤为本题答案．解法3 如图建立空间直角坐标系O －xyz ，设正方体的棱长为2，则对角线l 的方向向量可取为).2,2,2(-=→l对图①，有),1,0,1()0,0,1()1,0,0(MN ),0,1,1()0,0,1()0,1,0(MP --=--=-=-=→--→--.0,0MNP l MN l MP l 面得由⊥=⋅=⋅→--→→--→对图②，有),1,2,1()2,0,1()1,2,2(MN =---=→--.0不垂直与面知由MNP l N M l ≠⋅→---→对图③，有),1,1,2()1,0,2()0,1,0(MP -=--=→--.l l 不垂直与面知由MNP 0MP ≠→--→对图④，有),0,2,2()1,0,2()1,2,0(MN ),1,0,1()1,0,2()2,0,1(MP -=---=--=---=→--→--.0,0MNP l MN l MP l 面得由⊥=⋅=⋅→--→→--→对图⑤，有),1,2,1()2,0,1()1,2,0(MN ),2,1,1()2,0,1(),0,1,2(MP -=---==--=→--→--.MNP 0MN ,0MP 面得由⊥=⋅=⋅→--→→--→l l l综合得本题答案为①④⑤．从解法3可以看到；应用向量法讨论两直线是否垂直十分方便，操作也比较简单，无须多动脑筋，只需要计算正确即可．[答案] ①④⑤ 三、解答题17．已知函数f(x)=2sinx(sinx+cosx)． (Ⅰ)求函数f(x)的最小正周期和最大值；(Ⅱ)在给出的直角坐标系中，画出函数y=f(x 在区间⎥⎦⎤⎢⎣⎡ππ-2,2上的图象．[命题意图] 本小题主要考查三角函数的性质和恒等变形的基础知识，同时考查动手画图的技能．作为三角函数的解答题，力求较全面地覆盖三角函数的基础知识，因此，试题的设计给出一个三角函数的解析式，通过运用和角与倍角的三角函数公式，变形为单个三角函数的表达式，从而求出它的周期和最值．恒等变形过程强调通性通法，以适应文科考生的实际．在这个基础上要求作出这个函数的图像，强化了作图技能的考查，倡导考生重视实践，学会动手操作．[解题思路] 首先把给出的函数解析式变形为单个三角函数的表达式，再按问题的要求答题．,42x sin 21 4sin 2cos 4cos 2sin 21 2sin 2cos 1 cos sin 2sin 2f(x) 12⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+=+-=+=πππx x xx x x x 解法.21,)x (f +π最大值为的最小正周期为所以函数.42sin 21 4sin 42sin 2 4x cos 22sinx )cos (sin sin 2)( 2⎪⎭⎫ ⎝⎛-+=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⋅=+=ππππx x x x x x f 解法.21,)x (f +π最大值为的最小正周期为所以函数（Ⅱ）解由（Ⅰ）知上的图像是在区间故函数⎥⎦⎤⎢⎣⎡ππ-=2，2)x (f y18．如图，在直三棱柱,C B A ABC 111中-底面是等腰直角三角形，∠ACB=90°．侧棱B A CC ED ,2AA 111与分别是、=的中点，点E 在平面ABD 上的射影是△ABD 的重心G ．(Ⅰ)求B A 1与平面ABD 所成角的大小(结果用反三角函数值表示)；.)Ⅱ(1的距离到平面求点AED A[命题意图] 本小题主要考查线面关系和直三棱柱等基础知识，同时考查空间想象能力和推理运算能力．新课程的立体几何教材分为(A)、(B)两个版本，即传统的逻辑推理体系和向量运算方法．为了．适应不同地区的选用情况，前几年高考的立体几何试题是命制出(甲)、(乙)两道平行题目由考生选作．今年试验改变这种做法，原课程与新课程统一命制一道通用的试题，基本要求是用传统方法或向量方法，解题难度相当．于是，试题的知识载体定位于直棱柱．理科用直三棱柱，文科用正四棱柱．理科试题中的图形实际上是半个正方体，它的原型是正方体的一个性质：“若点M 是正方体ABCD D C B A 1111-的棱D D 1的中点，则正方体的中心O 在截面AMC 上的射影恰好是△AMC 的重心”．试题基本上是采用其逆命题，且只给出半个正方体，把问题提为“正方体的一条对角线与截面所成的角”，隐蔽了上述性质，提高了对考生空间想像力和推理能力的要求，以期更好地考查考生的数学能力．[解题思路] 本题(Ⅰ)的基本解法是先求出三棱柱的底面边长，可以在直三棱柱中求解，也可以补形成正四棱柱或直平行六面体求解，思维层次高者可以发现EB=DF 避开计算，通过线段比求角的三角函数值．(Ⅱ)问的解法用等积法最为简便．运用向量方法则(Ⅰ)问较易，(Ⅱ)问较难，总体难度相当．(Ⅰ)解法1 如图，连结BG ，则BG 是BE 在面ABD 的射影，即∠EBG 是B A 1与平面ABD 所成的角．设F 为AB 中点，连结EF 、FC ，因为D 、E 分别是B 、A CC 11的中点，又DC⊥平面ABC ，所以CDEF 为矩形．连结DF ，G 是△ADB 的重心，故G∈DF．在直角三角形EFD 中，.3FD 1EF ,FD 31FD FG EF 22===⋅=知由.36321,2=⨯==EG ED 于是.3EB ,32B A ,22AB ,2ED FC 1=====则因为.323136EB EG EBG sin =⋅==∠所以.32arcsinABD B A 1所成的角是平面即解法2 同解法1图．AEB ，D ADB E V V --=因为所以 AB·DF·EG=AB·EF·DE，其中EF=1．,x 22FB CF DE x,BC ====则设.1x 21FB DB DF ,x 1DB 222222+=-=+=所以.DF 32EG ,DF 92DF 32DF 31EG 22==⋅=即又,DE DF 322=所以x 221x 21322=⎪⎭⎫⎝⎛+即,02x 3x 2=+-整理得),,12(x x 舍去与题设矛盾解得==.36142132EG =+⨯⋅=则,31x 22BE 2=+⎪⎪⎭⎫⎝⎛=而.323/36BE EG EBG sin ===∠所以,ABCH H C B A , 31111-行六面体将直三棱柱补形成直平如图解法H H 1取的中点P,连结PD,PA,PB,则ABDP 是平行四边形,PB 必过△ADB 的重心．.PB Q A ,EG //Q A ,Q A ,PA ,PB 31PQ 1111⊥=故则连结截取 ,QB B A PQ P A 221221-=-所以.PB 31PB 31PB 32PQ QB P A B A 222222121=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=-=-即,x 2PD AB ,1x PA DA BD ,x BC 2222222==+====则设 ,BD 2AB 2AD PB ,ABDP 2222+=+中在平行四边行。

(新课标)高考数学模拟系列(二)试题理新人教A版

12023年高考模拟系列试卷（二）数学试题【新课标版】（理科）1．本试卷分第一卷（阅读题）和第二卷（表达题）两局部。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．作答时，将答案写在答题卡上。

写在本试卷上无效。

3．考试完毕后，将本试卷和答题卡一并交回。

第一卷（选择题，共60分）一、此题共12小题，每题5分，共60分，在每题给出的四个选项中只有一个选项是符合题目要求的1、设集合{}21,M x x x =-≤∈R ，{}21,02N y y x x ==-+≤≤，那么()RM N ⋂等于（）A ．RB ．{}|1x x R x ∈≠且C ．{}1D ．∅2、在复平面内，复数2013ii 1iz =+-表示的点所在的象限是（） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限3、假设sin601233,log cos60,log tan 30a b c ===，那么（）A ．a b c >>B ．b c a >>C ．c b a >>D ．b a c >>4、设数列{}n a 是公差不为零的等差数列，它的前n 项和为n S ，且1S 、2S 、4S 成等比数列，那么41a a 等于（） A ．6B ．7C ．4D ．35、已知点()1,0A -和圆222x y +=上一动点P ，动点M 满足2MA AP =，那么点M 的轨迹方程是（）A ．()2231x y -+=B ．223()12x y -+=C ．2231()22x y -+= D ．223122x y ⎛⎫+-= ⎪⎝⎭6、命题“存在,αβ∈R ，使22sin()sin()sin sin αβαβαβ+-≥-”的否认为（）A ．任意,αβ∈R ，使22sin()sin()sin sin αβαβαβ+-≥- B ．任意,αβ∈R ，使22sin()sin()sin sin αβαβαβ+-<- C ．存在,αβ∈R ，使22sin()sin()sin sin αβαβαβ+-<- D ．存在,αβ∈R ，使22sin()sin()sin sin αβαβαβ+-≤- 7、设a b <，函数()()2y x a x b =--的图象可能是（）28、程序框图如下：如果上述程序运行的结果S 的值比2023小，假设使输出的S 最大，那么判断框中应填入（） A ．10k ≤ B ．10k ≥ C ．9k ≤ D ．9k ≥9、图为一个空间几何体的三视图，其中俯视图是下边一个等边三角形，其内切圆的半径是1，正视图和侧视图是上边两个图形，数据如图，那么此几何体的体积是（）A ．1533π+B ．21533π+C ．3033π+D ．43033π+ 10、在9212x x ⎛⎫- ⎪⎝⎭的展开式中，常数项为（）A ．5376-B ．5376C ．84-D ．8411、如果点P 在平面区域220140x y x x y -+≤⎧⎪≥-⎨⎪+-≤⎩上，点Q 在曲线（x －1）2＋(y －1)2＝1上，那么|PQ |的最小值为（）A ．5－1B ．355 C ．3515- D ．523－1 12、已知椭圆C ：22221(0)x ya b a b+=>>的左右焦点为12,F F ，过2F 的直线与圆222()()x a y b b -+-=相切于点A ，并与椭圆C 交与不同的两点P ，Q ，如图，假设A 为线段PQ 的靠近P 的三等分点，那么椭圆的离心率为（）3A ．23B ．33C ．53D ．73第二卷(非选择题，共90分)二、填空题：本大题共4小题，每题4分，共16分，把答案填在题中横线上 13、由曲线23y x =-和直线2y x =所围成的面积为。

2006年高考数学模拟题与参考答案

２０年第２０６期
中学数学教学
４３
在
若
分别为— — ．
一，号数的一常值
如
，
ＡＣＢ（＝
．
３，ＤＢ
曼
箬；
１．（詈）４若 ∈（・，数：ｏ０１＞２）则函：ｌ（一 ’ 的ｇ）
解集是— — ．１．理）离散型随机变量的分布列如表，５（设则
．
７
Ｉ．８Ｊ
（一Ｐ（）则下列结论不正确的是（）Ｋ，
Ａ．（一Ｏ）１Ｈ（ｒ一ｌ）
．
）
（一）
３若集合Ｍ一｛ —Ｌ，－ｚ，．ｌｒｘＣ｝Ｎ一｛ｌｌ一３ｌ ≥６ ∈Ｒ｝全集Ｕ＝Ｒ，Ｍ的真子集个数是。，则ｒＣＮ３
）
Ｄ｜２Ｏ（，）
ｌ．（＋５ ”的展开式中各项二项式系数之和１若１ｘ）为，７５ ”的展开式中各项系数之和为ｂ则（ｘ＋）
５函数 —Ｌ１在区间（，）．ｒｍ’ ＯＩ上是（
Ａ单调增函数．
）
１五的为Ｊｊ明刀值（但‘
（等差数列｝， “ ＋“ ＋Ⅱ 一３，文）中若．４９“ ＋“
＋ａ一２，。７则前９项的和Ｓ等于（
Ａ＿６６Ｂ９９（．４：】４
９正方形ＡＤ— Ａ。。Ｄ，中，Ｐ在侧面．ＢＣＢＣ，点ＢＣ．及其边界上运动，ＣＢ・并保持ＡＰ上ＢＤ．则动点Ｐ，

2006年广东高考数学模拟试题

图，四棱锥ＰＡＢＤ的底面是正－Ｃ
（抛物线的一部分Ｄ）
方形，侧面ＰＤ是边长为１的正Ａ三角形，且侧面ＰＤ上底面ＡＡＣＥ为侧棱ＰＢＤ，Ｄ的中点．Ａ
维普资讯
胁
毹
（）：Ｅ＿平面ＰＤ；１求证ＡＬＣ
（３Ａ）９（）３Ｂｌ（）１Ｃ－３（－９Ｄ）３
ｃｓＡｏ２）与向量二（０＝２）的夹角为了，＂ＩＴ，其中Ａ、、ＢＣ是
Ｊ
６）．是定义在Ｒ上且以３为周期的偶函数，且２０），则方程ｆｘ＝区间（，）的个数的最小值＝ｉ）Ｏ在０６内解
１．（小题满分１５本３分）已知向量ｍ＝ｓ２１（ｎＡ，一ｉ
（）ｘ３ｉＣ２＝ｓｘｎ
（与的取值有关Ｄ）
５把直线一ｙ０按向量０（ｌ２平移后，得直．２＝：一，）－所
线与＋一＝切，实圆｝相则数Ａ值）的为（
∈Ｒ）若当０， ≤ ≤ 时，
二
４若０７，２．＜则ｘ与３ｉ／＂ｓｘ的大小关系为（ｎ
（２＞ｓｘＡ）ｘ３ｉｎ（２＜ｓｘＢ）ｘ３ｉｎ
ｍ・ｉ）ｍ－）０有实数解，ｓｘ＋１ｎｆｌ＞则实数ｍ的取值范围是三、解答题：本大题共６小题。８共０分．解答应写出文字说明、证明过程或演算步骤．
任意ｎ２＞Ｉ，总有３４、Ⅱ、２Ｓ成等差数列，Ｓ一，一ｔ
￣ｌｌｍＳ｜（ｉ）

2006年贵州省高考理科数学试题(真题与答案解析)

2006年全国统一高考数学试卷Ⅱ（理科）一、选择题（共12小题，每小题5分，满分60分）D．3．（5分）=（）．C4．（5分）如图，PA、PB、DE分别与⊙O相切，若∠P=40°，则∠DOE等于（）度．5．（5分）已知△ABC的顶点B，C在椭圆+y2=1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC ．D7．（5分）如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和．过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=（）8．（5分）函数y=f（x）的图象与函数g（x）=log2x（x＞0）的图象关于原点对称，则f（x）的表达式为（）．C9．（5分）已知双曲线的一条渐近线方程为，则双曲线的离心率为（）．C D．11．（5分）设S n是等差数列{a n}的前n项和，若，则=（）．C D．12．（5分）函数的最小值为（）二、填空题（共4小题，每小题4分，满分16分）13．（4分）（2012•肇庆一模）在的展开式中常数项为_________（用数字作答）．14．（4分）已知△ABC的三个内角A、B、C成等差数列，且AB=1，BC=4，则边BC上的中线AD的长为_________．15．（4分）（2012•甘肃一模）过点的直线l将圆（x﹣2）2+y2=4分成两段弧，当劣弧所对的圆心角最小时，直线l的斜率k=_________．16．（4分）（2014•江苏一模）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在[2500，3000）（元）月收入段应抽出_________人．三、解答题（共6小题，满分74分）17．（12分）已知向量，，．（1）若，求θ；（2）求的最大值．19．（12分）某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．（1）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；（2）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率．20．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AB=BC，D、E分别为BB1、AC1的中点．（I）证明：ED为异面直线BB1与AC1的公垂线；（II）设，求二面角A 1﹣AD﹣C1的大小．24．（12分）设函数f（x）=（x+1）ln（x+1）．若对所有的x≥0，都有f（x）≥ax成立，求实数a的取值范围．25．（14分）已知抛物线x2=4y的焦点为F，A、B是抛物线上的两动点，且．过A、B两点分别作抛物线的切线，设其交点为M．（Ⅰ）证明为定值；（Ⅱ）设△ABM的面积为S，写出S=f（λ）的表达式，并求S的最小值．27．（12分）设数列{a n}的前n项和为S n，且方程x2﹣a n x﹣a n=0有一根为S n﹣1，n=1，2，3，…．（1）求a1，a2；（2）猜想数列{S n}的通项公式，并给出严格的证明．2006年全国统一高考数学试卷Ⅱ（理科）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）D．所以最小正周期为3．（5分）=（）．C4．（5分）如图，PA、PB、DE分别与⊙O相切，若∠P=40°，则∠DOE等于（）度．∠AOB=×5．（5分）（2014•四川二模）已知△ABC的顶点B，C在椭圆+y2=1上，顶点A是椭圆的一个焦点，且椭圆的另．D7．（5分）如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和．过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=（），AB'=所成的角为，A'B'=．C与9．（5分）（2011•普宁市模拟）已知双曲线的一条渐近线方程为，则双曲线的离心率为（）．C D．由渐近线方程可得11．（5分）（2010•锦州二模）设S n是等差数列{a n}的前n项和，若，则=（）．C D．，代入中∴12．（5分）函数的最小值为（）二、填空题（共4小题，每小题4分，满分16分）13．（4分）（2012•肇庆一模）在的展开式中常数项为45（用数字作答）．14．（4分）已知△ABC的三个内角A、B、C成等差数列，且AB=1，BC=4，则边BC上的中线AD的长为．∴由余弦定理定理可得故答案为：15．（4分）（2012•甘肃一模）过点的直线l将圆（x﹣2）2+y2=4分成两段弧，当劣弧所对的圆心角最小时，直线l的斜率k=．．16．（4分）（2014•江苏一模）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在[2500，3000）（元）月收入段应抽出25人．按分层抽样应抽出三、解答题（共6小题，满分74分）17．（12分）已知向量，，．（1）若，求θ；（2）求的最大值．，化简）因为，所以）因为时，的最大值为19．（12分）某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．（1）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；（2）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率．，，这两个事件是互斥的，根据互斥事件的答：==20．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AB=BC，D、E分别为BB1、AC1的中点．（I）证明：ED为异面直线BB1与AC1的公垂线；（II）设，求二面角A 1﹣AD﹣C1的大小．EO C C EO=AC=，EF==，FE=24．（12分）设函数f（x）=（x+1）ln（x+1）．若对所有的x≥0，都有f（x）≥ax成立，求实数a的取值范围．25．（14分）已知抛物线x2=4y的焦点为F，A、B是抛物线上的两动点，且．过A、B两点分别作抛物线的切线，设其交点为M．（Ⅰ）证明为定值；（Ⅱ）设△ABM的面积为S，写出S=f（λ）的表达式，并求S的最小值．的方程，联立方程求得交点坐标，求得和，进而可求得•，则易得切线（（=，=（（2[S=∵，即，==+2=+2=）S=（）27．（12分）设数列{a n}的前n项和为S n，且方程x2﹣a n x﹣a n=0有一根为S n﹣1，n=1，2，3，…．（1）求a1，a2；（2）猜想数列{S n}的通项公式，并给出严格的证明．．，﹣）﹣．，=+．，==对所有正整数参与本试卷答题和审题的老师有：wdlxh；wsj1012；zlzhan；zhwsd；yhx01248；涨停；wdnah；minqi5；qiss；翔宇老师；liuerq；xintrl；congtou；298520；jj2008（排名不分先后）菁优网2014年6月6日。

2006年高考理科数学试题及答案(全国卷2)

2006年普通高等学校招生全国统一考试文科数学（全国卷Ⅰ）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3到10页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

3．本卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A 、B 互斥，那么球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B 相互独立，那么其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ，那么334R V π=n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径k n kk n n P P C k P --=)1()(一．选择题（1）设集合M={x|x 2-x<0},N={x||x|<2},则（A ）M φ=N （B ）M M N =（C ）M N M =（D ）R N M =（2）已知函数y=e x 的图象与函数y=f(x)的图象关于直线y=x 对称，则（A ）f(2x)=e 2x (x )R ∈ （B ）f(2x)=ln2lnx(x>0)（C ）f(2x)=2e 2x (x )R ∈（D ）f(2x)= lnx+ln2(x>0)（3）双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m=（A ）-41 （B ）-4 (C)4 （D ）41 （4）如果(m 2+i)(1+mi)是实数,则实数m=（A ）1（B ）-1（C ）2（D ）-2（5）函数f(x)=tan(x+4π)的单调递增区间为（A ）(k π-2π, k π+2π),k Z ∈ （B ）(k π, (k+1)π),k Z ∈(C) (k π-43π, k π+4π),k Z ∈ （D ）(k π-4π, k π+43π),k Z ∈（6）∆ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，若a 、b 、c ，且c=2a ，则cosB=（A ）41 （B ）43 （C ）42 （D ）32（7）已知各顶点都在一个球面上的正四棱锥高为4，体积为16，则这个球的表面积是（A ）16 π （B ）20π （C ）24π （D ）32π（8）抛物线y=-x 2上的点到4x+3y-8=0直线的距离的最小值是（A ）34 （B ）57 （C ）58 （D ）3（9）设平面向量a 1、a 2、a 3的和a 1+a 2+a 3=0，如果平面向量b 1、b 2、b 3满足|b i |=2|a i |，且a i 顺时针旋转30︒后与同向，其中i=1、2、3，则（A ）-b 1+b 2+b 3=0 （B ）b 1-b 2+b 3=0（C ）b 1+b 2-b 3=0 （D ）b 1+b 2+b 3=0（10）设{a n }是公差为正数的等差数列，若a 1+a 2+a 3=15，a 1a 2a 3=80，则a 11+a 12+a 13=（A ）120 （B ）105 （C ）90 （D ）75（11）用长度分别为2、3、4、5、6(单位:cm)的细木棒围成一个三角形(允许连接,但不允许折断),能够得到期的三角形面积的最大值为（A ）85cm 2（B ）610cm 2（C ）355cm 2（D ）20cm 2（12）设集合I={1，2，3，4，5}，选择I 的两个非空子和B ，要使B 中的最小的数大于A 中最大的数，则不同的选择方法共有（A ）50种（B ）49种（C ）48种（D ）47种第Ⅱ卷注意事项：1．用钢笔或圆珠笔直接答在试题卷上。

2006年高考数学模拟试题(二)

ห้องสมุดไป่ตู้．
— —
一
１（
＇），则
—
３函ｌＩ；１的义是）．数 —。ｘ一）定域（－鞋ｌ
Ａｆ１Ｕ一ｘｏ．专，）（ｃ，。）
１（ｃ１３一 × ），。。
１
ｎ一。（用数字作答．）设数列｛的前项和为Ｓ，Ｓ＝ｎ｝则９（用数字作答）．
（
）．一ｎ若
）．
一２则Ｄ的最小值等于，
１．离心率等于ｌｐ（中２ ≤ ９１ ≤ ９Ｐ，４ｏｑ其ｇ ≤ｐ，≤ｑ，ｑ ∈Ｎ的不同形状的双曲线个数为）．１．给定实数，义［为不大于的最大整数，５定］｛为ｚ的小数部分，｝且一［］｝则下列结＋｛，论： —ｌＥ３ ① ＜ｘ ≤ ；ＸＥ３ ② －ｘ是周期函数； ③ ］是偶函数；一１｛＜１中不正确的 ④ ＜｝．其
的展开式中，含项的系数等于－４０则实数ｎ８，的值等于（）．
＆１２
７．已知函数，）（一ｃｓ，ｏ若经过该函数图象上的一个最大值点与一个最小值点的直线的最大斜率等于√ ，，）３则（的最小正周期是（）．
一
苏
、
如果在ｚ上存在点Ｍ，使线段Ｏ的垂直平分线Ｍ经过Ｆ，则椭圆离心率的取值范围是（）．
Ｌ１ｒ１，
‘
＆ｒ１，１
Ｌ‘
ｃｆ，１．等１

2006年高考数学模拟试题(二)

Ｂ．ｒ
厶
）．
６把函数 — ｃ一ｓｘ的图像向左平移．ｏｉｎ，个单位（，１ｍ＞Ｏ，得的图像关于轴对）所称。ｍ的最小值是（则
．
ｃ
ｏ
Ｄ．
ｏ
ｌ．径为４的球面上有Ａ、Ｃ、四点，２半Ｂ、Ｄ且满足
１．中学有高一学生４０人，二学生３０４某０高０
）．
Ａ．题 “ 命声或为假
Ｂ命题 “ ｐ且ｑ为真 ”
．
人。三学生３０人。通过分层抽样抽高０现取０个样本容量为ｎ的样本。知每个学已生被抽到的概率为０２则ｎ．。一－．
Ｉ．３
ｌ．Ｆ（，）（，）设Ｊ一ｃｏ、ｃｏ是椭圆＋一１
（＞６Ｏ的两个焦点，是以ＦＦ为直ｎ＞）Ｐ２径的圆与椭圆的一个交点。ＰＦＦ２若１ —
＇Ｃ．３：２４
。
ｎ１
５ＰＦ。椭圆的离心率为（则
号丙ｌ概为三各一次・答格的率，人答，及
则三人中只有一人答及格的概率为
（）．
＝ｌ，ｓ。Ｏ则的值为（）．八５Ｒ５Ｃ１０Ｄ．能确定５９．Ｏ不
ＡＢｃＤ上不．－．．都对嘉以
１．图２南北方向的公路ＺＡ地在公路的ｓ如。，

2006年高考数学模拟题及参考答案

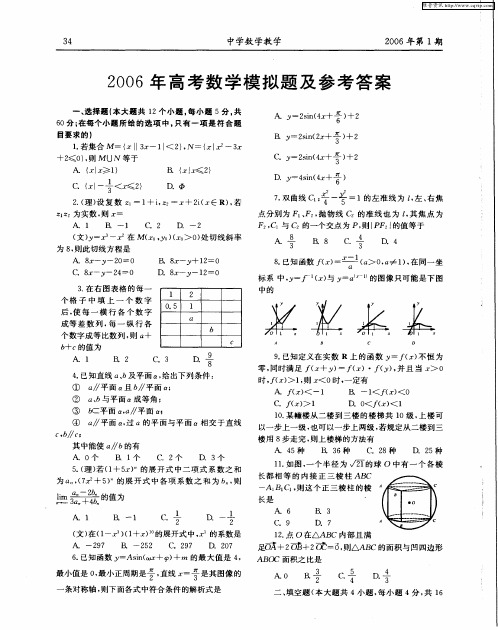
直角梯形，ＡＤ∥ ＢＡＢＣ．
ｊＢＡＢ— ＡＤ— ＰＢ一ＩＣ，
（）４若函数 —ｌｏ
定义域是｛ｌ≤ ８．）
的值域是｛ ≤ ３，它的Ｙｆ｝则
９
（）函数一２１若的定义域是｛ｌ０．它的 ≤ ）则值域是｛ ≤１；Ｙｌ）
Ｊｎ
且ａｂ一÷ ，６３５４４Ｓ一Ｓ：１．
Ｊ
（）１求数列｛｝的通项公式；
（）Ｔ＝ｂ＋ｂ＋ … ＋ｂ．２求ｌ２
（）（－Ｘ）１的展开式中，的系数是文在１。（＋）
八一２７９Ｂ一２２５Ｃ．２７９Ｄ．２７０
长个棱一这的１ＡＢ：是Ｄ ◎ ｆＩ八．＼１．三Ｊ棱Ｉ，ｌ柱＿ｌ，；则 — 正． … 三至＝．７
２００６年第１期
分，把答案写在题中横线上）
２ｊｌｚ一＋＞Ｏ
中学数学教学
３５
（）厂）１求（的单调递增区间；（）２是否存在实数ａ使＿）（。Ｏ上单调，厂（在一。，］
．
１．３已知实数、、足条件ｘ－４Ｏ则ｙｚ满＋ｙ＞ｊ
为８则此切线方程是，
八８ — 一２０Ｏ
Ｉ３．
８ｃ号Ｄ４．．
Ｂ８． — ＋１＝０２Ｄ．８ — 一１＝０２
８已知函数，）ｘ（＞Ｏ口１，同一坐．（：— １ａ－，≠ ）在

06年数学高考模拟试题(2).doc

06年数学高考模拟试题(2)第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题；每小题5分，共60分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．（1）与向量(12,5)a =平行的单位向量为（）A ．125(,)1313-B ．125(,)1313--C ．125(,)1313或125(,)1313--D ．125(,)1313±±（2）函数2log (2)y x =+的定义域为（）A.．(,1)(3,)-∞-+∞ B ．(,1][3,)-∞-+∞C ．(2,1]--D ．(2,1][3,)--+∞（3）某地区高中分三类：A 类校共有学生4000人，B 类校共有学生2000人，C 类校共有学生3000人。

现欲抽样分析某次考试的情况，若抽取900份试卷进行分析，则从A 类校抽取的试卷份数应为（）A ．450份B ．400份C ．300份D ．200份（4）已知直线m 、n 和平面α，则m ∥n 的一个必要条件是（）A ．m ∥α，n ∥α Ｂ．m ⊥α，n ⊥α C ．m ∥α，n ⊂α D ．m 、n 与α成等角（5）若正数b a 、满足3++=b a ab ，则b a +的取值范围是（）A ．),9[+∞ Ｂ．),6[+∞ C ．]9,0( D ．)6,0(（6）设双曲线22221x y a b-=(0,0)a b >>的实轴长、虚轴长、焦距成等比数列，则双曲线的离心率为（）A ．2 B ．12C D （7）若函数y =f (x ) (x ∈R )满足f (x +2)=f (x )，且x ∈(－1,1]时，f (x )=|x |．则函数y =f (x )的图象与函数y =log 4|x |的图象的交点的个数为（）A ．3B ．4C ．6D ．8 （8）已知点P 是抛物线22y x =上的动点，点P 在y 轴上的射影是M ，点A 的坐标是7(,4)2A ，则||||PA PM +的最小值是（）A ．112 B ．4 C ．92D ．5 （9）已知函数()y f x =的图象与函数21xy -=-的图象关于直线y x =对称，则(3)f 的值为（）A ．1B ．1-C ．2D ．2-（10）能够使得圆222410x y x y +-++=上恰有两个点到直线20x y c ++=距离等于1的c 的一个值为（）A ．2C ．3 D．（11）关于x 的不等式ax-b >0的解集是(1,+∞)，则关于x 的不等式02>-+x bax 的解集是（） A ．(-∞,-1)∪(2,+∞) B ．(-1,2) C ．(1,2) D ．(-∞,1)∪(2,+∞)（12）由0，1，2，…，9这十个数字组成的、无重复数字的四位数中，个位数字与百位数字之差的绝对值等于8的个数为（）A.180B.196C.210D.224第Ⅱ卷(非选择题，共90分)二、填空题：本大题共4小题；每小题4分，共16分．把答案填在题中横线上．（13）如图，已知点E 是棱长为2的正方体1AC 的棱1AA 的中点，则点A 到平面EBD 的距离等于_____________．（14）若123n a n =++++，则数列1{}na 的前n 项和n S =_____________．（15）已知1sincos,222θθ+=则cos2θ= ．（16）有两个向量1(1,0)e =，2(0,1)e =，今有动点P ，从0(1,2)P -开始沿着与向量12e e +相同的方向作匀速直线运动，速度为12||e e +；另一动点Q ，从0(2,1)Q --开始沿着与向量1232e e +相同的方向作匀速直线运动，速度为12|32|e e +．设P 、Q 在时刻0t =秒时分别在0P 、0Q 处，则当00PQ P Q ⊥时，t = 秒．三、解答题：本大题6小题，共74分．解答应写出文字说明，证明过程或演算步骤． (17)(本小题满分12分)某厂生产的A 产品按每盒10件进行包装，每盒产品均需检验合格后方可出厂．质检办法规定：从每盒10件A 产品中任抽4件进行检验，若次品数不超过1件，就认为该盒产品合格；否则，就认为该盒产品不合格．已知某盒A 产品中有2件次品．（1）求该盒产品被检验合格的概率；（2）若对该盒产品分别进行两次检验，求两次检验得出的结果不一致的概率．1A 1B 1C 1D DC BAE(18)(本小题满分12分)已知偶函数f (x )=cos θsin x －sin(x －θ)+(tan θ－2)sin x －sin θ的最小值是0，求f (x )的最大值及此时x 的集合．(19) (本小题满分12分)如图，直三棱柱111ABC A B C -中，112AB AC AA ==，90BAC ∠=，D 为棱1BB 的中点．（Ⅰ）求异面直线1C D 与1A C 所成的角；（Ⅱ）求证：平面1A DC ⊥平面ADC ．(20) (本小题满分12分)已知二次函数f (x )满足：①在x =1时有极值； ②图象过点(0,-3)，且在该点处的切线与直线2x +y =0平行．（I ）求f (x )的解析式；（II ）求函数g (x )=f (x 2)的单调递增区间。

2006年高中数学篇目索引上海市甘泉外国语中学资料室提供

2006年高中数学篇目索引上海市甘泉外国语中学资料室提供由一道高考题反思解析几何的教学/展国培（江苏省靖江市第一中学）//中学数学（武汉）.—2006，no. 1.—P.10由一堂探索性问题专题课想到的/霍乙光，翟小军（江苏省东海高级中学）//中学数学（武汉）.—2006，no. 1.—P.14用导数的几何意义求切线方程的另一“误区”/孟祥礼，孟祥东//中学数学（武汉）.—2006，no. 1.—P.26试论类比推理在数学解题中的几个误区/黄加卫（浙江省湖州市第一中学）//中学数学（武汉）.—2006，no. 1.—P.30一类视角最值问题的变式与高考题/任念兵//中学数学（武汉）.—2006，no. 1.—P.39完全四边形的一条性质及应用/沈文选（湖南师范大学数学系）//中学数学（武汉）.—2006，no. 1.—P.44对一道求值域题的“三思”/苗大勇（河南省舞阳县第一高级中学）//中学生数学（北京）.—2006，no. 1.—P.26让数学教育体现更多的人文关怀——高中学生写数学周记的尝试与思考/谢志庆（武汉市第十一中学）//数学通报（北京）.—2006，no. 1.—P.15新课标背景下的高中数学情境创设策略的探讨/刘允忠（浙江省宁波市北仑区明港中学）//数学通报（北京）.—2006，no. 1.—P.18对高中实验教材中一些问题的商榷/韩裕娜（华南师范大学数学系）//数学通报（北京）.—2006，no. 1.—P.25学生为什么不善于利用几何意义解题——从一道二次函数题学生解答受阻谈起/王国栋（北京一零一中学）//数学通报（北京）.—2006，no. 1.—P.28摆线的课件制作/王怀昌（山东省枣庄市第三中学）//数学通报（北京）.—2006，no.1.—P.40变式教学诱发一题多解/陈迪军（湖北省大冶市第一中学）//数学通报（北京）.—2006，no. 1.—P.44“取倒数”技巧的妙用/刘祖希，苏希常（苏州市第一中学）//数学通报（北京）.—2006，no. 1.—P.49从一道高考题的解答谈分析讨论思想/孙芸（江苏省海们锡类中学）//数学通报（北京）.—2006，no. 1.—P.54数学教学中有效“问题情境“的创设及案例分析/应之中（浙江省丽水中学）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.9课堂教学要呈现“教学本质“/陈柏良（浙江绍兴市高级中学）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.11例谈用本原性问题驱动数学概念教学/杨玉东（上海教育科学研究院），李伟峰（上海市建平世纪中学）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.15课例：用二分法求方程的近似解/张国良（江苏前黄高级中学）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.21一个优美三角结论的秒用/任伟芳（浙江宁波鄞州高级中学）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.33高考数学模拟新题集锦/本刊试题研究组//中学数学教学参考（陕西）.—2006，no. 1-2.—P.39三角函数高考题回顾与展望/季青等//中学数学教学参考（陕西）.—2006，no. 1-2.—P.952006年上海市普通高等学校春季招生数学试题/本刊//中学数学教学参考（陕西）.—2006，no. 1-2.—P.98高一数学第一学期阶段测评题/金良（山西省长治学院附属太行中学）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.101高二数学第一学期阶段测评题/张世林，田宏梅（湖北省巴东一中）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.104圆锥曲线的几何性质/刘康宁（西安铁一中）//中学数学教学参考（陕西）.—2006，no. 1-2.—P.107高中信息安全与密码课程的一次教学尝试/陈言（福建省福州格致中学）//数学教学（上海）.—2006，no. 2.—P.4学生的质疑是数学教学的珍贵资源/申治国（河南省滑县教师进修学校高中部）//数学教学（上海）.—2006，no. 2.—P.36对数学选择题的思考/周齐/（上海市震旦中学）//数学教学（上海）.—2006，no.2.—P.15对一道不等式习题的探究性学习/陈天雄（福建省莆田第五中学）//数学教学（上海）.—2006，no. 2.—P.16高中“问题解决学习”的一次实践/万自成（上海市奉贤区前桥中学）//数学教学（上海）.—2006，no. 2.—P.19对函数中几个易误易混的剖析/刘智强（浙江省绍兴市稽山中学）//数学教学（上海）.—2006，no. 2.—P.25例说几何中的形外发展策略/许冬云（江苏省南通高等师范学校）//数学教学（上海）.—2006，no. 2.—P.29例谈立体几何中探索性问题的向量解法/朱永厂（江苏省南京师范大学附中江宁校区）//数学教学（上海）.—2006，no. 2.—P.31激活试题的裂变效应/岳荫巍（北京市同仁中学）//数学教学（上海）.—2006，no.2.—P.34函数原来还可以这样教——学习高中数学新课程手迹/王鹏远（北大附中）//数学通报（北京）.—2006，no. 2.—P.16奇思秒想自然来——从点到直线的距离公式推导所想到的/黄坪（上海市曹杨二中）//数学教学（上海）.—2006，no. 2.—P.28一堂概率统计课的片断实录——让学生的“异想”延伸/蒋映（重庆市江北区203中学）//数学教学（上海）.—2006，no. 2.—P.33到两点距离之积是常数的点的轨迹之研究——高二数学研究性学习一例/朱华根（浙江省华维外国语学校）//数学教学（上海）.—2006，no. 2.—P.37通过类比联想寻找解题思路和方法/李爱清（曲阜师范大学附中）//数学教学（上海）.—2006，no. 2.—P.40巧用构造图形法解题/任伟芳（浙江省宁波市鄞洲高级中学）//数学教学（上海）.—2006，no. 2.—P.43一个征解问题的证明与加强及引申/李成龙（江苏省沫阳县选远中学）//数学教学（上海）.—2006，no. 2.—P.50浅谈数学教学如何适应社会网络化趋势/杨建湖（湖南湘潭教育学院）//数学教学通讯：上半月（重庆）.—2006，no. 2.—P.4感受·体验·感悟/叶亚美（江苏省无锡市惠山区教育局教研室）//数学教学通讯：上半月（重庆）.—2006，no. 2.—P.19一节意外的探究性习题课/李怀忠（甘肃省景泰县京华高级中学教研室//数学教学通讯：上半月（重庆）.—2006，no. 2.—P.26探析高考创新试题“新”的特点/虞关寿（浙江省绍兴鲁迅中学）//数学教学通讯：上半月（重庆）.—2006，no. 2.—P.60新课程标准下的数学教学应处理好六种关系/肖林元（江苏省南京市教研室）//中学数学（湖北）.—2006，no. 2.—P.1两圆的“公共弦”——探究性教学案例/戴海林（浙江省瑞安中学）//中学数学（湖北）.—2006，no. 2.—P.14一类圆锥曲线关于焦点弦问题的新解法/王立新（西北师范大学数学与信息科学学院）//中学数学（湖北）.—2006，no. 2.—P.18剖析错解原因探究解题规律——对一道新颖的平面区域面积题的思考/孙芸（江苏省海门市锡类中学，曹军（江苏省海门师范学校）//中学数学（湖北）.—2006，no. 2.—P.28从近两年高考题看高考题趋势/李苑青（广西师范大学），江鸿（湖北大学数学系）//中学数学（湖北）.—2006，no. 2.—P.36解不定方程的常用技法/讲厚利（安徽省安庆市第一中学）//中等数学（天津）.—2006，no. 2.—P.6用不定方程解的个数解一类计数问题/孔祥新（浙江省绍兴市第一中学）//中等数学（天津）.—2006，no. 2.—P.16两道试题的解题/李成章（南开大学数学科学学院）//中等数学（天津）.—2006，no.2.—P.182005年全国高中数学联赛山东赛区预赛/本刊//中等数学（天津）.—2006，no. 2.—P.30椭圆标准方程的推导及启示/聂文喜（湖北省广水市第一中学）//中学生数学（北京）.—2006，no. 2.—P.6一道值得关注的高考选择题/赵优良（湖南省浏阳市田家炳实验中学）//中学生数学（北京）.—2006，no. 2.—P.19狄利克雷及其数学成就/沈杰（首都师范大学附属中学）//中学生数学（北京）.—2006，no. 2.—P.27一道概率题的联想/李禄俊（华东师大二附中）//中学生数学（北京）.—2006，no.2.—P.34直线划分平面得到的一组结论/曾经（浙江省泰顺县第一中学）//中学生数学（北京）.—2006，no. 2.—P.3函数概念的若干问题释疑/周永量（湖南省祁东育贤中学）//中学生数学（北京）.—2006，no. 3.—P.12高考反函数题型及解题技巧/姚祥尹（广东省佛冈一中）//中学生数学（北京）.—2006，no. 3.—P.14例谈高考数学创新题/白美林（江苏阜宁高等师范学校）//中学生数学（北京）.—2006，no. 3.—P.19分式不等式的一些证法/徐文兵（北京清华大学附属中学）//中学生数学（北京）.—2006，no. 3.—P.6证明三点共线问题的方法/黄全福（安徽省怀宁县江镇中学//中学生数学（北京）.—2006，no. 3.—P.6角元塞瓦定理及其应用（二）/李成章（南开大学数学科学学院）//中学生数学（北京）.—2006，no. 3.—P.5巧用齐次化与非齐次化的思想解不等式赛题/徐文兵（清华大学附属中学）//中等数学（天津）.—2006，no. 3.—P.14关于给定有限项的数列的通项公式——也谈数列通项公式的探究/许承厚（华东师范大学数学系）//数学教学（上海）.—2006，no. 3.—P.10也谈“一次意犹未尽的关于根式的探究”/孔志培（浙江省舟山市南海实验学校）//数学教学（上海）.—2006，no. 3.—P.10一道平面几何题数据的一般化探究/茹双林（上海市格致中学）//数学教学（上海）.—2006，no. 3.—P.13由物理现象探求圆锥曲线切线的性质/虞关寿（浙江省绍兴鲁迅中学）//数学教学（上海）.—2006，no. 3.—P.14构造性方法解题——简约而不简单/黄加卫（浙江省湖州市第一中学）//数学教学（上海）.—2006，no. 3.—P.22数学史中勾股定理的证明/朱哲（浙江师范大学数理学院）//数学教学（上海）.—2006，no. 3.—P.43新课程背景下对数学课堂教学的几点思考/袁以武（广东省广州市东山区教育局教研室）//数学教学通讯（重庆）.—2006，no. 3.—P.5注重解题反思发展学生能力/汪纯中（华东师范大学课程与数学系）//数学教学通讯（重庆）.—2006，no. 3.—P.7寻求信息技术与数学教学的结合点/钱炎（江苏省梅村高级中学）//数学教学通讯（重庆）.—2006，no. 3.—P.13谈高中数学概念教学中问题情境的创设/曾庆宝（广西富川县民族中学）//数学教学通讯（重庆）.—2006，no. 3.—P.10点睛：燃起学生理性思维的火花/章珏（江苏省无锡市第一中学）//数学教学通讯（重庆）.—2006，no. 3.—P.18例谈估算的若干策略/丁勇，母建军（江苏省苏州市木渎第二中学）//数学教学通讯（重庆）.—2006，no. 3.—P.46关于函数对称性的几个结论/杨在强（重庆市綦江中学）//数学教学通讯（重庆）.—2006，no. 3.—P.53对一道课本例题例答的不同看法/王太和，解晋（江苏省海安高级中学）//数学教学通讯（重庆）.—2006，no. 3.—P.55和算法内容相关的高考试题/王惠春（江苏省常熟市练塘中学）//数学教学通讯（重庆）.—2006，no. 3.—P.562005年全国高中数学联赛解答题第三题的别解/吕峰波（浙江嘉兴一中）//数学教学通讯（重庆）.—2006，no. 3.—P.64几何视角下的等比数列求和公式/汪晓勤（华东师范大学数学系）//中学数学教学参考（陕西）.—2006，no. 3.—P.12双曲线为什么有渐近线——关于数学概念教学的几点体会/李建军（湖北省长阳县一中）//中学数学教学参考（陕西）.—2006，no. 3.—P.14二次式系数绝对值和最大值/陈云烽（中山大学数计学院数学系）//中学数学教学参考（陕西）.—2006，no. 3.—P.18由函数方程确定的抽象函数的性质/陈甬（浙江省宁波市华茂外国语学校）//中学数学教学参考（陕西）.—2006，no. 3.—P.22高考数学复习的话题与认识/裴光亚（湖北省武汉市教育科学研究院）//中学数学教学参考（陕西）.—2006，no. 3.—P.26数列高考题回顾与展望/张仁达等（本刊试题研究组）//中学数学教学参考（陕西）.—2006，no. 3.—P.35四面题/武履新（西安铁一中）//中学数学教学参考（陕西）.—2006，no. 3.—P.48一个数学多媒体辅助教学的实验与反思/孙建洪（浙江师范大学数理学院硕士）//中学数学教学参考（陕西）.—2006，no. 3.—P.55运动与数学教学/黄安成（江苏省睢宁高级中学）//中学数学（武汉）.—2006，no.3.—P.1双曲线为什么有渐进线/李建军（湖北省长阳县一中）//中学数学（武汉）.—2006，no. 3.—P.6注重题后反思培养学生思维品质/章建春，杨波（浙江省富阳中学）//中学数学（武汉）.—2006，no. 3.—P.10解析几何中减少运算量的常用方法/王芝平，张月超（北京宏志中学）//中学数学（武汉）.—2006，no. 3.—P.15一类对函数恒成立问题的解法/杨志明（湖北省黄石二中）//中学数学（武汉）.—2006，no. 3.—P.24高考否定性命题的解题策略/杨炼（浙江省嵊州市第二中学）//中学数学（武汉）.—2006，no. 3.—P.30巧用曲线系推广高考题/向显元，林文国（湖北省当阳市第二高中）//中学数学（武汉）.—2006，no. 3.—P.44数学变式教学中的闪光点/余继光（浙江省绍兴柯桥中学）//上海中学数学（上海）.—2006，no. 3.—P.1直线中的对称问题的教学设计/汪晓晶（上海市松江一中）//上海中学数学（上海）.—2006，no. 3.—P.2特殊化方法在解高考题中的三种功能/章显联（浙江省绍兴鲁迅中学）//上海中学数学（上海）.—2006，no. 3.—P.6关于设计数学教学情景的思考/穆晓东（上海市长宁区教育学院）//上海中学数学（上海）.—2006，no. 3.—P.14数学教学中要处理好三种关系/干亚清（上海市金山区教师进修学院）//上海中学数学（上海）.—2006，no. 3.—P.18不要轻易相信视觉和直觉/徐洁绮（上海师范大学课程与教学论研究生）//上海中学数学（上海）.—2006，no. 3.—P.27注重基础关注学习方式的转变——2006年上海市春季高考数学试卷回眸/杨家政（上海市闵行区教师进修学院）//上海中学数学（上海）.—2006，no. 3.—P.35幂不等式及其应用/王风春（上海市宝山区教师进修学院）//上海中学数学（上海）.—2006，no. 3.—P.48解读上海数学新课程标准的德育/文卫星（上海市七宝中学）//数学通报（北京）.—2006，no. 4.—P.4新课程实施中数学推理能力培养的几点思考/宁连华（南京师范大学数学系）//数学通报（北京）.—2006，no. 4.—P.7处理好数学教学中的几个关系/王永建（南京教学研究室）//数学通报（北京）.—2006，no. 4.—P.16一类求取值范围问题的解法/姜坤崇（山东省邹平县教育局教研室）//数学通报（北京）.—2006，no. 4.—P.27使用高中数学新教材的几点感想/田彦武（宁夏银川市第九中学）//数学通报（北京）.—2006，no. 4.—P.30一道课本例题的研究性学习/刘品德（广东省江门市江海中学）//数学通报（北京）.—2006，no. 4.—P.35谈谈数学类比/唐逢春（山东省博兴第一中学）//数学通报（北京）.—2006，no.4.—P.44一道高考题的推广与圆锥曲线切线的几何作法/王芝平（北京宏志中学）//数学通报数学（北京）.—2006，no. 4.—P.51改进一个含参的多变量分式不等式/黄道军（湖北省宣恩一中）//数学通报（北京）.—2006，no. 4.—P.58椭圆参数方程的应用/赵建勋（河北省正定中学）//中学生数学（北京）.—2006，no.4.—P.4用好奇函数的性质 f (0)=0/刘祖希（江苏省苏州市第一中学）//中学生数学（北京）.—2006，no. 4.—P.6逆用两个不等式解集的等式/甘大旺（浙江省宁波市北仓区明港中学）//中学生数学（北京）.—2006，no. 4.—P.9巧用方程根解题两例/沈杰（首都师范大学附中）//中学生数学（北京）.—2006，no. 4.—P.15例谈估算的若干策略/母建平（江苏省苏州市木渎第二中学）//中学生数学（北京）.—2006，no. 4.—P.22在逐层递进学生思维自然发展/周根龙（江苏省如皋高等师范学校）//中学数学教学参考（陕西）.—2006，no. 4.—P.10“优双曲线”性质的探索/王玉新（江苏省徐州第一中学）//中学数学教学参考（陕西）.—2006，no. 4.—P.20高三数学回扣课本复习指南（续）/陈永林等（山东省诸城市第一中学）//中学数学教学参考（陕西）.—2006，no. 4.—P.29立体几何高考题回顾与展望/崔菊敏（本刊试题研究组）//中学数学教学参考（陕西）.—2006，no. 4.—P.34概率与统计高考题回顾与展望/赵晓玲（陕西师范大学附中）//中学数学教学参考（陕西）.—2006，no. 4.—P.41数学教师科研选题的原则与策略/李袆（山西师范大学数学与计算机科学学院）//中学数学教学参考（陕西）.—2006，no. 4.—P.50导致排列组合问题解题困难的因素/沈金兴（华东师范大学04级数学教育硕士）//中学数学教学参考（陕西）.—2006，no. 4.—P.54发挥例题教学课的潜能/李广修（江苏省无锡市第一中学）//数学教学（上海）.—2006，no. 4.—P.5《数学归纳法及应用举例》第一课的教学设计/张晓斌，张斌//数学教学（上海）.—2006，no. 4.—P.7浅谈物理素材在数学教学中的作用/任念兵（上海市育才中学）//数学教学（上海）.—2006，no. 4.—P.10对2005年一道上海春季高考试题的再认识/岳荫巍（北京市同仁中学）//数学教学（上海）.—2006，no. 4.—P.40对一道高考创新题的探究/佟成军（江苏省海州高级中学）//数学教学（上海）.—2006，no. 4.—P.46从两道轨迹谈共线点的向量解法/柏仁俊（湖北省武汉中学）//中学数学（湖北）.—2006，no. 4.—P.20高考导致问题透视/李昭平（安徽省太湖中学）//中学数学（湖北）.—2006，no. 4.—P.24构造辅助圆解题举隅/夏智红（武汉市第一中学）//中学数学（湖北）.—2006，no.4.—P.29整数剩余类在高中数学中的应用举隅/王峰（安徽省临泉一中）//中学数学（湖北）.—2006，no. 4.—P.47用平面发向量解立体几何体/张家瑞（江苏省苏州市迅达培训学校）//中等数学（天津）.—2006，no. 4.—P.6用换元法证明不等式/雷动良（湖南省动江师范学校）//中等数学（天津）.—2006，no. 4.—P.16三道竞赛题的统一证明/李康海（浙江省永康一中）//中等数学（天津）.—2006，no.4.—P.232005年中国西部数学奥林匹克/本刊//中等数学（天津）.—2006，no. 4.—P.282005年全国高中数学联赛四川省初赛/本刊//中等数学（天津）.—2006，no. 4.—P.312005年河南省数学竞赛（高二）/本刊//中等数学（天津）.—2006，no. 4.—P.34从认知规律谈高中数学的概念教学/慕泽刚（重庆市渝西中学）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.4问题探究创新——浅谈“问题”的探究性学习/胡坚（浙江省浦江中学）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.11浅谈例题的教学价值及选择/仁武（江苏省阴江室青阳中学）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.16新课程理念下学生创新思维的培养/金学顺（浙江温岭大溪中学）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.19美国高中数学课标中探究式学习两例/吴有昌（华南师范大学数学科学学院）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.27例析解析几何中范围问题的求解策略/朱智昌（江苏省泰洲市刁铺中学）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.31导数问题的常用类型与解法/曾庆宝（广西富川民族中学）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.34透过三角形的“心”展望高考走势/朱书华（江苏省前黄高级中学）//数学教学通讯：上半月（重庆）.—2006，no. 5.—P.44函数的周期性与图象对称性的相互关系/江国新（湖北省大芫冶市第一中学）//中学生数学（北京）.—2006，no. 5.—P.3一道数据处理试题与基尼系数/玲珑居士//中学生数学（北京）.—2006，no. 5.—P.16赏析几道以图表为背景的题/夏万保（江苏省栗阳市南渡高级中学）//中学生数学（北京）.—2006，no. 5.—P.19例析结论开放的探索性问题/李瑛华（山东省宁阳四中）//中学生数学（北京）.—2006，no. 5.—P.21第九届北京高中数学知识应用竞赛决赛试题及参考解答/本刊//中学生数学（北京）.—2006，no. 5.—P.24解题后的反思/杨万兵（江苏省盐城市第一中学）//中学生数学（北京）.—2006，no.5.—P.32怎样计算椭圆的面积/何苗（北京市昌平一中）//中学生数学（北京）.—2006，no.5.—P.34教学创新课例：抛物线的概念和标准方程/黄安成（江苏省睢宁高级中学）//中学数学教学参考（陕西）.—2006，no. 5.—P.16一类等比数列的讨论/陈云烽（中山大学数计学院）//中学数学教学参考（陕西）.—2006，no. 5.—P.25双曲线一个几何性质的应用性研究/吕中伟（江苏省常熟市常熟中学）//中学数学教学参考（陕西）.—2006，no. 5.—P.322006年高考数学模拟试题（一）/刘康宁（陕西省西安市铁一中），费瑛（西安交通大学二附中）//中学数学教学参考（陕西）.—2006，no. 5.—P.342006年高考数学模拟试题（二）/王华民（江苏省无锡市滨湖区教研中心）//中学数学教学参考（陕西）.—2006，no. 5.—P.38“排列、组合和二项式定理”测评题/金良（山西省长治学院附属太行中学），王毓量（甘肃省庆城县长庆一中）//中学数学教学参考（陕西）.—2006，no. 5.—P.43二项式定理及其应用/丘健（陕西省咸阳市育才中学）//中学数学教学参考（陕西）.—2006，no. 5.—P.45立体几何中画图、识图、用图的调查与反思/陆建（江苏省滨海中学）//中学数学教学参考（陕西）.—2006，no. 5.—P.522005年全国高中数学联赛加试第二题的探讨/王扬（广东省深圳市育才中学）//中等数学（天津）.—2006，no. 5.—P.102005年全国高中数学联赛福建赛区预赛/本刊//中等数学（天津）.—2006，no. 5.—P.292005年河北省高中数学竞赛/本刊//中等数学（天津）.—2006，no. 5.—P.33数学奥林匹克高中训练题（88）/本刊//中等数学（天津）.—2006，no. 5.—P.40澄清概率中的几个问题/孔凡海（南京市第一中学）//中学数学（湖北）.—2006，no.5.—P.7注重解题反思发展学生能力/汪纯中（华东师范大学课程与教学系）//中学数学（湖北）.—2006，no. 5.—P.9几何画板技术与教学实际的整合——“抛物线的性质”第二课时教学案例/饶庆军（浙江师范大学研究生学院）//中学数学（湖北）.—2006，no. 5.—P.13用平面向量巧解一题/佟成军（江苏省海州高级中学）//中学数学（湖北）.—2006，no. 5.—P.44确定圆锥曲线焦点的一种方法/张小凯（浙江省象山中学）//中学数学（湖北）.—2006，no. 5.—P.45从一道经典的外国数学竞赛题到两个优美的三角不等式/邓军民（广东省广东市育才中学）//中学数学（湖北）.—2006，no. 5.—P.46数学解题中优化运算的途径/刘海东（河北省三河市第一中学）//中学数学（湖北）.—2006，no. 5.—P.7数学考试的心理障碍分析及对策/刘绍周（江苏省武进高级中学）//上海中学数学（上海）.—2006，no. 5.—P.13从一道高考试题看应用题复习教学/韩保席（江苏省吴江市高级中学）//上海中学数学（上海）.—2006，no. 5.—P.16高中数学常见学习心理障碍的分析/汪晓晶（上海市松江一中）//上海中学数学（上海）.—2006，no. 5.—P.20高中数学研究性学习的实践和认识/金鑫华（上海市金山区教师进修学院）//上海中学数学（上海）.—2006，no. 5.—P.22三垂线定理及其逆定理的数学实践与思考/孙秉正（安徽师范大学02级教育硕士）//上海中学数学（上海）.—2006，no. 5.—P.24高中学生自主学习下知识整合的途径初探/徐根弟（上海市金山中学）//上海中学数学（上海）.—2006，no. 5.—P.28以思想方法为纽带，促进学生提高学力/张菊英（上海师大二附中）//上海中学数学（上海）.—2006，no. 5.—P.322006年高考模拟试卷（理科）/本刊//上海中学数学（上海）.—2006，no. 5.—P.37解谈2005年高考导数试题/王惠丰（浙江省牌头中学）//上海中学数学（上海）.—2006，no. 5.—P.40从一堂高三最值问题复习想到的/张劲松（人民教育出版社）//数学教学（上海）.—2006，no. 5.—P.9由0．001的差异引发的思考/张闽（上海市第三女子中学）//数学教学（上海）.—2006，no. 5.—P.18例说平面几何命题在空间的拓展/金婉芬（浙江省台洲市椒江第五中学）//数学教学（上海）.—2006，no. 5.—P.24愿函数与反函数图象交点问题的探究/钱文颖，邵春和（上海市卢湾高级中学）//数学教学（上海）.—2006，no. 5.—P.26几何三大难题的不能与“解决”/何莎莎（上海市育才中学：华东师大数学系03级教育硕士）//数学教学（上海）.—2006，no. 5.—P.38谈高中数学对形式化的处理——数学课程一个理念的落实/王林全（华南师范大学数学科学学院）//数学通报（北京）.—2006，no. 5.—P.17一个分式不等式的再推广/宋庆（南昌大学附属中学）//数学通报（北京）.—2006，no. 5.—P.29在体验中“做”数学——记一次椭圆概念新授课/潘建国（江苏如皋市丁堰市中学）//数学通报（北京）.—2006，no. 5.—P.35立体几何中交汇型试题/俞新龙（浙江省绍兴县越崎中学）//数学通报（北京）.—2006，no. 5.—P.38与时具进大胆创新——“互叠法”证明不等式的发现与解题联想/孙建斌（福建泉洲市永春县科委）//数学通报（北京）.—2006，no. 5.—P.44例说“错题”及其教育功能/方均斌（浙江温州师院）//数学通报（北京）.—2006，no. 5.—P.54也谈一类竞赛不等式的创新证法/刘南薪（江西省都昌县第一中学）//数学通报（北京）.—2006，no. 5.—P.56如何评课：数学课程资源层面的透视/喻平（南京师范大学数学与计算机科学学院）//中学数学教学参考（陕西）.—2006，no. 6.—P.5数学课堂教学设计的艺术/陈柏良（浙江省绍兴市高级中学）//中学数学教学参考（陕西）.—2006，no. 6.—P.8在反思中提升学生的数学学习能力/朱桌君（江苏省天一中学）//中学数学教学参考（陕西）.—2006，no. 6.—P.18在双基模块的基础上构建双基平台——高三复习课“抽象函数”教学实录/文卫星（上海市七宝中学）//中学数学教学参考（陕西）.—2006，no. 6.—P.21一道全国高中联赛向量题推广的新视角/岳建良（陕西师范大学数学与信息科学学院2003级教育硕士//中学数学教学参考（陕西）.—2006，no. 6.—P.30本刊第三届中学生数学智能通讯赛试题/本刊//中学数学教学参考（陕西）.—2006，no. 6.—P.38构造思想渗透教学的一次实验研究/黄加卫（浙江省湖州市第一中学）//中学数学教学参考（陕西）.—2006，no. 6.—P.49帕普斯的几何命题与三角公式/汪晓勤（上海华东师范大学数学系）//中学数学教学参考（陕西）.—2006，no. 6.—P.54数学教育现代化的重新定义/顾冷沅（上海市教育科学研究院）//中学数学教学参考（陕西）.—2006，no. 6.—P.62拨开云雾见明月——求无棱二面角的一堂习题课/杨陈勇（浙江余姚市第八中学）//中学数学（湖北）.—2006，no. 6.—P.8一个立几模块的教学/王晓明（浙江省宁波中学）//中学数学（湖北）.—2006，no.6.—P.15谈数学问题的转化/胡清峰（湖北大学数学与计算机科学学院）//中学数学（湖北）.—2006，no. 6.—P.28例说用坐标法解立体几何问题/昌明（江苏省扬州大学附属中学）//中学数学（湖北）.—2006，no. 6.—P.35一些分式不等式及其斜率解释/沈华（湖北大学数学系）//中学数学（湖北）.—2006，no. 6.—P.44二项式系数的性质的数学实践与反思/林静（上海师大附中）//上海中学数学（上海）.—2006，no. 6.—P.4一堂复数的三角形式的研究课/翁灵玲（上海同济大学第一附属中学）//上海中学数学（上海）.—2006，no. 6.—P.10在课堂教学中发展学生数学思维/余缨缨（上海市中国中学）//上海中学数学（上海）.—2006，no. 6.—P.22。

2006年高考理科数学试卷及答案(全国卷2)

2006 高考理科数学试题全国 II 卷
理科试题
本试卷分第Ｉ卷（选择题）和第ＩＩ卷（非选择题）两部分。第Ｉ卷１至２页。第
ＩＩ卷３至４页。考试结束后，将本试卷和答题卡一并交回。
第Ｉ卷
注意事项：
１．答题前，考生在答题卡上务必用黑色签字笔将自己的姓名、准考号填写清楚，
并贴好条形码。请认真核准条形码上的准考证号、姓名和科目。
圆的另外一个焦点在 BC 边上，则 ΔABห้องสมุดไป่ตู้ 的周长是
（A） 2 3
（B）6
（C） 4 3
（D）12
（6）函数 y = ln x +1(x > 0) 的反函数为
（A） y = ex+1(x ∈ R)
（B） y = ex−1(x ∈ R)
（C） y = ex+1(x > 1)
（D） y = ex−1(x > 1)
线；（II）设 AA1 = AC = 2 AB, 求二面角 A1 − AD − C1 的大小。
（20）（本小题１２分）设函数 f (x) = (x +1) ln(x +1).若对所有的 x ≥ 0,
E
都有 f (x) ≥ ax 成立，求实数 a 的取值范围。
C
（21）（本小题满分为１４分）已知抛物线 x2 = 4 y 的焦点为 F，A、B
（B） 4π
（C） π 4
（D） π 2
（3）
(1
3 − i)2
=
（A） 3 i 2
（B） − 3 i 2
（C） i
（D） −i
（4）过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积
的比为
（A） 3 16

2006年黑龙江高考第二次摸拟考试数学理

2006年黑龙江省高考第二次摸拟考试理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟。

第Ⅰ卷1至3页，第Ⅱ卷4至6页。

考试结束后，将本试卷和答题卡一并交回。

考试公式：如果事件A 、B 互斥，那么，P （A ＋B ）＝P （A ）＋P （B ）如果事件A 、B 相互独立，那么，P （A ·B ）＝P （A ）·P （B ）如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率Pn (k )=C k n P k (1-P )n-k球的表面积公式：S ＝4πR 2，其中R 表示球的半径球的体积公式：V =34πR 3，其中R 表示球的半径第Ⅰ卷注意事项：1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上.3.本卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

一、选择题1.复数()212i iz -+=所对应的点位于复平面的 2．在边长为1的正三角形ABC 中，·的值为 A ．21 B ．－21 C ．21或－21D ．不确定3．若x ∈(－2π,2π),则方程sin x =tan x 的实根的个数为A ．1B ．2C ．3D ．44．已知函数f (x )=lg xx-+11,若f (a )＝b ，则f (-a )＝ A ．bB ．-bC ．b1 D ．-b1 5．(x 2－x2)3的展开式中的常数项为 A ．6 B ．－6 C ．12 D ．－126．已知集合A ＝{1，－2，3}，B ＝{－4，5，6，－7}。

分别从两个集合中各取一个元素作为点的坐标，则平面直角坐标系中，位于第一、第二象限内不同点的个数为 A ．18 B ．16 C ．10 D ．147．在等差数列中{a n }中，a 1+a 2+a 3=1，a 28+a 29+a 30=165，则此数列前30项的和为 A.．810 B ．830 C ．850 D ．8708．如果不等式f (x )=Asin(ωx+φ)(A >0,ω>0),f (1)=0则A ．f (x -1)一定是奇函数B ．f (x -1)一定是偶函数D ．f (x +1)一定是奇函数D ．f (x +1)一定是偶函数 9．如果不等式｜x －a ｜<1成立的充分不必要条件是21<x <23，则实数a 的取值范围是 A ．21<a <23B ．21≤a ≤23C ．a <21或a >23D ．a ≤21或a ≥2310．已知向量a 、b 均为非零向量，现把向量a ，b ，3a －2b 的起点移至同一点，则这三个向量终点的位置关系一定是 A ．恰好有两个点重合 B ．恰好三个点重合 C ．三点共线 D ．以上都不对11．在2006年前，我国实行的《中华人民共和国个人所和税法》规定起征点为800元，即公民全民工资、薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纲税所得额。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ＣＰ且ｑ．
ＤＰ或ｑ．
４已知点Ａ（，）Ｂ（，）将线段ＯＡＢ各等．１Ｏ，１，Ａ、分，Ｏ设Ａ上从左至右的第ｋ个分点为Ａ，ＡＢ上从下至上的第ｋ个分点为Ｂ１ ≤ ）过点Ａ（ ≤ ，且垂直于－的直线为ｚ，交ｚＰ，丁轴ＯＢ于则点
Ｂ［，ｏ６＋ｏ）
ｎ以上都不对
Ｃ＝ｉ２詈）Ｄ —｜ｘ７．ｓ＋ｙｎ．ｓ＿ｙｎ＿ｒ。）
２设集合Ｍ一｛＿一２＜０ＥＲ）Ｎ一｛ｌ．｛ｘ￣，丁，１＜ｌ
２工， ∈Ｒ｝则（，
八ＭＵＮ＝Ｍ
Ａ．３Ｒ４Ｃ５
）．
Ｄ．６
在每小题所给的四个选项中．只有一项是符合题
目要求的）
９若圆－＋一（＞０至少能盖住函数ｆＣ）．丁ｒ）ｒ一
ｖ
１下列函数中，．图象关于直线－＝｛对称的是丁
（点，￣ｓ筹一大点和个值则ｒｎ
）．
的取值范围是（
Ａｓ２号）１ —ｉ２詈）．ｉｎ一３ｓ．ｎ一
Ａ［／，ｏ．ｖｏ＋ｏ）３
Ｃ［７＋ｏ）．２【ｏ，
八ａ或ｎ％０＞２
Ｃ＜口２Ｏ＜
）．
Ｂａ．＝０或 “ ＝２
ｎ ≤ “ ２Ｏ ≤
，０、２
．
—
１．４若双曲线一
１的一条准线恰为圆工＋。
．
— —
８若数列｛｝．ｎ的通项公式为一５昔）一（
４ ÷ ）（ＥＮ）｛｝最大项为第项，（ｎ，的口最小
１设Ｆ工一厂）／一）Ｅ，一【号Ｉ０（）＿＋（，ＲＩ７．（ｘ，是一
函数Ｆ（的单调递增区问，Ｆ（的图象按向）将）量口７０平移得到一个新的函数Ｇ（的图一（【），）
象，Ｇ（的单调递减区间必定是（则））．
动点Ｐａ６在不等式组‘ ｘ ≤ｏ（，）｛－ｋ，所表示
【Ｏ ≥
）．
Ｒ ≤ 一１６２或 ≥
Ｄ一１６２． ≤ ≤
的平面区域内部及边界上运动．则
围是（）．
的取值范
６由数字１２３ … ，．，，，９组成的三位数中，各位数字按
）．
珏ＭｎＮ＝Ｍ
Ｃ（ｃＭ）．ＲｎＮ＝ＯＤ（ｃ．Ｍ）ｎＮ＝Ｒ３给出两个命题：：Ｘｌ的充要条件是为正实．Ｐｌ — 数；：ｑ存在反函数的函数一定是单调函数．下列则复合命题中真命题是（
ＡＰ且ｑ．
严格递增（１６）如“ ５ ” 或严格递减（４１）如“ ２ ” 顺序排列的个数是（
Ａ．２１０
Ａ．２＋。）［，。Ｃ［，］．一２２题中横线上）
Ｉ（。，］３．。一２ｎ（。一２ｌ［，。一。，］＿２＋。）Ｊ
）．
Ａ一］Ｂ号．．，［［Ｃ］．，Ｄ警［警．］［
１．１过点Ｍ（２ｏ的直线与椭圆＋＝ｌ交于－，）。
Ｐ，。点，段ＰＰ的中点为Ｐ．直线ｍ的Ｐ两线．ｚ设
ＢＰ或ｑ
应试操练
析式为一、值域为｛，｝同族函数” 有１４的“ 共
维普资讯
应试操练
②
２高考数学模拟试题（）Ｏ６年Ｏ二
命题人：蕲春一中宋春雨审稿人：浠水一中陈火森
一
、
选择题（本大题共１２小题，每小题５分，６，共Ｏ分
项为第Ｙ项，＿则丁＋等于（
， ‘ ）、Ｉ
＋２＝０的一条切线，ｋ等于ｘ则
１．５若一系列函数的解析式相同、值域相同，其定义但域不同，则称这些函数为“ 同族函数” 那么函数解，
羹奇一旱¨ ．奇＿ ⑥
维普资讯
）．
Ｃ０２４Ｄ．１２６
１６３８．１
二、空题（填本大题共４小题，１共６分．把答案填写在１．在（＋口）３若１－的展开式中的系数为一８，丁Ｏ则
ａ
—
７原点Ｏ和点Ｐ（，）．１１分别在直线－丁＋ —ｎ＝０的两侧，ａ的取值范围是（则
Ａ圆上．
＆椭圆上
４ —０
Ｃ双曲线上
Ｄ．抛物线七
交Ｍ、Ｎ两点．Ｍ、关于直线Ｘ— —Ｏ对称，且Ｎ
５已一÷一＋＋（）＋３．知妇。ｘ是Ｒ上的单凋＋２
增函数，ｂ的取值范围是（则
６一１６２＜或＞
Ｃ～１＜２＜６
在同一（）．
斜率为ｋ（ｔ）直线Ｏ１ ≠Ｏ，Ｐ的斜率为ｋ，ｋ是则２ｚ
的值为（）．
Ａ２ＲＣＤ一１．２．喜．
１．直线２若工ｌ与圆。＋＋＋丁＿＋
ｆ — ＋２Ｏ是 ≥ ，

2006年高考数学模拟试题(二)

2006年高考数学模拟试题(一)

2006年高考理科数学摸拟试题解析样本1

(新课标)高考数学模拟系列(二)试题 理 新人教A版

2006年高考数学模拟题与参考答案

2006年广东高考数学模拟试题

2006年贵州省 高考理科数学试题(真题与答案解析)

2006年高考理科数学试题及答案(全国卷2)

2006年高考数学模拟试题(二)

2006年高考数学模拟试题(二)

2006年高考数学模拟题及参考答案

06年数学高考模拟试题(2).doc

2006年高中数学篇目索引 上海市甘泉外国语中学资料室提供

2006年高考理科数学试卷及答案(全国卷2)

最新2006年高考试题与答案-全国卷2数学理

2006年黑龙江高考第二次摸拟考试数学理

(新课标)高考数学模拟系列(二)试题理新人教A版

2006年贵州省高考理科数学试题(真题与答案解析)

2006年高中数学篇目索引上海市甘泉外国语中学资料室提供