反比例函数与几何综合(同步)
中考反比例函数与几何综合
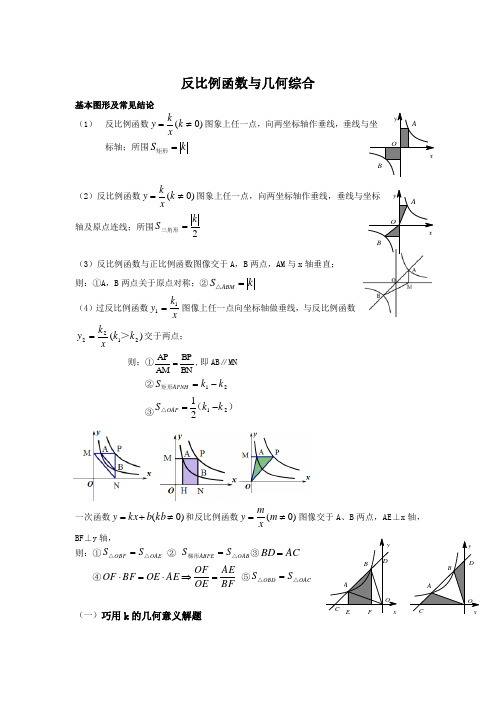
Oy xBAABxy O反比例函数与几何综合基本图形及常见结论 (1) 反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴;所围k S =矩形(2)反比例函数)0(≠=k xky 图象上任一点,向两坐标轴作垂线,垂线与坐标轴及原点连线;所围2k S =三角形(3)反比例函数与正比例函数图像交于A ,B 两点,AM 与x 轴垂直; 则:①A ,B 两点关于原点对称;②k S ABM =△(4)过反比例函数xk y 11=图像上任一点向坐标轴做垂线,与反比例函数)(2122k k xk y >=交于两点; 则:①BNBP AM AP =,即AB ∥MN②21k k S APNH -=矩形③)(△2121k k S OAP -=一次函数)0(≠+=kb b kx y 和反比例函数)0(≠=m xmy 图像交于A 、B 两点,AE ⊥x 轴,BF ⊥y 轴,则:①OAE OBF S S △△= ② OAB ABFE S S △梯形=③AC BD =④BFAEOE OF AE OE BF OF =⇒⋅=⋅ ⑤OACOBD S S △△=(一)巧用k 的几何意义解题y x ABO CDy xDC F EO B A例1.函数y=和y=在第一象限内的图象如图,点P 是y=的图象上一动点,PC ⊥x 轴于点C ,交y=的图象于点B .给出如下结论:①△ODB 与△OCA 的面积相等;②PA 与PB 始终相等;③四边形PAOB 的面积大小不会发生变化;④CA=AP .其中所有正确结论的序号是________。
迁移练习1(1).如图,双曲线)0x (k>=xy 经过Rt △OAB 斜边OB 的中点D ,与AB 交于点C .若△OBC 面积为3,则k =_______迁移练习1(2)..双曲线)0x (k>=xy 经过矩形OABC 边AB 的中点F ,交BC 于点E ; 若梯形OEBA 的面积为9,则k=________。
九年级数学上册《反比例函数与几何综合运用》教案、教学设计

例题:在直角坐标系中,已知点A(2, 3)和点B(-2, -3),求反比例函数y = k/x的图像上距离点A和点B相等的点C的坐标。
4.探究题:引导学生探究反比例函数与一次函数、二次函数的相互转化,提高学生对函数知识的综合运用能力。
(1)导入:通过实际情境引入反比例函数,让学生感受反比例函数在生活中的应用;
(2)新课:讲解反比例函数的定义、性质、图像,并结合几何图形进行展示;
(3)巩固:设计典型习题,让学生运用反比例函数知识解决问题,巩固所学;
(4)拓展:引导学生将反比例函数与一次函数、二次函数相互转化,解决复杂问题;
(5)实践:设计实际问题,让学生将反比例函数与几何知识综合运用,提高解决问题的能力;
2.提高题:设计一些反比例函数与一次函数、二次函数相结合的问题,提高学生解决问题的能力;
3.实践题:结合实际问题,让学生运用反比例函数知识解决几何综合问题。
在学生完成练习的过程中,我会及时给予反馈和指导,帮助学生找到问题所在,提高解题能力。
(五)总结归纳
在课堂尾声,我会对本节课的内容进行总结归纳,强调以下几点:
二、学情分析
九年级的学生已经具备了一定的数学基础,掌握了函数的基本概念和性质,能够运用一次函数和二次函数解决一些实际问题。在此基础上,他们对反比例函数的学习将更加深入和系统。然而,学生对反比例函数的理解和应用能力还存在一定的局限性,特别是将反比例函数与几何知识综合运用时,可能会遇到一定的困难。因此,在教学过程中,教师需要关注以下几点:
1.反比例函数的定义、性质和图像;
2.反比例函数在实际问题中的应用;
3.反比例函数与一次函数、二次函数的相互转化;
专题九-反比例函数与几何的综合应用

在物理学中,一些物理量之间可能存在反比例关系,如电阻与电流、压力与面积等。通过运用反 比例函数的性质,可以更好地理解和解决这些物理问题。
反比例函数在经济学中的应用
在经济学中,一些经济指标之间可能存在反比例关系,如价格与需求量、成本与产量等。通过运 用反比例函数的性质,可以对这些经济指标进行更准确的预测和分析。
如长度、面积等。
利用反比例函数性质建立关系
02
根据反比例函数的性质,结合几何图形的特点,建立所求最值
与相关量之间的关系。
求解最值
03
通过求解反比例函数的最值,得到所求几何量的最值。
判定存在性问题
根据题意列出方程或不等式
01
根据题目条件,列出与几何图形相关的方程或不等式
。
利用反比例函数性质分析解的情况
反比例关系在圆中的应用
在圆中,当一个圆的半径增加时,其 面积会按平方比例增加,但其周长只 会按线性比例增加。这种关系虽然不 是严格的反比例关系,但也可以用于 解决一些与圆相关的问题。
解题技巧与实例分析
通过利用圆的性质和上述关系, 可以求解一些与圆相关的问题。 例如,已知一个圆的半径和另一 个圆的面积或周长,可以求解未 知圆的半径或面积等。
仔细阅读题目要求,明确题意 ,避免答非所问。
合理安排答题顺序
先做易做的题目,确保会做的 题目不丢分,再攻克难题。
控制答题时间
每道题目分配合理的时间,避 免时间不够用或浪费过多时间
。
检查答案
做完题目后要认真检查答案, 确保没有遗漏或错误。
THANKS FOR WATCHING
感谢您的观看
解题技巧与实例分析
对于其他几何图形中的反比例关系问题,可以通过设定未知数、利用几何图形的性质和反比例关系来求解。 需要注意的是,在解题过程中要仔细分析题目条件和数据特点,选择合适的解题方法和思路。
(完整版)反比例函数与几何的综合应用及答案

专训1 反比例函数与几何的综合应用名师点金:解反比例函数与几何图形的综合题,一般先设出几何图形中的未知数,然后结合函数的图象用含未知数的式子表示出几何图形与图象的交点坐标,再由函数解析式及几何图形的性质写出含未知数及待求字母系数的方程(组),解方程(组)即可得所求几何图形中的未知量或函数解析式中待定字母的值.反比例函数与三角形的综合1.如图,一次函数y =kx +b 与反比例函数y =x 6(x>0)的图象交于A(m ,6),B(3,n)两点.(1)求一次函数的解析式;(2)根据图象直接写出使kx +b<x 6成立的x 的取值范围; (3)求△AOB 的面积.(第1题)2.如图,点A ,B 分别在x 轴、y 轴上,点D 在第一象限内,DC ⊥x 轴于点C ,AO=CD =2,AB =DA =,反比例函数y =x k(k >0)的图象过CD 的中点E.(1)求证:△AOB ≌△DCA ; (2)求k 的值;(3)△BFG 和△DCA 关于某点成中心对称,其中点F 在y 轴上,试判断点G 是否在反比例函数的图象上,并说明理由.(第2题)反比例函数与四边形的综合 反比例函数与平行四边形的综合3.如图,过反比例函数y =x 6(x >0)的图象上一点A 作x 轴的平行线,交双曲线y =-x 3(x <0)于点B ,过B 作BC ∥OA 交双曲线y =-x 3(x <0)于点D ,交x 轴于点C ,连接AD 交y 轴于点E ,若OC =3,求OE 的长.(第3题)反比例函数与矩形的综合4.如图,矩形OABC 的顶点A ,C 的坐标分别是(4,0)和(0,2),反比例函数y =x k(x>0)的图象过对角线的交点P 并且与AB ,(第4题)BC 分别交于D ,E 两点,连接OD ,OE ,DE ,则△ODE 的面积为________. 5.如图,在平面直角坐标系中,矩形OABC 的对角线OB ,AC 相交于点D ,且BE ∥AC ,AE ∥OB.(1)求证:四边形AEBD 是菱形;(2)如果OA =3,OC =2,求出经过点E 的双曲线对应的函数解析式.(第5题)反比例函数与菱形的综合6.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与x 轴平行,A ,B 两点的纵坐标分别为3,1,反比例函数y =x 3的图象(第6题)经过A ,B 两点,则菱形ABCD 的面积为( ) A .2 B .4 C .2 D .47.如图,在平面直角坐标系中,菱形ABCD 的顶点C 与原点O 重合,点B 在y 轴的正半轴上,点A 在反比例函数y =x k(k>0,x>0)的图象上,点D 的坐标为(4,3).(1)求k 的值;(2)若将菱形ABCD 沿x 轴正方向平移,当菱形的顶点D 落在反比例函数y =x k(k>0,x>0)的图象上时,求菱形ABCD 沿x 轴正方向平移的距离.(第7题)反比例函数与正方形的综合8.如图,在平面直角坐标系中,点O 为坐标原点,正方形OABC 的边OA ,OC分别在x 轴,y 轴上,点B 的坐标为(2,2),反比例函数y =x k(x >0,k ≠0)的图象经过线段BC 的中点D(1)求k 的值;(2)若点P(x ,y)在该反比例函数的图象上运动(不与点D 重合),过点P 作PR ⊥y 轴于点R ,作PQ ⊥BC 所在直线于点Q ,记四边形CQPR 的面积为S ,求S 关于x 的函数解析式并写出x 的取值范围.(第8题)反比例函数与圆的综合(第9题)9.如图,双曲线y =x k(k>0)与⊙O 在第一象限内交于P ,Q 两点,分别过P ,Q 两点向x 轴和y 轴作垂线,已知点P 的坐标为(1,3),则图中阴影部分的面积为________.10.如图,反比例函数y =x k(k <0)的图象与⊙O 相交.某同学在⊙O 内做随机扎针试验,求针头落在阴影区域内的概率.(第10题)专训2 全章热门考点整合应用名师点金:反比例函数及其图象、性质是历年来中考的热点,既有与本学科知识的综合,也有与其他学科知识的综合,题型既有选择、填空,也有解答类型.其热门考点可概括为:1个概念,2个方法,2个应用及1个技巧.1个概念:反比例函数的概念1.若y =(m -1)x |m|-2是反比例函数,则m 的取值为( )A .1B .-1C .±1D .任意实数 2.某学校到县城的路程为5 km ,一同学骑车从学校到县城的平均速度v(km /h )与所用时间t(h )之间的函数解析式是( )A .v =5tB .v =t +5C .v =t 5D .v =5t3.判断下面哪些式子表示y 是x 的反比例函数: ①xy =-31;②y =5-x ;③y =5x -2;④y =x 2a(a 为常数且a ≠0). 其中________是反比例函数.(填序号) 2个方法:画反比例函数图象的方法4.已知y 与x 的部分取值如下表: x … -6 -5 -4 -3 -2 -11 2 3 4 5 6…y… 1 1.21.52 3 6 -6-3-2-1.5 -1.2-1…析式;(2)画出这个函数的图象.求反比例函数解析式的方法5.已知反比例函数y =x k的图象与一次函数y =x +b 的图象在第一象限内相交于点A(1,-k +4).试确定这两个函数的解析式.6.如图,已知A(-4,n),B(2,-4)是一次函数y =kx +b 的图象和反比例函数y =x m的图象的两个交点.求:(1)反比例函数和一次函数的解析式;(2)直线AB 与x 轴的交点C 的坐标及△AOB 的面积;(3)方程kx +b -x m=0的解(请直接写出答案);(4)不等式kx +b -x m<0的解集(请直接写出答案).(第6题)2个应用反比例函数图象和性质的应用7.画出反比例函数y =x 6的图象,并根据图象回答问题: (1)根据图象指出当y =-2时x 的值;(2)根据图象指出当-2<x<1且x ≠0时y 的取值范围; (3)根据图象指出当-3<y<2且y ≠0时x 的取值范围.反比例函数的实际应用8.某厂仓库储存了部分原料,按原计划每小时消耗2吨,可用60小时.由于技术革新,实际生产能力有所提高,即每小时消耗的原料量大于计划消耗的原料量.设现在每小时消耗原料x(单位:吨),库存的原料可使用的时间为y(单位:小时).(1)写出y 关于x 的函数解析式,并求出自变量的取值范围.(2)若恰好经过24小时才有新的原料进厂,为了使机器不停止运转,则x 应控制在什么范围内?1个技巧:用k 的几何性质巧求图形的面积9.如图,A ,B 是双曲线y =x k(k ≠0)上的两点,过A 点作AC ⊥x 轴,交OB 于D 点,垂足为C.若△ADO 的面积为1,D 为OB 的中点,则k 的值为( )A .34B .38C .3D .4(第9题)(第10题)10.如图,过x 轴正半轴上的任意一点P 作y 轴的平行线交反比例函数y =x 2和y =-x 4的图象于A ,B 两点,C 是y 轴上任意一点,则△ABC 的面积为________.11.如图是函数y =x 3与函数y =x 6在第一象限内的图象,点P 是y =x 6的图象上一动点,PA ⊥x 轴于点A ,交y =x 3的图象于点C ,PB ⊥y 轴于点B ,交y =x 3的图象于点D.(1)求证:D 是BP 的中点; (2)求四边形ODPC 的面积.(第11题)答案1.解:(1)∵A(m ,6),B(3,n)两点在反比例函数y =x 6(x>0)的图象上, ∴m =1,n =2,即 A(1,6),B(3,2).又∵A(1,6),B(3,2)在一次函数y =kx +b 的图象上, ∴2=3k +b ,6=k +b ,解得b =8,k =-2,即一次函数解析式为y =-2x +8.(第1题)(2)根据图象可知使kx +b<x 6成立的x 的取值范围是0<x<1或x>3.(3)如图,分别过点A ,B 作AE ⊥x 轴,BC ⊥x 轴,垂足分别为E ,C ,设直线AB 交x 轴于D 点.令-2x +8=0,得x =4,即D(4,0). ∵A(1,6),B(3,2),∴AE =6,BC =2.∴S △AOB =S △AOD -S △ODB =21×4×6-21×4×2=8.2.(1)证明:∵点A ,B 分别在x 轴,y 轴上,点D 在第一象限内,DC ⊥x 轴于点C ,∴∠AOB =∠DCA =90°.在Rt △AOB 和Rt △DCA 中,∵AB =DA ,AO =DC ,∴Rt △AOB ≌Rt △DCA. (2)解:在Rt △ACD 中,∵CD =2,DA =, ∴AC ==1.∴OC =OA +AC =2+1=3. ∴D 点坐标为(3,2).∵点E 为CD 的中点,∴点E 的坐标为(3,1).∴k =3×1=3. (3)解:点G 在反比例函数的图象上.理由如下:∵△BFG 和△DCA 关于某点成中心对称, ∴△BFG ≌△DCA.∴FG =CA =1,BF =DC =2,∠BFG =∠DCA =90°.∵OB =AC =1,∴OF =OB +BF =1+2=3.∴G 点坐标为(1,3). ∵1×3=3,∴点G(1,3)在反比例函数的图象上.3.解:∵BC ∥OA ,AB ∥x 轴,∴四边形ABCO 为平行四边形. ∴AB =OC =3.设Aa 6,则Ba 6,∴(a -3)·a 6=-3.∴a =2. ∴A(2,3),B(-1,3).∵OC =3,C 在x 轴负半轴上,∴C(-3,0), 设直线BC 对应的函数解析式为y =kx +b , 则-k +b =3,-3k +b =0,解得.9∴直线BC 对应的函数解析式为y =23x +29. 解方程组,3得y1=3,x1=-1,.3∴D23.设直线AD 对应的函数解析式为y =mx +n , 则,3解得.9∴直线AD 对应的函数解析式为y =83x +49. ∴E49.∴OE =49.4.415点拨:因为C(0,2),A(4,0),由矩形的性质可得P(2,1),把P 点坐标代入反比例函数解析式可得k =2,所以反比例函数解析式为y =x 2.因为D点的横坐标为4,所以AD =42=21.因为点E 的纵坐标为2,所以2=CE 2,所以CE =1,则BE =3.所以S △ODE =S 矩形OABC -S △OCE -S △BED -S △OAD =8-1-49-1=415.5.(1)证明:∵BE ∥AC ,AE ∥OB , ∴四边形AEBD 是平行四边形.∵四边形OABC 是矩形,∴DA =21AC ,DB =21OB ,AC =OB. ∴DA =DB.∴四边形AEBD 是菱形. (2)解:如图,连接DE ,交AB 于F , ∵四边形AEBD 是菱形,∴DF =EF =21OA =23,AF =21AB =1.∴E ,19.设所求反比例函数解析式为y =x k, 把点E ,19的坐标代入得1=29,解得k =29. ∴所求反比例函数解析式为y =2x 9.(第5题)(第7题)6.D7.解:(1)如图,过点D 作x 轴的垂线,垂足为F. ∵点D 的坐标为(4,3),∴OF =4,DF =3.∴OD =5. ∴AD =5.∴点A 的坐标为(4,8).∴k =xy =4×8=32.(2)将菱形ABCD 沿x 轴正方向平移,使得点D 落在函数y =x 32(x>0)的图象上点D ′处,过点D ′作x 轴的垂线,垂足为F ′.∵DF =3,∴D ′F ′=3.∴点D ′的纵坐标为3.∵点D ′在y =x 32的图象上,∴3=x 32,解得x =332,即OF ′=332.∴FF ′=332-4=320.∴菱形ABCD 沿x 轴正方向平移的距离为320.8.解:(1)∵正方形OABC 的边OA ,OC 分别在x 轴,y 轴上,点B 的坐标为(2,2),∴C(0,2).∵D 是BC 的中点,∴D(1,2).∵反比例函数y =x k(x >0,k ≠0)的图象经过点D ,∴k =2.(2)当P 在直线BC 的上方,即0<x <1时,∵点P(x ,y)在该反比例函数的图象上运动,∴y =x 2.∴S 四边形CQPR =CQ ·PQ =x ·-22=2-2x ;当P 在直线BC 的下方,即x >1时,同理求出S 四边形CQPR =CQ ·PQ =x ·x 2=2x -2,综上,S =2-2x (0<x <1).2x -2(x >1),9.410.解:∵反比例函数的图象关于原点对称,圆也关于原点对称,故阴影部分的面积占⊙O 面积的41,则针头落在阴影区域内的概率为41.1.B 2.C 3.①③④4.解:(1)反比例函数:y =-x 6.(2)如图所示.(第4题)5.解:∵反比例函数y =x k的图象经过点A(1,-k +4),∴-k +4=1k ,即-k +4=k ,∴k =2,∴A(1,2).∵一次函数y =x +b 的图象经过点A(1,2),∴2=1+b ,∴b =1.∴反比例函数的解析式为y =x 2,一次函数的解析式为y =x +1.6.解:(1)将B(2,-4)的坐标代入y =x m ,得-4=2m ,解得m =-8.∴反比例函数的解析式为y =x -8.∵点A(-4,n)在双曲线y =x -8上,∴n =2.∴A(-4,2).把A(-4,2),B(2,-4)的坐标分别代入y =kx +b ,得2k +b =-4,-4k +b =2,解得b =-2.k =-1,∴一次函数的解析式为y =-x -2.(2)令y =0,则-x -2=0,x =-2.∴C(-2,0).∴OC =2.∴S △AOB =S △AOC +S △BOC =21×2×2+21×2×4=6.(3)x 1=-4,x 2=2.(4)-4<x<0或x>2.7.解:如图,由观察可知:(1)当y =-2时,x =-3;(2)当-2<x<1且x ≠0时,y<-3或y>6;(3)当-3<y<2且y ≠0时,x<-2或x>3.(第7题)点拨:解决问题时,画出函数图象.由图象观察得知结果.由图象解决相关问题,一定要注意数形结合,学会看图.8.解:(1)库存原料为2×60=120(吨),根据题意可知y 关于x 的函数解析式为y =x 120.由于生产能力提高,每小时消耗的原料量大于计划消耗的原料量,所以自变量的取值范围是x>2.(2)根据题意,得y ≥24,所以x 120≥24.解不等式,得x ≤5,即每小时消耗的原料量应控制在大于2吨且不大于5吨的范围内.点拨:(1)由“每小时消耗的原料量×可使用的时间=原料总量”可得y 关于x 的函数解析式.(2)要使机器不停止运转,需y ≥24,解不等式即可.(第9题)9.B 点拨:如图,过点B 作BE ⊥x 轴于点E ,∵D 为OB 的中点,∴CD 是△OBE 的中位线,则CD =21BE.设Ax k ,则B2x k ,CD =4x k ,AD =x k -4x k .∵△ADO 的面积为1,∴21AD ·OC =1,即214x k ·x =1.解得k =38.10.311.(1)证明:∵点P 在双曲线y =x 6上,∴设P 点坐标为,m 6.∵点D 在双曲线y =x 3上,BP ∥x 轴,D 在BP 上,∴D 点坐标为,m 3.∴BD =m 3,BP =m 6,故D 是BP 的中点.(2)解:由题意可知S △BOD =23,S △AOC =23,S 四边形OBPA =6.∴S 四边形ODPC =S 四边形OBPA -S △BOD -S △AOC =6-23-23=3.。
反比例函数与几何综合
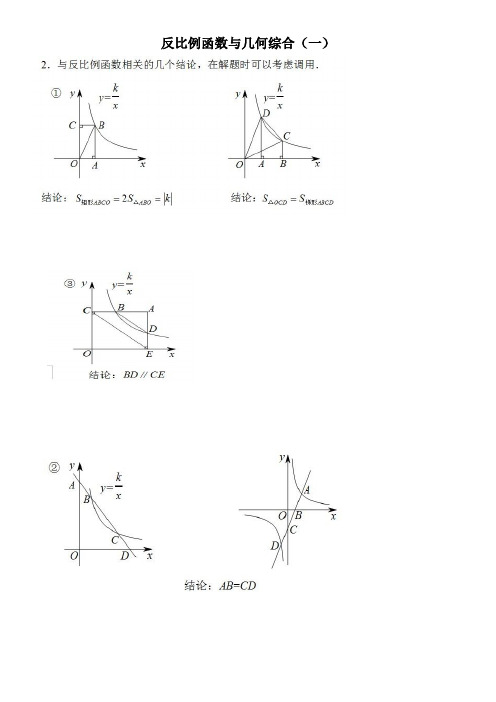
反比例函数与几何综合(一)反比例函数与一次函数、几何图形综合题类型一 反比例函数与一次函数综合 1. 已知反比例函数y =kx的图象过点A (3,1).(1)求反比例函数的解析式;(2) 若一次函数y =ax +6(a ≠0)的图象与反比例函数的图象只有一个交点,求一次函数的解析式.2. 如图,直线y =2x +4与反比例函数y =kx 的图象相交于A (-3,a )和B 两点.(1)求k 的值;(2)直线y =m (m >0)与直线AB 相交于点M ,与反比例函数y =kx的图象相交于点N .若MN =4,求m 的值.第2题图3. 如图,已知A (-4,n ),B (2,-4)是一次函数y =kx +b 和反比例函数y =mx 的图象的两个交点.(1)求一次函数和反比例函数的解析式; (2)求△AOB 的面积;(3)观察图象,直接写出方程kx +b -mx=0的解.第3题图4. 如图,已知直线y =kx 与双曲线y =4x (x >0)相交于点A (2,m ),将直线y =kx 向下平移2个单位长度后与y 轴相交于点B ,与双曲线交于点C ,连接AB 、AC .第4题图(1)求直线BC 的函数表达式; (2)求△ABC 的面积.类型二 反比例函数与几何图形综合5. 如图,已知,A (0,4),B (-3,0),C (2,0),D 为B 点关于AC 的对称点,反比例函数y =kx 的图象经过D 点.(1)证明四边形ABCD 为菱形; (2)求此反比例函数的解析式;(3)已知在y =kx的图象(x >0)上有一点N ,y 轴正半轴上有一点M ,且四边形ABMN 是平行四边形,求M 点的坐标.第5题图6. 如图,在平面直角坐标系中,Rt △AOB 的斜边OA 在x 轴的正半轴上,∠OBA =90°,且tan ∠AOB =12,OB =25,反比例函数y =kx的图象经过点B .(1)求反比例函数的表达式;(2)若△AMB 与△AOB 关于直线AB 对称,一次函数y =mx +n 的图象过点M 、A ,求一次函数的表达式.第6题图类型三 反比例函数与一次函数、几何图形综合7. 如图,双曲线y =kx (x >0)经过△OAB 的顶点A 和OB 的中点C ,AB ∥x 轴,点A 的坐标为(4,6),连接AC 交x 轴于D ,连接BD . (1)确定k 的值;(2)求直线AC 的解析式;(3)判断四边形OABD 的形状,并说明理由; (4)求△OAC 的面积.第7题图8. 如图,直线y =-x +b 与反比例函数y =kx 的图象相交于A (1,4),B 两点,延长AO 交反比例函数图象于点C ,连接OB .(1)求k 和b 的值;(2)直接写出一次函数值小于反比例函数值的自变量x 的取值范围;(3)在y 轴上是否存在一点P ,使S △PAC =25S △AOB ?若存在,请求出点P 坐标;若不存在,请说明理由.第8题图。
反比例函数与几何图形的综合

反比例函数与几何图形的小综合题型一反比例函数与三角形结合1.(2020•沙坪坝区校级月考)如图,一次函数y=x+32分别与x轴、y轴交于A、B两点,点P为反比例函数y=kx(k≠0,x<0)图象上一点,过点P作y轴的垂线交直线AB交于C,作PD⊥PC交直线AB于D,若AC•BD=7,则k的值为()A.﹣2B.﹣3C.−72D.−92【点睛】设P(m,n).则AC=√2n,BD=−√2m,构建方程求出mn的值即可.【解析】解:设P(m,n).则AC=√2n,BD=−√2m,∵AC•BD=7,∴﹣2mn=7,∴mn=−72,∴k=−72.故选:C.2.如图,在平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(2,4),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在反比例函数y=kx的图象上,则k的值为12.【解析】解:∵OB在x轴上,∠ABO=90°,点A的坐标为(2,4),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在反比例函数y=kx的图象上,∴点C的坐标为(6,2),∴2=k6,解得,k=12,3.(2020•薛城区期中)在平面直角坐标系xOy 中,将一块含有45°角的直角三角板如图放置,直角顶点C 的坐标为(1,0),顶点A 的坐标为(0,2),顶点B 恰好落在第一象限的双曲线上,现将直角三角板沿x 轴正方向平移,当顶点A 恰好落在该双曲线上时停止运动,则此时点C 的对应点C ′的坐标为 (52,0) .【解析】解:过点B 作BD ⊥x 轴于点D ,∵∠ACO +∠BCD =90°,∠OAC +∠ACO =90°, ∴∠OAC =∠BCD ,在△ACO 与△BCD 中,{∠OAC =∠BCD∠AOC =∠BDC AC =BC ,∴△ACO ≌△BCD (AAS )∴OC =BD ,OA =CD ,∵A (0,2),C (1,0)∴OD =3,BD =1,∴B (3,1),∴设反比例函数的解析式为y =kx,将B (3,1)代入y =k x,∴k =3,∴y =3x,∴把y =2代入y =3x ,∴x =32,当顶点A 恰好落在该双曲线上时,此时点A 移动了32个单位长度,∴C 也移动了32个单位长度,此时点C 的对应点C ′的坐标为( 52,0)故答案为(52,0).4.(2020•盐湖区期末)如图,在平面直角坐标系中,边长为4的等边△OAB 的OA 边在x 轴的正半轴上,反比例函数y =kx (x >0)的图象经过AB 边的中点C ,且与OB 边交于点D ,则点D 的坐标为 (√3,3) .【解析】解:∵△AOB 是等边三角形,边长为4,∴B (2,2√3),∵BC =CA ,∴C (3,√3),把点C 坐标代入y =k x上,得到k =3√3,∵直线OB 的解析式为y =√3x , 由{y =√3xy =3√3x,解得{x =√3y =3或{x =−√3y =−3(舍弃)∴D (√3,3),故答案为(√3,3). 题型二 反比例函数与四边形结合5.(2020•北海期末)如图,矩形ABCD 在第一象限,AB 在x 轴的正半轴上,AB =3,BC =1,直线y =12x ﹣1经过点C 交x 轴于点E ,双曲线y =kx经过点D ,则k 的值为( )A .1B .2C .3D .4【解析】解:根据矩形的性质知点C 的纵坐标是y =1,∵直线y =12x ﹣1经过点C ,∴1=12x ﹣1, 解得,x =4,即点C 的坐标是(4,1).∵矩形ABCD 在第一象限,AB 在x 轴正半轴上,AB =3,BC =1,∴D (1,1),∵双曲线y =kx 经过点D ,∴k =xy =1×1=1,即k 的值为1.故选:A .6.(2020•秀洲区二模)平面直角坐标系中,菱形AOBC 的位置如图所示,点A 在x 轴负半轴上,B (1,√3),反比例函数y =kx 在第二象限的图象经过点C ,则k = −√3 .【点睛】根据菱形的性质可以求得点C 的坐标,再根据点C 在反比例函数图象上,从而可以求得k 的值.【解析】解:∵点A在x轴负半轴上,B(1,√3),∴OB=2,点C的纵坐标是√3,∴OA=2,∵四边形AOBC是菱形,点A在x轴的负半轴,∴点C的坐标为(﹣1,√3),∵反比例函数y=kx在第二象限的图象经过点C,∴√3=k−1,得k=−√3,故答案为:−√3.7.如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,BE∥AC,AE∥OB,函数y=kx(k>0,x>0)的图象经过点E,若点A、C的坐标分别为(3,0),(0,2),则k的值为92.【解析】解:∵BE∥AC,AE∥OB,∴四边形AEBD是平行四边形,∵四边形OABC是矩形,C的坐标为(0,2),∴DA=12AC,DB=12OB,AC=OB,AB=OC=2,∴DA=DB,∴四边形AEBD是菱形;连接DE,交AB于F,如图所示:∵四边形AEBD是菱形,∴AB与DE互相垂直平分,∵OA=3,OC=2,∴EF=DF=12OA=32,AF=12AB=1,3+32=92,∴点E坐标为:(92,1).∵函数y=kx(k>0,x>0)的图象经过点E,∴k=92×1=92,故答案为:92.8.(2020•盘龙区二模)如图,在平面直角坐标系中,反比例函数y=kx(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN 的最小值是2√26.【解析】解:∵正方形OABC的边长是6,∴点M的横坐标和点N的纵坐标为6,∴M (6,k 6),N (k6,6),∴BN =6−k 6,BM =6−k 6,∵△OMN 的面积为10,∴6×6−12×6×k 6−12×6×k 6−12×(6−k6)2=10,∴k =24,∴M (6,4),N (4,6),作M 关于x 轴的对称点M ′,连接NM ′交x 轴于P ,则NM ′的长=PM +PN 的最小值,∵AM =AM ′=4,∴BM ′=10,BN =2,∴NM ′=√BM′2+BN 2=√102+22=2√26,故答案为2√26.巩固练习1.(2020•铜山区二模)如图,矩形ABCD 的边BC 在x 轴的负半轴上,顶点D (a ,b )在反比例函数y =kx的图象上,直线AC 交y 轴点E ,且S △BCE =4,则k 的值为( )A .﹣16B .﹣8C .﹣4D .﹣2【解析】解:D (a ,b ),则CO =﹣a ,CD =AB =b ,∵矩形ABCD 的顶点D 在反比例函数y =kx (x <0)的图象上,∴k =ab ,∵△BCE 的面积是4,∴12×BC ×OE =4,即BC ×OE =8,∵AB ∥OE ,∴BC OC=AB EO,即BC •EO =AB •CO ,∴8=b ×(﹣a ),即ab =﹣8,∴k =﹣8故选:B .2.(2020•九龙坡区校级期末)如图,已知反比例函数y =ax和一次函数y =kx +b 的图象相交于点A (﹣1,y 1)、B (4,y 2)两点,则不等式ax ≤kx +b 的解集为( )A .x ≤﹣1或x ≥4B .﹣1≤x ≤4C .x ≤4D .x ≤﹣1或.0<x ≤4【解析】解:不等式a x≤kx +b 的解集就是反比例函数值小于或等于一次函数值的自变量的取值范围,观察图象可得:第二象限x ≤﹣1,第四象限0<x ≤4,故选:D .3.(2020•深圳模拟)如图,点A 是双曲线y =3x上的动点,连结AO 并延长交双曲线于点B ,将线段AB 绕B 顺时针旋转60°得到线段BC ,点C 在双曲线y =kx上的运动,则k = ﹣9 .【解析】解:∵双曲线y =3x 关于原点对称,∴点A 与点B 关于原点对称.∴OA =OB .连接OC ,AC ,如图所示.∵将线段AB 绕B 顺时针旋转60°得到线段BC ,∴△ABC 是等边三角形,OA =OB ,∴OC ⊥AB ,∠BAC =60°,∴tan ∠OAC =OCOA =√3,∴OC =√3OA .过点A 作AE ⊥y 轴,垂足为E ,过点C 作CF ⊥y 轴,垂足为F ,∵AE ⊥OE ,CF ⊥OF ,OC ⊥OA ,∴∠AEO =∠OFC ,∠AOE =90°﹣∠FOC =∠OCF ,∴△AEO ∽△OFC .∴AE OF=EO FC=AO OC.∵OC =√3OA ,∴OF =√3AE ,FC =√3EO .设点A 坐标为(a ,b ),∵点A 在第一象限,∴AE =a ,OE =b .∴OF =√3AE =√3a ,FC =√3EO =√3b .∵点A 在双曲线y =3x上,∴ab =3.∴FC •OF =√3b •√3a =3ab =9,设点C 坐标为(x ,y ),∵点C 在第四象限,∴FC =x ,OF =﹣y .∴FC •OF =x •(﹣y )=﹣xy =9.∴xy =﹣9.∵点C 在双曲线y =kx 上,∴k =xy =﹣9.故答案为:﹣9.4.(2020•普陀区二模)如图,在平面直角坐标系xOy 中,△ABC 的顶点A 、C 在坐标轴上,点B 的坐标是(2,2).将△ABC 沿x 轴向左平移得到△A 1B 1C 1,点B 1落在函数y =−6x 的图象上.如果此时四边形AA 1C 1C 的面积等于552,那么点C 1的坐标是 (﹣5,112) .【解析】解:如图,∵点B 的坐标是(2,2),BB 1∥AA 1,∴点B 1的纵坐标为2, 又∵点B 1落在函数y =−6x 的图象上,∴当y =2时,x =﹣3,∴BB 1=AA 1=5=CC 1,又∵四边形AA 1C 1C 的面积等于552,∴AA 1×OC =552,∴OC =112,∴点C 1的坐标是(﹣5,112).故答案为:(﹣5,112).5.(2020•九龙坡区校级期末)如图,菱形OABC 在直角坐标系中,点A 的坐标为(52,0),对角线OB =2√5,反比例函数y =kx (k ≠0,x >0)经过点C .则k 的值为 3 .【解析】解:∵四边形OABC 是菱形,∴OA =AB =BC =CO ,设点C 的坐标为(a ,b ),∵点A 的坐标为(52,0),对角线OB =2√5,∴点B 的坐标为(a +52,b ),OC =52,∴{a 2+b 2=(52)2(a +52)2+b 2=(2√5)2,解得a =32,b =2,∴ab =32×2=3,∵反比例函数y =kx (k ≠0,x >0)经过点C ,点C 的坐标为(a ,b ),∴b =ka ,∴k =ab =3. 故答案为:3.6.以矩形ABCD 两条对角线的交点O 为坐标原点,以平行于两边的方向为坐标轴,建立如图所示的平面直角坐标系,BE ⊥AC ,垂足为E .若双曲线y =32x(x >0)经过点D ,则OB •BE 的值为 3 .【解析】解:如图,∵双曲线y =32x (x >0)经过点D ,∴S △ODF =12k =34, 则S △AOB =2S △ODF =32,即12OA •BE =32,∴OA •BE =3,∵四边形ABCD 是矩形,∴OA =OB ,∴OB •BE =3,故答案为:3.7.(2020•通辽)如图,在平面直角坐标系中,反比例函数y =k x(k >0)的图象与半径为5的⊙O 交于M 、N 两点,△MON 的面积为3.5,若动点P 在x 轴上,则PM +PN 的最小值是 5√2 .【解析】解:如图设点M (a ,b ),N (c ,d ),∴ab =k ,cd =k ,∵点M,N在⊙O上,∴a2+b2=c2+d2=25,作出点N关于x轴的对称点N'(c,﹣d),∴S△OMN=12k+12(b+d)(a﹣c)−12k=3.5,∴bc﹣ad=7,∴kca−kac=7,∴ac=k(c2−a2)7,同理:bd=k(b2−d2)7,∴ac﹣bc=k(c2−a2)7−k(b2−d2)7=k7[(c2+d2)﹣(a2+b2)]=0,∵M(a,b),N'(c,﹣d),∴MN'2=(a﹣c)2+(b+d)2=a2+b2+c2+d2﹣2ac+2bd=a2+b2+c2+d2﹣2(ac﹣bd)=50,∴MN'=5√2,故答案为:5√2。
反比例函数与几何综合(一)(含答案)

学生做题前请先回答以下问题问题1:思考反比例函数与几何综合的处理思路是什么?问题2:什么是关键点?问题3:将函数特征与几何特征联系起来的桥梁是什么?问题4:围绕关键点以及横平竖直线段长将几何特征与函数特征结合分析时有几种方式?分别是什么?以下是问题及答案,请对比参考:问题1:思考反比例函数与几何综合的处理思路是什么?答:反比例函数与几何综合的处理思路:①从关键点入手.通过关键点坐标和横平竖直线段长的互相转化可将函数特征和几何特征综合在一起进行研究.②对函数特征和几何特征进行转化、组合,列方程求解.若借助反比例函数模型,能快速将函数特征转化为几何特征.问题2:什么是关键点?答:关键点是几何图形与函数图象的交点,在处理反比例函数与几何综合的问题时从关键点入手分析.问题3:将函数特征与几何特征联系起来的桥梁是什么?答:通过关键点坐标与横平竖直线段长的相互转化,可将函数特征与几何特征综合起来一起进行研究.问题4:围绕关键点以及横平竖直线段长将几何特征与函数特征结合分析时有几种方式?分别是什么?答:可以采用两种方式:①根据函数特征设出坐标,表达线段长,利用几何特征建等式;②根据几何特征设出线段长,表达坐标,代入函数建立等式.反比例函数与几何综合(一)一、单选题(共8道,每道12分)1.如图,直线与双曲线在第一象限内的交点为R,与x轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积之比为4:1,则k的值为( )A. B.C.2D.3答案:B解题思路:试题难度:三颗星知识点:反比例函数与几何综合2.如图,均是等腰直角三角形,点在反比例函数的图象上,斜边都在x轴上,则点的坐标是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:反比例函数与几何综合3.如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x 轴,y轴上,反比例函数(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为( )A.(1,14)B.(2,8)C.(2,7)D.(1,16)答案:C解题思路:试题难度:三颗星知识点:反比例函数与几何综合4.如图,矩形ABCD的顶点D在反比例函数(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为( )A.-6B.-8C.-9D.-12答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合5.如图,在反比例函数的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数的图象上运动.若tan∠CAB=2,则k的值为( )A.2B.4C.6D.8答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合6.如图,直线与双曲线交于点A,将直线向上平移4个单位长度后,与y轴交于点C,与双曲线交于点B,若OA=3BC,则k的值为( )A.3B.6C. D.答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合7.如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=,反比例函数在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )A.60B.80C.30D.40答案:D解题思路:试题难度:三颗星知识点:反比例函数与几何综合8.直线y=-2x-2与反比例函数的图象交于点A,与x轴交于点B,过点B作x 轴垂线交双曲线于点C,若AB=AC,则k的值为( )A.-1B.-2C.-4D.-8答案:C解题思路:试题难度:三颗星知识点:反比例函数与几何综合。
反比例函数与几何综合

一、反比例函数的定义函数ky x=(k 为常数,0k ≠)叫做反比例函数,其中k 叫做比例系数,x 是自变量,y 是函数,自变量x 的取值范围是不等于0的一切实数.二、反比例函数的图象反比例函数ky x=(k 为常数,0k ≠)的图象由两条曲线组成,每条曲线随着x 的不断增大(或减小)越来越接近坐标轴,反比例函数的图象属于双曲线.反比例函数k y x =与ky x=-(0k ≠)的图象关于x 轴对称,也关于y 轴对称.三、反比例函数的性质反比例函数ky x=(k 为常数,0k ≠)的图象是双曲线; 当0k >时,函数图象的两个分支分别位于第一、三象限内,它们关于原点对称,在每一个象限内,y 随x 的增大而减小;当0k <时,函数图象的两个分支分别位于第二、四象限内,它们关于原点对称,在每一个象限内,y 随x 的增大而增大.注意:⑴反比例函数ky x=(0k ≠)的取值范围是0x ≠.因此,①图象是断开的两条曲线,画图象时,不要把两个分支连接起来. ②叙述反比例函数的性质时,一定要加上“在每一个象限内”,如当0k >时,双曲线ky x=的两支分别在一、三象限,在每一个象限内,y 随x 的增大而减小.这是由于0x ≠,即0x >或0x <的缘故.如果笼统地叙述为0k <时,y 随x 的增大而增大就是错误的.⑵由于反比例函数中自变量x 和函数y 的值都不能为零,所以图象和x 轴、y 轴都没有交点,但画图时要体现出图象和坐标轴无限贴近的趋势. ⑶在画出的图象上要注明函数的解析式.四、反比例函数解析式的求法反比例函数的解析式(0)ky k x=≠中,只有一个系数k ,确定了k 的值,也就确定了反比例函数的解析式.因此,只需给出一组x 、y 的对应值或图象上一点的坐标,利用待定系数法,即可确定反比例函数的解析式.五、比例系数k 的几何意义过反比例函数()0ky k x=≠,图象上一点()P x y ,,做两坐标轴的垂线,两垂足、原点、P 点组成一个矩形,矩形的面积S x y xy k =⋅==.一、反比例函数与几何综合【例1】 如图,11POA ∆、212P A A ∆都是等腰直角三角形,点1P 、2P 在函数4y x=(0x >)的图像上,斜边1OA 、12A A 、都在x 轴上,求点2A 的坐标.【巩固】如图所示,()()111222P x y P x y ,,,,……,()n n n P x y ,在函数()90y x x=>的图象上,11OP A ∆,212P A A ∆,323P A A ∆,…,1n n n P A A -∆,…都是等腰直角三角形,斜边1121n n OA A A A A -,,…,都在x 轴上,则12n y y y +++=…______________.【例2】 如图,如果函数y x =-与4y x=-的图像交于A ,B 两点,过点A 作AC 垂直于y 轴,垂足为点C ,求BOC ∆的面积.【巩固】如图,一次函数y kx b =+的图像与反比例函数my x=的图像交于(21)(1)A B n -,,,两点. (1)试确定上述反比例函数和一次函数的表达式; (2)求AOB ∆的面积.【例3】 如图,直线y kx b =+与反比例函数()0k y x x=<′的图象相交于点A 、点B ,与x 轴交于点C ,其中点A 的坐标为()24-,,点B 的横坐标为4-. (1)试确定反比例函数的关系式;(2)求AOC ∆的面积.【巩固】如图,在直角坐标系xOy 中,一次函数1y k x b =+的图像与反比例函数2k y x=的图像交于()()143A B m ,,,两点. (1)求一次函数的解析式; (2)求AOB ∆的面积.【例4】 两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x=的图象上,PC x ⊥轴于点C ,交1y x =的图象于点A ,PD y ⊥轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①ODB ∆与OCA ∆的面积相等; ②四边形PAOB 的面积不会发生变化; ③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分).【巩固】如图,点A 、B 在反比例函数ky x=(0k >)的图象上,且点A 、B 的横坐标分别为a 和2a (0a >)AC x ⊥轴,垂足为C ,AOC ∆的面积为2. (1)求反比例函数的解析式;(2)若点(a -,1y ),(2a -,2y )也在反比例函数的图象上,试比较1y 与2y 的大小; (3)求AOB ∆的面积.【例5】 已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B C ,重合),过F 点的反比例函数(0)ky k x=>的图象与AC 边交于点E .(1)求证:AOE △与BOF △的面积相等;(2)记OEF ECF S S S =-△△,求当k 为何值时,S 有最大值,最大值为多少?(3)请探索:是否存在这样的点F ,使得将CEF △沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.【巩固】两个反比例函数1k y x =和()2120ky k k x=>>在第一象限内的图象如图所示,动点P 在1k y x =的图象上,PC x ⊥轴于点C ,交2k y x =的图象于点A ,PD y ⊥轴于点D ,交2ky x=的图象于点B .⑴求证:四边形PAOB 的面积是定值; ⑵当23PA PC =时,求DBBP的值; ⑶若点P 的坐标为()52,,OAB ABP ∆∆,的面积分别记为OAB S ∆、ABP S ∆,设ABP OAB S S S ∆∆-=.①求1k 的值;②当2k 为何值时,S 有最大值,最大值为多少?k 2x【例6】 如图,反比例函数8y x=的图象过矩形OABC 的顶点B ,OA 、OC 分别在x 轴、y 轴的正半轴上,:2:1OA OC =.(1)设矩形OABC 的对角线交于点E ,求出E 点的坐标;(2)若直线2y x m =+平分矩形OABC 面积,求m 的值.【巩固】如图,已知正方形OABC 的面积为9,点O 为坐标原点,点A 在x 轴上,点C 在y 轴上,点B 在函数ky x=(0k >,0x >)的图像上,点P (m ,n )为其双曲线上的任一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F ,并设矩形OEPF 和正方形OABC 不重合部分的面积为S .⑴求B 点的坐标和k 的值;⑵当92S =时,求P 点坐标;⑶写出S 关于m 的函数关系式.【例7】 若一次函数21y x =-和反比例函数2ky x=的图象都经过点(1,1). (1)求反比例函数的解析式;(2)已知点A 在第三象限,且同时在两个函数的图象上,求点A 的坐标; (3)利用(2)的结果,若点B 的坐标为(2,0),且以点A O B P ,,,为顶点的四边形是平行四边形,请你直接写出点P 的坐标.【巩固】如图,点()1A m m+,,()31B m m+-,都在反比例函数kyx=的图象上.(1)求m k,的值;(2)如果M为x轴上一点,N为y轴上一点,以点A B M N,,,为顶点的四边形是平行四边形,试求直线MN的函数表达式.【巩固】已知(1)A m-,与(2B m+,是反比例函数kyx=图象上的两个点.(1)求k的值;(2)若点(10)C-,,则在反比例函数kyx=图象上是否存在点D,使得以A B C D,,,四点为顶点的四边形为梯形?若存在,求出点D的坐标;若不存在,请说明理由.【例8】如图,已知反比例函数12yx=的图象和一次函数7y kx=-的图象都经过点()2P m,.①求这个一次函数的解析式;②如果等腰梯形ABCD的顶点A B,在这个一次函数图象上,顶点C D,在这个反比例函数图象上,两底AD,BC与y轴平行,且A和B的横坐标分别为a和2a+,求a的值。
[数学]-专题26 反比例函数与几何综合题型归纳(原版)
![[数学]-专题26 反比例函数与几何综合题型归纳(原版)](https://img.taocdn.com/s3/m/bc1b13d9dbef5ef7ba0d4a7302768e9950e76e63.png)
专题26 反比例函数与几何综合题型归纳(原卷版)类型一反比例函数与三角形综合1.(2022秋•岚山区校级期末)如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,点A在反比例函数y=6x(x>0)的图象上,则经过点B的反比例函数解析式为()A.y=−1x B.y=−2x C.y=−4x D.y=−6x2.(2022秋•金水区校级期末)如图,已知直角三角形ABO中,AO=√3,将△ABO绕点O点旋转至△A'B'O的位置,且A'在OB的中点,B'在反比例函数y=kx上,则k的值为.3.(2022秋•荔湾区校级期末)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=k x过A,B两点,过点C作CD∥y轴交双曲线于点D,若S△BCD=16,则k的值是.4.(2023•南海区模拟)如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1,A2,A3,A4,A5分别作x轴的垂线与反比例函数y=2x(x≠0)的图象相交于点P1,P2,P3,P4,P5,得直角三角形OP1A1,A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为S1,S2,S3,S4,S5,则S2022=.5.(2022秋•桥西区校级期末)如图,一次函数y1=k1x+b的图像与反比例函数y2=k2x(x>0)的图像相交于A(m,6),B(6,1)两点,且与x轴,y轴交于点M,N.(1)填空:k2=;m=;在第一象限内,当y1>y2时,x的取值范围为;(2)连接OA,OB,求△AOB的面积;(3)点E在线段AB上,过点E作x轴的垂线,交反比例函数图像于点F,若EF=2,求点F的坐标.6.(2022秋•龙泉驿区期末)某班在“图形与坐标”的主题学习中,第四学习小组提出如下背景“如图,在平面直角坐标系中,将一个边长为2的等边三角形ABC沿x轴平移(边AB在x轴上,点C在x轴上方),其中A(a,0),三角形ABC与反比例函数y=2√3x(x>0)交于点D,E两点(点D在点E左边)”,让其他小组提出问题,请你解答:(1)第一小组提出“当a=2时,求点D的坐标”;(2)第二小组提出“若AD=CE,求a的值”;(3)第三小组提出“若将点E绕点A逆时针旋转60°至点E′,点E′恰好也在y=2√3x(x>0)上,求a的值”.7.(2022秋•南山区期末)如图:△AOB为等腰直角三角形,斜边OB在x轴上,S△OAB=4,一次函数y1=kx+b(k≠0)的图象经过点A交y轴于点C,反比例函数y2=kx(x>0)的图象也经过点A.(1)求反比例函数的解析式;(2)若CD=2AD,求△COD的面积;(3)当y1<y2时对应的自变量的取值范围是.(请直接写出答案)8.(2022秋•老城区校级期中)如图,已知:直线y=12x与双曲线y=kx(k>0)交于A,B两点,且点A的横坐标为4,若双曲线y=kx(k>0)上一点C的纵坐标为8,连接AC.(1)填空:k的值为8;点B的坐标为;点C的坐标为.(2)直接写出关于的不等式12x−kx≥0的解集;(3)求三角形AOC的面积.9.(2022秋•虹口区校级期中)如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=1x和y=9x在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=1x的图象于点C,联结AC,若△ABC是等腰三角形,求k的值.类型二反比例函数与平行四边形综合10.(2022秋•襄都区校级期末)如图,反比例函数y=kx的图象经过平行四边形ABCD对角线的交点P.知A,C,D,三点在坐标轴上,BD⊥DC,平行四边形ABCD的面积为6,则k的值为()A.﹣6B.﹣5C.﹣4D.﹣311.(2022秋•滨城区校级期末)如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=−2x上,顶点C在y=9x上,则平行四边形OABC的面积是.12.(2022秋•平城区校级月考)如图,在平面直角坐标系中,已知平行四边形ABOC的面积为6,边OB在x轴上,顶点A、C分别在反比例函数y=kx(x<0)和y=2x(x>0)的图象上,则k﹣2的值为()A.﹣4B.4C.﹣6D.613.(2022秋•高新区期末)如图,在平面直角坐标中,平行四边形ABCD顶点A的坐标为(1,0),点D在反比例函数y=−6x的图象上,点B,C在反比例函数y=kx(x>0)的图象上,CD与y轴交于点E,若DE=CE,∠DAO=45°,则k的值为.14.(2022•湘潭县校级模拟)如图,在平面直角坐标系Oxy 中,函数y =kx (其中x <0)的图象经过平行四边形ABOC 的顶点A ,函数y =8x(其中x >0)的图象经过顶点C ,点B 在x 轴上,若点C 的横坐标为2,△AOC 的面积为6. (1)求k 的值;(2)求直线AB 的解析式.类型三 反比例函数与矩形综合15.(2022秋•永城市期末)如图,直线y =﹣x +3与坐标轴分别相交于A ,B 两点,过A ,B 两点作矩形ABCD ,AB =2AD ,双曲线y =kx 在第一象限经过C ,D 两点,则k 的值是( )A .6B .274C .272D .2716.(2022秋•岚山区校级期末)如右图,已知矩形OABC 的面积为1003,它的对角线OB 与双曲线y =kx 相交于点D ,且OB :OD =5:3,则k =( )A .10B .20C .6D .1217.(2022秋•达川区期末)如图,矩形AOBC 的边OA =3,OB =4,动点F 在边BC 上(不与B 、C 重合),过点F 的反比例函数y =k x的图象与边AC 交于点E ,直线EF 分别与y 轴和x 轴相交于点D 和G .给出下列命题:①若k =6,则△OEF 的面积为92;②若k =218,则点C 关于直线EF 的对称点在x 轴上; ③满足题设的k 的取值范围是0<k ≤12;④若DE ⋅EG =256,则k =2; 其中正确的命题个数是( )A .1个B .2个C .3个D .4个18.(2023•黔江区一模)如图,矩形ABCD 中,点A 在双曲线y =−8x 上,点B ,C 在x 轴上,延长CD 至点E ,使CD =2DE ,连接BE 交y 轴于点F ,连接CF ,则△BFC 的面积为( )A .5B .6C .7D .819.(2022秋•荔城区校级期末)如图,点A 为双曲线y =−2x 在第二象限上的动点,AO 的延长线与双曲线的另一个交点为B ,以AB 为边的矩形ABCD 满足AB :BC =4:3,对角线AC ,BD 交于点P ,设P的坐标为(m,n),则m,n满足的关系式为.20.(2022秋•滕州市校级期末)如图,矩形OABC与反比例函数y1=k1x(k1是非零常数,x>0)的图象交于点M,N,反比例函数y2=k2x(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则2k2﹣2k1=.21.(2022秋•长安区校级期末)如图,矩形ABCD顶点坐标分别为A(1,1),B(2,1),CB=2.(1)若反比例函数y=kx与的图象过点D,则k=.(2)若反比例函数与矩形ABCD的边CD、CB分别交于点E、点F,且△CEF的面积是,则反比例函数的表达式为.(3)若反比例函数y=kx(x>0)的图象将矩形边界上横、纵坐标均为整数的点恰好等分成了两组,使两组点分别在双曲线两侧,则k的取值范围是.22.(2022秋•松原期末)如图,在平面直角坐标系中,四边形OABC为矩形,点C、A分别在x轴和y轴的正半轴上,点D为AB的中点.一次函数y=﹣3x+6的图象经过点C、D,反比例函数y=kx(x>0)的图象经过点B,求k的值.23.(2022•礼县校级模拟)如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数y=k1x(x>0)的图象经过线段OB的中点D,并与AB、BC分别交于点B、F.一次函数y=k2x+b的图象经过E、F两点.(1)分别求出一次函数和反比例函数的表达式.(2)点P是x轴上一动点,当PE+PF的值最小时,求点P的坐标.25.(2022春•姑苏区校级月考)如图,在以O为原点的平面直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B(a,b)在第一象限,四边形OABC是矩形,反比例函数y=kx(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=2CE.(1)求证:BD=2AD;(2)若四边形ODBE的面积是6,求k的值.类型四反比例函数与菱形综合26.(2022秋•江北区校级期末)如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=kx(k≠0,x>0)的图象同时经过顶点C、D.若点C的横坐标为10,BE=3DE,则k的值为()15 4D.10A.15B.6C.27.(2022•珠海校级三模)如图,菱形ABCD 的顶点分别在反比例函数y =k 1x (k 1>0)和y =k2x 的图象上,且∠ADC =120°,则k 2k 1的值是( )A .﹣3B .−13C .√3D .−√3328.(2022秋•岚山区校级期末)如图,O 为坐标原点,点C 在x 轴上.四边形OABC 为菱形,D 为菱形对角线AC 与OB 的交点,反比例函数y =kx 在第一象限内的图象经过点A 与点D ,若菱形OABC 的面积为24√2,则点A 的坐标为 .29.(2022秋•福州期末)如图,四边形ABOC 为菱形,∠BOC =60°,反比例函数y =kx (x <0)的图象经过点B ,交AC 边于点P ,若△BOP 的面积为4√3,则点A 的坐标为 .30.(2022秋•通川区期末)如图,在平面直角坐标系中,点A 的坐标是(5,0),函数y =kx (x >0)的图象经过菱形OABC 的顶点C ,若OB •AC =40,则k 的值为 .31.(2023•西山区校级开学)如图,在平面直角坐标系中,菱形ABCD 的顶点C 与原点O 重合,点B 在y 轴的正半轴上,点A 在反比例函数y =k x(k >0,x >0)的图象上,点D 的坐标为(4,3). (1)求反比例函数的关系式;(2)设点M 在反比例函数图象上,连接MA 、MD ,若△MAD 的面积是菱形ABCD 面积的14,求点M的坐标.类型五 反比例函数与正方形综合32.(2022秋•东港市期末)如图,在平面直角坐标系中,一次函数y =43x +4的图象与x 轴,y 轴分别交于点B ,A ,以线段AB 为边作正方形ABCD ,且点C 在反比例函数y =k x (x <0)的图象上,则k 的值为( )A .﹣21B .21C .﹣24D .2433.(2022秋•龙岗区校级期末)如图,反比例函数y =k x(x >0)图象经过正方形OABC 的顶点A ,BC 边与y 轴交于点D ,若正方形OABC 的面积为12,BD =2CD ,则k 的值为( )A .3B .185C .165D .10334.(2022秋•济南期末)如图,在直角坐标系中,正方形的中心在原点O ,且正方形的一组对边与x 轴平行,点P (4a ,a )是反比例函数y =k x(k >0)的图象上与正方形的一个交点,若图中阴影部分的面积等于16,则k 的值为( )A .16B .1C .4D .﹣1635.(2022•南关区校级模拟)如图,正方形ABCO 和正方形CDEF 的顶点B 、E 在双曲线y =6x(x >0)上,连接OB 、OE 、BE ,则S △OBE 的值为( )A .2B .2.5C .3D .3.536.(2022•绿园区校级模拟)如图,在平面直角坐标系中,大、小两个正方形的一个顶点均为坐标原点,两边分别在x 轴,y 轴的正半轴上,若经过小正方形的顶点A 的函数y =kx (x >0)的图象与大正方形的一边交于点B (1,3),则阴影部分的面积为( ) A .6B .3C .32D .3−√337.(2022秋•徐汇区期末)点A 、M 在函数y =1x (x >0)图象上,点B 、N 在函数y =−3x (x <0)图象上,分别过A 、B 作x 轴的垂线,垂足为D 、C ,再分别过M 、N 作线段AB 的垂线,垂足为Q 、P ,若四边形ABCD 与四边形MNPQ 均为正方形,则正方形MNPQ 的面积是 .38.(2022秋•薛城区期末)如图,点B 是反比例函数y =k x图象上的一点,矩形OABC 的周长是20,正方形OCDF 与正方形BCGH 的面积之和为68,则k 的值为 .39.(2022春•姑苏区校级期中)如图,在平面直角坐标系中,反比例函数y =kx (x >0)的图象与边长等于6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,△MON 的面积是16,动点P 从原点出发,以每秒2个单位长度的速度沿x 轴向右运动,记运动时间为t ,当t = s 时,PM +PN 最小.40.(2022•香洲区校级三模)如图,反比例函数y =k x(k ≠0,x >0)的图象过点B ,E ,四边形ODEF 和ABCD 是正方形,顶点F 在x 轴的正半轴上,A ,D 在y 轴正半轴上,点C 在边DE 上,延长BC 交x 轴于点G .若AB =2,则四边形CEFG 的面积为 .41.(2022秋•蚌山区月考)如图,两个边长分别为a ,b (a >b )的正方形连在一起,三点C ,B ,F 在同一直线上,反比例函数y =kx 在第一象限的图象经过小正方形右下顶点E .若OB 2﹣BE 2=8,则(1)S 正方形OABC﹣S 正方形DEFB = ;(2)k 的值是 .42.(2022•九龙坡区自主招生)如图,在平面直角坐标系中,已知点A的坐标为(0,4),点B的坐标为(2,0),连结AB,以线段AB为边在第一象限内作正方形ABCD,直线BD:y=ax+b交双曲线y= kx(k≠0)于D、E两点,连结CE.(1)求双曲线y=kx(k≠0)和直线BD的解析式;(2)求△BEC的面积;(3)请直接写出不等式ax+b>kx的解集.43.(2022•东湖区期中)如图,在平面直角坐标系中,正方形OABC的顶点O在坐标原点,顶点A在y 轴上,顶点C在x轴上,反比例函数y=k的图象过AB边上一点E,与BC边交于点D,BE=2,OE=10.(1)求k的值;(2)直线y=ax+b过点D及线段AB的中点F,点P是直线OF上一动点,当PD+PC的值最小时,直接写出这个最小值.44.(2021秋•榆林)如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(0,2),以线段AB为一边在第一象限内作平行四边形ABCD,其顶点D(3,1)在反比例函数y=kx(x>0)的图象上.(1)求证:四边形ABCD是正方形;(2)设将正方形ABCD沿x轴向左平移m(m>0)个单位后,得到正方形A′B′C′D′,点C的对应点C′恰好落在反比例函数y=kx(x>0)的图象上,求m的值.45.(2022秋•宝山区校级期中)如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数y=kx(k>0,x>0)图象上,点P是函数y=kx(k>0,x>0)图象上异于点B的任意一点,过点P分别作x轴、y轴的垂线,垂足分别为点E、F.设矩形OEPF和正方形OABC不重合部分的面积为S.(1)点B的坐标是,k=;(2)当S=92,求点P的坐标;(3)求出S关于m的函数关系式.46.(2022秋•武功县期末)如图,在平面直角坐标系中,A(﹣1,2),B(﹣1,﹣2),以AB为边向右作正方形ABCD,边AD、BC分别与y轴交于点E、F,反比例函数y=kx(k≠0)的图象经过点D.(1)求反比例函数的表达式;(2)在反比例函数的图象上是否存在点P,使得△PEF的面积等于正方形ABCD面积的一半?若存在,请求出点P的坐标;若不存在,请说明理由.47.(2022•靖江市校级模拟)如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=kx(k>0)的图象经过BC边的中点D(3,1).(1)直接写出这个反比例函数的表达式;(2)若△ABC与△EFG关于点M成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.①直接写出OF的长、对称中心点M的坐标;②连接AF,BE,证明四边形ABEF是正方形.。
反比例与几何综合应用(讲义)

反比例函数与几何综合(讲义)一、知识点睛反比例函数与几何综合的解题思路:1. 抓住_______.“关键点”是信息汇聚点,通常是_________和________的______.通过___________和____________的互相转化可将_________与_________综合在一起进行研究. 2. 梳理题干中的条件,__________.3. 集中到___________或__________建等式求解. 二、精讲精练1. 如图,已知第一象限内的图象是反比例函数1y x=图象的一个分支,第二象限内的图象是反比例函数2y x=-图象的一个分支,在x 轴上方有一条平行于x 轴的直线l 与它们分别交于点A ,B ,过点A ,B 作x 轴的垂线,垂足分别为点C ,D .若四边形ACDB 的周长为8,且AB <AC ,则点A 的坐标是_____________.第1题图 第2题图 第4题图2. 如图,正方形OAPB 的顶点B 以及等腰直角三角形AFD 的顶点A ,D 在坐标轴上,点P ,F 在函数9y x=(x >0)的图象上,则点F 的坐标为________.3. 正方形A 1B 1P 1P 2的顶点P 1,P 2在反比例函数2y x=(x >0)的图象上,顶点A 1,B 1分别在x 轴、y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数xy 2=(x >0)的图象上,顶点A 2在x 轴的正半轴上,则点P 3的坐标为____________.4. 如图,已知动点A 在函数4y x=(x >0)的图象上,AB x ⊥轴于点B ,AC y⊥轴于点C ,延长CA 至点D ,使AD =AB ,延长BA 至点E ,使AE =AC .直线DE 分别交x 轴、y 轴于点P ,Q .当QE :DP =4:9时,图中阴影部分的面积等于_________.5. 如图,□A B C D 的顶点A ,B 的坐标分别是A (-1,0),B (0,-2),顶点C ,D 在双曲线ky x=(x >0)上,边AD 交y 轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k=_______.第5题图6.如图,点A(x1,y1),B(x2,y2)均在双曲线kyx=(x>0)的图象上,且214x x-=,122y y-=.分别过点A,B向x轴、y轴作垂线段,垂足分别为C,D,E,F.AC与BF相交于点G,若四边形FOCG的面积为2,五边形AEODB的面积为14,则双曲线的解析式为____________________.7.如图,双曲线kyx=经过点A(2,2)与点B(4,m),则△AOB的面积为___________.第7题图第8题图8.如图,正比例函数y=kx(k>0)与反比例函数1yx=的图象交于A,C两点,过点A作x轴的垂线,交x轴于点B,过点C作x轴的垂线,交x轴于点D.连接AD,BC,则四边形ABCD的面积为____________.9.两个反比例函数kyx=(k>1)和1yx=在第一象限内的图象如图所示,点P 在kyx=的图象上,PC⊥x轴于点C,交1yx=的图象于点A,PD⊥y轴于点D,交1yx=的图象于点B,当点P在kyx=的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是____________(填写序号).10.如图,一次函数y ax b=+的图象与x轴、y轴交于A,B两点,与反比例函数kyx=的图象交于C,D两点,过C,D两点分别作y轴,x轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论: ①△DEF 与△CEF 的面积相等;②△AOB ∽△FOE ; ③△DCE ≌△CDF ;④AC =BD .其中正确的结论是____________(填写序号).第10题图 第11题图11. 如图,M为双曲线y =M 作x 轴、y 轴的垂线,分别交直线y =-x +m 于D ,C 两点,若直线y =-x +m 与y 轴交于点A ,与x 轴交于点B ,则AD ·BC 的值为_____.12. 如图,直线y =-x +6与x 轴、y 轴分别交于A ,B 两点,P 是反比例函数4y x=(x >0)图象上位于直线下方的一点,过点P 作x 轴的垂线,垂足为点M ,交AB 于点E ,过点P 作y 轴的垂线,垂足为点N ,交AB 于点F .则AF BE ⋅=________.【参考答案】 知识点睛1.关键点,函数图象,几何图形,交点,关键点坐标,横平竖直线段长,函数特征,几何特征2.依次转化3.函数特征,几何特征精讲精练1.(13,3)2.(32+32-+) 3.11) 4.1335.12 6.6y x= 7.38.2 9.①②④ 10.①②④ 11.12.8。
反比例函数与几何综合 (通用版)(含答案)

反比例函数与几何综合(通用版)试卷简介:反比例函数与几何综合一、单选题(共8道,每道10分)1.如图,在平面直角坐标系中,直线y=-3x+3与x轴,y轴分别交于A,B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是( )A.1B.2C.3D.4答案:B解题思路:如图,作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F.根据题意可得,A(1,0),B(0,3),△CEB≌△BOA≌△AFD.∴BE=OA=DF=1,CE=OB=AF=3,∴OF=OE=4,∴C(3,4),D(4,1),k=1×4=4.∵平移后点C的纵坐标为4,∴平移后点C的横坐标为1,∴a=3-1=2.试题难度:三颗星知识点:反比例函数与几何综合2.如图,反比例函数(x>0)的图象与矩形OABC的边AB,BC分别交于点E,F,且AE=BE, 则△OEF的面积为( )A.3B.C. D.答案:C解题思路:由反比例函数常用模型知道,若点E是BA中点,则点F是线段BC的中点,,,,∴.试题难度:三颗星知识点:反比例函数与几何综合3.如图,正方形ABCD的边AB在x轴的正半轴上,C(2,1),D(1,1).反比例函数的图象与边BC交于点E,与边CD交于点F.已知BE:CE=3:1,则DF:FC等于( )A.4:1B.3:1C.2:1D.1:1答案:D解题思路:方法一:易知点E,则反比例函数为,∴点,,∴DF:FC=1:1.方法二:如图,延长CD交y轴于点G,连接FE,BG.由反比例函数常见模型,可知FE∥BG,∴△CFE∽△CGB,∴,∵,易求∴DF:FC=1:1.试题难度:三颗星知识点:反比例函数与几何综合4.如图,在函数(x<0)和(x>0)的图象上,分别有A,B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,已知,,则线段AB的长度为( )A. B.C. D.答案:D解题思路:由,得.∴两反比例函数的解析式为,设B点坐标为(t>0),∵AB∥x轴,∴A点坐标为.由题意,可证得Rt△AOC∽Rt△OBC,∴OC:BC=AC:OC,即,∴,∴,,∴.试题难度:三颗星知识点:反比例函数与几何综合5.如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(8,4).将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数的解析式为( )A. B.C. D.答案:B解题思路:只需求出点D的坐标即可.如图,连接OB,∵∴∵OC=AB=4,∴CD=2,即点D(2,4),∴.试题难度:三颗星知识点:反比例函数与几何综合6.如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B,C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将菱形OABC沿直线OD翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且.若某反比例函数的图象经过点,则这个反比例函数的解析式为( )A. B.C. D.答案:D解题思路:连接CD,由折叠性质可知,,∴点A与点D重合.如图所示:根据题意可求得,点B的坐标为,∴点的坐标为,∴经过点的反比例函数的解析式为.试题难度:三颗星知识点:反比例函数与几何综合7.如图,直线与双曲线(k>0)在第一象限内的交点为R,与x轴的交点为P,与y轴的交点为Q;作RM⊥x轴于点M,若△OPQ与△PRM的面积之比为4:1,则k的值为( )A. B.C.2D.3答案:B解题思路:由题意可知点,点易知△OPQ与△MPR相似,且相似比为2:1,∴,∴点,则试题难度:三颗星知识点:反比例函数与几何综合8.函数y=x的图象与函数的图象在第一象限内交于点B,点C是函数在第一象限图象上的一个动点,当△OBC的面积为3时,点C的坐标是( )A. B.C. D.答案:D解题思路:在x轴上找到点D使得△OBD的面积为3,过点D作OB的平行线,根据平行线间的距离处处相等及同底等高转化面积可知,平行线与反比例函数图象的交点即为要求的点C.如图,CD∥OB,由,点B的纵坐标为2,得OD=3,∴D(3,0).由CD∥OB可设直线CD的函数解析式为y=x+b,把D点坐标代入可得b=-3,∴直线CD的函数解析式为y=x-3.联立直线CD和反比例函数的解析式可求得C(4,1).同理可求得,直线的函数解析式为y=x+3,联立直线和反比例函数的解析式可求得.试题难度:三颗星知识点:反比例函数与几何综合二、填空题(共2道,每道10分)9.如图,矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,直线经过点C,交x轴于点E,双曲线经过点D,则k=____.答案:1解题思路:∵点C的纵坐标为1,则点,∴OB=4,∵AB=3,BC=1,∴D(1,1),∴.试题难度:知识点:反比例函数图象上点的坐标特征10.如图,已知四边形ABCD是平行四边形,BC=2AB.A,B两点的坐标分别是(-1,0),(0,2),C,D两点在反比例函数(k<0)的图象上,则k=____.答案:-12解题思路:题目当中关键点是点C和点D,我们需要建立等式来求解,题干中给出建等式的信息有三点:①点C,D都在反比例函数的图象上;②四边形ABCD是平行四边形,可以利用对边相等等条件建立等式;③BC=2AB,可以用来建等式.设点C的坐标是,过点C作x轴的垂线,过点D作y轴的垂线,两垂线交于点E,如图所示:易证得△CED≌△BOA,则DE=1,CE=2,∴点D的坐标是.∵点D在反比例函数的图象上,∴(此时利用①②两个条件);由于DA=BC=2AB=,点D,点A(-1,0),构造直角三角形,利用勾股定理可以得到,整理我们可以得到,将其代入可以得到,∵,∴,∴.试题难度:一颗星知识点:反比例函数与几何综合第 11 页共 11 页。
反比例函数与几何的综合应用(教案)

四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《反比例函数与几何的综合应用》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要根据面积或比例来求解问题的情况?”比如,我们如何根据已知的长和宽来求解矩形的面积。这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索反比例函数在几何问题中的奥秘。
3.重点难点解析:在讲授过程中,我会特别强调反比例函数的性质和图像,以及它在几何问题中的应用这两个重点。对于难点部分,比如反比例函数与一次函数的交点求解,我会通过具体例题和逐步解析来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与反比例函数在几何问题中应用相关的实际问题。
三、教学难点与重点
1.教学重点
(1)反比例函数的定义及其性质:反比例函数的定义,图像特点,以及其在实际中的应用。
举例:y = k/x(k≠0),解释k的取值对函数图像的影响,如k>0时图像位于一、三象限,k<0时图像位于二、四象限。
(2)反比例函数与其他函数的交点问题:分析反比例函数与一次函数、二次函数的交点情况,掌握求解方法。
(二)新课讲授(用时10形如y = k/x(k≠0)的函数,它的图像是一条经过原点的曲线。反比例函数在解决与比例相关的问题时非常重要。
2.案例分析:接下来,我们来看一个具体的案例。这个案例将展示如何利用反比例函数来求解矩形的面积,以及它如何帮助我们解决实际问题。
此外,我在课堂上尝试引导同学们提出问题、分析问题并解决问题,目的是培养他们的独立思考能力。但从实际情况来看,同学们在这一方面的表现还不够理想。因此,我计划在接下来的教学中,进一步加强这方面的训练,鼓励同学们敢于提问、善于提问。
反比例函数+反比例函数与几何的综合应用课件+2022--2023学年沪科版数学九年级上册

求出旋转后的对应点,关注点与反比例函数图象之间的位置关系,即可轻松解题.
例
如图直线
y
1 2
x
1
与反比例函数 y
k x
(x<0)的图象交于点A,与x轴交于点B,BC垂直于
y
x轴,交双曲线于点C,若AB=AC,求k的值.
分析
△ABC为等腰三角形
C点的纵坐标可以用k来表示
过点A作AD垂直于BC
C
A
D
B
O
例函数图象恰好过点D时,求此反比例函数解析式.
y
E
解答 设DB与y轴交于点F,
∴DF=DB﹣BF=4﹣1=3,
∴D(﹣3,4), k
设反比例解析式为y=x , ∴k=﹣3×4=﹣12. ∴此反比例函数解析式是y=﹣12.
x
D
y k x
B
F
C
OA
x
三角形的旋转与反比例函数相结合,一般处理方法,考虑图形的旋转实质上为点的旋转,
D
EC
20
8
C.(3, 3 ) D.(3, 3 )
B AF
O
x
解答 如图,过点C作CF⊥AB于点F,
∵四边形ABCD是菱形, ∴AB=BC,CD∥AB,
∵∠CEA=90°, ∴∠EAB=90°,又∵∠CEA=90°,CF⊥AB,
∴四边形CEAF是矩形, ∴AE=CF,CE=AF,
∵点B的横坐标为5,AE=2CE, ∴AB=BC=5,CF=2CE,BF=5﹣CE,
AB=4,△ABC的面积为2,将△ABC以点B为旋转中心,顺时针旋转90°得到△DBE,一反比
例函数图象恰好过点D,求此反比例函数解析式.
分析
点A绕着点B顺时针旋转90度得到点D
北师大版九年级上册数学 反比例函数与几何综合(同步)

模块一 反比例函数k 的几何意义1.反比例函数k 的几何意义:如图,在反比例函数图象上任选一点,向两坐标轴作垂线,垂线与坐标轴所围成矩形的面积为k 。
如图二,所围成三角形的面积为2k2.如图,四条双曲线1C 、2C 、3C 、4C 对应的函数解析式分别为:1k y x =、2k y x =、3k y x =、4ky x=,那么1k 、2k 、3k 、4k 的大小顺序为1234k k k k <<<模块二 反比例函数与面积的综合1.若所求图形面积是规则图形,则可以按照相应图形的面积公式直接计算2.若所求图形面积是不规则图形,则采用割补法3.转化面积时,注意观察是否需要使用反比例函数k 的几何意义模块三 反比例函数与其他几何问题1.反比例函数与等腰三角形(1).涉及一般等腰三角形存在性的问题,注意需要分类讨论, (2).如果有等腰直角三角形或者等边三角形,注意考虑它的特殊性质 2.利用k 的几何意义进行面积转化 (1).如图直线AB 与反比例函数ky x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCD OBD OAC S S S S ∆∆∆∆=--,此方法是绝大部分学生选用的方法。
但是,从效率来讲,就比较低Oy xBAABx y OC C 3C 2C 1G F E D CB A Oyx反比例函数与几何综合 新知学习(2).如图,过点A 、B 作x 轴的垂线,垂足分别为E 、F ,则根据k 的几何意义可得,OBF OAE S S ∆∆=,而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形,所以OAB ABFE S S ∆=梯形,此方法的好处,在于方便,快捷,不易出错。
3.k 的几何意义与双曲线的对称性 (1).如图一,直线AB 与反比例函数ky x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCA OCB ODB ODA S S S S S ∆∆∆∆∆=+=+,此两种方法是绝大部分学生选用的方法。
反比例函数与几何综合

个性化教案教学目标1、熟练掌握反比例函数的性质与图像特征2、强化反比例函数与其它几何问题的综合分析方法。
难点重点重难点:反比例函数与几何综合问题的分析教学内容一、反比例函数的定义函数kyx=(k为常数,0k≠)叫做反比例函数,其k中叫做比例系数,x是自变量,y是函数,自变量x的取值范围是不等于0的一切实数.二、反比例函数的图象反比例函数kyx=(k为常数,0k≠)的图象由两条曲线组成,每条曲线随着x的不断增大(或减小)越来越接近坐标轴,反比例函数的图象属于双曲线.反比例函数kyx=与kyx=-(0k≠)的图象关于x轴对称,也关于y轴对称.三、反比例函数的性质反比例函数kyx=(k为常数,0k≠)的图象是双曲线;当0k>时,函数图象的两个分支分别位于第一、三象限内,它们关于原点对称,在每一个象限内,y 随x的增大而减小;当0k<时,函数图象的两个分支分别位于第二、四象限内,它们关于原点对称,在每一个象限内,y 随x的增大而增大.注意:⑴反比例函数kyx=(0k≠)的取值范围是0x≠.因此,①图象是断开的两条曲线,画图象时,不要把两个分支连接起来.②叙述反比例函数的性质时,一定要加上“在每一个象限内”,如当0k>时,双曲线kyx=的两支分别在一、三象限,在每一个象限内,y随x的增大而减小.这是由于0x≠,即0x>或0x<的缘故.如果笼统地叙述为0k<时,y随x的增大而增大就是错误的.⑵由于反比例函数中自变量x和函数y的值都不能为零,所以图象和x轴、y轴都没有交点,但画图时要体现出图象和坐标轴无限贴近的趋势.⑶在画出的图象上要注明函数的解析式.四、反比例函数解析式的求法反比例函数的解析式(0)ky kx=≠中,只有一个系数k,确定了k的值,也就确定了反比例函数的解析式.因此,只需给出一组x、y的对应值或图象上一点的坐标,利用待定系数法,即可确定反比例函数的解析式.五、比例系数k 的几何意义过反比例函数()0ky k x=≠,图象上一点()P x y ,,做两坐标轴的垂线,两垂足、原点、P 点组成一个矩形,矩形的面积S x y xy k =⋅==.一、反比例函数与几何综合【例1】 已知点(1,3)在函数ky x=(0x >)的图像上,矩形ABCD 的边BC 在x 轴上,E 是对角线BD 的 中点,函数ky x=(0x >)的图像经过A 、E 两点,若45ABD ∠=︒,求E 点的坐标. EDCBAOxy【例2】 如图,点A (m ,1m +),B (3m +,1m -)都在反比例函数ky x=的图象上. (1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点,以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式.BAOyx例题精讲【例3】 如图,11POA ∆、212P A A ∆都是等腰直角三角形,点1P 、2P 在函数4y x=(0x >)的图像上,斜边1OA 、12A A 、都在x 轴上,求点2A 的坐标.A 2A 1P 2P 1Oxy【例4】 如图,P 是函数12y x=(0x >)图象上一点,直线1y x =-+交x 轴于点A ,交y 轴于点B ,PM Ox ⊥轴于M ,交AB 于E ,PN Oy ⊥轴于N ,交AB 于F .求AF BE ⋅的值.EF P N B M AxyO【例5】 已知:等腰三角形OAB 在直角坐标系中的位置如图,点A 的坐标为()333-,,点B 的坐标为()60-,. (1)若三角形OAB 关于y 轴的轴对称图形是三角形OA B '',请直接写出A 、B 的对称点A '、B '的坐标;(2)若将三角形OAB 沿x 轴向右平移a 个单位,此时点A 恰好落在反比例函数63y x=的图像上,求a 的值;(3)若三角形OAB 绕点O 按逆时针方向旋转α度(090α<<).当α=30 时点B 恰好落在反比例函数ky x=的图像上,求k 的值.-6OBxy A【例6】 过原点作直线交双曲线ky x=(0k >)于点A 、C ,过A 、C 分别作两坐标轴的平行线,围成矩形 ABCD ,如图所示.⑴知矩形ABCD 的面积等于8,求双曲线的解析式;⑵若已知矩形ABCD 的周长为8,能否由此确定双曲线的解析式?如果能够确定,请予求出;如果不能确定,试说明原因.CBAD xy O【例7】 如图,已知正方形OABC 的面积为9,点O 为坐标原点,点A 在x 轴上,点C 在y 轴上,点B 在函数ky x=(0k >,0x >)的图像上,点P (m ,n )为其双曲线上的任一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F ,并设矩形OEPF 和正方形OABC 不重合部分的面积为S .⑴求B 点的坐标和k 的值;⑵当92S =时,求P 点坐标;⑶写出S 关于m 的函数关系式.P S F EOC BAyx【例8】 已知图中的曲线是反比例函数5m y x-=(m 为常数)图象的一支. ⑴这反比例函数图象的另一支在第几象限?常数m 的取值范围是什么?⑵若该函数的图象与正比例函数2y x =的图象在第一象内限的交点为A ,过A 点作x 轴的垂线,垂足为B ,当OAB ∆的面积为4时,求点A 的坐标及反比例函数的解析式.Oyx【例9】 两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x=的图象上,PC x ⊥轴于点C ,交1y x =的图象于点A ,PD y ⊥轴于点D ,交1y x =的图象于点B ,当点P 在k y x=的图象上运动时,以下结论: ①ODB ∆与OCA ∆的面积相等; ②四边形PAOB 的面积不会发生变化; ③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分).y=k x P By=1xx yOCDA【例10】 两个反比例函数1k y x =和()2120k y k k x=>>在第一象限内的图象如图所示,动点P 在1k y x =的图象上,PC x ⊥轴于点C ,交2k y x =的图象于点A ,PD y ⊥轴于点D ,交2ky x=的图象于点B .⑴求证:四边形PAOB 的面积是定值; ⑵当23PA PC =时,求DBBP的值; ⑶若点P 的坐标为()52,,OAB ABP ∆∆,的面积分别记为OAB S ∆、ABP S ∆,设ABP OAB S S S ∆∆-=.①求1k 的值;②当2k 为何值时,S 有最大值,最大值为多少?y=k 2xy=k 1xP DyxO CBA【例11】 如图,点A 、B 在反比例函数ky x=(0k >)的图象上,且点A 、B 的横坐标分别为a 和2a (0a >)AC x ⊥轴,垂足为C ,AOC ∆的面积为2. (1)求反比例函数的解析式;(2)若点(a -,1y ),(2a -,2y )也在反比例函数的图象上,试比较1y 与2y 的大小; (3)求AOB ∆的面积.xyOCBA【例12】 已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与B C ,重合),过F 点的反比例函数(0)ky k x=>的图象与AC 边交于点E .(1)求证:AOE △与BOF △的面积相等;(2)记OEF ECF S S S =-△△,求当k 为何值时,S 有最大值,最大值为多少?(3)请探索:是否存在这样的点F ,使得将CEF △沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.xyFECBAO【例13】 如图,反比例函数8y x=的图象过矩形OABC 的顶点B ,OA 、OC 分别在x 轴、y 轴的正半轴上,:2:1OA OC =.(1)设矩形OABC 的对角线交于点E ,求出E 点的坐标; (2)若直线2y x m =+平分矩形OABC 面积,求m 的值.yxOC B A【例14】 若一次函数21y x =-和反比例函数2ky x=的图象都经过点(1,1). (1)求反比例函数的解析式;(2)已知点A 在第三象限,且同时在两个函数的图象上,求点A 的坐标; (3)利用(2)的结果,若点B 的坐标为(2,0),且以点A O B P ,,,为顶点的四边形是平行四边形,请你直接写出点P 的坐标.yxFECBAO【例15】 如图,点()1A m m +,,()31B m m +-,都在反比例函数ky x=的图象上. (1)求m k ,的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A B M N ,,,为顶点的四边形是平行四边形,试求直线MN 的函数表达式.yxOBA【例16】 已知(1)A m -,与(233)B m +,是反比例函数ky x=图象上的两个点. (1)求k 的值;(2)若点(10)C -,,则在反比例函数ky x=图象上是否存在点D ,使得以A B C D ,,,四点为顶点的四边形为梯形?若存在,求出点D 的坐标;若不存在,请说明理由.yxBA-111-1C【例17】 如图,已知反比例函数12y x=的图象和一次函数7y kx =-的图象都经过点()2P m ,.①求这个一次函数的解析式;②如果等腰梯形ABCD 的顶点A B ,在这个一次函数图象上,顶点C D ,在这个反比例函数图象上,两底AD ,BC 与y 轴平行,且A 和B 的横坐标分别为a 和2a +,求a 的值。
反比例函数与几何综合
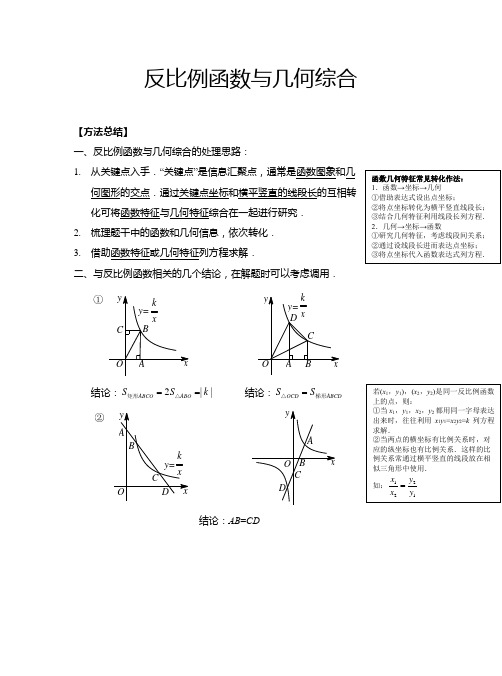
反比例函数与几何综合【方法总结】一、反比例函数与几何综合的处理思路:1. 从关键点入手.“关键点”是信息汇聚点,通常是函数图象和几何图形的交点.通过关键点坐标和横平竖直的线段长的互相转化可将函数特征与几何特征综合在一起进行研究. 2. 梳理题干中的函数和几何信息,依次转化. 3. 借助函数特征或几何特征列方程求解.二、与反比例函数相关的几个结论,在解题时可以考虑调用.结论: 结论:结论:AB =CD①2||ABO ABCO S S k ==△矩形OCD ABCD S S =△梯形②结论:BD ∥CE 【典型例题】1. 如图,在x 轴正半轴上依次截取,过分别作x 轴的垂线与的图象相交于点,得直角三角形.求这5个直角三角形的面积之和.2. 如图,A ,B 是双曲线(k <0)上的点,且A ,B 两点的横坐标分别为a ,2a ,线段AB 的延长线交x 轴于点C .若S △AOC =9,则k =________.3. 如图,反比例函数的图象经过矩形OABC 对角线的交点M ,分别与AB ,BC 相交于点D ,E .若四边形ODBE 的面积为6,则k 的值为________.③112233445OA A A A A A A A A ====12345,,,,A A A A A 2y x=12345,,,,P P P P P 11122233344455,,,,OPA A P A A P A A P AA P A ky x=0ky x x=>()4. 如图,若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数()的图象上,则点E 的坐标是________.5. 如图,直线与双曲线(x >0)交于点.将直线向右平移个单位后,与双曲线(x >0)交于点,与x 轴交于点,若,则k =________.6. 如图,在平面直角坐标系中有Rt △ABC ,∠CAB =90°,AB =AC ,A (-1,0),B (1,1),将△ABC 沿x 轴的正方向平移,在第一象限内B ,C 两点的对应点B 1,C 1正好落在反比例函数的图象上,则k =__________.1y x=0x>43x y =k y x =A 43x y =92ky x =B C 2AO BC=xky x=7. 如图,平行四边形OABC 的顶点O 在坐标原点,顶点A ,C 在反比例函数(x >0)的图象上,点A 的横坐标为4,点B 的横坐标为6,且平行四边形OABC 的面积为9,则k 的值为_________.8. 如图,一次函数的图象与x 轴,y 轴分别交于A ,B 两点,与反比例函数的图象交于C ,D 两点,过C ,D 两点分别作y 轴,x 轴的垂线,垂足为点E ,F ,连接CF ,DE .有下列四个结论: ①△DEF 与△CEF 的面积相等;②△AOB ∽△FOE ;③△DCE ≌△CDF ;④AC =BD . 其中正确的结论序号是___________.k y x=y ax b =+ky x=。
反比例函数与几何图像综合
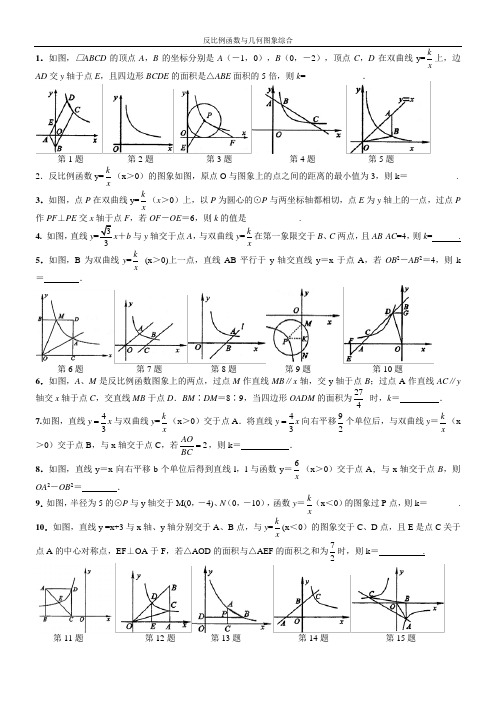
1.如图,□ABCD 的顶点A ,B 的坐标分别是A (-1,0),B (0,-2),顶点C ,D 在双曲线y=kx上,边AD 交y 轴于点E ,且四边形BCDE 的面积是△ABE 面积的5倍,则k =_____________.第1题 第2题 第3题 第4题 第5题2.反比例函数y=kx(x >0)的图象如图,原点O 与图象上的点之间的距离的最小值为3,则k =___________.3.如图,点P 在双曲线y=kx(x >0)上,以P 为圆心的⊙P 与两坐标轴都相切,点E 为y 轴上的一点,过点P作PF ⊥PE 交x 轴于点F ,若OF -OE =6,则k 的值是____________.4. 如图,直线y 33x +b 与y 轴交于点A ,与双曲线y =kx在第一象限交于B 、C 两点,且AB ·AC =4,则k = .5.如图,B 为双曲线y =kx(x >0)上一点,直线AB 平行于y 轴交直线y =x 于点A ,若OB 2-AB 2=4,则k= .第6题 第7题 第8题 第9题 第10题轴交x 轴于点C ,交直线MB 于点D .BM ∶DM =8∶9,当四边形OADM 的面积为274时,k = .7.如图,直线43y x =与双曲线y =k x (x >0)交于点A .将直线43y x =向右平移92个单位后,与双曲线y =kx(x>0)交于点B ,与x 轴交于点C ,若2AOBC=,则k = _____ .8.如图,直线y =x 向右平移b 个单位后得到直线l ,l 与函数y =6x(x >0)交于点A ,与x 轴交于点B ,则OA 2-OB 2= .9.如图,半径为5的⊙P 与y 轴交于M(0,-4)、N (0,-10),函数y =kx(x <0)的图象过P 点,则k =_______.10.如图,直线y =x+3与x 轴、y 轴分别交于A 、B 点,与y =kx(x <0)的图象交于C 、D 点,且E 是点C 关于点A 的中心对称点,EF ⊥OA 于F ,若△AOD 的面积与△AEF 的面积之和为72时,则k = .第11题 第12题 第13题 第14题 第15题11.如图,正方形ABCD 的边BC在x 轴负半轴上,E(-6,n)是对角线AC 的中点,函数y =kx(x <0)的图象经过D 、E 两点,则k =_________.12.如图,已知双曲线y =kx(k >0)经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若△OBC的面积为3,则k =_________.13.如图,已知点A 、B 在双曲线y=kx(k >0)上,AC ⊥x 轴于点C ,BD ⊥y 轴于点D ,AC 与BD 交于点P ,P是AC 的中点,若△ABP 的面积为3,则k =_______________.14.如图,直线y =kx +b 与x 轴、y 轴交于点A 、B ,与双曲线10y x=交于C ,若BC =2AB ,则S △AOB =______________.15.如图,y =k x (k <0)与直线y =-x +(k +1)交于A 、C 两点,AB ⊥x 轴于B 点,且S △ABO =32,则S △ABC =________.16. 过点A (1,2)的直线与双曲线xy 2=在第一象限内交于点P ,直线AO 交双曲线的另一分支于点B ,且点C (2,1).(1)如图,当点P 与C 重合时,P A 、PB 分别交y 轴于点E 、F .求证:CE =CF ;(2)当点P 异于A 、C 时,探究∠P AC 与∠PBC 的数量关系,请直接写出结论不必证明.17.如图,正方形AOCB 的边长为4,反比例函数的图象过点E (3,4). (1)求反比例函数的解析式;(2)反比例函数的图象与线段BC 交于点D ,直线12y x b =-+过点D ,与线段(3)连接OF ,OE ,探究∠AOF 与∠EOC 的数量关系,并证明.。
反比例函数与几何综合

反比例函数与几何综合
连接中考:
反比例函数在中考中通常以填空和压轴题形式出现:通常会结合几何图形一起考查,或者解答题中结合常见的动点、平移、存在性问题等形式出现,一般难度较大,对学生的知识要求比较高!
知识点睛:
反比例函数与几何综合的处理思路
1从关键点入手:从关键点坐标和横平竖直线段长的相互转化,可将函数特征与几何特征综合在一起研究;
2对函数特征和几何特征进行转化、组合,列方程求解,若借助反比例模型,能快速将函数特征转化成几何特征与反比例特征相关的几个模型,在解题时可以考虑调用。
经典例题:
勾股定理中常见的玄图又出现了,解答此类题目几何特征与函数特征都十分重要,反比例函数综合题中常用的方法有:1设点法(设而不求)2特殊值法3转化法等,学生在学习反比例时特别要注意知识点间结合的综合运用!。
反比例函数与几何的综合应用讲义+2023-2024学年人教版数学九年级下册

反比例函数与几何的综合应用点石成金解反比例函数与几何图形的综合题,一般先设出几何图形中的未知量,然后结合函数的图象用代数式表示出几何图形与图象的交点坐标,再由函数解析式及几何图形的性质写出含未知数及待定字母的方程(组) ,解方程(组) 即可得所求几何图形中的未知量或函数解析式中待定字母的值.经典实例剖析如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y=k(k为常数,k≠0)的图象经x过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.(1)求函数y=k的表达式,并直接写出E、F两点的坐标;x(2)求△AEF的面积.分析:(1)根据正方形的性质,以及函数上点的坐标特征可求点D的坐标为(1,2),根据待定系数法可求反比例函数表达式,进一步得到E、F两点的坐标;(2)过点F作FG⊥AB,与AB的延长线交于点G,根据两点间的距离公式可求AE=1,FG=3,再根据三角形面积公式可求△AEF的面积.解:(1)∵正方形OABC的边长为2,∴点D的纵坐标为2,即y=2,将y=2代入y=2x,得x=1,∴点D的坐标为(1,2),的图象经过点D,∵函数y=kx,∴2=k1解得k =2,∴函数y =k x 的表达式为y =2x ,∴E (2,1),F (﹣1,﹣2);(2)过点F 作FG ⊥AB ,与BA 的延长线交于点G ,∵E (2,1),F (﹣1,﹣2),∴AE =1, FG =2﹣(﹣1)=3,∴△AEF 的面积为:12AE •FG =12×1×3=32.分类训练应用1 反比例函数与三角形的综合1.如图,一次函数y =kx +94(k 为常数,k ≠0)的图象与反比例函数y =m x (m 为常数,m ≠0)的图象在第一象限交于点A (1,n ),与x 轴交于点B (﹣3,0).(1)求一次函数和反比例函数的解析式.(2)点P 在x 轴上,△ABP 是以AB 为腰的等腰三角形,请直接写出点P 的坐标.应用2 反比例函数你与四边形的综合类型1 反比例函数与平行四边形的综合2.如图,一次函数y =kx +b 的图象与反比例函数y =m x 的图象相交于A (﹣1,4),B (a ,﹣1)两点.(1)求反比例函数和一次函数的表达式;的图象于点Q,连接PQ.当(2)点P(n,0)在x轴负半轴上,连接AP,过点B作BQ∥AP,交y=mxBQ=AP时,求n的值.类型2反比例函数与矩形的综合(k<0)的图象与矩形ABCO的边相交于E、F两点,且BE=2AE,E(﹣1,3.如图,反比例函数y=kx2).(1)求直线EF的解析式;(2)连接EF,求△BEF的面积.类型3反比例函数与菱形的综合4.如图,在直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反(k>0,x>0)的图象上,点D的坐标为(4,3).比例函数y=kx(1)求k的值.(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在该函数的图象上时,求菱形ABCD沿x轴正方向平移的距离.类型4反比例函数与正方形的综合5.如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,(x>0,k≠0)的图象经过线段BC的中点D.点B的坐标为(2,2),反比例函数y=kx(1)求k的值;(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.应用3反比例函数与菱形、正方形的综合6.如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=2OB,反比例函数y=27x 在第一象限的图象经过正方形的顶点C.(1)求点C的坐标;(2)如图2,将正方形ABCD沿x轴向右平移得到正方形A'B'CD',点A'恰好落在反比例函数的图象上,求此时点D'的坐标;(3)在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.应用4 反比例函数与正六边形的综合(k>0,x>0)7.如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数y=kx的图象上,边CD在x轴上,点B在y轴上,已知CD=2.(1)点A是否在该反比例函数的图象上?请说明理由;(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标;(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模块一 反比例函数k 的几何意义1.反比例函数k 的几何意义:如图,在反比例函数图象上任选一点,向两坐标轴作垂线,垂线与坐标轴所围成矩形的面积为k 。
如图二,所围成三角形的面积为2k2.如图,四条双曲线1C 、2C 、3C 、4C 对应的函数解析式分别为:1k y x =、2k y x =、3k y x =、4ky x=,那么1k 、2k 、3k 、4k 的大小顺序为1234k k k k <<<模块二反比例函数与面积的综合1.若所求图形面积是规则图形,则可以按照相应图形的面积公式直接计算2.若所求图形面积是不规则图形,则采用割补法3.转化面积时,注意观察是否需要使用反比例函数k 的几何意义模块三反比例函数与其他几何问题1.反比例函数与等腰三角形(1).涉及一般等腰三角形存在性的问题,注意需要分类讨论, (2).如果有等腰直角三角形或者等边三角形,注意考虑它的特殊性质 2.利用k 的几何意义进行面积转化 (1).如图直线AB 与反比例函数ky x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCD OBD OAC S S S S ∆∆∆∆=--,此方法是绝大部分学生选用的方法。
但是,从效率来讲,就比较低Oy xBAABx y OC 4C 3C 2C 1G F E D CB A Oyx反比例函数与几何综合 新知学习(2).如图,过点A 、B 作x 轴的垂线,垂足分别为E 、F ,则根据k 的几何意义可得,OBF OAE S S ∆∆=,而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形,所以OAB ABFE S S ∆=梯形,此方法的好处,在于方便,快捷,不易出错。
3.k 的几何意义与双曲线的对称性 (1).如图一,直线AB 与反比例函数ky x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCA OCB ODB ODA S S S S S ∆∆∆∆∆=+=+,此两种方法是绝大部分学生选用的方法。
常规方法,费时、费力、而且还易计算出错。
(2).如图二,我们知道反比例函数的图象是双曲线,关于原点成中心对称,那么延长BO 交双曲线于点E ,连接AE 、则OB OE =,OAB OAE S S ∆∆=,因此可以将OAE ∆的面积转化为梯形的面积一.反比例函数k 的几何意义1.利用k 的几何意义求参数的数值或比较参数大小【例1】 如图,点P 在反比例函数的图像上,过P 点作PA x ⊥轴于A 点,作PB y ⊥轴于B 点,矩形OAPB 的面积为9,则该反比例函数的解析式为yxABOCDyx DC FEO B ADCBAOyxExyOABCDOA B Pxy基础演练【练一练】反比例函数xky =的图像如图所示,点M 是该函数图像上一点,MN 垂直于x 轴,垂足是点N ,如果2MON S ∆=,则k 的值为()A. 2B. 2-C. 4D. 4-【例2】 如图,在Rt AOB ∆中,点A 是直线y x m =+与双曲线my x=在第一象限的交点,且2AOB S ∆=,则m 的值是_____.【例3】 如图,正比例函数y kx =和y ax =(0a >)的图像与反比例函数ky x=(0k >)的图像分别相交于A 点和C 点.若Rt AOB ∆和Rt COD ∆的面积分别为1S 和2S ,则1S 与2S 的关系是()A .12S S >B .1S =2SC .1S <2SD .不能确定【练一练】在函数ky x=(0x >)的图像上取三点A 、B 、C ,由这三点分别向x 轴、y 轴作垂线,设矩形12AA OA 、12BB OB 、12CC OC 的面积分别为A S 、B S 、C S ,试比较三者大小.NM Oxy OCBAyxOyxDBCAy xOC 1B 1A 1C 2B 2A 2CBA【解析】设点A 的坐标为(a ,b ),因为点A 在双曲线k y x =上,所以k b a =,即ab k =.因为A 在第一象限内,所以11A S OA A A ab k=⋅==,同理可得A B C S S S k===.由此我们可以得到一个结论: 在反比例函数ky x =(0k ≠)中,具有矩形面积的不变性,即121212AA OA BB OB CC OC S S S k ===.在此基础上可以推得:梯形面积的不变性,即2211AA B B AA B BS S =由上题结论可推得:梯形面积与三角形面积的不变性:AOBABFE S S ∆=梯形1122ABFOC ACOE ABFOC ACOE BDOF ABFOC ACO BOF AOBABFE S S S S S S S S S S ∆=-=--=--=梯形 【答案】A B C S S S == 2.反比例函数与方程的思想 【例4】 已知点(1,3)在函数ky x=(0x >)的图像上,矩形ABCD 的边BC 在x 轴上,E 是对角线BD 的中点,函数ky x=(0x >)的图像经过A 、E 两点,若45ABD ∠=︒,求E 点的坐标.【解析】方程的思想无处不在,涉及到函数问题的时候,主要是通过等量关系去建立方程,本题方法不唯一【答案】点(1,3)在函数ky x =的图像上,3k =.又E 也在函数k y x =的图像上,故设E 点的坐标为(m ,3m ).过E 点作EF x ⊥轴于F ,则3EF m =.又E 是对角线BD 的中点,62AB CD EF m ===.故A 点的纵坐标为6m ,代入3y x =中,得A 点坐标为 (2m ,6m ). 因此22m m BF OF OB m =-=-=.由45ABD ∠=︒,得45EBF ∠=︒,BF EF =.即有32m m =.解得6m =±.而0m >,故6m =.则E 点坐标为 (6,62).ED xyA BC OF EDxyA B C O二.反比例函数与面积的综合1.一般面积问题【例5】 在平面直角坐标系中,函数ky x=(0x >,常数0k >)的图象经过点A (1,2),B (m ,n ),(1m >),过点B 作y 轴的垂线,垂足为C .若ABC ∆的面积为2,求点B 的坐标.【练一练】如图,直线y kx b =+与反比例函数()10k y x x=<′的图象相交于点A 、点B ,与x 轴交于点C ,其中点A 的坐标为()24-,,点B 的横坐标为4-. (1)试确定反比例函数的关系式; (2)求AOC ∆的面积.【例6】 如图,点A 、B 是双曲线3y x=上的点,分别经过A 、B 两点向x 轴、y 轴作垂线段,若1S =阴影,则12S S +=【练一练】如图,在反比例函数2y x=(0x >)的图象上,有点1P ,2P ,3P ,4P 它们的横坐标依次为1,2,3,4.分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影部分的面积从左到右依次为1S ,2S ,3S ,求123S S S ++.xyAB C OCB A Oxy S 2S 1OBA yx S 3S 2S 1yx4312P 4P 3P 2P 1y =2x【练一练】已知A B C D E,,,,是反比例函数16yx=()0x>图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形,则这五个橄榄形的面积总和是(用含π的代数式表示)【例7】如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数kyx=(0k>,0x>)的图像上,点P(m,n)为其双曲线上的任一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.⑴求B点的坐标和k的值;⑵当92S=时,求P点坐标;⑶写出S关于m的函数关系式.【练一练】如图,反比例函数8yx=的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,:2:1OA OC=.(1)设矩形OABC的对角线交于点E,求出E点的坐标;(2)若直线2y x m=+平分矩形OABC面积,求m的值.y=16xEDCBAyx OyxEPBFCAOyxBAOC2.利用k 的几何意义进行面积转化【例8】 如图,在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A ,,,,分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P ,,,,,得直角三角形1112233344455OP A A P A A P A A P A A P A 2,,,,,并设其面积分别为12345S S S S S ,,,,,则5S 的值为.【例9】 两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在ky x =的图象上,PC x ⊥轴于点C ,交1y x =的图象于点A ,PD y ⊥轴于点D ,交1y x =的图象于点B ,当点P 在ky x=的图象上运动时,以下结论:①ODB ∆与OCA ∆的面积相等; ②四边形PAOB 的面积不会发生变化; ③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是(把你认为正确结论的序号都填上,少填或错填不给分).【练一练】如图,点A 、B 在反比例函数ky x=(0k >)的图象上,且点A 、B 的横坐标分别为a 和2a (0a >)AC x ⊥轴,垂足为C ,AOC ∆的面积为2.(1)求反比例函数的解析式;(2)若点(a -,1y ),(2a -,2y )也在反比例函数的图象上,试比较1y 与2y 的大小; (3)求AOB ∆的面积.y=2xA 5A 4A 3A 2A 1O yxP5P 4P 3P 2P 1y xy=k xy=1xDBP ACO BAOyxDCEBAOyx【练一练】如图,已知双曲线()0ky k x=>经过直角三角形OAB 斜边OB 的中点D ,与直角边AB 相交于点C .若OBC ∆的面积为3,则k =__________.3.k 的几何意义与双曲线的对称性 【例10】 直线y kx =(0k >)与双曲线4y x=交于11(,)A x y 、22(,)B x y 两点,则122127x y x y -的值等于_____________【练一练】已知反比例函数8y x=上两点A ,B 的横坐标分别为2-,8,则OAB ∆的面积为三.反比例函数与其他几何问题【例11】 如图,已知反比例函数12k y x=的图象与一次函数2y k x b =+的图象交于A B ,两点,()1122A n B ⎛⎫-- ⎪⎝⎭,,,.(1)求反比例函数和一次函数的解析式;(2)在x 轴上是否存在点P ,使AOP ∆为等腰三角形?若存在,请你直接写出P 点的坐标;若不存在,请说明理由.【例12】 如图,11POA ∆、212P A A ∆都是等腰直角三角形,点1P 、2P 在函数4y x=(0x >)的图像上,斜边1OA 、12A A 、都在x 轴上,求点2A 的坐标.OEDCBAxyOyxBAA 2A 1P 2P 1Oxy【题1】 (2013•六盘水)下列图形中,阴影部分面积最大的是()A .C .D .A B. C.D.【题2】 (2013•南宁)如图,直线y=与双曲线y=(k >0,x >0)交于点A ,将直线y=向上平移4个单位长度后,与y 轴交于点C ,与双曲线y=(k >0,x >0)交于点B ,若OA=3BC ,则k 的值为()A 3B. 6 C. D.【题3】 如图,正方形OABC ,ADEF 的顶点A 、D 、C 在坐标轴上,点F 在AB 上,点B 、E 在函数1(0)y x x=>的图象上,则点E 的坐标是【题4】 (2013•自贡)如图,在函数的图象上有点P1、P2、P3…、Pn 、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn 、Pn+1分别作x 轴、y 轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn ,则S1=_________,Sn=___________.(用含n 的代数式表示)F EOCA BD xy 课后作业【题5】 (2013•娄底)如图,已知A 点是反比例函数的图象上一点,AB⊥y 轴于B ,且△ABO 的面积为3,则k 的值为___________.【题6】 (2013•内江)如图,反比例函数(x >0)的图象经过矩形OABC 对角线的交点M ,分别于AB 、BC 交于点D 、E ,若四边形ODBE 的面积为9,则k 的值为()A 1B. 2 C.3D. 4【题7】 已知反比例函数2ky x=和一次函数21y x =-,一次函数的图象经过(,)a b 、(1,)a b k ++两点 ⑴求反比例函数的解析式⑵如图,已知A 点在第一象限且同时在上述两个函数的图象上,求A 点坐标;⑶利用⑵的结果,请问:在x 轴上是否存在点P ,使AOP ∆为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由。
