广东省广州市培正中学2014届高三数学12月月考试题 理
广东省各地2014届高三数学上学期 期末考试试题分类汇编 三角函数

5π12-π32Oy x广东省各地2014届高三上学期期末考试数学理试题分类汇编三角函数一、选择、填空题题1、(佛山市2014届高三教学质量检测(一))设函数sin 23cos2y x x =+的最小正周期为T ,最大值为A ,则A .T π=,2A =B . T π=,2A =C .2T π=,2A =D .2T π=,2A = 答案:C2、(广州市2014届高三1月调研测试).函数()()sin f x A x ωϕ=+(0A >,0ω>,2πϕ<)的部分图象如图1所示,则函数()y f x =对应的解析式为 A .sin 26y x π⎛⎫=+ ⎪⎝⎭B .sin 26y x π⎛⎫=-⎪⎝⎭C .cos 26y x π⎛⎫=+ ⎪⎝⎭D .cos 26y x π⎛⎫=-⎪⎝⎭答案:A3、(增城市2014届高三上学期调研)已知3177cos ,45124x x πππ⎛⎫+=<< ⎪⎝⎭,则2sin 22sin 1tan x xx+=-(A )2875- (B )2875 (C )21100- (D )21100答案:A4、(省华附、省实、广雅、深中四校2014届高三上学期期末)函数()sin()(0,0)f x A x A ωθω=+>>的部分图象如图所示,则()f x = A .π2sin(2)6x - B. π2sin(2)3x -C. π2sin(4)3x +D. π2sin(4)6x +答案:B5、(江门市2014届高三调研考试)在ABC ∆中,3=c ,045=A ,075=B ,则=a .答案:26、(汕头市2014届高三上学期期末教学质量监测)已知函数①x x y cos sin +=,②x x y cos sin 22=,则下列结论正确的是( )A .两个函数的图象均关于点(,0)4π-成中心对称B .两个函数的图象均关于直线4x π=-对称C .两个函数在区间(,)44ππ-上都是单调递增函数D .可以将函数②的图像向左平移4π个单位得到函数①的图像答案:C7、(中山市2014届高三上学期期末考试)已知20πα<<,=+)6cos(πα53,则=αcos答案:410+8、(珠海市2014届高三上学期期末)已知1cos 3ϕ=-()0ϕπ<<,则sin 2ϕ=答案:9、(珠海市2014届高三上学期期末)在△ABC 中,A :B :C =1:2:3,则a :b :c 等于( ) A 、1:2:3 B 、3:2:1C 、1 2D 、2 1 答案:C10、(珠海一中等六校2014届高三第三次联考)如果函数sin 2cos 2y x a x =+的图象关于直线8x π=-对称,那么a 等于( C )A.2B.-2C.1D.-1答案:C 二、解答题 1、(佛山市2014届高三教学质量检测(一))在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,且a =,B C =. (Ⅰ) 求cos B 的值;(Ⅱ) 设函数()()sin 2f x x B =+,求6f π⎛⎫⎪⎝⎭的值. 【解析】解法1:(Ⅰ) 因为B C =,所以c b =,……………………………………2分又a =, 所以222cos 2a c b B ac+-=, ……………………………3分23b = ………………………………………………4分=……………………………………………5分 解法2:∵a =,∴sin A B =…………………………………2分∵B C =,且A B C ++=π,所以sin 2B B =………………………3分又2sin cos B B B =……………………4分 ∵sin 0B ≠,∴cos B =.………………………………………5分 (Ⅱ)由(Ⅰ)得sin B ==,…………………………………………7分 (注:直接得到sin B =) 所以sin 63f B ππ⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭ ……………………………………………8分 sin cos cos sin 33B B ππ=+ ……………………………10分12=………………………………11分=………………………………………12分 2、(广州市2014届高三1月调研测试)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c,且cos 2A C += (1)求cos B 的值;(2)若3a =,b =c 的值.解:(1)在△ABC 中,A B C π++=.………………………………………1分所以coscos 22A C Bπ+-= …………………………………………………2分sin23B ==.………………………………………………3分 所以2cos 12sin2BB =- …………………………………………………………5分 13=.………………………………………………………………7分(2)因为3a =,b =1cos 3B =,由余弦定理2222cos b a c ac B =+-,……………………………………………9分 得2210c c -+=.…………………………………………………………………11分 解得1c =.………………………………………………………………………12分 3、(增城市2014届高三上学期调研) 已知函数()()2sin cos sin .f x x x x =-(1)当0x π<<时,求()f x 的最大值及相应的x 值; (2)利用函数y=sin x 的图象经过怎样的变换得到f(x)的图象.解(1)()()22sin cos sin 2sin cos 2sin f x x x x x x x =-=- 1分sin 2cos 21x x =+- 3分214x π⎛⎫=+- ⎪⎝⎭ 5分∵0x π<<,∴92444x πππ<+<6分 所以当242x ππ+=时,即8x π=时 7分f(x)1所以f(x)1,相应的x 的值8x π= 8分(2)函数y=sin x 的图象向左平移4π个单位, 9分 把图象上的点横坐标变为原来的12倍, 10分11分最后把图象向下平移1个单位得到y 214x π⎛⎫=+- ⎪⎝⎭的图象 12分方法2:把函数y=sin x 图象上的点横坐标变为原来的12倍 9分 把函数x 的图象向左平移8π个单位, 10分11分最后把图象向下平移1个单位得到y 214x π⎛⎫=+- ⎪⎝⎭的图象 12分4、(省华附、省实、广雅、深中四校2014届高三上学期期末)在ABC 中,三个内角,,A B C 所对的边分别为,a ,.b c222)2b c a bc +-=,2B A =. (1) 求tan A ; (2) 设ππ(2sin(),1),(sin(),1),44m B n B =-=+-求m n ⋅的值. 解: (1)2223()2,b c a bc +-=222cos2b c a A bc +-∴== (2)分0π,A <<sinA ∴==…………………………………………… 4分sintan cos AA A== ………………………………………………………6分(2)(解法一)ππ(2sin(),1),(sin(),1),44m B n B =-=+-ππ2sin()sin()144m n B B ∴⋅=-+- (7)分2(cos sin )(cos sin )122B B B B =⨯-⨯+-22cos sin 1B B =-- (9)分22sin .B =- (10)分2B A =,sin sin 22sin cos 3B A A A ∴===16.9m n ⋅=- (12)分(2)(解法二)ππ(2sin(),1),(sin(),1),44m B n B =-=+-ππ2sin()sin()144m n B B ∴⋅=-+- (7)分πππ2cos ()sin()1244B B ⎡⎤=--+-⎢⎥⎣⎦ππ2cos()sin()144B B =++-πsin(2)12B =+-cos 21B =- (9)分22sin .B =- (10)分2B A =,sin sin 22sin cos B A A A ∴===16.9m n ⋅=- (12)分(2)(解法三)2B A =,sin sin 22sin cos B A A A ∴===21cos cos 212sin .3B A A ==-=- (9)分π4(2sin(),1)sin ),1)(,1),43m B B B ∴=-=-=- (10)分π4(sin(),1)(cos ),1)(1).426n B B B =+-=+-=- (11)分4161.39m n +∴⋅=--=- ………………………12分5、(江门市2014届高三调研考试)已知1)2cos 2sin 3(2cos2)(-+=xx x x f ,R x ∈. ⑴ 求)(x f 的最小正周期;⑵ 设α、)2, 0(πβ∈,2)(=αf ,58)(=βf ,求)(βα+f 的值. 解:⑴x x x f cos sin 3)(+=……2分,)6sin(2π+=x ……4分,)(x f 的最小正周期π2=T ……5分⑵因为2)6sin(2=+πα,1)6sin(=+πα,3266ππαπ<+<……6分, 所以26ππα=+,3πα=……7分,58)6sin(2=+πβ,54)6sin(=+πβ,3266ππβπ<+<……8分,因为2354<,所以266ππβπ<+<,53)6cos(=+πβ……9分,所以ββππβαβαcos 2)2sin(2)6sin(2)(=+=++=+f ……10分, 6sin)6sin(26cos)6cos(2]6)6cos[(2ππβππβππβ+++=-+=……11分,5433+=……12分。
广东省各地2014届高三上学期期末考试数学理试题分类汇编:立体几何
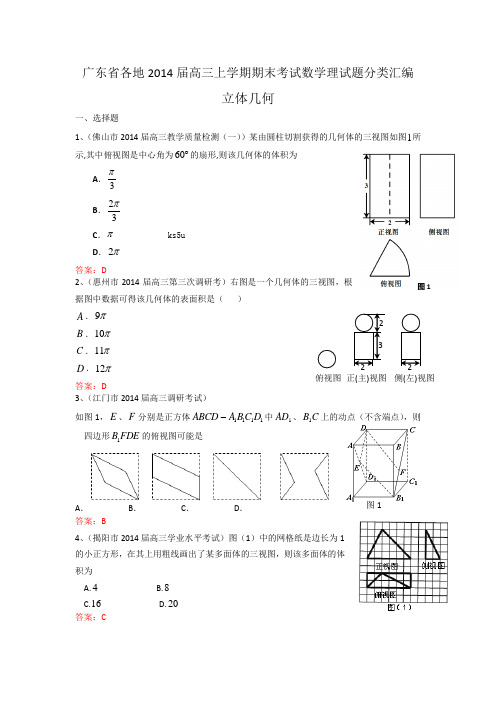
图1图1广东省各地2014届高三上学期期末考试数学理试题分类汇编立体几何一、选择题1、(佛山市2014届高三教学质量检测(一))某由圆柱切割获得的几何体的三视图如图1所示,其中俯视图是中心角为60︒的扇形,则该几何体的体积为A .3πB .23πC .π ks5uD .2π答案:D 2、(惠州市2014届高三第三次调研考)右图是一个几何体的三视图,根据图中数据可得该几何体的表面积是( )A .9πB .10πC .11πD .12π答案:D 3、(江门市2014届高三调研考试)如图1,E 、F 分别是正方体1111D C B A ABCD -中1AD 、C B 1上的动点(不含端点),则四边形FDE B 1的俯视图可能是A .B .C .D . 答案:B4、(揭阳市2014届高三学业水平考试)图(1)中的网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为A.4B.8C.16D.20 答案:C俯视图正(主)视图 侧(左)视图5、(汕头市2014届高三上学期期末教学质量监测)三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视 图(如图所示)的面积为8,则侧视图的面积为( )A. 8B. 4C.答案:C 6、(肇庆市2014届高三上学期期末质量评估)某几何体的三视图如图2所示(单位:cm), 则其体积和表面积分别是( )A. 6π3cm 和12(1)π+2cmB. 6π3cm 和12π2cm C. 12π3cm 和12(1)π+2cm D. 12π3cm 和12π2cm答案:A 7、(中山市2014届高三上学期期末考试)把边长为1的正方形ABCD 沿对角线BD 折起,使得平面⊥ABD 平面CBD ,形成三棱锥ABD C -的正视图与俯视图如下图所示,则侧视图的面积为 ( )A BC D . 答案:B8、(珠海市2014届高三上学期期末)一个四棱锥的三视图如图所示,其中主视图是腰长为1的等腰直角三角形,则这个几何体的体积是( ) A 、12 B 、1 C 、23D 、2 答案:A 9、(珠海一中等六校2014届高三第三次联考)已知正方形ABCD 的对角线AC 与BD 相交于E 点,将ACD ∆沿对角线AC 折起,使得平面ABC ⊥平面ADC (如图),则下列命题中正确的为( C )A. 直线AB ⊥直线CD, 且直线AC ⊥直线BDB. 直线AB ⊥平面BCD ,且直线AC ⊥平面BDEC. 平面ABC ⊥平面BDE ,且平面ACD ⊥平面BDED. 平面ABD ⊥平面BCD ,且平面ACD ⊥平面BDE 答案:C10、(东莞市2014届高三上学期期末调研测试)一个空间几何体的正视图与侧视图都是边长为2的正三角形,俯视图是半径为1的圆,则该几何体的体积是答案:A 二、填空题1、(省华附、省实、广雅、深中四校2014届高三上学期期末)某几何体的三视图如图所示,其中正(主)视图与侧(左)视图的边界均为直角三角形,俯视图的边界为直角梯形,则该几何体的体积为 .答案:8 2、(江门市2014届高三调研考试)若α、β是不重合的平面,a 、b 、c 是互不相同的空间直线,则下列命题中为真命题的是 .(写出所有真命题的序号) ① 若α//a ,α//b ,则b a // ② 若α//c ,α⊥b ,则b c ⊥解法二图ABCD PEFH. .ACDB EF图5 图6ABCD PEF③ 若α⊥c ,β//c ,则βα⊥④ 若α⊂b ,α⊂c 且b a ⊥,c a ⊥,则α⊥a答案:②③(对1个3分,错1个2-分)三、解答题 1、(佛山市2014届高三教学质量检测(一))如图5,矩形ABCD 中,12AB =,6AD =,E 、F 分别为CD 、AB 边上的点,且3DE =,4BF =,将BCE ∆沿BE 折起至PBE ∆位置(如图6所示),连结AP 、EF 、PF ,其中PF =(Ⅰ)求证:PF ⊥平面ABED ; (Ⅱ)求直线AP 与平面PEF 所成角的正弦值.【解析】(Ⅰ)由翻折不变性可知,6PB BC ==,9PE CE ==,在PBF ∆中,222201636PF BF PB +=+==,所以PF BF⊥ ……………2分 在图1中,易得EF ==………3分在PEF ∆中,222612081EF PF PE +=+==,所以PF EF ⊥ …………………4分 又BF EF F = ,BF ⊂平面ABED ,EF ⊂平面ABED ,所以PF ⊥平面ABED . ………………6分(注:学生不写BF EF F = 扣1分)(Ⅱ)方法一:以D 为原点,建立空间直角坐标系D xyz -如图所示,则()6,0,0A ,(6,8,P , ()0,3,0E ,()6,8,0F ,所以(0,,25AP = ,(0,0,FP =,()6,5,0EF = , …………8分设平面PEF 的法向量为(),,x y z =n ,则0FP EF ⎧⋅=⎪⎨⋅=⎪⎩n n ,即0650z x y ⎧=⎪⎨+=⎪⎩,解得560x y z ⎧=-⎪⎨⎪=⎩ 令6y =-,得()5,6,0=-n ,……………………………………………12分设直线AP 与平面PEF 所成角为θ,则sin AP AP θ⋅===nn. 所以直线AP 与平面PEF. ……………………14分 方法二:过点A 作AH EF ⊥于H ,由(Ⅰ)知PF ⊥平面ABED ,而AH ⊂平面ABED所以PF AH ⊥,又EF PF F = ,EF ⊂平面PEF ,PF ⊂平面PEF , 所以AH ⊥平面PEF ,所以APH ∠为直线AP 与平面PEF 所成的角. ………………………9分 在Rt APF ∆中,AP ===…………………………11分在AEF ∆中,由等面积公式得AF ADAH EF ⋅==………………………………13分 在Rt APH ∆中,sin AH APH AP ∠===所以直线AP 与平面PEF. ………………………14分 2、(广州市2014届高三1月调研测试)在如图6的几何体中,平面CDEF 为正方形,平面ABCD 为等腰梯形,AB ∥CD ,BC AB 2=,60ABC ︒∠=,AC FB ⊥.(1)求证:⊥AC 平面FBC ;(2)求直线BF 与平面ADE 所成角的正弦值.(1)证明1:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得BC AC 3=.……………………………2分 所以222AC BC AB +=.所以BC AC ⊥.………………………………………………………………3分 因为AC FB ⊥,BF BC B = ,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .……………………………………………………………4分证明2:因为60ABC ︒∠=,设BAC α∠=()0120α<<,则120ACB α∠=-.在△ABC 中,由正弦定理,得()sin sin 120BC ABαα=- .……………………1分 因为BC AB 2=,所以()sin 1202sin αα-=.整理得tan 3α=,所以30α=.……………………………………………2分 所以BC AC ⊥.………………………………………………………………3分 因为AC FB ⊥,BF BC B = ,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .…………………………………………………4分(2)解法1:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C = ,所以⊥FC 平面ABCD .……………………………6分取AB 的中点M ,连结MD ,ME ,因为ABCD 是等腰梯形,且BC AB 2=,60DAM ∠=,所以MD MA AD ==.所以△MAD 是等边三角形,且ME BF .………………7分取AD 的中点N ,连结MN ,NE ,则MN AD ⊥.………8分 因为MN ⊂平面ABCD ,ED FC ,所以ED MN ⊥. 因为AD ED D = ,所以MN ⊥平面ADE . ……………9分 所以MEN ∠为直线BF 与平面ADE 所成角. ……………10分 因为NE ⊂平面ADE ,所以MN ⊥NE .…………………11分因为2MN AD =,ME ==,……………………………12分 在Rt △MNE中,sin MN MEN ME ∠==.………………………………13分 所以直线BF 与平面ADE14分 解法2:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C = ,所以⊥FC 平面ABCD .……………………………………6分所以CA ,CB ,CF 两两互相垂直,建立如图的空间直角坐标系xyz C -.………………………7分 因为ABCD 是等腰梯形,且BC AB 2=,60ABC ︒∠= 所以CB CD CF ==.不妨设1BC =,则()0,1,0B ,()0,0,1F,)A,1,02D ⎫-⎪⎪⎝⎭,1,12E ⎫-⎪⎪⎝⎭, 所以()0,1,1BF =-,1,022DA ⎛⎫= ⎪ ⎪⎝⎭,()0,0,1DE = .………………………9分设平面ADE 的法向量为=()x,y,z n ,则有0,0.DA DE ⎧⋅=⎪⎨⋅=⎪⎩ n n即0,20.y x z +=⎪=⎩ 取1x =,得=n ()1,是平面ADE 的一个法向量.…………………………11分 设直线BF 与平面ADE 所成的角为θ,则sin cos ,4BF BF BF ⋅θ=〈〉===n n n.………………13分 所以直线BF 与平面ADE 所成角的正弦值为4.………………………………14分 3、(增城市2014届高三上学期调研)如图3,边长为2的正方形ABCD ,E,F 分别是AB,BC 的中点,将△AED , △DCF 分别沿DE,DF 折起,使A,C 两点重合于A '。
广东省广州市重点中学高三12月月考(数学理)

广东省广州市重点中学高三12月月考(数学理)第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知0tan cos <∙θθ,那么角θ是( )A .第一或第二象限角B .第二或第三象限角C .第三或第四象限角D .第一或第四象限角2、圆4)2()2(22=++-y x 截直线02=-+y x 所得的弦长等于( ) A.22 B.2 C.6 D.53.已知函数()f x =M ,()ln(1)g x x =+的定义域为N ,则M N =( )A .{|1}x x >-B .{|1}x x <C .{|11}x x -<<D .∅4.一个水平放置的图形的斜二测直观图是一个底角为045,腰和上底都为1的等腰梯形,则原平面图的面积是( )A .22+B .221+ C222+. D . 21+ 5.已知O 是ABC △所在平面内一点,D 为BC 边中点,且02=++OC OB OA , 那么( ) A .AO OD =B .2AO OD =C .3AO OD =D .2AO OD =6.设椭圆12222=+n y m x 、双曲线12222=-n y m x 、抛物线x n m y )(22+=(其中0>>n m )的离心率分别为321,,e e e ,则 ( ) A .321e e e > B .321e e e < C .123e e e =D .123e e e 与大小不确定7.若不等式组220x y x y y x y a-0⎧⎪+⎪⎨⎪⎪+⎩≥,≤,≥,≤表示的平面区域是一个三角形,则a 的取值范围是( )A .43a ≥B .01a <≤C .413a ≤≤D .01a <≤或43a ≥ 8.对于函数①()lg(21)f x x =-+,②2()(2)f x x =-,③()cos(2)f x x =+,判断如下三个命题的真假:命题甲:(2)f x +是偶函数;命题乙:()f x 在()-∞2,上是减函数,在(2)+∞,上是增函数;命题丙:(2)()f x f x +-在()-∞+∞,上是增函数. 能使命题甲、乙、丙均为真的所有函数的序号是( ) A .①③B .①②C .③D .②第II 卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
2014年广东省广州市高考数学二模(理科)试题及参考答案

试卷类型:A2014年广州市普通高中毕业班综合测试(二)数学(理科)2014.4 本试卷共4页,21小题, 满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式是13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 若复数z 满足 i 2z =,其中i 为虚数单位,则z 的虚部为A .2-B .2C .2-iD .2i 2.若函数()y f x =是函数3x y =的反函数,则12f ⎛⎫⎪⎝⎭的值为A .2log 3-B .3log 2-C .19D 3.命题“对任意x ∈R ,都有32x x >”的否定是A .存在0x ∈R ,使得3200x x >B .不存在0x ∈R ,使得3200x x > C .存在0x ∈R ,使得3200x x ≤ D .对任意x ∈R ,都有32x x ≤4. 将函数()2cos 2(f x x x x =+∈R )的图象向左平移6π个单位长度后得到函数 ()y g x =,则函数()y g x =A .是奇函数B .是偶函数C .既是奇函数又是偶函数D .既不是奇函数,也不是偶函数图1俯视图侧视图正视图5.有两张卡片,一张的正反面分别写着数字0与1,另一张的正反面分别写着数字2与3, 将两张卡片排在一起组成两位数,则所组成的两位数为奇数的概率是 A .16 B .13 C .12D .38 6.设12,F F 分别是椭圆()2222:10x y C a b a b+=>>的左、右焦点,点P 在椭圆C 上,线段1PF的中点在y 轴上,若1230PF F ︒∠=,则椭圆C 的离心率为 A .16 B .13CD7.一个几何体的三视图如图1,则该几何体的体积为A .6π4+B .12π4+C .6π12+D .12π12+ 8.将正偶数2,4,6,8,按表1的方式进行排列,记ij a 表示第i 行第j 列的数,若2014ij a =,则i j +的值为A .257B .256C .254D .253 表1 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.不等式2210x x --<的解集为 .10.已知312nx x ⎛⎫- ⎪⎝⎭的展开式的常数项是第7项,则正整数n 的值为 .11.已知四边形ABCD 是边长为a 的正方形,若2,2DE EC CF FB ==,则A E A F ⋅的值 为 .12.设,x y 满足约束条件 220,840,0,0.x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩若目标函数()0,0z ax by a b =+>>的最大值为8,则ab 的最大值为 .D CB A a 图3重量/克0.0320.02452515O 13.已知[]x 表示不超过x 的最大整数,例如[][]1.52,1.51-=-=.设函数()[]f x x x ⎡⎤=⎣⎦, 当[)0,(x n n ∈∈N *)时,函数()f x 的值域为集合A ,则A 中的元素个数为 . (二)选做题(14~15题,考生从中选做一题)14.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线,(x a t t y t =-⎧⎨=⎩为参数)与圆1cos ,(sin x y θθθ=+⎧⎨=⎩为参数)相切,切点在第一象限,则实数a 的值为 .15.(几何证明选讲选做题)在平行四边形ABCD 中,点E 在线段AB 上,且 12A E EB =,连接,DE AC ,AC 与DE 相交于点F ,若△AEF 的面积为1 cm 2,则 △AFD 的面积为 cm 2.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)如图2,在△ABC 中,D 是边AC 的中点, 且1AB AD ==,BD =. (1) 求cos A 的值; (2)求sin C 的值. 图2 17.(本小题满分12分)一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样 本,称出它们的重量(单位:克),重量分组区间为(]5,15,(]15,25,(]25,35,(]35,45, 由此得到样本的重量频率分布直方图,如图3. (1)求a 的值;(2)根据样本数据,试估计盒子中小球重量的平均值;(注:设样本数据第i 组的频率为i p ,第i 组区间的中点值为i x ()1,2,3,,i n =,则样本数据的平均值为112233n n X x p x p x p x p =++++. (3)从盒子中随机抽取3个小球,其中重量在(]5,15内的小球个数为ξ,求ξ的分布列和数学期望.FE D CB18.(本小题满分14分) 如图4,在五面体ABCDEF 中,四边形ABCD 是边长为2的正方形,EF ∥平面ABCD , 1EF =,,90FB FC BFC ︒=∠=,AE =(1)求证:AB ⊥平面BCF ;(2)求直线AE 与平面BDE 所成角的正切值. 图4 19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,且10a =,对任意n ∈N *,都有()11n n na S n n +=++. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足22log log n n a n b +=,求数列{}n b 的前n 项和n T .20.(本小题满分14分)已知定点()0,1F 和直线:1l y =-,过点F 且与直线l 相切的动圆圆心为点M ,记点M 的轨迹为曲线E .(1) 求曲线E 的方程;(2) 若点A 的坐标为()2,1, 直线1:1(l y kx k =+∈R ,且0)k ≠与曲线E 相交于,B C 两 点,直线,AB AC 分别交直线l 于点,S T . 试判断以线段ST 为直径的圆是否恒过两个 定点? 若是,求这两个定点的坐标;若不是,说明理由. 21.(本小题满分14分)已知函数()ln (,f x a x bx a b =+∈R )在点()()1,1f 处的切线方程为220x y --=. (1)求,a b 的值; (2)当1x >时,()0kf x x+<恒成立,求实数k 的取值范围; (3)证明:当n ∈N *,且2n ≥时,22111322ln 23ln 3ln 22n n n n n n--+++>+.2014年广州市普通高中毕业班综合测试(二)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力对照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.分.二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.9.1,12⎛⎫- ⎪⎝⎭10.8 11.2a12.4 13.222n n -+141 15.3三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分) (1)解:在△ABD 中,1AB AD ==,3BD =,∴222cos 2AB AD BD A AB AD+-=⋅⋅2221112113+-⎝⎭==⨯⨯. ……………4分(2)解:由(1)知,1cos 3A =,且0A <<π,∴sin A ==. ……………6分 ∵D 是边AC 的中点,∴22AC AD ==.在△ABC 中,222222121cos 22123AB AC BC BC A AB AC +-+-===⋅⋅⨯⨯,………8分解得3BC =……………10分 由正弦定理得,sin sin BC ABA C=, ……………11分∴1sin sin AB AC BC⋅===. ……………12分17.(本小题满分12分)(1) 解:由题意,得()0.020.0320.018101x +++⨯=, ……………1分 解得0.03x =. ……………2分 (2)解:50个样本小球重量的平均值为0.2100.32200.3300.184024.6X =⨯+⨯+⨯+⨯=(克). ……………3分由样本估计总体,可估计盒子中小球重量的平均值约为24.6克. ……………4分(3)解:利用样本估计总体,该盒子中小球重量在(]5,15内的概率为0.2,则13,5B ξ⎛⎫⎪⎝⎭. ……………5分 ξ的取值为0,1,2,3, ……………6分()30346405125P C ξ⎛⎫=== ⎪⎝⎭,()2131448155125P C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭, ()2231412255125P C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭,()3331135125P C ξ⎛⎫=== ⎪⎝⎭. ……………10分 ∴ξ的分布列为:……………11分∴6448121301231251251251255E ξ=⨯+⨯+⨯+⨯=. ……………12分 (或者13355E ξ=⨯=)18.(本小题满分14分)(1)证明:取AB 的中点M ,连接EM ,则1AM MB ==,∵EF ∥平面ABCD ,EF ⊂平面ABFE ,平面ABCD 平面ABFE AB =,M OH FED C B ∴EF ∥AB ,即EF ∥MB . ……………1分 ∵EF =MB 1=∴四边形EMBF 是平行四边形. ……………2分 ∴EM ∥FB ,EM FB =.在Rt △BFC 中,2224FB FC BC +==,又FB FC =,得FB =∴EM = ……………3分在△AME中,AE =1AM =,EM = ∴2223AM EM AE +==,∴AM EM ⊥. ……………4分 ∴AM FB ⊥,即AB FB ⊥. ∵四边形ABCD 是正方形,∴AB BC ⊥. ……………5分 ∵FB BC B =,FB ⊂平面BCF ,BC ⊂平面BCF ,∴AB ⊥平面BCF . ……………6分 (2)证法1:连接AC ,AC 与BD 相交于点O ,则点O 是AC 的中点, 取BC 的中点H ,连接,OH EO ,FH , 则OH ∥AB ,112OH AB ==. 由(1)知EF ∥AB ,且12EF AB =,∴EF ∥OH ,且EF OH =.∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO F H == .……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF ,∴FH AB ⊥. ……………8分∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD . ……………9分 ∴EO ⊥平面ABCD . ∵AO ⊂平面ABCD ,∴EO ⊥AO . ……………10分 ∵AO BD ⊥,,EOBD O EO =⊂平面EBD ,BD ⊂平面EBD ,∴AO ⊥平面EBD . ……………11分 ∴AEO ∠是直线AE 与平面BDE 所成的角. ……………12分 在Rt △AOE中,tan AOAEO EO∠== ……………13分 ∴直线AE 与平面BDE……………14分证法2:连接AC ,AC 与BD 相交于点O ,则点O 取BC 的中点H ,连接,OH EO ,FH , 则OH ∥AB ,112OH AB ==.由(1)知EF ∥AB ,且12EF AB =, ∴EF ∥OH ,且EF OH =. ∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH ==. ……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF , ∴FH AB ⊥.∵FH BC ⊥,,ABBC B AB =⊂平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD .∴EO ⊥平面ABCD . ……………8分 以H 为坐标原点,BC 所在直线为x 轴,OH 所在直线为y 轴,HF 所在直线为z 轴, 建立空间直角坐标系H xyz -,则()1,2,0A -,()1,0,0B ,()1,2,0D --,()0,1,1E -.∴()1,1,1AE =-,()2,2,0BD =--,()1,1,1BE =--. ……………9分 设平面BDE 的法向量为=n (),,x y z ,由n 0BD ⋅=,n 0BE ⋅=, 得220x y --=,0x y z --+=,得0,z x y ==-.令1x =,则平面BDE 的一个法向量为=n ()1,1,0-. ……………10分 设直线AE 与平面BDE 所成角为θ, 则sin θ=cos ,n AE⋅=n AE nAE=. ……………11分∴cos 3θ==,sin tan cos θθθ== ……………13分 ∴直线AE 与平面BDE……………14分19.(本小题满分14分)(1)解法1:当2n ≥时,()11n n na S n n +=++,()()111n n n a S n n --=+-,……1分 两式相减得()()()11111n n n n na n a S S n n n n +---=-++--, ……………3分即()112n n n na n a a n +--=+,得12n n a a +-=. ……………5分 当1n =时,21112a S ⨯=+⨯,即212a a -=. ……………6分 ∴数列{}n a 是以10a =为首项,公差为2的等差数列.∴()2122n a n n =-=-. ……………7分 解法2:由()11n n na S n n +=++,得()()11n n n n S S S n n +-=++, ……………1分 整理得,()()111n n nS n S n n +=+++, ……………2分 两边同除以()1n n +得,111n nS S n n+-=+. ……………3分 ∴数列n S n ⎧⎫⎨⎬⎩⎭是以101S =为首项,公差为1的等差数列. ∴011nS n n n=+-=-. ∴()1n S n n =-. ……………4分 当2n ≥时,()()()111222n n n a S S n n n n n -=-=----=-. ……………5分 又10a =适合上式, ……………6分 ∴数列{}n a 的通项公式为22n a n =-. ……………7分 (2)解法1:∵22log log n n a n b +=,∴221224n an n n b n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++()0122142434144n n n n --=+⨯+⨯++-⋅+⋅,①()1231442434144n n n T n n -=+⨯+⨯++-⋅+⋅,② ……………11分 ①-②得0121344444n nn T n --=++++-⋅14414n nn -=-⋅-()13413n n -⋅-=. ……………13分 ∴()131419n n T n ⎡⎤=-⋅+⎣⎦. ……………14分 解法2:∵22log log n n a n b +=,∴221224n an n n b n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++()0122142434144n n n n --=+⨯+⨯++-⋅+⋅.由()12311n nx x x x x x x x+-++++=≠-, ……………11分两边对x 取导数得,012123n x x x nx-++++=()()12111n n nx n x x +-++-. ………12分令4x =,得()()0122114243414431419n n n n n n --⎡⎤+⨯+⨯++-⋅+⋅=-⋅+⎣⎦. ……………13分 ∴ ()131419nn T n ⎡⎤=-⋅+⎣⎦. ……………14分 20.(本小题满分14分)(1)解法1:由题意, 点M 到点F 的距离等于它到直线l 的距离,故点M 的轨迹是以点F 为焦点, l 为准线的抛物线. (1)分∴曲线E 的方程为24x y =. ……………2分 解法2:设点M 的坐标为(),x y ,依题意,得1MF y =+,1y =+, ……………1分化简得24x y =.∴曲线E 的方程为24x y =. ……………2分(2) 解法1: 设点,B C 的坐标分别为()()1122,,,x y x y ,依题意得,2211224,4x y x y ==.由21,4,y kx x y =+⎧⎨=⎩消去y 得2440xkx --=, 解得1,22x k ==±.∴12124,4x x k x x +==-. ……………3分直线AB 的斜率2111111124224ABx y x k x x --+===--, 故直线AB 的方程为()12124x y x +-=-. ……………4分令1y =-,得1822x x =-+, ∴点S 的坐标为182,12x ⎛⎫-- ⎪+⎝⎭. ……………5分 同理可得点T 的坐标为282,12x ⎛⎫-- ⎪+⎝⎭. ……………6分∴()()()121212888222222x x ST x x x x -⎛⎫=---= ⎪++++⎝⎭ ()()()121212121288248x x x x x xx x x x k k---===+++. ……………7分 ∴2ST=()()()2221212122221614k x x x x x x kkk+-+-==. ……………8分设线段ST 的中点坐标为()0,1x -,则()()()12012124418822222222x x x x x x x ++⎛⎫=-+-=- ⎪++++⎝⎭ ()()()1212444444222248k k x x x x k k++=-=-=-+++. ……………9分∴以线段ST 为直径的圆的方程为()2222114x y ST k ⎛⎫+++= ⎪⎝⎭()2241k k +=. ……………10分展开得()()22222414414k x x y k k k++++=-=. ……………11分 令0x =,得()214y +=,解得1y =或3y =-. ……………12分 ∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分 解法2:由(1)得抛物线E 的方程为24x y =.设直线AB 的方程为()112y k x -=-,点B 的坐标为()11,x y ,由()112,1,y k x y ⎧-=-⎨=-⎩解得122,1.x k y ⎧=-⎪⎨⎪=-⎩∴点S 的坐标为122,1k ⎛⎫-- ⎪⎝⎭. …………3分由()1212,4,y k x x y ⎧-=-⎨=⎩消去y ,得2114840x k x k -+-=, 即()()12420x x k --+=,解得2x =或142x k =-. ……………4分 ∴1142x k =-,22111114414y x k k ==-+. ∴点B 的坐标为()211142,441k k k --+. ……………5分同理,设直线AC 的方程为()212y k x -=-, 则点T 的坐标为222,1k ⎛⎫-- ⎪⎝⎭,点C 的坐标为()222242,441k k k --+. …………6分 ∵点,B C 在直线1:1l y kx =+上,∴()()()()()()22222211212121214414414242kk k k k k k k k k k k k -+--+---==----121k k =+-.∴121k k k +=+. ……………7分 又()211144142k k k k -+=-1+,得()21111214442412k k kk k k k k k -=-=+--, 化简得122kk k =. ……………8分 设点(),P x y 是以线段ST 为直径的圆上任意一点,则0SP TP ⋅=, ……………9分 得()()122222110x x y y k k ⎛⎫⎛⎫-+-++++= ⎪⎪⎝⎭⎝⎭, ……………10分 整理得,()224410x x y k+-++=. ……………11分 令0x =,得()214y +=,解得1y =或3y =-. ……………12分 ∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分 21.(本小题满分14分)(1)解:∵()ln f x a x bx =+, ∴()af x b x'=+. ∵直线220x y --=的斜率为12,且过点11,2⎛⎫- ⎪⎝⎭, ……………1分∴()()11,211,2f f ⎧=-⎪⎪⎨⎪'=⎪⎩即1,21,2b a b ⎧=-⎪⎪⎨⎪+=⎪⎩解得11,2a b ==-. ……………3分(2)解法1:由(1)得()ln 2xf x x =-. 当1x >时,()0k f x x +<恒成立,即ln 02x k x x -+<,等价于2ln 2x k x x <-. ……………4分令()2ln 2x g x x x =-,则()()ln 11ln g x x x x x '=-+=--. ……………5分 令()1ln h x x x =--,则()111x h x x x-'=-=. 当1x >时,()0h x '>,函数()h x 在()1,+∞上单调递增,故()()10h x h >=. ……………6分 从而,当1x >时,()0g x '>,即函数()g x 在()1,+∞上单调递增, 故()()112g x g >=. ……………7分 因此,当1x >时,2ln 2x k x x <-恒成立,则12k ≤. ……………8分 ∴所求k 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分解法2:由(1)得()ln 2x f x x =-. 当1x >时,()0k f x x +<恒成立,即ln 02x kx x-+<恒成立. ……………4分 令()ln 2x k g x x x =-+,则()222112222k x x kg x x x x -+'=--=-.方程2220x x k -+=(﹡)的判别式48k ∆=-.(ⅰ)当0∆<,即12k >时,则1x >时,2220x x k -+>,得()0g x '<, 故函数()g x 在()1,+∞上单调递减. 由于()()110,2ln 21022kg k g =-+>=-+>,则当()1,2x ∈时,()0g x >,即ln 02x kx x-+>,与题设矛盾. …………5分 (ⅱ)当0∆=,即12k =时,则1x >时,()()2222121022x x x g x x x --+'=-=-<. 故函数()g x 在()1,+∞上单调递减,则()()10g x g <=,符合题意. ………6分 (ⅲ) 当0∆>,即12k <时,方程(﹡)的两根为1211,11x x =<=>, 则()21,x x ∈时,()0g x '>,()2,x x ∈+∞时,()0g x '<. 故函数()g x 在()21,x 上单调递增,在()2,x +∞上单调递减, 从而,函数()g x 在()1,+∞上的最大值为()2222ln 2x kg x x x =-+. ………7分 而()2222ln 2x k g x x x =-+2221ln 22x x x <-+, 由(ⅱ)知,当1x >时,1ln 022x x x-+<, 得2221ln 022x x x -+<,从而()20g x <. 故当1x >时,()()20g x g x ≤<,符合题意. ……………8分 综上所述,k 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分(3)证明:由(2)得,当1x >时,1ln 022x x x -+<,可化为21ln 2x x x -<, …10分又ln 0x x >, 从而,21211ln 111x x x x x >=---+. ……………11分 把2,3,4,,x n =分别代入上面不等式,并相加得,11111111111112ln 23ln 3ln 32435211n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++>-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪--+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭……………12分 111121n n =+--+ ……………13分223222n n n n--=+. ……………14分。
广东省广州市2014届高三调研测试数学理试题-Word版附答案

广州市2014届高三年级调研测试 试卷类型:A数 学(理 科) 2014.1本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:锥体体积公式13V Sh =,其中S 为锥体的底面积,h 为锥体的高.一.选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i 为虚数单位, 则复数i2i-的模等于A B C .3 D .52.设集合{}0322=--=x x x A ,{}12==x x B ,则B A 等于A .{}1-B .{}1,3C .{}1,1,3-D .R 3.已知向量(3,1)=a ,(,2)x =-b ,(0,2)=c ,若()⊥-a b c ,则实数x 的值为 A .43 B .34 C .34- D .43- 4.定义在R 上的函数()f x 满足2log (16), 0,()(1), 0,x x f x f x x -≤⎧=⎨->⎩则()3f 的值为A .4-B .2C .2log 13D .45.函数()()sin f x A x ωϕ=+(0A >,0ω>,2πϕ<)的部分图象如图1所示,则函数()y f x =对应的解析式为A .sin 26y x π⎛⎫=+ ⎪⎝⎭B .sin 26y x π⎛⎫=- ⎪⎝⎭C .cos 26y x π⎛⎫=+⎪⎝⎭D .cos 26y x π⎛⎫=-⎪⎝⎭6.执行如图2的程序框图,如果输入的N 的值是6,那么输出的p 的值是A .15B .105C .120D .7207.若点(1,0)A 和点(4,0)B 到直线l 的距离依次为1和2,则这样的直线有A .1条B .2条C .3条D .4条8.对于实数a 和b ,定义运算“*”:a *2221, ,, .a ab a b b b ab a b ⎧-+-≤⎪=⎨->⎪⎩设()()21f x x =-*()1x -,且关于x 的方程为()()f x m m =∈R 恰有三个互不相等的实数根1x ,2x ,3x ,则321x x x ⋅⋅的取值范围是 A .1,032⎛⎫-⎪⎝⎭ B .1,016⎛⎫- ⎪⎝⎭ C .10,32⎛⎫ ⎪⎝⎭D .10,16⎛⎫⎪⎝⎭ 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9.在等比数列{}n a 中,若1323a a a =⋅,则4a = .10.若x ,y 满足约束条件0,0,1,3412,x y x y x y ≥⎧⎪≥⎪⎨-≥-⎪⎪+≤⎩则x y +的最大值为_______.ks5u11.如图3,设D 是图中边长为4的正方形区域,E 是D 内函数2y x =图象下方的点构成的区域.在D 内随机取一点,则该点落在E 中的概率为 . 12.已知点P 在曲线4e 1x y =+(其中e 为自然对数的底数)上,α为曲线在点P 处的切线的倾斜角,则αtan 的取值范围是 .13.有4名优秀学生A ,B ,C ,D 全部被保送到甲,乙,丙3所学校,每所学校至少去一名,则不同的保送方案共有 种.(二)选做题(14~15题,考生只能从中选做一题)B14.(几何证明选讲选做题)如图4,AC 为⊙O 的直径,OB AC ⊥,弦BN 交AC 于点M .若OC =1OM =,则MN 的长为 . 15.(坐标系与参数方程选讲选做题)若点(,)P x y 在曲线2cos sin x y θθ=-+⎧⎨=⎩(θ为参数,θ∈R )上,则y x 的取值范围是 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c,且cos 23A C +=. (1)求cosB 的值;(2)若3a =,b =c 的值.ks5u17.(本小题满分12分)空气质量指数PM2.5 (单位:3/m μg )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:从甲城市2013年9月份的30天中随机抽取15天的PM2.5日均浓度指数数据茎叶图如图5所示. (1)试估计甲城市在2013年9月份30天的空气质量类别为优或良的天数; (2)在甲城市这15个监测数据中任取2个,设X 为空气质量类别为优或良的天数,求X 的分布列及数学期望.18.(本小题满分14分)在如图6的几何体中,平面CDEF 为正方形,平面ABCD 为等腰梯形,AB ∥CD ,BC AB 2=,60ABC ︒∠=,AC FB ⊥.(1)求证:⊥AC 平面FBC ;3 2 0 45 56 47 6 9 78 8 0 79 1 8 0 9 图5(2)求直线BF 与平面ADE 所成角的正弦值. 19.(本小题满分14分)已知数列{a n }满足135a =,1321n n n a a a +=+,*n ∈N .(1)求证:数列1 1 n a ⎧⎫-⎨⎬⎩⎭为等比数列; (2)是否存在互不相等的正整数m ,s ,t ,使m ,s ,t 成等差数列,且1m a -,1s a -,1t a -成等比数列?如果存在,求出所有符合条件的m ,s ,t ;如果不存在,请说明理由.20.(本小题满分14分)设函数()313f x x ax =-()0a >,()221g x bx b =+-. (1)若曲线()x f y =与()x g y =在它们的交点()c ,1处有相同的切线,求实数a ,b 的值; (2)当12ab -=时,若函数()()()h x f x g x =+在区间()0,2-内恰有两个零点,求实数a 的取值范围;(3)当1a =,0b =时,求函数()()()h x f x g x =+在区间[]3,+t t 上的最小值.21.(本小题满分14分)如图7,已知椭圆C 的方程为()222210x y a b a b +=>>,双曲线12222=-by a x 的两条渐近线为21,l l .过椭圆C 的右焦点F 作直线l ,使1l l ⊥,又l 与2l 交于点P ,设l 与椭圆C 的两个交点由上至下 依次为A ,B .(1)若1l 与2l 的夹角为60°,且双曲线的焦距为4,求椭圆C 的方程;(2)求||||AP FA 的最大值.图7广州市2014届高三年级调研测试 数学(理科)试题参考答案及评分标准说明:1.参考答案及评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 解:(1)在△ABC 中,A B C π++=.………………………………………………………………1分所以coscos22A C Bπ+-= …………………………………………………………………………2分sin2B ==3分 所以2cos 12sin2BB =- ……………………………………………………………………………5分 13=.………………………………………………………………………………………7分 (2)因为3a =,b =1cos 3B =,由余弦定理2222cos b a c ac B =+-,………………………………………………………………9分 得2210c c -+=.……………………………………………………………………………………11分 解得1c =.……………………………………………………………………………………………12分8 A17.(本小题满分12分) 解:(1)由茎叶图可知,甲城市在2013年9月份随机抽取的15天中的空气质量类别为优或良的天数为5天.…………………………………………………………………………………………………1分 所以可估计甲城市在2013年9月份30天的空气质量类别为优或良的天数为10天.…………2分 (2)X 的取值为0,1,2,………………………………………………………………………………3分因为()02510215C C 30C 7P X ===,………………………………………………………………………5分 ()11510215C C 101C 21P X ===,………………ks5u …………………………………………7分()20510215C C 22C 21P X ===.…………………………………………………………………………9分所以X 的分布列为:所以数学期望321221170=⨯+⨯+⨯=EX .…………………………………………………12分18.(本小题满分14分)(1)证明1:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得BC AC 3=.……………………………………………………2分所以222AC BC AB +=.所以BC AC ⊥.………………………………………………………………………………………3分因为AC FB ⊥,BF BC B =,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .………………………………………………………………………………4分 证明2:因为60ABC ︒∠=,设BAC α∠=()0120α<<,则120ACB α∠=-.在△ABC 中,由正弦定理,得()sin sin 120BC ABαα=-.…………………………………………1分 因为BC AB 2=,所以()sin 1202sin αα-=.整理得tan 3α=,所以30α=.…………………………………………………………………2分 所以BC AC ⊥.………………………………………………………………………………………3分 因为AC FB ⊥,BF BC B =,BF 、BC ⊂平面FBC ,……………………10分所以⊥AC 平面FBC .………………………………………………………………………………4分(2)解法1:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C =,所以⊥FC 平面ABCD .……………………………………………………6分取AB 的中点M ,连结MD ,ME ,因为ABCD 是等腰梯形,且BC AB 2=,60DAM ∠=, 所以MD MA AD ==.所以△MAD 是等边三角形,且MEBF .…………………………7分取AD 的中点N ,连结MN ,NE ,则MN AD ⊥.………8分 因为MN ⊂平面ABCD ,ED FC ,所以ED MN ⊥.因为ADED D =,所以MN ⊥平面ADE . ……………9分所以MEN ∠为直线BF 与平面ADE 所成角. ……………10分 因为NE ⊂平面ADE ,所以MN ⊥NE .…………………11分因为2MN AD =,ME ==,…………………………………………12分 在Rt △MNE中,sin 4MN MEN ME ∠==.……………………………………………………13分 所以直线BF 与平面ADE所成角的正弦值为4.………ks5u …………………14分 解法2:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C =,所以⊥FC 平面ABCD .……………………………………………………6分所以CA ,CB ,CF 两两互相垂直,建立如图的空间直角坐标系xyz C -.………………………7分 因为ABCD 是等腰梯形,且BC AB 2=,60ABC ︒∠= 所以CB CD CF ==.不妨设1BC =,则()0,1,0B ,()0,0,1F,)A,1,02D ⎫-⎪⎪⎝⎭,1,12E ⎫-⎪⎪⎝⎭, 所以()0,1,1BF =-,31,02DA ⎛⎫= ⎪⎪⎝⎭,()0,0,1DE =.………………………………………9分设平面ADE 的法向量为=()x,y,z n ,则有0,0.DA DE ⎧⋅=⎪⎨⋅=⎪⎩n n即0,20.y x z +=⎪=⎩取1x =,得=n ()1,是平面ADE 的一个法向量.………………………………………11分 设直线BF 与平面ADE 所成的角为θ, 则)()1,3,0sin cos,22BF BF BF -⋅θ=〈〉===n n n13分 所以直线BF 与平面ADE ………………………………………………14分 19.(本小题满分14分) 解:(1)因为1321n n n a a a +=+,所以111233n n a a +=+.…………………………………………………1分 所以1111113n n a a +⎛⎫-=- ⎪⎝⎭.……………………………ks5u ……………………3分 因为135a =,则11213a -=.…………………………………………………………………………4分所以数列11n a ⎧⎫-⎨⎬⎩⎭是首项为32,公比为31的等比数列.…………………………………………5分(2)由(1)知,112121333n n n a -⎛⎫-=⨯= ⎪⎝⎭,所以332n n na =+.……………………………………7分 假设存在互不相等的正整数m ,s ,t 满足条件,则有()()()22,111.s m t m t s a a a +=⎧⎪⎨-=--⎪⎩……………………………………………………………………9分 由332n n n a =+与()()()2111s m t a a a -=--,得2333111323232s m t sm t ⎛⎫⎛⎫⎛⎫-=-- ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭.……………………………………………………10分 即232323343m tm t s s ++⨯+⨯=+⨯.……………………………………………………………11分因为2m t s +=,所以3323mts+=⨯.……………………………………………………………12分因为3323m t s +≥=⨯,当且仅当m t =时等号成立,这与m ,s ,t 互不相等矛盾.……………………………………………………………………13分 所以不存在互不相等的正整数m ,s ,t 满足条件.……………………………………………14分 20.(本小题满分14分) 解:(1)因为()313f x x ax =-,()221g x bx b =+-, 所以()2f x x a '=-,()2g x bx '=.…………………………………………………………………1分 因为曲线()x f y =与()x g y =在它们的交点()c ,1处有相同切线, 所以()()11g f =,且()()11g f '='。
广东省广州市2014届高三调研测试数学理试题 PDF版含答案

115~150 中度污染
150~250 重度污染
>250 严重污染
从甲城市 2013 年 9 月份的 30 天中随机抽取 15 天的 PM2.5 日均浓度指数数据茎叶图如图 5 所示. (1)试估计甲城市在 2013 年 9 月份 30 天的空气质量类别为优或良的天数; (2)在甲城市这 15 个监测数据中任取 2 个,设 X 为空气质量类别为优或良 的天数,求 X 的分布列及数学期望. 3 5 6 7 8 9 204 5 4 697 807 1809 图5
C
B
M O N
A
.
图4 .
y x 2 cos ( 为参数, R )上,则 的取值范围是 x y sin
三、解答题:本大题共 6 小题,满分 80 分.解答须写出文字说明、证明过程和演算步骤. 16. (本小题满分 12 分) 在△ ABC 中,角 A , B , C 所对的边分别为 a , b , c ,且 cos (1)求 cos B 的值; (2)若 a 3 , b 2 2 ,求 c 的值.
1 Sh ,其中 S 为锥体的底面积, h 为ቤተ መጻሕፍቲ ባይዱ体的高. 3
一.选择题:本大题共 8 小题,每小题 5 分,满分 40 分.在每小题给出的四个选项中,只有一项是符 合题目要求的. 1.已知 i 为虚数单位, 则复数
i 的模等于 2i
C.
A. 5
B. 3
3 3
D.
5 5
2.设集合 A x x 2 x 3 0 , B x x 1 ,则 A B 等于
试卷类型:A
广州市 2014 届高三年级调研测试
数 学(理 科)
本试卷共 4 页,21 小题,满分 150 分.考试用时 120 分钟.
广东省各地2014届高三11月模拟数学理试题分类汇编三角函数

广东省各地2014届高三11月模拟数学理试题分类汇编三角函数一、选择题1、(广州市培正中学2014届高三11月月考)把函数sin()3y x π=+图象上所有点向右平移3π个单位,再将所得图象的横坐标变为原来的12倍(纵坐标不变),得图象的解析式是s i n ()(0,)y x ωϕωϕπ=+><,则 ( )1.,23A πωϕ==- .2,3B πωϕ== .2,0C ωϕ== 2.2,3D πωϕ==答案:C2、(广州增城市2014届高三上学期调研).已知3177c o s ,45124x x πππ⎛⎫+=<<⎪⎝⎭,则2s i n 22s i n1t a n x x x+=-(A )2875- (B )2875(C )21100- (D )21100答案:A3、(河源市东江中学2014届高三11月月考到函数y =cos 2x -sin 2x 的图像,只需将函数y =f (x )的图像( )A .向左平移π2个单位长度B .向右平移π2个单位长度C .向左平移π4个单位长度D .向右平移π4个单位长度答案:C4、(河源市东江中学2014届高三11月月考)已知△ABC 中,,,A B C ∠∠∠的对边分别为,,a b c 若62a c ==+且75A ∠=,则 b =( )A .2B .423+C .423-D .62- 答案:A5、(揭阳一中、潮州金山中学2014届高三上学期期中联考)将函数sin()3y x π=-的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变), 再将所得的图象向左平移3π个单位,得到的图象对应的解析式是( ) A .1sin2y x = B .1sin()22y x π=-C.1sin()26y x π=- D.sin(2)6y x π=-答案:C6、(汕头市聿怀中学2014届高三上学期期中考试)若tan 2α=,则2sin cos sin 2cos αααα-+的值为A .0B .34C .1D .54答案:B7、(汕头市潮师高级中学2014届高三上学期期中)在△ABC 中,a b c ,,分别为角A B C ,,所对边,若2cos a b C =,则此三角形一定是( ) A .正三角形 B .直角三角形 C .等腰三角形D .等腰或直角三角形答案:C8、(中山一中2014届高三上学期第二次统测)化简2001sin 352sin 20-=A .12 B .12- C . 1- D . 1 答案:B二、填空题1、(广东省宝安中学等七校2014届高三第二次联考)已知ABC ∆的内角A B C ,,的对边分别为a b c ,,,且26120c b B ===︒,,,则ABC ∆的面积等于________.答案:322、(广州市培正中学2014届高三11月月考)函数()2s i ns i n ()3f x x x π=⋅-的值域是 . 答案:31,22⎡⎤-⎢⎥⎣⎦ 3、(河源市东江中学2014届高三11月月考) 已知324ππβα<<<,()()123cos ,sin 135αβαβ-=+=-,则sin 2α等于 答案:4、(惠州市2014届高三上学期第二次调研)若tan()2πα-=,则sin 2α= .xy π6π35π63- 3O答案:54-5、(江门市2014届高三调研)在ABC ∆中,3=c ,045=A ,075=B ,则=a .答案:26、(揭阳一中、潮州金山中学2014届高三上学期期中联考) 在====∠∆AC BC AB A ABC 则中,若,7,5,1200答案:37、(汕头市聿怀中学2014届高三上学期期中考试)已知53)4sin(=-x π,则x 2sin 的值为 . 答案:7258、(中山一中2014届高三上学期第二次统测)在ABC ∆中,=23AB ,=2AC ,0=60C , 则BC = 答案:49、(珠海一中等六校2014届高三上学期第二次联考) 如图是函数()sin(),(0,0,||)2f x A x A πωϕωϕ=+>><的图象,则其解析式是____________. 答案:3sin(2)3y x π=+三、解答题1、(广东省百所高中2014届高三11月联考) 已知函数(1)求5()4f π的值; (2)设,求的值。
广东省广州市2014届高三年级调研测试(理数)试卷及答案

广州市2014届高三年级调研测试数 学(理 科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:锥体体积公式13V Sh =,其中S 为锥体的底面积,h 为锥体的高.一.选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i 为虚数单位, 则复数i2i-的模等于 A .5 B .3 C .33 D .552.设集合{}0322=--=x x x A ,{}12==x x B ,则B A 等于A .{}1-B .{}1,3C .{}1,1,3-D .R 3.已知向量(3,1)=a ,(,2)x =-b ,(0,2)=c ,若()⊥-a b c ,则实数x 的值为 A .43 B .34 C .34- D .43- 4.定义在R 上的函数()f x 满足2log (16), 0,()(1), 0,x x f x f x x -≤⎧=⎨->⎩则()3f 的值为A .4-B .2C .2log 13D .45.函数()()sin f x A x ωϕ=+(0A >,0ω>,2πϕ<)的部分图象如图1所示,则函数()y f x =对应的解析式为 A .sin 26y x π⎛⎫=+ ⎪⎝⎭ B .sin 26y x π⎛⎫=- ⎪⎝⎭C .cos 26y x π⎛⎫=+ ⎪⎝⎭D .cos 26y x π⎛⎫=- ⎪⎝⎭6.执行如图2的程序框图,如果输入的N 的值是6,那么输出的p 的值是 A .15 B .105 C .120 D .7207.若点(1,0)A 和点(4,0)B 到直线l 的距离依次为1和2,则这样的直线有A .1条B .2条C .3条D .4条8.对于实数a 和b ,定义运算“*”:a *2221, ,, .a ab a b b b ab a b ⎧-+-≤⎪=⎨->⎪⎩设()()21f x x =-*()1x -,且关于x 的方程为()()f x m m =∈R 恰有三个互不相等的实数根1x ,2x ,3x ,则321x x x ⋅⋅的取值范围是 A .1,032⎛⎫-⎪⎝⎭ B .1,016⎛⎫- ⎪⎝⎭ C .10,32⎛⎫⎪⎝⎭D .10,16⎛⎫ ⎪⎝⎭二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.在等比数列{}n a 中,若1323a a a =⋅,则4a = .10.若x ,y 满足约束条件0,0,1,3412,x y x y x y ≥⎧⎪≥⎪⎨-≥-⎪⎪+≤⎩则x y +的最大值为_______.O xy1π611π12图1 O x y 24-2图3是否开始 1,1==p k p p k =⋅?k N <输出p 图22k k =+输入N结束11.如图3,设D 是图中边长为4的正方形区域,E 是D 内函数2y x =图象下方的点构成的区域.在D 内随机取一点,则该点落在E 中的概率为 . 12.已知点P 在曲线4e 1xy =+(其中e 为自然对数的底数)上,α为曲线在点P 处的切线的倾斜角,则αtan 的取值范围是 .13.有4名优秀学生A ,B ,C ,D 全部被保送到甲,乙,丙3所学校,每所学校至少去一名,则不同的保送方案共有 种.(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图4,AC 为⊙O 的直径,OB AC ⊥,弦BN 交AC 于点M .若3OC =,1OM =,则MN 的长为 . 15.(坐标系与参数方程选讲选做题)若点(,)P x y 在曲线2cos sin x y θθ=-+⎧⎨=⎩(θ为参数,θ∈R )上,则y x 的取值范围是 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且3cos 23A C +=. (1)求cos B 的值;(2)若3a =,22b =,求c 的值. 17.(本小题满分12分)空气质量指数PM2.5 (单位:3/m μg )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:PM2.5日均浓度0~35 35~75 75~115 115~150 150~250 >250空气质量类别优 良 轻度污染 中度污染 重度污染 严重污染从甲城市2013年9月份的30天中随机抽取15天的PM2.5日均浓度指数数据茎叶图如图5所示. (1)试估计甲城市在2013年9月份30天的空气质量类别为优或良的天数;3 2 0 4ABCOM N图4(2)在甲城市这15个监测数据中任取2个,设X 为空气质量类别为优或良的天数,求X 的分布列及数学期望.18.(本小题满分14分)在如图6的几何体中,平面CDEF 为正方形,平面ABCD 为等腰梯形,AB ∥CD ,BC AB 2=,60ABC ︒∠=,AC FB ⊥.(1)求证:⊥AC 平面FBC ;(2)求直线BF 与平面ADE 所成角的正弦值. 19.(本小题满分14分)已知数列{a n }满足135a =,1321n n n a a a +=+,*n ∈N . (1)求证:数列1 1 n a ⎧⎫-⎨⎬⎩⎭为等比数列; (2)是否存在互不相等的正整数m ,s ,t ,使m ,s ,t 成等差数列,且1m a -,1s a -,1t a -成等比数列?如果存在,求出所有符合条件的m ,s ,t ;如果不存在,请说明理由.20.(本小题满分14分)设函数()313f x x ax =-()0a >,()221g x bx b =+-. (1)若曲线()x f y =与()x g y =在它们的交点()c ,1处有相同的切线,求实数a ,b 的值; (2)当12ab -=时,若函数()()()h x f x g x =+在区间()0,2-内恰有两个零点,求实数a 的取值范围; (3)当1a =,0b =时,求函数()()()h x f x g x =+在区间[]3,+t t 上的最小值.21.(本小题满分14分)如图7,已知椭圆C 的方程为()222210x y a b a b +=>>,双曲线12222=-by a x 的两条渐近线为21,l l .过椭圆C 的右焦点F 作直线l ,使1l l ⊥,又l 与2l 交于点P ,设l 与椭圆C 的两个交点由上至下依次为A ,B .yAP l 1图6ABCDE F(1)若1l 与2l 的夹角为60°,且双曲线的焦距为4,求椭圆C 的方程;(2)求||||AP FA 的最大值.图7数学(理科)参考答案及评分标准说明:1.参考答案及评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 解:(1)在△ABC 中,A B C π++=.………………………………………………………………1分 所以coscos 22A C Bπ+-= …………………………………………………………………………2分 3sin23B ==.………………………………………………………………………3分 所以2cos 12sin2BB =- ……………………………………………………………………………5分 13=.………………………………………………………………………………………7分 (2)因为3a =,22b =,1cos 3B =,由余弦定理2222cos b a c ac B =+-,………………………………………………………………9分 得2210c c -+=.……………………………………………………………………………………11分 解得1c =.……………………………………………………………………………………………12分题号 1 2 3 4 5 6 7 8 答案 D C A D A B C A 题号 9 10 11 12 13 14 15 答案 3 4 13 [)01,- 36 1 33,33⎡⎤-⎢⎥⎣⎦17.(本小题满分12分) 解:(1)由茎叶图可知,甲城市在2013年9月份随机抽取的15天中的空气质量类别为优或良的天数为5天.…………………………………………………………………………………………………1分 所以可估计甲城市在2013年9月份30天的空气质量类别为优或良的天数为10天.…………2分 (2)X 的取值为0,1,2,………………………………………………………………………………3分因为()02510215C C 30C 7P X ===,………………………………………………………………………5分 ()11510215C C 101C 21P X ===,……………………………………………………………………………7分()20510215C C 22C 21P X ===.…………………………………………………………………………9分所以X 的分布列为:X0 1 2P73 2110 212所以数学期望32212221101730=⨯+⨯+⨯=EX .…………………………………………………12分18.(本小题满分14分)(1)证明1:因为BC AB 2=,60ABC ︒∠=,在△ABC 中,由余弦定理可得BC AC 3=.……………………………………………………2分 所以222AC BC AB +=.所以BC AC ⊥.………………………………………………………………………………………3分 因为AC FB ⊥,BF BC B =,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .………………………………………………………………………………4分证明2:因为60ABC ︒∠=,设BAC α∠=()0120α<<,则120ACB α∠=-.在△ABC 中,由正弦定理,得()sin sin 120BC ABαα=-.…………………………………………1分 因为BC AB 2=,所以()sin 1202sin αα-=.整理得3tan 3α=,所以30α=.…………………………………………………………………2分 所以BC AC ⊥.………………………………………………………………………………………3分 因为AC FB ⊥,BF BC B =,BF 、BC ⊂平面FBC ,所以⊥AC 平面FBC .………………………………………………………………………………4分……………………10分(2)解法1:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C =,所以⊥FC 平面ABCD .……………………………………………………6分取AB 的中点M ,连结MD ,ME ,因为ABCD 是等腰梯形,且BC AB 2=,60DAM ∠=, 所以MD MA AD ==.所以△MAD 是等边三角形,且MEBF .…………………………7分取AD 的中点N ,连结MN ,NE ,则MN AD ⊥.………8分 因为MN ⊂平面ABCD ,ED FC ,所以ED MN ⊥.因为ADED D =,所以MN ⊥平面ADE . ……………9分所以MEN ∠为直线BF 与平面ADE 所成角. ……………10分 因为NE ⊂平面ADE ,所以MN ⊥NE .…………………11分因为32MN AD =,222ME MD DE AD =+=,…………………………………………12分 在Rt △MNE 中,6sin 4MN MEN ME ∠==.……………………………………………………13分 所以直线BF 与平面ADE 所成角的正弦值为64.………………………………………………14分 解法2:由(1)知,⊥AC 平面FBC ,FC ⊂平面FBC ,所以FC AC ⊥.因为平面CDEF 为正方形,所以FC CD ⊥.因为AC CD C =,所以⊥FC 平面ABCD .……………………………………………………6分所以CA ,CB ,CF 两两互相垂直,建立如图的空间直角坐标系xyz C -.………………………7分因为ABCD 是等腰梯形,且BC AB 2=,60ABC ︒∠=所以CB CD CF ==.不妨设1BC =,则()0,1,0B ,()0,0,1F ,()3,0,0A,31,,022D ⎛⎫- ⎪ ⎪⎝⎭,31,,122E ⎛⎫- ⎪ ⎪⎝⎭, 所以()0,1,1BF =-,31,,022DA ⎛⎫=⎪ ⎪⎝⎭,()0,0,1DE =.………………………………………9分MN ABCD EFx AB CDEFyz设平面ADE 的法向量为=()x,y,z n ,则有0,0.DA DE ⎧⋅=⎪⎨⋅=⎪⎩n n 即30,220.y x z ⎧+=⎪⎨⎪=⎩取1x =,得=n ()1,3,0-是平面ADE 的一个法向量.………………………………………11分 设直线BF 与平面ADE 所成的角为θ, 则()()0,1,11,3,06sin cos ,422BF BF BF --⋅θ=〈〉===n n n.……………………………13分 所以直线BF 与平面ADE 所成角的正弦值为64.………………………………………………14分 19.(本小题满分14分) 解:(1)因为1321n n n a a a +=+,所以111233n n a a +=+.…………………………………………………1分所以1111113n n a a +⎛⎫-=- ⎪⎝⎭.…………………………………………………………………………3分 因为135a =,则11213a -=.…………………………………………………………………………4分 所以数列11n a ⎧⎫-⎨⎬⎩⎭是首项为32,公比为31的等比数列.…………………………………………5分(2)由(1)知,112121333n n n a -⎛⎫-=⨯= ⎪⎝⎭,所以332nn n a =+.……………………………………7分 假设存在互不相等的正整数m ,s ,t 满足条件,则有()()()22,111.s m t m t s a a a +=⎧⎪⎨-=--⎪⎩……………………………………………………………………9分 由332n n n a =+与()()()2111s m t a a a -=--,得2333111323232s m t sm t ⎛⎫⎛⎫⎛⎫-=-- ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭.……………………………………………………10分 即232323343m tm t s s ++⨯+⨯=+⨯.……………………………………………………………11分因为2m t s +=,所以3323m t s+=⨯.……………………………………………………………12分因为332323m t m t s ++≥=⨯,当且仅当m t =时等号成立,这与m ,s ,t 互不相等矛盾.……………………………………………………………………13分 所以不存在互不相等的正整数m ,s ,t 满足条件.……………………………………………14分 20.(本小题满分14分) 解:(1)因为()313f x x ax =-,()221g x bx b =+-, 所以()2f x x a '=-,()2g x bx '=.…………………………………………………………………1分 因为曲线()x f y =与()x g y =在它们的交点()c ,1处有相同切线, 所以()()11g f =,且()()11g f '='。
【Word版2014广州二模】广东省广州市2014届高三普通高中毕业班综合测试(二)数学理试题 Word版含答案

试卷类型:A2014年广州市普通高中毕业班综合测试(二)数学(理科)2014.4 本试卷共4页,21小题, 满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:锥体的体积公式是13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 若复数z 满足 i 2z =,其中i 为虚数单位,则z 的虚部为A .2-B .2C .2-iD .2i2.若函数()y f x =是函数3xy =的反函数,则12f ⎛⎫⎪⎝⎭的值为A .2log 3-B .3log 2-C .19D 3.命题“对任意x ∈R ,都有32x x >”的否定是A .存在0x ∈R ,使得3200x x >B .不存在0x ∈R ,使得3200x x >C .存在0x ∈R ,使得3200x x ≤ D .对任意x ∈R ,都有32x x ≤4. 将函数()2cos 2(f x x x x =+∈R )的图象向左平移6π个单位长度后得到函数 ()y g x =,则函数()y g x =A .是奇函数B .是偶函数C .既是奇函数又是偶函数D .既不是奇函数,也不是偶函数图1俯视图侧视图正视图5.有两张卡片,一张的正反面分别写着数字0与1,另一张的正反面分别写着数字2与3, 将两张卡片排在一起组成两位数,则所组成的两位数为奇数的概率是 A .16 B .13 C .12 D .386.设12,F F 分别是椭圆()2222:10x y C a b a b+=>>的左、右焦点,点P 在椭圆C 上,线段1PF的中点在y 轴上,若1230PF F ︒∠=,则椭圆C 的离心率为 A .16 B .13C.6 D.37.一个几何体的三视图如图1,则该几何体的体积为A .6π4+B .12π4+C .6π12+D .12π12+ 8.将正偶数2,4,6,8, 按表1的方式进行 排列,记ij a 表示第i 行第j 列的数,若2014ij a =,则i j +的值为A .257B .256C .254D .253 表1 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.不等式2210x x --<的解集为 .10.已知312nx x ⎛⎫- ⎪⎝⎭的展开式的常数项是第7项,则正整数n 的值为 .11.已知四边形ABCD 是边长为a 的正方形,若2,2DE EC CF FB == ,则A E A F ⋅的值为 .12.设,x y 满足约束条件 220,840,0,0.x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩若目标函数()0,0z ax by a b =+>>的最大值为8,则ab 的最大值为 .D CB A a 图3重量/克0.0320.02452515O 13.已知[]x 表示不超过x 的最大整数,例如[][]1.52,1.51-=-=.设函数()[]f x x x ⎡⎤=⎣⎦,当[)0,(x n n ∈∈N *)时,函数()f x 的值域为集合A ,则A 中的元素个数为 .(二)选做题(14~15题,考生从中选做一题)14.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线,(x a t t y t =-⎧⎨=⎩为参数)与 圆1cos ,(sin x y θθθ=+⎧⎨=⎩为参数)相切,切点在第一象限,则实数a 的值为 .15.(几何证明选讲选做题)在平行四边形ABCD 中,点E 在线段AB 上,且 12A E EB =,连接,DE AC ,AC 与DE 相交于点F ,若△AEF 的面积为1 cm 2,则 △AFD 的面积为 cm 2.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)如图2,在△ABC 中,D 是边AC 的中点, 且1AB AD ==,BD =(1) 求cos A 的值; (2)求sin C 的值. 图2 17.(本小题满分12分)一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样 本,称出它们的重量(单位:克),重量分组区间为(]5,15,(]15,25,(]25,35,(]35,45, 由此得到样本的重量频率分布直方图,如图3. (1)求a 的值;(2)根据样本数据,试估计盒子中小球重量的平均值;(注:设样本数据第i 组的频率为i p ,第i 组区间的中点值为i x ()1,2,3,,i n = ,则样本数据的平均值为112233n n X x p x p x p x p =++++ . (3)从盒子中随机抽取3个小球,其中重量在(]5,15内的小球个数为ξ,求ξ的分布列和数学期望.FE D CB18.(本小题满分14分) 如图4,在五面体ABCDEF 中,四边形ABCD 是边长为2的正方形,EF ∥平面ABCD ,1EF =,,90FB FC BFC ︒=∠=,AE =(1)求证:AB ⊥平面BCF ;(2)求直线AE 与平面BDE 所成角的正切值. 图4 19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,且10a =,对任意n ∈N *,都有()11n n na S n n +=++. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足22log log n n a n b +=,求数列{}n b 的前n 项和n T .20.(本小题满分14分)已知定点()0,1F 和直线:1l y =-,过点F 且与直线l 相切的动圆圆心为点M ,记点M 的轨迹为曲线E .(1) 求曲线E 的方程;(2) 若点A 的坐标为()2,1, 直线1:1(l y kx k =+∈R ,且0)k ≠与曲线E 相交于,B C 两 点,直线,AB AC 分别交直线l 于点,S T . 试判断以线段ST 为直径的圆是否恒过两个 定点? 若是,求这两个定点的坐标;若不是,说明理由. 21.(本小题满分14分)已知函数()ln (,f x a x bx a b =+∈R )在点()()1,1f 处的切线方程为220x y --=. (1)求,a b 的值; (2)当1x >时,()0kf x x+<恒成立,求实数k 的取值范围; (3)证明:当n ∈N *,且2n ≥时,22111322ln 23ln 3ln 22n n n n n n--+++>+ .2014年广州市普通高中毕业班综合测试(二)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力对照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.分.二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.9.1,12⎛⎫- ⎪⎝⎭10.8 11.2a12.4 13.222n n -+141 15.3三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分) (1)解:在△ABD 中,1AB AD ==,3BD=, ∴222cos 2AB AD BD A AB AD+-=⋅⋅2221112113+-⎝⎭==⨯⨯. ……………4分(2)解:由(1)知,1cos 3A =,且0A <<π,∴sin 3A ==. ……………6分 ∵D 是边AC 的中点,∴22AC AD ==.在△ABC 中,222222121cos 22123AB AC BC BC A AB AC +-+-===⋅⋅⨯⨯,………8分解得3BC =……………10分 由正弦定理得,sin sin BC ABA C=, ……………11分∴1sin sin 3AB AC BC⋅===. ……………12分17.(本小题满分12分)(1) 解:由题意,得()0.020.0320.018101x +++⨯=, ……………1分 解得0.03x =. ……………2分 (2)解:50个样本小球重量的平均值为0.2100.32200.3300.184024.6X =⨯+⨯+⨯+⨯=(克). ……………3分由样本估计总体,可估计盒子中小球重量的平均值约为24.6克. ……………4分(3)解:利用样本估计总体,该盒子中小球重量在(]5,15内的概率为0.2,则13,5B ξ⎛⎫⎪⎝⎭. ……………5分 ξ的取值为0,1,2,3, ……………6分()30346405125P C ξ⎛⎫=== ⎪⎝⎭,()2131448155125P C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭, ()2231412255125P C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭,()3331135125P C ξ⎛⎫=== ⎪⎝⎭. ……………10分∴ξ的分布列为:……………11分 ∴6448121301231251251251255E ξ=⨯+⨯+⨯+⨯=. ……………12分 (或者13355E ξ=⨯=)18.(本小题满分14分)(1)证明:取AB 的中点M ,连接EM ,则1AM MB ==,∵EF ∥平面ABCD ,EF ⊂平面ABFE ,平面ABCD 平面ABFE AB =,M OH FED C B ∴EF ∥AB ,即EF ∥MB . ……………1分 ∵EF =MB 1=∴四边形EMBF 是平行四边形. ……………2分 ∴EM ∥FB ,EM FB =.在Rt △BFC 中,2224FB FC BC +==,又FB FC =,得FB =∴EM =……………3分在△AME中,AE =1AM =,EM =∴2223AM EM AE +==,∴AM EM ⊥. ……………4分 ∴AM FB ⊥,即AB FB ⊥. ∵四边形ABCD 是正方形,∴AB BC ⊥. ……………5分 ∵FB BC B = ,FB ⊂平面BCF ,BC ⊂平面BCF ,∴AB ⊥平面BCF . ……………6分 (2)证法1:连接AC ,AC 与BD 相交于点O ,则点O 是AC 的中点, 取BC 的中点H ,连接,OH EO ,FH , 则OH ∥AB ,112OH AB ==. 由(1)知EF ∥AB ,且12EF AB =,∴EF ∥OH ,且EF OH =.∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1E O F H == .……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF ,∴FH AB ⊥. ……………8分∵FH BC ⊥,,AB BC B AB =⊂ 平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD . ……………9分 ∴EO ⊥平面ABCD . ∵AO ⊂平面ABCD ,∴EO ⊥AO . ……………10分 ∵AO BD ⊥,,EO BD O EO =⊂ 平面EBD ,BD ⊂平面EBD , ∴AO ⊥平面EBD . ……………11分 ∴AEO ∠是直线AE 与平面BDE 所成的角. ……………12分 在Rt △AOE中,tan AOAEO EO∠== ……………13分 ∴直线AE 与平面BDE. ……………14分证法2:连接AC ,AC 与BD 相交于点O ,则点O 取BC 的中点H ,连接,OH EO ,FH , 则OH ∥AB ,112OH AB ==.由(1)知EF ∥AB ,且12EF AB =, ∴EF ∥OH ,且EF OH =. ∴四边形EOHF 是平行四边形.∴EO ∥FH ,且1EO FH ==. ……………7分 由(1)知AB ⊥平面BCF ,又FH ⊂平面BCF , ∴FH AB ⊥.∵FH BC ⊥,,AB BC B AB =⊂ 平面ABCD ,BC ⊂平面ABCD ,∴FH ⊥平面ABCD .∴EO ⊥平面ABCD . ……………8分 以H 为坐标原点,BC 所在直线为x 轴,OH 所在直线为y 轴,HF 所在直线为z 轴,建立空间直角坐标系H xyz -,则()1,2,0A -,()1,0,0B ,()1,2,0D --,()0,1,1E -.∴()1,1,1AE =- ,()2,2,0BD =-- ,()1,1,1BE =--. ……………9分设平面BDE 的法向量为=n (),,x y z ,由n 0BD ⋅= ,n 0BE ⋅=,得220x y --=,0x y z --+=,得0,z x y ==-.令1x =,则平面BDE 的一个法向量为=n ()1,1,0-. ……………10分 设直线AE 与平面BDE 所成角为θ,则sin θ=cos , n AE ⋅=n AEnAE=. ……………11分∴cos 3θ==,sin tan cos θθθ== ……………13分 ∴直线AE 与平面BDE. ……………14分19.(本小题满分14分)(1)解法1:当2n ≥时,()11n n na S n n +=++,()()111n n n a S n n --=+-,……1分 两式相减得()()()11111n n n n na n a S S n n n n +---=-++--, ……………3分即()112n n n na n a a n +--=+,得12n n a a +-=. ……………5分 当1n =时,21112a S ⨯=+⨯,即212a a -=. ……………6分 ∴数列{}n a 是以10a =为首项,公差为2的等差数列.∴()2122n a n n =-=-. ……………7分 解法2:由()11n n na S n n +=++,得()()11n n n n S S S n n +-=++, ……………1分 整理得,()()111n n nS n S n n +=+++, ……………2分 两边同除以()1n n +得,111n nS S n n+-=+. ……………3分 ∴数列n S n ⎧⎫⎨⎬⎩⎭是以101S =为首项,公差为1的等差数列. ∴011nS n n n=+-=-. ∴()1n S n n =-. ……………4分 当2n ≥时,()()()111222n n n a S S n n n n n -=-=----=-. ……………5分 又10a =适合上式, ……………6分 ∴数列{}n a 的通项公式为22n a n =-. ……………7分 (2)解法1:∵22log log n n a n b +=, ∴221224na n n nb n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++ ()0122142434144n n n n --=+⨯+⨯++-⋅+⋅ ,①()1231442434144n n n T n n -=+⨯+⨯++-⋅+⋅ ,② ……………11分①-②得0121344444n nn T n --=++++-⋅ 14414n nn -=-⋅-()13413n n -⋅-=.……………13分 ∴()131419nn T n ⎡⎤=-⋅+⎣⎦. ……………14分 解法2:∵22log log n n a n b +=, ∴221224na n n nb n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++ ()0122142434144n n n n --=+⨯+⨯++-⋅+⋅ .由()12311n nx x x x x x x x+-++++=≠- , ……………11分两边对x 取导数得,012123n x x x nx-++++=()()12111n n nx n x x +-++-. ………12分令4x =,得()()0122114243414431419n n n n n n --⎡⎤+⨯+⨯++-⋅+⋅=-⋅+⎣⎦ . ……………13分 ∴ ()131419nn T n ⎡⎤=-⋅+⎣⎦. ……………14分 20.(本小题满分14分)(1)解法1:由题意, 点M 到点F 的距离等于它到直线l 的距离,故点M 的轨迹是以点F 为焦点, l 为准线的抛物线. ……………1分 ∴曲线E 的方程为24x y =. ……………2分 解法2:设点M 的坐标为(),x y ,依题意, 得1MF y =+,1y =+, ……………1分 化简得24x y =.∴曲线E 的方程为24x y =. ……………2分 (2) 解法1: 设点,B C 的坐标分别为()()1122,,,x y x y ,依题意得,2211224,4x y x y ==.由21,4,y kx x y =+⎧⎨=⎩消去y 得2440x kx --=,解得1,2422k x k ±==± ∴12124,4x x k x x +==-. ……………3分直线AB 的斜率2111111124224ABx y x k x x --+===--, 故直线AB 的方程为()12124x y x +-=-. ……………4分 令1y =-,得1822x x =-+,∴点S 的坐标为182,12x ⎛⎫-- ⎪+⎝⎭. ……………5分 同理可得点T 的坐标为282,12x ⎛⎫-- ⎪+⎝⎭. ……………6分 ∴()()()121212888222222x x ST x x x x -⎛⎫=---= ⎪++++⎝⎭ ()()()121212121288248x x x x x x x x x x kk---===+++. ……………7分 ∴2ST=()()()2221212122221614k x x x x x x k k k +-+-==. ……………8分设线段ST 的中点坐标为()0,1x -,则()()()12012124418822222222x x x x x x x ++⎛⎫=-+-=- ⎪++++⎝⎭ ()()()1212444444222248k k x x x x kk++=-=-=-+++. ……………9分 ∴以线段ST 为直径的圆的方程为()2222114x y ST k ⎛⎫+++= ⎪⎝⎭()2241k k +=. ……………10分展开得()()22222414414k x x y k k k++++=-=. ……………11分 令0x =,得()214y +=,解得1y =或3y =-. ……………12分 ∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分 解法2:由(1)得抛物线E 的方程为24x y =.设直线AB 的方程为()112y k x -=-,点B 的坐标为()11,x y ,由()112,1,y k x y ⎧-=-⎨=-⎩解得122,1.x k y ⎧=-⎪⎨⎪=-⎩∴点S 的坐标为122,1k ⎛⎫-- ⎪⎝⎭. …………3分 由()1212,4,y k x x y ⎧-=-⎨=⎩消去y ,得2114840x k x k -+-=,即()()12420x x k --+=,解得2x =或142x k =-. ……………4分 ∴1142x k =-,22111114414y x k k ==-+. ∴点B 的坐标为()211142,441k k k --+. ……………5分 同理,设直线AC 的方程为()212y k x -=-, 则点T 的坐标为222,1k ⎛⎫-- ⎪⎝⎭,点C 的坐标为()222242,441k k k --+. …………6分 ∵点,B C 在直线1:1l y kx =+上,∴()()()()()()22222211212121214414414242k k k k k k k k k k k k k -+--+---==----121k k =+-.∴121k k k +=+. ……………7分 又()211144142k k k k -+=-1+,得()21111214442412k k kk k k k k k -=-=+--,化简得122kk k =. ……………8分 设点(),P x y 是以线段ST 为直径的圆上任意一点,则0SP TP ⋅=, ……………9分得()()122222110x x y y k k ⎛⎫⎛⎫-+-++++= ⎪⎪⎝⎭⎝⎭, ……………10分 整理得,()224410x x y k+-++=. ……………11分 令0x =,得()214y +=,解得1y =或3y =-. ……………12分 ∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分 21.(本小题满分14分)(1)解:∵()ln f x a x bx =+, ∴()af x b x'=+. ∵直线220x y --=的斜率为12,且过点11,2⎛⎫- ⎪⎝⎭, ……………1分∴()()11,211,2f f ⎧=-⎪⎪⎨⎪'=⎪⎩即1,21,2b a b ⎧=-⎪⎪⎨⎪+=⎪⎩解得11,2a b ==-. ……………3分(2)解法1:由(1)得()ln 2x f x x =-. 当1x >时,()0k f x x +<恒成立,即ln 02x kx x-+<,等价于2ln 2x k x x <-.……………4分令()2ln 2x g x x x =-,则()()ln 11ln g x x x x x '=-+=--. ……………5分令()1ln h x x x =--,则()111x h x x x-'=-=. 当1x >时,()0h x '>,函数()h x 在()1,+∞上单调递增,故()()10h x h >=. ……………6分 从而,当1x >时,()0g x '>,即函数()g x 在()1,+∞上单调递增, 故()()112g x g >=. ……………7分 因此,当1x >时,2ln 2x k x x <-恒成立,则12k ≤. ……………8分∴所求k 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分解法2:由(1)得()ln 2x f x x =-. 当1x >时,()0k f x x +<恒成立,即ln 02x kx x-+<恒成立. ……………4分 令()ln 2x kg x x x=-+,则()222112222k x x k g x x x x -+'=--=-.方程2220x x k -+=(﹡)的判别式48k ∆=-.(ⅰ)当0∆<,即12k >时,则1x >时,2220x x k -+>,得()0g x '<, 故函数()g x 在()1,+∞上单调递减.由于()()110,2ln 21022kg k g =-+>=-+>, 则当()1,2x ∈时,()0g x >,即ln 02x kx x-+>,与题设矛盾. …………5分(ⅱ)当0∆=,即12k =时,则1x >时,()()2222121022x x x g x x x--+'=-=-<.故函数()g x 在()1,+∞上单调递减,则()()10g x g <=,符合题意. ………6分 (ⅲ) 当0∆>,即12k <时,方程(﹡)的两根为1211,11x x =<=+>, 则()21,x x ∈时,()0g x '>,()2,x x ∈+∞时,()0g x '<. 故函数()g x 在()21,x 上单调递增,在()2,x +∞上单调递减, 从而,函数()g x 在()1,+∞上的最大值为()2222ln 2x kg x x x =-+. ………7分 而()2222ln 2x k g x x x =-+2221ln 22x x x <-+, 由(ⅱ)知,当1x >时,1ln 022x x x-+<, 得2221ln 022x x x -+<,从而()20g x <. 故当1x >时,()()20g x g x ≤<,符合题意. ……………8分 综上所述,k 的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分(3)证明:由(2)得,当1x >时,1ln 022x x x-+<,可化为21ln 2x x x -<, …10分 又ln 0x x >, 从而,21211ln 111x x x x x >=---+. ……………11分 把2,3,4,,x n = 分别代入上面不等式,并相加得,11111111111112ln 23ln 3ln 32435211n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++>-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪--+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭……………12分 111121n n =+--+ ……………13分 223222n n n n--=+. ……………14分。
2014年普通高等学校招生全国统一考试数学理试题(广东卷,含答案)

2014年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,0,1}M =-,{0,1,2}N =,则M N =A. {0,1} B . {1,0,2}- C. {1,0,1,2}- D . {1,0,1}-2.已知复数Z 满足(34)25i z +=,则Z= A. 34i -+ B. 34i -- C . 34i +D. 34i -3.若变量,x y 满足约束条件121y xx y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为m 和n ,则m n -=A.5B.6C.7D.84.若实数k 满足09k <<,则曲线221259x y k -=-与曲线221259x y k -=-的A. 焦距相等B. 实半轴长相等C. 虚半轴长相等D. 离心率相等5.已知向量()1,0,1a =-,则下列向量中与a 成60︒夹角的是A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)6.已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别是小学 初中高中 年级OA.200,20B.100,20C.200,10D.100,107.若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,l l l l l l ⊥⊥⊥,则下面结论一定正确的是 A.14l l ⊥ B.14//l l C.14,l l 既不垂直也不平行D.14,l l 的位置关系不确定 8.设集合(){}12345=,,,,{1,0,1},1,2,3,4,5i A x x x x x x i ∈-=,那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为A.60B.90C.120D.130二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题) 9.不等式521≥++-x x 的解集为 。
2014年广东高考理科数学试题含答案(Word版)

答案: C 提示 : 画出可行域(略), 易知在点(2,1) (−1, −1)处目标函数 最小值m = −3,∴ M − m = 6, 选 C.
4.若实数 k 满足 0 < k < 9, 则曲线 A 离心率相等
别取得最大值M = 3,
x2 y2 x2 y2 − = 1 曲线 − = 1的 25 9 − k 25 − k 9
B.
a 成 60° 夹角的是
C. 0,-1,1 D. -1,0,1
-1,1,0
1,-1,0
答案 : B 提示 : 1 = ,即 12 + 02 + (−1) 2 ⋅ 12 + (−1) 2 + 0 2 2 (1, 0, −1) ⋅ (1, −1, 0) 两向 1 的夹角余弦值为 , 从而夹角为600 ,∴ 选 B. 2
6、已知某地区中小学生人数和近视情况 别如 1 和 用 层抽样的方法抽取 2%的学生进行调查 则样本容 A. 200,20 B. 100,20 C. 200,10 D. 100,10
2 所示 为了解该地区中小学生的近视形成原因 和抽取的高中生近视人数 别为
答案 : A 提示 : 样本容 为(3500 + 4500 + 2000) ⋅ 2% = 200,
.
+ 2 在点 (0,3) 处的 线方程为 答案 : 5 x + y − 3 = 0
提示 : y ' = −5e −5 x ,∴ y '
x =0
= − 5,∴ 所求 线方程为y − 3 = −5 x,即5 x + y − 3 = 0 .
.
11.从 0,1,2,3,4,5,6,7,8,9 中任取七个 的数 则 七个数的中位数是 6 的概率为 1 答案 : 6 提示 : 要使6为取出的7个数中的中位数, 则取出的数中必有3个 大于6,
2014年广东卷数学试题及答案(理)

2014年普通高等学校招生全国统一考试(广东卷)数学理一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{1,0,1},{0,1,2},M N =-=则M N ⋃=A .{1,0,1}- B. {1,0,1,2}- C. {1,0,2}- D. {0,1}2.已知复数Z 满足(34)25,i z +=则Z=A .34i - B. 34i + C. 34i -- D. 34i -+3.若变量,x y 满足约束条件121y x x y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为M 和m ,则M-m=A .8 B.7 C.6 D.54.若实数k 满足09,k <<则曲线221259x y k -=-与曲线221259x y k -=-的 A .离心率相等 B.虚半轴长相等 C. 实半轴长相等 D.焦距相等5.已知向量()1,0,1,a =-则下列向量中与a 成60︒夹角的是A .(-1,1,0) B. (1,-1,0) C. (0,-1,1) D. (-1,0,1)6、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为A 、200,20B 、100,20C 、200,10D 、100,107、若空间中四条两两不同的直线1234,,,l l l l ,满足122334,,,l l l l l l ⊥⊥⊥,则下列结论一定正确的是A .14l l ⊥B .14//l lC .14,l l 既不垂直也不平行D .14,l l 的位置关系不确定8.设集合(){}12345=,,,,1,0,1,1,2,3,4,5i A x x x x x x i ∈-=,那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为A .60 B90 C.120 D.130二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9.不等式521≥++-x x 的解集为 。
培正中学2014届高三11月月考数学试卷(理)

培正中学2014届高三11月月考数学试卷(理)一、选择题:本大题共8个小题,每小题5分,共40分.每小题给出的四个选项中只有一项是符合题目要求的.1. 已知A 、B 均为集合{}1,3,5,7,9U =的子集,且{}3AB =,{}()9U B A =ð,则A 等于( ) {}.1,3A {}.3,7,9B {}.3,5,9C {}.3,9D2. “1a =”是“(1)(2)0a a --=”成立的 ( ).A 充分非必要条件 .B 必要非充分条件 .C 充要条件 .D 既不充分也不必要条件3. 552log 10log 0.25+= ( ) .0A .1B .2C .4D4. 函数2ln(1)34x y x x +=--+的定义域为 ( ).(4,1)A -- .(4,1)B - .(1,1)C - .(1,1]D -5. 把函数sin()3y x π=+图象上所有点向右平移3π个单位,再将所得图象的横坐标变为原来的12倍(纵坐标不变),得图象的解析式是sin()(0,)y x ωϕωϕπ=+><,则 ( )1.,23A πωϕ==- .2,3B πωϕ== .2,0C ωϕ== 2.2,3D πωϕ== 6.已知向量a 、b 满足||1,()(2)0a a b a b =+⋅-=,则||b 的取值范围为A .[1,2]B .[2,4]C .11[,]42 D .1[,1]27、如图,E 、F 分别为棱长为1的正方体的棱11A B 、11B C 的中点,点G 、H 分别为面对角线AC 和棱1DD 上的动点(包括端点),则下列关于四面体E FGH -的体积正确的是 ( )A )此四面体体积既存在最大值,也存在最小值;B )此四面体的体积为定值;C )此四面体体积只存在最小值;D )此四面体体积只存在最大值。
8. 在直角坐标系中,如果不同两点A(a ,b),B(—a ,一b)都在函数y=h (x )的图象上, 那么称[A ,B]为函数h(x)的一组“友好点”([A,B]与[B,A]看作一组).已知定义在),0[+∞上的函数f(x)满足ABCD 1A1B 1C1DE FG H第7题图f (x+2)= 2f (x),且当x ∈[0,2]时,f(x)=sin 2πx.则函数⎩⎨⎧<≤---≤<=08,;80),()(x x x x f x g 的“友好点”的组数为 (A) 4(B)5 (C) 6 (D)7二、填空题(本大题共7小题, 分为必做题和选做题两部分.每小题5分, 满分30分) (一)必做题: 第9至13题为必做题, 每道试题考生都必须作答. 9、若bi ia-=-11,其中b a ,都是实数,i 是虚数单位,则bi a += . 10、函数()2sin sin()3f x x x π=⋅-的值域是 .11、已知数列{}n a 的前n 项和21n n S a =-,则数列{}n a 的通项公式为n a = .*()n N ∈12、如图:底面直径为2的圆柱被与底面成030二面角的平面所截,截面是一个椭圆, 则此椭圆的焦距为 .13. 对于三次函数32()f x ax bx cx d =+++(0a ≠),给出定义:设()f x '是函数()y f x =的导数,()f x ''是函数()f x '的导数,若方程()0f x ''=有实数解0x ,则称点00(,())x f x 为函数()y f x =的“拐点”,某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心. 给定函数32115()33212f x x x x =-+-,请你根据上面探究结果,解答以下问题: (1)函数32115()33212f x x x x =-+-的对称中心坐标为 ______ ;(2)计算1232012()()()()2013201320132013f f f f ++++= __________ .(二)选做题: 第14、15题为选做题, 考生只能选做其中一题, 两题全答的, 只计前一题的得分。
培正中学高三数学第二次月考试卷(理科)

培正中学高三数学第二次月考试卷(理科)A、 B、 C、 D、8.若,则的最小值为( )A、7B、C、D、5二、填空题:(每小题5分,满分30分)(一)必做题(9~13题)9.不等式的解集为 .10.从1 ,2 ,3 ,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率为11.已知是递增等比数列,,则此数列的公比q= .12.若命题存在,使是假命题,则实数m的取值范围为 .13. 已知实数a 0,函数若,则a的值为 .(二)选做题(14~15题,考生从中选做一题,如果两题都做了,只批改第14题)14. 在极坐标系中,曲线与的交点的极坐标为 .15. 如图1所示,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC= .三、解答题:(共6小题,满分80分)16.(本小题12分)已知向量,,设函数 .(1) 求的最小正周期; (2) 求在上的最大值和最小值.17. (本小题13分) 某校100名学生期中考试语文成绩的频率分布直方图如图2所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1) 求图中a的值;(2) 根据频率分布直方图,估计这100名学生语文成绩的平均分;(3) 若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应的分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.分数段[50,60)[60,70)[70,80)[80,90)x:y1:12:13:44:518. (本小题14分) 如图3所示,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中ADAB,CD∥AB,AB=4,CD=2,侧面PAD 是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.(1) 求证:DE∥平面PBC;(2) 求三棱锥A-PBC的体积.19.(本题13分) 已知a为实常数,是定义在R上的奇函数,当x0时,,若对一切成立,求实数a的取值范围。
广东省广州市培正中学2024届高三上学期第一次模拟测试数学试题 (2)

一、单选题二、多选题1.若,则( )A.B.C.D.2. 已知函数,函数的图象与曲线有3个不同的交点,其横坐标依次为,,,设,则的取值范围为( )A.B.C.D.3.已知球半径为,设是球面上四个点,其中,则棱锥的体积的最大值为( )A.B.C.D.4. 复数,则( )A.B.C.D.5. 医学上用基于SEIR 流行病传播模型测算基本传染数(也叫基本再生数)来衡量传染性的强弱,基本传染数可表示为.计算基本传染数需要确定的参数有:(1)参数:,即需要知道第一例病例发生的时间(确定起点以便计算t ),以及之后某一时刻的累计病例数,时间t 的单位为天数;(2)参数和ρ:只要确定了潜伏期TE 和传染期TI ,和ρ就都确定了.已知2022年2月15日某地发现首例A 型传染性病例,到2022年3月28日累计A 型传染性病例数达到425例.取,,根据上面的公式计算这41天A型传染性基本传染数约为(注:参考数据:)( )A .2.63B .2.78C .2.82D .3.046. 任意大于1的正整数m 的三次幂均可“分裂”成m 个连续奇数的和,如:,,,…,按此规律,若分裂后,其中有一个奇数是2019,则m 的值是( )A .46B .45C .44D .437.的展开式中的各项系数和为243,则该展开式中的系数为( )A.B .46C .61D .1908.直线平面,直线平面,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件9. 已知函数在区间上的零点个数为,函数在区间上的所有零点的和记为.则下述正确的是( )A.B.C .在区间上任意两零点的差大于D .在区间上任意两相邻零点的差大于10.设函数,,则下列说法正确的有( )A .不等式的解集为;B.函数在单调递增,在单调递减;C .当时,总有恒成立;D.若函数有两个极值点,则实数广东省广州市培正中学2024届高三上学期第一次模拟测试数学试题 (2)广东省广州市培正中学2024届高三上学期第一次模拟测试数学试题 (2)三、填空题四、解答题11. 若关于的方程在区间上有且只有一个解,则的值可能为( )A.B.C .0D .112.已知函数,则下列说法正确的是( )A .的值域为B .的图像关于点中心对称C.的最小正周期为D.的增区间为()13. 若的展开式中存在常数项,则常数项为_________.14.若函数的图象经过点和,且当时,恒成立,则实数a 的取值范围是______.15. 为庆祝中国共产党成立100周年,某志愿者协会开展“党史下乡”宣讲活动,准备派遣10名志愿者去三个乡村开展宣讲,每名志愿者只去一个乡村,每个乡村至少安排3个志愿者,则不同的安排方法共有________种.(用数字作答)16.已知函数(1)若不等式对任意的恒成立,求的取值范围;(2)当时,记的最小值为,正实数,,满足,证明:.17.已知二次函数(1)若为偶函数,求的值;(2)判定函数在区间内是否有零点,请说明理由;(3)已知函数存在最小值,求的最大值.18. 已知四棱锥如图所示,其中,均为等边三角形,二面角为直二面角,点为线段的中点,点是线段上靠近的三等分点,平面.(1)求证:;(2)若,求直线与平面所成角的正弦值.19. 在①,②这两个条件中任选一个作为已知条件,然后解答问题.在中,角A ,B ,C 的对边分别为a ,b ,c ,______.(1)求角A ;(2)若,,求的BC 边上的中线AD 的长.20.已知点,,动点的轨迹曲线满足,,过点的直线交曲线于、两点.(1)求的值,并写出曲线的方程;(2)求△面积的最大值.21. “黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”江南梅雨的点点滴滴都流润着浓洌的诗情每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q镇年梅雨季节的降雨量单位:的频率分布直方图,试用样本频率估计总体概率,解答下列问题:Ⅰ“梅实初黄暮雨深”假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率;Ⅱ“江南梅雨无限愁”在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元而乙品种杨梅的亩产量亩与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为元,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润万元的期望更大?需说明理由降雨量亩产量500700600400。
《广东省广州市培正中学二零一六届高三数学12月月考试题理新人教a版》.doc

培正中学2014届高三12月月考数学试卷(理)(问卷)总分:150分 考试用时:120分钟一、选择题:每小题5分,共40分.每小题给出的四个选项中只有一项是符合题目要求的.己知 R 是实数集,M ={x\x(2-x)<0},N = {y\y = 4T^},则 N C C R M =(若a,b 为实数,则“0<ab< 1”是“bv 丄”的( )a(B)必要而不充分条件7.数列{。
“}的首项为 3, {b fl }为等差数列且=a H+} -a n (n e N*).若则$ = -2,/?10 = 12 ,1.(A) (1,2)(O [0,2](D) [1,2]2.(A)充分而不必要条件(0充要条件(D) 即不充分也不必要条件3.复数磊的烛复数在复平面内对应的点在((A)第一彖限4. (B)第二彖限如图所示,一•个空间儿何体的主视图和左视图都是边长为1的正(C) 第三象限(D)形,俯视图是一个总径为1的圆,那么这个儿何体的全而积为((B) 2TI3(D)-TT25. 某地区决定从12名人学生村官中选3个人担任乡长助理,则甲、至少有1人入选,乙没有入选的不同选法的种数位为( )(A) 220 (B) 165(C)84 (D).816. 在平而直角坐标系xOy 中,已知圆=16上冇且只冇四个点到直线3兀-4y+c = 0的距离为2,则实数f 的収值范围为()(A) -10<c<10 (C) c > 10< -10(A) 4兀 (0 3兀(B)-10<c<10(D) c > 10 或c v -10n+l(A) 0 (0 8 (D) 11 第四象限)左视图8.过双曲线C:2%2-2_ = 1(/?>0)的左顶点P作斜率为1的直线若/与双曲线C的两条渐近线分别相交于点Q,R, liOP + OR = 2OQ,则双曲线C的离心率是(二、填空题(木大题共7小题,分为必做题和选做题两部分.每小题5分,满分30分) (-)必做题:第9至13题为必做题,每道试题考生都必须作答.9.己知随机变量g 服从正态分布M2,;),且戶(§<4)=0.8,贝IJ 戶(0V§V2)等 于 •r r1 i ILLI t 110・ 已知d =1, b =2, Q 与b 的夹角为120° , a + b +c = 0 ,则d 与c 的夹角为 ______________11 > J ? (1+丁4 - F )dx = ________________ ;_x-4y + 3<0,12. 设O 为坐标原点,点M 坐标为(2,1),若N(x,y)满足不等式组:(2x+y —12 5 0,则x> 1, OM • ON 的最大值为 __________________ ,1- | x-11,^ e (-oo,2)13. 若函数f (x) = < 1,则函数F(x) = xf(x)-1零点个数-/(x-2),xe[2,+oo)为 _______________ .(二)选做题:第14、15题为选做题,考主只能选做其中一题,两题全答的,只计前一题 的得分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
培正中学2014届高三12月月考数学试卷(理)(问卷)总分:150分 考试用时:120分钟一、选择题:每小题5分,共40分.每小题给出的四个选项中只有一项是符合题目要求的. 1.已知R 是实数集,}1|{},0)2(|{-==<-=x y y N x x x M ,则RN C M ⋂=( ) (A) ()1,2 (B) ∅ (C) []0,2 (D) []1,22. 若,a b 为实数,则“01ab <<”是“1b a<”的( ) (A) 充分而不必要条件 (B) 必要而不充分条件 (C) 充要条件 (D) 即不充分也不必要条件 3.复数ii437++的共轭复数在复平面内对应的点在( ) (A) 第一象限 (B) 第二象限(C) 第三象限 (D) 第四象限4.如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为( )(A)4π (B)2π (C)3π (D)3π25.某地区决定从12名大学生村官中选3个人担任乡长助理,则甲、丙至少有1人入选,乙没有入选的不同选法的种数位为 ( )(A)220 (B) 165 (C)84(D).816.在平面直角坐标系xOy 中,已知圆1622=+y x 上有且只有四个点到直线043=+-c y x 的距离为2,则实数c 的取值范围为( ) (A) 1010<<-c (B)1010≤≤-c(C) 10≥c 或10-≤c (D)10>c 或10-<c7. 数列{}n a 的首项为3,{}n b 为等差数列且1(*)n n n b a a n N +=-∈.若则3102,12b b =-=,则8a =( )(A) 0 (B) 3 (C)8 (D) 118.过双曲线C :()22210y x b b-=>的左顶点P 作斜率为1的直线l ,若l 与双曲线C 的两条渐近线分别相交于点R Q ,,且2=+,则双曲线C 的离心率是( )图1COPBA(C)2(D)3二、填空题(本大题共7小题, 分为必做题和选做题两部分.每小题5分, 满分30分) (一)必做题: 第9至13题为必做题, 每道试题考生都必须作答.9.已知随机变量ξ服从正态分布N (2,σ2),且P (ξ<4)=0.8,则P (0<ξ<2)等于 .10. 已知a r =1,b r =2,a r 与b r 的夹角为120°,0a b c ++=r r r r ,则a r 与c r的夹角为 .11、02dx -=⎰( .12.设O 为坐标原点,点M 坐标为)1,2(,若),(y x N 满足不等式组:⎪⎩⎪⎨⎧≥≤-+≤+-,1,0122,034x y x y x 则⋅的最大值为 .13. 若函数⎪⎩⎪⎨⎧+∞∈--∞∈--=),2[),2(31)2,(|,1|1)(x x f x x x f ,则函数1)()(-=x xf x F 零点个数为 .(二)选做题: 第14、15题为选做题, 考生只能选做其中一题, 两题全答的, 只计前一题的得分。
14.(坐标系与参数方程选做题)已知两曲线参数方程分别为2cos sin x y θθ=⎧⎨=⎩(0)θπ<≤和2x ty t=⎧⎨=⎩ (t ∈)R ,它们的交点坐标为___________. 15.(几何证明选讲选做题)如图1,过圆O 外一点P 分别作圆的切线和割线交圆于,A B ,且7PB =,C 是圆上一点使得5BC =,BAC APB ∠=∠,则AB =___________.三、解答题: 本大题共6小题, 满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本题满分12分) 已知x x x f 2sin 4)32cos()(+-=π(1)求函数的最小正周期及单调递增区间; (2)若⎥⎦⎤⎢⎣⎡∈2,0πx ,求函数的最大值及最小值。
17.(本小题满分12分)某班学生春假需要选择春游线路,已知甲寝室与乙寝室各有6位同学,每人选择一条线路。
甲寝室选择去乌镇游玩的有1人,选择去横店游玩的有5人,乙寝室选择去乌镇游玩的有2人,选择去横店游玩的有4人,现从甲寝室、乙寝室中各任选2人分析游玩线路问题.(1)求选出的4 人均选择游玩横店的概率;(2)设ξ为选出的4个人中选择游玩乌镇的人数,求ξ的分布列和数学期望E ξ18.(本小题14分)设数列{}n a 是公差不为0的等差数列,n S 为前n 项和,满足1253,2,a a a 成等差数列,6010=S 。
(1)求数列{}n a 的通项公式及前n 项和n S ;(2)试求所有正整数m ,使212m ma a ++为数列{}n a 中的项。
19.(本小题满分14分)已知矩形11A ACC 中,4,21==AC AA ,B 是AC 上动点,过B 作11//AA BB 交11C A 于1B ,沿1BB 将矩形11B BCC 折起,连接AC ,11C A 。
(1) 求三棱柱体积的最大值.(2) 满足条件(1)时,D 为AC 中点,求证⊥1AC 面BD A 1.(3) 满足条件(1)(2)时,E 为1CC 中点,求二面角A 1—BD —E 的大小.20.(本小题满分14分)已知中心在原点的椭圆的一个焦点)22,0(1-F ,又过点(1,0)-,且离心率e 满足32,e ,34成等比数列. (1)求椭圆的方程;(2)试问是否存在直线l ,使l 与椭圆交于不同的两点M 、N ,且线段MN 恰被直线21-=x 平分?若存在,求出l 的倾斜角的取值范围;若不存在,请说明理由.21.(本小题满分14分)已知函数32()ln()2f x x x=++,()ln g x x =. (1)求函数()f x 的单调区间; (2)如果关于x 的方程1()2g x x m =+有实数根,求实数m 的取值范围; (3)是否存在正数k ,使得关于x 的方程()()f x kg x =有两个不相等的实根?如果存在,求的k 取值范围,如果不存在,说明理由?培正中学2014届高三12月月考数学试卷(理)(参考答案)总分:150分 考试用时:120分钟一、选择题:每小题5分,共40分.每小题给出的四个选项中只有一项是符合题目要求的.二、填空题(本大题共7小题, 分为必做题和选做题两部分.每小题5分, 满分30分) 9. 0.3 ; 10. 90; 11. +2π; 12. 12 ; 13. 3 ;14.三、解答题: 本大题共6小题, 满分80分.解答须写出文字说明、证明过程和演算步骤. 16.解:(1)1()cos 222(1cos 2)232cos 222)23f x x x x x x x π=++-=-+=-+学科网 (3分)最小正周期ππ==22T (4分) 由223222πππππ+≤-≤-k x k ,得12512ππππ+≤≤-k x k递增区间是⎥⎦⎤⎢⎣⎡+-125,12ππππk k ,Z k ∈ (7分) (2)⎥⎦⎤⎢⎣⎡∈2,0πx ,32323πππ≤-≤-x , 1)32sin(23≤-≤-πx (10分) 23213)(,212)23(3)(max min +=+⨯==+-⨯=x f x f (14分)17.解:(Ⅰ)设“从甲寝室选出的2人选横店”为事件A ,“从乙寝室选出的2人选横店”为事件B .由于事 件A 、B 相互独立, 且,.………………4分所以选出的4人均选择横店的概率为…………………………… 6分(Ⅱ)设可能的取值为0,1,2,3.得,,…………… 12分的分布列为 的数学期望 18.解:(1)设数列}{n a 首项1a ,公差d ,则d a d a d a a a 132112111123+=+++=+ (2分) d a d a a 82)4(22115+=+=则)82(213211d a d a +=+ 0321=+d a (4分) 且6045102910101110=+=⨯+=d a d a S 解得n n n n n S n a d a n n 422)1()3(,52,2,321-=⨯++-⨯=-==-= (7分)(2)526)52(4)52(52]2)52[(522)32(222221-+-+-=-+-=-+-=++m m m m m m m a a m m 52612526452-+-=-++-=m m m m (10分)要使1212+++m m a a 也是}{n a 的项,则526-m 为整数。
522152612,1-⨯=-=-+-=m m m 是第二项512352612,2-⨯=-=-+-=m m m 是第一项5821152612,3-⨯==-+-=m m m 是第八项572952612,4-⨯==-+-=m m m 是第七项所有的正整数m 为4,3,2,1 (14分) 19.解:(1)依题意,三棱柱为直三棱柱,1AA S V ABC ⨯=∆柱体 (2分)ABC AC AB S ABC ∠⋅=∆sin 21要使体积最大,ABC ∆面积最大,只有当AC AB ABC ==∠,90时,面积最大。
此时22221=⨯⨯=S 422=⨯=最大V (4分) (2)D 为AC 的中点,则22tan 11==∠AA AD D AA ,22222tan 11===∠AC CC CAC 则11CAC D AA ∠=∠ 那么︒=∠+∠9011ADA CAC D A AC 11⊥ (6分) 又BD AC ⊥1所以BD A AC 11平面⊥ (8分) (3)D 为AC 的中点,AC BD ⊥,则11ACC A BD 面⊥DE A 1∠为二面角E BD A --1所成的平面角。
(10分)6242211=+=+=AD AA D A322=+=CE DC DE 3212111=+=E C C A E A (12分) 中在三角形DE A 121221E A DE D A =+ 则︒=∠901DE A所以二面角E BD A --1的大小为︒90 (14分) 21. 解:(1)∵34,,32e 成等比数列 ∴34322⨯=e 232=e 设),(y x p 是椭圆上任意一点,依椭圆的定义得99,322249)22(2222=+=+++y x y y x 化简得 即1922=+y x 为所求椭圆方程。
…………5分(2)假设l 存在,因l 与直线21-=x 相交,不可能垂直x 轴 因此可设l 的方程为:m kx y +=由整理得得消去9)(9,992222=++⎩⎨⎧=++=m kx x y y x mkx y 0)9(2)9(222=-+++m kmx x k ①方程①有两个不等的实数根∴090)9)(9(44222222<-->-+-=∆k m m k m k 即 ②…………………………7分设两个交点M 、N 的坐标分别为),)(,(2211y x y x ∴92221+-=+k kmx x ∵线段MN 恰被直线21-=x 平分 ∴192221221-=+-+=-k km x x 即 ∵0≠k ∴kk m 292+= ③ 把③代入②得 0)9()29(222<+-+k k k∵092>+k ∴229104k k+-< ∴32>k 解得3>k 或3-<k ∴直线l 的倾斜角范围为)32,2()2,3(ππππ⋃ ……………………………………15分22.解:(1)323()ln()(22f x x x x =++>-,且0)x ≠, 221222()232f x x x x x '=-=-++,令'()0f x =,解得:1x =-或3.()f x ,'()f x 随x 变化情况如下表:x -(1,0)- (0,3) (3,)+∞'()f x +0 - -0 +()f x ↗↘↘↗∴()f x 的单调递增区间是(3,12--)和(3,+∞),单调递减区间是(1,0-)和(0,3)。
