最后一卷二答案
广东省中山市普通高中2024届高三最后一卷语文试卷含解析
2024年高考语文模拟试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
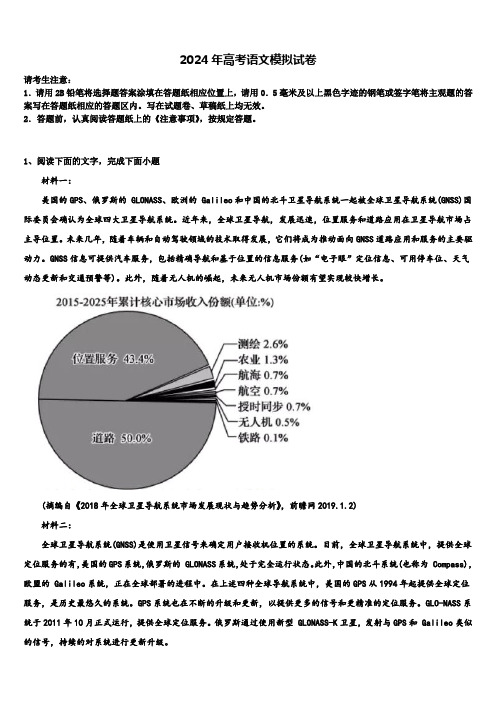
1、阅读下面的文字,完成下面小题材料一:美国的GPS、俄罗斯的 GLONASS、欧洲的 Galileo和中国的北斗卫星导航系统一起被全球卫星导航系统(GNSS)国际委员会确认为全球四大卫星导航系统。
近年来,全球卫星导航,发展迅速,位置服务和道路应用在卫星导航市场占主导位置。
未来几年,随着车辆和自动驾驶领域的技术取得发展,它们将成为推动面向GNSS道路应用和服务的主要驱动力。
GNSS信息可提供汽车服务,包括精确导航和基于位置的信息服务(如“电子眼”定位信息、可用停车位、天气动态更新和交通预警等)。
此外,随着无人机的崛起,未来无人机市场份额有望实现较快增长。
(摘编自《2018年全球卫星导航系统市场发展现状与趋势分析》,前瞻网2019.1.2)材料二:全球卫星导航系统(GNSS)是使用卫星信号来确定用户接收机位置的系统。
目前,全球卫星导航系统中,提供全球定位服务的有,美国的GPS系统,俄罗斯的 GLONASS系统,处于完全运行状态。
此外,中国的北斗系统(也称为 Compass),欧盟的 Galileo系统,正在全球部署的进程中。
在上述四种全球导航系统中,美国的GPS从1994年起提供全球定位服务,是历史最悠久的系统。
GPS系统也在不断的升级和更新,以提供更多的信号和更精准的定位服务。
GLO-NASS系统于2011年10月正式运行,提供全球定位服务。
俄罗斯通过使用新型 GLONASS-K卫星,发射与GPS和 Galileo类似的信号,持续的对系统进行更新升级。
北斗系统于2011年12月开始,提供有限的初始服务,2012年9月正式公布。
公布之初,北斗的空间段包括15颗卫星,向亚太地区提供区域定位服务。
安徽省合肥市第一中学2023届高三最后一卷英语答案

合肥一中2023届高三最后一卷英语参考答案第一部分听力(共两节,满分30分)1-5. BCBCA 6-10. BACCA11-15. CABCB 16-20. BCBAA第二部分阅读(共两节,满分50分)第一节(共15小题;每小题2.5分,满分37.5分)21-25. DCDDA 26-30. BACDC 31-35. BBCAB第二节(共5小题;每小题2.5分,满分12.5分)36-40. GBEFD第三部分语言运用(共两节,满分30分)第一节(共15小题;每小题1分,满分15分)41-45. CABAD 46-50. CBDAB 51-55. CBACD第二节(共10小题;每小题1.5分, 满分15分)56. was staged 57. tickets 58. When 59. paid 60. a61. traditional 62. to explore 63. has built 64. who 65. with第四部分写作(共两节,满分40分)第一节(满分15分)略第二节(满分25分)略部分答案详解:A篇【导语】语篇类型:应用文主题语境:人与社会文章呈现了四部电影的网络评语。
21.D. 细节理解题。
根据题干“ a natural disaster”定位到All That Breathes一节中第一句“Thecarefully-made documentary All That Breathes is set in the climate catastrophe of the failing river and crowded neighborhoods of New Delhi.” 可得答案为D。
22.C. 细节理解题。
根据题干定位到Guillermo del Toro’s Pinocchio和Abbott Elementary两节,在这两节的最后都有“— Aisha Harris”字样,说明两段评语为同一人所写,可得答案为C。
安徽省合肥市第一中学高三最后一卷数学答案和解析

合肥一中2023届高三最后一卷数学参考答案1.解析:因为][0,2,2,0A B ⎡⎤==-⎣⎦所以{}(){}0,0R A B A B x Rx ⋂=⋂=∈≠∣ð.故选:C .2.解析:因为1z =+,所以1z =,故z 的虚部是.故选:A .3.解析:5x =,故0.155 5.75 6.5y =⨯+=,经计算可得被污损的数据为6.4,答案选B .4.解析:曲线1:sin 2cos22C y x x π⎛⎫=+=⎪⎝⎭,把1:cos2C y x =上各点的横坐标缩短到原来的23,纵坐标不变,可得cos3y x =的图象;再把得到的曲线向左平移18π个单位长度,可以得到曲线25:cos 3cos 366C y x x ππ⎛⎫⎛⎫=--=+ ⎪ ⎪⎝⎭⎝⎭的图象,故选:C.5.解析:设直线1y =与y 轴交点为M ,由对称性,易知MFA 为直角三角形,且1602AFM AFB ∠∠== ,2AF FM ∴=,即1212p +=,去绝对值,解得23p =或6,p =∴抛物线的准线方程为13y =-或3y =-.故选:C.6.解析:一方面,考虑{}Ω,,,a b c d =含有等可能的样本点,{}{}{},,,,,A a b B a c C a d ===.则()()()()()()11,24P A P B P C P AB P BC P AC ======,故,,A B C 两两独立,但()1148P ABC =≠,故此时,()()()()P ABC P A P B P C =不成立.另一方面,考虑{}Ω1,2,3,4,5,6,7,8=含有等可能的样本点,{}{}{}1,2,3,4,3,4,5,6,4,6,7,8A B C ===.则()()()()11,28P A P B P C P ABC ====()111822P AC =≠⨯,故,A C 不独立,也即,,A B C 两两独立不成立.综上,“,,A B C 两两独立”是“()()()()P ABC P A P B P C =”的既不充分也不必要条件.故选D.7.解析:作AQ 垂直下半平面于,作AH x ⊥轴于H ,连接,HQ QB .设11,,,(0)A m B m m m m ⎛⎫⎛⎫--> ⎪ ⎪⎝⎭⎝⎭由题可知60AHQ ∠= ,则11,,22AH QH AQ m m m ===,两点间距离公式可得222144QB m m =+.22222144AB AQ QB m m =+=+≥,当且仅当22m =时,AB 取最小值2.故选A.8.解析:因为()1f x +为偶函数,所以()()11f x f x +=-+①,所以()f x 的图象关于直线1x =轴对称,因为()()11f x g x --=等价于()()11f x g x --=②,又()()31f x g x -+=③,②+③得()()132f x f x -+-=④,即()()132f x f x +++=,即()()22f x f x +=-,所以()()4f x f x +=,故()f x 的周期为4,又()()13g x f x =--,所以()g x 的周期也为4,故选项B 正确,①代入④得()()132f x f x ++-=,故()f x 的图象关于点()2,1中心对称,且()21f =,故选项A 正确,易得()()01,41f f ==,且()()132f f +=,故()()()()12344f f f f ++==,故20221()5054(1)(2)2021(1)i f i f f f ==⨯++=+∑,因为()1f 与()3f 值不确定,故选项C 错误,因为()()31f x g x -+=,所以()()()()()()10,30,013,211g g g f g f ===-=-,所以()()()()022130g g f f ⎡⎤+=-+=⎣⎦,故()()()()01230g g g g +++=,故2023()50600i g i ==⨯=∑,所以选项D 正确,故选C .9.解析:A.()()22AD AF AB AF ED =+=+,故A 错误;B.因为()()2,22||AB EA AB EA FA AB FA AB EB AB ⊥⋅+=⋅=⋅= ,故B 正确;C.()()11,22BC CD FE BC BC CD FE FE ⋅=⋅= ,又BC FE =,所以()()BC CD FE BC CD FE ⋅=⋅ ,故C正确;D.AE 在CB方向上的投影向量为()3322AE CB CB AE CB CB CB e CB CB⋅=⋅=-=,故D 错误.故选BC .10.解析:由切线长定理易得12l r r =+,A 正确.由勾股定理知()()222121212(2)4R r r r r r r =+--=,解得R =,B 正确.()()()222122222221212121212124422S R R R S r r r r r r r r l r r r r ππππ===+++++++.()()33212222222121212121212442331233R R V R R V r r r r r r r r h r r r r ππππ===++++++.所以1122,C S V S V =正确.1122212212122122231S r r r r S r r r r r r ==≤++++,当且仅当12r r =时等号成立,这与圆台的定义矛盾,故D 错误.综上,答案为ABC .11.解析:以BC 为x 轴,DA 为y 轴建系,则()(0,0,D A 可以求得动点M 的轨迹方程:22302x y y +-=.这是一个圆心在点0,4P ⎛⎫ ⎪ ⎪⎝⎭,半径为34的圆(不含原点)D A 项:()1,0B -,所以max 193||4BM BP r =+=.故A 错误B项:2222||1||11424CB MB MC MD MD ⎛⎫⋅=-=-≤-=- ⎪ ⎪⎝⎭ .故B 正确C 项:易知直线:10AB x y -+=,故1328ABM M AB S AB d -=≤.故C 错误D 项:易知cos MBC ∠取最小值,当且仅当MBC ∠取最大值,也即BM 与P 相切时.此时3tan 24MBC ∠=,故221tan 132cos 191tan2MBCMBC MBC ∠∠∠-==+.故D 正确.故选:BD.12.解析:由sin 0,cos 0x x >>得()f x 的定义域为2,2,2k k k Z πππ⎛⎫+∈ ⎪⎝⎭,当0,2x π⎛⎫∈ ⎪⎝⎭时,3,2x πππ⎛⎫+∈ ⎪⎝⎭不在定义域内,故()()f x f x π+=不成立,易知()f x 的最小正周期为2π,故选项A 错误,又()22222cos log cos 2sin log sin 2f x x x x x f x π⎛⎫-=⋅+⋅=⎪⎝⎭,所以()f x 的图象关于直线4x π=对称,所以选项B 正确,因为()222222sin log sin cos log cos f x x x x x =⋅+⋅,设2sin t x =,所以函数转化为()()()()()()2222log 1log 1,0,1,log log 1g t t t t t t g t t t =⋅+-⋅-∈='--,所以()0g t '>得,()0g t '<得102t <<,所以()g t 在10,2⎛⎫ ⎪⎝⎭上单调递减,在1,12⎛⎫ ⎪⎝⎭上单调递增,故min 1()12g t g ⎛⎫==- ⎪⎝⎭,即min ()1f x =-,故选项C 正确,因为()g t 在10,2⎛⎫ ⎪⎝⎭上单调递减,在1,12⎛⎫ ⎪⎝⎭上单调递增,由2sin t x =,令210sin 2x <<得20sin 2x <<,又()f x 的定义域为2,2,2k k k Z πππ⎛⎫+∈ ⎪⎝⎭,解得22,4k x k k Z πππ<<+∈,因为2sin t x =在2,24k k πππ⎛⎫+ ⎪⎝⎭上单调递增,所以()f x 的单调递减区间为2,2,4k k k Z πππ⎛⎫+∈ ⎪⎝⎭,同理函数的递增区间为2,2,42k k k Z ππππ⎛⎫++∈⎪⎝⎭,所以选项D 正确,故选BCD.13.解析:因为22(1)y x =-',所以曲线11xy x+=-在点()2,3-处的切线斜率为2,所以切线方程为()322y x +=-,即27y x =-,即270x y --=.14.解析:法1:()tan tan tan 1,tan tan tan tan 11tan tan αβαβαβαβαβ++==-∴+=-- .()()()cos sin 1tan tan tan tan 2cos cos βααβαβαβαβ--+∴=-++=.法2:(特殊值法)令38παβ==,易得答案.15.解析:0.255205.2550.250.0025510.0199=+++=+=- .16.解析:设双曲线的右焦点为2F ,根据双曲线方程知,2c =.直线过原点,由对称性,原点O 平分线段原点AB ,又原点O 平分线段2,FF ∴四边形2AFBF 为平行四边形.ABF 和2ABF 中,分别有中位线,,OP BF OQ AF ∥∥,,,OP OQ AF BF ⊥∴⊥∴ 四边形2AFBF 为矩形,2BFF ∴ 为直角三角形.不妨设B 在第一象限,设直线AB 倾斜角为2θ,则2,32ππθ⎡⎫∈⎪⎢⎣⎭,且OFB OBF ∠∠θ==,在Rt 2BFF中可得:22124cos 4sin ,2cos 2sin 4c a BF BF e a θθπθθθ∴=-=-∴===-⎛⎫- ⎪⎝⎭,2,,,3264ππππθθ⎡⎫⎡⎫∈∴∈⎪⎪⎢⎢⎣⎭⎣⎭ ,易知()14f θπθ=⎛⎫- ⎪⎝⎭在,64ππθ⎡⎫∈⎪⎢⎣⎭上为增函数,)11,4e ∞πθ∴=∈+⎛⎫- ⎪⎝⎭17.解析:(1)因为1cos 3B =,所以2222sin 1cos 2costan 222cos 2A CB AC B A C ++++=++()()1cos 1cos 21cos A C B A C -++=+++1cos 1cos 821cos 3B B B ++=+=-.(2)因为ABC S =1122sin 223ac B ac =⋅=,所以6ac =再由余弦定理知,2222cos b a c ac B =+-,即222614263c c ⎛⎫=+-⨯⨯ ⎪⎝⎭,也即4220360c c -+=,解得c =c =.18.解析:(1)因为21342n n n n S S S a +++=-,所以()21132n n n n n S S S S a +++-=--,即2132n n na a a ++=-所以()()()()()()21111111223222220n n n n n n n n n n n n n a a a a a a a a a a a a a ++++++++---=----=---=(为常数)所以数列{}12n n a a +-是等差数列.(2)由(1)知121221n n a a a a +-=-=,即121n n a a +=+.也即()1121n n a a ++=+,又112a +=,所以11222n n n a -+=⋅=..所以()()()()1222112122121n n n n n n n b n n n n n n a +⎡⎤++===-⎢+⋅+⋅++⎢⎥⎣⎦.∴数列{}n b 的前n 项和()12231111111212222232212n n n T n n +⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-⎢⎥ ⎪ ⎪ ⎪⋅⋅⋅⋅⋅+⋅⎝⎭⎝⎭⎢⎥⎝⎭⎣⎦()()1111121121212n n n n +⎡⎤=-=-⎢⎥⋅+⋅+⋅⎢⎥⎣⎦19.(1)补全四面体PQRS 如图,即证:PQ SR ⊥取SR 的中点M ,正四面体中各个面均为正三角形,故,PM SR QM SR ⊥⊥,又PM QM M ⋂=,所以SR ⊥面PQM .又PQ ⊂面PQM ,所以PQ SR ⊥.(2)在QSR 的中心建系如图:则()(33,,,0,,02222S P R Q ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭1,0,,,33623A C ⎛⎛- ⎪ ⎪⎝⎭⎝⎭,31,,022K ⎛⎫-- ⎪ ⎪⎝⎭,.设面ACK 的法向量为(),,n x y z = ,则00n AC n AK ⎧⋅=⎪⎨⋅=⎪⎩,解得()n =- ,又33,,22PQ ⎛=- ⎝ ,所以22sin cos ,11n PQ θ== .20.解析:(1)设事件A 为“小周在这三个月集齐三款模型”,则()3333111034500A P A ⎛⎫== ⎪⎝⎭.(2)1,2,,12X = ,由题意得()()1911,2,,111010k P X k k -⎛⎫=== ⎪⎝⎭ ,()1191210P X ⎛⎫== ⎪⎝⎭11111199()12101010k k k E X -=⎛⎫⎛⎫=+⋅ ⎪⎪⎝⎭⎝⎭∑,错位相减求得最后结果为()11910910E X ⎛⎫=-⋅ ⎪⎝⎭.21.解析:(1)将()1,1M 代入,可以求得243b =.联立22314410x y x y ⎧+=⎪⎨⎪+-=⎩,得24610x x --=.设()()1122,,,A x y B x y ,则12262AB x =-=,又易知点M 到直线l的距离为2,故ABM的面积4ABM S = ..(2)设()()1122,,,A x y B x y ,联立22314410x y x ty ⎧+=⎪⎨⎪+-=⎩得()223230t y ty +--=,则1221222333t y y t y y t ⎧+=⎪⎪+⎨-⎪=⎪+⎩,11sin ,sin 22ABM PQM S AM BM AMB S PM QM PMQ ∠∠== ,又sin sin PMQ AMB∠∠=所以5PQM ABM S S = 等价于5PM QM AM BM =,也即5QM AM BMPM=5QM AMBMPM =即1251313x x -=-,也即129115x x --=,也即1295ty ty --=,也即223935t t =+,解得322t =±.22.解析:(1)()ln f x x ax =-'在()0,∞+上有两个变号零点,即ln xa x=有两个不等实根,设()()2ln 1ln ,x x g x g x x x-'==,故()g x 在()0,e 上单调递增,在(),e ∞+上单调递减,所以max 1()g x e=,且()10g =,又(),0x g x ∞+→+→,故10a e<<,且121x e x <<<,所以()2111111ln 12f x x x ax x =--+,又11ln x a x =,所以()21111111111ln 11ln 1ln 122x f x x x x x x x x x =-⋅⋅-+=-+,设()()1ln 1,1,2h x x x x x e =-+∈,所以()()1ln 102h x x =-<',所以()h x 在()1,e 上单调递减,所以()1,02e h x ⎛⎫∈-⎪⎝⎭,所以()11,02e f x ⎛⎫∈- ⎪⎝⎭.(2)法一:ln 0x ax -=的两个实根12,x x ,所以1122ln ,ln x ax x ax ==,所以()2121ln ln x x a x x -=-,得:2121ln ln x x a x x -=-,设21x t x =,又1202x x <<,所以2t >,要证:2128x x <,即证:123ln2ln 2ln x x +<,即证:123ln22ax ax +<,即证:()2123ln2a x x ->,即证:()212121ln ln 23ln2x x x x x x -->-,即证:2211212ln 3ln2x x xx x x -⋅>-,即证:22121121ln 3ln21x x x x x x -⋅>-,即证:21ln 3ln21t t t -⋅>-,设()()212ln 321ln ,(2),,(2)1(1)t t t t t t t t t t t ϕϕ+---=⋅>-'=>-,设()()()()222111112ln 3,(2),20t t F t t t t F t tt t t+-=+-->=--=>',所以()F t 在()2,∞+上单调递增,所以()()32ln202F t F >=->,所以()0t ϕ'>,所以()t ϕ在()2,∞+上单调递增,所以()()23ln2t ϕϕ>=,所以21ln 3ln21t t t -⋅>-,所以2128x x <成立.法二:ln 0x ax -=的两个实根12,x x ,所以1122ln ,ln x ax x ax ==,所以2211ln ln x x x x =,设21x t x =,又1202x x <<,所以2t >,.由2211ln ln x x x x =可得:12ln ln ln ,ln 11t t tx x t t ==--,.要证:2128x x <,即证:123ln2ln 2ln x x +<,即证:ln 2ln 3ln211t t t t t +<--,即证:21ln 3ln21t t t -⋅>-设()()212ln 321ln ,(2),,(2)1(1)t t t t t t t t t t t ϕϕ+---=⋅>-'=>-,设()()()()222111112ln 3,(2),20t t F t t t t F t tt t t+-=+-->=--=>',所以()F t 在()2,∞+上单调递增,所以()()32ln202F t F >=->,所以()0t ϕ'>,所以()t ϕ在()2,∞+上单调递增,所以()()23ln2t ϕϕ>=,所以21ln 3ln21t t t -⋅>-,所以2128x x <成立.法三:由(1)知:10a e<<,且121x e x <<<,()ln xg x x=在()0,e 上单调递增,在(),e ∞+上单调递减,又1122x x x <<,且()()12g x g x a ==,所以()()()2112g x g x g x =<,所以1111ln ln22x x x x <,所以211ln ln2x x <,所以2112x x <,所以112x <<,又()ln222g =,所以ln202a <<,又ln2ln424=,即()()24g g =,所以24x >,因为122x x <,所以212284x x x <<,故2128x x <.。
2024届高考考前最后一卷(新课标II卷)数学答案

2024届高考考前最后一卷(新课标II 卷)数学·全解全析及评分标准一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.B 【解析】因为2{|5240}{0,1,2,3,4,8}A x x x N ,,{2,0,2,4},B 所以{0,2,4}A B .故选B . 2.C 【解析】令i(,)z a b a b R ,则i 2(i)3i 1a b a b ,所以23b b ,解得1b .故选C .3.D 【解析】因为12AC CB ,所以1(),2OC OA OB OC 所以3115(1,2)(3,0)(,2)2222OC OA OB ,所以54(,33OC ,所以点C 的坐标为54(,33.故选D . 4.A 【解析】用抽签的方式确定这四个节目的出场顺序有44A 种方法,小提琴合奏与管弦乐合奏不相邻的排列有2223A A 种方法,由古典概型,得小提琴合奏与管弦乐合奏不相邻的概率222344A A 1A 2P .故选A . 5.D【解析】由题意,知34a .由3a ,10,62a 成等差数列,得63202aa ,所以632a ,所以等比数列{}n a 的公比2q ,所以3121a a q ,438a a q ,47364a a q ,所以14773a a a .故选D .6.C 【解析】设椭圆C 的半焦距为(0)c c ,因为点Q 在x 轴上,且1223PQ PF PF ,所以13,所以114 .由13 ,得121233PQ PF PF ,所以1212()()33PQ PF PF PQ ,即121233F Q QF,所以122F Q QF ,即12||2||F Q QF .因为PQ 平分12F PF ,所以1122||||2||||1PF F Q PF QF . 又12||||2PF PF a ,所以14||3a PF,22||3a PF . 在12PF F △中,由余弦定理的推论,得222222221212122124220()((2)4||||||1339cos 42162||||42339a a a c c PF PF F F F PF a a a PF PF,化简,得2223c a ,即椭圆C 的离心率e .故选C .7.B 【解析】二次函数2y x x 图象的对称轴是直线2x,当2x时,2y x x 单调递减,2e xxy 也单调递减,当2x时,2y x x 单调递增,2e xxy 也单调递增.因为2e nnn a 中的自变量n 为正整数,所以由*10,n n a a N ,得1921222,所以2119 ,所以“21 ”是“*10,n n a a N ”的必要不充分条件.故选B . 8.A 【解析】1e 1ln(0)x x m m m等价于ln e 1ln(1)ln x m x m , 令ln e x m t ,则1ln(1)(ln )t x t x ,即ln ln(1)1t t x x . 而ln y x x 在(0,) 上单调递增,所以1t x ,即e 1x m x ,即1e xx m . 令1()((1,))e x x f x x,则2()exxf x ,当(1,2)x 时,()0,()f x f x 单调递增, 当(2,)x 时,()0,()f x f x 单调递减,所以()f x 在2x 处取得极大值,即最大值为21(2)e f ,所以21e m.故选A . 二、选择题:本题共3小题,每小题6分,共18分。
高三最后一卷语文试题现代文阅读练习二及答案解析

谷之夜师陀辞别了晚霞,马降入弥漫着雾的狭谷,一股潮气冷冷的扑上脸来,正是春三月。
溪谷间悄寂无声,是飞鸟已经绝迹的时候。
极目一望,四围枯草荒烟,三两声犬吠,像发于邃古。
想起是草木同荆蓁的世界,颇觉苍凉了。
但已远遁大红大绿的攘夺,而就洪荒溟蒙的境地。
望望天色,星斗像结串的铃儿,在风声里簌簌的摇荡。
只听见那马打着响鼻,是已经疲劳不堪,但依然载着人,困顿的迈着步,在昏暗的夜色中达达前进。
狭谷里只有蹄声,岑寂和懒倦。
而这越走越长的路,它将把我们引到哪里去呢?行走于这样荒芜的山里,是早已将一切交付于马了。
转过山脚,是一座被山洪冲毁了的石桥。
向前望着的时候,那年幼的勤务兵忽然狂喜的喊道:“啊,火!”是红色的火,在山坳那里一明,接着又暗淡了下去。
像兽类的长啸的唿哨,这时突然响过山谷。
马吃惊的打着虎坐,耸起了鬃鬣,险哉!这就往旁边一跳,几乎要跳下溪去。
于是那火光,便真有些不平常了,是求神的香炷,是强盗的火号,或者是人家吗?这沉默着的时候,那勤务兵伏倒鞍桥上,终于听出。
“啥个舅子!”他惊魂未定的说。
风从岭上吹来,可以听见幽微的铃声。
这路就不再是无限遥远的渺茫的长途,可以寻到人迹了。
那么那是怎样的人家呢,那我们现在正循踪而往的,那住在这古老的石桥左近,将收留我这来自远方的人的?向前走着,不久便在一座牧羊者的石屋前面停住。
掌灯照我们上去的是牧人,一个四十岁上下的老者,那老人穿着一件羊皮短褐,鞋是古代的样式,很顽固的家伙,走动咯咯的响。
由那宽厚的双肩,看得出他是不怕小毛病的人。
“这样的孱头货,”他推了一下那马的颈项说:“它不会比我跑的快!”这小屋,几乎是全用石头建造,地是用灰石捶成,平坦的,三合土的一般,然而更增深了冷清的气息。
在潮湿的后壁下筑着泥炕。
墙角那里,有一小泥灶,上边齐整的挂着食具。
灶下放着木墩,是从一株大树的下部锯下来,供切面菜之用的,可是上面蒙着灰土,大约已经好久不曾用过。
羊舍主人将小油灯挂到墙上,在炕上坐下,手指伸进一只黑磁的小罐里摸索着,捻碎了一撮烟草。
2024届合肥一中最后一卷数学答案

合肥一中2024届高三最后一卷数学参考答案1.已知向量(2,3)a =,(1,3)b − ,则2a b −= ( )A .2B .3C .4D .5【答案解析】2(2,3)(2,6)(4,3),25a b a b −=−−=−−=,选D 2.已知复数z 满足(1)2z i i ⋅+=−,则=z ( ) A .i 2321+ B .i 2321− C .i 2321−− D .i 2321+− 【答案解析】2131312222iz i z i i−==−=++,,∴选A3.已知焦点在x,焦距为,则该椭圆的方程为( ) A .2213x y += B .2219x y += C .22197x y += D .2213628x y +=【答案解析】22223,9,927,197x y a a b c a =====−=+=,选C4.已知等比数列{}n a 的前n 项和为n S ,且314S =,32a =,则4a =( ) A .1 B .23或-1 C .23− D .23−或1 【答案解析】由3S =14,3a =2,12q ∴=或41,3q a =−∴=23−或1,∴选D5.已知α为三角形的内角,且cos α=, 则sin 2α=( )A C D【答案解析】sin2α= B6.甲乙丙丁戊5名同学坐成一排参加高考调研,若甲不在两端且甲乙不相邻的不同排列方式的个数为( )A .36种B .48种C .54种D .64种【答案解析】先考虑甲乙不相邻的不同排列方式数,再减去甲站在一端且甲乙不相邻的排列方式数,所以总数为321133423336A A A A A −=种,选A 7.已知四棱锥P ABCD −的各顶点在同一球面上,若2224AD AB BC CD ====,PAB ∆为正三角形,且面PAB ⊥面ABCD ,则该球的表面积为( )A .13π B .16π C .523π D .20π【答案解析】如图,2OE FG AE ===,222221323R OE AE ∴=+=+=, 25243S R ππ∴==,故选C. 8.过(0,)M p 且倾斜角为((,))2πααπ∈的直线l 与曲线2:2C x py =交于,A B 两点,分别过,A B 作曲线C 的两条切线12,l l ,若12,l l 交于N ,若直线MN 的倾斜角为β.则tan()αβ−的最小值为( )ABC. D.【答案解析】如图设00(,)N x y ,则AB l 为00()x x p y y =+且过(0,)M p ,0y p ∴=−且, 又设'2tan pk x β==−,'2k k ∴=− , tan tan tan()1tan tan αβαβαβ−∴−=+, 当且仅当k ==”成立,故选Ctan x kpα=''2()()1k k k k k k−==−+−≥+9. 下表是某人上班的年收入(单位:万元)与上班年份的一组数据: 年份x 1 2 3 4 5 6 7 收入y2.93.33.64.44.85.25.9则下列命题正确的有( ) A .年收入的均值为4.3 B .年收入的方差为1.2 C .年收入的上四分位数为5D .若y 与x 可用回归直线方程 0.5y x a =+来模拟,则 2.3a = 【答案解析】30.14.37=,A 正确; 21.9610.490.010.250.812.567.081.277s ++++++==≠,B 错误;70.75 5.25×=,所以上四分位数为5.2,C 错误;0.5 4.30.54 2.3ay x =−=−×=,D 正确; 故选AD 10.已知函数2()cos sin (0)f x x x x ωωωω=−>,则下列命题正确的有( )A .当2ω=时,524x π=是()y f x =的一条对称轴 B .若12|()()|2f x f x −=,且12min ||x x π−=,则12ω= C .存在(0,1)ω∈,使得的图像向左平移6π个单位得到的函数为偶函数 D .若()f x 在[0,]π上恰有5个零点,则ω的范围为7[2,)3【答案解析】1()sin(2)62f x x πω=+− 对于A ,当2ω=时,1()sin(4)62f xx π=+−,51()242f π=−, 524x π∴= 不是()y f x =的一条对称轴,对于B ,由题意知,2T π=,12ω∴=对于C ,11()sin(2())sin(2)62362g x x x ππωππωω=++−=++−, 若()g x 为偶函数,则362k ωππππ+=+,∴,矛盾对于D ,令t =2[,2]666x πππωωπ+∈+,由题意知,2529[,)66ππ∈ 7[2,)3ω∴∈故选BD11.已知函数()x f x e =,,则下列命题正确的有( ) A .若()g x ax ≥恒成立,则1a e≤−B .若()y f x =与1y ax =−相切,则2a e =C .存在实数a 使得()y f x ax =−和()y g x ax =+有相同最小值D .存在实数a 使得方程()f x x a −=与()x g x a +=有相同的根且所有的根构成等差数列 【答案解析】对于A ,由()g x ax ≥得,令,则'2ln 1()x h x x−= ∴ ()y h x =在(0,)e 单调递减,(,)e +∞单调递增,∴min 1()()a h x h e e≤==−对于B ,设切点为00(,)xP x e ,则切线方程为000()xxy e e x x −=−,即000(1)x x y e x e x =+−,又1y ax =−,000(1)1x x e ae x = ∴ −=− ,(1ln )1()a a ∴−=−∗ 2a e = 不满足式,∴B 错,对于C ,易知当1a =时()y f x ax =−和()y g x ax =+有相同最小值1,13k ω=+26πωπ+()ln g x x =−的ln x a x ≤−ln ()x h x x =−()∗的对于D ,令()()x h x f x x e x =−=−,令()()ln x g x x x x ϕ=+=−,则(),()h x x ϕ的图象大致如下:设交点为(,())M m h m ,易知01m <<,由图象知,当直线y a =与曲线()y h x =和曲线()y x ϕ=共有三个不同的交点时,直线y a =必经过点(())M m h m ,,即().a h m =因为()()h m m ϕ=,所以ln m e m m m −=−,即2ln 0m e m m −+=.令()()()h x x a h m ϕ===,得x m ln e x x x e m −=−=−,解得m x m x e =或.由01m <<得1m m e <<.所以当直线y a =与曲线()y h x =和()y x ϕ=共有三个不同的交点时, 从左到右的三个交点的横坐标依次为ln m ,m ,m e .因为2+ln =0m e m m −,即+ln =2m e m m ,所以ln m ,m ,m e 成等差数列, 故选ACD12.已知集合2{|20}A x N x x =∈−−≤,集合22{|(21)0}B x x a x a a =−+++=,若B A ⊆,则a =___________.【答案解析】{0,1,2}A =,{,1}B a a =+,由B A ⊆得0a =或1a =13.过(1,2)P 的直线l 被曲线2240x x y −+=所截得的线段长度为l 的方程为___________ .【答案解析】当斜率不存在时1x =满足题意;当斜率存在时,设直线l :2(1)y k x −=−,由题意知圆心到直线的距离为1得34k =−∴1x =或34110x y +−=14.在ABC ∆中,设,,A B C 所对的边分别为,,a b c ,且,tan sin sin ,b c A B C ≠=+则以下结论正确的有____(5)__________.(1)2(0,);11a b c∈+(2)2(11a b c∈+(3));2b ca +∈ (4)(2b c a +∈(5)).a ∈+∞【答案解析】222222222222222222222222222,2,cos cos ()cos 2cos ()cos ,cos ()(1cos )0,0,cos cos ()cos 2cos ,,2a a b c b c bc A A a b c A bc A b c A b c a Aa abc A b c A Aa b c A bc A b c a b c a a =+=++=++=+++−+−+=+−==+>=+−+>>15. 正方体1111ABCD A B C D −的棱长为2,P 是线段1A B 上的动点.(1)求证:平面11BDD B ⊥平面11A BC ; (2)1PB 与平面11A BCPB 的长. 【答案解析】(1)证明:由题,1DD ⊥面1111A B C D ,四边形1111A B C D 为正方形,所以1111111,AC B D AC DD ⊥⊥,而111111,B D DD D B D ∩=⊂面11BDD B ,1DD ⊂面11BDD B ,所以11AC ⊥面11BDD B ,而11AC ⊂面11A BC ,所以平面11BDD B ⊥平面11A BC .…………………………………………………………………………6分(2)设1B 在面11A BC 上的射影点为E ,连接1,EP EB ,11A BC S ∆=, 111111B A BC B A B C V V −−=,即1111222332EB ×=××××,得1EB =,设1PB 与平面11A BC 所成的角的大小为θ,则11sinEB PB θ==所以1PB =,在1BPB ∆中,由余弦定理得,2221112cos4PB BB PB BB PB π=+−××,即224PB =+−,解得PB =分16.甲和乙进行中国象棋比赛,每局甲赢或输的概率分别为0.8,0.2,且每局比赛相互独立.(1)若比赛采取三局两胜制,且乙已经赢得比赛,则比赛需要的局数X 的数学期望()E X 为多少?(保留小数点后一位)(2)由于甲、乙实力悬殊,乙提出“甲赢5局之前乙赢2局则乙胜”,求乙胜的概率. 【答案解析】(1)()0.20.20.20.80.20.80.20.20.104P A =×+××+××=, 所以()0.20.20.820.20.2()23 2.615 2.60.1040.104E X ××××=×+×≈≈.………………7分(2)设00.2p =,则2112131402000300040005000223400000()[(1)][(1)][(1)][(1)][12(1)3(1)4(1)5(1)]0.048.6160.34464.P A p C p p p C p p p C p p p C p p p p p p p p =+−+−+−+−=+−+−+−+−=×=……………………………………………………………………………………………15分17. ()()x a f x e a R −=∈.(1)若()f x 的图象在点00(,())A x f x 处的切线经过原点,求0x ; (2)对任意的[)0,x ∈+∞,有()sin f x x ≥,求a 的取值范围. 【答案解析】 (1)()x af x e −′=,所以00000()x a x ae f x e −−−′==−,所以01x =;………………5分(2)即()sin 00x aex x −−≥∀≥,令()sin x a g x e x −=−,若0a ≤,则0,1,()sin 1sin 0,x a x a x a e g x e x x −−−≥≥=−≥−≥合题;…………7分若0,()cos ,x a a g x e x −′>=− 令()(),h x g x ′=则()sin ,x a h x e x −′=+当0x π≤≤时,()0,()h x g x ′′>递增,而2(0)10,()0,2aag e g e ππ−−′′=−<=>所以,存在唯一的0(0,)[0,],2x ππ∈⊆使得000()cos 0,x a g x e x −′=−=所以,当00x x <<时,()0,()g x g x ′<递减,当0x x π<<时,()0,()g x g x ′>递增,故00000()()sin cos sin 0,x ag x g x ex x x −==−=−≥极小所以00,4x π<≤此时,00ln cos ,x a x −=故00ln cos 4a x x π=−≤−即ln 2042a π<≤+; ……………………………………………………………………………………………11分当x π>时,ln 2142()sin 1110x x ax ag x e x eee π−−−−=−≥−≥−≥−>,因而ln 202a π<≤+合题; 综上所述,a 的取值范围是求ln 2(,].42π−∞+………………………………………15分 18.已知双曲线2222:1(0,0)y x C a b a b−=>>的上焦点为,下顶点为A ,渐近线方程是y =,直线23y =与y轴交于B 点,过B 点的直线交双曲线上支于,P Q 两点,,AP AQ 分别交直线23y =于,M N 两点,O 坐标原点.(1)求C 的方程;(2)求证:,,,M N O A 四点共圆; (3)求(2)中的圆的半径r 的取值范围. 【答案解析】(1)由题,222ac a b c b==+=,解得2242a b ==,,所以C 的方程为221.42y x −=…………………………………………………………4分(2)(方法一)设11222(,),(,),:3P x y Q x y PQ y kx =+,代入22142y x −=,化简整理得22432(2)039k x kx −+−=,有222122016324(2)0990k k k x x −≠∆=−−−>>,解得21629k <<, 112:2y AP yx x +=−,令23y =得11836M x x y =+,同理22836N x x y =+, 12121212121221212128864||||36369(2)(2)6464168649(2)(2)99()39x x x x BM BN y y y y x x x x y y k x x k x x =×=++++==+++++,2216||||(2),||||||||,339BO BA BO BA BM BN =×+==所以,,,M N O A 四点共圆.……………………………………………………………………………………12分(2)(方法二)设,OM AN 的倾斜角分别为,αβ.由对称性,不妨设PQ 的斜率0k >,此时,αβ均为锐角,所以,,,M N O A 四点共圆AOM ANM π⇔∠+∠=()παβπ⇔++=,,(0,)22ππαβαβ⇔+=∈tan tan 1αβ⇔=1OM AN k k ⇔=设11222(,),(,),:3P x y Q x y PQ y kx =+,代入22142y x −=,化简整理得 22432(2)039k x kx −+−=,有222122016324(2)0990k k k x x −≠∆=−−−>>,解得21629k <<, 122329(2)x x k =−−,12243(2)kx x k +=−−, 112:2y AP yx x +=−,令23y =得11836M x x y =+,同理22836N x x y =+, 1124OM y k x +=,222AN AQy k k x +==, 1212121288()()223344OM AN kx kx y y k k x x x x ++++== 2121212864()3914k x x k x x x x +++=, 所以,,,M N O A 四点共圆.……………………………………………………………12分(3)设圆心为T ,则121212121212212121,44488363633382()438643()39T T y x x x x x x x y y kx kx kx x x x k k x x k x x =− +==+=+ ++ ++++=+++(,1),5(3T k r ∴−=…………………………………………………………17分19.给定自然数n 且2n ≥,设12,,,n x x x 均为正数,1n i i x T ==∑(T 为常数), 11.n i n i i nx x T x T x −==−−∑如果函数()f x 满足:在区间I 上恒有()0f x ′′>,则称函数()f x 为凸函数.凸函数()f x 具有性质:1111()()n ni i i i f x f x n n ==≥∑∑,. (1)判断(),(0,1)1x f x x x =∈−是否为凸函数,并证明; (2)设(1,2,,),i i x y i n T== 证明:111111n n y y n −≤−−−; (3)求n nx T x −的最小值. 【答案解析】(1)()2312(),()0,(0,1)(1)1f x f x x x x ′′′==>∈−−,所以()f x 在(0,1)上为凸函数. …………………………………………………………………………………………4分(2)(1,2,,)i x y i n = 为正数,11111n n n i i i i i i x y x T T =====∑∑∑,即11n i i y ==∑, 由11n i n i i n x x T x T x −==−−∑,得11,11i n n i n i x x TT x x T T −==−−∑ 即1111n i n i i n y y y y −==−−∑, 所以11111111111111()(1)()(1)111111111n i n n n n i i n i i n n i i i n i i i y y y y n f y n f y n y y y n y n n −−−−=−====−−==≥−=−=−−−−−−−−∑∑∑∑∑, 01(1,2,,)i y i n <<= ,所以111111111n n n n n y y n y y y n −−−−≤=−−−−, 即111111n n y y n −≤−−−,所以111111n n y y n −≤−−−.……………………………10分 (3)11111n n n n n n n x x y T x T x y y T===−−−−−关于n y 在(0,1)递增, 由(2)解得min ()3)n y n =≥;当2n =时,12n y ≥.所以min 3)n n x n T x =≥ − ;当2n =时也成立. 当3n ≥时,当且仅当12111n n y y y y n −−=====− 时取“=”;当2n =时,当且仅当1212y y ==时取“=”. 所以n n x T x −分。
2024年江苏省徐州市中考考前数学最后一卷+答案解析

2024年江苏省徐州市中考考前数学最后一卷一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.“坎宁安数”是以英国数学家坎宁安的名字命名的,能写成形式的数字,2024是一个坎宁安数,因为下列各数中均含有“2024”,其中最小的是()A.2024B.C.D.2.下列图形中,既是轴对称图形又是中心对称图形的是()A. B.C.D.3.在单词数学中字母“a ”出现的频率是()A.B.C.D.4.下列运算正确的是()A. B.C.D.5.以下是小李记录的自己一周内每天校外锻炼的时间单位:分钟,,则下列关于小李该周每天校外锻炼时间的描述,正确的是()A.众数为62分钟B.中位数为62分钟C.平均数为70分钟D.方差为06.分式是刻画数量关系和变化规律的一类重要的代数式,我们学习了分式的概念、基本性质和运算.回顾学习分式的过程,常常是先回顾分数的概念、分数的基本性质和分数的运算法则,然后推广得到分式的概念、分式的基本性质和分式的运算法则.这种研究方法主要体现的数学思想是()A.归纳思想 B.类比思想C.数学抽象D.数形结合思想7.将二次函数的图象先向上平移3个单位长度,再向右平移2个单位长度后得到的图象的顶点坐标是()A.B.C.D.8.中,,,,将绕点A旋转得到,连接CD、CE,在旋转过程中,面积的最大值是()A. B. C.15 D.18二、填空题:本题共10小题,每小题3分,共30分。
9.因式分解:__________.10.第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数字218000000用科学记数法表示为_____.11.如果,则的值为_____.12.如图,CE,CF是正六边形的两条对角线,则的大小为_______.13.已知关于x的分式方程的解为正数,则m的取值范围是___________.14.如图,在中,,点D为AB边的中点,于E,若,则AC的长为_________.15.如图,点A,B,C,D在上,,,则________.16.黄金分割比是让无数科学家、数学家、艺术家为之着迷的数字.黄金矩形的长宽之比为黄金分割比,即矩形的短边为长边的倍.黄金分割比能够给画面带来美感,令人愉悦,在很多艺术品以及大自然中都能找到它.比如蜗牛壳的螺旋中就隐藏了黄金分割比.如图,用黄金矩形ABCD框住整个蜗牛壳,之后作正方形ABFE,得到黄金矩形CDEF,再作正方形DEGH,得到黄金矩形CFGH……,这样作下去,我们以每个小正方形边长为半径画弧线,然后连接起来,就是黄金螺旋.已知,则阴影部分的面积为_____.17.如图,矩形OABC的顶点A在反比例函数的图象上,顶点B、C在第一象限,对角线轴,交y轴于点若矩形OABC的面积是16,,则__________.18.如图,在矩形ABCD中,点E是边AD上一点,连接BE,过点E作BC的垂线,垂足为F,的角平分线分别交EF,EC于点G,若,,,则GH的长为_______.三、计算题:本大题共2小题,共12分。
2024年湖南省长沙一中高考数学最后一卷+答案解析

2024年湖南省长沙一中高考数学最后一卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则()A.B.C.D.2.若复数z 满足,则z 可以为()A.B.C. D.3.已知随机变量X 服从正态分布,且,,则()A.B.C.D.4.已知直线,圆O :,则“”是“直线l 上存在点P ,使点P 在圆O内”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件5.在平行四边形ABCD 中,,点P 为该平行四边形所在平面内的任意一点,则的最小值为()A.6 B.8C.10D.126.地震震级通常是用来衡量地震释放能量大小的数值,里氏震级最早是由查尔斯里克特提出的,其计算基于地震波的振幅,计算公式为,其中M 表示某地地震的里氏震级,A 表示该地地震台测振仪记录的地震波的最大振幅,表示这次地震中的标准地震振幅.假设在一次地震中,某地地震台测振仪记录的地震波的最大振幅为5000,且这次地震的标准地震振幅为,则该地这次地震的里氏震级约为参考数据:A.级B.级C.级D.级7.已知双曲线的左、右焦点分别为,,P 为C 的渐近线上一点.若的面积为,则C 的离心率为()A.B.2C.D.8.已知正方体的棱长为2,M 是棱的中点,空间中的动点P 满足,且,则动点P 的轨迹长度为()A. B.3 C. D.二、多选题:本题共3小题,共18分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知函数,则下列说法正确的是()A.的最大值为2B.函数的图象关于直线对称C.不等式的解集为D.若在区间上单调递增,则的取值范围是10.某校在运动会期间进行了一场“不服来战”对抗赛,由篮球专业的1名体育生组成甲组,3名非体育生的篮球爱好者组成乙组,两组进行对抗比赛.具体规则为甲组的同学连续投球3次,乙组的同学每人各投球1次.若甲组同学和乙组3名同学的命中率依次分别为,则()A.乙组同学恰好命中2次的概率为B.甲组同学恰好命中2次的概率小于乙组同学恰好命中2次的概率C.甲组同学命中次数的方差为D.乙组同学命中次数的数学期望为11.设无穷数列的前n项和为,且若存在,使成立,则()A.B.C.不等式的解集为D.对任意给定的实数p,总存在,当时,三、填空题:本题共3小题,每小题5分,共15分。
2024年安徽省合肥市中考“最后一卷”模拟英语试题(含听力原文+答案 无听力音频)

2024年合肥市中考“最后一卷”(模拟卷)英语试题注意事项:1.本试卷共四部分,十大题,满分120分,考试时间120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。
3.请务必在“答题卷”上答题,在“试题卷”上答题无效。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
第一部分听力(共四大题,满分20分)Ⅰ.短对话理解(共5小题;每小题1分,满分5分)你将听到五段对话,每段对话后有一个小题。
请在每小题所给的A、B、C三个选项中选出一个最佳选项。
每段对话读两遍。
1. What’s Daming’s favorite festival?A. B. C.2. What does the boy want?A. B. C.3. How will the weather be tomorrow?A. Rainy.B. Snowy.C. Sunny.4. What does the girl want to do?A. Watch a movie.B. Play some sports.C. Have a picnic.5. Where are the two speakers?A. In a market.B. In a museum.C. In a bank.Ⅱ.长对话理解(共5小题;每小题1分,满分5分)你将听到两段对话,每段对话后有几个小题。
请在每小题所给的A、B、C三个选项中选出一个最佳选项。
每段对话读两遍。
听下面一段对话,回答第6至7小题。
6. How many clubs are there in the school?A. 2.B. 3.C. 4.7. What does Jane think of the sports club?A. Fun.B. Tiring.C. Difficult.听下面一段对话,回答第8至10小题。
8. What’s the matter with the man?A. He has a cold.B. He has a headache.C. He has a toothache.9. How long has he been like this?A. For one day.B. For two days.C. For a week.10. What does the doctor advise him to do?A. Take some medicine.B. Have some rest.C. Drink hot water.Ⅲ.短文理解(共5小题;每小题1分,满分5分)你将听到一篇短文,短文后有五个小题。
【中考预测卷】2023年中考考前最后一卷-数学(全国通用)(含答案)

2023年中考考前最后一卷数学(考试时间:120分钟试卷满分:120分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)........A .10x −≤<或1x ≥ C .1x ≤−或1x ≥第Ⅱ卷(非选择题 共90分)二、填空题(本大题共6个小题,每小题3分,共18分,直接填写答案.)甲、乙两组数据的方差分别为22,s s 甲乙,则2s 甲______________2s 乙(填“>”,“<”或“=”).14.点()()1122,,,A x y B x y 在一次函数(2)1y a x =−+的图像上,当12x x >时,12y y <,则a的取值范围是____________.15.如图,ABC∆中,D为BC的中点,E是AD上一点,连接BE并延长交AC于F,BE AC=,且9BF=,6CF=,那么AF的长度为__.16.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图)就是一例.这个三角形给出了(a+b)n(n=1,2,3,4,5,6)的展开式的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数,等等.有如下四个结论:①(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;②当a=-2,b=1时,代数式a3+3a2b+3ab2+b3的值是-1;③当代数式a4+4a3b+6a2b2+4ab3+b4的值是0时,一定是a=-1,b=1;④(a+b)n的展开式中的各项系数之和为2n.上述结论中,正确的有______(写出序号即可).三、解答题(本大题共个8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)17.(6分)解不等式组211 3.x xx≥−⎧⎨+≤⎩,①②请结合题意填空,完成本题的解答.(1)解不等式①,得___________;(2)解不等式②,得___________;(3)把不等式①和②的解集在数轴上表示出来:(4)原不等式组的解集为___________请结合上述信息,解答下列问题:(1)共有名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是(2)补全调查结果条形统计图;(3)小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.20.(10分)如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高α(1)求证:A ACF ∠=∠; (2)若8AC =,4cos 5ACF ∠=,求BF 及DE 22.(10分)某商店购进了一种消毒用品,进价为每件的销售量y (件)与每件售价x (元)之间存在一次函数关系(其中数).当每件消毒用品售价为9元时,每天的销售量为11元时,每天的销售量为95件.于点G,交直线CD于点F.(1)当矩形ABCD是正方形时,以点F为直角顶点在正方形ABCD的外部作等腰直角三角形CFH,连接EH.①如图1,若点E在线段BC上,则线段AE与EH之间的数量关系是________,位置关系是_________;②如图2,若点E在线段BC的延长线上,①中的结论还成立吗?如果成立,请给予证明;如果不成立,请说明理由;(2)如图3,若点E在线段BC上,以BE和BF为邻边作BEHF,M是BH中点,连BC=,求GM的最小值.接GM,3AB=,22023年中考考前最后一卷数学·参考答案第Ⅰ卷一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)二、填空题(本大题共6小题,每小题3分,共18分)17.(6分)【详解】(1)解:移项得:21x x −≥− 解得:1x ≥−…………….. 1 分 故答案为:1x ≥−; (2)移项得:31x ≤−, 解得:2x ≤,…………….. 2 分 故答案为:2x ≤;(3)把不等式①和②的解集在数轴上表示出来:……………..4 分(4)所以原不等式组的解集为:12x −≤≤,……………..6 分 故答案为:12x −≤≤. 18. (6分) (4)(3)解:把“礼仪”“陶艺”“园艺”“厨艺”及“编程画树状图如下:共有25种等可能的结果,其中小刚和小强两人恰好选到同一门课程的结果有∴小刚和小强两人恰好选到同一门课程的概率为51255=. (6)20.(10分)【详解】(1)解:过点D作DE BC⊥,交BC的延长线于点E,在Rt ADF 中,3DF x =Rt ABC △中,【详解】(1)解:∵Rt ABC △中,90ACB ∠=︒, ∴∠A +∠B =∠ACF +∠BCF =90°, ∵BE CD =, ∴∠B =∠BCF ,∴∠A =∠ACF ; ……………..2 分 (2)∵∠B =∠BCF ,∠A =∠ACF22.(10分)【详解】(1)解:设y 与x 之间的函数关系式为()0y kx b k =+≠,根据题意得: 91051195k b k b +=⎧⎨+=⎩,解得:5150k b =−⎧⎨=⎩,∴y 与x 之间的函数关系式为5150y x =−+;……………..2 分(2)解:(-5x +150)(x -8)=425,整理得:2383450x x −+=,解得:1213,25x x ==,……………..4 分∵8≤x ≤15,∴若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为13元;……………..6 分(3)解:根据题意得:()()()851508w y x x x =−=−+−251901200x x =−+−()2519605x =−−+……………..8 分∵8≤x ≤15,且x 为整数,当x <19时,w 随x 的增大而增大,∴当x =15时,w 有最大值,最大值为525.……………..10 分答:每件消毒用品的售价为15元时,每天的销售利润最大,最大利润是525元. 23.(11分) 2212x x +=()43k ∴−∵x 1+x 2=4【详解】解:(1)①∵四边形ABCD为正方形,∴AB=BC,∠ABC=∠BCD=90°,即∠BAE+∠AEB=90°,∵AE⊥BF,∴∠CBF+∠AEB=90°,∴∠CBF=∠BAE,又AB=BC,∠ABE=∠BCF=90°,∴△ABE≌△BCF(AAS),∴BE=CF,AE=BF,∵△FCH为等腰直角三角形,∴FC=FH=BE,FH⊥FC,而CD⊥BC,∴FH∥BC,∴四边形BEHF为平行四边形,∴BF∥EH且BF=EH,∴AE=EH,AE⊥EH,故答案为:相等;垂直;……………..2 分②成立,…………….. 3分理由是:当点E在线段BC的延长线上时,同理可得:△ABE≌△BCF(AAS),∴BE=CF,AE=BF,……………..4 分。
湖南省长沙市第一中学2024届高考最后一卷语文试题试题(含答案)

长沙市一中2024届高考最后一卷语文试卷本试卷总分150分,考试时间150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,18分)阅读下面的文字,完成1~5题。
材料一:读《中国不高兴》,令我想起了一件事,几年前,一位在南京大学当教授的朋友对我说,中国公共理性话语危机已经严重到了非采取行动不可的程度,他想编一本给大学生用的写作课本,帮助训练他们基本的逻辑说理能力,力求避免过度简单化,浮泛空论,巡回论证,无凭据推理,谩骂、粗口、唱衰等说理方式。
学校教育的一个重要部分是语言教育,不只是训练读写的技能,更是通过学习使用文字语言,养成公共说理的理性思考习惯。
只有说理的社会才是正派、宽容的社会,需要尊重与自己意见不同的说理对方。
对对手要宽容、厚道,陈述对方的论辩时应该尽量做到全面、准确、心平气和,不要一开口,就是“我不高兴”“我生气”。
这些都是《中国不高兴》作者们需要补的功课。
许多读者受蛊惑而浑然不觉,他们虽受过教育,但缺乏基本的理性辨析能力,这是不是意味着学校教育中有了严重的疏忽和失败?公共说理不是吵架,不是如《中国不高兴》作者们所说的那样,要“刺激”什么人或者要出什么气。
吵架越成功,说理越失败。
吵架是一种恶性激化人际意见对立的话语行为,而说理的目的恰恰是要尽量消除人际意见对立,化解分歧。
公共说理是要通过交流、说服来达成共识。
公共说理是公共文明的成就,也是形成良好社会关系、民主政治秩序的根本条件。
中国的公共说理机制还不健全,提高公共话语理性的自觉性应该成为各阶段学校教育的一个重要项目。
(摘编自徐贲《“不高兴”先生要学会说理》)材料二:三联生活周刊:随着近年网络暴力事件影响越来越大,人们不禁开始怀念起20年前的中国互联网环境。
适应性联考高三最后一卷语文现代文阅读试题二及答案解析

额尔古纳河右岸迟子建我是雨和雪的老熟人了,我有九十岁了。
雨雪看老了我,我也把它们给看老了。
如今夏季的雨越来越稀疏,冬季的雪也逐年稀薄了。
它们就像我身下的已被磨得脱了毛的狍皮褥子,那些浓密的绒毛都随风而逝了,留下的是岁月的累累瘢痕。
坐在这样的褥子上,我就像守着一片碱场的猎手,可我等来的不是那些竖着美丽犄角的鹿,而是裹挟着沙尘的狂风。
西班他们刚走,雨就来了。
在这之前,连续半个多月,太阳每天早晨都是红着脸出来,晚上黄着脸落山,一整天身上一片云彩都不拔。
①炽热的阳光把河水给舔瘦了,向阳山坡的草也被晒得弯了腰了。
我不怕天旱,但我怕玛克辛姆的哭声。
柳莎到了月圆的日子会哭泣,而玛克辛姆呢,他一看到大地旱得出现弯曲的裂缝,就会蒙面大哭。
好像那裂缝是毒蛇,会要了他的命。
可我不怕这样的裂缝,在我眼中它们就是大地的闪电。
安草儿在雨中打扫营地。
我问安草儿,布苏是不是个缺雨的地方,西班下山还得带着雨?安草儿直了直腰,伸出舌头舔了舔雨滴,冲我笑了。
他一笑,眼角和脸颊的皱纹也跟着笑了——眼角笑出的是菊花纹,脸颊笑出的是葵花纹。
雨水洒下来,他那如花的皱纹就像是含着露珠。
我们这个乌力楞只剩下我和安草儿了,其他人都在早晨时乘着卡车,带着家当和驯鹿下山了。
以往我们也下山,早些年去乌启罗夫,近年来到激流乡,用鹿茸和皮张换来酒、盐、肥皂、糖和茶等东西,然后再回到山上。
但这次他们下山却是彻底离开大山了。
他们去的那个地方叫布苏,帕日格告诉我,布苏是个大城镇,靠着山,山下建了很多白墙红顶的房子,那就是他们定居的住所。
山脚下还有一排鹿圈,用铁丝网拦起,驯鹿从此将被圈养起来。
我不愿意睡在看不到星星的屋子里,我这辈子是伴着星星度过黑夜的。
如果午夜梦醒时我望见的是漆黑的屋顶,我的眼睛会瞎的;②我的驯鹿没有犯罪,我也不想看到它们蹲进“监狱”。
听不到那流水一样的鹿铃声,我一定会耳聋的;我的腿脚习惯了坑坑洼洼的山路,如果让我每天走在城镇平坦的小路上,它们一定会疲软得再也负载不起我的身躯,使我成为一个瘫子;我一直呼吸着山野清新的空气,如果让我去闻布苏的汽车放出的那些“臭屁”,我一定就不会喘气了。
2024年湖北省武汉市华中师大一附中高考数学最后一卷+答案解析

2024年湖北省武汉市华中师大一附中高考数学最后一卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.设复数,则的虚部是()A.1B.C.iD.2.设双曲线C:的右焦点为F,过F作双曲线的一条渐近线的垂线,垂足为H,若为坐标原点,则双曲线C的离心率为()A. B.3 C.2 D.3.若命题“,”是假命题,则x不能等于()A. B.0 C.1 D.4.若函数向左平移个单位后在区间上单调递增,则()A. B. C. D.5.已知数列的前n项和为,若是等差数列,且,,则()A.1B.C.10D.6.如图,在中,,,D是CB边的中点,过点C作于点E,延长CE交AB于点F,则()A.B.C.D.7.()A. B. C. D.8.如图所示是一个以AB为直径,点S为圆心的半圆,其半径为4,F为线段AS的中点,其中C,D,E是半圆圆周上的三个点,且把半圆的圆周分成了弧长相等的四段,若将该半圆围成一个以S为顶点的圆锥的侧面,则在该圆锥中下列结果正确的是()A.为正三角形B.平面CEFC.平面CEFD.点D到平面CEF的距离为二、多选题:本题共3小题,共18分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得6分,部分选对的得2分,有选错的得0分。
9.设函数,则下列结论正确的是()A.存在实数使得B.方程有唯一正实数解C.方程有唯一负实数解D.有负实数解10.已知随机事件A,B满足,,则下列结论正确的是()A. B. C. D.11.设点是抛物线上任意一点,过点A作抛物线的两条切线,分别交抛物线于点和点,则下列结论正确的是()A. B.C. D.直线BC与抛物线相切三、填空题:本题共3小题,每小题5分,共15分。
12.已知曲线在点处的切线的倾斜角为,则a的值为______.13.已知,,若有且只有一组数对满足不等式,则实数a的取值集合为______.14.在三棱锥中,,且记直线PA,PC与平面ABC所成角分别为,,已知,当三棱锥的体积最小时,则三棱锥外接球的表面积为______.四、解答题:本题共5小题,共77分。
2024届广东高考考前最后一卷化学试题+答案

2024届高考考前最后一卷(广东卷)化学本试卷共8页,20小题,满分100分。
考试用时75分钟。
注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名、准考证号填写在答题卡上。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
可能用到的相对原子质量:H 1 C 12 O 16 V 51 Ni 59一、选择题:本题共16小题,共44分。
第1~10小题,每小题2分;第11~16小题,每小题4分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.中华文化源远流长,如下是“2023年度全国十大考古新发现”中各遗址出土的文物,主要由金属材料制成的是()A.玉璜B.金覆面C.象牙质铲形器D.珐华彩莲纹梅瓶2.新材料产业是战略性、基础性、先导性产业,事关现代化经济体系建设大局。
下列说法正确的是()A.集成电路产业基础原料电子级多晶硅属于分子晶体B.超级钢是一种新型合金,其熔点和强度均低于纯铁C.离子液体在室温或稍高于室温下能导电,属于离子化合物D.高分子分离膜可用于海水淡化,淡化原理利用的是海水和淡水密度不同3.广东人文底蕴深厚,非物质文化遗产种类繁多,下列说法不正确的是()Fe O可作为脸谱油彩中的红色颜料A.潮汕英歌舞——34B.佛山醒珠——制作原料竹篾的主要成分为天然高分子化合物C.粤绣——面料所用丝绸的主要成分为蛋白质D.上漖龙舟——凿刻各种规格咬口的过程中没有新物质生成4.实验室制备乙酸乙酯的过程中,下列实验操作不正确的是()A .向试管中加入药品和用品B .乙酸乙酯的生成C .乙酸乙酯的收集D .乙酸乙酯的分离5.锂硫电池因能量密度更高,可能会逐渐取代锂离子电池。
2024年中考考前最后一卷英语(山东济南卷)(全解全析)

Wear your socks on your hands for the next three rounds.
Act like your favorite teacher for the next 30 seconds.
Chair Racing
You do need space for this activity. Chair racing is fun as well as challenging. Divide the group into two teams. Now ask one member of the team to sit on a chair while the otherscarry it to the finish line!
A.Big Ben.B.Oxford Street.C.Tower Bridge.
20.What can tourists do near the Palace?
A.Enjoy the whole city.B.Do some shopping.C.Drink a free coffee.
1.C 2.C 3.C 4.A 5.B 6.B 7.A 8.C 9.A 10.B
B.The bottle is full of water.
C.I saw the bottle half full of water.
4.A.Li Hua speaks English like Americans.
B.Li Hua comes from America.
C.Li Hua likes English very much.
12.When was Amelia born?
合肥一中 2024 届高三最后一卷 地理答案

合肥一中2024届高三最后一卷地理参考答案1.D 2.C 3.B 4.A 5.D 6.A 7.C 8.D 9.C 10.A 11.A 12.C 13.A 14.D 15.D 16.A 17. (1)气候干旱(特别是冬春季节),蒸发强烈;地形较低洼,地下水位高,土壤水分易被蒸发;不合理灌溉。
(每点3分,答2点得6分)(2)沟底地势较低,便于蓄积地表水;(因开挖含盐量高的表层土壤)沟处土壤盐分较低;沟内覆土压实,减少土壤水分蒸发,保持土壤温度。
(每点2分,答3点得6分)(3)在寒冬时节抽取地下咸水灌溉,在地表形成冰层;春季气温回升,结冰咸水最先融化、下渗,把将地表大部分盐分带到地下;等气温继续回升至零摄氏度,地表结冰的淡水融化,又起到淋洗地表盐分的作用。
(每点2分,答3点得6分)18.(1)白垩纪岩石层主要是由单细胞浮游生物的遗骸构成,说明当时主要为海洋环境。
(4分)(2)地质历史时期多佛白崖位于海平面以下时,大量的藻类遗体堆积形成白色的石灰岩;由于地壳抬升或者海水下降等原因露出海面;裸露的白色石灰岩,长年累月遭受海浪的侵蚀作用,形成陡峭的海蚀崖、海蚀柱等海浪侵蚀地貌。
(每点2分,答3点得6分)(3)2012年初寒潮天气降雨(雪)量大,大量雨(雪)水进入岩石裂隙;并出现冻结,水结冰膨胀,导致整块岩石松动,在重力作用下,岩石崩塌滑落。
(每点3分,答2点得6分)19. (1)青藏高原冰川融化(北极地区冰盖消融),地表岩石(水域)裸露,吸收太阳辐射,产生更多的地面长波辐射,近地面大气温度升高;(3分)近地面大气通过对流活动和传导,使地表与上层大气能量交换更频繁,大气温度快速上升。
(每点3分,答2点得6分)(2)北极地区海冰融化导致海水蒸发量增加,对大气产生潜热输送;水汽是一种重要的温室气体,大气中水汽增加使空气吸收更多地面长波辐射,从而使大气逆辐射增强并使近地面升温。
(每点2分,答2点得4分)(3)采取相关科学研究和监测预报;建设抗御水旱灾害的水利工程;开展灾害保险业务;改种高热量资源需求的作物类型或品种等。
2024年江苏省淮安市中考考前数学最后一卷+答案解析

2024年江苏省淮安市中考考前数学最后一卷一、选择题:本题共8小题,每小题3分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列为正数的是()A. B. C.0 D.2.下列运算正确的是()A. B.C. D.3.如图,直线,直线和,交于C、D两点,P为CD上一点,且,,则的度数为()A. B.无法确定 C. D.4.在数轴上表示不等式的解集,正确的是()A. B.C. D.5.若一个正n边形的内角和为,则它的每个外角度数是()A. B. C. D.6.已知一次函数的图象如图所示,则b的取值范围是()A. B. C. D.7.《千里江山图》是宋代王希孟的作品,如图,它的局部画面装裱前是一个长为米,宽为米的矩形,装裱后,整幅图画宽与长的比是8:13,且四周边衬的宽度相等,则边村的宽度应是多少米?设边衬的宽度为x米,根据题意可列方程()A. B. C. D.8.如图1,中,点P从点C出发,沿折线匀速运动,连接AP,设点P的运动距离为x,AP的长为y,y关于x的函数图象如图2所示,则当点P为BC的中点时,AP的长为()A. B. C. D.5二、填空题:本题共8小题,每小题3分,共24分。
9.将8240000000用科学记数法可表示为__________.10.如图,点A、在数轴上对应的数分别是和3,则AB的长度为_____.11.为了解我国中学生课外阅读的情况,应采用的调查方式是______填写“普查”或“抽查”12.点在第四象限,则x的取值范围是_______.13.如图,正方形ABCD的两条对角线相交于点O,点E在BD上,且则的度数为________.14.如图,AB为的直径,点C在上,且,过点C的弦CD与线段OB相交于点E,满足,连接AD,则__________15.如图,将矩形ABCD绕点A旋转,使点B的对应点恰好落在BD上.若连接,则的长为__________.16.如图,反比例函数的图象与的两边AB、BC分别交于点、,已知轴,点A在y轴上,点C在x轴上,F为BC的中点,则__________.三、计算题:本大题共1小题,共6分。
【中考卷】浙江省绍兴市2021届中考英语最后一卷(二)含答案与解析

浙江省绍兴市2021届中考最后一卷(二)英语(考试时间:120分钟试卷满分:120分)注意事项:1. 试题的答案书写在答题卡上,不得在试卷上直接作答。
2. 作答前认真阅读答题卡上的注意事项。
3. 考试结束,由监考人员将试题和答题卡一并收回。
第I卷(70分)(一)听力部分(共25分)一、听力(本题有15小题,第一节每小题1分,第二、三节每小题2分,共计25分)第一节:听小对话,回答问题听下面5段对话,每段对话后有1个问题根据你所听到的对话和问题,从A、B、C三个选项中选出正确答案,并把答题卡上对应题目的答案标号涂黑。
1.Where is the closest bank?A.It’s opposite the hospital.B.It’s behind the hospital.C.It’s in front of the hospital.2.What does David want to be when he finishes university?A.A pilot. B.A doctor. C.A computer programmer.3.What time is it now?A.It’s 10:00 p.m.B.It’s 10:30 p.m.C.It’s 11:00 p.m.4.How was the weather yesterday?A.It was sunny. B.It was rainy. C.It was windy.5.Who did Jennifer go to see three weeks ago?A.Her uncle. B.Her aunt. C.Her cousin.第二节:听较长对话,回答问题。
根据你所听到的长对话,从A、B、C三个选项中选出正确答案,并把答题卡上对应题目的答案标号涂黑。
听下面一段对话,回答第6和7小题。
6.What is Paul's model ship made of?A.Metal. B.Glass. C.Wood.7.Where will they make the model ship?A.At school. B.At Paul's house. C.At Jane's house.听下面一段对话,回答第8和10小题。
2021-2022年高三高考最后一卷语文试题含答案

2021-2022年高三高考最后一卷语文试题含答案一、语言文字运用(15分)1.下列词语中加点的字,每对读音都相同的一组是(3分)A.仓猝./憔悴.一摞./落.脚点契.合/雕阑玉砌.B.弓弦./船舷.坼.裂/开小差.强.迫/强.词夺理C.怂.恿/悚.然干涸./和.稀泥秕.谷/如丧考妣.D.危殆./怠.慢皎.洁/广角.镜蒹葭./汗流浃.背2.下列各句中,没有语病的一句是(3分)A.上海市动物疾控中心对近期打捞上来的黄浦江上游漂浮死猪抽检的34份留存样品进行了禽流感专项检测,未发现禽流感病毒。
B.有些地方的公款吃喝现象从来就没有停止过,官员们只是变得更加小心,将“阵地”从社会酒店转移到内部食堂、私人会所。
C. 当今世界,自主知识产权所占比重是衡量一个国家科学发展水平的标志,而科学技术进步与否是国家富强的重要标志。
D.的确,我们很难简单地概括出中国文学的传统,但谁又会否认先秦文学中的《诗经》、《楚辞》不是后人难以超越的高峰?3.下面一段文字是从哪五个方面来介绍“H7N9型禽流感”的?请简要概括。
(不超过30字)(5分)xx3月底在上海和安徽两地率先发现的H7N9型禽流感是一种新型禽流感,是全球首次发现的新亚型流感。
在流行病学史不详的情况下,根据临床表现、辅助检查和实验室检测结果,特别是从患者呼吸道分泌物标本中分离出H7N9禽流感病毒,或H7N9禽流感病毒核酸检测阳性,可以诊断。
经调查,H7N9禽流感病毒基因来自于东亚地区野鸟和中国上海、浙江、江苏鸡群的基因重配。
被该病毒感染者均在早期出现发热、咳嗽、少痰、肌肉酸痛等症状;后期病情发展迅速,表现为重症肺炎,体温大多持续在39度以上,死亡率较高。
至xx5月,对人感染H7N9禽流感患者的密切接触者进行追踪,均未发现流感样症状。
4.阅读漫画,完成问题。
(5分)(1)给这幅漫画加个标题。
(不能用“无题”)(2分)(2)这幅漫画形象地提醒人们:。
(3分)二、文言文阅读(19分)阅读下面的文言文,完成5~8题。
2023 年合肥市中考“最后一卷”(模拟卷) 语文试题答案

2023年合肥市中考“最后一卷”(模拟卷)语文试题答案及评分标准一、(35分)1.①兔从狗窦入,雉从梁上飞②山气日夕佳,飞鸟相与还③感时花溅泪,恨别鸟惊心④晓雾将歇,猿鸟乱鸣⑤无可奈何花落去,似曾相识燕归来(共10分。
每空1分,有漏字、添字、错别字的,该空不得分)2.(1)ǎi dǎo衙(3分,每空1分)(2)A(3分)(3)指说粗鲁话;说话粗野,没礼貌。
(2分,意思对即可)(4)明朝或明代想象力\浪漫主义桀骜不驯、疾恶如仇、本领高强、爱憎分明、忠贞不贰、勇敢机智等(共5,每空1分,孙悟空形象任意三个词即可)。
3.①七言律诗②颔联③颈联④首联⑤继承和发扬我国优秀传统文化⑥史册⑦国家⑧邀请函尊敬的刘老师:我们班将于5月12日下午2:30在本班教室开展古诗词赏析展示活动,真诚地邀请您参加并给予指导。
(或“想邀请您做评委,期待您莅临指导。
”)九(1)班:小丽2023年5月8日(共12分,①—④题,每空1分;⑤题2分;⑥-⑦题每空1分;⑧题共4分,格式2分,内容2分)二、(55分)【一】(22分)4.BCAD(4分,位置对1处,可得1分)5.①“牧羊人”朝“月亮门”消失的地方惆怅张望;②“牧羊人”和施工队一起捡砖石为修复“月亮门”而努力;③“牧羊人”因“月亮门”成功修缮心泛涟漪。
(6分,每点2分,意思对即可)6.(1)示例一:动作描写,“伸出”“顶倒”两个动词,形象生动地写出了大风刮倒“月亮门”的过程,突出风大、猛烈。
示例二:拟人,使用“伸出”“顶倒”两词语,赋予“大风”以人的动作,突出大风风势之大、凶猛。
(2分,意思对即可)(2)运用比喻的修辞手法,形象生动地写出在大风中倒塌的“月亮门”的颓败景状,极富画面感,表达了老方的惆怅之情。
(2分,意思对即可)7.不能删去。
第④段主要写了长城上十号敌台的现状;交代了其是新广武村的名胜景点这一事实;既丰富了文章内容,又为下文迎来大批游客做铺垫。
若删去,会使得后文情节显得不连贯、突兀。
