数字电路与数字电子技术-课后答案第七章
数字电子技术基础课后答案全解

数字电子技术基础课后答案全解第3章逻辑代数及逻辑门【3-1】填空1、与模拟信号相比,数字信号的特点是它的离散性。
一个数字信号只有两种取值分别表示为0和12、布尔代数中有三种最基本运算:与、或和非,在此基础上又派生出五种基本运算,分别为与非、或非、异或、同或和与或非。
3、与运算的法则可概述为:有“0”出0,全“1”出1;类似地或运算的法则为有”1”出”1”,全”0”出”0”4、摩根定理表示为:AB=AB;AB=AB。
5、函数表达式Y=ABCD,则其对偶式为Y=(AB)CD。
6、根据反演规则,若Y=ABCDC,则Y(ABCD)C7、指出下列各式中哪些是四变量ABCD的最小项和最大项。
在最小项后的()里填入mi,在最大项后的()里填入Mi,其它填某(i为最小项或最大项的序号)。
(1)A+B+D(某);(2)ABCD(m7);(3)ABC(某)(4)AB(C+D)(某);(5)ABCD(M9);(6)A+B+CD(某);8、函数式F=AB+BC+CD写成最小项之和的形式结果应为成最大项之积的形式结果应为m(3,6,7,11,12,13,14,15),写M(0,1,2,4,5,8,9,10)9、对逻辑运算判断下述说法是否正确,正确者在其后()内打对号,反之打某。
(1)若某+Y=某+Z,则Y=Z;(某)(2)若某Y=某Z,则Y=Z;(某)(3)若某Y=某Z,则Y=Z;(√)【3-2】用代数法化简下列各式(1)F1=ABCAB1(2)F2=ABCDABDACDAD(3)F3ACABCACDCD(4)F4ABC(ABC)(ABC)ACD【3-3】用卡诺图化简下列各式ABC(1)F1BCABABC(2)F2ABBCBCABCAB(3)F3ACACBCBC(4)F4ABCABDACDCDABCACDABACBCAD第1页/共46页或ABACBC(5)F5ABCACABD(6)F6ABCDABCADABCABACBDABCCD(7)F7ACABBCDBDABDABCD(8)F8ACACBDBDABDBDABCDABCDABCDABCD(9)F9A(CD)BCDACDABCDCDCD(10)F10=F10ACABBCDBECDECABACBDEC【3-4】用卡诺图化简下列各式(1)P1(A,B,C)=m(0,1,2,5,6,7)ABACBCm(0,1,2,3,4,6,7,8,9,10,11,14)ACADBCDABBC ADBD(2)P2(A,B,C,D)=(3)P3(A,B,C,D)=m(0,1,,4,6,8,9,10,12,13,14,15)(4)P4(A,B,C,D)=M1M7ABCBCD【3-5】用卡诺图化简下列带有约束条件的逻辑函数(1)P1A,B,C,Dm(3,6,8,9,11,12)d(0,1,2,13,14,15)ACBDBCD(或ACD)(2)P2(A,B,C,D)=m(0,2,3,4,5,6,11,12)(8,9,10,13,14,15)dBCBCD(3)P3=ACDABCDABCDADACDBCD(或ABD)AB+AC=0(4)P4=ABCDABCDAB(ABCD为互相排斥的一组变量,即在任何情况下它们之中不可能两个同时为1)【3-6】已知:Y1=ABACBDY2=ABCDACDBCDBC用卡诺图分别求出Y1Y2,Y1Y2,Y1Y2。
数字电子技术课后答案

数字电子技术基础答案第1章自测题 1.1填空题1. 100011.11 00110101.01110101 11110.01 1E.42. 43. n 24. 逻辑代数 卡诺图5.)(D C B A F )(D C B A F +='6.))((C B D C B A F7. 代数法 卡诺图8. 1 1.2判断题1. √2.√3. × 1.3选择题 1.B 2.C 3.C1.4 A F =1⊙B AB F 2 B A F +=3 1.51.6 C L =1.7 AB C B A BC Y 习题1.1 当000012 A A A ,7A 到3A 有1个不为0时,就可以被十进制8整除 1.2 (a)AC BC AB F ++=1 (b )B A AB F +=2(c)C B A S ⊕⊕= AC BC AB C 0 1.3略1.4 (1) )(B A D C F )(1 ))((1B A D C F ++='(2) )(B A B A F )(2 ))((2B A B A F ++='(3) E D C B A F 3 DE C AB F ='3(4) )()(4D A B A C E A F )())()((4D A C AB E A F +++='1.5 C B A F ⊕⊕=1.6 (1) B A C B C A L (2) D B C B D C A L (3) AD L (4) E ABCD L (5) 0 L 1.7 C B A BC A C AB ABC C B A L ),,( 1.8(1) ABD D A C F 1 (2) BC AB AC F 2(3) C A B A B A F 3 (有多个答案) (4) C B D C AB C A CD F +++=4 (5) C B A ABD C B A D B A F 5 (6) 16 F 1.9 (1) AD D C B B A F 1 (2) B A AC F 2(3) D A D B C B F 3 (4) B C F 4 1.10 (1) C A B F 1 (2) B C F 2(3) D A B C F 3 (4) C B A D B D C F 4 1.11 C A B A D F1.12 (1) D B A D C A D C B F 1(多种答案) (2) C B BCD D C D B F 2 (3) C B C A D C F 3 (4) A B F 4 (5) BD D B F 5 (6) C B D A D C A F 6(多种答案) (7) C A D B F 7(多种答案) (8) BC D B F 8(多种答案) (9) B D C F 9 1.13 略第2章自测题 2.1 判断题1. √2. √3. ×4. √5. √6. √7. ×8. √9. × 10√ 2.2 选择题1.A B 2.C D 3.A 4.B 5.B 6.A B D 7.C 8.A C D 9.A C D 10.B 习题2.1解:ABC Y =12.2解:(a)mA 234.0503.012=-=-=C CES CC BS R U V I βBS mA 1.0537.06I I B <=-=∴三极管处于放大状态,)V (711.05012=⨯⨯-=-=C B CC O R I V u β。
数字电子技术基础习题册答案
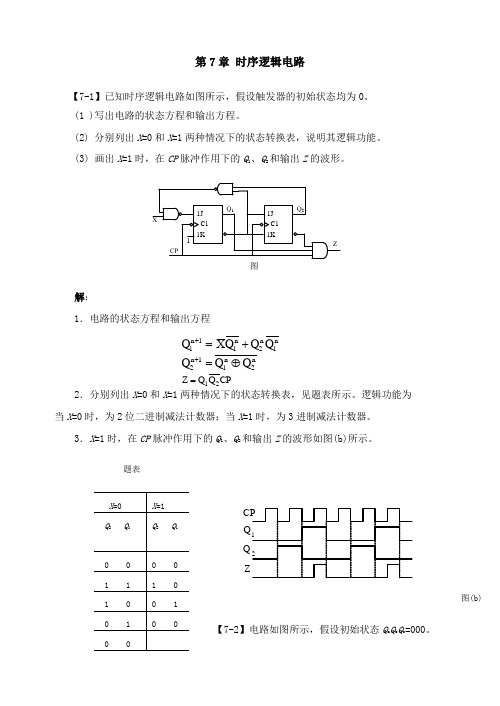
第7章 时序逻辑电路【7-1】已知时序逻辑电路如图所示,假设触发器的初始状态均为0。
(1 )写出电路的状态方程和输出方程。
(2) 分别列出X =0和X =1两种情况下的状态转换表,说明其逻辑功能。
(3) 画出X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形。
1J 1KC11J 1KC1Q 1Q 2CPXZ1图解:1.电路的状态方程和输出方程n 1n2n 11n 1Q Q Q X Q +=+n 2n 11n 2Q Q Q ⊕=+ CP Q Q Z 21=2.分别列出X =0和X =1两种情况下的状态转换表,见题表所示。
逻辑功能为 当X =0时,为2位二进制减法计数器;当X =1时,为3进制减法计数器。
3.X =1时,在CP 脉冲作用下的Q 1、Q 2和输出Z 的波形如图(b)所示。
题表Q Q Z图(b)【7-2】电路如图所示,假设初始状态Q a Q b Q c =000。
(1) 写出驱动方程、列出状态转换表、画出完整的状态转换图。
(2) 试分析该电路构成的是几进制的计数器。
Q c图解:1.写出驱动方程1a a ==K J ncn a b b Q Q K J ⋅== n b n a c Q Q J = n a c Q K = 2.写出状态方程n a 1n a Q Q =+ n a n a n a n a n c n a 1n b Q Q Q QQ Q Q +=+ nc n a n c n b n a 1n b Q Q Q Q Q Q +=+3.列出状态转换表见题表,状态转换图如图(b)所示。
图7.2(b)表7.2状态转换表CP na nbc Q Q Q 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1 4 1 0 0 5 1 0 16 0 0 0n4.由FF a 、FF b 和FF c 构成的是六进制的计数器。
【7-3】在二进制异步计数器中,请将正确的进位端或借位端(Q 或Q )填入下表解:题表7-3下降沿触发 由 Q 端引出进位 由Q 端引出借位触发方式 加法计数器 减法计数器上升沿触发 由Q 端引出进位 由Q 端引出借位【7-4】电路如图(a)所示,假设初始状态Q 2Q 1Q 0=000。
《数字电子技术基础》课后习题答案

BC A
00
01
11
10
0
0
0
0
0
1
0
1
1
1
则表达结果 Y 的表达式为:
逻辑电路如下:
技能题:
3.20:解:根据题意,A、B、C、D 变量的卡诺图如下:
CD AB
00
01
11
10
00
0
0
0
0
编辑版 word
01
0
0
0
0
11
0
1
1
1
10
0
0
0
0
电路图如下:
编辑版 word
第四章:
自测题:
一、 2、输入信号,优先级别最高的输入信号 7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C
第六章:
自测题:
一、 1、存储,组合逻辑,存储 3、时钟 CP,时钟 CP,时钟 CP,时钟 CP 9、4,4
二、 2、√ 9、×
三、 3、C 8、D
练习题:
6.2、
(1)输出方程
Y Q2n
(2)驱动方程
n
J0 Q2
J1 K1 Q0n
K0 1
J 2 Q1nQ0n
(3)状态方程
K2 1
Q0n1
练习题:
4.1;解:(a) (b)
,所以电路为同或门
,所以电路为与门。
4.5、解:当 M=0 时,
, 所以此时电路输出反码。
,同理可推:
当 M=1 时,
, 所以此时电路输出原码。
,同理可推:
4.7、Y ABC D ABCD ABC ABC D ABCD ABC D BD ABC BC D
数字电路与数字电子技术 课后答案第七章

第七章 时序逻辑电路1.电路如图P7.1所示,列出状态转换表,画出状态转换图和波形图,分析电路功能。
图P7.1 解:(1)写出各级的W .Z 。
D 1=21Q Q ,D 2=Q 1,Z=Q 2CP( 2 ) 列分析表( 3 ) 状态转换表(4)状态转换图和波形图。
图7.A1本电路是同步模3计数器。
2. 已知电路状态转换表如表P7.1所示,输入信号波形如图P7.2所示。
若电路的初始状态为Q2Q1 = 00,试画出Q2Q1的波形图(设触发器的下降沿触发)。
Q 2 Q 1 D 2 D 1 Q 2n+1 Q 1n+1 Z0 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 1 1 1 0 1 0 1Q 2 Q 1 Q 2n+1 Q 1n+1 Z0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1CPCP X Q 1 0Q 2 0 Z CP Q 1 0 Q 1 0Z ( b ) Q 2 Q 1 /Z( a )011解:由状态转换表作出波形图3. 试分析图P7.3所示电路,作出状态转换表及状态转换图,并作出输入信号为0110111110相应的输出波形(设起始状态Q 2Q 1 = 00)。
( a )( b )解:(1)写W .Z 列分析表J K( 2 )CPX图P7.3CPX Q 1 0 Q 1 0 Z图P7.A2(3)作出输出波形图:1 根据状态转换表,作出状态的响应序列,设y = Q 2Q 1 X : 0 1 1 0 1 1 1 1 1 0 y n : 0 02 1 0 2 13 3 3 y n+1: 0 2 1 0 2 1 3 3 3 0 Z : 1 1 1 1 1 1 1 0 0 12 根据状态响应序列画响应的输出波形。
4.。
X :Z :0 0 0 0 0 0 0 0 0 0 1 1 0 0 … 解:(1)建立原始的状态转换图和状态转换表 设:A --- 输入“0”以后的状态。
数字电子技术习题答案

习题答案第一章数制和码制1.数字信号和模拟信号各有什么特点?答:模拟信号——量值的大小随时间变化是连续的。
数字信号——量值的大小随时间变化是离散的、突变的(存在一个最小数量单位△)。
2.在数字系统中为什么要采用二进制?它有何优点?答:简单、状态数少,可以用二极管、三极管的开关状态来对应二进制的两个数。
3.二进制:0、1;四进制:0、1、2、3;八进制:0、1、2、3、4、5、6、7;十六进制:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
4.(30.25)10=( 11110.01)2=( 1E.4)16。
(3AB6)16=( 0011101010110110)2=(35266)8。
(136.27)10=( 10001000.0100)2=( 88.4)16。
5.B E6.ABCD7.(432.B7)16=( 010*********. 10110111)2=(2062. 556)8。
8.二进制数的1和0代表一个事物的两种不同逻辑状态。
9.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
这种表示法称为原码。
10.正数的反码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
11.正数的补码与原码相同,负数的补码即为它的反码在最低位加1形成。
12.在二进制数的前面增加一位符号位。
符号位为0表示正数;符号位为1表示负数。
正数的反码、补码与原码相同,负数的反码即为它的正数原码连同符号位按位取反。
负数的补码即为它的反码在最低位加1形成。
补码再补是原码。
13.A:(+1011)2的反码、补码与原码均相同:01011;B: (-1101)2的原码为11101,反码为10010,补码为10011.14.A: (111011)2 的符号位为1,该数为负数,反码为100100,补码为100101. B: (001010)2 的符号位为0,该数为正,故反码、补码与原码均相同:001010.15.两个用补码表示的二进制数相加时,和的符号位是将两个加数的符号位和来自最高有效数字位的进位相加,舍弃产生的进位得到的结果就是和的符号。
数字电子技术第7章习题答案

数字电子技术第7章习题答案
1. 什么是逻辑门?
答:逻辑门是数字电路中的基本组件,用于对输入进行逻辑运算并产生输出。
2. 列举几种常见的逻辑门。
答:与门、或门、非门、异或门、与非门、或非门等。
3. 什么是真值表?
答:真值表是一种用来展示逻辑函数输入与输出关系的表格,其中列出了所有可能的输入和对应的输出。
4. 什么是逻辑电路?
答:逻辑电路是指由逻辑门组成的电路,用于对输入进行逻辑运算并产生输出。
5. 什么是卡诺图?
答:卡诺图是一种用于最小化逻辑函数的图形化工具,通过将函数的真值表转化为图形,可快速找到最小化的逻辑表达式。
6. 什么是多路复用器?
答:多路复用器是一种数字电路,可以选择不同的输入并将其发送到一个输出线上。
7. 什么是解码器?
答:解码器是一种数字电路,用于将二进制数字输入转换为对应的输出,通常用于驱动其他数字电路中的寄存器、计数器等。
8. 什么是编码器?
答:编码器是一种数字电路,用于将多个输入端连接到一个二进制数字输出端,也可以实现将多个开关等输入转换为一个数字信号输出。
9. 什么是计数器?
答:计数器是一种数字电路,可用于记录电路所经过的时间或事件数量,通常用于计时器、频率计等应用。
10. 什么是触发器?
答:触发器是一种数字电路,可用于存储和控制数字信号,通常用于存储器、寄存器等应用。
数字电子技术习题及答案

第一章 数字逻辑基础1-1. 将下列的二进制数转换成十进制数(1)、1011,(2)、10101,(3)、11111,(4)、1000011-2. 将下列的十进制数转换成二进制数(1)、8,(2)、27,(3)、31,(4)、1001-3. 完成下列的数制转换(1)、(255)10=( )2=( )16=( )8421BCD(2)、(11010)2=( )16=( )10=( )8421BCD(3)、(3FF )16=( )2=( )10=( )8421BCD(4)、(1000 0011 0111)8421BCD =()10=()2=()161-4. 完成下列二进制的算术运算(1)、1011+111,(2)、1000-11,(3)、1101×101,(4)、1100÷100 1-5. 设:AB Y 1=,B A Y 1+=,B A Y 1⊕=。
已知A 、B 的波形如图题1-5所示。
试画出Y 1、Y 2、Y 3对应A 、B 的波形。
图题1-51-6选择题1.以下代码中为无权码的为 。
A . 8421BCD 码B . 5421BCD 码C . 余三码D . 格雷码2.以下代码中为恒权码的为 。
A .8421BCD 码B . 5421BCD 码C . 余三码D . 格雷码3.一位十六进制数可以用 位二进制数来表示。
A . 1B . 2C . 4D . 164.十进制数25用8421BCD码表示为。
A.10 101B.0010 0101C.100101D.101015.在一个8位的存储单元中,能够存储的最大无符号整数是。
A.(256)10B.(127)10C.(FF)16D.(255)106.与十进制数(53.5)10等值的数或代码为。
A.(0101 0011.0101)8421BCDB.(35.8)16C.(110101.1)2D.(65.4)87.矩形脉冲信号的参数有。
A.周期B.占空比C.脉宽D.扫描期8.与八进制数(47.3)8等值的数为:A. (100111.011)2B.(27.6)16C.(27.3 )16D. (100111.11)29. 常用的BCD码有。
第7章数字电子技术MULTISIM仿真实验2.

第7章 数字电子技术Multisim仿真实验
(1) 设计要求:设计一个火灾报警控制电路。该报警系 统设有烟感、温感和紫外线感三种不同类型的火灾探测器。 为了防止误报警,只有当其中两种或两种以上的探测器发出 火灾探测信号时,报警系统才产生控制信号。
(2) 探测器发出的火灾探测信号有两种可能:一种是高 电平(1),表示有火灾报警;一种是低电平(0),表示无火灾 报警。设A、B、C分别表示烟感、温感和紫外线感三种探 测器的探测信号,为报警电路的输入信号;设Y为报警电路 的输出。在逻辑转换仪面板上根据设计要求列出真值表,如 图7-8所示。
第7章 数字电子技术Multisim仿真实验
2.实验原理 译码是编码的逆过程。译码器就是将输入的二进制代码 翻译成输出端的高、低电平信号。3线-8线译码器74LS138有 3个代码输入端和8个信号输出端。此外还有G1、G2A、G2B使 能控制端,只有当G1 = 1、G2A = 0、G2B = 0时,译码器才 能正常工作。 7段LED数码管俗称数码管,其工作原理是将要显示的十 进制数分成7段,每段为一个发光二极管,利用不同发光段 的组合来显示不同的数字。74LS48是显示译码器,可驱动共 阴极的7段LED数码管。
第7章 数字电子技术Multisim仿真实验
4.实验步骤 (1) 按图7-12连接电路。双击字信号发生器图标,打开 字信号发生器面板,按图7-14所示的内容设置字信号发生器 的各项内容。 (2) 打开仿真开关,不断单击字信号发生器面板上的单 步输出Step按钮,观察输出信号与输入代码的对应关系,并 记录下来。 (3) 按图7-13连接电路。双击字信号发生器图标,打开 字信号发生器面板,按图7-15所示的内容设置字信号发生器 的各项内容。
第7章 数字电子技术Multisim仿真实验
数字电子技术基础数电第六版阎石课后答案第七章

数字电子技术基础数电第六版阎石课后答案第七章第七章:逻辑门和逻辑代数1. 本章节内容概述本章介绍了逻辑门和逻辑代数的基础知识。
首先介绍了逻辑电平和逻辑门的概念,然后详细介绍了与门、或门、非门等基本逻辑门的原理、特性和应用。
接着介绍了与非门、或非门、异或门等组合逻辑门的原理和应用。
最后介绍了逻辑代数的基本概念和运算规则。
2. 逻辑门逻辑门是数字电子电路中使用的基本元件,用于进行逻辑运算。
逻辑门有多种类型,其中最基本的有与门(AND)、或门(OR)和非门(NOT)。
2.1 与门(AND)与门是一种逻辑门,其输出信号仅在所有输入信号都为高电平时才为高电平,否则为低电平。
与门的逻辑符号如下:AND gateAND gate2.2 或门(OR)或门是一种逻辑门,其输出信号在任何输入信号中有一个或多个为高电平时就为高电平,只有所有输入信号都为低电平时才为低电平。
或门的逻辑符号如下:OR gateOR gate2.3 非门(NOT)非门是一种逻辑门,其输出信号和输入信号相反。
当输入信号为低电平时,输出信号为高电平;当输入信号为高电平时,输出信号为低电平。
非门的逻辑符号如下:NOT gateNOT gate3. 组合逻辑门除了基本逻辑门之外,还有一些由基本逻辑门组合而成的组合逻辑门,例如与非门(NAND)、或非门(NOR)和异或门(XOR)等。
3.1 与非门(NAND)与非门是由与门和非门组成的组合逻辑门。
其输出信号在所有输入信号都为高电平时为低电平,否则为高电平。
与非门的逻辑符号如下:NAND gateNAND gate3.2 或非门(NOR)或非门是由或门和非门组成的组合逻辑门。
其输出信号在任何输入信号中有一个或多个为高电平时为低电平,只有所有输入信号都为低电平时才为高电平。
或非门的逻辑符号如下:NOR gateNOR gate3.3 异或门(XOR)异或门是一种比较特殊的组合逻辑门,其输出信号在输入信号中有奇数个高电平时为高电平,否则为低电平。
数字电子技术课后习题答案

ABACBC
BC
A
00 01 11 10
00
1
0
1
11
0
1
0
Y ABC
❖ 3.13某医院有一、二、三、四号病室4间,每室设有 呼叫按钮,同时在护士值班室内对应的装有一号、 二号、三号、四号4个指示灯。
❖ 现要求当一号病室的按钮按下时,无论其它病室的 按钮是否按下,只有一号灯亮。当一号病室的按钮 没有按下而二号病室的按钮按下时,无论三、四号 病室的按钮是否按下,只有二号灯亮。当一、二号 病室的按钮都未按下而三号病室的按钮按下时,无 论四号病室的按钮是否按下,只有三号灯亮。只有 在一、二、三号病室的按钮均未按下四号病室的按 钮时,四号灯才亮。试用优先编码器74148和门电路 设计满足上述控制要求的逻辑电路,给出控制四个 指示灯状态的高、低电平信号。
HP RI/BIN
I0
0/ Z1 0 10 ≥1
I1
1/ Z1 1 11
I2
2/ Z1 2 12 18
YS
I3
3/ Z1 3 13
I4
4/ Z1 4 14
YEX
I5
5/ Z1 5 15
I6
6/ Z1 6 16
I7
7/ Z1 7 17
Y0
V18
Y1
ST
E N
Y2
(b)
74148
(a)引脚图;(b)逻辑符号
A
00 01 11 10
00
0
0
1
11
1
0
1
Y AB BC AC
由于存在AC 项,不存在相切的圈,故无冒险。
❖ 4.1在用或非门组成的基本RS触发器中,已知 输入SD 、RD的波形图如下,试画出输出Q, Q
数字电子技术应用基础习题答案赵景波数字电子技术书后习题参考答案

第1章习题答案一、填空题 1、模拟、数字 2、高、低3、逻辑、逻辑、逻辑、与逻辑、或逻辑、非逻辑4、基数、位权、基、位权5、8421、2421、余3、格雷6、进位制、数、按位权展开求和7、除2取余、乘2取整8、二进、二进制、三位、四位 9、8、4、2、1、二进制、0~9 10、原码、反码、补码、补码11、分配、结合、交换、反演、非非 12、或项、与项13、最小项、相邻、最小项、一位变量 14、“1”、“0” 二、判断题1、错2、错3、错4、对5、错6、错7、对 三、选择题1、B2、C3、B4、A四、简答题1、答:数字信号是离散的,模拟信号是连续的,这是它们的最大区别。
它们之中,数字电路的抗干扰能力较强。
2、答:数制是指计数的进制,如二进制码、十进制码和十六进制码等等码制是指不同的编码方式,如各种BCD 码、循环码等。
在本书介绍的范围内,8421BCD 码和2421BCD 码属于有权码余3码和格雷码属于无权码。
3、答:用卡诺图化简时,合并的小方格应组成正方形或长方形,同时满足相邻原则。
利用卡诺图化简逻辑函数式的步骤如下:①根据变量的数目,画出相应方格数的卡诺图;②根据逻辑函数式,把所有为“1”的项画入卡诺图中;③用卡诺圈把相邻最小项进行合并,合并时就遵照卡诺圈最大化原则;④根据所圈的卡诺圈,消除圈内全部互非的变量,每一个圈作为一个“与”项,将各“与”项相或,即为化简后的最简与或表达式。
五、计算题1、(1)C B A + (2)B C A + (3)BC B A AB ++ (4)C B D C B A ++2、(1)(365)10=(101101101)2=(555)8=(16D )16 (2)(11101.1)2=(29.5)10=(35.4)8=(1D.8)16(3)(57.625)10=(71.5)8=(39.A )163、(1)D C AD Y += (2)AD B C B A Y ++=(3)C B BC B A Y ++= (4)D B A ACD BC A D C A Y +++=第2章习题答案一、填空题1、门电路、与门、或门2、异或、同或3、开关、双极、单极、双极、单极4、或非、有1出1,全0出0、与非5、图腾、高电平“1”、低电平“0”、“1”、“0”、高阻6、三态、OC7、TTL 、CMOS 、CMOS8、PMOS 、NMOS 、输入、输出、控制 9、并、并、并 10、“与”、悬空、“或”、低、高、低、悬空 二、判断题 1、对 2、错三、选择题1、B2、D3、B四、分析题1、F 1是与门电路,F 2是或门电路,波形如下图所示。
数字电子技术基础课后习题答案第7章习题答案

题7.1.1 可编程阵列逻辑(PAL)由、和组成。
答:输入缓冲器、与阵列、或阵列输出题7.1.2 通用阵列逻辑(GAL)由、和组成。
答:输入缓冲器、与阵列、或阵列输出逻辑宏单元题7.1.3 可编程阵列逻辑(PAL)可组成种典型的输出组态。
(A)2 (B)3 (C)4 (D)5答:C题7.1.4 通用阵列逻辑(GAL)的输出逻辑宏单元可组成种典型的输出组态。
(A)2 (B)3 (C)4 (D)5答:D题7.1.5 在系统编程器件(isp)和早期的EEPROM在编程方面,前者脱离了束缚。
(A)软件平台(B)编程器(C)电源(D)刷新电路答:B题7.1.6 单片通用阵列逻辑(GAL)的输出逻辑宏单元编程为寄存器组态时,只能应用在场合。
(A)同步时序电路(B)异步时序电路(C)复位电路(D)移位寄存器答:A、D题7.2.1 在系统可编程逻辑器件采用编程单元。
(A)E2CMOS (B)熔丝(C)SRAM (D)隧道型浮栅单元答:A题7.2.2 EPM7000S系列提供的共享乘积项有和。
(A)共享扩展(B)并联扩展(C)串联扩展(D)缓冲扩展答A、B题7.2.3 输入输出单元即可以编程为输入或输出,还可以编程为。
答:双向题7.2.4 编程I/O控制块输出缓冲器的输出电压摆率,可提供较高的。
(A)克服毛刺(B)并联扩展(C)转换速度(D)减低功耗答:C题7.2.5 ispLSI1000系列的ORP可提供GLB到IOC的信号。
(A)输入(B)中间(C)输出(D)时钟答:C题7.2.6 CPLD具有较高的性能,并具有如下特点。
(A)单片多系统(B)异步时序电路(C)动态刷新(D)丰富的查找表8081题7.3.1 现场可编程门阵列(FPGA )静态时无 ,称之为 。
(A) 功耗 (B) 电流(C) 零功耗器件 (D) 有源器件答:A 、C题7.3.2 CPLD 的信号通路固定,系统速度可以 。
FPGA 的内连线是分布在逻辑单元周围,而且编程的种类和编程点很多,使布线相当灵活,但在系统速度方面低于 。
第7章 数字电路基础

编码种类
十进制数
8421 0000
2421 0000
5421 0000
余3码 0011
格雷码 0000
0
1 2
3 4 5 6 7
0001 0010
0011 0100 0101 0110 0111
0001 0010
0011 0100 0101 0110 0111
0001 0010
第七章 数字电路基础
实际的矩形脉冲往往与理想的矩形脉冲 不同,即脉冲的前沿与脉冲的后沿都不是陡 直的,如图8-5所示。
图8-5实际矩形脉冲的主要参数
第七章 数字电路基础
实际的矩形脉冲可以用如下的五个参数来描述
• 脉冲的幅度Um:脉冲的底部到脉冲的顶部之间的变化量。 • 脉 冲 的 宽 度 t w : 从 脉 冲 前 沿 的 0.5Um 到 脉 冲 后 沿 的 0.5Um两点之间的时间间隔称为脉冲的宽度,又可以称为 脉冲的持续时间。 • 脉冲的重复周期T:在重复的周期信号中两个相邻脉冲 对应点之间的时间间隔称为脉冲的重复周期。 • 脉冲的上升时间t r :指脉冲的上升沿从0.1Um 上升到 0.9Um所用的时间。 • 脉冲的下降时间t f :指脉冲的下降沿从0.9Um下降到 0.1Um所用的时间。
第七章 数字电路基础
逻辑代数中的几个问题
逻辑代数中的变量和常量 逻辑代数与普通代数相似,有变量也有常量。 变量用大写英文字母A、B、C„表示,称为逻辑变量 。每个逻辑变量的取值只有“0”和“1”两种。 逻辑代数中的常量,只有两个“0”和“1”。 与普通代数不同的是这里的“0”和“1”不再表示数 值的大小,而是代表两种不同的逻辑状态。 例如可以用“1”和“0”表示开关的“闭合”与“断 开”;信号的“有”和“无”;“高电平”与“低电平” ;“是”与“非”等。究竟代表什么意义,要视具体情况 而定。
《数字电子技术基础》课后习题答案

《数字电子技术基础》课后习题答案《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1) 十六进制转二进制: 4 5 C0100 0101 1100二进制转八进制:010 001 011 1002 13 4十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2) 十六进制转二进制: 6 D E . C 80110 1101 1110 . 1100 1000二进制转八进制:011 011 011 110 . 110 010 0003 3 3 6 . 6 2十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1 758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3) 十六进制转二进制:8 F E . F D1000 1111 1110. 1111 1101二进制转八进制:100 011 111 110 . 111111 0104 3 7 6 . 7 7 2十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*1 6-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(4376.772)8=(2302.98828125)10(4) 十六进制转二进制:7 9 E . F D0111 1001 1110 . 1111 1101二进制转八进制:011 110 011 110 . 111 111 0103 6 3 6 . 7 7 2十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16 -2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1 950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD (45.36)10=(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10=(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10=(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则二、2、×4、×三、1、B3、D5、C练习题:2.2:(4)解:Y=AB̅+BD+DCE+A̅D=AB̅+BD+AD+A̅D+DCE=AB̅+BD+D+DCE=AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A ̅+B ̅+C ̅)(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A ̅+B ̅+C ̅+DE ) =[(A ̅+B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A ̅+B ̅+C ̅+DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE 2.3:(2)证明:左边=A +A ̅(B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A ̅+(B +C)̅̅̅̅̅̅̅̅̅̅=A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A̅B +AB ̅)⨁C = (A̅B +AB ̅)C ̅+ (A ̅B +AB ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A ̅BC ̅+AB ̅C ̅)+A ̅B ̅̅̅̅⋅AB̅̅̅̅̅⋅C =A̅BC ̅+AB ̅C ̅+(A +B ̅)(A ̅+B )C =A̅BC ̅+AB ̅C ̅+(AB +A ̅B ̅)C =A̅BC ̅+AB ̅C ̅+ABC +A ̅B ̅C 右边= ABC +(A +B +C )AB ̅̅̅̅⋅BC ̅̅̅̅⋅CA̅̅̅̅ =ABC +(A +B +C )[(A̅+B ̅)(B ̅+C ̅)(C ̅+A ̅)] =ABC +(A +B +C )(A̅B ̅+A ̅C ̅+B ̅+B ̅C ̅)(C ̅+A ̅)=ABC +(A +B +C )(A̅B ̅C ̅+A ̅C ̅+B ̅C ̅+A ̅B ̅) =ABC +AB̅C ̅+A ̅BC ̅+A ̅B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B ̅C ̅)(A ̅+BC) 2.5(3)Y ̅=A ̅B ̅(C ̅+D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C ̅D ̅(A ̅+B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC ̅+AB ̅C +A ̅BC 2.7:(1)Y =A ̅B ̅+B ̅C ̅+AC +B ̅C 卡诺图如下: B C A 00 0111100 1 1 1111所以,Y=B̅+AC2.8:(2)画卡诺图如下:B C A 0001 11 100 1 1 0 11 1 1 1 1Y(A,B,C)=A+B̅+C̅2.9:(1)画Y(A,B,C,D)=∑m(0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:CDAB00 01 11 1000 1 1 1 101 1 111 ×××10 1 ××Y (A,B,C,D )=A̅B ̅+D ̅ 2.10:(3)解:化简最小项式: Y =AB +(A̅B +C ̅)(A ̅B ̅+C ) =AB +(A̅B A ̅B ̅+A ̅BC +A ̅B ̅C ̅+C ̅C ) =AB (C +C̅)+A ̅BC +A ̅B ̅C ̅ =ABC +ABC ̅+A ̅BC +A ̅B ̅C ̅ =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5) 2.13:(3)Y =AB̅+BC ̅+AB ̅C ̅+ABC ̅D ̅ =AB̅(1+C ̅)+BC ̅(1+AD ̅) =AB̅+BC ̅ =AB̅+BC ̅̿̿̿̿̿̿̿̿̿̿̿̿ = AB̅̅̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:B C A 00 01 11 10 0 0 0 1 0 1 0 1 1 1Y =AB +AC +BC=AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC ̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=(A ̅+B ̅)(A ̅+C ̅)(B ̅+C ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅+B ̅̅̅̅̅̅̅̅̅+A ̅+C ̅̅̅̅̅̅̅̅̅+B ̅+C ̅̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空;二、1、√8、√;三、1、A4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A ̅B ̅1̅̅̅̅̅̅=A +B +0=A +B(e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y1=A+B+0̅̅̅̅̅̅̅̅̅̅̅̅̅=A+B̅̅̅̅̅̅̅̅(c) Y3=A+B+1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y6=A⋅0+B⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y1=A⨁B⋅C=(A̅B+AB̅)C=A̅BC+AB̅C3.8、解:输出高电平时,带负载的个数2020400===IHOHOH I I NG 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===ILOLOL I I NG 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B ̅EN=0时,Y 1=A ̅, Y 2=B3.17根据题意,设A为具有否决权的股东,其余两位股东为B、C,画卡诺图如下,BCA00 01 11 100 0 0 0 01 0 1 1 1则表达结果Y的表达式为:Y=AB+AC=AB+AC̿̿̿̿̿̿̿̿̿̿̿̿=AB̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A、B、C、D变量的卡诺图如下:CD AB00 01 11 1000 0 0 0 001 0 0 0 011 0 1 1 110 0 0 0 0Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC ̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、3、√4、√三、5、A7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅B +B ̅̅̅̅̅̅̅̅̅̅̅=A ̅+B̅̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
阎石《数字电子技术基础》(第6版)章节题库-第7章 脉冲波形的产生和整形电路【圣才出品】

第7章脉冲波形的产生和整形电路一、选择题1.为了提高多谐振荡器频率的稳定性,最有效的方法是()。
A.提高电容、电阻的精度B.提高电源的稳定度C.采用石英晶体振荡器C.保持环境温度不变【答案】C【解析】石英晶体多谐振荡器的振荡频率取决于石英晶体的固有谐振频率,而与外接电阻、电容无关,具有极高的频率稳定性。
2.已知时钟脉冲频率为f cp,欲得到频率为0.2f cp的矩形波应采用()A.五进制计数器B.五位二进制计数器C.单稳态触发器C.多谐振荡器【答案】A【解析】频率变为原来的五分之一,是五分频,只需要每五次脉冲进一位即可实现。
3.在图7-1用555定时器组成的施密特触发电路中,它的回差电压等于()A.5VB.2VC.4VD.3V图7-1【答案】B【解析】555组成的施密特触发器中,当不接外接电压时,得到电路的回差电压为2V CC/3-V cc/3=V cc/3;5脚为外部参考电压输入V CO,如果参考电压由外接的电压V CO供给,这时V T+=V CO;V T-=V CO/2,回差电压为V CO/2=4V/2=2V,可以通过改变V CO值可以调节回差电压的大小。
4.电路如下图7-2(图中为上升沿JK触发器),触发器当前状态Q3Q2Q1为“100”,请问在时钟作用下,触发器下一状态(Q3Q2Q1)为()。
图7-2A.“101”B.“100”C.“011”D.“000”【答案】C【解析】JK触发器特征方程为Q n+1=JQ_n+K_Q n,由图7-2可得,三个触发器的驱动方程均为J=K=1,即特性方程均为Q n+1=Q_n,Q1的时钟是CP,Q2的时钟是Q1,Q3的时钟是Q2,当前Q3Q2Q1的状态是100,由于触发器在上升沿被触发,CP上升沿Q1状态被触发,变为1;同时触发了Q2,Q2变为1;同理Q3为0。
5.多谐振荡器可产生的波形是()A.正弦波B.矩形脉冲C.三角波D.锯齿波【答案】B【解析】“多谐”指矩形波中除了基波成分外,还含有丰富的高次谐波成分。
《数字电子技术基础》课后习题答案

《数字电路与逻辑设计》作业教材:《数字电子技术基础》(高等教育出版社,第2版,2012年第7次印刷)第一章:自测题:一、1、小规模集成电路,中规模集成电路,大规模集成电路,超大规模集成电路5、各位权系数之和,1799、01100101,01100101,01100110;11100101,10011010,10011011二、1、×8、√10、×三、1、A4、B练习题:1.3、解:(1)十六进制转二进制:45 C010*********二进制转八进制:010*********2134十六进制转十进制:(45C)16=4*162+5*161+12*160=(1116)10所以:(45C)16=(10001011100)2=(2134)8=(1116)10(2)十六进制转二进制:6D E.C8011011011110.11001000二进制转八进制:011011011110.1100100003336.62十六进制转十进制:(6DE.C8)16=6*162+13*161+14*160+13*16-1+8*16-2=(1758.78125)10所以:(6DE.C8)16=(011011011110. 11001000)2=(3336.62)8=(1758.78125)10(3)十六进制转二进制:8F E.F D100011111110.11111101二进制转八进制:100011111110.1111110104376.772十六进制转十进制:(8FE.FD)16=8*162+15*161+14*160+15*16-1+13*16-2=(2302.98828125)10所以:(8FE.FD)16=(100011111110.11111101)2=(437 6.772)8=(2302.98828125)10 (4)十六进制转二进制:79E.F D011110011110.11111101二进制转八进制:011110011110.1111110103636.772十六进制转十进制:(79E.FD)16=7*162+9*161+14*160+15*16-1+13*16-2=(1950. 98828125)10所以:(8FE.FD)16=(011110011110.11111101)2=(3636.772)8=(1950.98828125)101.5、解:(74)10 =(0111 0100)8421BCD=(1010 0111)余3BCD(45.36)10 =(0100 0101.0011 0110)8421BCD=(0111 1000.0110 1001 )余3BCD(136.45)10 =(0001 0011 0110.0100 0101)8421BCD=(0100 0110 1001.0111 1000 )余3BCD (374.51)10 =(0011 0111 0100.0101 0001)8421BCD=(0110 1010 0111.1000 0100)余3BCD1.8、解(1)(+35)=(0 100011)原= (0 100011)补(2)(+56 )=(0 111000)原= (0 111000)补(3)(-26)=(1 11010)原= (1 11101)补(4)(-67)=(1 1000011)原= (1 1000110)补第二章:自测题:一、1、与运算、或运算、非运算3、代入规则、反演规则、对偶规则 二、 2、×4、× 三、 1、B 3、D5、C练习题:2.2:(4)解:Y =AB̅+BD +DCE +A D =AB̅+BD +AD +A D +DCE =AB̅+BD +D +DCE =AB̅+D (B +1+CE ) =AB̅+D (8)解:Y =(A +B ̅+C )(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅(A +B ̅+C +DE ) =[(A +B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅+(D ̅+E ̅)̅̅̅̅̅̅̅̅̅̅](A +B ̅+C +DE ) =(ABC +DE )(ABC ̅̅̅̅̅̅+DE ) =DE2.3:(2)证明:左边=A +A (B +C)̅̅̅̅̅̅̅̅̅̅̅̅ =A +A +(B +C)̅̅̅̅̅̅̅̅̅̅ =A +B̅C ̅ =右式所以等式成立(4)证明:左边= (A B +AB̅)⨁C = (A B +AB ̅)C + (A B +AB̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅C = (A BC +AB ̅C )+A B ̅̅̅̅⋅AB̅̅̅̅⋅C =A BC +AB̅C +(A +B ̅)(A +B )C =A BC +AB̅C +(AB +A B ̅)C =A BC +AB̅C +ABC +A B ̅C 右边= ABC +(A +B +C )AB̅̅̅̅⋅BC ̅̅̅̅⋅CA ̅̅̅̅ =ABC +(A +B +C )[(A +B̅)(B ̅+C )(C +A )]=ABC +(A +B +C )(A B̅+A C +B ̅+B ̅C )(C +A ) =ABC +(A +B +C )(A B̅C +A C +B ̅C +A B ̅) =ABC +AB̅C +A BC +A B ̅C 左边=右边,所以等式成立 2.4(1)Y ′=(A +B̅C )(A +BC) 2.5(3)Y ̅=A B ̅̅̅̅(C +D ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ C D ̅̅̅̅̅(A +B ̅)̅̅̅̅̅̅̅̅̅̅̅̅̅̅ 2.6:(1)Y =AB +AC +BC=AB (C +C̅)+AC (B +B ̅)+BC (A +A ̅) =ABC +ABC̅+AB ̅C +A ̅BC 2.7:(1)Y =A B̅+B ̅C +AC +B ̅C 卡诺图如下:所以,Y =B2.8:(2)画卡诺图如下:Y(A,B,C)=A +B̅+C2.9:(1)画Y (A,B,C,D )=∑m (0,1,2,3,4,6,8)+∑d(10,11,12,13,14)如下:Y (A,B,C,D )=A B̅+D ̅2.10:(3)解:化简最小项式:Y =AB +(A B +C )(A B̅+C ) =AB +(A B A B̅+A BC +A B ̅C +C C ) =AB (C +C )+A BC +A B̅C =ABC +ABC ̅+A BC +A B ̅C =∑m (0,3,6,7)最大项式:Y =∏M(1,2,4,5)2.13:(3)Y =AB̅+BC +AB ̅C +ABC D ̅ =AB̅(1+C )+BC (1+AD ̅) =AB ̅+BC =AB ̅+BC ̿̿̿̿̿̿̿̿̿̿̿̿ = AB ̅̅̅∙BC ̅̅̅̅̅̅̅̅̅̅̅技能题:2.16 解:设三种不同火灾探测器分别为A 、B 、C ,有信号时值为1,无信号时为0,根据题意,画卡诺图如下:Y =AB +AC +BC =AB +AC +BC ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿ =AB ̅̅̅̅⋅AC̅̅̅̅⋅BC ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =(A +B ̅)(A +C )(B ̅+C )̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ =A +B ̅̅̅̅̅̅̅̅+A +C ̅̅̅̅̅̅̅̅+B ̅+C̅̅̅̅̅̅̅̅第三章:自测题:一、1、饱和,截止7、接高电平,和有用输入端并接,悬空; 二、 1、√ 8、√; 三、 1、A 4、D练习题:3.2、解:(a)因为接地电阻4.7k Ω,开门电阻3k Ω,R>R on ,相当于接入高电平1,所以Y =A B 1̅̅̅̅̅̅=A +B +0=A +B (e) 因为接地电阻510Ω,关门电0.8k Ω,R<R off ,相当于接入高电平0,所以、 Y =A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A ̅⋅B ̅∙1̅̅̅̅̅̅̅̅̅̅=A +B +0=A +B3.4、解:(a) Y 1=A +B +0̅̅̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅(c) Y 3=A +B +1̅̅̅̅̅̅̅̅̅̅̅̅̅=1̅=0(f) Y 6=A ⋅0+B ⋅1̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=B̅3.7、解:(a) Y 1=A⨁B ⋅C =(A B +AB̅)C =A B C +AB ̅C3.8、解:输出高电平时,带负载的个数2020400===IH OH OH I I N G 可带20个同类反相器输出低电平时,带负载的个数78.1745.08===IL OL OL I I N G 反相器可带17个同类反相器3.12EN=1时,Y 1=A , Y 2=B̅ EN=0时,Y 1=A̅, Y 2=B3.17根据题意,设A 为具有否决权的股东,其余两位股东为B 、C ,画卡诺图如下,则表达结果Y 的表达式为:Y =AB +AC =AB +AC ̿̿̿̿̿̿̿̿̿̿̿=AB ̅̅̅̅⋅AC̅̅̅̅̅̅̅̅̅逻辑电路如下:技能题:3.20:解:根据题意,A 、B 、C 、D 变量的卡诺图如下:Y =ABC +ABD =ABC +ABD ̿̿̿̿̿̿̿̿̿̿̿̿̿̿̿=ABC̅̅̅̅̅̅⋅ABD ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅电路图如下:第四章:自测题:一、2、输入信号,优先级别最高的输入信号7、用以比较两组二进制数的大小或相等的电路,A>B 二、 3、√ 4、√ 三、 5、A 7、C练习题:4.1;解:(a) Y =A⨁B +B ̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +AB ̅+B ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=A B +B ̅̅̅̅̅̅̅̅̅̅̅=A +B ̅̅̅̅̅̅̅̅=AB ,所以电路为与门。
数字电路与数字电子技术课后答案第七章

第七章 时序逻辑电路1.电路如图P7.1所示,列出状态转换表,画出状态转换图和波形图,分析电路功能。
图P7.1 解:(1)写出各级的W.Z 。
D 1=21Q Q ,D 2=Q 1,Z=Q 2CP( 2 ) 列分析表( 3 ) 状态转换表(4图7.A1 本电路是同步模3计数器。
2. 已知电路状态转换表如表P7.1所示,输入信号波形如图P7.2所示。
若电路的初始状态为Q2Q1 = 00,试画出Q2Q1的波形图(设触发器的下降沿触发)。
Q 2 Q 1 D 2 D 1 Q 2n+1 Q 1n+1 Z 0 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 1 1 1 0 1 0 1Q 2 Q 1 Q 2n+1 Q 1n+1 Z 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1 CP表P7.1 XQ 2 Q 1 0 1 00 01 10 11 01/1 10/0 10/0 01/1 11/1 10/0 11/000/1n+1n+1CP XQ 1 0 Q 2 0 Z 图P7.2 CPQ 1 0 Q 1 0 Z ( b ) Q 2 Q 1 /Z( a )01/0 11/1 10/1 00/0解:由状态转换表作出波形图3. 试分析图P7.3所示电路,作出状态转换表及状态转换图,并作出输入信号为0110111110相应的输出波形(设起始状态Q 2Q 1 = 00)。
( a )( b )解:(1)写W.Z 列分析表J 1 = XQ 2 J 2 = X Z =12Q Q XK 1 = X K 2 =1Q X( 2 ) 作出状态转换表及状态转换图XQ 2 Q 10 1 00 01 00/1 00/1 10/1 11/1 X Q 2 Q 1 J 2 K 2 J 1 K 1 Q 2n+1 Q 1n+1 Z 0 0 0 0 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 0 0 1 0 11 0 1 1 0 0 0 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1 1 1 0 1 0 1 1 0 CP X图P7.3CP X Q 1 0 Q 1 0Z 图P7.A2 0 /10 /1 0 /1 1/1 1/1 0/1 01 11 00(3)作出输出波形图:1 根据状态转换表,作出状态的响应序列,设y = Q 2Q 1 X : 0 1 1 0 1 1 1 1 1 0 y n : 0 02 1 0 2 13 3 3 y n+1: 0 2 1 0 2 1 3 3 3 0 Z : 1 1 1 1 1 1 1 0 0 12 根据状态响应序列画响应的输出波形。
精品课件-数字电子技术(第四版)(江晓安)-第七章

X () X (t)
第七章 脉冲波形的产生与变换
7
7.2 555定时电路 7.2.1 基本组成
555集成电路主要由3个5 kΩ电阻组成的分压器、 两个高精度电压比较器、 一个基本RS触发器、 一个作 为放电通路的管子及输出驱动电路组成, 其结构框图如 图 7-2 所示。
第七章 脉冲波形的产生与变换
T T1 T2
第七章 脉冲波形的产生与变换
35
而T1和T2分别为
T1
R1
R2
U DD C 1n
U DD
1 3
U
DD
2 3
U
D
D
R1 R2 C 1n2
T2
0 R2C 1n
0
2 3
U
DD
1 3 UDD
R2C 1n2
T (R1 2R2 ) C 1n2 0.7(R1 2R2 )C
第七章 脉冲波形的产生与变换
19
三要素如下:
uC (0 ) 0 uC () UDD
RC
由于比较器A、B的存在,uC不可能充至UDD。当uC充
至大于 平,
13RUS触DD 发器处,但于小保23于持UD态D ,即QQ=1,0
时,UA=UB均为低电 ,电路
仍处于uO=高电平,放电管仍处于截止,电容继续u充C 电23。U当DD 时,UA=1,UB=0,则Q=0,Q=1,uO=0,放电管导通, 电容通
电管V导通,这段时间我们称为第一暂稳态期。
第七章 脉冲波形的产生与变换
进入第二暂稳态期,放电过程为
uC uC
(0 ) 2 3
() 0
U
DD
放 R2C
第七章 脉冲波形的产生与变换
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字电路与数字电子技术-课后答案第七章第七章时序逻辑电路1.电路如图P7.1所示,列出状态转换表,画出状态转换图和波形图,分析电路功能。
CP图P7.1解:(1)写出各级的W.Z。
D1=21Q Q,D2=Q1,Z=Q2CP( 2 ) 列分析表Q2 Q1D2D1Q2n+1Q1n+1Z( 3 ) 状态转换表Q2 Q1Q2n+1Q1n+1(4)状态转换图和波形图。
图7.A1本电路是同步模3计数器。
2. 已知电路状态转换表如表P7.1所示,输入信号波形如图P7.2所示。
若电路的初始状态为Q2Q1 = 00,试画出Q2Q1的波形图(设触发器的下降沿触发)。
CPQ 1 0 Q 1 0 Z Q 2 Q 1 /Z 01/0 11/1 10/1 00/03. 试分析图P7.3所示电路,作出状态转换表及状态转换图,并作出输入信号为0110111110相应的输出波形(设起始状态Q2Q1 = 00)。
( a )( b )CP解:(1)写W.Z列分析表J1 = XQ2J2 = X Z =12Q Q XK 1 = X K 2 =1Q X( 2 ) 作出状态转换表及状态转换图(31 根据状态转换表,作出状态的响应序列,设y = Q 2Q 1X : 0 1 1 0 1 1 1 1 1 0 y n : 0 0 2 1 0 2 1 3 3 3 y n+1: 0 2 1 0 2 1 3 3 3 0 Z : 1 1 1 1 1 1 1 0 0 1X Q 2 Q 1 0 1 00 00/1 10/1 X Q 2 Q 1 J 2 K 2 J 1 K 1 Q 2n+1 Q 1n+1 Z 0 0 0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 /1 0 /1 0 /10111 10 002 根据状态响应序列画响应的输出波形。
4. 设计一个“1 1 1 1”序列信号检测器,设输入信号为X ,输出信号为Z 。
X :0 0 1 1 0 0 0 1 1 1 1 1 0 1 … Z :0 0 0 0 0 0 0 0 0 0 1 1 0 0 … 解:(1)建立原始的状态转换图和状态转换表 设:A --- 输入“0”以后的状态。
B --- 输入1个“1”以后的状态。
C --- 输入2个“1”以后的状态。
D --- 输入3个“1”以后的状态。
E --- 输入4个“1”以后的状态。
画出状态转换图及状态转换表0 /0 0/1B E A CP X Q 2 0(2)状态化简:画出化简后的状态转换图和状态转换表。
(3)状态分配:画出分配后的状态转换表和状态转换图设:A —00 B —01 C —11 D —100 /0 0 /0 1/01/1BD CA X y 20 1 A B A/0 A/0 B/0 C/0 0 /0 0 /0 1/0 1/1 0111 0010 XQ 2Q 1 0 1 00 01 00/0 00/0 01/011/0(4)画出动作卡诺图,触发器选型,确定电路激励输入,确定外输出Z。
图P7.A4(d )选用JK触发器,J是a必圈0必不圈,其余无关,K是β必圈1必不圈,其余无关。
J2 = XQ1J2 =2Q X Z =12Q Q XK2 =X K1=X+Q2 =2Q X(5)画出逻辑电路图XQ2Q10 100XQ2Q10 100XQ2Q10 100α图P7.A4( e )5. 已知某计数器电路中图P7.4所示,分析它是几进制计数器,并画出工作波形,设电路初始状态Q 2Q 1 = 00。
图P7.4 解:列出分析表:D 1=1Q ,D 2=21Q ⊕Q设计数器为4进制计数器,画出工作波形图如下:Q 2 Q 1 D 2 D 1 Q 2n+1Q 1n+1 00 01 11 10 CP6. 分析图P7.5所示计数器电路,画出状态转换图,说明是几进制计数器,有无自启功能。
图P7.5解:(1)写出激励函数,列分析表J1=32Q Q J2=1Q J3=Q2Q1K1=1 K2= 31Q Q =Q1+Q3K3=1设计数器是具有自启动能力的模4计数器。
7.分析图P7.6所示计数器电路,写出各级出发器特征方程,画出状态转换图,说明电路是否具有自启动能力。
图P7.6( 2 ) 画出状态转换图000 001 111110 100101010 011解:(1) 写出激励函数,列分析表J 1=1 J 2 = Q 13Q J 3 = Q 2Q 1K 1=1 K 2= Q 13Q K 3 = Q 1(2)写出各级触发器特征方程,画出状态转换图。
Q 1 n+1 = [1Q ]CP ↓Q 2 n+1 = [Q13Q 2Q +231Q Q Q ]CP ↓ Q 3 n+1 = [Q 2Q 13Q +1Q Q 3] CP ↓ Q 3 Q 2 Q 1 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 1 0 1 1 1 000 001 110111 010设计数器是具有自启能力的模6计数器。
8. 用JK触发器设计同步模9 加法计数器。
解:(1)列出状态转换表,画出动作卡诺图Q4 Q3Q2 Q1Q4n+1Q3n+1Q2n+1Q1n+1W4W3W2W1Z0 0 1 1 0 0 01 0 0 1α0图P7.A8( a )(2) 由动作卡诺图写出各触发器的激励函数。
J 4 = Q 3Q 2Q 1 J 3 = Q 2Q 1 J 2 = Q 1 J 1 =4Q Z = Q 4K 4 = 1 K 3 = Q 2Q 1 K 2 = Q 1 K 1 =1图P7.A8( b )Q 4 Q 3Q 2 Q 1 0001 11 10 00 01 0 0 X 1 0 0 X(3)检查是否具有自启能力。
具有自启动能力(4)画出逻辑电路图Q 4 Q 3 Q 2 Q 1 J 4 K 4 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+1Z 1 0 0 1 0 1 0 0 1 1 0 1 0 0 1 0 1 11 11 11 11 10 10 10 0000 0110 0000 0010 0001 1101 1110 0101 1011 01001100 1000 0011 00000000 0111图P7.A8( d )9. 用D 触发器设计模7同步加法计数器。
解:(1) 画出状态转换卡诺图,求出激励函数。
由于D 触发器Q n+1 = D ,所以可以Q n+1直接求出D 。
Q3 Q2 Q1 00 01 11 10 0 0 Q3 Q2 Q1 00 01 11 100 1 Q3 Q2 Q1 00 01 11 10 0 0 Q3 Q2 Q1 00 01 11 10 1 1 Q3 Q2 Q1 00 01 11 10001/0 011/0图P7.A9( a )D 3 = Q 32Q +Q 2Q 1 D 2 = 2Q Q 1+3Q Q 21QD 1 = 3Q 1Q +2Q 1Q Z = Q 3Q 2 (2)检查是否自启动具有自启动能力 (3)画出逻辑电路图Q 3 Q 2 Q 1 D 3 D 2 D 1 10 10 11 1010 10000 101 111 100 110 001 10 011010图P7.A9( c )10. 用JK 触发器设计模7同步减法计数器 解:(1)列出状态转换表,画出动作卡诺图Q 3 Q 2 Q 1 Q 3n+1 Q 2n+1 Q 1n+1 W 3 W 2 W 1 Z 1 1 1 1 1 0 1 1 β 0 Q3 Q2Q3 Q2 Q1 00 01 11 10 X β Q3 Q2 Q1 00 01 11 10 X 0 Q3 Q2图P7.A10( a )(2)根据动作卡诺图求出激励函数J 3=2Q J 2=2Q +3Q =31Q Q J 1=1 Z=23Q QK 3=2Q 1Q K 2=1Q K 1=Q 2+Q 3=32Q Q (3)检查是否自启动具有自启动能力 (4)画出逻辑电路图Q 3 Q 2 Q 1 J 3 K 3 J 2 K 2 11 10 1011000 010 111 011 001 110 10 100 101图P7.A10( c )11.用JK 触发器设计一个可控计数器,X=0为7进制同步加法计数,X=1为模5同步加法计数。
解:(1)画出状态转换卡诺图,从而画出动作卡诺图X Q 3 Q 2 Q 1 00 01 11 10 00 01 001 101000 001 010 110 xxx X Q 3 Q 2 Q 1 00 01 11 10 0001 0 0 0 0 α α X X Q 3 Q 2 Q 1 00 01 11 10 00 01 0 0 β 0 0 1 X X Q 3 Q 2 Q 1 00 01 11 10 00 01 αα0α β β X β图P7.A11( a )图P7.A11( a )(2)根据动作卡诺图求出激励函数J 3 = Q 2Q 1 J 2 = Q 1 J 1 =3Q +X 2Q =23Q X •QK 3 = X K 2 = Q 1+Q 3 =31Q Q K 1=1(3) 检查是否自启动有自启动能力(4) 画出逻辑电路图 X Q 3 Q 2 Q 1 J 3 K 3 J 2 K 2 J 1 K 1 Q 3n+1 Q 2n+1 Q 1n+10 1 1 1 1 0 1 1 X= 0,1 X= 0,1 X= 0,1 X= 0 X= 1 011 110000 101 001 100 010图P7.A11( c )12. ,设计同步计数器(1) (2)解:(1) 1画出状态转换卡诺图,采用D 触发器 Q A Q B Q C Q D 0 0 0 0 0 0 01 0 1 Q A Q B Q C Q D 0 0 0 0 0 0 01图P7.A12 ( 1 )(a )2 从次态卡诺图求出激励函数D A=Q A C Q+Q A D Q+A Q Q C Q DD B=C Q Q D+Q B D QD C= Q C D Q+Q B C Q Q DD D=D Q3 检查是否自启动本计数器具有自启动能力4 画出逻辑电路图Q A Q B Q C Q D D A D B D C D D Q A n+1 Q B n+1 Q C n+1 Q D n+1 0 0 1 0 0 0 1 11011 0000 0001 0011 1111 1110 1101 0100 1100 1001 1000 0101 0110 0111 1010 0010图P7.A12 ( 1 )( c )(2) 画出状态转换卡诺图,从而得到动作卡诺图Q A Q B Q C Q D 00 01 11 10 00 01 0001 0101 1101 1001 0100 0110 1110 Q A Q B Q C Q D 00 01 11 10 00 01 0 0 1 1 0 0 Q A Q B Q C Q D00 01 11 10 00 0 0 0 0 0 1 Q A Q B Q C Q D 00 01 11 10 00 1 1 1 1 0 0 Q A Q B Q C Q D 00 01 11 10 00 0 1 1 0 1 1图P7.A12 ( 2 )(a )(3) 采用JK触发器在动作卡诺图上求出各触发器激励函数.J A = Q B C Q D Q J B = Q C D Q J C =B Q Q DK A =00B Q K B = Q A K C = Q B Q DJ D = Q B Q C+ A Q B Q C Q= C B ACBQ QQ•QQK D = Q B C Q+B Q Q C = C BCB QQ•QQ(4) 检查是否自启动Q A Q B Q C Q D J A K A J B K B J C K C J D K D Q A n+1Q B n+1Q C n+1Q D n+11 0 0 1 0 1 0 1 1 00 0 0 0 1 111011000 000010010001 0011 00101111 11101011图P7.A12 ( 2 )( b )电路具有自启动能力(5)画出逻辑电路图图P7.A12 ( 2 )( c )13.分析图P7.7所示电路逻辑功能,画出状态转换图,说明电路是否具有自启动能力图P7.7解:本电路是异步时序电路,用特征方程法进行分析(1) 写出各触发器的激励函数及特征方程J1 = K1 = 1 J2 = Q3 J3 =1 J4 = K4 = 1CP1= CP↓K2 = 1 K3 = Q2CP4 = Q3↓CP2 = Q1↓CP3 = CP↓Z =CPQQQQ4321Q1n+1 = [1Q]CP↓Q2n+1 = [Q32Q]Q1↓Q3n+1 = [3Q+2Q Q3] CP↓= [3Q+2Q] CP↓= [23Q Q] CP↓Q4n+1 = [4Q] Q3↓,画出转换图表P7.A13Q4 Q3Q2 Q1Q4n+1Q3n+1Q2n+1Q1n+10 0 0 0 01 0 10 1 0 1 01 0 00 1 1 0 1 00011010100000001100010101101111 1101010000111110本电路是异步模8计数器,有自启动能力14.分析图P7.8所示电路,写出特征方程,画出状态转换图及在CP作用下Q1,Q2,Q3,Q4和F的工作波形.图P7.8解:(1) 写出各触发器的激励函数,列分析表J1= K1=1 J2=431QQ•Q=1Q(Q3+Q4) J3 = Q41QK2 = 1Q K3 =2Q1QJ4 =2Q3Q F=4Q3Q2Q1QK 4 =Q(2) 根据分析表画出状态转换图表P7.A14 Q A Q B Q C Q D J A K A J B K B J C K C J D K D Q A n+1 Q B n+1 Q C n+1 Q D n+1 F 0 0 0 0 1 1 0 1 0 1 1 1 1 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 0 0 0 1 0 1101 0001 1000 1001 0010 0011 0100 0111 0101 1010 1100 0110 1011 0000 1111 1110图P7.A14 ( a )(3) 写出特征方程画出在CP 作用下各触发器和F 工作波形图P7.A14 ( b )Q 1n+1 = [1Q ]↓Q 2n+1 = [1Q (Q 3+Q 4) 2Q +Q 1Q 2] CP ↓ Q 3n+1 = [Q 41Q 3Q +12Q Q Q 3]↓ Q 4n+1 = [2Q 3Q 4Q +Q 1Q 4] CP ↓15. 分析图P7.9所示电路,并画出在CP 作用下Q 2输出与CP 之间的关系Q 10 Q 2 0图P7.9解:(1) 写出特征方程Q1n+1 = [1Q][Q2+CP]↑当Q3=1时, CP1 =CP↑,即CP1=CP↓Q2n+1 = [1Q] Q1↑当Q3 = 0时, CP1=CP↑Q3n+1 = [1Q] Q1↑根据特征方程画出工作波形图(1)画波形图CPQ1图P7.A15CP脉冲与Q2之间的关系是Q2的周期为3.5 T CP (T CP为CP的周期)16. 分析图P7.10所示电路,写出特征方程,并画出在CP作用下,输出a、b、c、d、e、f 下的各点波形,说明该电路完成什么逻辑功能。
