北京育英中学九年级上册期末精选试卷检测题
北京育英中学化学初三化学上册期末试卷(含答案)

北京育英中学化学上册期末试卷(含答案)一、九年级化学上册选择题1.A、B、C三种物质各15g,在一定条件下充分反应后生成新物质D30g;若增加10gA,反应停止后,只有物质C剩余。
根据上述条件推断下列说法中正确的是A.第一次反应停止后,B 剩余9gB.反应中所消耗的A 和B的质量比是3:2C.第二次反应停止后,D 的质量为50gD.反应中所消耗的A 和C的质量比是5:32.已知反应前后分子变化的微观示意图如下所示。
下列说法正确的是A.此反应中有三种氧化物B.此反应中反应物的质量比是1:2C.该反应是置换反应D.反应前后原子的种类和个数都不变3.有18.6g的NaOH和Na2CO3固体混合物,已知Na元素与C元素的质量比是23:3,把该固体全部加入到盛有100g的足量稀硫酸的烧杯中,充分反应后,烧杯里残留物质的质量是114.2g。
则原NaOH和Na2CO3固体混合物中钠元素的质量是()A.9.2g B.6.9g C.4.6g D.2.3g4.在一定条件下,在一个密闭容器内发生某反应,测得反应过程中各物质的质量如下表所示,下列说法错误的是物质a b c d反应前质量1010102(g)反应后质量待测2212(g)A.该反应是化合反应,d可能是催化剂B.a、b两种物质中元素种类一定与c物质中元素种类相同C.b物质可能是单质D.反应后a物质的质量为3g5.如图实验装置进行的相应实验,达不到实验目的是()A.用如图所示装置除去CO2中含有的少量HCl气体B.用如图所示的装置证明可燃物燃烧需要与氧气接触C.用如图所示装置制取少量CO2气体D.在实验室中,用如图所示装置除去少量黄河水中的泥沙6.将氯酸钾和二氧化锰的混合物30克置于试管中,加热一段时间后冷却称量剩余固体为20.4克。
将此剩余固体加入足量水充分溶解(二氧化锰不溶于水)后过滤,滤渣经洗涤干燥后称得质量为5克。
下列说法正确的是:A.参加反应的氯酸钾质量为25克B.停止加热后剩余固体中含有两种物质C.生成氧气质量为9.6克D.反应过程中固体中二氧化锰的质量分数不变7.下表列出了除去物质中少量杂质的方法,其中错误的是选项物质所含杂质除去杂质的方法A CO2CO点燃B CO2O2将气体通过灼热的铜网C Cu Zn加入过量的稀盐酸,过滤,洗涤,干燥D FeCl2溶液CuCl2加入过量的铁粉,过滤A.A B.B C.C D.D8.下列四个图像分别表示四个化学兴趣小组活动中的数据及处理情况,其中正确的是A.高温煅烧一定质量的石灰石B.加热一定质量的高锰酸钾固体C.相同质量的铁粉和锌粉分别加入到足量的稀硫酸中D.向一定质量的过氧化氢溶液加入二氧化锰固体9.下列除去少量杂质的方法正确的是()A.CO2气体(CO):点燃 B.MnO2固体(KCl):加水过滤C.Fe粉中含少量铜:加盐酸 D.CO气体(CO2):通入水10.科学实验是人类获取科学知识,验证科学理论的重要手段,其中,对实验现象的正确描述很重要,以下实验现象描述正确的是A.红磷在空气中燃烧,产生大量白色的烟雾B.CO还原氧化铁,可观察到红棕色粉末逐渐变黑C.铁与硫酸铜溶液反应,可观察到浅绿色溶液变成蓝色D.向滴有植物油的水中加入洗洁精,振荡后得到澄清透明的溶液11.能正确反映相关实验过程中量的变化的图像是A.A B.B C.C D.D12.以下归纳和总结完全正确的一组是A、对现象的认识B、对安全的认识①气体压缩,气体分子之间的间隔变小②活性炭除去异味,活性炭具有吸附性③电解水时正极与负极产生的气体质量比为1:2①点燃可燃性气体前一定要验纯②煤矿矿井要保持通风、严禁烟火③家中天然气泄漏赶紧打开排风扇C、对鉴别除杂方法的认识D、对人物贡献的认识①区分硬水和软水,加肥皂水后搅拌②除去CO2中少量CO,通入足量灼热的氧化铜③除去CaO中CaCO3,高温充分煅烧①拉瓦锡--测定空气组成②门捷列夫--元素周期表③张青莲--测定水的组成A.A B.B C.C D.D13.下列四种图像中,能正确反映对应变化关系的是:A.加热一定质量的高锰酸钾固体B.电解一定量的水C.木炭在高温下和氧化铜反应D.用两份完全相同的过氧化氢溶液分别制取氧气14.某纯净物在氧气中燃烧生成水和二氧化碳两种物质,实验测得1.6g该纯净物在氧气中燃烧后,可生成3.6g水和4.4g二氧化碳,则该纯净物的组成为()A.只含有碳、氢元素B.含有碳、氢、氧三种元素C.肯定含有碳、氢元素,可能含有氧元素D.无法判断15.取一定质量的碳酸钙,高温加热一段时间后,得到碳酸钙和氧化钙的固体混合物,其中碳、氧元素质量比为1:5,那么该固体混合物中碳酸钙和氧化钙的质量比为A.7:25 B.50:21 C.21:50 D.25:1416.下图为某反应的微观示意图,下列说法错误..的是A.x=2B.该反应中有4种氧化物C.反应前后原子的种类、个数、质量都不变D.若反应中甲、乙的分子个数比为1∶2时,则无物质戊生成17.如图所示中能正确反映对应变化关系的是A.电解水一段时间B.加热氯酸钾制氧气C.加热一定量高锰酸钾D.红磷在密闭容器内燃烧18.某密闭容器中有X、O2、CO2和 H2O四种物质,在一定条件下充分反应,测得反应前后各物质的质量如下表。
2024年北京初三九年级上学期数学期末考《圆的综合》

2024年1月九上期末——圆的综合1.【东城】24.如图,AB 为⊙O 的直径,点C 在⊙O 上,∠ACB 的平分线CD 交⊙O 于点D.过点D 作DE ∥AB ,交CB 的延长线于点E .(1)求证:直线DE 是⊙O 的切线;(2)若∠BAC =30°,BC =CD 的长.2.【西城】24.如图,AB 是O 的直径,AB BC =,AC 交O 于点D ,点F 在OD 的延长线上且12FAD ABC ∠=∠.(1)求证:AF 是O 的切线;(2)若8AF =,4DF =,求AC 的长.3.【海淀】25.如图,AB 为半圆O 的直径,点C ,D 在半圆O 上,直线CM 与半圆O 相切于点C ,//CM AD .(1)若MCD ∠α=,求COA ∠的大小(用含α的式子表示);(2)过点O 作OE CD ⊥交CM 于点E ,交CD 于点F ,若//CD AB ,6AB =,求CE 的长.4.【朝阳】24.如图,AC ,BD 是圆内接四边形ABCD 的对角线,AC ⊥BD 于点E ,BD 平分∠ADC .(1)求∠BAD 的度数;(2)点P 在DB 的延长线上,P A 是该圆的切线.①求证:PC 是该圆的切线;②若PA =AC =3,直接写出PD 的长.5.【石景山】24.如图,在ABC △中,AB AC =,以AB 为直径的O 交BC 于点D ,交AC 于点E ,点F 在AC 的延长线上,12CBF BAC ∠=∠.(1)求证:BF 是O 的切线;(2)若5AB =,1tan 2CBF ∠=,求CE 的长.6.【丰台】24.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O 交BC 于点D ,作DE ⊥AC 交AC 于点E ,延长ED 与AB 的延长线交于点F .(1)求证:DE 是⊙O 的切线;(2)若△ABC 为等边三角形,AE=3,求⊙O 半径的长.7.【昌平】24.如图,AB 是⊙O 的直径,点C 在⊙O 上,点D 为 AC 的中点,过点D 作⊙O 的切线,交BC 延长线于点P ,连接OD 交AC 于点E .(1)求证:四边形DECP 是矩形;(2)作射线AD 交BC 的延长线于点F ,若tan ∠CAB =43,BC =6,求DF 的长.8.【通州】25.如图,点C 在以AB 为直径的O 上,CD 平分ACB ∠交O 于点D ,交AB 于点E ,过点D 作DF AB ∥交CO 的延长线于点F .(1)求证:直线DF 是O 的切线;(2)若30A ∠=︒,43AC =,求DF 的长.24题图9.【房山】24.如图,AB是⊙O的直径,AC,BC是弦,点D在AB的延长线上,且DCB DAC∠=∠,⊙O的切线AE与DC的延长线交于点E.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,30∠=︒,求AE的长.D10.【大兴】24.如图,AB是⊙O的直径,点C在⊙O上,连接AC,BC,过点O作OD⊥BC于点D,过点C作直线CE交OD的延长线于点E,使得∠E=∠B.(1)求证:CE是⊙O的切线.(2)若DE=6,CE=35,求OD的长.11.【门头沟】25.如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.(1)求证:∠BAD=∠DAE;(2)若AB=6,AD=5,求DF的长.12.【燕山】24.如图,在△ABC中,∠ACB=90°,点D在AB上,以AD为直径作⊙O与BC相切于点E,连接DE并延长交AC的延长线于点F.(1)求证:AF=AD;(2)若CE=4,CF=2,求⊙O的半径.13.【顺义】25.如图,AB为⊙O的弦,点C为AB的中点,CO的延长线交⊙O于点D,连接AD,BD,过点D作⊙O的切线交AO的延长线于点E.(1)求证:DE∥AB;(2)若⊙O的半径为3,tan∠ADC=,求DE的长.14.【密云】24.如图,⊙O是△ABC的外接圆,∠ABC=45°,连接OC交AB于点E,过点A作OC的平行线交BC延长线于点D.(1)求证:AD是⊙O的切线;(2)若⊙O的半径为4,AD=6,求线段CD的长.15.【平谷】24.如图,AB 为⊙O 的直径,弦CD ⊥AB 于H ,连接AC 、AD ,过点A 作⊙O 的切线与∠ADC 的平分线相交于点E ,DE 交AB 于点G ,交AC 于点F ,交⊙O 于点M ,连接AM .(1)求证:AC=AD ;(2)若22tan =∠AMD ,CD=4,求AF 长.。
北京市海淀区育英中学2020—2021学年第一学期期末考试九年级数学试卷
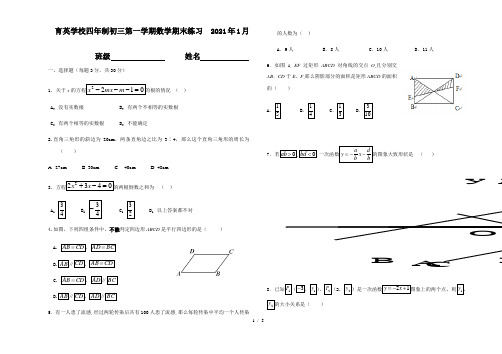
1 / 5育英学校四年制初三第一学期数学期末练习 2021年1月班级 姓名一、选择题(每题3分,共30分)1. 关于x 的方程0122=---m mx x 的根的情况 ( )A . 没有实数根B . 有两个不相等的实数根C . 有两个相等的实数根D . 不能确定2.直角三角形的斜边为20cm ,两条直角边之比为3∶4,那么这个直角三角形的周长为( )A . 27cm B. 30cm C. 40cm D. 48cm 3. 方程04322=-+x x的两根倒数之和为 ( )A .43 B . 43-C .23D . 以上答案都不对4.如图,下列四组条件中,不能..判定四边形ABCD 是平行四边形的是( ) A. CD AB =,BC AD = B.AB ∥CD ,CD AB =C. CD AB =,AD ∥BCD.AB ∥CD ,AD ∥BC5.有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中平均一个人传染的人数为( ) A .9人B .8人C .10人D .11人6.如图1, EF 过矩形ABCD 对角线的交点O ,且分别交AB .CD 于E 、F ,那么阴影部分的面积是矩形ABCD 的面积的( )A .51 B .41 C .31 D .1037.若0ab >,0bd <,一次函数a dy x b b=--的图象大致形状是 ( ) 8.已知1P (3-,1y ),2P (2,2y )是一次函数21y x =-+图象上的两个点,则1y ,2y 的大小关系是( )yOA yBCD2 / 5A .12y y >B .12y y <C .12y y =D .不能确定 9.如图,已知长方形ABCD 中,AB =3cm ,AD =9cm ,将此长方形折叠,使点B 与点D 重合,折痕为EF ,则△ABE 的面积为( ) A .3cm 2 B .4cm 2 C .6cm 2 D .12cm 210. 如图,某电信公司提供了A B ,两种方案的移动通讯费用y (元)与通话时间x (元)之间的关系,则以下说法错误..的是( ) A .若通话时间少于120分,则A 方案比B 方案便宜20元 B .若通话时间超过200分,则B 方案比A 方案便宜12元 C .若通讯费用为60元,则B 方案比A 方案的通话时间多 D .若两种方案通讯费用相差10元,则通话时间是145分或185分二、填空题(每题3分,共24分) 第12题图 11.方程)3(5)3(2-=-x x x 的根是____________.12. 在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直, 则绳端离旗杆底端的距离(BC )有5米.则旗杆的高度____.13. 如果方程0622=--+k kx x的一个根是-3,那么另一个根是____,k =______.14. 如图,Rt △ABC 中,∠BAC=90°,D ,E ,F 分别为AB ,BC ,AC 的中点,已知DF =5,则AE = .15.将直线23y x =--向左平移2个单位得到直线解析式 .16. 如图是某汽车行驶的路程s (km)与时间t (min)的函数关系图.当16≤ t ≤30时,s 与t 的函数关系式为 .17. 如图,直线1l :1y x =+与直线2l :y mx n =+相交于点P (a ,2),则关于x 的不等式1x +≥mx n +的解集为 ./minS /km40127050 30250y (元)A 方案B 方案3 / 518.正方形ABCD 的边长为4,点M ,N 在对角线AC 上(可与点A ,C 重合),MN =2,点P ,Q 在正方形的边上.下面四个结论中, ①存在无数个四边形PMQN 是平行四边形; ②存在无数个四边形PMQN 是菱形; ③存在无数个四边形PMQN 是矩形; ④至少存在一个四边形PMQN 是正方形. 所有正确结论的序号是 .三、解答题(19题5分,20题4分,21、22、23、24 、25题都是每题6分,26题7分,共46分)19.解方程: 25140x x +-=20.工人师傅做铝合金窗框分为下面三个步骤:(1)先截出两对符合规格的铝合金窗料(如图1所示),使AB CD EF GH ==,; (2)摆放成图2的四边形,则这时窗框的形状是______形;其依据是______.(3)将直角尺靠窗框的一个角(如图3所示),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4所示),说明窗框合格,这时窗框是______形,其依据是______.21.在平面直角坐标系xOy 中,一次函数的图象经过点A (1,-3)和B (2,0).(1)求这个一次函数的解析式;(2)若以O 、A 、B 、C 为顶点的四边形为平行四边形,则点C 的坐标为 (直接写出答案).22.已知关于x 的方程2(2)20(0)mx m x m -++=≠.(1)求证:方程总有两个实数根;(2)若方程的两个实数根是整数,求正整数m 的值.图1 图2 图3 图423.某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年(13年的可变成本为__________万元;(2)如果该养殖户第3年的养殖成本为7.146万元,24.已知:如图,在菱形ABCD中,BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.(1)判断四边形EBCF的形状,并证明;(2)若AF=9, CF=3,求CD的长.25.A和点B,点C轴上一定点,其坐标为C(1,0),一个动点P从原点出发沿O-B-A-C-O方向移动,连结PC。
2024年北京初三九年级上学期数学期末考《几何综合》
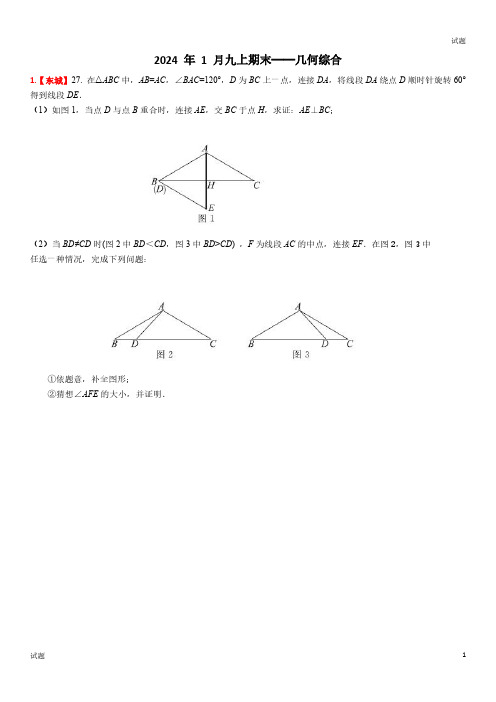
2024年1月九上期末——几何综合1.【东城】27.在△ABC中,AB=AC,∠BAC=120°,D为BC上一点,连接DA,将线段DA绕点D顺时针旋转60°得到线段DE.(1)如图1,当点D与点B重合时,连接AE,交BC于点H,求证:AE⊥BC;(2)当BD≠CD时(图2中BD<CD,图3中BD>CD),F为线段AC的中点,连接EF.在图2,图3中任选一种情况,完成下列问题:①依题意,补全图形;②猜想∠AFE的大小,并证明.2.【西城】27.在ABC △中,90ACB ∠=︒,AC BC =,CM AB ⊥于点M .点P 在射线CM 上,连接AP ,作CD AP ⊥于点D .连接MD ,作CE MD ⊥于点E ,作//DF AB 交直线CE 于点F ,连接MF .图1图2备用图(1)当点P 在线段CM 上时,在图1中补全图形,并直接写出ADM ∠的度数;(2)当点P 在线段CM 的延长线上时,利用图2探究线段DF 与AM 之间的数量关系,并证明;(3)取线段MF 的中点K ,连接BK ,若8AC =,直接写出线段BK 的长的最小值.3.【海淀】27.如图,在ABC △中,AB AC =,点D ,E 分别在边AC ,BC 上,连接DE ,EDC B ∠∠=.(1)求证:ED EC =;(2)连接BD ,点F 为BD 的中点,连接AF ,EF .①依题意补全图形;②若AF EF ⊥,求BAC ∠的大小.4.【朝阳】27.已知线段AB 和点C ,将线段AC 绕点A 逆时针旋转α(0°<α<90°),得到线段AD ,将线段BC 绕点B 顺时针旋转180°-α,得到线段BE ,连接DE ,F 为DE 的中点,连接AF ,BF .(1)如图1,点C 在线段AB 上,依题意补全图1,直接写出∠AFB 的度数;(2)如图2,点C 在线段AB 的上方,写出一个α的度数,使得3AF =成立,并证明.图1图25.【石景山】27.如图,在Rt ACB △中,90ACB ∠=°,60BAC ∠=°.D 是边BA 上一点(不与点B 重合且12BD BA <),将线段CD 绕点C 逆时针旋转60°得到线段CE ,连接DE ,AE .(1)求CAE ∠的度数;(2)F 是DE 的中点,连接AF 并延长,交CD 的延长线于点G ,依题意补全图形.若G ACE ∠=∠,用等式表示线段FG ,AF ,AE 之间的数量关系,并证明.6.【丰台】27.已知在△ABC中,AB=AC,0°<∠BAC<90°,将线段AC绕点A逆时针旋转α得到线段AD,连接BD,CD.(1)如图1,当∠BAC=α时,∠ABD=(用含有α的式子表示);(2)如图2,当α=90°时,连接BD,作∠BAD的角平分线交BC的延长线于点F,交BD于点E,连接DF.①依题意在图2中补全图形,并求∠DBC的度数;②用等式表示线段AF,CF,DF之间的数量关系,并证明.7.【昌平】27.在△ABC中,AB=AC,∠BAC=90°,点M为BC的中点,连接AM,点D为线段CM上一动点,过点D作DE⊥BC,且DE=DM,(点E在BC的上方),连接AE,过点E作AE的垂线交BC边于点F.(1)如图1,当点D为CM的中点时,①依题意补全图形;②直接写出BF和DE的数量关系为______________;(2)当点D在图2的位置时,用等式表示线段BF与DE之间的数量关系,并证明.图1图227题图127题图28.【通州】27.如图,ABC △中,90ACB ∠=︒,AC BC =,点D 在AB 的延长线上,取AD 的中点F ,连结CD 、CF ,将线段CD 绕点C 顺时针旋转90︒得到线段CE ,连结AE 、BE .(1)依题意,请补全图形;(2)判断BE 、CF 的数量关系及它们所在直线的位置关系,并证明.9.【房山】27.如图,在等边三角形ABC 中,E ,F 分别是BC ,AC 上的点,且BE CF =,AE ,BF 交于点G .(1)AGF ∠=°;(2)过点A 作AD ∥BC (点D 在AE 的右侧),且AD BC =,连接DG .①依题意补全图形;②用等式表示线段AG ,BG 与DG 的数量关系,并证明.10.【大兴】27.在△ABC中,∠BAC=90°,AB=AC,点P为BA的延长线上一点,连接PC,以点P为中心,将线段PC顺时针旋转90°得到线段PD,连接BD.(1)依题意补全图形;(2)求证:∠ACP=∠DPB;(3)用等式表示线段BC,BP,BD之间的数量关系,并证明.11.【门头沟】27.如图,Rt△ABC中,∠ACB=90°,CA=CB,过点C在△ABC外作射线CP,且∠ACP=α,点A关于CP的对称点为点D,连接AD,BD,CD,其中AD,BD分别交射线CP于点M,N.(1)依题意补全图形;(2)当α=30°时,直接写出∠CNB的度数;(3)当0°<α<45°时,用等式表示线段BN,CM之间的数量关系,并证明.12.【燕山】27.如图,△ABC为等边三角形,点M为AB边上一点(不与点A,B重合),连接CM,过点A作AD⊥CM于点D,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.(1)依题意补全图形,直接写出∠AEB的大小,并证明;(2)连接ED并延长交BC于点F,用等式表示BF与FC的数量关系,并证明.13.【顺义】27.在菱形ABCD中,∠B=60°,点P是对角线AC上一点(不与点A重合),点E,F分别是边AB,AD上的点,且∠EPF=60°,射线PE,PF分别与DA,BA的延长线交于点M,N.(1)如图1,若点P与C重合,且PA平分∠EPF,求证:AM=AN;(2)连接BP,若∠ABP=45°,BP=3,且PA不平分∠EPF.①依题意补全图2;②用等式表示线段AM,AN的数量关系,并证明.14.【密云】27.如图,在Rt△ABC中,∠ACB=90°,AC=BC.点D为AB边上的一点,将线段CD绕点C逆时针旋转90°得到线段CE,连接AE、BE.(1)依据题意,补全图形;(2)直接写出∠A C E+∠B C D的度数;(3)若点F为BD中点,连接CF交AE于点P,用等式表示线段A E与CF之间的数量关系,并证明.15.【平谷】27.如图,△ABC中,AC=BC,∠ACB=90°,D为AB边中点,E为△ABC外部射线CD上一点,连接AE,过C作CF⊥AE于F.(1)依题意补全图形,(2)找出图中与∠EAD相等的角,并证明;(3)连接DF,猜想∠CFD的度数,并证明.。
【物理】北京市九年级上册期末精选试卷检测题

【物理】北京市九年级上册期末精选试卷检测题一、初三物理电流和电路易错压轴题(难)1.在“探究串联电路中电流的特点”实验中,小明连接了如图所示的电路,闭合开关后,发现两个小灯泡都不发光,电流表没示数,检查发现各连线接触良好.(1)于是小明提出用导线两端依次连接ab、ac、ad两点的设计方案,其中用导线连接哪两点间不合适?答:________ (选填“ab”、“ac”或“ad”).(2)当小明用导线连接ab时,两灯泡不发光;连接ac时,小灯泡1L不发光,小灯泡2L 很亮,然后又熄灭.那么,原电路中的故障是________,小灯泡2L又熄灭的原因可能是_____________.(3)此时,同组的小红提出用电压表检查电路,你认为小红的方案可行吗?答:________(选填“可行”或“不可行”).【答案】ad L1断路电路中电流太大,灯丝被烧断可行【解析】【分析】【详解】(1)于是小明提出用导线两端依次连接ab、ac、ad两点的设计方案,连接ab两点可以检查电流表有没有故障,再连接ac两点,就可以检查L1、L2有没有故障,连接ad两点,电路短路,可能会损坏电源,所以连接ad两点不合适;(2)当小明用导线连接ab时,两灯泡不发光,说明电流表完好;连接ac时,小灯泡1L 不发光,小灯泡2L很亮,然后又熄灭.那么,原电路中的故障是L1断路,小灯泡2L又熄灭的原因可能是电路中电流太大,灯丝被烧断.(3)此时,同组的小红提出用电压表检查电路,小红的方案可行,可以分别把电压表接在ab之间、ac之间,看电压表的示数即可.2.现有两只小灯泡L1、L2,它们的额定电压分别为2.5V和3.8V.(1)如图甲是小明测定灯泡L1额定功率的实物电路图(不完整).①请用笔画线代替导线将实物电路图连接完整_____.②闭合开关前,应将滑动变阻器的滑片P移到__端(选填“A”或“B”).闭合开关后发现:小灯泡不亮,电流表示数为零,而电压表示数接近电源电压。
北京市第一学期期末九年级语文考试卷含答案.doc

北京市第一学期期末九年级语文考试卷含答案姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、语言表达(共4题)1.阅读下面的文字,完成第(1)—(2)题。
我区的琉璃渠村始建于公元1264年,是经历了辽、金、元、明、清五个朝代的千年古村。
村子的东头紧邻石担路,在村东入口处建有一座三官阁过街楼,过街楼上专门供奉着天官、地官、水官,以保一方平安。
过街楼正面朝向东方,匾额题写的是“带河”。
过街楼背面朝向西方,匾额题写的是“砺山”成语有“带砺山河”一词。
“带河”指黄河细得像条衣带,“砺山”指泰评卷人得分山小得像块磨刀石,这实际上是不可能发生的。
所以此成语多比喻时间久远,江山永固。
(1)根据“琉璃渠村示意图”回答,过街楼的匾额为什么东面是“带河”,西面是“砺山”?答:____________(节选自鲁迅《孔乙己》)【答案】丁举人会说什么?(不超过50字)答案示例:孔乙己,你还有脸出来呢?读了多少年的四书五经,怎么还是偷,虽然是书吧,然而总之是偷啊,活该!难度:偏难知识点:课文内容理解4.阅读下面两则材料【材料一】传统的匾额被称作古建筑的灵魂,是最能体现中国古代建筑文化和建筑特色的一种装饰构件。
以其多变的式样,精湛的书法,精炼的内容与建筑群落相互辉映,和谐统一,成为建筑中不可分割的部分。
匾额悬挂于屋檐之下、门楣之上,位于门的正中,突出一个“____________【答案】1.①正,②伸张正义。
2. “还我河山”属于言志类,表明岳飞抗金收复中原的理想“武侯祠”属于说明类,说明这座建筑的功能是祭祀诸葛亮用的。
3. 示例:(1)山高水长。
(2)因为东面是历史悠久的永定河,西面是广袤的燕山山脉。
难度:偏难知识点:综合性学习二、填空题(共6题)1.阅读下面的文字,请文成(1)—(2)题。
(不超过50字)成语是经过长期锤炼而形成的汉语言文化精髓,它的主要来源是:①寓言故事,如狐假虎威;②神话传说,如夸父逐日;③诗文创作,如老骥伏枥;④历史故事,如破釜沉舟。
北京版初三上学期期末物理试卷及解答参考

北京版物理初三上学期期末自测试卷(答案在后面)一、单项选择题(本大题有10小题,每小题3分,共30分)1、在下列关于光现象的描述中,正确的是:A、光在同种均匀介质中沿直线传播B、光的折射现象只会发生在光从空气进入水中时C、光从水中斜射入空气中时,折射角小于入射角D、光速在真空中比在水中要快2、下列关于力的说法中,正确的是:A、力的作用是相互的,但两个物体之间的作用力大小总是不相等的B、一个物体受到的力越大,它的加速度也越大,但加速度的方向与力的方向无关C、物体受到的合力为零时,物体可能处于静止状态,也可能处于匀速直线运动状态D、摩擦力总是阻碍物体运动的方向3、下列关于光现象的说法中,正确的是:A、太阳光通过三棱镜后,可以分解成七种颜色的光,这是光的色散现象。
B、手电筒的光束可以照亮很远的路面,说明光在空气中的传播速度很快。
C、平静的水面可以反射出清晰的物体像,这是因为光发生了折射。
D、在屏幕上看到的电影画面是实际光线会聚形成的,所以电影屏幕应该是凹面镜。
4、关于机械能的说法,以下不正确的是:A、物体在斜面上匀速下滑时,重力势能减小,动能不变。
B、抛出去的篮球在上升过程中,动能减小,重力势能增大。
C、用弹簧测力计竖直向上提起重物时,弹簧测力计的示数逐渐减小。
D、自行车在水平路面上匀速行驶时,其机械能保持不变。
5、一个物体从静止开始沿水平面加速运动,5秒内通过了25米的距离。
假设水平面是光滑的,不计空气阻力,下列关于该物体的描述正确的是:A、物体的加速度是5 m/s²B、物体的速度是5 m/sC、物体的动能是125 JD、物体的动量是25 kg·m/s6、一个质量为2 kg的物体,从高度h处自由落下,不考虑空气阻力。
当物体落地时,下列关于物体动能的描述正确的是:A、物体的动能是mghB、物体的动能是mgh/2mgℎ)C、物体的动能是(12mgℎ)D、物体的动能是(mgℎ+127、在下列关于物理量的描述中,正确的是:A、速度是表示物体运动快慢的物理量,单位是米每秒(m/s)。
北京育英中学数学九年级上册期末试卷(含答案)

北京育英中学数学九年级上册期末试卷(含答案) 一、选择题1.下列方程中,是关于x 的一元二次方程的为( )A .2210x x += B .220x x --= C .2320x xy -= D .240y -= 2.已知34a b =(0a ≠,0b ≠),下列变形错误的是( ) A .34a b = B .34a b = C .43b a = D .43a b =3.如图,ABC ∆与A B C '''∆是以坐标原点O 为位似中心的位似图形,若点A 是OA '的中点,ABC ∆的面积是6,则A B C '''∆的面积为( )A .9B .12C .18D .24 4.如图,CD 为O 的直径,弦AB CD ⊥于点E ,2DE =,8AB =,则O 的半径为( )A .5B .8C .3D .105.在△ABC 中,若|sinA ﹣12|+2cosB )2=0,则∠C 的度数是( ) A .45°B .75°C .105°D .120° 6.若直线l 与半径为5的O 相离,则圆心O 与直线l 的距离d 为( )A .5d <B .5d >C .5d =D .5d ≤ 7.如图,△ABC 内接于⊙O ,连接OA 、OB ,若∠ABO =35°,则∠C 的度数为( )A.70°B.65°C.55°D.45°8.下列说法中,不正确的是()A.圆既是轴对称图形又是中心对称图形B.圆有无数条对称轴C.圆的每一条直径都是它的对称轴D.圆的对称中心是它的圆心9.下列函数中属于二次函数的是( )A.y=12x B.y=2x2-1 C.y=23x+D.y=x2+1x+110.在一个不透明的口袋中装有3个红球和2个白球,它们除颜色不同外,其余均相同.把它们搅匀后从中任意摸出1个球,则摸到红球的概率是()A.14B.34C.15D.3511.方程2x x=的解是()A.x=0 B.x=1 C.x=0或x=1 D.x=0或x=-1 12.不透明袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是()A.13B.14C.15D.1613.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是()A.2332π-B.233π-C.32π-D.3π-14.2的相反数是()A.12-B.12C.2D.2-15.如图,AB为O的直径,C为O上一点,弦AD平分BAC∠,交BC于点E,6AB=,5AD=,则AE的长为()A .2.5B .2.8C .3D .3.2二、填空题16.若△ABC ∽△A′B′C′,∠A =50°,∠C =110°,则∠B′的度数为_____.17.如图,为了测量某棵树的高度,小明用长为2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m ,与树相距15m ,则树的高度为_________m.18.如图,A 、B 、C 是⊙O 上三点,∠ACB =30°,则∠AOB 的度数是_____.19.如图,四边形ABCD 内接于⊙O ,AB 是⊙O 的直径,过点C 作⊙O 的切线交AB 的延长线于点P ,若∠P =40°,则∠ADC =____°.20.如图,已知O 的半径为2,ABC ∆内接于O ,135ACB ∠=,则AB =__________.21.在泰州市举行的大阅读活动中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20 cm ,则它的宽为________cm .(结果保留根号)22.在△ABC 中,∠C =90°,cosA =35,则tanA 等于 . 23.如图是二次函数2y ax bx c =++的部分图象,由图象可知不等式20ax bx c ++>的解集是_______.24.如图,∠C=∠E=90°,AC=3,BC=4,AE=2,则AD=_________ .25.如图,曲线AB 是顶点为B ,与y 轴交于点A 的抛物线y =﹣x 2+4x +2的一部分,曲线BC 是双曲线k y x=的一部分,由点C 开始不断重复“A ﹣B ﹣C ”的过程,形成一组波浪线,点P (2018,m )与Q (2025,n )均在该波浪线上,则mn =_____.26..甲、乙、丙、丁四位同学在五次数学测验中他们成绩的平均分相等,方差分别是2.3,3.8,5.2,6.2,则成绩最稳定的同学是______.27.如图示,在Rt ABC ∆中,90ACB ∠=︒,3AC =,3BC =,点P 在Rt ABC ∆内部,且PAB PBC ∠=∠,连接CP ,则CP 的最小值等于______.28.已知正方形ABCD 边长为4,点P 为其所在平面内一点,PD 5,∠BPD =90°,则点A 到BP 的距离等于_____.29.二次函数y =ax 2+bx +c (a ,b ,c 为常数,且a ≠0)的图像上部分点的横坐标x 和纵 坐标y 的对应值如下表x … -1 0 1 2 3 … y … -3 -3 -1 39 …关于x 的方程ax 2+bx +c =0一个负数解x 1满足k <x 1<k +1(k 为整数),则k =________.30.若二次函数24y x x =-的图像在x 轴下方的部分沿x 轴翻折到x 轴上方,图像的其余部分保持不变,翻折后的图像与原图像x 轴上方的部分组成一个形如“W ”的新图像,若直线y =-2x +b 与该新图像有两个交点,则实数b 的取值范围是__________ 三、解答题31.解下列一元二次方程.(1)x 2+x -6=0;(2)2(x -1)2-8=0.32.如图,在矩形ABCD 中,E 是BC 上一点,连接AE ,将矩形沿AE 翻折,使点B 落在CD 边F 处,连接AF ,在AF 上取一点O,以点O 为圆心,OF 为半径作⊙O 与AD 相切于点P .AB=6,BC=33(1)求证:F 是DC 的中点.(2)求证:AE=4CE.(3)求图中阴影部分的面积.33.如图,四边形 ABCD 为矩形.(1)如图1,E 为CD 上一定点,在AD 上找一点F ,使得矩形沿着EF 折叠后,点D 落在 BC 边上(尺规作图,保留作图痕迹);(2)如图2,在AD 和CD 边上分别找点M ,N ,使得矩形沿着MN 折叠后BC 的对应边B' C'恰好经过点D ,且满足B' C' ⊥BD(尺规作图,保留作图痕迹);(3)在(2)的条件下,若AB =2,BC =4,则CN = .34.小亮晚上在广场散步,图中线段AB 表示站立在广场上的小亮,线段PO 表示直立在广场上的灯杆,点P 表示照明灯的位置.(1)请你在图中画出小亮站在AB 处的影子BE ;(2)小亮的身高为1.6m ,当小亮离开灯杆的距离OB 为2.4m 时,影长为1.2m ,若小亮离开灯杆的距离OD =6m 时,则小亮(CD )的影长为多少米?35.如图①,在矩形ABCD 中,BC =60cm .动点P 以6cm /s 的速度在矩形ABCD 的边上沿A →D 的方向匀速运动,动点Q 在矩形ABCD 的边上沿A →B →C 的方向匀速运动.P 、Q 两点同时出发,当点P 到达终点D 时,点Q 立即停止运动.设运动的时间为t (s ),△PDQ 的面积为S (cm 2),S 与t 的函数图象如图②所示.(1)AB = cm ,点Q 的运动速度为 cm /s ;(2)在点P 、Q 出发的同时,点O 也从CD 的中点出发,以4cm /s 的速度沿CD 的垂直平分线向左匀速运动,以点O 为圆心的⊙O 始终与边AD 、BC 相切,当点P 到达终点D 时,运动同时停止.①当点O 在QD 上时,求t 的值;②当PQ 与⊙O 有公共点时,求t 的取值范围.四、压轴题36.已知在ABC 中,AB AC =.在边AC 上取一点D ,以D 为顶点、DB 为一条边作BDF A ∠=∠,点E 在AC 的延长线上,ECF ACB ∠=∠.(1)如图(1),当点D 在边AC 上时,请说明①FDC ABD ∠=∠;②DB DF =成立的理由.(2)如图(2),当点D 在AC 的延长线上时,试判断DB 与DF 是否相等?37.在长方形ABCD 中,AB =5cm ,BC =6cm ,点P 从点A 开始沿边AB 向终点B以1/cm s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动.如果P 、Q 分别从A 、B 同时出发,当点Q 运动到点C 时,两点停止运动.设运动时间为t 秒.(1)填空:______=______,______=______(用含t 的代数式表示);(2)当t 为何值时,PQ 的长度等于5cm ?(3)是否存在t 的值,使得五边形APQCD 的面积等于226cm ?若存在,请求出此时t 的值;若不存在,请说明理由.38.如图,Rt △ABC ,CA ⊥BC ,AC =4,在AB 边上取一点D ,使AD =BC ,作AD 的垂直平分线,交AC 边于点F ,交以AB 为直径的⊙O 于G ,H ,设BC =x .(1)求证:四边形AGDH 为菱形;(2)若EF =y ,求y 关于x 的函数关系式;(3)连结OF ,CG .①若△AOF 为等腰三角形,求⊙O 的面积;②若BC =3,则30CG+9=______.(直接写出答案).39.如图,抛物线2()20y ax x c a =++<与x 轴交于点A 和点B (点A 在原点的左侧,点B 在原点的右侧),与y 轴交于点C ,3OB OC ==.(1)求该抛物线的函数解析式.(2)如图1,连接BC ,点D 是直线BC 上方抛物线上的点,连接OD ,CD .OD 交BC 于点F ,当32COF CDF S S =::时,求点D 的坐标.(3)如图2,点E 的坐标为(03)2-,,点P 是抛物线上的点,连接EB PB PE ,,形成的PBE △中,是否存在点P ,使PBE ∠或PEB ∠等于2OBE ∠?若存在,请直接写出符合条件的点P 的坐标;若不存在,请说明理由.40.如图,抛物线2y x bx c =-++与x 轴的两个交点分别为(1,0)A ,(30)B ,.抛物线的对称轴和x 轴交于点M .(1)求这条抛物线对应函数的表达式;(2)若P 点在该抛物线上,求当PAB △的面积为8时,求点P 的坐标.(3)点G 是抛物线上一个动点,点E 从点B 出发,沿x 轴的负半轴运动,速度为每秒1个单位,同时点F 由点M 出发,沿对称轴向下运动,速度为每秒2个单位,设运动的时间为t .①若点G 到AE 和MF 距离相等,直接写出点G 的坐标.②点C 是抛物线的对称轴上的一个动点,以FG 和FC 为边做矩形FGDC ,直接写出点E 恰好为矩形FGDC 的对角线交点时t 的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据一元二次方程的定义,一元二次方程有三个特点:(1)只含有一个未知数;(2)未知数的最高次数是2;(3)是整式方程.要判断一个方程是否为一元二次方程,先看它是否为整式方程,若是,再对它进行整理.如果能整理为ax 2+bx +c =0(a ≠0)的形式,则这个方程就为一元二次方程.【详解】解:A.2210x x +=,是分式方程, B.220x x --=,正确,C.2320x xy -=,是二元二次方程,D.240y -=,是关于y 的一元二次方程,故选B【点睛】此题主要考查了一元二次方程的定义,关键是掌握一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;方程中如果有分母,那么分母中无未知数; ②只含有一个未知数; ③未知数的最高次数是2.2.B解析:B【解析】【分析】根据两内项之积等于两外项之积对各项分析判断即可得解.【详解】 解:由34a b =,得出,3b=4a, A.由等式性质可得:3b=4a ,正确;B.由等式性质可得:4a=3b ,错误;C. 由等式性质可得:3b=4a ,正确;D. 由等式性质可得:4a=3b ,正确.故答案为:B.【点睛】本题考查的知识点是等式的性质,熟记等式性质两内项之积等于两外项之积是解题的关键. 3.D解析:D【解析】【分析】根据位似图形的性质,再结合点A 与点A '的坐标关系可得出两个三角形的相似比,再根据面积比等于相似比的平方即可得出答案.【详解】解:∵△ABC 与△A B C '''是以坐标原点O 为位似中心的位似图形,且A 为O A '的中心, ∴△ABC 与△A B C '''的相似比为:1:2;∵位似图形的面积比等于相似比的平方,∴△A B C '''的面积等于4倍的△ABC 的面积,即4624⨯=.故答案为:D.【点睛】本题考查的知识点是位似图形的性质,位似是特殊的相似,熟记位似图形的面积比等于相似比的平方是解题的关键.4.A解析:A【解析】【分析】作辅助线,连接OA ,根据垂径定理得出AE=BE=4,设圆的半径为r ,再利用勾股定理求解即可.【详解】解:如图,连接OA ,设圆的半径为r ,则OE=r-2,∵弦AB CD ⊥,∴AE=BE=4,由勾股定理得出:()22242r r =+-,解得:r=5,故答案为:A.【点睛】本题考查的知识点主要是垂径定理、勾股定理及其应用问题;解题的关键是作辅助线,灵活运用勾股定理等几何知识点来分析、判断或解答. 5.C解析:C【解析】 【分析】根据非负数的性质列出关系式,根据特殊角的三角函数值求出∠A 、∠B 的度数,根据三角形内角和定理计算即可.【详解】由题意得,sinA-12=0,22-cosB=0, 即sinA=122, 解得,∠A=30°,∠B=45°,∴∠C=180°-∠A-∠B=105°,故选C.【点睛】本题考查的是非负数的性质的应用、特殊角的三角函数值的计算和三角形内角和定理的应用,熟记特殊角的三角函数值是解题的关键.6.B解析:B【解析】【分析】直线与圆相离等价于圆心到直线的距离大于半径,据此解答即可.【详解】解:∵直线l与半径为5的O相离,∴圆心O与直线l的距离d满足:5d .故选:B.【点睛】本题考查了直线与圆的位置关系,属于应知应会题型,若圆心到直线的距离为d,圆的半径为r,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交. 7.C解析:C【解析】【分析】根据三角形的内角和定理和等腰三角形等边对等角求得∠O的度数,再进一步根据圆周角定理求解.【详解】解:∵OA=OB,∠ABO=35°,∴∠BAO=∠ABO=35°,∴∠O=180°-35°×2=110°,∴∠C=12∠O=55°.故选:C.【点睛】本题考查三角形的内角和定理、等腰三角形的性质,圆周角定理.能理解同弧所对的圆周角等于圆心角的一半是解决此题的关键.8.C解析:C【解析】【分析】圆有无数条对称轴,但圆的对称轴是直线,故C圆的每一条直线都是它的对称轴的说法是错误的本题不正确的选C,理由:圆有无数条对称轴,其对称轴都是直线,故任何一条直径都是它的对称轴的说法是错误的,正确的说法应该是圆有无数条对称轴,任何一条直径所在的直线都是它的对称轴故选C【点睛】此题主要考察对称轴图形和中心对称图形,难度不大9.B解析:B【解析】【分析】根据反比例函数的定义,二次函数的定义,一次函数的定义对各选项分析判断后利用排除法求解.【详解】解:A. y=12x是正比例函数,不符合题意;B. y=2x2-1是二次函数,符合题意;C. yD. y=x2+1x+1不是二次函数,不符合题意.故选:B.【点睛】本题考查了二次函数的定义,解题关键是掌握一次函数、二次函数、反比例函数的定义.10.D解析:D【解析】【分析】根据题意即从5个球中摸出一个球,概率为3 5 .【详解】摸到红球的概率=33 235=+,故选:D.【点睛】此题考查事件的简单概率的求法,正确理解题意,明确可能发生的总次数及所求事件发生的次数是求概率的关键.11.C解析:C【分析】根据因式分解法,可得答案.【详解】解:2x x=,方程整理,得,x2-x=0因式分解得,x(x-1)=0,于是,得,x=0或x-1=0,解得x1=0,x2=1,故选:C.【点睛】本题考查了解一元二次方程,因式分解法是解题关键.12.A解析:A【解析】【分析】根据红球的个数以及球的总个数,直接利用概率公式求解即可.【详解】因为共有6个球,红球有2个,所以,取出红球的概率为2163 P==,故选A.【点睛】本题考查了简单的概率计算,正确把握概率的计算公式是解题的关键. 13.B解析:B【解析】【分析】根据菱形的性质得出△DAB是等边三角形,进而利用全等三角形的判定得出△ABG≌△DBH,得出四边形GBHD的面积等于△ABD的面积,进而求出即可.【详解】连接BD,∵四边形ABCD是菱形,∠A=60°,∴∠ADC=120°,∴∠1=∠2=60°,∴△DAB 是等边三角形,∵AB=2,∴△ABD,∵扇形BEF 的半径为2,圆心角为60°,∴∠4+∠5=60°,∠3+∠5=60°,∴∠3=∠4,设AD 、BE 相交于点G ,设BF 、DC 相交于点H ,在△ABG 和△DBH 中,2{34A AB BD ∠=∠=∠=∠,∴△ABG ≌△DBH (ASA ),∴四边形GBHD 的面积等于△ABD 的面积,∴图中阴影部分的面积是:S 扇形EBF -S △ABD=2602123602π⨯-⨯=23π 故选B . 14.D解析:D【解析】【分析】根据相反数的概念解答即可.【详解】2的相反数是-2,故选D .15.B解析:B【解析】【分析】连接BD,CD,由勾股定理求出BD 的长,再利用ABD BED ,得出DE DB DB AD =,从而求出DE 的长,最后利用AE AD DE =-即可得出答案.【详解】连接BD,CD∵AB为O的直径90ADB∴∠=︒22226511 BD AB AD∴=-=-∵弦AD平分BAC∠11CD BD∴==CBD DAB∴∠=∠ADB BDE∠=∠ABD BED∴DE DBDB AD∴=11511=解得115DE=115 2.85AE AD DE∴=-=-=故选:B.【点睛】本题主要考查圆周角定理的推论及相似三角形的判定及性质,掌握圆周角定理的推论及相似三角形的性质是解题的关键.二、填空题16.20°【解析】【分析】先根据三角形内角和计算出∠B的度数,然后根据相似三角形的性质得到∠B′的度数.【详解】解:∵∠A=50°,∠C=110°,∴∠B=180°﹣50°﹣110°=20°解析:20°【解析】【分析】先根据三角形内角和计算出∠B的度数,然后根据相似三角形的性质得到∠B′的度数.【详解】解:∵∠A=50°,∠C=110°,∴∠B=180°﹣50°﹣110°=20°,∵△ABC∽△A′B′C′,∴∠B′=∠B=20°.故答案为20°.【点睛】本题考查了相似三角形的性质,如果两个三角形相似,那么它们的对应角相等,对应边成比例,它们对应面积的比等于相似比的平方.17.7【解析】设树的高度为m,由相似可得,解得,所以树的高度为7m解析:7【解析】设树的高度为x m,由相似可得6157262x+==,解得7x=,所以树的高度为7m18.60°【解析】【分析】直接利用圆周角定理,即可求得答案.【详解】∵A、B、C是⊙O上三点,∠ACB=30°,∴∠AOB的度数是:∠AOB =2∠ACB=60°.故答案为:60°.【点解析:60°【解析】【分析】直接利用圆周角定理,即可求得答案.【详解】∵A、B、C是⊙O上三点,∠ACB=30°,∴∠AOB的度数是:∠AOB=2∠ACB=60°.故答案为:60°.【点睛】考查了圆周角定理的运用,同弧或等弧所对的圆周角等于圆心角的一半.19.115°【解析】【分析】根据过C点的切线与AB的延长线交于P点,∠P=40°,可以求得∠OCP和∠OBC的度数,又根据圆内接四边形对角互补,可以求得∠D的度数,本题得以解决.【详解】解:连解析:115°【解析】【分析】根据过C点的切线与AB的延长线交于P点,∠P=40°,可以求得∠OCP和∠OBC的度数,又根据圆内接四边形对角互补,可以求得∠D的度数,本题得以解决.【详解】解:连接OC,如右图所示,由题意可得,∠OCP=90°,∠P=40°,∴∠COB=50°,∵OC=OB,∴∠OCB=∠OBC=65°,∵四边形ABCD是圆内接四边形,∴∠D+∠ABC=180°,∴∠D=115°,故答案为:115°.【点睛】本题考查切线的性质、圆内接四边形,解题的关键是明确题意,找出所求问题需要的条件.20.【解析】分析:根据圆内接四边形对边互补和同弧所对的圆心角是圆周角的二倍,可以求得∠AOB的度数,然后根据勾股定理即可求得AB的长.详解:连接AD、AE、OA、OB,∵⊙O的半径为2,△AB解析:22【解析】分析:根据圆内接四边形对边互补和同弧所对的圆心角是圆周角的二倍,可以求得∠AOB 的度数,然后根据勾股定理即可求得AB的长.详解:连接AD、AE、OA、OB,∵⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,∴∠ADB=45°,∴∠AOB=90°,∵OA=OB=2,∴2,故答案为:2点睛:本题考查三角形的外接圆和外心,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.21.()【解析】设它的宽为xcm.由题意得.∴ .点睛:本题主要考查黄金分割的应用.把一条线段分割为两部分,使其中较长部分与全长之比等于较短部分与较长部分之比,其比值是一个无理数,即,近似值约解析:(10510)【解析】设它的宽为x cm.由题意得51x=.:202x= .∴10510点睛:本题主要考查黄金分割的应用.把一条线段分割为两部分,使其中较长部分与全长之-51,近似值约为0.618. 22..【解析】试题分析:∵在△ABC 中,∠C =90°,cosA =,∴.∴可设.∴根据勾股定理可得.∴.考点:1.锐角三角函数定义;2.勾股定理. 解析:43. 【解析】 试题分析:∵在△ABC 中,∠C =90°,cosA =35,∴35AC AB =. ∴可设35AC k AB k ==,.∴根据勾股定理可得4BC k =. ∴44tanA 33BC k AC k ===. 考点:1.锐角三角函数定义;2.勾股定理.23.【解析】【分析】求方程的解即是求函数图象与x 轴的交点坐标,因为图像具有对称性,知道一个坐标,就可求出另一个,分析x 轴上方的图象可得结果.【详解】由图像可知,二次函数的对称轴x=2,图像与x解析:15x -<<【解析】【分析】求方程的解即是求函数图象与x 轴的交点坐标,因为图像具有对称性,知道一个坐标,就可求出另一个,分析x 轴上方的图象可得结果.【详解】由图像可知,二次函数的对称轴x=2,图像与x 轴的一个交点为5,所以,另一交点为2-3=-1. ∴x 1=-1,x 2=5. ∴不等式20ax bx c ++>的解集是15x -<<.故答案为15x -<<【点睛】要了解二次函数性质与图像,由于图像的开口向下,所以,有两个交点,知一易求另一个,本题属于基础题.24..【解析】试题分析:由∠C=∠E=90°,∠BAC=∠DAE 可得△ABC ∽△ADE ,根据相似三角形的对应边的比相等就可求出AD 的长.试题解析:∵∠C=∠E=90°,∠BAC=∠DAE ∴△AB解析:10 3.【解析】试题分析:由∠C=∠E=90°,∠BAC=∠DAE可得△ABC∽△ADE,根据相似三角形的对应边的比相等就可求出AD的长.试题解析:∵∠C=∠E=90°,∠BAC=∠DAE∴△ABC∽△ADE∴AC:AE=BC:DE∴DE=83∴103AD=考点: 1.相似三角形的判定与性质;2.勾股定理.25.24【解析】【详解】点B是抛物线y=﹣x2+4x+2的顶点,∴点B的坐标为(2,6),2018÷6=336…2,故点P离x轴的距离与点B离x轴的距离相同,∴点P的坐标为(2018,6),解析:24【解析】【详解】点B是抛物线y=﹣x2+4x+2的顶点,∴点B的坐标为(2,6),2018÷6=336…2,故点P离x轴的距离与点B离x轴的距离相同,∴点P的坐标为(2018,6),∴m=6;点B(2,6)在kyx=的图象上,∴k=6;即12yx=,2025÷6=337…3,故点Q离x轴的距离与当x=3时,函数12yx=的函数值相等,又 x =3时,1243y ==, ∴点Q 的坐标为(2025,4),即n =4,∴mn =6424.⨯=故答案为24.【点睛】本题主要考查了反比例函数图象上的点的坐标特征以及二次函数的图象与性质.本题是一道找规律问题.找到点P 、Q 在A ﹣B ﹣C 段上的对应点是解题的关键.26.甲【解析】【分析】方差反映了一组数据的波动情况,方差越小越稳定,据此可判断.【详解】∵2.3<3.8<5.2<6.2,∴,∴成绩最稳定的是甲.故答案为:甲.【点睛】本题考查了方差解析:甲【解析】【分析】方差反映了一组数据的波动情况,方差越小越稳定,据此可判断.【详解】∵2.3<3.8<5.2<6.2,∴2222甲乙丁丙<<<S S S S ,∴成绩最稳定的是甲.故答案为:甲.【点睛】本题考查了方差的概念,正确理解方差所表示的意义是解题的关键.27.【解析】【分析】首先判定直角三角形∠CAB=30°,∠ABC=60°,,然后根据,得出∠ACB+∠PAC+∠PBC=∠APB=120°,定角定弦,点P 的轨迹是以AB 为弦,圆周角为120°的圆弧解析:72- 【解析】 【分析】首先判定直角三角形∠CAB=30°,∠ABC=60°,()22223323AB AC BC =+=+=,然后根据PAB PBC ∠=∠,得出∠ACB+∠PAC+∠PBC=∠APB=120°,定角定弦,点P 的轨迹是以AB 为弦,圆周角为120°的圆弧上,如图所示,当点C 、O 、P 在同一直线上时,CP 最小,构建圆,利用勾股定理,即可得解.【详解】∵90ACB ∠=︒,3AC =,3BC =, ∴()22223323AB AC BC =+=+=∴∠CAB=30°,∠ABC=60°∵PAB PBC ∠=∠,∠PAB+∠PAC=30°∴∠ACB+∠PAC+∠PBC=∠APB=120°∴定角定弦,点P 的轨迹是以AB 为弦,圆周角为120°的圆弧上,如图所示,当点C 、O 、P 在同一直线上时,CP 最小∴CO ⊥AB ,∠COB=60°,∠ABO=30°∴OB=2,∠OBC=90°∴()2222237OC OB BC =+=+= ∴72CP OC OP =-=-故答案为72-.【点睛】此题主要考查直角三角形中的动点综合问题,解题关键是找到点P 的位置.28.或【解析】【分析】由题意可得点P在以D为圆心,为半径的圆上,同时点P也在以BD为直径的圆上,即点P是两圆的交点,分两种情况讨论,由勾股定理可求BP,AH的长,即可求点A到BP的距离.【详解】解析:335+或335-【解析】【分析】由题意可得点P在以D为圆心,5为半径的圆上,同时点P也在以BD为直径的圆上,即点P是两圆的交点,分两种情况讨论,由勾股定理可求BP,AH的长,即可求点A到BP 的距离.【详解】∵点P满足PD=5,∴点P在以D为圆心,5为半径的圆上,∵∠BPD=90°,∴点P在以BD为直径的圆上,∴如图,点P是两圆的交点,若点P在AD上方,连接AP,过点A作AH⊥BP,∵CD=4=BC,∠BCD=90°,∴BD=2∵∠BPD=90°,∴BP22BD PD-3,∵∠BPD=90°=∠BAD,∴点A,点B,点D,点P四点共圆,∴∠APB=∠ADB=45°,且AH⊥BP,∴∠HAP=∠APH=45°,∴AH=HP,在Rt△AHB中,AB2=AH2+BH2,∴16=AH2+(AH)2,∴AHAH,若点P在CD的右侧,同理可得AH,综上所述:AH.【点睛】本题是正方形与圆的综合题,正确确定点P是以DBD为直径的圆的交点是解决问题的关键.29.-3【解析】【分析】首先利用表中的数据求出二次函数,再利用求根公式解得x1,再利用夹逼法可确定x1 的取值范围,可得k.【详解】解:把x=0,y=-3,x=1,y=-1,x=-1,y=-3解析:-3【解析】【分析】首先利用表中的数据求出二次函数,再利用求根公式解得x1,再利用夹逼法可确定x1的取值范围,可得k.【详解】解:把x=0,y=-3,x=1,y=-1,x=-1,y=-3代入y=ax2+bx+c得3 1 3ca b c a b c-=⎧⎪-=++⎨⎪-=-+⎩,解得113abc=⎧⎪=⎨⎪=-⎩,∴y=x²+x-3,∵△=b2-4ac=12-4×1×(-3)=13,∴x=122ba-±-±=,∵1x<0,∴1x=−1<0,∵-4≤-3,∴133222-≤-≤-, ∴-3≤−1−13≤ 2.5-, ∵整数k 满足k <x 1<k+1,∴k=-3,故答案为:-3.【点睛】本题考查了二次函数的图象和性质,解题的关键是求出二次函数的解析式.30.【解析】【分析】当直线y=-2x+b 处于直线m 的位置时,此时直线和新图象只有一个交点A ,当直线处于直线n 的位置时,此时直线与新图象有三个交点,当直线y=-2x+b 处于直线m 、n 之间时,与该新图解析:18b -<<【解析】【分析】当直线y=-2x+b 处于直线m 的位置时,此时直线和新图象只有一个交点A ,当直线处于直线n 的位置时,此时直线与新图象有三个交点,当直线y=-2x+b 处于直线m 、n 之间时,与该新图象有两个公共点,即可求解.【详解】解:设y=x 2-4x 与x 轴的另外一个交点为B ,令y=0,则x=0或4,过点B (4,0), 由函数的对称轴,二次函数y=x 2-4x 翻折后的表达式为:y=-x 2+4x ,当直线y=-2x+b 处于直线m 的位置时,此时直线和新图象只有一个交点A ,当直线处于直线n 的位置时,此时直线n 过点B (4,0)与新图象有三个交点, 当直线y=-2x+b 处于直线m 、n 之间时,与该新图象有两个公共点,当直线处于直线m 的位置:联立y=-2x+b 与y=x 2-4x 并整理:x 2-2x-b=0,则△=4+4b=0,解得:b=-1;当直线过点B 时,将点B 的坐标代入直线表达式得:0=-8+b ,解得:b=8,故-1<b <8;故答案为:-1<b <8.【点睛】本题考查的是二次函数综合运用,涉及到函数与x 轴交点、几何变换、一次函数基本知识等内容,本题的关键是确定点A 、B 两个临界点,进而求解.三、解答题31.(1)123;2x x =-=;(2)123;1x x ==-【解析】【分析】(1)利用因式分解法解一元二次方方程;(2)用直接开平方法解一元二次方程.【详解】解:(1)x 2+x -6=0;(3)(2)0x x +-=∴123;2x x =-=(2)2(x -1)2-8=0.22(1)8x -=2(1)4x -=12x -=±∴123;1x x ==-【点睛】本题考查直接开平方法和因式分解法解一元二次方程,掌握解题技巧正确计算是本题的解题关键.32.(1)见解析;(2)见解析;(3)2 【解析】【分析】(1)易求DF 长度即可判断;(2)通过30°角所对的直角边等于斜边一半证得AE=2EF ,EF=2CE 即可得;(3)先证明△OFG 为等边三角形,△OPG 为等边三角形,即可确定扇形圆心角∠POG 和∠GOF 的大小均为60°,所以两扇形面积相等, 通过割补法得出最后阴影面积只与矩形OPDH 和△OGF 有关,根据面积公式求出两图形面积即可.【详解】(1)∵AF=AB=6,AD=BC=∴DF=3,∴CF=DF=3,∴F 是CD 的中点(2)∵AF=6, DF=3,∴∠DAF=30°,∴∠EAF=30◦ ,∴AE=2EF;∴∠EFC=30◦ ,EF=2CE,∴AE=4CE(3)如图,连接OP,OG,作OH⊥FG,∵∠AFD=60°,OF=OG,∴△OFG为等边三角形,同理△OPG为等边三角形,∴∠POG=∠FOG=60°,OH=33 OG ,∴S扇形OPG=S扇形OGF,∴S阴影=(S矩形OPDH-S扇形OPG-S△OGH)+(S扇形OGF-S△OFG)=S矩形OPDH-32S△OFG=313 2323222,即图中阴影部分的面积3 .【点睛】本题考查了正方形的性质,等边三角形的性质及解直角三角形,涉及知识点较多,综合性较强,根据条件,结合图形找准对应知识点是解答此题的关键.33.(1)图见解析(2)图见解析(351【解析】【分析】(1)以点E为圆心,以DE长为半径画弧,交BC于点D′,连接DD′,作DD′的垂直平分线交AD于点F即可;(2)先作射线BD,然后过点D作BD的垂线与BC的延长线交于点H,作∠BHD的角平分线交CD于点N,交AD于点M,在HD上截取HC′=HC,然后在射线C′D上截取C′B′=BC,此时的M、N即为满足条件的点;(3)在(2)的条件下,根据AB=2,BC=4,即可求出CN的长.【详解】(1)如图,点F为所求;(2)如图,折痕MN、矩形A’B’C’D’为所求;(3)在(2)的条件下,∵AB=2,BC=4,∴BD=5∵BD⊥B′C′,∴BD⊥A′D′,得矩形DGD′C′.∴DG=C′D′=2,∴BG=5设CN的长为x,CD′=y.则C′N=x,D′N=2−x,BD′=4−y,∴(4−y)2=y2+(5)2,解得y5.(2−x)2=x25)2解得x =512-. 故答案为:51-. 【点睛】 本题考查了作图−复杂作图、矩形的性质、翻折变换,解决本题的关键是掌握矩形的性质.34.(1)如图,BE 为所作;见解析;(2)小亮(CD )的影长为3m .【解析】 【分析】(1)根据光是沿直线传播的道理可知在小亮由B 处沿BO 所在的方向行走到达O 处的过程中,连接PA 并延长交直线BO 于点E ,则可得到小亮站在AB 处的影子;(2)根据灯的光线与人、灯杆、地面形成的两个直角三角形相似解答即可.【详解】(1)如图,连接PA 并延长交直线BO 于点E ,则线段BE 即为小亮站在AB 处的影子:(2)延长PC 交OD 于F ,如图,则DF 为小亮站在CD 处的影子,AB =CD =1.6,OB =2.4,BE =1.2,OD =6,∵AB ∥OP ,∴△EBA ∽△EOP , ∴,AB EB OP EO =即1.6 1.2,1.2 2.4OP =+ 解得OP =4.8,∵CD ∥OP ,∴△FCD ∽△FPO ,∴CD FD OP FO =,即1.64.86FD FD =+, 解得FD =3答:小亮(CD )的影长为3m .【点睛】 本题考查的是相似三角形的判定及性质,解答此题的关键是根据题意画出图形,构造出相似三角形,再根据相似三角形的性质解答.35.(1)30,6;(2)①4571532-≤t 1532+ 【解析】。
北京育英中学化学初三化学上册期末试卷(含答案)

北京育英中学化学上册期末试卷(含答案)一、九年级化学上册选择题 1.下列有关图象中不正确的是A .图①是一定量的碳在过量的氧气中燃烧B .图②是加热高锰酸钾制取氧气C .图③是镁条在密闭容器中燃烧D .图④是活性炭与氧化铜粉末在高温下恰好完全反应 2.已知:22Mg OH M O (gO+H ),CaCO 3高温CaO+CO 2↑。
取12.9gMg (OH )2和CaCO 3的混合物,加热,剩余固体质量随时间变化如图所示。
下列说法错误的是A .x 点剩余固体成分为CaCO 3、MgO 和Mg (OH )2B .y 点剩余固体中镁元素质量为1.2gC .z 点发生的反应为CaCO 3高温CaO+CO 2↑D .若剩余固体中钙元素的质量分数为36.0%,则剩余固体的成分为CaCO 3和MgO 3.将过氧化氢溶液平均分成两等份a 和b ,只向b 中加入少量二氧化锰,另一份微微加热。
则放出氧气的质量(m )与反应时间(t )的关系的图象正确的是( )A .B .C.D.4.已知由CuS、CuSO3、CuSO4组成的混合物中,硫元素的质量分数为x,则混合物中氧元素的质量分数为A.1-3xB.1-2xC.1-xD.无法计算5.铜元素有多种氧化物,如CuO、Cu2O。
称取14.4g仅含Cu、O两种元素的固体样品、采用如下图装置实验(夹持装置省略)。
测得实验前后装置B增重4.4g。
查资料可知:碱石灰由NaOH和CaO组成,其作用是吸收H2O和CO2。
下列说法正确的是()A.装置B的作用是吸收反应生成的H2O和CO2B.若缺少装置C,则实验所得Cu、O个数比偏高C.根据实验数据进行计算,可以确定该固体为Cu2OD.实验开始前应先关闭K2,打开K1,让CO通一段时间6.如图所示为硫化氢(H2S)与氧气反应的微观示意图。
下列说法正确的是()A.甲中硫、氢元素质量比为1:2B.丙代表的是纯净物C.34g硫化氢完全燃烧至少需48g氧气D.生成物的分子个数比为2:2:17.下列图象不能正确反映其变化过程的是()A.镁在装有空气的密闭容器内燃烧B.电解水生成气体的体积C.加热氯酸钾和二氧化锰的混合物制取氧气D.把铁钉放入硫酸铜溶液中8.下列图像能正确反映对应的实验操作的是()A.加热氯酸钾和二氧化锰的混合物制取氧气B.一定量的红磷在密封容器中燃烧C.向一定质量的二氧化锰中加入过氧化氢溶液D.碳和氧化铜的固体混合物在高温条件下反应9.下列推理不正确的是①燃烧过程中伴随着发光放热,所以有发光放热现象的变化一定是燃烧②由同种分子构成的物质为纯净物,但纯净物不一定由同种分子构成③单质只含一种元素,所以含一种元素的物质一定是单质④物理变化没有新物质生成,所以没有新物质生成的变化一定是物理变化⑤氧化物都含有氧元素,所以含有氧元素的化合物一定是氧化物A.①②③⑤B.①②⑤C.①③⑤D.①④⑤10.化学中常借助曲线图来表示某种变化过程,如有人分别画出了下列的四个曲线图,下列有关曲线图的说法正确的是A.图①是红磷在装有空气的密闭容器中燃烧B.图②是硝酸铵溶于水时溶液温度的变化C.图③是用一定量的双氧水制取氧气D.图④是电解水一段时间11.某校学习小组利用石灰石与稀盐酸反应,收集并测定 CO2的体积(如图所示)。
北京市九年级上册期末数学试卷及答案(5)
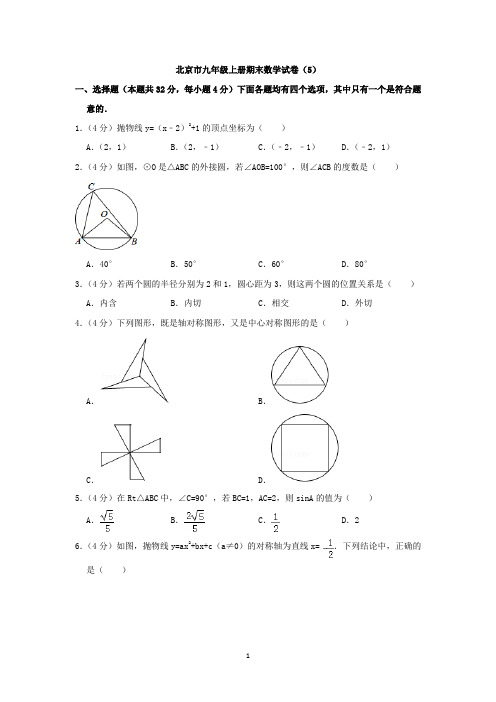
北京市九年级上册期末数学试卷(5)一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.1.(4分)抛物线y=(x﹣2)2+1的顶点坐标为()A.(2,1)B.(2,﹣1)C.(﹣2,﹣1)D.(﹣2,1)2.(4分)如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是()A.40°B.50°C.60°D.80°3.(4分)若两个圆的半径分别为2和1,圆心距为3,则这两个圆的位置关系是()A.内含B.内切C.相交D.外切4.(4分)下列图形,既是轴对称图形,又是中心对称图形的是()A.B.C.D.5.(4分)在Rt△ABC中,∠C=90°,若BC=1,AC=2,则sinA的值为()A.B.C.D.26.(4分)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=.下列结论中,正确的是()A.a<0B.当x<﹣时,y随x的增大而增大C.a+b+c>0D.当x=﹣时,y的最小值是7.(4分)如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC 以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是()A.(0,0)B.(1,0)C.(1,﹣1)D.(2.5,0.5)8.(4分)若抛物线y=(x﹣2m)2+3m﹣1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,则m的取值范围是()A.m<2 B.m>2 C.m D.m二、填空题(本题共16分,每小题4分)9.(4分)如图,△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD=2,DB=3,DE=1,则BC的长是.10.(4分)把抛物线y=x2向右平移1个单位,再向下平移3个单位,得到抛物线y= .11.(4分)如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转α角后得到△A′B′C,当点A的对应点A'落在AB边上时,旋转角α的度数是度,阴影部分的面积为.12.(4分)在平面直角坐标系xOy中,过点A(6,5)作AB⊥x轴于点B.半径为r(0<r <5)的⊙A与AB交于点C,过B点作⊙A的切线BD,切点为D,连接DC并延长交x轴于点E.(1)当r=时,EB的长等于;(2)点E的坐标为(用含r的代数式表示).三、解答题(本题共30分,每小题5分)13.(5分)计算:2sin60°+3tan30°﹣2tan60°﹣cos45°.14.(5分)已知:二次函数y=x2+bx﹣3的图象经过点A(2,5).(1)求二次函数的解析式;(2)求二次函数的图象与x轴的交点坐标;(3)将(1)中求得的函数解析式用配方法化成y=(x﹣h)2+k的形式.15.如图,在梯形ABCD中,AB∥DC,∠A=90°,点P在AD边上,且PC⊥PB.若AB=6,DC=4,PD=2,求PB的长.16.列方程或方程组解应用题:“美化城市,改善人民居住环境”是城市建设的一项重要内容.某市近年来,通过植草、栽树、修建公园等措施,使城区绿地面积不断增加,2011年底该市城区绿地总面积约为75公顷,截止到2013年底,该市城区绿地总面积约为108公顷,求从2011年底至2013年底该市城区绿地总面积的年平均增长率.17.如图,为了估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BD,∠ACB=45°,∠ADB=30°,并且点B,C,D在同一条直线上.若测得CD=30米,求河宽AB(结果精确到1米,取1.73,取1.41).18.如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,cosA=.(1)求OC的长;(2)点E,F在⊙O上,EF∥AB.若EF=16,直接写出EF与AB之间的距离.四、解答题(本题共20分,每小题5分)19.(5分)设二次函数y1=x2﹣4x+3的图象为C1,二次函数y2=ax2+bx+c(a≠0)的图象与C1关于y轴对称.(1)求二次函数y2=ax2+bx+c的解析式;(2)当﹣3<x≤0时,直接写出y2的取值范围;(3)设二次函数y2=ax2+bx+c(a≠0)图象的顶点为点A,与y轴的交点为点B,一次函数y3=kx+m(k,m为常数,k≠0)的图象经过A,B两点,当y2<y3时,直接写出x的取值范围.20.(5分)如图,在矩形ABCD中,E是CD边上任意一点(不与点C,D重合),作AF⊥AE 交CB的延长线于点F.(1)求证:△ADE∽△ABF;(2)连接EF,M为EF的中点,AB=4,AD=2,设DE=x,①求点M到FC的距离(用含x的代数式表示);②连接BM,设BM2=y,求y与x之间的函数关系式,并直接写出BM的长度的最小值.21.(5分)如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)求证:DE是⊙O的切线;(2)若=,求cos∠ABC的值.22.(5分)阅读下面材料:定义:与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形.问题:⊙O的半径为1,画一个⊙O的关联图形.在解决这个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的(它是非封闭的形),它们都是⊙O的关联图形.而图2中以P,Q为端点的一条曲线就不是⊙O的关联图形.参考小明的发现,解决问题:(1)在下列几何图形中,⊙O的关联图形是(填序号);①⊙O的外切正多边形;②⊙O的内接正多边形;③⊙O的一个半径大于1的同心圆.(2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是;(3)在图2中,当⊙O的关联图形的弧长最小时,经过D,E两点的直线为y= ;(4)请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.(7分)已知:二次函数y=x2﹣mx+m+1(m为常数).(1)若这个二次函数的图象与x轴只有一个公共点A,且A点在x轴的正半轴上.①求m的值;②四边形AOBC是正方形,且点B在y轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B,C两点,求平移后的图象对应的函数解析式;(2)当0≤x≤2时,求函数y=x2﹣mx+m+1的最小值(用含m的代数式表示).24.(7分)已知:△ABC,△DEF都是等边三角形,M是BC与EF的中点,连接AD,BE.(1)如图1,当EF与BC在同一条直线上时,直接写出AD与BE的数量关系和位置关系;(2)△ABC固定不动,将图1中的△DEF绕点M顺时针旋转α(0°≤α≤90°)角,如图2,判断(1)中的结论是否仍然成立,若成立,请加以证明;若不成立,说明理由;(3)△ABC固定不动,将图1中的△DEF绕点M旋转α(0°≤α≤90°)角,作DH⊥BC 于点H.设BH=x,线段AB,BE,ED,DA所围成的图形面积为S.当AB=6,DE=2时,求S 关于x的函数关系式,并写出相应的x的取值范围.25.(8分)已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.(1)①填空:二次函数图象的对称轴为;②求二次函数的解析式;(2)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标;(3)点E在x轴的正半轴上,∠OAE>45°,点O与点O′关于EC所在直线对称.作ON⊥EO′于点N,交EC于点M.若EM•EC=32,求点E的坐标.北京市九年级上册期末数学试卷答案(5)一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的.1.(4分)抛物线y=(x﹣2)2+1的顶点坐标为()A.(2,1)B.(2,﹣1)C.(﹣2,﹣1)D.(﹣2,1)【分析】抛物线的顶点式为:y=a(x﹣h)2+k,其顶点坐标是(h,k),可以确定抛物线的顶点坐标.【解答】解:抛物线y=(x﹣2)2+1是以抛物线的顶点式给出的,其顶点坐标为:(2,1).故选:A.【点评】本题考查的是抛物线的性质,根据抛物线的顶点式确定抛物线的顶点坐标.2.(4分)如图,⊙O是△ABC的外接圆,若∠AOB=100°,则∠ACB的度数是()A.40°B.50°C.60°D.80°【分析】已知⊙O是△ABC的外接圆,∠AOB=100°,根据圆周角定理可求得∠ACB的度数.【解答】解:∵⊙O是△ABC的外接圆,∠AOB=100°,∴∠ACB=∠AOB=×100°=50°.故选:B.【点评】本题主要考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角是所对的圆心角的一半.3.(4分)若两个圆的半径分别为2和1,圆心距为3,则这两个圆的位置关系是()A.内含B.内切C.相交D.外切【分析】由两个圆的半径分别为2和1,圆心之间的距离是3,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.【解答】解:∵两个圆的半径分别为2和1,圆心之间的距离是3,又∵2+1=3,∴这两个圆的位置关系是外切.故选:D.【点评】此题考查了圆与圆的位置关系.解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.4.(4分)下列图形,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误;B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;C、此图形旋转180°后能与原图形重合,此图形是中心对称图形,不是轴对称图形,故此选项错误;D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.故选:D.【点评】此题主要考查了中心对称图形与轴对称的定义,根据定义得出图形形状是解决问题的关键.5.(4分)在Rt△ABC中,∠C=90°,若BC=1,AC=2,则sinA的值为()A.B.C.D.2【分析】首先利用勾股定理求得AB的长度,然后利用三角函数的定义求解.【解答】解:在直角△ABC中,AB==,则sinA===.故选:A.【点评】本题考查三角函数的定义,理解定义是关键.6.(4分)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=.下列结论中,正确的是()A.a<0B.当x<﹣时,y随x的增大而增大C.a+b+c>0D.当x=﹣时,y的最小值是【分析】根据抛物线开口方向可对A进行判断;根据当抛物线开口向上,在对称轴左侧y 随x的增大而减小的性质可对B进行判断;观察函数图象得到当x=1时,y<0,则可对C 进行判断;先根据对称轴方程得到a=b,再由抛物线开口向上,函数有最小值=,然后约分后即可对D进行判断.【解答】解:A、抛物线开口向上,则a>0,所以A选项错误;B、抛物线开口向上,对称轴为直线x=,则x<﹣时,y随x的增大而减小,所以B选项错误;C、当x=1时,y<0,即a+b+c<0,所以C选项错误;D、对称轴为直线x=﹣=,则a=b,因为抛物线开口向上,所以函数有最小值==,所以D选项正确.故选:D.【点评】本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=﹣,函数有最小值;抛物线与y轴的交点坐标为(0,c);当b2﹣4ac>0,抛物线与x轴有两个交点;当b2﹣4ac=0,抛物线与x轴有一个交点;当b2﹣4ac<0,抛物线与x轴没有交点.也考查了二次函数的性质.7.(4分)如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC 以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是()A.(0,0)B.(1,0)C.(1,﹣1)D.(2.5,0.5)【分析】先根据旋转的性质得到点A的对应点为点D,点B的对应点为点E,再根据旋转的性质得到旋转中心在线段AD的垂直平分线,也在线段BE的垂直平分线,即两垂直平分线的交点为旋转中心,而易得线段BE的垂直平分线为直线x=1,线段AD的垂直平分线为以AD为对角线的正方形的另一条对角线所在的直线.【解答】解:∵将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,∴点A的对应点为点D,点B的对应点为点E,作线段AD和BE的垂直平分线,它们的交点为P(1,﹣1),∴旋转中心的坐标为(1,﹣1).故选:C.【点评】本题考查了坐标与图形变化﹣旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.8.(4分)若抛物线y=(x﹣2m)2+3m﹣1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,则m的取值范围是()A.m<2 B.m>2 C.m D.m【分析】根据二次函数y=(x﹣2m)2+3m﹣1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,则当x=2m时,y1<y2,由此即可解决问题.【解答】解:∵抛物线y=(x﹣2m)2+3m﹣1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,∴当x=2m时,y1<y2,∴3m﹣1<2m+1,∴m<2,所以m的取值范围是m<2.故选:A.【点评】此题考查了抛物线与x轴交点,得出当x=2m时,y<2m+1是解题关键.二、填空题(本题共16分,每小题4分)9.(4分)如图,△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD=2,DB=3,DE=1,则BC的长是 2.5 .【分析】首先由DE∥BC,可证得△ADE∽△ABC,进而可根据相似三角形得到的比例线段求得BC的长.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴DE:BC=AD:AB,∵AD=2,DB=3,∴AB=AD+BD=5,∴1:BC=2:5,∴BC=2.5,故答案为:2.5.【点评】本题考查了相似三角形的性质和判定,关键是求出相似后得出比例式,题目比较典型,难度适中.10.(4分)把抛物线y=x2向右平移1个单位,再向下平移3个单位,得到抛物线y= x2﹣2x﹣2 .【分析】根据向右平移横坐标加,向下平移纵坐标减求出平移后的抛物线的顶点坐标,然后利用顶点式写出即可.【解答】解:∵抛物线y=x2向右平移1个单位,再向下平移3个单位,∴平移后的抛物线的顶点坐标为(1,﹣3),∴所得抛物线为y=(x﹣1)2﹣3=x2﹣2x﹣2.故答案为:x2﹣2x﹣2.【点评】本题考查了二次函数图象与几何变换,利用顶点的变化确定抛物线解析式的变化更简便.11.(4分)如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转α角后得到△A′B′C,当点A的对应点A'落在AB边上时,旋转角α的度数是60 度,阴影部分的面积为.【分析】连接CA′,证明三角形AA′C是等边三角形即可得到旋转角α的度数,再利用旋转的性质求出扇形圆心角以及△CDB′的两直角边长,进而得出图形面积即可.【解答】解:∵AC=A′C,且∠A=60°,∴△ACA′是等边三角形.∴∠ACA′=60°,∴∠A′CB=90°﹣60°=30°,∵∠CA′D=∠A=60°,∴∠CDA′=90°,∵∠B′CB=∠A′CB′﹣∠A′CB=90°﹣30°=60°,∴∠CB′D=30°,∴CD=CB′=CB=×2=1,∴B′D==,∴S△CDB′=×CD×DB′=×1×=,S扇形B′CB==,则阴影部分的面积为:﹣,故答案为:﹣.【点评】此题主要考查了扇形面积应用以及三角形面积求法和勾股定理应用等知识,本题的关键是弄清所求的阴影面积等于扇形减去三角形面积12.(4分)在平面直角坐标系xOy中,过点A(6,5)作AB⊥x轴于点B.半径为r(0<r <5)的⊙A与AB交于点C,过B点作⊙A的切线BD,切点为D,连接DC并延长交x轴于点E.(1)当r=时,EB的长等于;(2)点E的坐标为(6±,0)(用含r的代数式表示).【分析】(1)连接AD,根据AD=AC=,AB=5,∠ADB=90°,可知CD是AB边上的中线,等于斜边的一半,所以∠CAD=∠ADC=∠ACD=∠ECB=60°,EC=2BC=5,根据EB=即可得出结论;(2))根据BC=AB﹣AC=5﹣r可知C(6,5﹣r),过点D作x轴的垂线,垂足为F,根据勾股定理可知DB2=AB2﹣AD2=25﹣r2;由相似三角形的判定定理得出△ABD∽△BDF,故可得出DF及BF的值,再根据DF∥AB得出△BCE∽△FDE,故=,解得BE=,再根据B点坐标即可得出结论.【解答】解:(1)连接AD,∵AD=AC=,AB=5,∠ADB=90°,∴CD是AB边上的中线,等于斜边的一半,∴∠CAD=∠ADC=∠ACD=∠ECB=60°.∴EC=2BC=5,EB==;故答案为:;(2)∵BC=AB﹣AC=5﹣r,∴C(6,5﹣r),过点D作x轴的垂线,垂足为F,∵AB=5,∠ADB=90°,AD=r,∴DB2=AB2﹣AD2=25﹣r2;∵DF⊥x轴,AB⊥x轴,∴DF∥AB,∴∠BDF=∠ABD,∠BFD=∠ADB=90°,∴△ABD∽△BDF,∴===,∴DF=•DB=×=,同理,BF=,∵DF∥AB,∴△BCE∽△FDE,∴=,即=,解得BE=,∴E(6+,0)或(6﹣,0).故答案为:(6±,0).【点评】本题考查的是圆的综合题,涉及到直角三角形的性质、相似三角形的判定与性质、切线的性质等知识,难度适中.三、解答题(本题共30分,每小题5分)13.(5分)计算:2sin60°+3tan30°﹣2tan60°﹣cos45°.【分析】首先把特殊角的三角函数值代入,然后计算求解即可.【解答】解:原式=2×+3×﹣2×﹣=﹣.【点评】本题考查了特殊角的三角函数值,正确记忆函数值是关键.14.(5分)已知:二次函数y=x2+bx﹣3的图象经过点A(2,5).(1)求二次函数的解析式;(2)求二次函数的图象与x轴的交点坐标;(3)将(1)中求得的函数解析式用配方法化成y=(x﹣h)2+k的形式.【分析】(1)直接把A点坐标代入y=x2+bx﹣3可求出b,从而确定二次函数的解析式;(2)根据抛物线与x轴的交点解方程x2+2x﹣3=0,即可得到二次函数的图象与x轴的交点坐标;(3)利用配方法求解.【解答】解:(1)∵二次函的图象经过点A(2,5),∴4a+2b﹣3=5,解得b=2,∴二次函数的解析式为y=x2+2x﹣3;(2)令y=0,则x2+2x﹣3=0,解得x1=﹣3,x2=1,∴二次函数的图象与x轴的交点坐标为(﹣3,0)和(1,0);(3)y=x2+2x﹣3=(x+1)2﹣4.【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.15.如图,在梯形ABCD中,AB∥DC,∠A=90°,点P在AD边上,且PC⊥PB.若AB=6,DC=4,PD=2,求PB的长.【分析】先根据等角的余角相等得到∠DCP=∠APB,则可判断△PCD∽△BPA,利用相似比可得到PA=12,然后利用勾股定理计算PB.【解答】解:∵在梯形ABCD中,AB∥CD,∠A=90°,∴∠D=90°.∴∠DCP+∠DPC=90°,∵CP⊥PB,∴∠BPC=90°,∴∠DPC+∠APB=90°,∴∠DCP=∠APB,∴△PCD∽△BPA,∴=,即=,∴PA=12,在Rt△PBA中,AB=6,PA=12,∴PB==6.【点评】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了三角形相似的判定与性质.16.列方程或方程组解应用题:“美化城市,改善人民居住环境”是城市建设的一项重要内容.某市近年来,通过植草、栽树、修建公园等措施,使城区绿地面积不断增加,2011年底该市城区绿地总面积约为75公顷,截止到2013年底,该市城区绿地总面积约为108公顷,求从2011年底至2013年底该市城区绿地总面积的年平均增长率.【分析】设从2011年底至2013年底该市城区绿地总面积的年平均增长率是x,由增长率问题的数量关系建立方程求出其解即可.【解答】解:设从2011年底至2013年底该市城区绿地总面积的年平均增长率是x,由题意,得75(1+x)2=108解得:x1=0.2=20%,x2=﹣2.2(舍去).答:从2011年底至2013年底该市城区绿地总面积的年平均增长率是20%.【点评】本题考查了运用增长率问题的数量关系解实际问题的运用,一元二次方程的解法的运用,解答时增长率问题的数量关系建立方程是关键.17.如图,为了估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BD,∠ACB=45°,∠ADB=30°,并且点B,C,D在同一条直线上.若测得CD=30米,求河宽AB(结果精确到1米,取1.73,取1.41).【分析】设河宽AB为x米.分别解直角三角形ABC和直角三角形ABD即可求出x的值.【解答】解:设河宽AB为x米.∵AB⊥BC,∴∠ABC=90°.∵在Rt△ABC中,∠ACB=45°,∴AB=BC=x.∵在Rt△ABD中,∠ADB=30°,∴BD=AB=x,∴CD=BD﹣BC=x﹣x,∴x﹣x=30解得x=15+15≈41.答:河宽AB约为41米.【点评】本题考查了解直角三角形的应用,解此类题目的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.18.如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,cosA=.(1)求OC的长;(2)点E,F在⊙O上,EF∥AB.若EF=16,直接写出EF与AB之间的距离.【分析】(1)由垂径定理求得AC=6;然后通过解Rt△AOC来求OC的长度;(2)需要分类讨论:EF在圆心是下方和EF在圆心的上方两种情况.【解答】解:(1)∵AB是⊙O的弦,OC⊥AB于C,AB=12,∴AC=AB=6.∵在Rt△AOC中,∠ACO=90°,cosA=,∴OA=10,∴OC==8;(2)设直线CO交EF于点D,连接OE.∵EF∥AB,∴OD⊥EF,ED=EF=8.∴在直角△OED中,根据勾股定理得到:OD===6.如图1,CD=OC﹣OD=8﹣6=2;如图2,CD=OC,+OD=8+6=14;综上所述,EF与AB之间的距离是2或14.【点评】本题考查了解直角三角形,勾股定理和垂径定理.解(2)题时,要分类讨论,不要漏解.四、解答题(本题共20分,每小题5分)19.(5分)设二次函数y1=x2﹣4x+3的图象为C1,二次函数y2=ax2+bx+c(a≠0)的图象与C1关于y轴对称.(1)求二次函数y2=ax2+bx+c的解析式;(2)当﹣3<x≤0时,直接写出y2的取值范围;(3)设二次函数y2=ax2+bx+c(a≠0)图象的顶点为点A,与y轴的交点为点B,一次函数y3=kx+m(k,m为常数,k≠0)的图象经过A,B两点,当y2<y3时,直接写出x的取值范围.【分析】(1)求出抛物线C1的顶点坐标,再根据关于y轴对称的点的横坐标互为相反数,纵坐标相同求出抛物线C2的顶点坐标,然后利用顶点式形式写出即可;(2)作出函数图象,然后根据图形写出y2的取值范围即可;(3)根据函数图象写出抛物线C2在直线AB的下方部分的x的取值范围即可.【解答】解:(1)二次函数y1=x2﹣4x+3=(x﹣2)2﹣1图象的顶点(2,﹣1),关于y轴的对称点坐标为(﹣2,﹣1)所以,所求的二次函数的解析式为y2=(x+2)2﹣1,即y2=x2+4x+3;(2)如图,﹣3<x≤0时,y2的取值范围为:﹣1≤y2≤3;(3)y2<y3时,﹣2<x<0.【点评】本题考查了二次函数图象与几何变换,利用顶点的变化确定抛物线解析式的变化更简便.20.(5分)如图,在矩形ABCD中,E是CD边上任意一点(不与点C,D重合),作AF⊥AE 交CB的延长线于点F.(1)求证:△ADE∽△ABF;(2)连接EF,M为EF的中点,AB=4,AD=2,设DE=x,①求点M到FC的距离(用含x的代数式表示);②连接BM,设BM2=y,求y与x之间的函数关系式,并直接写出BM的长度的最小值.【分析】(1)根据矩形的性质可得∠DAB=∠ABC=∠C=∠D=90°,再求出∠ABF=∠D=90°,根据同角的余角相等求出∠DAE=∠BAF,然后根据两组角对应相等的两个三角形相似证明;(2)①取FC的中点H,连接MH,根据三角形的中位线平行于第三边并且等于第三边的一半可得MH∥DC,MH=EC,然后表示出EC,即可得解;②根据相似三角形对应边成比例列式求出BF,再表示出FH,BH,然后利用勾股定理列式整理即可得到y与x的关系式,再根据二次函数的最值问题解答.【解答】(1)证明:∵在矩形ABCD中,∠DAB=∠ABC=∠C=∠D=90°,∴∠ABF=∠D=90°,∵AF⊥AE,∴∠EAF=∠BAF+∠EAB=90°,∵∠DAE+∠EAB=∠DAB=90°,∴∠DAE=∠BAF,又∵∠D=∠ABF=90°,∴△ADE∽△ABF;(2)解:①如图,取FC的中点H,连接MH,∵M为EF的中点,∴MH∥DC,MH=EC,∵在矩形ABCD中,∠C=90°,∴MH⊥FC,即MH是点M到FC的距离,∵DE=x,DC=AB=4,∴EC=4﹣x,∴MH=EC=2﹣x,即点M到FC的距离为MH=2﹣x;②∵△ADE∽△ABF,∴=,∴=,∴BF=2x,FC=2+2x,FH=CH=1+x,∴BH=|BF﹣HF|=|x﹣1|,∵MH=2﹣x,∴在Rt△MHB中,BM2=BH2+MH2=(2﹣x)2+(x﹣1)2=x2﹣4x+5,∴y=x2﹣4x+5(0<x<4)∵y=x2﹣4x+5=(x2﹣x+)+5﹣=(x﹣)2+,当x=时,BM2有最小值,此时,BM的最小值是.【点评】本题是相似形综合题,主要利用了相似三角形的判定与性质,三角形的中位线平行于第三边并且等于第三边的一半,勾股定理,二次函数的最值问题,难点在于(2)作辅助线构造出三角形的中位线.21.(5分)如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)求证:DE是⊙O的切线;(2)若=,求cos∠ABC的值.【分析】(1)如图,连接OC.欲证DE是⊙O的切线,只需证得OC⊥DE;(2)由=,可设CE=2k(k>0),则DE=3k,在Rt△DAE中,由勾股定理求得AE==2k.则tan∠E==.所以在Rt△OCE中,tan∠E==.在Rt△AOD中,由勾股定理得到OD==k,故cos∠ABC=cos∠AOD==.【解答】(1)证明:如图,连接OC.∵AD是过点A的切线,AB是⊙O的直径,∴AD⊥AB,∴∠DAB=90°.∵OD∥BC,∴∠1=∠2,∠3=∠4.∵OC=OB,∴∠2=∠4.∴∠1=∠3.在△COD和△AOD中,,∴△COD≌△AOD(SAS)∴∠OCD=∠DAB=90°,即OC⊥DE于点C.∵OC是⊙O的半径,∴DE是⊙O的切线;(2)解:由=,可设CE=2k(k>0),则DE=3k,∴AD=DC=k.∴在Rt△DAE中,AE==2k.∴tan∠E==.∵在Rt△OCE中,tan∠E==.∴=,∴OC=OA=.∴在Rt△AOD中,OD==k,∴cos∠ABC=cos∠AOD==.【点评】本题考查了切线的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.22.(5分)阅读下面材料:定义:与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形.问题:⊙O的半径为1,画一个⊙O的关联图形.在解决这个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的(它是非封闭的形),它们都是⊙O的关联图形.而图2中以P,Q为端点的一条曲线就不是⊙O的关联图形.参考小明的发现,解决问题:(1)在下列几何图形中,⊙O的关联图形是①③(填序号);①⊙O的外切正多边形;②⊙O的内接正多边形;③⊙O的一个半径大于1的同心圆.(2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是2π;(3)在图2中,当⊙O的关联图形的弧长最小时,经过D,E两点的直线为y= ﹣x﹣;(4)请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).【分析】(1)根据与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形,可得答案;(2)根据圆的关联图形周长,可得封闭的关联图形,根据圆的关联图形的周长最小是它本身,可得答案;(3)根据⊙O的关联图形的弧长最小,可得DE是圆O的切线,可得答案;(4)根据圆的关联图形的长度小于2π,可得圆的关联图形是非封闭的,可得答案.【解答】解:(1)①⊙O的外切正多边形与圆的所有切线和割线都有公共点,故①说法正确;②⊙O的内接正多边形与圆的有的切线没有公共点,故②说法错误;③⊙O的一个半径大于1的同心圆与圆的所有切线和割线都有公共点,故③说法正确;故答案为:①③;(2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G是它本身,图形G的周长的最小值是2π,故答案为:2π;(3)由当⊙O的关联图形的弧长最小时,得DE是圆的一条切线且OD=OE,设DE的解析式是y=﹣x+b,由DE于圆相切,得.解得b=﹣,故答案为:y=﹣x﹣;(4)如图:画图形是非封闭的,l长度=π+2:.【点评】本题考查了圆的综合题,利用了圆的关联图形的定义:与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形,圆的关联图形可以是封闭的,可以是非封闭的,封闭的关联图形周长的最小时是它本身,非封闭的关联图形的长度最小时半圆加两条与圆相切且等于半径的线段.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.(7分)已知:二次函数y=x2﹣mx+m+1(m为常数).(1)若这个二次函数的图象与x轴只有一个公共点A,且A点在x轴的正半轴上.①求m的值;②四边形AOBC是正方形,且点B在y轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B,C两点,求平移后的图象对应的函数解析式;(2)当0≤x≤2时,求函数y=x2﹣mx+m+1的最小值(用含m的代数式表示).【分析】(1)①根据二次函数x2﹣mx+m+1的图象与x轴只有一个公共点A,可得判别式为0,依此可得关于m的方程,求解即可;②由①得点A的坐标为(2,0).根据正方形的性质可得点B的坐标为(0,﹣2),点C的坐标为(2,﹣2).根据待定系数法可求平移后的图象对应的函数解析式;(2)分三种情况:(ⅰ)当<0,即m<0时;(ⅱ)当0≤≤2,即0≤m≤4时;(ⅲ)当>2,即m>4时;讨论可求函数y=x2﹣mx+m+1的最小值.【解答】解:(1)①∵二次函数y=x2﹣mx+m+1的图象与x轴只有一个公共点A,∴△=m2﹣4×1×(m+1)=0.整理,得m2﹣3m﹣4=0,解得m1=4,m2=﹣1,又∵点A在x轴的正半轴上,∴m=4,②由①得点A的坐标为(2,0).。
海淀九年级第一学期期末练习物理试卷(带解析)

海淀九年级第一学期期末练习物理试卷(带解析)学校:___________姓名:___________班级:___________考号:___________一、单选题1下列用品中,通常情况下属于绝缘体的是A.铁钉子B.塑料笔杆C.不锈钢勺D.铁质炒菜锅2小明按照图中所示的电路图连接电路,闭合开关S后,发现两只灯泡都不亮,且电流表的示数为零,电压表的示数接近电源两端的电压。
若电路中只有一处故障,则这个故障可能是A.灯泡L1短路B.灯泡L1断路C.灯泡L2断路D.灯泡L2短路3.如图所示的四个电路图中,能正确反映出如图所示实物电路连接关系的是( )A.B.C.D.4如图所示的四个电路中,闭合开关S,三盏灯为并联关系的是5如图所示的电路图中,开关S闭合后能用电压表正确测出灯L2两端电压的是6如图所示的四个电路中,已知定值电阻R1和R2的阻值大小关系为R1>R2。
在这四个电路中,电路的等效电阻最小的是7如图甲所示的电路中,在M、N两点间接入滑动变阻器,要求闭合开关S后,在滑片P向左滑动的过程中,灯泡的亮度逐渐变亮。
在图乙所示的四种接法中,可能实现上述要求的是8如图所示的电路中,电源两端的电压保持不变。
灯泡L上标有“6V 3W” (灯丝电阻随温度变化可忽略不计),R1为定值电阻,滑动变阻器R2的最大阻值为60Ω,电压表V的量程为0~15V,电流表的量程为0~0.6A。
闭合开关S后,在调节滑动变阻器滑片位置的过程中,保证两电表的示数均不超过其量程,灯泡L两端的电压也不超过其额定电压。
在此调节过程中,其中一电表的示数曾达到其刻度的最大值,电压表示数的最大值与最小值之比为5:4,在电压表的示数出现最大值和最小值的这两种状态下滑动变阻器的电功率相等,且灯泡在其中一种状态下能正常工作。
下列说法中正确的是A.定值电阻R1的电功率最小值为0.75WB.滑动变阻器接入电路中的阻值调节范围是12Ω~60ΩC.电流表示数变化的范围是0.4 A ~0.5 AD.电路的总电功率最大值为10.5W9如图所示电路中,电源两端的电压不变,闭合开关S后,滑动变阻器的滑片P从a端向b端滑动的过程中A.电流表、电压表的示数都减小B.电流表、电压表的示数都增大C.电流表的示数增大、电压表的示数减小D.电流表的示数减小、电压表的示数增大10在图中所示的事例中,符合安全用电原则的是11.关于电功和电功率,下列说法中正确的是( )A.电功率是表示电流做功多少的物理量B.电流通过用电器所做的电功越多,这个用电器的电功率一定越大C.额定功率越大的用电器,正常工作时电流通过它所做的电功一定越多D.用电器工作过程中的实际电功率可能小于它的额定功率12现有两个不同规格的灯泡分别标有“PZ 220V-40W”和“PZ 220V-100W”,它们正常发光时的电阻分别为R1、R2。
北京16区九年级上学期期末考试卷(2020年1月)-1.海淀期末九年级调研(数学)参考答案(1)

2
2
∴当 BE 4 时, CF 的最大值为 8.
24. 解:(1)依题意,设点 A(x, y) , B(x,0) , C(0, y) (x 0, y 0) .
∴ AB y , AC x .
∵ AB AC ,
∴x y.
∵点 A 在直线 y 1 x 3 上, 22
∴点 A 的坐标为 A(3,3) .
所有可能情况如下:
(1,1),(1,2),(1,3),(2,1),(2,2), (2,3),(3,1),(3,2),(3,3).
(2)由(1)可得:标号之和分别为 2,3,4,3,4,5,4,5,6.
4 P( 和为奇数) = 9 ,
5 P( 和为偶数) = 9 . 因为 4 5 ,所以不公平.
99 23. 解:(1)如图,
(2)解:如图,连接 BC,连接 BE 交 OC 于点 F. ∵AB 是 A O 的直径,
数学参考答案 第 4 页(共 7 页)
D E
AO
C M
B
∴∠ACB=∠AEB=90°.
∵AB=10,AC= 4 5 ,
2
∴BC= AB2 AC2 102 4 5 2 5 .
∵OC∥AD, ∴∠BFO=∠AEB=90°. ∴∠CFB=90°,F 为线段 BE 中点. ∵∠CBE=∠EAC=∠CAB,∠CFB=∠ACB, ∴△CFB∽△BCA. ∴ CF BC .
∴ (x 1)2 4 .
∴ x 1 2或x 1 2 .
∴ x1 3, x2 1 .
18.证明:∵ EAC DAB ,
∴ EAC BAE DAB BAE .
∴ BAC DAE .
∵ AB AC , AD AE
∴ △ABC ∽ △ADE .
【物理】北京育英中学九年级上册期末精选试卷检测题

【物理】北京育英中学九年级上册期末精选试卷检测题一、初三物理电流和电路易错压轴题(难)1.小明利用如图所示的电路“探究串、并联电路中电流的关系“.(1)探究串联电路中电流的关系.①用笔画线代替导线将开关S3连入电路中________.(要求:只闭合开关S3后,R1、R2以及电流表串联;导线不许交叉)②小明将S3闭合后,发现电流表均无示数.于是他用一只电压表对电路故障(电路中只有一处故障)进行了检测,将电压表接在R1两端时,电压表与电流表均无示数;接在R2两端时,电压表有示数,电流表无示数.电路中的故障是________.小明排除故障后继续实验,读出了电路中各电流表的示数,得到了串联电路中电流的关系是:串联电路中各处电流相等.(2)完成上述实验后,小明继续探究并联电路中电流的关系.①各开关的连接情况是________(填写各开关断开或闭合).②分析实验中各电流表的读数(如图所示),可知并联电路中电流的关系是________:.③电阻R1:R2=________.(3)为了验证结论的普遍性,你可以采用的方法是:________.(拓展)在电源电压不变的情况下,小明两次实验中电路消耗的最大功率与最小功率之比P最大:P最小=________.【答案】R2断路闭合S1、S2断开S3并联电路干路电流等于各支路电流的和1:2改变电源电压9:2【解析】【分析】(1)按从电源正极依次连接,一条路径将所有用电器连接起来;(2)闭合开关后,电流表无示数,说明电路故障为断路;电压表的示数接近电源电压,说明电压表的正负接线柱与电源两极相连;(3)通过开关的断开与闭合判断出并联电路;(4)根据实验数据得到并联电路电流的规律;(5)多次测量找普遍规律,可以改变电源电压;(6)根据电功率的公式算出两次电功率的比值。
【详解】(1)①按从电源正极依次把各个元件连接起来,组成了一条电流的路径,电路连接如图所示:②闭合开关后,电流表无示数,说明电路故障为断路;将电压表接在R1两端时,电压表与电流表均无示数;接在R2两端时,电压表有示数,电流表无示数,说明与电压表并联的R2断路;(2)①闭合开关S1、S2,断开开关S3,电路有两条路径,组成并联电路;②由实物图可知电流表选用0-3A的量程,I1=2.4A,I2=1.6A,I3=0.8A,则I1=I2+I3即并联电路干路电流等于各支路电流的和;③并联电路中各个支路的电压相等,在电压相等的情况下电流和电阻成反比,即R1:R2=I3:I2=0.8A:1.6A=1:2;(3)为了验证结论的普遍性,应多次测量,可以采用的方法是:改变电源电压;在电源电压不变的情况下,并联时的总电阻最大,串联时的总电阻最小,根据可知并联时总功率最大,串联时总功率最小,最大功率和最小功率之比。
北京育英中学化学初三化学上册期末试卷(含答案)
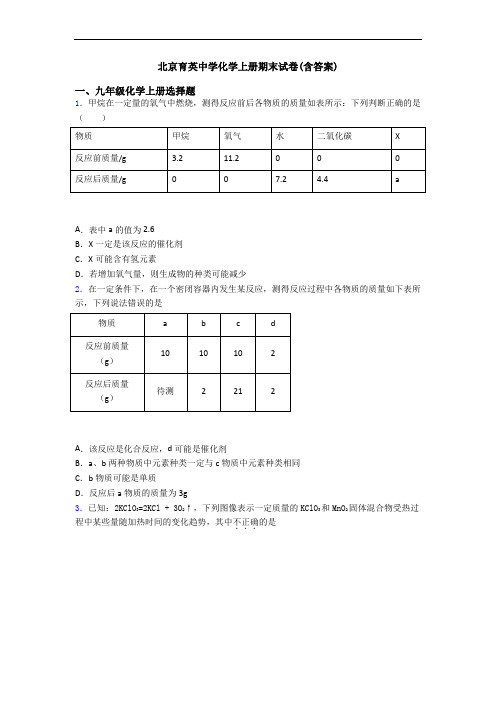
北京育英中学化学上册期末试卷(含答案)一、九年级化学上册选择题1.甲烷在一定量的氧气中燃烧,测得反应前后各物质的质量如表所示:下列判断正确的是()A.表中a的值为2.6B.X一定是该反应的催化剂C.X可能含有氢元素D.若增加氧气量,则生成物的种类可能减少2.在一定条件下,在一个密闭容器内发生某反应,测得反应过程中各物质的质量如下表所示,下列说法错误的是A.该反应是化合反应,d可能是催化剂B.a、b两种物质中元素种类一定与c物质中元素种类相同C.b物质可能是单质D.反应后a物质的质量为3g3.已知:2KClO3=2KCl + 3O2↑,下列图像表示一定质量的KClO3和MnO2固体混合物受热过程中某些量随加热时间的变化趋势,其中不正确...的是A.A B.B C.C D.D4.将2.8 g铁粉放入一定量的硫酸与硫酸铜的混合溶液中,三者恰好完全反应,除去其中的不溶物,再将所得的溶液蒸干,最后可得固体( )A.3.2 g B.7.6 g C.8.0 g D.15.2 g5.图中表示一定量的木炭和氧化铜固体混合物受热过程中,某变量随加热时间的变化趋势,其中纵坐标表示()A.固体的质量 B.固体中氧化铜的质量 C.二氧化碳的质量 D.固体中铜元素的质量分数6.往12g铝和铁的混合物中加入足量的稀硫酸,充分反应后,产生1g氢气,则混合物中铝的质量分数为A.62.3% B.63.2% C.36.8% D.37.7%7.下列物质鉴别方法,错误的是A.用水鉴别生石灰和石灰石 B.用MnO2鉴别蒸馏水和双氧水C.用燃着的木条鉴别H2和CH4 D.用澄清石灰水鉴别CO和CO28.根据下图所示实验分析得出的结论中,不正确的是( )A.二氧化碳与水反应生成碳酸B.与电源正极相连接的玻璃管中生成的气体是氧气C.不同物质着火点不同D.向小试管中加入适量干冰,看到U型管中左侧液面上升,右侧液面下降9.下列图像能正确反映对应变化关系的是()A.向一定量的二氧化锰中加入过氧化氢溶液B.加热一定量的高锰酸钾固定C.向碳酸钙固体中逐滴加入稀盐酸至过量D .将水通电电解一段时间10.美国普度大学研发出一种制备氢气的新工艺,流程如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京育英中学九年级上册期末精选试卷检测题一、初三数学 一元二次方程易错题压轴题(难)1.如图1,平面直角坐标系xOy 中,等腰ABC ∆的底边BC 在x 轴上,8BC =,顶点A 在y 的正半轴上,2OA =,一动点E 从(3,0)出发,以每秒1个单位的速度沿CB 向左运动,到达OB 的中点停止.另一动点F 从点C 出发,以相同的速度沿CB 向左运动,到达点O 停止.已知点E 、F 同时出发,以EF 为边作正方形EFGH ,使正方形EFGH 和ABC ∆在BC 的同侧.设运动的时间为t 秒(0t ≥).(1)当点H 落在AC 边上时,求t 的值;(2)设正方形EFGH 与ABC ∆重叠面积为S ,请问是存在t 值,使得9136S =?若存在,求出t 值;若不存在,请说明理由;(3)如图2,取AC 的中点D ,连结OD ,当点E 、F 开始运动时,点M 从点O 出发,以每秒25OD DC CD DO ---运动,到达点O 停止运动.请问在点E 的整个运动过程中,点M 可能在正方形EFGH 内(含边界)吗?如果可能,求出点M 在正方形EFGH 内(含边界)的时长;若不可能,请说明理由.【答案】(1)t=1;(2)存在,143t =,理由见解析;(3)可能,3455t ≤≤或4533t ≤≤或35t ≤≤理由见解析 【解析】【分析】(1)用待定系数法求出直线AC 的解析式,根据题意用t 表示出点H 的坐标,代入求解即可;(2)根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4,用待定系数法求出直线AB 的解析式,求出点H 落在BC 边上时的t 值,求出此时重叠面积为169﹤9136,进一步求出重叠面积关于t 的表达式,代入解t 的方程即可解得t 值;(3)由已知求得点D (2,1),AC=结合图形分情况讨论即可得出符合条件的时长.【详解】(1)由题意,A(0,2),B(-4,0),C(4,0),设直线AC 的函数解析式为y=kx+b ,将点A 、C 坐标代入,得:402k b b +=⎧⎨=⎩,解得:122k b ⎧=-⎪⎨⎪=⎩, ∴直线AC 的函数解析式为122y x =-+, 当点H 落在AC 边上时,点E(3-t ,0),点H (3-t ,1),将点H 代入122y x =-+,得: 11(3)22t =--+,解得:t=1; (2)存在,143t =,使得9136S =. 根据已知,当点F 运动到点O 停止运动前,重叠最大面积是边长为1的正方形的面积,即不存在t ,使重叠面积为9136S =,故t ﹥4, 设直线AB 的函数解析式为y=mx+n ,将点A 、B 坐标代入,得:402m n n -+=⎧⎨=⎩,解得:122m n ⎧=⎪⎨⎪=⎩, ∴直线AC 的函数解析式为122y x =+, 当t ﹥4时,点E (3-t ,0)点H (3-t ,t-3),G(0,t-3), 当点H 落在AB 边上时,将点H 代入122y x =+,得: 13(3)22t t -=-+,解得:133t =; 此时重叠的面积为221316(3)(3)39t -=-=, ∵169﹤9136,∴133﹤t ﹤5, 如图1,设GH 交AB 于S ,EH 交AB 于T,将y=t-3代入122y x =+得:1322t x -=+, 解得:x=2t-10,∴点S(2t-10,t-3), 将x=3-t 代入122y x =+得:11(3)2(7)22y t t =-+=-, ∴点T 1(3,(7))2t t --,∴AG=5-t ,SG=10-2t ,BE=7-t ,ET=1(7)2t -, 211(7)24BET S BE ET t ∆==-, 21(5)2ASG S AG SG t ∆==- 所以重叠面积S=AOB BET ASG S S S ∆∆∆--=4-21(7)4t --2(5)t -=2527133424t t -+-, 由2527133424t t -+-=9136得:1143t =,29215t =﹥5(舍去), ∴143t =;(3)可能,35≤t≤1或t=4. ∵点D 为AC 的中点,且OA=2,OC=4,∴点D (2,1),AC=255易知M 点在水平方向以每秒是4个单位的速度运动;当0﹤t ﹤12时,M 在线段OD 上,H 未到达D 点,所以M 与正方形不相遇; 当12﹤t ﹤1时, 12+12÷(1+4)=35秒, ∴t =35时M 与正方形相遇,经过1÷(1+4)=15秒后,M 点不在正方行内部,则3455t ≤≤; 当t=1时,由(1)知,点F 运动到原E 点处,M 点到达C 处;当1≤t≤2时,当t=1+1÷(4-1)=43秒时,点M 追上G 点,经过1÷(4-1)=13秒,点M 都在正方形EFGH 内(含边界),4533t ≤≤ 当t=2时,点M 运动返回到点O 处停止运动,当 t=3时,点E 运动返回到点O 处, 当 t=4时,点F 运动返回到点O 处,当35t ≤≤时,点M 都在正方形EFGH 内(含边界),综上,当3455t ≤≤或4533t ≤≤或35t ≤≤时,点M 可能在正方形EFGH 内(含边界).【点睛】本题考查了一次函数与几何图形的综合,涉及求一次函数的解析式、正方形的性质、直角三角形的性质、不规则图形的面积、解一元二次方程等知识,解答的关键是认真审题,提取相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,进而推理、探究、发现和计算.2.已知关于x 的方程x 2﹣(2k +1)x +k 2+1=0.(1)若方程有两个不相等的实数根,求k 的取值范围;(2)若方程的两根恰好是一个矩形两邻边的长,且k =2,求该矩形的对角线L 的长.【答案】(1)k >34;(215 【解析】【分析】(1)根据关于x 的方程x 2-(2k +1)x +k 2+1=0有两个不相等的实数根,得出△>0,再解不等式即可;(2)当k=2时,原方程x 2-5x+5=0,设方程的两根是m 、n ,则矩形两邻边的长是m 、n ,利用根与系数的关系得出m+n=5,mn=5,22m n +,利用完全平方公式进行变形即可求得答案.【详解】解:(1)∵方程x 2-(2k +1)x +k 2+1=0有两个不相等的实数根,∴Δ=[-(2k +1)]2-4×1×(k 2+1)=4k -3>0,∴k >34; (2)当k =2时,原方程为x 2-5x +5=0,设方程的两个根为m ,n ,∴m +n =5,mn =5,==.【点睛】本题考查了根的判别式、根与系数的关系、矩形的性质等,一元二次方程根的情况与判别式△的关系:(1)△>0时,方程有两个不相等的实数根;(2)△=0时,方程有两个相等的实数根;(3)△<0时,方程没有实数根.3.已知关于x 的一元二次方程()221210m x m x +-+=有两个不相等的实数根. (1)求实数m 的取值范围;(2)若原方程的两个实数根分别为1x ,2x ,且满足1212215x x x x +=-,求m 的值.【答案】(1)14m <且0m ≠;(2)15m =- 【解析】【分析】(1)根据一元二次方程的定义和判别式的意义得到:()22140m m ∴∆=-->且20m ≠,然后求出两个不等式解集的公共部分即可.(2)利用根与系数的关系得到12221m x x m -+=, 1221x x m =,加上14m <且0m ≠,则可判断10x <,20x <,所以1212215x x x x --=-,2221215m m m--=-,然后解方程求出m 即可得到满足条件的m 的值.【详解】(1)因为方程()221210m x m x +-+=有两个不相等的实数根, ()221240m m ∴∆=-->,解得14m <; 又因为是一元二次方程,所以20m ≠,0m ∴≠.m ∴的取值范围是14m <且0m ≠.(2)1x ,2x 为原方程的两个实数根,12221m x x m -∴+=,1221x x m = 14m <且0m ≠,122210m x x m -∴+=<,12210x x m=>,10x ∴<,20x <. 1212215x x x x +=-,1212215x x x x --=-,2221215m m m -∴-=-,215210m m ∴--=,解得113m =,215m =-, 14m <且0m ≠,113m ∴=不合题意,舍去,15m ∴=-. 【点睛】 此题主要考查一元一次方程的定义和判别式的意义,正确理解概念和熟练运用根的判别式是解题的关键.4.某连锁超市派遣调查小组在春节期间调查某种商品的销售情况,下面是调查后小张与其 他两位成员交流的情况.小张:“该商品的进价为 24元/件.”成员甲:“当定价为 40元/件时,每天可售出 480件.”成员乙:“若单价每涨 1元,则每天少售出 20件;若单价每降 1元,则每天多售出 40件.” 根据他们的对话,请你求出要使该商品每天获利 7680元,应该怎样合理定价?【答案】要使该商品每天获利7680元,应定价为36元/件、40元/件或48元/件【解析】【分析】设每件商品定价为x 元,则在每件40元的基础上涨价时每天的销售量是[]48020(40)x --件,每件商品的利润是(24)x -元,在每件40元的基础上降价时每天的销量是[]48040(40)x +-件,每件的利润是(24)x -元,从而可以得到答案.【详解】解:设每件商品定价为x 元.①当40x ≥时,[](24)48020(40)7680x x ---= ,解得:1240,48;x x ==②当40x <时,[](24)48040(40)7680x x -+-=,解得:1236,40x x ==(舍去),.答:要使该商品每天获利7680元,应定价为36元/件、40元/件或48元/件.【点睛】本题考查的是一元二次方程中的升降价对销售量产生影响方面的应用,用含有未知数的代数式表示销售量是这一类题的关键.5.如图直线y =kx +k 交x 轴负半轴于点A ,交y 轴正半轴于点B ,且AB =2(1)求k的值;(2)点P从A出发,以每秒1个单位的速度沿射线AB运动,过点P作直线AB的垂线交x轴于点Q,连接OP,设△PQO的面积为S,点P运动时间为t,求S与t的函数关系式,并直接写出t的取值范围;(3)在(2)的条件下,当P在AB的延长线上,若OQ+AB=7(BQ﹣OP),求此时直线PQ的解析式.【答案】(1)k32)当0<t<12时,S=12•OQ•P y=12(1﹣2t3=﹣3 2t2+34t.当t>12时,S=12OQ•P y=12(2t﹣13=323.(3)直线PQ的解析式为y 353.【解析】【分析】(1)求出点B的坐标即可解决问题;(2)分两种情形①当0<t<12时,②当t>12时,根据S=12OQ•P y,分别求解即可;(3)根据已知条件构建方程求出t,推出点P,Q的坐标即可解决问题.【详解】解:(1)对于直线y=kx+k,令y=0,可得x=﹣1,∴A(﹣1,0),∴OA=1,∵AB=2,∴OB223AB OA-=∴k3(2)如图,∵tan ∠BAO =3OB OA= ∴∠BAO =60°,∵PQ ⊥AB ,∴∠APQ =90°,∴∠AQP =30°,∴AQ =2AP =2t , 当0<t <12时,S =12•OQ •P y =12(1﹣2t 3323. 当t >12时,S =12OQ •P y =12(2t ﹣1)•32t =32t 2﹣34t . (3)∵OQ +AB 7(BQ ﹣OP ),∴2t ﹣1+22221373(21)(1)24t t t +--+ ∴2t +1271t t -+∴4t 2+4t +1=7t 2﹣7t +7,∴3t 2﹣11t +6=0,解得t =3或23(舍弃), ∴P (1233Q (5,0), 设直线PQ 的解析式为y =kx +b ,则有133250k b k b ⎧+=⎪⎨⎪+=⎩解得353k b ⎧=⎪⎪⎨⎪=⎪⎩,∴直线PQ 的解析式为35333y x =-+. 【点睛】 本题属于一次函数综合题,考查了一次函数的性质,三角形的面积,无理方程等知识,解题的关键是学会利用参数构建方程解决问题.二、初三数学 二次函数易错题压轴题(难)6.如图,抛物线y =﹣x 2+bx +c 与x 轴交于A ,B 两点,其中A (3,0),B (﹣1,0),与y 轴交于点C ,抛物线的对称轴交x 轴于点D ,直线y =kx +b 1经过点A ,C ,连接CD . (1)求抛物线和直线AC 的解析式:(2)若抛物线上存在一点P ,使△ACP 的面积是△ACD 面积的2倍,求点P 的坐标; (3)在抛物线的对称轴上是否存在一点Q ,使线段AQ 绕Q 点顺时针旋转90°得到线段QA 1,且A 1好落在抛物线上?若存在,求出点Q 的坐标;若不存在,请说明理由.【答案】(1)2y x 2x 3=-++;3y x =-+ ;(2)(﹣1,0)或(4,﹣5);(3)存在;(1,2)和(1,﹣3)【解析】【分析】(1)将点A ,B 坐标代入抛物线解析式中,求出b ,c 得出抛物线的解析式,进而求出点C 的坐标,再将点A ,C 坐标代入直线AC 的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD =AD ,进而判断出△ABC 的面积和△ACP 的面积相等,即可得出结论;(3)分点Q 在x 轴上方和在x 轴下方,构造全等三角形即可得出结论.【详解】解:(1)把A (3,0),B (﹣1,0)代入y =﹣x 2+bc +c 中,得93010b c b c -++=⎧⎨--+=⎩, ∴23b c =⎧⎨=⎩, ∴抛物线的解析式为y =﹣x 2+2x +3,当x =0时,y =3,∴点C 的坐标是(0,3),把A(3,0)和C(0,3)代入y=kx+b1中,得11303k bb+=⎧⎨=⎩,∴113kb=-⎧⎨=⎩∴直线AC的解析式为y=﹣x+3;(2)如图,连接BC,∵点D是抛物线与x轴的交点,∴AD=BD,∴S△ABC=2S△ACD,∵S△ACP=2S△ACD,∴S△ACP=S△ABC,此时,点P与点B重合,即:P(﹣1,0),过B点作PB∥AC交抛物线于点P,则直线BP的解析式为y=﹣x﹣1①,∵抛物线的解析式为y=﹣x2+2x+3②,联立①②解得,1xy=-⎧⎨=⎩或45xy=⎧⎨=-⎩,∴P(4,﹣5),∴即点P的坐标为(﹣1,0)或(4,﹣5);(3)如图,①当点Q在x轴上方时,设AC与对称轴交点为Q',由(1)知,直线AC的解析式为y=﹣x+3,当x=1时,y=2,∴Q'坐标为(1,2),∵Q'D=AD=BD=2,∴∠Q'AB=∠Q'BA=45°,∴∠AQ'B=90°,∴点Q'为所求,②当点Q在x轴下方时,设点Q(1,m),过点A1'作A1'E⊥DQ于E,∴∠A 1'EQ =∠QDA =90°, ∴∠DAQ +∠AQD =90°,由旋转知,AQ =A 1'Q ,∠AQA 1'=90°, ∴∠AQD +∠A 1'QE =90°, ∴∠DAQ =∠A 1'QE , ∴△ADQ ≌△QEA 1'(AAS ), ∴AD =QE =2,DQ =A 1'E =﹣m , ∴点A 1'的坐标为(﹣m +1,m ﹣2), 代入y =﹣x 2+2x +3中, 解得,m =﹣3或m =2(舍), ∴Q 的坐标为(1,﹣3),∴点Q 的坐标为(1,2)和(1,﹣3).【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,三角形“k ”字型全等,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.7.如图1,抛物线2:C y x =经过变换可得到抛物线()1111:C y a x x b =-,1C 与x 轴的正半轴交于点1A ,且其对称轴分别交抛物线C 、1C 于点1B 、1D ,此时四边形111D OB A 恰为正方形;按上述类似方法,如图2,抛物线()1111:C y a x x b =-经过变换可得到抛物线()2222:C y a x x b =-,2C 与x 轴的正半轴交于点2A ,且对称轴分别交抛物线1C 、2C 于点2B 、2D ,此时四边形222OB A D 也恰为正方形;按上述类似方法,如图3,可得到抛物线()3333:C y a x x b =-与正方形333OB A D ,请探究以下问题: (1)填空:1a = ,1b = ; (2)求出2C 与3C 的解析式;(3)按上述类似方法,可得到抛物线():n n n n C y a x x b =-与正方形n n n OB A D (1n ≥).①请用含n 的代数式直接表示出n C 的解析式;②当x 取任意不为0的实数时,试比较2018y 与2019y 的函数值的大小关系,并说明理由.【答案】(1)11a =,12b =;(2)22132y x x =-,23126y x x =-;(3)①()2212123n n y x x n -=-≥⨯,②20182019y y >. 【解析】 【分析】(1)求与x 轴交点A 1坐标,根据正方形对角线性质表示出B 1的坐标,代入对应的解析式即可求出对应的b 1的值,写出D 1的坐标,代入y 1的解析式中可求得a 1的值; (2)求与x 轴交点A 2坐标,根据正方形对角线性质表示出B 2的坐标,代入对应的解析式即可求出对应的b 2的值,写出D 2的坐标,代入y 2的解析式中可求得a 2的值,写出抛物线C 2的解析式;再利用相同的方法求抛物线C 3的解析式;(3)①根据图形变换后二次项系数不变得出a n =a 1=1,由B 1坐标(1,1)、B 2坐标(3,3)、B 3坐标(7,7)得B n 坐标(2n -1,2n -1),则b n =2(2n -1)=2n +1-2(n ≥1),写出抛物线C n 解析式.②根据规律得到抛物线C 2015和抛物线C 2016的解析式,用求差法比较出y 2015与y 2016的函数值的大小. 【详解】解:(1)y 1=0时,a 1x (x -b 1)=0, x 1=0,x 2=b 1, ∴A 1(b 1,0),由正方形OB 1A 1D 1得:OA 1=B 1D 1=b 1, ∴B 1(12b ,12b ),D 1(12b ,12b-), ∵B 1在抛物线c 上,则12b =(12b )2, 解得:b 1=0(不符合题意),b 1=2, ∴D 1(1,-1),把D 1(1,-1)代入y 1=a 1x (x -b 1)中得:-1=-a 1, ∴a 1=1,故答案为1,2;(2)当20y =时,有()220a x x b -=, 解得2x b =或0x =,()22,0A b ∴. 由正方形222OB A D ,得2222B D OA b ==,222,22b b B ⎛⎫∴ ⎪⎝⎭,222,22bb D ⎛⎫- ⎪⎝⎭.2B 在抛物线1C 上,2222222b b b ⎛⎫∴=- ⎪⎝⎭. 解得24b =或20b =(不合舍去),()22,2D ∴-2D 在抛物线2C 上,()22224a ∴-=-.解得212a =. 2C ∴的解析式是()2142y x x =-,即22122y x x =-. 同理,当30y =时,有()330a x x b -=, 解得3x b =,或0x =.()33,0A b ∴.由正方形333OB A D ,得3333B D OA b ==,333,22b b B ⎛⎫∴ ⎪⎝⎭,333,22bb D ⎛⎫- ⎪⎝⎭.3B 在抛物线2C 上,2333122222b b b⎛⎫∴=-⋅ ⎪⎝⎭. 解得312b =或30b =(不合舍去),()36,6D ∴-3D 在抛物线3C 上,()366612a ∴-=-.解得316a =. 3C ∴的解析式是()31126y x x =-,即23126y x x =-.(3)解:①n C 的解析式是()2212123n n y x x n -=-≥⨯. ②由①可得2201820161223y x x =-⨯,2201920171223y x x =-⨯. 当0x ≠时,220182019201620171110233y y x >⎛⎫-=-⎪⎝⎭, 20182019y y ∴>.【点睛】本题是二次函数与方程、正方形的综合应用,将函数知识与方程、正方形有机地结合在一起.这类试题一般难度较大.解这类问题关键是善于将函数问题转化为方程问题,善于利用正方形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.就此题而言:①求出抛物线与x 轴交点坐标⇔把y =0代入计算,把函数问题转化为方程问题;②利用正方形对角线相等且垂直平分表示出对应B 1、B 2、B 3、B n 的坐标;③根据规律之间得到解析式是关键.8.如图,顶点为M 的抛物线y =ax 2+bx +3与x 轴交于A (﹣1,0),B 两点,与y 轴交于点C ,过点C 作CD ⊥y 轴交抛物线于另一点D ,作DE ⊥x 轴,垂足为点E ,双曲线y =6x(x >0)经过点D ,连接MD ,BD . (1)求抛物线的表达式;(2)点N ,F 分别是x 轴,y 轴上的两点,当以M ,D ,N ,F 为顶点的四边形周长最小时,求出点N ,F 的坐标;(3)动点P 从点O 出发,以每秒1个单位长度的速度沿OC 方向运动,运动时间为t 秒,当t 为何值时,∠BPD 的度数最大?【答案】(1)y =﹣x 2+2x +3;(2)N (57,0),F (0,53);(3)t =9﹣15 【解析】 【分析】(1)由已知求出D 点坐标,将点A (-1,0)和D (2,3)代入y=ax 2+bx+3即可;(2)作M关于y轴的对称点M',作D关于x轴的对称点D',连接M'D'与x轴、y轴分别交于点N、F,则以M,D,N,F为顶点的四边形周长最小即为M'D'+MD的长;(3)设P(0,t),作△PBD的外接圆N,当⊙N与y轴相切时,∠BPD的度数最大;【详解】解;(1)C(0,3)∵CD⊥y,∴D点纵坐标是3.∵D在y=6x上,∴D(2,3),将点A(﹣1,0)和D(2,3)代入y=ax2+bx+3,∴a=﹣1,b=2,∴y=﹣x2+2x+3;(2)M(1,4),B(3,0),作M关于y轴的对称点M',作D关于x轴的对称点D',连接M'D'与x轴、y轴分别交于点N、F,则以M,D,N,F为顶点的四边形周长最小即为M'D'+MD的长;∴M'(﹣1,4),D'(2,﹣3),∴M'D'直线的解析式为y=﹣73x+53,∴N(57,0),F(0,53);(3)设P(0,t).∵△PBO 和△CDP 都是直角三角形, tan ∠CDP =32t -,tan ∠PBO =3t,令y =tan ∠BPD =3233123t t t t -+--, ∴yt 2+t ﹣3yt +6y ﹣9=0, △=﹣15y 2+30y +1=0时,y =15415-+舍)或y 15415+,∴t =32﹣12×1y,∴t =9﹣15 ∴P (0,9﹣15. 【点睛】本题考查二次函数的图象及性质;熟练掌握二次函数的图象及性质,利用轴对称求最短距离,学会利用辅助圆解决问题,属于中考压轴题.9.定义:对于已知的两个函数,任取自变量x 的一个值,当0x ≥时,它们对应的函数值相等;当0x <时,它们对应的函数值互为相反数,我们称这样的两个函数互为相关函数.例如:正比例函数y x =,它的相关函数为(0)(0)x x y x x ≥⎧=⎨-<⎩. (1)已知点()5,10A -在一次函数5y ax =-的相关函数的图像上,求a 的值; (2)已知二次函数2142y x x =-+-. ①当点3,2B m ⎛⎫ ⎪⎝⎭在这个函数的相关函数的图像上时,求m 的值; ②当33x -≤≤时,求函数2142y x x =-+-的相关函数的最大值和最小值.(3)在平面直角坐标系中,点M 、N 的坐标分别为1,12⎛⎫-⎪⎝⎭、9,12⎛⎫⎪⎝⎭,连结MN .直接写出线段MN 与二次函数24y x x n =-++的相关函数的图像有两个公共点时n 的取值范围.【答案】(1)1;(2)①22- ;②max 432y =,min 12y =-;(3)31n -<≤-,514n <≤【解析】 【分析】(1)先求出5y ax =-的相关函数,然后代入求解,即可得到答案;(2)先求出二次函数的相关函数,①分为m <0和m ≥0两种情况将点B 的坐标代入对应的关系式求解即可; ②当-3≤x <0时,y=x 2-4x+12,然后可 此时的最大值和最小值,当0≤x≤3时,函数y=-x 2+4x-12,求得此时的最大值和最小值,从而可得到当-3≤x≤3时的最大值和最小值; (3)首先确定出二次函数y=-x 2+4x+n 的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n 的值,然后结合函数图象可确定出n 的取值范围. 【详解】解:(1)根据题意,一次函数5y ax =-的相关函数为5,(0)5,(0)ax x y ax x -≥⎧=⎨-+<⎩,∴把点()5,10A -代入5y ax =-+,则(5)510a -⨯-+=,∴1a =;(2)根据题意,二次函数2142y x x =-+-的相关函数为2214,(0)214,(0)2x x x y x x x ⎧-+-≥⎪⎪=⎨⎪-+<⎪⎩,①当m <0时,将B (m ,32)代入y=x 2-4x+12得m 2-4m+1322=,解得:m=2 当m≥0时,将B (m ,32)代入y=-x 2+4x-12得:-m 2+4m-12=32,解得:或m=2.综上所述:m=2-或m=2+或m=2-②当-3≤x <0时,y=x 2-4x+12,抛物线的对称轴为x=2,此时y 随x 的增大而减小, ∴当3x =-时,有最大值,即2143(3)4(3)22y =--⨯-+=, ∴此时y 的最大值为432. 当0≤x≤3时,函数y=-x 2+4x 12-,抛物线的对称轴为x=2, 当x=0有最小值,最小值为12-, 当x=2时,有最大值,最大值y=72. 综上所述,当-3≤x≤3时,函数y=-x 2+4x 12-的相关函数的最大值为432,最小值为12-;(3)如图1所示:线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有1个公共点.∴当x=2时,y=1,即-4+8+n=1,解得n=-3.如图2所示:线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有3个公共点.∵抛物线y=x 2-4x-n 与y 轴交点纵坐标为1, ∴-n=1,解得:n=-1.∴当-3<n≤-1时,线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有2个公共点. 如图3所示:线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有3个公共点.∵抛物线y=-x 2+4x+n 经过点(0,1), ∴n=1.如图4所示:线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有2个公共点.∵抛物线y=x 2-4x-n 经过点M (12-,1), ∴14+2-n=1,解得:n=54. ∴1<n≤54时,线段MN 与二次函数y=-x 2+4x+n 的相关函数的图象恰有2个公共点. 综上所述,n 的取值范围是-3<n≤-1或1<n≤54. 【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了二次函数的图象和性质、函数图象上点的坐标与函数解析式的关系,求得二次函数y=-x 2+4x+n 的相关函数与线段MN 恰好有1个交点、2个交点、3个交点时n 的值是解题的关键.10.如图,在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠交x 轴于点(2,0),(3,0)A B -,交y 轴于点C ,且经过点(6,6)D --,连接,AD BD .(1)求该抛物线的函数关系式;(2)△ANM 与ABD ∆是否相似?若相似,请求出此时点M 、点N 的坐标;若不存在,请说明理由;(3)若点P 是直线AD 上方的抛物线上一动点(不与点,A D 重合),过P 作//PQ y 轴交直线AD 于点Q ,以PQ 为直径作⊙E ,则⊙E 在直线AD 上所截得的线段长度的最大值等于 .(直接写出答案)【答案】(1)2113442y x x =--+;(2)点M (0,32)、点N (34,0)或点M (0,32),N (-3,0)或点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32);(3)QH 有最大值,当x=2-时,其最大值为125. 【解析】 【分析】(1)用交点式函数表达式得:y=a (x-2)(x+3),将点D 坐标代入上式即可求解; (2)分∠MAB=∠BAD 、∠MAB=∠BDA ,两种大情况、四种小情况,分别求解即可; (3)根据题意,利用二次函数的性质和三角函数,QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+=23392055x x --+,即可求解. 【详解】解:(1)用交点式函数表达式得:y=a (x-2)(x+3), 将点D 坐标代入上式并解得:14a =-, 故函数的表达式为:2113442y x x =--+…①, 则点C (0,32); (2)由题意得:AB=5,AD=10,BD=35, ①∠MAN=∠ABD 时, (Ⅰ)当△ANM ∽△ABD 时,直线AD 所在直线的k 值为34,则直线AM 表达式中的k 值为34-,则直线AM 的表达式为:3(2)4y x =--,故点M (0,32),AD AB AM AN =,则AN=54,则点N (34,0);(Ⅱ)当△AMN ∽△ABD 时, 同理可得:点N (-3,0),点M (0,32), 故点M (0,32)、点N (34,0)或点M (0,32),N (-3,0); ②∠MAN=∠BDA 时,(Ⅰ)△ABD ∽△NMA 时,∵AD ∥MN ,则tan ∠MAN=tan ∠BDA=12, AM :y=12-(x-2),则点M (-1,32)、点N (-3,0); (Ⅱ)当△ABD ∽△MNA 时,AD BD AM AN =,即3535=, 解得:AN=94, 故点N (14-,0)、M (-1,32); 故:点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32); 综上,点M (0,32)、点N (34,0)或点M (0,32),N (-3,0)或点M (-1,32)、点N (-3,0)或N (14-,0)、M (-1,32); (3)如图所示,连接PH ,由题意得:tan ∠PQH=43,则cos ∠PQH=35, 则直线AD 的表达式为:y=3342x -,设点P (x ,2113442x x --+),则点Q (x ,3342x -), 则QH=PQcos ∠PQH=35PQ=352113(442x x --+33)42x -+ =23392055x x --+ =2312(2)205x -++, ∵3020-<, 故QH 有最大值,当x=2-时,其最大值为125. 【点睛】本题考查的是二次函数综合应用,涉及到一次函数、圆的基本知识,解直角三角形,相似三角形的判定和性质,其中(2)需要分类求解共四种情况,避免遗漏.三、初三数学 旋转易错题压轴题(难)11.已知:如图①,在矩形ABCD 中,3,4,AB AD AE BD ==⊥,垂足是E .点F 是点E 关于AB 的对称点,连接AF 、BF .(1)求AF 和BE 的长;(2)若将ABF 沿着射线BD 方向平移,设平移的距离为m (平移距离指点B 沿BD 方向所经过的线段长度).当点F 分别平移到线段AB AD 、上时,直接写出相应的m 的值. (3)如图②,将ABF 绕点B 顺时针旋转一个角1(080)a a ︒<<︒,记旋转中ABF 为''A BF ,在旋转过程中,设''A F 所在的直线与直线AD 交于点P ,与直线BD 交于点Q .是否存在这样的P Q 、两点,使DPQ 为等腰三角形?若存在,求出此时DQ 的长;若不存在,请说明理由.【答案】(1)129,55AF BF ==;(2)95m =或165m =;(3)存在4组符合条件的点P 、点Q ,使DPQ 为等腰三角形; DQ 的长度分别为2或25891055或35105【解析】【分析】(1)利用矩形性质、勾股定理及三角形面积公式求解;(2)依题意画出图形,如图①-1所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;(3)在旋转过程中,等腰△DPQ有4种情形,分别画出图形,对于各种情形分别进行计算即可.【详解】(1)∵四边形ABCD是矩形,∴∠BAD=90°,在Rt△ABD中,AB=3,AD=4,由勾股定理得:BD=2222345AB AD+=+=,∵S△ABD12=BD•AE=12AB•AD,∴AE=AB AD3412 BD55⋅⨯==,∵点F是点E关于AB的对称点,∴AF=AE125=,BF=BE,∵AE⊥BD,∴∠AEB=90°,在Rt△ABE中,AB=3,AE125 =,由勾股定理得:BE2222129355 AB AE⎛⎫=-=-=⎪⎝⎭;(2)设平移中的三角形为△A′B′F′,如图①-1所示:由对称点性质可知,∠1=∠2.BF=BE95 =,由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′95 =,①当点F′落在AB上时,∵AB∥A′B′,∴∠3=∠4,根据平移的性质知:∠1=∠4,∴∠3=∠2,∴BB′=B′F′95=,即95m=;②当点F′落在AD上时,∵AB∥A′B′,AB⊥AD,∴∠6=∠2,A′B′⊥AD,∵∠1=∠2,∠5=∠1,∴∠5=∠6,又知A′B′⊥AD,∴△B′F′D为等腰三角形,∴B′D=B′F′95 =,∴BB′=BD-B′D=5-91655=,即m165=;(3)存在.理由如下:∵四边形ABCD是矩形,∴∠BAD=90°,∵AE⊥BD,∴∠AEB=90°,∠2+∠ABD=90°,∠BAE+∠ABD=90°,∴∠2=∠BAE,∵点F是点E关于AB的对称点,∴∠1=∠BAE,∴∠1=∠2,在旋转过程中,等腰△DPQ依次有以下4种情形:①如图③-1所示,点Q落在BD延长线上,且PD=DQ,则∠Q=∠DPQ,∴∠2=∠Q+∠DPQ=2∠Q,∵∠1=∠3+∠Q,∠1=∠2,∴∠3=∠Q,∴A′Q=A′B=3,∴F′Q=F′A′+A′Q=1227355+=,在Rt△BF′Q中,由勾股定理得:BQ=2222927910 BF F Q555⎛⎫⎛⎫+=+=⎪ ⎪⎝⎭⎝⎭'',∴DQ=BQ-BD=9105 5-;②如图③-2所示,点Q落在BD上,且PQ=DQ,则∠2=∠P,∵∠1=∠2,∴∠1=∠P,∴BA′∥PD,则此时点A′落在BC边上.∵∠3=∠2,∴∠3=∠1,∴BQ=A′Q,∴F′Q=F′A′-A′Q=125-BQ,在Rt△BQF′中,由勾股定理得:BF′2+F′Q2=BQ2,即:222 91255BQ BQ⎛⎫⎛⎫+-=⎪ ⎪⎝⎭⎝⎭,解得:158 BQ=,∴DQ= BD-BQ=5-1525 88=;③如图③-3所示,点Q落在BD上,且PD=DQ,则∠3=∠4.∵∠2+∠3+∠4=180°,∠3=∠4,∴∠4=90°-12∠2.∵∠1=∠2,∴∠4=90°-12∠1,∴∠A′QB=∠4=90°-12∠1,∴∠A′QB=∠A′BQ,∴A′Q=A′B=3,∴F′Q=A′Q-A′F′=3-123 55=,在Rt△BF′Q中,由勾股定理得:222293310 BF F Q55⎛⎫⎛⎫+=+=⎪ ⎪⎝⎭⎝⎭'',∴DQ=BQ-BD=310 5-④如图④-4所示,点Q落在BD上,且PQ=PD,则∠2=∠3.∵∠1=∠2,∠3=∠4,∠2=∠3,∴∠1=∠4,∴BQ=BA′=3,∴DQ=BD-BQ=5-3=2.综上所述,存在4组符合条件的点P、点Q,使△DPQ为等腰三角形,DQ的长度分别为:2或25891055或35105【点睛】本题是四边形综合题目,主要考查了矩形的性质、轴对称的性质、平移的性质、旋转的性质、勾股定理、等腰三角形的性质等知识点;第(3)问难度很大,解题关键是画出各种旋转图形,依题意进行分类讨论.12.已知抛物线y=ax2+bx-3a-5经过点A(2,5)(1)求出a和b之间的数量关系.(2)已知抛物线的顶点为D点,直线AD与y轴交于(0,-7)①求出此时抛物线的解析式;②点B为y轴上任意一点且在直线y=5和直线y=-13之间,连接BD绕点B逆时针旋转90°,得到线段BC,连接AB、AC,将AB绕点B顺时针旋转90°,得到线段BH.截取BC的中点F和DH的中点G.当点D、点H、点C三点共线时,分别求出点F和点G的坐标.【答案】(1)a+2b=10;(2)①y= 2x2+4x-11,②G147305+,91305+),F1(305-21-8,33305-4+),G2(47-3058,91-305-8),F2(305218,33-305-4)【解析】【分析】(1)把点A坐标代入抛物线y=ax2+bx-3a-5即可得到a和b之间的数量关系;(2)①求出直线AD的解析式,与抛物线y=ax2+bx-3a-5联立方程组,根据直线与抛物线有两个交点,结合韦达定理求出a ,b ,即可求出解析式; ②作AI ⊥y 轴于点I ,HJ ⊥y 轴于点J.设B (0,t ),根据旋转性质表示粗H 、D 、C 坐标,应含t 式子表示直线AD 的解析式,根据D 、H 、C 三点共线,把点C 坐标代入求出131305t -+=,231-305t -=,分两类讨论,分别求出G 、F 坐标。
