大学物理答案
大学物理试题及答案 13篇

大学物理试题及答案 1物理试题及答案1一、选择题1. 下列哪个物理量是标量?A. 加速度B. 动量C. 荷电量D. 质量答案:D2. 以下哪一项是描述物体向心加速度的?A. F = mV^2/RB. F = maC. F = GmM/R^2D. F = -kx答案:A3. 以下哪种基本力被用于原子核内?A. 弱相互作用力B. 强相互作用力C. 电磁力D. 万有引力答案:B4. 如果一个物体以匀速直线运动,哪些物理量会保持不变?A. 动量B. 加速度C. 动能D. 势能答案:A5. 加速度和质量都是矢量量,因为它们有什么共同之处?A. 它们都可以用标量表示B. 它们都受到相同的力C. 它们都有方向D. 它们都可以用向量表示答案:C二、填空题6. 一个物体从7m/s的速度以匀加速度减速到0m/s,它移动的距离为_____。
答案:(7^2)/2a7. 假设你跳下一个10米高的建筑物,你从地上跳起的速度至少要是_____。
答案:14m/s8. 当电荷增加_____倍,电场的力就增加了相同的倍数。
答案:两倍9. 加速度是速度的_____,速度是位移的_____。
答案:导数,导数10. 能量的单位是_____,它也等于1焦耳。
答案:耗三、解答题11. 题目:一个1000磅的汽车从初始速度60英里/小时匀加速度减速50英里/小时,它会相撞的距离有多远?解答:首先,将速度转换为英尺/秒,即60英里/小时=88英尺/秒,50英里/小时=73.3英尺/秒;通过减去初始速度和最终速度,可以算出减速度,即-5.1英尺/秒^2;将所得的值代入公式,S = (v_f^2 - v_i^2)/2a,算出S = 263英尺。
12. 题目:一颗飞船以7km/s的速度飞行,绕月球公转,它的圆周半径是6000公里。
求该飞船的向心加速度。
解答:首先,将速度转化为米/秒,即7 x 1000 = 7000米/秒;其次,将圆周半径转化为米,即6000 x 1000 = 6 x 10^6米;最后,应用公式a = v^2/r,将所得的值代入,得到a = 6.12 m/s^2。
《大学物理》各章练习题及答案解析

《大学物理》各章练习题及答案解析第1章 质点运动学一、选择题:1.以下五种运动中,加速度a保持不变的运动是 ( D ) (A) 单摆的运动。
(B) 匀速率圆周运动。
(C) 行星的椭圆轨道运动。
(D) 抛体运动。
(E) 圆锥摆运动。
2.下面表述正确的是( B )(A)质点作圆周运动,加速度一定与速度垂直; (B) 物体作直线运动,法向加速度必为零; (C)轨道最弯处法向加速度最大; (D)某时刻的速率为零,切向加速度必为零。
3.某质点做匀速率圆周运动,则下列说法正确的是( C )(A)质点的速度不变; (B)质点的加速度不变 (C)质点的角速度不变; (D)质点的法向加速度不变4.一运动质点在某瞬时位于矢径()y x r , 的端点处,其速度大小为( D )()()(()22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx D C dtrd B dt drA5. 一质点在平面上运动,运动方程为:j t i t r222+=,则该质点作( B )(A)匀速直线运动 (B)匀加速直线运动(C)抛物线运动 (D)一般曲线运动6.一质点做曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,s 表示路程,a t 表示切向加速度,对下列表达式,正确的是( B )(A)dt dr v = (B) dt ds v = (C) dtdv a = (D) dt vd a t=7. 某质点的运动方程为 3723+-=t t X (SI ),则该质点作 [ D ](A)匀加速直线运动,加速度沿 x 轴正方向; (B)匀加速直线运动,加速度沿 x 轴负方向; (C)变加速直线运动.加速度沿 x 轴正方向; (D)变加速直线运动,加速度沿 x 轴负方向8.一质点沿x 轴运动,其运动方程为()SI t t x 3235-=,当t=2s 时,该质点正在( A )(A)加速 (B)减速 (C)匀速 (D)静止1.D2. B3. C4.D5.B ,6B ,7A 8 A二 、填空题1. 一质点的运动方程为x =2t ,y =4t 2-6t ,写出质点的运动方程(位置矢量)j t t i t r)64(22-+=,t =1s 时的速度j i v22+=,加速度j a 8=,轨迹方程为x x y 32-=。
大学物理简答试题及答案

大学物理简答试题及答案一、简述牛顿第一定律的内容及其物理意义。
答案:牛顿第一定律,也称为惯性定律,指出一切物体在没有受到外力作用时,总保持静止状态或匀速直线运动状态。
其物理意义在于,物体具有惯性,即维持其运动状态不变的性质,除非有外力作用于它。
二、解释什么是光的干涉现象,并给出一个生活中的例子。
答案:光的干涉现象是指两束或多束相干光波在空间中相遇时,由于光波的叠加,会在某些区域出现光强增强,在另一些区域出现光强减弱的现象。
生活中的例子包括肥皂泡上出现的彩色条纹,这是由于光在肥皂泡的前后表面反射后发生干涉造成的。
三、请说明电磁感应定律的内容及其应用。
答案:电磁感应定律,也称为法拉第电磁感应定律,指出当穿过闭合电路的磁通量发生变化时,电路中就会产生感应电动势。
其应用非常广泛,例如发电机就是利用电磁感应定律将机械能转换为电能的设备。
四、描述热力学第一定律,并解释其在热力学过程中的意义。
答案:热力学第一定律,也称为能量守恒定律,表明在一个孤立系统中,能量既不能被创造也不能被消灭,只能从一种形式转换为另一种形式,其总量保持不变。
在热力学过程中,这意味着系统与外界交换的热量和做功的总和等于系统内能的变化。
五、简述波粒二象性的概念及其在量子力学中的重要性。
答案:波粒二象性是指微观粒子如电子、光子等,既表现出波动性也表现出粒子性的特性。
在量子力学中,波粒二象性是基本的物理现象,它揭示了物质和能量在微观尺度上的行为,是量子力学理论构建的基础之一。
六、解释什么是相对论效应,并举例说明其在高速运动中的体现。
答案:相对论效应是指在相对论中,由于物体的速度接近光速,会出现时间膨胀、长度收缩等现象。
例如,高速运动的粒子相对于静止观察者的时间会变慢,这就是时间膨胀效应的体现。
七、阐述开普勒第三定律的内容及其在天文学中的应用。
答案:开普勒第三定律,也称为调和定律,指出所有行星绕太阳公转的轨道的半长轴的立方与公转周期的平方成正比。
大学物理试题及答案

大学物理试题及答案一、选择题(每题2分,共10分)1. 根据牛顿第三定律,作用力与反作用力的大小关系是:A. 相等B. 不相等C. 有时相等,有时不相等D. 无法确定2. 物体的惯性只与物体的:A. 质量有关B. 速度有关C. 位置有关D. 形状有关3. 根据能量守恒定律,以下哪种情况是可能发生的?A. 一个静止的物体突然加速运动,没有外力作用B. 一个物体在没有外力作用下速度减慢C. 一个物体在没有外力作用下速度保持不变D. 一个物体在没有外力作用下从静止变为运动4. 波的干涉现象说明波具有:A. 粒子性B. 波动性C. 能量D. 动量5. 根据热力学第二定律,以下哪个过程是不可能自发发生的?A. 热量从高温物体传向低温物体B. 热量从低温物体传向高温物体C. 气体自发膨胀D. 气体自发收缩二、填空题(每空1分,共10分)6. 根据麦克斯韦方程组,电场的高斯定律可以表示为:_________。
7. 在理想气体状态方程 PV=nRT 中,P 代表_______,V 代表_______,n 代表_______,R 是_______常数,T 代表_______。
8. 根据量子力学的不确定性原理,粒子的位置和动量不能同时被精确测量,这一原理由_______提出。
9. 光的双缝干涉实验展示了光的_______性。
10. 根据爱因斯坦的相对论,当物体的速度接近光速时,其质量会随着速度的增加而_______。
三、简答题(每题5分,共20分)11. 解释什么是光电效应,并简述其基本原理。
12. 描述牛顿运动定律的第二定律,并给出一个生活中的例子。
13. 解释什么是热力学温标,并简述其与摄氏温标的区别。
14. 简述什么是电磁感应,并给出一个实际应用的例子。
四、计算题(每题15分,共30分)15. 一个质量为2kg的物体在水平面上以5m/s²的加速度加速运动。
求作用在物体上的力的大小。
16. 一个理想气体在等压过程中,从体积V1=2m³增加到V2=4m³,温度从T1=300K增加到T2=600K。
大学物理教材习题答案

⼤学物理教材习题答案第⼀章质点运动习题解答⼀、分析题1.⼀辆车沿直线⾏驶,习题图1-1给出了汽车车程随时间的变化,请问在图中标出的哪个阶段汽车具有的加速度最⼤。
答: E 。
位移-速度曲线斜率为速率,E 阶段斜率最⼤,速度最⼤。
2.有⼒P 与Q 同时作⽤于⼀个物体,由于摩擦⼒F 的存在⽽使物体处于平衡状态,请分析习题图1-2中哪个可以正确表⽰这三个⼒之间的关系。
答: C 。
三个⼒合⼒为零时,物体才可能处于平衡状态,只有(C )满⾜条件。
3.习题图1-3(a )为⼀个物体运动的速度与时间的关系,请问习题图1-3(b )中哪个图可以正确反映物体的位移与时间的关系。
答:C 。
由v-t 图可知,速度先增加,然后保持不变,再减少,但速度始终为正,位移⼀直在增加,且三段变化中位移增加快慢不同,根据v-t 图推知s-t 图为C 。
三、综合题:1.质量为的kg 50.0的物体在⽔平桌⾯上做直线运动,其速率随时间的变化如习题图1-4所⽰。
问:(1)设s 0=t 时,物体在cm 0.2=x 处,那么s 9=t 时物体在x ⽅向的位移是多少?(2)在某⼀时刻,物体刚好运动到桌⼦边缘,试分析物体之后的运动情况。
解:(1)由v-t 可知,0~9秒内物体作匀减速直线运动,且加速度为:220.8cm/s 0.2cm/s 4a == 由图可得:0 2.0cm s =,00.8cm/s v =, 1.0cm/s t v =-,则由匀减速直线运动的位移与速度关系可得:22002() t a s s v v -=- 2200()/2t s v v a s =-+ 22[0.8( 1.0)]/20.2 2.0cm =--?+1.1c m =(2)当物体运动到桌⼦边缘后,物体将以⼀定的初速度作平抛运动。
2.设计师正在设计⼀种新型的过⼭车,习题图1- 5为过⼭车的模型,车的质量为0.50kg ,它将沿着图⽰轨迹运动,忽略过⼭车与轨道之间的摩擦⼒。
大学物理活页答案(振动和波)

大学物理活页答案(振动和波部分)第一节 简谐振动1. D2.D3.B4.B5.B6.A7. X=0.02cos (52π−π2) 8. 2:1 9. 0.05m -37° 10. π or 3π 11. 012.解: 周期 3/2/2=ω=πT s , 振幅 A = 0.1 m , 初相 φ= 2π/3, v max = A = 0.3π m/s ,a max = 2A = 0.9π2 m/s 2 .13.提示:旋转矢量法(1)x =0.1cos (πt −π2)(2)x =0.1cos (πt +π3) (3)x =0.1cos (πt +π)14. (1)x =0.08cos (π2t +π3)t=1 x=-0.069m F=-kx=−m ω2x =2.7×10−4(2)π3=π2t t=0.67s第二节 振动能量和振动的合成1. D2.D3.D4.B5.B6. )(212121k k m k k +=νπ 提示:弹簧串联公式等效于电阻并联 7. 0.02m 8. π 0 提示:两个旋转矢量反向9. 402hz10. A=0.1m 位相等于113° 提示:两个旋转矢量垂直。
11. mv 0=(m +M)v ′ 12kA 2=1(m+M)v ′22 A=0.025m ω=√k m+M =40 x=0.025cos (40t −π/2)12. x=0.02cos (4t +π/3)x (m) ω π/3 π/3 t = 0 0.04 0.08 -0.04 -0.08 O A A机械波第一节 简谐波1. B2. A3.D4.C5.A (注意图缺:振幅A=0.01m )6.B7. 503.2 8. a 向下 b 向上 c 向上 d 向下 (追赶前方质元)9. π 10. 4π 或011.解:(1) )1024cos(1.0x t y π-π=)201(4cos 1.0x t -π= (SI) (2) t 1 = T /4 = (1 /8) s ,x 1 = λ /4 = (10 /4) m 处质点的位移)80/4/(4cos 1.01λ-π=T y m 1.0)818/1(4cos 1.0=-π= (3) 振速 )20/(4sin 4.0x t ty -ππ-=∂∂=v . )4/1(212==T t s ,在 x 1 = λ /4 = (10 /4) m 处质点的振速 26.1)21sin(4.02-=π-ππ-=v m/s 12.λ=0.4m u =0.05 k =ωu =2πλ=5π ω=π4 ϕ0=π2−2πT ∙T 2=−π2 y (x,t )=0.06cos (π4t −5πx −π2) y (0.2,t )=0.06cos (π4t −3π2)13. 210)cos sin 3(21-⨯-=t t y P ωω 210)]cos()21cos(3(21-⨯π++π-=t t ωω )3/4cos(1012π+⨯=-t ω (SI). 波的表达式为:]2/234cos[1012λλω-π-π+⨯=-x t y )312cos(1012π+π-⨯=-λωx t (SI) 第二节 波的干涉 驻波 电磁波1.D2.C3. D4.B5.B6.A7.C8. y =−2Acos (ωt ) ðy ðt =2Aωsin (ωt)9. 2A (提示:两振动同相)10. 0.5m 11. Acos2π(t T −x λ) A12. > 70.8hz 13. 7.96×10-2 W/m 214.解:(1) 反射点是固定端,所以反射有相位突变π,且反射波振幅为A ,因此反 射波的表达式为 ])//(2cos[2π+-π=T t x A y λ(2) 驻波的表达式是 21y y y += )21/2cos()21/2cos(2π-ππ+π=T t x A λ (3) 波腹位置: π=π+πn x 21/2λ, λ)21(21-=n x , n = 1, 2, 3, 4,… 波节位置: π+π=π+π2121/2n x λ λn x 21= , n = 1, 2, 3, 4,…15.解:(1) 与波动的标准表达式 )/(2cos λνx t A y -π= 对比可得: ν = 4 Hz , λ = 1.50 m , 波速 u = λν = 6.00 m/s(2) 节点位置 )21(3/4π+π±=πn x )21(3+±=n x m , n = 0,1,2,3, …(3) 波腹位置 π±=πn x 3/44/3n x ±= m , n = 0,1,2,3, …。
大学物理考试题及答案

大学物理考试题及答案一、选择题1. 下列关于力的描述,正确的是()。
A. 力是物体间的相互作用,具有大小和方向。
B. 力的作用是相互的,作用力和反作用力大小相等,方向相反。
C. 力的作用效果与力的作用点有关。
D. 以上选项均正确。
答案:D2. 物体做匀速直线运动时,下列说法正确的是()。
A. 物体的速度不变。
B. 物体的加速度为零。
C. 物体所受合力为零。
D. 以上选项均正确。
答案:D3. 关于功的定义,下列说法正确的是()。
A. 功是力和力的方向的乘积。
B. 功是力和力的方向的点积。
C. 功等于力的大小乘以物体在力的方向上的位移。
D. 功是力对物体所做的功。
答案:C4. 根据牛顿第二定律,下列说法正确的是()。
A. 物体的加速度与作用力成正比。
B. 物体的加速度与物体的质量成反比。
C. 加速度的方向与作用力的方向相同。
D. 以上选项均正确。
答案:D5. 波长为λ的光波在介质中的波速为v,那么在真空中该光波的波速为()。
A. vB. λ/vC. 3×10^8 m/sD. 2×10^8 m/s答案:C二、填空题1. 物体在水平面上受到的摩擦力与物体对水平面的压力成正比,比例系数为_________。
答案:摩擦系数2. 一个质量为2kg的物体,受到一个10N的水平力作用,加速度为_________。
答案:5 m/s^23. 一个电路中,电阻R1为10Ω,电阻R2为20Ω,当它们串联时,总电阻为_________。
答案:30Ω4. 一束光从空气射入水中,如果水的折射率为1.33,那么光线的传播方向将_________。
答案:改变5. 一个半径为R的圆形线圈,通以电流I,放在均匀磁场中,线圈所受的磁力矩大小为_________。
答案:μ = I * (πR^2)三、计算题1. 一个质量为0.5kg的物体,受到一个斜向上的力F,大小为20N,与水平方向成30度角,求物体的加速度。
解:首先分解力F为水平分量和垂直分量。
大学物理答案完整版

作业1 (静电场一)1.关于电场强度定义式,下列说法中哪个是正确的?[ ] A .场强E 的大小与试探电荷0q 的大小成反比。
B .对场中某点,试探电荷受力F 与0q 的比值不因0q 而变。
C .试探电荷受力F 的方向就是场强E 的方向。
D .若场中某点不放试探电荷0q ,则0F =,从而0E =。
答案: 【B 】[解]定义。
场强的大小只与产生电场的电荷以及场点有关,与试验电荷无关,A 错;如果试验电荷是负电荷,则试验电荷受的库仑力的方向与电场强度方向相反,C 错;电荷产生的电场强度是一种客观存在的物质,不因试验电荷的有无而改变,D 错;试验电荷所受的库仑力与试验电荷的比值就是电场强度,与试验电荷无关,B 正确。
2.一个质子,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示,已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示哪个正确?[ ]答案: 【D 】[解]a m E q=,质子带正电且沿曲线作加速运动,有向心加速度和切线加速度。
存在向心加速度,即有向心力,指向运动曲线弯屈的方向,因此质子受到的库仑力有指向曲线弯屈方向的分量,而库仑力与电场强度方向平行(相同或相反),因此A 和B 错;质子沿曲线ACB 运动,而且是加速运动,所以质子受到的库仑力还有一个沿ACB 方向的分量(在C 点是沿右上方),而质子带正电荷,库仑力与电场强度方向相同,所以,C 错,D 正确。
3.带电量均为q +的两个点电荷分别位于X 轴上的a +和a -位置,如图所示,则Y 轴上各点电场强度的表示式为E = ,场强最大值的位置在y = 。
答案:j y a qyE 23220)(2+=πε,2/a y ±= [解]21E E E += )(422021y a q E E +==πε关于y 轴对称:θcos 2,01E E E y x ==j y a qyj E E y 23220)(2+==∴πε沿y 轴正向的场强最大处0=dydEy y a y y a dy dE 2)(23)(25222322⨯+-+∝-- 2/a y = 2/a y ±=处电场最强。
大学物理答案第一章
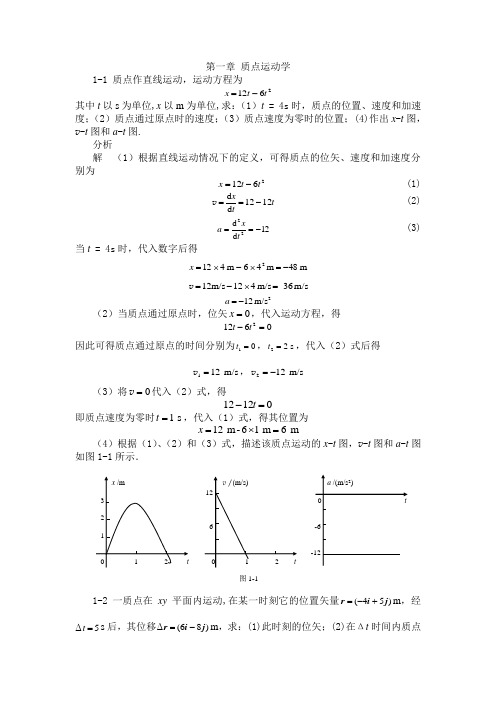
第一章 质点运动学1-1 质点作直线运动,运动方程为2612t t x -=其中t 以s 为单位,x 以m 为单位,求:(1)t = 4s 时,质点的位置、速度和加速度;(2)质点通过原点时的速度;(3)质点速度为零时的位置;(4)作出x -t 图,v -t 图和a -t 图.分析解 (1)根据直线运动情况下的定义,可得质点的位矢、速度和加速度分别为2612t t x -= (1)t tx 1212d d -==v (2) 12d d 22-==tx a (3) 当t = 4s 时,代入数字后得m 48m 46m 4122-=⨯-⨯=xm/s -36m/s 412m/s 12=⨯-=v2m/s 12-=a(2)当质点通过原点时,位矢0=x ,代入运动方程,得06122=-t t因此可得质点通过原点的时间分别为01=t ,s 22=t ,代入(2)式后得m/s 121=v ,m/s 122-=v(3)将0=v 代入(2)式,得01212=-t即质点速度为零时s 1=t ,代入(1)式,得其位置为m 6m 16-m 12=⨯=x(4)根据(1)、(2)和(3)式,描述该质点运动的x -t 图,v -t 图和a -t 图如图1-1所示.1-2 一质点在xy 平面内运动,在某一时刻它的位置矢量)54(j i r +-=m ,经5Δ=t s 后,其位移)86(Δj i r -=m ,求:(1)此时刻的位矢;(2)在Δt 时间内质点图1-1的平均速度.(i 、j 分别为x 、y 方向的单位矢.)分析解 (1)据题意,在t t ∆+时刻,该质点的位矢为m 32m )8-(6m )54(1)(j i j i j i r r r -=++-=∆+=(2)在Δt 时间内质点的平均速度为m/s )1.6-(1.2m/s 586j i j i r v =-=∆∆=t 1-3 质点在xy 平面上运动,运动方程为t y t x 4sin ,4cos 3ππ== 其中t 以s 为单位,x ,y 以m 为单位.(1)求质点运动轨道的正交坐标方程并在xy 平面上绘出质点的轨道;(2)求出质点的速度和加速度表示式,由此求出质点在轨道上运动的方向并证明质点的加速度指向坐标原点;(3)求t = 1 s 时质点的位置和速度与加速度的大小和方向.分析解 (1)质点的运动方程为 t x 43πcos = (1) t y 4πsin = (2) (1)式两边同乘以3并平方后与(2)式的平方相加,得正交坐标方程为 1322=+y x 上式表明质点的运动轨道是一个椭圆,如图1-2所示.(2)由(1)和(2)式可得质点速度和加速度的x ,y 方向分量分别为t t x 443d d ππsin -==x v (3) t t y 44d d ππcos ==y v (4) t t a x 4163d d 2ππcos -==x v (5) t t a y 416d d 2ππsin -==yv (6)则质点速度为 j i v t t 44443ππππcos sin +-= 当t =0时,由运动方程(1)和(2)式,得知质点位于横坐标上3的位置,图1-2由(3)和(4)式,知040>==πy x v v ,,即表明质点在椭圆上沿反时针方向运动. 质点加速度为 j i a 2t t 41641632ππππsin cos --= 由(1)和(2)式得t 时刻质点的位矢为j i r t t 44ππsin cos += (7) 位矢r 与x 轴的夹角ϕ由下式确定:t x y 433πϕtan tan == 而加速度a 与x 轴的夹角α则由下式确定:t a a x y433παtan tan == 即有ϕαtan tan =,注意到在曲线运动中加速度始终指向曲线凹的一侧,则得πϕα+=,表明a 与r 方向相反,指向原点,如图1-2所示.(3)当t = 1 s 时,由(1)--(2)式得m 26=x m 22=y m/s 86π-=x v m/s 82π=y v 22m/s 326π-=x a 22m/s 322π-=y a 速度的大小 m/s 42π=+=2y 2xv v v 速度v 与x 轴的夹角θ则由下式确定:33-==x yv v θtan 注意到此时v x <0,v y >0,则 πθ6533=-=)a r c t a n (. 加速度的大小 22m/s 162π=+=2y 2x a a a对于夹角α有 33==x ya a αtan 又因a x <0,a y <0,则 πα6733==)a r c t a n (. 1-4 质点沿直线运动,其速度2323++=t t v ,如果t = 2时,x = 4,求t = 3时质点的位置、速度和加速度.(其中v 以m/s 为单位,t 以s 为单位,x 以m 为单位)分析解 速度表示式对t 积分,得034241d x t t t t x +++==⎰v 将t = 2 s 时,x = 4 m 代入上式,得积分常数120-=x m ,则1224134-++=t t t x 速度表示式对t 求导数,得t t ta 63d d 2+==v 因此t = 3 s 时质点的位置、速度和加速度分别为m 2541m 12m 32m 3m 34134.=-⨯++⨯=x m/s 56m/s 2m/s 33m/s 323=+⨯+=v2222m/s 45m/s 36m/s 33=⨯+⨯=a1-5 质点沿直线运动,加速度24t a -=,如果当t = 3时,x = 9,v = 2,求质点的运动方程.(其中a 以m/s 2为单位,t 以s 为单位,x 以m 为单位,v 以m/s 为单位)分析解 加速度表示式对t 积分,得03431d v v ++-==⎰t t t a 0242121d x t t t t x +++-==⎰0v v 将t =3 s 时,x = 9 m ,v = 2 m/s 代入以上二式,得积分常数m/s 10-=v ,7500.=x m ,则14313-+-=t t v 750212124.+-+-=t t t x 1-6 质点以不变的速率5m/s 运动,速度的方向与x 轴间夹角等于t 弧度(t为时间的数值),当t = 0时,x = 0,y = 5m ,求质点的运动方程及轨道的正交坐标方程,并在xy 平面上描画出它的轨道.分析解 设质点的速率为v ,与x 轴间夹角为t 弧度,则速度的分量为t t x x cos v v ==d d t ty y s i n v v ==d d 以上两式分别积分,得1C t x +=sin v 2C t y +-=c o s v初始条件为t = 0时,x = 0,y = 5m ,代入以上两式后,得01=C m 102=C因此运动方程为t x sin 5= 105+-=t y cos从中消去t ,得质点运动轨道的正交坐标方程为251022=-+)(y x这是圆心在y 轴上10m 处的圆,半径为5m ,如图1-3所示.1-7 在离水面高度为h 的岸上,有人用绳子拉船靠岸,人以0v 的速率收绳,求当船离岸边的距离为s 时,船的速度和加速度.分析解 选如图1-4所示的直角坐标系,设t 时刻绳长为l ,船的速度为v ,则此时船的x ,y 方向坐标分别为22h l x -= h y =由速度定义得0d d d d ===th t y y v t l hl l t x d d d d 22-===x v v图1-3 图1-4因绳长l 随时间减小的速率等于人的收绳速率,即0d d v =-tl ,则当s x =时,船的速度为022022v v v s h s h l l+-=--= 其中负号表明船的速度方向沿x 轴的负向.又由加速度的定义得0d d ==t a yy v2023222022d d d d v v v x )(h l h h l l t t a a x --=⎪⎪⎭⎫ ⎝⎛--=== 当s x =时,加速度为 2032v sh a -= 其中负号表明船的加速度方向也沿x 轴的负向,且船作变加速直线运动.1-8 当物体以非常高的速度穿过空气时,由空气阻力产生的反向加速度大小与物体速度的平方成正比,即2v k a -=,其中k 为常量.若物体不受其它力作用沿x 方向运动,通过原点时的速度为0v ,试证明在此后的任意位置x 处其速度为x k -=e 0v v分析证 根据加速度的定义,得2v v k a t-==d d 因 tt x x t a d d d d d d d d v v v v ===,代入上式,整理后得 x d d 1-k v v= 应用初始条件0=x 时,0v v =,上式两边分别对v 和x 积分⎰⎰-=x x 0d d 10k v v vv 得 kx -=0v v ln 即有 x k -=e 0v v1-9 一支气枪竖直向上发射,发射速度为29.4m /s ,若发射两粒子弹的间隔时间为4s ,求二子弹将在距发射点多高的地方彼此相遇?分析解 以发射点为原点,竖直向上为y 坐标正向,第一粒子弹发射后的t 时刻,其位置为20121gt t y -=v (1) 其中0v 为发射速度,第二粒子弹此时(设4>t s )的位置为2024214)()(---=t g t y v (2) 当二子弹相遇时,21y y =,由(1)和(2)式得s 5s 2s 8942920=+=+=..g t v 将上式代入(1)式,得m 524m 58921m 5429212201...=⨯⨯-⨯=-=gt t y v 1-10 A 车通过某加油站后其行驶路程x 与时间t 的关系可以表示为24.02t t x +=(其中t 以s 为单位,x 以m 为单位)在A 车离开10 s 后B 车通过该加油站时速度为12 m/s ,且具有与A 车相同的加速度.求:(1)B 车离开加油站后追上A 车所需时间;(2)两车相遇时各自的速度.分析解 (1)令B 车通过该加油站时0=t ,则A 车的运动方程为2A 1040102)(.)(+++=t t xB 车的运动方程为2B 4012t t x .+=两车相遇时有B A x x =,由以上两式得2240121040102t t t t .)(.)(+=+++解得 s 30=t(2)根据速度的定义,相遇时两车速度分别为m/s 3410802d d A A =+⨯+==)(.t tx v m/s 368012d d B B =+==t tx .v 1-11 一升降机以加速度1.22m /s 2上升,当上升速度为2.44m /s 时,有一螺帽自升降机的天花板松落,天花板与升降机底面相距2.74m ,计算:(1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离. 分析解 (1)以升降机外固定柱子为参考系,竖直向上为y 坐标正向,螺帽松落时升降机底面位置为原点.螺帽松落后从m 7420.=y 处以初速度m /s4420.=v 作竖直上抛运动,升降机底面则从原点以同样的初速度作向上的加速运动,加速度2m/s 221.=a ,它们的运动方程分别为螺帽: 200121gt t y y -+=v 底面: 20221at t y +=v 螺帽落到底面上时,21y y =,由以上两式可得s 0.705s 22189742220=+⨯=+=...a g y t (2)螺帽相对于升降机外固定柱子的下降距离为m 7150m 70508921m 7050442 2122010.....=⨯⨯+⨯-=+-=-=gt t y y s v 1-12 一小球自h = 4.9m 处落到一倾角θ= 45°的斜面上,设小球与斜面碰撞后速率不变,方向如图所示.求小球第二次与斜面碰撞时,离第一次碰撞处的距离L 为若干? 分析 解 以小球与斜面第一次相撞点为原点取直角坐标系如图1-5所示.第一次相撞后小球作平抛运动,初速度为0v .此前,小球为自由落体,因此有 gh 20=v小球作平抛运动的运动方程为t x 0v = 221gt y = 由于斜面倾角θ= 45°,当小球第二次碰到斜面时,应有y x =,则由以上二式解得 gt 02v =两次碰撞点之间的距离为m 27.7m 459444200=︒⨯=====sin .sin sin sin sin θθθθh g t x L 2v v 1-13 消防队员用水龙头喷射10 m 外的着火竖墙,水龙头每分钟喷水量为图1-5280 kg ,水喷出时速度为26 m/s ,与地面交角为45º。
大学物理试题及参考答案

大学物理试题及参考答案一、选择题(每题3分,共30分)1. 光在真空中的传播速度是:A. 3×10^8 m/sB. 3×10^5 km/sC. 3×10^7 m/sD. 3×10^6 km/s2. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成反比,其数学表达式为:A. F = maB. a = F/mC. F = ma^2D. a = F^2/m3. 以下哪种波是横波?A. 声波B. 电磁波C. 光波D. 地震波4. 根据热力学第一定律,能量守恒,其数学表达式为:A. ΔU = Q + WB. ΔU = Q - WC. U = Q + WD. U = Q - W5. 以下哪种现象不属于电磁感应?A. 法拉第电磁感应定律B. 洛伦兹力C. 自感D. 互感6. 根据麦克斯韦方程组,以下哪个方程描述了变化的磁场产生电场?A. 高斯定律B. 法拉第电磁感应定律C. 安培定律D. 麦克斯韦方程7. 以下哪种物质的热传导率最高?A. 木头B. 铜C. 玻璃D. 空气8. 根据量子力学,海森堡不确定性原理表明:A. 粒子的位置和动量可以同时精确测量B. 粒子的位置和动量不能同时精确测量C. 粒子的能量和时间可以同时精确测量D. 粒子的能量和动量可以同时精确测量9. 根据相对论,以下哪种效应描述了时间膨胀?A. 洛伦兹收缩B. 钟慢效应C. 质能等价D. 质量增加效应10. 以下哪种设备不是利用电磁波工作的?A. 微波炉B. 收音机C. 光纤通信D. 温度计二、填空题(每题2分,共20分)1. 牛顿第三定律指出,作用力和反作用力大小相等,方向相反,并且作用在不同的物体上。
2. 光的波长、频率和速度之间的关系可以用公式 c = λν 来表示。
3. 根据欧姆定律,电流 I = V/R,其中 V 代表电压,R 代表电阻。
4. 热力学第二定律表明,不可能从单一热源吸热使之完全转化为功而不产生其他效果。
大学物理课后习题答案

大学物理课后习题答案(共15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--1—1 一质点在xOy 平面上运动,运动方程为2135,342x t y t t t s x y m =+=+-式中以计,,以计。
(1)以时间t 为变量,写出质点位置矢量的表示式; (2)计算第1秒内质点的位移;(3)计算0t = s 时刻到4t = s 时刻内的平均速度;(4)求出质点速度矢量表示式,计算4t = s 时质点的速度; (5)计算0t = s 到4t = s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算4t = s 是质点的加速度。
(位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式)解:(1) 质点t 时刻位矢为:j t t i t r⎪⎭⎫ ⎝⎛-+++=4321)53(2(m)(2) 第一秒内位移 j y y i x x r)()(01011-+-=∆)(5.33)101(3)01(21)01(32m j i j i +=⎥⎦⎤⎢⎣⎡-+--=(3) 前4秒内平均速度 )s m (53)2012(411-⋅+=+=∆∆=j i j i t r V(4) 速度)s m ()3(3d d 1-⋅++==j t i tr V ∴ )s m (73)34(314-⋅+=++=j i j i V(5) 前4秒平均加速度)s m (43704204-⋅=-=--=∆∆=j j V V t V a(6) 加速度)s m ()s m (d d 242--⋅=⋅==j a j tV a1—2 质点沿直线运动,速度32132()v t t m s -=++,如果当时t=2 s 时,x=4 m,求:t=3 s 时质点的位置、速度和加速度。
解:23d d 23++==t t txv c t t t c t v x x +++=+==⎰⎰241d d 34 当t =2时x =4代入求证 c =-12 即1224134-++=t t t x tt tv a t t v 63d d 23223+==++= 将t =3s 代入证)s m (45)s m (56)(414123133--⋅=⋅==a v m xP .31 1—9 一个半径R= m 的圆盘,可依绕一个水平轴自由转动,一根轻绳子饶在盘子的边缘,其自由端拴一物体。
大学物理简答试题及答案

大学物理简答试题及答案一、简述牛顿第一定律的内容及其意义。
答案:牛顿第一定律,也称为惯性定律,指出在没有外力作用的情况下,物体将保持静止状态或匀速直线运动状态。
这一定律的意义在于它揭示了物体的惯性特性,即物体倾向于保持其运动状态不变,除非有外力作用于它。
这为物理学中力和运动的关系提供了基本的理解框架。
二、解释什么是光的干涉现象,并给出一个实际应用的例子。
答案:光的干涉现象是指两束或多束相干光波在空间某一点相遇时,它们的振幅相加形成新的光波的现象。
这种相加可以是相长的,也可以是相消的,取决于两束光波的相位差。
干涉现象的一个实际应用是光学干涉仪,它可以用来测量物体的微小位移或者表面粗糙度。
三、阐述电磁感应定律的基本原理及其在现代科技中的应用。
答案:电磁感应定律,由法拉第提出,描述了变化的磁场能够在导体中产生电动势的现象。
当磁场发生变化时,会在导体中产生一个与磁场变化率成正比的电动势。
这一原理在现代科技中应用广泛,如发电机、变压器和感应加热等设备。
四、描述热力学第一定律的主要内容,并解释其在能量守恒中的应用。
答案:热力学第一定律,也称为能量守恒定律,表明在一个封闭系统中,能量既不能被创造也不能被消灭,只能从一种形式转换为另一种形式。
在热力学过程中,系统吸收的热量与对外做的功之和等于系统内能的增加。
这一定律在热机设计、能量转换效率分析等方面有着重要的应用。
五、简述波粒二象性的概念及其在量子力学中的重要性。
答案:波粒二象性是指微观粒子如电子、光子等,既表现出波动性也表现出粒子性的特性。
这一概念是量子力学的基础之一,它揭示了物质的双重性质,对于理解原子和分子结构、化学反应以及量子信息等领域具有重要意义。
六、解释什么是相对论,并简述其在现代物理学中的意义。
答案:相对论是由爱因斯坦提出的理论,包括狭义相对论和广义相对论两部分。
狭义相对论主要处理在没有引力作用下的高速运动物体,而广义相对论则将引力视为时空的弯曲。
大学物理课后习题答案(高教版 共三册)

由 得则
7、在xy平面内有一运动质点,其运动学方程为:(SI) 则t时刻其速度为多少?其切向加速度的大小为多少?该质点运动的轨 迹是什么? 解:(1)
(2)速率: (3)两式平方后相加,, 轨迹为一半径为10m的圆。
8、一条河在某一段直线岸边有A、B两个码头,相距 1km ,甲、乙两人 需要从码头A到码头B,再立即由B返回。甲划船前去,船相对河水的速 度 4km/h,而乙沿岸步行,步行速度也为 4km/h ,如河水流速为 2km/h ,方向从A到B,试推算甲比乙晚多少分钟回到码头A? 解:由A到B船对地的速度大小:
2、质点在一直线上运动,其坐标与时间有如下关系: (SI) (A 为常 数),则在任意时刻 t 质点的加速度为多少?什么时刻质点的速度为零? 解:(1)
(SI) (2)令
有 得 (SBiblioteka ) (K=0,1,2……)3、一质点沿X 方向运动,其加速度随时间变化关系为:a=3+2t (SI), 如果初始时质点的速度 为 5m/s ,则当 t 为 3s 时,质点的速度为多少? 解:由
由B到A船对地的速度大小: 甲由A到B再回到A所需时间: 乙由A到B再回到A所需时间:
所以甲比乙晚十分钟回到码头A 。
9、轮船在水上以相对于水的速度航行,水流速度为,人相对于甲板以 速度行走。如人相对于岸静止,则、和的关系是怎样的? 解:
即 的关系为:
第一章 运动学
1、质点的运动方程为 (SI),则在t 由 0 至 4s 的时间间隔内,质点的位 移大小为多少?在 t 由0 到 4s 的时间间隔内质点走过的路程为多少? 解:本题质点在x方向作直线运动
(1) t1=0时,=0 t2=4(s) 时, =(m) ∴位移大小(m) (2 ) 令 得t=3 (s ) 即t=3 (s )时,质点拐弯沿x轴负向运动,则0~4(s)内质点走过 的路程:
大学物理大一试题及答案

大学物理大一试题及答案一、选择题(每题3分,共30分)1. 光在真空中的传播速度是多少?A. 299,792,458 m/sB. 299,792,458 km/sC. 3.0 x 10^8 m/sD. 3.0 x 10^5 km/s答案:C2. 牛顿第一定律描述的是:A. 物体的加速度与作用力成正比B. 物体的加速度与作用力成反比C. 物体在没有外力作用下保持静止或匀速直线运动D. 物体在受到外力作用下保持静止或匀速直线运动答案:C3. 以下哪个不是电磁波?A. 无线电波B. 微波C. 可见光D. 声波答案:D4. 根据热力学第一定律,系统内能的增加等于:A. 系统吸收的热量B. 系统释放的热量C. 系统吸收的热量与对外做功之和D. 系统释放的热量与对外做功之和答案:C5. 一个物体的质量为2kg,受到的重力是:A. 19.6 NB. 9.8 NC. 39.2 ND. 4.9 N答案:A6. 以下哪个是波动现象?A. 电子的轨道运动B. 光的反射C. 光的折射D. 光的干涉答案:D7. 根据库仑定律,两个点电荷之间的力与它们电荷量的乘积成正比,与它们距离的平方成反比。
这个定律是由哪位科学家提出的?A. 牛顿B. 法拉第C. 库仑D. 麦克斯韦答案:C8. 以下哪个量不是矢量?A. 速度B. 力C. 功D. 温度答案:D9. 根据能量守恒定律,能量既不能被创造也不能被消灭,只能从一种形式转化为另一种形式。
这个定律是:A. 热力学第一定律B. 热力学第二定律C. 能量守恒定律D. 动量守恒定律答案:C10. 光的波长与频率的关系是:A. 波长与频率成正比B. 波长与频率成反比C. 波长与频率无关D. 波长与频率成正比或反比,取决于介质答案:B二、填空题(每题2分,共20分)1. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成_________。
答案:反比2. 光年是_________的单位。
大学物理考试题目及答案

大学物理考试题目及答案一、选择题(每题3分,共30分)1. 光在真空中的传播速度是多少?A. 3×10^8 m/sB. 3×10^4 m/sC. 3×10^5 m/sD. 3×10^6 m/s答案:A2. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成反比。
这一定律的数学表达式是什么?A. F = maB. F = m/aC. a = F/mD. a = mF答案:A3. 一个物体从静止开始自由下落,其下落的高度h与时间t之间的关系是什么?A. h = gt^2B. h = 1/2 gt^2C. h = 2gtD. h = gt答案:B4. 电场强度的定义式是:A. E = F/qB. E = qFD. E = F/g答案:A5. 一个理想的气体经历等压变化时,其体积与温度的关系遵循什么定律?A. 查理定律B. 盖-吕萨克定律C. 阿伏加德罗定律D. 波义耳定律答案:B6. 根据能量守恒定律,一个封闭系统的总能量是:A. 增加的B. 减少的C. 不变的D. 无法确定的答案:C7. 波长为λ的光波在介质中的折射率为n,当光波从真空进入该介质时,其波速会:A. 增加B. 减少C. 不变D. 先增加后减少答案:B8. 一个电路中的电流I与电阻R之间的关系由欧姆定律描述,该定律的数学表达式是什么?A. I = V/RB. I = VRD. I = V + R答案:A9. 根据热力学第一定律,一个系统的内能变化等于它与外界交换的热量和它对外做的功之和。
如果一个系统吸收了热量并且对外做功,那么它的内能将会:A. 增加B. 减少C. 不变D. 无法确定答案:A10. 两个点电荷之间的相互作用力遵循:A. 库仑定律B. 牛顿定律C. 高斯定律D. 毕奥-萨伐尔定律答案:A二、填空题(每题4分,共20分)11. 一个物体的质量为2kg,受到的力为10N,根据牛顿第二定律,它的加速度是 _______ m/s²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 5 章 机械波5-1 一个余弦横波以速度 u 沿 x 轴正向传播, t 时刻波形曲线如图所示.试分别指出图中 A 、B 、 C 各质点在该 时刻的 运动方向 。
A ;B; C。
答: 下 上 上5-2 关于振动和波 , 下面几句叙述中正确的是[ ](A) 有机 械振 动就一定 有机械波; (B) 机械波 的频率与波 源的振动 频率相同; (C) 机械波的波速 与波源的振 动速度相同; (D) 机械波的波速与波源的振动速度总是不相等的。
答: (B)5-3 一平面简谐波的表达式为y =0.25cos(125t -0.37x )(SI),其角频率u 2u 2338= = == 17.0m1255-4 频率为 500Hz 的波,其波速为 350m/s ,相位差为 2π/3 的两点之间的 距离为_。
x解: ∆=2x, x ==0.233m2波速 u = ,波长 =解:=125rads -1 ;u =0.37,u = 0.37=338ms5-5 一平面简谐波沿x轴负方向传播。
已知在x=-1m处质点的振动方程为y= A cos(t +) (SI) ,若波速为u,则此波的表达式为。
1x答:y = A cos[(t + 1+ x) + ](SI) uu5-6 一平面简谐波沿Ox轴正方向传播,t = 0 时刻的波形图如图所示,则P处介质质点的振动方程是[ ]。
(A) y = 0.10cos(4t + 1) (SI);(B) y = 0.10cos(4t - 1) (SI);(C) y = 0.10cos(2t + 1) (SI);(D) y = 0.10cos(2t + 1) (SI)。
P6解:答案为(A)u确定圆频率:由图知=10m,u=20m/s ,得= 2= 2u = 4A 确定初相:原点处质元t=0时,y P0= 0.05= A、v00,所以=5-7 一平面简谐波的表达式为y = A cos[(t - x/u)] ,其中- x/u表示;-x/u表示;y表示。
答:-x / u是表示x处的质点比原点处的质点多振动的时间( x > 0 表明x 处的质点比坐标原点处的质点少振动x / u的时间,x < 0 表明x处的质点比坐标原点处的质点多振动x / u的时间)。
- x/ u是表示x处的质点超前于坐标原点的相位(x > 0 表明x处的质点在相位上落后于坐标原点,x < 0 表明x处的质点在相位上超前于坐标原点)。
y 表示x处的质点在t时刻离开平衡位置的位移。
5-8 已知波源的振动周期为4.00×10-2 s,波的传播速度为300 m·s-1,波沿x轴正方向传播,则位于x1 = 10.0 m 和x2 = 16.0 m 的两质点振动相位差的大小为。
答:=2x2-x1 = 2x2 - x1 =8uT 35-9 一列平面简谐波沿x轴正向无衰减地传播,波的振幅为2×10-3 m,周期为0.01 s,波速为400 m∙s-1。
当t = 0 时x轴原点处的质元正通过平衡位置向y轴正方向运动,则该简谐波的表达式为。
答:波沿x轴正向无衰减地传播,所以简谐波的表达式为y = A cos[(t - x)+]的形式。
u其中= 2= 200;由x =0、v 0,知= -,代入上式,得y=210 cos[200(t-400)- 2]m5-10 一简谐波,振动周期T =1/ 2 s ,波长 =10 m,振幅A = 0.1 m. 当t = 0 时刻,波源振动的位移恰好为正方向的最大值.若坐标原点和波源重合,且波沿Ox轴正方向传播,求:(1)此波的表达式;(2)t1 =T/4时刻,x1 =/4处质点的位移;(3)t2 =T/2时刻,x1 =/4处质点振动速度。
解:(1) O点的振动方程为y = A cos(2π t +) = 0.1cos(2π t + 0) = 0.1cos(4πt) m向x轴正向传播的波的波动方程为y = 0.1cos(4πt - 2π x ) = 0.1cos(4πt - πx )(SI)5(2) 将t=T4=18s, x = 4=2.5m代入波动方程,得位移y = 0.1cos(4 π1- π 2.5) =0.1m(3) 质点振动速度为v =y = -0.14πsin(4πt - πx ) m/st 585将t = 2 = 4s,x = 4 =2.5m 代入上式,得速度1πv = -0.4 πsin(4 π - 2.5) ms -1 = -0.4π m s -1 = - 1.26ms -15-11 如图,一平面波在介质中以波速 u = 10 m ·s -1沿 x 轴负方向传播,已 知 A 点的振动方程为 y = 410-2 cos (3πt +/3)[SI ]。
(1)以A 点为坐标原点,写出波函数;(2)以距 A 点 5m 处的B 点为坐标原点,写出波函数;(3)A 点 左侧 2m 处质 点的振动方程; 该点超 前于 A 点的相位 。
x1) y = 410-2cos[3π(t + x)+ ]m5-12 图示一平面简谐波在 t = 1.0 s 时刻的波形图,波的振幅为 0.20 m ,周 期为 4.0 s ,求(1)坐标原点处质点的振动方程;(2)若OP =5.0m ,写出波函 数;(3)写出图中 P 点处质点的振动方程。
解:3)4y = 410-2 cos[3π(t - 4]m x =-2 -x =0 = -9153,即比A 点相位落后 30.20解: 如图所示为 t =0 时 的波形图 ,可 见 t =0 原点 处质 点 在负 的 最大 位移 处 ,所 以 =。
(1) 坐标原点处质点的振动方程为y = 0.2cos( t +)m2) 波函数为y = 0.2cos[(t - x ) +]m3) P 点 的坐标 x =5.0m 代入 上式,得 P 点的 振动方程为y = 0.2cos( t )m5-13 已 知一列机械波的 波速为 u , 频 率为 , 沿着 x 轴负方 向传播.在 x 轴的正坐标上有两个点 x 1和 x 2.如果 x 1<x 2 , 则 x 1和x 2的相位差1 -2为[]答: (B )5-14 如图所示,一简谐波沿 BP 方向传播,它在 B 点引起的振动方程为 y 1 = A 1 cos 2 πt 。
另一简谐波 沿 CP 方 向传播 , 它 在 C 点 引 起 的振 动方 程 为 y = A cos (2 πt+ π)。
P 点与 B 点相距 0.40 m ,与 C 点相距 0.50 m 。
波速均为 u =0.20 m s -1。
则两波在 P 的 相 位 差 为 。
(A) 0 (B)2(x 1 -x 2) u(C) (D)2(x 2 -x 1) uo xx2x习题 5-12 解题用图习题 5-13 解答用图答:= - - 2CP- BP CP- BP0.50-0.40= - 2= - 2= 0uT0.205-15 如图所示,S 1和 S 2为两相干波源,它们的振动方向均垂直于图面,发出波 长为的简谐波,P 点是两列波相遇区域中的一点,已知 S 1P =2,S 2P = 2.2, 两列波在 P 点发生相消干涉.若 S 1的振动方程为 y 1=A cos(t +/2),则S 2的振 动方程为 [ ]5-17 如图所示,两列波长均为的相干简谐波分别习通题过5图-1中6解的答O用1图和 O 2点,通过 O 1 点的 简谐 波在 M 1 M 2 平面 反射后,与通 过 O 2 点的简 谐波在 P 点 相遇。
假 定波 在 M 1 M 2 平 面 反射 时 有 由 半波 损 失。
O 1 和 O 2 两 点 的振 动 方 程为 y = A cost 和 y = A cost ,且 O m +mP =8, OP =3(为波 长),求 :(1) 两列波分别在 P 点引起的振动的方程;(A) y 2 = A cos(t -) ;(B) y = A cos(t -) ;(C) y 2 = A cos(t +); (D) y = A cos(t - 0.1) 。
答: 答案为(D ) 。
设 S 2 的振动方成为 y 2 = A cos(t +2) ,在 P 点两波的相位差为=- -2S P -S P2.2- 2= - - 2 =22解得2 = 1.9可记为2 = -0.1。
5-16 如图所示,S 为点波源,振动方向垂直 于纸面,S 1和S 2是屏AB 上的两个狭缝,S 1 S 2= a 。
SS ⊥AB ,并且 SS 1=b 。
x 轴以S 为坐标原点, 并且垂直于 AB 。
在AB 左侧,波长为1;在ABb S 1A aS S2x x右侧,波长为 2 。
求 x 轴 上两波相遇点的 相位差。
解:如解答用图 所示, 坐标为 x 的 P 点,两列波引起的分振动的相位差为 S1S2a2P (x ) x= 2πa 2 +b 2 - b 1 x - x 2 + a 2B习题5-16解答用图S(2)两列波在P 点合振动的强度(假定两列波在传播或反射过程中均不衰减)。
解:(1) O1在P 点引起的振动为y1= A cos[πt - 28+] = A cos(πt +)O2在P 点引起的振动为y2= A[cosπt - 23] = A cos t(2)在P 点二振动反相,合振动的振幅为0,I A2,所以P 点合振动的强度为0。
5-18 在驻波中,两个相邻波节间各质点的振动[ ](A) 振幅相同,相位相同.(B) 振幅不同,相位相同.(C) 振幅相同,相位不同.(D) 振幅不同,相位不同.答:(B)5-19 在波长为的驻波中,相对同一波节距离为/8 两点的振幅和相位分别为答:(B)(A) 相等和 0;(B) 相等和;(C) 不等和 0;(D) 不等和。
[ ]5-20 一静止的报警器,其频率为1000 Hz,有一汽车以79.2 km 的时速驶向和背离报警器时,坐在汽车里的人听到报警声的频率分别是和(设空气中声速为340 m·s-1) 。
解:汽车速度为v = 792003600= 22m∙s-1第 8 章 气体动理论8-1 容器中储有 1mol 的氮气,压强为 1.33Pa ,温度为 7℃,则(1)1 m 3 中氮气的分子数为多少? (2)容器中的氮气的密度为多少 ?解:( 1) 由 p = n kT 得n = p= 3.44×1020 m -3VkT(2)由理想气体状态方程,得= M = p = 1.6 ×10-5 kg ·m -3。
V RT8-2 质量为4.4g 的二氧化碳气体,体积为 1×10-3m 3,温度为 -23C ,试分 别用真实气体的状态方程与理想气体的状态方程计算二氧化碳的压强是多少? 并将两种结果进行比较。
