广东省阳江市高一下学期数学期中考试试卷

合集下载

广东省阳江市高一下学期数学期中考试试卷

广东省阳江市高一下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2017高二上·日喀则期中) ﹣401是等差数列﹣5，﹣9，﹣13…的第（）项．A . 98B . 99C . 100D . 1012. （2分） (2015高三上·潍坊期中) 如图，在△ABC上，D是BC上的点，且AC=CD，2AC= AD，AB=2AD，则sinB等于（）A .B .C .D .3. （2分） (2019高一上·利辛月考) 在中，，，，那么的面积为（）A .B .C .D .4. （2分） (2019高一上·葫芦岛月考) 将代数式因式分解的结果为（）A . (x+5)(x－1)B . (x－5)(x+1)C . (x+5)(x+1)D . (x－5)(x－1)5. （2分） (2017高一下·宿州期中) 设x＞0，y＞0，满足 + =4，则x+y的最小值为（）A . 4B .C . 2D . 96. （2分） (2016高三上·黄冈期中) 设a1 ， a2 ，…，a50是从﹣1，0，1这三个整数中取值的数列，若a1+a2+…+a50=9，且（a1+1）2+（a2+1）2+…+（a50+1）2=107，则a1 ， a2 ，…，a50中有0的个数为（）A . 10B . 11C . 12D . 137. （2分）设ABC的一个顶点是A(3,-1),的平分线所在直线方程分别为x=0,y=x , 则直线BC的方程为（）A . y=2x+5B . y=2x+2C . y=3x+5D . y=-x+8. （2分）双曲线x2-y2=4左支上一点P(a,b)到直线y=x的距离为，则a+b=（）A . 2B . -2C . 4D . -49. （2分） (2018高二上·汕头期末) 知数列满足，，则的前10项和等于（）A .B .C .D .10. （2分）(2016·韶关模拟) 等比数列{an}前n项和为Sn ，若S2=6，S4=30，则S6=（）A . 62B . 64C . 126D . 128二、多选题 (共2题；共6分)11. （3分） (2019高二上·中山月考) 数列的前项和为，若数列的各项按如下规律排列：，以下运算和结论正确的是（）A .B . 数列是等比数列C . 数列的前项和为D . 若存在正整数，使，则12. （3分） (2020高一下·邢台期中) 在三角形中，下列命题正确的有（）A . 若，，，则三角形有两解B . 若，则一定是钝角三角形C . 若，则一定是等边三角形D . 若，则的形状是等腰或直角三角形三、填空题 (共4题；共4分)13. （1分） (2017高一下·泰州期中) 两条平行线l1：3x+4y=2与l2：ax+4y=7的距离为________．14. （1分）(2017·吉林模拟) 艾萨克•牛顿（1643年1月4日﹣1727年3月31日）英国皇家学会会长，英国著名物理学家，同时在数学上也有许多杰出贡献，牛顿用“作切线”的方法求函数f（x）零点时给出一个数列{xn}：满足，我们把该数列称为牛顿数列．如果函数f（x）=ax2+bx+c（a＞0）有两个零点1，2，数列{xn}为牛顿数列，设，已知a1=2，xn＞2，则{an}的通项公式an=________．15. （1分）(2018·如皋模拟) 已知均为正数，，，则的最小值为________.16. （1分） (2019高三上·西湖期中) 已知的内角的对边分别为 .若，的面积为，则面积的最大值为________.四、解答题 (共6题；共60分)17. （10分）求两条平行直线4x﹣3y﹣1=0和8x﹣6y+1=0之间的距离．18. （10分）(2017·甘肃模拟) 在△ABC中，a，b，c分别是角A，B，C的对边，且b，c是关于x的一元二次方程x2+mx﹣a2+b2+c2=0的两根．（1）求角A的大小；（2）已知a= ，设B=θ，△ABC的面积为y，求y=f（θ）的最大值．19. （10分）(2020·南京模拟) 设，记.（1）求；（2）记，求证：恒成立.20. （10分） (2018高一上·徐州期中) 已知函数f（x）=mx2+（1-3m）x-4，m∈R.（1）当m=1时，求f（x）在区间[-2，2]上的最大值和最小值.（2）解关于x的不等式f（x）＞-1.（3）当m＜0时，若存在x0∈（1，+∞），使得f（x）＞0，求实数m的取值范围.21. （10分） (2016高二上·浦东期中) 已知各项为正的数列{an}是等比数列，a1=2，a5=32，数列{bn}满足：对于任意n∈N* ，有a1b1+a2b2+…+anbn=（n﹣1）•2n+1+2．（1）求数列{an}的通项公式；（2）令f（n）=a2+a4+…+a2n，求的值；（3）求数列{bn}通项公式，若在数列{an}的任意相邻两项ak与ak+1之间插入bk（k∈N*）后，得到一个新的数列{cn}，求数列{cn}的前100项之和T100．22. （10分） (2017高二下·沈阳期末) 在△ABC中，a、b、c分别为角A、B、C的对边，且，（1）求的度数；（2）若，，求b和c的值．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、多选题 (共2题；共6分)11-1、12-1、三、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、四、解答题 (共6题；共60分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、21-3、22-1、22-2、第11 页共11 页。

广东省阳江市高一下学期期中数学试卷(理科)

广东省阳江市高一下学期期中数学试卷（理科）姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分） (2019高一上·南昌月考) 若，则点位于（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限2. （2分） (2018高一上·阜城月考) 直线经过原点和，则它的倾斜角是（）A . 45°B . 135°C . 45° 或135°D . −45°3. （2分）如果角α的终边过点（2sin60°，﹣2cos60°），则sinα的值等于（）A .B . ﹣C . ﹣D . ﹣4. （2分）以点和为直径两端点的圆的方程是（）A .B .C .D .5. （2分）已知弧度数为2的圆心角所对的弦长也是2，则这个圆心角所对的弧长是（）A . 2B .C . 2sin1D . sin26. （2分） (2018高一下·河南月考) 已知 ,则（）A .B .C .D .7. （2分）点P（x ， y，z）满足 =2，则点P在（）A . 以点（1，1，-1）为圆心，以2为半径的圆上B . 以点（1，1，-1）为中心，以2为棱长的正方体上C . 以点（1，1，-1）为球心，以2为半径的球面上D . 无法确定8. （2分） (2017高一下·安庆期末) 为了得到函数y=sin（2x﹣）的图象，可以将函数y=sin2x的图象（）A . 向右平移个单位B . 向右平移个单位C . 向左平移个单位D . 向左平移个单位9. （2分）“”是“直线与直线互相垂直”的（）A . 充要条件；B . 充分不必要条件；C . 必要不充分条件；D . 既不充分也不必要条件.10. （2分） (2017高一下·嘉兴期末) 若α是第四象限角，cosα= ，则sinα=（）A . ﹣B .C . ﹣D .二、填空题 (共4题；共5分)11. （2分） (2018高一上·台州期末) =________弧度，它是第________象限的角.12. （1分）若sinα＜0，且tanα＞0，则α是第1 象限角．13. （1分） (2016高二下·深圳期中) 已知点A（﹣2，0），B（0，4）到直线l：x+my﹣1=0的距离相等，则m的值为________．14. （1分）(2020·重庆模拟) 已知，则 ________.三、解答题 (共4题；共40分)15. （5分）已知=（m，cos），=（sin， n），函数f（x）=•，函数f（x）的图象过点（，4）和点（﹣， 0）（1）求函数f（x）的解析式；（2）用“五点法”作出函数f（x）在一个周期内的图象．16. （10分） (2018高一上·鹤岗月考) 已知函数（）的最小正周期为，且其图象关于直线对称.（1）求和的值；（2）若，，求的值.17. （10分） (2016高二上·长春期中) 已知直线过定点P（2，1）．（1）求经过点P且在两坐标轴上的截距相等的直线方程；（2）若过点P的直线l与x轴和y轴的正半轴分别交于A，B两点，求△AOB面积的最小值及此时直线l的方程．18. （15分） (2019高二上·砀山月考) 已知圆经过两点，且圆心在直线上，直线的方程为。

广东高一高中数学期中考试带答案解析

广东高一高中数学期中考试班级:___________ 姓名：___________ 分数：___________一、选择题1.化为弧度制为（）A．B．C．D．2.已知角的终边经过点P(4，－3)，则的值等于( )A．B．C．D．3.函数的定义域为（）A．R B．[1，10]C．D．（1，10）4.函数是（）A．最小正周期为的奇函数B．最小正周期为的偶函数C．最小正周期为的奇函数D．最小正周期为的偶函数5.已知向量，向量，且与的夹角为，则在方向上的投影是（）A．B．C．D．6.为了得到函数的图象，只需把函数的图象（）A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向右平移个长度单位7.设，则（）A．B．C．D．8.在中，有命题①；②；③若，则为等腰三角形；④若，则为锐角上述命题正确的是（）A①② B①④ C②③ D②③④9.设是定义域为，最小正周期为的函数。

若，则等于（）A．1B．C．0D．10.数列的通项公式，其前项和为，则等于( )A．1006B．2012C．503D．0二、填空题1.某学校高一、高二、高三年级的学生人数之比为，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高一年级抽取 _ ；2.已知，则________；3.已知，,且,则；4.函数在区间上的最小值为________；5.如图，在中，，，则= ，= ；三、解答题1.如图，设、是平面内相交成角的两条数轴，、分别是与轴、轴正方向同向的单位向量。

若向量，则把有序实数对叫做向量在坐标系中的坐标。

若，则=2.已知（1）若的夹角为45°，求；（2）若，求与的夹角．3.已知．（1）化简；（2）若，且是第二象限角，求的值．4.设函数（1）求解析式；（2）求函数的单调递减区间；（3）在给出的直角坐标系中用“五点作图法”画出函数在上的图像．（要求列表、描点、连线）5.已知等差数列首项，公差为，且数列是公比为4的等比数列，（1）求；（2）求数列的通项公式及前项和；（3）求数列的前项和．6.已知函数．（1）求函数的零点；（2）若方程在上有解，求实数的取值范围．7.已知数列的前项和为，且．(1)求数列的通项公式；(2)令，数列的前项和为，若不等式对任意恒成立，求实数的取值范围．广东高一高中数学期中考试答案及解析一、选择题1.化为弧度制为（）A．B．C．D．【答案】A【解析】因为180度是π弧度，那么可知故答案为A.【考点】弧度制与角度制的互化点评：本试题考查了弧度制的概念，以及弧度和角度的互化，同时考查了运算能力，属于基础题。

广东省阳江市第三中学2021-2022学年高一下学期期中考试数学试题

阳江三中2021-2022学年下学期高一数学期中考试题考试时间：120分钟；命题：李永贵2022.4.26一、单选题(共8小题，每小题5分，满分40分）1．化简→→→→+++DE CD BC AB （）A ．0B ．A EC ．0D ．EA2．sin 27cos18cos 27sin18︒︒+︒︒=（）A ．2B ．2C ．12D ．23．已知向量)41,21(=→a ，()2,b m =- ，若a 与b 共线，则b = （）AB C D ．4．计算ii i -++)2)(1-（（）A ．i-3B ．i+3C ．i31+-D ．i31--5．已知点()1,2A -和向量()1,3a = ，且2AB a =，则点B 的坐标为（）A ．(1,8)B ．(0,5)C ．(3,4)--D ．(3,4)6．ABC 中，角,,A B C 所对的边分别为a b c ，，.若3A π=，32a c ==，，则sin C =（）A ．3B ．3C ．3D ．3±7．将曲线C 1：2sin 23y x π⎛⎫=+ ⎪⎝⎭上的点向右平移6π个单位长度，再将各点横坐标缩短为原来的12，纵坐标不变，得到曲线C 2，则C 2的方程为（）A ．2sin 4y x=B ．2sin 43y x π⎛⎫=- ⎪⎝⎭C ．2sin y x =D ．2sin 3y x π⎛⎫=- ⎪⎝⎭8．平面向量a 与b的夹角为135°，已知()1,1a =- ，2b = ，则a b -= 的（）A B ．2C ．D二、多选题(共4小题，每小题5分，满分20分）9．已知()1,3a =，()2,1b =- ，下列计算正确的是（）A ．()1,4a b +=-B ．()3,2a b -=C ．()1,2b a -=D ．()1,2a b --=10．在ABC 中，三个内角分别为A ，B ，C ，下列结论正确的是（）A ．()sin sinBC A +=恒成立B ．若2220a b c +->，则ABC 一定是锐角三角形C ．若sin sin A B >，则A B>D ．若cos cos a A b B =，则三角形ABC 必是等腰直角三角形11．已知向量a ，b均为单位向量，且2b a - ，则以下结论正确的是（）A ．a b⊥B ．2a b +=C ．a b -=D ．,60a b 〈〉=︒12．设复数122z =-+，则以下结论正确的是（）.A ．02=z B ．2z z=C ．31z =D ．2022z z=三、填空题(共4小题，每小题5分，满分20分）13．已知向量,a b 的夹角为60︒，且||1,||2a b ==，则(2)a a b ⋅+= ____________．14．如图，已知两座灯塔A 、B 与C ，灯塔A 在C 的北偏东20°，灯塔B在C 的南偏东40°，则灯塔A 与灯塔B 的距离为______km ．15．函数5tan(2)12y x π=+的定义域是______________16．已知复数z 满足1z =，则22z i +-的最大值为______.四、解答题(共6小题，第17小题满分10分，其它小题满分各12分，共70分）17．求m 为何实数时，复数()226215i z m m m m =+-+--是：(1)实数；(2)纯虚数；（3）对应的点在第一象限内；18．如图，在ABC 中，角60A = ，D 为边AC 上一点，且31BC =，21BD =，20CD =求：(1)sin CDB ∠的值；(2)边AD 的长.19．已知函数()214f x x π⎛⎫=-+ ⎪⎝⎭(1)求()f x 的最小正周期和最大值；(2)将()f x 的图像向右平移8π个单位得到函数()g x 的图象，求()g x 在[]0π，上的零点.20．已知ABC 的内角,,A B C 的对边分别为,,a b c ，满足()()2sin 2sin 2sin a b A b a B c C -+-=.(1)求角C 的大小；(2)若tan 2A =，求()sin 2A C -的值.21．在ABC 中，2AB =，1AC =，2ACB π∠=，D 是线段BC 上一点，且12BD DC = ，F 为线段AB 上一点.(1)设AB a = ，AC b = ，AD xa yb =+.求x y -；(2)若F 为线段AB 的中点，求CF FA ⋅的值；22．已知()()()sin ,sin sin a x x b x x f x a b ==-=⋅，，，(1)求f (x )的单调递增区间；(2)△ABC 中，角A ，B ，C 所对的边为a ，b ，c ．若()32f A =，4a =，求△ABC 周长的取值范围．2021-2022学年下学期高一数学期中考试题参考答案题号123456789101112答案BA B D ABADABACACBC1．B2．A3．B4.D5．A 【详解】因为向量()1,3a = ，且2AB a =，所以()2,6AB = .设(),B x y ，则()()1,22,6x y +-=，解得：18x y =⎧⎨=⎩，即()1,8B .6．B7．A 【详解】解：将2sin 23y x π⎛⎫=+ ⎪⎝⎭向右平移6π个单位长度得到2sin 22sin 263y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦，再将2sin 2y x =各点横坐标缩短为原来的12，纵坐标不变得到2sin 4y x =。

广东省阳江市高一下学期数学期中考试试卷

广东省阳江市高一下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）(2019·云南模拟) 在等比数列中，若，，成等差数列，则数列的公比为（）A . 0或1或-2B . 1或2C . 1或-2D . -22. （2分） (2018高一下·唐山期末) ①45化为二进制数为；②一个总体含有1000个个体（编号为0000，0001，…，0999），采用系统抽样从中抽取一个容量为50的样本，若第一个抽取的编号为0008，则第六个编号为0128；③已知，，为三个内角，，的对边，其中， , ，则这样的三角形有两个解.以上说法正确的个数是（）A . 0B . 1C . 2D . 33. （2分） (2016高一下·南市期末) 已知向量 =（3，4），则与方向相同的单位向量是（）A . （，）B . （，）C . （﹣﹣，）D . （4，3）4. （2分） (2018高二下·黑龙江期中) 下列结论正确的是（）A . 若，则B . 若，则C . 若，则D . 若，则5. （2分）在△ABC中，角A，B，C所对的边分别为a，b，c，若，则△ABC的形状为（）A . 直角三角形B . 等腰三角形C . 等腰直角三角形D . 等腰或直角三角形6. （2分） (2018高二上·湛江月考) 若两个正实数满足，则的最小值为（）A .B .C .D .7. （2分）平面向量与夹角为60°，，，则（）A .B . 12C . 4D . 28. （2分）不等式ax2+bx+c＜0的解集为空集，则（）A . a＜0，△＞0B . a＜0，△≥0C . a＞0，△≤0D . a＞0，△≥09. （2分） (2019高二上·石河子月考) 在数列中，已知，，且满足，则（）A .B .C .D .10. （2分）已知，，且.现给出如下结论：①；②；③；④.其中正确结论的序号是（）A . ①③B . ①④C . ②③D . ②④二、双空题 (共4题；共4分)11. （1分） (2018高三上·龙泉驿月考) 、分别为双曲线左、右支上的点，设是平行于轴的单位向量，则的最小值为________．12. （1分） (2017高一下·西安期末) △ABC中，a•cosA=b•cosB，则该三角形的形状为________．13. （1分）(2017·鄂尔多斯模拟) 已知实数x、y满足，则的取值范围为________．14. （1分）数列{an}中，a1=1，且a1•a2•…•an=n2 （n≧2），则an=________．三、解答题 (共6题；共55分)15. （5分） (2017高一上·巢湖期末) 已知向量 =（﹣2，4）， =（﹣1，﹣2）．（1）求，的夹角的余弦值；（2）若向量﹣λ 与2 + 垂直，求λ的值．16. （10分）(2016·陕西模拟) 在△ABC中，角A、B、C所对的边分别为a，b，c．已知a+c=3 ，b=3．（1）求cosB的最小值；（2）若 =3，求A的大小．17. （10分） (2018高二上·成都月考) 在等差数列中，，其前项和为，等比数列的各项均为正数，，公比为，且，．（Ⅰ）求与．（Ⅱ）设数列满足，求的前项和．18. （10分）(2016·太原模拟) 函数f（x）=|x+1|﹣|2﹣x|．（1）解不等式f（x）＜0；（2）若m，n∈R+，，求证：n+2m﹣f（x）＞0恒成立．19. （10分） (2019高三上·珠海月考) 已知函数 .（1）当时，求函数的最小值和最大值（2）设△ABC的对边分别为，且， ,若，求的值.20. （10分） (2019高二上·温州期中) 已知是递增的等差数列，，是方程x2－5x＋6＝0的根.（1）求的通项公式；（2）求数列的前项和.四、填空题 (共2题；共2分)21. （1分）满足arccos（x2）＞arccos（2x）的实数x的取值范围是________22. （1分） (2016高三上·辽宁期中) 已知向量 =（1，2）， =（1，0）， =（3，4），若λ为实数，（+λ ）⊥ ，则λ的值为________．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、双空题 (共4题；共4分)11-1、12-1、13-1、14-1、三、解答题 (共6题；共55分)15-1、15-2、16-1、16-2、17-1、18-1、18-2、19-1、19-2、20-1、20-2、四、填空题 (共2题；共2分) 21-1、22-1、。

广东省阳江市高一下学期数学期中考试试卷

广东省阳江市高一下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）中，,,则A .B .C .D .2. （2分） (2016高二上·桂林期中) 在△ABC中，若，，B=120°，则a等于（）A .B . 2C .D .3. （2分） (2019高二上·宝坻月考) 已知四个实数成等差数列，五个实数成等比数列，则（）A . 8B . －8C . ±8D .4. （2分）已知函数,等差数列的公差为2,且f(a2+a4+a6+a8+a10)=4,若,则n=（）A . 10B . 8C . 6D . 55. （2分） (2018高二上·新乡月考) 已知数列{an}是公差为2的等差数列，且成等比数列，则为（）A . -2B . -3C . 2D . 36. （2分） (2020高一下·驻马店期末) 已知，，，若，则最大值为（）A .B .C .D .7. （2分） (2016高一上·厦门期中) 已知f（x）= 满足对任意x1≠x2都有＜0成立，那么a的取值范围是（）A . （0，1）B .C .D .8. （2分）在△ABC中，=，=，若点D满足=2，则=（）A . +B . -C . -D . +9. （2分）(2018·凉山模拟) 在中，分别是内角的对边，若，，，则的面积等于（）A . 3B .C .D .10. （2分） (2016高二上·西安期中) 已知数列{an}的前n项和Sn=n2﹣4n+2，则|a1|+|a2|+…+|a10|等于（）A . 66B . 65C . 61D . 5611. （2分）用a代表红球，b代表蓝球，c代表黑球，由加法原理及乘法原理，从1个红球和1个蓝球中取出若干个球的所有取法可由（1+a）（1+b）的展开式1+a+b+ab表示出来，如：“1”表示一个球都不取、“a”表示取出一个红球，而“ab”则表示把红球和蓝球都取出来．以此类推，下列各式中，其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球，且所有的蓝球都取出或都不取出的所有取法的是（）A . （1+a+a2+a3+a4+a5）（1+b5）（1+c）5B . （1+a5）（1+b+b2+b3+b4+b5）（1+c）5C . （1+a）5（1+b+b2+b3+b4+b5）（1+c5）D . （1+a5）（1+b）5（1+c+c2+c3+c4+c5）12. （2分） (2019高一下·巴音郭楞月考) 在中三内角A，B，C的对边分别为a，b，c，且，，则角C的大小是（）A . 或B .C .D .二、填空题 (共4题；共4分)13. （1分） (2018高三上·广东月考) 已知向量，若且方向相反，则________.14. （1分） (2019高二下·绍兴期中) 已知函数在上为增函数，则的取值范围为 ________15. （1分） (2019高二上·岳阳月考) 在中，内角，，所对的边分别为，，，若，且，则的面积为________.16. （1分） (2017高二下·河北期末) 已知数列满足，，则最小值为________．三、解答题 (共6题；共50分)17. （10分）(2017·福州模拟) 已知a、b、c分别为△ABC的内角A、B、C的对边，btanA=2asinB．（1）求A；（2）若a= ，2b﹣c=4，求△ABC的面积．18. （5分） (2019高一下·哈尔滨月考) 设正项数列的前项和满足 .（1）求的通项公式;（2）设，求数列的前项和 .19. （10分）已知点O（0，0）、A（1，2）、B（4，5），向量 = +t ．（Ⅰ）t为何值时，点P在x轴上？（Ⅱ）t为何值时，点P在第二象限？（Ⅲ）四边形ABPO能否为平行四边形？若能，求出t的值；若不能，说明理由．20. （5分） (2016高一上·佛山期中) 某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出场单价就降低0.02元，根据市场调查，销售商一次订购量不会超过600件．（1）设一次订购x件，服装的实际出厂单价为p元，写出函数p=f（x）的表达式；（2）当销售商一次订购多少件服装时，该厂获得的利润最大？其最大利润是多少？21. （10分） (2019高三上·赤峰月考) 各项为正数的数列满足：， .（1）求的通项公式；（2）求证： .22. （10分） (2019高三上·江西月考) 已知函数 . （1）求函数的单调区间；（2）若，，试证： .参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共50分) 17-1、17-2、18-1、18-2、19-1、20-1、20-2、21-1、21-2、22-1、22-2、第11 页共11 页。

广东省阳江市高一下学期数学期中联考试卷

广东省阳江市高一下学期数学期中联考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2017高一下·张家口期末) 已知点（x0 ， y0）在x2+y2=r2（r＞0）外，则直线x0x+y0y=r2与圆x2+y2=r2的位置关系为（）A . 相交B . 相切C . 相离D . 相交、相切、相离三种情况均有可能2. （2分）△ABC中，已知，则A的度数等于（）A .B .C .D .3. （2分） (2019高一下·广德期中) 已知数列中，，，若，则（）A . 1008B . 1009C . 1010D . 20204. （2分）已知直线与平行，则的值是（）A . 1或3B . 1或5C . 3或5D . 1或25. （2分）△ABC中，若，则△ABC的形状为（）A . 直角三角形B . 等腰三角形C . 等边三角形D . 锐角三角形6. （2分） (2019高一下·广德期中) 已知数列中，，（），则（）A .B . 0C .D .7. （2分） (2019高一下·广德期中) 过可作两条直线与圆相切，则k的取值范围为（）A .B . 或C . 或D .8. （2分） (2019高一下·广德期中) 设等比数列中，前n项和为，已知，，则等于（）B .C .D .9. （2分）在中,,则此三角形解的情况是（）A . 一解B . 两解C . 一解或两解D . 无解10. （2分） (2019高一下·广德期中) 已知是递增数列，对任意的，都有恒成立，则的取值范围是（）A .B .C .D .11. （2分） (2019高一下·广德期中) 如图，已知A(4,0)、B(0,4)，从点P(2，0)射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是（）B .C . 6D .12. （2分） (2019高一下·广德期中) 已知的图象与x轴、y轴有三个不同的交点，有一个圆恰好经过这三个点，则此圆与坐标轴的另一个交点是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分）(2017·扬州模拟) 若复数z满足（2﹣i）z=1+i，则复数z在复平面上对应的点在第________象限．14. （1分） (2019高一下·广德期中) 如图，渔船甲位于岛屿的南偏西方向的处，且与岛屿相距12海里，渔船乙以10海里/小时的速度从岛屿出发沿正北方向航行，若渔船甲同时从处出发沿北偏东的方向追赶渔船乙，刚好用2小时追上．则 =________.15. （1分） (2019高一下·广德期中) 若直线与圆交于M、N两点，且M、N两点关于直线对称，则 ________.16. （1分） (2019高一下·广德期中) 已知三角形中，边上的高与边长相等，则的最大值是________．三、解答题 (共6题；共60分)17. （10分）从椭圆E： + =1（a＞b＞0）上一点M向x轴作垂线，垂足恰为左焦点F1 ，点A、B 是椭圆与x轴正半轴、y轴正半轴的交点，且AB∥OM，|F1A|= ．（1）求该椭圆的离心率；（2）若P是该椭圆上的动点，右焦点为F2 ，求• 的取值范围．（3）若直线y=kx+m与椭圆E有两个交点P和Q，且原点O总在以PQ为直径的圆的内部，求实数m的取值范围．18. （10分） (2016高二上·湖南期中) 已知命题p：方程 =1表示双曲线，命题q：x∈（0，+∞），x2﹣mx+4≥0恒成立，若p∨q是真命题，且綈（p∧q）也是真命题，求m的取值范围．19. （15分） (2019高二上·上海月考) 已知方程的曲线是圆C，（1）若直线l：与圆C相交于M、N两点，且（O为坐标原点），求实数m的值；（2）当时，设T为直线n：上的动点，过T作圆C的两条切线TG、TH，切点分别为G、H，求四边形TGCH而积的最小值.20. （5分）已知直线l：kx﹣y+1+2k=0（k∈R）．（1）证明：直线l过定点；（2）若直线l不经过第四象限，求k的取值范围；（3）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值及此时直线l的方程．21. （10分） (2019高二下·嘉兴期中) 已知点是抛物线的焦点，是抛物线在第一象限内的点，且，(I) 求点的坐标；(II)以为圆心的动圆与轴分别交于两点，延长分别交抛物线于两点；①求直线的斜率；②延长交轴于点，若，求的值.22. （10分） (2019高二上·辽源期中) 如图，己知抛物线，直线交抛物线于两点，是抛物线外一点，连接分别交地物线于点，且 .（1）若，求点的轨迹方程.（2）若，且平行x轴，求面积.参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分) 17-1、17-2、17-3、18-1、19-1、19-2、20-1、20-2、20-3、21-1、22-1、22-2、。

阳江市数学高一下期中提高练习(含解析)

一、选择题1．(0分)[ID ：12424]圆224470x y x y +--+=上的动点P 到直线0x y +=的最小距离为（）A ．1B ．221-C ．22D ．22．(0分)[ID ：12421]设l 为直线，,αβ是两个不同的平面，下列命题中正确的是( ) A ．若//l α，//l β，则//αβB ．若l α⊥，l β⊥，则//αβC ．若l α⊥，//l β，则//αβD ．若αβ⊥，//l α，则l β⊥3．(0分)[ID ：12416]水平放置的ABC 的斜二测直观图如图所示，若112A C ＝，111A B C △的面积为22，则AB 的长为（）A 2B ．17C ．2D ．84．(0分)[ID ：12376]设α表示平面，a ，b 表示直线，给出下列四个命题：①a α//，a b b α⊥⇒//；②a b //，a b αα⊥⇒⊥；③a α⊥，a b b α⊥⇒⊂；④a α⊥，b a b α⊥⇒//，其中正确命题的序号是（）A ．①②B ．②④C ．③④D ．①③5．(0分)[ID ：12355]已知点A （1，2），B （3，1），则线段AB 的垂直平分线的方程是（）A ．4x 2y 5+=B ．4x 2y 5-=C ．x 2y 5+=D ．x 2y 5-= 6．(0分)[ID ：12350]四棱锥P ABCD -的底面ABCD 为正方形，PA ⊥底面ABCD ，2AB =，72PA =，若该四棱锥的所有顶点都在同一球面上，则该球的表面积为（）A ．812πB ．814πC ．65πD ．652π 7．(0分)[ID ：12330]椭圆22221(0)x y a b a b+=>>的左右焦点分别是1F 、2F ，以2F 为圆心的圆过椭圆的中心，且与椭圆交于点P ，若直线1PF 恰好与圆2F 相切于点P ，则椭圆的离心率为（）A 31+B 31C ．22D 51- 8．(0分)[ID ：12394]如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是( )A ．B ．C ．D ．9．(0分)[ID ：12388]一个几何体的三视图如图所示，则该几何体的表面积为（）A ．3πB ．4πC ．2π+4D ．3π+410．(0分)[ID ：12428]在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30，则该长方体的体积为（）A ．8B ．62C ．82D ．8311．(0分)[ID ：12338]某几何体的三视图如图所示（单位：cm ），其俯视图为等边三角形，则该几何体的体积（单位：3cm ）是（）A ．3B 1033C ．23D 83312．(0分)[ID ：12385]一锥体的三视图如图所示,则该棱锥的最长棱的棱长为 ( )A ．√33B ．√17C ．√41D ．√4213．(0分)[ID ：12368]α，β是两个不重合的平面，在下列条件中，可判断平面α，β平行的是（）A ．m ，n 是平面α内两条直线，且//m β，//n βB ．α内不共线的三点到β的距离相等C ．α，β都垂直于平面γD ．m ，n 是两条异面直线，m α⊂，n β⊂，且//m β，//n α14．(0分)[ID ：12363]若圆锥的高等于底面直径，则它的底面积与侧面积之比为 A ．1∶2B ．1∶3C ．1∶5D ．3∶215．(0分)[ID ：12361]如图，正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，线段B 1D 1上有两个动点E 、F ，且EF=12．则下列结论中正确的个数为①AC ⊥BE ；②EF ∥平面ABCD ；③三棱锥A ﹣BEF 的体积为定值；④AEF ∆的面积与BEF ∆的面积相等，A ．4B ．3C ．2D ．1二、填空题16．(0分)[ID ：12488]经过两条直线2310x y ++=和340x y -+=的交点，并且平行于直线3470x y +-=的直线方程是________.17．(0分)[ID ：12477]已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M 分别是线段AB 、AD 、AA 1的中点，又P 、Q 分别在线段A 1B 1、A 1D 1上，且A 1P ＝A 1Q ＝x (0<x <1).设平面MEF ∩平面MPQ＝l ，现有下列结论：①l ∥平面ABCD ；②l ⊥AC ；③直线l 与平面BCC 1B 1不垂直；④当x 变化时，l 不是定直线.其中不成立的结论是________.(写出所有不成立结论的序号)18．(0分)[ID ：12476]已知A ，B ，C ，D 是同一球面上的四个点，其中ABC ∆是正三角形，AD ⊥平面ABC ，26AD AB ==，则该球的体积为_________.19．(0分)[ID ：12474]如图，在长方形ABCD 中，2AB =，1BC =，E 为DC 的中点，F 为线段EC （端点除外）上一动点，现将AFD 沿AF 折起，使平面ABD ⊥平面ABC ，在平面ABD 内过点D 作DK AB ⊥，K 为垂足，设AK t =，则t 的取值范围是__________．20．(0分)[ID ：12447]在一个密闭的容积为1的透明正方体容器内装有部分液体，如果任意转动该正方体，液面的形状都不可能是三角形，那么液体体积的取值范围是．21．(0分)[ID ：12446]底面边长为2的正三棱柱111ABC A B C -被不平行于底面的平面MNP 所截，其中3AM =，4BN =，5PC =，则多面体ABC MNP -体积为________22．(0分)[ID ：12440]圆台的两个底面面积之比为4：9，母线与底面的夹角是60°，轴截面的面积为1803_____．23．(0分)[ID ：12495]正四棱锥S -ABCD 2S 、A 、B 、C 、D 都在同一个球面上，则该球的体积为______．24．(0分)[ID ：12433]已知点(,)P x y 是直线4(0)y kx k =-->上的一个动点，PA ，PB 是圆22:20C x y y +-=的两条切线，A ，B 是切点，若四边形PACB 的面积的最小值为2，则实数k 的值为__________．25．(0分)[ID ：12502]直线:l y x b =+与曲线2:1C y x =-有两个公共点，则b 的取值范围是______.三、解答题26．(0分)[ID ：12602]如图，四棱锥P －ABCD 的底面ABCD 是平行四边形，BA ＝BD ＝2，AD ＝2，PA ＝PD ＝5，E ，F 分别是棱AD ，PC 的中点．（1）证明：EF ∥平面PAB ；（2）若二面角P －AD －B 为60°．①证明：平面PBC ⊥平面ABCD ；②求直线EF 与平面PBC 所成角的正弦值．27．(0分)[ID ：12597]已知点(3,3)M ，圆22:(1)(2)4C x y -+-=.（1）求过点M 且与圆C 相切的直线方程；（2）若直线40()ax y a -+=∈R 与圆C 相交于A ，B 两点，且弦AB 的长为23实数a 的值.28．(0分)[ID ：12574]已知平面内两点(8,6),(2,2)A B -.（1）求AB 的中垂线方程；（2）求过点(2,3)P -且与直线AB 平行的直线l 的方程．29．(0分)[ID ：12558]在直角坐标系中，射线OA: x －y=0（x≥0），OB: x+2y=0（x≥0），过点P(1,0)作直线分别交射线OA 、OB 于A 、B 两点.（1）当AB 中点为P 时，求直线AB 的方程；（2）当AB 中点在直线12y x =上时，求直线AB 的方程. 30．(0分)[ID ：12581]已知过点A (0，1)且斜率为k 的直线l 与圆C ：(x －2)2＋(y －3)2＝1交于M ，N 两点．(1)求k 的取值范围；(2)若OM ON ⋅＝12，其中O 为坐标原点，求|MN |.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．B2．B3．B4．B5．B6．B7．B8．A9．D10．C11．B12．C13．D14．C15．B二、填空题16．【解析】【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为：故答案为：【点睛】本题17．④【解析】【详解】连接BDB1D1∵A1P＝A1Q＝x∴PQ∥B1D1∥BD∥EF则PQ∥平面ME F又平面MEF∩平面MPQ＝l∴PQ∥ll∥EF∴l∥平面ABCD故①成立；又EF⊥AC∴l⊥AC故18．【解析】【分析】取正的外心为过作平面的垂线在上取点使得即得是三棱锥外接球球心求出球半径可得体积【详解】如图是外心延长线与交于点是中点过作平面取∵平面ABC ∴到的距离相等∴是三棱锥外接球球心∴所以故答19．【解析】当位于的中点点与中点重合随点到点由得平面则又则因为所以故综上的取值范围为点睛:立体几何中折叠问题要注重折叠前后垂直关系的变化不变的垂直关系是解决问题的关键条件20．【解析】【分析】【详解】试题分析：如图正方体ABCD-EFGH此时若要使液面不为三角形则液面必须高于平面EHD且低于平面AFC而当平面EHD平行水平面放置时若满足上述条件则任意转动该正方体液面的形状21．【解析】【分析】将多面体分为四棱锥与三棱锥两部分相加求和即可【详解】如图将多面体分为四棱锥与三棱锥两部分其中四棱锥的高为为梯形则故多面体体积为故答案为：【点睛】本题主要考查了多面体体积的求解方法根据22．【解析】【分析】首先通过两个底面面积之比为得到半径比设出上底半径为下底半径为由因为母线与底面的夹角是得到母线长为高为就可以根据轴截面的面积解出代公式求出侧面积即可【详解】圆台的两个底面面积之比为则半23．【解析】如图过S作SO1⊥平面ABCD由已知=1在Rt△SO1C中∵SC＝∴∴O1S＝O1A＝O1B ＝O1C＝O1D故O1是过SABCD点的球的球心∴球的半径为r＝1∴球的体积为点睛：与球有关的组合24．【解析】分析：画出图形（如图）根据圆的性质可得然后可将问题转化为切线长最小的问题进而转化为圆心到直线距离的最小值的问题处理详解：根据题意画出图形如下图所示由题意得圆的圆心半径是由圆的性质可得四边形的25．【解析】【分析】由题意曲线表示以原点为圆心1为半径的半圆根据图形得出直线与半圆有两个公共点时抓住两个关键点一是直线与圆相切时二是直线过时分别求出的值即可确定的范围【详解】如图所示是个以原点为圆心1为三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．B解析：B【解析】【分析】先求出圆心到直线0x y +=的距离，根据距离的最小值为d r -，即可求解.【详解】由圆的一般方程可得22(2)(2)1x y -+-=，圆心到直线的距离d ==所以圆上的点到直线的距离的最小值为1.故选B.【点睛】本题主要考查了点到直线的距离，圆的方程，属于中档题.2．B解析：B【解析】A 中，,αβ也可能相交；B 中，垂直与同一条直线的两个平面平行，故正确；C 中，,αβ也可能相交；D 中，l 也可能在平面β内.【考点定位】点线面的位置关系3．B解析：B【解析】【分析】依题意由111A B C △的面积为114B C =，所以8BC =，2AC =，根据勾股定理即可求AB ．【详解】依题意，因为111A B C △的面积为所以11111sin 452AC B C ︒=⨯⋅=111222B C ⨯⨯⨯，解得114B C =，所以8BC =，2AC =，又因为AC BC ⊥，由勾股定理得：AB ====故选B ．【点睛】本题考查直观图还原几何图形，属于简单题. 利用斜二测画法作直观图，主要注意两点：一是与x 轴平行的线段仍然与x '轴平行且相等；二是与y 轴平行的线段仍然与y '轴平行且长度减半. 4．B解析：B【解析】【分析】【详解】①a ∥α，a ⊥b ⇒b 与α平行，相交或b ⊂α，故①错误；②若a ∥b ，a ⊥α，由直线与平面垂直和判定定理得b ⊥α，故②正确；③a ⊥α，a ⊥b ⇒b 与α平行，相交或b ⊂α，故③错误；④若a ⊥α，b ⊥α，则由直线与平面垂直的性质得a ∥b ，故④正确．故选B ．5．B解析：B【解析】【分析】【详解】因为线段AB 的垂直平分线上的点(),x y 到点A ，B 的距离相等，=．即：221244x x y y +-++- 229612x x y y =+-++-，化简得：425x y -=．故选B ．6．B解析：B【解析】【分析】根据题意可知，该四棱锥的外接球即为其所在长方体的外接球，根据公式即可求得.【详解】根据题意，为方便说明，在长方体中找出该四棱锥如图所示：由图可知在长方体中的四棱锥P ABCD -完全满足题意，故该四棱锥的外接球即是长方体的外接球，故外接球半径222722294R ⎛⎫++ ⎪⎝⎭==，故该球的表面积为28144S R ππ==. 故选：B .【点睛】本题考查四棱锥外接球的问题，关键的步骤是将问题转化为求长方体的外接球. 7．B解析：B【解析】【分析】根据椭圆的定义可知12||||2PF PF a +=，又1PF 恰好与圆2F 相切于点P ，可知2||PF c =且12PF PF ⊥，即可列出方程求椭圆的离心率.【详解】由1PF 恰好与圆2F 相切于点P ，可知2||PF c =，且 12PF PF ⊥，又12||||2PF PF a +=，可知1||2PF a c =-，在12Rt PF F ∆中，222(2)4a c c c -+=，即2222a ac c -=所以2220,(0,1)e e e +-=∈，解得21231e -+==，故选：B【点睛】本题主要考查了椭圆的定义，椭圆的简单几何性质，圆的切线的性质，属于中档题. 8．A解析：A【解析】【分析】利用线面平行判定定理可知B 、C 、D 均不满足题意，从而可得答案．【详解】对于B 项，如图所示，连接CD ，因为AB ∥CD ，M ，Q 分别是所在棱的中点，所以MQ ∥CD ，所以AB ∥MQ ，又AB ⊄平面MNQ ，MQ ⊂平面MNQ ，所以AB ∥平面MNQ ，同理可证，C ，D 项中均有AB ∥平面MNQ . 故选：A.【点睛】本题考查空间中线面平行的判定定理，利用三角形中位线定理是解决本题的关键，属于中档题．9．D解析：D 【解析】该几何体为半圆柱，底面为半径为1的半圆，高为2，因此表面积为π×12+12×2π×1×2+2×2=3π+4 ,选D.10．C解析：C 【解析】【分析】首先画出长方体1111ABCD A B C D -，利用题中条件，得到130AC B ∠=，根据2AB =，求得123BC =，可以确定122CC =，之后利用长方体的体积公式求出长方体的体积. 【详解】在长方体1111ABCD A B C D -中，连接1BC ，根据线面角的定义可知130AC B ∠=，因为2AB =，所以123BC =，从而求得122CC =，所以该长方体的体积为222282V =⨯⨯=，故选C. 【点睛】该题考查的是长方体的体积的求解问题，在解题的过程中，需要明确长方体的体积公式为长宽高的乘积，而题中的条件只有两个值，所以利用题中的条件求解另一条边的长就显得尤为重要，此时就需要明确线面角的定义，从而得到量之间的关系，从而求得结果.11．B解析：B 【解析】由题意可知该几何体为正三棱柱去掉一个小三棱锥，1104323333V =-⋅⋅=. 故选：B.12．C解析：C 【解析】试题分析：该几何体为一个侧面与底面垂直，底面为正方形的四棱锥（如图所示），其中底面ABCD 边长为4，侧面PAD ⊥平面ABCD ，点P 在底面的射影为E ，所以PE ⊥AD,DE =1,AE =4,PE =4,所以PA =√PE 2+AE 2=5,PB =√PE 2+BE 2=√41,PC =√PE 2+CE 2=√33,PD =√PE 2+DE 2=√17,底面边长为4，所以最长的棱长为√41，故选C.考点：简单几何体的三视图．13．D解析：D【解析】【分析】A中，根据面面平行的判定定理可得：α∥β或者α与β相交．B中，根据面面得位置关系可得：α∥β或者α与β相交．C中，则根据面面得位置关系可得：α∥β或者α与β相交．D中，在直线n上取一点Q，过点Q作直线m 的平行线m′，所以m′与n是两条相交直线，m′⊂β，n⊂β，且m′∥β，n∥α，根据面面平行的判定定理可得α∥β，即可得到答案．【详解】由题意，对于A中，若m，n是平面α内两条直线，且m∥β，n∥β，则根据面面平行的判定定理可得：α∥β或者α与β相交．所以A错误．对于B中，若α内不共线的三点到β的距离相等，则根据面面得位置关系可得：α∥β或者α与β相交．所以B错误．对于C中，若α，β都垂直于平面γ，则根据面面得位置关系可得：α∥β或者α与β相交．所以C错误．对于D中，在直线n上取一点Q，过点Q作直线m 的平行线m′，所以m′与n是两条相交直线，m′⊂β，n⊂β，且m′∥β，n∥α，根据面面平行的判定定理可得α∥β，所以D正确．故选D．【点睛】本题主要考查了平面与平面平行的判定与性质的应用，其中解答中灵活运用平面与平面平行额判定与性质进行判定是解答的关键，着重考查学生严密的思维能力和空间想象能力，属于基础题．14．C解析：C【解析】【分析】由已知，求出圆锥的母线长，进而求出圆锥的底面面积和侧面积，可得答案【详解】设圆锥底面半径为r，则高h＝2r，∴其母线长l＝r．∴S侧＝πrl＝πr2，S底＝πr故选C．【点睛】本题考查的知识点是旋转体，圆锥的表面积公式，属于基础题．15．B解析：B【解析】试题分析：①中AC⊥BE，由题意及图形知，AC⊥面DD1B1B，故可得出AC⊥BE，此命题正确；②EF∥平面ABCD，由正方体ABCD-A1B1C1D1的两个底面平行，EF在其一面上，故EF 与平面ABCD 无公共点，故有EF ∥平面ABCD ，此命题正确；③三棱锥A-BEF 的体积为定值，由几何体的性质及图形知，三角形BEF 的面积是定值，A 点到面DD1B1B 距离是定值，故可得三棱锥A-BEF 的体积为定值，此命题正确；④由图形可以看出，B 到线段EF 的距离与A 到EF 的距离不相等，故△AEF 的面积与△BEF 的面积相等不正确考点：1．正方体的结构特点；2．空间线面垂直平行的判定与性质二、填空题16．【解析】【分析】先求出两相交直线的交点设出平行于直线的直线方程根据交点在直线上求出直线方程【详解】联立直线的方程得到两直线的交点坐标平行于直线的直线方程设为则所以直线的方程为：故答案为：【点睛】本题解析：1934011x y ++= 【解析】【分析】先求出两相交直线的交点，设出平行于直线3470x y +-=的直线方程，根据交点在直线上，求出直线方程. 【详解】联立直线的方程23103470x y x y ++=⎧⎨+-=⎩，得到两直线的交点坐标135(,)1111-，平行于直线3470x y +-=的直线方程设为340x y c ++=，则1353()4()+01111c ⋅-+⋅= 所以直线的方程为：1934011x y ++= 故答案为：1934011x y ++= 【点睛】本题考查了直线的交点，以及与已知直线平行的直线方程，考查了学生概念理解，转化与划归的能力，属于基础题.17．④【解析】【详解】连接BDB1D1∵A1P ＝A1Q ＝x ∴PQ ∥B1D1∥BD ∥EF 则P Q ∥平面MEF 又平面MEF∩平面MPQ ＝l ∴PQ ∥ll ∥EF ∴l ∥平面ABCD 故①成立；又EF ⊥AC ∴l ⊥AC 故解析：④ 【解析】【详解】连接BD ，B 1D 1，∵A 1P ＝A 1Q ＝x ，∴PQ ∥B 1D 1∥BD ∥EF ，则PQ ∥平面MEF ，又平面MEF ∩平面MPQ ＝l ，∴PQ ∥l ，l ∥EF ， ∴l ∥平面ABCD ，故①成立；又EF ⊥AC ，∴l ⊥AC ，故②成立；∵l ∥EF ∥BD ，故直线l 与平面BCC 1B 1不垂直，故③成立；当x 变化时，l 是过点M 且与直线EF 平行的定直线，故④不成立．即不成立的结论是④.18．【解析】【分析】取正的外心为过作平面的垂线在上取点使得即得是三棱锥外接球球心求出球半径可得体积【详解】如图是外心延长线与交于点是中点过作平面取∵平面ABC ∴到的距离相等∴是三棱锥外接球球心∴所以故答解析：323π【解析】【分析】取正ABC 的外心为M ，过M 作平面ABC 的垂线，在上取点O ，使得12OM AD =，即得O 是三棱锥A BCD -外接球球心，求出球半径可得体积．【详解】如图，M 是ABC ∆外心，AM 延长线与BC 交于点E ，E 是BC 中点，过M 作MO ⊥平面ABC ，取12OM AD =， ∵AD ⊥平面ABC ，∴//MO AD ，O 到,A D 的距离相等，∴O 是三棱锥A BCD -外接球球心，233332AM =⨯⨯=3OM =，∴22223(3)23OA OM AM =+=+=，所以2344()(23)32333V OA πππ==⨯=．故答案为：323π．【点睛】本题考查求球的体积，解题关键是作出外接球球心．三棱锥外接球球心在过各面中点且与面垂直的直线上．19．【解析】当位于的中点点与中点重合随点到点由得平面则又则因为所以故综上的取值范围为点睛:立体几何中折叠问题要注重折叠前后垂直关系的变化不变的垂直关系是解决问题的关键条件解析：1,12⎛⎫⎪⎝⎭【解析】当F 位于DC 的中点，点D 与AB 中点重合，1t =．随F 点到C 点，由CB AB ⊥，CB DK ⊥，得CB ⊥平面ADB ，则CB BD ⊥．又2CD =，1BC =，则3BD =．因为1AD =，2AB =，所以AD BD ⊥，故12t =．综上，t 的取值范围为1,12⎛⎫⎪⎝⎭．点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.20．【解析】【分析】【详解】试题分析：如图正方体ABCD-EFGH 此时若要使液面不为三角形则液面必须高于平面EHD 且低于平面AFC 而当平面EHD 平行水平面放置时若满足上述条件则任意转动该正方体液面的形状解析：15,66⎛⎫⎪⎝⎭【解析】【分析】【详解】试题分析：如图，正方体ABCD-EFGH ，此时若要使液面不为三角形，则液面必须高于平面EHD ，且低于平面AFC ．而当平面EHD 平行水平面放置时，若满足上述条件，则任意转动该正方体，液面的形状都不可能是三角形．所以液体体积必须＞三棱柱G-EHD 的体积16，并且＜正方体ABCD-EFGH 体积-三棱柱B-AFC 体积15166-=考点：1．棱柱的结构特征；2．几何体的体积的求法21．【解析】【分析】将多面体分为四棱锥与三棱锥两部分相加求和即可【详解】如图将多面体分为四棱锥与三棱锥两部分其中四棱锥的高为为梯形则故多面体体积为故答案为：【点睛】本题主要考查了多面体体积的求解方法根据解析：3【解析】【分析】将多面体ABC MNP -分为四棱锥N ACPM -与三棱锥N ABC -两部分相加求和即可. 【详解】如图, 将多面体ABC MNP -分为四棱锥N ACPM -与三棱锥N ABC -两部分. 其中四棱锥N ACPM -的高为2sin 603⨯︒=.ACPM 为梯形. 则()3521833323N ACPM V -+⨯=⨯=123434323N ABC V -=⨯=. 故多面体ABC MNP -834343+=故答案为：43【点睛】本题主要考查了多面体体积的求解方法,根据多面体的特征分为两个棱锥计算即可.属于中档题.22．【解析】【分析】首先通过两个底面面积之比为得到半径比设出上底半径为下底半径为由因为母线与底面的夹角是得到母线长为高为就可以根据轴截面的面积解出代公式求出侧面积即可【详解】圆台的两个底面面积之比为则半解析：360π【解析】【分析】首先通过两个底面面积之比为4:9，得到半径比，设出上底半径为2k，下底半径为3k，由因为母线与底面的夹角是60，得到母线长为2k，高为3k.就可以根据轴截面的面积k=，代公式求出侧面积即可.解出6【详解】圆台的两个底面面积之比为4:9，则半径比为2:3所以设圆台的上底半径为2k，下底半径为3k，由于母线与底面的夹角是60，所以母线长为2k3k.由于轴截面的面积为1803，所以()46318032k k k+⨯=，解得6k =.所以圆台的上底半径为12，下底半径为18.母线长为12. 所以圆台的侧面积为()121812360ππ+⨯=. 故答案为：360π 【点睛】本题主要考查圆台的性质以及圆台的侧面积，同时考查了线面成角问题，属于中档题.23．【解析】如图过S 作SO1⊥平面ABCD 由已知=1在Rt△SO1C 中∵SC＝∴∴O1S＝O1A ＝O1B ＝O1C ＝O1D 故O1是过SABCD 点的球的球心∴球的半径为r ＝1∴球的体积为点睛：与球有关的组合解析：43π【解析】如图，过S 作SO 1⊥平面ABCD ，由已知1112O C AC ==1.在Rt △SO 1C 中， ∵ SC ＝2 ，∴ 22111SO SC O C =-=，∴ O 1S ＝O 1A ＝O 1B ＝O 1C ＝O 1D ，故O 1是过S ，A ，B ，C ，D 点的球的球心，∴ 球的半径为r ＝1， ∴ 球的体积为34433r π=π.点睛：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.24．【解析】分析：画出图形（如图）根据圆的性质可得然后可将问题转化为切线长最小的问题进而转化为圆心到直线距离的最小值的问题处理详解：根据题意画出图形如下图所示由题意得圆的圆心半径是由圆的性质可得四边形的解析：【解析】分析：画出图形（如图），根据圆的性质可得2PBCPACB S S =四边形，然后可将问题转化为切线长最小的问题，进而转化为圆心到直线距离的最小值的问题处理．详解：根据题意画出图形如下图所示．由题意得圆22:20C x y y +-=的圆心()0,1，半径是1r =，由圆的性质可得2PBCPACB S S =四边形，四边形PACB 的最小面积是2，∴PBC S的最小值112S rd ==（d 是切线长）， ∴2d =最小值，∵圆心到直线的距离就是PC 的最小值，2221251k+==+又0k >， ∴2k =．点睛：本题考查圆的性质、切线长定理的运用，解题时注意转化思想方法的运用，结合题意将问题逐步转化为点到直线的距离的问题处理．25．【解析】【分析】由题意曲线表示以原点为圆心1为半径的半圆根据图形得出直线与半圆有两个公共点时抓住两个关键点一是直线与圆相切时二是直线过时分别求出的值即可确定的范围【详解】如图所示是个以原点为圆心1为解析：2⎡⎣【解析】【分析】由题意，曲线2:1C y x =-表示以原点为圆心，1为半径的半圆，根据图形得出直线:l y x b =+与半圆有两个公共点时抓住两个关键点，一是直线:l y x b =+与圆相切时，二是直线:l y x b =+过()1,0A -时分别求出b 的值，即可确定b 的范围。

广东省阳江市高一下学期数学期中考试试卷

广东省阳江市高一下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）(2017·运城模拟) 设集合U={0，1，2，3，4，5}，A={1，2，3}，B={x∈Z|x2﹣5x+4≥0}，则A∩（∁UB）=（）A . {1，2，3}B . {1，2}C . {2，3}D . {2}2. （2分）函数的奇偶性为（）A . 既奇又偶函数B . 偶函数C . 非奇非偶函数D . 奇函数3. （2分）(2020·海南模拟) 如图是二次函数的部分图象，则函数的零点所在的区间是（）A .B .C .D .4. （2分）(2017·内江模拟) 已知向量 =（1，﹣2）， =（1，1）， = + ， = ﹣λ ，如果⊥ ，那么实数λ=（）A . 4B . 3C . 2D . 15. （2分） sin（﹣150°）的值为（）A .B .C .D .6. （2分） (2016高二上·福州期中) 在△ABC中，sin2A≤sin2B+sin2C﹣sinBsinC，则A的取值范围是（）A . （0， ]B . [ ，π）C . （0， ]D . [ ，π）7. （2分） (2016高二下·桂林开学考) 设，若，则 =（）A .B .C .D .8. （2分） (2019高一下·上海月考) 若，且，那么是（）A . 直角三角形B . 等边三角形C . 等腰三角形D . 等腰直角三角形9. （2分）已知O是△ABC外接圆的圆心，A、B、C为△ABC的内角，若，则m 的值为（）A . 1B . sinAC . cosAD . tanA10. （2分）在中，已知 ,，那么是（）三角形.A . 等腰三角形B . 直角三角形C . 等边三角形D . 等腰直角三角形二、填空题 (共7题；共7分)11. （1分） (2019高三上·上海月考) 已知集合，则=________.12. （1分） (2019高一下·嘉定月考) 已知，则 ________.13. （1分）(2017·虹口模拟) 设函数f（x）= ，则当x≤﹣1时，则f[f（x）]表达式的展开式中含x2项的系数是________．14. （1分） (2019高二上·成都期中) 抛物线上一点到抛物线准线的距离为，点关于轴的对称点为，为坐标原点，的内切圆与切于点，点为内切圆上任意一点，则的取值范围为________．15. （1分）(2016·江苏) 已知{an}是等差数列，Sn是其前n项和.若a1+a22= - 3，S5=10，则a9的值是________.16. （1分）(2020·海南模拟) 已知函数，若函数只有一个零点，且，则实数的取值范围________.17. （1分） (2015高一下·天门期中) 在△ABC中，若c2＞a2+b2 ，则△ABC必是________（填锐角，钝角，直角）三角形．三、解答题 (共5题；共60分)18. （10分）如图，已知A1B1C1﹣ABC是正三棱柱，D是AC中点．（1）证明AB1∥平面DBC1；（2）假设AB1⊥BC1 ， BC=2，求线段AB1在侧面B1BCC1上的射影长．19. （10分）已知，在中，分别为内角所对的边，且对满足．（1）求角的值；（2）若，求面积的最大值．20. （10分） (2017高一下·济南期末) 已知函数．（1）求函数f（x）的最小正周期和单调增区间；（2）函数f（x）的图象可以由函数y=sin2x（x∈R）的图象经过怎样的变换得到？21. （15分） (2017高一下·嘉兴期末) 数列{an}满足：a1=1，an+1+（﹣1）nan=2n﹣1．（1）求a2，a4，a6；（2）设bn=a2n，求数列{bn}的通项公式；（3）设Sn为数列{an}的前n项和，求S2018．22. （15分） (2019高一上·北京月考) 已知关于的不等式，解集为 . （1）若或，求的值.（2）解关于的不等式， .参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题；共7分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题；共60分)18-1、19-1、19-2、20-1、20-2、21-1、21-2、21-3、22-1、22-2、。

广东省阳江市高一下学期期中数学试卷

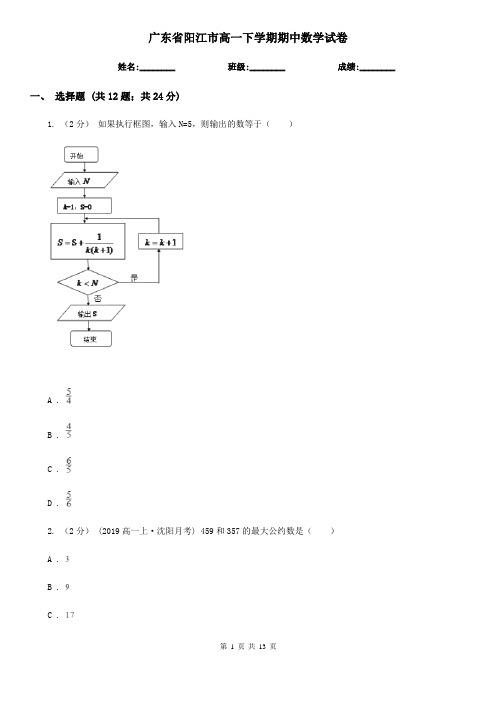
广东省阳江市高一下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）如果执行框图，输入N=5，则输出的数等于（）A .B .C .D .2. （2分） (2019高一上·沈阳月考) 459和357的最大公约数是（）A .B .C .D .3. （2分） (2018高一下·唐山期末) 某校高一学生进行测试，随机抽取20名学生的测试成绩，绘制茎叶图如图所示，则这组数据的众数和中位数分别为（）A . 86，77B . 86，78C . 77，77D . 77，784. （2分） (2017高二下·成都开学考) 执行如图所示的程序框图，则输出S的值为（）A .B .C . 0D .5. （2分）(2013·陕西理) 某单位有840名职工，现采用系统抽样方法，抽取42人做问卷调查，将840人按1，2，…，840随机编号，则抽取的42人中，编号落入区间[481，720]的人数为（）A . 11B . 12C . 13D . 146. （2分） (2017高二下·黑龙江期末) 对变量x ， y有观测数据（xi ， yi）（i=1，2，3，4，5），得表1；对变量u ， v有观测数据（ui ， vi）（i=1，2，3，4，5），得表2．由这两个表可以判断（）表1：x12345y 2.9 3.3 3.6 4.4 5.1表2：u12345v2520211513A . 变量x与y正相关，u与v正相关B . 变量x与y负相关，u与v正相关C . 变量x与y负相关，u与v负相关D . 变量x与y正相关，u与v负相关7. （2分）下列四个数中，数值最小的是（）A . 10111（2）B . 101（5）C . 25（10）D . 1B（16）8. （2分） (2016高一下·咸阳期末) 已知某种彩票发行1000000张，中奖率为0.001，则下列说法正确的是（）A . 买1张肯定不中奖B . 买1000张一定能中奖C . 买1000张也不一定能中奖D . 买1000张一定恰有1张能中奖9. （2分） (2018高二下·黑龙江期中) 10张奖券中有3张是有奖的,某人从中不放回地依次抽两张,则在第一次抽到中奖券的条件下,第二次也抽到中奖券的概率为（）A .B .C .D .10. （2分）将两个数a=2010，b=2011交换使得a=2011，b=2010，下面语句正确一组是（）A .B .C .D .11. （2分）在25件同类产品中，有2件次品，从中任取3件产品，其中不可能事件为（）A . 3件都是正品B . 至少有1次品C . 3件都是次品D . 至少有1件正品12. （2分） (2017高二下·资阳期末) 根据如下样本数据：x34567y 4.0 2.50.5﹣0.5﹣2.0得到的回归方程为 =bx+a．若a=8.4，则估计x，y的变化时，若x每增加1个单位，则y就（）A . 增加1.2个单位B . 减少1.5个单位C . 减少2个单位D . 减少1.2个单位二、填空题 (共4题；共4分)13. （1分）若输入x=﹣25，则下列算法语句运行后输出的结果为________．14. （1分） (2019高三上·安顺模拟) 某学校高一、高二、高三年级的学生人数成等差数列，现用分层抽样的方法从这三个年级中抽取90人，则应从高二年级抽取的学生人数为________.15. （1分）从1，2，3，4，5这五个数中一次随机取两个数，则其中一个数是另一个的两倍的概率为________．16. （1分） (2018高一下·平顶山期末) 一个项目由15个专家评委投票表决，剔除一个最高分96，一个最低分58后所得到的平均分为92，方差为16，那么原始得分的方差为________．三、解答题 (共6题；共45分)17. （5分）用秦九韶算法计算多项式f（x）=12+35x﹣8x2+79x3+6x4+5x5+3x6在x=﹣4时的V4值．18. （10分） (2018高一下·安徽期末) 某企业根据供销合同生产某种型号零件10万件，规定：零件长度(单位：毫米)在区间内，则为一等品；若长度在或内，则为二等品；否则为不合格产品.现从生产出的零件中随机抽取100件作样本，其长度数据的频率分布直方图如图所示.（1）试估计该样本的平均数；（2）根据合同，企业生产的每件一等品可获利10元，每件二等品可获利8元，每件不合格产品亏损6元，若用样本估计总体，试估算该企业生产这批零件所获得的利润.19. （5分）(2017·漳州模拟) 漳州水仙鳞茎硕大，箭多花繁，色美香郁，素雅娟丽，有“天下水仙数漳州”之美誉．现某水仙花雕刻师受雇每天雕刻250粒水仙花，雕刻师每雕刻一粒可赚1.2元，如果雕刻师当天超额完成任务，则超出的部分每粒赚1.7元；如果当天未能按量完成任务，则按实际完成的雕刻量领取当天工资．（I）求雕刻师当天收入（单位：元）关于雕刻量n（单位：粒，n∈N）的函数解析式f（n）；（Ⅱ）该雕刻师记录了过去10天每天的雕刻量n（单位：粒），整理得如表：以10天记录的各雕刻量的频率作为各雕刻量发生的概率．（ⅰ）求该雕刻师这10天的平均收入；（ⅱ）求该雕刻师当天收入不低于300元的概率．20. （5分）读下列所给程序，依据程序画出程序框图，并说明其功能.INPUT “输入三个正数a ， b ， c＝”；a ， b ， cIF a＋b>c AND a＋c>b AND b＋c>a THENp＝(a＋b＋c)/2S＝SQR(p*(p－a)*(p－b)*(p－c))PRINT “三角形的面积S＝”SELSEPRINT “构不成三角形”END IFEND．21. （10分） (2016高二上·孝感期中) 解答题（1）在边长为1的正方形ABCD内任取一点M，求事件“|AM|≤1”的概率；（2）某班在一次数学活动中，老师让全班56名同学每人随机写下一对都小于1的正实数x、y，统计出两数能与1构成锐角三角形的三边长的数对（x，y）共有12对，请据此估计π的近似值（精确到0.001）．22. （10分） (2017高一下·兰州期中) 甲、乙二人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判断题4个．甲、乙二人依次各抽一题．（1）甲抽到选择题、乙抽到判断题的概率是多少？（2）甲、乙二人中至少有一人抽到选择题的概率是多少？参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共45分) 17-1、18-1、18-2、19-1、20-1、21-1、21-2、22-1、22-2、。

广东阳江市数学高一下期中测试(培优练)

一、选择题1．(0分)[ID ：12423]已知三棱锥D ABC -的外接球的表面积为128π，4,42AB BC AC ===，则三棱锥D ABC -体积的最大值为（）A ．2732B ．10863+C ．1663+D ．3221663+ 2．(0分)[ID ：12407]下列命题正确的是（）A ．经过三点确定一个平面B ．经过一条直线和一个点确定一个平面C ．两两相交且不共点的三条直线确定一个平面D ．四边形确定一个平面3．(0分)[ID ：12405]三棱锥P -ABC 中，P A ⊥平面ABC ，AB ⊥BC ，P A =2，AB =BC =1，则其外接球的表面积为（）A ．6πB ．5πC ．4πD ．3π4．(0分)[ID ：12404]已知直线m 、n 及平面α，其中m ∥n ，那么在平面α内到两条直线m 、n 距离相等的点的集合可能是：（1）一条直线；（2）一个平面；（3）一个点；（4）空集。

其中正确的是（）A ．（1）（2）（3）B ．（1）（4）C ．（1）（2）（4）D ．（2）（4）5．(0分)[ID ：12401]已知(2,0)A -，(0,2)B ，实数k 是常数，M ，N 是圆220x y kx ++=上两个不同点，P 是圆220x y kx ++=上的动点，如果M ，N 关于直线10x y --=对称，则PAB ∆面积的最大值是（）A ．32-B ．4C ．6D ．32+6．(0分)[ID ：12381]对于平面、β、γ和直线a 、b 、m 、n ,下列命题中真命题是( ) A ．若,,,,a m a n m n αα⊥⊥⊂⊂,则a α⊥B ．若//,a b b α⊂,则//a αC ．若//,,,a b αβαγβγ==则//a bD ．若,,//,//a b a b ββαα⊂⊂,则//βα7．(0分)[ID ：12373]已知m 和n 是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m ⊥β的是( )A ．α⊥β，且m ⊂αB ．m ⊥n ，且n ∥βC ．α⊥β，且m ∥αD ．m ∥n ，且n ⊥β8．(0分)[ID ：12372]已知正四面体ABCD 中，M 为棱AD 的中点，设P 是BCM ∆（含边界）内的点，若点P 到平面ABC ，平面ACD ，平面ABD 的距离相等，则符合条件的点P （）A ．仅有一个B ．有有限多个C ．有无限多个D ．不存在9．(0分)[ID ：12354]已知圆M:x 2+y 2−2ay =0(a >0)截直线x +y =0所得线段的长度是2√2，则圆M 与圆N:(x −1)2+(y −1)2=1的位置关系是（）A ．内切B ．相交C ．外切D ．相离10．(0分)[ID ：12352]已知直线20ax y a +-+=在两坐标轴上的截距相等，则实数(a = )A ．1B ．1-C ．2-或1D ．2或111．(0分)[ID ：12349]已知三棱锥S ABC -的每个顶点都在球O 的表面上，ABC ∆是边长为43的等边三角形，SA ⊥平面ABC ，且SB 与平面ABC 所成的角为6π，则球O 的表面积为（）A ．20πB ．40πC ．80πD ．160π12．(0分)[ID ：12340]某几何体的三视图如图所示，则该几何体的体积为( )A ．12B ．18C ．24D ．30 13．(0分)[ID ：12396]若a ＞b ＞0，0＜c ＜1，则A ．log a c ＜log b cB ．log c a ＜log c bC ．a c ＜b cD ．c a ＞c b 14．(0分)[ID ：12418]如图，正四面体ABCD 中，,EF 分别是线段AC 的三等分点，P 是线段AB 的中点，G 是线段BD 的动点，则( )A ．存在点G ，使PG EF ⊥成立B ．存在点G ，使FG EP ⊥成立C ．不存在点G ，使平面EFG ⊥平面ACD 成立D ．不存在点G ，使平面EFG ⊥平面ABD 成立 15．(0分)[ID ：12406]圆心在x +y =0上，且与x 轴交于点A （-3，0）和B （1，0）的圆的方程为（）A ．22(1)(1)5x y ++-=B ．22(1)(1)5x y -++=C ．22(1)(1)5x y -++=D ．22(1)(1)5x y ++-=二、填空题16．(0分)[ID ：12463]已知圆22:20(0)M x y ay a +-=>截直线0x y +=所得线段的长度是22，则圆M 与圆22:(1)(1)1N x y -+-=的位置关系是_________．17．(0分)[ID ：12458]已知圆22(1)16x y ++=，点(1,0),(1,0)E F -，过(1,0)E -的直线1l 与过(1,0)F 的直线2l 垂直且圆相交于,A C 和,B D ，则四边形ABCD 的面积的取值范围是_________.18．(0分)[ID ：12523]已知在直角梯形ABCD 中，AB AD ⊥，CD AD ⊥，224AB AD CD ===，将直角梯形ABCD 沿AC 折叠，使平面BAC ⊥平面DAC ，则三棱锥D ABC -外接球的体积为__________．19．(0分)[ID ：12443]已知B 与点()1,2,3A 关于点()0,1,2M -对称，则点B 的坐标是______．20．(0分)[ID ：12442]正三棱柱的底面边长为，高为2，则它的外接球的表面积为．21．(0分)[ID ：12441]如上图所示，在正方体1111ABCD A B C D -中，,M N 分别是棱1AB CC 、的中点，1MB P ∆的顶点P 在棱1CC 与棱11C D 上运动，有以下四个命题：A ．平面1MB P 1ND ⊥； B ．平面1MB P ⊥平面11ND A ；C ．∆1MB P 在底面ABCD 上的射影图形的面积为定值；D ．∆1MB P 在侧面11D C CD 上的射影图形是三角形．其中正确命题的序号是__________.22．(0分)[ID ：12500]如图，AB 是底面圆O 的直径,点C 是圆O 上异于A 、B 的点，PO 垂直于圆O 所在的平面，且1,2PO OB BC ===，点E 在线段PB 上，则CE OE +的最小值为________.23．(0分)[ID ：12437]在正方体1111ABCD A B C D -中，①BD 平面11CB D ②直线AD 与1CB 所成角的大小为60︒③1AA BD ⊥ ④平面11A BC ∥平面1ACD请把所有正确命题的序号填在横线上________．24．(0分)[ID ：12456]已知四面体ABCD 的外接球球心O 在棱CD 上，AB=3，CD=2，则A 、B 两点在四面体ABCD 的外接球上的球面距离是________.25．(0分)[ID ：12468]如图：点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动，则下列四个命题：①三棱锥1A D PC -的体积不变； ②1A P ∥面1ACD ；③1DPBC ；④面1PDB 面1ACD ．其中正确的命题的序号是__________.三、解答题26．(0分)[ID ：12605]如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，平面PBD ⊥平面ABCD ，2AD =，25PD =，4AB PB ==，60BAD ∠=︒.（1）求证：AD PB ⊥；（2）E 是侧棱PC 上一点，记PE PCλ=，当PB ⊥平面ADE 时，求实数λ的值 27．(0分)[ID ：12576]已知圆C 过点()1,1A ，()3,1B -，圆心C 在直线250x y --=上，P 是直线34100x y -+=上任意一点．（1）求圆C 的方程；（2）过点P 向圆C 引两条切线，切点分别为M ，N ，求四边形PMCN 的面积的最小值．28．(0分)[ID ：12616]如图所示的等腰梯形ABCD 中，//AB CD ，12AB AD BC CD a ====，E 为CD 中点．若沿AE 将三角形DAE 折起，并连接DB ，DC ，得到如图所示的几何体D-ABCE ，在图中解答以下问题：（1）设G 为AD 中点，求证：//DC 平面GBE ；（2）若平面DAE ⊥平面ABCE ，且F 为AB 中点，求证：DF AC ⊥．29．(0分)[ID ：12577]如图，在梯形ABCD 中，AB CD ∥，1AD DC BC ===，60ABC ∠=︒，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，1CF =.(1)证明：BC ⊥平面ACFE ；(2)设点M 在线段EF 上运动，平面MAB 与平面FCB 所成锐二面角为θ，求cos θ的取值范围.30．(0分)[ID ：12535]如图所示，直角梯形ABCD 中，//AD BC ，,AD AB ⊥22,AB BC AD ===四边形EDCF 为矩形，2DE =，平面EDCF ⊥ABCD .（1）求证：//DF 平面ABE ；（2）求二面角B EF D --二面角的正弦值；（3）在线段BE 上是否存在点P ，使得直线AP 与平面BEF 所成角的正弦值为66，若存在，求出线段BP的长，若不存在，请说明理由.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．D2．C3．A4．C5．D6．C7．D8．A9．B10．D11．C12．C13．B14．C15．A二、填空题16．相交【解析】【分析】根据直线与圆相交的弦长公式求出的值结合两圆的位置关系进行判断即可【详解】解：圆的标准方程为则圆心为半径圆心到直线的距离圆截直线所得线段的长度是即则圆心为半径圆的圆心为半径则即两个17．【解析】【分析】由题可知而过的弦过圆心时最长与垂直时最短据此则可以确定四边形的面积的取值范围【详解】由题知直线过圆心故设圆心到直线的距离为则所以所以四边形的面积;故答案为:【点睛】本题主要考查直线与18．【解析】结合题意画出折叠后得到的三棱锥如图所示由条件可得在底面中取AB的中点OAC的中点E连OCOE则∵∴∵平面平面∴平面∴又∴∴∴点O为三棱锥外接球的球心球半径为2∴答案：点睛：（1）本题是一道关19．【解析】【分析】根据空间直角坐标系中点坐标公式求结果【详解】设B则所以所以的坐标为【点睛】本题考查空间直角坐标系中点坐标公式考查基本分析求解能力属基础题20．【解析】试题分析：由正三棱柱底面边长为得底面所在平面截其外接球所成圆半径为又由高为则球心到圆的球心距为根据球心距截面圆半径球半径构成的直角三角形满足勾股定理我们易得半径满足：已知求得正三棱柱外接球所21．【解析】由正方体的几何性质对4个命题进行判断对于A当动点P与点重合时以等腰三角形与不垂直所以不能得出平面A为假命题；对于B易证所以平面所以平面⊥平面故B为真命题；对于C在底面上的射影图形的面积为定值22．【解析】【分析】首先求出即有将三棱锥展开当三点共线时值最小可证为中点从而可求从而得解【详解】在中所以同理所以在三棱锥中将侧面绕旋转至平面使之与平面共面如图所示当共线时取得最小值又因为所以垂直平分即为23．①③④【解析】【分析】利用线面平行的判定定理判断①；由异面直线所成角判断②；由线面垂直的性质判断③；由面面平行的判定定理判断④【详解】对于①如下图所示由于则四边形为平行四边形则面面所以平面故①正确；24．【解析】【分析】根据球心到四个顶点距离相等可推断出O为CD的中点且OA＝OB＝OC ＝OD进而在△A0B中利用余弦定理求得cos∠AOB的值则∠AOB可求进而根据弧长的计算方法求得答案【详解】解：球心25．①②④【解析】对于①因为从而平面故上任意一点到平面的距离均相等以为顶点平面为底面则三棱锥的体积不变正确；对于②连接容易证明且相等由于①知：平面平面所以可得面②正确；对于③由于平面若则平面则为中点与动三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．D解析：D【解析】【分析】先求出球心O 到底面距离的最大值，从而可求顶点D 到底面的距离的最大值，利用该最大值可求体积的最大值.【详解】设外接球的球心为O ，半径为R ，则24128R ππ=，故42R =设球心O 在底面上的投影为E ，因为OA OC OB ==，故E 为ABC ∆的外心.因为4AB BC ==，42AC =222AC AB BC =+，故ABC ∆为直角三角形，故E 为AC 的中点，所以2226OE OA AE =-=，设D 到底面ABC 的距离为h ，则2642h OE R ≤+=所以三棱锥D ABC -的体积的最大值为(1132216644264232+⨯⨯⨯⨯=. 故选：D.【点睛】几何体的外接球、内切球问题，关键是球心位置的确定，必要时需把球的半径放置在可解的几何图形中，注意球心在底面上的投影为底面外接圆的圆心．如果球心的位置不易确定，则可以把该几何体补成规则的几何体，便于球心位置和球的半径的确定．2．C解析：C【解析】【分析】根据确定一个平面的公理及推论即可选出.【详解】A 选项，根据平面基本性质知，不共线的三点确定一个平面，故错误；B 选项，根据平面基本性质公理一的推论，直线和直线外一点确定一个平面，故错误；C 选项，根据公理一可知，不共线的三点确定一个平面，而两两相交且不共点的三条直线，在三个不共线的交点确定的唯一平面内，所以两两相交且不共点的三条直线确定一个平面，正确；选项D,空间四边形不能确定一个平面，故错误；综上知选C.【点睛】本题主要考查了平面的基本性质公理一及其推论，属于中档题.3．A解析：A【解析】分析：将三棱锥的外接球转化为以,,AP AB BC 为长宽高的长方体的外接球，从而可得球半径，进而可得结果.详解：因为PA ⊥平面AB ，,AB BC ⊂平面ABC ，PA BC ∴⊥，,PA AB AB BC ⊥⊥，所以三棱锥的外接球，就是以,,AP AB BC 为长宽高的长方体的外接球，外接球的直径等于长方体的对角线，即2R ==246R ππ=，故选A.点睛：本题主要考查三棱锥外接球表面积的求法，属于难题.要求外接球的表面积和体积，关键是求出求的半径，求外接球半径的常见方法有：①若三条棱两垂直则用22224R a b c =++（,,a b c 为三棱的长）；②若SA ⊥面ABC （SA a =），则22244R r a =+（r 为ABC ∆外接圆半径） ③可以转化为长方体的外接球；④特殊几何体可以直接找出球心和半径.4．C解析：C【解析】【分析】根据题意，对每一个选项进行逐一判定，不正确的只需举出反例，正确的作出证明，即可得到答案.【详解】如图（1）所示，在平面内不可能由符合题的点；如图（2），直线,a b 到已知平面的距离相等且所在平面与已知平面垂直，则已知平面为符合题意的点；如图（3），直线,a b 所在平面与已知平面平行，则符合题意的点为一条直线，综上可知（1）（2）（4）是正确的，故选C.【点睛】本题主要考查了空间中直线与平面之间的位置关系，其中熟记空间中点、线、面的位置关系是解答此类问题的关键，着重考查了空间想象能力，以及推理与论证能力，属于基础题. 5．D解析：D【解析】【分析】根据圆上两点,M N 关于直线10x y --=对称，可知圆心在该直线上，从而求出圆心坐标与半径，要使得PAB ∆面积最大，则要使得圆上点P 到直线AB 的距离最大，所以高最大为3212+，PAB S ∆最大值为32 【详解】由题意，圆x 2+y 2+kx=0的圆心（-2k ，0）在直线x-y-1=0上， ∴-2k -1=0，∴k=-2,∴圆x 2+y 2+kx=0的圆心坐标为（1，0），半径为1 ∵A （-2，0），B （0，2），∴直线AB 的方程为2x -+2y =1，即x-y+2=0 ∴圆心到直线AB 32. ∴△PAB 面积的最大值是1321322||(1)222222AB +=⨯=2 故选D ．【点睛】主要考查了与圆有关的最值问题，属于中档题.该题涉及到圆上动点到定直线（圆与直线相离）的最大距离.而圆上动点到定直线的最小距离为圆心到直线距离减去半径，最大距离为圆心到直线距离加上半径.6．C解析：C【解析】【分析】【详解】若由线面垂直的判定定理知,只有当和为相交线时,才有错误；若此时由线面平行的判定定理可知,只有当在平面外时,才有错误；由面面平行的性质定理:若两平面平行,第三个平面与他们都相交,则交线平行,可判断,若//αβ，a αγ⋂=，b βγ=，则//a b 为真命题, 正确；若此时由面面平行的判定定理可知,只有当、为相交线时,才有//,D βα错误.故选C.考点：考查直线与直线，直线与平面，平面与平面的位置关系. 7．D解析：D【解析】【分析】根据所给条件，分别进行分析判断，即可得出正确答案.【详解】解：αβ⊥且m α⊂⇒m β⊂或//m β或m 与β相交，故A 不成立；m n ⊥且//n β⇒m β⊂或//m β或m 与β相交，故B 不成立；αβ⊥且//m α⇒m β⊂或//m β或m 与β相交，故C 不成立；//m n 且n β⊥⇒m β⊥，故D 成立；故选：D【点睛】本题考查直线与平面的位置关系，线面垂直判定，属于基础题.8．A解析：A【解析】【分析】根据正四面体的对称性分析到平面ABC ，平面ACD ，平面ABD 的距离相等的点的轨迹，与BCM ∆所在平面的公共部分即符合条件的点P .【详解】在正四面体ABCD 中，取正三角形BCD 中心O ，连接AO ，根据正四面体的对称性，线段AO 上任一点到平面ABC ，平面ACD ，平面ABD 的距离相等，到平面ABC ，平面ACD ，平面ABD 的距离相等的点都在AO 所在直线上，AO 与BCM ∆所在平面相交且交于BCM ∆内部，所以符合题意的点P 只有唯一一个.故选：A【点睛】此题考查正四面体的几何特征，对称性，根据几何特征解决点到平面距离问题，考查空间想象能力.9．B解析：B【解析】化简圆M:x 2+(y −a)2=a 2⇒M(0,a),r 1=a ⇒M 到直线x +y =0的距离d =√2⇒ (√2)2+2=a 2⇒a =2⇒M(0,2),r 1=2，又N(1,1),r 2=1⇒|MN|=√2⇒|r 1−r 2|<|MN|< |r 1+r 2|⇒两圆相交. 选B10．D解析：D【解析】【分析】根据题意讨论直线它在两坐标轴上的截距为0和在两坐标轴上的截距不为0时，求出对应a 的值，即可得到答案．【详解】由题意，当2a 0-+=，即a 2=时，直线ax y 2a 0+-+=化为2x y 0+=，此时直线在两坐标轴上的截距都为0，满足题意；当2a 0-+≠，即a 2≠时，直线ax y 2a 0+-+=化为122x y a a a+=--，由直线在两坐标轴上的截距相等，可得2a 2a a-=-，解得a 1=；综上所述，实数a 2=或a 1=．故选：D ．【点睛】本题主要考查了直线方程的应用，以及直线在坐标轴上的截距的应用，其中解答中熟记直线在坐标轴上的截距定义，合理分类讨论求解是解答的关键，着重考查了运算与求解能力，属于基础题.11．C解析：C【解析】【分析】根据线面夹角得到4SA =，计算ABC ∆的外接圆半径为42sin a r A ==，2222SA R r ⎛⎫=+ ⎪⎝⎭，解得答案. 【详解】 SA ⊥平面ABC ，则SB 与平面ABC 所成的角为6SBA π∠=，故4SA =.ABC ∆的外接圆半径为42sin a r A ==，设球O 的半径为R ，则2222SA R r ⎛⎫=+ ⎪⎝⎭，解得25R =，故球O 的表面积为2480R ππ=. 故选：C .【点睛】本题考查了三棱锥的外接球问题，意在考查学生的计算能力和空间想象能力.12．C解析：C【解析】试题分析：由三视图可知，几何体是三棱柱消去一个同底的三棱锥，如图所示，三棱柱的高为5，消去的三棱锥的高为3，三棱锥与三棱柱的底面为直角边长分别为3和4的直角三角形，所以几何体的体积为V =12×3×4×5−13×12×3×4×3=24，故选C ．考点：几何体的三视图及体积的计算．【方法点晴】本题主要考查了几何体的三视图的应用及体积的计算，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答的难点在于根据几何体的三视图还原出原几何体和几何体的度量关系，属于中档试题．13．B解析：B【解析】试题分析：对于选项A ，a b 1gc 1gc log c ,log c lg a lg b==，01c <<，10gc ∴<，而0a b >>，所以lg lg a b >，但不能确定lg lg a b 、的正负，所以它们的大小不能确定;对于选项B ，c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >，两边同乘以一个负数1lg c改变不等号方向，所以选项B 正确;对于选项C ，利用c y x =在第一象限内是增函数即可得到c c a b >，所以C 错误;对于选项D ，利用xy c =在R 上为减函数易得a b c c <，所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较；若底数不同,可考虑利用中间量进行比较. 14．C解析：C【解析】【分析】利用空间中线线、线面、面面间的位置关系对选项进行一一验证，即可得答案．【详解】正四面体ABCD 中，,E F 分别是线段AC 的三等分点，P 是线段AB 的中点，G 是直线BD 的动点，在A 中，不存在点G ，使PG EF ⊥成立，故A 错误；在B 中，不存在点G ，使FG EP ⊥成立，故B 错误；在C 中，不存在点G ，使平面EFG ⊥平面ACD 成立，故C 正确；在D 中，存在点G ，使平面EFG ⊥平面ABD 成立，故D 错误.故选：C.【点睛】本题考查命题真假的判断、考查空间中线线、线面、面面间的位置关系，考查转化与化归思想，考查空间想象能力．15．A解析：A【解析】【分析】由题意得：圆心在直线x=-1上，又圆心在直线x+y=0上，故圆心M 的坐标为（-1，1），再由点点距得到半径。

广东省阳江市高一下学期期中数学试卷

广东省阳江市高一下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） P是所在平面内一点，，则P点一定在（）A . 内部B . 在直线AC上C . 在直线AB上D . 在直线BC上2. （2分）若，且，则下列不等式一定成立的是（）A .B .C .D .3. （2分）在等差数列{an}中，a5=33，a45=153，则201是该数列的第（）项．A . 60B . 61C . 62D . 634. （2分） (2018高二上·武邑月考) 若等比数列{an}的前n项和Sn＝2010n＋t(t为常数)，则a1的值为（）A . 2008B . 2009C . 2010D . 20115. （2分）若数列{an}的通项公式为an=2n+5，则此数列是（）A . 公差为2的等差数列B . 公差为5的等差数列C . 首项为5的等差数列D . 公差为n的等差数列6. （2分）(2018·枣庄模拟) 要得到函数的图象，只需将函数的图象（）A . 向左平移个单位B . 向左平移个单位C . 向右平移个单位D . 向右平移个单位7. （2分）下列命题正确的是（）A . 若a>b，则B . 若，则C . 若，则a>bD . 若a>b，则a-c>b-c8. （2分）(2018·佛山模拟) 设满足约束条件，则的最小值为（）A . 4B . 0C . 2D . -49. （2分） (2018高一下·平原期末) 如图，测量河对岸的塔高时，可以选与塔底在同一水平面内的两个观测点与，测得米，并在测得塔顶的仰角为，则塔的高度为（）A . 米B . 米C . 米D . 米10. （2分）函数的值域为（）A .B .C .D .11. （2分）(2017·衡水模拟) 已知函数y=2sinx的定义域为[a，b]，值域为[﹣2，1]，则b﹣a的值不可能是（）A .B . πC . 2πD .12. （2分） (2016高三上·翔安期中) 如果数列{an}的前n项和Sn= an﹣3，那么这个数列的通项公式是（）A . an=2（n2+n+1）B . an=3×2nC . an=3n+1D . an=2×3n二、填空题 (共4题；共4分)13. （1分）(2018·河北模拟) 已知向量，的夹角为，且，则 ________．14. （1分） (2016高三上·六合期中) 设Sn为数列{an}的前n项和，Sn=kn2+n，n∈N* ，其中k是常数．若对于任意的m∈N* ， am ， a2m ， a4m成等比数列，则k的值为________．15. （1分）(2017·天津) 若a，b∈R，ab＞0，则的最小值为________．16. （1分）(2017·黑龙江模拟) 如图，A，B，C，D为平面四边形ABCD的四个内角，若A+C=180°，AB=6，BC=4，CD=5，AD=5，则四边形ABCD面积是________．三、解答题 (共6题；共60分)17. （10分）(2017·盐城模拟) 设△ABC面积的大小为S，且3 • =2S．（1）求sinA的值；（2）若C= ，• =16，求AC．18. （10分） (2016高一下·亭湖期中) 已知cosθ=﹣，θ∈（，π），求（1）sinθ的值（2） cos（﹣θ ）的值．19. （10分） (2016高一上·启东期末) 如图所示，我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪，两个三角形地块PAB与QAD种植花卉，一个三角形地块CPQ设计成水景喷泉，四周铺设小路供居民平时休闲散步，点P在边BC上，点Q在边CD上，记∠PAB=a．（1）当∠PAQ= 时，求花卉种植面积S关于a的函数表达式，并求S的最小值；（2）考虑到小区道路的整体规划，要求PB+DQ=PQ，请探究∠PAQ是否为定值，若是，求出此定值，若不是，请说明理由．20. （10分） (2017高三下·黑龙江开学考) 已知数列{an}满足a1=1，an+1=2an+1（n∈N*）．（1）求数列{an}的通项公式；（2）设Sn为数列{ }的前n项和，求证：1≤Sn＜4．21. （10分）(2019·郓城模拟) 设数列满足．（1）求的通项公式；（2）求数列的前项和．22. （10分） (2016高一上·荆州期中) 某自来水厂的蓄水池存有400吨水，水厂每小时可向蓄水池中注水60吨，同时蓄水池又向居民小区不间断供水，t小时内供水总量为吨，（0≤t≤24）（1）从供水开始到第几小时时，蓄水池中的存水量最少？最少水量是多少吨？（2）若蓄水池中水量少于80吨时，就会出现供水紧张现象，请问：在一天的24小时内，有几小时出现供水紧张现象．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、第11 页共11 页。