中考模拟题八

合集下载

深圳市中考数学模拟试卷（八）含答案解析

广东省深圳市中考数学模拟试卷（八）一、选择题．（本题共10小题，每小题3分，共30分，在每小题所给出的选项中，只有一项符合题目要求）1．2的倒数是（）A．B．﹣C．2 D．﹣22．12月13日，嫦娥二号成功飞抵距地球约700万公里远的深空，7 000 000用科学记数法表示为（）A．7×105B．7×106C．70×106D．7×1073．如图，OA⊥OB，若∠1=40°，则∠2的度数是（）A．20° B．40°C．50°D．60°4．下列立体图形中，俯视图是正方形的是（）A．B．C．D．5．二次函数y=﹣2（x﹣1）2+3的图象的顶点坐标是（）A．（1，3）B．（﹣1，3） C．（1，﹣3） D．（﹣1，﹣3）6．某校九年级开展“光盘行动”宣传活动，各班级参加该活动的人数统计结果如下表，对于这组统计数据，下列说法中正确的是（）班级1班2班3班4班5班6班人数52 60 62 54 58 62A．极差是40 B．众数是60 C．平均数是58 D．中位数是587．已知A（﹣1，y1），B（2，y2）两点在双曲线y=上，且 y1＞y2，则m的取值范围是（）A．m＜0 B．m＞0 C．m＞﹣D．m＜﹣8．圆锥底面圆的半径为3cm，其侧面展开图是半圆，则圆锥母线长为（）A．3cm B．6cm C．9cm D．12cm9．△ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a2+b2=c2，那么下列结论正确的是（）A．csinA=a B．bcosB=c C．atanA=b D．ctanB=b10．若正比例函数y=mx（m≠0），y随x的增大而减小，则它和二次函数y=mx2+m的图象大致是（）A．B．C．D．二.填空题．（本大题共6小题，每小题4分，共24分）11．如图，⊙O的直径AB与弦CD垂直，且∠BAC=40°，则∠BOD=．12．从1，2，3这三个数字中任意取出两个不同的数字，则取出的两个数字都是奇数的概率是．13．一次函数y=kx+1的图象经过（1，2），则反比例函数的图象经过点（2，）．14．点P在线段AB的垂直平分线上，PA=7，则PB=．15．如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为（6，0），⊙P的半径为，则点P的坐标为．16．如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AG=13，CF=6，则四边形BDFG的周长为．三.解答题（一）（本大题共3小题，每小题6分，共18分）17．计算：|﹣2|+﹣4sin45°﹣1﹣2．18．化简：÷（1﹣）．19．如图：已知D、E分别在AB、AC上，AB=AC，∠B=∠C，求证：BE=CD．四、解答题（二）（本大题3小题，每小题7分，共21分）20．为响应我市“中国梦”•“宜宾梦”主题教育活动，某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛，评选出一、二、三等奖和优秀奖．小明同学根据获奖结果，绘制成如图所示的统计表和数学统计图．等级频数频率一等奖 a 0.1二等奖10 0.2三等奖 b 0.4优秀奖15 0.3请你根据以上图表提供的信息，解答下列问题：（1）a=，b=，n=．（2）学校决定在获得一等奖的作者中，随机推荐两名作者代表学校参加市级比赛，其中王梦、李刚都获得一等奖，请用画树状图或列表的方法，求恰好选中这二人的概率．21．4月20日，我省芦山县发生7.0级强烈地震，造成大量的房屋损毁，急需大量帐篷．某企业接到任务，须在规定时间内生产一批帐篷．如果按原来的生产速度，每天生产120顶帐篷，那么在规定时间内只能完成任务的90%．为按时完成任务，该企业所有人员都支援到生产第一线，这样，每天能生产160顶帐篷，刚好提前一天完成任务．问规定时间是多少天？生产任务是多少顶帐篷？22．宜宾是国家级历史文化名城，大观楼是标志性建筑之一（如图①）．喜爱数学实践活动的小伟查资料得知：大观楼始建于明代（一说是唐代韦皋所建），后毁于兵火，乾隆乙酉年（1765年）重建，它是我国目前现存最高大、最古老的楼阁之一．小伟决定用自己所学习的知识测量大观楼的高度．如图②，他利用测角仪站在B处测得大观楼最高点P的仰角为45°，又前进了12米到达A处，在A处测得P的仰角为60°．请你帮助小伟算算大观楼的高度．（测角仪高度忽略不计，≈1.7，结果保留整数）．五、解答题（三）（本大题3小题，每小题9分，共27分）23．如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°．得到△ADE，连接BD，CE交于点F．（1）求证：△ABD≌△ACE；（2）求∠ACE的度数；（3）求证：四边形ABFE是菱形．24．数学活动﹣﹣求重叠部分的面积．问题情境：数学活动课上，老师出示了一个问题：如图1，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合，DE经过点C，DF交AC于点C．求重叠部分（△DCG）的面积．（1）思考：请解答老师提出的问题．（2）合作交流：“希望”小组受此问题的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图2，求出重叠部分（△DGH）的面积，请写出解答过程．（3）提出问题：老师要求各小组向“希望”小组学习，将△DEF绕点D旋转，再提出一个求重叠部分面积的问题．“爱心”小组提出的问题是：如图3，将△DEF绕点D旋转，DE，DF分别交AC于点M，N，使DM=MN，求重叠部分（△DMN）的面积．任务：请解决“爱心”小组所提出的问题，直接写出△DMN的面积是．25．如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a＞0），经过点A和x轴正半轴上的点B，AO=OB=2，∠AOB=120°．（1）求这条抛物线的表达式；（2）连接OM，求∠AOM的大小；（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．广东省深圳市中考数学模拟试卷（八）参考答案与试题解析一、选择题．（本题共10小题，每小题3分，共30分，在每小题所给出的选项中，只有一项符合题目要求）1．2的倒数是（）A．B．﹣C．2 D．﹣2【考点】倒数．【分析】根据倒数的概念求解．【解答】解：2的倒数是．故选A．【点评】主要考查倒数的定义，要求熟练掌握．需要注意的是倒数的性质：负数的倒数是负数，正数的倒数是正数，0没有倒数．倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．2．12月13日，嫦娥二号成功飞抵距地球约700万公里远的深空，7 000 000用科学记数法表示为（）A．7×105B．7×106C．70×106D．7×107【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于7 000 000有7位，所以可以确定n=7﹣1=6．【解答】解：7 000 000=7×106．故选B．【点评】此题考查科学记数法表示较大的数的方法，准确确定a与n值是关键．3．如图，OA⊥OB，若∠1=40°，则∠2的度数是（）A．20° B．40°C．50°D．60°【考点】余角和补角．【专题】计算题．【分析】根据互余两角之和为90°即可求解．【解答】解：∵OA⊥OB，∠1=40°，∴∠2=90°﹣∠1=90°﹣40°=50°．故选C．【点评】本题考查了余角的知识，属于基础题，掌握互余两角之和等于90°是解答本题的关键．4．下列立体图形中，俯视图是正方形的是（）A．B．C．D．【考点】简单几何体的三视图．【分析】根据从上面看得到的图形是俯视图，可得答案．【解答】解；A、正方体的俯视图是正方形，故A正确；B、圆柱的俯视图是圆，故B错误；C、三棱锥的俯视图是三角形，故C错误；D、圆锥的俯视图是圆，故D错误，故选：A．【点评】本题考查了简单几何体的三视图，从上面看得到的图形是俯视图．5．二次函数y=﹣2（x﹣1）2+3的图象的顶点坐标是（）A．（1，3）B．（﹣1，3） C．（1，﹣3） D．（﹣1，﹣3）【考点】二次函数的性质．【分析】根据二次函数顶点式解析式写出顶点坐标即可．【解答】解：二次函数y=﹣2（x﹣1）2+3的图象的顶点坐标为（1，3）．故选A．【点评】本题考查了二次函数的性质，熟练掌握利用顶点式解析式写出顶点坐标的方法是解题的关键．6．某校九年级开展“光盘行动”宣传活动，各班级参加该活动的人数统计结果如下表，对于这组统计数据，下列说法中正确的是（）班级1班2班3班4班5班6班人数52 60 62 54 58 62A．极差是40 B．众数是60 C．平均数是58 D．中位数是58【考点】众数；算术平均数；中位数；极差．【分析】分别计算该组数据的众数、平均数、中位数及极差后，选择正确的答案即可．【解答】解：A．极差是62﹣52=10，故此选项错误；B．62出现了2次，最多，所以众数为62，故此选项错误；C． =（52+60+62+54+58+62）÷6=58；故此选项正确；D．∵6个数据按大小排列后为：52，54，58，60，62，62；∴中位数为：（60+58）÷2=59；故此选项错误；故选：C．【点评】此题主要考查了平均数、众数、中位数及极差的知识，解题时分别计算出众数、中位数、平均数及极差后找到正确的选项即可．7．已知A（﹣1，y1），B（2，y2）两点在双曲线y=上，且 y1＞y2，则m的取值范围是（）A．m＜0 B．m＞0 C．m＞﹣D．m＜﹣【考点】反比例函数图象上点的坐标特征．【专题】计算题．【分析】将A（﹣1，y1），B（2，y2）两点分别代入双曲线y=，求出 y1与y2的表达式，再根据 y1＞y2则列不等式即可解答．【解答】解：将A（﹣1，y1），B（2，y2）两点分别代入双曲线y=得，y1=﹣2m﹣3，y2=，∵y1＞y2，∴﹣2m﹣3＞，解得m＜﹣，故选：D．【点评】本题考查了反比例函数图象上点的坐标特征，要知道，反比例函数图象上的点符合函数解析式．8．圆锥底面圆的半径为3cm，其侧面展开图是半圆，则圆锥母线长为（）A．3cm B．6cm C．9cm D．12cm【考点】圆锥的计算．【专题】压轴题．【分析】首先求得圆锥的底面周长，然后根据圆的周长公式即可求得母线长．【解答】解：圆锥的底面周长是：6πcm，设母线长是l，则lπ=6π，解得：l=6．故选B．【点评】考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．9．△ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a2+b2=c2，那么下列结论正确的是（）A．csinA=a B．bcosB=c C．atanA=b D．ctanB=b【考点】勾股定理的逆定理；锐角三角函数的定义．【分析】由于a2+b2=c2，根据勾股定理的逆定理得到△ABC是直角三角形，且∠C=90°，再根据锐角三角函数的定义即可得到正确选项．【解答】解：∵a2+b2=c2，∴△ABC是直角三角形，且∠C=90°．A、sinA=，则csinA=a．故本选项正确；B、cosB=，则cosBc=a．故本选项错误；C、tanA=，则=b．故本选项错误；D、tanB=，则atanB=b．故本选项错误．故选A．【点评】本题考查了锐角三角函数的定义和勾股定理的逆定理．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．10．若正比例函数y=mx（m≠0），y随x的增大而减小，则它和二次函数y=mx2+m的图象大致是（）A．B．C．D．【考点】二次函数的图象；正比例函数的图象．【专题】压轴题．【分析】根据正比例函数图象的性质确定m＜0，则二次函数y=mx2+m的图象开口方向向下，且与y轴交于负半轴．【解答】解：∵正比例函数y=mx（m≠0），y随x的增大而减小，∴该正比例函数图象经过第二、四象限，且m＜0．∴二次函数y=mx2+m的图象开口方向向下，且与y轴交于负半轴．综上所述，符合题意的只有A选项．故选A．【点评】本题考查了二次函数图象、正比例函数图象．利用正比例函数的性质，推知m＜0是解题的突破口．二.填空题．（本大题共6小题，每小题4分，共24分）11．如图，⊙O的直径AB与弦CD垂直，且∠BAC=40°，则∠BOD=80°．【考点】圆周角定理；垂径定理．【分析】根据垂径定理可得点B是中点，由圆周角定理可得∠BOD=2∠BAC，继而得出答案．【解答】解：∵，⊙O的直径AB与弦CD垂直，∴=，∴∠BOD=2∠BAC=80°．故答案为：80°．【点评】此题考查了圆周角定理，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半．12．从1，2，3这三个数字中任意取出两个不同的数字，则取出的两个数字都是奇数的概率是．【考点】列表法与树状图法．【专题】压轴题．【分析】首先列出树状图，可以直观的看出总共有几种情况，再找出都是奇数的情况，根据概率公式进行计算即可．【解答】解：如图所示：取出的两个数字都是奇数的概率是： =，故答案为：．【点评】此题主要考查了画树状图，以及概率公式，关键是正确画出树状图．13．一次函数y=kx+1的图象经过（1，2），则反比例函数的图象经过点（2，）．【考点】反比例函数图象上点的坐标特征；一次函数图象上点的坐标特征．【专题】压轴题．【分析】把点（1，2）代入一次函数解析式求得k的值．然后利用反比例函数图象上点的坐标特征来填空．【解答】解：∵一次函数y=kx+1的图象经过（1，2），∴2=k+1，解得，k=1．则反比例函数解析式为y=，∴当x=2时，y=．故答案是：．【点评】本题考查了一次函数、反比例函数图象上点的坐标特征．利用待定系数法求得一次函数解析式是解题的关键．14．点P在线段AB的垂直平分线上，PA=7，则PB=7．【考点】线段垂直平分线的性质．【分析】根据线段垂直平分线的性质得出PA=PB，代入即可求出答案．【解答】解：∵点P在线段AB的垂直平分线上，PA=7，∴PB=PA=7，故答案为：7．【点评】本题考查了对线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．15．如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，⊙P与x轴交于O，A两点，点A的坐标为（6，0），⊙P的半径为，则点P的坐标为（3，2）．【考点】垂径定理；坐标与图形性质；勾股定理．【专题】压轴题；探究型．【分析】过点P作PD⊥x轴于点D，连接OP，先由垂径定理求出OD的长，再根据勾股定理求出PD的长，故可得出答案．【解答】解：过点P作PD⊥x轴于点D，连接OP，∵A（6，0），PD⊥OA，∴OD=OA=3，在Rt△OPD中，∵OP=，OD=3，∴PD===2，∴P（3，2）．故答案为：（3，2）．【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．16．如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AG=13，CF=6，则四边形BDFG的周长为20．【考点】菱形的判定与性质；直角三角形斜边上的中线；勾股定理．【专题】压轴题．【分析】首先可判断四边形BGFD是平行四边形，再由直角三角形斜边中线等于斜边一半，可得BD=FD，则可判断四边形BGFD是菱形，设GF=x，则AF=13﹣x，AC=2x，在Rt△ACF中利用勾股定理可求出x的值．【解答】解：∵AG∥BD，BD=FG，∴四边形BGFD是平行四边形，∵CF⊥BD，∴CF⊥AG，又∵点D是AC中点，∴BD=DF=AC，∴四边形BGFD是菱形，设GF=x，则AF=13﹣x，AC=2x，∵在Rt△ACF中，∠CFA=90°，∴AF2+CF2=AC2，即（13﹣x）2+62=（2x）2，解得：x=5，故四边形BDFG的周长=4GF=20．故答案为：20．【点评】本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质，解答本题的关键是判断出四边形BGFD是菱形．三.解答题（一）（本大题共3小题，每小题6分，共18分）17．计算：|﹣2|+﹣4sin45°﹣1﹣2．【考点】实数的运算；负整数指数幂；特殊角的三角函数值．【专题】计算题．【分析】原式第一项利用绝对值的代数意义化简，第二项化为最简二次根式，第三项利用特殊角的三角函数值计算，最后一项利用负指数幂法则计算即可得到结果．【解答】解：原式=2+2﹣4×﹣1=1．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．18．化简：÷（1﹣）．【考点】分式的混合运算．【分析】先因式分解再约分求解即可．【解答】解：÷（1﹣）=×，=．【点评】本题主要考查了分式的混合运算，解题的关键是熟记因式分解的几种方法．19．如图：已知D、E分别在AB、AC上，AB=AC，∠B=∠C，求证：BE=CD．【考点】全等三角形的判定与性质．【专题】证明题．【分析】要证明BE=CD，把BE与CD分别放在两三角形中，证明两三角形全等即可得到，而证明两三角形全等需要三个条件，题中已知一对边和一对角对应相等，观察图形可得出一对公共角，进而利用ASA可得出三角形ABE与三角形ACD全等，利用全等三角形的对应边相等可得证．【解答】证明：在△ABE和△ACD中，，∴△ABE≌△ACD（ASA），∴BE=CD（全等三角形的对应边相等）．【点评】此题考查了全等三角形的判定与性质，全等三角形的判定方法为：SSS；SAS；ASA；AAS；HL（直角三角形判定全等的方法），常常利用三角形的全等来解决线段或角相等的问题，在证明三角形全等时，要注意公共角及公共边，对顶角等隐含条件的运用．四、解答题（二）（本大题3小题，每小题7分，共21分）20．为响应我市“中国梦”•“宜宾梦”主题教育活动，某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛，评选出一、二、三等奖和优秀奖．小明同学根据获奖结果，绘制成如图所示的统计表和数学统计图．等级频数频率一等奖 a 0.1二等奖10 0.2三等奖 b 0.4优秀奖15 0.3请你根据以上图表提供的信息，解答下列问题：（1）a=5，b=20，n=144．（2）学校决定在获得一等奖的作者中，随机推荐两名作者代表学校参加市级比赛，其中王梦、李刚都获得一等奖，请用画树状图或列表的方法，求恰好选中这二人的概率．【考点】列表法与树状图法；频数（率）分布表；扇形统计图．【专题】图表型．【分析】（1）首先利用频数、频率之间的关系求得参赛人数，然后乘以一等奖的频率即可求得a 值，乘以三等奖的频率即可求得b值，用三等奖的频率乘以360°即可求得n值；（2）列表后即可将所有情况全部列举出来，从而求得恰好抽中者两人的概率；【解答】解：（1）观察统计表知，二等奖的有10人，频率为0.2，故参赛的总人数为10÷0.2=50人，a=50×0.1=5人，b=50×0.4=20．n=0.4×360°=144°，故答案为：5，20，144；（2）列表得：A B C 王李A ﹣AB AC A王A李B BA ﹣BC B王B李C CA CB ﹣C王C李王王A 王B 王C ﹣王李李李A 李B 李C 李王﹣∵共有20种等可能的情况，恰好是王梦、李刚的有2种情况，∴恰好选中王梦和李刚两位同学的概率P==．【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．21．4月20日，我省芦山县发生7.0级强烈地震，造成大量的房屋损毁，急需大量帐篷．某企业接到任务，须在规定时间内生产一批帐篷．如果按原来的生产速度，每天生产120顶帐篷，那么在规定时间内只能完成任务的90%．为按时完成任务，该企业所有人员都支援到生产第一线，这样，每天能生产160顶帐篷，刚好提前一天完成任务．问规定时间是多少天？生产任务是多少顶帐篷？【考点】二元一次方程组的应用．【专题】应用题．【分析】设规定时间为x天，生产任务是y顶帐篷，根据不提速在规定时间内只能完成任务的90%，即提速后刚好提前一天完成任务，可得出方程组，解出即可．【解答】解：设规定时间为x天，生产任务是y顶帐篷，由题意得，，解得：．答：规定时间是6天，生产任务是800顶帐篷．【点评】本题考查了二元一次方程组的应用，解答本题的关键是仔细审题，设出未知数，利用等量关系得出方程组，难度一般．22．宜宾是国家级历史文化名城，大观楼是标志性建筑之一（如图①）．喜爱数学实践活动的小伟查资料得知：大观楼始建于明代（一说是唐代韦皋所建），后毁于兵火，乾隆乙酉年（1765年）重建，它是我国目前现存最高大、最古老的楼阁之一．小伟决定用自己所学习的知识测量大观楼的高度．如图②，他利用测角仪站在B处测得大观楼最高点P的仰角为45°，又前进了12米到达A处，在A处测得P的仰角为60°．请你帮助小伟算算大观楼的高度．（测角仪高度忽略不计，≈1.7，结果保留整数）．【考点】解直角三角形的应用-仰角俯角问题．【专题】应用题．【分析】设大观楼的高OP=x，在Rt△POB中表示出OB，在Rt△POA中表示出OA，再由AB=12米，可得出方程，解出即可得出答案．【解答】解：设大观楼的高OP=x，在Rt△POB中，∠OBP=45°，则OB=OP=x，在Rt△POA中，∠OAP=60°，则OA==x，由题意得，AB=OB﹣OA=12m，即x﹣x=12，解得：x=18+6，故大观楼的高度OP=18+6≈28（米）．答：大观楼的高度约为28米．【点评】本题考查了解直角三角形的应用，要求学生能借助仰角构造直角三角形并解直角三角形，注意方程思想的运用．五、解答题（三）（本大题3小题，每小题9分，共27分）23．如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°．得到△ADE，连接BD，CE交于点F．（1）求证：△ABD≌△ACE；（2）求∠ACE的度数；（3）求证：四边形ABFE是菱形．【考点】全等三角形的判定与性质；菱形的判定；旋转的性质．【专题】证明题．【分析】（1）根据旋转角求出∠BAD=∠CAE，然后利用“边角边”证明△ABD和△ACE全等．（2）根据全等三角形对应角相等，得出∠ACE=∠ABD，即可求得．（3）根据对角相等的四边形是平行四边形，可证得四边形ABFE是平行四边形，然后依据邻边相等的平行四边形是菱形，即可证得．【解答】（1）证明：∵△ABC绕点A按逆时针方向旋转100°，∴∠BAC=∠DAE=40°，∴∠BAD=∠CAE=100°，又∵AB=AC，∴AB=AC=AD=AE，在△ABD与△ACE中∴△ABD≌△ACE（SAS）．（2）解：∵∠CAE=100°，AC=AE，∴∠ACE=（180°﹣∠CAE）=（180°﹣100°）=40°；（3）证明：∵∠BAD=∠CAE=100°AB=AC=AD=AE，∴∠ABD=∠ADB=∠ACE=∠AEC=40°．∵∠BAE=∠BAD+∠DAE=140°，∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°，∴∠BAE=∠BFE，∴四边形ABFE是平行四边形，∵AB=AE，∴平行四边形ABFE是菱形．【点评】此题考查了全等三角形的判定与性质，等腰三角形的性质、旋转的性质以及菱形的判定，熟练掌握全等三角形的判定与性质是解本题的关键．24．数学活动﹣﹣求重叠部分的面积．问题情境：数学活动课上，老师出示了一个问题：如图1，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合，DE经过点C，DF交AC于点C．求重叠部分（△DCG）的面积．（1）思考：请解答老师提出的问题．（2）合作交流：“希望”小组受此问题的启发，将△DEF绕点D旋转，使DE⊥AB交AC于点H，DF交AC于点G，如图2，求出重叠部分（△DGH）的面积，请写出解答过程．（3）提出问题：老师要求各小组向“希望”小组学习，将△DEF绕点D旋转，再提出一个求重叠部分面积的问题．“爱心”小组提出的问题是：如图3，将△DEF绕点D旋转，DE，DF分别交AC于点M，N，使DM=MN，求重叠部分（△DMN）的面积．任务：请解决“爱心”小组所提出的问题，直接写出△DMN的面积是．【考点】几何变换综合题．【分析】（1）确定点G为AC的中点，从而△ADC为等腰三角形，其底边AC=8，底边上的高GD=BC=3，从而面积可求；（2）本问解法有多种，解答中提供了三种不同的解法．基本思路是利用相似三角形、勾股定理求解；（3）对于爱心小组提出的问题，如答图4所示，作辅助线，利用相似三角形、勾股定理、等腰三角形的性质，列方程求解．【解答】解：（1）【思考】∵∠ACB=90°，D是AB的中点，∴DC=DA=DB，∴∠B=∠DCB．又∵△ABC≌△FDE，∴∠FDE=∠B．∴∠FDE=∠DCB，∴DG∥BC．∴∠AGD=∠ACB=90°，∴DG⊥AC．又∵DC=DA，∴G是AC的中点，∴CG=AC=×8=4，DG=BC=×6=3，∴S△DGC=CG•DG=×4×3=6．（2）【合作交流】如下图所示：∵△ABC≌△FDE，∴∠B=∠1．∵∠C=90°，ED⊥AB，∴∠A+∠B=90°，∠A+∠2=90°，∴∠B=∠2，∴∠1=∠2，∴GH=GD．∵∠A+∠2=90°，∠1+∠3=90°，∴∠A=∠3，∴AG=GD，∴AG=GH，即点G为AH的中点．在Rt△ABC中，AB===10，∵D是AB中点，∴AD=AB=5．在△ADH与△ACB中，∵∠A=∠A，∠ADH=∠ACB=90°，∴△ADH∽△ACB，∴，即，解得DH=，∴S△DGH=S△ADH=××DH•AD=××5=．（3）【提出问题】解决“希望”小组提出的问题．如答图4，过点D作DK⊥AC于点K，则DK∥BC，又∵点D为AB中点，∴DK=BC=3．∵DM=MN，∴∠MND=∠MDN，由（2）可知∠MDN=∠B，∴∠MND=∠B，又∵∠DKN=∠C=90°，∴△DKN∽△ACB，∴，即，得KN=．设DM=MN=x，则MK=x﹣．在Rt△DMK中，由勾股定理得：MK2+DK2=MD2，即：（x﹣）2+32=x2，解得x=，∴S△DMN=MN•DK=××3═．【点评】本题是几何综合题，考查了相似三角形、全等三角形、等腰三角形、勾股定理、图形面积计算、解方程等知识点．题干信息量大，篇幅较长，需要认真读题，弄清题意与作答要求．试题以图形旋转为背景，在旋转过程中，重叠图形的形状与面积不断发生变化，需要灵活运用多种知识予以解决，有利于培养同学们的研究与探索精神，激发学习数学的兴趣，是一道好题．25．如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a＞0），经过点A和x轴正半轴上的点B，AO=OB=2，∠AOB=120°．（1）求这条抛物线的表达式；（2）连接OM，求∠AOM的大小；（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．【考点】二次函数综合题．【专题】压轴题．【分析】（1）根据AO=OB=2，∠AOB=120°，求出A点坐标，以及B点坐标，进而利用待定系数法求二次函数解析式；（2）根据（1）中解析式求出M点坐标，再利用锐角三角函数关系求出∠FOM=30°，进而得出答案；（3）分别根据当△ABC1∽△AOM以及当△C2BA∽△AOM时，利用相似三角形的性质求出C点坐标即可．【解答】解：（1）过点A作AE⊥y轴于点E，∵AO=OB=2，∠AOB=120°，∴∠AOE=30°，∴OE=，AE=1，∴A点坐标为：（﹣1，），B点坐标为：（2，0），将两点代入y=ax2+bx得：，解得：，∴抛物线的表达式为：y=x2﹣x；（2）过点M作MF⊥OB于点F，∵y=x2﹣x=（x2﹣2x）=（x2﹣2x+1﹣1）=（x﹣1）2﹣，∴M点坐标为：（1，﹣），∴tan∠FOM==，∴∠FOM=30°，∴∠AOM=30°+120°=150°；（3）当点C在x轴负半轴上时，则∠BAC=150°，而∠ABC=30°，此时∠C=0°，故此种情况不存在；当点C在x轴正半轴上时，∵AO=OB=2，∠AOB=120°，∴∠ABO=∠OAB=30°，∴AB=2EO=2，当△ABC1∽△AOM，∴=，∵MO==，∴=，解得：BC1=2，∴OC1=4，∴C1的坐标为：（4，0）；当△C2BA∽△AOM，∴=，∴=，解得：BC2=6，∴OC2=8，∴C2的坐标为：（8，0）．综上所述，△ABC与△AOM相似时，点C的坐标为：（4，0）或（8，0）．【点评】此题主要考查了锐角三角函数的应用以及待定系数法求二次函数解析式和相似三角形的性质等知识，利用分类讨论思想以及数形结合得出是解题关键．。

2024年河北省唐山市路北区中考模拟预测地理试题(原卷版)

2024年八年级模拟检测地理试卷2024.05注意事项：1.本次测试满分60分，时间为60分钟。

2.答卷前，用0.5mm黑色签字笔填写学校、班级、姓名及考生号，并用2B铅笔把对应考生号的标号涂黑。

3.选择题选出答案后，用2B铅笔在答题卡上对应题目的答案标号涂黑；非选择题用0.5mm黑色签字笔作答；答案写在答题卡各题指定区域内的相应位置上；不准使用涂改液。

涉及作图的题目，用2B铅笔画图。

答在试卷上无效。

4.保持答题卡的整洁，不要折叠答题卡。

一、选择题：本大题共25小题，每小题1分，共25分。

在每小题给出的四个选项中，只有一项符合题目要求。

传统民居是人类适应自然、与自然和谐相处的结果。

我国地域辽阔，传统民居呈现诸多不同。

读图，完成下面小题。

1. ②④省区的简称分别是（）A. 陕、秦B. 内、滇C. 秦、滇D. 藏、云2. 以下说法与①②③④四省区的传统民居特点相对应的是（）A. “游动的家”“竹木的家”“地下的家”“石头的家”B. “地下的家”“游动的家”“竹木的家”“石头的家”C. “地下的家”“石头的家”“竹木的家”“游动的家”D. “游动的家”“地下的家”“石头的家”“竹木的家”3. 传统民居建筑风格的差异告诉我们（）A. ①地区雨水多较潮湿，植被繁茂B. ②地区黄土层非常厚，干燥少雨C ③地区建造搬迁方便，适合游牧 D. ④地区当地土层浅薄，林木稀少北极东北航道沟通亚洲与欧洲、连接太平洋与大西洋，是“冰上丝绸之路”的重要组成部分。

下图为北极东北航道和传统航道示意图。

据此，完成下面小题。

4. 北极航道越来越具有现实价值，其主要原因是（）A. 北极沿岸多港口B. 传统航道拥堵C. 印度洋海盗猖獗D. 全球气候变暖5. 与传统航道相比，“冰上丝绸之路”的优势是（）A. 贸易市场较大B. 沿途补给便利C. 缩短航程D. 顺风顺水6. 由中国大连沿传统航道到鹿特丹要依次经过（）A. 红海一苏伊士运河一土耳其海峡B. 南海一霍尔木兹海峡一地中海C. 红海一直布罗陀海峡一地中海D. 南海一马六甲海峡一苏伊士运河北京时间2023年1月1日早晨,浙江舟山（30°N,122°E ）朱家尖海滩迎来新年第一缕阳光。

2020届信阳市新县中考数学模拟试卷(八)(有答案)(加精)

河南省信阳市新县中考数学模拟试卷（八）一、选择题（每小题3分，共24分）1．2的相反数是（）A．2 B．﹣2 C．D．2．未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题．将8450亿元用科学记数法表示为（）A．0.845×1012元B．8.45×1011元C．8.45×1012元D．84.5×1010元3．如图，直线BD∥EF，AE与BD交于点C，若∠ABC=30°，∠BAC=75°，则∠CEF的大小为（）A．60°B．75°C．90°D．105°4．已知一元二次方程x2﹣6x+c=0有一个根为2，则另一根为（）A．2 B．3 C．4 D．85．有19位同学参加歌咏比赛，所得的分数互不相同，取得前10位同学进入决赛．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学的（）A．平均数B．中位数C．众数D．方差6．如图所示为某几何体的示意图，则该几何体的主视图应为（）A．B．C．D．7．在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作⊙O交BC于点M、N，⊙O与AB、AC相切，切点分别为D、E，则⊙O的半径和∠MND的度数分别为（）A．2，22.5°B．3，30°C．3，22.5°D．2，30°8．如图，△AOB为等腰三角形，顶点A的坐标（2，），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（）A．（，） B．（，）C．（，）D．（，4）二、填空题（每小题3分，共21分）9．25的算术平方根是．10．如图，AB∥CD，∠ABE=60°，∠F=50°，则∠E的度数为度．11．若不等式组的解集为3≤x≤4，则不等式ax+b＜0的解集为．12．若根式有意义，则双曲线y=与抛物线y=x2+2x+2﹣2k的交点在第象限．13．如图，有四张卡片（形状、大小和质地都相同），正面分别写有字母A、B、C、D和一个不同的算式，将这四张卡片背面向上洗匀，从中随机抽取两张卡片，这两张卡片上的算式只有一个正确的概率是．14．如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为．15．如图，在△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，F是BC的中点．若动点E以2cm/s 的速度从A点出发，沿着A→B→A的方向运动，设运动时间为t（s）（0≤t≤3），连接EF，当t为s时，△BEF是直角三角形．三、解答题（本大题共8小题，满分75分）16．先化简，再求值：（+2﹣x）÷，其中x满足x2﹣4x+3=0．17．我市民营经济持续发展，2013年城镇民营企业就业人数突破20万．为了解城镇民营企业员工每月的收入状况，统计局对全市城镇民营企业员工2013年月平均收入随机抽样调查，将抽样的数据按“2000元以内”、“2000～4000元”、“4000～6000元”和“6000元以上”分为四组，进行整理，分别用A，B，C，D表示，得到下面两幅不完整的统计图．由图中所给出的信息解答下列问题：（1）本次抽样调查的员工有人，在扇形统计图中x的值为，表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是；（2）将不完整的条形统计图补充完整，并估计我市2013年城镇民营企业20万员工中，每月的收入在“2000～4000元”的约多少人？（3）统计局根据抽样数据计算得到，2013年我市城镇民营企业员工月平均收入为4872元，请你结合上述统计的数据，谈一谈用平均数反映月收入情况是否合理？18．已知：如图，▱ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E．（1）求证：△AOD≌△EOC；（2）连接AC，DE，当∠B=°和∠AEB=°时，四边形ACED是正方形？请说明理由．19．天塔是天津市的标志性建筑之一，某校数学兴趣小组要测量天塔的高度，如图，他们在点A处测得天塔最高点C的仰角为45°，再往天塔方向前进至点B处测得最高点C的仰角为54°，AB=112m，根据这个兴趣小组测得的数据，计算天塔的高度CD（tan36°≈0.73，结果保留整数）．20．如图，直线y=kx+k（k≠0）与双曲线交于C、D两点，与x轴交于点A．（1）求n的取值范围和点A的坐标；=4，求双曲线的解析式；（2）过点C作CB⊥y轴，垂足为B，若S△ABC（3）在（1）（2）的条件下，若AB=，求点C和点D的坐标，并根据图象直接写出反比例函数的值小于一次函数的值时，自变量x的取值范围．21．某品牌手机去年每台的售价y（元）与月份x之间满足函数关系：y=﹣50x+2600，去年的月销量p（万台）与月份x之间成一次函数关系，其中1﹣6月份的销售情况如下表：月份（x）1月2月3月4月5月6月销售量（p） 3.9万台 4.0万台 4.1万台 4.2万台 4.3万台 4.4万台（1）求p关于x的函数关系式；（2）求该品牌手机在去年哪个月的销售金额最大？最大是多少万元？（3）今年1月份该品牌手机的售价比去年12月份下降了m%，而销售量也比去年12月份下降了1.5m%．今年2月份，经销商决定对该手机以1月份价格的“八折”销售，这样2月份的销售量比今年1月份增加了1.5万台．若今年2月份这种品牌手机的销售额为6400万元，求m 的值．22．问题背景：已知在△ABC中，AB边上的动点D由A向B运动（与A，B不重合），点E与点D同时出发，由点C沿BC的延长线方向运动（E不与C重合），连接DE交AC于F，点H是线段AF上一点．（1）初步尝试：如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等，求证：HF=AH+CF．小王同学发现可以由以下两种思路解决此问题：思路一：过点D作DG∥BC，交AC于点G，先证GH=AH，再证GF=CF，从而证得结论成立；思路二：过点E作EM⊥AC，交AC的延长线于点M，先证CM=AH，再证HF=MF，从而证得结论成立；请你任选一种思路，完整地书写本小题的证明过程（如用两种方法作答，则以第一种方法评分）（2）类比探究：如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且点D，E的运动速度之比是：1，求的值．（3）延伸拓展：如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记=m，且点D，E的运动速度相等，试用含m的代数式表示（直接写出结果，不必写解答过程）23．如图，在平面直角坐标系xOy中，二次函数y=ax2+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．（1）求该二次函数的解析式；（2）如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；（3）如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．河南省信阳市新县中考数学模拟试卷（八）参考答案与试题解析一、选择题（每小题3分，共24分）1．2的相反数是（）A．2 B．﹣2 C．D．【考点】相反数．【分析】根据相反数的定义求解即可．【解答】解：2的相反数为：﹣2．故选：B．2．未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题．将8450亿元用科学记数法表示为（）A．0.845×1012元B．8.45×1011元C．8.45×1012元D．84.5×1010元【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：8450亿元用科学记数法表示为8.45×1011，故选：B．3．如图，直线BD∥EF，AE与BD交于点C，若∠ABC=30°，∠BAC=75°，则∠CEF的大小为（）A．60°B．75°C．90°D．105°【考点】平行线的性质；三角形内角和定理．【分析】先根据三角形外角的性质求出∠1的度数，再由平行线的性质即可得出结论．【解答】解：∵∠1是△ABC的外角，∠ABC=30°，∠BAC=75°，∴∠1=∠ABC+∠BAC=30°+75°=105°，∵直线BD∥EF，∴∠CEF=∠1=105°．故选D．4．已知一元二次方程x2﹣6x+c=0有一个根为2，则另一根为（）A．2 B．3 C．4 D．8【考点】根与系数的关系．【分析】利用根与系数的关系来求方程的另一根．【解答】解：设方程的另一根为α，则α+2=6，解得α=4．故选C．5．有19位同学参加歌咏比赛，所得的分数互不相同，取得前10位同学进入决赛．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学的（）A．平均数B．中位数C．众数D．方差【考点】统计量的选择．【分析】因为第10名同学的成绩排在中间位置，即是中位数．所以需知道这19位同学成绩的中位数．【解答】解：19位同学参加歌咏比赛，所得的分数互不相同，取得前10位同学进入决赛，中位数就是第10位，因而要判断自己能否进入决赛，他只需知道这19位同学的中位数就可以．故选：B．6．如图所示为某几何体的示意图，则该几何体的主视图应为（）A．B．C．D．【考点】简单组合体的三视图．【分析】几何体的主视图就是从正面看所得到的图形，注意所有的看到的棱都应表现在主视图中．【解答】解：从正面看可得到图形．故选A．7．在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作⊙O交BC于点M、N，⊙O与AB、AC相切，切点分别为D、E，则⊙O的半径和∠MND的度数分别为（）A．2，22.5°B．3，30°C．3，22.5°D．2，30°【考点】切线的性质；等腰直角三角形．【分析】首先连接AO，由切线的性质，易得OD⊥AB，即可得OD是△ABC的中位线，继而求得OD的长；根据圆周角定理即可求出∠MND的度数．【解答】解：连接OA，∵AB与⊙O相切，∴OD⊥AB，∵在等腰直角三角形ABC中，AB=AC=4，O为BC的中点，∴AO⊥BC，∴OD∥AC，∵O为BC的中点，∴OD=AC=2；∵∠DOB=45°，∴∠MND=∠DOB=22.5°，故选A．8．如图，△AOB为等腰三角形，顶点A的坐标（2，），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（）A．（，） B．（，）C．（，）D．（，4）【考点】坐标与图形变化-旋转．【分析】过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，根据点A的坐标求出OC、AC，再利用勾股定理列式计算求出OA，根据等腰三角形三线合一的性质求出OB，根据旋转的性质可得BO′=OB，∠A′BO′=∠ABO，然后解直角三角形求出O′D、BD，再求出OD，然后写出点O′的坐标即可．【解答】解：如图，过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，∵A（2，），∴OC=2，AC=，由勾股定理得，OA===3，∵△AOB为等腰三角形，OB是底边，∴OB=2OC=2×2=4，由旋转的性质得，BO′=OB=4，∠A′BO′=∠ABO，∴O′D=4×=，BD=4×=，∴OD=OB+BD=4+=，∴点O′的坐标为（，）．故选：C．二、填空题（每小题3分，共21分）9．25的算术平方根是5．【考点】算术平方根．【分析】根据算术平方根的定义即可求出结果，算术平方根只有一个正根．【解答】解：∵52=25，∴25的算术平方根是5．故答案为：5．10．如图，AB∥CD，∠ABE=60°，∠F=50°，则∠E的度数为10度．【考点】平行线的性质；三角形的外角性质．【分析】先根据平行线的性质求出∠CDE的度数，再由三角形外角的性质即可得出结论．【解答】解：∵AB∥CD，∠ABE=60°，∠F=50°，∴∠CDE=∠ABE=60°，∴∠E=∠CDE﹣∠F=60°﹣50°=10°．故答案为：10．11．若不等式组的解集为3≤x≤4，则不等式ax+b＜0的解集为x＞．【考点】解一元一次不等式组；不等式的解集；解一元一次不等式．【分析】求出每个不等式的解集，根据找不等式组解集的规律找出不等式组的解集，即可求出a，b的值，代入求出不等式的解集即可．【解答】解：∵解不等式①得：x≥，解不等式②得：x≤﹣a，∴不等式组的解集为：≤x≤﹣a，∵不等式组的解集为3≤x≤4，∴=3，﹣a=4，b=6，a=﹣4，∴﹣4x+6＜0，x＞，故答案为：x＞12．若根式有意义，则双曲线y=与抛物线y=x2+2x+2﹣2k的交点在第二象限．【考点】二次根式有意义的条件．【分析】根据被开方数大于等于0，分母不等于0可得2﹣2k＞0，再根据反比例函数的性质确定出反比例函数图象的位置，求出抛物线对称轴为直线x=﹣1，与y轴的交点在正半轴，确定出抛物线图象不在第四象限，从而判断出交点的位置．【解答】解：由题意得：2﹣2k＞0，解得：k＜1，∴2k﹣2＜0，∴双曲线y=在第二、四象限，∵抛物线y=x2+2x+2﹣2k的对称轴为直线x=﹣=﹣1，与y轴的交点为（0，2﹣2k），在y轴正半轴，∴抛物线y=x2+2x+2﹣2k的图象不经过第四象限，∴双曲线y=与抛物线y=x2+2x+2﹣2k的交点在第二象限．故答案为：二．13．如图，有四张卡片（形状、大小和质地都相同），正面分别写有字母A、B、C、D和一个不同的算式，将这四张卡片背面向上洗匀，从中随机抽取两张卡片，这两张卡片上的算式只有一个正确的概率是．【考点】列表法与树状图法．【分析】首先此题需要两步完成，直接运用树状图法或者采用列表法，再根据列举求出所用可能数，再求出只有一次正确的情况数根据概率公式解答即可．【解答】解：列表如下：第1次第2次A B C DA BA CA DAB AB CB DBC AC BC DCD AD BD CD由表可知一共有12种情况，其中抽取的两张卡片上的算式只有一个正确的有8种，所以两张卡片上的算式只有一个正确的概率=，故答案为：．14．如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为π+1．【考点】旋转的性质；正方形的性质；扇形面积的计算．【分析】根据旋转的性质作出图形，再利用勾股定理列式求出正方形的对角线，然后根据点A运动的路径线与x轴围成的面积为三个扇形的面积加上两个直角三角形的面积，列式计算即可得解．【解答】解：如图，∵正方形ABCD的边长为1，∴对角线长：=，点A运动的路径线与x轴围成的面积为：+++×1×1+×1×1=π+π+π++=π+1．故答案为：π+1．15．如图，在△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，F是BC的中点．若动点E以2cm/s 的速度从A点出发，沿着A→B→A的方向运动，设运动时间为t（s）（0≤t≤3），连接EF，当t为1s或3s或s或s时，△BEF是直角三角形．【考点】相似三角形的判定与性质；勾股定理的逆定理；三角形中位线定理．【分析】先利用含30度的直角三角形三边的关系得到AC=2，AB=4，然后讨论：当∠BFE=90°时，则EF∥AC，则可利用EF为△ABC的中位线得到AE=AB=2，于是可计算出t=1（s）或t=3（s）；当∠FEB=90°，则证明△BEF∽△BCA，利用相似比可计算出BE=，则AE=，于是可计算出t=（s）或t=（s）．【解答】解：∵∠ACB=90°，∠ABC=60°，BC=2cm，∴AC=BC=2，AB=2BC=4，当∠BFE=90°时，则EF∥AC，∵F是BC的中点，∴EF为△ABC的中位线，∴AE=AB=2，∴t==1（s）或t==3（s）；当∠FEB=90°，∵∠FBE=∠ABC，∠BEF=∠C，∴△BEF∽△BCA，∴=，即=，解得BE=，∴AE=4﹣=，∴t==（s）或t==（s），综上所述，t的值为1s或3s或s或s．故答案为1s或3s或s或．三、解答题（本大题共8小题，满分75分）16．先化简，再求值：（+2﹣x）÷，其中x满足x2﹣4x+3=0．【考点】分式的化简求值；解一元二次方程-因式分解法．【分析】通分相加，因式分解后将除法转化为乘法，再将方程的解代入化简后的分式解答．【解答】解：原式=÷=•=﹣，解方程x2﹣4x+3=0得，（x﹣1）（x﹣3）=0，x1=1，x2=3．当x=1时，原式无意义；当x=3时，原式=﹣=﹣．17．我市民营经济持续发展，2013年城镇民营企业就业人数突破20万．为了解城镇民营企业员工每月的收入状况，统计局对全市城镇民营企业员工2013年月平均收入随机抽样调查，将抽样的数据按“2000元以内”、“2000～4000元”、“4000～6000元”和“6000元以上”分为四组，进行整理，分别用A，B，C，D表示，得到下面两幅不完整的统计图．由图中所给出的信息解答下列问题：（1）本次抽样调查的员工有500人，在扇形统计图中x的值为14，表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是21.6°；（2）将不完整的条形统计图补充完整，并估计我市2013年城镇民营企业20万员工中，每月的收入在“2000～4000元”的约多少人？（3）统计局根据抽样数据计算得到，2013年我市城镇民营企业员工月平均收入为4872元，请你结合上述统计的数据，谈一谈用平均数反映月收入情况是否合理？【考点】条形统计图；用样本估计总体；扇形统计图；加权平均数．【分析】（1）根据B组的人数是300，对应的百分比是60%，据此即可求得调查的总人数，然后利用百分比的意义求得x的值，利用360°乘以对应的比例求得圆心角的度数；（2）利用调查的总人数减去其它组的人数求得C组的人数，从而补全直方图，利用总人数20万乘以对应的比例求得每月的收入在“2000～4000元”的人数；（3）判断平均数是有代表性即可．【解答】解：（1）本次抽样调查的人数是300÷60%=500（人），x=100×=14，表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是360°×=21.6°；故答案是：500，14，21.6°；（2）C组的人数是500﹣30﹣300﹣70=100（人），估计我市2013年城镇民营企业20万员工中，每月的收入在“2000～4000元”的约有：20×=12（万人）；（3）不合理，因为平均数不能代表大多数人的收入，应该用中位数或众数代表．18．已知：如图，▱ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E．（1）求证：△AOD≌△EOC；（2）连接AC，DE，当∠B=45°和∠AEB=45°时，四边形ACED是正方形？请说明理由．【考点】平行四边形的性质；全等三角形的判定与性质；正方形的判定．【分析】（1）首先根据O是CD的中点，可得DO=CO，再证明∠D=∠OCE，然后可利用ASA定理证明△AOD≌△EOC；（2）当∠B=45°和∠AEB=45°时，四边形ACED是正方形；首先证明∠BAE=90°，然后证明AC 是BE边上的中线，根据直角三角形的性质可得AC=CE，然后利用等腰三角形的性质证明AC⊥BE，可得结论．【解答】（1）证明：∵O是CD的中点，∴DO=CO，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠D=∠OCE，在△ADO和△ECO中，∴△AOD≌△EOC（ASA）；（2）解：当∠B=45°和∠AEB=45°时，四边形ACED是正方形，∵∠B=45°和∠AEB=45°，∴∠BAE=90°，∵△AOD≌△EOC，∴AO=EO，∵DO=CO，∴四边形ACED是平行四边形，∴AD=CE，∵四边形ABCD是平行四边形，∴AD=BC，∴BC=CE，∵∠BAE=90°，∴AC=CE，∴平行四边形ACED是菱形，∵∠B=∠AEB，BC=CE，∴AC⊥BE，∴四边形ACED是正方形．故答案为：45，45．19．天塔是天津市的标志性建筑之一，某校数学兴趣小组要测量天塔的高度，如图，他们在点A处测得天塔最高点C的仰角为45°，再往天塔方向前进至点B处测得最高点C的仰角为54°，AB=112m，根据这个兴趣小组测得的数据，计算天塔的高度CD（tan36°≈0.73，结果保留整数）．【考点】解直角三角形的应用-仰角俯角问题．【分析】首先根据题意得：∠CAD=45°，∠CBD=54°，AB=112m，在Rt△ACD中，易求得BD=AD ﹣AB=CD﹣112；在Rt△BCD中，可得BD=CD•tan36°，即可得CD•tan36°=CD﹣112，继而求得答案．【解答】解：根据题意得：∠CAD=45°，∠CBD=54°，AB=112m，∵在Rt△ACD中，∠ACD=∠CAD=45°，∴AD=CD，∵AD=AB+BD，∴BD=AD﹣AB=CD﹣112（m），∵在Rt△BCD中，tan∠BCD=，∠BCD=90°﹣∠CBD=36°，∴tan36°=，∴BD=CD•tan36°，∴CD•tan36°=CD﹣112，∴CD=≈≈415（m）．答：天塔的高度CD约为：415m．20．如图，直线y=kx+k（k≠0）与双曲线交于C、D两点，与x轴交于点A．（1）求n的取值范围和点A的坐标；=4，求双曲线的解析式；（2）过点C作CB⊥y轴，垂足为B，若S△ABC（3）在（1）（2）的条件下，若AB=，求点C和点D的坐标，并根据图象直接写出反比例函数的值小于一次函数的值时，自变量x的取值范围．【考点】反比例函数与一次函数的交点问题．【分析】（1）由反比例函数图象位于第二、四象限，得到比例系数小于0列出关于n的不等式，求出不等式的解集即可得到n的范围，对于直线解析式，令y=0求出x的值，确定出A的坐标即可；（2）设C（a，b），表示出三角形ABC的面积，根据已知的面积列出关于a与b的关系式，利用反比例函数k的几何意义即可求出k的值，确定出反比例解析式；（3）由CB垂直于y轴，得到B，C纵坐标相同，即B（0，b），在直角三角形AOB中，由AB 与OA的长，利用勾股定理求出OB的长，确定出B坐标，进而确定出C坐标，将C代入直线解析式求出k的值，确定出一次函数解析式，与反比例解析式联立求出D的坐标，由C，D两点的横坐标，利用图象即可求出反比例函数的值小于一次函数的值时，自变量x的取值范围．【解答】解：（1）由图象得：n+1＜0，解得：n＜﹣1，由y=kx+k，令y=0，解得：x=﹣1，则A坐标为（﹣1，0）；（2）设C（a，b），=a•（﹣b）=4，∵S△ABC∴ab=﹣8，∵点C在双曲线上，∴y=﹣；（3）∵CB⊥y轴，∴B（0，b），在Rt△AOB中，AB=，OA=1，根据勾股定理得：OB=4，∴B（0，﹣4），∴C（2，﹣4），将C代入直线y=kx+k中，得：2k+k=﹣4，即k=﹣，∴直线AC解析式为y=﹣x﹣，联立直线与反比例解析式得：，解得：或，∴D（﹣3，），则由图象可得：当x＜﹣3或0＜x＜2时，反比例函数的值小于一次函数的值．21．某品牌手机去年每台的售价y（元）与月份x之间满足函数关系：y=﹣50x+2600，去年的月销量p（万台）与月份x之间成一次函数关系，其中1﹣6月份的销售情况如下表：月份（x）1月2月3月4月5月6月销售量（p） 3.9万台 4.0万台 4.1万台 4.2万台 4.3万台 4.4万台（1）求p关于x的函数关系式；（2）求该品牌手机在去年哪个月的销售金额最大？最大是多少万元？（3）今年1月份该品牌手机的售价比去年12月份下降了m%，而销售量也比去年12月份下降了1.5m%．今年2月份，经销商决定对该手机以1月份价格的“八折”销售，这样2月份的销售量比今年1月份增加了1.5万台．若今年2月份这种品牌手机的销售额为6400万元，求m 的值．【考点】二次函数的应用．【分析】（1）直接利用待定系数法求一次函数解析式即可；（2）利用销量×售价=销售金额，进而利用二次函数最值求法求出即可；（3）分别表示出1，2月份的销量以及售价，进而利用今年2月份这种品牌手机的销售额为6400万元，得出等式求出即可．【解答】解：（1）设p=kx+b，把p=3.9，x=1；p=4.0，x=2分别代入p=kx+b中，得：，解得：，∴p=0.1x+3.8；（2）设该品牌手机在去年第x个月的销售金额为w万元，w=（﹣50x+2600）（0.1x+3.8）=﹣5x2+70x+9880=﹣5（x﹣7）2+10125，当x=7时，w最大=10125，答：该品牌手机在去年七月份的销售金额最大，最大为10125万元；（3）当x=12时，y=2000，p=5，1月份的售价为：2000（1﹣m%）元，则2月份的售价为：0.8×2000（1﹣m%）元；1月份的销量为：5×（1﹣1.5m%）万台，则2月份的销量为：[5×（1﹣1.5m%）+1.5]万台；∴0.8×2000（1﹣m%）×[5×（1﹣1.5m%）+1.5]=6400，解得：m1%=（舍去），m2%=，∴m=20，答：m的值为20．22．问题背景：已知在△ABC中，AB边上的动点D由A向B运动（与A，B不重合），点E与点D同时出发，由点C沿BC的延长线方向运动（E不与C重合），连接DE交AC于F，点H是线段AF上一点．（1）初步尝试：如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等，求证：HF=AH+CF．小王同学发现可以由以下两种思路解决此问题：思路一：过点D作DG∥BC，交AC于点G，先证GH=AH，再证GF=CF，从而证得结论成立；思路二：过点E作EM⊥AC，交AC的延长线于点M，先证CM=AH，再证HF=MF，从而证得结论成立；请你任选一种思路，完整地书写本小题的证明过程（如用两种方法作答，则以第一种方法评分）（2）类比探究：如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且点D，E的运动速度之比是：1，求的值．（3）延伸拓展：如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记=m，且点D，E的运动速度相等，试用含m的代数式表示（直接写出结果，不必写解答过程）【考点】三角形综合题．【分析】（1）过点D作DG∥BC，交AC于点G，先证明△ADG是等边三角形，得出GD=AD=CE，再证明GH=AH，由ASA证明△GDF≌△CEF，得出GF=CF，即可得出结论；（2）过点D作DG∥BC，交AC于点G，先证出AH=GH=GD，AD=GD，由题意AD=CE，得出GD=CE，再证明△GDF≌△CEF，得出GF=CF，即可得出结论；（3）过点D作DG∥BC，交AC于点G，先证出DG=DH=AH，再证明△ADG∽△ABC，△ADG ∽△DGH，△DGH∽△ABC，得出=m，=m，=m，证出△DFG∽△EFC，得出=m，即可得出结果．【解答】（1）证明（选择思路一）：过点D作DG∥BC，交AC于点G，如图1所示：则∠ADG=∠B，∠AGD=∠ACB，∵△ABC是等边三角形，∴∠A=∠B=∠ACB=60°，∴∠ADG=∠AGD=∠A，∴△ADG是等边三角形，∴GD=AD=CE，∵DH⊥AC，∴GH=AH，∵DG∥BC，∴∠GDF=∠CEF，∠DGF=∠ECF，在△GDF和△CEF中，，∴△GDF≌△CEF（ASA），∴GF=CF，∴GH+GF=AH+CF，即HF=AH+CF；（2）解：过点D作DG∥BC，交AC于点G，如图2所示：则∠ADG=∠B=90°，∵∠BAC=∠ADH=30°，∴∠HGD=∠HDG=60°，∴AH=GH=GD，AD=GD，根据题意得：AD=CE，∴GD=CE，∵DG∥BC，∴∠GDF=∠CEF，∠DGF=∠ECF，在△GDF和△CEF中，，∴△GDF≌△CEF（ASA），∴GF=CF，∴GH+GF=AH+CF，即HF=AH+CF，∴=2；（3）解：=，理由如下：过点D作DG∥BC，交AC于点G，如图3所示：则∠ADG=∠B，∠AGD=∠ACB，AD=EC，∵AB=AC，∠BAC=36°，∴∠ACB=∠B=∠ADG=∠AGD=72°，∵∠ADH=∠BAC=36°，∴AH=GH，∠DHG=72°=∠AGD，∴DG=DH=AH，△ADG∽△ABC，△ADG∽△DGH，∴=m，=m，∴△DGH∽△ABC，∴=m，∴=m，∵DG∥BC，∴△DFG∽△EFC，∴=m，∴==m，即=m，∴=，∴=+1=．23．如图，在平面直角坐标系xOy中，二次函数y=ax2+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．（1）求该二次函数的解析式；（2）如图1，连结BC，在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；（3）如图2，若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，求△BDP面积的最大值及此时点P的坐标．【考点】二次函数综合题．【分析】（1）采用待定系数法求得二次函数的解析式；（2）先求得直线BC的解析式为y=x﹣4，则可设E（m，m﹣4），然后分三种情况讨论即可求得；（3）利用△PBD的面积S=S梯形﹣S△BOD﹣S△PFD即可求得．【解答】解：（1）∵二次函数y=ax2+bx﹣4（a≠0）的图象与x轴交于A（﹣2，0）、C（8，0）两点，∴，解得，∴该二次函数的解析式为y=x2﹣x﹣4；（2）由二次函数y=x2﹣x﹣4可知对称轴x=3，∴D（3，0），∵C（8，0），∴CD=5，由二次函数y=x2﹣x﹣4可知B（0，﹣4），设直线BC的解析式为y=kx+b，∴，解得，∴直线BC的解析式为y=x﹣4，设E（m，m﹣4），当DC=CE时，EC2=（m﹣8）2+（m﹣4）2=CD2，即（m﹣8）2+（m﹣4）2=52，解得m1=8﹣2，m2=8+2（舍去），∴E（8﹣2，﹣）；当DC=DE时，ED2=（m﹣3）2+（m﹣4）2=CD2，即（m﹣3）2+（m﹣4）2=52，解得m3=0，m4=8（舍去），∴E （0，﹣4）；当EC=DE 时，（m ﹣8）2+（m ﹣4）2=（m ﹣3）2+（m ﹣4）2解得m 5=5.5， ∴E （，﹣）．综上，存在点E ，使得△CDE 为等腰三角形，所有符合条件的点E 的坐标为（8﹣2，﹣）、（0，﹣4）、（，﹣）．（3）过点P 作y 轴的平行线交x 轴于点F ， ∵P 点的横坐标为m ，∴P 点的纵坐标为m 2﹣m ﹣4，∵△PBD 的面积S=S 梯形﹣S △BOD ﹣S △PFD =m [4﹣（m 2﹣m ﹣4）]﹣（m ﹣3）[﹣（m 2﹣m ﹣4）]﹣×3×4 =﹣m 2+m=﹣（m ﹣）2+∴当m=时，△PBD 的最大面积为，∴点P 的坐标为（，﹣）．。

2020年苏州市中考数学模拟试卷(八)

2020年苏州市中考数学模拟试卷(八)一、选择题:本大题共10小题,每小题3分，共30分.1．﹣2的绝对值为（）A．B．C．﹣2D．22．已知一组数据为7，2，5，x，8，它们的平均数是5，则这组数据的方差为（）A．3B．4.5C．5.2D．63．成人每天维生素D的摄入量约为0.0000046克．数据“0.0000046”用科学记数法表示为（）A．46×10﹣7B．4.6×10﹣7C．4.6×10﹣6D．0.46×10﹣54．如图，AC与BD交于点O，AB∥CD，∠AOB＝105°，∠B＝30°，则∠C的度数为（）A．45°B．55°C．60°D．75°(第4题) (第5题)5．如图，在⊙O中，∠BAC＝15°，∠ADC＝20°，则∠ABO的度数为（）A．70°B．55°C．45°D．35°6．某工厂计划生产300个零件，由于采用新技术，实际每天生产零件的数量是原计划的2倍，因此提前5天完成任务．设原计划每天生产零件x个，根据题意，所列方程正确的是（）A．5B．5C．5D．57．如图，直线y＝x+b和y＝kx+2与x轴分别交于点A（﹣2，0），点B（3，0），则解集为（）A．x＜﹣2B．x＞3C．x＜﹣2或x＞3D．﹣2＜x＜3(第7题) (第8题)8．一座楼梯的示意图如图所示，BC是铅垂线，CA是水平线，BA与CA的夹角为θ．现要在楼梯上铺一条地毯，已知CA＝4米，楼梯宽度1米，则地毯的面积至少需要（）A．米2B．米2C．（4）米2 D．（4+4tanθ）米29．如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是（）A．2.5B．3C．4D．510．如图1，若△ABC内一点P满足∠P AC＝∠PBA＝∠PCB，则点P为△ABC的布洛卡点．三角形的布洛卡点是法国数学家和数学教育家克洛尔于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡重新发现，并用他的名字命名．问题：已知在等腰直角三角形DEF中，如图2，∠EDF＝90°，若点Q为△DEF的布洛卡点，DQ＝1，则EQ+FQ＝（）A．5B．4C．D．二、填空题:本大题共8小题,每小题3分，共24分.把答案直接填在答题卡相应位置上．．．．．．．．. 11．计算：（2a2）2＝．12．分解因式：m2﹣4m+4＝．13．若二次根式有意义，则x的取值范围是．14．已知关于x，y的方程组的解满足x+y＝5，则k的值为．15．四边形具有不稳定性．如图，矩形ABCD按箭头方向变形成平行四边形A'B'C'D'，当变形后图形面积是原图形面积的一半时，则∠A'＝．(第15题) (第16题) 16．如图，转盘中6个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针落在阴影部分的概率为．(第17题) (第18题)17．已知三个边长分别为2cm，3cm，5cm的正方形如图排列，则图中阴影部分的面积为．18．如图，⊙O半径为，正方形ABCD内接于⊙O，点E在上运动，连接BE，作AF⊥BE，垂足为F，连接CF．则CF长的最小值为．三、解答题:本大题共10小题,共76分.把解答过程写在答题卡相应位置上．．．．．．．．,解答时应写出必要的计算过程、推演步骤或文字说明。

2023年上海市中考语文模拟试题(八)

中考仿真试卷（八）一、文言文阅读（36分）（一）默写与运用。

（12分）1.旧时茅店社林边，________________。

（辛弃疾《西江月·夜行黄沙道中》）2.锺子期曰：“善哉乎鼓琴，________________。

”（《伯牙鼓琴》）3. ________________，长沟流月去无声。

（陈与义《临江仙·夜登小阁忆洛中旧游》）4.苏轼在《水调歌头》下片以“________________，_____________”两句用对偶句式来宽慰，表现了他达观的处事态度，同时寄托对未来的希望。

（二）阅读下面的诗文，完成5-11题。

（24分）。

黄鹤楼崔颢昔人已乘黄鹤去，此地空余黄鹤楼。

黄鹤一去不复返，白云千载空悠悠。

晴川历历汉阳树，芳草萋萋鹦鹉洲。

日暮乡关何处是，烟波江上使人愁。

5.诗中“历历”的意思是_____________________。

（2分）6.对诗中流露的思想情感理解不正确的一项是（）（3分）A.怅然若失之感B.岁月沧桑之感C.忘我陶醉之情D.思乡念家之意【甲】予观夫巴陵胜状，在洞庭一湖。

衔远山，吞长江，浩浩汤汤，横无际涯；朝晖夕阴，气象万千。

此则岳阳楼之大观也，前人之述备矣。

然则北通巫峡，南极潇湘，迁客骚人，多会于此，览物之情，得无异乎？若夫霪雨霏霏，连月不开，阴风怒号，浊浪排空；日星隐曜，山岳潜形；商旅不行，樯倾楫摧；薄暮冥冥，虎啸猿啼。

登斯楼也，则有去国怀乡，忧谗畏讥，满目萧然，感极而悲者矣。

至若春和景明，波澜不惊，上下天光，一碧万顷；沙鸥翔集，锦鳞游泳；岸芷汀兰，郁郁青青。

而或长烟一空，皓月千里，浮光跃金，静影沉璧，渔歌互答，此乐何极！登斯楼也，则有心旷神怡，宠辱偕忘，把酒临风，其喜洋洋者矣。

【乙】登南昌滕王阁，赣大水西来注北阁与水称杰①然大观。

然不若武昌黄鹤楼。

虽水与滕王来去不殊，而楼制工巧奇丽，立黄鹄矶上，且三面临水，又西对晴川楼、汉阳城为佳。

总之有不如岳州岳阳楼。

2020-2021学年江苏省苏州市九年级中考英语模拟试卷(八)及答案

苏州市中考英语模拟试卷（八）（满分100分考试时间100分钟）一、单项填空(共15小题；每小题1分，满分15分)从A、B、C、D四个选项中，选出可以填人空白处的最佳选项。

( ) 1．一Who’s that girl?一You mean one at the corner of the building? That’S Jack’S daughter．A．a B．the C．an D．不填( ) 2．We students have a holiday every summer．A．two months B．two month’s C．two-month D．two-months( ) 3．一Why don’t we take a little break?一Haven’t we just had ?A．it B．one C．this D．that( ) 4．He the TV a 1ittle because his father was asleep．A．turned up B．turned on C．turned off D．turned down( ) 5．—I hear the Smiths have gone to Hainan for a holiday．—Really? How nice! Do you know when they ?A．left B．was leavingC．has left D．had left( ) 6．一Amy，do you know if Daniel to the farm with us tomorrow even if it ?—Sorry，I’ve no idea．A．will go；will rain B．will go；rainsC．goes；will rain D．goes；rains( ) 7．一Would you please the paper for me and see if there are any spelling Mistakes?一Of course 1 will．A．1ook around B．1ook into C．look up D．1ook through( ) 8．一Do you know ?—I’m not sure．Maybe an artist?A．what the man with long hair is B．what is the man with long hairC．who the man with long hair is D．who is the man with long hair( ) 9．一Hello，Sam．This is Tommy．What are you doing?一I’m watching a match．It started at 7：00 P.m．and on for another hour．A．has been B．was C．will be D．had been( )10．一Have you got anything to do this afternoon, Lucy and Lily?一Yes，of us are going to the home for the elderly．A．each B．either C．both D．a11( )11．Many Chinese students think science subjects are foreign languages．A．more difficult as B．much difficult thanC．1ess difficult than D．so difficult as( )12．一Are you sure you have to? It’s been very late．I don’t know I can do it if not now．A．where B．why C．how D．when( )13．I’ll never forget those places of interest I have visited in the past 10 years·A．where B．what C．which D．in which( )14．About the journalists (记者)are waiting here．They are waiting for thenewest information about the missing plane．A．two hundred of B．two hundredC．hundred of D．two hundreds of( )15．一Hello，Jack! Haven’t seen you for a long time!一John!A．How old are you? B．How are you?C．How’s that? D．How time flies!二、完形填空(共10小题；每小题1分，满分10分)先通读下面的短文，掌握其大意，然后在每小题所给的A、B、C、D四个选项中，选出可以填入空白处的最佳选项。

江苏省2022年初三中考英语模拟试题(八)及答案详解

D.return; don't have to; keep
11.---What is your key to success?
---I believe that nothing difficult will beif I put all my effort into it.
A. by the wayB. in thiswayC. on the wayD. in theway
A. Counting sheep all night B. Like a piece of wood
C. Dreaming all nightD. Like the early bird
二、词汇
A.请根据括号中的中文提示、英文释义或句意，写出句中所缺单词，使句子通顺。
1.She____________(后悔)takingpart in the club activitybecause she learned nothing from it.
5.--How many mistakes did you make in the test,Daniel?
-- _______. I got full marks this time.
A. NoneB. NothingC. No oneD. Nobody
6.--- Is this restaurant as good as you expected？--- No．I have never had ___________ meal．
4. Rubbish needs to be ____________(put things into different groups) before you throw it away.

东营市英语中考模拟试题八及答案

东营市英语中考模拟试题八及答案2018年东营市英语中考模拟试题八及答案中考临近，不知道大家是否全都了解中考考试的题目类型和结构?下面是店铺整理的最新中考模拟试题，希望能帮到你。

2018年东营市中考模拟试题八英语试题(总分120分考试时间120分钟)注意事项：1、本试题分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷8页为选择题，65分;第Ⅱ卷4页为非选择题，55分;共120分。

考试时间为120分钟。

2、答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上。

考试结束，试题和答题卡一并收回。

3、第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑。

如需改动，必须先用橡皮擦干净，再改涂其它答案。

4、听力填表题为第Ⅱ卷的第四大题，在试卷第9页上。

第Ⅰ卷 (选择题，共65分)一、听力选择(共15小题，计15分;每小题约有8秒钟的答题时间)(一) 录音中有五个句子，每个句子听两遍，然后从每小题A、B、C中选出能对每个句子做出适当反应的答语。

1. A. It’s Friday B. It’s eight o’clock C. It’s June 122. A. With her parents B. sorry, I don’t know C. It’s cold here.3. A. It doesn’t matter. B. That’s nothing C. No problem.4. A. Never mind. B. Sorry to hear that. C. Much better5. A. Oh, wonderful, indeed. B. By taking a No. 3 bus. C. I went there alone.(二)录音中有五组对话，听对话两遍后，从每小题A、B、C中选出能回答所给问题的正确答案。

6. How does Bob’s father usually go to work?A. By bus.B. By bike.C. On foot.7. What time did the class begin?A. At 8:05.B. At 8:10.C. At 8: 15.8. What is the woman probably?A. A teacherB. A doctorC. A saleswoman9. Where does the girl want to go?A. To the teaching building.B. To the library.C. T o the computer room.10. What does the girl mean?A. Everyone can work out the problem.B. Jim is good at math.C. Nobody can work out the problem.(三)录音中有一段对话，听对话两遍后，从每小题A、B、C中选出能回答所给问题的正确答案。

八年级生物中考模拟试题(一)

八年级生物模拟试题（一）一、单项选择题(共18小题，每小题2分，共36分)21.初夏的天河湿地公园景色宜人。

你看：风吹芦苇，水草依依，随风摇曳；鱼儿在水草间嬉戏；野鸭子追逐着小鱼，专注着寻觅着美食。

赏此美景，勿忘所学，下列说法错误的是A.在水草→小鱼→野鸭这条食物链中，野鸭体内的有毒物质和能量最多B.该湿地公园中的所有生物及其生活的环境共同构成生态系统C.该生态系统有一定自动调节能力，一般各种生物的数量和所占的比例是相对稳定的D.天河湿地公园中的鱼儿、野鸭属于生态系统中的消费者22.下图为呼伦贝尔草原生态系统碳循环模式图，甲、乙、丙、丁表示生态系统的成分，①②③为生理过程，以下说法正确的是A.生态系统内的能量是沿着乙→丙→丁→甲流动的B.乙生物的细胞内都含有线粒体、叶绿体两种能量转换器C.甲通过生理过程①将系统外的能量输入到系统内D.过程③中的碳以二氧化碳形式进行传递23.用光学显微镜观察人体口腔上皮细胞临时装片，部分操作步骤和观察到的物像如下图，有关说法正确的是A.当图1 中的物镜由甲转换到乙后，视野中细胞数目变多，视野变暗B.图2 中a、b 两个步骤滴加的液体分别是生理盐水和碘液C.图3 中口腔上皮细胞的细胞核颜色深是因为其中含有染色体D.图3 中口腔上皮细胞叠加是在盖盖玻片时操作不当造成的24.“孔融让梨” 体现了中华民族的传统美德，下列有关“梨”的描述正确的是A.梨树花开后要形成果实和种子必须完成的两个生理过程是开花和传粉B.构成梨树细胞的细胞膜有保护和控制物质进出的作用C.梨树比人体多了系统这一结构层次D.梨树由受精卵细胞分裂和分化导致细胞内遗传物质发生了变化25.下列对绿色植物植株、花、果实和种子示意图的叙述，不正确的是A.图乙中的③可发育成图丙中的①B.新植物的幼体是由图丁中的①②③④组成C.图甲中①和②分别是由图丁中的②和①发育而来的D.图丁中结构④的数量和功能与玉米种子对应结构都不同26．“有收无收在于水，收多收少在于肥”，植物生长需要水和无机盐，下列说法错误的是A.水分在植物体内运输和散失的主要途径为：根部成熟区的导管→茎中的导管→叶中的导管→气孔→大气B.若孙悟同学家种植的玉米出现植株矮小瘦弱、叶片发黄现象，则可能需要补充氮肥C.在移栽植物的过程中有时需要给植物打针输液，主要目的是为植物提供水和无机盐D.没有绿色植物的蒸腾作用，生物圈中的水循环就无法进行27．图甲和图乙分别表示菜豆种子萌发成幼苗的各阶段示意图和该过程中体内有机物含量变化示意图，下列相关叙述错误的是A.图甲所示过程需要适量的水分、充足的空气、适宜的温度等外部条件B.图甲所示过程前期所需营养由子叶提供C.图乙b点才长出幼叶，所以ab段无光合作用D.图乙bc段有机物含量上升，是因为幼苗光合作用的合成量大于呼吸作用的消耗量28.如图表示人体内部分血管及血流方向，下列说法错误的是A.A和C血管中的成分可能是一样的B.如果A血管内流的是静脉血，C血管内流的一定是动脉血C.若B是毛细血管，A、C可能都是小动脉D.B血管管壁只有一层上皮细胞构成，适于进行物质交换29.下列有关人体结构与功能相适应的叙述，错误的是A.肺泡壁和毛细血管壁都是由一层扁平上皮细胞构成，利于肺泡与血液进行气体交换B.小肠中有多种消化液，利于小肠消化食物C.心房与心室之间、心室与动脉之间、静脉血管中都有瓣膜，可防止血液倒流D.神经元的突起末端与多个神经元的突起相连，便于接受刺激，产生并传递兴奋30.下面是反应某些生命活动和生理功能的坐标曲线图，叙述不正确的是A.图甲表示人体脑部和生殖器官与全身相对生长速率的比较曲线，曲线②表示生殖器官的生长B.图乙表示某种气体在血液中流经各器官的含量变化，如果B表示的器官是肺，则该气体是二氧化碳C.图丙表示光照强度、二氧化碳浓度对光合作用强度的影响。

2023年中考语文模拟测试卷8((有答案)

荆州市2023初中毕业生学业水平检测命题大赛（语文）试卷一、基础与运用（22分）1.下列词语中加点字的读音，全部正确的一项是（）A. 恐吓．（xià）稽．（qǐ）首妥帖．（tiē）吹毛求疵．（cī）B. 盘桓．（huán）叱咄．（duō）两栖．（qī）间．不容发（jiàn）C. 驾驭．（yù）诘．难（jié）濒．临（bīn）混．为一谈（hùn）D. 惩．戒（chéng）荫．庇（yìn）炽．热 (zhì) 拈．轻怕重(niān)2.下列词语中，没有错别字的一项是（）A. 推祟劝戒取义成仁不屑置辩B. 要诀雷霆身临奇境哗众取宠C. 涉猎隐匿如座针毡无精打采D. 寂寥诡谲味同嚼蜡铢两悉称3.下列加点成语使用正确的一项是( )A. 国际马拉松比赛首次在荆门激情开跑。

在这场万众瞩目．．．．的比赛中，荆门人以奔跑的姿势跑进春天，拥抱春天。

B. 撒贝宁主持的《开讲啦》节目鲜为人知．．．．，在此节目中，其青春活泼的主持风格深受广大青少年朋友的青睐。

C. 近期在东洲岛举行的焰火表演晚会中，璀璨夺目的焰火以及具有衡阳地方特色的民俗表演让人们拍手称快．．．．。

D. 在建国70周年即将到来之际，我们深情缅怀革命前辈，虽然他们早已离开人世，但他们的恩情我们一直铭记于心，耿耿于怀．．．．。

4.按顺序排列下面的语句，组成语意连贯的一段话。

排序正确的一项是（）①一夜枕上听雨，辗转不能成寐，清晨推窗望去，雨却停了。

②院子中，一丛绿树被染得浓阴如墨。

③初到江南，就碰上了梅雨季节。

④朦胧的墨绿中，清晰地闪着点点火红的花朵，给这雨后空朗的清晨增添了不少的生气。

⑤浓云尚未散开，低低压着房檐。

⑥空中还飘着若有若无的雨丝，天地间弥漫着一层层湿漉漉、静悄悄青黛色雾霭。

A.③①②④⑤⑥B.②④⑤⑥①③C.③①⑤⑥②④D.⑤⑥③①②④5．下列有关文学、文化常识表述不正确的一项是（）A．《关雎》《子衿》都是古老的恋歌，出自我国第一部诗歌总集《诗经》。

2020年苏州市中考英语模拟试题(八)及答案

2020年苏州市初三英语模拟试题（八）一、单项填空(共15小题;每小题7分，满分15分)请认真阅读下面各题，从题中所给的A、B、C、D四个选项中.选出最佳选项。

( )1.―Morning, Mr. Johnson! Here is message for you. girl left it to you just now.―Really? But I don't know anyone in this city.A. a; TheB. the; AC. the; TheD. a; A( )2. For the first time, I found great fun to achieve something through hard work.A. itB. thatC. thisD. one( )3. Give me a chance, I'll give you a wonderful surprise.A. ifB. orC. andD. while( )4.―You look very pretty, if I say so.一Thanks a lot for saying that.A. mustB. mayC. willD. have to( )5. She drove so fast at the turning that the car almost went the road.A. onB. alongC. fromD. off( )6.―Can John play soccer with us, Mrs. Black?一One moment, please. He on the phone to his cousin.A. talksB. talkedC. talkingD.is talking( )7. Are you alone? I just want a word with you.A. singleB. privateC. newD. certain( )8. Your support is important to our work. you can do helps.A. HoweverB. WhoeverC. WhateverD. Wherever( )9.―Xiao Zhou can always some special ways to make his talk shows popular in China.一Yeah. He is very smart and creative.A. go well withB. work closely withC. come up withD. catch up with( )10.―The dishes in this restaurant must be very expensive.―Don't worry. You can enjoy yourself. It's my .A. timeB. treatC. taskD. taste( )11.―It is reported that cancer can be controlled at a temperature lower than 110℃below zero.―Really? nice surpriseA. HowB. WhatC. What aD. What an( )12.―I really want to relax myself. Could we see City Danger tonight.一Sure!The actor the hero used to be a teacher. I like him very much.A. who playB. which playsC. who playsD. that play( )13. . British scientist Steven Hawking opened an account(账号)on China’s Weibo on April 12th.A. To our shameB. To our surpriseC. To our pityD. To our sorry( )14. ―Could you tell me ? ―At 8 : 00 p. m.A. when will the train leaveB. when the train will leaveC. where the train will goD. where will the train go( )15.―It was a wonderful trip. So, which city did you like better, Paris or Rome?一. There were good things and bad things about them.A. It's hard to sayB. I didn't get itC. You must be kiddingD. Couldn't be better二、完形填空(共10 小题;每小题1分，满分10分)请认真阅读下面短文.从短文后各题所给的A、B、C、D四个选项中，选出最佳选项。

模拟卷08_2020年安徽中考英语最新题型冲刺卷(原卷版)_

A.secretB.requestC.energyD.pride
9.Daniel asked his teacher ________.
A.where could he join his favourite club
B.what would the life be like on Mars in the future
安徽省2019-2020大联考中招模拟试题（八）
一、单项填空（10小题，每小题1分，共10分）（小题变为10小题，分值减少5分）
从每小题所给的A、B、C、D四个选项中选出一个可以填入空白处的最佳选项。
1.Although there is ________ ugly wound on Nancy’s face, she doesn’t care about it.
C.whether the rainbow appears after the rain in summer
D.how many people will come to the meeting this coming Saturday
10.—Excuse me. Would you mind my using your dictionary for a short time?
Gloria
Hi, Amy. My tip is to have a big noticeboard …
21. A. prepareB. continueC. regretD. forget
22. A. sadB. goodC. angryD. terrible
23. A. billB. diaryC. scoreD. promise
13. A.plantedB.collectedC.carriedD.boiled

广东省东莞市虎门镇成才实验学校2023年中考数学模拟试题8

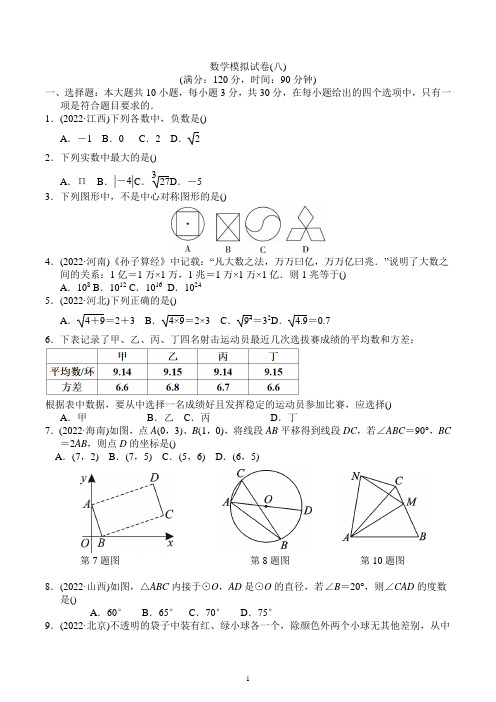
数学模拟试卷(八)(满分：120分，时间：90分钟)一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2022·江西)下列各数中，负数是()A ．－1B ．0C ．2D ． 2 2．下列实数中最大的是() A ．Π B ．||－4C ．327D ．－53．下列图形中，不是中心对称图形的是()4．(2022·河南)《孙子算经》中记载：“凡大数之法，万万曰亿，万万亿曰兆．”说明了大数之间的关系：1亿＝1万×1万，1兆＝1万×1万×1亿．则1兆等于()A ．108B ．1012C ．1016D ．10245．(2022·河北)下列正确的是()A ．4＋9＝2＋3B ．4×9＝2×3C ．94＝32D ． 4.9＝0.76．下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择()A ．甲B ．乙C ．丙D ．丁7．(2022·海南)如图，点A (0，3)、B (1，0)，将线段AB 平移得到线段DC ，若∠ABC ＝90°，BC＝2AB ，则点D 的坐标是()A ．(7，2)B ．(7，5)C ．(5，6)D ．(6，5)第7题图第8题图第10题图8．(2022·山西)如图，△ABC 内接于⊙O ，AD 是⊙O 的直径，若∠B ＝20°，则∠CAD 的度数是()A ．60°B ．65°C ．70°D ．75°9．(2022·北京)不透明的袋子中装有红、绿小球各一个，除颜色外两个小球无其他差别，从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么第一次摸到红球、第二次摸到绿球的概率是()A．14B．13C．12D．3410．(2022·天津)如图，在△ABC中，AB＝AC，若M是BC边上任意一点，将△ABM绕点A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是() A．AB＝AN B．AB∥NC C．∠AMN＝∠ACN D．MN⊥AC二、填空题：本大题共5小题，每小题3分，共15分．11. a是方程2x2＝x＋4的一个根，则代数式4a2－2a的值是___.12. 因式分解：2x2－8xy＋8y2＝__________.13．(2022·滨州)若m＋n＝10，mn＝5，则m2＋n2的值为____.14．(2022·滨州)在Rt△ABC中，若∠C＝90°，AC＝5，BC＝12，则sin A的值为_____. 15．(2022·青海)木材加工厂将一批木料按如图所示的规律依次摆放，则第n个图中共有木料__________根．三、解答题(一)：本大题共3小题，每小题8分，共24分．16．(2022·河池)计算：||－2 2－3－1－4×2＋(π－5)0.17．(2022·苏州)解方程：xx＋1＋3x＝1.18．某校学生利用双休时间去距学校10 km的炎帝故里参观，一部分学生骑自行车先走，过了20 min后，其余学生乘汽车沿相同路线出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度和汽车的速度．四、解答题(二)：本大题共3小题，每小题9分，共27分．19．(2022·大庆)如图，在四边形ABDF中，点E，C为对角线BF上的两点，AB＝DF，AC＝DE，EB＝CF.连接AE，CD.(1)求证：四边形ABDF是平行四边形；(2)若AE＝AC，求证：AB＝DB.20．(2022·陕西)有五个封装后外观完全相同的纸箱，且每个纸箱内各装有一个西瓜，其中，所装西瓜的重量分别为6 kg，6 kg，7 kg，7 kg，8 kg.现将这五个纸箱随机摆放．(1)若从这五个纸箱中随机选1个，则所选纸箱里西瓜的重量为6 kg的概率是____；(2)若从这五个纸箱中随机选2个，请利用列表或画树状图的方法，求所选两个纸箱里西瓜的重量之和为15 kg的概率．21．阅读下列“问题”与“提示”后，将解方程的过程补充完整，求出x的值．【问题】解方程：x2＋2x＋4x2＋2x－5＝0.【提示】可以用“换元法”解方程．解：设x2＋2x＝t(t≥0)，则有x2＋2x＝t2，原方程可化为：t2＋4t－5＝0.五、解答题(三)：本大题共2小题，每小题12分，共24分．22．(2022·河南)如图，反比例函数y ＝k x (x >0)的图象经过点A (2，4)和点B ，点B 在点A 的下方，AC 平分∠OAB ，交x 轴于点C .(1)求反比例函数的表达式；(2)请用无刻度的直尺和圆规作出线段AC 的垂直平分线；(要求：不写作法，保留作图痕迹)(3)线段OA 与(2)中所作的垂直平分线相交于点D ，连接CD .求证：CD ∥AB .23．(2021·江西)如图1，四边形ABCD 内接于⊙O ，AD 为直径，过点C 作CE ⊥AB 于点E ，连接AC .(1)求证：∠CAD ＝∠ECB ；(2)若CE 是⊙O 的切线，∠CAD ＝30°，连接OC ，如图2.①请判断四边形ABCO 的形状，并说明理由；②当AB ＝2时，求AD ，AC 与CD ︵围成阴影部分的面积．。

2024届重庆市八中学中考英语模拟预测题含答案

2024届重庆市八中学中考英语模拟预测题含答案注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

Ⅰ. 单项选择1、(2012甘肃白银)I think every student should go to school________，but some of them are always late．A．by the timeB．on timeC．for a timeD．at times2、Many college students go to West China to help local people, ______ they may find a good job in big cities. A．because B．if C．although D．after3、For your ________, you mustn't get out of the car in the wild animal park.A．choice B．chance C．safety D．mistake4、Mr. Li ____ to give a talk in our school yesterday.A．invites B．is invited C．was invited D．invited5、—Have you seen ______ movie Nice To Meet You?—Yes, it's ______ wonderful one.A．a, the B．the; a C．the; the D．a; a6、--Could you tell me ?--Next Monday.A．when you will go to Beijing B．when will you go to BeijingC．how will you go to Beijing7、In this exam, you’re asked to write a composition of about ________.A．90-words B．90-word C．90 words D．90 word’s8、To my surprise, I ________ from hundreds of students to make a speech to teachers, parents and fellow students. A．were chosen B．was chosenC．chose D．will be chosen9、一When did you leave your office yesterday?一I finished the project.A．Until B．While C．When D．Not until10、—Do you believe that paper is made _____ wood?—Yes, I do. And you can see that books are made ______ paper.A．from; from B．from; of C．of; from D．of; ofⅡ. 完形填空11、完形填空，阅读下面的短文，根据短文内容从各题所给的A、B、C、D四个选项中，选出一个可以填入空白处的最佳选项，使短文完整、通顺，并在答题卡上将该标号涂黑。

2020年中考数学模拟试题(八)有答案

2020年中考模拟试题（八）数学注意事项：1. 本试卷共8页，26个小题，满分为120分，考试时间为120分钟。

2. 根据阅卷需要，本试卷中的所有试题均按要求在答题卡上作答，答在本试卷上的答案无效。

3. 考试结束后，将本试卷保管好并将答题卡上交。

一、选择题（本大题包括10个小题，每小题3分，共30分，每小题只有一个正确选项，请在答题卡上将代表正确答案的字母用2B铅笔涂黑）1．下列各数，最小的数是（）A．﹣2020B．0C．D．﹣12．下面运算中，结果正确的是（）A．5ab﹣3b＝2a B．（﹣3a2b）2＝6a4b2C．a3•b÷a＝a2b D．（2a+b）2＝4a2+b23．新冠病毒疫情发生以来，我国邮政快递企业调配全网资源，迅速开通了国际和国内的航线，畅通陆路运输，全力保障武汉等重点地区的应急救援物资和人民群众日常基本生活物资运递，截止至2020年4月14日，累计为援鄂医疗队免费寄递物品19.71万件．其中数值19.71万可用科学记数法表示为（）A．1.971×109B．19.71×104C．0.1971×106D．1.971×105 4．下列图形既是轴对称图形又是中心对称图形的是（）A．B．C．D．5．如图所示的主视图和俯视图，其对应的几何体（阴影所示如图）可以是下列（）A．B．C．D．6．某单位向一所希望小学赠送1080本课外书，现用A、B两种不同的包装箱进行包装，单独使用B型包装箱比单独使用A型包装箱可少用6个；已知每个B型包装箱比每个A型包装箱可多装15本课外书．若设每个A型包装箱可以装书x本，则根据题意列得方程为（）A．B．C．D．7．如图，矩形ABCD的顶点A和对称中心均在反比例函数y＝（k≠0，x＞0）上，若矩形ABCD的面积为12，则k的值为（）A．12 B．6C．4D．38．如图，直线PQ是矩形ABCD的一条对称轴，点E在AB边上，将△ADE沿DE折叠，点A恰好落在CE与PQ的交点F处，若S△DEC＝4，则AD的长为（）A．4B．2C．4D．29．函数y＝x2+2bx+6的图象与x轴两个交点的横坐标分别为x1，x2，且x1＞1，x2﹣x1＝4，当1≤x≤3时，该函数的最小值m与b的关系式是（）A．m＝2b+5B．m＝4b+8C．m＝6b+15D．m＝﹣b2+4 10．如图，棱长均为1的直三棱柱ABC﹣A1B1C1中，F是棱AC的中点．动点P从点A出发，沿着A→B→C的路线在该棱柱的棱上运动，运动到点C就停止．设点P运动的路程为x，y＝FP+PB1，则y关于x的函数图象大致为（）A．B．C．D．二、填空题（本题包括7个小题，每小题3分，共21分，将答案直接填在答题卡对应题的横线上）11．在函数y＝中，自变量x的取值范围是．12．分解因式：a2b+4ab+4b＝．13．如图，菱形OABC的边长为2，且点A、B、C在⊙O上，则劣弧的长度为．14．关于x的方程x2﹣（3k+1）x+2k2+2k＝0，若等腰三角形△ABC一边长为a＝6，另两边长b，c为方程两个根，则△ABC的周长为．15．如图，已知AB是⊙O的直径，弦CD交AB于点E，∠CEA＝30°，OF⊥CD，垂足为点F，DE＝5，OF＝1，那么CD＝．16．如图，矩形ABCD中，AB＝4，BC＝6，点P是矩形ABCD内一动点，且S△P AB＝S△PCD，则PC+PD的最小值为．17．如图，菱形OAA1B1的边长为1，∠AOB＝60°，以对角线OA1为一边，在如图所示的一侧作相同形状的菱形OA1A2B2，再依次作菱形OA2A3B3，菱形OA3A4B4，……，则菱形OA2019A2020B2020的边长为．三、解答题(本题包括9个小题，共69分，请在答题卡上写出各题解答的文字说明、证明过程或计算步骤）18．计算：（π﹣3.14）0+﹣2sin45°+﹣（﹣1）2020；19．先化简，再求值：÷（﹣x+1），请从不等式组的整数解中选择一个合适的值代入求值．20．小锤和豆花要测量校园里的一块四边形场地ABCD（如图所示）的周长，其中边BC上有水池及建筑遮挡，没有办法直接测量其长度．小锤经测量得知AB＝AD＝5m，∠A＝60°，DC＝13m，∠ABC＝150°．豆花说根据小锤所得的数据可以求出CB的长度．你同意豆花的说法吗？若同意，请求出CB的长度；若不同意，请说明理由．21．在新中国成立70周年之际，某校开展了“校园文化艺术”活动，活动项目有：书法、绘画、声乐和器乐，要求全校学生人人参加，并且每人只能参加其中一项活动．政教处在该校学生中随机抽取了100名学生进行调查和统计，并绘制了如图两幅不完整的统计图，请结合图中相关数据解答下列问题：（1）请补全条形统计图和扇形统计图；（2）该校初中学生中，参加“书法”项目的学生所占的百分比是多少？（3）若该校共有1500人，请估计其中参加“器乐”项目的高中学生有多少人？（4）经政教处对所有参加“绘画”项目的作品进行评比，共选出2名初中学生和2名高中学生的最佳作品，学校决定从这4名学生中随机抽取2人作为学生会“绘画社团”的团长，那么正好抽到一名初中学生和一名高中学生的概率是多少？22．如图，放置在水平桌面上的台灯灯臂AB长为42cm，灯罩BC长为32cm，底座厚度为2cm，灯臂与底座构成的∠BAD＝60°．使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？23．预防新型冠状病毒期间，某种消毒液A地需要6吨，B地需要10吨，正好M地储备有7吨，N地储备有9吨．市预防新型冠状病毒领导小组决定将这16吨消毒液调往A地和B地．消毒液的运费价格如表（单位：元/吨）．设从M地调运x（0＜x≤6）吨到A地．（1）求调运16吨消毒液的总运费y关于x的函数关系式；（2）求出总运费最低的调运方案，最低运费为多少？A地B地终点起点M地70120N地458024．（1）【证法回顾】证明：三角形中位线定理．已知：如图1，DE是△ABC的中位线．求证：．（填写要求证的结论）证明：添加辅助线：如图1，在△ABC中，延长DE（D、E分别是AB、AC的中点）到点F，使得EF＝DE，连接CF，请继续完成证明过程；（2）【问题解决】如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD 边上的点，若AG＝2，DF＝3，∠GEF＝90°，求GF的长．25．如图F为⊙O上的一点，过点F作⊙O的切线与直径AC的延长线交于点D，过圆上的另一点B作AO的垂线，交DF的延长线于点M，交⊙O于点E，垂足为H，连接AF，交BM于点G．（1）求证：△MFG为等腰三角形．（2）若AB∥MD，求证：FG2＝EG•MF．（3）在（2）的条件下，若DF＝6，tan∠M＝，求AG的长．26．如图，抛物线y＝x2﹣（a+1）x+a与x轴交于A，B两点（点A位于点B的左侧），与y轴的负半轴交于点C．（1）求点B的坐标．（2）若△ABC的面积为6．①求这条抛物线相应的函数解析式；②在拋物线上是否存在一点P，使得∠POB＝∠CBO？若存在，请求出点P的坐标；若不存在，请说明理由．2020年中考数学模拟试题（八）参考答案一．选择题（共10小题）1．下列各数，最小的数是（）A．﹣2020B．0C．D．﹣1【分析】由于正数大于0，0大于负数，要求最小实数，只需比较﹣2020与﹣1即可．【解答】解：∵﹣2020＜﹣1＜0＜，∴最小的数是﹣2020．故选：A．2．下面运算中，结果正确的是（）A．5ab﹣3b＝2a B．（﹣3a2b）2＝6a4b2C．a3•b÷a＝a2b D．（2a+b）2＝4a2+b2【分析】根据合并同类项、积的乘方、单项式的除法和完全平方公式判断即可．【解答】解：A、5ab与﹣3b不是同类项，不能合并，选项错误，不符合题意；B、（﹣3a2b）2＝9a4b2，选项错误，不符合题意；C、a3•b÷a＝a2b，选项正确，符合题意；D、（2a+b）2＝4a2+4ab+b2，选项错误，不符合题意；故选：C．3．新冠病毒疫情发生以来，我国邮政快递企业调配全网资源，迅速开通了国际和国内的航线，畅通陆路运输，全力保障武汉等重点地区的应急救援物资和人民群众日常基本生活物资运递，截止至2020年4月14日，累计为援鄂医疗队免费寄递物品19.71万件．其中数值19.71万可用科学记数法表示为（）A．1.971×109B．19.71×104C．0.1971×106D．1.971×105【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：19.71万＝19710000＝1.971×105，故选：D．4．下列图形既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、是轴对称图形，不是中心对称图形，故此选项不合题意；B、是轴对称图形，不是中心对称图形，故此选项不合题意；C、不是轴对称图形，是中心对称图形，故此选项不合题意；D、既是轴对称图形，又是中心对称图形，故此选项符合题意．故选：D．5．如图所示的主视图和俯视图，其对应的几何体（阴影所示如图）可以是下列（）A．B．C．D．【分析】根据几何体的主视图确定A、B、C选项，然后根据俯视图确定D选项即．【解答】解：A、B、D选项的主视图符合题意；C选项的主视图和俯视图都不符合题意，D选项的俯视图符合题意，综上：对应的几何体为D选项中的几何体．故选：D．6．某单位向一所希望小学赠送1080本课外书，现用A、B两种不同的包装箱进行包装，单独使用B型包装箱比单独使用A型包装箱可少用6个；已知每个B型包装箱比每个A型包装箱可多装15本课外书．若设每个A型包装箱可以装书x本，则根据题意列得方程为（）A．B．C．D．【分析】关键描述语：单独使用B型包装箱比单独使用A型包装箱可少用6个；可列等量关系为：所用B型包装箱的数量＝所用A型包装箱的数量﹣6，由此可得到所求的方程．【解答】解：根据题意，得：．故选：C．7．如图，矩形ABCD的顶点A和对称中心均在反比例函数y＝（k≠0，x＞0）上，若矩形ABCD的面积为12，则k的值为（）A．12B．6C．4D．3【分析】设点A的坐标，利用矩形的面积，表示矩形的边长，再根据对称中心表示E的坐标，由点A、E都在反比例函数的图象上，由反比例函数k的几何意义求解即可．【解答】解：设矩形的对称中心为E，连接OA、OE，过E作EF⊥OC垂足为F，∵点E是矩形ABCD的对称中心，∴BF＝FC＝BC，EF＝AB，设OB＝a，AB＝b，∵ABCD的面积为12，∴BC＝，BF＝FC＝，∴点E（a+，b），∵S△AOB＝S△EOF＝k，∴ab＝（a+）×b＝k，即：ab＝6＝k，故选：B．8．如图，直线PQ是矩形ABCD的一条对称轴，点E在AB边上，将△ADE沿DE折叠，点A恰好落在CE与PQ的交点F处，若S△DEC＝4，则AD的长为（）A．4B．2C．4D．2【分析】根据矩形的性质和折叠的性质可得∠ADE＝∠EDF＝∠CDF＝30°，再根据三角形面积公式可求AD的长．【解答】解：∵四边形ABCD是矩形，∴∠A＝90°，∵直线PQ是矩形ABCD的一条对称轴，∴∠DGF＝90°，CD∥PQ，DG＝AD，由折叠得∠EFD＝∠A＝90°，DF＝AD，∠EDF＝∠ADE，∴∠CFD＝90°，∵EF＝CF，∴∠EDF＝∠CDF，∴∠ADE＝∠EDF＝∠CDF＝30°，∴EF＝DF，∴EC＝AD，∵S△DEC＝4，∴AD×AD÷2＝4，解得AD＝2．故选：D．9．函数y＝x2+2bx+6的图象与x轴两个交点的横坐标分别为x1，x2，且x1＞1，x2﹣x1＝4，当1≤x≤3时，该函数的最小值m与b的关系式是（）A．m＝2b+5B．m＝4b+8C．m＝6b+15D．m＝﹣b2+4【分析】由韦达定理得：x1•x2＝6，而x2﹣x1＝4，求出x1、x2的值，函数的对称轴为直线x＝（x1+x2）＝＜3，故当1≤x≤3时，函数在x＝3时，取得最小值，即可求解．【解答】解：函数y＝x2+2bx+6的图象与x轴两个交点的横坐标分别为x1，x2，∴x1•x2＝6，而x2﹣x1＝4，解得：x1＝﹣2±（舍去负数），则x2＝2+，∵x1+x2＝﹣2b，∴b＝﹣；函数的对称轴为直线x＝（x1+x2）＝＜3，故当1≤x≤3时，函数在x＝3时，取得最小值，即m＝y＝x2+2bx+6＝15+6b，故选：C．10．如图，棱长均为1的直三棱柱ABC﹣A1B1C1中，F是棱AC的中点．动点P从点A出发，沿着A→B→C的路线在该棱柱的棱上运动，运动到点C就停止．设点P运动的路程为x，y＝FP+PB1，则y关于x的函数图象大致为（）A．B．C．D．【分析】根据图象的对称性，确定图象的对称性即可求解．【解答】解：由题意知，FP+PB1关于BB1对称，故可知y关于x的函数图象关于直线x＝1对称，故选：B．二．填空题（共7小题）11．在函数y＝中，自变量x的取值范围是x≥0且x≠3．【分析】根据被开方数是非负数且分母不等于零，可得答案．【解答】解：由题意，得x≥0且x﹣3≠0，解得x≥0且x≠3，故答案为：x≥0且x≠3．12．分解因式：a2b+4ab+4b＝b（a+2）2．【分析】原式提取b，再利用完全平方公式分解即可．【解答】解：原式＝b（a2+4a+4）＝b（a+2）2，故答案为：b（a+2）213．如图，菱形OABC的边长为2，且点A、B、C在⊙O上，则劣弧的长度为π．【分析】连接OB，根据菱形性质求出OB＝OC＝BC，求出△BOC是等边三角形，求出∠COB＝60°，根据弧长公式求出即可．【解答】解：连接OB，∵四边形OABC是菱形，∴OC＝BC＝AB＝OA＝2，∴OC＝OB＝BC，∴△OBC是等边三角形，∴∠COB＝60°，∴劣弧的长为＝π，故答案为：π．14．关于x的方程x2﹣（3k+1）x+2k2+2k＝0，若等腰三角形△ABC一边长为a＝6，另两边长b，c为方程两个根，则△ABC的周长为16或22．【分析】先计算判别式的值得到△＝（k﹣1）2≥0，利用求根公式得到x1＝k+1，x2＝2k，根据等腰三角形的性质讨论：当k+1＝2k或k+1＝6或2k＝6时，分别计算出对应的k的值得到b、c的值，然后根据三角形三边的关系和三角形周长的定义求解．【解答】解：根据题意得△＝（3k+1）2﹣4（2k2+2k）＝（k﹣1）2≥0，所以x＝，则x1＝k+1，x2＝2k，当k+1＝2k时，解得k＝1，则b、c的长为2，而2+2＜6，不合题意舍去；当k+1＝6时，解得k＝5，则2k＝10，此时三角形的周长为6+6+10＝22；当2k＝6时，解得k＝3，则k+1＝4，此时三角形的周长为6+6+4＝16．综上所述，△ABC的周长为16或22．故答案为16或22．15．如图，已知AB是⊙O的直径，弦CD交AB于点E，∠CEA＝30°，OF⊥CD，垂足为点F，DE＝5，OF＝1，那么CD＝．【分析】根据AB是⊙O的直径，OF⊥CD，和垂径定理可得CF＝DF，再根据30度角所对直角边等于斜边一半，和勾股定理即可求出EF的长，进而可得CD的长．【解答】解：∵AB是⊙O的直径，OF⊥CD，根据垂径定理可知：CF＝DF，∵∠CEA＝30°，∴∠OEF＝30°，∴OE＝2，EF＝，∴DF＝DE﹣EF＝5﹣，∴CD＝2DF＝10﹣2．故答案为：10﹣2．16．如图，矩形ABCD中，AB＝4，BC＝6，点P是矩形ABCD内一动点，且S△P AB＝S△PCD，则PC+PD的最小值为2．【分析】依据S△P AB＝S△PCD，即可得出点P在BC的垂直平分线上，进而得到PB＝PC，当点B，P，D在同一直线上时，BP+PD的最小值等于对角线BD的长，依据勾股定理求得BD的长，即可得到PC+PD的最小值为2．【解答】解：∵点P是矩形ABCD内一动点，且S△P AB＝S△PCD，AB＝CD，∴点P到AB的距离等于点P到CD的距离，∴点P在BC的垂直平分线上，∴PB＝PC，∴PC+PD＝BP+PD，当点B，P，D在同一直线上时，BP+PD的最小值等于对角线BD的长，又∵AB＝CD＝4，BC＝6，∴对角线BD＝＝＝2，∴PC+PD的最小值为2，故答案为：2．17．如图，菱形OAA1B1的边长为1，∠AOB＝60°，以对角线OA1为一边，在如图所示的一侧作相同形状的菱形OA1A2B2，再依次作菱形OA2A3B3，菱形OA3A4B4，……，则菱形OA2019A2020B2020的边长为（）2019．【分析】根据图形的变化发现规律即可求解．【解答】解：∵菱形OAA1B的边长为1，∠AOB＝60°，对角线OA1为：2cos30°•OA＝；∴菱形OA1A2B2的边长为：菱形OA2A3B3的边长为（）2菱形OA3A4B4的边长为（）3……，发现规律：则菱形OA2019A2020B2020的边长为（）2019．故答案为：（）2019．三．解答题（共23小题）18．（1）计算：（﹣）﹣1+﹣|π﹣3|﹣；（2）因式分解：a3﹣2a2b+ab2．【分析】（1）原式利用负整数指数幂法则，绝对值的代数意义，二次根式性质，以及特殊角的三角函数值计算即可求出值；（2）原式提取公因式，再利用完全平方公式分解即可．【解答】解：（1）原式＝﹣3+﹣（π﹣3）﹣＝﹣3+﹣π+3﹣＝﹣π；（2）原式＝a（a2﹣2ab+b2）＝a（a﹣b）2．19．（1）计算：（π﹣3.14）0+﹣2sin45°+﹣（﹣1）2020；（2）先化简，再求值：÷（﹣x+1），请从不等式组的整数解中选择一个合适的值代入求值．【分析】（1）直接利用零指数幂的性质以及二次根式的性质、负整数指数幂的性质分别化简得出答案；（2）直接利用将括号里面通分运算，再利用分式的混合运算法则计算得出答案．【解答】解：（1）原式＝1+﹣1﹣2×+﹣1＝﹣1；（2）原式＝＝＝＝，由不等式组，解得：﹣2≤x≤2，∵x+1≠0，（2+x）（2﹣x）≠0，∴x≠﹣1，x≠±2，∴当x＝0时，原式＝＝1．（或当x＝1时，原式＝＝）．20．小锤和豆花要测量校园里的一块四边形场地ABCD（如图所示）的周长，其中边BC上有水池及建筑遮挡，没有办法直接测量其长度．小锤经测量得知AB＝AD＝5m，∠A＝60°，DC＝13m，∠ABC＝150°．豆花说根据小锤所得的数据可以求出CB的长度．你同意豆花的说法吗？若同意，请求出CB的长度；若不同意，请说明理由．【分析】直接利用等边三角形的判定方法得出△ABD是等边三角形，再利用勾股定理得出答案．【解答】解：同意豆花的说法．理由：连接BD，∵AB＝AD＝5m，∠A＝60°，∴△ABD是等边三角形，∴BD＝5m，∠ABD＝60°，∵∠ABC＝150°，∴∠DBC＝90°，∵DC＝13m，BD＝5m，∴CB＝＝12（m）．答：CB的长度为12m．21．在新中国成立70周年之际，某校开展了“校园文化艺术”活动，活动项目有：书法、绘画、声乐和器乐，要求全校学生人人参加，并且每人只能参加其中一项活动．政教处在该校学生中随机抽取了100名学生进行调查和统计，并绘制了如图两幅不完整的统计图，请结合图中相关数据解答下列问题：（1）请补全条形统计图和扇形统计图；（2）该校初中学生中，参加“书法”项目的学生所占的百分比是多少？（3）若该校共有1500人，请估计其中参加“器乐”项目的高中学生有多少人？（4）经政教处对所有参加“绘画”项目的作品进行评比，共选出2名初中学生和2名高中学生的最佳作品，学校决定从这4名学生中随机抽取2人作为学生会“绘画社团”的团长，那么正好抽到一名初中学生和一名高中学生的概率是多少？【分析】（1）求出参加高中声乐的人数即可补充条形统计图；由参加器乐和声乐的总人数看分别求出其所占的百分比则扇形统计图可补充完整；（2）首先求出参加各个项目的初中总人数即可得到参加“书法”项目的学生所占的百分比；（3）求出参加“器乐”项目的高中学生所占百分比，即可估计1500名学生中参加“器乐”项目的高中学生的人数；（4）记两名高中学生为A，B，两名初中学生为a，b．列表得到所有可能结果，进而可求出正好抽到一名初中学生和一名高中学生的概率．【解答】解：（1）补全条形统计图和扇形统计图如下：（2）．答：该校初中学生中，参加“书法”项目的学生占45%．（3）（人）．答：该校参加“器乐”项目的高中学生约有375人．（4）记两名高中学生为A，B，两名初中学生为a，b．列表如下：A B a bA（A，B）（A，a）（A，b）B（B，A）（B，a）（B，b）a（a，A）（a，B）（a，b）b（b，A）（b，B）（b，a）由上表可知，共有12种等可能结果，其中能抽到一名初中学生和一名高中学生的结果有8种，∴P（抽到一名初中学生和一名高中学生）＝．答：正好抽到一名初中学生和一名高中学生的概率是．22．如图，放置在水平桌面上的台灯灯臂AB长为42cm，灯罩BC长为32cm，底座厚度为2cm，灯臂与底座构成的∠BAD＝60°．使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？【分析】过点B作BM⊥CE于点M，BF⊥DA于点F，在Rt△BCM和Rt△ABF中，通过解直角三角形可求出CM、BF的长，再由CE＝CM+BF+ED即可求出CE的长．【解答】解：过点B作BM⊥CE于点M，BF⊥DA于点F，如图所示．在Rt△BCM中，BC＝32cm，∠CBM＝30°，∴CM＝BC•sin∠CBM＝16cm．在Rt△ABF中，AB＝42cm，∠BAD＝60°，∴BF＝AB•sin∠BAD＝21cm．∵∠ADC＝∠BMD＝∠BFD＝90°，∴四边形BFDM为矩形，∴MD＝BF，∴CE＝CM+MD+DE＝CM+BF+ED＝16+21+2＝21+18（cm）．答：此时灯罩顶端C到桌面的高度CE是（21+18）cm．23．预防新型冠状病毒期间，某种消毒液A地需要6吨，B地需要10吨，正好M地储备有7吨，N地储备有9吨．市预防新型冠状病毒领导小组决定将这16吨消毒液调往A地和B地．消毒液的运费价格如表（单位：元/吨）．设从M地调运x（0＜x≤6）吨到A地．（1）求调运16吨消毒液的总运费y关于x的函数关系式；（2）求出总运费最低的调运方案，最低运费为多少？A地B地终点起点M地70120N地4580【分析】（1）根据题意即可得调运16吨消毒液的总运费y关于x的函数关系式；（2）根据一次函数的性质即可求出总运费最低的调运方案和最低运费．【解答】解：（1）由题意可知：y＝70x+120（7﹣x）+45（6﹣x）+80[（9﹣（6﹣x）]＝﹣15x+1350（0＜x≤6）．（2）由（1）的函数可知：k＝﹣15＜0，所以函数的值随x的增大而减小，当x＝6时，有最小值y＝﹣15×6+1350＝1260（元）．答：总运费最低的调运方案是从M地调运6吨到A地，1吨到B地，最低运费为1260元．24．（1）【证法回顾】证明：三角形中位线定理．已知：如图1，DE是△ABC的中位线．求证：DE∥BC，DE＝BC．（填写要求证的结论）证明：添加辅助线：如图1，在△ABC中，延长DE（D、E分别是AB、AC的中点）到点F，使得EF＝DE，连接CF，请继续完成证明过程；（2）【问题解决】如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD 边上的点，若AG＝2，DF＝3，∠GEF＝90°，求GF的长．【分析】（1）利用“边角边”证明△ADE和△CEF全等，根据全等三角形对应边相等可得AD＝CF，然后判断出四边形BCFD是平行四边形，根据平行四边形的性质可得；（2）先判断出△AEG≌△DEH（ASA）进而判断出EF垂直平分GH，即可得出结论．【解答】解：DE∥BC，DE＝BC，证明：如图，延长DE到点F，使得EF＝DE，连接CF在△ADE和△CFE中，，∴△ADE≌△CFE（SAS），∴∠A＝∠ECF，AD＝CF，∴CF∥AB，又∵AD＝BD，∴CF＝BD，∴四边形BCFD是平行四边形，∴DE∥BC，DE＝BC．故答案为：DE∥BC，DE＝BC．（2）如图2，延长GE、FD交于点H，∵E为AD中点，∴EA＝ED，且∠A＝∠EDH＝90°，在△AEG和△DEH中，，∴△AEG≌△DEH（ASA），∴AG＝HD＝2，EG＝EH，∵∠GEF＝90°，∴EF垂直平分GH，∴GF＝HF＝DH+DF＝2+3＝5．25．如图F为⊙O上的一点，过点F作⊙O的切线与直径AC的延长线交于点D，过圆上的另一点B作AO的垂线，交DF的延长线于点M，交⊙O于点E，垂足为H，连接AF，交BM于点G．（1）求证：△MFG为等腰三角形．（2）若AB∥MD，求证：FG2＝EG•MF．（3）在（2）的条件下，若DF＝6，tan∠M＝，求AG的长．【分析】（1）连接OF，利用等角的余角相等证明∠MFG＝∠MGF即可解决问题．（2）连接EF．证明△EGF∽△FGM，可得结论，（3）连接OB．证明∠M＝∠FOD，推出tan∠M＝tan∠FOD＝＝，由DF＝6，推出OF＝8，再由tan∠M＝tan∠ABH＝＝，假设AH＝3k，BH＝4k，则AB＝BG＝5k，GH＝k，AG＝k，在Rt△OHB中，根据OH2+BH2＝OB2，构建方程即可解决问题．【解答】（1）证明：连接OF．∵DM是⊙O的切线，∴DM⊥OF，∴∠MFG+∠OF A＝90°，∵BM⊥AD，∴∠AHG＝90°，∴∠OAF+∠AGH＝90°，∵OF＝OA，∴∠OF A＝∠OAF，∵∠MGF＝∠AGH，∴∠MFG＝∠AGF，∴MF＝MG，∴△MFG是等腰三角形．（2）证明：连接EF．∵AB∥DM，∴∠MF A＝∠F AB，∵∠F AB＝∠FEG，∠MFG＝∠MGF，∴∠FEG＝∠MFG，∵∠EGF＝∠MGF，∴△EGF∽△FGM，∴＝，∴FG2＝EG•GM，∵MF＝MG，∴FG2＝EG•MF．（3）解：连接OB．∵∠M+∠D＝90°，∠FOD+∠D＝90°，∴∠M＝∠FOD，∴tan M＝tan∠FOD＝＝，∵DF＝6，∴OF＝8，∵DM∥AB，∴∠M＝∠ABH，∴tan M＝tan∠ABH＝＝，∴可以假设AH＝3k，BH＝4k，则AB＝BG＝5k，GH＝k，AG＝k，在Rt△OHB中，∵OH2+BH2＝OB2，∴（8﹣3k）2+（4k）2＝82，解得k＝，∴AG＝．26．如图，抛物线y＝x2﹣（a+1）x+a与x轴交于A，B两点（点A位于点B的左侧），与y 轴的负半轴交于点C．（1）求点B的坐标．（2）若△ABC的面积为6．①求这条抛物线相应的函数解析式；②在拋物线上是否存在一点P，使得∠POB＝∠CBO？若存在，请求出点P的坐标；若不存在，请说明理由．【分析】（1）令y＝0，解方程可求出点A坐标为（a，0），点B坐标为（1，0）；（2）①由（1）可得，点A的坐标为（a，0），点C的坐标为（0，a），a＜0，再由△ABC 的面积得到a的值即可；②本题分两种情况讨论：当点P在x轴上方时，直线OP的函数表达式为y＝3x，则直线与抛物线的交点P可求出；当点P在x轴下方时，直线OP的函数表达式为y＝﹣3x，则直线与抛物线的交点P即可求出．【解答】解：（1）当y＝0时，x2﹣（a+1）x+a＝0，解得x1＝1，x2＝a．∵点A位于点B的左侧，与y轴的负半轴交于点C，∴a＜0，∴点B坐标为（1，0）．（2）①由（1）可得，点A的坐标为（a，0），点C的坐标为（0，a），a＜0，∴AB＝1﹣a，OC＝﹣a，∵△ABC的面积为6，∴，∴a1＝﹣3，a2＝4．∵a＜0，∴a＝﹣3，∴y＝x2+2x﹣3．②存在，理由如下：∵点B的坐标为（1，0），点C的坐标为（0，﹣3），∴设直线BC的解析式为y＝kx﹣3，则0＝k﹣3，∴k＝3．∵∠POB＝∠CBO，∴当点P在x轴上方时，直线OP∥直线BC，∴直线OP的函数解析式y＝3x，则∴（舍去），，∴点的P坐标为当点P在x轴下方时，直线OP'与直线OP关于x轴对称，则直线OP'的函数解析式为y＝﹣3x，则∴（舍去），，∴点P'的坐标为综上可得，点P的坐标为或．。

福州市福清市中考数学模拟试卷（八）含答案解析

福建省福州市福清市中考数学模拟试卷（八）一.选择题（共10小题，每小题4分，满分40分；在每小题给出的四个选项中，只有一项是符合题目要求的．）1．（4分）下列函数的解析式中是一次函数的是（）A．y=B．y=x+1 C．y=x2+1 D．y=2．（4分）当k＞0时，正比例函数y=kx的图象大致是（）A． B． C． D．3．（4分）在下列性质中，平行四边形不一定具有的是（）A．对边相等B．对边平行C．对角互补D．内角和为360°4．（4分）如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（）A．5 B．10 C．6 D．85．（4分）在一次数学阶段考试中，某小组7名同学的成绩（单位：分）分别是65，80，70，90，95，100，70，这组数据的众数是（）A．90 B．85 C．80 D．706．（4分）甲，乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（）A．甲的波动比乙的波动大B．乙的波动比甲的波动大C．甲，乙的波动大小一样D．甲，乙的波动大小无法确定7．（4分）已知一次函数y=（m﹣1）x﹣4的图象经过（2，4），则m的值为（）A．7 B．5 C．8 D．28．（4分）一次函数y=2x+1的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限9．（4分）如图，下列四组条件中．不能判定四边形ABCD是平行四边形的是（）A．AB=DC，AD=BC B．AB∥DC，AD∥BC C．AB∥DC，AD=BC D．AB∥DC，AB=DC10．（4分）如图是某学校全体教职工年龄的频数分布直方图（统计中采用“上限不在内”的原则，如年龄为36岁统计在36≤x＜38小组，而不在34≤x＜36小组），根据图形提供的信息，下列说法中错误的是（）A．该学校教职工总人数是50人B．年龄在40≤x＜42小组的教职工人数占学校教职工人数的20%C．教职工年龄的中位数一定落在40≤x＜42这一组D．教职工年龄的众数一定在38≤x＜40这一组二．填空题（本题共6题，每小题4分，满分24分）11．（4分）正比例函数y=﹣5x中，y随着x的增大而．12．（4分）已知函数y=﹣x+3，当x=时，函数值为0．13．（4分）在矩形ABCD中，再增加条件（只需填一个）可使矩形ABCD 成为正方形．14．（4分）有一组数据如下：3，a，4，6，7，它们的平均数是5，那么a=．15．（4分）将直线向下平移3个单位，得到直线．16．（4分）某招聘考试分笔试和面试两种．其中笔试按60%、面试按40%计算加权平均数作为总成绩．小明笔试成绩为90分．面试成绩为85分，那么小明的总成绩为分．三．解答题（共8小题，满分86分.）17．（8分）已知：函数y=（1﹣3k）x+2k﹣1，试回答：（1）k为何值时，图象过原点？（2）k为何值时，y随x的增大而增大？18．（8分）已知样本数据为1，2，3，4，5，求这个样本的：（1）平均数；（2）方差S2．（提示：S2= [x1﹣）2+（x2﹣）2+（x3﹣）2+（x4﹣）2+（x5﹣）2]）19．（10分）已知一次函数的图象经过A（﹣2，﹣3），B（1，3）两点．（1）求这个一次函数的解析式；（2）试判断点P（﹣1，1）是否在这个一次函数的图象上；（3）求此函数与x轴、y轴围成的三角形的面积．20．（10分）在矩形ABCD中，两条对角线相交于O，∠AOB=60°，AB=2，求AD 的长．21．（12分）为了培养学生勤俭节约的意识，从小养成良好的生活习惯．某校随机抽查部分初中生对勤俭节约的态度（态度分为：赞成、无所谓、反对），并对抽查对象的态度绘制成了图1和图2两个统计图（统计图不完整），请根据图中的信息解答下列问题：（1）此次共抽查名学生；（2）持反对意见的学生人数占整体的%，无所谓意见的学生人数占整体的%；（3）估计该校1200名初中生中，大约有名学生持反对态度．22．（12分）如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．（1）求证：△BEC≌△DFA；（2）求证：四边形AECF是平行四边形．23．（12分）某商场欲购进果汁饮料和碳酸饮料共50箱，果汁饮料毎箱进价为55元，售价为63元；碳酸饮料毎箱进价为36元，售价为42元；设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注，总利润=总售价﹣总进价），（1）设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；（2）求总利润W关于x的函数关系式；（3）如果购进两种饮料的总费用不超过2000元，那么该商场如何进货才能获利最多？并求出最大利润．24．（14分）如图，直线L：与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4），动点M从A点以每秒1个单位的速度沿x轴向左移动．（1）求A、B两点的坐标；（2）求△COM的面积S与M的移动时间t之间的函数关系式；（3）当t为何值时△COM≌△AOB，并求此时M点的坐标．福建省福州市福清市中考数学模拟试卷（八）参考答案与试题解析一.选择题（共10小题，每小题4分，满分40分；在每小题给出的四个选项中，只有一项是符合题目要求的．）1．（4分）下列函数的解析式中是一次函数的是（）A．y=B．y=x+1 C．y=x2+1 D．y=【解答】解：A、是反比例函数，故此选项错误；B、是一次函数，故此选项正确；C、是二次函数，故此选项错误；D、不是一次函数，故此选项错误；故选：B．2．（4分）当k＞0时，正比例函数y=kx的图象大致是（）A． B． C． D．【解答】解：正比例函数的图象是一条经过原点的直线，且当k＞0时，经过一、三象限．故选：A．3．（4分）在下列性质中，平行四边形不一定具有的是（）A．对边相等B．对边平行C．对角互补D．内角和为360°【解答】解：A、平行四边形的对边相等，故A选项正确；B、平行四边形的对边平行，故B选项正确；C、平行四边形的对角相等不一定互补，故C选项错误；D、平行四边形的内角和为360°，故D选项正确；故选：C．4．（4分）如图：在菱形ABCD中，AC=6，BD=8，则菱形的边长为（）A．5 B．10 C．6 D．8【解答】解：设AC与BD相交于点O，由菱形的性质知：AC⊥BD，OA=AC=3，OB=BD=4在Rt△OAB中，AB===5所以菱形的边长为5．故选：A．5．（4分）在一次数学阶段考试中，某小组7名同学的成绩（单位：分）分别是65，80，70，90，95，100，70，这组数据的众数是（）A．90 B．85 C．80 D．70【解答】解：依题意得70出现了2次，次数最多，故这组数据的众数是70．故选：D．6．（4分）甲，乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（）A．甲的波动比乙的波动大B．乙的波动比甲的波动大C．甲，乙的波动大小一样D．甲，乙的波动大小无法确定【解答】解：根据方差的意义，甲样本的方差大于乙样本的方差，故甲的波动比乙的波动大．故选：A．7．（4分）已知一次函数y=（m﹣1）x﹣4的图象经过（2，4），则m的值为（）A．7 B．5 C．8 D．2【解答】解：∵一次函数y=（m﹣1）x﹣4的图象经过点A（2，4），∴4=2（m﹣1）﹣4，解得m=5．故选：B．8．（4分）一次函数y=2x+1的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：∵k=2＞0，图象过一三象限，b=1＞0，图象过第二象限，∴直线y=2x+1经过一、二、三象限，不经过第四象限．故选：D．9．（4分）如图，下列四组条件中．不能判定四边形ABCD是平行四边形的是（）A．AB=DC，AD=BC B．AB∥DC，AD∥BC C．AB∥DC，AD=BC D．AB∥DC，AB=DC【解答】解：根据平行四边形的判定，A、B、D均符合是平行四边形的条件，C 则不能判定是平行四边形．故选：C．10．（4分）如图是某学校全体教职工年龄的频数分布直方图（统计中采用“上限不在内”的原则，如年龄为36岁统计在36≤x＜38小组，而不在34≤x＜36小组），根据图形提供的信息，下列说法中错误的是（）A．该学校教职工总人数是50人B．年龄在40≤x＜42小组的教职工人数占学校教职工人数的20%C．教职工年龄的中位数一定落在40≤x＜42这一组D．教职工年龄的众数一定在38≤x＜40这一组【解答】解：A、该学校教职工总人数是4+6+11+10+9+6+4=50（人），故正确；B、在40≤x＜42小组的教职工人数占该学校全体教职工总人数的比例是：×100%=20%，故正确；C、教职工年龄的中位数一定落在40≤x＜42这一组，正确；D、教职工年龄的众数一定在38≤x＜40这一组．错误．故选：D．二．填空题（本题共6题，每小题4分，满分24分）11．（4分）正比例函数y=﹣5x中，y随着x的增大而减小．【解答】解：∵正比例函数y=﹣5x中k=﹣5＜0，∴y随着x的增大而减小．故答案为：减小．12．（4分）已知函数y=﹣x+3，当x=3时，函数值为0．【解答】解：当y=0时，﹣x+3=0，解得：x=3．故答案为：3．13．（4分）在矩形ABCD中，再增加条件AB=BC（只需填一个）可使矩形ABCD 成为正方形．【解答】解：∵AB=BC，∴矩形ABCD为正方形，故答案为：AB=BC．14．（4分）有一组数据如下：3，a，4，6，7，它们的平均数是5，那么a=5．【解答】解：由题意知，3，a，4，6，7的平均数是5，则=5，∴a=25﹣3﹣4﹣6﹣7=5．故答案为：5．15．（4分）将直线向下平移3个单位，得到直线y=x﹣3．【解答】解：原直线的k=，b=0；向下平移3个单位长度得到了新直线，那么新直线的k=，b=0﹣3=﹣3．∴新直线的解析式为y=x﹣3．故答案为：y=x﹣316．（4分）某招聘考试分笔试和面试两种．其中笔试按60%、面试按40%计算加权平均数作为总成绩．小明笔试成绩为90分．面试成绩为85分，那么小明的总成绩为88分．【解答】解：∵笔试按60%、面试按40%，∴总成绩是（90×60%+85×40%）=88（分）；故答案为：88．三．解答题（共8小题，满分86分.）17．（8分）已知：函数y=（1﹣3k）x+2k﹣1，试回答：（1）k为何值时，图象过原点？（2）k为何值时，y随x的增大而增大？【解答】解：（1）∵y=（1﹣3k）x+2k﹣1经过原点（0，0），∴0=（1﹣3k）×0+2k﹣1，解得，k=0.5，即当k=0.5时，图象过原点；（2）∵函数y=（1﹣3k）x+2k﹣1，y随x的增大而增大，∴1﹣3k＞0，解得，k＜，即当k＜时，y随x的增大而增大．18．（8分）已知样本数据为1，2，3，4，5，求这个样本的：（1）平均数；（2）方差S2．（提示：S2= [x1﹣）2+（x2﹣）2+（x3﹣）2+（x4﹣）2+（x5﹣）2]）【解答】解：（1）=（1+2+3+4+5）=3；（2）S2= [（1﹣3）2+（2﹣3）2+（3﹣3）2+（4﹣3）2+（5﹣3）2]=2．19．（10分）已知一次函数的图象经过A（﹣2，﹣3），B（1，3）两点．（1）求这个一次函数的解析式；（2）试判断点P（﹣1，1）是否在这个一次函数的图象上；（3）求此函数与x轴、y轴围成的三角形的面积．【解答】解：（1）设一次函数的表达式为y=kx+b，则，解得：k=2，b=1．∴函数的解析式为：y=2x+1．（2）将点P（﹣1，1）代入函数解析式，1≠﹣2+1，∴点P不在这个一次函数的图象上．（3）当x=0，y=1，当y=0，x=﹣，此函数与x轴、y轴围成的三角形的面积为：×1×=．20．（10分）在矩形ABCD中，两条对角线相交于O，∠AOB=60°，AB=2，求AD 的长．【解答】解：∵四边形ABCD是矩形，∴OA=OB=OC=OD，∠BAD=90°，∵∠AOB=60°，∴△AOB是等边三角形，∴OB=AB=2，∴BD=2BO=4，在Rt△BAD中，AD=．21．（12分）为了培养学生勤俭节约的意识，从小养成良好的生活习惯．某校随机抽查部分初中生对勤俭节约的态度（态度分为：赞成、无所谓、反对），并对抽查对象的态度绘制成了图1和图2两个统计图（统计图不完整），请根据图中的信息解答下列问题：（1）此次共抽查200名学生；（2）持反对意见的学生人数占整体的10%，无所谓意见的学生人数占整体的15%；（3）估计该校1200名初中生中，大约有120名学生持反对态度．【解答】解：（1）根据题意得：=200（名），答：此次共抽查了200名学生；（2）持反对意见的学生人数是200﹣150﹣30=20（名），持反对意见的学生人数占整体的×100%=10%；无所谓意见的学生人数占整体的×100%=15%；故答案为：10%，15%；（3）根据题意得：1200×10%=120（名），答：大约有120名学生持反对态度．故答案为：120．22．（12分）如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．（1）求证：△BEC≌△DFA；（2）求证：四边形AECF是平行四边形．【解答】证明：（1）∵四边形ABCD是矩形，∴AB=CD，AD=BC，又∵E、F分别是边AB、CD的中点，∴BE=DF，∵在△BEC和△DFA中，，∴△BEC≌△DFA（SAS）．（2）由（1）得，CE=AF，AD=BC，故可得四边形AECF是平行四边形．23．（12分）某商场欲购进果汁饮料和碳酸饮料共50箱，果汁饮料毎箱进价为55元，售价为63元；碳酸饮料毎箱进价为36元，售价为42元；设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注，总利润=总售价﹣总进价），（1）设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；（2）求总利润W关于x的函数关系式；（3）如果购进两种饮料的总费用不超过2000元，那么该商场如何进货才能获利最多？并求出最大利润．【解答】解：（1）y与x之间的函数关系式为y=50﹣x；（2）W=（63﹣55）x+（42﹣36）（50﹣x），整理得：W=2x+300；（3）根据题意得：55x+36（50﹣x）≤2000整理得：19x≤200．∴x≤10．∴x的最大值为10．又∵W=2x+300，W随着x的增大而增大．∴当x=10时，W有最大值，最大值为320．24．（14分）如图，直线L：与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4），动点M从A点以每秒1个单位的速度沿x轴向左移动．（1）求A、B两点的坐标；（2）求△COM的面积S与M的移动时间t之间的函数关系式；（3）当t为何值时△COM≌△AOB，并求此时M点的坐标．【解答】解：（1）对于直线AB：，当x=0时，y=2；当y=0时，x=4，则A、B两点的坐标分别为A（4，0）、B（0，2）；（2）∵C（0，4），A（4，0）∴OC=OA=4，=×4×（4﹣t）=8﹣2t；当0≤t≤4时，OM=OA﹣AM=4﹣t，S△OCM=×4×（t﹣4）=2t﹣8；当t＞4时，OM=AM﹣OA=t﹣4，S△OCM（3）分为两种情况：①当M在OA上时，OB=OM=2，△COM≌△AOB．∴AM=OA﹣OM=4﹣2=2∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位，所需要的时间是2秒钟；M（2，0），②当M在AO的延长线上时，OM=OB=2，则M（﹣2，0），此时所需要的时间t=[4﹣（﹣2）]/1=6秒，即M点的坐标是（2，0）或（﹣2，0）．。