沪教版数学六上《分数的乘法》word教案

合集下载

六年级数学上册 2.5 分数的乘法教案沪教版五四制

2.5 分数的乘法第（1）课时课题：书法---写字基本知识课型：新授课教学目标：1、初步掌握书写的姿势，了解钢笔书写的特点。

2、了解我国书法发展的历史。

3、掌握基本笔画的书写特点。

重点：基本笔画的书写。

难点：运笔的技法。

教学过程：一、了解书法的发展史及字体的分类：1、介绍我国书法的发展的历史。

2、介绍基本书体：颜、柳、赵、欧体，分类出示范本，边欣赏边讲解。

二、讲解书写的基本知识和要求：1、书写姿势：做到“三个一”：一拳、一尺、一寸（师及时指正）2、了解钢笔的性能：笔头富有弹性；选择出水顺畅的钢笔；及时地清洗钢笔；选择易溶解的钢笔墨水，一般要固定使用，不能参合使用。

换用墨水时，要清洗干净；不能将钢笔摔到地上，以免笔头折断。

三、基本笔画书写1、基本笔画包括：横、撇、竖、捺、点等。

2、教师边书写边讲解。

3、学生练习，教师指导。

（姿势正确）4、运笔的技法：起笔按，后稍提笔，在运笔的过程中要求做到平稳、流畅，末尾处回锋收笔或轻轻提笔，一个笔画的书写要求一气呵成。

在运笔中靠指力的轻重达到笔画粗细变化的效果，以求字的美观、大气。

5、学生练习，教师指导。

（发现问题及时指正）四、作业：完成一张基本笔画的练习。

板书设计：写字基本知识、一拳、一尺、一寸我的思考：通过导入让学生了解我国悠久的历史文化，激发学生学习兴趣。

这是书写的起步，让学生了解书写工具及保养的基本常识。

基本笔画书写是整个字书写的基础，必须认真书写。

课后反思：学生书写的姿势还有待进一步提高，要加强训练，基本笔画也要加强训练。

总第（2）课时课题：书写练习1课型：新授课教学目标：1、教会学生正确书写“杏花春雨江南”6个字。

2、使学生理解“杏花春雨江南”的意思，并用钢笔写出符合要求的的字。

重点：正确书写6个字。

难点：注意字的结构和笔画的书写。

教学过程：一、小结课堂内容，评价上次作业。

二、讲解新课：1、检查学生书写姿势和执笔动作（要求做到“三个一”）。

2、书写方法是：写一个字看一眼黑板。

沪教版小学数学六上2.7分数运算的应用word教案 (3)

分数的应用教学目标1. 知识目标：本节课是在学习了分数的有关概念，分数的加减乘除的运算，分数与小数的互化与运算的基础上的一节复习课。

2. 能力目标：通过整理和复习，提高学生的分析能力和计算能力。

3. 情感目标：通过生活中的数学，激发学生学习的兴趣。

进一步培养学生观察，分析，概括的逻辑思维能力。

发展他们思维的灵活性和解决实际问题的能力。

教学流程设计教学过程一、创设情境，切入课题甲,乙两家水果店都经营生梨的批发生意。

因互相竞争,都挂出牌子:5元3斤。

甲水果店的电子秤坏了,只能用手算,结果是用分数表示的。

乙水果店使用电子秤。

(电子秤精确到角)。

提示：电子秤是用小数表示的，且结果保留一位小数甲的生梨乙的生梨单价(元/斤) 买的重量(斤)二．设问质疑，探究尝试问题1：小丽在两家水果店都买了4斤生梨,请问:她在两家付的钱一样吗?在哪家付的钱多,多多少?(结果精确到角)问题2：一个月后,两家水果店都恰好销售出600斤生梨。

请问:乙水果店多赚了多少元?问题3：甲水果店的生梨进货价是1.3元/斤。

售出价:5元3斤,一天生意结束后赚了55元。

请问:一天卖出多少斤?课堂小结情景引入学习新知例题讲解2.请我们班级同学家中在去年买房的同学举手。

然后请其中一位同学将家里买房的价格叙述如下：去年买房者:每平方米元上海市房价从去年至今年普涨了1/5提问:(1)今年这套房子每平方米已涨到多少元?(2)房子总面积是：若今年买的话,总价要多付多少元?(3)买房子时还要付总价的3/200的契税,若现在买这套房子一共需要付多少元? 3.本界雅典奥运会，中国跃居世界第二。

创出了佳绩。

以上是中俄两国奖牌数的情况表。

学生由以上信息，分小组合作，自己编几道分数的应用题。

例如问：（1）中国的获得的金牌数是奖牌数的几分之几?(2) 俄罗斯获得的金牌数是中国金牌数的几分之几? 思考题中俄奖牌数情况表10203040中国俄罗斯国家奖牌数金牌银牌铜牌1714272738以下一段文字摘自10月9日的新闻晚报:今年的国庆”十.一”黄金周又恰逢上海旅游节,全市三千多家商业网点共实现销售额24.6亿元,比去年增加了1/6。

六年级数学上册《分数乘法》教案（精选11篇）

六年级数学上册《分数乘法》教案（精选11篇）六年级数学上册《分数乘法》篇1设计说明：1.重视学生的实践操作。

动手实践是学生学习数学的主要方式之一，它能加深学生对抽象的数学知识的理解。

在本设计中，教师为学生提供充分的动手操作的机会，学生通过分一分、算一算等活动，进一步体会分数乘整数的意义，同时还可以进一步体会“分数乘整数时，分子和整数相乘，分母不变”的道理。

2.实现数学学习的个性化。

本设计充分挖掘学生潜力，留给学生充足的时间和空间，放手让学生联系已有知识经验，自主探究计算方法，极大程度地发挥了学生学习的主体性和主动性。

学生在自主探究中产生了多种算法，让学生通过尝试、感悟、体验、探索，总结出“能约分的先约分，再计算比较简便”这一最优的计算方法。

学生自主构建知识，充分体现了“不同的人学习不同的数学”的理念。

课前准备：教师准备PPT学生准备彩色纸剪贴画长方形纸条教学过程：第1课时分数乘整数的意义及其计算方法⊙复习引入，提出问题1.把8+8+8+8+8改成乘法算式。

(8_5)2.把0.5+0.5+0.5改成乘法算式。

(0.5_3)3.列式计算。

(1)5个12是多少?(12_5)(2)12个1.5是多少?(1.5_12)4.提出问题。

师：3个是多少，能不能用算式_3来表示呢?今天，我们就一起来学习分数乘法。

(板书课题：分数乘整数的意义及其计算方法)设计意图：通过复习整数乘法和小数乘法，引出分数乘法问题，不仅自然地过渡到下一个环节，而且激发了学生探究新知的欲望。

⊙合作交流，探究新知：1.探究分数乘整数的意义，初步感知分数乘整数的计算方法。

课件出示问题：1个占整张纸条的，3个占整张纸条的几分之几?(1)引导学生分析问题。

你们打算用什么方法来解决这个问题?怎样获得最后的计算结果?(2)小组内讨论、交流。

(3)全班汇报。

预设：①图示法计算。

把一个长方形纸条看作单位“1”，把它平均分成5份，其中的一份就是一个，是，3份就是3个，如下图：3个是。

沪教版数学六年级上册2.5《分数的乘法》教学设计

沪教版数学六年级上册2.5《分数的乘法》教学设计一. 教材分析分数的乘法是小学数学中的一个重要概念，也是学生学习分数运算的基础。

沪教版数学六年级上册2.5《分数的乘法》一课，通过实例引入分数的乘法运算，让学生掌握分数乘法的计算法则，并能够灵活运用。

教材中通过具体的例题和练习，帮助学生理解和掌握分数乘法运算，培养学生的运算能力和逻辑思维能力。

二. 学情分析六年级的学生已经掌握了分数的基本概念和加减法运算，但对分数的乘法运算可能还存在一定的困难。

因此，在教学过程中，需要结合学生的实际情况，通过生动的实例和丰富的练习，让学生理解和掌握分数的乘法运算。

三. 教学目标1.知识与技能目标：让学生掌握分数的乘法运算方法，能够正确进行分数的乘法计算。

2.过程与方法目标：通过实例引入和练习，培养学生的运算能力和逻辑思维能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的团队合作意识和自主学习能力。

四. 教学重难点1.重点：分数的乘法运算方法。

2.难点：理解和掌握分数乘法运算的计算法则，能够灵活运用。

五. 教学方法1.情境教学法：通过生动的实例和实际问题，引发学生的思考和探究，激发学生的学习兴趣。

2.引导发现法：教师引导学生发现分数乘法运算的规律和方法，培养学生的逻辑思维能力。

3.练习法：通过丰富的练习，让学生巩固和掌握分数的乘法运算。

六. 教学准备1.教具准备：黑板、粉笔、多媒体教学设备。

2.学具准备：练习本、笔。

七. 教学过程1.导入（5分钟）教师通过一个实际问题，如“小明有2/3的苹果，小红的苹果是小明的3/2倍，请问小红有多少苹果？”引发学生的思考，进而引入分数的乘法运算。

2.呈现（10分钟）教师通过具体的例题，如2/3 × 3/4，引导学生发现分数乘法运算的规律，讲解分数乘法运算的计算法则。

3.操练（10分钟）学生分组进行练习，教师巡回指导。

每组完成几道分数乘法的题目，教师选取部分题目进行讲解和分析。

上海市六年级秋季班数学教案-4-分数的乘法-学生版

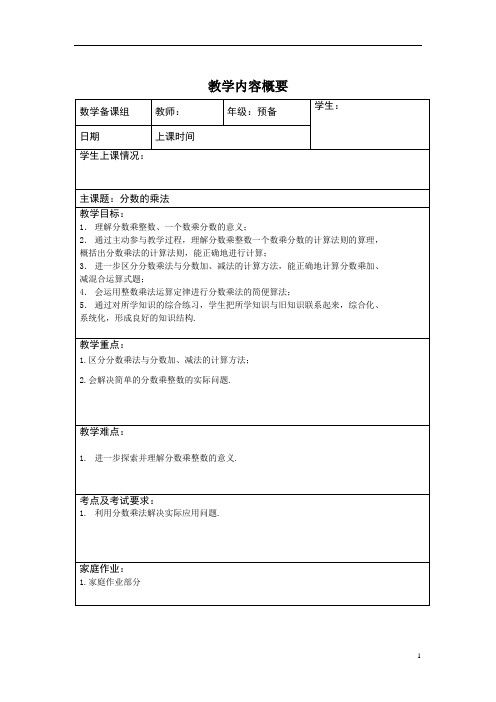
教学内容概要学生：数学备课组教师：年级：预备日期上课时间学生上课情况：主课题：分数的乘法教学目标：1．理解分数乘整数、一个数乘分数的意义；2．通过主动参与教学过程，理解分数乘整数一个数乘分数的计算法则的算理，概括出分数乘法的计算法则，能正确地进行计算；3．进一步区分分数乘法与分数加、减法的计算方法，能正确地计算分数乘加、减混合运算式题；4．会运用整数乘法运算定律进行分数乘法的简便算法；5．通过对所学知识的综合练习，学生把所学知识与旧知识联系起来，综合化、系统化，形成良好的知识结构.教学重点：1.区分分数乘法与分数加、减法的计算方法；2.会解决简单的分数乘整数的实际问题.教学难点：1.进一步探索并理解分数乘整数的意义.考点及考试要求：1.利用分数乘法解决实际应用问题.家庭作业：1.家庭作业部分教学内容【前课回顾】回忆一下我们分数到目前都讲了哪些内容？【知识精讲】知识点1 分数乘法的意义一般地，由于分数pq的意义是将_________________________________，于是我们把两个分数相乘p m q n ⨯的意义规定为：在分数p q 的基础上，以pq为总体，“再”等分为______份而取其中__________份，其结果是p mq n⨯⨯，即 p m q n ⨯=p m q n⨯⨯（0q ≠，0n ≠）. 知识点2 分数与分数相乘的方法两个分数相乘，将________________作积的分子，_________________作积的分母. 知识点3 整数与分数相乘的方法整数与分数相乘，______________________作积的分子，分母____________.【基础巩固】一、计算题 1、口算。

① 13 ×0= ；② 14 × 25 = ；③ 56 ×12= ；④ 712 × 314= ； ⑤45× 35 = ；⑥411 × 114 = ；⑦ 23 × 910 = ；⑧ 425×100= .2、能简算的要简算。

沪教版6年级数学上册第2章第6讲：真分数的乘法(教案)

沪教版6年级数学上册第2章第6讲：真分数的乘法（教案）第6讲：真分数的乘法（教案）导入前一节我们已经学习了分数的加减运算，同样地，分数之间也可以进行乘法运算。

那么分数乘法运算的基本方法是什么呢？首先我们从下面的一个例题入手，来共同探讨分数乘法的具体方法：例题：如图所示，取一个边长为1的正方形，首先竖着将它平均分成5等分，取其中的4份，涂上灰色，则灰色部分是原正方形的几分之几？接着，再横着将这个正方形平均分成3份，取其中的2份，涂上黄色，则此时黄色部分是原正方形的几分之几？那么灰色和黄色重叠的部分是原正方形的几分之几？解析：竖着将正方形分成5等份，取其中的4份涂上灰色，因为5份中，灰色占了4份，所以灰色部分正好是原来正方形的4； 5横着再将正方形平均分成3等份，取其中的2份涂上黄色，因为3份中，黄色占了2份，所以黄色部分正好是原正方形的2； 34，此时如果我们将灰色部分看成一个总体，横5那么灰色和黄色重叠部分是整个正方形的几分之几呢？通过刚才的分析，我们知道灰色部分占整个正方形的着将整个正方形平均分成3等份的同时，也将灰色部分平均分成了3等份，并且灰色和黄色重叠部分也占整个灰色部分的24242，所以灰色和黄色重叠部分就表示的，即：×。

那么它们的乘积是多少呢？353538，所以：15428×= 5315观察图形我们不难发现，两次总共将整个正方形平均分成了15份，其中二者重叠部分占了8份，所以重叠部分应该是原正方形的从中我们能够总结出什么规律呢？一：真分数的乘法在上面的例题中，我们得到了下列等式：428×= 5315观察等号两边三个分数的分子和分母，我们不难发现它们存在这样的关系：分子：4×2=8 分母：5×3=15由此可见：两个分数相乘，将分子相乘的积作为结果的分子，分母相乘的积作为结果的分母。

注意：分数相乘得到的结果能约分的一定要约分，必须化成最简分数。

沪教版小学数学六上2.9分数的乘法word教案 (1)

分数的乘法教学目标:1．掌握分数乘法的法则，并会利用法则进行分数乘法的计算,体会转化的思想。

2．理解分数乘法的法则的合理性，培养求真务实的精神。

3．增强团队合作能力、集体荣誉感和民族荣誉感。

教学重点：准确运用分数乘法法则进行计算。

教学难点：对分数乘法法则的理解。

教学方法：猜想、讨论、引导、总结。

教学工具:电脑、投影仪。

教学过程:导语:举世瞩目的2007世界夏季特奥会已经结束了，但是它的口号“你赢我也赢”却已经成为了上海市民的流行语，我想它也应该成为我们班级同学的流行语，希望我们班的同学都能“你行我也行” 。

下面，老师就有一个问题,看看我们班的同学谁最行! 特奥会前夕，宣传委员小明要为学校的宣传栏制作几张宣传海报，其中一张的长是43米、宽是53米，小明很想知道这张海报的面积是多少平方米，你能告诉他吗？分析：根据长方形的面积公式可知，应该是43×53。

如何计算呢？同学猜想。

教师准备了两种方法加以解释。

方法一：用纸做图,说明分数乘法法则的合理性。

将一张正方形的纸平均分成四份，取其中的三份，再把这三份平均分成五份,取其中的三份,即将这张纸平均分成了二十份,而取了其中的九份。

方法二：运用分数与除法的关系将43×53转化成整数的运算,说明分数乘法法则的合理性。

因为 43×53=（3÷4）×（3÷5） =3×3÷4÷5=（3×3）÷（4×5） =5433⨯⨯ 所以 43×53=5433⨯⨯ 分数乘法的运算法则：两个分数相乘，将分子相乘的积作积的分子，分母相乘的积作积的分母。

用字母表示为: )0n ,0q (nq m p n m q p ≠≠⨯⨯=⨯。

练习（口答）：3121.1⨯ 5132.2⨯ 4345.3⨯ 3165.4⨯ 4375.5⨯ 321311.6⨯ 3158.7⨯ 5283.8⨯ 例题：计算5283.1⨯ 7125.2⨯ 补充；如果是一个分数和一个整数相乘，可以把整数看作分母是1的分数，于是有：整数与分数相乘，整数与分数的分子的积作积的分子，分母不变。

沪教版6年级数学上册第2章第7讲：带分数的乘法(教案)

第7讲：假分数和带分数的乘法（教案）一：假分数的乘法在上一节我们学习了真分数的乘法，我们知道当两个真分数相乘时，分子与分子相乘作为积的分子，分母与分母相乘作为积的分母。

同样地，当两个假分数相乘时，也可以遵循真分数相乘的运算法则进行。

看下面的例题：例题：计算。

（1）825512⨯ （2）314724⨯练习：计算（1）5225⨯ （2）8934⨯ （3）251645⨯（4）613131056⨯⨯ （5）7991267⨯⨯二：带分数的乘法那么如果在进行分数乘法时，其中一个因数是带分数，又该如何进行计算呢？看下面的例题：例题：计算下列各式。

（1）51363⨯ （2）51×263解析：在进行带分数的乘法运算时，我们一般首先将带分数化成假分数，然后再按照分数乘法的规则进行计算。

解：（1）51231231233===63636318⨯⨯⨯⨯ （2）51575735×2===63636318⨯⨯⨯练习1：计算下列各式。

（1）5332124⨯ （2）212353⨯（3）531311211⨯⨯ （4）411511322⨯⨯随堂训练一：填空 1、916的49是_________；25的34是________； 2、一本绳子长57米，它的72是________米； 3、316千克的83是_______千克；316千克增加81千克后是_________千克； 4、=⨯953536________；=⨯47711_______；=⨯113921________； 5、=⨯⨯321125512_________；二：计算 ①23910⨯ ②313113512⨯⨯ ③23171761⨯④321910⨯ ⑤31589⨯ ⑥211173652⨯⨯。

沪教版小学数学六上2.7分数运算的应用word教案 (2)

分数运算的应用课题分数运算的应用课型新授三维目标掌握分数运算的几种基本运用；学会寻找文字中的关键信息联想到相应的数学问题，选用适当的方法解决之。

通过分数运算应用的学习，培养独立探究、合作交流的学习方式。

通过学习方式的培养，加深了解“学以致用”的道理，促进良好的学习态度的形成。

教学重点熟练掌握分数运算的几种基本运用。

教学难点学会寻找应用文字中的关键字词，从而能转化成较易理解的数学语言达到能够利用分数运算解决现实问题的目的。

策略方法老师讲授与学生独立探究、合作交流相结合。

流程和环节师生双边活动设计教师学生一、引入看到这张图片，让大家想到了？大家都知道明年上海就要举行世博会那大家知不知道上海是在什么时候确定成为2010年世博会主办城市的？学生看幻灯片生：世博二、新授例1：2002年12月3日，在摩纳哥举行国际展览局第132次大会，确定上海为2010年世博会主办城市。

在最后一轮投票，共有88个成员国参加了投票，中国上海赢得了54票，成为2010年世博会主办城市。

问：（1）上海在这一轮投票中，得票数占总投票数的几分之几？这就是我们今天所要学习的应用我们之前所学分数运算的相关知识来解决生活中的一些学生看幻灯片学生回答问题。

揭示课题：分数运算的应用（板书）数学来源于生活又运用于生活。

（2）其他城市的得票数是总投票数的几分之几？解：（1）442788548854==÷ 答：上海在这一轮投票中，得票数占总投票数的4427 。

（2）()44178834885488==÷- 答：其他城市的得票数是总投票数的4417。

分析小结：1．观察4427 和4417你发现了什么？它们的和是？那么解法2：1-4427=44172．归纳解应用题的步骤：审题----找关键句列式计算写答3．应用题类型1：求一个数是另一个数的几分之几用除法。

用字母表示： a 是b 的几分之几可表示为b ÷a 。

秋上海教育版数学六上2.5《分数的乘法》word教案

教案设计
教学目标：
1、理解分数乘法的意义，掌握分数乘法运算的法则；
2、在探索新知识的过程中培养学生分析问题、归纳总结、解决问题的能力；
3、培养学生学习数学的兴趣，了解从“一般”到“特殊”的数学思想方法。

教学重点和难点：
理解分数乘法的意义；掌握分数乘法运算的法则。

教学过程：
一、复习引入： 1、复习：
整数的乘法意义和法则。

2、思考：
如图，取边长为1
5
4。

将这5
4
看成一个总体，再三等
分，取其中的两份，这两份表
示54的3
2
即（3254⨯）。

问深色部分占这个正方形的几分之几? 1583254=⨯
二、学习新课：
1、概念辨析：
问：分数乘法的意义？两分数相乘的计算法则？（学生自己归纳总结）两个分数相乘，将分子相乘的积作分子，分母相乘的积作分母。

2、例题分析：例题1 计算：
（1） 3165⨯( 用图例说明此算式的意义) （２） 5
2
83⨯（约分可简化计
算）
（３）211354⨯ （４）612
5
⨯
（５）10312⨯ （６）5
1
1310⨯
（７）4
321253
⨯ 例题２一辆装满２０吨货物的卡车，货物总量的
12
5
是服装。

在服装类的货物中，童装又占了8
3
，问：这辆卡车装运的童装有多少吨？
8138258312520==⨯⨯吨
三、课堂小结：
分数乘法的意义、乘法法则等四、作业布置：完成练习册习题2.5。

沪教小学数学六年级上册2.9分数的乘法word教案2

分数的乘法教学目标1. 知识目标：理解分数乘法的意义，掌握分数乘法运算的法则。

2. 能力目标：在探索新知识的过程中培养学生分析问题、归纳总结、解决问题的能力。

3. 情感目标：培养学生学习数学的兴趣，了解从“一般”到“特殊”的数学思想方法。

教学重点和难点：理解分数乘法的意义；掌握分数乘法运算的法则。

教学用具准备：实物投影仪，投影仪，尺，PPT课件。

教学流程设计：教学过程：一、复习引入：1.复习：整数的乘法意义和法则。

2.思考：如图，取边长为1的正方形，将一边5等分，取其中的4份，着色部分是正方形的54。

将这54看成一个总体，再三等分，取其中的两份，这两份表示54的32即（3254⨯）。

问深色部分占这个正方形的几分之几? 1583254=⨯二、学习新课： 1.概念辨析：问：分数乘法的意义？两分数相乘的计算法则？（学生自己归纳总结）两个分数相乘，将分子相乘的积作分子，分母相乘的积作分母。

2.例题分析：例题1 计算：（1） 3165⨯( 用图例说明此算式的意义) （2） 5283⨯（约分可简化计算）（3）211354⨯ （4）6125⨯（5）10312⨯（6）511310⨯（7）4321253⨯ 例题2 一辆装满20吨货物的卡车，货物总量的125是服装。

在服装类的货物中，童装又占了83，问：这辆卡车装运的童装有多少吨？53251⨯⨯==吨20312888三、课堂小结：分数乘法的意义、乘法法则等四、作业布置：练习册习题2.5五、教学设计说明及反思：这是六年级第一章第五节，学生是在已掌握整数的四则运算，分数的意义和性质和分数的加减法基础上进一步学习分数的乘法，同时为以后学习分数的除法作准备。

首先让学生复习整数乘法的意义和法则；然后结合分数的意义通过分割正方形来引导学生自己总结出分数乘法的意义和法则，在此过程中培养学生分析问题、归纳总结、解决问题的能力；最后根据自己总结出来的法则进行分数乘法的运算练习，在设计题目是注意到因数可以有真分数、假分数、带分数、整数，乘法中可以约分等各种情况，此外通过一道应用题来检验同学学生对分数乘法的意义理解和综合应用能力。

沪教版(上海)六年级数学第一学期：2.5 分数的乘法教案

分数的乘法【教学目标】1．知识和技能：使学生理解分数乘整数的意义，掌握分数乘整数的计算方法。

使学生能够应用分数乘整数的计算法则，比较熟练的进行计算。

通过观察比较，培养学生的抽象概括能力。

知道分数乘整数的意义，学会分数乘整数的计算方法。

2．过程与方法：经历分数乘整数的意义及计算法则的形成过程，体验归纳概括的数学思想和方法。

在进行分数乘整数的计算过程中，能够感知计算方法。

3．情感、态度和价值观：通过引导学生探究知识间的内在联系，激发学生学习兴趣，感悟数学知识的魅力，领会数学美。

【教学重难点】1．使学生理解分数乘整数的意义。

掌握分数乘整数的计算方法；2．引导学生总结分数乘整数的计算方法。

【教学过程】一、铺垫孕伏1．出示复习题。

（投影片）（1）整数乘法的意义是什么？（2）列式并说出算式中的被乘数、乘数各表示什么？5个12是多少？ 9个11是多少？ 8个6是多少？（3）计算：=++636261________； =++103103103________。

计算103103103++时向学生提问：这道题的什么特点？计算时把什么做分子？使学生看到三个加数都相同，计算时3个3连加的结果做分子，分母不变。

2．引出课题。

分数加法是否也有简便算法？今天我们学习分数乘法。

（板书课题：分数乘整数）二、探究新知1．教学分数乘整数的意义。

（1）分析演示：师：每人吃92块蛋糕，每人吃的够一块吗？（不够一块）接着出示三个扇形图。

问：一个人吃了92块，三个人吃了几个92块？使学生从图中看到三个人吃了3个92块。

让学生用以前学过的知识解答3个人一共吃了多少块？（教师在3个扇形下面画出大括号并标出？块）订正时教师板书：92＋92＋92=9222++=96=32（块），（教师将3个双层扇形图片拼成一个一块蛋糕的32图片。

）（2）观察引导：这道题3个加数有什么特点？使学生看到3个加数的分数相同。

教师问：求三个相同分数的和怎样列式比较简便呢？引导学生列出乘法算式。

2017年秋六年级数学上册 2.5 分数的乘法(1)教案沪教版五四制

分数的乘法
课题
（）分数的乘法
设计
依据
（注：只在开始新章节教学课必填）
教材章节分析：这是六年级第一章第五节，学生是在已掌握整数的四则运算，分数的意义和性质和分数的加减法基础上进一步学习分数的乘法，同时为以后学习分数的除法作准备。首先让学生复习整数乘法的意义和法则；然后结合分数的意义通过分割正方形来引导学生自己总结出分数乘法的意义和法则，在此过程中培养学生分析问题、归纳总结、解决问题的能力；最后根据自己总结出来的法则进行分数乘法的运算练习，在设计题目是注意到因数可以有真分数、假分数、带分数、整数，乘法中可以约分等各种情况，此外通过一道应用题来检验同学学生对分数乘法的意义理解和综合应用能力。
学生学情分析：
课型
新授课
教
学
目
标
理解分数乘法的意义，掌握分数乘法运算的法则；在探索新知识的过程中培养学生分析问题、归纳总结、解决问题的能力；培养学生学习数学的兴趣，了解从“一般”到“特殊”的数学思想方法。
重点
分数乘法的法则。
难点
分数乘法的运算。
教学
准备
分数的意义、分数的加减运算
学生活动形式
教学过程
设计意图
、本课成功与不足及其改进措施：
课外
作业
1.计算：
（）×；（）×；（）×；（）×。
2.计算：
（）×；（）×；（）×；（）×；
（）×；（）×。
拓展练习：
计算×时，以下方法正确的是（）。
（）×；（）××＝＝；（）×（＋）×＝×＋×＝。
哪一种较简便！
预习
要求
教学后记与反思
、课堂时间消耗：教师活动分钟；学生活动分钟）
、本课时实际教学效果自评（满分分）：分

沪教版(五四制)六年级上册教案：2.5(2)分数的乘法

课题2.5（2）分数的乘法设计依据（注：只在开始新章节教学课必填）教材章节分析：学生学情分析：课型新授课教学目标理解分数乘法的意义，掌握分数乘法运算的法则；在探索新知识的过程中培养学生分析问题、归纳总结、解决问题的能力；培养学生学习数学的兴趣，了解从“一般”到“特殊”的数学思想方法。

重点分数乘法的法则。

难点分数乘法的运算。

教学准备分数的意义、分数的加减运算学生活动形式教学过程设计意图课题引入：课前练习一：1.计算：（口答） 34 ×12 38 9×13 3 89 ×18 19 611 ×13 211 45 ×4 31523 ×321 课前练习二：2.计算：（1）313 ×25 ；（2）920 ×18；（3）1124 ×815 ；（4）157 ×423。

课前练习三：3.说一说下列算式所表示的意义：（1）56 ×2；（2）45 ×23。

（求一个数的几分之几（或几倍）是多少用乘法计算。

）新课探索一：1.列式计算：（1）12的23 是多少？（2)24的138 倍多少？（3）123 的34是多少？（4）4是12的几分之几？执教：年级：学科：施教时间：第周星期第课时上海市横沙中学2016学年第一学期课堂教学设计方案新课探索二：例1：一个集装厢内装有20吨的货物，货物总量的512是服装，在服装类货物中，童装又占了38，这个集装厢装运的童装有多少吨？课内练习一：1. 计算：（1）118 ×125 ；（2）217 ×415 ；（3）825 ×1916 ；（4）5－223 ；（5）1916×8；（6）612 －334。

课内练习二：2.（1）23 千克的14 是多少千克？（2）38 米的23是多少米？课内练习三：4.小杰每天看电视56小时，五天共看电视多少小时？课内练习四：6.小杰家本月初买了25千克大米，到月底吃掉了其中的25，本月小杰家共吃了多少千克大米？课内练习四：6.小杰家本月初买了25千克大米，到月底吃掉了其中的25，本月小杰家共吃了多少千克大米？知识呈现：根据分数乘法的意义，“求一个数的几分之几（或几倍）是多少”用乘法。

2017年秋六年级数学上册 2.5 分数的乘法(2)教案沪教版五四制

难点
分数乘法的运算。
教学
准备
分数的意义、分数的加减运算
学生活动形式
教学过程
设计意图
课题引入：课前练习一：
.计算：（口答）
××××××
课前练习二：
.计算：
（）×；（）×；（）×；（）×。
课前练习三：
.说一说下列算式所表示的意义：
（）×；（）×。
（求一个数的几分之几（或几倍）是多少用乘法计算。）
新课探索一：
课内练习三：
.小杰每天看电视小时，五天共看电视多少小时？
课内练习四：
.小杰家本月初买了千克大米，到月底吃掉了其中的，本月小杰家共吃了多少千克大米？
课内练习四：
.小杰家本月初买了千克大米，到月底吃掉了其中的，本月小杰家共吃了多少千克大米？
知识呈现：
根据分数乘法的意义，“求一个数的几分之几（或几倍）是多少”用乘法。
分数的乘法
课题
（）分数的乘法
设计
依据
（注：只在开始新章节教学课必填）
教材章节分析：
学生学情分析：
课型
新授课
教
学
目
标
理解分数乘法的意义，掌握分数乘法运算的法则；在探索新知识的过程中培养学生分析问题、归纳总结、解决问题的能力；培养学生学习数学的兴趣，了解从“一般”到“特殊”的数学思想方法。
重点
分数乘法的法则。
课堂小结：根据分数乘法的意义，“求一个数的几分之几（或几倍）是多少”用乘法。
课外
作业
.计算：
（）×；（）×；（）＋；（）－；（）×；
（）×；（）×；（）－。
.一个长方形的长是米，宽是米，它的面积是多少平方米？
.计算：
（）吨的是多少吨？（）千克的是多少千克？

沪教版六年级上册数学教学设计分数乘除混合运算

分数乘除混合运算教学目的：1．使学生知道整数乘法的运算定律对分数乘法同样适用。

2．使学生能够运用所学的运算定律进行一些简便运算。

3．使学生知道在运算时应用了哪些运算定律，以培养学生的思维能力。

教学重点：运用所学的运算定律进行一些简便运算。

教学难点：会简算。

教学过程：一、复习指名说一说在整数乘法中都学过了哪些运算定律（乘法交换律、乘法结合律、乘法分配律）。

学生说出字母表达式或用语言叙述都可以。

对说出字母表达式的学生，最好让他们再说一说每个运算定律是什么意思。

二、探索获取1．整数乘法运算定律推广到分数乘法。

出示下面三组算式，让学生说一说每组算式的左右两边有什么样的关系。

×○×（×）×14 ○×（×14）（＋）×30 ○×30＋×30先让学生观察每组中的两个算式有什么特点。

然后算出左右两边的得数，看看每组的两个算式有什么样的关系，并分别做出结论。

可以做出“整数乘法的交换律对于分数乘法也适用”的结论。

最后做出“整数乘法的交换律、结合律和分配律，对于分数乘法同样适用”的结论。

让学生用字母表示每一个运算定律。

教师板书：a×b＝b×a（a×b）×c＝a×（b×c）（a＋b）×c＝a×c＋b×c教师：“这三个等式中的字母可以表示什么数？”（整数、小数、分数。

）2．教学例6（运用乘法运算定律使分数乘法计算简便）教师：“我们已经知道应用乘法运算定律可以使一些整数、小数的乘法计算简便，在分数乘法中应用运算定律也可以使一些计算简便。

”先让学生自己做，然后订正。

比较哪种方法简单。

3．做教科书第32页的练一练。

先让学生独立计算，教师巡视，了解学生掌握的情况，集体订正时，对于每一道题都指名说一说是应用了什么运算定律。

如果学生困难比较大，教师可以适当提示。