第八章连接件计算
第八章 剪切与连接件的实用计算

t1
t1
P
,试校核销钉的强度。
(a)
P 解: 销钉受力如图b所示
(b) 剪切面
P
d B A
d
t1
t
t1
P 2
挤压面
P 2
P
P
m n
(b)
剪切强度校核
受剪面为 m—m 和 n—n面
由截面法得两个面上的剪力
m
P 2
Q
n
P
P 2
Q
P Q 2 受剪面的面积为
d A 4
2
受剪面上的名义剪应力为
Q
P 2
根钢轨在距离为纵向间距 S
T1
的两个横截面上压(拉)力
T ' 2Q'
Q'
之差。
T ' T1 T
s
S 假想钢轨在接触面上处处传 递剪应力 τ ' ,接触面的宽 度为 b 。 T
T1
T ' ' bs
T ' 2Q'
Q'
s
'
Q S* z max bI z
T
S
T1
S z max 为一根钢轨的横截面
d
4Q u
15.3mm
二、挤压的实用计算 螺栓与钢板相互接触 的侧面上,发生的彼 此间的局部承压现象, 称为挤压。
P
P
P
P
受剪面 在接触面上的压力, 称为挤压力,并记为 Pbs 。
挤压面
挤压破坏的两种形式 (1)螺栓压扁 (2)钢板在孔缘压皱
在挤压近似计算中,假设 名义挤压应力 的计算式为
c
z1 M z
M1
08第八章-连接件的实用计算

n
F
n
3、变形特点
构件沿两组平行力系的交界面发 生相对错动。
(合力)
工程 力学 连接件的实用计算 第八章 4、连接处破坏四种形式:
第二章 汇交力系 工程力学
(合力) F n
(1) 剪切破坏 沿铆钉的剪切面剪断,如沿n– n面剪断 。 (2) 挤压破坏 铆钉与钢板在相互接触面上因挤压而使 连接溃压松动,发生破坏。 n (3) 拉伸破坏 钢板在受铆钉孔削弱的截面处,应力增 大,易在连接处拉断。 (4) 剪豁(3-3截面),边距大于孔径2倍可避 免
Me F
h l b
Me
d
h
解:(1) 键的受力分析如图
d F Me 2
2 M e 2 2 103 F 3 57kN d 0 10
工程 力学 连接件的实用计算 第八章 (2)校核剪切强度
第二章 汇交力系 工程力学
Me
h l
F
FS F
FS
b
A
d
F 57 103 6 28.6MPa A bl 20 100 10
第二章 汇交力系 工程力学
FS A
m
F
m
[] 为材料的许用切应力
F
剪切面
[ ]
u
n
m m
u
- 剪切极限应力
F
n - 安全系数
工程 力学 连接件的实用计算 第八章
第二章 汇交力系 工程力学
§8-3
一、挤压的概念
挤压的实用计算
1、受力特点 在外力的作用下,连接件和被连接 件在接触面上将相互压紧,这种局部受 压的情况称为挤压。 2、变形特点 在接触处的局部区域产生塑性变 形或压溃。
武汉理工大学材料力学课件8 组合变形及连接部分的计算--JK

若横截面周边具有棱角,则无需确定中性轴的位置,直 接根据梁的变形情况,确定最大拉应力和最大压应力点 的位置。 D D
1 1
z
z D2 y 中性轴
D2
y
中性轴
强度条件:
()若 [ t ] [ c ] [ ], 则 1 (2)若 [ t ] [ c ], 则
t ,max [ t ] ,
z
c ,max
FN M max [ c ] A Wz
(1)若F 的作用点在杆的一对称轴上, F M 则强度条件为: [ t ] t , max A Wz 其中 M Fe
c ,max
F M [ c ] A Wz
23
(2) 若F 的作用点不在杆的任一对称轴上
FN My A Iz
z
c ,max
(2)若 t ] [ c ] [ ] , [
则
FN M max [ c ] A Wz
max Max { t ,max , c ,max } [ ]
20
[例8-3-1] 最大吊重为 P=20kN的简易吊车,如图所 示,AB为工字A3钢梁,许用应力[σ]=100MPa,试选 T YA 择工字梁型号。 Ty XA D
另外, 和 的正负号可由My和 Mz引起的变形是拉 8 还是压直接判断。
sin cos 则,F引起的应力为: M ( I z I y) y z
二、中性轴的位置 令(y0,z0)是中性轴上任一点,则有: 显然,中性轴是一条通过坐标原点的直线, 设其与z轴的夹角为α,则有:
A Tx
C
B F
A
30° 2m
C
1m
材料力学第八章 剪切与联接件的实用计算

* z
I zb
Fbs bs Abs
宽度方向均布 矩形 高度方向抛物线 分布 薄壁 圆环
FN t At
3 FQ 圆形 4 FQ max max 2 A 3 A FQ 工字形型钢 max 2 FQ A max Iz 发生在中心轴上 ( * )d S z max
材料力学
第8章 剪切与连接件的实用计算 符号 正负号 FN与横截面外法线 方向一致为正,反 之为负. 拉为正、压为负 右手螺旋法则
内力
内力计算
轴力等于截面的一 侧所有外力的代数 和. 扭矩等于截面的一 侧所有外力偶矩的 代数和. 剪力等于截面的一 侧所有外力的代数 和. 弯矩等于截面的一 侧所有外对该截面 形心力矩的代数和.
FN
满足 满足
FN2 FN2 2 130 103 t2 =114MPa≤[ ]=160MPa At2 (b 2d ) 3 (0.11 2 0.017) 0.01
主板满足,盖板亦满足,故该连接头满足强度要求
材料力学
第8章 剪切与连接件的实用计算
例题1 图示对接铆接接头,每边铆钉数n=3,已知F=130kN,主板 =1cm, b 11cm,盖板1 =0.7cm,d 1.7cm,[ ]=160MPa,[ ]=120MPa, [ bs ]=300MPa,试校核该接头的强度。重新布置铆钉位置
材料力学
第8章 剪切与连接件的实用计算
第八章 剪切与连接件的实用计算
材料力学
第8章 剪切与连接件的实用计算
• • • • • •
本章主要内容 强度计算的实用计算方法 搭接铆接(单剪) 对接铆接(双剪) 铆钉群连接 其它连接
材料力学
第8章 剪切与连接件的实用计算
8 连接件的实用计算

当接触面为圆柱面时(如铆钉与钉孔间的接 触面), Abs应取圆孔或圆钉的直径平面面积。
Abs = dl
例8.1 拖车挂钩用销钉连接,已知挂钩部分的钢板厚度 拖车挂钩用销钉连接, t = 8mm,销钉的材料为20钢,其许用切应力 τ]=60MPa ,许 销钉的材料为20 销钉的材料为20钢 其许用切应力[ 用挤压应力[σ 用挤压应力 σbs]=100MPa,拖车的拉力F=18KN。试选择销 。 钉的直径。
工程力学
第八章
连接件的实用计算
工程力学
第八章 连接件的实用计算
工程力学
第八章
连接件的实用计算
第八章 连接件的实用计算 §8-1 连接件的概念 §8-2 剪切的实用计算 §8-3 挤压的实用计算
工程力学
第八章
连接件的实用计算
§8-1 连接件的概念
一、基本概念
工程中经常需要把一些构件连接起来,起连接作用 的构件称为连接件。
工程力学 ② 按挤压强度条件进行设计 销钉的挤压面的计算面积 Abs = dt 挤压力为
Fbs = F 2
第八章
连接件的实用计算
由挤压强度条件
Fbs F 18 ×103 N σ bs = = = = 81.5 MPa < [σ bs ] −3 −3 Abs 2dt 2 × (8 ×10 m) × (13.8 ×10 m)
① 校核剪切强度
Fs F 12 ×103 N = 7.14 MPa < [τ ] τ= = = A bl (0.028 m) × (0.06 m)
工程力学
第八章
连接件的实用计算
② 校核挤压强度
Fbs F 12 × 103 N σ bs = = = = 25 MPa < [σ bs ] 2 h Abs ⋅ l 0.008 × 0.06 m 2
第8章 连接件的实用计算

它与钢材在纯剪应力状态时的容许剪应力显 然是不同的。
例题1 图示冲床的最大冲压力为400KN,被冲剪钢板的剪切极限 应力为 [ ] = 300MPa ,试求此冲床所能冲剪钢板的最大厚度
t。已知 d=34mm。
钢板
冲头 t
d 冲模
解:剪切面是钢板内被
F
冲头冲出的圆柱体
的侧面:
A dt
冲孔所需要的冲剪力: F
F ≥ A[ ]
故
F 400×103
A ≤ [ ] = 300×106
1.33 103 m2
t
即
t
1.33 103
d
0.1245m
12.45mm
剪切面
剪切与挤压的实用计算
挤压面——相互压紧 部分的接触面
(1)挤压力
F
Fbs = F
剪切与挤压的实用计算
Abs d
剪切与挤压的实用计算
As
bs
Fbs Abs
[ bs]
注意:利用强度条件进行剪切和挤压强度计算时,
首先应弄清楚,哪个是受剪面哪个是挤压面?几
个剪切面、几个挤压面?
剪切与挤压的实用计算
剪切与挤压的实用计算
(榫齿连接)思考:指出下图中的剪切面和挤压面 位置,写出各剪切面面积和计算挤压面面积。
剪切 A=ab
挤压 Abs=eb
连接件的失效形式
(1) 沿着剪切面发生的剪切破坏
剪切面:发生相对错动的截面 称为剪切面或受剪面。
(合力)
P n
n P
(合力)
(2) 构件与连接件的接触面上(挤压面)因挤压 而松动。
(3)钢板在受螺栓孔削弱的截面处被拉断。
第八章组合变形及连接部分的计算-资料

z
tg Iy tg
Iz
M
y
(2) 对于圆形、正方形等截面 Iy=Iz ,所以有 = 。
z
tg Iy tg
Iz
M
y
梁发生平面弯曲,正应力可用合成弯矩 M 按正应力计算公式计算
z
tg Iy tg
Iz
M
y
梁的挠曲线一般仍是一条空间曲线,故梁的扰曲线方程仍应分别 按两垂直面内的弯曲来计算,不能直接用合成弯矩进行计算。
四、 强度分析
中性轴
作平行于中性轴的两直线分别与
D1 z
o
横截面周边相切于 D1 、D2两点
,D1 、D2 两点分别为横截面上
最大拉应力点和最大压应力点。
D2
y
D1
D1
oz
D2
y
中性轴
z o
D2
y
中性轴
对于矩形、工字形等有两个相互垂直的对称轴的截面梁横截面的
最大正应力发生在截面的棱角处。 可根据梁的变形情况,直接确定截面上最大拉,压应力点的
x
P1
m
x
y
m
z x
My
m
y
P1 在 m—m 面内产生的弯矩为 My = P1 x (使梁在 XZ 平面内弯曲,y 为中性轴)
P2 a
m
z
x
P1
m
x
y
m
MZ z x
My
m
y
P2 在 m—m 面内产生的弯矩为 MZ = P2 (x-a) (使梁在 XY 平面内弯曲,z 为中性轴)
二 、 梁横截面上的应力分析 (任意点 C(y, z) 的正应力)
第八章_组合变形与连接件的实用计算

y
z
10
A bh 50106 m2
Wy
1 6
b2h
1 6
52
10 10 9
4.17 10 8 m3
Wz
1 6
bh2
1 6
510 2
10 9
8.33 10 8 m3
5
危险点在切槽截 max
FN A
My Wy
Mz Wz
面的左上角。
1000 5105
x
max
My Wy
Mz Wz
F1
6 F1 2L 6 F2L
hb2
bh2
L
L
y
1、内力分析 2、应力分析 3、强度计算
max
9.979MPa
max
9.979MPa
§8-3 拉伸(或压缩)与弯曲
Ⅰ.横向力与轴向力共同作用
一、受力特点
作用在杆件上的外力既有轴向拉( 压 )力,
还有横向力
F1
F1 产生弯曲变形 F2
F2
F2 产生拉伸变形
二、变形特点 杆件将发生拉伸 (压缩 ) 与弯曲组合变形
三、内力分析 横截面上内力
1、拉(压) :轴力 FN
2、弯曲
弯矩 MZ 剪力 FS
MZ z
0
x
FN
y
因为引起的剪应力较小,故一般不考虑。
四、应力分析
横截面上任意一点 ( z, y) 处的
正应力计算公式为
1 、拉伸正应力
' FN
A
2、弯曲正应力
'' Mz y
工程力学课后习题答案第八章连接件的实用计算
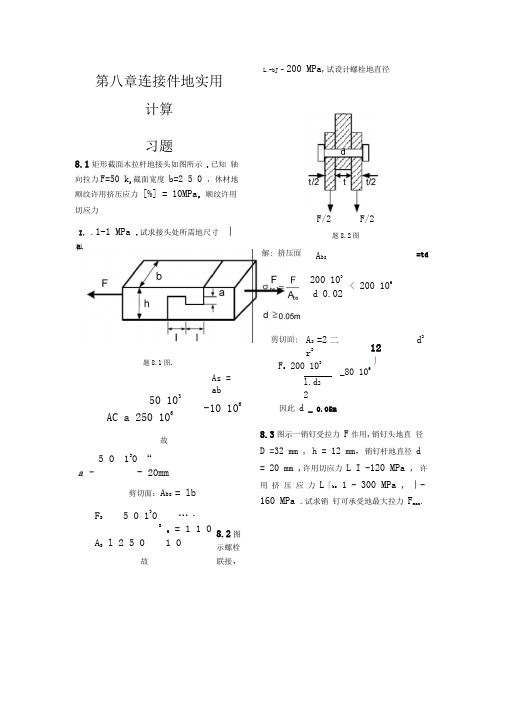
8.3图示一销钉受拉力 F 作用,销钉头地直 径D =32 mm , h = 12 mm ,销钉杆地直径 d = 20 mm ,许用切应力 L I -120 MPa , 许用 挤 压 应 力 L 「bs 1 - 300 MPa , 丨-160 MPa .试求销 钉可承受地最大拉力 F max .8.2图示螺栓联接,第八章连接件地实用计算 习题8.1矩形截面木拉杆地接头如图所示 .已知 轴向拉力F=50 k ,截面宽度 b=2 5 0 ,休材地顺纹许用挤压应力 [%] = 10MPa ,顺纹许用切应力 a . L.-bJ -200 MPa ,试设计螺栓地直径I. .1-1 MPa .试求接头处所需地尺寸 丨和 A bsd 0.02题8.1图.200 103A s =2二 r 2 As = ab50 103AC a 250 106-10 106F/2 F/2题8.2图F s 200 103l.d 2 2=td< 200 10612丿d 2_80 106因此 d _ 0.05m故5 0 130 “ a - - 20mm250 10剪切面:A bs = lbF S5 0 130 …・S6 = 1 1 0 A S l 2 5 0 1 0 故已知外力F =200 kN , 板厚度t =20 mm,板与螺栓地材料相同,其许用切应力丨.1-80 MPa ,许用挤压应力解:1 h D - I|hrZZZ/////.-d-*\\、\\题8.3图.拉杆头部地切应力拉杆头部D2 -d2F s 二A s - ":dhAs 二dh 挤压应力3.14 20 10” 12 10120 106N =90.4KN 乞F maxF =%Abs=% 兀(D2-d2)=300 心0*3.= 587.8 KN _Fmax所以应取F =90.4 KN ;F ■d 290.4 KN_3223.14 20 10 m2题8.4图.解:先考虑受剪切力时地情况,在钢板和铆钉都达到许用剪切应力时,. F S兀 2由一,A Q = na s和a s = —d 得,n =a s 2s d4将L I - 140MPa,d = 0.020m代入上式,得n 二n a s-UF S-bs3160 10兀2TT314 2 6qd _… 4 0.020 140 10A bsA bs = n a bs〉a bs = dt得_ a bs 事bs dt 竽bs _S4^再尬代入上式,得F Fa bs -上bJ dt 士bs1160"030.020 0.01 320 106由以上两式可以确定铆钉地个数为四个,下=3.64 :::=2.5 ::3=72.0MP 确定排列方式为(n1为一行中铆钉个数)8.4图示两块钢板用直径d = 20 mm地铆钉搭接,钢板与铆钉材料相同.已知F ^1 6 0 !两板尺寸相同,厚度t =10 mm , 宽度b =1 2 0 ,m许用拉应力kr】=1 6 0 M R许a用切应力I. )-140 MPa ,许用挤压应力L「bs丄320 MPa ,试求所需要地铆钉数,并加以排列,然后校核板地拉伸强度.F NA -山兀得,n1-l- |,A = 0.01 0.12 = 0.0012m2,a bs = 0.0002m2代入上式得160汉103 '0.0012_------ 6. 160"06£ =10.0002—1k6所以每排只排一个,共四排,在此种排列情况下,强度符合条件8.5图示直径为 30 mm 地心轴上安装着一 个手摇柄,杆与轴之间有一个键K,键长36mm,截面为正方形,边长8 mm,材料地许用切 应力LI -5 6 0 MP 锻用挤压应力L 「bs 1 = 200 MPa ,试求手摇柄右端 F 地最 大许可值.30mm解:挤压面为 傀=4 36 = 144mm 2故最大挤压应力为F bs "bs A bs =Abs bbs li 44m m 2x 20°MP a= 28.8kN剪切面为 A = 8^36=288mm 故最大剪切应力为F s= Ab 】 = 288mm 2 汉560MPa=161.28kN由于 F bs ::: Fs ,所以取 F bs 二 28.2kN , 由力矩平衡条件,得15 F bs -750 F = 0F =576N手摇柄右端F 地最大许为576N.8.6图示冲床地冲头,在F 力地作用下,冲剪 钢板,设板厚t =10 mm ,板材料地剪切强度 极限-b =360 MPq 当需冲剪一个直径 d -20 mm 地圆孔,试计算所需地冲力 F 等 于多少?解:剪切面S 二二dt由于b因此F ss ■: dt750mm题8.5图.F - ■ dt 3.14 0.02m 0.01m 360 106p a钢板。
材料力学 孙训方

与y的夹角。
14
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
tanq
Iy Iz
tan
这就表明,只要 Iy≠Iz ,中性轴的方向
就不与合成弯矩M的矢量重合,亦即合
成弯矩M 所在的纵向面不与中性轴垂直, 或者说,梁的弯曲方向不与合成弯矩M 所在的纵向面重合。正因为这样,通常 把这类弯曲称为斜弯曲(oblique
29
z
inertia)。
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
显然当梁的横截面具有一个对称轴时,这个对称轴和它垂
直的形心轴都是形心主惯性轴,外力产生的弯矩作用在包含其
中任何一根轴的纵向面内时梁都发生平面弯曲。
下节讲述对于没有对称轴的截面确定主惯性轴和主惯性矩
的相关问题。
键连接(图b)中,键主要受剪切及挤压。
7
材 料 力 学 Ⅰ 电 子 教 案
第八章 组合变形及连接部分的计算
工程计算中常按连接件和构件在连接处可能产生的破
坏情况,作一些简化的计算假设(例如认为螺栓和铆钉的 受剪面上切应力均匀分布)得出名义应力(nominal stress), 然后与根据在相同或类似变形情况下的破坏试验结果所确 定的相应许用应力比较,从而进行强度计算。这就是所谓
第八章 组合变形及连接部分的计算
2. 作梁的计算简图(图b),并分别作水平弯曲和竖直弯曲
的弯矩图—My 图和Mz 图(图c ,d)。
21
材 料 力 学 Ⅰ 电 子 教 案
3. 确定此梁的危险截面。
A截面上My最大,MyA=0.642 qa2,该截面上Mz虽不是最大,但
因工字钢Wy<<Wz ,故A截面是可能的危险截面。 D 截面上Mz 最大: MzD=0.456 qa2 , 且 MyD= 0.444 qa2,
第八章 钢结构的连接计算

第八章钢结构的连接计算连接设计应符合安全可靠、节省钢材、构造简单、制造安装方便等原则。
钢结构的连接方法有:焊缝连接、螺栓连接和铆钉连接。
我们主要讲焊缝连接、普通螺栓连接、摩擦型高强度螺栓连接。
第一节焊接连接焊缝连接的优点是构造简单,节省钢材,制造方便,易于自动化操作,生产效率高。
缺点是焊缝附近的部位材质变脆,产生焊接残余应力和残余变形,焊缝连接的韧性和塑性较差,脆性较大,疲劳确定较低。
焊接方法有:电弧焊、电渣焊、电阻焊,钢结构常用的是电弧焊。
电弧焊又分手工电弧焊、自动焊或半自动焊。
对接焊缝可使传力直接、构造简单、节省盖板和焊缝钢材,但要求尺寸精确,通常要求在板件边缘开坡口。
角焊缝位于板件边缘,受力情况复杂,引起应力集中和受力不均匀,但下料和装配时不用对板件开坡口,尺寸要求稍低,使用灵活,制造方便。
焊缝连接也有缺陷如裂纹、焊瘤、烧穿、弧坑、气孔、加渣、咬边、未熔合、未焊透等,焊缝质量分三级:一级、二级、三级。
三级焊缝只要求对全部焊缝作外观检查,符合三级质量标准,二级、一级焊缝还要求一定数量的超声波或射线、拍片检验并符合相应质量级别的质量标准。
I形、V形、U形、X形、单边V形、单边U 形、K 形等,分别根据钢板厚度而定。
对接焊缝应在两端设置引弧板。
无法放置引弧板时,对接焊缝计算长度应按实际长度减去10mm (一端5mm )。
对接焊缝承受轴心力应按公式(8-1)计算强度w c w t w f f t l N ,)/(≤=σ (8-1)其中:l w -焊缝计算长度,当有引弧板时取板件宽度b ,当无引弧板时,取b -10mm ;t -在对接接头中为被连接钢板中的较小厚度,在T 形或角接接头中为对接焊缝所在钢板的厚度;w t f 、w c f -对接焊缝的抗拉强度设计值、抗压强度设计值。
对接焊缝承受弯矩、剪力和轴心拉力;w t w w w w f tl Nt l M A N W M ≤+=+=26σ (8-2) w v w w w f tl Vt I VS ≤==5.1τ (8-3) 对称工字形截面构件的直焊缝连接,当承受弯矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在局部面积上的受压称为挤压或承压。相当复杂 的问题。
工程上对螺栓连接的强度计算,均采用直接实验为 依据的实用计算。
一、剪切的实用计算
1.剪切的工程实例
铆钉连接
螺栓连接
销轴连接
榫连接
平键连接
焊接连接
*受力特征:
杆件受到两个大小相等,方 向相反、作用线垂直于杆的 轴线并且相互平行且相距很 近的力的作用。
F/2
F/2
挤压面 Abs :直径等于d,高度为接
触高度的半圆柱表面。
挤压应力 bs :挤压面上分布的正应力。
*挤压实用计算方法: 假设挤压应力在整个挤压面上均匀分布。
bs
Fbs Abs
挤压面面积的计算:
1、平面接触(如平键):挤压面面积等于实际的承压面积。
hl Abs 2
h——平键高度 l——平键长度
t1=5mm, d=15mm, 材 料 许 用 剪 应 力 [τ]
=60MPa, 许用挤压应力[σbs]=200MPa, 试校核
t1 销钉的强度。
解:(1)剪应力强度
Ft
F
FS
F 2
9kN
d
FS As
4 9 103
152
51MPa [ ]
F/2
FS
(2)挤压强度
F/2
F FS
F
bs
Fbs Abs
155 .7MPa
3
F t(b
d)
110 103 1 (85 16)
159.4MPa
综上,接头安全。 123
F
F
F
t t
d
F/4
123
图示拉杆头和拉杆的横截面均为圆形,拉杆头的剪 切面积A=( B )。
A.Dh √B.dh C.d 2 4 D. D2 d 2 4
图示木接头中剪切面积为( D )。 A.l B.lb C.2l √D.2lb
F F
剪切面
*变形特征:
杆件沿两力之间的截面发生错动,直至破坏(小矩形
)。
剪切面:发生错动的面。
单剪 有一个剪切面的杆件,如铆钉。
一个剪切面
Fs
双剪:有两个剪切面的杆件,如螺栓。
F F/2
F/2
求应力(切应力): *实用计算方法:根据构件破坏的可能性,以直接试验 为基础,以较为近似的名义应力公式进行构件的强度计 算。
F
F
F
F
一个剪切面 两个剪切面
某钢桁架的一结点如图。斜杆A由两个 63mm6mm的等边角钢组成,受力F=140kN
的作用。该斜杆用螺栓连接在厚度为=10mm
的结点板上,螺栓直径为d=16mm。已知角钢、 结点板和螺栓的材料均为Q235钢,许用应力为
[]=170MPa , []=130MPa ,
[bs]=300MPa。试选择螺栓个数,并校核斜杆
图示木杆接头,已知轴向力F=50kN,截面
宽度b=250mm,木材的顺纹挤压容许应力
[σbs]=10MPa,须纹许用切应力[τ]=1MPa。 试根据剪切和挤压强度确定接头的尺寸L和a。
b F
a
LL
挤压面
F 剪切面
FS F
F
A lb
L
F
b
50103 250 1
200mm
F
bs
F h
b F
l
键:连接轴和轴上的传动件(如齿轮、皮带轮等),使轴 和传动件不发生相对转动,以传递扭矩。
2、柱面接触(如铆钉):挤压面面积为实际的承压面积在其直径 平面上的投影。 挤压强度条件:
bs
Fb Abs
[ bs ]
F F
Abs d
d——铆钉或销钉直径, ——接触柱面的长度
*挤压强度条件:
(3)主板拉断的校核。
I
F/n
F/n
F/n F/n
危险截面为I-I截面。
F
主板的强度条件为(忽略
应力集中的影响):
I
t
max
(b
F 2d )t1
[ ]
F F/2
F
b
2d
[ ]t1
0.17m 17cm
作业: 8-26,8-25
u
解得
d 4FS 0.0153m 15.3mm
π u
二、挤压概念及其实用计算
挤压:连接件和被连接件在接触面上相互压紧的现象。
F
F/2
F/2
F/2
F/2
F
挤压引起的可能的破坏:在接触表面产生过大的塑性变形、
压碎或连接件(如销钉)被压扁。
F
*挤压强度问题(以销为例) 挤压力(中间部分):
Fbs F
组合变形 与连接件的计算
2021年4月6日
§8-5 连接件的实用计算法
以螺栓(或铆钉)连接为例,
F
F
F
m
m F
F
F
螺栓破坏实验表明,连接处的破坏可能性有三种: (1)螺栓在两侧与钢板接触面的压力F作用下,将沿mm截面被剪断;
(2)螺栓与钢板在相互接触面上因挤压而使连接松动; (3)钢板在受螺栓孔削弱的截面处被拉断。
名义切应力:假设切应力在整个剪切面上均匀分布。
Fs
As
剪切强度条件:
FS [ ]
AS
名义许用切应力
可解决三类问题: 1、选择截面尺寸; 2、确定最大许可载荷, 3、强度校核。
在假定的前提下进行 实物或模型实验,确 定许用应力。可在有 关的设计规范中查到, 它与钢材在纯剪应力 状态时的许用切应力 显然是不同的。
校核bs 挤 压FAbb强ss 度2(92参M照Pa上页[图bs)] 螺栓Fbs满足Fn挤, 压强A度bs 条件 d
校核角钢的拉伸强度
对应最弱截面m-m的轴力
F
Fbs Fbs Fbs
FN,max 140 kN
Amm 1266 mm 2
角钢横截面m-m上的拉应力
FN,max 111MPa [ ]
Fbs Abs
F ba
bs
a F
b bs
50103 20mm 250 10
图示悬臂梁,有两块木板钉成T型截面,铁钉的许 用剪力[FS]=800N。求铁钉的间距。
解:
1.8kN 200
50
162.5
z 200
50 Iz=113.54×106mm4 τ
τ
FS
S
* z
bI z
1800 20050 (225162.5) 50113.54106
为 [bs ] 10MPa 。试求接头处所需的尺寸L和 。
F
b
F
LL
解:剪切面如图所示。剪 切面面积为:
F/2 F
As Lb
剪切面
由剪切强度条件:
F/2
Fs F / 2 [ ]
As Lb
由挤压强度条件:
L F
2b[ j ]
100mm
bs
Fbs Abs
F /2
b
[ bs ]
F 2b[ bs ]
即
1.33103 m2
1.33 103
t
0.1245m 12.45mm
d
F 剪切面
图示的销钉连接中,构件A通过安全销C将力偶矩传 递到构件B。已知荷载F=2kN,加力臂长l=1.2m, 构 件 B 的 直 径 D=65mm , 销 钉 的 极 限 切 应 力 u=200MPa。试求安全销所需的直径d。
A的拉伸强度。
选择螺栓个数的问题:先从剪切强度条件选择螺栓 个数,然后用挤压强度条件来校核。
F A
当各螺栓直径相同,且外力作用线
过该组螺栓截面的形心时,可假定
每个螺栓的受力相等,对每个螺栓
(总数为n)
FS
F/ 2
n
F 2n
剪切强度条件
F
FS AS
2n π d2
130MPa
4
得 n 2.68
取 n3
,[
jy
]
280
MPa
b
F。
若F=250KN,试求(1)每边所需的铆钉个数n;
(2)若铆钉按图(b)排列,所需板宽b为多少?
F
F
F
F
图(a)
F
F
图(b)
解: 可能造成的破坏:
(1)因铆钉被剪断而使铆接被破坏;
(2)铆钉和板在钉孔之间相互挤压过大,而使铆接被 破坏;
(3)因板有钉孔,在截面被削弱处被拉断。
可采用假设的计算方法: 假定每个铆钉所受的力都是一样的。
(1)铆钉剪切计算
F/2n
F/n
Fs
F/2n
F/2n
Fs A
F / 2n
1 d 2
[ j ]
4
2F
n d 2[ j ] 3.98
(2)铆钉的挤压计算
jy
Fb Ajy
F /n t1d
[ jy ]
n F
t1d[ jy ]
3.72
因此取 n=4.
10mm
齿轮与轴由平键(b=16mm,h=10mm,)连接,它 传递的扭矩m=1600Nm,轴的直径d=50mm,键的许 用切应力为[]= 80M Pa ,许用挤压应力为[ bs]=
240M Pa,试设计键的长度。
m
h
2
解:键的受力分析如图
F
FS
ቤተ መጻሕፍቲ ባይዱ
Fbs
2m d
2 1600 0.05
64kN
h AQ L
m F
b
d
切应力和挤压应力的强度条件
FS Lb
[ ] [L1]
FS
b
