广东省某重点中学2013届高三数学理二轮复习之圆锥曲线练习二答案不全 (1)
2013广东揭阳二模数学答案(理科)

5.方茴说:“那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢,就算喜欢也是偷偷摸摸的。
”6.方茴说:“我觉得之所以说相见不如怀念,是因为相见只能让人在现实面前无奈地哀悼伤痛,而怀念却可以把已经注定的谎言变成童话。
”7.在村头有一截巨大的雷击木,直径十几米,此时主干上唯一的柳条已经在朝霞中掩去了莹光,变得普普通通了。
8.这些孩子都很活泼与好动,即便吃饭时也都不太老实,不少人抱着陶碗从自家出来,凑到了一起。
9.石村周围草木丰茂,猛兽众多,可守着大山,村人的食物相对来说却算不上丰盛,只是一些粗麦饼、野果以及孩子们碗中少量的肉食。
1.“噢,居然有土龙肉,给我一块!”2.老人们都笑了,自巨石上起身。
而那些身材健壮如虎的成年人则是一阵笑骂,数落着自己的孩子,拎着骨棒与阔剑也快步向自家中走去。
3.石村不是很大,男女老少加起来能有三百多人,屋子都是巨石砌成的,简朴而自然。
揭阳市2013年高中毕业班高考第二次模拟考数学(理科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数.一.选择题:BCDA DACC解析:1.由210x-≥得0x ≥,[0,)A ∴=+∞,故选B .2.由(12)1ai i bi +=-得1,12a b ⇒=-=-||a bi ⇒+==选C . 3.设(,)B x y ,由3AB a =得1659x y +=⎧⎨-=⎩,所以选D .4.由129m a a a a =+++得5(1)93637m d a d m -==⇒=,选A .5.依题意可知该几何体的直观图如右上图,其体积为.3112322111323-⨯⨯⨯⨯⨯=,故选D. 6.令()ln(1)g x x x =-+,则1'()111xg x x x =-=++,由'()0,g x >得0,x >即函数()g x 在(0,)+∞上单调递增,由'()0g x <得10x -<<,即函数()g x 在(1,0)-上单调递减,所以当0x =时,函数()g x 有最小值,min ()(0)0g x g ==,于是对任意的(1,0)(0,)x ∈-+∞,有()0g x ≥,故排除B 、D,因函数()g x 在(1,0)-上单调递减,则函数()f x 在(1,0)-上递增,故排除C,所以答案选A.7.四名学生中有两名分在一所学校的种数是24C ,顺序有33A 种,而甲乙被分在同一所学校的有33A 种,所以不同的安排方法种数是23343330C A A -=.故选C .8. 因21(3)(2)()55(3)(2)1n n n a f f n n n n ⎛⎫+-+== ⎪++++-⎝⎭11()()23f f n n =-++,故5.方茴说:“那时候我们不说爱,爱是多么遥远、多么沉重的字眼啊。
2013年广州二模理科数学试题附详细解答(纯WORD版)
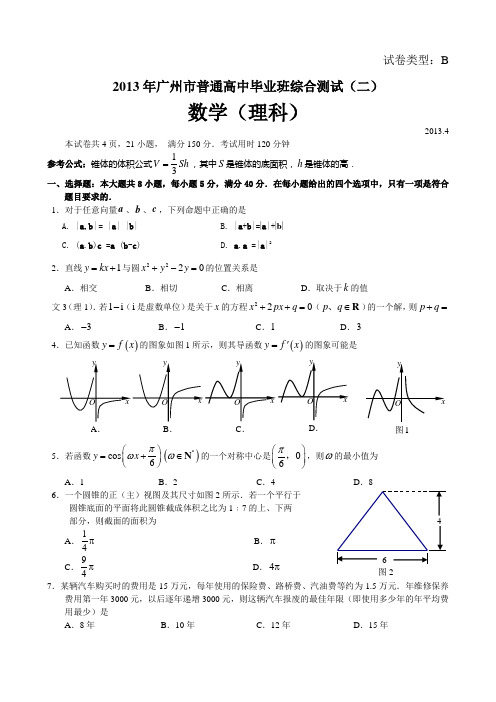
试卷类型:B2013年广州市普通高中毕业班综合测试(二)数学(理科)2013.4本试卷共4页,21小题, 满分150分.考试用时120分钟 参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.对于任意向量a 、b 、c ,下列命题中正确的是A. |a.b | = |a | |b |B. |a +b |=|a |+|b |C. (a .b )c =a (b -c )D. a .a =|a |22.直线1y kx =+与圆2220x y y +-=的位置关系是A .相交B .相切C .相离D .取决于k 的值文3(理1).若1i -(i 是虚数单位)是关于x 的方程220x px q ++=(p q ∈R 、)的一个解,则p q += A .3- B .1- C .1 D .34.已知函数()y f x =的图象如图1所示,则其导函数()y f x '=的图象可能是5.若函数cos 6y x πω⎛⎫=+⎪⎝⎭()*ω∈N 的一个对称中心是06π⎛⎫ ⎪⎝⎭,,则ω的最小值为A .1B .2C .4D .86.一个圆锥的正(主)视图及其尺寸如图2所示.若一个平行于 圆锥底面的平面将此圆锥截成体积之比为1﹕7的上、下两 部分,则截面的面积为A .14π B .π C .94π D .4π7.某辆汽车购买时的费用是15万元,每年使用的保险费、路桥费、汽油费等约为1.5万元.年维修保养费用第一年3000元,以后逐年递增3000元,则这辆汽车报废的最佳年限(即使用多少年的年平均费用最少)是A .8年B .10年C .12年D .15年图1A .B .C .D .图2- 2 -8.记实数1x ,2x ,…,n x 中的最大数为{}12max ,,n x x x …,,最小数为{}12min ,,n x x x …,,则{}{}2max min 116x x x x +-+-+=,, A .34 B .1 C .3 D .72二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9.某商场销售甲、乙、丙三种不同型号的钢笔,甲、乙、丙三种型号钢笔的数量之比依次为2﹕3﹕4.现用分层抽样的方法抽出一个容量为n 的样本,其中甲型钢笔有12支,则此样本容量n = . 10.已知 α为锐角,且3c o s 45απ⎛⎫+= ⎪⎝⎭,则 sin α= . 11.用0,1,2,3,4,5这六个数字,可以组成 个没有重复数字且能被5整除的五位数(结果用数值表示).12.已知函数()22f x x x =-,点集()()(){}M x y f x f y =+,≤2,()()(){}N x y f x f y =-,≥0,则M N 所构成平面区域的面积为 .13.数列}{n a 的项是由1或2构成,且首项为1,在第k 个1和第1k +个1之间有21k -个2,即数列}{n a 为:1,2,1,2,2,2,1,2,2,2,2,2,1,…,记数列}{n a 的前n 项和为n S ,则20S = ;2013S = . (二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)在△ABC 中,D 是边AC 的中点,点E 在线段BD 上,且满足13BE BD =,延长AE 交BC 于点F ,则BFFC的值为 . 15.(坐标系与参数方程选做题)在极坐标系中,已知点1,2A π⎛⎫ ⎪⎝⎭,点P 是曲线2sin 4cosρθθ=上任意一点,设点P 到直线cos 10ρθ+=的距离为d ,则PA d +的最小值为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)某单位有A 、B 、C 三个工作点,需要建立一个公共无线网络发射点O ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为80AB =m ,70BC =m ,50CA =m .假定A 、B 、C 、O 四点在同一平面内. (1)求BAC ∠的大小;(2)求点O 到直线BC 的距离.已知正方形ABCD 的边长为2,E F G H 、、、分别是边AB BC CD DA 、、、的中点.(1)在正方形ABCD 内部随机取一点P,求满足||PH <(2)从A B C D E F G H 、、、、、、、这八个点中,随机选取两个点,记这两个点之间的距离为ξ,求随机变量ξ的分布列与数学期望E ξ.18.(本小题满分14分)等边三角形ABC 的边长为3,点D 、E 分别是边AB 、AC 上的点,且满足AD DB =12CE EA =(如图3).将△ADE 沿DE 折起到△1A DE 的位置,使二面角1A DE B --成直二面角,连结1A B 、1A C(如图4).(1)求证:1A D ⊥平面BCED ;(2)在线段BC 上是否存在点P ,使直线1PA 与平面1A BD 所成的角为60?若存在,求出PB 的长,若不存在,请说明理由.- 4 -已知0a >,设命题p :函数()2212f x x ax a =-+-在区间[]0,1上与x 轴有两个不同的交点;命题q :()g x x a ax =--在区间()0,+∞上有最小值.若()p q ⌝∧是真命题,求实数a 的取值范围.20.(本小题满分14分)经过点()0,1F 且与直线1y =-相切的动圆的圆心轨迹为M .点A 、D 在轨迹M 上,且关于y 轴对称,过线段AD (两端点除外)上的任意一点作直线l ,使直线l 与轨迹M 在点D 处的切线平行,设直线l 与轨迹M 交于点B 、C . (1)求轨迹M 的方程;(2)证明:BAD CAD ∠=∠; (3)若点D 到直线AB,且△ABC 的面积为20,求直线BC 的方程. 21.(本小题满分14分)设n a 是函数()321f x x n x =+-()*n ∈N 的零点.(1)证明:01n a <<; (2)证明:1n n <+1232n a a a +++< .2013年广州市普通高中毕业班综合测试(二)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力对照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共8小题,每小题5分,满分40分.1、分析:|||||||cos ,|a b a b a b =<> ;由向量加法的几何意义||||||a b a b ++ …;()a b c是与c 平行的向量,()a b c 是与a 平行的向量;D 正确,即22||a a a a ==2、分析:圆2220x y y +-=即22(1)1x y +-=,圆心为(0,1),半径1r =,圆心到直线1y kx =+即10kx y -+=得距离0d ==,即直线经过圆心,故直线与圆相交3、分析:因为1i -是方程220x px q ++=的一个解,所以2(1i)2(1i)0p q -+-+=,整理得(2)(22)i 0p q p ++--=,解得1p =-,2q =,所以1p q +=4、分析:用排除法,当0x >时,()f x 单调递减,故此时()0f x '<,即()f x '的图象在x 轴下方,排除B 、D ;当0x <时,()f x 先增后减再增,故此时()0()0()0f x f x f x '''>→<→>,排除C ;A 正确5、分析:由题意cos()066ππω⨯+=,代入检验2ω=适合6、分析:圆锥直观图如图,设截面圆半径为r ,所截小圆锥的高为h ,由题意2221131173433r hr h πππ=⨯⨯-,化简2836r h =,又由三角形相似得34r h =,即34h r =, 联立解得294r =,故截面圆面积为294r ππ=7、分析:设使用了n 年,则年平均费用为- 6 -15(1.50.3)(1.520.3)(1.530.3)(1.50.3)n n++++⨯++⨯+++⨯15 1.50.3(123)n n n++++++=(1)15 1.50.32n n n n+++⨯=150.31.65 1.652n n =+++…当且仅当150.32n n =时,即2100n =,10n =取到最小值 8、分析:2min{1,1,6}x x x x +-+-+的图象如下图中的红色部分,其最大值2max{min{1,1,6}}x x x x +-+-+在两直线16y x y x =+⎧⎨=-+⎩的交点处取到,解得交点坐标为57(,)22,即最大值为72二、填空题:本大题查基本知识和基本运算,体现选择性.共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.第13题第一个空2分,第二个空3分.9.54 10.1011.216 12.2π 13.36;3981 14.14 159、分析:设乙型号x 支,丙型号y 支,则12234x y==,得18x =,24y =,则样本容量12182454n =++= 10、分析:因为02πα<<,所以3444πππα<+<,又3cos()45πα+=,所以4sin()45πα+==, 故sin sin[()]44ππαα=+- sin()cos cos()sin 4444ππππαα=+-+435252=⨯-⨯=11、分析:因为该五位数能被5整除,所以其末位是0或5,若末位是0,则从1,2,3,4,5中任取4个数字填前4位,有45A 5432120=⨯⨯⨯=种;若末位是5,因为0不能在首位,先从1,2,3,4中任取1个数字填首位,有14C 种,再将余下的3个数字连同0共4个数字排在中间三个数位,有34A 种,故末位是5的有1344C A 443296=⨯⨯⨯=种;综上,满足条件的五位数共有12096216+=种12、分析:2222{(,)|()()2}{(,)|222}{(,)|(1)(1)4}M x y f x f y x y x x y y x y x y =+=-+-=-+-剟M 表示以(1,1)为圆心,半径2r =的圆及其内部;2222{(,)|()()0}{(,)|220}{(,)|(1)(1)}{(,)|1||1|}N x y f x f y x y x x y y x y x y x y x y =-=--+=--=--厖 …N 表示两条相交直线构成的两个部分;在同一坐标系中画出上述两个图形,其公共部分如图中阴影部分所示,其面积21222S ππ=⨯=13、分析:2036S =;截至第21k -个 2 时,共有2(121)[135(21)]2k k k k k k k +-+++++-=+=+ 项,估计2k k +的值,当44k =时,共21980k k +=项,要达到2013项,只需从其后续的取1个1,32个 2,故201344(187)451(13587)23224526439812S +=⨯+++++⨯+⨯=+⨯+= 14、分析:如图,作//DH BC ,交AF 于G ,交AB 于H ,设HG x =,因为D 是AC 中点,所以G 、H 分别是AF 、AB 中点,所以2BF x =,又BEF ∆∽DEG ∆,又13BE BD =,所以24GD BF x ==,5HD HG GD x =+=,由中位线知10BC x =,1028FC BC BF x x x =-=-=,所以2184BF x FC x ==15、分析:点(1,)2A π的平面直角坐标为(0,1)A ,由2sin 4cos ρθθ=得22sin 4cos ρθρθ=,即其平面直角坐标方程为24y x =(抛物线),由cos 10ρθ+=得10x +=,(恰是抛物线的准线),作图如下:由抛物线定义知||||||PA d PA PF +=+,(F 为抛物线的焦点(1,0))由两点之间线段最短知,当P 移动到直线AF 与抛物线的交点'P 时||||PA PF +最小,此时- 8 -|||||||'||'|||PA d PA PF P A P F AF +=+=+=三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题主要考查解三角形等基础知识,考查正弦定理与余弦定理的应用,本小题满分12分) 解:(1)在△ABC 中,因为80AB =m ,70BC =m ,50CA =m ,由余弦定理得222cos 2AB AC BC BAC AB AC+-∠=⨯⨯ ……………………………………………………2分2228050701280502+-==⨯⨯. ……………………………3分因为BAC ∠为△ABC 的内角,所以3BAC π∠=.……………………………………………………4分 (2)方法1:因为发射点O 到A 、B 、C 三个工作点的距离相等,所以点O 为△ABC 外接圆的圆心.……………………………………………………………………5分 设外接圆的半径为R ,在△ABC 中,由正弦定理得2sin BCR A=, ……………………………………………………………7分 因为70BC =,由(1)知3A π=,所以sin 2A =.所以2R ==,即R =8分 过点O 作边BC 的垂线,垂足为D ,…………………………9分在△OBD中,OB R ==703522BC BD ===,所以OD ===……………………………………11分 所以点O 到直线BCm .……………………………………………………………12分 方法2:因为发射点O 到A 、B 、C 三个工作点的距离相等, 所以点O 为△ABC 外接圆的圆心.……………………5分 连结OB ,OC ,过点O 作边BC 的垂线,垂足为D , …………………6分 由(1)知3BAC π∠=, 所以3BOC 2π∠=. 所以3BOD π∠=.………………………………………9分在Rt △BOD 中,703522BC BD ===,所以35tan tan 60BD OD BOD ===∠.…………………………………………11分 所以点O 到直线BC的距离为3m .……………………………………………………………12分 17.(本小题主要考查几何概型、随机变量的分布列与数学期望等基础知识,考查运算求解能力与数据处理能力等,本小题满分12分)解:(1)这是一个几何概型.所有点P 构成的平面区域是正方形ABCD 的内部,其面积是224⨯=…1’满足||PH <P 构成的平面区域是以HABCD 内部的公共部分,它可以看作是由一个以H圆心角为2π的扇形HEG 的内部(即四分之一个圆)与两个 直角边为1的等腰直角三角形(△AEH 和△DGH )内部 构成. ……………………………………………………………2分其面积是2112111422π⨯π⨯+⨯⨯⨯=+.………………3分所以满足||PH <112484π+π=+.………………………………………………………4分 (2)从A B C D E F G H 、、、、、、、这八个点中,任意选取两个点,共可构成28C 28=条不同的线段.……………………………………5分其中长度为1的线段有84条,长度为2的线段有6有8条,长度为的线段有2条.所以ξ所有可能的取值为12.……………………………………………………7分 且()821287P ξ===,(41287P ξ===, ()6322814P ξ===,(82287P ξ===,(212814P ξ===. ………………………………………9分所以随机变量ξ的分布列为:随机变量ξ的数学期望为……10分- 10 -21321127714714E ξ=⨯++⨯+57+=.………12分 18.(本小题主要考查空间直线与平面垂直、直线与平面所成角等基础知识,考查空间想象能力和运算求解能力等,本小题满分14分)证明:(1)因为等边△ABC 的边长为3,且AD DB=12CE EA =, 所以1AD =,2AE =. 在△ADE 中,60DAE ∠=,由余弦定理得DE 因为222AD DE AE +=, 所以AD DE ⊥.折叠后有1A D DE ⊥.……………………………………………………………………………………2分因为二面角1A DE B --是直二面角,所以平面1A DE ⊥平面BCED . …………………………3分 又平面1A DE 平面BCED DE =,1A D ⊂平面1A DE ,1A D DE ⊥, 所以1A D ⊥平面BCED . ………………………………………………………………………………4分 (2)解法1:假设在线段BC 上存在点P ,使直线1PA 与平面1A BD 所成的角为60.如图,作PH BD ⊥于点H ,连结1A H 、1A P .………………5分 由(1)有1A D ⊥平面BCED ,而PH ⊂平面BCED ,所以1A D ⊥PH .…………………………………………………6分又1A D BD D = ,所以PH ⊥平面1A BD .…………………………………………………………………………………7分 所以1PA H ∠是直线1PA 与平面1A BD 所成的角. ……………………………………………………8分 设PB x =()03x ≤≤,则2x BH =,PH x =.…………………………………………………9分 在Rt △1PA H 中,160PA H ∠=,所以112A H x =.………………………………………………10分 在Rt △1A DH 中,11A D =,122DH x =-.………………………………………………………11分 由22211A D DH A H +=,得222111222x x ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭.………………………………………………………12分解得52x =,满足03x ≤≤,符合题意.……………………………………………………………13分 所以在线段BC 上存在点P ,使直线1PA 与平面1A BD 所成的角为60,此时52PB =.………14分解法2:由(1)的证明,可知ED DB ⊥,1A D ⊥平面BCED .以D 为坐标原点,以射线DB 、DE 、1DA 分别为x 轴、y 轴、z 轴的正半轴,建立空间直角坐标系D xyz -如图. …………………………………………………………5分设2PB a =()023a ≤≤,则BH a =,PH =,2DH a =-. ……………………6分 所以()10,0,1A,()2,0P a -,()E .…………7分所以()12,,1PA a =-.……………………………………………………………………8分因为ED ⊥平面1A BD ,所以平面1A BD的一个法向量为()DE =.……………………………………………………9分因为直线1PA 与平面1A BD 所成的角为60,所以11sin 60PA DE PA DE =2==…………………………………………11分 解得54a =. ……………………………………………………………………12分 即522PB a ==,满足023a ≤≤,符合题意. ……………………………………………………13分所以在线段BC 上存在点P ,使直线1PA 与平面1A BD 所成的角为60,此时52PB =.………14分19.(本小题主要考查二次函数的交点与分段函数的最值、常用逻辑用语等基础知识,考查数形结合思想、分类讨论思想和运算求解能力、抽象概括能力等,本小题满分14分) 解:要使函数()2212f x x ax a =-+-在[]0,1上与x 轴有两个不同的交点,必须()()0101,0.f f a ⎧⎪⎪⎨<<⎪⎪∆>⎩≥0,≥0,……………………………………………………………2分- 12 -即()()2,1224012412a a a a a -⎧⎪-⎪⎨<<⎪⎪--->⎩≥0,≥0,0.………………………………………………4分112a <≤.112a <≤时,函数()2212f x x ax a =-+-在[]0,1上与x 轴有两个不同的交点.…5分 下面求()g x x a ax =--在()0,+∞上有最小值时a 的取值范围:方法1因为()()()1,,1,.a x a x a g x a x a x a --⎧⎪=⎨-++<⎪⎩≥…………………………………………………………6分①当1a >时,()g x 在()0,a 和[),a +∞上单调递减,()g x 在()0,+∞上无最小值;……………7分 ②当1a =时,()1,,21,1.x g x x x -⎧=⎨-+<⎩≥1()g x 在()0,+∞上有最小值1-;………8分 ③当01a <<时,()g x 在()0,a 上单调递减,在[),a +∞上单调递增,()g x 在()0,+∞上有最小值()2g a a =-.…………………………………………………………9分所以当01a <≤时,函数()g x 在()0,+∞上有最小值.……………………………………………10分方法2:因为()()()1,,1,.a x a x a g x a x a x a --⎧⎪=⎨-++<⎪⎩≥…………………………………………………………6分因为0a >,所以()10a -+<.所以函数()()110y a x a x a =-++<<是单调递减的.………………………………………………7分 要使()g x 在()0,+∞上有最小值,必须使()21y a x a =--在[),a +∞上单调递增或为常数.……8分 即10a -≥,即1a ≤.……………………………………………………………………………………9分 所以当01a <≤时,函数()g x 在()0,+∞上有最小值. ……………………………………………10分 若()p q ⌝∧是真命题,则p ⌝是真命题且q 是真命题,即p 是假命题且q 是真命题.……………11分所以101,,20 1.a a a ⎧<>⎪⎨⎪<⎩≤或 …………………………………………………………………………12分解得01a <或112a <≤. ………………………………………………………………………13分故实数a的取值范围为(11,12⎛⎤⎤ ⎥⎦⎝⎦.…………………………………………………………14分 20.(本小题主要考查动点的轨迹和直线与圆锥曲线的位置关系、导数的几何意义等基础知识,考查运算求解能力和推理论证能力等,本小题满分14分)解:(1)方法1:设动圆圆心为(),x y1y =+.…………………………1分整理,得24x y =.所以轨迹M 的方程为24x y =.…………………………………………………2分 方法2:设动圆圆心为P ,依题意得点P 到定点()0,1F 的距离和点P 到定直线1y =-的距离相等, 根据抛物线的定义可知,动点P 的轨迹是抛物线.……………………………………………………1分 且其中定点()0,1F 为焦点,定直线1y =-为准线.所以动圆圆心P 的轨迹M 的方程为24x y =.………………………………………………………2分 (2)由(1)得24x y =,即214y x =,则12y x '=. 设点2001,4D x x ⎛⎫⎪⎝⎭,由导数的几何意义知,直线l 的斜率为012BC k x =.…………………………3分由题意知点2001,4A x x ⎛⎫- ⎪⎝⎭.设点2111,4C x x ⎛⎫ ⎪⎝⎭,2221,4B x x ⎛⎫ ⎪⎝⎭, 则2212120121114442BCx x x x k x x x -+===-,即1202x x x +=.4分因为2210101011444ACx x x x k x x --==+,2220202011444ABx x x x k x x --==+.……………………………5分由于()120102020444AC AB x x x x x x x k k +---+=+==,即AC AB k k =-.……6分 所以BAD CAD ∠=∠.…………………………………………………………7分 (3)方法1:由点D 到AB,可知BAD ∠45= .………………………………8分 不妨设点C 在AD 上方(如图),即21x x <,直线AB 的方程为:()20014y x x x -=-+. A B CDOxylE- 14 -由()20021,44.y x x x x y ⎧-=-+⎪⎨⎪=⎩解得点B 的坐标为()20014,44x x ⎛⎫-- ⎪⎝⎭.……………………………………………………………10分 所以)()00042AB x x =---=-.由(2)知CAD BAD ∠=∠45=,同理可得02AC =+.………………………………11分 所以△ABC的面积200012244202S x =⨯-⨯+=-=, 解得03x =±.……………………………………………………………………12分 当03x =时,点B 的坐标为11,4⎛⎫- ⎪⎝⎭,32BC k =, 直线BC 的方程为()13142y x -=+,即6470x y -+=.…………………………………………13分 当03x =-时,点B 的坐标为497,4⎛⎫- ⎪⎝⎭,32BC k =-, 直线BC 的方程为()493742y x -=-+,即6470x y +-=. ……………………………………14分 方法2:由点D 到ABAD ,可知BAD ∠45= .…………………………………8分 由(2)知CAD BAD ∠=∠45= ,所以CAB ∠90=,即AC AB ⊥.由(2)知104AC x x k -=,204AB x x k -=. 所以1020144AC ABx x x xk k --=⨯=-.即()()102016x x x x --=-. ① 由(2)知1202x x x +=. ②不妨设点C 在AD 上方(如图),即21x x <,由①、②解得10204,4.x x x x =+⎧⎨=-⎩…………………………10分因为02AB ==-,同理02AC =+. ……………………………………………………11分以下同方法1. 21.(本小题主要考查函数的零点、函数的导数和不等式的证明等基础知识,考查运算求解能力和推理论证能力等,本小题满分14分)证明:(1)因为()010f =-<,()210f n =>,且()f x 在R 上的图像是一条连续曲线,所以函数()f x 在()01,内有零点.………………………………………………………………………1分 因为()2230f x x n '=+>,所以函数()f x 在R 上单调递增.………………………………………………………………………2分 所以函数()f x 在R 上只有一个零点,且零点在区间()01,内. 而n a 是函数()f x 的零点,所以01n a <<.…………………………………………………………3分 (2)先证明左边的不等式:因为3210n n a n a +-=, 由(1)知01n a <<,所以3n n a a <.………………………………………………………………4分 即231n n n n a a a -=<.所以211n a n >+.…………………………………………………………5分 所以1222211111211n a a a n +++>++++++ .…………………6分 以下证明222111112111n n n +++≥++++ . ① 方法1(放缩法):因为()21111111n a n n n n n >≥=-+++,…………………………………………7分 所以1211111111223341n a a a n n ⎛⎫⎛⎫⎛⎫⎛⎫+++>-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭1111n n n =-=++.…………………………………9分 方法2(数学归纳法):1)当1n =时,2111111=++,不等式①成立. 2)假设当n k =(*k ∈N )时不等式①成立,即222111112111k k k +++≥++++ .- 16 -那么()222211111121111k k +++++++++ ()21111k k k ≥++++. 以下证明()()()21111111k k k k k ++≥+++++. ② 即证()()()21111111k kk k k +≥-+++++.即证22112232k k k k ≥++++.由于上式显然成立,所以不等式②成立. 即当1n k =+时不等式①也成立.根据1)和2),可知不等式①对任何*n ∈N 都成立. 所以121n na a a n +++>+ .…………………………………………………9分 再证明右边的不等式:当1n =时,()31f x x x =+-.由于31113102228f ⎛⎫⎛⎫=+-=-< ⎪ ⎪⎝⎭⎝⎭,3333111044464f ⎛⎫⎛⎫=+-=> ⎪ ⎪⎝⎭⎝⎭, 所以11324a <<.………………………………………………………………10分 由(1)知01n a <<,且3210n n a n a +-=,所以32211n n a a n n -=<. ……………………………11分 因为当2n ≥时,()2111111n n n n n<=---,…………………………………………………………12分 所以当2n ≥时,12342311111114223341n a a a a a n n ⎛⎫⎛⎫⎛⎫+++++<++-+-++- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ 113122n =+-<. 所以当*n ∈N 时,都有1232n a a a +++<. 综上所述,1n n <+1232n a a a +++< .……………………………………………………………14分。
2013年高三理科数学二模试题(惠州有答案)

2013年高三理科数学二模试题(惠州有答案)骞夸笢鐪佹儬宸炲競2013悊绉戯級2013.4 85鍒嗭紝婊″垎40€椤规槸绗﹀悎棰樼洰瑕佹眰鐨勶紟1鐨勫畾涔夊煙涓洪泦鍚圡锛岄泦鍚圢锛?锛屽垯锛?锛夛紟A锛?B锛嶯C锛?D锛嶮2銆佸凡鐭ユき鍦鍊嶏紝鍒欐き鍦嗙殑绂诲績鐜囩瓑浜庯紙锛夛紟A锛?B锛?C锛?D锛?3猴級锛岄偅涔堣緭鍑虹殑锛?锛夛紟锛★紟2450 2500 锛o紟2550 锛わ紟2652 4銆佽嫢鏇茬嚎鐨勪竴鏉″垏绾?涓庣洿绾?鍨傜洿锛屽垯鍒囩嚎鐨勬柟绋嬩负锛?锛夛紟A銆?銆€B銆?C銆?D銆?5銆佹柟绋?鏈夊疄鏍圭殑姒傜巼涓猴紙锛夛紟A銆?B銆?C銆?D銆?6銆佸凡鐭?锛夛紟A銆佽嫢鈭?锛屽垯銆€B 銆佽嫢鈭?锛屽垯鈭?C銆佽嫢锛屽垯鈭?銆€D銆佽嫢锛屽垯7銆佷竴寮犳?鈥濆浘妗堬紝?銆?锛屽壀鍘婚儴鍒嗙殑闈㈢Н涓?锛?鑻?锛屽垯鐨勫浘璞℃槸锛?锛夛紟8銆佸皢鍑芥暟鐨勫浘璞″厛鍚戝乏骞崇Щ锛岀劧鍚庡皢鎵€寰楀浘璞′笂鎵€鏈夌偣鐨勬í鍧愭爣鍙樹负鍘熸潵鐨?鍊嶏紙绾靛潗鏍囦笉鍙橈級锛屽垯鎵?锛夛紟A锛?B锛?C锛?D 锛??10鍒嗭級浜屻€佸~绌洪ч??3锝?5锛屼笁棰樺叏绛旂殑锛屽彧璁$畻鍓嶄袱棰樺緱鍒嗭紟姣忓皬棰?鍒嗭紝婊″垎30鍒嗭紟9銆佸凡鐭ュ悜閲?锛?锛岃嫢锛屽垯瀹炴暟鐨勫€肩瓑浜?锛?10銆佸凡鐭?锛屽垯= 锛?11銆??锛?12銆佸嚱鏁?鐢变笅琛ㄥ畾涔夛細鑻?锛?锛?锛屽垯锛?13銆?鍧愭爣绯讳笌鍙傛暟鏂圭▼閫夊仛棰?鏇茬嚎锛?涓婄殑鐐瑰埌鏇茬嚎锛?锛?14銆?涓嶇瓑寮忛€?宸茬煡瀹炴暟婊¤冻锛屽垯鐨勬渶澶у€间负锛?15銆?鍑犱?濡傚浘锛屽钩琛屽洓杈瑰舰锛岃嫢鐨勯潰?cm , 鍒??cm 锛?涓夈€佽Вч??0鍒嗭紟瑙g瓟椤诲啓鍑烘?16?2?鐨勫墠椤瑰拰涓?, 宸茬煡锛?锛?锛堚厾锛夋眰棣栭」鍜屽叕姣?鐨勫€硷紱锛堚叀锛夎嫢锛屾眰鐨勫€硷紟17?2鍒嗭級璁惧嚱鏁?锛?锛堚厾锛夋眰鍑芥暟鐨勬渶?锛堚叀锛夊綋鏃讹紝鐨勬渶澶у€间负2锛屾眰鐨勫€硷紝骞舵眰鍑??18樻弧鍒?4у皬鐩稿悓鐨?4粦鐞冿紟锛堚厾锛夐噰鍙栨斁鍥炴娊鏍锋柟寮忥紝浠庝腑鎽稿嚭涓や釜鐞冿紝?锛堚叀锛夐噰鍙栦笉鏀惧洖鎶芥牱屾柟宸? 锛?19?4鍒嗭級濡傚浘锛屽凡鐭ュ洓妫遍敟鐨?搴曢潰鏄骞抽潰, 锛?鐐?涓?鐨勪腑鐐癸紟锛堚厾锛夋眰璇侊細骞抽潰锛?锛堚叀锛夋眰浜岄潰瑙?20?4鍒嗭級缁欏畾鍦哖: 鍙婃姏鐗?绾縎: ,杩囧渾蹇?浣滅洿绾?,姝ょ洿绾夸笌涓婅堪涓ゆ洸绾??璁颁负,濡傛灉绾?娈??姹傜洿绾?鐨勬柟绋? 21?4欢鐨勫嚱鏁?鏋勬垚鐨勯泦鍚堬細鈥溾憼鏂圭▼鏈夊疄鏁版牴锛涒憽鍑芥暟鐨?婊¤冻鈥濓紟?礌锛屽苟璇存槑鐞嗙敱锛?鍏锋湁涓嬮潰鐨勬€ц川锛氳嫢鐨勫畾涔夊煙涓篋锛屽垯瀵逛簬浠绘剰[m锛宯] D锛岄兘瀛樺湪[m锛宯]锛屼娇寰楃瓑寮?鎴愮珛鈥濓紝璇曠敤杩欎竴鎬ц川璇佹槑锛氭柟绋?鍙??鐨勫疄鏁版牴锛屾眰璇侊細瀵逛簬瀹氫箟鍩熶腑浠绘剰鐨?锛屽綋锛屼笖鏃讹紝锛?骞夸笢鐪佹儬宸炲競2013冪瓟妗?007.11 涓€銆侀€夋嫨棰橈細棰樺彿1銆佽В鏋愶細锛孨锛?锛?鍗?锛庣瓟妗堬細锛?2銆佽В锛屽張锛??锛?3銆佽В鏋愶細绋嬪簭鐨勮繍琛岀粨鏋滄槸锛庣瓟妗堬細锛?4銆佽В鏋愶細涓庣洿绾?鍨傜洿鐨勫垏绾?鐨勬枩鐜囧繀涓?锛岃€?锛屾墍浠ワ紝鍒囩偣涓?锛庡垏绾夸负锛屽嵆锛岀瓟妗堬細锛?5銆佽В鏋愶細鐢变竴鍏冧簩娆℃柟绋嬫湁瀹炴牴鐨勬潯浠?锛岃€?锛岀敱鍑犱綍姒傜巼寰楁锛庣瓟妗堬細锛?6銆佽В鏋愶細濡傛灉涓ゆ??姝g‘锛?锛屾墍浠?锛?7銆佽В鏋愶?锛岀瓟妗堬細锛?8銆佽В鏋愶細鐨勫浘璞″厛鍚戝乏骞崇Щ锛屾í鍧愭爣鍙樹负鍘熸潵鐨?鍊?锛庣瓟妗堬細锛??棰樺彿9銆佽В鏋愶細鑻?锛屽垯锛岃В寰?锛?10銆佽В?锛?11銆佽В鏋愶細12銆佽В鏋愶細浠?锛屽垯锛屼护锛屽垯锛?浠?锛屽垯锛屼护锛屽垯锛?浠?锛屽垯锛屼护锛屽垯锛?鈥︼紝鎵€浠?锛?13銆佽В鏋愶細锛?锛涘垯鍦嗗績鍧愭爣涓?锛?锛?蹇冨埌鐩寸嚎鐨勮窛绂讳负锛?14銆佽В鏋愶細鐢辨煰瑗夸笉绛夊紡锛岀瓟妗堬細锛?15銆佽В鏋愶細鏄剧劧涓?涓虹浉浼间笁瑙掑舰锛屽張锛屾墍浠??cm 锛?涓夈€佽Вч??0鍒嗭紟瑙g瓟椤诲啓鍑烘?16銆佽В: (鈪? , 鈥︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?鈭?锛屸€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?4鍒?瑙e緱锛庘€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?6鍒?(鈪?鐢?,寰楋細, 鈥︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?鈭?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?10鍒?鈭?锛庘€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?12鍒?17銆佽В锛氾紙1锛?鈥?2鍒?鍒?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?涓斿綋鏃??鍗?涓?愬紑鍖洪棿涓嶆墸鍒嗭級锛庘€︹€︹€?鍒?锛?锛夊綋鏃?锛屽綋锛屽嵆鏃?锛?鎵€浠?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?涓?酱锛?鈥︹€︹€︹€︹€︹€︹€?2鍒?18銆佽В锛?锛堚厾锛夎В娉曚竴锛氣€滄湁鏀惧洖鎽镐袱娆★紝棰滆壊涓嶅悓鈥濇寚鈥滃厛鐧藉啀榛戔€濇垨鈥滃厛榛戝啀鐧解€濓紝蹭笉鍚屸€濅负浜嬩欢锛屸€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭碘€绉嶅彲鑳斤紝鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?瑙f硶浜岋細鈥滄湁鏀惧洖鎽稿彇?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛庘€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鈭粹€滄湁鏀惧洖鎽镐袱娆★紝棰滆壊涓嶅悓鈥濈殑姒傜巼涓?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛屼緷棰樻剰寰楋細锛?锛?锛庘€︹€︹€︹€?0鍒?鈭?锛屸€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?锛庘€︹€︹€︹€︹€︹€︹€︹€?4鍒?19銆?鈪?璇佹槑:杩炵粨锛?涓?浜や簬鐐?锛岃繛缁?.鈥︹€︹€︹€︹€︹€︹€︹€︹€?鍒?? 鈭?鏄?鐨勪腑鐐? 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鐐?涓?鐨勪腑鐐? 鈭?. 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?骞抽潰骞抽潰, 鈭?骞抽潰. 鈥︹€︹€︹€︹€︹€?6鍒?(鈪?瑙f硶涓€: 骞抽潰, 骞抽潰,鈭?. 锛屸埓. 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?7鍒?? 鈭?. 锛?鈭?骞抽潰. 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?浣?锛屽瀭瓒充负锛岃繛鎺?锛屽垯, 鎵€浠?. 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?10鍒?,鈭?锛?. 鍦≧t鈻?涓? = 锛屸€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?12鍒?鈭?.鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?13鍒?鈭翠簩闈. 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?14鍒?瑙f硶浜岋細濡傚浘锛屼互鐐?鐨勫瀭鐩村钩鍒嗙嚎鎵€鍦ㄧ洿绾夸负杞达紝鎵€鍦ㄧ洿绾夸负杞达紝鎵€鍦ㄧ洿绾夸负杞达紝寤?锛屸€︹€︹€︹€︹€?鍒?鍒?锛?, 锛?鈭?锛?鈥︹€︹€︹€︹€?鍒?璁惧钩闈??, 鐢?锛屽緱锛?浠?锛屽垯锛屸埓. 鈥︹€︹€︹€︹€︹€︹€?鍒?骞抽潰, 骞抽潰, 鈭?. 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?锛屸埓. ?鈭?. 锛屸埓骞抽潰.鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?9鍒?鈭??, 锛庘€︹€︹€︹€︹€︹€︹€?10鍒?鈭?锛?鈭?锛?鈥︹€︹€︹€︹€︹€︹€︹€?12鍒?鈭?锛庘€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?13鍒?. 鈥︹€︹€︹€︹€︹€︹€︹€︹€?14鍒?20銆佽В:鍦?鐨勬柟绋嬩负,鍒欏叾鐩村緞闀?,鍦嗗績涓?,璁?鐨勬柟绋嬩负,鍗?,浠e叆鎶涚墿绾挎柟绋嬪緱: ,璁?锛?鏈?, 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鍒?. 鈥︹€︹€︹€︹€︹€︹€︹€?鍒?鏁?鈥?鍒?, 鈥︹€︹€︹€?7鍒?. 鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?8鍒?? , 鈥︹€︹€︹€︹€?10鍒?鎵€浠?锛屽嵆, 锛屸€︹€︹€︹€︹€?12鍒?鍗筹細鏂圭▼涓?鎴?. 鈥︹€︹€︹€︹€︹€︹€?4鍒?21銆佽В锛?锛?锛夊洜涓?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鎵€浠?锛屾弧瓒虫潯浠?. 鈥︹€︹€︹€︹€︹€︹€?鍒?鍙堝洜涓哄綋鏃讹紝锛屾墍浠ユ柟绋?鏈夊疄鏁版牴锛?鎵€浠ュ嚱鏁?冪礌锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?锛?锛夊亣璁炬柟绋?瀛樺湪涓や釜瀹炴暟鏍?锛夛紝鍒?锛屸€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?鍒?涓嶅Θ璁?浣垮緱绛夊紡鎴愮珛锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€?鍒?鍥犱负锛屾墍浠?锛屼笌宸茬煡鐭涚浘锛?鎵€浠ユ柟绋?︹€︹€︹€︹€︹€?0鍒?锛?锛屽洜涓?鎵€浠?锛屾墍浠?锛?鍙堝洜涓?锛屾墍浠ュ嚱鏁?涓哄噺鍑芥暟锛?鈥︹€︹€︹€︹€︹€︹€︹€?1鍒?鎵€浠?锛?鈥︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€︹€?2鍒?鎵€浠?锛屽嵆锛?鈥︹€︹€︹€?3鍒?鎵€浠?锛?鈥?4鍒?。
2013年理科全国各省市高考真题——圆锥曲线(带答案)

2013年全国各省市理科数学—圆锥曲线1、2013山东理T9.过点(3,1)作圆(x-1)2+y 2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为 (A )2x+y-3=0 (B )2x-y-3=0 (C )4x-y-3=0 (D )4x+y-3=0 2、2013重庆理T7.已知圆()()221:231C x y -+-=,圆()()222:349C x y -+-=,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则PM PN +的最小值为( )A 、4 B1 C 、6-3、2013全国理T8.椭圆22:143x y C +=的左、右顶点分别为12,A A ,点P 在C 上且直线2PA 的斜率的取值范围是[]2,1--,那么直线1PA 斜率的取值范围是(A )1324⎡⎤⎢⎥⎣⎦, (B )3384⎡⎤⎢⎥⎣⎦, (C )112⎡⎤⎢⎥⎣⎦, (D )314⎡⎤⎢⎥⎣⎦,4、2013新课标I 理10.已知椭圆E :)0(12222>>=+b a by a x 的右焦点为)03(,F ,过点F 的直线交椭圆E 于A 、B 两点。
若AB 的中点坐标为)11(-,,则E 的方程为A1364522=+y x B 1273622=+y x C 1182722=+y x D 191822=+y x 5、2013浙江理T9.如图,21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点,B A ,分别是1C ,2C 在第二、四象限的公共点。
若四边形21BF AF 为矩形,则2C 的离心率是A. 2B. 3C.23 D.266、2013辽宁理T15.已知椭圆2222:1(0)x y C a b a b+=>>的左焦点为,F C 与过原点的直线相交于,A B 两点,4,.10,6,cos ABF ,5AF BF AB AF C e ==∠=连接若则的离心率= .7、2013上海理T9.设AB 是椭圆Γ的长轴,点C 在Γ上,且4CBA π∠=,若AB=4,BC =Γ的两个焦点之间的距离为________8、2013福建理14. 椭圆()01:2222>>=+Γb a by a x 的左右焦点分别为21,F F ,焦距为c 2,若直线()c x y +=3与椭圆的一个交点满足12212F MF F MF ∠=∠,则该椭圆的离心率等于_____9、2013江苏T12.在平面直角坐标系xOy 中,椭圆C 的标准方程为)0,0(12222>>=+b a b y a x ,右焦点为F ,右准线为l ,短轴的一个端点为B ,设原点到直线BF 的距离为1d ,F 到l 的距离为2d ,若126d d =,则椭圆C 的离心率为 .10、2013新课标I 理T4.已知双曲线C :)0,0(12222>>=-b a b y a x 的离心率为25,则C的渐近线方程为(A )x y 41±= (B )x y 31±= (C ) x y 21±= (D )x y ±=11、2013北京理T6.若双曲线22221x y a b-=A. y =±2xB. y =C.12y x =±D.y x = 12、2013福建理T3.双曲线1422=-y x 的顶点到渐进线的距离等于( )A. 52B.54C. 552D.55413、2013广东理T7.已知中心在原点的双曲线C 的右焦点为()3,0F ,离心率等于32,在双曲线C 的方程是 ( )A . 2214x = B .22145x y -= C .22125x y -= D .2212x =14、2013天津理T5. 已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线与抛物线22(0)px p y =>的准线分别交于A , B 两点, O 为坐标原点. 若双曲线的离心率为2, △AOB 则p =(A) 1(B)32(C) 2 (D) 315、2013湖北理T5.已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=的( )A.实轴长相等B.虚轴长相等C.焦距相等D. 离心率相等16、2013江苏T3.双曲线191622=-y x 的两条渐近线的方程为 . 17、2013陕西理T11. 双曲线22116x y m-=的离心率为54, 则m 等于 .18、2013湖南理T14.设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点,P 是C上一点,若216,PF PF a +=且12PF F ∆的最小内角为30 ,则C 的离心率为___。
广东省12大市高三数学 二模文试题分类汇编9 圆锥曲线 理

广东省12大市2013届高三二模数学(理)试题分类汇编9:圆锥曲线一、选择题 1 .(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD 版))设F 1,F 2是椭圆)0(12222>>=+b a b y a x 的左右焦点,若直线x =m a (m >1)上存在一点P,使ΔF 2PF 1是底角为300的等腰三角形,则m 的取值范围是( )A D .2 .(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))已知双曲线22221x y a b-=的渐近线方程为y =,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )A .12B .2C D .13 .(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD 版))方程||||169x x y y +=-1的曲线即为函数y=f(x)的图象,对于函数y=f(x),有如下结论:①f(x)在R 上单调递减;②函数F(x)=4f(x)+3x 不存在零点;③函数y=f(x)的值域是R;④f(x)的图象不经过第一象限,其中正确的个数是 ( ) A .1个 B .2个 C .3个 D .4个 4 .(广东省惠州市2013届高三4月模拟考试数学理试题(WORD 版))设抛物线的顶点在原点,准线方程为-2,x =则抛物线的方程是( )A .28y x = B .28y x =-C .24y x =-D .24y x =二、填空题5 .(广东省韶关市2013届高三4月第二次调研测试数学理试题)设点P 是双曲线22221(0,0)x y a b a b-=>>与圆2222x y a b +=+在第一象限的交点,其中12,F F 分别是双曲线的左、右焦点,若21tan 3PF F ∠=,则双曲线的离心率为______________.6 .(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)下图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽________米.7 .(广东省揭阳市2013年高中毕业班第二次高考模拟考试理科数学试题)过双曲线221916x y -=的右焦点,且平行于经过一、三象限的渐近线的直线方程是 ________. 三、解答题8.(广东省肇庆市2013届高三4月第二次模拟数学(理)试题)设椭圆22221(0,0)x y a b b a+=>>的离心率为12,其左焦点E 与抛物线21:4C x y =-的焦点相同.(Ⅰ)求此椭圆的方程;(Ⅱ)若过此椭圆的右焦点F 的直线与曲线C 只有一个交点P ,则(1)求直线的方程;(2)椭圆上是否存在点(,)M x y ,使得12MPF S ∆=,若存在,请说明一共有几个点;若不存在,请说明理由.9.(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD 版))已知抛物线C:y 2=4x, F 是抛物线的焦点,设A(x 1,y 1),B(x 2 ,y 2)是C 上异于 原点O 的两个不重合点,OA 丄OB,且AB 与x 轴交于点T(1) 求x 1x 2的值; (2) 求T 的坐标;(3) 当点A 在C 上运动时,动点R 满足:FR FB FA =+,求点R 的轨迹方程.10.(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))已知动点M 到点(0,1)F 的距离与到直线4y =的距离之和为5. (1)求动点M 的轨迹E 的方程,并画出图形;(2)若直线:l y x m =+与轨迹E 有两个不同的公共点,A B ,求m 的取值范围; (3)在(2)的条件下,求弦长||AB 的最大值.11.(广东省韶关市2013届高三4月第二次调研测试数学理试题)已知椭圆)(1122221 >=-+a a y a x 的左右焦点为21,F F ,抛物线C:px y 22=以F 2为焦点且与椭圆相交于点()11,M x y 、N()22,x y ,点M 在x轴上方,直线1F M 与抛物线C 相切.(1)求抛物线C 的方程和点M 、N 的坐标;(2)设A,B 是抛物线C 上两动点,如果直线MA ,MB 与y 轴分别交于点,P Q . MPQ ∆是以MP ,MQ 为腰的等腰三角形,探究直线AB 的斜率是否为定值?若是求出这个定值,若不是说明理由.12.(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)已知动点(,)P x y 与两个定点(1,0),(1,0)M N -的连线的斜率之积等于常数λ(0λ≠) (1)求动点P 的轨迹C 的方程;(2)试根据λ的取值情况讨论轨迹C 的形状;(3)当2λ=时,对于平面上的定点(E F ,试探究轨迹C 上是否存在点P ,使得120EPF ∠=︒,若存在,求出点P 的坐标;若不存在,说明理由.13.(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD 版))在平面直角坐标系xoy 中,动点在椭圆C 1:2212x y +=上,动点Q 是动圆C 2:222(12)x y r r +=<<上一点.(1)求证:动点P 到椭圆C 1的右焦点的距离与到直线x=2的距离之比等于椭圆的离心率;(2)设椭圆C1上的三点1122(,),(,)A x y B C x y 与点F(1,0)的距离成等差数列,线段AC 的垂直平分线是否经过一个定点为?请说明理由.(3)若直线PQ 与椭圆C 1和动圆C 2均只有一个公共点,求P 、Q 两点的距离|PQ|的最大值. 14.(广东省揭阳市2013年高中毕业班第二次高考模拟考试理科数学试题)如图(6)已知抛物线2:2(0)C y px p =>的准线为l ,焦点为F,圆M 的圆心在x 轴的正半轴上,且与y 轴相切.过原点作倾斜角为3π的直线t ,交l 于点A,交圆M 于点B,且||||2AO OB ==. (1)求圆M 和抛物线C 的方程;(2)设,G H 是抛物线C 上异于原点O 的两个不同点,且0OG OH ⋅=,求GOH ∆面积的最小值; (3)在抛物线C 上是否存在两点Q P ,关于直线()():10m y k x k =-≠对称?若存在,求出直线m 的方程,若不存在,说明理由.15.(广东省江门佛山两市2013届高三4月教学质量检测(佛山二模)数学理试题)在平面直角坐标系内,动圆C过定点()1,0F,且与定直线1x=-相切.(1)求动圆圆心C的轨迹2C的方程;(2)中心在O的椭圆1C的一个焦点为F,直线过点(4,0)M.若坐标原点O关于直线的对称点P在曲线2C上,且直线与椭圆1C有公共点,求椭圆1C的长轴长取得最小值时的椭圆方程.16.(广东省惠州市2013届高三4月模拟考试数学理试题(WORD版))已知中心在原点O,焦点在x轴上,的椭圆过点).(1)求椭圆的方程;(2)设不过原点O的直线与该椭圆交于P、Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求OPQ∆面积的取值范围.17.(广东省广州市2013届高三4月综合测试(二)数学理试题(WORD 版))经过点()0,1F 且与直线1y =-相切的动圆的圆心轨迹为M .点A 、D 在轨迹M 上,且关于y 轴对称,过线段AD (两端点除外)上的任意一点作直线,使直线与轨迹M 在点D 处的切线平行,设直线与轨迹M 交于点B 、C .(1)求轨迹M 的方程;(2)证明:BAD CAD ∠=∠; (3)若点D 到直线ABABC 的面积为20,求直线BC 的方程.18.(广东省潮州市2013届高三第二次模拟考试数学(理)试题)设椭圆22221(0)x y a b a b+=>>的左右顶点分别为(2,0),(2,0)A B -,离心率e =过该椭圆上任一点P 作PQ x ⊥轴,垂足为Q ,点C 在QP 的延长线上,且||||QP PC =.(1)求椭圆的方程; (2)求动点C 的轨迹E 的方程;(3)设直线AC (C 点不同于,A B )与直线2x =交于点R ,D 为线段RB 的中点,试判断直线CD 与曲线E 的位置关系,并证明你的结论.广东省13大市2013届高三二模数学(理)试题分类汇编9:圆锥曲线参考答案一、选择题 1. A 2. A 3. D4. 【解析】抛物线的准线方程为-2,x =,∴抛物线的开口向右.设抛物线的标准方程为y 22(0)px p =>,则其准线方程为2p x =-, ∴22p-=-,解得4,p = ∴抛物线的标准方程为y 28x =.故选A . 二、填空题6. 7. 双曲线221916x y -=的右焦点为(5,0),渐近线的方程为43y x =±,所以所求直线方程为4(5),3y x =-即43200x y --=.三、解答题8.解:(Ⅰ)抛物线C 的焦点为(1,0)E -,它是题设椭圆的左焦点.离心率为112b =,所以,2b =.由2221b a -=求得a =因此,所求椭圆的方程为22143x y += (*) (Ⅱ)(1)椭圆的右焦点为(1,0)F ,过点F 与y 轴平行的直线显然与曲线C 没有交点.设直线的斜率为k ,① 若0k =,则直线0y =过点(1,0)F 且与曲线C 只有一个交点(0,0),此时直线的方程为0y =;② 若0k ≠,因直线过点(1,0)F ,故可设其方程为(1)y k x =-,将其代入24y x =-消去y ,得22222(2)0k x k x k --+=.因为直线与曲线C 只有一个交点P ,所以判别式22224(2)40k k k --⋅=,于是1k =±,从而直线的方程为1y x =-或1y x =-+.因此,所求的直线的方程为0y =或1y x =-或1y x =-+.(2)由(1)可求出点P 的坐标是(0,0)或(1,2)-或(1,2)--. ①若点P 的坐标是(0,0),则1PF =.于是12MPF S ∆==112y ⨯⨯,从而1y =±,代入(*)式联立: 221431x y y ⎧+=⎪⎨⎪=⎩或221431x y y ⎧+=⎪⎨⎪=-⎩,求得x =此时满足条件的点M 有4个: ,,1,1⎫⎛⎫⎫⎛⎫--⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎭⎝⎭⎭⎝⎭. ②若点P 的坐标是(1,2)-,则PF =点M 到直线:1y x =-+于是有11122MPF S y ∆==⨯-,从而112x y +-=±, 与(*)式联立:22143112x y x y ⎧+=⎪⎪⎨⎪+-=⎪⎩或22143112x y x y ⎧+=⎪⎪⎨⎪+-=-⎪⎩解之,可求出满足条件的点M 有4个:,,1115,714⎛⎫- ⎪⎝⎭,31,2⎛⎫- ⎪⎝⎭. ③ 若点P 的坐标是(1,2)--,则PF =,点(,)M x y 到直线:1y x =-是有11122MPF S y ∆==⨯-,从而112x y --=±, ④ 与(*)式联立:22143112x y x y ⎧+=⎪⎪⎨⎪--=⎪⎩或22143112x y x y ⎧+=⎪⎪⎨⎪--=-⎪⎩,解之,可求出满足条件的点M 有4个:,,1115,714⎛⎫⎪⎝⎭,31,2⎛⎫--⎪⎝⎭.综合①②③,以上12个点各不相同且均在该椭圆上,因此,满足条件的点M共有12个.图上椭圆上的12个点即为所求.9.10.11.解:(1)由椭圆方程得半焦距1)1(c 22=--a a =所以椭圆焦点为),( ,01F )01(21-F 又抛物线C 的焦点为)0,2(p ,2,12==∴p p x y C 42=∴:∵),(11y x M 在抛物线C 上, ∴1214x y =,直线M F 1的方程为)1(111++=x x y y 代入抛物线C 得22211(1)4(1),y x x x +=+22114(1)4(1)x x x x +=+即 22111(1)0,x x x x x ∴-++= ∵1F M 与抛物线C 相切,04)121221=-+∆∴x x =(,11,x ∴= ∴ M、N 的坐标分别为(1,2)、(1,-2) (2)直线AB 的斜率为定值—1. 证明如下:设11(,)A x y ,22(,)B x y ,(1,2)M ,A 、B 在抛物线24y x =上,∴211222244241y x y x ⎧=⎪=⎨⎪=⨯⎩①②③由①-③得,1112412MA y k x y -==-+④由②-③得,2222412MB y k x y -==-+④因为MPQ ∆是以MP,MQ 为腰的等腰三角形,所以MA MB k k =-由MAMB k k =-得11222124122412y x y y x y -⎧=-⎪-+⎪⎨-⎪=-⎪-+⎩ 化简整理, 得12211121222244422444y y y y x y y y y x -+-=-+⎧⎨-+-=-+⎩⑥⑦由⑥-⑦得:12124()4()y y x x -=--1212414y y k x x --∴===--为定值解法二:设211(,)4y A y ,222(,)4y B y则121214AM y k y -=-142y =+,242BMk y =+ 因为MPQ ∆是以MP,MQ 为腰的等腰三角形,所以MA MB k k =- 即1244022y y +=++ 所以121240(2)(2)y y y y ++=++所以,由1240y y ++=得 124y y +=- 所以,21222144AB y y k y y -=-2122214()y y y y -=-124y y =+44=- 1.=- 所以,直线AB 的斜率为定值,这个定值为 1.- 12.解、(Ⅰ)由题设可知;PN PM ,的斜率存在且不为0,所以λ=-⋅+11x y x y ,即)0(122≠=-y y x λ(Ⅱ)讨论如下:(1)当0>λ时,轨迹C 为中心在原点,焦点在x 轴上的双曲线(除去顶点)(2)当01<<-λ时,轨迹C 为中心在原点,焦点在x 轴上的椭圆(除去长轴两个端点) (3)当1-=λ时,轨迹C 为以原点为圆心,1为半径的圆(除去点(-1,0),(1,0)) (4)当1-<λ时,轨迹C 为中心在原点,焦点在y 轴上的椭圆(除去短轴两个端点)(Ⅲ)、当2=λ时,轨迹C 的方程为)0(1222≠=-y y x ,显然定点E 、F 为其左右焦点.假设存在这样的点P,使得0120=∠EPF ,记θ=∠EPF ,32,,===EF n PF m PE ,那么在EPF ∆中:⎪⎪⎩⎪⎪⎨⎧-+===-+⇒=-∆θθcos 2)32(sin 2142222222mn n m mn S mn n m n m EPF整理可得:8)cos 1(2=-θmn ,所以38120cos 14cos 140=-=-=θmn所以332233821120sin 210=⨯⨯==∆mn S EPF 又因为332322121=⨯⨯=⨯⨯=∆P P EPF y y EF S所以,32=P y 故,32±=P y 代入椭圆的方程可得:)0(123222≠=⎪⎭⎫⎝⎛±-y x P所以311±=P x ,所以满足题意的点P 有四个,坐标分别为)32,311(,)32,311(-,)32,311(-,)32,311(--13.14. 解:(1)∵1cos 602122p OA ==⨯=,即2p =, ∴所求抛物线的方程为24y x =∴设圆的半径为r,则122cos 60OB r =⋅=,∴圆的方程为22(2)4x y -+=(2) 设()()1122,,,G x y H x y ,由0OG OH ⋅=得02121=+y y x x ∵2211224,4y x y x ==,∴1216x x =, ∵12GOH S OG OH ∆=,∴()()222222*********GOHS OG OH x y x y ∆==++=()()2211221444x x x x ++=()()21212121214164x x x x x x x x ⎡⎤+++⎣⎦≥()212121214164x x x x x x ⎡⎤+⋅⎣⎦=256 ∴16GOH S ∆≥,当且仅当122x x ==时取等号, ∴GOH ∆面积最小值为16(3) 设()()4433,,,y x Q y x P 关于直线m 对称,且PQ 中点()00,y x D ∵ ()()4433,,,y x Q y x P 在抛物线C 上,∴2233444,4y x y x ==两式相减得:()()()3434344y y y y x x -+=- ∴343434444PQx x y y k y y k -+=⋅==--,∴02y k =-∵()00,y x D 在()():10m y k x k =-≠上 ∴010x =-<,点()00,y x D 在抛物线外∴在抛物线C 上不存在两点Q P ,关于直线m 对称15. ⑴由题可知,圆心C 到定点()1,0F 的距离与到定直线1x =-的距离相等由抛物线定义知,C 的轨迹2C 是以()1,0F 为焦点,直线1x =-为准线的抛物线 (确定“曲线是抛物线”1分,说明抛物线特征1分) 所以动圆圆心C 的轨迹2C 的方程为24y x = ⑵解法1、设(,)P m n ,则OP 中点为(,)22m n , 因为O P 、两点关于直线(4)y k x =-对称,所以(4)221n m k n k m⎧=-⎪⎪⎨⎪⋅=-⎪⎩,即80km n k m nk -=⎧⎨+=⎩,解之得2228181k m k k n k ⎧=⎪⎪+⎨⎪=-⎪+⎩(中点1分,方程组2分,化简1分) 将其代入抛物线方程,得:222288()411k k k k-=⋅++,所以21k = 联立 2222(4)1y k x x y ab =-⎧⎪⎨+=⎪⎩,消去y ,得:2222222()8160b a x a x a a b +-+-=由2222222(8)4()(16)0a b a a a b ∆=--+-≥,得2216a b +≥, 注意到221b a =-,即2217a ≥,所以a ≥,即2a ≥因此,椭圆1C.此时椭圆的方程为22+1171522x y =解法2、设2,4m P m ⎛⎫⎪⎝⎭ ,因为O P 、两点关于直线对称,则=4OM MP =,即4=,解之得4m =± 即(4,4)P ±,根据对称性,不妨设点P 在第四象限,且直线与抛物线交于,A B .则11AB OPk k =-=,于是直线方程为4y x =-(斜率1分,方程1分)联立 222241y x x y ab =-⎧⎪⎨+=⎪⎩,消去y ,得:2222222()8160b a x a x a a b +-+-=由2222222(8)4()(16)0a b a a a b ∆=--+-≥,得2216a b +≥, 注意到221b a =-,即2217a ≥,所以a ≥,即2a ≥因此,椭圆1C . 此时椭圆的方程为22+1171522x y =16.解:(1)由题意可设椭圆方程为22221x y a b+=(0)a b >>,则222112c a a b ⎧=⎪⎪⎨⎪+=⎪⎩, , 解的21a b =⎧⎨=⎩,所以,椭圆方程为2214x y += (2)由题意可知,直线的斜率存在且不为0,故可设直线的方程为(0)y kx m m =+≠,1,12,2(),()P x y Q x y ,由2214y kx m x y =+⎧⎪⎨+=⎪⎩ 消去y 得222(14)84(1)0k x kmx m +++-=, 则22222226416(14)(1)16(41)0k b k b b k m ∆=-+-=-+>,且122814km x x k -+=+,21224114m x x k-=+ 故2212121212()()()y y kx m kx m k x x km x x m =++=+++. 因为直线OP ,PQ ,OQ 的斜率依次成等比数列,所以,2221121222112()y y k x x km x x m k x x x x +++⋅==,即22228014k m m k-+=+, 又0m ≠,所以214k =,即12k =± 由于直线OP ,OQ 的斜率存在,且△>0,得202m <<且21m ≠. 设d 为点O 到直线的距离,则11122OPQ S d PQ m x ∆=⋅=⋅, 所以OPQ S ∆的取值范围为(0,1)17. (本小题主要考查动点的轨迹和直线与圆锥曲线的位置关系、导数的几何意义等基础知识,考查运算求解能力和推理论证能力等,本小题满分14分)解:(1)方法1:设动圆圆心为(),x y ,依题意得整理,得24x y =.所以轨迹M 的方程为24x y =方法2:设动圆圆心为P ,依题意得点P 到定点()0,1F 的距离和点P 到定直线1y =-的距离相等, 根据抛物线的定义可知,动点P 的轨迹是抛物线 且其中定点()0,1F 为焦点,定直线1y =-为准线. 所以动圆圆心P 的轨迹M 的方程为24x y = (2)由(1)得24x y =,即214y x =,则12y x '=. 设点2001,4D x x ⎛⎫⎪⎝⎭,由导数的几何意义知,直线的斜率为012BC k x =由题意知点2001,4A x x ⎛⎫- ⎪⎝⎭.设点2111,4C x x ⎛⎫ ⎪⎝⎭,2221,4B x x ⎛⎫⎪⎝⎭,则2212120121114442BCx x x x k x x x -+===-,即1202x x x +=A B CDOxylE因为2210101011444ACx x x x k x x --==+,2220202011444AB x x x x k x x --==+由于()120102020444AC AB x x x x x x x k k +---+=+==,即AC AB k k =- 所以BAD CAD ∠=∠(3)方法1:由点D 到ABBAD ∠45= 不妨设点C 在AD 上方(如图),即21x x <,直线AB 的方程为:()20014y x x x -=-+. 由()20021,44.y x x x x y ⎧-=-+⎪⎨⎪=⎩解得点B 的坐标为()20014,44x x ⎛⎫-- ⎪⎝⎭)()042x ---=-.由(2)知CAD BAD ∠=∠45=,同理可得2AC =+ 所以△ABC的面积20122244202S x =⨯-⨯+=-=, 解得03x =±当03x =时,点B 的坐标为11,4⎛⎫- ⎪⎝⎭,32BCk =, 直线BC 的方程为()13142y x -=+,即6470x y -+= 当03x =-时,点B 的坐标为497,4⎛⎫- ⎪⎝⎭,32BCk =-, 直线BC 的方程为()493742y x -=-+,即6470x y +-= 方法2:由点D 到ABBAD ∠45= 由(2)知CAD BAD ∠=∠45=,所以CAB ∠90=,即AC AB ⊥. 由(2)知104AC x x k -=,204AB x x k -=.所以1020144AC AB x x x x k k --=⨯=-. 即()()102016x x x x --=-. ① 由(2)知1202x x x +=. ②不妨设点C 在AD 上方(如图),即21x x <,由①、②解得10204,4.x x x x =+⎧⎨=-⎩2=-,同理2AC =+ 以下同方法1.18.解析:(1)由题意可得2a =,2c e a ==,∴c =∴2221b a c =-=,所以椭圆的方程为2214x y += (2)设(,)C x y ,00(,)P x y ,由题意得002x x y y =⎧⎨=⎩,即0012x xy x =⎧⎪⎨=⎪⎩,又220014x y +=,代入得221()142x y +=,即224x y +=. 即动点C 的轨迹E 的方程为224x y += (3)设(,)C m n ,点R 的坐标为(2,)t , ∵,,A C R 三点共线,∴//AC AR ,而(2,)AC m n =+,(4,)AR t =,则4(2)n t m =+, ∴42nt m =+, ∴点R 的坐标为4(2,)2n m +,点D 的坐标为2(2,)2nm +, ∴直线CD 的斜率为222(2)22244nn m n n mn m k m m m -+-+===---,而224m n +=,∴224m n -=-, ∴2mn m k n n==--, ∴直线CD 的方程为()m y n x m n -=--,化简得40mx ny +-=, ∴圆心O 到直线CD 的距离2d r ====, 所以直线CD 与圆O 相切。
广东省2013届高三最新理科试题精选(37套含13大市区的二模)分类汇编9圆锥曲线

广东省2013届高三最新理科试题精选(37套含13大市区的二模)分类汇编9:圆锥曲线一、选择题1 .(广东省韶关市2013届高三第三次调研考试数学(理科)试题(word 版) )椭圆221x my +=的焦点在y轴上,长轴长是短轴长的两倍,则m 的值为 ( )A .14B .12C .2D .4【答案】A2 .(广东省湛江一中等“十校”2013届高三下学期联考数学(理)试题)定义:关于x 的不等式||x A B-<的解集叫A 的B 邻域.已知2a b +-的a b +邻域为区间(2,8)-,其中a b 、分别为椭圆12222=+by a x 的长半轴和短半轴.若此椭圆的一焦点与抛物线x y 542=的焦点重合,则椭圆的方程为( )A .13822=+y xB .14922=+y xC .18922=+y xD .191622=+y x【答案】B3 .(广东省海珠区2013届高三上学期综合测试一数学(理)试题)已知椭圆()2222:10x y C a b a b+=>>的,双曲线221x y -=的渐近线与椭圆C 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C 的方程为.A 22184x y += .B 221126x y += .C 221168x y += .D 221205x y +=【答案】B4 .(广东省潮州市2013届高三上学期期末教学质量检测数学(理)试题)若抛物线22y px =的焦点与双曲线22122x y -=的右焦点重合,则p 的值为 ( )A .2-B .2C .4-D .4【答案】D 双曲线22122x y -=的右焦点为(2,0),所以抛物线22y px =的焦点为(2,0),则4p =.5 .(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD 版))设F 1,F 2是椭圆)0(12222>>=+b a b y a x 的左右焦点,若直线x =m a (m >1)上存在一点P,使ΔF 2PF 1是底角为300的等腰三角形,则m 的取值范围是( )A D .【答案】A6 .(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))已知双曲线22221x y a b-=的渐近线方程为y =,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )A .12B C D .1【答案】A7 .(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD 版))方程||||169x x y y +=-1的曲线即为函数y=f(x)的图象,对于函数y=f(x),有如下结论:①f(x)在R 上单调递减;②函数F(x)=4f(x)+3x 不存在零点;③函数y=f(x)的值域是R;④f(x)的图象不经过第一象限,其中正确的个数是 ( ) A .1个 B .2个 C .3个 D .4个 【答案】D二、填空题8 .(广东省珠海一中等六校2013届高三第一次联考数学(理)试题)已知双曲线22221(0b 0)x y a a b-=>,>和椭圆22x y =1169+有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为____________.【答案】22143x y -= 9.(广东省深圳市南山区2013届高三上学期期末考试数学(理)试题)已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为20x y +=,则双曲线的离心率e 的值为__________ .【答案】10.(广东省汕头市第四中学2013届高三阶段性联合考试数学(理)试题)双曲线的焦点在x 轴上,实轴长为4,离心率为3,则该双曲线的标准方程为___,渐近线方程为___.【答案】221432x y -= y =± 11.(广东省汕头市2013届高三3月教学质量测评数学(理)试题)已知动点P 在抛物线y 2=4x 上,那么使得点P 到定点Q(2,,-1)的距离与点P 到抛物线焦点的距离之和最小的点P 的坐标为___【答案】)1,41(-12.(广东省梅州市2013届高三3月总复习质检数学(理)试题)已知双曲线22221(0,0)x y a b a b-=>>的两条近线的夹角为3π,则双曲线的离心率为___【答案】13.(广东省茂名市实验中学2013届高三下学期模拟(二)测试数学(理)试题(详解))已知点A 是抛物线C 1:y 2=2px(p>0)与双曲线C 2:22221(0,0)x y a b a b-=>>的一条渐近线的交点,若点A 到抛物线C 1的准线的距离为p,则双曲线的离心率等于____【答案】14.(广东省茂名市2013届高三第一次模拟考试数学(理)试题)已知双曲线221x ky -=的一个焦点是0),则其渐近线方程为________.【答案】2y x =±;15.(广东省揭阳市2013届高三3月第一次高考模拟数学(理)试题(含解析))已知圆C 经过直线220x y -+=与坐标轴的两个交点,且经过抛物线28y x =的焦点,则圆C 的方程为______________.【答案】22115()()222x y -+-=[或2220x y x y +---=];易得圆心坐标为11(,)22,半径为r =, 故所求圆的方程为22115()()222x y -+-=【或2220x y x y +---=. 】16.(广东省江门市2013年高考模拟考试(即一模)数学(理)试题 )在平面直角坐标系Oxy 中,若双曲线14222=+-m y m x 的焦距为8,则=m _______. 【答案】3(未排除4-,给3分)17.(2013年广东省佛山市普通高中高三教学质量检测(一)数学(理)试题)已知抛物线24x y =上一点P到焦点F 的距离是5,则点P 的横坐标是_____.【答案】4±18.(广东省韶关市2013届高三4月第二次调研测试数学理试题)设点P 是双曲线22221(0,0)x y a b a b-=>>与圆2222x y a b +=+在第一象限的交点,其中12,F F 分别是双曲线的左、右焦点,若21tan 3PF F ∠=,则双曲线的离心率为______________.【答案】19.(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)下图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽________米.【答案】20.(广东省揭阳市2013年高中毕业班第二次高考模拟考试理科数学试题)过双曲线221916x y -=的右焦点,且平行于经过一、三象限的渐近线的直线方程是 ________.【答案】双曲线221916x y -=的右焦点为(5,0),渐近线的方程为43y x =±,所以所求直线方程为4(5),3y x =-即43200x y --=.三、解答题21.(广东省韶关市2013届高三第三次调研考试数学(理科)试题(word 版) )在平面直角坐标系xoy 中,设点F (1,0),直线l :1x =-,点P 在直线l 上移动,R 是线段PF 与y 轴的交点,,RQ FP PQ l ⊥⊥.(Ⅰ)求动点Q 的轨迹的方程;(Ⅱ) 记Q 的轨迹的方程为E ,过点F 作两条互相垂直的曲线E 的弦AB 、CD ,设AB 、CD 的中点分别为N M ,.求证:直线MN 必过定点)0,3(R .【答案】解:(Ⅰ)依题意知,直线l 的方程为:1x =-.点R 是线段FP 的中点,且RQ ⊥FP ,∴RQ 是线段FP 的垂直平分线∴PQ 是点Q 到直线l 的距离.∵点Q 在线段FP 的垂直平分线,∴PQ QF =故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x => (Ⅱ) 设()()B B A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y则⎪⎩⎪⎨⎧==)2(4)1(422BB A A x y x y(1)—(2)得k y y B A 4=+,即ky M 2=, 代入方程)1(-=x k y ,解得122+=kx M .所以点M 的坐标为222(1,)k k+同理可得:N 的坐标为2(21,2)k k +-. 直线MN 的斜率为21kkx x y y k N M N M MN -=--=,方程为 )12(1222---=+k x kk k y ,整理得)3()1(2-=-x k k y , 显然,不论k 为何值,(3,0)均满足方程, 所以直线MN 恒过定点R (3,0).1422.(广东省汕头一中2013年高三4月模拟考试数学理试题 )在平面直角坐标系中,已知点()2,0A、()2,0B -,P 是平面内一动点,直线PA 、PB 的斜率之积为34-.(1)求动点P 的轨迹C 的方程;(2)过点1,02⎛⎫⎪⎝⎭作直线l 与轨迹C 交于E 、F 两点,线段EF 的中点为M ,求直线MA 的斜率k 的取值范围.2013年4月汕头一中高三模拟考【答案】(1)依题意,有3224PA PB y y k k x x ⋅=⋅=--+(2x ≠±), ----------------------------- 化简得: 22143x y += (2x ≠±),为所求动点P 的轨迹C 的方程------------------------(2)依题意,可设(,)M x y 、(,)E x m y n ++、(,)F x m y n --,则有 2222()()143()()143x m y n x m y n ⎧+++=⎪⎪⎨--⎪+=⎪⎩, 两式相减,得4430014342EF mx n n x y k m y x -+=⇒==-=-, 由此得点M 的轨迹方程为:226830x y x +-=(0x ≠).------------------------------ 设直线MA :2x my =+(其中1m k=),则 22222(68)211806830x my m y my x y x =+⎧⇒+++=⎨+-=⎩, ------------------------------ 故由22(21)72(68)0||8m m m ∆=-+≥⇒≥,即18k≥, 解得:k 的取值范围是11,88⎡⎤-⎢⎥⎣⎦. ---------------------------23.(广东省汕头一中2013年高三4月模拟考试数学理试题 )已知抛物线C :212x y =,过焦点F 的动直线l 交抛物线于A 、B 两点,O 为坐标原点. (1)求证:OA OB ⋅为定值;(2)设M 是线段AB 的中点,过M 作x 轴的垂线交抛物线C 于点N ,证明:抛物线C 在点N 处的切线与AB 平行.【答案】(1)设直线l 的方程为:18y kx =+,()11,A x y ,()22,B x y . ------------------------- 由21218x y y kx ⎧=⎪⎪⎨⎪=+⎪⎩得:2110264x kx --=,∴12116x x =- ------------------------∴()2121212123464OA OB x x y y x x x x ⋅=+=+=-为定值---------------------------- (2)由(1)得:点M 的横坐标为4k ,∴点N 的横坐标为4k----------------------------∵'4y x = ∴4'|k x y k == ----------------------------∴平行另解:设()00,N x y ,则12024x x k x +==,220028k y x ==---------------------------- 设抛物线C 在点N 处的切线为284k k y m x ⎛⎫-=- ⎪⎝⎭ 由228412k k y m x x y⎧⎛⎫-=- ⎪⎪⎪⎝⎭⎨⎪=⎪⎩得:2202816m mk k x x -+-= ------------------------------- ∴22404816m mk k ⎛⎫∆=--= ⎪⎝⎭,解得:m k = ------------------------------- ∴平行24.(广东省东莞市2013届高三第二次模拟数学理试题)已知椭圆22122:1(0)x y C a b a b+=>>的离心率为e =直线:2l y x =+与以原点为圆心、以椭圆1C 的短半轴长为半径的圆O 相切. (1)求椭圆C 1的方程;(2)设椭圆1C 的左焦点为1F ,右焦点为2F ,直线1l 过点1F ,且垂直于椭圆的长轴,动直线2l 垂直于1l ,垂足为点P ,线段2PF 的垂直平分线交2l 于点M ,求点M 的轨迹2C 的方程;(3)设2C 与x 轴交于点Q ,不同的两点R 、S 在2C 上,且满足0=⋅,求||QS 的取值范围.【答案】解:(1)由直线:2l y x =+与圆222xy b +=相切,b =,即b =由e =,得222213b e a =-=,所以a =所以椭圆的方程是221:132x y C +=(2)由条件,知2||||MF MP =,即动点M 到定点2F 的距离等于它到直线1:1l x =-的距离,由抛物线的定义得点M 的轨迹2C 的方程是x y 42=(3)由(2),知(0,0)Q ,设221212,,,44y y R y S y ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭, ∴222121121,,,44y y y QR y RS y y ⎛⎫⎛⎫-==- ⎪ ⎪⎝⎭⎝⎭由0=⋅RS QR ,得()()222121121016y y y y y y -+-=∵12y y ≠,∴21116y y y ⎛⎫=-+⎪⎝⎭,∴222121256323264y y y =++≥=,当且仅当2121256y y =,即14y =±时等号成立 又||y QS ⎛== ,∵2264y ≥,∴当2264y =,即28y =±时,min ||QS =故||QS 的取值范围是)⎡+∞⎣25.(广东省肇庆市2013届高三上学期期末统一检测数学(理)试题)已知两圆222212:20,:(1)4C x y x C x y +-=++=的圆心分别为12,C C ,P 为一个动点,且12||||PC PC +=(1)求动点P 的轨迹M 的方程;(2)是否存在过点(2,0)A 的直线l 与轨迹M 交于不同的两点C 、D,使得11||||C C C D =?若存在,求直线l 的方程;若不存在,请说明理由.【答案】解:(1)两圆的圆心坐标分别为1(1,0),C 和2(1,0)C -∵1212||||||2PC PC C C +=>=∴根据椭圆的定义可知,动点P 的轨迹为以原点为中心,1(1,0),C 和2(1,0)C -为焦点,长轴长为2a =的椭圆, 1,1a c b ====∴椭圆的方程为2212x y +=,即动点P 的轨迹M 的方程为2212x y += (2)(i)当直线l 的斜率不存在时,易知点(2,0)A 在椭圆M 的外部,直线l 与椭圆M 无交点,所以直线l 不存在.(ii)设直线l 斜率存在,设为k ,则直线l 的方程为(2)y k x =-由方程组2212(2)x y y k x ⎧+=⎪⎨⎪=-⎩得2222(21)8820k x k x k +-+-=①依题意28(21)0k ∆=-->解得22k -<<当k <<时,设交点1122(,),(,)C x y D x y ,CD 的中点为00(,)N x y ,方程①的解为12x x == ,则212024221x x k x k +==+ ∴2002242(2)22121k ky k x k k k ⎛⎫-=-=-= ⎪++⎝⎭要使11||||C C C D =,必须1C N l ⊥,即11C N k k ⋅=-∴222212114021kk k k k --+⋅=--+,即2102k k -+=② ∵1114102∆=-⨯=-<或,∴2102k k -+=无解所以不存在直线,使得11||||C C C D =综上所述,不存在直线l ,使得11||||C C C D =26.(广东省深圳市南山区2013届高三上学期期末考试数学(理)试题)已知椭圆2222:1(0)x y C a b a b+=>>的,. (1)求椭圆C 的方程;(2)设直线l 与椭圆C 交于A B ,两点,坐标原点O 到直线l 求AOB △面积的最大值.【答案】(2)设11()A x y ,,22()B x y ,.27.(广东省汕头市东山中学2013届高三下学期入学摸底考试数学(理)试题)己知斜率为1的直线l 与双曲线2222:1x y C a b-=(0a >,0b >),相交于B 、D 两点,且BD 的中点为(1,3)M(1)求双曲线C 的离心率;(2)设C 的右顶点为A ,右焦点为F ,||||17DF BF ⋅=,证明:过A 、B 、D 三点的圆与x 轴相切.【答案】解:(1)由题设知,直线l 的方程为2y x =+代入双曲线C 的方程,并化简得:2222222()440b a x a x a a b ----=设11(,)B x y ,22(,)D x y ,则212224a x x b a +=-,22212224a a b x x b a+⋅=- ①由(1,3)M 为BD 的中点知:1212x x +=,故2221412a b a ⋅=-,即223b a = ② 所以2223c a a -=,即224c a = 故2c e a==所以双曲线C 的离心率为2e =(注:本题也可用点差法解决)(2)由①、②知,双曲线C 的方程为:22233x y a -=(,0)A a ,(2,0)F a ,122x x +=,2124302a x x +⋅=-<1|||2|BF x a =-同理2|||2|DF x a =-2222121212|||||(2)(2)||42()||864||548|BF DF x a x a x x a x x a a a a a a ⋅=--=-++=----=++又因为||||17DF BF ⋅= 且25480a a ++> 所以254817a a ++= 解得:1a =,95a =-(舍去)12|||6BD x x -连结MA ,则由(1,0)A ,(1,3)M 知||3MA =,从而||||||MA MB MD ==,且MA x ⊥轴, 因此以M 为圆心,MA 为半径的圆经过A 、B 、D 三点,且在点A 处与x 轴相切. 所以过A 、B 、D 三点的圆与x 轴相切28.(广东省汕头市东山中学2013届高三第二次模拟考试数学(理)试题(详解))已知直线033=+-y x 经过椭圆C :12222=+by a x (0>>b a )的一个顶点B 和一个焦点F .⑴求椭圆的标准方程;⑵设P 是椭圆C 上动点,求||||||PB PF -的取值范围,并求||||||PB PF -取最小值时点P 的坐标.【答案】【答案】⑴依题意,)1 , 0(B ,)0 , 3(-F , 所以1=b ,3=c ,222=+=c b a ,所以椭圆的标准方程为1422=+y x 5分. ⑵||||||||0BF PB PF ≤-≤,当且仅当||||PB PF =时,0||||||=-PB PF ,当且仅当P 是直线BF 与椭圆C 的交点时,||||||||BF PB PF =- ,2||=BF ,所以||||||PB PF -的取值范围是]2 , 0[ . 设) , (n m P ,由||||PB PF =得013=++n m ,由⎪⎩⎪⎨⎧=++=+0131422n m n m ,解得⎩⎨⎧-==10n m 或⎪⎪⎩⎪⎪⎨⎧=-=13111338n m , 所求点P 为)1 , 0(-P 和)1311, 1338(-P . 29.(广东省汕头市第四中学2013届高三阶段性联合考试数学(理)试题)在平面直角坐标系xOy 中,动点P到两点(0),0)的距离之和等于4,设点P 的轨迹为曲线C ,直线l 过点(1,0)E -且与曲线C 交于A ,B 两点.(1)求曲线C 的轨迹方程;(2)是否存在△AOB 面积的最大值,若存在,求出△AOB 的面积;若不存在,说明理由.【答案】解.(Ⅰ)由椭圆定义可知,点P 的轨迹C是以(0),0)为焦点,长半轴长为2 的椭圆.故曲线C 的方程为2214x y +=(Ⅱ)存在△AOB 面积的最大值因为直线l 过点(1,0)E -,可设直线l 的方程为 1x my =-或0y =(舍).则221,4 1.x y x my ⎧+=⎪⎨⎪=-⎩整理得 22(4)230m y my +--= 由22(2)12(4)0m m ∆=++>. 设1122()()A x y B x y ,,,.解得1y =2y =. 则21||y y -=因为1212AOB S OE y y ∆=⋅-= 设1()g t t t=+,t =t ≥.则()g t在区间)+∞上为增函数.所以()g t ≥.所以AOB S ∆≤当且仅当0m =时取等号,即max ()AOB S ∆=. 所以AOB S ∆30.(广东省汕头市2013届高三3月教学质量测评数学(理)试题)〔本小题满分14分)如图.已知椭圆22221(0)x y a b a b +=>>的长轴为AB,过点B 的直线l 与x 轴垂直,椭圆的离心率e =,F 为椭圆的左焦点且11AF F B =1 .(I)求椭圆的标准方程; (II)设P 是椭圆上异于A 、B 的任意一点,PH⊥x 轴,H 为垂足,延长HP 到点Q 使得HP=PQ.连接AQ 并延长交直线l 于点M.N 为MB 的中点,判定直线QN 与以AB 为直径的圆O 的位置关系.【答案】解:(Ⅰ)易知A )0,(a -, B )0,(a )0,(1c F -1)()0,(11=+⋅-=⋅∴c a c a F AF1222==-∴b c a又23=e 43122222=-==∴aa a c e ,解得42=a1422=+∴y x 所求椭圆方程为:(Ⅱ)设),(00y x P 则)2,(00y x Q )22(≠-≠x x 及 2200+=∴x y k AQ 所以直线AQ 方程)2(22:00++=x x y y )28,2(00+∴x y M )24,2(00+∴x y N 42222420000000-=--+=∴x y x x y x y k QN又点P 的坐标满足椭圆方程得到:442020=+y x ,所以 202044y x -=-200200024242y x y y x x y x k QN -=-=-=∴ ∴直线 QN 的方程:)(22000x x y x y y --=- 化简整理得到:442202000=+=+y x y y x x 即4200=+y y x x 所以 点O 到直线QN 的距离244220=+=y x d∴直线QN 与AB 为直径的圆O 相切.31.(广东省梅州市2013届高三3月总复习质检数学(理)试题)(本小题满分14分)已知F 1,F 2分别是椭圆C:22221(0)y x a b a b+=>>的上、下焦点,其中F 1也是抛物线C 1:24x y =的焦点,点M 是C 1与C 2在第二象限的交点,且15||3MF =. (1)求椭圆C 1的方程;(2)已知A(b,0),B(0,a),直线y=kx(k>0)与AB 相交于点D,与椭圆C 1相交于点E,F 两点,求四边形AEBF 面积的最大值. 【答案】32.(广东省茂名市实验中学2013届高三下学期模拟(二)测试数学(理)试题(详解))如图,已知点M0(x0,y0)是椭圆C:222yx=1上的动点,以M0为切点的切线l0与直线y=2相交于点P.(1)过点M0且l0与垂直的直线为l1,求l1与y轴交点纵坐标的取值范围;(2)在y轴上是否存在定点T,使得以PM0为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,说明理由.【答案】解:(1)由椭圆得:y =,'y =1222(22)x x ---切线的斜率为所以,直线l 1的方程为:000)y y x x -=-,与y 轴交点纵坐标为因为011x -≤≤,所以,2001x ≤≤,200222x ≤-≤,所以,当切点在第一、二象限时l 1与y 轴交点纵坐标的取值范围为:0y ≤≤,则对称性可知 l 1与y 轴交点纵坐标的取值范围为:22y -≤≤. (2)依题意,可得∠PTM 0=90°,设存在T(0,t),M 0(x 0,y 0)由(1)得点P 的坐标(220000222y y x x -+,2),由00PT M T =可求得t=1所以存在点T(0,1)满足条件.33.(广东省茂名市2013届高三第一次模拟考试数学(理)试题)已知椭圆1C :22221x y a b+= (0a b >>)的离心率为3,连接椭圆的四个顶点得到的四边形的面积为.(1)求椭圆1C 的方程;(2)设椭圆1C 的左焦点为1F ,右焦点为2F ,直线1l 过点1F 且垂直于椭圆的长轴,动直线2l 垂直1l 于点P ,线段2PF 的垂直平分线交2l 于点M ,求点M 的轨迹2C 的方程;(3)设O 为坐标原点,取2C 上不同于O 的点S ,以OS 为直径作圆与2C 相交另外一点R ,求该圆面积的最小值时点S 的坐标.【答案】解:(1)解:由e =得223a c =,再由222c a b =-,解得a =由题意可知1222a b ⋅⋅=,即a b ⋅=解方程组2a ab ⎧=⎪⎨⎪=⎩得a b ==所以椭圆C 1的方程是22132x y += (2)因为2MP MF =,所以动点M 到定直线1:1l x =-的距离等于它到定点2F (1,0)的距离,所以动点M 的轨迹2C 是以1l 为准线,2F 为焦点的抛物线,所以点M 的轨迹2C 的方程为24y x =(3)因为以OS 为直径的圆与2C 相交于点R ,所以∠ORS = 90°,即0OR SR ⋅= 设S (1x ,1y ),R (2x ,2y ),SR =(2x -1x ,2y -1y ),OR =(2x ,2y )所以222221*********()()()()016y y y OR SR x x x y y y y y y -⋅=-+-=+-= 因为12y y ≠,20y ≠,化简得12216y y y ⎛⎫=-+⎪⎝⎭所以221222256323264y y y =++≥=, 当且仅当2222256y y =即22y =16,y 2=±4时等号成立 圆的直径|OS===因为21y ≥64,所以当21y =64即1y =±8时,min OS =, 所以所求圆的面积的最小时,点S 的坐标为(16,±8)34.(广东省揭阳市2013届高三3月第一次高考模拟数学(理)试题(含解析))如图(6),设点)0,(1c F -、)0,(2c F 分别是椭圆)1(1:222>=+a y ax C 的左、右焦点,P 为椭圆C 上任意一点,且12PF PF ⋅uuu r uuu r 最小值为0.(1)求椭圆C 的方程;(2)若动直线12,l l 均与椭圆C 相切,且12//l l ,试探究在x 轴上是否存在定点B ,点B 到12,l l 的距离之积恒为1?若存在,请求出点B 坐标;若不存在,请说明理由.图(6)F 2F 1oyx【答案】解:(1)设),(y x P ,则有),(1y c x PF +=,),(2y c x P F -=[]a a x c x aa c y x PF PF ,,11222222221-∈-+-=-+=⋅ 由12PF PF ⋅uuu r uuu r最小值为0得210122=⇒=⇒=-a c c , ∴椭圆C 的方程为1222=+y x(2)①当直线12,l l 斜率存在时,设其方程为,y kx m y kx n =+=+ 把1l 的方程代入椭圆方程得222(12)4220k x mkx m +++-=∵直线1l 与椭圆C 相切,∴2222164(12)(22)0k m k m ∆=-+-=,化简得2212m k =+同理,2212n k =+∴22m n =,若m n =,则12,l l 重合,不合题意,∴m n =- 设在x 轴上存在点(,0)B t ,点B 到直线12,ll 的距离之积为1,则1=,即2222||1k t m k -=+,--- 把2212k m +=代入并去绝对值整理,22(3)2k t -=或者22(1)0k t -=前式显然不恒成立;而要使得后式对任意的k R ∈恒成立则210t -=,解得1t =±;---------------------------------------------------------②当直线12,l l 斜率不存在时,其方程为x =和x =,定点(1,0)-到直线12,l l 的距离之积为1)1-+=;定点(1,0)到直线12,l l 的距离之积为1)1=; 综上所述,满足题意的定点B 为(1,0)-或(1,0)35.(广东省江门市2013年高考模拟考试(即一模)数学(理)试题 )已知椭圆C 的中心在原点O ,离心率23=e ,右焦点为)0 , 3( F . ⑴求椭圆C 的方程;⑵设椭圆的上顶点为A ,在椭圆C 上是否存在点P ,使得向量OA OP +与FA 共线?若存在,求直线AP 的方程;若不存在,简要说明理由.【答案】解:⑴设椭圆C 的方程为22221(0)x y a b a b+=>>,椭圆C 的离心率23=e ,右焦点为)0 , 3( F ,∴c c a ==, 222a b c =+,∴2,1,a b c ===,故椭圆C 的方程为2214x y += ⑵假设椭圆C 上是存在点P (00,x y ),使得向量OA OP +与FA 共线,00(,1)OP OA x y +=+,(FA =,∴011y +=,即001)x y =+,(1) 又点P (00,x y )在椭圆2214x y +=上,∴220014x y += (2)由⑴、⑵组成方程组解得0001x y =⎧⎨=-⎩,或0017x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴(0,1)P -,或1()7P , 当点P 的坐标为(0,1)-时,直线AP 的方程为0y =,当点P的坐标为1()7P 时,直线AP440y -+=, 故直线AP 的方程为0y =440y -+=36.(广东省华附、省实、深中、广雅四校2013届高三上学期期末联考数学(理)试题)已知焦点在x 轴上的双曲线C 的两条渐近线过坐标原点,且两条渐近线与以点D (0, 2 )为圆心,1为半径的圆相切,又知双曲线C 的一个焦点与D 关于直线y =x 对称. (Ⅰ)求双曲线C 的方程;(Ⅱ)设直线y =mx +1与双曲线C 的左支交于A ,B 两点,另一直线l 经过M (-2,0)及AB 的中点,求直线l 在y 轴上的截距b 的取值范围;(Ⅲ)若Q 是双曲线C 上的任一点,F 1F 2为双曲线C 的左,右两个焦点,从F 1引∠F 1QF 2的平分线的垂线,垂足为N ,试求点N 的轨迹方程.【答案】解:(Ⅰ)设双曲线C 的渐近线方程为y =kx ,则kx -y =0∵该直线与圆x 2+(y - 2 )2=1相切,有|- 2 |k 2+ 1= 1 ⇒ k =±1. ∴双曲线C 的两条渐近线方程为y =±x , 故设双曲线C 的方程为 x 2a 2-y 2a2 = 1 .易求得双曲线C 的一个焦点为 ( 2 ,0),∴2a 2=2,a 2=1.∴双曲线C 的方程为x 2-y 2=1.(Ⅱ)由 ⎩⎨⎧ y =mx +1 x 2-y 2=1得(1-m 2)x 2-2mx -2=0.令f (x )= (1-m 2)x 2-2mx -2直线与双曲线左支交于两点,等价于方程f (x )=0在(-∞,0)上有两个不等实根. 因此 ⎩⎪⎨⎪⎧ △>02m 1-m 2 <0-21-m 2>0解得1<m <2 .又AB 中点为(m 1-m 2 ,11-m2 ),∴直线l 的方程为y =1-2m 2+m +2 (x +2). 令x =0,得b =2-2m 2+m +2=2-2(m -14 )2+178.∵1<m < 2 ,∴-2(m -14 )2+178 ∈ (-2+ 2 , 1),∴b ∈ (-∞,-2- 2 )∪(2,+∞).(Ⅲ)若Q 在双曲线的右支上,则延长2QF 到T ,使||||1QF QT =, 若Q 在双曲线的左支上,则在QF 2上取一点T ,使| QT |=|QF 1 |.根据双曲线的定义| TF 2 |=2,所以点T 在以F 2( 2 ,0)为圆心,2为半径的圆上,即点T 的轨迹方程是(x - 2 )2+y 2=4 (x ≠ 0) ①由于点N 是线段F 1T 的中点,设N (x ,y ),T (x T ,y T ).则 ⎩⎪⎨⎪⎧ x =x T- 2 2 y =y T2,即 ⎩⎨⎧ x T=2x + 2y T= 2y .代入①并整理得点N 的轨迹方程为x 2+y 2=1.(x ≠ -22) (或者用几何意义得到| NO |=12| F 2T |=1, 得点N 的轨迹方程为x 2+y 2=1.)37.(广东省海珠区2013届高三上学期综合测试一数学(理)试题)(本小题满分14分)设抛物线()2:20C x py p =>的焦点为F ,()()000,0A x y x ≠是抛物线C 上的一定点.(1)已知直线l 过抛物线C 的焦点F ,且与C 的对称轴垂直,l 与C 交于,Q R 两点, S 为C 的准线上一点,若QRS ∆的面积为4,求p 的值;(2)过点A 作倾斜角互补的两条直线AM ,AN ,与抛物线C 的交点分别为()11,,M x y ()22,N x y .若直线AM ,AN 的斜率都存在,证明:直线MN 的斜率等于抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率.【答案】(本小题主要考查直线、抛物线、对称等知识,考查数形结合、化归与转化、方程的思想方法,考查数学探究能力以及运算求解能力) 解: (1)由题设0,2p F ⎛⎫ ⎪⎝⎭,设1,,2p Q x ⎛⎫ ⎪⎝⎭则1,2p R x ⎛⎫- ⎪⎝⎭QR =2p ===.∴由QRS ∆的面积为4,得:1242p p ⨯⨯=,得: 2.p =(2)由题意()100,A x y -首先求抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率.解法一:设抛物线在1A 处的切线的斜率为k ,则其方程为()00y k x x y =++ 联立()0022y k x x y x py⎧=++⎪⎨=⎪⎩得2002220x pkx px k py ---=将2002py x =代入上式得:2200220x pkx px k x ---=()()22002420pk px k x ∆=-++=即2220020p k px k x ++= 即()200pk x += 得0.x k p=-即抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率为0.x p-解法二:由22x py =得212y x p=, ∴'x y p=∴抛物线C 在点A 关于对称轴的对称点()100,A x y -处的切线的斜率为0.x p-再求直线MN 的斜率.解法一:设直线AM 的斜率为1k ,则由题意直线AN 的斜率为1k -直线AM 的的方程为()010y y k x x -=-,则直线AN 的的方程为()010y y k x x -=--.联立()21002x py y k x x y ⎧=⎪⎨=-+⎪⎩得221100220x pk x pk x x -+-=(1)方程(1)有两个根01,x x ,∴()()2210102420pk px k x ∆=--->∴0,1x =0112x x pk +=,即1102x pk x =-,同理可得2102x pk x =--直线MN 的斜率222121122121222MNx x y y x x p p k x x x x p --+===--0022x x p p-==- ∴直线MN 的斜率等于抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率解法二:AM AN k k =-01020102y y y y x x x x --∴=--- 将222012012,,222x x x y y y p p p ===分别代入上式得:2222001201022222x x x x p p p p x x x x --=---, 整理得0122x x x =+∴直线MN 的斜率222121122121222MNx x y y x x p p k x x x x p --+===--0022x x p p-==- ∴直线MN 的斜率等于抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率.38.(广东省广州市2013届高三调研测试数学(理)试题)如图5, 已知抛物线2P yx :=,直线AB 与抛物线P 交于A B ,两点,OA OB ^,OA OB OC uu r uu u r uuu r+=,OC 与AB 交于点M .(1) 求点M 的轨迹方程;求四边形AOBC 的面积的最小值.,考查数形结合、函数与方程、化归与转化的数学思想方法,以及推理论证能力、运算求解能力、创新意识) 解法一:(1)解:设()()()221122M x y A y y B y y ,,,,,, ∵OA OB OC +=, ∴M 是线段AB 的中点 ∴()222121212222yy y y y y x +-+==,①122y y y +=. ② ∵OA OB ⊥, ∴0OA OB ⋅=. ∴2212120y y y y += 依题意知120y y ≠,∴121y y =-. ③把②、③代入①得:2422y x +=,即()2112y x =- ∴点M 的轨迹方程为()2112yx =- (2)解:依题意得四边形AOBC 是矩形,∴四边形AOBC 的面积为S OA OB ==⋅===∵22121222y y y y +≥=,当且仅当12y y =时,等号成立,∴2S ≥=∴四边形AOBC 的面积的最小值为2 解法二:(1)解:依题意,知直线OA OB ,的斜率存在,设直线OA 的斜率为k , 由于OA OB ⊥,则直线OB 的斜率为1k-故直线OA 的方程为y kx =,直线OB 的方程为1y x k=-. 由2y kx y x ,.⎧=⎨=⎩ 消去y ,得220k x x -=.解得0x =或21x k=∴点A 的坐标为211k k ,⎛⎫⎪⎝⎭同理得点B 的坐标为()2k k ,- ∵OA OB OC +=, ∴M 是线段AB 的中点 设点M 的坐标为()x y ,,则221212k k x k k y ,.⎧+⎪=⎪⎪⎨⎪-⎪=⎪⎩消去k ,得()2112yx =- ∴点M 的轨迹方程为()2112y x =-(2)解:依题意得四边形AOBC 是矩形, ∴四边形AOBC 的面积为S OA OB==⋅=≥2=当且仅当221kk=,即21k =时,等号成立 ∴四边形AOBC 的面积的最小值为239.(广东省广州市2013届高三3月毕业班综合测试试题(一)数学(理)试题)已知椭圆1C 的中心在坐标原点,两个焦点分别为1(2,0)F -,2F ()20,,点(2,3)A 在椭圆1C 上,过点A 的直线L 与抛物线22:4C x y =交于B C ,两点,抛物线2C 在点B C ,处的切线分别为12l l ,,且1l 与2l 交于点P .(1) 求椭圆1C 的方程;(2) 是否存在满足1212PF PF AF AF +=+的点P ? 若存在,指出这样的点P 有几个(不必求出点P 的坐标); 若不存在,说明理由.【答案】(本小题主要考查椭圆、抛物线、曲线的切线等基础知识,考查数形结合、函数与方程、化归与转化的数学思想方法,以及推理论证能力、运算求解能力、创新意识)(1) 解法1:设椭圆1C 的方程为22221x y a b+=()0a b >>,依题意: 222222231,4.a b a b ⎧+=⎪⎨⎪=+⎩解得: 2216,12.a b ⎧=⎪⎨=⎪⎩ ∴ 椭圆1C 的方程为2211612x y += 解法2:设椭圆1C 的方程为22221x y a b+=()0a b >>,根据椭圆的定义得1228a AF AF =+=,即4a =,∵2c =, ∴22212b a c =-=∴椭圆1C 的方程为2211612x y += (2)解法1:设点)41,(211x x B ,)41,(222x x C ,则))(41,(212212x x x x --=, )413,2(211x x BA --=, ∵C B A ,,三点共线, (苏元高考吧:) ∴BC BA // ∴()()()222211211113244x x x x x x ⎛⎫--=-- ⎪⎝⎭,化简得:1212212x x x x ()+-=. ① 由24xy =,即214y x ,=得y '=12x ∴抛物线2C 在点B 处的切线1l 的方程为)(2411121x x x x y -=-,即211412x x x y -=. ② 同理,抛物线2C 在点C 处的切线2l 的方程为 222412x x x y -=. ③ 设点),(y x P ,由②③得:=-211412x x x 222412x x x -, 而21x x ≠,则 )(2121x x x += 代入②得 2141x x y =, 则212x x x +=,214x x y =代入 ① 得 1244=-y x ,即点P 的轨迹方程为3-=x y . 若1212PF PF AF AF +=+ ,则点P 在椭圆1C 上,而点P 又在直线3-=x y 上, ∵直线3-=x y 经过椭圆1C 内一点(3,0), ∴直线3-=x y 与椭圆1C 交于两点∴满足条件1212PF PF AF AF +=+ 的点P 有两个 解法2:设点),(11y x B ,),(22y x C ,),(00y x P ,由24xy =,即214y x ,=得y '=12x ∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=∵21141x y =, ∴112y x x y -= .∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点),(),,(2211y x C y x B 的坐标都满足方程y x xy -=002∵经过),(),,(2211y x C y x B 的直线是唯一的, ∴直线L 的方程为y x xy -=002, ∵点)3,2(A 在直线L 上, ∴300-=x y ∴点P 的轨迹方程为3-=x y若1212PF PF AF AF +=+ ,则点P 在椭圆1C 上,又在直线3-=x y 上, ∵直线3-=x y 经过椭圆1C 内一点(3,0), ∴直线3-=x y 与椭圆1C 交于两点∴满足条件1212PF PF AF AF +=+ 的点P 有两个解法3:显然直线L 的斜率存在,设直线L 的方程为()23y k x =-+,由()2234y k x x y ,,⎧=-+⎪⎨=⎪⎩消去y ,得248120x kx k -+-=设()()1122B x y C x y ,,,,则12124812x x k x x k ,+==- 由24xy =,即214y x ,=得y '=12x∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-,即2111212x y x x y -+= ∵21141x y =, ∴211124x y x x =-.同理,得抛物线2C 在点C 处的切线2l 的方程为222124x y x x =- 由211222124124x y x x x y x x ,,⎧=-⎪⎪⎨⎪=-⎪⎩解得121222234x x x k x x y k ,.⎧+==⎪⎪⎨⎪==-⎪⎩ ∴()223P k k ,-∵1212PF PF AF AF +=+,∴点P 在椭圆22111612x y C :+=上 ∴()()2222311612k k -+=.化简得271230k k --=.(*)由()2124732280Δ=-⨯⨯-=>,可得方程(*)有两个不等的实数根. ∴满足条件的点P 有两个40.(广东省潮州市2013届高三上学期期末教学质量检测数学(理)试题)已知点(4,0)M 、(1,0)N ,若动点P 满足6||MN MP NP =⋅.(1)求动点P 的轨迹C ; (2)在曲线C 上求一点Q ,使点Q 到直线l :2120x y +-=的距离最小.【答案】解:(1)设动点(,)P x y ,又点(4,0)M 、(1,0)N ,∴(4,)MP x y =-,(3,0)MN =-,(1,)NP x y =- 由6||MN MP NP =⋅,得3(4)x --=∴222(816)4(21)4x x x x y -+=-++,故223412x y +=,即22143x y +=,∴轨迹C 是焦点为(1,0)±、长轴长24a =的椭圆;评分说明:只求出轨迹方程,没有说明曲线类型或交代不规范的扣1分. (2)椭圆C 上的点Q 到直线l 的距离的最值等于平行于直线l :2120x y +-= 且与椭圆C 相切的直线1l 与直线l 的距离. 设直线1l 的方程为20(12)x y m m ++=≠-由22341220x y x y m ⎧+=⎨++=⎩,消去y 得2242120x mx m ++-= (*). 依题意得0∆=,即0)12(16422=--m m ,故216m =,解得4m =±.当4m =时,直线1l :240x y ++=,直线l 与1l 的距离5d ==.当4m =-时,直线1l :240x y +-=,直线l 与1l 的距离d ==<,故曲线C 上的点Q 到直线l 当4m =-时,方程(*)化为24840x x -+=,即2(1)0x -=,解得1x =. 由1240y +-=,得32y =,故3(1,)2Q . ∴曲线C 上的点3(1,)2Q 到直线l 的距离最小 41.(广东省肇庆市2013届高三4月第二次模拟数学(理)试题)设椭圆22221(0,0)x y a b b a+=>>的离心率为12,其左焦点E 与抛物线21:4C x y =-的焦点相同.(Ⅰ)求此椭圆的方程;(Ⅱ)若过此椭圆的右焦点F 的直线与曲线C 只有一个交点P ,则(1)求直线的方程;(2)椭圆上是否存在点(,)M x y ,使得12MPF S ∆=,若存在,请说明一共有几个点;若不存在,请说明理由.【答案】解:(Ⅰ)抛物线C 的焦点为(1,0)E -,它是题设椭圆的左焦点.离心率为112b =,所以,2b =.由2221b a -=求得a =因此,所求椭圆的方程为22143x y += (*)(Ⅱ)(1)椭圆的右焦点为(1,0)F ,过点F 与y 轴平行的直线显然与曲线C 没有交点.设直线的斜率为k ,① 若0k =,则直线0y =过点(1,0)F 且与曲线C 只有一个交点(0,0),此时直线 的方程为0y =;② 若0k ≠,因直线过点(1,0)F ,故可设其方程为(1)y k x =-,将其代入24y x =-消去y ,得22222(2)0k x k x k --+=.因为直线与曲线C 只有一个交点P ,所以判别式22224(2)40k k k --⋅=,于是1k =±,从而直线的方程为1y x =-或1y x =-+.因此,所求的直线的方程为0y =或1y x =-或1y x =-+.(2)由(1)可求出点P 的坐标是(0,0)或(1,2)-或(1,2)--. ①若点P 的坐标是(0,0),则1PF =.于是12MPF S ∆==112y ⨯⨯,从而1y =±,代入(*)式联立: 221431x y y ⎧+=⎪⎨⎪=⎩或221431x y y ⎧+=⎪⎨⎪=-⎩,求得x =此时满足条件的点M 有4个: ,,1,1⎫⎛⎫⎫⎛⎫--⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎭⎝⎭⎭⎝⎭. ②若点P 的坐标是(1,2)-,则PF =点M 到直线:1y x =-+于是有11122MPF S y ∆==⨯-,从而112x y +-=±, 与(*)式联立:22143112x y x y ⎧+=⎪⎪⎨⎪+-=⎪⎩或22143112x y x y ⎧+=⎪⎪⎨⎪+-=-⎪⎩解之,可求出满足条件的点M 有4个:,,1115,714⎛⎫- ⎪⎝⎭,31,2⎛⎫- ⎪⎝⎭. ③ 若点P 的坐标是(1,2)--,则PF =,点(,)M x y 到直线:1y x =-是有11122MPF S y ∆==⨯-,从而112x y --=±,与(*)式联立:22143112x yx y⎧+=⎪⎪⎨⎪--=⎪⎩或22143112x yx y⎧+=⎪⎪⎨⎪--=-⎪⎩,解之,可求出满足条件的点M有4个:,,1115,714⎛⎫⎪⎝⎭,31,2⎛⎫--⎪⎝⎭.综合①②③,以上12个点各不相同且均在该椭圆上,因此,满足条件的点M共有12个.图上椭圆上的12个点即为所求.42.(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD版))已知抛物线C:y2=4x, F 是抛物线的焦点,设A(x1,y1),B(x2 ,y2)是C上异于原点O的两个不重合点,OA丄OB,且AB与x轴交于点T(1) 求x1x2的值;(2) 求T的坐标;(3) 当点A在C上运动时,动点R满足:FRFBFA=+,求点R的轨迹方程.【答案】F的距43.(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))已知动点M到点(0,1) y=的距离之和为5.离与到直线4(1)求动点M的轨迹E的方程,并画出图形;=+与轨迹E有两个不同的公共点,A B,求m的取值范围;(2)若直线:l y x mAB的最大值.(3)在(2)的条件下,求弦长||【答案】44.(广东省韶关市2013届高三4月第二次调研测试数学理试题)已知椭圆)(1122221 >=-+a a y a x 的左右焦点为21,F F ,抛物线C:px y 22=以F 2为焦点且与椭圆相交于点()11,M x y 、N ()22,x y ,点M 在x轴上方,直线1F M 与抛物线C 相切.(1)求抛物线C 的方程和点M 、N 的坐标;(2)设A,B 是抛物线C 上两动点,如果直线MA ,MB 与y 轴分别交于点,P Q . MPQ ∆是以MP ,MQ 为腰的等腰三角形,探究直线AB 的斜率是否为定值?若是求出这个定值,若不是说明理由.【答案】解:(1)由椭圆方程得半焦距1)1(c 22=--a a =所以椭圆焦点为),( ,01F )01(21-F 又抛物线C 的焦点为)0,2(p ,2,12==∴p p x y C 42=∴: ∵),(11y x M 在抛物线C 上, ∴1214x y =,直线M F 1的方程为)1(111++=x x y y 代入抛物线C 得22211(1)4(1),y x x x +=+22114(1)4(1)x x x x +=+即 22111(1)0,x x x x x ∴-++= ∵1F M 与抛物线C 相切,04)121221=-+∆∴x x =(,11,x ∴= ∴ M、N 的坐标分别为(1,2)、(1,-2) (2)直线AB 的斜率为定值—1. 证明如下:设11(,)A x y ,22(,)B x y ,(1,2)M ,A 、B 在抛物线24y x =上,∴211222244241y x y x ⎧=⎪=⎨⎪=⨯⎩①②③由①-③得,1112412MA y k x y -==-+④由②-③得,2222412MB y k x y -==-+④因为MPQ ∆是以MP,MQ 为腰的等腰三角形,所以MA MB k k =-由MAMB k k =-得11222124122412y x y y x y -⎧=-⎪-+⎪⎨-⎪=-⎪-+⎩ 化简整理,。
广东省某重点中学2013届高三数学理二轮复习之广州二模答题综合练习 含答案

1.已知函数f(x)=3sin ωx-cos ωx(x∈R,ω>0)的最小正周期为6π。
(1)求f错误!的值;(2)设α,β∈错误!,f错误!=-错误!,f(3β+2π)=错误!,求cos(α+β)的值π个单位,再将所有点的横坐标缩短到原(3)将函数f(x)先向左平移32π)的值域。
来的错误!得到g(x),求函数g(x),在区间(0,6ks5uMEBOC AP3.(本小题满分14分)如图所示,⊥PA 平面ABC ,点C 在以AB 为直径的⊙O 上,30=∠CBA ,2PA AB,点E 为线段PB 的中点,点M 在AB 弧上,且OM ∥AC .(Ⅰ)求证:平面MOE ∥平面PAC ; (Ⅱ)求证:平面PAC ⊥平面PCB ;(Ⅲ)设二面角M BP C --的大小为θ,求cos θ的值.ks5u4.(本小题满分14分)设函数,)(2xe a ax x xf ++=其中常数e R a ,∈为自然对数的底数.(1)若,2=a 求函数)(x f 的图象在1-=x 处的切线的方程; (2)若函数)(x f 的极大值为3,求a 的值及)(x f 的极小值.1.已知函数f(x)=错误!sin ωx-cos ωx(x∈R,ω>0)的最小正周期为6π.(1)求f错误!的值;(2)设α,β∈错误!,f错误!=-错误!,f(3β+2π)=65,求cos(α+β)的值(3)将函数f(x)先向左平移32π个单位,再将所有点的横坐标缩短到原来的错误!得到g(x),求函数g(x),在区间(0,6π)的值域.1.解:(1)f(x)=错误!sin ωx-cos ωx=2错误!=2sin错误!。
…………………… 2分∵函数f(x)的最小正周期为6π,∴T=错误!=6π,即ω=错误!. ……………………3分∴f(x)=2sin错误!. ∴f错误!=2sin错误!=2sin错误!=3 .……………………4分(2)f错误!=2sin错误!=2sin α=-错误!,∴sinα=-错误!t……………………5分]f (3β+2π)=2sin 错误!=2sin 错误!=2cos β=错误!, ∴cos β=错误!。
2013年理科全国各省市高考真题——圆锥曲线(解答题带答案)

2013年全国各省市理科数学—圆锥曲线1、2013大纲理T21.(本小题满分12分)已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为12F F ,,离心率为3,直线2y =与C 。
(I )求a ,b ;(II )设过2F 的直线l 与C 的左、右两支分别相交于,A B 两点,且11AF BF =,证明:22AF AB BF 、、成等比数列。
2、2013新课标I 理T20.(本小题满分12分)已知圆M :1)1(22=++y x ,圆N :9)1(22=+-y x ,动圆P 与圆M 外切并与圆N 内切,圆心P 的轨迹为曲线C .(Ⅰ)求C 的方程;(Ⅱ)l 是与圆P ,圆M 都相切的一条直线,l 与曲线C 交于A ,B 两点,当圆P 的半径最长时,求AB .3、2013新课标Ⅱ理T20.(本小题满分12分)平面直角坐标系xoy 中,过椭圆M :)0(12222>>=+b a by a x 右焦点的直线03=-+y x 交M 于A 、B 两点,P 为AB 的中点,且OP 的斜率为21。
(Ⅰ)求M 的方程(Ⅱ)C 、D 为M 上的两点,若四边形ACBD 的对角线CD ⊥AB ,求四边形ACBD 面积的最大值。
4、2013辽宁理T20.(本小题满分12分)如图,抛物线()()2212002:4,:20.,C x y C x py p M x y C ==->点在抛物线上,1M C 过作()0,,.1A B M O A B O x =的切线,切点为为原点时,重合于当1-.2MA 切线的斜率为(I )P 求的值;(II )2M C AB N 当在上运动时,求线段中点的轨迹方程(),,.A B O O 重合于时中点为5、2013北京理T19. (本小题共14分)已知A 、B 、C 是椭圆W :2214x y +=上的三个点,O 是坐标原点. (I)当点B 是W 的右顶点,且四边形OABC 为菱形时,求此菱形的面积. (II)当点B 不是W 的顶点时,判断四边形OABC 是否可能为菱形,并说明理由.6、2013重庆理T21.如题(21)图,椭圆的中心为原点O ,长轴在x 轴上,离心率2e =,过左焦点1F 作x 轴的垂线交椭圆于,A A '两点,4AA '=。
2013广东高考卷(理科数学)试题及详解

专业课原理概述部分一、选择题(每题1分,共5分)1. 设集合A={x|x²3x+2=0},则A中元素的个数为()A. 0B. 1C. 2D. 32. 若函数f(x)=2x3在区间(a,+∞)上单调递增,则实数a的取值范围是()A. a≥1B. a≤1C. a≥1D. a≤13. 执行右边的程序框图,若输入的x值为2,则输出y的值为()A. 6B. 8C. 10D. 124. 若向量a=(3,4),b=(1,2),则2a+3b的模长是()A. 7B. 9C. 11D. 135. 在△ABC中,角A、B、C的对边分别为a、b、c,若sin2A+sin2B+sin2C=3,则△ABC是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 不等边三角形二、判断题(每题1分,共5分)1. 若a>b,则ac²>bc²。
()2. 两个平行线之间的距离处处相等。
()3. 若函数f(x)在区间(a,b)上单调递增,则f'(x)>0。
()4. 三角形的面积等于底乘以高的一半。
()5. 任何两个实数的和都是实数。
()三、填空题(每题1分,共5分)1. 已知函数f(x)=x²2x+1,则f(1)=______。
2. 若向量a=(2,3),则向量a的模长|a|=______。
3. 在平面直角坐标系中,点P(2,3)关于x轴的对称点坐标为______。
4. 若等差数列{an}的公差为2,首项为1,则第10项a10=______。
5. 若sinθ=1/2,且θ为锐角,则cosθ=______。
四、简答题(每题2分,共10分)1. 简述函数的单调性定义。
2. 解释什么是平面向量的坐标表示。
3. 请写出三角形面积公式。
4. 请列举三种不同的数列。
5. 简述反函数的定义及其性质。
五、应用题(每题2分,共10分)1. 已知函数f(x)=3x²4x+1,求f(x)在区间(1,2)上的最大值。
广东省某重点中学2013届高三数学理二轮复习之圆锥曲线练习二答案不全 (1)

2013届高三二轮复习 圆锥曲线专题二 2013—4—6椭圆,双曲线,抛物线——基本量及其基本性质1、若R ∈k ,则“3>k "是“方程13322=+--k y k x 表示双曲线”的 ( )A.充分不必要条件 B 。
必要不充分条件 C 。
充要条件D.既不充分也不必要条件2、直线l :x -2y +2=0过椭圆左焦点F 1和一个顶点B ,则该椭圆的离心率为( )A.错误! B 。
错误! C 。
错误!D.错误!3、设P 是双曲线22a x -92y =1上一点,双曲线的一条渐近线方程为3x-2y =0,F 1、F 2分别是双曲线的左、右焦点.若|PF 1|=3,则|PF 2|等于 ( )(A)1或5 (B)6 (C)7 (D )94、椭圆错误!+错误!=1的离心率为错误!,则k 的值为 ( )A .-21B .21C .-错误!或21 D.错误!或215、已知双曲线221xmy +=的虚轴长是实轴长的2倍,则实数m 的值是( )A .4B .14C .14-D .4- 6、已知F 1、F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|,则cos ∠F 1PF 2= ( )A 。
错误!B 。
错误! C.错误!D 。
错误!7、设椭圆C 1的离心率为错误!,焦点在x 轴上且长轴长为26,若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为 ( )A 。
错误!-错误!=1 B.错误!-错误!=1C.错误!-错误!=1 D 。
错误!-错误!=18、F 是抛物线y =14x 2的焦点,P 是该抛物线上的动点,若|PF |=2,则点P 的坐标是 ( )A .(3,94) B .(±2,1) C .(1,4) D .(0,0)9、已知点P 在抛物线y 2=4x 上,则点P 到直线l 1:4x -3y +6=0的距离和到直线l 2:x =-1的距离之和的最小值为 ( )A.3716B 。
广东省13大市高三上学期期末数学(理)试题分类汇编13:圆锥曲线 Word版含答案.pdf

广东省13大市2013届高三上期末考数学理试题分类汇编 圆锥曲线 一、填空、选择题 1、(潮州市2013届高三上学期期末)若抛物线的焦点与双曲线的右焦点重合,则的值为 A. B. C. D. 答案:D 2、(佛山市2013届高三上学期期末)已知抛物线上一点P到焦点的距离是,则点P的横坐标是_____. 3、(广州市2013届高三上学期期末)圆上到直 线的距离为的点的个数是 _ . 答案: 分析:圆方程化为标准式为,其圆心坐标, 半径,由点到直线的距离公式得圆心到直线的距离,由右图 所示,圆上到直线的距离为的点有4个. 4、(广州市2013届高三上学期期末)在区间和分别取一个数,记为, 则方程表示焦点在轴上且离心率小于的椭圆的概率为 A. B. C. D. 答案:B 5、(惠州市2013届高三上学期期末)已知双曲线的一个焦点与抛物线的焦点重合,且双曲线的离心率等于,则该双曲线的方程为____ 答案: 6、(江门市2013届高三上学期期末)以抛物线的顶点为中心、焦点为一个顶点且离心率的双曲线的标准方程是 A. B. C. D. 答案:A 7、(茂名市2013届高三上学期期末)已知双曲线的一个焦点是(),则其渐近线方程为 . 8、(湛江市2013届高三上学期期末)已知点A是抛物线C1:y2=2px(p>0)与双曲线C2:的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线的离心率等于____ 答案: 解析: 9、(肇庆市2013届高三上学期期末)圆心在直线上的圆C与轴交于两点、,则圆C的方程为__________. 解析:直线AB的中垂线方程为,代入,得,故圆心的坐标为,再由两点间的距离公式求得半径,∴ 圆C的方程为直线的倾斜角的取值范围是( ) A. B. C. D. (a>0,b>0)的左、右焦点,过F1的直线与的左、右两支分别交于A,B两点.若 | AB | : | BF2 | : | AF2 |=3 : 4 : 5,则双曲线的离心率为 . 答案: 13、(江门市2013届高三上学期期末)与圆:关于直线:对称的圆的方程是 . 二、解答题 1、(潮州市2013届高三上学期期末)已知点、,若动点满足. (1)求动点的轨迹; (2)在曲线上求一点,使点到直线:的距离最小. 解:(1)设动点,又点、, ∴,,. ……… 3分 由,得, ……… 4分 ∴,故,即, ∴轨迹是焦点为、长轴长的椭圆; ……… 7分 评分说明:只求出轨迹方程,没有说明曲线类型或交代不规范的扣分. (2)椭圆上的点到直线的距离的最值等于平行于直线: 且与椭圆相切的直线与直线的距离. 设直线的方程为. ……… 8分 由,消去得 (*). 依题意得,即,故,解得. 当时,直线:,直线与的距离. 当时,直线:,直线与的距离. 由于,故曲线上的点到直线的距离的最小值为.…12分 当时,方程(*)化为,即,解得. 由,得,故. ……… 13分 ∴曲线上的点到直线的距离最小. ……… 14分 2、(佛山市2013届高三上学期期末)设椭圆的左右顶点分别为,离心率.作轴,垂足为,点在的延长线上,且.的轨迹的方程; (3)设直线(点不同于)与直线交于点,为线段的中点,试判断直线与曲线的位置关系,并证明你的结论.解析:,,∴, -----------------2分, 所以椭圆的方程为.-----------------4分,,由题意得,即, -----------------6分,代入得,即.的轨迹的方程为.-----------------8分,点的坐标为, ∵三点共线,∴, 而,,则,∴, ∴点的坐标为,点的坐标为, -----------------10分的斜率为, 而,∴, ∴, -----------------12分的方程为,化简得, ∴圆心到直线的距离, 所以直线与圆相切.-----------------14分如图5, 已知抛物线,直线与抛物线交于两点, ,,与交于点. 求点的轨迹方程; 求四边形的面积的最小值. 解法一: (1)解:设, ∵, ∴是线段的中点. …………… 2分 ∴,① …………… 3分 . ② …………… 4分 ∵, ∴. ∴. …………… 5分 依题意知, ∴. ③ …………… 6分 把②、③代入①得:,即. …………… 7分 ∴点的轨迹方程为. …………… 8分 (2)解:依题意得四边形是矩形, ∴四边形的面积为 …………… 9分 . …………… 11分 ∵,当且仅当时,等号成立, …………… 12分 ∴. …………… 13分 ∴四边形的面积的最小值为. …………… 14分 解法二: (1)解:依题意,知直线的斜率存在,设直线的斜率为, 由于,则直线的斜率为. …………… 1分 故直线的方程为,直线的方程为. 由 消去,得. 解得或. …………… 2分 ∴点的坐标为. …………… 3分 同理得点的坐标为. …………… 4分 ∵, ∴是线段的中点. …………… 5分 设点的坐标为, 则 …………… 6分 消去,得. …………… 7分 ∴点的轨迹方程为. …………… 8分 (2)解:依题意得四边形是矩形, ∴四边形的面积为 …………… 9分 ………… 10分 …………… 11分 . …………… 12分 当且仅当,即时,等号成立. …………… 13分 ∴四边形的面积的最小值为. …………… 14分 4、(惠州市2013届高三上学期期末)设椭圆的右焦点为直线与轴交于点若(其中为坐标原点). (1)求椭圆的方程;(2)设是椭圆上的任一点,为圆的任意一条直径、为直径的两个端点),求的最大值.(1)由题设知,,………………………………1分 由得解得椭圆的方程为(2)圆, 则 ………………………………………………6分 …………………………………………7分 .………………………………………………………………8分 从而求的最大值转化为求的最大值是椭圆上的任一点,设,,即,.…………………12分 因为,所以当时,取最大值的最大值为, 因为的中点坐标为,所以 ………………………………………6分 所以…………………………………7分 .………………………………………9分 因为点在圆上,所以,即.………………10分 因为点在椭圆上,所以,即.…………………………11分 所以.……………………………………12分 因为,所以当时,.………………………14分 方法3:①若直线的斜率存在,设的方程为,………………………6分 由,解得.……………………………………………7分 因为是椭圆上的任一点,, 所以,即, …………………………………9分 所以. ……………………………………10分 因为,所以当时,取最大值的斜率不存在,此时的方程为,由,解得或. 不妨设,,. …………………………………………12分 因为是椭圆上的任一点,, 所以,即,. 所以. 因为,所以当时,取最大值的最大值为中,,,是平面上一点,使三角形的周长为. ⑴求点的轨迹方程; ⑵在点的轨迹上是否存在点、,使得顺次连接点、、、所得到的四边形是矩形?若存在,请求出点、的坐标;若不存在,请简要说明理由 解:⑴依题意,……1分, ,所以,点的轨迹是椭圆……2分, ,……3分,所以,,,椭圆的方程为……4分,因为是三角形,点不在直线上(即不在轴上),所以点的轨迹方程为()……5分. ⑵根据椭圆的对称性,是矩形当且仅当直线经过原点,且是直角……6分,此时(或)……7分, 设,则……9分,解得,……10分,所以有2个这样的矩形,对应的点、分别为、或、……12分. 6、(茂名市2013届高三上学期期末)已知椭圆: ()的离心率为,连接椭圆的四个顶点得到的四边形的面积为. (1)求椭圆的方程; (2)设椭圆的左焦点为,右焦点为,直线过点且垂直于椭圆的长轴,动直线垂直于点,线段的垂直平分线交于点M,求点M的轨迹的方程; (3)设O为坐标原点,取上不同于O的点S,以OS为直径作圆与相交另外一点R,求该圆面积的最小值时点S的坐标. 解:(1)解:由,得,再由,解得 …………1分 由题意可知,即 …………………………2分 解方程组得 ………………………………3分 所以椭圆C1的方程是 ……………………………………3分 (2)因为,所以动点到定直线的距离等于它到定点(1,0)的距离,所以动点的轨迹是以为准线,为焦点的抛物线,…6分 所以点的轨迹的方程为 ……………………………………7分 (3)因为以为直径的圆与相交于点,所以∠ORS=90°,即 …………………………………………………………………………8分 设S (,),R(,),=(-,-),=(,) 所以 因为,,化简得 ……………………10分 所以, 当且仅当即=16,y2=±4时等号成立. ………………12分 圆的直径|OS|=因为≥64,所以当=64即=±8时,, ………13分 所以所求圆的面积的最小时,点S的坐标为(16,±8)……………14分 已知点是圆上的动点,圆心为,是圆内的定点;的中垂线交于点. (1)求点的轨迹的方程; (2)若直线交轨迹于与轴、轴都不平行)两点,为的中点,求的值(为坐标系原点). (1)解:由条件知: 1分 2分 3分 4分 所以点的轨迹是以为焦点的椭圆 5分 6分 所以点的轨迹的方程是 7分 解:设,则 8分 9分 10分 11分 13分 14分 或解:设,直线的方程为 则 8分 9分 10分 将代入椭圆方程得: 11分 12分 13分 所以 14分 =1上的动点,以M0为切点的切线l0与直线y=2相交于点P。
广东省某重点中学2013届高三数学理二轮复习之圆锥曲线复习(2) 含答案

1、 已知椭圆221102x y m m +=-- 的长轴在y 轴上,且焦距为4,则 m 等于 ( ) A .4 B 。
5 C.7 D 。
8 2、(2012年高考(福建理))已知双曲线22214x y b-=的右焦点与抛物线212y x =的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )A .5B .42C .3D .53、(2012年高考(陕西理))右图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽_______米。
4、设P 是圆2236x y +=上一动点,A 点坐标为(20,0).当P 在圆上运动时,线段PA 的中点M 的轨迹方程为_____________6、(2010深圳二模理)如图,已知点)0,2(-C ,直线4:0-=x l 与x 轴交于点A ,动点P 到直线0l 的距离为d ,且PC d 2=. (Ⅰ)求动点P 的轨迹E 的方程;(Ⅱ)设过点A 的直线l 交轨迹E 于M 、N 两点,且CN CM ⊥,求直线l 的方程.xyKs5uACOyxpd11.解:(Ⅰ)如图,设),(y x P ,PC d 2= ,22)2(24y x x ++⋅=+∴ ……3分平方整理得:8222=+y x , ∴点p 的轨迹方程为122=+y x 。
………5分联立8)4(2148)4(22222=++⇒⎪⎩⎪⎨⎧=++=x k x y x x k y 即083216)21(2222=-+++k x k x k……………7分0)832)(21(4)16(2222>-+-=∆k k k0)14)(21(8224>-+-∴k k k,化简得:212<k ……① 设),(),,(2211y x N y x M ,则2221222121832,2116k k x x k k x x +-=⋅+-=+,……9分),2(),,2(2211y x CN y x CM +=+= ,又CN CM ⊥,0=⋅∴CN CM0)2)(2(2121=+++∴y y x x ,即0)4)(4()2)(2(21221=+++++x x k x x ,0)41(4))(21(2)1(2222212=++++++∴k x x k x x k …………………11分0)41(42116)21(221832)1(2222222=+++-⋅+++-⋅+∴k kk k k k k 化简得:412=k 符合① …………………13分∴直线l 的方程是:)4(21+=x y 或)4(21+-=x y ……Ks5u………14分。
2013年广东汕头高考二模数学(理)试题Word版(含答案)

汕头市2013年普通高中高三教学质量测评试题(二) 理 科 数 学 一、选择题1. 算数z 满足()2z i i i -=+,则z =A .1i --B .1i -C .13i -+D .12i -2.已知集合{{}|,|31M x y N x x ===-≤≤,且,M N 都是全集U 的子集,则右边韦恩图中阴影部分表示的集合为 A.{}|1x x ≤B .{}|31x x -≤≤ C.{|3x x -≤≤D.{|1x x ≤≤3. 执行右边的框图,若输出的结果为12,则输入的实数x 的值是A .14B .32 C.2 D4.如图所示,图中曲线方程为21y x =-,用定积分表达围成封闭图形(阴影部分)的面积是5.给出平面区域G ,如图所示,其中(5,3),(2,1),(1,5)A B C ,若使目标函数(0)z ax y a =+>取得最小值的最优解有无穷多个,则a 的值为A .12B .23 C .2 D .46.某三棱锥的三视图如图所示,该三棱锥的体积是A .403 B.3 C .503 D.67.已知数列{}{},n n a b 都是公差为1的等差数列,其首项分别为1,a b 且*1111125,,,a b a b a b N +=>∈,则数列{}n b 的前10项和等于A .55B .70C .85D .1008.关于二项式2013(1)x -有下列命题:(1)该二项展开式中非常数项的系数和是1;(2)该二项展开式中第六项为620072013C x ;(3)该二项展开式中系数最大的项是第1007项;(4)当2014x =时,2013(1)x -除以2014的余数是2013。
其中正确命题有A .1个B .2个C .3个D .4个 二、填空题(一)必做题(9-13题) 9.某学校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程序的破坏,但可见部分如下图,据此可以了解分数在[50,60)的频率为 ,并且推算全班人数为 。
广东省11大市2013年高三数学一模试题分类汇编13:圆锥曲线(理科).pdf

广东省11大市2013年高三数学(理)一模试题分类汇编 圆锥曲线 一、填空、选择题 1、(广州市2013届高三3月毕业班综合测试试题(一))直线截圆所得劣弧所对的圆心角是 A. B. C. D. 答案:D 2、(江门市2013届高三2月高考模拟)在平面直角坐标系中,若双曲线的焦距为,则 . 答案:3 3、(揭阳市2013届高三3月第一次高考模拟)已知圆C经过直线与坐标轴的两个交点,且经过抛物线的焦点,则圆C的方程为 .圆心坐标为,半径为【或. 】 4、(梅州市2013届高三3月总复习质检)已知双曲线的两条近线的夹角为,则双曲线的离心率为___ 答案: 5、(汕头市2013届高三3月教学质量测评)已知动点P在抛物线y2=4x 上,那么使得点P到定点Q(2,,-1)的距离与点P到抛物线焦点的距离之和最小的点P的坐标为___ 答案: 6、(韶关市2013届高三调研考试)若方程表示双曲线,则实数k的取值范围是( )A、-1<k<1B、k>0C、k≤0D、k>1或k<-1 答案:A 7、(深圳市2013届高三2月第一次调研考试)双曲线的实轴长是虚轴长的倍,则 A. B. C. D. 答案:D 【解析】 8、(肇庆市2013届高三3月第一次模拟考试)若圆与直线相切,其圆心在轴的左侧,则 9、(佛山市2013届高三教学质量检测(一))已知抛物线上一点P到焦点的距离是,则点P的横坐标是_____. 10、(茂名市2013届高三第一次高考模拟考试)已知双曲线的一个焦点是(),则其渐近线方程为 . 11、(湛江市2013届高三高考测试(一))已知点A是抛物线C1:y2=2px(p>0)与双曲线C2:的一条渐近线的交点,若点A到抛物线C1的准线的距离为p,则双曲线的离心率等于____ 答案: 解析: 二、解答题 1、(广州市2013届高三3月毕业班综合测试试题(一))已知椭圆的中心在坐标原点,两个焦点分别为,,点在椭圆 上,过点的直线与抛物线交于两点,抛物线在点处的切线分别为,且与交于点. (1) 求椭圆的方程; (2) 是否存在满足的点? 若存在,指出这样的点有几个(不必求出点的坐标); 若不存在,说明理由. 解法1:设椭圆的方程为, 依题意: 解得: ……………2分 ∴ 椭圆的方程为. …………3分 解法2:设椭圆的方程为, 根据椭圆的定义得,即, …………1分 ∵, ∴. ……………2分 ∴ 椭圆的方程为. ……………3分 (2)解法1:设点,,则, , ∵三点共线, ∴. ……………4分 ∴, 化简得:. ① ……………5分 由,即得. …………6分 ∴抛物线在点处的切线的方程为,即. ② 同理,抛物线在点处的切线的方程为 . ③………8分 设点,由②③得:, 而,则 . ……………9分 代入②得 , ……………10分 则,代入 ① 得 ,即点的轨迹方程为.……………11分 若 ,则点在椭圆上,而点又在直线上, ………12分 ∵直线经过椭圆内一点, ∴直线与椭圆交于两点. ……………13分 ∴满足条件 的点有两个. …………14分 解法2:设点,,, 由,即得. ……………4分 ∴抛物线在点处的切线的方程为, 即. ……………5分 ∵, ∴ . ∵点在切线上, ∴. ① …………6分 同理, . ② ……………7分 综合①、②得,点的坐标都满足方程.……8分 ∵经过的直线是唯一的, ∴直线的方程为, ……………9分 ∵点在直线上, ∴. ……………10分 ∴点的轨迹方程为. ……………11分 若 ,则点在椭圆上,又在直线上,…12分 ∵直线经过椭圆内一点, ∴直线与椭圆交于两点. ……………13分 ∴满足条件 的点有两个. ……………14分 解法3:显然直线的斜率存在,设直线的方程为, 由消去,得. ………4分 设,则. ……………5分 由,即得. ……………6分 ∴抛物线在点处的切线的方程为,即.…7分 ∵, ∴. 同理,得抛物线在点处的切线的方程为. ……………8分 由解得 ∴. ……………10分 ∵, ∴点在椭圆上. ……………11分 ∴. 化简得.(*) ……………12分 由, ……………13分 可得方程(*)有两个不等的实数根. ∴满足条件的点有两个. ……………14分 2、(江门市2013届高三2月高考模拟)已知椭圆的中心在原点,离心率焦点. ⑴求椭圆的方程;,在椭圆,使得向量与共线?若存在,求直线的方程;若不存在,简要说明理由. 解:⑴设椭圆的方程, 1分 椭圆的离心率焦点, , , , 3分 故椭圆的方程. 4分 ⑵假设椭圆(),使得向量与共线, 5分 ,, ,即,(1) 6分 又点()在椭圆 (2) 7分 由⑴、⑵组成方程组解得,或, 9分 ,或, 10分 当点的坐标为时,直线的方程为, 当点的坐标为时,直线的方程为, 故直线的方程为或. 12分 3、(揭阳市2013届高三3月第一次高考模拟)如图(6),设点、分别是椭圆 的左、右焦点,为椭圆上任意一点,且最小值为. (1)求椭圆的方程均与椭圆,试探究在轴上是 否存在定点,点到的距离之积恒为1?若存在,请求出点坐标; 若不存在,请说明理由. 解:(1)设,则有,-------------1分 -----------------2分 由最小值为得,-------------------3分 ∴椭圆的方程为.---------------------------------------------4分 (2)①当直线斜率存在时,设其方程为--------------------5分 把的方程代入椭圆方程得 ∵直线与椭圆相切,∴,化简得 -------------------------------------------------------------------------------------7分 同理,-----------------------------------------------------------------------------8分 ∴,若,则重合,不合题意,∴-----------------------9分 设在轴上存在点,点到直线的距离之积为1,则 ,即,--------------------------------------10分 把代入并去绝对值整理, 或者 前式显然不恒成立;而要使得后式对任意的恒成立 则,解得;----------------------------------------------------------------------12分 ②当直线斜率不存在时,其方程为和,---------------------------13分 定点到直线的距离之积为; 定点到直线的距离之积为; 综上所述,满足题意的定点为或 --------------------------------------------14分 4、(梅州市2013届高三3月总复习质检)已知F1,F2分别是椭圆C:的上、下焦点,其中F1也是抛物线C1:的焦点,点M是C1与C2在第二象限的交点,且。
广东省13大市区高三数学 最新试题精选二模分类汇编9 圆锥曲线 理

广东省2013届高三最新理科试题精选(37套含13大市区的二模)分类汇编9:圆锥曲线一、选择题1 .(广东省韶关市2013届高三第三次调研考试数学(理科)试题(word 版) )椭圆221x my +=的焦点在y 轴上,长轴长是短轴长的两倍,则m 的值为 ( )A .14B .12C .2D .4【答案】A2 .(广东省湛江一中等“十校”2013届高三下学期联考数学(理)试题)定义:关于x 的不等式||x A B-<的解集叫A 的B 邻域.已知2a b +-的a b +邻域为区间(2,8)-,其中a b 、分别为椭圆12222=+by a x 的长半轴和短半轴.若此椭圆的一焦点与抛物线x y 542=的焦点重合,则椭圆的方程为( )A .13822=+y xB .14922=+y xC .18922=+y xD .191622=+y x【答案】B3 .(广东省海珠区2013届高三上学期综合测试一数学(理)试题)已知椭圆()2222:10x y C a b a b+=>>,双曲线221x y -=的渐近线与椭圆C 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C 的方程为.A 22184x y += .B 221126x y += .C 221168x y += .D 221205x y +=【答案】B4 .(广东省潮州市2013届高三上学期期末教学质量检测数学(理)试题)若抛物线22y px =的焦点与双曲线22122x y -=的右焦点重合,则p 的值为 ( )A .2-B .2C .4-D .4【答案】D 双曲线22122x y -=的右焦点为(2,0),所以抛物线22y px =的焦点为(2,0),则4p =.5 .(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD 版))设F 1,F 2是椭圆)0(12222>>=+b a b y a x 的左右焦点,若直线x =m a (m >1)上存在一点P,使ΔF 2PF 1是底角为300的等腰三角形,则m 的取值范围是( )A D .【答案】A6 .(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))已知双曲线22221x y a b-=的渐近线方程为y =,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )A .12B .2C .2D .1【答案】A7 .(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD 版))方程||||169x x y y +=-1的曲线即为函数y=f(x)的图象,对于函数y=f(x),有如下结论:①f(x)在R 上单调递减;②函数F(x)=4f(x)+3x 不存在零点;③函数y=f(x)的值域是R;④f(x)的图象不经过第一象限,其中正确的个数是 ( ) A .1个 B .2个 C .3个 D .4个 【答案】D二、填空题 8 .(广东省珠海一中等六校2013届高三第一次联考数学(理)试题)已知双曲线22221(0b 0)x y a a b -=>,>和椭圆22x y =1169+有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为____________.【答案】22143x y -=9.(广东省深圳市南山区2013届高三上学期期末考试数学(理)试题)已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为20x y +=,则双曲线的离心率e 的值为__________ .10.(广东省汕头市第四中学2013届高三阶段性联合考试数学(理)试题)双曲线的焦点在x 轴上,实轴长为4,离心率为3,则该双曲线的标准方程为___,渐近线方程为___.【答案】221432x y -= y =±11.(广东省汕头市2013届高三3月教学质量测评数学(理)试题)已知动点P 在抛物线y 2=4x 上,那么使得点P 到定点Q(2,,-1)的距离与点P 到抛物线焦点的距离之和最小的点P 的坐标为___【答案】)1,41(-12.(广东省梅州市2013届高三3月总复习质检数学(理)试题)已知双曲线22221(0,0)x y a b a b-=>>的两条近线的夹角为3π,则双曲线的离心率为___13.(广东省茂名市实验中学2013届高三下学期模拟(二)测试数学(理)试题(详解))已知点A 是抛物线C 1:y 2=2px(p>0)与双曲线C 2:22221(0,0)x y a b a b-=>>的一条渐近线的交点,若点A 到抛物线C 1的准线的距离为p,则双曲线的离心率等于____14.(广东省茂名市2013届高三第一次模拟考试数学(理)试题)已知双曲线221x ky -=的一个焦点是),则其渐近线方程为________.【答案】2y x =±;15.(广东省揭阳市2013届高三3月第一次高考模拟数学(理)试题(含解析))已知圆C 经过直线220x y -+=与坐标轴的两个交点,且经过抛物线28y x =的焦点,则圆C 的方程为______________.【答案】22115()()222x y -+-=[或2220x y x y +---=];易得圆心坐标为11(,)22,半径为r =, 故所求圆的方程为22115()()222x y -+-=【或2220x y x y +---=. 】16.(广东省江门市2013年高考模拟考试(即一模)数学(理)试题 )在平面直角坐标系Oxy 中,若双曲线14222=+-m y m x 的焦距为8,则=m _______.【答案】3(未排除4-,给3分)17.(2013年广东省佛山市普通高中高三教学质量检测(一)数学(理)试题)已知抛物线24x y =上一点P 到焦点F 的距离是5,则点P 的横坐标是_____.【答案】4± 18.(广东省韶关市2013届高三4月第二次调研测试数学理试题)设点P 是双曲线22221(0,0)x y a b a b-=>>与圆2222x y a b +=+在第一象限的交点,其中12,F F 分别是双曲线的左、右焦点,若21tan 3PF F ∠=,则双曲线的离心率为______________.19.(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)下图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽________米.【答案】20.(广东省揭阳市2013年高中毕业班第二次高考模拟考试理科数学试题)过双曲线221916x y -=的右焦点,且平行于经过一、三象限的渐近线的直线方程是 ________.【答案】双曲线221916x y -=的右焦点为(5,0),渐近线的方程为43y x =±,所以所求直线方程为4(5),3y x =-即43200x y --=.三、解答题 21.(广东省韶关市2013届高三第三次调研考试数学(理科)试题(word 版) )在平面直角坐标系xoy 中,设点F (1,0),直线l :1x =-,点P 在直线l 上移动,R 是线段PF 与y 轴的交点,,RQ FP PQ l ⊥⊥.(Ⅰ)求动点Q 的轨迹的方程;(Ⅱ) 记Q 的轨迹的方程为E ,过点F 作两条互相垂直的曲线E 的弦AB 、CD ,设AB 、CD 的中点分别为N M ,.求证:直线MN 必过定点)0,3(R .【答案】解:(Ⅰ)依题意知,直线l 的方程为:1x =-.点R 是线段FP 的中点,且RQ ⊥FP ,∴RQ 是线段FP 的垂直平分线∴PQ 是点Q 到直线l 的距离.∵点Q 在线段FP 的垂直平分线,∴PQ QF =故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x => (Ⅱ) 设()()B B A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y则⎪⎩⎪⎨⎧==)2(4)1(422BB A A x y x y(1)—(2)得k y y B A 4=+,即ky M 2=, 代入方程)1(-=x k y ,解得122+=kx M .所以点M 的坐标为222(1,)k k+同理可得:N 的坐标为2(21,2)k k +-. 直线MN 的斜率为21kkx x y y k N M N M MN -=--=,方程为 )12(1222---=+k x kk k y ,整理得)3()1(2-=-x k k y , 显然,不论k 为何值,(3,0)均满足方程, 所以直线MN 恒过定点R (3,0).1422.(广东省汕头一中2013年高三4月模拟考试数学理试题 )在平面直角坐标系中,已知点()2,0A 、()2,0B -,P 是平面内一动点,直线PA 、PB 的斜率之积为34-.(1)求动点P 的轨迹C 的方程;(2)过点1,02⎛⎫⎪⎝⎭作直线l 与轨迹C 交于E 、F 两点,线段EF 的中点为M ,求直线MA 的斜率k 的取值范围.2013年4月汕头一中高三模拟考 【答案】(1)依题意,有3224PA PB y y k k x x ⋅=⋅=--+(2x ≠±), ----------------------------- 化简得: 22143x y += (2x ≠±),为所求动点P 的轨迹C 的方程------------------------ (2)依题意,可设(,)M x y 、(,)E x m y n ++、(,)F x m y n --,则有2222()()143()()143x m y n x m y n ⎧+++=⎪⎪⎨--⎪+=⎪⎩,两式相减,得443004342EF mx n n x y k m y x -+=⇒==-=-, 由此得点M 的轨迹方程为:226830x y x +-=(0x ≠).------------------------------ 设直线MA :2x my =+(其中1m k=),则 22222(68)211806830x my m y my x y x =+⎧⇒+++=⎨+-=⎩, ------------------------------ 故由22(21)72(68)0||8m m m ∆=-+≥⇒≥,即18k≥, 解得:k 的取值范围是11,88⎡⎤-⎢⎥⎣⎦. ---------------------------23.(广东省汕头一中2013年高三4月模拟考试数学理试题 )已知抛物线C :212x y =,过焦点F 的动直线l 交抛物线于A 、B 两点,O 为坐标原点. (1)求证:OA OB ⋅为定值;(2)设M 是线段AB 的中点,过M 作x 轴的垂线交抛物线C 于点N ,证明:抛物线C 在点N 处的切线与AB 平行.【答案】(1)设直线l 的方程为:18y kx =+,()11,A x y ,()22,B x y . ------------------------- 由21218x y y kx ⎧=⎪⎪⎨⎪=+⎪⎩得:2110264x kx --=,∴12116x x =- ------------------------ ∴()2121212123464OA OB x x y y x x x x ⋅=+=+=-为定值---------------------------- (2)由(1)得:点M 的横坐标为4k ,∴点N 的横坐标为4k----------------------------∵'4y x = ∴4'|k x y k == ----------------------------∴平行另解:设()00,N x y ,则12024x x k x +==,220028k y x == ---------------------------- 设抛物线C 在点N 处的切线为284k k y m x ⎛⎫-=- ⎪⎝⎭由228412k k y m x x y⎧⎛⎫-=- ⎪⎪⎪⎝⎭⎨⎪=⎪⎩得:2202816m mk k x x -+-= ------------------------------- ∴22404816m mk k ⎛⎫∆=--= ⎪⎝⎭,解得:m k = -------------------------------∴平行24.(广东省东莞市2013届高三第二次模拟数学理试题)已知椭圆22122:1(0)x y C a b a b+=>>的离心率为e =,直线:2l y x =+与以原点为圆心、以椭圆1C 的短半轴长为半径的圆O 相切. (1)求椭圆C 1的方程;(2)设椭圆1C 的左焦点为1F ,右焦点为2F ,直线1l 过点1F ,且垂直于椭圆的长轴,动直线2l 垂直于1l ,垂足为点P ,线段2PF 的垂直平分线交2l 于点M ,求点M 的轨迹2C 的方程;(3)设2C 与x 轴交于点Q ,不同的两点R 、S 在2C 上,且满足0=⋅,求||QS 的取值范围.【答案】解:(1)由直线:2l y x =+与圆222x y b +=相切,b =,即b =由e =,得222213b e a =-=,所以a =所以椭圆的方程是221:132x y C +=(2)由条件,知2||||MF MP =,即动点M 到定点2F 的距离等于它到直线1:1l x =-的距离,由抛物线的定义得点M 的轨迹2C 的方程是x y 42=(3)由(2),知(0,0)Q ,设221212,,,44y y R y S y ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭, ∴222121121,,,44y y y QR y RS y y ⎛⎫⎛⎫-==- ⎪ ⎪⎝⎭⎝⎭由0=⋅,得()()222121121016y y y y y y -+-=∵12y y ≠,∴21116y y y ⎛⎫=-+⎪⎝⎭,∴222121256323264y y y =++≥=,当且仅当2121256y y =,即14y =±时等号成立 又||y QS ⎛== ,∵2264y ≥,∴当2264y =,即28y =±时,min ||QS =故||QS 的取值范围是)⎡+∞⎣25.(广东省肇庆市2013届高三上学期期末统一检测数学(理)试题)已知两圆222212:20,:(1)4C x y x C x y +-=++=的圆心分别为12,C C ,P 为一个动点,且12||||PC PC +=(1)求动点P 的轨迹M 的方程;(2)是否存在过点(2,0)A 的直线l 与轨迹M 交于不同的两点C 、D,使得11||||C C C D =?若存在,求直线l 的方程;若不存在,请说明理由.【答案】解:(1)两圆的圆心坐标分别为1(1,0),C 和2(1,0)C - ∵1212||||||2PC PC C C +=>=∴根据椭圆的定义可知,动点P 的轨迹为以原点为中心,1(1,0),C 和2(1,0)C -为焦点,长轴长为2a =的椭圆, 1,1a c b ====∴椭圆的方程为2212x y +=,即动点P 的轨迹M 的方程为2212x y += (2)(i)当直线l 的斜率不存在时,易知点(2,0)A 在椭圆M 的外部,直线l 与椭圆M 无交点,所以直线l 不存在.(ii)设直线l 斜率存在,设为k ,则直线l 的方程为(2)y k x =-由方程组2212(2)x y y k x ⎧+=⎪⎨⎪=-⎩得2222(21)8820k x k x k +-+-=①依题意28(21)0k ∆=-->解得22k -<<当22k -<<时,设交点1122(,),(,)C x y D x y ,CD 的中点为00(,)N x y ,方程①的解为221222884242k k x x k k ==++ ,则212024221x x k x k +==+ ∴2002242(2)22121k ky k x k k k ⎛⎫-=-=-= ⎪++⎝⎭ 要使11||||C C C D =,必须1C N l ⊥,即11C N k k ⋅=-∴222212114021kk k kk --+⋅=--+,即2102k k -+=②∵1114102∆=-⨯=-<或,∴2102k k -+=无解所以不存在直线,使得11||||C C C D =综上所述,不存在直线l ,使得11||||C C C D =26.(广东省深圳市南山区2013届高三上学期期末考试数学(理)试题)已知椭圆2222:1(0)x y C a b a b+=>>,. (1)求椭圆C 的方程 (2)设直线l 与椭圆C 交于A B ,两点,坐标原点O 到直线l求AOB △面积的最大值.【答案】(2)设11()A x y ,,22()B x y ,.27.(广东省汕头市东山中学2013届高三下学期入学摸底考试数学(理)试题)己知斜率为1的直线l 与双曲线2222:1x y C a b-=(0a >,0b >),相交于B 、D 两点,且BD 的中点为(1,3)M(1)求双曲线C 的离心率;(2)设C 的右顶点为A ,右焦点为F ,||||17DF BF ⋅=,证明:过A 、B 、D 三点的圆与x 轴相切. 【答案】解:(1)由题设知,直线l 的方程为2y x =+代入双曲线C 的方程,并化简得:2222222()440b a x a x a a b ----=设11(,)B x y ,22(,)D x y ,则212224a x x b a +=-,22212224a a b x x b a +⋅=- ①由(1,3)M 为BD 的中点知:1212x x +=,故2221412a b a ⋅=-,即223b a = ②所以2223c a a -=,即224c a = 故2ce a==所以双曲线C 的离心率为2e = (注:本题也可用点差法解决)(2)由①、②知,双曲线C 的方程为:22233x y a -=(,0)A a ,(2,0)F a ,122x x +=,2124302a x x +⋅=-<1|||2|BF x a =-同理2|||2|DF x a =-2222121212|||||(2)(2)||42()||864||548|BF DF x a x a x x a x x a a a a a a ⋅=--=-++=----=++又因为||||17DF BF ⋅= 且25480a a ++> 所以254817a a ++= 解得:1a =,95a =-(舍去)12|||6BD x x -==连结MA ,则由(1,0)A ,(1,3)M 知||3MA =,从而||||||MA MB MD ==,且MA x ⊥轴,因此以M 为圆心,MA 为半径的圆经过A 、B 、D 三点,且在点A 处与x 轴相切. 所以过A 、B 、D 三点的圆与x 轴相切 28.(广东省汕头市东山中学2013届高三第二次模拟考试数学(理)试题(详解))已知直线033=+-y x 经过椭圆C :12222=+by a x (0>>b a )的一个顶点B 和一个焦点F .⑴求椭圆的标准方程;⑵设P 是椭圆C 上动点,求||||||PB PF -的取值范围,并求||||||PB PF -取最小值时点P 的坐标. 【答案】【答案】⑴依题意,)1 , 0(B ,)0 , 3(-F , 所以1=b ,3=c ,222=+=c b a ,所以椭圆的标准方程为1422=+y x 5分. ⑵||||||||0BF PB PF ≤-≤,当且仅当||||PB PF =时,0||||||=-PB PF ,当且仅当P 是直线BF 与椭圆C 的交点时,||||||||BF PB PF =- ,2||=BF ,所以||||||PB PF -的取值范围是]2 , 0[ . 设) , (n m P ,由||||PB PF =得013=++n m ,由⎪⎩⎪⎨⎧=++=+0131422n m n m ,解得⎩⎨⎧-==10n m 或⎪⎪⎩⎪⎪⎨⎧=-=13111338n m ,所求点P 为)1 , 0(-P 和)1311, 1338(-P . 29.(广东省汕头市第四中学2013届高三阶段性联合考试数学(理)试题)在平面直角坐标系xOy 中,动点P到两点(0),0)的距离之和等于4,设点P 的轨迹为曲线C ,直线l 过点(1,0)E -且与曲线C 交于A ,B 两点.(1)求曲线C 的轨迹方程;(2)是否存在△AOB 面积的最大值,若存在,求出△AOB 的面积;若不存在,说明理由.【答案】解.(Ⅰ)由椭圆定义可知,点P 的轨迹C是以(0),0)为焦点,长半轴长为2 的椭圆.故曲线C 的方程为2214x y +=(Ⅱ)存在△AOB 面积的最大值因为直线l 过点(1,0)E -,可设直线l 的方程为 1x my =-或0y =(舍).则221,4 1.x y x my ⎧+=⎪⎨⎪=-⎩整理得 22(4)230m y my +--= 由22(2)12(4)0m m ∆=++>. 设1122()()A x y B x y ,,,.解得1y =2y =. 则21||y y -=因为1212AOB S OE y y ∆=⋅-= 设1()g t t t=+,t =t ≥.则()g t在区间)+∞上为增函数.所以()g t ≥.所以AOB S ∆≤当且仅当0m =时取等号,即max ()AOB S ∆=. 所以AOB S ∆30.(广东省汕头市2013届高三3月教学质量测评数学(理)试题)〔本小题满分14分)如图.已知椭圆22221(0)x y a b a b +=>>的长轴为AB,过点B 的直线l 与x 轴垂直,椭圆的离心率e =,F 为椭圆的左焦点且11AF F B =1 .(I)求椭圆的标准方程; (II)设P 是椭圆上异于A 、B 的任意一点,PH⊥x 轴,H 为垂足,延长HP 到点Q 使得HP=PQ.连接AQ 并延长交直线l 于点M.N 为MB 的中点,判定直线QN 与以AB 为直径的圆O 的位置关系.【答案】解:(Ⅰ)易知A )0,(a -, B )0,(a )0,(1c F - 1)()0,(11=+⋅-=⋅∴c a c a F AF1222==-∴b c a又23=e 43122222=-==∴aa a c e ,解得42=a 1422=+∴y x 所求椭圆方程为:(Ⅱ)设),(00y x P 则)2,(00y x Q )22(≠-≠x x 及 2200+=∴x y k AQ 所以直线AQ 方程)2(22:00++=x x y y)28,2(00+∴x y M )24,2(00+∴x y N 42222420000000-=--+=∴x y x x y x y k QN又点P 的坐标满足椭圆方程得到:442020=+y x ,所以 202044y x -=-200200024242y x y y x x y x k QN -=-=-=∴ ∴直线 QN 的方程:)(22000x x y x y y --=- 化简整理得到:442202000=+=+y x y y x x 即4200=+y y x x 所以 点O 到直线QN 的距离244220=+=y x d∴直线QN 与AB 为直径的圆O 相切.31.(广东省梅州市2013届高三3月总复习质检数学(理)试题)(本小题满分14分)已知F 1,F 2分别是椭圆C:22221(0)y x a b a b+=>>的上、下焦点,其中F 1也是抛物线C 1:24x y =的焦点,点M 是C 1与C 2在第二象限的交点,且15||3MF =. (1)求椭圆C 1的方程;(2)已知A(b,0),B(0,a),直线y=kx(k>0)与AB 相交于点D,与椭圆C 1相交于点E,F 两点,求四边形AEBF 面积的最大值. 【答案】32.(广东省茂名市实验中学2013届高三下学期模拟(二)测试数学(理)试题(详解))如图,已知点M0(x0,y0)是椭圆C:222yx=1上的动点,以M0为切点的切线l0与直线y=2相交于点P.(1)过点M0且l0与垂直的直线为l1,求l1与y轴交点纵坐标的取值范围;(2)在y轴上是否存在定点T,使得以PM0为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,说明理由.【答案】解:(1)由椭圆得:y ='y =1222(22)x x ---切线的斜率为,所以,直线l 1的方程为:000)y y x x -=-,与y 轴交点纵坐标为因为011x -≤≤,所以,2001x ≤≤,200222x ≤-≤,所以,当切点在第一、二象限时l 1与y 轴交点纵坐标的取值范围为:02y ≤≤,则对称性可知 l 1与y 轴交点纵坐标的取值范围为:22y -≤≤. (2)依题意,可得∠PTM 0=90°,设存在T(0,t),M 0(x 0,y 0)由(1)得点P 的坐标(220000222y y x x -+,2),由00PT M T =可求得t=1所以存在点T(0,1)满足条件.33.(广东省茂名市2013届高三第一次模拟考试数学(理)试题)已知椭圆1C :22221x y a b+= (0a b >>),连接椭圆的四个顶点得到的四边形的面积为(1)求椭圆1C 的方程;(2)设椭圆1C 的左焦点为1F ,右焦点为2F ,直线1l 过点1F 且垂直于椭圆的长轴,动直线2l 垂直1l 于点P ,线段2PF 的垂直平分线交2l 于点M ,求点M 的轨迹2C 的方程;(3)设O 为坐标原点,取2C 上不同于O 的点S ,以OS 为直径作圆与2C 相交另外一点R ,求该圆面积的最小值时点S 的坐标.【答案】解:(1)解:由3e =,得223a c =,再由222c a b =-,解得2a =由题意可知1222a b ⋅⋅=,即a b ⋅解方程组2a ab ⎧=⎪⎨⎪=⎩得a b ==所以椭圆C 1的方程是22132x y +=(2)因为2MP MF =,所以动点M 到定直线1:1l x =-的距离等于它到定点2F (1,0)的距离,所以动点M 的轨迹2C 是以1l 为准线,2F 为焦点的抛物线, 所以点M 的轨迹2C 的方程为24y x =(3)因为以OS 为直径的圆与2C 相交于点R ,所以∠ORS = 90°,即0OR SR ⋅= 设S (1x ,1y ),R (2x ,2y ),SR =(2x -1x ,2y -1y ),OR =(2x ,2y )所以222221*********()()()()016y y y OR SR x x x y y y y y y -⋅=-+-=+-= 因为12y y ≠,20y ≠,化简得12216y y y ⎛⎫=-+⎪⎝⎭所以221222256323264y y y =++≥=, 当且仅当2222256y y =即22y =16,y 2=±4时等号成立 圆的直径|OS===因为21y ≥64,所以当21y =64即1y =±8时,min OS =, 所以所求圆的面积的最小时,点S 的坐标为(16,±8)34.(广东省揭阳市2013届高三3月第一次高考模拟数学(理)试题(含解析))如图(6),设点)0,(1c F -、)0,(2c F 分别是椭圆)1(1:222>=+a y ax C 的左、右焦点,P 为椭圆C 上任意一点,且12PF PF ⋅uuu r uuu r 最小值为0.(1)求椭圆C 的方程;(2)若动直线12,l l 均与椭圆C 相切,且12//l l ,试探究在x 轴上是否存在定点B ,点B 到12,l l 的距离之积恒为1?若存在,请求出点B 坐标;若不存在,请说明理由.图(6)F 2F 1oyx【答案】解:(1)设),(y x P ,则有),(1y c x P F +=,),(2y c x P F -=[]a a x c x aa c y x PF PF ,,11222222221-∈-+-=-+=⋅ 由12PF PF ⋅uuu r uuu r最小值为0得210122=⇒=⇒=-a c c , ∴椭圆C 的方程为1222=+y x(2)①当直线12,l l 斜率存在时,设其方程为,y kx m y kx n =+=+ 把1l 的方程代入椭圆方程得222(12)4220k x mkx m +++-=∵直线1l 与椭圆C 相切,∴2222164(12)(22)0k m k m ∆=-+-=,化简得2212m k =+同理,2212n k =+∴22m n =,若m n =,则12,l l 重合,不合题意,∴m n =- 设在x 轴上存在点(,0)B t ,点B 到直线12,ll 的距离之积为1,则1=,即2222||1k t m k -=+,--- 把2212k m +=代入并去绝对值整理,22(3)2k t -=或者22(1)0k t -=前式显然不恒成立;而要使得后式对任意的k R ∈恒成立则210t -=,解得1t =±;---------------------------------------------------------②当直线12,l l 斜率不存在时,其方程为x =和x =,定点(1,0)-到直线12,l l 的距离之积为1)1-+=;定点(1,0)到直线12,l l 的距离之积为1)1=; 综上所述,满足题意的定点B 为(1,0)-或(1,0)35.(广东省江门市2013年高考模拟考试(即一模)数学(理)试题 )已知椭圆C 的中心在原点O ,离心率23=e ,右焦点为)0 , 3( F . ⑴求椭圆C 的方程;⑵设椭圆的上顶点为A ,在椭圆C 上是否存在点P ,使得向量OA OP +与FA 共线?若存在,求直线AP 的方程;若不存在,简要说明理由.【答案】解:⑴设椭圆C 的方程为22221(0)x y a b a b+=>>,椭圆C 的离心率23=e ,右焦点为)0 , 3( F ,∴c c a ==, 222a b c =+,∴2,1,a b c ===,故椭圆C 的方程为2214x y += ⑵假设椭圆C 上是存在点P (00,x y ),使得向量OA OP +与FA 共线,00(,1)OP OA x y +=+,(FA =,∴011y +=,即001)x y =+,(1) 又点P (00,x y )在椭圆2214x y +=上,∴220014x y += (2)由⑴、⑵组成方程组解得0001x y =⎧⎨=-⎩,或0017x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴(0,1)P -,或1()7P , 当点P 的坐标为(0,1)-时,直线AP 的方程为0y =,当点P的坐标为1()7P 时,直线AP440y -+=, 故直线AP 的方程为0y =440y -+=36.(广东省华附、省实、深中、广雅四校2013届高三上学期期末联考数学(理)试题)已知焦点在x轴上的双曲线C 的两条渐近线过坐标原点,且两条渐近线与以点D (0, 2 )为圆心,1为半径的圆相切,又知双曲线C 的一个焦点与D 关于直线y =x 对称. (Ⅰ)求双曲线C 的方程;(Ⅱ)设直线y =mx +1与双曲线C 的左支交于A ,B 两点,另一直线l 经过M (-2,0)及AB 的中点,求直线l 在y 轴上的截距b 的取值范围;(Ⅲ)若Q 是双曲线C 上的任一点,F 1F 2为双曲线C 的左,右两个焦点,从F 1引∠F 1QF 2的平分线的垂线,垂足为N ,试求点N 的轨迹方程.【答案】解:(Ⅰ)设双曲线C 的渐近线方程为y =kx ,则kx -y =0 ∵该直线与圆x 2+(y - 2 )2=1相切,有|- 2 |k 2+ 1= 1 ⇒ k =±1. ∴双曲线C 的两条渐近线方程为y =±x , 故设双曲线C 的方程为 x 2a 2-y 2a2 = 1 .易求得双曲线C 的一个焦点为 ( 2 ,0),∴2a 2=2,a 2=1.∴双曲线C 的方程为x 2-y 2=1.(Ⅱ)由 ⎩⎨⎧ y =mx +1 x 2-y 2=1得(1-m 2)x 2-2mx -2=0.令f (x )= (1-m 2)x 2-2mx -2直线与双曲线左支交于两点,等价于方程f (x )=0在(-∞,0)上有两个不等实根. 因此 ⎩⎪⎨⎪⎧ △>02m 1-m <0-21-m 2>0解得1<m <2 .又AB 中点为(m 1-m 2 ,11-m2 ),zxxk∴直线l 的方程为y =1-2m 2+m +2 (x +2). 令x =0,得b =2-2m 2+m +2=2-2(m -14 )2+178.∵1<m < 2 ,∴-2(m -14 )2+178 ∈ (-2+ 2 , 1),∴b ∈ (-∞,-2- 2 )∪(2,+∞).(Ⅲ)若Q 在双曲线的右支上,则延长2QF 到T ,使||||1QF QT =, 若Q 在双曲线的左支上,则在QF 2上取一点T ,使| QT |=|QF 1 |.根据双曲线的定义| TF 2 |=2,所以点T 在以F 2( 2 ,0)为圆心,2为半径的圆上,即点T 的轨迹方程是(x - 2 )2+y 2=4 (x ≠ 0) ①由于点N 是线段F 1T 的中点,设N (x ,y ),T (x T ,y T ).则 ⎩⎪⎨⎪⎧ x =x T- 2 2 y =y T2,即 ⎩⎨⎧ x T=2x + 2y T= 2y .代入①并整理得点N 的轨迹方程为x 2+y 2=1.(x ≠ -22) (或者用几何意义得到| NO |=12 | F 2T |=1, 得点N 的轨迹方程为x 2+y 2=1.)37.(广东省海珠区2013届高三上学期综合测试一数学(理)试题)(本小题满分14分)设抛物线()2:20C x py p =>的焦点为F ,()()000,0A x y x ≠是抛物线C 上的一定点.(1)已知直线l 过抛物线C 的焦点F ,且与C 的对称轴垂直,l 与C 交于,Q R 两点, S 为C 的准线上一点,若QRS ∆的面积为4,求p 的值;(2)过点A 作倾斜角互补的两条直线AM ,AN ,与抛物线C 的交点分别为()11,,M x y ()22,N x y .若直线AM ,AN 的斜率都存在,证明:直线MN 的斜率等于抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率.【答案】(本小题主要考查直线、抛物线、对称等知识,考查数形结合、化归与转化、方程的思想方法,考查数学探究能力以及运算求解能力) 解: (1)由题设0,2p F ⎛⎫ ⎪⎝⎭,设1,,2p Q x ⎛⎫ ⎪⎝⎭则1,2p R x ⎛⎫- ⎪⎝⎭2p ===.∴由QRS ∆的面积为4,得:1242p p ⨯⨯=,得: 2.p =(2)由题意()100,A x y -首先求抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率.解法一:设抛物线在1A 处的切线的斜率为k ,则其方程为()00y k x x y =++ 联立()0022y k x x y x py⎧=++⎪⎨=⎪⎩得2002220x pkx px k py ---=将2002py x =代入上式得:2200220x pkx px k x ---=()()22002420pk px k x ∆=-++=即2220020p k px k x ++= zxxk 即()200pk x += 得0.x k p=-即抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率为0.x p-解法二:由22x py =得212y x p=, ∴'x y p=∴抛物线C 在点A 关于对称轴的对称点()100,A x y -处的切线的斜率为0.x p-再求直线MN 的斜率.解法一:设直线AM 的斜率为1k ,则由题意直线AN 的斜率为1k -直线AM 的的方程为()010y y k x x -=-,则直线AN 的的方程为()010y y k x x -=--.联立()21002x py y k x x y ⎧=⎪⎨=-+⎪⎩得221100220x pk x pk x x -+-=(1)方程(1)有两个根01,x x ,∴()()2210102420pk px k x ∆=--->∴0,1x =0112x x pk +=,即1102x pk x =-,同理可得2102x pk x =--直线MN 的斜率222121122121222MNx x y y x x p p k x x x x p --+===--0022x x p p-==- ∴直线MN 的斜率等于抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率解法二:AM AN k k =- zxxk01020102y y y y x x x x --∴=--- 将222012012,,222x x x y y y p p p ===分别代入上式得:2222001201022222x x x x p p p p x x x x --=---, 整理得0122x x x =+∴直线MN 的斜率222121122121222MNx x y y x x p p k x x x x p --+===--0022x x p p-==- ∴直线MN 的斜率等于抛物线C 在点A 关于对称轴的对称点1A 处的切线的斜率.38.(广东省广州市2013届高三调研测试数学(理)试题)如图5, 已知抛物线2P y x :=,直线AB 与抛物线P 交于A B ,两点,OA OB ^,OA OB OC uu r uu u r uu u r+=,OC 与AB 交于点M .(1) 求点M 的轨迹方程;求四边形AOBC 的面积的最小值.,考查数形结合、函数与方程、化归与转化的数学思想方法,以及推理论证能力、运算求解能力、创新意识) 解法一:(1)解:设()()()221122M x y A y y B y y ,,,,,, ∵OA OB OC +=, ∴M 是线段AB 的中点 ∴()222121212222yy y y y y x +-+==,①122y y y +=. ② ∵OA OB ⊥, ∴0OA OB ⋅=.∴2212120y y y y +=依题意知120y y ≠,∴121y y =-. ③把②、③代入①得:2422y x +=,即()2112y x =- ∴点M 的轨迹方程为()2112yx =- (2)解:依题意得四边形AOBC 是矩形,∴四边形AOBC 的面积为S OA OB ==⋅===∵22121222y y y y +≥=,当且仅当12y y =时,等号成立,∴2S ≥=∴四边形AOBC 的面积的最小值为2 解法二:(1)解:依题意,知直线OA OB ,的斜率存在,设直线OA 的斜率为k , 由于OA OB ⊥,则直线OB 的斜率为1k-故直线OA 的方程为y kx =,直线OB 的方程为1y x k=-. 由2y kx y x ,.⎧=⎨=⎩ 消去y ,得220k x x -=. 解得0x =或21x k=∴点A 的坐标为211k k ,⎛⎫⎪⎝⎭同理得点B 的坐标为()2k k ,- ∵OA OB OC +=, ∴M 是线段AB 的中点 设点M 的坐标为()x y ,,则221212k k x k k y ,.⎧+⎪=⎪⎪⎨⎪-⎪=⎪⎩消去k ,得()2112yx =- ∴点M 的轨迹方程为()2112y x =-(2)解:依题意得四边形AOBC 是矩形, ∴四边形AOBC 的面积为S OA OB==⋅=≥2=当且仅当221kk=,即21k =时,等号成立 ∴四边形AOBC 的面积的最小值为239.(广东省广州市2013届高三3月毕业班综合测试试题(一)数学(理)试题)已知椭圆1C 的中心在坐标原点,两个焦点分别为1(2,0)F -,2F ()20,,点(2,3)A 在椭圆1C 上,过点A 的直线L 与抛物线22:4C x y =交于B C ,两点,抛物线2C 在点B C ,处的切线分别为12l l ,,且1l 与2l 交于点P .(1) 求椭圆1C 的方程;(2) 是否存在满足1212PF PF AF AF +=+的点P ? 若存在,指出这样的点P 有几个(不必求出点P 的坐标); 若不存在,说明理由.【答案】(本小题主要考查椭圆、抛物线、曲线的切线等基础知识,考查数形结合、函数与方程、化归与转化的数学思想方法,以及推理论证能力、运算求解能力、创新意识)(1) 解法1:设椭圆1C 的方程为22221x y a b+=()0a b >>,依题意: 222222231,4.a ba b ⎧+=⎪⎨⎪=+⎩解得: 2216,12.a b ⎧=⎪⎨=⎪⎩ ∴ 椭圆1C 的方程为2211612x y += 解法2:设椭圆1C 的方程为22221x y a b +=()0a b >>,根据椭圆的定义得1228a AF AF =+=,即4a =,∵2c =, ∴22212b a c =-=∴椭圆1C 的方程为2211612x y +=(2)解法1:设点)41,(211x x B ,)41,(222x x C ,则))(41,(212212x x x x BC --=, )413,2(211x x --=, ∵C B A ,,三点共线, (苏元高考吧:) ∴BC BA // ∴()()()222211211113244x x x x x x ⎛⎫--=-- ⎪⎝⎭,化简得:1212212x x x x ()+-=. ① 由24x y =,即214y x ,=得y '=12x ∴抛物线2C 在点B 处的切线1l 的方程为)(2411121x x x x y -=-,即211412x x x y -=. ② 同理,抛物线2C 在点C 处的切线2l 的方程为 222412x x x y -=. ③ 设点),(y x P ,由②③得:=-211412x x x 222412x x x -, 而21x x ≠,则 )(2121x x x += 代入②得 2141x x y =, 则212x x x +=,214x x y =代入 ① 得 1244=-y x ,即点P 的轨迹方程为3-=x y .若1212PF PF AF AF +=+ ,则点P 在椭圆1C 上,而点P 又在直线3-=x y 上, ∵直线3-=x y 经过椭圆1C 内一点(3,0), ∴直线3-=x y 与椭圆1C 交于两点∴满足条件1212PF PF AF AF +=+ 的点P 有两个 解法2:设点),(11y x B ,),(22y x C ,),(00y x P ,由24x y =,即214y x ,=得y '=12x ∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=∵21141x y =, ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① 同理, 20202y x x y -=. ② 综合①、②得,点),(),,(2211y x C y x B 的坐标都满足方程y x xy -=002∵经过),(),,(2211y x C y x B 的直线是唯一的, ∴直线L 的方程为y x xy -=002, ∵点)3,2(A 在直线L 上, ∴300-=x y ∴点P 的轨迹方程为3-=x y若1212PF PF AF AF +=+ ,则点P 在椭圆1C 上,又在直线3-=x y 上, ∵直线3-=x y 经过椭圆1C 内一点(3,0), ∴直线3-=x y 与椭圆1C 交于两点∴满足条件1212PF PF AF AF +=+ 的点P 有两个 解法3:显然直线L 的斜率存在,设直线L 的方程为()23y k x =-+,由()2234y k x x y ,,⎧=-+⎪⎨=⎪⎩消去y ,得248120x kx k -+-=设()()1122B x y C x y ,,,,则12124812x x k x x k ,+==- 由24x y =,即214y x ,=得y '=12x∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-,即2111212x y x x y -+= ∵21141x y =, ∴211124x y x x =-. 同理,得抛物线2C 在点C 处的切线2l 的方程为222124x y x x =- 由211222124124x y x x x y x x ,,⎧=-⎪⎪⎨⎪=-⎪⎩解得121222234x x x k x x y k ,.⎧+==⎪⎪⎨⎪==-⎪⎩ ∴()223P k k ,-∵1212PF PF AF AF +=+,∴点P 在椭圆22111612x y C :+=上 ∴()()2222311612k k -+=.化简得271230k k --=.(*)由()2124732280Δ=-⨯⨯-=>,可得方程(*)有两个不等的实数根. ∴满足条件的点P 有两个40.(广东省潮州市2013届高三上学期期末教学质量检测数学(理)试题)已知点(4,0)M 、(1,0)N ,若动点P 满足6||MN MP NP =⋅.(1)求动点P 的轨迹C ; (2)在曲线C 上求一点Q ,使点Q 到直线l :2120x y +-=的距离最小.【答案】解:(1)设动点(,)P x y ,又点(4,0)M 、(1,0)N , ∴(4,)MP x y =-,(3,0)MN =-,(1,)NP x y =-由6||MN MP NP =⋅,得3(4)x --=∴222(816)4(21)4x x x x y -+=-++,故223412x y +=,即22143x y +=,∴轨迹C 是焦点为(1,0)±、长轴长24a =的椭圆;评分说明:只求出轨迹方程,没有说明曲线类型或交代不规范的扣1分. (2)椭圆C 上的点Q 到直线l 的距离的最值等于平行于直线l :2120x y +-= 且与椭圆C 相切的直线1l 与直线l 的距离. 设直线1l 的方程为20(12)x y m m ++=≠-由22341220x y x y m ⎧+=⎨++=⎩,消去y 得2242120x mx m ++-= (*). 依题意得0∆=,即0)12(16422=--m m ,故216m =,解得4m =±.当4m =时,直线1l :240x y ++=,直线l 与1l 的距离d ==.当4m =-时,直线1l :240x y +-=,直线l 与1l 的距离d ==.由于55<,故曲线C 上的点Q 到直线l 的距离的最小值为5当4m =-时,方程(*)化为24840x x -+=,即2(1)0x -=,解得1x =. 由1240y +-=,得32y =,故3(1,)2Q . ∴曲线C 上的点3(1,)2Q 到直线l 的距离最小 41.(广东省肇庆市2013届高三4月第二次模拟数学(理)试题)设椭圆22221(0,0)x y a b b a+=>>的离心率为12,其左焦点E 与抛物线21:4C x y =-的焦点相同.(Ⅰ)求此椭圆的方程;(Ⅱ)若过此椭圆的右焦点F 的直线与曲线C 只有一个交点P ,则(1)求直线的方程;(2)椭圆上是否存在点(,)M x y ,使得12MPF S ∆=,若存在,请说明一共有几个点;若不存在,请说明理由.【答案】解:(Ⅰ)抛物线C 的焦点为(1,0)E -,它是题设椭圆的左焦点.离心率为112b =,所以,2b =.由2221b a -=求得a =因此,所求椭圆的方程为22143x y += (*)(Ⅱ)(1)椭圆的右焦点为(1,0)F ,过点F 与y 轴平行的直线显然与曲线C 没有交点.设直线的斜率为k ,① 若0k =,则直线0y =过点(1,0)F 且与曲线C 只有一个交点(0,0),此时直线 的方程为0y =;② 若0k ≠,因直线过点(1,0)F ,故可设其方程为(1)y k x =-,将其代入24y x =-消去y ,得22222(2)0k x k x k --+=.因为直线与曲线C 只有一个交点P ,所以判别式22224(2)40k k k --⋅=,于是1k =±,从而直线的方程为1y x =-或1y x =-+.因此,所求的直线的方程为0y =或1y x =-或1y x =-+.(2)由(1)可求出点P 的坐标是(0,0)或(1,2)-或(1,2)--. ①若点P 的坐标是(0,0),则1PF =.于是12MPF S ∆==112y ⨯⨯,从而1y =±,代入(*)式联立: 221431x y y ⎧+=⎪⎨⎪=⎩或221431x y y ⎧+=⎪⎨⎪=-⎩,求得x =此时满足条件的点M 有4个: ,,1,1⎫⎛⎫⎫⎛⎫--⎪ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎭⎝⎭⎭⎝⎭. ②若点P 的坐标是(1,2)-,则PF =点M 到直线:1y x =-+于是有11122MPF S y ∆==⨯-,从而112x y +-=±, 与(*)式联立:22143112x y x y ⎧+=⎪⎪⎨⎪+-=⎪⎩或22143112x y x y ⎧+=⎪⎪⎨⎪+-=-⎪⎩解之,可求出满足条件的点M 有4个:,,1115,714⎛⎫- ⎪⎝⎭,31,2⎛⎫- ⎪⎝⎭. ③ 若点P 的坐标是(1,2)--,则PF =,点(,)M x y 到直线:1y x =-是有11122MPF S y ∆==⨯-,从而112x y --=±,与(*)式联立:22143112x yx y⎧+=⎪⎪⎨⎪--=⎪⎩或22143112x yx y⎧+=⎪⎪⎨⎪--=-⎪⎩,解之,可求出满足条件的点M有4个:,,1115,714⎛⎫⎪⎝⎭,31,2⎛⎫--⎪⎝⎭.综合①②③,以上12个点各不相同且均在该椭圆上,因此,满足条件的点M共有12个.图上椭圆上的12个点即为所求.42.(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD版))已知抛物线C:y2=4x, F 是抛物线的焦点,设A(x1,y1),B(x2 ,y2)是C上异于原点O的两个不重合点,OA丄OB,且AB与x轴交于点T(1) 求x1x2的值;(2) 求T的坐标;(3) 当点A在C上运动时,动点R满足:FRFBFA=+,求点R的轨迹方程.【答案】F的43.(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))已知动点M到点(0,1) y=的距离之和为5.距离与到直线4(1)求动点M的轨迹E的方程,并画出图形;=+与轨迹E有两个不同的公共点,A B,求m的取值范围;(2)若直线:l y x mAB的最大值.(3)在(2)的条件下,求弦长||【答案】44.(广东省韶关市2013届高三4月第二次调研测试数学理试题)已知椭圆)(1122221 >=-+a a y a x 的左右焦点为21,F F ,抛物线C:px y 22=以F 2为焦点且与椭圆相交于点()11,M x y 、N()22,x y ,点M在x 轴上方,直线1F M 与抛物线C 相切.(1)求抛物线C 的方程和点M 、N 的坐标;(2)设A,B 是抛物线C 上两动点,如果直线MA ,MB 与y 轴分别交于点,P Q . MPQ ∆是以MP ,MQ 为腰的等腰三角形,探究直线AB 的斜率是否为定值?若是求出这个定值,若不是说明理由.【答案】解:(1)由椭圆方程得半焦距1)1(c 22=--a a = 所以椭圆焦点为),( ,01F )01(21-F 又抛物线C 的焦点为)0,2(p ,2,12==∴p p x y C 42=∴: ∵),(11y x M 在抛物线C 上, ∴1214x y =,直线M F 1的方程为)1(111++=x x y y 代入抛物线C 得22211(1)4(1),y x x x +=+22114(1)4(1)x x x x +=+即 22111(1)0,x x x x x ∴-++= ∵1F M 与抛物线C 相切,04)121221=-+∆∴x x =(,11,x ∴= ∴ M、N 的坐标分别为(1,2)、(1,-2) (2)直线AB 的斜率为定值—1. 证明如下:设11(,)A x y ,22(,)B x y ,(1,2)M ,A 、B 在抛物线24y x =上,∴211222244241y x y x ⎧=⎪=⎨⎪=⨯⎩①②③由①-③得,1112412MA y k x y -==-+④由②-③得,2222412MB y k x y -==-+④因为MPQ ∆是以MP,MQ 为腰的等腰三角形,所以MA MB k k =-由MAMB k k =-得11222124122412y x y y x y -⎧=-⎪-+⎪⎨-⎪=-⎪-+⎩ 化简整理,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013届高三二轮复习 圆锥曲线专题二 2013-4-6 椭圆,双曲线,抛物线——基本量及其基本性质
1、若R ∈k ,则“3>k ”是“方程
13
32
2=+--k y k x 表示双曲线”的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 2、直线l :x -2y +2=0过椭圆左焦点F 1和一个顶点B ,则该椭圆的离心率为( )
A.15
B.25
C.55 D .255
3、设P 是双曲线22
a x -9
2
y =1上一点,双曲线的一条渐近线方程为3x -2y =0,F 1、F 2分别
是双曲线的左、右焦点.若|PF 1|=3,则|PF 2|等于 ( )
(A)1或5 (B)6 (C)7
(D)9
4、椭圆x 29+y 24+k =1的离心率为4
5,则k 的值为 ( )
A .-21
B .21
C .-19
25或21
D.19
25或21
5、已知双曲线221x my +=的虚轴长是实轴长的2倍,则实数m 的值是( ) A .4 B .
14 C .1
4
- D .4- 6、已知F 1、F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|, 则cos ∠F 1PF 2= ( ) A.1
4
B.35
C.3
4
D.4
5
7、设椭圆C 1的离心率为5
13,焦点在x 轴上且长轴长为26,若曲线C 2上的点到椭圆C 1的两
个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为 ( ) A.x 242-y 2
32=1 B.x 2132-y 2
52=1 C.x 232-y 2
4
2=1
D.x 2132-y 2
12
2=1 8、F 是抛物线y =1
4x 2的焦点,P 是该抛物线上的动点,若|PF |=2,则点P 的坐标是 ( )
A .(3,9
4
) B .(±2,1) C .(1,4) D .(0,0)
9、已知点P 在抛物线y 2=4x 上,则点P 到直线l 1:4x -3y +6=0的距离和到直线l 2:x =-1的距离之和的最小值为 ( ) A.37
16
B.11
5
C .2
D .3
10、等轴双曲线的一个焦点是1(0,4)F ,
则它的标准方程为 _________ ,渐近线方程为 _______ .
11、(2009广东卷理)巳知椭圆G 的中心在坐标原点,长轴在x , 且G 上一点到G 的两个焦点的距离之和为12,则椭圆G 的方程为 12、(2007·江苏)在平面直角坐标系xOy 中,已知△ABC 顶点A (-4,0)和C (4,0),
顶点B 在椭圆x 225+y 2
9=1上,则sin A +sin C sin B
=________
13、短轴长为5,离心率e =2
3
的椭圆的两焦点为F 1,F 2,过F 1作直线交椭圆于A ,
B 两点,则△ABF 2的周长为_________________
14、已知双曲线kx 2-y 2=1的一条渐近线与直线2x +y +1=0垂直,
那么双曲线的离心率为________________,渐近线方程为________________
15、(1)已知抛物线2
2(0)y px p =>,过其焦点且斜率为1的直线交抛物线与A 、B 两点,
若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为____________
(2)设已知抛物线C 的顶点在坐标原点,焦点为F (1,0),直线l 与抛物线C 相交于A ,B
两点.若AB 的中点为(2,2),则直线l 的方程为________.
16、以抛物线2
:8C y x =上的一点A 为圆心作圆,若该圆经过抛物线C 的顶点和焦点, 那么该圆的方程为 .
17、(1)过点(2,-2)且与双曲线2
2x -y 2=1有公共渐近线的双曲线方程为__________
(2)渐近线方程为034=±y x ,且过点()
32,3-的双曲线方程为_____________ 18、求中心在原点,以坐标轴为对称轴,满足下列条件的椭圆标准方程: (1)椭圆过点(3,0),且离心率e =6
3; __________________ ks5u
(2)两个焦点的坐标分别是(2,0)-、(2,0),并且经过点5
3(,)22
- ;_______________
(3)经过两点12)P P 、; ________________________
(4)经过点)2,3(-,与椭圆14
92
2=+y x 有共同焦点. _________________。
