揭阳一中2012-2013高二下学期第一次阶段考试文数

合集下载

广东省揭阳一中2012-2013学年高二下学期第一次阶段考理综试题.pdf

揭阳第一中学2012—2013学年高二级第二学期第一次段考理科综合可能用到的相对原子质量： H—1 C—12 N—14 O—16 Na—23 Cl—35.5 C．调整能量在生态系统中流动的方向 D．使物质能够尽快地循环流动 2．某生态系统中有ab、c、d四种生物，构成食物链a→b→c，d为分解者，下图是该生态系统中能量流入b处发生的一系列变化示意图，下列说法错误的是A．图中的甲表示b的同化能量，乙表示b用于生长．发育和繁殖的能量 B．蘑菇可参与丁过程 C．当生态系统处于相对稳定状态时，b的种群数量一般处于值 D．图中d的能量不全部来自b生物 4．如图是可持续发展战略中对森林的两种开发模式ⅠⅡ，其中叙述不正确的是A．完全砍伐后再种植的树通常具有一样的树龄和种类 B．选择性砍伐使森林变得更有层次和多样性 C．选择Ⅱ模式更有利于森林的可持续发展 D．进行大面积砍伐，让其自身恢复．基因工程与蛋白质工程的区别是A．基因工程需对基因进行分子水平操作，蛋白质工程不对基因进行操作 B．基因工程合成自然界已存在的蛋白质，蛋白质工程可以合成自然界不存在的蛋白质 C．基因工程是分子水平操作，蛋白质工程是细胞水平(或性状水平)的操作 D．基因工程完全不同于蛋白质工程．下图表示基因工程中获取水稻某目的基因的不同方法。

下列相关叙述中正确的是 A．这三种方法都用到酶，都是在体外进行 B．①②③碱基对的排列顺序均相同 C．图示ab、c三种方法均属人工合成法 D．方法a不遵循中心法则下列化合物沸点比较错误的是A．烷＞乙烷＞甲烷 B．1—氯戊烷＜1—氯丙烷 C．氯烷＞烷 D．正戊烷＞异戊烷＞新戊烷 A．C4H10和C20H42 B．邻二甲苯和对二甲苯 C．C4H8和C3H6 D．一溴乙烷和1,2—二溴乙烷 10．下列操作达不到预期目的的是 ① 石油分馏时把温度计插入受热的液体中 ② 用酸性高锰酸钾溶液除去乙炔中含有的H2S ③将苯和溴水混合后加入铁粉制取溴苯 ④苯 A．只有①② B．只有③④ C．只有①③ D．①②③④下列有机反应中，不属于取代反应的是A．＋Cl2＋HCl B．2CH3CH2OH＋O22CH3CHO＋2H2O C．ClCH2CH===CH2＋ NaOHHOCH2CH===CH2＋NaCl D．＋HO—NO2＋H2O关于物体的动量和动能下列说法中正确的是A．一物体的动量不变其动能一定不变B．一物体的动能不变其动量一定不变 C．两物体的动量相等,其动能一定相等D．两物体的动能相等,其动量一定相等一个阻值为2Ω的线圈在匀强磁场中转动产生的交变电动势为e=10sin20(tV），当该线圈与一阻值为8Ω的电阻组成闭合回路时，下列说法正确的是A．t=0时，线圈平面位于中性面 B．t=0时，穿过线圈的磁通量为0 C．电阻的热功率为16W D．用电压表测路端电压时读数为V 15．温度传感器广泛应用于空调．电冰箱等家用电器中，它是利用热敏电阻的阻值随着温度变化的特性来工作的。

广东省揭阳一中高二政治下学期第一次段考试题新人教版

揭阳一中2012—2013学年度下学期高二段考一政治一．单项选择题（第1-11题为地理,第12-23为历史,第24-35为政治,共35题, 每小题4分，共140分）24.如果孔子生活在我们的时代，并周游列国。

请想象一下，孔子在奥巴马连任后去白宫拜访，可能阐述的合理观点是①中国文化，已经成为世界性文化②中华民族爱好和平，高举和平、发展、合作的旗帜③文化具有多样性，必须尊重各民族文化一律平等原则④世界各国文化只有交流、借鉴、包容，才能走向趋同A．①②B．②③C．①③D．②④25.作家莫言获2012年诺贝尔文学奖，“莫言热”迅速席卷社会，图书脱销、网络热推、出版加印、改编电影……一位工程师在2007年随意注册的白酒商标“莫言醉”也卖出了1000万元的高价。

这体现了A．文化必然带来经济效益B．文化与经济的发展亦步亦趋C．文化与经济相互交融D．文化是一定经济、政治的反映26.一部被认为诋毁伊斯兰先知穆罕默德的14分钟电影预告片，引发中东大规模反美浪潮，四位外交官付出生命的代价。

从中应该领悟到A．传统习俗对人们的物质和精神生活产生持久的影响B．传统文化具有相对稳定性C．尊重文化多样性是实现世界文化繁荣的必然要求D．必须尊重各民族文化一律平等的原则27.2012年4月29日，英威廉王子与相恋多年的女友凯特的皇家婚礼在伦敦威斯敏斯特大教堂举行。

1900余名各国政要出席了婚礼，全球有20亿人通过电视收看了实况。

英国各界都希望把这场婚事大肆操办一下，以便利用这一机会，展示英国的老派文化、老派传统，展示英国文化的风采。

这一事实说明①大众传媒已日益成为文化传播的重要手段②大众传媒已取代旧的传媒③观察人们的社会行为，可以从中看到历史上的和现实中的文化④英国皇家婚礼是英国民族文化的集中展示A．①②B．③④C．②④D．①③28.文化之所以能增强人的精神力量，是因为其A.使人深受震撼、力量倍增B.成为心灵的火炬、前进的旗帜C.具有特殊的感染力和感召力D.激励人们不断创造美好的幸福生活29.下列关于传统文化的说法，不正确的是A.传统文化渗透在现实生活中的各个领域B.传统文化带有自己民族的色彩C.传统文化打上了历史的烙印D.传统文化只存在于历史中30.近年来，我国重化工业和石油等资源勘探开采业对近海海域生态环境造成较大污染，已经对海产品养殖和捕捞带来威胁。

广东省揭阳一中2013-高二下学期期中学业水平测试数学文试题

揭阳第一中学2013—2014学年度第二学期高二级期中考试文科数学试题参考公式：用最小二乘法计算回归直线方程：y bx a =+，其中：2121121)())((xn xy x n yx x xy y x xb ni ini ii ni ini i i--=---=∑∑∑∑====, x b y a -=一．选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{1,2,3,4}U =, }1{=A ,}4,2{=B , 则A (UB )=A ．}1{B ． }3{C ．}3,1{D ．}3,2,1{2．已知函数()2030x x x fx x log ,,⎧>=⎨≤⎩, 则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是( ) A ．9 B ．19 C ．9- D ．19- 3．已知等差数列}{n a 的前n 项和为n S ，若34512a a a ++=，则7S 的值为 ( )A ．56B ．42C ．28D ．14 4．函数()(2)xf x x e =-的单调递增区间是A ．(,1)-∞B ．（0，2）C ．（1，3）D ．(1,)+∞5．函数2()2xf x e x =+-的零点的个数为 ( ) A ． 1 B ．2 C ．3 D ． 4 6．如图1，程序结束输出s 的值是( )A ．30B ．55C ．91D ．1407．已知实数,x y 满足11y xx y y ≤⎧⎪+≤⎨⎪≥-⎩，则目标函数2z x y =-的最大值为( )A ．3-B ．12C ．5D ．68．已知双曲线221(0)5x y m m -=>的右焦点F(3，0)，则此双曲线的离心率为( )A ．6B ．2 C ．32 D ．349．为了解儿子身高与其父亲身高的关系，随机抽取5对父子身高数据如下则y 对x 的线性回归方程为（）A ．1882y x =+ B ．176y = C ．1y x =- D ．1y x =+ 10．设二次函数2()4()f x ax x c x =-+∈R 的值域为[0,)+∞，则19c a+的最小值为( )A ．3B ．92 C ．5 D ．7二．填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分. 11．在区间[]1,2-上任意取一个数x ，则[]0,1x ∈的概率为 . 12、命题“x ∃∈R ，2450x x ++≤”的否定是 . 13．已知向量a ，b 都是单位向量，且a b 12=，则2-a b 的值为 . 14．观察下列不等式：1<+<<；… 则第5个不等式为．三．解答题：本大题共6小题，满分80分．解答应写出文字说明、证明过程或演算步骤. 15．（本小题满分12分）已知函数2f x x x ()sin sin π⎛⎫=-+⎪⎝⎭. （1）求函数)(x f y =的单调递增区间；（2）若4f ()πα-=，求)42(πα+f 的值.16．（本小题满分12分）为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：喜爱打篮球不喜爱打篮球合计男生 20 5 25 女生 10 15 25 合计302050（１）用分层抽样的方法在喜欢打篮球的学生中抽６人，其中男生抽多少人？（２）在上述抽取的６人中选２人，求恰有一名女生的概率.（３）为了研究喜欢打蓝球是否与性别有关，由公式22()()()()()n ad bc K a d c d a c b d -=++++计算出28.333K ≈，那么你能否有99.5%的把握认为是否喜欢打篮球与性别有关？附临界值表：2()P K k ≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 k2.0722.7063.8415.0246.6357.87910.82817.（本小题满分14分）在三棱锥S ABC -中，90SAB SAC ACB ∠=∠=∠=,1,3,22AC BC SB ===.(1) 证明:BC SC ⊥(2) 求点A 到平面SCB 的距离。

广东省揭阳一中高二数学下学期第一次段考试卷文(含解

广东省揭阳一中2014-2015学年高二下学期第一次段考数学试卷（文科）一、选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=}，则图中阴影部分所表示的集合是（）A．{x|0≤x＜1} B．{x|0≤x≤1}C．{x|1＜x＜2} D．{x|1＜x≤2}2．命题“若x2＜1，则﹣1＜x＜1”的逆否命题是（）A．若x2≥1，则x≥1或x≤﹣1 B．若﹣1＜x＜1，则x2＜1C．若x＞1或x＜﹣1，则x2＞1 D．若x≥1或x≤﹣1，则x2≥13．如图所示的框图输出结果为（）A．1023 B．1024 C．511 D．20474．函数f（x）=（x2﹣2x）e x的图象大致是（）A．B．C．D．5．设M=（其中0＜x＜y），则M，N，P的大小关系为（）A．M＜N＜P B．N＜P＜M C．P＜M＜N D．P＜N＜M6．观察下列各式：1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，可以得出的一般结论是（）A．n+（n+1）+（n+2）+…+（3n﹣2）=n2B．n+（n+1）+（n+2）+…+（3n﹣2）=（2n ﹣1）2C．n+（n+1）+（n+2）+…+（3n﹣1）=n2D．n+（n+1）+（n+2）+…+（3n﹣1）=（2n ﹣1）27．在平面直角坐标系中，不等式（a为常数）表示平面区域的面积为9，则的最小值为（）A．﹣1 B．C．D．﹣8．已知F1、F2是双曲线C：﹣=1（a＞0，b＞0）的左右焦点，P是双曲线C上一点，且|PF1|+|PF2|=6a，△PF1F2的最小内角为30°，则双曲线C的离心率e为（）A．B．2C．D．9．若方程x3﹣3x+m=0在[0，2]上有解，则实数m的取值范围是（）A．[﹣2，2] B．[0，2] C．[﹣2，0] D．（﹣∞，﹣2）∪（2，+∞）10．对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f″（x）是f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数g（x）=，则g（）+g（）+…+g（）（）A．2011 B．2012 C．2013 D．2014二、填空题：（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）.11．已知a，b∈R，i是虚数单位．若（a+i）（1+i）=bi，则a+bi=．12．若函数f（x）=在x=1处取极值，则a=．13．已知双曲线x2﹣=1与抛物线y2=2px（p＞0）有一个公共的焦点F，且两曲线的一个交点为M，若|MF|=5，则点M的横坐标为．14．记等差数列{a n}的前n项的和为S n，利用倒序求和的方法得：；类似地，记等比数列{b n}的前n项的积为T n，且，试类比等差数列求和的方法，将T n表示成首项b1，末项b n与项数n的一个关系式，即T n=．三、解答题（本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤）15．已知函数f（x）=2cos2x+sin2x﹣4cosx．（Ⅰ）求的值；（Ⅱ）求f（x）的最大值和最小值．16．如图，四棱锥P﹣ABCD的底面ABCD是边长为2的菱形，∠BAD=60°，已知PB=PD=2，PA=．（1）证明：PC⊥BD；（2）若E为PA的中点，求三棱锥E﹣ABC的体积．17．研究某新药的疗效，利用简单随机抽样法给100个患者服用此药，跟踪调查后得如下表的数据．无效有效合计男性患者15 35 50女性患者4 46 50合计19 81 100请问：（1）请分别估计服用该药品男患者和女患者中有效者所占的百分比？（2）是否有99%的把握认为服用此药的效果与患者的性别有关？（写出必要过程）（3）根据（2）的结论，能否提出更好的调查方法来更准确估计服用该药的患者中有效者所占的比例？说明理由．参考附表：K2=，期中n﹣a+b+c+dP（K2≥k0）0.50 0.40 0.25 0.15 0.10k0 0.455 0.708 1.323 2.072 2.706P（K2≥k0）0.05 0.025 0.010 0.005 0.001k0 3.841 5.024 6.635 7.879 10.82818．已知数列{a n}为等差数列，a3=5，a7=13，数列{b n}的前n项和为S n，且有S n=2b n﹣1．1）求{a n}、{b n}的通项公式；2）若c n=a n b n，{c n}的前n项和为T n，求T n．19．已知椭圆的右焦点为F（2，0），M为椭圆的上顶点，O为坐标原点，且△MOF是等腰直角三角形．（Ⅰ）求椭圆的方程；（Ⅱ）过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1，k2，且k1+k2=8，证明：直线AB过定点（）．20．已知函数f（x）=lnx﹣kx+1（k∈R）（Ⅰ）当k=1时，求函数f（x）的单调区间；（Ⅱ）若f（x）≤0恒成立，试确定实数k的取值范围；（Ⅲ）证明：+++…+＜（n∈N*且n＞1）广东省揭阳一中2014-2015学年高二下学期第一次段考数学试卷（文科）一、选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）．1．设全集U是实数集R，集合A={y|y=3x，x＞0}，B={x|y=}，则图中阴影部分所表示的集合是（）A．{x|0≤x＜1} B．{x|0≤x≤1}C．{x|1＜x＜2} D．{x|1＜x≤2}考点：Venn图表达集合的关系及运算．专题：集合．分析：欲求出图中阴影部分所表示的集合，先要弄清楚它表示的集合是什么，由图知，阴影部分表示的集合中的元素是在集合B中的元素但不在集合A中的元素组成的，即B∩C R A．解答：解：由图可知，图中阴影部分所表示的集合是B∩C R A，∵A={y|y=3x，x＞0}=（1，+∞），∴C R A=（﹣∞，1]，B={x|y=}，∴2x﹣x2≥0，解得0≤x≤2，即B=[0，2]，∴B∩C R A=[0，1]故选：B．点评：本小题主要考查Venn图表达集合的关系及运算、二次不等式的解法等基础知识，属于基础题．2．命题“若x2＜1，则﹣1＜x＜1”的逆否命题是（）A．若x2≥1，则x≥1或x≤﹣1 B．若﹣1＜x＜1，则x2＜1C．若x＞1或x＜﹣1，则x2＞1 D．若x≥1或x≤﹣1，则x2≥1考点：四种命题．分析：根据逆否命题的定义，直接写出答案即可，要注意“且”形式的命题的否定．解答：解：原命题的条件是““若x2＜1”，结论为“﹣1＜x＜1”，则其逆否命题是：若x≥1或x≤﹣1，则x2≥1．故选D．点评：解题时，要注意原命题的结论“﹣1＜x＜1”，是复合命题“且”的形式，否定时，要用“或”形式的符合命题．3．如图所示的框图输出结果为（）A．1023 B．1024 C．511 D．2047考点：程序框图．专题：算法和程序框图．分析：由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．解答：解：当i=1时，满足进行循环的条件，执行循环体后：S=1，i=1；当i=1时，满足进行循环的条件，执行循环体后：S=3，i=2；当i=2时，满足进行循环的条件，执行循环体后：S=7，i=3；当i=3时，满足进行循环的条件，执行循环体后：S=15，i=4；当i=4时，满足进行循环的条件，执行循环体后：S=31，i=5；当i=5时，满足进行循环的条件，执行循环体后：S=63，i=6；当i=6时，满足进行循环的条件，执行循环体后：S=127，i=7；当i=7时，满足进行循环的条件，执行循环体后：S=255，i=8；当i=8时，满足进行循环的条件，执行循环体后：S=511，i=9；当i=9时，满足进行循环的条件，执行循环体后：S=1023，i=10；当i=10时，不满足进行循环的条件，故输出的S值为：1023，故选：A点评：本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．4．函数f（x）=（x2﹣2x）e x的图象大致是（）A．B．C．D．考点：函数的图象与图象变化．专题：数形结合．分析：本题是选择题，可采用排除法进行逐一排除，根据f（0）=0可知图象经过原点，以及根据导函数大于0时原函数单调递增，求出单调增区间，从而可以进行判定．解答：解：因为f（0）=（02﹣2×0）e0=0，排除C；因为f'（x）=（x2﹣2）e x，解f'（x）＞0，所以或时f（x）单调递增，排除B，D．点评：本题主要考查了利用导数研究函数的单调性，以及函数的图象等基础知识，考查了排除法，属于基础题．5．设M=（其中0＜x＜y），则M，N，P的大小关系为（）A．M＜N＜P B．N＜P＜M C．P＜M＜N D．P＜N＜M考点：基本不等式．分析：由基本不等式可得N＞P且M＞N，可得答案．解答：解：由基本不等式可得≥，∵0＜x＜y，∴＞，∴N＞P，再由基本不等式可得M=＞====N，∴P＜N＜M，故选：D．点评：本题考查基本不等式比较式子的大小，属基础题．6．观察下列各式：1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，可以得出的一般结论是（）A．n+（n+1）+（n+2）+…+（3n﹣2）=n2B．n+（n+1）+（n+2）+…+（3n﹣2）=（2n ﹣1）2C．n+（n+1）+（n+2）+…+（3n﹣1）=n2D．n+（n+1）+（n+2）+…+（3n﹣1）=（2n ﹣1）2考点：归纳推理．专题：规律型．分析：分析已知中1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，各式子左右两边的形式，包括项数，每一个式子第一数的值等，归纳分析后，即可得到结论．解答：解：1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，由上述式子可以归纳：左边每一个式子均有2n﹣1项，且第一项为n，则最后一项为3n﹣2右边均为2n﹣1的平方点评：归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．7．在平面直角坐标系中，不等式（a为常数）表示平面区域的面积为9，则的最小值为（）A．﹣1 B．C．D．﹣考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用平面区域的面积求出a，的几何意义为区域内的点到定点D（﹣4，2）的斜率，利用数形结合即可得到结论．解答：解：作出不等式组对应的平面区域如图：则a＞0，由，解得，即C（a，﹣a），由，解得，即A（a，a），则对应的平面区域的面积S=，解得a=3，即A（3，3），C（3，﹣3），则的几何意义为区域内的点到定点D（﹣4，2）的斜率，由图象知，CD的斜率最小，此时=，故选：D点评：本题主要考查线性规划的应用以及斜率的求解，根据面积公式求出a的取值是解决本题的关键．8．已知F1、F2是双曲线C：﹣=1（a＞0，b＞0）的左右焦点，P是双曲线C上一点，且|PF1|+|PF2|=6a，△PF1F2的最小内角为30°，则双曲线C的离心率e为（）A．B．2C．D．考点：双曲线的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：利用双曲线的定义和已知即可得出|PF1|，|PF2|，进而确定最小内角，再利用余弦定理和离心率计算公式即可得出．解答：解：设|PF1|＞|PF2|，则|PF1|﹣|PF2|=2a，又|PF1|+|PF2|=6a，解得|PF1|=4a，|PF2|=2a．则∠PF1F2是△PF1F2的最小内角为30°，∴（2a）2=（4a）2+（2c）2﹣2×4a×2c×，∴，解得e=．故选：C．点评：熟练掌握双曲线的定义、离心率计算公式、余弦定理是解题的关键．9．若方程x3﹣3x+m=0在[0，2]上有解，则实数m的取值范围是（）A．[﹣2，2] B．[0，2] C．[﹣2，0] D．（﹣∞，﹣2）∪（2，+∞）考点：函数在某点取得极值的条件；一元二次方程的根的分布与系数的关系．专题：计算题；数形结合．分析：因为是方程有解，转化为函数在[0，2]的函数值，利用导数求解即可．解答：解：由题意方程x3﹣3x+m=0在[0，2]上有解，则﹣m=x3﹣3x，x∈[0，2]求函数的值域即得实数m的取值范围令y=x3﹣3x，x∈[0，2]y'=3x2﹣3令y'＞0，解得x＞1，故此函数在[0，1]上减，在[1，2]上增，又x=1，y=﹣2；x=2，y=2；x=0，y=0∴函数y=x3﹣3x，x∈[0，2]的值域是[﹣2，2]故﹣m∈[﹣2，2]，∴m∈[﹣2，2]，故选A点评：本题考查学生对一元三次方程的图象的认识，以及对函数值正负与图象关系的利用10．对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f″（x）是f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．设函数g（x）=，则g（）+g（）+…+g（）（）A．2011 B．2012 C．2013 D．2014考点：导数的运算．专题：导数的概念及应用．分析：求出原函数的导函数，再求出导函数的导函数，由导函数的导函数等于0求出x的值，可得g（1﹣x）+g（x）=2，从而得到g（）+g（）+…+g（）的值．解答：解：∵g（x）=，∴g′（x）=x2﹣x﹣3，由g″（x）=2x﹣1=0，得x=．∴g（）=1∴g（x）的对称中心为（，1），∴g（1﹣x）+g（x）=2，∴g（）+g（）=g（）+g（）=…=2g（）=2g（）=2．∴g（）+g（）+…+g（）=2013故选C．点评：本题是新定义题，考查了函数导函数的零点的求法，考查了函数的性质，解答的关键是寻找函数值所满足的规律，是中档题．二、填空题：（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）.11．已知a，b∈R，i是虚数单位．若（a+i）（1+i）=bi，则a+bi=1+2i．考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：利用复数的乘法展开等式的左边，通过复数的相等，求出a，b的值即可得到结果．解答：解：因为（a+i）（1+i）=bi，所以a﹣1+（a+1）i=bi，所以，解得a=1，b=2，所以a+bi=1+2i．故答案为：1+2i．点评：本题考查复数代数形式的混合运算，复数相等条件的应用，考查计算能力．12．若函数f（x）=在x=1处取极值，则a=3．考点：利用导数研究函数的极值．专题：计算题；压轴题．分析：先求出f′（x），因为x=1处取极值，所以1是f′（x）=0的根，代入求出a即可．解答：解：f′（x）==．因为f（x）在1处取极值，所以1是f′（x）=0的根，将x=1代入得a=3．故答案为3点评：考查学生利用导数研究函数极值的能力．13．已知双曲线x2﹣=1与抛物线y2=2px（p＞0）有一个公共的焦点F，且两曲线的一个交点为M，若|MF|=5，则点M的横坐标为3．考点：双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：根据双曲线和考查抛物线的性质，求出p，再根据抛物线的定义，到焦点的距离与到准线的距离相等，得到x0+=5，解得即可．解答：解：∵抛物线y2=2px（p＞0）的焦点为F（，0）．双曲线x2﹣=1的焦点为（2，0）或（﹣2，0），∴=2，∵两曲线的一个交点为M，设点M的横坐标x0，|MF|=5，∴x0+=5，∴x0=5﹣=3，故答案为：3．点评：本题考查双曲线和考查抛物线的焦点，以及抛物线的定义，到焦点的距离与到准线的距离相等，考查学生的计算能力，比较基础．14．记等差数列{a n}的前n项的和为S n，利用倒序求和的方法得：；类似地，记等比数列{b n}的前n项的积为T n，且，试类比等差数列求和的方法，将T n表示成首项b1，末项b n与项数n的一个关系式，即T n=．考点：类比推理．专题：探究型．分析：等差数列与等比数列的定义的区别在于差与比，故类比倒序相加求和，可知倒序相乘求积，再利用等比数列的性质，即可得到结论．解答：解：由题意，T n=b1b2…b n①，倒序为T n=b n b n﹣1…b1②，①×②可得=（b1b2…b n）（b n b n﹣1…b1）=∵∴故答案为：点评：本题考查类比推理，解题的关键是类比解题的方法，类比倒序相加求和，可知倒序相乘求积．三、解答题（本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤）15．已知函数f（x）=2cos2x+sin2x﹣4cosx．（Ⅰ）求的值；（Ⅱ）求f（x）的最大值和最小值．考点：三角函数的最值；二倍角的余弦．专题：三角函数的求值．分析：（Ⅰ）把x=代入到f（x）中，利用特殊角的三角函数值求出即可；（Ⅱ）利用同角三角函数间的基本关系把sin2x变为1﹣cos2x，然后利用二倍角的余弦函数公式把cos2x变为2cos2x﹣1，得到f（x）是关于cosx的二次函数，利用配方法把f（x）变成二次函数的顶点式，根据cosx的值域，利用二次函数求最值的方法求出f（x）的最大值和最小值即可．解答：解：（Ⅰ）=；（Ⅱ）f（x）=2（2cos2x﹣1）+（1﹣cos2x）﹣4cosx=3cos2x﹣4cosx﹣1=，因为cosx∈[﹣1，1]，所以当cosx=﹣1时，f（x）取最大值6；当时，取最小值﹣．点评：考查学生灵活运用同角三角函数间的基本关系及二倍角的余弦函数公式化间求值，此题以三角函数为平台，考查二次函数求最值的方法．16．如图，四棱锥P﹣ABCD的底面ABCD是边长为2的菱形，∠BAD=60°，已知PB=PD=2，PA=．（1）证明：PC⊥BD；（2）若E为PA的中点，求三棱锥E﹣ABC的体积．考点：棱柱、棱锥、棱台的体积；棱锥的结构特征．专题：空间位置关系与距离．分析：（1）连接BD，AC交于O点，由已知得PO⊥BD，BD⊥AC，从而BD⊥面PAC，由此能证明BD⊥PC．（2）由V E﹣ABC=V B﹣AEC，利用等积法能求出三棱锥E﹣ABC的体积．解答：（1）证明：连接BD，AC交于O点，∵PB=PD，∴PO⊥BD，又∵ABCD是菱形，∴BD⊥AC，而AC∩PO=O，∴BD⊥面PAC，∴BD⊥PC．（2）解：由（1）知BD⊥面PAC，==3，∴V E﹣ABC=V B﹣AEC===．点评：本题考查异面直线垂直的证明，考查三棱锥的体积的求法，解题时要注意空间思维能力的培养．17．研究某新药的疗效，利用简单随机抽样法给100个患者服用此药，跟踪调查后得如下表的数据．无效有效合计男性患者15 35 50女性患者4 46 50合计19 81 100请问：（1）请分别估计服用该药品男患者和女患者中有效者所占的百分比？（2）是否有99%的把握认为服用此药的效果与患者的性别有关？（写出必要过程）（3）根据（2）的结论，能否提出更好的调查方法来更准确估计服用该药的患者中有效者所占的比例？说明理由．参考附表：K2=，期中n﹣a+b+c+dP（K2≥k0）0.50 0.40 0.25 0.15 0.10k0 0.455 0.708 1.323 2.072 2.706P（K2≥k0）0.05 0.025 0.010 0.005 0.001k0 3.841 5.024 6.635 7.879 10.828考点：独立性检验的应用．专题：应用题．分析：（1）根据列联表可求得服用该药品男患者和女患者中有效者所占的人数，再求比例；（2）计算K2，同临界值表进行比较，得到有多大把把握认为服用此药的效果与患者的性别有关；（3）计算服用该药的患者中有效者无效者的比例，来判断分层抽样是否更切合实际．解答：解：（1）利用简单随机抽样法给50个患者服用此药，男性有35位有效，因此服用该药品男患者中有效者所占的百分比==70%．给50个患者服用此药，女性有46位有效，因此服用该药品男患者中有效者所占的百分比=92%．（2）根据所给的数据代入求观测值的公式得到K2=≈7.86由于93967＞6.635，所以有99%的把握认为服用此药的效果与患者的性别有关．（3）由（2）得结论知，服用此药的效果与患者的性别有关，并且从样本数据中能看出该地区男性比女性有效的比例有明显差异，因此在调查时，先确定此病的患者中男、女的比例，再把患者分成男、女两层并采用分层抽样方法比采用简单随机抽样的方法更好．点评：本题考查独立性检验的应用及分层抽样．本题解题的关键是正确代入所给的数据，求出观测值，这里不需要把观测值同临界值进行比较，是一个基础题．18．已知数列{a n}为等差数列，a3=5，a7=13，数列{b n}的前n项和为S n，且有S n=2b n﹣1．1）求{a n}、{b n}的通项公式；2）若c n=a n b n，{c n}的前n项和为T n，求T n．考点：数列的求和；等差数列的性质．专题：等差数列与等比数列．分析：（1）由已知条件利用等差数列的通项公式能求出首项和公差，由此能求出a n=2n ﹣1（n∈N*）；由S n=2b n﹣1，能推导出{b n}是首项为1公比为2的等比数列，由此求出（n∈N*）．（2）由，利用错位相减法能求出{c n}的前n项和为T n．解答：解：（1）∵{a n}是等差数列，且a3=5，a7=13，设公差为d．∴，解得∴a n=1+2（n﹣1）=2n﹣1（n∈N*）在{b n}中，∵S n=2b n﹣1当n=1时，b1=2b1﹣1，∴b1=1当n≥2时，由S n=2b n﹣1及S n﹣1=2b n﹣1﹣1，得b n=2b n﹣2b n﹣1，∴b n=2b n﹣1∴{b n}是首项为1公比为2的等比数列∴（n∈N*）（2）∵，∴①②①﹣②得==1+4（2n﹣1﹣1）﹣（2n﹣1）•2n=﹣3﹣（2n﹣3）•2n∴（n∈N*）点评：本题考查数列的前n项和的求法，解题时要认真审题，注意错位相减法的合理运用．19．已知椭圆的右焦点为F（2，0），M为椭圆的上顶点，O为坐标原点，且△MOF是等腰直角三角形．（Ⅰ）求椭圆的方程；（Ⅱ）过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1，k2，且k1+k2=8，证明：直线AB过定点（）．考点：直线与圆锥曲线的关系；椭圆的标准方程．专题：圆锥曲线的定义、性质与方程．分析：（Ⅰ）由△MOF是等腰直角三角形，得c2=b2=4，再根据a2=b2+c2可求得a；（Ⅱ）分情况讨论：（1）当直线AB的斜率存在时，设AB的方程为：y=kx+m，联立直线AB 方程与椭圆方程消掉y得x的二次方程，由韦达定理及k1+k2=8可得关于k，m的关系式，消m代入直线AB方程可求得定点坐标；（2）若直线AB的斜率不存在，设AB方程为x=x0，由已知可求得AB方程，易验证其过定点；解答：（Ⅰ）解：由△MOF是等腰直角三角形，得c2=b2=4，a2=8，故椭圆方程为：=1．（Ⅱ）证明：（1）若直线AB的斜率存在，设AB的方程为：y=kx+m，依题意得m≠±2，设A（x1，y1），B（x2，y2），由，得（1+2k2）x2+4kmx+2m2﹣8=0，则．由已知 k1+k2=8，可得，所以，即．所以，整理得．故直线AB的方程为，即y=k（）﹣2．所以直线AB过定点（）．（2）若直线AB的斜率不存在，设AB方程为x=x0，设A（x0，y0），B（x0，﹣y0），由已知，得．此时AB方程为，显然过点（）．综上，直线AB过定点（）．点评：本题考查直线与圆锥曲线的位置关系、椭圆标准方程的求解，考查分类讨论思想，考查学生分析问题解决问题的能力．20．已知函数f（x）=lnx﹣kx+1（k∈R）（Ⅰ）当k=1时，求函数f（x）的单调区间；（Ⅱ）若f（x）≤0恒成立，试确定实数k的取值范围；（Ⅲ）证明：+++…+＜（n∈N*且n＞1）考点：利用导数求闭区间上函数的最值；利用导数研究函数的单调性．专题：导数的综合应用．分析：（Ⅰ）由函数f（x）的定义域为（0，+∞），f′（x）=．能求出函数f（x）的单调区间．（Ⅱ）由（1）知k≤0时，f（x）在（0，+∞）上是增函数，而f（1）=1﹣k＞0，f（x）≤0不成立，故k＞0，又由（1）知f（x）的最大值为f（），由此能确定实数k的取值范围．（Ⅲ）由（2）知，当k=1时，有f（x）≤0在（0，+∞）恒成立，且f（x）在（1，+∞）上是减函数，f（1）=0，即lnx＜x﹣1在x∈[2，+∞）上恒成立，由此能够证明+++…+＜（n∈N*且n＞1）解答：解：（Ⅰ）易知f（x）的定义域为（0，+∞），又f′（x）=当0＜x＜1时，f′（x）＞0；当x＞1时，f′（x）＜0∴f（x）在（0，1）上是增函数，在（1，+∞）上是减函数．（Ⅱ）当k≤0时，f（1）=1﹣k＞0，不成立，故只考虑k＞0的情况又f′（x）=当k＞0时，当0＜x＜时，f′（x）＞0；当时，f′（x）＜0在上是增函数，在时减函数，此时要使f（x）≤0恒成立，只要﹣lnk≤0 即可解得：k≥1．（Ⅲ）当k=1时，有f（x）≤0在（0，+∞）恒成立，且f（x）在（1，+∞）上是减函数，f（1）=0，即lnx＜x﹣1在x∈（1，+∞）上恒成立，令x=n2，则lnn2＜n2﹣1，即2lnn＜（n﹣1）（n+1），∴（n∈N*且n＞1）∴+++…+＜=即：+++…+＜（n∈N*且n＞1）成立．点评：本题考查函数单调区间的求法，确定实数的取值范围，不等式的证明．考查化归与转化、分类与整合的数学思想，培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识．。

广东省揭阳一中2012-2013学年高二下学期第一次段考生物试题Word版含答案

揭阳第一中学2012—2013学年高二级第二学期第一次段考生物可能用到的相对原子质量： H—1 C—12 N—14 O—16 Na—23 Cl—35.5一．单项选择题（本题包括16小题，每小题4分，共64分。

每小题给出的四个选项中，只有一个选项符合题目要求）1．稻田中农民要拔掉稗草，鱼塘中要不断清除肉食性的“黑鱼”，用生态学观点看这是为了A．保持生态平衡 B．保持生物群落的单一性C．调整能量在生态系统中流动的方向 D．使物质能够尽快地循环流动2．某生态系统中有a、b、c、d四种生物，构成食物链a→b→c，d为分解者，下图是该生态系统中能量流入b处发生的一系列变化示意图，下列说法错误的是A．图中的甲表示b的同化能量，乙表示b用于生长．发育和繁殖的能量B．蘑菇可参与丁过程C．当生态系统处于相对稳定状态时，b的种群数量一般处于K值2D．图中d的能量不全部来自b生物3．由于“赤潮”的影响，一条4Kg重的杂食性海洋鱼死亡，假如该杂食性的食物有1/2来自植物，1/4来自草食鱼类，1/4来自以草食鱼类为食的小型肉食鱼类，按能量流动效率20%计算，该杂食性鱼从出生到死亡，共需海洋植物A．120㎏ B．160㎏ C．60㎏ D．100㎏4．如图是可持续发展战略中对森林的两种开发模式Ⅰ、Ⅱ，其中叙述不正确的是A．完全砍伐后再种植的树通常具有一样的树龄和种类B．选择性砍伐使森林变得更有层次和多样性C．选择Ⅱ模式更有利于森林的可持续发展D．进行大面积砍伐，让其自身恢复ks5u5．基因工程与蛋白质工程的区别是A．基因工程需对基因进行分子水平操作，蛋白质工程不对基因进行操作B．基因工程合成自然界已存在的蛋白质，蛋白质工程可以合成自然界不存在的蛋白质C．基因工程是分子水平操作，蛋白质工程是细胞水平(或性状水平)的操作D．基因工程完全不同于蛋白质工程6．下图表示基因工程中获取水稻某目的基因的不同方法。

下列相关叙述中正确的是A．这三种方法都用到酶，都是在体外进行B．①②③碱基对的排列顺序均相同C．图示a、b、c三种方法均属人工合成法D．方法a不遵循中心法则二．双项选择题（本题包括9小题，每小题6分，共54分。

【语文】广东省揭阳一中2012-2013学年高二下学期第一次段考试题

92届高二（下）第一次阶段考试语文试卷、基础题（21分）1 .下列词语中加点字的读音完全相同的一组是（） A . 帆船藩篱梵文人仰马翻万物蕃息B . 角斗绝招咀嚼一觉醒来倔头倔脑 C. 汛期温驯徇情出言不逊以身殉职 D . 俯瞰抚育胸脯釜底抽薪辅车相依2. 下列句子中加点成语的使用不准确一项是（） A. 北京时间2月16日，第21届冬奥会双人滑比赛在加拿大温哥华举行了自由滑比赛，中国组合申雪与赵宏博不孚众望.，以总分216.57分获得金牌。

B. 从实数轴上的“雁翅排开”，发展到复平面上的“烘云托月”，无论数的概念怎样扩大，零的特殊地位始终不变。

C.刘翔低调或者说“哀兵”策略固然是为了减轻自己肩上的压力，但是有外国媒体一针. 见血地指出，如今刘翔的问题或许并不是脚，而是在心理上。

D.—项社会调查显示，如果丈夫的收入低于妻子，一部分男性难免会自惭形秽.，甚至无端对自己进行心理折磨。

3. 下列各句中没有语病的一句是（）A 在这次会晤中，麦奇杰和杨旭代表广药向戚务生介绍了广药集团入主广州足球和全力争取广州队冲超，还将广州足球打造成“城市名片”也已经写入了政府工作报告中。

B. 北京市发改委制定的三大下调医药费用的举措，让饱受看病贵、看病难现象的百姓感受到了一丝暖意。

C. 文章对环境污染问题作了比较具体的分析，同时也概括地介绍了关于环境科学的基本知识，人们对环境科学引起了重视。

D.生活方式，是人类行为活动的空间展现，包含人的学习生活、职业生活、家庭生活、闲暇生活、社会交往等内容。

从生活方式上，大体可以看出一个人的文化素养和思想品位。

4.下列文字，依文意排列，顺序最恰当的选项是（） _, , , ，其为我书其大概焉。

②凡工之所不能画者 ④其物象意趣，登临之乐，览者各自得焉若乃升于高以望江山之远近，①吾亦不能言也③嬉于水而逐鱼鸟之浮沉A、①④②③B、②①④③5、下列加点字的意思，解释不正确的一项是（A、然常患不得极吾乐于其间者B、轩裳圭组劳.吾形于外C、累于此者既佚.矣，幸无患D、吾尝用于时矣，而讫无称焉，宜去二也6.下列各组加点字的用法和意义，相同的一组是C③④②①D④①②③）忧虑，担心劳累通“逸”，安逸至今A 、 ①一日天子恻然哀之，赐其.骸骨B 、 ①使得与.此五物偕返于田庐C ①乃以难强之筋骸，贪过分之荣禄D ①吾负三宜去，虽无五物，其去宜矣，复何7、选出下列各组中是宾语前置的句子（） A 六一，何谓也?C 老于此五物之间、古诗文阅读（ 25 分）一）阅读下面的文言文，完成嘉靖三十九年六月，忽有贼迤逦从西北来，大举袭入潮阳①，自号为兵。

广东省揭阳一中高二数学第一次阶段性测试题文【会员独享】

揭阳第一中学2011—2012学年度第一学期高二级阶段考试（一）文科数学试卷一、选择题。

（每小题5分，共8小题，共40分） 1、已知数列{n a }的通项公式是n a ＝252+n n(n ∈*N )，则数列的第5项为（） A.110 B.16 C.15 D.122、在△ABC 中，a b c 、、分别是三内角A B C 、、的对边, ︒=︒=45,75C A ,2b =,则此三角形的最小边长为（）A ．46 B ．322 C ．362 D ． 423、设S n 是等差数列｛a n ｝的前n 项和，若S 3S 6＝13，则S 6S 12＝( )A ．310B. 13C. 18D. 194、在ABC ∆中，a b c 、、分别是三内角A B C 、、的对边，且22sin sin (sin sin )sin A C A B B -=-，则角C 等于( ) A ．6π B ．3π C ．56π D ．23π 5、已知等差数列{}n a 的前n 项和为n S ，若5418a a -=，则8S 等于（）A ．72B ．54C ．36D ．186、设βα,是三角形ABC 的两个锐角，且,1tan tan <βα则△ABC 的形状是（）A 、钝角三角形B 、直角三角形C 、锐角三角形D 、任意三角形 7、在等差数列{}n a 中，20111-=a ，其前n 项的和为n S ．若20102008220102008S S-=，则=2011S ( ) A ．2010- B. 2010 C ．2011 D ．2011- 8、一直角三角形三边长a b c 、、成等比数列，且a b c <<，则( )A.三边长之比为3：4：5B.三边长之比为1:3:3C.较大锐角的余弦值为512- D.2c ab = 9、设等差数列{}n a 的前n 项和为n S ，若39S =，636S =，则789a a a ++=（）A.63B.45C.36D.2710、已知等比数列{}n a 满足0,1,2,n a n >=，且25252(3)n n a a n -⋅=≥，则当1n ≥时，2123221l o g l o g l o g n a a a -+++=（） A. (21)n n - B. 2(1)n + C. 2n D. 2(1)n -二、填空题。

广东省揭阳一中2012-2013学年高二下学期期中数学文试题

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------揭阳一中2012-2013学年度第二学期高二级期中考试文科数学试题参考公式：2121121)())((xn xy x n yx x xy y x xb ni ini ii ni ini i i--=---=∑∑∑∑====, x b y a -=一．选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合{1,2,3,4,5}U =，{1,2,3}A =，{3,4,5}B =，则C U ()A B I 等于（）A ．{1,2,3,4,5}B ．{1,2,4,5}C ．{1,2,5}D ．{3} 2．设p 、q 是简单命题，则“p 或q 是假命题” 是 “非 p 为真命题”的（）A ．充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 非充分非必要条件 3. 若01x y <<<，则（）A ．33y x <B ．33>x y C ．44log log x y < D ．11()()44x y<4．已知等比数列{}n a 满足122336a a a a +=+=，，则7a =（）A ．64B ．81C ．128D ．2435．函数xe x xf )3()(-=的单调递增区间是（）----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------A. )2,(-∞ B.(0,3) C.(1,4) D. ),2(+∞ 6则y 对x 的线性回归方程为（）A ．1y x =-B ．1y x =+C ．1882y x =+D ．176y = 7. 通过随机询问由22()()()()()n ad bc K a d c d a c b d -=++++ 算得，22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表：参照附表，得到的正确结论是（） A ．有99%以上的把握认为“爱好该项运动与性别有关” B ．有99%以上的把握认为“爱好该项运动与性别无关”C ．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”D ．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关”----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------8. 已知函数：c bx x x f ++=2)(，其中：40,40≤≤≤≤c b ，记函数)(x f 满足条件：(2)12(2)4f f ≤⎧⎨-≤⎩为事件为A ，则事件A 发生的概率为（） A ．14 B ．58 C ．12 D ．389．若直线:10 (0,0)l ax by a b ++=>>始终平分圆M ：228210x y x y ++++=的周长，则14a b+的最小值为（）A ．8B ．12C ．16D ．2010. 设曲线1*()n y x n N +=∈在点（1，1）处的切线与x 轴的交点的横坐标为n x ,则12n x x x ⋅⋅⋅的值为（）A ．1n B ． 11n + C ． 1nn + D ． 1 二．填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卡相应横线上.11. 某班有学生48人，现用系统抽样的方法，抽取一个容量为4的样本，知座位号分别为6，30，42的同学都在样本中，那么样本中另一位同学的座位号应该是．12.已知双曲线2214x y -=，则其渐近线方程为_________, 离心率为________.13. 某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮练习，每人投10次，投中的次数如下表：则以上两组数据的方差中较小的一个为2s = .----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------14（,m n 都是正整数，且,m n 互质），通过推理可推测m 、n 的值，则-m n = .三、解答题：本大题共6小题，共80分. 解答应写出必要的文字说明、证明过程或演算步骤.15.（本小题满分12分）已知函数()=cos )f x x x π--. (1) 求函数()f x 的最小正周期和值域； (2) 若α是第二象限角，且2()=-33f πα-,试求cos 21+cos 2-sin 2ααα的值. 16.（本小题满分12分）我区高三期末统一测试中某校的数学成绩分组统计如下表：----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------（2）若我区参加本次考试的学生有600（3）若该校教师拟从分数不超过60的概率．17.（本小题满分14分）已知如图：平行四边形ABCD 中，6BC =所在平面与平面ABCD 垂直，G ，H 分别是DF ，（1）求证：GH ∥平面CDE ；（2）若2,CD DB ==F-ABCD 18.（本小题满分14分）已知椭圆（a ＞b ＞0）的离心率为12，以原点为圆心，椭圆短半轴长半径的圆与直线相切.(1)求椭圆的方程；(2)设直线320l x y -=:与椭圆在x 轴上方的一个交点为P ，F 是椭圆的右焦点，试探究以PF 为直径的圆与以椭圆长轴为直径的圆的位置关系. 19.（本小题满分14分）306090120150----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------已知数列{}n a 满足111111n na a +-=--,且10a =.（1）求数列{}n a 的通项公式；（2）设=2nn n b n a ⋅，求数列{}n b 的前n 项和n S ；（3）设n c =，记1nn kk T c==∑，证明：1n T <.20.（本小题满分14分）已知函数1()ln f x a x x=-.(a R ∈) （1）当1a =-时，试确定函数()f x 在其定义域内的单调性；（2）求函数()f x 在(0,]e 上的最小值；（3）试证明：11(1)( 2.718,)n e e n N n+*+>=∈.揭阳一中2012-2013学年度第二学期高二级期中考试文科数学参考答案及评分说明一．选择题：BACAD CACCB 二．填空题：11. 18，12. x y 21±=、213.25，14. 41----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------三．解答题：15解：（1）∵()=cos )f x x x π-=cos x x ----------------------------------------2分=12(cos )2x x 2cos()3x π=+-------------------4分 ∴函数()f x 的最小正周期2T π=,值域为[-2,2].--------------------------6分 (2)由2()=-33f πα-得22cos 3α=-，1cos 3α=-，------------7分 ∵α是第二象限角∴sin α===分 ∴27cos 22cos19αα=-=-，-----------------------------------9分sin 22sin cos 9ααα==-，---------------- -------------10分 ∴cos 21+cos 2-sin 2ααα712--=--------------- ------------12分16.解：（1）由频率分布表得31000.03M ==, -------1分----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------HGDEFAC所以100(333715)42m =-+++=，---------2分420.42100n ==， 0.030.030.370.420.151N =++++=．---------3分直方图如右---------5分（2）由题意知，全区90分以上学生估计为4215600342100+⨯=人．---------7分（3）设考试成绩在(]0,30内的3人分别为A 、B 、C ；考试成绩在(]30,60内的3人分别为a 、b 、c ，从不超过60分的6人中，任意抽取2人的结果有： (A ，B)，(A ，C)，(A ，a)，(A ，b)，(A ，c)， (B ，C)，(B ，a)，(B ，b)，(B ，c)，(C ，a)，(C ，b)，(C ，c)，(a ，b)，(a ，c)，(b ，c)共有15个. ---------10分设抽取的2人的分数均不大于30分为事件D ．则事件D 含有3个结果： (A ，B)，(A ，C) ，(B ，C) ---------11分∴31()155P D == ．---------12分 17. （1）证明：∵//EF AD ,//AD BC ∴//EF BC 且EF AD BC ==∴四边形EFBC 是平行四边形 ∴H 为FC 的中点-------------2分又∵G 是FD 的中点----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有--------------------------------------------∴//HG CD ---------------------------------------4分 ∵HG ⊄平面CDE ，CD ⊂平面CDE∴GH ∥平面CDE ------------------------------7分（2）解：∵平面ADEF ⊥平面ABCD ，交线为AD且FA ⊥AD ， ∴FA ⊥平面ABCD .---------------------------------------------------9分∵6BC =, ∴6FA = 又∵2,CD DB ==，222CD DB BC +=∴BD ⊥CD----------------------------------------------------------------------------------------11分∴ ABCDSCD BD =⋅＝∴ F ABCD V -=13ABCDS FA ⋅＝163⨯=分 18. 解：（1）由于e=12∴2a c = --------- 1分又b == ∴22223,33b a c c =-== ---------3分 221,4c a ∴== --------- 4分所以椭圆的方程为：13422=+y x ---------5分----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有-------------------------------------------- (2)由（1）可知，直线与椭圆的一个交点为)23,1(P ，)0,1(F则以PF 为直径的圆方程是2239(1)()416x y -+-=，圆心为⎪⎭⎫⎝⎛431，，半径为43 ---------9分以椭圆长轴为直径的圆的方程是422=+y x ，圆心是()0,0，半径是2 --------- 11分两圆心距为43-24543122==⎪⎭⎫ ⎝⎛+，所以两圆内切. --------- 14分19．解：（1）由111111n n a a +-=--，知数列1{}1na -是首项为1，公差为1的等差数列，-----2分∴1111nn n a =+-=-， ------------------------------------3分 ∴11n a n=-.------------------------------------------------------------------------4分（2）由（1）得=2n n n b n a ⋅=12(1-)=(-1)2n nn n n⋅∴n S =234-12+22+32+---+-2)+-1)n nn n ⋅⋅⋅⋅（2（2---------------------------①--------5分345+12=2+22+32+---+-2)+-1)n n n S n n ⋅⋅⋅⋅（2（2-------------------②--------6分①-②得234+1-S =2+2+2+---+-1)n n n n ⋅2-（2=21+1+12(2-1)-(-1)2=(2-)2-4n n n n n -∴n S =+1(-2)2+4n n .----------------------------------------------------------------------------------8分----------------------------------------------------------------------------------------------------------------------------------------------------------------------------精品word 文档值得下载值得拥有-------------------------------------------- （3）由（1）得n c ===---------------------------------10分=----------------------------------------------------------------12分∴11n nn k k k T c ====∑∑1(n =+++- 1=分 20．解：（1）当1a =-时，1()ln f x x x=+，(0,)x ∈+∞，则22111'()x f x x x x-=-+=，---------------------------------------------------1分 ∵当01x <<时，'()0f x <，当1x >时，'()0f x >∴函数()f x 在(0,1)上单调递减，在(1,)+∞上单调递增。

精品解析：广东省揭阳第一中学2012届高三第一次阶段考试数学(文)试题

【试题总体说明】该卷是阶段性考试,考查内容是集合、简易逻辑、不等式、函数与导数,试卷难度中等偏上,难度系数大约0.55～0.6,符合高考试卷难度要求,题型较为全面，同时关注能力以及应用考查,通过考查能够发现学生学习情况以及存在的问题,便于在以后的教学中进行弥补；集合的相关知识考查有点偏少,试卷难易题的比例适中，能较好的调动学生的学习积极性.总的来看,还是一份较很好的的试卷。

揭阳一中2011—2012学年度高三平时测试一数学（文科）解析第I卷（选择题）(50分）一、选择题：本大题共10小题,每小题5分，满分50分．在每小题给出的四个选项中,只有一项是符合题目要求的．1．已知}2,1{=A，}2A 为（）xB,则BR≤1|{<∈=xA。

}2,1{ B.}1{ C.}2{≥x|x{≤1|≤xx D。

}1答案：B解析：考查集合的概念和运算，是简单题。

2．不等式0232>x的解集是（）-x-A。

11x或}3>x C。

}1|{<-x<x D。

x|<{<x{-|x或}3->x B。

1-xx答案:B<}1{<3|解析:考查一元二次不等式的求解,是简单题。

3．下列命题中的真命题是（）A.x ∃∈R ，使得 sin cos 1.5x x +=B.(0,),1xx ex ∀∈+∞>+C 。

(,0),23xx x ∃∈-∞<D.(0,),sin cos x x x π∀∈>答案:B解析：在选项A 中考查三角函数的值域、因为,sin cos x x +=2sin()2 1.414 1.54x π+≤≈<在选项B 中考查指数函数、导数的运用,设'()1,()10,xx f x ex f x e =--∴=->所以,f （x)在(0，+∞）上单调增,所以，()(0)0,1xf x f ex >=∴>+; C 、D 可以用图像排除. 本题还考查了数形结合与简易逻辑，是中档题.4．函数)10(||<<=a x xa y x的图象的大致形状是( )答案:D解析:该题只要讨论x>0与x<0即可得出,0,0x x a x y a x ⎧>=⎨-<⎩,考查绝对值化为分段函数常用方法,另外考查指数函数图象,是中档题.，高&考%资(源#网]5．某种商品的零售价2007年比2005年上涨25％，由于采取措施控制物价结果使2009年的物价仅比2005年上涨10％，那么2009年比2007年的物价下降（）A 。

揭阳一中2012年度高三上期中联考数学(文)考试及答案

广东省潮州金中-揭阳一中2012届高三第一学期期中联考数学（文科）本试卷共20小题，满分150分．考试用时120分钟．第I 卷（选择题）（50分）一、选择题：本大题共10 小题，每小题5分，满分50分.每小题给出地四个选项中，只有一项是符合题目要求.1．已知全集U =R ，集合A ={x x |＜3}，B ={x x 3log |＞0}，则A C U B =（） A ．{x |1＜x ＜3}B ．{x |1≤x ＜3} C ．{x |x ＜3}D ．{x |x ≤1}2．已知a ，b ，c ∈R，命题“若a b c ++=3，则222a b c ++≥3”地否命题是（）A ．若a +b+c≠3，则222a b c ++<3B ．若a+b+c=3，则222a b c ++<3C ．若a +b+c≠3，则222a b c ++≥3D ．若222a b c ++≥3，则a+b+c=3 3.2(sin cos )1y x x =+-是（）A. 最小正周期为2π地奇函数B.最小正周期为2π地偶函数C. 最小正周期为π地奇函数D. 最小正周期为π地偶函数４．已知a 、b 是实数，则“a>1，且b>1”是“a+b>2，且1>ab ”地（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分且必要条件 D ．既不充分也不必要条件 5．若20,AB BC AB ABC ⋅+=∆则是（） A ．锐角三角形 B ．直角三角形C ．钝角三角形D ．等腰直角三角形6．曲线x x x f ln )(=在点1=x 处地切线方程为（）A.22+=x yB.22-=x yC.1-=x yD.1+=x y 7．若方程()20f x -=在(,0)-∞内有解，则()y f x =地图象是（）8．要得到函数)53sin(2π-=x y 地图象，只需将函数x y 3sin 2=地图象（）A ．向左平移5π个单位 B ．向右平移5π个单位 C ．向左平移15π个单位 D ．向右平移15π个单位9．已知31)4sin(=-πα，则)4cos(απ+地值等于( )A ．232B ．232-C ．31D ．31-10．对任意实数,x y ，定义运算x y ax by cxy *=++，其中,,a b c 是常数，等式右边地运算是通常地加法和乘法运算.已知123,234*=*=，并且有一个非零常数m ，使得对任意实数x ,都有x m x *=，则m 地值是（）A.4-B.4C.5-D.6第II 卷（非选择题）（100分）二、填空题：本大题共4小题，每小题5分，满分20分． 11．函数5||4)(--=x x x f 地定义域为_____________12．已知函数⎩⎨⎧≥+-<=)4(,2)1()4(,2)(x x f x x f x , 则(5)f = _____________.13．已知单位向量21,e e 地夹角为60，则=-12e14．已知实数x,y 满足2943,31x y x y z x y x +≤⎧⎪-≤-=--⎨⎪≥⎩则地最小值是三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．15.（本题满分12分）已知函数x x x f cos sin )(-=，R x ∈．（1）求函数)(x f 地最小正周期；（2）若函数)(x f 在0x x =处取得最大值，求)3()2()(000x f x f x f ++ 地值.16．（本题满分12分）已知命题2:12640p x x --<，22:210q x x a -+-≤, 若p ⌝是q ⌝地必要而不充分条件，求正实数a 地取值范围 17．（本题满分14分）已知向量m =),1,4sin3(x n =)4cos ,4(cos 2xx . （1）若m ·n =1,求)3cos(π+x 地值；（2）记函数f(x)= m ·n ，在ABC ∆中，角A,B,C 地对边分别是a,b,c ，且满足,cos cos )2(C b B c a =-求f(A)地取值范围.18．（本题满分14分）设21)(axe xf x+=，其中0>a （Ⅰ）当34=a 时，求)(x f 地极值点；（Ⅱ）若)(x f 为R 上地单调函数，求a 地取值范围.19．（本题满分14分）某工厂生产一种产品地成本费由三部分组成：① 职工工资固定支出12500元； ② 原材料费每件40元；③ 电力与机器保养等费用为每件x 05.0元，其中x 是该厂生产这种产品地总件数. （1）把每件产品地成本费)(x P （元）表示成产品件数x 地函数，并求每件产品地最低成本费；（2）如果该厂生产地这种产品地数量x 不超过3000件，且产品能全部销售．根据市场调查：每件产品地销售价)(x Q 与产品件数x 有如下关系：x x Q 05.0170)(-=，试问生产多少件产品，总利润最高？（总利润=总销售额—总地成本）20. （本题满分14分）已知函数()2.2xxaf x =-将()y f x =地图象向右平移2个单位，得到()yg x =地图象．（1）求函数()y g x =地解析式；(2) 若函数()y h x =与函数()y g x =地图象关于直线1y =对称，求函数()y h x =地解析式；(3)设1()()(),F x f x h x a=+已知()F x 地最小值是m ，且2m >+ 求实数a 地取值范围．广东省潮州金中-揭阳一中2012届高三第一学期期中联考数学（文科）参考答案及评分标准1-10 DACAB CDDDB11．[)()+∞⋃,55,412．12 1314．－1715．解：（1）)4sin(2cos sin )(π-=-=x x x x f ， ………………3分()f x ∴地最小正周期为2π………………6分（2）依题意，4320ππ+=k x （Z k ∈）， ………………8分由周期性，)3()2()(000x f x f x f ++12)49cos 49(sin )23cos 23(sin )43cos 43(sin-=-+-+-=ππππππ………………12分16．解:∴p:(x-16)(x+4)<0,-4<x<16,………………………3分[][](1)0x a -+≤q:x-(1-a)∴≤≤a>01-a x 1+a …………6分p ⌝是q ⌝地必要而不充分条件p ∴是q 地充分而不必要条件 1415116a a a -≤-⎧∴∴≥⎨+≥⎩,∴正实数a 地取值范围[15,)+∞…………12分17．解：（1）∵m ·n =1 即14cos 4cos 4sin32=+xx x ……………………2分即1212cos 212sin 23=++x x ∴21)62sin(=+πx ……………………4分 ∴21)21(21)62(sin 21)3cos(22=∙-=+-=+ππx x …………7分（2）∵,cos cos )2(C b B c a =-由正弦定理得BcocC B C A sin cos )sin sin 2(=-∴C B B C B A cos sin cos sin cos sin 2=- ∴)sin(cos sin 2C B B A +=………………9分 ∵π=++C B A∴,0sin ,sin )sin(≠=+A A C B 且∴,3,21cos π==B B ………………11分∴320π<<A∴2626πππ<+<A ∴1)62sin(21<+<πA …………………12分又∵f(x)= m ·n ＝21)62sin(++πx∴21)62sin()(++=πA A f∴23)(1<<A f故函数f(A)地取值范围是).23,1(…………………14分18．解：对)(x f 求导得222)1(21)('ax axax e x f x+-+= ①……………2分（Ⅰ）当34=a 时，若,03840)('2=+-=x x x f ，则解得.21,2321==x x ……………4分综合①,可知所以,231=x 是极小值点,212=x 是极大值点.……………8分（II ）若)(x f 为R 上地单调函数，则)('x f 在R 上不变号，结合①与条件a>0，知0122≥+-ax ax 在R 上恒成立，……………10分因此0)1(4442≤-=-=∆a a a a 由此并结合0>a ，知10≤<a . 所以a 地取值范围为{}.10≤<a a ……………14分19．解：（1）12500()400.05P x x x=++……3分由基本不等式得()4090P x ≥=………5分当且仅当125000.05x x =，即500x =时，等号成立 ……6分 ∴12500()400.05P x x x=++，成本地最小值为90元． ……7分（2）设总利润为y 元，则125001301.0)()(2-+-=-=x x x xP x xQ y 29750)650(1.02+--=x ……………12分当650x =时,max 29750y =……………13分答：生产650件产品时，总利润最高，最高总利润为29750元. ……14分20.解：(1)由题设，()g x (2)f x =-2222x x a --=-．………3分(2)设(,)()x y y h x =在地图象上，11(,)()x y y g x =在地图象上，则112x x y y =⎧⎨=-⎩，（5分）2(),2()y g x y g x ∴-==-即22()222x x a h x --=-+．……………6分（3）由题设，21()2xx F x a =-+22222x x a ---+＝111()2(41)242x x a a -+-+0a ≠①当0a <时，有114a -0<，410a -<，而2x 0>，12x 0>，()2F x ∴<，这与()F x 地最小值2m >+矛盾；……8分②当104a <≤时，有114a -0>，410a -≤，此时()F x 在R 上是增函数，故不存在最小值；……………9分③当4a ≥时，有114a -0≤，410a ->，此时()F x 在R 上是减函数，故不存在最小值；……………10分 ④当144a <<时，有114a -0>，410a ->，()2F x ≥．……………11分当且仅当2x =时取得等号， …………12分()F x 取最小值m=2又2m >144a <<，得(4)(41)744144a a a a --⎧>⎪⎪⎨⎪<<⎪⎩1212,21244a a a ⎧<<⎪⎪∴<<⎨⎪<<⎪⎩……………14分版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.Zzz6Z 。

广东揭阳一中12-13学年高二下第一次阶段考试--语文.

揭阳一中2012-2013学年高二下学期第一次阶段考试语文试题一、基础题（21分）1．下列词语中加点字的读音完全相同的一组是（）A．帆．船藩．篱梵．文人仰马翻．万物蕃．息B．角．斗绝．招咀嚼．一觉．醒来倔．头倔脑C．汛．期温驯．徇．情出言不逊．以身殉．职D．俯．瞰抚．育胸脯．釜．底抽薪辅．车相依2. 下列句子中加点成语的使用不准确一项是( )A．北京时间2月16日，第21届冬奥会双人滑比赛在加拿大温哥华举行了自由滑比赛，中国组合申雪与赵宏博不孚众望．．．．，以总分216.57分获得金牌。

B．从实数轴上的“雁翅排开”，发展到复平面上的“烘云托月．．．．”，无论数的概念怎样扩大，零的特殊地位始终不变。

C．刘翔低调或者说“哀兵”策略固然是为了减轻自己肩上的压力，但是有外国媒体一针．．见血．．地指出，如今刘翔的问题或许并不是脚，而是在心理上。

D．一项社会调查显示，如果丈夫的收入低于妻子，一部分男性难免会自惭形秽．．．．，甚至无端对自己进行心理折磨。

3．下列各句中没有语病的一句是（）A．在这次会晤中，麦奇杰和杨旭代表广药向戚务生介绍了广药集团入主广州足球和全力争取广州队冲超，还将广州足球打造成“城市名片”也已经写入了政府工作报告中。

B．北京市发改委制定的三大下调医药费用的举措，让饱受看病贵、看病难现象的百姓感受到了一丝暖意。

C．文章对环境污染问题作了比较具体的分析，同时也概括地介绍了关于环境科学的基本知识，人们对环境科学引起了重视。

D．生活方式，是人类行为活动的空间展现，包含人的学习生活、职业生活、家庭生活、闲暇生活、社会交往等内容。

从生活方式上，大体可以看出一个人的文化素养和思想品位。

4．下列文字，依文意排列，顺序最恰当的选项是（）若乃升于高以望江山之远近，，，，，其为我书其大概焉。

①吾亦不能言也②凡工之所不能画者③嬉于水而逐鱼鸟之浮沉④其物象意趣，登临之乐，览者各自得焉A、①④②③B、②①④③C、③④②①D、④①②③5、下列加点字的意思，解释不正确的一项是（）A、然常患．不得极吾乐于其间者忧虑，担心B、轩裳圭组劳．吾形于外劳累C、累于此者既佚．矣，幸无患通“逸”，安逸D、吾尝用于时矣，而讫．无称焉，宜去二也至今6．下列各组加点字的用法和意义，相同的一组是（）A、①一日天子恻然哀之，赐其．骸骨②愚人之所以为愚，其．皆出于此乎？B、①使得与．此五物偕返于田庐②于是携酒与．鱼，复游于赤壁之下C、①乃以．难强之筋骸，贪过分之荣禄②乘彼垝垣，以．望复关。

揭阳市2012届高中毕业班高考第一次模拟考(文数)

揭阳市2012年高中毕业班第一次高考模拟考试题数学（文科）本试卷共4页，21小题，满分150分．考试用时120分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液，不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁，考试结束后，将试卷和答题卡一并交回，参考公式：锥体的体积公式；Sh V 31=,其中S 是锥体的底面积，h 为锥体的高线性回归方程a x b yˆˆˆ+=中系数计算公式211)())((ˆx xy y x x b ini i i ni ---=∑∑==22121xn xxn y x ini i i ni --=∑∑==,.ˆˆx b y a-=其中,表示样本均值．一．选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．己知集合},{},11|{m B x x A =≤≤-=若A∩B=B，则m 的取值范围是A ．（-∞，-1]B ．[1，+∞）C ．[-1，1]D ．（-∞，-1]∪[1，+∞）2．设复数z 满足zi= 2+2i （i 是虚数单位），则z 的共轭复数是 A.2-2i B.2+2i C.-2+2i D.-2-2i 3．运行图1所示的程序，可得A 的输出值为 A ． 30 B ． 20 C ．10 D ．-10 4．160sin 80sin 20cos 10sin +的值为100cos .A 23.B 21.C 10cos .D5．以双曲线1322=-y x 的焦点为顶点，顶点为焦点的椭圆的离心率为， 21.A 33.B 23.C 41.D6．设n S 为等比数列}{n a 的前n 项和,若11=a ,公比2=q ,962=-+k k S S ,则k 的值为A ．6B ．5C ．4D ．37．从一个正方体中截去部分几何体，得到的几何体的三视图及尺寸 (单位：cm)如图2所示，则此几何体的体积是3322.cm A 3647.cm B 3323.cm C 38.cm D 8．在同一坐标系内，设不等式1||||≤+y x 围成的封闭区域为M ，曲线12222=+y x 围成的封闭区域为N ，向区域M 中随机投一点P（该点落在区域M 内任何一点是等可能的），则点P 落在区域N 内的概率为．π4.A 8.πB 4.πC 16.πD 9．若直线1=+by ax ,过点)sin ,(cos ααM ,则1.22≥+b a A 1.22≤+b a B 111.22≤+b a C 111.22≥+ba D 10.设a ○L b 表示选择a 和b 两数之较大者的运算，且a ○L a a a ,=○S b 表示选择a 和b 中较小者的运算，且a ○S a =a ,下列三个结论 a ①○L b b =○L a a ②○L b (○L a c ()=○L )b ○L c .a ③○S b (○L a c ()=○S )b ○L a (○S )c 其中正确的是 A.①、③. B.②、③ C.①、② D.①、②、③二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题(11-13题)11．已知函数)sin()(ϕω+=x A x f （其中20,0,0πϕω<<>>A )的部分图象如图3示．则函数)(x f y =的最小正周期为______，=)0(f __________ 12.在正三角形ABC 中，D 是BC 上的点，AB=3，BD =1，则=⋅AD AC ________ 13.设函数xx x f -+=1lg 21)(，则=+++)109()102()101(f f f ______(二)选做题（14、15题，考生只能从中选做一题）14.（几何证明选讲选做题）如图3所示，AB 与⊙O 切于点B ，AO 交⊙O 于点C 、D ，且AO=5，AB=4，则⊙O 的半径长=_____．则△ABD 的面积是___________．15.(坐标系与参数方程选做题)在直角坐标系xoy 中，已知曲线C 的参数方程是⎩⎨⎧=-=θθsin 22cos 2y x （θ是参数），若以O 为极点，x 轴的正半轴为极轴建立极坐标系，则曲线C 的极坐标方程可写为_______三．解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程和演算步骤． 16.（本小题满分12分）已知△ABC 中，角A 、B 、C 的对边分别B C A a c b a 2,1,=+=、、，△ABC 的面积433=S(1)求b 的长； (2)求C 2cos 的值．17.（本小题满分12分）近年来，随着以煤炭为主的能源消耗大幅攀升、机动车保有量急剧增加，某市空气中的“pm2.5”（直径小于等于2.5微米的颗粒物）的含量呈逐年上升的趋势，图5是根据该市环保部门提供的2007年至2011年该市“pm2.5"年均浓度值画成的散点图，（为便于计算把2007年编号为1，2008年编号为2，……，2011年编号为5．） (1)以“pm2.5”年均浓度值为因变量，年份的编号为自变量，利用散点图提供的数据，用最小二乘法求出该市“pm2.5”年均浓度值与年份编号之间的线性回归方程a bx yˆˆ+= (2)按世界卫生组织(WHO)过渡期一1的标准，空气中“pm2.5”的年均浓度限值为35微克／立方米，该市若不采取措施，试预测从2012年起，几年后该市空气中“pm2.5”的年均浓度值将超过世界卫生组织(WHO)过渡期一1设定的限值．（温馨提示：答题前请仔细阅读卷首所给的计算公式及说明．） 18．（本小题满分14分）如图5，已知四棱锥P-ABCD 中90=∠=∠ABC DAB ，2,1====AD PA BC AB ，PA⊥平面ABCD ．(1)求PC 与平面PAB 所成角的正切值； (2)求证：平面PAC⊥平面PCD.19．（本小题满分14分）已知函数3x y =在点))(,(*3N n n n ∈处的切线与x 轴的交点为)0,(n a ,令i ni n a S ∑==1(1)用n 表示n a ,并求n S (2)求：ini S 11∑= (3)设23741-++++=n n a a a a p ，82141210+++++=n n a a a a Q ，其中 ,2,1=n 试比较n p 与n Q 的大小，并证明你的结论；20.（本小题满分14分）如图6，已知点)1,0(A ，A B '),2,1(是点A 关于直线x y =的对称点，P 为x 轴上的动点． (1)求||||PB PA +的最小值；(2)已知抛物线C 的顶点为原点O ，焦点在x 轴，且过点B ，⊙M 的圆心M 在抛物线C 上运动，且过点A'，D ，E 为⊙M 与y 轴的两个交点，试探究三角形A'DE 的面积是否随圆心M 的变化而变化？若没有变化，求出三角形A'DE 的面积． 21．（本小题满分14分）已知函数).(ln )(R a x a x x f ∈+=(1)当1-=a 时，求函数)(x f y =的最小值；(2)若0>a ，证明对+∈∀R x x 21,，总有)2(2)()(2121x x f x f x f +≤+成立；(3)设221)2()()(x x a x f x F ++-=，试确定函数)(x F y =在[1，e]上的零点个数．参考答案一、选择题：CBCCA BBCAD 解析：1．}11|{≤≤-=x x A ，]1,1[-∈⇒=M B B A ，选C ． 2.i ii z 22)1(2-=+=，故选B. 3. A=20*2-30=10,选 C.4．原式2160cos 20sin 80sin 20cos 80cos ==+=，故选C ． 5．易知椭圆中21,1,2=⇒==e c a ，故选A ． 6．由962=-+k k S S ，得,5232962396)22(1112=⇒=⇒=⋅⇒=+=++++k a a a k k k k k k 选B ．7．该几何体的直观图是棱长为2的正方体截去一角：其体积3364711121312cm V =⨯⨯⨯⨯-= 故选B ．8．如图区域M 的面积2=M S ，区域N 的面积2π=N S ，由几何概型的概率公式可得所求的概率为⋅4π选C ． 9．点)sin ,(cos ααM 在单位圆上，由直线1=+by ax ，过点M 得111|100|222222≥+⇒≥+⇒≤+-⨯+⨯b a b a b a b a 故选A ．10.由题设知结论①显然成立，对于②，先求b 、c 中的最大者再与.a 中的最大者，再与c 求较大者结果是一样的，即均为.a 、b 、c 中的最大者，对于③，先设.a 为.a 、b 、c 中的最小者，这样a ○S b ○L c=a ，而(a ○S b)○L (a ○S c)=a ，这时结论成立，若b 或c 为cb a 、、中的最小者，比如b ，这时a ○S (b ○L c)=a ○S c ，而(a ○S b )○L (a ○S c )=a ○S c ，故结论③也成立，综上得正确答案为D ．二.填空题：11．π、（2分）2（3分） 12. 6 13．2914．3、（2分）548（3分） 15.θρcos 4-= 解析：11.由图象易得πππ=-=)885(2T ，)42sin(2)(π+=x x f ，故2)0(=f 12..6120cos ||||9||)(02=⋅+=⋅+=+⋅=⋅C 13.若)1,0(,21∈x x ，且则1)1)(1(lg1)()(212121=--+=+x x x x x f x f故,29214)21(4)109()102()101(=+=+=+++f f f f 14.解法一：过点B 作AD 的垂线，垂足为E ，由AO=5，AB=4得OB=OD=3．由512=⇒⋅=⋅BE AB BO BE AO 54821=⋅=∴∆BE AD S ABD解法二：过点D 作DE⊥AE 于E ，由DE B //0，得524583=⨯=⇒=DE AD AO DE OB 54821=⋅=∴∆DE AB S ABD15.在直角坐标系xoy 中，曲线C 是以点(-2，0)为圆心，以2为半径的圆，如图设),(θρP 是曲线C 上任意一点，在Rt△OPA 中，易得θθπρcos 4)cos(-=-=OA ，即曲线C 的极坐标方程为.cos 4θρ-=三，解答题：16.解：(1)π=++=+C B A B C A ,2 3π=∴B ………………1分433sin 21==B ac S ………………3分 32314332sin 2=⨯⨯==∴B a S c ………………5分由余弦定理得721691cos 22=⨯-+=-+=B ac c a b 7=∴b ………………7分 (2)由正弦定理知：C c B b sin sin =142137233sin sin =⨯==∴b B c C ………………9分 C C 2sin 212cos -=∴1413)14213(212-=⨯-=………………12分 17．解：(1)由散点图可得，变量 i i y x ,组成的一组数据为(1，13)，(2，15)，(3，20)，(4，22)，(5，25)193==∴y x ， ……3分1.3210)1()2(623110)4()1()6()2(ˆ22222=+++-+-⨯+⨯+⨯+-⨯-+-⨯-=b……5分7.931.319ˆ=⨯-=-=x b y a……6分 ∴所求回归方程为7.91.3ˆ+=x y……7分 (2)由357.91.3>+x ，得16.8>x ……9分 N x ∈∴x 的最小值为9，……10分故可预测从2012年起，3年后该市空气中“pm2.5”的年均浓度值将超过世界卫生组织( WHO)过渡期1设定的限值．…………12分18.解：(1)解法一：∵PA⊥平面ABCD ，BC ⊂平面ABCD ∴BC ⊥PA …………………1分又∵BC⊥AB，PA∩AB=A ∴BC⊥平面PAB……………2分又∵BC ⊂平面PBC,∴平面PBC ⊥平面PAB ……………3分在平面PAB 内过点A 作AE ⊥PB 于E,则AE ⊥平面PBC, ∴AE 的长为点A 到与平面PAC 的距离………………5分在Rt△PAB ,51,222=+=∴==AB PA PB AB PA ………………6分552512=⨯=⋅=∴PB AB PA AE ………7分解法二：∵PA⊥平面ABCD ，AD ⊂平面ABCD ∴AD⊥PA …………………1分又∵DA⊥AB，PA∩AB=A ∴AD⊥平面PAB ………………2分∵BC⊥AB ∴BC∥AD ∴BC⊥平面PAB ∴BC ⊥PB ………………3分在Rt△PAB ,51,222=+=∴==AB PA PB AB PA ………………4分设点A 到平面PBC 的距离为h ，则由PBC A ABC P V V --=，得h S PA S PBC ABC ⋅=⋅∆∆PBCABC S PA S h ∆∆⋅=∴5522121=⋅⋅⋅=BC PB PABC AB …………………7分(2)证法一：过点C 作CE∥AB 交AD 于点E ，∵DA⊥AB ∴DA⊥EC，且AE =BC =1．………………9分∵AD =2，∴E 为AD 的中点，∴EC 为AD 的垂直平分线，………………10分∴CD=AC，∵△ABC 为等腰直角三角形，∴∠BAC=450…………………11分∴∠DAC =∠ADC=450．∴∠DCA=900，即DC⊥AC，………………12分又∵PA⊥平面ABCD ，CD ⊂平面ABCD ∴CD⊥PA………………13分且PA∩AC=A ,∴CD⊥平面PAC ，∵CD ⊂面PDC ．∴平面PAC⊥平面PCD………………14分证法二：∵PA⊥平面ABCD ，CD ⊂平面ABCD ∴CD⊥PA，………9分又)()(+⋅+=⋅ ⋅+⋅+⋅+⋅=00cos 21135cos 210135cos 21=⨯+⨯++⨯⨯= …………11分⊥∴ ,即AC⊥DC，………12分又∵PA⊥平面ABCD ，CD ⊂平面ABCD ∴CD⊥PA，且PA∩AC=A ∴CD⊥平面PAC ，∵CD ⊂面PDC ，∴平面PAC⊥平面PCD.………………14分 19.解：(1)23x y ='∴函数3x y =在点),(3n n 处的切线方程为)(323n x n n y -=-………2分令0=y ，得323n n n x =+-= 32n a n =∴，*N n ∈………3分 ∵数列}{n a 是首项321=a ，公差32=d 的等差数列，2)(1n n a a n S +=∴2)3232(n n +=3)1(+=n n ………5分 (2))1(31+=n n S n)111(3+-=n n ………6分 )111(3)]111()3121()211[(3111+-=+-++-+-=∴∑=n n n S i i ………8分 (3)∵23741,,,,-n a a a a 组成以1a 为首项，以d 3为公差的等差数列………9分82141210,,,,+n a a a a 组成以10a 为首项，以2d 为公差的等差数列，…………………10分n n n n n d n n na P n 313232)1(221-=-+=⋅-+=∴………11分 d n n na Q n 22)1(10⋅-+=n n n n n 632323232022+=-+=………12分)19(31)632(3122-=+--=-n n n n n n Q P n n ………13分∴对于正整数n ，当20≥n 时，n n Q P >;当n=19时，n n Q P = 当181≤≤n 时，n n Q P <………………14分 19．解：(1)设点)1,0.(A 关于x 轴的对称点为A 1，则A 1的坐标为)1,0(-………1分于是||||||||||11B A PB PA PB PA ≥+=+当且仅当A 、P 、B 三点共线是取等号，……3分这时|PA|+|PB|取得最小值………………4分224)12(1|||)||(|21min +=++==+∴B A PB PA（2）解法一：依题意知点),0,1(A '………7分设抛物线C 的方程为)0(22>=p px y 由抛物线C 过点B 得,122=⇒=p p 即抛物线C 的方程为x y 22=………8分过点M 作y 轴的垂线，垂足为G ，则点G 平分DE ，设圆心为M(m ，n)，则,12)1(||||||2222222+-=-+-=-'=m n m n m MG A M DG ………10分,2||,1||,22==∴=DE DG m n ………………12分即当M 运动时，弦DE 的长不随圆心M 的变化而变化，又∵点A'到y 轴的距离不变，∴三角形A'DE 的面积不随圆心M 的变化而变化，……13分11||21=⨯⨯='∆DE S DE A ………14分解法二：依题意知点),0,1(A '………7分设抛物线C 的方程为)0(22>=p px y 由抛物线C 过点B 得,122=⇒=p p 即抛物线C 的方程为x y 22=………8分设圆的圆心为),(n m M ∵圆M 过点)0,1(A '∴圆的方程为2222)1()()(n m n y m x +-=-+-………9分令0=x 得，,01222=-+-m ny y∵点),(n m M 在抛物线x y 22=上，m n 22=∴0)1)(1(01222=+---⇒=-+-∴n y n y n ny y设2121),,0(),,0(y y y E y D >则1,121-=+=n y n y221=-∴y y ，即2||=DE即当M 运动时，弦DE 的长不随圆心M 的变化而变化，……………12分又∵点A'到y 轴的距离不变，∴三角形A'DE 的面积不随圆心M 的变化而变化；………………13分11||21=⨯⨯='∆DE S DE A ………14分解法三：依题意知点),0,1(A '………7分设抛物线C 的方程为)0(22>=p px y 由抛物线C 过点B 得,122=⇒=p p 即抛物线C 的方程为x y 22=………8分设圆的圆心为),(n m M ∵圆M 过点)0,1(A '∴圆的方程为2222)1()()(n m n y m x +-=-+-………9分令0=x 得，,01222=-+-m ny y22484a am n +-=∆∵点),(n m M 在抛物线x y 22=上， m n 22=∴ 4=∆∴，设2121),,0(),,0(y y y E y D >由求根公式得1,122221-=+=+=n y n n y 221=-∴y y 即2||=DE∴当M 运动时，弦长|DE|为定值，…………………12分又∵点A'到y 轴的距离不变，∴三角形A'DE 的面积不随圆心M 的变化而变化，……13分11||21=⨯⨯='∆DE S DE A ………14分解法四：依题意知点),0,1(A '………7分设抛物线C 的方程为)0(22>=p px y 由抛物线C 过点B 得,122=⇒=p p 即抛物线C 的方程为x y 22=………8分设圆的圆心为),(n m M ∵圆M 过点)0,1(A '∴圆的方程为2222)1()()(n m n y m x +-=-+-………9分令0=x 得，,01222=-+-m ny y设),0(),,0(21y E y D则n y y 221=+，,12.21-=m y y212212214)()(y y y y y y ⋅-+=-∴484)12(4)2(22+-=--=m n m n又∵点),(n m M 在抛物线x y 22=上，,22m n =∴,4)y (221=-∴y 2||21=-y y ………12分∴当M 运动时，弦长|DE|为定值，又∵点A'到y 轴的距离不变，………………13分 ∴三角形A'DE 的面积不随圆心M 的变化而变化，11||21=⨯⨯='∆DE S DE A ………14分 21.解：(1)当1-=a 时，x x x f ln )(-=令0)(='x f ，得0111=-=-xx x ，得1=x ………1分当)1,0(∈x 时，0)(<'x f ，当0)(),,1(>'+∞∈x f x∴当1=x 时，函数x x x f ln )(-=有最小值，1)1()(min ==f x f ………3分(2)证明：x a x x f ln )(+=)2(2)()(212]x x f x f x f +-+∴)2ln 2(2ln ln 21212211x x a x x x a x x a x +++-+++= )2ln 2ln ln (2121x x x x a +-+=)2ln (ln 2121x x x x a +-=………4分 +∈R x x 21,22121x x x x +≤∴ 02ln ln 2121≤+-∴x x x x ………6分又.0>a 0)2ln (ln 2121≤+-∴x x x x a 即对+∈∀R x x 21,，总有)2(2)()(2121x x f x f x f +≤+成立，………7分(3)解法一：函数)(x F y =的零点，即方程0)(=x F 的实根，将方程0)(=x F 化为x x x x a -=-221)ln (………8分由(1)知0ln =/-x x xx xx a ln 212--=∴………9分令xx x x x g ln 21)(2--=，则22)ln ()11)(21()ln )(1()(x x x x x x x x x g ------='.2)ln ()1ln 21)(1(x x x x x -+--=………11分 ],1[.e x ∈01ln 21,01>+->-∴x x x 0)(>'∴x g ，即函数)(x g 在[1，e]上为增函数，………12分21)1()(min -==∴g x g ，)1(22121)()(22max --=--==e e e e e e e g x g ………13分 ∴当)1(22212--≤≤-e e e a 时，方程0)(=x F 有一个实根，函数)(x F y =有一个零点；当21-<a 或)1(222-->e e e a 时,方程0)(=x F 没有实根,函数)(x F y =没有零点．……l4分解法二：x a x a x x F -+-+=)1(ln 21)(2 x a x x a x a x x F ))(1(1)(--=--+='∴………8分当1≤a 时，对0)(],,1[≥'∈∀x F e x 恒成立，即函数)(x F y =在[1，e]单调递增，则当0)()1(≤⋅e F F ，即0]21)1()[21(2≤+--+e e e a a 时，函数)(x F y =在[1，e]上有唯一零点，结合1≤a ，解得)1(22212--≤≤-e e e a ………10分当e a ≤<1时，函数)(x F y =,在),1(a 单调递减，在),(e a 单调递增， ,021)1(<--=a F ,01221)1(21)(22<+-<---=e e e e a e e F ∴函数)(x F y =在[1，e]上无零点．………12分当e a >时，函数)(x F y =在[1，e]单调递减，,021)1(<--=a F ∴函数⋅=)(x F y 在[1，e]上无零点，………13分综上可知，当)1(22212--≤≤-e e e a 时，函数)(x F y =有一个零点，当21-<a 或)1(222-->e e e a 时，函数)(x F y =没有零点．………14分。

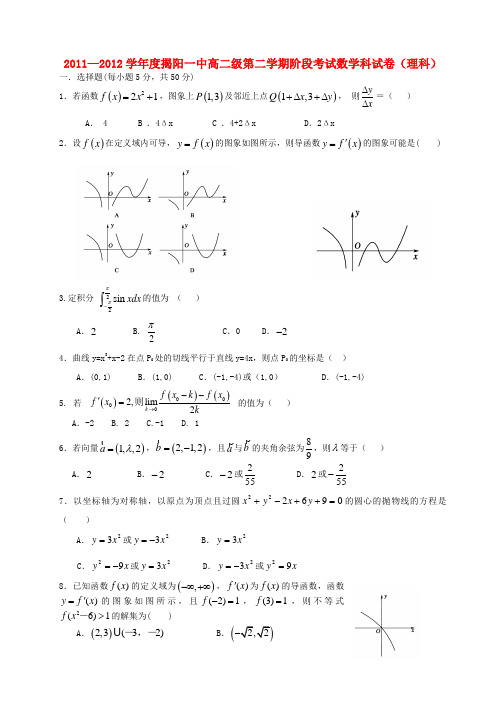
广东省揭阳一中高二数学下学期第一次段考题理新人教A版

2011—2012学年度揭阳一中高二级第二学期阶段考试数学科试卷（理科）一．选择题(每小题5分，共50分)1．若函数()221f x x =+，图象上()1,3P 及邻近上点()1,3Q x y +∆+∆，则yx∆∆＝（） A ． 4 B ．4Δx C ．4+2Δx D ．2Δx2．设()f x 在定义域内可导，()y f x =的图象如图所示，则导函数()y f x '=的图象可能是( )3.定积分22sin xdx ππ-⎰的值为（）A ．2 B.2πC ．0D ．2- 4．曲线y=x 3+x-2在点P 0处的切线平行于直线y=4x ，则点P 0的坐标是（） A ．(0,1) B ．(1,0) C ．(-1,-4)或（1,0） D ．(-1,-4)5.若的值为（）A ．-2 B. 2 C.-1 D. 16．若向量()1,,2a λ=，()2,1,2b =-，且a 与b 的夹角余弦为98，则λ等于（）A ．2B ．2-C ．2-或552 D ．2或552-7．以坐标轴为对称轴，以原点为顶点且过圆096222=++-+y x y x 的圆心的抛物线的方程是（）A ．23x y =或23x y -= B ．23x y =C ．x y 92-=或23x y = D ．23x y -=或x y 92=8．已知函数()f x 的定义域为(),-∞+∞，()f x '为()f x 的导函数，函数()y f x '=的图象如图所示，且(2)1f -=，(3)1f =，则不等式2(6)1f x >－的解集为( ) A ．()2,3(32)－，－B．(()()()00002,lim 2k f x k f x f x k→--'=则C ．()2,3D．((),2,-∞+∞二．填空题（每小题5分，共20分）9．函数sin ()xf x x=的导函数为_________. 10.设若0lg ,0,()8,0,ax x f x x tdt x >⎧⎪=⎨+≤⎪⎩⎰((1))1f f =，则a ＝_________. 11.函数x e x x f )3()(-=的单调递增区间是_________.12．从如图所示的长方形区域内任取一个点(),M x y ，则点M 取自图中非阴影部分的概率为_________.13．设双曲线22221x y a b-=（0a <,0b >）的渐近线与抛物线21y x =+相切，则该双曲线的离心率等于_________.14．已知函数()sin cos 4f x f x x π⎛⎫'=+⎪⎝⎭，则()4f π=_________. 三．解答题：（本大题共6小题，共80分）15.（本小题满分12分）已知函数x x x f 3)(3-=，过点)6,2(-P 作曲线)(x f y =的切线的方程，求切线方程．16.（本小题满分12分）已知函数()()211ln 2f x x ax a x =-+-，其中1a >，讨论函数()f x 的单调性. 17. （本小题满分14分）某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益．通过对市场的预测，当对两项投入都不大于3(百万元)时，每投入x (百万元)广告费，增加的销售额可近似的用函数21214y x x =-+(百万元)来计算；每投入x (百万元)技术改造费用，增加的销售额可近似的用函数3221253y x x x =-++(百万元)来计算．现该公司准备共投入3(百万元)，分别用于广告投入和技术改造投入，请设计一种资金分配方案，使得该公司的销售额最大． (参考数据：2≈1.41，3≈1.73)18．（本小题满分14分）已知函数bx ax x x f ++=23)(在1x =处有极值2-．（1）求常数a 、b ；（2）求曲线()yf x =与x 轴所包围的面积。